1. INTRODUCTION
1.1. General
For the last few years, or so, a sudden and strong interest for strongly magnetized plasmas has emerged on an international scale within the inertial confinement fusion (ICF) dedicated community. Certainly, it is related to the very stringent conditions demanded by a successful laser driven implosion of the thermonuclear pellet, as evidenced by the last national ignition facility (NIF) campaign at Lawrence Livermore National Laboratory (LLNL) – Livermore.
Simultaneously, very encouraging demonstration of a nearly steady, on a ns-time scale, kilo-Tesla magnetic field resulting from a laser irradiated coil (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Shiraga, Nishimura and Azechi2013) has prompted the perspective of using strong applied magnetic (B) intensities to control the laser–plasma interaction, itself.
In this context, it appears highly timely to survey the diagnostics of magnetized plasmas. We try to fulfill this goal by focusing attention on:
• Faraday rotation
• Inverse Faraday effect (IFE)
• Thomson scattering (TS)
• Combined Stark–Zeeman line broadening of hydrogenic transitions (dipolar)
• Proton and heavier ion stopping in dense and arbitrary magnetized plasmas and as a prerequisite, we first survey the commonly used parameters in a no field situation (B = 0) and a magnetized one (B ≠ 0) (Potekhin & Chabrier, Reference Potekhin and Chabrier2012).
1.2. General parameters
The state of a free-electron gas is determined by the electron number density n e and temperature T. Instead of n e it is convenient to introduce the dimensionless density parameter r s = a e/a 0, where a 0 is the Bohr radius and a e = (4/3πn e)−1/3. The parameter r s can be quickly evaluated from the relations 
${r_{\rm s}} = 1.1723n_{24}^{ - 1/3} = ({{\rm \rho} _0}/{\rm \rho} {)^{1/3}}$, where n 24 ≡ n e/1024 cm−3 and ρ0 = 2.6752(A/Z)g/cm3. The analogous density parameter for the ions is 
${R_{\rm S}} = {a_{\rm i}}{m_{\rm i}}{(Ze)^2}/{\hbar ^2} = 1822.89A{Z^{7/3}}{r_{\rm s}}$, where m i is the ion mass and a i ≡ (4/3πn i)−1/3 is the ion sphere radius while electron degeneracy is θ = T/T F. In the nonrelativistic limit, 
${T_{\rm F}} \approx 1.163 \times {10^6}r_{\rm s}^{ - 2} \,K$, and
$${\rm \theta} = 0.543\;{r_{\rm s}}/{\Gamma _{\rm e}},$$where
$${\Gamma _{\rm e}} \equiv \displaystyle{{{e^2}} \over {{a_{\rm e}}{k_{\rm B}}T}} \approx \displaystyle{{22.747} \over {{T_6}}}{\left( {{{\rm \rho} _6}\displaystyle{Z \over A}} \right)^{1/3}}$$The strength of the Coulomb interaction of nonrelativistic ions is characterized by the Coulomb coupling parameter
$${\rm \Gamma} = \displaystyle{{{{(Ze)}^2}} \over {{a_{\rm i}}{k_{\rm B}}T}} = {{\rm \Gamma} _{\rm e}}{Z^{5/3}},$$where T 6 ≡ T/106 K.
1.3. Magnetic parameters
Convenient dimensionless parameters that characterize the magnetic field in a plasma are the ratios of the electron cyclotron energy 
$\hbar\!{{\rm \omega}_{\rm c}}$ to the Hartree unit of energy, to the electron rest energy, and to k BT:
$${{\rm \gamma} _{\rm m}} = {\hbar^3}B/m_{\rm e}^2 c{e^3} = B/{B_0},$$where B 0 = 2.3505 × 109G,
$$b = \displaystyle{{\hbar{{\rm \omega}_{\rm c}}} \over {{m_{\rm e}}{c^2}}} = {\rm \alpha} _{\rm f}^2 {{\rm \gamma} _{\rm m}} = \displaystyle{B \over {4.414 \times {{10}^{13}}G}},$$
where 
${{\rm \alpha} _{\rm f}} = {e^2}/\hbar \!c$ is the fine-structure constant, and
$${\rm \zeta} = \hbar\!{{\rm \omega}_{\rm c}}/{k_{\rm B}}T \approx 134.34{B_{12}}/{T_6}$$
where B 12 ≡ B/1012G. The magnetic length 
$a_{\rm m} = (\hbar \!c/eB)^{1/2}$
$={a_0}/\sqrt {{{\rm \gamma} _{\rm m}}} $ gives a characteristic transverse scale of the electron wave function.
For the ions, the cyclotron energy is 
$\hbar\!{{\rm \omega}_{{\rm ci}}} = Z({m_{\rm e}}/{m_{\rm i}})\hbar\!{{\rm \omega}_{\rm c}}$, and the parameter analogous of ζ is
$${{\rm \zeta} _{\rm i}} = \hbar\!{{\rm \omega}_{{\rm ci}}}/{k_{\rm B}}T \approx 0.0737(Z/A){B_{12}}/{T_6}.$$Another important parameter is the ratio of the ion cyclotron frequency to the plasma frequency,
$${\rm \beta} = {{\rm \omega} _{{\rm ci}}}{\rm /}{{\rm \omega} _{\rm p}} = {{\rm \zeta} _{\rm i}}/{\rm \eta} \approx 0.0094{B_{12}}\sqrt {{{\rm \rho} _6}}. $$2. FARADAY ROTATION
In 1845 Michael Faraday discovered that a longitudinal magnetic field can rotate the polarization direction of light passing through transparent dielectric material. That discovery was, in fact, the first empirical connection between light and magnetism.
In interstellar space, Faraday rotation is most easily seen in linearly polarized radio beams traversing a region of magnetized plasma. The resulting rotation Δθ of the beam's polarization direction is given by 
${\rm \Re} {{\rm \lambda} ^2}$, where λ is the radio wavelength and 
${\rm \Re} $, the so-called rotation measure, is an integral over the observer's line of sight to the radio source.
In Gaussian units, it is given by
$${\rm \Re} = ({e^3}/2{\rm \pi} {m^2}{c^4})\int {n_{\rm e}}(s){B_{\rm s}}(s)ds,$$where n e is the local density of free electrons, m is the electron mass, and B s is the local magnetic field's component along the line of sight.
3. THE IFE
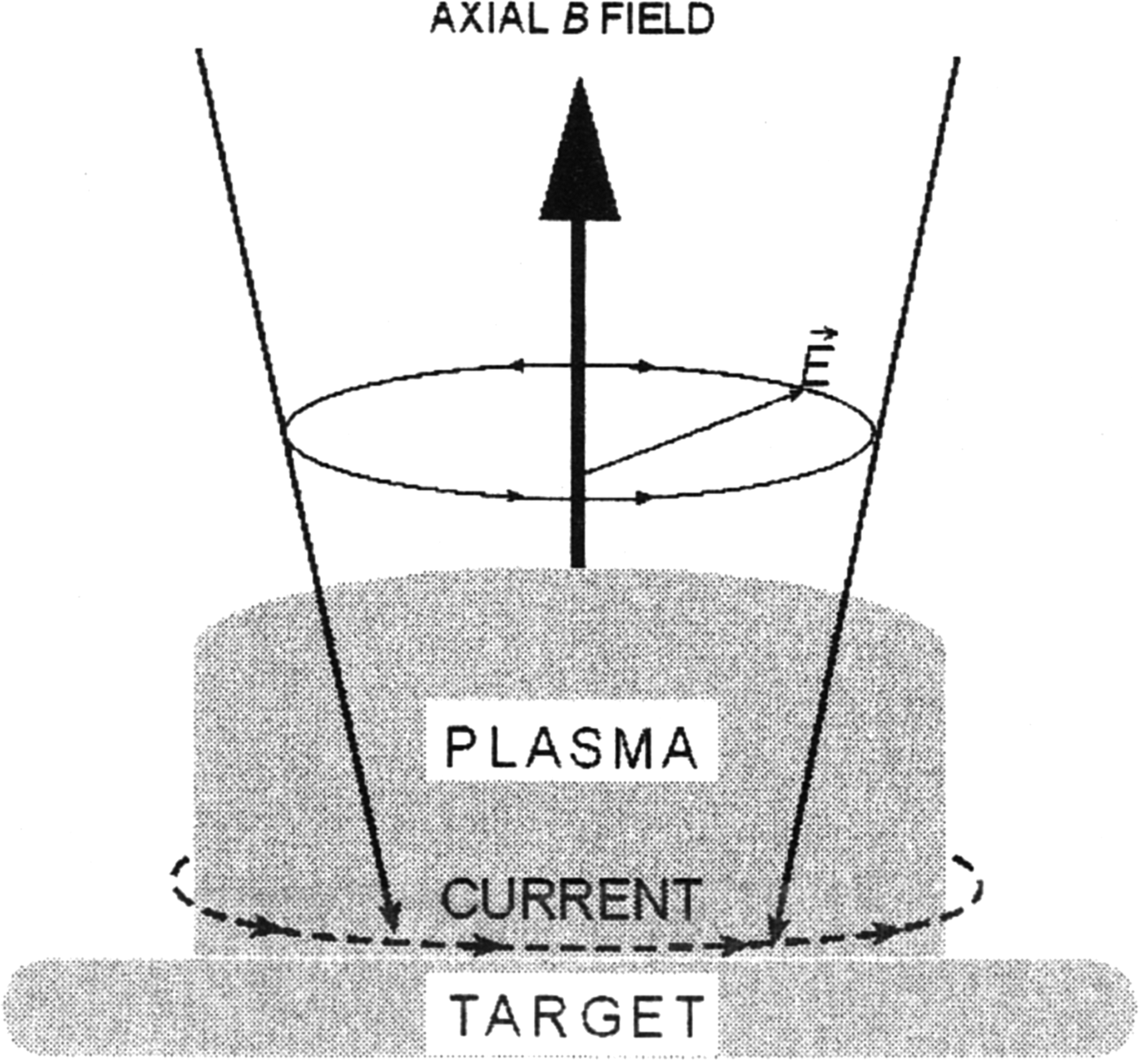
The IFE is the phenomenon where a magnetic field is created in a medium due to the rotation of the electric field (Eliezer, Reference Eliezer2002). In particular, a circularly polarized laser can induce a magnetic field in the plasma. The magnetic field arises because the electrons quiver with the oscillating electric field of the incoming laser light, and if the laser is circularly polarized then the electrons describe a circular motion. The net effect of this is a circular current on the edge of the plasma, which generates the magnetic field (see Fig. 1).
Fig. 1. A schematic presentation of the inverse Faraday effect (after (Eliezer, Reference Eliezer2002)).
A simple (order of magnitude) calculation for the magnetic field created by the IFE in cold plasma is now developed. The motion of the electrons in an applied electric field is, according to linearized law,
$$\displaystyle{{\partial v} \over {\partial t}} = - \displaystyle{e \over {{m_{\rm e}}}}{\bf E}$$where v is the electron velocity and E is the applied electric field in the plasma, as a result of the absorbed laser energy. The ions are considered immobile. The electric field is incident in the z-direction and is circularly polarized in the x–y plane:
$${\bf E} = {E_0}\left( {\displaystyle{{{\hat {\bf x}} + {\bf {i}}{\hat {\bf y}}} \over {\sqrt 2}}} \right)\exp [ - i({\rm \omega} t - kz)]$$
where 
${\hat {\bf x}}$ and 
${\hat {\bf y}}$ are unit vectors in the x- and y-directions, respectively.
Substituting (3) into (2), one gets the solution for the electron (fluid) velocity:
$${\bf v} = {v_0}\left( {\displaystyle{{ - { \hat {\bf x}} + {\bf {i}}{\hat {\bf y}}} \over {\sqrt 2}}} \right)\exp [ - i({\rm \omega} t - kz)],\quad {v_0} = \displaystyle{{e{E_0}} \over {{m_{\rm e}}{\rm \omega}}} $$The electrons also satisfy the continuity equation
$$\displaystyle{{\partial {n_{\rm e}}} \over {\partial t}} = - \nabla \cdot ({n_{\rm e}}{\bf v}).$$The density is assumed to consist of a background (n 0) and perturbed (n 1) components
$${n_{\rm e}} = {n_0} + {n_1}\quad \quad {n_0}\,{\gg}\, {n_1}$$
where n 0 does not depend on time and n 1 ≈ exp (−iωt). Since 
$\nabla \cdot {\bf v} = 0$, the continuity Eq. (5) yields
$$i{\rm \omega} {n_1} = {\bf v} \cdot (\nabla {n_0}).$$The electric current, which in this approximation is a second-order perturbed value, is obtained by using (4) and (7):
$${\bf J} = - e\langle {n_1}{\bf v}\rangle = \langle {\displaystyle{{ie} \over {\rm \omega}} ({\bf v} \cdot \nabla {n_0}){\bf v}} \rangle = \displaystyle{{{e^3}E_0^2} \over {2{m_{\rm e}}{{\rm \omega} ^3}}}\nabla {n_0} \times {\hat {\bf z}}$$
where 〈〉 is the time average over the fast oscillations and 
${ \hat {\bf z}}$ is the unit vector in the z-direction. Note that the wave vector of the electromagnetic field is parallel to 
${\hat {\bf z}}$. From Eq. (8) one can see that the electric current J has a contribution from the density gradient in the x–y plane (mainly from the edge of the plasma) and it points in the toroidal direction. This current produces an axial magnetic field (i.e., in the z-direction) according to Maxwell's equation (Gaussian units):
$$\nabla \times {\bf B} = \displaystyle{{4{\rm \pi}} \over c}{\bf J},$$which in order of magnitude is given by
$$B = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^3}}}\displaystyle{e \over {mc}} \vert E{ \vert ^2}$$where ωp is the electron plasma frequency. This may be expressed in terms of the laser light intensity I L by
$${I_{\rm L}} = \displaystyle{c \over {4{\rm \pi}}} \vert E{ \vert ^2}.$$Thus, we find the axial poloidal magnetic field
$$\displaystyle{B \over {gauss}} = 2 \times {10^{ - 10}}\displaystyle{{{I_{\rm L}}} \over {W/{\rm c}{{\rm m}^2}}}{\left( {\displaystyle{{\rm \lambda} \over {1\,{\rm \mu m}}}} \right)^3}\left( {\displaystyle{n \over {{{10}^{21}}\,{\rm c}{{\rm m}^{ - 3}}}}} \right).$$where λ is the laser wavelength. For instance, taking λ = 1 µm, as for a neodymium laser, and n = 1021 cm−3, with I L = 1016W/cm2, gives B = 2 × 106 Gauss. As a second example, suppose λ = 10 µm, as in a CO2 laser, n = 1019cm−3, and I L = 1014W/cm2. We kept I Lλ2 constant in the two examples, as this seems to be the case in practice. For this example, B = 2 × 105 gauss.
This derivation highlights a classical dipole approximation.
Using ponderomotive forces (Lehner, Reference Lehner1994), it was suggested that the induced magnetic field is not linear with I L, as given by the classical IFE (10), but B is proportional to the square root of I L. Moreover, the constant of proportionality is significantly larger than in the classical approach. In this formalism the electric current is a first-order effect rather than a second-order perturbation value. In the non-relativistic domain the axial magnetic field, can thus be written as
$$\eqalign{B & = {B_{\rm c}}\left( {\displaystyle{{{{\rm \omega} _{{\rm pe}}}} \over {\rm \omega}}} \right)\left( {\displaystyle{{e{E_0}} \over {{m_{\rm e}}{\rm \omega} c}}} \right) \cr & \approx 6.5 \times {10^5}{\left( {\displaystyle{{{n_{\rm e}}} \over {{n_{\rm e}}c}}} \right)^{1/2}}{\left( {\displaystyle{{{I_{\rm L}}} \over {{{10}^{14}}\,{\rm Watt}/{\rm c}{{\rm m}^2}}}} \right)^{1/2}}.}$$This formula fits some experiments (Horovitz et al., Reference Horovitz, Eliezer, Ludminski, Henis, Moshe, Shpitalnik and Arad1997) in the domain of I L ≈ 1010 W/cm2. However, for ~1014 Watt/cm2 the experimental values are larger than those estimated by Eq. (11).
It has also been stressed (Talin et al., Reference Talin, Kaftandjian and Klein1975) that the IFE strongly relies on angular momentum transfer between radiation field and plasma as evidenced by a Kubo response function formalism. Up to now, experiments have not yet been discriminated amongst the above theory proposals.
Apparently, the very first manifestations of IFE in plasmas have been identified with a Klystron source of waves (Deschamps et al., Reference Deschamps, Fitaire and Lagoute1970).
Currently, high power lasers are used.
Magnetic fields in excess of 7 MG have been measured with high spatial and temporal precision during interactions of a circularly polarized laser pulse with an underdense helium plasma at intensities up to 1019 Watt/cm2 (Najmudin et al., Reference Najmudin, Tatarakis, Pukhov, Clark, Clarke, Dangor, Faure, Malka, Neely, Santala and Krushelnik2001). The fields, while of the form expected from the IFE for a cold plasma, are much larger than expected, and have a duration approaching that of the high intensity laser pulse (<3 psec). These observations can be explained by particle-in-cell (PIC) simulations in 3D. The simulations show that the magnetic field is generated by fast electrons which spiral around the axis of the channel created by the laser field.
More generally, 3D PIC simulations allow for a detailed analysis of a given experiment, while deeper theoretical investigations are still lacking in this area of magnetized plasmas.
4. PLASMA SCATTERING OF ELECTROMAGNETIC RADIATION: TS
4.1. General
It is well-known that electromagnetic radiation is emitted by an accelerated charge. An important example of this phenomenon occurs when the acceleration is induced in the first place by an electromagnetic wave. This interaction, when the incident radiation is of sufficiently low frequency ω so that 
$\hbar\!{\rm \omega} $ is much less than mc 2, the rest energy of the charge, is generally referred to as TS.Footnote 1 It is the extension of the theory to include the simultaneous scattering from a large number of free positive and negative charges, that is, the plasma, and the experimental application of scattering, which are the topics of concern.
For a single charge the angular distribution of intensity, the frequency, and the phase of the scattered radiation depend on the orbit of that charge relative to the observer. Equally, for a large group of charges the scattered spectrum is related to the orbits of all those charges, or rather in practice, to some average taken over the probable behavior of the group. From the spectrum of radiation scattered from a plasma we may in principle determine the electron and ion temperatures and densities, the direction and magnitude of a magnetic field in the plasma, and in general, information about all fluctuations (waves, instabilities) within the plasma. In reality, we are of course limited by the radiation sources available to us; the cross-section for scattering is so small that measurements on laboratory plasmas were not possible at all until the advent of high-power lasers. The first measurements were by the scattering of radio waves from the ionosphere in the late 1950s.
4.2. Stokes parameters for TS in magnetized plasma
We consider the scattering of a plane monochromatic electromagnetic wave by an electron located at the origin of a Cartesian coordinate system, in a cold collisionless plasma in a uniform magnetic field. Let B be a uniform static magnetic field pointing in the direction of the z-axis, 
${\bf B} = B{\hat {\bf z}}$, where 
${\hat {\bf z}}$ represents the unit vector and B denotes the field strength (Chou & Chen, Reference Chou and Chen1994).
The propagation vector k of the incident electromagnetic wave makes an angle α with the static magnetic field, and is lying in the xz-plane as shown in Figure 2.
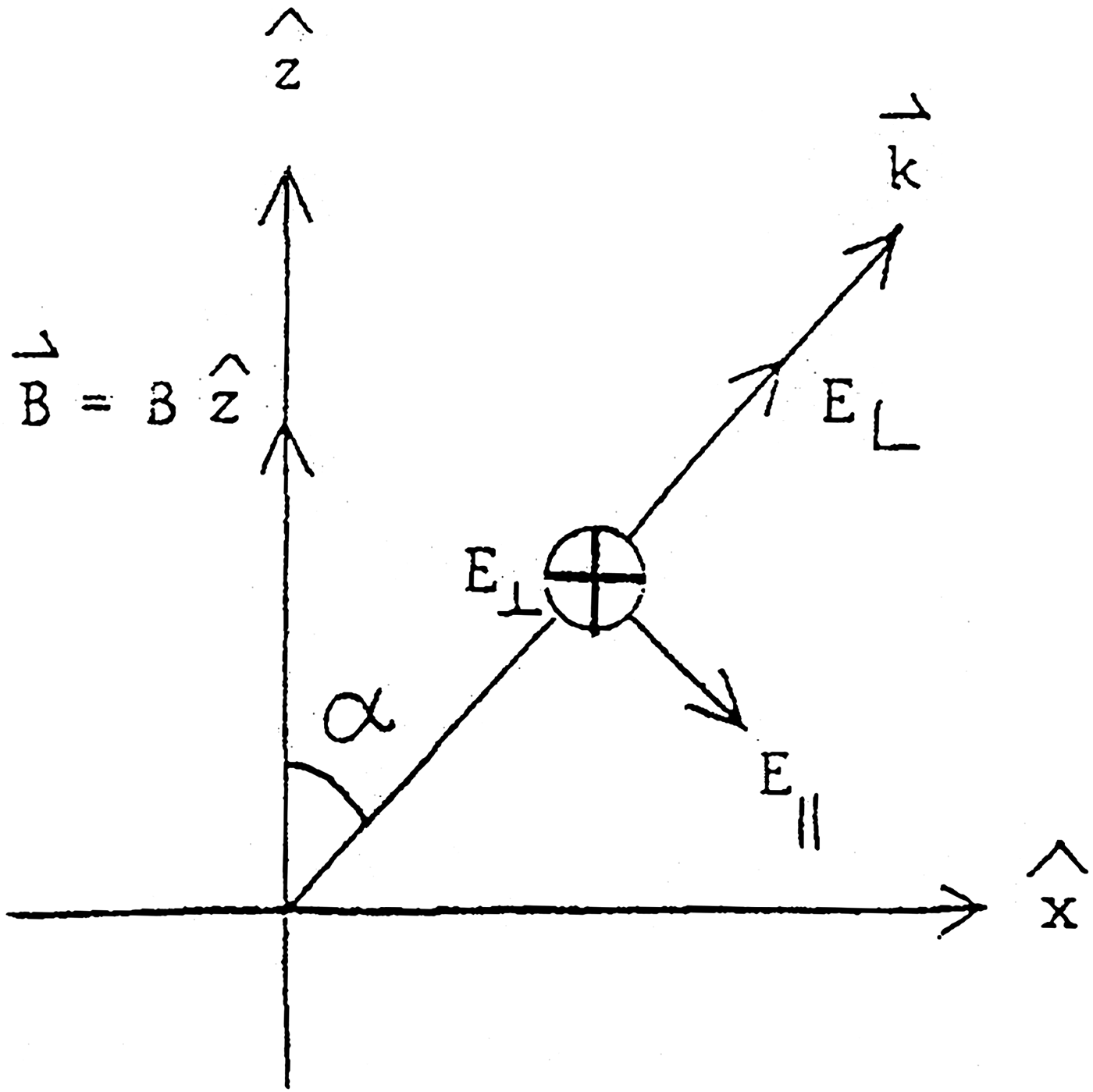
Fig. 2. Thomson scattering in a magnetized plasma. 
${E_{\rm \parallel}} $ is in xz-plane, E ⊥ is perpendicular to xz-plane, E L is along the propagation vector k, 
${\rm \alpha} \lt ({\bf k},{\bf B})$, B denotes a static uniform magnetic field.
To calculate the polarization parameters due to magnetic TS we first resolve the E(t) vector of the incident wave into parallel 
$({E_{\rm \parallel}} (t))$ and perpendicular (E ⊥(t)) components with respect to the xz-plane formed by the static external magnetic field B and the direction of propagation of the incident wave. The intensity of the incident wave may therefore be written in terms of these two transverse components and the longitudinal component E L in the direction of propagation
$${{\bf E}^{\ast}} \cdot {\bf E} = E_{\rm \parallel} ^{\ast} {E_{\rm \parallel}} + E_ \bot ^{\ast} {E_ \bot} + E_{\rm L}^{\ast} {E_{\rm L}}\;\comma$$as shown in Figure 2,
The Stokes parameters which describe the intensity and polarization of the incident electromagnetic wave propagating in a magnetized plasma will now be written in terms of the parallel and perpendicular electric field components 
${E_{\rm \parallel}} $ and E ⊥ as
$$\eqalign{I \equiv & \,{S_0} = E_{\rm \parallel} ^{\ast} {E_{\rm \parallel}} + E_ \bot ^{\ast} {E_ \bot}, \cr Q \equiv & \,{S_1} = E_{\rm \parallel} ^{\ast} {E_{\rm \parallel}} - E_ \bot ^{\ast} {E_ \bot}, \cr U \equiv &\, {S_2} = E_{\rm \parallel} ^{\ast} {E_ \bot} + E_ \bot ^{\ast} {E_{\rm \parallel}} \cr V \equiv & \,{S_3} = - i(E_{\rm \parallel} ^{\ast} {E_ \bot} + E_ \bot ^{\ast} {E_{\rm \parallel}} ).} $$ We note that for electromagnetic waves propagating in a plasma, there is generally, also an electric field in the direction of propagation, namely, the longitudinal component 
${E_{\rm L}} = {E_{\rm L}}{ \hat {\bf k}}$ where 
${ \hat {\bf k}}$ is a unit vector in the direction of propagation.
The first Stokes parameter I simply gives the intensity of the radiation, the second Q and third U specify the linear polarization, and the fourth V, the circular polarization. The effect of the magnetized plasma on the scattered radiation may then be determined by the following set of Stokes parameters in a symbolic matrix form
$$\vec M^{\prime} = \displaystyle{{r_0^2} \over {{R^2}}}\vec M \cdot \vec S,$$where
$$\eqalign{& \vec S = (I,Q,U,V) = ({S_0},{S_1},{S_2},{S_3}), \cr & \vec S^{\prime} = (I^{\prime},Q^{\prime},U^{\prime},V^{\prime}) = ({{S^{\prime}}_0},{{S^{\prime}}_1},{{S^{\prime}}_2},{{S^{\prime}}_3})} $$are the 4-vectors constructed with the Stokes parameters for the incident and scattered radiation, with
$$\eqalign{{r_0} &= {e^2}/m{c^2}\;\cr &= 2.83 \times {10^{ - 13}}\,{\rm cm}}$$
${ \hat {\bf r}} = {\bf R}$/R a unit vector directed from the position of the charge to the observation point, and R is the distance between the two points.
If the incident wave is linearly polarized with its electric field perpendicular to the external magnetic field, the scattered wave is in general elliptically polarized. The polarization of the scattered wave becomes linear only if the observation is made in the plane perpendicular to the magnetic field in view of azimuthal symmetry of the scattering relative to the static magnetic field. The Stokes parameters of the scattered radiation are significantly reduced in the regime of low frequency and strong magnetic field (Ωc ≪ ω ≪ ωc) due to the presence of the magnetized plasma. Plasma effects are relatively small and insensitive to the value of 
$ \vee ( \vee \equiv {\rm \omega} _{\rm p}^2 /{{\rm \omega} ^2})$ as long as ∨ ≪ 1.
For TS in a cold magnetized plasma, the total cross-section may thus be cast in the form 
$(u = {\rm \omega} _{\rm c}^2 /{{\rm \omega} ^2})$$
$$\eqalign{{{\rm \sigma }_{\rm \lambda }}({\rm \omega },B) = & \displaystyle{{{\sigma _{\rm T}}} \over {[1 + K_{\rm \lambda }^2 ({\rm \alpha }) + L_{\rm \lambda }^2 ({\rm \alpha })]}} \times \left\{ {{{[{k_{\rm \lambda }}({\rm \alpha })\sin {\rm \alpha } + {L_{\rm \lambda }}({\rm \alpha })\cos {\rm \alpha }]}^2}} \right. \cr & \quad + \displaystyle{1 \over {{{(1 - u)}^2}}}[1 - {u^{1/2}}{({K_{\rm \lambda }}({\rm \alpha })\cos {\rm \alpha } - {L_{\rm \lambda }}({\rm \alpha })\sin {\rm \alpha }]^2} \cr & \quad + \left. {\displaystyle{1 \over {{{(1 - u)}^2}}}{{[{u^{1/2}} - {K_{\rm \lambda }}({\rm \alpha })\cos {\rm \alpha } - {L_{\rm \lambda }}({\rm \alpha })\sin {\rm \alpha }]}^2}} \right\},} $$
where α is the angle of incidence relative to the static magnetic field B and 
${{\rm \sigma} _{\rm T}} = 8{\rm \pi} r_0^2 /3$ denotes the canonical Thomson cross-section, where
$${K_{\rm \lambda}} ({\rm \alpha} ) = \displaystyle{{2{u^{1/2}}(1 - \vee )\cos {\rm \alpha}} \over {u\!\mathop {\sin} \nolimits^2 {\rm \alpha} - {{( - 1)}^{\rm \lambda}} \sqrt {{u^2}\mathop {\sin} \nolimits^4 {\rm \alpha} + 4u{{(1 - \vee )}^2}\mathop {\cos} \nolimits^2 {\rm \alpha}}}}, $$and
$${L_{\rm \lambda}} ({\rm \alpha} ) = \displaystyle{{2{u^{1/2}} \vee \sin {\rm \alpha}} \over {2(1 - \vee ) - u\mathop {\sin} \nolimits^2 {\rm \alpha} + {{( - 1)}^{\rm \lambda}} \sqrt {{u^2}\mathop {\sin} \nolimits^4 {\rm \alpha} + 4u{{(1 - \vee )}^2}\mathop {\cos} \nolimits^2 {\rm \alpha}}}} $$with λ = 1 mode designating the extraordinary wave and λ = 2 mode the ordinary wave.
The 
$r_0^2 $-scaling of σλ(ω, B) thus highlights a m −2 dependence featuring an overwhelming electron contribution to TS, while the e 4-dependence demonstrates that only very highly charged ion could substantially contribute to TS. We have in this way documented incoherent scattering by independent electrons.
Correlated (Coherent) redistribution of incoming radiation should be expected in a hot plasma. Up to now, that situation has only been taken up in the highly dilute magnetized plasmas encountered in Tokamak-like machines, (Sheffield, Reference Sheffield1975). TS in dense and magnetized plasmas of ICF concern seems to be still awaiting for a dedicated treatment. A very recent experimental demonstration of TS in a magnetized plasma had just appeared (Kenmochi et al., Reference Kenmochi, Minami, Takahashi, Mizuuchi, Kobayashi, Nagasaki, Nakamura, Okada, Yamamoto, Oshima, Konoshima, Shi, Zang, Kasajima and Sano2014).
5. STARK–ZEEMAN BROADENING OF HYDROGENIC TRANSITIONS
The standard impact formalism (Griem, Reference Griem1964; Bekefi el al., Reference Bekefi, Deutsch, Ya’ akobi and Bekefi1976) for line broadening by plasma may be easily extended to take into account the full es-structure of the static patterns in presence of combined Stark and Zeeman effects.
Then the light intensity polarized along a unit vector 
${ \hat {\bf e}}$ may be written
$$\eqalign{I({\rm \omega}, {\hat {\bf e}}) = &\, {{\rm \pi} ^{ - 1}}{\rm Re}\int W(\vec F)d\vec F\sum\limits_{i,j,k,l} \langle {n_{\rm i}} \vert { \hat {\bf e}} \cdot \vec R \vert {n_{\rm j}}\rangle \cr & \quad \times \langle n^{\prime}k \vert { \hat{\bf e}} \cdot \vec R \vert nl\rangle \langle {n_{\rm i}} \vert \langle {n_{\rm j}} \vert \{ i[{\rm \omega} - {\hbar^{\!\!- 1}}({H_{\rm n}} - {H_{{\rm n^{\prime}}}})]\cr & \quad - {{\rm \phi} _{{\rm nn^{\prime}}}}{\} ^{ - 1}}\vert nl\rangle \vert n^{\prime}k\rangle,} $$
with 
$\vec R$ the optical electron position vector. H n[H n′] is the atomic Hamiltonian taking into account the full static electromagnetic perturbation operating on the sublevels |n i〉 and |n l〉 of the upper state (n)[|n j〉 and |n k〉 of the lower state (n′)] of the line. ϕnn′ denotes the electron collision (or relaxation) operator.
As in most line-broadening theories, the ions are regarded as infinitely massive classical particles over the time of interest (static ion approximation). Moreover, it may be shown that the low-frequency microfield distribution 
$W(\vec F)$ is rigorously unaffected in presence of a magnetic field of any strength when Doppler broadening is negligible in a thermal plasma. Therefore, it remains to evaluate the ϕnn′ matrix elements. We restrict our attention to a sufficiently high electron density, such that the Larmor radius remains greater than the corresponding Debye length, that is,
$${r_{\rm G}}/{{\rm \lambda} _{\rm D}} = 4.544 \times {10^{ - 3}}N_{\rm e}^{1/2} /H \ge 1,$$where N e is in cm–3 and H in gauss.
The electron–atom interaction may then be evaluated with the usual monopole–dipole approximation and a straight-line trajectory for the perturbing electron traveling in the Debye sphere surrounding the emitter.
Relative strength of Stark to Zeeman line shift features
$$\eqalign{{\rm \tau} = &\, \displaystyle{3 \over 2}n(n - 1)e{a_0}{E_0}/\displaystyle{{(n - 1)e\hbar H} \over {2mc}} = \displaystyle{3 \over 2}n{A_0} \cr {A_0} = \,&\, 3.43 \times {10^{ - 7}}N_{\rm e}^{2/3} [{\rm c}{{\rm m}^{ - 3}}]/H} $$
for the 
${\rm \cal H}$-atom like emitter.
Pure Stark broadening is retrieved with τ ≫ 1 (large n and N e moderate H. Line profiles depend on the direction of observation. The magnetic field 
$\vec H$ polarizes the emitted light.
Averaging the usual impact profiles around the direction of the magnetic field, yields the complete profiles including averages on the plasma microfield, which are polarized either along or transverse to the magnetic field. This procedure is illustrated in Figures 3 and 4, (Nguyen - Hoe et al., Reference Nguyen – Hoe, Drawin and Herman1967) for the H α lines of atomic hydrogen observed either parallel or perpendicular to 
$\vec H$ and expressed in terms of the polarized intensities by the relations
$$\eqalign{& {I_{\rm \parallel}} (\Delta {\rm \lambda} ) = \displaystyle{1 \over 2}[I(\Delta {\rm \lambda}, { \hat {\bf x}}) + I(\Delta {\rm \lambda}, { \hat {\bf y}})] \cr & {I_ \bot} (\Delta {\rm \lambda} ) = \displaystyle{1 \over 2}[{I_{\rm \parallel}} (\Delta {\rm \lambda}, {\hat {\bf x}}) + I(\Delta {\rm \lambda}, {\hat {\bf z}})].} $$
Fig. 3. Calculated H α profile observed longitudinally N e = 1015 cm−3; T = 104K, H = 103Γ (τ = 15.44) (1), H = 2 × 104Γ (τ = 0.7715) (2), H = 4 × 104Γ (τ = 0.3857) (3), H = 6 × 104Γ (τ = 0.2638) (4) [after Nguyen-Hoe et al. (Reference Nguyen – Hoe, Drawin and Herman1967)].
Fig. 4. Calculated H α profile observed transversally N e = 1015 cm−3; T = 104 K, H = 1 × 103Γ (τ = 15.44) (1), H = 2 × 104Γ (τ = 0.7715) (2), H = 4 × 104Γ (τ = 0.3857) (3), H = 6 × 104Γ (τ = 0.2638) (4) [after Nguyen-Hoe et al. (Reference Nguyen – Hoe, Drawin and Herman1967)].
In Figures 3 and 4 the abscissa α = Δλ/E 0 is scaled with the Holtsmark field
$${E_0} = \displaystyle{{2.603Z_P^{1/3} eN_{\rm e}^{2/3}} \over {4{\rm \pi} {{\rm \epsilon} _0}}}$$where N p denotes the perturbed density N p = N e/Z p.
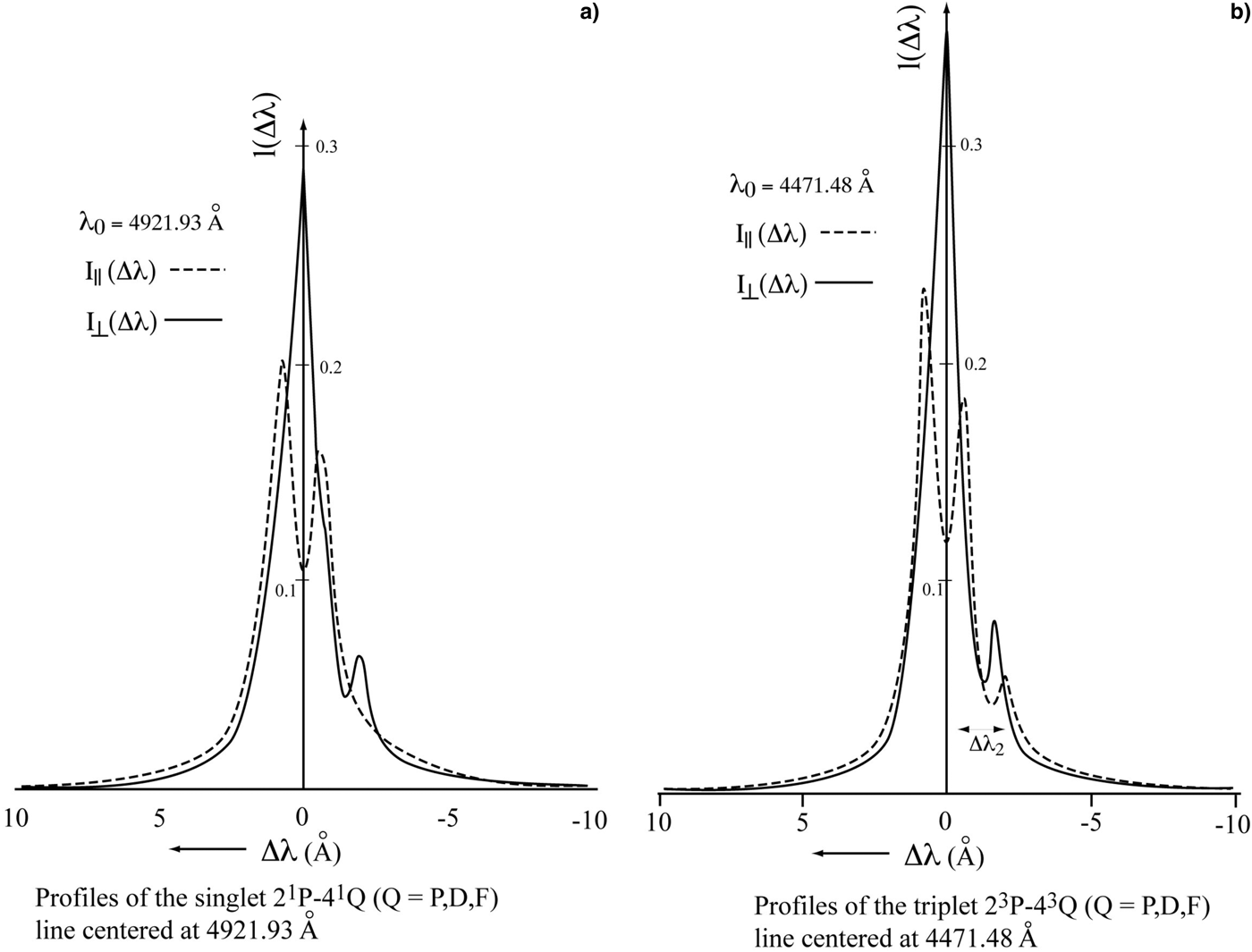
The same line of reasoning applies to the well-known hydrogenic lines 2P–4Q(Q = P,D,F) located at 4471 and 4921 Å in the spectrum of neutral helium (Deutsch, Reference Deutsch1970).
Corresponding polarized profiles are exhibited on Figure 5.
Fig. 5. Balmer-like transitions in neutral Helium. N e = 6 × 1015cm−3, T e = 2 × 104 K, H(G) = 7 × 104 [after Deutsch (Reference Deutsch1970)].
At first sight, the given profiles show a structure which looks very different from the isolated-line Lorentz triplet and from the hydrogen H β line broadened in the presence of a strong magnetic field with the same (N e,T e) values.
More precisely, the parallel intensities 
${I_{\rm \parallel}} (\Delta {\rm \lambda} )$ keep their central peaks 2P–4D and 2P–4F. The perpendicular intensities I ⊥(Δλ) again exhibit this structure, but with a strong asymmetry. The second peak of 
${I_{\rm \parallel}} (\Delta {\rm \lambda} )$ may be surely attributed to the 2P–4F maximum, as would be shown in a plot of 
$I(\Delta {\rm \lambda}, { \hat {\bf z}})$ (polarized along the magnetic field and free from the σ components) with the same two-peaked structure.
Another striking result is the absence of σ components on the 2P–4D side and the appearance of a weak σ component on the 23P − 43F side only, located at
$$\Delta {{\rm \lambda} _z} = {{\rm \lambda} ^2} \times 4.688 \times {10^{ - 13}}B,\quad {\rm \tau} = 0.9$$where λz and λ are in angstroms, and B in gauss (see Fig. 6). This feature is easily explained by the interpenetration of the 2P–4D and 2P–4F static patterns in the presence of a strong Zeeman effect and also by the dominating electron-impact effect in the line center, at the vicinity of the 2P–4D maximum. This behavior is more pronounced for the 41Q sublevels, which have a stronger mutual interaction, than for the 43Q ones. In fact, the line-center broadening of these partially degenerate lines is the result of a competition between Zeeman, static Stark, and electron-impact broadening.
Fig. 6. Energy loss of α particles moving parallel to B as a function of dimensionless speed u, N e = 1021 cm−3, T = 5 keV, B = 5 and 10 MG, [after Cereceda et al. (Reference Cereceda, Deutsch, Deperetti, Sabatier and Nersisyan2000)].
As a by-product it clearly appears that even a strong Zeeman effect cannot be studied with a linear superposition of Lorentz triplets to each component of the static Stark pattern.
These considerations have been very recently extended to high-Z emitters (Iglesias, Reference Iglesias2013) submitted to a combined Stark–Zeeman broadening mechanism, through a global algorithm presentation.
6. ION STOPPING IN MAGNETIZED PLASMA: A DIELECTRIC APPROACH
For many years, a high level of sophisticated and theory activity has been devoted to the stopping of nonrelativistic charged particles in arbitrary magnetized plasmas (see for instance Nersisyan et al., Reference Nersisyan, Toepffer and Zwicknagel2007). However, the experimental vindication of this work is still badly missing. In order to promote a basic science approach easing quantitative studies of ion-magnetized plasma target, we intend to pinpoint – a few conspicuous trends suggested by theory or simulation studies.
6.1. Projectile velocity V ≥ V the
At V ≥ V the, target thermal electron velocity, one expects target ions to remain as a negligible contribution to the ion projectile showing down.
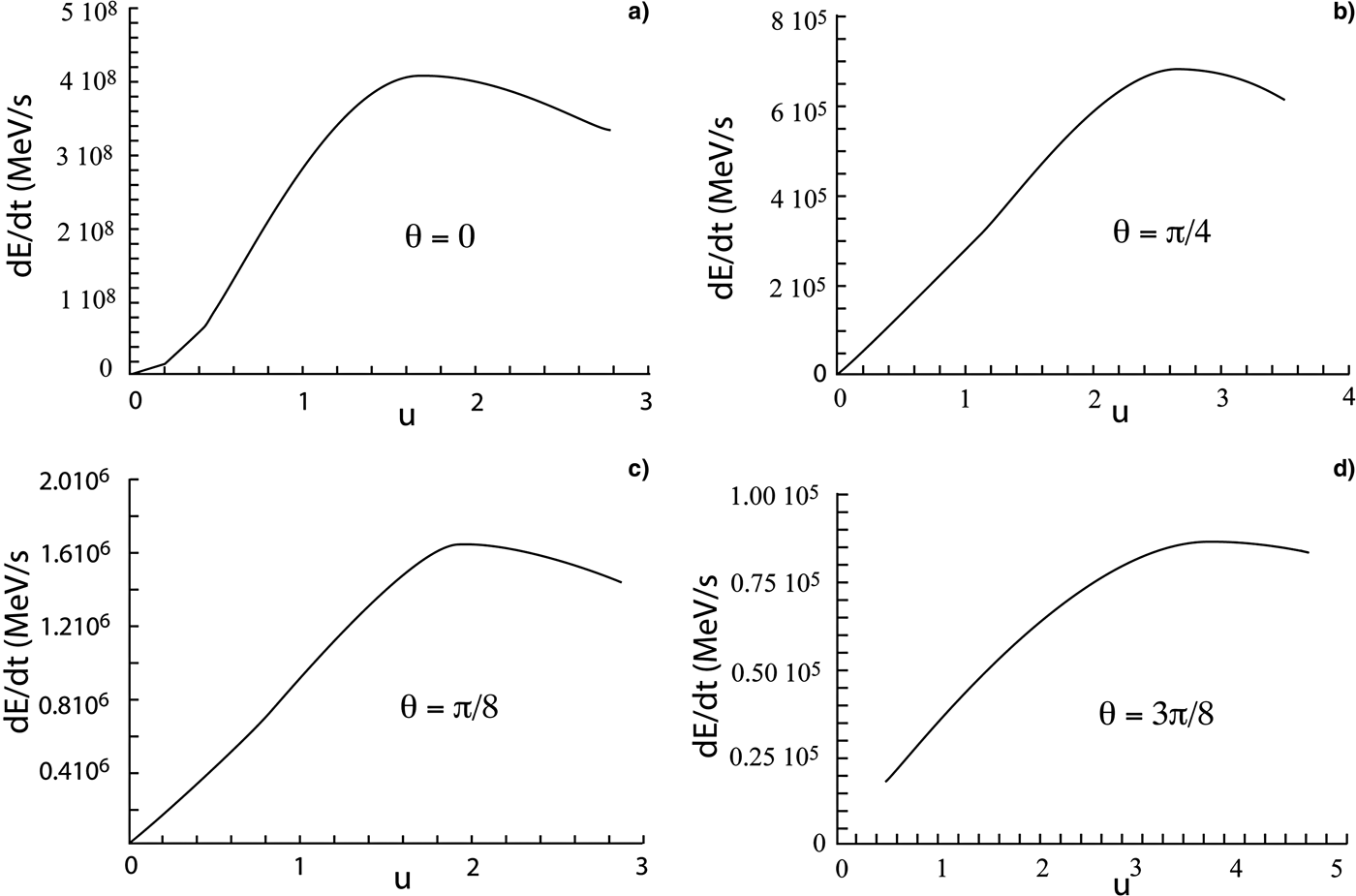
A first look at 
$\vec V{\rm \parallel} \vec B$, steady applied magnetic field, one observes (see Fig. 6) a marked shift at u = V/V the >1 of the maximum projectile stopping, toward the right of its usual location at u ~ 1 for B = 0.
Usually, one uses a finite series representation (Cereceda et al., Reference Cereceda, Deutsch, Deperetti, Sabatier and Nersisyan2000), with a large number of terms (here L = 250 in the stopping expression (Ichimaru, Reference Ichimaru1973)
$$\eqalign{\displaystyle{{dE} \over {dt}} = & \displaystyle{{{q^2}} \over {2{{\rm \pi} ^2}{{\epsilon} _0}}}\int_0^{{{\rm k}_{ \bot {\rm max}}}} d{k_ \bot} \cdot \int_0^\infty d{k_{\rm \parallel}} \sum\nolimits_{\ell = - {\rm L}}^{\rm L} {k_ \bot} J_l^2 ({k_ \bot} {{\rm \rho} _{\rm L}}) \cr & \times \displaystyle{{{k_ \bot} {v_ \bot} + \ell {{\rm \omega} _{\rm c}}} \over {{k^2}}}{I_{\rm m}}\left( {\displaystyle{{ - 1} \over {{\epsilon} ({\bf k},{k_ \bot} {v_ \bot} + \ell {{\rm \omega} _{\rm c}})}}} \right).} $$where q is the projectile charge, ωc its cyclotron frequency and ρL = V ⊥/ωc, its Larmor radius, in terms of the usual longitudinal dielectric function.
Another striking trend is the slowing down θ-dependence, where θ denotes the angle between 
$\vec V$ and 
$\vec B$. It features a monotone decay with increasing θ (see Fig. 7).
Fig. 7. Energy loss of α particles moving at angle θ with respect to B as a function of dimensionless speed u = V/V the. (a) θ = 0, (b) θ = π, (c) θ = π/4, (d) θ = 3π/8. N e = 1021 cm−3, T e = 5 keV, B = 500 T [after Cereceda et al. (Reference Cereceda, Deperetti and Deutsch2005)].
6.2. V < V the
The low ion velocity slowing down (LIVSD) regime is also endowed with specific behaviors. When a simple kinetic-theoretic approach is applied to this regime, one easily faces basic conceptual difficulties (Nersisyan et al., Reference Nersisyan, Toepffer and Zwicknagel2007) for θ = 0 and π/2. A first and preliminary step out of this dilemma is to work within a hydrodynamic framework. We thus implement a radically novel approach to LIVSD when the projectile velocity ν remains smaller than the target electron thermal νthe. We, thus consider ion stopping
$$S(V) \equiv \displaystyle{{d{E_{\rm b}}} \over {dx}}(V),$$near ν = 0. The ratio S(V)/V usually monitors a linear stopping profile, up to 100 keV/a.m.u in cold matter. Similar trends are also reported in highly ionized plasma with B = 0 or B ≠ 0.
From now on, we intend to make use of a very powerful connection between very low velocity ion stopping and particle diffusion through Einstein characterization of ion mobility associated with thermal electron fluctuations in target, around the slow ion projectile visualized as an impurity immersed in a dense and homogeneous electron fluid.
Technically, we are then led to use the recently proposed and exact Dufty–Berkovsky relationship
$$\mathop {\lim} \limits_{\nu \to 0} \displaystyle{{S(V)} \over V} = {k_{\rm B}}{T_{\rm e}}{D^{ - 1}},$$connecting the ratio of stopping to ν in the zero velocity limit with the ion diffusion coefficient D in the target.
In a magnetized plasma D can be readily expressed in terms of Green–Kubo integrands (GKI) involving field fluctuations in the target electron fluid, under the form
$$D = \displaystyle{{{c^2}} \over {{B^2}}}\int_0^\infty d{\rm \tau} \langle {\bf E}({\rm \tau} ) \cdot {\bf E}(0)\rangle $$in terms of an equilibrium canonical average of the two-point autocorrelation function for fluctuating electric fields.
At this juncture we need to frame the GKI in suitable magnetized one-component plasma (OCP) models for the transverse and parallel geometry, respectively. This procedure implies that the slowly incoming ions are evolving against a background of faster fluctuating target electrons (v < V the) providing the OCP rigid neutralizing background thus validating the OCP assumption.
Moreover, restricting to proton projectiles impacting the electron–proton plasma we immediately perceive the pertinence of the diffusion-based LIVSD as phrased by Eq. (23).
First, the proton beam can easily self-diffuse amongst its target homologues, while the same mechanism experienced by target electrons allow them to drag ambipolarly the incoming proton projectiles.
So, the transverse electron LIVSD can either be monitored by the well-known classical diffusion D ⊥ ~ B −2, or by the Bohm-like hydrodynamic one with D ⊥ ~ B −1. In the first case, momentum conservation at the level of the electron–ion pair implies that the ions will diffuse with the same coefficient as the electrons. On the other hand, the hydro Bohm diffusion across B is operated through clumps with a large number of particles involved in this collective process.
So, exploring first the ωb ≥ ωp domain, one can explicit the parallel and B-independent diffusion
$$D_{\rm \parallel} ^{(0)} = \displaystyle{{2\sqrt {\rm \pi} V_{{\rm thi}}^2} \over {{\nu _{\rm c}}}}{\rm \sim O}({\rm \omega} _{\rm b}^0 ),$$
yielding back readily the unmagnetized (B = 0) LIVSD where 
$V_{{\rm thi}}^2 = {k_{\rm B}}T/{M_{\rm i}}$, and νc = ωpεpln(1/εp) in terms of the redefined dimensionless plasma parameter 
${{\rm \varepsilon} _{\rm p}} = 1/{n_{\rm e}}{\rm \lambda} _{\rm D}^3 $, and λD, the Debye length, in a beam-plasma system taken as globally neutral with νc/ωb ≪ 1.
At the same level of approximation transverse diffusion reads as
$$D_ \bot ^{(0)} = \displaystyle{{r_{\rm L}^2 {\nu _{\rm c}}} \over {3\sqrt {\rm \pi}}} {\rm \sim} {\rm O}({\rm \omega} _{\rm b}^{ - 2} )$$in terms of Larmor radius r L = V thi/ωb.
With higher B values (ωb ≫ ωp) one reaches the transverse hydro Bohm regime featuring (Marchetti et al., Reference Marchetti, Kirkpatrick and Dorfman1984)
$${D_ \bot} = D_ \bot ^0 + \displaystyle{{0.5V_{{\rm thi}}^2} \over {{{\rm \omega} _{\rm b}}}}{\rm \epsilon} _{\rm p}^2 {[\ln (1/{{\rm \varepsilon} _{\rm p}})]^{3/2}}\comma$$while parallel diffusion retains a ωb-dependence through
$$D_{\rm \parallel} ^{(0)} = \displaystyle{{{\Gamma ^{5/2}}} \over {{{\rm \omega} _{\rm p}}{a^2}}}{\left( {\displaystyle{3 \over {\rm \pi}}} \right)^{1/2}}\left[ {0.5\;\ln (1 + {X^2}) - 0.3 + \displaystyle{{0.0235} \over {{r^2}}}} \right]\comma$$
where 
$\Gamma = {a^2}/3{\rm \lambda} _{\rm D}^2 $ with a = (3/4πn e)1/3, r = ωp/ωb and 
$X = 1/\sqrt 3 {\Gamma ^{3/2}} \lt 1$ encompasses, most if not all, situations of practical interest.
When electron diffusion is considered, v the should be used in Eq. (26) and the above ambipolar process has to be implemented.
The D ⊥ and 
${D_{\rm \parallel}} $ expressions introduced in Eqs (26) and (27) are expected to document a strong anisotropy between transverse and parallel slowing down. However, in both cases, B-dependence is obviously increasing with B 2 (classical) or B (Bohm-like). The temperature behavior is much more intriguing, as respectively displayed on Figures 8 and 9 for transverse and parallel LIVSD. One, then witnesses a monotonous increase for transverse stopping (Fig. 8) contrasted to a monotonous decay for parallel counterpart (Fig. 9).
Fig. 8. Proton transverse LIVSD in a dense plasma (n = 1021 cm−3 and B = 1010 G). (a) Electron stopping, (b) ion stopping, [after Deutsch & Popoff (Reference Deutsch and Popoff2008)].
Fig. 9. Proton parallel LIVSD in a dense plasma (n = 1021 cm−3 and B = 1010 G). (a) Electron stopping (B ≠ 0), (b) ion stopping (B ≠ 0), (c) ion stopping (B = 0), (d) electron stopping (B = 0) [after Deutsch & Popoff (Reference Deutsch and Popoff2008)].
We thus implemented the very simple LIVSD expression (23) to the, a priory very involved ion beam-arbitrarily magnetized plasma interaction. We used transverse and parallel diffusion coefficients in suitably framed magnetized OCP with target electrons building up the corresponding neutralizing background. Thus, we reached analytic LIVSD transverse and parallel expressions.
Finally, we investigate the stopping power of an ion in a magnetized electron plasma in a model of binary collisions (BC) between ions and magnetized electrons, in which the Coulomb interaction is treated up to second-order as a perturbation to the helical motion of the electrons. The calculations are done with the help of an improved BC theory which is uniformly valid for any strength of the magnetic field and where the second-order two-body forces are treated in the interaction in Fourier space without specifying the interaction potential. The stopping power is explicitly calculated for a regularized and screened potential which is both of finite range and less singular than the Coulomb interaction at the origin. Closed expressions are derived for mono-energetic electrons, which are then folded with the velocity distributions of the electrons. The resulting stopping power is evaluated for isotropic Maxwell velocity distributions of the electrons. The accuracy and validity of the present model have been studied by comparisons with the classical trajectory Monte Carlo numerical simulations.
Finally, with a view toward possible experiments envisioned at LULI (Palaiseau) or TITAN (Livermore) with PW-laser produced protons, we propose to check at B = 20 T, the θ = 0 and π/2 data obtained with the present kinetic-elaborated formalism (Fig. 10).
Fig. 10. Proton stopping in a magnetized electron–proton plasma (n e = 1018 cm−3; T = 10 eV). (a) θ = 0, (b) θ = π/2.
7. SUMMARIES
Out of the above surveyed diagnostics for dense and magnetized plasmas of ICF interest, we stress emphasis on the following suggestions:
• The IFE needs a basic theory simulation revisitation in order to match quantitatively present day available experimental vindication.
• TS in a magnetized plasma is presently restricted to dilute and Tokamak-like situations. It has to be extended to dense and hot plasmas envisioned for ICF.
• Combined Stark–Zeeman line broadening requires to be adapted to high-Z elements (Iglesias, Reference Iglesias2013) and eventually compared with fine and hyperfine line splitting. Moreover the spiraling of perturbing charges around the emitter has to be tackled for Larmor radii smaller than Debye lengths.
As far as we know, the above panorama of potentially available diagnostics for strongly magnetized ICF-like plasmas is here critically displayed for the first time. Such a presentation is primarily motivated by novel experimental achievements (Fujioka et al., Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Shiraga, Nishimura and Azechi2013) allowing for a very efficient and nearly steady magnetization process, far beyond those previously proposed for magnetized target fusion (for instance Cereceda et al., Reference Cereceda, Deutsch, Deperetti, Sabatier and Nersisyan2000).
We hope that the above speculations could be appreciated as timely ones in view of the increasing interest within the inertial fusion community for the investigation of ultra-dense plasmas exposed to kilo Teslas steady magnetic fields. In particular, it is highly likely that an imposed magnetization on inertial pellet could allow for a better control of its compression in a large setup of the NIF–LeMegaJoule (LMJ) class.
