Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T14:19:28.279Z Has data issue: false hasContentIssue false
  • English
  • Français

The diagnostics of density distribution for inhomogeneous dense DT plasmas using fast protons

Published online by Cambridge University Press:  16 June 2008

X.-M. Li ,
B.-F. Shen ,
X.-M. Zhang ,
Z.-Y. Jin  and
F.-C. WANG
X.-M. Li*
Affiliation:
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai, China
B.-F. Shen
Affiliation:
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai, China
X.-M. Zhang
Affiliation:
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai, China
Z.-Y. Jin
Affiliation:
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai, China
F.-C. WANG
Affiliation:
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai, China
*
Address correspondence and reprint requests to: Xue-Mei Li, State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, the Chinese Academy of Sciences, Shanghai 201800, China. Email: xmlee0102@yahoo.com.cn
Rights & Permissions [Opens in a new window]

Abstract

The density distribution of inhomogeneous dense deuterium-tritium plasmas in laser fusion is revealed by the energy loss of fast protons going through the plasma. In our simulation of a plasma density diagnostics, the fast protons used for the diagnostics may be generated in the laser-plasma interaction. Dividing a two-dimensional area into grids and knowing the initial and final energies of the protons, we can obtain a large linear and ill-posed equation set for the densities of all grids, which is solved with the Tikhonov regularization method. We find that the accuracy of the set plan with four proton sources is better than those of the set plans with less than four proton sources. Also we have done the density reconstruction especially for four proton sources with and without assuming circularly symmetrical density distribution, and find that the accuracy is better for the reconstruction assuming circular symmetry. The error is about 9% when no noise is added to the final energy for the reconstruction of four proton sources assuming circular symmetry. The accuracies for different random noises to final proton energies with four proton sources are also calculated.

Keywords

Density distributionDT plasmaFast protonsL-curveTikhonov regularization method
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 2 , June 2008 , pp. 139 - 145
Copyright
Copyright © Cambridge University Press 2008

1. INTRODUCTION

For relatively low plasma densities, several methods of plasma diagnostics, such as laser interferometry (Belyaev et al., Reference Belyaev, Basko, Sharkov, Cherkasov and Fertman1996), Thomson scattering (Snyder et al., Reference Snyder, Crawford and Fincke2000), and spectroscopic measurements (Morgan et al., Reference Morgan, Griem and Elton1994), have been successfully applied. With the increase of the plasma density, the optical depth of the plasma volume becomes excessively high when the plasma areal density is beyond 1021/cm2 (Golubev et al., Reference Golubev, Basko, Fertman, Kozodaev, Mesheryakov, Sharkov, Vishnevskiy, Fortov, Kulish, Gryaznov, Mintsev, Golubev, Pukhov, Smirnov, Funk, Stoewe, Stetter, Flierl, Hoffmann, Jacoby and Iosilevski1998; Wetzler et al., Reference Wetzler, Suss, Stockl, Tauschwitz and Hoffmann1997). So the techniques above no longer work well. At the same time, fast protons generated during the interaction of ultraintense (I > 1019 W/cm2) short laser pulses with thin solid targets become effective for the diagnostics of dense plasmas because of their large stopping range in plasmas, small source size, short duration, and large number density.

The generation of fast protons (Dong et al., Reference Dong, Sheng and Yu2003; Mora, Reference Mora2003; Silva et al., Reference Silva, Marti, Davies, Fonseca, Ren, Tsung and Mori2004; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernãndez2006; Yin et al., Reference Yin, Albright, Hegelich and Fernandez2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Willi et al., Reference Willi, Toncian, Borghesi, Fuchs, D'Humieres, Antici, Audebert, Brambrink, Cecchetti, Pipahl and Romagnani2007) has been studied in many papers and the generation of quasi-monoenergetic protons is dominated (Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernãndez2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Willi et al., Reference Willi, Toncian, Borghesi, Fuchs, D'Humieres, Antici, Audebert, Brambrink, Cecchetti, Pipahl and Romagnani2007). There are also many proton imaging techniques which allow the distribution of electromagnetic fields in plasmas and around laser-irradiated targets to be explored (Ruhl et al., Reference Ruhl, Cowan and Pegoraro2006; Borghesi et al., Reference Borghesi, Schiavi, Campbell, Haines, Willi, MacKinnon, Gizzi, Galimberti, Clarke and Ruhl2001, Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2002, Reference Borghesi, Schiavi, Campbell and Haines2003, Reference Borghesi, Audebert, Bulanov, Cowan, Fuchs, Gauthier, MacKinnon, Patel, Pretzler, Romagnani, Schiavi, Toncian and Willi2005, Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007) and the density gradient of the laser-driven implosion target to be obtained using the angle deflection from the density impact on the protons (Mackinnon et al., Reference Mackinnon, Patel, Borghesi, Clarke, Freeman, Habara, Hatchett, Hey, Hicks, Kar, Key, King, Lancaster, Neely, Nikkro, Norreys, Notley, Phillips, Romagnani, Snavely, Stephens and Town2006). The researches above have been done with the thickness of the probed targets much smaller than the collisional stopping distance for the protons employed, so the energy loss of the protons (Borghesi et al., Reference Borghesi, Schiavi, Campbell, Haines, Willi, MacKinnon, Gizzi, Galimberti, Clarke and Ruhl2001, Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2002, Reference Borghesi, Schiavi, Campbell and Haines2003, 2005, 2007) is mainly due to the electromagnetic fields they have passed through. In the following, we will focus on the impact of background electrons' collision on the protons, ignoring that of the electromagnetic fields, which is right for much denser and thicker plasmas. Therefore, we can use fast protons for the density diagnostics for extremely dense plasmas, such as in the case of laser fusion.

Neglecting the self-generated electromagnetic fields by the proton beams, which is appropriate when the proton number is low or protons move together with electrons of equal number (Califano et al., Reference Califano, Pegoraro and Bulanov2003), we can consider only the energy loss induced by collisions between particles. The interaction physics for the protons is simpler than that for the electrons when they are going through the deuterium-tritium (DT) plasmas, because the deflection angle for protons is much smaller than that for electrons and the mean transverse dispersion distance for the protons is much smaller than the corresponding propagating distance in DT plasmas. Therefore, fast protons can be supposed to go through the probed plasma straightly (Bloembergen & Heerden, Reference Bloembergen and Heerden1951; Smith, Reference Smith1947; Nardi et al., Reference Nardi, Maron and Hoffmann2007; Li et al., Reference Li, Shen, Zha, Zhang, Jin and Wang2006), which makes it easier to use the Coulomb energy loss as a method of plasma density diagnostics.

The density of the order of 1019/cm3 in homogeneous plasma has been obtained through the above method with one single proton beam (Golubev et al., Reference Golubev, Basko, Fertman, Kozodaev, Mesheryakov, Sharkov, Vishnevskiy, Fortov, Kulish, Gryaznov, Mintsev, Golubev, Pukhov, Smirnov, Funk, Stoewe, Stetter, Flierl, Hoffmann, Jacoby and Iosilevski1998). We will demonstrate the way of revealing the density distribution of inhomogeneous plasmas after knowing the coulomb energy loss of fast proton beams. The method of obtaining the density distribution of the two-dimensional (2D) slice plasma will be demonstrated in Sections 3, 4, and 5. A brief discussion of the plasma density diagnostics will be presented at the end. When more proton sources are used, the experiment will be more difficult, although the accuracy of revealing will be improved. So the number of the proton sources will be as few as possible. In this paper, no more than four proton sources will be used.

2. THEORY AND FORMULAS

The studied 2D slice area is divided into many grids, for example, N = 14 × 14 as shown in Figure 1, N is the picture element of the area. The set plan of four proton sources is displayed in Figure 1.

Fig. 1. The zone studied is the square of 210 µm × 210 µm extending from 390 µm to 600 µm on both the x axis and the y axis and divided into 196 grids. The coordinates of the proton sources represented by four quadrangles are (0, 195), (0, 495), (0, 990), and (390, 0). The distance between the proton energy detectors and the studied zone is about 1 mm. (This figure is only the sketch map, not represents the actual size.)

Because protons propagate in a DT plasma almost without any angle deflection (Bloembergen & Heerden, Reference Bloembergen and Heerden1951; Smith, Reference Smith1947; Nardi et al., Reference Nardi, Maron and Hoffmann2007; Li et al., Reference Li, Shen, Zha, Zhang, Jin and Wang2006), the stopping power for fast protons in the plasma is (Atzeni & Meyer-ter-vehn, Reference Atzeni and Meyer-ter-vehn2004; Hoffmann et al., Reference Hoffmann, Weyrich, Wahl, Gardes, Bimbot and Fleurier1990; Meyer-ter-Vehn et al., Reference Meyer-ter-vehn, Witkowski, Bock, Hoffmann, Hofmann, Muller, Arnold and Mulser1990; Deutsch et al., Reference Deutsch, Maynard, Bimbot, Gardes, Dellanegra, Dumail, Kubica, Richard, Rivet, Servajean, Fleurier, Sanba, Hoffmann, Weyrich and Wahl1989)

(1)
{dE_p \over dx} = - {4\pi \, \lpar e^2 / 4 \pi \varepsilon_0\rpar ^2 \over m_e v_p^2} n_{\rm fe} L_{\rm fe} \quad L_{\rm fe} = \ln {2\, m_e v_p^2 \over \hbar \omega_p}.

Here v p and E p are the velocity and the kinetic energy of fast protons in the probing beam, respectively, n fe is the density of free electrons in the plasma, L fe is the coulomb logarithm, ɛ0 is the permittivity of free space, ωp = (4πn fee 2/m e)1/2 is the plasma frequency, and m e and −e are the electron mass and charge, respectively (international system of unit is used in our calculation).

The conditions under what the first equation is feasible are: (1) the incident proton velocity v p is much higher than the thermal velocity of plasma electrons v e = (2T e/m e)1/2 (Smith, Reference Smith1947), (2) the energy of the protons is more than 0.1 MeV, so that the capture and loss of the electron can be neglected, and the effective charge of the protons is always one (Livingston & Beth, Reference Livingston and Beth1937), (3) the protons are nonrelativistic, so the relativistic effect can be neglected. The three conditions are completely satisfied in this paper as described below, where proton energy E p is several MeVs and plasma temperature T e is much smaller than 10 keV before the ignition laser is used in fast ignition. Because the DT plasma is fully ionized, only free electrons play an important role.

Assuming that the plasma density is uniform inside each grid and the propagating length in a grid for a probing proton is l, and using E p = m pv p2/2 in the nonrelativistic limit, Eq. (1) can be integrated to:

(2)
n_{\rm fe} l = \lpar E_{\,p0}^2 - E_{\,p0}^2\rpar \times a\comma \;

with

(3)
a={1 \over 4\pi \, \lpar e^2 / 4\pi \varepsilon_0\rpar ^2 L_{\rm fe}}{m_e \over m_p}\comma \;

where E p0 and E p1 are the initial and final energies of the protons, respectively. A remarkable feature of the above expression is that, provided that E p0 and E p1 are given, the expression contains only one unknown quantity, that is, the density of free electrons n fe.

When the probing proton beam propagates in the inhomogeneous plasmas in a specific direction, the equation for the densities of all grids is

(4)
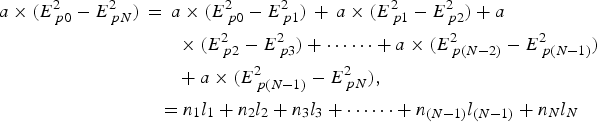
\eqalign{a \times \lpar E_{\,p0}^2 - E_{\,pN}^2 \rpar & \,=\, a \times \lpar E_{\,p0}^2 - E_{\,p1}^2 \rpar \,+\, a \times \lpar E_{\,p1}^2 - E_{\,p2}^2 \rpar + a \cr & \qquad \times \lpar E_{\,p2}^2 - E_{\,p3}^2\rpar + \cdots \cdots + a \times \lpar E_{\,p\lpar N - 2\rpar }^2 - E_{\,p\lpar N - 1\rpar }^2 \rpar \cr & \qquad +a \times \lpar E_{\,p\lpar N - 1\rpar }^2 - E_{\,pN}^2 \rpar, \cr & \quad = n_1 l_1 + n_2 l_2 + n_3 l_3 + \cdots \cdots + n_{\lpar N - 1\rpar } l_{\lpar N - 1\rpar } + n_N l_N}

n 1, n 2, n 3 …… n (N−1),n N are the densities of each grid respectively, l 1,l 2,l 3…l (N−1),l N are the distances of this proton beam propagating in each grid.

3. TIKHONOV' REGULARIZATION METHODS SOLVING THE ILL-POSED EQUATION SET

In order to reveal the density distribution, we should have M (M ≥ N) linear equations of the densities of all grids. So M sets of initial and final protons energies should be known. Then we will obtain the following large linear equation set,

(5)
\hbox{Ax} = \hbox{b}\comma \;

with

\eqalign{\hbox{A} &= \left(\matrix{l_{11} & l_{12} & l_{13} & \cdots & l_{1 N} \cr l_{21} & l_{22} & l_{23} & \cdots & l_{2 N} \cr l_{31} & l_{32} & l_{33} & \cdots & l_{3 N} \cr \cdots & \cdots & \cdots & \cdots & \cdots \cr l_{M1} & l_{M2} & l_{M3} & \cdots & l_{M N}}\right)\comma \; \hbox{x} = \left(\matrix{n_1 \cr n_2 \cr n_3 \cr \vdots \cr n_N}\right)\ \hbox{and }\cr \hbox{ b} & = \hbox{a} \times \Delta \hbox{E}^{2} = a \times \left(\matrix{E^2_{10} - E^2_{1\, N} \cr E^2_{20} - E^2_{2\, N} \cr E^2_{30} - E^2_{3\, N} \cr \vdots \cr E^2_{M0} - E^2_{MN}} \right).}

The matrix A can be calculated as long as the probed area, the initial position, and the propagating direction of proton beams are known. Unfortunately, the condition number of this matrix is usually very large and consequentially Eq. (5) is quite ill-posed. So it is not easy to reveal the accurate plasma density distribution by solving this equation set, even quite accurate final proton energies are measured (Xiao et al., Reference Xiao, Yu, Wang, Shi and Li2003). In order to reveal accurately the density distribution with the use of Eq. (5), the Tikhonov regularization method which is very popular in other similar inverse problems (Xiao et al., Reference Xiao, Yu, Wang, Shi and Li2003) can be used. Here we have to solve λ for the minimized question,

(6)
\min \left\{ \vert \vert \hbox{Ax} - \hbox{b} \vert \vert_2^2 + \lambda^2 \hbox{I}^{2}\right\} \comma \;

where I is the unit matrix, λ is regularization factor, AT is the transpose of the matrix A. So, x can be obtained from the equation set

(7)
\lpar \hbox{A}^{\rm T} \hbox{A} + \lambda \hbox{I}^{2}\rpar \hbox{x} = \hbox{A}^{\rm T} \hbox{b}.

So Eq. (5) can be solved with the right λ and the corresponding x. The ways finding the right λ include the Newton algorithm and the fast algorithm based on the deviation principle of L-curve (Xiao et al., Reference Xiao, Yu, Wang, Shi and Li2003). The error of revealing can be described as (Xiao et al., Reference Xiao, Yu, Wang, Shi and Li2003)

(8)
Er = \hbox{norm} \lpar \hbox{D}^{\prime} - \hbox{D}\rpar /\hbox{norm}\lpar \hbox{D}\rpar \comma \;

where D is the simulated density matrix and D′ is the revealed density matrix.

4. NUMERICAL SIMULATIONS

4.1. The Set Plan for the Numerical Simulation

The 2D dense plasma slice considered has the density of the order 1025/cm3. The studied zone extends from 390 µm to 600 µm both on x direction and y direction in our coordinate system. The density distribution we will study has the expression

(9)
n = \left\{\matrix{10^{25}/\hbox{cm}^3 \times \exp\lpar - k/36\rpar & k \lt 60 \cr 0\hfill & k \geq 60}\right\}\comma \;

where k is the distance between the position and the center of the area (495, 495). So the plasma densities of all grids are assumed as the densities of the center of each grid. With this way, a simulated density matrix D of 196 elements is obtained.

Four identical proton sources are placed at (0, 195), (0, 495), (0, 990), and (390, 0), respectively, with the mono-energy of 17 MeV. If the proton energy is too low, the proton beams have already exhausted before leaving the plasmas which makes the measurements of final proton energies incorrect; if the energy is too high, the differences of final energies of different proton beams are too small after propagating through the plasmas which makes the measurements of final energies too difficult to be obtained. The energy detectors facing the four proton sources are around 1 mm away from probed area and the number (M) of the detectors is always not smaller than N. The matrix A obtained this way has a condition number of 1.7 × 103, so Eq. (5) is quite ill-posed.

4.2. The Calculation for the Density Distribution

4.2.1. The Calculation for the Density Reconstruction Without Assuming Circularly Symmetrical Density Distribution

The final energies of each proton beam in specific directions are calculated analytically using Eqs. (1) and (9) for the simulated plasma density, so that an energy matrix of M = 218 elements is given. With this vector and using the Tikhonov regularization method based on deviation principle of L-curve, the revealed density matrix D′ of 196 elements is obtained and the simulated plasma density profile can be repeated to some degree. The contour lines of the simulated density D are shown in Figure 2, also the contour lines of the revealed density D′ are shown in Figure 3. Comparing the two figures, we find that Figure 3 can reflect the correct density distribution. In the zone where the simulated plasmas appear, the revealed density is a little smaller than the simulated one, and on the same order of 1025/cm3. The error can be described as Er = 21% (Xiao et al., Reference Xiao, Yu, Wang, Shi and Li2003). The accuracy is found to be improved slightly after we have done the density reconstruction for 1600 grids and same four proton sources. And only with more proton sources, the accuracy can be improved with more grids. So we will do the reconstruction with 196 grids in the following for the simplicity of the experiment with less proton energy detectors and the rapidity of the calculation.

Fig. 2. The contour lines of the simulated density distribution. (The density values are the product of the value of each contour line and 1025/cm3, and this will apply to the figures in the following).

Fig. 3. The contour lines of the revealed density distribution without noise when the numbers of the grids and the protons sources are 196 and 4 respectively, the error of revealing is described as Er = 21%.

Radio-Chromic Film (RCF) is one kind of energy detectors and has been used for high-flux proton detection in several laser–plasma experiments (Borghesi et al., Reference Borghesi, Schiavi, Campbell, Haines, Willi, MacKinnon, Gizzi, Galimberti, Clarke and Ruhl2001, Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke, Pegoraro, Ruhl and Bulanov2002, Reference Borghesi, Schiavi, Campbell and Haines2003, Reference Breschi, Borghesi, Campbell, Galimberti, Giulietti, Gizzi, Romagnani, Schiavi and Willi2005, 2007). The uncertainty of the measurement is no more than 5% (McLaughlin et al., Reference McLaughlin, Chen, Soares, Miller, Van Dyk and Lewis1991), even can decrease to 2% in some measurement (Nichiporov et al., Reference Nichiporov, Kostjuchenko, Puhl, Bensen, Desrosiers, Dich, McLaughlin, Kojima, Coursey and Zink1995; Christopher, Reference Christopher2007). So we add two kinds of random noises to the final proton energies:

(10)
\eqalignno{\hbox{E}_{\,final}^{\prime} &= \hbox{E}_{\,final} \times \lpar 1 - 0.02 \times \hbox{rand} \lpar \hbox{size} \lpar \hbox{E}_{\,final}\rpar \rpar \rpar \comma \; \cr \hbox{E}_{\,final}^{\prime} &= \hbox{E}_{\,final} \times \lpar 1 - 0.05 \times \hbox{rand} \lpar \hbox{size} \lpar \hbox{E}_{\,final}\rpar \rpar \rpar.}

The corresponding revealing errors are 26% and 37%, also the contour lines of calculated densities are shown in Figures 4 and 5, respectively.

Fig. 4. The contour lines of the revealed density distribution for four proton sources with noises level of 2% added to the final proton energies. The error of revealing is described as Er = 26%.

Fig. 5. The contour lines of the revealed density distribution for four proton sources with noises level of 5% added to the final proton energies. The error of revealing is described as Er = 37%.

We also calculate the errors for two (M = 200) and three (M = 200) proton sources without noises to final proton energies, which are 47% and 39%. So more proton sources are used, more improved accuracy will be reached.

4.2.2. The Calculation for the Density Reconstruction Assuming Circularly Symmetrical Density Distribution

When we assume the circularly symmetrical density distribution for the density reconstruction, unknown variables for the densities of all grids will decrease a lot, that is, from 196 to 25. Errors of revealing are described as Er = 9%, 12%, and 22% for four proton sources without and with two kinds of noises (2% and 5%) to the final proton energies, respectively, and also the contour lines of calculated densities are shown in Figures 6, 7, and 8, respectively. Compared with the ones (21%, 26%, and 37%) without the circular symmetry, all of the three kinds of revealing errors (without and with two kinds of noises to the final proton energies) have decreased more than ten percents. So assuming circularly symmetrical density distribution is better for the density reconstruction.

Fig. 6. The contour lines of the revealed density distribution for the four proton sources assuming circular symmetry without noise to the final proton energies. The error of revealing is described as Er = 9%.

Fig. 7. The contour lines of the revealed density distribution for four proton sources with noises level of 2% added to the final proton energies and assuming circular symmetry. The error of revealing is described as Er = 12%.

Fig. 8. The contour lines of the revealed density distribution for four proton sources with noises level of 5% added to the final proton energies and assuming circular symmetry. The error of revealing is described as Er = 22%.

With the assumption of circularly symmetrical density distribution, we also do the density reconstruction for one proton source (M = 200) without and with two kinds of noises (2% and 5%) to the final proton energies, the errors are 11%, 19%, and 36%. From the comparison of the revealing errors of one and those of four proton sources, we can find that the errors are almost the same when no noises are added to final energies, and that the accuracy of four proton sources is better than that of one proton source when noises are added to final proton energies. When the level of the noises increases, the difference between the accuracies of one and four proton sources also increases. Because the set plan with one proton source is easier for the performance of the experiment, one proton source can also be suitable for low level noise while doing the density reconstruction assuming circular symmetry.

5. DISCUSSION

In order to describe the accuracy better, the errors at the radius of k = 15 µm and k = 30 µm are calculated for the set plan in Figure 6, which are both described as Er = 8%. So the accuracies are on the same level as the average accuracy with error described as Er = 9%. For the density reconstructions of four proton sources without assuming circular symmetry, the revealed density distributions give incorrect results for some area at large radius where the simulated plasma doesn't exit, but the values of revealed density there are very small, as shown in Figures 3, 4, and 5.

When the density reconstruction assuming circularly symmetrical density distribution is done, we should be careful of the locations where the four proton sources are put. If they are put at circularly symmetrical locations, the efficient number of proton sources will be smaller than four and the accuracy will not reach the normal level as obtained in this paper.

6. CONCLUSION

Particular properties of the protons generated in the laser-plasma interaction have made protons suitable for the diagnostics of dense plasmas. Our diagnostics of the density distribution of the inhomogeneous plasma is suitable for the dense and thick plasmas, especially in the case of laser fusion. From the Coulomb energy loss of protons propagating in the inhomogenous plasmas, we obtain the large linear and ill-posed equation set for each grid density, solved with the Tikhonov regularization method, which is very popular in other inverse problems. The accuracy will increase with the number of proton sources. Because of the difficulty in the experiment, no more than four proton sources are used in this paper. We mainly do the density reconstruction for four proton sources without and with two kinds of noises (2% and 5%) to final proton energies. The revealing errors are 21%, 26%, and 37%, respectively. Furthermore, the accuracy of the density reconstruction assuming circularly symmetrical density distribution is better than that of the reconstruction without assuming the circular symmetry and the revealing errors are 9%, 12%, and 22% for four proton sources without and with two kinds of noises (2% and 5%) to the final proton energies.

ACKNOWLEDGMENTS

This work is supported by National Natural Science Foundation of China (Project 10675155) and the 973 program (No. 2006CB806004). We also would like to express our thanks to Japan–Korea–China Cooperative project on “High Energy Density Sciences for Laser Fusion Energy.”

References

REFERENCES

Atzeni, S. & Meyer-ter-vehn, J. (2004). The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter. Oxford: Oxford Science.CrossRefGoogle Scholar
Belyaev, A.G., Basko, M., Sharkov, B., Cherkasov, A. & Fertman, A. (1996). Diagnostics of plasma target for ion beam: target interaction experiments. Fusion Engin. Design 32–33, 557–560.Google Scholar
Bloembergen, N. & Heerden, P.J.V. (1951). The range and straggling of protons between 35 and 120 Mev. Phys. Rev 83, 561–566.CrossRefGoogle Scholar
Borghesi, M., Schiavi, A., Campbell, D.H., Haines, M.G., Willi, O., MacKinnon, A.J., Gizzi, L.A., Galimberti, M., Clarke, R.J. & Ruhl, H. (2001). Proton imaging: a diagnostic for inertial confinement fusion/fast ignitor studies. Plasma Phys. Contr. Fusion 43, 267–276.CrossRefGoogle Scholar
Borghesi, M., Campbell, D.H., Schiavi, A., Haines, M.G., Willi, O., MacKinnon, A.J., Patel, P., Gizzi, L.A., Galimberti, M., Clarke, R.J., Pegoraro, F., Ruhl, H. & Bulanov, S. (2002). Phys. Plasmas 9, 2214–2220.CrossRefGoogle Scholar
Borghesi, M., Schiavi, A., Campbell, D.H. & Haines, M.G. (2003). Proton imaging detection of transient electromagnetic fields in laser-plasma interactions (invited). Rev. Sci. Instr. 74, 1688–1693.CrossRefGoogle Scholar
Borghesi, M., Audebert, P., Bulanov, S.V., Cowan, T., Fuchs, J., Gauthier, J.C., MacKinnon, A.J., Patel, P.K., Pretzler, G., Romagnani, L., Schiavi, A., Toncian, T. & Willi, O. (2005). High-intensity laser-plasma interaction studies employing laser-driven proton probes. Laser Part. Beams 23, 291–295.CrossRefGoogle Scholar
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–167.CrossRefGoogle Scholar
Breschi, E., Borghesi, M., Campbell, D.H., Galimberti, M., Giulietti, D., Gizzi, L.A., Romagnani, L., Schiavi, A. & Willi, O. (2004). Spectral and angular characterization of laser-produced proton beams from dosimetric measurements. Laser Part. Beams 22, 393–397.CrossRefGoogle Scholar
Califano, F., Pegoraro, F. & Bulanov, S.V. (2003). Propagation of a short proton beam through a thin plasma slab. Phys. Rev. E 68, 066406.CrossRefGoogle Scholar
Christopher, G.S. (2007). Radiochromic film dosimetry. Rad. Measur. 41, S100–S116.Google Scholar
Deutsch, C., Maynard, G., Bimbot, R., Gardes, D., Dellanegra, S., Dumail, M., Kubica, B., Richard, A., Rivet, M.F., Servajean, A., Fleurier, C., Sanba, A., Hoffmann, D.H.H., Weyrich, K. & Wahl, H. (1989). Ion beam-plasma interaction: A standard model approach. Nucl. Instr. & Meth. Phys. Res. A 278, 38–43.CrossRefGoogle Scholar
Dong, Q.L., Sheng, Z.M. & Yu, M.Y. (2003). Optimization of ion acceleration in the interaction of intense femtosecond laser pulses with ultrathin foils. Phys. Rev. E 68, 026408.CrossRefGoogle ScholarPubMed
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Golubev, A., Basko, M., Fertman, A., Kozodaev, A., Mesheryakov, N., Sharkov, B., Vishnevskiy, A., Fortov, V., Kulish, M., Gryaznov, V., Mintsev, V., Golubev, E., Pukhov, A., Smirnov, V., Funk, U., Stoewe, S., Stetter, M., Flierl, H.P., Hoffmann, D.H.H., Jacoby, J. & Iosilevski, I. (1998). Dense plasma diagnostics by fast proton beams. Phys. Rev. E 57, 3363–3367.CrossRefGoogle Scholar
Hegelich, B.M., Albright, B.J., Cobble, J., Flippo, K., Letzring, S., Paffett, M., Ruhl, H., Schreiber, J., Schulze, R.K. & Fernãndez, J.C. (2006). Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 439, 441–444.CrossRefGoogle ScholarPubMed
Hoffmann, D.H.H., Weyrich, K., Wahl, H., Gardes, D., Bimbot, R. & Fleurier, C. (1990). Energy loss of heavy ions in a plasma target. Phys. Rev. A 42, 2313–2321.CrossRefGoogle Scholar
Li, X.M., Shen, B.F., Zha, X.J., Zhang, X.M., Jin, Z.Y. & Wang, F.C. (2006). The energy deposition and propagation of fast ions in ultra-dense plasmas. Acta Phys. Sinica 55, 2313–2321.Google Scholar
Livingston, M.S. & Beth, H.A. (1937). Nuclear physics C. nuclear dynamics, experimental. Rev. Mod. Phys. 9, 000245.CrossRefGoogle Scholar
Mackinnon, A.J., Patel, P.K., Borghesi, M., Clarke, R.C., Freeman, R.R., Habara, H., Hatchett, S.P. & Hey, D., Hicks, D.G., Kar, S., Key, M.H., King, J.A., Lancaster, K., Neely, D., Nikkro, A., Norreys, P.A., Notley, M.M., Phillips, T.W., Romagnani, L., Snavely, R.A., Stephens, R.B. & Town, R.P.J. (2006). Proton radiography of a laser-driven implosion. Phys. Rev. Lett. 97, 045001.CrossRefGoogle ScholarPubMed
McLaughlin, W.L., Chen, Y.D., Soares, C.G., Miller, A., Van Dyk, G. & Lewis, D.F. (1991). Sensitometry of the response of a new radiochromic film dosimeter to gamma radiation and electron beams. Nucl. Instr. & Meth. Phys. Res. A 302 165–176.CrossRefGoogle Scholar
Meyer-ter-vehn, J., Witkowski, S., Bock, R., Hoffmann, D.H.H., Hofmann, I., Muller, R.W., Arnold, R. & Mulser, P. (1990). Accelerator and target studies for heavy ion fusion at the Gesellschaft-fur-Schwerionenforschung. Phys. Fluids B 2, 1313–1317.CrossRefGoogle Scholar
Mora, P. (2003). Plasma Expansion into a Vacuum. Phys. Rev. Lett. 90, 185002.CrossRefGoogle ScholarPubMed
Morgan, C.A., Griem, H.R. & Elton, R.C. (1994). Spectroscopic measurements of electron density and temperature in polyacetal-capillary-discharge plasmas. Phys. Rev. E 49, 2282–2291.CrossRefGoogle ScholarPubMed
Nardi, E., Maron, Y. & Hoffmann, D.H.H. (2007). Plasma diagnostics by means of the scattering of electrons and proton beams. Laser Part. Beams 25, 489–495.CrossRefGoogle Scholar
Nichiporov, D., Kostjuchenko, V., Puhl, J.M., Bensen, D.L., Desrosiers, M.F., Dich, C.E., McLaughlin, W.L., Kojima, T., Coursey, B.M. & Zink, S. (1995). Investigation of applicability of alanine and radiochromic detectors to dosimetry of proton clinical beams. Appl. Rad. Isotopes 46, 1355–1362.CrossRefGoogle ScholarPubMed
Ruhl, H., Cowan, T. & Pegoraro, F. (2006). The generation of images of surface structures by laser-accelerated protons. Laser Part. Beams 24, 181–184.CrossRefGoogle Scholar
Silva, L.O., Marti, M., Davies, J.R., Fonseca, R.A., Ren, C., Tsung, F.S. & Mori, W.B. (2004). proton shock acceleration in laser-plasma interactions. Phys. Rev. Lett. 92, 015002.CrossRefGoogle ScholarPubMed
Smith, J.H. (1947). Theoretical range-energy values for protons in air and aluminum. Phys. Rev. 71, 32–33.CrossRefGoogle Scholar
Snyder, S.C., Crawford, D.M. & Fincke, J.R. (2000). Dependence on the scattering angle of the electron temperature and electron density in Thomson-scattering measurements on an atmospheric-pressure plasma jet. Phys. Rev. E 61, 1920–1924.CrossRefGoogle Scholar
Wetzler, H., Suss, W., Stockl, C., Tauschwitz, A. & Hoffmann, D.H.H. (1997). Density diagnostics of an argon plasma by heavy ion beams and spectroscopy. Laser Part. Beams 15, 449–459.CrossRefGoogle Scholar
Willi, O., Toncian, T., Borghesi, M., Fuchs, J., D'Humieres, E., Antici, P., Audebert, P., Brambrink, E., Cecchetti, C., Pipahl, A. & Romagnani, L. (2007). Laser triggered micro-lens for focusing and energy selection of MeV protons. Laser Part. Beams 25, 71–77.CrossRefGoogle Scholar
Xiao, T.Y., Yu, S.G. & Wang, Y.F. (2003). The Numerical Computation for the Inverse Problems. (Shi, Z.C. and Li, Y.S.), Beijing: The Science Press of China.Google Scholar
Yin, L., Albright, B.J., Hegelich, B.M. & Fernandez, J.C. (2006). GeV laser ion acceleration from ultrathin targets: The laser break-out afterburner. Laser Part. Beams 24, 291–298.CrossRefGoogle Scholar
Figure 0

Fig. 1. The zone studied is the square of 210 µm × 210 µm extending from 390 µm to 600 µm on both the x axis and the y axis and divided into 196 grids. The coordinates of the proton sources represented by four quadrangles are (0, 195), (0, 495), (0, 990), and (390, 0). The distance between the proton energy detectors and the studied zone is about 1 mm. (This figure is only the sketch map, not represents the actual size.)

Figure 1

Fig. 2. The contour lines of the simulated density distribution. (The density values are the product of the value of each contour line and 1025/cm3, and this will apply to the figures in the following).

Figure 2

Fig. 3. The contour lines of the revealed density distribution without noise when the numbers of the grids and the protons sources are 196 and 4 respectively, the error of revealing is described as Er = 21%.

Figure 3

Fig. 4. The contour lines of the revealed density distribution for four proton sources with noises level of 2% added to the final proton energies. The error of revealing is described as Er = 26%.

Figure 4

Fig. 5. The contour lines of the revealed density distribution for four proton sources with noises level of 5% added to the final proton energies. The error of revealing is described as Er = 37%.

Figure 5

Fig. 6. The contour lines of the revealed density distribution for the four proton sources assuming circular symmetry without noise to the final proton energies. The error of revealing is described as Er = 9%.

Figure 6

Fig. 7. The contour lines of the revealed density distribution for four proton sources with noises level of 2% added to the final proton energies and assuming circular symmetry. The error of revealing is described as Er = 12%.

Figure 7

Fig. 8. The contour lines of the revealed density distribution for four proton sources with noises level of 5% added to the final proton energies and assuming circular symmetry. The error of revealing is described as Er = 22%.