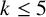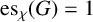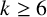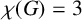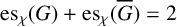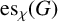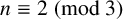1 Introduction
If
${\mathcal I}$
is a graph invariant and G a graph, then it is natural to consider the minimum number of vertices of G whose removal results in an induced subgraph
$G'$
with
${\mathcal I}(G') \ne {\mathcal I}(G)$
or with
$E(G') = \emptyset $
(see [Reference Alikhani and Piri2]). Let us call this number the
${\mathcal I}$
-stability number of G and denote it by
$vs_{\mathcal I}(G)$
. Similarly, one may be interested in the minimum number of edges that have to be removed in order to obtain a spanning subgraph
$G'$
with
${\mathcal I}(G') \ne {\mathcal I}(G)$
or with
$E(G') = \emptyset $
. In this case let us call the minimum number of edges the
${\mathcal I}$
-stability index of G and denote it by
$es_{\mathcal I}(G)$
.
Here we consider the
$\chi $
-stability index
${\mathrm {es}_{\chi }}$
, spelled out as chromatic stability index. The
$\chi $
-stability index
${\mathrm {es}_{\chi }}(G)$
of a graph G with at least one edge is thus the minimum number of edges of G whose removal results in a graph with chromatic number smaller than that of G. If
$E(G) = \emptyset $
, then
${\mathrm {es}_{\chi }}(G) = 0$
. In some papers the term ‘chromatic edge-stability number’ is used, but in our general framework and since the investigation of the
$\chi '$
-stability number was initiated in [Reference Alikhani and Piri2], this earlier terminology would be confusing.
The
$\chi $
-stability index was first studied by Staton [Reference Staton10], who provided upper bounds
${\mathrm {es}_{\chi }}$
for regular graphs in terms of the size of the graph. The invariant was subsequently investigated in [Reference Arumugam, Sahul Hamid, Muthukamatchi, Balakrishnan and Madhavan3, Reference Brešar, Klavžar and Movarraei4, Reference Kemnitz, Marangio and Movarraei8]. We continue this line of the research, focusing on the following three open problems on the chromatic stability index.
Problem 1.1 [Reference Akbari, Klavžar, Movarraei and Nahvi1, Reference Arumugam, Sahul Hamid, Muthukamatchi, Balakrishnan and Madhavan3].
Characterise graphs G with
${\mathrm {es}_{\chi }}(G)=1$
.
Problem 1.2 [Reference Akbari, Klavžar, Movarraei and Nahvi1].
Characterise graphs G with
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G})=2$
.
In [Reference Akbari, Klavžar, Movarraei and Nahvi1] it was proved that if G is a graph of order n with
$r=\chi (G)$
, then
$$ \begin{align} {\mathrm{es}_{\chi}}(G)\leq\begin{cases} \lfloor{n}/{r}\rfloor\lfloor{n}/{r}+1\rfloor \quad & \mbox{if } n\equiv r-1 \pmod r, \\ \lfloor{n}/{r}\rfloor^2 \quad & \text{otherwise}.\\ \end{cases} \end{align} $$
Problem 1.3 [Reference Akbari, Klavžar, Movarraei and Nahvi1].
Characterise graphs that attain the upper bound in (1.1).
In the rest of this section we recall definitions needed in this paper. In Section 2 we consider graphs G with
${\mathrm { es}_{\chi }}(G) = 1$
and construct examples which demonstrate that a known characterisation of k-regular graphs G with
${\mathrm {es}_{\chi }}(G) = 1$
does not extend to
$k\ge 6$
. Then, in Section 3, we characterise graphs G with
$\chi (G)=3$
for which
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G}) = 2$
. In the concluding section we obtain necessary structural conditions on graphs G which attain the upper bound in (1.1). The conditions are proved to be sufficient when
$n\equiv 2 \pmod 3$
and
$\chi (G)=3$
.
The chromatic number
$\chi (G)$
of a graph G is the smallest integer k such that G admits a proper colouring of its vertices using k colours. Unless stated otherwise, we will assume that the colours are from the set
$[k] = \{1,\ldots , k\}$
. A
$\chi (G)$
-colouring (or simply
$\chi $
-colouring) of G is a proper colouring using
$\chi (G)$
colours. In a colouring of G, a set of vertices having the same colour form a colour class. If c is a k-colouring of G with colour classes
$C_1, \ldots , C_k$
, then we will identify c with
$(C_1,\ldots , C_k)$
, that is, we will say that c is a colouring
$(C_1,\ldots , C_k)$
. When we wish to emphasise that these colour classes correspond to c, we will denote them by
$(C_1^c,\ldots , C_k^c)$
. If c is a colouring of G and
$A\subseteq V(G)$
, then let
$c(A) = \bigcup _{a\in A} c(a)$
. Let
$c^*(G)$
denote the cardinality of a smallest colour class among all
$\chi $
-colourings of G. If
$c^*(G) = 1$
, then we say that G has a singleton colour class. The chromatic bondage number
$\rho (G)$
of G denotes the minimum number of edges between two colour classes among all
$\chi $
-colourings of a graph G. Clearly
${\mathrm {es}_{\chi }}(G)\leq \rho (G)$
.
For
$v\in V(G)$
, let
$d_G(v)$
and
$N_G(v)$
denote the degree and the open neighbourhood of v in G, respectively. If
$A\subseteq V(G)$
, then let
$N_G(A)=(\bigcup _{v\in A}N_G(v))\backslash A$
. For
$A,B\subseteq V(G)$
, let
$E[A,B]$
be the set of edges which have one endpoint in A and the other in B, and let
$e(A,B)=|E[A,B]|$
. The subgraph of G induced by
$A\subseteq V(G)$
will be denoted by
$G[A]$
. The girth
$g(G)$
of a graph G is the length of a shortest cycle in G. The order of a largest complete subgraph in G is the clique number
$\omega (G)$
of G. The complement of G is denoted by
$\overline {G}$
.
2 On Problem 1.1
Problem 1.1, which asks for a characterisation of graphs G with
${\mathrm {es}_{\chi }}(G)=1$
, has been independently posed in [Reference Arumugam, Sahul Hamid, Muthukamatchi, Balakrishnan and Madhavan3, Problem 2.18] and [Reference Akbari, Klavžar, Movarraei and Nahvi1, Problem 5.3]. The two equivalent reformulations of the condition
${\mathrm {es}_{\chi }}(G)=1$
from the next proposition are from [Reference Kemnitz, Marangio and Movarraei8, Proposition 2.2] and [Reference Arumugam, Sahul Hamid, Muthukamatchi, Balakrishnan and Madhavan3, Remark 2.15], respectively. To be self-contained, we include a simple proof of the result.
Proposition 2.1. If G is a graph with
$\chi (G) \ge 2$
, then the following claims are equivalent:
-
(i)
${\mathrm {es}_{\chi }}(G)=1$
; -
(ii)
$\rho (G) = 1$
; -
(iii) G admits a
$\chi (G)$
-colouring
$(C_1, \ldots , C_{\chi (G)})$
, where
$|C_1| = 1$
and
$e(C_1,C_2) = 1$
.
Proof. Let
${\mathrm {es}_{\chi }}(G)=1$
and let
$e=uv\in E(G)$
be an edge such that
$\chi (G-e) = \chi (G) - 1$
. If c is a
$(\chi (G) - 1)$
-colouring of
$G-e$
, then
$c(u) = c(v)$
, for otherwise c would be a proper colouring of G (using only
$\chi (G) - 1$
colours). Recolouring u with a new colour yields a colouring of G as required by (iii). Hence (i) implies (iii). The implication (iii)
$\Rightarrow $
(ii) is obvious and (ii)
$\Rightarrow $
(i) follows from the fact already noted that
${\mathrm {es}_{\chi }}(G) \le \rho (G)$
.
Although Proposition 2.1 formally gives two characterisations of graphs G with
${\mathrm {es}_{\chi }}(G)=1$
, it should be understood that Problem 1.1 asks for a structural characterisation of such graphs. The next result gives a partial solution of the problem.
Theorem 2.2 [Reference Akbari, Klavžar, Movarraei and Nahvi1, Theorem 4.4].
Let G be a connected, k-regular graph with
$k\leq 5$
. Then
${\mathrm {es}_{\chi }}(G)=1$
if and only if G is
$K_2$
, G is an odd cycle, or
$\chi (G)>3$
and
$c^{\star }(G) = 1$
.
The second part of [Reference Akbari, Klavžar, Movarraei and Nahvi1, Problem 5.3] says: ‘In particular, for the regular case extend the classification of Theorem 2.2 to
$k>5$
.’ We do not solve the problem, but demonstrate in the rest of the section that (i) the problem appears difficult and (ii)
$k=5$
is the threshold for regular graphs. Let X be the graph drawn in Figure 1.
Figure 1 The graph X.
Proposition 2.3. The graph X is a
$6$
-regular graph with
$\chi (X)=4$
,
$c^{\star }(X) = 1$
and
${\mathrm {es}_{\chi }}(X) = 2$
.
Proof. Since
$\omega (X)=4$
, we have
$\chi (X)\geq 4$
. We give a 4-colouring c of X as follows:
$c(w)=4$
,
$c(v_1)=c(u_3)=c(u_6)=1$
,
$c(v_3)=c(u_2)=c(u_5)=2$
,
$c(v_2)=c(u_1)=c(u_4)=3$
. Since colour 4 is used exactly once,
$\chi (X)=4$
and
$c^*(X)=1$
. It remains to prove that
${\mathrm {es}_{\chi }}(X) = 2$
.
Let
$X'$
be the graph obtained from X by deleting the edges
$wv_1, wu_6$
. Then we can get a 3-colouring
$c'$
of
$X'$
as follows:
$c'(w) = c'(v_1) = c'(u_3) = c'(u_6) = 1$
,
$c'(v_3) = c'(u_2) = c'(u_5) = 2$
,
$c'(v_2) = c'(u_1) = c'(u_4) = 3$
. Hence
${\mathrm {es}_{\chi }}(X) \le 2$
.
Suppose now by contrast that
${\mathrm {es}_{\chi }}(X) = 1$
. Then by Proposition 2.1(iii), there exists a colouring
$c = (C_1, C_2, C_3, C_4)$
, such that
$|C_1| = 1$
and
$e(C_1, C_2)=1$
. Since
$X[\{v_1,v_2,v_3,w\}]\cong K_4$
, we have
$c(w)=1$
or
$c(v_i)=1$
for some
$i\in [3]$
. If
$c(w)=1$
, then
$\chi (X[N(w)])=3 $
and colour 2 appears only once in
$N(w)$
. But this is impossible because
$X[v_1,v_2,v_3]\cong K_3$
and
$X[u_2,u_4,u_6]\cong K_3$
. If
$c(w)\ne 1$
, then by symmetry we may without loss of generality assume that
$c(v_1)=1$
. Then we consider the colouring of
$N(v_1)$
. If
$c(u_5)\neq c(v_3)$
, say
$c(u_5)=a\in \{2,3,4\}$
and
$c(v_3)=b\in \{2,3,4\}\backslash \{a\}$
, then
$c(v_2)=c(u_1)=c=\{2,3,4\}\backslash \{a,b\}$
,
$c(w)=a$
and
$c(u_2)=b$
, contradicting the fact that
$e(C_1, C_2)=1$
. If
$c(u_5)=c(v_3)$
, say
$c(u_5)=c(v_3)=a\in \{2,3,4\}$
, then
$c(v_2)=b\in \{2,3,4\}\backslash \{a\}$
and
$c(w)=c=\{2,3,4\}\backslash \{a,b\}$
. Since
$\{w,v_2,u_5\}\subseteq N(u_6)$
, we have
$c(u_6)=1$
, contradicting the fact that
$|C_1| = 1$
. So
${\mathrm {es}_{\chi }}(G)\geq 2$
and we are done.
Proposition 2.3 shows that Theorem 2.2 does not extend to
$6$
-regular graphs. On the other hand, consider the following example to see that there exist
$4$
-chromatic,
$6$
-regular (and higher regularity) graphs with
${\mathrm {es}_{\chi }}(G)=1$
. A graph
$G=C(n; a_0,a_1, \ldots , a_k)$
is called a circulant if
$$ \begin{align*}V(G)=[n] \quad\mbox{and}\quad E(G)=\{(i,j): |i-j|\in\{a_0, a_1, \ldots, a_k\} \pmod n\},\end{align*} $$
where
$1\leq a_0<a_1<\cdots <a_k\leq n/2$
. If
$a_k<n/2$
, then G is a
$(2k+2)$
-regular graph; otherwise, G is
$(2k + 1)$
-regular. In [Reference Dobrynin, Melnikov and Pyatkin5, Theorem 2.1], Dobrynin et al. constructed 4-critical r-regular circulants for
$r\in \{6,8,10\}$
. (Recall that a graph G with
$\chi (G)=k$
is called edge-critical (or simply k-critical) if its chromatic number is strictly less than k after removing any edge.) Hence these regular graphs satisfy
${\mathrm {es}_{\chi }}(G)=1$
.
3 On Problem 1.2
Let G be a graph with
${\mathrm {es}_{\chi }}(G)=1$
and
$\chi (G)=r$
. We say that a
$\chi $
-colouring of G is a good colouring if it satisfies the conditions of Proposition 2.1(iii). Let
$\mathcal {C}(G)$
be the set of good colourings of G. If
$c = (C^c_1, \ldots , C^c_r) \in \mathcal {C}(G)$
, then we may always without loss of generality assume that
$|C^c_1|=1$
and
$e(C^c_1, C^c_2)=1$
.
Clearly,
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G}) = 2$
holds if and only if
${\mathrm {es}_{\chi }}(G) = {\mathrm { es}_{\chi }}(\overline {G}) = 1$
. We first characterise disconnected graphs G for which
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G}) = 2$
.
Proposition 3.1. Let G be a graph with components
$G_1, \ldots ,G_s$
,
$s\ge 2$
, and let
$\mathcal {G}=\{G_i:\ \chi (G_i)=\chi (G), \ i\in [s]\}$
. Then
${\mathrm { es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G})=2$
if and only if
-
(i)
$|\mathcal {G}|=1$
and
${\mathrm {es}_{\chi }}(G_i)=1$
for
$G_i\in \mathcal {G}$
, and -
(ii) there exists a
$G_j$
such that
${\mathrm {es}_{\chi }}(\overline {G_j})=1$
, or there exist components
$G_j$
and
$G_k$
,
$j\neq k$
, such that
$c^*(\overline {G_j})=1$
and
$c^*(\overline {G_k})=1$
.
Proof. The following fact is essential for the rest of the argument: if c is a proper colouring of
$\overline {G}$
, then
$c(V(G_i))\cap c(V(G_j)) = \emptyset $
for every
$i, j\in [s]$
,
$i\ne j$
. If G satisfies (i) and (ii), then (i) yields
${\mathrm {es}_{\chi }}(G)=1$
, while (ii) gives
${\mathrm { es}_{\chi }}(\overline {G})=1$
. Conversely, suppose that
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G})=2$
. Then
${\mathrm { es}_{\chi }}(G)=1$
and
${\mathrm {es}_{\chi }}(\overline {G})=1$
. If
$|\mathcal {G}|\geq 2$
or
${\mathrm {es}_{\chi }}(G_i)\geq 2$
for any
$G_i\in \mathcal {G}$
, then
$\chi (G - e)=\chi (G)$
for any
$e\in E(G)$
, a contradiction. This means that (i) holds. Since
${\mathrm { es}_{\chi }}(\overline {G})=1$
, there exists an a edge
$\overline {e}\in E(\overline {G})$
such that
$\chi (\overline {G} - \overline {e})<\chi (\overline {G})$
. We consider two cases for the edge
$\overline {e}$
. If
$\overline {e}\in E(\overline {G_j})$
for some
$j\in [s]$
, then
${\mathrm {es}_{\chi }}(\overline {G_j})=1$
. In the other case the two endpoints of
$\overline {e}$
lie in different components, say in
$G_j$
and in
$G_k$
,
$j\ne k$
. But then
$c^*(\overline {G_j})=1$
and
$c^*(\overline {G_k})=1$
. Thus (ii) holds as well.
In the main result of this section we now characterise connected graphs G with
$\chi (G)=3$
for which
${\mathrm {es}_{\chi }}(G)+{\mathrm { es}_{\chi }}(\overline {G})=2$
.
Theorem 3.2. Let G be a connected graph of order n, with
$\chi (G)=3$
. Then
${\mathrm {es}_{\chi }}(G)+{\mathrm {es}_{\chi }}(\overline {G})=2$
if and only if
-
(i) all odd cycles in G share one edge,
-
(ii)
$c^*(\overline {G})=1$
, -
(iii)
$\chi (\overline {G})\geq \lceil {n}/{2}\rceil $
, -
(iv) if n is even,
$\chi (\overline {G})={n}/{2}$
and
$||C^c_2|-|C^c_3||=1$
for each
$c = (C_1^c, C_2^c, C_3^c)\in \mathcal {C}(G)$
, then
$g(G)=3$
and for any proper colouring of
$\overline {G}$
, if
$\{x_1,x_2,x_3\}$
is a colour class, then
$d_{G}(v)\geq 2$
for each
$v\in N_G(\{x_1,x_2,x_3\})$
.
Proof.
Necessity. Since
${\mathrm {es}_{\chi }}(G)=1$
and
$\chi (G)=3$
, there is an edge
$e\in E(G)$
such that
$G - e$
has no odd cycles. So (i) holds. It was observed in [Reference Akbari, Klavžar, Movarraei and Nahvi1, Lemma 4.3] that
${\mathrm {es}_{\chi }}(G)=1$
implies
$c^*(G)=1$
, hence (ii) holds. Let
$c = (C^c_1,C^c_2, C^c_3)\in \mathcal {C}(G)$
. We have
$\omega (\overline {G})\geq \lfloor {n}/{2}\rfloor $
since
$|C^c_1|=1$
. So,
$\chi (\overline {G})\geq \omega (\overline {G})\geq \lceil {n}/{2}\rceil $
when n is even. When n is odd and
$\omega (\overline {G})={(n-1)}/{2}$
, we have
$|C^c_2|=|C^c_3|={(n-1)}/{2}$
and
$\overline {G}[C^c_2]\cong K_{C^c_2}$
,
$\overline {G}[C^c_3]\cong K_{C^c_3}$
. Note that for any proper colouring of
$\overline {G}$
, there is at most one colour class with three vertices and there must be fewer than three vertices in other colour classes. By Proposition 2.1(iii), there exists a
$\chi $
-colouring of
$\overline {G}$
such that some colour class has exactly one vertex. Then
$\chi (\overline {G})\geq {(n+1)}/{2}=\lceil {n}/{2}\rceil $
.
Suppose now that n is even,
$\chi (\overline {G})={n}/{2}$
and
$||C^c_2|-|C^c_3||=1$
for any
$c = (C_1^c, C_2^c, C_3^c)\in \mathcal {C}(G)$
. Let
$C^c_1=\{x_1\}$
and let
$x_2$
be the vertex of
$C^c_2$
such that
$x_1x_2\in E(G)$
. Let
$\bar {c}\in \mathcal {C}(\overline {G})$
and let the colour set used by
$\bar {c}$
be
$[{n}/{2}]$
. We claim that
$\bar {c}(x_1)=\bar {c}(x_2)$
and
$\bar {c}(x_1)\in \bar {c}(C^c_3)$
. Notice that
$x_1$
is in
$\overline {G}$
adjacent to all vertices of
$C^c_2$
except
$x_2$
. If
$|C^c_2|-|C^c_3|=1$
, then
$|C^c_2|={n}/{2}$
. Then the claim holds because
$\chi (\overline {G})= {n}/{2} = |\bar {c}(C^c_2)|$
. Suppose next that
$|C^c_3|-|C^c_2|=1$
. Then
$|C^c_3|={n}/{2}$
and
$|C^c_2|={(n-2)}/{2}$
. We have
$|\bar {c}(C^c_3)| = {n}/{2}$
. If
$\bar {c}(x_1)\neq \bar {c}(x_2)$
, then
$\bar {c}(x_1\cup C^c_2)=[{n}/{2}]$
, contradicting the fact that
$\bar {c}\in \mathcal {C}(\overline {G})$
because there is no singleton colour class. Hence
$\bar {c}(x_1)=\bar {c}(x_2)$
and
$\bar {c}(x_1)\in \bar {c}(C^c_3)$
since
$\bar {c}(C^c_3)=[{n}/{2}]$
. Thus
$g(G)=3$
. We can set
$x_3\in C^c_3$
and
$\bar {c}(x_1)=\bar {c}(x_2)=\bar {c}(x_3)=1$
in the following. Suppose there is a vertex
$v\in N_G(\{x_1,x_2,x_3\})$
such that
$d_G(v)=1$
. If
$|C^c_2|-|C^c_3|=1$
, then
$C^c_2\subseteq N_{\overline {G}}(v)$
when
$v\in N_G(x_1)$
,
$(C^c_2\backslash \{x_2\})\cup x_3\subseteq N_{\overline {G}}(v)$
when
$v\in N_G(x_2)$
and
$V(G)\backslash \{x_3\}= N_{\overline {G}}(v)$
when
$v\in N_G(x_3)$
. Thus
$\chi (\overline {G})>{n}/{2}$
when
$v\in N_G(x_1)\cup N_G(x_2)$
, a contradiction. When
$v\in N_G(x_3)$
, we may assume without loss of generality that
$\bar {c}(C^c_3)=[ {(n-2)}/{2}]$
. Then
$\bar {c}(v)={n}/{2}$
since
$x_2\in N_{\overline {G}}(v)$
. But every colour in
$[({n-2)}/{2}]$
appears exactly twice in
$N_{\overline {G}}(v)$
, contradicting the fact that
$\bar {c}\in \mathcal {C}(\overline {G})$
. If
$|C^c_3|-|C^c_2|=1$
, then
$\chi (\overline {G})>{n}/{2}$
when
$v\in N_G(x_3)$
and
$\bar {c}\notin \mathcal {C}(\overline {G})$
when
$v\in N_G(x_1)\cup N_G(x_2)$
by the same analysis as above, a contradiction.
Sufficiency. Suppose an edge e is shared by all odd cycles of G. Then
$\chi (G -e)\leq 2$
. Hence
${\mathrm {es}_{\chi }}(G)=1$
by definition. Suppose
$\chi (\overline {G})\geq \lceil {n}/{2}\rceil $
. In [Reference Akbari, Klavžar, Movarraei and Nahvi1, Lemma 4.2] it was proved that if
$\chi (\overline {G})\geq {(n+2)}/{2}$
, then
${\mathrm {es}_{\chi }}(\overline {G})=1$
. So we may assume
$\chi (\overline {G})=\lceil {n}/{2}\rceil $
in the following.
Suppose first that n is odd. Let
$\bar {c}$
be a proper colouring of
$\overline {G}$
. Since
$\chi (\overline {G})=\lceil {n}/{2}\rceil ={(n+1)}/{2}$
, the complement
$\overline {G}$
has a singleton colour class under
$\bar {c}$
. If
$\overline {G}$
has two singleton colour classes under
$\bar {c}$
, then
$\rho (\overline {G})=1$
. Otherwise, other colour classes have exactly two vertices. Since G is connected,
$\Delta (\overline {G})<n-1$
, thus
$\rho (\overline {G})=1$
. Suppose next that n is even. We have
$||C^c_2|-|C^c_3||=1$
for any
$c_i\in \mathcal {C}(G)$
since
$\chi (\overline {G})={n}/{2}$
. Since
$c^*(\overline {G})=1$
, there is a proper colouring such that some colour class contains three vertices. Let
$\bar {c}$
be the proper colouring and
$\bar {c}(x_1)=\bar {c}(x_2)=\bar {c}(x_3)$
, where
$x_s\in C^c_s $
for
$s\in [3]$
. Let
$\{\alpha ,\beta \}=\{2,3\}$
. If
$|C^c_\alpha |-|C^c_\beta |=1$
, then
$|C^c_\alpha |={n}/{2}$
and
$|C^c_\beta |={(n-2)}/{2}$
. Since
$\chi (\overline {G})={n}/{2}$
, we may assume
$\bar {c}(C^c_\alpha )=[{n}/{2}]$
and
${n}/{2}\notin C^c_\beta $
, say
$\bar {c}(u)={n}/{2}$
. Since G is connected and
$d_G(v)\geq 2$
for any
$v\in N_G(\{x_1,x_2,x_3\})$
, we have
$N_{C^c_\beta }(u)\backslash \{x_\beta \}\neq \emptyset $
or
$\{x_1,x_\beta \}\subseteq N_G(u)$
. Thus
$\rho (\overline {G})=1$
, and by Proposition 2.1 we conclude that
${\mathrm {es}_{\chi }}(\overline {G})=~1$
.
4 On Problem 1.3
Obviously, when
$r=2$
, the upper bound in (1.1) is attained if and only if the graph in question is a complete bipartite graph in which the orders of its bipartition sets differ by at most one. For an arbitrary r we have the following result.
Theorem 4.1. Let G be a graph of order n and with
$r=\chi (G)$
.
-
(i) Suppose that
$n\equiv r-1 \pmod r$
and
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor $
. Then for any r-colouring
$(C_1,\ldots , C_r)$
of G, where
$|C_1|\leq \cdots \leq |C_r|$
,-
(1)
$|C_1|=\lfloor {n}/{r}\rfloor $
and
$|C_2|=\cdots =|C_r|=\lfloor {n}/{r}+1\rfloor $
; -
(2) if
$2\leq i\leq r$
, then
$G[C_1\cup C_i]$
is a complete bipartite graph with bipartition
$(C_1, C_i)$
; -
(3) if
$v\in C_i$
and
$j\in [r]\backslash \{i\}$
, then
$e(v, C_j)\geq \lfloor {n}/{r}\rfloor $
.
-
-
(ii) Suppose that
$n\not \equiv r-1 \pmod r$
and
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{r}\rfloor ^2$
. Then for any r-colouring
$(C_1,\ldots , C_r)$
of G, where
$|C_1|\leq \cdots \leq |C_r|$
,-
(1)
$|C_1|=|C_2|=\lfloor {n}/{r}\rfloor $
; -
(2) if
$|C_i|=\lfloor {n}/{r}\rfloor $
,
$v\in C_i$
and
$j\in [r]\backslash \{i\}$
, then
$e(v, C_j)\geq \lfloor {n}/{r}\rfloor $
; -
(3) if
$|C_i|>\lfloor {n}/{r}\rfloor $
, then
$\sum _{v_s\in C_i} \ell _s\geq {\lfloor {n}/{r}\rfloor }^2$
, where
$$ \begin{align*}\ell_s=\min\{e(v_s, C_j):\ v_s\in C_i, j\in[r]\backslash \{i\}\}.\end{align*} $$
-
Proof. (i) Consider an r-colouring
$(C_1,\ldots , C_r)$
of G, where
$|C_1|\leq \cdots \leq |C_r|$
.
(1) Since
$n\equiv r-1 \pmod r$
, we have
$n = r\lfloor n/r\rfloor + r -1$
. From here it was deduced in the proof of [Reference Akbari, Klavžar, Movarraei and Nahvi1, Theorem 2.1] that there exists at least one pair of colour classes,
$C_i$
and
$C_j$
,
$i<j$
, such that
$|C_i|+|C_j|\leq \lfloor {n}/{r}\rfloor +\lfloor {n}/{r}+1\rfloor $
. Since
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor $
, we have
$|C_i|=\lfloor {n}/{r}\rfloor $
and
$|C_j|=\lfloor {n}/{r}+1\rfloor $
. Moreover,
$i=1$
and
$|C_k|\geq \lfloor {n}/{r}+1\rfloor $
for
$2\leq k\leq r$
, since otherwise
${\mathrm {es}_{\chi }}(G)\leq |C_1||C_2|\leq \lfloor {n}/{r}\rfloor ^2$
, a contradiction. Thus
$|C_2|=\cdots =|C_r|=\lfloor {n}/{r}+1\rfloor $
because
$n = r\lfloor n/r\rfloor + r -1$
.
(2) and (3) Observe that
$G[C_1\cup C_i]$
is a complete bipartite graph with bipartition
$(C_1, C_i)$
for any
$2\leq i\leq r$
, since otherwise
${\mathrm {es}_{\chi }}(G)\leq |C_1||C_i|\leq \lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor -1$
, a contradiction. Therefore,
$e(v, C_j)\geq \lfloor {n}/{r}\rfloor $
when
$v\in C_1$
or
$j=1$
. If
$e(v, C_j)<\lfloor {n}/{r}\rfloor $
for some
$v\in C_i$
and
$j\in [r]\backslash \{i\}$
(
$i,j>1$
), then by deleting the edge set
$E(v, C_j)\cup E(C_i\backslash \{v\}, C_1)$
, we get an
$(r-1)$
-colouring with the colour class set
$\{C_1\cup (C_i\backslash \{v\}), C_2,\ldots ,C_j\cup \{v\},\ldots , C_r\}\backslash \{C_i\}$
. Notice that
$|E(v, C_j)\cup E(C_i\backslash \{v\}, C_1)|<\lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor $
. Thus
${\mathrm {es}_{\chi }}(G)< \lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor $
, a contradiction.
(ii) Suppose
$n\not \equiv r-1 \pmod r$
and
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{r}\rfloor ^2$
. Consider an r-colouring
$(C_1,\ldots , C_r)$
of G, where
$|C_1|\leq |C_2|\leq \cdots \leq |C_r|$
.
(1) By the proof of [Reference Akbari, Klavžar, Movarraei and Nahvi1, Theorem 2.1], there exists at least one pair of colour classes,
$C_i$
and
$C_j$
(
$i\leq j$
), in which
$|C_i|+|C_j|\leq 2\lfloor {n}/{r}\rfloor $
. Since
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{r}\rfloor ^2$
, we have
$|C_i|=|C_j|=\lfloor {n}/{r}\rfloor $
. Moveover,
$|C_k|\geq \lfloor {n}/{r}\rfloor $
for
$1\leq k\leq r$
, since otherwise
${\mathrm {es}_{\chi }}(G)\leq |C_1||C_2|< \lfloor {n}/{r}\rfloor ^2$
, a contradiction. Thus
$|C_1|=|C_2|=\lfloor {n}/{r}\rfloor $
.
(2) and (3) Suppose
$|C_i|=\lfloor {n}/{r}\rfloor $
and there exists some
$v\in C_i$
and
$j\in [r]\backslash \{i\}$
such that
$e(v, C_j)<\lfloor {n}/{r}\rfloor $
. We take a colour class
$C_k$
with
$\lfloor {n}/{r}\rfloor $
vertices, which is different from
$C_i$
. This is possible because
$|C_1|=|C_2|=\lfloor {n}/{r}\rfloor $
. Note that k and j are not necessarily distinct. We delete the edge set
$E(v, C_j)\cup E(C_i\backslash \{v\}, C_k)$
and get an
$(r-1)$
-colouring with colour class set
$\{C_1, \ldots , C_k\cup (C_i\backslash \{v\}), \ldots ,C_j\cup \{v\},\ldots , C_r\}\backslash \{C_i\}$
. Notice that
$|E(v, C_j)\cup E(C_i\backslash \{v\}, C_k)|<\lfloor {n}/{r}\rfloor ^2$
. Thus
${\mathrm {es}_{\chi }}(G)< \lfloor {n}/{r}\rfloor ^2$
, a contradiction.
Suppose
$|C_i|>\lfloor {n}/{r}\rfloor $
and
$\sum _{v_s\in C_i}\ell _s< {\lfloor {n}/{r}\rfloor }^2$
, where
$\ell _s$
is defined as in the statement of the theorem. Let
$C^s$
be one of the corresponding colour classes when
$\ell _s$
is taken for
$v_s$
. Then for any
$v_s\in C_i$
, we delete the edge set
$E(v_s, C^s)$
and get an
$(r-1)$
-colouring by putting
$v_s$
in
$C^s$
. Thus
${\mathrm {es}_{\chi }}(G)< \lfloor {n}/{r}\rfloor ^2$
, a contradiction.
Recall that a graph colouring
$(C_1,\ldots , C_k)$
is equitable [Reference Erdős and Fiedler6] if
$| |C_i| - |C_j| | \le 1$
for all
$i\ne j$
. Hence all the colourings from Theorem 4.1(i) are equitable, and consequently the corresponding extremal graphs have the same chromatic number and the equitable chromatic number. (See [Reference Heckel7, Reference Li and Zhang9] for a couple of recent investigations of the equitable chromatic number.)
Theorem 4.2. Let G be a graph of order n, where
$n\equiv 2 \pmod 3$
and with
$\chi (G)=3$
. If any
$3$
-colouring of G satisfies (1)–(3) of Theorem 4.1(i), then
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{3}\rfloor \lfloor {n}/{3}+1\rfloor $
.
Proof. Let c be a
$3$
-colouring of G satisfying (1)–(3) of Theorem 4.1(i). Let
$\{i,j\}=\{2,3\}$
. For
$v\in C_i$
we may let
$e(v, C_j)=\lfloor {n}/{3}\rfloor $
(as adding edges to a graph cannot decrease its
$\chi $
-stability index). Since for any
$e\in E(G)$
, e lies in exactly
$\lfloor {n}/{3}\rfloor $
subgraphs
$K_3$
, the graph
$G - e$
has at most
$\lfloor {n}/{3}\rfloor $
fewer subgraphs isomorphic to
$K_3$
than G. Let
$F\subseteq E(G)$
with
$|F|=\lfloor {n}/{3}\rfloor \lfloor {n}/{3}+1\rfloor -1$
. Then the graph
$G\backslash F$
has at most
$\lfloor {n}/{3}\rfloor (\lfloor {n}/{3}\rfloor \lfloor {n}/{3}+1\rfloor -1)$
fewer subgraphs
$K_3$
than G. But G has
$\lfloor {n}/{3}\rfloor \lfloor {n}/{3}\rfloor \lfloor {n}/{3}+1\rfloor $
subgraphs
$K_3$
, so that
$G\backslash F$
has at least one subgraph
$K_3$
and consequently
$\chi (G\backslash F)=3$
. Hence,
${\mathrm {es}_{\chi }}(G)=\lfloor {n}/{3}\rfloor \lfloor {n}/{3}+1\rfloor $
.
Let G be a graph with n vertices and
$r=\chi (G)$
. Note that when
$r=5$
and
$n\equiv 4 \pmod 5$
, the conditions (1)–(3) in Theorem 4.1(i) are not sufficient. Let
$G_{12}$
be the graph from Figure 2, and let
$G_{14}$
be obtained from
$G_{12}$
by adding two new vertices
$u_0$
and
$v_0$
and connecting
$u_0$
and
$v_0$
to all vertices of
$G_{12}$
. Then we have the following result.
Figure 2 The graph
$G_{12}$
. Colour available online.
Proposition 4.3. The graph
$G_{14}$
satisfies conditions (1)–(3) of Theorem 4.1(i), but
${\mathrm { es}_{\chi }}(G_{14})<\lfloor {n}/{r}\rfloor \lfloor {n}/{r}+1\rfloor =6$
.
Proof. We first show that
$\chi (G_{14})=5$
. Let
$A=\{a,b,c\}$
,
$B=\{u,v,w\}$
,
$C=\{1,2,3\}$
, and
$D=\{x,y,z\}$
. We claim that
$\chi (G_{14})=5$
and that
$G_{14}$
has a unique
$5$
-colouring. By means of a computer search (using SageMath), we found all independent sets of
$G_{14}$
with at least three vertices, A, B, C, D,
$\{b,u,1,z\}$
, and each
$X\subseteq \{b,u,1,z\}$
with
$|X|=3$
. So, if any three vertices of
$\{b,u,1,z\}$
have the same colour under some proper colouring
$c:V(G_{14})\rightarrow [k]$
of
$G_{14}$
, then
$k\geq 6$
. Thus
$\chi (G_{14})=5$
and the unique
$5$
-colouring has colour classes
$\{u_0,v_0\}$
, A, B, C, D. Therefore, the graph
$G_{14}$
satisfies conditions (1)–(3) of Theorem 4.1(i).
On the other hand, by deleting the edges
$cv$
,
$aw$
,
$3y$
and
$2x$
(coloured orange in the figure), we can get a
$4$
-colouring with colour classes
$\{u_0,v_0\}$
,
$\{a,c,v,w\}$
,
$\{b,u,1,z\}$
,
$\{2,3,x,y\}$
. Therefore,
${\mathrm {es}_{\chi }}(G_{14})\leq 4$
.
