INTRODUCTION
Interactions between fiscal and monetary policy in the determination of the price level have been the object of a great deal of new research in recent years. One relatively new strand of research, the fiscal theory of the price level (FTPL), asserts that fiscal policy can have an important influence on the price level in models in which one might expect prices to depend only on monetary variables. An extreme specific case of FTPL asserts that, in certain specific circumstances, fiscal variables can fully determine the price level independently of monetary variables.1
For a long list of references on the fiscal theory of prices, see Woodford (2001), Cochrane (1999), Cochrane (2005), and Buiter (2002).
Clearly, this extreme result is the polar opposite of the monetarist contention that the price level and the inflation rate depend primarily on monetary variables. It is thus not surprising that the fiscal theory approach has aroused a great deal of debate and controversy. These debates consider various aspects of the theory. One point of debate concerns the extreme specific case, in which the price level follows an explosive path. McCallum (2001) has argued that this fiscalist equilibrium is an implausible “bubble equilibrium.”
The influence of fiscal variables on the price level is, however, not limited to extreme cases in which the system is nonstationary. In a local analysis around a unique steady state (Leeper 1991) made an important distinction between “active” and “passive” policies (the precise definitions will be given below). In a standard model, he showed that two combinations, either (i) active monetary and passive fiscal policy or (ii) active fiscal and passive monetary policy yield determinacy, that is, a unique stationary rational expectations equilibrium (REE). In case (i), the usual monetarist view that inflation depends only on monetary policy is confirmed. However, case (ii) is fiscalist in the sense that fiscal policy, in addition to monetary policy, has an effect on the inflation rate. Leeper 1991) also showed that the steady state is indeterminate, with multiple stationary solutions, when both policies are passive, whereas the economy is explosive when both policies are active.2
It should be pointed out that the FTPL does not predict that the “fiscalist” solution will always be followed, regardless of fiscal and monetary policies. For example, in the active monetary/passive fiscal policy regime, there is general agreement that the appropriate solution is the monetarist solution.
Another point of controversy concerns the nature of the intertemporal budgetconstraint of the government. Buiter (2002) argues that FTPL, which does not impose this constraint as an identity, can lead to inconsistencies or anomalies, and therefore should be rejected as a “starting point for further research in monetary economics.” Buiter recommends restricting attention to Ricardian “fiscal-financial-monetary programmes” in which the government's intertemporal budget constraint “holds for all admissible sequences” of relevant variables. Woodford [e.g., see Woodford (2002) and Woodford (2003b, pp. 315–316)] argues against this position and for the validity of non-Ricardian fiscal policies in which the government need only satisfy its intertemporal budget constraint in equilibrium. Particular examples are the extreme case described earlier and the active fiscal/passive monetary regime of Leeper (1991), in which fiscal policy is non-Ricardian because taxes respond only weakly to debt levels.
The significance of FTPL continues to be debated. Two recent papers by Bassetto (2002) and Niepelt (2004) readdress the significance of FTPL by strengthening the notion of rationality used in the earlier literature. Bassetto (2002) casts the analysis in terms of a market game that generates REE as sequential equilibria of the game. He finds that versions of FTPL can emerge as a sequential equilibrium, which takes account of out-of-equilibrium behavior in a Bayesian fully rationalist way. In contrast, Niepelt (2004) strengthens the notion of REE in the literature on FTPL by requiring that the equilibrium also fully incorporates past optimal choices. Niepelt shows that debt valuation according to FTPL is inconsistent with his refined notion of REE.3
Niepelt also suggests a different definition of FTPL in terms of valuation of flows.
Strengthening the notion of rationality is not the only possible way to assess the implications of FTPL. Such approaches require even more information and coordination than the usual notion of REE on the part of the economic agents. In this paper, we take a very different approach by modeling out-of-equilibrium behavior as being boundedly rational in a specific sense. We employ the learning approach to macroeconomics, which has been developed in recent years4
See Evans and Honkapohja (2001) for a recent treatise. Surveys of the literature are provided, for example, in Evans and Honkapohja (1999), Marimon (1997), and Sargent (1983).
The learning processes that we consider are to be interpreted as a description of how private agents would plausibly update their forecast rules over time as new data become available. Thus, we are describing how learning by private agents might proceed, in a decentralized market economy, if the agents use statistical methods for estimation and forecasting. In general, stability is a joint property of the equilibrium under consideration and the learning rule followed by agents. However, the learning rules we consider employ standard econometric procedures, that is, least-squares (LS) regressions in stochastic models and sample means in nonstochastic models.5
The sample mean can, of course, be regarded as least squares regression on a constant.
In many standard models, the REE of interest are indeed locally stable under these learning rules. This holds, for example, for the usual solutions of the Cagan model of inflation, the Samuelson overlapping generations model of money and the real business cycle model, and it holds for the New Keynesian model when appropriate interest-rate policies are followed. If an equilibrium is unstable under LS learning, then we regard it as one that would not be attainable. In such circumstances, depending on the outcome, a policy maker would do well to change its policy to ensure convergence to the equilibrium. Of course, in the unstable case, faced with increasing forecast errors, private agents (and policy makers) may alter their perceived functional form and updating rules, but there is no reason to expect this to redirect them to the equilibrium being considered.6
If an alternative convergent learning rule exists, the policy maker could in principle try to induce agents to coordinate on using a such rule. However, achieving this coordination is likely to be far more difficult than changing fiscal or monetary policies.
The version of the model under learning that we consider specifies household consumption and money demands as functions of the nominal interest rate and expected inflation over the coming period. These are obtained from the Euler equations that characterize the household optimal decisions under subjective expectations. In the deterministic cases, we employ the resulting nonlinear model for our analysis. However, in stochastic cases, the analysis is based on the linearized model around a nonstochastic steady state, which is standard practice.
Agents' expectations of inflation are based on a forecast function that is revised over time in accordance with adaptive LS learning. Given these expectations, the short-run state of the economy at each time is given by the temporary equilibrium. Our household behavior is boundedly rational in two respects. First, in contrast to “rational expectations” the parameters of the forecast function are not known a priori to be at their equilibrium values, although when learning is stable they will converge to these values asymptotically. Second, the decision rules of the agents do not explicitly consider expectations of variables at more distant horizons.
Using this framework, we investigate both the rational explosive inflation paths studied by McCallum (2001), and the classification of fiscal and monetary policies proposed by Leeper (1991), for stability of the REE under LS learning.7
In independent work, McCallum (2003a) considers stability under LS learning of the fiscalist bubble solution using a simplified linear model. He does not analyze the case of interest rate rules.
If, instead, fiscal policy is active and monetary policy is passive, the fiscalist solution, in which fiscal variables affect the price level, is stable under LS learning, in line with FTPL. This is one of our most striking results because real balances are affected by the rule for setting lump-sum taxes. Hence, Ricardian equivalence fails in a setting where the traditional view would expect it to be satisfied. In this regime, taxes respond only weakly to debt and the interest rate responds only weakly to inflation. Nevertheless, the REE in question is both stochastically stationary and attainable by boundedly rational agents who follow LS learning rules.
In both of the cases just described, the stable REE is the unique stationary solution. For other combinations of monetary and fiscal policy, the results are intriguing: for some parameter values, all REE are unstable under LS learning, whereas for other parameter values there is incipient convergence to an explosive path. Taken together, our results clearly indicate that policy formulation should incorporate the implications of the stability properties, under LS learning, of the different REE.
THE MODEL
We consider a stochastic optimizing model that is close to Leeper (1991) and McCallum (2001). For the basic model, notation and specification of monetary and fiscal policy rules we follow Leeper, but we use McCallum's more general class of utility functions and also his timing in which utility depends on beginning of period money balances.8
The question of whether beginning- or end-of-period real balances is used leads to subtle differences in the model and can in some cases have major implications; compare Carlstrom and Fuerst (2001).
Households are assumed to maximize

Here cs denotes consumption in period s and ms = Ms/Ps, where Ms is the money supply and Ps is the price level at s. Note that real money balances enter utility as
. The household's budget constraint is

where bs = Bs/Ps, πs = Ps/Ps−1 is the gross inflation rate and τs is real lump-sum taxes. Note that Bs is the end of period s nominal stock of bonds. Rs−1 is the gross nominal interest rate on bonds, set at time s−1 but paid in the beginning of period s. The household has a constant endowment y of consumer goods each period. Throughout the paper, we assume 0 < σ2 < 1.
We assume that there is a constant flow of government purchases g ≥ 0. As shown in Appendix A.1, household optimality and market clearing conditions imply the Fisher equation

and the equation for money market equilibrium, in period t,
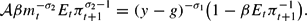
Assuming a lower bound on real bonds, the transversality condition implies

Equations (2) and (3) are usually derived under RE but, as argued in Appendix A.1, they also can be assumed to hold in a temporary equilibrium with given subjective expectations. As noted in the Introduction, these equations as decision rules of the agents do not explicitly consider expectations of variables at more distant horizons. However, we verify that the household transversality condition and the intertemporal budget constraint of the government are satisfied along the learnable temporary equilibrium paths that converge to an REE.
The specification of the model is completed by giving the government budget constraint and policy rules. The government budget constraint is Bt+Mt+τtPt = gPt+Mt−1+Rt−1Bt−1, which in real terms can be written
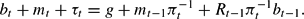
For fiscal policy, we use Leeper's tax rule
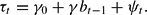
Monetary policy is given either by Leeper's interest rate rule

or by a simple fixed money supply rule
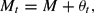
as in Sims (1999) or McCallum (2001). Here ψt and θt are exogenous random shocks, which for simplicity are iid with mean zero. We remark that the government nominal bond supply is jointly determined with the equilibrium price level by the government budget constraint once the tax and monetary policy rules have been specified.
In the terminology of Leeper (1991), fiscal policy is “active” if |β−1−γ| > 1 and “passive” if |β−1−γ| < 1, whereas under (7) monetary policy is active if |αβ| > 1 and passive if |αβ| < 1. For the empirically realistic case 0≤γ≤β−1 active (passive, respectively) fiscal policy means that additional tax revenue from a small increase in the steady state level of debt is insufficient (sufficient, respectively) to cover the increased interest payments. Under the interest rate rule (7), with α > 0, active monetary policy means that a small increase in the steady-state inflation rate leads to an increase in the real interest rate. As noted by Sims (1999), it is also natural to refer to monetary policy as active if the policy rule (8) is followed in place of (7).
We want to consider the RE solutions under different policy regimes and then to analyze their stability under LS learning. Leeper emphasized the cases of AM/PF (active monetary/passive fiscal policy) and AF/PM (active fiscal/passive monetary policy) in which, as discussed later, there is a unique stationary solution. We will be particularly interested in these cases but also will consider explosive regimes of the model and regimes with indeterminacy, that is, with multiple stationary solutions.
BUBBLES AND THE FISCAL THEORY OF PRICES
We begin our analysis with consideration of a prominent case of the fiscal theory of prices in which, under a constant money supply, the price level path is determined by fiscal policy. For example, see Sims (1999) or McCallum (2001). In this section, we use a nonstochastic version of the model in which ψt ≡ 0 and θt ≡ 0. Monetary policy is given by (8) and fiscal policy is given by (6) with γ = 0. Thus, policy reduces to

which is a special case in which both monetary and fiscal policy are active.
With a nonstochastic model it is natural to assume point expectations, so that (3) becomes

With constant nominal money stock, we can write
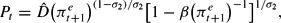
where
.
Consider first the perfect foresight solutions. We take as given the initialmoney stock and the initial value of bonds redeemed R0B0. With a constant money supply and taxes, we have B1+τP1 = gP1+R0B0 in period 1. Under perfect foresight, we have
for t ≥ 1 and so (5) reduces to

for t ≥ 2. This equation is explosive and will violate the transversality conditions unless b1 = B1/P1 =(τ−g)/(β−1−1). With R0B0 given as an initial condition this equation uniquely determines, under perfect foresight, the price level P1 through (τ−g)/(1−β) = R0B0/P1. Under perfect foresight, the price equation (9) becomes
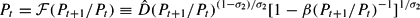
for t ≥ 1. We remark that the right-hand side of (10) is strictly increasing in Pt+1/Pt and therefore the equation can be solved uniquely for Pt given Pt+1 (and vice versa). However, there is no explicit closed-form solution.
The equation (10) has a steady state at
but is explosive and will diverge unless initial conditions happen to be such that
. However, for 0<σ2 < 1 and initial
we obtain an explosive price path Pt → ∞ that is consistent with the transversality conditions and the equilibrium equations. In this “fiscalist” equilibrium, the price level P1 = R0B0(1−β)/(τ−g) is entirely determined by fiscal variables and Pt follows an explosive “bubble” price path despite a constant money stock.
McCallum (2001) argues that this solution is less plausible than an alternative “bubble-free” monetarist solution
and bt = 0 for all t = 1, 2, 3, …, in which (with our timing) the level of real taxes τt adjusts to satisfy τ1 = g+R0B0/P1 and τt = g for t = 2, 3, …. One way to interpret McCallum's view, as he acknowledges, is as an argument that fiscal policy must be Ricardian, that is, must satisfy the government intertemporal budget constraint for all feasible sequences, not just for equilibrium sequences. [For a related argument see Buiter (2002).] However, the status of the fiscalist solution in this model remains controversial.
Fiscalist Case Under Learning
We now take a different tack, which nonetheless comes to the same conclusion as McCallum (2001), that is, that the fiscalist solution is not plausible in the case under scrutiny. We suppose that the government can indeed commit to τt = τ for all t = 1, 2, 3, …, so that the only equilibrium perfect foresight price path is the explosive fiscalist solution given earlier. However, we drop the perfect foresight assumption and ask if the price path is learnable under a natural adaptive learning rule that is closely related to LS.
In a temporary equilibrium (9), agents make a forecast of the relevant variable πt+1, for which they are assumed to employ a suitable parametric model. In each period, agents estimate the key parameter, using the available data, and employ the estimated model to make their forecast
. The temporary equilibrium then generates a new data point, and in the following period agents update their parameter estimate and make forecasts using the reestimated model. The issue of interest is whether the estimated parameter converges asymptotically so that the economy converges to the perfect foresight path over time.
We first note that, using (10), Pt → ∞ implies that πt+1 → ∞ along the perfect foresight path.9
If instead we had Pt → ∞ and
where
, the right-hand side of (10) would tend to a finite value. This is a contradiction. (If
, there would be deflation, that is, Pt+1 < Pt for sufficiently large t, which would violate the assumption Pt → ∞.)
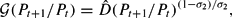
it can be seen that

Thus, for Pt+1/Pt large,
provides a good approximation to
. Solving
gives
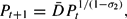
where
. For all large Pt, along a fiscalist path, forecasts based on (11) would be close to the perfect foresight value of Pt+1.
We therefore endow private agents with the Perceived Law of Motion (PLM)
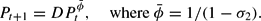
We assume that agents know the growth rate parameter
, but do not know D (equal to
under RE) and must estimate D from the data. Under this PLM the ratio
provides the relevant data for estimating the unknown constant D. Allowing the estimation of both D and ϕ would require a stochastic framework because otherwise there is insufficient information to identify two parameters.10
It can be shown that when both D and ϕ are unknown the equilibrium fails to be E-stable, which indicates that instability would arise in a stochastic setup of the model. Learning in terms of some other parameters could also be considered without changing the results as E-stability is invariant to smooth 1−1 transformations of the parameters.
is known, then this clearly would cast doubt on the plausibility of the fiscal theory in this policy setting.
Our learning rule specifies that the estimate Dt is updated as follows:
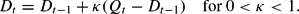
This rule adjusts the estimate in the direction of the most recent value of the ratio Qt. The rule (12) is a standard constant gain learning rule for estimating an unknown constant. The “gain” κ is usually taken to be a small positive value.11
In stochastic models, a decreasing gain such as κt = t−1 would normally be used. In this case the rule would be a recursive form for estimating an unknown constant by least squares.
Under this learning rule, forecasts of prices are given by
and
, so that expected inflation is given by12
We are here treating the information set at the time expectations are formed as including Pt−1 but not Pt. (However, including current Pt in the information set would not make the price bubble paths stable.)
. Substituting this forecast into (9) and solving for Qt yields
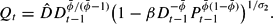
Thus, the system under learning consists of (12), (13), and the definitional equation
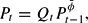
and the fiscalist solution is stable under the learning rule (12) if
as t → ∞.
PROPOSITION 1.Under constant taxes and fixed money supply, the explosive fiscalist price path is locally unstable under the learning rule (12) for all 0 < κ < 1.
Proof. Suppose to the contrary that
as t → ∞. Then Pt → ∞ under the system (12), (13), and (14), so that
. For large Pt, Dt approximately follows
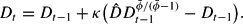
This equation has the fixed point
, but it is easily seen that
is unstable under (15) since
, where
This instability result indicates a lack of robustness of the perfect foresight price path, to small deviations, under a simple LS learning rule of a type that is known to yield stability in other contexts, and contrasts with cases here in which analogous learning rules converge.
We close this section with two remarks.
First, the contribution of Proposition 1 is not that it shows the possibility of an REE being unstable under LS learning. This possibility is well known. In some cases, instability under learning is due to a PLM specified in terms of a variable that explodes. For example, Bullard (1994) and Schönhofer (1996) give an example of instability in an overlapping generations model with constant money growth. Their instability result depends on a specification of LS updating in which the regressor follows an explosive path, and the solution becomes stable when the updating rule is instead specified in terms of the inflation rate.13
See Section 14.5 of Evans and Honkapohja (2001) for details.
Second, the instability result relies on using natural but simple rules for decision making and learning. These decision rules are discussed in Appendix A.1. In particular, the household demand for real balances depends only on the interest rate and the expected rate of inflation over the coming period. More elaborate decision (and learning) rules can be imagined in which households choose their money demands based on a forecast of the whole future price path.14
However, our decision rule is natural because it ensures that the household attempts each period to meet the first-order condition for maximizing utility given by the usual Euler equation.Monetarist Solution Under Learning
We now consider LS learning stability of the monetarist solution. We set this case up by assuming that the government pays off the debt immediately, never resorting to bond finance thereafter. (We continue to assume that money supply is constant.) Clearly, this is an extreme form of Ricardian policies.15
McCallum (2001) points out that the monetarist solution is an REE even if the government attempts to implement a non-Ricardian fiscal policy because fully rational agents would not have a positive demand for bonds in this REE.
The solution of interest is the steady state

It is easily seen that this is the unique steady state solution for πt. We refer to this as the monetarist solution and we now investigate its stability under (constant-gain) LS learning. A natural learning rule treats the equilibrium inflation rate as an unknown constant ζ to be estimated.16
Equivalently, in analogy with the previous section, agents have the PLM Pt = ζPt−1 and forecast
,
so that
.
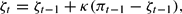
with expected inflation given by
. Again, κ is a small positive constant.
Writing the nonlinear model (9) as
, we have
so that our system becomes
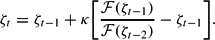
The monetarist solution is locally stable under (17) if ζt → 1 from nearby starting points as t → ∞. The relevant stability condition is easily obtained by looking at the linearized second-order difference equation. This yields
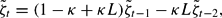
where
and
. Using standard results, the linearized system is stable if |κL| < 1 and |1−κ+κL| < 1+κL. Since L > 0 these inequalities hold for κ > 0 sufficiently small. We conclude as follows:
PROPOSITION 2. Under constant money supply and Ricardian fiscal policy, the monetarist solution is locally stable under the learning rule (16) for all κ > 0 sufficiently small.
We conjecture that the monetarist solution is in fact globally stable under our simple learning rule. We have not investigated this because it is not central to the message of this paper. There are a number of examples of global stability results in the learning literature. In particular, for the standard overlapping generations model of money, Wenzelburger (2002) has recently developed a relatively complicated learning rule under which the monetary steady state is globally stable.
Discussion
Propositions 1 and 2 cast doubt on the plausibility of FTPL for the special case of constant money and taxes. If the government follows non-Ricardian policies and the money supply is held fixed, the only REE is the explosive price bubble path, but this equilibrium is not stable under (constant-gain) LS learning. The economy under the specified learning rule may follow some explosive path for a period of time, but this path will not converge to the fiscalist solution.
However, there are other policy regimes in which FTPL has been proposed as the relevant solution. In particular, Leeper (1991) studied situations in which the inflation rate is affected by government tax and bond variables but with finite steady state inflation. We now turn to an analysis of LS learning under policy rules (6) and (7) based on a linearization around the steady state of the model with random shocks. We will be particularly interested in the policy regimes in which the interaction of monetary and fiscal policy rules leads to a unique stationary solution under RE, but we also will consider other policy regimes.
LINEARIZED MODEL WITH STOCHASTIC SHOCKS
We thus return to monetary policy following an interest rate rule, with the system specified by (2), (3), (5), and the policy rules given by (6) and (7). This is a stochastic, nonlinear system with exogenous shocks, lagged endogenous variables and expectations of future quantities that are themselves nonlinear functions of the endogenous economic variables.17
One might be tempted to initially examine a nonstochastic version of the model, but as will become evident, for assessing the FTPL it is essential to look at the stochastic system. The fiscalist equilibrium is a bivariate VAR with feedback from both endogenous variables. To capture these dynamics, LS learning must be conducted in a stochastic setting in order to avoid asymptotic perfect multicollinearity. For a discussion of this point, see Section 3c of Evans and Honkapohja (1998).
In Appendix A.2, we show that the linearized system takes the form
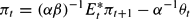

where
denotes inflation expectations formed at t. The notation
is used to emphasize that the reduced form (18)–(19) applies whether or not expectations are rational. The coefficients φ1, …, φ4 are given in Appendix A.2.18
These reduced form equations are identical to the reduced form given by Leeper, but with coefficients that differ slightly because of differences in timing and the more general utility function used here. See Leeper (1991), p. 136.
Linear stochastic expectations models such as (18)–(19) may or may not have a unique stationary REE, depending on the parameters. When there is a unique stationary RE solution, the steady state of the model is said to be (locally) “determinate” (the terminology “regular” is also used). When there are multiple stationary RE solutions, the steady state (or model) is called “indeterminate” (or “irregular”), and when there are no stationary RE solutions the steady state of the model is called “explosive.”19
Conditions for determinacy and indeterminacy (equivalently regularity and irregularity) are given, for example, in Blanchard and Kahn (1980), Chapter 3 of Farmer (1999) and Chapter 10, Appendix 2, of Evans and Honkapohja (2001).
In univariate one-step ahead forward-looking models with positive feedback, there is a simple connection between determinacy of a steady state and the stability of the unique stationary solution under LS learning.20
This is sometimes thought of as a reversal of dynamics in going from RE, or perfect foresight, to learning.
Sections 4.1 and 4.2 consider, respectively, determinacy and LS learnability of the different REE. Section 4.3 combines these analyses into an overall assessment of the plausibility of the FTPL.
Determinacy of the Different Equilibria
For models such as (18)–(19) the REE can be represented as vector autoregressions (VARs) depending also on exogenous variables, and by stationarity we mean that the VAR is asymptotically covariance stationary in the usual time-series sense. In the current context, stationarity is equivalent to the solution being nonexplosive in conditional mean. We begin by considering the determinate cases, which motivates the monetarist and fiscalist solutions, and present the fully general treatment a bit later.
In Appendix A.3, it is shown that the determinate case arises when either |αβ| > 1 and |β−1−γ| < 1, that is, active monetary policy and passive fiscal policy (AM/PF), or |αβ| < 1 and |β−1−γ| > 1, that is, active fiscal policy and passive monetary policy AM/PM. As shown in Appendix A.3, either condition |αβ| > 1 or |β−1−γ| > 1 leads to a linear restriction of the form
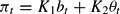
when nonexplosiveness of the solution is imposed. This equation together with (19) defines the unique stationary solution in the determinate case.
In the AM/PF regime, we obtain K1 = 0 and K2=−α−1, so that
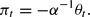
We will refer to this solution as the “monetarist solution,” as πt is independent of both bt−1 and ψt. In the AF/PM regime, we obtain
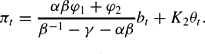
From (21) and (19), it is apparent that inflation now depends on bt−1 and ψt as well as on monetary policy. We therefore refer to this REE as the “fiscalist solution.”
In addition to the determinate cases, two other regimes are possible, depending on policy parameters. If |αβ| < 1 and |β−1−γ| < 1, so that both policies are passive, the model is indeterminate and there are multiple stationary solutions, which include the monetarist, the fiscalist REE and, as shown here, a class of nonfundamental solutions. If |αβ| > 1 and |β−1−γ| > 1, so that both policies are active, the model is explosive, and there are no stationary solutions.21
In this case requiring nonexplosiveness would impose two linear restrictions of the form (20). Because these are independent conditions, they can hold for all t only with probability 0.

Determinate, indeterminate and explosive regions.
We now systematically examine the possible REE. Introducing vector notation yt =(πt, bt)′, the linearized model (18)–(19) can be written
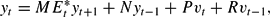
where

Using the method of undetermined coefficients, we consider equilibria of the form
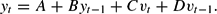
The form (23) excludes exogenous sunspot variables by assumption (we will briefly consider such solutions later). Computing the expectation22
We make the frequently employed assumption that when agents compute forecasts, using the PLM, they observe current values of the exogenous variables, but only lagged values of the endogenous variables. It can be shown that the key results do not change under the alternative information assumption that agents also observe current endogenous variables.
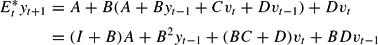
and inserting into (22) we obtain

The possible solutions to (A, B, C, D) can then be obtained by requiring that (23) and (25) describe the same random process.
Equivalently, we can use the terminology from the study of LS learning and E-stability, so that the guess (23) is the PLM and equation (25) is the Actual Law of Motion (ALM). The mapping from the PLM to the ALM is
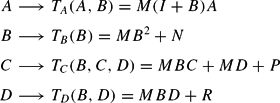
and the fixed points of this mapping correspond to REE of the form (23).
The second component of the mapping gives a quadratic matrix equation in B, which can have more than one solution. Given any solution for B, the first component gives the unique solution A = 0, provided that I−M(I+B) is nonsingular. Similarly, for given B the third and fourth components of the mapping are linear equations for C and D. Imposing the zero elements of M and N in the matrix quadratic for B, three types of equilibria can easily be shown to emerge:23
A Mathematica program with the details is available on request.
PROPOSITION 3. There are three types of REE, I. the monetarist solution, II. the fiscalist solution and III. nonfundamental solutions, taking the form (23), as listed below.
- I. B = N, C = P and D = R with A = 0. This is the monetarist solution identified earlier in the determinate case.
- II. , where χ =(βγ−1)φ1−βφ2, A = 0 and C and D are also uniquely determined by the fixed point.24This is a way of representing the fiscalist solution identified above in the determinate case. Although this may appear to be a complicated representation, it can be verified that the eigenvalues of B are 0 and αβ. The zero eigenvalue corresponds to the static linear relationship (21) between πt and bt, which can be used to obtain alternative representations of the REE irrespective of stationarity (see Appendix A.3).
Explicit formulas for C and D are available on request. This assumes χ≠0.
- III. , A = 0. For C and D the solution is not unique. For D there is a two-dimensional continuum and, given a value for D, the equation for C also yields a two-dimensional continuum. We call this class of solutions the non-fundamental solutions, because of the indeterminacy in the C and D coefficients.25We remark that this solution set can be expanded to allow for dependence on an exogenous sunspot variable.
Note that this value of B is equal to J−1 in Appendix A.3. If both eigenvalues of J have absolute values greater than one, there is indeterminacy and this entire class of solutions is stationary.
The next proposition summarizes the determinacy properties of the different solutions shown in the preceding proposition.
PROPOSITION 4. (i) Under AM/PF policy, the monetarist solution is stationary while the fiscalist solution and nonfundamental solutions are explosive. (ii) Under AF/PM policy, the fiscalist solution is stationary while the monetarist solution and nonfundamental solutions are explosive. (iii) Under PM/PF policy, all the REE are stationary. (iv) Under AM/AF policy, all solutions are explosive.26
The stationarity properties of the different REE are direct consequences of the earlier discussion in the text and in Appendix A.3.
We now turn to an examination of whether these solutions are stable under learning.
Stability Under LS Learning
In stochastic setups of type (22), in a temporary equilibrium with possibly nonrational expectations, agents need to make forecasts of endogenous variables in the next period. Agents are assumed to employ a parametric class of stochastic processes for the endogenous variables, the PLM (23), to estimate its parameters using past data and to make their forecasts using the estimated model. More specifically, agents use recursive least squares (RLS) to estimate the parameters ξ =(A, B, C, D) of the PLM (23) from past data. Thus, at time t, agents have estimates ξt =(At, Bt, Ct, Dt) and these are used to make forecasts
in (24) with ξ replaced by ξt. These forecasts together with yt−1, vt and vt−1 determine yt according to (22). In the following period t+1 the estimates ξt are updated using RLS to ξt+1 and the additional data point. An REE is said to be locally stable under LS learning if ξt locally converges to an REE as t → ∞.27
In the indeterminate case, “locally stable” means local convergence under RLS to the set of fixed points.
The phrase “locally stable under LS learning” can be made precise in several different senses. First, for initial parameter estimates in an appropriate compact set strictly containing the fixed point of interest, there is convergence with probability that can be made arbitrarily close to one if the adaption speed is sufficiently slow. Second, by adding a projection facility to the algorithm that constrains parameter estimates to a suitable compact set, one can obtain probability one convergence.28
Various positive probability of convergence results without a projection facility also can be stated.
In this context, E-stability is known to give the conditions for local convergence under LS learning for stationary (and in many cases for nonstationary) REE. In contrast, if E-stability of the REE does not hold, with some additional mild assumptions one can show that LS learning converges with probability zero even for initial estimates arbitrarily close to the RE values. To define E-stability, given PLM parameters ξ let T(ξ) denote the corresponding values of the ALM given by the mapping (26). The three types of RE solutions, given in Proposition 3, correspond to fixed points of this map. The RE solution (or solution set) of interest is E-stable if it is a locally asymptotically stable fixed point of the differential equation
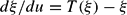
operating under the notional time u.
We now present the results giving stability under LS learning of the different solutions. Appendix A.4 establishes the result by examining E-stability for the different RE solutions.
PROPOSITION 5. Assume that the REE of interest is stationary. (I) The monetarist solution is locally stable under LS learning if

(II) The fiscalist solution is locally stable under LS learning if

and (III) The nonfundamental solutions are not locally stable under LS learning.
We next examine how the conditions for stability under LS learning related to the earlier determinacy results and then turn to the implications for FTPL.
Economic Implications
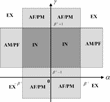
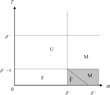
Looking at the economic model, it is evident that the most natural policy rules entail the parameter restrictions α > 0 and γ ≥ 0. α > 0 means that the nominal interest rate responds positively to current inflation and γ > 0 means that the lump-sum tax responds positively to beginning-of-period debt bt−1. In the case γ = 0, taxes are set independently of the debt level. Realistic values of γ would also appear to be below β−1, since γ > β−1 implies that, at the non-stochastic steady state, any shock to debt levels would lead to a tax increase that would more than pay off the debt, including interest, within one period. We therefore focus on the region α > 0 and β−1 > γ ≥ 0 of the policy parameter space.
Figure 2 shows the results on learning and E-stability for the monetarist and fiscalist solutions in this part of the parameter space. In the figure, M indicates that the monetarist solution is locally stable under LS learning. F indicates that the fiscalist solution is locally stable and U indicates that neither solution is locally stable under LS learning. In the region marked F, stability of the fiscalist solution is fragile, as discussed later. In none of the areas are both solutions simultaneously locally stable under LS learning. In the shaded region, defined by α > β−1 and 0≤γ < β−1−1, the solutions are not stationary.

Regions of E-stable REE.
Within the parameter region described by Figure 2, the AM/PF regime lies within region M. In this regime, the monetarist equilibrium is the unique stationary solution and it is also locally stable under LS learning. In the AF/PM regime, which coincides with region F, the fiscalist REE is the unique stationary solution and is locally stable under LS learning.29
Note that active monetary policy requires α > β−1. This is a somewhat stronger condition than given by the usual formulation of the “Taylor principle.”
Cases in which policy leads to unstable REE under learning have appeared in the literature, see in particular the treatment of interest rate pegging by Howitt (1992) and Evans and Honkapohja (2003).
The shaded explosive region with policy combination AM/AF is divided into two cases with either the fiscalist or the monetarist solution being stable under LS learning. We emphasize that our results are local: they are valid in a neighborhood of the steady state and here suggest an incipient tendency for the economy under LS learning to follow the indicated explosive equilibrium. We now briefly discuss the nonlinear dynamics in the explosive region.
Consider the monetarist solution in the nonlinear model. In this solution, the inflation rate is stationary, while bonds bt explode at rate β−1−γ (in the mean). Because the temporary equilibrium equation for πt is independent of bonds, the monetarist solution is E-stable for univariate PLMs throughout the (shaded) explosive region in Figure 2. Moreover, the transversality condition for bt is satisfied because β(β−1−γ) < 1. However, this is only a weak form of E-stability. Our linearization suggests that with VAR-type PLMs (23), stability of the monetarist solution holds only in the shaded region M. We remark that there are two technical complications with this last argument. First, as bt is explosive, the linearization coefficients change over time. This is unlikely to matter because the coefficients that change, φ1 and φ2, do not affect the E-stability conditions. Second, LS learning would include one explosive regressor. However, in related setups, this has not been found to be a difficulty, see Section 9.6 of Evans and Honkapohja (2001) and the references therein.
In the fiscalist solution, both bt and πt are explosive. πt grows away from the steady state at rate αβ. Initially bt also grows at this rate, as can be seen from the relation (21). However, asymptotically the growth rate of bt becomes β−1−γ, which can be seen from the nonlinear bond equation (5) by making use of approximations of money demand and
for large πt. The transversality condition for bt is satisfied throughout the shaded explosive region, provided γ > 0.31
Even if agents believe that bt will continue to grow forever at rate αβ, their perceived transversality condition is satisfied provided α < β−2.

This is a linear system in which the bt equation has become effectively decoupled from πt. The coefficients of the endogenous variables are the same as in (18)–(19) with φ1 = φ2 = φ4 = 0. Applying the analysis of Section 4.2, it can be seen that DTA has an eigenvalue larger than one, indicating a failure of E-stability of the fiscalist solution. These results suggest that in the shaded explosive region F, the fiscalist solution is E-stable in a region near the steady state but at some point loses stability along an explosive path.
In summary, we have found that when there is a unique stationary REE (the determinate case), this REE is stable under LS learning. Depending on the values of policy parameters α and γ the solution is either monetarist or fiscalist. When there are multiple stationary REE, there is no learnable REE. These results provide support for FTPL in the specific case of active fiscal and passive monetary policy AM/PM. In commenting on the results of our paper, Woodford (2003a) considers the AF/PM regime the “primary case with which the literature on FTPL has been concerned.” In the AM/PF case the REE chosen by LS learning is the monetarist solution. This is one of the points noted by McCallum (2003a), (2003b) in his discussion of our results. Woodford (2003a) contends that the monetarist solution in this region is consistent with the predictions of FTPL. Intriguingly, in the explosive region F, there is some support for FTPL in the sense that the incipient E-stability property of the fiscalist solution corresponds to the fact that the fiscalist solution has a less explosive bond growth rate than does the monetarist solution.32
This accords with an interpretation of FTPL that predicts selection only of solutions with the least explosive growth rate for real public debt. This interpretation also would pick the monetarist solution in the shaded region M.
We close this section with a brief discussion of the connection of the results of this section and those of Section 3. In Section 3, monetary policy is given by a fixed money rule, whereas in the framework of this section an interest rate rule is used instead. Strictly speaking, these rules are non-nested. However, they can be compared (under perfect foresight) as follows. Assuming high values of πt and using (10), we obtain
and hence
. Also using the Fisher equation πt+1 = βRt yields
. This can be compared to the interest rate rule (7) and it is immediate that dRt/dπt → ∞ as πt → ∞. Thus, the fixed money supply is like a very active (large α) interest rate policy. Because in Section 3 we also have γ = 0, this in effect places us at the lower boundary of the shaded M region, where the fiscalist solution is unstable and the monetarist solution is stable under LS learning. Note that although the transversality condition is not satisfied at the boundary γ = 0, it holds for arbitrarily small γ > 0.
CONCLUSIONS
We have considered local stability under LS learning of the RE solutions in a simple stochastic optimizing monetary model in which the interaction between monetary and fiscal policy is central. Our first finding was that in the case of constant money supply and constant taxes, the equilibrium explosive price paths dictated by FTPL are not locally stable under LS learning. In contrast, if fiscal policy is Ricardian, then the monetarist equilibrium is locally stable under LS learning. These results appear to cast doubt on the plausibility of FTPL in this policy setting.
We then examined an alternative setting in which interest rates are set as a linear function of inflation and taxes are set as a linear function of real debt. The usual monetarist solution is locally stable under LS learning in the active monetary/passive fiscal policy regime in which it is the unique stationary solution. However, the fiscalist solution, in which inflation depends on debt and on tax shocks, is stable under LS learning for a plausible subregion of the active fiscal/passive monetary regime, in which the fiscalist solution is the unique stationary solution. This provides some support for FTPL.
There also are regions of plausible policy parameter values in which the economy is indeterminate, with multiple stationary solutions. However, in this parameter domain none of the REE are locally stable under LS learning.
Overall, our results provide significant, although limited, support for the fiscalist solution. Whether the fiscalist solution emerges under learning depends on the joint fiscal and monetary policy regime. Careful consideration of the interaction of these policies is therefore required to understand the qualitative characteristics of inflation and debt dynamics. Naturally, local stability under natural learning rules is only a minimal criterion in policy design. Examination of sizes of the domains of attraction would be important in practical applications.
APPENDIX
HOUSEHOLD OPTIMALITY CONDITIONS AND TEMPORARY EQUILIBRIUM
Define the variables Wt+1=mt+bt and xt+1=mt. Following Chow (1996), Section 2.3, introduce the Lagrange multipliers λt for the budget constraint and μt for the equation xt+1=mt and write the Lagrangian
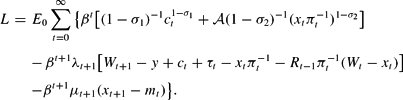
Here Wt, xt are the state and ct, mt the control variables.
The first-order conditions are
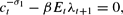

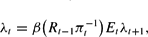
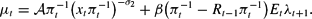
In addition, the optimal choices satisfy the transversality conditions (4).33
The transversality condition for the household is limt →∞βt(mt+bt) = 0, as consumption in this model is constant. As noted by McCallum (2001), provided bonds have a (possibly negative) lower bound, this is equivalent to (4).
These equations hold under RE, but they also hold for an optimizing agent who is solving a dynamic optimization problem under his subjective expectations. We now derive the consumption and money demand equations under subjective expectations. Substituting (A.3) into (A.4), one eliminates Etλt+1. Advancing the resulting equation and using (A.1) and (A.2) leads to
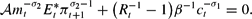
We use
to emphasize that (A.5) holds for subjective as well as RE.
To derive the Euler equation for consumption, combine (A.1) and (A.3) to obtain
and
. Assuming that all agents have identical expectations, market clearing implies that ct=y−g for all agents. It is, therefore, natural to assume that agents forecast their future consumption as ct+1=y−g. We arrive at the consumption schedule

The temporary equilibrium is obtained by imposing market clearing ct=y−g, which immediately gives the Fisher equation
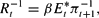
which under RE is (2). The equation for money market equilibrium is
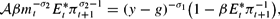
which, together with money supply rule (8), determines the current price level, for given expectations, in a temporary equilibrium. Under RE, we arrive at (3). If instead monetary policy is conducted using the interest rate rule (7), the money supply becomes endogenous and, given expectations, is jointly determined with the interest rate and price level.
LINEARIZATION OF THE MODEL
Rearranging (34), we can write money market clearing as
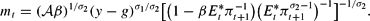
Its linearization at the nonstochastic steady state π is

where
, or
. Here
and
denote the deviations from the steady state.
Linearizing the Fisher relation (A.6) at the steady state π, R, we get
, where
is the deviation from the nonstochastic steady state. This can be substituted into money demand to yield
. Then linearize the budget constraint, taking note that mt is a function of Rt:
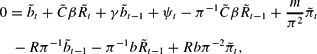
where π, b, R are the steady state values. We also note that
as a result of centering.
Collecting everything together, we have the two Leeper-type equations
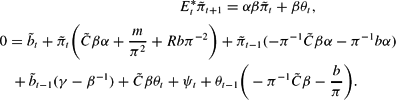
Equation (A.9) implicitly specifies the coefficients φ1, φ2, φ3, φ4 of equation (19). The nonstochastic steady state values are given by equations

DETERMINACY CONDITIONS
For either specification, the system under RE can be rewritten as

or

where ηt+1=πt+1−Etπt+1 and

The eigenvalues of J are (αβ)−1 and (β−1−γ)−1. The model has one predetermined and one free variable and thus determinacy requires that exactly one of these eigenvalues has absolute value less than one and the other greater than one. Imposing non-explosiveness gives a linear restriction between πt, bt and θt corresponding to the root with absolute value less than one. This restriction is obtained as follows. Diagonalize J as J=QΛQ−1, where Λ=diag((αβ)−1, (β−1−γ)−1). Explicit computation using Mathematica gives

Letting (xt, zt)′=Q−1(πt, bt)′, we have
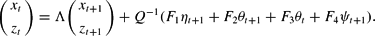
Let (C1, C2)′=−Q−1F3. If |(αβ)−1| < 1 then nonexplosiveness of the solution requires that Etxt+1=αβ(xt+C1θt) = 0, as otherwise |Etxt+s| → ∞ as s → ∞. This gives the restriction xt+C1θt = 0. Using xt=πt we obtain the static linear relationship satisfied by the monetarist solution. If |(β−1−γ)−1| < 1, then analogously nonexplosiveness requires that zt+C2θt = 0. Using zt as the linear function of πt and bt specified earlier gives the static linear relationship satisfied by the fiscalist solution.
Finally, we remark that in Section 4.1 the fiscalist solution II can be shown to satisfy the fiscalist static relationship whether or not the model is determinate. Because the matrix B is singular, one row is proportional to the other row and it can be verified that the proportionality factor is
, which is the same as the coefficient in (21).
PROOF OF PROPOSITION 5
The proposition is established by considering the E-stability conditions. First we note that the B component in this differential equation is nonlinear, with local stability determined by its linearization at the fixed point of interest. The B, C and D components are matrix-valued and need to be vectorized. Moreover, it is seen that the B component of (27) is an independent subsystem, the A and D subsystems, respectively, depend on B, and the C subsystem depends on both B and D. The stability conditions for (27) can be given in terms of the following matrices:

where [otimes ] denotes the Kronecker product and
,
, and soon denote the values of A, B etc. at the different REE in Proposition 3.
The E-stability condition for REE of type I and II is that the real parts of all eigenvalues of all four matrices DiTi, i=A, B, C, D, are less than one. For the class of nonfundamental solutions III, the matrices DCTC and DDTD will have some eigenvalues equal to one, because of the continuum of solutions. A necessary condition for E-stability is that the other eigenvalues of the four matrices have real parts less than one.
The explicit E-stability conditions for the three types of REE can be analytically computed using Mathematica (routines available on request). We give details for the monetarist solution and summarize the E-stability conditions in the other cases.
I. The monetarist solution: Inserting M and the value of
in the monetarist solution, we get

and DCTC = DDTD = 0. The eigenvalues of DATA are 0 and (αβ)−1. The nonzero eigenvalue of DBTB is (β−1−γ)/αβ. This yields the E-stability conditions given.
II. The fiscalist solution: The nonzero eigenvalues of DiTi, i=A, B, C, D, are 1+(γ+1−β−1)/αβ, 1+(γ−β−1)/αβ, and 2+(γ−β−1)/αβ. This yields the E-stability conditions given. Although the matrix
depends on φ1 and φ2, the eigenvalues of DiTi, i=A, B, C, D, are in fact independent of φ1 and φ2, as can be verified using Mathematica.
III. The nonfundamental solutions are not E-stable, as DBTB has an eigenvalue equal to 2.
An earlier version was presented in the CEPR-CREI conference on fiscal policy in Barcelona (May 2002) and in various meetings and seminars. We thank the audiences, Stefanie Albanesi, Ben McCallum, Mike Woodford, the referees, and the Associate Editor for their comments. Financial support from the U.S. National Science Foundation Grant No. 0136848 and from grants by the Academy of Finland, Bank of Finland, Yrjö Jahnsson Foundation, and Nokia Group is gratefully acknowledged. The research was to a large extent done while the second author was affiliated with the Research Unit on Economic Structures and Growth, University of Helsinki.