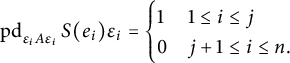1 Introduction
The notion of right rejective subcategories was introduced by Iyama and plays a crucial role in the proof of the finiteness theorem for representation dimensions of artin algebras [Reference Iyama13]. Right rejective subcategories are a special class of coreflective subcategories which appear in the classical theory of localizations of abelian categories. It is known that right rejective subcategories provide effective tools to study representation-finite orders [Reference Iyama12, Reference Iyama14, Reference Rump19]. A subcategory
![]() $\mathcal {C}'$
of an additive category
$\mathcal {C}'$
of an additive category
![]() $\mathcal {C}$
is called a right rejective subcategory if for each
$\mathcal {C}$
is called a right rejective subcategory if for each
![]() $X \in \mathcal {C}$
, there exists a monic right
$X \in \mathcal {C}$
, there exists a monic right
![]() $\mathcal {C}'$
-approximation of X. We call a chain of cosemisimple right rejective (respectively, coreflective) subcategories a right rejective (respectively, coreflective) chain.
$\mathcal {C}'$
-approximation of X. We call a chain of cosemisimple right rejective (respectively, coreflective) subcategories a right rejective (respectively, coreflective) chain.
Quasi-hereditary algebras were introduced by Cline, Parshall, and Scott to explore highest weight categories arising from the study of semisimple complex Lie algebras and algebraic groups [Reference Coulembier5, Reference Scott20]. As a distinguished class of quasi-hereditary algebras, Ringel [Reference Ringel18] introduced right-strongly quasi-hereditary algebras which frequently appear in the representation theory of algebras [Reference Cline, Parshall and Scott7, Reference Cline, Parshall and Scott8, Reference Geiss, Leclerc and Schröer10, Reference Kalck and Karmazyn16, Reference Tsukamoto21]. It is known that special right rejective chains called total right rejective chains, are characterized by right-strongly quasi-hereditary algebras.
Proposition 1.1 ([Reference Tsukamoto22, Theorem 3.22])
Let A be an artin algebra and
![]() $(e_{1},e_{2},\ldots , e_{n})$
a complete set of primitive orthogonal idempotents of A. Let
$(e_{1},e_{2},\ldots , e_{n})$
a complete set of primitive orthogonal idempotents of A. Let
![]() $\varepsilon _{i}:=e_{i} + \cdots + e_{n}$
. Then the following statements are equivalent.
$\varepsilon _{i}:=e_{i} + \cdots + e_{n}$
. Then the following statements are equivalent.
-
(1) The following chain is a total right rejective chain.
 $$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
$$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
-
(2)
 $A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a heredity chain (namely A is a quasi-hereditary algebra), and the following chain is a coreflective chain.
$A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a heredity chain (namely A is a quasi-hereditary algebra), and the following chain is a coreflective chain.  $$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset0. \end{align*} $$
$$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset0. \end{align*} $$
-
(3)
 $A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a right-strongly heredity chain (namely A is a right-strongly quasi-hereditary algebra).
$A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a right-strongly heredity chain (namely A is a right-strongly quasi-hereditary algebra).
Ágoston et al. [Reference Ágoston, Dlab and Wakamatsu1] introduced neat algebras as a generalization of quasi-hereditary algebras. As an analog of Proposition 1.1, we give characterizations for
![]() $\mathsf {proj}\, A$
to admit a right rejective chain using neat algebras. For an idempotent e of A, let
$\mathsf {proj}\, A$
to admit a right rejective chain using neat algebras. For an idempotent e of A, let
![]() $S(e):=eA/eJ$
, where J is the Jacobson radical of A.
$S(e):=eA/eJ$
, where J is the Jacobson radical of A.
Theorem 1.2 (Theorem 3.5)
Let A be an artin algebra and
![]() $(e_{1},e_{2},\ldots , e_{n})$
a complete set of primitive orthogonal idempotents of A. Let
$(e_{1},e_{2},\ldots , e_{n})$
a complete set of primitive orthogonal idempotents of A. Let
![]() $\varepsilon _{i}:=e_{i} + \cdots + e_{n}$
. Then the following statements are equivalent.
$\varepsilon _{i}:=e_{i} + \cdots + e_{n}$
. Then the following statements are equivalent.
-
(1) The following chain is a right rejective chain.
(1.1) $$ \begin{align} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align} $$
$$ \begin{align} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align} $$
-
(2)
 $A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a neat chain (namely A is a neat algebra), and the following chain is a coreflective chain.
$A> A\varepsilon _{2} A > \cdots > A \varepsilon _{n} A >0$
is a neat chain (namely A is a neat algebra), and the following chain is a coreflective chain.  $$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
$$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
-
(3) For each
 $i \in [1, n]$
,
$i \in [1, n]$
,
 $\operatorname {pd}\nolimits _{\varepsilon _{i} A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
holds.
$\operatorname {pd}\nolimits _{\varepsilon _{i} A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
holds.
By focusing on the condition (3) in Theorem 1.2, we give sufficient conditions (see Theorem 3.9) for the right rejective chain (1.1) to be a total right rejective chain. Moreover, we prove that the following classes of algebras satisfy the sufficient conditions.
-
• Nakayama algebras with heredity ideals (Proposition 3.13).
-
• Locally hereditary algebras (Proposition 3.16).
-
• Algebras of global dimension at most two (Proposition 3.17).
Therefore, we have the following result.
Theorem 1.3 (Theorem 3.12)
Nakayama algebras with heredity ideals, locally hereditary algebras and algebras of global dimension at most two are right-strongly quasi-hereditary.
Notation
Throughout this paper, A is a basic artin algebra. Let
![]() $J=J(A)$
be the Jacobson radical of A. By a module, we mean a finitely generated right A-module. Let
$J=J(A)$
be the Jacobson radical of A. By a module, we mean a finitely generated right A-module. Let
![]() $\operatorname {pd}\nolimits _{A} M$
denote the projective dimension of an A-module M. We write
$\operatorname {pd}\nolimits _{A} M$
denote the projective dimension of an A-module M. We write
![]() $\mathsf {mod}\, A$
for the category of finitely generated right A-modules and
$\mathsf {mod}\, A$
for the category of finitely generated right A-modules and
![]() $\mathsf {proj}\, A$
for the full subcategory of
$\mathsf {proj}\, A$
for the full subcategory of
![]() $\mathsf {mod}\, A$
consisting of projective A-modules. For
$\mathsf {mod}\, A$
consisting of projective A-modules. For
![]() $M \in \mathsf {mod}\, A$
, let
$M \in \mathsf {mod}\, A$
, let
![]() $\mathsf {add}\, M$
denote the full subcategory of
$\mathsf {add}\, M$
denote the full subcategory of
![]() $\mathsf {mod}\, A$
whose objects are direct summands of finite direct sums of M.
$\mathsf {mod}\, A$
whose objects are direct summands of finite direct sums of M.
2 Right rejective chains
In this section, we recall the definition of right rejective chains and collect related results (see [Reference Iyama13, Reference Iyama15
] for details). By a subcategory, we always mean a full subcategory which is closed under isomorphisms. For a subcategory
![]() $\mathcal {C}'$
of an additive category
$\mathcal {C}'$
of an additive category
![]() $\mathcal {C}$
, we call a morphism
$\mathcal {C}$
, we call a morphism
![]() $f: Y \to X$
in
$f: Y \to X$
in
![]() $\mathcal {C}$
a right
$\mathcal {C}$
a right
![]() $\mathcal {C}'$
-approximation of X if
$\mathcal {C}'$
-approximation of X if
![]() $Y \in \mathcal {C}'$
and
$Y \in \mathcal {C}'$
and
![]() $\mathcal {C}(-, f): \mathcal {C}(-, Y) \rightarrow \mathcal {C}(-, X)$
is an epimorphism on
$\mathcal {C}(-, f): \mathcal {C}(-, Y) \rightarrow \mathcal {C}(-, X)$
is an epimorphism on
![]() $\mathcal {C}'$
. Dually, we define a left
$\mathcal {C}'$
. Dually, we define a left
![]() $\mathcal {C}'$
-approximation.
$\mathcal {C}'$
-approximation.
Definition 2.1 Let
![]() $\mathcal {C}$
be an additive category and
$\mathcal {C}$
be an additive category and
![]() $\mathcal {C}'$
a subcategory of
$\mathcal {C}'$
a subcategory of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
-
(1) We call
 $\mathcal {C}'$
a coreflective subcategory of
$\mathcal {C}'$
a coreflective subcategory of
 $\mathcal {C}$
if for any
$\mathcal {C}$
if for any
 $X\in \mathcal {C}$
, there exists a right
$X\in \mathcal {C}$
, there exists a right
 $\mathcal {C}'$
-approximation
$\mathcal {C}'$
-approximation
 $f \in \mathcal {C}\left (Y,X\right )$
of X such that
$f \in \mathcal {C}\left (Y,X\right )$
of X such that
 $\mathcal {C}(-, f): \mathcal {C}(-, Y) \rightarrow \mathcal {C}(-, X)$
is an isomorphism on
$\mathcal {C}(-, f): \mathcal {C}(-, Y) \rightarrow \mathcal {C}(-, X)$
is an isomorphism on
 $\mathcal {C}'$
.
$\mathcal {C}'$
. -
(2) We call
 $\mathcal {C}'$
a right rejective subcategory of
$\mathcal {C}'$
a right rejective subcategory of
 $\mathcal {C}$
if for any
$\mathcal {C}$
if for any
 $X\in \mathcal {C}$
, there exists a right
$X\in \mathcal {C}$
, there exists a right
 $\mathcal {C}'$
-approximation of X such that it is a monomorphism in
$\mathcal {C}'$
-approximation of X such that it is a monomorphism in
 $\mathcal {C}$
.
$\mathcal {C}$
.
Dually, reflective subcategories and left rejective subcategories are defined.
Right rejective subcategories are coreflective subcategories, but the converse does not hold in general.
To define a right rejective chain, we need the notion of cosemisimple subcategories. Let
![]() $\mathcal {J}_{\mathcal {C}}$
be the Jacobson radical of
$\mathcal {J}_{\mathcal {C}}$
be the Jacobson radical of
![]() $\mathcal {C}$
. For a subcategory
$\mathcal {C}$
. For a subcategory
![]() $\mathcal {C}'$
of
$\mathcal {C}'$
of
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
![]() $[\mathcal {C}']$
denote the ideal of
$[\mathcal {C}']$
denote the ideal of
![]() $\mathcal {C}$
consisting of morphisms which factor through some object of
$\mathcal {C}$
consisting of morphisms which factor through some object of
![]() $\mathcal {C}'$
, and let
$\mathcal {C}'$
, and let
![]() $\mathcal {C}/[\mathcal {C}']$
denote the factor category.
$\mathcal {C}/[\mathcal {C}']$
denote the factor category.
Definition 2.2 Let
![]() $\mathcal {C}$
be an additve category. A subcategory
$\mathcal {C}$
be an additve category. A subcategory
![]() $\mathcal {C}'$
of
$\mathcal {C}'$
of
![]() $\mathcal {C}$
is called a cosemisimple subcategory of
$\mathcal {C}$
is called a cosemisimple subcategory of
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $\mathcal {J}_{\mathcal {C}/[\mathcal {C}']}=0$
holds.
$\mathcal {J}_{\mathcal {C}/[\mathcal {C}']}=0$
holds.
We recall characterizations of coreflective subcategories, right rejective subcategories and cosemisimple right rejective subcategories of
![]() $\mathsf {proj}\, A$
. We write
$\mathsf {proj}\, A$
. We write
![]() $\operatorname {gldim}\nolimits A$
for the global dimension of A.
$\operatorname {gldim}\nolimits A$
for the global dimension of A.
Proposition 2.3 ([Reference Iyama15, Theorem 3.2])
Let A be an artin algebra and
![]() $\varepsilon $
an idempotent of A. Then the following statements hold.
$\varepsilon $
an idempotent of A. Then the following statements hold.
-
(1)
 $\mathsf {add} \varepsilon A$
is a coreflective subcategory of
$\mathsf {add} \varepsilon A$
is a coreflective subcategory of
 $\mathsf {proj}A$
if and only if
$\mathsf {proj}A$
if and only if
 $A\varepsilon \in \mathsf {proj}\, \varepsilon A \varepsilon $
.
$A\varepsilon \in \mathsf {proj}\, \varepsilon A \varepsilon $
. -
(2)
 $\mathsf {add} \varepsilon A$
is a right rejective subcategory of
$\mathsf {add} \varepsilon A$
is a right rejective subcategory of
 $\mathsf {proj}A$
if and only if
$\mathsf {proj}A$
if and only if
 $A \varepsilon A \in \mathsf {add} \varepsilon A$
as a right A-module. In this case,
$A \varepsilon A \in \mathsf {add} \varepsilon A$
as a right A-module. In this case,
 $\operatorname {gldim}\nolimits \varepsilon A \varepsilon \le \operatorname {gldim}\nolimits A$
holds.
$\operatorname {gldim}\nolimits \varepsilon A \varepsilon \le \operatorname {gldim}\nolimits A$
holds. -
(3)
 $\mathsf {add} \varepsilon A$
is a cosemisimple right rejective subcategory of
$\mathsf {add} \varepsilon A$
is a cosemisimple right rejective subcategory of
 $\mathsf {proj}A$
if and only if
$\mathsf {proj}A$
if and only if
 $e J \in \mathsf {add} \varepsilon A$
as a right A-module, where
$e J \in \mathsf {add} \varepsilon A$
as a right A-module, where
 $e:=1- \varepsilon $
. In this case, the inclusion
$e:=1- \varepsilon $
. In this case, the inclusion
 $e J\to e A$
is a right
$e J\to e A$
is a right
 $\mathsf {add}\, \varepsilon A$
-approximation of
$\mathsf {add}\, \varepsilon A$
-approximation of
 $eA$
.
$eA$
.
Now, we introduce the notion of coreflective chains, right rejective chains and total right rejective chains.
Definition 2.4 Let
![]() $\mathcal {C}$
be an additve category. Let
$\mathcal {C}$
be an additve category. Let
be a chain of subcategories of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
-
(1) (2.1) is called a coreflective chain (of length n) if
 $\mathcal {C}_{i+1}$
is a cosemisimple coreflective subcategory of
$\mathcal {C}_{i+1}$
is a cosemisimple coreflective subcategory of
 $\mathcal {C}_{i}$
for each
$\mathcal {C}_{i}$
for each
 $1 \le i \le n$
.
$1 \le i \le n$
. -
(2) (2.1) is called a right rejective chain (of length n) if
 $\mathcal {C}_{i+1}$
is a cosemisimple right rejective subcategory of
$\mathcal {C}_{i+1}$
is a cosemisimple right rejective subcategory of
 $\mathcal {C}_{i}$
for each
$\mathcal {C}_{i}$
for each
 $1 \le i \le n$
.
$1 \le i \le n$
. -
(3) (2.1) is called a total right rejective chain (of length n) if the following conditions hold for each
 $1 \le i \le n$
:
$1 \le i \le n$
:-
(a)
 $\mathcal {C}_{i+1}$
is a right rejective subcategory of
$\mathcal {C}_{i+1}$
is a right rejective subcategory of
 $\mathcal {C}$
and
$\mathcal {C}$
and -
(b)
 $\mathcal {C}_{i+1}$
is a cosemisimple subcategory of
$\mathcal {C}_{i+1}$
is a cosemisimple subcategory of
 $\mathcal {C}_{i}$
.
$\mathcal {C}_{i}$
.
-
One can easily check that total right rejective chains are right rejective chains, and right rejective chains are coreflective chains. However, the converses do not always hold. We refer to Example 3.6 which shows that right rejective chains are not necessarily total right rejective chains.
If
![]() $\mathsf {proj}\, A$
has a right rejective chain, then we give an upper bound of the global dimension of A.
$\mathsf {proj}\, A$
has a right rejective chain, then we give an upper bound of the global dimension of A.
Proposition 2.5 ([Reference Iyama15, Theorem 3.3])
Let A be an artin algebra. If
![]() $\mathsf {proj} A$
admits a right rejective chain of length n, then the global dimension of A is at most
$\mathsf {proj} A$
admits a right rejective chain of length n, then the global dimension of A is at most
![]() $2n-2$
.
$2n-2$
.
Remark 2.6 The length of a right rejective chain of
![]() $\mathsf {proj}\, A$
is bounded by the number of indecomposable direct summands of A, or equivalently the number of isomorphism classes of simple A-modules. Hence, if A has m simple modules and
$\mathsf {proj}\, A$
is bounded by the number of indecomposable direct summands of A, or equivalently the number of isomorphism classes of simple A-modules. Hence, if A has m simple modules and
![]() $\mathsf {proj}\, A$
admits a right rejective chain, then the global dimension of A is at most
$\mathsf {proj}\, A$
admits a right rejective chain, then the global dimension of A is at most
![]() $2m-2$
by Proposition 2.5.
$2m-2$
by Proposition 2.5.
Total right rejective chains are closely related to right-strongly quasi-hereditary algebras which are a special class of quasi-hereditary algebras. We recall the definitions of quasi-hereditary algebras and right-strongly quasi-hereditary algebras (see [Reference Coulembier5, Reference Dlab and Ringel9] and [Reference Ringel18], for details). We call an idempotent ideal
![]() $A\varepsilon A$
a heredity ideal of A if
$A\varepsilon A$
a heredity ideal of A if
![]() $A \varepsilon A \in \mathsf {proj}\, A$
and
$A \varepsilon A \in \mathsf {proj}\, A$
and
![]() $\varepsilon A \varepsilon $
is semisimple.
$\varepsilon A \varepsilon $
is semisimple.
Definition 2.7 Let A be an artin algebra.
-
(1) ([Reference Coulembier5, Reference Dlab and Ringel9]) We call A a quasi-hereditary algebra if there exists a chain of idempotent ideals
(2.2)such that $$ \begin{align} A =A\varepsilon_{1} A> A\varepsilon_{2} A > \cdots > A \varepsilon_{n} A >A \varepsilon_{n+1} A=0 \end{align} $$
$$ \begin{align} A =A\varepsilon_{1} A> A\varepsilon_{2} A > \cdots > A \varepsilon_{n} A >A \varepsilon_{n+1} A=0 \end{align} $$
 $A \varepsilon _{i}A/A\varepsilon _{i+1}A $
is a heredity ideal of
$A \varepsilon _{i}A/A\varepsilon _{i+1}A $
is a heredity ideal of
 $A /A\varepsilon _{i+1}A$
for each
$A /A\varepsilon _{i+1}A$
for each
 $1 \le i \le n$
. In this case, (2.2) is called a heredity chain.
$1 \le i \le n$
. In this case, (2.2) is called a heredity chain.
-
(2) ([Reference Ringel18]) We call A a right-strongly quasi-hereditary algebra if there exists a chain of idempotent ideals
such that $$ \begin{align*} A=A\varepsilon_{1} A> A\varepsilon_{2} A > \cdots > A \varepsilon_{n} A >A \varepsilon_{n+1} A=0 \end{align*} $$
$$ \begin{align*} A=A\varepsilon_{1} A> A\varepsilon_{2} A > \cdots > A \varepsilon_{n} A >A \varepsilon_{n+1} A=0 \end{align*} $$
 $A\varepsilon _{i}A \in \mathsf {proj}\, A$
and
$A\varepsilon _{i}A \in \mathsf {proj}\, A$
and
 $\varepsilon _{i}A \varepsilon _{i}/ \varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i}$
is semisimple for each
$\varepsilon _{i}A \varepsilon _{i}/ \varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i}$
is semisimple for each
 $1 \le i \le n$
.
$1 \le i \le n$
.
Since
![]() $-\otimes _{A}A/A\varepsilon _{i+1}A$
preserves projective modules, right-strongly quasi-hereditary algebras are quasi-hereditary algebras. We give a characterization of right-strongly quasi-hereditary algebras by total right rejective chains.
$-\otimes _{A}A/A\varepsilon _{i+1}A$
preserves projective modules, right-strongly quasi-hereditary algebras are quasi-hereditary algebras. We give a characterization of right-strongly quasi-hereditary algebras by total right rejective chains.
Proposition 2.8 ([Reference Tsukamoto22, Theorem 3.22])
Let A be an artin algebra. Then A is a right-strongly quasi-hereditary algebra if and only if
![]() $\mathsf {proj}\, A$
admits a total right rejective chain.
$\mathsf {proj}\, A$
admits a total right rejective chain.
3 Main results
In this section, we give characterizations of right rejective chains and constructions of total right rejective chains. Moreover, using the constructions, we provide total right rejective chains for several classes of algebras.
3.1 Characterizations of right rejective chains
In this subsection, using neat algebras, we give characterizations of
![]() $\mathsf {proj}\, A$
admitting a right rejective chain.
$\mathsf {proj}\, A$
admitting a right rejective chain.
For an idempotent e of A,
![]() $S(e)$
stands for a semisimple A-module
$S(e)$
stands for a semisimple A-module
![]() $eA/eJ$
. Let
$eA/eJ$
. Let
![]() $P(e)$
denote a projective cover of
$P(e)$
denote a projective cover of
![]() $S(e)$
. In the following, we fix a complete set
$S(e)$
. In the following, we fix a complete set
![]() $(e_{1},e_{2},\ldots , e_{n})$
of primitive orthogonal idempotents of A. Then, we have a complete set
$(e_{1},e_{2},\ldots , e_{n})$
of primitive orthogonal idempotents of A. Then, we have a complete set
![]() $\{S(e_{i}) \mid 1 \le i \le n \}$
of representatives of isomorphism classes of simple A-modules. Let
$\{S(e_{i}) \mid 1 \le i \le n \}$
of representatives of isomorphism classes of simple A-modules. Let
![]() $\varepsilon _{i}:=e_{i} + \cdots +e_{n}$
for
$\varepsilon _{i}:=e_{i} + \cdots +e_{n}$
for
![]() $1 \le i \le n$
and
$1 \le i \le n$
and
![]() $\varepsilon _{n+1}:=0$
. We recall the definition of neat algebras (see [Reference Ágoston, Dlab and Wakamatsu1] for details). A typical example of a neat algebra is a quasi-hereditary algebra.
$\varepsilon _{n+1}:=0$
. We recall the definition of neat algebras (see [Reference Ágoston, Dlab and Wakamatsu1] for details). A typical example of a neat algebra is a quasi-hereditary algebra.
Definition 3.1 [Reference Ágoston, Dlab and Wakamatsu1]
Let A be an artin algebra.
-
(1) An idempotent e of A is called a neat idempotent if
 $\operatorname {Ext}\nolimits _{A}^{i}(S(e), S(e))=0$
holds for each
$\operatorname {Ext}\nolimits _{A}^{i}(S(e), S(e))=0$
holds for each
 $i \ge 1$
. We call
$i \ge 1$
. We call
 $(e_{1},e_{2},\ldots , e_{n})$
a neat sequence if
$(e_{1},e_{2},\ldots , e_{n})$
a neat sequence if
 $e_{i}$
is a neat idempotent of
$e_{i}$
is a neat idempotent of
 $\varepsilon _{i}A\varepsilon _{i}$
for each
$\varepsilon _{i}A\varepsilon _{i}$
for each
 $1 \le i \le n$
.
$1 \le i \le n$
. -
(2) An algebra A is called a neat algebra if there exists a neat sequence.
We give an upper bound of the global dimension of a neat algebra.
Proposition 3.2 ([Reference Ágoston, Dlab and Wakamatsu1, Proposition 2])
If A is a neat algebra with a neat sequence
![]() $(e_{1},e_{2},\ldots , e_{n})$
, then the global dimension of A is at most
$(e_{1},e_{2},\ldots , e_{n})$
, then the global dimension of A is at most
![]() $2^{n}-2$
.
$2^{n}-2$
.
We reformulate neat algebras in terms of a chain of strong idempotent ideals. Recall that an idempotent ideal
![]() $A \varepsilon A$
is called a strong idempotent ideal (or stratifying ideal) of A if
$A \varepsilon A$
is called a strong idempotent ideal (or stratifying ideal) of A if
![]() $\operatorname {Ext}\nolimits _{A/A\varepsilon A}^{j}(X, Y) \cong \operatorname {Ext}\nolimits _{A}^{j}(X, Y)$
holds for each
$\operatorname {Ext}\nolimits _{A/A\varepsilon A}^{j}(X, Y) \cong \operatorname {Ext}\nolimits _{A}^{j}(X, Y)$
holds for each
![]() $X, Y \in \mathsf {mod}\, (A/ A \varepsilon A)$
and
$X, Y \in \mathsf {mod}\, (A/ A \varepsilon A)$
and
![]() $j \ge 1$
(see [Reference Auslander, Platzeck and Todorov3] and [Reference Conde6] for details).
$j \ge 1$
(see [Reference Auslander, Platzeck and Todorov3] and [Reference Conde6] for details).
Proposition 3.3 Let A be an artin algebra. Then A is a neat algebra with a neat sequence
![]() $(e_{1},e_{2},\ldots , e_{n})$
if and only if a chain of idempotent ideals
$(e_{1},e_{2},\ldots , e_{n})$
if and only if a chain of idempotent ideals
satisfies that
![]() $\varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is a strong idempotent ideal of
$\varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is a strong idempotent ideal of
![]() $\varepsilon _{i}A\varepsilon _{i}$
and
$\varepsilon _{i}A\varepsilon _{i}$
and
![]() $\varepsilon _{i} A\varepsilon _{i}/ \varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is semisimple for each
$\varepsilon _{i} A\varepsilon _{i}/ \varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is semisimple for each
![]() $1 \le i \le n$
. In this case, we call (3.1) a neat chain.
$1 \le i \le n$
. In this case, we call (3.1) a neat chain.
Proof. Let e be an idempotent of A and
![]() $\varepsilon :=1 -e$
. It suffices to show that e is a neat idempotent of A if and only if
$\varepsilon :=1 -e$
. It suffices to show that e is a neat idempotent of A if and only if
![]() $A\varepsilon A$
is a strong idempotent ideal and
$A\varepsilon A$
is a strong idempotent ideal and
![]() $A/A\varepsilon A$
is semisimple. Indeed, one can apply this claim to each subalgebra
$A/A\varepsilon A$
is semisimple. Indeed, one can apply this claim to each subalgebra
![]() $\varepsilon _{i}A \varepsilon _{i}$
. By [Reference Ágoston, Dlab and Wakamatsu1, Proposition 1.1], e is a neat idempotent of A if and only if it satisfies that (a) the multiplication map:
$\varepsilon _{i}A \varepsilon _{i}$
. By [Reference Ágoston, Dlab and Wakamatsu1, Proposition 1.1], e is a neat idempotent of A if and only if it satisfies that (a) the multiplication map:
![]() $A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A \to A \varepsilon A$
is an isomorphism, (b)
$A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A \to A \varepsilon A$
is an isomorphism, (b)
![]() $\operatorname {Tor}\nolimits _{j}^{\varepsilon A \varepsilon }(A \varepsilon , \varepsilon A)=0$
for each
$\operatorname {Tor}\nolimits _{j}^{\varepsilon A \varepsilon }(A \varepsilon , \varepsilon A)=0$
for each
![]() $j \ge 1$
and (c)
$j \ge 1$
and (c)
![]() $e A \varepsilon A e=eJe$
. Moreover, by [Reference Conde6, Remark 2.1.2(a)], the conditions (a) and (b) are equivalent to the condition that
$e A \varepsilon A e=eJe$
. Moreover, by [Reference Conde6, Remark 2.1.2(a)], the conditions (a) and (b) are equivalent to the condition that
![]() $A \varepsilon A$
is a strong idempotent ideal of A. Thus we show that the condition (c) holds if and only if
$A \varepsilon A$
is a strong idempotent ideal of A. Thus we show that the condition (c) holds if and only if
![]() $A/A \varepsilon A$
is semisimple. The “only if” part holds since
$A/A \varepsilon A$
is semisimple. The “only if” part holds since
![]() $A/ A\varepsilon A \cong eAe / eA \varepsilon A e = eAe/ J(eAe)$
. We show the “if” part. By
$A/ A\varepsilon A \cong eAe / eA \varepsilon A e = eAe/ J(eAe)$
. We show the “if” part. By
![]() $\varepsilon =1-e$
, we obtain that
$\varepsilon =1-e$
, we obtain that
![]() $eA\varepsilon A e \subseteq eJe$
. Since
$eA\varepsilon A e \subseteq eJe$
. Since
![]() $A/ A \varepsilon A $
is semisimple, so is
$A/ A \varepsilon A $
is semisimple, so is
![]() $eAe/e A \varepsilon A e$
. Thus
$eAe/e A \varepsilon A e$
. Thus
![]() $0=J(eAe/eA\varepsilon Ae) =J(eAe)/eA\varepsilon Ae$
, and hence the assertion holds.▪
$0=J(eAe/eA\varepsilon Ae) =J(eAe)/eA\varepsilon Ae$
, and hence the assertion holds.▪
By Proposition 3.3, we reprove the following result.
Corollary 3.4 ([Reference Ágoston, Dlab and Wakamatsu1, Corollary in
 $\S$
0])
$\S$
0])
Any quasi-hereditary algebra is a neat algebra.
Proof. We assume that A is a quasi-hereditary algebra. Then there exists a heredity chain
We show that this chain is a neat chain. By definition,
![]() $\varepsilon _{i} A\varepsilon _{i}/ \varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is semisimple. Thus it suffices from Proposition 3.3 to prove that
$\varepsilon _{i} A\varepsilon _{i}/ \varepsilon _{i} A \varepsilon _{i+1} A \varepsilon _{i}$
is semisimple. Thus it suffices from Proposition 3.3 to prove that
![]() $\varepsilon _{i}A \varepsilon _{i+1}A \varepsilon _{i}$
is a strong idempotent ideal of
$\varepsilon _{i}A \varepsilon _{i+1}A \varepsilon _{i}$
is a strong idempotent ideal of
![]() $\varepsilon _{i}A \varepsilon _{i}$
for each
$\varepsilon _{i}A \varepsilon _{i}$
for each
![]() $1 \le i\le n$
. By
$1 \le i\le n$
. By
![]() $A \varepsilon _{i}A/A\varepsilon _{i+1}A \in \mathsf {proj}\, (A/ A \varepsilon _{i+1}A)$
, it follows from [Reference Auslander, Platzeck and Todorov3, Proposition 5.2] that
$A \varepsilon _{i}A/A\varepsilon _{i+1}A \in \mathsf {proj}\, (A/ A \varepsilon _{i+1}A)$
, it follows from [Reference Auslander, Platzeck and Todorov3, Proposition 5.2] that
![]() $A \varepsilon _{i}A/A\varepsilon _{i+1}A$
is a strong idempotent ideal of
$A \varepsilon _{i}A/A\varepsilon _{i+1}A$
is a strong idempotent ideal of
![]() $A/A\varepsilon _{i+1}A$
. Since
$A/A\varepsilon _{i+1}A$
. Since
we obtain that
![]() $\operatorname {Ext}\nolimits _{A/A \varepsilon _{i}A}^{j}(X, Y) \cong \operatorname {Ext}\nolimits _{A/A\varepsilon _{i+1}A}^{j}(X, Y)$
for each
$\operatorname {Ext}\nolimits _{A/A \varepsilon _{i}A}^{j}(X, Y) \cong \operatorname {Ext}\nolimits _{A/A\varepsilon _{i+1}A}^{j}(X, Y)$
for each
![]() $X, Y \in \mathsf {mod}\, (A/A \varepsilon _{i}A)$
and
$X, Y \in \mathsf {mod}\, (A/A \varepsilon _{i}A)$
and
![]() $j \ge 1$
. Thus,
$j \ge 1$
. Thus,
![]() $A \varepsilon _{i}A$
is inductively a strong idempotent ideal of A for each
$A \varepsilon _{i}A$
is inductively a strong idempotent ideal of A for each
![]() $2 \le i\le n$
. Since
$2 \le i\le n$
. Since
![]() $A \varepsilon _{i+1}A$
is a strong idempotent ideal of A, it follows from [Reference Auslander, Platzeck and Todorov3, Theorem 2.1] that
$A \varepsilon _{i+1}A$
is a strong idempotent ideal of A, it follows from [Reference Auslander, Platzeck and Todorov3, Theorem 2.1] that
![]() $\varepsilon _{i}A \varepsilon _{i+1}A \varepsilon _{i}$
is also a strong idempotent ideal of
$\varepsilon _{i}A \varepsilon _{i+1}A \varepsilon _{i}$
is also a strong idempotent ideal of
![]() $\varepsilon _{i}A \varepsilon _{i}$
. Hence the assertion holds.▪
$\varepsilon _{i}A \varepsilon _{i}$
. Hence the assertion holds.▪
We give characterizations for
![]() $\mathsf {proj}\, A$
to admit a right rejective chain.
$\mathsf {proj}\, A$
to admit a right rejective chain.
Theorem 3.5 Let A be an artin algebra. Then the following statements are equivalent.
-
(1) The following chain is a right rejective chain.
 $$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
$$ \begin{align*} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align*} $$
-
(2) A is a neat algebra with a neat sequence
 $(e_{1}, e_{2}, \ldots , e_{n})$
and the following chain is a coreflective chain. (3.2)
$(e_{1}, e_{2}, \ldots , e_{n})$
and the following chain is a coreflective chain. (3.2) $$ \begin{align} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align} $$
$$ \begin{align} \mathsf{proj}\, A \supset \mathsf{add}\, \varepsilon_{2} A \supset \cdots \supset \mathsf{add}\, \varepsilon_{n} A \supset 0. \end{align} $$
-
(3) For each
 $1 \le i \le n$
,
$1 \le i \le n$
,
 $\operatorname {pd}\nolimits _{\varepsilon _{i} A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
holds.
$\operatorname {pd}\nolimits _{\varepsilon _{i} A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
holds.
Proof. By an equivalence
![]() $\operatorname {Hom}\nolimits _{A}(\varepsilon _{i}A, -) : \mathsf {add}\, \varepsilon _{i}A \xrightarrow {\sim } \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
, we obtain that
$\operatorname {Hom}\nolimits _{A}(\varepsilon _{i}A, -) : \mathsf {add}\, \varepsilon _{i}A \xrightarrow {\sim } \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
, we obtain that
![]() $\mathsf {add}\, \varepsilon _{i+1}A$
is a cosemisimple right rejective (respectively, coreflective) subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A$
is a cosemisimple right rejective (respectively, coreflective) subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
if and only if
$\mathsf {add}\, \varepsilon _{i}A$
if and only if
![]() $\mathsf {add}\, \varepsilon _{i+1}A\varepsilon _{i}$
is a cosemisimple right rejective (respectively, coreflective) subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A\varepsilon _{i}$
is a cosemisimple right rejective (respectively, coreflective) subcategory of
![]() $\mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
.
$\mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
.
(1)
![]() $\Leftrightarrow $
(3): We consider an exact sequence in
$\Leftrightarrow $
(3): We consider an exact sequence in
![]() $\mathsf {mod}\, \varepsilon _{i}A\varepsilon _{i}$
$\mathsf {mod}\, \varepsilon _{i}A\varepsilon _{i}$
If
![]() $\mathsf {add}\, \varepsilon _{i+1} A$
is a cosemisimple right rejective subcategory of
$\mathsf {add}\, \varepsilon _{i+1} A$
is a cosemisimple right rejective subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
, then
$\mathsf {add}\, \varepsilon _{i}A$
, then
![]() $e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{i+1} A\varepsilon _{i}$
by Proposition 2.3(3). Thus
$e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{i+1} A\varepsilon _{i}$
by Proposition 2.3(3). Thus
![]() $\operatorname {pd}\nolimits _{\varepsilon _{i}A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
. Conversely, we assume that
$\operatorname {pd}\nolimits _{\varepsilon _{i}A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
. Conversely, we assume that
![]() $\operatorname {pd}\nolimits _{\varepsilon _{i}A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
. Then
$\operatorname {pd}\nolimits _{\varepsilon _{i}A\varepsilon _{i}} S(e_{i})\varepsilon _{i} \le 1$
. Then
![]() $e_{i}J\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
. Since
$e_{i}J\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
. Since
![]() $e_{i}A\varepsilon _{i}$
is not a direct summand of
$e_{i}A\varepsilon _{i}$
is not a direct summand of
![]() $e_{i}J\varepsilon _{i}$
, we have
$e_{i}J\varepsilon _{i}$
, we have
![]() $e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{i+1} A\varepsilon _{i}$
. Hence
$e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{i+1} A\varepsilon _{i}$
. Hence
![]() $\mathsf {add}\, \varepsilon _{i+1} A$
is a cosemisimple right rejective subcategory of
$\mathsf {add}\, \varepsilon _{i+1} A$
is a cosemisimple right rejective subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
by Proposition 2.3(3). Thus the assertion holds.
$\mathsf {add}\, \varepsilon _{i}A$
by Proposition 2.3(3). Thus the assertion holds.
(1)
![]() $\Rightarrow{}$
(2): Since right rejective chains are coreflective chains, it suffices to show that the chain
$\Rightarrow{}$
(2): Since right rejective chains are coreflective chains, it suffices to show that the chain
![]() $A>A \varepsilon _{2}A > \cdots > A \varepsilon _{n}A >0$
is a neat chain by Proposition 3.3. Due to our assumption,
$A>A \varepsilon _{2}A > \cdots > A \varepsilon _{n}A >0$
is a neat chain by Proposition 3.3. Due to our assumption,
![]() $\mathsf {add}\, \varepsilon _{i+1}A$
is a right rejective subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A$
is a right rejective subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
. By Proposition 2.3(2), we obtain that
$\mathsf {add}\, \varepsilon _{i}A$
. By Proposition 2.3(2), we obtain that
![]() $\varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
for each
$\varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A\varepsilon _{i}$
for each
![]() ${1 \le i \le n}$
. Thus
${1 \le i \le n}$
. Thus
![]() $\varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i}$
is a strong idempotent ideal of
$\varepsilon _{i} A\varepsilon _{i+1}A \varepsilon _{i}$
is a strong idempotent ideal of
![]() $\varepsilon _{i}A\varepsilon _{i}$
by [Reference Auslander, Platzeck and Todorov3, Proposition 5.2]. Let
$\varepsilon _{i}A\varepsilon _{i}$
by [Reference Auslander, Platzeck and Todorov3, Proposition 5.2]. Let
![]() $\mathcal {C}:=\mathsf {add}\, \varepsilon _{i}A/ [\mathsf {add}\, \varepsilon _{i+1}A]$
. Then
$\mathcal {C}:=\mathsf {add}\, \varepsilon _{i}A/ [\mathsf {add}\, \varepsilon _{i+1}A]$
. Then
![]() $\mathcal {J}_{\mathcal {C}}=0$
holds by cosemisimplicity. Since
$\mathcal {J}_{\mathcal {C}}=0$
holds by cosemisimplicity. Since
![]() $J(\varepsilon _{i}A \varepsilon _{i}/ \varepsilon _{i}A \varepsilon _{i+1} A \varepsilon _{i})=J(\operatorname {End}\nolimits _{\mathcal {C}}(\varepsilon _{i}A)) = \mathcal {J}_{\mathcal {C}}(\varepsilon _{i}A, \varepsilon _{i}A)=0$
, we have the assertion.
$J(\varepsilon _{i}A \varepsilon _{i}/ \varepsilon _{i}A \varepsilon _{i+1} A \varepsilon _{i})=J(\operatorname {End}\nolimits _{\mathcal {C}}(\varepsilon _{i}A)) = \mathcal {J}_{\mathcal {C}}(\varepsilon _{i}A, \varepsilon _{i}A)=0$
, we have the assertion.
(2)
![]() $\Rightarrow{}$
(1): Since (3.2) is a coreflective chain,
$\Rightarrow{}$
(1): Since (3.2) is a coreflective chain,
![]() $\mathsf {add}\, \varepsilon _{i+1}A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A$
is a cosemisimple subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
. Hence, it is enough to show that
$\mathsf {add}\, \varepsilon _{i}A$
. Hence, it is enough to show that
![]() $\mathsf {add}\, \varepsilon _{i+1}A$
is a right rejective subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A$
is a right rejective subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
for each
$\mathsf {add}\, \varepsilon _{i}A$
for each
![]() $1 \le i \le n-1$
. By Proposition 2.3(2), we prove that
$1 \le i \le n-1$
. By Proposition 2.3(2), we prove that
![]() $\varepsilon _{i}A \varepsilon _{i+1}A\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
. Since A is a neat algebra with a neat sequence
$\varepsilon _{i}A \varepsilon _{i+1}A\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
. Since A is a neat algebra with a neat sequence
![]() $(e_{1}, e_{2}, \ldots , e_{n})$
, it follows from Proposition 3.3 that
$(e_{1}, e_{2}, \ldots , e_{n})$
, it follows from Proposition 3.3 that
![]() $\varepsilon _{i}A\varepsilon _{i+1}A\varepsilon _{i}$
is a strong idempotent ideal of
$\varepsilon _{i}A\varepsilon _{i+1}A\varepsilon _{i}$
is a strong idempotent ideal of
![]() $\varepsilon _{i}A\varepsilon _{i}$
. Due to our assumption,
$\varepsilon _{i}A\varepsilon _{i}$
. Due to our assumption,
![]() $\mathsf {add}\, \varepsilon _{i+1}A$
is a coreflective subcategory of
$\mathsf {add}\, \varepsilon _{i+1}A$
is a coreflective subcategory of
![]() $\mathsf {add}\, \varepsilon _{i}A$
. Thus,
$\mathsf {add}\, \varepsilon _{i}A$
. Thus,
![]() $\varepsilon _{i}A \varepsilon _{i+1} \in \mathsf {proj}\, \varepsilon _{i+1}A \varepsilon _{i+1}$
by Proposition 2.3(1). Since
$\varepsilon _{i}A \varepsilon _{i+1} \in \mathsf {proj}\, \varepsilon _{i+1}A \varepsilon _{i+1}$
by Proposition 2.3(1). Since
![]() $\varepsilon _{i}A\varepsilon _{i+1}A\varepsilon _{i}$
is a strong idempotent ideal of
$\varepsilon _{i}A\varepsilon _{i+1}A\varepsilon _{i}$
is a strong idempotent ideal of
![]() $\varepsilon _{i}A\varepsilon _{i}$
and
$\varepsilon _{i}A\varepsilon _{i}$
and
![]() $\varepsilon _{i}A \varepsilon _{i+1} \in \mathsf {proj}\, \varepsilon _{i+1}A\varepsilon _{i+1}$
, it follows from [Reference Auslander, Platzeck and Todorov3, Corollary 3.8(b), Proposition 5.2] that
$\varepsilon _{i}A \varepsilon _{i+1} \in \mathsf {proj}\, \varepsilon _{i+1}A\varepsilon _{i+1}$
, it follows from [Reference Auslander, Platzeck and Todorov3, Corollary 3.8(b), Proposition 5.2] that
![]() $\varepsilon _{i}A \varepsilon _{i+1}A\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
. Thus the proof is complete.▪
$\varepsilon _{i}A \varepsilon _{i+1}A\varepsilon _{i} \in \mathsf {proj}\, \varepsilon _{i}A \varepsilon _{i}$
. Thus the proof is complete.▪
We give an example of a right rejective chain using Theorem 3.5.
Example 3.6 Let A be the algebra defined by the quiver

with relations
![]() $\alpha \beta \gamma \alpha $
and
$\alpha \beta \gamma \alpha $
and
![]() $\gamma \alpha \beta $
. Then we can check that
$\gamma \alpha \beta $
. Then we can check that
![]() ${\operatorname {pd}\nolimits _{A} S(e_{1})=1}$
,
${\operatorname {pd}\nolimits _{A} S(e_{1})=1}$
,
![]() $\operatorname {pd}\nolimits _{\varepsilon _{2}A\varepsilon _{2}} S(e_{2})\varepsilon _{2}=1$
and
$\operatorname {pd}\nolimits _{\varepsilon _{2}A\varepsilon _{2}} S(e_{2})\varepsilon _{2}=1$
and
![]() $\operatorname {pd}\nolimits _{\varepsilon _{3}A\varepsilon _{3}} S(e_{3})\varepsilon _{3}=0$
. Thus
$\operatorname {pd}\nolimits _{\varepsilon _{3}A\varepsilon _{3}} S(e_{3})\varepsilon _{3}=0$
. Thus
![]() $\mathsf {proj}\, A \supset \mathsf {add}\, (e_{2}+e_{3})A \supset \mathsf {add}\, e_{3} A \supset 0$
is a right rejective chain by Theorem 3.5. However, this is not a total right rejective chain since
$\mathsf {proj}\, A \supset \mathsf {add}\, (e_{2}+e_{3})A \supset \mathsf {add}\, e_{3} A \supset 0$
is a right rejective chain by Theorem 3.5. However, this is not a total right rejective chain since
![]() $Ae_{3}A \cong P(e_{3})^{\oplus 2} \oplus P(e_{3})/P(e_{3})J^{2} \not \in \mathsf {proj}\, A$
.
$Ae_{3}A \cong P(e_{3})^{\oplus 2} \oplus P(e_{3})/P(e_{3})J^{2} \not \in \mathsf {proj}\, A$
.
In the rest of this subsection, we give constructions of total right rejective chains using Theorem 3.5. We need the following two lemmas.
Lemma 3.7 Let e and
![]() $\varepsilon $
be idempotents of A such that
$\varepsilon $
be idempotents of A such that
![]() $\mathsf {add}\, eA \subset \mathsf {add}\, \varepsilon A$
. If
$\mathsf {add}\, eA \subset \mathsf {add}\, \varepsilon A$
. If
![]() $\varphi :Y \to X$
is a right
$\varphi :Y \to X$
is a right
![]() $\mathsf {add}\, eA \varepsilon $
-approximation of
$\mathsf {add}\, eA \varepsilon $
-approximation of
![]() $X \in \mathsf {proj}\, \varepsilon A \varepsilon $
, then
$X \in \mathsf {proj}\, \varepsilon A \varepsilon $
, then
![]() $\varphi \otimes _{\varepsilon A \varepsilon }\varepsilon A: Y\otimes _{\varepsilon A \varepsilon }\varepsilon A \to X\otimes _{\varepsilon A \varepsilon }\varepsilon A$
is a right
$\varphi \otimes _{\varepsilon A \varepsilon }\varepsilon A: Y\otimes _{\varepsilon A \varepsilon }\varepsilon A \to X\otimes _{\varepsilon A \varepsilon }\varepsilon A$
is a right
![]() $\mathsf {add}\, eA$
-approximation of
$\mathsf {add}\, eA$
-approximation of
![]() $X \otimes _{\varepsilon A\varepsilon }\varepsilon A$
.
$X \otimes _{\varepsilon A\varepsilon }\varepsilon A$
.
Proof. Let
![]() $f \in \operatorname {Hom}\nolimits _{A}(eA, X \otimes _{\varepsilon A \varepsilon } \varepsilon A)$
. Then
$f \in \operatorname {Hom}\nolimits _{A}(eA, X \otimes _{\varepsilon A \varepsilon } \varepsilon A)$
. Then
![]() $f \otimes _{A}A\varepsilon : eA \otimes _{A}A\varepsilon \to X \otimes _{\varepsilon A \varepsilon } \varepsilon A\otimes _{A}A \varepsilon $
. Since
$f \otimes _{A}A\varepsilon : eA \otimes _{A}A\varepsilon \to X \otimes _{\varepsilon A \varepsilon } \varepsilon A\otimes _{A}A \varepsilon $
. Since
![]() $\varphi $
is a right
$\varphi $
is a right
![]() $\mathsf {add}\, eA\varepsilon $
-approximation, there exists
$\mathsf {add}\, eA\varepsilon $
-approximation, there exists
![]() $\varphi ' : eA \otimes _{A} A \varepsilon \to Y$
such that
$\varphi ' : eA \otimes _{A} A \varepsilon \to Y$
such that
![]() $\alpha (f \otimes _{A} A \varepsilon ) = \varphi \varphi '$
, where
$\alpha (f \otimes _{A} A \varepsilon ) = \varphi \varphi '$
, where
![]() $\alpha : X \otimes _{\varepsilon A \varepsilon } \varepsilon A \otimes _{A} A\varepsilon \to X$
is an isomorphism. Let
$\alpha : X \otimes _{\varepsilon A \varepsilon } \varepsilon A \otimes _{A} A\varepsilon \to X$
is an isomorphism. Let
![]() $\beta : eA \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A \to eA$
be an isomorphism via
$\beta : eA \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A \to eA$
be an isomorphism via
![]() $ea \otimes b\varepsilon \otimes \varepsilon c \mapsto eab \varepsilon c$
. Then
$ea \otimes b\varepsilon \otimes \varepsilon c \mapsto eab \varepsilon c$
. Then
![]() $(\alpha \otimes _{\varepsilon A \varepsilon } \varepsilon A) (f \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A)= f \beta $
holds. Since
$(\alpha \otimes _{\varepsilon A \varepsilon } \varepsilon A) (f \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A)= f \beta $
holds. Since
![]() $(\varphi \otimes _{\varepsilon A \varepsilon } \varepsilon A) (\varphi ' \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=(\varphi \varphi ' \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=(\alpha \otimes _{\varepsilon A \varepsilon } \varepsilon A ) (f \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=f$
, we have the assertion.▪
$(\varphi \otimes _{\varepsilon A \varepsilon } \varepsilon A) (\varphi ' \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=(\varphi \varphi ' \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=(\alpha \otimes _{\varepsilon A \varepsilon } \varepsilon A ) (f \otimes _{A} A \varepsilon \otimes _{\varepsilon A \varepsilon } \varepsilon A) \beta ^{-1}=f$
, we have the assertion.▪
Lemma 3.8 Let
![]() $\varepsilon $
be an idempotent of A such that
$\varepsilon $
be an idempotent of A such that
![]() $\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
![]() $\mathsf {proj}\, A$
. If
$\mathsf {proj}\, A$
. If
![]() $\varphi : P \to Q$
is a monomorphism in
$\varphi : P \to Q$
is a monomorphism in
![]() $\mathsf {add}\, \varepsilon A$
, then
$\mathsf {add}\, \varepsilon A$
, then
![]() $\operatorname {Ker}\nolimits \varphi \in \mathsf {mod}\, (A/A \varepsilon A)$
.
$\operatorname {Ker}\nolimits \varphi \in \mathsf {mod}\, (A/A \varepsilon A)$
.
Proof. Let
![]() $\varphi : P \to Q$
be a monomorphism in
$\varphi : P \to Q$
be a monomorphism in
![]() $\mathsf {add}\, \varepsilon A$
. We show that
$\mathsf {add}\, \varepsilon A$
. We show that
![]() $\operatorname {Hom}\nolimits _{A}(\varepsilon A,\operatorname {Ker}\nolimits \varphi )=0$
. Let
$\operatorname {Hom}\nolimits _{A}(\varepsilon A,\operatorname {Ker}\nolimits \varphi )=0$
. Let
![]() $\psi \in \operatorname {Hom}\nolimits _{A}(\varepsilon A, \operatorname {Ker}\nolimits \varphi )$
. Then, we have a composition map
$\psi \in \operatorname {Hom}\nolimits _{A}(\varepsilon A, \operatorname {Ker}\nolimits \varphi )$
. Then, we have a composition map
such that
![]() $\varphi i \psi =0$
holds. Since
$\varphi i \psi =0$
holds. Since
![]() $\varphi : P \to Q$
is a monomorphism in
$\varphi : P \to Q$
is a monomorphism in
![]() $\mathsf {add}\, \varepsilon A$
, we have
$\mathsf {add}\, \varepsilon A$
, we have
![]() ${i \psi =0}$
. Hence
${i \psi =0}$
. Hence
![]() $\psi =0$
holds.▪
$\psi =0$
holds.▪
Now, we give constructions of total right rejective chains.
Theorem 3.9 Let A be an artin algebra and
a chain of subcategories. Then the chain (3.3) is a total right rejective chain if one of the following two conditions is satisfied.
-
(1) For each
 $1 \le i \le n$
,
$1 \le i \le n$
,
 $e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
and
$e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
and
 $A \varepsilon _{n}A \in \mathsf {proj}\, A$
hold.
$A \varepsilon _{n}A \in \mathsf {proj}\, A$
hold. -
(2) Assume that there exists
 $1 \le j \le n-1$
such that If
$1 \le j \le n-1$
such that If $$ \begin{align*} \operatorname{pd}\nolimits_{\varepsilon_{i}A \varepsilon_{i}} S(e_{i})\varepsilon_{i}= \begin{cases} 1&1 \le i \le j\\ 0&j+1 \le i \le n. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{pd}\nolimits_{\varepsilon_{i}A \varepsilon_{i}} S(e_{i})\varepsilon_{i}= \begin{cases} 1&1 \le i \le j\\ 0&j+1 \le i \le n. \end{cases} \end{align*} $$
 $\varphi : P \to Q$
is a monomorphism in
$\varphi : P \to Q$
is a monomorphism in
 $\mathsf {add}\, \varepsilon _{i+1}A\varepsilon _{i}$
, then
$\mathsf {add}\, \varepsilon _{i+1}A\varepsilon _{i}$
, then
 $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, \varepsilon _{i} A \varepsilon _{i}$
for all
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, \varepsilon _{i} A \varepsilon _{i}$
for all
 $1 \le i \le n-1$
.
$1 \le i \le n-1$
.
Proof. First, we assume (1). Then
![]() $e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
implies that
$e_{i}J\varepsilon _{i} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
implies that
![]() $\operatorname {pd}\nolimits _{\varepsilon _{i}A \varepsilon _{i}} S(e_{i})\varepsilon _{i} \leq 1$
holds. Thus, by Theorem 3.5, (3.3) is a right rejective chain. Since
$\operatorname {pd}\nolimits _{\varepsilon _{i}A \varepsilon _{i}} S(e_{i})\varepsilon _{i} \leq 1$
holds. Thus, by Theorem 3.5, (3.3) is a right rejective chain. Since
![]() $\varphi _{j}: e_{j}J \varepsilon _{j} \to e_{j}A \varepsilon _{j}$
is a right
$\varphi _{j}: e_{j}J \varepsilon _{j} \to e_{j}A \varepsilon _{j}$
is a right
![]() $\mathsf {add}\, \varepsilon _{j+1}A \varepsilon _{j}$
-approximation by Proposition 2.3(3), it follows from Lemma 3.7 that a composition map of
$\mathsf {add}\, \varepsilon _{j+1}A \varepsilon _{j}$
-approximation by Proposition 2.3(3), it follows from Lemma 3.7 that a composition map of
![]() $\varphi _{j} \otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A: e_{j}J \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A \to e_{j}A \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A$
and an isomorphism
$\varphi _{j} \otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A: e_{j}J \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A \to e_{j}A \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A$
and an isomorphism
![]() $e_{j}A \varepsilon _{j} \otimes _{\varepsilon _{j}A \varepsilon _{j}}\varepsilon _{j}A \to e_{j}A$
is a right
$e_{j}A \varepsilon _{j} \otimes _{\varepsilon _{j}A \varepsilon _{j}}\varepsilon _{j}A \to e_{j}A$
is a right
![]() $\mathsf {add}\, \varepsilon _{j+1}A$
-approximation of
$\mathsf {add}\, \varepsilon _{j+1}A$
-approximation of
![]() $e_{j}A$
. By
$e_{j}A$
. By
![]() $e_{j}J\varepsilon _{j} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{j}$
, we obtain that
$e_{j}J\varepsilon _{j} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{j}$
, we obtain that
![]() $e_{j}J \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A \in \mathsf {add}\, \varepsilon _{n}A$
. Take a minimal right
$e_{j}J \varepsilon _{j}\otimes _{\varepsilon _{j}A \varepsilon _{j}} \varepsilon _{j}A \in \mathsf {add}\, \varepsilon _{n}A$
. Take a minimal right
![]() $\mathsf {add}\, \varepsilon _{j+1}A$
-approximation
$\mathsf {add}\, \varepsilon _{j+1}A$
-approximation
![]() $\varphi ^{\prime }_{j}: P' \to e_{j}A$
of
$\varphi ^{\prime }_{j}: P' \to e_{j}A$
of
![]() $e_{j}A$
. Then
$e_{j}A$
. Then
![]() $P' \in \mathsf {add}\, \varepsilon _{n}A$
. On the other hand, we have that
$P' \in \mathsf {add}\, \varepsilon _{n}A$
. On the other hand, we have that
![]() $\varepsilon _{n} J \varepsilon _{n} =0$
since
$\varepsilon _{n} J \varepsilon _{n} =0$
since
![]() $\varepsilon _{n} J \varepsilon _{n} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{n}$
and
$\varepsilon _{n} J \varepsilon _{n} \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{n}$
and
![]() $\varepsilon _{n} A \varepsilon _{n}$
is an indecomposable
$\varepsilon _{n} A \varepsilon _{n}$
is an indecomposable
![]() $\varepsilon _{n} A \varepsilon _{n}$
-module. Thus, we obtain that
$\varepsilon _{n} A \varepsilon _{n}$
-module. Thus, we obtain that
![]() $A\varepsilon _{n}A$
is a heredity ideal of A since
$A\varepsilon _{n}A$
is a heredity ideal of A since
![]() $A \varepsilon _{n}A \in \mathsf {proj}\, A$
. By [Reference Burgess and Fuller4, Lemma 1.7],
$A \varepsilon _{n}A \in \mathsf {proj}\, A$
. By [Reference Burgess and Fuller4, Lemma 1.7],
![]() $\varphi ^{\prime }_{j}$
is a monomorphism, and hence the assertion holds.
$\varphi ^{\prime }_{j}$
is a monomorphism, and hence the assertion holds.
Next, we assume (2). We show that (3.3) is a total right rejective chain by induction on n. If
![]() $n=1$
, then this is clear. Let
$n=1$
, then this is clear. Let
![]() $n \ge 2$
. If
$n \ge 2$
. If
![]() $j=1$
, then
$j=1$
, then
![]() $\varepsilon _{2}A\varepsilon _{2}$
satisfies (1). Thus, we obtain a total right rejective chain of
$\varepsilon _{2}A\varepsilon _{2}$
satisfies (1). Thus, we obtain a total right rejective chain of
![]() $\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
. If
$\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
. If
![]() $j>1$
, then we also have a total right rejective chain of
$j>1$
, then we also have a total right rejective chain of
![]() $\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
by induction hypothesis. Since
$\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
by induction hypothesis. Since
![]() $\operatorname {pd}\nolimits S(e_{1})=1$
, it follows from Proposition 2.3(3) that
$\operatorname {pd}\nolimits S(e_{1})=1$
, it follows from Proposition 2.3(3) that
![]() $\mathsf {add}\, \varepsilon _{2}A$
is a cosemisimple right rejective subcategory of
$\mathsf {add}\, \varepsilon _{2}A$
is a cosemisimple right rejective subcategory of
![]() $\mathsf {proj}\, A$
. Since an equivalence
$\mathsf {proj}\, A$
. Since an equivalence
![]() $\mathsf {add}\, \varepsilon _{i}A \varepsilon _{2} \simeq \mathsf {add}\, \varepsilon _{i}A$
holds for each
$\mathsf {add}\, \varepsilon _{i}A \varepsilon _{2} \simeq \mathsf {add}\, \varepsilon _{i}A$
holds for each
![]() $2 \le i \le n$
, the chain of subcategories
$2 \le i \le n$
, the chain of subcategories
satisfies that
![]() $\mathsf {add}\, \varepsilon _{2}A$
is a cosemisimple right rejective subcategory of
$\mathsf {add}\, \varepsilon _{2}A$
is a cosemisimple right rejective subcategory of
![]() $\mathsf {proj}\, A$
and
$\mathsf {proj}\, A$
and
![]() $\mathsf {add}\, \varepsilon _{2} A \supset \cdots \supset \mathsf {add}\, \varepsilon _{n} A \supset 0$
is a total right rejective chain. Thus, each minimal right
$\mathsf {add}\, \varepsilon _{2} A \supset \cdots \supset \mathsf {add}\, \varepsilon _{n} A \supset 0$
is a total right rejective chain. Thus, each minimal right
![]() $\mathsf {add}\, \varepsilon _{i}A$
-approximation
$\mathsf {add}\, \varepsilon _{i}A$
-approximation
![]() $\varphi : P \to Q$
of
$\varphi : P \to Q$
of
![]() $Q \in \mathsf {add}\, \varepsilon _{2}A$
is a monomorphism in
$Q \in \mathsf {add}\, \varepsilon _{2}A$
is a monomorphism in
![]() $\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
. Since
$\mathsf {proj}\, \varepsilon _{2}A\varepsilon _{2}$
. Since
![]() $\mathsf {add}\, \varepsilon _{2} A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon _{2} A$
is a cosemisimple subcategory of
![]() $\mathsf {proj}\, A$
, there exists
$\mathsf {proj}\, A$
, there exists
![]() $l \ge 0$
such that
$l \ge 0$
such that
![]() $\operatorname {Ker}\nolimits \varphi \cong S(e_{1})^{\oplus l}$
by Lemma 3.8. Suppose to the contrary that
$\operatorname {Ker}\nolimits \varphi \cong S(e_{1})^{\oplus l}$
by Lemma 3.8. Suppose to the contrary that
![]() $l>0$
. Due to our assumption, we have that
$l>0$
. Due to our assumption, we have that
![]() $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
. Thus
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
. Thus
![]() $S(e_{1}) \in \mathsf {proj}\, A$
, a contradiction. Hence, the proof is complete.▪
$S(e_{1}) \in \mathsf {proj}\, A$
, a contradiction. Hence, the proof is complete.▪
We give a naive sufficient condition for
![]() $\mathsf {proj}\, A$
to satisfy the condition (1) in Theorem 3.9.
$\mathsf {proj}\, A$
to satisfy the condition (1) in Theorem 3.9.
Corollary 3.10 Keep the notation in (3.3). If
![]() $\operatorname {pd}\nolimits _{\varepsilon _{i}A \varepsilon _{i}} S(e_{i}) \varepsilon _{i} =0$
holds for each
$\operatorname {pd}\nolimits _{\varepsilon _{i}A \varepsilon _{i}} S(e_{i}) \varepsilon _{i} =0$
holds for each
![]() $1\le i \le n$
, then A satisfies the condition (1) in Theorem
3.9
. In particular, the chain (3.3) is a total right rejective chain.
$1\le i \le n$
, then A satisfies the condition (1) in Theorem
3.9
. In particular, the chain (3.3) is a total right rejective chain.
Proof. Since
![]() $e_{i}J\varepsilon _{i} =0 \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
, it is enough to prove
$e_{i}J\varepsilon _{i} =0 \in \mathsf {add}\, \varepsilon _{n} A \varepsilon _{i}$
, it is enough to prove
![]() $A \varepsilon _{n} A \in \mathsf {proj}\, A$
. By
$A \varepsilon _{n} A \in \mathsf {proj}\, A$
. By
![]() $\operatorname {rad}\nolimits _{A}(\varepsilon _{i}A, e_{i}A) =e_{i}J\varepsilon _{i}=0$
, we obtain that
$\operatorname {rad}\nolimits _{A}(\varepsilon _{i}A, e_{i}A) =e_{i}J\varepsilon _{i}=0$
, we obtain that
![]() $\operatorname {Hom}\nolimits _{A}(P(e_{n}), e_{i}J)=0$
holds for each
$\operatorname {Hom}\nolimits _{A}(P(e_{n}), e_{i}J)=0$
holds for each
![]() $1 \le i \le n$
. Hence
$1 \le i \le n$
. Hence
![]() $A \varepsilon _{n}A =(e_{1} + \cdots +e_{n})A \varepsilon _{n}A =\varepsilon _{n}A \in \mathsf {add}\, \varepsilon _{n}A$
.▪
$A \varepsilon _{n}A =(e_{1} + \cdots +e_{n})A \varepsilon _{n}A =\varepsilon _{n}A \in \mathsf {add}\, \varepsilon _{n}A$
.▪
The following examples show that the conditions (1) and (2) in Theorem 3.9 are independent.
Example 3.11
-
(1) Let A be the algebra defined by the quiver
with relations
 $\alpha \beta $
and
$\alpha \beta $
and
 $\gamma \alpha $
. Then we can easily check that the complete set
$\gamma \alpha $
. Then we can easily check that the complete set
 $(e_{1}, e_{2}, e_{3})$
of primitive orthogonal idempotents satisfies the condition (1). However, it dose not satisfy the condition (2). Indeed,
$(e_{1}, e_{2}, e_{3})$
of primitive orthogonal idempotents satisfies the condition (1). However, it dose not satisfy the condition (2). Indeed,
 $\varphi : P(e_{2})\to P(e_{3})$
is a monomorphism in
$\varphi : P(e_{2})\to P(e_{3})$
is a monomorphism in
 $\mathsf {add}\, (e_{2}+e_{3})A$
and
$\mathsf {add}\, (e_{2}+e_{3})A$
and
 $\operatorname {Ker}\nolimits \varphi \not \in \mathsf {proj}\, A$
.
$\operatorname {Ker}\nolimits \varphi \not \in \mathsf {proj}\, A$
.
-
(2) Let A be the algebra defined by the quiver
with relations
 $\alpha \beta , \alpha \gamma , \delta \beta $
, and
$\alpha \beta , \alpha \gamma , \delta \beta $
, and
 $\delta \gamma $
. Then we can check that the complete set
$\delta \gamma $
. Then we can check that the complete set
 $(e_{1}, e_{2}, e_{3})$
of primitive orthogonal idempotents satisfies the condition (2). However, it dose not satisfy the condition (1) since
$(e_{1}, e_{2}, e_{3})$
of primitive orthogonal idempotents satisfies the condition (2). However, it dose not satisfy the condition (1) since
 $e_{1}J \cong P(e_{2}) \oplus P(e_{3}) \not \in \mathsf {add}\, \varepsilon _{3}A$
.
$e_{1}J \cong P(e_{2}) \oplus P(e_{3}) \not \in \mathsf {add}\, \varepsilon _{3}A$
.
3.2 Application
In this subsection, we construct total right rejective chains for three classes of algebras: Nakayama algebras with heredity ideals, locally hereditary algebras and algebras of global dimension at most two. Hence, these algebras are right-strongly quasi-hereditary algebras by Proposition 2.8.
The following theorem is a main result of this subsection.
Theorem 3.12 The following classes of algebras are right-strongly quasi-hereditary algebras.
-
(1) Nakayama algebras with heredity ideals.
-
(2) Locally hereditary algebras.
-
(3) Algebras of global dimension at most two.
It is known that algebras in Theorem 3.12 are quasi-hereditary by [Reference Burgess and Fuller4, Proposition 2.3], [Reference Burgess and Fuller4, Proposition 1.6] and [Reference Dlab and Ringel9, Theorem 2]. Hence, Theorem 3.12 is a refinement of their results. Moreover, Theorem 3.12(3) is proven in [Reference Tsukamoto22, Theorem 4.1].
In the rest of this subsection, we give a proof of Theorem 3.12. First, we construct right rejective chains and total right rejective chains for Nakayama algebras. We say that an algebra A is a Nakayama algebra if every indecomposable projective module and every indecomposable injective module are uniserial.
Proposition 3.13 Let A be a Nakayama algebra. Then the following statements hold.
-
(1) If A has a simple projective module or a heredity ideal, then
 $\mathsf {proj}\, A$
admits a total right rejective chain.
$\mathsf {proj}\, A$
admits a total right rejective chain. -
(2) If
 $\operatorname {gldim}\nolimits A<\infty $
, then
$\operatorname {gldim}\nolimits A<\infty $
, then
 $\mathsf {proj}\, A$
admits a right rejective chain.
$\mathsf {proj}\, A$
admits a right rejective chain.
Proof. Let A be a Nakayama algebra and
![]() $\varepsilon $
an idempotent of A. Note that
$\varepsilon $
an idempotent of A. Note that
![]() $\varepsilon A \varepsilon $
is also a Nakayama algebra since
$\varepsilon A \varepsilon $
is also a Nakayama algebra since
![]() $\operatorname {Hom}\nolimits _{A}(\varepsilon A, -)$
is an exact and dense functor. We may assume that A is connected and fix a complete set
$\operatorname {Hom}\nolimits _{A}(\varepsilon A, -)$
is an exact and dense functor. We may assume that A is connected and fix a complete set
![]() $(e_{1},e_{2},\ldots , e_{n})$
of primitive orthogonal idempotents. By [Reference Anderson and Fuller2, Theorem 32.4], we can order the primitive idempotents such that there are projective covers
$(e_{1},e_{2},\ldots , e_{n})$
of primitive orthogonal idempotents. By [Reference Anderson and Fuller2, Theorem 32.4], we can order the primitive idempotents such that there are projective covers
for each
![]() $1 \le i \le n-1$
and
$1 \le i \le n-1$
and
if
![]() $e_{1}J \neq 0$
.
$e_{1}J \neq 0$
.
(1) If A has a simple projective module
![]() $S(e)$
, then
$S(e)$
, then
![]() $(1-e)A(1-e)$
is also a Nakayama algebra with a simple projective module by [Reference Anderson and Fuller2, Theorem 32.4]. It follows from Corollary 3.10 that
$(1-e)A(1-e)$
is also a Nakayama algebra with a simple projective module by [Reference Anderson and Fuller2, Theorem 32.4]. It follows from Corollary 3.10 that
![]() $\mathsf {proj}\, A$
admits a total right rejective chain.
$\mathsf {proj}\, A$
admits a total right rejective chain.
We assume that there exists a heredity ideal of A. We prove that A satisfies the condition (1) in Theorem 3.9 by induction on n. If
![]() $n=1$
, then this is clear. Let
$n=1$
, then this is clear. Let
![]() $n \geq 2$
. We assume that A has no simple projective modules. Then
$n \geq 2$
. We assume that A has no simple projective modules. Then
![]() $e_{i}J \neq 0$
holds for each
$e_{i}J \neq 0$
holds for each
![]() $1 \le i \le n$
. By (3.4) and (3.5), we obtain an exact sequence
$1 \le i \le n$
. By (3.4) and (3.5), we obtain an exact sequence
![]() $e_{i} A \to e_{i+1}J \to 0$
for each
$e_{i} A \to e_{i+1}J \to 0$
for each
![]() $1 \le i \le n$
, where
$1 \le i \le n$
, where
![]() $e_{n+1}:=e_{1}$
. Since A has a heredity ideal, we may assume that
$e_{n+1}:=e_{1}$
. Since A has a heredity ideal, we may assume that
![]() $Ae_{n}A$
is a heredity ideal of A. Then we have a composition map
$Ae_{n}A$
is a heredity ideal of A. Then we have a composition map
![]() $e_{n}A \to e_{1} J \to e_{1}A$
. Since
$e_{n}A \to e_{1} J \to e_{1}A$
. Since
![]() $Ae_{n}A$
is a heredity ideal of A, this composition map is a monomorphism by [Reference Burgess and Fuller4, Lemma 1.7]. Thus, we obtain that
$Ae_{n}A$
is a heredity ideal of A, this composition map is a monomorphism by [Reference Burgess and Fuller4, Lemma 1.7]. Thus, we obtain that
![]() $e_{n}A \cong e_{1} J \neq 0$
, and hence
$e_{n}A \cong e_{1} J \neq 0$
, and hence
![]() $\operatorname {pd}\nolimits S(e_{1})=1$
. Let
$\operatorname {pd}\nolimits S(e_{1})=1$
. Let
![]() $\varepsilon _{2}:=1-e_{1}$
. Then
$\varepsilon _{2}:=1-e_{1}$
. Then
![]() $\varepsilon _{2} A e_{n} A\varepsilon _{2} \in \mathsf {proj}\, \varepsilon _{2} A \varepsilon _{2}$
and
$\varepsilon _{2} A e_{n} A\varepsilon _{2} \in \mathsf {proj}\, \varepsilon _{2} A \varepsilon _{2}$
and
![]() $e_{n} J(\varepsilon _{2} A\varepsilon _{2})e_{n}=e_{n}J(A)e_{n}=0$
hold. Thus,
$e_{n} J(\varepsilon _{2} A\varepsilon _{2})e_{n}=e_{n}J(A)e_{n}=0$
hold. Thus,
![]() $\varepsilon _{2} A\varepsilon _{2}$
is a Nakayama algebra with a heredity ideal
$\varepsilon _{2} A\varepsilon _{2}$
is a Nakayama algebra with a heredity ideal
![]() $\varepsilon _{2} A e_{n} A\varepsilon _{2}$
. By induction hypothesis,
$\varepsilon _{2} A e_{n} A\varepsilon _{2}$
. By induction hypothesis,
![]() $\varepsilon _{2} A \varepsilon _{2}$
satisfies the condition (1) in Theorem 3.9. Since
$\varepsilon _{2} A \varepsilon _{2}$
satisfies the condition (1) in Theorem 3.9. Since
![]() $A e_{n} A \in \mathsf {proj}\, A$
and
$A e_{n} A \in \mathsf {proj}\, A$
and
![]() $e_{1} J \in \mathsf {add}\, e_{n} A$
, we have the assertion.
$e_{1} J \in \mathsf {add}\, e_{n} A$
, we have the assertion.
(2) Let A be an algebra of finite global dimension. By (1), we assume that A has no simple projective modules. Take an indecomposable projective module
![]() $e_{i}A$
such that its Loewy length
$e_{i}A$
such that its Loewy length
![]() $LL(e_{i}A)$
is maximal. By (3.4) and (3.5), we have
$LL(e_{i}A)$
is maximal. By (3.4) and (3.5), we have
![]() $LL(e_{i-1}A)\ge LL(e_{i}A)-1$
. If
$LL(e_{i-1}A)\ge LL(e_{i}A)-1$
. If
![]() $LL(e_{i-1}A)=LL(e_{i}A)-1$
, then
$LL(e_{i-1}A)=LL(e_{i}A)-1$
, then
![]() $\operatorname {pd}\nolimits S(e_{i})=1$
. Thus, we assume that
$\operatorname {pd}\nolimits S(e_{i})=1$
. Thus, we assume that
![]() $LL(e_{i-1}A)>LL(e_{i}A)-1$
. Then
$LL(e_{i-1}A)>LL(e_{i}A)-1$
. Then
![]() $LL(e_{i-1}A)=LL(e_{i}A)$
by maximality of
$LL(e_{i-1}A)=LL(e_{i}A)$
by maximality of
![]() $LL(e_{i}A)$
. By
$LL(e_{i}A)$
. By
![]() $\operatorname {gldim}\nolimits A <\infty $
, A is non-self-injective. Therefore, we obtain a simple module with projective dimension exactly one by replacing
$\operatorname {gldim}\nolimits A <\infty $
, A is non-self-injective. Therefore, we obtain a simple module with projective dimension exactly one by replacing
![]() $e_{i}A$
with
$e_{i}A$
with
![]() $e_{i-1}A$
and repeating this argument. Let
$e_{i-1}A$
and repeating this argument. Let
![]() $S(e)$
be the simple module with projective dimension one. Since it follows from Proposition 2.3(2) that
$S(e)$
be the simple module with projective dimension one. Since it follows from Proposition 2.3(2) that
![]() $\operatorname {gldim}\nolimits (1-e)A(1-e) \le \operatorname {gldim}\nolimits A<\infty $
, we inductively obtain that A satisfies the condition (3) in Theorem 3.5. Hence,
$\operatorname {gldim}\nolimits (1-e)A(1-e) \le \operatorname {gldim}\nolimits A<\infty $
, we inductively obtain that A satisfies the condition (3) in Theorem 3.5. Hence,
![]() $\mathsf {proj}\, A$
admits a right rejective chain.▪
$\mathsf {proj}\, A$
admits a right rejective chain.▪
We give applications of Proposition 3.13. In [Reference Gustafson11, Theorem], it is shown that if A is a Nakayama algebra with n simple modules and
![]() $\operatorname {gldim}\nolimits A < \infty $
, then
$\operatorname {gldim}\nolimits A < \infty $
, then
![]() $\operatorname {gldim}\nolimits A \le 2n-2$
. We give another proof by Proposition 3.13. Moreover, we give a refinement of [Reference Burgess and Fuller4, Proposition 2.3].
$\operatorname {gldim}\nolimits A \le 2n-2$
. We give another proof by Proposition 3.13. Moreover, we give a refinement of [Reference Burgess and Fuller4, Proposition 2.3].
Corollary 3.14 Let A be a Nakayama algebra. Then the following statements hold.
-
(1) The following statements are equivalent.
-
(a)
 $\operatorname {gldim}\nolimits A <\infty $
.
$\operatorname {gldim}\nolimits A <\infty $
. -
(b) A is a neat algebra.
-
(c)
 $\mathsf {proj}\, A$
admits a right rejective chain.
$\mathsf {proj}\, A$
admits a right rejective chain.
In this case, if A has n simple modules, then
 $\operatorname {gldim}\nolimits A \le 2n-2$
.
$\operatorname {gldim}\nolimits A \le 2n-2$
. -
-
(2) The following statements are equivalent.
-
(a) A has a heredity ideal.
-
(b) A is a quasi-hereditary algebra.
-
(c) A is a right-strongly quasi-hereditary algebra.
-
Proof. (1) (c)
![]() $\Rightarrow{}$
(b) and (b)
$\Rightarrow{}$
(b) and (b)
![]() $\Rightarrow{}$
(a) follow from Theorem 3.5 and Proposition 3.2, respectively. (a)
$\Rightarrow{}$
(a) follow from Theorem 3.5 and Proposition 3.2, respectively. (a)
![]() $\Rightarrow{}$
(c) follows from Proposition 3.13(2). Moreover, if A has n simple modules, then
$\Rightarrow{}$
(c) follows from Proposition 3.13(2). Moreover, if A has n simple modules, then
![]() $\operatorname {gldim}\nolimits A \le 2n-2$
by Remark 2.6.
$\operatorname {gldim}\nolimits A \le 2n-2$
by Remark 2.6.
(2) (c)
![]() $\Rightarrow{}$
(b) and (b)
$\Rightarrow{}$
(b) and (b)
![]() $\Rightarrow{}$
(a) are clear. By Proposition 3.13(1), if A has a heredity ideal, then
$\Rightarrow{}$
(a) are clear. By Proposition 3.13(1), if A has a heredity ideal, then
![]() $\mathsf {proj}\, A$
has a total right rejective chain. Thus, (a)
$\mathsf {proj}\, A$
has a total right rejective chain. Thus, (a)
![]() $\Rightarrow{}$
(c) holds by Proposition 2.8.▪
$\Rightarrow{}$
(c) holds by Proposition 2.8.▪
In Corollary 3.14, (2)
![]() $\Rightarrow{}$
(1) clearly holds. However, the converse does not hold in general. Indeed, Example 3.6 satisfies the equivalent conditions in Corollary 3.14(1), but it does not satisfy the equivalence conditions in Corollary 3.14(2).
$\Rightarrow{}$
(1) clearly holds. However, the converse does not hold in general. Indeed, Example 3.6 satisfies the equivalent conditions in Corollary 3.14(1), but it does not satisfy the equivalence conditions in Corollary 3.14(2).
Next, we prove that locally hereditary algebras satisfy the conditions (1) and (2) in Theorem 3.9. An algebra A is called a locally hereditary algebra if each nonzero morphism between indecomposable projective A-modules is a monomorphism (see [Reference Martinez-Villa17] for details). We need the following lemma.
Lemma 3.15 Let A be a nonsemisimple locally hereditary algebra. Then the following statements hold.
-
(1) Let e be a primitive idempotent of A and
 $\varepsilon :=1-e$
. Assume that
$\varepsilon :=1-e$
. Assume that
 $\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
 $\mathsf {proj}\, A$
. If
$\mathsf {proj}\, A$
. If
 $\varphi : P \to Q$
is a monomorphism in
$\varphi : P \to Q$
is a monomorphism in
 $\mathsf {add}\, \varepsilon A$
, then
$\mathsf {add}\, \varepsilon A$
, then
 $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
.
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
. -
(2)
 $\operatorname {soc}\nolimits A \in \mathsf {proj}\, A$
holds. In particular, there exists a simple projective module.
$\operatorname {soc}\nolimits A \in \mathsf {proj}\, A$
holds. In particular, there exists a simple projective module. -
(3) There exists a simple module such that its projective dimension is exactly one.
Proof. (1) Let
![]() $\varphi : P \to Q$
be a monomorphism in
$\varphi : P \to Q$
be a monomorphism in
![]() $\mathsf {add}\, \varepsilon A$
. Since
$\mathsf {add}\, \varepsilon A$
. Since
![]() $\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
![]() $\mathsf {proj}\, A$
, there exists
$\mathsf {proj}\, A$
, there exists
![]() $l \ge 0$
such that
$l \ge 0$
such that
![]() $\operatorname {Ker}\nolimits \varphi \cong S(e)^{\oplus l}$
by Lemma 3.8. Thus
$\operatorname {Ker}\nolimits \varphi \cong S(e)^{\oplus l}$
by Lemma 3.8. Thus
![]() $\rho ^{\oplus l}: P(e)^{\oplus l} \to \operatorname {Ker}\nolimits \varphi $
is a projective cover of
$\rho ^{\oplus l}: P(e)^{\oplus l} \to \operatorname {Ker}\nolimits \varphi $
is a projective cover of
![]() $\operatorname {Ker}\nolimits \varphi $
, where
$\operatorname {Ker}\nolimits \varphi $
, where
![]() $\rho : P(e) \to S(e)$
is a projective cover of
$\rho : P(e) \to S(e)$
is a projective cover of
![]() $S(e)$
. On the other hand, there exists an indecomposable direct summand
$S(e)$
. On the other hand, there exists an indecomposable direct summand
![]() $P'$
of P such that
$P'$
of P such that
![]() $S(e)$
is a direct summand of
$S(e)$
is a direct summand of
![]() $\operatorname {soc}\nolimits P'$
. Let
$\operatorname {soc}\nolimits P'$
. Let
![]() $\iota : S(e) \to P'$
be the inclusion. Then a composition map
$\iota : S(e) \to P'$
be the inclusion. Then a composition map
![]() $\iota \rho : P(e) \to P'$
is a nonzero morphism between indecomposable projective modules. Since
$\iota \rho : P(e) \to P'$
is a nonzero morphism between indecomposable projective modules. Since
![]() $\iota \rho $
is a monomorphism,
$\iota \rho $
is a monomorphism,
![]() $\rho $
is an isomorphism. Thus
$\rho $
is an isomorphism. Thus
![]() $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
.
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
.
(2) Let
![]() $\operatorname {soc}\nolimits A =S(e_{i_{1}}) \oplus \cdots \oplus S(e_{i_{t}})$
, where
$\operatorname {soc}\nolimits A =S(e_{i_{1}}) \oplus \cdots \oplus S(e_{i_{t}})$
, where
![]() $S(e_{i_{j}})$
is a simple module. For each
$S(e_{i_{j}})$
is a simple module. For each
![]() $1 \le j \le t$
, there exists an indecomposable projective module
$1 \le j \le t$
, there exists an indecomposable projective module
![]() $P_{j}$
such that
$P_{j}$
such that
![]() $S(e_{i_{j}})$
is a direct summand of
$S(e_{i_{j}})$
is a direct summand of
![]() $\operatorname {soc}\nolimits P_{j}$
. Since a composition map of a projective cover
$\operatorname {soc}\nolimits P_{j}$
. Since a composition map of a projective cover
![]() $p : P(e_{i_{j}}) \to S(e_{i_{j}})$
and the inclusion
$p : P(e_{i_{j}}) \to S(e_{i_{j}})$
and the inclusion
![]() $S(e_{i_{j}}) \to P_{j}$
is a monomorphism, p is an isomorphism. Thus
$S(e_{i_{j}}) \to P_{j}$
is a monomorphism, p is an isomorphism. Thus
![]() $\operatorname {soc}\nolimits A \in \mathsf {proj}\, A$
.
$\operatorname {soc}\nolimits A \in \mathsf {proj}\, A$
.
(3) We show that there exists an indecomposable projective module P such that its Loewy length
![]() $LL (P)$
is two. If
$LL (P)$
is two. If
![]() $LL(A)=2$
, then this is clear. We assume that
$LL(A)=2$
, then this is clear. We assume that
![]() $LL (A)\ge 3$
. Let Q be an indecomposable projective module with
$LL (A)\ge 3$
. Let Q be an indecomposable projective module with
![]() $LL (Q)=:l \ge 3$
. Then
$LL (Q)=:l \ge 3$
. Then
![]() $QJ^{l-2}/QJ^{l-1}\cong S(e_{i_{1}}) \oplus \cdots \oplus S(e_{i_{s}}) \neq 0$
. Note that there exists
$QJ^{l-2}/QJ^{l-1}\cong S(e_{i_{1}}) \oplus \cdots \oplus S(e_{i_{s}}) \neq 0$
. Note that there exists
![]() $1 \le j \le s$
such that
$1 \le j \le s$
such that
![]() $S(e_{i_{j}}) \not \in \mathsf {proj}\, A$
. Thus,
$S(e_{i_{j}}) \not \in \mathsf {proj}\, A$
. Thus,
![]() $LL(P(e_{i_{j}})) \ge 2$
. Since a composition map of
$LL(P(e_{i_{j}})) \ge 2$
. Since a composition map of
![]() $P(e_{i_{j}}) \to QJ^{l-2}$
and
$P(e_{i_{j}}) \to QJ^{l-2}$
and
![]() $QJ^{l-2} \to Q$
is a monomorphism, so is
$QJ^{l-2} \to Q$
is a monomorphism, so is
![]() $P(e_{i_{j}}) \to QJ^{l-2}$
. Since
$P(e_{i_{j}}) \to QJ^{l-2}$
. Since
![]() $LL( P(e_{i_{j}}))\le 2$
,
$LL( P(e_{i_{j}}))\le 2$
,
![]() $P(e_{i_{j}})$
is a desired projective module. Thus, we obtain
$P(e_{i_{j}})$
is a desired projective module. Thus, we obtain
![]() $\operatorname {pd}\nolimits S(e_{i_{j}})=1$
since it follows from (2) that
$\operatorname {pd}\nolimits S(e_{i_{j}})=1$
since it follows from (2) that
![]() $\operatorname {soc}\nolimits P(e_{i_{j}}) \in \mathsf {proj}\, A$
.▪
$\operatorname {soc}\nolimits P(e_{i_{j}}) \in \mathsf {proj}\, A$
.▪
Now, we state the following proposition.
Proposition 3.16 Any locally hereditary algebra satisfies the conditions (1) and (2) in Theorem
3.9
. Namely, if A is a locally hereditary algebra, then
![]() $\mathsf {proj}\, A$
admits a total right rejective chain.
$\mathsf {proj}\, A$
admits a total right rejective chain.
Proof. Let A be a locally hereditary algebra. If A is semisimple, then it clearly satisfies the conditions (1) and (2) in Theorem 3.9. Thus, we assume that A is not semisimple. First, we show that A satisfies the condition (1). By Lemma 3.15(2), there exists a simple module
![]() $S(e)$
such that
$S(e)$
such that
![]() $\operatorname {pd}\nolimits S(e)=0$
. Let
$\operatorname {pd}\nolimits S(e)=0$
. Let
![]() $\varepsilon :=1-e$
. Then
$\varepsilon :=1-e$
. Then
![]() $\varepsilon A \varepsilon $
is also a locally hereditary algebra by an equivalence of categories
$\varepsilon A \varepsilon $
is also a locally hereditary algebra by an equivalence of categories
![]() $\mathsf {add}\, \varepsilon A \simeq \mathsf {proj}\, \varepsilon A\varepsilon $
. Due to Corollary 3.10, A inductively satisfies the condition (1) in Theorem 3.9.
$\mathsf {add}\, \varepsilon A \simeq \mathsf {proj}\, \varepsilon A\varepsilon $
. Due to Corollary 3.10, A inductively satisfies the condition (1) in Theorem 3.9.
Next, we show that A satisfies the condition (2). By Lemma 3.15(3), there exists a simple module
![]() $S(e)$
with
$S(e)$
with
![]() $\operatorname {pd}\nolimits S(e)=1$
. Let
$\operatorname {pd}\nolimits S(e)=1$
. Let
![]() $\varepsilon :=1-e$
. Then
$\varepsilon :=1-e$
. Then
![]() $\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
$\mathsf {add}\, \varepsilon A$
is a cosemisimple subcategory of
![]() $\mathsf {proj}\, A$
by Proposition 2.3(3). For each monomorphism
$\mathsf {proj}\, A$
by Proposition 2.3(3). For each monomorphism
![]() $\varphi : P\to Q$
in
$\varphi : P\to Q$
in
![]() $\mathsf {add}\, \varepsilon A$
, we obtain that
$\mathsf {add}\, \varepsilon A$
, we obtain that
![]() $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
by Lemma 3.15(1). Since
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
by Lemma 3.15(1). Since
![]() $\varepsilon A \varepsilon $
is also a locally hereditary algebra, A inductively satisfies the condition (2) in Theorem 3.9.▪
$\varepsilon A \varepsilon $
is also a locally hereditary algebra, A inductively satisfies the condition (2) in Theorem 3.9.▪
Finally, we show the following proposition. This proposition is proven in [Reference Iyama15, Theorem 3.6] and [Reference Tsukamoto22, Theorem 4.1]. In this paper, we give a proof using Theorem 3.9.
Proposition 3.17 If
![]() $\operatorname {gldim}\nolimits A \leq 2$
, then
$\operatorname {gldim}\nolimits A \leq 2$
, then
![]() $\mathsf {proj}\, A$
admits a total right rejective chain.
$\mathsf {proj}\, A$
admits a total right rejective chain.
Proof. If
![]() $\operatorname {gldim}\nolimits A \le 1$
, then A is a locally hereditary algebra. Thus, the assertion follows from Proposition 3.16. We assume that
$\operatorname {gldim}\nolimits A \le 1$
, then A is a locally hereditary algebra. Thus, the assertion follows from Proposition 3.16. We assume that
![]() $\operatorname {gldim}\nolimits A =2$
. Let S be an A-module such that its length
$\operatorname {gldim}\nolimits A =2$
. Let S be an A-module such that its length
![]() $\ell (S)$
is minimal among A-modules with the projective dimension one. We show that S is a simple module. Suppose to the contrary that S is not simple. Then there exists an exact sequence
$\ell (S)$
is minimal among A-modules with the projective dimension one. We show that S is a simple module. Suppose to the contrary that S is not simple. Then there exists an exact sequence
![]() $0 \to S' \to S \to S/S' \to 0$
such that
$0 \to S' \to S \to S/S' \to 0$
such that
![]() $S' \neq 0$
and
$S' \neq 0$
and
![]() $S/S' \neq 0$
. Since
$S/S' \neq 0$
. Since
![]() $\operatorname {pd}\nolimits S'\le \max \{\operatorname {pd}\nolimits S, \operatorname {pd}\nolimits S/S' -1\} = 1$
, it follows from the assumption on S that
$\operatorname {pd}\nolimits S'\le \max \{\operatorname {pd}\nolimits S, \operatorname {pd}\nolimits S/S' -1\} = 1$
, it follows from the assumption on S that
![]() $\operatorname {pd}\nolimits S'=0$
. Thus, we have
$\operatorname {pd}\nolimits S'=0$
. Thus, we have
![]() $\operatorname {pd}\nolimits S/S' \le \max \{\operatorname {pd}\nolimits S, \operatorname {pd}\nolimits S' +1\} = 1$
. By the assumption on S, we have
$\operatorname {pd}\nolimits S/S' \le \max \{\operatorname {pd}\nolimits S, \operatorname {pd}\nolimits S' +1\} = 1$
. By the assumption on S, we have
![]() $\operatorname {pd}\nolimits S/S'=0$
, a contradiction. Thus S is a simple module. We put
$\operatorname {pd}\nolimits S/S'=0$
, a contradiction. Thus S is a simple module. We put
![]() $S(e):=S$
and
$S(e):=S$
and
![]() $\varepsilon :=1-e$
. Then
$\varepsilon :=1-e$
. Then
![]() $\mathsf {add}\, \varepsilon A$
is a cosemisimple right rejective subcategory of
$\mathsf {add}\, \varepsilon A$
is a cosemisimple right rejective subcategory of
![]() $\mathsf {proj}\, A$
by Proposition 2.3(3). Let
$\mathsf {proj}\, A$
by Proposition 2.3(3). Let
![]() $\varphi : P \to Q$
be a monomorphism in
$\varphi : P \to Q$
be a monomorphism in
![]() $\mathsf {add}\, \varepsilon A$
. Then, we have an exact sequence in
$\mathsf {add}\, \varepsilon A$
. Then, we have an exact sequence in
![]() $\mathsf {mod}\, A$
.
$\mathsf {mod}\, A$
.
By
![]() $\operatorname {gldim}\nolimits A = 2$
, we have that
$\operatorname {gldim}\nolimits A = 2$
, we have that
![]() $\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
. Since
$\operatorname {Ker}\nolimits \varphi \in \mathsf {proj}\, A$
. Since
![]() $\operatorname {gldim}\nolimits \varepsilon A \varepsilon \le \operatorname {gldim}\nolimits A=2$
by Proposition 2.3(2), we inductively obtain that A satisfies the condition (2) in Theorem 3.9. Hence, we have the assertion.▪
$\operatorname {gldim}\nolimits \varepsilon A \varepsilon \le \operatorname {gldim}\nolimits A=2$
by Proposition 2.3(2), we inductively obtain that A satisfies the condition (2) in Theorem 3.9. Hence, we have the assertion.▪
Now we are ready to prove Theorem 3.12.
Acknowledgment
The author would like to express her deep gratitude to Takahide Adachi and Ryoichi Kase for stimulating discussions and helpful comments.