2.1 Flow configurations

We consider an incompressible turbulent channel flow with bulk velocity $u_{b}$ and wall velocity zero, in which an array of $N_{par}$ solid non-rotating spherical particles is moving with a constant streamwise velocity, $0.9u_{b}$ . The dimensions of the channel, $u_{b}$ , and the viscosity $\unicode[STIX]{x1D708}$ are the same as in the reference flow without particles. The unladen reference simulation is case S2 from Vreman & Kuerten (Reference Vreman and Kuerten2014), a high-resolution long-time simulation of an incompressible turbulent channel flow in a standard domain and at standard Reynolds number. For explanatory reasons, we also consider a laminar channel flow, which has lower bulk velocity and is modified by an array of particles with velocity zero.

Streamwise, normal and spanwise directions are denoted by $x_{1}$ , $x_{2}$ and $x_{3}$ respectively, while time is denoted by $t$ . The channel half-width $H$ is equal to 1, the friction velocity of the unladen turbulent flow, $u_{\unicode[STIX]{x1D70F},0}$ , is equal to 1, $\unicode[STIX]{x1D708}=1/180$ , so that $Re_{\unicode[STIX]{x1D70F},0}=u_{\unicode[STIX]{x1D70F},0}H/\unicode[STIX]{x1D708}=180$ . All results in this paper are non-dimensionalized using $H$ and $u_{\unicode[STIX]{x1D70F},0}$ , which implies that $\unicode[STIX]{x1D708}=1/180$ in each case. The distance to the nearest wall is indicated by $y$ . The superscript $+$ applied to a length indicates a division by $1/180$ , the thickness of the viscous sublayer in the unladen flow. Thus $y^{+}=180(1-|x_{2}|)$ in each case. The spatial domain is given by $\unicode[STIX]{x1D6FA}_{0}=[0,L_{1}]\times [-1,1]\times [0,L_{3}]$ . The flow is periodic in the $x_{1}$ and $x_{3}$ directions. In the turbulent flow cases, $L_{1}=4\unicode[STIX]{x03C0}$ , $L_{3}=4\unicode[STIX]{x03C0}/3$ and $u_{b}=15.66$ , while in the laminar flow case $L_{1}=4\unicode[STIX]{x03C0}/18$ , $L_{3}=4\unicode[STIX]{x03C0}/36$ and $u_{b}=3$ . The translative velocity of the particles is indicated by $\boldsymbol{u}^{p}$ . In this paper, all particles have the same fixed $\boldsymbol{u}^{p}$ and zero angular velocity.

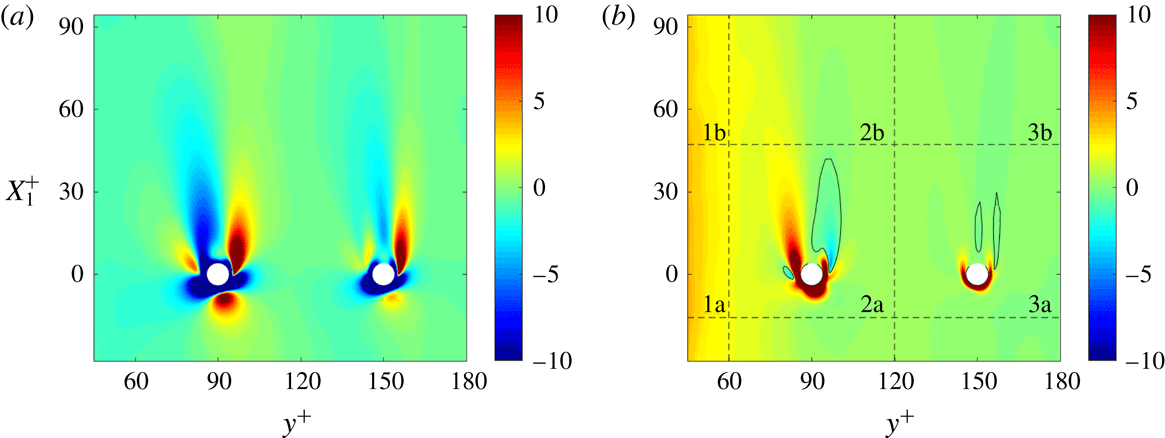
Figure 1. The structure of the particle array in three cross-sections of one-third of the flow domain in the streamwise direction ( $0\leqslant x_{1}\leqslant L_{1}/3$ ):  $x_{3}=\unicode[STIX]{x03C0}/36\approx 0.087$ , $x_{3}=3\unicode[STIX]{x03C0}/36\approx 0.262$ and $x_{2}=-1/2$ . The demarcation lines indicate the much smaller flow domain of the laminar case.

The array in the turbulent flow contains 1728 spherical particles of diameter $d_{p}=2/45$ ( $d_{p}^{+}=8$ ) and is sketched in figure 1 (only the first two rows (8 particles) of this array are used in the laminar flow). The particle radius is denoted by $r_{0}=d_{p}/2$ , and the overall particle volume fraction is 0.00075. The particle configuration originates from a nearly cubical pattern of $36\times 4\times 12$ particles with pitch size $\unicode[STIX]{x03C0}/9$ in the streamwise and spanwise directions and pitch size $1/3$ in the normal direction. This nearly cubical pattern is modified by shifting the odd rows in the spanwise direction by $-\unicode[STIX]{x03C0}/36$ and the even rows by $\unicode[STIX]{x03C0}/36$ , in order to reduce the effect of neighbouring particles on the streamwise oriented wake behind each particle. The $x_{2}$ coordinates of the particles are $\pm 1/6$ and $\pm 1/2$ . From a statistical point of view there are only two types of particles: the particles at $y^{+}=90$ and those at $y^{+}=150$ , also indicated by $p=1$ and $p=2$ , respectively. Thus for each type there are many statistically equivalent particle positions ( $1728/2$ ), which is an advantage for the computation of accurate statistics in the particle frame of reference. More numerical and physical reasons for this specific configuration will be given in § 2.4.

Table 1. A characterization of the unladen flow turbulence at the particle positions and a few particle Reynolds numbers based on unladen flow quantities.

Several unladen flow quantities and particle Reynolds numbers of the particles based on unladen flow velocities are specified in table 1 for the two distinct particle positions. The mean velocity, turbulence kinetic energy, turbulence dissipation rate and Kolmogorov length scale of the mean flow are denoted by $\overline{u}_{1,0}$ , $K_{0}$ , $\unicode[STIX]{x1D716}_{0}$ and $\unicode[STIX]{x1D702}_{0}$ , respectively. The particle Reynolds numbers due to the mean and fluctuating relative velocities are defined by $Re_{p,mean}=(\overline{u}_{1,0}-u_{1}^{p})d_{p}/\unicode[STIX]{x1D708}$ and $Re_{p,tur}=(2K_{0})^{1/2}d_{p}/\unicode[STIX]{x1D708}$ , respectively, where $\overline{u}_{1,0}$ and $K_{0}$ are the mean velocity and turbulence kinetic energy of the unladen flow. The total particle Reynolds number is defined by $R_{tot}=(Re_{p,mean}^{2}+Re_{p,tur}^{2})^{1/2}$ . For the laminar case, the (mean and total) particle Reynolds numbers are equal to 27 ( $p=1$ ) and 35 ( $p=2$ ). The corresponding relative velocities are obtained by dividing these Reynolds numbers by eight ( $d_{p}/\unicode[STIX]{x1D708}=8/u_{\unicode[STIX]{x1D70F},0}$ ).

2.2 Governing equations

The incompressible Navier–Stokes equations in Cartesian coordinates read

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{j}u_{j}=0, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}u_{i}=-\unicode[STIX]{x2202}_{j}(u_{i}u_{j})-\unicode[STIX]{x2202}_{j}q+\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{j}^{2}u_{i}+a_{i}. & \displaystyle\end{eqnarray}$$

The symbols $\unicode[STIX]{x2202}_{t}$ and $\unicode[STIX]{x2202}_{j}$ denote $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$ and $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{j}$ , respectively. Throughout the paper, the convention of summation over repeated indices in products is used, unless mentioned otherwise. The streamwise, wall-normal and spanwise Cartesian velocity components are denoted by $u_{1}$ , $u_{2}$ and $u_{3}$ , respectively. The symbol $q$ denotes the periodic part of the pressure divided by the fluid density. The streamwise component of the acceleration term $\boldsymbol{a}$ is equal to $(a_{1},0,0)$ , and $-a_{1}$ represents the non-periodic part of the streamwise component of the pressure gradient divided by the density. It only depends on time and is adjusted to maintain a constant $u_{b}$ , which is defined as the streamwise fluid velocity averaged over the fluid domain ( $\unicode[STIX]{x1D6FA}_{0}$ minus the volumes occupied by the particles). The boundary conditions imposed on the fluid velocity at solid surfaces are $\boldsymbol{u}=0$ at the channel walls ( $x_{2}=\pm 1$ ) and $\boldsymbol{u}=\boldsymbol{u}^{p}$ at the surfaces of the particles.

For use in later sections, we define the fluid stress tensor $\unicode[STIX]{x1D748}$ and strain rate $\unicode[STIX]{x1D64E}$ :

(2.3a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{ij}=-q\unicode[STIX]{x1D6FF}_{ij}+2\unicode[STIX]{x1D708}\unicode[STIX]{x1D61A}_{ij},\quad \unicode[STIX]{x1D61A}_{ij}={\textstyle \frac{1}{2}}(\unicode[STIX]{x2202}_{j}u_{i}+\unicode[STIX]{x2202}_{i}u_{j}). & & \displaystyle\end{eqnarray}$$

The force exerted by the fluid stress $\unicode[STIX]{x1D70E}_{ij}$ on a particle is defined by

(2.4) $$\begin{eqnarray}\displaystyle F_{i}^{p}=\int _{S_{p}}\unicode[STIX]{x1D70E}_{ij}n_{j}\,\text{d}S, & & \displaystyle\end{eqnarray}$$

where $S_{p}$ is the surface of the particle, and $\boldsymbol{n}$ is the normal vector pointing into the fluid. Note that $F_{i}^{p}$ does not include the contribution of the non-periodic part of the streamwise pressure gradient. The actual force exerted by the fluid on the particle is equal to $\unicode[STIX]{x1D70C}F_{i}^{p}+\unicode[STIX]{x1D70C}a_{i}\unicode[STIX]{x03C0}d_{p}^{3}/6$ .

For each particle, a spherical coordinate system is attached to the particle centre ( $\boldsymbol{x}^{p}$ ) such that

(2.5) $$\begin{eqnarray}\displaystyle \boldsymbol{x}-\boldsymbol{x}^{p}=\left[\begin{array}{@{}l@{}}r\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719}\\ r\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719}\\ r\cos \unicode[STIX]{x1D703}\end{array}\right], & & \displaystyle\end{eqnarray}$$

where $r$ is the radial coordinate, $\unicode[STIX]{x1D703}$ the polar angle and $\unicode[STIX]{x1D719}$ the azimuthal angle. Thus the polar axis is aligned to the spanwise direction of the channel. The spherical velocity components in the frame of the reference moving with the particle are denoted by $u_{r}$ , $u_{\unicode[STIX]{x1D703}}$ and $u_{\unicode[STIX]{x1D719}}$ .

2.3 Numerical method

We employ the solver NSpheres (Vreman Reference Vreman2017), an MPI-parallel body-fitted incompressible Navier–Stokes solver for flows with multiple moving spheres. Around each spherical particle, the Navier–Stokes equations in spherical coordinates are solved on a staggered spherical grid attached to the particle. The spherical grids are overset on a staggered Cartesian grid. The Navier–Stokes equations are discretized using second-order accurate central differencing in space with third-order interpolations from Cartesian to spherical grids and vice versa. In principle, the interpolation data structure and interpolation coefficients are updated each time step. However, in the present case we avoid this by using a Cartesian grid that formally moves with the same constant velocity as the particle array. Thus we use the Galilean invariant property of the Navier–Stokes equations, and solve $u_{1}-u_{1}^{p}$ instead of $u_{1}$ , while we impose $u_{1}-u_{1}^{p}=-u_{1}^{p}$ at the channel walls. In the post-processing, we obtain $u_{1}$ by adding $u_{1}^{p}$ to the solution for $u_{1}-u_{1}^{p}$ . The temporal discretization is explicit, except for the $\unicode[STIX]{x1D719}$ direction on the spherical grids. Since, due to the viscous time step restriction, the time step is proportional to the square of the grid size, the formally first-order temporal discretization error reduces with the same rate as the spatial discretization error if the grid is refined. The pressure Poisson equation is iteratively solved using the BICGstab method (van der Vorst Reference van der Vorst1992) and a tolerance $10^{-5}$ for the maximum norm of the residual. The augmented matrix method (Henshaw Reference Henshaw1994; Vreman Reference Vreman2016) is used to overcome the singularity due to the formally unspecified absolute level of the pressure.

We call this numerical method, which is fully described in Vreman (Reference Vreman2017), numerical method A. For validation purposes, we additionally consider a slightly modified method, numerical method B, which differs in three aspects from method A. First, for the convective terms, the forward Euler temporal discretization is replaced by the second-order Adams–Bashforth method. The latter scheme was also used in Vreman (Reference Vreman2016), and its implementation is straightforward for cases in which the spherical grids do not move with respect to the Cartesian grid. Second, the tolerance for the maximum residual error in the Poisson equation is reduced to $10^{-6}$ . Third, another variant of the augmented matrix method is used, in which the augmented variable is added to the system before the matrix is normalized by dividing each row by its diagonal element. Thus in the system after normalization, the coefficient of the augmented variable in each row is no longer equal to 1, but equal to the reciprocal of the diagonal element before normalization. The coefficients of the augmented variable influence how (inevitable) errors in the velocity divergence are distributed in space. In method A, the velocity divergence error in the cells touching the poles does not converge formally to zero in the limit of zero grid size and zero tolerance, while it does in method B. However, in practice the divergence error at the poles occurring if method A is used can be so small that the maximum error of the divergence seems to converge to zero upon grid refinement: see Vreman (Reference Vreman2017). Furthermore, finite errors restricted to the poles are not expected to deteriorate the convergence of quantities integrated over a finite surface or a volume, since the surface or volume of the region where the divergence has a small finite value converges to zero upon grid refinement.

Table 2. Overview of the particle-resolved simulations.

An overview of five particle-resolved simulations is shown in table 2. T stands for simulations of the turbulent flow and L for the simulation of the laminar flow. Case T1 is the main simulation, cases T2, T3 and T4 are introduced for validation purposes. The comparison in the next subsection will show that, for the present purposes, method A is sufficiently accurate (compared to method B), and that the discretization errors and statistical errors in the results of T1 are sufficiently small.

We proceed to specify the main simulation, T1, which was performed using numerical method A. The number of grid cells of the Cartesian grid is $1152\times 216\times 384$ . The uniform grid sizes in the streamwise and spanwise directions, $\unicode[STIX]{x0394}x_{1}^{+}$ and $\unicode[STIX]{x0394}x_{3}^{+}$ , are both equal to 1.96. The grid is stretched in the $x_{2}$ direction, such that $\unicode[STIX]{x0394}x_{2}^{+}$ linearly increases from approximately $0.5$ to $2$ for $0\leqslant y^{+}\leqslant 60$ over $48$ points and is equal to $2$ for $60\leqslant y^{+}\leqslant 180$ . Each spherical grid cell has $30\times 48\times 96$ cells and extends from $r_{0}^{+}=4$ to $r_{b}^{+}\approx 7r_{0}^{+}=28$ . The radius of the spherical holes in the Cartesian domain is set to $r_{a}=(r_{0}+r_{b})/2$ . The radial stretching function specified in Vreman (Reference Vreman2016) is used, such that the radial grid size $\unicode[STIX]{x0394}r^{+}$ is equal to $0.26$ at $r_{0}$ and $2$ at $r_{b}$ . The smallest radial grid size is called $h_{1}$ . The total number of grid cells ( $N_{tot}$ ) is approximately 343 million; 72 % of them belong to the spherical domains.

The total number of grid points in case T1 is not small, but if it had been simulated with one of the more common Cartesian methods for particle-resolved simulations, which typically use uniform cubical grids, 35 billion points would have been required to reach the same small mesh size near the particles. Thus, the overset grid method allows the number of grid points to be reduced by a factor of 100 for this volume fraction. However, the method needs an iterative method to solve the Poisson equation, and this consumes more than 90 % of the CPU time.

Simulation T1 was run on 432 processors. Each processor computed the flow on one block of the Cartesian grid and on the spherical grids of four particles. Thus the Cartesian domain was decomposed into 432 blocks, 36 blocks in the $x_{1}$ direction and 12 in the $x_{3}$ direction. The time step was equal to $3.5\times 10^{-5}$ , slightly lower than the viscous stability restriction. The velocity field was initialized using the parabolic profile and the perturbation specified in Vreman (Reference Vreman2014). This initial condition leads to a fast transition, such that the flow becomes turbulent well before $t=t_{1}=5$ . The end time of the simulation was $t=t_{2}=25$ . Complete spatial fields were stored each 0.07 time unit. The statistical averaging was performed by a post-processing program, which used all stored fields between $t=t_{1}$ and $t=t_{2}$ . The total simulation time of case T1 was approximately 0.7 million CPU hours, corresponding to approximately 10 weeks in wall clock time. In this case, the number of time steps was approximately 0.7 million, and on average the number of iterations of the Poisson solver was approximately 170 per time step.

The other cases do not require much additional explanation. All settings are the same as in case 1, except those mentioned in this paragraph. In case T2, each spherical and Cartesian grid is coarser by a factor of 2 in each direction, while the time step is four times larger. The end time could be taken larger in this case, because the simulation required much less CPU time than T1, due to the coarser grid and larger time step. Case T3 is based on the same run as case T1, but $t_{2}$ is smaller, such that the length of the time interval for statistical averaging ( $t_{2}-t_{1}$ ) is more than twice as small as in case 1. Case T4 is the same as case T3, except that method B has been used instead of method A. Furthermore, simulation T4 was started from the field at $t_{1}=5$ of case T3. Finally, L1 is the laminar case. The resolution and method in L1 are the same as in T1, but the initial condition of L1 is a parabolic profile without perturbations, and the domain is much smaller, such that precisely the first two rows (eight particles) of the particle array fit into the domain. The averaged quantities were computed from the last field. We verified that near the end of the simulation the solution was steady in the entire domain. Thus the last field of L1 does indeed correspond to a steady fully laminar flow.

2.4 Relevance of flow case

To limit the computing time without compromising on the near-wall resolution of the DNS, we did not place particles in the near-wall region, where the Cartesian grid is non-uniform. In the outer layer of the spherical grid around the particle $\unicode[STIX]{x0394}r^{+}\approx 2$ , $(r\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{+}\approx 2$ and the maximum $((r\sin \unicode[STIX]{x1D703})\unicode[STIX]{x0394}\unicode[STIX]{x1D719})^{+}\approx 2$ , thus if we placed a particle at for example $y^{+}=30$ there would be locations close to the wall where the wall-normal grid size would effectively be two wall units, while in the present case the wall-normal grid size at the wall is four times smaller (0.5 wall unit). Sufficient near-wall resolution would be obtained if the number of radial grid cells were increased by a factor of 4 in each direction or, alternatively, if the radial extent of the spherical grids were reduced in combination with a uniform Cartesian grid of grid size half a wall unit. The better option would probably be the latter one, but it would still imply a huge increase of the required CPU time (by approximately a factor of 15). Another option would be to use an immersed boundary method in combination with a fast Poisson solver on a uniform cubical grid of 5 billion cells (16 grid cells per particle diameter). However, this would probably reduce the accuracy of the numerical solution near the particles, for two reasons. First, the grid size near the particle surfaces would be twice as large as in the present T1. Second, for at least one common type of immersed boundary method, Stein, Guy & Thomases (Reference Stein, Guy and Thomases2017) have shown that the pressure and viscous stresses close to the surface of the particle do not converge pointwise to the correct values, although the particle force (which is not a pointwise quantity) does converge to the correct value.

Despite the restrictions imposed on location and velocity of the particles, the present flow case is interesting and new. The local 3-D inhomogeneity of the flow makes it a rich problem. It is a well-controlled configuration that facilitates an accurate computation of local statistics, even at locations very close to the particles. The particles are exposed to turbulence produced by real physical mechanisms in near-wall turbulence. As such this is a step forward compared with studies of particles in decaying isotropic turbulence (since the turbulence then depends on the initial condition) or forced isotropic turbulence (since the turbulence then depends on the forcing term). Our aim is to investigate how turbulent flow responds to particles, how energy exchange mechanisms are modified, in particular in the vicinity the particles. Even without particles in the near-wall region, the turbulence appears to be significantly modified in the entire flow (including the near-wall region). We wish to understand how a small volume fraction of particles can significantly influence the amount and character of the turbulence everywhere in the flow. We will find that the present PR-DNS confirms important findings and explanations hitherto only based on interpretations from experiments and point-particle simulations of vertical channel flows with freely moving particles (see §§ 3.1 and 6). Thus we expect that our conclusions regarding the 3-D statistical structure of the turbulence around the particles in the present configuration are somehow also valid for solid particles falling through turbulence, for example air turbulence generated by vertical channel walls (Kulick et al. Reference Kulick, Fessler and Eaton1994) or acoustic woofers at the edges of the set-up (Hwang & Eaton Reference Hwang and Eaton2006; Tanaka & Eaton Reference Tanaka and Eaton2010).

As mentioned in the Introduction, the present case of particles with a fixed velocity is a relevant limit for particles at high Stokes numbers caused by high inertia. In the copper particle experiments performed by Kulick et al. (Reference Kulick, Fessler and Eaton1994), the particle–fluid mass density ratio was approximately 7000, while the modified Stokes response time was roughly 8000 times larger than the wall unit time scale ( $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}/u_{\unicode[STIX]{x1D70F}}$ ). We could have allowed free rotation of the particles in our case, but this would have been inconsistent with the previous argument that our case is relevant for cases with very high particle inertia. Furthermore, Zeng, Balachandar & Fischer (Reference Zeng, Balachandar and Fischer2005) found that the effect of sphere rotation on drag and lift forces is small, and it is the mean particle drag force that will be shown to cause most of the turbulence attenuation and anisotropy increase observed in the present case (§ 6).

For finite inertia and free motion of particles in the normal direction, the particles would be subjected to a larger range of the particle Reynolds number than in the present case. A larger range of the particle Reynolds number is interesting from a physical point of view, but higher particle Reynolds numbers lead to thinner no-slip particle boundary layers and the need for a smaller grid size near the particles. It is remarked that also in the present case the instantaneous particle Reynolds number is not constant. Based on the unladen flow velocity the (95 % probability) range of the instantaneous Reynolds number is from 0 to 50.

2.5 Definition of fixed-frame averaged quantities

The basic averaging operator in the fixed frame is denoted by an overbar and defined as the average over time and the two periodic directions ( $x_{1}$ and $x_{3}$ ). Thus the fixed-frame statistics are functions of the wall-normal direction only ( $0\leqslant y^{+}\leqslant 180$ ; for each $y^{+}$ , the statistics are based on the two planes $x_{2}=\pm (1-y^{+}/180)$ ). The corresponding fluid phase-weighted averaging operator applied to an arbitrary function $f$ on $\unicode[STIX]{x1D6FA}_{0}$ is defined by

(2.6) $$\begin{eqnarray}\displaystyle \langle f\rangle _{}=\overline{\unicode[STIX]{x1D712}f}/\overline{\unicode[STIX]{x1D712}}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D712}$ is the commonly known indicator function of the fluid, equal to $1$ in the fluid and $0$ inside the solid phase. In addition, we define $\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D712}}$ , which is the volume fraction of the fluid after averaging, and we define the Reynolds stress tensor by

(2.7) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D619}_{ij}=\langle u_{i}u_{j}\rangle _{}-\langle u_{i}\rangle _{}\langle u_{j}\rangle _{}. & & \displaystyle\end{eqnarray}$$

Often, the basic averaging operator is a Reynolds (or statistical) averaging operator, which can be the present overbar, averaging over time only (Ishii Reference Ishii1975) or averaging over an ensemble of realizations (Zhang & Prosperetti Reference Zhang and Prosperetti1997; Drew & Passman Reference Drew and Passman1999). These operators satisfy the Reynolds conditions, which are (i) linearity, (ii) invariance of constant fields, (iii) commutation with derivatives and (iv) $\overline{\overline{f_{1}}f_{2}}=\overline{f_{1}}\;\overline{f_{2}}$ for arbitrary functions $f_{1}$ and $f_{2}$ on $\unicode[STIX]{x1D6FA}_{0}$ . It is stressed that the fluid phase-weighted averaging operator does not inherit condition (iii), the commutation condition. Furthermore, if a local volume averaging operator is used, for example the operator defined by Anderson & Jackson (Reference Anderson and Jackson1967) and Jackson (Reference Jackson1997), an operator very similar to the Gaussian spatial convolution filter later used in large-eddy simulation, then the fourth Reynolds condition is not satisfied. However, for the fluid phase-weighted average, condition (iv) is satisfied, and this implies $\unicode[STIX]{x1D619}_{ij}=\langle u_{i}^{\prime }u_{j}^{\prime }\rangle _{}$ , where $u_{i}^{\prime }=u_{i}-\langle u_{i}\rangle$ is the velocity fluctuation.

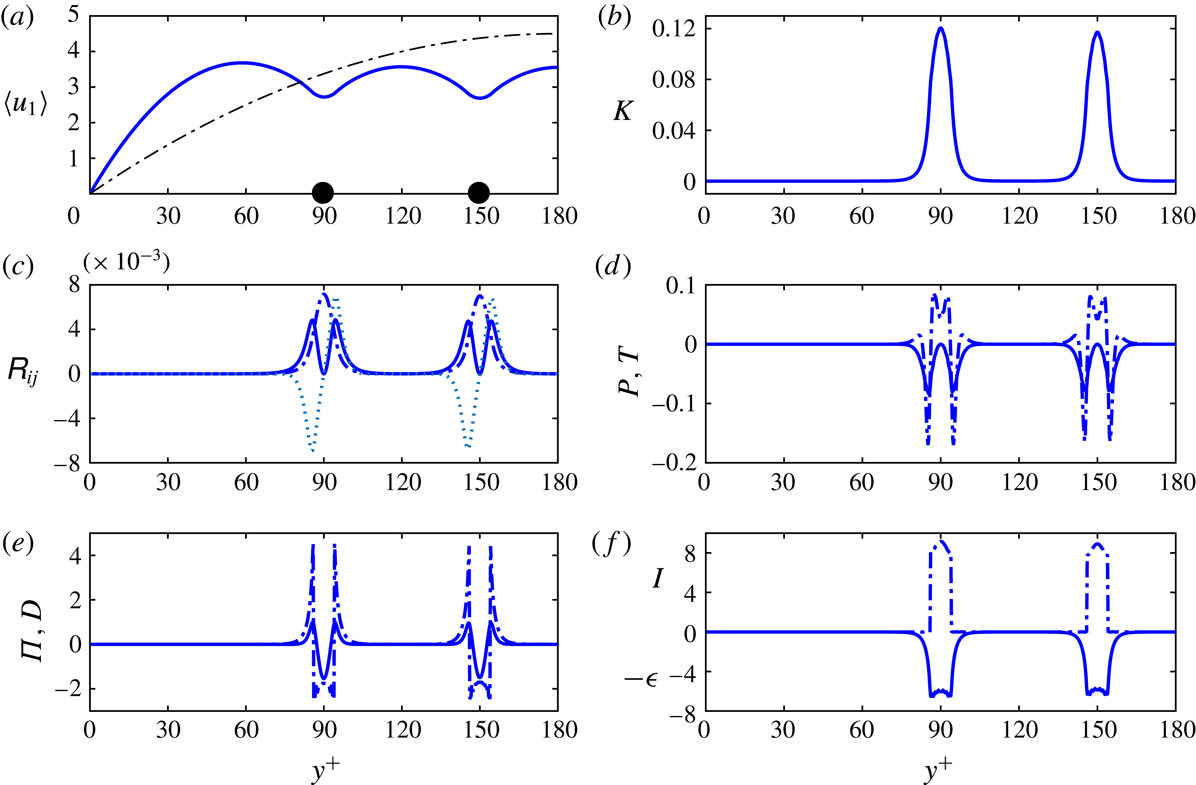
The fixed-frame turbulence kinetic energy (TKE) is defined by $K_{}=(\unicode[STIX]{x1D619}_{ii})/2$ . For Reynolds averaging, the TKE equation for incompressible two-phase flow has been derived by Kataoka & Serizawa (Reference Kataoka and Serizawa1989). Using PR-DNS of turbulent bubbly channel flow, Santarelli et al. (Reference Santarelli, Roussel and Fröhlich2016) evaluated all the distinct terms in this equation, which are together called the TKE budget. In fact, the TKE equation can also be derived in an alternative way, without assuming incompressibility and Reynolds condition (iv); see appendix A. The resulting form is not only more general (also applicable in the context of local spatial averaging), but it also resembles how the actual evaluation of terms is performed in this paper, namely without explicit usage of any fluctuation field. We drop the phase subscript used in appendix A, and write the equations for the fluid phase in an incompressible particle-laden flow as

(2.8) $$\begin{eqnarray}\displaystyle 0=-\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\langle u_{j}\rangle _{}), & & \displaystyle\end{eqnarray}$$

(2.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D6FC}\langle u_{i}\rangle _{}) & = & \displaystyle -\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\langle u_{i}\rangle _{}\langle u_{j}\rangle _{})-\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D619}_{ij})\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D6FC}\langle q\rangle _{})+\unicode[STIX]{x2202}_{j}(2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{})-\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}\langle a_{i}\rangle _{},\end{eqnarray}$$

(2.10) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}K_{}=C_{}+P_{}+T_{}+\unicode[STIX]{x1D6F1}_{}+D_{}-\unicode[STIX]{x1D716}_{}+I+B_{}. & & \displaystyle\end{eqnarray}$$

The last equation is the TKE equation, in which $C_{}$ is convective transport, $P_{}$ turbulence production, $T_{}$ turbulent transport, $\unicode[STIX]{x1D6F1}_{}$ pressure diffusion, $D_{}$ viscous diffusion, $\unicode[STIX]{x1D716}_{}$ turbulence dissipation, $I=I_{1}+I_{2}$ the interfacial term and $B_{}$ body-force production:

(2.11) $$\begin{eqnarray}\displaystyle & \displaystyle C_{}=-\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\langle u_{j}\rangle K), & \displaystyle\end{eqnarray}$$

(2.12) $$\begin{eqnarray}\displaystyle & \displaystyle P_{}=-\unicode[STIX]{x1D619}_{ij}\unicode[STIX]{x2202}_{j}\langle u_{i}\rangle _{}, & \displaystyle\end{eqnarray}$$

(2.13) $$\begin{eqnarray}\displaystyle & \displaystyle T_{}=-\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}_{j}\left(\frac{1}{2}\unicode[STIX]{x1D6FC}\langle u_{i}u_{i}u_{j}\rangle _{}-\frac{1}{2}\unicode[STIX]{x1D6FC}\langle u_{i}\rangle \langle u_{i}\rangle \langle u_{j}\rangle -\unicode[STIX]{x1D6FC}\langle u_{i}\rangle _{}\unicode[STIX]{x1D619}_{ij}-\unicode[STIX]{x1D6FC}\langle u_{j}\rangle _{}K_{}\right), & \displaystyle\end{eqnarray}$$

(2.14) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{}=-\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\langle qu_{j}\rangle _{}-\unicode[STIX]{x1D6FC}\langle q\rangle _{}\langle u_{j}\rangle _{}), & \displaystyle\end{eqnarray}$$

(2.15) $$\begin{eqnarray}\displaystyle & \displaystyle D_{}=\frac{2\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x2202}_{j}(\unicode[STIX]{x1D6FC}\langle u_{i}\unicode[STIX]{x1D61A}_{ij}\rangle _{}-\unicode[STIX]{x1D6FC}\langle u_{i}\rangle _{}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{}), & \displaystyle\end{eqnarray}$$

(2.16) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{}=2\unicode[STIX]{x1D708}(\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle _{}-\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{}), & \displaystyle\end{eqnarray}$$

(2.17) $$\begin{eqnarray}\displaystyle & \displaystyle I_{1}=\frac{1}{\unicode[STIX]{x1D6FC}}(\langle u_{i}\rangle _{}\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}-\overline{u_{i}\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}), & \displaystyle\end{eqnarray}$$

(2.18) $$\begin{eqnarray}\displaystyle & \displaystyle I_{2}=-\langle \unicode[STIX]{x1D70E}_{ij}\rangle _{}(\langle \unicode[STIX]{x2202}_{j}u_{i}\rangle _{}-\unicode[STIX]{x2202}_{j}\langle u_{i}\rangle _{}), & \displaystyle\end{eqnarray}$$

(2.19) $$\begin{eqnarray}\displaystyle & \displaystyle B_{}=\langle u_{i}a_{i}\rangle _{}-\langle u_{i}\rangle _{}\langle a_{i}\rangle _{}. & \displaystyle\end{eqnarray}$$

This form is the basis for the numerical implementation of the fixed-frame TKE equation in the present paper. The gradient of the indicator function is a generalized function (Drew & Passman Reference Drew and Passman1999),

(2.20) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}=n_{j}\unicode[STIX]{x1D6FF}_{fs}, & & \displaystyle\end{eqnarray}$$

where $\boldsymbol{n}$ is the normal vector perpendicular to the interface, pointing from the solid to the fluid region, and $\unicode[STIX]{x1D6FF}_{fs}$ a delta function on $\unicode[STIX]{x1D6FA}_{0}$ , infinitely large on the fluid–solid interface and zero otherwise. The non-commutation term $I_{2}$ can be rewritten as

(2.21) $$\begin{eqnarray}\displaystyle I_{2}=-\frac{1}{\unicode[STIX]{x1D6FC}}\langle \unicode[STIX]{x1D70E}_{ij}\rangle _{}(\langle u_{i}\rangle _{}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}-\overline{u_{i}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}). & & \displaystyle\end{eqnarray}$$

Further discussion of the formulation of the fixed-frame TKE equation and the description of its numerical implementation can be found in appendix B.

2.6 Definition of moving-frame averaged quantities

An analysis based on averaging in the (non-rotating) frame of reference of the particle (the moving frame) provides useful insight into the mechanisms of a turbulent particle-laden flow. If the particles do not move relative to each other, the averaging operator required for such an analysis is relatively simple. Thus in the frame of reference moving with $u_{i}^{p}$ , we define $\langle \cdot \rangle _{\text{M}}$ as the operator that averages over time and over all particle frames that are statistically equivalent. In the present configuration, there are only two statistically different particle frames ( $p=1$ and $p=2$ ). The statistical quantities due to this averaging are 3-D functions, constant in time, but dependent on all three spatial coordinates. For any fluid variable $f$ , the fluctuation $f^{\prime \prime }$ is defined by $f^{\prime \prime }=f-\langle f\rangle _{\text{M}}$ . The fluid velocity in the frame of reference of the particle is denoted by $w_{i}=u_{i}-u_{i}^{p}$ .

The averaged equations for the fluid phase in the translative frame of reference of particle $p$ are given by

(2.22) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{j}\langle w_{j}\rangle _{\text{M}}=0, & & \displaystyle\end{eqnarray}$$

(2.23) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}\langle w_{i}\rangle _{\text{M}} & = & \displaystyle -\unicode[STIX]{x2202}_{j}(\langle w_{i}\rangle _{\text{M}}\langle w_{j}\rangle _{\text{M}})-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D619}_{\text{M}ij}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x2202}_{i}\langle q\rangle _{\text{M}}+2\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{j}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}+\langle a_{i}\rangle _{\text{M}}+\unicode[STIX]{x2202}_{t}\langle u_{i}^{p}\rangle _{\text{M}},\end{eqnarray}$$

(2.24) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{t}K_{\text{M}}=C_{\text{M}}+P_{\text{M}}+T_{\text{M}}+\unicode[STIX]{x1D6F1}_{\text{M}}+D_{\text{M}}-\unicode[STIX]{x1D716}_{\text{M}}+J_{\text{M}}+B_{\text{M}}. & & \displaystyle\end{eqnarray}$$

In these equations,

(2.25) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D619}_{\text{M}ij}=\langle w_{i}w_{j}\rangle _{\text{M}}-\langle w_{i}\rangle _{\text{M}}\langle w_{j}\rangle _{\text{M}}=\langle w_{i}^{\prime \prime }w_{j}^{\prime \prime }\rangle _{\text{M}}, & & \displaystyle\end{eqnarray}$$

while the turbulence kinetic energy $K_{\text{M}}$ is $\unicode[STIX]{x1D619}_{\text{M}ii}/2$ , and the terms in the TKE equation (2.24) are defined by

(2.26) $$\begin{eqnarray}\displaystyle & \displaystyle C_{\text{M}}=-\unicode[STIX]{x2202}_{j}(\langle w_{j}\rangle _{\text{M}}K_{\text{M}}), & \displaystyle\end{eqnarray}$$

(2.27) $$\begin{eqnarray}\displaystyle & \displaystyle P_{\text{M}}=-\unicode[STIX]{x1D619}_{\text{M}ij}\unicode[STIX]{x2202}_{j}\langle w_{i}\rangle _{\text{M}}, & \displaystyle\end{eqnarray}$$

(2.28) $$\begin{eqnarray}\displaystyle T_{\text{M}} & = & \displaystyle -\unicode[STIX]{x2202}_{j} (\!{\textstyle \frac{1}{2}}\langle w_{i}w_{i}w_{j}\rangle _{\text{M}}-{\textstyle \frac{1}{2}}\langle w_{i}\rangle _{\text{M}}\langle w_{i}\rangle _{\text{M}}\langle w_{j}\rangle _{\text{M}}\nonumber\\ \displaystyle & & \displaystyle -\,\langle w_{i}\rangle _{\text{M}}\unicode[STIX]{x1D619}_{\text{M}ij}-\langle w_{j}\rangle _{\text{M}}K_{\text{M}}\!)=-{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}_{j}\langle w_{i}^{\prime \prime }w_{i}^{\prime \prime }w_{j}^{\prime \prime }\rangle _{\text{M}},\end{eqnarray}$$

(2.29) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\text{M}}=-\unicode[STIX]{x2202}_{j}(\langle qw_{j}\rangle _{\text{M}}-\langle q\rangle _{\text{M}}\langle w_{j}\rangle _{\text{M}})=-\unicode[STIX]{x2202}_{j}\langle q^{\prime \prime }w_{j}^{\prime \prime }\rangle _{\text{M}}, & & \displaystyle\end{eqnarray}$$

(2.30) $$\begin{eqnarray}\displaystyle D_{\text{M}} & = & \displaystyle \unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{j}^{2}K_{\text{M}}-\unicode[STIX]{x1D708}(\langle (\unicode[STIX]{x2202}_{i}w_{j})(\unicode[STIX]{x2202}_{j}w_{i})\rangle _{\text{M}}-\langle \unicode[STIX]{x2202}_{i}w_{j}\rangle _{\text{M}}\langle \unicode[STIX]{x2202}_{j}w_{i}\rangle _{\text{M}})\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{j}(\langle w_{i}\unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}-\langle w_{i}\rangle _{\text{M}}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}})=2\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{j}\langle w_{i}^{\prime \prime }\unicode[STIX]{x1D61A}_{ij}^{\prime \prime }\rangle _{\text{M}},\end{eqnarray}$$

(2.31) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{\text{M}}=2\unicode[STIX]{x1D708}(\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}-\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}})=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}^{\prime \prime }\unicode[STIX]{x1D61A}_{ij}^{\prime \prime }\rangle _{\text{M}}, & \displaystyle\end{eqnarray}$$

(2.32) $$\begin{eqnarray}\displaystyle & \displaystyle J_{\text{M}}=-\langle w_{i}\unicode[STIX]{x2202}_{t}u_{i}^{p}\rangle _{\text{M}}+\langle w_{i}\rangle _{\text{M}}\langle \unicode[STIX]{x2202}_{t}u_{i}^{p}\rangle _{\text{M}}=-\langle w_{i}^{\prime \prime }\unicode[STIX]{x2202}_{t}{u_{i}^{p}}^{\prime \prime }\rangle _{\text{M}}, & \displaystyle\end{eqnarray}$$

(2.33) $$\begin{eqnarray}\displaystyle & \displaystyle B_{\text{M}}=\langle w_{i}a_{i}\rangle _{\text{M}}-\langle w_{i}\rangle _{\text{M}}\langle a_{i}\rangle _{\text{M}}=\langle w_{i}^{\prime \prime }a_{i}^{\prime \prime }\rangle _{\text{M}}. & \displaystyle\end{eqnarray}$$

In each of the equations (2.25) and (2.28)–(2.33), the form in which the terms are numerically evaluated is given first, followed by an expression in terms of fluctuations. The former expressions would also provide a valid TKE equation if $\langle \cdot \rangle _{\text{M}}$ did not satisfy the fourth Reynolds condition. The term $C_{\text{M}}$ is the convection term, and $P_{\text{M}}$ is turbulence production, $T_{\text{M}}$ turbulent transport, $\unicode[STIX]{x1D6F1}_{\text{M}}$ pressure diffusion, $D_{\text{M}}$ viscous diffusion, $\unicode[STIX]{x1D716}_{\text{M}}$ turbulence dissipation, $J_{\text{M}}$ a term due to particle acceleration and $B_{\text{M}}$ body-force production. In the present case, the left-hand sides of (2.23)–(2.24) are zero, and $\unicode[STIX]{x2202}_{t}u_{i}^{p}=0$ so that $J_{\text{M}}=0$ . Apart from the occurrence of $J_{\text{M}}$ , this TKE equation has the same form as the single-phase TKE equation for cases with a 3-D mean flow.

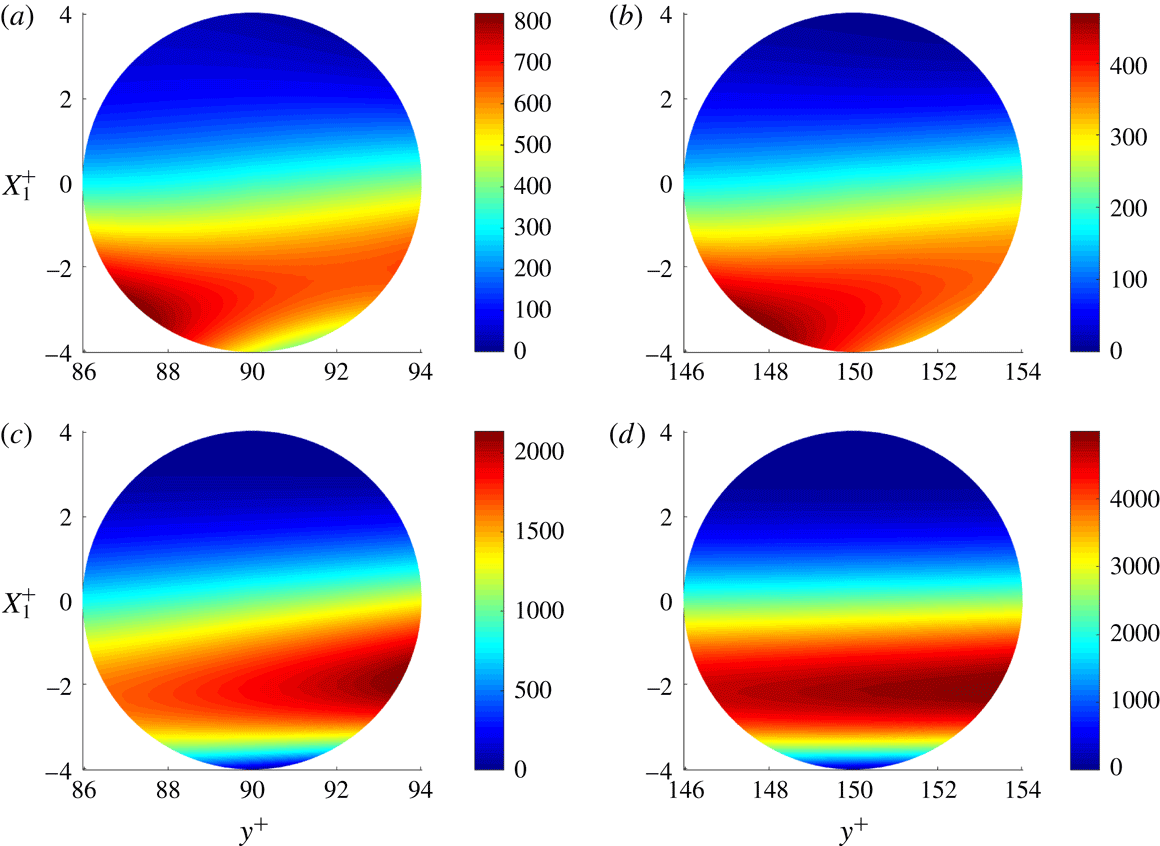
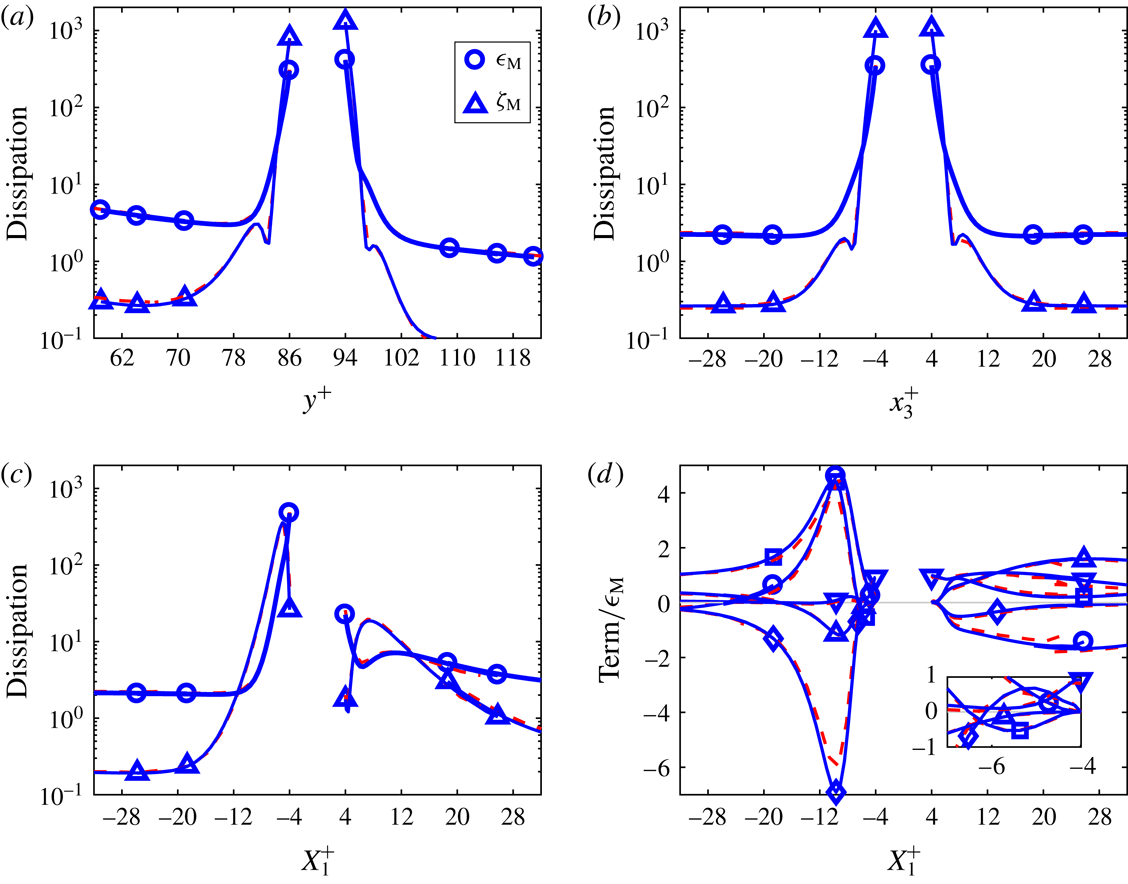
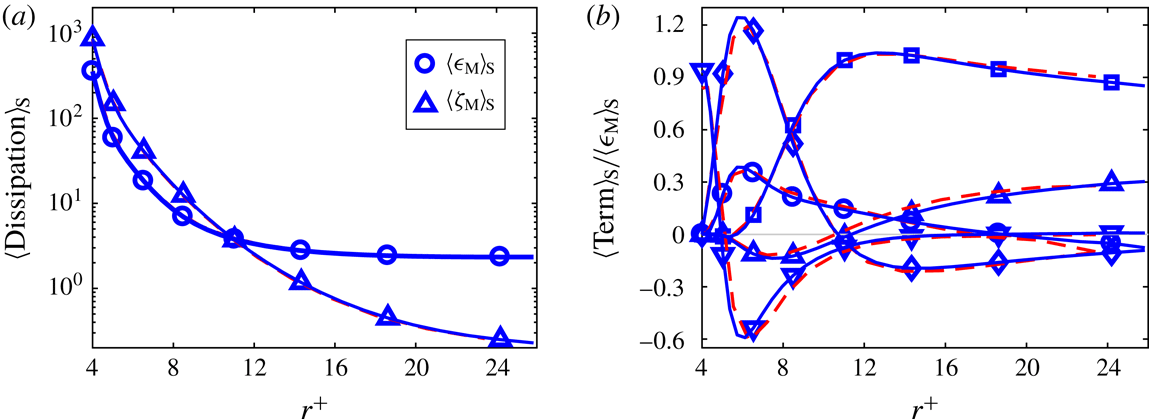
Since there are only two statistically different types of particles, the 3-D domain can be decomposed in 1728/2 statistically equivalent rectangular blocks. The size of each block is $L_{1}/18\times H\times L_{3}/24$ . The output of the post-processing program is a series of statistical quantities defined on a 3-D domain of the size of one block, which we call the reference block. Each moving-frame statistical quantity is determined at the cell centres of the active Cartesian cells and at the cell centres of the spherical cells. In addition to the evaluations of each term at the cell centres, the terms $D_{\text{M}}$ and $\unicode[STIX]{x1D716}_{\text{M}}$ are also explicitly computed at the centres of the cell faces on the particle surfaces. The numerical implementation of the moving-frame TKE equation is further described in appendix C. The numerical implementation employs the TKE equation in spherical coordinates, which is also derived in this appendix since we could not find that form in the literature.

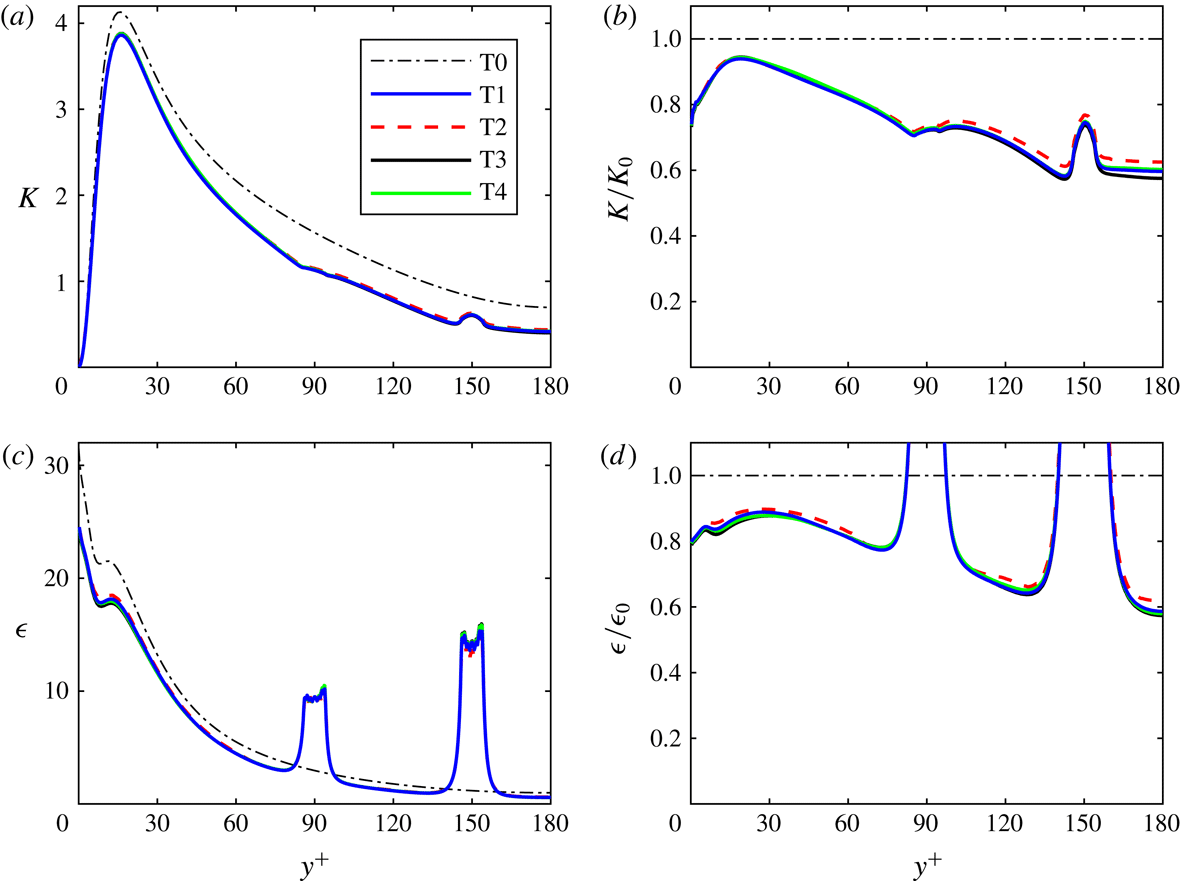
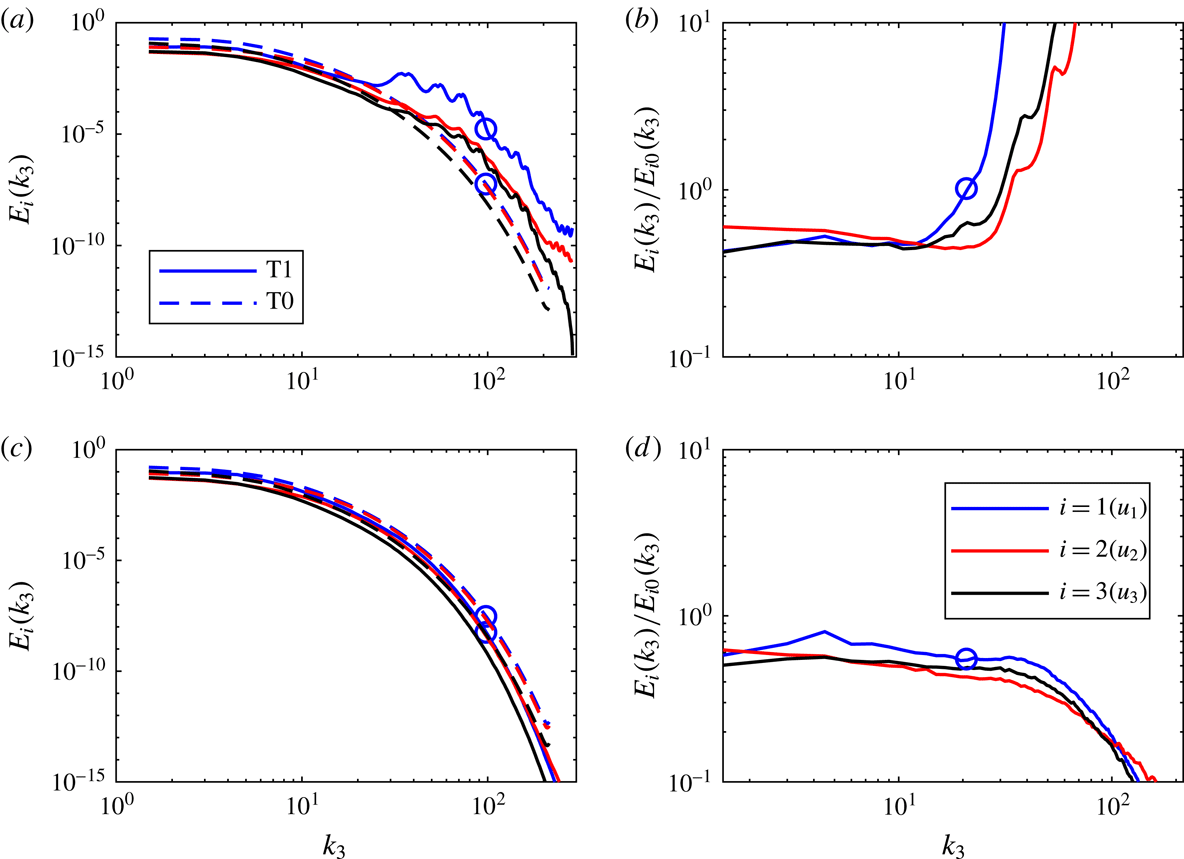
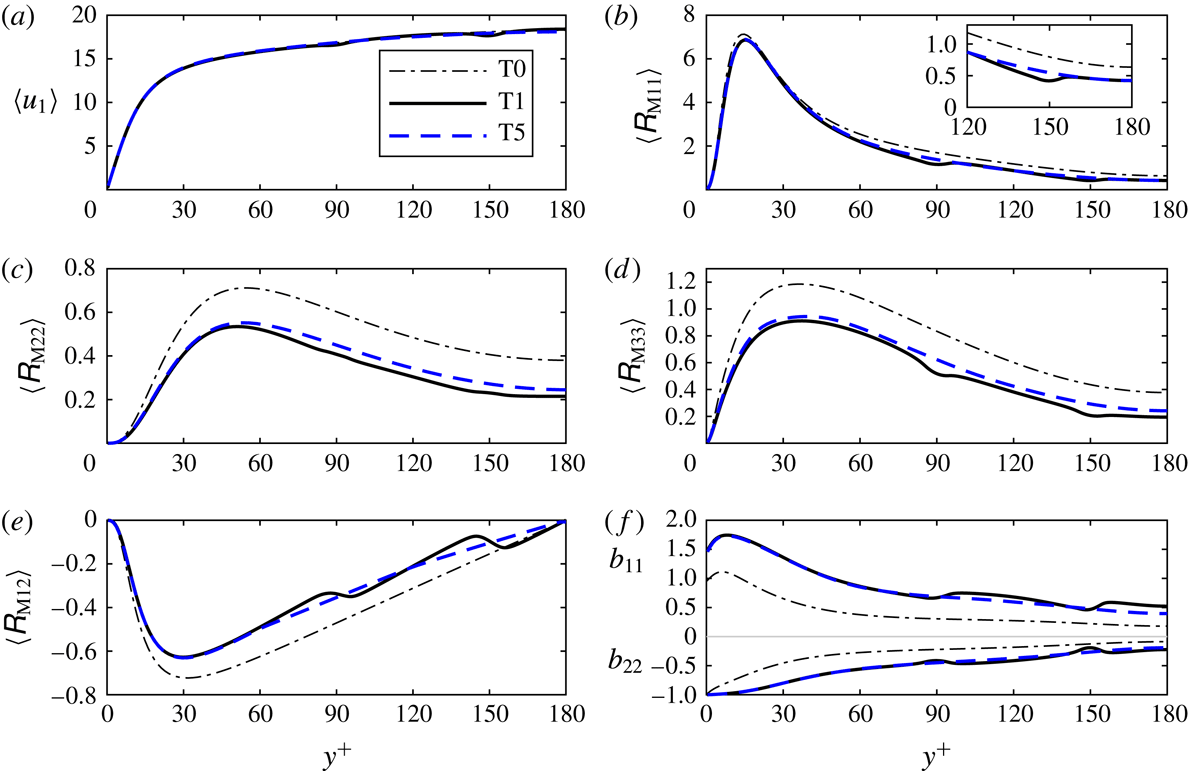
Figure 2. Fixed-frame statistics from cases T1 (blue solid), T2 (red dashed), T3 (black solid), T4 (green solid) and the unladen case T0 (thin black dash-dotted). (a,b) Turbulence kinetic energy $K$ before (a) and after (b) normalization with its unladen counterpart ( $K_{0}$ ). (c,d) Turbulence dissipation rate before (c) and after (d) normalization with its unladen counterpart ( $\unicode[STIX]{x1D716}_{0}$ ).

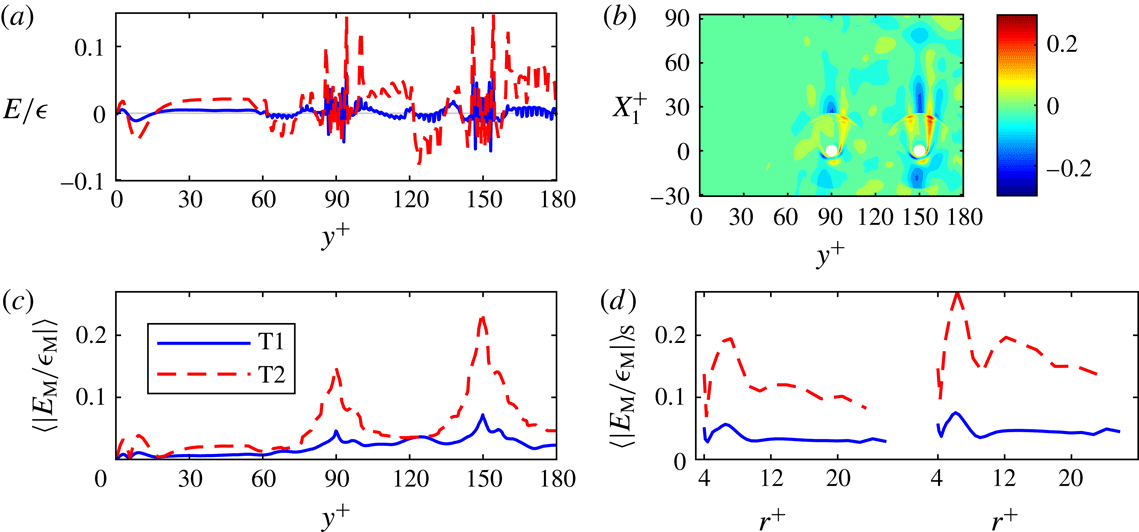
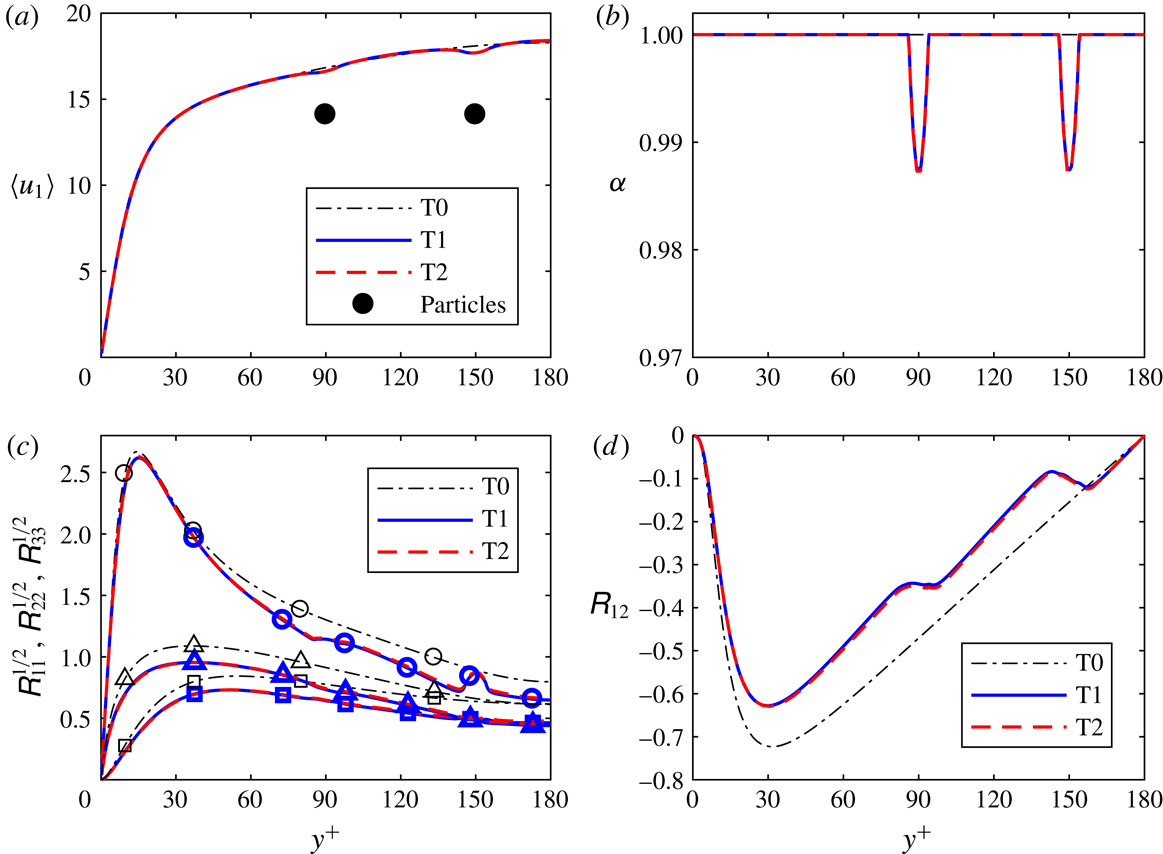
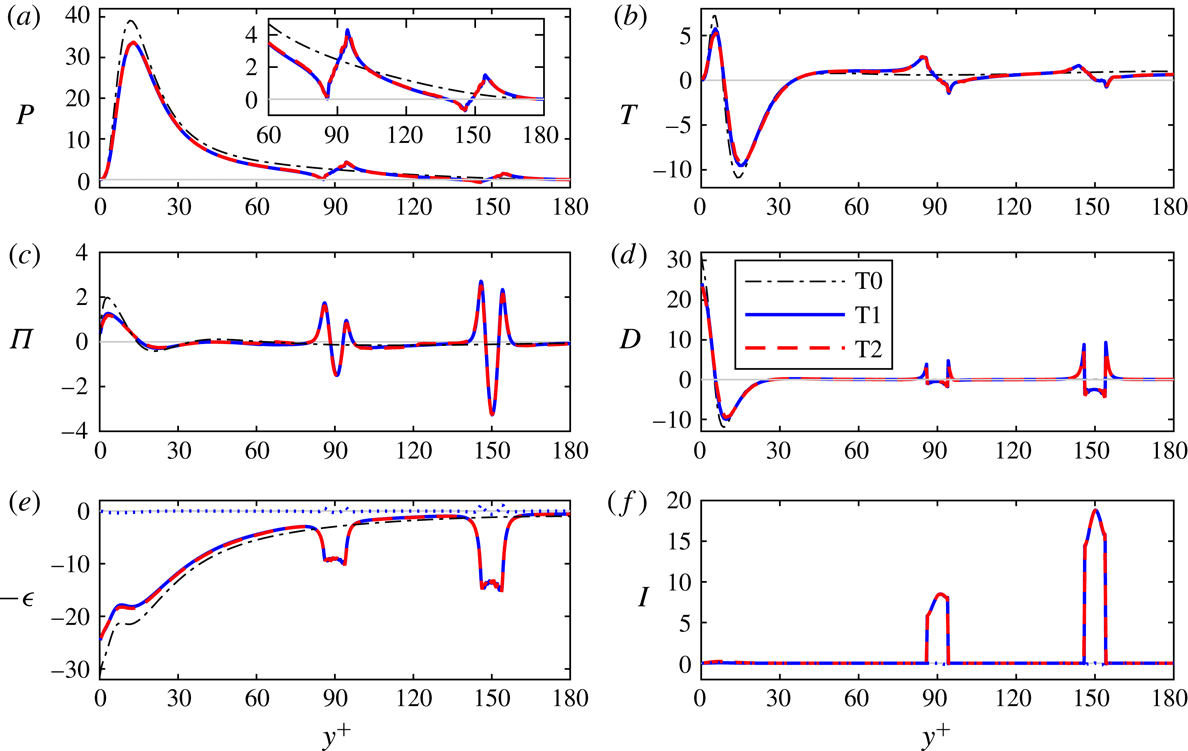
2.7 Validation

Representative results of simulations T1, T2, T3 and T4 of the turbulent case are shown in figures 2 and 3 and table 3. Case T0 denotes the unladen turbulent channel flow, while $E$ and $E_{\text{M}}$ denote the fixed-frame and moving-frame budget errors, the sums of all terms on the right-hand sides of the discretized forms of (2.10) and (2.24), respectively. The reasonably small discrepancies between fine-grid simulation T1 and coarse-grid simulation T2 are primarily caused by discretization errors in T2 and to a lesser extent caused by statistical errors in T1. Furthermore, profiles shown in the next sections will confirm that also for the individual Reynolds stresses and the individual budget terms the differences between T1 and T2 are quite small for the fixed-frame terms (figures 5 and 6) and reasonably small for the moving-frame terms (figures 13 and 14). It is concluded that the simulation on the finest grid, T1, is sufficiently accurate for our purposes. A more extensive discussion of the validation results can be found in appendix D.

Table 3. Statistics of the forces on the particles. The numbers for cases T1 and L1 have been multiplied by 100. For T2, T3 and T4, the relative differences with respect to T1 are shown. Root-mean-square denoted by r.m.s.

Figure 3. (a) Relative fixed-frame budget error $E/\unicode[STIX]{x1D716}$ . (b) Relative moving-frame budget error $E_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ in a symmetry plane cutting through the particles for case T1. (c) Planar average of $|E_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}|$ . (d) Spherical surface average of $|E_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}|$ as a function of the radius, which is the distance to the particle centre, for particles at $y^{+}=90$ (left subplot) and for particles at $y^{+}=150$ (right subplot). (a,c,d) Fine-grid case T1 (blue solid) and coarse-grid case T2 (red dashed).

3.1 Fixed-frame results of the turbulent case

Before we show the results for the TKE budget of the turbulent case, we show and discuss the results of a number of basic statistical quantities. The mean velocity and fluid volume fraction profiles are shown in figure 4. The mean velocity seems to be largely unaffected by the particles, a finding that is consistent with experimental results (Kulick et al. Reference Kulick, Fessler and Eaton1994). The wall-friction velocity $u_{\unicode[STIX]{x1D70F}}$ , derived from the mean velocity profile, and the corresponding $Re_{\unicode[STIX]{x1D70F}}$ are $0.979$ and 176, respectively (for both T1 and T2), 2 % smaller than the unladen values, $u_{\unicode[STIX]{x1D70F},0}$ and $Re_{\unicode[STIX]{x1D70F},0}$ . Since in this case the particles are concentrated at two $y^{+}$ locations, we do see a somewhat lower mean fluid velocity around these particle locations. The overall particle volume fraction is 0.00075, but due to the structure of the array, the mean particle volume fraction, which is a function of $y^{+}$ , peaks at 0.0128 (at $y^{+}=90$ and $y^{+}=150$ ). According to figure 4(c), all three turbulence intensities are attenuated, while the wall-normal and spanwise intensities decrease relatively more than the streamwise one. These observations are also consistent with experimental findings (Kulick et al. Reference Kulick, Fessler and Eaton1994; Kussin & Sommerfeld Reference Kussin and Sommerfeld2002). Furthermore, the Reynolds shear stress is weakened by the particles (figure 4 d).

Despite the small changes in the mean velocity profile, the turbulence kinetic energy $K$ is significantly attenuated for all $y^{+}$ ; see figure 2 in the previous section. The strongest attenuation is observed at the centre line, where $K$ has reduced to approximately 60 % of its unladen value. Surprisingly, a clear local maximum of $K$ is observed at $y^{+}=150$ , while a bump in the profile is observed $y^{+}=90$ . Figure 4(c) reveals that the local maximum in $K$ at the second particle location is mainly caused by $\unicode[STIX]{x1D619}_{11}$ , the streamwise component of the Reynolds stress. Later on in this paper, we will explain the local maxima of $K$ and $\unicode[STIX]{x1D619}_{11}$ at $y^{+}=150$ (§§ 3.2 and 5). Figure 2 also shows a decrease of the turbulence dissipation rate $\unicode[STIX]{x1D716}$ , but not at all locations; around the $y^{+}$ locations of the particles, $\unicode[STIX]{x1D716}$ is strongly enhanced.

Figure 5. Fixed-frame turbulence kinetic energy budget: (a) standard production (the inset zooms in on the channel core), (b) turbulent transport, (c) pressure diffusion, (d) viscous diffusion, (e) turbulence dissipation and (f) interface term $I$ . Fine-grid case T1 (blue solid), coarse-grid case T2 (red dashed) and unladen case T0 (thin black dash-dotted). The blue dotted lines in (e,f) represent the small cross-term contribution to the turbulence dissipation rate ( $\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}_{i}u_{j})^{\prime }(\unicode[STIX]{x2202}_{j}u_{i})^{\prime }\rangle$ ) and the small commutator contribution to the interfacial term ( $I_{2}$ ), respectively.

The profiles of all terms in the fixed-frame TKE budget are shown in figure 5. Compared to the unladen flow, all terms are reduced in the near-wall region, except the interfacial term $I$ of course, which is zero in the unladen flow and in the near-wall region of the particle-laden flow. The term $B$ , which is negligible ( ${<}0.002$ ), and the convection term $C$ , which is zero because (2.8) implies $\langle u_{2}\rangle _{}=0$ , are not shown. Furthermore, we observe that a large part of the strongly enhanced turbulence dissipation rate near the particles is compensated by the large and positive $I$ , which apparently represents production of turbulence kinetic energy by the presence of particles. This is consistent with the findings of Santarelli et al. (Reference Santarelli, Roussel and Fröhlich2016), who found $I\approx \unicode[STIX]{x1D716}$ in the core of the channel, for turbulent channel flow with (freely moving) bubbles at larger particle volume fraction ( ${\geqslant}0.003$ ) and at much larger particle Reynolds number. A positive $I$ means that the particles produce turbulence kinetic energy. One could imagine that fluctuating bubbles inject energy into the TKE equation. However, in the present case the particle velocity fluctuation is zero. Thus the large interfacial term must have another cause in this case.

At this point, it is useful to consider the composition of the interfacial term in more detail. On particle surfaces, the instantaneous velocity $\boldsymbol{u}$ is equal to the velocity of the particles $u_{i}^{p}$ . Since the latter is constant and the same for all particles, the two contributions to the interfacial term, $I_{1}$ and $I_{2}$ (2.17)–(2.18), can be simplified to

(3.1) $$\begin{eqnarray}\displaystyle & \displaystyle I_{1}=\frac{1}{\unicode[STIX]{x1D6FC}}(\langle u_{i}\rangle _{}-u_{i}^{p})\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}, & \displaystyle\end{eqnarray}$$

(3.2) $$\begin{eqnarray}\displaystyle & \displaystyle I_{2}=-\frac{1}{\unicode[STIX]{x1D6FC}}(\langle u_{i}\rangle _{}-u_{i}^{p})\langle \unicode[STIX]{x1D70E}_{ij}\rangle _{}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}. & \displaystyle\end{eqnarray}$$

Apparently, $I_{1}$ and $I_{2}$ are inner products of vectors with $\langle \boldsymbol{u}\rangle _{}-\boldsymbol{u}^{p}$ , the mean relative velocity between the phases, so that they both vanish if the mean relative velocity is zero. Thus, for particles with constant velocity, the turbulence kinetic energy produced by the interfacial term is a direct consequence of a non-zero mean relative velocity. According to equation (B 5) in appendix B, $I_{1}$ and $I_{2}$ are both zero if $\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}=0$ , i.e. for all $y^{+}$ for which the plane parallel to the wall is not intersected by an interfacial surface. Thus, in this case, $I$ is precisely non-zero in the two intervals with width $d_{p}$ centred around the two particle locations. The form of (3.2) suggests that $I_{2}$ is small if the variation of $\unicode[STIX]{x1D6FC}$ is small. Indeed, figure 5(f) shows that $I_{2}$ is negligible compared to $I$ .

Figure 6. Fixed-frame statistics for the laminar case L1: (a) mean streamwise velocity (blue solid), (b) turbulence kinetic energy, (c) Reynolds stresses $\unicode[STIX]{x1D619}_{22}$ (solid), $\unicode[STIX]{x1D619}_{33}$ (dash-dotted) and $\unicode[STIX]{x1D619}_{12}$ (dotted), (d) standard production (solid) and turbulent transport (dash-dotted), (e) pressure diffusion (solid) and viscous diffusion (dash-dotted) and (f) turbulence dissipation (solid) and interfacial term (dash-dotted). Panel (a) also includes the unladen laminar velocity profile (thin dash-dotted) and the particle velocity (black circles).

The placement of all particles at two specific $x_{2}$ positions leads to sudden changes in the different particle terms. The particle volume fraction $1-\unicode[STIX]{x1D6FC}$ is not continuously differentiable at the edges of the particles (the particle locations plus or minus $d_{p}/2$ ). This gives rise to strong discontinuities in $I$ at these locations, discontinuities which are balanced by the discontinuities in the viscous diffusion term $D$ . Another effect is that the non-zero transport terms, $T$ , $\unicode[STIX]{x1D6F1}$ and $D$ , change sign around the particles, and that even the production changes sign, at least near $y^{+}=150$ (see inset of figure 5 a). Thus the particles have a strong locally disturbing effect on all conventional terms in the turbulence kinetic energy equation. We will discuss the local effects of particles on the surrounding turbulence in more detail in §§ 4 and 6.

The quantity $\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}$ , which appears in (3.1) and (2.17), is proportional to the force exerted by the fluid on the particles as a function of $x_{2}$ . In fact $-\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}$ is the interfacial term in the mean momentum (2.9), and therefore we call this term the mean drag loading (the mean density of the drag force exerted by the particles on the fluid). We derive an estimate for the level of $\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}$ around $x_{2}^{p}$ . For this purpose, we define a thin volumetric slice $V_{s}=[0,L_{1}]\times [-x_{2}^{p}-r_{0},x_{2}^{p}+r_{0}]\times [0,L_{3}]$ around $x_{2}^{p}$ . The particle volume fraction in this slice is denoted by $\unicode[STIX]{x1D6FC}_{s}$ and is equal to $432V_{p}/(d_{p}L_{1}L_{3})$ , where $V_{p}=\unicode[STIX]{x03C0}d_{p}^{3}/6$ . For $x_{2}\approx x_{2}^{p}$ ,

(3.3) $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}} & {\approx} & \displaystyle \frac{1}{d_{p}}\int _{x_{2}^{p}-r_{0}}^{x_{2}^{p}+r_{0}}\overline{\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712}}\,\text{d}x_{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{d_{p}L_{1}L_{3}(t_{2}-t_{1})}\int _{t_{1}}^{t_{2}}\int _{0}^{L_{1}}\int _{x_{2}^{p}-r_{0}}^{x_{2}^{p}+r_{0}}\int _{0}^{L_{3}}(\unicode[STIX]{x1D70E}_{ij}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D712})\,\text{d}x_{3}\,\text{d}x_{2}\,\text{d}x_{1}\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{432}{d_{p}L_{1}L_{3}}\text{mean}(F_{i}^{p})=\frac{\unicode[STIX]{x1D6FC}_{s}}{V_{p}}\text{mean}(F_{i}^{p}).\end{eqnarray}$$

Since the mean of $F_{1}^{p}$ is expected to have the same sign as $\langle u_{1}\rangle -u_{1}^{p}$ , and the wall-normal and spanwise components of the mean relative velocity are zero, the interfacial term $I\approx I_{1}$ in the budget is expected to be positive. In particular, equation (3.1) is approximated by

(3.4) $$\begin{eqnarray}\displaystyle I_{1}\approx \frac{\unicode[STIX]{x1D6FC}_{s}}{V_{p}}(\langle u_{1}\rangle -u_{1}^{p})\;\text{mean}(F_{1}^{p})\approx 185(\langle u_{1}\rangle -u_{1}^{p})\;\text{mean}(F_{1}^{p}), & & \displaystyle\end{eqnarray}$$

for $x_{2}\approx x_{2}^{p}$ . This equation would in fact reduce to the model for the interfacial term in bubbly flows proposed by Throsko & Hassan (Reference Throsko and Hassan2001) and tested by Santarelli et al. (Reference Santarelli, Roussel and Fröhlich2016) if we replaced $F_{1}^{p}$ by the standard model expression for the particle drag force. To evaluate this approximation for $I_{1}$ , we use the PR-DNS values for $F_{1}^{p}$ listed in table 3. Furthermore, we use the PR-DNS values for $\langle u_{1}\rangle -u_{1}^{p}$ at $y^{+}=90$ and $y^{+}=150$ , which are 2.53 and 3.60 respectively. Thus we obtain $I\approx I_{1}\approx 7.6$ and $I\approx 16.8$ , and the comparison with figure 5(f) shows that these are indeed good approximations of the average heights of the two peaks in the interfacial term.

3.2 Fixed-frame results of the laminar case

In the previous section, we observed a surprising peak in $K$ around $y^{+}=150$ , a very strong enhancement of $\unicode[STIX]{x1D716}$ around $y^{+}=90$ and $y^{+}=150$ , and in the same regions a large production of turbulence kinetic energy by the interfacial term even though the particle velocity fluctuation is zero. Are these remarkable observations caused by true turbulence or do laminar effects play a role? How much of $K$ and $\unicode[STIX]{x1D716}$ is truly turbulent? While definitive answers to these questions will be given in § 5, we address a related question in this subsection, namely whether the remarkable features also persist in a laminar channel flow past a particle array. We therefore consider the results of case L1, in which, in order to keep the flow laminar and the relative particle velocity roughly the same, the fluid bulk velocity was reduced to 3, and the velocity of the particle array was set to 0. The fluid-weighted averaging operator $\langle \cdot \rangle$ was applied to the steady state reached by this flow.

The results of simulation L1 are shown in figure 6. It appears that the turbulence kinetic energy is non-zero around the particles, although the flow is laminar and steady. This is in line with the work of Mehrabadi et al. (Reference Mehrabadi, Tenneti, Garg and Subramaniam2015), who observed a non-zero TKE in PR-DNS of laminar flow past an array of fixed particles. Due to the laminar flow disturbance around the particle, each velocity component is subject to spatial variation in planes parallel to the wall, which implies a non-zero spatial fluctuation with respect to the planar average. According to figure 6(b,c), $K$ is much larger than $\unicode[STIX]{x1D619}_{22}$ and $\unicode[STIX]{x1D619}_{33}$ , which implies $\unicode[STIX]{x1D619}_{11}\approx 2K$ . This very strong anisotropy must be due to the wakes behind the particles, which reduce the streamwise velocity considerably below $\langle u_{1}\rangle$ in a rather large region. Because $\unicode[STIX]{x1D619}_{22}$ is very small, the Reynolds shear stress $\unicode[STIX]{x1D619}_{12}$ is also small (although it is non-zero: see figure 6 c). This also explains the peak near the second particle position and the bump around the first particle position in figure 2(a). The latter is a bump because the level of the increase in $K$ due to laminar effects is rather small compared to the background turbulence at the first particle position.

It appears that the interfacial term and the turbulence dissipation rate are larger than $\unicode[STIX]{x1D6F1}$ and $D$ and much larger than $P$ and $T$ . Thus in this case we have $I\approx \unicode[STIX]{x1D716}$ (the interfacial production of $K$ is balanced by the dissipation of $K$ ), although the profile of $I$ is thinner and has a slightly larger peak than that of $\unicode[STIX]{x1D716}$ . In view of the modest value of $K$ (only 0.12), it is surprising how large $I$ and $\unicode[STIX]{x1D716}$ are near the particle locations, of the same order as in the turbulent flow around $y^{+}=90$ (figure 5 e,f).

With respect to the local distortions by the particles, there is a strong similarity between cases L1 and T1, not only for $I$ and $\unicode[STIX]{x1D716}$ , but also for the shape distortions of $P$ and the transport terms around the particle positions. Thus laminar effects can significantly contribute to $K$ and $\unicode[STIX]{x1D716}$ , and several similarities between L1 and T1 suggest that laminar effects have an important effect on turbulence statistics in the turbulent case too.

4.1 Mean flow and Reynolds stresses

Figure 7 shows the contours of the streamwise and wall-normal mean velocity components and the turbulence kinetic energy $K_{M}$ on the symmetry plane $X_{3}=0$ of the reference 3-D block ( $X_{i}=x_{i}-x_{i}^{p}$ ). This symmetry plane includes the centres of the two statistically different particles. In this plane, $\langle u_{3}\rangle _{\text{M}}=0$ , and $\unicode[STIX]{x2202}_{3}\langle u_{1}\rangle _{\text{M}}=0$ . In the planes $X_{2}=0$ through the particles, the structure of $\langle u_{3}\rangle _{\text{M}}$ is similar to the structure of $\langle u_{2}\rangle _{\text{M}}$ in figure 7(b). In figure 7(c), we observe a region of relatively low turbulence kinetic energy around each particle. These regions are elongated in the streamwise direction and include the rather long wakes behind the particles. The Reynolds shear stress $\unicode[STIX]{x1D619}_{\text{M}12}$ in this plane (figure 7 d) has, on top of the negative background Reynolds shear stress, a quadrant type of structure around each particle: negative near the left front and right rear and positive near the right front and left rear. The structures at the rear occur in the free shear layers at both sides of the wake behind each particle and their sign tends to be opposite to the sign of the local shear component $\langle \unicode[STIX]{x1D61A}_{12}\rangle _{\text{M}}$ .

Figure 7. Contours of moving-frame statistics in the plane $X_{3}=0$ (case T1). (a) Mean streamwise velocity $\langle u_{1}\rangle _{\text{M}}-u_{1}^{p}$ . (b) Mean wall-normal velocity $\langle u_{2}\rangle _{\text{M}}$ . (c) Turbulence kinetic energy $K_{\text{M}}$ . (d) Reynolds shear stress $\unicode[STIX]{x1D619}_{\text{M}12}$ .

Figure 8. Contours of moving-frame Reynolds stresses in the plane $X_{3}=0$ (case T1). (a) $\unicode[STIX]{x1D619}_{\text{M}11}$ . (b) $\unicode[STIX]{x1D619}_{\text{M}22}$ . (c) $\unicode[STIX]{x1D619}_{\text{M}33}$ . (d) Anisotropy coefficient $b_{\text{M}11}$ .

The four non-zero components of the Cartesian Reynolds stress tensor in the plane $X_{3}=0$ are shown in figure 8. The distortion of the turbulence by the particles is clearly not entirely symmetric about the $y^{+}=90$ and $y^{+}=150$ axes through the particles. All three diagonal components are substantially suppressed around the particles, while the wake structures created by the particles persist further downstream for $\unicode[STIX]{x1D619}_{\text{M}11}$ than for $\unicode[STIX]{x1D619}_{\text{M}22}$ and $\unicode[STIX]{x1D619}_{\text{M}33}$ (the latter two quantities recover more quickly than $\unicode[STIX]{x1D619}_{\text{M}11}$ and the mean streamwise velocity). However, somewhat downstream of the particles (around $X_{1}^{+}\approx 10$ ) and on the right side ( $y^{+}\approx 100$ for $p=1$ and $y^{+}\approx 160$ for $p=2$ ) we observe local maxima of $\unicode[STIX]{x1D619}_{\text{M}11}$ (see figure 8 a, less easy to discern for $p=2$ than for $p=1$ ). These local maxima appear inside a region of enhanced anisotropy of the turbulence (see figure 8 d), where the streamwise component of the anisotropy tensor, $b_{\text{M}11}=-1+3\unicode[STIX]{x1D619}_{\text{M}11}/(\unicode[STIX]{x1D619}_{\text{M}11}+\unicode[STIX]{x1D619}_{\text{M}22}+\unicode[STIX]{x1D619}_{\text{M}33})$ , is shown. We observe that the anisotropy is strongly modified near the particles, but while $b_{\text{M}11}$ is increased in some regions, it is reduced in other regions. Near the fronts and the rears of the particles, $b_{\text{M}11}$ approaches $-1$ since there $u_{1}^{\prime \prime }$ is the particle wall-normal component and therefore vanishes faster than $u_{2}^{\prime \prime }$ and $u_{3}^{\prime \prime }$ if the particle surface is approached. At the sides of the particle in this plane, $u_{2}^{\prime \prime }$ is the particle wall-normal component. Thus at those locations values of $b_{\text{M}22}$ approach $-1$ and, as a consequence, $b_{\text{M}11}$ (and $b_{\text{M}33}$ ) increase. We observe that the low $b_{\text{M}11}$ at the rears and the high $b_{\text{M}11}$ at the sides are transported downstream. Thus the wake has a long core of relatively low $b_{\text{M}11}$ , embraced by a hull of relatively high  $b_{\text{M}11}$ .

Figure 9. Moving-frame TKE budget in the plane $X_{3}=0$ (case T1). Positive values of production $P_{\text{M}}$ (red dash-dotted, contour levels 2, 5, 20 and 100). Negative production $P_{\text{M}}$ (blue dashed) and minus the dissipation rate $-\unicode[STIX]{x1D716}_{\text{M}}$ (blue solid), both for contour levels $-$ 2, $-$ 5, $-$ 20 and $-$ 100. The arrows represent the total transport flux vector (for each coordinate direction, the odd numbered points are skipped).

4.2 TKE budget

An overview of the moving-frame TKE budget in the same plane is shown in figure 9. The dissipation is enhanced around the particles, but the production is too, while negative production occurs as well. Arrows are used to visualize the total transport flux vector, the vector inside the divergence in $C_{\text{M}}+T_{\text{M}}+\unicode[STIX]{x1D6F1}_{\text{M}}+D_{\text{M}}$ ( $C_{\text{M}}$ is also a transport term, because it can be written in divergence form). We observe a background flow of turbulence kinetic energy in the positive $x_{1}$ and positive $x_{2}$ directions. This background flow is dominated by $\langle w_{1}\rangle K_{\text{M}}$ in the $x_{1}$ direction and by $\langle u_{i}^{\prime \prime }u_{i}^{\prime \prime }u_{2}^{\prime \prime }\rangle _{\text{M}}/2$ in the $x_{2}$ direction.

Figure 10. Contours of moving-frame TKE budget in the plane $X_{3}=0$ (case T1), all clipped to the range $[-10,10]$ ; most dark red (dark blue) regions contain peaks much higher than 10 (much lower than $-$ 10). (a) Convection term $C_{\text{M}}$ . (b) Production term $P_{\text{M}}$ . (c) Turbulent transport term $T_{\text{M}}$ . (d) Pressure diffusion term $\unicode[STIX]{x1D6F1}_{\text{M}}$ . (e) Viscous diffusion term $D_{\text{M}}$ . (f) Minus turbulence dissipation rate $-\unicode[STIX]{x1D716}_{\text{M}}$ .

Table 4. Extrema of the terms in the moving average budget and $\unicode[STIX]{x1D701}_{\text{M}}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}$ on the spherical grids for particle types $p=1$ and $p=2$ . From case T1.

Contour plots of the six individual terms of the moving-frame turbulence kinetic energy budget are shown in figure 10. Note that for clarity of the figure, the values have been clipped to a rather narrow range, the dark red (dark blue) coloured regions typically include values much larger than 10 (lower than $-$ 10). The term due to the forcing by the streamwise pressure gradient, $B_{\text{M}}$ , is negligible and therefore not shown. For each term and particle, the extrema over the entire spherical grid around the particle are listed in table 4 (the very large maxima of $D_{\text{M}}$ and $\unicode[STIX]{x1D716}_{\text{M}}$ , which should formally be the same, numerical differ by approximately 7 % for $p=1$ and 8 % for $p=2$ .)

Regions where the first transport term ( $C_{\text{M}}$ ) injects turbulence kinetic energy are observed near the front and the sides, while regions where it consumes turbulence kinetic energy are observed near the sides and the rear. Comparison of figure 10(a–c) shows that, in the neighbourhood of the particle, the role of convection is more important than the role of the turbulent transport term $T_{\text{M}}$ . The pressure diffusion term, $\unicode[STIX]{x1D6F1}_{\text{M}}$ , another transport term, also strongly injects turbulence kinetic energy in regions at the front and at the sides (it is the second largest locally productive effect in the TKE budget: see table 4), although the strongly positive region near the front is very thin. Also near the front, but slightly further away from the particle surface, there is a pronounced region of negative pressure diffusion. The fourth transport term is the viscous diffusion term, $D_{\text{M}}$ , which becomes very large in a thin layer attached to the particle surface. The terms of the TKE budget that attain the largest values are $D_{\text{M}}$ and $\unicode[STIX]{x1D716}_{\text{M}}$ , whose absolute extrema are attained at the particle surfaces. These are also the only two terms of the TKE budget that are non-zero on the particles. That all the other terms are zero on the particles is not discernible in figure 10 (because the range in this plot is restricted to $[-10,10]$ , which is only a few per cent of $\unicode[STIX]{x1D716}_{\text{M}}$ on the particle surface), but it can be seen in (the inset of) figure 13(d) (forthcoming). While $D_{M}$ and $\unicode[STIX]{x1D716}_{M}$ are very large on and close to the particles, they rapidly decay away from the particles, $D_{M}$ even more rapidly than $\unicode[STIX]{x1D716}_{M}$ , as the dark (red) layers at the front and sides of the particle are thinner in figure 10(e) than the corresponding dark blue layers in figure 10(f).

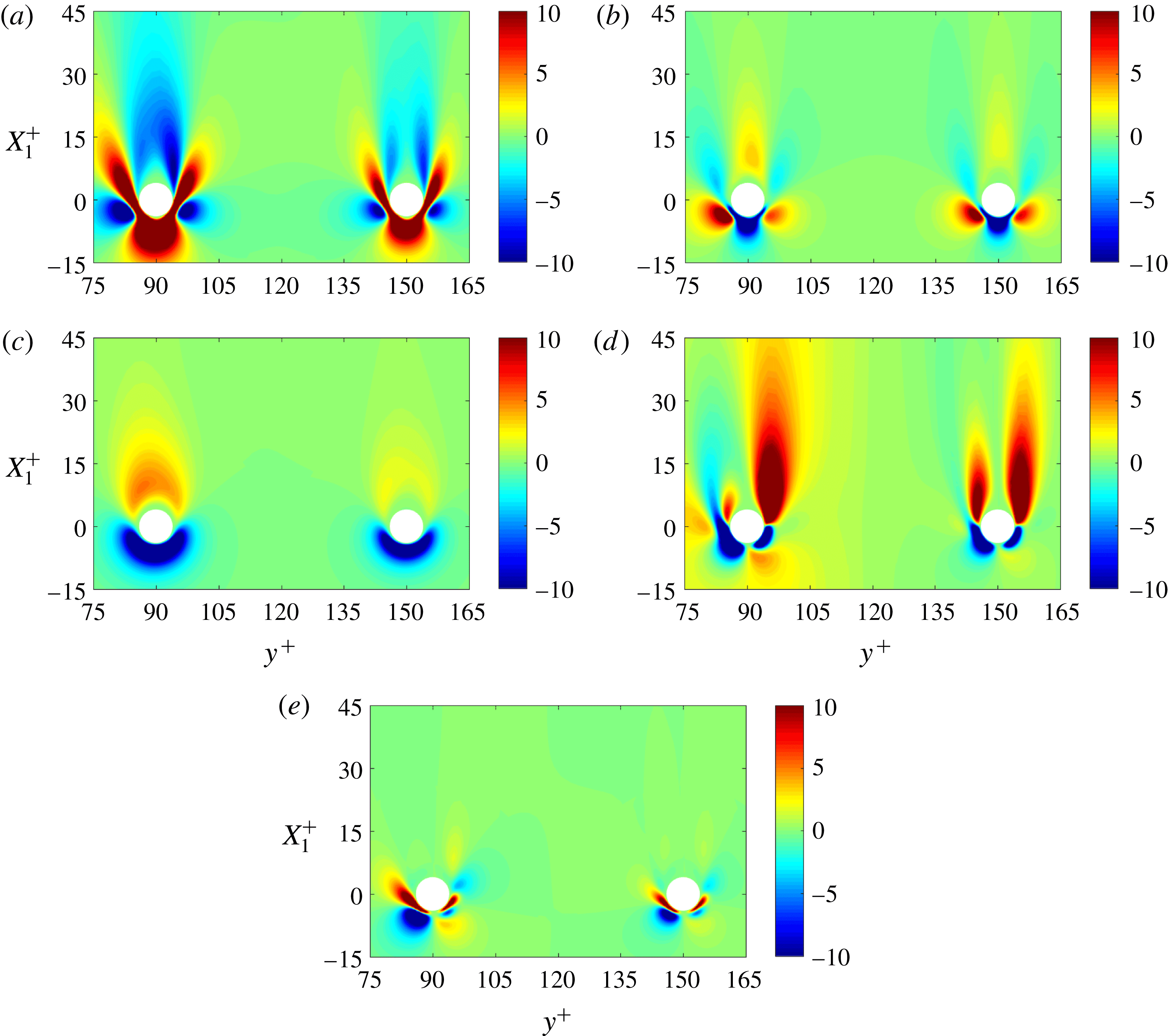
Figure 11. Decomposition of $P_{\text{M}}$ in the plane $X_{3}=0$ (case T1). Contours of the non-zero contributions, all clipped to the range $[-10,10]$ ; most dark red (dark blue) regions contain peaks much higher than 10 (much lower than $-$ 10). (a) $-\unicode[STIX]{x1D619}_{\text{M}11}\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}$ . (b)  $-\unicode[STIX]{x1D619}_{\text{M}22}\langle \unicode[STIX]{x1D61A}_{22}\rangle _{\text{M}}$ . (c) $-\unicode[STIX]{x1D619}_{\text{M}33}\langle \unicode[STIX]{x1D61A}_{33}\rangle _{\text{M}}$ . (d) $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}$ . (e) $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{1}\langle u_{2}\rangle _{\text{M}}$ .

4.3 Turbulence production

The turbulence production term, $P_{\text{M}}$ , is positive everywhere in simple turbulent flows, but in this flow we see a region of strongly negative production near the front and the sides of each particle, and also a region of weakly negative production in the wake further away from the first particle. The region of negative production at the front has a thin neck, and before the flow reaches this neck it goes through a region with enhanced positive turbulence production. The decomposition of the production term is shown in figure 11. In this symmetry plane, there are five non-zero contributions to the production term: $-\unicode[STIX]{x1D619}_{\text{M}11}\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}$ , $-\unicode[STIX]{x1D619}_{\text{M}22}\langle \unicode[STIX]{x1D61A}_{22}\rangle _{\text{M}}$ , $-\unicode[STIX]{x1D619}_{\text{M}33}\langle \unicode[STIX]{x1D61A}_{33}\rangle _{\text{M}}$ , $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}$ and $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{1}\langle u_{2}\rangle _{\text{M}}$ .

Near the front of the particle, perpendicular to the particle surface, there is a nearly streamwise oriented axis where $\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}+\unicode[STIX]{x2202}_{1}\langle u_{2}\rangle _{\text{M}}=0$ . Combining this with the approximation $\unicode[STIX]{x1D619}_{\text{M}22}\approx \unicode[STIX]{x1D619}_{\text{M}33}$ implying $b_{\text{M}22}\approx b_{\text{M}33}\approx -b_{\text{M}11}/2$ , the production on this axis is approximated by

(4.1) $$\begin{eqnarray}\displaystyle P_{\text{M}} & {\approx} & \displaystyle -\unicode[STIX]{x1D619}_{\text{M}11}\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}-\unicode[STIX]{x1D619}_{\text{M}22}\langle \unicode[STIX]{x1D61A}_{22}\rangle _{\text{M}}-\unicode[STIX]{x1D619}_{\text{M}33}\langle \unicode[STIX]{x1D61A}_{33}\rangle _{\text{M}}\nonumber\\ \displaystyle & = & \displaystyle -b_{\text{M}11}\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}-b_{\text{M}22}\langle \unicode[STIX]{x1D61A}_{22}\rangle _{\text{M}}-b_{\text{M}33}\langle \unicode[STIX]{x1D61A}_{33}\rangle _{\text{M}}\nonumber\\ \displaystyle & {\approx} & \displaystyle -b_{\text{M}11}(\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}+\langle \unicode[STIX]{x1D61A}_{22}\rangle _{\text{M}}/2+\langle \unicode[STIX]{x1D61A}_{33}\rangle _{\text{M}}/2)\nonumber\\ \displaystyle & = & \displaystyle -b_{\text{M}11}\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}/2.\end{eqnarray}$$

On this axis, the mean flow must decelerate ( $\langle \unicode[STIX]{x1D61A}_{11}\rangle _{\text{M}}<0$ ), which implies that $P_{\text{M}}$ has the same sign as the streamwise anisotropy $b_{\text{M}11}$ . Because of the anisotropy of the background turbulence $b_{\text{M}11}>0$ when the turbulence starts to approach the particle, and therefore the production is first enhanced in the deceleration zone. However, closer to the particle $b_{\text{M}11}$ becomes negative because the streamwise component is the normal component in the turbulent structure impinging on the front of the particle (see figure 8 d). As a consequence $P_{\text{M}}$ becomes strongly negative.

The regions of negative production at the sides of each particle are attributed to strongly positive $\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}$ . To explain the positive correlation between $\unicode[STIX]{x1D619}_{\text{M}12}$ and $\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}$ , we consider the region of negative $\unicode[STIX]{x1D619}_{\text{M}12}$ at the front-right side of the second particle: see figure 7(d). There is no perfect symmetry, but near the front there is an approximate symmetry about the axis $y^{+}=150$ . Near the particle surface and somewhat to the right of the symmetry line, there is a region where $\unicode[STIX]{x1D619}_{\text{M}12}>0$ (see figure 8 d), $\langle u_{1}\rangle _{\text{M}}$ increases with increasing $x_{2}$ (figure 8 a). Thus $\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}}>0$ and this provides a negative contribution to $P_{\text{M}}$ .

However, how can $\unicode[STIX]{x1D619}_{\text{M}12}$ become positive at this point? This cannot be due to the convection of the background $\unicode[STIX]{x1D619}_{\text{M}12}$ , because the background $\unicode[STIX]{x1D619}_{\text{M}12}$ is negative. To explain this, we choose a point near to the previous point, also on the $X_{3}=0$ plane, but closer to the approximate-symmetry axis, where $\unicode[STIX]{x1D619}_{\text{M}12}$ is rising or has just become positive. At this point we consider the turbulent structures with positive $u_{1}^{\prime \prime }$ , which tend to bend to the right, since $\langle u_{2}\rangle _{\text{M}}$ is slightly positive. The structures with positive $u_{1}^{\prime \prime }$ have relatively large inertia and therefore they will approach the particle very closely before they bend, so that $q^{\prime \prime }$ tends to be positive. After they have bent, their $u_{1}^{\prime \prime }$ and $u_{2}^{\prime \prime }$ are still relatively large, so that the fluctuating shear rate $\unicode[STIX]{x1D61A}_{12}^{\prime \prime }$ also tends to be positive. This implies a positive correlation of $q^{\prime \prime }$ and $\unicode[STIX]{x1D61A}_{12}^{\prime \prime }$ at this point, in other words a positive pressure term $\langle q^{\prime \prime }\unicode[STIX]{x1D61A}_{12}^{\prime \prime }\rangle _{\text{M}}$ , which appears in the transport equation of $\unicode[STIX]{x1D619}_{12}$ . If the correlation is sufficiently strong to overrule other mechanisms in that equation, for example negative production of $\unicode[STIX]{x1D619}_{\text{M}12}$ , then $\unicode[STIX]{x1D619}_{\text{M}12}$ becomes positive indeed.

In the wakes of both particles we see two wings of positive production, although the left wing in the wake of the first particle is relatively short. Each pair of wings (or in three dimensions each asymmetrically annular region of enhanced $P_{\text{M}}$ in the wake) corresponds to regions in an annular free shear layer where, as mentioned above, $\unicode[STIX]{x1D619}_{\text{M}12}$ and $\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle$ have opposite signs, so that $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle$ is positive and can enhance $P_{\text{M}}$ . In fact, $-\unicode[STIX]{x1D619}_{\text{M}12}\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle$ appears in the production term of the $\unicode[STIX]{x1D619}_{\text{M}11}$ equation and not in those of the $\unicode[STIX]{x1D619}_{\text{M}22}$ and $\unicode[STIX]{x1D619}_{\text{M}33}$ equations. Furthermore, the wings of positive production at the right sides of the particles are stronger than those on the left. It seems that the right wings are responsible for the occurrence of maxima of $\unicode[STIX]{x1D619}_{\text{M}11}$ and large values of $b_{11}$ at $y^{+}\approx 100$ and $y^{+}\approx 160$ (see figure 8). If the particle Reynolds number based on the mean relative velocity were larger than a few hundred, then positive production in the wake would be expected since the particle wake would be unstable, for laminar free-stream flow and probably also for turbulent free-stream flow. However, in this case the particle Reynolds number remains moderate (maximum 50). Therefore, we do not attribute the positive $P_{\text{M}}$ in the wake to classical particle wake instability but to the interaction between the channel flow turbulence and the mean velocity gradients created by the particle.

Figure 12. Contours of moving-frame dissipation terms on the particle surface, viewed from a point on the polar axis (case T1). Turbulence dissipation rate $\unicode[STIX]{x1D716}_{\text{M}}$ on particles at $y^{+}=90$ (a) and $y^{+}=150$ (b). Mean flow dissipation rate $\unicode[STIX]{x1D701}_{\text{M}}$ on particles at $y^{+}=90$ (c) and $y^{+}=150$ (d).

4.4 Dissipation rates

The dissipation structure of kinetic energy near the particle is quantified by two quantities: the turbulence dissipation rate $\unicode[STIX]{x1D716}_{\text{M}}$ and the dissipation rate of mean flow kinetic energy, defined by $\unicode[STIX]{x1D701}_{\text{M}}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}\langle \unicode[STIX]{x1D61A}_{ij}\rangle _{\text{M}}$ . The latter is not a term in the moving-frame TKE equation, but it is part of the fixed-frame turbulence dissipation rate, as we will see in § 5. The contours of $\unicode[STIX]{x1D716}_{\text{M}}$ and $\unicode[STIX]{x1D701}_{\text{M}}$ on the two particle surfaces, the entire hemispheres at one side of the symmetry plane $X_{3}=0$ , are shown in figure 12. The hemispheres appear as circles as we view the hemispheres along the polar axes, which are perpendicular to $X_{3}=0$ . Thus the centre of each circle shown corresponds to the point on the polar line $\unicode[STIX]{x1D703}=0$ at radius $r=r_{0}$ . Since the unladen $\unicode[STIX]{x1D716}_{\text{M}}$ is only 2.96 at $y^{+}=90$ and 1.17 at $y^{+}=150$ (see table 1), there are locations on the particle surface, in particular at the front and at the sides, where $\unicode[STIX]{x1D716}_{\text{M}}$ exceeds the unladen value by a factor of more than 100. However, the maximum of $\unicode[STIX]{x1D701}_{\text{M}}$ is even larger than $\unicode[STIX]{x1D716}_{\text{M}}$ , more than twice as large for $p=1$ , and more than eight times as large for $p=2$ (see table 4). Compared to the first particle, the turbulence around the second particle is weaker, so that the maximum of $\unicode[STIX]{x1D716}_{\text{M}}$ is lower, but the particle Reynolds number $Re_{p,tot}$ is larger (table 1), which leads to a larger maximum of $\unicode[STIX]{x1D701}_{\text{M}}$ .

Figure 13. Profiles of moving-frame statistics for particle $p=1$ from fine-grid simulation T1 (blue solid) and coarse-grid simulation T2 (red dashed). The turbulence dissipation rate $\unicode[STIX]{x1D716}_{\text{M}}$ (circles) and the mean flow dissipation rate $\unicode[STIX]{x1D701}_{\text{M}}$ (triangles) on three axes through the particle centre: the $x_{2}$ axis (a), the $x_{3}$ axis (b) and the $x_{1}$ axis (c). TKE budget terms divided by $\unicode[STIX]{x1D716}_{\text{M}}$ on the $x_{1}$ axis are shown in (d): $C_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ (circles), $P_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ (squares), $T_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ (upward triangles), $\unicode[STIX]{x1D6F1}_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ (diamonds) and $D_{\text{M}}/\unicode[STIX]{x1D716}_{\text{M}}$ (downward triangles); the inset zooms in on the region near the front of the particle.

At the channel walls, $\unicode[STIX]{x1D701}_{\text{M}}=\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}_{2}\langle u_{1}\rangle _{\text{M}})^{2}$ . This is far away from particles, so that at $y^{+}=0$ , $\unicode[STIX]{x1D701}_{\text{M}}$ is virtually identical to the dissipation rate of the fixed-frame mean flow kinetic energy, defined by

(4.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}\rangle \langle \unicode[STIX]{x1D61A}_{ij}\rangle , & & \displaystyle\end{eqnarray}$$

and likewise the difference between $\unicode[STIX]{x1D716}_{\text{M}}$ and $\unicode[STIX]{x1D716}$ is negligible at the wall. Thus at the wall, we find $\unicode[STIX]{x1D701}_{\text{M}}\approx 176$ , approximately six times larger than $\unicode[STIX]{x1D716}_{\text{M}}$ at the wall. Thus also at that solid surface, the mean flow dissipation rate is much larger than the turbulence dissipation rate. It is possible to express the wall viscous length scale $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$ as a function of $\unicode[STIX]{x1D708}$ and the value of $\unicode[STIX]{x1D701}$ at the wall ( $\unicode[STIX]{x1D701}_{w}$ ): $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D701}_{w})^{1/4}$ . This expression is fully analogous to the expression for the Kolmogorov length scale, since the latter is obtained if $\unicode[STIX]{x1D701}_{w}$ is replaced by $\unicode[STIX]{x1D716}$ . It seems a logical step to also define a particle surface viscous length scale by $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708},p}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D701}_{\text{M}s})^{1/4}$ , where $\unicode[STIX]{x1D701}_{\text{M}s}$ denotes $\unicode[STIX]{x1D701}_{\text{M}}$ on the particle surface. This length scale depends on the position on the particle surface, and it is minimum at the location where $\unicode[STIX]{x1D701}_{\text{M}s}$ is maximum (a location on the surface of the second particle: see figure 12 d). This maximum is approximately 5000, so that the minimum $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708},p}$ equals $0.44\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708},0}$ , which is larger than $0.26\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708},0}$ , the grid spacing at the particle surface in case T1. Thus, although $\unicode[STIX]{x1D701}_{\text{M}}$ attains very large values at the particle surface, the small length scale associated with $\unicode[STIX]{x1D701}_{\text{M}}$ is resolved in case T1.

Figure 14. Profiles of spherical surface averages of moving-frame statistics for particle $p=1$ from fine-grid simulation T1 (blue solid) and coarse-grid simulation T2 (red dashed). (a) The turbulence dissipation rate $\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (circles) and the mean flow dissipation rate $\langle \unicode[STIX]{x1D701}_{\text{M}}\rangle _{\text{S}}$ (triangles) as a function of $r^{+}$ (the distance to the particle). (b) TKE budget terms divided by $\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ : $\langle C_{\text{M}}\rangle _{\text{S}}/\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (circles), $\langle P_{\text{M}}\rangle _{\text{S}}/\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (squares), $\langle T_{\text{M}}\rangle _{\text{S}}/\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (upward triangles), $\langle \unicode[STIX]{x1D6F1}_{\text{M}}\rangle _{\text{S}}/\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (diamonds) and $\langle D_{\text{M}}\rangle _{\text{S}}/\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ (downward triangles).

Profiles of both dissipation rates on the three Cartesian axes through the centre of the first particle are shown in figure 13. These profiles consist of overlapping segments from the spherical and Cartesian grids. Figure 13(a–c) shows that $\unicode[STIX]{x1D701}_{\text{M}}$ decays faster than $\unicode[STIX]{x1D716}_{\text{M}}$ with increasing distance from the particle. Furthermore, figure 13(c) indicates that $\unicode[STIX]{x1D716}_{\text{M}}$ and $\unicode[STIX]{x1D701}_{\text{M}}$ are much lower in the wake than the maxima at the sides (figure 13 a,b), but also that in the wake the radii of the regions where $\unicode[STIX]{x1D716}_{\text{M}}$ and $\unicode[STIX]{x1D701}_{\text{M}}$ are elevated extend to relatively far away from the particle. Figure 13(d) illustrates that, locally, the absolute values of convection, turbulence production and pressure diffusion terms can be much larger than the turbulence dissipation rate.

To further quantify the effects of the moving-frame statistics, it is useful to reduce them to one-dimensional profiles. This can be done in several ways: one way to do this is illustrated in figure 14, another way is introduced in the next section. The spherical surface average $\langle \cdot \rangle _{\text{S}}$ reduces the 3-D statistics to profiles that are only a function of the distance to the particle centre. The operator denotes averaging over the surface of the sphere with radius $r$ and with the same centre as the particle. The spherical surface average of the TKE budget in the moving frame of the first particle is shown in figure 14(b), after division by $\langle \unicode[STIX]{x1D716}_{\text{M}}\rangle _{\text{S}}$ , which is shown in figure 14(a). Figure 14(b) looks somewhat similar to the radial budget shown in Vreman (Reference Vreman2016). In that paper, isotropic turbulence with zero mean flow over the particle was simulated, and apart from small effects of the cubical structure of the dilute array, the statistical variation in polar and azimuthal directions did not play a role there. This implied that there was no convection term. Furthermore, there was also no energy produced by shear, but the production was due to a stochastic forcing of the large scales. However, that production term did look similar to $\langle P_{\text{M}}\rangle _{\text{S}}$ shown in figure 14(b), while also the radial profiles of pressure diffusion and viscous transport were qualitatively similar to those shown in figure 14(b). In contrast, transport had a different shape: it was positive near the particle, in fact similar to $\langle C_{\text{M}}\rangle _{\text{S}}$ in the present case, while the present $\langle T_{\text{M}}\rangle _{\text{S}}$ is negative close to the particle. In figure 14(b), the dominant transport term is turbulent transport for $r^{+}>13.5$ , convection for $9.5<r^{+}<13.5$ , pressure diffusion for $5<r^{+}<9.5$ , and viscous diffusion for $r_{0}^{+}=4<r^{+}<5$ .