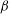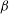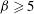1. Introduction
Cell membranes consist of different lipid molecules and proteins and they form a heterogeneous two-dimensional surface (Singer et al. Reference Singer and Nicolson1972; Engelman Reference Engelman2005). Sphingolipid and cholesterol-rich microdomains of the membrane, sometimes called rafts, diffuse on the membrane surface (Simons & Ikonen Reference Simons and Ikonen1997). The important roles played by rafts in different cell biological processes have been the focus of many studies on membrane biology and biophysics in the past (Brown & London Reference Brown and London1998; Ikonen Reference Ikonen2001). Recent studies put the proposed mechanisms of emergence of raft domains under scrutiny; however, the fact that there are cholesterol-rich microdomains that play a crucial role in cell functions is still valid. Furthermore, the motion or diffusion of these heterogeneous submicrometre size domains in the surrounding membrane surface is crucial for the cell functionality.
The size of the microdomains in cell membranes is of the order of a tenth of a micrometre, which makes it difficult to observe them under the optical microscope in live conditions. On the other hand, giant unilamellar vesicles (GUVs) consisting of phase-separated liquid-ordered and disordered domains are simpler model systems for cell membranes (Dietrich et al. Reference Dietrich, Bagatolli, Volovyk, Thompson, Levi, Jacobson and Gratton2001). These GUVs have domains that are rich in saturated lipids and cholesterol, have sizes in micrometre range (so that they can be observed via optical microscope) and move in the membrane surface.
In his pioneering work, Saffman (Reference Saffman1976) employed a hydrodynamic model to obtain the drag on a protein molecule moving in an incompressible lipid membrane sheet of viscosity
![]() ${\it\eta}$
and thickness
${\it\eta}$
and thickness
![]() $h$
. The protein was considered to be a rigid cylinder of height
$h$
. The protein was considered to be a rigid cylinder of height
![]() $h$
. The space above and below the membrane was filled up with a liquid of viscosity
$h$
. The space above and below the membrane was filled up with a liquid of viscosity
![]() ${\it\mu}_{s}$
that is less than the membrane viscosity
${\it\mu}_{s}$
that is less than the membrane viscosity
![]() ${\it\eta}$
. For the case when the cylinder radius
${\it\eta}$
. For the case when the cylinder radius
![]() $a$
is much smaller than the ratio
$a$
is much smaller than the ratio
![]() ${\it\eta}h/{\it\mu}_{s}$
the translational diffusion coefficient of the cylinder obtained by Saffman (Reference Saffman1976) is
${\it\eta}h/{\it\mu}_{s}$
the translational diffusion coefficient of the cylinder obtained by Saffman (Reference Saffman1976) is
where
![]() $k_{B}$
is Boltzmann’s constant,
$k_{B}$
is Boltzmann’s constant,
![]() $T$
is absolute temperature and
$T$
is absolute temperature and
![]() ${\it\gamma}$
is Euler’s constant. Later the diffusion coefficient for a rigid cylindrical particle of an arbitrary size was computed by Hughes, Pailthorpe & White (Reference Hughes, Pailthorpe and White1981) and Petrov & Schwille (Reference Petrov and Schwille2008). Evans & Sackmann (Reference Evans and Sackmann1988) obtained the diffusion constant of a rigid disk moving along a supported lipid bilayer. They considered the effect of the supporting fluid on the lipid bilayer with a momentum dissipation term proportional to the membrane fluid velocity in the momentum equation. In contrast, Stone & Ajdari (Reference Stone and Ajdari1998) obtained the diffusion coefficient for a rigid circular domain of the same thickness as that of a supported lipid bilayer by considering the viscous force of the supporting fluid on the lipid bilayer with a body force term in the corresponding momentum equation.
${\it\gamma}$
is Euler’s constant. Later the diffusion coefficient for a rigid cylindrical particle of an arbitrary size was computed by Hughes, Pailthorpe & White (Reference Hughes, Pailthorpe and White1981) and Petrov & Schwille (Reference Petrov and Schwille2008). Evans & Sackmann (Reference Evans and Sackmann1988) obtained the diffusion constant of a rigid disk moving along a supported lipid bilayer. They considered the effect of the supporting fluid on the lipid bilayer with a momentum dissipation term proportional to the membrane fluid velocity in the momentum equation. In contrast, Stone & Ajdari (Reference Stone and Ajdari1998) obtained the diffusion coefficient for a rigid circular domain of the same thickness as that of a supported lipid bilayer by considering the viscous force of the supporting fluid on the lipid bilayer with a body force term in the corresponding momentum equation.
When the domain is rigid and its size is small compared to the hydrodynamic length scale (
![]() $a\ll {\it\eta}h/{\it\mu}_{s}$
), the domain diffusion constant depends on the domain radius as
$a\ll {\it\eta}h/{\it\mu}_{s}$
), the domain diffusion constant depends on the domain radius as
![]() $\ln (1/a)$
(Saffman & Delbrück Reference Saffman and Delbrück1975; Saffman Reference Saffman1976). This has been validated experimentally (Hughes et al.
Reference Hughes, Pailthorpe, White and Sawyer1982; Peters & Cherry Reference Peters and Cherry1982; Lee & Petersen Reference Lee and Petersen2003; Cicuta, Keller & Veatch Reference Cicuta, Keller and Veatch2007). However, the experiments by Gambin et al. (Reference Gambin, Lopez-Esparza, Reffay, Sierecki, Gov, Genest, Hodges and Urbach2006) show that for a large range of protiens and protien clusters, the diffusion constant varies as
$\ln (1/a)$
(Saffman & Delbrück Reference Saffman and Delbrück1975; Saffman Reference Saffman1976). This has been validated experimentally (Hughes et al.
Reference Hughes, Pailthorpe, White and Sawyer1982; Peters & Cherry Reference Peters and Cherry1982; Lee & Petersen Reference Lee and Petersen2003; Cicuta, Keller & Veatch Reference Cicuta, Keller and Veatch2007). However, the experiments by Gambin et al. (Reference Gambin, Lopez-Esparza, Reffay, Sierecki, Gov, Genest, Hodges and Urbach2006) show that for a large range of protiens and protien clusters, the diffusion constant varies as
![]() $1/a$
, in contrast to
$1/a$
, in contrast to
![]() $\ln (1/a)$
as predicted by the theoretical results of Saffman & Delbrück (Reference Saffman and Delbrück1975) and Saffman (Reference Saffman1976). In support of the experimental results of Gambin et al. (Reference Gambin, Lopez-Esparza, Reffay, Sierecki, Gov, Genest, Hodges and Urbach2006), Naji, Levine & Pincus (Reference Naji, Levine and Pincus2007) reported that the membrane deformation in the neighbourhood of the particle reduces the diffusion constant. By using mesoscopic simulations Guigas & Weiss (Reference Guigas and Weiss2006) reported that the domain diffusion varies as
$\ln (1/a)$
as predicted by the theoretical results of Saffman & Delbrück (Reference Saffman and Delbrück1975) and Saffman (Reference Saffman1976). In support of the experimental results of Gambin et al. (Reference Gambin, Lopez-Esparza, Reffay, Sierecki, Gov, Genest, Hodges and Urbach2006), Naji, Levine & Pincus (Reference Naji, Levine and Pincus2007) reported that the membrane deformation in the neighbourhood of the particle reduces the diffusion constant. By using mesoscopic simulations Guigas & Weiss (Reference Guigas and Weiss2006) reported that the domain diffusion varies as
![]() $\ln (1/a)$
for the smaller domains, and when the domain size is larger than the hydrodynamic length scale the domain diffusion constant depends on the domain size as
$\ln (1/a)$
for the smaller domains, and when the domain size is larger than the hydrodynamic length scale the domain diffusion constant depends on the domain size as
![]() $1/a^{2}$
. However, the experimental results of Klingler & McConnell (Reference Klingler and McConnell1993) and Cicuta et al. (Reference Cicuta, Keller and Veatch2007) support the prediction of Hughes et al. (Reference Hughes, Pailthorpe and White1981) that the diffusion constant varies as
$1/a^{2}$
. However, the experimental results of Klingler & McConnell (Reference Klingler and McConnell1993) and Cicuta et al. (Reference Cicuta, Keller and Veatch2007) support the prediction of Hughes et al. (Reference Hughes, Pailthorpe and White1981) that the diffusion constant varies as
![]() $1/a$
when the domain radius is large compared to the hydrodynamic length scale.
$1/a$
when the domain radius is large compared to the hydrodynamic length scale.
In general, the liquid-ordered domains in vesicles or protein-rich microdomains in a cell membrane are large compared to the size of proteins; they are not rigid but rather fluid-like and their viscosity differs from the viscosity of the surrounding membrane. Towards this Ramachandran et al. (Reference Ramachandran, Komura, Imai and Seki2010) modelled the microdomain as a circular liquid domain with zero thickness moving in a 2D liquid membrane sheet. They obtained the finite diffusion coefficient of the liquid domain by considering the effect of surrounding fluid above and below the membrane plane through a momentum decay term in the momentum equation. Also recently, Seki, Ramachandran & Komura (Reference Seki, Ramachandran and Komura2011) obtained the diffusion coefficient of a liquid disk moving on a supported membrane sheet when the viscosities of the liquid disk and the membrane are the same. Seki, Mogre & Komura (Reference Seki, Mogre and Komura2014) studied the diffusion of a circular liquid domain moving along one of the monolayers with viscosity identical to the domain viscosity while considering the frictional resistance between the monolayers of the lipid bilayer. When the viscosity contrast, defined as the ratio of the difference between the viscosities of the domain and the surrounding membrane and the domain viscosity, is either zero or small, Fujitani (Reference Fujitani2011, Reference Fujitani2012, Reference Fujitani2013) derived approximate analytical expressions for the drag force on the liquid domain and thus the diffusion coefficient. To compute values of the drag force, certain integrals had to be evaluated numerically or further approximations had to be made.
All the above studies suffer from the limitation that either the domains are rigid, or they are too small in comparison to the hydrodynamic length scale, or they have very little viscosity contrast with the surrounding membrane. In the actual experimental scenario of the domains moving in a vesicle, none of these holds. For example, the domains have sizes in the
![]() ${\rm\mu}$
m range, their viscosity is approximately five times that of the surrounding disordered membrane and certainly the domains are not rigid. Recently, Aliaskarisohi et al. (Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010), have studied the diffusion of domains in a spherical vesicle surface and obtained an approximate series solution for the diffusion coefficient for a liquid domain. The authors observe that the diffusion of the domains is suppressed due to the confinement to the vesicle surface and the diffusion is dominated by the dissipation into the bulk fluid. The authors also mention the difficulty in applying their analysis to the case of a flat membrane as a large number of terms need to be retained in the series solution, leading to difficulty in numerical inversion of a matrix of extremely large size. The works of Aliaskarisohi et al. (Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010), Fujitani (Reference Fujitani2011, Reference Fujitani2012, Reference Fujitani2013) and Seki et al. (Reference Seki, Ramachandran and Komura2011, Reference Seki, Mogre and Komura2014) assumed the no-slip boundary condition at the membrane-surrounding fluid and the domain–membrane interfaces.
${\rm\mu}$
m range, their viscosity is approximately five times that of the surrounding disordered membrane and certainly the domains are not rigid. Recently, Aliaskarisohi et al. (Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010), have studied the diffusion of domains in a spherical vesicle surface and obtained an approximate series solution for the diffusion coefficient for a liquid domain. The authors observe that the diffusion of the domains is suppressed due to the confinement to the vesicle surface and the diffusion is dominated by the dissipation into the bulk fluid. The authors also mention the difficulty in applying their analysis to the case of a flat membrane as a large number of terms need to be retained in the series solution, leading to difficulty in numerical inversion of a matrix of extremely large size. The works of Aliaskarisohi et al. (Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010), Fujitani (Reference Fujitani2011, Reference Fujitani2012, Reference Fujitani2013) and Seki et al. (Reference Seki, Ramachandran and Komura2011, Reference Seki, Mogre and Komura2014) assumed the no-slip boundary condition at the membrane-surrounding fluid and the domain–membrane interfaces.
To understand the effect of different fluid viscosity on the domain diffusion in a lipid bilayer, Cicuta et al. (Reference Cicuta, Keller and Veatch2007) recorded the diffusion of circular liquid domains on the surface of GUVs. They reported that the diffusion coefficient of the circular liquid domain varies with the domain size and it is independent of the membrane viscosity when the membrane viscosity is less than the domain viscosity. In contrast, when the domain viscosity is less than the membrane viscosity, they observed that the domain diffusion depends on the membrane viscosity and the domain size. The experimental and theoretical observations of Cicuta et al. (Reference Cicuta, Keller and Veatch2007) and Aliaskarisohi et al. (Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010) motivated us to study the motion of a circular liquid domain moving in a flat liquid membrane sheet of different viscosity.
In our study, the membrane sheet spans to infinity, and the domain and the membrane are assumed to have the same thickness, remain flat and be surrounded by liquid of a different viscosity that spans to infinity above and below the membrane sheet. All the liquids are incompressible and subject to low-Reynolds-number flow such that the motion is governed by Stokes’ equation. The drag on the domain is obtained by solving Stokes’ equation for the two-dimensional membrane as well as the surrounding three-dimensional fluid. The resulting expressions for the drag force involve a set of dual integral equations, of Fredholm second kind. We employ a discrete collocation method (Atkinson Reference Atkinson1997) with approximations based on Chebyshev polynomials to numerically solve the dual integral equations.
Our computation of the drag coefficient (and mobility) is valid for arbitrary viscosity contrast between the domain and membrane as well as the membrane and fluid subject to the condition that the surrounding membrane curvature can be neglected. The numerical solution procedure is valid for arbitrary size, in principle. However, in practice, we obtain high accuracy when the Boussinesq number is larger than five. Our computation agrees with the experimental observation that when the domains are more viscous than their surrounding, the diffusion coefficient is almost independent of the viscosity contrast. However, for negative viscosity contrast, the dimensionless mobility (or equivalently the diffusion constant) is larger than the mobility when the domains are more viscous, it is sensitive to the viscosity contrast, and it does not vary logarithmically with the Boussinesq number. In fact, the mobility varies non-monotonically with the Boussinesq number when the viscosity contrast is large and negative. This is unlike the behaviour observed when the domains are more viscous or rigid. To our knowledge, this is a new observation and experiments need to be conducted to demonstrate the behaviour observed here for negative viscosity contrast. Upon choosing a suitable composition from the ternary phase diagram of a saturated lipid, an unsaturated lipid and cholesterol, we can prepare GUVs with coexisting liquid-ordered and disordered phases in which domains consisting of ordered phase are embedded in the disordered surrounding (Veatch & Keller Reference Veatch and Keller2005). In this case the viscosity contrast is positive. Further, by selecting different compositions along the tie-line of the ternary phase diagram of Veatch & Keller (Reference Veatch and Keller2005), we can make domains enriched with disordered phase in a surrounding consisting of ordered phase. In this scenario the viscosity contrast becomes negative and it is possible to prepare experimental systems in which the viscosity contrast is less than
![]() $-5$
(i.e. large in magnitude).
$-5$
(i.e. large in magnitude).
2. Problem formulation
A circular liquid domain of size
![]() $a$
and viscosity
$a$
and viscosity
![]() ${\it\eta}_{d}$
moves with velocity
${\it\eta}_{d}$
moves with velocity
![]() $U$
along
$U$
along
![]() $X$
-axis in a flat fluid membrane sheet of viscosity
$X$
-axis in a flat fluid membrane sheet of viscosity
![]() ${\it\eta}_{m}$
. The space above and below the domain and membrane sheet is occupied by a liquid with viscosity
${\it\eta}_{m}$
. The space above and below the domain and membrane sheet is occupied by a liquid with viscosity
![]() ${\it\mu}_{s}$
. A schematic diagram of the system is shown in figure 1. All the fluids considered are incompressible and undergo low-Reynolds-number flow.
${\it\mu}_{s}$
. A schematic diagram of the system is shown in figure 1. All the fluids considered are incompressible and undergo low-Reynolds-number flow.

Figure 1. Schematic diagram of a circular liquid domain of size
![]() $a$
and thickness
$a$
and thickness
![]() $h$
moving with velocity
$h$
moving with velocity
![]() $U$
along the
$U$
along the
![]() $X$
-axis in a membrane sheet of the same thickness. The viscosities of the domain, the surrounding membrane and the surrounding fluid are
$X$
-axis in a membrane sheet of the same thickness. The viscosities of the domain, the surrounding membrane and the surrounding fluid are
![]() ${\it\eta}_{d}$
,
${\it\eta}_{d}$
,
![]() ${\it\eta}_{m}$
and
${\it\eta}_{m}$
and
![]() ${\it\mu}_{s}$
, respectively. The schematic diagram on the right is the sectional view in the
${\it\mu}_{s}$
, respectively. The schematic diagram on the right is the sectional view in the
![]() $x{-}z$
plane. Both the membrane and the surrounding fluid span to infinity in their respective directions.
$x{-}z$
plane. Both the membrane and the surrounding fluid span to infinity in their respective directions.
The governing equations for various domains are as follows. For the 3D fluid above (
![]() $z>0$
) and below (
$z>0$
) and below (
![]() $z<h$
) the membrane sheet, including the domain, we have
$z<h$
) the membrane sheet, including the domain, we have
where
![]() $\boldsymbol{v}(r,{\it\theta},z)=(v_{r},v_{{\it\theta}},v_{z})$
and
$\boldsymbol{v}(r,{\it\theta},z)=(v_{r},v_{{\it\theta}},v_{z})$
and
![]() $p(r,{\it\theta},z)$
are the velocity and pressure fields in the surrounding fluid, respectively. The
$p(r,{\it\theta},z)$
are the velocity and pressure fields in the surrounding fluid, respectively. The
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() $\boldsymbol{{\rm\nabla}}$
are the Laplacian and the gradient operators, respectively. For the membrane and domain liquid (
$\boldsymbol{{\rm\nabla}}$
are the Laplacian and the gradient operators, respectively. For the membrane and domain liquid (
![]() $-h\leqslant z\leqslant 0$
), the variation of the quantities across the thickness direction is precluded due to its molecular structure. Further, because of the symmetry about the mid-plane of the membrane we assume that the velocity in the
$-h\leqslant z\leqslant 0$
), the variation of the quantities across the thickness direction is precluded due to its molecular structure. Further, because of the symmetry about the mid-plane of the membrane we assume that the velocity in the
![]() $z$
direction is zero. Thus for the in-plane motion in the domain and the surrounding membrane we have (Saffman Reference Saffman1976)
$z$
direction is zero. Thus for the in-plane motion in the domain and the surrounding membrane we have (Saffman Reference Saffman1976)
where
![]() $\boldsymbol{u}(r,{\it\theta})=(u_{r},\;u_{{\it\theta}},\;0)$
and
$\boldsymbol{u}(r,{\it\theta})=(u_{r},\;u_{{\it\theta}},\;0)$
and
![]() ${\it\Pi}(r,{\it\theta})$
are the velocity and pressure fields, respectively, and
${\it\Pi}(r,{\it\theta})$
are the velocity and pressure fields, respectively, and
![]() ${\it\sigma}$
is the traction (or drag) applied on the top and bottom surfaces of the membrane and domain by the surrounding fluid. No-slip boundary conditions at the membrane-surrounding liquid and domain–membrane interfaces are applied and the velocity decays to zero at infinity for both the membrane and the surrounding fluid. Note that the no-slip boundary condition at the membrane-surrounding liquid interface leads to the following relations between the velocity fields in the surrounding fluid and the domain/membrane:
${\it\sigma}$
is the traction (or drag) applied on the top and bottom surfaces of the membrane and domain by the surrounding fluid. No-slip boundary conditions at the membrane-surrounding liquid and domain–membrane interfaces are applied and the velocity decays to zero at infinity for both the membrane and the surrounding fluid. Note that the no-slip boundary condition at the membrane-surrounding liquid interface leads to the following relations between the velocity fields in the surrounding fluid and the domain/membrane:
The incompressibility conditions for the surrounding and membrane fluids are separately imposed (see equation (2.8) of Saffman (Reference Saffman1976) and equation (2.22) of Fujitani (Reference Fujitani2011)). However, it is worth mentioning that as both the domain and its surrounding are assumed to be incompressible fluids, the in-plane flow field must be divergence-free at the domain boundary. This condition has not been imposed in the present study.
Equations (2.1) and (2.2), along with the boundary conditions, can be solved analytically for the pressure and velocity fields by exploiting the rotational symmetry about the
![]() $z$
-axis and use of Fourier and Hankel transforms (Saffman Reference Saffman1976; Fujitani Reference Fujitani2011). The contributions to the drag force on the circular liquid domain moving with a steady velocity
$z$
-axis and use of Fourier and Hankel transforms (Saffman Reference Saffman1976; Fujitani Reference Fujitani2011). The contributions to the drag force on the circular liquid domain moving with a steady velocity
![]() $U$
come from the tangential components of the tractions applied to the domain by the surrounding membrane at the cylindrical interface (at
$U$
come from the tangential components of the tractions applied to the domain by the surrounding membrane at the cylindrical interface (at
![]() $r=a$
) and by the surrounding fluid at the top and bottom circular interfaces of radius
$r=a$
) and by the surrounding fluid at the top and bottom circular interfaces of radius
![]() $a$
. The expression for the magnitude of the drag force is given by the integral
$a$
. The expression for the magnitude of the drag force is given by the integral
where
![]() $\tilde{r}=r/a$
dimensionless radial distance and
$\tilde{r}=r/a$
dimensionless radial distance and
![]() $A(z)$
is an as yet undetermined function. The details of the derivation of (2.4) have been omitted here to avoid repetition. They are available in Fujitani (Reference Fujitani2011). The quantity
$A(z)$
is an as yet undetermined function. The details of the derivation of (2.4) have been omitted here to avoid repetition. They are available in Fujitani (Reference Fujitani2011). The quantity
![]() $A(z)$
is obtained, in principle, by solving the following two integral equations:
$A(z)$
is obtained, in principle, by solving the following two integral equations:
and
where
![]() $c$
is an unknown constant,
$c$
is an unknown constant,
![]() ${\it\beta}={\it\eta}_{m}/(2{\it\mu}_{s}a)$
is the Boussinesq number representing the ratio between the membrane drag and surrounding fluid drag,
${\it\beta}={\it\eta}_{m}/(2{\it\mu}_{s}a)$
is the Boussinesq number representing the ratio between the membrane drag and surrounding fluid drag,
![]() ${\it\epsilon}=({\it\eta}_{d}-{\it\eta}_{m})/{\it\eta}_{d}$
denotes the relative viscosity contrast between the domain and the surrounding membrane, and
${\it\epsilon}=({\it\eta}_{d}-{\it\eta}_{m})/{\it\eta}_{d}$
denotes the relative viscosity contrast between the domain and the surrounding membrane, and
![]() $\text{J}_{i}(z)$
is the Bessel function of
$\text{J}_{i}(z)$
is the Bessel function of
![]() $i$
th order and first kind. Note that, typically,
$i$
th order and first kind. Note that, typically,
![]() $0\leqslant {\it\epsilon}\leqslant 1$
, and
$0\leqslant {\it\epsilon}\leqslant 1$
, and
![]() ${\it\epsilon}=0$
indicates that the domain and membrane have same viscosity while
${\it\epsilon}=0$
indicates that the domain and membrane have same viscosity while
![]() ${\it\epsilon}=1$
implies that the domain is rigid or the membrane viscosity is very small in comparison to the domain viscosity. Further, for
${\it\epsilon}=1$
implies that the domain is rigid or the membrane viscosity is very small in comparison to the domain viscosity. Further, for
![]() ${\it\epsilon}<0$
the surrounding membrane has higher viscosity than the domain, which is not the case in general. However, it is possible to make two-phase lipid bilayer vesicles in the laboratory with appropriately chosen lipid composition such that the domain viscosity is smaller than the surrounding. A typical value of
${\it\epsilon}<0$
the surrounding membrane has higher viscosity than the domain, which is not the case in general. However, it is possible to make two-phase lipid bilayer vesicles in the laboratory with appropriately chosen lipid composition such that the domain viscosity is smaller than the surrounding. A typical value of
![]() ${\it\epsilon}$
is
${\it\epsilon}$
is
![]() $4/5$
and
$4/5$
and
![]() $0.2<{\it\beta}<1000$
(considering
$0.2<{\it\beta}<1000$
(considering
![]() $10^{-9}<{\it\eta}_{m}<10^{-6}~\text{N}~\text{s}~\text{m}^{-1}$
and
$10^{-9}<{\it\eta}_{m}<10^{-6}~\text{N}~\text{s}~\text{m}^{-1}$
and
![]() $0.5<a<2.5~{\rm\mu}\text{m}$
(Brooks et al.
Reference Brooks, Fuller, Frank and Robertson1999; Cicuta et al.
Reference Cicuta, Keller and Veatch2007; Aliaskarisohi et al.
Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010; Stanich et al.
Reference Stanich, Honerkamp-Smith, Putzel, Warth, Lamprecht, Mandal, Mann, Hua and Keller2013)).
$0.5<a<2.5~{\rm\mu}\text{m}$
(Brooks et al.
Reference Brooks, Fuller, Frank and Robertson1999; Cicuta et al.
Reference Cicuta, Keller and Veatch2007; Aliaskarisohi et al.
Reference Aliaskarisohi, Tierno, Dhar, Khattari, Blaszczynski and Fischer2010; Stanich et al.
Reference Stanich, Honerkamp-Smith, Putzel, Warth, Lamprecht, Mandal, Mann, Hua and Keller2013)).
Equations (2.4)–(2.6) complete the description to obtain the drag force on the domain, and subsequently the diffusion coefficient or mobility of the domain. However, the main difficulty lies in solving the dual integral equations (2.5) and (2.6), particularly when the viscosity contrast is neither zero nor unity. For
![]() ${\it\epsilon}=0$
, the solution to the integral equation (2.5) is exact and is given by
${\it\epsilon}=0$
, the solution to the integral equation (2.5) is exact and is given by
![]() $A(z)=2acU\,\text{J}_{1}(z)/{\rm\pi}z$
, and through the subsequent use of (2.6) the constant
$A(z)=2acU\,\text{J}_{1}(z)/{\rm\pi}z$
, and through the subsequent use of (2.6) the constant
![]() $c$
can be evaluated. For
$c$
can be evaluated. For
![]() ${\it\epsilon}\ll 1$
, Fujitani (Reference Fujitani2011) obtained a semi-analytical solution to (2.5). However, when
${\it\epsilon}\ll 1$
, Fujitani (Reference Fujitani2011) obtained a semi-analytical solution to (2.5). However, when
![]() ${\it\epsilon}$
is not very small, the dual integral equations (2.5) and (2.6) are not analytically tractable. To our knowledge, no numerical solution is available either. We develop a simple algorithm to obtain a numerical solution to (2.5) and (2.6) using the discrete collocation method (Atkinson Reference Atkinson1997) and Chebyshev polynomials. We first introduce a new variable
${\it\epsilon}$
is not very small, the dual integral equations (2.5) and (2.6) are not analytically tractable. To our knowledge, no numerical solution is available either. We develop a simple algorithm to obtain a numerical solution to (2.5) and (2.6) using the discrete collocation method (Atkinson Reference Atkinson1997) and Chebyshev polynomials. We first introduce a new variable
![]() $B(z)=zA(z)$
and rewrite (2.5) and (2.6) as
$B(z)=zA(z)$
and rewrite (2.5) and (2.6) as
and
where
Equation (2.7) is in the form of a Fredholm equation of second kind. The drag force in terms of the new variable
![]() $B(z)$
is
$B(z)$
is
The expression (2.10) for the drag force in terms of the new variable
![]() $B(z)$
eliminates the possibility of the integrand taking prohibitively large values when
$B(z)$
eliminates the possibility of the integrand taking prohibitively large values when
![]() $z$
is large, making the numerical computation of the integral easier. In the following, we describe the numerical solution procedure for (2.7) and (2.8).
$z$
is large, making the numerical computation of the integral easier. In the following, we describe the numerical solution procedure for (2.7) and (2.8).
3. Numerical solution of Fredholm integral equation
To solve (2.7), we need to map the infinite domain
![]() $[0,\infty )$
to a finite domain (see Collocation Theorem 2.6.2 of Zemyan (Reference Zemyan2012)). To achieve this, we define the change of variable
$[0,\infty )$
to a finite domain (see Collocation Theorem 2.6.2 of Zemyan (Reference Zemyan2012)). To achieve this, we define the change of variable
![]() $z=\tan [(X+1){\rm\pi}/4]$
, and rewrite (2.7) and (2.8) as
$z=\tan [(X+1){\rm\pi}/4]$
, and rewrite (2.7) and (2.8) as
and
respectively. In the above
![]() $t(Y)=\tan [(Y+1){\rm\pi}/4]$
and the values of
$t(Y)=\tan [(Y+1){\rm\pi}/4]$
and the values of
![]() $X$
and
$X$
and
![]() $Y$
lie in the finite domain
$Y$
lie in the finite domain
![]() $[-1,1]$
.
$[-1,1]$
.
Now we can approximate
![]() $B(X)$
using a set of
$B(X)$
using a set of
![]() $n$
linearly independent functions that are continuous in
$n$
linearly independent functions that are continuous in
![]() $[-1,1]$
(Zemyan Reference Zemyan2012). We choose Chebyshev polynomials for this purpose:
$[-1,1]$
(Zemyan Reference Zemyan2012). We choose Chebyshev polynomials for this purpose:
where
![]() $T_{i}(X)$
is the Chebyshev polynomial of first kind with degree
$T_{i}(X)$
is the Chebyshev polynomial of first kind with degree
![]() $i$
. Note that the number of collocation points is same as the number of Chebyshev polynomials used to approximate
$i$
. Note that the number of collocation points is same as the number of Chebyshev polynomials used to approximate
![]() $B(X)$
. By substituting (3.3) into (3.1), we obtain
$B(X)$
. By substituting (3.3) into (3.1), we obtain
The most convenient choice of the collocation points for (3.4) are the zeros of the
![]() $n$
th degree Chebyshev polynomial, and with this choice we obtain a system of
$n$
th degree Chebyshev polynomial, and with this choice we obtain a system of
![]() $n$
linear equations with
$n$
linear equations with
![]() $n$
unknown Chebyshev coefficients:
$n$
unknown Chebyshev coefficients:
where
![]() $\bar{\unicode[STIX]{x1D651}}$
and
$\bar{\unicode[STIX]{x1D651}}$
and
![]() $\bar{\unicode[STIX]{x1D64F}}$
are
$\bar{\unicode[STIX]{x1D64F}}$
are
![]() $n\times n$
matrices with elements
$n\times n$
matrices with elements
![]() $v_{i,j}=\int _{-1}^{1}\,\text{d}Y\sec ^{2}[(Y+1){\rm\pi}/4]M(z_{j},t)\times T_{i-1}(Y)$
and
$v_{i,j}=\int _{-1}^{1}\,\text{d}Y\sec ^{2}[(Y+1){\rm\pi}/4]M(z_{j},t)\times T_{i-1}(Y)$
and
![]() $t_{i,j}=T_{i-1}(X_{j})$
, respectively, and
$t_{i,j}=T_{i-1}(X_{j})$
, respectively, and
![]() $X_{j}$
are the collocation points. The elements of the
$X_{j}$
are the collocation points. The elements of the
![]() $n\times 1$
array
$n\times 1$
array
![]() $\boldsymbol{b}$
of Chebyshev coefficients are
$\boldsymbol{b}$
of Chebyshev coefficients are
![]() $b_{i}=B_{i}{\rm\pi}/2acU$
, and
$b_{i}=B_{i}{\rm\pi}/2acU$
, and
![]() $r_{j}=\text{J}_{1}(z_{j})$
are the elements of the
$r_{j}=\text{J}_{1}(z_{j})$
are the elements of the
![]() $n\times 1$
array
$n\times 1$
array
![]() $\boldsymbol{R}$
.
$\boldsymbol{R}$
.
We use the Gauss–Chebyshev quadrature method (Mason & Handscomb Reference Mason and Handscomb2010) to compute the elements
![]() $v_{i,j}$
:
$v_{i,j}$
:
where the
![]() $Y_{k}$
are the zeros of the
$Y_{k}$
are the zeros of the
![]() $n$
th degree Chebyshev polynomial. Substituting the expression
$n$
th degree Chebyshev polynomial. Substituting the expression
![]() $v_{i,j}$
obtained from (3.6) into (3.5) and solving for
$v_{i,j}$
obtained from (3.6) into (3.5) and solving for
![]() $\boldsymbol{b}$
, we obtain the Chebyshev coefficients
$\boldsymbol{b}$
, we obtain the Chebyshev coefficients
![]() $B_{i}$
in terms of the unknown constant
$B_{i}$
in terms of the unknown constant
![]() $c$
. To calculate
$c$
. To calculate
![]() $c$
, we substitute the Chebyshev polynomial approximation of function
$c$
, we substitute the Chebyshev polynomial approximation of function
![]() $B(X)$
, given by (3.3), into (3.2) and obtain
$B(X)$
, given by (3.3), into (3.2) and obtain
 $$\begin{eqnarray}c=4{\it\mu}_{s}a\left/\left\{\frac{{\rm\pi}}{n}\mathop{\sum }_{i=1}^{n}\mathop{\sum }_{k=1}^{n}\left[\frac{\displaystyle \sqrt{1-Y_{k}^{2}}\sec ^{2}\left[(Y_{k}+1)\frac{{\rm\pi}}{4}\right]b_{i}T_{i-1}(Y_{k})\text{J}_{1}(Y_{k})}{t_{k}^{2}(1+{\it\beta}t_{k})}\right]\right\}\right..\end{eqnarray}$$
$$\begin{eqnarray}c=4{\it\mu}_{s}a\left/\left\{\frac{{\rm\pi}}{n}\mathop{\sum }_{i=1}^{n}\mathop{\sum }_{k=1}^{n}\left[\frac{\displaystyle \sqrt{1-Y_{k}^{2}}\sec ^{2}\left[(Y_{k}+1)\frac{{\rm\pi}}{4}\right]b_{i}T_{i-1}(Y_{k})\text{J}_{1}(Y_{k})}{t_{k}^{2}(1+{\it\beta}t_{k})}\right]\right\}\right..\end{eqnarray}$$
Note that we use the Gauss–Chebyshev quadrature method to compute the integral appearing in (3.2). Using the results of (3.5) and (3.7), and substituting (3.3) into (2.10), we obtain the approximation to the drag force
![]() $F$
on the circular liquid domain of radius
$F$
on the circular liquid domain of radius
![]() $a$
as
$a$
as
We decompose the domain of integration appearing in (3.8) into two parts:
Exploiting the boundedness of
![]() $T_{i}(\boldsymbol{\cdot })$
and the exponentially decaying behaviour
$T_{i}(\boldsymbol{\cdot })$
and the exponentially decaying behaviour
![]() $\text{J}_{2}(z\tilde{r})$
for large
$\text{J}_{2}(z\tilde{r})$
for large
![]() $z$
, we choose a
$z$
, we choose a
![]() $U_{L}<\infty$
such that the second integral in (3.9) is small and can be neglected in comparison with the first integral. Finally, the expression for the drag force becomes
$U_{L}<\infty$
such that the second integral in (3.9) is small and can be neglected in comparison with the first integral. Finally, the expression for the drag force becomes
The above integral is evaluated using Simpson’s rule.
4. Results and discussion
To compute the drag force
![]() $F$
using (3.10), we need to choose the number of Chebyshev polynomials (or collocation points)
$F$
using (3.10), we need to choose the number of Chebyshev polynomials (or collocation points)
![]() $n$
, the upper limit of integration
$n$
, the upper limit of integration
![]() $U_{L}$
, and the step size
$U_{L}$
, and the step size
![]() $h$
in Simpson’s rule. Furthermore, we need to choose an appropriate value of
$h$
in Simpson’s rule. Furthermore, we need to choose an appropriate value of
![]() $\tilde{r}$
larger than but close to unity to replace the limit
$\tilde{r}$
larger than but close to unity to replace the limit
![]() $\tilde{r}\rightarrow 1^{+}$
. We carry out convergence studies for the drag force
$\tilde{r}\rightarrow 1^{+}$
. We carry out convergence studies for the drag force
![]() $F$
with respect to the parameters. Further, we compute the error in the drag force for two limiting cases in which the analytical solution is available. They are
$F$
with respect to the parameters. Further, we compute the error in the drag force for two limiting cases in which the analytical solution is available. They are
![]() ${\it\epsilon}=0$
(viscosity of domain and membrane are the same (Fujitani Reference Fujitani2011)) and
${\it\epsilon}=0$
(viscosity of domain and membrane are the same (Fujitani Reference Fujitani2011)) and
![]() ${\it\epsilon}=1$
(the domain is rigid (Hughes et al.
Reference Hughes, Pailthorpe and White1981; Petrov & Schwille Reference Petrov and Schwille2008)).
${\it\epsilon}=1$
(the domain is rigid (Hughes et al.
Reference Hughes, Pailthorpe and White1981; Petrov & Schwille Reference Petrov and Schwille2008)).
4.1. Validation of the numerical method for a domain with the same viscosity as the surrounding membrane (
 ${\it\epsilon}=0$
) and a rigid domain (
${\it\epsilon}=0$
) and a rigid domain (
 ${\it\epsilon}=1$
)
${\it\epsilon}=1$
)
For
![]() ${\it\epsilon}=0$
the viscosities of the domain and the surrounding membrane are the same. In this case, from (2.7) we obtain
${\it\epsilon}=0$
the viscosities of the domain and the surrounding membrane are the same. In this case, from (2.7) we obtain
![]() $B(X)=2acU\,\text{J}_{1}(X)/{\rm\pi}$
and the drag force on the liquid domain given by (Fujitani Reference Fujitani2011)
$B(X)=2acU\,\text{J}_{1}(X)/{\rm\pi}$
and the drag force on the liquid domain given by (Fujitani Reference Fujitani2011)
where
 $$\begin{eqnarray}c={\displaystyle \frac{{\rm\pi}{\it\mu}_{s}a}{\displaystyle \int _{0}^{\infty }\,\text{d}z{\displaystyle \frac{\text{J}_{1}^{2}(z)}{(z^{2}+{\it\beta}z^{3})}}}}.\end{eqnarray}$$
$$\begin{eqnarray}c={\displaystyle \frac{{\rm\pi}{\it\mu}_{s}a}{\displaystyle \int _{0}^{\infty }\,\text{d}z{\displaystyle \frac{\text{J}_{1}^{2}(z)}{(z^{2}+{\it\beta}z^{3})}}}}.\end{eqnarray}$$
In figure 2 we present the variation in the ratio
![]() $F/2cU$
computed numerically using (3.10) with respect to the parameters
$F/2cU$
computed numerically using (3.10) with respect to the parameters
![]() $U_{L}$
,
$U_{L}$
,
![]() $1/h$
,
$1/h$
,
![]() $\tilde{r}$
and
$\tilde{r}$
and
![]() $n$
. Note that the integral
$n$
. Note that the integral
![]() $\lim _{\tilde{r}\rightarrow 1^{+}}\int _{0}^{\infty }\,\text{d}z\,\text{J}_{1}(z)\text{J}_{2}(\tilde{r}z)=1$
, and consequently the ratio
$\lim _{\tilde{r}\rightarrow 1^{+}}\int _{0}^{\infty }\,\text{d}z\,\text{J}_{1}(z)\text{J}_{2}(\tilde{r}z)=1$
, and consequently the ratio
![]() $F/2cU$
is unity and independent of
$F/2cU$
is unity and independent of
![]() ${\it\beta}$
. Upon observing the convergence and the closeness of the ratio to unity we find the following parameter values:
${\it\beta}$
. Upon observing the convergence and the closeness of the ratio to unity we find the following parameter values:
![]() $n=12\,000,\tilde{r}=1.009$
,
$n=12\,000,\tilde{r}=1.009$
,
![]() $U_{L}=6000,h=0.05$
. However, we also find from figure 2(d) that the ratio is closest to unity for
$U_{L}=6000,h=0.05$
. However, we also find from figure 2(d) that the ratio is closest to unity for
![]() $n=4000$
as well. Thus to save computational time we finally choose
$n=4000$
as well. Thus to save computational time we finally choose
![]() $n=4000,\tilde{r}=1.009,U_{L}=6000$
and
$n=4000,\tilde{r}=1.009,U_{L}=6000$
and
![]() $h=0.05$
for calculating the drag force.
$h=0.05$
for calculating the drag force.

Figure 2. Variation of
![]() $F/2cU$
for
$F/2cU$
for
![]() ${\it\epsilon}=0$
(a) with
${\it\epsilon}=0$
(a) with
![]() $U_{L}$
for
$U_{L}$
for
![]() $\tilde{r}=1.009$
,
$\tilde{r}=1.009$
,
![]() $n=4000,h=0.05$
, (b) with
$n=4000,h=0.05$
, (b) with
![]() $1/h$
for
$1/h$
for
![]() $\tilde{r}=1.009,n=4000,U_{L}=6000$
, (c) with
$\tilde{r}=1.009,n=4000,U_{L}=6000$
, (c) with
![]() $\tilde{r}$
for
$\tilde{r}$
for
![]() $n=4000,U_{L}=6000,h=0.05$
and (d) with
$n=4000,U_{L}=6000,h=0.05$
and (d) with
![]() $n$
for
$n$
for
![]() $\tilde{r}=1.009,U_{L}=6000,h=0.05$
.
$\tilde{r}=1.009,U_{L}=6000,h=0.05$
.
After fixing these parameters, we compute the constant
![]() $c$
using (3.7) and compare it with the exact solution (4.2) for different
$c$
using (3.7) and compare it with the exact solution (4.2) for different
![]() ${\it\beta}$
. The integral in (4.2) is evaluated using the software Mathematica. In figure 3(a,b), we present the variation in the error in
${\it\beta}$
. The integral in (4.2) is evaluated using the software Mathematica. In figure 3(a,b), we present the variation in the error in
![]() $c$
and percentage error in
$c$
and percentage error in
![]() $F/{\it\mu}_{s}aU$
with
$F/{\it\mu}_{s}aU$
with
![]() ${\it\beta}$
. We observe that up to
${\it\beta}$
. We observe that up to
![]() ${\it\beta}=10^{7}$
the error in
${\it\beta}=10^{7}$
the error in
![]() $c$
is small and the percentage error in
$c$
is small and the percentage error in
![]() $F$
is below 0.05 %. Thus we claim that our method can approximate the drag force on the liquid domain accurately.
$F$
is below 0.05 %. Thus we claim that our method can approximate the drag force on the liquid domain accurately.

Figure 3. Error in calculation of constant
![]() $c$
versus
$c$
versus
![]() $\log {\it\beta}$
for
$\log {\it\beta}$
for
![]() ${\it\epsilon}=0$
. The parameters are
${\it\epsilon}=0$
. The parameters are
![]() $n=4000,\,U_{L}=6000$
and
$n=4000,\,U_{L}=6000$
and
![]() $h=0.05$
.
$h=0.05$
.
For the case of a rigid domain, Petrov & Schwille (Reference Petrov and Schwille2008) derived a simple analytical expression for the drag force for the solution developed by Hughes et al. (Reference Hughes, Pailthorpe and White1981). In figure 4 we present the variation of the error in dimensionless drag force (
![]() $F/{\it\mu}_{s}aU$
) for
$F/{\it\mu}_{s}aU$
) for
![]() ${\it\beta}=10$
calculated using (3.10) with respect to the parameters
${\it\beta}=10$
calculated using (3.10) with respect to the parameters
![]() $U_{L},\,1/h,\,\tilde{r}$
and
$U_{L},\,1/h,\,\tilde{r}$
and
![]() $n$
. The drag force computed by Petrov & Schwille (Reference Petrov and Schwille2008) has been taken as the benchmark. We observe that the error is minimum when
$n$
. The drag force computed by Petrov & Schwille (Reference Petrov and Schwille2008) has been taken as the benchmark. We observe that the error is minimum when
![]() $\tilde{r}=1.014$
,
$\tilde{r}=1.014$
,
![]() $n=4000$
,
$n=4000$
,
![]() $h=0.06$
and
$h=0.06$
and
![]() $U_{L}=6000$
and we choose these parameter values for computing the drag force on the domain. The variation of the error and the percentage error in the dimensionless drag force
$U_{L}=6000$
and we choose these parameter values for computing the drag force on the domain. The variation of the error and the percentage error in the dimensionless drag force
![]() $F/{\it\mu}_{s}aU$
with respect to
$F/{\it\mu}_{s}aU$
with respect to
![]() ${\it\beta}$
have been presented in figure 5(a,b), respectively. The error initially decreases with
${\it\beta}$
have been presented in figure 5(a,b), respectively. The error initially decreases with
![]() ${\it\beta}$
and then increases almost linearly. However, the percentage error asymptotically reaches a constant value of around 2.5 % (see inset of figure 5
b). Further, the percentage error is large for
${\it\beta}$
and then increases almost linearly. However, the percentage error asymptotically reaches a constant value of around 2.5 % (see inset of figure 5
b). Further, the percentage error is large for
![]() ${\it\beta}$
less than 5, and is around 5 % or below for
${\it\beta}$
less than 5, and is around 5 % or below for
![]() ${\it\beta}$
larger than 5. Thus we say that our method is accurate for larger values of
${\it\beta}$
larger than 5. Thus we say that our method is accurate for larger values of
![]() ${\it\beta}$
when
${\it\beta}$
when
![]() ${\it\epsilon}$
is unity.
${\it\epsilon}$
is unity.

Figure 4. Variation of the error in
![]() $F/{\it\mu}_{s}aU$
(a) with
$F/{\it\mu}_{s}aU$
(a) with
![]() $U_{L}$
for
$U_{L}$
for
![]() $\tilde{r}=1.014$
,
$\tilde{r}=1.014$
,
![]() $n=4000,h=0.06$
, (b) with
$n=4000,h=0.06$
, (b) with
![]() $1/h$
for
$1/h$
for
![]() $\tilde{r}=1.014$
,
$\tilde{r}=1.014$
,
![]() $n=4000,U_{L}=6000$
, (c) with
$n=4000,U_{L}=6000$
, (c) with
![]() $\tilde{r}$
for
$\tilde{r}$
for
![]() $n=4000,U_{L}=6000,h=0.06$
and (d) with
$n=4000,U_{L}=6000,h=0.06$
and (d) with
![]() $n$
for
$n$
for
![]() $\tilde{r}=1.014$
,
$\tilde{r}=1.014$
,
![]() $U_{L}=6000$
,
$U_{L}=6000$
,
![]() $h=0.06$
. In all the above cases
$h=0.06$
. In all the above cases
![]() ${\it\beta}=10$
and
${\it\beta}=10$
and
![]() ${\it\epsilon}=1$
.
${\it\epsilon}=1$
.

Figure 5. Variation of the error and percentage error in
![]() $F/{\it\mu}_{s}aU$
versus
$F/{\it\mu}_{s}aU$
versus
![]() ${\it\beta}$
for
${\it\beta}$
for
![]() ${\it\epsilon}=1$
. The parameters are
${\it\epsilon}=1$
. The parameters are
![]() $n=4000,\tilde{r}=1.014,U_{L}=6000,h=0.06$
.
$n=4000,\tilde{r}=1.014,U_{L}=6000,h=0.06$
.
For
![]() ${\it\epsilon}$
other than zero or unity, we do not have any analytical or existing results to compare. We carry out convergence studies for the drag force with respect to the parameters
${\it\epsilon}$
other than zero or unity, we do not have any analytical or existing results to compare. We carry out convergence studies for the drag force with respect to the parameters
![]() $U_{L}$
,
$U_{L}$
,
![]() $h$
,
$h$
,
![]() $\tilde{r}$
and
$\tilde{r}$
and
![]() $n$
for a few values of
$n$
for a few values of
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\beta}$
and obtain the same parameter values at convergence. The values of
${\it\beta}$
and obtain the same parameter values at convergence. The values of
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\beta}$
selected for convergence studies lie in a large range. Thus for subsequent studies we select
${\it\beta}$
selected for convergence studies lie in a large range. Thus for subsequent studies we select
![]() $n=4000,\tilde{r}=1.014,U_{L}=6000$
,
$n=4000,\tilde{r}=1.014,U_{L}=6000$
,
![]() $h=0.06$
.
$h=0.06$
.
4.2. Drag on the domain for arbitrary
 ${\it\epsilon}$
${\it\epsilon}$
In figure 6(a,b) we present the variation of the dimensionless drag force with the Boussinesq number
![]() ${\it\beta}$
for several values of the viscosity contrast
${\it\beta}$
for several values of the viscosity contrast
![]() ${\it\epsilon}$
between the domain and surrounding membrane. The values of
${\it\epsilon}$
between the domain and surrounding membrane. The values of
![]() ${\it\epsilon}$
are chosen such that the domain characteristic varies from highly viscous to one having very low viscosity with respect to the surrounding membrane. For example,
${\it\epsilon}$
are chosen such that the domain characteristic varies from highly viscous to one having very low viscosity with respect to the surrounding membrane. For example,
![]() ${\it\epsilon}=0.8$
implies
${\it\epsilon}=0.8$
implies
![]() ${\it\eta}_{d}/{\it\eta}_{m}=5$
, and for
${\it\eta}_{d}/{\it\eta}_{m}=5$
, and for
![]() ${\it\epsilon}=-20$
we obtain
${\it\epsilon}=-20$
we obtain
![]() ${\it\eta}_{d}/{\it\eta}_{m}=1/21$
. We have chosen
${\it\eta}_{d}/{\it\eta}_{m}=1/21$
. We have chosen
![]() ${\it\beta}$
to vary between 5 and 1000, for most cases, as this lies within the range of its possible values. Further, we obtained accuracy of 95 % or more in the computation of the drag force above
${\it\beta}$
to vary between 5 and 1000, for most cases, as this lies within the range of its possible values. Further, we obtained accuracy of 95 % or more in the computation of the drag force above
![]() ${\it\beta}=5$
in the previous subsection. From figure 6, we observe that, for any specified
${\it\beta}=5$
in the previous subsection. From figure 6, we observe that, for any specified
![]() ${\it\epsilon}$
, the dimensionless drag force increases with
${\it\epsilon}$
, the dimensionless drag force increases with
![]() ${\it\beta}$
. An increasing
${\it\beta}$
. An increasing
![]() ${\it\beta}$
implies increasing surrounding membrane viscosity
${\it\beta}$
implies increasing surrounding membrane viscosity
![]() ${\it\eta}_{m}$
for fixed surrounding fluid viscosity and domain radius. Thus the drag force should increase with
${\it\eta}_{m}$
for fixed surrounding fluid viscosity and domain radius. Thus the drag force should increase with
![]() ${\it\beta}$
in this scenario.
${\it\beta}$
in this scenario.

Figure 6. Variation of
![]() $F/{\it\mu}_{s}aU$
with the Boussinesq number
$F/{\it\mu}_{s}aU$
with the Boussinesq number
![]() ${\it\beta}$
for different viscosity contrast
${\it\beta}$
for different viscosity contrast
![]() ${\it\epsilon}$
. The parameters chosen are
${\it\epsilon}$
. The parameters chosen are
![]() $n=4000,\tilde{r}=1.014$
,
$n=4000,\tilde{r}=1.014$
,
![]() $U_{L}=6000$
,
$U_{L}=6000$
,
![]() $h=0.06$
.
$h=0.06$
.
We observe from figure 6(a) that for positive
![]() ${\it\epsilon}$
the dimensionless drag force does not change significantly with
${\it\epsilon}$
the dimensionless drag force does not change significantly with
![]() ${\it\epsilon}$
. The same is true for
${\it\epsilon}$
. The same is true for
![]() $-1\leqslant {\it\epsilon}\leqslant 1$
. Note that when
$-1\leqslant {\it\epsilon}\leqslant 1$
. Note that when
![]() ${\it\epsilon}$
changes from 0 to unity the domain behaviour changes from having the same viscosity as the surrounding membrane to near rigid. During this drastic change in the domain behaviour the diffusion coefficient does not change. In this scenario, the domains diffuse in a membrane of low viscosity. A similar observation was also made by Cicuta et al. (Reference Cicuta, Keller and Veatch2007) in their experimental study.
${\it\epsilon}$
changes from 0 to unity the domain behaviour changes from having the same viscosity as the surrounding membrane to near rigid. During this drastic change in the domain behaviour the diffusion coefficient does not change. In this scenario, the domains diffuse in a membrane of low viscosity. A similar observation was also made by Cicuta et al. (Reference Cicuta, Keller and Veatch2007) in their experimental study.
For large and negative
![]() ${\it\epsilon}$
the domain viscosity is much smaller than that of the surrounding membrane. In this scenario, we observe a significant drop in the drag force for all
${\it\epsilon}$
the domain viscosity is much smaller than that of the surrounding membrane. In this scenario, we observe a significant drop in the drag force for all
![]() ${\it\beta}$
(see figure 6
b). From figure 7(a), we also observe that the ratio between the drag forces on the rigid and liquid domains increases with
${\it\beta}$
(see figure 6
b). From figure 7(a), we also observe that the ratio between the drag forces on the rigid and liquid domains increases with
![]() ${\it\beta}$
initially and then decreases. The drop is most significant in the intermediate range of
${\it\beta}$
initially and then decreases. The drop is most significant in the intermediate range of
![]() ${\it\beta}$
, between approximately 10 and 100. Again, from figure 7(a) we observe that the drag forces on the rigid and the liquid domains are almost the same
${\it\beta}$
, between approximately 10 and 100. Again, from figure 7(a) we observe that the drag forces on the rigid and the liquid domains are almost the same
![]() $-1\leqslant {\it\epsilon}\leqslant 1$
(data for
$-1\leqslant {\it\epsilon}\leqslant 1$
(data for
![]() ${\it\epsilon}=-1$
not presented).
${\it\epsilon}=-1$
not presented).

Figure 7. (a) Variation of drag force on the liquid domain, relative to the drag force on a rigid domain of the same size, with the Boussinesq number
![]() ${\it\beta}$
for three different values of viscosity contrast
${\it\beta}$
for three different values of viscosity contrast
![]() ${\it\epsilon}$
. (b) Mobility with respect to
${\it\epsilon}$
. (b) Mobility with respect to
![]() ${\it\beta}$
for
${\it\beta}$
for
![]() ${\it\beta}\geqslant 5$
and comparison with the results of Saffman (Reference Saffman1976) and Hughes et al. (Reference Hughes, Pailthorpe and White1981). For large and negative
${\it\beta}\geqslant 5$
and comparison with the results of Saffman (Reference Saffman1976) and Hughes et al. (Reference Hughes, Pailthorpe and White1981). For large and negative
![]() ${\it\epsilon}$
, significant departure from the logarithmic behaviour is observed.
${\it\epsilon}$
, significant departure from the logarithmic behaviour is observed.
Hughes et al. (Reference Hughes, Pailthorpe and White1981) have predicted that mobility varies linearly with
![]() ${\it\beta}$
for small
${\it\beta}$
for small
![]() ${\it\beta}$
. Due to the large percentage error in our results for
${\it\beta}$
. Due to the large percentage error in our results for
![]() ${\it\beta}\leqslant 5$
, we do not attempt a quantitative comparison of mobility with the asymptotic behaviour predicted by Hughes et al. (Reference Hughes, Pailthorpe and White1981). However, we do observe that the absolute error is less for
${\it\beta}\leqslant 5$
, we do not attempt a quantitative comparison of mobility with the asymptotic behaviour predicted by Hughes et al. (Reference Hughes, Pailthorpe and White1981). However, we do observe that the absolute error is less for
![]() ${\it\beta}\ll 1$
and the mobility varies linearly with
${\it\beta}\ll 1$
and the mobility varies linearly with
![]() ${\it\beta}$
in this regime (not shown). Finally, in figure 7(b), we present the dimensionless mobility variation with
${\it\beta}$
in this regime (not shown). Finally, in figure 7(b), we present the dimensionless mobility variation with
![]() ${\it\beta}$
for different
${\it\beta}$
for different
![]() ${\it\epsilon}$
. For a rigid domain (
${\it\epsilon}$
. For a rigid domain (
![]() ${\it\epsilon}=1$
) our results agree with the logarithmic behaviour (
${\it\epsilon}=1$
) our results agree with the logarithmic behaviour (
![]() $U/F\approx \ln (2{\it\beta})$
) predicted by Saffman (Reference Saffman1976) and Hughes et al. (Reference Hughes, Pailthorpe and White1981). When the domain is not rigid, but the viscosity contrast
$U/F\approx \ln (2{\it\beta})$
) predicted by Saffman (Reference Saffman1976) and Hughes et al. (Reference Hughes, Pailthorpe and White1981). When the domain is not rigid, but the viscosity contrast
![]() ${\it\epsilon}$
is less than unity in magnitude, the mobility for the liquid domain is close to that for the rigid domain. However, for large and negative
${\it\epsilon}$
is less than unity in magnitude, the mobility for the liquid domain is close to that for the rigid domain. However, for large and negative
![]() ${\it\epsilon}$
, that is when the surrounding membrane is significantly more viscous than the domain, the mobility is significantly different and does not vary as
${\it\epsilon}$
, that is when the surrounding membrane is significantly more viscous than the domain, the mobility is significantly different and does not vary as
![]() $\ln (2{\it\beta})$
. The dimensionless mobility initially increases with
$\ln (2{\it\beta})$
. The dimensionless mobility initially increases with
![]() ${\it\beta}$
and subsequently decreases but is always larger than the mobility for the rigid domain. To the best of our knowledge, such a behaviour has not been predicted previously. It is possible to design experiments by choosing a ternary lipid mixture of ordered and disordered lipids and cholesterol of suitable composition to obtain domains of significantly lower viscosity than the surrounding. Ternary phase diagrams presented in figures 8–10 of Veatch & Keller (Reference Veatch and Keller2005) can provide guidance to choosing such compositions.
${\it\beta}$
and subsequently decreases but is always larger than the mobility for the rigid domain. To the best of our knowledge, such a behaviour has not been predicted previously. It is possible to design experiments by choosing a ternary lipid mixture of ordered and disordered lipids and cholesterol of suitable composition to obtain domains of significantly lower viscosity than the surrounding. Ternary phase diagrams presented in figures 8–10 of Veatch & Keller (Reference Veatch and Keller2005) can provide guidance to choosing such compositions.
5. Conclusions
In this paper, we develop a simple numerical solution procedure involving the discrete collocation method and Chebyshev polynomials for the dual integral equations, of Fredholm second kind, that compute the drag force (and the diffusion coefficient) on a liquid microdomain diffusing in a two-dimensional lipid bilayer membrane. We first validate our method with the existing results for the cases when either the domain is rigid or the domain and the surrounding membrane have the same viscosity. For the general case of arbitrary viscosity contrast between the domain and surrounding membrane, the drag force is almost independent of the viscosity contrast between the domain and the surrounding membrane for a more viscous domain, whereas it varies significantly with the viscosity contrast for a less viscous domain. Further, unlike the rigid domain, the mobility of the domain does not vary logarithmically with the Boussinesq number for larger values of the latter. The mobility initially increases with the Boussinesq number and then decreases but is always larger than that for the rigid domain. In our solution of the dual integral equations, we do not make any assumptions. Accordingly, unlike the earlier studies, our methodology of computing the drag force and diffusion coefficient is valid for arbitrary viscosity contrast between the domain and membrane and for any domain size subject to the condition that the Boussinesq number should be larger than 5 for good accuracy. A study of the diffusion behaviour and drag on a microdomain for such a large range of viscosity contrast between the domain and the surrounding membrane is now possible.
Acknowledgements
The authors acknowledge the financial support from the Department of Science and Technology and the Department of Biotechnology, Government of India, through grant nos. DST/ME/20120003 and DBT/ME/2015034, respectively. The authors thank R. Lakhan for his assistance in drawing the schematic diagram and A. Anand for discussions on the numerical solution of the dual integral equations. S.L.D. was a visiting professor at the Indian Institute Technology Delhi when the manuscript was submitted and revised.