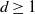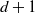1. Introduction
Throughout this paper the d-dimensional standard orthogonal simplex (see e.g. [Reference Hofrichter, Jost and Tran5]) is defined as
We also denote the interior of ![]() $\mathcal{S}_d$
, the Borel
$\mathcal{S}_d$
, the Borel ![]() $\sigma$
-algebra, and the Lebesgue measure on
$\sigma$
-algebra, and the Lebesgue measure on ![]() $\mathcal{S}_d$
by
$\mathcal{S}_d$
by ![]() $\mathcal{S}_d^o$
,
$\mathcal{S}_d^o$
, ![]() $\mathcal{B} (\mathcal{S}_d)$
, and
$\mathcal{B} (\mathcal{S}_d)$
, and ![]() $\lambda_d$
respectively. Let
$\lambda_d$
respectively. Let ![]() $E_0=(0,0,\ldots,0)$
be the origin, and let
$E_0=(0,0,\ldots,0)$
be the origin, and let ![]() $E_1=(1,0,\ldots,0)$
,
$E_1=(1,0,\ldots,0)$
, ![]() $E_2=(0,1,0,\ldots,0), \ldots, E_d=(0,\ldots,0,1)$
be the standard orthonormal basis vectors in
$E_2=(0,1,0,\ldots,0), \ldots, E_d=(0,\ldots,0,1)$
be the standard orthonormal basis vectors in ![]() $\mathbb{R}^d$
, which are also the vertices of
$\mathbb{R}^d$
, which are also the vertices of ![]() $\mathcal{S}_d$
.
$\mathcal{S}_d$
.
For some initial point ![]() $Z_0\in \mathcal{S}_d$
, we consider the following random iteration:
$Z_0\in \mathcal{S}_d$
, we consider the following random iteration:
where
•
 $\xi_n$
,
$\xi_n$
,  $n=0,1,2,\ldots,$
are independent copies of some random variable
$n=0,1,2,\ldots,$
are independent copies of some random variable  $\xi$
with support in [0, 1],
$\xi$
with support in [0, 1],•
 $\Theta_n$
,
$\Theta_n$
,  $n=0,1,2,\ldots,$
are discrete random vectors such that
where
$n=0,1,2,\ldots,$
are discrete random vectors such that
where \[\mathbb{P} (\Theta_n= E_j\mid Z_0,Z_1,\ldots,Z_n;\ \xi_n ) = p_j(Z_n), \quad j=0,1,2,\ldots,d,\]
\[\mathbb{P} (\Theta_n= E_j\mid Z_0,Z_1,\ldots,Z_n;\ \xi_n ) = p_j(Z_n), \quad j=0,1,2,\ldots,d,\]
 $p=(p_1,p_2,\ldots,p_d)$
(sometimes referred to as a probability choice function) is a given mapping (which is the same for all n) from
$p=(p_1,p_2,\ldots,p_d)$
(sometimes referred to as a probability choice function) is a given mapping (which is the same for all n) from  $\mathcal{S}_d$
to itself such that
$\mathcal{S}_d$
to itself such that  $p_j\colon \mathcal{S}_d\to [0,1], j=1,2,\ldots d$
are Borel-measurable functions, and
$p_j\colon \mathcal{S}_d\to [0,1], j=1,2,\ldots d$
are Borel-measurable functions, and  $p_0(z) \coloneqq 1-\sum_{j=1}^dp_j(z)$
for all
$p_0(z) \coloneqq 1-\sum_{j=1}^dp_j(z)$
for all  $z\in\mathcal{S}_d$
.
$z\in\mathcal{S}_d$
.
The aforementioned model originates from Sethuraman’s construction of the Dirichlet distribution (see [Reference Sethuraman10]) for the case where ![]() $p_1,p_2,\ldots,p_d$
are positive constants. Sethuraman proved that if
$p_1,p_2,\ldots,p_d$
are positive constants. Sethuraman proved that if
•
 $\xi\sim \text{Beta}(1,\gamma)$
, where
$\xi\sim \text{Beta}(1,\gamma)$
, where  $\gamma$
is some positive constant,
$\gamma$
is some positive constant,•
 $\Theta$
is a discrete random vector such that
$\Theta$
is a discrete random vector such that  $\mathbb{P}(\Theta=E_j)=p_j$
for
$\mathbb{P}(\Theta=E_j)=p_j$
for  $j=1,2,\ldots,d$
, and
$j=1,2,\ldots,d$
, and  $p_0=1-p_1-\cdots-p_d>0$
,
$p_0=1-p_1-\cdots-p_d>0$
,•
 $Z\sim\text{Dirichlet}(p_1\gamma,p_2\gamma,\ldots,p_d\gamma,p_0\gamma)$
, and
$Z\sim\text{Dirichlet}(p_1\gamma,p_2\gamma,\ldots,p_d\gamma,p_0\gamma)$
, and•
 $Z, \Theta, \xi$
are jointly independent,
$Z, \Theta, \xi$
are jointly independent,
then
Here ![]() $\text{Beta}(a,b)$
denotes the usual Beta distribution with the probability density function
$\text{Beta}(a,b)$
denotes the usual Beta distribution with the probability density function
![]() $\Gamma$
is the Gamma function, and
$\Gamma$
is the Gamma function, and ![]() $\text{Dirichlet}(\alpha_1,\alpha_2,\ldots,\alpha_d,\alpha_{d+1})$
denotes the Dirichlet distribution with the probability density function
$\text{Dirichlet}(\alpha_1,\alpha_2,\ldots,\alpha_d,\alpha_{d+1})$
denotes the Dirichlet distribution with the probability density function
 \[f(z_1,z_2,\ldots,z_d)=\dfrac{\Gamma \big(\sum_{i=1}^{d+1}\alpha_i\big)}{\prod_{i=1}^{d+1} \Gamma(\alpha_i)}\bigg(1-\sum_{i=1}^d z_i\bigg)^{\alpha_{d+1}-1}\prod_{i=1}^{d}z^{\alpha_i-1}_i,\quad (z_1,z_2,\ldots,z_d)\in \mathcal{S}_d^o.\]
\[f(z_1,z_2,\ldots,z_d)=\dfrac{\Gamma \big(\sum_{i=1}^{d+1}\alpha_i\big)}{\prod_{i=1}^{d+1} \Gamma(\alpha_i)}\bigg(1-\sum_{i=1}^d z_i\bigg)^{\alpha_{d+1}-1}\prod_{i=1}^{d}z^{\alpha_i-1}_i,\quad (z_1,z_2,\ldots,z_d)\in \mathcal{S}_d^o.\]
Consequently, the stationary distribution of the Markov chain ![]() $\{Z_n\}_{n\ge0}$
corresponding to Sethuraman’s model is
$\{Z_n\}_{n\ge0}$
corresponding to Sethuraman’s model is ![]() $\text{Dirichlet}(p_1\gamma,p_2\gamma,\ldots, p_d\gamma, p_0\gamma)$
. Further extensions, where
$\text{Dirichlet}(p_1\gamma,p_2\gamma,\ldots, p_d\gamma, p_0\gamma)$
. Further extensions, where ![]() $\xi\sim \text{Beta}(k,\gamma)$
for some positive integer k, and
$\xi\sim \text{Beta}(k,\gamma)$
for some positive integer k, and ![]() $\Theta$
has a quasi-Bernoulli distribution, were studied by Hitczenko and Letac in [Reference Hitczenko and Letac4].
$\Theta$
has a quasi-Bernoulli distribution, were studied by Hitczenko and Letac in [Reference Hitczenko and Letac4].
In [Reference Diaconis and Freedman3], Diaconis and Freedman reconsidered Sethuraman’s model from the point of view of random iterated functions, and also studied the case where p(z) depends on ![]() $z\in \mathcal{S}_1=[0,1]$
. Other models in
$z\in \mathcal{S}_1=[0,1]$
. Other models in ![]() $\mathcal{S}_1$
with various special cases of p(z) and
$\mathcal{S}_1$
with various special cases of p(z) and ![]() $\xi$
were studied in [Reference McKinlay and Borovkov7], [Reference Pacheco-González8], and [Reference Ramli and Leng9]. Inspired by the work of Diaconis and Freedman, Ladjimi and Peigné in their recent work [Reference Ladjimi and Peigné6] studied iterated random functions with place-dependent probability choice functions, and demonstrated several applications to the one-dimensional model where
$\xi$
were studied in [Reference McKinlay and Borovkov7], [Reference Pacheco-González8], and [Reference Ramli and Leng9]. Inspired by the work of Diaconis and Freedman, Ladjimi and Peigné in their recent work [Reference Ladjimi and Peigné6] studied iterated random functions with place-dependent probability choice functions, and demonstrated several applications to the one-dimensional model where ![]() $\xi\sim \text{Uniform}[0,1]$
, and p(z) is a Hölder-continuous function in [0, 1].
$\xi\sim \text{Uniform}[0,1]$
, and p(z) is a Hölder-continuous function in [0, 1].
In [Reference McKinlay and Borovkov7], McKinlay and Borovkov gave a general condition for the ergodicity of the one-dimensional Markov chain ![]() $\{Z_n\}_{n\ge0}$
in
$\{Z_n\}_{n\ge0}$
in ![]() $\mathcal{S}_1$
. By solving integral equations, they derived a closed-form expression for the stationary density function in the case where
$\mathcal{S}_1$
. By solving integral equations, they derived a closed-form expression for the stationary density function in the case where ![]() $\xi\sim \text{Beta}(1,\gamma)$
, and p(z) is a piecewise continuous function on [0, 1]. In particular, if
$\xi\sim \text{Beta}(1,\gamma)$
, and p(z) is a piecewise continuous function on [0, 1]. In particular, if ![]() $p(z)=(1-c)z+b(1-z), b,c\in (0,1]$
, then the stationary distribution is
$p(z)=(1-c)z+b(1-z), b,c\in (0,1]$
, then the stationary distribution is ![]() $\text{Beta}(b\gamma, c\gamma)$
.
$\text{Beta}(b\gamma, c\gamma)$
.
The model, also known in the literature as a stick-breaking process, a stochastic give-and-take (see [Reference DeGroot and Rao2], [Reference McKinlay and Borovkov7]) or a Diaconis–Freedman chain (see [Reference Ladjimi and Peigné6]) has many applications in other fields such as human genetics, robot coverage algorithms, random search, etc. For further discussions, we refer the reader to [Reference DeGroot and Rao2], [Reference Ramli and Leng9], and [Reference McKinlay and Borovkov7].
The rest of the paper is organized as follows. In Section 2 we give an extension of the ergodicity criterion of McKinlay and Borovkov to higher-dimensional simplexes under certain assumptions on p(z) and ![]() $\xi$
. In Section 3, in the case where
$\xi$
. In Section 3, in the case where ![]() $\xi$
is Beta-distributed while the probability choice function p(z) linearly depend on z, we prove that the limiting distribution of the chain is a Dirichlet distribution. Finally, in Section 4, we consider a history-dependent random walk model in [0, 1] based on urn-type schemes. Using martingales and coupling techniques, we show that the random walk converges in distribution to an arcsine random variable.
$\xi$
is Beta-distributed while the probability choice function p(z) linearly depend on z, we prove that the limiting distribution of the chain is a Dirichlet distribution. Finally, in Section 4, we consider a history-dependent random walk model in [0, 1] based on urn-type schemes. Using martingales and coupling techniques, we show that the random walk converges in distribution to an arcsine random variable.
2. Existence of the limiting distribution
To prove the ergodicity of the Markov chain ![]() $\{Z_n\}_{n\ge 0}$
, we will make use of the following result.
$\{Z_n\}_{n\ge 0}$
, we will make use of the following result.
Proposition 1. (Theorems 1.3 and 2.1 in [Reference Borovkov1]) Let ![]() $Z_n, n=0,1,2,\ldots$
be a Markov chain on a measurable state space
$Z_n, n=0,1,2,\ldots$
be a Markov chain on a measurable state space ![]() $(\mathcal{X},\mathfrak{B})$
such that, for
$(\mathcal{X},\mathfrak{B})$
such that, for ![]() $n\ge 1$
,
$n\ge 1$
, ![]() $\mathbb{P}(Z_n\in A\mid Z_0=z)$
is a measurable function of
$\mathbb{P}(Z_n\in A\mid Z_0=z)$
is a measurable function of ![]() $z\in \mathcal{X}$
when
$z\in \mathcal{X}$
when ![]() $A\in \mathfrak{B}$
is fixed, while it is a probability measure of A when z is fixed.
$A\in \mathfrak{B}$
is fixed, while it is a probability measure of A when z is fixed.
Then ![]() $Z_n$
is ergodic if there exists a subset
$Z_n$
is ergodic if there exists a subset ![]() $V\in \mathfrak{B}$
,
$V\in \mathfrak{B}$
, ![]() $q>0$
, a probability measure
$q>0$
, a probability measure ![]() $\varphi$
on
$\varphi$
on ![]() $(\mathcal{X},\mathfrak{B})$
, and some positive integer
$(\mathcal{X},\mathfrak{B})$
, and some positive integer ![]() $n_0$
such that
$n_0$
such that
(a)
 $\mathbb{P}(\tau_V<\infty\mid Z_0=z)=1$
for all
$\mathbb{P}(\tau_V<\infty\mid Z_0=z)=1$
for all  $z\in \mathcal{X}$
, where
$z\in \mathcal{X}$
, where  $\tau_V=\inf\{n\ge 1\colon Z_n\in V\}$
,
$\tau_V=\inf\{n\ge 1\colon Z_n\in V\}$
,(b)
 $\sup_{z\in V} \mathbb{E} (\tau_V\mid Z_0=z )<\infty$
,
$\sup_{z\in V} \mathbb{E} (\tau_V\mid Z_0=z )<\infty$
,(c)
 $\mathbb{P}(Z_{n_0}\in B\mid Z_0=z)\ge q \varphi(B)$
for all
$\mathbb{P}(Z_{n_0}\in B\mid Z_0=z)\ge q \varphi(B)$
for all  $B\in \mathfrak{B}$
and
$B\in \mathfrak{B}$
and  $z \in V$
,
$z \in V$
,(d)
 $\gcd \{n\colon \mathbb{P}(Z_{n}\in B\mid Z_0=z)\ge q \varphi(B)\}=1$
for
$\gcd \{n\colon \mathbb{P}(Z_{n}\in B\mid Z_0=z)\ge q \varphi(B)\}=1$
for  $z \in V$
.
$z \in V$
.
Moreover, if the above conditions are fulfilled, then there exists a unique invariant measure ![]() $\mu$
such that the distribution of
$\mu$
such that the distribution of ![]() $Z_n$
converges to
$Z_n$
converges to ![]() $\mu$
in total variation norm.
$\mu$
in total variation norm.
For each ![]() $z=(z_1,z_2\ldots,z_d)\in \mathcal{S}_d$
, we define
$z=(z_1,z_2\ldots,z_d)\in \mathcal{S}_d$
, we define ![]() $z_{0}=1-z_1-z_2-\cdots-z_d$
. Note that the set of all
$z_{0}=1-z_1-z_2-\cdots-z_d$
. Note that the set of all ![]() $(z_0,z_1,z_2\ldots,z_d)$
, where
$(z_0,z_1,z_2\ldots,z_d)$
, where ![]() $(z_1,z_2\ldots,z_d)\in {\mathcal S}_d$
, constitutes the standard d-simplex in
$(z_1,z_2\ldots,z_d)\in {\mathcal S}_d$
, constitutes the standard d-simplex in ![]() $\mathbb{R}^{d+1}$
.
$\mathbb{R}^{d+1}$
.
Assumption 1. There exist ![]() $\delta\in(0,{{{1}/{2^d}}})$
and
$\delta\in(0,{{{1}/{2^d}}})$
and ![]() $s,t\in(\delta^{1/d},1-\delta^{1/d})$
,
$s,t\in(\delta^{1/d},1-\delta^{1/d})$
, ![]() $s<t$
such that
$s<t$
such that
(i)
 $\mathbb{P}(\xi \lt 1-\delta)\coloneqq 1-\eta<1$
,
$\mathbb{P}(\xi \lt 1-\delta)\coloneqq 1-\eta<1$
,(ii) there is an
 $\varepsilon \gt 0$
such that, for any
$\varepsilon \gt 0$
such that, for any  $1\le k\le d$
and any
$1\le k\le d$
and any  $0\le j_1 \lt j_2 \lt \cdots \lt j_k\le d$
, we have
$0\le j_1 \lt j_2 \lt \cdots \lt j_k\le d$
, we have
 \[\inf_{\overset{z\in \mathcal{S}_d,}{ z_{j_1}+\cdots+z_{j_k}\le \delta}}\ \sum_{l=1}^k p_{j_l}(z)\ge \varepsilon,\]
\[\inf_{\overset{z\in \mathcal{S}_d,}{ z_{j_1}+\cdots+z_{j_k}\le \delta}}\ \sum_{l=1}^k p_{j_l}(z)\ge \varepsilon,\]
(iii) there is
 $c \gt 0$
such that, for all
$c \gt 0$
such that, for all  $B\in \mathcal{B}([0,1])$
,
$B\in \mathcal{B}([0,1])$
,  $B\subset [s(1-t)^{d-1}-\delta,t]\cup[(1-t)^{d}-\delta,1-s]$
, we have
where
$B\subset [s(1-t)^{d-1}-\delta,t]\cup[(1-t)^{d}-\delta,1-s]$
, we have
where \[\mathbb{P}(\xi\in B)\gt c\lambda(B),\]
\[\mathbb{P}(\xi\in B)\gt c\lambda(B),\]
 $\lambda$
is the Lebesgue measure on
$\lambda$
is the Lebesgue measure on  $[0,1].$
$[0,1].$
Remark 1. Condition (i) is quite natural in order to avoid the absorption of ![]() $Z_n$
at the boundary of
$Z_n$
at the boundary of ![]() $\mathcal{S}_d$
. For
$\mathcal{S}_d$
. For ![]() $d=1$
, the above conditions are very similar to the assumptions (E1–E2–E3) of McKinlay and Borovkov in [Reference McKinlay and Borovkov7]. However, in contrast to our condition (iii), McKinlay and Borovkov require that
$d=1$
, the above conditions are very similar to the assumptions (E1–E2–E3) of McKinlay and Borovkov in [Reference McKinlay and Borovkov7]. However, in contrast to our condition (iii), McKinlay and Borovkov require that ![]() $\xi$
has a density on
$\xi$
has a density on ![]() $[s-\delta,t]$
and
$[s-\delta,t]$
and ![]() $[1-t-\delta,1-s]$
. Also, observe that in condition (iii) the intervals are properly defined (though they may overlap).
$[1-t-\delta,1-s]$
. Also, observe that in condition (iii) the intervals are properly defined (though they may overlap).

Figure 1. Illustration of ![]() $V_j$
,
$V_j$
, ![]() $j=0,1,2$
in case
$j=0,1,2$
in case ![]() $d=2$
.
$d=2$
.
For ![]() $j=0,1,\ldots,d$
define
$j=0,1,\ldots,d$
define
In particular,
 \[V_0=\Bigg\{z=(z_1,\ldots, z_d)\in\mathcal{S}_d\colon \sum_{j=1}^d z_j\le \delta \Bigg\}.\]
\[V_0=\Bigg\{z=(z_1,\ldots, z_d)\in\mathcal{S}_d\colon \sum_{j=1}^d z_j\le \delta \Bigg\}.\]
For each ![]() $x=(x_1,x_2,\ldots,x_d)\in (0,1)^d$
, also define
$x=(x_1,x_2,\ldots,x_d)\in (0,1)^d$
, also define ![]() $T\colon (0,1)^d\to\mathcal{S}_d^o$
by setting
$T\colon (0,1)^d\to\mathcal{S}_d^o$
by setting
 \[T(x)=\Bigg(x_1\prod_{j=2}^d (1-x_j),\ x_2\prod_{j=3}^d (1-x_j), \ldots, x_{d-1}(1-x_d),\ x_d\Bigg).\]
\[T(x)=\Bigg(x_1\prod_{j=2}^d (1-x_j),\ x_2\prod_{j=3}^d (1-x_j), \ldots, x_{d-1}(1-x_d),\ x_d\Bigg).\]
Note that T is a homeomorphism from ![]() $(0,1)^d$
to
$(0,1)^d$
to ![]() $\mathcal{S}_d^o$
, and its inverse
$\mathcal{S}_d^o$
, and its inverse ![]() $T^{-1}$
for each
$T^{-1}$
for each
is given by
Let ![]() $z=(z_1,\ldots,z_d)$
,
$z=(z_1,\ldots,z_d)$
, ![]() $u=(u_1,\ldots,u_d)\in\mathcal{S}_d$
,
$u=(u_1,\ldots,u_d)\in\mathcal{S}_d$
, ![]() $z_0=1-\sum_{k=1}^d z_k$
, and
$z_0=1-\sum_{k=1}^d z_k$
, and ![]() $u_0=1-\sum_{k=1}^d u_k$
. For each
$u_0=1-\sum_{k=1}^d u_k$
. For each ![]() $j=1,2,\ldots,d$
we define the following functions:
$j=1,2,\ldots,d$
we define the following functions:
If ![]() $z_0\neq 0$
then the map
$z_0\neq 0$
then the map ![]() $G_z$
is invertible; moreover, its inverse can be computed as
$G_z$
is invertible; moreover, its inverse can be computed as
For some two real numbers s and t, such that ![]() $0<s<t<1$
, define
$0<s<t<1$
, define
 \begin{align*}K&\coloneqq \Bigg\{ (u_1,\ldots,u_d)\in\mathcal{S}_d\colon s\le\dfrac{u_j}{1-\sum_{l=j+1}^d u_l}\le t, j=1,2,\ldots,d \Bigg\}=T \big([s,t]^d\big).\end{align*}
\begin{align*}K&\coloneqq \Bigg\{ (u_1,\ldots,u_d)\in\mathcal{S}_d\colon s\le\dfrac{u_j}{1-\sum_{l=j+1}^d u_l}\le t, j=1,2,\ldots,d \Bigg\}=T \big([s,t]^d\big).\end{align*}
The proof of the following lemma is given in the Appendix.
Lemma 1. Assume that ![]() $\delta\in (0,{{{1}/{2^d}}})$
,
$\delta\in (0,{{{1}/{2^d}}})$
, ![]() $s,t\in (\delta^{1/d},1-\delta^{1/d})$
and
$s,t\in (\delta^{1/d},1-\delta^{1/d})$
and ![]() $s<t$
.
$s<t$
.
(a) If
 $z\in V_0$
, then
$z\in V_0$
, then
 \[G^{-1}_z(K) \subset T ([s(1-t)^{d-1}-\delta,t]^d ).\]
\[G^{-1}_z(K) \subset T ([s(1-t)^{d-1}-\delta,t]^d ).\]
(b) If
 $z\in V_k$
with
$z\in V_k$
with  $k\in \{1,2,\ldots, d\}$
, then
$k\in \{1,2,\ldots, d\}$
, then
 \[G_{R_k(z)}^{-1}\circ R_k(K)\subset T \big([(1-t)^{d}-\delta,1-s]\times[s(1-t)^{d-1}-\delta,t]^{d-1}\big).\]
\[G_{R_k(z)}^{-1}\circ R_k(K)\subset T \big([(1-t)^{d}-\delta,1-s]\times[s(1-t)^{d-1}-\delta,t]^{d-1}\big).\]
Theorem 1. Assume that all the conditions in Assumption 1 are fulfilled. Then the Markov chain ![]() $\{Z_n\}_{n\ge0}$
converges in distribution.
$\{Z_n\}_{n\ge0}$
converges in distribution.
Proof. (Step 1) We define
 \[V=\bigcup_{j=0}^dV_j.\]
\[V=\bigcup_{j=0}^dV_j.\]
From part (i) of Assumption 1 it follows that ![]() $\mathbb{P}(Z_1\in V\mid Z_0=z)\ge \mathbb{P}(\xi\ge 1-\delta)=\eta>0$
for all
$\mathbb{P}(Z_1\in V\mid Z_0=z)\ge \mathbb{P}(\xi\ge 1-\delta)=\eta>0$
for all ![]() $z\in \mathcal{S}_d$
. Therefore, for all
$z\in \mathcal{S}_d$
. Therefore, for all ![]() $z\in \mathcal{S}_d$
, given
$z\in \mathcal{S}_d$
, given ![]() $Z_0=z$
, the random variable
$Z_0=z$
, the random variable ![]() $\tau_{V}=\inf\{n\ge 1\colon Z_n\in V\}$
is stochastically dominated by a geometric random variable with parameter
$\tau_{V}=\inf\{n\ge 1\colon Z_n\in V\}$
is stochastically dominated by a geometric random variable with parameter ![]() $\eta$
, thus yielding
$\eta$
, thus yielding
Hence conditions (a) and (b) from the statement of Proposition 1 are satisfied.
(Step 2) Throughout the rest of the proof we let Const. denote some positive constant. From the definition of ![]() $\{Z_n\}_{n\ge 0}$
, we observe that
$\{Z_n\}_{n\ge 0}$
, we observe that
where
 \begin{align*} (\zeta_{1},\ldots,\zeta_{d})&\coloneqq T(\xi_0,\ldots,\xi_{d-1}),\\* \zeta_0 &\coloneqq \prod_{j=0}^{d-1}(1-\xi_j)=1-\sum_{j=1}^d \zeta_j.\end{align*}
\begin{align*} (\zeta_{1},\ldots,\zeta_{d})&\coloneqq T(\xi_0,\ldots,\xi_{d-1}),\\* \zeta_0 &\coloneqq \prod_{j=0}^{d-1}(1-\xi_j)=1-\sum_{j=1}^d \zeta_j.\end{align*}
For ![]() $1\le k\le d$
and
$1\le k\le d$
and ![]() $0\le j_1<j_2<\cdots<j_k\le d$
, define
$0\le j_1<j_2<\cdots<j_k\le d$
, define
Let ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
. Then, if
$B\in \mathcal{B}(\mathcal{S}_d)$
. Then, if ![]() $Z_0=z\in V_0$
and
$Z_0=z\in V_0$
and ![]() $\Theta_{0}=E_1, \Theta_{1}=E_2,\ldots, \Theta_{d-1}=E_d$
, then
$\Theta_{0}=E_1, \Theta_{1}=E_2,\ldots, \Theta_{d-1}=E_d$
, then ![]() $Z_{j}\in U_{j+1,j+2,\ldots,d}$
for
$Z_{j}\in U_{j+1,j+2,\ldots,d}$
for ![]() $j=0,1,\ldots,d$
. Therefore, from part (ii) of Assumption 1 it follows that
$j=0,1,\ldots,d$
. Therefore, from part (ii) of Assumption 1 it follows that
 \begin{align}&\mathbb{P} (Z_d\in B\mid Z_0=z) \notag \\[5pt]
& \quad \ge \mathbb{P} (Z_d\in B\cap K, (\Theta_{0},\Theta_{1},\ldots,\Theta_{d-1})=(E_1,E_2,\ldots,E_d)\mid Z_0=z ) \notag \\[5pt]
& \quad \ge\Bigg[\prod_{l=1}^d \inf_{z\in U_{l,l+1,\ldots,d}}\Bigg(\sum_{j=l}^dp_j(z) \Bigg)\Bigg]\times \mathbb{P}(\zeta_0 z + \zeta_1 E_1+\cdots+\zeta_{d} E_{d} \in B\cap K ) \notag \\[5pt]
& \quad \ge \varepsilon^d \mathbb{P}((\zeta_0 z_1+\zeta_1, \zeta_0 z_2+\zeta_2,\ldots,\zeta_0 z_d+\zeta_d)\in B\cap K) \notag \\[5pt]
& \quad = \varepsilon^d \mathbb{P}((\zeta_1,\ldots,\zeta_d)\in G^{-1}_z(B\cap K))=\varepsilon^d \mathbb{P}((\xi_0,\ldots,\xi_{d-1})\in T^{-1}\circ G^{-1}_z(B\cap K)).\end{align}
\begin{align}&\mathbb{P} (Z_d\in B\mid Z_0=z) \notag \\[5pt]
& \quad \ge \mathbb{P} (Z_d\in B\cap K, (\Theta_{0},\Theta_{1},\ldots,\Theta_{d-1})=(E_1,E_2,\ldots,E_d)\mid Z_0=z ) \notag \\[5pt]
& \quad \ge\Bigg[\prod_{l=1}^d \inf_{z\in U_{l,l+1,\ldots,d}}\Bigg(\sum_{j=l}^dp_j(z) \Bigg)\Bigg]\times \mathbb{P}(\zeta_0 z + \zeta_1 E_1+\cdots+\zeta_{d} E_{d} \in B\cap K ) \notag \\[5pt]
& \quad \ge \varepsilon^d \mathbb{P}((\zeta_0 z_1+\zeta_1, \zeta_0 z_2+\zeta_2,\ldots,\zeta_0 z_d+\zeta_d)\in B\cap K) \notag \\[5pt]
& \quad = \varepsilon^d \mathbb{P}((\zeta_1,\ldots,\zeta_d)\in G^{-1}_z(B\cap K))=\varepsilon^d \mathbb{P}((\xi_0,\ldots,\xi_{d-1})\in T^{-1}\circ G^{-1}_z(B\cap K)).\end{align}
(Step 3) For ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
and
$B\in \mathcal{B}(\mathcal{S}_d)$
and ![]() $z\in V_0$
, from part (iii) of Assumption 1 and Lemma 1, we have
$z\in V_0$
, from part (iii) of Assumption 1 and Lemma 1, we have
We shall demonstrate below that
Indeed, for any injective continuously differentiable map ![]() $Q\colon K\to [0,1]^d$
and any measurable subset
$Q\colon K\to [0,1]^d$
and any measurable subset ![]() $A\subset K$
,
$A\subset K$
,
We also observe that
 \begin{align*}\det\bigg(\dfrac{\partial}{\partial u} G_z^{-1}(u)\bigg)
& =\det\begin{pmatrix}1+\dfrac{z_1}{z_0} && \quad \dfrac{z_1}{z_0} && \quad \dfrac{z_1}{z_0}&& \quad \cdots && \quad \dfrac{z_1}{z_0}\\[15pt]
\dfrac{z_2}{z_0} && \quad 1+\dfrac{z_2}{z_0} && \quad \dfrac{z_2}{z_0} && \quad \cdots && \quad \dfrac{z_2}{z_0}\\[15pt]
\vdots && \quad \vdots && \quad \ddots && \quad \cdots && \quad \vdots \\[15pt]
\dfrac{z_{d-1}}{z_0} && \quad \cdots & & \dfrac{z_{d-1}}{z_0} && \quad 1+\dfrac{z_{d-1}}{z_0} && \quad \dfrac{z_{d-1}}{z_0}\\[15pt]
\dfrac{z_d}{z_0} && \quad \cdots && \quad \dfrac{z_d}{z_0} && \quad \dfrac{z_d}{z_0} && \quad 1+\dfrac{z_d}{z_0}\end{pmatrix}\displaybreak\\
& =\det\begin{pmatrix}1+\dfrac{z_1}{z_0}& \quad -1 & \quad -1 & \quad -1 & \quad \cdots & \quad -1\\[15pt]
\dfrac{z_2}{z_0} & \quad 1 & \quad 0 & \quad 0 & \quad \cdots & \quad 0\\[15pt]
\dfrac{z_3}{z_0} & \quad 0 & \quad 1 & \quad 0 & \quad \cdots & \quad 0\\[10pt]
\vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \cdots & \quad \vdots \\[5pt]
\dfrac{z_{d-1}}{z_0} & \quad 0& \quad \cdots & \quad 0 & \quad 1 & \quad 0\\[15pt]
\dfrac{z_d}{z_0} & \quad 0 & \quad \cdots & \quad 0 & \quad 0 & \quad 1\end{pmatrix}\\[8pt]
& =1+\dfrac{z_1}{z_0}+\dfrac{z_2}{z_0}+\cdots+\dfrac{z_d}{z_0}\\[6pt]
& =\dfrac{1}{z_0}\\[6pt]
& \ge 1,\end{align*}
\begin{align*}\det\bigg(\dfrac{\partial}{\partial u} G_z^{-1}(u)\bigg)
& =\det\begin{pmatrix}1+\dfrac{z_1}{z_0} && \quad \dfrac{z_1}{z_0} && \quad \dfrac{z_1}{z_0}&& \quad \cdots && \quad \dfrac{z_1}{z_0}\\[15pt]
\dfrac{z_2}{z_0} && \quad 1+\dfrac{z_2}{z_0} && \quad \dfrac{z_2}{z_0} && \quad \cdots && \quad \dfrac{z_2}{z_0}\\[15pt]
\vdots && \quad \vdots && \quad \ddots && \quad \cdots && \quad \vdots \\[15pt]
\dfrac{z_{d-1}}{z_0} && \quad \cdots & & \dfrac{z_{d-1}}{z_0} && \quad 1+\dfrac{z_{d-1}}{z_0} && \quad \dfrac{z_{d-1}}{z_0}\\[15pt]
\dfrac{z_d}{z_0} && \quad \cdots && \quad \dfrac{z_d}{z_0} && \quad \dfrac{z_d}{z_0} && \quad 1+\dfrac{z_d}{z_0}\end{pmatrix}\displaybreak\\
& =\det\begin{pmatrix}1+\dfrac{z_1}{z_0}& \quad -1 & \quad -1 & \quad -1 & \quad \cdots & \quad -1\\[15pt]
\dfrac{z_2}{z_0} & \quad 1 & \quad 0 & \quad 0 & \quad \cdots & \quad 0\\[15pt]
\dfrac{z_3}{z_0} & \quad 0 & \quad 1 & \quad 0 & \quad \cdots & \quad 0\\[10pt]
\vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \cdots & \quad \vdots \\[5pt]
\dfrac{z_{d-1}}{z_0} & \quad 0& \quad \cdots & \quad 0 & \quad 1 & \quad 0\\[15pt]
\dfrac{z_d}{z_0} & \quad 0 & \quad \cdots & \quad 0 & \quad 0 & \quad 1\end{pmatrix}\\[8pt]
& =1+\dfrac{z_1}{z_0}+\dfrac{z_2}{z_0}+\cdots+\dfrac{z_d}{z_0}\\[6pt]
& =\dfrac{1}{z_0}\\[6pt]
& \ge 1,\end{align*}
where the second matrix is obtained from the first one by subtracting the first column from each of the remaining columns, and then we use the Schur determinant identity, i.e.
 \[\det {\begin{pmatrix}C&\quad D\\[3pt] E& \quad F\end{pmatrix}}=\det(F)\cdot \det(C-DF^{-1}E)\]
\[\det {\begin{pmatrix}C&\quad D\\[3pt] E& \quad F\end{pmatrix}}=\det(F)\cdot \det(C-DF^{-1}E)\]
when F is invertible; here F is the ![]() $d-1$
square identity matrix,
$d-1$
square identity matrix, ![]() $C=[1+z_1/z_0]$
, etc. Furthermore,
$C=[1+z_1/z_0]$
, etc. Furthermore,
 \begin{align*}& \det\bigg(\dfrac{\partial}{\partial v} T^{-1}(v)\bigg)\\
&\quad =\det\begin{pmatrix}\dfrac{1}{1-\sum_{j=2}^d v_j} & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} & \quad \cdots & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} \\[18pt]
0 & \quad \dfrac{1}{1-\sum_{j=3}^d v_j} & \quad \dfrac{v_2}{\big(1-\sum_{j=3}^d v_j\big)^2} & \quad \cdots & \quad \dfrac{v_2}{\big(1-\sum_{j=3}^d v_j\big)^2} \\[15pt]
\vdots & \quad \vdots & \quad \ddots & \quad \cdots & \quad \vdots \\[5pt]
0 & \quad \cdots & \quad 0 & \quad \dfrac{1}{1-v_d} & \quad \dfrac{v_{d-1}}{(1-v_d)^2}\\[15pt]
0& \quad \cdots & \quad 0 & \quad 0 & \quad 1\end{pmatrix}\\[5pt]
&\quad=\Bigg[ \prod_{j=1}^d \Bigg(1- \sum_{l=j+1}^d v_l\Bigg)\Bigg]^{-1}\\[5pt]
&\quad \ge 1.\end{align*}
\begin{align*}& \det\bigg(\dfrac{\partial}{\partial v} T^{-1}(v)\bigg)\\
&\quad =\det\begin{pmatrix}\dfrac{1}{1-\sum_{j=2}^d v_j} & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} & \quad \cdots & \quad \dfrac{v_1}{\big(1-\sum_{j=2}^d v_j\big)^2} \\[18pt]
0 & \quad \dfrac{1}{1-\sum_{j=3}^d v_j} & \quad \dfrac{v_2}{\big(1-\sum_{j=3}^d v_j\big)^2} & \quad \cdots & \quad \dfrac{v_2}{\big(1-\sum_{j=3}^d v_j\big)^2} \\[15pt]
\vdots & \quad \vdots & \quad \ddots & \quad \cdots & \quad \vdots \\[5pt]
0 & \quad \cdots & \quad 0 & \quad \dfrac{1}{1-v_d} & \quad \dfrac{v_{d-1}}{(1-v_d)^2}\\[15pt]
0& \quad \cdots & \quad 0 & \quad 0 & \quad 1\end{pmatrix}\\[5pt]
&\quad=\Bigg[ \prod_{j=1}^d \Bigg(1- \sum_{l=j+1}^d v_l\Bigg)\Bigg]^{-1}\\[5pt]
&\quad \ge 1.\end{align*}
Therefore inequality (3) is obtained by applying (4) to the map ![]() $Q=T^{-1}\circ G^{-1}_z$
.
$Q=T^{-1}\circ G^{-1}_z$
.
Combining (1), (2), and (3), we conclude that for each ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
and
$B\in \mathcal{B}(\mathcal{S}_d)$
and ![]() $z\in V_0$
$z\in V_0$
(Step 4) For each ![]() $k\in \{1,2,\ldots,d\}$
,
$k\in \{1,2,\ldots,d\}$
, ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
, and
$B\in \mathcal{B}(\mathcal{S}_d)$
, and ![]() $z\in V_k$
, we have
$z\in V_k$
, we have
 \begin{align*}& \mathbb{P}(Z_d\in B\mid Z_0=z) \\[5pt]
& \quad \ge \mathbb{P}(Z_d\in B\cap (K), (\Theta_{0},\ldots,\Theta_{d-1})= (E_0,E_1,\ldots,E_{k-1},E_{k+1},\ldots, E_{d}) \mid Z_0=z)\\[5pt]
& \quad \ge \text{Const.}\ \mathbb{P}(R_k^{-1}\circ G_{R_k(z)}(\zeta_1,\zeta_2,\ldots,\zeta_d) \in B\cap K )\\[5pt]
& \quad =\text{Const.}\ \mathbb{P}( (\zeta_1,\ldots,\zeta_{d})\in G_{R_k(z)}^{-1}\circ R_k(B\cap K ) )\\[5pt]
& \quad =\text{Const.}\ \mathbb{P}( (\xi_0,\xi_1,\ldots,\xi_{d-1})\in T^{-1} \circ G_{R_k(z)}^{-1}\circ R_k(B\cap K ) ),\end{align*}
\begin{align*}& \mathbb{P}(Z_d\in B\mid Z_0=z) \\[5pt]
& \quad \ge \mathbb{P}(Z_d\in B\cap (K), (\Theta_{0},\ldots,\Theta_{d-1})= (E_0,E_1,\ldots,E_{k-1},E_{k+1},\ldots, E_{d}) \mid Z_0=z)\\[5pt]
& \quad \ge \text{Const.}\ \mathbb{P}(R_k^{-1}\circ G_{R_k(z)}(\zeta_1,\zeta_2,\ldots,\zeta_d) \in B\cap K )\\[5pt]
& \quad =\text{Const.}\ \mathbb{P}( (\zeta_1,\ldots,\zeta_{d})\in G_{R_k(z)}^{-1}\circ R_k(B\cap K ) )\\[5pt]
& \quad =\text{Const.}\ \mathbb{P}( (\xi_0,\xi_1,\ldots,\xi_{d-1})\in T^{-1} \circ G_{R_k(z)}^{-1}\circ R_k(B\cap K ) ),\end{align*}
where we use the fact that, for ![]() $u\in \mathcal{S}_d$
and
$u\in \mathcal{S}_d$
and ![]() $z\in V_k$
,
$z\in V_k$
,
Similarly to the inequalities (2) and (3), we have
It follows that for each ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
,
$B\in \mathcal{B}(\mathcal{S}_d)$
, ![]() $k=1,2,\ldots,d$
and
$k=1,2,\ldots,d$
and ![]() $z\in V_k$
,
$z\in V_k$
,
Next, we define the probability measure ![]() $\varphi$
as
$\varphi$
as
for each ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
. From (5) and (6), we can conclude that condition (c) in Proposition 1 is verified.
$B\in \mathcal{B}(\mathcal{S}_d)$
. From (5) and (6), we can conclude that condition (c) in Proposition 1 is verified.
(Step 5) For each ![]() $B\in \mathcal{B}(\mathcal{S}_d)$
and
$B\in \mathcal{B}(\mathcal{S}_d)$
and ![]() $z\in V$
,
$z\in V$
,
 \begin{align*}\mathbb{P}(Z_{d+1}\in B\mid Z_0=z)& \ge \mathbb{P}(Z_{d+1}\in B, Z_1\in V |Z_0=z)\\[3pt]
&= \mathbb{P}(Z_{d+1}\in B\mid Z_1\in V,Z_0=z)\cdot \mathbb{P}(Z_1\in V\mid Z_0=z) \\[3pt]
&\ge \eta \mathbb{P}(Z_{d+1}\in B\mid Z_1\in V )\\[3pt]
&\ge \text{Const.}\ \lambda_d (B\cap K).\end{align*}
\begin{align*}\mathbb{P}(Z_{d+1}\in B\mid Z_0=z)& \ge \mathbb{P}(Z_{d+1}\in B, Z_1\in V |Z_0=z)\\[3pt]
&= \mathbb{P}(Z_{d+1}\in B\mid Z_1\in V,Z_0=z)\cdot \mathbb{P}(Z_1\in V\mid Z_0=z) \\[3pt]
&\ge \eta \mathbb{P}(Z_{d+1}\in B\mid Z_1\in V )\\[3pt]
&\ge \text{Const.}\ \lambda_d (B\cap K).\end{align*}
Since ![]() $\gcd\{d,d+1\}=1$
, condition (d) in Proposition 1 is also fulfilled. □
$\gcd\{d,d+1\}=1$
, condition (d) in Proposition 1 is also fulfilled. □
3. Beta walks with linearly place-dependent probabilities
Suppose that the conditions of Assumption 1 are fulfilled. Since convergence in total variation implies convergence in distribution, as ![]() $n\to\infty$
,
$n\to\infty$
, ![]() $Z_n$
converges in distribution to a random vector Z having the invariant measure. By the definition of the invariant measure
$Z_n$
converges in distribution to a random vector Z having the invariant measure. By the definition of the invariant measure
where ![]() $\Theta$
is a discrete random vector satisfying
$\Theta$
is a discrete random vector satisfying
and ![]() $\xi$
is independent of Z and
$\xi$
is independent of Z and ![]() $\Theta$
.
$\Theta$
.
Lemma 2. Assume that
•
 $p=(p_1,p_2,\ldots, p_d)$
is a Borel-measurable probability choice function and
$p=(p_1,p_2,\ldots, p_d)$
is a Borel-measurable probability choice function and  $\Theta$
satisfies (8),
$\Theta$
satisfies (8),•
 $\xi$
is independent of Z and
$\xi$
is independent of Z and  $\Theta$
,
$\Theta$
,• Z and
 $\xi$
have the probability density functions f and g respectively (with respect to Lebesgue measures
$\xi$
have the probability density functions f and g respectively (with respect to Lebesgue measures  $\lambda_d$
and
$\lambda_d$
and  $\lambda_1$
).
$\lambda_1$
).
Then (7) holds if and only if f and g satisfy the following equation:
 \begin{equation}f(z)=\sum_{j=0}^d T_j(z) \quad \lambda_d\hbox{-}{a.e.\ on}\ \mathcal{S}_d,\end{equation}
\begin{equation}f(z)=\sum_{j=0}^d T_j(z) \quad \lambda_d\hbox{-}{a.e.\ on}\ \mathcal{S}_d,\end{equation}
where
 \begin{align*}T_0(z_1,z_2,\ldots,z_d)&=\int_{z_1+z_2+\cdots+z_d}^1\dfrac{1}{u^d}\, f\bigg(\dfrac{z_1}{u},\dfrac{z_2}{u},\ldots,\dfrac{z_d}{u}\bigg)p_0\bigg( \dfrac{z_1}{u},\dfrac{z_2}{u},\ldots,\dfrac{z_d}{u}\bigg)g(1-u)\,\text{d} u,\\[5pt]
T_j(z_1,z_2,\ldots,z_d)&=\int_{1-z_j}^1\dfrac{1}{u^d} f\bigg(\dfrac{z_1}{u},\ldots, \dfrac{z_{j-1}}{u},\dfrac{z_j-1+u}{u},\dfrac{z_{j+1}}{u},\ldots,\dfrac{z_d}{u}\bigg)\\[5pt]
& \quad\,\times p_j\bigg(\dfrac{z_1}{u},\ldots, \dfrac{z_{j-1}}{u},\dfrac{z_j-1+u}{u},\dfrac{z_{j+1}}{u},\ldots,\dfrac{z_d}{u}\bigg)g(1-u)\,\text{d} u\end{align*}
\begin{align*}T_0(z_1,z_2,\ldots,z_d)&=\int_{z_1+z_2+\cdots+z_d}^1\dfrac{1}{u^d}\, f\bigg(\dfrac{z_1}{u},\dfrac{z_2}{u},\ldots,\dfrac{z_d}{u}\bigg)p_0\bigg( \dfrac{z_1}{u},\dfrac{z_2}{u},\ldots,\dfrac{z_d}{u}\bigg)g(1-u)\,\text{d} u,\\[5pt]
T_j(z_1,z_2,\ldots,z_d)&=\int_{1-z_j}^1\dfrac{1}{u^d} f\bigg(\dfrac{z_1}{u},\ldots, \dfrac{z_{j-1}}{u},\dfrac{z_j-1+u}{u},\dfrac{z_{j+1}}{u},\ldots,\dfrac{z_d}{u}\bigg)\\[5pt]
& \quad\,\times p_j\bigg(\dfrac{z_1}{u},\ldots, \dfrac{z_{j-1}}{u},\dfrac{z_j-1+u}{u},\dfrac{z_{j+1}}{u},\ldots,\dfrac{z_d}{u}\bigg)g(1-u)\,\text{d} u\end{align*}
for ![]() $j=1,2,\ldots,d$
. (The integrals above are understood in the Lebesgue sense.)
$j=1,2,\ldots,d$
. (The integrals above are understood in the Lebesgue sense.)
Proof. Denote ![]() $\tilde Z=(1-\xi) Z + \xi \Theta$
. For each
$\tilde Z=(1-\xi) Z + \xi \Theta$
. For each ![]() $z\in \mathcal{S}_d$
, we have
$z\in \mathcal{S}_d$
, we have
 \begin{align}\mathbb{P}(\tilde Z\le y)& =\int_0^1 \sum_{j=0}^d\mathbb{P}( u Z + ({1-u}) \Theta\le {y}, \Theta=E_j) g(1-u) \,\text{d} u \notag \\*& = \sum_{j=0}^d \int_{\mathcal{S}_d\times [0,1]}\textbf{1}_{\{ z \le {{u}^{-1}}(y-(1-u)E_j) \}}f(z)p_j(z)g(1-u) \,\text{d} z\,\text{d} u,\end{align}
\begin{align}\mathbb{P}(\tilde Z\le y)& =\int_0^1 \sum_{j=0}^d\mathbb{P}( u Z + ({1-u}) \Theta\le {y}, \Theta=E_j) g(1-u) \,\text{d} u \notag \\*& = \sum_{j=0}^d \int_{\mathcal{S}_d\times [0,1]}\textbf{1}_{\{ z \le {{u}^{-1}}(y-(1-u)E_j) \}}f(z)p_j(z)g(1-u) \,\text{d} z\,\text{d} u,\end{align}
where for ![]() $y=(y_1,y_2,\ldots,y_d)$
,
$y=(y_1,y_2,\ldots,y_d)$
, ![]() $z=(z_1,z_2,\ldots,z_d)\in \mathcal{S}_d$
, we write
$z=(z_1,z_2,\ldots,z_d)\in \mathcal{S}_d$
, we write ![]() $z\le y$
if
$z\le y$
if ![]() $z_j\le y_j$
for all
$z_j\le y_j$
for all ![]() $j=1,2,\ldots,d$
.
$j=1,2,\ldots,d$
.
For each ![]() $j\in \{0,1,\ldots, d\}$
,
$j\in \{0,1,\ldots, d\}$
, ![]() $u\in(0,1)$
, and
$u\in(0,1)$
, and ![]() $y\in \mathcal{S}_d^o$
, changing the variable
$y\in \mathcal{S}_d^o$
, changing the variable ![]() $x=\varphi(z)\coloneqq uz+(1-u)E_j$
we have
$x=\varphi(z)\coloneqq uz+(1-u)E_j$
we have
 \begin{align} &\int_{\mathcal{S}_d}\textbf{1}_{\{z \le{{u}^{-1}}(y-(1-u)E_j) \}}f(z)p_j(z)\,\text{d} z \notag \\[5pt]
& \quad =\int_{\varphi(\mathcal{S}_d)}\textbf{1}_{\{ x \le y \}}f(\varphi^{-1}(x))p_j(\varphi^{-1}(x))\textsf{D} \varphi^{-1}(x) \,\text{d} x \notag\\[5pt]
&\quad =\int_{\{x\in \mathcal{S}_d \colon 0 \le x\le y, 1-u\le x_j\le 1\}}\dfrac{1}{u^d}f\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg)p_j\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg) \,\text{d} x,\end{align}
\begin{align} &\int_{\mathcal{S}_d}\textbf{1}_{\{z \le{{u}^{-1}}(y-(1-u)E_j) \}}f(z)p_j(z)\,\text{d} z \notag \\[5pt]
& \quad =\int_{\varphi(\mathcal{S}_d)}\textbf{1}_{\{ x \le y \}}f(\varphi^{-1}(x))p_j(\varphi^{-1}(x))\textsf{D} \varphi^{-1}(x) \,\text{d} x \notag\\[5pt]
&\quad =\int_{\{x\in \mathcal{S}_d \colon 0 \le x\le y, 1-u\le x_j\le 1\}}\dfrac{1}{u^d}f\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg)p_j\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg) \,\text{d} x,\end{align}
where ![]() $\textsf{D}\varphi^{-1}$
denotes the Jacobian of
$\textsf{D}\varphi^{-1}$
denotes the Jacobian of ![]() $\varphi^{-1}$
. Combining (10) and (11), and applying Fubini’s theorem, we obtain
$\varphi^{-1}$
. Combining (10) and (11), and applying Fubini’s theorem, we obtain
 \begin{align*} &\mathbb{P}(\tilde Z\le y)\\*&\ =\int_{\{x\in \mathcal{S}_d\ \colon 0\le x\le y \}}\Bigg[\sum_{j=0}^d\int_{1-x_j}^1 \dfrac{1}{u^d}f\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg)p_j\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg) g(1-u) \,\text{d} u\Bigg] \,\text{d} x.\end{align*}
\begin{align*} &\mathbb{P}(\tilde Z\le y)\\*&\ =\int_{\{x\in \mathcal{S}_d\ \colon 0\le x\le y \}}\Bigg[\sum_{j=0}^d\int_{1-x_j}^1 \dfrac{1}{u^d}f\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg)p_j\bigg( \dfrac{1}{u}(x-(1-u)E_j) \bigg) g(1-u) \,\text{d} u\Bigg] \,\text{d} x.\end{align*}
Therefore
 \begin{align*}\tilde{f}(z) \coloneqq \sum_{j=0}^d\int_{1-z_j}^1 \dfrac{1}{u^d} f\bigg( \dfrac{1}{u}(z-(1-u)E_j) \bigg) p\bigg( \dfrac{1}{u}(z-(1-u)E_j) \bigg) g(1-u) \,\text{d} u = \sum_{j=0}^d T_j(z)\end{align*}
\begin{align*}\tilde{f}(z) \coloneqq \sum_{j=0}^d\int_{1-z_j}^1 \dfrac{1}{u^d} f\bigg( \dfrac{1}{u}(z-(1-u)E_j) \bigg) p\bigg( \dfrac{1}{u}(z-(1-u)E_j) \bigg) g(1-u) \,\text{d} u = \sum_{j=0}^d T_j(z)\end{align*}
is a probability density function of ![]() $\tilde Z$
, which is unique up to a set of measure zero. Hence,
$\tilde Z$
, which is unique up to a set of measure zero. Hence, ![]() $f(z)=\tilde f(z)$
for almost all
$f(z)=\tilde f(z)$
for almost all ![]() $z\in \mathcal{S}_d$
, and the lemma is thus proved. □
$z\in \mathcal{S}_d$
, and the lemma is thus proved. □
Theorem 2. Assume that
(a)
 $\xi\sim \text{Beta}(1,\gamma)$
, where
$\xi\sim \text{Beta}(1,\gamma)$
, where  $\gamma>0$
is some constant,
$\gamma>0$
is some constant,(b)
 $p=(p_1,p_2,\ldots,p_d)\colon \mathcal{S}_d\to \mathcal{S}_d$
is defined by
where
$p=(p_1,p_2,\ldots,p_d)\colon \mathcal{S}_d\to \mathcal{S}_d$
is defined by
where \[p_k(z_1,z_2, \ldots,z_d)=\beta_k(1-z_k) +\bigg( 1-\sum_{j=1}^{d+1}\beta_j+\beta_k \bigg) z_k, \quad k=1,2,\ldots,d,\]
\[p_k(z_1,z_2, \ldots,z_d)=\beta_k(1-z_k) +\bigg( 1-\sum_{j=1}^{d+1}\beta_j+\beta_k \bigg) z_k, \quad k=1,2,\ldots,d,\]
 $\beta_k>0$
and
$\beta_k>0$
and  $\sum_{j=1}^{d+1}\beta_j-\beta_k<1$
for
$\sum_{j=1}^{d+1}\beta_j-\beta_k<1$
for  $k=1,2,\ldots,d+1$
,
$k=1,2,\ldots,d+1$
,(c)
 $Z\sim \text{Dirichlet}(\beta_1\gamma,\beta_2\gamma,\ldots,\beta_d\gamma, \beta_{d+1}\gamma)$
.
$Z\sim \text{Dirichlet}(\beta_1\gamma,\beta_2\gamma,\ldots,\beta_d\gamma, \beta_{d+1}\gamma)$
.
Then ![]() $Z\overset{d}{=} (1-\xi) Z + \xi \Theta$
, and thus
$Z\overset{d}{=} (1-\xi) Z + \xi \Theta$
, and thus ![]() $Z_n$
converges to a Dirichlet distribution by Theorem 1 and Lemma 2.
$Z_n$
converges to a Dirichlet distribution by Theorem 1 and Lemma 2.
Proof. Let f and g, respectively, be the probability density functions of
It suffices to check that f and g satisfy the integral equation (9).
We have
 \begin{align*}T_0(z_1,\ldots,z_d) &= \dfrac{\Gamma \big(\gamma \sum_{j = 1}^{d + 1} \beta_j\big)}{\prod_{j = 1}^{d + 1} \Gamma (\beta_j\gamma )}\prod_{j = 1}^d z_j^{\beta _j\gamma - 1}\int_{\sum_{j = 1}^d z_j}^1 \bigg( u - \sum_{j = 1}^d z_j \bigg)^{\gamma\beta_{d + 1} - 1} u^{-\gamma \big(\sum_{j = 1}^{d + 1} \beta_j - 1 \big)-1}\\[6pt]
& \quad\, \times\Bigg[\gamma\beta_{d+1} u -\gamma\Bigg(\sum_{j=1}^{d+1}\beta_j-1\Bigg)\Bigg(u-\sum_{j = 1}^d z_j\Bigg)\Bigg]\,\text{d} u\\[6pt]
&=\dfrac{\Gamma \big(\gamma \sum_{j = 1}^{d + 1} \beta_j\big)}{\prod_{j = 1}^{d + 1} \Gamma (\beta_j\gamma )} \Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma}\prod_{j=1}^d z_j^{\beta_j\gamma-1},\end{align*}
\begin{align*}T_0(z_1,\ldots,z_d) &= \dfrac{\Gamma \big(\gamma \sum_{j = 1}^{d + 1} \beta_j\big)}{\prod_{j = 1}^{d + 1} \Gamma (\beta_j\gamma )}\prod_{j = 1}^d z_j^{\beta _j\gamma - 1}\int_{\sum_{j = 1}^d z_j}^1 \bigg( u - \sum_{j = 1}^d z_j \bigg)^{\gamma\beta_{d + 1} - 1} u^{-\gamma \big(\sum_{j = 1}^{d + 1} \beta_j - 1 \big)-1}\\[6pt]
& \quad\, \times\Bigg[\gamma\beta_{d+1} u -\gamma\Bigg(\sum_{j=1}^{d+1}\beta_j-1\Bigg)\Bigg(u-\sum_{j = 1}^d z_j\Bigg)\Bigg]\,\text{d} u\\[6pt]
&=\dfrac{\Gamma \big(\gamma \sum_{j = 1}^{d + 1} \beta_j\big)}{\prod_{j = 1}^{d + 1} \Gamma (\beta_j\gamma )} \Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma}\prod_{j=1}^d z_j^{\beta_j\gamma-1},\end{align*}
where we use the fact that
Similarly, for ![]() $k=1,2,\ldots,d$
, we also obtain that
$k=1,2,\ldots,d$
, we also obtain that
 \[T_k(z_1,\ldots,z_d)=\dfrac{\Gamma\big(\gamma\sum_{j=1}^{d+1}\beta_j\big)}{\prod_{j=1}^{d+1}\Gamma(\beta_j \gamma)}\Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma-1}z_k\prod_{j=1}^d z_j^{\beta_j\gamma-1}.\]
\[T_k(z_1,\ldots,z_d)=\dfrac{\Gamma\big(\gamma\sum_{j=1}^{d+1}\beta_j\big)}{\prod_{j=1}^{d+1}\Gamma(\beta_j \gamma)}\Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma-1}z_k\prod_{j=1}^d z_j^{\beta_j\gamma-1}.\]
Therefore
 \begin{equation*} \sum_{k=0}^dT_k(z_1,\ldots,z_d)=\dfrac{\Gamma\big(\gamma\sum_{j=1}^{d+1}\beta_j\big)}{\prod_{j=1}^{d+1}\Gamma(\beta_j \gamma)}\Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma-1}\prod_{j=1}^d z_j^{\beta_j\gamma-1}=f(z_1,z_2,\ldots,z_d).\end{equation*}
\begin{equation*} \sum_{k=0}^dT_k(z_1,\ldots,z_d)=\dfrac{\Gamma\big(\gamma\sum_{j=1}^{d+1}\beta_j\big)}{\prod_{j=1}^{d+1}\Gamma(\beta_j \gamma)}\Bigg(1-\sum_{j=1}^d z_j \Bigg)^{\beta_{d+1}\gamma-1}\prod_{j=1}^d z_j^{\beta_j\gamma-1}=f(z_1,z_2,\ldots,z_d).\end{equation*}
□
We want to conclude this section with the following observations.
• If
 $d=1$
, then
$d=1$
, then  $p_1(z)=\beta_1(1-z)+(1-\beta_2)z$
. This is, in fact, the one-dimensional case considered by McKinlay and Borovkov in [Reference McKinlay and Borovkov7].
$p_1(z)=\beta_1(1-z)+(1-\beta_2)z$
. This is, in fact, the one-dimensional case considered by McKinlay and Borovkov in [Reference McKinlay and Borovkov7].• If
 $d\ge 1$
and
$d\ge 1$
and  $\sum_{j=1}^{d+1}\beta_j=1$
, then we obtain the model considered by Sethuraman in [Reference Sethuraman10].
$\sum_{j=1}^{d+1}\beta_j=1$
, then we obtain the model considered by Sethuraman in [Reference Sethuraman10].
4. Random walks in [0, 1] based on urn-type schemes
Let ![]() $h\colon [0,1]\to\mathbb{R}_+$
be some non-random measurable function. In this section we will study a random walk on the unit interval
$h\colon [0,1]\to\mathbb{R}_+$
be some non-random measurable function. In this section we will study a random walk on the unit interval ![]() $\mathcal{S}_1=[0,1]$
with the following properties.
$\mathcal{S}_1=[0,1]$
with the following properties.
(1) At time
 $n=0,1,2,\ldots,$
the system is characterized by
$n=0,1,2,\ldots,$
the system is characterized by  $Z_n\in [0,1]$
(location of the particle) and two positive numbers
$Z_n\in [0,1]$
(location of the particle) and two positive numbers  $L_n$
and
$L_n$
and  $R_n$
. We assume that
$R_n$
. We assume that  $R_0=L_0=1$
.
$R_0=L_0=1$
.(2) At time
 $n+1$
, with probability
$n+1$
, with probability  ${{{L_n}/{(L_n+R_n)}}}$
the quantity
${{{L_n}/{(L_n+R_n)}}}$
the quantity  $L_n$
increases by
$L_n$
increases by  $h(Z_n)$
, i.e. a function of the distance from 0 to the current position of the particle, and then the particle jumps to a new location
$h(Z_n)$
, i.e. a function of the distance from 0 to the current position of the particle, and then the particle jumps to a new location  $Z_{n+1}$
, which is uniformly distributed on the interval
$Z_{n+1}$
, which is uniformly distributed on the interval  $(0,Z_n)$
. With the complementary probability
$(0,Z_n)$
. With the complementary probability  ${{{R_n}/{(L_n+R_n)}}}$
, the quantity
${{{R_n}/{(L_n+R_n)}}}$
, the quantity  $R_n$
increases by
$R_n$
increases by  $h(1-Z_n)$
, i.e. a function of the distance from 1 to the current position of the particle, and then the particle jumps to a new location
$h(1-Z_n)$
, i.e. a function of the distance from 1 to the current position of the particle, and then the particle jumps to a new location  $Z_{n+1}$
, uniformly distributed on the interval
$Z_{n+1}$
, uniformly distributed on the interval  $(Z_n,1)$
.
$(Z_n,1)$
.
One can think of ![]() $L_n$
and
$L_n$
and ![]() $R_n$
as numbers of two different kinds of balls in an urn, and the direction of the walk is governed by the kind of ball that is drawn randomly from the urn at time n. The number of balls of the chosen type then increases by yet another random quantity, depending on the position of the walk. The number of balls in our model can, in general, be non-integer; however, this is allowed for the generalized Pólya urn models.
$R_n$
as numbers of two different kinds of balls in an urn, and the direction of the walk is governed by the kind of ball that is drawn randomly from the urn at time n. The number of balls of the chosen type then increases by yet another random quantity, depending on the position of the walk. The number of balls in our model can, in general, be non-integer; however, this is allowed for the generalized Pólya urn models.
Formally, we can write the model as the following recursion: let ![]() $Z_0\in(0,1)$
be some non-random quantity, and for
$Z_0\in(0,1)$
be some non-random quantity, and for ![]() $n=1,2,\ldots$
let
$n=1,2,\ldots$
let
 \begin{equation}\begin{aligned}Z_{n}&= Z_{n-1} \xi_n\cdot \textbf{1}_{\{U_{n}<{{{L_{n-1}}/{(L_{n-1}}}+R_{n-1})}\}}+[Z_{n-1}+(1-Z_{n-1})\,\xi_n]\cdot \textbf{1}_{\{U_n\ge {{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\\[5pt]
L_n&= L_{n-1} +h(Z_{n-1})\cdot \textbf{1}_{\{U_n<{{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\\[5pt]
R_n&= R_{n-1}+h (1-Z_{n-1})\cdot \textbf{1}_{\{U_n\ge {{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\end{aligned}\end{equation}
\begin{equation}\begin{aligned}Z_{n}&= Z_{n-1} \xi_n\cdot \textbf{1}_{\{U_{n}<{{{L_{n-1}}/{(L_{n-1}}}+R_{n-1})}\}}+[Z_{n-1}+(1-Z_{n-1})\,\xi_n]\cdot \textbf{1}_{\{U_n\ge {{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\\[5pt]
L_n&= L_{n-1} +h(Z_{n-1})\cdot \textbf{1}_{\{U_n<{{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\\[5pt]
R_n&= R_{n-1}+h (1-Z_{n-1})\cdot \textbf{1}_{\{U_n\ge {{{L_{n-1}}/{(L_{n-1}}}+R_{n-1}})\}},\end{aligned}\end{equation}
where ![]() $\{\xi_n,U_n\}_{n=1}^\infty$
is a set of i.i.d. uniform U[0, 1] random variables. Since the probabilities of jumps to the left (and right, respectively) depend on
$\{\xi_n,U_n\}_{n=1}^\infty$
is a set of i.i.d. uniform U[0, 1] random variables. Since the probabilities of jumps to the left (and right, respectively) depend on ![]() $(L_n, R_n)$
, the distribution of
$(L_n, R_n)$
, the distribution of ![]() $Z_{n+1}$
is generally dependent on the whole history of the random walk up to time n. Also, let
$Z_{n+1}$
is generally dependent on the whole history of the random walk up to time n. Also, let
and note that ![]() $Z_n$
is
$Z_n$
is ![]() $\mathcal{F}_n$
-measurable, while
$\mathcal{F}_n$
-measurable, while ![]() $L_n$
and
$L_n$
and ![]() $R_n$
are
$R_n$
are ![]() $\mathcal{G}_n$
-measurable.
$\mathcal{G}_n$
-measurable.
If ![]() $h(x)\equiv 0$
, then
$h(x)\equiv 0$
, then ![]() $L_n$
and
$L_n$
and ![]() $R_n$
do not change with time, and
$R_n$
do not change with time, and ![]() $Z_n$
is a Markov chain satisfying Theorem 2 with
$Z_n$
is a Markov chain satisfying Theorem 2 with ![]() $\gamma=1$
and
$\gamma=1$
and
so ![]() $Z_n$
converges in distribution to
$Z_n$
converges in distribution to
If ![]() $h(x)\equiv \beta$
for some constant
$h(x)\equiv \beta$
for some constant ![]() $\beta>0$
, then the process
$\beta>0$
, then the process ![]() $(L_n,R_n)$
is the classical Pólya urn. We conjecture that under some regularity conditions on the function h, the random walk
$(L_n,R_n)$
is the classical Pólya urn. We conjecture that under some regularity conditions on the function h, the random walk ![]() $Z_n$
converges either almost surely to a Bernoulli random variable, or weakly to some non-trivial distribution with full support on [0, 1] (compare with Section 2.1 in [Reference Diaconis and Freedman3]). Even though we were not able to deal with the general case, there is one non-trivial situation where we have explicit results, as follows.
$Z_n$
converges either almost surely to a Bernoulli random variable, or weakly to some non-trivial distribution with full support on [0, 1] (compare with Section 2.1 in [Reference Diaconis and Freedman3]). Even though we were not able to deal with the general case, there is one non-trivial situation where we have explicit results, as follows.
In the remaining part of this section we consider only the case where
It turns out that even in this seemingly ‘simple’ case, there are challenges to rigorously obtaining the limiting distribution (see Theorem 3 below).
Lemma 3. We have
(a)
 $\limsup_{n\to\infty} {{{L_{n}}/{R_{n}}}}\le 4$
and
$\limsup_{n\to\infty} {{{L_{n}}/{R_{n}}}}\le 4$
and  $\limsup_{n\to\infty} {{{R_{n}}/{L_{n}}}}\le 4$
almost surely,
$\limsup_{n\to\infty} {{{R_{n}}/{L_{n}}}}\le 4$
almost surely,(b)
 $L_n\to\infty$
and
$L_n\to\infty$
and  $R_n\to\infty$
almost surely as
$R_n\to\infty$
almost surely as  $n\to\infty$
.
$n\to\infty$
.
Proof. First of all, observe that the probability that the sequence ![]() $Z_n$
eventually becomes monotone is zero, namely
$Z_n$
eventually becomes monotone is zero, namely
Since ![]() $R_n$
is non-decreasing in n and
$R_n$
is non-decreasing in n and ![]() $L_n\le L_0+n$
, we have
$L_n\le L_0+n$
, we have
Since
by Lévy’s extension to the Borel–Cantelli lemma the event in the above display happens infinitely often with probability 1, hence there are infinitely many ns for which ![]() $Z_n$
decreases. By the identical argument,
$Z_n$
decreases. By the identical argument, ![]() $Z_n$
cannot eventually become increasing.
$Z_n$
cannot eventually become increasing.
Let us prove part (a) now. We know that ![]() $Z_n$
makes a.s. infinitely many steps to the left as well as to the right. Hence there exists a sequence of finite stopping times with respect to the filtration
$Z_n$
makes a.s. infinitely many steps to the left as well as to the right. Hence there exists a sequence of finite stopping times with respect to the filtration ![]() $\mathcal{G}$
:
$\mathcal{G}$
:
 \begin{align*}\tau_1&=0,\\[4pt]
\eta_i&=\inf\{n>\tau_i\colon Z_n\ge Z_{n-1}\},\\[4pt]
\tau_{i+1}&=\inf\{n>\eta_{i}\colon Z_n
< Z_{n-1}\},\end{align*}
\begin{align*}\tau_1&=0,\\[4pt]
\eta_i&=\inf\{n>\tau_i\colon Z_n\ge Z_{n-1}\},\\[4pt]
\tau_{i+1}&=\inf\{n>\eta_{i}\colon Z_n
< Z_{n-1}\},\end{align*}
for ![]() $i=1,2,\ldots.$
Moreover,
$i=1,2,\ldots.$
Moreover,
![]() $\tau_n,\eta_n\to\infty$
as
$\tau_n,\eta_n\to\infty$
as ![]() $n\to\infty$
, and
$n\to\infty$
, and
for each ![]() $i=2,3,\ldots$
(note that, in fact, the probability of the event
$i=2,3,\ldots$
(note that, in fact, the probability of the event ![]() $Z_n=Z_{n-1}$
is zero).
$Z_n=Z_{n-1}$
is zero).
Observe that, for each ![]() $k\ge 1$
and
$k\ge 1$
and ![]() $1\le \ell\le k-1$
,
$1\le \ell\le k-1$
,
 \begin{align*}& \{\eta_i=k,\ \tau_i=k-\ell\}\\[6pt]
&\quad =\{Z_k\ge Z_{k-1},\ Z_{k-1}< Z_{k-2}<\cdots<Z_{k-\ell}, \tau_i=k-\ell\}\\[6pt]
& \quad =\bigg\{U_k\ge \dfrac{ L_{k-1}}{L_{k-1}+R_{k-1}},\ U_{k-1} \lt \dfrac{ L_{k-2}}{L_{k-2}+R_{k-2}}, \ldots,U_{k-\ell+1} \lt \dfrac{ L_{k-\ell}}{L_{k-\ell}+R_{k-\ell}},\ \tau_i=k-\ell\bigg\}.\end{align*}
\begin{align*}& \{\eta_i=k,\ \tau_i=k-\ell\}\\[6pt]
&\quad =\{Z_k\ge Z_{k-1},\ Z_{k-1}< Z_{k-2}<\cdots<Z_{k-\ell}, \tau_i=k-\ell\}\\[6pt]
& \quad =\bigg\{U_k\ge \dfrac{ L_{k-1}}{L_{k-1}+R_{k-1}},\ U_{k-1} \lt \dfrac{ L_{k-2}}{L_{k-2}+R_{k-2}}, \ldots,U_{k-\ell+1} \lt \dfrac{ L_{k-\ell}}{L_{k-\ell}+R_{k-\ell}},\ \tau_i=k-\ell\bigg\}.\end{align*}
However, ![]() $L_{k-j}$
and
$L_{k-j}$
and ![]() $R_{k-j}$
depend only on
$R_{k-j}$
depend only on ![]() $L_{k-j-1}$
,
$L_{k-j-1}$
, ![]() $R_{k-j-1}$
,
$R_{k-j-1}$
, ![]() $Z_{k-j-1}$
, and
$Z_{k-j-1}$
, and ![]() $U_{k-j}$
,
$U_{k-j}$
, ![]() $j=1,2,\ldots,\ell$
(see (12)). Hence the event above is
$j=1,2,\ldots,\ell$
(see (12)). Hence the event above is ![]() $\sigma(U_1,\ldots,U_k,\xi_1,\ldots,\xi_{k-2})$
-measurable, and it is thus independent of
$\sigma(U_1,\ldots,U_k,\xi_1,\ldots,\xi_{k-2})$
-measurable, and it is thus independent of ![]() $\xi_{k-1}$
; as a result
$\xi_{k-1}$
; as a result ![]() $V_{i+1}\coloneqq \xi_{\eta_i-1}$
is independent of
$V_{i+1}\coloneqq \xi_{\eta_i-1}$
is independent of
On the other hand, since ![]() $\eta_{i-1}-1\le \eta_i-2$
,
$\eta_{i-1}-1\le \eta_i-2$
, ![]() $V_i$
is
$V_i$
is ![]() $\mathcal{H}_i$
-measurable. So
$\mathcal{H}_i$
-measurable. So ![]() $\{V_i\}_{i=1}^\infty$
is an i.i.d. sequence of Uniform[0, 1] random variables.
$\{V_i\}_{i=1}^\infty$
is an i.i.d. sequence of Uniform[0, 1] random variables.
We have
hence, due to the monotonicity of ![]() $R_n$
,
$R_n$
,
 \[R_{\eta_i}\ge \sum_{k=1}^{i} [1-V_{k+1}].\]
\[R_{\eta_i}\ge \sum_{k=1}^{i} [1-V_{k+1}].\]
By the strong law of large numbers
 \[\lim_{k\to\infty} \dfrac 1k \sum_{i=1}^k [1-V_{i+1}]=\dfrac 12\quad \text{a.s.,}\]
\[\lim_{k\to\infty} \dfrac 1k \sum_{i=1}^k [1-V_{i+1}]=\dfrac 12\quad \text{a.s.,}\]
hence
Next, for ![]() $i\in\mathbb{N}$
, we have
$i\in\mathbb{N}$
, we have
 \begin{align*}L_{\tau_{i+1}-1}-L_{\eta_i-1}&=0,\\[5pt]
L_{\eta_i-1}-L_{\tau_i-1}&=Z_{\tau_i-1}(1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2})\\[5pt]
&\le 1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\le \tilde V_i,\end{align*}
\begin{align*}L_{\tau_{i+1}-1}-L_{\eta_i-1}&=0,\\[5pt]
L_{\eta_i-1}-L_{\tau_i-1}&=Z_{\tau_i-1}(1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2})\\[5pt]
&\le 1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\le \tilde V_i,\end{align*}
where
 \begin{align*}\tilde V_i&= [1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2} ]\\[5pt]
& \quad\, +\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\\[5pt]
&\quad\, +\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\tilde\xi^{(i)}_{\eta_i+1}+\cdots\\[5pt]
&=1+\sum_{k=\tau_i}^{\eta_i-2} \xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{k}+\sum_{k=\eta_i-1}^{\infty}\xi_{\tau_i}\cdots\xi_{\eta_i-2}\cdot\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\cdots\tilde\xi^{(i)}_{k}\end{align*}
\begin{align*}\tilde V_i&= [1+\xi_{\tau_i}+\xi_{\tau_i}\xi_{\tau_i+1}+\cdots+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2} ]\\[5pt]
& \quad\, +\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}+\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\\[5pt]
&\quad\, +\xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{\eta_i-2}\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\tilde\xi^{(i)}_{\eta_i+1}+\cdots\\[5pt]
&=1+\sum_{k=\tau_i}^{\eta_i-2} \xi_{\tau_i}\xi_{\tau_i+1}\cdots\xi_{k}+\sum_{k=\eta_i-1}^{\infty}\xi_{\tau_i}\cdots\xi_{\eta_i-2}\cdot\tilde\xi^{(i)}_{\eta_i-1}\tilde\xi^{(i)}_{\eta_i}\cdots\tilde\xi^{(i)}_{k}\end{align*}
and ![]() $\tilde\xi^{(i)}_k$
,
$\tilde\xi^{(i)}_k$
, ![]() $i,k\in\mathbb{N}$
are i.i.d. copies of
$i,k\in\mathbb{N}$
are i.i.d. copies of ![]() $\xi$
, independent of everything else. By construction,
$\xi$
, independent of everything else. By construction, ![]() $\tilde V_i$
is a
$\tilde V_i$
is a ![]() $\tilde{\mathcal{H}_i}$
-measurable random variable, where
$\tilde{\mathcal{H}_i}$
-measurable random variable, where
On the other hand, one can easily show that the variables ![]() $\xi_{\tau_{i+1}+j}$
,
$\xi_{\tau_{i+1}+j}$
, ![]() $\tilde{\xi}^{(i+1)}_{j+1}$
,
$\tilde{\xi}^{(i+1)}_{j+1}$
, ![]() $j=0,1,2,\ldots,$
are independent of
$j=0,1,2,\ldots,$
are independent of ![]() $\tilde{\mathcal{H}_i}$
, and therefore
$\tilde{\mathcal{H}_i}$
, and therefore ![]() $\tilde V_{i+1}$
is independent of
$\tilde V_{i+1}$
is independent of ![]() $\tilde{\mathcal{H}_i}$
. Consequently,
$\tilde{\mathcal{H}_i}$
. Consequently, ![]() $\tilde V_i$
,
$\tilde V_i$
, ![]() $i=1,2,\ldots,$
are independent random variables with expectation
$i=1,2,\ldots,$
are independent random variables with expectation
 \[\mathbb{E}\Bigg[1+ \sum_{k=1}^{\infty} \Bigg(\prod_{i=1}^k \xi_i\Bigg)\Bigg]=2,\]
\[\mathbb{E}\Bigg[1+ \sum_{k=1}^{\infty} \Bigg(\prod_{i=1}^k \xi_i\Bigg)\Bigg]=2,\]
and hence by the strong law we have
 \[\lim_{k\to\infty} \dfrac 1k \sum_{i=1}^k \tilde V_i=2\quad\text{a.s.,}\]
\[\lim_{k\to\infty} \dfrac 1k \sum_{i=1}^k \tilde V_i=2\quad\text{a.s.,}\]
yielding
Combining this with (13), and taking into account that ![]() $\eta_i\to\infty$
, we get
$\eta_i\to\infty$
, we get
Due to the symmetry, the complementary inequality can be proved identically.
Let us now prove part (b). From part (a) we obtain that a.s. either both ![]() $L_n$
and
$L_n$
and ![]() $R_n$
increase to
$R_n$
increase to ![]() $\infty$
, or both stay bounded, i.e.
$\infty$
, or both stay bounded, i.e. ![]() $\sup_{n\ge0}L_n<\infty$
and
$\sup_{n\ge0}L_n<\infty$
and ![]() $\sup_{n\ge0}R_n<\infty$
for all n. Let us show that the latter case a.s. cannot happen. Again, from (a) we get that a.s. there exists a (random) N such that, for
$\sup_{n\ge0}R_n<\infty$
for all n. Let us show that the latter case a.s. cannot happen. Again, from (a) we get that a.s. there exists a (random) N such that, for ![]() $n\ge N$
,
$n\ge N$
,
As a result, for ![]() $n\ge N$
, we have for
$n\ge N$
, we have for ![]() $S_n=L_n+R_n$
$S_n=L_n+R_n$
 \begin{align*}& \mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n\bigg)\\[4pt]
& \quad =\mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)+\mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[4pt]
&\quad \geq\mathbb{P}\bigg(R_{n+1}-R_n>\dfrac 14\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)+\mathbb{P}\bigg(L_{n+1}-L_n>\dfrac 14\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[4pt]
&\quad =\mathbb{P}\bigg(R_{n+1}-R_n>\dfrac 14,\ Z_{n+1}>Z_n\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)\\[4pt]
&\quad \quad\, +\mathbb{P}\bigg(L_{n+1}-L_n > \dfrac 14,\ Z_{n+1}<Z_n\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[5pt]
&\quad \geq \dfrac 12 \cdot\dfrac 15+\dfrac 12 \cdot\dfrac 15\\[6pt]
&\quad =\dfrac 15>0.\end{align*}
\begin{align*}& \mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n\bigg)\\[4pt]
& \quad =\mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)+\mathbb{P}\bigg(S_{n+1}-S_n>\dfrac 14\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[4pt]
&\quad \geq\mathbb{P}\bigg(R_{n+1}-R_n>\dfrac 14\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)+\mathbb{P}\bigg(L_{n+1}-L_n>\dfrac 14\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[4pt]
&\quad =\mathbb{P}\bigg(R_{n+1}-R_n>\dfrac 14,\ Z_{n+1}>Z_n\mid {\mathcal F}_n, Z_n\le \dfrac12\bigg)\\[4pt]
&\quad \quad\, +\mathbb{P}\bigg(L_{n+1}-L_n > \dfrac 14,\ Z_{n+1}<Z_n\mid {\mathcal F}_n, Z_n> \dfrac12\bigg)\\[5pt]
&\quad \geq \dfrac 12 \cdot\dfrac 15+\dfrac 12 \cdot\dfrac 15\\[6pt]
&\quad =\dfrac 15>0.\end{align*}
Since ![]() $S_n$
is non-decreasing for any n, this implies that
$S_n$
is non-decreasing for any n, this implies that ![]() $S_n\to\infty$
a.s., contradicting the assumption that both
$S_n\to\infty$
a.s., contradicting the assumption that both ![]() $L_n$
and
$L_n$
and ![]() $R_n$
remain bounded. □
$R_n$
remain bounded. □
converges almost surely to ![]() $\zeta_{\infty}\in(0,1)$
as
$\zeta_{\infty}\in(0,1)$
as ![]() $n\to\infty$
.
$n\to\infty$
.
Remark 2. Lemma 3 implies only that
Proof of Lemma 4. We introduce the quantity
which will be shown to be a supermartingale. Indeed,
 \begin{align*}& \mathbb{E} (W_{n+1}|\mathcal{F}_n )\\[5pt]
&\quad =\dfrac{L_n}{L_n+R_n}\mathbb{E}\bigg(W_{n+1} \mid U_{n+1}<\dfrac{L_{n}}{L_n+R_n},\mathcal{F}_n \bigg)\\[5pt]
&\quad\quad\, +\dfrac{R_n}{L_n+R_n}\mathbb{E}\bigg(W_{n+1} \mid U_{n+1}>\dfrac{L_n}{L_n+R_n},\mathcal{F}_n\bigg)\\[5pt]
& \quad = \dfrac{L_n}{L_n+R_n}\int_{0}^{Z_n} \dfrac{1}{Z_n}\bigg[ \bigg(\dfrac{1}{2}-\dfrac{L_n+Z_n+u}{L_n+R_n+Z_n} \bigg)^2+\dfrac{1}{L_n+R_n+Z_n}\bigg]\,\text{d} u\\[5pt]
& \quad\quad\, + \dfrac{R_{n}}{L_n+R_{n}}\int_{Z_n}^{1} \dfrac{1}{1-Z_n}\bigg[\bigg(\dfrac{1}{2}-\dfrac{L_n+u}{L_n+R_n+1-Z_n} \bigg)^2+\dfrac{1}{L_n+R_n+1-Z_n}\bigg]\,\text{d} u\\[5pt]
&\quad = \dfrac{L_n}{L_n + R_n}\dfrac{3 ( {L_n - R_n} )^2 + 12 ( {L_n - R_n} )Z_n + 12 ( {L_n + R_n + Z_n} ) + 13Z_n^2}{12 ( L_n + R_n + Z_n )^2}\\[5pt]
&\quad\quad\, + \dfrac{R_n}{L_n + R_n}\dfrac{3 ( {L_n - R_n} )^2 + 12 ( {L_n - R_n} )Z_n + 12 ( {L_n + R_n + Z_n} ) + 13(1-Z_n)^2}{12 ( L_n + R_n + 1-Z_n )^2}.\end{align*}
\begin{align*}& \mathbb{E} (W_{n+1}|\mathcal{F}_n )\\[5pt]
&\quad =\dfrac{L_n}{L_n+R_n}\mathbb{E}\bigg(W_{n+1} \mid U_{n+1}<\dfrac{L_{n}}{L_n+R_n},\mathcal{F}_n \bigg)\\[5pt]
&\quad\quad\, +\dfrac{R_n}{L_n+R_n}\mathbb{E}\bigg(W_{n+1} \mid U_{n+1}>\dfrac{L_n}{L_n+R_n},\mathcal{F}_n\bigg)\\[5pt]
& \quad = \dfrac{L_n}{L_n+R_n}\int_{0}^{Z_n} \dfrac{1}{Z_n}\bigg[ \bigg(\dfrac{1}{2}-\dfrac{L_n+Z_n+u}{L_n+R_n+Z_n} \bigg)^2+\dfrac{1}{L_n+R_n+Z_n}\bigg]\,\text{d} u\\[5pt]
& \quad\quad\, + \dfrac{R_{n}}{L_n+R_{n}}\int_{Z_n}^{1} \dfrac{1}{1-Z_n}\bigg[\bigg(\dfrac{1}{2}-\dfrac{L_n+u}{L_n+R_n+1-Z_n} \bigg)^2+\dfrac{1}{L_n+R_n+1-Z_n}\bigg]\,\text{d} u\\[5pt]
&\quad = \dfrac{L_n}{L_n + R_n}\dfrac{3 ( {L_n - R_n} )^2 + 12 ( {L_n - R_n} )Z_n + 12 ( {L_n + R_n + Z_n} ) + 13Z_n^2}{12 ( L_n + R_n + Z_n )^2}\\[5pt]
&\quad\quad\, + \dfrac{R_n}{L_n + R_n}\dfrac{3 ( {L_n - R_n} )^2 + 12 ( {L_n - R_n} )Z_n + 12 ( {L_n + R_n + Z_n} ) + 13(1-Z_n)^2}{12 ( L_n + R_n + 1-Z_n )^2}.\end{align*}
Substituting
or equivalently
we obtain that
where
 \begin{align*}r_0(\zeta,z)&=-24z \zeta^3+36z \zeta^2+12\,\zeta^3-18z\zeta-24\zeta^2+3z+15\zeta-3\\[4pt]
&=-3(2\zeta-1)^2(\zeta z+(1-z)(1-\zeta)),\\[4pt]
r_1(\zeta,z)&=-30\,{z}^{2}{\zeta}^{2}-12\,z{\zeta}^{3}+30\,{z}^{2}\zeta+24\,z{\zeta}^{2}+6\,{\zeta}^{3}\\[4pt]
&\quad\, -7\,{z}^{2}-38\,z\zeta-12\,{\zeta}^{2}+14\,z+13\,\zeta-7,\\[4pt]
r_2(\zeta,z)&=10\,{z}^{3}\zeta-12\,{z}^{2}{\zeta}^{2}-5\,{z}^{3}-9\,{z}^{2}\zeta+7\,{z}^{2}-19\,z\zeta+4\,z+6\,\zeta-6,\\[4pt]
r_3(\zeta,z)&=-z ( 6\,{z}^{3}{\zeta}^{2}-6\,{z}^{3}\zeta-12\,{z}^{2}{\zeta}^{2}-17\,{z}^{3}-12\,{z}^{2}\zeta\\[4pt]
&\quad\, +6\,z{\zeta}^{2}+28\,{z}^{2}+30\,z\zeta-23\,z-6\,\zeta+12 ),\\[4pt]
r_4(\zeta,z)&=-6\,{z}^{2} ( 1-z ) (z^2+2z\zeta(1-z)+1 ),\\[4pt]
r_5(\zeta,z)&=-6z^4 ( 1- z )^2.\end{align*}
\begin{align*}r_0(\zeta,z)&=-24z \zeta^3+36z \zeta^2+12\,\zeta^3-18z\zeta-24\zeta^2+3z+15\zeta-3\\[4pt]
&=-3(2\zeta-1)^2(\zeta z+(1-z)(1-\zeta)),\\[4pt]
r_1(\zeta,z)&=-30\,{z}^{2}{\zeta}^{2}-12\,z{\zeta}^{3}+30\,{z}^{2}\zeta+24\,z{\zeta}^{2}+6\,{\zeta}^{3}\\[4pt]
&\quad\, -7\,{z}^{2}-38\,z\zeta-12\,{\zeta}^{2}+14\,z+13\,\zeta-7,\\[4pt]
r_2(\zeta,z)&=10\,{z}^{3}\zeta-12\,{z}^{2}{\zeta}^{2}-5\,{z}^{3}-9\,{z}^{2}\zeta+7\,{z}^{2}-19\,z\zeta+4\,z+6\,\zeta-6,\\[4pt]
r_3(\zeta,z)&=-z ( 6\,{z}^{3}{\zeta}^{2}-6\,{z}^{3}\zeta-12\,{z}^{2}{\zeta}^{2}-17\,{z}^{3}-12\,{z}^{2}\zeta\\[4pt]
&\quad\, +6\,z{\zeta}^{2}+28\,{z}^{2}+30\,z\zeta-23\,z-6\,\zeta+12 ),\\[4pt]
r_4(\zeta,z)&=-6\,{z}^{2} ( 1-z ) (z^2+2z\zeta(1-z)+1 ),\\[4pt]
r_5(\zeta,z)&=-6z^4 ( 1- z )^2.\end{align*}
One can show that ![]() $\max_{x,y\in [0,1]} r_i(x,y)\le 0$
for
$\max_{x,y\in [0,1]} r_i(x,y)\le 0$
for ![]() $i=0,2,3,4,5$
. From the assertion of Lemma 3,
$i=0,2,3,4,5$
. From the assertion of Lemma 3, ![]() $\varepsilon_n\to 0$
almost surely as
$\varepsilon_n\to 0$
almost surely as ![]() $n\to\infty$
, and one can show that
$n\to\infty$
, and one can show that ![]() $\max_{x,y\in [0,1]} r_0(x,y)+r_1(x,y)\varepsilon \le 0$
for
$\max_{x,y\in [0,1]} r_0(x,y)+r_1(x,y)\varepsilon \le 0$
for ![]() $0\le \varepsilon< 0.5$
. Hence
$0\le \varepsilon< 0.5$
. Hence ![]() $W_n$
is a supermartingale. Therefore, by Doob’s martingale convergence theorem, a.s. there exists
$W_n$
is a supermartingale. Therefore, by Doob’s martingale convergence theorem, a.s. there exists ![]() $ W_{\infty}\coloneqq \lim_{n\to\infty} W_n$
. Observe that
$ W_{\infty}\coloneqq \lim_{n\to\infty} W_n$
. Observe that
 \[\zeta_n\in \Bigg\{\dfrac12-\sqrt{W_n-\dfrac1{L_n+R_n}}-\dfrac{Z_n}{L_n+R_n},\dfrac12+\sqrt{W_n-\dfrac1{L_n+R_n}}-\dfrac{Z_n}{L_n+R_n}\Bigg\}.\]
\[\zeta_n\in \Bigg\{\dfrac12-\sqrt{W_n-\dfrac1{L_n+R_n}}-\dfrac{Z_n}{L_n+R_n},\dfrac12+\sqrt{W_n-\dfrac1{L_n+R_n}}-\dfrac{Z_n}{L_n+R_n}\Bigg\}.\]
On the other hand, note that
as ![]() $n\to\infty$
. As a result,
$n\to\infty$
. As a result, ![]() $\limsup_{n\to\infty} \zeta_n=\liminf_{n\to\infty} \zeta_n=\!:\,\zeta_{\infty}$
almost surely. □
$\limsup_{n\to\infty} \zeta_n=\liminf_{n\to\infty} \zeta_n=\!:\,\zeta_{\infty}$
almost surely. □
Lemma 5. ![]() $\zeta_{\infty}=\frac{1}{2}$
almost surely.
$\zeta_{\infty}=\frac{1}{2}$
almost surely.
Proof. Suppose ![]() $\mathbb{P}(\zeta_{\infty}=1/2)<1$
. Then there exists
$\mathbb{P}(\zeta_{\infty}=1/2)<1$
. Then there exists ![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that ![]() $\mathbb{P}(|\zeta_{\infty}-1/2|>\varepsilon)>0$
. Let us denote the stopping time
$\mathbb{P}(|\zeta_{\infty}-1/2|>\varepsilon)>0$
. Let us denote the stopping time
Since ![]() $\mathbb{P}(|\zeta_{\infty}-1/2|>\varepsilon)>0$
, there exists m such that
$\mathbb{P}(|\zeta_{\infty}-1/2|>\varepsilon)>0$
, there exists m such that ![]() $\mathbb{P}(\tau_m=\infty)>0$
. Let us consider
$\mathbb{P}(\tau_m=\infty)>0$
. Let us consider ![]() $Y_{n}=W_{n\wedge \tau_m}$
.
$Y_{n}=W_{n\wedge \tau_m}$
. ![]() $Y_n$
is also a supermartingale, hence there exists
$Y_n$
is also a supermartingale, hence there exists ![]() $Y_{\infty}=\lim_{n\to\infty}Y_n$
as well. From (14) it follows that
$Y_{\infty}=\lim_{n\to\infty}Y_n$
as well. From (14) it follows that
where
 \begin{align*}\rho_n &=\dfrac{1}{(1+\varepsilon_n Z_n)^2 (1+\varepsilon_n(1-Z_n))^2}( {r}_1(\zeta_n,Z_n)+{r_2}(\zeta_n,Z_n)\varepsilon_n+\cdots +r_5(\zeta_n,Z_n) \varepsilon_n^4\\[6pt]
& \quad\, - (1+(1-Z_n)Z_n\varepsilon_n )(2+\varepsilon_n+(1-Z_n)Z_n\varepsilon_n^2)r_0(\zeta_n,Z_n) ) .\end{align*}
\begin{align*}\rho_n &=\dfrac{1}{(1+\varepsilon_n Z_n)^2 (1+\varepsilon_n(1-Z_n))^2}( {r}_1(\zeta_n,Z_n)+{r_2}(\zeta_n,Z_n)\varepsilon_n+\cdots +r_5(\zeta_n,Z_n) \varepsilon_n^4\\[6pt]
& \quad\, - (1+(1-Z_n)Z_n\varepsilon_n )(2+\varepsilon_n+(1-Z_n)Z_n\varepsilon_n^2)r_0(\zeta_n,Z_n) ) .\end{align*}
Furthermore, ![]() $|\rho_n|$
is bounded by a non-random constant. This fact implies that, for
$|\rho_n|$
is bounded by a non-random constant. This fact implies that, for ![]() $N>0$
,
$N>0$
,
 \[\mathbb{E}( W_{m+N} )-\mathbb{E}( W_{m} )=\dfrac{1}{6}\mathbb{E}\Bigg(\sum_{n=m}^{m+N} \varepsilon_n( r_0(\zeta_n,Z_n)+O(\varepsilon_n))\Bigg).\]
\[\mathbb{E}( W_{m+N} )-\mathbb{E}( W_{m} )=\dfrac{1}{6}\mathbb{E}\Bigg(\sum_{n=m}^{m+N} \varepsilon_n( r_0(\zeta_n,Z_n)+O(\varepsilon_n))\Bigg).\]
Therefore
 \begin{equation}\mathbb{E}( Y_{\infty} )-\mathbb{E}( Y_{m} )=\dfrac{1}{6}\mathbb{E}\Bigg(\sum_{n=m}^{\tau_m} \varepsilon_n(r_0(\zeta_n,Z_n)+O(\varepsilon_n))\Bigg).\end{equation}
\begin{equation}\mathbb{E}( Y_{\infty} )-\mathbb{E}( Y_{m} )=\dfrac{1}{6}\mathbb{E}\Bigg(\sum_{n=m}^{\tau_m} \varepsilon_n(r_0(\zeta_n,Z_n)+O(\varepsilon_n))\Bigg).\end{equation}
Note that
Hence, combining with Remark 2, it follows that on the event ![]() $\{\tau_m=\infty\}$
$\{\tau_m=\infty\}$
for large enough n. Since ![]() $\mathbb{P}(\tau_m=\infty)>0$
and
$\mathbb{P}(\tau_m=\infty)>0$
and ![]() $\varepsilon_n\ge {{{1}/{(2+n)}}}$
, the left-hand side of (15) is finite while the right-hand side is divergent. This contradiction proves the lemma. □
$\varepsilon_n\ge {{{1}/{(2+n)}}}$
, the left-hand side of (15) is finite while the right-hand side is divergent. This contradiction proves the lemma. □
Theorem 3. As ![]() $n\to\infty$
,
$n\to\infty$
, ![]() $Z_n$
converges in distribution to a
$Z_n$
converges in distribution to a ![]() $\text{Beta}(\frac12,\frac12)$
random variable.
$\text{Beta}(\frac12,\frac12)$
random variable.
Proof. Let us fix a small ![]() $\varepsilon>0$
. By Lemma 5 there exists a (random) N such that
$\varepsilon>0$
. By Lemma 5 there exists a (random) N such that
for all ![]() $n\ge N$
. Fix a large non-random
$n\ge N$
. Fix a large non-random ![]() $N_0$
. For this fixed
$N_0$
. For this fixed ![]() $N_0$
we couple
$N_0$
we couple ![]() $\{{Z_n}\}_{n\ge 0}$
with two random walks
$\{{Z_n}\}_{n\ge 0}$
with two random walks ![]() $\{\tilde{Z_n}\}_{n\ge 0}$
and
$\{\tilde{Z_n}\}_{n\ge 0}$
and ![]() $\{\hat Z_n\}_{n\ge 0}$
defined as follows.
$\{\hat Z_n\}_{n\ge 0}$
defined as follows.
• For
 $0\le n \le N_0$
, set
$0\le n \le N_0$
, set  $\tilde{Z_n} = \hat Z_n =Z_{n}.$
$\tilde{Z_n} = \hat Z_n =Z_{n}.$
• For
 $n\ge N_0$
, set
and
$n\ge N_0$
, set
and \[\tilde Z_{n+1}=\begin{cases}\xi_{n+1} \tilde Z_n & \text{if} \ U_{n+1}\le \dfrac{1}{2}-\varepsilon,\\[12pt]\tilde Z_n+\xi_{n+1} (1-\tilde Z_n) & \text{if} \ U_{n+1}>\dfrac{1}{2}-\varepsilon,\end{cases}\]
\[\tilde Z_{n+1}=\begin{cases}\xi_{n+1} \tilde Z_n & \text{if} \ U_{n+1}\le \dfrac{1}{2}-\varepsilon,\\[12pt]\tilde Z_n+\xi_{n+1} (1-\tilde Z_n) & \text{if} \ U_{n+1}>\dfrac{1}{2}-\varepsilon,\end{cases}\]
 \[\hat Z_{n+1}=\begin{cases} \xi_{n+1} \hat Z_n & \text{if} \ U_{n+1}\le \dfrac{1}{2}+\varepsilon,\\[12pt]\hat Z_n+\xi_{n+1} (1-\hat Z_n) & \text{if} \ U_{n+1}> \dfrac{1}{2}+\varepsilon.\end{cases}\]
\[\hat Z_{n+1}=\begin{cases} \xi_{n+1} \hat Z_n & \text{if} \ U_{n+1}\le \dfrac{1}{2}+\varepsilon,\\[12pt]\hat Z_n+\xi_{n+1} (1-\hat Z_n) & \text{if} \ U_{n+1}> \dfrac{1}{2}+\varepsilon.\end{cases}\]
Let ![]() $A_{N_0}=\{N\le N_0\}$
.
$A_{N_0}=\{N\le N_0\}$
.
Assume that for some ![]() $n\ge N_0$
,
$n\ge N_0$
, ![]() $\hat Z_n\le Z_n\le \tilde Z_{n}$
(this is definitely true for
$\hat Z_n\le Z_n\le \tilde Z_{n}$
(this is definitely true for ![]() $n=N_0$
). We observe that on
$n=N_0$
). We observe that on ![]() $A_{N_0}$
:
$A_{N_0}$
:
• When
 $\tilde Z_n$
chooses left,
$\tilde Z_n$
chooses left,  $Z_n$
also chooses left since
In this case,
$Z_n$
also chooses left since
In this case, \[ U_{n+1}\le \dfrac12-\varepsilon<\dfrac{L_n}{L_n+R_n}. \]
\[ U_{n+1}\le \dfrac12-\varepsilon<\dfrac{L_n}{L_n+R_n}. \]
 $Z_{n+1}=\xi_{n+1}Z_n\le \xi_{n+1}\tilde Z_n = \tilde Z_{n+1}$
. When
$Z_{n+1}=\xi_{n+1}Z_n\le \xi_{n+1}\tilde Z_n = \tilde Z_{n+1}$
. When  $\tilde Z_n$
chooses right,
$\tilde Z_n$
chooses right,  $Z_n$
might choose left or right, but we still have
$Z_n$
might choose left or right, but we still have
 \[ Z_{n+1}\le Z_n+\xi_{n+1}(1-Z_n)\le \tilde Z_n+\xi_{n+1}(1-\tilde Z_n) = \tilde Z_{n+1}. \]
\[ Z_{n+1}\le Z_n+\xi_{n+1}(1-Z_n)\le \tilde Z_n+\xi_{n+1}(1-\tilde Z_n) = \tilde Z_{n+1}. \]
• When
 $Z_n$
chooses left,
$Z_n$
chooses left,  $\hat Z_n$
also chooses left since
In this case,
$\hat Z_n$
also chooses left since
In this case, \[ U_{n+1}\le \dfrac{L_n}{L_n+R_n}
< \dfrac12+\varepsilon. \]
\[ U_{n+1}\le \dfrac{L_n}{L_n+R_n}
< \dfrac12+\varepsilon. \]
 $Z_{n+1}=\xi_{n+1}Z_n\ge \xi_{n+1}\hat Z_n = \hat Z_{n+1}$
. When
$Z_{n+1}=\xi_{n+1}Z_n\ge \xi_{n+1}\hat Z_n = \hat Z_{n+1}$
. When  $Z_n$
chooses right,
$Z_n$
chooses right,  $\hat Z_n$
might choose left or right, but we still have
$\hat Z_n$
might choose left or right, but we still have
 \[ \hat Z_{n+1}\le \hat Z_n+\xi_{n+1}(1-\hat Z_n)\le Z_n+\xi_{n+1}(1- Z_n) = Z_{n+1}. \]
\[ \hat Z_{n+1}\le \hat Z_n+\xi_{n+1}(1-\hat Z_n)\le Z_n+\xi_{n+1}(1- Z_n) = Z_{n+1}. \]
By induction, we obtain that on ![]() $A_{N_0}$
for all
$A_{N_0}$
for all ![]() $n\ge 0$
,
$n\ge 0$
, ![]() $\hat Z_{n}\le Z_n\le \tilde Z_{n}$
. Therefore we have
$\hat Z_{n}\le Z_n\le \tilde Z_{n}$
. Therefore we have
for all ![]() $n\ge0$
and
$n\ge0$
and ![]() $x\in [0,1]$
. On the other hand, by Theorem 2,
$x\in [0,1]$
. On the other hand, by Theorem 2, ![]() $\tilde Z_{n}$
and
$\tilde Z_{n}$
and ![]() $\hat Z_{n}$
converge weakly to
$\hat Z_{n}$
converge weakly to ![]() $\text{Beta}(\frac{1}{2}+\varepsilon,\frac{1}{2}-\varepsilon)$
and
$\text{Beta}(\frac{1}{2}+\varepsilon,\frac{1}{2}-\varepsilon)$
and ![]() $\text{Beta}(\frac{1}{2}-\varepsilon,\frac{1}{2}+\varepsilon)$
respectively, as
$\text{Beta}(\frac{1}{2}-\varepsilon,\frac{1}{2}+\varepsilon)$
respectively, as ![]() $n\to\infty$
. Since
$n\to\infty$
. Since ![]() $\varepsilon$
is arbitrarily small and
$\varepsilon$
is arbitrarily small and ![]() $\mathbb{P}(A_{N_0})\to 1$
as
$\mathbb{P}(A_{N_0})\to 1$
as ![]() $N_0\to\infty$
, the theorem is proved. □
$N_0\to\infty$
, the theorem is proved. □
Appendix A
Proof of Lemma 1.
(a) For ![]() $u=(u_1,\ldots,u_d)\in K$
and
$u=(u_1,\ldots,u_d)\in K$
and ![]() $z=(z_1,\ldots,z_d)\in V_0$
, define
$z=(z_1,\ldots,z_d)\in V_0$
, define
Note that ![]() $u_0\le 1-u_d\le 1-\delta \le z_0$
,
$u_0\le 1-u_d\le 1-\delta \le z_0$
, ![]() $z_j\le 1-z_0\le \delta$
, and thus
$z_j\le 1-z_0\le \delta$
, and thus
for ![]() $j=1,2,\ldots,d$
. Therefore, for
$j=1,2,\ldots,d$
. Therefore, for ![]() $j=1,2,\ldots,d$
, we have
$j=1,2,\ldots,d$
, we have
 \begin{align*} s(1-t)^{d-1}-\delta & \le v_j\le \dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}=\dfrac{ u_j-z_j{{{u_0}/{z_0}}}}{ 1-\sum_{l=j+1}^d u_l+\sum_{l=j+1}^d z_l{{{u_0}/{z_0}}}}\\[5pt]
& \le \dfrac{u_j}{ 1-\sum_{l=j+1}^d u_l}\le t.\end{align*}
\begin{align*} s(1-t)^{d-1}-\delta & \le v_j\le \dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}=\dfrac{ u_j-z_j{{{u_0}/{z_0}}}}{ 1-\sum_{l=j+1}^d u_l+\sum_{l=j+1}^d z_l{{{u_0}/{z_0}}}}\\[5pt]
& \le \dfrac{u_j}{ 1-\sum_{l=j+1}^d u_l}\le t.\end{align*}
This implies that ![]() $v=G_z^{-1}(u)\in K_0$
for each
$v=G_z^{-1}(u)\in K_0$
for each ![]() $u\in K$
and
$u\in K$
and ![]() $z\in V_0$
, where we denote
$z\in V_0$
, where we denote
 \begin{equation*} K_0=\Bigg\{(v_1,\ldots,v_d)\in\mathcal{S}_d\colon s(1-t)^{d-1}-\delta\le\dfrac{v_j}{1-\sum_{l=j+1}^d v_l}\le t, j=1,2,\ldots,d \Bigg\}.\end{equation*}
\begin{equation*} K_0=\Bigg\{(v_1,\ldots,v_d)\in\mathcal{S}_d\colon s(1-t)^{d-1}-\delta\le\dfrac{v_j}{1-\sum_{l=j+1}^d v_l}\le t, j=1,2,\ldots,d \Bigg\}.\end{equation*}
Observe that ![]() $T^{-1}(K_0)=[s(1-t)^{d-1}-\delta,t]^d$
. Thus
$T^{-1}(K_0)=[s(1-t)^{d-1}-\delta,t]^d$
. Thus ![]() $T^{-1}\circ G^{-1}_z(K) \subset [s(1-t)^{d-1}-\delta,t]^d$
.
$T^{-1}\circ G^{-1}_z(K) \subset [s(1-t)^{d-1}-\delta,t]^d$
.
(b) For ![]() $u\in K, z\in V_k$
, let
$u\in K, z\in V_k$
, let
 \begin{align*} \hspace*{24pt} v&=(v_1,v_2,\ldots,\ldots,v_k)\\[4pt] & \coloneqq G_{R_k(z)}^{-1}(R_k(u))\\[4pt]
&\,\,=\bigg(u_{0}-z_{0}\dfrac{u_k}{z_k}, u_1-z_1\dfrac{u_k}{z_k},\ldots,u_{k-1}-z_{k-1}\dfrac{u_k}{z_k},u_{k+1}-z_{k+1}\dfrac{u_k}{z_k},\ldots, u_{d}-z_{d}\dfrac{u_k}{z_k}\bigg).\end{align*}
\begin{align*} \hspace*{24pt} v&=(v_1,v_2,\ldots,\ldots,v_k)\\[4pt] & \coloneqq G_{R_k(z)}^{-1}(R_k(u))\\[4pt]
&\,\,=\bigg(u_{0}-z_{0}\dfrac{u_k}{z_k}, u_1-z_1\dfrac{u_k}{z_k},\ldots,u_{k-1}-z_{k-1}\dfrac{u_k}{z_k},u_{k+1}-z_{k+1}\dfrac{u_k}{z_k},\ldots, u_{d}-z_{d}\dfrac{u_k}{z_k}\bigg).\end{align*}
Note that ![]() $z_l\le 1-z_k \le \delta$
for
$z_l\le 1-z_k \le \delta$
for ![]() $l\in\{0,2,\ldots,d\}\setminus \{k\}$
and
$l\in\{0,2,\ldots,d\}\setminus \{k\}$
and ![]() $u_{k} \le {\max\{u_d,1-u_d\}} \le {1-\delta}\le {z_k}.$
Therefore we observe the following.
$u_{k} \le {\max\{u_d,1-u_d\}} \le {1-\delta}\le {z_k}.$
Therefore we observe the following.
(i) For
 $k+1\le j\le d$
,
$k+1\le j\le d$
,
 \[\dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}=\dfrac{ u_j-z_j{{{u_k}/{z_k}}}}{ 1-\sum_{l=j+1}^d u_l+\sum_{l=j+1}^d z_l{{{u_k}/{z_k}}}} \le \dfrac{u_j}{ 1-\sum_{l=j+1}^d u_l}\le t\]
\[\dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}=\dfrac{ u_j-z_j{{{u_k}/{z_k}}}}{ 1-\sum_{l=j+1}^d u_l+\sum_{l=j+1}^d z_l{{{u_k}/{z_k}}}} \le \dfrac{u_j}{ 1-\sum_{l=j+1}^d u_l}\le t\]
and
 \begin{align*}\dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}& \ge v_j = u_j-z_j\dfrac{u_k}{z_k}\ge u_j-z_j\ge s(1-t)^{d-1}-\delta.\end{align*}
\begin{align*}\dfrac{v_j}{ 1-\sum_{l=j+1}^d v_l}& \ge v_j = u_j-z_j\dfrac{u_k}{z_k}\ge u_j-z_j\ge s(1-t)^{d-1}-\delta.\end{align*}
(ii) For
 $j=1$
, we have
$j=1$
, we have
 \begin{align*} \dfrac{v_{1}}{ 1-\sum_{l=2}^{d} v_l }& =\dfrac{ u_0-z_0{{{u_k}/{z_k}}}}{ u_0+\sum_{l=1}^d z_l{{{u_k}/{z_k}}}}\\[4pt]
& =1-\dfrac{{u_k}}{ \big(1-\sum_{l=1}^d u_l\big)z_k+{u_k}\sum_{l=1}^d z_l}\\[4pt]
& \le 1-\dfrac{u_k} { \big(1-\sum_{l=k}^d u_l\big)z_k+{u_k}}\\[4pt]
& \le 1-\dfrac{u_k} { 1-\sum_{l=k+1}^d u_l }\\[4pt]
&\le 1-s\end{align*}
\begin{align*} \dfrac{v_{1}}{ 1-\sum_{l=2}^{d} v_l }& =\dfrac{ u_0-z_0{{{u_k}/{z_k}}}}{ u_0+\sum_{l=1}^d z_l{{{u_k}/{z_k}}}}\\[4pt]
& =1-\dfrac{{u_k}}{ \big(1-\sum_{l=1}^d u_l\big)z_k+{u_k}\sum_{l=1}^d z_l}\\[4pt]
& \le 1-\dfrac{u_k} { \big(1-\sum_{l=k}^d u_l\big)z_k+{u_k}}\\[4pt]
& \le 1-\dfrac{u_k} { 1-\sum_{l=k+1}^d u_l }\\[4pt]
&\le 1-s\end{align*}
and
 \begin{align*}& \dfrac{v_{1}}{ 1-\sum_{l=2}^{d} v_l } \ge v_1= u_0-z_0\dfrac{u_k}{z_k}\ge (1-t)^d-\delta.\end{align*}
\begin{align*}& \dfrac{v_{1}}{ 1-\sum_{l=2}^{d} v_l } \ge v_1= u_0-z_0\dfrac{u_k}{z_k}\ge (1-t)^d-\delta.\end{align*}
(iii) For
 $2\le j\le k$
,
$2\le j\le k$
,
 \[\hspace*{-15pt}s(1-t)^{d-1}-\delta \le v_j \le \dfrac{v_j}{ 1-\sum_{l=j+1}^{d} v_l }=\dfrac{ u_{j-1}-z_{j-1}\ {u_k}/{z_k}}{ 1-\sum_{l=j}^d u_l+\sum_{l=j}^d z_l\ {u_k}/{z_k}} \le \dfrac{u_{j-1}}{ 1-\sum_{l=j}^d u_l}\le t.\]
\[\hspace*{-15pt}s(1-t)^{d-1}-\delta \le v_j \le \dfrac{v_j}{ 1-\sum_{l=j+1}^{d} v_l }=\dfrac{ u_{j-1}-z_{j-1}\ {u_k}/{z_k}}{ 1-\sum_{l=j}^d u_l+\sum_{l=j}^d z_l\ {u_k}/{z_k}} \le \dfrac{u_{j-1}}{ 1-\sum_{l=j}^d u_l}\le t.\]
(c) Therefore
Acknowledgement
We would like to thank the anonymous referees for a very careful reading of our manuscript and their useful comments, which substantially improved the paper. We also would like to thank Andrew R. Wade for useful suggestions. The research of SV is partially supported by grants from the Swedish Research Council (VR2014-5147) and the Crafoord Foundation.