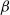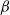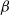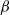1. Introduction
Let
![]() $X_{t}$
(
$X_{t}$
(
![]() $t=0,1,2,\ldots$
) be a Markov chain on the state space
$t=0,1,2,\ldots$
) be a Markov chain on the state space
![]() $\textsf{X}$
with n-step transition probability measure
$\textsf{X}$
with n-step transition probability measure
![]() $P^{n}$
and stationary distribution
$P^{n}$
and stationary distribution
![]() $\pi$
. If the n-step probability measures
$\pi$
. If the n-step probability measures
![]() $P^{n}$
converge in total variation norm to the stationary probability measure
$P^{n}$
converge in total variation norm to the stationary probability measure
![]() $\pi$
at rate
$\pi$
at rate
![]() $r^{n}$
(for some
$r^{n}$
(for some
![]() $r>1$
), that is,
$r>1$
), that is,
the Markov chain is said to be geometrically ergodic. It is well known that for stationary Markov chains, geometric ergodicity implies that so-called
![]() $\beta$
-mixing coefficients (or coefficients of absolute regularity)
$\beta$
-mixing coefficients (or coefficients of absolute regularity)
![]() $\beta(n)$
, to be defined formally in Section 2, converge to zero at the same rate,
$\beta(n)$
, to be defined formally in Section 2, converge to zero at the same rate,
![]() $\lim_{n\to\infty}r^{n}\beta(n)=0$
(see e.g. [Reference Doukhan8, page 89], [Reference Bradley2, Theorem 3.7], or [Reference Bradley3, Theorem 21.19]). For initial distributions other than the stationary one, a similar mixing result has been obtained by Liebscher [Reference Liebscher16, Proposition 4].
$\lim_{n\to\infty}r^{n}\beta(n)=0$
(see e.g. [Reference Doukhan8, page 89], [Reference Bradley2, Theorem 3.7], or [Reference Bradley3, Theorem 21.19]). For initial distributions other than the stationary one, a similar mixing result has been obtained by Liebscher [Reference Liebscher16, Proposition 4].
We are interested in counterparts of these mixing results when the convergence in (1) takes place at a rate r(n) slower than geometric, that is,
When (2) holds with suitably defined rates r(n) slower than geometric, the Markov chain is called subgeometrically ergodic. The main result of this note establishes that for both stationary and other initial distributions, subgeometric ergodicity implies
![]() $\beta$
-mixing with subgeometrically decaying mixing coefficients, that is,
$\beta$
-mixing with subgeometrically decaying mixing coefficients, that is,
![]() $\lim_{n\to\infty}\tilde{r}(n)\beta(n)=0$
for some rate function
$\lim_{n\to\infty}\tilde{r}(n)\beta(n)=0$
for some rate function
![]() $\tilde{r}(n)$
.
$\tilde{r}(n)$
.
To illustrate some common rate functions, consider the expression
In the case
![]() $\alpha,\beta,c,d>0$
the four terms above satisfy
$\alpha,\beta,c,d>0$
the four terms above satisfy
![]() ${\textrm{e}}^{dn}/{\textrm{e}}^{cn^{\gamma}}\to\infty$
,
${\textrm{e}}^{dn}/{\textrm{e}}^{cn^{\gamma}}\to\infty$
,
![]() ${\textrm{e}}^{cn^{\gamma}}/(1+n)^{\beta}\to\infty$
, and
${\textrm{e}}^{cn^{\gamma}}/(1+n)^{\beta}\to\infty$
, and
![]() $(1+n)^{\beta}/(1+\ln(n))^{\alpha}\to\infty$
as
$(1+n)^{\beta}/(1+\ln(n))^{\alpha}\to\infty$
as
![]() $n\to\infty$
, and this hierarchy can be used to define different growth rates. Ordered from the fastest to the slowest growth rate, a growth rate is called geometric (sometimes also exponential) if the dominant term is
$n\to\infty$
, and this hierarchy can be used to define different growth rates. Ordered from the fastest to the slowest growth rate, a growth rate is called geometric (sometimes also exponential) if the dominant term is
![]() ${\textrm{e}}^{dn}$
(with
${\textrm{e}}^{dn}$
(with
![]() $d>0$
; note that
$d>0$
; note that
![]() ${\textrm{e}}^{dn}=r^{n}$
with
${\textrm{e}}^{dn}=r^{n}$
with
![]() $r>1$
if and only if
$r>1$
if and only if
![]() $d>0$
), subexponential if the dominant term is
$d>0$
), subexponential if the dominant term is
![]() ${\textrm{e}}^{cn^{\gamma}}$
(
${\textrm{e}}^{cn^{\gamma}}$
(
![]() $c>0$
and above
$c>0$
and above
![]() $d=0$
), polynomial if the dominant term is
$d=0$
), polynomial if the dominant term is
![]() $(1+n)^{\beta}$
(
$(1+n)^{\beta}$
(
![]() $\beta>0$
,
$\beta>0$
,
![]() $c=d=0$
), and logarithmic if the dominant term is
$c=d=0$
), and logarithmic if the dominant term is
![]() $(1+\ln(n))^{\alpha}$
(
$(1+\ln(n))^{\alpha}$
(
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\beta=c=d=0$
).
$\beta=c=d=0$
).
We next provide some brief background on
![]() $\beta$
-mixing and subgeometric ergodicity. The notion of
$\beta$
-mixing and subgeometric ergodicity. The notion of
![]() $\beta$
-mixing (or absolute regularity) was introduced by Volkonskii and Rozanov [Reference Volkonskii and Rozanov29, Reference Volkonskii and Rozanov30], who attributed it to Kolmogorov. The surveys by Bradley [Reference Bradley1, Reference Bradley2], the monograph by Doukhan [Reference Doukhan8], and the three-volume series by Bradley [Reference Bradley3] specialized on (the various different concepts of) mixing and contain a wealth of further references. As for subgeometric ergodicity, the first subgeometric ergodicity results for general state space Markov chains were obtained by Nummelin and Tuominen [Reference Nummelin and Tuominen21] and Tweedie [Reference Tweedie24]; the subgeometric rate functions r(n) considered were introduced by Stone and Wainger [Reference Stone and Wainger22]. Tuominen and Tweedie [Reference Tuominen and Tweedie23] gave a set of conditions that imply the convergence in (2) and, in particular, formulated a sequence of so-called drift conditions to establish subgeometric ergodicity. Subsequent work by Fort and Moulines [Reference Fort and Moulines9, Reference Fort and Moulines10], Jarner and Roberts [Reference Jarner and Roberts11], and Douc et al. [Reference Douc, Fort, Moulines and Soulier6] led to a formulation of a single drift condition to ensure subgeometric ergodicity, paralleling the use of a Foster–Lyapunov drift condition to establish geometric ergodicity (see e.g. [Reference Meyn and Tweedie19, Chapter 15]).
$\beta$
-mixing (or absolute regularity) was introduced by Volkonskii and Rozanov [Reference Volkonskii and Rozanov29, Reference Volkonskii and Rozanov30], who attributed it to Kolmogorov. The surveys by Bradley [Reference Bradley1, Reference Bradley2], the monograph by Doukhan [Reference Doukhan8], and the three-volume series by Bradley [Reference Bradley3] specialized on (the various different concepts of) mixing and contain a wealth of further references. As for subgeometric ergodicity, the first subgeometric ergodicity results for general state space Markov chains were obtained by Nummelin and Tuominen [Reference Nummelin and Tuominen21] and Tweedie [Reference Tweedie24]; the subgeometric rate functions r(n) considered were introduced by Stone and Wainger [Reference Stone and Wainger22]. Tuominen and Tweedie [Reference Tuominen and Tweedie23] gave a set of conditions that imply the convergence in (2) and, in particular, formulated a sequence of so-called drift conditions to establish subgeometric ergodicity. Subsequent work by Fort and Moulines [Reference Fort and Moulines9, Reference Fort and Moulines10], Jarner and Roberts [Reference Jarner and Roberts11], and Douc et al. [Reference Douc, Fort, Moulines and Soulier6] led to a formulation of a single drift condition to ensure subgeometric ergodicity, paralleling the use of a Foster–Lyapunov drift condition to establish geometric ergodicity (see e.g. [Reference Meyn and Tweedie19, Chapter 15]).
The rest of the paper proceeds as follows. Section 2 contains necessary mathematical preliminaries. Section 3 reviews the relation of geometric ergodicity and
![]() $\beta$
-mixing, while the corresponding results in the subgeometric case are given in Section 4. The general results obtained are exemplified in Section 5, where subgeometric ergodicity and
$\beta$
-mixing, while the corresponding results in the subgeometric case are given in Section 4. The general results obtained are exemplified in Section 5, where subgeometric ergodicity and
![]() $\beta$
-mixing results for the self-exciting threshold autoregressive model are presented. Section 6 concludes the paper and all proofs are given in an Appendix.
$\beta$
-mixing results for the self-exciting threshold autoregressive model are presented. Section 6 concludes the paper and all proofs are given in an Appendix.
2. Preliminaries
To formalize the discussion in the Introduction, consider
![]() $X_{t}$
(
$X_{t}$
(
![]() $t=0,1,2,\ldots$
), a time-homogeneous discrete-time Markov chain on a general measurable state space
$t=0,1,2,\ldots$
), a time-homogeneous discrete-time Markov chain on a general measurable state space
![]() $(\textsf{X},\mathcal{B}(\textsf{X}))$
. Comprehensive treatments of the relevant Markov chain theory can be found in [Reference Meyn and Tweedie19] or [Reference Douc, Moulines, Priouret and Soulier7]. Let
$(\textsf{X},\mathcal{B}(\textsf{X}))$
. Comprehensive treatments of the relevant Markov chain theory can be found in [Reference Meyn and Tweedie19] or [Reference Douc, Moulines, Priouret and Soulier7]. Let
![]() $\mu$
be any initial measure on
$\mu$
be any initial measure on
![]() $\mathcal{B}(\textsf{X})$
, and suppose that
$\mathcal{B}(\textsf{X})$
, and suppose that
![]() $X_{0}$
has distribution
$X_{0}$
has distribution
![]() $\mu$
. Denote the transition probabilities by
$\mu$
. Denote the transition probabilities by
![]() $P(x\,;\,A)$
(
$P(x\,;\,A)$
(
![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
,
![]() $A\in\mathcal{B}(\textsf{X})$
) and let
$A\in\mathcal{B}(\textsf{X})$
) and let
![]() $(\Omega,\mathcal{F},\mathbb{P}_{\mu})$
denote the probability space of the Markov process
$(\Omega,\mathcal{F},\mathbb{P}_{\mu})$
denote the probability space of the Markov process
![]() $\{X_{0},X_{1},\ldots\}$
. As usual,
$\{X_{0},X_{1},\ldots\}$
. As usual,
![]() $\mathbb{P}_{x}$
denotes the probability measure corresponding to a fixed initial value
$\mathbb{P}_{x}$
denotes the probability measure corresponding to a fixed initial value
![]() $X_{0}=x$
and
$X_{0}=x$
and
![]() $P^{n}(x\,;\,A)=\mathbb{P}_{x}(X_{n}\in A)$
(
$P^{n}(x\,;\,A)=\mathbb{P}_{x}(X_{n}\in A)$
(
![]() $x\in\textsf{X}$
,
$x\in\textsf{X}$
,
![]() $A\in\mathcal{B}(\textsf{X})$
) signifies the n-step transition probability measure.
$A\in\mathcal{B}(\textsf{X})$
) signifies the n-step transition probability measure.
Next consider the rate of convergence of the n-step probability measures
![]() $P^{n}$
to the stationary probability measure
$P^{n}$
to the stationary probability measure
![]() $\pi$
. To this end, for any two probability measures
$\pi$
. To this end, for any two probability measures
![]() $\lambda_{1}$
and
$\lambda_{1}$
and
![]() $\lambda_{2}$
on
$\lambda_{2}$
on
![]() $(\textsf{X},\mathcal{B}(\textsf{X}))$
, the total variation distance is defined as
$(\textsf{X},\mathcal{B}(\textsf{X}))$
, the total variation distance is defined as
where the last supremum runs over all
![]() $\mathcal{B}(\textsf{X})$
-measurable functions
$\mathcal{B}(\textsf{X})$
-measurable functions
![]() $h\colon \textsf{X}\to\mathbb{R}$
bounded in absolute value by 1 and
$h\colon \textsf{X}\to\mathbb{R}$
bounded in absolute value by 1 and
![]() $\lambda_{i}(h)=\int_{\textsf{X}}\lambda_{i}({\textrm{d}} x)h(x)<\infty$
. The n-step probability measures
$\lambda_{i}(h)=\int_{\textsf{X}}\lambda_{i}({\textrm{d}} x)h(x)<\infty$
. The n-step probability measures
![]() $P^{n}$
converge in total variation norm to the stationary probability measure
$P^{n}$
converge in total variation norm to the stationary probability measure
![]() $\pi$
at rate r(n),
$\pi$
at rate r(n),
![]() $n\geq 0$
, if
$n\geq 0$
, if
If (3) holds, we say that the Markov chain
![]() $X_{t}$
is ergodic with rate r(n); geometric ergodicity obtains when
$X_{t}$
is ergodic with rate r(n); geometric ergodicity obtains when
![]() $r(n)=r^{n}$
for some
$r(n)=r^{n}$
for some
![]() $r>1$
.
$r>1$
.
To define the
![]() $\beta$
-mixing coefficients, let
$\beta$
-mixing coefficients, let
![]() $\mathcal{F}_{k}^{l}$
,
$\mathcal{F}_{k}^{l}$
,
![]() $0\leq k\leq l\leq\infty$
, signify the
$0\leq k\leq l\leq\infty$
, signify the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\{X_{k},\ldots,X_{l}\}$
. For the stochastic process
$\{X_{k},\ldots,X_{l}\}$
. For the stochastic process
![]() $\{X_{0},X_{1},\ldots\}$
, the
$\{X_{0},X_{1},\ldots\}$
, the
![]() $\beta$
-mixing coefficients
$\beta$
-mixing coefficients
![]() $\beta(n)$
,
$\beta(n)$
,
![]() $n=1,2,\ldots,$
are defined by ([Reference Doukhan8, Section 1.1], [Reference Bradley3, Chapter 3])
$n=1,2,\ldots,$
are defined by ([Reference Doukhan8, Section 1.1], [Reference Bradley3, Chapter 3])
 \begin{align*}\beta(n) & =\dfrac{1}{2}\sup_{m\in\mathbb{N}}\sup\sum_{i=1}^{I}\sum_{j=1}^{J}|\mathbb{P}_{\mu}(A_{i}\cap B_{j})-\mathbb{P}_{\mu}(A_{i})\mathbb{P}_{\mu}(B_{j})|\\& =\sup_{m\in\mathbb{N}}\mathbb{E}_{\mu}\biggl[\sup_{B\in\mathcal{F}_{n+m}^{\infty}}|\mathbb{P}_{\mu}(B\mid\mathcal{F}_{0}^{m})-\mathbb{P}_{\mu}(B)|\biggr],\end{align*}
\begin{align*}\beta(n) & =\dfrac{1}{2}\sup_{m\in\mathbb{N}}\sup\sum_{i=1}^{I}\sum_{j=1}^{J}|\mathbb{P}_{\mu}(A_{i}\cap B_{j})-\mathbb{P}_{\mu}(A_{i})\mathbb{P}_{\mu}(B_{j})|\\& =\sup_{m\in\mathbb{N}}\mathbb{E}_{\mu}\biggl[\sup_{B\in\mathcal{F}_{n+m}^{\infty}}|\mathbb{P}_{\mu}(B\mid\mathcal{F}_{0}^{m})-\mathbb{P}_{\mu}(B)|\biggr],\end{align*}
where
![]() $\mathbb{N}=\{0,1,2,\ldots\}$
, and in the first expression for
$\mathbb{N}=\{0,1,2,\ldots\}$
, and in the first expression for
![]() $\beta(n)$
the second supremum is taken over all pairs of (finite) partitions
$\beta(n)$
the second supremum is taken over all pairs of (finite) partitions
![]() $\{A_{1},A_{2},\ldots,A_{I}\}$
and
$\{A_{1},A_{2},\ldots,A_{I}\}$
and
![]() $\{B_{1},B_{2},\ldots,B_{J}\}$
of
$\{B_{1},B_{2},\ldots,B_{J}\}$
of
![]() $\Omega$
such that
$\Omega$
such that
![]() $A_{i}\in\mathcal{F}_{0}^{m}$
for each i and
$A_{i}\in\mathcal{F}_{0}^{m}$
for each i and
![]() $B_{j}\in\mathcal{F}_{n+m}^{\infty}$
for each j. For our purposes it is convenient to use the following alternative expression obtained by Davydov ([Reference Davydov5, Proposition 1; note that his definition of
$B_{j}\in\mathcal{F}_{n+m}^{\infty}$
for each j. For our purposes it is convenient to use the following alternative expression obtained by Davydov ([Reference Davydov5, Proposition 1; note that his definition of
![]() $\beta(n)$
includes an additional factor of 2]):
$\beta(n)$
includes an additional factor of 2]):
where
![]() $\mu P^{m}(\cdot)=\int_{\textsf{X}}\mu({\textrm{d}} x)P^{m}(x\,;\,\cdot)$
denotes the distribution of
$\mu P^{m}(\cdot)=\int_{\textsf{X}}\mu({\textrm{d}} x)P^{m}(x\,;\,\cdot)$
denotes the distribution of
![]() $X_{m}$
(
$X_{m}$
(
![]() $m=1,2,\ldots$
;
$m=1,2,\ldots$
;
![]() $\mu P^{0}=\mu$
). For a stationary Markov chain (i.e. one with initial distribution
$\mu P^{0}=\mu$
). For a stationary Markov chain (i.e. one with initial distribution
![]() $\pi$
), the
$\pi$
), the
![]() $\beta$
-mixing coefficients can be expressed simply as
$\beta$
-mixing coefficients can be expressed simply as
Process
![]() $X_{t}$
is said to be
$X_{t}$
is said to be
![]() $\beta$
-mixing (or sometimes absolutely regular) if
$\beta$
-mixing (or sometimes absolutely regular) if
![]() $\lim_{n\rightarrow\infty}\beta(n)=0$
. As with the convergence in (3), the rate of this convergence is of interest, and in what follows we seek for results of the form
$\lim_{n\rightarrow\infty}\beta(n)=0$
. As with the convergence in (3), the rate of this convergence is of interest, and in what follows we seek for results of the form
![]() $\lim_{n\rightarrow\infty}r(n)\beta(n)=0$
with some rate function r(n).
$\lim_{n\rightarrow\infty}r(n)\beta(n)=0$
with some rate function r(n).
3. The geometric case
We start by briefly discussing the relation of geometric ergodicity and
![]() $\beta$
-mixing; although these results are well known, comparing them with the subgeometric case will be illuminating. For a stationary Markov chain (i.e. one with initial distribution
$\beta$
-mixing; although these results are well known, comparing them with the subgeometric case will be illuminating. For a stationary Markov chain (i.e. one with initial distribution
![]() $\pi$
), this relation is particularly simple. As was first shown by Nummelin and Tuominen [Reference Nummelin and Tuominen20, Theorem 2.1], a geometrically ergodic Markov chain satisfies, for some
$\pi$
), this relation is particularly simple. As was first shown by Nummelin and Tuominen [Reference Nummelin and Tuominen20, Theorem 2.1], a geometrically ergodic Markov chain satisfies, for some
![]() $r>1$
,
$r>1$
,
![]() $\lim_{n\rightarrow\infty}r^{n}\int\pi({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
; given expression (5), the
$\lim_{n\rightarrow\infty}r^{n}\int\pi({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
; given expression (5), the
![]() $\beta$
-mixing property immediately follows and the mixing coefficients satisfy
$\beta$
-mixing property immediately follows and the mixing coefficients satisfy
![]() $\lim_{n\rightarrow\infty}r^{n}\beta(n)=0$
. Statements of this result can be found for instance in [Reference Doukhan8, page 89], [Reference Bradley2, Theorem 3.7], and [Reference Bradley3, Theorem 21.19]. For initial distributions other than the stationary one, a corresponding result seems to have first appeared in [Reference Liebscher16, Proposition 4].
$\lim_{n\rightarrow\infty}r^{n}\beta(n)=0$
. Statements of this result can be found for instance in [Reference Doukhan8, page 89], [Reference Bradley2, Theorem 3.7], and [Reference Bradley3, Theorem 21.19]. For initial distributions other than the stationary one, a corresponding result seems to have first appeared in [Reference Liebscher16, Proposition 4].
To facilitate comparison with the subgeometric case, we present the ergodicity and mixing results as consequences of a particular drift criterion; as is discussed in [Reference Meyn and Tweedie19], this is how geometric ergodicity is often established. We use the following traditional Foster–Lyapunov-type geometric drift condition (see [Reference Meyn and Tweedie19, Theorem 15.0.1]). Here
![]() $\boldsymbol{1}_{C}(\cdot)$
signifies the indicator function of a set C. As a technical remark, note that in this condition we assume the function V to be everywhere finite (i.e.
$\boldsymbol{1}_{C}(\cdot)$
signifies the indicator function of a set C. As a technical remark, note that in this condition we assume the function V to be everywhere finite (i.e.
![]() $V \colon \textsf{X}\rightarrow[1,\infty)$
) and such that
$V \colon \textsf{X}\rightarrow[1,\infty)$
) and such that
![]() $\sup_{x\in C}V(x)<\infty$
. In contrast, in [Reference Meyn and Tweedie19, Theorem 15.0.1] it is only assumed that V is extended-real-valued (i.e.
$\sup_{x\in C}V(x)<\infty$
. In contrast, in [Reference Meyn and Tweedie19, Theorem 15.0.1] it is only assumed that V is extended-real-valued (i.e.
![]() $V \colon \textsf{X}\rightarrow[1,\infty]$
) and finite at some point
$V \colon \textsf{X}\rightarrow[1,\infty]$
) and finite at some point
![]() $x_{0}\in\textsf{X}$
. Our stronger requirements hold in most practical applications and lead to more transparent exposition and proofs.
$x_{0}\in\textsf{X}$
. Our stronger requirements hold in most practical applications and lead to more transparent exposition and proofs.
Condition Drift–G. Suppose there exist a petite set C, constants
![]() $b<\infty$
,
$b<\infty$
,
![]() $\beta>0$
, and a measurable function
$\beta>0$
, and a measurable function
![]() $V \colon \textsf{X}\rightarrow[1,\infty)$
such that
$V \colon \textsf{X}\rightarrow[1,\infty)$
such that
![]() $\sup_{x\in C}V(x)<\infty$
, satisfying
$\sup_{x\in C}V(x)<\infty$
, satisfying
For the definition of a ‘petite set’ appearing in this condition, and for the concepts of irreducibility and aperiodicity in the theorem below, we refer the reader to [Reference Meyn and Tweedie19]. Theorem 1 summarizes the relation between geometric ergodicity and
![]() $\beta$
-mixing.
$\beta$
-mixing.
Theorem 1. Suppose
![]() $X_{t}$
is a
$X_{t}$
is a
![]() $\psi$
-irreducible and aperiodic Markov chain and that Condition Drift–G holds. Then
$\psi$
-irreducible and aperiodic Markov chain and that Condition Drift–G holds. Then
-
(a)
 $X_{t}$
is geometrically ergodic, that is, for some
$X_{t}$
is geometrically ergodic, that is, for some
 $r_{1}>1$
,
$r_{1}>1$
,
 $\lim_{n\rightarrow\infty}r_{1}^{n}\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
for all
$\lim_{n\rightarrow\infty}r_{1}^{n}\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
for all
 $x\in\textsf{X}$
.
$x\in\textsf{X}$
.
Suppose further that the initial state
![]() $X_{0}$
has distribution
$X_{0}$
has distribution
![]() $\mu$
such that
$\mu$
such that
![]() $\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. Then
$\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. Then
-
(b) for some
 $r_{2}>1$
,
$r_{2}>1$
,
 $\lim_{n\rightarrow\infty}r_{2}^{n}\int_{\textsf{X}}\mu({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
,
$\lim_{n\rightarrow\infty}r_{2}^{n}\int_{\textsf{X}}\mu({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
, -
(c)
 $X_{t}$
is
$X_{t}$
is
 $\beta$
-mixing and the mixing coefficients satisfy, for some
$\beta$
-mixing and the mixing coefficients satisfy, for some
 $r_{3}>1$
,
$r_{3}>1$
,
 $\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
.
$\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
.
Moreover:
-
(d) In the stationary case (
 $\mu=\pi$
) condition
$\mu=\pi$
) condition
 $\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed, (b) and (c) hold with
$\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed, (b) and (c) hold with
 $r_{2}=r_{3}$
, and (b) and (c) are equivalent.
$r_{2}=r_{3}$
, and (b) and (c) are equivalent.
Parts (a) and (b) are very well known (see e.g. [Reference Meyn and Tweedie19, Theorem 15.0.1] for part (a) and [Reference Nummelin and Tuominen20, Theorem 2.3] for part (b)) and so is also the mixing result in the stationary case (see the references given earlier). Part (c) for general initial distributions was obtained by Liebscher [Reference Liebscher16, Proposition 4], although our formulation is somewhat different from his (our formulation and proof avoid the use of so-called ‘Q-geometric ergodicity’ employed by Liebscher; for completeness, our proof of Theorem 1, which may be of independent interest, is provided in the supplementary material). Part (d) elaborates parts (b) and (c) as well as their relation in the stationary case.
4. The subgeometric case
We seek a counterpart of Theorem 1 in which the geometric rate
![]() $r^{n}$
is replaced by some slower rate function; such rate functions were already exemplified in the Introduction. More formally, the subgeometric rate functions we consider are defined as follows (see e.g. [Reference Nummelin and Tuominen21] and [Reference Douc, Fort, Moulines and Soulier6]). Let
$r^{n}$
is replaced by some slower rate function; such rate functions were already exemplified in the Introduction. More formally, the subgeometric rate functions we consider are defined as follows (see e.g. [Reference Nummelin and Tuominen21] and [Reference Douc, Fort, Moulines and Soulier6]). Let
![]() $\Lambda_{0}$
be the set of positive non-decreasing functions
$\Lambda_{0}$
be the set of positive non-decreasing functions
![]() $r_{0} \colon \mathbb{N}\rightarrow[1,\infty)$
such that
$r_{0} \colon \mathbb{N}\rightarrow[1,\infty)$
such that
![]() $\ln[r_{0}(n)]/n$
decreases to zero as
$\ln[r_{0}(n)]/n$
decreases to zero as
![]() $n\rightarrow\infty$
. The class of subgeometric rate functions, denoted by
$n\rightarrow\infty$
. The class of subgeometric rate functions, denoted by
![]() $\Lambda$
, consists of positive functions
$\Lambda$
, consists of positive functions
![]() $r \colon \mathbb{N}\rightarrow(0,\infty)$
for which there exists some
$r \colon \mathbb{N}\rightarrow(0,\infty)$
for which there exists some
![]() $r_{0}\in\Lambda_{0}$
such that
$r_{0}\in\Lambda_{0}$
such that
Typical examples are obtained of rate functions r for which these inequalities hold with (for notational convenience, we set
![]() $\ln(0)=0$
)
$\ln(0)=0$
)
The rate function
![]() $r_{0}(n)$
is called subexponential when
$r_{0}(n)$
is called subexponential when
![]() $c>0$
, polynomial when
$c>0$
, polynomial when
![]() $c=0$
and
$c=0$
and
![]() $\beta>0$
, and logarithmic when
$\beta>0$
, and logarithmic when
![]() $\beta=c=0$
and
$\beta=c=0$
and
![]() $\alpha>0$
.
$\alpha>0$
.
In analogy with the geometric case, subgeometric ergodicity and mixing results are most conveniently obtained by verifying an appropriate drift condition. The following drift condition for subgeometric ergodicity is adapted from [Reference Douc, Moulines, Priouret and Soulier7, Definition 16.1.7]. A somewhat more general drift condition, for instance allowing for V to be extended-real-valued, is given in [Reference Douc, Fort, Moulines and Soulier6].
Condition Drift–SubG. Suppose there exist a petite set C, a constant
![]() $b<\infty$
, a concave increasing continuously differentiable function
$b<\infty$
, a concave increasing continuously differentiable function
![]() $\phi \colon [1,\infty)\rightarrow(0,\infty)$
satisfying
$\phi \colon [1,\infty)\rightarrow(0,\infty)$
satisfying
![]() $\lim_{v\rightarrow\infty}\phi'(v)=0$
, and a measurable function
$\lim_{v\rightarrow\infty}\phi'(v)=0$
, and a measurable function
![]() $V \colon \textsf{X}\rightarrow[1,\infty)$
such that
$V \colon \textsf{X}\rightarrow[1,\infty)$
such that
![]() $\sup_{x\in C}V(x)<\infty$
and
$\sup_{x\in C}V(x)<\infty$
and
Note that if
![]() $\phi(v)=\eta v$
(
$\phi(v)=\eta v$
(
![]() $\eta>0$
), then one obtains Condition Drift–G (but assumption
$\eta>0$
), then one obtains Condition Drift–G (but assumption
![]() $\lim_{v\rightarrow\infty}\phi'(v)=0$
rules this out; as we are interested in subgeometric rates of ergodicity, assuming this means no loss of generality; see [Reference Douc, Moulines, Priouret and Soulier7, Remark 16.1.8]).
$\lim_{v\rightarrow\infty}\phi'(v)=0$
rules this out; as we are interested in subgeometric rates of ergodicity, assuming this means no loss of generality; see [Reference Douc, Moulines, Priouret and Soulier7, Remark 16.1.8]).
Following Douc et al. [Reference Douc, Fort, Moulines and Soulier6] we next introduce a rate function, denoted by
![]() $r_{\phi}$
. First define the function
$r_{\phi}$
. First define the function
where
![]() $\phi$
is as in Condition Drift–SubG. The definition implies that
$\phi$
is as in Condition Drift–SubG. The definition implies that
![]() $H_{\phi}$
is a non-decreasing, concave, and differentiable function on
$H_{\phi}$
is a non-decreasing, concave, and differentiable function on
![]() $[1,\infty)$
, and it has an inverse
$[1,\infty)$
, and it has an inverse
![]() $H_{\phi}^{-1} \colon [0,\infty)\rightarrow[1,\infty)$
which is increasing and differentiable (see [Reference Douc, Fort, Moulines and Soulier6, Section 2.1]). Thus we can define the rate function
$H_{\phi}^{-1} \colon [0,\infty)\rightarrow[1,\infty)$
which is increasing and differentiable (see [Reference Douc, Fort, Moulines and Soulier6, Section 2.1]). Thus we can define the rate function
Douc et al. [Reference Douc, Fort, Moulines and Soulier6, Lemma 2.3 and Proposition 2.5] showed that this rate function is subgeometric and that Condition Drift–SubG implies the convergence (3) at rate
![]() $r_{\phi}(n)$
.
$r_{\phi}(n)$
.
Theorem 2 summarizes the relation between subgeometric ergodicity and
![]() $\beta$
-mixing. Here
$\beta$
-mixing. Here
![]() $\lfloor k\rfloor$
denotes the integer part of the real number k.
$\lfloor k\rfloor$
denotes the integer part of the real number k.
Theorem 2. Suppose
![]() $X_{t}$
is a
$X_{t}$
is a
![]() $\psi$
-irreducible and aperiodic Markov chain and that Condition Drift–SubG holds. Then
$\psi$
-irreducible and aperiodic Markov chain and that Condition Drift–SubG holds. Then
-
(a)
 $X_{t}$
is subgeometrically ergodic with rate
$X_{t}$
is subgeometrically ergodic with rate
 $r_{\phi}(n)$
, that is,
$r_{\phi}(n)$
, that is,
 \begin{align*} & \lim_{n\rightarrow\infty}r_{\phi}(n)\Vert P^{n}(x\,;\,\cdot)- \\&
\pi(\cdot)\Vert =0 \end{align*}
for all
\begin{align*} & \lim_{n\rightarrow\infty}r_{\phi}(n)\Vert P^{n}(x\,;\,\cdot)- \\&
\pi(\cdot)\Vert =0 \end{align*}
for all
 $x\in\textsf{X}$
.
$x\in\textsf{X}$
.
Suppose further that the initial state
![]() $X_{0}$
has distribution
$X_{0}$
has distribution
![]() $\mu$
such that
$\mu$
such that
![]() $\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. Then
$\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. Then
-
(b)
 $\lim_{n\rightarrow\infty}r_{\phi}(n)\int\mu({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
,
$\lim_{n\rightarrow\infty}r_{\phi}(n)\int\mu({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
, -
(c)
 $X_{t}$
is
$X_{t}$
is
 $\beta$
-mixing and the mixing coefficients satisfy
$\beta$
-mixing and the mixing coefficients satisfy
 $\lim_{n\rightarrow\infty}\tilde{r}_{\phi}(n)\beta(n)=0$
for any rate function
$\lim_{n\rightarrow\infty}\tilde{r}_{\phi}(n)\beta(n)=0$
for any rate function
 $\tilde{r}_{\phi}(n)$
such that
$\tilde{r}_{\phi}(n)$
such that
 $\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
where
$\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
where
 $n_{1}=\lfloor n/2\rfloor$
.
$n_{1}=\lfloor n/2\rfloor$
.
Moreover:
-
(d) In the stationary case (
 $\mu=\pi$
) condition
$\mu=\pi$
) condition
 $\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed, (b) and (c) hold with
$\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed, (b) and (c) hold with
 $r_{\phi}(n)=\tilde{r}_{\phi}(n)$
, and (b) and (c) (with
$r_{\phi}(n)=\tilde{r}_{\phi}(n)$
, and (b) and (c) (with
 $r_{\phi}(n)=\tilde{r}_{\phi}(n)$
) are equivalent.
$r_{\phi}(n)=\tilde{r}_{\phi}(n)$
) are equivalent. -
(e) If
 $r_{\phi}(n)$
satisfies (6) with
$r_{\phi}(n)$
satisfies (6) with
 $r_{\phi,0}(n)=(1+\ln(n))^{\alpha}\cdot(1+n)^{\beta}\cdot {\textrm{e}}^{cn^{\gamma}}$
and
$r_{\phi,0}(n)=(1+\ln(n))^{\alpha}\cdot(1+n)^{\beta}\cdot {\textrm{e}}^{cn^{\gamma}}$
and
 $\tilde{r}_{\phi}(n)$
satisfies (6) with
$\tilde{r}_{\phi}(n)$
satisfies (6) with
 $\tilde{r}_{\phi,0}(n)=(1+\ln(n))^{\alpha}\cdot(1+n)^{\beta}\cdot {\textrm{e}}^{\tilde{c}n^{\gamma}}$
for some
$\tilde{r}_{\phi,0}(n)=(1+\ln(n))^{\alpha}\cdot(1+n)^{\beta}\cdot {\textrm{e}}^{\tilde{c}n^{\gamma}}$
for some
 $0<\tilde{c}<c2^{-\gamma}$
, then
$0<\tilde{c}<c2^{-\gamma}$
, then
 $\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
.
$\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
.
Of the results in Theorem 2, part (a) is given in Proposition 2.5 of [Reference Douc, Fort, Moulines and Soulier6]. Part (b) can be obtained by combining Theorem 4.1 of [Reference Tuominen and Tweedie23] and Proposition 2.5 of [Reference Douc, Fort, Moulines and Soulier6], but in the proof we make use of [Reference Nummelin and Tuominen21]. Part (c) is new and illuminates the relation between subgeometrically ergodic Markov chains and their
![]() $\beta$
-mixing properties, thereby providing a counterpart of a result obtained by Liebscher [Reference Liebscher16, Proposition 4] in the case of geometric ergodicity. Part (d) is analogous to its counterpart in Theorem 1 and provides further insight into parts (b) and (c), whereas part (e) makes part (c) more concrete in the case of the most common rate functions. For completeness, we give a detailed proof in the Appendix.
$\beta$
-mixing properties, thereby providing a counterpart of a result obtained by Liebscher [Reference Liebscher16, Proposition 4] in the case of geometric ergodicity. Part (d) is analogous to its counterpart in Theorem 1 and provides further insight into parts (b) and (c), whereas part (e) makes part (c) more concrete in the case of the most common rate functions. For completeness, we give a detailed proof in the Appendix.
As discussed in [Reference Douc, Fort, Moulines and Soulier6, Section 2.3] and [Reference Meitz and Saikkonen17, Theorem 1], there is a connection between the function
![]() $\phi$
and the rate function
$\phi$
and the rate function
![]() $r_{\phi}$
, which can be used to find out the latter in particular cases. For instance, polynomial rate functions are associated with cases where the function
$r_{\phi}$
, which can be used to find out the latter in particular cases. For instance, polynomial rate functions are associated with cases where the function
![]() $\phi$
is of the form
$\phi$
is of the form
![]() $\phi(v)=cv^{\alpha}$
with
$\phi(v)=cv^{\alpha}$
with
![]() $\alpha\in(0,1)$
and
$\alpha\in(0,1)$
and
![]() $c\in(0,1]$
, and then the rate obtained is
$c\in(0,1]$
, and then the rate obtained is
![]() $r_{\phi}(n)=n^{\alpha/(1-\alpha)}$
(an alternative form is
$r_{\phi}(n)=n^{\alpha/(1-\alpha)}$
(an alternative form is
![]() $r_{\phi}(n)=n^{\kappa-1}$
with
$r_{\phi}(n)=n^{\kappa-1}$
with
![]() $\kappa=1+\alpha/(1-\alpha)$
already given by Jarner and Roberts [Reference Jarner and Roberts11]). In the subexponential case the function
$\kappa=1+\alpha/(1-\alpha)$
already given by Jarner and Roberts [Reference Jarner and Roberts11]). In the subexponential case the function
![]() $\phi$
is such that
$\phi$
is such that
![]() $v/\phi(v)$
goes to infinity slower than polynomially so that a possibility, given in [Reference Meitz and Saikkonen17, Theorem 1], is
$v/\phi(v)$
goes to infinity slower than polynomially so that a possibility, given in [Reference Meitz and Saikkonen17, Theorem 1], is
![]() $\phi(v)=c(v+v_{0})/[\ln(v+v_{0})]^{\alpha}$
for some
$\phi(v)=c(v+v_{0})/[\ln(v+v_{0})]^{\alpha}$
for some
![]() $\alpha,c,v_{0}>0$
. This results in the rate
$\alpha,c,v_{0}>0$
. This results in the rate
![]() $r_{\phi}(n)=({\textrm{e}}^{d})^{n^{1/(1+\alpha)}}$
for some
$r_{\phi}(n)=({\textrm{e}}^{d})^{n^{1/(1+\alpha)}}$
for some
![]() $d>0$
, which is faster than polynomial. A logarithmic rate is an example of a rate slower than polynomial. Then the function
$d>0$
, which is faster than polynomial. A logarithmic rate is an example of a rate slower than polynomial. Then the function
![]() $\phi$
is of the form
$\phi$
is of the form
![]() $\phi(v)=c[1+\ln(v)]^{\alpha}$
for some
$\phi(v)=c[1+\ln(v)]^{\alpha}$
for some
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $c\in(0,1]$
, and the resulting rate is
$c\in(0,1]$
, and the resulting rate is
![]() $r_{\phi}(n)=[\ln(v)]^{\alpha}$
(see [Reference Douc, Fort, Moulines and Soulier6, Section 2.3]).
$r_{\phi}(n)=[\ln(v)]^{\alpha}$
(see [Reference Douc, Fort, Moulines and Soulier6, Section 2.3]).
Theorem 2 (or 1) also provides information about the moments of the stationary distribution of
![]() $X_{t}$
. Specifically, once part (a) of Theorem 2 (or 1) has been established, one can deduce from Condition Drift–SubG (or Drift–G) and Theorem 14.3.7 of [Reference Meyn and Tweedie19] that
$X_{t}$
. Specifically, once part (a) of Theorem 2 (or 1) has been established, one can deduce from Condition Drift–SubG (or Drift–G) and Theorem 14.3.7 of [Reference Meyn and Tweedie19] that
![]() $\int_{\textsf{X}}\pi({\textrm{d}} x)\phi(V(x))<\infty$
(or
$\int_{\textsf{X}}\pi({\textrm{d}} x)\phi(V(x))<\infty$
(or
![]() $\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
). This can be very useful when one aims to apply limit theorems developed for
$\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
). This can be very useful when one aims to apply limit theorems developed for
![]() $\beta$
-mixing processes, where moment conditions are typically assumed.
$\beta$
-mixing processes, where moment conditions are typically assumed.
We close this section by noting that Condition Drift–SubG can also be used to obtain more general ergodicity results than provided in Theorem 2. Without going into details, we only mention that Theorem 2.8 of [Reference Douc, Fort, Moulines and Soulier6] and Theorem 1 of [Reference Meitz and Saikkonen17] show how a stronger form of ergodicity, called (f,r)-ergodicity, can be established.
5. Example
To illustrate our results we consider the self-exciting threshold autoregressive (SETAR) model studied by Chan et al. [Reference Chan, Petruccelli, Tong and Woolford4]. These authors analyzed the model
where
![]() $-\infty=r_{0}<\cdots<r_{M}=\infty$
, and for each
$-\infty=r_{0}<\cdots<r_{M}=\infty$
, and for each
![]() $j=1,\ldots,M$
,
$j=1,\ldots,M$
,
![]() $\{W_{t}(\,j)\}$
is an independent and identically distributed mean zero sequence independent of
$\{W_{t}(\,j)\}$
is an independent and identically distributed mean zero sequence independent of
![]() $\{W_{t}(i)\}$
,
$\{W_{t}(i)\}$
,
![]() $i\neq j$
, and with
$i\neq j$
, and with
![]() $W_{t}(\,j)$
having a density that is positive on the whole real line. They considered the following conditions:
$W_{t}(\,j)$
having a density that is positive on the whole real line. They considered the following conditions:
and showed that the SETAR model is ergodic if and only if one of the conditions (8a)–(8e) holds [Reference Chan, Petruccelli, Tong and Woolford4, Theorem 2.1]. Moreover, if
![]() $\mathbb{E}[\vert W_{t}(\,j)\vert]<\infty$
for each j, they showed that condition (8a) ensures geometric ergodicity [Reference Chan, Petruccelli, Tong and Woolford4, Theorem 2.3]. To our knowledge, in the cases (8b)–(8e) no results regarding the rate of ergodicity have as yet appeared in the literature and our Theorem 4(b) below indicates that geometric ergodicity may not always hold without stronger assumptions. Related to this, we note that Meyn and Tweedie [Reference Meyn and Tweedie19, Section 11.4.3 and Section B.2] discussed the (geometric) ergodicity of the SETAR model (7), reproducing the ergodicity result of [Reference Chan, Petruccelli, Tong and Woolford4, Theorem 2.1] as their Proposition 11.4.5. On their page 541, Meyn and Tweedie [Reference Meyn and Tweedie19] also stated that (our additions in brackets) ‘in the interior of the parameter space [the union of (8a)–(8e)] we are able to identify geometric ergodicity in Proposition 11.4.5 … the stronger form [geometric ergodicity] is actually proved in that result’ but no formal proof is given for this statement.
$\mathbb{E}[\vert W_{t}(\,j)\vert]<\infty$
for each j, they showed that condition (8a) ensures geometric ergodicity [Reference Chan, Petruccelli, Tong and Woolford4, Theorem 2.3]. To our knowledge, in the cases (8b)–(8e) no results regarding the rate of ergodicity have as yet appeared in the literature and our Theorem 4(b) below indicates that geometric ergodicity may not always hold without stronger assumptions. Related to this, we note that Meyn and Tweedie [Reference Meyn and Tweedie19, Section 11.4.3 and Section B.2] discussed the (geometric) ergodicity of the SETAR model (7), reproducing the ergodicity result of [Reference Chan, Petruccelli, Tong and Woolford4, Theorem 2.1] as their Proposition 11.4.5. On their page 541, Meyn and Tweedie [Reference Meyn and Tweedie19] also stated that (our additions in brackets) ‘in the interior of the parameter space [the union of (8a)–(8e)] we are able to identify geometric ergodicity in Proposition 11.4.5 … the stronger form [geometric ergodicity] is actually proved in that result’ but no formal proof is given for this statement.
We consider rates of ergodicity and
![]() $\beta$
-mixing in case (8d) when the autoregressive coefficients
$\beta$
-mixing in case (8d) when the autoregressive coefficients
![]() $\theta(1)$
and
$\theta(1)$
and
![]() $\theta(M)$
equal unity. For intuition, note that due to non-zero intercept terms
$\theta(M)$
equal unity. For intuition, note that due to non-zero intercept terms
![]() $\varphi(1)$
and
$\varphi(1)$
and
![]() $\varphi(M)$
, both the first and the last regimes exhibit non-stationary random-walk-type behavior with a drift. As the intercept terms satisfy
$\varphi(M)$
, both the first and the last regimes exhibit non-stationary random-walk-type behavior with a drift. As the intercept terms satisfy
![]() $\varphi(M)<0<\varphi(1)$
, the drift is increasing in the first regime and decreasing in the last regime. This feature prevents the process
$\varphi(M)<0<\varphi(1)$
, the drift is increasing in the first regime and decreasing in the last regime. This feature prevents the process
![]() $y_{t}$
from exploding to (plus or minus) infinity, thereby providing intuition why ergodicity can hold true. It is noteworthy that ergodicity is in no way dependent on the behavior of the process in the middle regimes (
$y_{t}$
from exploding to (plus or minus) infinity, thereby providing intuition why ergodicity can hold true. It is noteworthy that ergodicity is in no way dependent on the behavior of the process in the middle regimes (
![]() $2,\ldots,M-1$
), which can exhibit stationary, random-walk-type (with or without drift), or even explosive behavior.
$2,\ldots,M-1$
), which can exhibit stationary, random-walk-type (with or without drift), or even explosive behavior.
In their results, Chan et al. [Reference Chan, Petruccelli, Tong and Woolford4] allowed for regime-dependent distributions for the error term
![]() $W_{t}(\,j)$
. To obtain our results for the case (8d), we strengthen the assumptions on the error term and, in particular, assume that the error distribution is the same in each regime (this stronger assumption is needed to apply the results mentioned in the proof of Theorem 3 below, and relaxing it appears less than straightforward). To compensate, we obtain results for a model more general than the SETAR model (7) with (8d). Specifically, we formulate our results in terms of the general non-linear autoregressive model
$W_{t}(\,j)$
. To obtain our results for the case (8d), we strengthen the assumptions on the error term and, in particular, assume that the error distribution is the same in each regime (this stronger assumption is needed to apply the results mentioned in the proof of Theorem 3 below, and relaxing it appears less than straightforward). To compensate, we obtain results for a model more general than the SETAR model (7) with (8d). Specifically, we formulate our results in terms of the general non-linear autoregressive model
where the function
![]() $g \colon \mathbb{R}\rightarrow\mathbb{R}$
and the error term
$g \colon \mathbb{R}\rightarrow\mathbb{R}$
and the error term
![]() $\varepsilon_{t}$
satisfy the following conditions:
$\varepsilon_{t}$
satisfy the following conditions:
(A1) g is a measurable function with the property
![]() $|g(x)|\rightarrow\infty$
as
$|g(x)|\rightarrow\infty$
as
![]() $|x|\rightarrow\infty$
and such that there exist positive constants r and
$|x|\rightarrow\infty$
and such that there exist positive constants r and
![]() $M_{0}$
such that
$M_{0}$
such that
(A2)
![]() $\{\varepsilon_{t},\,t=1,2,\ldots\}$
is a sequence of independent and identically distributed mean zero random variables that is independent of
$\{\varepsilon_{t},\,t=1,2,\ldots\}$
is a sequence of independent and identically distributed mean zero random variables that is independent of
![]() $X_{0}$
and the distribution of
$X_{0}$
and the distribution of
![]() $\varepsilon_{1}$
has a (Lebesgue) density that is bounded away from zero on compact subsets of
$\varepsilon_{1}$
has a (Lebesgue) density that is bounded away from zero on compact subsets of
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Model (9) with conditions (A1) and (A2) is a special case of models considered by Fort and Moulines [Reference Fort and Moulines10, Section 2.2], Douc et al. [Reference Douc, Fort, Moulines and Soulier6, Section 3.3], and Meitz and Saikkonen [Reference Meitz and Saikkonen17, Sections 3-4]. These authors considered much more general models, but for clarity of presentation we have simplified the model as much as possible while still being able to obtain results for the SETAR model (7) with (8d) (papers [Reference Fort and Moulines10] and [Reference Douc, Fort, Moulines and Soulier6] considered a multivariate version of (9) whereas [Reference Meitz and Saikkonen17] considered a higher-order generalization of (9); the inequality constraint for the function g in condition (A1) is also more general in these papers, where it is only required that
![]() $|g(x)| \leq (1-r|x|^{-\rho})|x|$
for some
$|g(x)| \leq (1-r|x|^{-\rho})|x|$
for some
![]() $0<\rho\leq2$
).
$0<\rho\leq2$
).
The following theorem establishes ergodicity and
![]() $\beta$
-mixing results for model (9) with varying rates of convergence. The proof (in the Appendix) makes use of results in [Reference Fort and Moulines10], [Reference Douc, Fort, Moulines and Soulier6], and [Reference Meitz and Saikkonen17] to obtain rates of ergodicity, as well as Theorems 1 and 2 above to obtain rates of
$\beta$
-mixing results for model (9) with varying rates of convergence. The proof (in the Appendix) makes use of results in [Reference Fort and Moulines10], [Reference Douc, Fort, Moulines and Soulier6], and [Reference Meitz and Saikkonen17] to obtain rates of ergodicity, as well as Theorems 1 and 2 above to obtain rates of
![]() $\beta$
-mixing (only the subgeometric mixing results in parts (b) and (c) are new).
$\beta$
-mixing (only the subgeometric mixing results in parts (b) and (c) are new).
Theorem 3. Consider model (9) with conditions (A1) and (A2).
-
(a) If
 $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]<\infty$
for some
 ${z_{0}>0}$
, then
${z_{0}>0}$
, then
 $X_{t}$
is geometrically ergodic with convergence rate
$X_{t}$
is geometrically ergodic with convergence rate
 $r(n)=r_{1}^{n}$
for some
$r(n)=r_{1}^{n}$
for some
 $r_{1}>1$
. Moreover, if the initial state
$r_{1}>1$
. Moreover, if the initial state
 $X_{0}$
has a distribution such that
$X_{0}$
has a distribution such that
 $\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
for some
 $z>0$
, then
$z>0$
, then
 $X_{t}$
is also
$X_{t}$
is also
 $\beta$
-mixing and the mixing coefficients satisfy, for some
$\beta$
-mixing and the mixing coefficients satisfy, for some
 $r_{3}>1$
,
$r_{3}>1$
,
 $\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
.
$\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
. -
(b) If
 $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|^{\kappa_{0}}}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|^{\kappa_{0}}}]<\infty$
for some
 ${z_{0}>0}$
and
${z_{0}>0}$
and
 ${\kappa_{0}\in(0,1)}$
, then
${\kappa_{0}\in(0,1)}$
, then
 $X_{t}$
is subexponentially ergodic with convergence rate
$X_{t}$
is subexponentially ergodic with convergence rate
 $r(n)=({\textrm{e}}^{c})^{n^{\kappa_{0}}}$
(for some
$r(n)=({\textrm{e}}^{c})^{n^{\kappa_{0}}}$
(for some
 $c>0$
). Moreover, if the initial state
$c>0$
). Moreover, if the initial state
 $X_{0}$
has a distribution such that
$X_{0}$
has a distribution such that
 $\mathbb{E}[{\textrm{e}}^{z|X_{0}|^{\kappa_{0}}}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z|X_{0}|^{\kappa_{0}}}]<\infty$
for some
 $z>0$
, then
$z>0$
, then
 $X_{t}$
is also
$X_{t}$
is also
 $\beta$
-mixing and the mixing coefficients satisfy, for some
$\beta$
-mixing and the mixing coefficients satisfy, for some
 $\tilde{c}>0$
,
$\tilde{c}>0$
,
 $\lim_{n\rightarrow\infty}({\textrm{e}}^{\tilde{c}})^{n^{\kappa_{0}}}\beta(n)=0$
.
$\lim_{n\rightarrow\infty}({\textrm{e}}^{\tilde{c}})^{n^{\kappa_{0}}}\beta(n)=0$
. -
(c) If
 $\mathbb{E}[|\varepsilon_{1}|^{s_{0}}]<\infty$
for either
$\mathbb{E}[|\varepsilon_{1}|^{s_{0}}]<\infty$
for either
 $s_{0}=2$
or
$s_{0}=2$
or
 $s_{0}\geq4$
, then
$s_{0}\geq4$
, then
 $X_{t}$
polynomially ergodic with convergence rate
$X_{t}$
polynomially ergodic with convergence rate
 $r(n)=n^{s_{0}-1}$
. Moreover, if the initial state
$r(n)=n^{s_{0}-1}$
. Moreover, if the initial state
 $X_{0}$
has distribution such that
$X_{0}$
has distribution such that
 $\mathbb{E}[|X_{0}|^{s_{0}}]<\infty$
, then
$\mathbb{E}[|X_{0}|^{s_{0}}]<\infty$
, then
 $X_{t}$
is also
$X_{t}$
is also
 $\beta$
-mixing and the mixing coefficients satisfy
$\beta$
-mixing and the mixing coefficients satisfy
 $\lim_{n\rightarrow\infty}n^{s_{0}-1}\beta(n)=0$
.
$\lim_{n\rightarrow\infty}n^{s_{0}-1}\beta(n)=0$
.
Theorem 3 shows that there is a trade-off between rates of ergodicity and
![]() $\beta$
-mixing and finiteness of moments of the error term. The fastest geometric rate is obtained when
$\beta$
-mixing and finiteness of moments of the error term. The fastest geometric rate is obtained when
![]() $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]<\infty$
(
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]<\infty$
(
![]() $z_{0}>0$
), so that
$z_{0}>0$
), so that
![]() $\varepsilon_{1}$
has finite moments of all orders and the slowest polynomial rate is obtained when only
$\varepsilon_{1}$
has finite moments of all orders and the slowest polynomial rate is obtained when only
![]() $\mathbb{E}[\varepsilon_{1}^{2}]<\infty$
. As discussed after Theorem 2, we also have
$\mathbb{E}[\varepsilon_{1}^{2}]<\infty$
. As discussed after Theorem 2, we also have
![]() $\int_{\textsf{X}}\pi({\textrm{d}} x)\phi(V(x))<\infty$
so that there is a similar trade-off between these convergence rates and finiteness of moments of the stationary distribution (expressions of V and
$\int_{\textsf{X}}\pi({\textrm{d}} x)\phi(V(x))<\infty$
so that there is a similar trade-off between these convergence rates and finiteness of moments of the stationary distribution (expressions of V and
![]() $\phi$
are available in the proof of Theorem 3).
$\phi$
are available in the proof of Theorem 3).
Above it was mentioned that [Reference Fort and Moulines10], [Reference Douc, Fort, Moulines and Soulier6], and [Reference Meitz and Saikkonen17] considered (subgeometric) ergodicity of models more general than (9) with conditions (A1) and (A2). Making use of our Theorems 1 and 2, subgeometric rates of
![]() $\beta$
-mixing can easily be obtained for these more general models too. We omit the details for brevity.
$\beta$
-mixing can easily be obtained for these more general models too. We omit the details for brevity.
In a series of papers, Veretennikov and co-authors also considered the model (9) with function g satisfying
![]() $|g(x)|\leq(1-r|x|^{-\rho})|x|$
for some
$|g(x)|\leq(1-r|x|^{-\rho})|x|$
for some
![]() $1\leq\rho\leq2$
. Using methods very different from ours, they obtained results on subgeometric ergodicity and subgeometric rates for
$1\leq\rho\leq2$
. Using methods very different from ours, they obtained results on subgeometric ergodicity and subgeometric rates for
![]() $\beta$
-mixing coefficients. The cases
$\beta$
-mixing coefficients. The cases
![]() $1<\rho<2$
and
$1<\rho<2$
and
![]() $\rho=2$
are considered in [Reference Veretennikov27], [Reference Klokov and Veretennikov14, Reference Klokov and Veretennikov15], and [Reference Klokov13] and are shown to lead to subgeometric rates. For the case
$\rho=2$
are considered in [Reference Veretennikov27], [Reference Klokov and Veretennikov14, Reference Klokov and Veretennikov15], and [Reference Klokov13] and are shown to lead to subgeometric rates. For the case
![]() $\rho=1$
relevant for the SETAR example, these papers refer to [Reference Veretennikov25, Reference Veretennikov26] and [Reference Veretennikov and Gulinskii28]. A result corresponding to our Theorem 3(a) can be found in [Reference Veretennikov and Gulinskii28, Theorem 1], but subgeometric rates, such as those in our Theorem 3 parts (b) and (c), do not seem to be established in the case
$\rho=1$
relevant for the SETAR example, these papers refer to [Reference Veretennikov25, Reference Veretennikov26] and [Reference Veretennikov and Gulinskii28]. A result corresponding to our Theorem 3(a) can be found in [Reference Veretennikov and Gulinskii28, Theorem 1], but subgeometric rates, such as those in our Theorem 3 parts (b) and (c), do not seem to be established in the case
![]() $\rho=1$
.
$\rho=1$
.
We now specialize the results above to the SETAR model (7) with (8d). It is easy to see that this model, with the function g in (9) defined as
 $$g(x)=\sum_{j=1}^{M}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}$$
$$g(x)=\sum_{j=1}^{M}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}$$
(with
![]() $\boldsymbol{1}\{\cdot\}$
denoting the indicator function), satisfies the condition in (A1). Namely, for x large enough and positive we have
$\boldsymbol{1}\{\cdot\}$
denoting the indicator function), satisfies the condition in (A1). Namely, for x large enough and positive we have
![]() $\lvert g(x)\rvert=g(x)=x+\varphi(M)=\lvert x\rvert-(-\varphi(M))$
, whereas for x small enough and negative we have
$\lvert g(x)\rvert=g(x)=x+\varphi(M)=\lvert x\rvert-(-\varphi(M))$
, whereas for x small enough and negative we have
![]() $\lvert g(x)\rvert=-g(x)=-x-\varphi(1)=\lvert x\rvert-\varphi(1)$
, so that the inequality in (A1) holds for
$\lvert g(x)\rvert=-g(x)=-x-\varphi(1)=\lvert x\rvert-\varphi(1)$
, so that the inequality in (A1) holds for
![]() $M_{0}>\max\{|r_{1}|,|r_{M-1}|\}$
and
$M_{0}>\max\{|r_{1}|,|r_{M-1}|\}$
and
![]() $r=\min\{\varphi(1),-\varphi(M)\}$
(and the supremum condition is obviously satisfied).
$r=\min\{\varphi(1),-\varphi(M)\}$
(and the supremum condition is obviously satisfied).
Part (a) of the next theorem simply restates the result of Theorem 3 for the SETAR model (7) with (8d), whereas part (b) establishes that geometric ergodicity cannot hold under the weaker moment assumptions of Theorem 3 parts (b) and (c).
Theorem 4. Consider the SETAR model (7) with the parameters satisfying (8d) and the error terms satisfying
![]() $W_{t}(\,j)=\varepsilon_{t}$
(
$W_{t}(\,j)=\varepsilon_{t}$
(
![]() $j=1,\ldots,M$
) with
$j=1,\ldots,M$
) with
![]() $\varepsilon_{t}$
as in (A2).
$\varepsilon_{t}$
as in (A2).
-
(a) Sufficient conditions for geometric, subexponential, and polynomial ergodicity and
 $\beta$
-mixing of
$\beta$
-mixing of
 $X_{t}$
are as in parts (a), (b), and (c) of Theorem 3, respectively.
$X_{t}$
are as in parts (a), (b), and (c) of Theorem 3, respectively. -
(b) If
 $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
 ${z_{0}>0}$
, then
${z_{0}>0}$
, then
 $X_{t}$
is not geometrically ergodic.
$X_{t}$
is not geometrically ergodic.
Theorem 4(b) shows that for the SETAR model (7) with (8d), the subgeometric rates of Theorem 3 parts (b) and (c) cannot be improved to a geometric rate unless stronger moment assumptions are made regarding the error term. This result is obtained by making use of a necessary condition for geometric ergodicity of certain specific type of Markov chains in [Reference Jarner and Tweedie12] (using their necessary condition to obtain this result appears possible only in case (8d) out of (8a)–(8e)).
6. Conclusion
In this note we have shown that subgeometrically ergodic Markov chains are
![]() $\beta$
-mixing with subgeometrically decaying mixing coefficients. Although this result is simple, it should prove very useful in obtaining rates of mixing in situations where geometric ergodicity cannot be established. An illustration using the popular self-exciting threshold autoregressive model showed how our results can yield new subgeometric rates of mixing.
$\beta$
-mixing with subgeometrically decaying mixing coefficients. Although this result is simple, it should prove very useful in obtaining rates of mixing in situations where geometric ergodicity cannot be established. An illustration using the popular self-exciting threshold autoregressive model showed how our results can yield new subgeometric rates of mixing.
Acknowledgements
The authors thank the Academy of Finland for financial support, and the editors and an anonymous referee for useful comments and suggestions.
Appendix A. Proofs
This Appendix contains the proofs of Theorems 2–4; proof of Theorem 1 is provided in the supplementary material. Proofs of Theorems 1 and 2 make use of the following handy inequality for the
![]() $\beta$
-mixing coefficients due to Liebscher [Reference Liebscher16, Proposition 3]. (Note that our Lemma A.1 below includes an additional factor of
$\beta$
-mixing coefficients due to Liebscher [Reference Liebscher16, Proposition 3]. (Note that our Lemma A.1 below includes an additional factor of
![]() $\frac{1}{2}$
compared to Liebscher’s Proposition 3; see our expression for
$\frac{1}{2}$
compared to Liebscher’s Proposition 3; see our expression for
![]() $\beta(n)$
in (4) and his equation (27).) Again,
$\beta(n)$
in (4) and his equation (27).) Again,
![]() $\lfloor k\rfloor$
denotes the integer part of the real number k.
$\lfloor k\rfloor$
denotes the integer part of the real number k.
Lemma A.1. Suppose
![]() $X_{t}$
is a Markov chain with stationary distribution
$X_{t}$
is a Markov chain with stationary distribution
![]() $\pi$
and that the initial state
$\pi$
and that the initial state
![]() $X_{0}$
has distribution
$X_{0}$
has distribution
![]() $\mu$
. Then
$\mu$
. Then
where
![]() $n_{1}=\lfloor n/2\rfloor$
.
$n_{1}=\lfloor n/2\rfloor$
.
In the proof below, notation
![]() $\mathbb{E}_{\mu}[\cdot]$
is used for the conditional expectation of a
$\mathbb{E}_{\mu}[\cdot]$
is used for the conditional expectation of a
![]() $\mathcal{F}_{0}^{\infty}$
-measurable random variable conditioned on the initial state
$\mathcal{F}_{0}^{\infty}$
-measurable random variable conditioned on the initial state
![]() $X_{0}$
with distribution
$X_{0}$
with distribution
![]() $\mu$
. When conditioning is on
$\mu$
. When conditioning is on
![]() $X_{0}=x$
the notation
$X_{0}=x$
the notation
![]() $\mathbb{E}_{x}[\cdot]$
is used; these are connected via
$\mathbb{E}_{x}[\cdot]$
is used; these are connected via
![]() $\mathbb{E}_{\mu}[\cdot]=\int_{\textsf{X}}\mu({\textrm{d}} x)\mathbb{E}_{x}[\cdot]$
. We also define the concept of return time to a measurable set A as
$\mathbb{E}_{\mu}[\cdot]=\int_{\textsf{X}}\mu({\textrm{d}} x)\mathbb{E}_{x}[\cdot]$
. We also define the concept of return time to a measurable set A as
![]() $\tau_{A}=\inf\{ n\geq 1 \colon X_{n}\in A\} $
.
$\tau_{A}=\inf\{ n\geq 1 \colon X_{n}\in A\} $
.
Proof of Theorem 2. First note that, due to the assumed irreducibility and aperiodicity, the petite set C in Condition Drift–SubG is small [Reference Meyn and Tweedie19, Theorem 5.5.7]. We first show that
 \begin{equation}\sup_{x\in C}\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1} r_{\phi}(k)\Biggr]<\infty;\end{equation}
\begin{equation}\sup_{x\in C}\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1} r_{\phi}(k)\Biggr]<\infty;\end{equation}
by Theorem 2.1 of Tuominen and Tweedie [Reference Tuominen and Tweedie23] this implies the subgeometric ergodicity in (a) (for related results implying (a); see also [Reference Nummelin and Tuominen21, Theorem 2.7(i)], [Reference Tweedie24, Theorem 1(iii)], [Reference Douc, Fort, Moulines and Soulier6, Proposition 2.5]). Douc et al. [Reference Douc, Fort, Moulines and Soulier6, Proposition 2.1 and Lemma 2.3] showed that Condition Drift–SubG implies the existence of a sequence of drift functions
![]() $V_{k}(x)$
,
$V_{k}(x)$
,
![]() $k=0,1,2,\ldots,$
such that, for
$k=0,1,2,\ldots,$
such that, for
![]() $k\geq 0$
,
$k\geq 0$
,
where
![]() $\tilde{b}=br_{\phi}(1)(r_{\phi}(0))^{-2}$
(see their Proposition 2.1 and the top of page 1358) and
$\tilde{b}=br_{\phi}(1)(r_{\phi}(0))^{-2}$
(see their Proposition 2.1 and the top of page 1358) and
![]() $r_{\phi}\in\Lambda$
(see their Lemma 2.3). Applying Proposition 11.3.2 of [Reference Meyn and Tweedie19] with
$r_{\phi}\in\Lambda$
(see their Lemma 2.3). Applying Proposition 11.3.2 of [Reference Meyn and Tweedie19] with
![]() $Z_{k}=V_{k}(X_{k})$
,
$Z_{k}=V_{k}(X_{k})$
,
![]() $f_{k}(x)=r_{\phi}(k)$
,
$f_{k}(x)=r_{\phi}(k)$
,
![]() $s_{k}(x)=\tilde{b}r_{\phi}(k)\boldsymbol{1}_{C}(x)$
, and stopping time
$s_{k}(x)=\tilde{b}r_{\phi}(k)\boldsymbol{1}_{C}(x)$
, and stopping time
![]() $\tau_{C}$
, we obtain ([Reference Douc, Fort, Moulines and Soulier6, Proposition 2.2] also states this conclusion; note also that by their equation (2.2) we have
$\tau_{C}$
, we obtain ([Reference Douc, Fort, Moulines and Soulier6, Proposition 2.2] also states this conclusion; note also that by their equation (2.2) we have
![]() $V_{0}(x)\leq V(x)$
)
$V_{0}(x)\leq V(x)$
)
 \begin{align}\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1} r_{\phi}(k)\Biggr]& \leq V(x)+\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}\tilde{b}r_{\phi}(k)\boldsymbol{1}_{C}(x)\Biggr] \notag \\[3pt] &=V(x)+\tilde{b}r_{\phi}(0)\boldsymbol{1}_{C}(x) \notag \\[3pt]& =V(x)+b\dfrac{r_{\phi}(1)}{r_{\phi}(0)}\boldsymbol{1}_{C}(x).\end{align}
\begin{align}\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1} r_{\phi}(k)\Biggr]& \leq V(x)+\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}\tilde{b}r_{\phi}(k)\boldsymbol{1}_{C}(x)\Biggr] \notag \\[3pt] &=V(x)+\tilde{b}r_{\phi}(0)\boldsymbol{1}_{C}(x) \notag \\[3pt]& =V(x)+b\dfrac{r_{\phi}(1)}{r_{\phi}(0)}\boldsymbol{1}_{C}(x).\end{align}
By condition
![]() $\sup_{x\in C}V(x)<\infty$
(in Condition Drift–SubG), we obtain (10). Now Theorem 2.1 of [Reference Tuominen and Tweedie23] ensures that
$\sup_{x\in C}V(x)<\infty$
(in Condition Drift–SubG), we obtain (10). Now Theorem 2.1 of [Reference Tuominen and Tweedie23] ensures that
![]() $\lim_{n\to\infty}r_{\phi}(n)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
, so the subgeometric ergodicity in (a) is established (note that as
$\lim_{n\to\infty}r_{\phi}(n)\Vert P^{n}(x\,;\,\cdot)-\pi(\cdot)\Vert =0$
, so the subgeometric ergodicity in (a) is established (note that as
![]() $V_{0}(x)\leq V(x)$
holds with V(x) assumed everywhere finite, the set S(f,r) in Theorem 2.1 of [Reference Tuominen and Tweedie23] coincides with
$V_{0}(x)\leq V(x)$
holds with V(x) assumed everywhere finite, the set S(f,r) in Theorem 2.1 of [Reference Tuominen and Tweedie23] coincides with
![]() $\textsf{X}$
, so the aforementioned convergence holds for all
$\textsf{X}$
, so the aforementioned convergence holds for all
![]() $x\in\textsf{X}$
).
$x\in\textsf{X}$
).
To prove (b), suppose the initial state
![]() $X_{0}$
has distribution
$X_{0}$
has distribution
![]() $\mu$
such that
$\mu$
such that
![]() $\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. We will use Theorems 2.7(i,ii) and 2.2 of [Reference Nummelin and Tuominen21], but first we obtain a property of the rate function
$\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
. We will use Theorems 2.7(i,ii) and 2.2 of [Reference Nummelin and Tuominen21], but first we obtain a property of the rate function
![]() $r_{\phi}(z)$
(which is well known for members of
$r_{\phi}(z)$
(which is well known for members of
![]() $\Lambda_{0}$
but not for members of
$\Lambda_{0}$
but not for members of
![]() $\Lambda$
). Recall that
$\Lambda$
). Recall that
![]() $r_{\phi}(z)=(H_{\phi}^{-1})'(z)=\phi\circ H_{\phi}^{-1}(z)$
so that
$r_{\phi}(z)=(H_{\phi}^{-1})'(z)=\phi\circ H_{\phi}^{-1}(z)$
so that
![]() $r_{\phi}'(z)/r_{\phi}(z)=\phi'\circ H_{\phi}^{-1}(z)$
. As
$r_{\phi}'(z)/r_{\phi}(z)=\phi'\circ H_{\phi}^{-1}(z)$
. As
![]() $\phi'$
is non-increasing (see [Reference Douc, Fort, Moulines and Soulier6, first paragraph of Section 2.1]) and
$\phi'$
is non-increasing (see [Reference Douc, Fort, Moulines and Soulier6, first paragraph of Section 2.1]) and
![]() $H_{\phi}^{-1}$
is increasing, it follows that
$H_{\phi}^{-1}$
is increasing, it follows that
![]() $r_{\phi}'(z)/r_{\phi}(z)=\phi'\circ H_{\phi}^{-1}(z)$
is non-increasing. Therefore the function
$r_{\phi}'(z)/r_{\phi}(z)=\phi'\circ H_{\phi}^{-1}(z)$
is non-increasing. Therefore the function
is also non-increasing. Following the proof of Lemma 1 of Stone and Wainger [Reference Stone and Wainger22] (which relies only on their property (iii) on their page 326) yields the desired property
![]() $r_{\phi}(m+n)\leq r_{\phi}(m)r_{\phi}(n)$
for all
$r_{\phi}(m+n)\leq r_{\phi}(m)r_{\phi}(n)$
for all
![]() $m,n>0$
.
$m,n>0$
.
Using this property we now obtain
 $$r_{\phi}(\tau_{C})\leq r_{\phi}(1)r_{\phi}(\tau_{C}-1)\leq r_{\phi}(1)\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k) ,$$
$$r_{\phi}(\tau_{C})\leq r_{\phi}(1)r_{\phi}(\tau_{C}-1)\leq r_{\phi}(1)\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k) ,$$
and further that
 $$\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}}r_{\phi}(k)\Biggr]\leq(r_{\phi}(1)+1)\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k)\Biggr]\quad\text{and}\quad\mathbb{E}_{x}[r_{\phi}(\tau_{C})]\leq r_{\phi}(1)\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k)\Biggr]$$
$$\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}}r_{\phi}(k)\Biggr]\leq(r_{\phi}(1)+1)\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k)\Biggr]\quad\text{and}\quad\mathbb{E}_{x}[r_{\phi}(\tau_{C})]\leq r_{\phi}(1)\mathbb{E}_{x}\Biggl[\sum_{k=0}^{\tau_{C}-1}r_{\phi}(k)\Biggr]$$
(see [Reference Tuominen and Tweedie23, equations (5) and (14)]). The former result together with (10) implies that condition (2.12) of Theorem 2.7(i) of [Reference Nummelin and Tuominen21] is satisfied. The latter result together with (11) yields
and, as
![]() $\mathbb{E}_{\mu}[r_{\phi}(\tau_{C})]=\int_{\textsf{X}}\mu({\textrm{d}} x)\mathbb{E}_{x}[r_{\phi}(\tau_{C})]$
, the assumed bound
$\mathbb{E}_{\mu}[r_{\phi}(\tau_{C})]=\int_{\textsf{X}}\mu({\textrm{d}} x)\mathbb{E}_{x}[r_{\phi}(\tau_{C})]$
, the assumed bound
![]() $\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
implies
$\int_{\textsf{X}}\mu({\textrm{d}} x)V(x)<\infty$
implies
so the condition in Theorem 2.7(ii) of [Reference Nummelin and Tuominen21] is satisfied. Therefore, by Theorems 2.7(i,ii) and 2.2 of [Reference Nummelin and Tuominen21],
Next consider part (d). In the stationary case (
![]() $\mu=\pi$
), the desired result
$\mu=\pi$
), the desired result
follows from the last remark in Theorem 2.2 of [Reference Nummelin and Tuominen21] (and condition
![]() $\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed). Thus (b) holds in the stationary case. Regarding part (c) in the stationary case, note from (5) that now
$\int_{\textsf{X}}\pi({\textrm{d}} x)V(x)<\infty$
is not needed). Thus (b) holds in the stationary case. Regarding part (c) in the stationary case, note from (5) that now
![]() $\beta(n)=\int\pi({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi\Vert $
,
$\beta(n)=\int\pi({\textrm{d}} x)\Vert P^{n}(x\,;\,\cdot)-\pi\Vert $
,
![]() $n=1,2,\ldots,$
so (b) and (c) are clearly equivalent (and hold with the same rate
$n=1,2,\ldots,$
so (b) and (c) are clearly equivalent (and hold with the same rate
![]() $r_{\phi}(n)$
).
$r_{\phi}(n)$
).
To prove (c), use Lemma A.1 to obtain the inequality
 \begin{align*}& \tilde{r}_{\phi}(n)\beta(n) \\[3pt] &\quad \leq\dfrac{\tilde{r}_{\phi}(n)}{r_{\phi}(n_{1})}\biggl[ \dfrac{1}{2}r_{\phi}(n_{1})\int\pi({\textrm{d}} x)\Vert P^{n_{1}}(x\,;\,\cdot)-\pi\Vert +\dfrac{3}{2}r_{\phi}(n_{1})\int\mu({\textrm{d}} x)\Vert P^{n_{1}}(x\,;\,\cdot)-\pi\Vert \biggr].\end{align*}
\begin{align*}& \tilde{r}_{\phi}(n)\beta(n) \\[3pt] &\quad \leq\dfrac{\tilde{r}_{\phi}(n)}{r_{\phi}(n_{1})}\biggl[ \dfrac{1}{2}r_{\phi}(n_{1})\int\pi({\textrm{d}} x)\Vert P^{n_{1}}(x\,;\,\cdot)-\pi\Vert +\dfrac{3}{2}r_{\phi}(n_{1})\int\mu({\textrm{d}} x)\Vert P^{n_{1}}(x\,;\,\cdot)-\pi\Vert \biggr].\end{align*}
The term in square brackets converges to zero as
![]() $n\to\infty$
by parts (b) and (d) and, by assumption,
$n\to\infty$
by parts (b) and (d) and, by assumption,
![]() $\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
. This establishes (c).
$\limsup_{n\rightarrow\infty}\tilde{r}_{\phi}(n)/r_{\phi}(n_{1})<\infty$
. This establishes (c).
To prove (e), it suffices to note that
where the first and the last ratio on the right-hand side are bounded from above uniformly in n due to (6), and that
where the three ratios on the right-hand side are clearly bounded from below uniformly in n by some constant larger than zero.
![]()
Proof of Theorem 3. The ergodicity results of parts (a) and (b) could be obtained using results in [Reference Douc, Fort, Moulines and Soulier6, Section 3.3] and those in part (c) using results in [Reference Fort and Moulines10, Section 2.2]; for clarity of presentation, we will in all parts rely on the results in [Reference Meitz and Saikkonen17]. Model (9) with conditions (A1) and (A2) is a special case of the model considered in [Reference Meitz and Saikkonen17] (with
![]() $p=\rho=1$
in that paper). The assumptions made in [Reference Meitz and Saikkonen17] holds due to (A2) and the moment conditions assumed in parts (a)–(c) of Theorem 3. Therefore we can make use of Theorems 2 and 3 in [Reference Meitz and Saikkonen17] to obtain suitable ergodicity results.
$p=\rho=1$
in that paper). The assumptions made in [Reference Meitz and Saikkonen17] holds due to (A2) and the moment conditions assumed in parts (a)–(c) of Theorem 3. Therefore we can make use of Theorems 2 and 3 in [Reference Meitz and Saikkonen17] to obtain suitable ergodicity results.
(a) In this case Assumption 2(a) of [Reference Meitz and Saikkonen17] holds with
![]() $\kappa_{0}=1$
and we apply their Theorem 2(ii). From the proof of that theorem (case
$\kappa_{0}=1$
and we apply their Theorem 2(ii). From the proof of that theorem (case
![]() $p=1$
) it can be seen that Condition Drift–G holds with
$p=1$
) it can be seen that Condition Drift–G holds with
![]() $V(x)={\textrm{e}}^{b_{1}|x|}$
for some
$V(x)={\textrm{e}}^{b_{1}|x|}$
for some
![]() $b_{1}\in(0,z_{0})$
, which can be chosen as small as desired. From Theorem 2(ii) of [Reference Meitz and Saikkonen17] we obtain that
$b_{1}\in(0,z_{0})$
, which can be chosen as small as desired. From Theorem 2(ii) of [Reference Meitz and Saikkonen17] we obtain that
![]() $X_{t}$
is geometrically ergodic with convergence rate
$X_{t}$
is geometrically ergodic with convergence rate
![]() $r(n)=({\textrm{e}}^{c})^{n}$
(for some
$r(n)=({\textrm{e}}^{c})^{n}$
(for some
![]() $c>0$
), i.e.
$c>0$
), i.e.
![]() $r(n)=r_{1}^{n}$
for some
$r(n)=r_{1}^{n}$
for some
![]() $r_{1}>1$
. To obtain results on
$r_{1}>1$
. To obtain results on
![]() $\beta$
-mixing, we next apply Theorem 1 of the present paper. If the initial state
$\beta$
-mixing, we next apply Theorem 1 of the present paper. If the initial state
![]() $X_{0}$
has distribution such that
$X_{0}$
has distribution such that
![]() $\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
for some
![]() $z>0$
(and noting that above
$z>0$
(and noting that above
![]() $b_{1}$
can be chosen small enough so that
$b_{1}$
can be chosen small enough so that
![]() $b_{1}\leq z$
holds), then by Theorem 1
$b_{1}\leq z$
holds), then by Theorem 1
![]() $X_{t}$
is
$X_{t}$
is
![]() $\beta$
-mixing and the mixing coefficients satisfy, for some
$\beta$
-mixing and the mixing coefficients satisfy, for some
![]() $r_{3}>1$
,
$r_{3}>1$
,
![]() $\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
.
$\lim_{n\rightarrow\infty}r_{3}^{n}\beta(n)=0$
.
(b) In this case Assumption 2(a) of [Reference Meitz and Saikkonen17] holds with
![]() $\kappa_{0}\in(0,1)$
and we apply their Theorem 2(i). From the proof of that theorem (case
$\kappa_{0}\in(0,1)$
and we apply their Theorem 2(i). From the proof of that theorem (case
![]() $p=1$
) it can be seen that Condition Drift–SubG holds with
$p=1$
) it can be seen that Condition Drift–SubG holds with
![]() $V(x)={\textrm{e}}^{b_{1}|x|^{\kappa_{0}}}$
(for some
$V(x)={\textrm{e}}^{b_{1}|x|^{\kappa_{0}}}$
(for some
![]() $b_{1}\in(0,\beta_{0})$
, which can be chosen as small as desired) and
$b_{1}\in(0,\beta_{0})$
, which can be chosen as small as desired) and
![]() $\phi(v)=c_{0}(v+v_{0})(\ln(v+v_{0}))^{-\alpha}$
(for some
$\phi(v)=c_{0}(v+v_{0})(\ln(v+v_{0}))^{-\alpha}$
(for some
![]() $c_{0},v_{0}>0$
and
$c_{0},v_{0}>0$
and
![]() $\alpha=1/\kappa_{0}-1$
). From Theorem 2(i) of [Reference Meitz and Saikkonen17] we obtain that
$\alpha=1/\kappa_{0}-1$
). From Theorem 2(i) of [Reference Meitz and Saikkonen17] we obtain that
![]() $X_{t}$
is subexponentially ergodic with convergence rate
$X_{t}$
is subexponentially ergodic with convergence rate
![]() $r(n)=({\textrm{e}}^{c})^{n^{\kappa_{0}}}$
(for some
$r(n)=({\textrm{e}}^{c})^{n^{\kappa_{0}}}$
(for some
![]() $c>0$
). To obtain results on
$c>0$
). To obtain results on
![]() $\beta$
-mixing, we next apply Theorem 2 of the present paper. If the initial state
$\beta$
-mixing, we next apply Theorem 2 of the present paper. If the initial state
![]() $X_{0}$
has distribution such that
$X_{0}$
has distribution such that
![]() $\mathbb{E}[{\textrm{e}}^{z|X_{0}|^{\kappa_{0}}}]<\infty$
for some
$\mathbb{E}[{\textrm{e}}^{z|X_{0}|^{\kappa_{0}}}]<\infty$
for some
![]() $z>0$
(and noting that above
$z>0$
(and noting that above
![]() $b_{1}$
can be chosen small enough so that
$b_{1}$
can be chosen small enough so that
![]() $b_{1}\leq z$
holds), then by Theorem 2
$b_{1}\leq z$
holds), then by Theorem 2
![]() $X_{t}$
is
$X_{t}$
is
![]() $\beta$
-mixing and the mixing coefficients satisfy, for any
$\beta$
-mixing and the mixing coefficients satisfy, for any
![]() $\tilde{c}\in(0,z2^{-\kappa_{0}})$
,
$\tilde{c}\in(0,z2^{-\kappa_{0}})$
,
![]() $\lim_{n\rightarrow\infty}\tilde{r}(n)\beta(n)=0$
with
$\lim_{n\rightarrow\infty}\tilde{r}(n)\beta(n)=0$
with
![]() $\tilde{r}(n)=({\textrm{e}}^{\tilde{c}})^{n^{\kappa_{0}}}$
.
$\tilde{r}(n)=({\textrm{e}}^{\tilde{c}})^{n^{\kappa_{0}}}$
.
(c) In this case Assumption 2(b) of [Reference Meitz and Saikkonen17] holds with either
![]() $s_{0}=2$
or
$s_{0}=2$
or
![]() $s_{0}\geq4$
and we apply their Theorem 3(ii) (in which exactly the cases
$s_{0}\geq4$
and we apply their Theorem 3(ii) (in which exactly the cases
![]() $s_{0}=2$
and
$s_{0}=2$
and
![]() $s_{0}\geq4$
are available). From the proof of that theorem (the end of step 4 and case
$s_{0}\geq4$
are available). From the proof of that theorem (the end of step 4 and case
![]() $p=1$
) it can be seen that Condition Drift–SubG holds with
$p=1$
) it can be seen that Condition Drift–SubG holds with
![]() $V(x)=1+|x|^{s_{0}}$
and
$V(x)=1+|x|^{s_{0}}$
and
![]() $\phi(v)=cv^{\alpha}$
(for some
$\phi(v)=cv^{\alpha}$
(for some
![]() $c>0$
and
$c>0$
and
![]() $\alpha=1-1/s_{0}$
). From Theorem 3(ii) of [Reference Meitz and Saikkonen17] we obtain that
$\alpha=1-1/s_{0}$
). From Theorem 3(ii) of [Reference Meitz and Saikkonen17] we obtain that
![]() $X_{t}$
is polynomially ergodic with convergence rate
$X_{t}$
is polynomially ergodic with convergence rate
![]() $r(n)=n$
(
$r(n)=n$
(
![]() $s_{0}=2$
) or
$s_{0}=2$
) or
![]() $r(n)=n^{s_{0}-1}$
(
$r(n)=n^{s_{0}-1}$
(
![]() $s_{0}\geq4$
). To obtain results on
$s_{0}\geq4$
). To obtain results on
![]() $\beta$
-mixing, we next apply Theorem 2 of the present paper. If the initial state
$\beta$
-mixing, we next apply Theorem 2 of the present paper. If the initial state
![]() $X_{0}$
has distribution such that
$X_{0}$
has distribution such that
![]() $\mathbb{E}[|X_{0}|^{s_{0}}]<\infty$
, then
$\mathbb{E}[|X_{0}|^{s_{0}}]<\infty$
, then
![]() $X_{t}$
is
$X_{t}$
is
![]() $\beta$
-mixing and the mixing coefficients satisfy
$\beta$
-mixing and the mixing coefficients satisfy
![]() $\lim_{n\rightarrow\infty}n\beta(n)=0$
(
$\lim_{n\rightarrow\infty}n\beta(n)=0$
(
![]() $s_{0}=2$
) or
$s_{0}=2$
) or
![]() $\lim_{n\rightarrow\infty}n^{s_{0}-1}\beta(n)=0$
(
$\lim_{n\rightarrow\infty}n^{s_{0}-1}\beta(n)=0$
(
![]() $s_{0}\geq4$
).
$s_{0}\geq4$
).
![]()
Proof of Theorem 4. Part (a) follows immediately from Theorem 3 and the discussion preceding it, noting that the SETAR model (7) with (8d) satisfies the condition in (A1). To prove (b), assume that
![]() $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
![]() ${z_{0}>0}$
but that
${z_{0}>0}$
but that
![]() $X_{t}$
would be geometrically ergodic. We will use results of [Reference Jarner and Tweedie12] to show that this leads to a contradiction. To this end, note that for the SETAR model (7) with the parameters satisfying (8d), the function g in our equation (9) equals
$X_{t}$
would be geometrically ergodic. We will use results of [Reference Jarner and Tweedie12] to show that this leads to a contradiction. To this end, note that for the SETAR model (7) with the parameters satisfying (8d), the function g in our equation (9) equals
 $$g(x)=\sum_{j=1}^{M}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\},$$
$$g(x)=\sum_{j=1}^{M}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\},$$
which can be written as
 \begin{align*}g(x) & =[\varphi(1)+x]\boldsymbol{1}\{x\leq r_{1}\}+[\varphi(M)+x]\boldsymbol{1}\{r_{M-1}<x\} \\[3pt] &\quad +{ \sum_{j=2}^{M-1}}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}\\[3pt] &=x+\varphi(1)\boldsymbol{1}\{x\leq r_{1}\}+\varphi(M)\boldsymbol{1}\{r_{M-1} \lt x\} \\[3pt] &\quad +{ \sum_{j=2}^{M-1}}[\varphi(\,j)+\theta(\,j)x-x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}\end{align*}
\begin{align*}g(x) & =[\varphi(1)+x]\boldsymbol{1}\{x\leq r_{1}\}+[\varphi(M)+x]\boldsymbol{1}\{r_{M-1}<x\} \\[3pt] &\quad +{ \sum_{j=2}^{M-1}}[\varphi(\,j)+\theta(\,j)x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}\\[3pt] &=x+\varphi(1)\boldsymbol{1}\{x\leq r_{1}\}+\varphi(M)\boldsymbol{1}\{r_{M-1} \lt x\} \\[3pt] &\quad +{ \sum_{j=2}^{M-1}}[\varphi(\,j)+\theta(\,j)x-x]\boldsymbol{1}\{x\in(r_{j-1},r_{j}]\}\end{align*}
or as
![]() $g(x)=x+\tilde{g}(x)$
, where
$g(x)=x+\tilde{g}(x)$
, where
![]() $\tilde{g}(x)$
is bounded. Also recall that it is assumed that the error terms satisfy
$\tilde{g}(x)$
is bounded. Also recall that it is assumed that the error terms satisfy
![]() $W_{t}(\,j)=\varepsilon_{t}$
(
$W_{t}(\,j)=\varepsilon_{t}$
(
![]() $j=1,\ldots,M$
) with
$j=1,\ldots,M$
) with
![]() $\varepsilon_{t}$
as in (A2). These facts show that the SETAR model (7) with (8d) can be expressed in the form of equation (3) in Jarner and Tweedie [Reference Jarner and Tweedie12] so that
$\varepsilon_{t}$
as in (A2). These facts show that the SETAR model (7) with (8d) can be expressed in the form of equation (3) in Jarner and Tweedie [Reference Jarner and Tweedie12] so that
![]() $X_{t}$
is what [Reference Jarner and Tweedie12] call a ‘random-walk-type Markov chain’. (Note also that this holds only in case (8d) out of (8a)–(8e).) Theorem 2.2 of [Reference Jarner and Tweedie12] shows that a necessary condition for the geometric ergodicity of a random-walk-type Markov chain
$X_{t}$
is what [Reference Jarner and Tweedie12] call a ‘random-walk-type Markov chain’. (Note also that this holds only in case (8d) out of (8a)–(8e).) Theorem 2.2 of [Reference Jarner and Tweedie12] shows that a necessary condition for the geometric ergodicity of a random-walk-type Markov chain
![]() $X_{t}$
with stationary probability measure
$X_{t}$
with stationary probability measure
![]() $\pi$
is that there exists a
$\pi$
is that there exists a
![]() $z>0$
such that
$z>0$
such that
![]() $\int_{{\mathbb{R}}}\,{\textrm{e}}^{z|x|}\pi({\textrm{d}} x)<\infty$
. This can be shown to be in contradiction with our assumption that
$\int_{{\mathbb{R}}}\,{\textrm{e}}^{z|x|}\pi({\textrm{d}} x)<\infty$
. This can be shown to be in contradiction with our assumption that
![]() $\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
$\mathbb{E}[{\textrm{e}}^{z_{0}|\varepsilon_{1}|}]=\infty$
for all
![]() ${z_{0}>0}$
, as follows.
${z_{0}>0}$
, as follows.
Suppose
![]() $z>0$
is such that
$z>0$
is such that
![]() $\int_{{\mathbb{R}}}\,{\textrm{e}}^{z|x|}\pi({\textrm{d}} x)<\infty$
and assume that
$\int_{{\mathbb{R}}}\,{\textrm{e}}^{z|x|}\pi({\textrm{d}} x)<\infty$
and assume that
![]() $X_{0}$
, and hence also
$X_{0}$
, and hence also
![]() $X_{1}$
, has the stationary distribution
$X_{1}$
, has the stationary distribution
![]() $\pi$
. Thus
$\pi$
. Thus
![]() $\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
and
$\mathbb{E}[{\textrm{e}}^{z|X_{0}|}]<\infty$
and
![]() $\mathbb{E}[{\textrm{e}}^{z|X_{1}|}]<\infty$
. As
$\mathbb{E}[{\textrm{e}}^{z|X_{1}|}]<\infty$
. As
![]() $0<{\textrm{e}}^{zx}\leq {\textrm{e}}^{z|x|}$
and
$0<{\textrm{e}}^{zx}\leq {\textrm{e}}^{z|x|}$
and
![]() $0<{\textrm{e}}^{-zx}\leq {\textrm{e}}^{z|x|}$
, it follows that
$0<{\textrm{e}}^{-zx}\leq {\textrm{e}}^{z|x|}$
, it follows that
![]() $\mathbb{E}[{\textrm{e}}^{zX_{0}}]$
,
$\mathbb{E}[{\textrm{e}}^{zX_{0}}]$
,
![]() $\mathbb{E}[{\textrm{e}}^{-zX_{0}}]$
,
$\mathbb{E}[{\textrm{e}}^{-zX_{0}}]$
,
![]() $\mathbb{E}[{\textrm{e}}^{zX_{1}}]$
, and
$\mathbb{E}[{\textrm{e}}^{zX_{1}}]$
, and
![]() $\mathbb{E}[{\textrm{e}}^{-zX_{1}}]$
are all positive and finite. As
$\mathbb{E}[{\textrm{e}}^{-zX_{1}}]$
are all positive and finite. As
![]() $X_{1}=X_{0}+\tilde{g}(X_{0})+\varepsilon_{1}$
with
$X_{1}=X_{0}+\tilde{g}(X_{0})+\varepsilon_{1}$
with
![]() $X_{0}$
and
$X_{0}$
and
![]() $\varepsilon_{1}$
independent,
$\varepsilon_{1}$
independent,
![]() $\mathbb{E}[{\textrm{e}}^{zX_{1}}]=\mathbb{E}[{\textrm{e}}^{zX_{0}}\,{\textrm{e}}^{z\tilde{g}(X_{0})}]\mathbb{E}[{\textrm{e}}^{z\varepsilon_{1}}]$
(due to the non-negativity of the exponential function, this holds whether the expectations involved are finite or equal
$\mathbb{E}[{\textrm{e}}^{zX_{1}}]=\mathbb{E}[{\textrm{e}}^{zX_{0}}\,{\textrm{e}}^{z\tilde{g}(X_{0})}]\mathbb{E}[{\textrm{e}}^{z\varepsilon_{1}}]$
(due to the non-negativity of the exponential function, this holds whether the expectations involved are finite or equal
![]() $+\infty$
). As
$+\infty$
). As
![]() $0<\mathbb{E}[{\textrm{e}}^{zX_{0}}],\mathbb{E}[{\textrm{e}}^{zX_{1}}]<\infty$
and
$0<\mathbb{E}[{\textrm{e}}^{zX_{0}}],\mathbb{E}[{\textrm{e}}^{zX_{1}}]<\infty$
and
![]() $\tilde{g}(X_{0})$
is bounded, this implies that
$\tilde{g}(X_{0})$
is bounded, this implies that
![]() $0<\mathbb{E}[{\textrm{e}}^{z\varepsilon_{1}}]<\infty$
. An analogous argument yields that
$0<\mathbb{E}[{\textrm{e}}^{z\varepsilon_{1}}]<\infty$
. An analogous argument yields that
![]() $0<\mathbb{E}[{\textrm{e}}^{-z\varepsilon_{1}}]<\infty$
. Finally, non-negativity of the random variables involved implies that
$0<\mathbb{E}[{\textrm{e}}^{-z\varepsilon_{1}}]<\infty$
. Finally, non-negativity of the random variables involved implies that
yielding a contradiction.
![]()