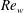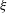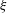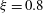1. Introduction
Internal tides are formed in the ocean by the interaction of the barotropic tide with topographic features. As internal tides propagate, they steepen due to nonlinearity and disperse into trains of internal solitary waves. Ultimately, these waves interact with the continental or nearshore slope, where they steepen further and eventually break. Prior to breaking, the dynamics of shoaling internal solitary waves are described well by the weakly nonlinear, weakly dispersive Korteweg–deVries (KdV) equation (Helfrich & Melville Reference Helfrich and Melville2006). In shallow water and during and after breaking, however, KdV theory breaks down and non-analytical methods must be used to describe internal wave dynamics.
Although field observations of shoaling and breaking internal waves have been made in the past (Klymak & Moum Reference Klymak and Moum2003; Scotti & Pineda Reference Scotti and Pineda2004; Shroyer, Moum & Nash Reference Shroyer, Moum and Nash2009; Davis & Monismith Reference Davis and Monismith2011; Nam & Send Reference Nam and Send2011; Walter et al. Reference Walter, Woodson, Arthur, Fringer and Monismith2012, Reference Walter, Woodson, Leary and Monismith2014), these results are limited by the spatial and temporal resolution of field data. For this reason, a wide range of numerical and laboratory studies have explored the breaking process of internal solitary waves on slopes in more idealized domains. These studies have examined shoaling and breaking mechanisms, as well as the formation of upslope surges of dense water that are referred to as bores or boluses (Wallace & Wilkinson Reference Wallace and Wilkinson1988; Helfrich Reference Helfrich1992; Lamb Reference Lamb2002; Vlasenko & Hutter Reference Vlasenko and Hutter2002; Venayagamoorthy & Fringer Reference Venayagamoorthy and Fringer2007). Of particular interest has been a classification of breaking mechanisms across the full parameter space of incoming wave and slope conditions. Boegman, Ivey & Imberger (Reference Boegman, Ivey and Imberger2005) created one such classification using the internal Iribarren number
where
![]() $s$
is the bathymetric slope,
$s$
is the bathymetric slope,
![]() $a$
is the wave amplitude and
$a$
is the wave amplitude and
![]() $L_{w}$
is the solitary wavelength. Aghsaee, Boegman & Lamb (Reference Aghsaee, Boegman and Lamb2010) expanded this classification, defining surging, collapsing, plunging and fission breaker types based on several time scales associated with breaking. Including smaller, more realistic slopes
$L_{w}$
is the solitary wavelength. Aghsaee, Boegman & Lamb (Reference Aghsaee, Boegman and Lamb2010) expanded this classification, defining surging, collapsing, plunging and fission breaker types based on several time scales associated with breaking. Including smaller, more realistic slopes
![]() $s=O(0.01)$
allowed Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010) to capture fission breakers, which were not included in Boegman et al.’s (Reference Boegman, Ivey and Imberger2005) classification. During fission, the rear face of the initial wave separates into a train of solitary waves of elevation that propagate up the slope as boluses. Fission has been observed in the field (Shroyer et al.
Reference Shroyer, Moum and Nash2009) and with a two-dimensional field-scale numerical model (Bourgault et al.
Reference Bourgault, Blokhina, Mirshak and Kelley2007a
).
$s=O(0.01)$
allowed Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010) to capture fission breakers, which were not included in Boegman et al.’s (Reference Boegman, Ivey and Imberger2005) classification. During fission, the rear face of the initial wave separates into a train of solitary waves of elevation that propagate up the slope as boluses. Fission has been observed in the field (Shroyer et al.
Reference Shroyer, Moum and Nash2009) and with a two-dimensional field-scale numerical model (Bourgault et al.
Reference Bourgault, Blokhina, Mirshak and Kelley2007a
).
Much of the interest in internal wave interaction with bottom topography stems from Munk & Wunsch’s (Reference Munk and Wunsch1998) claim that turbulence due to breaking internal waves at boundaries accounts for a significant sink of energy in the ocean. In addition, turbulent mixing caused by breaking internal waves has implications for nearshore distributions of temperature, nutrients, and larvae (Pineda Reference Pineda1994; Leichter et al.
Reference Leichter, Wing, Miller and Denny1996; Omand et al.
Reference Omand, Leichter, Franks, Guza, Lucas and Feddersen2011), as well as sediment transport (Bourgault et al.
Reference Bourgault, Morsilli, Richards, Neumeier and Kelley2014) and dissolved oxygen variability (Walter et al.
Reference Walter, Woodson, Leary and Monismith2014). For these reasons, the mixing associated with breaking internal waves on slopes has also been an active area of research. Several studies have quantified the ‘mixing efficiency’, or the proportion of initial wave energy that contributes to irreversible mixing of the density field. Michallet & Ivey (Reference Michallet and Ivey1999) used laboratory experiments to calculate the mixing efficiency as a function of the ratio between the length scale of the wave and the length scale of the slope. They found that for small values of this ratio (small slopes), breaking is not vigorous and the mixing efficiency is low. For large vales of this ratio (large slopes), the mixing efficiency is again low because most of the incoming energy is reflected off of the slope. The mixing efficiency peaks around 25 % for intermediate values of the ratio, when the most vigorous breaking occurs. Boegman et al. (Reference Boegman, Ivey and Imberger2005) also recast Michallet & Ivey’s (Reference Michallet and Ivey1999) results in terms of the internal Iribarren number, and found that the peak mixing efficiency occurs when
![]() ${\it\xi}\approx 0.8$
, corresponding to plunging breakers. However, Bourgault & Kelley (Reference Bourgault and Kelley2007b
) found that the results of Michallet & Ivey (Reference Michallet and Ivey1999) were likely affected by dissipation due to sidewall friction.
${\it\xi}\approx 0.8$
, corresponding to plunging breakers. However, Bourgault & Kelley (Reference Bourgault and Kelley2007b
) found that the results of Michallet & Ivey (Reference Michallet and Ivey1999) were likely affected by dissipation due to sidewall friction.
Estimates of the mixing efficiency have also been made for other internal wave-breaking mechanisms. Hult, Troy & Koseff (Reference Hult, Troy and Koseff2011) used novel laboratory techniques to measure the mixing efficiency of internal waves interacting with a bathymetric ridge. Specifically, they separated the mixing efficiency into different regions of the flow, including the interface, where breaking occurs, and the lower layer, where flow interacts with the bottom boundary. They found a local mixing efficiency of 10–17 % at the interface, where wave breaking contributes to turbulent mixing, and no mixing in the lower layer, where boundary-induced turbulence exists but has no density gradients to mix. This resulted in an overall mixing efficiency of 4–7 % for the entire domain. Fringer & Street (Reference Fringer and Street2003) used a high-resolution numerical model to calculate the mixing efficiency of breaking internal waves in deep water. Using the formulation of Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995), they found a maximum instantaneous mixing efficiency of
![]() $0.36\pm 0.02$
. Using the formulation of Michallet & Ivey (Reference Michallet and Ivey1999), they found a ‘bulk’ mixing efficiency of
$0.36\pm 0.02$
. Using the formulation of Michallet & Ivey (Reference Michallet and Ivey1999), they found a ‘bulk’ mixing efficiency of
![]() $0.42\pm 0.07$
. Fringer & Street (Reference Fringer and Street2003) also provide a summary of mixing efficiency values from previous studies in their table 1. In addition, Fringer & Street (Reference Fringer and Street2003) examined the dynamics of the breaking process, and found that progressive internal waves break due to an initial two-dimensional instability (either Kelvin–Helmholtz billows or Rayleigh–Taylor instability) that is uniform in the lateral (cross-stream) direction. These initial instabilities create unstable stratification that leads to a secondary convective instability in the lateral direction. This secondary instability manifests itself in the form of streamwise vorticity, or ‘longitudinal rolls’ that significantly affect dissipation and mixing in the domain.
$0.42\pm 0.07$
. Fringer & Street (Reference Fringer and Street2003) also provide a summary of mixing efficiency values from previous studies in their table 1. In addition, Fringer & Street (Reference Fringer and Street2003) examined the dynamics of the breaking process, and found that progressive internal waves break due to an initial two-dimensional instability (either Kelvin–Helmholtz billows or Rayleigh–Taylor instability) that is uniform in the lateral (cross-stream) direction. These initial instabilities create unstable stratification that leads to a secondary convective instability in the lateral direction. This secondary instability manifests itself in the form of streamwise vorticity, or ‘longitudinal rolls’ that significantly affect dissipation and mixing in the domain.
Numerical modelling has been used extensively to study shoaling and breaking internal waves on slopes both at the field (Lamb Reference Lamb2002; Bourgault et al. Reference Bourgault, Blokhina, Mirshak and Kelley2007a ; Vlasenko & Stashchuk Reference Vlasenko and Stashchuk2007; Walter et al. Reference Walter, Woodson, Arthur, Fringer and Monismith2012) and laboratory (Vlasenko & Hutter Reference Vlasenko and Hutter2002; Venayagamoorthy & Fringer Reference Venayagamoorthy and Fringer2007; Aghsaee et al. Reference Aghsaee, Boegman and Lamb2010) scales. While field-scale models are able of capturing realistic wave and slope conditions, they fail to resolve the small-scale processes associated with breaking. Conversely, laboratory-scale models begin to resolve breaking processes but fail to capture realistic wave and slope conditions. Several high-resolution three-dimensional modelling studies have examined turbulence and mixing during internal wave generation and breaking on critical slopes. These include the direct numerical simulations (DNS) of Gayen & Sarkar (Reference Gayen and Sarkar2010) and the large-eddy simulations (LES) of Gayen & Sarkar (Reference Gayen and Sarkar2011). However, most previous modelling studies of breaking internal waves on slopes have used two-dimensional domains that suppress the three-dimensional variability of the breaking process seen in these studies and in Fringer & Street (Reference Fringer and Street2003), thus preventing the accurate calculation of breaking energetics.
The present study uses DNS to examine the dynamics of breaking internal solitary waves on slopes. We capture the three-dimensional structure of wave–slope interaction and breaking, and examine the effects of this structure on dissipation and mixing. Section 2 introduces the governing equations and computational setup, while § 3 describes the general structure and energetics of breaking. We examine the three-dimensional flow features induced by breaking and their effects on wave structure and energetics in § 4. The effects of initial wave amplitude and bathymetric slope are discussed in § 5. Finally, we discuss the geophysical application of our results in § 6.
2. Governing equations and computational set-up
We solve the Navier–Stokes equations with the Boussinesq approximation given by

Figure 1. The domain used to study breaking internal waves on slopes. (a) The initial stratification, where
![]() ${\it\rho}_{1}=985\ \text{kg}\ \text{m}^{-3}$
,
${\it\rho}_{1}=985\ \text{kg}\ \text{m}^{-3}$
,
![]() ${\it\rho}_{2}=1015\ \text{kg}\ \text{m}^{-3}$
and
${\it\rho}_{2}=1015\ \text{kg}\ \text{m}^{-3}$
and
![]() ${\it\delta}=2\ \text{cm}$
. The parameters
${\it\delta}=2\ \text{cm}$
. The parameters
![]() $a_{0}$
,
$a_{0}$
,
![]() $L_{w}$
,
$L_{w}$
,
![]() $h_{1}$
, and
$h_{1}$
, and
![]() $h_{2}$
are shown in table 1. (b) The physical dimensions of the domain and a coarse example of the orthogonal curvilinear grid (without vertical stretching). Here,
$h_{2}$
are shown in table 1. (b) The physical dimensions of the domain and a coarse example of the orthogonal curvilinear grid (without vertical stretching). Here,
![]() $L_{s}=1.675\ \text{m}$
and the lateral (
$L_{s}=1.675\ \text{m}$
and the lateral (
![]() $x_{2}$
, into the page) width of the domain is
$x_{2}$
, into the page) width of the domain is
![]() $W=0.1\ \text{m}$
. The parameters
$W=0.1\ \text{m}$
. The parameters
![]() $L$
,
$L$
,
![]() $H$
, and
$H$
, and
![]() $s$
are shown in table 1. The radius of curvature of the rounded bottom at the beginning of the slope is 3 m.
$s$
are shown in table 1. The radius of curvature of the rounded bottom at the beginning of the slope is 3 m.
For all simulations, the initial stratification is given by
where the reference density
![]() ${\it\rho}_{0}=1000\ \text{kg}\ \text{m}^{-3}$
, the density difference between the top and bottom layer
${\it\rho}_{0}=1000\ \text{kg}\ \text{m}^{-3}$
, the density difference between the top and bottom layer
![]() ${\rm\Delta}{\it\rho}={\it\rho}_{2}-{\it\rho}_{1}=30\ \text{kg}\ \text{m}^{-3}$
, the upper layer depth
${\rm\Delta}{\it\rho}={\it\rho}_{2}-{\it\rho}_{1}=30\ \text{kg}\ \text{m}^{-3}$
, the upper layer depth
![]() $h_{1}=0.3\ \text{m}$
, the interface thickness
$h_{1}=0.3\ \text{m}$
, the interface thickness
![]() ${\it\delta}=2\ \text{cm}$
and
${\it\delta}=2\ \text{cm}$
and
![]() ${\it\alpha}=0.99$
. A solitary wave of depression is created in the domain by initializing the interface with a half-Gaussian at the left boundary (e.g. Fringer Reference Fringer2003; Bourgault et al.
Reference Bourgault, Blokhina, Mirshak and Kelley2007a
). This interface
${\it\alpha}=0.99$
. A solitary wave of depression is created in the domain by initializing the interface with a half-Gaussian at the left boundary (e.g. Fringer Reference Fringer2003; Bourgault et al.
Reference Bourgault, Blokhina, Mirshak and Kelley2007a
). This interface
![]() ${\it\zeta}$
is given by
${\it\zeta}$
is given by
where
![]() $a_{0}$
and
$a_{0}$
and
![]() $L_{0}$
are the initial amplitude and length scale of the half-Gaussian, respectively. An initial perturbation
$L_{0}$
are the initial amplitude and length scale of the half-Gaussian, respectively. An initial perturbation
![]() ${\it\zeta}^{\prime }R$
, where
${\it\zeta}^{\prime }R$
, where
![]() ${\it\zeta}^{\prime }=1\ \text{mm}$
and
${\it\zeta}^{\prime }=1\ \text{mm}$
and
![]() $R\in \{-1,1\}$
is a uniformly distributed random number, is also added to the interface to trigger lateral instabilities during breaking.
$R\in \{-1,1\}$
is a uniformly distributed random number, is also added to the interface to trigger lateral instabilities during breaking.
Seven wave cases are considered here, and summarized in table 1. Following Troy & Koseff (Reference Troy and Koseff2005), we classify each case in terms of the wave Reynolds number
![]() $\mathit{Re}_{w}=a^{2}{\it\omega}_{0}/{\it\nu}$
, where
$\mathit{Re}_{w}=a^{2}{\it\omega}_{0}/{\it\nu}$
, where
![]() $a$
is the amplitude of the initial solitary wave after it has formed, and was found to be approximately
$a$
is the amplitude of the initial solitary wave after it has formed, and was found to be approximately
![]() $a_{0}/2$
. The wave frequency
$a_{0}/2$
. The wave frequency
![]() ${\it\omega}_{0}$
is estimated as
${\it\omega}_{0}$
is estimated as
![]() $c_{0}/{\it\lambda}$
, where
$c_{0}/{\it\lambda}$
, where
![]() $c_{0}=\sqrt{g^{\prime }h_{1}h_{2}/H}$
is the linear phase speed of an internal wave in a two-layer fluid (
$c_{0}=\sqrt{g^{\prime }h_{1}h_{2}/H}$
is the linear phase speed of an internal wave in a two-layer fluid (
![]() $g^{\prime }=g{\rm\Delta}{\it\rho}/{\it\rho}_{0}$
is the reduced gravity) and
$g^{\prime }=g{\rm\Delta}{\it\rho}/{\it\rho}_{0}$
is the reduced gravity) and
![]() ${\it\lambda}\approx 2L_{w}$
is the wavelength. The solitary wavelength
${\it\lambda}\approx 2L_{w}$
is the wavelength. The solitary wavelength
![]() $L_{w}$
is calculated as (Michallet & Ivey Reference Michallet and Ivey1999)
$L_{w}$
is calculated as (Michallet & Ivey Reference Michallet and Ivey1999)
where
![]() ${\it\eta}$
is the displacement of the
${\it\eta}$
is the displacement of the
![]() ${\it\rho}={\it\rho}_{0}$
isopycnal from
${\it\rho}={\it\rho}_{0}$
isopycnal from
![]() $h_{1}$
. Here,
$h_{1}$
. Here,
![]() $L_{w}$
was found to be approximately 1.2 m for all cases. Case 3 is considered the base case with
$L_{w}$
was found to be approximately 1.2 m for all cases. Case 3 is considered the base case with
![]() ${\it\nu}=10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
and
${\it\nu}=10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
and
![]() $\mathit{Re}_{w}=208$
. To facilitate direct comparison of dissipation and mixing between cases,
$\mathit{Re}_{w}=208$
. To facilitate direct comparison of dissipation and mixing between cases,
![]() ${\it\nu}$
is changed relative to the base case in order to maintain a constant
${\it\nu}$
is changed relative to the base case in order to maintain a constant
![]() $\mathit{Re}_{w}$
. The wave Reynolds number is proportional to
$\mathit{Re}_{w}$
. The wave Reynolds number is proportional to
![]() $(a/{\it\delta}_{S})^{2}$
, where
$(a/{\it\delta}_{S})^{2}$
, where
![]() ${\it\delta}_{S}=\sqrt{2{\it\nu}/{\it\omega}_{0}}$
is the Stokes’ boundary-layer thickness. Thus, we maintain a constant initial wave amplitude to Stokes’ boundary-layer thickness ratio for each case. For all cases, the Prandtl number
${\it\delta}_{S}=\sqrt{2{\it\nu}/{\it\omega}_{0}}$
is the Stokes’ boundary-layer thickness. Thus, we maintain a constant initial wave amplitude to Stokes’ boundary-layer thickness ratio for each case. For all cases, the Prandtl number
![]() $\mathit{Pr}=1$
such that
$\mathit{Pr}=1$
such that
![]() ${\it\kappa}={\it\nu}$
. Following Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010), we also calculate the internal Iribarren number
${\it\kappa}={\it\nu}$
. Following Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010), we also calculate the internal Iribarren number
![]() ${\it\xi}$
for each case and classify the breaker type, as shown in table 1.
${\it\xi}$
for each case and classify the breaker type, as shown in table 1.
Table 1. The solitary wave cases considered in this study in terms of the domain length
![]() $L$
, the domain height
$L$
, the domain height
![]() $H$
, the upper-layer depth
$H$
, the upper-layer depth
![]() $h_{1}$
, the lower-layer depth
$h_{1}$
, the lower-layer depth
![]() $h_{2}$
, the amplitude of the initial half-Gaussian
$h_{2}$
, the amplitude of the initial half-Gaussian
![]() $a_{0}$
, the length scale of the initial half-Gaussian
$a_{0}$
, the length scale of the initial half-Gaussian
![]() $L_{0}$
, the bottom slope
$L_{0}$
, the bottom slope
![]() $s$
, the kinematic viscosity
$s$
, the kinematic viscosity
![]() ${\it\nu}$
, the Stokes’ boundary-layer thickness
${\it\nu}$
, the Stokes’ boundary-layer thickness
![]() ${\it\delta}_{S}$
, the internal Iribarren number
${\it\delta}_{S}$
, the internal Iribarren number
![]() ${\it\xi}$
and the breaker type (S
${\it\xi}$
and the breaker type (S
![]() $=$
surging, C
$=$
surging, C
![]() $=$
collapsing, P
$=$
collapsing, P
![]() $=$
plunging, F
$=$
plunging, F
![]() $=$
fission).
$=$
fission).

The boundary conditions for all velocity components are no-slip on the bottom wall and free-slip on the top, left and right walls. The density field has a gradient-free boundary condition on the top, bottom, left and right walls. All variables are periodic in the lateral (
![]() $x_{2}$
) direction. Each simulation was run on an orthogonal curvilinear grid generated using the open-source software gridgen (available online at https://code.google.com/p/gridgen-c/). Cases 1, 3, 4 and 5 were computed on a grid of size
$x_{2}$
) direction. Each simulation was run on an orthogonal curvilinear grid generated using the open-source software gridgen (available online at https://code.google.com/p/gridgen-c/). Cases 1, 3, 4 and 5 were computed on a grid of size
![]() $N_{1}\times N_{2}\times N_{3}=1152\times 96\times 128\approx 14\times 10^{6}$
points. To account for different length domains,
$N_{1}\times N_{2}\times N_{3}=1152\times 96\times 128\approx 14\times 10^{6}$
points. To account for different length domains,
![]() $N_{1}=1024$
for case 2 (
$N_{1}=1024$
for case 2 (
![]() ${\approx}13\times 10^{6}$
points),
${\approx}13\times 10^{6}$
points),
![]() $N_{1}=1408$
for case 6 (
$N_{1}=1408$
for case 6 (
![]() ${\approx}17\times 10^{6}$
points) and
${\approx}17\times 10^{6}$
points) and
![]() $N_{1}=2048$
for case 7 (
$N_{1}=2048$
for case 7 (
![]() ${\approx}25\times 10^{6}$
points). Grid stretching of the form
${\approx}25\times 10^{6}$
points). Grid stretching of the form
![]() ${\rm\Delta}x_{i}^{k}=r{\rm\Delta}x_{i}^{k+1}$
, where
${\rm\Delta}x_{i}^{k}=r{\rm\Delta}x_{i}^{k+1}$
, where
![]() $r$
is the stretching factor and
$r$
is the stretching factor and
![]() $k$
is the index of the grid point, is employed in the horizontal (
$k$
is the index of the grid point, is employed in the horizontal (
![]() $x_{1}$
) and vertical (
$x_{1}$
) and vertical (
![]() $x_{3}$
) directions to increase resolution in the breaking region. Grid spacing in the lateral (
$x_{3}$
) directions to increase resolution in the breaking region. Grid spacing in the lateral (
![]() $x_{2}$
) direction is constant. In the horizontal direction, stretching is applied from
$x_{2}$
) direction is constant. In the horizontal direction, stretching is applied from
![]() $x_{1}=0$
to
$x_{1}=0$
to
![]() $L_{s}$
with
$L_{s}$
with
![]() $r=1.01$
, concentrating
$r=1.01$
, concentrating
![]() $N_{1}-128$
points (approximately 90 %) into the sloping region. The grid is also stretched slightly in
$N_{1}-128$
points (approximately 90 %) into the sloping region. The grid is also stretched slightly in
![]() $x_{1}$
in the sloping region to maintain orthogonality. In the vertical direction, stretching is performed twice. First, grid points are concentrated toward the bottom with
$x_{1}$
in the sloping region to maintain orthogonality. In the vertical direction, stretching is performed twice. First, grid points are concentrated toward the bottom with
![]() $r=1.02$
in order to resolve the flow near the wall. Second, 100 of 128 points (78 %) are concentrated in the bottom 35 % of the domain with
$r=1.02$
in order to resolve the flow near the wall. Second, 100 of 128 points (78 %) are concentrated in the bottom 35 % of the domain with
![]() $r=1.07$
in order to resolve the interface and lower layer during breaking. The resulting grid resolution at the interface in the breaking region is approximately
$r=1.07$
in order to resolve the interface and lower layer during breaking. The resulting grid resolution at the interface in the breaking region is approximately
![]() ${\rm\Delta}x_{1}\times {\rm\Delta}x_{2}\times {\rm\Delta}x_{3}=4\ \text{mm}\times 1\ \text{mm}\times 2\ \text{mm}$
. Near the bottom wall, the vertical coordinate is measured in wall units
${\rm\Delta}x_{1}\times {\rm\Delta}x_{2}\times {\rm\Delta}x_{3}=4\ \text{mm}\times 1\ \text{mm}\times 2\ \text{mm}$
. Near the bottom wall, the vertical coordinate is measured in wall units
![]() $x_{3}^{+}=x_{3}/{\it\delta}_{S}$
. The vertical resolution near the wall is therefore
$x_{3}^{+}=x_{3}/{\it\delta}_{S}$
. The vertical resolution near the wall is therefore
![]() ${\rm\Delta}x_{3}^{+}={\rm\Delta}x_{3}/{\it\delta}_{S}<1$
. In the worst-case scenario, the grid spacing is found to be within approximately one order of magnitude (a factor of 13) of the Kolmogorov length scale
${\rm\Delta}x_{3}^{+}={\rm\Delta}x_{3}/{\it\delta}_{S}<1$
. In the worst-case scenario, the grid spacing is found to be within approximately one order of magnitude (a factor of 13) of the Kolmogorov length scale
![]() ${\it\eta}_{k}$
(defined in § 4.2). For further discussion of grid resolution, see § 4.2.
${\it\eta}_{k}$
(defined in § 4.2). For further discussion of grid resolution, see § 4.2.
A time step of
![]() ${\rm\Delta}t=0.003\ \text{s}$
was used for all simulations. The number of time steps varied by case, and was 20 000 for cases 1–5, 30 000 for case 6 and 37 000 for case 7. Simulations were run on the US Army Research Lab DoD Supercomputing Research Center (ARL DSRC) supercomputer Harold using 432 processors (cases 1, 3, 4 and 5), 384 processors (case 2), 528 processors (case 6), and 768 processors (case 7). With a computation time of approximately 10 s per time step, this resulted in wall-clock simulation times of 56 h (24 000 CPU hours; cases 1, 3, 4 and 5), 56 h (21 000 CPU hours; case 2), 83 h (44 000 CPU hours; case 6) and 103 h (79 000 CPU hours; case 7).
${\rm\Delta}t=0.003\ \text{s}$
was used for all simulations. The number of time steps varied by case, and was 20 000 for cases 1–5, 30 000 for case 6 and 37 000 for case 7. Simulations were run on the US Army Research Lab DoD Supercomputing Research Center (ARL DSRC) supercomputer Harold using 432 processors (cases 1, 3, 4 and 5), 384 processors (case 2), 528 processors (case 6), and 768 processors (case 7). With a computation time of approximately 10 s per time step, this resulted in wall-clock simulation times of 56 h (24 000 CPU hours; cases 1, 3, 4 and 5), 56 h (21 000 CPU hours; case 2), 83 h (44 000 CPU hours; case 6) and 103 h (79 000 CPU hours; case 7).
3. Physical description of breaking
3.1. Energy definitions
We define the volume-integrated kinetic and potential energy in the domain as
In the absence of boundary fluxes, the background potential energy evolves according to
where
![]() ${\it\phi}_{d}$
is the rate of change of the background potential energy due to irreversible density changes within the domain. The total potential energy evolves according to
${\it\phi}_{d}$
is the rate of change of the background potential energy due to irreversible density changes within the domain. The total potential energy evolves according to
where
![]() ${\it\phi}_{z}=g\!\int _{V}\!{\it\rho}u_{3}\text{d}V$
is the reversible buoyancy flux and
${\it\phi}_{z}=g\!\int _{V}\!{\it\rho}u_{3}\text{d}V$
is the reversible buoyancy flux and
![]() ${\it\phi}_{i}=({\it\kappa}g/{\it\rho}_{0})\!\int _{A}({\it\rho}_{top}-{\it\rho}_{bottom})\text{d}A$
is the irreversible change from internal to potential energy. In the definition of
${\it\phi}_{i}=({\it\kappa}g/{\it\rho}_{0})\!\int _{A}({\it\rho}_{top}-{\it\rho}_{bottom})\text{d}A$
is the irreversible change from internal to potential energy. In the definition of
![]() ${\it\phi}_{i}$
,
${\it\phi}_{i}$
,
![]() ${\it\rho}_{top}$
and
${\it\rho}_{top}$
and
![]() ${\it\rho}_{bottom}$
are the densities on the top and bottom boundaries of the domain, respectively, and
${\it\rho}_{bottom}$
are the densities on the top and bottom boundaries of the domain, respectively, and
![]() $A$
is the corresponding surface area of the boundary. It follows that
$A$
is the corresponding surface area of the boundary. It follows that
From (3.5), it becomes clear that the background potential energy changes only due to molecular diffusion of the density field, or irreversible diapycnal mixing. Reversible changes in the density field are due to ‘stirring’ processes. These changes are available for exchange with the kinetic energy field and are contained in
![]() ${\it\phi}_{z}$
. This exchange can be seen in the evolution equation for the kinetic energy,
${\it\phi}_{z}$
. This exchange can be seen in the evolution equation for the kinetic energy,
where the volume-integrated dissipation is defined as
Finally, the total energy in the domain
![]() $E_{T}$
evolves according to
$E_{T}$
evolves according to
For energy quantities
![]() $E$
and their rates of change
$E$
and their rates of change
![]() $\text{d}E/\text{d}t$
(specifically, those shown in figure 3
a,b respectively), the volume of integration
$\text{d}E/\text{d}t$
(specifically, those shown in figure 3
a,b respectively), the volume of integration
![]() $V$
is chosen as the entire computational domain in order to capture the evolution of the solitary wave over the full simulation. However, for irreversible energy quantities
$V$
is chosen as the entire computational domain in order to capture the evolution of the solitary wave over the full simulation. However, for irreversible energy quantities
![]() ${\it\epsilon},{\it\phi}_{d}$
and
${\it\epsilon},{\it\phi}_{d}$
and
![]() ${\it\phi}_{i}$
,
${\it\phi}_{i}$
,
![]() $V$
is restricted to the sloping region of the domain (
$V$
is restricted to the sloping region of the domain (
![]() $x_{1}>L_{s}$
; see figure 4) to eliminate effects that occur prior to shoaling and breaking. We note that in the calculation of
$x_{1}>L_{s}$
; see figure 4) to eliminate effects that occur prior to shoaling and breaking. We note that in the calculation of
![]() ${\it\phi}_{d}$
, the background density field
${\it\phi}_{d}$
, the background density field
![]() ${\it\rho}(x_{3}^{\ast })$
is still calculated for the entire domain, but only integrated over the sloping region. Thus,
${\it\rho}(x_{3}^{\ast })$
is still calculated for the entire domain, but only integrated over the sloping region. Thus,
![]() ${\it\phi}_{d}$
may be thought of as the contribution of the sloping region to the total irreversible mixing in the domain.
${\it\phi}_{d}$
may be thought of as the contribution of the sloping region to the total irreversible mixing in the domain.
In what follows, we present normalized values of the above energetics quantities. Specifically, energy quantities
![]() $E$
have the initial value
$E$
have the initial value
![]() $E_{0}$
removed and are then normalized by the absolute value of the minimum available potential energy
$E_{0}$
removed and are then normalized by the absolute value of the minimum available potential energy
![]() $|E_{a,min}|$
. Rates of energy change
$|E_{a,min}|$
. Rates of energy change
![]() $\text{d}E/\text{d}t$
are normalized by the absolute value of the minimum rate of change of available potential energy
$\text{d}E/\text{d}t$
are normalized by the absolute value of the minimum rate of change of available potential energy
![]() $|(\text{d}E_{a}/\text{d}t)_{min}|$
. The minimum absolute value is used in both cases because
$|(\text{d}E_{a}/\text{d}t)_{min}|$
. The minimum absolute value is used in both cases because
![]() $E_{a,min}<0$
and
$E_{a,min}<0$
and
![]() $(\text{d}E_{a}/\text{d}t)_{min}<0$
. All other energy flux quantities are normalized by the maximum dissipation
$(\text{d}E_{a}/\text{d}t)_{min}<0$
. All other energy flux quantities are normalized by the maximum dissipation
![]() ${\it\epsilon}_{max}$
for the given case. Time is normalized in all figures by the wave period
${\it\epsilon}_{max}$
for the given case. Time is normalized in all figures by the wave period
![]() $T=2{\rm\pi}/{\it\omega}_{0}\approx 76\ \text{s}$
.
$T=2{\rm\pi}/{\it\omega}_{0}\approx 76\ \text{s}$
.

Figure 2. Snapshots in time of density structure (left column) and velocity structure (right column) for breaking wave case 3. Results are averaged in the lateral (
![]() $x_{2}$
) direction. In the left column, black corresponds to
$x_{2}$
) direction. In the left column, black corresponds to
![]() ${\it\rho}={\it\rho}_{0}+{\rm\Delta}{\it\rho}/2$
and white corresponds to
${\it\rho}={\it\rho}_{0}+{\rm\Delta}{\it\rho}/2$
and white corresponds to
![]() ${\it\rho}={\it\rho}_{0}-{\rm\Delta}{\it\rho}/2$
. The lower layer (
${\it\rho}={\it\rho}_{0}-{\rm\Delta}{\it\rho}/2$
. The lower layer (
![]() ${\it\rho}>{\it\rho}_{0}$
) is shown in grey the right column as well. Dots labelled a–i in figures 3, 5, 14, 15 and 23–25 correspond to the labels shown here.
${\it\rho}>{\it\rho}_{0}$
) is shown in grey the right column as well. Dots labelled a–i in figures 3, 5, 14, 15 and 23–25 correspond to the labels shown here.
3.2. General structure and energetics
We begin with a physical description of the wave-breaking process in terms of density and velocity structure (figure 2) and energetics (figure 3). This description is based on the results of case 3, but is representative of the results for all cases. Initially, a solitary wave of depression forms and propagates toward the slope. As the leading face of the wave moves over the slope, downslope velocities in the lower layer are concentrated in the thin region between the bottom and the interface (figure 2 a). Simultaneously, the rear face of the wave steepens because the upslope velocity under the rear shoulder of the wave is proportional to the local height of the lower layer (figure 2 b). Ultimately, the downslope velocity under the trough and the upslope velocity under the rear face interact, causing the shear that leads to the breaking event (figure 2 c). After breaking, dense water surges up the slope in the form of a bore or bolus (figure 2 d–h). Once this surge reaches its maximum upslope location, it then recedes back down the slope (figure 2 i).

Figure 3. Volume-integrated energy results for breaking wave case 3. (a) Energy quantities
![]() $E_{k}$
,
$E_{k}$
,
![]() $E_{p}$
,
$E_{p}$
,
![]() $E_{b}$
,
$E_{b}$
,
![]() $E_{a}$
and
$E_{a}$
and
![]() $E_{t}$
, all normalized by
$E_{t}$
, all normalized by
![]() $|E_{a,min}|$
. (b) Reversible energy evolution quantities
$|E_{a,min}|$
. (b) Reversible energy evolution quantities
![]() $\text{d}E_{k}/\text{d}t$
and
$\text{d}E_{k}/\text{d}t$
and
![]() $\text{d}E_{a}/\text{d}t$
, both normalized by
$\text{d}E_{a}/\text{d}t$
, both normalized by
![]() $|(\text{d}E_{a}/\text{d}t)_{min}|$
. (c) Irreversible energy evolution quantities
$|(\text{d}E_{a}/\text{d}t)_{min}|$
. (c) Irreversible energy evolution quantities
![]() ${\it\epsilon}$
,
${\it\epsilon}$
,
![]() ${\it\phi}_{d}$
, and
${\it\phi}_{d}$
, and
![]() ${\it\phi}_{i}$
normalized by
${\it\phi}_{i}$
normalized by
![]() ${\it\epsilon}_{max}$
. Dots labelled a–i correspond to time snapshots from figure 2.
${\it\epsilon}_{max}$
. Dots labelled a–i correspond to time snapshots from figure 2.
The energetics of the wave are closely related to its structure. This can be seen in figure 3, where the labelled dots correspond to the snapshots shown in figure 2. Initially, the wave gains kinetic energy at the expense of available potential energy as it forms and propagates toward the slope (figure 3
a, point a). Available potential (kinetic) energy then increases (decreases) as the wave steepens and reaches a maximum (minimum) at the breakpoint (figure 3
a, point b). During the breaking event, kinetic energy again rises at the expense of available potential energy until the upslope surge begins (figure 3
a, points b–d). The upslope surge leads to an increase in available potential energy at the expense of kinetic energy until the dense water reaches its maximum upslope location (figure 3
a, points d–h). Then, the dense water recedes back downslope, gaining kinetic energy at the expense of available potential energy (figure 3
a, points h–i). Throughout the wave propagation and breaking event,
![]() $\text{d}E_{k}/\text{d}t$
and
$\text{d}E_{k}/\text{d}t$
and
![]() $\text{d}E_{a}/\text{d}t$
nearly mirror each other (figure 3
b), owing to the exchange of energy through the reversible buoyancy flux
$\text{d}E_{a}/\text{d}t$
nearly mirror each other (figure 3
b), owing to the exchange of energy through the reversible buoyancy flux
![]() ${\it\phi}_{z}$
.
${\it\phi}_{z}$
.

Figure 4. Regions used for dissipation calculations. Region I is the upper layer, where
![]() ${\it\rho}<{\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2$
. Region II is the interior, where
${\it\rho}<{\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2$
. Region II is the interior, where
![]() ${\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2\leqslant {\it\rho}\leqslant {\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
(the dashed line shows the location of the initial density interface). Region III is the lower layer, where
${\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2\leqslant {\it\rho}\leqslant {\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
(the dashed line shows the location of the initial density interface). Region III is the lower layer, where
![]() ${\it\rho}>{\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. Region IV is the BBL, where
${\it\rho}>{\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. Region IV is the BBL, where
![]() $x_{3}<-d+{\it\delta}_{S}$
in the breaking region and
$x_{3}<-d+{\it\delta}_{S}$
in the breaking region and
![]() $d$
is the local depth of the bottom boundary. The non-sloping region is not included in dissipation calculations. Note that regions are not shown to scale and that the boundaries of regions I, II and III move with the flow while region IV is fixed in time.
$d$
is the local depth of the bottom boundary. The non-sloping region is not included in dissipation calculations. Note that regions are not shown to scale and that the boundaries of regions I, II and III move with the flow while region IV is fixed in time.
Dissipation and irreversible mixing, shown in figure 3(c), result in an imperfect exchange between kinetic and available potential energy. Dissipation
![]() ${\it\epsilon}$
begins as the wave interacts with the slope and is sustained throughout the breaking event, with several peaks. The first peak occurs during the strong downslope flow prior to the breakpoint (figure 3
c, point b). The second peak occurs after breaking as the surge of dense water forms and propagates upslope (figure 3
c, point f). The third peak occurs as dense water from the upslope surge recedes back downslope (figure 3
c, point h). Irreversible mixing occurs throughout the simulation, but is only elevated above the background value after breaking occurs. We therefore define an effective mixing rate
${\it\epsilon}$
begins as the wave interacts with the slope and is sustained throughout the breaking event, with several peaks. The first peak occurs during the strong downslope flow prior to the breakpoint (figure 3
c, point b). The second peak occurs after breaking as the surge of dense water forms and propagates upslope (figure 3
c, point f). The third peak occurs as dense water from the upslope surge recedes back downslope (figure 3
c, point h). Irreversible mixing occurs throughout the simulation, but is only elevated above the background value after breaking occurs. We therefore define an effective mixing rate
as the rate of mixing above the background value.
The effects of dissipation and irreversible mixing are apparent in the background potential energy and total energy profiles (figure 3
a). The background potential energy increases monotonically throughout the simulation, but increases at a faster rate after breaking (after approximately
![]() $t/T=0.25$
) due to elevated mixing. This increase in background potential energy accounts for the separation between the available potential energy and potential energy curves. The total energy in the system initially increases due to background mixing. However, it ultimately decreases as the effect of mixing is overwhelmed by that of dissipation.
$t/T=0.25$
) due to elevated mixing. This increase in background potential energy accounts for the separation between the available potential energy and potential energy curves. The total energy in the system initially increases due to background mixing. However, it ultimately decreases as the effect of mixing is overwhelmed by that of dissipation.

Figure 5. Dissipation breakdown by region and mixing efficiency for breaking wave case 3. (a) Total dissipation
![]() ${\it\epsilon}$
, bottom-boundary dissipation
${\it\epsilon}$
, bottom-boundary dissipation
![]() ${\it\epsilon}_{IV}$
, interior dissipation
${\it\epsilon}_{IV}$
, interior dissipation
![]() ${\it\epsilon}_{II}$
, and effective irreversible mixing
${\it\epsilon}_{II}$
, and effective irreversible mixing
![]() ${\it\phi}_{e}$
as a function of time, all normalized by
${\it\phi}_{e}$
as a function of time, all normalized by
![]() ${\it\epsilon}_{max}$
. (b) The cumulative dissipation in the bottom boundary region
${\it\epsilon}_{max}$
. (b) The cumulative dissipation in the bottom boundary region
![]() ${\it\epsilon}_{cum,IV}$
and in the interior region
${\it\epsilon}_{cum,IV}$
and in the interior region
![]() ${\it\epsilon}_{cum,II}$
. The total cumulative dissipation
${\it\epsilon}_{cum,II}$
. The total cumulative dissipation
![]() ${\it\epsilon}_{cum}$
is shown as well. Values are normalized by
${\it\epsilon}_{cum}$
is shown as well. Values are normalized by
![]() ${\it\epsilon}_{tot}$
. (c) The instantaneous mixing efficiency
${\it\epsilon}_{tot}$
. (c) The instantaneous mixing efficiency
![]() ${\it\eta}$
and bulk mixing efficiency
${\it\eta}$
and bulk mixing efficiency
![]() ${\it\eta}_{B}$
. Dots labelled a–i correspond to time snapshots from figure 2.
${\it\eta}_{B}$
. Dots labelled a–i correspond to time snapshots from figure 2.
3.3. Interior and bottom boundary energetics
In order to understand the sources of dissipation in the domain, we separate the total dissipation
![]() ${\it\epsilon}$
into four regions, as shown in figure 4. Therefore,
${\it\epsilon}$
into four regions, as shown in figure 4. Therefore,
where
![]() ${\it\epsilon}_{I}$
is the dissipation in the upper layer,
${\it\epsilon}_{I}$
is the dissipation in the upper layer,
![]() ${\it\epsilon}_{II}$
is the dissipation in the interior,
${\it\epsilon}_{II}$
is the dissipation in the interior,
![]() ${\it\epsilon}_{III}$
is the dissipation in the lower layer and
${\it\epsilon}_{III}$
is the dissipation in the lower layer and
![]() ${\it\epsilon}_{IV}$
is the dissipation in the bottom boundary layer (BBL). The upper layer (region I) is defined as the region above the density interface where
${\it\epsilon}_{IV}$
is the dissipation in the bottom boundary layer (BBL). The upper layer (region I) is defined as the region above the density interface where
![]() ${\it\rho}<{\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2$
, and the lower layer (region III) is defined as the region below the density interface where
${\it\rho}<{\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2$
, and the lower layer (region III) is defined as the region below the density interface where
![]() ${\it\rho}>{\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. The interior (region II) is defined as the region around the density interface where
${\it\rho}>{\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. The interior (region II) is defined as the region around the density interface where
![]() ${\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2\leqslant {\it\rho}\leqslant {\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. The bottom boundary region (region IV) is defined as a fixed number of grid cells above the bottom wall. This number was chosen such that
${\it\rho}_{0}-0.99{\rm\Delta}{\it\rho}/2\leqslant {\it\rho}\leqslant {\it\rho}_{0}+0.99{\rm\Delta}{\it\rho}/2$
. The bottom boundary region (region IV) is defined as a fixed number of grid cells above the bottom wall. This number was chosen such that
![]() $x_{3}<-d+{\it\delta}_{S}$
in the breaking region, where
$x_{3}<-d+{\it\delta}_{S}$
in the breaking region, where
![]() $d$
is the local depth of the bottom boundary. Figure 5 shows the dissipation in these regions, both instantaneously (figure 5
a) and cumulatively (figure 5
b). The cumulative dissipation, or the total energy lost to dissipation up to time
$d$
is the local depth of the bottom boundary. Figure 5 shows the dissipation in these regions, both instantaneously (figure 5
a) and cumulatively (figure 5
b). The cumulative dissipation, or the total energy lost to dissipation up to time
![]() $t$
, is defined as
$t$
, is defined as
where
![]() $R$
is the region. The total energy lost to dissipation over the course of the simulation is therefore
$R$
is the region. The total energy lost to dissipation over the course of the simulation is therefore
The dissipation in the upper and lower layer regions are not shown in figure 5 because they contribute negligibly to the total dissipation.
The first and third peaks in the total dissipation in figure 5(a) correspond to peaks in the bottom-boundary dissipation. As discussed in § 3.2, these peaks are associated with the strong downslope flow of dense water in a thin region between the interface and the bottom (figure 5 a, points b and h, respectively). The second peak in the total dissipation corresponds to the peak in interior dissipation as well as the peak in irreversible mixing. These peaks occur after breaking when dense water surges upslope, suggesting that they are due to the billows that form at the interface during this time (figure 5 a, points d–g). The third peak in total dissipation also corresponds with a smaller peak in interior dissipation and slightly elevated mixing (figure 5 a, points h,i). This is associated with the interaction of the downslope flow of dense water from the initial surge interacting with upslope flow under the next wave crest (figure 2 h,i). Cumulatively, dissipation at the bottom boundary accounts for roughly 67 % of the total dissipation in the domain, while dissipation in the interior accounts for roughly 33 % for case 3. Furthermore, the relative contribution of interior dissipation to total dissipation increases after the breakpoint (figure 5 b, point b).
We do not separate irreversible mixing into the regions shown in figure 4 because
![]() ${\it\phi}_{d}$
is defined as a volume-integrated quantity. Although
${\it\phi}_{d}$
is defined as a volume-integrated quantity. Although
![]() $\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{j}\partial x_{j}$
in (3.5) can be positive or negative,
$\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{j}\partial x_{j}$
in (3.5) can be positive or negative,
![]() ${\it\phi}_{d}$
is guaranteed to be positive (Winters et al.
Reference Winters, Lombard, Riley and D’Asaro1995). Breaking up the vertical portion
${\it\phi}_{d}$
is guaranteed to be positive (Winters et al.
Reference Winters, Lombard, Riley and D’Asaro1995). Breaking up the vertical portion
![]() $\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{3}^{2}$
of
$\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{3}^{2}$
of
![]() $\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{j}\partial x_{j}$
, however, allows
$\partial ^{2}{\it\rho}(x_{3}^{\ast })/\partial x_{j}\partial x_{j}$
, however, allows
![]() ${\it\phi}_{d}$
to be negative because density gradients may be arbitrarily cut off by region boundaries. Horizontal separation of the domain into the sloping region (where energetics are calculated) and non-sloping region is allowable in this case because horizontal gradients are negligibly affected by this cutoff. In fact, the value of
${\it\phi}_{d}$
to be negative because density gradients may be arbitrarily cut off by region boundaries. Horizontal separation of the domain into the sloping region (where energetics are calculated) and non-sloping region is allowable in this case because horizontal gradients are negligibly affected by this cutoff. In fact, the value of
![]() ${\it\phi}_{d}$
calculated when integrating over both the sloping and non-sloping regions (not shown) is essentially the same as
${\it\phi}_{d}$
calculated when integrating over both the sloping and non-sloping regions (not shown) is essentially the same as
![]() ${\it\phi}_{d}$
calculated over the sloping region alone. Separating irreversible mixing into the regions in figure 4 using the current method would require sorting the density field separately in each region. Alternatively, Scotti & White (Reference Scotti and White2014) provide a local measure of mixing, based on a local definition of the available potential energy, that would allow for isolated calculations of mixing in arbitrary regions. A full analysis using this method is a topic of future work.
${\it\phi}_{d}$
calculated over the sloping region alone. Separating irreversible mixing into the regions in figure 4 using the current method would require sorting the density field separately in each region. Alternatively, Scotti & White (Reference Scotti and White2014) provide a local measure of mixing, based on a local definition of the available potential energy, that would allow for isolated calculations of mixing in arbitrary regions. A full analysis using this method is a topic of future work.
3.4. Mixing efficiency
There are two major energy pathways for a breaking internal wave, both of which result in irreversible energy loss. The initial energy of the wave is either (i) exchanged between kinetic energy and available potential energy and ultimately lost to dissipation, or (ii) converted to background potential energy through diffusion of the density field. Dissipation and irreversible mixing, therefore, act as the only possible sinks of initial wave energy. The mixing efficiency measures their relative magnitudes. Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) define the instantaneous mixing efficiency as the instantaneous fraction of irreversible energy exchange that goes into mixing of the density field. Here, we calculate this quantity as
Similarly to Michallet & Ivey (Reference Michallet and Ivey1999) and Fringer & Street (Reference Fringer and Street2003), we also account for the cumulative effects of dissipation and mixing by calculating the bulk mixing efficiency
 $$\begin{eqnarray}{\it\eta}_{B}=\frac{\displaystyle \int _{0}^{t_{max}}{\it\phi}_{e}\text{d}t}{\displaystyle \int _{0}^{t_{max}}({\it\phi}_{e}+{\it\epsilon})\text{d}t}=\frac{{\it\phi}_{e,tot}}{{\it\phi}_{e,tot}+{\it\epsilon}_{tot}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}_{B}=\frac{\displaystyle \int _{0}^{t_{max}}{\it\phi}_{e}\text{d}t}{\displaystyle \int _{0}^{t_{max}}({\it\phi}_{e}+{\it\epsilon})\text{d}t}=\frac{{\it\phi}_{e,tot}}{{\it\phi}_{e,tot}+{\it\epsilon}_{tot}},\end{eqnarray}$$
where
![]() ${\it\phi}_{e,tot}$
is defined in the same way as
${\it\phi}_{e,tot}$
is defined in the same way as
![]() ${\it\epsilon}_{tot}$
in (3.14).
${\it\epsilon}_{tot}$
in (3.14).
The mixing efficiency results for case 3 are shown in figure 5(c). The instantaneous mixing efficiency decreases prior to breaking (figure 5 c, point a) and reaches a minimum at the breakpoint (figure 5 c, point b). This decrease corresponds to the first peak in dissipation that is caused by strong downslope flow under the leading edge of the wave. The instantaneous mixing efficiency then begins to increase after breaking, and reaches its peak of 0.31 during the upslope surge of dense water (figure 5 c, points c–g). This corresponds to the increase and peak in irreversible mixing. As the dense water reaches its maximum upslope location and begins to recede (figure 5 c, points h–i), the instantaneous mixing efficiency decreases again and levels out around the bulk value of 0.14. This decrease corresponds to the third peak in dissipation that is caused by downslope flow of dense water near the bottom. Note that we are not concerned with the instantaneous mixing efficiency near the beginning of the simulation, when a lack of dissipation causes its value to approach unity. This phenomenon was also observed by Smyth & Winters (Reference Smyth and Winters2003) during the preturbulent phase of breaking Holmboe waves and Kelvin–Helmholtz instabilities.
We acknowledge that the domain-integrated definitions of the mixing efficiency used here combine a variety of dissipation and mixing mechanisms, such as boundary-layer and free shear flow, into one value. In addition, our definitions fail to separate the mean and turbulent components of dissipation and mixing, which undoubtedly contribute to the bulk mixing efficiency in differing amounts. A local definition of mixing efficiency, such as that provided by Scotti & White (Reference Scotti and White2014), would allow for this separation. However, we choose to use the domain-integrated definition here in order to facilitate comparison with previous work, such as that of Fringer & Street (Reference Fringer and Street2003), and particularly Michallet & Ivey (Reference Michallet and Ivey1999) and Boegman et al. (Reference Boegman, Ivey and Imberger2005) (see § 5.2).
4. Three-dimensional dynamics
4.1. Lateral variability
Internal wave breaking introduces three-dimensionality to the flow field. This three-dimensionality manifests itself in the form of lateral (cross-stream) variability, and is an important component of the structure and energetics discussed above (Fringer & Street Reference Fringer and Street2003). Figure 6 depicts the three-dimensional evolution of the flow over the course of a breaking event, displaying isosurfaces of density (
![]() ${\it\rho}={\it\rho}_{0}$
) and longitudinal vorticity
${\it\rho}={\it\rho}_{0}$
) and longitudinal vorticity
![]() ${\it\omega}_{1}$
. The density structure is initially two-dimensional (figure 6
a), and remains two-dimensional until after breaking has occurred (figure 6
b,c). Lateral variability is then evident at two distinct locations within the domain: (i) in the interior within a density overturn and (ii) near the bottom at the ‘nose’ of the upslope surge (figure 6
d,e). Although they appear in different locations, both of these instabilities occur in regions of unstable stratification. A more detailed view of this lateral variability is shown in figure 7.
${\it\omega}_{1}$
. The density structure is initially two-dimensional (figure 6
a), and remains two-dimensional until after breaking has occurred (figure 6
b,c). Lateral variability is then evident at two distinct locations within the domain: (i) in the interior within a density overturn and (ii) near the bottom at the ‘nose’ of the upslope surge (figure 6
d,e). Although they appear in different locations, both of these instabilities occur in regions of unstable stratification. A more detailed view of this lateral variability is shown in figure 7.

Figure 6. Snapshots in time of the three-dimensional structure of breaking wave case 3. Isosurfaces of
![]() ${\it\rho}={\it\rho}_{0}$
(red),
${\it\rho}={\it\rho}_{0}$
(red),
![]() ${\it\omega}_{1}/{\it\omega}_{0}=27$
(blue), and
${\it\omega}_{1}/{\it\omega}_{0}=27$
(blue), and
![]() ${\it\omega}_{1}/{\it\omega}_{0}=-27$
(green) are shown. Blue and green isosurfaces of streamwise vorticity
${\it\omega}_{1}/{\it\omega}_{0}=-27$
(green) are shown. Blue and green isosurfaces of streamwise vorticity
![]() ${\it\omega}_{1}/{\it\omega}_{0}$
represent longitudinal rolls. Labels (a–i) correspond to the same times as in figure 2.
${\it\omega}_{1}/{\it\omega}_{0}$
represent longitudinal rolls. Labels (a–i) correspond to the same times as in figure 2.

Figure 7. A zoomed-in view of figure 6(e) showing the development of lateral variability during breaking.

Figure 8. A zoomed-in view of figure 6(g) showing vortex interaction during the upslope surge.
In the interior, strong shear at the interface leads to billows that are initially two-dimensional. However, since the billows create unstable stratification, they are susceptible to cross-stream convective instability. Specifically, dense fluid sinks and less-dense fluid rises, creating cross-stream plumes within the billow. These plumes generate streamwise vorticity
![]() ${\it\omega}_{1}$
, as illustrated in figure 9(a), which shows an
${\it\omega}_{1}$
, as illustrated in figure 9(a), which shows an
![]() $x_{2}{-}x_{3}$
slice through the billow in figures 6(e) and 7 (see figure 13
e for the location of the slice). This mechanism of streamwise vorticity generation is the same as that discussed by Fringer & Street (Reference Fringer and Street2003) for breaking internal waves in deep water and Winters & D’Asaro (Reference Winters and D’Asaro1994) and Dörnbrack (Reference Dörnbrack1998) for critical layers. Unstable stratification is also created at the bottom boundary by the no-slip condition; the dense nose of the upslope surge is raised above the bottom, allowing less dense water to flow underneath. Again, cross-stream plumes develop as dense fluid sinks and less dense fluid rises, generating streamwise vorticity
$x_{2}{-}x_{3}$
slice through the billow in figures 6(e) and 7 (see figure 13
e for the location of the slice). This mechanism of streamwise vorticity generation is the same as that discussed by Fringer & Street (Reference Fringer and Street2003) for breaking internal waves in deep water and Winters & D’Asaro (Reference Winters and D’Asaro1994) and Dörnbrack (Reference Dörnbrack1998) for critical layers. Unstable stratification is also created at the bottom boundary by the no-slip condition; the dense nose of the upslope surge is raised above the bottom, allowing less dense water to flow underneath. Again, cross-stream plumes develop as dense fluid sinks and less dense fluid rises, generating streamwise vorticity
![]() ${\it\omega}_{1}$
. Figure 9(b) depicts these plumes in an
${\it\omega}_{1}$
. Figure 9(b) depicts these plumes in an
![]() $x_{2}{-}x_{3}$
slice through the nose of the upslope surge in figures 6(e) and 7 (see figure 13
e for the location of the slice). The plumes are visible in three dimensions as ‘lobes and clefts’, an instability that is typical of gravity currents and was first studied by Simpson (Reference Simpson1972). More recently, Härtel, Carlsson & Thunblom (Reference Härtel, Carlsson and Thunblom2000) used a linear-stability analysis to examine the lobe and cleft instability mechanism and predict the wavelength of the most unstable mode. Following Fringer & Street (Reference Fringer and Street2003), we will refer to the streamwise vortex tubes created by cross-stream instabilities as longitudinal rolls.
$x_{2}{-}x_{3}$
slice through the nose of the upslope surge in figures 6(e) and 7 (see figure 13
e for the location of the slice). The plumes are visible in three dimensions as ‘lobes and clefts’, an instability that is typical of gravity currents and was first studied by Simpson (Reference Simpson1972). More recently, Härtel, Carlsson & Thunblom (Reference Härtel, Carlsson and Thunblom2000) used a linear-stability analysis to examine the lobe and cleft instability mechanism and predict the wavelength of the most unstable mode. Following Fringer & Street (Reference Fringer and Street2003), we will refer to the streamwise vortex tubes created by cross-stream instabilities as longitudinal rolls.
Ultimately, the longitudinal rolls from both sources interact. As the upslope surge continues, more longitudinal rolls develop within billows at the interface, and are stretched and tilted by the mean (laterally-averaged) flow. The rolls under the nose experience similar stretching and tilting until vortices from the two sources interact (figure 6
f,g). This interaction, of which a more detailed view is shown in figure 8, is indicative of turbulence and corresponds to elevated interior dissipation and mixing in the domain (figure 5, points f–g). As the upslope surge continues, the longitudinal rolls are dissipated (figure 6
h,i). The growth and decay of turbulence is shown in figure 10, which depicts the
![]() $x_{2}{-}x_{3}$
slice shown in figure 9(b) over time. The strongest turbulence is seen in figure 10(g), after which the turbulence decays (figure 10
i,j). Note that more lateral variability is generated as the downslope flow of dense water from the initial surge interacts with upslope flow under the next wave crest (figure 6
h). This corresponds to the second, smaller peak in interior dissipation and mixing in figure 5(a), but is not seen in the slice shown in figure 10.
$x_{2}{-}x_{3}$
slice shown in figure 9(b) over time. The strongest turbulence is seen in figure 10(g), after which the turbulence decays (figure 10
i,j). Note that more lateral variability is generated as the downslope flow of dense water from the initial surge interacts with upslope flow under the next wave crest (figure 6
h). This corresponds to the second, smaller peak in interior dissipation and mixing in figure 5(a), but is not seen in the slice shown in figure 10.

Figure 9. An
![]() $x_{2}{-}x_{3}$
slice through the billow (a) and nose of the upslope surge (b) in figure 6(e). Slice locations are shown in figure 13(e) by sections
$x_{2}{-}x_{3}$
slice through the billow (a) and nose of the upslope surge (b) in figure 6(e). Slice locations are shown in figure 13(e) by sections
![]() $E_{1}{-}E_{1}^{\prime }$
and
$E_{1}{-}E_{1}^{\prime }$
and
![]() $E_{2}{-}E_{2}^{\prime }$
, respectively. Shading represents the density field using the same color scale as figure 2. Arrows represent velocity vectors (
$E_{2}{-}E_{2}^{\prime }$
, respectively. Shading represents the density field using the same color scale as figure 2. Arrows represent velocity vectors (
![]() $u_{2},u_{3}$
). Bold contour lines represent
$u_{2},u_{3}$
). Bold contour lines represent
![]() ${\it\rho}/{\it\rho}_{0}=1.005$
in (a) and
${\it\rho}/{\it\rho}_{0}=1.005$
in (a) and
![]() ${\it\rho}/{\it\rho}_{0}=1.011$
in (b) and depict cross-stream plumes developing due to unstable stratification. Streamwise vorticity is shown by blue (
${\it\rho}/{\it\rho}_{0}=1.011$
in (b) and depict cross-stream plumes developing due to unstable stratification. Streamwise vorticity is shown by blue (
![]() ${\it\omega}_{1}/{\it\omega}_{0}=18$
) and green (
${\it\omega}_{1}/{\it\omega}_{0}=18$
) and green (
![]() ${\it\omega}_{1}/{\it\omega}_{0}=-18$
) contour lines, similar to figure 6. Here
${\it\omega}_{1}/{\it\omega}_{0}=-18$
) contour lines, similar to figure 6. Here
![]() $d$
is the local depth at the slice.
$d$
is the local depth at the slice.

Figure 10. An
![]() $x_{2}{-}x_{3}$
slice through section
$x_{2}{-}x_{3}$
slice through section
![]() $E_{2}{-}E_{2}^{\prime }$
in figure 13(e) at different time snapshots. Shading represents the density field using the same color scale as figure 2. Streamwise vorticity is shown by blue (
$E_{2}{-}E_{2}^{\prime }$
in figure 13(e) at different time snapshots. Shading represents the density field using the same color scale as figure 2. Streamwise vorticity is shown by blue (
![]() ${\it\omega}_{1}/{\it\omega}_{0}=18$
) and green (
${\it\omega}_{1}/{\it\omega}_{0}=18$
) and green (
![]() ${\it\omega}_{1}/{\it\omega}_{0}=-18$
) contour lines, as in figure 9. Here
${\it\omega}_{1}/{\it\omega}_{0}=-18$
) contour lines, as in figure 9. Here
![]() $d$
is the local depth at the slice. Labels (f–i) correspond to the time snapshots from figures 2 and 6. Time point
$d$
is the local depth at the slice. Labels (f–i) correspond to the time snapshots from figures 2 and 6. Time point
![]() $j$
is not shown in other figures, and corresponds to
$j$
is not shown in other figures, and corresponds to
![]() $t/T=0.63$
.
$t/T=0.63$
.
4.2. Resolution requirements
In order to resolve the turbulence that develops during wave breaking, certain grid-resolution requirements are placed on our simulations. First, we must resolve the large-scale sources of turbulence, including the shear stress created by the no-slip bottom boundary condition and regions of unstable stratification. Figure 11 shows vertical profiles of laterally averaged horizontal velocity
![]() $u_{1}$
and density
$u_{1}$
and density
![]() ${\it\rho}/{\it\rho}_{0}$
, where the vertical coordinate is shown in wall units
${\it\rho}/{\it\rho}_{0}$
, where the vertical coordinate is shown in wall units
![]() $x_{3}^{+}=x_{3}/{\it\delta}_{S}$
to emphasize the near-wall flow. Profiles are shown within the thin region of downslope flow between the interface and the bottom as the wave approaches the slope (figure 11
a) and under the nose of the upslope surge (figure 11
b). These examples were chosen to represent extreme near-bottom gradients experienced during the simulations. It is clear in both cases that the flow near the bottom is well-resolved. By visual inspection, we also conclude that the initially two-dimensional (
$x_{3}^{+}=x_{3}/{\it\delta}_{S}$
to emphasize the near-wall flow. Profiles are shown within the thin region of downslope flow between the interface and the bottom as the wave approaches the slope (figure 11
a) and under the nose of the upslope surge (figure 11
b). These examples were chosen to represent extreme near-bottom gradients experienced during the simulations. It is clear in both cases that the flow near the bottom is well-resolved. By visual inspection, we also conclude that the initially two-dimensional (
![]() $x_{1}{-}x_{3}$
) sources of unstable stratification are well-resolved in our domain.
$x_{1}{-}x_{3}$
) sources of unstable stratification are well-resolved in our domain.

Figure 11. Vertical (
![]() $x_{3}$
) profiles of laterally-averaged horizontal velocity
$x_{3}$
) profiles of laterally-averaged horizontal velocity
![]() $u_{1}$
(●) and density
$u_{1}$
(●) and density
![]() ${\it\rho}/{\it\rho}_{0}$
(○). (a) A vertical profile corresponding to section
${\it\rho}/{\it\rho}_{0}$
(○). (a) A vertical profile corresponding to section
![]() $A{-}A^{\prime }$
in figure 13(a). (b) A vertical profile corresponding to section
$A{-}A^{\prime }$
in figure 13(a). (b) A vertical profile corresponding to section
![]() $E_{2}{-}E_{2}^{\prime }$
(through the nose of the upslope surge) in figure 13(e). In both plots,
$E_{2}{-}E_{2}^{\prime }$
(through the nose of the upslope surge) in figure 13(e). In both plots,
![]() $u_{1}$
is normalized by the maximum value over the full profile, and the vertical coordinate is shown in wall units
$u_{1}$
is normalized by the maximum value over the full profile, and the vertical coordinate is shown in wall units
![]() $x_{3}^{+}=x_{3}/{\it\delta}_{S}$
measured upward from the bottom. Note the difference in the range of the vertical axes.
$x_{3}^{+}=x_{3}/{\it\delta}_{S}$
measured upward from the bottom. Note the difference in the range of the vertical axes.
In addition to resolving the large scales of the flow during wave breaking, resolving the turbulence cascade to smaller scales places an even stricter resolution requirement on our simulations. In order to demonstrate adequate resolution of the turbulence cascade, we define turbulence quantities as a departure from the lateral average. Specifically,
![]() $u_{i}=\overline{u}_{i}+u_{i}^{\prime }$
where
$u_{i}=\overline{u}_{i}+u_{i}^{\prime }$
where
![]() $u_{i}$
is the full velocity,
$u_{i}$
is the full velocity,
![]() $\overline{u}_{i}$
is the laterally averaged velocity, and
$\overline{u}_{i}$
is the laterally averaged velocity, and
![]() $u_{i}^{\prime }$
is the fluctuation about the lateral average. The density is decomposed in the same way,
$u_{i}^{\prime }$
is the fluctuation about the lateral average. The density is decomposed in the same way,
![]() ${\it\rho}=\overline{{\it\rho}}+{\it\rho}^{\prime }$
. Figure 12 shows lateral spectra of the vertical velocity anomaly
${\it\rho}=\overline{{\it\rho}}+{\it\rho}^{\prime }$
. Figure 12 shows lateral spectra of the vertical velocity anomaly
![]() $E_{33}(k_{2})$
, where
$E_{33}(k_{2})$
, where
![]() $k_{2}$
is the lateral wavenumber, for case 3 at four successive times after wave breaking has occurred. These spectra are averaged over the breaking region (
$k_{2}$
is the lateral wavenumber, for case 3 at four successive times after wave breaking has occurred. These spectra are averaged over the breaking region (
![]() $0.68\leqslant x/L\leqslant 0.85$
) in both the BBL (the bottom 10 vertical grid cells) and the interior (
$0.68\leqslant x/L\leqslant 0.85$
) in both the BBL (the bottom 10 vertical grid cells) and the interior (
![]() $40\leqslant N_{3}\leqslant 75$
, which corresponds to
$40\leqslant N_{3}\leqslant 75$
, which corresponds to
![]() $-0.93\leqslant x_{3}/d\leqslant -0.81$
in figure 10). Results for the lateral spectra of the density anomaly
$-0.93\leqslant x_{3}/d\leqslant -0.81$
in figure 10). Results for the lateral spectra of the density anomaly
![]() ${\it\rho}^{\prime }$
in the same region are similar and are therefore not presented. Shortly after breaking, a spectral peak emerges in both the BBL and the interior at the observed wavenumber of the initial instability (see figure 9). This peak is clearly well resolved, with a normalized wavenumber of approximately 0.04. Over time, more broadband spectra are observed, with a cascade to smaller scales from the initial peak at the ‘injection’ scale. These results are comparable with those presented by Caulfield & Peltier (Reference Caulfield and Peltier2000) (their figure 16) for DNS of stratified shear flow. While the development of turbulence in the BBL and the interior is similar, figure 12 shows that turbulence grows faster in the BBL, resulting in a fully turbulent spectrum at an earlier time. However, the overall magnitude of the turbulence is larger in the interior than in the BBL. Note that the magnitudes of the spectral peaks change with time due to the passing of the breaking wave through the averaging area and the resulting change in total turbulent kinetic energy. Ultimately, we must compare the grid resolution in our simulations to the Kolmogorov length scale, which we calculate here as
${\it\rho}^{\prime }$
in the same region are similar and are therefore not presented. Shortly after breaking, a spectral peak emerges in both the BBL and the interior at the observed wavenumber of the initial instability (see figure 9). This peak is clearly well resolved, with a normalized wavenumber of approximately 0.04. Over time, more broadband spectra are observed, with a cascade to smaller scales from the initial peak at the ‘injection’ scale. These results are comparable with those presented by Caulfield & Peltier (Reference Caulfield and Peltier2000) (their figure 16) for DNS of stratified shear flow. While the development of turbulence in the BBL and the interior is similar, figure 12 shows that turbulence grows faster in the BBL, resulting in a fully turbulent spectrum at an earlier time. However, the overall magnitude of the turbulence is larger in the interior than in the BBL. Note that the magnitudes of the spectral peaks change with time due to the passing of the breaking wave through the averaging area and the resulting change in total turbulent kinetic energy. Ultimately, we must compare the grid resolution in our simulations to the Kolmogorov length scale, which we calculate here as
![]() ${\it\eta}_{k}=({\it\nu}^{3}/{\it\epsilon}^{\prime })^{1/4}$
. The local turbulent dissipation is defined as
${\it\eta}_{k}=({\it\nu}^{3}/{\it\epsilon}^{\prime })^{1/4}$
. The local turbulent dissipation is defined as
where
![]() $s_{ij}^{\prime }=((\partial u_{i}^{\prime }/\partial x_{j})+(\partial u_{j}^{\prime }/\partial x_{i}))/2$
. We find that in the worst case scenario, the grid spacing is roughly one order of magnitude (a factor of 13) larger than
$s_{ij}^{\prime }=((\partial u_{i}^{\prime }/\partial x_{j})+(\partial u_{j}^{\prime }/\partial x_{i}))/2$
. We find that in the worst case scenario, the grid spacing is roughly one order of magnitude (a factor of 13) larger than
![]() ${\it\eta}_{k}$
.
${\it\eta}_{k}$
.

Figure 12. Lateral spectra of the vertical velocity anomaly
![]() $E_{33}(k_{2})$
(in
$E_{33}(k_{2})$
(in
![]() $\text{m}^{3}\ \text{s}^{-2}$
) in both the BBL (a) and the interior (b). Spectra are shown at four successive times corresponding to snapshots (d–g) in figures 2 and 6. The observed wavenumber of the initial instability
$\text{m}^{3}\ \text{s}^{-2}$
) in both the BBL (a) and the interior (b). Spectra are shown at four successive times corresponding to snapshots (d–g) in figures 2 and 6. The observed wavenumber of the initial instability
![]() $(\cdots )$
is shown as well. The lateral wavenumber
$(\cdots )$
is shown as well. The lateral wavenumber
![]() $k_{2}$
is normalized by the lateral grid spacing
$k_{2}$
is normalized by the lateral grid spacing
![]() ${\rm\Delta}x_{2}$
.
${\rm\Delta}x_{2}$
.
4.3. Three-dimensionality
As discussed in the previous section, our desire to accurately capture three-dimensional effects places a strict resolution requirement on the simulations. By comparing the three-dimensional results with those of a similar two-dimensional simulation, we can determine the relative importance of capturing these effects. Here, we present results from a two-dimensional version of breaking wave case 3 that differs from the three-dimensional version only in the number of lateral grid points, which is reduced from 96 to 1, suppressing lateral variability in the simulation. Figure 13 shows the density structure of the two-dimensional simulation (left column) and an
![]() $x_{1}{-}x_{3}$
slice through the centre of the three-dimensional simulation (right column) for comparison. The structure of the waves is essentially the same prior to breaking (figure 13
a,b), and even during the breaking event and beginning of the upslope surge (figure 13
c,d), before lateral variability develops in the three-dimensional simulation. However, as the billows at the interface evolve, the two-dimensional and three-dimensional results differ (figure 13
e–i). Rather than breaking down due to lateral instability as they do in the three-dimensional simulation, the billows continue to grow and interact with one another, giving rise to the ‘inverse energy cascade’ of two-dimensional turbulence that is not realistic for a breaking internal wave. Similar differences were found by Aghsaee et al. (Reference Aghsaee, Boegman, Diamessis and Lamb2012) when comparing their high-resolution two-dimensional numerical model results with the inherently three-dimensional laboratory experiments of Boegman et al. (Reference Boegman, Ivey and Imberger2005).
$x_{1}{-}x_{3}$
slice through the centre of the three-dimensional simulation (right column) for comparison. The structure of the waves is essentially the same prior to breaking (figure 13
a,b), and even during the breaking event and beginning of the upslope surge (figure 13
c,d), before lateral variability develops in the three-dimensional simulation. However, as the billows at the interface evolve, the two-dimensional and three-dimensional results differ (figure 13
e–i). Rather than breaking down due to lateral instability as they do in the three-dimensional simulation, the billows continue to grow and interact with one another, giving rise to the ‘inverse energy cascade’ of two-dimensional turbulence that is not realistic for a breaking internal wave. Similar differences were found by Aghsaee et al. (Reference Aghsaee, Boegman, Diamessis and Lamb2012) when comparing their high-resolution two-dimensional numerical model results with the inherently three-dimensional laboratory experiments of Boegman et al. (Reference Boegman, Ivey and Imberger2005).

Figure 13. Snapshots in time of the density structure for two-dimensional (left column) and three-dimensional (right column) versions of breaking wave case 3 using the same colour scale as figure 2. The three-dimensional result is depicted by an
![]() $x_{1}{-}x_{3}$
slice through
$x_{1}{-}x_{3}$
slice through
![]() $x_{2}/W=0.5$
, the lateral centreline of the domain. Labels (a–i) correspond to the same times as in figures 2 and 6. The lines in panels (a) and (e), right column, are the locations of the
$x_{2}/W=0.5$
, the lateral centreline of the domain. Labels (a–i) correspond to the same times as in figures 2 and 6. The lines in panels (a) and (e), right column, are the locations of the
![]() $x_{2}{-}x_{3}$
slices shown in figures 9 and 10 and of the vertical (
$x_{2}{-}x_{3}$
slices shown in figures 9 and 10 and of the vertical (
![]() $x_{3}$
) profiles shown in figure 11.
$x_{3}$
) profiles shown in figure 11.
Following Fringer & Street (Reference Fringer and Street2003), we can quantify the three-dimensionality introduced to the flow after the breaking event by partitioning the total kinetic energy
![]() $E_{k}$
into its component parts
$E_{k}$
into its component parts
such that
![]() $E_{k}=E_{1}+E_{2}+E_{3}$
. Here,
$E_{k}=E_{1}+E_{2}+E_{3}$
. Here,
![]() $V$
is the volume of the entire computational domain. The normalized departure from two-dimensionality is then given by
$V$
is the volume of the entire computational domain. The normalized departure from two-dimensionality is then given by
The discrepancy between the kinetic energy in the two- and three-dimensional simulations can be attributed to the longitudinal rolls that are present and contribute to dissipation in the three-dimensional simulation, but are suppressed in the two-dimensional simulation. This is shown in figure 15, which presents the dissipation and mixing results for both simulations. Dissipation in the three-dimensional simulation
![]() ${\it\epsilon}_{3D}$
departs from the two-dimensional result
${\it\epsilon}_{3D}$
departs from the two-dimensional result
![]() ${\it\epsilon}_{2D}$
when the longitudinal rolls form (figure 15
a, point d). Dissipation is then larger in the three-dimensional simulation throughout the breaking process, with a peak difference of roughly 30 % at
${\it\epsilon}_{2D}$
when the longitudinal rolls form (figure 15
a, point d). Dissipation is then larger in the three-dimensional simulation throughout the breaking process, with a peak difference of roughly 30 % at
![]() $t/T=0.36$
and a slightly smaller difference of roughly 25 % at
$t/T=0.36$
and a slightly smaller difference of roughly 25 % at
![]() $t/T=0.51$
. Figure 15(b) shows the dissipation breakdown between the interior and bottom boundary regions (as defined in § 3.3 and shown in figure 4) for both simulations as well. The peak difference in dissipation between the two- and three-dimensional results at
$t/T=0.51$
. Figure 15(b) shows the dissipation breakdown between the interior and bottom boundary regions (as defined in § 3.3 and shown in figure 4) for both simulations as well. The peak difference in dissipation between the two- and three-dimensional results at
![]() $t/T=0.36$
occurs predominantly in the interior region where
$t/T=0.36$
occurs predominantly in the interior region where
![]() ${\it\epsilon}_{3D,II}$
is nearly 50 % larger than
${\it\epsilon}_{3D,II}$
is nearly 50 % larger than
![]() ${\it\epsilon}_{2D,II}$
. At
${\it\epsilon}_{2D,II}$
. At
![]() $t/T=0.51$
, more comparable differences are seen in both the interior and bottom boundary regions;
$t/T=0.51$
, more comparable differences are seen in both the interior and bottom boundary regions;
![]() ${\it\epsilon}_{3D,II}$
is roughly 30 % larger than
${\it\epsilon}_{3D,II}$
is roughly 30 % larger than
![]() ${\it\epsilon}_{2D,II}$
, while
${\it\epsilon}_{2D,II}$
, while
![]() ${\it\epsilon}_{3D,IV}$
is roughly 20 % larger than
${\it\epsilon}_{3D,IV}$
is roughly 20 % larger than
![]() ${\it\epsilon}_{2D,IV}$
. Figure 15(a) also shows the effective irreversible mixing rate for the two-dimensional simulation
${\it\epsilon}_{2D,IV}$
. Figure 15(a) also shows the effective irreversible mixing rate for the two-dimensional simulation
![]() ${\it\phi}_{e,2D}$
and the three-dimensional simulation
${\it\phi}_{e,2D}$
and the three-dimensional simulation
![]() ${\it\phi}_{e,3D}$
. The peak mixing is higher in the two-dimensional simulation, and is larger throughout most of the breaking event, with a peak difference of roughly 30 % at
${\it\phi}_{e,3D}$
. The peak mixing is higher in the two-dimensional simulation, and is larger throughout most of the breaking event, with a peak difference of roughly 30 % at
![]() $t/T=0.42$
. As discussed by Fringer & Street (Reference Fringer and Street2003), this increased mixing is attributed to the inverse energy cascade of two-dimensional turbulence. Because density overturns are not broken down by longitudinal rolls, they are able to grow and interact, creating sharper density gradients and increased surface area for interfacial diffusion. Overall, the three-dimensional simulation has roughly 8 % more dissipation and 20 % less mixing than the two-dimensional simulation, resulting in a 20 % smaller bulk mixing efficiency.
$t/T=0.42$
. As discussed by Fringer & Street (Reference Fringer and Street2003), this increased mixing is attributed to the inverse energy cascade of two-dimensional turbulence. Because density overturns are not broken down by longitudinal rolls, they are able to grow and interact, creating sharper density gradients and increased surface area for interfacial diffusion. Overall, the three-dimensional simulation has roughly 8 % more dissipation and 20 % less mixing than the two-dimensional simulation, resulting in a 20 % smaller bulk mixing efficiency.

Figure 15. Dissipation and irreversible mixing for two- and three-dimensional versions of breaking wave case 3. (a) Dissipation for the two-dimensional case
![]() ${\it\epsilon}_{2D}$
and three-dimensional case
${\it\epsilon}_{2D}$
and three-dimensional case
![]() ${\it\epsilon}_{3D}$
, as well as effective irreversible mixing for the two-dimensional case
${\it\epsilon}_{3D}$
, as well as effective irreversible mixing for the two-dimensional case
![]() ${\it\phi}_{e,2D}$
and three-dimensional case
${\it\phi}_{e,2D}$
and three-dimensional case
![]() ${\it\phi}_{e,3D}$
. (b) The dissipation breakdown by region as defined in § 3.3, including dissipation in the bottom boundary region for the two-dimensional case
${\it\phi}_{e,3D}$
. (b) The dissipation breakdown by region as defined in § 3.3, including dissipation in the bottom boundary region for the two-dimensional case
![]() ${\it\epsilon}_{2D,IV}$
and three-dimensional case
${\it\epsilon}_{2D,IV}$
and three-dimensional case
![]() ${\it\epsilon}_{3D,IV}$
, as well as dissipation in the interior region for the two-dimensional case
${\it\epsilon}_{3D,IV}$
, as well as dissipation in the interior region for the two-dimensional case
![]() ${\it\epsilon}_{2D,II}$
and three-dimensional case
${\it\epsilon}_{2D,II}$
and three-dimensional case
![]() ${\it\epsilon}_{3D,II}$
. Both plots are normalized by the maximum dissipation in the three-dimensional simulation
${\it\epsilon}_{3D,II}$
. Both plots are normalized by the maximum dissipation in the three-dimensional simulation
![]() ${\it\epsilon}_{3D,max}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
${\it\epsilon}_{3D,max}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
Owing to the effect of three-dimensional flow features (i.e. longitudinal rolls) on dissipation and mixing, a grid-resolution study was performed to ensure that our energetics results are grid independent. Keeping the
![]() $x_{1}{-}x_{3}$
grid and domain width
$x_{1}{-}x_{3}$
grid and domain width
![]() $W$
constant, we varied the number of lateral grid points
$W$
constant, we varied the number of lateral grid points
![]() $N_{2}$
in order to better resolve the lateral variability discussed in § 4.1. Figure 16 shows the maximum instantaneous and bulk mixing efficiencies for case 3 as a function of
$N_{2}$
in order to better resolve the lateral variability discussed in § 4.1. Figure 16 shows the maximum instantaneous and bulk mixing efficiencies for case 3 as a function of
![]() $N_{2}$
. As expected, both quantities are overestimated by the two-dimensional simulation (
$N_{2}$
. As expected, both quantities are overestimated by the two-dimensional simulation (
![]() $N_{2}=1$
). However, once lateral variability is resolved using a three-dimensional simulation, interior dissipation increases due to the presence of longitudinal rolls, and irreversible mixing decreases due to the lack of two-dimensional turbulence, leading to a decrease in mixing efficiency. The maximum instantaneous and bulk mixing efficiencies are relatively unaffected by increased lateral resolution for the three-dimensional grids tested. Both values have converged to the reported values of
$N_{2}=1$
). However, once lateral variability is resolved using a three-dimensional simulation, interior dissipation increases due to the presence of longitudinal rolls, and irreversible mixing decreases due to the lack of two-dimensional turbulence, leading to a decrease in mixing efficiency. The maximum instantaneous and bulk mixing efficiencies are relatively unaffected by increased lateral resolution for the three-dimensional grids tested. Both values have converged to the reported values of
![]() ${\it\eta}=0.31$
and
${\it\eta}=0.31$
and
![]() ${\it\eta}_{B}=0.14$
for
${\it\eta}_{B}=0.14$
for
![]() $N_{2}=96$
, confirming that our results are grid independent.
$N_{2}=96$
, confirming that our results are grid independent.

Figure 16. Maximum instantaneous mixing efficiency
![]() ${\it\eta}_{max}$
(○) and bulk mixing efficiency
${\it\eta}_{max}$
(○) and bulk mixing efficiency
![]() ${\it\eta}_{B}$
(●) as a function of the number of lateral grid points
${\it\eta}_{B}$
(●) as a function of the number of lateral grid points
![]() $N_{2}$
for breaking wave case 3. The
$N_{2}$
for breaking wave case 3. The
![]() $x_{1}{-}x_{3}$
grid and the domain width
$x_{1}{-}x_{3}$
grid and the domain width
![]() $W$
are held constant.
$W$
are held constant.
5. Effects of wave amplitude and bathymetric slope
5.1. General structure and energetics
While the discussion of breaking wave case 3 in §§ 3 and 4 is generally applicable to all of the cases in table 1, several conditions may change the structure and energetics of the breaking process. Here, we consider the effects of initial wave amplitude
![]() $a$
and bathymetric slope
$a$
and bathymetric slope
![]() $s$
on breaking dynamics. As shown in table 1, cases 1, 3, 4 and 5 have a constant bathymetric slope
$s$
on breaking dynamics. As shown in table 1, cases 1, 3, 4 and 5 have a constant bathymetric slope
![]() $s$
, and thus vary only in the initial amplitude of the wave
$s$
, and thus vary only in the initial amplitude of the wave
![]() $a$
. This results in different wave breaker types that are classified by Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010). Figure 17 shows the density structure of breaking wave cases 1 (surging breaker) and 4 (plunging breaker) for comparison with case 3 (collapsing breaker). For smaller incoming waves, the rear face of the wave does not have enough momentum to overcome the downslope flow under the leading face, resulting in a relatively weak surging breaker (figure 17
a). For larger waves, the rear face has enough momentum to plunge over the downslope flow under the leading face, resulting in a more vigorous plunging breaker (figure 17
c). Case 3 represents a collapsing breaker (figure 17
b), for which the rear face of the wave steepens, but is swept backward before it is able to plunge.
$a$
. This results in different wave breaker types that are classified by Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010). Figure 17 shows the density structure of breaking wave cases 1 (surging breaker) and 4 (plunging breaker) for comparison with case 3 (collapsing breaker). For smaller incoming waves, the rear face of the wave does not have enough momentum to overcome the downslope flow under the leading face, resulting in a relatively weak surging breaker (figure 17
a). For larger waves, the rear face has enough momentum to plunge over the downslope flow under the leading face, resulting in a more vigorous plunging breaker (figure 17
c). Case 3 represents a collapsing breaker (figure 17
b), for which the rear face of the wave steepens, but is swept backward before it is able to plunge.

Figure 17. Snapshots in time of density structure for breaking wave cases 1, 3 and 4 just after the break point (left column), and during the upslope surge (right column). (a) Depicts case 1, a surging breaker, (b) depicts case 3, a collapsing breaker and (c) depicts case 4, a plunging breaker. Results are averaged in the lateral (
![]() $x_{2}$
) direction.
$x_{2}$
) direction.
For a given bathymetric slope, the incoming wave amplitude has a clear effect on the energetics of the breaking process. While the shape of the energy profiles is similar for each case, the magnitudes are increased with increasing
![]() $a$
. Furthermore, the dissipation breakdowns are similar in shape to that shown for case 3 in figure 5. That is, the dissipation is dominated by three peaks. The first and third peaks correspond to strong downslope flow in the bottom boundary region, first under the leading edge of the wave and then as dense water from the upslope surge recedes back downslope. The second peak in dissipation corresponds to the peaks in interior dissipation and irreversible mixing that are caused by density overturns and the formation of longitudinal rolls during breaking and the upslope surge.
$a$
. Furthermore, the dissipation breakdowns are similar in shape to that shown for case 3 in figure 5. That is, the dissipation is dominated by three peaks. The first and third peaks correspond to strong downslope flow in the bottom boundary region, first under the leading edge of the wave and then as dense water from the upslope surge recedes back downslope. The second peak in dissipation corresponds to the peaks in interior dissipation and irreversible mixing that are caused by density overturns and the formation of longitudinal rolls during breaking and the upslope surge.
Cases 2, 3, 6 and 7 have a constant amplitude
![]() $a$
and are used to study the effect of varying bathymetric slope. The results for cases 2 (
$a$
and are used to study the effect of varying bathymetric slope. The results for cases 2 (
![]() $s=0.3$
) and 6 (
$s=0.3$
) and 6 (
![]() $s=0.15$
) are not shown due to their similarity with those of case 3 (
$s=0.15$
) are not shown due to their similarity with those of case 3 (
![]() $s=0.218$
) in figure 2. However, the structure and energetics of case 7 (
$s=0.218$
) in figure 2. However, the structure and energetics of case 7 (
![]() $s=0.05$
) are significantly different than those of cases 1–6 because its low slope results in a fission breaker. Figure 18 shows snapshots in time of the density structure for case 7. Here, rather than breaking in the sense of a surging, collapsing, or plunging breaker, the initial solitary wave of depression disperses into a train of rank-ordered solitary waves of elevation (boluses) that propagate up the slope (figure 18
a,b). The ‘fission’ occurs in figure 18(c), when a patch of dense fluid is pinched off of the leading wave of elevation, leading to density overturns at the interface. These density overturns interact with the trailing solitary waves as they propagate up the slope and eventually dissipate (figure 18
d–h). This structure is strikingly similar to that shown in figure 3 of Helfrich (Reference Helfrich1992), which depicts experimental results with the same wave amplitude and bathymetric slope as case 7.
$s=0.05$
) are significantly different than those of cases 1–6 because its low slope results in a fission breaker. Figure 18 shows snapshots in time of the density structure for case 7. Here, rather than breaking in the sense of a surging, collapsing, or plunging breaker, the initial solitary wave of depression disperses into a train of rank-ordered solitary waves of elevation (boluses) that propagate up the slope (figure 18
a,b). The ‘fission’ occurs in figure 18(c), when a patch of dense fluid is pinched off of the leading wave of elevation, leading to density overturns at the interface. These density overturns interact with the trailing solitary waves as they propagate up the slope and eventually dissipate (figure 18
d–h). This structure is strikingly similar to that shown in figure 3 of Helfrich (Reference Helfrich1992), which depicts experimental results with the same wave amplitude and bathymetric slope as case 7.
The dissipation breakdown for case 7 is shown in figure 19. Here, we see an almost entirely different energy profile than in cases 1, 3 and 6. Initially, dissipation rises due to downslope flow in the bottom-boundary region under the leading edge of the initial wave of depression (figure 19
a, points a–c). The only major peak in dissipation and mixing occurs after the density overturns created by the fission event have had time to grow and spread along the interface (figure 19
a, points c–d). After this peak, a lower level of dissipation and mixing is sustained as the train of solitary waves moves up the slope (figure 19
a, points e–h), creating smaller density overturns along the interface. This corresponds to a sustained period of elevated instantaneous mixing efficiency. Helfrich (Reference Helfrich1992) also observed ‘enhanced’ mixing due to the runup of boluses after breaking. Although breaking occurs over a relatively longer period of time in case 7 than in cases 3 and 6, the cumulative percentages of bottom-boundary dissipation (60 %) and interior dissipation (36 %) are similar (figure 19
b). We note that some dissipation (4 %) also occurs in the lower layer, which was not true for other cases (see figure 5), and accounts for the small gap between
![]() ${\it\epsilon}_{cum}$
and
${\it\epsilon}_{cum}$
and
![]() ${\it\epsilon}_{cum,II}+{\it\epsilon}_{cum,IV}$
in figure 19.
${\it\epsilon}_{cum,II}+{\it\epsilon}_{cum,IV}$
in figure 19.

Figure 19. Dissipation breakdown by region and mixing efficiency for breaking wave case 7. (a) Total dissipation
![]() ${\it\epsilon}$
, bottom-boundary dissipation
${\it\epsilon}$
, bottom-boundary dissipation
![]() ${\it\epsilon}_{IV}$
, interior dissipation
${\it\epsilon}_{IV}$
, interior dissipation
![]() ${\it\epsilon}_{II}$
, and effective irreversible mixing
${\it\epsilon}_{II}$
, and effective irreversible mixing
![]() ${\it\phi}_{e}$
as a function of time, all normalized by
${\it\phi}_{e}$
as a function of time, all normalized by
![]() ${\it\epsilon}_{max}$
. (b) The cumulative dissipation in the bottom boundary region
${\it\epsilon}_{max}$
. (b) The cumulative dissipation in the bottom boundary region
![]() ${\it\epsilon}_{cum,IV}$
and in the interior region
${\it\epsilon}_{cum,IV}$
and in the interior region
![]() ${\it\epsilon}_{cum,II}$
. The total cumulative dissipation
${\it\epsilon}_{cum,II}$
. The total cumulative dissipation
![]() ${\it\epsilon}_{cum}$
is shown as well. Values are normalized by
${\it\epsilon}_{cum}$
is shown as well. Values are normalized by
![]() ${\it\epsilon}_{tot}$
. (c) The instantaneous mixing efficiency
${\it\epsilon}_{tot}$
. (c) The instantaneous mixing efficiency
![]() ${\it\eta}$
and bulk mixing efficiency
${\it\eta}$
and bulk mixing efficiency
![]() ${\it\eta}_{B}$
. Dots labelled a–h correspond to time snapshots from figure 18.
${\it\eta}_{B}$
. Dots labelled a–h correspond to time snapshots from figure 18.
5.2. Dissipation, mixing and mixing efficiency
The combined effect of wave amplitude and bathymetric slope is described by the internal Iribarren number
![]() ${\it\xi}$
, as defined in § 1. This parameter has been used in the past to classify internal wave breaker types (Boegman et al.
Reference Boegman, Ivey and Imberger2005; Aghsaee et al.
Reference Aghsaee, Boegman and Lamb2010) and mixing efficiency (Boegman et al.
Reference Boegman, Ivey and Imberger2005). Here, we consider the variation of dissipation, irreversible mixing and mixing efficiency with
${\it\xi}$
, as defined in § 1. This parameter has been used in the past to classify internal wave breaker types (Boegman et al.
Reference Boegman, Ivey and Imberger2005; Aghsaee et al.
Reference Aghsaee, Boegman and Lamb2010) and mixing efficiency (Boegman et al.
Reference Boegman, Ivey and Imberger2005). Here, we consider the variation of dissipation, irreversible mixing and mixing efficiency with
![]() ${\it\xi}$
, noting that
${\it\xi}$
, noting that
![]() $\mathit{Re}_{w}$
is held constant in our simulations. Figure 20(a,b) shows peak and total values of dissipation and mixing as a function of the internal Iribarren number for all cases. We see a general decrease in dissipation and mixing with increasing
$\mathit{Re}_{w}$
is held constant in our simulations. Figure 20(a,b) shows peak and total values of dissipation and mixing as a function of the internal Iribarren number for all cases. We see a general decrease in dissipation and mixing with increasing
![]() ${\it\xi}$
. However, a distinction exists between constant slope (varying amplitude) cases and constant amplitude (varying slope) cases. Both peak and total values of dissipation and mixing increase more rapidly with decreasing
${\it\xi}$
. However, a distinction exists between constant slope (varying amplitude) cases and constant amplitude (varying slope) cases. Both peak and total values of dissipation and mixing increase more rapidly with decreasing
![]() ${\it\xi}$
for constant slope cases than for constant amplitude cases because larger amplitude waves have more initial energy to expend.
${\it\xi}$
for constant slope cases than for constant amplitude cases because larger amplitude waves have more initial energy to expend.

Figure 20. Dissipation, mixing and mixing efficiency results. (a) Peak and (b) total dissipation (○) and mixing (●) as functions of the internal Iribarren number
![]() ${\it\xi}$
. (c) Bulk mixing efficiency (●) as a function of the internal Iribarren number
${\it\xi}$
. (c) Bulk mixing efficiency (●) as a function of the internal Iribarren number
![]() ${\it\xi}$
. The mixing efficiency results of Boegman et al. (Reference Boegman, Ivey and Imberger2005) using the data of Michallet & Ivey (Reference Michallet and Ivey1999) are shown in grey for comparison. (d) The fraction
${\it\xi}$
. The mixing efficiency results of Boegman et al. (Reference Boegman, Ivey and Imberger2005) using the data of Michallet & Ivey (Reference Michallet and Ivey1999) are shown in grey for comparison. (d) The fraction
![]() $f_{2D}$
of total dissipation (○) and mixing (●) accounted for by the laterally averaged flow as a function of the internal Iribarren number
$f_{2D}$
of total dissipation (○) and mixing (●) accounted for by the laterally averaged flow as a function of the internal Iribarren number
![]() ${\it\xi}$
. (e) Bulk mixing efficiency
${\it\xi}$
. (e) Bulk mixing efficiency
![]() ${\it\eta}_{B}$
versus wave Reynolds number
${\it\eta}_{B}$
versus wave Reynolds number
![]() $\mathit{Re}_{w}$
for the data of Michallet & Ivey (Reference Michallet and Ivey1999). ( f) Bulk mixing efficiency
$\mathit{Re}_{w}$
for the data of Michallet & Ivey (Reference Michallet and Ivey1999). ( f) Bulk mixing efficiency
![]() ${\it\eta}_{B}$
as a function of internal Iribarren number
${\it\eta}_{B}$
as a function of internal Iribarren number
![]() ${\it\xi}$
for our simulations (black) and interpolated from the data of Michallet & Ivey (Reference Michallet and Ivey1999) for
${\it\xi}$
for our simulations (black) and interpolated from the data of Michallet & Ivey (Reference Michallet and Ivey1999) for
![]() $\mathit{Re}_{w}=208$
(grey). In (a)–(d), constant slope (varying amplitude) cases 1, 3, 4 and 5 are connected with a solid line, while constant amplitude (varying slope) cases 2, 3, 6 and 7 are connected with a dashed line.
$\mathit{Re}_{w}=208$
(grey). In (a)–(d), constant slope (varying amplitude) cases 1, 3, 4 and 5 are connected with a solid line, while constant amplitude (varying slope) cases 2, 3, 6 and 7 are connected with a dashed line.
The mixing efficiency is a measure of the relative magnitudes of dissipation and mixing, and is plotted as a function of the internal Iribarren number in figure 20(c). Despite the decrease in both peak and total dissipation and mixing with increasing
![]() ${\it\xi}$
, the bulk mixing efficiency does not follow this trend. Rather,
${\it\xi}$
, the bulk mixing efficiency does not follow this trend. Rather,
![]() ${\it\eta}_{B}$
is found to increase for larger and smaller values of
${\it\eta}_{B}$
is found to increase for larger and smaller values of
![]() ${\it\xi}$
, with a minimum for intermediate values of
${\it\xi}$
, with a minimum for intermediate values of
![]() ${\it\xi}$
and a spike around
${\it\xi}$
and a spike around
![]() ${\it\xi}=0.8$
. We note that the peak instantaneous mixing efficiency (not shown) varies similarly between
${\it\xi}=0.8$
. We note that the peak instantaneous mixing efficiency (not shown) varies similarly between
![]() ${\it\eta}_{max}=0.1{-}0.4$
with a spike of
${\it\eta}_{max}=0.1{-}0.4$
with a spike of
![]() ${\it\eta}_{max}=0.3$
around
${\it\eta}_{max}=0.3$
around
![]() ${\it\xi}=0.8$
. Previous work by Boegman et al. (Reference Boegman, Ivey and Imberger2005), using the data of Michallet & Ivey (Reference Michallet and Ivey1999), has shown that the bulk mixing efficiency
${\it\xi}=0.8$
. Previous work by Boegman et al. (Reference Boegman, Ivey and Imberger2005), using the data of Michallet & Ivey (Reference Michallet and Ivey1999), has shown that the bulk mixing efficiency
![]() ${\it\eta}_{B}$
peaks around 0.25 for
${\it\eta}_{B}$
peaks around 0.25 for
![]() ${\it\xi}\approx 0.8$
, and decreases for both larger and smaller
${\it\xi}\approx 0.8$
, and decreases for both larger and smaller
![]() ${\it\xi}$
values. Their data is plotted in figure 20(c) for comparison. Although our values are similar, there is a discrepancy in the shape of the
${\it\xi}$
values. Their data is plotted in figure 20(c) for comparison. Although our values are similar, there is a discrepancy in the shape of the
![]() ${\it\eta}_{B}$
versus
${\it\eta}_{B}$
versus
![]() ${\it\xi}$
curve. Specifically, we see a minimum mixing efficiency, rather than a maximum, for intermediate Iribarren numbers, and we appear to overestimate mixing efficiency for both the largest and smallest Iribarren number case.
${\it\xi}$
curve. Specifically, we see a minimum mixing efficiency, rather than a maximum, for intermediate Iribarren numbers, and we appear to overestimate mixing efficiency for both the largest and smallest Iribarren number case.
The discrepancy between our results and those of Michallet & Ivey (Reference Michallet and Ivey1999) and Boegman et al. (Reference Boegman, Ivey and Imberger2005) can be explained by a Reynolds number (
![]() $\mathit{Re}_{w}$
) effect. While we maintain a constant
$\mathit{Re}_{w}$
) effect. While we maintain a constant
![]() $\mathit{Re}_{w}=208$
in our simulations and vary
$\mathit{Re}_{w}=208$
in our simulations and vary
![]() ${\it\xi}$
, Michallet & Ivey (Reference Michallet and Ivey1999) varied
${\it\xi}$
, Michallet & Ivey (Reference Michallet and Ivey1999) varied
![]() $\mathit{Re}_{w}$
and
$\mathit{Re}_{w}$
and
![]() ${\it\xi}$
simultaneously. Figure 20(e) shows Michallet & Ivey’s (Reference Michallet and Ivey1999) mixing efficiency data as a function of
${\it\xi}$
simultaneously. Figure 20(e) shows Michallet & Ivey’s (Reference Michallet and Ivey1999) mixing efficiency data as a function of
![]() $\mathit{Re}_{w}$
, revealing that their mixing efficiency values generally increase with wave Reynolds number. In order to see how mixing efficiency varies strictly as a function of
$\mathit{Re}_{w}$
, revealing that their mixing efficiency values generally increase with wave Reynolds number. In order to see how mixing efficiency varies strictly as a function of
![]() ${\it\xi}$
, the effect of
${\it\xi}$
, the effect of
![]() $\mathit{Re}_{w}$
must be removed. Assuming
$\mathit{Re}_{w}$
must be removed. Assuming
![]() ${\it\eta}_{B}=f(\mathit{Re}_{w},{\it\xi})$
, we remove the
${\it\eta}_{B}=f(\mathit{Re}_{w},{\it\xi})$
, we remove the
![]() $\mathit{Re}_{w}$
effect from their data by creating an interpolant for
$\mathit{Re}_{w}$
effect from their data by creating an interpolant for
![]() ${\it\eta}_{B}$
in
${\it\eta}_{B}$
in
![]() $\mathit{Re}_{w}{-}{\it\xi}$
space, and calculating
$\mathit{Re}_{w}{-}{\it\xi}$
space, and calculating
![]() ${\it\eta}_{B}$
for a single value of
${\it\eta}_{B}$
for a single value of
![]() $\mathit{Re}_{w}$
. The result is shown in figure 20( f) for
$\mathit{Re}_{w}$
. The result is shown in figure 20( f) for
![]() $\mathit{Re}_{w}=208$
and compared with the seven values of
$\mathit{Re}_{w}=208$
and compared with the seven values of
![]() ${\it\xi}$
studied here. Accounting for Reynolds number effects in the laboratory data leads to a better agreement in the shape of the
${\it\xi}$
studied here. Accounting for Reynolds number effects in the laboratory data leads to a better agreement in the shape of the
![]() ${\it\eta}_{B}$
versus
${\it\eta}_{B}$
versus
![]() ${\it\xi}$
relationship with our results. Specifically, the bulk mixing efficiency from the experiments also peaks near
${\it\xi}$
relationship with our results. Specifically, the bulk mixing efficiency from the experiments also peaks near
![]() ${\it\xi}=0.8$
and increases for larger Iribarren numbers.
${\it\xi}=0.8$
and increases for larger Iribarren numbers.
Although our results qualitatively agree with those of Michallet & Ivey (Reference Michallet and Ivey1999) when accounting for Reynolds number effects, a difference still exists for the lowest Iribarren number case, which has a larger mixing efficiency than the laboratory data. This is likely an effect of dissipation due to sidewall friction on the results of Michallet & Ivey (Reference Michallet and Ivey1999). Because Michallet & Ivey (Reference Michallet and Ivey1999) did not account for sidewall friction in their calculations, they overestimated the incident wave energy and underestimated the reflected wave energy off the slope (Bourgault & Kelley Reference Bourgault and Kelley2007b
). This led to an overestimation of the total energy lost during breaking, and therefore an underestimation of mixing efficiency (see equation (12), Bourgault & Kelley Reference Bourgault and Kelley2007b
). This effect was likely largest for the case with the lowest slope and therefore the longest distance over which sidewall dissipation could act. Because our computational domain does not have sidewalls (we use periodic boundary conditions in the lateral direction), sidewall dissipation does not affect our results, leading to a larger mixing efficiency for the lowest Iribarren number (lowest slope) case. The general difference in magnitude between our mixing efficiency results and those in the laboratory could occur for a number of reasons. In particular, we are unable to run our simulations until the waves come to rest as in the laboratory experiments because this would require a much larger domain and simulation time that would lead to computational requirements beyond our capabilities. Furthermore, unlike the laboratory experiments in which the mixing efficiency is computed with bulk energy changes, we calculate
![]() ${\it\eta}_{B}$
using direct calculations of
${\it\eta}_{B}$
using direct calculations of
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\phi}_{d}$
. Finally, it is difficult to exactly match the initial stratification in the laboratory experiments.
${\it\phi}_{d}$
. Finally, it is difficult to exactly match the initial stratification in the laboratory experiments.
For the low value of
![]() $\mathit{Re}_{w}$
considered here, we find that the mixing efficiency is controlled by the two-dimensionality of the flow. This follows from the discussion in § 4.3, where we found a higher mixing efficiency for a two-dimensional simulation when compared with a similar three-dimensional simulation due to the suppression of longitudinal rolls. Along these lines, we would expect the mixing efficiency to depend on the degree of two-dimensionality in a given wave-breaking case. We quantify the two-dimensionality of the flow as the fraction
$\mathit{Re}_{w}$
considered here, we find that the mixing efficiency is controlled by the two-dimensionality of the flow. This follows from the discussion in § 4.3, where we found a higher mixing efficiency for a two-dimensional simulation when compared with a similar three-dimensional simulation due to the suppression of longitudinal rolls. Along these lines, we would expect the mixing efficiency to depend on the degree of two-dimensionality in a given wave-breaking case. We quantify the two-dimensionality of the flow as the fraction
![]() $f_{2D}$
of total dissipation or mixing that is due to the laterally averaged flow. Thus,
$f_{2D}$
of total dissipation or mixing that is due to the laterally averaged flow. Thus,
![]() $f_{2D}=\overline{{\it\epsilon}}_{tot}/{\it\epsilon}_{tot}$
for dissipation and
$f_{2D}=\overline{{\it\epsilon}}_{tot}/{\it\epsilon}_{tot}$
for dissipation and
![]() $f_{2D}=\overline{{\it\phi}}_{e,tot}/{\it\phi}_{e,tot}$
for mixing, where
$f_{2D}=\overline{{\it\phi}}_{e,tot}/{\it\phi}_{e,tot}$
for mixing, where
![]() $\overline{{\it\epsilon}}$
is defined as in (3.9) but using the laterally averaged velocity
$\overline{{\it\epsilon}}$
is defined as in (3.9) but using the laterally averaged velocity
![]() $\overline{u}_{i}$
and
$\overline{u}_{i}$
and
![]() $\overline{{\it\phi}}_{e}$
is defined with
$\overline{{\it\phi}}_{e}$
is defined with
![]() ${\it\phi}_{d}$
as in (3.5) but using the laterally averaged density
${\it\phi}_{d}$
as in (3.5) but using the laterally averaged density
![]() $\overline{{\it\rho}}$
. These quantities are displayed in figure 20(d), and show a similar dependence on
$\overline{{\it\rho}}$
. These quantities are displayed in figure 20(d), and show a similar dependence on
![]() ${\it\xi}$
as
${\it\xi}$
as
![]() ${\it\eta}_{B}$
. It is clear that
${\it\eta}_{B}$
. It is clear that
![]() $f_{2D}$
increases for larger and smaller values of
$f_{2D}$
increases for larger and smaller values of
![]() ${\it\xi}$
, with a minimum for intermediate values of
${\it\xi}$
, with a minimum for intermediate values of
![]() ${\it\xi}$
and a peak around
${\it\xi}$
and a peak around
![]() ${\it\xi}=0.8$
. As in Boegman et al. (Reference Boegman, Ivey and Imberger2005), the peak near
${\it\xi}=0.8$
. As in Boegman et al. (Reference Boegman, Ivey and Imberger2005), the peak near
![]() ${\it\xi}=0.8$
is due to the occurrence of plunging breakers, which introduce more available potential energy to the flow than collapsing breakers with similar internal Iribarren numbers. This also increases the two-dimensionality of the flow because the initial plunging motion does not vary in the lateral direction. Ultimately, a physical explanation of the dependence of mixing efficiency on two-dimensionality depends on the mechanisms of lateral instability during breaking, which are functions of
${\it\xi}=0.8$
is due to the occurrence of plunging breakers, which introduce more available potential energy to the flow than collapsing breakers with similar internal Iribarren numbers. This also increases the two-dimensionality of the flow because the initial plunging motion does not vary in the lateral direction. Ultimately, a physical explanation of the dependence of mixing efficiency on two-dimensionality depends on the mechanisms of lateral instability during breaking, which are functions of
![]() $\mathit{Re}_{w}$
,
$\mathit{Re}_{w}$
,
![]() ${\it\xi}$
and the non-dimensional interface thickness
${\it\xi}$
and the non-dimensional interface thickness
![]() ${\it\delta}/{\it\lambda}$
.
${\it\delta}/{\it\lambda}$
.
6. Geophysical application
6.1. Reynolds number effects
The small spatial scale of the simulations presented here must be considered when assessing the geophysical relevance of the results. The present simulations can be related to geophysical flows using the turbulence activity number (or buoyancy Reynolds number)
![]() $\mathit{Re}_{b}={\it\epsilon}^{\prime }/{\it\nu}N^{2}$
. This quantity can also be written as a ratio of the Ozmidov length scale
$\mathit{Re}_{b}={\it\epsilon}^{\prime }/{\it\nu}N^{2}$
. This quantity can also be written as a ratio of the Ozmidov length scale
![]() $L_{o}=({\it\epsilon}^{\prime }/N^{3})^{1/2}$
to the Kolmogorov length scale
$L_{o}=({\it\epsilon}^{\prime }/N^{3})^{1/2}$
to the Kolmogorov length scale
![]() ${\it\eta}_{k}$
as
${\it\eta}_{k}$
as
![]() $L_{o}/{\it\eta}_{k}=\mathit{Re}_{b}^{3/4}$
. Here,
$L_{o}/{\it\eta}_{k}=\mathit{Re}_{b}^{3/4}$
. Here,
![]() $N$
is calculated conservatively using the initial stratification. A maximum
$N$
is calculated conservatively using the initial stratification. A maximum
![]() $\mathit{Re}_{b}$
of approximately two is reached for the current simulations, indicating a relatively small separation between the largest and smallest scales of turbulence. Based on the work of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005), such a flow is classified in the ‘diffusive’ regime of stratified turbulence. Geophysical flows, on the other hand, usually have
$\mathit{Re}_{b}$
of approximately two is reached for the current simulations, indicating a relatively small separation between the largest and smallest scales of turbulence. Based on the work of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005), such a flow is classified in the ‘diffusive’ regime of stratified turbulence. Geophysical flows, on the other hand, usually have
![]() $\mathit{Re}_{b}$
values that are one to many orders of magnitude higher, indicating a larger separation of scales. Such flows are classified in the ‘intermediate’ or ‘energetic’ regimes of stratified turbulence by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). Examples of
$\mathit{Re}_{b}$
values that are one to many orders of magnitude higher, indicating a larger separation of scales. Such flows are classified in the ‘intermediate’ or ‘energetic’ regimes of stratified turbulence by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). Examples of
![]() $\mathit{Re}_{b}$
calculations in the field include Davis & Monismith (Reference Davis and Monismith2011), Walter et al. (Reference Walter, Woodson, Arthur, Fringer and Monismith2012) and Walter (Reference Walter2014) for nonlinear internal waves in the coastal environment, as well as (Bouffard & Boegman Reference Bouffard and Boegman2013, see figure 7) for the stratified region of Lake Erie.
$\mathit{Re}_{b}$
calculations in the field include Davis & Monismith (Reference Davis and Monismith2011), Walter et al. (Reference Walter, Woodson, Arthur, Fringer and Monismith2012) and Walter (Reference Walter2014) for nonlinear internal waves in the coastal environment, as well as (Bouffard & Boegman Reference Bouffard and Boegman2013, see figure 7) for the stratified region of Lake Erie.
The low Reynolds number of our simulations has several consequences for the interpretation of the results. In particular, dissipation in the boundary layer is much greater than that in the interior over the course of the wave-breaking event. For a higher-Reynolds-number flow, we would expect more energetic turbulence in the interior and therefore a larger relative contribution of the interior dissipation to the total dissipation. For example, in field observations of breaking internal waves in Monterey Bay, California, Walter et al. (Reference Walter, Woodson, Arthur, Fringer and Monismith2012) found dissipation values on the same order of magnitude in the interior as in the boundary layer. More energetic turbulence in the interior would also increase the turbulent contribution to the irreversible mixing
![]() ${\it\phi}_{e}$
, which in our simulations is roughly the same magnitude as the background mixing term
${\it\phi}_{e}$
, which in our simulations is roughly the same magnitude as the background mixing term
![]() ${\it\phi}_{i}$
. In addition, the boundary-layer dissipation in our simulations is largely due to the two-dimensional flow (figure 15
b) because boundary-layer turbulence does not develop until after breaking and is confined to a small region. For a higher Reynolds number flow, we would expect more energetic turbulence to develop sooner in the boundary layer, that is, during the initial downslope flow under the leading edge of the wave in figure 2(a,b).
${\it\phi}_{i}$
. In addition, the boundary-layer dissipation in our simulations is largely due to the two-dimensional flow (figure 15
b) because boundary-layer turbulence does not develop until after breaking and is confined to a small region. For a higher Reynolds number flow, we would expect more energetic turbulence to develop sooner in the boundary layer, that is, during the initial downslope flow under the leading edge of the wave in figure 2(a,b).
Aghsaee et al. (Reference Aghsaee, Boegman and Lamb2010) considered the effect of Reynolds number on the internal wave-breaking mechanism, focusing on the scale of the boundary-layer instability that triggers breaking relative to the wave scale. They found that increasing the Reynolds number reduced both the relative size and growth rate of vortices shed from the boundary layer, thus reducing the effect of boundary-layer separation on wave breaking. This allowed the breaker type to change from collapsing to plunging (for the same internal Iribarren number) because the steepening rear face was no longer swept backwards by the separated downslope flow and was able to plunge forward. It is therefore likely that increasing the Reynolds number would also modify how the mixing efficiency of breaking internal waves varies with the internal Iribarren number, although the specific effect is unknown.
6.2. Preturbulent mixing
In addition to the effects described above, the Reynolds number also sets the relative contribution of preturbulent mixing to total mixing during the wave-breaking event. It is expected that as the Reynolds number increases, preturbulent mixing will contribute less to the total mixing because turbulent mixing will play a larger role. We demonstrate this by rerunning case 3 and increasing
![]() ${\it\nu}$
by factors of 2, 4 and 6 with
${\it\nu}$
by factors of 2, 4 and 6 with
![]() ${\it\kappa}={\it\nu}$
(thus reducing the Reynolds number by factors of 2, 4 and 6). Figure 21(a) shows total and laterally averaged irreversible mixing values for case 3 with the original viscosity and diffusivity
${\it\kappa}={\it\nu}$
(thus reducing the Reynolds number by factors of 2, 4 and 6). Figure 21(a) shows total and laterally averaged irreversible mixing values for case 3 with the original viscosity and diffusivity
![]() ${\it\nu}_{0}={\it\kappa}_{0}=1\times 10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
, and with
${\it\nu}_{0}={\it\kappa}_{0}=1\times 10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
, and with
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
increased by a factor of 4. Figure 21(b) shows the fraction of total mixing that occurs in the preturbulent stage as a function of
${\it\kappa}$
increased by a factor of 4. Figure 21(b) shows the fraction of total mixing that occurs in the preturbulent stage as a function of
![]() ${\it\kappa}$
, where the turbulent transition is defined as the point in time when
${\it\kappa}$
, where the turbulent transition is defined as the point in time when
![]() ${\it\phi}_{e}$
departs from
${\it\phi}_{e}$
departs from
![]() $\overline{{\it\phi}}_{e}$
. Reducing the Reynolds number delays the onset of lateral variability during breaking. Thus, higher fractions of the peak and total mixing values are due to mixing in the preturbulent stage. We expect that increasing the Reynolds number of our simulations further would allow the turbulent transition to occur earlier in the shoaling and breaking event. This would likely reduce the large values of the mixing efficiency seen in figure 5 prior to breaking because the mixing efficiency would be less affected by preturbulent mixing. Extending our results to higher Reynolds numbers is the subject of future work.
$\overline{{\it\phi}}_{e}$
. Reducing the Reynolds number delays the onset of lateral variability during breaking. Thus, higher fractions of the peak and total mixing values are due to mixing in the preturbulent stage. We expect that increasing the Reynolds number of our simulations further would allow the turbulent transition to occur earlier in the shoaling and breaking event. This would likely reduce the large values of the mixing efficiency seen in figure 5 prior to breaking because the mixing efficiency would be less affected by preturbulent mixing. Extending our results to higher Reynolds numbers is the subject of future work.

Figure 21. Irreversible mixing results for case 3 with increased viscosity
![]() ${\it\nu}$
and diffusivity
${\it\nu}$
and diffusivity
![]() ${\it\kappa}={\it\nu}$
(lower Reynolds number). (a) Total and laterally averaged irreversible mixing values (
${\it\kappa}={\it\nu}$
(lower Reynolds number). (a) Total and laterally averaged irreversible mixing values (
![]() ${\it\phi}_{e}$
and
${\it\phi}_{e}$
and
![]() $\overline{{\it\phi}}_{e}$
, respectively) for case 3 with the original viscosity and diffusivity
$\overline{{\it\phi}}_{e}$
, respectively) for case 3 with the original viscosity and diffusivity
![]() ${\it\nu}_{0}={\it\kappa}_{0}=1\times 10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
, and with
${\it\nu}_{0}={\it\kappa}_{0}=1\times 10^{-6}\ \text{m}^{2}\ \text{s}^{-1}$
, and with
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
increased by a factor of 4. Dots labelled c–i correspond to time snapshots from figures 2 and 6. (b) The fraction of total mixing that occurs in the preturbulent stage
${\it\kappa}$
increased by a factor of 4. Dots labelled c–i correspond to time snapshots from figures 2 and 6. (b) The fraction of total mixing that occurs in the preturbulent stage
![]() ${\it\phi}_{e,PT}/{\it\phi}_{e,tot}$
as a function of
${\it\phi}_{e,PT}/{\it\phi}_{e,tot}$
as a function of
![]() ${\it\kappa}$
, where the turbulent transition is defined as the point in time when
${\it\kappa}$
, where the turbulent transition is defined as the point in time when
![]() ${\it\phi}_{e}$
departs from
${\it\phi}_{e}$
departs from
![]() $\overline{{\it\phi}}_{e}$
.
$\overline{{\it\phi}}_{e}$
.
6.3. Local versus global energetics
Despite the Reynolds number differences between geophysical flows and the flow simulated here, qualitative comparisons can still be made. To better relate the global (volume-integrated) energy quantities discussed thus far to what might be observed by a moored instrument during a breaking internal wave event in the field, we calculate local turbulence dissipation and buoyancy flux values at specific locations within the domain. Local turbulence quantities are defined as a departure from the lateral average as in § 4.2, and local turbulent dissipation
![]() ${\it\epsilon}^{\prime }$
is defined as in (4.1). The local turbulent buoyancy flux is defined similarly as
${\it\epsilon}^{\prime }$
is defined as in (4.1). The local turbulent buoyancy flux is defined similarly as
Figure 22 shows the maximum local turbulent dissipation over the wave-breaking event for case 3. Turbulent dissipation is maximized after the breakpoint in the region of the upslope surge due to the presence of longitudinal rolls. Some turbulent dissipation is also evident offshore of the breakpoint due to the downslope return flow after the upslope surge. Figures 23–25 show the density and velocity structure as well as turbulence quantities over time at the three cross-shore ‘virtual mooring’ locations in figure 22 for case 3, as would be measured at fixed moorings in the field. The density structure is depicted with a profile over time, while turbulence quantities are shown for two locations, one in the BBL (defined as the second grid cell from the bottom) and one in the interior (defined as the stratified region of the flow). These local results are presented in comparison with the global results for case 3, including
![]() ${\it\epsilon},{\it\phi}_{e}$
and
${\it\epsilon},{\it\phi}_{e}$
and
![]() $\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, the volume-integrated turbulent dissipation. Global quantities are divided by the volume of the sloping region of the domain to facilitate direct dimensional comparison with local quantities. The along-slope velocity at the boundary-layer measurement location
$\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, the volume-integrated turbulent dissipation. Global quantities are divided by the volume of the sloping region of the domain to facilitate direct dimensional comparison with local quantities. The along-slope velocity at the boundary-layer measurement location
![]() $u_{s,BL}$
is also shown to relate energetics quantities to the phase of the flow. We do not distinguish between positive and negative values of
$u_{s,BL}$
is also shown to relate energetics quantities to the phase of the flow. We do not distinguish between positive and negative values of
![]() $b$
, only whether its absolute value is elevated above zero, indicating turbulent vertical transport of density. Furthermore, we do not calculate the local mixing efficiency because the flow is not in local equilibrium. This implies that some of the turbulent buoyancy flux is reversible and is therefore not a true measure of mixing.
$b$
, only whether its absolute value is elevated above zero, indicating turbulent vertical transport of density. Furthermore, we do not calculate the local mixing efficiency because the flow is not in local equilibrium. This implies that some of the turbulent buoyancy flux is reversible and is therefore not a true measure of mixing.

Figure 22. The locations of virtual moorings M1, M2 and M3 in figures 23–25, respectively. Included is the maximum (over the entire wave-breaking event) local turbulent dissipation
![]() ${\it\epsilon}_{max}^{\prime }(x_{1},x_{3})$
(in
${\it\epsilon}_{max}^{\prime }(x_{1},x_{3})$
(in
![]() $\text{m}^{2}\ \text{s}^{-3}$
) for breaking wave case 3 shown on a
$\text{m}^{2}\ \text{s}^{-3}$
) for breaking wave case 3 shown on a
![]() $\log _{10}$
scale, as well as the initial pycnocline (– –), the cross-shore location of the breakpoint ( ▿ ) and the cross-shore location of the formation of the upslope surge (♢).
$\log _{10}$
scale, as well as the initial pycnocline (– –), the cross-shore location of the breakpoint ( ▿ ) and the cross-shore location of the formation of the upslope surge (♢).

Figure 23. A comparison of local energetics to volume-integrated (global) energetics at
![]() $x/L=0.67$
(M1 in figure 22) for case 3. (a) Density as a function of depth and time using the same colour scale as figure 2. (b) The along-slope velocity at the boundary-layer measurement location
$x/L=0.67$
(M1 in figure 22) for case 3. (a) Density as a function of depth and time using the same colour scale as figure 2. (b) The along-slope velocity at the boundary-layer measurement location
![]() $u_{s,BL}$
(in
$u_{s,BL}$
(in
![]() $\text{m}\ \text{s}^{-1}$
) as a function of time. (c) and (d) Local turbulent dissipation
$\text{m}\ \text{s}^{-1}$
) as a function of time. (c) and (d) Local turbulent dissipation
![]() ${\it\epsilon}^{\prime }$
and buoyancy flux
${\it\epsilon}^{\prime }$
and buoyancy flux
![]() $b$
, both in
$b$
, both in
![]() $\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
$\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
![]() ${\it\epsilon}$
, effective mixing rate
${\it\epsilon}$
, effective mixing rate
![]() ${\it\phi}_{e}$
, and turbulent dissipation
${\it\phi}_{e}$
, and turbulent dissipation
![]() $\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
$\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
![]() $\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
$\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.

Figure 24. A comparison of local energetics to volume-integrated (global) energetics at
![]() $x/L=0.76$
(M2 in figure 22) for case 3. (a) Density as a function of depth and time using the same colour scale as figure 2. (b) The along-slope velocity at the boundary-layer measurement location
$x/L=0.76$
(M2 in figure 22) for case 3. (a) Density as a function of depth and time using the same colour scale as figure 2. (b) The along-slope velocity at the boundary-layer measurement location
![]() $u_{s,BL}$
(in
$u_{s,BL}$
(in
![]() $\text{m}\ \text{s}^{-1}$
) as a function of time. (c) and (c) Local turbulent dissipation
$\text{m}\ \text{s}^{-1}$
) as a function of time. (c) and (c) Local turbulent dissipation
![]() ${\it\epsilon}^{\prime }$
and buoyancy flux
${\it\epsilon}^{\prime }$
and buoyancy flux
![]() $b$
, both in
$b$
, both in
![]() $\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
$\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
![]() ${\it\epsilon}$
, effective mixing rate
${\it\epsilon}$
, effective mixing rate
![]() ${\it\phi}_{e}$
, and turbulent dissipation
${\it\phi}_{e}$
, and turbulent dissipation
![]() $\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
$\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
![]() $\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
$\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.

Figure 25. A comparison of local energetics to volume-integrated (global) energetics at
![]() $x/L=0.83$
(M3 in figure 22) for case 3. (a) Shows density as a function of depth and time using the same color scale as figure 2. (b) Shows the along-slope velocity at the boundary layer measurement location
$x/L=0.83$
(M3 in figure 22) for case 3. (a) Shows density as a function of depth and time using the same color scale as figure 2. (b) Shows the along-slope velocity at the boundary layer measurement location
![]() $u_{s,BL}$
(in
$u_{s,BL}$
(in
![]() $\text{m}\ \text{s}^{-1}$
) as a function of time. (c,d) Local turbulent dissipation
$\text{m}\ \text{s}^{-1}$
) as a function of time. (c,d) Local turbulent dissipation
![]() ${\it\epsilon}^{\prime }$
and buoyancy flux
${\it\epsilon}^{\prime }$
and buoyancy flux
![]() $b$
, both in
$b$
, both in
![]() $\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
$\text{m}^{2}\ \text{s}^{-3}$
, in the BBL region (c) and the interior region (d). The vertical location of the interior measurement is shown by a dotted line in (a). (e) Volume-integrated (global) dissipation
![]() ${\it\epsilon}$
, effective mixing rate
${\it\epsilon}$
, effective mixing rate
![]() ${\it\phi}_{e}$
, and turbulent dissipation
${\it\phi}_{e}$
, and turbulent dissipation
![]() $\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
$\int _{V}{\it\epsilon}^{\prime }\text{d}V$
, all divided by the volume of the sloping region of the domain to give units of
![]() $\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
$\text{m}^{2}\ \text{s}^{-3}$
. Dots labelled a–i correspond to time snapshots from figures 2 and 6.
Figures 23–25 show distinctly different signals depending on the cross-shore (
![]() $x_{1}$
) location of the virtual mooring relative to the breakpoint of the wave and the vertical (
$x_{1}$
) location of the virtual mooring relative to the breakpoint of the wave and the vertical (
![]() $x_{3}$
) location of the turbulence measurement. Furthermore, these local signals correspond to different parts of the global dissipation and mixing signal. The magnitudes of the strongest local turbulence signals are generally larger than the global signal. Specifically, the turbulent dissipation and buoyancy flux signals at M2 and M3 are between one and two orders of magnitude greater than the corresponding global signals. We are therefore concerned only with the shape of the turbulence signals, and do not attempt to relate them quantitatively to the global result. The magnitudes of the strongest local dissipation signals do, however, compare well with those observed in the laboratory by Hult et al. (Reference Hult, Troy and Koseff2011) for breaking internal waves over a ridge, which are on the order of
$x_{3}$
) location of the turbulence measurement. Furthermore, these local signals correspond to different parts of the global dissipation and mixing signal. The magnitudes of the strongest local turbulence signals are generally larger than the global signal. Specifically, the turbulent dissipation and buoyancy flux signals at M2 and M3 are between one and two orders of magnitude greater than the corresponding global signals. We are therefore concerned only with the shape of the turbulence signals, and do not attempt to relate them quantitatively to the global result. The magnitudes of the strongest local dissipation signals do, however, compare well with those observed in the laboratory by Hult et al. (Reference Hult, Troy and Koseff2011) for breaking internal waves over a ridge, which are on the order of
![]() $10^{-4}$
or
$10^{-4}$
or
![]() $10^{-5}\ \text{m}^{2}\ \text{s}^{-3}$
. Owing to the difficulty of measuring local turbulent buoyancy flux in the laboratory, such values are not available for comparison (Hult et al.
Reference Hult, Troy and Koseff2011).
$10^{-5}\ \text{m}^{2}\ \text{s}^{-3}$
. Owing to the difficulty of measuring local turbulent buoyancy flux in the laboratory, such values are not available for comparison (Hult et al.
Reference Hult, Troy and Koseff2011).
Figure 23 shows the results from M1, which is located just downslope of the breakpoint. The density record shows the passage of a nonlinear wave prior to breaking. However, a relatively weak turbulence signal is seen here because most turbulence activity occurs upslope after breaking. A small spike in dissipation is seen in the boundary layer as the wave moves up the slope, and elevated dissipation and buoyancy flux are seen at the end of the event in the interior as dense water from the upslope surge flows back down the slope and interacts with the next wave crest. Figure 24 shows the results from M2, which is located upslope of the breakpoint and near the beginning of the upslope surge. Here, relatively strong signals are seen in both the BBL and the interior. Near the boundary, a peak in dissipation associated with the lobe–cleft instability at the front of the upslope surge is seen first. Then, a second peak is seen as dense water from the upslope surge flows back down the slope. In the interior, an extended period of elevated dissipation and buoyancy flux is seen after the upslope surge passes the mooring. This period is associated with the breakdown of billows at the interface due to lateral instability. These billows are evident in the density record in figure 24(a). A similar density structure was observed in the field by Walter et al. (Reference Walter, Woodson, Arthur, Fringer and Monismith2012, figure 4a) during the passage of an upslope propagating internal bore. The ‘bores’ in their study are the result of breaking internal waves on the nearshore slope in southern Monterey Bay, California. Figure 25 shows the results from M3, which is further up the slope. Here, we again see a relatively strong signal, but one that is different in shape than at M2. The density record shows the passage of the upslope surge; this is associated with peaks in dissipation both in the BBL and the interior, as well as elevated buoyancy flux in the interior.
The along-slope velocity at the boundary-layer measurement location was shown in figures 23(b), 24(b) and 25(b) in order to relate turbulent dissipation and buoyancy flux to the phase of the flow. At each virtual mooring, dissipation and buoyancy flux are enhanced at times of flow reversal from downslope (or zero flow) to upslope, specifically during the initial upslope surge of the breaking wave, and when the downslope flow from the upslope surge interacts with the next wave crest. Enhanced dissipation is also seen at mooring M2 during the downslope flow from the upslope surge. Similar trends were observed in the LES of Gayen & Sarkar (Reference Gayen and Sarkar2011) and in the field observations of Aucan et al. (Reference Aucan, Merrifield, Luther and Flament2006) at Kaena Ridge, Hawaii, both of which examined the phasing of near-bottom turbulence generated by internal tidal flow over a slope.
We acknowledge that the first peak in global dissipation in our simulations is attributed to laminar dissipation at the bottom boundary because turbulence has not yet developed. Therefore, this peak is not captured by the turbulence signal at any of the virtual moorings. This is evident in figures 23(e), 24(e) and 25(e), which show a time series of the global (volume-integrated) turbulent dissipation
![]() $\int _{V}{\it\epsilon}^{\prime }\text{d}V$
. Turbulent dissipation does not develop anywhere in the domain until breaking occurs. It can also be noted that turbulent dissipation is absent near the bottom boundary offshore of the wave-breaking location in figure 22, which shows the maximum turbulent dissipation
$\int _{V}{\it\epsilon}^{\prime }\text{d}V$
. Turbulent dissipation does not develop anywhere in the domain until breaking occurs. It can also be noted that turbulent dissipation is absent near the bottom boundary offshore of the wave-breaking location in figure 22, which shows the maximum turbulent dissipation
![]() ${\it\epsilon}_{max}^{\prime }$
over the course of breaking wave case 3 as a function of
${\it\epsilon}_{max}^{\prime }$
over the course of breaking wave case 3 as a function of
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{3}$
. In a higher-Reynolds-number flow, we would expect the first peak in global dissipation to also appear in the turbulent dissipation signal corresponding to the initial downslope flow under the leading edge of the wave. The turbulence signals seen at M1 and M2 would likely be modified to include this peak, while the signal at M3 would likely not change because of its position upslope of the initial density interface.
$x_{3}$
. In a higher-Reynolds-number flow, we would expect the first peak in global dissipation to also appear in the turbulent dissipation signal corresponding to the initial downslope flow under the leading edge of the wave. The turbulence signals seen at M1 and M2 would likely be modified to include this peak, while the signal at M3 would likely not change because of its position upslope of the initial density interface.
Comparison of local and global energetics allows us to determine which mooring location provides a signal that is most representative of the internal wave-breaking event as a whole. Through inspection of figures 23–25, we find that this is mooring M2, which is located offshore of the intersection of the initial pycnocline with the slope, and onshore of the breakpoint and formation of the upslope surge (see figure 22). Mooring M2 captures both peaks in dissipation after breaking; the first peak is due to the passing of the upslope surge, while the second peak is due to its return flow downslope. Furthermore, M2 captures elevated dissipation and buoyancy flux in the interior associated with the breakdown of billows at the interface. In a more turbulent flow, M2 would likely also capture turbulent dissipation in the bottom boundary under the leading edge of the wave. From this single mooring location, one could potentially characterize dissipation and mixing for the entire breaking event. The same is not true for moorings M1 and M3. In the current simulations, mooring M1 is too far downslope to capture any relevant signal, although it would likely capture the initial peak in bottom-boundary dissipation in a more turbulent flow. Mooring M3 captures the upslope surge in both the bottom boundary and interior regions, but it is not representative of the event as a whole. These results imply that the cross-shore placement of field moorings relative to the breaking location and the vertical placement of instruments are critical to the interpretation of breaking internal wave observations.
7. Conclusion
Using DNS, we have simulated the three-dimensional structure of breaking internal solitary waves on slopes. Our study includes seven cases with varying initial wave amplitude, bathymetric slope, and internal Iribarren number, but constant wave Reynolds number. For each case, the structure and energetics of wave breaking were analysed, and wave energetics were separated into different regions of the flow. On average, bottom-boundary dissipation accounted for roughly 63 % of total dissipation in the domain, while the interior dissipation accounted for roughly 35 %. Peaks in dissipation were caused by strong shear due to downslope flow over the no-slip bottom boundary, as well as strong shear and density overturns at the interface during breaking and the upslope surge. Peaks in interior dissipation and irreversible mixing were found to correspond with three-dimensionality in the flow field associated with wave breaking. This three-dimensionality manifested itself in the form of a lateral (cross-stream) instability in two specific locations: the interface and the bottom. At the interface, unstable stratification was created by density overturns during breaking and the upslope surge, driving a cross-stream convective instability. At the bottom, unstable stratification was created under the nose of the upslope surge, which was raised above the no-slip bottom wall, leading to the lobe and cleft instability typical of gravity currents. Longitudinal rolls (streamwise vorticity) developed and grew from both of these sources, ultimately interacting to enhance interior dissipation and irreversible mixing. By comparing our results with those of a similar two-dimensional simulation, we quantified the effect of lateral variability on wave breaking. The two-dimensional simulation underestimated dissipation by as much as 30 % while overestimating irreversible mixing by as much as 30 %. Overall, the three-dimensional simulation had roughly 8 % more dissipation and 20 % less mixing than the two-dimensional simulation. These differences were attributed to the suppression of longitudinal rolls in the two-dimensional simulation and the inverse cascade of two-dimensional turbulence, respectively, and highlight the importance of capturing three-dimensional effects when considering the structure and energetics of breaking internal waves on slopes.
An additional goal of this study was to examine the variation in the structure and energetics of breaking internal waves with the initial amplitude of the wave and the bathymetric slope. The combined effect of these two parameters was considered in terms of the internal Iribarren number
![]() ${\it\xi}$
. We found that both peak and total values of dissipation and irreversible mixing decrease with increasing
${\it\xi}$
. We found that both peak and total values of dissipation and irreversible mixing decrease with increasing
![]() ${\it\xi}$
. However, the bulk mixing efficiency increases for larger and smaller values of
${\it\xi}$
. However, the bulk mixing efficiency increases for larger and smaller values of
![]() ${\it\xi}$
, with a minimum for intermediate values of
${\it\xi}$
, with a minimum for intermediate values of
![]() ${\it\xi}$
and a peak near
${\it\xi}$
and a peak near
![]() ${\it\xi}=0.8$
for plunging breakers. This trend was explained by the degree of two-dimensionality in the flow. Bulk mixing efficiency results were found to agree with those of Boegman et al. (Reference Boegman, Ivey and Imberger2005) when the effect of
${\it\xi}=0.8$
for plunging breakers. This trend was explained by the degree of two-dimensionality in the flow. Bulk mixing efficiency results were found to agree with those of Boegman et al. (Reference Boegman, Ivey and Imberger2005) when the effect of
![]() $\mathit{Re}_{w}$
was removed and the effect of sidewall friction was considered. Our results indicate that the mixing efficiency might be more appropriately classified as a function of both the wave slope and the bathymetric slope, as in Aghsaee et al.’s (Reference Aghsaee, Boegman and Lamb2010) figure 6 for internal wave breaker types. It must be noted, however, that performing such a study using high-resolution, three-dimensional numerical simulations would require a great deal of computational effort.
$\mathit{Re}_{w}$
was removed and the effect of sidewall friction was considered. Our results indicate that the mixing efficiency might be more appropriately classified as a function of both the wave slope and the bathymetric slope, as in Aghsaee et al.’s (Reference Aghsaee, Boegman and Lamb2010) figure 6 for internal wave breaker types. It must be noted, however, that performing such a study using high-resolution, three-dimensional numerical simulations would require a great deal of computational effort.
Our average bulk mixing efficiency value of 0.16 and average peak instantaneous mixing efficiency value of 0.29 were found to be lower than Fringer & Street’s (Reference Fringer and Street2003) averages of 0.42 and 0.36, respectively, likely due to the presence of the bottom boundary. However, our bulk mixing efficiency values were found to be slightly higher than Hult et al.’s (Reference Hult, Troy and Koseff2011) values of 0.04–0.07 because some boundary-driven turbulence contributed to the mixing in our domain, while boundary-driven turbulence was confined to the well-mixed bottom layer in their experiments.
Finally, we examined the geophysical application of our results and considered the effects of Reynolds number on dissipation and mixing. Specifically, we found that increasing the Reynolds number led to a decrease in preturbulent mixing. In order to better relate our volume-integrated results to what might be observed during a breaking internal wave event in the field, we also calculated local turbulent dissipation and buoyancy flux values for different ‘virtual moorings’. We found distinctly different turbulence signals at each mooring, and showed that a mooring placed upslope of the breakpoint but downslope of the intersection of the pycnocline and the bottom provided results that were the most representative of dissipation and mixing over the event as a whole. This could assist in the interpretation of existing field measurements of breaking internal waves on slopes.
Acknowledgements
R.S.A. gratefully acknowledges the support of the Stanford Graduate Fellowship (SGF). R.S.A. and O.B.F. gratefully acknowledge the support of ONR grant N00014-08-1-0904 (scientific officers Dr C. Linwood Vincent, Dr T. Paluszkiewicz, and Dr S. Harper). We gratefully acknowledge the US Army Research Laboratory DoD Supercomputing Resource Center for computer time on Harold and especially thank the diligent staff at CCAC (Consolidated Customer Assistance Center) for their support. We also thank O. Murray of ONR for ensuring our access to these resources. Lastly, we thank three anonymous reviewers for their thoughtful and constructive comments that led to substantial improvement of the manuscript.