1. Introduction
Synthetic magnetic fluids, also known as ferrofluids, are stable colloidal suspensions consisting of the carrier liquid (kerosene, water or mineral oil) and magnetic (iron, cobalt, nickel etc.) nanoparticles. The most widely studied ferrofluids, however, are based on colloidal magnetite
$(\text{Fe}_{3}\text{O}_{4})$
. Generally, the suspended ultra-fine magnetite particles with diameter
$d_{p}$
of the order of 10 nm are coated with a surfactant layer preventing them from forming aggregates. Due to demagnetisation and chemical sorption effects there is also a layer of demagnetised magnetite of thickness
${\sim}$
1 nm at the boundary of the magnetic core.
Studies on the magnetic properties of such colloids have been conducted since the 1930s (Elmore Reference Elmore1938) but they intensified noticeably, starting from the 1960s and 1970s (Finlayson Reference Finlayson1970; Bogatyrev & Shaidurov Reference Bogatyrev and Shaidurov1976), when the industrial production of magnetic fluids became possible. Currently, a significant body of literature exists devoted to the properties of ferrofluids, see, for example, Rosensweig (Reference Rosensweig1979, Reference Rosensweig1985), Bashtovoy, Berkovsky & Vislovich (Reference Bashtovoy, Berkovsky and Vislovich1988), Blums, Cebers & Maiorov (Reference Blums, Cebers and Maiorov1997), Odenbach (Reference Odenbach2009) and references therein. In the absence of a magnetic field, magnetic moments of individual particles in a ferrofluid are randomly oriented so that the fluid has no net magnetisation. However, when placed in a magnetic field, they orient along the applied field and the fluid becomes magnetised. The degree of magnetisation depends on the strength of the applied field and the local temperature and concentration of magnetic particles. Driven by the Kelvin force that arises, a magnetised fluid tends to flow toward regions with a stronger magnetic field. Such a fluid motion is referred to as magnetoconvection. It does not require gravity to be initiated in a non-uniformly heated fluid and can be conveniently controlled by varying the applied external magnetic field (Schwab, Hildebrandt & Stierstadt Reference Schwab, Hildebrandt and Stierstadt1983; Tangthieng et al. Reference Tangthieng, Finlayson, Maulbetsch and Cader1999; Bozhko & Putin Reference Bozhko and Putin2003, Reference Bozhko and Putin2009; Zablotsky, Mezulis & Blums Reference Zablotsky, Mezulis and Blums2009). Therefore it is considered to be an important alternative to gravitational convection in heat exchange systems where natural convection cannot arise due to the lack of gravity (orbital stations) (Odenbach Reference Odenbach1995; Bozhko & Putin Reference Bozhko and Putin2009) or extreme confinement (microelectronics) (Matsuki & Murakami Reference Matsuki and Murakami1987; Mukhopadhyay et al. Reference Mukhopadhyay, Ganguly, Sen and Puri2005; Koji, Hideaki & Masahiro Reference Koji, Hideaki and Masahiro2007; Lian, Xuan & Li Reference Lian, Xuan and Li2009). Thus in the current study we focus on features of a pure magnetic convection by setting the gravitational acceleration to zero in the governing equations. This also allows us to reduce the number of governing parameters of the problem to keep this paper to a reasonable length. The results we have obtained for mixed magneto-gravitational convection regimes will be reported in a separate publication.
Consistent with our previous studies (Suslov Reference Suslov2008; Suslov et al. Reference Suslov, Bozhko, Sidorov and Putin2012) we consider a planar geometry: a fluid layer confined by long and wide non-magnetic plates. The choice of such a classical geometry is dictated by a number of factors. Firstly, it is a common prototype configuration for realistic heat exchangers. Secondly, it allows one to make significant analytical and computational progress without being overwhelmed by geometrical details. Thirdly, this geometry is relatively easy to realise in experiments. An alternative setup that has been extensively studied numerically consists of two coaxial co-rotating or differentially rotating cylinders (e.g. Zebib Reference Zebib1996; Tagg & Weidman Reference Tagg and Weidman2007; Altmeyer et al. Reference Altmeyer, Hoffmann, Leschhorn and Lücke2010). However as mentioned in Suslov et al. (Reference Suslov, Bozhko, Putin and Sidorov2010) experimental implementation of such a geometry is somewhat more complicated and the magnetic field applied in this case is necessarily non-uniform, which complicates the understanding of basic thermomagnetic mechanisms that are of interest here.
There are a number of motivating factors for this study stemming from experimental observations reported by our collaborators (Bozhko & Putin Reference Bozhko and Putin1991; Bozhko et al. Reference Bozhko, Pilugina, Putin, Shupenik, Suhanovsky and Schelykalov1998; Bozhko & Putin Reference Bozhko and Putin2003; Suslov et al. Reference Suslov, Bozhko, Sidorov and Putin2012). In particular, it has been observed that when a normal magnetic field is applied to a sufficiently wide and long ferrofluid layer the convection patterns arising near the edges of the experimental layer differ drastically in both orientation and behaviour from their counterparts in the central part of the layer. Namely, while the most prominent pattern in the middle part of the layer is stationary, propagating structures have been detected near the edges that form some angle with the boundary, see figure 9 in Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012). The exact reasons for such a different behaviour of a ferrofluid near the edges of the flow domain remain unclear to date and our present study explores one of the plausible explanations. At the boundary between magnetic (ferrofluid) and non-magnetic (container wall) media the magnetic field lines inevitably refract, which is the consequence of Maxwell’s boundary conditions for a magnetic field, see § 2. As a result, even if the applied magnetic field is assumed to be normal to the layer, which was the case in the majority of previous studies (e.g. Finlayson Reference Finlayson1970; Suslov Reference Suslov2008), the field lines necessarily curve near the layer edges so that they are effectively ‘sucked into’ the magnetic medium. Such a behaviour of magnetic field lines near the borders is very sensitive to the minor details of the border geometry and its defects so that it is virtually impossible to know what the local inclination angle of the magnetic field is. To render the problem tractable to analysis we resort to the following compromise: we still consider an infinitely wide and long layer of fluid and assume that the applied field is uniform, but we allow its arbitrary inclination with respect to the plane of the layer. Effectively, this adds two field direction angles to the standard problem’s parameter list, see § 2.
Since ferrofluids do not retain magnetisation in the absence of an externally applied magnetic field they are sometimes classified as superparamagnets rather than ferromagnets (Albrecht et al. Reference Albrecht, Bührer, Fähnle, Maier, Platzek and Reske1997). The next motivating factor for our current study is to demonstrate that such a terminology might be misleading if used blindly. We will show that even though the governing equations used to describe the behaviour of ferrofluids (see § 2) are indeed similar to those typically used for natural paramagnetic fluids such as oxygen (e.g. Ageikin Reference Ageikin1950; Huang, Edwards & Gray Reference Huang, Edwards and Gray1997), flow instability patterns predicted using these equations in ferrofluids are qualitatively different from those found in paramagnetic fluids. We will show in § 4 that this distinction is brought about by a nonlinearity of the magnetic field inside a layer of ferrofluid, which is caused by a field inclination and a much stronger degree of ferrofluid magnetisation compared to that of paramagnetic fluids. This in turn leads to another methodological motivation of our current study: in contrast to paramagnetic fluids the flow stability characteristics of ferrofluids depend sensitively on the actual values of their magnetic susceptibilities, which vary widely with the magnitude of the applied field. Therefore special care should be taken when comparing computational and experimental results for ferrofluids to make sure that the analysis has been performed for fluid properties that vary in a way consistent with experimental conditions. This aspect of theoretical ferrofluid research has received insufficient attention in the previously reported studies and will be detailed in § 3. Remarkably, in contrast to the previous studies of magnetoconvection arising in a normal field (Finlayson Reference Finlayson1970; Suslov Reference Suslov2008) we will show that the magnitude of the applied inclined magnetic field becomes an additional governing parameter of the problem.
Prior to proceeding with presenting our results we should stress that ferrofluids are complex multi-component colloidal systems and treating them as monofluids with spatially uniform properties cannot be justified in general. There is a growing body of evidence that effects such as gravitational sedimentation (Bozhko & Tynjala Reference Bozhko and Tynjala2005; Bozhko et al. Reference Bozhko, Putin, Sidorov and Suslov2013) and thermophoresis (Völker & Odenbach Reference Völker and Odenbach2003; Lange Reference Lange2004; Ryskin & Pleiner Reference Ryskin and Pleiner2004, Reference Ryskin and Pleiner2007) of magnetic nano-particles as well as magnetoviscosity (e.g. Bashtovoy et al. Reference Bashtovoy, Berkovsky and Vislovich1988; Odenbach & Raj Reference Odenbach and Raj2000; Odenbach Reference Odenbach2002a ,Reference Odenbach b , Reference Odenbach2004; Odenbach & Müller Reference Odenbach and Müller2005; Pop & Odenbach Reference Pop and Odenbach2006; Engler, Borin & Odenbach Reference Engler, Borin and Odenbach2009) can significantly affect experimentally observed ferrofluid flows. The detailed set of specific assumptions and physical conditions under which the governing equations considered in § 2 are expected to be accurate has been discussed in Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012) and will be justified in §§ 2–4. Here we just state that we assume that the concentration of the magnetic phase remains uniform in the current study and therefore we will only investigate the influence of the thermal and magnetic fields on the flow structure. Such a simplified approach appears to be reasonable, at least in the initial study, since the time scale for establishing thermosolutal gradients is significantly longer than that of the development of a thermomagnetic instability, and sedimentation effects are not present due to the lack of gravity.
The rest of the paper is organised as follows. The linearised perturbation equations are given in § 5 and their Squire-transformed form is interpreted in § 6. Their numerical solutions, the values of the determined critical parameters and a physical interpretation based on perturbation energy considerations are presented in § 7. Concluding remarks are given in § 8.
2. Problem formulation and governing equations
We will follow the major steps of the analysis presented in Finlayson (Reference Finlayson1970) and Suslov (Reference Suslov2008). Namely, a linear flow stability analysis will be used to shed light on the physical mechanisms of the observed convection and to provide parametric guidance for further quantitative experimental study of fully nonlinear convection states driven by complex mechanisms in thin layers of ferro-colloids.
Consider a layer of a ferromagnetic fluid that fills the gap between two infinitely long and wide parallel non-magnetic plates as shown in figure 1. The plates are separated by the distance
$2d$
and are maintained at constant different temperatures
$T_{\ast }\pm {\rm\Theta}$
. An external uniform magnetic field,
$\boldsymbol{H}^{e}=(H_{x}^{e},H_{y}^{e},H_{z}^{e})$
such that
$|\boldsymbol{H}^{e}|=H^{e}$
, where
$H_{x}^{e}=H^{e}\cos {\it\delta}$
,
$H_{y}^{e}=H^{e}\sin {\it\delta}\cos {\it\gamma}$
and
$H_{z}^{e}=H^{e}\sin {\it\delta}\sin {\it\gamma}$
, is applied at an arbitrary inclination to the layer. This field causes an internal magnetic field
$\boldsymbol{H}$
such that
$|\boldsymbol{H}|=H$
within the layer. The external field induces fluid magnetisation
$\boldsymbol{M}$
such that
$|\boldsymbol{M}|=M$
, which is assumed to be co-directed with the internal magnetic field:
$\boldsymbol{M}={\it\chi}_{\ast }\boldsymbol{H}$
, where
${\it\chi}_{\ast }$
is the integral magnetic susceptibility of the fluid. As discussed, for example, in Odenbach (Reference Odenbach2004) and references therein this is true if the magnetic particle size does not exceed
$d_{p}\sim 13$
nm (the estimations based on the experimental data, see § 3, show that for the fluid used in the cited experiments the average value of
$d_{p}$
satisfies this condition). In this case the ratio of the Brownian particle magnetisation relaxation time
${\it\tau}_{B}=(4{\rm\pi}d_{p}^{3}{\it\eta}_{\ast })/(k_{B}T)$
, where
$k_{B}=1.38\times 10^{-23}~\text{J}~\text{K}^{-1}$
is the Boltzmann constant, to the viscous time
${\it\tau}_{v}={\it\rho}_{\ast }d^{2}/{\it\eta}_{\ast }$
characterising the macroflow development is
${\it\tau}_{B}/{\it\tau}_{v}\sim 10^{-5}$
. Here,
${\it\rho}_{\ast }$
is the fluid density and
${\it\eta}_{\ast }$
is the dynamic viscosity. Thus it is safe to assume that the orientation of the magnetic moments of individual particles, and thus of the fluid magnetisation, follows the direction of a local magnetic field. The orientation of magnetic particle aggregates, however, can in principle be affected by the mechanical torque due to the local shear of the flow so that they can misalign with the local magnetic field. Yet the experiments reported in Odenbach & Müller (Reference Odenbach and Müller2005) show that such a misalignment only becomes noticeable for shear rates exceeding 15 s
$^{-1}$
while the shear rate for typical convection flows that are of interest here are of the order of 0.1 s
$^{-1}$
or even smaller. Therefore the misalignment of the magnetisation and magnetic field vectors can be safely neglected. We also assume that the fluid magnetisation depends only on magnetic field and temperature, which is the case when the concentration of magnetic particles remains uniform in experiments (we do not consider gravitational sedimentation, thermo- or magneto-phoresis of solid particles).
Figure 1. Sketch of the problem geometry. The vector of external magnetic field,
$\boldsymbol{H}^{e}$
, forms angles
${\it\delta}$
and
${\it\gamma}$
with the coordinate axes.
We choose the right-hand system of coordinates
$(x,y,z)$
with the origin in the mid-plane of the layer in such a way that the plates are located at
$x=\pm d$
and the
$y$
and
$z$
axes are parallel to the plates. Assuming that the temperature difference
$2{\rm\Theta}$
between the walls is sufficiently small, we adopt the Boussinesq approximation of the continuity, Navier–Stokes and thermal energy equations, which are complemented with Maxwell’s equations for the magnetic field:
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\rho}_{\ast }\frac{\partial \boldsymbol{v}}{\partial t}+{\it\rho}_{\ast }\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}p+{\it\eta}_{\ast }{\rm\nabla}^{2}\boldsymbol{v}+{\it\mu}_{0}M\boldsymbol{{\rm\nabla}}H, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial T}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}T={\it\kappa}_{\ast }{\rm\nabla}^{2}T, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{{\rm\nabla}}\times \boldsymbol{H}=0,\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{B}=0,\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{B}={\it\mu}_{0}(\boldsymbol{M}+\boldsymbol{H}),\quad \boldsymbol{M}=\frac{M(H,T)}{H}\boldsymbol{H}. & \displaystyle\end{eqnarray}$$
In the above equations
$\boldsymbol{v}$
is the velocity vector with the respective components
$(u,v,w)$
in the
$x$
,
$y$
and
$z$
directions,
$t$
is time,
$T$
is the temperature,
$p$
is the pressure,
$\boldsymbol{B}$
is the magnetic flux density,
${\it\kappa}_{\ast }$
is the thermal diffusivity of the fluid, and
${\it\mu}_{0}=4{\rm\pi}\times 10^{-7}~\text{H}~\text{m}^{-1}$
is the magnetic constant. The subscript
$\ast$
denotes the values of the fluid properties evaluated at the reference temperature
$T_{\ast }$
and reference internal magnetic field
$H_{\ast }$
(to be defined in § 4). In writing (2.2) we assume that the fluid remains Newtonian. It has been found in experiments of Bogatyrev & Gilev (Reference Bogatyrev and Gilev1984) that this is a reasonable approximation for fluids with the concentration of solid phase not exceeding
$f=0.1$
. The more recent measurements (however with different fluids) reviewed in Odenbach (Reference Odenbach2002b
, chap. 4) have indicated that ferrofluids placed in a magnetic field can also behave as Bingham fluids with a non-zero yield stress that increases approximately quadratically with the applied magnetic field. However the yield-stress magnitude remains very small for the field strength range relevant to the current study so that the Newtonian fluid approximation is well justified here.
As shown by numerous studies cited in § 1 the viscosity of concentrated ferrofluids depends on the applied magnetic field and the local flow shear that influence the concentration of aggregates formed as a result of a dipole interaction between magnetised particles. In general, both the average and local values of viscosity can vary. Even though many experiments aiming at quantifying such a dependence have been reported in the literature (e.g. Odenbach Reference Odenbach2002a ; Odenbach & Müller Reference Odenbach and Müller2005; Pop & Odenbach Reference Pop and Odenbach2006), the data collected in these experiments cannot be used directly to model flows in geometries and conditions that are significantly different from those of rheological experiments. Fortunately, in our study the reference layer-average fluid viscosity only enters the non-dimensional governing equations in combination with other fluid properties, forming the magnetic Rayleigh number (see § 3). We allow its value to vary over a wide range, which effectively includes all experimental conditions even though the exact value of magnetoviscosity remains unknown. The unknown variation of the local viscosity and other fluid properties subject to the action of the locally varying magnetic field and shear presents a more daunting problem. It is well known (e.g. Suslov & Paolucci Reference Suslov and Paolucci1995a ,Reference Suslov and Paolucci b ) that, if sufficiently large, such a variation can strongly influence the structure of the flow and its stability. Yet to make analytical progress in the absence of a quantitative rheological model we are forced to neglect these spatial variations of fluid properties in (2.2). This is consistent with a widely used Boussinesq thermal approximation adapted for magnetic fluids (Bashtovoy et al. Reference Bashtovoy, Berkovsky and Vislovich1988) and is expected to be reasonable if the temperature and magnetic field variation across the layer remain small. The qualitative agreement between the computational results and the experimental observations reported in our previous work (Suslov et al. Reference Suslov, Bozhko, Sidorov and Putin2012) indicates that indeed such a simplification preserves sufficient accuracy of the model and makes it tractable. We provide a further discussion and a quantitative justification of this simplification in §§ 3 and 4.
The last term in (2.2) represents a ponderomotive (Kelvin) force that acts on a magnetised fluid in a non-uniform magnetic field, driving it toward regions with a stronger magnetic field as discussed in Bashtovoy et al. (Reference Bashtovoy, Berkovsky and Vislovich1988). In order to close the problem, a magnetic equation of state is required, which is assumed to be in the simplest linear form valid for small temperature and field variations within the layer,
$$\begin{eqnarray}M=M_{\ast }+{\it\chi}{\rm\Delta}H-K{\rm\Delta}T,\quad {\rm\Delta}H\equiv H-H_{\ast },\quad {\rm\Delta}T\equiv T-T_{\ast }.\end{eqnarray}$$
Here
$H_{\ast }$
and
$M_{\ast }={\it\chi}_{\ast }H_{\ast }$
are the magnitude of the magnetic field and the magnetisation at the location with temperature
$T_{\ast }$
,
${\it\chi}=\partial M/\partial H|_{(H_{\ast },T_{\ast })}$
is the differential magnetic susceptibility and
$K=\partial M/\partial T|_{(H_{\ast },T_{\ast })}$
is the pyromagnetic coefficient. Using (2.6) we rewrite (2.5) as
$$\begin{eqnarray}\displaystyle \boldsymbol{M}=\frac{{\it\chi}H+({\it\chi}_{\ast }-{\it\chi})H_{\ast }-K{\rm\Delta}T}{H}\boldsymbol{H}. & & \displaystyle\end{eqnarray}$$
Subsequently, eliminating the magnetisation in favour of the magnetic field, we obtain from (2.4b )
$$\begin{eqnarray}(1+{\it\chi})\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{H}+\frac{({\it\chi}_{\ast }-{\it\chi})H_{\ast }-K{\rm\Delta}T}{H}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{H}-\boldsymbol{{\rm\nabla}}H\boldsymbol{\cdot }\boldsymbol{e})-K\boldsymbol{{\rm\nabla}}T\boldsymbol{\cdot }\boldsymbol{e}=0,\end{eqnarray}$$
where
$\boldsymbol{e}=(e_{1},e_{2},e_{3})\equiv \boldsymbol{H}/H$
is the unit vector in the direction of the magnetic field. This equation shows that thermomagnetic coupling occurs mostly when the magnetic field and the temperature gradient have components in the same direction.
It is convenient to redefine pressure
$p$
entering the momentum equation (2.2) so that it includes both a hydrostatic component and a Kelvin force potential (see also Odenbach Reference Odenbach2002a
, pp. 86, 87). In order to do this we use (2.6) to write
$$\begin{eqnarray}\displaystyle {\it\mu}_{0}M\boldsymbol{{\rm\nabla}}H & = & \displaystyle {\it\mu}_{0}[M_{\ast }+{\it\chi}{\rm\Delta}H-K{\rm\Delta}T]\boldsymbol{{\rm\nabla}}H\nonumber\\ \displaystyle & = & \displaystyle {\it\mu}_{0}\boldsymbol{{\rm\nabla}}\left[M_{\ast }H+{\textstyle \frac{1}{2}}{\it\chi}{\rm\Delta}H^{2}\right]-{\it\mu}_{0}K{\rm\Delta}T\boldsymbol{{\rm\nabla}}H.\end{eqnarray}$$
We will demonstrate in § 7.4 that only the non-potential component
$$\begin{eqnarray}F_{K}=-{\it\mu}_{0}K{\rm\Delta}T\boldsymbol{{\rm\nabla}}H\end{eqnarray}$$
of the Kelvin force can lead to the destabilisation of a static mechanical equilibrium and result in magnetoconvection. Upon introducing the modified pressure
$$\begin{eqnarray}P=p-{\it\mu}_{0}\left[M_{\ast }H+{\textstyle \frac{1}{2}}{\it\chi}{\rm\Delta}H^{2}\right]\!,\end{eqnarray}$$
(2.2) is written as
$$\begin{eqnarray}{\it\rho}_{\ast }\frac{\partial \boldsymbol{v}}{\partial t}+{\it\rho}_{\ast }\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}P+{\it\eta}_{\ast }{\rm\nabla}^{2}\boldsymbol{v}-{\it\mu}_{0}K{\rm\Delta}T\boldsymbol{{\rm\nabla}}H.\end{eqnarray}$$
We impose the standard no-slip/no-penetration and thermal boundary conditions
$$\begin{eqnarray}\boldsymbol{v}=\mathbf{0},\quad {\rm\Delta}T=\pm {\rm\Theta}\quad \text{at }x=\mp d\end{eqnarray}$$
for velocity and temperature, respectively. The magnetic boundary conditions are
$$\begin{eqnarray}(\boldsymbol{H}^{e}-\boldsymbol{H})\times \boldsymbol{n}=\mathbf{0},\quad (\boldsymbol{B}^{e}-\boldsymbol{B})\boldsymbol{\cdot }\boldsymbol{n}=0\quad \text{at }x=\pm d,\end{eqnarray}$$
where superscript
$e$
denotes fields outside the layer and
$\boldsymbol{n}=(1,0,0)$
is the normal vector to the walls. Using (2.8), condition (2.14b
) is rewritten as
$$\begin{eqnarray}\left[\left((1+{\it\chi})H+({\it\chi}_{\ast }-{\it\chi})H_{\ast }\pm K{\rm\Theta}\right)\boldsymbol{e}-\boldsymbol{H}^{e}\right]\boldsymbol{\cdot }\boldsymbol{n}=0\quad \text{at }x=\pm d.\end{eqnarray}$$
3. Non-dimensionalisation and problem parameters
The governing equations and boundary conditions are non-dimensionalised using
$$\begin{eqnarray}\displaystyle \displaystyle (x,y,z)=d(x^{\prime },y^{\prime },z^{\prime }),\quad \boldsymbol{v}=\frac{{\it\kappa}_{\ast }}{d}\boldsymbol{v}^{\prime },\quad t=\frac{d^{2}}{{\it\kappa}_{\ast }}t^{\prime },\quad P=\frac{{\it\rho}_{\ast }{\it\kappa}_{\ast }^{2}}{d^{2}}P^{\prime },\quad {\rm\Delta}T={\rm\Theta}{\it\theta}^{\prime },\qquad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \displaystyle \boldsymbol{H}=\frac{K{\rm\Theta}}{1+{\it\chi}}\boldsymbol{H}^{\prime },~H=\frac{K{\rm\Theta}}{1+{\it\chi}}H^{\prime },~\boldsymbol{M}=\frac{K{\rm\Theta}}{1+{\it\chi}}\boldsymbol{M}^{\prime },\quad M=\frac{K{\rm\Theta}}{1+{\it\chi}}M^{\prime }. & & \displaystyle\end{eqnarray}$$
Then omitting primes for simplicity of notation, we obtain
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{v}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{v}=-\boldsymbol{{\rm\nabla}}P+\mathit{Pr}{\rm\nabla}^{2}\boldsymbol{v}-Ra_{m}\mathit{Pr}{\it\theta}\boldsymbol{{\rm\nabla}}H, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial {\it\theta}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}={\rm\nabla}^{2}{\it\theta}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\times \boldsymbol{H}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (1+{\it\chi})(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{H}-\boldsymbol{{\rm\nabla}}{\it\theta}\boldsymbol{\cdot }\boldsymbol{e})+\frac{({\it\chi}_{\ast }-{\it\chi})N-(1+{\it\chi}){\it\theta}}{H}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{H}-\boldsymbol{{\rm\nabla}}H\boldsymbol{\cdot }\boldsymbol{e})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{M}=[{\it\chi}H+({\it\chi}_{\ast }-{\it\chi})N-(1+{\it\chi}){\it\theta}]\boldsymbol{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \left[\left((1+{\it\chi})(H\pm 1)+({\it\chi}_{\ast }-{\it\chi})N\right)\boldsymbol{e}-\boldsymbol{H}^{e}\right]\boldsymbol{\cdot }\boldsymbol{n}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{v}=\mathbf{0},\quad {\it\theta}=\mp 1\quad \text{at }x=\pm 1. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}Ra_{m}=\frac{{\it\mu}_{0}K^{2}{\rm\Theta}^{2}d^{2}}{{\it\eta}_{\ast }{\it\kappa}_{\ast }(1+{\it\chi})},\quad \mathit{Pr}=\frac{{\it\eta}_{\ast }}{{\it\rho}_{\ast }{\it\kappa}_{\ast }},\quad N=\frac{H_{\ast }(1+{\it\chi})}{K{\rm\Theta}}.\end{eqnarray}$$
The magnetic Rayleigh number
$Ra_{m}$
characterises the importance of magnetic forces, Prandtl number
$\mathit{Pr}$
characterises the ratio of viscous and thermal diffusion transport, and parameter
$N$
represents the non-dimensional magnetic field at the reference location.
Typical parameter values that are reported in the recent experiments (Suslov et al.
Reference Suslov, Bozhko, Sidorov and Putin2012; Bozhko et al.
Reference Bozhko, Putin, Sidorov and Suslov2013) are listed in table 1. Based on physical quantities listed in this table we estimate the value of Prandtl number
$\mathit{Pr}$
to be around 55 and use this for our computations. Note, however, that our previous results (Suslov Reference Suslov2008) for a normal field have been reported in terms of magnetic Grashof number for
$\mathit{Pr}=130$
. However, this does not prevent us from performing a meaningful comparison of the current and past results because in the case of pure magnetoconvection (in the absence of gravity) considered here the critical values of
$Ra_{m}$
are found to be invariant with respect to the values of Prandtl number. Thus for comparison with the previous results we simply use the relationship
$$\begin{eqnarray}Gr_{m}(\mathit{Pr})=\frac{Ra_{m}}{\mathit{Pr}},\end{eqnarray}$$
where
$Ra_{m}$
is the invariant value reported in the current paper and
$\mathit{Pr}$
is the value of Prandtl number used elsewhere.
Table 1. The typical values of experimental parameters and properties of the ferrofluid manufactured in the Scientific Laboratory of Practical Ferromagnetic Fluids, Ivanovo, Russia under Technical Conditions 229-001-02068195-2002 and used in experiments reported in Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012) and Bozhko et al. (Reference Bozhko, Putin, Sidorov and Suslov2013).
Among other important physical quantities characterising the field-dependent magnetic properties of the fluid are the differential and integral magnetic susceptibilities
${\it\chi}$
and
${\it\chi}_{\ast }$
and pyromagnetic coefficient
$K$
, which depend on the applied magnetic field and the temperature. The pyromagnetic coefficient
$K$
only enters the governing equations as a component of the non-dimensional groups (3.10) so that its exact value is not required for the current analysis, see a similar discussion of fluid viscosity in § 2. However we will see in § 4 that the magnitude of
$K$
(and thus of parameter
$N$
) can be conveniently used to distinguish between paramagnetic and ferromagnetic fluids. At the same time, the values of magnetic susceptibilities
${\it\chi}$
and
${\it\chi}_{\ast }$
are important problem parameters entering the governing equations directly. It is a common practice to estimate them from the Langevin magnetisation law
$$\begin{eqnarray}M_{L}(H)=M_{\infty }L({\it\xi}),\quad L({\it\xi})=\coth {\it\xi}-\frac{1}{{\it\xi}},\quad {\it\xi}={\it\mu}_{0}{\rm\pi}\frac{M_{s}d_{p}^{3}H}{6k_{B}T},\end{eqnarray}$$
where
$M_{\infty }$
is the experimentally measured saturation magnetisation of the fluid,
$L({\it\xi})$
is Langevin’s function and
${\it\xi}$
is Langevin’s parameter. Here
$M_{s}$
is the saturation magnetisation of a magnetic phase at a given temperature and
$d_{p}^{3}$
is the average cube of the diameter of a magnetised core of solid particles. Due to the Curie effect (demagnetisation of a ferromagnetic fluid with increasing temperature) and thermal expansion of the carrier fluid, the saturation magnetisation of magnetic material and ferrofluid vary as
$$\begin{eqnarray}\displaystyle & \displaystyle M_{s}=M_{s\ast }\frac{1-{\it\beta}_{2}T^{2}}{1-{\it\beta}_{2}T_{\ast }^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{\infty }=M_{\infty \ast }\frac{1-{\it\beta}_{2}T^{2}}{1-{\it\beta}_{2}T_{\ast }^{2}}(1-{\it\beta}_{\ast }(1-f)(T-T_{\ast })), & \displaystyle\end{eqnarray}$$
${\it\beta}_{\ast }$
is the coefficient of thermal expansion of the carrier fluid,
${\it\beta}_{2}$
is the Curie coefficient and
$f$
is the volume fraction of the magnetic phase. In this study, magnetite particles with
$M_{s\ast }=480~\text{kA}~\text{m}^{-1}$
and
${\it\beta}_{2}=8\times 10^{-7}~\text{K}^{-2}$
at reference temperature
$T_{\ast }=293$
K are considered, which correspond to the experimental fluids referred to in the previous publications (Suslov Reference Suslov2008; Suslov et al.
Reference Suslov, Bozhko, Sidorov and Putin2012; Bozhko et al.
Reference Bozhko, Putin, Sidorov and Suslov2013). The fluid saturation magnetisation measured at
$T_{\ast }=293$
K was
$M_{\infty \ast }=43~\text{kA}~\text{m}^{-1}$
.
However, both experimental measurements and molecular dynamics simulations show that the magnetisation law of a realistic ferrofluid deviates significantly from the Langevin dependence. The main reason for this is that Langevin’s law assumes no inter-particle interactions, which is not the case for experimental fluids with magnetic phase concentration as high as
$f=0.1$
. A comprehensive review of this issue is given in Ivanov et al. (Reference Ivanov, Kantorovich, Reznikov, Holm, Pshenichnikov, Lebedev, Chremos and Camp2007). There the authors showed that a significant improvement of the accuracy of the magnetisation law for a ferrofluid is obtained via the use of the so-called second-order modified mean field (MMF2) model that is essentially a two-term expansion of the Weiss mean field model (Weiss Reference Weiss1907; Tsebers Reference Tsebers1982). It is obtained by replacing the Langevin parameter
${\it\xi}$
with
$$\begin{eqnarray}\bar{{\it\xi}}={\it\mu}_{0}{\rm\pi}\frac{M_{s}d_{p}^{3}\bar{H}}{6k_{B}T},\quad \bar{H}=H+\frac{1}{3}M_{L}(H)\left(1+\frac{1}{48}\frac{\text{d}M_{L}(H)}{\text{d}H}\right).\end{eqnarray}$$
Here
$\bar{H}$
is the effective magnetic field that takes into account mean magnetic interactions between particles in a concentrated magnetic fluid.
The only physical quantity that remains unknown in the above formulae is the average cube of the diameter of magnetised particle cores. This quantity depends strongly on the (unknown) size dispersion of nano-particles and their aggregates present in the fluid. Thus
$d_{p}^{3}$
was determined by matching the predictions of the initial differential magnetic susceptibility
$\lim _{H\rightarrow 0}{\it\chi}(H)$
of the fluid with its experimentally determined value
${\it\chi}=3$
(Pshenichnikov Reference Pshenichnikov2007; Lebedev & Lysenko Reference Lebedev and Lysenko2011). It turned out that the MMF2 model produces this value if
$d_{p}^{3}\approx 1.64\times 10^{-24}~\text{m}^{3}$
.
Even though the MMF2 model is shown to produce accurate values for magnetic properties of a ferrofluid, it requires the value of a local magnetic field
$H$
as an input. However, this quantity depends on the geometry of the problem considered. For example, it was shown in Suslov (Reference Suslov2008) that when an external magnetic field
$H^{e}$
is applied perpendicularly to an infinite differentially heated layer of a ferrofluid bounded by parallel non-magnetic plates the internal magnetic field in the mid-plane of the layer is
$H_{\ast }=H^{e}/(1+{\it\chi}_{\ast })$
. The values of
$H_{\ast }$
and the corresponding fluid magnetisation
$M_{\ast }$
are shown in figure 2(c) for the experimental range of external magnetic field
$0\leqslant H^{e}\leqslant 35~\text{kA}~\text{m}^{-1}$
. If the magnetic field is applied obliquely then the relationship between the external and internal fields becomes much more complicated, see § 4. However, in this study we are mostly interested in the qualitative behaviour of the system for relatively small field inclination angles
$0^{\circ }\leqslant {\it\delta}\leqslant 15^{\circ }$
. Therefore the data presented in figure 2 for
${\it\delta}=0^{\circ }$
will suffice for parameter estimation purposes.
Figure 2. The comparison of magnetic fluid properties defined using Langevin’s law and the MMF2 model for
${\it\delta}=0^{\circ }$
and
$T_{\ast }=293$
K (
${\rm\Theta}=7.5$
K is chosen in (d)).
The comparison of relevant quantities obtained using Langevin and MMF2 models given in figure 2 demonstrates that Langevin’s law systematically underestimates the values of the magnetic susceptibilities and the pyromagnetic coefficient. Thus we use MMF2 curves to choose the range of parameters for which the numerical results will be presented. As seen from figure 2(a) the values of magnetic susceptibilities change over the range of the applied magnetic field from
$({\it\chi},{\it\chi}_{\ast })=(3,3)$
to just below
$({\it\chi},{\it\chi}_{\ast })=(1.5,2.5)$
. Thus we will report the numerical results for these two pairs of values. We also note that the previous numerical results are available (see Suslov Reference Suslov2008) for
$({\it\chi},{\it\chi}_{\ast })=(5,5)$
. Therefore, for comparison purposes we will also perform computations for this pair of parameters as well as for
$({\it\chi},{\it\chi}_{\ast })=(3,5)$
. Note that as discussed in Finlayson (Reference Finlayson1970) and Suslov (Reference Suslov2008),
${\it\chi}={\it\chi}_{\ast }$
along the linear segment of the magnetisation curve. However,
${\it\chi}<{\it\chi}_{\ast }$
when the fluid’s magnetisation approaches saturation. Therefore, by choosing different values of the differential and integral magnetic susceptibilities, we investigate the effect of nonlinearity of the magnetisation law on flow stability.
As mentioned previously, the value of the pyromagnetic coefficient
$K$
enters the definition of magnetic Rayleigh number. In this study the data from figure 2(b) are not used to limit the computational range of
$Ra_{m}$
but, rather, are presented here to enable the design of chambers for future experiments where the thickness of the gap between the walls will need to be chosen so that it results in the values of parameters close to critical ones reported in this study.
Figure 2(d) shows the values of the normally applied non-dimensional external magnetic field
$H^{e\prime }$
and the corresponding reference internal magnetic field
$N_{0}=N|_{{\it\delta}=0^{\circ }}$
(here we use a prime to denote a non-dimensional external field in figure 2(d) and to distinguish it from the dimensional external field
$H^{e}$
; however, for simplicity of notation we will use
$H^{e}$
to denote the non-dimensional field in the subsequent text). These parameters are not independent. It has been shown in Suslov (Reference Suslov2008) that
$$\begin{eqnarray}H^{e\prime }=(1+{\it\chi}_{\ast })N_{0}\end{eqnarray}$$
when
${\it\delta}=0^{\circ }$
. It is also known that neither of these two parameters affects the stability characteristics of the flow when the magnetic field is perpendicular to the layer if the magnetisation law is linear (Finlayson Reference Finlayson1970; Suslov Reference Suslov2008). However, when the nonlinearity of magnetisation is taken into account and when the field is applied obliquely the role of these parameters becomes non-trivial. It will be demonstrated in § 4 that whenever
${\it\delta}\neq 0^{\circ }$
the magnetic field lines within the layer curve. This curvature will be shown to be responsible for a qualitative change in the behaviour of the perturbation fields compared to that observed when
${\it\delta}=0^{\circ }$
. The relationship between parameters
$N$
and
$H^{e\prime }$
for a general oblique field cannot be given explicitly (apart from some limiting cases discussed in § 4) yet it is still well approximated by (3.16). It is convenient to use
$N_{0}$
for expressing solutions for magnetic field within the layer symbolically and
$H^{e\prime }$
for parameterising the numerical stability results. Figure 2(d) shows that for all experimentally relevant conditions the value of
$H^{e\prime }$
(and
$N_{0}$
) remains large and close to constant for fixed temperature difference
$2{\rm\Theta}$
between the walls. Therefore we choose
$H^{e\prime }=100$
in our computations, which is close to the values achieved in experiments. Our calculations show that the numerical stability results become almost independent of
$H^{e\prime }$
when its value exceeds 40 (this is the case when the temperature difference between the walls does not exceed about 30 K, which is the experimental maximum). We also present some selected results for
$H^{e\prime }=10$
. This would correspond to the temperature difference
${\rm\Delta}T$
between the walls of more than
$100^{\circ }$
, which is experimentally unachievable with the fluids used in the referenced experiments. However, such a value of
$H^{e\prime }$
could be realistic for a stronger magnetisable fluid (e.g. one with a higher concentration of magnetic particles and thus with a larger pyromagnetic coefficient). Therefore, we present the numerical results for
$H^{e\prime }=10$
as well, which allows us to see more clearly the peculiar qualitative effects brought about by the inclination of a magnetic field and the resulting curvature of magnetic field lines (see figure 5
a,c below).
4. Basic flow
We look for steady motionless solutions of (3.2)–(3.9) in the form
$$\begin{eqnarray}\boldsymbol{v}_{0}=\mathbf{0},\quad {\it\theta}_{0}={\it\theta}_{0}(x),\quad P_{0}=P_{0}(x),\quad \boldsymbol{H}_{0}=(H_{x0}(x),H_{y0}(x),H_{z0}(x)).\end{eqnarray}$$
They should satisfy
$$\begin{eqnarray}\text{D}P_{0}=-Ra_{m}\mathit{Pr}{\it\theta}_{0}e_{10}\text{D}H_{x0},\quad \text{D}^{2}{\it\theta}_{0}=0,\end{eqnarray}$$
$$\begin{eqnarray}\text{D}\left(\left(1+\frac{M_{0}}{H_{0}}\right)H_{x0}\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\text{D}H_{y0}=0,\quad \text{D}H_{z0}=0,\end{eqnarray}$$
and the boundary conditions
$$\begin{eqnarray}{\it\theta}_{0}=\pm 1,\quad H_{y0}=H_{y}^{e},\quad H_{z0}=H_{z}^{e},\end{eqnarray}$$
$$\begin{eqnarray}\left(1+\frac{M_{0}}{H_{0}}\right)H_{x0}=H_{x}^{e}\quad \text{at }x=\mp 1,\end{eqnarray}$$
where
$H_{0}\equiv \sqrt{H_{x0}^{2}+H_{y0}^{2}+H_{z0}^{2}}$
,
$M_{0}\equiv \sqrt{M_{x0}^{2}+M_{y0}^{2}+M_{z0}^{2}}$
and
$\text{D}\equiv \text{d}/\text{d}x$
. Upon introducing the unit vector
$\boldsymbol{e}_{0}(x)\equiv (e_{10}(x),e_{20}(x),e_{30}(x))=\left(H_{x0}/H_{0},H_{y0}/H_{0},H_{z0}/H_{0}\right)$
in the direction of the magnetic field the basic flow solutions of (4.2) are written as
$$\begin{eqnarray}{\it\theta}_{0}=-x\quad \text{and}\quad P_{0}=Ra_{m}\mathit{Pr}\int _{0}^{x}\bar{x}e_{10}\text{D}H_{x0}\,\text{d}\bar{x}+C,\end{eqnarray}$$
where
$C$
is an arbitrary constant. Equations (4.4) along with boundary conditions (4.5) result in expressions for tangential components of the magnetic field that are constant inside the fluid layer,
$H_{y0}(x)=H_{y}^{e}$
and
$H_{z0}(x)=H_{z}^{e}$
. In view of (3.7) and (4.6), equation(4.3) is integrated to obtain a nonlinear algebraic equation for the
$x$
-component of the unperturbed magnetic field
$$\begin{eqnarray}\left((1+{\it\chi})(H_{0}-{\it\theta}_{0})+({\it\chi}_{\ast }-{\it\chi})N\right)H_{x0}=H_{x}^{e}H_{0}.\end{eqnarray}$$
It is known (e.g. Suslov Reference Suslov2008) that for a perpendicular field when
$\boldsymbol{e}_{0}=(1,0,0)$
the basic flow component of the magnetic field in the
$x$
direction across the layer is given by
$H_{x0}=N_{0}-x$
, where
$N_{0}$
is defined by (3.16). However, when the external field is applied obliquely a nonlinear equation (4.8) does not have a closed-form solution and has to be solved numerically. Yet by evaluating this equation at the reference position
$x=0$
we obtain exact expressions for the magnetic field and its
$x$
component there:
$$\begin{eqnarray}H_{x0}(0)=N_{0}\cos {\it\delta},\quad N\equiv H_{0}(0)=N_{0}\cos {\it\delta}\sqrt{1+(1+{\it\chi}_{\ast })^{2}\tan ^{2}{\it\delta}}.\end{eqnarray}$$
It follows from (4.9) and (3.16) that the magnetic field in the mid-plane of the layer monotonically increases from
$N_{0}$
for a normal field to
$H^{e}$
when the applied field is tangential to the layer.
Taking into account that
$N_{0}\gg x$
as discussed in § 3 the solution of (4.8) can also be written asymptotically as
$$\begin{eqnarray}\displaystyle \frac{H_{x0}^{a}}{N_{0}\cos {\it\delta}} & = & \displaystyle 1-\frac{1+{\it\chi}}{(1+{\it\chi}_{\ast })^{3}\sin ^{2}{\it\delta}+(1+{\it\chi})\cos ^{2}{\it\delta}}\frac{N}{N_{0}}\frac{x}{N_{0}}\nonumber\\ \displaystyle & & \displaystyle +\,\sin ^{2}{\it\delta}\frac{(1+{\it\chi})^{2}(1+{\it\chi}_{\ast })^{3}\!\left(\displaystyle \frac{N^{2}}{N_{0}^{2}}+\displaystyle \frac{1}{2}\frac{{\it\chi}_{\ast }-{\it\chi}}{1+{\it\chi}_{\ast }}\cos ^{2}{\it\delta}\!\right)}{((1+{\it\chi}_{\ast })^{3}\sin ^{2}{\it\delta}+(1+{\it\chi})\cos ^{2}{\it\delta})^{3}}\frac{x^{2}}{N_{0}^{2}}+o\!\left(\frac{x^{2}}{N_{0}^{2}}\!\right)\!.\qquad\end{eqnarray}$$
A similar asymptotic approach was used in Hennenberg et al. (Reference Hennenberg, Wessow, Slavtchev, Desaive and Scheild2006) to determine the approximate expression for the magnetic field in a layer of magnetic fluid subject to longitudinal temperature gradient (in contrast to the transverse gradient considered here).
If the magnetisation law is linear, that is if
${\it\chi}={\it\chi}_{\ast }$
, the above expression simplifies to
$$\begin{eqnarray}\frac{H_{x0}^{a}}{N_{0}\cos {\it\delta}}=1-\frac{x}{N}+(1+{\it\chi})^{2}\sin ^{2}{\it\delta}\frac{N_{0}^{2}}{N^{2}}\frac{x^{2}}{N^{2}}+o\left(\frac{x^{2}}{N^{2}}\right).\end{eqnarray}$$
The first two terms in the asymptotic solution (4.11) are equivalent to expression (9) given in Huang et al. (Reference Huang, Edwards and Gray1997) for a magnetic field in a layer of paramagnetic fluid with
${\it\chi}={\it\chi}_{\ast }\ll 1$
. However, the nonlinearity of the magnetic field in the layer was fully neglected in Huang et al. (Reference Huang, Edwards and Gray1997). As seen from expressions (4.10) and (4.11) this is only true when
$N_{0}\rightarrow \infty$
, that is when pyromagnetic coefficient
$K\rightarrow 0$
, see definition (3.10). This is shown to be a good approximation in the case of paramagnetic fluids (Huang et al.
Reference Huang, Edwards and Gray1997); however,
$K$
is large in the current problem, see figure 2(b). Therefore
$N_{0}$
is finite and the nonlinearity of the magnetic field inside the layer of ferromagnetic fluid cannot be ignored. This is confirmed by fully nonlinear numerical solutions for the magnetic field shown for the finite values of
${\it\chi}={\it\chi}_{\ast }=3$
in figure 3. The degree of nonlinearity increases with decreasing value of the applied magnetic field provided that the value of the pyromagnetic coefficient does not vary significantly. Yet the three-term asymptotic solution (4.10) remains robust, providing accuracy within 1–2 % of the numerically computed values in all regimes considered.
Figure 3. Numerical solution for the magnitude
$H_{0}$
of the undisturbed magnetic field (a,d) and its cross-layer component
$H_{x0}$
(b,e), for
$H^{e}=100$
(a,c),
$H^{e}=10$
(d,e),
${\it\chi}={\it\chi}_{\ast }=3$
and various field inclination angles
${\it\delta}$
. (c,e) The corresponding relative error of the asymptotic solution (4.10).
Importantly, figure 3 demonstrates that the relative deviation of the magnetic field within the layer from its average value cannot exceed
$1/N_{0}$
. Using the data presented in figure 2(d) one then concludes that the field varies within the layer by less than 4 %. This is a natural measure of the error that is introduced in the model considered by assuming that the field-dependent fluid properties remain constant in (2.2).
Once the magnetic field within the layer is determined the unperturbed fluid magnetisation is computed using
$$\begin{eqnarray}M_{0}={\it\chi}H_{0}+({\it\chi}_{\ast }-{\it\chi})N-(1+{\it\chi}){\it\theta}_{0}.\end{eqnarray}$$
Typical distributions of the magnetisation and magnetic pressure across the layer are shown in figure 4. Both figures 3 and 4 demonstrate that the field inclination leads to a noticeable difference between the magnitudes of the cross-layer components of magnetic and magnetisation fields and their full magnitudes. This difference is more pronounced near the cold wall, which introduces an asymmetry in basic flow fields that will be shown to influence the stability results qualitatively. The other observation is that the magnitude of the external magnetic field influences the fields inside the layer: weaker oblique external fields lead to a stronger nonlinearity of internal fields (compare the top and bottom rows in figures 3 and 4). The symmetry-breaking effect of the field inclination is also evident in the behaviour of the magnetic pressure
$P_{0}$
shown in figure 4(c,f). As the field inclination angle increases, the pressure near the cold wall grows with respect to that near the hot wall. As will be discussed later this leads to the preferential shift of instability structures toward the hot wall, which introduces a further asymmetry and qualitative change in stability characteristics compared to the normal field case considered in Finlayson (Reference Finlayson1970) and Suslov (Reference Suslov2008).
Figure 4. Numerical solution for the magnitude
$M_{0}$
of the undisturbed fluid magnetisation (a,d), its cross-layer component
$M_{x0}$
(b,e) and magnetic pressure
$P_{0}$
(c,f), for
$H^{e}=100$
(a–c),
$H^{e}=10$
(d–f),
${\it\chi}={\it\chi}_{\ast }=3$
and various field inclination angles
${\it\delta}$
.
The behaviour of magnetic field lines inside a layer of ferrofluid is shown in figure 5(a,c). In contrast to the case of a normal field considered in Finlayson (Reference Finlayson1970) and Suslov (Reference Suslov2008), the non-dimensional magnitude (relative to the fluid magnetisation) of the obliquely applied field strongly affects the geometry of magnetic lines. The curvature of magnetic lines is especially pronounced in stronger magnetisable fluids (plot (c) as contrasted to plot (a)). This has a profound effect on the distribution of the normal non-potential component
$F_{K0}=-{\it\theta}_{0}(\text{d}H_{0}/\text{d}x)$
of the non-dimensional Kelvin force, which can be viewed as a magnetic buoyancy force. It is shown in figure 5(b,d). Such a force is positive near the left wall and negative near the right wall, which corresponds to an inherently unstable situation when hot fluid near
$x=-1$
is forced to flow toward the cold wall at
$x=1$
and vice versa. This situation is similar to an unstably stratified layer of a regular fluid heated from below in a downward gravitational field. Yet such similarity is complete only if the external magnetic field is normal to the layer. In this case, similar to its gravitational counterpart, the magnetic buoyancy is a linear function of the cross-layer coordinate
$x$
and its non-dimensional value is independent of the strength of the applied field, see dashed lines in figure 5(b,d). However, when an oblique field of the same magnitude is applied to the layer at least three qualitative differences arise due to the nonlinearity of the induced internal field. Firstly, the magnetic buoyancy force becomes more uniform across the layer so that the onset of thermomagnetic instability is expected to be delayed compared to the normal field situation. Secondly, the magnetic buoyancy force becomes a function of the magnitude of the applied magnetic field. Thirdly, and most importantly, the nonlinearity of the internal magnetic field leads to the situation where the layer that is unstably stratified with respect to magnetic buoyancy is effectively reduced to a sublayer in the vicinity of the hot wall, see figure 5(d). Therefore, in contrast to the case of a normal field, the cross-layer symmetry of the instability structures that arise is broken. In the following sections we will establish and quantify the physical features of instability patterns that are brought about by the inclination of an external field and were not found in the previous studies reported in Finlayson (Reference Finlayson1970) and Suslov (Reference Suslov2008).
Figure 5. Refraction of magnetic lines (a,c) and the distribution of the Kelvin force (b,d) in a layer of magnetic fluid heated from the left for the field inclination angles
${\it\delta}=10^{\circ }$
(solid line),
${\it\delta}=0^{\circ }$
(dashed line),
${\it\gamma}=0^{\circ }$
,
${\it\chi}={\it\chi}_{\ast }=3$
,
$H^{e}=100$
(a,b) and
$H^{e}=10$
(c,d).
5. Linearised perturbation equations
In order to investigate linear stability of the basic state discussed in § 4 with respect to infinitesimal disturbances that are assumed to be periodic in the
$y$
and
$z$
directions we consider a standard normalform representation of the perturbed quantities and write them as
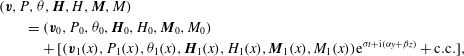$$\begin{eqnarray}\displaystyle & & \displaystyle (\boldsymbol{v},P,{\it\theta},\boldsymbol{H},H,\boldsymbol{M},M)\nonumber\\ \displaystyle & & \displaystyle \qquad =(\boldsymbol{v}_{0},P_{0},{\it\theta}_{0},\boldsymbol{H}_{0},H_{0},\boldsymbol{M}_{0},M_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,[(\boldsymbol{v}_{1}(x),P_{1}(x),{\it\theta}_{1}(x),\boldsymbol{H}_{1}(x),H_{1}(x),\boldsymbol{M}_{1}(x),M_{1}(x))\text{e}^{{\it\sigma}t+\text{i}({\it\alpha}y+{\it\beta}z)}+\text{c.c.}],\qquad\end{eqnarray}$$
where
${\it\sigma}={\it\sigma}^{R}+\text{i}{\it\sigma}^{I}$
is the complex amplification rate,
${\it\alpha}$
and
${\it\beta}$
are real wavenumbers in the
$y$
and
$z$
directions, respectively, and c.c. denotes the complex conjugate of the expression in square brackets. To satisfy (3.5) identically, it is convenient to introduce a perturbation
${\it\phi}_{1}(x)\text{e}^{{\it\sigma}t+\text{i}({\it\alpha}y+{\it\beta}z)}$
of the magnetic potential so that
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{H}_{1}=[\text{D}{\it\phi}_{1},\text{i}{\it\alpha}{\it\phi}_{1},\text{i}{\it\beta}{\it\phi}_{1}]^{\text{T}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H_{1}=\boldsymbol{H}_{1}\boldsymbol{\cdot }\boldsymbol{e}_{0}=e_{10}\text{D}{\it\phi}_{1}+\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30}){\it\phi}_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{M}_{1}={\it\chi}\boldsymbol{H}_{1}-(1+{\it\chi}){\it\theta}_{1}\boldsymbol{e}_{0}+\frac{(1+{\it\chi}){\it\theta}_{0}-({\it\chi}_{\ast }-{\it\chi})N}{H_{0}}(H_{1}\boldsymbol{e}_{0}-\boldsymbol{H}_{1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{1}=\boldsymbol{M}_{1}\boldsymbol{\cdot }\boldsymbol{e}_{0}={\it\chi}H_{1}-(1+{\it\chi}){\it\theta}_{1}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}0=\text{D}u_{1}+\text{i}({\it\alpha}v_{1}+{\it\beta}w_{1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}u_{1}+\mathit{Pr}({\it\alpha}^{2}+{\it\beta}^{2}-\text{D}^{2})u_{1}+\text{D}P_{1}+\,e_{10}Ra_{m}\mathit{Pr}\text{D}H_{x0}\,{\it\theta}_{1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,Ra_{m}\mathit{Pr}{\it\theta}_{0}e_{10}\text{D}^{2}{\it\phi}_{1}+\displaystyle Ra_{m}\mathit{Pr}{\it\theta}_{0}\left(\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30})+(1-e_{10}^{2})\frac{\text{D}H_{x0}}{H_{0}}\right)\text{D}{\it\phi}_{1}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\text{i}Ra_{m}\mathit{Pr}{\it\theta}_{0}e_{10}({\it\alpha}e_{20}+{\it\beta}e_{30})\frac{\text{D}H_{x0}}{H_{0}}{\it\phi}_{1}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}v_{1}+\mathit{Pr}({\it\alpha}^{2}+{\it\beta}^{2}-\text{D}^{2})v_{1}+\text{i}{\it\alpha}P_{1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{i}{\it\alpha}Ra_{m}\mathit{Pr}{\it\theta}_{0}e_{10}\text{D}{\it\phi}_{1}-{\it\alpha}Ra_{m}\mathit{Pr}{\it\theta}_{0}({\it\alpha}e_{20}+{\it\beta}e_{30}){\it\phi}_{1}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}w_{1}+\mathit{Pr}({\it\alpha}^{2}+{\it\beta}^{2}-\text{D}^{2})w_{1}+\text{i}{\it\beta}P_{1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{i}{\it\beta}Ra_{m}\mathit{Pr}{\it\theta}_{0}e_{10}\text{D}{\it\phi}_{1}-{\it\beta}Ra_{m}\mathit{Pr}{\it\theta}_{0}({\it\alpha}e_{20}+{\it\beta}e_{30}){\it\phi}_{1}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}{\it\theta}_{1}+\text{D}{\it\theta}_{0}u_{1}+({\it\alpha}^{2}+{\it\beta}^{2}-\text{D}^{2}){\it\theta}_{1}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0=(\text{D}^{2}-{\it\alpha}^{2}-{\it\beta}^{2}){\it\phi}_{1}+(1-e_{10}^{2})\left(\frac{{\it\chi}_{\ast }-{\it\chi}}{1+{\it\chi}}N-{\it\theta}_{0}\right)\frac{\text{D}^{2}{\it\phi}_{1}}{H_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\bigg[e_{10}\left(\frac{{\it\chi}_{\ast }-{\it\chi}}{1+{\it\chi}}N-{\it\theta}_{0}\right)\left(2\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30})+3(1-e_{10}^{2})\frac{\text{D}H_{x0}}{H_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(1-e_{10}^{2})\text{D}{\it\theta}_{0}\bigg]\frac{\text{D}{\it\phi}_{1}}{H_{0}}-\bigg[\left(\frac{{\it\chi}_{\ast }-{\it\chi}}{1+{\it\chi}}N-{\it\theta}_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left({\it\alpha}^{2}+{\it\beta}^{2}-({\it\alpha}e_{20}+{\it\beta}e_{30})^{2}+\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30})(1-3e_{10}^{2})\frac{\text{D}H_{x0}}{H_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30})e_{10}\text{D}{\it\theta}_{0}\bigg]\frac{{\it\phi}_{1}}{H_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\left(\text{i}({\it\alpha}e_{20}+{\it\beta}e_{30})+(1-e_{10}^{2})\frac{\text{D}H_{x0}}{H_{0}}\right){\it\theta}_{1}-e_{10}\text{D}{\it\theta}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}u_{1}=v_{1}=w_{1}={\it\theta}_{1}=0\quad \text{at }x=\pm 1.\end{eqnarray}$$
A perturbation of a magnetic field within a fluid layer causes perturbation of the external magnetic field for non-magnetic boundaries as discussed in Finlayson (Reference Finlayson1970). If there are no induced currents outside the layer and a non-magnetic medium (air) fills the surrounding space, then the external magnetic field has a potential
${\it\phi}_{1}^{e}(x)\exp ({\it\sigma}t+\text{i}{\it\alpha}y+\text{i}{\it\beta}z)$
, which, as follows from (2.4) and (2.5), satisfies Laplace’s equation
$$\begin{eqnarray}(\text{D}^{2}-{\it\alpha}^{2}-{\it\beta}^{2}){\it\phi}_{1}^{e}=0,\end{eqnarray}$$
in the regions
$x<-1$
and
$x>1$
. A physically relevant bounded solution can be written as
$$\begin{eqnarray}{\it\phi}_{1}^{e}(x)=\left\{\begin{array}{@{}ll@{}}A\exp \left(\sqrt{{\it\alpha}^{2}+{\it\beta}^{2}}x\right),\quad & x<-1\\ B\exp \left(-\sqrt{{\it\alpha}^{2}+{\it\beta}^{2}}x\right),\quad & x>1.\end{array}\right.\end{eqnarray}$$
Upon taking into account (2.5), the linearisation of the magnetic boundary conditions (2.14) leads to
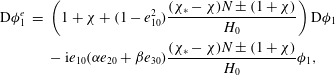$$\begin{eqnarray}\displaystyle \text{D}{\it\phi}_{1}^{e} & = & \displaystyle \left(1+{\it\chi}+(1-e_{10}^{2})\frac{({\it\chi}_{\ast }-{\it\chi})N\pm (1+{\it\chi})}{H_{0}}\right)\text{D}{\it\phi}_{1}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}e_{10}({\it\alpha}e_{20}+{\it\beta}e_{30})\frac{({\it\chi}_{\ast }-{\it\chi})N\pm (1+{\it\chi})}{H_{0}}{\it\phi}_{1},\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}_{1}^{e}={\it\phi}_{1}\quad \text{at }x=\pm 1.\end{eqnarray}$$
After eliminating
$A$
and
$B$
from (5.11) and (5.13) we obtain the boundary conditions for
${\it\phi}_{1}$
at
$x=\pm 1$
:
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+{\it\chi}+(1-e_{10}^{2})\frac{({\it\chi}_{\ast }-{\it\chi})N\pm (1+{\it\chi})}{H_{0}}\right)\text{D}{\it\phi}_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad \pm \,\sqrt{{\it\alpha}^{2}+{\it\beta}^{2}}{\it\phi}_{1}-\text{i}e_{10}({\it\alpha}e_{20}+{\it\beta}e_{30})\frac{({\it\chi}_{\ast }-{\it\chi})N\pm (1+{\it\chi})}{H_{0}}{\it\phi}_{1}=0.\end{eqnarray}$$
6. Squire’s transformation
Upon using the generalised Squire’s transformations
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}(x,y,z)=(\bar{x},\widetilde{y},\widetilde{z}),\quad {\it\theta}_{0}=\widetilde{{\it\theta}}_{0},\quad H_{x0}=\widetilde{H}_{x0},\quad H_{0}=\widetilde{H}_{0},\quad {\it\sigma}=\widetilde{{\it\sigma}},\quad {\it\alpha}^{2}+{\it\beta}^{2}=\widetilde{{\it\alpha}}^{2},\\ {\it\beta}=\widetilde{{\it\beta}},\quad u_{1}=\widetilde{u},\quad {\it\alpha}v_{1}+{\it\beta}w_{1}=\widetilde{{\it\alpha}}\widetilde{v},\quad w_{1}=\widetilde{w},\quad {\it\theta}_{1}=\widetilde{{\it\theta}},\quad P_{1}=\widetilde{P},\quad {\it\phi}_{1}=\widetilde{{\it\phi}},\\ Ra_{m}=\widetilde{Ra}_{m},\quad \mathit{Pr}=\widetilde{\mathit{Pr}},\quad N=\widetilde{N},\quad {\it\chi}=\widetilde{{\it\chi}},\quad {\it\chi}_{\ast }=\widetilde{{\it\chi}}_{\ast },\\ e_{10}=\widetilde{e}_{10},\quad {\it\alpha}e_{20}+{\it\beta}e_{30}=\widetilde{{\it\alpha}}\widetilde{e}_{20},\end{array}\!\!\!\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}0=\text{D}\widetilde{u}+\text{i}\widetilde{{\it\alpha}}\widetilde{v},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{{\it\sigma}}\widetilde{u}+\widetilde{\mathit{Pr}}(\widetilde{{\it\alpha}}^{2}-\text{D}^{2})\widetilde{u}+\text{D}\widetilde{P}+\widetilde{e}_{10}\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\text{D}\widetilde{H}_{x0}\widetilde{{\it\theta}}+\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}\widetilde{e}_{10}\text{D}^{2}\widetilde{{\it\phi}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}\left[\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}+(1-\widetilde{e}_{10}^{2})\frac{\text{D}\widetilde{H}_{x0}}{\widetilde{H}_{0}}\right]\text{D}\widetilde{{\it\phi}}-\text{i}\widetilde{{\it\alpha}}\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}\widetilde{e}_{10}\widetilde{e}_{20}\frac{\text{D}\widetilde{H}_{x0}}{\widetilde{H}_{0}}\widetilde{{\it\phi}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{{\it\sigma}}\widetilde{v}+\widetilde{\mathit{Pr}}(\widetilde{{\it\alpha}}^{2}-\text{D}^{2})\widetilde{v}+\text{i}\widetilde{{\it\alpha}}\widetilde{P}+\widetilde{{\it\alpha}}\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}(\text{i}\widetilde{e}_{10}\text{D}\widetilde{{\it\phi}}-\widetilde{{\it\alpha}}\widetilde{e}_{20}\widetilde{{\it\phi}})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{{\it\sigma}}\widetilde{w}+\widetilde{\mathit{Pr}}(\widetilde{{\it\alpha}}^{2}-\text{D}^{2})\widetilde{w}+\text{i}\widetilde{{\it\beta}}\widetilde{P}+\,\widetilde{{\it\beta}}\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}(\text{i}\widetilde{e}_{10}\text{D}\widetilde{{\it\phi}}-\widetilde{{\it\alpha}}\widetilde{e}_{20}\widetilde{{\it\phi}})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{{\it\sigma}}\widetilde{{\it\theta}}+\text{D}\widetilde{{\it\theta}}_{0}\widetilde{u}+(\widetilde{{\it\alpha}}^{2}-\text{D}^{2})\widetilde{{\it\theta}}=0,\end{eqnarray}$$
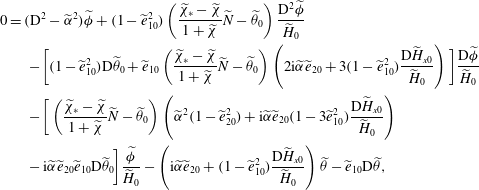$$\begin{eqnarray}\displaystyle & & \displaystyle 0=(\text{D}^{2}-\widetilde{{\it\alpha}}^{2})\widetilde{{\it\phi}}+(1-\widetilde{e}_{10}^{2})\left(\frac{\widetilde{{\it\chi}}_{\ast }-\widetilde{{\it\chi}}}{1+\widetilde{{\it\chi}}}\widetilde{N}-\widetilde{{\it\theta}}_{0}\right)\frac{\text{D}^{2}\widetilde{{\it\phi}}}{\widetilde{H}_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\bigg[(1-\widetilde{e}_{10}^{2})\text{D}\widetilde{{\it\theta}}_{0}+\widetilde{e}_{10}\left(\frac{\widetilde{{\it\chi}}_{\ast }-\widetilde{{\it\chi}}}{1+\widetilde{{\it\chi}}}\widetilde{N}-\widetilde{{\it\theta}}_{0}\right)\left(2\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}+3(1-\widetilde{e}_{10}^{2})\frac{\text{D}\widetilde{H}_{x0}}{\widetilde{H}_{0}}\right)\bigg]\frac{\text{D}\widetilde{{\it\phi}}}{\widetilde{H}_{0}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\bigg[\left(\frac{\widetilde{{\it\chi}}_{\ast }-\widetilde{{\it\chi}}}{1+\widetilde{{\it\chi}}}\widetilde{N}-\widetilde{{\it\theta}}_{0}\right)\left(\widetilde{{\it\alpha}}^{2}(1-\widetilde{e}_{20}^{2})+\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}(1-3\widetilde{e}_{10}^{2})\frac{\text{D}\widetilde{H}_{x0}}{\widetilde{H}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}\widetilde{e}_{10}\text{D}\widetilde{{\it\theta}}_{0}\bigg]\frac{\widetilde{{\it\phi}}}{\widetilde{H}_{0}}-\left(\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}+(1-\widetilde{e}_{10}^{2})\frac{\text{D}\widetilde{H}_{x0}}{\widetilde{H}_{0}}\right)\widetilde{{\it\theta}}-\widetilde{e}_{10}\text{D}\widetilde{{\it\theta}},\end{eqnarray}$$
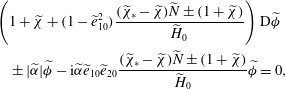$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\widetilde{{\it\chi}}+(1-\widetilde{e}_{10}^{2})\frac{(\widetilde{{\it\chi}}_{\ast }-\widetilde{{\it\chi}})\widetilde{N}\pm (1+\widetilde{{\it\chi}})}{\widetilde{H}_{0}}\right)\text{D}\widetilde{{\it\phi}}\nonumber\\ \displaystyle & & \displaystyle \quad \pm \,|\widetilde{{\it\alpha}}|\widetilde{{\it\phi}}-\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{10}\widetilde{e}_{20}\frac{(\widetilde{{\it\chi}}_{\ast }-\widetilde{{\it\chi}})\widetilde{N}\pm (1+\widetilde{{\it\chi}})}{\widetilde{H}_{0}}\widetilde{{\it\phi}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{u}=\widetilde{v}=\widetilde{w}=\widetilde{{\it\theta}}=0\quad \text{at }\bar{x}=\pm 1.\end{eqnarray}$$
Equation (6.4) is obtained by multiplying (5.5) by
${\it\alpha}$
, (5.6) by
${\it\beta}$
, adding them together, and dividing the result by
$\widetilde{{\it\alpha}}$
. Note that only (6.5) contains
$\widetilde{w}$
and
$\widetilde{{\it\beta}}$
and thus it can be solved for any particular value of
$\widetilde{{\it\beta}}$
after
$\widetilde{{\it\sigma}}$
,
$\widetilde{P}$
and
$\widetilde{{\it\phi}}$
are found from (6.2)–(6.4), (6.6) and (6.7), which form an equivalent two-dimensional problem obtained by formally setting
$\widetilde{w}=\widetilde{{\it\beta}}=0$
. It is important to note though that the notion of an equivalent two-dimensional problem in the current context is somewhat different from that arising in problems dealing with non-magnetic fluids. The reason is that even if
$\widetilde{w}$
and
$\widetilde{{\it\beta}}$
are set to zero in the above Squire-transformed equations the external magnetic field remains three-dimensional. In general it still has three non-zero components in the
$x$
,
$y$
and
$z$
directions and thus it needs to be described using two coordinate angles
${\it\delta}$
and
${\it\gamma}$
that act as independent control parameters of the problem. The above transformations simply mean that we conveniently view the
$y$
direction as the periodicity direction of the perturbation structures that arise, while the vector of the applied magnetic field can be arbitrarily oriented. More specifically, the axes of the instability rolls are considered to be always parallel to the
$z$
axis in figure 1 so that
${\it\gamma}=0^{\circ }$
(
${\it\gamma}=90^{\circ }$
) means that the magnetic field has a component in the plane of the fluid layer that is perpendicular (parallel) to the roll axes. The values of
$0^{\circ }<{\it\gamma}<90^{\circ }$
are interpreted accordingly. For the sake of brevity in the following sections we will for convenience refer to instability patterns computed using the above transformed equations for
${\it\gamma}=0^{\circ }$
and
${\it\gamma}=90^{\circ }$
as transverse and longitudinal rolls, respectively, while patterns obtained for all other values of
${\it\gamma}$
will be referred to as oblique rolls. We will also refer to angle
${\it\delta}$
as the field inclination angle and angle
${\it\gamma}$
as the angle between the axes of the instability rolls and the in-layer component of the applied magnetic field.
7. Numerical results
7.1. Discretisation
Equations (6.2)–(6.7) are discretised using the pseudo-spectral Chebyshev collocation method as introduced in Ku & Hatziavramidis (Reference Ku and Hatziavramidis1984), Hatziavramidis & Ku (Reference Hatziavramidis and Ku1985) and implemented in Suslov & Paolucci (Reference Suslov and Paolucci1995a
,Reference Suslov and Paolucci
b
). This spatial approximation converges exponentially quickly so that 71 collocation points used in the current computations guarantee that all digits in the reported numerical results are significant and accurate. Upon discretisation and exclusion of (6.5), which is the only equation containing
${\it\beta}$
, the system of (6.2)–(6.7) results in a generalised algebraic eigenvalue problem for the complex amplification rate
$\widetilde{{\it\sigma}}$
$$\begin{eqnarray}(\widetilde{{\it\sigma}}\unicode[STIX]{x1D653}+\unicode[STIX]{x1D654})\boldsymbol{q}=\mathbf{0},\end{eqnarray}$$
where
$\unicode[STIX]{x1D653}$
and
$\unicode[STIX]{x1D654}=Y(\widetilde{{\it\sigma}},\widetilde{Ra}_{m},\widetilde{\mathit{Pr}},\widetilde{{\it\chi}},\widetilde{{\it\chi}}_{\ast };{\it\delta},{\it\gamma})$
are matrices and eigenvector
$\boldsymbol{q}$
contains the discretised components of
$(\widetilde{u},\widetilde{v},\widetilde{P},\widetilde{{\it\theta}},\widetilde{{\it\phi}})^{\text{T}}$
. The eigenvalue problem is solved using the Matlab (MATLAB 2013) function eig. Once both
$\widetilde{{\it\sigma}}$
and
$\boldsymbol{q}$
are found (6.5) is written as
$$\begin{eqnarray}\left(\mathit{Pr}\left(\text{D}^{2}-\widetilde{{\it\alpha}}^{2}\right)-\widetilde{{\it\sigma}}\right)\widetilde{w}=\text{i}\widetilde{{\it\beta}}\left(\widetilde{P}+\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}\left(\widetilde{e}_{10}\text{D}\widetilde{{\it\phi}}+\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{20}\widetilde{{\it\phi}}\right)\right)\end{eqnarray}$$
and solved for
$\widetilde{w}$
. The inverse Squire’s transformation (6.1) then recovers full three-dimensional solutions for perturbations.
7.2. Check of numerical accuracy
In order to test the numerical code, the critical values for the magnetic convection threshold in a perpendicular (
${\it\delta}=0^{\circ }$
) external magnetic field with magnitude
$H^{e}=100$
for the case of
$\widetilde{\mathit{Pr}}=130$
and
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=4$
have been computed using relation (3.11), and the critical values
$\widetilde{Gr}_{mc}=1.387$
and
$\widetilde{{\it\alpha}}_{c}=1.928$
are obtained, which agree well with the values of
$\widetilde{Gr}_{mc}=1.385$
and
$\widetilde{{\it\alpha}}_{c}=1.95$
computed from the corresponding data reported in Finlayson (Reference Finlayson1970). The magnetic convection threshold for
$\widetilde{\mathit{Pr}}=130$
and
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=5$
is also determined and the critical values
$\widetilde{Gr}_{mc}=1.3981$
and
$\widetilde{{\it\alpha}}_{c}=1.9365$
are obtained, which are identical to those reported in Suslov (Reference Suslov2008). As an additional check the critical values of
$\widetilde{Ra}_{mc}=160.543$
and
$\widetilde{{\it\alpha}}_{c}=1.8045$
were computed for the normal field
$H^{e}=100$
in the limit of a paramagnetic fluid with
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=10^{-3}$
. These values are in excellent agreement with the respective values of
$2568.476/16=160.530$
and
$3.609/2=1.8045$
reported in Huang et al. (Reference Huang, Edwards and Gray1997) (the coefficients of
$1/16$
and
$1/2$
are due to the differences between the non-dimensionalisation scales used).
7.3. Flow stability characteristics
The numerical values of critical parameters for thermomagnetic convection arising in magnetic fields of various orientations and intensities are given in tables 2–4. The data in the tables warrant a number of general conclusions.
Table 2. The critical values of
$\widetilde{Ra}_{m}$
,
$\widetilde{{\it\alpha}}$
and disturbance wave speed
$\widetilde{c}=-\widetilde{{\it\sigma}}^{I}/\widetilde{{\it\alpha}}$
and the corresponding perturbation energy integrals
${\rm\Sigma}_{k}$
and
${\rm\Sigma}_{m1}$
for magnetoconvection at
${\it\delta}=0^{\circ }$
,
$H^{e}=100$
(odd-numbered lines),
$H^{e}=10$
(even-numbered lines) and various values of
$\widetilde{{\it\chi}}$
and
$\widetilde{{\it\chi}}_{\ast }$
.
Table 3. Same as table 2 but for transverse rolls at
${\it\delta}=10^{\circ }$
and
${\it\gamma}=0^{\circ }$
.
Table 4. Same as table 2 but for longitudinal rolls at
${\it\delta}=10^{\circ }$
and
${\it\gamma}=90^{\circ }$
.
The magneto-convective instability arising in a normal field remains stationary regardless of the specific magnetic properties of the fluid and the magnitude of the applied magnetic field. This is in agreement with the findings previously reported, for example, in Finlayson (Reference Finlayson1970), Huang et al. (Reference Huang, Edwards and Gray1997) and Suslov (Reference Suslov2008). However, in contrast to all previous studies, the instability threshold
$\widetilde{Ra}_{mc}$
is found to depend not only on the values of the magnetic susceptibilities
${\it\chi}$
and
${\it\chi}_{\ast }$
but also on the magnitude of the applied magnetic field, namely, the decrease of the characteristic non-dimensional field parameter
$N$
promotes instability and increases the wavelength of the patterns that arise. This dependence, however, remains relatively weak: the largest difference between the critical values of magnetic Rayleigh numbers and wavenumbers is found to be under 3.5 % and 1.5 %, respectively, for a fluid with the highest degree of magnetisation investigated (
${\it\chi}={\it\chi}_{\ast }=5$
) when the external magnetic field is changed by a factor of 10. The comparison of the current results with our previous study (Suslov Reference Suslov2008) shows that the dependence of the critical parameters on the magnitude of the magnetic field is traced back to the form of the constitutive magnetisation (2.7). Its linearisation used in all previous studies cited above eliminates the dependence of the threshold values on the amplitude of the normal magnetic field. However, as shown in § 4 such an idealisation is only robust for the case of paramagnetic fluids with small magnetic susceptibilities but it should not be expected to be uniformly valid for realistic ferromagnetic fluids.
If the dependence of the fluid magnetisation on the magnitude of the applied magnetic field remains linear,
$\!$
that is if
${\it\chi}\approx {\it\chi}_{\ast }$
, see figure 2,
$\!$
then the magnetoconvection threshold parameters decrease monotonically with the values of magnetic susceptibilities to their limiting values
$(\widetilde{Ra}_{mc},\widetilde{{\it\alpha}}_{c})\approx (160.5,1.805)$
that are independent of the magnitude of the applied magnetic field. However, when the fluid magnetisation approaches saturation so that
${\it\chi}<{\it\chi}_{\ast }$
, the variation of the differential and integral susceptibilities have opposite influences on the threshold: the decrease of
${\it\chi}$
at fixed
${\it\chi}_{\ast }$
promotes instability while the decrease of
${\it\chi}_{\ast }$
at fixed
${\it\chi}$
delays it. In realistic ferrofluids, however, the values of both
${\it\chi}$
and
${\it\chi}_{\ast }$
decrease with the increasing magnetic field, but at different rates, see figure 2(a). Therefore, it is not straightforward to anticipate what the overall effect of a changing magnetic field on the convection onset could be and one needs to rely on the specific computational results. In particular, the data in table 2 show that the critical value of magnetic Rayleigh number decreases by more than 10 % when progressively stronger magnetic field is applied to a layer of experimental ferrofluid with the initial susceptibilities
${\it\chi}={\it\chi}_{\ast }\approx 3$
that are reduced to
${\it\chi}\approx 1.5$
and
${\it\chi}_{\ast }\approx 2.5$
during a typical experimental run.
It is remarkable that, as seen from tables 3 and 4, when an oblique magnetic field is applied to the layer the trends described above are reversed even for small field inclination angles
${\it\delta}$
: now the decrease of
${\it\chi}$
at fixed
${\it\chi}_{\ast }$
delays instability while the decrease of
${\it\chi}_{\ast }$
at fixed
${\it\chi}$
promotes it. This indicates the qualitative difference between the instability mechanisms present in normal and oblique fields that we will discuss in more detail in the following sections. The numerical data given in tables 2–4 also demonstrate a very strong stabilisation effect of the field inclination compared to the normal field situation that is further illustrated in figures 6(a) and 8(a). Such a stabilisation is observed regardless of the specific magnetic properties of the fluid for all investigated values of
${\it\chi}$
and
${\it\chi}_{\ast }$
.
Figure 6. (a) Critical magnetic Rayleigh number
$\widetilde{Ra}_{mc}$
and (b) wavenumber
$\widetilde{{\it\alpha}}_{c}$
as functions of the field inclination angle
${\it\delta}$
for transverse rolls at
$H^{e}=10$
and
${\it\gamma}=0^{\circ }$
. The respective plots for
$H^{e}=100$
are indistinguishable within the figure resolution.
An even more striking effect of the field inclination is evident from the data presented in table 3: the transverse instability rolls computed for
${\it\gamma}=0^{\circ }$
become oscillatory resulting in waves propagating along the direction of the field component that is tangential to the plane of the fluid layer. This is a somewhat unexpected result given that the unperturbed problem possesses a full planar symmetry with no preferred direction. Moreover Huang et al. (Reference Huang, Edwards and Gray1997) even argued that the instability in this problem can only be stationary. The resolution of this apparent paradox is prompted by the comparative computational data presented in table 3 for
$H^{e}=10$
and
$H^{e}=100$
and by figure 7. They show that the magnitude of the disturbance wave speed
$|\widetilde{c}|=\left|{\it\sigma}^{I}/\widetilde{{\it\alpha}}_{c}\right|$
is approximately inversely proportional to the magnitude of the applied magnetic field
$H^{e}$
, which in turn is proportional to the field parameter
$N$
characterising the nonlinearity of the magnetic field distribution within a layer. It is assumed in Huang et al. (Reference Huang, Edwards and Gray1997) that
$N\rightarrow \infty$
and effectively postulated that the magnetic field within the layer varies linearly. No unsteady patterns were found there. Therefore, we conclude that the main reason for the appearance of oscillatory instability in the current problem is the nonlinearity of the magnetic field within the ferrofluid layer as has been discussed in § 4.
Figure 7. Critical wave speed
$\widetilde{c}=-\widetilde{{\it\sigma}}^{I}/\widetilde{{\it\alpha}}_{c}$
as a function of the field inclination angle
${\it\delta}$
for transverse rolls at
${\it\gamma}=0^{\circ }$
for (a)
$H^{e}=10$
and (b)
$H^{e}=100$
.
Figure 8. Same as figure 6 but for longitudinal rolls at
${\it\gamma}=90^{\circ }$
.
The values of the threshold parameters for longitudinal rolls computed for
${\it\gamma}=90^{\circ }$
are given in table 4. Remarkably, they remain strictly stationary for all values of the governing parameters. Figure 8(a) shows that, similar to the critical magnetic Rayleigh number for transverse rolls, the one for longitudinal rolls increases quickly with the field inclination angle
${\it\delta}$
. However, for all non-zero angles it remains smaller than that of transverse rolls. This is consistent with findings of Huang et al. (Reference Huang, Edwards and Gray1997) for paramagnetic fluids and confirms an experimental fact that the axes of thermomagnetic rolls appearing away from the boundaries always align with the tangential component of the magnetic field since this configuration is found to be less stable than a transverse one. Having said this, we emphasise that even though longitudinal rolls are always expected to dominate the observed instability patterns, the possibility of the existence of transverse rolls should not be ignored for at least two reasons. Firstly, unlike in paramagnetic fluids, in ferrofluids they are qualitatively different from their longitudinal counterparts as they are unsteady. They are also characterised by a wavenumber that depends sensitively on the field inclination angle, see figure 6(b), while the wavenumber of longitudinal rolls remains almost constant as the field inclination is increased, see figure 8(b). Secondly, near the boundaries of a layer the longitudinal rolls may be suppressed due to the geometry of the boundary or other influences that are not present in unbounded domains so that oscillatory transverse rolls might be preferred. The experimental observations reported in our previous work (Suslov et al.
Reference Suslov, Bozhko, Sidorov and Putin2012) (see figures 9 and 11 there) indeed indicate that this might have been the case in the near-boundary regions of a finite experimental enclosure.
Given that the two limiting cases of transverse and longitudinal rolls have qualitatively different characteristics it is of interest to investigate how and at what value of the intermediate angle the transition between stationary and oscillatory patterns occurs. Thus we have computed the stability characteristics of oblique rolls for various values of magnetic susceptibilities and field inclination angles. These are presented in figures 9–11. They confirm that both the critical magnetic Rayleigh number and wavenumber increase continuously and monotonically from longitudinal to transverse rolls and the rate at which they do grows quickly with the field inclination angle. The only exception is the behaviour of the wavenumber for relatively large field inclination angles when it reaches its maximum value for oblique rolls forming an angle of about 45
$^{\circ }$
with the tangential field component and then starts decreasing. Of particular interest is the behaviour of the disturbance wave speed. It grows continuously from zero for longitudinal rolls to its maximum for transverse rolls; however, the most rapid growth is observed for
${\it\gamma}\lesssim 50^{\circ }$
and
${\it\gamma}\gtrsim 130^{\circ }$
. This suggests that if the value of magnetic Rayleigh number is gradually increased in an experiment then the stationary rolls aligned with the tangential component of the field will appear first. Subsequently, they would be unsteadily modulated by a periodic pattern forming an angle of about
$40$
–
$45^{\circ }$
with the axes of the stationary rolls. A further increase of magnetic Rayleigh number would lead to the increase of the modulation frequency and wavenumber and to the re-orientation of the modulating pattern so that it would become closer to orthogonal with respect to the original stationary rolls.
Figure 9. (a) Critical magnetic Rayleigh number
$\widetilde{Ra}_{mc}$
, (b) wavenumber
$\widetilde{{\it\alpha}}_{c}$
and (c) wave speed
$\tilde{c}$
as functions of the azimuthal angle
${\it\gamma}$
for various angles
${\it\delta}$
for
$H^{e}=100$
and
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=5$
.
Figure 10. Same as figure 9 but for
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=3$
.
Figure 11. Same as figure 9 but for
$\widetilde{{\it\chi}}=1.5$
and
$\widetilde{{\it\chi}}_{\ast }=2.5$
.
It is also noteworthy that the
$\widetilde{Ra}_{mc}$
and
$\widetilde{{\it\alpha}}_{c}$
curves are symmetric with respect to the
${\it\gamma}=90^{\circ }$
line, while the
$\widetilde{c}_{c}$
line is centro-symmetric with respect to
$(\widetilde{c}_{c},{\it\gamma})=(0,90^{\circ })$
. To shed light on why this is so refer to figure 5(a,c) where the concave south–west/north–east magnetic field lines are shown for
${\it\gamma}=0^{\circ }$
. If
${\it\gamma}$
is changed to
$180^{\circ }$
the magnetic field lines re-orient to become north–west/south–east and convex. As has been discussed above, the appearance of oscillatory disturbances is a consequence of the nonlinearity of the magnetic field. Therefore we conclude that it is this change of the curvature of magnetic lines in the plane perpendicular to the roll axes that is responsible for the change of the sign of the disturbance wave speed.
7.4. Perturbation energy balance
To confirm the physical nature of the observed instabilities it is instructive to consider the mechanical energy balance in a way similar to that used for example in Hart (Reference Hart1971), Suslov & Paolucci (Reference Suslov and Paolucci1995a
), Suslov, Bozhko & Putin (Reference Suslov, Bozhko, Putin, Indeitsev and Krivtsov2008) and Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012). We multiply the momentum equations (6.3) and (6.4) by the complex-conjugate velocity components
$\bar{u}$
and
$\bar{v}$
, respectively, add them together and integrate by parts across the layer using the boundary conditions (6.9) and the continuity equation (6.2) to obtain
$$\begin{eqnarray}\widetilde{{\it\sigma}}{\rm\Sigma}_{k}={\rm\Sigma}_{vis}+{\rm\Sigma}_{m1}+{\rm\Sigma}_{m2},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle {\rm\Sigma}_{k} & = & \displaystyle \int _{-1}^{1}\underbrace{(|\widetilde{u}|^{2}+|\widetilde{v}|^{2})}_{E_{k}}\text{d}\bar{x}>0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Sigma}_{vis} & = & \displaystyle \int _{-1}^{1}\underbrace{-\widetilde{\mathit{Pr}}(\widetilde{{\it\alpha}}^{2}(|\widetilde{u}|^{2}+|\widetilde{v}|^{2})+|\text{D}\widetilde{u}|^{2}+|\text{D}\widetilde{v}|^{2})}_{E_{vis}}\text{d}\bar{x}=-1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Sigma}_{m1} & = & \displaystyle \int _{-1}^{1}\underbrace{-\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\text{D}\widetilde{H}_{x0}\widetilde{e}_{10}\widetilde{{\it\theta}}\bar{\widetilde{u}}}_{E_{m1}}\text{d}\bar{x},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Sigma}_{m2} & = & \displaystyle \int _{-1}^{1}E_{m2}\text{d}\bar{x}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{m2} & = & \displaystyle -\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\text{D}\widetilde{H}_{x0}\bar{\widetilde{u}}\frac{\widetilde{{\it\theta}}_{0}}{\widetilde{H}_{0}}\left((1-\widetilde{e}_{10}^{2})\text{D}\widetilde{{\it\phi}}-\,\text{i}\widetilde{{\it\alpha}}\widetilde{e}_{10}\widetilde{e}_{20}\widetilde{{\it\phi}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\widetilde{Ra}_{m}\widetilde{\mathit{Pr}}\widetilde{{\it\theta}}_{0}\left(\widetilde{e}_{10}\bar{\widetilde{u}}\text{D}^{2}\widetilde{{\it\phi}}+\text{i}\widetilde{{\it\alpha}}(\widetilde{e}_{10}\bar{\widetilde{v}}+\widetilde{e}_{20}\bar{\widetilde{u}})\text{D}\widetilde{{\it\phi}}-\widetilde{{\it\alpha}}^{2}\widetilde{e}_{20}\bar{\widetilde{v}}\widetilde{{\it\phi}}\right).\end{eqnarray}$$
Given that
${\rm\Sigma}_{k}$
is positive definite, the perturbation energy balance (7.3) determines the complex growth rate
${\it\sigma}$
of linear instability. It does not contain the modified pressure
$P$
as it integrates to zero identically. This confirms that the potential component of the Kelvin force included in
$P$
indeed has no effect on the stability of a layer of ferromagnetic fluid as has been stated in § 2. The viscous dissipation contribution to the energy perturbation balance is always negative and, given that the eigenfunctions of the linearised problem are defined up to a multiplicative constant, we scale them in such a way that
${\rm\Sigma}_{vis}\equiv -1$
. The remaining two terms are of magnetic nature. As discussed in Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012),
${\rm\Sigma}_{m1}$
represents the variation of fluid magnetisation (and thus of the local Kelvin force) due to the thermal perturbations while
${\rm\Sigma}_{m2}$
describes the energy contribution associated with the induced magnetic field variations. Separating the real (Re) and imaginary (Im) parts of (7.3) we obtain at the critical point
$$\begin{eqnarray}0=\text{Re}({\rm\Sigma}_{m1}+{\rm\Sigma}_{m2})-1,\quad \widetilde{{\it\sigma}}^{I}{\rm\Sigma}_{k}=\text{Im}({\rm\Sigma}_{m1}+{\rm\Sigma}_{m2}).\end{eqnarray}$$
The energy terms with positive real parts promote instability, while the ones with negative suppress it. Equation (7.6b ) demonstrates that the nature of the detected oscillatory instabilities is purely magnetic.
Tables 2–4 contain numerical data for various perturbation energy terms that enable us to draw a number of general conclusions. Firstly, the magnitude of the kinetic energy term
${\rm\Sigma}_{k}$
never exceeds the value of about 10 % of the viscous dissipation, while the magnitude of the magnetic contribution
${\rm\Sigma}_{m1}$
always exceeds the dissipation value. This confirms that the instability is of magnetic rather than hydrodynamic or thermal nature and that the visible fluid motion triggered by the instability is not the main recipient of the energy supplied to the system (in experiments such as those described in Suslov et al. (Reference Suslov, Bozhko, Sidorov and Putin2012) the energy is supplied by heat exchangers attached to the layer walls). Secondly, since Re(
${\rm\Sigma}_{m1}$
) is always positive we conclude that the specific mechanism triggering the instability is the thermally induced variation of fluid magnetisation. Thirdly, since Re
$({\rm\Sigma}_{m1})>1$
then, according to (7.6a
), Re
$({\rm\Sigma}_{m2})<0$
. This means that the variation of the applied magnetic field caused by perturbations always plays a stabilising role. In summary, the analysis of mechanical energy balance shows that the energy received by the system through a thermal exchange with the ambient is mostly spent on varying the local magnetisation of the fluid. In turn the latter triggers fluid motion, which is an observable signature of instability. The remaining part of the received energy is spent on modifying the magnetic field. Since the variation of magnetic field is not limited to the interior of the layer this energy largely leaves it and thus cannot be used for supporting a mechanical instability within the system.
Typical distributions of the perturbation energy integrands for instability patterns arising in normal and oblique fields are shown in figures 12 and 13, respectively. Since the integrand behaviour for longitudinal rolls is found to be qualitatively similar to that for stationary rolls arising in a normal field, only the results for transverse rolls are presented here. As expected, the viscous dissipation
$E_{vis}$
occurs mostly near the solid boundaries and the kinetic energy
$E_{k}$
of perturbations is maximised near the centre of the layer. Figures 12(b) and 13(b) show that the magnetisation variation effect
$E_{m1}$
plays a destabilising role uniformly across the complete width of the layer and with the maximum near its centre. On the other hand, the stabilising effect of magnetic field modification
$E_{m2}$
is most pronounced near the walls of the layer. This is intuitively expected since the internal magnetic field near the walls defines the external field via the field-matching boundary conditions (5.12) and (5.13). The overall role of the
$E_{m1}$
and
$E_{m2}$
effects does not change in the oblique field; however, the field inclination introduces a noticeable asymmetry. The maximum of the destabilising influence shifts toward the hot wall: compare the locations of the maxima of the dash-dotted lines in figures 12(b) and 13(b). This is because the unstable magnetic buoyancy stratification in oblique fields is more pronounced near the hot wall, see figure 5(b,d) and the discussion in § 4. While the magnitude of Re
$(E_{m1})$
determines whether the instability is present, figure 13(c) shows that it is the magnitude of Im
$(E_{m2})$
that predominantly defines the sign of
$\widetilde{{\it\sigma}}^{I}$
and thus the propagation direction of transverse and oblique rolls.
Figure 12. Disturbance energy integrands at the critical point of magnetoconvection threshold
$\widetilde{Ra}_{mc}=176.8$
,
$\widetilde{{\it\alpha}}_{c}=1.909$
at
$H^{e}=10$
,
${\it\delta}={\it\gamma}=0^{\circ }$
and
${\it\chi}={\it\chi}_{\ast }=3$
.
Figure 13. Same as figure 12 but for
$\widetilde{Ra}_{mc}=548.4$
,
$\widetilde{{\it\alpha}}_{c}=2.135$
,
${\it\delta}=10^{\circ }$
.
7.5. Perturbation fields
To complete this report we present the plots of typical perturbation fields arising in normal and inclined magnetic fields. The mechanism driving convection is straightforward to see from figure 14 for a normal field. Consider, for example, the region near
$y=3$
. There the thermal perturbation
${\it\theta}_{1}$
leads to local cooling. As a result this region becomes more strongly magnetised, see figure 14(c) for
$M_{1}$
, and the fluid there is driven toward the hot wall where the basic magnetic field is stronger, see figure 3(a,d). This is reflected in the plot of the velocity field (figure 14
a) showing that indeed cool fluid flows toward the hot wall (from right to left) there. This situation is similar to gravitational convection arising in a fluid heated from below.
Figure 14. Perturbation eigenfunctions of (a) the fluid velocity
$\boldsymbol{v}_{1}=(u,v)$
, (b) temperature
${\it\theta}_{1}$
, (c) magnetisation
$M_{1}$
and (d) magnetic field
$H_{1}$
, for magnetoconvection at
$H^{e}=10$
,
${\it\delta}={\it\gamma}=0^{\circ }$
and
$\widetilde{{\it\chi}}=\widetilde{{\it\chi}}_{\ast }=3$
at the critical point
$\widetilde{Ra}_{mc}=176.8$
,
$\widetilde{{\it\alpha}}_{c}=1.909$
. The field values increase from black to white.
When the applied magnetic field is inclined the mechanism driving convection remains the same, even though it is less straightforward to recognise it from figure 15. The thermal and magnetisation perturbation cells align with the applied magnetic field and so does the main fluid flow direction.
Figure 15. Same as figure 14 but for
$\widetilde{Ra}_{mc}=548.4$
,
$\widetilde{{\it\alpha}}_{c}=2.135$
,
${\it\delta}=10^{\circ }$
.
It is noteworthy that the perturbation cells for magnetic field
$H_{1}$
corresponding to transverse rolls do not align with the rest of the perturbation field, see figure 15(d). They also become asymmetric. At the same time the structure of the perturbation fields for longitudinal rolls in an inclined field (not shown) remains very similar to that seen in figure 14 for a normal field. Therefore, it is logical to conclude that the phase shift between the magnetic field
$H_{1}$
and the rest of the perturbation fields is responsible for the change of the instability character to oscillatory for transverse and oblique rolls.
8. Conclusions
In the current study the stability of a differentially heated layer of ferrofluid has been analysed and contrasted to that of a layer of paramagnetic fluid considered previously in Huang et al. (Reference Huang, Edwards and Gray1997). The magnetic properties of a ferrofluid have been estimated using the experimental data and the modified mean field model that has been shown to be more accurate than the classical Langevin’s law of magnetisation (Pshenichnikov Reference Pshenichnikov2007; Lebedev & Lysenko Reference Lebedev and Lysenko2011). In contrast to the linear distribution of magnetic field that exists in a layer of a paramagnetic fluid, the magnetic field in a layer of a ferrofluid varies nonlinearly. The nonlinear distributions of unperturbed magnetic and magnetisation fields have been derived asymptotically and computed numerically for a range of fluid properties corresponding to realistic ferrofluids, including that used in previous experiments (Suslov et al. Reference Suslov, Bozhko, Sidorov and Putin2012). It has been shown that unlike in paramagnetic fluids such distributions in ferrofluids depend not only on the inclination of the applied magnetic field, but also on its magnitude.
The field nonlinearity found in ferrofluids is responsible for breaking the symmetry, which in turn results in several qualitative differences between instabilities detected in para- and ferromagnetic fluids. In particular, it is shown that in ferromagnetic fluids the instability arises preferentially near the hot wall bounding the layer. This is traced back to the curvature of the magnetic field lines inside a ferrofluid layer. The instability leading to the appearance of oblique and transverse rolls in a ferrofluid is found to be oscillatory, which is not the case in paramagnetic fluids. Even though, similar to paramagnetic fluids, our linear stability analysis demonstrates that stationary longitudinal rolls are least stable, the possibility of the existence of propagating oblique and transverse rolls cannot be disregarded in experimental studies, especially those concerned with flows in finite geometries where the proximity of solid boundaries can suppress longitudinal rolls. The cited experimental observations indeed indicate that. Moreover, our preliminary results of weakly nonlinear analysis of perturbed thermomagnetic flows that will be reported elsewhere indicate that the bifurcation leading to the appearance of stationary longitudinal rolls is supercritical. However, this might not be the case for propagating oblique and transverse patterns where the degree of symmetry breaking is generally higher than for longitudinal rolls. Therefore it may be possible that the character of a bifurcation leading to non-stationary convection patterns could change to subcritical, at least in some parametric regions. In this case, in a realistic experiment, stationary longitudinal and finite-amplitude propagating oblique patterns can co-exist and interact. Even if it is confirmed that the bifurcation for travelling patterns remains supercritical so that non-stationary flow structures appear at necessarily larger governing parameters than the critical values for longitudinal rolls, they will still be experimentally observable in the form of time-dependent small-amplitude modulations of the main stationary structures once and thus cannot be disregarded.
Disturbance energy considerations have been used to determine that the physical cause of the detected instabilities is the variation of fluid magnetisation due to thermal disturbances. However, the related variation of a magnetic field is found to draw energy from the perturbed field, thus playing a stabilising role. It is also found that it is this magnetic field variation effect that determines the propagation direction of oblique and transverse instability patterns in a ferrofluid layer in inclined magnetic fields.
Acknowledgements
The authors would like to thank Professors G. F. Putin and A. A. Bozhko and Mr A. S. Sidorov of the Physics Department at Perm State National Research University, Russia for discussing the relevance of the presented computational results to the experimental studies currently conducted in their group.
