INTRODUCTION
Optimal growth models usually make the assumption of a constant and strictly positive utility social discount rate. This practice has long been questioned, but is still widely used, maybe because of the lack of a convincing alternative.
The first doubt goes back at least to the well-known criticisms by Ramsey and Harrod of a strictly positive utility social discount rate [Ramsey (1928), Harrod (1948)], and has led to the so-called undiscounted utilitarianism. But Koopmans (1960) has stressed the drawbacks of this approach: it usually leads to unrealistically high optimal saving rates for the present and near-future generations, and so to a sacrifice of the present and of the near future instead of the supposed sacrifice of the far future implied by a positive discount rate. Nevertheless, the temptation of a zero rate of discount is still very present as far as the environment is concerned because of the very long horizon often involved in environmental matters1
Obviously, the time horizon is especially long for problems such as global warming or nuclear waste disposal.
The usual approach has been challenged by authors arguing that the utility discount rate should be neither constant and positive nor zero but should be decreasing in the course of time. They claim that empirical evidence supports that decrease. Harvey (1994), Heal (1998), Loewenstein and Prelec (1992), Laibson (1996, 1997), and Barro (1999) propose formulas of decreasing discounting justified by considerations of individual psychology. But the choice of a utility discount rate in normative models is an ethical one, as stressed by Heal (1998) and Ayong Le Kama (2001), and it is less than obvious that a social planner should only reflect in this choice the representative consumer's psychology. Gollier (2002a, 2002b) and Weitzman (1998) justify decreasing discounting in a partial equilibrium setup by the uncertainty on the future growth rate of the economy or on the future interest rate. Li and Löfgren (2000) study an economy with heterogeneous agents differing by their utility discount rate (constant and exogenous) but identical in all other respects. They show that this economy behaves as if there was a unique representative agent with a decreasing discount rate, tending in the long run toward the rate of the more patient agent. Here, the decreasing discount rate is not an assumption but a consequence of the heterogeneity.
Another strand of literature, disconnected from environmental concerns, studies the question of habit formation, and introduces a utility discount factor depending on present and past consumption levels [Epstein (1987), Becker, Boyd, and Sung (1989), Obstfeld (1990), Das (2003)]. Obstfeld (1990) gives a formal treatment of the simple optimal growth model with this utility discount factor, and concludes that most of the time this assumption does not qualitatively change the optimal growth paths, in comparison with the case of an exogenous constant discount rate.
We want here to extend Obstfeld's approach to a growth model in which environment matters [Pittel (2002) has the same objective in a different framework]. We consider two ways by which the environmental quality could affect the social intertemporal welfare: the usual direct effect of the current level of environmental quality on instantaneous utility (amenity effect), and a less usual indirect effect of current and past levels of environmental quality on the utility discount factor. This discount factor now depends on the path of environmental quality through time. Utility is no longer time-separable, tastes are intertemporally dependent. The discount rate depends on the current state of the environment. In addition, we make the assumption of a positive marginal impatience: the discount rate increases with the level of the environmental quality.
It is possible to rationalize this ethical choice of an endogenous utility discount rate depending on the environmental quality and increasing with it by a sustainable development motive. Society could express in this way a form of intergenerational altruism, consisting in deciding to discount the future at a rate all the lower because the environmental quality is low. That could be a way of introducing sustainability concerns in optimal growth models.2
It could be interesting to study the market economy, where private agents, unaware of sustainability concerns or considering the environmental quality as an externaliy, would discount exponentially, and to look at the way the optimal solutions with endogenous discounting could be implemented.
We then try to elucidate the consequences of such an ethical choice. These consequences are very hard to assess in complex growth models with capital accumulation. Thus, we use a simple framework in which consumption directly comes from the use of environmental services, and so directly causes environmental degradation.3
It is in some sense the worst possible case: there exists neither technical progress enhancing the transformation of environmental services into consumption, nor substitution possibilities between environmental services and manmade capital. There is no means of improving the environmental quality except by natural regeneration. In such a framework, consumption and environmental quality necessarily evolve together in the long run: both increase, or both decrease, or both converge toward a stationary state.
We first study the evolution of the economy and the environment with an exogenous and constant discount rate (Section 2), as a benchmark for the study of the endogenous utility discount case. We present and discuss in Section 3 the assumptions made about the endogenous discount factor and their consequences, and then characterize all the types of optimal paths that the economy can follow under these assumptions. We show that the convergence of the environmental quality toward a steady state occurs only for a very special configuration of the parameters in the exogenous discounting case, whereas it occurs generically in the endogenous discounting one. This happens for a utility discount rate becoming sufficiently high when the environmental quality is high and sufficiently low when the environmental quality is poor. Section 4 concludes.
THE ECONOMY WITH A CONSTANT DISCOUNT RATE
The Model
We introduce an optimal growth model with an environmental asset. This asset can be seen as natural capital or as the environmental quality. It is valued both as a source of consumption of environmental services and as a stock of amenities. The stock of environmental asset S is depleted by consumption C, but regenerates itself at a rate m > 0 taken as constant for simplification. Its dynamics is then described by:

The objective of the social planner is to maximize the present value of the life-time utility of the representative consumer over an infinite horizon. The representative consumer derives felicity4
We follow the convention of Arrow and Kurz (1970) in referring to the subutility functions as felicities. In contrast, the term utility always refers to the planner's intertemporal objective.
and
represent some consumption and environmental quality paths respectively. The social planner seeks to maximize:

subject to:

Assumption 1. The felicity function u(.) is continuous, twice differentiable, and possesses the following properties:5
uC and uS are the first partial derivatives of the function u(.) with respect to its arguments C and S. uCC is likewise the second partial derivative, using obvious notation.
The constant-value Hamiltonian of the previous problem is:

where
is the co-state variable associated with the environmental quality. The first order necessary conditions then give us:


where
, and the transversality condition writes:

ϕ(C, S)≡SuS/CuC>0 by assumption 1 is the ratio of the values of environmental quality and consumption, both evaluated at their marginal felicity. ϕ(.) then reflects the “relative preference for the environment” of the representative agent.
Differentiation of equation (4a) with respect to time leads to the following result:
where η1 = CuCC/uC < 0 is the elasticity of the marginal felicity of consumption with respect to the level of consumption and η2=SuCS/uC[lEg ]0 is the elasticity of the marginal felicity with respect to the level of environmental quality. Substituting this relationship into (4b) yields:

The Balanced Growth Path (BGP)
Existence of a BGP
Given the equation of motion of the environmental quality (1), if the growth rate of the environmental quality is constant along the optimal path, then the ratio C/S is also constant, which indicates that C and S grow at the same rate. Let g be this common rate. We have C/S=m−g. Substituting g into (5) leads to:

Therefore, the feasibility of the BGP, that is the constancy of g, requires:
Assumption 2. (i) The elasticities of the marginal felicity of consumption with respect to consumption, η1, and environmental quality, η2, are constant; (ii) the relative preference for the environment is constant, that is,
.6
Smulders and Gradus (1996) show that (ii) is a necessary condition for the existence of a balanced growth path when the stock of environmental resource is a source of felicity.
These restrictions7
Despite the lack of generality that these restrictions imply, they allow us to study the effect of endogenous discounting in a framework where the benchmark—the case with constant and exogenous discounting—consists in a balanced growth path.

where σ=−1/η1>0 is the intertemporal elasticity of substitution of consumption.
Assumption 3. σ<1.
This assumption is sufficient to ensure the concavity of the felicity function.8
We see easily that the necessary and sufficient condition for concavity is
σ<1 is then sufficient, and we restrict ourselves to this case for technical reasons (see later).
It is easy to show that, with the specification of the felicity function (6), the growth rate along the BGP is:

which may be positive or negative, depending on the parameters.9
The growth rate of consumption and environmental quality along the BGP will be positive if the natural regeneration and the preference for the environment are sufficiently high, and if the discount rate is low enough.
In addition, as S is evolving along the BGP at the rate g and λ at the rate ρ−m−ϕ(m−g), the transversality condition (4c) is fulfilled if and only if (g−m)(1+ϕ)<0, that is, g<m. Given that we have assumed σ<1, the upper bound of g is strictly lower than m: g≤σm<m. The transversality condition is always satisfied.
Properties of the BGP
Introducing the stationary variable x=C/S, we easily show, using the equation of motion of the environmental quality (1) and equation (5), that the dynamic system characterizing the evolution of the economy and the environment reduces to a single equation in x,

where
is the stationary ratio of consumption to environmental quality along the BGP. By (1) and (7), we have:

Equation (8) is unstable. If the x ratio is higher than
the environmental quality will be consumed completely, and if on the contrary it is lower, the environmental quality will grow without bounds and consumption will be driven to zero. The x ratio then takes from the initial time its stationary value
and initial consumption is
THE ECONOMY WITH AN ENDOGENOUS DISCOUNT RATE
The Model
We now introduce an economy in which the social planner uses a discount factor based on the historical path of the environmental quality. In all other respects, the economy is the same as in the previous section. The intertemporal discounted utility function, with variable discount rate, of a representative consumer is now given by:

where the felicity function u(.) satisfies assumptions 1, 2 and 3. The future felicities are discounted at time t with a discount factor equal to
where Δt≥0 is assumed to depend on the past and current levels of the environmental quality, as described by the following equation:

∀St, is the utility discount rate at time t.10
The preference structure, as specified in (10), is recursive in the sense that Δ is allowed to depend on the past and current levels of the environmental quality, as described by equation (11). Thus, a change in the present level of environmental quality will not only have an effect on the current level of felicity but also on the entire future felicity stream.
In the case of an endogenous discounting depending on the past and current levels of consumption, there is considerable disagreement over whether the marginal discount rate should be positive or negative [see Obstfeld (1990)]. Loosely speaking, a positive marginal rate means that rich people are more impatient than poor ones. This assumption is frequently made in the literature related to the question of habit formation, but never satisfactorily justified [see Epstein (1987)]. Obstfeld (1990) justifies his adoption of this assumption by the fact that it is necessary for the convergence of his model. Das (2003) shows that this is not a general property of models with habit formation, which can, under some additional assumptions, be stable even with a negative marginal discount rate. Whatever the psychological explanations that underline each approach, our view is that the final choice is normative. Moreover, we think that the fact that impatience should be increasing or decreasing with the consumption of private goods doesn't imply anything about how impatience should evolve with the public natural capital.11
This is the reason why our model does not reduce to the familiar AK framework of the endogenous growth theory, even if it seems formally identical: the AK model deals with manmade capital, which is a private good, while we want to study endogenous discounting depending on the natural capital, which is a public or at least a merit good.
Assumption 4. θ′(S)>0 and θ′′(S)<0, ∀S>0.
Our choice of a discount rate increasing with the environmental quality is justified by the outcomes of the current debate about discounting and the environment [see Portney and Weyant (1999) for a comprehensive view of this debate]. The main point is to find how to take into account the welfare of the far future generations properly, that the traditional exogenous exponential discounting makes quite irrelevant, without sacrificing the welfare of the present ones; or, as has been stressed by Chichilnisky (1996), how to avoid any dictatorship of the present and of the future. One possible way is to use hyperbolic (decreasing) discounting, but it leads to time-inconsistent choices. Our approach allows us to avoid this. In this context, the positive marginal discount rate reflects the sustainability motive that here underlies endogenous discounting: concerned by intergenerational equity, the society chooses to discount at a rate all the smaller since the environmental quality is low, because in this case environmental questions become pressing. The idea is that an endogenous discounting with a positive marginal discount rate depending on the level of the environmental quality should help to prevent or to limit further deteriorations of the environment.
Following Obstfeld (1990), we consider Δt as a second state variable that accounts for accumulated impatience.12
Because of the nonconstant discount rate, Pontryagin's maximum principle cannot be applied directly. We need this state variable to solve the problem within the standard optimal control approach.

The social planner's program is therefore to maximize (10) subjects to (1) and (12) together with the initial conditions (S0 and Δ0 given) and nonnegativity constraints (Ct≥0, St≥0).
The constant-value Hamiltonian of the social planner's problem is:

where
is the co-state variable associated with environmental quality, and
is the co-state variable associated with the “stock of accumulated impatience” [Obstfeld (1990)].
Applying Pontryagin's maximum principle, we get the following first-order necessary conditions for optimality:



where
and
[thus
], together with the transversality condition:13
On the transversality conditions in infinite horizon problems, see Michel (1982).

Note that, as Obstfeld (1990) points out, when μ converges to a definite long term value, as will be the case later, the third equation (14c) of this system can be integrated into:

which means that μt corresponds to the discounted present value of the future flow of felicities from the standpoint of time t. Given that we have assumed a negative felicity function, we also have μt≤0.
We prove in the Appendix that assumptions 3 and 4 ensure the strict concavity of the maximized Hamiltonian
with respect to S and Δ. So the necessary conditions are also sufficient for an optimum [Seierstad and Sydsaeter (1987)].
We now reduce the system (14a)–(14c) into a more tractable one. Following Palivos, Wang, and Zhang (1997), recall that, along the optimal path,
Because the social planner's program considered here is autonomous,
thus, the Hamiltonian is independent of time along the optimal path. This and the transversality condition (15) imply that
∀t along the optimal path. We can therefore deduce:

The system (14a)–(14b) then writes


The Optimal Paths
Given assumptions 1 and 2, the differentiation of the first-order condition (18a) with respect to time yields:

Substituting the dynamics of the environmental quality (1) and the first-order condition (18b) into this equation, we show that the dynamics of consumption along the optimal path is:

where ε(S)=Sθ′(S)/θ(S) is the elasticity of the utility discount rate θ(.) with respect to the environmental quality. ε(S) is positive under assumption 4. If we reintroduce the variable x=C/S, the dynamic system characterizing the evolution of this economy is given by the motion of the ratio of consumption to environmental quality along the optimal path:

together with the one of the environmental quality (1).
Let us assume that the utility discount rate is bounded:
Assumption 5. (i)
is finite, and (ii)
The first part of this assumption seems reasonable: it means that when the environmental quality becomes very high the discount rate remains bounded.
can be interpreted as the utility discount rate that the social planner would choose if economic activity did not harm environmental quality, which could remain always high. The second part of this assumption just introduces the notation used for the lower bound of the utility discount rate, eventually equal to zero.14
An example of discount rate statisfying assumptions 4 and 5, with
is:

Now we can study all the types of optimal scenarios that can occur with endogenous discounting, given the parameters of the economy.
The stationary state
Let us first look at the existence of a stationary state of the dynamic system (1) and (20).
A stationary solution (x*, S*) of this dynamic system is characterized by
Thus, equation (1) implies x*=m. Substituting this into (20), we easily see that stationary solutions are values S* satisfying the following equation:

Assumption 6. ε′(S)≤0, ∀S.
This assumption demands that the elasticity of the utility discount rate is decreasing in S. It seems reasonable, and in addition it is necessary to ensure the stability of the stationary solution (see later).
PROPOSITION 1. Under assumptions 1–6, there exists a unique stationary equilibrium (x*, S*) characterized by:

if and only if
and
that is, if and only if the upper bound of the utility discount rate is high enough vis-à-vis the relative preference for the environment and the natural regeneration rate and the lower bound low enough.15
If
the second part of this condition is always fulfilled.
Proof. Let us consider the function f(S)=m[1+ϕ+(σ/(1−σ))ε(S)]>0, which corresponds to the RHS of (21). A solution S* of (21) will be such that θ(S*) = f(S*). We know, by assumptions 4 and 5, that θ(S) is strictly increasing from its lower bound
(eventually equal to zero) to its upper bound
In addition, f(S) is positive, and we have f′(S)=m(σ/(1−σ))ε′(S)≤0 under assumption 6. Palivos et al. (1997) show (Lemma 1, p. 212) that under assumption 5(i) we have limS→∞Sθ′(S) = 0, that is, limS→∞ε(S) = 0. Then f(S) decreases monotically for S = 0 to +∞ from f(0) = m[1+ϕ+(σ/(1−σ))ε(0)] to m(1+ϕ). There exists, therefore, a unique value S* such that θ(S*)=f(S*) if and only if
which reduces to
and
PROPOSITION 2. Under assumptions 1–6, the unique stationary equilibrium (x*, S*) is a saddlepoint.
Proof. We can show that the Jacobian matrix of the dynamic system (1) and (20) is:

We then have trJ=θ(S*)>0 and:

because ε′(S*)≤0 by assumption 6 and θ′(S*)>0 by assumption 4.
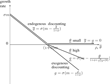
Propositions 1 and 2 state that endogenous discounting associated with a high upper bound of the utility discount rate and a small lower bound of this rate leads to the convergence of the economy toward a locally stable stationary state. In the exogenous discounting case, there is a unique configuration of the parameters ensuring g = 0: the discount rate must satisfy ρ =(1 + ϕ)m, whereas the existence of a stationary state is generic in the endogenous discounting case. In addition, the steady state is unstable in the exogenous case, whereas it is saddlepath stable in the endogenous one. This result means that endogenous discounting with a utility discount rate becoming sufficiently high when the environmental quality is high and sufficiently low when the environment is very depleted allows society to stabilize the environmental quality, which would either collapse or grow infinitely with exogenous discounting. See Figure 1, in which the
curve is growing, and admits
as an asymptote.16
We show easily that the locus
is a curve x(S) increasing in S from
to
It will be shown later that limS→∞ε(S) = 0. So
In addition, it is straightforward to show that the locus
is concave.

The convergence toward a stationary state. Case $\overline{\protect\theta} >m(1+\protect\phi)$, that is, $\overline{x}>m$ and $\protect\underline{\protect\theta} \leq f(0)$, that is, $\protect\underline{x}\leq m$.
More technically, this result shows that the endogenous discounting allows a stabilization of the environmental quality when the bounds of the discount function are such that the range of feasible values of the ratio of consumption to environmental quality includes the regenerative capacity of the environment, m. That is: for
S∈[0, +∞[, a necessary condition for the existence of a stationary solution is
Let us now characterize the optimal paths when no stationary solution exists.
The asymptotically balanced growth path
Adapting Palivos et al. (1997), we say that a solution of the system (1) and (20) is an asymptotically balanced growth path if
exists and is finite (the path is nondegenerate if this limit is strictly positive) and if
. Palivos et al. (1997) show that necessary conditions for the existence of an asymptotically balanced growth solution of this type of problem is an asymptotically constant discount rate and an asymptotically constant elasticity of marginal felicity. These two conditions are by assumption fulfilled here. We then obtain the following:
PROPOSITION 3. Under assumptions 1–6, there exists a unique nondegenerate asymptotically balanced growth path characterized by:

if and only if
that is, the upper bound of the utility discount rate is low enough vis-à-vis the relative preference for the environment and the natural regeneration rate. If,
we have a degenerate asymptotically balanced growth path with
Proof. Let us suppose that there exists a constant and strictly positive growth rate
such that
We then have
Because
, we have limt→∞S=+∞ and assumption 5(i) can be used. As shown by Palivos et al. (1997) (Lemma 1, p. 212), we then have limS→∞ε(S)=0. The long term of the system (1) and (20) is then given by:

from which we deduce (23). By construction, this solution is valid if and only if
that is,
. The case
is straightforward.
We may notice that the asymptotic growth rate
is exactly the same as the balanced growth rate g of the problem with exogenous discounting, provided that
[see equation (7)]. Then if the upper bound of the utility discount rate is exactly the rate that would be chosen by the social planner in the case of exogenous discounting, the endogenous discounting economy follows in the long run the same path as the exogenous one, provided that this rate is low enough.
The system (1) and (20) is a dynamic system involving two variables: the environmental quality S, which grows asymptotically at a constant rate, and the ratio of consumption to environmental quality x, which is stationary in the long run. Moreover, equation (20) makes the growth rate of x depend on the level of S, and so S cannot be easily eliminated to obtain a system involving two variables stationary in the long run. Nevertheless, we obtain the following results.
PROPOSITION 4. Under assumption 1–6, if the upper bound of the utility discount rate is low enough (i.e., if
), then along the asymptotically balanced growth path: (i) x is lower than its long run value, that is,
∀t; (ii) the growth rate of the environmental quality is higher than its long run value, that is,
∀t.
Proof. It is easy to show that equation (20) can be rewritten as:

This equation shows that for any given value of x such that
and x diverges, which is impossible. We therefore deduce that
∀t (this shows the first part of the proposition). We then have
.
Propositions 3 and 4 indicate that endogenous discounting associated with an upper bound of the utility discount rate relatively low leads to an asymptotically balanced growth path, and that in the short run the environmental quality grows faster than in the long run at the expense of lower consumption. Society is less impatient to consume in the short run than in the long run, as long as the environmental quality is not high enough. See Figure 2.

The asymptotically balanced growth path. Case $\overline{\protect\theta} \leq m(1+\protect\phi)$, that is, $\overline{x}\leq m$.
The asymptotical depletion of the environmental quality
We now consider the last feasible case. This case involves a high lower bound of the utility discount rate, such that
PROPOSITION 5. Under assumptions 1–6, if
(i.e., if the lower bound of the utility discount rate is high enough vis-à-vis the preference for the environment and the natural regeneration rate), an asymptotical depletion of the environmental quality occurs, with:

Proof. When the environmental quality decreases toward 0, the long term of the system (1) and (20) is given by:

from which we deduce (24). By construction, this solution is valid if and only if
that is,
.
PROPOSITION 6. Under assumptions 1–6, if
then along the path of asymptotical depletion of the environmental quality: (i) x is higher than its long run value, that is,
∀t; (ii) the environmental quality decreases more quickly than in the long run, that is,
∀t.
Proof. It is easy to show that equation (20) can be rewritten as:

This equation shows that if
and x converges toward zero, which is impossible given the properties of the felicity function. We therefore deduce that
∀t (this shows the first part of the proposition). We then have
.
Propositions 5 and 6 indicate that when the discount rate is bounded from below at a high value, the optimal solution is an asymptotical depletion of the environmental quality, because the society's impatience remains high whatever the level of the natural capital. Furthermore, impatience is higher in the short run than in the long run, because the environmental quality is higher and impatience increases with it. This implies that in the short run environmental quality decreases faster, which allows the society to consume more. See Figure 3. In this case, the ratio of consumption to environmental quality is always higher than the regenerative capacity of the environment m.

The asymptotical depletion of the environmental quality. Case $\protect\underline{\protect\theta} >f(0)$, that is, $\protect\underline{x}>m$.
CONCLUDING REMARKS
This paper has introduced an endogenous utility discount rate depending on the state of the environmental quality. Even if there is a disagreement over whether the marginal discount rate should be positive or negative, in the context of the habit formation literature in which the discount rate depends on consumption for a private motive, we make the assumption of a positive marginal discount rate depending on the state of the environment to reflect the social motive of sustainability. In the context of the long-lasting debate about discounting and the environment, this expresses the fact that if the society is concerned by intergenerational equity, it will choose to discount at a rate all the smaller, because the environmental quality is low.
We show within this framework that under both exogenous and endogenous discounting three qualitatively different scenarios can occur: growth of consumption and the environmental quality to infinity, decrease to zero, and convergence toward a positive steady state (see Figure 4). This last scenario occurs with endogenous discounting when the discount rate is allowed to vary between bounds
and
with
large enough and
small enough, whereas in the exogenous case it occurs only for a discount rate exactly equal to (1+ϕ)m, a razor-edge case. So a stabilization of the environmental quality is more likely to occur with endogenous discounting.

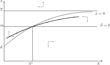
The growth rate as a function of $\protect\rho $ (exogenous discounting) and $\overline{\protect\theta} $ (endogenous discounting).
This methodology can be used in applied cost-benefit analysis. Although implying a utility discount rate decreasing in the course of time if environmental conditions worsen, it avoids the problem of time inconsistency and gives a new justification to this decrease.
APPENDIX
PROOF OF THE STRICT CONCAVITY OF THE MAXIMIZED HAMILTONIAN WITH RESPECT TO S AND Δ
The constant value Hamiltonian is given by equation (13) and the first-order condition for optimality with respect to C is given by equation (14a) and writes
With our specification of the felicity function (6), this equation gives us the following expression for the optimal consumption:

We have

So:

and:

from which we easily deduce:

Given that by equation (16) we have
assumptions 3 and 4 ensure that
We thank El Hadji Fall and Philippe Michel for their valuable comments. Any remaining shortcomings are our responsibility.