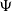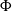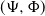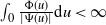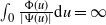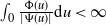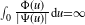1. Introduction
Continuous-state branching processes with immigration (CBI processes) were defined by Kawazu and Watanabe [Reference Kawazu and Watanabe23]. They are scaling limits of Galton–Watson Markov chains with immigration; see e.g. [Reference Kawazu and Watanabe23, Theorem 2.2]. Recent years have seen renewed interest in this class of Markov processes. They appear for example as strong solutions of some stochastic differential equations (SDEs) with jumps (see Dawson and Li [Reference Dawson and Li9]); from a more applied point of view, they form an important subclass of the so-called affine processes, which are known in the financial mathematics setting for modeling interest rates (see [Reference Duffie, Filipović and Schachermayer11]). We mention for instance the works in this direction of Jiao et al. [Reference Jiao, Ma and Scotti21] and Barczy et al. [Reference Barczy, Ben Alaya, Kebaier and Pap2], where certain CBI processes are studied from a statistical point of view.
The asymptotic behaviors of Galton–Watson processes with immigration have been extensively studied since the seventies. We refer to the works of Cohn [Reference Cohn8], Heathcote [Reference Heathcote19], Heyde [Reference Heyde20], Pakes [Reference Pakes31], and Seneta [Reference Seneta34], and to their references. Transience and recurrence of CBI processes have been characterized by Duhalde et al. [Reference Duhalde, Foucart and Ma10]. Fine properties of the stationary distributions of CBI processes, when they exist, have also been recently established in Chazal et al. [Reference Chazal, Loeffen and Patie7] and Keller-Ressel and Mijatovic [Reference Keller-Ressel and Mijatović24]. In the case where no stationary distribution exists, less attention has been paid to limit theorems for CBI processes. It will certainly not be surprising that the results found in the seventies for Galton–Watson processes with immigration have counterparts in the continuous-state and continuous-time framework. A year after the founding work of Kawazu and Watanabe, Pinsky published a short note [Reference Pinsky32], without proof, on the limits of CBI processes. We believe it is of interest to write down some details and resume in this article the study of limit theorems for CBI processes initiated by Pinsky.
We start by proving an almost-sure (a.s.) convergence for CBI processes by adapting Grey’s approach [Reference Grey17] to the framework with immigration (Theorem 2). We then provide a general nonlinear renormalization in law (Theorem 4). To the best of our knowledge this latter renormalization does not appear in the literature about Galton–Watson processes with immigration. We explain now our main results. Denote respectively by
$\Psi$
and
$\Phi$
the branching and immigration mechanisms; we will recall their definitions in the next section. In the case of supercritical branching, we show the existence of two distinct a.s. asymptotic regimes according to the convergence/divergence of the integral
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
. When this integral converges, i.e.
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$
, the branching dynamics takes precedence over immigration and directs the divergence of the process towards infinity. More precisely, under the classical
$L\ln L$
moment assumption (also called the Kesten–Stigum condition) over the branching Lévy measure, the CBI process grows at the same exponential rate as the pure branching process. On the other hand, when it diverges, i.e.
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, immigration is so substantial that the branching, although supercritical, is somehow overtaken. Thus, the process typically grows faster than the pure branching process on the event of its non-extinction.
A similar dichotomy occurs more generally for non-critical CBI processes when we consider their long-term behavior in law. Our main contribution is to design a nonlinear time-dependent renormalization in law of a non-critical CBI(
$\Psi,\Phi$
) process
$(Y_t,t\geq 0)$
satisfying
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
. We shall find (see Theorem 4) a deterministic function
$\lambda \mapsto r_t(\lambda)$
depending only on
$\Psi$
and
$\Phi$
such that
\begin{equation} r_t(1/Y_t)\underset{t\rightarrow \infty}{\longrightarrow} \textrm{e}_1 \text{ in law,}\end{equation}
where
$\textrm{e}_1$
is a standard exponential random variable. The latter renormalization is actually equivalent to the following property; see Corollary 1. Given two independent CBI
$(\Psi,\Phi)$
processes
$(Y_t,t\geq 0)$
and
$(\tilde{Y}_t,t\geq 0)$
such that
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, one has
\begin{equation}\frac{Y_t}{\tilde{Y}_t}\underset{t\rightarrow \infty}{\longrightarrow} \Lambda \text{ in law,}\end{equation}
where
$\mathbb{P}(\Lambda=0)=\mathbb{P}(\Lambda=\infty)=\frac{1}{2}$
. As a consequence of (2), we shall see that no function
$(\eta(t),t\geq 0)$
exists such that
$\eta(t)Y_t$
converges in law towards a nondegenerate random variable (i.e. one whose support is not contained in
$\{0,\infty\}$
). This has been shown by Cohn [Reference Cohn8] in the setting of discrete time and space. The meaning of the limit in law (1) will be made more explicit by introducing further assumptions on the rate of divergence of the integral
$\int_0 \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
, namely on the speed at which
$\int_\varepsilon \frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
goes to
$\infty$
as
$\varepsilon$
goes to 0. In the same vein as Pakes (see [Reference Pakes31]), we design three regimes of divergence: slow (S), log (L), and fast (F). Each corresponds to a specific renormalization and a specific limiting law. The faster the integral diverges, the more the branching dynamics is overtaken by immigration. This is reflected by the different renormalizations occurring in the three regimes. In particular, in the fast case (F) the branching mechanism plays no role in the renormalization. Pinsky’s result [Reference Pinsky32, Theorem 2], which corresponds to the subcritical case under the condition (S), now has a proof (see Remark 9–ii), and a misprint in his statement is corrected.
Notation: By
$\overset{d}{\longrightarrow}$
and
$\overset{p}{\longrightarrow}$
, respectively, we denote convergence in law and convergence in probability. We use the relation symbol
$\sim$
when the ratio of the two terms on the two sides of it converges to 1 (if either of the two terms is random, the convergence holds a.s.). The probability measure and its expectation are denoted by
$\mathbb{P}$
and
$\mathbb{E}$
. For any
$x\geq 0$
,
$\mathbb{P}_x$
denotes the law of a CBI process started from x. The integrability of a function f in a neighborhood of 0 is denoted by
$\int_0 f(x)\textrm{d} x<\infty$
(similarly
$\int^{\infty} f(x)\textrm{d} x<\infty$
denotes the integrability of f in a neighborhood of
$\infty$
). Last, we denote functions, either deterministic or random, vanishing in the limit by o(1).
The paper is organized as follows. First we recall in Section 2 the definition of a CBI process and some of its most fundamental properties. Our main results are stated in Section 3. We first establish in Section 3.1 the a.s. convergence results in the supercritical case. Then, Section 3.2 is devoted to the study of convergence in law in the non-critical case when
$\int_0\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
. We define the three regimes (S), (L), (F) in Section 3.3. The last section treats some critical branching mechanisms having certain regular variation properties.
2. Preliminaries
Here we recall the definition of a CBI process and some of its fundamental properties. Our main references are Chapter 3 of Li’s book [Reference Li29] and Chapter 12 of Kyprianou’s book [Reference Kyprianou26]. We say that a random variable is nondegenerate if its support is not contained in
$\{0,\infty\}$
and proper if it is finite a.s.
Write
$\pi$
and
$\nu$
for two
$\sigma$
-finite nonnegative measures on
$(0,\infty)$
satisfying respectively
$\int^\infty_0 (z\wedge z^2) \,\pi(\textrm{d}z)<\infty$
and
$\int^\infty_0 (1\wedge z) \,\nu(\textrm{d}z)<\infty$
. Consider a triple
$(\sigma,b, \beta)$
such that
$\sigma\geq 0$
,
$b\in \mathbb{R}$
, and
$\beta\geq 0$
. Let
$\Psi$
be the Laplace exponent of a spectrally positive Lévy process with finite mean (here we assume
$|\Psi'(0+)|<\infty$
, so that in particular the CBI process does not explode) and whose characteristic triple is
$(b,\sigma,\pi)$
. Let
$\Phi$
be the Laplace exponent of a subordinator with drift
$\beta$
and Lévy measure
$\nu$
. These are specified by the Lévy–Khinchine formula
\begin{align*}\Psi(q)&=bq+\frac{1}{2}\sigma^{2}q^{2}+\int_{0}^{\infty}(e^{-qu}-1+qu)\pi(\textrm{d} u),\quad q\geq0.\end{align*}
So
$\Psi$
is convex (i.e.,
$\Psi''(q)\geq 0$
for all
$q\geq 0$
) with
$\Psi(0)=0$
. Similarly,
\begin{align*}\Phi(q)&=\beta q+\int_{0}^{\infty}(1-e^{-qu})\nu(\textrm{d} u),\quad q\geq0.\end{align*}
So
$\Phi$
is a concave, continuous, strictly increasing function with
$\Phi(0)=0$
.
A CBI process with branching and immigration mechanisms
$\Psi$
and
$\Phi$
is a strong Markov process
$(Y_{t}, t\geq 0)$
taking values in
$[0,\infty)$
whose transition kernels are characterized by their Laplace transforms. So for
$\lambda\geq 0$
and
$x\in \mathbb{R}_{+}$
,
\begin{equation}\mathbb{E}_x\big[e^{-\lambda Y_{t}}\big]=\exp \left(\!-xv_{t}(\lambda)-\int_{0}^{t}\Phi(v_{s}(\lambda))\textrm{d} s\right),\end{equation}
where the map
$t\mapsto v_{t}(\lambda)$
is the solution to the differential equation
\begin{equation} \frac{\partial}{\partial t}v_{t}(\lambda)=-\Psi(v_{t}(\lambda)), \quad v_{0}(\lambda)=\lambda. \end{equation}
Note that
$v_{t+s}(\lambda)=v_t(v_s(\lambda))$
from the Markov property.
The existence and unicity of CBI processes have been established in [Reference Kawazu and Watanabe23, Theorem 1.1].
Recently Dawson and Li [Reference Dawson and Li9] (see also [Reference Jiao22]) have shown that any CBI process is the strong solution of a certain SDE with jumps.
Suppose that
$(\Omega,\mathscr{F}_t,\mathbb{P})$
is a filtered probability space satisfying the usual hypotheses. Let
$\{B_t\}_{t\ge0}$
be an
$(\mathscr{F}_t)$
-Brownian motion. Let
$N_0(\textrm{d}s,\textrm{d}z,\textrm{d}u)$
and
$N_1(\textrm{d}s, \textrm{d}u)$
denote two
$(\mathscr{F}_t)$
-Poisson random measures on
$(0,\infty)^3$
and
$(0,\infty)^2$
with intensities
$\textrm{d}s \,\pi(\textrm{d}z)\,\textrm{d}u$
and
$\textrm{d}s \,\nu(\textrm{d}z)$
. We assume that the Brownian motion and the Poisson random measures are independent of each other. Let
$\tilde N_0(\textrm{d}s,\textrm{d}z,\textrm{d}u)$
be the corresponding compensated measure of
$N_0$
, namely
$\tilde N_0(\textrm{d}s,\textrm{d}z,\textrm{d}u)\,{:\!=}\, N_0(\textrm{d}s,\textrm{d}z,\textrm{d}u)-\textrm{d}s \,\pi(\textrm{d}z)\,\textrm{d}u.$
The SDE
\begin{equation}\begin{split} Y_t = Y_0&+\sigma\int_0^t \sqrt{Y_{s}} \,\textrm{d}B_s\\[4pt] &+\int_0^t\int_{0}^\infty\int_0^{Y_{s-}} z\,\tilde{N}_0(\textrm{d}s, \textrm{d}z, \textrm{d}u)+\int_0^t(\beta-bY_s)\textrm{d}s+\int_0^t\int_{0}^\infty zN_1(\textrm{d}s, \textrm{d}z)\end{split}\end{equation}
admits a unique strong solution whose law is that of a CBI process with branching mechanism
$\Psi$
and immigration mechanism
$\Phi$
. When there is no immigration, that is to say
$\Phi \equiv 0$
, the drift
$\beta$
and the Poisson random measure
$N_1$
vanish and the process
$(Y_t,t\geq 0)$
solving (5) is a continuous-state branching process (CB process) with branching mechanism
$\Psi$
. When
$\Psi\equiv 0$
, only the immigration part remains and
$(Y_t,t\geq 0)$
is a subordinator with Laplace exponent
$\Phi$
. Lastly, we recall that a (sub-)critical CB
$(\Psi)$
process conditioned on non-extinction is a CBI
$(\Psi,\Phi)$
process with
$\Phi=\Psi'-\Psi'(0+)$
; see Lambert [Reference Lambert27], Li [Reference Li28, Theorem 4.1], and Fittipaldi and Fontbona [Reference Fittipaldi and Fontbona14]. From now on, unless explicitly stated otherwise, we consider processes with immigration, namely
$\Phi(q)>0$
for all
$q>0$
.
Recall the form of the function
$\Psi$
and notice that
$b=\Psi'(0+)$
. A CBI process is said to be critical, subcritical, or supercritical accordingly as
$b=0$
,
$b>0$
, or
$b<0$
. Note that
$\Psi$
has at most two roots. Introduce
\begin{eqnarray*}\rho=\inf\{z>0, \Psi(z)\geq 0\}, \quad \inf\varnothing=\infty. \end{eqnarray*}
We see that
$\rho=0$
if
$b\geq 0$
and
$\rho>0$
if
$b<0$
. In particular,
$\rho=\infty$
if and only if
$-\Psi$
is the Laplace exponent of a subordinator. By (4), if
$0<\lambda<\rho$
(resp.
$\lambda>\rho$
), then
$v_{t}(\lambda)\in[\lambda,\rho]$
is increasing (resp.
$v_{t}(\lambda)\in[\rho,\lambda]$
is decreasing) in t. Then (4) implies
\begin{equation} \int_{v_{t}(\lambda)}^{\lambda}\frac{\textrm{d} z}{\Psi(z)}=t, \quad\forall t\in[0,\infty),\quad \forall \lambda\in(0,\infty)/\{\rho\}.\end{equation}
Recall
$\bar{v}_t\,{:\!=}\,\underset{\lambda \rightarrow \infty}{\lim \uparrow} v_{t}(\lambda)\in [0, \infty]$
and set
$\bar{v}\,{:\!=}\,\underset{t \rightarrow \infty}{\lim \downarrow} \bar{v}_{t}\in [0, \infty].$
Grey shows in [Reference Grey17] that
\begin{equation}\bar{v}_t<\infty \text{ for all } t>0 \text{ if and only if } \int^{\infty}\frac{\textrm{d} q}{\Psi(q)}<\infty \text{ (Grey's condition)}.\end{equation}
Note that
$\rho\leq \bar{v}$
, and if
$\bar{v}<\infty$
then
$\bar{v}=\rho$
.
Recall (3). Define the map
$r_{t}(\lambda)\,{:\!=}\,\int_{0}^{t}\Phi(v_{s}(\lambda))\textrm{d} s$
. A simple change of variable gives
\begin{equation}r_{t}(\lambda)=\begin{cases} \int_{v_t(\lambda)}^{\lambda}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u & \text{ if } \Psi \not\equiv 0, \\ \\[-7pt] t\Phi(\lambda) & \text{ if } \Psi \equiv 0.\end{cases}\end{equation}
Then (3) can also be written as
\begin{equation}\mathbb{E}_x\big[e^{-\lambda Y_{t}}\big]=\exp \left(\!-xv_{t}(\lambda)-r_t(\lambda) \right).\end{equation}
Note also that for any
$t\geq 0$
and any
$n\in \mathbb{N}$
,
$Y_t=Y_t^{1}+\cdots+Y_t^{n}$
in law, where
$((Y_t^{i})_{t\geq 0}, 1\leq i\leq n)$
are independent and identically distributed copies of a CBI
$(\Psi,\frac{1}{n}\Phi)$
process. Thus, in particular,
$Y_t$
has an infinitely divisible law on
$\mathbb{R}_+$
, and
$\lambda\mapsto r_t(\lambda)$
is the Laplace exponent of a subordinator (with no killing term). For any
$t\geq 0$
, we set
\begin{equation*}r_t(\infty)=\int_{\bar{v}_t}^{\infty}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\in (0,\infty],\end{equation*}
where
$\bar{v}_t\,{:\!=}\,\underset{\lambda \rightarrow \infty}{\lim} \uparrow v_t(\lambda)$
, with the convention that if
$\int^{\infty}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\infty$
then
$r_t(\infty)=\infty$
for all
$t>0$
. From (8), we easily check that
$r_t(\infty)<\infty$
as soon as
$\int^{\infty}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u<\infty$
. Letting
$\lambda$
tend to
$\infty$
in (9) readily implies that
$r_t(\infty)<\infty$
if and only if
$\mathbb{P}_x(Y_t=0)>0$
. We refer the reader interested in the zero-set of CBI processes to [Reference Foucart and Uribe Bravo16].
We refer to [Reference Li29, Section 3.2] for proofs of the following technical statements; see also [Reference Grey17]. We gather in the next lemma analytical results on the map
$\lambda\mapsto v_{t}(\lambda)$
and its inverse (whenever it exists).
Lemma 1. The map
$\lambda\mapsto v_{t}(\lambda)$
is strictly increasing on
$[0,\infty)$
. For any
$t\geq 0$
, let
$\lambda\mapsto v_{-t}(\lambda)$
be the inverse map of
$\lambda\mapsto v_t(\lambda)$
. This is a strictly increasing function, well-defined on
$[0,\bar{v}_{t})$
, which satisfies for all
$s, t\geq 0$
and
$0\leq \lambda<\bar{v}_{s+t}$
\begin{equation*}v_{-(s+t)}(\lambda)=v_{-s}(v_{-t}(\lambda)).\end{equation*}
For
$0\leq \lambda<\bar{v}_{t}$
such that
$\Psi(\lambda)\neq 0$
, by (6) one has
\begin{equation} \int_{\lambda}^{v_{-t}(\lambda)}\frac{\textrm{d} z}{\Psi(z)}=\int_{v_{t}(v_{-t}(\lambda))}^{v_{-t}(\lambda)}\frac{\textrm{d} z}{\Psi(z)}=t.\end{equation}
In particular, in the supercritical case, i.e.
$b\in(\!-\infty, 0)$
, for
$\lambda\in (0,\rho)$
\begin{eqnarray}\frac{\partial v_{-t}(\lambda)}{\partial t}=\Psi(v_{-t}(\lambda)), \quad v_{0}(\lambda)=\lambda.\end{eqnarray}
The map
$t\mapsto v_{-t}(\lambda)$
is decreasing, and by letting
$t\rightarrow\infty$
in (10) we see that
$v_{-t}(\lambda)\underset{t\rightarrow \infty}{\longrightarrow} 0$
.
Moreover,
$v_{-(t+u)}(\lambda)/v_{-t}(\lambda)\underset{t\rightarrow \infty}{\longrightarrow} e^{bu}$
for any
$u\geq0$
.
The following theorem was announced by Pinsky [Reference Pinsky32] and provides some initial information on the growth rate. It has been established in the (sub-)critical case by Li (see [Reference Li29, Theorem 3.20, p. 66]) and by Keller-Ressel and Mijatović (see [Reference Keller-Ressel and Mijatović24, Appendix]).
Theorem 1. (Pinsky [Reference Pinsky32], Li [Reference Li29]) Let
$(Y_{t}, t\geq 0)$
be a CBI process with
$|\Psi'(0+)|<\infty$
. Set
$\tau(t)=e^{bt}$
if
$b<0$
and
$\tau(t)=1$
if
$b\geq 0$
. The process
$(\tau(t)Y_{t}, t\geq 0)$
converges in law, as
$t\rightarrow \infty$
, towards a proper random variable if and only if
\begin{equation*}\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty.\end{equation*}
If
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, then for all
$z\geq 0$
,
$\mathbb{P}_x(\tau(t)Y_{t}\leq z)\underset{t\rightarrow \infty }\longrightarrow 0$
; that is to say,
$(\tau(t)Y_{t}, t\geq 0)$
converges to
$\infty$
in probability.
Our paper aims to enrich the above Theorem 1 by studying a.s. limits in the supercritical case and finding new results on the growth rates when
$\Psi$
is non-critical and
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
. It is clear that a supercritical CBI process
$(Y_t,t\geq 0)$
is transient, i.e.
$Y_t\underset{t\rightarrow \infty}{\longrightarrow} \infty$
a.s. The properties of transience and recurrence for subcritical and critical CBI processes have been studied in Duhalde et al. [Reference Duhalde, Foucart and Ma10]. It is established in [Reference Duhalde, Foucart and Ma10, Theorem 3] that a (sub-)critical CBI
$(\Psi,\Phi)$
process is recurrent or transient accordingly as
\begin{eqnarray}\mathcal{E}\,{:\!=}\,\int_0 \frac{\textrm{d} x}{\Psi(x)}\exp\left(\!-\int_{x}^{1}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)=\infty \quad \mbox{or}\ <\infty.\end{eqnarray}
We see that the integral
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
plays a crucial role in this integral test. In particular, it is worth noticing that in the (sub-)critical case, the divergence of
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
is necessary for the CBI process to be transient, but not sufficient.
The notion of regularly varying functions will be used in several places. Recall that a function R is regularly varying at
$\infty$
(resp. at 0) with index
$\theta\in \mathbb{R}$
if for any
$\lambda>0$
\begin{equation*}\frac{R(\lambda x)}{R(x)}\rightarrow\lambda^{\theta} \quad \text{ as } x\rightarrow \infty \ (\text{resp.} 0).\end{equation*}
The function R is said to be slowly varying if
$\theta=0$
. If R is regularly varying with index
$\theta$
, then R has the form
$R(x)=x^{\theta}L(x)$
for all
$x\geq 0$
with L a slowly varying function. We stress that such functions occur naturally in the study of this subject; for instance, in the supercritical case, i.e.
$b\in(\!-\infty,0)$
, Lemma 1 ensures that the function
$t\mapsto v_{-\ln(t)}(\lambda)$
is regularly varying at
$\infty$
with index b. We refer the reader to Bingham et al. [Reference Bingham, Goldie and Teugels4] for a reference on regularly varying functions.
3. Results
3.1. Almost-sure limits
This section deals with the so-called Seneta–Heyde norming for CBI processes. We refer to Seneta [Reference Seneta34] and Heyde [Reference Heyde20] for the seminal papers in the discrete setting; see also Lambert [Reference Lambert27]. For the case where no immigration is taken into account, i.e.
$\Phi\equiv 0$
, this study was carried out by Grey [Reference Grey17] and Bingham [Reference Bingham5]. We refer the reader for instance to the end of Chapter 12 of Kyprianou’s book [Reference Kyprianou26].
Recall
$\rho \in [0,\infty]$
(the largest root of
$\Psi$
), the map
$t\mapsto v_{-t}(\lambda)$
, and its equation (11).
Theorem 2. Let
$(Y_{t}, t\geq 0)$
be a CBI
$(\Psi, \Phi)$
process with a supercritical branching mechanism
$\Psi$
, i.e.
$b<0$
. Let
$0<\lambda<{{\rho}}$
. Then the following hold:
-
(i) If
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$
, then
$v_{-t}(\lambda)Y_t\underset{t\rightarrow \infty}{\longrightarrow} W^{\lambda}$
$\mathbb{P}_x$
-a.s., where
$W^{\lambda}$
is a nondegenerate proper random variable with Laplace exponent
(13)
\begin{equation}\mathbb{E}_x\left[e^{-\theta W^{\lambda}}\right]=\exp\left(\!-xv_{-\frac{\ln\theta}{b}}(\lambda)+\int_{0}^{v_{-\frac{\ln\theta}{b}}(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)\!.\end{equation}
-
(ii) If
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, then
$v_{-t}(\lambda)Y_t\underset{t\rightarrow \infty}{\longrightarrow} \infty$
$\mathbb{P}_x$
-a.s.
Remark 1.
-
(i) It is worth mentioning that Grey [Reference Grey17, Theorem 2] found the same a.s. renormalization
$v_{-t}(\lambda)$
for the supercritical process without immigration, i.e. with
$\Phi\equiv 0$
, on the event of non-extinction. See also Duquesne and Labbé [Reference Duquesne and Labbé12, Lemma 2.2] for the expression for the Laplace transform (13) with
$\Phi\equiv 0$
. As explained in the introduction, Theorem 2 reflects the fact that two regimes occur according to the convergence or divergence of the integral
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u$
. In Case (i), the branching dictates the growth of the process; in Case (ii) it is overwhelmed by the immigration. Moreover, when
$\int^\infty (x\ln x) \pi(\textrm{d} x)<\infty$
, we have
$v_{-t}(\lambda)\underset{t\rightarrow \infty}{\sim} K_{\lambda}e^{bt}$
for some constant
$K_\lambda>0$
. So in this case, as mentioned in the introduction, the CBI process grows a.s. exponentially fast. -
(ii) In the non-critical case,
$|\Psi(u)|\underset{u\rightarrow 0}{\sim} |b|u$
, and the condition
$\int_0\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$
is equivalent to
$\int^{\infty}\ln\!(u)\nu(\textrm{d} u)=\infty$
, where
$\nu$
is the immigration measure
$\nu$
; see Remark 7 below.
Proof. The proof follows from a simple adaptation of Grey’s martingales (see [Reference Grey17]) to the setting of CBI processes. Consider
$(Y_{t}, t\geq 0)$
, a CBI
$(\Psi, \Phi)$
process. Recall (9). Fix
$\lambda \in (0, \rho)$
. For every
$t\geq 0$
, set
\begin{equation*}\kappa_{\lambda}(t)\,{:\!=}\,\exp\left(\int_{\lambda}^{v_{-t}(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right).\end{equation*}
We show that the process
$(M_t^{\lambda}, t\geq 0)$
defined for any
$t\geq 0$
by
$M^{\lambda}_{t}=\kappa_{\lambda}(t)\exp\left(\!-v_{-t}(\lambda)Y_{t}\right)$
is a positive martingale. The random variables
$M^{\lambda}_{t}$
are plainly integrable, and for any
$s,t\geq 0$
,
\begin{align*}\mathbb{E}[M_{t+s}^{\lambda}|\mathscr{F}_t]&=\kappa_{\lambda}(t+s)\mathbb{E}[\exp(\!-v_{-(t+s)}(\lambda)Y_{t+s})\lvert Y_t] \qquad \text{(by the Markov property)}&\\[2pt] &=\kappa_{\lambda}(t+s)\exp\left(\!-Y_tv_s(v_{-(t+s)}(\lambda))-\int_{v_s(v_{-(t+s)}(\lambda))}^{v_{-(t+s)}(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)&\\[2pt] &=\kappa_{\lambda}(t+s)\exp\left(\int_{v_{-(t+s)}(\lambda)}^{v_{-t}(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)\exp\big(\!-Y_tv_{-t}(\lambda)\big) &\\[2pt] &=\kappa_{\lambda}(t)\exp\big(\!-Y_tv_{-t}(\lambda)\big)=M_t^{\lambda},& \end{align*}
where the second equality follows from (9) and the third from the fact that
\begin{equation*} v_s(v_{-(t+s)}(\lambda))=v_s(v_{-s}\circ v_{-t}(\lambda))=v_{-t}(\lambda).\end{equation*}
In particular, we see that the process
$(e^{-v_{-t}(\lambda)Y_{t}(x)}, t\geq 0)$
is a positive supermartingale. This implies that the process
$(v_{-t}(\lambda)Y_{t}, t\geq 0)$
converges, as t goes to infinity,
$\mathbb{P}_x$
-a.s. in
$\bar{\mathbb{R}}_{+}{\,{:\!=}\,[0,\infty]}$
. Denote its limit by
$W^{\lambda}$
. We shall see that it is infinite a.s. in Case (ii).
Since
$\Psi$
is supercritical, one has
$\rho>0$
, and
$\Psi(u)<0$
for
$0<u<\rho$
. By Lemma 1, we know that when
$0<\lambda<\rho$
,
$v_{-t}(\lambda)\underset{t\rightarrow \infty}\longrightarrow 0$
. For fixed
$\theta> 0$
, we choose t large enough so that
$v_{-t}(\lambda), \theta v_{-t}(\lambda)\in (0,\rho)$
. Recall that by assumption
$b\in (\!-\infty,0)$
. Then it can be established from Equations (4) and (10) (see e.g. [Reference Duquesne and Labbé12, Lemma 2.2] and [Reference Li29, Theorem 3.13] for details) that
\begin{equation}v_t(\theta v_{-t}(\lambda))\underset{t\rightarrow \infty}\longrightarrow v_{-\frac{\ln \theta}{b}}(\lambda).\end{equation}
Note that the above convergence holds no matter the sign of
$-\frac{\ln \theta}{b}$
. By (9), one has for all
$t\geq 0$
\begin{equation*} \mathbb{E}_x\big[e^{-\theta v_{-t}(\lambda)Y_{t}}\big]=\exp\left(\!-xv_t(\theta v_{-t}(\lambda))-r_t(\theta v_{-t}(\lambda))\right),\end{equation*}
and by letting t go to
$\infty$
in the right-hand side above we get the expression (13) for the Laplace transform of
$W^{\lambda}$
. It is not hard to see that
\begin{equation*}v_{-\frac{\ln \theta}{b}}(\lambda)\in(0,\rho)\end{equation*}
as
$\int_0\frac{\textrm{d} z}{\Psi(z)}=-\infty$
and
$\int_\lambda^\rho\frac{\textrm{d} z}{\Psi(z)}=-\infty$
. In fact, if
$\rho<\infty$
, then
$\Psi(\rho)=0$
; if
$\rho=\infty$
, then
$-\Psi$
is the Laplace exponent of a subordinator, which implies that
$\int^{\infty}\frac{\textrm{d} z}{\Psi(z)}=-\infty$
. Moreover, by (10),
\begin{equation}v_{-\frac{\ln \theta}{b}}(\lambda)\underset{\theta \rightarrow 0}\longrightarrow 0 \quad \text{ and } \quad v_{-\frac{\ln \theta}{b}}(\lambda)\underset{\theta \rightarrow \infty}\longrightarrow \rho.\end{equation}
Using the first convergence in (15), we observe that if
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$
, then
$W^{\lambda}<\infty$
$\mathbb{P}_x$
-a.s. Applying the second convergence in (15) and the fact that
$\int^{\rho}\frac{\textrm{d} u}{\Psi(u)}=-\infty$
, we get
\begin{equation*}\mathbb{P}(W^{\lambda}_x=0)=\exp\left(\!-x\rho+\int_{0}^{\rho}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)=0.\end{equation*}
If
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, then
$\int_{0}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=-\infty$
, as
$\Psi(u)<0$
for
$0<u<\rho$
. We get from (13) that
$\mathbb{E}_x[e^{-\theta W^{\lambda}}]=0$
for any
$\theta>0$
; therefore
$W^{\lambda}=\infty$
a.s.
The next theorem sheds some light on what limit theorems can be expected in the case
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
.
Theorem 3. Let
$(Y_t,t\geq 0)$
be a supercritical CBI
$(\Psi,\Phi)$
process. Assume
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
. For any positive deterministic function
$(\eta(t),t\geq 0)$
, if
$(\eta(t)Y_t,t\geq 0)$
converges a.s., then its limit is either 0 a.s. or
$\infty$
a.s.
Remark 2. Theorem 3 eliminates the hope of finding any law of large numbers and can be seen as a starting point for a study through nonlinear renormalizations; see Section 3.2 below.
Proof. We shall use the framework of flow of SDEs as in Dawson and Li [Reference Dawson and Li9]. We recall that by replacing, in the SDE (5), the Brownian motion
$(B_t,t\geq 0)$
by a white noise
$M(\textrm{d} s,\textrm{d} u)$
(see [Reference Dawson and Li9, Reference Li and Ma30] for details), one can consider on the same probability space the SDEs
\begin{equation}\begin{split} Y^{(n)}_t(x)&= x+\sigma\int_n^{n+t} \int_0^{Y^{(n)}_{s}(x)} \, M(\!\textrm{d}s,\textrm{d}u)+\int_n^{n+t}\int_{0}^\infty\int_0^{Y^{(n)}_{s-}(x)} z\,\tilde{N}_0(\!\textrm{d}s, \textrm{d}z, \textrm{d}u) \\[3pt] &\quad +\int_n^{n+t}(\beta-bY^{(n)}_s(x))\textrm{d}s+\int_n^{n+t}\int_{0}^\infty zN_1(\!\textrm{d}s, \textrm{d}z).\end{split}\end{equation}
These SDEs are known to have pathwise unique solutions. More precisely, this provides a sequence of flows of CBI
$(\Psi,\Phi)$
processes
$\left\{Y^{(n)}_t(x), x\geq0, t\geq0, n\geq 0\right\}$
such that for any
$n\in \mathbb{N}$
and any
$x\geq y\geq 0$
,
$\left(Y^{(n)}_t(x)-Y^{(n)}_t(y),t\geq 0\right)$
is a CB process started from
$x-y$
with branching mechanism
$\Psi$
and is independent of
$\left\{Y_t^{(n)}(y),t\geq0\right\}$
. We denote by
$(Y_t(x),t\geq 0)$
the process
$\left(Y_t^{(0)}(x),t\geq 0\right)$
, the solution to (16) for
$n=0$
. Pathwise uniqueness implies that
$Y_t^{(n)}(Y_n(x))=Y_{n+t}(x)$
for any
$x\geq 0$
,
$t\geq 0$
, and
$n\in \mathbb{N}$
a.s. Let
$X_t^{(n)}(x)=Y_t^{(n)}(x)-Y_t^{(n)}(0)$
. Then
\begin{eqnarray*}Y_{n+t}(0)=X^{(n)}_{t}(Y_n(0))+Y^{(n)}_{t}(0).\end{eqnarray*}
By Theorem 2(ii),
$v_{-t}(\lambda)Y^{(n)}_t(0)\underset{t\rightarrow \infty}{\longrightarrow} \infty$
a.s., and applying Theorem 2(i) to the CB
$(\Psi)$
process
$\left(X^{(n)}_{t}(Y_n(0)),t\geq 0\right)$
(see Remark 1(i)), we get
$v_{-t}(\lambda)X^{(n)}_{t}(Y_n(0))\underset{t\rightarrow \infty}{\longrightarrow} W^{\lambda}$
for some finite random variable
$W^{\lambda}$
. Hence
\begin{eqnarray}\frac{Y_{n+t}(0)}{Y^{(n)}_t(0)}=1+\frac{X^{(n)}_{t}(Y_n(0))}{Y^{(n)}_t(0)}\underset{t\rightarrow \infty}{\longrightarrow} 1\quad\mbox{a.s.}\end{eqnarray}
Assume that there exists some
$\eta(t)>0$
such that
$\eta(t)Y_t(0)\underset{t\rightarrow \infty}{\longrightarrow} V_0$
a.s. Then by (17),
$\eta(n+t)Y^{(n)}_t(0)\underset{t\rightarrow \infty}{\longrightarrow} V_0$
a.s., and for
$\ell\in\mathbb{N}$
,
$\eta(n+l)Y^{(n)}_{\ell}(0)\underset{\ell\rightarrow \infty}{\longrightarrow} V_0$
a.s. However, by iteration, it is not hard to see that for
$\ell\geq1$
,
\begin{align*}Y^{(n)}_{\ell}(0)&= X_{\ell-1}^{(n+1)}\Big(Y_1^{(n)}(0)\Big)+Y_{\ell-1}^{(n+1)}(0)\\[3pt] &=\sum_{k=1}^{\ell} X_{\ell-k}^{(n+k)}\Big(Y_1^{(n+k-1)}(0)\Big),\quad \Big(Y_0^{(n+\ell)}(0)=0\Big)\end{align*}
where
$\left\{X_{\cdot}^{(k)}\Big(Y_1^{(k-1)}(0)\Big)\right\}_{k=1}^\infty$
is a sequence of independent CB(
$\Psi$
) processes.
By the above iteration, for fixed n,
$\left\{Y^{(n)}_{\ell}(0),\ell\geq1\right\}$
is measurable with respect to the
$\sigma$
-algebra
$\mathcal{G}_n$
generated by the sequence of independent processes
\begin{equation*}\left\{ X_t^{(k)}\left(Y_1^{(k-1)}(0)\right)\,{:}\, t\geq0 \right\}_{k=n}^\infty.\end{equation*}
Since, for any n,
$\eta(n+l)Y^{(n)}_{\ell}(0)\underset{\ell\rightarrow \infty}{\longrightarrow} V_0$
a.s., we immediately have that
$V_0$
is measurable with respect to the tail
$\sigma$
-algebra generated by the same sequence of independent processes
$\left\{X_t^{(k)} \left(Y_1^{(k-1)}(0)\right)\,{:}\, t\geq0\right\}_{k=1}^\infty$
, i.e.
$\cap_{n=1}^\infty \mathcal{G}_n$
.
Kolmogorov’s zero–one law (see e.g. [Reference Durrett13, Theorem 2.5.1]) asserts that
$V_0$
is a constant or infinite a.s. Assume that
$V_0$
is a finite positive constant a.s. Since
$Y^{(n)}_{\cdot}(0)$
has the same distribution as
$Y_{\cdot}(0)$
, we immediately have that
$\eta(t)Y^{(n)}_t(0)\underset{t\rightarrow \infty}{\longrightarrow} V_0$
a.s. Then
$\eta(n+t)/\eta(t)\underset{t\rightarrow \infty}{\longrightarrow}1$
, which implies that
$\eta(t)\sim L(e^t)$
for some slowly varying function L at
$\infty$
. However recalling that
$v_{-\ln t}$
is a regularly varying function with index b (see Lemma 1), we have that
$v_{-t}(\lambda)\sim e^{bt}L^*(e^{t})$
as t goes to
$\infty$
, where
$L^*(\cdot)$
is a slowly varying function at
$\infty$
and thus
$v_{-t}(\lambda)/\eta(t)\rightarrow 0$
. This leads to a contradiction. Thus
$V_0$
is 0 a.s. or
$\infty$
a.s.
3.2. A general limit in law for non-critical CBI processes when
$\int_0\frac{\Phi(\textbf{\textit{u}})}{|\Psi(\textbf{\textit{u}})|}\textrm{d} \textbf{\textit{u}}=\infty$
This section focuses on the study of the long-term behavior of CBI
$(\Psi,\Phi)$
processes satisfying the condition
\begin{equation}\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty. \end{equation}
By Theorem 1, in this case
$Y_t$
converges in law to
$\infty$
as t goes to
$\infty$
. We give a finer description of the behavior of
$Y_t$
through distributional, rather than a.s., limit theorems. In this section, we prove the main convergence theorem below, which provides a nonlinear time-dependent renormalization in law of any non-critical CBI process. The three different regimes of convergence in law mentioned in the introduction are designed in Section 3.3 below.
Recall the definition of
$r_t(\lambda)$
in (8) and that
$r_t(\infty)=\infty$
if and only if
$\mathbb{P}_x(Y_t=0)=0$
for all
$t>0$
. In the next theorem, we take the convention
$1/0=\infty$
.
Theorem 4. Assume (18) holds and
$\Psi$
is non-critical (
$b\neq 0$
). Then, for all
$x\geq 0$
, we have
\begin{equation}r_t(1/Y_t)\,{:\!=}\,\int_{v_{t}(1/Y_t)}^{1/Y_t} \frac{\Phi(u)}{\Psi(u)}\textrm{d} u\stackrel{d}\longrightarrow \textrm{e}_1, \text{ as } t\rightarrow \infty \text{ under } \mathbb{P}_{x},\end{equation}
where
$\textrm{e}_1$
is an exponential random variable with parameter 1.
Remark 3. The law of the limiting distribution in (19) does not depend on the initial state x of the CBI process. It justifies the perception that in the regime (18), the dynamics is governed in the long term by the immigration part and not by the branching part.
Proof. Recall the equations (3) and (9).
Step 1: We claim that for fixed
$\lambda>0$
,
$r_t(\lambda)\rightarrow\infty$
as
$t\rightarrow\infty$
. In fact, in the subcritical case,
$\Psi(u)>0$
for
$u>0$
. By (6),
$v_t(\lambda)\downarrow 0$
as
$t\to\infty$
, for any fixed
$\lambda>0$
. According to (18) and the second equality of (8), we have that
$r_{t}(\lambda)\rightarrow\infty$
as
$t\to\infty.$
In the supercritical case, still by (6),
$v_t(\lambda)\rightarrow \rho$
as
$t\to\infty$
for fixed
$\lambda>0$
. Then
$\Phi(v_t(\lambda))\rightarrow\Phi(\rho)>0$
as
$t\rightarrow\infty$
. Combining this with the first equality of (8), we obtain that
$r_t(\lambda)\rightarrow\infty$
as
$t\rightarrow\infty$
.
Step 2: Recall that
$\lambda\mapsto r_{t}(\lambda)$
is the Laplace exponent of a subordinator with no killing term. For all t,
$r_t(0)=0$
, and
$r_t$
is strictly decreasing in
$\lambda$
. So we can define
$\lambda\mapsto c_{t}(\lambda)$
as the inverse of
$\lambda \mapsto r_{t}(\lambda)$
. Fix
$\lambda>0$
. By Step 1, for any small
$\varepsilon>0$
, we can find sufficiently large t such that
$r_t(\varepsilon)>\lambda=r_{t}(c_{t}(\lambda))$
, which implies that
$c_t(\lambda)<\varepsilon$
. Thus
\begin{equation}c_t(\lambda)\underset{t\rightarrow\infty}{\rightarrow} 0,\text{ and } v_t(c_t(\lambda))\underset{t\rightarrow\infty}{\rightarrow} 0.\end{equation}
The second limit follows from (18) and the second equality of (8) (replacing
$\lambda$
by
$c_t(\lambda)$
).
Step 3: Notice that we can equivalently show that for any
$\lambda\geq0$
and
$\theta>0$
,
\begin{eqnarray}\lim_{t\to\infty}\mathbb{E}_x\big[e^{-\theta c_t(\lambda)Y_t}\big]=e^{-\lambda}.\end{eqnarray}
In fact, if (21) holds, then
$c_t(\lambda)Y_t$
converges in distribution to a random variable Z such that
$\mathbb{P}(Z=\infty)=1-\mathbb{P}(Z=0)=1-e^{-\lambda}.$
Therefore, for
$\lambda>0$
,
\begin{equation}\mathbb{P}(r_{t}(1/Y_t)>\lambda)=\mathbb{P}(1/Y_{t}> c_{t}(\lambda))=\mathbb{P}(c_{t}(\lambda)Y_t<1)\underset{t\rightarrow \infty}{\longrightarrow} e^{-\lambda},\end{equation}
which implies (19).
Step 4: Note that
\begin{equation}\mathbb{E}_x\big[e^{-\theta c_t(\lambda)Y_t}\big]=\exp{\left(\!-xv_{t}(\theta c_t(\lambda))-r_t(\theta c_t(\lambda))\right)}\end{equation}
and
\begin{align}r_t(\theta c_t(\lambda))&=\int_{v_t(\theta c_t(\lambda))}^{\theta c_t(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u \nonumber\\[3pt] &={\int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u}+\underbrace{\int_{v_{t}(c_t(\lambda))}^{c_t(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u}_{=r_{t}(c_t(\lambda))=\lambda}+{\int_{v_{t}(\theta c_t(\lambda))}^{v_{t}(c_t(\lambda))}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u.}\end{align}
So to obtain (21), it suffices to prove that as
$t\rightarrow \infty$
,
\begin{equation}v_t(\theta c_t(\lambda))\rightarrow0\end{equation}
and
\begin{eqnarray} \int_{c_t(\lambda)}^{\theta {c_t(\lambda)}}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\rightarrow0,\quad \int_{v_t(c_t(\lambda))}^{v_t(\theta c_t(\lambda))}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\rightarrow0.\end{eqnarray}
By the monotonicity of
$\Phi$
, we have, for small enough y,
\begin{eqnarray}\left|\int_{\theta y}^{y}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right|\leq \max(\Phi(y),\Phi(\theta y))\left|\int_{\theta y}^{y}\frac{1}{\Psi(u)}\textrm{d} u\right|.\end{eqnarray}
On the one hand
\begin{equation*} \max(\Phi({y}),\Phi(\theta y))\underset{y\rightarrow 0}\longrightarrow 0\end{equation*}
as
$\Phi$
is continuous and
$\Phi(0)=0$
. On the other hand, since
$\Psi$
is non-critical, there exists some constant
$h>0$
such that
$|\Psi(u)|\geq hu$
for u close enough to 0. This implies that
\begin{eqnarray} \bigg|\int_{\theta y}^{y}\frac{1}{\Psi(u)}\textrm{d} u\bigg|\leq \frac{|\ln\theta|}{h}, \end{eqnarray}
when y is small enough. Then by (27) and (20),
\begin{eqnarray}\bigg|\int_{c_t(\lambda)}^{\theta {c_t(\lambda)}}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\bigg|\leq \max(\Phi(c_t(\lambda)),\Phi(\theta c_t(\lambda)))\frac{|\ln\theta|}{h}\underset{t\rightarrow \infty}{\longrightarrow} 0.\end{eqnarray}
So the first convergence in (26) is proved.
Note that
\begin{align*}\int_{v_t(c_t(\lambda))}^{v_t(\theta c_t(\lambda))}\frac{\textrm{d} u}{\Psi(u)}&=\int_{v_t(c_t(\lambda))}^{c_t(\lambda)}\frac{\textrm{d} u}{\Psi(u)}+\int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{\textrm{d} u}{\Psi(u)}+\int_{\theta c_t(\lambda)}^{ v_t(\theta c_t(\lambda))}\frac{\textrm{d} u}{\Psi(u)}\nonumber\\[3pt] &= t+\int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{\textrm{d} u}{\Psi(u)}-t\nonumber\\[3pt] &= \int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{\textrm{d} u}{\Psi(u)},\end{align*}
which implies that
$v_t(\theta c_t(\lambda))\to 0$
as
$t\to\infty$
, since
$v_t(c_t(r))\to 0$
by (20) and
\begin{equation*}\left|\int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{\textrm{d} u}{\Psi(u)}\right|\leq\ln\theta/h\end{equation*}
by (28). So the convergence in (25) is proved. Then
\begin{eqnarray*}\bigg|\int_{v_t(c_t(\lambda))}^{v_t(\theta c_t(\lambda))}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\bigg| &\leq &\max\{\Phi(v_t(c_t(\lambda))),\Phi(v_t(\theta c_t(\lambda)))\}\left|\int_{v_t(c_t(\lambda))}^{v_t(\theta c_t(\lambda))}\frac{1}{\Psi(u)}\textrm{d} u\right|\nonumber\\[3pt] &=&\max\{\Phi(v_t(c_t(\lambda))),\Phi(v_t(\theta c_t(\lambda)))\}\left|\int_{c_t(\lambda)}^{\theta c_t(\lambda)}\frac{1}{\Psi(u)}\textrm{d} u\right|,\end{eqnarray*}
which goes to 0 similarly as in (29). Then the second convergence in (26) is proved. So both conditions (25) and (26) hold, and we can conclude that (19) holds.
Remark 4. Note that Steps 1 and 2 also work for the critical case. But Step 4 requires
$b\neq 0.$
However, the same line of argument as in this proof will be used in Section 3.4, where we focus on the study of the critical case.
We now provide a corollary leading to a more intuitive probabilistic understanding of Theorem 4. In particular it will shed new light on Theorem 3. We take the convention
$0/0=0\times \infty=0$
.
Corollary 1. Assume (18) and that
$\Psi$
is non-critical. Let
$(Y_t,t\geq 0)$
and
$(\tilde{Y}_t,t\geq 0)$
be two independent CBI
$(\Psi,\Phi)$
processes started from 0.
Then
\begin{equation}Y_t/\tilde{Y}_t\underset{t\rightarrow \infty}{\longrightarrow} \Lambda\ in\ law\end{equation}
where
$\Lambda$
has law
$\mathbb{P}(\Lambda=0)=1-\mathbb{P}(\Lambda=\infty)=1/2$
. Moreover, there is no deterministic renormalization
$(\eta(t),t\geq 0)$
such that
$(\eta(t)Y_t,t\geq 0)$
converges in law towards a nondegenerate random variable.
Proof. By a similar argument as in Equation (22), since for any
$\lambda>0$
,
$c_t(\lambda)Y_t\underset{t\rightarrow \infty}{\longrightarrow} Z$
in law with Z such that
$\mathbb{P}(Z=\infty)=1-\mathbb{P}(Z=0)=1-e^{-\lambda}$
, one has for any
$\theta>0$
that
\begin{equation*}\mathbb{P}(r_t(\theta/Y_t)>\lambda)=\mathbb{P}(c_t(\lambda)Y_t<\theta)\underset{t\rightarrow \infty}{\longrightarrow} e^{-\lambda}=\mathbb{P}(\!\textrm{e}_1>\lambda),\end{equation*}
with
$\textrm{e}_1$
a standard exponential random variable. Hence, for any
$\theta\geq 0$
and for any
$t\geq 0$
, we apply (9) to obtain
\begin{align*}\mathbb{E}\left[e^{-\theta\frac{{Y}_t}{\tilde Y_t}}\right]=\mathbb{\tilde E}_0\left[{\mathbb{E}}_0\left[e^{-\frac{\theta}{\tilde Y_t}{Y}_t}\Big|\tilde Y_t\right]\right]&= \mathbb{\tilde E}\left[\mathbb{E}\left[e^{- r_t(\theta/\tilde Y_t)}\Big|\tilde Y_t\right]\right]\\[3pt] &=\mathbb{\tilde E}\left[e^{-r_t(\theta /\tilde Y_t)}\right]\underset{t\rightarrow \infty}{\longrightarrow}\mathbb{E}\left[e^{-\textrm{e}_1}\right]=\frac{1}{2}.\end{align*}
Therefore
$Y_t/\tilde{Y}_t\underset{t\rightarrow \infty}{\longrightarrow} \Lambda$
in law with
$\mathbb{P}(\Lambda=0)=\frac{1}{2}$
and
$\mathbb{P}(\Lambda=\infty)=\frac{1}{2}$
.
We show now that there is no renormalization in law. For the sake of contradiction, assume that there exists
$(\eta(t),t\geq 0)$
such that
$\eta(t)Y_t\underset{t\rightarrow \infty}{\longrightarrow} V$
in law with V a nondegenerate random variable. Let
$b>a>0$
be any two values such that
$\mathbb{P}(V\in[a,b])>0.$
Then
\begin{equation*}\varliminf_{t\to\infty}\mathbb{P}\left(\frac{\eta(t){Y}_t}{\eta(t)\tilde{Y}_t}=\frac{{Y}_t}{\tilde{Y}_t}\in[a/b, b/a]\right)>0,\end{equation*}
but this is in contradiction to (30). Thus necessarily V is degenerate.
Remark 5. The statement of Corollary 1 holds for CBI processes started from arbitrary initial values. Indeed if
$(Y_t(x),t\geq 0)$
and
$(\tilde{Y}_t(y),t\geq 0)$
are two independent CBI
$(\Psi,\Phi)$
processes started respectively at x and y, then for any
$t\geq 0$
,
$Y_t(x)=X_t(x)+Y_t(0)$
with
$(X_t(x),t\geq 0)$
a CB
$(\Psi)$
process started from x and independent of
$(Y_t(0),t\geq 0)$
. Similarly
$\tilde{Y}_t(y)=\tilde{X}_t(y)+\tilde{Y}_t(0)$
with
$(\tilde{X}_t(y),t\geq 0)$
a CB
$(\Psi)$
process started from y and independent of
$(\tilde Y_t(0),t\geq 0)$
. One checks that
\begin{align*}\frac{Y_t(x)}{\tilde{Y}_t(y)}=\frac{Y_t(0)\left(1+X_t(x)/Y_t(0)\right)}{\tilde{Y}_t(0)\left(1+\tilde{X}_t(y)/\tilde{Y}_t(0)\right)}\overset{p}{\sim} \frac{Y_t(0)}{\tilde{Y}_t(0)} \text{ as } t\rightarrow \infty.\end{align*}
Indeed, on the one hand if
$\Psi$
is (sub-)critical then both
$\tilde{X}_t(x)$
and
$X_t(y)$
converge towards 0 a.s., and by Theorem 1,
$Y_t(0)$
and
$\tilde{Y}_t(0)$
go towards
$\infty$
in probability. On the other hand if
$\Psi$
is supercritical then by Theorem 2, for any
$x\geq 0$
,
\begin{equation*}\frac{X_t(x)}{Y_t(0)}=\frac{v_{-t}(\lambda)X_t(x)}{v_{-t}(\lambda)Y_t(0)}\underset{t\rightarrow \infty}{\longrightarrow} 0 \quad \text{ a.s.}\end{equation*}
3.3. Three different regimes
Since the renormalization in Theorem 4 is nonlinear and time-dependent, it is rather an intricate problem, at first sight, to deduce from it which explicit growth rates are possible. We design here different regimes for which (18) holds and the rate can be found explicitly. This establishes and completes [Reference Pinsky32, Theorem 2].
3.3.1. Definition of the regimes and preliminary calculations
Recall
$\lambda \mapsto c_t(\lambda)$
, the inverse of
\begin{equation*}\lambda\ma2psto r_t(\lambda)=\int_{v_t(\lambda)}^{\lambda}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u.\end{equation*}
Theorem 4 indicates that
$Y_t$
should grow at the speed of
$1/c_t(\lambda)$
as
$t\rightarrow \infty$
. However, the magnitude of
$c_t(\lambda)$
is rather involved and deserves careful analysis. We shall simplify (19) to more straightforward forms by imposing some additional conditions.
To start with, let us fix some constant
$\lambda_0$
such that
$\lambda_0\in(0,\infty)$
in the (sub-)critical case and
$\lambda_0\in(0,\rho)$
in the supercritical case. Put
\begin{eqnarray} \varphi(\lambda)=\int_\lambda^{\lambda_0} \frac{\textrm{d} u}{|\Psi(u)|},\qquad 0<\lambda<\lambda_0. \end{eqnarray}
By assumption
$|\Psi'(0+)|<\infty$
and thus
$\varphi(\lambda)\rightarrow\infty$
as
$\lambda\rightarrow0$
. The mapping
$\varphi\,{:}\,(0,\lambda_0)\;\rightarrow\;(0,\infty)$
is strictly decreasing, and we write g for its inverse mapping. It is easy to see that g is a strictly decreasing continuous function on
$(0,\infty)$
, and
\begin{equation}\lim_{x\to\infty}g(x)=0,\quad \lim_{x\to0}g(x)=\lambda_0.\end{equation}
By (6), if
$b\geq0$
, then
$\Psi\geq 0$
and
\begin{align}\varphi(v_t(\lambda))&=\int_{v_t(\lambda)}^{\lambda} \frac{\textrm{d} u}{\Psi(u)}+\int_\lambda^{\lambda_0} \frac{\textrm{d} u}{\Psi(u)}=t+\varphi(\lambda).&\end{align}
Similarly if
$b<0$
, then
$\Psi(u)\leq 0$
for
$0 \leq u\leq \rho$
, and provided that
$v_t(\lambda)\in (0,\lambda_0)$
,
\begin{align}\varphi(v_t(\lambda))&=-\int_{v_t(\lambda)}^{\lambda} \frac{\textrm{d} u}{\Psi(u)}-\int_\lambda^{\lambda_0} \frac{\textrm{d} u}{\Psi(u)}=-t+\varphi(\lambda).&\end{align}
Applying g to both sides implies that if
$b\geq 0$
, then
\begin{eqnarray}v_t(\lambda)=g(\varphi(\lambda)+t) ,\qquad 0<\lambda<\lambda_0, \ t>0,\end{eqnarray}
and if
$b<0$
and
$v_t(\lambda)\in(0,\rho)$
, then
\begin{eqnarray}v_t(\lambda)=g(\varphi(\lambda)-t) ,\qquad 0<\lambda<\lambda_0, \ t>0.\end{eqnarray}
Then, for any
$x,y>0$
such that
$\Psi$
never attains zero between x and y, we obtain by a change of variable that
\begin{equation}\int_x^y\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\int_{g(\varphi(x))}^{g(\varphi(y))}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\int_{\varphi(y)}^{\varphi(x)}\Phi(g(u))\textrm{d} u.\end{equation}
Inspired by Pinsky [Reference Pinsky32, Theorem 2], we introduce the following function to characterize the divergence of the integral in (18):
\begin{equation}H(x)\,{:\!=}\,\left\{ \begin{array}{l@{\quad}l}\displaystyle\frac{1}{|b|}\int_{e^{-x}}^1\frac{\Phi(u)}{u}\textrm{d} u & \mbox{if } b\in(\!-\infty,0)\cup(0,\infty),\\\\\displaystyle\int_{g(x)}^{\lambda_0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u & \mbox{if }b=0, \\\end{array}\right. \quad x\geq 0,\end{equation}
where H(0) takes the value
$\lim_{x\to 0}H(x)=0$
(using (32)). It is not hard to check that the condition (18) is equivalent to
$H(x)\underset{x\rightarrow \infty}{\longrightarrow}\infty$
. Based on (31), a simple calculation shows that H
$^{\prime}$
is strictly decreasing and
$H'(x)\rightarrow0$
as
$x\rightarrow\infty$
. We now introduce different regimes of speed of divergence of the function H at
$\infty$
. We refer the reader to Bingham et al. [Reference Bingham, Goldie and Teugels4] for a reference on these functions. The following three modes of convergence to 0 of H
$^{\prime}$
correspond to different possible modes of divergence of H:
(S) Slow divergence:
$xH'(x)\rightarrow0$
as
$x\rightarrow\infty$
and
$H(x)\rightarrow\infty$
.
(L) Log divergence:
$xH'(x)\rightarrow a$
for some constant
$a>0$
as
$x\rightarrow\infty$
.
(F) Fast divergence:
$xH'(x)\rightarrow\infty$
as
$x\rightarrow\infty$
and H
$^{\prime}$
is regularly varying at
$\infty$
.
Note that Conditions (L) and (F) always entail
$H(x)\longrightarrow \infty$
as x goes to
$\infty$
, while the limit
$xH'(x)\rightarrow0$
as
$x\rightarrow\infty$
in Condition (S) does not guarantee it. Since
$H'(x)\rightarrow0$
as
$x\rightarrow\infty$
, Condition (F) can be given in the following equivalent form:
\begin{eqnarray} H'(x)=x^{-\delta}\frac{1}{ L(x)}, \end{eqnarray}
where L is slowly varying at
$\infty$
and
$0\leq\delta\leq 1$
, and if
$\delta=0$
,
$L(x)\rightarrow\infty$
as
$x\rightarrow\infty$
; if
$\delta=1$
,
$L(x)\rightarrow0$
as
$x\rightarrow\infty$
.
Let h be the inverse map of
$1/H'$
. Under (39) with
$\delta>0$
,
$t\mapsto h(t)$
is regularly varying with index
$1/\delta$
at
$\infty$
, i.e.
$h(t)\sim t^{1/\delta}L^*(t)$
for some slowly varying function
$L^*(t)$
. Moreover, since
$H'(x)\rightarrow0$
as
$x\rightarrow\infty$
, we have
\begin{equation}\lim_{t\to\infty}h(t)=\infty.\end{equation}
It may be difficult to verify the three conditions. We provide a proposition below to study the asymptotic behaviors of H and
$H'.$
For this purpose, recall the immigration mechanism
\begin{equation*}\Phi(q)=\beta q+\int_{0}^{\infty}(1-e^{-qu})\nu(\textrm{d} u).\end{equation*}
As observed by Pinsky [Reference Pinsky32, p. 244], for a non-critical CBI process, a faster rate of divergence in (18) implies heavier tails of the Lévy measure
$\nu(\textrm{d} u)$
. The following result specifies this idea.
Proposition 1. Assume that
$b\neq 0$
and
$H(x)\rightarrow\infty$
as
$x\rightarrow\infty$
. Denote by
$\bar{\nu}$
the tail of
$\nu$
: for all
$u\geq 0$
,
$\bar{\nu}(u)=\nu([u,\infty))$
. Then
\begin{eqnarray*}H(x)\sim\frac{1}{|b|}\int_{1}^{e^{x}}\frac{\bar{\nu}(u)}{u}\textrm{d} u,\quad \text{ as }x\rightarrow \infty.\end{eqnarray*}
Moreover,
$H'(x)=\Phi(e^{-x})/|b|$
for any
$x\geq 0$
, and if
$u\mapsto \bar\nu(u)$
is slowly varying at
$\infty$
, then
\begin{eqnarray*}H'(x)\sim \bar{\nu}(e^x)/|b| \quad \text{ as }x\rightarrow \infty.\end{eqnarray*}
Remark 6. The tail
$u\mapsto\bar\nu(u)$
is slowly varying at
$\infty$
if and only if
$\Phi$
is slowly varying at 0; see [Reference Bingham, Goldie and Teugels4, Theorem 8/1/6, p. 333].
Proof. Note that
$\Phi(u)/u=\beta+\int_0^{\infty} e^{-ut}\bar{\nu}(t)\textrm{d} t$
. A simple calculation shows that for
$z\in(0,1)$
,
\begin{align*}\int_{z}^1\frac{\Phi(u)}{u}\textrm{d} u &=\beta(1-z)+\int_0^{\infty}\frac{\bar{\nu}(u)}{u}(e^{-zu}-e^{-u})\textrm{d} u\\[3pt] &=\beta(1-z)+\bigg(\int_0^1+\int_1^{\infty}\bigg)\frac{\bar{\nu}(u)}{u}(e^{-zu}-e^{-u})\textrm{d} u.\end{align*}
Since
\begin{equation*}\int_0^1u\nu(\textrm{d} u)<\infty, \qquad \int_1^{\infty} \frac{\bar{\nu}(u)}{u}e^{-u}\textrm{d} u<\infty, \quad \text{and} \qquad \int_{0+}\frac{\Phi(u)}{u}\textrm{d} u=\infty,\end{equation*}
we have that as
$z\rightarrow0$
,
\begin{eqnarray}\int_{z}^1\frac{\Phi(u)}{u}\textrm{d} u\sim \int_1^{\infty}\frac{\bar{\nu}(u)}{u}e^{-zu}\textrm{d} u,\end{eqnarray}
which implies
$\int_1^x \frac{\bar{\nu}(u)}{u}\textrm{d} u\rightarrow\infty$
as
$x\rightarrow \infty$
. It is not hard to see that
$\int_1^x \frac{\bar{\nu}(u)}{u}\textrm{d} u$
is also slowly varying at
$\infty$
. It follows from a Tauberian theorem (see e.g. Bertoin [Reference Bertoin3, p. 10]) that
\begin{eqnarray} \int_1^x \frac{\bar{\nu}(u)}{u}\textrm{d} u\sim\int_1^{\infty} \frac{\bar{\nu}(u)}{u}e^{-u/x}\textrm{d} u, \quad x\rightarrow\infty. \end{eqnarray}
The first result follows from (41) and (42). For the second result, note that
$H'(x)=\Phi(e^{-x})/|b|$
. Without loss of generality, we can assume that the parameter
$\beta$
in
$\Phi$
equals zero. Applying the Tauberian theorem implies that if
$\bar{\nu}(x)\sim \ell(x)$
for some slowly varying function
$\ell$
at
$\infty$
, then
\begin{equation*}\frac{\Phi(u)}{u}\sim \frac{1}{u}\ell(1/u)\end{equation*}
as u goes 0. Hence we have
$H'(x)\sim \bar{\nu}(e^x)/|b|$
,
$x\rightarrow \infty.$
Remark 7. By letting z go to 0 in (41), we see that
$\int_{0}\frac{\Phi(x)}{x}\textrm{d} x=\infty$
if and only if
$\int^{\infty}\frac{\bar{\nu}(u)}{u}\textrm{d} u=\infty$
; the latter is equivalent to
$\int^{\infty}_1\ln x\ \nu(\textrm{d} x)=\infty$
.
Proposition 1 allows us to reformulate the three regimes, in the non-critical case, in terms of the tail of the immigration measure
$\nu$
when the latter has a slowly varying tail:
(S) Slow divergence:
$\bar{\nu}(x)\ln x \rightarrow 0$
as
$x\rightarrow\infty$
and
$\int^{\infty}_1\frac{\bar{\nu}(x)}{x}=\infty$
.
(L) Log divergence:
$\bar{\nu}(x)\ln x \rightarrow c$
for some constant
$c>0$
as
$x\rightarrow\infty$
.
(F) Fast divergence:
$\bar{\nu}(x)\ln x \rightarrow \infty$
as
$x\rightarrow\infty$
.
The constant c in the regime (L) matches with
$a|b|$
where
$a\,{:\!=}\,\underset{x\rightarrow \infty}{\lim} xH'(x)$
. We give below some examples of explicit immigration measures
$\nu$
for which the three different regimes may occur in the non-critical cases.
Example 1. Let
$b\in(\!-\infty,0)\cup(0,\infty)$
.
-
1. If
as
\begin{equation*}\bar{\nu}(x)\sim\frac{1}{\ln x\ln\ln x}\end{equation*}
$x\rightarrow\infty$
, then
$H(x)\sim(\ln\ln x)/|b|$
and
$H'(x)\sim1/(|b|x\ln x)$
. Condition (S) is satisfied. This example corresponds to Example 3 of null-recurrent CBI process in [Reference Duhalde, Foucart and Ma10].
-
2. If
$\bar{\nu}(x)\sim c/{\ln x}$
for some constant
$c>0$
, as
$x\rightarrow\infty$
, then
$H'(x)\sim c/(|b|x)$
. Condition (L) is satisfied. -
3. If
(with
\begin{equation*}\bar{\nu}(x)\sim\frac{\ln\ln x}{(\ln x)^\delta}\end{equation*}
$0<\delta\leq1$
) as
$x\rightarrow\infty,$
then
$H'(x)\sim (x^{-\delta}\ln x)/|b|$
. If, as
$x\rightarrow\infty$
,
$\bar{\nu}(x)\sim1/(\ln\ln x)$
, then
$H'(x)\sim1/(|b|\ln x)$
. Both cases satisfy Condition (F).
Remark 8. Recall the integral test
$\mathcal{E}<\infty$
or
$\mathcal{E}=\infty$
for transience or recurrence of (sub-)critical CBI processes given in (12). Plainly, by a change of variable,
$\mathcal{E}=\int^{\infty}e^{-H(x)}\textrm{d} x$
. If (F) holds, or (L) is satisfied with
$a>1$
, then
$\mathcal{E}<\infty$
and the process is transient. In the case (S), or (L) with
$a\leq 1$
,
$\mathcal{E}=\infty$
and the process is null-recurrent.
We state now a side result on the growth rate of a subordinator whose Laplace exponent is slowly varying at 0.
Proposition 2. Let
$(I_t,t\geq 0)$
be a subordinator with Laplace exponent
$\Phi$
. Assume that
$\Phi$
is slowly varying at 0; then
\begin{equation*}t\Phi(1/I_t)\overset{d}{\longrightarrow} \textrm{e}_1 \text{ as } t\to \infty.\end{equation*}
Proof. This is reminiscent of Steps 1 and 2 in the proof of Theorem 4. Observe that the stated convergence holds if and only if, for all
$\lambda>0$
,
\begin{equation*}\mathbb{P}(t\Phi(1/I_t)>\lambda)=\mathbb{P}(I_t<1/\Phi^{-1}(\lambda/t))=\mathbb{P}(\Phi^{-1}(\lambda/t)I_t<1)\underset{t\rightarrow \infty}{\longrightarrow} e^{-\lambda}.\end{equation*}
The latter will occur if for any
$\theta>0$
,
$\mathbb{E}[e^{-\theta \Phi^{-1}(\lambda/t)I_t}]\underset{t\rightarrow \infty}{\longrightarrow} e^{-\lambda}$
. Since
$\Phi$
is slowly varying at 0 and
$\Phi^{-1}(\lambda/t)\longrightarrow 0$
as
$t\to \infty$
, we have
\begin{equation*}\frac{t}{\lambda}\Phi(\theta \Phi^{-1}(\lambda/t))=\frac{\Phi(\theta \Phi^{-1}(\lambda/t))}{\Phi( \Phi^{-1}(\lambda/t))}\underset{t\rightarrow \infty}{\longrightarrow} 1.\end{equation*}
Therefore
\begin{equation*}\mathbb{E}[e^{-\theta \Phi^{-1}(\lambda/t)I_t}]=e^{-t\Phi(\theta \Phi^{-1}(\lambda/t))}\underset{t\rightarrow \infty}{\longrightarrow} e^{-\lambda},\end{equation*}
which finishes the proof.
In the next subsection, we study how the convergence results can be made explicit by combining Theorem 4 and the three conditions. These results can be seen as the continuous analogues of those in [Reference Pakes31].
3.3.2. Non-critical case
Consider a non-critical CBI process
$(Y_t, t\geq 0)$
, i.e.
$b\neq0$
. Recall
$v_{-t}(\lambda)$
defined by (11) and
$\lambda_0$
given in (31). Set
\begin{equation*}\rho_t\,{:\!=}\,\left\{ \begin{array}{l}1 \quad \mbox{ if } b>0,\\ \\[-7pt] v_{-t}(\lambda_0) \quad \mbox{ if }b<0. \\\end{array}\right.\end{equation*}
From Theorem 1 and Theorem 2(ii), if (18) holds, then
$\rho_tY_{t}$
converges to
$\infty$
at least in probability.
Theorem 5. Assume that
$b\neq0$
.
-
(i) If Condition (S) holds, let
for
\begin{equation*}m(x)\,{:\!=}\,\exp \left(\int_{1/x}^1\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)\end{equation*}
$x>0$
. Then
(43)where U is uniformly distributed on [0,1].
\begin{equation}\frac{\ln \rho_tY_t}{t}\overset{p}{\longrightarrow}0\quad \text{ and }\quad m(\rho_tY_t)/m(e^{|b|t})\stackrel{d}{\longrightarrow} U \quad \text{ as }t\to\infty,\end{equation}
-
(ii) If Condition (L) holds, then
(44)where
\begin{eqnarray}\frac{\ln \rho_tY_t}{t}\overset{d}{\longrightarrow}|b|U_L \quad \text{ as }t\to\infty,\end{eqnarray}
\begin{equation*}\mathbb{P}(U_L\leq \lambda)=\left(\frac{\lambda}{1+\lambda}\right)^a, \quad \lambda\geq0.\end{equation*}
-
(iii) If Condition (F) holds (i.e. (39) holds with
$0\leq \delta\leq 1$
), then
In particular, if
\begin{equation*}\frac{\ln Y_t}{t}\overset{p}{\longrightarrow}\infty\quad\mbox{and}\quad t\Phi(1/Y_t)\overset{d}{\longrightarrow}\textrm{e}_1 \quad \text{ as }t\to\infty.\end{equation*}
$0<\delta\leq 1$
in (39), then we have
(45)
\begin{equation} h(t)= t^{1/\delta}L^*(t)\quad\text{and}\quad\frac{\ln Y_t}{h(|b|t)}\overset{d}{\longrightarrow}U_F \quad \text{ as }t\to\infty,\end{equation}
where
$L^*$
is some slowly varying function at
$\infty$
and
$U_F$
follows the extreme distribution given by
$\mathbb{P}(U_F\leq \lambda)=\exp(\!-1/\lambda^{\delta})$
,
$\lambda\geq0$
.
Remark 9.
-
(i) We observe from Proposition 2 that in the fast regime (F), the branching part plays essentially no role in the growth of the non-critical CBI
$(\Psi,\Phi)$
process, since it has the same growth rate as the immigration subordinator
$(I_t,t\geq 0)$
. -
(ii) The statement (i) of Theorem 5 is given in Pinsky [Reference Pinsky32, Theorem 2], but with some errors. The corrected convergence from [Reference Pinsky32, Theorem 2] reads as follows:
We will first prove the following lemmas.
\begin{equation*}\mathbb{P}_x(m(X_t)/m(e^{ct})\geq u^{-1})\to u, \qquad \forall 0< u\leq 1, \quad \text{ as } t\to\infty.\end{equation*}
Lemma 2. Assume that
$b\neq0$
. Then
\begin{equation*}\varphi(\lambda)\underset{\lambda \rightarrow 0}{\sim}-\frac{1}{|b|}\ln \lambda,\end{equation*}
\begin{equation*} -\ln g(x)\underset{x \rightarrow\infty}{\sim} |b|x,\end{equation*}
and
\begin{eqnarray*} \ln{v_t(\lambda_t)}\sim-b(t+\varphi(\lambda_t)) \quad\mbox{if}\ b>0; \qquad \ln{v_t(\rho_t\lambda_t)}\sim\ln \lambda_t\quad\mbox{if}\ b<0, \end{eqnarray*}
for any
$\lambda_t\rightarrow0+$
as
$t\rightarrow\infty$
.
Proof. Note that
\begin{equation*}\varphi(\lambda)=\int_{\lambda}^{\lambda_0}\frac{\textrm{d} u}{|\Psi(u)|}\underset{\lambda \rightarrow 0}{\sim}\int_{\lambda}^{\lambda_0}\frac{\textrm{d} u}{|b|u}\underset{\lambda \rightarrow 0}{\sim}-\frac{1}{|b|}\ln \lambda.\end{equation*}
Since g is the inverse function of
$\varphi,$
we have
$ -\ln g(x)\underset{x \rightarrow\infty}{\sim} |b|x. $
If
$b>0$
, we establish the last statement by plugging
$x=\varphi(\lambda_t)+t$
into (35). Now we turn to
$b<0$
. It follows from (14) and (15) that
\begin{eqnarray*}v_t(\rho_t\lambda)\underset{t\rightarrow \infty}\longrightarrow v_{-\frac{\ln\lambda}{b}}(\lambda_0)\quad\mbox{and}\quad v_{-\frac{\ln\lambda}{b}}(\lambda_0)\underset{\lambda \rightarrow 0}\longrightarrow 0.\end{eqnarray*}
Recall that
$\lambda\mapsto v_t(\rho_t\lambda)$
is non-decreasing. Recall also that if
$b>0$
then
$\rho_t \equiv 1$
; if
$b<0$
then
$\lim_{t\to\infty}\rho_t=0.$
Thus we have
$\rho_t\lambda_t, v_t(\rho_t\lambda_t)\in(0,\lambda_0)$
for sufficiently large t. Then by (36),
\begin{eqnarray}v_t(\rho_t\lambda_t)=g(\varphi(\rho_t\lambda_t)-t)\end{eqnarray}
for large t. Recall that
$\rho_t=v_{-t}(\lambda_0)$
. By (10), we obtain
\begin{eqnarray*}\varphi(\rho_t\lambda_t)-t=\int_{\rho_t\lambda_t}^{\rho_t}(\!-1/\Psi(u))\textrm{d} u\sim \int_{\rho_t\lambda_t}^{\rho_t}(\!-1/bu)\textrm{d} u=\frac{\ln \lambda_t}{b}, \quad \mbox{as}\ t\rightarrow\infty.\end{eqnarray*}
Putting
$x=\varphi(\rho_t\lambda_t)-t$
into
$\ln g(x)\sim bx\,(x\rightarrow\infty)$
and using (46), we get the last statement for
$b<0$
.
Lemma 3. If
$b<0$
, then
$\ln\rho_t\sim bt$
as
$t\rightarrow\infty$
.
Proof. Recall from Lemma 1 that
$\rho_{t+s}/\rho_t\rightarrow e^{bs}$
as
$t\rightarrow\infty$
. Consider the function
$\rho_{\ln t}$
on
$(1,\infty)$
. We observe that
$\rho_{\ln t}$
is regularly varying with index b at
$\infty$
. By Bingham et al. [Reference Bingham, Goldie and Teugels4, Proposition 1.3.6(i)], we have
$ \ln \rho_{\ln t}\sim b\ln t\ (t\rightarrow\infty). $
Proof. (Proof of Theorem 5.) Recall that under the assumption (18), the process
$(Y_t, t\geq 0)$
goes to infinity in probability. By the Skorokhod representation theorem, there is a probability space on which is defined a process whose one-dimensional laws are those of
$(Y_{t},t\geq 0)$
, which tends to
$\infty$
a.s. when t goes towards
$\infty$
. See [Reference Blackwell and Dubins6, Corollary] for a continuous-time version of the Skorokhod representation theorem, and apply it at time
$t=\infty$
. In the supercritical case, we apply the Skorokhod representation theorem to the bivariate process
$(Y_{t},\rho_{t}Y_{t})_{t\geq 0}$
, so that on a certain probability space, copies of both coordinates go to infinity a.s. We stress that our aim is to establish some convergences in law. One can equivalently work along an arbitrary sequence
$(t_n)_{n\geq 1}$
which tends to
$\infty$
and apply the usual Skorokhod representation theorem.
By the definition of H and Theorem 4,
\begin{equation}\textrm{sgn}(b)\Big[H(\!-\ln v_t(1/Y_t))-H(\ln Y_t)\Big]=(1+o(1))\int_{v_t(1/Y_t)}^{1/Y_t}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u \overset{d}{\longrightarrow}\textrm{e}_1. \end{equation}
-
(i) Applying first the mean value theorem, and then Condition (S), we see that there exists
$\theta_t$
between
$\ln Y_t$
and
$-\ln v_t(1/Y_t)$
such that
(48)We start with
\begin{align} H(\!-\!\ln v_t(1/Y_t))-H(\ln Y_t)&=\int_{\ln Y_t}^{-\ln v_t(1/Y_t)}\frac{uH'(u)}{u}\textrm{d} u\nonumber\\&=H'(\theta_t)\theta_t\ln\bigg(\!-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\bigg)\nonumber\\&= o(1)\ln\bigg(\!-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\bigg). \end{align}
$b>0$
. In this case,
for sufficiently large t. Then a comparison between (47) and (48) implies that
\begin{equation*}-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\geq1\end{equation*}
It follows from Lemma 2 with
\begin{equation*}-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\overset{p}\rightarrow+\infty.\end{equation*}
$\lambda_t=1/Y_t$
that
Based on the results above, again using Condition (S), there exists
\begin{eqnarray*}\frac{\ln Y_t}{t}\overset{p}{\rightarrow}0\quad\mbox{and}\quad-\ln v_t(1/Y_t)\overset{p}{\sim}bt,\quad t\rightarrow\infty.\end{eqnarray*}
$\theta'_t$
between bt and
$-\ln v_t(1/Y_t)$
such that
(49)Note that
\begin{align} H(\!-\ln v_t(1/Y_t))-H(bt) = H'(\theta'_t)\theta'_t\ln\Big(\!-\frac{\ln v_t(1/Y_t)}{bt}\Big)\overset{p}{\rightarrow}0,\quad t\rightarrow\infty. \end{align}
Combining this with (47) and (49), we have that
\begin{eqnarray*}\frac{m(Y_t)}{m(e^{bt})}={\exp\left(\int^{e^{-bt}}_{1/Y_t}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\right)}={\exp\{(H(\ln Y_t)-H(bt))(1+o(1))\}}.\end{eqnarray*}
We now turn to
\begin{equation*}\frac{m(Y_t)}{m(e^{bt})}\overset{d}{\rightarrow}\exp(\!-\textrm{e}_1).\end{equation*}
$b<0$
. In this case,
for sufficiently large t. A comparison between (47) and (48) implies that
\begin{equation*}0<-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\leq1\end{equation*}
It follows from Lemma 2 with
\begin{equation*}-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\overset{p}\rightarrow0.\end{equation*}
$\lambda_t=1/(\rho_tY_t)$
and Lemma 3 that
Proceeding as in the case with
\begin{eqnarray*}-\ln v_t(1/Y_t)\overset{p}{\sim}\ln\rho_tY_t\quad\mbox{and}\quad\ln Y_t\overset{p}{\sim}-bt,\quad t\rightarrow\infty.\end{eqnarray*}
$b>0$
, we have that
\begin{equation*}\frac{m(\rho_tY_t)}{m(e^{-bt})}\overset{d}{\rightarrow}\exp(\!-\textrm{e}_1).\end{equation*}
-
(ii) By Condition (L),
Using Lemma 2 with
\begin{eqnarray*}H(\!-\ln v_t(1/Y_t))-H(\ln Y_t)=\int_{\ln Y_t}^{-\ln v_t(1/Y_t)}H'(u)\textrm{d} u\sim a\int ^{-\ln v_t(1/Y_t)}_{\ln Y_t}\frac{\textrm{d} u}{u},\quad t\rightarrow\infty.\end{eqnarray*}
$\lambda_t=1/Y_t$
if
$b>0$
, and using Lemma 2 with
$\lambda_t=1/(\rho_tY_t)$
and Lemma 3 if
$b<0$
, we obtain
Then by (47), we have Theorem 5(ii).
\begin{eqnarray*}\textrm{sgn}(b)\int ^{-\ln v_t(1/Y_t)}_{\ln Y_t}\frac{\textrm{d} u}{u}=\textrm{sgn}(b)\ln\bigg(\!-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\!\bigg)=\ln \bigg(\!1+\frac{|b|t}{\ln \rho_tY_t}(1+o(1))\!\bigg)+o(1).\end{eqnarray*}
-
(iii) The mean value theorem for integrals shows that there is some
$\bar\theta_t$
between
$\ln Y_t$
and
$-\ln v_t(1/Y_t)$
such that
By Condition (F) and (47), we have that
\begin{eqnarray*} H(\!-\ln v_t(1/Y_t))-H(\ln Y_t)=H'(\bar\theta_t)\bar\theta_t\ln\bigg(\!-\frac{\ln v_t(1/Y_t)}{\ln Y_t}\bigg). \end{eqnarray*}
$-\ln v_t(1/Y_t)\overset{p}{\sim}\ln Y_t.$
Then it follows from Lemma 2 (together with Lemma 3 if
$b<0$
) that
(50)Applying (35), (36), and (37), we obtain, for large t,
\begin{equation}t/\ln Y_t\overset{p}{\rightarrow}0 \quad\mbox{and}\quad t/\varphi(1/Y_t)\overset{p}{\rightarrow}0,\quad t\rightarrow\infty.\end{equation}
(51)Note that
\begin{eqnarray}\int_{v_t(1/Y_t)}^{1/Y_t}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\left\{ \begin{array}{l}\displaystyle\int^{\varphi(1/Y_t)+t}_{\varphi(1/Y_t)}\Phi(g(u))\textrm{d} u \quad \mbox{ if } b>0,\\\\\displaystyle \int^{\varphi(1/Y_t)-t}_{\varphi(1/Y_t)}\Phi(g(u))\textrm{d} u \quad \mbox{ if } b<0.\end{array}\right.\end{eqnarray}
$\Phi(g(u))=bH'(\!-\ln g(u))$
.
By the fact that
$ -\ln g(u)\sim |b|u$
as
$u\rightarrow\infty$
and Condition (F), we have that
$\Phi(g(u))$
is regularly varying at
$\infty$
; see [Reference Resnick33, Proposition 0.8(iv)]. In the rest of the proof, we deal only with
$b>0$
. The proof for
$b<0$
is quite similar and therefore omitted.
By changing variable and applying a mean value theorem to the right-hand side of (51), we obtain
\begin{align} \int_{v_t(1/Y_t)}^{1/Y_t}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u &=\varphi(1/Y_t)\int^{t/\varphi(1/Y_t)+1}_{1}\Phi(g(\varphi(1/Y_t)u)) \textrm{d} u\nonumber\\[2pt]&= t\Phi(g(\varphi(1/Y_t){\hat\theta}_t)) \quad\quad\big(\text{for some } {\hat\theta}_t\in(1,t/\varphi(1/Y_t)+1)\big)\nonumber\\[2pt] &\sim t\Phi(g(\varphi(1/Y_t))) \qquad (t\rightarrow\infty).\end{align}
The validity of the last equivalence is proved as follows: using (50), we have
$\theta_t\overset{p}{\to}1$
as
$t\rightarrow\infty.$
Since
$\Phi \circ g$
is regularly varying, the last equivalence holds by locally uniform convergence; see e.g. [Reference Bingham, Goldie and Teugels4, Theorem 1.2.1]. Then
$t\Phi(1/Y_t)= t\Phi(g(\varphi(1/Y_t)))\overset{d}{\rightarrow}\textrm{e}_1$
from Theorem 4.
Now we focus on the case when
$\delta>0$
in (39). Note that
$H'(x)=\frac{1}{b}\Phi(e^{-x})$
. Since h is the inverse function of
$1/H'$
, we have
$H'(h(x))=1/x$
for any
$x>b/\Phi(1).$
Then by Karamata’s theorem (see [Reference Resnick33, p. 23]), the statement on h(t) in (45) holds.
For
$\lambda>0$
, we again use
$H'(x)=\frac{1}{b}\Phi(e^{-x})$
, and apply (39) and (40) to obtain that
\begin{eqnarray*}\frac{H'(\!\ln Y_t)}{H'(h(bt)\lambda)} =t\Phi(1/Y_t) \frac{H'(h(bt))}{H'(h(bt)\lambda)}\overset{d}{\rightarrow}{\lambda^\delta}\textrm{e}_1 \quad \text{ as }t\to\infty. \end{eqnarray*}
Hence,
$ \mathbb{P}(\!\ln Y_t/h(bt)\leq\lambda)=\mathbb{P}(H'(\!\ln Y_t))/H'(h(bt)\lambda)\geq1)\underset{t\rightarrow \infty}\longrightarrow\exp(\!-1/\lambda^\delta)$
.
3.4. On the critical case
The study of the critical case, i.e.
$b=\Psi'(0+)=0$
, is more involved, as
$v_t(\lambda)$
may have different asymptotics as
$t\rightarrow \infty$
and
$\lambda\rightarrow 0$
depending on the behavior of
$\Psi$
near 0. We make the following assumption on the Lévy measure
$\pi$
in the branching mechanism: suppose that
$\pi$
satisfies
\begin{eqnarray} \bar{\pi}(u)\underset{u\rightarrow\infty}{\sim} -\frac{1}{\Gamma(\!-\alpha)}u^{-1-\alpha}\ell(u), \end{eqnarray}
where
$\bar{\pi}(u)=\pi(u,\infty)$
for
$u>0$
,
$0<\alpha<1$
, and
$\ell$
is slowly varying at
$\infty$
. By [Reference Bingham, Goldie and Teugels4, Theorem 8.1.6], the above assumption is equivalent to
\begin{eqnarray} \Psi(\lambda)\underset{\lambda \rightarrow 0}{\sim} \lambda^{1+\alpha}\ell(1/\lambda). \end{eqnarray}
Recall that
$\varphi$
is defined by (31) and g is the inverse function of
$\varphi$
. It follows from Karamata’s theorem (see [Reference Resnick33, p. 17, p. 23]) that
\begin{eqnarray}\varphi(\lambda)\sim\frac{\lambda^{-\alpha}}{\alpha \ell(1/\lambda)}\quad \text{and} \quad g(1/\lambda)\sim\lambda^{1/\alpha}\ell^*(1/\lambda), \quad \text{ as }\lambda\rightarrow0,\end{eqnarray}
where
$\ell^*$
is slowly varying at
$\infty$
. We denote by
$\Phi^{-1}$
the inverse function of
$\Phi$
.
Theorem 6. Assume that
$b=0$
and (53) holds.
-
(i) If Condition (S) holds, let m(x) be defined as in (43). Then
where V is uniformly distributed on
\begin{eqnarray*}\frac{m(Y_t)}{m(1/g(t))}\stackrel{d}{\longrightarrow} V \text{ as }t\to\infty,\end{eqnarray*}
$[0,1].$
-
(ii) If Condition (L) holds, then
where
\begin{equation*}g(t)Y_t\overset{d}{\longrightarrow}V_L \text{ as }t\to\infty,\end{equation*}
$\mathbb{E}\big[e^{-\lambda V_L}\big]=(1+\lambda^\alpha)^{-a}$
for all
$\lambda\geq 0.$
-
(iii) If Condition (F) holds with
$\delta>0$
in (39), then
(56)where
\begin{equation} \varrho_tY_t\overset{d}{\longrightarrow}V_F \quad \text{ as }t\to\infty, \end{equation}
$\mathbb{E}\big[e^{-\theta V_F}\big]=\exp(\!-\theta^{\delta\alpha})$
for all
$\theta\geq 0$
, with
$\varrho_t=\Phi^{-1}(1/t)= t^{-1/(\delta\alpha)}\bar{\ell}(t) \text{ as }t\to\infty$
for some slowly varying function
$\bar{\ell}$
at
$\infty$
.
If Condition (F) holds with
$\delta=0$
in (39), then
$t\Phi(1/Y_t)\overset{d}{\longrightarrow}\textrm{e}_1 \text{ as }t\to\infty$
.
Remark 10. When
$\delta\in (0,1]$
, the convergence (56) is equivalent to the following:
$t\Phi(1/Y_t)\overset{d}{\longrightarrow}V_F^{-\delta\alpha}$
as t goes to
$\infty$
. Indeed, for any
$\lambda>0$
, the property of regular variation of
$\varrho_t$
implies that
\begin{align*}&\mathbb{P}(t\Phi(1/Y_t)\geq \lambda)\\
&=\mathbb{P}(\Phi(1/Y_t)\geq \lambda/t)=\mathbb{P}(1/Y_t\geq\varrho_{t/\lambda})\\
&=\mathbb{P}(\varrho_{t/\lambda}Y_t\leq 1)\sim \mathbb{P}\big(\lambda^{1/(\delta\alpha)}\varrho_tY_t\leq 1\big)\underset{t \to \infty}\to\mathbb{P}\big(V_F\leq \lambda^{-1/(\delta\alpha)}\big)=\mathbb{P}((V_F)^{-\delta\alpha}\geq \lambda).\end{align*}
Since the random variable
$V_F$
has a stable law,
$(V_F)^{-\delta\alpha}$
is not a standard exponential random variable. Therefore, unlike in the non-critical cases (see Theorem 5(iii)), for which
$t\Phi(1/Y_t)\overset{d}{\longrightarrow}\textrm{e}_1$
holds when Condition (F) holds, no matter what value
$\delta\in [0,1]$
takes, in the critical case the convergence to
$\textrm{e}_1$
holds only for
$\delta=0.$
Proof. We start with some observations. By (35) and (37), we have
\begin{eqnarray} \int_{v_t(\lambda)}^\lambda\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\int^{t+\varphi(\lambda)}_{\varphi(\lambda)}\Phi(g(u))\textrm{d} u,\quad H(x)=\int^x_{\varphi(\lambda_0)}\Phi(g(u))\textrm{d} u. \end{eqnarray}
Then
$H'(x)=\Phi(g(x)).$
Note that we will use H
$^{\prime}$
(x) or
$\Phi(g(x))$
in different contexts.
It was mentioned in Remark 4 that Steps 1 and 2 in the proof of Theorem 4 still hold for the critical case. That is to say, recalling
$r_t(\lambda)$
defined by (8) and
$\lambda\mapsto c_{t}(\lambda)$
its inverse, for any fixed
$\lambda>0$
we have
$c_t(\lambda){\rightarrow} 0$
and
$v_t(c_t(\lambda)){\rightarrow} 0$
as
$t\rightarrow\infty$
. Therefore
$\varphi(c_t(\lambda))\to\infty \text{ as } t\to\infty$
.
-
(i) From (57) with
$\lambda$
replaced by
$c_t(\lambda)$
, by the mean value theorem, there exists
$\hat\theta_t$
between
$\varphi(c_t(\lambda))$
and
$t+\varphi(c_t(\lambda))$
such that
(58)Together with Condition (S), this yields
\begin{eqnarray}\lambda=\int_{v_t(c_t(\lambda))}^{c_t(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\int^{t+\varphi(c_t(\lambda))}_{\varphi(c_t(\lambda))}\Phi (g (u))\textrm{d} u=\hat\theta_t H'(\hat\theta_t){\ln} \bigg(\frac{t+\varphi(c_t(\lambda))}{\varphi(c_t(\lambda))}\bigg).\end{eqnarray}
$\varphi(c_t(\lambda))/t\rightarrow0$
as
$t\rightarrow\infty.$
Then, still by the mean value theorem and Condition (S), we obtain
(59)which goes to 0 as
\begin{equation}\int^{v_t(\theta c_t(\lambda))}_{v_t(c_t(\lambda))}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\int^{t+\varphi(c_t(\lambda))}_{t+\varphi(\theta c_t(\lambda))}\Phi \circ g (u)\textrm{d} u=o(1)\ln \bigg(\frac{t+\varphi( c_t(\lambda))}{t+\varphi(\theta c_t(\theta\lambda))}\bigg),\end{equation}
$\varphi$
is regularly varying with index
$-\alpha$
by (55). Similarly
Hence, by (24), (23), and (22),
\begin{equation*}\int_{\theta c_t(\lambda)}^{c_t(\lambda)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\rightarrow0.\end{equation*}
(60)Applying the same transformation as in (59) to (60) shows that
\begin{eqnarray}\int_{v_{t}(1/Y_t)}^{1/Y_t} \frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\int^{t+\varphi(1/Y_t)}_{\varphi(1/Y_t)}\Phi (g(u)) \textrm{d} u\stackrel{d}\longrightarrow \textrm{e}_1 \quad \text{ as } t\rightarrow\infty.\end{eqnarray}
$\varphi(1/Y_t)/t\overset{p}{\rightarrow}0\text{ as } t\,{\rightarrow}\,\infty$
. Again using Condition (S), we have
(61)Therefore, combining the above two displays (60) and (61) yields
\begin{eqnarray}\int_{g(t)}^{v_t(1/Y_t)}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u=\int_{t+\varphi(1/Y_t)}^{t}\Phi (g(u)) \textrm{d} u=o(1)\ln \Big(\frac{t}{t+\varphi(1/Y_t)}\Big)\overset{p}{\rightarrow}0.\end{eqnarray}
This allows one to conclude that (i) holds.
\begin{equation*}-\ln\Big(\frac{m(Y_t)}{m(1/g(t))}\Big)=\int_{g(t)}^{1/Y_t}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u\overset{d}{\longrightarrow}\textrm{e}_1.\end{equation*}
-
We shall study the two terms in the exponential one by one. As
\begin{eqnarray*} \mathbb{E}_x\big[e^{-\lambda g(t)Y_t}\big]= \exp\Big\{\!-xv_t(g(t)\lambda)-\int^{t+\varphi(\lambda g(t))}_{\varphi(\lambda g(t))}\Phi (g(u))\textrm{d} u\Big\}. \end{eqnarray*}
$t\rightarrow\infty$
,
$g(t)\to0$
and consequently
$v_t(g(t)\lambda)\rightarrow0$
. By Condition (L),
which converges to
\begin{eqnarray*}\int^{t+\varphi(\lambda g(t))}_{\varphi(\lambda g(t))}\Phi \circ g(u)\textrm{d} u\sim a\int^{t+\varphi(\lambda g(t))}_{\varphi(\lambda g(t))}\frac{\textrm{d} x}{x}=a\ln\Big(\frac{\varphi(g(t))+\varphi(\lambda g(t))}{\varphi(\lambda g(t))}\Big),\end{eqnarray*}
$a\ln(\lambda^{\alpha}+1)$
by (55). So the statement in (ii) holds.
-
(iii) Applying the same proof as in (58), we have from Condition (F) that
(62)
\begin{equation}t/\varphi(c_t(\lambda))\rightarrow0 \quad \text{ as } t\rightarrow\infty.\end{equation}
Since
$\varphi$
is regularly varying with index
$-\alpha$
(see (55)),
$\varphi(\theta c_t(\lambda))/\varphi(c_t(\lambda))\rightarrow \theta^{-\alpha}$
for
$\theta>0.$
Then
$t/\varphi(\theta c_t(\lambda))\rightarrow0$
.
We also note that
$H'=\Phi \circ g$
is regularly varying by (39). Based on the above results, a similar proof as in (52) shows that for any
$\theta>0$
,
\begin{eqnarray}\int_{v_{t}(\theta c_t(\lambda))}^{\theta c_t(\lambda)} \frac{\Phi(u)}{\Psi(u)}\textrm{d} u\sim t \Phi\circ g(\varphi(\theta c_t(\lambda)))=t\Phi(\theta c_t(\lambda)) \quad \text{ as }t\rightarrow\infty.\end{eqnarray}
Letting
$\theta=1$
and
$\lambda=1$
, by the definition of
$r_t(1),c_t(1)$
, the left term in the equivalence relation above equals 1, and so we have
\begin{equation}t\Phi(c_t(1))\rightarrow1 \quad \text{ as } t\rightarrow\infty.\end{equation}
If (39) holds, then
$\Phi=H'\circ \varphi$
is regularly varying with index
$\delta\alpha$
at 0 by (55) and [Reference Resnick33, Proposition 0.8(iv)]. Using the above two displays,
\begin{eqnarray*}\int_{v_{t}(\theta c_t(1))}^{\theta c_t(1)} \frac{\Phi(u)}{\Psi(u)}\textrm{d} u\sim t \Phi(c_t(1))\frac{\Phi(\theta c_t(1))}{\Phi(c_t(1))}\sim \theta^{\delta\alpha}, \quad \text{ as }t\to\infty.\end{eqnarray*}
As
$c_t(1)\to 0$
, we also have
$v_{t}(\theta c_t(1))\to 0$
thanks to the above display. Then, using (23) and (24), we conclude that
\begin{equation*}\mathbb{E}_x\big[e^{-\theta c_t(1) Y_t}\big]\rightarrow e^{-\theta^{\delta\alpha}}\end{equation*}
as
$t\to\infty.$
By [Reference Resnick33, Proposition 0.8(v)], the map
$\Phi^{-1}$
is regularly varying with index
$1/(\delta\alpha)$
at 0, and by (64), we have that
$c_t(1)=\Phi^{-1}(\Phi(c_t(1)))\sim\Phi^{-1}(1/t)$
. Thus the first result in (iii) holds.
If
$\Phi \circ g$
is slowly varying at
$\infty$
, then
$\Phi \circ g (\varphi(u))$
is slowly varying at 0 by (55). Then it follows from (63) that
$\mathbb{E}_x[e^{-\theta c_t(\lambda) Y_t}]\rightarrow e^{-\lambda}$
as
$t\rightarrow\infty$
. As in (22), we have (19) in this case. The second half of (iii) follows the very similar proof of Theorem 5(iii) and we omit it.
Remark 11. Recall that in the critical case when
$\Phi=\Psi'$
, the CBI
$(\Psi,\Phi)$
process has the same law as the CB(
$\Psi$
) processes conditioned on non-extinction. Moreover, we readily check that
$\int_0\frac{\Psi'(u)}{\Psi(u)}\textrm{d} u=\infty$
. It follows that
$H'(x)=\Psi'(g(x))$
for all x.
We apply now Theorem 1 and Theorem 6 to the case of stable branching and immigration mechanisms, for which explicit calculations can be made.
Corollary 2. (Stable case) Assume
$\Psi(q)=dq^{\alpha+1}$
for
$d>0$
and
$\alpha\in (0,1]$
, and
$\Phi(q)=d'q^{\beta}$
for
$d'>0$
and
$\beta\in (0,1]$
. Then the following hold:
-
(i) If
$\beta/\alpha>1$
, then
$Y_t\overset{d}{\longrightarrow} Y_\infty \text{ as } t\rightarrow \infty$
, where
$Y_\infty$
has Laplace transform
for any
\begin{equation*}\mathbb{E}\big[e^{-\lambda Y_\infty}\big]=e^{-\frac{\lambda^{\beta-\alpha}}{\beta-\alpha}}\end{equation*}
$\lambda \geq 0$
.
-
(ii) If
$\beta/\alpha=1$
, then
$t^{-\frac{1}{\alpha}}Y_t\overset{d}{\longrightarrow} (\alpha d)^{\frac{1}{\alpha}}V_L \text{ as } t\rightarrow \infty$
, where
$V_L$
has Laplace transform
for any
\begin{equation*}\mathbb{E}\big[e^{-\lambda V_L}\big]=\frac{1}{(1+\lambda^{\alpha})^{\frac{d'}{\alpha d}}}\end{equation*}
$\lambda\geq 0$
.
-
(iii) If
$\beta/\alpha<1$
, then
$t^{-\frac{1}{\beta}}Y_t\overset{d}{\longrightarrow} (d')^{1/\beta}V_F\text{ as } t\rightarrow \infty,$
where
$V_F$
has Laplace transform
$\mathbb{E}\big[e^{-\lambda V_F}\big]=e^{-\lambda^{\beta}}$
for any
$\lambda\geq 0$
.
Remark 12. When
$\beta=\alpha$
, the specific case
$d'=(\alpha+1)d$
, which corresponds to
$\Phi=\Psi'$
, has been studied by Kyprianou and Pardo [Reference Kyprianou and Pardo25, Lemma 3] using other techniques.
Proof. First notice that
$\int_{0}\frac{\Phi(u)}{\Psi(u)}\textrm{d} u =\infty$
if and only if
$\frac{\beta}{\alpha}\leq 1$
. The statement (i) is a direct consequence of Theorem 1. Let
$\lambda_0=1$
; we compute
\begin{equation*}\varphi(x)=\frac{1}{\alpha d}\left(\frac{1}{x^{\alpha}}-1\right) \quad \text{and} \quad g(x)=\left(\frac{1}{\alpha dx+1}\right)^{\frac{1}{\alpha}}\end{equation*}
for
$x>0$
. Moreover,
\begin{equation*}x\Phi(g(x))\sim \frac{d'}{(\alpha d)^{\beta/\alpha}}x^{1-\beta/\alpha}\end{equation*}
as x goes to
$\infty$
. If
$\beta/\alpha=1$
then Condition (L) is fulfilled for
$a=\frac{d'}{\alpha d}$
, and we deduce the statement (ii) from Theorem 6. If
$\beta/\alpha<1$
, then Condition (F) and (39) are fulfilled with
$\delta=\frac{\beta}{\alpha}$
. Theorem 6 also applies.
We have focused our study on CBI processes whose branching Lévy measure has finite mean, i.e.
$\Psi'(0+)=b\in \mathbb{R}$
or equivalently
$\int^{\infty}_1 z\pi(\textrm{d} z)<\infty$
. The proofs of Theorem 4 and Corollary 1, however, do not make use of this assumption. Thus they also hold in the case of a non-explosive supercritical CBI
$(\Psi,\Phi)$
process with
$\Psi'(0+)=-\infty$
. A similar dichotomy occurs in the long-term behavior, depending on whether
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u<\infty$
or
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
when
$b=-\infty$
. In the first case, some a.s. nonlinear renormalizations can be found; see [Reference Grey18] and Foucart and Ma [Reference Foucart and Ma15] for the case without immigration. In the case
$\int_{0}\frac{\Phi(u)}{|\Psi(u)|}\textrm{d} u=\infty$
, there exist regimes similar to those found in Section 3.3; see [Reference Barbour and Pakes1] for the case of processes with discrete state space.
Acknowledgements
The authors thank the anonymous referees for helpful comments.
Funding Information
C. F. is supported by the French National Research Agency (ANR): LABEX MME-DII (ANR11-LBX-0023-01). C. M. is supported by the NSFC of China (11871032) and GXNSF (2018GXNSFAA050031). L. Y. is supported by the NSFC of China (11801458).
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process for this article.
