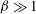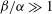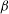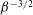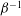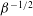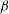1 Introduction
Complex fluids and soft materials are typically viscoelastic: they can exhibit the mechanical response of a viscous liquid or an elastic solid, depending on the time scale of an applied deformation (Larson Reference Larson1999). Small-amplitude oscillatory shear (SAOS) rheometry is a standard method to characterize viscoelasticity, wherein a sample is exposed to a weak time-periodic shear deformation at a specified strain amplitude. The stress in the material is proportional to the strain amplitude and oscillates with the same waveform as the imposed deformation. The stress contains contributions that are in phase and out of phase with the strain, from which the linear storage (elastic) and loss (viscous) moduli of the material, respectively, are determined. Nonlinear viscoelastic properties, such as shear thinning or shear thickening, and normal stress differences, are often characterized via a large-amplitude steady shear test. In such an experiment, the stress depends nonlinearly on the strain amplitude.
There has been significant recent interest in large-amplitude oscillatory shear (LAOS) as a rheometric protocol to quantify transient, nonlinear viscoelasticity of complex fluids (Hyun et al. Reference Hyun, Kim, Ahn and Lee2002, Reference Hyun, Wilhelm, Klein, Cho, Nam, Ahn, Lee, Ewoldt and McKinley2011). It should be noted, however, that theoretical (Bird, Warner & Evans Reference Bird, Warner and Evans1971) and experimental (Philippoff Reference Philippoff1966) investigations of LAOS rheology are, in fact, decades old. In LAOS, a complex fluid is exposed to a strong shear deformation whose amplitude typically varies sinusoidally in time. The measured stress is not proportional to the strain amplitude and is not sinusoidal (although it is normally periodic), indicating nonlinear mechanical response. The stress is usually decomposed into a series of temporal Fourier modes, which underlies the technique of Fourier-transform rheology (Wilhelm Reference Wilhelm2002). This approach can be used to fit parameters from nonlinear constitutive models to LAOS data (Gurnon & Wagner Reference Gurnon and Wagner2012). Ewoldt, Hosoi & McKinley (Reference Ewoldt, Hosoi and McKinley2008) propose an alternative decomposition using Chebyshev polynomials. Rogers and co-workers interpret LAOS data as a ‘sequence of physical processes,’ which does not require the stress waveform to be expanded in orthogonal basis functions of time (Rogers et al. Reference Rogers, Erwin, Vlassopoulos and Cloitre2011; Rogers & Lettinga Reference Rogers and Lettinga2012). Theoretical studies have computed the LAOS dynamics of popular constitutive relations, including the Giesekus (Gurnon & Wagner Reference Gurnon and Wagner2012), co-rotational Maxwell (Giacomin et al. Reference Giacomin, Bird, Johnson and Mix2011), Doi–Edwards (Pearson & Rochefort Reference Pearson and Rochefort1982), and fourth-order fluid (Bharadwaj & Ewoldt Reference Bharadwaj and Ewoldt2014) models. Only the first few Fourier modes of the stress are computed in those works. This adequately describes the material dynamics at small to moderate strain amplitude. However, many harmonic modes can be excited at large strain amplitude: for instance, experiments on emulsions have measured overtones up to the 151st order (Hyun et al. Reference Hyun, Wilhelm, Klein, Cho, Nam, Ahn, Lee, Ewoldt and McKinley2011). A physical understanding of the material dynamics encoded in such an experimental data set is not apparent. Moreover, it is plainly impractical to calculate this many overtones from Fourier decomposition of a constitutive relation. This motivates the need for an alternative modelling approach to LAOS at large strain amplitude, which we refer to as the ‘strongly nonlinear’ regime of LAOS. The central goal of this article is to take a step in that direction. This will be accomplished through singular asymptotic analysis of the strongly nonlinear LAOS dynamics of a paradigmatic complex fluid model; namely, a dilute suspension of nearly spherical particles that undergo rotational Brownian motion in an oscillatory shear flow.
The equations governing the LAOS rheology of the model material under consideration are presented in § 2. In § 3 we perform an asymptotic analysis that elucidates the physics of the strongly nonlinear regime of LAOS. This article is concluded with a discussion in § 4.
2 Governing equations
Consider a homogeneous suspension of identical rigid spheroids in an incompressible Newtonian fluid. The particles are free of external forces and torques but are subject to rotational Brownian motion. The suspension is dilute; hydrodynamic interactions between particles can be ignored. An ambient linear flow with velocity gradient tensor
${\it\bf\Gamma}$
is impressed on the material. The particles are sufficiently small that inertial effects are negligible. Define
$\boldsymbol{p}$
as a unit vector coaxial with the axis of revolution of a particle. In the absence of Brownian rotation
$\boldsymbol{p}$
evolves deterministically according to Jeffery’s equation (Jeffery Reference Jeffery1922). The effect of Brownian rotation necessitates a statistical description of the particle orientation. Let
${\it\psi}(\boldsymbol{p},t)$
be an orientation probability density function, such that
${\it\psi}(\boldsymbol{p},t)\,\text{d}{\it\varpi}$
is the probability that a particle is oriented within the differential solid angle
$\text{d}{\it\varpi}$
about
${\it\varpi}$
at time
$t$
. The admissible values of
$\boldsymbol{p}$
span the surface of a unit sphere; hence, at all times
$\int _{{\it\varpi}}{\it\psi}(\boldsymbol{p},t)\,\text{d}{\it\varpi}=1$
. The probability density function satisfies the conservation, or Fokker–Planck, equation (Brenner & Condiff Reference Brenner and Condiff1974)
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\psi}}{\partial t}+\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\boldsymbol{\cdot }(\dot{\boldsymbol{p}}{\it\psi})=0,\quad \text{where }\dot{\boldsymbol{p}}=(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\boldsymbol{\cdot }({\it\bf\Omega}+\mathscr{B}\unicode[STIX]{x1D640})\boldsymbol{\cdot }\boldsymbol{p}-D\boldsymbol{{\rm\nabla}}_{\boldsymbol{p}}\ln {\it\psi}, & & \displaystyle\end{eqnarray}$$
in which
$D$
is the rotational diffusivity,
$\unicode[STIX]{x1D644}$
is the identity tensor,
${\it\bf\Omega}$
and
$\unicode[STIX]{x1D640}$
are the vorticity and rate of strain tensors, respectively (anti-symmetric and symmetric parts of
${\it\bf\Gamma}$
, respectively), and
$\mathscr{B}=(r^{2}-1)/(r^{2}+1)$
is the Bretherton constant, with
$r$
the spheroid aspect ratio. The first term of
$\dot{\boldsymbol{p}}$
represents the evolution of the particle’s axis of rotational symmetry in the imposed flow. The second term is a diffusive flux due to rotational Brownian motion, which acts to smoothen gradients in probability density. For nearly spherical particles,
$r\approx 1$
, the probability density is expanded as (Leal & Hinch Reference Leal and Hinch1972, hereafter ‘LH72’)
$$\begin{eqnarray}\displaystyle {\it\psi}(\boldsymbol{p},t)=\frac{1}{4{\rm\pi}}[1+\mathscr{B}\boldsymbol{p}\boldsymbol{p}\boldsymbol{ : }\unicode[STIX]{x1D63E}(t)+O(\mathscr{B}^{2})], & & \displaystyle\end{eqnarray}$$
where
$\mathscr{B}\ll 1$
is the small parameter. The microstructure tensor
$\unicode[STIX]{x1D63E}$
, which describes the non-equilibrium particle orientation, is second rank, symmetric, traceless, and evolves in time according to
$$\begin{eqnarray}\displaystyle \frac{\partial \unicode[STIX]{x1D63E}}{\partial t}+\unicode[STIX]{x1D63E}\boldsymbol{\cdot }{\it\bf\Omega}-{\it\bf\Omega}\boldsymbol{\cdot }\unicode[STIX]{x1D63E}=3\unicode[STIX]{x1D640}-6D\unicode[STIX]{x1D63E}. & & \displaystyle\end{eqnarray}$$
The left-hand side of (2.3) is a co-rotational, or Jaumann, derivative. Thus, in a frame of reference rotating with
${\it\bf\Omega}$
the microstructure is forced to align along the principal axes of the straining component of the linear flow (first term on the right-hand side), and relaxes under Brownian rotation on a time scale
${\it\tau}=1/(6D)$
(second term on the right-hand side). The Jaumann derivative couples the evolution of temporal modes in
$\unicode[STIX]{x1D63E}$
, which drives the complex microstructure dynamics under LAOS. Microstructural evolution equations similar to (2.3) occur for complex fluids comprising weakly elastic spheres (Goddard & Miller Reference Goddard and Miller1967); weakly charged spherical particles surrounded by thin electric double layers (Russel Reference Russel1978); slightly deformed, high-viscosity drops (Rallison Reference Rallison1980); and spherical, surfactant-coated drops (Vlahovska, Blawzdziewicz, & Loewenberg Reference Vlahovska, Blawzdziewicz and Loewenberg2002). We therefore view (2.3) as a paradigmatic micro-mechanical model for LAOS, which contains the effects of memory, relaxation, distortion via strain, and advective coupling of temporal modes. Further, (2.3) bears close resemblance to the co-rotational Maxwell model.
Consider a two-dimensional oscillatory shear flow
$\dot{{\it\gamma}}\cos ({\it\omega}t)y\boldsymbol{e}_{x}$
, where
$x,y,z$
are Cartesian coordinates,
$\boldsymbol{e}_{x}$
is a unit vector along the
$x$
axis,
$\dot{{\it\gamma}}$
is the strain-rate amplitude, and
${\it\omega}$
is the angular oscillation frequency. The assumption that the flow around the particle evolves instantaneously requires that the time scale of momentum diffusion at the particle scale,
$l^{2}/{\it\nu}$
, is much smaller than the oscillation time,
$1/{\it\omega}$
; that is,
${\it\omega}l^{2}/{\it\nu}\ll 1$
. Here
$l$
is the characteristic linear dimension of the particle, and
${\it\nu}$
is the kinematic viscosity of the fluid. The particle orientation is isotropic initially,
$\unicode[STIX]{x1D63E}=0$
at
$t=0$
. Under these conditions, the microstructure tensor takes the form
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63E}=A(t)(\boldsymbol{e}_{x}\boldsymbol{e}_{x}-\boldsymbol{e}_{y}\boldsymbol{e}_{y})+B(t)(\boldsymbol{e}_{x}\boldsymbol{e}_{y}+\boldsymbol{e}_{y}\boldsymbol{e}_{x}), & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{e}_{y}$
is a unit vector along the
$y$
axis. The particle contribution to the shear stress,
${\it\sigma}_{xy}$
, first normal stress difference,
$N_{1}$
, and second normal stress difference,
$N_{2}$
of the suspension are (LH72)
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\sigma}_{xy}={\it\eta}c\dot{{\it\gamma}}\left[\left(\frac{5}{2}+\frac{26}{147}{\it\epsilon}^{2}\right)\cos ({\it\omega}t)+\frac{2{\it\epsilon}^{2}}{5{\it\beta}}B(t)\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{1}={\it\sigma}_{xx}-{\it\sigma}_{yy}=\frac{4{\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}}{5{\it\beta}}A(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{2}={\it\sigma}_{yy}-{\it\sigma}_{zz}=2{\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}\left[\cos ({\it\omega}t)\frac{B(t)}{7}-\frac{A(t)}{5{\it\beta}}\right], & \displaystyle\end{eqnarray}$$
${\it\eta}$
is the solvent viscosity,
$c$
is the (small) particle volume fraction,
${\it\epsilon}=r-1$
, and
${\it\beta}=\dot{{\it\gamma}}{\it\tau}$
is a Weissenberg number. Note that
${\it\beta}$
is often termed a rotary Péclet number, e.g. Brenner & Condiff (Reference Brenner and Condiff1974). Evidently, the non-equilibrium microstructure components
$A(t)$
and
$B(t)$
directly relate to observable rheological quantities. The expressions (2.5)–(2.7) are correct to first order in
$c$
; presumably, the next contribution in
$c$
is
$O(c^{2})$
, arising from two-particle hydrodynamic interactions. The
$O(\mathscr{B}^{2})$
orientation microstructure perturbation for a single particle (2.2), which contains a fourth rank tensor contribution, would result in an
$o({\it\epsilon}^{2})$
contribution to the stress. (Note that
$\mathscr{B}={\it\epsilon}(r+1)/(r^{2}+1)$
.) Since
$r\approx 1$
by definition (and thus
${\it\epsilon}\ll 1$
and
$\mathscr{B}\ll 1$
), the
$O(\mathscr{B}^{2})$
orientation microstructure yields a stress contribution that is smaller than that arising from the
$O(\mathscr{B})$
microstructure calculated here.
Substitution of the above forms of the shear flow and microstructure tensor into (2.3) returns two first-order differential equations for
$A(t)$
and
$B(t)$
,
$$\begin{eqnarray}\displaystyle \frac{\text{d}A}{\text{d}t}+\frac{A}{{\it\tau}}=\dot{{\it\gamma}}\cos ({\it\omega}t)B,\quad \text{and}\quad \frac{\text{d}B}{\text{d}t}+\frac{B}{{\it\tau}}+\dot{{\it\gamma}}\cos ({\it\omega}t)A=\frac{3}{2}\dot{{\it\gamma}}\cos ({\it\omega}t), & & \displaystyle\end{eqnarray}$$
in which the coupling of shear stress (
$B$
) and normal stresses (
$A$
) arises solely through the co-rotational derivative. Equation (2.8) is subject to the initial conditions
$A=B=0$
at
$t=0$
. From (2.8) the following second-order equation for
$B(\bar{t})$
is obtained,
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}^{2}B}{\text{d}\bar{t}^{2}}+\left[\frac{1}{{\it\beta}^{2}}\left(1+{\it\alpha}\tan \left(\frac{{\it\alpha}\bar{t}}{{\it\beta}}\right)\right)+\cos ^{2}\left(\frac{{\it\alpha}\bar{t}}{{\it\beta}}\right)\right]B\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{1}{{\it\beta}}\left[2+{\it\alpha}\tan \left(\frac{{\it\alpha}\bar{t}}{{\it\beta}}\right)\right]\frac{\text{d}B}{\text{d}\bar{t}}=\frac{3}{2{\it\beta}}\cos \left(\frac{{\it\alpha}\bar{t}}{{\it\beta}}\right),\end{eqnarray}$$
where
$\bar{t}=\dot{{\it\gamma}}t$
is a dimensionless time and
${\it\alpha}={\it\omega}{\it\tau}$
is a dimensionless frequency, or Deborah number. Note that
$\dot{{\it\gamma}}$
is the frequency of the free oscillations in
$B(t)$
under steady shear, arising from the time-periodic orientation, or (degenerate) Jeffery orbit, of a nearly spherical particle spinning with the ambient angular velocity. Equation (2.9) describes the oscillations of
$B$
, and hence shear stress, which are forced by the periodic flow and damped by Brownian rotation.
The SAOS rheology is calculated from (2.8) via a regular perturbation expansion of
$B(t)$
in
${\it\beta}$
, yielding
$$\begin{eqnarray}\displaystyle B(t)=\frac{3{\it\beta}}{2(1+{\it\alpha}^{2})}[\cos ({\it\omega}t)+{\it\alpha}\sin ({\it\omega}t)]+O({\it\beta}^{3}), & & \displaystyle\end{eqnarray}$$
where we have used
${\it\alpha}\bar{t}/{\it\beta}={\it\omega}t$
. To leading order,
$B(t)$
is proportional to the flow strength (
${\it\beta}$
) and oscillates at the frequency of the shear, with an amplitude and phase shift that are determined by the value of
${\it\alpha}$
. The component of
$B(t)$
in phase (out of phase) with the strain rate is the viscous (elastic) contribution to the shear stress. The
$O({\it\beta}^{3})$
correction contains a frequency-tripled overtone (
$3{\it\omega}$
) and a fundamental mode (
${\it\omega}$
). Using (2.10) with (2.8) yields
$$\begin{eqnarray}\displaystyle A(t)=\frac{3{\it\beta}^{2}}{4(1+{\it\alpha}^{2})}\left[1+\frac{1-2{\it\alpha}^{2}}{1+4{\it\alpha}^{2}}\cos (2{\it\omega}t)+\frac{3{\it\alpha}}{1+4{\it\alpha}^{2}}\sin (2{\it\omega}t)\right]+O({\it\beta}^{4}). & & \displaystyle\end{eqnarray}$$
For weak shear
$A(t)$
is
$O({\it\beta}^{2})$
to leading order and contains a frequency-doubled overtone (
$2{\it\omega}$
) and a steady contribution. Thus, the normal stress differences oscillate about a non-zero mean at twice the frequency of the shear flow. The
$O({\it\beta}^{4})$
correction is comprised of a frequency-quadrupled overtone (
$4{\it\omega}$
), a frequency-doubled overtone, and a steady contribution. The leading term of the normal stress differences, and the ratio of the first correction to the leading term of the shear stress are both
$O({\it\beta}^{2})$
; this scaling regime has been termed medium-amplitude oscillatory shear (MAOS) rheology (Onogi, Masuda & Matsumoto Reference Onogi, Masuda and Matsumoto1970; Pearson & Rochefort Reference Pearson and Rochefort1982; Hyun & Wilhelm Reference Hyun and Wilhelm2009; Swan, Furst & Wagner Reference Swan, Furst and Wagner2014). Note that expressions akin to (2.10) and (2.11) are given in LH72.
3 Strongly nonlinear LAOS: asymptotic analysis
We now analyse strongly nonlinear LAOS, where the strain-rate amplitude
${\it\beta}\gg 1$
, and the strain amplitude
${\it\beta}/{\it\alpha}\gg 1$
. A formal solution for
$B(t)$
(and
$A(t)$
), valid at arbitrary
${\it\alpha}$
and
${\it\beta}$
, can be cast in integral form (LH72; Vlahovska et al.
Reference Vlahovska, Blawzdziewicz and Loewenberg2002). However, this integral must be evaluated numerically, in general. Here, we derive an asymptotic solution that yields considerable physical insight into the strongly nonlinear regime. This asymptotic solution for
${\it\beta}\gg 1$
and
${\it\beta}/{\it\alpha}\gg 1$
is the main original contribution of the present work; recall that LH72 considered weak oscillatory shear,
${\it\beta}\ll 1$
. A naive expansion,
$$\begin{eqnarray}\displaystyle B(\bar{t})=B_{0}(\bar{t})+B_{1}(\bar{t}){\it\beta}^{-1}+O({\it\beta}^{-2}), & & \displaystyle\end{eqnarray}$$
fails because
$B_{1}$
contains a secular term that grows in time, in contrast to the bounded oscillation obtained from numerical solution of the problem. This regular expansion assumes that relaxation of the microstructure (via rotational Brownian motion) is always subdominant to shear-driven orientation at
${\it\beta}\gg 1$
. However, the cumulative action of weak instantaneous relaxation will have a leading-order effect at sufficiently long times,
$\bar{t}\sim O({\it\beta})$
. The usual method to overcome this difficulty is a multiple-scale, or two-timing, expansion, with a fast time
$\bar{t}$
and a slow time
$T=\bar{t}/{\it\beta}=t/{\it\tau}$
. That is, we expand
$B$
as
$$\begin{eqnarray}\displaystyle B(\bar{t},T)=B_{0}(\bar{t},T)+B_{1}(\bar{t},T){\it\beta}^{-1}+O({\it\beta}^{-2}). & & \displaystyle\end{eqnarray}$$
However, this expansion also fails as the solvability condition to remove secularity in
$B_{1}(\bar{t},T)$
contains the fast time
$\bar{t}$
. This occurs because the frequency of undamped oscillations, i.e. the strain rate
$\cos ({\it\alpha}T)$
, varies on the slow time
$T$
. The impasse is resolved using WKBJ theory (Hinch Reference Hinch1991), whence the following new fast time is introduced
$$\begin{eqnarray}\displaystyle s={\it\beta}\int ^{T}\cos ({\it\alpha}T^{\prime })\,\text{d}T^{\prime }=\frac{\dot{{\it\gamma}}}{{\it\omega}}\sin ({\it\omega}t). & & \displaystyle\end{eqnarray}$$
Notice that
$s$
is the instantaneous strain, which appears as the natural ‘time scale’ in strongly nonlinear LAOS. Thus, we pose the expansion
$$\begin{eqnarray}\displaystyle B(s,T)=B_{0}(s,T)+B_{1}(s,T){\it\beta}^{-1}+O({\it\beta}^{-2}). & & \displaystyle\end{eqnarray}$$
From (2.9), the leading term satisfies
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}B_{0}}{\partial s^{2}}+B_{0}=0,\quad B_{0}=0\quad \text{and}\quad \frac{\partial B_{0}}{\partial s}=\frac{3}{2}\quad \text{at }s=0. & & \displaystyle\end{eqnarray}$$
The solution is
$B_{0}=R(T)\text{e}^{\text{i}s}+\text{c.c.}$
, where c.c. denotes complex conjugate and
$R(T)$
is a slowly varying amplitude. The next term satisfies
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}B_{1}}{\partial s^{2}}+B_{1}=\frac{3}{2\cos ({\it\alpha}T)}-\frac{2}{\cos ({\it\alpha}T)}\frac{\partial }{\partial s}\left(\frac{\partial B_{0}}{\partial T}+B_{0}\right), & & \displaystyle\end{eqnarray}$$
subject to
$B_{1}=\partial B_{1}/\partial s=0$
at
$s=0$
. The second term on the right-hand side of (3.6) must vanish to eliminate the secular forcing, which yields
$R(T)=k\text{e}^{-T}$
, where
$k$
is a constant. Thus, the leading-order oscillations in
$B$
, and hence shear stress, are exponentially damped on the slow time, due to weak rotary diffusion. It is then readily found that
$$\begin{eqnarray}\displaystyle B_{0}=\frac{3}{2}\text{e}^{-T}\sin (s),\quad B_{1}=\frac{3}{2}\left[\frac{1}{\cos ({\it\alpha}T)}-\cos (s)\right]. & & \displaystyle\end{eqnarray}$$
The expansion (3.7) loses uniformity at
$\bar{t}\equiv \bar{t}_{0}={\rm\pi}{\it\beta}/2{\it\alpha}$
; the leading term
$B_{0}$
is finite whereas the correction
$B_{1}$
diverges. The imposed flow vanishes at this ‘turning point.’ Consequently, there is no vorticity to drive the Jeffery orbit; the microstructure evolves on a much slower time than
$1/\dot{{\it\gamma}}$
. Further, the LAOS condition
${\it\beta}\gg 1$
is temporarily invalidated; the system has entered a ‘turning region,’ where relaxation is a leading-order affect. To analyse the microstructure at the turning point we introduce a local, or inner, coordinate
$r={\it\beta}^{-{\it\delta}}(\bar{t}-\bar{t}_{0})$
. Recasting (2.9) in terms of
$r$
reveals that
${\it\delta}=1/2$
to bring relaxation into the leading-order dynamics. Thus, the turning region is of width
$\bar{t}-\bar{t}_{0}\sim O({\it\beta}^{1/2})$
, or
$O(\sqrt{{\it\tau}/\dot{{\it\gamma}}})$
in dimensional terms. This intermediate time scale is much longer than that of the Jeffery orbit (
$1/\dot{{\it\gamma}}$
), but much shorter than the oscillation period (
$2{\rm\pi}/{\it\omega}$
). In the turning region, (2.9) reduces to
$$\begin{eqnarray}\displaystyle \frac{\text{d}^{2}B}{\text{d}r^{2}}+\left(\frac{2}{{\it\beta}^{1/2}}-\frac{1}{r}\right)\frac{\text{d}B}{\text{d}r}+\left({\it\alpha}^{2}r^{2}-\frac{1}{{\it\beta}^{1/2}r}\right)B=-\frac{3{\it\alpha}}{2{\it\beta}^{1/2}}r+O({\it\beta}^{-1}). & & \displaystyle\end{eqnarray}$$
Here, we expand
$$\begin{eqnarray}\displaystyle B(r)=\tilde{B}_{0}(r)+\tilde{B}_{1/2}(r){\it\beta}^{-1/2}+O({\it\beta}^{-1}). & & \displaystyle\end{eqnarray}$$
Insertion of (3.9) into (3.8) shows that
$\tilde{B}_{0}$
satisfies a homogeneous equation, which matches to
$B_{0}$
from the prior ‘core’ region (3.7). This represents the decay of the initial microstructure; it cannot contribute to the long-time LAOS dynamics, which is our primary interest. Thus, we simply set
$\tilde{B}_{0}=0$
; thereby,
$\tilde{B}_{1/2}(r)$
satisfies
$$\begin{eqnarray}\displaystyle \frac{\text{d}^{2}\tilde{B}_{1/2}}{\text{d}r^{2}}-\frac{1}{r}\frac{\text{d}\tilde{B}_{1/2}}{\text{d}r}+{\it\alpha}^{2}r^{2}\tilde{B}_{1/2}=-\frac{3{\it\alpha}}{2}r, & & \displaystyle\end{eqnarray}$$
which has the solution
$$\begin{eqnarray}\displaystyle \tilde{B}_{1/2}(r) & = & \displaystyle \left[c_{0}+\frac{3}{2}\sqrt{\frac{{\rm\pi}}{{\it\alpha}}}S\left(\sqrt{\frac{{\it\alpha}}{{\rm\pi}}}r\right)\right]\cos \left(\frac{{\it\alpha}r^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\left[d_{0}+\frac{3}{2}\sqrt{\frac{{\rm\pi}}{{\it\alpha}}}C\left(\sqrt{\frac{{\it\alpha}}{{\rm\pi}}}r\right)\right]\sin \left(\frac{{\it\alpha}r^{2}}{2}\right),\end{eqnarray}$$
in which
$$\begin{eqnarray}\displaystyle S(z)=\int _{0}^{z}\sin \left(\frac{{\rm\pi}x^{2}}{2}\right)\,\text{d}x\quad \text{and}\quad C(z)=\int _{0}^{z}\cos \left(\frac{{\rm\pi}x^{2}}{2}\right)\,\text{d}x & & \displaystyle\end{eqnarray}$$
are the Fresnel sine and Fresnel cosine integrals, respectively. The constants
$c_{0}$
and
$d_{0}$
are found by matching
$\tilde{B}_{1/2}{\it\beta}^{-1/2}$
as
$r\rightarrow -\infty$
with (3.7) as
$T\rightarrow {\rm\pi}/2{\it\alpha}$
. This yields
$c_{0}=d_{0}=\sqrt{9{\rm\pi}/16{\it\alpha}}$
.
Sufficiently beyond the turning point, the reversed flow gains enough strength that the suspension enters another core region. Here, a new multiple-scale expansion proceeds as
$$\begin{eqnarray}\displaystyle B(s,T)=B_{0}(s,T)+{\it\beta}^{-1/2}B_{1/2}(s,T)+B_{1}(s,T){\it\beta}^{-1}+O({\it\beta}^{-3/2}), & & \displaystyle\end{eqnarray}$$
where the term
${\it\beta}^{-1/2}B_{1/2}$
is forced by the
$O({\it\beta}^{-1/2})$
term from the turning region. Inserting this expansion into (2.9) shows first that
$B_{0}$
is the same as in (3.7). Second,
$B_{1/2}$
satisfies the same equation and secularity condition as
$B_{0}$
. Third,
$B_{1}$
again satisfies (3.6). Thus, we find
$$\begin{eqnarray}\displaystyle B_{1/2}=\text{e}^{-(T-{\rm\pi}/2{\it\alpha})}[a_{0}\cos (s)+b_{0}\sin (s)],\quad B_{1}=\frac{3}{2\cos ({\it\alpha}T)}. & & \displaystyle\end{eqnarray}$$
Matching
$B_{1/2}$
as
$T\rightarrow {\rm\pi}/2{\it\alpha}$
with
$\tilde{B}_{1/2}$
as
$r\rightarrow \infty$
yields
$a_{0}=\sqrt{9{\rm\pi}/4{\it\alpha}}\mathscr{F}_{-}$
and
$b_{0}=\sqrt{9{\rm\pi}/4{\it\alpha}}\mathscr{F}_{+}$
, where
$$\begin{eqnarray}\displaystyle \mathscr{F}_{\pm }=\cos ({\it\beta}/{\it\alpha})\pm \sin ({\it\beta}/{\it\alpha}). & & \displaystyle\end{eqnarray}$$
The analysis of subsequent turning regions is practically identical. Let
$\bar{t}_{n}=(2n+1){\rm\pi}{\it\beta}/2{\it\alpha}$
be the
$n$
th turning point, with
$n=0,1,2,\ldots .$
The expansion of
$B(s,T)$
in the core region between
$\bar{t}_{n}$
and
$\bar{t}_{n+1}$
proceeds as before:
$B_{0}$
and
$B_{1}$
remain unchanged, and
$B_{1/2}$
is
$$\begin{eqnarray}\displaystyle B_{1/2}=\text{e}^{-(T-\bar{t}_{n}/{\it\beta})}[a_{n}\cos (s)+b_{n}\sin (s)], & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle a_{n}=a_{0}\mathop{\sum }_{m=0}^{n}(-1)^{m+n}\text{e}^{-m{\rm\pi}/{\it\alpha}},\quad b_{n}=b_{0}\mathop{\sum }_{m=0}^{n}\text{e}^{-m{\rm\pi}/{\it\alpha}}. & & \displaystyle\end{eqnarray}$$
The long-time limit (
$n\rightarrow \infty$
) is found via the identities
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m=0}^{\infty }(-1)^{m}\text{e}^{-m{\rm\pi}/{\it\alpha}}=(1+\text{e}^{-{\rm\pi}/{\it\alpha}})^{-1},\quad \mathop{\sum }_{m=0}^{\infty }\text{e}^{-m{\rm\pi}/{\it\alpha}}=(1-\text{e}^{-{\rm\pi}/{\it\alpha}})^{-1}. & & \displaystyle\end{eqnarray}$$
Further, using (3.17) as
$n\rightarrow \infty$
, the leading-order microstructure at the turning region
$\bar{t}_{n}$
for long times is
$(-1)^{n}\tilde{B}_{1/2}{\it\beta}^{-1/2}$
, where
$$\begin{eqnarray}\displaystyle \tilde{B}_{1/2}(r) & = & \displaystyle \left[c_{n}+\frac{3}{2}\sqrt{\frac{{\rm\pi}}{{\it\alpha}}}S\left(\sqrt{\frac{{\it\alpha}}{{\rm\pi}}}r\right)\right]\cos \left(\frac{{\it\alpha}r^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\left[d_{n}+\frac{3}{2}\sqrt{\frac{{\rm\pi}}{{\it\alpha}}}C\left(\sqrt{\frac{{\it\alpha}}{{\rm\pi}}}r\right)\right]\sin \left(\frac{{\it\alpha}r^{2}}{2}\right),\end{eqnarray}$$
Figure 1. Long-time periodic variation of
$B(t)$
at
${\it\beta}=50$
and
${\it\alpha}=1$
. Solid line is uniformly valid asymptotic solution, circles are numerical solution, and dashed line is the SAOS result (2.10). (a)
$B$
normalized by its maximum value
$B_{m}$
versus dimensionless time
${\it\omega}t$
. Dot-dashed line is strain rate
$\cos ({\it\omega}t)$
. (b) Lissajous curve of
$B$
versus dimensionless strain rate
$\cos ({\it\omega}t)$
.
in which
$r={\it\beta}^{-1/2}(\bar{t}-\bar{t}_{n})$
,
$c_{n}=c_{0}\mathscr{G}_{-}$
,
$d_{n}=d_{0}\mathscr{G}_{+}$
, and
$$\begin{eqnarray}\displaystyle \mathscr{G}_{\pm }=\frac{1+\text{e}^{2{\rm\pi}/{\it\alpha}}+2\text{e}^{{\rm\pi}/{\it\alpha}}[\cos (2{\it\beta}/{\it\alpha})\pm \sin (2{\it\beta}/{\it\alpha})]}{\text{e}^{2{\rm\pi}/{\it\alpha}}-1}. & & \displaystyle\end{eqnarray}$$
A long-time solution for
$B(t)$
that is uniformly valid to
$O({\it\beta}^{-1/2})$
is readily constructed from (3.16)–(3.20). This asymptotic solution is plotted alongside a numerical solution in figure 1(a) for
${\it\beta}=50$
and
${\it\alpha}=1$
. The numerical scheme integrates the first-order equations for
$A$
and
$B$
(2.8). Excellent agreement between the two is observed. The predicted rapid oscillations in microstructure punctuated by slower evolution in turning regions is evident. The latter coincide with times when the strain rate vanishes. The period of
$B(t)$
is
$2{\rm\pi}/{\it\omega}$
, as in SAOS (2.10). A Lissajous curve of
$B(t)$
versus strain rate is plotted in figure 1(b). In SAOS, a Lissajous curve is an ellipse. In LAOS, the turning regions correspond to a distorted ellipse near the origin. The rapid microstructure oscillations in the core regions are characterized by multiple self-intersections of the Lissajous curve. Note that a three-dimensional plot of
$B$
against strain rate and strain does not have intersections. The microstructure dynamics displayed in figure 1(a) are equivalent to the numerical computations of Vlahovska et al. (Reference Vlahovska, Blawzdziewicz and Loewenberg2002) for the shear-stress response of a high-viscosity, surfactant-coated drop in oscillatory shear: see figure 8(b) of that paper. This is expected; the non-equilibrium surfactant concentration distribution is described to leading order by a co-rotational Maxwell model for a high-viscosity drop.
With the asymptotic solution for
$B$
in hand, the evolution of
$A$
is readily found from (2.8). A long-time uniformly valid asymptotic solution for
$A$
is plotted in figure 2(a). The period of
$A$
is
${\rm\pi}/{\it\omega}$
. Thus, the normal stress differences oscillate at twice the rate of the shear stress. In MAOS, the Lissajous curve of
$A$
versus strain rate is a bow-tie shape (figure 2
b). In LAOS, the turning regions are represented by a shrunken bow-tie at the origin. The microstructure oscillations in the core regions result in self-intersections of the Lissajous curve. The Lissajous curve of
$A(B)$
is an even(odd) function of strain rate; hence, a Fourier decomposition of
$A(B)$
contains only even(odd) overtones of the fundamental frequency
${\it\omega}$
.
Figure 2. Long-time periodic variation of
$A(t)$
at
${\it\beta}=50$
and
${\it\alpha}=1$
. Line style is same as in figure 1, except that dashed line is the MAOS result (2.11). (a)
$[A(t)-A_{a}]/[A_{m}-A_{a}]$
versus dimensionless time
${\it\omega}t$
, where
$A_{a}$
and
$A_{m}$
are average and maximum values of
$A$
, respectively. (b) Lissajous curve of
$A$
versus dimensionless strain rate
$\cos ({\it\omega}t)$
.
Figure 3. Long-time maximum values
$A_{m}$
(squares) and
$B_{m}$
(circles) versus
${\it\beta}$
at
${\it\alpha}=1$
from numerical solution. Lines are asymptotic scaling predictions at small and large
${\it\beta}$
.
Our asymptotic analysis revealed that
$B\sim {\it\beta}^{-1/2}$
and
$A\sim 3/2+O({\it\beta}^{-3/2})$
in the strongly nonlinear regime,
${\it\beta}\gg 1$
and
${\it\beta}/{\it\alpha}\gg 1$
(figure 3). The resultant non-Newtonian shear stress
${\it\sigma}_{xy}\sim {\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}{\it\beta}^{-3/2}$
. In contrast,
${\it\sigma}_{xy}\sim {\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}{\it\beta}^{-2}$
for steady shear at
${\it\beta}\gg 1$
(LH72). Thus, there are distinct scalings for the abatement of shear stress for LAOS versus steady shear. The first normal stress difference
$N_{1}\sim {\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}{\it\beta}^{-1}$
under strongly nonlinear LAOS; the
${\it\beta}^{-1}$
scaling persists in steady shear (LH72). The second normal stress difference
$N_{2}\sim {\it\epsilon}^{2}{\it\eta}c\dot{{\it\gamma}}{\it\beta}^{-1/2}$
in LAOS, whereas a
${\it\beta}^{-1}$
scaling is predicted in steady shear at large
${\it\beta}$
(LH72). This suggests distinct scalings for the decay of the first and second normal stress differences in LAOS, whereas both decay as
${\it\beta}^{-1}$
for steady shear. Our predicted stress scalings originate from the microstructure dynamics in turning regions, where the strain rate vanishes and the strain is maximal. Thus, it is the times when the flow vanishes that dictate the LAOS rheology of this paradigmatic complex fluid.
The rapid variation of stress in a core region is caused by the reorientation of the microstructure with the ambient vorticity, at a rate
$\dot{{\it\gamma}}\cos ({\it\omega}t)$
(the strain rate) that is much larger than the oscillation frequency
${\it\omega}$
. Hence, the oscillatory flow is not responsible for these rapid stress oscillations; it merely modulates (slowly) the frequency thereof. The strain rate eventually becomes sufficiently small that the time scales for microstructure reorientation and relaxation are comparable; the system enters a turning region. This stress dynamic under LAOS should be exhibited by any complex fluid comprised of ‘co-rotational’ microstructure, which rotates with (half) the vorticity of the ambient shear (
$\mathscr{B}\ll 1$
): e.g. a nearly spherical Brownian particle, a slightly elastic sphere (Goddard & Miller Reference Goddard and Miller1967), a weakly charged sphere (Russel Reference Russel1978), a slightly deformed drop (Rallison Reference Rallison1980), or a surfactant-coated spherical drop (Vlahovska et al.
Reference Vlahovska, Blawzdziewicz and Loewenberg2002). In contrast, the orientation of a slender microstructure (
$\mathscr{B}\rightarrow 1$
, e.g. a rod) is equally affected by vorticity and strain: the microstructure spends long periods aligned with the flow, which are periodically interrupted by short tumbles between flow-aligned states. Hence, the strongly nonlinear LAOS rheology of materials comprised of slender microstructure will exhibit periods of almost constant shear stress between turning regions. We have recently analysed the LAOS rheology of the Giesekus model of entangled polymer solutions, wherein polymer chains are idealized as rigid dumbbells with anisotropic drag, which does indeed exhibit this behaviour (Khair Reference Khair2016). Also note that Leahy, Koch & Cohen (Reference Leahy, Koch and Cohen2015) have quantified the orientation dynamics of a spheroid constrained to rotate in the flow-gradient plane of a time-dependent shear flow, in the case of weak Brownian rotation. They find that the effective rotational diffusivity of a slender particle can be greatly enhanced by the flow.
4 Discussion
We quantified the dynamics of nearly spherical colloidal particles in oscillatory shear as a paradigm for strongly nonlinear LAOS rheology. A central conclusion is that the stress evolution is partitioned into core and turning regions, which represent distinct balances between physical effects. We believe that this will be a feature of strongly nonlinear LAOS that is exhibited by a host of complex fluids, beyond the model system studied here. The damped stress oscillation we predict within a core region is reminiscent of the damped oscillation in conservative dichroism (
${\rm\Delta}n^{\prime \prime }$
) and orientation angle (
${\it\chi}$
) measured via rheo-optical methods for suspensions of spheroidal particles during start-up of shear (Frattini & Fuller Reference Frattini and Fuller1986). This is unsurprising, since a turning region (that precedes a core region) in LAOS is akin to a transition between cessation and start-up of shear, with a strain rate that (to leading order) varies linearly in time, i.e. a ramp function. Further,
${\rm\Delta}n^{\prime \prime }$
and
${\it\chi}$
are related to the suspension microstructure via (Frattini & Fuller Reference Frattini and Fuller1986)
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle {\rm\Delta}n^{\prime \prime }/{\rm\Delta}n_{max}^{\prime \prime }=[\langle \sin ^{2}{\it\theta}\sin 2{\it\phi}\rangle ^{2}+\langle \sin ^{2}{\it\theta}\cos 2{\it\phi}\rangle ^{2}]^{1/2},\\ \displaystyle \tan (2{\it\chi})=\langle \sin ^{2}{\it\theta}\sin 2{\it\phi}\rangle /\langle \sin ^{2}{\it\theta}\cos 2{\it\phi}\rangle ,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where the angular brackets
$\langle \,\rangle$
denote an average over the orientation distribution
${\it\psi}$
;
${\rm\Delta}n_{max}^{\prime \prime }$
is the magnitude of the dichroism in the maximally flow-aligned state; and
${\it\theta}$
and
${\it\phi}$
are the polar and azimuthal angles measured from the vorticity and velocity axes of the ambient shear, respectively. Using (2.2) and (2.4), we find
${\rm\Delta}n^{\prime \prime }/{\rm\Delta}n_{max}^{\prime \prime }=4\mathscr{B}(A(t)^{2}+B(t)^{2})^{1/2}/5$
and
$\tan (2{\it\chi})=B(t)/A(t)$
. From the scalings in figure 3, we have
${\rm\Delta}n^{\prime \prime }/{\rm\Delta}n_{max}^{\prime \prime }\sim \mathscr{B}{\it\beta}$
at
${\it\beta}\ll 1$
, and
${\rm\Delta}n^{\prime \prime }/{\rm\Delta}n_{max}^{\prime \prime }\sim \mathscr{B}{\it\beta}^{0}$
at
${\it\beta}\gg 1$
, which represents an increase in dichroism with increasing
${\it\beta}$
, due to flow alignment of the microstructure. This trend is observed in the measurements of Vermant, Yang & Fuller (Reference Vermant, Yang and Fuller2001) on a dilute suspension of haematite particles under steady shear: see figure 7 in that paper. Those particles resemble prolate spheroids and were determined to possess a hydrodynamic aspect ratio of
$r=1.75$
(
$\mathscr{B}=0.51$
) with a polydispersity of 0.65. (Note that polydispersity itself can lead to temporal damping in
${\rm\Delta}n^{\prime \prime }$
and
${\it\chi}$
for non-Brownian suspensions, due to ‘phase mixing’ arising from variation in the period of a Jeffery orbit with aspect ratio (Vermant et al.
Reference Vermant, Yang and Fuller2001).) In particular, their measured
${\rm\Delta}n^{\prime \prime }$
appears to approach a plateau at high shear rates, consistent with our prediction at
${\it\beta}\gg 1$
. We also predict that
${\it\chi}\sim {\rm\pi}/4$
at
${\it\beta}\ll 1$
, and
${\it\chi}\sim {\it\beta}^{-1/2}$
at
${\it\beta}\gg 1$
. Again, the decrease in
${\it\chi}$
with growing
${\it\beta}$
is indicative of flow-driven alignment. The measurements of
${\it\chi}$
by Vermant et al. (Reference Vermant, Yang and Fuller2001) follow this trend, with
${\it\chi}$
approaching zero degrees at large shear rates. In steady shear,
$B\sim 1/{\it\beta}$
and
$A\sim {\it\beta}^{0}$
at large
${\it\beta}$
, which gives
${\it\chi}\sim {\it\beta}^{-1}$
; a different decay than under LAOS. In contrast,
${\rm\Delta}n^{\prime \prime }/{\rm\Delta}n_{max}^{\prime \prime }\sim \mathscr{B}{\it\beta}^{0}$
in steady and oscillatory shear at large
${\it\beta}$
. Thus, measurement of
${\it\chi}$
may be a sensitive indication of differences in microstructure for oscillatory versus steady shear at large Weissenberg number. A direct comparison of our predictions against rheo-optical measurements of a dilute suspension under oscillatory shear would be of clear interest. It is likely that many-body hydrodynamic interactions in a concentrated suspension could significantly alter the stress signal compared to that calculated here; nonetheless, the partitioning of stress evolution into core and turning regions should persist.
For the model system considered here, the stress attains a unique long-time periodic orbit, or state of ‘alternance’ (Giacomin et al. Reference Giacomin, Bird, Johnson and Mix2011), which is independent of the initial orientation configuration, since the microstructure satisfies a linear evolution equation (2.3). It is unclear if alternance is the sole outcome for nonlinear microstructural equations or nonlinear constitutive relations. Indeed, chaotic microstructure dynamics has been predicted for drops and vesicles in oscillatory and steady flow, respectively (Young et al. Reference Young, Blawzdziewicz, Cristini and Goodman2008; Aouane et al. Reference Aouane, Thiébaud, Benyoussef and Wagner2014). Moreover, experiments on polymer melts under LAOS reveal quasi-periodic or chaotic response at large strain (Hatzikiriakos & Dealy Reference Hatzikiriakos and Dealy1991; Adrian & Giacomin Reference Adrian and Giacomin1992), which has been attributed to a nonlinear coupling of viscoelasticity and dynamic wall slip (Graham Reference Graham1995). What are the necessary conditions for aperiodic stress dynamics to occur under LAOS? Does a unique mapping between input parameters (i.e. Weissenberg and Deborah numbers) and the observed stress waveform always exist? The resolution of these questions should advance our understanding of LAOS rheology and, more broadly, the nonlinear dynamics of complex fluids in time-dependent flows.
