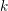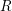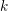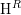Introduction
Let  $(R,\mathfrak{m},k)$ denote a local Noetherian ring
$(R,\mathfrak{m},k)$ denote a local Noetherian ring  $R$ with maximal ideal
$R$ with maximal ideal  $\mathfrak{m}$ and residue field
$\mathfrak{m}$ and residue field  $k$. Let
$k$. Let  $\operatorname{K}^{R}$ denote the Koszul complex on a minimal generating set of
$\operatorname{K}^{R}$ denote the Koszul complex on a minimal generating set of  $\mathfrak{m}$, and let
$\mathfrak{m}$, and let  $\operatorname{H}^{R}$ denote its homology. The Koszul complex
$\operatorname{H}^{R}$ denote its homology. The Koszul complex  $\operatorname{K}^{R}$ can be endowed with the structure of a differential graded (DG) algebra, and is the first step in constructing a DG algebra minimal free resolution of
$\operatorname{K}^{R}$ can be endowed with the structure of a differential graded (DG) algebra, and is the first step in constructing a DG algebra minimal free resolution of  $k$ over
$k$ over  $R$ (called a Tate resolution of
$R$ (called a Tate resolution of  $k$ over
$k$ over  $R$) through the process of adjoining DG algebra variables. It is thus natural to expect that the properties of the homology algebra
$R$) through the process of adjoining DG algebra variables. It is thus natural to expect that the properties of the homology algebra  $\operatorname{H}^{R}$ are related to other homological properties of
$\operatorname{H}^{R}$ are related to other homological properties of  $R$. Indeed, it is known that both the Gorenstein and complete intersection properties of
$R$. Indeed, it is known that both the Gorenstein and complete intersection properties of  $R$ can be characterized in terms of
$R$ can be characterized in terms of  $\operatorname{H}^{R}$.
$\operatorname{H}^{R}$.
Certain higher order homology operations on Koszul homology, introduced by Golod [Reference Golod10], can be used to characterize extremality in the growth of the minimal free resolution of  $k$ over
$k$ over  $R$. If
$R$. If  $R$ is Golod, then it has the property that for all finitely generated
$R$ is Golod, then it has the property that for all finitely generated  $R$-modules
$R$-modules  $M$ the Poincaré series
$M$ the Poincaré series  $\sum _{i\geqslant 0}\operatorname{rank}_{k}(\operatorname{Tor}_{i}^{R}(M,k))z^{i}$ are rational and share a common denominator, see Ghione and Gulliksen [Reference Ghione and Gulliksen9]. This property is also satisfied by other large classes of rings, and recent work of Rossi and Şega [Reference Rossi and Şega24] and Kustin, Şega, and Vraciu [Reference Kustin, Şega and Vraciu15] provides insight into the fact that the multiplicative structure of Koszul homology plays a role in establishing such results. In this paper we further explore how the structure of
$\sum _{i\geqslant 0}\operatorname{rank}_{k}(\operatorname{Tor}_{i}^{R}(M,k))z^{i}$ are rational and share a common denominator, see Ghione and Gulliksen [Reference Ghione and Gulliksen9]. This property is also satisfied by other large classes of rings, and recent work of Rossi and Şega [Reference Rossi and Şega24] and Kustin, Şega, and Vraciu [Reference Kustin, Şega and Vraciu15] provides insight into the fact that the multiplicative structure of Koszul homology plays a role in establishing such results. In this paper we further explore how the structure of  $\operatorname{H}^{R}$ can be used to derive rationality of Poincaré series and other homological properties of
$\operatorname{H}^{R}$ can be used to derive rationality of Poincaré series and other homological properties of  $R$. In particular, we give special attention in the graded case to the Koszul property.
$R$. In particular, we give special attention in the graded case to the Koszul property.
Recall that the Koszul homology of a Golod ring has trivial multiplication, see [Reference Golod10]. When  $R$ is not Golod, we find it useful to consider conditions on
$R$ is not Golod, we find it useful to consider conditions on  $\operatorname{H}^{R}$ that, to some extent, generalize the condition that multiplication is trivial. We require that cycles living “deep” enough in
$\operatorname{H}^{R}$ that, to some extent, generalize the condition that multiplication is trivial. We require that cycles living “deep” enough in  $\operatorname{K}^{R}$ (i.e., ones that are contained in
$\operatorname{K}^{R}$ (i.e., ones that are contained in  $\mathfrak{m}^{i}\operatorname{K}^{R}$ for large enough values of
$\mathfrak{m}^{i}\operatorname{K}^{R}$ for large enough values of  $i$) can be expressed, up to a boundary, in terms of certain cycles that have trivial products among themselves. More precisely, we consider the following conditions on
$i$) can be expressed, up to a boundary, in terms of certain cycles that have trivial products among themselves. More precisely, we consider the following conditions on  $\operatorname{K}^{R}$, depending on integers
$\operatorname{K}^{R}$, depending on integers  $t,b,s$:
$t,b,s$:
 ${\mathcal{Z}}_{t,b,s}$:
${\mathcal{Z}}_{t,b,s}$:There exists a finite set
 $Z\subseteq Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ such that
$Z\subseteq Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ such that  $zz^{\prime }=0$ in
$zz^{\prime }=0$ in  $Z(\operatorname{K}^{R})$ for all
$Z(\operatorname{K}^{R})$ for all  $z,z^{\prime }\in Z$ and for every
$z,z^{\prime }\in Z$ and for every  $v\in \mathfrak{m}^{s}\operatorname{K}^{R}$ there exists
$v\in \mathfrak{m}^{s}\operatorname{K}^{R}$ there exists  $m\in \mathbb{N}$ and
$m\in \mathbb{N}$ and  $z_{i}\in Z$,
$z_{i}\in Z$,  $u_{i}\in Z(\mathfrak{m}^{b}\operatorname{K}^{R})$ for each
$u_{i}\in Z(\mathfrak{m}^{b}\operatorname{K}^{R})$ for each  $i$ with
$i$ with  $1\leqslant i\leqslant m$, such that
$1\leqslant i\leqslant m$, such that  $v-\sum _{i=1}^{m}z_{i}u_{i}\in B(\mathfrak{m}^{s-1}\operatorname{K}^{R})$.
$v-\sum _{i=1}^{m}z_{i}u_{i}\in B(\mathfrak{m}^{s-1}\operatorname{K}^{R})$. ${\mathcal{P}}_{t}$:
${\mathcal{P}}_{t}$:There exists
 $[l]\in \operatorname{H}_{1}(\operatorname{K}^{R})$ such that for every
$[l]\in \operatorname{H}_{1}(\operatorname{K}^{R})$ such that for every  $z\in Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ there exists
$z\in Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ there exists  $z^{\prime }\in Z(\mathfrak{m}^{t-1}\operatorname{K}^{R})$ such that
$z^{\prime }\in Z(\mathfrak{m}^{t-1}\operatorname{K}^{R})$ such that  $z-z^{\prime }l\in B(\mathfrak{m}^{t-1}\operatorname{K}^{R})$.
$z-z^{\prime }l\in B(\mathfrak{m}^{t-1}\operatorname{K}^{R})$.
After setting some ground work in the first two sections, in Sections 3 and 4 we prove various homological implications of the conditions  ${\mathcal{Z}}_{t,b,s}$ and
${\mathcal{Z}}_{t,b,s}$ and  ${\mathcal{P}}_{t}$, under specific conditions on the integers
${\mathcal{P}}_{t}$, under specific conditions on the integers  $t,b,s$. The main results regarding these conditions are Theorems 3.1 and 4.2. We note that the hypotheses of Theorem 3.1 also require
$t,b,s$. The main results regarding these conditions are Theorems 3.1 and 4.2. We note that the hypotheses of Theorem 3.1 also require  $R$ to be artinian, while the hypotheses of Theorem 4.2 and its corollaries do not. The conclusions of these theorems and their corollaries are formulated in terms of vanishing of the natural maps
$R$ to be artinian, while the hypotheses of Theorem 4.2 and its corollaries do not. The conclusions of these theorems and their corollaries are formulated in terms of vanishing of the natural maps  $\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{j},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{i},k)$ induced by the inclusions
$\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{j},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{i},k)$ induced by the inclusions  $\mathfrak{m}^{j}\subseteq \mathfrak{m}^{i}$ for certain values of
$\mathfrak{m}^{j}\subseteq \mathfrak{m}^{i}$ for certain values of  $i$,
$i$,  $j$, as well as identifying Golod homomorphisms, establishing generation of the Yoneda algebra
$j$, as well as identifying Golod homomorphisms, establishing generation of the Yoneda algebra  $\operatorname{Ext}_{R}(k,k)$ in low degrees, and deducing rationality of Poincaré series. Our arguments utilize the DG algebra structure of the minimal free resolution of
$\operatorname{Ext}_{R}(k,k)$ in low degrees, and deducing rationality of Poincaré series. Our arguments utilize the DG algebra structure of the minimal free resolution of  $k$ over
$k$ over  $R$. This approach is inspired by, and generalizes, work of Levin and Avramov [Reference Levin and Avramov18], where homological properties of local Gorenstein artinian rings are derived from the fact that the Koszul homology algebra of such a ring is a Poincaré algebra.
$R$. This approach is inspired by, and generalizes, work of Levin and Avramov [Reference Levin and Avramov18], where homological properties of local Gorenstein artinian rings are derived from the fact that the Koszul homology algebra of such a ring is a Poincaré algebra.
For appropriate values of  $t$, the property
$t$, the property  ${\mathcal{P}}_{t}$ holds for the class of compressed Gorenstein artinian local rings discussed in [Reference Rossi and Şega24] and also for the class of compressed level local artinian rings of odd socle degree, see [Reference Kustin, Şega and Vraciu15]. In particular, our results in Section 4 can be used to recover the results of [Reference Rossi and Şega24] and [Reference Kustin, Şega and Vraciu15] regarding the fact that when the socle degree is different than three, these rings can be obtained as homomorphic images of a hypersurface, via a Golod homomorphism.
${\mathcal{P}}_{t}$ holds for the class of compressed Gorenstein artinian local rings discussed in [Reference Rossi and Şega24] and also for the class of compressed level local artinian rings of odd socle degree, see [Reference Kustin, Şega and Vraciu15]. In particular, our results in Section 4 can be used to recover the results of [Reference Rossi and Şega24] and [Reference Kustin, Şega and Vraciu15] regarding the fact that when the socle degree is different than three, these rings can be obtained as homomorphic images of a hypersurface, via a Golod homomorphism.
In Section 5 we show that the property  ${\mathcal{P}}_{2}$ is satisfied in the case of stretched artinian rings satisfying
${\mathcal{P}}_{2}$ is satisfied in the case of stretched artinian rings satisfying  $\mathfrak{m}^{3}\neq 0$ and
$\mathfrak{m}^{3}\neq 0$ and  $\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})\neq \operatorname{rank}_{k}(0:\mathfrak{m})$. The class of stretched Cohen–Macaulay local rings was considered by Sally in [Reference Sally25], where she proves that the Poincaré series of the residue field over such a ring is rational. A consequence of our results on generation in the Koszul homology algebra is that the Poincaré series of all finitely generated
$\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})\neq \operatorname{rank}_{k}(0:\mathfrak{m})$. The class of stretched Cohen–Macaulay local rings was considered by Sally in [Reference Sally25], where she proves that the Poincaré series of the residue field over such a ring is rational. A consequence of our results on generation in the Koszul homology algebra is that the Poincaré series of all finitely generated  $R$-modules over a stretched Cohen–Macaulay local ring
$R$-modules over a stretched Cohen–Macaulay local ring  $R$ are rational, sharing a common denominator. Theorem 5.4 also states that the Yoneda algebra
$R$ are rational, sharing a common denominator. Theorem 5.4 also states that the Yoneda algebra  $\operatorname{Ext}_{R}(k,k)$ of a stretched artinian local ring
$\operatorname{Ext}_{R}(k,k)$ of a stretched artinian local ring  $(R,\mathfrak{m},k)$ is generated in degree
$(R,\mathfrak{m},k)$ is generated in degree  $1$ if
$1$ if  $\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})\neq \operatorname{rank}_{k}(0:\mathfrak{m})$ and in degrees
$\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})\neq \operatorname{rank}_{k}(0:\mathfrak{m})$ and in degrees  $1$ and
$1$ and  $2$ if
$2$ if  $\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})=\operatorname{rank}_{k}(0:\mathfrak{m})$.
$\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})=\operatorname{rank}_{k}(0:\mathfrak{m})$.
For the remainder of the introduction, assume that  $R$ is a standard graded
$R$ is a standard graded  $k$-algebra. Let
$k$-algebra. Let  $\operatorname{K}^{R}$ denote the Koszul complex on a set of minimal generators of the irrelevant ideal of
$\operatorname{K}^{R}$ denote the Koszul complex on a set of minimal generators of the irrelevant ideal of  $R$ and let
$R$ and let  $\operatorname{H}^{R}$ denote the homology algebra of
$\operatorname{H}^{R}$ denote the homology algebra of  $\operatorname{K}^{R}$. The
$\operatorname{K}^{R}$. The  $k$-algebra
$k$-algebra  $R$ is said to be a Koszul algebra if the resolution of
$R$ is said to be a Koszul algebra if the resolution of  $k$ over
$k$ over  $R$ is linear, that is to say, the differentials in the minimal graded free resolution of
$R$ is linear, that is to say, the differentials in the minimal graded free resolution of  $k$ can be represented by matrices of linear forms (see e.g., [Reference Şega26] and [Reference Herzog and Iyengar12]). The algebra
$k$ can be represented by matrices of linear forms (see e.g., [Reference Şega26] and [Reference Herzog and Iyengar12]). The algebra  $\operatorname{H}^{R}$ is bigraded; when writing the bidegree
$\operatorname{H}^{R}$ is bigraded; when writing the bidegree  $(i,j)$ of an element, the index
$(i,j)$ of an element, the index  $i$ denotes homological degree and the index
$i$ denotes homological degree and the index  $j$ denotes internal degree. The linear strand of
$j$ denotes internal degree. The linear strand of  $\operatorname{H}^{R}$ is the set of elements of bidegree
$\operatorname{H}^{R}$ is the set of elements of bidegree  $(i,i+1)$, and the nonlinear strands are composed of elements of bidegree
$(i,i+1)$, and the nonlinear strands are composed of elements of bidegree  $(i,i+r)$ with
$(i,i+r)$ with  $r>1$. We say that the nonlinear strands of
$r>1$. We say that the nonlinear strands of  $\operatorname{H}^{R}$ are generated by a set
$\operatorname{H}^{R}$ are generated by a set  $\overline{Z}\subseteq \operatorname{H}^{R}$ if the nonlinear strands are contained in the ideal generated by
$\overline{Z}\subseteq \operatorname{H}^{R}$ if the nonlinear strands are contained in the ideal generated by  $\overline{Z}$ in
$\overline{Z}$ in  $\operatorname{H}^{R}$. If the nonlinear strands are generated by a subset
$\operatorname{H}^{R}$. If the nonlinear strands are generated by a subset  $\overline{Z}$ of the linear strand, it follows that
$\overline{Z}$ of the linear strand, it follows that  $\operatorname{H}^{R}$ is generated by the linear strand as a
$\operatorname{H}^{R}$ is generated by the linear strand as a  $k$-algebra.
$k$-algebra.
In Section 6 we interpret our earlier results in the graded setting, with special attention to the Koszul property. In particular, we obtain the following statements, which provide new homological criteria for verifying that an algebra is Koszul:
(1) If the nonlinear strands of
 $\operatorname{H}^{R}$ are generated by one element of bidegree
$\operatorname{H}^{R}$ are generated by one element of bidegree  $(1,2)$, then
$(1,2)$, then  $R$ is absolutely Koszul, hence Koszul. (See [Reference Iyengar and Römer14] or Section 6 regarding absolutely Koszul algebras.)
$R$ is absolutely Koszul, hence Koszul. (See [Reference Iyengar and Römer14] or Section 6 regarding absolutely Koszul algebras.)(2) If
 $R_{{\geqslant}3}=0$ and there exists a set of cycles
$R_{{\geqslant}3}=0$ and there exists a set of cycles  $Z$ representing elements in the linear strand in
$Z$ representing elements in the linear strand in  $\operatorname{H}^{R}$, with the property that
$\operatorname{H}^{R}$, with the property that  $zz^{\prime }=0$ in
$zz^{\prime }=0$ in  $Z(\operatorname{K}^{R})$ for all
$Z(\operatorname{K}^{R})$ for all  $z,z^{\prime }\in Z$ and such that the nonlinear strand of
$z,z^{\prime }\in Z$ and such that the nonlinear strand of  $\operatorname{H}^{R}$ is generated by
$\operatorname{H}^{R}$ is generated by  $\overline{Z}=\{[z]\mid z\in Z\}$, then
$\overline{Z}=\{[z]\mid z\in Z\}$, then  $R$ is Koszul.
$R$ is Koszul.
If  $R$ is Koszul, then part of the Koszul homology algebra
$R$ is Koszul, then part of the Koszul homology algebra  $\operatorname{H}^{R}$ is generated by elements in the linear strand; this point was made by Avramov, Conca, and Iyengar [Reference Avramov, Conca and Iyengar4] and Boocher et al. [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7]. More precisely, in [Reference Avramov, Conca and Iyengar4, Theorem 4.1] it is shown that if
$\operatorname{H}^{R}$ is generated by elements in the linear strand; this point was made by Avramov, Conca, and Iyengar [Reference Avramov, Conca and Iyengar4] and Boocher et al. [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7]. More precisely, in [Reference Avramov, Conca and Iyengar4, Theorem 4.1] it is shown that if  $R$ is Koszul then
$R$ is Koszul then  $\operatorname{H}_{i,j}^{R}=0$ for
$\operatorname{H}_{i,j}^{R}=0$ for  $j>2i$ and
$j>2i$ and  $\operatorname{H}_{i,2i}^{R}=(\operatorname{H}_{1,2}^{R})^{i}$ for all
$\operatorname{H}_{i,2i}^{R}=(\operatorname{H}_{1,2}^{R})^{i}$ for all  $i\geqslant 0$ and in [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7, Theorem 3.1] it is proved that one has also
$i\geqslant 0$ and in [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7, Theorem 3.1] it is proved that one has also  $\operatorname{H}_{i,2i-1}^{R}=(\operatorname{H}_{1,2}^{R})^{i-2}\operatorname{H}_{2,3}^{R}$ for all
$\operatorname{H}_{i,2i-1}^{R}=(\operatorname{H}_{1,2}^{R})^{i-2}\operatorname{H}_{2,3}^{R}$ for all  $i\geqslant 2$. Sections 6 and 7 provide some further insight into the connections between the fact that
$i\geqslant 2$. Sections 6 and 7 provide some further insight into the connections between the fact that  $R$ is Koszul and the structure of
$R$ is Koszul and the structure of  $\operatorname{H}^{R}$. In Proposition 6.2 we note that if
$\operatorname{H}^{R}$. In Proposition 6.2 we note that if  $R$ is Koszul then the nonlinear strands of
$R$ is Koszul then the nonlinear strands of  $\operatorname{H}^{R}$ are contained in the set of matric Massey products of
$\operatorname{H}^{R}$ are contained in the set of matric Massey products of  $\operatorname{K}^{R}$. However, generation of
$\operatorname{K}^{R}$. However, generation of  $\operatorname{H}^{R}$ by the linear strand (which implies that the nonlinear strands of
$\operatorname{H}^{R}$ by the linear strand (which implies that the nonlinear strands of  $\operatorname{H}^{R}$ are contained in the set of matric Massey products) does not imply that
$\operatorname{H}^{R}$ are contained in the set of matric Massey products) does not imply that  $R$ is Koszul. This can be seen by means of the example in 7.4, which relies on a ring from a paper of Roos [Reference Roos23]. (The fact that the linear strand need not generate
$R$ is Koszul. This can be seen by means of the example in 7.4, which relies on a ring from a paper of Roos [Reference Roos23]. (The fact that the linear strand need not generate  $\operatorname{H}^{R}$ as a
$\operatorname{H}^{R}$ as a  $k$-algebra when
$k$-algebra when  $R$ is Koszul is also noted in [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7, Remark 3.2].) On the other hand, 7.2 describes a Koszul algebra
$R$ is Koszul is also noted in [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7, Remark 3.2].) On the other hand, 7.2 describes a Koszul algebra  $R$ for which
$R$ for which  $\operatorname{H}^{R}$ has the same bigraded Hilbert series as the homology algebra of the ring of 7.4 and is also generated by the linear strand. It turns out that the ring in 7.2 satisfies the hypothesis of statement (2) above. This observation sheds some light on our effort to understand what distinguishes one homology algebra from the other in the two examples.
$\operatorname{H}^{R}$ has the same bigraded Hilbert series as the homology algebra of the ring of 7.4 and is also generated by the linear strand. It turns out that the ring in 7.2 satisfies the hypothesis of statement (2) above. This observation sheds some light on our effort to understand what distinguishes one homology algebra from the other in the two examples.
The examples in Section 7 utilize the Macaulay2 package DGAlgebras written by Frank Moore, which provides an efficient way to verify rings for which statements (1) or (2) hold; using this, we apply our Theorem 6.1 to the rings studied in Roos [Reference Roos23]. The last section also contains a concrete example of how our results can be used toward establishing homological properties of the ring and computations of Poincaré series, see 7.6.
Given the evidence that the properties considered in this paper show up in a large variety of situations, we hope that this study will be useful in further explorations of homological properties of local rings.
The work on this paper started during the 2015 Mathematical Research Communities program in Commutative Algebra, under the guidance of Liana Şega. The authors would also like to thank the other organizers of this program, Srikanth Iyengar, Karl Schwede, Gregory Smith, and Wenliang Zhang, for their support, and also the AMS staff that coordinated the program. Anjan Gupta joined the project following conversations during the conference in honor of Craig Huneke held in Ann Arbor in July 2016, and is thankful for support to travel to this conference from the Department of Mathematics at the University of Michigan and IIT Bombay.
1 Background
In this section we set notation and provide needed definitions, including that of a small homomorphism, for which we provide some preliminary results.
1.1. Let  $(R,\mathfrak{m},k)$ be a local ring and
$(R,\mathfrak{m},k)$ be a local ring and  $M$ a finite (meaning finitely generated)
$M$ a finite (meaning finitely generated)  $R$-module. Fix a minimal generating set of
$R$-module. Fix a minimal generating set of  $\mathfrak{m}$ and let
$\mathfrak{m}$ and let  $\operatorname{K}^{R}$ denote the Koszul complex on this set. Let
$\operatorname{K}^{R}$ denote the Koszul complex on this set. Let  $\operatorname{H}^{R}$ denote the homology algebra of
$\operatorname{H}^{R}$ denote the homology algebra of  $\operatorname{K}^{R}$. The complex
$\operatorname{K}^{R}$. The complex  $\operatorname{K}^{R}$ has a natural structure of a graded commutative algebra, and this structure is inherited by
$\operatorname{K}^{R}$ has a natural structure of a graded commutative algebra, and this structure is inherited by  $\operatorname{H}^{R}$. We denote by
$\operatorname{H}^{R}$. We denote by  $\operatorname{K}^{M}$ the Koszul complex
$\operatorname{K}^{M}$ the Koszul complex  $\operatorname{K}^{R}\otimes _{R}M$.
$\operatorname{K}^{R}\otimes _{R}M$.
The Poincaré series  $\operatorname{P}_{M}^{R}(z)$ of
$\operatorname{P}_{M}^{R}(z)$ of  $M$ is defined as
$M$ is defined as
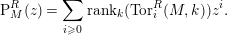 $$\begin{eqnarray}\operatorname{P}_{M}^{R}(z)=\mathop{\sum }_{i\geqslant 0}\operatorname{rank}_{k}(\operatorname{Tor}_{i}^{R}(M,k))z^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{M}^{R}(z)=\mathop{\sum }_{i\geqslant 0}\operatorname{rank}_{k}(\operatorname{Tor}_{i}^{R}(M,k))z^{i}.\end{eqnarray}$$ If  $\unicode[STIX]{x1D719}:(R,\mathfrak{m},k)\rightarrow (S,\mathfrak{n},k)$ is a surjective homomorphism of local rings then the following coefficientwise inequality holds
$\unicode[STIX]{x1D719}:(R,\mathfrak{m},k)\rightarrow (S,\mathfrak{n},k)$ is a surjective homomorphism of local rings then the following coefficientwise inequality holds
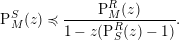 $$\begin{eqnarray}\operatorname{P}_{M}^{S}(z)\preccurlyeq \frac{\operatorname{P}_{M}^{R}(z)}{1-z(\operatorname{P}_{S}^{R}(z)-1)}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{M}^{S}(z)\preccurlyeq \frac{\operatorname{P}_{M}^{R}(z)}{1-z(\operatorname{P}_{S}^{R}(z)-1)}.\end{eqnarray}$$ If equality holds for  $M=k$ then we say that
$M=k$ then we say that  $\unicode[STIX]{x1D719}$ is a Golod homomorphism.
$\unicode[STIX]{x1D719}$ is a Golod homomorphism.
The homomorphism  $\unicode[STIX]{x1D719}$ induces maps
$\unicode[STIX]{x1D719}$ induces maps
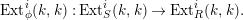 $$\begin{eqnarray}\operatorname{Ext}_{\unicode[STIX]{x1D719}}^{i}(k,k):\operatorname{Ext}_{S}^{i}(k,k)\rightarrow \operatorname{Ext}_{R}^{i}(k,k).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{\unicode[STIX]{x1D719}}^{i}(k,k):\operatorname{Ext}_{S}^{i}(k,k)\rightarrow \operatorname{Ext}_{R}^{i}(k,k).\end{eqnarray}$$ If  $\operatorname{Ext}_{\unicode[STIX]{x1D719}}^{\ast }(k,k)$ is surjective then we say
$\operatorname{Ext}_{\unicode[STIX]{x1D719}}^{\ast }(k,k)$ is surjective then we say  $\unicode[STIX]{x1D719}$ is small. Recall that if
$\unicode[STIX]{x1D719}$ is small. Recall that if  $\unicode[STIX]{x1D719}$ is Golod then
$\unicode[STIX]{x1D719}$ is Golod then  $\unicode[STIX]{x1D719}$ is small (cf. Avramov [Reference Avramov1, 3.5]).
$\unicode[STIX]{x1D719}$ is small (cf. Avramov [Reference Avramov1, 3.5]).
When  $R$ is artinian, specific conditions formulated in terms of the concepts above allow for an explicit computation of the series
$R$ is artinian, specific conditions formulated in terms of the concepts above allow for an explicit computation of the series  $\operatorname{P}_{k}^{R}(z)$.
$\operatorname{P}_{k}^{R}(z)$.
Lemma 1.2. Let  $(R,\mathfrak{m},k)$ be an artinian local ring with
$(R,\mathfrak{m},k)$ be an artinian local ring with  $\mathfrak{m}^{s+1}=0$. Let
$\mathfrak{m}^{s+1}=0$. Let  $n$ denote the minimal number of generators of
$n$ denote the minimal number of generators of  $\mathfrak{m}$ and let
$\mathfrak{m}$ and let  $a$ be the dimension of
$a$ be the dimension of  $\mathfrak{m}^{s}$.
$\mathfrak{m}^{s}$.
If the canonical projection  $R\rightarrow R/\mathfrak{m}^{s}$ is small and the ring
$R\rightarrow R/\mathfrak{m}^{s}$ is small and the ring  $R/\mathfrak{m}^{s}$ is Golod, then the Poincaré series of
$R/\mathfrak{m}^{s}$ is Golod, then the Poincaré series of  $k$ over
$k$ over  $R$ is rational, satisfying the formula:
$R$ is rational, satisfying the formula:
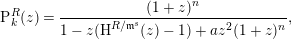 $$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\frac{(1+z)^{n}}{1-z(\operatorname{H}^{R/\mathfrak{m}^{s}}(z)-1)+az^{2}(1+z)^{n}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\frac{(1+z)^{n}}{1-z(\operatorname{H}^{R/\mathfrak{m}^{s}}(z)-1)+az^{2}(1+z)^{n}},\end{eqnarray}$$ where  $\operatorname{H}^{R/\mathfrak{m}^{s}}(z)$ stands for the Hilbert series (which is in this case a polynomial of degree
$\operatorname{H}^{R/\mathfrak{m}^{s}}(z)$ stands for the Hilbert series (which is in this case a polynomial of degree  $n$) of the Koszul homology algebra
$n$) of the Koszul homology algebra  $\operatorname{H}^{R/\mathfrak{m}^{s}}$.
$\operatorname{H}^{R/\mathfrak{m}^{s}}$.
Proof. As  $\mathfrak{m}^{s}\cong k^{a}$, we have
$\mathfrak{m}^{s}\cong k^{a}$, we have  $\operatorname{P}_{R/\mathfrak{m}^{s}}^{R}(z)=az\operatorname{P}_{k}^{R}(z)+1$.
$\operatorname{P}_{R/\mathfrak{m}^{s}}^{R}(z)=az\operatorname{P}_{k}^{R}(z)+1$.
Since  $R/\mathfrak{m}^{s}$ is Golod and
$R/\mathfrak{m}^{s}$ is Golod and  $R\rightarrow R/\mathfrak{m}^{s}$ is small,
$R\rightarrow R/\mathfrak{m}^{s}$ is small,  $R\rightarrow R/\mathfrak{m}^{s}$ is a Golod homomorphism by [Reference Şega26, 6.7]. Therefore, we have
$R\rightarrow R/\mathfrak{m}^{s}$ is a Golod homomorphism by [Reference Şega26, 6.7]. Therefore, we have
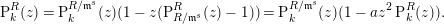 $$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)(1-z(\operatorname{P}_{R/\mathfrak{m}^{s}}^{R}(z)-1))=\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)(1-az^{2}\operatorname{P}_{k}^{R}(z)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)(1-z(\operatorname{P}_{R/\mathfrak{m}^{s}}^{R}(z)-1))=\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)(1-az^{2}\operatorname{P}_{k}^{R}(z)).\end{eqnarray}$$By rearranging, we have that
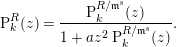 $$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\frac{\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)}{1+az^{2}\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{k}^{R}(z)=\frac{\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)}{1+az^{2}\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)}.\end{eqnarray}$$ Finally, since  $R/\mathfrak{m}^{s}$ is Golod, we have that
$R/\mathfrak{m}^{s}$ is Golod, we have that
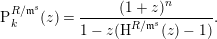 $$\begin{eqnarray}\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)=\frac{(1+z)^{n}}{1-z(\operatorname{H}^{R/\mathfrak{m}^{s}}(z)-1)}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{k}^{R/\mathfrak{m}^{s}}(z)=\frac{(1+z)^{n}}{1-z(\operatorname{H}^{R/\mathfrak{m}^{s}}(z)-1)}.\end{eqnarray}$$ In order to apply the lemma, we need to verify that the canonical projection  $R\rightarrow R/\mathfrak{m}^{s}$ is Golod or small. In [Reference Levin and Avramov18], Levin and Avramov prove that this homomorphism is Golod (thus small) whenever the artinian ring
$R\rightarrow R/\mathfrak{m}^{s}$ is Golod or small. In [Reference Levin and Avramov18], Levin and Avramov prove that this homomorphism is Golod (thus small) whenever the artinian ring  $R$ is Gorenstein. Their proof relies on the fact that
$R$ is Gorenstein. Their proof relies on the fact that  $\operatorname{H}^{R}$ is a Poincaré algebra when
$\operatorname{H}^{R}$ is a Poincaré algebra when  $R$ is Gorenstein. This leads us to believe that, more generally, the structure of the Koszul homology
$R$ is Gorenstein. This leads us to believe that, more generally, the structure of the Koszul homology  $\operatorname{H}^{R}$ can be used to understand the homological properties of the canonical projection
$\operatorname{H}^{R}$ can be used to understand the homological properties of the canonical projection  $R\rightarrow R/\mathfrak{m}^{s}$. The next lemma shows that matric Massey products play a role.
$R\rightarrow R/\mathfrak{m}^{s}$. The next lemma shows that matric Massey products play a role.
1.3. Let  $\unicode[STIX]{x1D711}:R\rightarrow S$ be a homomorphism of local rings. The usual products of
$\unicode[STIX]{x1D711}:R\rightarrow S$ be a homomorphism of local rings. The usual products of  $\operatorname{H}^{R}$ are understood to be the set of products
$\operatorname{H}^{R}$ are understood to be the set of products  $\operatorname{H}_{{\geqslant}1}^{R}\cdot \operatorname{H}_{{\geqslant}1}^{R}$. We denote by
$\operatorname{H}_{{\geqslant}1}^{R}\cdot \operatorname{H}_{{\geqslant}1}^{R}$. We denote by  $MH(\operatorname{K}^{R})$ the set of matric Massey products of
$MH(\operatorname{K}^{R})$ the set of matric Massey products of  $\operatorname{H}_{{\geqslant}1}^{R}$, as defined in [Reference May20]. This set of higher order homology operations is a submodule of
$\operatorname{H}_{{\geqslant}1}^{R}$, as defined in [Reference May20]. This set of higher order homology operations is a submodule of  $\operatorname{H}_{{\geqslant}1}^{R}$ and contains the usual products; see also [Reference Avramov2, (1.4.1)] for a more concise definition.
$\operatorname{H}_{{\geqslant}1}^{R}$ and contains the usual products; see also [Reference Avramov2, (1.4.1)] for a more concise definition.
The induced map  $\operatorname{H}(\operatorname{K}^{\unicode[STIX]{x1D711}}):\operatorname{H}(\operatorname{K}^{R})\rightarrow \operatorname{H}(\operatorname{K}^{S})$ satisfies
$\operatorname{H}(\operatorname{K}^{\unicode[STIX]{x1D711}}):\operatorname{H}(\operatorname{K}^{R})\rightarrow \operatorname{H}(\operatorname{K}^{S})$ satisfies  $\operatorname{H}(\operatorname{K}^{\unicode[STIX]{x1D711}})(MH(\operatorname{K}^{R}))\subseteq MH(\operatorname{K}^{S})$. By [Reference Avramov1, 4.6], if
$\operatorname{H}(\operatorname{K}^{\unicode[STIX]{x1D711}})(MH(\operatorname{K}^{R}))\subseteq MH(\operatorname{K}^{S})$. By [Reference Avramov1, 4.6], if  $\unicode[STIX]{x1D711}$ is small then the induced homomorphism
$\unicode[STIX]{x1D711}$ is small then the induced homomorphism
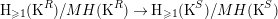 $$\begin{eqnarray}\operatorname{H}_{{\geqslant}1}(\operatorname{K}^{R})/MH(\operatorname{K}^{R})\rightarrow \operatorname{H}_{{\geqslant}1}(\operatorname{K}^{S})/MH(\operatorname{K}^{S})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}_{{\geqslant}1}(\operatorname{K}^{R})/MH(\operatorname{K}^{R})\rightarrow \operatorname{H}_{{\geqslant}1}(\operatorname{K}^{S})/MH(\operatorname{K}^{S})\end{eqnarray}$$is injective. From here we derive immediately the following statement:
Lemma. Let  $(R,\mathfrak{m},k)$ be a local ring with
$(R,\mathfrak{m},k)$ be a local ring with  $i\geqslant 0$. Consider the conditions:
$i\geqslant 0$. Consider the conditions:
(1) The canonical projection
 $R\rightarrow R/\mathfrak{m}^{i}$ is small;
$R\rightarrow R/\mathfrak{m}^{i}$ is small;(2)
 $\operatorname{H}_{{\geqslant}1}(\mathfrak{m}^{i}\operatorname{K}^{R})\subseteq MH(\operatorname{K}^{R})$.
$\operatorname{H}_{{\geqslant}1}(\mathfrak{m}^{i}\operatorname{K}^{R})\subseteq MH(\operatorname{K}^{R})$.
Then (1) implies (2). ◻
Example 7.4 in Section 7 shows that the implication (2) $\;\Longrightarrow \;$(1) does not hold when
$\;\Longrightarrow \;$(1) does not hold when  $i=2$. Ideally, one would like to replace condition (2) with a stronger one, that is equivalent to (1). While such a condition is not yet known, we identify in Sections 3 and 4 two conditions on Koszul homology that imply (1), for certain values of
$i=2$. Ideally, one would like to replace condition (2) with a stronger one, that is equivalent to (1). While such a condition is not yet known, we identify in Sections 3 and 4 two conditions on Koszul homology that imply (1), for certain values of  $i$.
$i$.
2 A property of the Tate resolution
The purpose of this section is to record in Proposition 2.8 a general property of the Tate resolution. This result will be used later, in the proof of one of the main theorems. We start with a description of the Tate resolution, and we invite the reader to consult [Reference Avramov3] for more details, in particular for the definition of a DG algebra. We then build the ingredients of the proof of the proposition by means of a couple of lemmas.
2.1. Adjunction of variables. Let  $B$ be a DG algebra over
$B$ be a DG algebra over  $R$ and suppose
$R$ and suppose  $z$ is a cycle in
$z$ is a cycle in  $B$. We embed
$B$. We embed  $B$ into a DG algebra
$B$ into a DG algebra  $B^{\prime }=B\langle y\rangle$ by freely adjoining a variable
$B^{\prime }=B\langle y\rangle$ by freely adjoining a variable  $y$ such that
$y$ such that  $\unicode[STIX]{x2202}(y)=z$ as follows:
$\unicode[STIX]{x2202}(y)=z$ as follows:
If  $|z|$ is even, the variable
$|z|$ is even, the variable  $y$ such that
$y$ such that  $\unicode[STIX]{x2202}(y)=z$ is called an exterior variable and satisfies
$\unicode[STIX]{x2202}(y)=z$ is called an exterior variable and satisfies  $y^{2}=0$. Denote by
$y^{2}=0$. Denote by  $k\langle y\rangle$ the exterior algebra over
$k\langle y\rangle$ the exterior algebra over  $k$ of a free
$k$ of a free  $k$-module on a generator of degree
$k$-module on a generator of degree  $|z|+1$. The differential on
$|z|+1$. The differential on  $B\langle y\rangle =B\otimes _{k}k\langle y\rangle$ is given by
$B\langle y\rangle =B\otimes _{k}k\langle y\rangle$ is given by
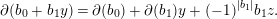 $$\begin{eqnarray}\unicode[STIX]{x2202}(b_{0}+b_{1}y)=\unicode[STIX]{x2202}(b_{0})+\unicode[STIX]{x2202}(b_{1})y+(-1)^{|b_{1}|}b_{1}z.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(b_{0}+b_{1}y)=\unicode[STIX]{x2202}(b_{0})+\unicode[STIX]{x2202}(b_{1})y+(-1)^{|b_{1}|}b_{1}z.\end{eqnarray}$$ If  $|z|>0$ is odd,
$|z|>0$ is odd,  $y$ is a divided powers variable. The
$y$ is a divided powers variable. The  $k$-algebra
$k$-algebra  $k\langle y\rangle$ on a divided powers variable
$k\langle y\rangle$ on a divided powers variable  $y$ is the free
$y$ is the free  $k$-module with basis
$k$-module with basis  $\{y^{(i)}:|y^{(i)}|=i|y|\}_{i\geqslant 0}$ and multiplication table
$\{y^{(i)}:|y^{(i)}|=i|y|\}_{i\geqslant 0}$ and multiplication table
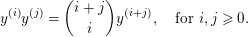 $$\begin{eqnarray}y^{(i)}y^{(j)}=\binom{i+j}{i}y^{(i+j)},\quad \text{for }i,j\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}y^{(i)}y^{(j)}=\binom{i+j}{i}y^{(i+j)},\quad \text{for }i,j\geqslant 0.\end{eqnarray}$$ We set  $y^{(1)}=y$,
$y^{(1)}=y$,  $y^{(0)}=1$, and
$y^{(0)}=1$, and  $y^{(i)}=0$ for
$y^{(i)}=0$ for  $i<0$. Forgetting the differentials,
$i<0$. Forgetting the differentials,  $B\langle y\rangle =B\otimes _{k}k\langle y\rangle$. If
$B\langle y\rangle =B\otimes _{k}k\langle y\rangle$. If  $z\in B$ is a cycle of positive odd degree, then
$z\in B$ is a cycle of positive odd degree, then
 $$\begin{eqnarray}\unicode[STIX]{x2202}\left(\mathop{\sum }_{i}b_{i}y^{(i)}\right)=\mathop{\sum }_{i}\unicode[STIX]{x2202}(b_{i})y^{(i)}+\mathop{\sum }_{i}(-1)^{|b_{i}|}b_{i}zy^{(i-1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}\left(\mathop{\sum }_{i}b_{i}y^{(i)}\right)=\mathop{\sum }_{i}\unicode[STIX]{x2202}(b_{i})y^{(i)}+\mathop{\sum }_{i}(-1)^{|b_{i}|}b_{i}zy^{(i-1)}\end{eqnarray}$$ is a differential on  $B\langle y\rangle$ that extends that of
$B\langle y\rangle$ that extends that of  $B$ and satisfies the Leibniz rule.
$B$ and satisfies the Leibniz rule.
The notation  $B\langle y_{1},\ldots ,y_{n}\rangle$ stands for the DG algebra obtained by repeated adjunction of variables as above.
$B\langle y_{1},\ldots ,y_{n}\rangle$ stands for the DG algebra obtained by repeated adjunction of variables as above.
2.2. The Tate resolution. Let  $x_{1},\ldots ,x_{n}$ be a minimal generating set for
$x_{1},\ldots ,x_{n}$ be a minimal generating set for  $\mathfrak{m}$ and
$\mathfrak{m}$ and  $\operatorname{K}^{R}$ the Koszul complex on
$\operatorname{K}^{R}$ the Koszul complex on  $x_{1},\ldots ,x_{n}$. Note that we can interpret
$x_{1},\ldots ,x_{n}$. Note that we can interpret  $\operatorname{K}^{R}$ as the DG algebra
$\operatorname{K}^{R}$ as the DG algebra
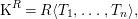 $$\begin{eqnarray}\operatorname{K}^{R}=R\langle T_{1},\ldots ,T_{n}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{K}^{R}=R\langle T_{1},\ldots ,T_{n}\rangle ,\end{eqnarray}$$ where  $T_{i}$ are degree 1 exterior variables (these exterior variables in degree 1 will be referred to as Koszul variables) with
$T_{i}$ are degree 1 exterior variables (these exterior variables in degree 1 will be referred to as Koszul variables) with  $\unicode[STIX]{x2202}(T_{i})=x_{i}$. One can continue to “kill” homology by adjoining variables to
$\unicode[STIX]{x2202}(T_{i})=x_{i}$. One can continue to “kill” homology by adjoining variables to  $\operatorname{K}^{R}$, following the construction in [Reference Avramov3, 6.3.1]. The resulting DG algebra
$\operatorname{K}^{R}$, following the construction in [Reference Avramov3, 6.3.1]. The resulting DG algebra  ${\mathcal{A}}$ is a minimal free resolution of
${\mathcal{A}}$ is a minimal free resolution of  $k$ over
$k$ over  $R$, often referred to as the Tate resolution of
$R$, often referred to as the Tate resolution of  $k$ over
$k$ over  $R$.
$R$.
Forgetting differentials,  ${\mathcal{A}}$ is a free
${\mathcal{A}}$ is a free  $R$-module: see [Reference Avramov3, Remark 6.2.1] for a description of the basis in terms of the variables adjoined. In particular, one can see that
$R$-module: see [Reference Avramov3, Remark 6.2.1] for a description of the basis in terms of the variables adjoined. In particular, one can see that  ${\mathcal{A}}$ is also a free
${\mathcal{A}}$ is also a free  $\operatorname{K}^{R}$-module.
$\operatorname{K}^{R}$-module.
2.3. Notation. We write  $\operatorname{K}$ for
$\operatorname{K}$ for  $\operatorname{K}^{R}$ when the ring
$\operatorname{K}^{R}$ when the ring  $R$ is understood. Since
$R$ is understood. Since  ${\mathcal{A}}$ is a free algebra over
${\mathcal{A}}$ is a free algebra over  $\operatorname{K}$, we consider a homogeneous
$\operatorname{K}$, we consider a homogeneous  $\operatorname{K}$-basis of
$\operatorname{K}$-basis of  ${\mathcal{A}}$. For each
${\mathcal{A}}$. For each  $j$, let
$j$, let  $\unicode[STIX]{x1D712}_{i,j}$ with
$\unicode[STIX]{x1D712}_{i,j}$ with  $1\leqslant i\leqslant q_{j}$ denote the elements of homological degree
$1\leqslant i\leqslant q_{j}$ denote the elements of homological degree  $j$ in this basis. If
$j$ in this basis. If  $z\in {\mathcal{A}}_{p}$, then we write
$z\in {\mathcal{A}}_{p}$, then we write  $z$ in terms of this basis as
$z$ in terms of this basis as
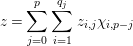 $$\begin{eqnarray}z=\mathop{\sum }_{j=0}^{p}\mathop{\sum }_{i=1}^{q_{j}}z_{i,j}\unicode[STIX]{x1D712}_{i,p-j}\end{eqnarray}$$
$$\begin{eqnarray}z=\mathop{\sum }_{j=0}^{p}\mathop{\sum }_{i=1}^{q_{j}}z_{i,j}\unicode[STIX]{x1D712}_{i,p-j}\end{eqnarray}$$ with  $z_{i,j}\in \operatorname{K}_{j}$ for each
$z_{i,j}\in \operatorname{K}_{j}$ for each  $j$.
$j$.
As usual,  $Z({\mathcal{A}})$ denotes the set of cycles of
$Z({\mathcal{A}})$ denotes the set of cycles of  ${\mathcal{A}}$ and
${\mathcal{A}}$ and  $B({\mathcal{A}})$ denotes the set of boundaries.
$B({\mathcal{A}})$ denotes the set of boundaries.
The following lemma provides the inductive step for our key lemma, Lemma 2.7, below.
Lemma 2.4. Let  $z\in Z_{p}({\mathcal{A}})$ and write it as in (2.3.1). Let
$z\in Z_{p}({\mathcal{A}})$ and write it as in (2.3.1). Let  $a$ be an integer with
$a$ be an integer with  $0\leqslant a\leqslant p$. Assume
$0\leqslant a\leqslant p$. Assume  $z_{i,j}\in \mathfrak{m}^{t}\operatorname{K}$ for all
$z_{i,j}\in \mathfrak{m}^{t}\operatorname{K}$ for all  $j$ with
$j$ with  $0\leqslant j\leqslant a-1$ and all
$0\leqslant j\leqslant a-1$ and all  $i$ with
$i$ with  $1\leqslant i\leqslant q_{j}$. Then
$1\leqslant i\leqslant q_{j}$. Then
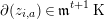 $$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})\in \mathfrak{m}^{t+1}\operatorname{K}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})\in \mathfrak{m}^{t+1}\operatorname{K}\end{eqnarray}$$ for all  $i$ with
$i$ with  $1\leqslant i\leqslant q_{a}.$
$1\leqslant i\leqslant q_{a}.$
Proof. Since  $z\in Z({\mathcal{A}})$, we have
$z\in Z({\mathcal{A}})$, we have  $\unicode[STIX]{x2202}(z)=0$. On the other hand we can compute
$\unicode[STIX]{x2202}(z)=0$. On the other hand we can compute  $\unicode[STIX]{x2202}(z)$ from (2.3.1), using the Leibniz rule; this yields:
$\unicode[STIX]{x2202}(z)$ from (2.3.1), using the Leibniz rule; this yields:
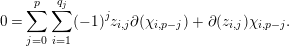 $$\begin{eqnarray}0=\mathop{\sum }_{j=0}^{p}\mathop{\sum }_{i=1}^{q_{j}}(-1)^{j}z_{i,j}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})+\unicode[STIX]{x2202}(z_{i,j})\unicode[STIX]{x1D712}_{i,p-j}.\end{eqnarray}$$
$$\begin{eqnarray}0=\mathop{\sum }_{j=0}^{p}\mathop{\sum }_{i=1}^{q_{j}}(-1)^{j}z_{i,j}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})+\unicode[STIX]{x2202}(z_{i,j})\unicode[STIX]{x1D712}_{i,p-j}.\end{eqnarray}$$ Let  $i$ be such that
$i$ be such that  $1\leqslant i\leqslant q_{a}$. We express all terms in the right-hand side of (2.4.1) in terms of the
$1\leqslant i\leqslant q_{a}$. We express all terms in the right-hand side of (2.4.1) in terms of the  $\operatorname{K}$-basis of
$\operatorname{K}$-basis of  ${\mathcal{A}}$, and collect the terms to compute the coefficient of each basis element in the sum. We see that the coefficient of
${\mathcal{A}}$, and collect the terms to compute the coefficient of each basis element in the sum. We see that the coefficient of  $\unicode[STIX]{x1D712}_{i,p-a}$ in this sum is
$\unicode[STIX]{x1D712}_{i,p-a}$ in this sum is
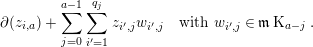 $$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})+\mathop{\sum }_{j=0}^{a-1}\mathop{\sum }_{i^{\prime }=1}^{q_{j}}z_{i^{\prime },j}w_{i^{\prime },j}\quad \text{with }w_{i^{\prime },j}\in \mathfrak{m}\operatorname{K}_{a-j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})+\mathop{\sum }_{j=0}^{a-1}\mathop{\sum }_{i^{\prime }=1}^{q_{j}}z_{i^{\prime },j}w_{i^{\prime },j}\quad \text{with }w_{i^{\prime },j}\in \mathfrak{m}\operatorname{K}_{a-j}.\end{eqnarray}$$ The coefficients  $w_{i^{\prime },j}$ come from expressing
$w_{i^{\prime },j}$ come from expressing  $\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})$ in terms of the
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})$ in terms of the  $\operatorname{K}$-basis, for
$\operatorname{K}$-basis, for  $j\leqslant a-1$. In particular,
$j\leqslant a-1$. In particular,  $w_{i^{\prime },j}\in \mathfrak{m}\operatorname{K}$ since
$w_{i^{\prime },j}\in \mathfrak{m}\operatorname{K}$ since  ${\mathcal{A}}$ is minimal. (Note that if
${\mathcal{A}}$ is minimal. (Note that if  $j\geqslant a$ then
$j\geqslant a$ then  $z_{i,j}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})$ does not have any contribution to the coefficient of
$z_{i,j}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-j})$ does not have any contribution to the coefficient of  $\unicode[STIX]{x1D712}_{i,p-a}$, for degree reasons.) These coefficients of
$\unicode[STIX]{x1D712}_{i,p-a}$, for degree reasons.) These coefficients of  $\unicode[STIX]{x1D712}_{i,p-a}$ must equal
$\unicode[STIX]{x1D712}_{i,p-a}$ must equal  $0$, hence
$0$, hence
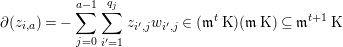 $$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})=-\mathop{\sum }_{j=0}^{a-1}\mathop{\sum }_{i^{\prime }=1}^{q_{j}}z_{i^{\prime },j}w_{i^{\prime },j}\in (\mathfrak{m}^{t}\operatorname{K})(\mathfrak{m}\operatorname{K})\subseteq \mathfrak{m}^{t+1}\operatorname{K}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i,a})=-\mathop{\sum }_{j=0}^{a-1}\mathop{\sum }_{i^{\prime }=1}^{q_{j}}z_{i^{\prime },j}w_{i^{\prime },j}\in (\mathfrak{m}^{t}\operatorname{K})(\mathfrak{m}\operatorname{K})\subseteq \mathfrak{m}^{t+1}\operatorname{K}\end{eqnarray}$$ for all  $i$ with
$i$ with  $1\leqslant i\leqslant q_{a}$.
$1\leqslant i\leqslant q_{a}$.
2.5. Let  $\widehat{R}$ denote the completion of
$\widehat{R}$ denote the completion of  $R$ with respect to
$R$ with respect to  $\mathfrak{m}$. We may write
$\mathfrak{m}$. We may write  $\widehat{R}=Q/I$, with
$\widehat{R}=Q/I$, with  $(Q,\mathfrak{n},k)$ a regular local ring and
$(Q,\mathfrak{n},k)$ a regular local ring and  $I\subseteq \mathfrak{n}^{2}$; this presentation is called a minimal Cohen presentation. We set
$I\subseteq \mathfrak{n}^{2}$; this presentation is called a minimal Cohen presentation. We set
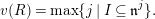 $$\begin{eqnarray}v(R)=\max \{j\mid I\subseteq \mathfrak{n}^{j}\}.\end{eqnarray}$$
$$\begin{eqnarray}v(R)=\max \{j\mid I\subseteq \mathfrak{n}^{j}\}.\end{eqnarray}$$As noted in [Reference Hoffmeier and Şega13], this integer is independent of the choice of the minimal Cohen presentation.
Remark 2.6. If  $v(R)\geqslant t+1$, that is,
$v(R)\geqslant t+1$, that is,  $I\subseteq \mathfrak{n}^{t+1}$, then the map
$I\subseteq \mathfrak{n}^{t+1}$, then the map
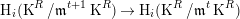 $$\begin{eqnarray}\operatorname{H}_{i}(\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R})\rightarrow \operatorname{H}_{i}(\operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}_{i}(\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R})\rightarrow \operatorname{H}_{i}(\operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R})\end{eqnarray}$$ induced by the canonical homomorphism  $\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R}\rightarrow \operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R}$ is zero for all
$\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R}\rightarrow \operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R}$ is zero for all  $i\geqslant 1$. In particular, we have: If
$i\geqslant 1$. In particular, we have: If  $\unicode[STIX]{x2202}(z)\in \mathfrak{m}^{t+1}\operatorname{K}^{R}$, then
$\unicode[STIX]{x2202}(z)\in \mathfrak{m}^{t+1}\operatorname{K}^{R}$, then  $z\in B(\operatorname{K}^{R})+\mathfrak{m}^{t}\operatorname{K}^{R}$ for all
$z\in B(\operatorname{K}^{R})+\mathfrak{m}^{t}\operatorname{K}^{R}$ for all  $z\in \operatorname{K}_{{\geqslant}1}^{R}$.
$z\in \operatorname{K}_{{\geqslant}1}^{R}$.
Indeed, to justify this statement it suffices to assume that  $R$ is complete, with
$R$ is complete, with  $R=Q/I$ as above. We can write
$R=Q/I$ as above. We can write  $\operatorname{K}^{R}=\operatorname{K}^{Q}\otimes _{Q}R$, where
$\operatorname{K}^{R}=\operatorname{K}^{Q}\otimes _{Q}R$, where  $\operatorname{K}^{Q}$ is the Koszul complex on a minimal generating set of
$\operatorname{K}^{Q}$ is the Koszul complex on a minimal generating set of  $\mathfrak{n}$ obtained by lifting the minimal generating set picked for
$\mathfrak{n}$ obtained by lifting the minimal generating set picked for  $\mathfrak{m}$. Since
$\mathfrak{m}$. Since  $I\subseteq \mathfrak{n}^{t+1}$ by assumption, we can make the identifications
$I\subseteq \mathfrak{n}^{t+1}$ by assumption, we can make the identifications  $\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R}=\operatorname{K}^{Q}/\mathfrak{n}^{t+1}\operatorname{K}^{Q}$ and
$\operatorname{K}^{R}/\mathfrak{m}^{t+1}\operatorname{K}^{R}=\operatorname{K}^{Q}/\mathfrak{n}^{t+1}\operatorname{K}^{Q}$ and  $\operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R}=\operatorname{K}^{Q}/\mathfrak{n}^{t}\operatorname{K}^{Q}$. The map in (2.6.1) can then be identified with the induced map
$\operatorname{K}^{R}/\mathfrak{m}^{t}\operatorname{K}^{R}=\operatorname{K}^{Q}/\mathfrak{n}^{t}\operatorname{K}^{Q}$. The map in (2.6.1) can then be identified with the induced map
 $$\begin{eqnarray}\operatorname{H}_{i}(\operatorname{K}^{Q}/\mathfrak{n}^{t+1}\operatorname{K}^{Q})\rightarrow \operatorname{H}_{i}(\operatorname{K}^{Q}/\mathfrak{n}^{t}\operatorname{K}^{Q})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}_{i}(\operatorname{K}^{Q}/\mathfrak{n}^{t+1}\operatorname{K}^{Q})\rightarrow \operatorname{H}_{i}(\operatorname{K}^{Q}/\mathfrak{n}^{t}\operatorname{K}^{Q})\end{eqnarray}$$ which is zero for all  $i\geqslant 1$ because the induced map
$i\geqslant 1$ because the induced map  $\operatorname{H}_{i}(\mathfrak{n}^{t+1}\operatorname{K}^{Q})\rightarrow \operatorname{H}_{i}(\mathfrak{n}^{t}\operatorname{K}^{Q})$ is zero for all
$\operatorname{H}_{i}(\mathfrak{n}^{t+1}\operatorname{K}^{Q})\rightarrow \operatorname{H}_{i}(\mathfrak{n}^{t}\operatorname{K}^{Q})$ is zero for all  $i\geqslant 0$, since
$i\geqslant 0$, since  $Q$ is regular (for example, see [Reference Şega26, Theorem 3.3]).
$Q$ is regular (for example, see [Reference Şega26, Theorem 3.3]).
We are now prepared to prove a key lemma; a reformulation of this will yield Proposition 2.8 below.
Lemma 2.7. Suppose  $(R,\mathfrak{m},k)$ is a local ring,
$(R,\mathfrak{m},k)$ is a local ring,  $\operatorname{K}$ is the Koszul complex on a minimal generating set
$\operatorname{K}$ is the Koszul complex on a minimal generating set  $x_{1},\ldots ,x_{n}$ of
$x_{1},\ldots ,x_{n}$ of  $\mathfrak{m}$, and
$\mathfrak{m}$, and  ${\mathcal{A}}$ is the Tate resolution of
${\mathcal{A}}$ is the Tate resolution of  $k$. Let
$k$. Let  $t\geqslant 1$ be an integer such that
$t\geqslant 1$ be an integer such that  $v(R)\geqslant t+1$. If
$v(R)\geqslant t+1$. If  $x\in {\mathcal{A}}$, then there exists
$x\in {\mathcal{A}}$, then there exists  $y\in \operatorname{K}_{1}{\mathcal{A}}$ such that
$y\in \operatorname{K}_{1}{\mathcal{A}}$ such that  $\unicode[STIX]{x2202}(x-y)\in \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}$.
$\unicode[STIX]{x2202}(x-y)\in \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}$.
Proof. Let  $x\in {\mathcal{A}}_{p+1}$. If
$x\in {\mathcal{A}}_{p+1}$. If  $p=0$, we may take
$p=0$, we may take  $y=x$ and the result follows trivially. Now assume
$y=x$ and the result follows trivially. Now assume  $p\geqslant 1$. Since
$p\geqslant 1$. Since  ${\mathcal{A}}$ is minimal, we have
${\mathcal{A}}$ is minimal, we have  $\unicode[STIX]{x2202}(x)=\sum x_{i}g_{i}$ with
$\unicode[STIX]{x2202}(x)=\sum x_{i}g_{i}$ with  $x_{i}\in \mathfrak{m}$ and
$x_{i}\in \mathfrak{m}$ and  $g_{i}\in {\mathcal{A}}_{p}$. Choosing
$g_{i}\in {\mathcal{A}}_{p}$. Choosing  $A_{i}\in \operatorname{K}_{1}$ such that
$A_{i}\in \operatorname{K}_{1}$ such that  $\unicode[STIX]{x2202}(A_{i})=x_{i}$, we have
$\unicode[STIX]{x2202}(A_{i})=x_{i}$, we have
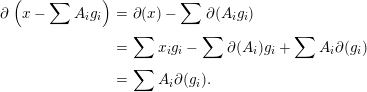 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}\left(x-\sum A_{i}g_{i}\right) & = & \displaystyle \unicode[STIX]{x2202}(x)-\sum \unicode[STIX]{x2202}(A_{i}g_{i})\nonumber\\ \displaystyle & = & \displaystyle \sum x_{i}g_{i}-\sum \unicode[STIX]{x2202}(A_{i})g_{i}+\sum A_{i}\unicode[STIX]{x2202}(g_{i})\nonumber\\ \displaystyle & = & \displaystyle \sum A_{i}\unicode[STIX]{x2202}(g_{i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}\left(x-\sum A_{i}g_{i}\right) & = & \displaystyle \unicode[STIX]{x2202}(x)-\sum \unicode[STIX]{x2202}(A_{i}g_{i})\nonumber\\ \displaystyle & = & \displaystyle \sum x_{i}g_{i}-\sum \unicode[STIX]{x2202}(A_{i})g_{i}+\sum A_{i}\unicode[STIX]{x2202}(g_{i})\nonumber\\ \displaystyle & = & \displaystyle \sum A_{i}\unicode[STIX]{x2202}(g_{i}).\nonumber\end{eqnarray}$$ Set  $y^{\prime }=\sum A_{i}g_{i}$. Then
$y^{\prime }=\sum A_{i}g_{i}$. Then  $y^{\prime }\in \operatorname{K}_{1}{\mathcal{A}}$ and
$y^{\prime }\in \operatorname{K}_{1}{\mathcal{A}}$ and  $\unicode[STIX]{x2202}(x-y^{\prime })\in \operatorname{K}_{1}{\mathcal{A}}$.
$\unicode[STIX]{x2202}(x-y^{\prime })\in \operatorname{K}_{1}{\mathcal{A}}$.
Apply Lemma 2.4 with  $z=\unicode[STIX]{x2202}(x-y^{\prime })$ and
$z=\unicode[STIX]{x2202}(x-y^{\prime })$ and  $a=1$ (noting that
$a=1$ (noting that  $z_{i,0}=0$ for all
$z_{i,0}=0$ for all  $i$ with
$i$ with  $1\leqslant i\leqslant q_{0}$, so the hypothesis is satisfied). For all
$1\leqslant i\leqslant q_{0}$, so the hypothesis is satisfied). For all  $i$ with
$i$ with  $0\leqslant i\leqslant q_{1}$ this yields
$0\leqslant i\leqslant q_{1}$ this yields  $\unicode[STIX]{x2202}(z_{i,1})\in \mathfrak{m}^{t+1}\operatorname{K}$ (indeed, this holds for all
$\unicode[STIX]{x2202}(z_{i,1})\in \mathfrak{m}^{t+1}\operatorname{K}$ (indeed, this holds for all  $t$ in Lemma 2.4, hence
$t$ in Lemma 2.4, hence  $\unicode[STIX]{x2202}(z_{i,1})=0$), and then Remark 2.6 shows
$\unicode[STIX]{x2202}(z_{i,1})=0$), and then Remark 2.6 shows
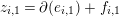 $$\begin{eqnarray}z_{i,1}=\unicode[STIX]{x2202}(e_{i,1})+f_{i,1}\end{eqnarray}$$
$$\begin{eqnarray}z_{i,1}=\unicode[STIX]{x2202}(e_{i,1})+f_{i,1}\end{eqnarray}$$ for some  $e_{i,1}\in \operatorname{K}_{2}$ and
$e_{i,1}\in \operatorname{K}_{2}$ and  $f_{i,1}\in \mathfrak{m}^{t}\operatorname{K}$. Consequently, we have:
$f_{i,1}\in \mathfrak{m}^{t}\operatorname{K}$. Consequently, we have:
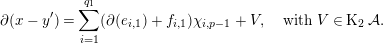 $$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime })=\mathop{\sum }_{i=1}^{q_{1}}(\unicode[STIX]{x2202}(e_{i,1})+f_{i,1})\unicode[STIX]{x1D712}_{i,p-1}+V,\quad \text{with }V\in \operatorname{K}_{2}{\mathcal{A}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime })=\mathop{\sum }_{i=1}^{q_{1}}(\unicode[STIX]{x2202}(e_{i,1})+f_{i,1})\unicode[STIX]{x1D712}_{i,p-1}+V,\quad \text{with }V\in \operatorname{K}_{2}{\mathcal{A}}.\end{eqnarray}$$ Now take  $y_{1}=\sum _{i=1}^{q_{1}}e_{i,1}\unicode[STIX]{x1D712}_{i,p-1}$ and we have:
$y_{1}=\sum _{i=1}^{q_{1}}e_{i,1}\unicode[STIX]{x1D712}_{i,p-1}$ and we have:
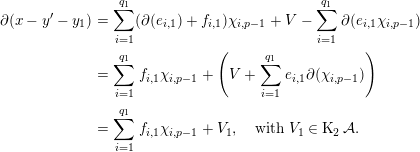 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(x-y^{\prime }-y_{1}) & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}(\unicode[STIX]{x2202}(e_{i,1})+f_{i,1})\unicode[STIX]{x1D712}_{i,p-1}+V-\mathop{\sum }_{i=1}^{q_{1}}\unicode[STIX]{x2202}(e_{i,1}\unicode[STIX]{x1D712}_{i,p-1})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}f_{i,1}\unicode[STIX]{x1D712}_{i,p-1}+\left(V+\mathop{\sum }_{i=1}^{q_{1}}e_{i,1}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-1})\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}f_{i,1}\unicode[STIX]{x1D712}_{i,p-1}+V_{1},\quad \text{with }V_{1}\in \operatorname{K}_{2}{\mathcal{A}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(x-y^{\prime }-y_{1}) & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}(\unicode[STIX]{x2202}(e_{i,1})+f_{i,1})\unicode[STIX]{x1D712}_{i,p-1}+V-\mathop{\sum }_{i=1}^{q_{1}}\unicode[STIX]{x2202}(e_{i,1}\unicode[STIX]{x1D712}_{i,p-1})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}f_{i,1}\unicode[STIX]{x1D712}_{i,p-1}+\left(V+\mathop{\sum }_{i=1}^{q_{1}}e_{i,1}\unicode[STIX]{x2202}(\unicode[STIX]{x1D712}_{i,p-1})\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{q_{1}}f_{i,1}\unicode[STIX]{x1D712}_{i,p-1}+V_{1},\quad \text{with }V_{1}\in \operatorname{K}_{2}{\mathcal{A}}.\nonumber\end{eqnarray}$$ Set  $m=\min \{p,n\}$, and let us assume inductively, for
$m=\min \{p,n\}$, and let us assume inductively, for  $a-1<m$, that we constructed
$a-1<m$, that we constructed  $y_{1},y_{2},\ldots ,y_{a-1}\in \operatorname{K}_{1}{\mathcal{A}}$ such that
$y_{1},y_{2},\ldots ,y_{a-1}\in \operatorname{K}_{1}{\mathcal{A}}$ such that
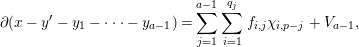 $$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1})=\mathop{\sum }_{j=1}^{a-1}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}+V_{a-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1})=\mathop{\sum }_{j=1}^{a-1}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}+V_{a-1},\end{eqnarray}$$ with  $f_{i,j}\in \mathfrak{m}^{t}\operatorname{K}$ and
$f_{i,j}\in \mathfrak{m}^{t}\operatorname{K}$ and  $V_{a-1}\in \operatorname{K}_{a}{\mathcal{A}}$. Applying again Lemma 2.4 and Remark 2.6, with
$V_{a-1}\in \operatorname{K}_{a}{\mathcal{A}}$. Applying again Lemma 2.4 and Remark 2.6, with  $z=\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1})$ we have that
$z=\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1})$ we have that
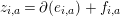 $$\begin{eqnarray}z_{i,a}=\unicode[STIX]{x2202}(e_{i,a})+f_{i,a}\end{eqnarray}$$
$$\begin{eqnarray}z_{i,a}=\unicode[STIX]{x2202}(e_{i,a})+f_{i,a}\end{eqnarray}$$ with  $e_{i,a}\in \operatorname{K}_{a+1}$ and
$e_{i,a}\in \operatorname{K}_{a+1}$ and  $f_{i,a}\in \mathfrak{m}^{t}\operatorname{K}_{a}$. Consequently, we can write
$f_{i,a}\in \mathfrak{m}^{t}\operatorname{K}_{a}$. Consequently, we can write
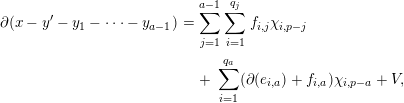 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1}) & = & \displaystyle \mathop{\sum }_{j=1}^{a-1}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{q_{a}}(\unicode[STIX]{x2202}(e_{i,a})+f_{i,a})\unicode[STIX]{x1D712}_{i,p-a}+V,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a-1}) & = & \displaystyle \mathop{\sum }_{j=1}^{a-1}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{q_{a}}(\unicode[STIX]{x2202}(e_{i,a})+f_{i,a})\unicode[STIX]{x1D712}_{i,p-a}+V,\nonumber\end{eqnarray}$$ with  $V\in \operatorname{K}_{a+1}{\mathcal{A}}$. Now take
$V\in \operatorname{K}_{a+1}{\mathcal{A}}$. Now take  $y_{a}=\sum _{i=1}^{q_{a}}e_{i,a}\unicode[STIX]{x1D712}_{i,p-a}$ and, as above, we get:
$y_{a}=\sum _{i=1}^{q_{a}}e_{i,a}\unicode[STIX]{x1D712}_{i,p-a}$ and, as above, we get:
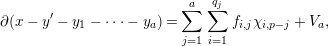 $$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a})=\mathop{\sum }_{j=1}^{a}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}+V_{a},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(x-y^{\prime }-y_{1}-\cdots -y_{a})=\mathop{\sum }_{j=1}^{a}\mathop{\sum }_{i=1}^{q_{j}}f_{i,j}\unicode[STIX]{x1D712}_{i,p-j}+V_{a},\end{eqnarray}$$ with  $V_{a}\in \operatorname{K}_{a+1}{\mathcal{A}}$. Note that
$V_{a}\in \operatorname{K}_{a+1}{\mathcal{A}}$. Note that  $V_{a}=0$ when
$V_{a}=0$ when  $a\geqslant m$, by degree reasons (if
$a\geqslant m$, by degree reasons (if  $p<n$) and since
$p<n$) and since  $K_{{>}n}=0$.
$K_{{>}n}=0$.
Set  $y=y^{\prime }+y_{1}+\cdots +y_{m}$. Then the cycle
$y=y^{\prime }+y_{1}+\cdots +y_{m}$. Then the cycle  $z=\unicode[STIX]{x2202}(x-y)$ satisfies the conclusions of our statement.
$z=\unicode[STIX]{x2202}(x-y)$ satisfies the conclusions of our statement.
We can now prove the useful decomposition property of the Tate resolution advertised above, which was inspired by the work in [Reference Levin and Avramov18].
Proposition 2.8. Let  $t\geqslant 1$ be an integer such that
$t\geqslant 1$ be an integer such that  $v(R)\geqslant t+1$, and let
$v(R)\geqslant t+1$, and let  ${\mathcal{A}}$ be the Tate resolution of
${\mathcal{A}}$ be the Tate resolution of  $k$ over
$k$ over  $R$. Denote by
$R$. Denote by  ${\mathcal{A}}^{\prime }$ the DG subalgebra of
${\mathcal{A}}^{\prime }$ the DG subalgebra of  ${\mathcal{A}}$ given by
${\mathcal{A}}$ given by
 $$\begin{eqnarray}{\mathcal{A}}^{\prime }=\{x\in {\mathcal{A}}\mid \unicode[STIX]{x2202}(x)\in \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}^{\prime }=\{x\in {\mathcal{A}}\mid \unicode[STIX]{x2202}(x)\in \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}\}.\end{eqnarray}$$ Then  ${\mathcal{A}}$ is generated by
${\mathcal{A}}$ is generated by  ${\mathcal{A}}^{\prime }$ as a
${\mathcal{A}}^{\prime }$ as a  $\operatorname{K}$-algebra, that is:
$\operatorname{K}$-algebra, that is:  ${\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}{\mathcal{A}}^{\prime }=\operatorname{K}{\mathcal{A}}^{\prime }$.
${\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}{\mathcal{A}}^{\prime }=\operatorname{K}{\mathcal{A}}^{\prime }$.
Proof. For  $x\in {\mathcal{A}}$, Lemma 2.7 provides an element
$x\in {\mathcal{A}}$, Lemma 2.7 provides an element  $y\in \operatorname{K}_{1}{\mathcal{A}}$ such that
$y\in \operatorname{K}_{1}{\mathcal{A}}$ such that  $x-y\in {\mathcal{A}}^{\prime }$. A reformulation of Lemma 2.7 therefore gives that
$x-y\in {\mathcal{A}}^{\prime }$. A reformulation of Lemma 2.7 therefore gives that  ${\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}$. Applying this fact repeatedly, and noting that
${\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}$. Applying this fact repeatedly, and noting that  $\operatorname{K}_{n+1}=0$, we get:
$\operatorname{K}_{n+1}=0$, we get:
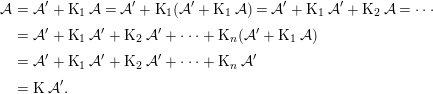 $$\begin{eqnarray}\displaystyle {\mathcal{A}} & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}({\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}})={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}=\cdots \nonumber\\ \displaystyle & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}({\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}})\nonumber\\ \displaystyle & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}{\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \operatorname{K}{\mathcal{A}}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}} & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}={\mathcal{A}}^{\prime }+\operatorname{K}_{1}({\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}})={\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}=\cdots \nonumber\\ \displaystyle & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}({\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}})\nonumber\\ \displaystyle & = & \displaystyle {\mathcal{A}}^{\prime }+\operatorname{K}_{1}{\mathcal{A}}^{\prime }+\operatorname{K}_{2}{\mathcal{A}}^{\prime }+\cdots +\operatorname{K}_{n}{\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \operatorname{K}{\mathcal{A}}^{\prime }.\nonumber\end{eqnarray}$$3 Generation by a special set
We continue with the notation of the previous sections for the Koszul complex and the Tate resolution of a local ring  $R$. In this section, we prove one of the main theorems, Theorem 3.1 below, and we point out its applications. In particular, these applications include a computation of the Poincaré series
$R$. In this section, we prove one of the main theorems, Theorem 3.1 below, and we point out its applications. In particular, these applications include a computation of the Poincaré series  $\operatorname{P}_{k}^{R}(z)$ and conditions under which the map
$\operatorname{P}_{k}^{R}(z)$ and conditions under which the map  $R\rightarrow R/\mathfrak{m}^{s}$ is Golod.
$R\rightarrow R/\mathfrak{m}^{s}$ is Golod.
Recall that the invariant  $v(R)$ was introduced in 2.5.
$v(R)$ was introduced in 2.5.
Theorem 3.1. Let  $(R,\mathfrak{m},k)$ be a local ring and let
$(R,\mathfrak{m},k)$ be a local ring and let  $s$ be an integer such that
$s$ be an integer such that  $\mathfrak{m}^{s+1}=0$. Let
$\mathfrak{m}^{s+1}=0$. Let  $t$ and
$t$ and  $b$ be integers such that
$b$ be integers such that  $s-t\leqslant b\leqslant s-1$ and
$s-t\leqslant b\leqslant s-1$ and  $v(R)\geqslant t+1\geqslant 2$, and assume that the following condition holds:
$v(R)\geqslant t+1\geqslant 2$, and assume that the following condition holds:
 ${\mathcal{Z}}_{t,b,s}$:
${\mathcal{Z}}_{t,b,s}$:There exists a finite set
 $Z\subseteq Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ such that
$Z\subseteq Z(\mathfrak{m}^{t}\operatorname{K}^{R})$ such that  $zz^{\prime }=0$ for all
$zz^{\prime }=0$ for all  $z,z^{\prime }\in Z$ and for every
$z,z^{\prime }\in Z$ and for every  $v\in \mathfrak{m}^{s}\operatorname{K}^{R}$ there exists
$v\in \mathfrak{m}^{s}\operatorname{K}^{R}$ there exists  $m\in \mathbb{N}$ and
$m\in \mathbb{N}$ and  $z_{i}\in Z$,
$z_{i}\in Z$,  $u_{i}\in Z(\mathfrak{m}^{b}\operatorname{K}^{R})$ for each
$u_{i}\in Z(\mathfrak{m}^{b}\operatorname{K}^{R})$ for each  $i$ with
$i$ with  $1\leqslant i\leqslant m$, such that
$1\leqslant i\leqslant m$, such that  $$\begin{eqnarray}v-\mathop{\sum }_{i=1}^{m}z_{i}u_{i}\in B(\mathfrak{m}^{s-1}\operatorname{K}^{R}).\end{eqnarray}$$
$$\begin{eqnarray}v-\mathop{\sum }_{i=1}^{m}z_{i}u_{i}\in B(\mathfrak{m}^{s-1}\operatorname{K}^{R}).\end{eqnarray}$$
The maps  $\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ induced by the inclusion
$\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ induced by the inclusion  $\mathfrak{m}^{s}\subseteq \mathfrak{m}^{b}$ are then zero for all
$\mathfrak{m}^{s}\subseteq \mathfrak{m}^{b}$ are then zero for all  $i\geqslant 0$.
$i\geqslant 0$.
We postpone the proof of the theorem in order to give some corollaries. Concrete examples for which these results can be applied are given in Section 7. We use below, and also in the next section, the following result of Rossi and Şega.
3.2. [Reference Rossi and Şega24, Lemma 1.2]
Let  $\unicode[STIX]{x1D705}:(R,\mathfrak{m},k)\rightarrow (\overline{R},\overline{\mathfrak{m}},k)$ be a surjective homomorphism of local rings. If there exists a positive integer
$\unicode[STIX]{x1D705}:(R,\mathfrak{m},k)\rightarrow (\overline{R},\overline{\mathfrak{m}},k)$ be a surjective homomorphism of local rings. If there exists a positive integer  $a$ such that:
$a$ such that:
(a) the map
 $\operatorname{Tor}_{i}^{R}(\overline{R},k)\rightarrow \operatorname{Tor}_{i}^{R}(\overline{R}/\overline{\mathfrak{m}}^{a},k)$ induced by the canonical quotient map
$\operatorname{Tor}_{i}^{R}(\overline{R},k)\rightarrow \operatorname{Tor}_{i}^{R}(\overline{R}/\overline{\mathfrak{m}}^{a},k)$ induced by the canonical quotient map  $\overline{R}\rightarrow \overline{R}/\overline{\mathfrak{m}}^{a}$ is zero for all positive
$\overline{R}\rightarrow \overline{R}/\overline{\mathfrak{m}}^{a}$ is zero for all positive  $i$, and
$i$, and(b) the map
 $\operatorname{Tor}_{i}^{\overline{R}}(\overline{\mathfrak{m}}^{2a},k)\rightarrow \operatorname{Tor}_{i}^{\overline{R}}(\overline{\mathfrak{m}}^{a},k)$ induced by the inclusion
$\operatorname{Tor}_{i}^{\overline{R}}(\overline{\mathfrak{m}}^{2a},k)\rightarrow \operatorname{Tor}_{i}^{\overline{R}}(\overline{\mathfrak{m}}^{a},k)$ induced by the inclusion  $\overline{\mathfrak{m}}^{2a}\subseteq \overline{\mathfrak{m}}^{a}$ is zero for all non-negative integers
$\overline{\mathfrak{m}}^{2a}\subseteq \overline{\mathfrak{m}}^{a}$ is zero for all non-negative integers  $i$,
$i$,
then  $\unicode[STIX]{x1D705}$ is a Golod homomorphism.
$\unicode[STIX]{x1D705}$ is a Golod homomorphism.
Corollary 3.3. Under the hypotheses of Theorem 3.1, if  $2b\geqslant s$ then the homomorphism
$2b\geqslant s$ then the homomorphism  $R\rightarrow R/\mathfrak{m}^{s}$ is Golod.
$R\rightarrow R/\mathfrak{m}^{s}$ is Golod.
Proof. We apply 3.2 to the natural projection  $\unicode[STIX]{x1D705}:R\rightarrow R/\mathfrak{m}^{s}$, with
$\unicode[STIX]{x1D705}:R\rightarrow R/\mathfrak{m}^{s}$, with  $\overline{R}=R/\mathfrak{m}^{s}$,
$\overline{R}=R/\mathfrak{m}^{s}$,  $\overline{\mathfrak{m}}=\mathfrak{m}/\mathfrak{m}^{s}$ and
$\overline{\mathfrak{m}}=\mathfrak{m}/\mathfrak{m}^{s}$ and  $a=b$. We need to check that conditions (a) and (b) hold. Since
$a=b$. We need to check that conditions (a) and (b) hold. Since  $2a=2b\geqslant s$, we have
$2a=2b\geqslant s$, we have  $\overline{\mathfrak{m}}^{2a}=0$, so condition 3.2(b) holds trivially. Theorem 3.1 gives that the induced maps
$\overline{\mathfrak{m}}^{2a}=0$, so condition 3.2(b) holds trivially. Theorem 3.1 gives that the induced maps  $\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ are zero for all
$\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ are zero for all  $i>0$, and this implies condition 3.2(a), since
$i>0$, and this implies condition 3.2(a), since  $R/\mathfrak{m}^{s}=\overline{R}$ and
$R/\mathfrak{m}^{s}=\overline{R}$ and  $R/\mathfrak{m}^{b}=\overline{R}/\overline{\mathfrak{m}}^{a}$.
$R/\mathfrak{m}^{b}=\overline{R}/\overline{\mathfrak{m}}^{a}$.
Remark 3.4. Let  $R=Q/I$ be a minimal Cohen presentation of
$R=Q/I$ be a minimal Cohen presentation of  $R$, with
$R$, with  $(Q,\mathfrak{n},k)$ a regular local ring. As first noted by Löfwall [Reference Löfwall19], the ring
$(Q,\mathfrak{n},k)$ a regular local ring. As first noted by Löfwall [Reference Löfwall19], the ring  $R$ is Golod whenever there exists an integer
$R$ is Golod whenever there exists an integer  $t$ such that
$t$ such that
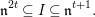 $$\begin{eqnarray}\mathfrak{n}^{2t}\subseteq I\subseteq \mathfrak{n}^{t+1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{n}^{2t}\subseteq I\subseteq \mathfrak{n}^{t+1}.\end{eqnarray}$$ Assume  $s$ and
$s$ and  $t$ are integers such that
$t$ are integers such that  $\mathfrak{m}^{s+1}=0$ and
$\mathfrak{m}^{s+1}=0$ and  $v(R)\geqslant t+1$, and so
$v(R)\geqslant t+1$, and so  $\mathfrak{n}^{s+1}\subseteq I\subseteq \mathfrak{n}^{t+1}$. If
$\mathfrak{n}^{s+1}\subseteq I\subseteq \mathfrak{n}^{t+1}$. If  $s<2t$, then the inclusions in (3.4.1) hold, and it follows that
$s<2t$, then the inclusions in (3.4.1) hold, and it follows that  $R$ is Golod. If
$R$ is Golod. If  $s=2t$ then
$s=2t$ then  $R$ is not necessarily Golod, but it follows that the quotient ring
$R$ is not necessarily Golod, but it follows that the quotient ring  $R/\mathfrak{m}^{s}=Q/(I+\mathfrak{n}^{s})$ is Golod.
$R/\mathfrak{m}^{s}=Q/(I+\mathfrak{n}^{s})$ is Golod.
Corollary 3.5. Assume the hypothesis of Theorem 3.1 is satisfied. If  $s=2t$ and
$s=2t$ and  $b=t$, then the hypotheses of Lemma 1.2 are satisfied, and thus
$b=t$, then the hypotheses of Lemma 1.2 are satisfied, and thus  $\operatorname{P}_{k}^{R}(z)$ satisfies the formula (1.2.1).
$\operatorname{P}_{k}^{R}(z)$ satisfies the formula (1.2.1).
Proof. The homomorphism  $R\rightarrow R/\mathfrak{m}^{s}$ is Golod by Theorem 3.1, and thus small (see 1.1). The ring
$R\rightarrow R/\mathfrak{m}^{s}$ is Golod by Theorem 3.1, and thus small (see 1.1). The ring  $R/\mathfrak{m}^{s}$ is Golod by Remark 3.4.
$R/\mathfrak{m}^{s}$ is Golod by Remark 3.4.
Proof of Theorem 3.1.
Let  $|Z|$ denote the cardinality of
$|Z|$ denote the cardinality of  $Z$. Let
$Z$. Let  $\{z_{1},\ldots ,z_{|Z|}\}$ be the cycles in
$\{z_{1},\ldots ,z_{|Z|}\}$ be the cycles in  $Z$ and let
$Z$ and let  ${\mathcal{I}}$ denote the set of all finite ordered lists of elements in
${\mathcal{I}}$ denote the set of all finite ordered lists of elements in  $\{1,\ldots ,|Z|\}$, including the empty set.
$\{1,\ldots ,|Z|\}$, including the empty set.
Let  $I\in {\mathcal{I}}$. If
$I\in {\mathcal{I}}$. If  $I=(i)$ has length
$I=(i)$ has length  $1$, we set
$1$, we set  $I^{-}=\emptyset$. If
$I^{-}=\emptyset$. If  $I=(i_{1},\ldots ,i_{r})$ has length
$I=(i_{1},\ldots ,i_{r})$ has length  $r\geqslant 2$, we set
$r\geqslant 2$, we set  $I^{-}=(i_{1},\ldots ,i_{r-1})$. We now define for each
$I^{-}=(i_{1},\ldots ,i_{r-1})$. We now define for each  $I\in {\mathcal{I}}$ an element
$I\in {\mathcal{I}}$ an element  $y_{I}\in {\mathcal{A}}$, where
$y_{I}\in {\mathcal{A}}$, where  ${\mathcal{A}}$ is the Tate resolution of
${\mathcal{A}}$ is the Tate resolution of  $k$ as in 2.2, such that
$k$ as in 2.2, such that
(1)
 $y_{I}=1\in {\mathcal{A}}_{0}$, if
$y_{I}=1\in {\mathcal{A}}_{0}$, if  $I=\emptyset$;
$I=\emptyset$;(2)
 $\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$, if
$\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$, if  $I=(i_{1},\ldots ,i_{r})$ with
$I=(i_{1},\ldots ,i_{r})$ with  $r\geqslant 1$.
$r\geqslant 1$.
The details of constructing these elements are as follows. If  $I=\emptyset$, we choose
$I=\emptyset$, we choose  $y_{I}$ as in (1). If
$y_{I}$ as in (1). If  $r=1$ and
$r=1$ and  $I=(i)$, we can choose
$I=(i)$, we can choose  $y_{I}\in {\mathcal{A}}$ such that
$y_{I}\in {\mathcal{A}}$ such that  $\unicode[STIX]{x2202}(y_{I})=z_{i}$, since
$\unicode[STIX]{x2202}(y_{I})=z_{i}$, since  $z_{i}\in Z$ is a cycle. Assuming that
$z_{i}\in Z$ is a cycle. Assuming that  $r\geqslant 2$ and the elements
$r\geqslant 2$ and the elements  $y_{I}$ have been defined for all
$y_{I}$ have been defined for all  $I\in {\mathcal{I}}$ of length
$I\in {\mathcal{I}}$ of length  $r-1$, we can construct elements
$r-1$, we can construct elements  $y_{I}$ satisfying (2) for
$y_{I}$ satisfying (2) for  $I=(i_{1},\ldots ,i_{r})$ by noting that
$I=(i_{1},\ldots ,i_{r})$ by noting that  $z_{i_{r}}y_{I^{-}}$ is a cycle, so such a
$z_{i_{r}}y_{I^{-}}$ is a cycle, so such a  $y_{I}$ exists since
$y_{I}$ exists since  ${\mathcal{A}}$ is acyclic. Indeed, we have
${\mathcal{A}}$ is acyclic. Indeed, we have
 $$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i_{r}}y_{I^{-}})=(-1)^{|z_{i_{r}}|}z_{i_{r}}\unicode[STIX]{x2202}(y_{I^{-}})=(-1)^{|z_{i_{r}}|}z_{i_{r}}z_{i_{r-1}}y_{(I^{-})^{-}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}(z_{i_{r}}y_{I^{-}})=(-1)^{|z_{i_{r}}|}z_{i_{r}}\unicode[STIX]{x2202}(y_{I^{-}})=(-1)^{|z_{i_{r}}|}z_{i_{r}}z_{i_{r-1}}y_{(I^{-})^{-}}=0,\end{eqnarray}$$ where the last equality is due to the hypothesis on the set  $Z$.
$Z$.
We identify the map  $\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ with the map
$\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{s},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{b},k)$ with the map  $H_{i}(\mathfrak{m}^{s}{\mathcal{A}})\rightarrow H_{i}(\mathfrak{m}^{b}{\mathcal{A}})$. In order to show this map is trivial for
$H_{i}(\mathfrak{m}^{s}{\mathcal{A}})\rightarrow H_{i}(\mathfrak{m}^{b}{\mathcal{A}})$. In order to show this map is trivial for  $i\geqslant 0$, we let
$i\geqslant 0$, we let  $x\in \mathfrak{m}^{s}{\mathcal{A}}_{c}$ for some
$x\in \mathfrak{m}^{s}{\mathcal{A}}_{c}$ for some  $c$ and must show that
$c$ and must show that  $x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$.
$x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$.
Set  $Y=\{y_{I}\in {\mathcal{A}}|I\in {\mathcal{I}}\}$. For
$Y=\{y_{I}\in {\mathcal{A}}|I\in {\mathcal{I}}\}$. For  $i,j\geqslant 0,$ define
$i,j\geqslant 0,$ define
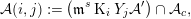 $$\begin{eqnarray}{\mathcal{A}}(i,j):=\left(\mathfrak{m}^{s}\operatorname{K}_{i}Y_{j}{\mathcal{A}}^{\prime }\right)\cap {\mathcal{A}}_{c},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(i,j):=\left(\mathfrak{m}^{s}\operatorname{K}_{i}Y_{j}{\mathcal{A}}^{\prime }\right)\cap {\mathcal{A}}_{c},\end{eqnarray}$$ where  $Y_{j}$ is the set of elements of
$Y_{j}$ is the set of elements of  $Y$ of degree
$Y$ of degree  $j$.
$j$.
Claim.
For  $i,j\geqslant 0$,
$i,j\geqslant 0$,
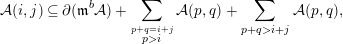 $$\begin{eqnarray}{\mathcal{A}}(i,j)\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathop{\sum }_{\stackrel{p+q=i+j}{p>i}}{\mathcal{A}}(p,q)+\mathop{\sum }_{p+q>i+j}{\mathcal{A}}(p,q),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(i,j)\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathop{\sum }_{\stackrel{p+q=i+j}{p>i}}{\mathcal{A}}(p,q)+\mathop{\sum }_{p+q>i+j}{\mathcal{A}}(p,q),\end{eqnarray}$$where only finitely many terms in this sum are not zero for degree reasons.
Proof of Claim.
To prove the inclusion, it suffices to consider elements of  ${\mathcal{A}}(i,j)$ of the form
${\mathcal{A}}(i,j)$ of the form  $vy_{I}a^{\prime }$ for some
$vy_{I}a^{\prime }$ for some  $v\in \mathfrak{m}^{s}\operatorname{K}_{i}$,
$v\in \mathfrak{m}^{s}\operatorname{K}_{i}$,  $a^{\prime }\in {\mathcal{A}}^{\prime }$ and
$a^{\prime }\in {\mathcal{A}}^{\prime }$ and  $y_{I}\in Y_{j}$, with
$y_{I}\in Y_{j}$, with  $I=(i_{1},\ldots ,i_{r})\in {\mathcal{I}}$ or
$I=(i_{1},\ldots ,i_{r})\in {\mathcal{I}}$ or  $I=\emptyset$; in the last case, we set
$I=\emptyset$; in the last case, we set  $r=0$. (Note that every element of
$r=0$. (Note that every element of  ${\mathcal{A}}(i,j)$ can be written as a sum of elements of this form.)
${\mathcal{A}}(i,j)$ can be written as a sum of elements of this form.)
By assumption there exist  $z_{\unicode[STIX]{x1D704},v}\in Z$ and
$z_{\unicode[STIX]{x1D704},v}\in Z$ and  $u_{\unicode[STIX]{x1D704},v}\in Z(\mathfrak{m}^{b}\operatorname{K})$ with
$u_{\unicode[STIX]{x1D704},v}\in Z(\mathfrak{m}^{b}\operatorname{K})$ with  $1\leqslant \unicode[STIX]{x1D704}\leqslant m$ such that
$1\leqslant \unicode[STIX]{x1D704}\leqslant m$ such that
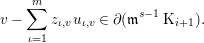 $$\begin{eqnarray}v-\mathop{\sum }_{\unicode[STIX]{x1D704}=1}^{m}z_{\unicode[STIX]{x1D704},v}u_{\unicode[STIX]{x1D704},v}\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1}).\end{eqnarray}$$
$$\begin{eqnarray}v-\mathop{\sum }_{\unicode[STIX]{x1D704}=1}^{m}z_{\unicode[STIX]{x1D704},v}u_{\unicode[STIX]{x1D704},v}\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1}).\end{eqnarray}$$ We need to show thus that  $(\sum _{\unicode[STIX]{x1D704}=1}^{m}z_{\unicode[STIX]{x1D704},v}u_{\unicode[STIX]{x1D704},v}+w)y_{I}{\mathcal{A}}^{\prime }$ is contained in the right-hand side of (3.5.1), for all
$(\sum _{\unicode[STIX]{x1D704}=1}^{m}z_{\unicode[STIX]{x1D704},v}u_{\unicode[STIX]{x1D704},v}+w)y_{I}{\mathcal{A}}^{\prime }$ is contained in the right-hand side of (3.5.1), for all  $w\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})$,
$w\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})$,  $z_{\unicode[STIX]{x1D704},v}\in Z$ and
$z_{\unicode[STIX]{x1D704},v}\in Z$ and  $u_{\unicode[STIX]{x1D704},v}\in Z(\mathfrak{m}^{b}\operatorname{K})$. Note that it suffices to prove this statement when
$u_{\unicode[STIX]{x1D704},v}\in Z(\mathfrak{m}^{b}\operatorname{K})$. Note that it suffices to prove this statement when  $m=1$. We assume thus that
$m=1$. We assume thus that  $v-z_{i_{r+1}}u\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})$ for some
$v-z_{i_{r+1}}u\in \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})$ for some  $z_{i_{r+1}}\in Z$ and
$z_{i_{r+1}}\in Z$ and  $u\in Z(\mathfrak{m}^{b}\operatorname{K})$ and we show that
$u\in Z(\mathfrak{m}^{b}\operatorname{K})$ and we show that  $vy_{I}{\mathcal{A}}^{\prime }$ is contained in the right-hand side of (3.5.1).
$vy_{I}{\mathcal{A}}^{\prime }$ is contained in the right-hand side of (3.5.1).
In what follows, we simplify the notation when  $I$ has length
$I$ has length  $1$ and we write
$1$ and we write  $y_{i}=y_{(i)}$. Define
$y_{i}=y_{(i)}$. Define  $I^{+}=(i_{1},\ldots ,i_{r},i_{r+1})$. Recall that we defined a set
$I^{+}=(i_{1},\ldots ,i_{r},i_{r+1})$. Recall that we defined a set  $I^{-}$ for any nonempty
$I^{-}$ for any nonempty  $I\in {\mathcal{I}}$. Although we do not define a set
$I\in {\mathcal{I}}$. Although we do not define a set  $\emptyset ^{-}$, we agree to set
$\emptyset ^{-}$, we agree to set  $y_{I^{-}}=z_{i_{r}}=y_{i_{r}}=0$ when
$y_{I^{-}}=z_{i_{r}}=y_{i_{r}}=0$ when  $I=\emptyset$. With this convention, note that the formula
$I=\emptyset$. With this convention, note that the formula  $\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$ also holds when
$\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$ also holds when  $I=\emptyset$, so we will not treat this case separately.
$I=\emptyset$, so we will not treat this case separately.
Note that
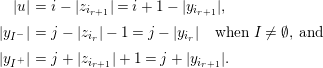 $$\begin{eqnarray}\displaystyle |u| & = & \displaystyle i-|z_{i_{r+1}}|=i+1-|y_{i_{r+1}}|,\nonumber\\ \displaystyle |y_{I^{-}}| & = & \displaystyle j-|z_{i_{r}}|-1=j-|y_{i_{r}}|\quad \text{when }I\neq \emptyset ,\;\text{and}\nonumber\\ \displaystyle |y_{I^{+}}| & = & \displaystyle j+|z_{i_{r+1}}|+1=j+|y_{i_{r+1}}|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |u| & = & \displaystyle i-|z_{i_{r+1}}|=i+1-|y_{i_{r+1}}|,\nonumber\\ \displaystyle |y_{I^{-}}| & = & \displaystyle j-|z_{i_{r}}|-1=j-|y_{i_{r}}|\quad \text{when }I\neq \emptyset ,\;\text{and}\nonumber\\ \displaystyle |y_{I^{+}}| & = & \displaystyle j+|z_{i_{r+1}}|+1=j+|y_{i_{r+1}}|.\nonumber\end{eqnarray}$$We now have
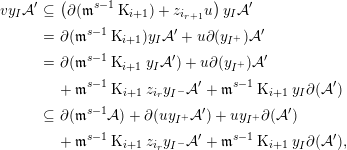 $$\begin{eqnarray}\displaystyle vy_{I}{\mathcal{A}}^{\prime } & \subseteq & \displaystyle \left(\unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})+z_{i_{r+1}}u\right)y_{I}{\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})y_{I}{\mathcal{A}}^{\prime }+u\unicode[STIX]{x2202}(y_{I^{+}}){\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}{\mathcal{A}}^{\prime })+u\unicode[STIX]{x2202}(y_{I^{+}}){\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}{\mathcal{A}})+\unicode[STIX]{x2202}(uy_{I^{+}}{\mathcal{A}}^{\prime })+uy_{I^{+}}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle vy_{I}{\mathcal{A}}^{\prime } & \subseteq & \displaystyle \left(\unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})+z_{i_{r+1}}u\right)y_{I}{\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1})y_{I}{\mathcal{A}}^{\prime }+u\unicode[STIX]{x2202}(y_{I^{+}}){\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}{\mathcal{A}}^{\prime })+u\unicode[STIX]{x2202}(y_{I^{+}}){\mathcal{A}}^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{s-1}{\mathcal{A}})+\unicode[STIX]{x2202}(uy_{I^{+}}{\mathcal{A}}^{\prime })+uy_{I^{+}}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime }),\nonumber\end{eqnarray}$$ where in line 2 we used the formula  $z_{i_{r+1}}y_{I}=\unicode[STIX]{x2202}(y_{I^{+}})$, in line 3 we used the Leibniz rule and the formula
$z_{i_{r+1}}y_{I}=\unicode[STIX]{x2202}(y_{I^{+}})$, in line 3 we used the Leibniz rule and the formula  $\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$, and in line 4 we used again the Leibniz rule and the fact that
$\unicode[STIX]{x2202}(y_{I})=z_{i_{r}}y_{I^{-}}$, and in line 4 we used again the Leibniz rule and the fact that  $u$ is a cycle.
$u$ is a cycle.
Consider the terms from the last line in the previous display. Since  $u\in Z(\mathfrak{m}^{b}\operatorname{K})$ and
$u\in Z(\mathfrak{m}^{b}\operatorname{K})$ and  $b\leqslant s-1$, we have
$b\leqslant s-1$, we have  $\unicode[STIX]{x2202}(\mathfrak{m}^{s-1}{\mathcal{A}})+\unicode[STIX]{x2202}(uy_{I^{+}}{\mathcal{A}}^{\prime })\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. Additionally, since
$\unicode[STIX]{x2202}(\mathfrak{m}^{s-1}{\mathcal{A}})+\unicode[STIX]{x2202}(uy_{I^{+}}{\mathcal{A}}^{\prime })\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. Additionally, since  $\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}$ by the definition of
$\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{t}\operatorname{K}_{1}{\mathcal{A}}$ by the definition of  ${\mathcal{A}}^{\prime }$, we have
${\mathcal{A}}^{\prime }$, we have  $uy_{I^{+}}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{b+t}\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}$ and
$uy_{I^{+}}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{b+t}\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}$ and  $\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{s-1+t}\operatorname{K}_{i+2}y_{I}{\mathcal{A}}$. Furthermore, since
$\mathfrak{m}^{s-1}\operatorname{K}_{i+1}y_{I}\unicode[STIX]{x2202}({\mathcal{A}}^{\prime })\subseteq \mathfrak{m}^{s-1+t}\operatorname{K}_{i+2}y_{I}{\mathcal{A}}$. Furthermore, since  $z_{i_{r}}=\unicode[STIX]{x2202}(y_{i_{r}})$, we have
$z_{i_{r}}=\unicode[STIX]{x2202}(y_{i_{r}})$, we have  $\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }\subseteq \mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }$. Thus
$\mathfrak{m}^{s-1}\operatorname{K}_{i+1}z_{i_{r}}y_{I^{-}}{\mathcal{A}}^{\prime }\subseteq \mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }$. Thus
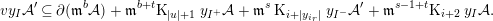 $$\begin{eqnarray}vy_{I}{\mathcal{A}}^{\prime }\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathfrak{m}^{b+t}\!\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}+\mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1+t}\!\operatorname{K}_{i+2}y_{I}{\mathcal{A}}.\end{eqnarray}$$
$$\begin{eqnarray}vy_{I}{\mathcal{A}}^{\prime }\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathfrak{m}^{b+t}\!\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}+\mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s-1+t}\!\operatorname{K}_{i+2}y_{I}{\mathcal{A}}.\end{eqnarray}$$ Using Proposition 2.8 and the facts  $b+t\geqslant s$ and
$b+t\geqslant s$ and  $t\geqslant 1$, we have
$t\geqslant 1$, we have
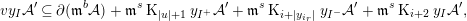 $$\begin{eqnarray}vy_{I}{\mathcal{A}}^{\prime }\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathfrak{m}^{s}\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s}\operatorname{K}_{i+2}y_{I}{\mathcal{A}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}vy_{I}{\mathcal{A}}^{\prime }\subseteq \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathfrak{m}^{s}\operatorname{K}_{|u|+1}y_{I^{+}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s}\operatorname{K}_{i+|y_{i_{r}}|}y_{I^{-}}{\mathcal{A}}^{\prime }+\mathfrak{m}^{s}\operatorname{K}_{i+2}y_{I}{\mathcal{A}}^{\prime },\end{eqnarray}$$ with the provision that if  $I=\emptyset$, the third term on the right of this inclusion is
$I=\emptyset$, the third term on the right of this inclusion is  $0$ by convention. Since
$0$ by convention. Since  $|u|=i+1-|y_{i_{r+1}}|$, we conclude
$|u|=i+1-|y_{i_{r+1}}|$, we conclude  $vy_{I}{\mathcal{A}}^{\prime }$ is contained in
$vy_{I}{\mathcal{A}}^{\prime }$ is contained in
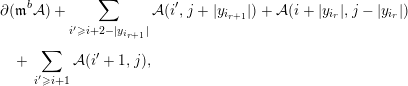 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathop{\sum }_{i^{\prime }\geqslant i+2-|y_{i_{r+1}}|}{\mathcal{A}}(i^{\prime },j+|y_{i_{r+1}}|)+{\mathcal{A}}(i+|y_{i_{r}}|,j-|y_{i_{r}}|)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{i^{\prime }\geqslant i+1}{\mathcal{A}}(i^{\prime }+1,j),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})+\mathop{\sum }_{i^{\prime }\geqslant i+2-|y_{i_{r+1}}|}{\mathcal{A}}(i^{\prime },j+|y_{i_{r+1}}|)+{\mathcal{A}}(i+|y_{i_{r}}|,j-|y_{i_{r}}|)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{i^{\prime }\geqslant i+1}{\mathcal{A}}(i^{\prime }+1,j),\nonumber\end{eqnarray}$$ with the caveat that we remove the term  ${\mathcal{A}}(i+|y_{i_{r}}|,j-|y_{i_{r}}|)$ from the right-hand sum when
${\mathcal{A}}(i+|y_{i_{r}}|,j-|y_{i_{r}}|)$ from the right-hand sum when  $I=\emptyset$. In the display above, the second and last terms of the right-hand side are sums of the form
$I=\emptyset$. In the display above, the second and last terms of the right-hand side are sums of the form  ${\mathcal{A}}(p,q)$ with
${\mathcal{A}}(p,q)$ with  $p+q>i+j$ and the third term is of the form
$p+q>i+j$ and the third term is of the form  ${\mathcal{A}}(p,q)$ with
${\mathcal{A}}(p,q)$ with  $p+q=i+j$ and
$p+q=i+j$ and  $p>i$. The Claim is thus proved.
$p>i$. The Claim is thus proved.
To finish the proof of the theorem, order the set  $M=\{(i,j)|i,j\geqslant 0\}$ as follows: Order the elements by
$M=\{(i,j)|i,j\geqslant 0\}$ as follows: Order the elements by  $i+j$ first, then by
$i+j$ first, then by  $i$ as a tiebreak. In other words:
$i$ as a tiebreak. In other words:
 $$\begin{eqnarray}(i,j)>(i^{\prime },j^{\prime })\;\Longleftrightarrow \;i+j>i^{\prime }+j^{\prime }\qquad \text{or}\qquad (i+j=i^{\prime }+j^{\prime }~\text{and}~i>i^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(i,j)>(i^{\prime },j^{\prime })\;\Longleftrightarrow \;i+j>i^{\prime }+j^{\prime }\qquad \text{or}\qquad (i+j=i^{\prime }+j^{\prime }~\text{and}~i>i^{\prime }).\end{eqnarray}$$ Recall that  $x\in \mathfrak{m}^{s}{\mathcal{A}}_{c}$ and we need to show
$x\in \mathfrak{m}^{s}{\mathcal{A}}_{c}$ and we need to show  $x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. Using Proposition 2.8, we know that
$x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. Using Proposition 2.8, we know that  $x\in \sum _{i=0}^{n}\mathfrak{m}^{s}\operatorname{K}_{i}{\mathcal{A}}^{\prime }$. Thus if
$x\in \sum _{i=0}^{n}\mathfrak{m}^{s}\operatorname{K}_{i}{\mathcal{A}}^{\prime }$. Thus if  $M_{0}=\{(i,0)\mid 0\leqslant i\leqslant n\}$, then
$M_{0}=\{(i,0)\mid 0\leqslant i\leqslant n\}$, then
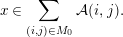 $$\begin{eqnarray}x\in \mathop{\sum }_{(i,j)\in M_{0}}{\mathcal{A}}(i,j).\end{eqnarray}$$
$$\begin{eqnarray}x\in \mathop{\sum }_{(i,j)\in M_{0}}{\mathcal{A}}(i,j).\end{eqnarray}$$ Using the Claim, we see that there exists a finite set  $M_{1}$ and an element
$M_{1}$ and an element
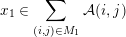 $$\begin{eqnarray}x_{1}\in \mathop{\sum }_{(i,j)\in M_{1}}{\mathcal{A}}(i,j)\end{eqnarray}$$
$$\begin{eqnarray}x_{1}\in \mathop{\sum }_{(i,j)\in M_{1}}{\mathcal{A}}(i,j)\end{eqnarray}$$ such that  $x-x_{1}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, and such that the smallest element of
$x-x_{1}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, and such that the smallest element of  $M_{1}$ is strictly larger (in the order described above) than the smallest element of
$M_{1}$ is strictly larger (in the order described above) than the smallest element of  $M_{0}$.
$M_{0}$.
Applying the Claim again, this time using  $x_{1}$, we see that there exists a finite set
$x_{1}$, we see that there exists a finite set  $M_{2}$ and an element
$M_{2}$ and an element  $x_{2}$ such that
$x_{2}$ such that
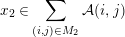 $$\begin{eqnarray}x_{2}\in \mathop{\sum }_{(i,j)\in M_{2}}{\mathcal{A}}(i,j)\end{eqnarray}$$
$$\begin{eqnarray}x_{2}\in \mathop{\sum }_{(i,j)\in M_{2}}{\mathcal{A}}(i,j)\end{eqnarray}$$ such that  $x_{1}-x_{2}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, hence
$x_{1}-x_{2}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, hence  $x-x_{2}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, and such that the smallest element of
$x-x_{2}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$, and such that the smallest element of  $M_{2}$ is strictly larger (in the order described above) than the smallest element of
$M_{2}$ is strictly larger (in the order described above) than the smallest element of  $M_{1}$. A repeated use of the argument ensures the construction of elements
$M_{1}$. A repeated use of the argument ensures the construction of elements  $x_{a}$ and sets
$x_{a}$ and sets  $M_{a}$ such that for each integer
$M_{a}$ such that for each integer  $a$ the smallest element of
$a$ the smallest element of  $M_{a}$ is greater than the smallest element of
$M_{a}$ is greater than the smallest element of  $M_{a-1}$ and such that
$M_{a-1}$ and such that  $x-x_{a}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. When
$x-x_{a}\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$. When  $a$ is sufficiently large (so that
$a$ is sufficiently large (so that  $p+q>c$ for all
$p+q>c$ for all  $(p,q)\in M_{a}$) one sees that, for degree reasons, we have
$(p,q)\in M_{a}$) one sees that, for degree reasons, we have  ${\mathcal{A}}(p,q)=0$ for all
${\mathcal{A}}(p,q)=0$ for all  $(p,q)\in M_{a}$, since the elements of
$(p,q)\in M_{a}$, since the elements of  ${\mathcal{A}}(p,q)$ are in
${\mathcal{A}}(p,q)$ are in  ${\mathcal{A}}_{c}$, with
${\mathcal{A}}_{c}$, with  $c$ fixed. We conclude that
$c$ fixed. We conclude that  $x_{a}=0$ for
$x_{a}=0$ for  $a$ sufficiently large, hence
$a$ sufficiently large, hence  $x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$.
$x\in \unicode[STIX]{x2202}(\mathfrak{m}^{b}{\mathcal{A}})$.
4 Generation by one element
We now turn our focus to the case where the Koszul homology algebra is generated by a single element. Namely, here we are concerned with rings that satisfy the following condition, depending on integers  $t$ and
$t$ and  $r$:
$r$:
 ${\mathcal{P}}_{t,r}:$
${\mathcal{P}}_{t,r}:$There exists
 $[l]\in \operatorname{H}_{r}(\operatorname{K})$ such that for every
$[l]\in \operatorname{H}_{r}(\operatorname{K})$ such that for every  $z\in Z(\mathfrak{m}^{t}\operatorname{K})$ there exists
$z\in Z(\mathfrak{m}^{t}\operatorname{K})$ there exists  $z^{\prime }\in Z(\mathfrak{m}^{t-1}\operatorname{K})$ such that
$z^{\prime }\in Z(\mathfrak{m}^{t-1}\operatorname{K})$ such that  $z-z^{\prime }l\in B(\mathfrak{m}^{t-1}\operatorname{K})$.
$z-z^{\prime }l\in B(\mathfrak{m}^{t-1}\operatorname{K})$.
Note that this condition is independent of the choice of the representative  $l$ of the class
$l$ of the class  $[l]\in \operatorname{H}_{r}(\operatorname{K})$.
$[l]\in \operatorname{H}_{r}(\operatorname{K})$.
Remark 4.1. The condition  ${\mathcal{P}}_{t,r}$ is particularly strong when the cycle
${\mathcal{P}}_{t,r}$ is particularly strong when the cycle  $l$ is not a minimal generator of
$l$ is not a minimal generator of  $Z_{r}(\operatorname{K})$. In this case, we can choose
$Z_{r}(\operatorname{K})$. In this case, we can choose  $l\in \mathfrak{m}Z_{r}(\operatorname{K})$. Since
$l\in \mathfrak{m}Z_{r}(\operatorname{K})$. Since  $\operatorname{K}$ is constructed using a minimal generating set for
$\operatorname{K}$ is constructed using a minimal generating set for  $\mathfrak{m}$, we have that any cycle in
$\mathfrak{m}$, we have that any cycle in  $Z_{r}(\operatorname{K})$ is also in
$Z_{r}(\operatorname{K})$ is also in  $\mathfrak{m}\operatorname{K}$ and thus in
$\mathfrak{m}\operatorname{K}$ and thus in  $Z_{r}(\mathfrak{m}\operatorname{K})$. Let
$Z_{r}(\mathfrak{m}\operatorname{K})$. Let  $i\geqslant 0$. We have thus
$i\geqslant 0$. We have thus  $lz^{\prime }\in \mathfrak{m}Z_{i}(\mathfrak{m}^{t}\operatorname{K})$ for all
$lz^{\prime }\in \mathfrak{m}Z_{i}(\mathfrak{m}^{t}\operatorname{K})$ for all  $z^{\prime }\in Z_{i-r}(\mathfrak{m}^{t-1}\operatorname{K})$. The hypothesis that
$z^{\prime }\in Z_{i-r}(\mathfrak{m}^{t-1}\operatorname{K})$. The hypothesis that  ${\mathcal{P}}_{t,r}$ holds then implies
${\mathcal{P}}_{t,r}$ holds then implies
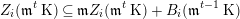 $$\begin{eqnarray}Z_{i}(\mathfrak{m}^{t}\operatorname{K})\subseteq \mathfrak{m}Z_{i}(\mathfrak{m}^{t}\operatorname{K})+B_{i}(\mathfrak{m}^{t-1}\operatorname{K})\end{eqnarray}$$
$$\begin{eqnarray}Z_{i}(\mathfrak{m}^{t}\operatorname{K})\subseteq \mathfrak{m}Z_{i}(\mathfrak{m}^{t}\operatorname{K})+B_{i}(\mathfrak{m}^{t-1}\operatorname{K})\end{eqnarray}$$ for all  $i$, and so by Nakayama’s Lemma, we have
$i$, and so by Nakayama’s Lemma, we have  $Z_{i}(\mathfrak{m}^{t}\operatorname{K})\subseteq B_{i}(\mathfrak{m}^{t-1}\operatorname{K})$, hence the induced map
$Z_{i}(\mathfrak{m}^{t}\operatorname{K})\subseteq B_{i}(\mathfrak{m}^{t-1}\operatorname{K})$, hence the induced map  $\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all
$\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all  $i\geqslant 0$.
$i\geqslant 0$.
When  $l$ is part of a minimal generating set for
$l$ is part of a minimal generating set for  $Z_{r}(\operatorname{K})$ and
$Z_{r}(\operatorname{K})$ and  $r$ is odd, we see below that a similar statement can be deduced, only that the complex
$r$ is odd, we see below that a similar statement can be deduced, only that the complex  $\operatorname{K}$ needs to be replaced with a larger complex.
$\operatorname{K}$ needs to be replaced with a larger complex.
We denote by  ${\mathcal{B}}$ the following DG algebra
${\mathcal{B}}$ the following DG algebra
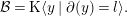 $$\begin{eqnarray}{\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle .\end{eqnarray}$$Theorem 4.2. Let  $(R,\mathfrak{m},k)$ be a local ring, let
$(R,\mathfrak{m},k)$ be a local ring, let  $t\geqslant 2$ be an integer, and
$t\geqslant 2$ be an integer, and  $r\geqslant 1$ be an odd integer. If
$r\geqslant 1$ be an odd integer. If  ${\mathcal{P}}_{t,r}$ holds, then the map
${\mathcal{P}}_{t,r}$ holds, then the map
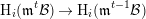 $$\begin{eqnarray}\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{B}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{B}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{B}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{B}})\end{eqnarray}$$ induced by the inclusion  $\mathfrak{m}^{t}{\hookrightarrow}\mathfrak{m}^{t-1}$ is zero for all
$\mathfrak{m}^{t}{\hookrightarrow}\mathfrak{m}^{t-1}$ is zero for all  $i\geqslant 0$.
$i\geqslant 0$.
Proof. We first prove two claims.
Claim 1.
For a cycle  $z\in K$, if
$z\in K$, if  $z=z^{\prime }+w$ with
$z=z^{\prime }+w$ with  $z^{\prime }\in \mathfrak{m}^{t}\operatorname{K}_{p}y^{(q)}$ and
$z^{\prime }\in \mathfrak{m}^{t}\operatorname{K}_{p}y^{(q)}$ and  $w\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}$, then
$w\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}$, then  $z^{\prime }\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})y^{(q)}$.
$z^{\prime }\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})y^{(q)}$.
Proof of Claim 1.
Set  $|z|=c$, hence
$|z|=c$, hence  $p+(r+1)q=c$. Write
$p+(r+1)q=c$. Write  $z^{\prime }=vy^{(q)}$ with
$z^{\prime }=vy^{(q)}$ with  $v\in \mathfrak{m}^{t}\operatorname{K}_{p}$. We have
$v\in \mathfrak{m}^{t}\operatorname{K}_{p}$. We have
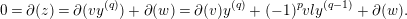 $$\begin{eqnarray}0=\unicode[STIX]{x2202}(z)=\unicode[STIX]{x2202}(vy^{(q)})+\unicode[STIX]{x2202}(w)=\unicode[STIX]{x2202}(v)y^{(q)}+(-1)^{p}vly^{(q-1)}+\unicode[STIX]{x2202}(w).\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x2202}(z)=\unicode[STIX]{x2202}(vy^{(q)})+\unicode[STIX]{x2202}(w)=\unicode[STIX]{x2202}(v)y^{(q)}+(-1)^{p}vly^{(q-1)}+\unicode[STIX]{x2202}(w).\end{eqnarray}$$ Since  $w\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}$ and
$w\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}$ and  $|w|=c$ we can write
$|w|=c$ we can write  $\unicode[STIX]{x2202}(w)=\sum _{i,j}k_{i}y^{(j)}$ with
$\unicode[STIX]{x2202}(w)=\sum _{i,j}k_{i}y^{(j)}$ with  $k_{i}\in \mathfrak{m}^{t}\operatorname{K}_{i}$, where the sum is taken over non-negative
$k_{i}\in \mathfrak{m}^{t}\operatorname{K}_{i}$, where the sum is taken over non-negative  $i,j$ with
$i,j$ with  $i+(r+1)j=c-1$, and
$i+(r+1)j=c-1$, and  $i\geqslant p$. Since
$i\geqslant p$. Since  $p+(r+1)q=c$, we must have
$p+(r+1)q=c$, we must have  $j<q$ for all such
$j<q$ for all such  $j$. Since
$j$. Since  $1,y,y^{(2)},y^{(3)},\ldots \,$ is a basis of
$1,y,y^{(2)},y^{(3)},\ldots \,$ is a basis of  ${\mathcal{B}}$ over
${\mathcal{B}}$ over  $\operatorname{K}$, we conclude from (4.2.1) that
$\operatorname{K}$, we conclude from (4.2.1) that  $\unicode[STIX]{x2202}(v)=0$, and hence
$\unicode[STIX]{x2202}(v)=0$, and hence  $v\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})$.
$v\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})$.
Claim 2.
If  $z^{\prime }\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})y^{(q)}$, then
$z^{\prime }\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})y^{(q)}$, then
 $$\begin{eqnarray}z^{\prime }\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{p+r+1}y^{(q-1)}.\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime }\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{p+r+1}y^{(q-1)}.\end{eqnarray}$$Proof of Claim 2.
Let  $z^{\prime }=vy^{(q)}$ with
$z^{\prime }=vy^{(q)}$ with  $v\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})$. The hypothesis of the theorem gives
$v\in Z_{p}(\mathfrak{m}^{t}\operatorname{K})$. The hypothesis of the theorem gives  $v-v^{\prime }l\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})$ for some
$v-v^{\prime }l\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})$ for some  $v^{\prime }\in Z_{p-r}(\mathfrak{m}^{t-1}\operatorname{K})$, and so
$v^{\prime }\in Z_{p-r}(\mathfrak{m}^{t-1}\operatorname{K})$, and so  $z^{\prime }-v^{\prime }ly^{(q)}\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})y^{(q)}$. An application of the Leibniz rule yields
$z^{\prime }-v^{\prime }ly^{(q)}\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})y^{(q)}$. An application of the Leibniz rule yields
 $$\begin{eqnarray}z^{\prime }-v^{\prime }ly^{(q)}=z^{\prime }-v^{\prime }\unicode[STIX]{x2202}(y^{(q+1)})=z^{\prime }-(-1)^{|v^{\prime }|}\unicode[STIX]{x2202}(v^{\prime }y^{(q+1)}),\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime }-v^{\prime }ly^{(q)}=z^{\prime }-v^{\prime }\unicode[STIX]{x2202}(y^{(q+1)})=z^{\prime }-(-1)^{|v^{\prime }|}\unicode[STIX]{x2202}(v^{\prime }y^{(q+1)}),\end{eqnarray}$$and therefore
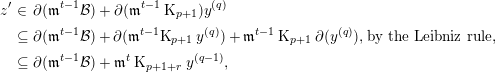 $$\begin{eqnarray}\displaystyle z^{\prime } & \in & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})y^{(q)}\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\!\operatorname{K}_{p+1}y^{(q)})+\mathfrak{m}^{t-1}\operatorname{K}_{p+1}\unicode[STIX]{x2202}(y^{(q)}),\text{by the Leibniz rule,}\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{p+1+r}y^{(q-1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z^{\prime } & \in & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\operatorname{K}_{p+1})y^{(q)}\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\unicode[STIX]{x2202}(\mathfrak{m}^{t-1}\!\operatorname{K}_{p+1}y^{(q)})+\mathfrak{m}^{t-1}\operatorname{K}_{p+1}\unicode[STIX]{x2202}(y^{(q)}),\text{by the Leibniz rule,}\nonumber\\ \displaystyle & \subseteq & \displaystyle \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{p+1+r}y^{(q-1)},\nonumber\end{eqnarray}$$which verifies Claim 2.
Now suppose  $z\in {\mathcal{B}}$ represents a nontrivial class in
$z\in {\mathcal{B}}$ represents a nontrivial class in  $\operatorname{H}_{c}(\mathfrak{m}^{t}{\mathcal{B}})$ and let
$\operatorname{H}_{c}(\mathfrak{m}^{t}{\mathcal{B}})$ and let  $p$ be the largest integer such that
$p$ be the largest integer such that  $z\in \mathfrak{m}^{t}\operatorname{K}_{p}{\mathcal{B}}$. Write
$z\in \mathfrak{m}^{t}\operatorname{K}_{p}{\mathcal{B}}$. Write  $z=\sum k_{i}y^{(j)}$, where the sum is taken over integers
$z=\sum k_{i}y^{(j)}$, where the sum is taken over integers  $i,j$ with
$i,j$ with  $i+(r+1)j=c$ and
$i+(r+1)j=c$ and  $i\geqslant p$, and
$i\geqslant p$, and  $k_{i}\in \mathfrak{m}^{t}\operatorname{K}_{i}$. Set
$k_{i}\in \mathfrak{m}^{t}\operatorname{K}_{i}$. Set  $z^{\prime }=k_{p}y^{(c-p/r+1)}$ and
$z^{\prime }=k_{p}y^{(c-p/r+1)}$ and  $w=z-z^{\prime }$. Then
$w=z-z^{\prime }$. Then  $z=z^{\prime }+w$ and the hypotheses of Claim 1 are satisfied. Putting together Claim 1 and Claim 2, we have:
$z=z^{\prime }+w$ and the hypotheses of Claim 1 are satisfied. Putting together Claim 1 and Claim 2, we have:
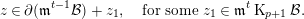 $$\begin{eqnarray}z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+z_{1},\quad \text{for some }z_{1}\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}.\end{eqnarray}$$
$$\begin{eqnarray}z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+z_{1},\quad \text{for some }z_{1}\in \mathfrak{m}^{t}\operatorname{K}_{p+1}{\mathcal{B}}.\end{eqnarray}$$ As  $z_{1}$ is also a cycle, we may repeat the argument for
$z_{1}$ is also a cycle, we may repeat the argument for  $z_{1}$, and so on. Inductively, we obtain
$z_{1}$, and so on. Inductively, we obtain  $z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{i}{\mathcal{B}}$ for all
$z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})+\mathfrak{m}^{t}\operatorname{K}_{i}{\mathcal{B}}$ for all  $i>p$. Since
$i>p$. Since  $\operatorname{K}_{i}=0$ for
$\operatorname{K}_{i}=0$ for  $i\gg 0$, we get
$i\gg 0$, we get  $z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})$.
$z\in \unicode[STIX]{x2202}(\mathfrak{m}^{t-1}{\mathcal{B}})$.
We recall below a result of Levin [Reference Levin17, Lemma 2].
4.3. Let  ${\mathcal{F}}$ be a differential graded
${\mathcal{F}}$ be a differential graded  $R$-algebra and
$R$-algebra and  ${\mathcal{E}}$ a differential graded
${\mathcal{E}}$ a differential graded  ${\mathcal{F}}$-module which is free as a graded
${\mathcal{F}}$-module which is free as a graded  ${\mathcal{F}}$-module (i. e. forgetting differentials) and such that
${\mathcal{F}}$-module (i. e. forgetting differentials) and such that  $\unicode[STIX]{x2202}({\mathcal{E}})\subseteq \mathfrak{m}{\mathcal{E}}$. Let
$\unicode[STIX]{x2202}({\mathcal{E}})\subseteq \mathfrak{m}{\mathcal{E}}$. Let  $M$,
$M$,  $N$ be
$N$ be  $R$-modules such that
$R$-modules such that  $\mathfrak{m}M\subseteq N\subseteq M$, and such that the canonical map
$\mathfrak{m}M\subseteq N\subseteq M$, and such that the canonical map  $N\otimes _{R}{\mathcal{E}}\rightarrow M\otimes _{R}{\mathcal{E}}$ is injective. If the induced homomorphism
$N\otimes _{R}{\mathcal{E}}\rightarrow M\otimes _{R}{\mathcal{E}}$ is injective. If the induced homomorphism  $\operatorname{H}(N\otimes _{R}{\mathcal{F}})\rightarrow \operatorname{H}(M\otimes _{R}{\mathcal{F}})$ is zero, then so is the induced homomorphism
$\operatorname{H}(N\otimes _{R}{\mathcal{F}})\rightarrow \operatorname{H}(M\otimes _{R}{\mathcal{F}})$ is zero, then so is the induced homomorphism  $\operatorname{H}(N\otimes _{R}{\mathcal{E}})\rightarrow \operatorname{H}(M\otimes _{R}{\mathcal{E}})$.
$\operatorname{H}(N\otimes _{R}{\mathcal{E}})\rightarrow \operatorname{H}(M\otimes _{R}{\mathcal{E}})$.
Corollary 4.4. If  ${\mathcal{P}}_{t,1}$ holds, then the following hold:
${\mathcal{P}}_{t,1}$ holds, then the following hold:
(1) The map
induced by the inclusion $$\begin{eqnarray}\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{t-1},k)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m}^{t-1},k)\end{eqnarray}$$ $\mathfrak{m}^{t}\subseteq \mathfrak{m}^{t-1}$ is zero for all
$\mathfrak{m}^{t}\subseteq \mathfrak{m}^{t-1}$ is zero for all  $i\geqslant 0$.
$i\geqslant 0$.(2) If
 $v(R)\geqslant t$, then the algebra
$v(R)\geqslant t$, then the algebra  $\operatorname{Ext}_{R}(k,k)$ is generated in degrees
$\operatorname{Ext}_{R}(k,k)$ is generated in degrees  $1$ and
$1$ and  $2$.
$2$.(3) If
 $t=2$, then the algebra
$t=2$, then the algebra  $\operatorname{Ext}_{R}(k,k)$ is generated in degree
$\operatorname{Ext}_{R}(k,k)$ is generated in degree  $1$.
$1$.
Proof. If  $l\notin \mathfrak{m}Z_{1}(\operatorname{K})$, we can then construct a minimal Tate resolution
$l\notin \mathfrak{m}Z_{1}(\operatorname{K})$, we can then construct a minimal Tate resolution  ${\mathcal{A}}$ of
${\mathcal{A}}$ of  $k$ over
$k$ over  $R$ by starting with the Koszul complex K, then adjoining a variable
$R$ by starting with the Koszul complex K, then adjoining a variable  $y$ with
$y$ with  $\unicode[STIX]{x2202}(y)=l$, and then the rest of the needed variables as described in 2.2. The description of the basis of
$\unicode[STIX]{x2202}(y)=l$, and then the rest of the needed variables as described in 2.2. The description of the basis of  ${\mathcal{A}}$ in [Reference Avramov3, Remark 6.2.1] shows that, forgetting differentials,
${\mathcal{A}}$ in [Reference Avramov3, Remark 6.2.1] shows that, forgetting differentials,  ${\mathcal{A}}$ is free over the algebra
${\mathcal{A}}$ is free over the algebra  ${\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle$. Using 4.3 and Theorem 4.2, we conclude that the induced map
${\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle$. Using 4.3 and Theorem 4.2, we conclude that the induced map
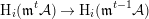 $$\begin{eqnarray}\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{A}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{A}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{A}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{A}})\end{eqnarray}$$ is zero for all  $i\geqslant 0$, and this yields the desired conclusion.
$i\geqslant 0$, and this yields the desired conclusion.
If  $l\in \mathfrak{m}Z_{1}(\operatorname{K})$, then by Remark 4.1 the induced map
$l\in \mathfrak{m}Z_{1}(\operatorname{K})$, then by Remark 4.1 the induced map  $\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all
$\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all  $i\geqslant 0$, and the conclusion follows again by applying Levin’s result in 4.3.
$i\geqslant 0$, and the conclusion follows again by applying Levin’s result in 4.3.
In view of (1), part (2) follows from [Reference Hoffmeier and Şega13], and part (3) from [Reference Roos.22, Corollary 1].
Corollary 4.5. Let  $(Q,\mathfrak{n},k)$ be a regular local ring, and
$(Q,\mathfrak{n},k)$ be a regular local ring, and  $I$ an ideal with
$I$ an ideal with  $I\subseteq \mathfrak{n}^{2}$, and consider the local ring
$I\subseteq \mathfrak{n}^{2}$, and consider the local ring  $(R,\mathfrak{m},k)$ defined by
$(R,\mathfrak{m},k)$ defined by  $R=Q/I$. Let
$R=Q/I$. Let  $h\in I\smallsetminus \mathfrak{n}I$ and let
$h\in I\smallsetminus \mathfrak{n}I$ and let  $L\in \operatorname{K}^{Q}$ such that
$L\in \operatorname{K}^{Q}$ such that  $\unicode[STIX]{x2202}(L)=h$. Let
$\unicode[STIX]{x2202}(L)=h$. Let  $l$ denote the image of
$l$ denote the image of  $L$ in
$L$ in  $\operatorname{K}=\operatorname{K}^{Q}\otimes _{Q}R$. Assume that
$\operatorname{K}=\operatorname{K}^{Q}\otimes _{Q}R$. Assume that  ${\mathcal{P}}_{t,1}$ holds, with
${\mathcal{P}}_{t,1}$ holds, with  $l$ as above.
$l$ as above.
If  $P=Q/(h)$, then the induced map
$P=Q/(h)$, then the induced map  $\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t-1},k)$ is zero for all
$\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t-1},k)$ is zero for all  $i\geqslant 0$.
$i\geqslant 0$.
Furthermore, let  $a$ be an integer such that
$a$ be an integer such that  $I\subseteq \mathfrak{n}^{a+1}$. If
$I\subseteq \mathfrak{n}^{a+1}$. If  $h\in I\smallsetminus \mathfrak{n}^{a+2}$ and
$h\in I\smallsetminus \mathfrak{n}^{a+2}$ and  $a+1\leqslant t\leqslant 2a$, then the canonical projection
$a+1\leqslant t\leqslant 2a$, then the canonical projection  $P\rightarrow R$ is a Golod homomorphism.
$P\rightarrow R$ is a Golod homomorphism.
Proof. The hypothesis implies that  $h$ is part of a minimal generating set of
$h$ is part of a minimal generating set of  $I$.
$I$.
Set  ${\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle$ and
${\mathcal{B}}=\operatorname{K}\langle y\mid \unicode[STIX]{x2202}(y)=l\rangle$ and  ${\mathcal{B}}^{\prime }=\operatorname{K}^{Q}\langle y\mid \unicode[STIX]{x2202}(y)=L\rangle$. Note that
${\mathcal{B}}^{\prime }=\operatorname{K}^{Q}\langle y\mid \unicode[STIX]{x2202}(y)=L\rangle$. Note that  ${\mathcal{B}}=$
${\mathcal{B}}=$ $({\mathcal{B}}^{\prime }\otimes _{Q}P)\otimes _{P}R$ and
$({\mathcal{B}}^{\prime }\otimes _{Q}P)\otimes _{P}R$ and  ${\mathcal{B}}^{\prime }\otimes _{Q}P$ is a minimal free resolution of
${\mathcal{B}}^{\prime }\otimes _{Q}P$ is a minimal free resolution of  $k$ over
$k$ over  $P$. We can identify thus the induced map
$P$. We can identify thus the induced map  $\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t-1},k)$ with the induced map
$\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{t-1},k)$ with the induced map  $\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{B}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{B}})$, and the latter is zero, by the theorem. Under the additional hypotheses in the last paragraph of the statement, it also follows that the induced map
$\operatorname{H}_{i}(\mathfrak{m}^{t}{\mathcal{B}})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}{\mathcal{B}})$, and the latter is zero, by the theorem. Under the additional hypotheses in the last paragraph of the statement, it also follows that the induced map  $\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{2a},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{a},k)$ is zero for all
$\operatorname{Tor}_{i}^{P}(\mathfrak{m}^{2a},k)\rightarrow \operatorname{Tor}_{i}^{P}(\mathfrak{m}^{a},k)$ is zero for all  $i\geqslant 0$, since
$i\geqslant 0$, since  $t\leqslant 2a$ and
$t\leqslant 2a$ and  $t-1\geqslant a$. Since
$t-1\geqslant a$. Since  $I\subseteq \mathfrak{n}^{a+1}$, [Reference Rossi and Şega24, Lemma 1.4] gives that the induced map
$I\subseteq \mathfrak{n}^{a+1}$, [Reference Rossi and Şega24, Lemma 1.4] gives that the induced map  $\operatorname{Tor}_{i}^{P}(R,k)\rightarrow \operatorname{Tor}_{i}^{P}(R/\mathfrak{m}^{a},k)$ is zero for all positive
$\operatorname{Tor}_{i}^{P}(R,k)\rightarrow \operatorname{Tor}_{i}^{P}(R/\mathfrak{m}^{a},k)$ is zero for all positive  $i$, and then applying 3.2 to the canonical projection
$i$, and then applying 3.2 to the canonical projection  $\unicode[STIX]{x1D705}:P\rightarrow R$ gives the final conclusion.
$\unicode[STIX]{x1D705}:P\rightarrow R$ gives the final conclusion.
Remark 4.6. The existence of a surjective Golod homomorphism from a complete intersection ring to the local ring  $R$ is a rather remarkable property: Using a result of Levin recorded in [Reference Avramov, Kustin and Miller6, Proposition 5.18], this property allows one to conclude that the Poincaré series of all finitely generated
$R$ is a rather remarkable property: Using a result of Levin recorded in [Reference Avramov, Kustin and Miller6, Proposition 5.18], this property allows one to conclude that the Poincaré series of all finitely generated  $R$-modules are rational, sharing a common denominator.
$R$-modules are rational, sharing a common denominator.
Compressed Gorenstein artinian local rings, and, more generally, compressed level artinian local rings are defined in terms of an extremal condition involving the length, embedding dimension, and the socle of the ring. We refer to [Reference Rossi and Şega24] and [Reference Kustin, Şega and Vraciu15] for the precise definitions. Such rings can be viewed as being “generic”, in a sense explained in more detail in [Reference Kustin, Şega and Vraciu15, Theorem 3.1], for example.
Remark 4.7. Let  $(R,\mathfrak{m},k)$ be a compressed Gorenstein local ring of socle degree
$(R,\mathfrak{m},k)$ be a compressed Gorenstein local ring of socle degree  $s\neq 3$ and assume
$s\neq 3$ and assume  $k$ is infinite. Set
$k$ is infinite. Set  $t=s+2-v(R)$ and
$t=s+2-v(R)$ and  $a=v(R)-1$. When
$a=v(R)-1$. When  $s\neq 3$, the inequalities
$s\neq 3$, the inequalities  $a+1\leqslant t\leqslant 2a$ follow from general properties of compressed Gorenstein rings, and more precisely from the fact that
$a+1\leqslant t\leqslant 2a$ follow from general properties of compressed Gorenstein rings, and more precisely from the fact that  $s=2v(R)-1$ or
$s=2v(R)-1$ or  $s=2v(R)-2$, as noted in [Reference Rossi and Şega24].
$s=2v(R)-2$, as noted in [Reference Rossi and Şega24].
The proof of [Reference Rossi and Şega24, Proposition 4.6] shows that  $Z_{n}(\mathfrak{m}^{t}\operatorname{K})\subseteq lZ_{n-1}(\mathfrak{m}^{t-1}\operatorname{K})$ for some cycle
$Z_{n}(\mathfrak{m}^{t}\operatorname{K})\subseteq lZ_{n-1}(\mathfrak{m}^{t-1}\operatorname{K})$ for some cycle  $l\in \operatorname{K}_{1}$, and [Reference Rossi and Şega24, Lemma 4.4] shows that the induced map
$l\in \operatorname{K}_{1}$, and [Reference Rossi and Şega24, Lemma 4.4] shows that the induced map  $\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all
$\operatorname{H}_{i}(\mathfrak{m}^{t}\operatorname{K})\rightarrow \operatorname{H}_{i}(\mathfrak{m}^{t-1}\operatorname{K})$ is zero for all  $i<n$, where
$i<n$, where  $n$ denotes the minimal number of generators of
$n$ denotes the minimal number of generators of  $\mathfrak{m}$. It follows that the ring
$\mathfrak{m}$. It follows that the ring  $R$ satisfies
$R$ satisfies  ${\mathcal{P}}_{t,1}$. We can then construct
${\mathcal{P}}_{t,1}$. We can then construct  $h\in I$ such that
$h\in I$ such that  $\unicode[STIX]{x2202}(L)=h$, where
$\unicode[STIX]{x2202}(L)=h$, where  $L$ is a preimage of
$L$ is a preimage of  $l$ in
$l$ in  $\operatorname{K}^{Q}$. With this data, the hypotheses of Corollary 4.5 are satisfied, hence we recover the main structural result in [Reference Rossi and Şega24] stating that
$\operatorname{K}^{Q}$. With this data, the hypotheses of Corollary 4.5 are satisfied, hence we recover the main structural result in [Reference Rossi and Şega24] stating that  $R$ is a homomorphic image of a hypersurface via a Golod homomorphism.
$R$ is a homomorphic image of a hypersurface via a Golod homomorphism.
Remark 4.8. The condition  ${\mathcal{P}}_{t,1}$ is also satisfied for compressed level artinian local rings of socle degree
${\mathcal{P}}_{t,1}$ is also satisfied for compressed level artinian local rings of socle degree  $s=2t-1$, with
$s=2t-1$, with  $s\neq 3$. This can be seen from the proof of [Reference Kustin, Şega and Vraciu15, Lemma 6.3] and [Reference Kustin, Şega and Vraciu15, Lemma 4.4]. The conclusion that such rings are homomorphic images of a hypersurface via a Golod homomorphism is established there using the results of [Reference Rossi and Şega24]. Corollary 4.5 recovers the same conclusion, as well.
$s\neq 3$. This can be seen from the proof of [Reference Kustin, Şega and Vraciu15, Lemma 6.3] and [Reference Kustin, Şega and Vraciu15, Lemma 4.4]. The conclusion that such rings are homomorphic images of a hypersurface via a Golod homomorphism is established there using the results of [Reference Rossi and Şega24]. Corollary 4.5 recovers the same conclusion, as well.
Another class of rings for which the condition  ${\mathcal{P}}_{t,1}$ holds is discussed in the next section.
${\mathcal{P}}_{t,1}$ holds is discussed in the next section.
5 Stretched Cohen–Macaulay local rings
Let  $(R,\mathfrak{m},k)$ be an artinian local ring. We set
$(R,\mathfrak{m},k)$ be an artinian local ring. We set
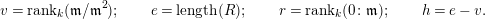 $$\begin{eqnarray}v=\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2});\qquad e=\text{length}(R);\qquad r=\operatorname{rank}_{k}(0:\mathfrak{m});\qquad h=e-v.\end{eqnarray}$$
$$\begin{eqnarray}v=\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2});\qquad e=\text{length}(R);\qquad r=\operatorname{rank}_{k}(0:\mathfrak{m});\qquad h=e-v.\end{eqnarray}$$ Note that  $\mathfrak{m}^{h+1}=0$. The ring
$\mathfrak{m}^{h+1}=0$. The ring  $R$ is said to be stretched if
$R$ is said to be stretched if  $h$ is the least integer
$h$ is the least integer  $i$ such that
$i$ such that  $\mathfrak{m}^{i+1}=0$. Assume further that
$\mathfrak{m}^{i+1}=0$. Assume further that  $R$ is not a field. Then
$R$ is not a field. Then  $R$ is stretched if and only if
$R$ is stretched if and only if  $\mathfrak{m}^{2}$ is principal. Sally [Reference Sally25] computed the series
$\mathfrak{m}^{2}$ is principal. Sally [Reference Sally25] computed the series  $\operatorname{P}_{k}^{R}(t)$ for a stretched artinian local ring
$\operatorname{P}_{k}^{R}(t)$ for a stretched artinian local ring  $R$ as follows:
$R$ as follows:
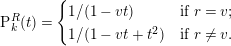 $$\begin{eqnarray}\operatorname{P}_{k}^{R}(t)=\left\{\begin{array}{@{}ll@{}}1/(1-vt)\quad & \text{if }r=v;\\ 1/(1-vt+t^{2})\quad & \text{if }r\neq v.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{P}_{k}^{R}(t)=\left\{\begin{array}{@{}ll@{}}1/(1-vt)\quad & \text{if }r=v;\\ 1/(1-vt+t^{2})\quad & \text{if }r\neq v.\end{array}\right.\end{eqnarray}$$ In this section we show that finitely generated  $R$-modules have rational Poincaré series as well, sharing a common denominator. The main result is Theorem 5.4; its proof involves an application of the results in Section 4.
$R$-modules have rational Poincaré series as well, sharing a common denominator. The main result is Theorem 5.4; its proof involves an application of the results in Section 4.
5.1. Structure of stretched artinian local rings. Assume that  $(R,\mathfrak{m},k)$ is a stretched artinian local ring, not a field. We further set
$(R,\mathfrak{m},k)$ is a stretched artinian local ring, not a field. We further set
 $$\begin{eqnarray}p=v-r\qquad \text{and}\qquad q=r-1.\end{eqnarray}$$
$$\begin{eqnarray}p=v-r\qquad \text{and}\qquad q=r-1.\end{eqnarray}$$ Assume that  $h\geqslant 3$. (The case
$h\geqslant 3$. (The case  $h\leqslant 2$ has been treated in [Reference Avramov, Iyengar and Şega5] and will be recalled later.) As described in [Reference Sally25], we choose elements
$h\leqslant 2$ has been treated in [Reference Avramov, Iyengar and Şega5] and will be recalled later.) As described in [Reference Sally25], we choose elements  $t,z_{1},\ldots ,z_{p},w_{1},\ldots ,w_{q}$ forming a minimal generating system of
$t,z_{1},\ldots ,z_{p},w_{1},\ldots ,w_{q}$ forming a minimal generating system of  $\mathfrak{m}$ such that the following hold:
$\mathfrak{m}$ such that the following hold:
(1)
 $\mathfrak{m}^{i}=(t^{i})$ for all
$\mathfrak{m}^{i}=(t^{i})$ for all  $i\geqslant 2$;
$i\geqslant 2$;(2) The elements
 $w_{1},\ldots ,w_{r-1},t^{h}$ form a basis of
$w_{1},\ldots ,w_{r-1},t^{h}$ form a basis of  $(0:\mathfrak{m})$; in particular,
$(0:\mathfrak{m})$; in particular,  $tw_{j}=0$ and
$tw_{j}=0$ and  $z_{i}w_{j}=0$ for all
$z_{i}w_{j}=0$ for all  $i$,
$i$,  $j$ with
$j$ with  $1\leqslant i\leqslant p$ and
$1\leqslant i\leqslant p$ and  $1\leqslant j\leqslant q$;
$1\leqslant j\leqslant q$;(3)
 $tz_{i}=0$ for all
$tz_{i}=0$ for all  $i$ with
$i$ with  $1\leqslant i\leqslant p$;
$1\leqslant i\leqslant p$;(4)
 $z_{i}z_{j}=a_{ij}t^{h}$, with
$z_{i}z_{j}=a_{ij}t^{h}$, with  $a_{ij}=0$ or
$a_{ij}=0$ or  $a_{ij}$ a unit of
$a_{ij}$ a unit of  $R$, for all
$R$, for all  $i$,
$i$,  $j$ with
$j$ with  $1\leqslant i,j\leqslant p$.
$1\leqslant i,j\leqslant p$.
(Note that there are no elements  $w_{i}$ if
$w_{i}$ if  $r=1$ and there are no elements
$r=1$ and there are no elements  $z_{i}$ if
$z_{i}$ if  $r=v$.)
$r=v$.)
If  $r\neq v$, let
$r\neq v$, let  $\overline{a_{ij}}$ denote the image of
$\overline{a_{ij}}$ denote the image of  $a_{ij}$ in
$a_{ij}$ in  $k=R/\mathfrak{m}$ and note that the matrix
$k=R/\mathfrak{m}$ and note that the matrix  $(\overline{a_{ij}})$ is invertible. Indeed, if this matrix is not invertible, then there exists an element
$(\overline{a_{ij}})$ is invertible. Indeed, if this matrix is not invertible, then there exists an element  $z=\sum _{i=1}^{p}b_{i}z_{i}$, with
$z=\sum _{i=1}^{p}b_{i}z_{i}$, with  $b_{i}\in R$ such that
$b_{i}\in R$ such that  $b_{i}$ is a unit for at least one index
$b_{i}$ is a unit for at least one index  $i$, and such that
$i$, and such that  $zz_{j}=0$ for all
$zz_{j}=0$ for all  $j$ for all
$j$ for all  $1\leqslant j\leqslant p$. This implies that
$1\leqslant j\leqslant p$. This implies that  $z\in (0:\mathfrak{m})$, hence
$z\in (0:\mathfrak{m})$, hence  $z\in (w_{1},\ldots ,w_{r-1},t^{h})$, contradicting the fact that
$z\in (w_{1},\ldots ,w_{r-1},t^{h})$, contradicting the fact that  $t,z_{1},\ldots ,z_{p},w_{1},\ldots ,w_{q}$ is a minimal generating set of
$t,z_{1},\ldots ,z_{p},w_{1},\ldots ,w_{q}$ is a minimal generating set of  $\mathfrak{m}$.
$\mathfrak{m}$.
The fact that the matrix  $(\overline{a_{ij}})$ is invertible also implies that for every
$(\overline{a_{ij}})$ is invertible also implies that for every  $i$ with
$i$ with  $1\leqslant i\leqslant p$ there exists an element
$1\leqslant i\leqslant p$ there exists an element  $y_{i}\in (z_{1},\ldots ,z_{p})$ such that
$y_{i}\in (z_{1},\ldots ,z_{p})$ such that
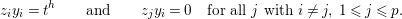 $$\begin{eqnarray}z_{i}y_{i}=t^{h}\qquad \text{and}\qquad z_{j}y_{i}=0\quad \text{for all }j\text{ with }i\neq j,\;1\leqslant j\leqslant p.\end{eqnarray}$$
$$\begin{eqnarray}z_{i}y_{i}=t^{h}\qquad \text{and}\qquad z_{j}y_{i}=0\quad \text{for all }j\text{ with }i\neq j,\;1\leqslant j\leqslant p.\end{eqnarray}$$ Since  $y_{i}\in (z_{1},\ldots ,z_{p})$ we also have
$y_{i}\in (z_{1},\ldots ,z_{p})$ we also have
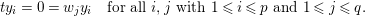 $$\begin{eqnarray}ty_{i}=0=w_{j}y_{i}\quad \text{for all }i,j\text{ with }1\leqslant i\leqslant p\text{ and }1\leqslant j\leqslant q.\end{eqnarray}$$
$$\begin{eqnarray}ty_{i}=0=w_{j}y_{i}\quad \text{for all }i,j\text{ with }1\leqslant i\leqslant p\text{ and }1\leqslant j\leqslant q.\end{eqnarray}$$5.2. Structure of Koszul homology. Let  $R$ be as in 5.1. We consider the Koszul complex
$R$ be as in 5.1. We consider the Koszul complex  $K^{R}$ on the set
$K^{R}$ on the set  $\{w_{1},\ldots ,w_{q},z_{1},\ldots ,z_{p},t\}$. As a DG algebra it can be described as the complex
$\{w_{1},\ldots ,w_{q},z_{1},\ldots ,z_{p},t\}$. As a DG algebra it can be described as the complex
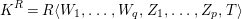 $$\begin{eqnarray}K^{R}=R\langle W_{1},\ldots ,W_{q},Z_{1},\ldots ,Z_{p},T\rangle\end{eqnarray}$$
$$\begin{eqnarray}K^{R}=R\langle W_{1},\ldots ,W_{q},Z_{1},\ldots ,Z_{p},T\rangle\end{eqnarray}$$ with  $\unicode[STIX]{x2202}(W_{i})=w_{i}$,
$\unicode[STIX]{x2202}(W_{i})=w_{i}$,  $\unicode[STIX]{x2202}(Z_{i})=z_{i}$ and
$\unicode[STIX]{x2202}(Z_{i})=z_{i}$ and  $\unicode[STIX]{x2202}(T)=t$.
$\unicode[STIX]{x2202}(T)=t$.
In what follows, we consider products of some of the variables  $W_{i}$ or
$W_{i}$ or  $Z_{i}$, with the index
$Z_{i}$, with the index  $i$ ranging over certain sets
$i$ ranging over certain sets  $I$. We adopt the convention that the product is equal to
$I$. We adopt the convention that the product is equal to  $1$ if
$1$ if  $I=\emptyset$; for example
$I=\emptyset$; for example  $Z_{1}\cdots Z_{p}=1$ if
$Z_{1}\cdots Z_{p}=1$ if  $p=0$. We set
$p=0$. We set
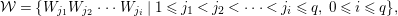 $$\begin{eqnarray}{\mathcal{W}}=\{W_{j_{1}}W_{j_{2}}\cdots W_{j_{i}}\mid 1\leqslant j_{1}<j_{2}<\cdots <j_{i}\leqslant q,\,0\leqslant i\leqslant q\},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}=\{W_{j_{1}}W_{j_{2}}\cdots W_{j_{i}}\mid 1\leqslant j_{1}<j_{2}<\cdots <j_{i}\leqslant q,\,0\leqslant i\leqslant q\},\end{eqnarray}$$ where  $W_{j_{1}}W_{j_{2}}\cdots W_{j_{i}}=1$ when
$W_{j_{1}}W_{j_{2}}\cdots W_{j_{i}}=1$ when  $i=0$.
$i=0$.
Lemma. Let  $s\geqslant 1$. Every cycle of
$s\geqslant 1$. Every cycle of  $Z_{s}(\mathfrak{m}^{2}K^{R})$ has the form
$Z_{s}(\mathfrak{m}^{2}K^{R})$ has the form
 $$\begin{eqnarray}\sum a_{W}t^{h}TZ_{1}\cdots Z_{p}W+V,\quad \text{with }V\in B_{s}(\mathfrak{m}K^{R})\text{ and }a_{W}\in R,\end{eqnarray}$$
$$\begin{eqnarray}\sum a_{W}t^{h}TZ_{1}\cdots Z_{p}W+V,\quad \text{with }V\in B_{s}(\mathfrak{m}K^{R})\text{ and }a_{W}\in R,\end{eqnarray}$$ where the sum ranges over all  $W\in {\mathcal{W}}$ with
$W\in {\mathcal{W}}$ with  $|W|=s-p-1$.
$|W|=s-p-1$.
Proof. If  $L=Z_{i_{1}}Z_{i_{2}}\cdots Z_{i_{m}}W_{j_{1}}W_{j_{2}}\cdots W_{j_{n}}$ with indices satisfying the inequalities
$L=Z_{i_{1}}Z_{i_{2}}\cdots Z_{i_{m}}W_{j_{1}}W_{j_{2}}\cdots W_{j_{n}}$ with indices satisfying the inequalities  $1\leqslant i_{1}<i_{2}<\cdots <i_{m}\leqslant p$ and
$1\leqslant i_{1}<i_{2}<\cdots <i_{m}\leqslant p$ and  $1\leqslant j_{1}<j_{2}<\cdots <j_{n}\leqslant q$, then the Leibniz rule and the fact that
$1\leqslant j_{1}<j_{2}<\cdots <j_{n}\leqslant q$, then the Leibniz rule and the fact that  $tw_{j}=0=tz_{i}$ for all
$tw_{j}=0=tz_{i}$ for all  $1\leqslant i\leqslant p$ and
$1\leqslant i\leqslant p$ and  $1\leqslant j\leqslant q$ imply that
$1\leqslant j\leqslant q$ imply that  $t\unicode[STIX]{x2202}(L)=0$. Consequently, another application of the Leibniz rule gives
$t\unicode[STIX]{x2202}(L)=0$. Consequently, another application of the Leibniz rule gives
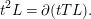 $$\begin{eqnarray}t^{2}L=\unicode[STIX]{x2202}(tTL).\end{eqnarray}$$
$$\begin{eqnarray}t^{2}L=\unicode[STIX]{x2202}(tTL).\end{eqnarray}$$ Since  $\mathfrak{m}^{2}=(t^{2})$, it suffices to consider cycles of the form
$\mathfrak{m}^{2}=(t^{2})$, it suffices to consider cycles of the form  $z=\sum _{L}a_{L}t^{2}TL$ with
$z=\sum _{L}a_{L}t^{2}TL$ with  $L$ ranging over all possible products
$L$ ranging over all possible products  $L$ as above (if
$L$ as above (if  $p=0=q$, then we only have one term where
$p=0=q$, then we only have one term where  $L=1$). Taking differentials, we have
$L=1$). Taking differentials, we have
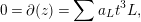 $$\begin{eqnarray}0=\unicode[STIX]{x2202}(z)=\sum a_{L}t^{3}L,\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x2202}(z)=\sum a_{L}t^{3}L,\end{eqnarray}$$ where the last equality follows again from the Leibniz rule and the fact that  $t\unicode[STIX]{x2202}(L)=0$, as noted above. Since the products
$t\unicode[STIX]{x2202}(L)=0$, as noted above. Since the products  $L$ are linearly independent over
$L$ are linearly independent over  $R$, we have
$R$, we have  $a_{L}t^{3}=0$ for all
$a_{L}t^{3}=0$ for all  $L$, and hence
$L$, and hence  $a_{L}=t^{h-2}b_{L}+c_{L}$, with
$a_{L}=t^{h-2}b_{L}+c_{L}$, with  $b_{L}\in R$ and
$b_{L}\in R$ and  $c_{L}\in (w_{1},\ldots ,w_{q},z_{1},\ldots ,z_{p})$. We have thus
$c_{L}\in (w_{1},\ldots ,w_{q},z_{1},\ldots ,z_{p})$. We have thus  $z=\sum _{L}b_{L}t^{h}TL$.
$z=\sum _{L}b_{L}t^{h}TL$.
Consider a cycle  $t^{h}TL$, with
$t^{h}TL$, with  $L$ as above. Set
$L$ as above. Set  $Z=Z_{i_{1}}Z_{i_{2}}\cdots Z_{i_{m}}$ and
$Z=Z_{i_{1}}Z_{i_{2}}\cdots Z_{i_{m}}$ and  $W=W_{j_{1}}W_{j_{2}}\cdots W_{j_{n}}$, so that
$W=W_{j_{1}}W_{j_{2}}\cdots W_{j_{n}}$, so that  $t^{h}TL=t^{h}TZW$. We show that
$t^{h}TL=t^{h}TZW$. We show that  $t^{h}TZW\in \unicode[STIX]{x2202}(\mathfrak{m}K^{R})$ whenever
$t^{h}TZW\in \unicode[STIX]{x2202}(\mathfrak{m}K^{R})$ whenever  $Z\neq Z_{1}Z_{2}\cdots Z_{p}$.
$Z\neq Z_{1}Z_{2}\cdots Z_{p}$.
Indeed, assume  $Z\neq Z_{1}Z_{2}\cdots Z_{p}$. In particular, we have
$Z\neq Z_{1}Z_{2}\cdots Z_{p}$. In particular, we have  $p\neq 0$. Without loss of generality, we may assume
$p\neq 0$. Without loss of generality, we may assume  $Z_{1}$ is not a factor in
$Z_{1}$ is not a factor in  $Z$. Then for any such
$Z$. Then for any such  $Z$ and any
$Z$ and any  $W$ as above we have:
$W$ as above we have:
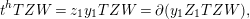 $$\begin{eqnarray}t^{h}TZW=z_{1}y_{1}TZW=\unicode[STIX]{x2202}(y_{1}Z_{1}TZW),\end{eqnarray}$$
$$\begin{eqnarray}t^{h}TZW=z_{1}y_{1}TZW=\unicode[STIX]{x2202}(y_{1}Z_{1}TZW),\end{eqnarray}$$ where the element  $y_{1}$ is as defined above, and the last equality follows from the Leibniz rule, in view of the relations in (5.1.1) and (5.1.2).
$y_{1}$ is as defined above, and the last equality follows from the Leibniz rule, in view of the relations in (5.1.1) and (5.1.2).
5.3. Generation of Koszul homology. We continue with the notation and hypotheses of 5.1 and 5.2. In addition, we assume  $r\neq v$, hence
$r\neq v$, hence  $p\neq 0$. We set:
$p\neq 0$. We set:
 $$\begin{eqnarray}{\mathcal{J}}_{1}=\{(i,j)\mid 1\leqslant i\leqslant j\leqslant p,a_{ij}\neq 0\}\text{; }{\mathcal{J}}_{2}=\{(i,j)\mid 1\leqslant i\leqslant j\leqslant p,a_{ij}=0\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}_{1}=\{(i,j)\mid 1\leqslant i\leqslant j\leqslant p,a_{ij}\neq 0\}\text{; }{\mathcal{J}}_{2}=\{(i,j)\mid 1\leqslant i\leqslant j\leqslant p,a_{ij}=0\}.\end{eqnarray}$$ Consider the following element in  $K_{1}^{R}$:
$K_{1}^{R}$:
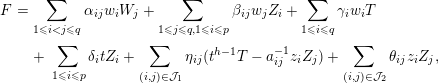 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \mathop{\sum }_{1\leqslant i<j\leqslant q}\unicode[STIX]{x1D6FC}_{ij}w_{i}W_{j}+\mathop{\sum }_{1\leqslant j\leqslant q,1\leqslant i\leqslant p}\unicode[STIX]{x1D6FD}_{ij}w_{j}Z_{i}+\mathop{\sum }_{1\leqslant i\leqslant q}\unicode[STIX]{x1D6FE}_{i}w_{i}T\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}\unicode[STIX]{x1D6FF}_{i}tZ_{i}+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{1}}\unicode[STIX]{x1D702}_{ij}(t^{h-1}T-a_{ij}^{-1}z_{i}Z_{j})+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{2}}\unicode[STIX]{x1D703}_{ij}z_{i}Z_{j},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \mathop{\sum }_{1\leqslant i<j\leqslant q}\unicode[STIX]{x1D6FC}_{ij}w_{i}W_{j}+\mathop{\sum }_{1\leqslant j\leqslant q,1\leqslant i\leqslant p}\unicode[STIX]{x1D6FD}_{ij}w_{j}Z_{i}+\mathop{\sum }_{1\leqslant i\leqslant q}\unicode[STIX]{x1D6FE}_{i}w_{i}T\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}\unicode[STIX]{x1D6FF}_{i}tZ_{i}+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{1}}\unicode[STIX]{x1D702}_{ij}(t^{h-1}T-a_{ij}^{-1}z_{i}Z_{j})+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{2}}\unicode[STIX]{x1D703}_{ij}z_{i}Z_{j},\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FC}_{ij}$,
$\unicode[STIX]{x1D6FC}_{ij}$,  $\unicode[STIX]{x1D6FD}_{ij}$,
$\unicode[STIX]{x1D6FD}_{ij}$,  $\unicode[STIX]{x1D6FE}_{i}$,
$\unicode[STIX]{x1D6FE}_{i}$,  $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$,  $\unicode[STIX]{x1D702}_{ij}$,
$\unicode[STIX]{x1D702}_{ij}$,  $\unicode[STIX]{x1D703}_{ij}\in R$. Recall that the elements
$\unicode[STIX]{x1D703}_{ij}\in R$. Recall that the elements  $a_{ij}$ were introduced in 5.1. The relations in 5.1 yield that
$a_{ij}$ were introduced in 5.1. The relations in 5.1 yield that  $F$ is a cycle.
$F$ is a cycle.
Lemma. Assume in addition that at least one of the coefficients  $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$,  $\unicode[STIX]{x1D702}_{ij}$, or
$\unicode[STIX]{x1D702}_{ij}$, or  $\unicode[STIX]{x1D703}_{ij}$ is a unit. If
$\unicode[STIX]{x1D703}_{ij}$ is a unit. If  $z$ is a cycle in
$z$ is a cycle in  $\mathfrak{m}^{2}K^{R}$, then
$\mathfrak{m}^{2}K^{R}$, then  $z=AF+A^{\prime }$ for some
$z=AF+A^{\prime }$ for some  $A\in Z(\mathfrak{m}K^{R})$ and
$A\in Z(\mathfrak{m}K^{R})$ and  $A^{\prime }\in B(\mathfrak{m}K^{R})$. In other words, condition
$A^{\prime }\in B(\mathfrak{m}K^{R})$. In other words, condition  ${\mathcal{P}}_{2,1}$ holds with
${\mathcal{P}}_{2,1}$ holds with  $l=F$.
$l=F$.
Proof. Using Lemma 5.2, we see that it suffices to consider cycles of the form  $t^{h}TZ_{1}\cdots Z_{p}W$, with
$t^{h}TZ_{1}\cdots Z_{p}W$, with  $W\in {\mathcal{W}}$. Now consider the following element, which can be seen to be a cycle in
$W\in {\mathcal{W}}$. Now consider the following element, which can be seen to be a cycle in  $\mathfrak{m}K^{R}$:
$\mathfrak{m}K^{R}$:
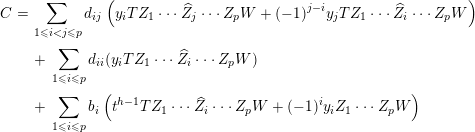 $$\begin{eqnarray}\displaystyle C & = & \displaystyle \mathop{\sum }_{1\leqslant i<j\leqslant p}d_{ij}\left(y_{i}TZ_{1}\cdots \widehat{Z}_{j}\cdots Z_{p}W+(-1)^{j-i}y_{j}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W\right)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}d_{ii}(y_{i}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}b_{i}\left(t^{h-1}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W+(-1)^{i}y_{i}Z_{1}\cdots Z_{p}W\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C & = & \displaystyle \mathop{\sum }_{1\leqslant i<j\leqslant p}d_{ij}\left(y_{i}TZ_{1}\cdots \widehat{Z}_{j}\cdots Z_{p}W+(-1)^{j-i}y_{j}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W\right)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}d_{ii}(y_{i}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{1\leqslant i\leqslant p}b_{i}\left(t^{h-1}TZ_{1}\cdots \widehat{Z}_{i}\cdots Z_{p}W+(-1)^{i}y_{i}Z_{1}\cdots Z_{p}W\right)\nonumber\end{eqnarray}$$ with  $d_{ij},b_{i}\in R$, where the notation
$d_{ij},b_{i}\in R$, where the notation  $\widehat{Z}_{j}$ indicates that the element
$\widehat{Z}_{j}$ indicates that the element  $Z_{j}$ is missing from the product. Set
$Z_{j}$ is missing from the product. Set
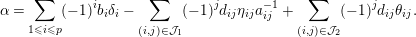 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\mathop{\sum }_{1\leqslant i\leqslant p}(-1)^{i}b_{i}\unicode[STIX]{x1D6FF}_{i}-\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{1}}(-1)^{j}d_{ij}\unicode[STIX]{x1D702}_{ij}a_{ij}^{-1}+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{2}}(-1)^{j}d_{ij}\unicode[STIX]{x1D703}_{ij}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\mathop{\sum }_{1\leqslant i\leqslant p}(-1)^{i}b_{i}\unicode[STIX]{x1D6FF}_{i}-\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{1}}(-1)^{j}d_{ij}\unicode[STIX]{x1D702}_{ij}a_{ij}^{-1}+\mathop{\sum }_{(i,j)\in {\mathcal{J}}_{2}}(-1)^{j}d_{ij}\unicode[STIX]{x1D703}_{ij}.\end{eqnarray}$$Then we have
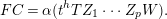 $$\begin{eqnarray}FC=\unicode[STIX]{x1D6FC}(t^{h}TZ_{1}\cdots Z_{p}W).\end{eqnarray}$$
$$\begin{eqnarray}FC=\unicode[STIX]{x1D6FC}(t^{h}TZ_{1}\cdots Z_{p}W).\end{eqnarray}$$ Since at least one of the coefficients  $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$,  $\unicode[STIX]{x1D702}_{ij}$, or
$\unicode[STIX]{x1D702}_{ij}$, or  $\unicode[STIX]{x1D703}_{ij}$ is a unit, we can choose the coefficients
$\unicode[STIX]{x1D703}_{ij}$ is a unit, we can choose the coefficients  $d_{ij}$ and
$d_{ij}$ and  $b_{i}$ such that
$b_{i}$ such that  $\unicode[STIX]{x1D6FC}$ is a unit. Then, if we take
$\unicode[STIX]{x1D6FC}$ is a unit. Then, if we take  $A=\unicode[STIX]{x1D6FC}^{-1}C$, we have
$A=\unicode[STIX]{x1D6FC}^{-1}C$, we have  $t^{h}TZ_{1}\cdots Z_{p}W=AF$.
$t^{h}TZ_{1}\cdots Z_{p}W=AF$.
Theorem 5.4. Let  $(R,\mathfrak{m},k)$ be a stretched artinian local ring with minimal Cohen presentation
$(R,\mathfrak{m},k)$ be a stretched artinian local ring with minimal Cohen presentation  $R=Q/I$, where
$R=Q/I$, where  $(Q,\mathfrak{n},k)$ is a regular local ring and
$(Q,\mathfrak{n},k)$ is a regular local ring and  $I\subseteq \mathfrak{n}^{2}$. Assume
$I\subseteq \mathfrak{n}^{2}$. Assume  $R$ is not a field.
$R$ is not a field.
Set  $v=\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})$ and
$v=\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})$ and  $r=\operatorname{rank}_{k}(0:\mathfrak{m})$. The following hold:
$r=\operatorname{rank}_{k}(0:\mathfrak{m})$. The following hold:
(1) If
 $r\neq v$, then
$r\neq v$, then  $I\not \subseteq \mathfrak{n}(I:\mathfrak{n})$ and we have:
$I\not \subseteq \mathfrak{n}(I:\mathfrak{n})$ and we have:(a) If
 $\mathfrak{m}^{3}\neq 0$, then the induced homomorphism
$\mathfrak{m}^{3}\neq 0$, then the induced homomorphism  $Q/(f)\rightarrow R$ is Golod for all
$Q/(f)\rightarrow R$ is Golod for all  $f\in I\smallsetminus \mathfrak{n}(I:\mathfrak{n})$.
$f\in I\smallsetminus \mathfrak{n}(I:\mathfrak{n})$.(b) The algebra
 $\operatorname{Ext}_{R}(k,k)$ is generated by its elements of degree
$\operatorname{Ext}_{R}(k,k)$ is generated by its elements of degree  $1$.
$1$.(c)
 $(1+t)^{v}(1-vt+t^{2})\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated
$(1+t)^{v}(1-vt+t^{2})\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated  $R$-modules
$R$-modules  $M$.
$M$.
(2) If
 $r=v$, then
$r=v$, then(a)
 $R$ is a Golod ring.
$R$ is a Golod ring.(b) The algebra
 $\operatorname{Ext}_{R}(k,k)$ is generated by its elements of degree
$\operatorname{Ext}_{R}(k,k)$ is generated by its elements of degree  $1$ and
$1$ and  $2$.
$2$.(c)
 $(1-vt)\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated
$(1-vt)\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated  $R$-modules
$R$-modules  $M$.
$M$.
Remark 5.5. If  $R$ is a stretched artinian local ring with
$R$ is a stretched artinian local ring with  $\mathfrak{m}^{3}=0$ and
$\mathfrak{m}^{3}=0$ and  $r\neq v$, then the hypotheses of [Reference Avramov, Iyengar and Şega5, Theorem 4.1] apply. In view of [Reference Avramov, Iyengar and Şega5, Theorem 1.4], we have that, after a faithfully flat extension, there exists a regular local ring
$r\neq v$, then the hypotheses of [Reference Avramov, Iyengar and Şega5, Theorem 4.1] apply. In view of [Reference Avramov, Iyengar and Şega5, Theorem 1.4], we have that, after a faithfully flat extension, there exists a regular local ring  $(Q,\mathfrak{n},k)$, an element
$(Q,\mathfrak{n},k)$, an element  $u\in \mathfrak{n}$, and a Golod surjective homomorphism
$u\in \mathfrak{n}$, and a Golod surjective homomorphism  $Q/(u^{2})\rightarrow R$. In this case, as noted in [Reference Avramov, Iyengar and Şega5], the ring
$Q/(u^{2})\rightarrow R$. In this case, as noted in [Reference Avramov, Iyengar and Şega5], the ring  $R$ is Koszul, in the sense that the associated graded ring with respect to
$R$ is Koszul, in the sense that the associated graded ring with respect to  $\mathfrak{m}$ is a Koszul algebra, implying in particular part (1b) of the theorem. In this case, one has
$\mathfrak{m}$ is a Koszul algebra, implying in particular part (1b) of the theorem. In this case, one has  $(1-vt+t^{2})\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated
$(1-vt+t^{2})\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated  $R$-modules
$R$-modules  $M$ [Reference Avramov, Iyengar and Şega5, Theorem 1.1], and in particular (1c) holds.
$M$ [Reference Avramov, Iyengar and Şega5, Theorem 1.1], and in particular (1c) holds.
Proof. Choose  $\widetilde{w}_{i}$,
$\widetilde{w}_{i}$,  $\widetilde{t}$,
$\widetilde{t}$,  $\widetilde{z}_{i}$ preimages of the elements
$\widetilde{z}_{i}$ preimages of the elements  $w_{i}$,
$w_{i}$,  $t$,
$t$,  $z_{i}$ in
$z_{i}$ in  $Q$. Let
$Q$. Let  $K^{R}$ be the Koszul complex described earlier, and let
$K^{R}$ be the Koszul complex described earlier, and let  $K^{Q}$ be the Koszul complex over
$K^{Q}$ be the Koszul complex over  $Q$ on the set
$Q$ on the set  $\{\widetilde{w}_{1},\ldots ,\widetilde{w}_{q},\widetilde{z}_{1},\ldots ,\widetilde{z}_{p},\widetilde{t}\}$, and note that
$\{\widetilde{w}_{1},\ldots ,\widetilde{w}_{q},\widetilde{z}_{1},\ldots ,\widetilde{z}_{p},\widetilde{t}\}$, and note that  $K^{R}=K^{Q}\otimes _{Q}R$, hence we can identify
$K^{R}=K^{Q}\otimes _{Q}R$, hence we can identify  $K^{R}$ with
$K^{R}$ with  $K^{Q}/IK^{Q}$.
$K^{Q}/IK^{Q}$.
(1) Assume  $r\neq v$ and
$r\neq v$ and  $\mathfrak{m}^{3}\neq 0$. In this case, the ideal
$\mathfrak{m}^{3}\neq 0$. In this case, the ideal  $I$ is generated by the elements
$I$ is generated by the elements
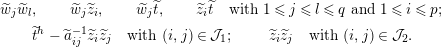 $$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{w}_{j}\widetilde{w}_{l},\qquad \widetilde{w}_{j}\widetilde{z}_{i},\qquad \widetilde{w}_{j}\widetilde{t},\qquad \widetilde{z}_{i}\widetilde{t}\quad \text{with }1\leqslant j\leqslant l\leqslant q\text{ and }1\leqslant i\leqslant p; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{t}^{h}-\widetilde{a}_{ij}^{-1}\widetilde{z}_{i}\widetilde{z}_{j}\quad \text{with }(i,j)\in {\mathcal{J}}_{1};\qquad \,\widetilde{z}_{i}\widetilde{z}_{j}\quad \text{with }(i,j)\in {\mathcal{J}}_{2}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{w}_{j}\widetilde{w}_{l},\qquad \widetilde{w}_{j}\widetilde{z}_{i},\qquad \widetilde{w}_{j}\widetilde{t},\qquad \widetilde{z}_{i}\widetilde{t}\quad \text{with }1\leqslant j\leqslant l\leqslant q\text{ and }1\leqslant i\leqslant p; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{t}^{h}-\widetilde{a}_{ij}^{-1}\widetilde{z}_{i}\widetilde{z}_{j}\quad \text{with }(i,j)\in {\mathcal{J}}_{1};\qquad \,\widetilde{z}_{i}\widetilde{z}_{j}\quad \text{with }(i,j)\in {\mathcal{J}}_{2}. & \displaystyle \nonumber\end{eqnarray}$$We also have
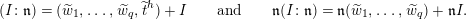 $$\begin{eqnarray}(I:\mathfrak{n})=(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q},\widetilde{t}^{h})+I\qquad \text{and}\qquad \mathfrak{n}(I:\mathfrak{n})=\mathfrak{n}(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q})+\mathfrak{n}I.\end{eqnarray}$$
$$\begin{eqnarray}(I:\mathfrak{n})=(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q},\widetilde{t}^{h})+I\qquad \text{and}\qquad \mathfrak{n}(I:\mathfrak{n})=\mathfrak{n}(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q})+\mathfrak{n}I.\end{eqnarray}$$ (Note that, if  $R$ is Gorenstein, then
$R$ is Gorenstein, then  $q=0$ and
$q=0$ and  $\mathfrak{n}(I:\mathfrak{n})=\mathfrak{n}I$.) In particular, note that
$\mathfrak{n}(I:\mathfrak{n})=\mathfrak{n}I$.) In particular, note that  $I\neq \mathfrak{n}(I:\mathfrak{n})$.
$I\neq \mathfrak{n}(I:\mathfrak{n})$.
Let  $f\in I\smallsetminus \mathfrak{n}(I:\mathfrak{n})$. Then we can choose elements
$f\in I\smallsetminus \mathfrak{n}(I:\mathfrak{n})$. Then we can choose elements  $\unicode[STIX]{x1D6FC}_{ij}$,
$\unicode[STIX]{x1D6FC}_{ij}$,  $\unicode[STIX]{x1D6FD}_{ij}$,
$\unicode[STIX]{x1D6FD}_{ij}$,  $\unicode[STIX]{x1D6FE}_{i}$,
$\unicode[STIX]{x1D6FE}_{i}$,  $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$,  $\unicode[STIX]{x1D702}_{ij}$,
$\unicode[STIX]{x1D702}_{ij}$,  $\unicode[STIX]{x1D703}_{ij}\in R$ in (5.3.1) such that at least one of the elements
$\unicode[STIX]{x1D703}_{ij}\in R$ in (5.3.1) such that at least one of the elements  $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$,  $\unicode[STIX]{x1D702}_{ij}$, or
$\unicode[STIX]{x1D702}_{ij}$, or  $\unicode[STIX]{x1D703}_{ij}$ is a unit, and such that we can lift the element
$\unicode[STIX]{x1D703}_{ij}$ is a unit, and such that we can lift the element  $F$ in (5.3.1) to an element
$F$ in (5.3.1) to an element  $L$ in
$L$ in  $K^{Q}$ with
$K^{Q}$ with  $\unicode[STIX]{x2202}(L)=f$. Then Lemma 5.3 shows that the ring
$\unicode[STIX]{x2202}(L)=f$. Then Lemma 5.3 shows that the ring  $R$ satisfies
$R$ satisfies  ${\mathcal{P}}_{2,1}$, with
${\mathcal{P}}_{2,1}$, with  $l=F$. Part (1a) follows then from Corollary 4.5 and (1b) follows from Corollary 4.4. Furthermore, the existence of a surjective Golod homomorphism onto
$l=F$. Part (1a) follows then from Corollary 4.5 and (1b) follows from Corollary 4.4. Furthermore, the existence of a surjective Golod homomorphism onto  $R$ from a hypersurface ring, together with formula (5.0.1) and a result of Levin, see [Reference Avramov, Kustin and Miller6, Proposition 5.18], prove (1c).
$R$ from a hypersurface ring, together with formula (5.0.1) and a result of Levin, see [Reference Avramov, Kustin and Miller6, Proposition 5.18], prove (1c).
Remark 5.5 explains the statements (1b) and (1c) when  $\mathfrak{m}^{3}=0$.
$\mathfrak{m}^{3}=0$.
(2) Assume now that  $r=v$, hence
$r=v$, hence  $p=0$. We see that the ideal
$p=0$. We see that the ideal  $I$ is then generated by the elements
$I$ is then generated by the elements
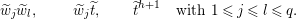 $$\begin{eqnarray}\widetilde{w}_{j}\widetilde{w}_{l},\qquad \,\widetilde{w}_{j}\widetilde{t},\qquad \widetilde{t}^{h+1}\quad \text{with }1\leqslant j\leqslant l\leqslant q.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{w}_{j}\widetilde{w}_{l},\qquad \,\widetilde{w}_{j}\widetilde{t},\qquad \widetilde{t}^{h+1}\quad \text{with }1\leqslant j\leqslant l\leqslant q.\end{eqnarray}$$ We set  $A=R/(w_{1},\ldots ,w_{q})$ and
$A=R/(w_{1},\ldots ,w_{q})$ and  $B=R/(t)$. Note that
$B=R/(t)$. Note that  $(A,\mathfrak{a},k)$ is a local ring with
$(A,\mathfrak{a},k)$ is a local ring with  $A\cong Q^{\prime }/(\unicode[STIX]{x1D70F}^{h+1})$, where
$A\cong Q^{\prime }/(\unicode[STIX]{x1D70F}^{h+1})$, where  $Q^{\prime }$ is the regular local ring
$Q^{\prime }$ is the regular local ring  $Q^{\prime }=Q/(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q})$ and
$Q^{\prime }=Q/(\widetilde{w}_{1},\ldots ,\widetilde{w}_{q})$ and  $\unicode[STIX]{x1D70F}$ is the image of
$\unicode[STIX]{x1D70F}$ is the image of  $\widetilde{t}$ in
$\widetilde{t}$ in  $Q^{\prime }$; in particular,
$Q^{\prime }$; in particular,  $A$ is a hypersurface. Also, note that
$A$ is a hypersurface. Also, note that  $(B,\mathfrak{b},k)$ is a local ring whose maximal ideal satisfies
$(B,\mathfrak{b},k)$ is a local ring whose maximal ideal satisfies  $\mathfrak{b}^{2}=0$. Then
$\mathfrak{b}^{2}=0$. Then  $R$ is isomorphic to the fiber product
$R$ is isomorphic to the fiber product  $A\times _{k}B$. Since
$A\times _{k}B$. Since  $A$ and
$A$ and  $B$ are both Golod rings, [Reference Lescot16, Théorème 4.1] implies that
$B$ are both Golod rings, [Reference Lescot16, Théorème 4.1] implies that  $R$ is a Golod ring, establishing (2a). Also, by [Reference Moore21], the algebra
$R$ is a Golod ring, establishing (2a). Also, by [Reference Moore21], the algebra  $\operatorname{Ext}_{R}(k,k)$ is then the coproduct of the algebras
$\operatorname{Ext}_{R}(k,k)$ is then the coproduct of the algebras  $\operatorname{Ext}_{A}(k,k)$ and
$\operatorname{Ext}_{A}(k,k)$ and  $\operatorname{Ext}_{B}(k,k)$; see loc. cit. for the definition of the coproduct. Since
$\operatorname{Ext}_{B}(k,k)$; see loc. cit. for the definition of the coproduct. Since  $\mathfrak{b}^{2}=0$, the Yoneda algebra
$\mathfrak{b}^{2}=0$, the Yoneda algebra  $\operatorname{Ext}_{B}(k,k)$ is generated by its elements of degree
$\operatorname{Ext}_{B}(k,k)$ is generated by its elements of degree  $1$. The Yoneda algebra of the hypersurface
$1$. The Yoneda algebra of the hypersurface  $A$ is generated in degrees
$A$ is generated in degrees  $1$ and
$1$ and  $2$. It follows that the coproduct is generated in degrees
$2$. It follows that the coproduct is generated in degrees  $1$ and
$1$ and  $2$, establishing (2b).
$2$, establishing (2b).
By a result of Ghione and Gulliksen [Reference Ghione and Gulliksen9] and formula 5.0.1, the fact that  $R$ is Golod implies that
$R$ is Golod implies that  $P_{M}^{R}(t)$ is rational, with denominator
$P_{M}^{R}(t)$ is rational, with denominator  $(1+t)^{v}(1-vt)$. The more precise denominator
$(1+t)^{v}(1-vt)$. The more precise denominator  $1-vt$ in (2c) requires additional discussion. To compute
$1-vt$ in (2c) requires additional discussion. To compute  $P_{M}^{R}(t)$ we use a method employed in the proof of [Reference Avramov, Iyengar and Şega5, Corollary 4.4]. By [Reference Dress and Krämer8, Rem. 3] one has
$P_{M}^{R}(t)$ we use a method employed in the proof of [Reference Avramov, Iyengar and Şega5, Corollary 4.4]. By [Reference Dress and Krämer8, Rem. 3] one has  $\unicode[STIX]{x1D6FA}_{2}^{R}(M)=K\oplus L$, where
$\unicode[STIX]{x1D6FA}_{2}^{R}(M)=K\oplus L$, where  $K$ is an
$K$ is an  $A$-module and
$A$-module and  $L$ is a
$L$ is a  $B$-module. Using further a formula in [Reference Dress and Krämer8, Thm. 2], we have
$B$-module. Using further a formula in [Reference Dress and Krämer8, Thm. 2], we have
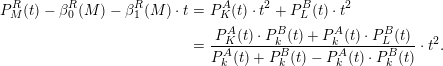 $$\begin{eqnarray}\displaystyle P_{M}^{R}(t)-\unicode[STIX]{x1D6FD}_{0}^{R}(M)-\unicode[STIX]{x1D6FD}_{1}^{R}(M)\cdot t & = & \displaystyle P_{K}^{A}(t)\cdot t^{2}+P_{L}^{B}(t)\cdot t^{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{P_{K}^{A}(t)\cdot P_{k}^{B}(t)+P_{k}^{A}(t)\cdot P_{L}^{B}(t)}{P_{k}^{A}(t)+P_{k}^{B}(t)-P_{k}^{A}(t)\cdot P_{k}^{B}(t)}\cdot t^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{M}^{R}(t)-\unicode[STIX]{x1D6FD}_{0}^{R}(M)-\unicode[STIX]{x1D6FD}_{1}^{R}(M)\cdot t & = & \displaystyle P_{K}^{A}(t)\cdot t^{2}+P_{L}^{B}(t)\cdot t^{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{P_{K}^{A}(t)\cdot P_{k}^{B}(t)+P_{k}^{A}(t)\cdot P_{L}^{B}(t)}{P_{k}^{A}(t)+P_{k}^{B}(t)-P_{k}^{A}(t)\cdot P_{k}^{B}(t)}\cdot t^{2}.\end{eqnarray}$$ Since  $A$ is a hypersurface, we have that
$A$ is a hypersurface, we have that  $P_{k}^{A}(t)=1/(1-t)$, and the Poincaré series of every finitely generated
$P_{k}^{A}(t)=1/(1-t)$, and the Poincaré series of every finitely generated  $A$-module can be written as a rational function with denominator
$A$-module can be written as a rational function with denominator  $1-t$, since every
$1-t$, since every  $A$-module
$A$-module  $M$ has an eventually periodic resolution. Since
$M$ has an eventually periodic resolution. Since  $\mathfrak{b}^{2}=0$ and
$\mathfrak{b}^{2}=0$ and  $\operatorname{rank}_{k}(\mathfrak{b}/\mathfrak{b}^{2})=v-1$, we have that
$\operatorname{rank}_{k}(\mathfrak{b}/\mathfrak{b}^{2})=v-1$, we have that  $P_{k}^{B}(t)=1/(1-(v-1)t)$ and the Poincaré series of every finitely generated
$P_{k}^{B}(t)=1/(1-(v-1)t)$ and the Poincaré series of every finitely generated  $B$-module can be written as a rational function with denominator
$B$-module can be written as a rational function with denominator  $1-(v-1)t$. Plugging these formulas into (5.5.1) we obtain that
$1-(v-1)t$. Plugging these formulas into (5.5.1) we obtain that  $P_{M}^{R}(t)$ can be written as a fraction with denominator
$P_{M}^{R}(t)$ can be written as a fraction with denominator  $1-vt$, establishing (2c).
$1-vt$, establishing (2c).
If  $(R,\mathfrak{m},k)$ is a
$(R,\mathfrak{m},k)$ is a  $d$-dimensional local Cohen–Macaulay ring of multiplicity
$d$-dimensional local Cohen–Macaulay ring of multiplicity  $e$, then
$e$, then  $R$ is said to be stretched if there exists a minimal reduction
$R$ is said to be stretched if there exists a minimal reduction  $\mathbf{x}=x_{1},\ldots ,x_{d}$ of
$\mathbf{x}=x_{1},\ldots ,x_{d}$ of  $\mathfrak{m}$ (that is, there exist
$\mathfrak{m}$ (that is, there exist  $d$ elements
$d$ elements  $x_{1},\ldots ,x_{d}$ of
$x_{1},\ldots ,x_{d}$ of  $\mathfrak{m}$ such that
$\mathfrak{m}$ such that  $\mathfrak{m}^{r+1}=(x_{1},\ldots ,x_{d})\mathfrak{m}^{r}$ for some non-negative integer
$\mathfrak{m}^{r+1}=(x_{1},\ldots ,x_{d})\mathfrak{m}^{r}$ for some non-negative integer  $r$) such that
$r$) such that  $R/(\mathbf{x})$ is stretched. Standard arguments allow us to reduce computations of Poincaré series over
$R/(\mathbf{x})$ is stretched. Standard arguments allow us to reduce computations of Poincaré series over  $R$ to computations over the stretched artinian local ring
$R$ to computations over the stretched artinian local ring  $R/(x_{1},\ldots ,x_{d})$, and we obtain:
$R/(x_{1},\ldots ,x_{d})$, and we obtain:
Corollary 5.6. Let  $(R,\mathfrak{m})$ be a stretched local Cohen–Macaulay ring of dimension
$(R,\mathfrak{m})$ be a stretched local Cohen–Macaulay ring of dimension  $d$ and type
$d$ and type  $r$. Set
$r$. Set  $\text{mult}(R)=e$ and
$\text{mult}(R)=e$ and  $\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})=v$. There exists then a polynomial
$\operatorname{rank}_{k}(\mathfrak{m}/\mathfrak{m}^{2})=v$. There exists then a polynomial  $d_{R}(t)\in \mathbb{Z}[t]$ such that
$d_{R}(t)\in \mathbb{Z}[t]$ such that  $d_{R}(t)\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated
$d_{R}(t)\operatorname{P}_{M}^{R}(t)\in \mathbb{Z}[t]$ for all finitely generated  $R$-modules
$R$-modules  $M$, where
$M$, where
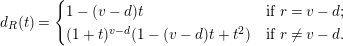 $$\begin{eqnarray}d_{R}(t)=\left\{\begin{array}{@{}ll@{}}1-(v-d)t\quad & \text{if }r=v-d;\\ (1+t)^{v-d}(1-(v-d)t+t^{2})\quad & \text{if }r\neq v-d.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}d_{R}(t)=\left\{\begin{array}{@{}ll@{}}1-(v-d)t\quad & \text{if }r=v-d;\\ (1+t)^{v-d}(1-(v-d)t+t^{2})\quad & \text{if }r\neq v-d.\end{array}\right.\end{eqnarray}$$6 Graded rings and Koszul algebras
We give here graded versions of the main statements. While our results have been stated so far for local rings, they can be stated similarly in the case that  $R=Q/I$, with
$R=Q/I$, with  $Q=k[x_{1},\ldots ,x_{n}]$ with
$Q=k[x_{1},\ldots ,x_{n}]$ with  $k$ a field and
$k$ a field and  $I$ a homogeneous ideal, and with
$I$ a homogeneous ideal, and with  $\mathfrak{m}$ denoting the irrelevant ideal
$\mathfrak{m}$ denoting the irrelevant ideal  $(x_{1},\ldots ,x_{n})$. Furthermore, in the graded case, the hypotheses can be formulated into more suggestive language, as we shall point out below, and in particular we obtain the applications to the study of the Koszul property mentioned in the introduction.
$(x_{1},\ldots ,x_{n})$. Furthermore, in the graded case, the hypotheses can be formulated into more suggestive language, as we shall point out below, and in particular we obtain the applications to the study of the Koszul property mentioned in the introduction.
Let  $R$ be as above, and let
$R$ be as above, and let  $\operatorname{K}$ denote the Koszul complex on the images of the variables. Let
$\operatorname{K}$ denote the Koszul complex on the images of the variables. Let  $\operatorname{H}$ denote the homology. Note that
$\operatorname{H}$ denote the homology. Note that  $\operatorname{K}$ and
$\operatorname{K}$ and  $\operatorname{H}$ are bigraded algebras. When we say that an element of
$\operatorname{H}$ are bigraded algebras. When we say that an element of  $\operatorname{K}$ or
$\operatorname{K}$ or  $\operatorname{H}$ has bidegree
$\operatorname{H}$ has bidegree  $(i,j)$, the entry
$(i,j)$, the entry  $i$ denotes homological degree and the entry
$i$ denotes homological degree and the entry  $j$ denotes internal degree. If
$j$ denotes internal degree. If  $[z]\in \operatorname{H}_{i,j}$ is nonzero we set
$[z]\in \operatorname{H}_{i,j}$ is nonzero we set
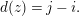 $$\begin{eqnarray}d(z)=j-i.\end{eqnarray}$$
$$\begin{eqnarray}d(z)=j-i.\end{eqnarray}$$ When looking at the Betti table of the resolution of  $R$ over
$R$ over  $Q$ given by Macaulay2 [Reference Grayson and Stillman11], which can be interpreted as also describing the graded Hilbert series of
$Q$ given by Macaulay2 [Reference Grayson and Stillman11], which can be interpreted as also describing the graded Hilbert series of  $\operatorname{H}$, the information
$\operatorname{H}$, the information  $d(z)=r$ indicates that the element
$d(z)=r$ indicates that the element  $[z]$ lies in the
$[z]$ lies in the  $r$th line (strand) of the table.
$r$th line (strand) of the table.
With this terminology, we can restate conditions  ${\mathcal{Z}}_{t,b,s}$ and
${\mathcal{Z}}_{t,b,s}$ and  ${\mathcal{P}}_{t,r}$ as follows:
${\mathcal{P}}_{t,r}$ as follows:
 ${\mathcal{P}}_{t,r}$ :
${\mathcal{P}}_{t,r}$ :There exists
 $[l]\in \operatorname{H}_{r}$ such that for every
$[l]\in \operatorname{H}_{r}$ such that for every  $[z]\in \operatorname{H}$ with
$[z]\in \operatorname{H}$ with  $d(z)\geqslant t$, there exists
$d(z)\geqslant t$, there exists  $[z^{\prime }]\in \operatorname{H}$ with
$[z^{\prime }]\in \operatorname{H}$ with  $d(z^{\prime })\geqslant t-1$ such that
$d(z^{\prime })\geqslant t-1$ such that  $[z]=[z^{\prime }][l]$.
$[z]=[z^{\prime }][l]$. ${\mathcal{Z}}_{t,b,s}$ :
${\mathcal{Z}}_{t,b,s}$ :There exists a set of cycles
 $Z$ in
$Z$ in  $\operatorname{K}$ with
$\operatorname{K}$ with  $d(z)\geqslant t$ for all
$d(z)\geqslant t$ for all  $z\in Z$ and
$z\in Z$ and  $zz^{\prime }=0$ for all
$zz^{\prime }=0$ for all  $z,z^{\prime }\in Z$, and such that for every
$z,z^{\prime }\in Z$, and such that for every  $[v]\in \operatorname{H}$ with
$[v]\in \operatorname{H}$ with  $d(v)=s$ there exists
$d(v)=s$ there exists  $m\in \mathbb{N}$ and
$m\in \mathbb{N}$ and  $z_{i}\in Z$,
$z_{i}\in Z$,  $[u_{i}]\in \operatorname{H}$ with
$[u_{i}]\in \operatorname{H}$ with  $d(z_{i})\geqslant b$ for each
$d(z_{i})\geqslant b$ for each  $1\leqslant i\leqslant m$, such that
$1\leqslant i\leqslant m$, such that  $[v]=\sum _{i=1}^{m}[z_{i}][u_{i}]$.
$[v]=\sum _{i=1}^{m}[z_{i}][u_{i}]$.
We now concentrate on the consequences of our results to the study of the Koszul property of  $R$. As recalled earlier, [Reference Roos.22, Corollary 1] shows that the map
$R$. As recalled earlier, [Reference Roos.22, Corollary 1] shows that the map  $\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m},k)$ induced by the inclusion
$\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m},k)$ induced by the inclusion  $\mathfrak{m}^{2}\subseteq \mathfrak{m}$ is zero for all
$\mathfrak{m}^{2}\subseteq \mathfrak{m}$ is zero for all  $i\geqslant 0$ if and only if the Yoneda algebra
$i\geqslant 0$ if and only if the Yoneda algebra  $\operatorname{Ext}_{R}(k,k)$ is generated in degree
$\operatorname{Ext}_{R}(k,k)$ is generated in degree  $1$. Since
$1$. Since  $R$ is a standard graded
$R$ is a standard graded  $k$-algebra, the last statement is equivalent to the fact that
$k$-algebra, the last statement is equivalent to the fact that  $R$ is a Koszul algebra.
$R$ is a Koszul algebra.
We also consider a property that is stronger than Koszulness. As defined in [Reference Iyengar and Römer14], a local (or graded) ring is said to be absolutely Koszul if the linearity defect of every finitely generated  $R$-module is finite. While we refer to [Reference Herzog and Iyengar12] for the original definition of linearity defect, we mention that a module
$R$-module is finite. While we refer to [Reference Herzog and Iyengar12] for the original definition of linearity defect, we mention that a module  $M$ has finite linearity defect if and only if it has a syzygy
$M$ has finite linearity defect if and only if it has a syzygy  $N$ whose associated graded module
$N$ whose associated graded module  $\operatorname{gr}_{\mathfrak{m}}(N)$ has a linear resolution over the associated graded ring
$\operatorname{gr}_{\mathfrak{m}}(N)$ has a linear resolution over the associated graded ring  $\operatorname{gr}_{\mathfrak{m}}(R)$. In the graded case, if
$\operatorname{gr}_{\mathfrak{m}}(R)$. In the graded case, if  $R$ is absolutely Koszul, then it is also Koszul, see [Reference Herzog and Iyengar12, Proposition 1.13].
$R$ is absolutely Koszul, then it is also Koszul, see [Reference Herzog and Iyengar12, Proposition 1.13].
As defined in the introduction, the linear strand of  $\operatorname{H}$ is the set of elements
$\operatorname{H}$ is the set of elements  $[z]$ with
$[z]$ with  $d(z)=1$. The nonlinear strands are composed of those elements with
$d(z)=1$. The nonlinear strands are composed of those elements with  $d(z)>1$. We say that the nonlinear strands of
$d(z)>1$. We say that the nonlinear strands of  $\operatorname{H}$ are generated by a set
$\operatorname{H}$ are generated by a set  $\overline{Z}$ with
$\overline{Z}$ with  $\overline{Z}\subseteq \operatorname{H}$ if the nonlinear strands are contained in the ideal generated by
$\overline{Z}\subseteq \operatorname{H}$ if the nonlinear strands are contained in the ideal generated by  $\overline{Z}$ in
$\overline{Z}$ in  $\operatorname{H}$. If the nonlinear strands are generated by a subset
$\operatorname{H}$. If the nonlinear strands are generated by a subset  $\overline{Z}$ of the linear strand, it follows that
$\overline{Z}$ of the linear strand, it follows that  $\operatorname{H}$ is generated by the linear strand as a
$\operatorname{H}$ is generated by the linear strand as a  $k$-algebra.
$k$-algebra.
Theorem 6.1. Assume one of the following conditions holds:
(1) There exists an element
 $[l]$ of bidegree
$[l]$ of bidegree  $(1,2)$ such that the nonlinear strands are generated by
$(1,2)$ such that the nonlinear strands are generated by  $[l]$, that is, every element in the nonlinear strands of
$[l]$, that is, every element in the nonlinear strands of  $\operatorname{H}$ is a multiple of
$\operatorname{H}$ is a multiple of  $[l]$.
$[l]$.(2)
 $R_{{\geqslant}3}=0$ and there exists a set of cycles
$R_{{\geqslant}3}=0$ and there exists a set of cycles  $Z$ representing elements in the linear strand, with the property that
$Z$ representing elements in the linear strand, with the property that  $zz^{\prime }=0$ for all
$zz^{\prime }=0$ for all  $z,z^{\prime }\in Z$, such that the set
$z,z^{\prime }\in Z$, such that the set  $\overline{Z}=\{[z]\mid z\in Z\}$ generates the nonlinear strand of
$\overline{Z}=\{[z]\mid z\in Z\}$ generates the nonlinear strand of  $\operatorname{H}$.
$\operatorname{H}$.
Then  $R$ is Koszul. Moreover,
$R$ is Koszul. Moreover,  $R$ is absolutely Koszul when (1) holds.
$R$ is absolutely Koszul when (1) holds.
Proof. If (1) holds, then  ${\mathcal{P}}_{2,1}$ holds. By Corollary 4.4, the induced maps
${\mathcal{P}}_{2,1}$ holds. By Corollary 4.4, the induced maps  $\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m},k)$ are zero. This implies that
$\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m},k)$ are zero. This implies that  $R$ is Koszul.
$R$ is Koszul.
One of the consequences of the hypothesis in (1) is that there are no elements in bidegree  $(1,i)$ with
$(1,i)$ with  $i>2$. Consequently, the ideal
$i>2$. Consequently, the ideal  $I$ is quadratic and
$I$ is quadratic and  $v(R)=2$. Let
$v(R)=2$. Let  $L$ denote a preimage of
$L$ denote a preimage of  $l$ in
$l$ in  $\operatorname{K}^{Q}$ and set
$\operatorname{K}^{Q}$ and set  $h=\unicode[STIX]{x2202}(L)$. Note that
$h=\unicode[STIX]{x2202}(L)$. Note that  $h\in I\smallsetminus \mathfrak{n}^{3}$. We can apply then Corollary 4.5 with
$h\in I\smallsetminus \mathfrak{n}^{3}$. We can apply then Corollary 4.5 with  $a=1$ and
$a=1$ and  $t=2$ to conclude that
$t=2$ to conclude that  $R$ is a homomorphic image of a quadratic hypersurface via a Golod homomorphism, hence
$R$ is a homomorphic image of a quadratic hypersurface via a Golod homomorphism, hence  $R$ is absolutely Koszul by [Reference Herzog and Iyengar12, Theorem 5.9].
$R$ is absolutely Koszul by [Reference Herzog and Iyengar12, Theorem 5.9].
If (2) holds, then  ${\mathcal{Z}}_{1,1,2}$ holds. We apply then the graded version of Theorem 3.1 to conclude that the induced map
${\mathcal{Z}}_{1,1,2}$ holds. We apply then the graded version of Theorem 3.1 to conclude that the induced map  $\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m},k)$ is zero, hence
$\operatorname{Tor}_{i}^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{i}^{R}(\mathfrak{m},k)$ is zero, hence  $R$ is Koszul.
$R$ is Koszul.
There exist Koszul algebras that do not satisfy either of the conditions of the theorem, since, as noted in [Reference Boocher, D’Alì, Grifo, Montaño and Sammartano7], the fact that  $R$ is Koszul does not necessarily imply that the Koszul homology is generated by the linear strand. On the other hand, the fact that
$R$ is Koszul does not necessarily imply that the Koszul homology is generated by the linear strand. On the other hand, the fact that  $R$ is Koszul does impose conditions on the Koszul homology; see the introduction for more details on known results. Of particular interest is the following reformulation of Lemma 1.3 from Section 1. The statement of this result was communicated to us orally by S. Iyengar, who arrived at it in work with L. Avramov and A. Conca.
$R$ is Koszul does impose conditions on the Koszul homology; see the introduction for more details on known results. Of particular interest is the following reformulation of Lemma 1.3 from Section 1. The statement of this result was communicated to us orally by S. Iyengar, who arrived at it in work with L. Avramov and A. Conca.
Proposition 6.2. If  $R$ is Koszul, then the nonlinear strands of
$R$ is Koszul, then the nonlinear strands of  $\operatorname{H}$ are contained in the set of matric Massey products MH
$\operatorname{H}$ are contained in the set of matric Massey products MH $(\operatorname{K})$.
$(\operatorname{K})$.
Proof. If  $R$ is Koszul, then the induced map
$R$ is Koszul, then the induced map  $\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m},k)$ is zero, hence the canonical projection
$\operatorname{Tor}_{\ast }^{R}(\mathfrak{m}^{2},k)\rightarrow \operatorname{Tor}_{\ast }^{R}(\mathfrak{m},k)$ is zero, hence the canonical projection  $R\rightarrow R/\mathfrak{m}^{2}$ is Golod, and thus small. Apply then Lemma 1.3 to see that
$R\rightarrow R/\mathfrak{m}^{2}$ is Golod, and thus small. Apply then Lemma 1.3 to see that  $\operatorname{H}_{{\geqslant}1}(\mathfrak{m}^{2}\operatorname{K})\subseteq MH(\operatorname{K})$.
$\operatorname{H}_{{\geqslant}1}(\mathfrak{m}^{2}\operatorname{K})\subseteq MH(\operatorname{K})$.
In the next section, we discuss an example of a graded algebra  $R$ with
$R$ with  $R_{{\geqslant}3}=0$ for which the nonlinear strand is generated by the linear strand, but
$R_{{\geqslant}3}=0$ for which the nonlinear strand is generated by the linear strand, but  $R$ is not Koszul, see 7.4. Thus, the converse of Proposition 6.2 does not hold. Stronger hypotheses on the generation of Koszul homology such as the ones in our theorem are thus needed in order to ensure
$R$ is not Koszul, see 7.4. Thus, the converse of Proposition 6.2 does not hold. Stronger hypotheses on the generation of Koszul homology such as the ones in our theorem are thus needed in order to ensure  $R$ is Koszul.
$R$ is Koszul.
7 Examples
We now proceed to give the relevant examples mentioned above. The computations here are done with the help of the Macaulay2 package DGAlgebras written by Frank Moore, but all computations can also be checked by hand (for example, see 7.6 below). In this section,  $k$ denotes a field of characteristic
$k$ denotes a field of characteristic  $0$.
$0$.
Let  $Q=k[X,Y,Z,U]$, and
$Q=k[X,Y,Z,U]$, and  $R=Q/\mathfrak{a}$ for an ideal
$R=Q/\mathfrak{a}$ for an ideal  $\mathfrak{a}$. Set
$\mathfrak{a}$. Set  $\mathfrak{m}=(x,y,z,u)$, with
$\mathfrak{m}=(x,y,z,u)$, with  $x,y,z,u$ the images of
$x,y,z,u$ the images of  $X,Y,Z,U$ in
$X,Y,Z,U$ in  $R$, respectively, and
$R$, respectively, and  $T_{1},\ldots ,T_{4}$ the degree one variables of the Tate complex mapping to
$T_{1},\ldots ,T_{4}$ the degree one variables of the Tate complex mapping to  $x,y,z,u$, respectively. As before,
$x,y,z,u$, respectively. As before,  $\operatorname{K}^{R}$ is the Koszul complex on
$\operatorname{K}^{R}$ is the Koszul complex on  $(x,y,z,u)$ and
$(x,y,z,u)$ and  $\operatorname{H}^{R}$ is its homology algebra. If
$\operatorname{H}^{R}$ is its homology algebra. If  $z\in \operatorname{K}^{R}$ is a cycle, we denote by
$z\in \operatorname{K}^{R}$ is a cycle, we denote by  $[z]$ its homology class in
$[z]$ its homology class in  $\operatorname{H}^{R}$. Recall (e.g., [Reference Roos23]) that
$\operatorname{H}^{R}$. Recall (e.g., [Reference Roos23]) that  $\operatorname{H}^{R}\cong \operatorname{Tor}^{Q}(R,k)$, and so the Betti table of
$\operatorname{H}^{R}\cong \operatorname{Tor}^{Q}(R,k)$, and so the Betti table of  $R$ over
$R$ over  $Q$ gives an indication in which bidegrees elements of
$Q$ gives an indication in which bidegrees elements of  $\operatorname{H}^{R}$ reside.
$\operatorname{H}^{R}$ reside.
We start by applying Theorem 6.1 to rings having the form  $R=Q/\mathfrak{a}$ where
$R=Q/\mathfrak{a}$ where  $\mathfrak{a}$ is an ideal generated by quadratic forms in
$\mathfrak{a}$ is an ideal generated by quadratic forms in  $(X,Y,Z,U)$; such rings were studied by Roos in [Reference Roos23]. We verify the conditions of Theorem 6.1 hold for 40+2=42 of the 104 rings in [Reference Roos23, Tables A–D], showing in particular that 40 of them are absolutely Koszul.
$(X,Y,Z,U)$; such rings were studied by Roos in [Reference Roos23]. We verify the conditions of Theorem 6.1 hold for 40+2=42 of the 104 rings in [Reference Roos23, Tables A–D], showing in particular that 40 of them are absolutely Koszul.
7.1. Consider the ring  $R$ which is case 66 in [Reference Roos23, Table C]:
$R$ which is case 66 in [Reference Roos23, Table C]:
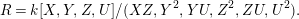 $$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(XZ,Y^{2},YU,Z^{2},ZU,U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(XZ,Y^{2},YU,Z^{2},ZU,U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$ We claim that the nonlinear strand of  $\operatorname{H}^{R}$ is generated by a single element in bidegree
$\operatorname{H}^{R}$ is generated by a single element in bidegree  $(1,2)$, that is, it satisfies Theorem 6.1(1). As a result, we can conclude that this ring is absolutely Koszul, hence Koszul. To do this, we use the Macaulay2 package DGAlgebras.
$(1,2)$, that is, it satisfies Theorem 6.1(1). As a result, we can conclude that this ring is absolutely Koszul, hence Koszul. To do this, we use the Macaulay2 package DGAlgebras.
In the following code, the set  $\mathtt{C}$ is a list of cycles whose images (given by
$\mathtt{C}$ is a list of cycles whose images (given by  $\mathtt{G}$) generate
$\mathtt{G}$) generate  $\mathtt{H}$ (
$\mathtt{H}$ ( $=\operatorname{H}^{R}$) as a
$=\operatorname{H}^{R}$) as a  $k$-algebra and
$k$-algebra and  $\mathtt{P}$ is the list of generators in
$\mathtt{P}$ is the list of generators in  $\mathtt{G}$ which are not in the linear strand. We define an ideal
$\mathtt{G}$ which are not in the linear strand. We define an ideal  $\mathtt{I}$ in
$\mathtt{I}$ in  $\mathtt{H}$ to be generated by the elements in
$\mathtt{H}$ to be generated by the elements in  $\mathtt{P}$ and all products
$\mathtt{P}$ and all products  $hk$ with
$hk$ with  $h,k\in \mathtt{G}$; this ideal is equal to the union of all nonlinear strands of
$h,k\in \mathtt{G}$; this ideal is equal to the union of all nonlinear strands of  $\mathtt{H}$, together with the zero element. Showing generation of the nonlinear strands by an element in bidegree
$\mathtt{H}$, together with the zero element. Showing generation of the nonlinear strands by an element in bidegree  $(1,2)$ now reduces to checking ideal containment.
$(1,2)$ now reduces to checking ideal containment.

In this example, we see that the homology class of the cycle  $N=zT_{1}+(y+u)T_{2}+(z+u)T_{3}+uT_{4}$ generates the nonlinear strands of
$N=zT_{1}+(y+u)T_{2}+(z+u)T_{3}+uT_{4}$ generates the nonlinear strands of  $\operatorname{H}^{R}$, hence by Theorem 6.1(1),
$\operatorname{H}^{R}$, hence by Theorem 6.1(1),  $R$ is absolutely Koszul.
$R$ is absolutely Koszul.
Moreover, a similar argument shows that 40 of the rings from [Reference Roos23, Tables A–D] have the nonlinear strand of their Koszul homology algebra generated by a single element in bidegree  $(1,2)$, and hence are absolutely Koszul rings; these are cases 1–4, 8–10, 23, 25–28, 49, 50, 52, 53, 66–68, 70, 72, 75–83, and isotopes 46va, 66v5, 68v, 71v4, 72v2e, 75v2, 78v1, 78v2e, 78v3v, and 81va from [Reference Roos23, Tables A–D]. Indeed, in all these cases we show that the homology class of the sum of generating cycles in bidegree
$(1,2)$, and hence are absolutely Koszul rings; these are cases 1–4, 8–10, 23, 25–28, 49, 50, 52, 53, 66–68, 70, 72, 75–83, and isotopes 46va, 66v5, 68v, 71v4, 72v2e, 75v2, 78v1, 78v2e, 78v3v, and 81va from [Reference Roos23, Tables A–D]. Indeed, in all these cases we show that the homology class of the sum of generating cycles in bidegree  $(1,2)$ found by DGAlgebras can be taken to be such a generator.
$(1,2)$ found by DGAlgebras can be taken to be such a generator.
The next example is a ring satisfying condition (2), but not condition (1), of Theorem 6.1.
7.2. Let  $R$ be the ring which is case 54 in [Reference Roos23]:
$R$ be the ring which is case 54 in [Reference Roos23]:
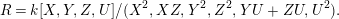 $$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2},XZ,Y^{2},Z^{2},YU+ZU,U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2},XZ,Y^{2},Z^{2},YU+ZU,U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$ The nonlinear strand of  $\operatorname{H}^{R}$ cannot be generated by a single element in bidegree
$\operatorname{H}^{R}$ cannot be generated by a single element in bidegree  $(1,2)$ as in the previous example, which can be seen by computing the Betti table for
$(1,2)$ as in the previous example, which can be seen by computing the Betti table for  $R$ over
$R$ over  $Q$:
$Q$:

and observing there is no way for an element in bidegree  $(4,6)$ to be a multiple of an element in bidegree
$(4,6)$ to be a multiple of an element in bidegree  $(1,2)$.
$(1,2)$.
Next, we use the package DGAlgebras again to show that the nonlinear strand of  $\operatorname{H}^{R}$ is generated by a finite set of classes of cycles with trivial self-multiplication, that is, the ring
$\operatorname{H}^{R}$ is generated by a finite set of classes of cycles with trivial self-multiplication, that is, the ring  $R$ satisfies condition (2) of Theorem 6.1.
$R$ satisfies condition (2) of Theorem 6.1.

In this example, the set Cyc is the desired generating set contained in the linear strand and its elements correspond to the following cycles:
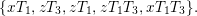 $$\begin{eqnarray}\{xT_{1},zT_{3},zT_{1},zT_{1}T_{3},xT_{1}T_{3}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{xT_{1},zT_{3},zT_{1},zT_{1}T_{3},xT_{1}T_{3}\}.\end{eqnarray}$$ The Macaulay2 code first checks  $\mathfrak{m}^{3}=0$, and then verifies that all the products of elements in Cyc are 0 and that the nonlinear strand I is contained in the ideal generated by Cls (the images in H of cycles in Cyc). A similar argument shows that the ring in case 71 of [Reference Roos23, Tables A–D] also satisfies Theorem 6.1(2); for that ring, one can show that the set Cyc=
$\mathfrak{m}^{3}=0$, and then verifies that all the products of elements in Cyc are 0 and that the nonlinear strand I is contained in the ideal generated by Cls (the images in H of cycles in Cyc). A similar argument shows that the ring in case 71 of [Reference Roos23, Tables A–D] also satisfies Theorem 6.1(2); for that ring, one can show that the set Cyc= $\{C_{0},C_{1},C_{2},C_{7},C_{8},C_{9},C_{11},C_{15}\}$ is the desired generating set with trivial self-multiplication.
$\{C_{0},C_{1},C_{2},C_{7},C_{8},C_{9},C_{11},C_{15}\}$ is the desired generating set with trivial self-multiplication.
Remark 7.3. Even among other rings with  $\mathfrak{m}^{3}=0$ in [Reference Roos23], there are limitations to Theorem 6.1(2): For example, the ring in case 71v16 of [Reference Roos23] has no generating set satisfying this condition, despite being Koszul. Using DGAlgebras as above, we see that the ring
$\mathfrak{m}^{3}=0$ in [Reference Roos23], there are limitations to Theorem 6.1(2): For example, the ring in case 71v16 of [Reference Roos23] has no generating set satisfying this condition, despite being Koszul. Using DGAlgebras as above, we see that the ring
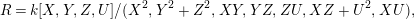 $$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2},Y^{2}+Z^{2},XY,YZ,ZU,XZ+U^{2},XU), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2},Y^{2}+Z^{2},XY,YZ,ZU,XZ+U^{2},XU), & & \displaystyle \nonumber\end{eqnarray}$$ has  $\mathfrak{m}^{3}=0$ and has
$\mathfrak{m}^{3}=0$ and has  $H^{R}$ generated by
$H^{R}$ generated by  $X_{1},\ldots ,X_{17}$ such that
$X_{1},\ldots ,X_{17}$ such that  $X_{13}^{2}\not =0$, hence the cycle corresponding to
$X_{13}^{2}\not =0$, hence the cycle corresponding to  $X_{13}$ cannot be a part of any set with trivial self-multiplication. However, without
$X_{13}$ cannot be a part of any set with trivial self-multiplication. However, without  $X_{13}$, we cannot generate the nonlinear strand:
$X_{13}$, we cannot generate the nonlinear strand:

Hence no set satisfying the conditions of Theorem 6.1(2) can exist for this ring, but  $R$ is Koszul by [Reference Roos23, Main Theorem].
$R$ is Koszul by [Reference Roos23, Main Theorem].
The next example shows that generation of  $\operatorname{H}^{R}$ by the linear strand alone cannot detect Koszulness of
$\operatorname{H}^{R}$ by the linear strand alone cannot detect Koszulness of  $R$.
$R$.
7.4. Consider the ring which is case 55 in [Reference Roos23]:
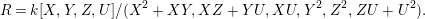 $$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2}+XY,XZ+YU,XU,Y^{2},Z^{2},ZU+U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R=k[X,Y,Z,U]/(X^{2}+XY,XZ+YU,XU,Y^{2},Z^{2},ZU+U^{2}). & & \displaystyle \nonumber\end{eqnarray}$$ The graded Betti table of  $R$ over
$R$ over  $Q$ is the same as for the ring in 7.2. Moreover, we see that
$Q$ is the same as for the ring in 7.2. Moreover, we see that  $\operatorname{H}^{R}$ is generated by the linear strand. This code can also be used to show the ring in 7.2 is generated by its linear strand.
$\operatorname{H}^{R}$ is generated by the linear strand. This code can also be used to show the ring in 7.2 is generated by its linear strand.

We see that  $\operatorname{H}^{R}$ has 6 generators in bidegree
$\operatorname{H}^{R}$ has 6 generators in bidegree  $(1,2)$ and 4 generators in bidegree
$(1,2)$ and 4 generators in bidegree  $(2,3)$, all in the linear strand; further, the resolution of
$(2,3)$, all in the linear strand; further, the resolution of  $k$ over
$k$ over  $R$ is not linear, hence
$R$ is not linear, hence  $R$ is not Koszul.
$R$ is not Koszul.
Remark 7.5. The Koszul homology algebras of the rings in 7.2 and 7.4 share the same Hilbert series and are both generated by the linear strand, yet one ring is Koszul and the other one is not. Thus, generation by the linear strand and “good” Hilbert series of the Koszul homology are not sufficient to decide whether the ring is Koszul. The particularities of the generation of certain nonlinear strands in the Koszul homology seem to be relevant factors in detecting good homological behavior.
We now showcase the applicability of our results with a nonquadratic example: a noncompressed level algebra of socle degree  $4$, with defining ideal generated in degree
$4$, with defining ideal generated in degree  $3$.
$3$.
7.6. Let  $Q=k[A,B,C,D]$, and let
$Q=k[A,B,C,D]$, and let  $I$ be the ideal
$I$ be the ideal
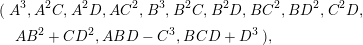 $$\begin{eqnarray}\displaystyle & & \displaystyle (A^{3},A^{2}C,A^{2}D,AC^{2},B^{3},B^{2}C,B^{2}D,BC^{2},BD^{2},C^{2}D,\nonumber\\ \displaystyle & & \displaystyle \quad AB^{2}+CD^{2},ABD-C^{3},BCD+D^{3} ),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (A^{3},A^{2}C,A^{2}D,AC^{2},B^{3},B^{2}C,B^{2}D,BC^{2},BD^{2},C^{2}D,\nonumber\\ \displaystyle & & \displaystyle \quad AB^{2}+CD^{2},ABD-C^{3},BCD+D^{3} ),\nonumber\end{eqnarray}$$ and set  $R=Q/I$. Write
$R=Q/I$. Write  $\mathfrak{m}$ for the maximal homogeneous ideal of
$\mathfrak{m}$ for the maximal homogeneous ideal of  $R$ and write
$R$ and write  $a,b,c,d$ for the images of the variables. As before we denote by
$a,b,c,d$ for the images of the variables. As before we denote by  $T_{1},\ldots ,T_{4}$ the variables of the Tate complex in degree one, mapping to
$T_{1},\ldots ,T_{4}$ the variables of the Tate complex in degree one, mapping to  $a,b,c,d$. One computes with Macaulay2 the Betti table of
$a,b,c,d$. One computes with Macaulay2 the Betti table of  $R$ over
$R$ over  $Q$:
$Q$:

Proposition 1. The following hold:
(1) The last strand of the Koszul homology
 $\operatorname{H}$ is generated by one element in
$\operatorname{H}$ is generated by one element in  $\operatorname{H}_{1,3}$.
$\operatorname{H}_{1,3}$.(2)
 $R\rightarrow R/\mathfrak{m}^{4}$ is a Golod homomorphism and
$R\rightarrow R/\mathfrak{m}^{4}$ is a Golod homomorphism and  $R/\mathfrak{m}^{4}$ is a Golod ring.
$R/\mathfrak{m}^{4}$ is a Golod ring.(3)
 $P_{k}^{R}(t)=(1+z)^{3}/1-z-12z^{2}-10z^{3}-z^{4}+2z^{5}$.
$P_{k}^{R}(t)=(1+z)^{3}/1-z-12z^{2}-10z^{3}-z^{4}+2z^{5}$.
To give a feel for how computations in  $\operatorname{H}^{R}$ are done by hand, and because the computations in this example are not too tedious, we give a proof that does not rely on the DGAlgebras package in Macaulay2.
$\operatorname{H}^{R}$ are done by hand, and because the computations in this example are not too tedious, we give a proof that does not rely on the DGAlgebras package in Macaulay2.
Proof. Using Macaulay2, we check that the reduced Gröbner basis of  $I$ with respect to the lexicographic order is composed of the elements:
$I$ with respect to the lexicographic order is composed of the elements:
 $$\begin{eqnarray}\displaystyle A^{3}, & A^{2}C,A^{2}D,AC^{2},B^{3},B^{2}C,B^{2}D,BC^{2},BD^{2},C^{2}D,AB^{2}+CD^{2}, & \displaystyle \nonumber\\ \displaystyle & ABD-C^{3}BCD+D^{3},BC^{3},AD^{3}+C^{4},D^{4},CD^{3},C^{5}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A^{3}, & A^{2}C,A^{2}D,AC^{2},B^{3},B^{2}C,B^{2}D,BC^{2},BD^{2},C^{2}D,AB^{2}+CD^{2}, & \displaystyle \nonumber\\ \displaystyle & ABD-C^{3}BCD+D^{3},BC^{3},AD^{3}+C^{4},D^{4},CD^{3},C^{5}. & \displaystyle \nonumber\end{eqnarray}$$ Using this information, one sees that  $c^{4}$ and
$c^{4}$ and  $acd^{2}$ generate the two-dimensional socle of
$acd^{2}$ generate the two-dimensional socle of  $R$.
$R$.
Note that the element  $k_{1}=(ac-bd)T_{1}+c^{2}T_{3}\in \operatorname{K}_{1,3}$ is a cycle. We show that its class
$k_{1}=(ac-bd)T_{1}+c^{2}T_{3}\in \operatorname{K}_{1,3}$ is a cycle. We show that its class  $[k_{1}]$ generates
$[k_{1}]$ generates  $\operatorname{H}_{4,8}$ and
$\operatorname{H}_{4,8}$ and  $\operatorname{H}_{3,7}$.
$\operatorname{H}_{3,7}$.
Claim 1.
 $\operatorname{H}_{4,8}$ is generated by the following two elements:
$\operatorname{H}_{4,8}$ is generated by the following two elements:
 $$\begin{eqnarray}[c^{4}T_{1}T_{2}T_{3}T_{4}],\qquad [acd^{2}T_{1}T_{2}T_{3}T_{4}].\end{eqnarray}$$
$$\begin{eqnarray}[c^{4}T_{1}T_{2}T_{3}T_{4}],\qquad [acd^{2}T_{1}T_{2}T_{3}T_{4}].\end{eqnarray}$$ This can be seen from the fact that  $c^{4},acd^{2}$ form a basis for the socle of
$c^{4},acd^{2}$ form a basis for the socle of  $R$.
$R$.
Claim 2.
 $\operatorname{H}_{3,7}$ is generated by the following element:
$\operatorname{H}_{3,7}$ is generated by the following element:  $[c^{4}T_{1}T_{3}T_{4}]$.
$[c^{4}T_{1}T_{3}T_{4}]$.
To verify this claim, note first that  $c^{4}T_{1}T_{3}T_{4}$ is a cycle. Then, compute the module of boundaries
$c^{4}T_{1}T_{3}T_{4}$ is a cycle. Then, compute the module of boundaries  $\mathfrak{m}^{3}\unicode[STIX]{x2202}(K_{4})$ as being generated by the classes of the following elements:
$\mathfrak{m}^{3}\unicode[STIX]{x2202}(K_{4})$ as being generated by the classes of the following elements:
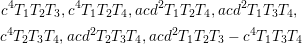 $$\begin{eqnarray}\displaystyle & \displaystyle c^{4}T_{1}T_{2}T_{3},c^{4}T_{1}T_{2}T_{4},acd^{2}T_{1}T_{2}T_{4},acd^{2}T_{1}T_{3}T_{4}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c^{4}T_{2}T_{3}T_{4},acd^{2}T_{2}T_{3}T_{4},acd^{2}T_{1}T_{2}T_{3}-c^{4}T_{1}T_{3}T_{4} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle c^{4}T_{1}T_{2}T_{3},c^{4}T_{1}T_{2}T_{4},acd^{2}T_{1}T_{2}T_{4},acd^{2}T_{1}T_{3}T_{4}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c^{4}T_{2}T_{3}T_{4},acd^{2}T_{2}T_{3}T_{4},acd^{2}T_{1}T_{2}T_{3}-c^{4}T_{1}T_{3}T_{4} & \displaystyle \nonumber\end{eqnarray}$$ and check that  $[c^{4}T_{1}T_{3}T_{4}]\notin \mathfrak{m}^{3}\unicode[STIX]{x2202}(K_{4})$. Since
$[c^{4}T_{1}T_{3}T_{4}]\notin \mathfrak{m}^{3}\unicode[STIX]{x2202}(K_{4})$. Since  $\dim \operatorname{H}_{3,7}=1$, this proves the claim.
$\dim \operatorname{H}_{3,7}=1$, this proves the claim.
Consider now the elements  $k_{2}=c^{2}T_{1}T_{2}T_{4}$ and
$k_{2}=c^{2}T_{1}T_{2}T_{4}$ and  $k_{3}=(bc+d^{2})T_{2}T_{3}T_{4}-b^{2}T_{1}T_{2}T_{4}$, and
$k_{3}=(bc+d^{2})T_{2}T_{3}T_{4}-b^{2}T_{1}T_{2}T_{4}$, and  $k_{4}=c^{2}T_{1}T_{4}$ which are also cycles. To verify that
$k_{4}=c^{2}T_{1}T_{4}$ which are also cycles. To verify that  $[k_{1}]$ generates
$[k_{1}]$ generates  $\operatorname{H}_{4,8}$ and
$\operatorname{H}_{4,8}$ and  $\operatorname{H}_{3,7}$, we note the following relations:
$\operatorname{H}_{3,7}$, we note the following relations:
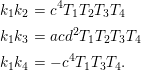 $$\begin{eqnarray}\displaystyle k_{1}k_{2} & = & \displaystyle c^{4}T_{1}T_{2}T_{3}T_{4}\nonumber\\ \displaystyle k_{1}k_{3} & = & \displaystyle acd^{2}T_{1}T_{2}T_{3}T_{4}\nonumber\\ \displaystyle k_{1}k_{4} & = & \displaystyle -c^{4}T_{1}T_{3}T_{4}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k_{1}k_{2} & = & \displaystyle c^{4}T_{1}T_{2}T_{3}T_{4}\nonumber\\ \displaystyle k_{1}k_{3} & = & \displaystyle acd^{2}T_{1}T_{2}T_{3}T_{4}\nonumber\\ \displaystyle k_{1}k_{4} & = & \displaystyle -c^{4}T_{1}T_{3}T_{4}.\nonumber\end{eqnarray}$$ We conclude that the ring  $R$ satisfies the graded version of condition
$R$ satisfies the graded version of condition  ${\mathcal{Z}}_{2,2,4}$, as stated in Section 6.
${\mathcal{Z}}_{2,2,4}$, as stated in Section 6.
Corollary 3.5, together with a usage of Macaulay2 for computing the Poincaré series of  $R/\mathfrak{m}^{4}$ over the polynomial ring, gives:
$R/\mathfrak{m}^{4}$ over the polynomial ring, gives:
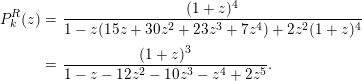 $$\begin{eqnarray}\displaystyle P_{k}^{R}(z) & = & \displaystyle \frac{(1+z)^{4}}{1-z(15z+30z^{2}+23z^{3}+7z^{4})+2z^{2}(1+z)^{4}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(1+z)^{3}}{1-z-12z^{2}-10z^{3}-z^{4}+2z^{5}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{k}^{R}(z) & = & \displaystyle \frac{(1+z)^{4}}{1-z(15z+30z^{2}+23z^{3}+7z^{4})+2z^{2}(1+z)^{4}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(1+z)^{3}}{1-z-12z^{2}-10z^{3}-z^{4}+2z^{5}}.\nonumber\end{eqnarray}$$Acknowledgments
We are grateful to J.-E. Roos and A. Conca, as well as the anonymous referee, for useful comments and suggestions.