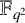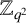1 Introduction
In number theory, a Sidon set (or Sidon sequence), named after the Hungarian mathematician Szimon Szidon, is a set
![]() $A = \lbrace a_0, a_1, a_2, \ldots \rbrace $
of natural numbers in which all pairwise sums
$A = \lbrace a_0, a_1, a_2, \ldots \rbrace $
of natural numbers in which all pairwise sums
![]() $a_i + a_j \; (i \leq j)$
are different. Sidon introduced the concept in his investigations of Fourier series. This notion has been generalised: in an abelian group G, a subset A is a
$a_i + a_j \; (i \leq j)$
are different. Sidon introduced the concept in his investigations of Fourier series. This notion has been generalised: in an abelian group G, a subset A is a
![]() $B_h[g]$
-set if, for any element x of G, the number of h-tuples of elements of A of sum x is less than or equal to g. The main problem in the study of Sidon sets is to find the largest number of elements a Sidon set can have which are smaller than some given number x.
$B_h[g]$
-set if, for any element x of G, the number of h-tuples of elements of A of sum x is less than or equal to g. The main problem in the study of Sidon sets is to find the largest number of elements a Sidon set can have which are smaller than some given number x.
There are several constructions of Sidon sets (for a complete summary, see [Reference O’Bryant9]). We will concentrate on the construction of Bose [Reference Bose1] using finite affine geometry. Let q be any prime power and
![]() $\gamma $
a generator of
$\gamma $
a generator of
![]() $\mathbb {F}_{q^2}^{\times }$
and define the set
$\mathbb {F}_{q^2}^{\times }$
and define the set
Bose [Reference Bose1] showed that
![]() $B(q,\gamma )$
is a Sidon set.
$B(q,\gamma )$
is a Sidon set.
The discrete logarithm function is defined by
 $$ \begin{align*} \mathrm{Log}_{\gamma} : ( \mathbb{F}_{q^2}^*, \times) & \longrightarrow (\mathbb{Z}_{q^2 - 1}, +) \\[-2pt] \gamma^k & \longmapsto \mathrm{Log}_{\gamma}(\gamma^k) = k. \end{align*} $$
$$ \begin{align*} \mathrm{Log}_{\gamma} : ( \mathbb{F}_{q^2}^*, \times) & \longrightarrow (\mathbb{Z}_{q^2 - 1}, +) \\[-2pt] \gamma^k & \longmapsto \mathrm{Log}_{\gamma}(\gamma^k) = k. \end{align*} $$
So the Sidon set
![]() $B(q,\gamma )$
is
$B(q,\gamma )$
is
![]() $B(q,\gamma ) = \{ \mathrm {Log}_{\gamma }(\alpha + a) : a \in \mathbb {F}_q \}.$
$B(q,\gamma ) = \{ \mathrm {Log}_{\gamma }(\alpha + a) : a \in \mathbb {F}_q \}.$
However, the condition
![]() $\gamma ^a-\gamma \in \mathbb {F}_{q}$
implies that
$\gamma ^a-\gamma \in \mathbb {F}_{q}$
implies that
![]() $(\gamma ^a-\gamma )^q=\gamma ^a-\gamma ,$
or equivalently
$(\gamma ^a-\gamma )^q=\gamma ^a-\gamma ,$
or equivalently
which means that
![]() $\gamma ^a$
is a root of the polynomial
$\gamma ^a$
is a root of the polynomial
![]() $f(x)=x^q-x+\beta $
where
$f(x)=x^q-x+\beta $
where
![]() $\beta =\gamma ^q+ \gamma $
. This fact will be used in our construction later.
$\beta =\gamma ^q+ \gamma $
. This fact will be used in our construction later.
We relate the Sidon sets constructed by Bose [Reference Bose1] with affine subspaces of
![]() $ \mathbb {F} _ {q ^ 2} $
of dimension one. We define Sidon arrays which are combinatorial objects giving a partition of the group
$ \mathbb {F} _ {q ^ 2} $
of dimension one. We define Sidon arrays which are combinatorial objects giving a partition of the group
![]() $\mathbb {Z} _{q ^ 2} $
as a union of Sidon sets. Sidon arrays are related to the Sidon spaces constructed in [Reference Roth, Raviv and Tamo10] and used there to describe cyclic subspace codes. We take a different approach inspired by Bose’s construction of Sidon sets. We also use linear recurring sequences to quickly obtain Bose-type Sidon sets without the need to use the discrete logarithm. Our method is as fast as the one described in [Reference Lindström7], at least when q is a prime.
$\mathbb {Z} _{q ^ 2} $
as a union of Sidon sets. Sidon arrays are related to the Sidon spaces constructed in [Reference Roth, Raviv and Tamo10] and used there to describe cyclic subspace codes. We take a different approach inspired by Bose’s construction of Sidon sets. We also use linear recurring sequences to quickly obtain Bose-type Sidon sets without the need to use the discrete logarithm. Our method is as fast as the one described in [Reference Lindström7], at least when q is a prime.
The article is organised as follows. In Section 2, we review facts about linearised polynomials and their relation with subspaces of
![]() $ \mathbb {F} _ {q ^ 2} $
defined over
$ \mathbb {F} _ {q ^ 2} $
defined over
![]() $\mathbb {F}_q$
and we prove our main result Theorem 2.5. In Section 3, we define the concept of Sidon array and we give some examples. Section 4 is devoted to the fast construction of Bose-type Sidon sets.
$\mathbb {F}_q$
and we prove our main result Theorem 2.5. In Section 3, we define the concept of Sidon array and we give some examples. Section 4 is devoted to the fast construction of Bose-type Sidon sets.
2 Linearised polynomials and Sidon sets
We start by recalling some elementary facts about linearised polynomials (for a detailed exposition, we refer to [Reference Lidl and Niederreiter6, Ch. 3]).
Let
![]() $\mathbb {F}_q$
and
$\mathbb {F}_q$
and
![]() $\mathbb {F}_{q^m}$
be the finite fields with q and
$\mathbb {F}_{q^m}$
be the finite fields with q and
![]() $q^m$
elements, respectively, where q is a prime or a prime power. Polynomials over
$q^m$
elements, respectively, where q is a prime or a prime power. Polynomials over
![]() $\mathbb {F}_{q^m}$
of the form
$\mathbb {F}_{q^m}$
of the form
 $$ \begin{align*} L(x):=\sum_{i=0}^{n}c_ix^{q^i}, \quad n \in \mathbb{N}, \end{align*} $$
$$ \begin{align*} L(x):=\sum_{i=0}^{n}c_ix^{q^i}, \quad n \in \mathbb{N}, \end{align*} $$
are often known as q-polynomials or linearised polynomials. This terminology stems from the following property: if F is an arbitrary extension field of
![]() $\mathbb {F}_{q^m}$
, then
$\mathbb {F}_{q^m}$
, then
 $$ \begin{align*} L(\alpha+\beta) & =L(\alpha)+ L(\,\beta)\quad \text{for all}\;\alpha, \beta \in F, \\ L(c\alpha) & =cL(\alpha)\quad \text{for all } c \in \mathbb{F}_{q} \;\text{and all } \alpha \in F. \end{align*} $$
$$ \begin{align*} L(\alpha+\beta) & =L(\alpha)+ L(\,\beta)\quad \text{for all}\;\alpha, \beta \in F, \\ L(c\alpha) & =cL(\alpha)\quad \text{for all } c \in \mathbb{F}_{q} \;\text{and all } \alpha \in F. \end{align*} $$
So these special polynomials induce linear transformations of
![]() $\mathbb {F}_{q^m}$
and
$\mathbb {F}_{q^m}$
and
![]() $\mathbb {F}_{q}$
. An important example of a linearised polynomial is the so-called trace polynomial
$\mathbb {F}_{q}$
. An important example of a linearised polynomial is the so-called trace polynomial
 $$ \begin{align*}\mathrm{Tr}(x)=\sum_{i=0}^{m-1}x^{q^i}\end{align*} $$
$$ \begin{align*}\mathrm{Tr}(x)=\sum_{i=0}^{m-1}x^{q^i}\end{align*} $$
defining the trace function of
![]() $\mathbb {F}_{q^m}$
over
$\mathbb {F}_{q^m}$
over
![]() $\mathbb {F}_{q}$
. The following well-known theorem shows the special character of the set of roots of a linearised polynomial.
$\mathbb {F}_{q}$
. The following well-known theorem shows the special character of the set of roots of a linearised polynomial.
Theorem 2.1 [Reference Lidl and Niederreiter6, Ch. 3]
Let
![]() $L(x)$
be a nonzero linearised polynomial over
$L(x)$
be a nonzero linearised polynomial over
![]() $\mathbb {F}_{q^m}$
and let the extension field
$\mathbb {F}_{q^m}$
and let the extension field
![]() $\mathbb {F}_{q^s}$
of
$\mathbb {F}_{q^s}$
of
![]() $\mathbb {F}_{q^m}$
contain all the roots of
$\mathbb {F}_{q^m}$
contain all the roots of
![]() $L(x)$
. Then each root of
$L(x)$
. Then each root of
![]() $L(x)$
has the same multiplicity, which is either
$L(x)$
has the same multiplicity, which is either
![]() $1$
or a power of q, and the roots form a linear subspace of
$1$
or a power of q, and the roots form a linear subspace of
![]() $\mathbb {F}_{q^s}$
, regarded as a vector space over
$\mathbb {F}_{q^s}$
, regarded as a vector space over
![]() $\mathbb {F}_{q}$
. Reciprocally, let U be a linear subspace of
$\mathbb {F}_{q}$
. Reciprocally, let U be a linear subspace of
![]() $\mathbb {F}_{q^m}$
, considered as a vector space over
$\mathbb {F}_{q^m}$
, considered as a vector space over
![]() $\mathbb {F}_{q}$
. Then for any nonnegative integer k, the polynomial
$\mathbb {F}_{q}$
. Then for any nonnegative integer k, the polynomial
 $$ \begin{align*}L(x)=\prod_{\beta \in U}(x-\beta)^k\end{align*} $$
$$ \begin{align*}L(x)=\prod_{\beta \in U}(x-\beta)^k\end{align*} $$
is a linearised polynomial over
![]() $\mathbb {F}_{q^m}.$
$\mathbb {F}_{q^m}.$
A polynomial of the form
![]() $A(x)=L(x)+\alpha $
, where
$A(x)=L(x)+\alpha $
, where
![]() $L(x)$
is a linearised polynomial over
$L(x)$
is a linearised polynomial over
![]() $\mathbb {F}_{q^m}$
and
$\mathbb {F}_{q^m}$
and
![]() $\alpha \in \mathbb {F}_{q^m}$
, is called an affine q-polynomial over
$\alpha \in \mathbb {F}_{q^m}$
, is called an affine q-polynomial over
![]() $\mathbb {F}_{q^m}$
. As in the case of linearised polynomials, there is an analogue of Theorem 2.1.
$\mathbb {F}_{q^m}$
. As in the case of linearised polynomials, there is an analogue of Theorem 2.1.
Theorem 2.2 [Reference Lidl and Niederreiter6, Ch. 3]
Let
![]() $A(x)$
be an affine q-polynomial over
$A(x)$
be an affine q-polynomial over
![]() $\mathbb {F}_{q^m}$
and let the extension field
$\mathbb {F}_{q^m}$
and let the extension field
![]() $\mathbb {F}_{q^s}$
of
$\mathbb {F}_{q^s}$
of
![]() $\mathbb {F}_{q^m}$
contain all the roots of
$\mathbb {F}_{q^m}$
contain all the roots of
![]() $A(x)$
. Then each root of
$A(x)$
. Then each root of
![]() $A(x)$
has the same multiplicity, which is either
$A(x)$
has the same multiplicity, which is either
![]() $1$
or a power of q, and the roots form an affine subspace of
$1$
or a power of q, and the roots form an affine subspace of
![]() $\mathbb {F}_{q^s}$
, regarded as a vector space over
$\mathbb {F}_{q^s}$
, regarded as a vector space over
![]() $\mathbb {F}_{q}$
. Reciprocally, let T be an affine subspace of
$\mathbb {F}_{q}$
. Reciprocally, let T be an affine subspace of
![]() $\mathbb {F}_{q^m}$
, considered as a vector space over
$\mathbb {F}_{q^m}$
, considered as a vector space over
![]() $\mathbb {F}_{q}$
. Then for any nonnegative integer k, the polynomial
$\mathbb {F}_{q}$
. Then for any nonnegative integer k, the polynomial
 $$ \begin{align*}A(x)=\prod_{\beta \in T}(x-\beta)^{q^k}\end{align*} $$
$$ \begin{align*}A(x)=\prod_{\beta \in T}(x-\beta)^{q^k}\end{align*} $$
is an affine q-polynomial over
![]() $\mathbb {F}_{q^m}.$
$\mathbb {F}_{q^m}.$
Remark 2.3. The polynomial
![]() $f(x)=x^q-x+\beta $
in Bose’s construction is an affine q-polynomial over
$f(x)=x^q-x+\beta $
in Bose’s construction is an affine q-polynomial over
![]() $\mathbb {F}_{q^2}$
, so it defines an affine line in
$\mathbb {F}_{q^2}$
, so it defines an affine line in
![]() $\mathbb {F}_{q^2}$
.
$\mathbb {F}_{q^2}$
.
In this paper, we are interested in the special case
![]() $L(x)=x^q+ax$
defined over
$L(x)=x^q+ax$
defined over
![]() $\mathbb {F}_{q^2}$
. If L splits completely over
$\mathbb {F}_{q^2}$
. If L splits completely over
![]() $\mathbb {F}_{q^2}$
, then its roots have multiplicity one and form a vector space of dimension one over
$\mathbb {F}_{q^2}$
, then its roots have multiplicity one and form a vector space of dimension one over
![]() $\mathbb {F}_{q}$
, that is to say a line, denoted by
$\mathbb {F}_{q}$
, that is to say a line, denoted by
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\mathcal {A}$
be the affine line associated to the affine q-polynomial
$\mathcal {A}$
be the affine line associated to the affine q-polynomial
![]() $A(x)=x^q+ax+b$
, when it splits completely over
$A(x)=x^q+ax+b$
, when it splits completely over
![]() $\mathbb {F}_{q^2}$
.
$\mathbb {F}_{q^2}$
.
Consider a line
![]() $\mathcal {L}\subset \mathbb {F}_{q^2}$
, that is,
$\mathcal {L}\subset \mathbb {F}_{q^2}$
, that is,
![]() $\mathcal {L} = \mathrm {Gen}(\theta ):=\lbrace a\theta : a \in \mathbb {F}_q \rbrace $
for some nonzero
$\mathcal {L} = \mathrm {Gen}(\theta ):=\lbrace a\theta : a \in \mathbb {F}_q \rbrace $
for some nonzero
![]() $\theta \in \mathbb {F}_{q^2}$
. Then for every
$\theta \in \mathbb {F}_{q^2}$
. Then for every
![]() $\delta \in \mathbb {F}_{q^2}{\setminus} \mathcal {L}$
, the set
$\delta \in \mathbb {F}_{q^2}{\setminus} \mathcal {L}$
, the set
![]() $\mathcal {A}:=\mathcal {L} + \delta $
is an affine line. Fix once and for all a primitive element
$\mathcal {A}:=\mathcal {L} + \delta $
is an affine line. Fix once and for all a primitive element
![]() $\gamma $
in
$\gamma $
in
![]() $\mathbb {F}_{q^2}^{\times }$
.
$\mathbb {F}_{q^2}^{\times }$
.
Before stating and proving our main result, we require the following simple lemma.
Lemma 2.4 [Reference Ganley4, page 323]
If
![]() $\alpha _1, \alpha _2, \alpha _3$
and
$\alpha _1, \alpha _2, \alpha _3$
and
![]() $\alpha _4 \in \mathbb {F}_q$
are distinct, then the relations
$\alpha _4 \in \mathbb {F}_q$
are distinct, then the relations
cannot hold simultaneously. In other words, any solution
![]() $ (\alpha _1, \alpha _2, \alpha _3, \alpha _4) \in \mathbb {F}_q^4$
of (2.1) satisfies
$ (\alpha _1, \alpha _2, \alpha _3, \alpha _4) \in \mathbb {F}_q^4$
of (2.1) satisfies
![]() $\alpha _1 \in \lbrace \alpha _3, \alpha _4\rbrace $
.
$\alpha _1 \in \lbrace \alpha _3, \alpha _4\rbrace $
.
Theorem 2.5. Let
![]() $\gamma $
be a primitive element in
$\gamma $
be a primitive element in
![]() $\mathbb {F}_{q^2}^{\times }$
and let
$\mathbb {F}_{q^2}^{\times }$
and let
![]() $\theta , \delta \in \mathbb {F}_{q^2}^{\times }$
be such that
$\theta , \delta \in \mathbb {F}_{q^2}^{\times }$
be such that
![]() $\delta \notin \mathcal {L} = \mathrm {Gen}(\theta )$
. Then the set
$\delta \notin \mathcal {L} = \mathrm {Gen}(\theta )$
. Then the set
where
![]() $\mathcal {A}:=\mathcal {L} + \delta $
, is a Sidon set modulo
$\mathcal {A}:=\mathcal {L} + \delta $
, is a Sidon set modulo
![]() $q^2 - 1$
.
$q^2 - 1$
.
Proof. Let
![]() $a_1, a_2, a_3, a_4 $
be any four different elements in
$a_1, a_2, a_3, a_4 $
be any four different elements in
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $a_1 + a_2 = a_3 + a_4$
. Since the sum is taken modulo
$a_1 + a_2 = a_3 + a_4$
. Since the sum is taken modulo
![]() $q^2-1$
and
$q^2-1$
and
![]() $\gamma $
is primitive, the powers of
$\gamma $
is primitive, the powers of
![]() $\gamma ^i$
are different for
$\gamma ^i$
are different for
![]() $1\leq i \leq q^2-1$
and
$1\leq i \leq q^2-1$
and
![]() $\gamma ^{a_1} \cdot \gamma ^{a_2} = \gamma ^{a_3} \cdot \gamma ^{a_4}$
.
$\gamma ^{a_1} \cdot \gamma ^{a_2} = \gamma ^{a_3} \cdot \gamma ^{a_4}$
.
Since the
![]() $\gamma ^{a_i}$
terms are different elements of
$\gamma ^{a_i}$
terms are different elements of
![]() $\mathbb {F}_{q^2}$
and by construction also belong to
$\mathbb {F}_{q^2}$
and by construction also belong to
![]() $\mathcal {A}$
, there exist distinct
$\mathcal {A}$
, there exist distinct
![]() $\alpha _1, \alpha _2, \alpha _3, \alpha _4 \in \mathbb {F}_q$
such that
$\alpha _1, \alpha _2, \alpha _3, \alpha _4 \in \mathbb {F}_q$
such that
![]() $(\alpha _1 \theta + \delta )(\alpha _2 \theta + \delta ) = (\alpha _3 \theta + \delta )(\alpha _4 \theta ~+~\delta )$
, that is,
$(\alpha _1 \theta + \delta )(\alpha _2 \theta + \delta ) = (\alpha _3 \theta + \delta )(\alpha _4 \theta ~+~\delta )$
, that is,
Equation (2.2) is equivalent to
By Lemma 2.4, the expressions
![]() $\alpha _1 \alpha _2 - \alpha _3 \alpha _4$
and
$\alpha _1 \alpha _2 - \alpha _3 \alpha _4$
and
![]() $\alpha _3 + \alpha _4 - \alpha _1 - \alpha _2$
are not zero simultaneously, so we can write
$\alpha _3 + \alpha _4 - \alpha _1 - \alpha _2$
are not zero simultaneously, so we can write
where
![]() $b = \alpha _1 \alpha _2 - \alpha _3 \alpha _4$
and
$b = \alpha _1 \alpha _2 - \alpha _3 \alpha _4$
and
![]() $a = \alpha _3 + \alpha _4 - \alpha _1 - \alpha _2$
. Since
$a = \alpha _3 + \alpha _4 - \alpha _1 - \alpha _2$
. Since
![]() ${b}/{a} \in \mathbb {F}_q$
, (2.3) implies
${b}/{a} \in \mathbb {F}_q$
, (2.3) implies
![]() $\delta \in \mathrm {Gen}(\theta )$
, which contradicts our hypothesis and proves our claim.
$\delta \in \mathrm {Gen}(\theta )$
, which contradicts our hypothesis and proves our claim.
Remark 2.6. Let us consider the linearised polynomial
![]() $ f (x) = x ^ q-x $
, which decomposes completely in
$ f (x) = x ^ q-x $
, which decomposes completely in
![]() $\mathbb {F}_{q^2}$
. Its roots are all the elements of
$\mathbb {F}_{q^2}$
. Its roots are all the elements of
![]() $\mathbb {F}_{q}$
, so the affine polynomial
$\mathbb {F}_{q}$
, so the affine polynomial
![]() $g(x) = f (x-a)$
is also reducible and
$g(x) = f (x-a)$
is also reducible and
Setting
![]() $\beta =a^q+a$
, a straightforward calculation shows that
$\beta =a^q+a$
, a straightforward calculation shows that
![]() $\beta $
has trace 0 and we get Bose’s construction as a particular case.
$\beta $
has trace 0 and we get Bose’s construction as a particular case.
Example 2.7. Let us consider
![]() $q=p=5$
. The polynomial
$q=p=5$
. The polynomial
![]() $ p(x) = x^2 + 4x + 2 $
is primitive over
$ p(x) = x^2 + 4x + 2 $
is primitive over
![]() $ \mathbb {F}_5 $
. Let
$ \mathbb {F}_5 $
. Let
![]() $\gamma $
be a root of
$\gamma $
be a root of
![]() $p(x)$
, so that
$p(x)$
, so that
![]() $\gamma $
is a primitive element. The polynomial
$\gamma $
is a primitive element. The polynomial
![]() $A(x)=x^5 + \gamma ^{16}x + \gamma ^{14}$
splits completely over
$A(x)=x^5 + \gamma ^{16}x + \gamma ^{14}$
splits completely over
![]() $\mathbb {F}_{5^2}$
with roots
$\mathbb {F}_{5^2}$
with roots
![]() $\lbrace \gamma ^4, \gamma ^6, \gamma ^{11}, \gamma ^{14}, \gamma ^{15} \rbrace $
, so the set
$\lbrace \gamma ^4, \gamma ^6, \gamma ^{11}, \gamma ^{14}, \gamma ^{15} \rbrace $
, so the set
![]() $\mathcal {S}:=\lbrace 4,6,11,14,15\rbrace $
is a Sidon set modulo
$\mathcal {S}:=\lbrace 4,6,11,14,15\rbrace $
is a Sidon set modulo
![]() $24$
.
$24$
.
3 Linearised polynomials and Sidon arrays
In this section, we define new objects which we have called Sidon arrays. We first make some further remarks on the linearised polynomials that appear in the construction of Sidon sets in the previous section. We need the following lemma giving conditions for the polynomial
![]() $x^q+ax$
to factorise completely over
$x^q+ax$
to factorise completely over
![]() $\mathbb {F}_{q^2}$
.
$\mathbb {F}_{q^2}$
.
Lemma 3.1 (see [Reference Lidl and Niederreiter6, Theorem 2.24 and Exercise 2.14])
The polynomial
![]() $L(x)=x^q+ax$
in
$L(x)=x^q+ax$
in
![]() $\mathbb {F}_{q^2}[x]$
splits completely over
$\mathbb {F}_{q^2}[x]$
splits completely over
![]() $\mathbb {F}_{q^2}$
if and only if there exists
$\mathbb {F}_{q^2}$
if and only if there exists
![]() $\beta \in \mathbb {F}_{q^2}$
such that
$\beta \in \mathbb {F}_{q^2}$
such that
![]() $a=\beta ^{q-1}$
.
$a=\beta ^{q-1}$
.
Using Lemma 3.1 and since
![]() $f(x)=b^{-q}\mathrm {Tr}(bx)=\prod _{i=1}^{q}(x-b^{-1}\lambda _i)$
, the roots of f can be written as
$f(x)=b^{-q}\mathrm {Tr}(bx)=\prod _{i=1}^{q}(x-b^{-1}\lambda _i)$
, the roots of f can be written as
![]() $\beta \lambda _j$
for
$\beta \lambda _j$
for
![]() $\beta $
a
$\beta $
a
![]() $(q + 1)$
th root of unity and
$(q + 1)$
th root of unity and
![]() $\lambda _j$
ranging over all trace zero elements in
$\lambda _j$
ranging over all trace zero elements in
![]() $\mathbb {F}_{q^2}$
.
$\mathbb {F}_{q^2}$
.
Remark 3.2. The roots of a q-polynomial of the form
![]() $x^q + ax $
form a vector subspace of dimension one over
$x^q + ax $
form a vector subspace of dimension one over
![]() $ \mathbb {F} _q $
and therefore an additive normal subgroup
$ \mathbb {F} _q $
and therefore an additive normal subgroup
![]() $ \mathcal {G} _a $
of
$ \mathcal {G} _a $
of
![]() $ \mathbb {F} _ {q ^ 2} $
with
$ \mathbb {F} _ {q ^ 2} $
with
![]() $ q $
elements. Thus,
$ q $
elements. Thus,
![]() $ \mathbb {F}_{q^2} $
is the union of
$ \mathbb {F}_{q^2} $
is the union of
![]() $ q $
different classes, that is,
$ q $
different classes, that is,
 $$ \begin{align*} \mathbb {F}_ {q^2} = \bigcup_{i = 1}^q (c_i + \mathcal{G}_a) \end{align*} $$
$$ \begin{align*} \mathbb {F}_ {q^2} = \bigcup_{i = 1}^q (c_i + \mathcal{G}_a) \end{align*} $$
with the convention that
![]() $ c_1 = 0 $
corresponds to the class of
$ c_1 = 0 $
corresponds to the class of
![]() $ \mathcal {G} _a $
.
$ \mathcal {G} _a $
.
By Theorem 2.2, the q elements of a class
![]() $c_i + \mathcal {G}_a$
are the roots of an affine polynomial of the form
$c_i + \mathcal {G}_a$
are the roots of an affine polynomial of the form
![]() $f(x)=x^q+ax+b$
. Since
$f(x)=x^q+ax+b$
. Since
![]() $c_i$
belongs to at least one line, there is a linearised polynomial
$c_i$
belongs to at least one line, there is a linearised polynomial
![]() $L(x)$
that has
$L(x)$
that has
![]() $c_i$
as one of its roots. By the description given above for the roots of
$c_i$
as one of its roots. By the description given above for the roots of
![]() $L(x)$
, we can also characterise the roots of the affine polynomial
$L(x)$
, we can also characterise the roots of the affine polynomial
![]() $f(x)$
as
$f(x)$
as
![]() $ \theta \lambda +\beta \mathcal {G}_0$
, where
$ \theta \lambda +\beta \mathcal {G}_0$
, where
![]() $\mathcal {G}_0$
is the additive subgroup in
$\mathcal {G}_0$
is the additive subgroup in
![]() $\mathbb {F}_{q^2}$
of trace zero elements,
$\mathbb {F}_{q^2}$
of trace zero elements,
![]() $\beta $
and
$\beta $
and
![]() $\theta $
are
$\theta $
are
![]() $(q+1)$
th roots of unity and
$(q+1)$
th roots of unity and
![]() $\lambda \in \mathcal {G}_0$
is such that
$\lambda \in \mathcal {G}_0$
is such that
![]() $\theta \lambda \notin \beta \mathcal {G}_0$
.
$\theta \lambda \notin \beta \mathcal {G}_0$
.
By Remark 3.2, the elements of
![]() $ \mathbb {F} _ {q ^ 2} $
can be organised in a
$ \mathbb {F} _ {q ^ 2} $
can be organised in a
![]() $ q \times q $
matrix
$ q \times q $
matrix
![]() $ \mathcal {S}$
such that the ith row is the class
$ \mathcal {S}$
such that the ith row is the class
![]() $ (c_i + \mathcal {G} _a) $
. Recall that the elements of
$ (c_i + \mathcal {G} _a) $
. Recall that the elements of
![]() $\mathcal {G} _a$
are of the form
$\mathcal {G} _a$
are of the form
![]() $\beta \lambda _j$
, where
$\beta \lambda _j$
, where
![]() $\beta $
is a
$\beta $
is a
![]() $(q + 1)$
th root of unity and
$(q + 1)$
th root of unity and
![]() $\lambda _j$
ranges over all trace zero elements in
$\lambda _j$
ranges over all trace zero elements in
![]() $\mathbb {F}_{q^2}$
. So the entries of
$\mathbb {F}_{q^2}$
. So the entries of
![]() $\mathcal {S}$
are
$\mathcal {S}$
are
![]() $s_{i,j}=c_i+\beta \lambda _j$
.
$s_{i,j}=c_i+\beta \lambda _j$
.
Definition 3.3. A Sidon array of order
![]() $ q $
is a matrix of order
$ q $
is a matrix of order
![]() $ q \times q $
whose entries are all integers in the interval
$ q \times q $
whose entries are all integers in the interval
![]() $ [0, q ^2-1] $
such that any row or column other than the first row and first column is a Sidon set modulo
$ [0, q ^2-1] $
such that any row or column other than the first row and first column is a Sidon set modulo
![]() $ q^2-1$
.
$ q^2-1$
.
From the comments and Remark 3.2, Sidon arrays of order
![]() $ q $
exist and they can be constructed as indicated above.
$ q $
exist and they can be constructed as indicated above.
Example 3.4. Let us consider
![]() $q=p=5$
. The polynomial
$q=p=5$
. The polynomial
![]() $ p(x) = x^2 + 4x + 2 $
is primitive over
$ p(x) = x^2 + 4x + 2 $
is primitive over
![]() $ \mathbb {F}_5 $
with root
$ \mathbb {F}_5 $
with root
![]() $\gamma $
. Take
$\gamma $
. Take
![]() $a=\gamma ^{16}$
. Then
$a=\gamma ^{16}$
. Then
![]() $\mathcal {G}_a=\lbrace 0, \gamma ^{19}\gamma ,\gamma ^7, \gamma ^{13} \rbrace $
is the set of roots of
$\mathcal {G}_a=\lbrace 0, \gamma ^{19}\gamma ,\gamma ^7, \gamma ^{13} \rbrace $
is the set of roots of
![]() $f(x)=x^5 + \gamma ^{16}x$
. The elements of
$f(x)=x^5 + \gamma ^{16}x$
. The elements of
![]() $\mathbb {F}_{q^2}$
can be organised as in Table 1.
$\mathbb {F}_{q^2}$
can be organised as in Table 1.
Table 1 A Sidon array modulo 25 before taking logarithms.

Taking logarithms, with the convention
![]() $ \mathrm {Log}_ \gamma (0) = 24 $
, gives Table 2.
$ \mathrm {Log}_ \gamma (0) = 24 $
, gives Table 2.
Table 2 A Sidon array modulo 25.

It can be verified that the table meets the conditions for a Sidon array. In fact, the second row corresponds to the set obtained in Example 2.7, as logarithms of the roots of the polynomial
![]() $A(x)=x^5 + \gamma ^{16}x + \gamma ^{14}$
.
$A(x)=x^5 + \gamma ^{16}x + \gamma ^{14}$
.
Sidon arrays are a refinement of the partitions in the case
![]() $ h = 2 $
introduced by Gilberto et al. [Reference Gilberto, Alberto and Velasquez5]. They proved the following theorem.
$ h = 2 $
introduced by Gilberto et al. [Reference Gilberto, Alberto and Velasquez5]. They proved the following theorem.
Theorem 3.5 [Reference Gilberto, Alberto and Velasquez5]
There is a partition of
![]() $\,\mathbb {Z}_{q^h}$
into
$\,\mathbb {Z}_{q^h}$
into
![]() $B_d$
sets modulo
$B_d$
sets modulo
![]() $q^h-1$
where d runs through the divisors of h.
$q^h-1$
where d runs through the divisors of h.
In our case, taking
![]() $h = 2$
, we have a partition of
$h = 2$
, we have a partition of
![]() $\mathbb {Z}_{q^2}$
modulo
$\mathbb {Z}_{q^2}$
modulo
![]() $q ^ 2-1$
as
$q ^ 2-1$
as
![]() $B_2$
sets, that is, Sidon sets.
$B_2$
sets, that is, Sidon sets.
A Golomb ruler
![]() $G_k$
of order k is an ordered set of k integers
$G_k$
of order k is an ordered set of k integers
![]() $(a_1, a_2, \ldots , a_k)$
such that
$(a_1, a_2, \ldots , a_k)$
such that
![]() $0 \leq a_1 < a_2 < \cdots < a_k$
and all the differences
$0 \leq a_1 < a_2 < \cdots < a_k$
and all the differences
![]() $\lbrace a_i - a_j \mid 1 \leq j < i \leq k\rbrace $
are distinct. A
$\lbrace a_i - a_j \mid 1 \leq j < i \leq k\rbrace $
are distinct. A
![]() $(v, k)$
-modular Golomb ruler is an ordered set of k integers
$(v, k)$
-modular Golomb ruler is an ordered set of k integers
![]() $(a_1, a_2, \ldots , a_k)$
such that
$(a_1, a_2, \ldots , a_k)$
such that
![]() $0 \leq a_1 < a_2 < \cdots < a_k$
and all the differences
$0 \leq a_1 < a_2 < \cdots < a_k$
and all the differences
![]() $\lbrace a_i - a_j \mid 1 \leq j < i \leq k,\; i \neq j \rbrace $
are distinct and nonzero modulo v.
$\lbrace a_i - a_j \mid 1 \leq j < i \leq k,\; i \neq j \rbrace $
are distinct and nonzero modulo v.
Sidon sets are widely used in the construction of Golomb rulers and modular Golomb rulers (see [Reference Caicedo, Martos and Trujillo2, Reference Davydov, Faina, Giulietti, Marcugini and Pambianco3, Reference Martos Ojeda, Delgado Ordoñez and Trujillo Solarte8]). In this context, disjoint Golomb rulers (see [Reference Xiu, Fan and Liang11]) are similar to Sidon arrays. This is another reason for our interest in Sidon arrays, since they could have similar properties and applications as disjoint Golomb Rulers.
4 Linear recurrences and fast construction of Sidon sets
We begin this section with the definition and properties of recurrence relations, which we need for our applications. For more details, see [Reference Lidl and Niederreiter6, Ch. 6].
Definition 4.1. Let
![]() $k \in \mathbb {N}$
. A sequence
$k \in \mathbb {N}$
. A sequence
![]() $s_0,s_1,\ldots $
of elements of
$s_0,s_1,\ldots $
of elements of
![]() $\mathbb {F}_q$
is called a linear recurring sequence of order k in
$\mathbb {F}_q$
is called a linear recurring sequence of order k in
![]() $\mathbb {F}_q$
if there are elements
$\mathbb {F}_q$
if there are elements
![]() $a,a_0,a_1,\ldots , a_{k-1} \in \mathbb {F}_q$
such that
$a,a_0,a_1,\ldots , a_{k-1} \in \mathbb {F}_q$
such that
The terms
![]() $s_0 , s_1,\ldots , s_{k-1}$
determining the sequence are called initial values. Equation (4.1) is called a linear recurrence relation of order k. If
$s_0 , s_1,\ldots , s_{k-1}$
determining the sequence are called initial values. Equation (4.1) is called a linear recurrence relation of order k. If
![]() $a=0$
it is called homogeneous, otherwise it is called nonhomogeneous. The vector
$a=0$
it is called homogeneous, otherwise it is called nonhomogeneous. The vector
![]() $(s_n, s_{n+1},\ldots , s_{n+k-1})$
is called an nth state vector; in particular,
$(s_n, s_{n+1},\ldots , s_{n+k-1})$
is called an nth state vector; in particular,
![]() $(s_0, s_{1},\ldots , s_{k-1})$
is called an initial state vector. Linear recurring sequences in
$(s_0, s_{1},\ldots , s_{k-1})$
is called an initial state vector. Linear recurring sequences in
![]() $\mathbb {F}_q$
are eventually periodic. More precisely, we have the following result.
$\mathbb {F}_q$
are eventually periodic. More precisely, we have the following result.
Theorem 4.2 (see [Reference Lidl and Niederreiter6, page 194])
If
![]() $s_0,s_1,\ldots $
is a linear recurring sequence in a finite field satisfying the linear recurrence relation (4.1) and if the coefficient
$s_0,s_1,\ldots $
is a linear recurring sequence in a finite field satisfying the linear recurrence relation (4.1) and if the coefficient
![]() $a_0$
is nonzero, then the sequence
$a_0$
is nonzero, then the sequence
![]() $s_0,s_1,\ldots $
is periodic.
$s_0,s_1,\ldots $
is periodic.
Suppose that the affine polynomial
![]() $ f (x) = x^q + ax + b $
factorises as a product of linear polynomials over
$ f (x) = x^q + ax + b $
factorises as a product of linear polynomials over
![]() $\mathbb {F}_{q^2}$
, so its roots lie on an affine line and therefore their discrete logarithms form a Sidon set modulo
$\mathbb {F}_{q^2}$
, so its roots lie on an affine line and therefore their discrete logarithms form a Sidon set modulo
![]() $q^2-1$
. As remarked above,
$q^2-1$
. As remarked above,
![]() $f(x)=\beta ^{-q} \mathrm {Tr}(\,\beta x+ \alpha )$
for some nonzero
$f(x)=\beta ^{-q} \mathrm {Tr}(\,\beta x+ \alpha )$
for some nonzero
![]() $\beta , \alpha \in \mathbb {F}_{q^2}$
. So if
$\beta , \alpha \in \mathbb {F}_{q^2}$
. So if
![]() $\theta $
is a root of
$\theta $
is a root of
![]() $f(x)$
, then it is also a root of
$f(x)$
, then it is also a root of
![]() $\mathrm {Tr}(\,\beta x+ \alpha )$
. We will use this fact to give a fast construction of Sidon sets without the need to take discrete logarithms.
$\mathrm {Tr}(\,\beta x+ \alpha )$
. We will use this fact to give a fast construction of Sidon sets without the need to take discrete logarithms.
Fix a primitive element
![]() $\gamma $
of
$\gamma $
of
![]() $\mathbb {F}_{q^2}$
and define the sequence
$\mathbb {F}_{q^2}$
and define the sequence
![]() $s_i:=\mathrm{Tr}(\,\beta \gamma ^i+\alpha ) \in \mathbb {F}_q$
. By the properties of the trace polynomial, it is easy to prove that the sequence
$s_i:=\mathrm{Tr}(\,\beta \gamma ^i+\alpha ) \in \mathbb {F}_q$
. By the properties of the trace polynomial, it is easy to prove that the sequence
![]() $s_i$
is periodic with period
$s_i$
is periodic with period
![]() $q^2-1$
and therefore a linear recurring sequence of order k in
$q^2-1$
and therefore a linear recurring sequence of order k in
![]() $\mathbb {F}_q$
for some k. The next theorem follows from the above discussion and the construction in Section 2.
$\mathbb {F}_q$
for some k. The next theorem follows from the above discussion and the construction in Section 2.
Theorem 4.3. Let
![]() $s_i$
be the sequence defined above. Then the set
$s_i$
be the sequence defined above. Then the set
![]() $\mathcal{S}$
defined by
$\mathcal{S}$
defined by
![]() $\mathcal {S}:=\lbrace i \pmod {q^2-1} \mid s_i = 0\rbrace $
is a Sidon set modulo
$\mathcal {S}:=\lbrace i \pmod {q^2-1} \mid s_i = 0\rbrace $
is a Sidon set modulo
![]() $q^2-1$
.
$q^2-1$
.
Although the definition of the set does not involve discrete logarithms, there is still the problem of evaluating the trace polynomial and calculating all the powers of the primitive element
![]() $\gamma $
. Using the fact that the sequence is recurrent, we can reduce our problem to calculate only the initial values of the recurrence, with the rest reduced to arithmetic on
$\gamma $
. Using the fact that the sequence is recurrent, we can reduce our problem to calculate only the initial values of the recurrence, with the rest reduced to arithmetic on
![]() $\mathbb {F}_q$
.
$\mathbb {F}_q$
.
Since
![]() $ \gamma $
is a primitive element, there exist
$ \gamma $
is a primitive element, there exist
![]() $ n_0 $
and
$ n_0 $
and
![]() $ m_0 $
such that
$ m_0 $
such that
![]() $ \beta = \gamma ^ {n_0} $
and
$ \beta = \gamma ^ {n_0} $
and
![]() $ \alpha = \gamma ^ {m_0} $
. In
$ \alpha = \gamma ^ {m_0} $
. In
![]() $\mathbb {F}_q$
,
$\mathbb {F}_q$
,
where
![]() $t_i:=\mathrm {Tr}(\gamma ^i)$
is the sequence given by the trace. Also,
$t_i:=\mathrm {Tr}(\gamma ^i)$
is the sequence given by the trace. Also,
![]() $ t_i $
is periodic with period
$ t_i $
is periodic with period
![]() $ q^2-1 $
.
$ q^2-1 $
.
Let
![]() $ p(x) = x^2-a_1x-a_0 \in \mathbb {F}_q[x] $
be the minimal polynomial of
$ p(x) = x^2-a_1x-a_0 \in \mathbb {F}_q[x] $
be the minimal polynomial of
![]() $ \gamma $
. Then we have
$ \gamma $
. Then we have
![]() $ \gamma ^2 = a_1 \gamma + a_0 $
and multiplying by
$ \gamma ^2 = a_1 \gamma + a_0 $
and multiplying by
![]() $ \gamma ^i $
gives
$ \gamma ^i $
gives
![]() $ \gamma ^{i + 2} = a_1 \gamma ^{i + 1} + a_0 \gamma ^i $
. Taking the trace on both sides,
$ \gamma ^{i + 2} = a_1 \gamma ^{i + 1} + a_0 \gamma ^i $
. Taking the trace on both sides,
That is, the recurrence has order
![]() $ 2 $
and the coefficients of the recurrence are the coefficients of the minimal polynomial
$ 2 $
and the coefficients of the recurrence are the coefficients of the minimal polynomial
![]() $ p(x) $
. So we only need to find the initial values
$ p(x) $
. So we only need to find the initial values
![]() $ t_0 $
and
$ t_0 $
and
![]() $ t_1 $
:
$ t_1 $
:
the last equation because
![]() $ \gamma $
and
$ \gamma $
and
![]() $ \gamma ^q $
are conjugates. Thus the sequence
$ \gamma ^q $
are conjugates. Thus the sequence
![]() $ s_i $
is completely determined. However, this is not yet an effective method because if
$ s_i $
is completely determined. However, this is not yet an effective method because if
![]() $ n_0 $
and
$ n_0 $
and
![]() $ m_0 $
are large, we need to calculate many terms of the recurrence
$ m_0 $
are large, we need to calculate many terms of the recurrence
![]() $t_i$
. Instead, we use the particular case
$t_i$
. Instead, we use the particular case
![]() $ \beta = 1 $
, that is, we consider the sequence
$ \beta = 1 $
, that is, we consider the sequence
![]() $ s_i = \mathrm {Tr} (x + \alpha ) = t_i + t_{m_0} $
. Set
$ s_i = \mathrm {Tr} (x + \alpha ) = t_i + t_{m_0} $
. Set
![]() $ b = t_ {m_0} $
so that
$ b = t_ {m_0} $
so that
![]() $ t_i = s_i-b $
. Substituting this in (4.2) gives
$ t_i = s_i-b $
. Substituting this in (4.2) gives
 $$ \begin{align*} s_{n+2}&= a_1(s_{n+1}-b)+a_0(s_n-b)+b \\[2pt] &= a_1s_{n+1}+a_0s_n+b(1-a_1-a_0) \\[2pt] &= a_1s_{n+1}+a_0s_n+bp(1). \end{align*} $$
$$ \begin{align*} s_{n+2}&= a_1(s_{n+1}-b)+a_0(s_n-b)+b \\[2pt] &= a_1s_{n+1}+a_0s_n+b(1-a_1-a_0) \\[2pt] &= a_1s_{n+1}+a_0s_n+bp(1). \end{align*} $$
From this discussion, we derive the following result.
Theorem 4.4. Let
![]() $ b \in \mathbb {F}_q $
and
$ b \in \mathbb {F}_q $
and
![]() $ f(x) = x ^ 2-a_1x-a_0 \in \mathbb {F}_q [x] $
be a primitive polynomial. Define the nonhomogeneous sequence
$ f(x) = x ^ 2-a_1x-a_0 \in \mathbb {F}_q [x] $
be a primitive polynomial. Define the nonhomogeneous sequence
![]() $ s_{n + 2} = a_1s_ {n + 1} + a_0s_n + a $
with
$ s_{n + 2} = a_1s_ {n + 1} + a_0s_n + a $
with
![]() $ s_0 = 2 + b $
,
$ s_0 = 2 + b $
,
![]() $ s_1 = -a_1 + b $
and
$ s_1 = -a_1 + b $
and
![]() $ a = bf (1) $
. Then the set
$ a = bf (1) $
. Then the set
![]() $ \mathcal {S}: = \lbrace i \pmod {(q ^ 2-1)} \mid s_i = 0 \rbrace $
is a Sidon set modulo
$ \mathcal {S}: = \lbrace i \pmod {(q ^ 2-1)} \mid s_i = 0 \rbrace $
is a Sidon set modulo
![]() $ q ^ 2-1 $
.
$ q ^ 2-1 $
.
The result of the previous theorem can be described algorithmically as shown in Algorithm 1.
Algorithm 1: SidonSets

Algorithm 1 requires calculation of
![]() $O(q^2)$
terms to form the period and the calculations being done in
$O(q^2)$
terms to form the period and the calculations being done in
![]() $\mathbb {F}_q$
. In [Reference Lindström7, Theorem 2.1], the author shows that Bose-type Sidon sets can be constructed without taking logarithms, only calculating certain powers and doing arithmetic modulo
$\mathbb {F}_q$
. In [Reference Lindström7, Theorem 2.1], the author shows that Bose-type Sidon sets can be constructed without taking logarithms, only calculating certain powers and doing arithmetic modulo
![]() $q^2-1$
, that is, with the same complexity. When
$q^2-1$
, that is, with the same complexity. When
![]() $q=p$
with p prime, [Reference Lindström7] also gives a fast criterion to construct primitive polynomials.
$q=p$
with p prime, [Reference Lindström7] also gives a fast criterion to construct primitive polynomials.
Example 4.5. Let us consider
![]() $q=p=5$
. The polynomial
$q=p=5$
. The polynomial
![]() $ p(x) = x^2 + 4x + 2 $
is irreducible over
$ p(x) = x^2 + 4x + 2 $
is irreducible over
![]() $ \mathbb {F}_5 $
and primitive. Taking
$ \mathbb {F}_5 $
and primitive. Taking
![]() $ b = 2 $
, we construct the first 25 terms of the sequence
$ b = 2 $
, we construct the first 25 terms of the sequence
![]() $ \{4, 1, 2, 4, 4, 0, 1, 0, 2, 1, 1, 3, 0, 3, 2, 0, 0, 4, 3, 4, 2, 3, 3, 1\} $
and get the set
$ \{4, 1, 2, 4, 4, 0, 1, 0, 2, 1, 1, 3, 0, 3, 2, 0, 0, 4, 3, 4, 2, 3, 3, 1\} $
and get the set
![]() $ \mathcal {S}: = \lbrace 5,7,12,15,16 \rbrace $
which is a Sidon set modulo
$ \mathcal {S}: = \lbrace 5,7,12,15,16 \rbrace $
which is a Sidon set modulo
![]() $ 24 $
. This can be found by considering the polynomial
$ 24 $
. This can be found by considering the polynomial
![]() $ x ^ 5 + \gamma ^ {20} x + \gamma ^ {19} $
with
$ x ^ 5 + \gamma ^ {20} x + \gamma ^ {19} $
with
![]() $ \gamma $
a root of
$ \gamma $
a root of
![]() $p(x)$
.
$p(x)$
.