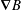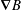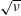1 Introduction
For birth alphas the magnetic drift due to the gradient of the magnetic field,
$\unicode[STIX]{x1D735}B$
, is more important than the electric or
$\boldsymbol{E}\times \boldsymbol{B}$
drift. However, no satisfactory analytic evaluation of collisional transport is presently available to test simulations of alpha transport in the presence of ripple when
$\unicode[STIX]{x1D735}B$
drift dominates. Here, it is demonstrated that in the weak ripple limit analytic expressions for the alpha fluxes can be obtained and used to place constraints on the ripple that can be tolerated, as well as be used to validate simulations.
In the presence of
$\unicode[STIX]{x1D735}B$
drift a narrow boundary layer must form just inside the trapped–passing boundary to allow the finite trapped response to match to the vanishing response of the well-confined passing alpha. The boundary layer always results in alpha particle and energy diffusivities proportional to the square root of the appropriate collision frequency,
$\unicode[STIX]{x1D708}$
. The behaviour is similar to the
$\sqrt{\unicode[STIX]{x1D708}}$
regime in stellarators as approximately treated by Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969) and Ho & Kulsrud (Reference Ho and Kulsrud1987), and more rigorously formulated by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), and recently applied to tokamaks by Catto (Reference Catto2018).
Physically the transport is expected to be a result of the sensitivity of trapped energetic alphas in tokamaks to ripple in the vicinity of their turning points (Goldston, White & Boozer Reference Goldston, White and Boozer1981; Linsker & Boozer Reference Linsker and Boozer1982; Yushmanov Reference Yushmanov1982, Reference Yushmanov1983; Mynick Reference Mynick1986; White Reference White2001). However, these latter references do not consider the collisional boundary layer analysis associated with the
$\unicode[STIX]{x1D735}B$
drifting barely trapped alphas and so obtain diffusivities linear in
$\unicode[STIX]{x1D708}$
or stochastic transport. By regarding collisions as a perturbation instead of on equal footing with the
$\unicode[STIX]{x1D735}B$
drift, they ignore the vital barely trapped alphas that their treatments are unable to properly handle.
The ripple
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717})$
due to
$N$
toroidal field coils is normally defined as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}=(B_{\max }-B_{\min })/(B_{\max }+B_{\min }), & & \displaystyle\end{eqnarray}$$
with
$B_{\max }$
and
$B_{\min }$
the maximum and minimum fields on the flux surface labelled by the poloidal flux function
$\unicode[STIX]{x1D713}$
, and
$\unicode[STIX]{x1D717}$
the poloidal angle variable. The ripple form
$$\begin{eqnarray}\displaystyle B=B_{0}[1-\unicode[STIX]{x1D700}(\unicode[STIX]{x1D713})\cos \unicode[STIX]{x1D717}-\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717})\cos (N\unicode[STIX]{x1D701})], & & \displaystyle\end{eqnarray}$$
is often used to obtain explicit results, with
$\unicode[STIX]{x1D700}$
the inverse aspect ratio,
$B_{0}$
the magnetic field at the magnetic axis,
$\unicode[STIX]{x1D701}$
the toroidal angle variable and
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717})$
a slow function of
$\unicode[STIX]{x1D717}$
. To avoid introducing ripple wells along the magnetic field
$\boldsymbol{B}$
,
$\unicode[STIX]{x1D6FF}\ll qN\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D700}$
must be assumed, where
$q$
is the safety factor and
$\unicode[STIX]{x1D700}/q\simeq B_{p}/B_{0}$
, with
$B_{p}$
the poloidal magnetic field. By considering the weak ripple limit, the departure from axisymmetry only matters for the radial magnetic drift.
The proportionality of the diffusivity to
$\sqrt{\unicode[STIX]{x1D708}}$
in the boundary layer treatments of Galeev et al. (Reference Galeev, Sagdeev, Furth and Rosenbluth1969), Ho & Kulsrud (Reference Ho and Kulsrud1987), Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), Catto (Reference Catto2018) is very different than the precession or tangential drift results of Goldston et al. (Reference Goldston, White and Boozer1981), Linsker & Boozer (Reference Linsker and Boozer1982), Yushmanov (Reference Yushmanov1982, Reference Yushmanov1983) and Mynick (Reference Mynick1986). They do not allow for the existence of a narrow collisional boundary layer that is necessary to make the perturbed trapped distribution function vanish at the trapped–passing boundary. In the
$\boldsymbol{E}\times \boldsymbol{B}$
toroidal precession, weak ripple case considered by Linsker & Boozer (Reference Linsker and Boozer1982) and Mynick (Reference Mynick1986) the heuristic particle diffusivity of their equations (27) and (4), respectively, is
$$\begin{eqnarray}\displaystyle D_{\text{LBM}}^{\text{tp}}\sim \unicode[STIX]{x1D700}^{1/2}(q^{2}N^{2}\unicode[STIX]{x1D708}/\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6FF}qN\unicode[STIX]{x1D70C}_{0}v_{0}/rN\unicode[STIX]{x1D714}\sqrt{qN})^{2}=[\unicode[STIX]{x1D708}Nq^{3}\unicode[STIX]{x1D6FF}^{2}\unicode[STIX]{x1D70C}_{0}^{2}v_{0}^{2}/\unicode[STIX]{x1D700}^{1/2}(r\,\unicode[STIX]{x1D714})^{2}]\propto \unicode[STIX]{x1D708}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}$
is the pitch angle scattering frequency of alphas off the background ions,
$\unicode[STIX]{x1D714}\sim cE_{r}/RB_{p}\sim cqE_{r}/rB_{0}$
is the precession frequency with
$E_{r}$
the radial component of the electric field
$\boldsymbol{E}$
and
$c$
the speed of light and
$v_{0}$
and
$\unicode[STIX]{x1D70C}_{0}$
are the birth speed and birth gyroradius of the alphas. Both Linsker & Boozer and Mynick use
$\unicode[STIX]{x1D700}^{1/2}$
as the trapped fraction, as there is no boundary layer in their calculation, and
$q^{2}N^{2}\unicode[STIX]{x1D708}/\unicode[STIX]{x1D700}$
as the effective collision frequency with a step size of
$\unicode[STIX]{x1D6FF}qN\unicode[STIX]{x1D70C}_{0}v_{0}/rN\unicode[STIX]{x1D714}\sqrt{qN}$
. However, the perturbed distribution functions as given by their equations (32) and (47), respectively, do not vanish at the trapped–passing boundary as required to match onto the vanishing trapped response. In addition, Linsker & Boozer (Reference Linsker and Boozer1982) realize they are assuming that the dominant transport contribution is from banana orbits with turning points away from the equatorial plane, while for the boundary layer evaluation to be presented here the barely trapped alphas dominate. Mynick (Reference Mynick1986) extends Linsker & Boozer to more general magnetic field perturbations, but continues to treat collisions perturbatively so no boundary layer is considered in the precession case. Yushmanov (Reference Yushmanov1983) extends his earlier work (Yushmanov Reference Yushmanov1982) to find the diffusivities by a perturbation technique that treats collisions as weak and therefore ignores boundary layer effects. Finally, the map used by Goldston et al. (Reference Goldston, White and Boozer1981) uses the radial step in their equation (8) that becomes infinite for the barely trapped and ignore collisions so can only study stochastic transport without any provision for a collisional boundary layer due to the barely trapped stalling at turning points where collisions and precession matter most. It is unclear how sensitive their ripple threshold estimate of
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}\leqslant (\unicode[STIX]{x1D700}/\unicode[STIX]{x03C0}qN)^{3/2}(\unicode[STIX]{x1D70C}_{0}\,\text{d}q/\text{d}r)^{-1}, & & \displaystyle\end{eqnarray}$$
is to these approximations, but some improvements were made by White et al. (Reference White, Goldston, Redi and Budny1996). Mynick (Reference Mynick1986) and White (Reference White2001) provide useful summaries of these results with (and without) precession.
In the following section a phenomenological estimate of the alpha diffusivity associated with the collisional narrow boundary layer formed by the presence of tangential
$\unicode[STIX]{x1D735}B$
drift. Then § 3 gives a detailed evaluation of all the terms in the transit averaged kinetic equation to be solved in the boundary layer. The solution of the kinetic equation using the results of Catto (Reference Catto2018) is given in § 4 for the
$\sqrt{\unicode[STIX]{x1D708}}$
regime, followed by the evaluation of the transport fluxes and diffusivities. The closing section presents a summary and discussion of key points. It stresses that collisional
$\sqrt{\unicode[STIX]{x1D708}}$
alpha losses are insensitive to the ripple near the equatorial plane on the outboard side where ripple is much stronger (Redi et al.
Reference Redi, Budny, McCune, Miller and White1996).
2 Phenomenological estimate and comparisons
Both Clebsch and Boozer (Reference Boozer1981) representations are employed to write
$\boldsymbol{B}$
as
$$\begin{eqnarray}\displaystyle \boldsymbol{B}=B\boldsymbol{b}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}=K(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}+G(\unicode[STIX]{x1D713})\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}+I(\unicode[STIX]{x1D713})\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}, & & \displaystyle\end{eqnarray}$$
with
$K(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717},\unicode[STIX]{x1D701})$
periodic in the poloidal and toroidal angle, and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D701}-q\unicode[STIX]{x1D717}, & & \displaystyle\end{eqnarray}$$
with
$q=q(\unicode[STIX]{x1D713})$
the safety factor. The preceding give
$$\begin{eqnarray}\displaystyle \boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=q\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D717}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}=q\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle B^{2}=(G+qI)\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}, & & \displaystyle\end{eqnarray}$$
as well as
$\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}=0=\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
, with
$G\,/qI\sim rB_{p}/qRB_{0}\sim \unicode[STIX]{x1D700}^{2}/q^{2}\ll 1$
.
The transit averaged drift kinetic equation need only be solved for the trapped since
$\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=0$
for the passing means that the perturbed passing distribution function vanishes (
$f_{p}=0$
). Here
$\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
is the radial magnetic drift due to the rippled magnetic field, with the overbar indicating transit averaging over the trapped,
$$\begin{eqnarray}\displaystyle \bar{A}=\frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\ell A/v_{\Vert }}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\ell /v_{\Vert }}=\frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D70F}A}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D70F}}=\frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}A/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}, & & \displaystyle\end{eqnarray}$$
with
$A$
arbitrary,
$\text{d}\unicode[STIX]{x1D70F}=\text{d}\ell /v_{\Vert }=\text{d}\unicode[STIX]{x1D717}/v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}$
and
$q\,\text{d}\unicode[STIX]{x1D717}=\text{d}\unicode[STIX]{x1D701}$
for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D701}-q\unicode[STIX]{x1D717}$
fixed (denoted by the subscript on the integral). The integrals are over a full bounce for trapped particles. For energetic alphas, the
$\boldsymbol{E}\times \boldsymbol{B}$
drift is small and can be ignored.
The usual transit averaged equation
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\frac{\unicode[STIX]{x2202}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}=\overline{C\{f_{t}\}}, & & \displaystyle\end{eqnarray}$$
must be solved for the trapped correction
$f_{t}=f_{t}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},v,\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E})$
to the slowing down distribution
$$\begin{eqnarray}\displaystyle f_{s}(\unicode[STIX]{x1D713},v)=\frac{S(\unicode[STIX]{x1D713})\unicode[STIX]{x1D70F}_{s}(\unicode[STIX]{x1D713})H(v_{0}-v)}{4\unicode[STIX]{x03C0}[v^{3}+v_{c}^{3}(\unicode[STIX]{x1D713})]}, & & \displaystyle\end{eqnarray}$$
where
$f=f_{s}+f_{t}$
with
$f_{t}\ll \,f_{s}$
,
$\unicode[STIX]{x1D707}=v_{\bot }^{2}/2B$
is the magnetic moment,
$\unicode[STIX]{x1D70E}=v_{\Vert }/|v_{\Vert }|$
is the sign of the parallel velocity
$v_{\Vert }=\sqrt{v^{2}-2\unicode[STIX]{x1D707}B}$
and the magnetic drift is
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{m}=\unicode[STIX]{x1D6FA}^{-1}[\unicode[STIX]{x1D707}\boldsymbol{b}\times \unicode[STIX]{x1D735}B+v_{\Vert }^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})]\simeq \unicode[STIX]{x1D6FA}^{-1}v_{\Vert }\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b}), & & \displaystyle\end{eqnarray}$$
where the final form is a useful approximate form for the magnetic drift as the parallel velocity correction is negligible. In addition,
$C$
is the alpha collision operator,
$S$
the alpha birth rate,
$\unicode[STIX]{x1D70F}_{s}$
is the slowing down time for the alphas,
$v_{c}$
is the critical speed at which the drag of the background ions and electrons on the alphas is equal and
$v_{0}$
is the alpha birth speed with
$H$
a Heaviside step function that vanishes for speeds
$v>v_{0}$
. The magnetic drift term in a flux surface,
$\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}$
, is dominated by the
$\unicode[STIX]{x1D735}B$
drift as curvature drift is small for the trapped.
The weak ripple limit means that the departure from axisymmetry only matters for the radial magnetic drift term. Everywhere else the axisymmetric limit
$$\begin{eqnarray}\displaystyle \boldsymbol{B}\rightarrow I(\unicode[STIX]{x1D713})\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}+\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713} & & \displaystyle\end{eqnarray}$$
is used with
$I=RB_{t}$
and
$R|\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}|=1$
, where
$R$
is the major radius and
$B_{t}\simeq B_{0}$
is the toroidal magnetic field. Therefore, except for a very small radial drift due to asymmetry, the alphas try to move on surfaces of constant drift kinetic canonical angular momentum
$$\begin{eqnarray}\displaystyle \bar{\unicode[STIX]{x1D713}}_{\ast }=\unicode[STIX]{x1D713}-I(\unicode[STIX]{x1D713})v_{\Vert }/\unicode[STIX]{x1D6FA}, & & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FA}=ZeB/Mc$
the alpha gyrofrequency.
Pitch angle scattering must be the dominant collisional process to get a boundary layer narrower than
$\unicode[STIX]{x1D700}^{1/2}$
. This balance between the strong
$\unicode[STIX]{x1D735}B$
drift of the alphas tangential to the flux surface and collisions, reduces the width
$w$
in pitch angle
$\unicode[STIX]{x1D706}$
of the boundary layer by enhancing the pitch angle scattering frequency
$\unicode[STIX]{x1D708}\sim v_{c}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}$
, with
$\unicode[STIX]{x1D70F}_{s}$
the slowing down time. Using
$$\begin{eqnarray}\displaystyle \overline{C\{f_{t}\}}\sim \unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}^{2}}\sim \frac{\unicode[STIX]{x1D708}f_{t}}{w^{2}}\sim \frac{Nqv_{0}^{2}f_{t}}{\unicode[STIX]{x1D6FA}_{0}\unicode[STIX]{x1D700}R^{2}}\sim \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\frac{\unicode[STIX]{x2202}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x2202}f_{t}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}\sim Nf_{t}$
due to the
$N$
coils, gives the normalized width of the boundary layer
$w$
to be
$$\begin{eqnarray}\displaystyle w\sim (r\,R\unicode[STIX]{x1D708}/N\unicode[STIX]{x1D70C}_{0}qv_{0})^{1/2}\ll \unicode[STIX]{x1D700}^{1/2}, & & \displaystyle\end{eqnarray}$$
indicating that the alphas must
$\unicode[STIX]{x1D735}B$
precess on a flux surface much faster than they pitch angle scatter off the ions. This condition for the boundary layer analysis to be valid is easily satisfied by alphas. The effective barely trapped fraction is estimated from this boundary layer width to be
$$\begin{eqnarray}\displaystyle F\sim w, & & \displaystyle\end{eqnarray}$$
with
$w\ll \unicode[STIX]{x1D700}^{1/2}$
requiring
$(N\unicode[STIX]{x1D70C}_{0}qv_{0}/R^{2}\unicode[STIX]{x1D708})^{1/2}\gg 1$
. For deuterium–tritium (D–T) with
$R=10~\text{m}$
,
$B=5T$
and
$T_{i}\simeq 10~\text{keV}$
and
$n_{e}\simeq 10^{14}~\text{cm}^{-3}$
,
$R/\unicode[STIX]{x1D70C}_{0}\sim 10^{2}$
and
$v_{0}/\unicode[STIX]{x1D708}R\sim 10^{6}$
, so a narrow boundary layer will occur. Then the effective drift decorrelation time for the alphas is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}\sim F^{2}/\unicode[STIX]{x1D708}\sim (rR/Nq\unicode[STIX]{x1D70C}_{0}v_{0}). & & \displaystyle\end{eqnarray}$$
The radial
$\unicode[STIX]{x1D735}B$
drift speed of the alphas is
$$\begin{eqnarray}\displaystyle V=\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}/RB_{p}\sim q\unicode[STIX]{x1D70C}_{0}v_{0}N\unicode[STIX]{x1D6FF}/r, & & \displaystyle\end{eqnarray}$$
and small decorrelation time limits the effective radial step size
$\unicode[STIX]{x1D6E5}$
to be
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}\sim V\unicode[STIX]{x1D70F}\sim R\unicode[STIX]{x1D6FF}. & & \displaystyle\end{eqnarray}$$
Consequently, the weak ripple diffusivity is
$$\begin{eqnarray}\displaystyle D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{weak}}\sim F\unicode[STIX]{x1D6E5}^{2}/\unicode[STIX]{x1D70F}\sim q^{1/2}\unicode[STIX]{x1D700}^{-1/2}N^{1/2}\unicode[STIX]{x1D6FF}^{2}v_{0}^{1/2}\unicode[STIX]{x1D70C}_{0}^{1/2}R\unicode[STIX]{x1D708}^{1/2}. & & \displaystyle\end{eqnarray}$$
This result will be justified in more detail by solving a boundary layer problem that allows the trapped distribution function
$f_{t}$
to vanish at the trapped–passing boundary.
The banana regime diffusivity is due to a combination of pitch angle scattering off the ions and electron drag and is found to be of order
$D_{\text{axi}}^{\text{ban}}\simeq 0.25q^{2}\unicode[STIX]{x1D70C}_{0}^{2}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}\ell n(v_{0}/v_{c})\sim q^{2}\unicode[STIX]{x1D70C}_{0}^{2}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}$
for D–T (Hsu, Catto & Sigmar Reference Hsu, Catto and Sigmar1990), giving
$$\begin{eqnarray}\displaystyle \frac{D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{weak}}}{D_{\text{axi}}^{\text{ban}}}\sim \left(\frac{v_{c}^{3/2}}{v_{0}^{3/2}}\right)\left(\frac{N^{1/2}\unicode[STIX]{x1D6FF}^{1/2}\unicode[STIX]{x1D700}^{1/2}}{q^{3/2}}\right)\frac{R\sqrt{v_{0}\unicode[STIX]{x1D70F}_{s}}}{\unicode[STIX]{x1D70C}_{0}^{3/2}}=\left(\frac{qN\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D700}}\right)^{1/2}\left(\frac{v_{c}R\,\unicode[STIX]{x1D6FF}}{v_{0}\unicode[STIX]{x1D70C}_{0}}\right)^{3/2}\frac{\unicode[STIX]{x1D700}\sqrt{v_{0}\unicode[STIX]{x1D70F}_{s}/R}}{q^{2}},\qquad & & \displaystyle\end{eqnarray}$$
for weak ripple (
$qN\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D700}$
). For this estimate, weak ripple transport will be larger than neoclassical for
$\unicode[STIX]{x1D6FF}\sim 10^{-3}$
, even though
$qN\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D700}$
, because
$R/\unicode[STIX]{x1D70C}_{0}\sim 10^{2}$
,
$v_{0}\unicode[STIX]{x1D70F}_{s}/R\sim 10^{6}$
, and
$v_{c}^{3/2}/v_{0}^{3/2}\sim 1/5$
. More specifically, weak ripple transport will occur and be larger than neoclassical whenever
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D700}}{qN}>\unicode[STIX]{x1D6FF}>\left(\frac{q\unicode[STIX]{x1D70C}_{0}v_{0}}{Rv_{c}}\right)^{3/4}\left(\frac{R}{N\unicode[STIX]{x1D700}v_{0}\unicode[STIX]{x1D70F}_{s}}\right)^{1/4}. & & \displaystyle\end{eqnarray}$$
These inequalities indicate that ripple levels of
$\unicode[STIX]{x1D6FF}\sim 10^{-3}$
are needed to keep ripple and neoclassical losses comparable. The ripple on the outboard or low field side of a tokamak is typically of this order, but it is much smaller on the high field side (Redi et al.
Reference Redi, Budny, McCune, Miller and White1996).
Ripple of
$\unicode[STIX]{x1D6FF}\sim 10^{-3}$
will also avoid seriously depleting the slowing down distribution function during
$\sqrt{\unicode[STIX]{x1D708}}$
regime transport as
$\unicode[STIX]{x1D70F}_{s}D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{weak}}/a^{2}\ll 1$
gives the constraint on the ripple of
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}<\left(\frac{v_{0}}{v_{c}}\right)^{3/4}\left(\frac{a}{R}\right)\left(\frac{r\,R}{Nq\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}}\right)^{1/4}. & & \displaystyle\end{eqnarray}$$
The detailed boundary layer evaluation performed in the § 4 indicates that the barely trapped alphas dominate
$\sqrt{\unicode[STIX]{x1D708}}$
regime collisional transport so that outboard ripple larger than
$\unicode[STIX]{x1D6FF}\sim 10^{-3}$
is tolerable.
Catto (Reference Catto2018) performed a boundary layer analysis for strong ripple (
$qN\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D700}$
) to find
$$\begin{eqnarray}\displaystyle D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{strong}}\sim (qv_{c}/v_{0})^{3/2}(\unicode[STIX]{x1D70C}_{0}v_{0}/\unicode[STIX]{x1D714}R)^{2}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D70F}_{s})^{1/2}, & & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D714}$
the rotation frequency due to a radial electric field. Comparing this to the small ripple result, but using a magnetic drift estimate of
$\unicode[STIX]{x1D714}R\sim v_{0}\unicode[STIX]{x1D70C}_{p0}/R\sim q\unicode[STIX]{x1D70C}_{0}v_{0}/R$
, gives
$$\begin{eqnarray}\displaystyle \frac{D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{weak}}}{D_{\sqrt{\unicode[STIX]{x1D708}}}^{\text{strong}}}\sim \frac{q^{1/2}N^{1/2}\unicode[STIX]{x1D6FF}^{2}}{\unicode[STIX]{x1D700}^{1/2}}\sim \left(\frac{qN\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D700}}\right)^{1/2}\unicode[STIX]{x1D6FF}^{3/2}, & & \displaystyle\end{eqnarray}$$
which is very small even if
$qN\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D700}$
, as might be expected. Unfortunately, retaining the
$\unicode[STIX]{x1D735}B$
drift in the strong ripple limit is not an analytically tractable limit so this estimate is likely to be too crude. Moreover, the large ripple limit treats only ripple trapped alphas in wells that are poloidally localized.
3 Transit averaged kinetic equation
Only the axisymmetric forms of the collision operator and drift within a flux surface are required in the kinetic equation. Neglecting curvature drift, they may be written as
$$\begin{eqnarray}\displaystyle \overline{C\{f_{t}\}}\simeq \frac{2v_{\unicode[STIX]{x1D706}}^{3}}{\displaystyle \unicode[STIX]{x1D70F}_{s}v^{3}\left(\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}/\unicode[STIX]{x1D709}\right)}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}\left[\unicode[STIX]{x1D706}\left(\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}\right)\frac{\unicode[STIX]{x2202}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}}\right], & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\simeq \frac{Mcv^{2}}{Ze}\frac{\displaystyle (\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})\left(\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\,\unicode[STIX]{x1D709}\right)}{\displaystyle \left(\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}/\unicode[STIX]{x1D709}\right)}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x1D707}B_{0}/v^{2}$
, and
$\unicode[STIX]{x1D709}^{2}=v_{\Vert }^{2}/v^{2}=1-2\unicode[STIX]{x1D707}B/v^{2}=1-\unicode[STIX]{x1D706}B/B_{0}\simeq 1-\unicode[STIX]{x1D706}(1-\unicode[STIX]{x1D700})-2\unicode[STIX]{x1D706}\unicode[STIX]{x1D700}\sin ^{2}(\unicode[STIX]{x1D717}/2)$
. The pitch angle scattering collision frequency is
$\unicode[STIX]{x1D708}=v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}\sim v_{c}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}$
, where
$$\begin{eqnarray}\displaystyle & \displaystyle v_{\unicode[STIX]{x1D706}}^{3}=\frac{3\unicode[STIX]{x03C0}^{1/2}T_{e}^{3/2}}{(2m)^{1/2}Mn_{e}}\mathop{\sum }_{i}Z_{i}^{2}n_{i}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{c}^{3}=\frac{3\unicode[STIX]{x03C0}^{1/2}T_{e}^{3/2}}{(2m)^{1/2}n_{e}}\mathop{\sum }_{i}\frac{Z_{i}^{2}n_{i}}{M_{i}}, & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{s}=\frac{3MT_{e}^{3/2}}{4(2\unicode[STIX]{x03C0}m)^{1/2}Z^{2}e^{4}n_{e}\ell n\unicode[STIX]{x1D6EC}}, & & \displaystyle\end{eqnarray}$$
with the electron and bulk ion densities and temperatures denoted by
$n_{j}$
and
$T_{j}$
, and
$m$
the electron mass and
$M_{i}$
the mass of an ion of charge
$Z_{i}$
. The density of slowing down alphas is
$$\begin{eqnarray}\displaystyle n_{s}=\int \text{d}^{3}vf_{s}=S\unicode[STIX]{x1D70F}_{s}\int _{0}^{v_{0}}\frac{v^{2}\,\text{d}v}{(v^{3}+v_{c}^{3})}=\frac{S\unicode[STIX]{x1D70F}_{s}}{3}\ell n[1+(v_{0}^{3}/v_{c}^{3})]\simeq S\unicode[STIX]{x1D70F}_{s}\ell n(v_{0}/v_{c}), & & \displaystyle\end{eqnarray}$$
where
$v_{0}^{3}/v_{c}^{3}\gg 1$
and
$v_{\unicode[STIX]{x1D706}}^{3}\,/\,v_{c}^{3}=3/5$
for the deuterium–tritium (D–T) reaction of interest here.
To evaluate the magnetic drift the divergence of an arbitrary vector
$\boldsymbol{A}$
is written as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{A}=\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}\left[\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\left(\frac{\boldsymbol{A}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}\left(\frac{\boldsymbol{A}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}\left(\frac{\boldsymbol{A}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)\right], & & \displaystyle\end{eqnarray}$$
giving
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC} & \simeq & \displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\nonumber\\ \displaystyle & = & \displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}\left[\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\left(\frac{Bv_{\Vert }}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}\left(\frac{v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)\right],\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713} & \simeq & \displaystyle \frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times (v_{\Vert }\boldsymbol{b})\nonumber\\ \displaystyle & = & \displaystyle -\frac{v_{\Vert }}{\unicode[STIX]{x1D6FA}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}\left[\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}\left(\frac{Bv_{\Vert }}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}\left(\frac{v_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\right)\right].\end{eqnarray}$$
As a result, neglecting curvature drift
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\simeq \frac{Mcv^{2}}{\displaystyle Ze\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\simeq -\frac{Mcv^{2}}{\displaystyle Ze\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}\oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}. & & \displaystyle\end{eqnarray}$$
Ripple only matters in the radial drift. Using
$2\unicode[STIX]{x1D709}\unicode[STIX]{x2202}\unicode[STIX]{x1D709}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\unicode[STIX]{x1D717}}=-N\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\sin [N(\unicode[STIX]{x1D6FC}+q\unicode[STIX]{x1D717})]$
, gives
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=\frac{McN\unicode[STIX]{x1D706}v^{2}}{2Ze}\frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}\sin [N(\unicode[STIX]{x1D6FC}+q\unicode[STIX]{x1D717})]}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}}. & & \displaystyle\end{eqnarray}$$
Then, using
$\sin [N(\unicode[STIX]{x1D6FC}+q\unicode[STIX]{x1D717})]=\sin (N\unicode[STIX]{x1D6FC})\cos (Nq\unicode[STIX]{x1D717})+\cos (N\unicode[STIX]{x1D6FC})\sin (Nq\unicode[STIX]{x1D717})$
, and noting that the term odd in
$\unicode[STIX]{x1D717}$
about the equatorial plane
$(\unicode[STIX]{x1D717}=0)$
vanishes, leaves
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}=\frac{McN\unicode[STIX]{x1D706}v^{2}\sin (N\unicode[STIX]{x1D6FC})}{2Ze}\frac{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}\cos (qN\unicode[STIX]{x1D717})}{\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}^{-1}}, & & \displaystyle\end{eqnarray}$$
giving the estimate
$\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}/RB_{p}\sim qN\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D6FF}/r$
used earlier.
Using the full bounce, large aspect ratio results
$$\begin{eqnarray}\displaystyle & \hspace{-28.00006pt}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}/\unicode[STIX]{x1D709}=8(2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706})^{-1/2}\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}=8(2\unicode[STIX]{x1D700})^{-1/2}\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}K(\unicode[STIX]{x1D705}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \hspace{-28.00006pt}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\text{d}\unicode[STIX]{x1D717}\unicode[STIX]{x1D709}=\frac{8\sqrt{2\unicode[STIX]{x1D700}}\unicode[STIX]{x1D705}^{2}}{\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}x\cos ^{2}x}{\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}}=\frac{8\sqrt{2\unicode[STIX]{x1D700}}[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]}{\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}}, & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\frac{\text{d}\unicode[STIX]{x1D717}}{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D717} & = & \displaystyle \frac{8}{(2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706})^{1/2}}\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x\frac{(1-2\unicode[STIX]{x1D705}^{2}\sin ^{2}x)}{\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}}\nonumber\\ \displaystyle & = & \displaystyle \frac{8}{(2\unicode[STIX]{x1D700})^{1/2}}\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}[2E(\unicode[STIX]{x1D705})-K(\unicode[STIX]{x1D705})],\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}\sin x=\sin (\unicode[STIX]{x1D717}/2)$
and the
$\unicode[STIX]{x1D6FC}$
subscript is a reminder that the integral is to be performed at fixed
$\unicode[STIX]{x1D6FC}$
. Here
$K(\unicode[STIX]{x1D705})$
and
$E(\unicode[STIX]{x1D705})$
are complete elliptic integrals of the first and second kind, respectively, with
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}^{2}=[1-(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D706}]/2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}, & & \displaystyle\end{eqnarray}$$
so that
$\unicode[STIX]{x1D705}=0$
are the deeply trapped and
$\unicode[STIX]{x1D705}=1$
the is the barely passing boundary. Using these results along with the barely trapped limits
$E(\unicode[STIX]{x1D705})\rightarrow 1+\cdots \,$
and
$K(\unicode[STIX]{x1D705})\rightarrow \ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})+\cdots \,$
, gives
$$\begin{eqnarray}\displaystyle \overline{C\{f_{t}\}}\simeq \frac{v_{\unicode[STIX]{x1D706}}^{3}}{4\unicode[STIX]{x1D70F}_{s}v^{3}\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}K(\unicode[STIX]{x1D705})}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}\left\{\frac{[E(\unicode[STIX]{x1D705})-(1-\unicode[STIX]{x1D705}^{2})K(\unicode[STIX]{x1D705})]}{\unicode[STIX]{x1D705}}\frac{\unicode[STIX]{x2202}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}}\right\}\underset{\unicode[STIX]{x1D705}\rightarrow 1}{\longrightarrow }\frac{(v_{\unicode[STIX]{x1D706}}^{3}/2\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}v^{3})}{\ell n[8/(1-\unicode[STIX]{x1D705})]}\frac{\unicode[STIX]{x2202}^{2}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{2}},\qquad & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\simeq \frac{v^{2}[2E(\unicode[STIX]{x1D705})-K(\unicode[STIX]{x1D705})]}{2\unicode[STIX]{x1D6FA}_{p}R^{2}K(\unicode[STIX]{x1D705})}\underset{\unicode[STIX]{x1D705}\rightarrow 1}{\longrightarrow }\frac{-v^{2}}{2\unicode[STIX]{x1D6FA}_{p}R^{2}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FA}_{p}=ZeB_{p}/Mc\simeq \unicode[STIX]{x1D700}\unicode[STIX]{x1D6FA}_{0}/q$
.
The integral appearing in
$\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}$
was evaluated in the
$Nq\gg 1$
limit in Linsker & Boozer (Reference Linsker and Boozer1982), Mynick (Reference Mynick1986) and White (Reference White2001), but their procedure is inadequate for the barely trapped (
$\unicode[STIX]{x1D705}\rightarrow 1$
) as the result is singular. Appendix A gives the asymptotic expansion for
$\unicode[STIX]{x1D705}\rightarrow 1$
that is found by more carefully expanding the
$\unicode[STIX]{x1D717}$
dependence of
$\unicode[STIX]{x1D709}$
about the turning point
$\unicode[STIX]{x1D717}_{t}$
, where
$$\begin{eqnarray}\displaystyle \sin (\unicode[STIX]{x1D717}_{t}/2)=\sqrt{[1-(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D706}]/2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D705}. & & \displaystyle\end{eqnarray}$$
Using
$\sin (\unicode[STIX]{x1D717}/2)=\unicode[STIX]{x1D705}\sin x$
leads to the form
$$\begin{eqnarray}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\frac{\text{d}\unicode[STIX]{x1D717}}{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6FF}\cos (qN\unicode[STIX]{x1D717}) & = & \displaystyle \frac{8}{(2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706})^{1/2}}\operatorname{Re}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\text{d}x\unicode[STIX]{x1D6FF}\text{e}^{\text{i}qN\unicode[STIX]{x1D717}}}{\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}}\nonumber\\ \displaystyle & \simeq & \displaystyle \frac{8\unicode[STIX]{x1D6FF}}{(2\unicode[STIX]{x1D700})^{1/2}}\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}\operatorname{Re}\{\text{e}^{\text{i}qN\unicode[STIX]{x1D717}_{t}}\tilde{K}(\unicode[STIX]{x1D705})\},\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle \widetilde{K}(\unicode[STIX]{x1D705})\equiv \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}/\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}, & & \displaystyle\end{eqnarray}$$
and where
$\unicode[STIX]{x1D6FF}\simeq \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0})$
is used since only the limit
$\unicode[STIX]{x1D705}\rightarrow 1\;(\unicode[STIX]{x1D717}\rightarrow \unicode[STIX]{x03C0})$
is of interest. Then changing to
$\unicode[STIX]{x1D717}$
by using
$\cos (\unicode[STIX]{x1D717}/2)\,\text{d}\unicode[STIX]{x1D717}=2\unicode[STIX]{x1D705}\cos x\,\text{d}x$
, the result from appendix A gives
$$\begin{eqnarray}\displaystyle \widetilde{K}(\unicode[STIX]{x1D705})\equiv \frac{1}{2}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}}{\sqrt{\unicode[STIX]{x1D705}^{2}-\sin ^{2}(\unicode[STIX]{x1D717}/2)}}\simeq \ell n\left(\frac{1}{qN\sqrt{2(1-\unicode[STIX]{x1D705})}}\right). & & \displaystyle\end{eqnarray}$$
Therefore, using
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0})$
,
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\simeq \frac{N\unicode[STIX]{x1D6FF}B_{0}v^{2}\ell n[2q^{2}N^{2}(1-\unicode[STIX]{x1D705})]}{2\unicode[STIX]{x1D6FA}_{0}\ell n[(1-\unicode[STIX]{x1D705})/8]}\cos (\unicode[STIX]{x03C0}qN)\sin (N\unicode[STIX]{x1D6FC}). & & \displaystyle\end{eqnarray}$$
Inserting the preceding
$\unicode[STIX]{x1D705}\rightarrow 1$
results into the transit averaged kinetic equation yields the equation that must be solved for the trapped
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{v_{\unicode[STIX]{x1D706}}^{3}}{2\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}v^{3}\ell n[8/(1-\unicode[STIX]{x1D705})]}\frac{\unicode[STIX]{x2202}^{2}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{2}}+\frac{qv^{2}}{2\unicode[STIX]{x1D6FA}_{0}Rr}\frac{\unicode[STIX]{x2202}f_{t}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{qNv^{2}\unicode[STIX]{x1D6FF}\ell n[2q^{2}N^{2}(1-\unicode[STIX]{x1D705})]\cos (\unicode[STIX]{x03C0}qN)}{2\unicode[STIX]{x1D6FA}_{0}r\ell n[(1-\unicode[STIX]{x1D705})/8]}RB_{p}\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\sin (N\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
In the section that follows this equation is solved for the trapped in the narrow boundary layer just inside the trapped–passing boundary.
4 Boundary layer analysis and transport fluxes
Fortunately, the weak ripple limit with the
$\unicode[STIX]{x1D735}B$
drift retained is analytically tractable, as will now be demonstrated. There is no need to assume poloidal localization since ripple trapping does not occur.
Defining
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}\equiv (1-\unicode[STIX]{x1D705})/8, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{t}\equiv \operatorname{Im}[H(\unicode[STIX]{x1D702})\text{e}^{\text{i}N\unicode[STIX]{x1D6FC}}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle k\equiv \frac{32qN\unicode[STIX]{x1D70F}_{s}v^{5}}{v_{\unicode[STIX]{x1D706}}^{3}\unicode[STIX]{x1D6FA}_{0}R^{2}}\gg 1, & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle L\equiv \frac{32\unicode[STIX]{x1D6FF}\,qN\,\unicode[STIX]{x1D70F}_{s}v^{5}\cos (\unicode[STIX]{x03C0}qN)}{\unicode[STIX]{x1D6FA}_{0}Rv_{\unicode[STIX]{x1D706}}^{3}}RB_{p}\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$
the boundary layer equation becomes of the form first considered by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017):
$$\begin{eqnarray}\displaystyle \frac{1}{\ell n(\unicode[STIX]{x1D702})}\frac{\unicode[STIX]{x2202}^{2}H}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{2}}-2\text{i}kH=-2L\frac{\ell n(16q^{2}N^{2}\unicode[STIX]{x1D702})}{\ell n(\unicode[STIX]{x1D702})}\simeq -2L, & & \displaystyle\end{eqnarray}$$
where for alphas it is not unreasonable to assume
$\ell n(\unicode[STIX]{x1D702}^{-1})\sim \ell n(k^{1/2})>\ell n(16q^{2}N^{2})$
as
$v_{0}^{4}\unicode[STIX]{x1D70F}_{s}\unicode[STIX]{x1D70C}_{0}/v_{\unicode[STIX]{x1D706}}^{3}R^{2}\ggg 4q^{3}N^{3}$
, and Im denotes imaginary part. Then, a boundary layer equation of the exact same form as in the strong ripple limit of Catto (Reference Catto2018) is obtained. There it is shown that the matched asymptotic solution vanishing at the trapped–passing boundary is
$$\begin{eqnarray}\displaystyle H=\frac{\text{i}L}{k}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}}-1]. & & \displaystyle\end{eqnarray}$$
Consequently,
$$\begin{eqnarray}\displaystyle f_{t}=B_{p}R^{2}\frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6FF}\cos (\unicode[STIX]{x03C0}qN)\operatorname{Re}\{[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}}-1]\text{e}^{\text{i}N\unicode[STIX]{x1D6FC}}\}, & & \displaystyle\end{eqnarray}$$
where
$f_{t}/f_{s}\sim R\unicode[STIX]{x1D6FF}/a\ll 1$
is required, with the minor radius,
$a$
, assumed to be roughly the radial scale length of the alpha density variation, and
$Re$
denoting the real part.
The alpha flux is evaluated from
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d}=\left\langle \int \text{d}^{3}v(Mv^{2}/2)^{d}f_{t}\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\right\rangle , & & \displaystyle\end{eqnarray}$$
where
$\langle \cdots \rangle$
is the flux surface average, with
$d=0$
for the alpha particle flux and
$d=1$
for the alpha energy flux. Ignoring curvature drift, using
$\text{d}^{3}v\rightarrow 2\unicode[STIX]{x03C0}(Bv^{2}/B_{0}\unicode[STIX]{x1D709})\,\text{d}v\,\text{d}\unicode[STIX]{x1D706}$
, performing the transit average first by holding
$\unicode[STIX]{x1D6FC}$
fixed and noting
$$\begin{eqnarray}\displaystyle \int _{-\unicode[STIX]{x1D717}_{t}}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}}{\boldsymbol{ B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\frac{B}{\unicode[STIX]{x1D709}}\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713} & = & \displaystyle \overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\int _{-\unicode[STIX]{x1D717}_{t}}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}}{\unicode[STIX]{x1D709}\,\boldsymbol{ b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}}\nonumber\\ \displaystyle & \simeq & \displaystyle \frac{2B_{0}}{\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D700}}}\sqrt{1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705}^{2}}K(\unicode[STIX]{x1D705})\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\frac{\text{d}\unicode[STIX]{x1D717}}{\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D717}},\qquad\end{eqnarray}$$
gives the alternate and more useful form of the fluxes to be
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d} & = & \displaystyle \left\langle \int \text{d}^{3}v(Mv^{2}/2)^{d}f_{t}\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\right\rangle \nonumber\\ \displaystyle & \simeq & \displaystyle 8\sqrt{2\unicode[STIX]{x1D700}}\int _{0}^{v_{0}}\text{d}vv^{2}\left(\frac{Mv^{2}}{2}\right)^{d}\left\langle \int _{0}^{1}\text{d}\unicode[STIX]{x1D705}\,f_{t}\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\,\ell n\left(\frac{8}{1-\unicode[STIX]{x1D705}}\right)\right\rangle ,\end{eqnarray}$$
where
$f_{t}\propto \exp (\text{i}N\unicode[STIX]{x1D6FC})$
is independent of
$\unicode[STIX]{x1D717}$
and the last form is for
$\unicode[STIX]{x1D705}\rightarrow 1$
. Inserting
$f_{t}$
and
$\overline{\boldsymbol{v}_{m}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}$
, and using
$$\begin{eqnarray}\displaystyle \frac{\ell n(v_{0}/v_{c})}{n_{s}}\frac{\unicode[STIX]{x2202}n_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\gg \frac{1}{v_{c}}\frac{\unicode[STIX]{x2202}v_{c}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\sim \frac{1}{n_{i}}\frac{\unicode[STIX]{x2202}n_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$
leaves
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d} & \simeq & \displaystyle -\frac{16\,B_{p}^{2}R^{2}qN\unicode[STIX]{x1D6FF}^{2}\cos ^{2}(\unicode[STIX]{x03C0}qN)}{\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x1D700}}\unicode[STIX]{x1D6FA}_{0}\ell n(v_{0}/v_{c})}\frac{\unicode[STIX]{x2202}n_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\int _{0}^{v_{0}}\frac{\text{d}vv^{4}}{v^{3}+v_{c}^{3}}\left(\frac{Mv^{2}}{2}\right)^{d}\nonumber\\ \displaystyle & & \displaystyle \times \operatorname{Re}\left\{\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D702}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}}-1]\ell n(16q^{2}N^{2}\unicode[STIX]{x1D702})\right\},\end{eqnarray}$$
where
$\langle \sin (N\unicode[STIX]{x1D6FC})\text{e}^{\text{i}N\unicode[STIX]{x1D6FC}}\rangle \simeq \text{i}/2$
is used. Letting
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D702}\sqrt{k\ell n(2k)}\propto v^{5/2}$
and defining
$$\begin{eqnarray}\displaystyle k_{0}\equiv \frac{32qN\unicode[STIX]{x1D70F}_{s}v_{0}^{5}}{v_{\unicode[STIX]{x1D706}}^{3}\unicode[STIX]{x1D6FA}_{0}R^{2}}\gg 1, & & \displaystyle\end{eqnarray}$$
then the fraction of barely trapped particles that contribute is proportional to
$$\begin{eqnarray}\displaystyle \operatorname{Re}\left\{\text{i}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D702}[\text{e}^{-(1-\text{i})\unicode[STIX]{x1D702}\sqrt{2k\ell n(\sqrt{2k})}}-1]\ell n(16q^{2}N^{2}\unicode[STIX]{x1D702})\right\}\simeq \frac{\ell n(\sqrt{k\ell n(2k)}/16q^{2}N^{2})}{2\sqrt{k\ell n(2k)}},\qquad & & \displaystyle\end{eqnarray}$$
with the speed weighting
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{v_{0}}\text{d}vv^{4}\left(\frac{Mv^{2}}{2}\right)^{d}\frac{\ell n[\sqrt{k\ell n(2k)}/16q^{2}N^{2}]}{(v^{3}+v_{c}^{3})\sqrt{k\ell n(2k)}}\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \frac{v_{0}^{2}\ell n[\sqrt{k_{0}\ell n(2k_{0})}/16q^{2}N^{2}]}{\sqrt{k_{0}\ell n(2k_{0})}}\left\{\begin{array}{@{}ll@{}}\ell n(v_{0}/v_{c}) & d=0\\ Mv_{0}^{2}/3 & d=1,\end{array}\right.\end{eqnarray}$$
thereby yielding the collisional particle and energy fluxes for the alphas
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{d} & \simeq & \displaystyle -\frac{B_{p}^{2}R^{3}q^{1/2}N^{1/2}\unicode[STIX]{x1D6FF}^{2}v_{\unicode[STIX]{x1D706}}^{3/2}\unicode[STIX]{x1D70C}_{0}^{1/2}\cos ^{2}(\unicode[STIX]{x03C0}qN)}{\unicode[STIX]{x03C0}\sqrt{\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}}v_{0}\ell n(v_{0}/v_{c})}\frac{\unicode[STIX]{x2202}n_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}\frac{\ell n[\sqrt{k_{0}\ell n(2k_{0})}/16q^{2}N^{2}]}{\sqrt{\ell n(2k_{0})}}\nonumber\\ \displaystyle & & \displaystyle \times \left\{\begin{array}{@{}ll@{}}\ell n(v_{0}/v_{c}) & d=0\\ Mv_{0}^{2}/3 & d=1.\end{array}\right.\end{eqnarray}$$
The flux implies that the particle diffusivity of the alphas is
$$\begin{eqnarray}\displaystyle D_{0}^{\text{weak}}=\frac{q^{1/2}N^{1/2}\unicode[STIX]{x1D6FF}^{2}v_{\unicode[STIX]{x1D706}}^{3/2}\unicode[STIX]{x1D70C}_{0}^{1/2}R}{2\unicode[STIX]{x03C0}v_{0}\sqrt{\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}\ell n(2k_{0})}}\ell n\left[\frac{\sqrt{k_{0}\ell n(2k_{0})}}{16q^{2}N^{2}}\right], & & \displaystyle\end{eqnarray}$$
while the alpha energy diffusivity is
$$\begin{eqnarray}\displaystyle D_{1}^{\text{weak}}=\frac{q^{1/2}N^{1/2}\unicode[STIX]{x1D6FF}^{2}v_{\unicode[STIX]{x1D706}}^{3/2}\unicode[STIX]{x1D70C}_{0}^{1/2}R}{3\unicode[STIX]{x03C0}v_{0}\sqrt{\unicode[STIX]{x1D700}\unicode[STIX]{x1D70F}_{s}\ell n(2k_{0})}}\frac{\ell n[\sqrt{k_{0}\ell n(2k_{0})}/16q^{2}N^{2}]}{\ell n(v_{0}/v_{c})}, & & \displaystyle\end{eqnarray}$$
where a coarse grain average is used to replace
$\cos ^{2}(\unicode[STIX]{x03C0}qN)$
by 1/2.
The first expression is the same as the estimate in § 2 within numerical and logarithmic factors that decrease the diffusivity since
$\unicode[STIX]{x1D708}=v_{\unicode[STIX]{x1D706}}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}\sim v_{c}^{3}/v_{0}^{3}\unicode[STIX]{x1D70F}_{s}$
. However, the boundary layer solution technique makes it clear that the ripple that matters is at the equatorial plane on the high field side since
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0})$
. Consequently, the weak ripple,
$\sqrt{\unicode[STIX]{x1D708}}$
transport regime seems unlikely to be an important consideration for the alphas since the details of the collisional boundary layer analysis presented here imply that these results are insensitive to the ripple near the low field side equatorial plane where the ripple is largest and typically approximately
$\unicode[STIX]{x1D6FF}\sim 10^{-3}$
. High field side ripple is substantially smaller. Therefore, adequately confined collisionless alpha orbits appears to be all that is required to keep collisional alpha confinement at axisymmetric neoclassical levels (Hsu et al.
Reference Hsu, Catto and Sigmar1990) in weakly rippled tokamak fields.
5 Summary and discussion
A fully self-consistent evaluation of alpha particle and energy transport fluxes for weak ripple (
$\unicode[STIX]{x1D700}>qN\unicode[STIX]{x1D6FF}$
) has been performed in the
$\sqrt{\unicode[STIX]{x1D708}}$
regime. The new features of this evaluation are a complete boundary layer analysis retaining collisions to enable the perturbed trapped distribution function to vanish at the trapped–passing boundary so it can properly match to the passing response and the careful treatment of the tangential magnetic
$\unicode[STIX]{x1D735}B$
drift on a flux surface so that the radial steps remain well behaved for the barely trapped alphas. The result places only mild constraints on ripple. These are necessary to satisfy to keep ripple transport comparable to neoclassical, while avoiding alpha depletion. Indeed, since the results are only sensitive to the ripple near the equatorial plane on the high field side it is likely that the losses are well below axisymmetric neoclassical transport losses (Hsu et al.
Reference Hsu, Catto and Sigmar1990).
The
$\sqrt{\unicode[STIX]{x1D708}}$
regime ripple restriction on the alpha energy loss to avoid depletion of the alphas just after birth found from
$\unicode[STIX]{x1D70F}_{s}D_{1}^{\text{weak}}/a^{2}\ll 1$
is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF} & \ll & \displaystyle \left[\frac{3\unicode[STIX]{x03C0}\ell n(v_{0}/v_{c})\sqrt{\ell n(2k_{0})}}{\ell n[\sqrt{k_{0}\ell n(2k_{0})}/16q^{2}N^{2}]}\right]^{1/2}\left(\frac{v_{0}}{v_{\unicode[STIX]{x1D706}}}\right)^{3/4}\left(\frac{a}{R}\right)\left(\frac{r\,R}{Nq\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}}\right)^{1/4}\nonumber\\ \displaystyle & {\sim} & \displaystyle 5\left(\frac{v_{0}}{v_{\unicode[STIX]{x1D706}}}\right)^{3/4}\left(\frac{a}{R}\right)\left(\frac{\unicode[STIX]{x1D700}R^{2}}{Nq\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D70F}_{s}}\right)^{1/4}\sim 10^{-2},\end{eqnarray}$$
with
$k_{0}\gg 1$
required for a narrow boundary layer, and
$$\begin{eqnarray}\displaystyle k_{0}=\frac{32qN\unicode[STIX]{x1D70C}_{0}v_{0}^{4}\unicode[STIX]{x1D70F}_{s}}{v_{\unicode[STIX]{x1D706}}^{3}R^{2}}\sim 10^{8}, & & \displaystyle\end{eqnarray}$$
for
$R/\unicode[STIX]{x1D70C}_{0}\sim 10^{2}$
,
$v_{0}\unicode[STIX]{x1D70F}_{s}/R\sim 10^{6}$
and
$v_{0}/v_{\unicode[STIX]{x1D706}}\sim 3$
. The
$\sqrt{\unicode[STIX]{x1D708}}$
regime results suggest that when the ripple is weak (
$\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D700}/qN$
), alpha energy depletion will be not be a issue in tokamaks because the collisional boundary layer analysis is dominated by the barely trapped particles and they are only sensitive to the very small ripple near the high field side equatorial plane (Redi et al.
Reference Redi, Budny, McCune, Miller and White1996). The analytic results obtained here can be used to validate a full simulation of the solution of the transit averaged equation for a more realistic model of collisional transport with strongly varying poloidal ripple. Based on the analytic results presented here, it seems likely that adequate confinement of collisionless alpha orbits will ensure that collisional
$\sqrt{\unicode[STIX]{x1D708}}$
alpha losses due to ripple will be small.
Acknowledgements
The work was supported the US Department of Energy grant DE-FG02-91ER-54109. The author very much appreciates the helpful comments and suggestions of the reviewers.
Appendix A. Asymptotic expansions for
$\unicode[STIX]{x1D705}\rightarrow 1$
To approximately expand the elliptic integral
$$\begin{eqnarray}\displaystyle K(\unicode[STIX]{x1D705})=\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}=\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}\cos ^{2}x} & & \displaystyle\end{eqnarray}$$
as
$\unicode[STIX]{x1D705}\rightarrow 1$
, expand
$\cos ^{2}x$
about
$x=\unicode[STIX]{x03C0}/2$
. Then letting
$z=-x+\unicode[STIX]{x03C0}/2$
gives
$$\begin{eqnarray}\displaystyle K(\unicode[STIX]{x1D705}) & \simeq & \displaystyle \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}(x-\unicode[STIX]{x03C0}/2)^{2}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}z/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}z^{2}}=\unicode[STIX]{x1D705}^{-1}\ell n[\unicode[STIX]{x1D705}z+\sqrt{\unicode[STIX]{x1D705}^{2}z^{2}+1-\unicode[STIX]{x1D705}^{2}}]|_{0}^{\unicode[STIX]{x03C0}/2},\end{eqnarray}$$
so as
$\unicode[STIX]{x1D705}\rightarrow 1$
,
$\ell n[\unicode[STIX]{x03C0}/\sqrt{1-\unicode[STIX]{x1D705}^{2}}]$
, which is close to
$K(\unicode[STIX]{x1D705})\rightarrow \ell n(4/\sqrt{1-\unicode[STIX]{x1D705}^{2}})+\cdots \,$
and recovered using
$$\begin{eqnarray}\displaystyle K(\unicode[STIX]{x1D705}) & = & \displaystyle \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}(x-\unicode[STIX]{x03C0}/2)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}\cos ^{2}x}-\int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x/\sqrt{1-\unicode[STIX]{x1D705}^{2}+\unicode[STIX]{x1D705}^{2}(x-\unicode[STIX]{x03C0}/2)^{2}}.\qquad\end{eqnarray}$$
Next use
$\sin (\unicode[STIX]{x1D717}/2)=\unicode[STIX]{x1D705}\sin x$
and
$\sin (\unicode[STIX]{x1D717}_{t}/2)=\unicode[STIX]{x1D705}$
to consider the form
$$\begin{eqnarray}\displaystyle \widetilde{K}(\unicode[STIX]{x1D705})\equiv \int _{0}^{\unicode[STIX]{x03C0}/2}\text{d}x\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}/\sqrt{1-\unicode[STIX]{x1D705}^{2}\sin ^{2}x}. & & \displaystyle\end{eqnarray}$$
Then changing to
$\unicode[STIX]{x1D717}$
by using
$\cos (\unicode[STIX]{x1D717}/2)\,\text{d}\unicode[STIX]{x1D717}=2\unicode[STIX]{x1D705}\cos x\,\text{d}x$
, gives
$$\begin{eqnarray}\displaystyle \widetilde{K}(\unicode[STIX]{x1D705})\equiv \frac{1}{2}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}}{\sqrt{\unicode[STIX]{x1D705}^{2}-\sin ^{2}(\unicode[STIX]{x1D717}/2)}}=\frac{1}{2}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}}{\sqrt{[\unicode[STIX]{x1D705}+\sin (\unicode[STIX]{x1D717}/2)][\unicode[STIX]{x1D705}-\sin (\unicode[STIX]{x1D717}/2)]}}. & & \displaystyle\end{eqnarray}$$
Expanding about
$\unicode[STIX]{x1D717}_{t}$
using
$$\begin{eqnarray}\displaystyle \sin (\unicode[STIX]{x1D717}/2)=\unicode[STIX]{x1D705}+\sqrt{1-\unicode[STIX]{x1D705}^{2}}(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})/2-\unicode[STIX]{x1D705}(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})^{2}/8+\cdots \,, & & \displaystyle\end{eqnarray}$$
yields
$$\begin{eqnarray}\displaystyle \widetilde{K}(\unicode[STIX]{x1D705}) & \simeq & \displaystyle \frac{1}{2}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\frac{\text{d}\unicode[STIX]{x1D717}\text{e}^{-\text{i}qN(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})}}{\sqrt{(\unicode[STIX]{x1D705}+\,\cdots )(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})[\sqrt{1-\unicode[STIX]{x1D705}^{2}}+\unicode[STIX]{x1D705}(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})/4+\,\cdots ]}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\unicode[STIX]{x1D705}}\int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\frac{\text{d}z\,\text{e}^{-\text{i}z}}{\sqrt{z(\unicode[STIX]{x1D6FF}+z)}},\end{eqnarray}$$
where
$z=qN(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})$
and
$\unicode[STIX]{x1D6FF}=4qN\sqrt{1-\unicode[STIX]{x1D705}^{2}}/\unicode[STIX]{x1D705}$
, with
$\unicode[STIX]{x1D717}_{t}\rightarrow \unicode[STIX]{x03C0}$
as
$\unicode[STIX]{x1D705}\rightarrow 1$
.
Integrate by parts using
$$\begin{eqnarray}\displaystyle \frac{1}{\sqrt{z(\unicode[STIX]{x1D6FF}+z)}}=\frac{\text{d}}{\text{d}z}\left[\ell n\left(\frac{2}{\unicode[STIX]{x1D6FF}}\sqrt{z(\unicode[STIX]{x1D6FF}+z)}+\frac{2z}{\unicode[STIX]{x1D6FF}}+1\right)-\ell n(\text{const.})\right], & & \displaystyle\end{eqnarray}$$
to find
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}\widetilde{K}(\unicode[STIX]{x1D705}) & \simeq & \displaystyle \int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\frac{\text{d}z\,\text{e}^{-\text{i}z}}{\sqrt{z(\unicode[STIX]{x1D6FF}+z)}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\text{d}z\,\text{e}^{-\text{i}z}\frac{\text{d}}{\text{d}z}\left\{\ell n\left[\frac{2}{\unicode[STIX]{x1D6FF}}\sqrt{z(\unicode[STIX]{x1D6FF}+z)}+\frac{2z}{\unicode[STIX]{x1D6FF}}+1\right]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\ell n\left[\frac{2qN\unicode[STIX]{x1D717}_{t}}{\unicode[STIX]{x1D6FF}}\left(\sqrt{1+\frac{\unicode[STIX]{x1D6FF}}{qN\unicode[STIX]{x1D717}_{t}}}+1\right)+1\right]\right\}\nonumber\\ \displaystyle & = & \displaystyle \ell n\left[\frac{2qN\unicode[STIX]{x1D717}_{t}}{\unicode[STIX]{x1D6FF}}\left(\sqrt{1+\frac{\unicode[STIX]{x1D6FF}}{qN\unicode[STIX]{x1D717}_{t}}}+1\right)+1\right]\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}\int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\text{d}z\,\text{e}^{-\text{i}z}\left\{\ell n\left[\frac{2z}{\unicode[STIX]{x1D6FF}}\left(\sqrt{1+\frac{\unicode[STIX]{x1D6FF}}{z}}+1\right)+1\right]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\ell n\left[\frac{2qN\unicode[STIX]{x1D717}_{t}}{\unicode[STIX]{x1D6FF}}\left(\sqrt{1+\frac{\unicode[STIX]{x1D6FF}}{qN\unicode[STIX]{x1D717}_{t}}}+1\right)+1\right]\right\}.\end{eqnarray}$$
Letting
$\unicode[STIX]{x1D6FF}\rightarrow 0$
leaves
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}\widetilde{K}(\unicode[STIX]{x1D705}) & \simeq & \displaystyle \ell n\left(\frac{4qN\unicode[STIX]{x1D717}_{t}}{\unicode[STIX]{x1D6FF}}\right)+\text{i}\int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\text{d}z\,\text{e}^{-\text{i}z}\ell n\left(\frac{z}{qN\unicode[STIX]{x1D717}_{t}}\right)\nonumber\\ \displaystyle & \simeq & \displaystyle \ell n\left(\frac{\unicode[STIX]{x03C0}}{\sqrt{2(1-\unicode[STIX]{x1D705})}}\right)+\text{i}\int _{0}^{qN\unicode[STIX]{x03C0}}\text{d}z\,\text{e}^{-\text{i}z}\ell n\left(\frac{z}{qN\unicode[STIX]{x03C0}}\right)\nonumber\\ \displaystyle & \simeq & \displaystyle \ell n\left(\frac{1}{qN\sqrt{2(1-\unicode[STIX]{x1D705})}}\right),\end{eqnarray}$$
where using
$y=z/qN\unicode[STIX]{x03C0}$
yields (Gradshteyn & Ryzhik Reference Gradshteyn and Ryzhik2007)
$$\begin{eqnarray}\displaystyle \text{i}\int _{0}^{qN\unicode[STIX]{x03C0}}\text{d}z\,\text{e}^{-\text{i}z}\ell n\left(\frac{z}{qN\unicode[STIX]{x03C0}}\right) & = & \displaystyle \text{i}\unicode[STIX]{x03C0}qN\int _{0}^{1}\text{d}y\text{e}^{-\text{i}\unicode[STIX]{x03C0}qNy}\ell ny\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{1}\text{d}y\ell ny\frac{\text{d}}{\text{d}y}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}qNy}-1)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\frac{\text{d}y}{y}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}qNy}-1)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\unicode[STIX]{x03C0}qN}\frac{\text{d}z}{z}(\text{e}^{-\text{i}z}-1)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\unicode[STIX]{x03C0}qN}\frac{\text{d}z}{z}(\cos z-1)-\text{i}\int _{0}^{\unicode[STIX]{x03C0}qN}\frac{\text{d}z}{z}\sin z\nonumber\\ \displaystyle & = & \displaystyle [Ci(\unicode[STIX]{x03C0}qN)-C-\ell n(\unicode[STIX]{x03C0}qN)]-\text{i}[Si(\unicode[STIX]{x03C0}qN)],\end{eqnarray}$$
where
$C=0.577215$
is Euler’s constant and
$$\begin{eqnarray}\displaystyle Si(x)=\int _{0}^{x}\frac{\text{d}t\sin t}{t}=si(x)+\frac{\unicode[STIX]{x03C0}}{2}, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle Ci(x)=C+\ell nx+\int _{0}^{x}\frac{\text{d}t(\cos t-1)}{t}. & & \displaystyle\end{eqnarray}$$
The preceding evaluation is very different from results (Linsker & Boozer Reference Linsker and Boozer1982; White Reference White2001) obtained by simply using
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}^{2}\simeq 2\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}[\sin (\unicode[STIX]{x1D717}_{t}/2)\cos (\unicode[STIX]{x1D717}_{t}/2)](\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})=\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}(\sin \unicode[STIX]{x1D717}_{t})(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717}) & & \displaystyle\end{eqnarray}$$
to write, for example,
$$\begin{eqnarray}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\frac{\text{d}\unicode[STIX]{x1D717}}{\unicode[STIX]{x1D709}}\cos (Nq\unicode[STIX]{x1D717}) & \simeq & \displaystyle \frac{4}{\sqrt{\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}\sin \unicode[STIX]{x1D717}_{t}}}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\text{d}\unicode[STIX]{x1D717}\frac{\cos (Nq\unicode[STIX]{x1D717})}{\sqrt{\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{4}{\sqrt{\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}\sin \unicode[STIX]{x1D717}_{t}}}\operatorname{Re}\left[\text{e}^{\text{i}qN\unicode[STIX]{x1D717}_{t}}\int _{0}^{\unicode[STIX]{x1D717}_{t}}\text{d}\unicode[STIX]{x1D717}\frac{\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}}{\sqrt{\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717}}}\right],\end{eqnarray}$$
for a complete bounce. Letting
$z=Nq(\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717})$
gives
$$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D717}_{t}}\text{d}\unicode[STIX]{x1D717}\frac{\text{e}^{\text{i}qN(\unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}_{t})}}{\sqrt{\unicode[STIX]{x1D717}_{t}-\unicode[STIX]{x1D717}}}=\frac{1}{\sqrt{Nq}}\int _{0}^{qN\unicode[STIX]{x1D717}_{t}}\text{d}z\frac{\text{e}^{-\text{i}z}}{\sqrt{z}}\simeq \frac{1}{\sqrt{Nq}}\int _{0}^{\infty }\text{d}z\frac{\text{e}^{-\text{i}z}}{\sqrt{z}}. & & \displaystyle\end{eqnarray}$$
Using (Magnus, Oberhettinger & Soni Reference Magnus, Oberhettinger and Soni1966)
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }\text{d}z\frac{\text{e}^{-\text{i}z}}{\sqrt{z}} & = & \displaystyle \int _{0}^{\infty }\text{d}z\frac{\cos z}{\sqrt{z}}-\text{i}\int _{0}^{\infty }\text{d}z\frac{\sin z}{\sqrt{z}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E4}(1/2)\left(\cos \frac{\unicode[STIX]{x03C0}}{4}-\text{i}\sin \frac{\unicode[STIX]{x03C0}}{4}\right)=\unicode[STIX]{x03C0}^{1/2}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4},\end{eqnarray}$$
yields
$$\begin{eqnarray}\displaystyle \oint _{\unicode[STIX]{x1D6FC}}\frac{\text{d}\unicode[STIX]{x1D717}}{\unicode[STIX]{x1D709}}\cos (Nq\unicode[STIX]{x1D717})\simeq \frac{2\sqrt{2\unicode[STIX]{x03C0}}}{\sqrt{\unicode[STIX]{x1D700}Nq\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}\sqrt{1-\unicode[STIX]{x1D705}^{2}}}}\cos \left(Nq\unicode[STIX]{x1D717}_{t}-\frac{\unicode[STIX]{x03C0}}{4}\right), & & \displaystyle\end{eqnarray}$$
where
$2\unicode[STIX]{x1D705}\sqrt{1-\unicode[STIX]{x1D705}^{2}}=2\sin (\unicode[STIX]{x1D717}_{t}/2)\cos (\unicode[STIX]{x1D717}_{t}/2)=\sin \unicode[STIX]{x1D717}_{t}$
and
$\unicode[STIX]{x1D717}_{t}\rightarrow \unicode[STIX]{x03C0}-2\sqrt{2(1-\unicode[STIX]{x1D705})}$
. Then (A 18) gives
$$\begin{eqnarray}\displaystyle \frac{\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}}{RB_{p}}\simeq \frac{\sqrt{\unicode[STIX]{x03C0}Nq\unicode[STIX]{x1D706}}v^{2}\unicode[STIX]{x1D6FF}\cos \left[(Nq-\frac{1}{4})\unicode[STIX]{x03C0}\right]}{4\unicode[STIX]{x1D6FA}_{0}rK(\unicode[STIX]{x1D705})\sqrt{\unicode[STIX]{x1D705}\sqrt{1-\unicode[STIX]{x1D705}^{2}}}}\sin (N\unicode[STIX]{x1D6FC})\sim \frac{q\unicode[STIX]{x1D70C}_{0}v_{0}\unicode[STIX]{x1D6FF}\sqrt{Nq}}{r}. & & \displaystyle\end{eqnarray}$$
Taking the
$\unicode[STIX]{x1D705}\rightarrow 1$
(
$\unicode[STIX]{x1D717}_{t}\rightarrow \unicode[STIX]{x03C0}$
) limit yields
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}\underset{\unicode[STIX]{x1D705}\rightarrow 1}{\longrightarrow }-RB_{p}\frac{\sqrt{\unicode[STIX]{x03C0}qN}\,v^{2}\unicode[STIX]{x1D6FF}\cos [(Nq\,-1/4)\unicode[STIX]{x03C0}]}{2^{5/4}\unicode[STIX]{x1D6FA}_{0}r(1-\unicode[STIX]{x1D705})^{1/4}\,\ell n[8/(1-\unicode[STIX]{x1D705})]}\sin (N\unicode[STIX]{x1D6FC}), & & \displaystyle\end{eqnarray}$$
which is singular! However, the result for
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}}$
should not be singular as
$\unicode[STIX]{x1D705}\rightarrow 1$
.
