It is a pleasure to participate in the discussion on Automated
Inference and the Future of Econometrics at the 20th anniversary mark of
Econometric Theory. Many factors appear to be fueling the growth
of computer-intensive inferential rules; some of these lie with theoretical
advances and with the current and predictable increases in computing power
and in availability of large data sets.
Among the many possible aspects, I wish to comment on three issues
related to this theme, with a view toward possible developments. These
comments are not intended to highlight some published work of mine, and
they are mostly nontechnical; I hope none of these features will be
seen as a liability by the reader.
The three issues, listed in increasing degree of importance, concern
the distinction between automation and computer aided decisions
(Section 1), model selection (Section 2), and learning (Section 3).
Conclusions are reported in Section 4.
1. AUTOMATION AND COMPUTER AIDED DECISIONS
The first aspect is wording. I perceive automated inference (AI) as
associated with artificial intelligence and expert systems. Many
computing-intensive procedures are instead of a different nature, which
I would classify as tools for computer aided decisions (CAD), to be
defined subsequently. This section argues that the two concepts are
different and that they may be fruitfully applied in different
situations. In particular AI is best suited for industrial
applications, CAD for scientific communication.
The phrase “automated inference” conveys the idea that
control over inference is left to a computer program or, more
precisely, that the econometrician does not have complete control over
inference. This concept is associated with artificial intelligence and
expert systems because whatever inferential rule is being applied, it
is used without the direct control of the econometrician. In the
following I will use the (common) acronym AI for both phrases.
Examples of AI are “black-box” procedures. Many black
boxes have been entertained in econometrics, especially in the past.
They include, e.g., automatic univariate autoregressive moving average
(ARMA) modeling, i.e., completely human-unaided computer software that
takes in data and that produces predictions using an ARMA model,
selected via a set of inference rules. More recent references include
some applications of Bayesian vector autoregressions with Minnesota
priors, which are close to being black boxes.
Automated procedures of this kind are also in use for fitting and
selecting artificial neural networks. Some selection methods, called
“pruning,” are typically computed before the optimization
(estimation) has been completed. These pruning procedures cannot be
restated as (quasi-) likelihood ratios and thus are not amenable to
direct statistical interpretation, at least using standard theory.
By contrast let us define by computer aided decisions (CAD) any
computer intensive inference procedure that is (in principle)
completely supervised by a human. Examples of CAD are abundant,
including plug-in bandwidth kernel density estimation, spectral
estimation and testing, indirect inference, Monte Carlo estimation,
model selection through information criteria or statistical tests, and
many more.
The common denominator to any definition of scientific methodology is
communication. For experimental sciences, scientific validity is
associated with replicability of experiments. For nonexperimental
sciences, replicability of experiments is replaced by replicability of
inference. To communicate, econometricians need to have complete
control over inference, and CAD is the elective method for large data
sets in macro- and micro-econometrics. A different situation exists in
financial econometrics; see the discussion that follows.
In fact, there are few reasons why the econometrician should give
away control over inference if the goal of the research project is
scientific communication, despite a possibly heavy computational
burden. If the key steps of inference are unknown to the
econometrician, there is little hope she or he can convince the
scientific community that the prompted inference is a sound one.
This reasoning connects with the aspiration of econometrics to help
economics become more scientific; this idea is at the basis of the
Constitution of the Econometric Society. Concerning the relation
between science and inference, Kim, De Marchi, and Morgan (1995) define the following four motivations for
testing in econometrics: (1) theory falsification, (2a) theory
consensus building, (2b) model quality control, (2c) matching specific
model characteristics with a subset of empirical data (my own wording).
Number (1) corresponds to Popperian theory falsification, number (2) to
theory confirmation.
Regardless of which school in philosophy of science one subscribes
to, it is hard to see which of the preceding activities one can
recommend to be left undisclosed, as in AI. For instance, in (2a),
tests are performed to assess the “accuracy and reliability of
[theory] performance in order to secure widespread support
for belief in that theory” (Kim et al.,
1995, p. 83); obviously this message cannot be conveyed if
inference (performed automatically) is not fully known.
On the other hand, one can see many advantages of AI in industrial
applications, where the main goal is on timely decision making. The
closest analogues to industrial quality control problems are found in
finance. In applied finance, timely forecasts on a vast number of
phenomena are needed to make buy/sell decisions, and automation is
a must more than an option. For obvious reasons, financial analysts are
also averse to communicating their inferences to competitors, and AI
rules prevail. Given that financial decision makers probably use AI,
this information could be used in model building; see Section 3.
2. MODEL SELECTION
Model selection has a long history in econometrics, possibly as long
as the history of econometrics itself. Many procedures are currently in
use for model selection, including information criteria (IC) and
hypothesis testing (HT). Sometimes model selection is an intermediate
step in an inference procedure, e.g., in a forecasting exercise. Other
times model selection is the main goal of inference; this happens,
e.g., when one wishes to compare several economic theories as
alternative explanations for the same set of data. In this case,
multiple comparison (MC) methods can be applied; these methods are not
presently as widespread in econometrics as in other sciences. Sections
2.1–2.3 report some comments on IC, HT, and MC.
2.1. Information Criteria
There has been substantial progress in the area of IC over the last
decades; see Rao and Wu (2001) for a recent
survey. Progress has been made in extending results to possibly
nonstationary time series processes; see Phillips (1996) and references therein for the extension of
Rissanen's theorem to the case of time-series prediction. IC,
although based on (quasi-)likelihood ratios (see Pötscher, 1991), treat models symmetrically,
unlike hypothesis testing. This is the key motivation used by Granger,
King, and White (1995) in advocating the use
of IC in comparison of economic theories.
One limitation of IC lies however with their characteristic of
estimators of the best model. No measure of strength of decision is
usually available, unless a Bayesian paradigm is used. Bayesian
analysis is however not the best suited method for communicating
inferences when the elicitation of a priori distributions is
subjective. Model averaging is not an option when inference is aimed at
selecting among economic theories.
In general, one would like to complement the choice of a model with a
likely (objective) assessment of whether this model is significantly
distant from alternative ones. If one is to choose among different
economic theories, this is particularly relevant.
Asymptotic probability statements on IC can be deduced from their
connection to HT and MC procedures, which are discussed in Sections 2.2
and 2.3. This is because IC, HT, and MC are all based on the same
(quasi-)likelihood theory. No investigation appears to exist in this
direction in the literature, and any attempt along this line will
probably be rewarded.
One other area where more theoretical contributions would be welcome
is comparison of IC procedures. These comparisons should be aimed at
selecting a single or at most a few best criteria. The many IC now in
use often generate conflicting decisions, with no clue on how to
resolve them.
At present, procedures are classified as efficient and/or
consistent (see Rao and Wu, 2001). Among
consistent criteria, no comparison is usually made on (higher order)
asymptotics, as in the case of parameter estimation.
Here one needs to define (higher order) asymptotics in this context.
As one possibility, consider two criterion functions
hjn(i), j = 1,2, based
on a sample of size n, where i =
1,…,p indicates different models
M1,…,Mp. Let
i0 be the index of the correct model. Consistency of
is usually proved by showing that
hjn(i0) =
Op(1) as n → ∞ whereas
hjn(i) =
O(nαj) →
∞ for i ≠ i0. The order
nαj could depend also on
i, but we assume for simplicity that it is uniform over
incorrect models. Assume that both h1n and
h2n are consistent. One could first
compare α1 and α2, where the criterion
that guarantees the fastest divergence should be favored.
Assume however that the two criteria h1n
and h2n are both consistent and have the
same divergence rate α1 = α2. One could
then study the ratio qn :=
h1n /h2n
− 1 to ascertain if qn is
asymptotically positive or negative. More generally one could study the
asymptotic distribution of qn and prefer
h1n to h2n if
Pr(qn ≥ 0) → η > ½.
These comparisons could give a handle on how to select a best
criterion, thus reducing the possibility of conflicting results.
2.2. Hypothesis Testing
Some selection procedures are based on HT. HT gives a probabilistic
framework within which one can measure strength of decisions. Let
Θ1 ⊂ Θ2 ⊂
··· ⊂ Θp be nested
parameter sets corresponding to models
M1,…,Mp. Some
common misconceptions on HT in model selection are the following: (i)
in nested models, a general to specific HT strategy is only associated
with testing Mj−1 in
Mj starting with j = p
and proceeding to j = 0 (called “testing-down”
strategy in the following discussion); (ii) HT may be applied only to
nested models that contain the true data generating process (DGP).
Consider (i). In several instances it has proved useful to consider a
general to specific strategy that tests Mi
in Mp starting with i = 0 and
proceeding up to p − 1. For later reference, call this
procedure a “testing-up” sequence. This strategy is still
general to specific, because each submodel is tested against the full
model Mp.
The testing-up sequence has been applied, e.g., when testing for
cointegration rank (see Johansen, 1992). Here
Mj indicates a vector autoregressive (VAR)
model with cointegration rank at most equal to j; let
LR(i| j) be the likelihood ratio test
comparing Mi and
Mj. For the testing-up procedure, as
sample size diverges, one has Pr(select
Mr) → 1 − α and Pr(select
Mi) → 0 for i <
r, where r is the true cointegration rank and α
is the size of each test in the sequence. These properties do not apply
to the testing-down procedure, because the limit distribution of
LR(j − 1| j) depends on which submodel
Mj−h contains the DGP,
h = 1,2,3,…,j − 1. Hence one sees that,
in a nonstationary setting, the testing-up procedure is recommended,
contrary to the common belief (i). Obviously, letting α decrease to
zero as sample size increases generates a consistent selection
criterion for cointegration rank.
Regarding issue (ii), it is important to note that hypothesis testing
can be defined and used also for comparing misspecified models that do
not contain the DGP, as shown by Vuong (1989)
for independent and identically distributed (i.i.d.) observations.
Extension of these results to dependent data and more than a pair of
models appears to be a fruitful line of future research.
A final word of caution concerns the distribution of the estimators
of the selected model, as shown in recent work by Leeb and
Pötscher (2003).
2.3. Multiple Comparisons
Consider finally the case when model selection is the main goal of
inference, i.e., one wishes to confront several economic theories with
the same set of data. In this context MC procedures may find wider
applications in econometrics; see Hsu (1996)
for an introduction to MC.
As a simple example, consider the usual regression setup with two
regressors,
Assume also that several competing theories exist on the explanation
of y. Theory 1 predicts that β1 > 0 and
β2 < 0, and theory 2 predicts that β1
= β2.
Of course one can compute the univariate t tests
tβ1=0,
tβ2=0, and
tβ1=β2 or the
corresponding confidence intervals. One can then combine these separate
inferences, using probability inequalities such as Bonferroni's
(this is called “deduced inference” in Hsu, 1996).
However, in principle, one would like to construct simultaneous
confidence intervals for β1, β2, and
β1 − β2 from the start, with
overall coverage probability not inferior to 95%. This is called
“direct inference” in Hsu (1996).
Note that the direct method can exploit the fact that we wish to have
three confidence intervals for a bivariate distribution of
,
where a hat indicates the regression estimator.
One possible simple direct inference method is Scheffé's
procedure, which states
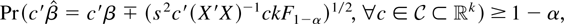
where F1−α is the 1 − α
quantile of an F(k,n − k)
distribution, and k is the number of regressors, in the
example equal to 2. One can form simultaneous confidence intervals for
any choice of
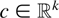
using
(s2c′(X′X)−1ckF1−α)1/2
as standard error. In our example we can choose c equal to
c1 := (1 : 0)′, c2 := (0
: 1)′, c3 := (1 : −1)′, obtaining
three confidence intervals I1,
I2, I3. If the lower endpoint
of I1 is greater than 0 one can assert
β1 > 0; similarly if the upper endpoint of
I2 is negative, one can assert β2
< 0. If finally I3 contains 0, then one can
assert β1 = β2. All these statements have
a joint error rate bounded by 5%.
Note that, if some new economic theory comes along—theory 3,
say, which predicts β1 + 2β2 =
1—one does not have to rework the confidence level of the
confidence intervals I1, I2,
I3 from the start, but just needs to construct one
more confidence interval I4 for β1 +
2β2 − 1.
This feature is both a strength and a weakness of
Scheffé's procedure. On one side it gives great flexibility
to add any other confidence interval; on the other hand a price is paid
in accommodating all these simultaneous confidence intervals. The price
is that some possibly less comprehensive procedure gives tighter bounds
for each confidence interval; see Hsu (1996).
MCs are widely used in analysis of variance (ANOVA) applications and
in regression models; for the application of Scheffé-like
procedures in nonlinear regression see, e.g., Johansen and Johnstone
(1990). It is possible that many of the
procedures within PcGets (see Granger and Hendry,
2005), could be (re)discussed or reorganized in this MC
perspective.
3. LEARNING
There appears to be an increasing decoupling among the fields of
economic theory (A), econometric theory (B), and applications (C); this
is how Mirowski (1995) describes the current
age dominated by “critical post-modernism.” Separately, the
three groups (A, B, C) “maintain a life of their own, through
their own journals, their own pedagogy, their forms of tacit
knowledge” (Mirowski, 1995, p. 29).
Although some degree of autonomy appears constructive (certain
“facts” survive changes in economic-theory regimes), a
complete separation appears to be contrary to the foundations of all
three fields and especially of econometrics (see Frisch, 1933).
One direction that may foster closer cooperation among the three
areas is given by the literature on learning, which challenges the
notion of rational expectations. Several papers have recently appeared
in this line; see, e.g., Guidolin and Timmermann (2003) and references therein.
In these economic models, agents form expectations as an
econometrician observing data. Advances in AI could thus help produce
better models, e.g., of investors' behavior in financial markets.
This may hopefully lead to a better understanding of the actual
mechanics of observed economic behavior (C) through the explicit
incorporation of the econometric model uncertainty (B) into the
economic model (A). It is not hard to foresee a high reward for
teamwork in this area in the future.
4. CONCLUSIONS
In this note I have tried to distinguish between AI and CAD. Both are
valuable: AI is better employed in industrial applications and finance,
whereas CAD is needed if one wishes to communicate inference, which is
at the basis of building economic science.
Information criteria in model selection give many interesting lines
of future research. At present there are many IC, and it is difficult
to select any single one. Moreover, for non-Bayesians, IC do not
provide measures of strength of inference.
Hypothesis testing is still a resource for econometricians, which
should be more fully exploited also in the selection of (possibly
misspecified) models. Multiple comparisons methods should also be more
fully explored in econometrics.
As always, the future of econometrics lies in working more closely
with economists; embedding AI rules for investors in economic models of
financial markets appears a promising area of development for the
economics of learning.
