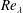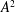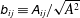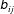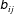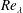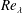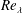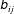1 Introduction
Velocity-gradient dynamics underlies many critical turbulence phenomena such as intermittency, multifractality, streamline topology, material-element deformation and scalar mixing (Soria et al.
Reference Soria, Sondergaard, Cantwell, Chong and Perry1994; Blackburn, Mansour & Cantwell Reference Blackburn, Mansour and Cantwell1996; Martín et al.
Reference Martín, Ooi, Chong and Soria1998b
; Suman & Girimaji Reference Suman and Girimaji2010; Danish, Suman & Girimaji Reference Danish, Suman and Girimaji2016). It is of fundamental interest to understand velocity-gradient dynamics and develop Lagrangian closure models that capture key turbulence features (Girimaji & Pope Reference Girimaji and Pope1990; Martín, Dopazo & Valiño Reference Martín, Dopazo and Valiño1998a
; Jeong & Girimaji Reference Jeong and Girimaji2003; Chevillard et al.
Reference Chevillard, Meneveau, Biferale and Toschi2008; Meneveau Reference Meneveau2011; Pereira, Moriconi & Chevillard Reference Pereira, Moriconi and Chevillard2018). The multifractal and intermittent nature of velocity gradients renders characterization of their dynamics quite challenging (Yakhot & Sreenivasan Reference Yakhot and Sreenivasan2005; Donzis, Yeung & Sreenivasan Reference Donzis, Yeung and Sreenivasan2008; Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015). It has been demonstrated in recent literature (Yakhot & Donzis Reference Yakhot and Donzis2017) that intermittency effects manifest even at Reynolds number
$Re_{\unicode[STIX]{x1D706}}\sim O(10)$
and are significant by
$Re_{\unicode[STIX]{x1D706}}\sim O(100)$
. To complement the findings of the above studies, the goal of this investigation is to establish the
$Re_{\unicode[STIX]{x1D706}}$
dependence of the internal structure of the velocity gradients and constituent dynamical processes. We demonstrate that such an examination leads to improved insight into important aspects of velocity-gradient dynamics, including a clear distinction between internal structure and magnitude effects.
We factorize the velocity-gradient tensor (
$\unicode[STIX]{x1D608}_{ij}$
) into the magnitude (
$A^{2}$
-Frobenius norm of
$\unicode[STIX]{x1D63C}$
) and normalized velocity-gradient tensor
$\unicode[STIX]{x1D657}$
(Girimaji & Speziale Reference Girimaji and Speziale1995; Bikkani & Girimaji Reference Bikkani and Girimaji2007; Bechlars & Sandberg Reference Bechlars and Sandberg2017):
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{ij}=\frac{\unicode[STIX]{x1D608}_{ij}}{A}\quad \text{where }A=\sqrt{A^{2}}=\sqrt{\unicode[STIX]{x1D608}_{mn}\unicode[STIX]{x1D608}_{mn}}. & & \displaystyle\end{eqnarray}$$
The tensor
$\unicode[STIX]{x1D657}$
is of intrinsic physical interest as it provides insight into many structural features of turbulence such as local streamline topology and the orientation between strain rate eigendirections and vorticity (Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Wang et al.
Reference Wang, Szalay, Aragón-Calvo, Neyrinck and Eyink2014). The tensor
$\unicode[STIX]{x1D623}_{ij}$
is mathematically bounded and thus expected to be more amenable to analysis and closure modelling. Furthermore, it is demonstrated that the processes requiring closure in the equations for
$\unicode[STIX]{x1D623}_{ij}$
and
$A^{2}$
are identical. Thus, the evolution of unbounded-
$A^{2}$
can be cast in terms of bounded-
$\unicode[STIX]{x1D623}_{ij}$
dynamics.
The goal of the present study is to exploit the bounded nature of the
$\unicode[STIX]{x1D623}_{ij}$
tensor to examine the velocity-gradient structure and non-local processes. We seek to:
(i) Develop appropriately scaled
$\unicode[STIX]{x1D623}_{ij}$
and
$A^{2}$
evolution equations and exhibit that the processes requiring closure in the two cases are similar.(ii) Examine the
$Re_{\unicode[STIX]{x1D706}}$
dependence of the velocity-gradient structure:
$\unicode[STIX]{x1D623}_{ij}$
-moments, probability density functions (PDFs) and invariants (
$q$
and
$r$
). Although
$q$
and
$r$
are bounded, the normalization does not guarantee self-similarity at different Reynolds numbers.(iii) Establish the
$Re_{\unicode[STIX]{x1D706}}$
dependence of the unclosed non-local pressure and viscous processes in the
$\unicode[STIX]{x1D623}_{ij}$
and
$A^{2}$
evolution equations conditioned upon
$q$
and
$r$
.
The work employs forced isotropic turbulence simulation data in the Taylor-scale Reynolds number range
$Re_{\unicode[STIX]{x1D706}}=1$
to
$588$
. The remainder of the paper is arranged as follows. Section 2 contains the evolution equations of
$A^{2}$
,
$\unicode[STIX]{x1D623}_{ij}$
and its invariants. A brief description of the data sets used in the study is given in § 3. The
$Re_{\unicode[STIX]{x1D706}}$
dependences of various velocity-gradient features are presented in § 4. The paper concludes in § 5 with a brief summary.
2 Governing equations
Differentiating the incompressible Navier Stokes equation with respect to spatial coordinates (
$x_{j}$
) yields the evolution equation of the velocity-gradient tensor (Cantwell Reference Cantwell1992),
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D608}_{ij})+\unicode[STIX]{x1D608}_{ik}\unicode[STIX]{x1D608}_{kj}=-\frac{\unicode[STIX]{x2202}^{2}p}{\unicode[STIX]{x2202}x_{i}\unicode[STIX]{x2202}x_{j}}+\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D608}_{ij}}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}x_{k}};\quad i,j=1,2,3. & & \displaystyle\end{eqnarray}$$
Using the incompressibility condition
$\unicode[STIX]{x1D608}_{ii}=0$
, the isotropic pressure Hessian term can be written as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D608}_{ik}\unicode[STIX]{x1D608}_{ki}=-\frac{\unicode[STIX]{x2202}^{2}p}{\unicode[STIX]{x2202}x_{i}\unicode[STIX]{x2202}x_{i}}. & & \displaystyle\end{eqnarray}$$
The non-local anisotropic pressure Hessian and the viscous diffusion term are
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D60F}_{ij}=-\frac{\unicode[STIX]{x2202}^{2}p}{\unicode[STIX]{x2202}x_{i}\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}^{2}p}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}x_{k}}\frac{\unicode[STIX]{x1D6FF}_{ij}}{3};\quad \unicode[STIX]{x1D61B}_{ij}=\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D608}_{ij}}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}x_{k}}. & & \displaystyle\end{eqnarray}$$
Thus, the velocity-gradient equation may be written as
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D608}_{ij}}{\text{d}t}+\unicode[STIX]{x1D608}_{ik}\unicode[STIX]{x1D608}_{kj}-\frac{1}{3}\unicode[STIX]{x1D608}_{mk}\unicode[STIX]{x1D608}_{km}\unicode[STIX]{x1D6FF}_{ij}=\unicode[STIX]{x1D60F}_{ij}+\unicode[STIX]{x1D61B}_{ij}. & & \displaystyle\end{eqnarray}$$
In a Lagrangian reference frame, the
$\unicode[STIX]{x1D608}_{ij}$
-dynamics depends upon the non-local pressure and viscous terms. One of the earliest attempts at developing closure models for velocity-gradient dynamics was made by Vieillefosse (Reference Vieillefosse1982) by neglecting the non-local terms. There have since been several Lagrangian velocity-gradient models that develop closure for
$\unicode[STIX]{x1D60F}_{ij}$
and
$\unicode[STIX]{x1D61B}_{ij}$
to replicate turbulence behaviour. However, the intermittent nature of the velocity-gradient magnitude renders the modelling rather challenging. Recently, Pereira et al. (Reference Pereira, Moriconi and Chevillard2018) have used multifractal considerations, to first model
$A^{2}$
and then determine the closure for
$\unicode[STIX]{x1D608}_{ij}$
-evolution.
We seek an alternative approach by segregating the evolution of the magnitude (
$A^{2}$
) from that of normalized velocity-gradient tensor
$\unicode[STIX]{x1D623}_{ij}$
as defined in (1.1). We propose that modelling
$\unicode[STIX]{x1D623}_{ij}$
first has advantages due to the boundedness of the tensor components. Further,
$\unicode[STIX]{x1D623}_{ij}$
is of intrinsic interest as it characterizes the orientation of velocity gradients and local flow structures.
2.1 Mathematical bounds of
$\unicode[STIX]{x1D623}_{ij}$
Longitudinal
$\unicode[STIX]{x1D623}_{ij}$
-components satisfy the incompressibility condition,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D623}_{ii}=\unicode[STIX]{x1D623}_{11}+\unicode[STIX]{x1D623}_{22}+\unicode[STIX]{x1D623}_{33}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \Rightarrow \unicode[STIX]{x1D623}_{33}=-(\unicode[STIX]{x1D623}_{11}+\unicode[STIX]{x1D623}_{22}). & \displaystyle\end{eqnarray}$$
By virtue of normalization, the following inequality holds true:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{11}^{2}+\unicode[STIX]{x1D623}_{22}^{2}+\unicode[STIX]{x1D623}_{33}^{2}\leqslant 1. & & \displaystyle\end{eqnarray}$$
Applying (2.6) in the above inequality we obtain the following constraint:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{11}^{2}+\unicode[STIX]{x1D623}_{22}^{2}+\unicode[STIX]{x1D623}_{11}\unicode[STIX]{x1D623}_{22}\leqslant {\textstyle \frac{1}{2}}. & & \displaystyle\end{eqnarray}$$
The bounds of
$\unicode[STIX]{x1D623}_{11}$
subject to the above constraint can be obtained as
$$\begin{eqnarray}\displaystyle {\textstyle \frac{1}{2}}\left(-\sqrt{2-3\unicode[STIX]{x1D623}_{22}^{2}}-\unicode[STIX]{x1D623}_{22}\right)\leqslant \unicode[STIX]{x1D623}_{11}\leqslant {\textstyle \frac{1}{2}}\left(\sqrt{2-3\unicode[STIX]{x1D623}_{22}^{2}}-\unicode[STIX]{x1D623}_{22}\right). & & \displaystyle\end{eqnarray}$$
Now let us examine the minimum possible value of the lower bound. Minimizing the lower bound yields a
$\unicode[STIX]{x1D623}_{22}$
value of
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{22}={\textstyle \frac{1}{\sqrt{6}}}. & & \displaystyle\end{eqnarray}$$
Similarly, the upper bound attains the maximum value when
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{22}=-{\textstyle \frac{1}{\sqrt{6}}}. & & \displaystyle\end{eqnarray}$$
Therefore,
$\unicode[STIX]{x1D623}_{11}$
or any other longitudinal velocity gradient is bounded as
$$\begin{eqnarray}\displaystyle -\sqrt{{\textstyle \frac{2}{3}}}\leqslant \unicode[STIX]{x1D623}_{ij}\leqslant \sqrt{{\textstyle \frac{2}{3}}}\quad \forall i=j. & & \displaystyle\end{eqnarray}$$
Transverse components can be the sole non-zero element in the velocity-gradient tensor. These components are only constrained by normalization and are therefore only limited by unity,
$$\begin{eqnarray}\displaystyle -1\leqslant \unicode[STIX]{x1D623}_{ij}\leqslant 1\quad \forall i\neq j. & & \displaystyle\end{eqnarray}$$
2.2 Evolution equations of
$A^{2}$
and
$\unicode[STIX]{x1D623}_{ij}$
Multiplying the velocity-gradient equation (2.4) through by
$\unicode[STIX]{x1D608}_{ij}/A^{3}$
yields
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D608}_{ij}}{A^{3}}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D608}_{ij})=-\frac{\unicode[STIX]{x1D608}_{ij}\unicode[STIX]{x1D608}_{ik}\unicode[STIX]{x1D608}_{kj}}{A^{3}}+\frac{1}{3A^{3}}\unicode[STIX]{x1D608}_{km}\unicode[STIX]{x1D608}_{mk}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D608}_{ij}+\frac{\unicode[STIX]{x1D608}_{ij}\unicode[STIX]{x1D60F}_{ij}}{A^{3}}+\frac{\unicode[STIX]{x1D608}_{ij}\unicode[STIX]{x1D61B}_{ij}}{A^{3}}. & & \displaystyle\end{eqnarray}$$
Using the incompressibility condition, we obtain the following equation:
$$\begin{eqnarray}\displaystyle \frac{1}{A^{3}}\frac{\text{d}A^{2}}{\text{d}t}=\frac{1}{A^{3}}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D608}_{ij}\unicode[STIX]{x1D608}_{ij})=-2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj}+2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D629}_{ij}+2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D70F}_{ij}, & & \displaystyle\end{eqnarray}$$
where the non-local physics is incumbent in the normalized anisotropic pressure Hessian and viscous diffusion terms:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D629}_{ij}=\frac{\unicode[STIX]{x1D60F}_{ij}}{A^{2}}\quad \text{and}\quad \unicode[STIX]{x1D70F}_{ij}=\frac{\unicode[STIX]{x1D61B}_{ij}}{A^{2}}. & & \displaystyle\end{eqnarray}$$
It is convenient to describe magnitude evolution in terms of
$\unicode[STIX]{x1D703}\equiv \text{log}(A^{2})$
:
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t^{\prime }}=I_{\unicode[STIX]{x1D703}}+{\mathcal{P}}_{\unicode[STIX]{x1D703}}+V_{\unicode[STIX]{x1D703}}; & & \displaystyle\end{eqnarray}$$
where the normalized time and inertial, pressure and viscous contributions are
$$\begin{eqnarray}\displaystyle t^{\prime }\triangleq At,\quad I_{\unicode[STIX]{x1D703}}=-2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj},\quad {\mathcal{P}}_{\unicode[STIX]{x1D703}}=2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D629}_{ij},\quad V_{\unicode[STIX]{x1D703}}=2\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D70F}_{ij}. & & \displaystyle\end{eqnarray}$$
Next we turn our attention to the evolution of the normalized tensor
$\unicode[STIX]{x1D623}_{ij}$
:
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D623}_{ij}}{\text{d}t}=\frac{\text{d}}{\text{d}t}\left(\frac{\unicode[STIX]{x1D608}_{ij}}{A}\right)=\frac{1}{A}\frac{\text{d}\unicode[STIX]{x1D608}_{ij}}{\text{d}t}-\frac{\unicode[STIX]{x1D608}_{ij}}{2}\left(\frac{1}{A^{3}}\frac{\text{d}A^{2}}{\text{d}t}\right)\!. & & \displaystyle\end{eqnarray}$$
Using (2.4), (2.15) and (2.19), the governing equation for
$\unicode[STIX]{x1D623}_{ij}$
is obtained in normalized time
$t^{\prime }$
:
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D623}_{ij}}{\text{d}t^{\prime }}=-\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj}+\unicode[STIX]{x1D629}_{ij}+\unicode[STIX]{x1D70F}_{ij}+\frac{1}{3}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{km}\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D623}_{ij}(\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{kn}-\unicode[STIX]{x1D629}_{mn}-\unicode[STIX]{x1D70F}_{mn})\unicode[STIX]{x1D623}_{mn}. & & \displaystyle\end{eqnarray}$$
The processes that require closure in the
$\unicode[STIX]{x1D623}_{ij}$
-equation – the non-local pressure term
$\unicode[STIX]{x1D629}_{ij}$
and viscous term
$\unicode[STIX]{x1D70F}_{ij}$
– are same as those in the
$A^{2}$
-equation. Although the boundedness of
$\unicode[STIX]{x1D629}_{ij}$
and
$\unicode[STIX]{x1D70F}_{ij}$
are not guaranteed, the requirement that
$\unicode[STIX]{x1D623}_{ij}$
be bounded renders modelling the pressure and viscous terms more tractable. Once the
$\unicode[STIX]{x1D623}_{ij}$
-evolution closure model equation is developed, the magnitude equation requires no further closure modelling.
2.3 Evolution of
$\unicode[STIX]{x1D623}_{ij}$
invariants
Let
$p,q$
and
$r$
represent the invariants of
$\unicode[STIX]{x1D657}$
:
$$\begin{eqnarray}\displaystyle p=-\unicode[STIX]{x1D623}_{ii}=0,\quad q=-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{mi},\quad r=-{\textstyle \frac{1}{3}}\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{ki}. & & \displaystyle\end{eqnarray}$$
These invariants are of interest as the local streamline structure can be classified into four distinct topologies based on
$q$
and
$r$
(Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990). Now, we seek equations for
$q$
and
$r$
. Using (2.20), the following equation for inner product of
$\unicode[STIX]{x1D657}$
is obtained
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t^{\prime }}(\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D623}_{nj}) & = & \displaystyle -2\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kn}\unicode[STIX]{x1D623}_{nj}+\frac{2}{3}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{km}\unicode[STIX]{x1D623}_{ij}+2\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D623}_{nj}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{kq}+\unicode[STIX]{x1D629}_{in}\unicode[STIX]{x1D623}_{nj}+\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D629}_{nj}\nonumber\\ \displaystyle & & \displaystyle -\,2\unicode[STIX]{x1D629}_{mq}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D623}_{nj}+\unicode[STIX]{x1D70F}_{in}\unicode[STIX]{x1D623}_{nj}+\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D70F}_{nj}-2\unicode[STIX]{x1D70F}_{mq}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{in}\unicode[STIX]{x1D623}_{nj}.\end{eqnarray}$$
Taking the trace of (2.22), the evolution equation of
$q$
is determined as
$$\begin{eqnarray}\displaystyle \frac{\text{d}q}{\text{d}t^{\prime }}=-3r+2q\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj}-\unicode[STIX]{x1D629}_{in}(\unicode[STIX]{x1D623}_{ni}+2q\unicode[STIX]{x1D623}_{in})-\unicode[STIX]{x1D70F}_{in}(\unicode[STIX]{x1D623}_{ni}+2q\unicode[STIX]{x1D623}_{in})=I_{q}+{\mathcal{P}}_{q}+V_{q}, & & \displaystyle\end{eqnarray}$$
where
$I_{q}$
,
${\mathcal{P}}_{q}$
and
$V_{q}$
represent inertial, pressure and viscous contributions towards the evolution of
$q$
:
$$\begin{eqnarray}\displaystyle I_{q}=-3r+2q\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj},\quad {\mathcal{P}}_{q}=-\unicode[STIX]{x1D629}_{in}(\unicode[STIX]{x1D623}_{ni}+2q\unicode[STIX]{x1D623}_{in}),\quad V_{q}=-\unicode[STIX]{x1D70F}_{in}(b_{ni}+2qb_{in}).\quad \qquad & & \displaystyle\end{eqnarray}$$
To obtain the equation of
$r$
, we first derive the equation for triple inner product of
$\unicode[STIX]{x1D657}$
using (2.20) and (2.22):
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t^{\prime }}(\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}) & = & \displaystyle -3\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{lk}\unicode[STIX]{x1D623}_{kn}\unicode[STIX]{x1D623}_{nj}+\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{lj}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{km}+3\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{mk}\unicode[STIX]{x1D623}_{kq}+ (\!\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D629}_{ln}\unicode[STIX]{x1D623}_{nj}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D629}_{nj}+\unicode[STIX]{x1D629}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}-3\unicode[STIX]{x1D629}_{mq}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}\! )+(\!\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D70F}_{ln}\unicode[STIX]{x1D623}_{nj}+\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D70F}_{nj}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70F}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}-3\unicode[STIX]{x1D70F}_{mq}\unicode[STIX]{x1D623}_{mq}\unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{ln}\unicode[STIX]{x1D623}_{nj}\! ).\end{eqnarray}$$
Applying the Cayley–Hamilton Theorem,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D623}_{il}\unicode[STIX]{x1D623}_{lk}\unicode[STIX]{x1D623}_{kj}+p\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj}+q\unicode[STIX]{x1D623}_{ij}+r\unicode[STIX]{x1D6FF}_{ij}=0, & & \displaystyle\end{eqnarray}$$
in the trace of (2.25), the evolution equation of
$r$
is obtained as follows:
$$\begin{eqnarray}\frac{\text{d}r}{\text{d}t^{\prime }}=\frac{2}{3}q^{2}+3r\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj}-\unicode[STIX]{x1D629}_{mn}(\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{ni}+3r\unicode[STIX]{x1D623}_{mn})-\unicode[STIX]{x1D70F}_{mn}(\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{ni}+3r\unicode[STIX]{x1D623}_{mn})=I_{r}+{\mathcal{P}}_{r}+V_{r},\end{eqnarray}$$
where the local (inertial and isotropic pressure), anisotropic pressure and viscous contributions in the evolution of
$r$
are
$$\begin{eqnarray}\displaystyle I_{r}={\textstyle \frac{2}{3}}q^{2}+3r\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ik}\unicode[STIX]{x1D623}_{kj},\quad {\mathcal{P}}_{r}=-\unicode[STIX]{x1D629}_{mn}(\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{ni}+3r\unicode[STIX]{x1D623}_{mn}),\quad V_{r}=-\unicode[STIX]{x1D70F}_{mn}(\unicode[STIX]{x1D623}_{im}\unicode[STIX]{x1D623}_{ni}+3r\unicode[STIX]{x1D623}_{mn}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The goal of the remainder of this paper is to use DNS data sets to establish the
$Re_{\unicode[STIX]{x1D706}}$
dependence of the statistics of
$\unicode[STIX]{x1D623}_{ij}$
,
$q$
and
$r$
. Then we will also characterize the effect of changing Reynolds number on unclosed pressure (
$\unicode[STIX]{x1D629}_{ij}$
) and viscous (
$\unicode[STIX]{x1D70F}_{ij}$
) processes by examining the evolution of
$q$
,
$r$
and
$\unicode[STIX]{x1D703}$
. The investigation of the unclosed invariants will yield further insight into velocity-gradient dynamics and provide guidance for developing closure models.
3 DNS data sets
DNS data sets used in this study have been obtained from the following sources: Donzis research group at Texas A
$\&$
M University (Donzis et al.
Reference Donzis, Yeung and Sreenivasan2008; Yakhot & Donzis Reference Yakhot and Donzis2017) and Johns Hopkins Turbulence Database (Li et al.
Reference Li, Perlman, Wan, Yang, Meneveau, Burns, Chen, Szalay and Eyink2008). These data sets have been widely used in the literature to study velocity-gradient dynamics, intermittency and anomalous scaling (Donzis et al.
Reference Donzis, Yeung and Sreenivasan2008; Donzis & Sreenivasan Reference Donzis and Sreenivasan2010; Johnson & Meneveau Reference Johnson and Meneveau2016; Yakhot & Donzis Reference Yakhot and Donzis2017). Twelve forced isotropic incompressible turbulence data sets with Taylor Reynolds number (
$Re_{\unicode[STIX]{x1D706}}$
) ranging from
$1$
to
$588$
are used in this work. The details of these simulations are shown in table 1. Here,
$$\begin{eqnarray}\displaystyle Re_{\unicode[STIX]{x1D706}}\equiv u^{\prime }\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708} & & \displaystyle\end{eqnarray}$$
where
$u^{\prime }$
is the root-mean-square (r.m.s.) velocity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity.
$\unicode[STIX]{x1D706}$
(Taylor microscale) and
$\unicode[STIX]{x1D716}$
(dissipation rate) are given by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}=(15\unicode[STIX]{x1D708}(u^{\prime })^{2}/\unicode[STIX]{x1D716})^{1/2},\quad \unicode[STIX]{x1D716}=2\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle . & & \displaystyle\end{eqnarray}$$
Here,
$k_{max}\unicode[STIX]{x1D702}$
is the highest resolved wavenumber (
$k_{max}$
) normalized by the Kolmogorov length scale (
$\unicode[STIX]{x1D702}$
). All the derivatives used in this study are calculated using spectral methods.
Table 1. Details of forced isotropic incompressible turbulence data sets used.
4 Results and discussion
We start by exhibiting the known features of velocity gradients as a function of Reynolds number – anomalous scaling of the normalized higher-order moments and increasingly stretched exponential tails of the probability density functions (PDFs). We then contrast the known
$\unicode[STIX]{x1D608}_{ij}$
behaviour against the
$\unicode[STIX]{x1D623}_{ij}$
moments and PDF. Then the
$Re_{\unicode[STIX]{x1D706}}$
dependence of various velocity-gradient dynamics processes conditioned on
$q$
and
$r$
is established.
4.1 Unnormalized velocity-gradient statistics
Figure 1. Even-order moments (
$M_{2n}$
for
$n=2,3,4,5,6$
) of
$\unicode[STIX]{x1D608}_{11}$
as a function of
$Re_{\unicode[STIX]{x1D706}}$
. Dashed lines represent Gaussian moments, i.e.
$M_{2n}^{G}=(2n-1)!!$
, for reference.
Even-order moments (
$M_{2n}^{A}$
for
$n=2,3,4,5,6$
) of the longitudinal velocity gradient (
$\unicode[STIX]{x1D608}_{11}=\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x$
) given by
$$\begin{eqnarray}\displaystyle M_{2n}^{A}=\frac{\overline{{\unicode[STIX]{x1D608}_{11}}^{2n}}}{\overline{{\unicode[STIX]{x1D608}_{11}}^{2}}^{n}} & & \displaystyle\end{eqnarray}$$
are plotted as a function of
$Re_{\unicode[STIX]{x1D706}}$
in figure 1. Here,
$\overline{(\,\,)}$
implies volume averaging. It is observed that for
$Re_{\unicode[STIX]{x1D706}}\leqslant 9$
, the moments are nearly Gaussian. For
$Re_{\unicode[STIX]{x1D706}}>9$
, the values of all the moments steadily increase with
$Re_{\unicode[STIX]{x1D706}}$
in agreement with the anomalous scaling observed by Yakhot & Donzis (Reference Yakhot and Donzis2017). Note that the
$Re_{\unicode[STIX]{x1D706}}$
-range considered in this study is much wider than that of Yakhot & Donzis (Reference Yakhot and Donzis2017). Anomalous scaling of the moments is a clear indication of the intermittent behaviour of
$\unicode[STIX]{x1D608}_{ij}$
. This observation is further reinforced in the PDF plots of velocity gradients.
Figure 2. PDF of velocity-gradient component (a)
$\unicode[STIX]{x1D608}_{11}/\sqrt{\langle A^{2}\rangle }$
(b)
$\unicode[STIX]{x1D608}_{12}/\sqrt{\langle A^{2}\rangle }$
for different
$Re_{\unicode[STIX]{x1D706}}$
.
The PDFs of
$\unicode[STIX]{x1D608}_{11}$
and
$\unicode[STIX]{x1D608}_{12}$
are shown in figure 2. As expected, at sufficiently high
$Re_{\unicode[STIX]{x1D706}}$
, the longitudinal and transverse PDFs exhibit stretched exponential tails that grow with increasing
$Re_{\unicode[STIX]{x1D706}}$
(Kailasnath, Sreenivasan & Stolovitzky Reference Kailasnath, Sreenivasan and Stolovitzky1992; Chevillard & Meneveau Reference Chevillard and Meneveau2006; Schumacher et al.
Reference Schumacher, Scheel, Krasnov, Donzis, Yakhot and Sreenivasan2014).
Another feature of turbulent flows relevant to this study is the dissipative anomaly (Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005). In the asymptotic limit of high
$Re_{\unicode[STIX]{x1D706}}$
, the normalized energy dissipation rate (
$\unicode[STIX]{x1D716}L/u^{\prime 3}$
) asymptotes to a constant value of approximately 0.4–0.45. Here,
$L$
is the integral length scale and
$u^{\prime }$
is the r.m.s. velocity. In other words, the normalized mean energy dissipation rate is independent of viscosity provided the value of
$Re_{\unicode[STIX]{x1D706}}$
is sufficiently high. The onset of this dissipative anomaly in forced isotropic turbulence is observed at
$Re_{\unicode[STIX]{x1D706}}\sim 200$
(Sreenivasan Reference Sreenivasan1998; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Donzis et al.
Reference Donzis, Sreenivasan and Yeung2005). We will invoke this result later in the study.
4.2 Normalized velocity-gradient statistics
Figure 3. Even-order moments (
$M_{2n}$
for
$n=2,3,4,5,6$
) of
$\unicode[STIX]{x1D623}_{11}$
as a function of
$Re_{\unicode[STIX]{x1D706}}$
. Dashed lines represent Gaussian moments, i.e.
$M_{2n}^{G}=(2n-1)!!$
for reference.
In this subsection, we investigate the statistical characteristics of the tensor
$\unicode[STIX]{x1D657}$
. The even-order moments of
$\unicode[STIX]{x1D623}_{11}$
are given by
$$\begin{eqnarray}\displaystyle M_{2n}^{b}=\frac{\overline{{\unicode[STIX]{x1D623}_{11}}^{2n}}}{\overline{{\unicode[STIX]{x1D623}_{11}}^{2}}^{n}}. & & \displaystyle\end{eqnarray}$$
Even-order moments (
$M_{2n}^{b}$
for
$n=2,3,4,5,6$
) of
$\unicode[STIX]{x1D623}_{11}$
at different
$Re_{\unicode[STIX]{x1D706}}$
are plotted in figure 3.
$\unicode[STIX]{x1D623}_{11}$
-moments are sub-Gaussian and nearly invariant across the entire
$Re_{\unicode[STIX]{x1D706}}$
-range. This behaviour is to be expected as
$\unicode[STIX]{x1D623}_{ij}$
is bounded by unity. This also clearly demonstrates the contrast between the Reynolds number scaling of
$\unicode[STIX]{x1D623}_{ij}$
and
$\unicode[STIX]{x1D608}_{ij}$
.
Figure 4. PDF of (a,b) normalized longitudinal velocity gradient
$\unicode[STIX]{x1D623}_{11}$
and (c,d) normalized transverse velocity gradient
$\unicode[STIX]{x1D623}_{12}$
for (a,c)
$Re_{\unicode[STIX]{x1D706}}=1{-}35$
and (b,d)
$Re_{\unicode[STIX]{x1D706}}=35$
–588.
We will next examine the PDFs of
$\unicode[STIX]{x1D623}_{ij}$
at different
$Re_{\unicode[STIX]{x1D706}}$
. In figure 4(a,c) we present
$\unicode[STIX]{x1D623}_{11}$
- and
$\unicode[STIX]{x1D623}_{12}$
-PDFs, respectively, over the lower range of Reynolds numbers (
$Re_{\unicode[STIX]{x1D706}}\leqslant 35$
). In this range, the PDF undergoes slight changes in shape with changing
$Re_{\unicode[STIX]{x1D706}}$
. Figure 4(b,d) show that for
$Re_{\unicode[STIX]{x1D706}}\geqslant 35$
, both
$\unicode[STIX]{x1D623}_{11}$
- and
$\unicode[STIX]{x1D623}_{12}$
-PDFs converge to a characteristic shape, which remains unchanged at higher
$Re_{\unicode[STIX]{x1D706}}$
. This statistical self-similarity is anticipated from the collapse of higher-order moments of
$\unicode[STIX]{x1D623}_{11}$
to constant values. Note that the minimum and maximum longitudinal (
$\unicode[STIX]{x1D623}_{11}$
) and transverse (
$\unicode[STIX]{x1D623}_{12}$
) velocity-gradient values are in accordance with the bounds obtained analytically in (2.12) and (2.13).
4.3 Invariants of normalized velocity-gradient tensor
Delving further, we examine the marginal PDFs of
$q$
and
$r$
in figures 5 and 6. Figure 5(a) shows that in the range where
$Re_{\unicode[STIX]{x1D706}}\leqslant 25$
, the
$q$
-PDF appears to have a characteristic shape but shows discernible statistical variation about this shape. For
$25\leqslant Re_{\unicode[STIX]{x1D706}}\leqslant 225$
(figure 5
b), the distribution shifts towards more negative values of
$q$
with increasing
$Re_{\unicode[STIX]{x1D706}}$
. In this range the probability of strain-dominated topology (
$q<0$
) increases, while that of rotation-dominated topology (
$q>0$
) decreases. This is due to the fact that viscosity affects the strain-dominated topologies more than rotation-dominated topologies and lower viscous influence at higher Reynolds numbers causes a higher percentage of strain-dominated topologies to be generated. Finally,
$q$
-PDF attains a self-similar shape for flows above
$Re_{\unicode[STIX]{x1D706}}\sim 200$
. In the middle range of
$Re_{\unicode[STIX]{x1D706}}\in (25,200)$
the PDF transitions from one characteristic shape to another.
Unlike
$q$
-PDF, the
$r$
-PDF shows only a subtle
$Re_{\unicode[STIX]{x1D706}}$
dependence. It may be noted from figure 6 that irrespective of the
$Re_{\unicode[STIX]{x1D706}}$
value,
$r$
-PDF peaks at
$r=0$
. The shape of
$r$
-PDF remains fairly unchanged while its peak increases with
$Re_{\unicode[STIX]{x1D706}}$
in the range
$Re_{\unicode[STIX]{x1D706}}\in (1,200)$
. It appears to be invariant above
$Re_{\unicode[STIX]{x1D706}}\sim 200$
. Note that the variation in
$r$
-PDF with
$Re_{\unicode[STIX]{x1D706}}$
is minimal compared to
$q$
-PDF.
Figure 5.
$q$
-PDF for (a)
$Re_{\unicode[STIX]{x1D706}}=1,6,9,14,18$
and
$25$
and for (b)
$Re_{\unicode[STIX]{x1D706}}=25,35,86,225,385,414$
and
$588$
.
Figure 6.
$r$
-PDF for (a)
$Re_{\unicode[STIX]{x1D706}}=1,6,9,14,18$
and
$25$
and for (b)
$Re_{\unicode[STIX]{x1D706}}=25,35,86,225,385,414$
and
$588$
.
Figure 7.
$q$
–
$r$
joint PDF filled contour plots for
$Re_{\unicode[STIX]{x1D706}}$
$=$
(a)
$1$
, (b)
$6$
, (c)
$9$
, (d)
$14$
, (e)
$18$
and (f)
$25$
.
$q$
–
$r$
joint PDF line contour plots for
$Re_{\unicode[STIX]{x1D706}}$
$=$
(g)
$25$
to
$225$
and (h)
$225$
to
$588$
. The contour levels are identical for all plots: the colour scheme for (a–f) is shown in (a).
The
$q$
–
$r$
joint PDFs are plotted in figure 7 for different
$Re_{\unicode[STIX]{x1D706}}$
. Figure 7(a–f) shows the variation in shape of the
$q$
–
$r$
joint PDF in the low-
$Re_{\unicode[STIX]{x1D706}}$
range. At
$Re_{\unicode[STIX]{x1D706}}=1$
, the joint PDF is fairly symmetric about the
$q$
-axis and does not have a preferential distribution along the zero-discriminant (restricted Euler) line in the fourth quadrant. In fact, at this
$Re_{\unicode[STIX]{x1D706}}$
the distribution resembles that of invariants of a Gaussian field (Pereira, Garban & Chevillard (Reference Pereira, Garban and Chevillard2016)). As
$Re_{\unicode[STIX]{x1D706}}$
increases in the range
$(1,9)$
, the
$q$
–
$r$
joint PDF changes shape significantly and begins to develop a high-density region along the zero-discriminant line. It acquires a teardrop-like shape around
$Re_{\unicode[STIX]{x1D706}}=9$
. This value is in the same range as the transition
$Re_{\unicode[STIX]{x1D706}}$
for onset of anomalous scaling of
$\unicode[STIX]{x1D608}_{ij}$
moments (Yakhot & Donzis (Reference Yakhot and Donzis2017)). For
$9<Re_{\unicode[STIX]{x1D706}}\leqslant 225$
, the contours undergo refinements in the teardrop shape. Figure 7(g) clearly depicts these changes, amounting to an increase in the probability of strain-dominated topologies with respect to rotation-dominated topologies with increasing
$Re_{\unicode[STIX]{x1D706}}$
. This reiterates the observation from the marginal PDF of
$q$
(figure 5). Finally, the joint PDF contours become invariant for
$Re_{\unicode[STIX]{x1D706}}>200$
, as shown in figure 7(h).
The joint
$q$
–
$r$
PDF exhibits three distinct ranges of variation with
$Re_{\unicode[STIX]{x1D706}}$
. In the range
$Re_{\unicode[STIX]{x1D706}}\in (1,10)$
, it shows significant qualitative variation from near-Gaussian behaviour to a teardrop-like shape. Small quantitative changes are evident in the contours for
$10\leqslant Re_{\unicode[STIX]{x1D706}}\leqslant 200$
. Finally, an invariant joint distribution in the characteristic teardrop shape is attained for
$Re_{\unicode[STIX]{x1D706}}\geqslant 200$
.
4.4 Evolution of
$\unicode[STIX]{x1D623}_{ij}$
-invariants and
$A^{2}$
Figure 8. Conditional averages of inertial (circles), pressure (triangles) and viscous (squares) contributions in (a)
$\langle \text{d}q/\text{d}t^{\prime }|q\rangle$
, (b)
$\langle \text{d}q/\text{d}t^{\prime }|r\rangle$
, (c)
$\langle \text{d}r/\text{d}t^{\prime }|q\rangle$
and (d)
$\langle \text{d}r/\text{d}t^{\prime }|r\rangle$
for different
$Re_{\unicode[STIX]{x1D706}}$
(refer to (2.23) and (2.27); colour scheme is given in (b)).
In this subsection we study the dynamics of
$q$
- and
$r$
-evolution which lays the foundation for modelling both
$\unicode[STIX]{x1D623}_{ij}$
and
$A^{2}$
. We also characterize the
$Re_{\unicode[STIX]{x1D706}}$
dependence of
$\unicode[STIX]{x1D703}$
-dynamics conditioned on
$q$
and
$r$
. We consider the
$Re_{\unicode[STIX]{x1D706}}$
range
$86$
–
$588$
in this subsection to understand the role of different turbulent processes in
$q$
,
$r$
-phase space.
The averages of inertial, pressure and viscous terms of
$\text{d}q/\text{d}t^{\prime }$
(2.23) conditioned on
$q$
and
$r$
are plotted in figure 8(a,b). The inertial and pressure terms conditioned on
$q$
show a
$Re_{\unicode[STIX]{x1D706}}$
dependence at low
$Re_{\unicode[STIX]{x1D706}}$
and attain nearly invariant forms for
$Re_{\unicode[STIX]{x1D706}}\geqslant 225$
. The viscous term conditioned on
$q$
shows a significant
$Re_{\unicode[STIX]{x1D706}}$
dependence at low
$Re_{\unicode[STIX]{x1D706}}$
values, but is nearly invariant in the higher range. All
$q$
-evolution terms conditioned on
$r$
appear to be completely insensitive to
$Re_{\unicode[STIX]{x1D706}}$
.
The conditional averages of local (inertial and isotropic pressure), anisotropic pressure and viscous contributions in
$\text{d}r/\text{d}t^{\prime }$
(as shown in (2.27)) are reasonably insensitive to
$Re_{\unicode[STIX]{x1D706}}$
, as shown in figure 8(c,d). The average viscous contributions (
$V_{r}$
) conditioned on both
$q$
and
$r$
are negligible in comparison to the other terms. This suggests that
$r$
-evolution is relatively impervious to viscosity and dominated by inertial and pressure terms. The fact that the probability distribution of
$r$
is nearly insensitive to
$Re_{\unicode[STIX]{x1D706}}$
(figure 6
b) is consistent with this inference.
Figure 9. Conditional averages of inertial (circles), pressure (triangles) and viscous (squares) contributions in the
$\unicode[STIX]{x1D703}$
-evolution equation conditioned on (a)
$q$
and (b)
$r$
for different
$Re_{\unicode[STIX]{x1D706}}$
(refer to (2.17); colour scheme as given in a).
The different processes in the
$\unicode[STIX]{x1D703}$
-evolution (as given in (2.17)) conditioned on
$q$
and
$r$
are plotted in figure 9(a,b). The average inertial term (
$I_{\unicode[STIX]{x1D703}}$
) is positive for almost all
$q$
and
$r$
values – implying that inertia is a source of
$A^{2}$
. The sign of the pressure contribution (
${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
) depends on the
$q$
and
$r$
values. Expectedly, the viscous term (
$V_{\unicode[STIX]{x1D703}}$
) is negative across all values of
$q$
and
$r$
, indicating that it is always a sink of
$A^{2}$
. Viscous effects are stronger in strain-dominated topologies (
$q<0$
) and weaker in rotation-dominated topologies (
$q>0$
). However, it is nearly independent of
$r$
. Overall, the conditionally averaged inertial and pressure processes in the
$\unicode[STIX]{x1D703}$
-equation appear to approach asymptotic behaviour at high
$Re_{\unicode[STIX]{x1D706}}$
$({\sim}200)$
. The viscous term on the other hand appears to have a discernible
$Re_{\unicode[STIX]{x1D706}}$
dependence throughout the
$Re_{\unicode[STIX]{x1D706}}$
range.
Figure 10. Conditional variance of pressure and viscous terms in the
$q$
-,
$r$
- and
$\unicode[STIX]{x1D703}$
-equations conditioned on
$q$
and
$r$
: (a)
$\text{Var}({\mathcal{P}}_{q}|q)$
versus
$q$
, (b)
$\text{Var}(V_{q}|q)$
versus
$q$
, (c)
$\text{Var}({\mathcal{P}}_{q}|r)$
versus
$r$
, (d)
$\text{Var}(V_{q}|r)$
versus
$r$
, (e)
$\text{Var}({\mathcal{P}}_{r}|q)$
versus
$q$
, (f)
$\text{Var}(V_{r}|q)$
versus
$q$
, (g)
$\text{Var}({\mathcal{P}}_{r}|r)$
versus
$r$
, (h)
$\text{Var}(V_{r}|r)$
versus
$r$
, (i)
$\text{Var}({\mathcal{P}}_{\unicode[STIX]{x1D703}}|q)$
versus
$q$
, (j)
$\text{Var}(V_{\unicode[STIX]{x1D703}}|q)$
versus
$q$
, (k)
$\text{Var}({\mathcal{P}}_{\unicode[STIX]{x1D703}}|r)$
versus
$r$
and (l)
$\text{Var}(V_{\unicode[STIX]{x1D703}}|r)$
versus
$r$
for different
$Re_{\unicode[STIX]{x1D706}}$
(colour scheme is given in a).
Finally, we plot the conditional variance of the unclosed pressure and viscous terms in the
$q$
-,
$r$
- and
$\unicode[STIX]{x1D703}$
-evolution equations in figure 10. The variance of the pressure term in
$q$
-evolution conditioned on both
$q$
and
$r$
have invariant forms irrespective of
$Re_{\unicode[STIX]{x1D706}}$
(figure 10
a,c). However, the conditional variance of the viscous contribution to
$\text{d}q/\text{d}t^{\prime }$
(figure 10
b,d) does not converge even in the high-
$Re_{\unicode[STIX]{x1D706}}$
limit. In fact, it shows a progressive increase in the magnitude of the variance with increasing
$Re_{\unicode[STIX]{x1D706}}$
. Similarly, the conditional variance of the anisotropic pressure contribution in the
$r$
-evolution is invariant with changing
$Re_{\unicode[STIX]{x1D706}}$
(figure 10
e,g). On the other hand, the variance of the viscous term increases with increasing
$Re_{\unicode[STIX]{x1D706}}$
(figure 10
f,h). We also observe that the variance of
${\mathcal{P}}_{\unicode[STIX]{x1D703}}$
conditioned on both
$q$
and
$r$
exhibits reasonable collapse, while that of
$V_{\unicode[STIX]{x1D703}}$
exhibits a distinct
$Re_{\unicode[STIX]{x1D706}}$
dependence, with the magnitude increasing with
$Re_{\unicode[STIX]{x1D706}}$
(figure 10
i–l).
Therefore, we find that conditional statistics (mean and variance) of the pressure contribution to
$q$
-,
$r$
- and
$\unicode[STIX]{x1D703}$
-evolution become nearly invariant for
$Re_{\unicode[STIX]{x1D706}}>200$
. The mean-viscous contribution to
$q$
- and
$r$
-evolution also exhibits self-similarity beyond
$Re_{\unicode[STIX]{x1D706}}>200$
. On the other hand, the conditional mean of the viscous term in
$\unicode[STIX]{x1D703}$
-evolution shows a quantitative increase in magnitude with
$Re_{\unicode[STIX]{x1D706}}$
. The conditional variance of pressure processes in
$q$
-,
$r$
- and
$\unicode[STIX]{x1D703}$
-evolution are independent of
$Re_{\unicode[STIX]{x1D706}}$
while that of the viscous contribution shows steady growth in magnitude with increasing
$Re_{\unicode[STIX]{x1D706}}$
. This implies that the
$Re_{\unicode[STIX]{x1D706}}$
dependence in the velocity-gradient dynamics is solely due to viscous effects, which is to be expected.
4.5 Lagrangian velocity-gradient modelling
One of the long-term goals of this work is to develop a Lagrangian stochastic model for velocity gradients along the lines of Girimaji & Pope (Reference Girimaji and Pope1990). The main distinction is that we plan to develop a model for
$\unicode[STIX]{x1D623}_{ij}$
-evolution rather than
$\unicode[STIX]{x1D608}_{ij}$
-evolution, as was the case in Girimaji & Pope (Reference Girimaji and Pope1990).
It is anticipated that
$\unicode[STIX]{x1D629}_{ij}$
and
$\unicode[STIX]{x1D70F}_{ij}$
will be more tractable than their
$\unicode[STIX]{x1D608}_{ij}$
-counterparts. The proposal is to decompose each term into a conditional mean and a stochastic (white noise) term:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D629}_{ij}(\unicode[STIX]{x1D657})=\langle \unicode[STIX]{x1D629}_{ij}|q,r,\unicode[STIX]{x1D657}\rangle +\unicode[STIX]{x1D629}_{ij}^{\prime }(q,r,\unicode[STIX]{x1D657}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70F}_{ij}(\unicode[STIX]{x1D657})=\langle \unicode[STIX]{x1D70F}_{ij}|q,r,\unicode[STIX]{x1D657}\rangle +\unicode[STIX]{x1D70F}_{ij}^{\prime }(q,r,\unicode[STIX]{x1D657}). & \displaystyle\end{eqnarray}$$
The conditional statistics (means and variances) established in this paper (figures 8–10) provide guidance for this model development. Once
$\unicode[STIX]{x1D629}_{ij}$
and
$\unicode[STIX]{x1D70F}_{ij}$
models are established, Lagrangian evolution equations for
$A^{2}$
and
$\unicode[STIX]{x1D608}_{ij}$
can be developed without the need for any further closures ((2.4) and (2.15)).
5 Summary and conclusions
The main objective of the work is to clearly characterize the
$Re_{\unicode[STIX]{x1D706}}$
dependence of the different aspects of velocity-gradient structure and dynamics. In the analysis, we segregate the velocity-gradient magnitude (
$A^{2}$
) from the normalized-gradient tensor
$\unicode[STIX]{x1D623}_{ij}$
. The
$\unicode[STIX]{x1D623}_{ij}$
-tensor and the evolution of its invariants are the subject of this study. Some of the key findings of this study are summarized below:
(i) Higher-order moments (
$M_{2n}^{b}$
) of
$\unicode[STIX]{x1D623}_{ij}$
do not show any statistically significant variation across the entire range of
$Re_{\unicode[STIX]{x1D706}}$
investigated in this study. This is in contrast with
$\unicode[STIX]{x1D608}_{ij}$
, which exhibits a significant increase of normalized moment values with increasing
$Re_{\unicode[STIX]{x1D706}}$
. Moreover,
$\unicode[STIX]{x1D608}_{ij}$
-PDFs exhibit a clear stretch in tails as
$Re_{\unicode[STIX]{x1D706}}$
increases, while
$\unicode[STIX]{x1D623}_{ij}$
-PDFs achieve self-similarity for
$Re_{\unicode[STIX]{x1D706}}>35$
.(ii) PDFs and joint PDFs of
$\unicode[STIX]{x1D623}_{ij}$
-invariants (
$q$
,
$r$
) are more sensitive to changing
$Re_{\unicode[STIX]{x1D706}}$
than individual
$\unicode[STIX]{x1D623}_{ij}$
-components:(a) The
$q$
–
$r$
joint PDF changes qualitatively for
$Re_{\unicode[STIX]{x1D706}}\in (1,10)$
from Gaussian to a teardrop shape.(b) For
$Re_{\unicode[STIX]{x1D706}}\in (10,200)$
, the
$q$
–
$r$
joint PDF and marginal PDFs undergo minor quantitative changes with increasing
$Re_{\unicode[STIX]{x1D706}}$
to accommodate an increasing proportion of strain-dominated topologies.(c) The
$q$
and
$r$
individual PDFs as well as the
$q$
–
$r$
joint PDF converge to the characteristic teardrop shape for
$Re_{\unicode[STIX]{x1D706}}>200$
. Note that this asymptotic behaviour is observed in a similar range of
$Re_{\unicode[STIX]{x1D706}}$
as the onset of the dissipative anomaly (Donzis et al.
Reference Donzis, Sreenivasan and Yeung2005).
(iii) Physical processes contributing to the evolution of
$\unicode[STIX]{x1D623}_{ij}$
-invariants and
$A^{2}$
are also examined:(a) For
$Re_{\unicode[STIX]{x1D706}}\geqslant 200$
, the conditional mean and variance of the unclosed pressure term in the evolution of
$q$
,
$r$
and
$\unicode[STIX]{x1D703}$
are independent of
$Re_{\unicode[STIX]{x1D706}}$
.(b) The mean-viscous contribution to
$q$
- and
$r$
- evolution shows asymptotic convergence for
$Re_{\unicode[STIX]{x1D706}}>200$
. The mean-viscous contribution to
$\unicode[STIX]{x1D703}$
-evolution does not vary qualitatively but shows a continued quantitative dependence on
$Re_{\unicode[STIX]{x1D706}}$
. The conditional variance of viscous term in all three evolution equations continue to exhibit a
$Re_{\unicode[STIX]{x1D706}}$
dependence.(c) It is surmised that viscous processes are the primary source of the
$Re_{\unicode[STIX]{x1D706}}$
dependence of
$A^{2}$
.
In future works, we plan to develop closure models for
$\unicode[STIX]{x1D629}_{ij}$
and
$\unicode[STIX]{x1D70F}_{ij}$
as a function of
$q$
and
$r$
. This will lead to a Lagrangian closure model for
$\unicode[STIX]{x1D623}_{ij}$
-evolution, and ultimately to
$A^{2}$
-evolution.
Acknowledgements
The authors would like to acknowledge Dr D. Donzis of Texas A&M University for providing the DNS data.
