1. Introduction
Let N(t), t ≩ 0, be a counting process with 𝔼 [N(t)] finite for all t ≩ 0. We are interested in the asymptotic behaviour of 𝔼 [N(t)] for large t. For example, if N(t) is a renewal process whose lifetime distribution is nonarithmetic and has a finite mean 1/λ, Blackwell’s renewal theorem, that 𝔼 [N(t + h) − N(t)] → λh for t →∞ and any finite h > 0, is a well-known result, and has been extended to Markov renewal processes (see e.g. [Reference Alsmeyer1] and [Reference Cinlar6]). This theorem motivates us to consider under what conditions it may hold for a general counting process on the probability space (, F, P).
To answer this question, we need a suitable description for the dynamics of a general counting process. There have been various studies of refinements and extensions of Blackwell’s renewal theorem (see e.g. [Reference Asmussen2], [Reference Daley and Mohan8], [Reference Daley and Vere-Jones9], and [Reference Feller10]), but they are based on independence or Markov assumptions on the counting process. Hence, such traditional approaches may not be suitable for the present problem. In this paper we use martingales to study this question. In general, a martingale is used to construct an unbiased purely random component of a stochastic process. For any counting process N(t) assumed to be right-continuous in t and with 𝔼 [N(t)] finite for finite t, a martingale M(t) typically arises in a semimartingale representation
$$N(t) = \Lambda (t) + M(t),\quad \quad t \ge 0,$$
where Λ(t) is a process of bounded variation. Here we must be careful about two things. One is the filtration 𝔽≡{Ft : t ≩ 0} to which N(·) ≡{N(t): t ≩ 0} is adapted; the other is the predictability of Λ(·) ≡{Λ(t): t ≩ 0} with respect to the filtration, where Λ(·)is said to be 𝔽-predictable (or simply predictable when 𝔽 is clear in the context) if it is measurable with respect to the σ -field P on × [0, ∞) generated by all left-continuous 𝔽-adapted real-valued processes for time t ∊ [0, ∞).
Remark 1.1. If a stochastic process X(·) ≡{X(t): t ≩ 0} is 𝔽-predictable, then X(t)is Ft −- measurable for all t ≩ 0, where Ft − = σ (∪s<t Fs)(see [Reference Jacod and Shiryaev12, Proposition I.2.4]). For convenience in this paper, we call X(·) satisfying the latter condition 𝔽-predictable in the weak sense.
Consider the filtration 
$${\mathbb {F}}{^N} \equiv \{ F_t^N:t \ge 0\} $$, where 
$${\mathcal {F}}_0-^X = {\mathcal {F}} = \sigma (R(0-))$$. When ∧ (·)is FN-predictable, both it and therefore the martingale M(·) are a.s. uniquely determined by virtue of the Doob–Meyer decomposition because N(·) is a submartingale (see e.g. [Reference Kallenberg13, Lemma 25.7]). Such predictable Λ(·)is called a compensator, and in this case Λ(t) is nondecreasing in t. Consequently, if Λ(t) is absolutely continuous with respect to Lebesgue measure, then we can write
$$\Lambda (t) = N(0) + \int_0^t {\lambda _u}{\kern 1pt} {\rm{d}}u,$$
where λt is a nonnegative process and can be predictable with respect to 𝔽N, and called a stochastic intensity. In particular, λt is called the hazard rate function when N(·) is a renewal process (see e.g. [Reference Bremaud4] and [Reference Jacod and Shiryaev12]). However, such λt may not be amenable to our asymptotic analysis except when λt is a deterministic function of t or its randomization, namely, N(·)is a Poisson or doubly stochastic Poisson process, either of which is less interesting for us. This may be the reason why the semimartingale representation (1.1) is little used in renewal theory.
In this paper, we study counting processes using martingales. However, we do not use the filtration 𝔽N; rather, we consider nonpredictable ∧ (·) that makes our asymptotic analysis tractable. To this end, we formally introduce the counting process and related notations. Let N(·) be a nonnegative integer-valued process such that N(t) is finite, nondecreasing, right-continuous, has left-hand limits in t and N(t) ≡ N(t) − N(t−) ≤ 1 at all t ≩ 0, where N(0−) = 0. Define the nth counting time of N(·)by tn −1 = inf{t ≩ 0: n ≤ N(t)}, n ≩ 1.
$${t_{n - 1}} = \inf \{ t \ge 0:n \le N(t)\} ,\quad \quad n \ge 1.$$
Since N(t) is finite for all t ≩ 0, the set {tn −1, n = 1, 2,...} has no finite accumulation point in [0, ∞). Thus, N(·) is a general orderly counting process. Unless stated otherwise, assume that t 0 = 0, and speak of N(·) as being nondelayed. Otherwise, if t 0 > 0, N(·) is said to be delayed. In either case, n ≤ N(t) if and only if tn −1 ≤ t.Let T 0 = t 0 and Tn = tn − tn −1 for n ≩ 1. Let R(t) be the residual time to the next counting instant at time t, that is,
$$R(t) = {T_0} + \sum\limits_{\ell = 1}^{N(t)} {T_\ell } - t,\quad \quad t \ge 0,$$
and define X(t) = (N(t), R(t)) for t ≩ 0, where
$$X(0) = \left( {\matrix{
{(1,{T_1})} & {{\kern 1pt} if\;{\kern 1pt} {t_0} = 0,} \cr
{(0,{T_0})} & {{\kern 1pt} if\;{\kern 1pt} {t_0} > 0.} \cr
} } \right.$$
From the definition of N(·), X(t) is right-continuous for all t ≩ 0, and has a left-limit for all t > 0. Hence, N(tn) = n + 1, R(tn−) = 0 and 
$$R({t_n}) = {T_{n + 1}}$$. Let 
$${\mathbb {F}}{^X} \equiv \{ F_t^X:t \ge 0\} $$, where
$${\mathcal {F}}_t^X = \sigma (\{ X(u):u \le t\} ),\quad \quad t \ge 0.$$
Observe that N(·) is predictable under this filtration, but R(·) need not be because R(t) cannot be 
$${\mathcal {F}}_{t - }^X$$-measurable when R(t−) = 0 unless all Tn are deterministic. If we replace R(t)by the attained time A(t) since the last arrival instant, we gain nothing because 𝔽X = 𝔽N in this case.
In what follows, we use a filtration 𝔽 ≡{Ft : t ≩ 0} to which X(·) ≡{X(t): t ≩ 0} is adapted, i.e. 
$${\mathcal {F}}_t^X \subset {F_t}$$ for all t ≩ 0; we denote this by 
$${\mathbb {F}}{^X} \le {\mathbb {F}}$$. For convenience, we set N(0−) = 0 and 
$${\mathcal {F}}_{0 - }^X = {{\mathcal {F}}_{0 - }} = \sigma (R(0 - ))$$ unless otherwise stated, where R(0−) = R(0) 1(N(0) = 0). In most cases, 𝔽 = 𝔽X is sufficient, but a larger 𝔽 is needed in Sections 5.1 and 5.2. For a stopping time τ, define ℱτ − by
$${{\mathcal {F}}_{\tau - }} = \sigma (\{ A \cap \{ t \lt \tau \} :A \in {{\mathcal {F}}_t},t \ge 0\} ).$$
Since tn is a stopping time with respect to 𝔽X, it is an 𝔽-stopping time. Hence, we have the following fact.
Lemma 1.1. (I.1.14 of [Reference Jacod and Shiryaev12].) For each n ≩ 0, tn is a stopping time and 
$${{\mathcal {F}}_{{t_n} - }}$$-measurable.
We make the following two assumptions throughout the paper unless stated otherwise.
(A1) X(0) = (1, T 1).
(A2) 𝔼 [Tn] < ∞ for n ≩ 1, where Tn > 0 almost surely by the orderliness of N(·).
We first consider a renewal process, as a pilot example. In this case we assume the following in addition to (A1) and (A2).
(A3) For n ≩ 1, Tn is independent of 
$${{\mathcal {F}}_{{t_{n - 1}} - }}$$, and T 1, T 2, ... are identically distributed, with the common distribution denoted by F. If 𝔽 = 𝔽X, then this condition is the same as T 1, T 2, ... being independent and identically distributed.
For such a renewal process, we derive a new semimartingale representation; it differs from the standard representation that uses the stochastic intensity function (see Theorem 2.1). This enables us to revisit Blackwell’s renewal theorem and consider some of its refinements and extensions. Based on these observations, we extend the semimartingale representation to a general counting process, for which we replace the key renewal assumption (A3) by
(A4) 𝔼 [N(t)] < ∞ for finite t ≩ 0.
We then give conditions under which an asymptotic result similar to Blackwell’s renewal theorem holds. In particular, Blackwell’s result extends quite naturally to the counting process which is generated by a stationary sequence of inter-arrival times, in other words, the counting process under a Palm distribution (see Corollary 5.2).
This paper has five more sections. In Section 2, we present a general framework for the new semimartingale representation. We apply it to a renewal process N(t), and consider its interpretation. In Section 3, we revisit Blackwell’s renewal theorem and some other asymptotic properties of 𝔼 [N(t)]. In Section 4, we show how the present approach can be used to derive limit properties of var N(t). In Section 5, a new semimartingale representation is derived for a general counting process, and Blackwell’s renewal theorem is extended under various scenarios. We give concluding remarks in Section 6. Some proofs are deferred to an appendix.
2. A semimartingale representation
As discussed in Section 1, our aim is to derive the semimartingale representation (1.1) for a general counting process N(·). We first consider this problem in a broader context.
2.1. Martingales from a general setting
Let 𝔽 ≡{ℱt : t ≩ 0} be a filtration, and let N(·) with N(0−) = 0 be the orderly counting process introduced in Section 1; let Y(·) ≡{Y(t): t ≩ 0} with Y(0−) ∊ F 0− be a real-valued stochastic process which is right-continuous and has left-limits. Assume the following.
(B1) N(t)is Ft −-measurable for all t ≩ 0, namely, N(·)is 𝔽-predictable in the weak sense (see Remark 1.1), and Y(·)is 𝔽-adapted.
(B2) For every t ≩ 0, N(t) increases if Y(t) = Y(t−).
(B3) For every t ≩ 0, Y(t) has a right-hand derivative, denoted Y ′ (t).
Note that (B2) does not exclude the case in which N(t) increases when Y(t) = Y(t−). Furthermore, define R(t)by(1.3), and let X(t) = (N(t), R(t)). Then it is not hard to see that (B1) implies that 𝔽X 𝔽.
Since t 0 = 0 only if N(0) = 1, it now follows easily from elementary calculus that
$$Y(t) = Y(0 - ) + \int_0^t Y'(u){\kern 1pt} {\rm{d}}u + \sum\limits_{n = 0}^{N(t) - 1} \Delta Y({t_n}),\quad \quad t \ge 0,$$
where ΔY(t) = Y(t) − Y(t−). Let
$${M_Y}(t){\kern 1pt} : = \sum\limits_{n = 0}^{N(t) - 1} (Y({t_n}) - {\kern 1pt} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}]),$$
$${D_Y}(t){\kern 1pt} : = \sum\limits_{n = 0}^{N(t) - 1} ({\mathbb {E}} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}] - Y({t_n} - )).$$
With these two functions we then have the following lemma.
Lemma 2.1. Assume that N(·) ≡{N(t): t ≩ 0} with N(0−) = 0 and Y(·) with Y(0−) ∊ ℱ 0− satisfy conditions (B1)–(B3). If 𝔽(|MY(t)|) < ∞ for all finite t ≩ 0, then MY(·) is an 𝔽-martingale, and
$$Y(t) = Y(0 - ) + \int_0^t Y'(u){\kern 1pt} {\rm{d}}u + {D_Y}(t) + {M_Y}(t),\quad \quad t \ge 0.$$
Remark 2.1. Since in (2.4) both the integration term and DY(t) are predictable in the weak sense at least, the representation (2.4)for Y(t) may be called a special semimartingale, since this terminology is used when the bounded variation component of a semimartingale is predictable (see [Reference Jacod and Shiryaev12, Chapter 1, Section 4c]).
Proof. Equation (2.4) follows immediately from (2.1). Thus, we only need to prove that MY(·) is an 𝔽-martingale. Since 𝔼 [|MY(t)|] < ∞ by assumption, this is done by showing that
$${\mathbb {E}} [{M_Y}(t)|{{\mathcal {F}}_s}] = {M_Y}(s),\quad \quad 0 \le s \lt t.$$
To this end, recall that tn is ℱtn −-measurable by Lemma 1.1. Since n + 1 ≤ N(t) if and only if tn ≤ t, we can write MY(t)as
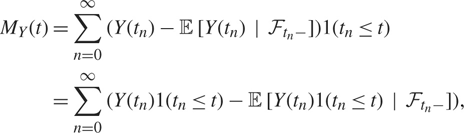$$\matrix{
{{M_Y}(t) = \sum\limits_{n = 0}^\infty (Y({t_n}) - {\mathbb {E}} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}])1({t_n} \le t)} \cr
{ = \sum\limits_{n = 0}^\infty (Y({t_n})1({t_n} \le t) - {\mathbb {E}} [Y({t_n})1({t_n} \le t)|{{\mathcal {F}}_{{t_n} - }}]),} \cr
} $$
where 1(·) is the indicator function of the statement ‘·’. Hence, 𝔼 [MY(t) | Fs] equals
$${M_Y}(s) + \sum\limits_{n = 0}^\infty {\mathbb {E}} (Y({t_n})1(s \lt {t_n} \le t) - {\mathbb {E}}[Y({t_n})1(s \lt {t_n} \le t)|{{\mathcal {F}}_{{t_n} - }}]|{{\mathcal {F}}_s}) = {M_Y}(s).$$
This proves (2.5), and therefore MY(·) is an 𝔽-martingale.
In what follows, we apply Lemma 2.1 with Y(·) chosen appropriately. For example, we can set Y(t) = N(t) because (B1)–(B3) are obviously satisfied. Then DY(t) ≡ N(t) and MY(t) ≡ 0 because N(·)is 𝔽-predictable, and substitution in (2.4) yields the identity Y(t) = N(t), and we should learn nothing. Thus, it is important to choose Y(·) suitably when applying Lemma 2.1.
2.2. Application to a renewal process
In our first application of Lemma 2.1 we find the semimartingale representation (1.1)for a renewal process N(·) defined by (A1)–(A3). This representation is used in establishing asymptotic properties of moments of N(t) including Blackwell’s renewal theorem in Section 3, and extended to a general counting process in Section 5. We first note the following well-known fact (see e.g. [Reference Feller10, Lemma in XI.1]).
Lemma 2.2. Conditions (A1)–(A3) imply (A4).
We choose a filtration 𝔽 such that 𝔽X ≼ 𝔽, where 𝔽X is defined through (1.4). Let Y(t) = N(t) − λR(t); such Y(·) clearly satisfies conditions (B1)–(B3). The idea behind this choice of Y(·) is to introduce a control parameter λ so that DY(t) vanishes. A similar idea is used for the queue length process of a many-server queue in [Reference Miyazawa16]. Indeed,
$${\mathbb {E}} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}] = N({t_n} - ) + 1 - \lambda {\mathbb {E}}({T_{n + 1}}) = N({t_n} - ) = Y({t_n} - ),\quad \quad n \ge 0,$$
and therefore DY(tn) vanishes, where N(0−) = 0; recall that ℱ 0− ={Ø, Ω}. Further, 𝔼[N(t)] < ∞ by Lemma 2.2, and the bound
$${\mathbb {E}}[|Y({t_n}) - {\mathbb {E}} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}]|] = {\mathbb {E}}[| - \lambda {T_{n + 1}} + 1|] \le 2 \lt \infty $$
implies that
$${\mathbb {E}}[|{M_Y}(t)|] \le \sum\limits_{n = 1}^\infty {\mathbb {E}} \{ |Y({t_n}) - {\mathbb {E}} [Y({t_n})|{{\mathcal {F}}_{{t_n} - }}]|\} {\mathbb {P}} ({t_{n - 1}} \le t) \le 2{\mathbb {E}} [N(t)] \lt \infty .$$
Hence, the next theorem follows from Lemma 2.1 because Y(0−) = 0 when R(0−) = 0.
Theorem 2.1. Let 𝔽 be a filtration such that 𝔽X ≼ 𝔽, and assume (A1)–(A3). Then the renewal process N(t) is expressible as
$$N(t) = \lambda (t + R(t)) + M(t),\quad \quad t \ge 0,$$
where
$$M(t) = \sum\limits_{n = 0}^{N(t) - 1} (1 - \lambda {T_{n + 1}}) = \sum\limits_{n = 1}^{N(t)} (1 - \lambda {T_n}),\quad \quad t \ge 0,$$
is an 𝔽-martingale.
Remark 2.2. N(·) is called a delayed renewal process when condition (A1) is replaced by X(0) = (0, T 0) with T 0 > 0, while (A2) and (A3) are unchanged. Let Y(t) = N(t) − λR(t)for t ≩ 0 and Y(0−) = R(0); then Y(0−) =−λT 0, and for t ≩ 0,
$${D_Y}(t) = 0,\quad \quad {M_Y}(t) = M(t).$$
Hence, by Lemma 2.1, (2.7) for the delayed renewal process becomes
$$N(t) = \lambda (t + R(t) - {T_0}) + M(t),\quad \quad t \ge 0.$$
In particular, if R(t) is stationary, then N(t) has stationary increments because
$$N(t) = \sum\limits_{0 \lt u \le t} 1(R(u - ) \ne R(u)).$$
Hence, (2.8) and T 0 = R(0) imply that M(t) also has stationary increments.
This remark shows that the delayed renewal process only changes the semimartingale representation (2.7) to have the extra term −λT 0 as in (2.8). Since T 0 is independent of all Tn for n ≩ 1by (A3) and the weak convergence of R(t) to its stationary distribution as t →∞ is key to our later arguments, the asymptotic results in Sections 3 and 4 are also valid for the delayed renewal process if T 0 has an appropriate finite moment. Since such extensions are obvious, we do not discuss them further below.
2.3. Interpretation of the semimartingale representation
By Theorem 2.1, we have the semimartingale representation (1.1) with
$$\Lambda (t) = \lambda [t + R(t)],$$
which is different from the compensator (1.2). This is not surprising because we have made a special semimartingale not for N(t)but for Y(t) ≡ N(t) − λR(t), where we recall the special martingale discussed in Remark 2.1. Further, the filtration is different, and (·) is not predictable because R(·) need not be predictable. Nevertheless, it suggests that the asymptotics of N(t) can be studied via a bias term λ[t + R(t)] and a pure noise term M(t).
Another feature of (2.7) is its relation to Wald’s identity. Define 
$${S_n} = \sum\nolimits_{\ell = 1}^n {T_\ell }$$ for n ≥1; then S N(tt ) = t + R(t), and therefore (2.7) can be written as
$${S_{N(t)}} - {\mathbb {E}} [T]N(t) = - {\mathbb {E}} [T]M(t),\quad \quad t \ge 0,$$
which immediately gives Wald’s identity, 𝔼[S N(t)] = 𝔼[T]𝔼[N(t)], since 𝔼[M(t)] = 𝔼[M(0)] = 0. This type of Wald’s identity is well known (see e.g. [Reference Asmussen2, Section V.6]).
It is interesting here that (2.9) says more. For example, the 𝔽-martingale −𝔼(T)M(t)is an error for estimating S N(t) by [𝔼(T)]N(t). To evaluate this error, we use certain facts concerning the quadratic variations of M(·) (see [Reference Van Der Vaart20] for their definitions).
Lemma 2.3. Under the assumptions of Theorem 2.1, if 𝔼(T 2) < ∞, the optional and predictable quadratic variations of M(·) are given for t ≩ 0 by
$$[M](t) = \sum\limits_{n = 1}^{N(t)} {(1 - \lambda {T_n})^2},$$
$$\langle M\rangle (t) = {\lambda ^2}\sigma _T^2N(t),$$
respectively, where 
$$\sigma _T^2$$ is the variance of T, and therefore
$${\mathbb {E}} [{M^2}(t)] = {\mathbb {E}} [\langle M\rangle (t)] = {\lambda ^3}\sigma _T^2(t + {\mathbb {E}} [R(t)]).$$
Proof. Since M(t) is piecewise constant and discontinuous at increasing instants of N(t), (2.10) is immediate from the definition of an optional quadratic variation (see e.g. [Reference Pang, Talreja and Whitt17, Theorem 3.1]). Since the predictable quadratic variation M (t) is defined as a predictable process for M 2(t) − M (t) to be a martingale, (2.11) is obtained from Lemma 2.1 with Y(t) = M 2(t). Its proof is detailed in Appendix A.1. Finally, (2.12) follows from (2.11) and (2.7).
Notice that N(·) is predictable, but TN (·) is not in our filtration F, while neither N(·) nor TN (·) are predictable in the filtration 𝔽N generated by N(·). This explains why [M](t) of (2.10)differs from M (t) of (2.11).
If 𝔼[T 2] < ∞, it follows from Lemma 2.3 and the inequality 𝔼 [R(t)] ≤ λ𝔼 [T 2]for t ≩ 0 (see e.g. [Reference Asmussen2, Proposition 6.2, p. 160]) that the expected quadratic error of (2.9)is
$${({\mathbb {E}} [T])^2}{\mathbb {E}} [{M^2}(t)] = \sigma _T^2\lambda (t + {\mathbb {E}} [R(t)]) \le \sigma _T^2(\lambda t + {\lambda ^2}{\mathbb {E}} [{T^2}]).$$
3. First moment asymptotics for a renewal process
We have asserted that the semimartingale representation (2.7) can be used to find the asymptotics of a renewal process N(t)for large t. In this subsection, we do so for the first moment under two scenarios that depend on the finiteness or otherwise of 𝔼 [T 2].
3.1. Blackwell’s renewal theorem, revisited
The first moment asymptotic is well known as Blackwell’s renewal theorem. In view of the representation (2.7), the asymptotic behaviour of 𝔼 [N(t)] is determined by that of 𝔼 [R(t)]. Taking this into account, we reformulate Blackwell’s renewal theorem as follows.
Lemma 3.1. For a renewal process N(·) satisfying assumptions (A1)–(A3), the following three conditions are equivalent.
(2a) The distribution of T is nonarithmetic, i.e. there is no Δ > 0 such that P(T ∊{nΔ : n ≩ 1}) = 1.
(2b) Blackwell’s renewal theorem holds, i.e. for each h > 0 and λ = 1/𝔼 [T],
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [N(t + h) - N(t)] = \lambda h.$$
(2c) R(t) has a limiting distribution as t →∞.
When one of these conditions holds, the limiting distribution of R(t) is given by
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {P}}(R(t) \le x) = \lambda \int_0^x {\mathbb {P}}(T > u){\kern 1pt} {\rm{d}}u.$$
Remark 3.1. In the delayed case, the nonarithmetic condition in (2a) is not necessary for R(t) to have a limiting distribution in (2c). Following equation (3.4) below, we give a direct proof that (2c) implies (2b), and hence of their equivalence in this case.
Proof. This lemma owes its proof to Feller’s key renewal theorem [Reference Feller10, Chapter XI]. By Blackwell’s renewal theorem, which is a special case of Feller’s key renewal theorem, (2a) implies (2b).
By Feller’s direct Riemann integrability argument, (2b) implies (2c) and (3.2) (see [Reference Feller10, Section XI.4]).
Finally, (2c) implies (2a) because (2c) does not hold if (2a) does not hold; equivalently, F is arithmetic.
Up to this point, the asymptotic behaviour of 𝔼 [N(t)] provided by Lemma 3.1 has nothing to do with the semimartingale representation (2.7). However, when seen from a sample path base, (2.7) can be viewed as a pre-limit renewal theorem. Taking its expectation yields
$${\mathbb {E}} [N(t)] = \lambda t + \lambda {\mathbb {E}} [R(t)],\quad \quad t \ge 0,$$
which is equivalent to Wald’s identity as discussed in Section 2.3. It is of interest here to see how Blackwell’s renewal theorem (3.1) can be obtained directly from (3.3) which provides information on R(t), namely, (3.1) holds if and only if
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [R(t + h) - R(t)] = 0.$$
If 𝔼 [T 2] < ∞, then (3.4) is immediate from (2c) because 
$${\mathbb {E}} [R(t)] \to {\textstyle{1 \over 2}}\lambda {\mathbb {E}}({T^2})$$
as t →∞. However, this argument fails when 𝔼 [T 2] =∞. Nevertheless, (3.4), equivalently (2b), is still obtained directly from (2c) using another semimartingale representation of N(t), as we now show.
Direct proof of (2b) and (3.2) from (2c). Let
$$\tilde R$$ be a random variable with the limit distribution of R(t). Apply Lemma 2.1 with Y(t) = N(t) −λv(v ∧ R(t)) for each fixed 
$$v \in {C_{\tilde R}}$$, where a ∧ b = min (a, b) for a, b ∊ ℝ, λv = 1/E [v ∧ T], and 
$${C_{\tilde R}}$$ is the set of all continuity points of the distribution of
$$\tilde R$$. Similarly to (2.6), we can check that DY(t) = 0 and Y ′ (t) = λv1(R(t) < v).
Then
$${M_v}(t){\kern 1pt} : = \sum\limits_{n = 1}^{N(t)} (1 - {\lambda _v}(v \wedge {T_n}))$$
is an 𝔽-martingale for the filtration 𝔽 such that 𝔽X 𝔽, and for v > 0,
$$N(t) = {\lambda _v}\int_0^t 1(R(u) \lt v){\kern 1pt} {\rm{d}}u + {\lambda _v}(v \wedge R(t)) + {M_v}(t).$$
Taking expectations in (3.5) yields
$${\mathbb {E}} [N(t)] = {\lambda _v}\int_0^t {\mathbb {P}}(R(u) \lt v){\kern 1pt} {\rm{d}}u + {\lambda _v}{\mathbb {E}} [v \wedge R(t)],\quad \quad t \ge 0,$$
and therefore, if (2c) holds, then, as u →∞, 𝕡(R(u) < v) converges to 
$$(\tilde R \lt v)$$, which equals 
$$(\tilde R \le v)$$ at continuity points 
$$v \in {C_{\tilde R}}$$, so for such υ,
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [N(t)]/t = {\lambda _v}{\mathbb {P}}(\tilde R \le v).$$
Since the left-hand side of this equation is independent of v, we have 
$${\lambda _v}{\mathbb {P}}(\tilde R \le v) = {\lambda ^*}$$ for some λ* and for all 
$$v \in {C_{\tilde R}}$$. Hence, we have
$${\mathbb {P}}(\tilde R \le v) = {{{\lambda ^*}} \over {{\lambda _v}}} = {\lambda ^*}{\mathbb {E}} [v \wedge T] = {\lambda ^*}{\mathbb {E}} [\int_0^v 1(T > x){\kern 1pt} {\rm{d}}x],$$
and this equality holds for all v ≩ 0 because the right-hand side is continuous in v. Letting v →∞ in (3.7) shows that 1 = λ *𝔼 [T]. Hence, λ * = 1/E [T] = λ. This and (3.7) yield (3.2). It follows from (3.6) and (3.7) that, for each h > 0 and 
$$v \in {C_{\tilde R}}$$,
$$\mathop {\lim }\limits_{t \to \infty } ({\mathbb {E}} [N(t + h)] - {\mathbb {E}} [N(t)]) = {\lambda _v}\mathop {\lim }\limits_{t \to \infty } \int_t^{t + h} {\mathbb {P}}(R(u) \lt v){\kern 1pt} {\rm{d}}u = \lambda h,$$
because υ ∧ R(t) is bounded by υ. Thus, (2c) implies (2b) and (3.2).
We show in Section 5 that the truncation technique used in this proof is useful for more general counting processes.
3.2. Infinite second moment case
When 𝔼[T 2] =∞, it is of interest to consider a refinement of the elementary renewal theorem 𝔼[N(t)] − λt = o(t). Sgibnev [Reference Sgibnev18] studied this problem, starting with the case of an arithmetic lifetime distribution. Here we consider it through the asymptotic behaviour of 𝔼 [R(t)] in (3.3). Recall first that, for some function z(·): ℝ+ ↦ ℝ, called a generator of Z(·), a solution Z of the general renewal equation of [Reference Feller10],
$$Z(t) = z(t) + \int_0^t Z(t - u){\kern 1pt} F({\rm{d}}u),\quad \quad t \ge 0,$$
is given by
$$Z(t) = {\mathbb {E}}[\int_0^t z(t - u){\kern 1pt} N({\rm{d}}u)].$$
We exhibit 𝔼[R(t)] as a solution of the general renewal equation. From (1.3), when tn −1 ≤ t < tn, R(t) = Tn − (t − tn −1), so choosing
$$z(t) = {\mathbb {E}} [(T - t){\kern 1pt} 1(T > t)],$$
and noting the fact that t n-1 and Tn are independent, we have
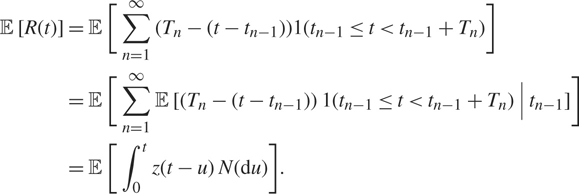$$\matrix{
{{\mathbb {E}} [R(t)] = {\kern 1pt} [\sum\limits_{n = 1}^\infty ({T_n} - (t - {t_{n - 1}}))1({t_{n - 1}} \le t \lt {t_{n - 1}} + {T_n})]} \hfill \cr
{ = {\mathbb {E}}{\kern 1pt} [\sum\limits_{n = 1}^\infty {\mathbb {E}} [({T_n} - (t - {t_{n - 1}})){\kern 1pt} 1({t_{n - 1}} \le t \lt {t_{n - 1}} + {T_n})|{t_{n - 1}}]]} \hfill \cr
{ = {\mathbb {E}} [\int_0^t z(t - u){\kern 1pt} N({\rm{d}}u)].} \hfill \cr
} $$
Thus, z(·) is indeed a generator for 𝔼 [R(t)]. To check the asymptotic behaviour of (3.10), the following lemma is useful (see also [Reference Sgibnev18] or [Reference Daley and Vere-Jones9, Exercise 4.4.5(c)]).
Lemma 3.2. (Sgibnev [Reference Sgibnev18], Theorem 4.) If in (3.8) the generator z(t) is nonnegative and nonincreasing in t ≩ 0, then the solution Z(·) satisfies
$$Z(t) \sim \lambda \int_0^t z(u){\kern 1pt} {\rm{d}}u,$$
where for functions f, g: ℝ+ ↦ ℝ, f (t)∼g(t) means limt →∞ f (t)/g(t) = 1.
It follows from Theorem 2.1 that (3.9), (3.10), and Lemma 3.2 yield
$${\mathbb {E}} [N(t)] - \lambda t = \lambda {\mathbb {E}} [R(t)] \sim \lambda \int_0^t \int_u^\infty {\mathbb {P}} (T > x){\kern 1pt} {\rm{d}}x{\kern 1pt} {\rm{d}}u$$
as shown in [Reference Sgibnev18, Theorem 5]. The asymptotic behaviour of (3.11) may be viewed as a doubly integrated tail of the distribution F of T (see e.g. [Reference Foss, Korshunov and Zachary11] for an integrated tail).
In this section, we have observed how the semimartingale representations (2.7) and (3.5) are helpful in elucidating the asymptotic behaviour of 𝔼 [N(t)]. One may wonder how the present approach might work for the asymptotic behaviour of higher moments of N(t). This is considered in Section 4.
It is also of interest to see how the approach works for more general counting processes. Observe that (2.7) holds if DY(t) of (2.3) vanishes, for which N(t) need not necessarily be a renewal process; we discuss this extension in Section 5, where the exposition is independent of the results in Section 4.
4. Second moment asymptotics
We consider the variance of the renewal process N(t), denoted var N(t). As shown below, the representation gives an alternative path for studying the asymptotic behaviour of var N(t). In particular, the martingale M(t) plays an important role in this case, and this contrasts with the first moment case.
Begin by using (2.7) with 𝔼[M(t)] = 0 to compute var N(t)in the form
$${\mathop{\rm var}}\, N(t) = {\lambda ^2}\,{\mathop{\rm var}}\, R(t) + 2\lambda {\mathbb {E}} [R(t)M(t)] + {\mathbb {E}} [{M^2}(t)].$$
From Lemma 2.3 we know that when 𝔼[T 2]is finite, 
$${\mathbb {E}} [{M^2}(t)] \sim {\lambda ^3}\sigma _T^2t$$. We therefore assume that 𝔼 [T 2] < ∞ because otherwise var N(t) is not finite. To study the asymptotic behaviour of var R(t), we consider 𝔼 [R 2(t)]; this function is the solution of the general renewal equation (3.8) with the generator (cf. around (3.9) above)
$$z(t) = {z_2}(t){\kern 1pt} : = {\mathbb {E}} [(T - t{)^2}{\kern 1pt} 1(T \gt t)] = \int_t^\infty {\mathbb {P}} 2x{\kern 1pt} (T > x){\kern 1pt} {\rm{d}}x.$$
Let
$$h(t) = \int_0^t {z_2}(u){\kern 1pt} {\rm{d}}u = t{\mathbb {E}} [(T - t)T{\kern 1pt} 1(T > t)] + {\textstyle{1 \over 3}}{\mathbb {E}} [(T \wedge t{)^3}].$$
Then Lemma 3.2 and 𝔼 [T 2] < ∞ yield, for t →∞,
$${\mathbb {E}} [{R^2}(t)] \sim \lambda h(t) \sim \left( {\matrix{
{\lambda t{z_2}(t) = {\rm{o}}(t)} & {{\kern 1pt} {\rm if}\;{\mathbb {E}} {\kern 1pt} [{T^3}] = \infty ,} \cr
{{1 \over 3}\lambda {\mathbb {E}} [{T^3}]} & {{\kern 1pt} {\rm if}\;{\mathbb {E}} {\kern 1pt} [{T^3}] \lt \infty .} \cr
} } \right.$$
Thus, 𝔼[R 2(t)] = o(t). On the other hand, by the Cauchy–Schwarz inequality,
$$|{\mathbb {E}}[R(t)M(t)]| \le \sqrt {{\mathbb {E}} [{R^2}(t)]{\kern 1pt} {\mathbb {E}} [{M^2}(t)]} \sim {\lambda ^2}\sqrt {t\sigma _T^2h(t)} .$$
Hence, because 𝔼[T 2] < ∞, the relations (4.1) and h(t) = o(t) yield the known result (e.g. [Reference Daley7, Section 2])
$${\rm{Var }}\,N(t) = {\lambda ^3}\sigma _T^2t + {\rm{o}}(t),\quad \quad t \to \infty .$$
We can refine (4.5) by evaluating 𝔼[R(t)M(t)], namely, using (4.3) and (4.4), we have the next result.
Proposition 4.1. Let N be a renewal process for which (A1)–(A3) hold. If 𝔼 [T 2] < ∞ and 𝔼 [T 3] =∞, then with z 2 defined by (4.2), the relation (4.5) is tightened to
$${\mathop{\rm var}}\, N(t) - {\lambda ^3}\sigma _T^2t = {\rm{O}}(t\sqrt {{z_2}(t)} ).$$
Now consider the case when 𝔼[T 3] < ∞. Then, from (4.3),
$$\mathop {\lim }\limits_{t \to \infty } {\mathop{\rm var}}\, R(t) = \mathop {\lim }\limits_{t \to \infty } \;h(t) - \mathop {\lim }\limits_{t \to \infty } {({\mathbb {E}} [R(t)])^2} = {\textstyle{1 \over 3}}\lambda {\mathbb {E}} [{T^3}] - {\textstyle{1 \over 4}}{\lambda ^2}{({\kern 1pt} [{T^2}])^2}.$$
To find the asymptotic behaviour of 𝔼[R(t)M(t)], we need the extra condition
$$\quad {\kern 1pt} (4a){\kern 1pt} \quad {\mathbb {E}} [R(t)] - C{\kern 1pt} \;is\;directly\;Riemann\;integrable\;on\;{\kern 1pt} [0,\infty ),$$
where 
$$C = {\textstyle{1 \over 2}}\lambda {\mathbb {E}} [{T^2}]$$. Then the following holds (the proof is given in Appendix A.2).
Lemma 4.1. Assume that (A1).(A3) and condition (4.7) hold. Then, if 𝔼 [T 3] < ∞,
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [R(t)M(t)] = {\textstyle{1 \over 2}}(\lambda {\mathbb {E}} [{T^2}] - {\lambda ^2}{\mathbb {E}} [{T^3}]) + {\textstyle{1 \over 2}}{\lambda ^3}\sigma _T^2{\mathbb {E}} [{T^2}].$$
Proposition 4.2. Assume that (A1)–(A3) and condition (4a) hold. Then, if 𝔼 [T 3] < ∞,
$${\mathop{\rm var}}\, N(t) - {\lambda ^3}\sigma _T^2t = - {\textstyle{2 \over 3}}{\lambda ^3}{\mathbb {E}} [{T^3}] + {\textstyle{5 \over 4}}{\lambda ^4}{({\mathbb {E}} [{T^2}])^2} - {\textstyle{1 \over 2}}{\lambda ^2}{\mathbb {E}} [{T^2}] + {\rm{o}}(1),\quad \quad t \to \infty .$$
Smith [Reference Smith19] first obtained this result under the condition that the distribution F of T is spread out.
Daley and Mohan [Reference Daley and Mohan8] proposed two conditions Aε and Bρ as below.
Condition Aε. For some ε ≩ 0,
$${\mathbb {E}} [R(t)] - C = {\rm{o}}({t^{ - 1 - \varepsilon }}),\quad \quad t \to \infty ,$$
Condition Bρ. F is strongly nonlattice, that is,
$$\mathop {\lim \quad inf}\limits_{|\theta | \to \infty } |1 - {\varphi _F}(\theta )| > 0,$$
and 0 < 𝔼[Tρ] < ∞ for some ρ ≩ 2, where φF is the characteristic function of F, namely, 
$${\varphi _F}(\theta ) = {\mathbb {E}} {[{\rm {e}}^{{\rm{i}}\theta T}}]$$ for θ ∊ ℝ with 
$${\rm{i}} = \sqrt { - 1} $$.
Now the spread out condition implies that F is strongly nonlattice (see e.g. [Reference Asmussen2, Chapter VII, Proposition 1.6]), so when 𝔼[T 3] < ∞, Condition Bρ [Reference Daley and Mohan8] is weaker than Smith’s assumption [Reference Smith19].
It is easy to see that (4.7) is satisfied if either Condition Aε holds for ε> 0 or Condition Bρ holds (see e.g. [Reference Daley and Mohan8, (2.5a)]). However a function f (t) = o(t −1) need not be directly Riemann integrable. Hence, (4.7) may be stronger than Condition A 0, though it is unclear whether this case can occur. On the other hand, [Reference Daley7, Corollary 1] shows that
$$\mathop {\lim }\limits_{t \to \infty } \int_0^t ({\mathbb {E}} [R(u)] - C){\kern 1pt} {\rm{d}}u\quad {\kern 1pt} \;{\rm{exists}}\;{\rm{and}}\;{\rm{is}}\;{\rm{finite}}{\kern 1pt} ,$$
if and only if 𝔼[T 3] < ∞. Thus, we may conjecture that 𝔼[T 3] < ∞ implies (4.7), but this is a hard problem because 𝔼 [R(t)] − C may oscillate wildly around the origin as t →∞. In other words, we do not know how to compare (4.7) with Condition A 0.
Thus, the semimartingale decomposition (2.7) can be used to study the asymptotic behaviour of a higher moment of N(t), but it appears to require an extra condition such as (4.7).
5. Extension to a general counting process
The present martingale approach is easily adapted to a general counting process as long as DY(t) of (2.3) vanishes. Here we consider such an extension, assuming (A1), (A2), and (A4). Recall that 𝔽X 𝔽 means that 
$${\mathcal {F}}_t^X \subset {{\mathcal {F}}_t}$$ for all t ≩ 0, where X(t) = (N(t), R(t)). Our basic idea is to use a condition similar to (2c) (see condition (5a) later).
First we introduce a random function to replace λ in (2.7) for v >0. Let
$$T_n^{(v)} = {T_n} \wedge v$$; define 
$${\tilde \lambda ^{(v)}}(t)$$ by
$${\tilde \lambda ^{(v)}}(t) = {1 \over {\mathbb {E}}{(T_{N(t)}^{(v)}|{{\mathcal {F}}_{{t_{N(t) - 1}} - }})}},\quad \quad t \ge 0,$$
equivalently,
$${\tilde \lambda ^{(v)}}(t) = {1 \over {\mathbb {E}}{(T_n^{(v)}|{{\mathcal {F}}_{{t_{n - 1}} - }})}},\quad \quad t \in [{t_{n - 1}},{t_n}),\;n = 1,2, \ldots .$$
Condition (A2) implies that 
$${\mathbb {E}} [T_n^{(v)}|{{\mathcal {F}}_{{t_{n - 1}} - }}]$$ is finite and positive, so 
$${\tilde \lambda ^{(v)}}(t)$$ is finite and bounded below by 1/v, and is therefore well defined.
Lemma 5.1. Let 𝔽 be a filtration such that 𝔽X ⪯ 𝔽, and assume (A1), (A2), and (A4). Then the counting process N(t) can be decomposed for each v > 0 via R(v)(t) = R(t) ∧ v as
$$N(t) = \int_0^t {\tilde \lambda ^{(v)}}(s){\kern 1pt} 1(R(s) \le v){\kern 1pt} {\rm{d}}s + {\tilde \lambda ^{(v)}}(t){R^{(v)}}(t) + {M^{(v)}}(t),$$
where
$${M^{(v)}}(t) = \sum\limits_{n = 1}^{N(t)} (1 - {\tilde \lambda ^{(v)}}({t_{n - 1}})T_n^{(v)}),\quad \quad t \ge 0,$$
is an F-martingale.
Remark 5.1. The left-hand side of (5.1) does not depend on v, and therefore the right-hand side is also independent of v (see (3.5) and arguments below it). We note that Lemma 5.1 holds for v =∞, and can be regarded as an extension of Theorem 2.1
Proof. Apply Lemma 2.1 with 
$$Y(t) = N(t) - {\tilde \lambda ^{(v)}}(t){R^{(v)}}(t)$$. Note that
$$Y'(t) = {\tilde \lambda ^{(v)}}(t){\kern 1pt} 1(R(t) \le v),\quad \quad {t_{n - 1}} \lt t \lt {t_n},$$
because 
$${\tilde \lambda ^{(v)}}(t)$$ is piecewise constant and R ′ (t) =−1for t ∊ (tn −1, tn). Then the facts that R (v) (tn −) = 0 
$${R^{(v)}}({t_n}) = T_{n + 1}^{(v)}$$, and 
$${\tilde \lambda ^{(v)}}({t_n})\, {\rm {is}} \,{\mathcal {F}}{_t}{_n}$$-measurable, imply that
$${D_Y}(t) = \sum\limits_{n = 0}^{N(t) - 1} {\mathbb {E}}(1 - {\tilde \lambda ^{(v)}}({t_n})T_{n + 1}^{(v)}|{{\mathcal {F}}_{{t_n} - }}) = \sum\limits_{n = 0}^{N(t) - 1} (1 - {\tilde \lambda ^{(v)}}({t_n}){\mathbb {E}}(T_{n + 1}^{(v)}|{{\mathcal {F}}_{{t_n} - }})) = 0.$$
On the other hand,
$${M_Y}(t) = 1 - {\tilde \lambda ^{(v)}}({t_0})T_1^{(v)} + \sum\limits_{n = 1}^{N(t) - 1} (1 - {\tilde \lambda ^{(v)}}({t_n})T_{n + 1}^{(v)}) = \sum\limits_{n = 1}^{N(t)} (1 - {\tilde \lambda ^{(v)}}({t_{n - 1}})T_n^{(v)}).$$
Finally, since
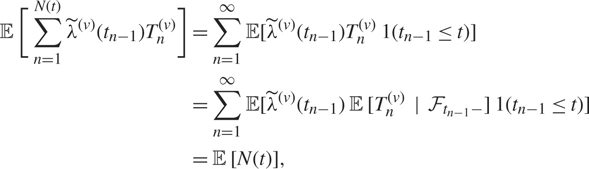$$\matrix{
{{\mathbb {E}} [\sum\limits_{n = 1}^{N(t)} {{\tilde \lambda }^{(v)}}({t_{n - 1}})T_n^{(v)}] = \sum\limits_{n = 1}^\infty {\mathbb {E}} [{{\tilde \lambda }^{(v)}}({t_{n - 1}})T_n^{(v)}{\kern 1pt} 1({t_{n - 1}} \le t)]} \hfill \cr
{ = \sum\limits_{n = 1}^\infty {\mathbb {E}} [{{\tilde \lambda }^{(v)}}({t_{n - 1}}){\kern 1pt} {\mathbb {E}} [T_n^{(v)}|{{\mathcal {F}}_{{t_{n - 1}} - }}]{\kern 1pt} 1({t_{n - 1}} \le t)]} \hfill \cr
{ = {\mathbb {E}} [N(t)],} \hfill \cr
} $$
then
$${\mathbb {E}}[|{M_Y}(t)|] \le {\mathbb {E}} [N(t)] + {\mathbb {E}} [\sum\limits_{n = 1}^{N(t)} {\tilde \lambda ^{(v)}}({t_{n - 1}})T_n^{(v)}] = 2{\mathbb {E}} [N(t)] \lt \infty .$$
Hence, M(v)(·) ≡ MY(·)is an 𝔽-martingale by Lemma 2.1, completing the proof of Lemma 5.1.
Thus, we have derived the semimartingale representation (5.1)for N(·) under the assump- tions (A1), (A2), and (A4). Using this representation, we extend Blackwell’s renewal theorem to a general counting process. To do this, we focus attention on condition (2c) of Lemma 3.1, of which the following can be viewed as its extended version.
(5a) There exists v > 0 such that as t →∞, both 
$${\mathbb {E}}[{\tilde \lambda ^{(v)}}(t){\kern 1pt} 1(R(t) \le v)]$$ and 
$${\mathbb {E}}[{\tilde \lambda ^{(v)}}(t){\kern 1pt} {R^{(v)}}(t)]$$ converge to finite positive limits.
Since 
$${\mathbb {E}} [T_{N(t)}^{(v)}|{{\mathcal {F}}_{{t_{N(t) - 1}} - }})$$ is bounded by v > 0, it may be easier to check condition (5a) via the weak convergence of 
$${\mathbb {E}} [T_{N(t)}^{(v)}|{{\mathcal {F}}_{{t_{N(t) - 1}} - }}]$$ as t →∞, but to do this we need an extra condition of uniform integrability: the following is sufficient for (5a).
(5b) There exists v > 0 such that:
(i) v is a continuity point of the limit distribution of R(v)(t), and
(ii)
$$({\mathbb {E}} [T_{N(t)}^{(v)}|{{\mathcal {F}}_{{t_{N(t) - 1}} - }}],{\kern 1pt} {R^{(v)}}(t))$$ has a limiting distribution as t →∞,(iii)
$$\{ {\tilde \lambda ^{(v)}}(t):t \ge 0\} $$ is uniformly integrable, i.e.
$$\mathop {\lim }\limits_{a \to \infty } \;\;\mathop {\sup }\limits_{t \ge 0} {\mathbb {E}}[{\tilde \lambda ^{(v)}}(t){\kern 1pt} 1({\tilde \lambda ^{(v)}}(t) > a)] = 0.$$
We now present a general conclusion from (5a).
Theorem 5.1. Under the assumptions of Lemma 5.1, if condition (5a) holds, then there exists λ> 0 such that
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [N(t)]/t = \lambda ,$$
and
$$\mathop {\lim }\limits_{t \to \infty } ({\mathbb {E}}[N(t + h)] - {\mathbb {E}}[N(t)]) = \lambda h,\quad \quad h \ge 0.$$
Proof. Let v > 0 be such that the expectations in condition (5a) converge; then by (5a) there exists finite λ(v) > 0 such that
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}}[{\tilde \lambda ^{(v)}}(t){\kern 1pt} 1(R(t) \le v)] = {\lambda ^{(v)}}.$$
Apply Lemma 5.1. Taking the expectation of (5.1) yields
$${\mathbb {E}} [N(t)] = \int_0^t {\mathbb {E}}[{\tilde \lambda ^{(v)}}(s){\kern 1pt} 1(R(s) \le v)]{\kern 1pt} {\rm{d}}s + {\mathbb {E}}[{\tilde \lambda ^{(v)}}(t){\kern 1pt} {R^{(v)}}(t)].$$
Divide both sides of this equation by t; letting t →∞ yields 
$$\mathop {\lim }\nolimits_{t \to \infty } {\mathbb {E}} [N(t)]/t = {\lambda ^{(v)}}$$. Now the left-hand side of this relation is independent of v, so λ(v) must also be independent of v: set λ =λ (v),giving (5.2). Equation (5.3) follows from (5.5) and (5a).
In applying Theorem 5.1 it is important to check conditions (5a) or (5b). Obviously, conditions (5b) are satisfied by a nonarithmetic renewal process (see assumptions (A1)–(A3)), for which 
$$T_n^{(v)}$$ is identically distributed and independent of 
$${{\mathcal {F}}_{{t_{n - 1}} - }}$$. We sketch two scenarios in which the two conditions are relaxed.
5.1. Modulated inter-arrival times
Let J(·) ≡{J(t): t ≩ 0} be a piecewise constant process on the state space S, which is a Polish space. Let t 0 = 0, and for n = 1, 2, ... let tn be the nth discontinuous instant of J(t); these instants generate the counting process N(·). As usual, let Tn = tn − tn −1, and for t ∊ [tn −1, tn)set R(t) = t − tn −1 and J(t) = J(tn −1). Define a joint process U(·) by
$$U(t) = (J(t),N(t),R(t)),\quad \quad t \ge 0.$$
Let 
$${\mathcal {F}}_t^U = \sigma (\{ U(s):s \le t\} )$$, and let 
$${\mathbb {F}}{^U} = \{ {\mathcal {F}}_t^U:t \ge 0\} $$; this is a filtration for U(·). Let 𝔽 = 𝔽U, then obviously 𝔽X ⪯ 𝔽 since X(t) = (N(t), R(t)). Assume the following conditions.
(M1) Tn is independent of 
$${{\mathcal {F}}_{{t_{n - 1}} - }}$$.
(M2) The distribution of Tn is nonarithmetic and determined by J(tn −1) ∊ S.
We refer to a process satisfying (M1) and (M2) as a modulated renewal process.A Markov- modulated renewal process is the special case in which {J(tn): n = 0, 1, ...} is a Markov chain. Let T(v)(x) be the conditional expectation of 
$$T_n^{(v)} \equiv v \wedge {T_n}$$ given J(tn −1) = x, that is, 
$${T^{(v)}}(x) = {\mathbb {E}} [T_n^{(v)}|J({t_{n - 1}}) = x]$$.
Corollary 5.1. For a modulated renewal process as defined above, if (i) S is countable, (ii) infx ∊S 𝔼 [T(x)] > 0, where T(x) = 𝔼 [Tn | J(tn −1) = x], and (iii) (J(t), R(t)) has a limit distribution as t →∞, then both (5.2) and Blackwell’s formula (5.3) hold with λ defined by
$$\lambda = {\mathbb {E}} [{1 \over {{T^{(v)}}(\tilde J)}}1(\tilde R \le v)] = {\mathbb {E}} [{1 \over {T(\tilde J)}}],$$
where 
$$(\tilde J,\tilde R)$$ is a random variable with the limit distribution of (J(t), R(t)), and v is any continuity point of the distribution of 
$$\tilde R$$.
Proof. From condition (iii), for a continuity point v of the distribution of 
$$\tilde R$$, and for a bounded function f: S ↦ 𝔽,
$$\matrix{
{\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}}[f(J(t)){\kern 1pt} 1(R(t) \le v)] = {\mathbb {E}}[f(\tilde J){\kern 1pt} 1(\tilde R \le v)],} \hfill \cr
{\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [f(J(t)){\kern 1pt} {R^{(v)}}(t)] = {\mathbb {E}} [f(\tilde J)(\tilde R \wedge v)].} \hfill \cr
} $$
By assumptions (i) and (ii) of the corollary, f (x)≔ 1/𝔽 [T(v)(x)] is continuous, bounded, and positive, where x is discrete, so we take a discrete topology. Thus, condition (5a) is satisfied, and therefore (5.2) and (5.3) are obtained by Theorem 5.1. Here, (5.6) is immediate from (5.4) in the proof of Theorem 5.1.
Remark 5.2. Under the conditions of Corollary 5.1, J(·) is piecewise continuous but no transition structure like that of a Markov chain is assumed: the restrictive conditions (i) and (ii) may be inconsistent with Markovianity. If S is a finite set, then (i) and (ii) automatically hold, and these may constitute circumstances when the present framework is useful. However, for a Markov-modulated renewal process, Blackwell’s formula (5.3) is obtained under a certain recurrence condition of J(t) without conditions (i) and (ii) (see e.g. [Reference Alsmeyer1]). In such a case the present approach would not be suitable.
5.2. Stationary inter-arrival times
Consider now the scenario in which {Tn : n ∊ 𝕫+} is a stationary sequence of positive reals with finite means, where ℤ+ is the set of all nonnegative integers. This sequence can be extended to a stationary sequence that starts at time −∞, and is well described by the Palm distribution P on a measurable space (Ω, ℱ). (We digress to note that in the point process literature, the Palm distribution is often notated as 𝕡0, and if need be, the distribution of a stationary point process, i.e. the distributions of counts on sets An are the same as for the translated sets An + t, are notated 𝕡. To be consistent with Sections 1–3 of this paper, we retain the notation 𝕡 for Palm distributions, and write 
$${\rm{\bar {\mathbb {P}}}}$$ for (count) stationary distributions as at (5.7) below.)
We introduce the standard formulation to describe {Tn} by a point process under (Ω, F, P) (see e.g. [Reference Baccelli and Brémaud3]). Let λ = 1/𝔼(T 0), and let {tn} be a two-sided random sequence such that t 0 = 0 and
$${t_n} = \left( {\matrix{
{{T_1} + \cdots + {T_n}} & {n > 0,} \cr
{ - ({T_{ - 1}} + \cdots + {T_{ - |n|}})} & {n \lt 0.} \cr
} } \right.$$
Define a point process N(·) on ℝ by
$$N(B) = \sum\limits_{n = - \infty }^\infty 1({t_n} \in B),\quad \quad B \in B().$$
Similarly to (1.3), define R(t) by
$$R(t) = \left\{ {\matrix{
{\sum\nolimits_{\ell = 1}^{N([0,t])} {{T_\ell } - t \quad t \ge 0,} } \hfill \cr
{\sum\nolimits_{\ell = 1}^{N((t,0))} {( - {T_{ - \ell }}) - t \quad t < 0.} } \hfill \cr
} } \right.$$
We can then construct a shift operator group {θt : t ∊ ℝ} on such that:
(S1) 
$${\theta _t} \circ A = \{ \omega \in \Omega :\theta _t^{ - 1}(\omega ) \in A\} $$,
(S2) the point process N is consistent with θt, that is, θt ∘ N(B) = N(B + t) for bounded B ∊ B(R) and B + t ={x + t ∊ R: x ∊ B}, and
(S3) for n ∊ 𝕫, 𝕡(θtn ∘ A) = 𝕡(A)for A ∊ F, where ℤ is the set of all integers.
Next define a probability measure 
$$\bar {\mathbb {P}} $$ on (Ω, ℱ) by
$$\bar {\mathbb {P}} (A) = \lambda {\mathbb {E}} [\int_0^{{T_1}} {\theta _t} \circ {1_A}{\kern 1pt} {\rm{d}}t],\quad \quad A \in F.$$
It is well known (see e.g. [Reference Baccelli and Brémaud3]) that N(·) is a stationary point process under 
$$\bar {\mathbb {P}} $$, and 
$$\bar {\mathbb {E}} [N(1)] = \lambda $$. Furthermore, we recover 𝕡 from 
$$\bar {\mathbb {P}} $$ by the so-called inversion formula: for each ε> 0,
$${\mathbb {P}}(A) = {1 \over {\lambda \varepsilon }}\bar {\mathbb {P}}\left[ {\int_0^\varepsilon {{\theta _{ - t}} \circ {1_A}N(dt)} } \right], \quad A \in {\mathcal {F}}.$$
We can now formulate Blackwell’s renewal theorem for the stationary sequence.
Corollary 5.2. Under assumptions (A1)–(A2), if (i) {Tn : n ∊ 𝕫} is a stationary and ergodic sequence under the Palm distribution 𝕡, (ii) 
$$\{ {\tilde \lambda ^{(v)}}(t):t \ge 0\} $$ is uniformly integrable under 𝕡, and (iii) the mixing condition
$$\mathop {\lim }\limits_{t \to \infty } \bar {\mathbb {P}}({\theta _{ - t}} \circ A,{t_1} \le u) = \bar {\mathbb {P}} (A)\bar {\mathbb {P}} ({t_1} \le u),\quad \quad A \in F,\;u \ge 0,$$
holds, then Blackwell’s formula (5.3) holds together with (5.2), and
$$\lambda = {1 \over {{\mathbb {E}} [{T_1}]}} = {\mathbb {E}} [{{1(R(0) \le v)} \over {{\mathbb {E}}[T_1^{(v)}|{{\mathcal {F}}_{0 - }}]}}],\quad \quad v \ge 0,$$
where the sets 
$${{\mathcal {F}}_t} = \sigma (\{ R(u):u \le t\} \cup \bigcup\nolimits_{n = - \infty }^\infty \{ {t_n} \le t\} )$$ define the filtration 𝔽 ≡{ℱt : t ∊ ℝ}.
Remark 5.3. The mixing condition (5.9)is used in [Reference Miyazawa14, Theorem 3.2].
Proof. Let ηn(Ω) = θtn (Ω )(Ω) be the shift operator on the sample space ; then
$$\matrix{
{{\eta _1} \circ ({{\tilde \lambda }^{(v)}}(t),{R^{(v)}}(t)) = ({1 \over {{\eta _1} \circ {\mathbb {E}} [T_n^{(v)}|{{\mathcal {F}}_{{t_{n - 1}} - }}]}},{\kern 1pt} {\eta _1} \circ {T_n} - (t - {\eta _1} \circ {t_{n - 1}}))} \hfill \cr
{ = ({1 \over {{\mathbb {E}} [T_n^{(v)}|{{\mathcal {F}}_{{t_n} - }}]}},{\kern 1pt} {T_{n + 1}} - (t - {t_n})),\quad \quad {t_n} \le t \lt {t_{n + 1}}.} \hfill \cr
} $$
Hence for n ∈ ℤ
$$\{ ({\tilde \lambda ^{(v)}}(t),{R^{(v)}}(t))black:{t_{n - 1}} \le t \lt {t_n}\} $$ is a stationary sequence under 𝕡, and
$$({\tilde \lambda ^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t)) = {\theta _t} \circ ({\tilde \lambda ^{(v)}}(t) \circ {\theta _{ - t}},{\kern 1pt} {R^{(v)}}(t) \circ {\theta _{ - t}})) = {\theta _t} \circ ({\tilde \lambda ^{(v)}}(0),{R^{(v)}}(0))$$
is a stationary process under 
$$\bar {\mathbb {P}} $$. Let f (x, y) be a nonnegative bounded continuous function on 
$${\mathbb {R}}_ + ^2$$; then by (5.9), for ε> 0,
$$\mathop {\lim }\limits_{t \to \infty } \overline {\mathbb {E}}[f({\tilde \lambda ^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t)){\kern 1pt} 1({t_1} \le \varepsilon )] = \overline {\mathbb {E}} [f({\tilde \lambda ^{(v)}}(0),{\kern 1pt} {R^{(v)}}(0))] \bar {\mathbb {P}} ({t_1} \le \varepsilon ).$$
On the other hand, by (5.8),
$$\matrix{
{|{\mathbb {E}} [f({{\tilde \lambda }^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t))] - {{\bar {\mathbb {E}} [f({{\tilde \lambda }^{(v)}}(t + {t_1}),{\kern 1pt} {R^{(v)}}(t + {t_1})){\kern 1pt} 1({t_1} \le \varepsilon )]} \over {\lambda \varepsilon }}|} \hfill \cr
{\quad \quad \le {{\parallel f\parallel } \over {\lambda \varepsilon }}\bar {\mathbb {E}} [N(\varepsilon ){\kern 1pt} 1(N(\varepsilon ) \ge 2)],} \hfill \cr
} $$
where 
$$\parallel f\parallel = \mathop {\sup }\nolimits_{(x,y) \in {\mathbb {R}}_ + ^2} |f(x,y)|$$. This and (5.9) imply that
$$\matrix{
{\mathop {\lim \;{\sup}}\limits_{t \to \infty } {\mathbb {E}} [f({{\tilde \lambda }^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t))]} \cr
{ \le \mathop {\limsup }\limits_{t \to \infty } {1 \over {\lambda \varepsilon }}\bar {\mathbb {E}} [\mathop {\rm sup }\limits_{s \in [0,\varepsilon )} f({{\tilde \lambda }^{(v)}}(t + s),{\kern 1pt} {R^{(v)}}(t + s)){\kern 1pt} 1({t_1} \le \varepsilon )] + {{\parallel f\parallel } \over {\lambda \varepsilon }}\bar {\mathbb {E}} [N(\varepsilon ){\kern 1pt} 1(N(\varepsilon ) \ge 2)]} \cr
{\quad = {1 \over {\lambda \varepsilon }}\bar {\mathbb {E}} [\mathop {\rm sup }\limits_{s \in [0,\varepsilon )} f({{\tilde \lambda }^{(v)}}(s),{\kern 1pt} {R^{(v)}}(s))]{\kern 1pt} \bar {\mathbb {P}} ({t_1} \le \varepsilon ) + {{\parallel f\parallel } \over {\lambda \varepsilon }}\bar {\mathbb {E}} [N(\varepsilon ){\kern 1pt} 1(N(\varepsilon ) \ge 2)].} \cr
} $$
Now
$$\mathop {\lim }\limits_{\varepsilon \downarrow 0} {{\bar {\mathbb {P}} ({t_1} \le \varepsilon )} \over {\lambda \varepsilon }} = 1\quad {\rm{and}}\quad \mathop {\lim }\limits_{\varepsilon \downarrow 0} {{\bar {\mathbb {E}} [N(\varepsilon ){\kern 1pt} 1(N(\varepsilon ) \ge 2)]} \over {\lambda \varepsilon }} = 0,$$
implying that
$$\mathop {\limsup }\limits_{t \to \infty } {\mathbb {E}}[f({\tilde \lambda ^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t))] \le \mathop {\lim }\limits_{\varepsilon \downarrow 0} \bar {\mathbb {E}} [\mathop {\sup }\limits_{s \in [0,\varepsilon )} f({\tilde \lambda ^{(v)}}(s),{\kern 1pt} {R^{(v)}}(s))] = \bar {\mathbb {E}} [f({\tilde \lambda ^{(v)}}(0),{\kern 1pt} {R^{(v)}}(0))],$$
by the right-continuity of 
$$f({\tilde \lambda ^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t))$$. Similarly, we have
$$\mathop {\liminf}\limits_{t \to \infty } {\mathbb {E}} [f({\tilde \lambda ^{(v)}}(t),{\kern 1pt} {R^{(v)}}(t))] \ge \bar {\mathbb {E}} [f({\tilde \lambda ^{(v)}}(0),{\kern 1pt} {R^{(v)}}(0))],$$
where
$$\bar {\mathbb {E}} [{\tilde \lambda ^{(v)}}(0){\kern 1pt} 1({R^{(v)}}(0) \le v)] = \lambda {\mathbb {E}} [{\tilde \lambda ^{(v)}}(0)T_1^{(v)}] = \lambda {\mathbb {E}} [{\tilde \lambda ^{(v)}}(0){\kern 1pt} {\mathbb {E}} [t_1^{(v)}|{{\mathcal {F}}_{0 - }}]] = \lambda \lt \infty .$$
Thus, by the uniform integrability assumption on 
$${\tilde \lambda ^{(v)}}(t)$$, condition (5a) is satisfied. Equation (5.10) is an immediate consequence of (5.7), completing the proof.
6. Concluding remarks
In this paper, we have used a certain martingale to give a new approach to Blackwell’s renewal theorem and its extensions for general counting processes. One may envisage applying this approach to other problems.
For example, consider a diffusion approximation of the renewal process N of Section 1 for which 𝔼 [T 2] < ∞. Scale N(t) −λt as 
$${\tilde N_n}(t){\kern 1pt} : = {n^{ - 1/2}}(N(nt) - \lambda nt)$$; this is called diffusion scaling. It is well known that 
$${\tilde N_n}( \cdot )$$ converges weakly to the Brownian motion B(t) with var 
$$B(t) = {\lambda ^3}\sigma _T^2t$$ in an appropriate function space with the Skorokhod topology. This is usually proved by the central limit theorem and a time change (see e.g. [Reference Chen and Yao5, Theorem 5.11] and [Reference Whitt21, Corollary 7.3.1]). To derive this result in the framework of this paper, let 
$${\tilde R_n}(t) = \lambda R(nt)/\sqrt n $$ and 
$${\tilde M_n}(t) = M(nt)/\sqrt n $$ then, by Theorem 2.1,
$${\tilde N_n}(t) = \lambda {\tilde R_n}(t) + {\tilde M_n}(t).$$
Observe that as 
$$n \to \infty ,{\rm{ }}{\tilde R_n}(t) \to 0$$ in probability because
$$\mathop {\lim \;{\rm sup}}\limits_{n \to \infty } {\mathbb {E}} [{\tilde R_n}(t)] \le \mathop {\limsup }\limits_{n \to \infty } \lambda {\mathbb {E}} [{T^2}]/\sqrt n = 0.$$
Further, Lemma 2.3 implies that
$$\mathop {\lim }\limits_{n \to \infty } \langle {\tilde M_n}(t)\rangle = \mathop {\lim }\limits_{n \to \infty } {{N(nt)} \over n}{\kern 1pt} {\lambda ^2}\sigma _T^2 = {\lambda ^3}\sigma _T^2t.$$
Hence (6.1) would imply that 
$${\tilde N_n}( \cdot )$$ converges weakly to the martingale with deterministic quadratic variation 
$$\sigma _T^2t$$, and this is just the Brownian motion B(t) with variance 
$$\sigma _T^2t$$ if the limiting process of 
$${\tilde N_n}( \cdot )$$ is continuous in time. To convert this argument into a formal proof, we should need to verify a technical condition, called C-tightness (see e.g. [Reference Whitt22, Theorem 2.1]); even without this, the above argument elucidates the mechanism of the diffusion approximation.
Thus, while the present approach is useful for studying counting processes, this may not be the case for studying stochastic models in applications. For example, counting processes appear as input data for stochastic models such as queueing and risk processes. In these applications, the semimartingale representation for a counting process may not be convenient because such stochastic processes are functionals of counting processes. In this situation, the general formulation in Section 2.1 would be useful if we can find an appropriate process Y(t), which may not be a counting process but includes it as one of components. The second author recently studied this type of application in [Reference Miyazawa16] and [Reference Miyazawa15] for diffusion approximations and tail asymptotics of the stationary distributions for queues and their networks. This may be a direction for future study.
Appendix
A.1. Proof of (2.11)
Apply Lemma 2.1 with Y(t) = M 2(t) for which Y ′ (t) = 0, and therefore
$$\matrix{
{\langle M\rangle (t) = {D_Y}(t)} \hfill \cr
{ = \sum\limits_{n = 0}^{N(t) - 1} ({\mathbb {E}} [{M^2}({t_n})|{{\mathcal {F}}_{{t_n} - }}] - {M^2}({t_n} - ))} \hfill \cr
{ = \sum\limits_{n = 0}^{N(t) - 1} ({\mathbb {E}} [(M({t_n} - ) + (1 - \lambda {T_{n + 1}}{{))}^2}|{{\mathcal {F}}_{{t_n} - }}] - {M^2}({t_n} - ))} \hfill \cr
{ = \sum\limits_{n = 0}^{N(t) - 1} {\mathbb {E}} [2M({t_n} - )(1 - \lambda {T_{n + 1}}) + {{(1 - \lambda {T_{n + 1}})}^2}|{{\mathcal {F}}_{{t_n} - }}]} \hfill \cr
{ = \sum\limits_{n = 0}^{N(t) - 1} {\mathbb {E}} [(1 - \lambda {T_{n + 1}}{)^2}]} \hfill \cr
{ = N(t){\mathbb {E}} [(1 - \lambda T{)^2}] = {\lambda ^2}\sigma _T^2N(t),} \hfill \cr
} $$
since 𝔼[Reference Alsmeyer1 − λTn +1 | ℱtn −] = 0. Thus, we have (2.11).
A.2. Proof of Lemma 4.1
The main idea of this proof is to apply the key renewal theorem. For this, recall that tN (t )−1 ≤ t < tN (t ), and rewrite R(t)M(t)as
$$R(t)M(t) = ({t_{N(t)}} - t)\sum\limits_{\ell = 1}^{N(t)} (1 - \lambda {T_\ell }) = {Z_1}(t) + {Z_2}(t),$$
where
$$\matrix{
{{Z_1}(t) = ({T_{N(t)}} + {t_{N(t) - 1}} - t)(1 - \lambda {T_{N(t)}}),} \cr
{{Z_2}(t) = ({T_{N(t)}} + {t_{N(t) - 1}} - t)\sum\limits_{\ell = 1}^{N(t) - 1} (1 - \lambda {T_\ell }).} \cr
} $$
We consider 𝔼(Z 1(t)) and 𝔼(Z 2(t)) separately. Let
$${z_3}(t) = {\kern 1pt} [(T - t)(1 - \lambda T){\kern 1pt} 1(T > t)],\quad \quad t \ge 0.$$
Then, much as for (3.10), the independence of tn −1 and Tn and the key renewal theorem (see e.g. [Reference Asmussen2, Example 2.6]) yield
$$\matrix{
{\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [{Z_1}(t)] = \mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [\sum\limits_{n = 1}^\infty ({T_n} - (t - {t_{n - 1}}))(1 - \lambda {T_n}){\kern 1pt} 1(0 \le t - {t_{n - 1}} \lt {T_n})]} \cr
{ = \mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [\sum\limits_{n = 1}^\infty {z_3}(t - {t_{n - 1}}){\kern 1pt} 1({t_{n - 1}} \le t)]} \cr
{ = \lambda \int_0^\infty {z_3}(u){\kern 1pt} {\rm{d}}u = \lambda {\mathbb {E}} [\int_0^T (T - u)(1 - \lambda T){\kern 1pt} {\rm{d}}u]} \cr
{ = {\textstyle{1 \over 2}}\lambda ({\mathbb {E}} [{T^2}] - \lambda {\mathbb {E}} [{T^3}]).} \cr
} $$
In considering 𝔼 [Z 2(t)], the limiting operations for the key renewal theorem are nested, so we use the extra condition (4.7). We prove that 𝔼 [T 3] < ∞ and that
$$\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [{Z_2}(t)] = {\textstyle{1 \over 2}}{\lambda ^3}{\mathbb {E}}({T^2})\sigma _T^2.$$
First, rewrite 𝔼[Z 2(t)] as
$$\matrix{
{{\mathbb {E}} [({T_{N(t)}} + {t_{N(t) - 1}} - t)\sum\limits_{\ell = 1}^{N(t) - 1} (1 - \lambda {T_\ell })]} \hfill \cr
{\quad \quad = {\mathbb {E}} [\sum\limits_{n = 1}^\infty ({t_n} - t)\sum\limits_{\ell = 1}^{n - 1} (1 - \lambda {T_\ell }){\kern 1pt} 1({t_{n - 1}} \le t \lt {t_n})]} \hfill \cr
{\quad \quad = {\mathbb {E}} [\sum\limits_{\ell = 1}^\infty (1 - \lambda {T_\ell })\sum\limits_{n = \ell + 1}^\infty ({t_n} - t){\kern 1pt} 1({t_{n - 1}} \le t \lt {t_n})]} \hfill \cr
{\quad \quad = {\mathbb {E}} [\sum\limits_{\ell = 1}^\infty (1 - \lambda {T_\ell }){V_\ell }(t){\kern 1pt} 1({t_{\ell - 1}} \le t)],} \hfill \cr
} $$
where
$${V_\ell }(t) = {\mathbb {E}} [\sum\limits_{n = \ell + 1}^\infty ({t_n} - t){\kern 1pt} 1({t_{n - 1}} \le t \lt {t_n})|{{\mathcal {F}}_{{t_{\ell - 1}}}}],\quad \quad t \ge 0,\ell \ge 1.$$
Let 
$$\tilde N( \cdot )$$ be an independent copy of N(·), let 
$${\tilde t_n}$$ be the nth counting epoch of the renewal process 
$$\tilde N( \cdot )$$ similar to N(⋅), and let 
$${\tilde T_n} = {\tilde t_n} - {\tilde t_{n - 1}}$$ for n ≩ 1, where 
$${\tilde t_0} = 0$$. Similarly, let 
$$\tilde R(t)$$ be the residual time to the next jump at time t. For t ≩ 0, define
$$\matrix{
{\tilde V(t|x) = {\mathbb {E}} [\sum\limits_{n = 2}^\infty ({{\tilde t}_n} - t)1({{\tilde t}_{n - 1}} \le t \lt {{\tilde t}_n})|{{\tilde T}_1} = x]} \cr
{ = {\mathbb {E}} [\sum\limits_{n = 2}^\infty ({{\tilde t}_n} - {{\tilde t}_1} - (t - {{\tilde t}_1}))1({{\tilde t}_{n - 1}} - {{\tilde t}_1} \le t - {{\tilde t}_1} \lt {{\tilde t}_n} - {{\tilde t}_1})|{{\tilde T}_1} = x].} \cr
} $$
Since the last formula is independent of 
$${\tilde T_1}$$ and represents the residual time to the next jump at time t − x, it equals 
$${\mathbb {E}} [\tilde R(t - x)]$$.
For notational convenience in what follows, define a function r(·)by
$$r(t) = \left{ {\matrix{
{{\mathbb {E}} [\tilde R(t)]} & {t \ge 0,} \cr
0 & {t \lt 0,} \cr
} } \right.$$
and let 
$$C = {\textstyle{1 \over 2}}\lambda {\mathbb {E}}({T^2})$$. Since, for n ≩ ℓ, tn − t is independent of 
$${{\mathcal {F}}_{{t_{\ell - 1}}}}$$,
$${V_\ell }(t) = \tilde V(t - {t_{\ell - 1}}|{T_\ell }) = r(t - ({t_{\ell - 1}} + {T_\ell })),\quad \quad t \ge 0.$$
Thus, (A.2) can be rewritten as
$${\mathbb {E}} [({T_{N(t)}} + {t_{N(t) - 1}} - t)\sum\limits_{\ell = 1}^{N(t) - 1} (1 - \lambda {T_\ell })] = {\mathbb {E}} [\sum\limits_{\ell = 1}^\infty (1 - \lambda {T_\ell })r(t - ({t_{\ell - 1}} + {T_\ell }))1({t_{\ell - 1}} \le t)].$$
Denote the right-hand side of (A.3)by W(t), and decompose it as
$$\matrix{
{{W_1}(t) = {\mathbb {E}} [\sum\limits_{\ell = 1}^\infty (\lambda {T_\ell } - 1)(C{\kern 1pt} 1({T_\ell } \le t - {t_{\ell - 1}}) - r(t - ({t_{\ell - 1}} + {T_\ell }))1({t_{\ell - 1}} \le t)],} \cr
{{W_2}(t) = C{\kern 1pt} {\mathbb {E}} [\sum\limits_{\ell = 1}^\infty (1 - \lambda {T_\ell })1({T_\ell } \le t - {t_{\ell - 1}})].} \cr
} $$
Define
$${w_1}(t) = {\mathbb {E}} [(\lambda T - 1)(C - r(t - T))1(T \le t)]\quad {\kern 1pt} and{\kern 1pt} \quad {w_2}(t) = C{\kern 1pt} {\mathbb {E}} [(1 - \lambda T)1(T \le t)].$$
It is readily checked that, for i = 1, 2, Wi(·) is the solution of the general renewal equation with the generator wi(·). Consider first w 1(t), and introduce
$$g(t) = \left\{ {\matrix{
{C - r(t)} & {t \ge 0,} \cr
0 & {t < 0,} \cr
} } \right.$$
so that from the definition of w 1,
$$\matrix{
{{w_1}(t) = {\mathbb {E}} [\lambda Tg(t - T)1(T \le t)] - {\mathbb {E}} [g(t - T)1(T \le t)]} \cr
{ = \lambda \int_0^\infty ug(t - u){\kern 1pt} F({\rm{d}}u) - \int_0^\infty g(t - u){\kern 1pt} F({\rm{d}}u).} \cr
} $$
Using the assumption at (4.7), we show that the last two integrals are directly Riemann integrable. To this end, let 
$$I_n^\delta (u) = (n\delta ,(n + 1)\delta ]$$ for Δ > 0 and u ≩ 0. Then
$$\mathop {\sup }\limits_{t \in I_n^\delta (0)} \int_0^\infty u{\kern 1pt} g(t - u){\kern 1pt} F({\rm{d}}u) \le \int_0^\infty u{\kern 1pt} \mathop {\sup }\limits_{t \in I_n^\delta } g(t - u){\kern 1pt} F({\rm{d}}u).$$
Similarly,
$$\int_0^\infty u\mathop {\inf }\limits_{t \in I_n^\delta } g(t - u){\kern 1pt} F({\rm{d}}u) \le \mathop {\inf }\limits_{t \in I_n^\delta (0)} \int_0^\infty u{\kern 1pt} g(t - u){\kern 1pt} F({\rm{d}}u).$$
Then, because |g| is bounded, 𝔼[T] < ∞, and for fixed u ≩ 0, g(t − u) is directly Riemann integrable for t ≩ u, the first integral 
$$\int_0^\infty ug(t - u){\kern 1pt} F({\rm{d}}u)$$ is directly Riemann integrable.
Similarly, the second integral 
$$\int_0^\infty g(t - u){\kern 1pt} F({\rm{d}}u)$$ is also directly Riemann integrable. Hence, w 1(t) is directly Riemann integrable. We then compute the integration on w 1:
$$\matrix{
{\int_0^s {w_1}(t){\kern 1pt} {\rm{d}}t = {\mathbb {E}} [\int_0^s (\lambda T - 1)g(t - T){\kern 1pt} 1(T \le t){\kern 1pt} {\rm{d}}t]} \hfill \cr
{ = {\mathbb {E}} [\int_0^{{{(s - T)}^ + }} (\lambda T - 1)g(u){\kern 1pt} 1(u \ge 0){\kern 1pt} {\rm{d}}u]} \hfill \cr
{ = {\mathbb {E}} [\int_0^s (\lambda T - 1)g(u){\kern 1pt} {\rm{d}}u] - {\mathbb {E}} [\int_{{{(s - T)}^ + }}^s (\lambda T - 1)g(u){\kern 1pt} {\rm{d}}u]} \hfill \cr
{ = {\mathbb {E}} [\int_{{{(s - T)}^ + }}^s (1 - \lambda T)g(u){\kern 1pt} {\rm{d}}u]} \hfill \cr
{ = \int_0^s {\mathbb {E}} [(1 - \lambda T)1(T > s - u)]g(u){\kern 1pt} {\rm{d}}u,} \hfill \cr
} $$
which is finite as s →∞ if 𝔼(T 2) < ∞ because |g(u)| is bounded by C. Furthermore, it is not hard to see that this integral converges to 0 as s →∞.
We next consider w 2(t). Then, since 𝔼(T 2) < ∞,
$${w_2}(t) = C{\kern 1pt} {\mathbb {E}} [(1 - \lambda T)(1 - 1(T > t))] = - C{\kern 1pt} {\mathbb {E}} [(1 - \lambda T)1(T > t)],$$
is directly Riemann integrable, and
$$\int_0^\infty {w_2}(t){\kern 1pt} {\rm{d}}t = \lambda C{\kern 1pt} {\mathbb {E}} [\int_0^\infty (T - {\mathbb {E}} [T])1(T > t){\kern 1pt} {\rm{d}}t] = \lambda C{\kern 1pt} \sigma _T^2.$$
Hence, w 1(t) + w 2(t) is directly Riemann integrable, and therefore the key renewal theorem and (A.4) yield
$$\matrix{
{\mathop {\lim }\limits_{t \to \infty } {\mathbb {E}} [({T_{N(t)}} + {t_{N(t) - 1}} - t)\sum\limits_{\ell = 1}^{N(t) - 1} (1 - \lambda {T_\ell })] = \lambda (\int_0^\infty {w_1}(t){\kern 1pt} {\rm{d}}t + \int_0^\infty {w_2}(t){\kern 1pt} {\rm{d}}t)} \cr
{ = \lambda \int_0^\infty {w_2}(t){\kern 1pt} {\rm{d}}t = {\lambda ^2}C{\kern 1pt} \sigma _T^2.} \cr
} $$
Recalling that 
$$C = {\textstyle{1 \over 2}}\lambda {\kern 1pt} [{T^2}]$$
, (A.1) follows. This proves Lemma 4.1.
Acknowledgements
We thank two anonymous referees for their helpful comments and suggestions. DJD’s work was done as an Honorary Professorial Associate at the University of Melbourne. MM’s work was partly supported by JSPS KAKENHI grant 16H027860001.
