1. Introduction
Transonic buffet and subsonic stall are two boundaries of the flight envelope of civil aircraft. Transonic buffet is an oscillation of the shock wave position over a wing caused by an interaction between a separated boundary layer and the shock wave. This oscillation induces variation of the aerodynamic forces which can be detrimental to aircraft handling. A thorough review of the state of knowledge about transonic buffet is presented by Giannelis, Vio & Levinski (Reference Giannelis, Vio and Levinski2017). On the other hand, subsonic stall occurs when flow separation causes a reduction of the lift forces as the wing angle of attack is increased. These phenomena involve complex physics, part of which is the occurrence of three-dimensional (3-D) flow features which are named buffet cells and stall cells, respectively. The stall cells are identified as a spanwise variation of the flow separation, while the buffet cells are a spanwise variation of the shock wave position, and thus of the shock induced flow separation.
Stall cells were observed experimentally (Gregory et al. Reference Gregory, Quincey, O'Reilly and Hall1971; Moss & Murdin Reference Moss and Murdin1971) since the 1970s. Most of these studies were carried out for a wing which spans the entire wind tunnel width, a set-up which is often considered as ‘two-dimensional’ (2-D). However, the flow becomes strongly 3-D when stall cells are present. Early studies suggested that the phenomenon might be caused by the side walls. However, the experimental results of Winkelmann & Barlow (Reference Winkelmann and Barlow1980) contradict this conclusion since the stall cells are observed over the entire span of wings of aspect ratios up to 12 and with free tips. They reported that the number of cells is proportional to the aspect ratio. Schewe (Reference Schewe2001) also reports the effect of the aspect ratio on the number of stall cells. Experiments by Broeren & Bragg (Reference Broeren and Bragg2001) of aerofoil with trailing edge, leading edge and thin aerofoil type of stall suggest that trailing edge separation is a necessary condition for the occurrence of stall cells. Yon & Katz (Reference Yon and Katz1998) obtained stall cells over a narrow range of angles of attack and discussed the unsteady nature of the stall cells. More recently, Dell'Orso & Amitay (Reference Dell'Orso and Amitay2018) carried out a parametric study of the effect of the angle of attack (![]() $\alpha$) and the Reynolds number
$\alpha$) and the Reynolds number ![]() $(Re = {\rho _{\infty }U_{\infty }c}/{\mu _{\infty }})$. They identified eight types of flow topologies from a full span separation (2-D) to the presence of one or two stall cells. From these results, the stall cells are observed above a given critical Reynolds number and angle of attack. They also observed conditions for which the topology oscillates in time between two types of flow topology. This might explain the fact that steady and unsteady stall cells are reported in the literature. Hence, the stall cells seem to be very sensitive to the flow conditions and are observed in the presence of a trailing edge separation. The stall cells can be steady or unsteady depending on the experiments. However, the measurement methods might also have a time-averaging effect and impact the visualization of an unsteady behaviour.
$(Re = {\rho _{\infty }U_{\infty }c}/{\mu _{\infty }})$. They identified eight types of flow topologies from a full span separation (2-D) to the presence of one or two stall cells. From these results, the stall cells are observed above a given critical Reynolds number and angle of attack. They also observed conditions for which the topology oscillates in time between two types of flow topology. This might explain the fact that steady and unsteady stall cells are reported in the literature. Hence, the stall cells seem to be very sensitive to the flow conditions and are observed in the presence of a trailing edge separation. The stall cells can be steady or unsteady depending on the experiments. However, the measurement methods might also have a time-averaging effect and impact the visualization of an unsteady behaviour.
Stall cells were computed by Bertagnolio, Sørensen & Rasmussen (Reference Bertagnolio, Sørensen and Rasmussen2005) for a wind turbine aerofoil with Reynolds-averaged Navier–Stokes (RANS) and unsteady Reynolds-averaged Navier–Stokes (URANS) simulations. Manni, Nishino & Delafin (Reference Manni, Nishino and Delafin2016) studied the stall cells over a wing with an aspect ratio equal to 10 at a Reynolds number of ![]() $1\times 10^{6}$ with URANS and delayed detached eddy simulation. Their URANS results showed stall cells with spanwise spacing of 1.4 to 1.8 chord length over a narrow range of angles of attack. Liu & Nishino (Reference Liu and Nishino2018) studied the unsteady behaviour of stall cells over a NACA0012 at a Reynolds number of
$1\times 10^{6}$ with URANS and delayed detached eddy simulation. Their URANS results showed stall cells with spanwise spacing of 1.4 to 1.8 chord length over a narrow range of angles of attack. Liu & Nishino (Reference Liu and Nishino2018) studied the unsteady behaviour of stall cells over a NACA0012 at a Reynolds number of ![]() $1.35\times 10^{5}$ and
$1.35\times 10^{5}$ and ![]() $1\times 10^{6}$. Previous work by the authors (Plante, Dandois & Laurendeau Reference Plante, Dandois and Laurendeau2019b), based on URANS simulations of an NACA4412 aerofoil at Reynolds
$1\times 10^{6}$. Previous work by the authors (Plante, Dandois & Laurendeau Reference Plante, Dandois and Laurendeau2019b), based on URANS simulations of an NACA4412 aerofoil at Reynolds ![]() $3.5\times 10^{5}$, showed the convection of the stall cells in the spanwise direction when the wing is swept. To the authors’ knowledge this is the first analysis of the stall cells phenomenon on swept wings.
$3.5\times 10^{5}$, showed the convection of the stall cells in the spanwise direction when the wing is swept. To the authors’ knowledge this is the first analysis of the stall cells phenomenon on swept wings.
Multiple models have been proposed for the origin of the phenomenon. Analyses based on the lifting line theory by Spalart (Reference Spalart2014) and Gross, Fasel & Gaster (Reference Gross, Fasel and Gaster2015) suggest that a negative slope of the lift versus the angle of attack is necessary to observe the stall cells. Analyses with lifting surface models (vortex lattice method) coupled with RANS data by Gallay & Laurendeau (Reference Gallay and Laurendeau2015) and Paul & Gopalarathnam (Reference Paul and Gopalarathnam2014) exhibit similar lift distributions. Kitsios et al. (Reference Kitsios, Rodríguez, Theofilis, Ooi and Soria2009) studied an ellipse and an NACA0015 aerofoil in stall conditions at a Reynolds number of 200 with global linear stability analyses. They found a non-oscillatory unstable mode with a spanwise wavenumber ![]() $\beta = 2{\rm \pi} /L_z = 1.0$. Rodríguez & Theofilis (Reference Rodríguez and Theofilis2011) linked this non-oscillating unstable global mode to the stall cells phenomenon. However, the existence of this mode has then been questioned by the later work of He et al. (Reference He, Gioria, Pérez and Theofilis2017), who were unable to recover the unstable global modes, and this with two different numerical approaches. Zhang & Samtaney (Reference Zhang and Samtaney2016) carried out similar stability analyses on an NACA0012 aerofoil at Reynolds numbers in a range from 400 to 1000. Besides the classical oscillatory modes, they identified an unstable non-oscillatory 3-D (
$\beta = 2{\rm \pi} /L_z = 1.0$. Rodríguez & Theofilis (Reference Rodríguez and Theofilis2011) linked this non-oscillating unstable global mode to the stall cells phenomenon. However, the existence of this mode has then been questioned by the later work of He et al. (Reference He, Gioria, Pérez and Theofilis2017), who were unable to recover the unstable global modes, and this with two different numerical approaches. Zhang & Samtaney (Reference Zhang and Samtaney2016) carried out similar stability analyses on an NACA0012 aerofoil at Reynolds numbers in a range from 400 to 1000. Besides the classical oscillatory modes, they identified an unstable non-oscillatory 3-D (![]() $\beta = 2$ and
$\beta = 2$ and ![]() $4$) mode on an aerofoil in a laminar regime but for slightly higher Reynolds numbers (between 800 and 1000). They associated this mode with a centrifugal instability of the recirculation bubble, present when the backflow velocity is larger than 20 % of the inflow velocity. In these articles, flows with a low Reynolds number of a few hundreds to a thousand were studied. As such, the literature lacks a proper relation between stall cells and a global instability for high Reynolds turbulent flows. The present paper has the purpose of providing this link using RANS models. This is done by carrying out 3-D URANS simulations and global stability analyses.
$4$) mode on an aerofoil in a laminar regime but for slightly higher Reynolds numbers (between 800 and 1000). They associated this mode with a centrifugal instability of the recirculation bubble, present when the backflow velocity is larger than 20 % of the inflow velocity. In these articles, flows with a low Reynolds number of a few hundreds to a thousand were studied. As such, the literature lacks a proper relation between stall cells and a global instability for high Reynolds turbulent flows. The present paper has the purpose of providing this link using RANS models. This is done by carrying out 3-D URANS simulations and global stability analyses.
Similar flow instabilities are reported for separation bubbles at low Reynolds numbers on various geometries. Separation bubbles on flat plates were analysed by Theofilis, Hein & Dallmann (Reference Theofilis, Hein and Dallmann2000) and Rodríguez & Theofilis (Reference Rodríguez and Theofilis2010). In the latter study a link to the structure of stall cells was proposed in relation with the above mentioned questionable computations in Rodríguez & Theofilis (Reference Rodríguez and Theofilis2011). Barkley, Gomes & Henderson (Reference Barkley, Gomes and Henderson2002) investigated a backward facing step and found a 3-D instability. They studied flows at Reynolds numbers within a range between 450 to 1050 based on the height of the step, and associated the 3-D unstable mode with a centrifugal instability thanks to the criterion of Bayly, Orszag & Herbert (Reference Bayly, Orszag and Herbert1988). Gallaire, Marquille & Ehrenstein (Reference Gallaire, Marquille and Ehrenstein2007) studied the flow over a bump at a Reynolds number of 400. They found a non-oscillatory mode causing the flow to become 3-D. A similar instability was found by Marquet et al. (Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009) for an ![]() $S$-shaped duct and by Picella et al. (Reference Picella, Loiseau, Lusseyran, Robinet, Cherubini and Pastur2018) in open-cavity flows. Finally, a 3-D non-oscillatory unstable mode was found for a shockwave boundary layer interaction by Robinet (Reference Robinet2007). These studies show that 3-D instabilities such as those found on aerofoils at low Reynolds numbers are also found on other configurations displaying recirculation bubbles.
$S$-shaped duct and by Picella et al. (Reference Picella, Loiseau, Lusseyran, Robinet, Cherubini and Pastur2018) in open-cavity flows. Finally, a 3-D non-oscillatory unstable mode was found for a shockwave boundary layer interaction by Robinet (Reference Robinet2007). These studies show that 3-D instabilities such as those found on aerofoils at low Reynolds numbers are also found on other configurations displaying recirculation bubbles.
Concerning transonic buffet, the 2-D phenomenon was investigated for an NACA0012 aerofoil by McDevitt & Okuno (Reference McDevitt and Okuno1985) for a wide range of Mach number and angles of attack at a Reynolds number of ![]() $1\times 10^{7}$. Strouhal numbers (
$1\times 10^{7}$. Strouhal numbers (![]() $St={fc}/{U_\infty }$) in a range from 0.06 to 0.07 were identified, and the buffet onset boundary in the Mach number – angle of attack plane was identified. Similar buffet frequencies were obtained by Benoit & Legrain (Reference Benoit and Legrain1987) for an RA16SC1 aerofoil and Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009) for the OAT15A aerofoil. The latter study is now widely used to validate numerical models. Recently, Brion et al. (Reference Brion, Dandois, Abart and Paillart2017) studied the OALT25, an aerofoil designed to promote laminar flow, with free transition and tripped boundary layer. They obtained Strouhal numbers of the order of 0.07 in the turbulent boundary layer case. From these experiments, turbulent transonic buffet is identified as a large amplitude oscillation of the shock position with a well-identified Strouhal number around 0.07.
$St={fc}/{U_\infty }$) in a range from 0.06 to 0.07 were identified, and the buffet onset boundary in the Mach number – angle of attack plane was identified. Similar buffet frequencies were obtained by Benoit & Legrain (Reference Benoit and Legrain1987) for an RA16SC1 aerofoil and Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009) for the OAT15A aerofoil. The latter study is now widely used to validate numerical models. Recently, Brion et al. (Reference Brion, Dandois, Abart and Paillart2017) studied the OALT25, an aerofoil designed to promote laminar flow, with free transition and tripped boundary layer. They obtained Strouhal numbers of the order of 0.07 in the turbulent boundary layer case. From these experiments, turbulent transonic buffet is identified as a large amplitude oscillation of the shock position with a well-identified Strouhal number around 0.07.
Many numerical studies of 2-D transonic buffet have been carried out. Le Balleur & Girodroux-Lavigne (Reference Le Balleur and Girodroux-Lavigne1989) and Edwards (Reference Edwards1993) used viscous–inviscid coupling strategies. However, the bulk of the numerical simulations reported in the literature is carried out with URANS models (Goncalves & Houdeville Reference Goncalves and Houdeville2004; Thiery & Coustols Reference Thiery and Coustols2006; Iovnovich & Raveh Reference Iovnovich and Raveh2012; Grossi, Braza & Hoarau Reference Grossi, Braza and Hoarau2014; Giannelis, Levinski & Vio Reference Giannelis, Levinski and Vio2018; Plante & Laurendeau Reference Plante and Laurendeau2019). These simulations identified frequencies in the range of those obtained experimentally. However, the simulations are found to be very sensitive to the numerical scheme and turbulence model. Large eddy simulations (LES) were carried out by Garnier & Deck (Reference Garnier and Deck2010) and Fukushima & Kawai (Reference Fukushima and Kawai2018) with excellent agreement with the experiment of Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009). However, such simulations are computationally very expensive. Hence, hybrid RANS–LES simulations were attempted (Deck Reference Deck2005; Huang et al. Reference Huang, Xiao, Liu and Fu2012; Grossi et al. Reference Grossi, Braza and Hoarau2014; Ishida et al. Reference Ishida, Ishiko, Hashimoto, Aoyama and Takekawa2016; Deck & Renard Reference Deck and Renard2020) and Ribeiro et al. (Reference Ribeiro, Singh, König, Fares, Zhang, Gopalakrishnan, Li and Chen2017) used the lattice Boltzmann method. These simulations predicted transonic buffet, but discrepancies to the experimental pressure distributions were found. Hence, URANS simulations reproduce the main feature of transonic buffet. However, the turbulence modelling has a strong effect on the quantitative results.
Three-dimensional transonic buffet is more complex. Most of the studies were carried out on half-wing body aircraft configuration. A broadband frequency content with a dominant frequency higher than the one of 2-D buffet was found experimentally (Roos Reference Roos1985; Dandois Reference Dandois2016; Koike et al. Reference Koike, Ueno, Nakakita and Hashimoto2016; Paladini et al. Reference Paladini, Dandois, Sipp and Robinet2019b; Masini, Timme & Peace Reference Masini, Timme and Peace2020). On such configurations, the convection of flow perturbations towards the wing tip was observed and buffet cells can be seen in the pressure-sensitive paint measurements of Sugioka et al. (Reference Sugioka, Koike, Nakakita, Numata, Nonomura and Asai2018). Numerical simulations of such configurations were carried out with URANS (Sartor & Timme Reference Sartor and Timme2016) and hybrid RANS–LES simulations (Brunet & Deck Reference Brunet and Deck2008; Ishida et al. Reference Ishida, Hashimoto, Ohmichi, Aoyama and Takekawa2017; Sartor & Timme Reference Sartor and Timme2017). Ohmichi, Ishida & Hashimoto (Reference Ohmichi, Ishida and Hashimoto2018) used dynamic mode decomposition and proper orthogonal decomposition to identify two dominant modes. One high-frequency mode (![]() $St\approx 0.2\text {--}0.6$) associated with buffet cells and one at
$St\approx 0.2\text {--}0.6$) associated with buffet cells and one at ![]() $St\approx 0.06$, coherent with 2-D buffet. Iovnovich & Raveh (Reference Iovnovich and Raveh2015) studied simplified swept wings closed by a symmetry plane and an extrapolation boundary condition to emulate an infinite swept wing. They observed buffet cells and an effect of the sweep angle on the buffet amplitude and frequency. Previous work by the authors (Plante et al. Reference Plante, Dandois and Laurendeau2019b) investigated infinite swept wings closed by periodic boundary conditions. Such simulations produced much more regular buffet cells and showed that buffet cells occur without any 3-D disturbance from the physical set-up, thus making this phenomenon a candidate for an explanation based on global stability analysis.
$St\approx 0.06$, coherent with 2-D buffet. Iovnovich & Raveh (Reference Iovnovich and Raveh2015) studied simplified swept wings closed by a symmetry plane and an extrapolation boundary condition to emulate an infinite swept wing. They observed buffet cells and an effect of the sweep angle on the buffet amplitude and frequency. Previous work by the authors (Plante et al. Reference Plante, Dandois and Laurendeau2019b) investigated infinite swept wings closed by periodic boundary conditions. Such simulations produced much more regular buffet cells and showed that buffet cells occur without any 3-D disturbance from the physical set-up, thus making this phenomenon a candidate for an explanation based on global stability analysis.
Transonic buffet was described as a feedback loop between the shock wave motion and acoustic waves generated near the trailing edge by Lee (Reference Lee1990). The description of the transonic buffet as a globally unstable mode was introduced by Crouch et al. (Reference Crouch, Garbaruk, Magidov and Travin2009) and further investigated by Iorio, González & Ferrer (Reference Iorio, González and Ferrer2014) and Sartor, Mettot & Sipp (Reference Sartor, Mettot and Sipp2015). Such analyses produce an accurate prediction of the buffet frequency and onset angle of attack angle. Three-dimensional global stability analyses were attempted by Iorio et al. (Reference Iorio, González and Ferrer2014), but an unstable mode specific to 3-D buffet was not found. Recently, global stability analysis was applied to infinite swept wings using a spanwise periodicity assumption (Crouch, Garbaruk & Strelets Reference Crouch, Garbaruk and Strelets2018, Reference Crouch, Garbaruk and Strelets2019; Paladini et al. Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a; Plante et al. Reference Plante, Dandois, Beneddine, Sipp and Laurendeau2019a) and fully 3-D analyses (Paladini Reference Paladini2018; He & Timme Reference He and Timme2020). Stability analysis has also been applied to the NASA Common Research Model by Timme (Reference Timme2018, Reference Timme2019, Reference Timme2020). These analyses exhibit unstable modes coherent with the occurrence of buffet cells, thus emphasising the phenomenological differences between 2-D and 3-D buffet.
This paper aims at showing that the buffet cell phenomenon occurring in transonic flow has the same origin as the stall cell one occurring during stall at low speed. In particular, we will show that a similar unstable global mode is at the origin of both phenomena and highlight discrepancies between linear dynamics predictions provided by global stability analyses and saturated nonlinear dynamics given by URANS simulations. In addition, the unstable global mode corresponding to the buffet/stall cell phenomenon is followed from low speed to transonic conditions to establish a close link between these two phenomena. First, the numerical methods are presented. Then, numerical solutions for low-speed stall and transonic buffet conditions are analysed. Linear global stability analyses around steady baseflow are presented and the transition from the linear to the nonlinear dynamic is investigated. Finally, the link between the two flow regimes is discussed.
2. Physical and numerical set-up
This section first describes the physical set-up studied in this paper. Then the governing equations and the numerical methods used to solve them are presented.
2.1. Configurations
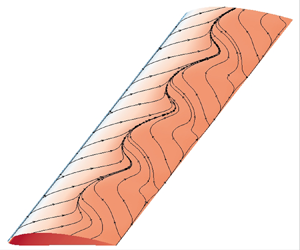
In this study, infinite swept wings are considered. Figure 1 shows the numerical set-up. Usually, aerodynamic analyses are carried out in a referential ![]() $(x,y,z)$ where the span of the wing is defined as the length
$(x,y,z)$ where the span of the wing is defined as the length ![]() $L_z$ along the
$L_z$ along the ![]() $z$ direction, and the sweep angle
$z$ direction, and the sweep angle ![]() $\delta$ is the angle between the
$\delta$ is the angle between the ![]() $z$-axis and the leading edge of the wing. With these definitions, the velocity in the
$z$-axis and the leading edge of the wing. With these definitions, the velocity in the ![]() $z$ direction is null and the free stream velocity is defined by its norm
$z$ direction is null and the free stream velocity is defined by its norm ![]() $V_{\infty ,3D}$ and the angle of attack
$V_{\infty ,3D}$ and the angle of attack ![]() $\alpha _{3D}$ (see figure 1). However, it is convenient for the present analysis to define another referential
$\alpha _{3D}$ (see figure 1). However, it is convenient for the present analysis to define another referential ![]() $(x',y',z')$ with
$(x',y',z')$ with ![]() $x'$ normal to the leading edge,
$x'$ normal to the leading edge, ![]() $y'=y$ and
$y'=y$ and ![]() $z'$ aligned with the leading edge. In this referential, the sweep angle becomes a sideslip angle applied to the free stream velocity
$z'$ aligned with the leading edge. In this referential, the sweep angle becomes a sideslip angle applied to the free stream velocity ![]() $V_{\infty ,3D}$.
$V_{\infty ,3D}$.

Figure 1. Infinite swept wing configuration.
Since the sweep angle will be changed in this article, we define the 2-D flow quantities as the conditions in the plane normal to the leading edge, i.e. in the plane ![]() $(x',y')$. Hence we get the relations
$(x',y')$. Hence we get the relations
For this study, the 2-D flow conditions are kept constant when the sweep angle changes to maintain the similarity. This means that the Mach number ![]() $M_{2D}$, the Reynolds number
$M_{2D}$, the Reynolds number ![]() $Re_{2D}$ and the angle of attack
$Re_{2D}$ and the angle of attack ![]() $\alpha _{2D}$ are kept constant. For convenience the 2-D subscripts are dropped (in the following
$\alpha _{2D}$ are kept constant. For convenience the 2-D subscripts are dropped (in the following ![]() $M = M_{2D}$,
$M = M_{2D}$, ![]() $Re = Re_{2D}$,
$Re = Re_{2D}$, ![]() $\alpha = \alpha _{2D}$, etc.) and the reference quantities are defined as
$\alpha = \alpha _{2D}$, etc.) and the reference quantities are defined as ![]() $V_{\infty } = V_{\infty ,2D} = 1.0$,
$V_{\infty } = V_{\infty ,2D} = 1.0$, ![]() $c = c_{2D} = 1.0$. For example, the Strouhal number is defined as
$c = c_{2D} = 1.0$. For example, the Strouhal number is defined as ![]() $St = {f c_{2D}}/{V_{\infty ,2D}} =f$. This is done to help the comparison of non-dimensional quantities based on these reference quantities when the sweep angle varies. The aspect ratio
$St = {f c_{2D}}/{V_{\infty ,2D}} =f$. This is done to help the comparison of non-dimensional quantities based on these reference quantities when the sweep angle varies. The aspect ratio ![]() $AR$ is defined as
$AR$ is defined as ![]() $AR={L_{z'}}/{c_{2D}} = L_{z'}$ and it should be noted that the baseline aerofoil is always retrieved in the plane
$AR={L_{z'}}/{c_{2D}} = L_{z'}$ and it should be noted that the baseline aerofoil is always retrieved in the plane ![]() $(x',y')$. The (
$(x',y')$. The (![]() $x',y',z'$) referential is more adapted for the present study, and therefore, it will be the only referential used throughout this paper. As such, the prime symbol is dropped for the sake of conciseness.
$x',y',z'$) referential is more adapted for the present study, and therefore, it will be the only referential used throughout this paper. As such, the prime symbol is dropped for the sake of conciseness.
The present paper focuses on two regimes: the subsonic stall regime and the transonic buffet regime. The subsonic study is based on the NACA4412 aerofoil at a Reynolds number ![]() $Re=350\,000$ and a Mach number
$Re=350\,000$ and a Mach number ![]() $M=0.2$ such that compressibility effects are negligible. This case is selected because it exhibits a trailing edge type of stall. The transonic case focuses on the ONERA OALT25 aerofoil at
$M=0.2$ such that compressibility effects are negligible. This case is selected because it exhibits a trailing edge type of stall. The transonic case focuses on the ONERA OALT25 aerofoil at ![]() $M=0.7352$ and
$M=0.7352$ and ![]() $Re=3\times 10^{6}$, such that the experimental 2-D results of Brion et al. (Reference Brion, Dandois, Abart and Paillart2017) can be used for comparison. This aerofoil was designed to promote laminarity and has been studied experimentally both with free transition and a boundary layer tripped at 7 % on both sides. With the tripped boundary layer, the buffet instability is similar to that of other turbulent aerofoils. In the present study, the laminar region is neglected and simulations are carried out in fully turbulent conditions. Hence, the experimental data with a tripped boundary layer are used to validate the numerical set-up for 2-D buffet computations. The final part of the paper is dedicated to a third aerofoil, the NACA0012, at a Reynolds number
$Re=3\times 10^{6}$, such that the experimental 2-D results of Brion et al. (Reference Brion, Dandois, Abart and Paillart2017) can be used for comparison. This aerofoil was designed to promote laminarity and has been studied experimentally both with free transition and a boundary layer tripped at 7 % on both sides. With the tripped boundary layer, the buffet instability is similar to that of other turbulent aerofoils. In the present study, the laminar region is neglected and simulations are carried out in fully turbulent conditions. Hence, the experimental data with a tripped boundary layer are used to validate the numerical set-up for 2-D buffet computations. The final part of the paper is dedicated to a third aerofoil, the NACA0012, at a Reynolds number ![]() $Re=1\times 10^{7}$ and various Mach numbers and angles of attack. This aerofoil is used to link the results from the two previous cases, since it allows us to track phenomena from the low Mach stall regime to the transonic buffet regime. This particular test case is selected since the experiments of McDevitt & Okuno (Reference McDevitt and Okuno1985) showed the transonic buffet in the high Mach range and this aerofoil is suitable to have a trailing edge type stall behaviour in the low Mach range. This makes it suitable to observe both the stall cells and the buffet cells. The aerofoils considered in this paper have a trailing edge thickness of 0.0025, 0.005 and 0.0025 chord units for the NACA4412, OALT25 and NACA0012 aerofoils, respectively.
$Re=1\times 10^{7}$ and various Mach numbers and angles of attack. This aerofoil is used to link the results from the two previous cases, since it allows us to track phenomena from the low Mach stall regime to the transonic buffet regime. This particular test case is selected since the experiments of McDevitt & Okuno (Reference McDevitt and Okuno1985) showed the transonic buffet in the high Mach range and this aerofoil is suitable to have a trailing edge type stall behaviour in the low Mach range. This makes it suitable to observe both the stall cells and the buffet cells. The aerofoils considered in this paper have a trailing edge thickness of 0.0025, 0.005 and 0.0025 chord units for the NACA4412, OALT25 and NACA0012 aerofoils, respectively.
2.2. Governing equations
2.2.1. Nonlinear model
In this study, the RANS equations are used to model the fluid flow. The one-equation Spalart–Allmaras turbulence model with the Edwards–Chandra modification is used to close the RANS equations system. This system reads in integral form
where ![]() $\boldsymbol {W} = [\rho , \rho u , \rho v , \rho w ,\rho e , \rho \tilde {\nu }]^{t}$ is the conservative variables vector,
$\boldsymbol {W} = [\rho , \rho u , \rho v , \rho w ,\rho e , \rho \tilde {\nu }]^{t}$ is the conservative variables vector, ![]() $\boldsymbol {V}$ is a diagonal matrix whose non-zero coefficients are the mesh cells volume and
$\boldsymbol {V}$ is a diagonal matrix whose non-zero coefficients are the mesh cells volume and ![]() $\boldsymbol {R}$ is the summation of the convective and viscous fluxes, and the source terms. In this article,
$\boldsymbol {R}$ is the summation of the convective and viscous fluxes, and the source terms. In this article, ![]() $z$-invariant solutions (all the derivatives of the flow variables with respect to
$z$-invariant solutions (all the derivatives of the flow variables with respect to ![]() $z$ are null) with
$z$ are null) with ![]() $w=0$ will be referred to as a 2-D solution, while
$w=0$ will be referred to as a 2-D solution, while ![]() $z$-invariant solutions with
$z$-invariant solutions with ![]() $w\neq 0$ will be referred to as 2.5-D solutions (Ghasemi, Mosahebi & Laurendeau Reference Ghasemi, Mosahebi and Laurendeau2014; Bourgault-Côté et al. Reference Bourgault-Côté, Ghasemi, Mosahebi and Laurendeau2017).
$w\neq 0$ will be referred to as 2.5-D solutions (Ghasemi, Mosahebi & Laurendeau Reference Ghasemi, Mosahebi and Laurendeau2014; Bourgault-Côté et al. Reference Bourgault-Côté, Ghasemi, Mosahebi and Laurendeau2017).
2.2.2. Linear model
Steady solutions ![]() $\boldsymbol {W}_0$ of (2.5), also known as baseflows, are computed to carry out global linear stability analyses (Sipp et al. Reference Sipp, Marquet, Meliga and Barbagallo2010; Theofilis Reference Theofilis2011; Taira et al. Reference Taira, Brunton, Dawson, Rowley, Colonius, McKeon, Schmidt, Gordeyev, Theofilis and Ukeiley2017). By definition, they satisfy
$\boldsymbol {W}_0$ of (2.5), also known as baseflows, are computed to carry out global linear stability analyses (Sipp et al. Reference Sipp, Marquet, Meliga and Barbagallo2010; Theofilis Reference Theofilis2011; Taira et al. Reference Taira, Brunton, Dawson, Rowley, Colonius, McKeon, Schmidt, Gordeyev, Theofilis and Ukeiley2017). By definition, they satisfy ![]() $\boldsymbol {R}(\boldsymbol {W}_\textbf {0})=0$, and under a first-order approximation, infinitesimal perturbations
$\boldsymbol {R}(\boldsymbol {W}_\textbf {0})=0$, and under a first-order approximation, infinitesimal perturbations ![]() $\boldsymbol {W}^{\prime }$ about a baseflow
$\boldsymbol {W}^{\prime }$ about a baseflow ![]() $\boldsymbol {W}_0$ are governed by the linearization of (2.5), which reads
$\boldsymbol {W}_0$ are governed by the linearization of (2.5), which reads
where ![]() ${\partial {\boldsymbol {R}}}/{\partial {\boldsymbol {W}}}|_{\boldsymbol {W}_0}$ is the Jacobian of the discretized RANS equations evaluated about the baseflow, including the turbulence model. Solutions in the form of normal modes are sought;
${\partial {\boldsymbol {R}}}/{\partial {\boldsymbol {W}}}|_{\boldsymbol {W}_0}$ is the Jacobian of the discretized RANS equations evaluated about the baseflow, including the turbulence model. Solutions in the form of normal modes are sought;
such that (2.6) reduces to the eigenproblem
Thus, the stability problem consists in computing eigenpairs of the Jacobian operator. The eigenvectors ![]() $\hat {\boldsymbol {W}}$ describe the spatial structure of the global modes and the eigenvalues
$\hat {\boldsymbol {W}}$ describe the spatial structure of the global modes and the eigenvalues ![]() $\lambda = \sigma +\textrm {i}\omega$ describe their time behaviour
$\lambda = \sigma +\textrm {i}\omega$ describe their time behaviour ![]() $(i = \sqrt {-1})$. For each mode, the real part
$(i = \sqrt {-1})$. For each mode, the real part ![]() $\sigma$ is its growth rate and
$\sigma$ is its growth rate and ![]() $\omega$ is its angular frequency.
$\omega$ is its angular frequency.
2.3. Numerical discretization and algorithms
2.3.1. Computational grids
Three-dimensional grids are obtained from the extrusion of baseline 2-D grids. Structured grids with an ![]() $O$-type topology are used. Table 1 reports the number of points on the aerofoil surface (
$O$-type topology are used. Table 1 reports the number of points on the aerofoil surface (![]() $n_i$), in the direction normal to the aerofoil surface (
$n_i$), in the direction normal to the aerofoil surface (![]() $n_j$), on the pressures side (
$n_j$), on the pressures side (![]() $n_{p.s.}$), on the suction side (
$n_{p.s.}$), on the suction side (![]() $n_{s.s.}$), on the trailing edge (
$n_{s.s.}$), on the trailing edge (![]() $n_{t.e.}$), the wall spacing (
$n_{t.e.}$), the wall spacing (![]() ${\rm \Delta} y_w$), the distance from the aerofoil surface to the far-field boundary condition (
${\rm \Delta} y_w$), the distance from the aerofoil surface to the far-field boundary condition (![]() ${\rm \Delta} y_{f.f.}$) and the spacing across the shockwave (
${\rm \Delta} y_{f.f.}$) and the spacing across the shockwave (![]() ${\rm \Delta} x_{s.f.}$).
${\rm \Delta} x_{s.f.}$).
Table 1. Characteristics of the grids.

2.3.2. Solution of the nonlinear model
In this paper, the ONERA-Airbus-Safran elsA (Cambier, Heib & Plot Reference Cambier, Heib and Plot2013) software is used to solve the (U)RANS equations. For this study, a cell-centred structured finite volume method is used. A second-order cell-centred scheme with scalar numerical dissipation is used for the discretization of the convective fluxes. Convergence towards steady-state solutions is accelerated using local time steps and geometrical multigrid with a LU-SSOR pseudo-time integration scheme. In some case, selective frequency damping (SFD) (Åkervik et al. Reference Åkervik, Brandt, Henningson, Hoepffner, Marxen and Schlatter2006; Jordi, Cotter & Sherwin Reference Jordi, Cotter and Sherwin2014, Reference Jordi, Cotter and Sherwin2015; Richez, Leguille & Marquet Reference Richez, Leguille and Marquet2016) or a Newton solver (Wales et al. Reference Wales, Gaitonde, Jones, Avitabile and Champneys2012; Busquet et al. Reference Busquet, Marquet, Richez, Juniper and Sipp2017) is used to force the convergence to a steady state. Time-accurate solutions are obtained by using a second-order dual time stepping approach.
2.3.3. Solution of the linear model
This study involves 3-D geometries for which ![]() $\boldsymbol {A}$ has a high dimension and a large bandwidth. Therefore, solving the eigenproblem is often too costly. But in our cases, the baseflows are always homogeneous in the spanwise direction, such that the method proposed by Schmid, de Pando & Peake (Reference Schmid, de Pando and Peake2017) and used by Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a) and Plante et al. (Reference Plante, Dandois, Beneddine, Sipp and Laurendeau2019a) for
$\boldsymbol {A}$ has a high dimension and a large bandwidth. Therefore, solving the eigenproblem is often too costly. But in our cases, the baseflows are always homogeneous in the spanwise direction, such that the method proposed by Schmid, de Pando & Peake (Reference Schmid, de Pando and Peake2017) and used by Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a) and Plante et al. (Reference Plante, Dandois, Beneddine, Sipp and Laurendeau2019a) for ![]() $n$-periodic arrays of fluid systems may be used to significantly reduce the cost of the eigenvalues computation. This method exploits the block-circulant structure of matrix
$n$-periodic arrays of fluid systems may be used to significantly reduce the cost of the eigenvalues computation. This method exploits the block-circulant structure of matrix ![]() $\boldsymbol {A}$, which takes the form
$\boldsymbol {A}$, which takes the form
 \begin{equation} \boldsymbol{A} =\begin{bmatrix} \boldsymbol{A}_0 & \boldsymbol{A}_1 & \boldsymbol{A}_2 & \ldots & \boldsymbol{A}_{n-1} \\ \boldsymbol{A}_{n-1} & \boldsymbol{A}_0 & \boldsymbol{A}_1 & \ldots & \boldsymbol{A}_{n-2} \\ \boldsymbol{A}_{n-2} & \boldsymbol{A}_{n-1} & \boldsymbol{A}_0 & \ldots & \boldsymbol{A}_{n-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{A}_1 & \boldsymbol{A}_2 & \boldsymbol{A}_3 & \ldots & \boldsymbol{A}_0\end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{A} =\begin{bmatrix} \boldsymbol{A}_0 & \boldsymbol{A}_1 & \boldsymbol{A}_2 & \ldots & \boldsymbol{A}_{n-1} \\ \boldsymbol{A}_{n-1} & \boldsymbol{A}_0 & \boldsymbol{A}_1 & \ldots & \boldsymbol{A}_{n-2} \\ \boldsymbol{A}_{n-2} & \boldsymbol{A}_{n-1} & \boldsymbol{A}_0 & \ldots & \boldsymbol{A}_{n-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{A}_1 & \boldsymbol{A}_2 & \boldsymbol{A}_3 & \ldots & \boldsymbol{A}_0\end{bmatrix} \end{equation}
when the degrees of freedom are properly indexed. As shown by Schmid et al. (Reference Schmid, de Pando and Peake2017), ![]() $\boldsymbol {A}$ can be transformed into a block diagonal matrix
$\boldsymbol {A}$ can be transformed into a block diagonal matrix
 \begin{equation} \hat{\boldsymbol{A}} = \begin{bmatrix} \hat{\boldsymbol{A}}_0 & 0 & \cdots & 0 \\ 0 & \hat{\boldsymbol{A}}_1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \hat{\boldsymbol{A}}_n-1 \end{bmatrix}\end{equation}
\begin{equation} \hat{\boldsymbol{A}} = \begin{bmatrix} \hat{\boldsymbol{A}}_0 & 0 & \cdots & 0 \\ 0 & \hat{\boldsymbol{A}}_1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \hat{\boldsymbol{A}}_n-1 \end{bmatrix}\end{equation}with
 \begin{equation} \hat{\boldsymbol{A}}_j = \sum_{k=0}^{n-1} \rho_j^{k} \boldsymbol{A}_k \end{equation}
\begin{equation} \hat{\boldsymbol{A}}_j = \sum_{k=0}^{n-1} \rho_j^{k} \boldsymbol{A}_k \end{equation}and
Eigenvalues of ![]() $\hat {\boldsymbol {A}}$ are also eigenvalues of
$\hat {\boldsymbol {A}}$ are also eigenvalues of ![]() $\boldsymbol {A}$ and each block matrix
$\boldsymbol {A}$ and each block matrix ![]() $\hat {\boldsymbol {A}}_{\boldsymbol {j}}$ can be treated separately, resulting in
$\hat {\boldsymbol {A}}_{\boldsymbol {j}}$ can be treated separately, resulting in ![]() $n$ separated eigenproblems of the size of a 2-D problem,
$n$ separated eigenproblems of the size of a 2-D problem,
The eigenvectors of ![]() $\boldsymbol {A}$ are then retrieved as
$\boldsymbol {A}$ are then retrieved as
This method implies solving the eigenproblem for all the ![]() $\hat {\boldsymbol {A}}_j$ matrices to get the stability result for all the
$\hat {\boldsymbol {A}}_j$ matrices to get the stability result for all the ![]() $n$ possible wavenumbers. However, the only difference between each
$n$ possible wavenumbers. However, the only difference between each ![]() $\hat {\boldsymbol {A}}_j$ matrix is the coefficients
$\hat {\boldsymbol {A}}_j$ matrix is the coefficients ![]() $\rho _j$ such that changing the value of
$\rho _j$ such that changing the value of ![]() $j$ or
$j$ or ![]() $n$ has the effect of changing the wavenumber. Hence, solving for the matrix
$n$ has the effect of changing the wavenumber. Hence, solving for the matrix ![]() $\hat {\boldsymbol {A}}_2$ is equivalent to solving
$\hat {\boldsymbol {A}}_2$ is equivalent to solving ![]() $\hat {\boldsymbol {A}}_1$ with
$\hat {\boldsymbol {A}}_1$ with ![]() $n$ divided by two. Therefore, in this study, the problem is only solved for the matrix
$n$ divided by two. Therefore, in this study, the problem is only solved for the matrix ![]() $\hat {\boldsymbol {A}}_1$ with various values of
$\hat {\boldsymbol {A}}_1$ with various values of ![]() $n$. This allows us to get the results over a continuous range of wavenumbers.
$n$. This allows us to get the results over a continuous range of wavenumbers.
This analysis yields results similar to the biGlobal stability analysis carried out by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) and He et al. (Reference He, Gioria, Pérez and Theofilis2017). However, this approach presents several advantages. In particular, it does not require tedious mathematical developments to include the periodicity assumption in the Jacobian matrix. This makes this approach suitable for the use of a black box computational fluid dynamics solver, in this case elsA.
The linear operator ![]() $\boldsymbol {A}$ is obtained with the fully discrete approach proposed by Mettot, Renac & Sipp (Reference Mettot, Renac and Sipp2014). This Jacobian is extracted with a second-order finite difference scheme as
$\boldsymbol {A}$ is obtained with the fully discrete approach proposed by Mettot, Renac & Sipp (Reference Mettot, Renac and Sipp2014). This Jacobian is extracted with a second-order finite difference scheme as
where ![]() $\epsilon$ is a small parameter and
$\epsilon$ is a small parameter and ![]() $\boldsymbol {u}$ are vectors chosen to efficiently compute every non-zero coefficient of the Jacobian matrix (see Beneddine (Reference Beneddine2017) for details). For the second-order finite volume scheme used in this study, the numerical stencils have a width of five grid cells. Hence,
$\boldsymbol {u}$ are vectors chosen to efficiently compute every non-zero coefficient of the Jacobian matrix (see Beneddine (Reference Beneddine2017) for details). For the second-order finite volume scheme used in this study, the numerical stencils have a width of five grid cells. Hence, ![]() $\boldsymbol {A}_3 = \boldsymbol {A}_4 = \cdots = \boldsymbol {A}_{n-3} = 0$, and all the non-zero block matrices
$\boldsymbol {A}_3 = \boldsymbol {A}_4 = \cdots = \boldsymbol {A}_{n-3} = 0$, and all the non-zero block matrices ![]() $\boldsymbol {A}_j$ (2.9) can be retrieved from a 3-D grid with only five grid cells in the spanwise direction (see Paladini et al. Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a; Plante et al. Reference Plante, Dandois, Beneddine, Sipp and Laurendeau2019a). Hence, the baseflows are computed as 2-D solutions and the grid is extruded to get the 3-D mesh for the extraction of the 3-D Jacobian
$\boldsymbol {A}_j$ (2.9) can be retrieved from a 3-D grid with only five grid cells in the spanwise direction (see Paladini et al. Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a; Plante et al. Reference Plante, Dandois, Beneddine, Sipp and Laurendeau2019a). Hence, the baseflows are computed as 2-D solutions and the grid is extruded to get the 3-D mesh for the extraction of the 3-D Jacobian ![]() $\boldsymbol {A}$. The spanwise spacing
$\boldsymbol {A}$. The spanwise spacing ![]() ${\rm \Delta} z$ must be imposed. Refinement study of this parameter will be presented, but no extra computational cost is associated with a change in
${\rm \Delta} z$ must be imposed. Refinement study of this parameter will be presented, but no extra computational cost is associated with a change in ![]() ${\rm \Delta} z$, which can therefore be chosen arbitrarily small. This Jacobian matrix is then reduced as
${\rm \Delta} z$, which can therefore be chosen arbitrarily small. This Jacobian matrix is then reduced as ![]() $\boldsymbol {\hat {A}_1}$ by assuming a given wavenumber in (2.11). The eigenproblems are then solved with the Arnoldi iteration method (Sorensen Reference Sorensen1992) coupled with a shift-and-invert strategy (Christodoulou & Scriven Reference Christodoulou and Scriven1988) to extract inner eigenvalues.
$\boldsymbol {\hat {A}_1}$ by assuming a given wavenumber in (2.11). The eigenproblems are then solved with the Arnoldi iteration method (Sorensen Reference Sorensen1992) coupled with a shift-and-invert strategy (Christodoulou & Scriven Reference Christodoulou and Scriven1988) to extract inner eigenvalues.
3. Unsteady Reynolds-averaged simulations
This section presents the results of URANS simulations for the low speed and transonic cases. These simulations are carried out to observe stall and buffet cells as well as the superposition between the 2-D transonic buffet mode and the buffet cells.
3.1. Subsonic stall
In this section the 2-D and 3-D simulations of the NACA4412 aerofoil at a Reynolds number of 350 000 are compared. Then the simulations of swept wings are presented.
3.1.1. Unswept  $\delta =0^{\circ }$ case
$\delta =0^{\circ }$ case
Let us first focus on the flow over an unswept wing in the post-stall regime. Figure 2 shows the lift polar in the unswept case (![]() $\delta =0^{\circ }$) for two kinds of simulations: 2-D solutions and 3-D solutions with an aspect ratio
$\delta =0^{\circ }$) for two kinds of simulations: 2-D solutions and 3-D solutions with an aspect ratio ![]() $AR=6$ and 113 spanwise grid points. The maximum lift coefficient of 1.57 is obtained for an angle of attack around
$AR=6$ and 113 spanwise grid points. The maximum lift coefficient of 1.57 is obtained for an angle of attack around ![]() $\alpha =14^{\circ }$ in both cases. For angles of attack higher than
$\alpha =14^{\circ }$ in both cases. For angles of attack higher than ![]() $16^{\circ }$ the flow solver failed to converge. This is caused by the occurrence of an instability linked to a vortex shedding. This is further discussed in § 4.1.4. In order to obtain steady-state 2-D solutions in this regime, the SFD method presented by Richez et al. (Reference Richez, Leguille and Marquet2016) and the Newton algorithm have been used. The SFD is used with a local time stepping algorithm and the cut-off frequency and damping coefficient were based on a parametric study to obtain solutions converged within machine accuracy. A value of the filter width
$16^{\circ }$ the flow solver failed to converge. This is caused by the occurrence of an instability linked to a vortex shedding. This is further discussed in § 4.1.4. In order to obtain steady-state 2-D solutions in this regime, the SFD method presented by Richez et al. (Reference Richez, Leguille and Marquet2016) and the Newton algorithm have been used. The SFD is used with a local time stepping algorithm and the cut-off frequency and damping coefficient were based on a parametric study to obtain solutions converged within machine accuracy. A value of the filter width ![]() $\varDelta = 1/74$ and the proportional controller coefficient
$\varDelta = 1/74$ and the proportional controller coefficient ![]() $\chi =50$ allowed the solution to converge, and the Courant–Friedrichs–Lewy number is set to 50 to compute the local time step in the LU-SSOR implicit scheme. To ensure consistency, it has been checked that both methods provide the same solution for several cases. Successive solutions are obtained by initialising each computation from the previous angle of attack. The lower branch of the lift polar is obtained by increasing the angle of attack up to values for which a converged solution could no longer be obtained. Then, by decreasing the angle of attack starting from these unconverged flow solutions, the solution method is able to converge on the lower branch of the lift curve. Every solution has been converged within machine accuracy. Two distinct solutions are found for some angles of attack. Such hysteresis phenomena of the discretized RANS equations were obtained by Wales et al. (Reference Wales, Gaitonde, Jones, Avitabile and Champneys2012) and Busquet et al. (Reference Busquet, Marquet, Richez, Juniper and Sipp2017) for the NACA0012 and the OA209 aerofoils, respectively. Grid convergence has been ensured by carrying out a 2-D simulation at an angle of attack of
$\chi =50$ allowed the solution to converge, and the Courant–Friedrichs–Lewy number is set to 50 to compute the local time step in the LU-SSOR implicit scheme. To ensure consistency, it has been checked that both methods provide the same solution for several cases. Successive solutions are obtained by initialising each computation from the previous angle of attack. The lower branch of the lift polar is obtained by increasing the angle of attack up to values for which a converged solution could no longer be obtained. Then, by decreasing the angle of attack starting from these unconverged flow solutions, the solution method is able to converge on the lower branch of the lift curve. Every solution has been converged within machine accuracy. Two distinct solutions are found for some angles of attack. Such hysteresis phenomena of the discretized RANS equations were obtained by Wales et al. (Reference Wales, Gaitonde, Jones, Avitabile and Champneys2012) and Busquet et al. (Reference Busquet, Marquet, Richez, Juniper and Sipp2017) for the NACA0012 and the OA209 aerofoils, respectively. Grid convergence has been ensured by carrying out a 2-D simulation at an angle of attack of ![]() $15^{\circ }$ with a grid refined by a factor 2 in both directions (1024 by 256 grid cells), resulting in non-significant differences in the pressure distribution.
$15^{\circ }$ with a grid refined by a factor 2 in both directions (1024 by 256 grid cells), resulting in non-significant differences in the pressure distribution.

Figure 2. Lift curve for the 2-D and 3-D steady solutions (NACA4412, ![]() $Re=350\,000$,
$Re=350\,000$, ![]() $M=0.2$,
$M=0.2$, ![]() $\delta =0^{\circ }$).
$\delta =0^{\circ }$).
For angles of attack over ![]() $14^{\circ }$ the 3-D lift coefficient is lower than the 2-D one. These solutions are obtained using a global time step and the SFD technique. The lower lift coefficient is associated with the presence of stall cells, as seen in figure 3 for an angle of attack of
$14^{\circ }$ the 3-D lift coefficient is lower than the 2-D one. These solutions are obtained using a global time step and the SFD technique. The lower lift coefficient is associated with the presence of stall cells, as seen in figure 3 for an angle of attack of ![]() $15^{\circ }$. Four steady stall cells are observed and the skin friction lines exhibit the ‘owl face’ shape reported in the literature. The left-hand part of this figure shows the result with a spanwise mesh refinement of a factor 2. No significant change in the result is noticeable, ensuring the grid convergence of the results. In this simulation, the wavenumber of the stall cell is
$15^{\circ }$. Four steady stall cells are observed and the skin friction lines exhibit the ‘owl face’ shape reported in the literature. The left-hand part of this figure shows the result with a spanwise mesh refinement of a factor 2. No significant change in the result is noticeable, ensuring the grid convergence of the results. In this simulation, the wavenumber of the stall cell is ![]() $4.2$. However, the periodic boundary conditions constrain the possible wavenumbers since the number of cells must be an integer. Hence, the only possible wavenumbers that may appear in the simulation are necessarily multiples of
$4.2$. However, the periodic boundary conditions constrain the possible wavenumbers since the number of cells must be an integer. Hence, the only possible wavenumbers that may appear in the simulation are necessarily multiples of ![]() $\beta _0=2{\rm \pi} /6$. There might therefore exist a discrepancy with respect to a truly infinite configuration, with
$\beta _0=2{\rm \pi} /6$. There might therefore exist a discrepancy with respect to a truly infinite configuration, with ![]() $AR=\infty$. A more accurate estimation of the most amplified wavenumber may be obtained by considering a larger aspect ratio. For this reason, a simulation with
$AR=\infty$. A more accurate estimation of the most amplified wavenumber may be obtained by considering a larger aspect ratio. For this reason, a simulation with ![]() $AR=12$ has also been run and eight stall cells were obtained. Therefore, the most amplified wavenumber is narrowed down to a value between
$AR=12$ has also been run and eight stall cells were obtained. Therefore, the most amplified wavenumber is narrowed down to a value between ![]() $14{\rm \pi} /12 \approx 3.7$ and
$14{\rm \pi} /12 \approx 3.7$ and ![]() $18{\rm \pi} /12 \approx 4.7$. This range will be compared with the result of linear stability analyses in § 4.1.
$18{\rm \pi} /12 \approx 4.7$. This range will be compared with the result of linear stability analyses in § 4.1.

Figure 3. Surface pressure coefficient and skin friction lines of 3-D steady solution with 224 (left-hand side) and 112 (right-hand side) spanwise grid cells (NACA4412, ![]() $M=0.2$,
$M=0.2$, ![]() $Re=350\,000$,
$Re=350\,000$, ![]() $\alpha =15^{\circ }$,
$\alpha =15^{\circ }$, ![]() $\delta =0^{\circ }$,
$\delta =0^{\circ }$, ![]() $L_z=6$).
$L_z=6$).
Since the 2-D solutions are particular cases where every derivative in the spanwise direction are null, they are also solutions of the 3-D discretized RANS equations. Hence these results demonstrate the existence of multiple solutions, the 2-D and the 3-D ones, for a given flow conditions. Such results are in agreement with those from Kamenetskiy et al. (Reference Kamenetskiy, Bussoletti, Hilmes, Venkatakrishnan, Wigton and Johnson2014).
3.1.2. Swept cases  $\delta >0^{\circ }$,
$\delta >0^{\circ }$,  $\alpha =15^{\circ }$
$\alpha =15^{\circ }$
A fixed value ![]() $\alpha =15^{\circ }$ is now considered and a sweep angle is added. In these conditions, the flow is unsteady and time-accurate simulations with a non-dimensional time step of 0.008 are carried out. Figure 4 shows the instantaneous pressure coefficient and the skin friction lines over wings swept at
$\alpha =15^{\circ }$ is now considered and a sweep angle is added. In these conditions, the flow is unsteady and time-accurate simulations with a non-dimensional time step of 0.008 are carried out. Figure 4 shows the instantaneous pressure coefficient and the skin friction lines over wings swept at ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$. Four stall cells are observed and the wavenumber is the same as for the unswept wing (
$30^{\circ }$. Four stall cells are observed and the wavenumber is the same as for the unswept wing (![]() $\beta = 4.2$). The topology of the stall cells also changes with the sweep angle, and the skin friction lines are now aligned in the cross-flow direction. This is associated with a spanwise convection of the stall cells. This induces a frequency proportional to the wavelength of the cells and their convection speed (
$\beta = 4.2$). The topology of the stall cells also changes with the sweep angle, and the skin friction lines are now aligned in the cross-flow direction. This is associated with a spanwise convection of the stall cells. This induces a frequency proportional to the wavelength of the cells and their convection speed (![]() $St = {V_C}/{\lambda _z}$). Table 2 summarizes all the wavelength and convection speed obtained for sweep angles of
$St = {V_C}/{\lambda _z}$). Table 2 summarizes all the wavelength and convection speed obtained for sweep angles of ![]() $0^{\circ }$,
$0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$. Figure 5 shows the definition of these quantities. For the simulations at a constant aspect ratio, the wavenumber is always 4.2. These results suggest that the sweep angle has no effect on the wavelength of the stall cells. However, as mentioned previously, this result is constrained by the wing aspect ratio. Finally, the convection speed observed in the URANS results is proportional to the sweep angle. These phenomena are also analysed using stability analyses in § 4.1.3.
$30^{\circ }$. Figure 5 shows the definition of these quantities. For the simulations at a constant aspect ratio, the wavenumber is always 4.2. These results suggest that the sweep angle has no effect on the wavelength of the stall cells. However, as mentioned previously, this result is constrained by the wing aspect ratio. Finally, the convection speed observed in the URANS results is proportional to the sweep angle. These phenomena are also analysed using stability analyses in § 4.1.3.

Figure 4. Instantaneous surface pressure coefficient and skin friction lines over a swept wing (NACA4412, ![]() $M=0.2$,
$M=0.2$, ![]() $Re=350\,000$,
$Re=350\,000$, ![]() $\alpha =15^{\circ }$,
$\alpha =15^{\circ }$, ![]() $L_z=6$): (a) sweep
$L_z=6$): (a) sweep ![]() $10^{\circ }$; (b) sweep
$10^{\circ }$; (b) sweep ![]() $20^{\circ }$; (c) sweep
$20^{\circ }$; (c) sweep ![]() $30^{\circ }$.
$30^{\circ }$.
Table 2. Stall cells convection frequency for several wing spans and sweep angles (NACA4412, ![]() $M=0.2$,
$M=0.2$, ![]() $Re=350\,000$,
$Re=350\,000$, ![]() $\alpha =15^{\circ }$).
$\alpha =15^{\circ }$).


Figure 5. Stall and buffet cells convection model.
3.2. Transonic buffet
This section analyses the transonic buffet on wings based on the OALT25 aerofoil at a Reynolds number ![]() $Re=3\times 10^{6}$, a Mach number of 0.7352 and an angle of attack of
$Re=3\times 10^{6}$, a Mach number of 0.7352 and an angle of attack of ![]() $4^{\circ }$. The non-dimensional time step is set to
$4^{\circ }$. The non-dimensional time step is set to ![]() $0.0105$. Simulations with the 2.5-D assumptions are first analysed. Then URANS results for 3-D infinite swept wings are presented.
$0.0105$. Simulations with the 2.5-D assumptions are first analysed. Then URANS results for 3-D infinite swept wings are presented.
3.2.1. Spanwise invariant solutions (2.5-D)
Figure 6 shows the time-averaged wall pressure coefficient of 2-D and 2.5-D simulations. The pressure coefficient on the pressure side and the trailing edge agree with the experiments of Brion et al. (Reference Brion, Dandois, Abart and Paillart2017) and the pressure of the supersonic plateau is also the same. This indicates that the Mach number and angle of attack are the same between the experiments and the simulations. However, the shock wave of the simulations is located further downstream compared with the experimental field. It is seen that the pressure distribution is the same for every sweep angle, except in the shock wave region. This shows that the flow fields in the ![]() $(x,y)$ plane remain close due to the fact that the upstream normal inflow conditions are kept constant when changing the sweep angle. The time evolution of the lift coefficient yields a Strouhal number of 0.075. The shock wave motion amplitude can be evaluated from the slope of the time-averaged pressure coefficient in the vicinity of the shock wave position. The largest buffet amplitude is observed for the unswept case and the buffet amplitude decreases as the sweep angle is increased. This relation between the sweep angle and the buffet amplitude is investigated with global stability analyses in § 4.2.3.
$(x,y)$ plane remain close due to the fact that the upstream normal inflow conditions are kept constant when changing the sweep angle. The time evolution of the lift coefficient yields a Strouhal number of 0.075. The shock wave motion amplitude can be evaluated from the slope of the time-averaged pressure coefficient in the vicinity of the shock wave position. The largest buffet amplitude is observed for the unswept case and the buffet amplitude decreases as the sweep angle is increased. This relation between the sweep angle and the buffet amplitude is investigated with global stability analyses in § 4.2.3.

Figure 6. Time-averaged wall pressure coefficient for spanwise invariant solution with several sweep angles (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha = 4^{\circ }$).
$\alpha = 4^{\circ }$).
3.2.2. Superposition between 2-D buffet mode and 3-D buffet cells
Figure 7 shows the instantaneous pressure coefficient and skin friction lines on swept wings of aspect ratio ![]() $AR = 6$ meshed with 168 spanwise grid cells. For the unswept wing and the wing swept at
$AR = 6$ meshed with 168 spanwise grid cells. For the unswept wing and the wing swept at ![]() $30^{\circ }$, a variation of the shock wave position is observed, forming the so-called buffet cells. For the unswept wing
$30^{\circ }$, a variation of the shock wave position is observed, forming the so-called buffet cells. For the unswept wing ![]() $(\delta =0^{\circ })$, spanwise structures are observed. However, the amplitude of the buffet cells is irregular and the number of buffet cells varies in time. As such, the wavenumber varies in time and the buffet cells appear and disappear at random spanwise location since there is no convection. This results in a flow that can seem chaotic but a dominant Strouhal number of 0.06 is observed. This is related to the frequency of a chordwise variation of the shock wave position and a variation of the buffet cells’ amplitude. The same frequency is observed for swept wings (
$(\delta =0^{\circ })$, spanwise structures are observed. However, the amplitude of the buffet cells is irregular and the number of buffet cells varies in time. As such, the wavenumber varies in time and the buffet cells appear and disappear at random spanwise location since there is no convection. This results in a flow that can seem chaotic but a dominant Strouhal number of 0.06 is observed. This is related to the frequency of a chordwise variation of the shock wave position and a variation of the buffet cells’ amplitude. The same frequency is observed for swept wings (![]() $\delta >0^{\circ }$). However, in these cases the number of buffet cells is constant and they are convected in the spanwise direction. Two cells are observed for a sweep angle of
$\delta >0^{\circ }$). However, in these cases the number of buffet cells is constant and they are convected in the spanwise direction. Two cells are observed for a sweep angle of ![]() $\delta =30^{\circ }$. This result is compared with the stability analysis results in § 4.2. Figure 7 also shows the instantaneous solution with 112 and 168 spanwise grid cells. The comparison of the two fields shows that the grid spacing is sufficient for this case since no significant differences are noticeable in the skin friction lines and the pressure coefficient.
$\delta =30^{\circ }$. This result is compared with the stability analysis results in § 4.2. Figure 7 also shows the instantaneous solution with 112 and 168 spanwise grid cells. The comparison of the two fields shows that the grid spacing is sufficient for this case since no significant differences are noticeable in the skin friction lines and the pressure coefficient.

Figure 7. Instantaneous surface pressure coefficient and skin friction lines for URANS simulations of infinite swept wings with two sweep angles (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$,
$\alpha =4^{\circ }$, ![]() $L_z=6$): (a)
$L_z=6$): (a) ![]() $\delta =0^{\circ }$; (b)
$\delta =0^{\circ }$; (b) ![]() $\delta =30^{\circ }$ (right-hand side, 112 spanwise grid cells; left-hand side, 168 spanwise grid cells).
$\delta =30^{\circ }$ (right-hand side, 112 spanwise grid cells; left-hand side, 168 spanwise grid cells).
Figure 8 shows the power spectral density of the sectional lift coefficient with 112, 168 and 224 spanwise grid cells. The sectional lift coefficient is extracted on a given chordwise wing section, the choice of this section has no effect since the buffet cells are convected in the spanwise direction. The sectional lift coefficient is sampled at every time step (0.0105 non-dimensional time unit) over a time frame of 630 non-dimensional time units. A periodogram with boxcar window and a single block is used to estimate the power spectral density, which yields a Strouhal number resolution of 0.00158. This method is used since the signals for the grid refinement study are too short to use a sufficient number of averaging blocks. This yields noisier spectra and estimation errors on the amplitude. Nevertheless, one can observe that the peak frequencies are the same. A dashed line is added to indicate the Strouhal number around 0.06 (the frequency observed for every sweep angle) and a dashed-dotted line indicates the Strouhal number of 0.135. The latter is associated with the convection of buffet cells, as it will be shown in this section. Another peak at a frequency of 0.135 could correspond to the nonlinear interaction between the two dominant modes (![]() $St = 0.135+0.055 = 0.19$).
$St = 0.135+0.055 = 0.19$).

Figure 8. Sectional lift coefficient power spectral density (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$,
$\alpha =4^{\circ }$, ![]() $\delta =30^{\circ }$).
$\delta =30^{\circ }$).
Figure 9 shows the power spectral density of the sectional and global lift coefficient with sweep angles of ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$. These spectra are evaluated using the Welch method with a Hann window and a 50 % overlap between the blocks. The signal length is of
$30^{\circ }$. These spectra are evaluated using the Welch method with a Hann window and a 50 % overlap between the blocks. The signal length is of ![]() $1\,260$ non-dimensional time units and nine blocks are used. The Welch method is used since the time series is longer than in the mesh refinement study. The sampling is done at every time step (0.0105 non-dimensional time units) for the sectional lift and every 10 time steps for the global lift. This yields a Strouhal number resolution of 0.0039. One can notice the frequency between
$1\,260$ non-dimensional time units and nine blocks are used. The Welch method is used since the time series is longer than in the mesh refinement study. The sampling is done at every time step (0.0105 non-dimensional time units) for the sectional lift and every 10 time steps for the global lift. This yields a Strouhal number resolution of 0.0039. One can notice the frequency between ![]() $St = 0.055$ and
$St = 0.055$ and ![]() $0.06$ indicated by a dashed line for every sweep angle in the global and sectional lift signals. Some harmonics of this frequency are also observed. This frequency is associated with a chordwise oscillation of the shock wave position which modulates the buffet cells amplitude (2-D oscillation). However, a second dominant frequency is observed in the sectional lift coefficient. The latter increases with the sweep angle and is due to the buffet cells convection in the spanwise direction. This second frequency is not observed in the spectrum of the global lift coefficient since the number of buffet cells is constant. For this reason, the variations of the lift coefficient associated with the convection are cancelled out when the lift coefficient is averaged along the span. Like in figure 8, the dashed line indicates the 2-D shock oscillation phenomenon while the dashed-dot lines indicates the buffet cells’ convection phenomenon. These two frequencies are further discussed in the next paragraph. Some harmonics of the buffet cells convection frequency are also observed. For instance the convection Strouhal number of 0.045 for a sweep angle of
$0.06$ indicated by a dashed line for every sweep angle in the global and sectional lift signals. Some harmonics of this frequency are also observed. This frequency is associated with a chordwise oscillation of the shock wave position which modulates the buffet cells amplitude (2-D oscillation). However, a second dominant frequency is observed in the sectional lift coefficient. The latter increases with the sweep angle and is due to the buffet cells convection in the spanwise direction. This second frequency is not observed in the spectrum of the global lift coefficient since the number of buffet cells is constant. For this reason, the variations of the lift coefficient associated with the convection are cancelled out when the lift coefficient is averaged along the span. Like in figure 8, the dashed line indicates the 2-D shock oscillation phenomenon while the dashed-dot lines indicates the buffet cells’ convection phenomenon. These two frequencies are further discussed in the next paragraph. Some harmonics of the buffet cells convection frequency are also observed. For instance the convection Strouhal number of 0.045 for a sweep angle of ![]() $10^{\circ }$ has a harmonic at 0.09, which is also the convection frequency for a sweep angle of
$10^{\circ }$ has a harmonic at 0.09, which is also the convection frequency for a sweep angle of ![]() $20^{\circ }$.
$20^{\circ }$.

Figure 9. Effect of the sweep angle on the global and sectional lift coefficient power spectral density (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$).
$\alpha =4^{\circ }$).
To visualize the unsteady behaviour of the flow, the pressure has been extracted along a line parallel to the leading edge. Figure 10 is a (![]() $z, t$) diagram showing this extraction of the pressure coefficient near
$z, t$) diagram showing this extraction of the pressure coefficient near ![]() ${x^{\prime }}/{c} = 0.43$ for the sweep angle of
${x^{\prime }}/{c} = 0.43$ for the sweep angle of ![]() $30^{\circ }$. Most of the time, the pressure is equal to the one on the supersonic plateau. However, two buffet cells periodically cross the extraction line because the amplitude of the cells changes in time. This occurs with a period
$30^{\circ }$. Most of the time, the pressure is equal to the one on the supersonic plateau. However, two buffet cells periodically cross the extraction line because the amplitude of the cells changes in time. This occurs with a period ![]() $T = 18.0$. This results in a Strouhal number equal to 0.055 (around the Strouhal number of 0.06 shown in figure 9). A Strouhal number of this order is observed for every sweep angle, as previously shown, thus suggesting that the variation of the buffet cells amplitude relates to a 2-D buffet mode. In addition, this figure allows us to follow the spanwise location of the buffet cells in time. Hence, the convection speed of the buffet cells can be extracted as the slope of an isocontour of pressure on this pressure map (here
$T = 18.0$. This results in a Strouhal number equal to 0.055 (around the Strouhal number of 0.06 shown in figure 9). A Strouhal number of this order is observed for every sweep angle, as previously shown, thus suggesting that the variation of the buffet cells amplitude relates to a 2-D buffet mode. In addition, this figure allows us to follow the spanwise location of the buffet cells in time. Hence, the convection speed of the buffet cells can be extracted as the slope of an isocontour of pressure on this pressure map (here ![]() $V_C = 0.4$) and the associated frequency can be computed with the wavelength of the buffet cells (
$V_C = 0.4$) and the associated frequency can be computed with the wavelength of the buffet cells (![]() $St = {V_C}/{\lambda _z}$). These quantities are schematized in figure 5 and reported for multiple sweep angles in table 3. Figure 11 shows the relation between the sweep angle and the convection speed. The cross-flow velocity varies in
$St = {V_C}/{\lambda _z}$). These quantities are schematized in figure 5 and reported for multiple sweep angles in table 3. Figure 11 shows the relation between the sweep angle and the convection speed. The cross-flow velocity varies in ![]() $\tan \delta$, meaning that the convection speed is proportional to the far field velocity projected along the leading edge. This proportionality is true for low-speed flow conditions as well. A fit coefficient of 0.7 is found for the buffet cells and 0.8 for the stall cells. More details are provided in Plante et al. (Reference Plante, Dandois and Laurendeau2019b). This relation between the sweep angle and the convection speed of the buffet cells is further analysed using stability analyses in § 4 for the stall and buffet conditions.
$\tan \delta$, meaning that the convection speed is proportional to the far field velocity projected along the leading edge. This proportionality is true for low-speed flow conditions as well. A fit coefficient of 0.7 is found for the buffet cells and 0.8 for the stall cells. More details are provided in Plante et al. (Reference Plante, Dandois and Laurendeau2019b). This relation between the sweep angle and the convection speed of the buffet cells is further analysed using stability analyses in § 4 for the stall and buffet conditions.

Figure 10. Extraction of the pressure on a line parallel to the leading edge near ![]() ${x^{\prime }}/{c} = 0.43$ (OALT25,
${x^{\prime }}/{c} = 0.43$ (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$,
$\alpha =4^{\circ }$, ![]() $\delta =30^{\circ }$).
$\delta =30^{\circ }$).
Table 3. Buffet cells convection frequency for several sweep angles (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$).
$\alpha =4^{\circ }$).


Figure 11. Convection speed of stall (NACA4412, ![]() $M=0.2$,
$M=0.2$, ![]() $Re=350\,000$,
$Re=350\,000$, ![]() $\alpha =15^{\circ }$) and buffet (OALT25,
$\alpha =15^{\circ }$) and buffet (OALT25, ![]() $M=0.7352$,
$M=0.7352$, ![]() $Re=3\times 10^{6}$,
$Re=3\times 10^{6}$, ![]() $\alpha =4^{\circ }$) cells.
$\alpha =4^{\circ }$) cells.
3.3. Partial conclusion
Three-dimensional flow features in the form of stall cells and buffet cells are observed with URANS modelling, in the low-speed stall regime and in the high-speed buffet regime, respectively. These phenomena can be obtained with a numerical set-up in which no disturbances are imposed by the initial conditions and the boundary conditions. This suggests that there is an instability inherent to these flow conditions. Moreover, the spanwise length of the cells remains approximately unchanged when the aspect ratio is increased. This suggests that there is a preferential wavenumber for these flow structures. However, finding a very accurate estimation of this wavenumber with URANS simulations would be computationally expensive since the aspect ratio constrains the number of cells which can be represented, and ![]() $AR$ needs to be increased to reduce the uncertainty with respect to the most amplified wavelength. As it will be shown in the next section, stability analyses are a more appropriate tool to address this point. Finally, both types of cells are convected with a velocity proportional to the free stream cross-flow velocity. This causes an unsteady behaviour which is superimposed to a 2-D unsteadiness in the case of the transonic buffet simulations. These flow behaviours are analysed with global linear stability analyses in the next section.
$AR$ needs to be increased to reduce the uncertainty with respect to the most amplified wavelength. As it will be shown in the next section, stability analyses are a more appropriate tool to address this point. Finally, both types of cells are convected with a velocity proportional to the free stream cross-flow velocity. This causes an unsteady behaviour which is superimposed to a 2-D unsteadiness in the case of the transonic buffet simulations. These flow behaviours are analysed with global linear stability analyses in the next section.
4. Global stability analyses
The second part of this study uses global stability analyses to identify linearly unstable modes which could explain the stall cells and buffet cells observed in § 3. Results for the low speed and transonic flow conditions are presented and discussed. Parameters characterising the size and intensity of the recirculation zones in the baseflows are provided as supplementary material to this article is available at https://doi.org/10.1017/jfm.2020.848.
4.1. Subsonic stall
Steady 2.5-D and 2-D solutions of the NACA4412 aerofoil at a Reynolds number of 350 000, a Mach number of 0.2, and multiple angles of attack and sweep angles are converged within machine accuracy. These solutions are used as baseflows for the stability analyses. For consistency with the previous section, most of the analyses are carried out for an angle of attack of ![]() $15^{\circ }$.
$15^{\circ }$.
4.1.1. Case  $\delta =0^{\circ }$ and
$\delta =0^{\circ }$ and  $\alpha =15^{\circ }$
$\alpha =15^{\circ }$
The following focuses on the case ![]() $\delta =0^{\circ }$ and
$\delta =0^{\circ }$ and ![]() $\alpha =15^{\circ }$. Figure 12 presents the eigenvalues spectra obtained for two values of
$\alpha =15^{\circ }$. Figure 12 presents the eigenvalues spectra obtained for two values of ![]() $\beta$. For both values, there is an unstable eigenvalue (positive real part) located along the real axis. This is a non-oscillatory unstable mode. A mode similar to this one has been observed by Zhang & Samtaney (Reference Zhang and Samtaney2016) for low-Reynolds laminar flow. But in the present case this mode is observed at an intermediate Reynolds number with the use of a steady RANS baseflow. This figure also shows the radius covered by the shift-and-invert Arnoldi strategy. Different shifts with various imaginary parts are used in the shift-and-invert strategy to ensure that modes with non-zero imaginary part are not missed. Figure 13 shows the growth rate of the steady unstable mode for a range of wavenumbers
$\beta$. For both values, there is an unstable eigenvalue (positive real part) located along the real axis. This is a non-oscillatory unstable mode. A mode similar to this one has been observed by Zhang & Samtaney (Reference Zhang and Samtaney2016) for low-Reynolds laminar flow. But in the present case this mode is observed at an intermediate Reynolds number with the use of a steady RANS baseflow. This figure also shows the radius covered by the shift-and-invert Arnoldi strategy. Different shifts with various imaginary parts are used in the shift-and-invert strategy to ensure that modes with non-zero imaginary part are not missed. Figure 13 shows the growth rate of the steady unstable mode for a range of wavenumbers ![]() $\beta$. Multiple values of
$\beta$. Multiple values of ![]() $\varDelta _z$ used in the extrusion of the grid are plotted to ensure that the grid is sufficiently refined. These results can be considered converged for every
$\varDelta _z$ used in the extrusion of the grid are plotted to ensure that the grid is sufficiently refined. These results can be considered converged for every ![]() $\beta$ with
$\beta$ with ![]() $\varDelta _z=0.002$. One can observe that the grid convergence is poorer in the high
$\varDelta _z=0.002$. One can observe that the grid convergence is poorer in the high ![]() $\beta$ range associated with small structures. This indicates that a finer grid is required to compute small flow structures, as expected. The grid spacing used in the URANS simulations (
$\beta$ range associated with small structures. This indicates that a finer grid is required to compute small flow structures, as expected. The grid spacing used in the URANS simulations (![]() $\varDelta _z = 0.054$) is well converged up to
$\varDelta _z = 0.054$) is well converged up to ![]() $\beta = 6$, covering the case with the maximum growth rate and the wavenumbers obtained in the URANS simulations. This is consistent with the grid convergence shown in figure 3.
$\beta = 6$, covering the case with the maximum growth rate and the wavenumbers obtained in the URANS simulations. This is consistent with the grid convergence shown in figure 3.

Figure 12. Eigenspectrum (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha$ =
$\alpha$ = ![]() $15.0^{\circ }$,
$15.0^{\circ }$, ![]() $\delta = 0.0^{\circ }$).
$\delta = 0.0^{\circ }$).

Figure 13. Effect of spanwise grid density and the wavenumber on the growth rate of the unstable mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha = 15.0^{\circ }$,
$\alpha = 15.0^{\circ }$, ![]() $\delta = 0.0^{\circ }$).
$\delta = 0.0^{\circ }$).
The maximum growth rate is obtained for a spanwise structure with ![]() $\beta \approx 4.4$. This corresponds to a wavelength
$\beta \approx 4.4$. This corresponds to a wavelength ![]() $\lambda _z \approx 1.43$, which is consistent with the value observed in the URANS simulations
$\lambda _z \approx 1.43$, which is consistent with the value observed in the URANS simulations ![]() $(\beta = 4.2)$. Indeed, in the simulations, the periodic boundary conditions constrained the possible wavenumbers to multiples of
$(\beta = 4.2)$. Indeed, in the simulations, the periodic boundary conditions constrained the possible wavenumbers to multiples of ![]() $\beta _0=2{\rm \pi} /AR$. Therefore, the wavelength of the URANS simulation is as close as possible to that predicted by the stability analysis, showing that this unstable mode is responsible for the formation of stall cells. Figure 14 shows the baseflow and the real part of the eigenvector
$\beta _0=2{\rm \pi} /AR$. Therefore, the wavelength of the URANS simulation is as close as possible to that predicted by the stability analysis, showing that this unstable mode is responsible for the formation of stall cells. Figure 14 shows the baseflow and the real part of the eigenvector ![]() $\widehat {\rho e}$ reconstructed in three dimensions with (2.14), and extracted on the aerofoil surface and the plane
$\widehat {\rho e}$ reconstructed in three dimensions with (2.14), and extracted on the aerofoil surface and the plane ![]() $z=0$. The instability is located in the shear layer and upstream of the separation line. The shape of this mode is consistent with the structure of the stall cells.
$z=0$. The instability is located in the shear layer and upstream of the separation line. The shape of this mode is consistent with the structure of the stall cells.

Figure 14. Flow visualization of the (a) baseflow and (b) 3-D unstable mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha = 15.0^{\circ }$,
$\alpha = 15.0^{\circ }$, ![]() $\delta = 0.0^{\circ }$): (a)
$\delta = 0.0^{\circ }$): (a) ![]() ${\rho e}/{\rho e_{\infty }}$ baseflow; (b) real part of the
${\rho e}/{\rho e_{\infty }}$ baseflow; (b) real part of the ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode ![]() $(\beta = 4.4) - St = 0.0$.
$(\beta = 4.4) - St = 0.0$.
4.1.2. Case  $\delta =0^{\circ }$ and varying
$\delta =0^{\circ }$ and varying  $\alpha$
$\alpha$
These stability analyses are carried out for several angles of attack for which a solution converged to machine accuracy can be obtained (figure 2). The 3-D unstable mode can be identified on the upper and lower branch of the lift polar hysteresis. Figure 15 shows the growth rate of this mode for the most amplified wavenumber of the two branches. The mode is unstable from an angle of attack of ![]() $14.15^{\circ }$ (the maximum lift) up to
$14.15^{\circ }$ (the maximum lift) up to ![]() $20.5^{\circ }$ (the last converged baseflow). On the lower branch, the growth rates are higher than for the upper one, but the mode is only unstable for angles of attack lower than
$20.5^{\circ }$ (the last converged baseflow). On the lower branch, the growth rates are higher than for the upper one, but the mode is only unstable for angles of attack lower than ![]() $16.9^{\circ }$. Above this angle, the mode becomes stable again, even though the flow is massively separated. Figure 16 shows the shape of the modes on the upper and lower branches. One can observe that the unstable mode is located around the region where the flow separates. For
$16.9^{\circ }$. Above this angle, the mode becomes stable again, even though the flow is massively separated. Figure 16 shows the shape of the modes on the upper and lower branches. One can observe that the unstable mode is located around the region where the flow separates. For ![]() $\alpha = 18^{\circ }$ the flow separates far from the leading edge. However, for the other angles of attack the separation is close to the leading edge. Hence, it is possible that the mode is no longer unstable past
$\alpha = 18^{\circ }$ the flow separates far from the leading edge. However, for the other angles of attack the separation is close to the leading edge. Hence, it is possible that the mode is no longer unstable past ![]() $\alpha = 16.9^{\circ }$ on the lower branch because the flow separation becomes fixed on the leading edge. This tends to validate the idea that stall cells are only observed with a trailing edge type of stall.
$\alpha = 16.9^{\circ }$ on the lower branch because the flow separation becomes fixed on the leading edge. This tends to validate the idea that stall cells are only observed with a trailing edge type of stall.

Figure 15. Effect of the angle of attack on the growth rate of the unstable mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\delta = 0.0^{\circ }$). (a) Upper branch of the lift hysteresis. (b) Lower branch of the lift hysteresis.
$\delta = 0.0^{\circ }$). (a) Upper branch of the lift hysteresis. (b) Lower branch of the lift hysteresis.

Figure 16. Flow visualization of the 3-D unstable mode for several angles of attack on the two branches of the lift hysteresis (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\delta = 0.0^{\circ }$). (a) Real part of the
$\delta = 0.0^{\circ }$). (a) Real part of the ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (![]() $\alpha =18^{\circ }$, upper branch,
$\alpha =18^{\circ }$, upper branch, ![]() $\beta = 5$) –
$\beta = 5$) – ![]() $St = 0.0$. (b) Real part of the
$St = 0.0$. (b) Real part of the ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (![]() $\alpha =20.5^{\circ }$, upper branch,
$\alpha =20.5^{\circ }$, upper branch, ![]() $\beta = 7.5$) –
$\beta = 7.5$) – ![]() $St = 0.0$. (c) Real part of the
$St = 0.0$. (c) Real part of the ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (![]() $\alpha =16.78^{\circ }$, lower branch,
$\alpha =16.78^{\circ }$, lower branch, ![]() $\beta = 8$) –
$\beta = 8$) – ![]() $St = 0.0$. (d) Real part of the
$St = 0.0$. (d) Real part of the ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode (![]() $\alpha =16.9^{\circ }$, lower branch,
$\alpha =16.9^{\circ }$, lower branch, ![]() $\beta = 5.5$) –
$\beta = 5.5$) – ![]() $St = 0.0$.
$St = 0.0$.
Works based on the lifting line theory by Spalart (Reference Spalart2014) and Gross et al. (Reference Gross, Fasel and Gaster2015) suggested that a negative slope of the ![]() $C_L-\alpha$ curve is a necessary condition for the occurrence of stall cells. Figure 15 shows the growth rate obtained in these flow conditions for different values of
$C_L-\alpha$ curve is a necessary condition for the occurrence of stall cells. Figure 15 shows the growth rate obtained in these flow conditions for different values of ![]() $\alpha$, and for the upper branch of the lift hysteresis, the most unstable eigenvalue crosses the imaginary axis at an angle of attack slightly below
$\alpha$, and for the upper branch of the lift hysteresis, the most unstable eigenvalue crosses the imaginary axis at an angle of attack slightly below ![]() $14.15^{\circ }$. This coincides with the maximum lift angle of attack in figure 2, which is therefore consistent with the negative
$14.15^{\circ }$. This coincides with the maximum lift angle of attack in figure 2, which is therefore consistent with the negative ![]() $C_L-\alpha$ slope criterion. However, the stability analysis of the lower branch of the lift hysteresis shows that the stall cell modes are stable for
$C_L-\alpha$ slope criterion. However, the stability analysis of the lower branch of the lift hysteresis shows that the stall cell modes are stable for ![]() $\alpha >16.9^{\circ }$, while the slope of the
$\alpha >16.9^{\circ }$, while the slope of the ![]() $C_L-\alpha$ curve is negative between
$C_L-\alpha$ curve is negative between ![]() $17.0^{\circ }$ and
$17.0^{\circ }$ and ![]() $17.4^{\circ }$ (see figure 2), which contradicts this criterion. Another conclusion of the analysis of Gross et al. (Reference Gross, Fasel and Gaster2015) is that the wavelength of the cells should be
$17.4^{\circ }$ (see figure 2), which contradicts this criterion. Another conclusion of the analysis of Gross et al. (Reference Gross, Fasel and Gaster2015) is that the wavelength of the cells should be ![]() $\lambda _z = -0.5({\partial C_L}/{\partial \alpha })$ with a discrete model or
$\lambda _z = -0.5({\partial C_L}/{\partial \alpha })$ with a discrete model or ![]() $\lambda _z = -({{\rm \pi} }/{4})({\partial C_L}/{\partial \alpha })$ with a continuous model. Since the linear instability occurs around the 2-D solution,
$\lambda _z = -({{\rm \pi} }/{4})({\partial C_L}/{\partial \alpha })$ with a continuous model. Since the linear instability occurs around the 2-D solution, ![]() ${\partial C_L}/{\partial \alpha }$ is taken as the slope of the 2-D lift polar around an angle of attack of
${\partial C_L}/{\partial \alpha }$ is taken as the slope of the 2-D lift polar around an angle of attack of ![]() $15.0^{\circ }$ (
$15.0^{\circ }$ (![]() $-2.52\ \textrm {rad}^{-1}$). With this slope, the wavelength should be 1.26 or 1.98 (
$-2.52\ \textrm {rad}^{-1}$). With this slope, the wavelength should be 1.26 or 1.98 (![]() $\beta =3.2$ and
$\beta =3.2$ and ![]() $5.0$, respectively). The values computed with the URANS (
$5.0$, respectively). The values computed with the URANS (![]() $\beta = 4.2$) simulations and the stability (
$\beta = 4.2$) simulations and the stability (![]() $\beta = 4.4$) analyses fall between the values predicted with this model. However, the
$\beta = 4.4$) analyses fall between the values predicted with this model. However, the ![]() $C_L-\alpha$ slope varies in the range of angles of attack studied with the global stability analysis and the values of
$C_L-\alpha$ slope varies in the range of angles of attack studied with the global stability analysis and the values of ![]() $\beta$ for which the flow is the most unstable does not vary significantly. This is in contradiction with the model proposed by Gross et al. (Reference Gross, Fasel and Gaster2015).
$\beta$ for which the flow is the most unstable does not vary significantly. This is in contradiction with the model proposed by Gross et al. (Reference Gross, Fasel and Gaster2015).
4.1.3. Effect of sweep at  $\alpha =15^{\circ }$
$\alpha =15^{\circ }$
The approach followed to carry out stability analyses also enables to study baseflow with ![]() $\delta \neq 0$. Figures 17(a) and 17(b) show the growth rate and frequency of the unstable mode with sweep angles of
$\delta \neq 0$. Figures 17(a) and 17(b) show the growth rate and frequency of the unstable mode with sweep angles of ![]() $0^{\circ }$,
$0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$,
$20^{\circ }$, ![]() $30^{\circ }$ and
$30^{\circ }$ and ![]() $40^{\circ }$. With these curves, it is possible to track the displacement of the most unstable eigenvalue with respect to the sweep angle. The frequency of the mode increases with the sweep and its growth rate decreases. For a sweep angle between
$40^{\circ }$. With these curves, it is possible to track the displacement of the most unstable eigenvalue with respect to the sweep angle. The frequency of the mode increases with the sweep and its growth rate decreases. For a sweep angle between ![]() $40^{\circ }$ and
$40^{\circ }$ and ![]() $50^{\circ }$, the mode becomes stable. The value of
$50^{\circ }$, the mode becomes stable. The value of ![]() $\beta$ for which the growth rate is maximum also slightly decreases as the sweep angle increases. The stability results are consistent with the URANS simulations from § 3. For example, the wavenumber observed in figure 3 in the unswept case is 4.2 with four stall cells. By accounting for the numerical constraint on the wavenumber (the domain size imposes the possible values of
$\beta$ for which the growth rate is maximum also slightly decreases as the sweep angle increases. The stability results are consistent with the URANS simulations from § 3. For example, the wavenumber observed in figure 3 in the unswept case is 4.2 with four stall cells. By accounting for the numerical constraint on the wavenumber (the domain size imposes the possible values of ![]() $\beta$), the actual wavenumber on an infinite domain is expected to be between 3.7 and 4.7. The modes with the maximum growth rate have
$\beta$), the actual wavenumber on an infinite domain is expected to be between 3.7 and 4.7. The modes with the maximum growth rate have ![]() $\beta$ between 4.0 and 4.4, hence within the expected range.
$\beta$ between 4.0 and 4.4, hence within the expected range.

Figure 17. Effect of the sweep angle on the growth rate and frequency of the 3-D unstable mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha = 15.0^{\circ }$; black, stability analysis; red, URANS simulations): (a) growth rate; (b) frequency.
$\alpha = 15.0^{\circ }$; black, stability analysis; red, URANS simulations): (a) growth rate; (b) frequency.
Figure 17(b) also shows the frequency obtained with URANS simulations (red points) and the frequency extrapolated from the trend of the convection speed (see figure 11) and the wavenumber (red lines). The frequencies observed in the URANS computations are well aligned with the frequency obtained with the global linear stability analysis. Hence, the linear stability analyses predict the behaviour of the stall cells.
4.1.4. 2-D wake instability mode
These analyses are now carried for ![]() $\beta = 0$, which corresponds to 2-D analyses. Such analyses are performed for several angles of attack. Figure 18 shows the part of the spectra where unstable modes are found. The mode becomes unstable for an angle of attack between
$\beta = 0$, which corresponds to 2-D analyses. Such analyses are performed for several angles of attack. Figure 18 shows the part of the spectra where unstable modes are found. The mode becomes unstable for an angle of attack between ![]() $16^{\circ }$ and
$16^{\circ }$ and ![]() $17^{\circ }$ for the upper branch (UB) of the lift hysteresis, and is unstable for the entire lower branch (LB). This is consistent with the need to use the SFD technique or a Newton solver to converge the baseflow for angles of attack above
$17^{\circ }$ for the upper branch (UB) of the lift hysteresis, and is unstable for the entire lower branch (LB). This is consistent with the need to use the SFD technique or a Newton solver to converge the baseflow for angles of attack above ![]() $16^{\circ }$, where it was observed that the local time stepping technique failed to converge. Figure 19 shows the eigenmodes for the upper and lower branch of the lift hysteresis at an angle of attack of
$16^{\circ }$, where it was observed that the local time stepping technique failed to converge. Figure 19 shows the eigenmodes for the upper and lower branch of the lift hysteresis at an angle of attack of ![]() $18^{\circ }$. The shape of these modes corresponds to a meandering of the wake which would lead to shedding of vortices in the nonlinear regime. The wavelength of this mode is larger for the lower branch, where the size of the separation is larger. As the angle of attack increases, the size of the separation region becomes larger and the Strouhal number based on the chord length (
$18^{\circ }$. The shape of these modes corresponds to a meandering of the wake which would lead to shedding of vortices in the nonlinear regime. The wavelength of this mode is larger for the lower branch, where the size of the separation is larger. As the angle of attack increases, the size of the separation region becomes larger and the Strouhal number based on the chord length (![]() $St_c$) decreases. However, the Strouhal number based on the frontal height of the separation zone (
$St_c$) decreases. However, the Strouhal number based on the frontal height of the separation zone (![]() $St_l = St_c l = St_c(x_{r}-x_{s})\sin \alpha$) stays constant around 0.2. This Strouhal number definition based on the separation height is inspired from the one of Yon & Katz (Reference Yon and Katz1998) and Zaman, McKinzie & Rumsey (Reference Zaman, McKinzie and Rumsey1989), but adapted to the case where the separation point
$St_l = St_c l = St_c(x_{r}-x_{s})\sin \alpha$) stays constant around 0.2. This Strouhal number definition based on the separation height is inspired from the one of Yon & Katz (Reference Yon and Katz1998) and Zaman, McKinzie & Rumsey (Reference Zaman, McKinzie and Rumsey1989), but adapted to the case where the separation point ![]() $x_{s}$ is not located at the leading edge but somewhere between the leading and the trailing edge; here the flow reattaches at the trailing edge (
$x_{s}$ is not located at the leading edge but somewhere between the leading and the trailing edge; here the flow reattaches at the trailing edge (![]() $x_{r} = 1.0$). This shows that the Strouhal number based on the separation height is the correct one and its value is close to the expected one for vortex shedding (Chabert, Dandois & Garnier Reference Chabert, Dandois and Garnier2016). Hence, for
$x_{r} = 1.0$). This shows that the Strouhal number based on the separation height is the correct one and its value is close to the expected one for vortex shedding (Chabert, Dandois & Garnier Reference Chabert, Dandois and Garnier2016). Hence, for ![]() $\alpha \gtrapprox 16.5^{\circ }$, the 3-D non-oscillating mode coexists with a 2-D wake instability mode, such that an unsteady behaviour should be observed in the URANS simulations. On the other hand, the case
$\alpha \gtrapprox 16.5^{\circ }$, the 3-D non-oscillating mode coexists with a 2-D wake instability mode, such that an unsteady behaviour should be observed in the URANS simulations. On the other hand, the case ![]() $\alpha =15^{\circ }$ was analysed in § 3.1, and consistently with the stability results (only the 3-D steady mode is unstable for this value of
$\alpha =15^{\circ }$ was analysed in § 3.1, and consistently with the stability results (only the 3-D steady mode is unstable for this value of ![]() $\alpha$), the unsteady computation converges toward a steady state. Hence, once again, the results of § 3 are consistent with the stability analyses.
$\alpha$), the unsteady computation converges toward a steady state. Hence, once again, the results of § 3 are consistent with the stability analyses.

Figure 18. Effect of the angle of attack on the spectra of the 2-D unstable mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\delta = 0.0^{\circ }$,
$\delta = 0.0^{\circ }$, ![]() $\beta = 0$).
$\beta = 0$).

Figure 19. Flow visualization of the (a,b) baseflow and (c,d) 2-D unstable mode on the two branches of the lift hysteresis (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha = 18.0^{\circ }$,
$\alpha = 18.0^{\circ }$, ![]() $\delta = 0.0^{\circ }$,
$\delta = 0.0^{\circ }$, ![]() $\beta = 0.0$). (a) The
$\beta = 0.0$). (a) The ![]() $u$ baseflow; upper branch of the lift hysteresis. (b) The
$u$ baseflow; upper branch of the lift hysteresis. (b) The ![]() $u$ baseflow; lower branch of the lift hysteresis. (c) Real part of the
$u$ baseflow; lower branch of the lift hysteresis. (c) Real part of the ![]() $\widehat {\rho u}$ eigenmode; upper branch of the lift hysteresis –
$\widehat {\rho u}$ eigenmode; upper branch of the lift hysteresis – ![]() $St = 0.92$. (d) Real part of the
$St = 0.92$. (d) Real part of the ![]() $\widehat {\rho u}$ eigenmode; lower branch of the lift hysteresis –
$\widehat {\rho u}$ eigenmode; lower branch of the lift hysteresis – ![]() $St = 0.49$.
$St = 0.49$.
4.1.5. Effect of sweep angle on the 2-D wake instability mode
The same stability analyses are now carried out for sweep angles of ![]() $0^{\circ }$,
$0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$ and an angle of attack of
$30^{\circ }$ and an angle of attack of ![]() $18^{\circ }$. Figure 20 shows the value of the growth rate and the Strouhal number of the wake instability mode for values of
$18^{\circ }$. Figure 20 shows the value of the growth rate and the Strouhal number of the wake instability mode for values of ![]() $\beta$ around zero. This unstable mode exists for large wavenumbers
$\beta$ around zero. This unstable mode exists for large wavenumbers ![]() $\beta$. In these figures, modes with a negative value of
$\beta$. In these figures, modes with a negative value of ![]() $\beta$ are shown. These modes can also be seen as modes with positive
$\beta$ are shown. These modes can also be seen as modes with positive ![]() $\beta$ and a negative frequency. One can observe that, as expected, the spectrum is symmetric with respect to the imaginary axis when the sweep angle is null. In this case, the baseflow indeed exhibits a zero spanwise velocity and perturbations may equivalently propagate (in terms of phase, the phase-speed being
$\beta$ and a negative frequency. One can observe that, as expected, the spectrum is symmetric with respect to the imaginary axis when the sweep angle is null. In this case, the baseflow indeed exhibits a zero spanwise velocity and perturbations may equivalently propagate (in terms of phase, the phase-speed being ![]() $v_\phi =\omega /\beta$) towards the inboard (negative
$v_\phi =\omega /\beta$) towards the inboard (negative ![]() $z$,
$z$, ![]() $v_\phi <0$) and outboard (positive
$v_\phi <0$) and outboard (positive ![]() $z$,
$z$, ![]() $v_{\phi }>0$) directions. If a positive sweep is considered, then a positive baseflow velocity in the
$v_{\phi }>0$) directions. If a positive sweep is considered, then a positive baseflow velocity in the ![]() $z$ direction is added and the phase of the perturbation is generally preferentially advected in this direction (in the case of a constant
$z$ direction is added and the phase of the perturbation is generally preferentially advected in this direction (in the case of a constant ![]() $W(x,y)=W$ baseflow velocity, one can show that the frequency
$W(x,y)=W$ baseflow velocity, one can show that the frequency ![]() $\omega$ (respectively, phase-speed
$\omega$ (respectively, phase-speed ![]() $v_\phi$) of a mode just shifts by an amount of
$v_\phi$) of a mode just shifts by an amount of ![]() $\beta W$ (respectively,
$\beta W$ (respectively, ![]() $W$), due to the Doppler shift). Therefore, a positive sweep generally tends to increase the frequency of 3-D perturbations and their phase speed. For exactly 2-D oscillating perturbations (as obtained for the wake instability mode), the phase velocity is infinite (positive or negative), even if sweep is added. It is also seen that, if the perturbations become slightly 3-D (
$W$), due to the Doppler shift). Therefore, a positive sweep generally tends to increase the frequency of 3-D perturbations and their phase speed. For exactly 2-D oscillating perturbations (as obtained for the wake instability mode), the phase velocity is infinite (positive or negative), even if sweep is added. It is also seen that, if the perturbations become slightly 3-D (![]() $\beta \neq 0$), then the outboard propagating 3-D perturbations are slightly more unstable than the inboard propagating ones. Note that the discussion would have been different if the group velocity (
$\beta \neq 0$), then the outboard propagating 3-D perturbations are slightly more unstable than the inboard propagating ones. Note that the discussion would have been different if the group velocity (![]() $v_g=\textrm {d}\omega /\textrm {d}\beta$) was considered, since the group velocity determines the speed of the envelope and fronts of a wave-packet and therefore better accounts for actual propagation of the perturbation: for this a convective/absolute stability analysis should be conducted following Huerre & Monkewitz (Reference Huerre and Monkewitz1990). But this is outside the scope of this paper.
$v_g=\textrm {d}\omega /\textrm {d}\beta$) was considered, since the group velocity determines the speed of the envelope and fronts of a wave-packet and therefore better accounts for actual propagation of the perturbation: for this a convective/absolute stability analysis should be conducted following Huerre & Monkewitz (Reference Huerre and Monkewitz1990). But this is outside the scope of this paper.

Figure 20. Effect of the wavenumber on the 2-D wake instability mode (NACA4412, ![]() $M = 0.2$,
$M = 0.2$, ![]() $Re = 350\,000$,
$Re = 350\,000$, ![]() $\alpha = 18.0^{\circ }$): (a) growth rate; (b) frequency.
$\alpha = 18.0^{\circ }$): (a) growth rate; (b) frequency.
4.2. Transonic buffet
The stability of baseflows obtained in the transonic regime for the OALT25 aerofoil at a Mach number of 0.7352 and a Reynolds number of ![]() $3\times 10^{6}$ is now studied. To begin with, the unswept case is analysed for several angles of attack. Then the effect of the sweep angle is analysed for a constant angle of attack of
$3\times 10^{6}$ is now studied. To begin with, the unswept case is analysed for several angles of attack. Then the effect of the sweep angle is analysed for a constant angle of attack of ![]() $4^{\circ }$. Finally, the 2-D case is analysed.
$4^{\circ }$. Finally, the 2-D case is analysed.
4.2.1. Effect of the angle of attack on the unswept case
Figure 21 shows the spectra obtained for ![]() $\beta = 2{\rm \pi}$ and
$\beta = 2{\rm \pi}$ and ![]() $\beta = 0$ for an angle of attack of
$\beta = 0$ for an angle of attack of ![]() $4^{\circ }$ and a sweep angle of
$4^{\circ }$ and a sweep angle of ![]() $0^{\circ }$. The cases where
$0^{\circ }$. The cases where ![]() $\beta$ tends to 0 are equivalent to the 2-D cases. As one can see, an unstable global mode is found at a Strouhal number of 0.075 when
$\beta$ tends to 0 are equivalent to the 2-D cases. As one can see, an unstable global mode is found at a Strouhal number of 0.075 when ![]() $\beta = 0$ (unsteady 2-D) and a Strouhal number of zero when
$\beta = 0$ (unsteady 2-D) and a Strouhal number of zero when ![]() $\beta = 2{\rm \pi}$ (non-oscillating 3-D). Hence, two unstable eigenmodes are found for these flow conditions. This result is analogous to that at low speed where both a stall cells and a wake instability mode were observed. It should be noted that the spectra are symmetric with respect to the real axis, due to the symmetry of the problem in the non-swept case (a wave may propagate in the positive and negative
$\beta = 2{\rm \pi}$ (non-oscillating 3-D). Hence, two unstable eigenmodes are found for these flow conditions. This result is analogous to that at low speed where both a stall cells and a wake instability mode were observed. It should be noted that the spectra are symmetric with respect to the real axis, due to the symmetry of the problem in the non-swept case (a wave may propagate in the positive and negative ![]() $z$ directions). Thus, an unsteady mode with a negative frequency is also observed. Following this analysis, figure 22(a) shows the effect of the wavenumber
$z$ directions). Thus, an unsteady mode with a negative frequency is also observed. Following this analysis, figure 22(a) shows the effect of the wavenumber ![]() $\beta$ on the growth rate of the non-oscillating unstable mode for several angles of attack. All the analyses are done with a spanwise grid spacing of
$\beta$ on the growth rate of the non-oscillating unstable mode for several angles of attack. All the analyses are done with a spanwise grid spacing of ![]() $0.002$. An analysis similar to the one shown in figure 13 has been carried out. It shows that refining the grid by a factor 100 does not change significantly the results for
$0.002$. An analysis similar to the one shown in figure 13 has been carried out. It shows that refining the grid by a factor 100 does not change significantly the results for ![]() $\beta$ up to 70 and for
$\beta$ up to 70 and for ![]() $\alpha = 4.0$ and
$\alpha = 4.0$ and ![]() $8.0$. It should also be noted that the spanwise grid spacing used in the URANS simulations (
$8.0$. It should also be noted that the spanwise grid spacing used in the URANS simulations (![]() $\varDelta _z = 0.035$) is properly converged for the range of unstable wavenumbers at an angle of attack of
$\varDelta _z = 0.035$) is properly converged for the range of unstable wavenumbers at an angle of attack of ![]() $4^{\circ }$. As for the subsonic stall case, a bump in the growth rate is observed for a medium wavelength around
$4^{\circ }$. As for the subsonic stall case, a bump in the growth rate is observed for a medium wavelength around ![]() $\beta =6.0$ for the low angle of attack. However, a second bump with a maximum growth rate at higher
$\beta =6.0$ for the low angle of attack. However, a second bump with a maximum growth rate at higher ![]() $\beta$ is obtained as the angle of attack increases. For the particular angle of attack of
$\beta$ is obtained as the angle of attack increases. For the particular angle of attack of ![]() $4.25^{\circ }$, the two bumps can clearly be distinguished. These results are similar to those obtained by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) and Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a) on the OAT15A aerofoil, where an intermediate-wavelength mode and a short-wavelength one were reported. Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) suspected that the short-wavelength might be too small to be relevant to a RANS framework. Figure 22(b) shows the spectra obtained for several
$4.25^{\circ }$, the two bumps can clearly be distinguished. These results are similar to those obtained by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) and Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a) on the OAT15A aerofoil, where an intermediate-wavelength mode and a short-wavelength one were reported. Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) suspected that the short-wavelength might be too small to be relevant to a RANS framework. Figure 22(b) shows the spectra obtained for several ![]() $\beta$ in-between the intermediate-wavelength and short-wavelength bumps at an angle of attack of
$\beta$ in-between the intermediate-wavelength and short-wavelength bumps at an angle of attack of ![]() $4.25^{\circ }$. One can notice that there is only one unstable eigenvalue for each
$4.25^{\circ }$. One can notice that there is only one unstable eigenvalue for each ![]() $\beta$. We do not observe a 2-mode switching, where the originally unstable mode would become stable while a previously stable mode would become unstable. This shows that these two bumps are in fact the same mode and not two separate modes which could have been both unstable for some angles of attack. Although this does not discard arguments on the physical relevance of the low-wavelength mode, the physical mechanism responsible for both these modes is the same. Figure 23 shows the
$\beta$. We do not observe a 2-mode switching, where the originally unstable mode would become stable while a previously stable mode would become unstable. This shows that these two bumps are in fact the same mode and not two separate modes which could have been both unstable for some angles of attack. Although this does not discard arguments on the physical relevance of the low-wavelength mode, the physical mechanism responsible for both these modes is the same. Figure 23 shows the ![]() $C_L-\alpha$ curve of the steady baseflow of the OALT25. As it is the case for the NACA4412, the angles of attack for which the linear stability shows an unstable 3-D mode corresponds to angles of attack where the
$C_L-\alpha$ curve of the steady baseflow of the OALT25. As it is the case for the NACA4412, the angles of attack for which the linear stability shows an unstable 3-D mode corresponds to angles of attack where the ![]() $C_L-\alpha$ slope is negative, in agreement with Gross et al. (Reference Gross, Fasel and Gaster2015). However, the slope of this curve around
$C_L-\alpha$ slope is negative, in agreement with Gross et al. (Reference Gross, Fasel and Gaster2015). However, the slope of this curve around ![]() $\alpha = 4^{\circ }$ and the most unstable wavelength does not match the predictions of the model of Gross et al. (Reference Gross, Fasel and Gaster2015). If one takes the slope between
$\alpha = 4^{\circ }$ and the most unstable wavelength does not match the predictions of the model of Gross et al. (Reference Gross, Fasel and Gaster2015). If one takes the slope between ![]() $5^{\circ }$ and
$5^{\circ }$ and ![]() $9^{\circ }$, wavenumbers of 6.5 and 4.13 are predicted with the discrete and continuous models, respectively. The unstable mode has a wavenumber
$9^{\circ }$, wavenumbers of 6.5 and 4.13 are predicted with the discrete and continuous models, respectively. The unstable mode has a wavenumber ![]() $\beta =6.0$, which is in the predicted range. However, as was the case for the subsonic mode, changes in the
$\beta =6.0$, which is in the predicted range. However, as was the case for the subsonic mode, changes in the ![]() $C_L-\alpha$ slope are not associated with changes in the wavelength predicted by stability analyses.
$C_L-\alpha$ slope are not associated with changes in the wavelength predicted by stability analyses.

Figure 21. Eigenspectrum in 2-D and 3-D (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha = 4.0^{\circ }$,
$\alpha = 4.0^{\circ }$, ![]() $\delta = 0.0^{\circ }$): (a)
$\delta = 0.0^{\circ }$): (a) ![]() $\beta = 0$; (b)
$\beta = 0$; (b) ![]() $\beta = 2{\rm \pi}$.
$\beta = 2{\rm \pi}$.

Figure 22. Effect of the wavenumber ![]() $\beta$ on the 3-D mode (OALT25,
$\beta$ on the 3-D mode (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\delta = 0.0^{\circ }$): (a) growth rate; (b) eigenspectrum (
$\delta = 0.0^{\circ }$): (a) growth rate; (b) eigenspectrum (![]() $\alpha = 4.25^{\circ }$).
$\alpha = 4.25^{\circ }$).

Figure 23. Lift coefficient of the steady 2-D flow (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\delta =0.0^{\circ }$).
$\delta =0.0^{\circ }$).
4.2.2. Sweep angle effect at  $\alpha =4^{\circ }$
$\alpha =4^{\circ }$
Figure 24(a) shows the effect of the sweep angle on the growth rate of the 3-D mode. As for the subsonic stall, the growth rate of the 3-D mode decreases as the sweep angle increases. From this trend, the mode becomes stable for a sweep angle slightly higher than ![]() $40^{\circ }$ and is stable at
$40^{\circ }$ and is stable at ![]() $50^{\circ }$. Also, the wavenumber for which the mode is the most unstable slightly decreases when the sweep angle increases. However, the wavenumber obtained in the swept URANS (
$50^{\circ }$. Also, the wavenumber for which the mode is the most unstable slightly decreases when the sweep angle increases. However, the wavenumber obtained in the swept URANS (![]() $\beta = 2.09$) simulations is not unstable in the stability analysis. It will be shown in § 5 that this discrepancy is due to nonlinear effects. Figure 24(b) shows the Strouhal number of the 3-D mode for sweep angles
$\beta = 2.09$) simulations is not unstable in the stability analysis. It will be shown in § 5 that this discrepancy is due to nonlinear effects. Figure 24(b) shows the Strouhal number of the 3-D mode for sweep angles ![]() $\delta$ of
$\delta$ of ![]() $0^{\circ }$,
$0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$,
$20^{\circ }$, ![]() $30^{\circ }$ and
$30^{\circ }$ and ![]() $40^{\circ }$ for a range of
$40^{\circ }$ for a range of ![]() $\beta$. As expected, the frequency increases with
$\beta$. As expected, the frequency increases with ![]() $\beta$ (smaller spanwise structures) and with the sweep angles (higher convection speed). The URANS results (red points) and the frequencies extrapolated from the convection speed of the URANS simulations (red lines) are plotted on this graph as well. The frequencies obtained by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) on the OAT15A aerofoil are also plotted. For the latter, the values have been corrected for the fact that the reference speed is taken as the speed normal to the leading edge instead of the free stream velocity. These curves match the stability results, even though the work of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) was performed on a different aerofoil. Hence, the linear stability is able to predict the convection speed of the cells, but because of the discrepancy on the wavenumber with respect to the URANS simulations, the frequency of the simulations is incorrectly predicted by the stability analyses. This is due to nonlinear effects that shift the wavelength of the cells (see § 5).
$\beta$ (smaller spanwise structures) and with the sweep angles (higher convection speed). The URANS results (red points) and the frequencies extrapolated from the convection speed of the URANS simulations (red lines) are plotted on this graph as well. The frequencies obtained by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) on the OAT15A aerofoil are also plotted. For the latter, the values have been corrected for the fact that the reference speed is taken as the speed normal to the leading edge instead of the free stream velocity. These curves match the stability results, even though the work of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) was performed on a different aerofoil. Hence, the linear stability is able to predict the convection speed of the cells, but because of the discrepancy on the wavenumber with respect to the URANS simulations, the frequency of the simulations is incorrectly predicted by the stability analyses. This is due to nonlinear effects that shift the wavelength of the cells (see § 5).

Figure 24. Effect of the sweep angle on the 3-D mode (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha = 4.0^{\circ }$; black, stability analysis; red, URANS simulations): (a) growth rate; (b) frequency.
$\alpha = 4.0^{\circ }$; black, stability analysis; red, URANS simulations): (a) growth rate; (b) frequency.
Figure 25 shows the baseflow with a sweep angle of ![]() $30^{\circ }$ and the real part of the
$30^{\circ }$ and the real part of the ![]() $\widehat {\rho e}$ 2-D and 3-D unstable modes. The two unstable modes are mostly located in the vicinity of the shock wave and in the shear layer. The 2-D mode displays the shape of the unstable mode reported in the 2-D buffet studies of Crouch et al. (Reference Crouch, Garbaruk, Magidov and Travin2009) and Sartor et al. (Reference Sartor, Mettot and Sipp2015). The 3-D mode has spanwise fluctuations in the shock foot and trailing edge region. Those are regions of flow separation. The shape of this mode is in line with the observations of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) and Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a).
$\widehat {\rho e}$ 2-D and 3-D unstable modes. The two unstable modes are mostly located in the vicinity of the shock wave and in the shear layer. The 2-D mode displays the shape of the unstable mode reported in the 2-D buffet studies of Crouch et al. (Reference Crouch, Garbaruk, Magidov and Travin2009) and Sartor et al. (Reference Sartor, Mettot and Sipp2015). The 3-D mode has spanwise fluctuations in the shock foot and trailing edge region. Those are regions of flow separation. The shape of this mode is in line with the observations of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) and Paladini et al. (Reference Paladini, Beneddine, Dandois, Sipp and Robinet2019a).

Figure 25. Flow visualization of the (a) baseflow, (b,c) 2-D and 3-D unstable modes (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha = 4.0^{\circ }$,
$\alpha = 4.0^{\circ }$, ![]() $\delta =30^{\circ }$). (a) The
$\delta =30^{\circ }$). (a) The ![]() ${\rho e}/{\rho e_{\infty }}$ baseflow. (b) Real part of the 2-D
${\rho e}/{\rho e_{\infty }}$ baseflow. (b) Real part of the 2-D ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode ![]() $(\beta = 0.0)$ –
$(\beta = 0.0)$ – ![]() $St = 0.075$. (c) Real part of the 3-D
$St = 0.075$. (c) Real part of the 3-D ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode
${\widehat {\rho e}}/{\rho e_{\infty }}$ eigenmode ![]() $(\beta = 5.0)$ –
$(\beta = 5.0)$ – ![]() $St = 0.356$.
$St = 0.356$.
4.2.3. 2-D buffet mode
Figure 26 shows the portion of the spectrum where the unsteady 2-D mode is located. One interesting point is that the unstable unsteady mode (2-D buffet) is only observed over a range of angles of attack between ![]() $3.75^{\circ }$ and
$3.75^{\circ }$ and ![]() $6.0^{\circ }$. The 3-D buffet mode becomes unstable at an angle of attack around
$6.0^{\circ }$. The 3-D buffet mode becomes unstable at an angle of attack around ![]() $3.75^{\circ }$ as well. However, it does not become stable again at higher angles of attack in the range studied in this paper. Hence, this mode is observed for transonic stall conditions, where the 2-D buffet is stable. Although this flow condition is an extreme one, which is not expected to be reached for a civil aircraft, this result suggests that the 3-D buffet can exist without the 2-D buffet phenomenon occurring. This is similar to the fact that the stall cells can be obtained without the wake instability mode.
$3.75^{\circ }$ as well. However, it does not become stable again at higher angles of attack in the range studied in this paper. Hence, this mode is observed for transonic stall conditions, where the 2-D buffet is stable. Although this flow condition is an extreme one, which is not expected to be reached for a civil aircraft, this result suggests that the 3-D buffet can exist without the 2-D buffet phenomenon occurring. This is similar to the fact that the stall cells can be obtained without the wake instability mode.

Figure 26. Effect of the angle of attack on the 2-D unstable mode (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\delta =0.0^{\circ }$,
$\delta =0.0^{\circ }$, ![]() $\beta = 0.0$).
$\beta = 0.0$).
Finally, it is possible to analyse the effect of ![]() $\beta$ on the 2-D buffet mode. Figure 27 shows this effect on the growth rate and the frequency for several sweep angles. These are modes with very large wavelengths of at least 10 chord lengths. It should be noted that the spectrum is symmetric with respect to the real axis for
$\beta$ on the 2-D buffet mode. Figure 27 shows this effect on the growth rate and the frequency for several sweep angles. These are modes with very large wavelengths of at least 10 chord lengths. It should be noted that the spectrum is symmetric with respect to the real axis for ![]() $\delta = 0^{\circ }$. But it is not the case for swept wings. Hence, the effect of
$\delta = 0^{\circ }$. But it is not the case for swept wings. Hence, the effect of ![]() $\beta$ on the growth rate and frequency is not the same for the positive and negative frequency. The 2-D buffet mode is more stable as the sweep angle increases. This is consistent with the fact that the buffet amplitude is lower when the sweep angle increases as shown in figure 6. Also,
$\beta$ on the growth rate and frequency is not the same for the positive and negative frequency. The 2-D buffet mode is more stable as the sweep angle increases. This is consistent with the fact that the buffet amplitude is lower when the sweep angle increases as shown in figure 6. Also, ![]() $\beta$ has an effect on the growth rate. Such results are similar to those of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) for the OAT15A aerofoil. However, they did not report the peak in the growth rate between
$\beta$ has an effect on the growth rate. Such results are similar to those of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) for the OAT15A aerofoil. However, they did not report the peak in the growth rate between ![]() $\beta = \pm 0.5$ and
$\beta = \pm 0.5$ and ![]() $\beta = \pm 0.6$. As verification, the case of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) has been executed with the numerical set-up of the present paper with similar results (see the Appendix). Hence, these peaks are not caused by any problem related to the stability method or its implementation, and their existence remains unexplained for the OALT25 aerofoil. Also, the inboard propagating modes (
$\beta = \pm 0.6$. As verification, the case of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) has been executed with the numerical set-up of the present paper with similar results (see the Appendix). Hence, these peaks are not caused by any problem related to the stability method or its implementation, and their existence remains unexplained for the OALT25 aerofoil. Also, the inboard propagating modes (![]() $\beta < 0$) are more unstable than the inboard propagating modes when the wing is swept. This behaviour is opposite to the tendency of the wake instability mode (figure 20).
$\beta < 0$) are more unstable than the inboard propagating modes when the wing is swept. This behaviour is opposite to the tendency of the wake instability mode (figure 20).

Figure 27. Effect of the wavenumber on the 2-D buffet mode (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha = 4.0^{\circ }$): (a) growth rate; (b) frequency.
$\alpha = 4.0^{\circ }$): (a) growth rate; (b) frequency.
4.3. Partial conclusion
The global linear stability analyses predict two unstable modes in the subsonic stall conditions. One which can be related to the stall cells (3-D) and the other to the shedding of vortices (2-D). The wavenumber, convection speed and frequency of the 3-D mode are consistent with the URANS results presented in § 3.1. The 2-D mode has the expected frequency with a Strouhal number based on the separation height of 0.2. However, multiple frequency and size of the vortices are identified for some flow conditions since multiple steady-state baseflows are found.
Two unstable modes are also identified in the transonic buffet regime. The first is associated with the 2-D buffet instability at a frequency around 0.07. The second leads to spanwise flow structures which can be associated with buffet cells. There is a discrepancy between the wavenumber predicted by the stability analyses and the URANS simulations. However, the frequency of this mode is that of 3-D structures convected at the same speed as those in the URANS simulations.
For the case of the NACA4412, two solution branches have been analysed. Such multiple solutions have been observed in the literature before (Wales et al. Reference Wales, Gaitonde, Jones, Avitabile and Champneys2012; Busquet et al. Reference Busquet, Marquet, Richez, Juniper and Sipp2017). Multiple baseflows were not found for the OALT25 aerofoil, however, they cannot be ruled out. Nevertheless such multiple solutions do not seem to be related to the occurrence of stall cells since an unstable stall cell mode is found at angles of attack where only one baseflow is found.
5. From linear to nonlinear regime
Section 3 analysed the nonlinear saturated regime. This was done by starting the solution from a non-converged RANS solution. Section 4 studied the behaviour of the solution in the linear regime around a fully converged RANS solution. This section investigates the transient between the two regimes. To do so, the steady baseflows are extruded to get a 3-D initial condition, and the URANS solver is run from this initial solution.
5.1. NACA4412 at  $\alpha =15^{\circ }$ and
$\alpha =15^{\circ }$ and  $\delta =0^{\circ }$
$\delta =0^{\circ }$
Figure 28 shows how the solution diverges from the steady 2-D baseflow towards the solution shown in § 3. As one can see, the flow diverges with four regular stall cells and the flow topology converges to the one shown previously. This corresponds to a wavenumber ![]() $\beta =4.2$ which is the wavenumber with the maximum growth rate allowable on this grid (see figure 17a), since the number of cells is constrained by the size of the domain. This result is consistent with the stability analysis.
$\beta =4.2$ which is the wavenumber with the maximum growth rate allowable on this grid (see figure 17a), since the number of cells is constrained by the size of the domain. This result is consistent with the stability analysis.

Figure 28. Snapshots of the surface pressure coefficient and skin friction lines of the URANS simulations (NACA4412, ![]() $M$ = 0.2,
$M$ = 0.2, ![]() $Re$ = 350 000,
$Re$ = 350 000, ![]() $\alpha = 15.0^{\circ }$,
$\alpha = 15.0^{\circ }$, ![]() $\delta = 0^{\circ }$,
$\delta = 0^{\circ }$, ![]() $L_z = 6$): (a)
$L_z = 6$): (a) ![]() $t = 68$; (b)
$t = 68$; (b) ![]() $t = 85$; (c)
$t = 85$; (c) ![]() $t = 102$.
$t = 102$.
5.2. OALT25 at  $\alpha =4^{\circ }$ and
$\alpha =4^{\circ }$ and  $\delta =20^{\circ }$
$\delta =20^{\circ }$
Similar analyses can be done for the transonic buffet case. Figure 29 shows three time samples of the URANS simulation with the extruded baseflow as the initial state and a sweep angle of ![]() $20^{\circ }$. One can observe that three-dimensionality occurs with the appearance of six buffet cells (
$20^{\circ }$. One can observe that three-dimensionality occurs with the appearance of six buffet cells (![]() $\beta = 6.28$), in agreement with the largest growth rate allowable for this computational domain (see figure 24a). However, the wavelength progressively increases towards the value observed in § 3. This shows that the stability analysis predicts the initial bifurcation from the baseflow to the presence of buffet cells. However, some nonlinear effects are responsible for the shift of wavelength observed such that the saturated regime is different from the value predicted by the linear model.
$\beta = 6.28$), in agreement with the largest growth rate allowable for this computational domain (see figure 24a). However, the wavelength progressively increases towards the value observed in § 3. This shows that the stability analysis predicts the initial bifurcation from the baseflow to the presence of buffet cells. However, some nonlinear effects are responsible for the shift of wavelength observed such that the saturated regime is different from the value predicted by the linear model.

Figure 29. Snapshots of the surface pressure coefficient and skin friction lines of the URANS simulations (OALT25, ![]() $M = 0.7352$,
$M = 0.7352$, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha = 4.0^{\circ }$,
$\alpha = 4.0^{\circ }$, ![]() $\delta = 20^{\circ }$,
$\delta = 20^{\circ }$, ![]() $L_z = 6$): (a)
$L_z = 6$): (a) ![]() $t = 68$; (b)
$t = 68$; (b) ![]() $t = 74$; (c)
$t = 74$; (c) ![]() $t = 89$.
$t = 89$.
6. Link between stall and buffet cells
Previous solutions were obtained for two different aerofoils, at two Reynolds numbers. To clearly establish a link between buffet cells and stall cells, the stability analyses are now carried out for an NACA0012 at a Reynolds number of ![]() $1\times 10^{7}$ and the unstable eigenvalues are tracked from the low-speed regime to the transonic one. The NACA0012 aerofoil at a high Reynolds number is selected since a trailing edge stall is expected at low Mach number and transonic buffet at higher speed (McDevitt & Okuno Reference McDevitt and Okuno1985). As the Mach number increases, the angle of attack is decreased in order to recover the stall and buffet onset conditions. Figure 30 shows the baseflow obtained for Mach numbers from 0.2 to 0.72. The flow topology at a Mach number of 0.2 is the one of a subsonic stall. Similar topology, but with a stronger flow acceleration and a weak shock wave near the leading edge are obtained for Mach numbers of 0.3 and 0.4. However, for Mach numbers higher than 0.5, the shock wave is stronger and flow separation occurs at the shock foot.
$1\times 10^{7}$ and the unstable eigenvalues are tracked from the low-speed regime to the transonic one. The NACA0012 aerofoil at a high Reynolds number is selected since a trailing edge stall is expected at low Mach number and transonic buffet at higher speed (McDevitt & Okuno Reference McDevitt and Okuno1985). As the Mach number increases, the angle of attack is decreased in order to recover the stall and buffet onset conditions. Figure 30 shows the baseflow obtained for Mach numbers from 0.2 to 0.72. The flow topology at a Mach number of 0.2 is the one of a subsonic stall. Similar topology, but with a stronger flow acceleration and a weak shock wave near the leading edge are obtained for Mach numbers of 0.3 and 0.4. However, for Mach numbers higher than 0.5, the shock wave is stronger and flow separation occurs at the shock foot.

Figure 30. Baseflow Mach number field at several Mach numbers and angle of attack (NACA0012, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\delta = 0^{\circ }$): (a)
$\delta = 0^{\circ }$): (a) ![]() $M = 0.2$ and
$M = 0.2$ and ![]() $\alpha = 18.2^{\circ }$; (b)
$\alpha = 18.2^{\circ }$; (b) ![]() $M = 0.3$ and
$M = 0.3$ and ![]() $\alpha = 15.0^{\circ }$; (c)
$\alpha = 15.0^{\circ }$; (c) ![]() $M = 0.4$ and
$M = 0.4$ and ![]() $\alpha = 12.0^{\circ }$; (d)
$\alpha = 12.0^{\circ }$; (d) ![]() $M = 0.5$ and
$M = 0.5$ and ![]() $\alpha = 7.9^{\circ }$; (e)
$\alpha = 7.9^{\circ }$; (e) ![]() $M = 0.6$ and
$M = 0.6$ and ![]() $\alpha = 6.15^{\circ }$; ( f)
$\alpha = 6.15^{\circ }$; ( f) ![]() $M = 0.72$ and
$M = 0.72$ and ![]() $\alpha = 3.5^{\circ }$.
$\alpha = 3.5^{\circ }$.
Figure 31(a) shows the growth rate of the 3-D unstable mode. For the low-speed cases, the maximum growth rate is found for ![]() $\beta$ around 4. This result is similar to the previous observations on the NACA4412 aerofoil, even though the Reynolds number is by far larger. For Mach numbers between 0.4 and 0.5, the flow topology changes significantly and so does the value of the most amplified
$\beta$ around 4. This result is similar to the previous observations on the NACA4412 aerofoil, even though the Reynolds number is by far larger. For Mach numbers between 0.4 and 0.5, the flow topology changes significantly and so does the value of the most amplified ![]() $\beta$. In this case
$\beta$. In this case ![]() $\beta$ is greater than 170. These are 3-D modes with a very small wavelength. As the Mach number increases, the value of
$\beta$ is greater than 170. These are 3-D modes with a very small wavelength. As the Mach number increases, the value of ![]() $\beta$ for which the 3-D mode is found decreases to reach a value of 100 for a Mach number of 0.6 and 50 for a Mach number of 0.72. This is consistent with the results of Crouch et al. (Reference Crouch, Garbaruk and Strelets2018), who reported only a short-wavelength mode for the NACA0012 aerofoil and not the intermediate-wavelength mode as on the OAT15A and OALT25. One major difference between the NACA0012 and the OALT25 aerofoils is the fact that there is only a flow separation in the shock foot area for the NACA0012, while the flow over the OALT25 also separates at the trailing edge. Figure 31(b) shows the growth rate of the 3-D mode normalized by the height of the separation
$\beta$ for which the 3-D mode is found decreases to reach a value of 100 for a Mach number of 0.6 and 50 for a Mach number of 0.72. This is consistent with the results of Crouch et al. (Reference Crouch, Garbaruk and Strelets2018), who reported only a short-wavelength mode for the NACA0012 aerofoil and not the intermediate-wavelength mode as on the OAT15A and OALT25. One major difference between the NACA0012 and the OALT25 aerofoils is the fact that there is only a flow separation in the shock foot area for the NACA0012, while the flow over the OALT25 also separates at the trailing edge. Figure 31(b) shows the growth rate of the 3-D mode normalized by the height of the separation ![]() $h_s$. By using this normalization, the maximum growth rates are located around
$h_s$. By using this normalization, the maximum growth rates are located around ![]() $\beta h_s\approx 0.25$ for every Mach number, which shows that this is the correct scaling length for this 3-D mode. The amplification factors are normalized by the same length scale. Two other scalings were attempted, namely a scaling by the separation length
$\beta h_s\approx 0.25$ for every Mach number, which shows that this is the correct scaling length for this 3-D mode. The amplification factors are normalized by the same length scale. Two other scalings were attempted, namely a scaling by the separation length ![]() $l_s$ and by the projection of the separation length in the direction normal to the inflow
$l_s$ and by the projection of the separation length in the direction normal to the inflow ![]() $l$ (see supplementary material to this article). By using the separation length, a proper scaling is obtained for the subsonic and transonic cases separately. But this scaling does not hold between these two flow regimes.
$l$ (see supplementary material to this article). By using the separation length, a proper scaling is obtained for the subsonic and transonic cases separately. But this scaling does not hold between these two flow regimes.

Figure 31. Effect of the Mach number and angle of attack on the growth rate of the 3-D mode (NACA0012, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\delta = 0^{\circ }$). (a) Normalized by the chord length. (b) Normalized by the separation height.
$\delta = 0^{\circ }$). (a) Normalized by the chord length. (b) Normalized by the separation height.
Figure 32 displays the eigenvectors at these flow conditions, indicating that the unstable modes are all located in the vicinity of the flow separation. For a Mach number larger than 0.5, a shock wave occurs in the baseflow. In these cases, the eigenmode reaches high values at the separation point and further downstream, but it does not propagate in the supersonic region upstream of the shock wave, contrary to subsonic cases.

Figure 32. Flow visualization of the 3-D ![]() ${\widehat {\rho e}}/{\rho e_{\infty }}$ unstable mode (NACA0012,
${\widehat {\rho e}}/{\rho e_{\infty }}$ unstable mode (NACA0012, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\delta = 0^{\circ }$): (a)
$\delta = 0^{\circ }$): (a) ![]() $M = 0.2$ and
$M = 0.2$ and ![]() $\alpha = 18.2^{\circ }$ –
$\alpha = 18.2^{\circ }$ – ![]() $St = 0.0$; (b)
$St = 0.0$; (b) ![]() $M = 0.3$ and
$M = 0.3$ and ![]() $\alpha = 15.0^{\circ }$ –
$\alpha = 15.0^{\circ }$ – ![]() $St = 0.0$; (c)
$St = 0.0$; (c) ![]() $M = 0.4$ and
$M = 0.4$ and ![]() $\alpha = 12.0^{\circ }$ –
$\alpha = 12.0^{\circ }$ – ![]() $St = 0.0$; (d)
$St = 0.0$; (d) ![]() $M = 0.5$ and
$M = 0.5$ and ![]() $\alpha = 7.9^{\circ }$ –
$\alpha = 7.9^{\circ }$ – ![]() $St = 0.0$; (e)
$St = 0.0$; (e) ![]() $M = 0.6$ and
$M = 0.6$ and ![]() $\alpha = 6.15^{\circ }$ –
$\alpha = 6.15^{\circ }$ – ![]() $St = 0.0$; ( f)
$St = 0.0$; ( f) ![]() $M = 0.72$ and
$M = 0.72$ and ![]() $\alpha = 3.5^{\circ }$ –
$\alpha = 3.5^{\circ }$ – ![]() $St = 0.0$.
$St = 0.0$.
In the case of the OALT25 aerofoil, the 3-D and 2-D modes become unstable around the same angle of attack. This may suggest that the two unstable modes are somewhat linked. For this reason, the angle of attack at which an unstable 2-D buffet mode appears has been searched for the NACA0012 at ![]() $M = 0.72$. Figure 33 shows the region of the spectra around which the unstable mode is expected. An unstable mode is present at an angle of attack of
$M = 0.72$. Figure 33 shows the region of the spectra around which the unstable mode is expected. An unstable mode is present at an angle of attack of ![]() $4.5^{\circ }$, but this mode is stable for lower angles of attack. This indicates that the 3-D buffet mode can be unstable (see unstable branch at
$4.5^{\circ }$, but this mode is stable for lower angles of attack. This indicates that the 3-D buffet mode can be unstable (see unstable branch at ![]() $\alpha =3.5^{\circ }$ in figure 31) without an underlying 2-D mode (figure 33).
$\alpha =3.5^{\circ }$ in figure 31) without an underlying 2-D mode (figure 33).

Figure 33. Effect of the angle of attack on the 2-D unstable mode (NACA0012, ![]() $M = 0.72$,
$M = 0.72$, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\delta =0.0^{\circ }$,
$\delta =0.0^{\circ }$, ![]() $\beta = 0.0$).
$\beta = 0.0$).
As it is the case for the NACA4412 and the OALT25 aerofoils, 3-D modes with a non-zero frequency are obtained when a sweep angle is added. Figure 34 shows the frequency of the 3-D modes with sweep angles of ![]() $\delta =0^{\circ }$,
$\delta =0^{\circ }$, ![]() $10^{\circ }$,
$10^{\circ }$, ![]() $20^{\circ }$ and
$20^{\circ }$ and ![]() $30^{\circ }$, and the scaling found previously. The angles of attack are slightly increased in comparison with previous results on the NACA0012 because the sweep angle has a stabilizing effect. As one can see, the frequency of these unstable modes is still proportional to the spanwise velocity. Moreover, the proportionality coefficients found for the NACA4412 and the OALT25 still hold for the NACA0012 in subsonic and transonic regimes, respectively.
$30^{\circ }$, and the scaling found previously. The angles of attack are slightly increased in comparison with previous results on the NACA0012 because the sweep angle has a stabilizing effect. As one can see, the frequency of these unstable modes is still proportional to the spanwise velocity. Moreover, the proportionality coefficients found for the NACA4412 and the OALT25 still hold for the NACA0012 in subsonic and transonic regimes, respectively.

Figure 34. Effect of the sweep angle on the 3-D mode frequency: (a) subsonic (NACA0012, ![]() $M=0.2$,
$M=0.2$, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\alpha = 18.5^{\circ }$); (b) transonic (NACA0012,
$\alpha = 18.5^{\circ }$); (b) transonic (NACA0012, ![]() $M=0.72$,
$M=0.72$, ![]() $Re = 10^{7}$,
$Re = 10^{7}$, ![]() $\alpha = 4.5^{\circ }$).
$\alpha = 4.5^{\circ }$).
Hence it is possible to follow a single and same unstable mode that represents stall cells in the subsonic regime and buffet cells in the transonic flow regime. This branch of modes exhibits the same features as those found separately for the NACA4412 and the OALT25 aerofoils. This also shows that the stall cell mode is present both at an intermediate (350 000) and high (![]() $1\times 10^{7}$) Reynolds number. Moreover, a scaling by the height of the separation bubble is proposed to link the size of the stall cells to that of the buffet cells.
$1\times 10^{7}$) Reynolds number. Moreover, a scaling by the height of the separation bubble is proposed to link the size of the stall cells to that of the buffet cells.
7. Conclusion
Three-dimensional flows over infinite swept configurations were obtained using URANS simulations for low-speed stall and transonic buffet conditions. The observed stall/buffet cells are steady for unswept wings, and convected in the spanwise direction when the wing is swept. This induces a frequency which can be related to the distance between two cells and their convection speed. In the case of the subsonic stall, this unsteadiness dominates the flow. However, it is superimposed to the 2-D buffet phenomenon at high-speed.
Global linear stability analyses of 2.5-D baseflows were carried out for subsonic stall and transonic buffet. An unstable 3-D mode was observed in both flow conditions. The frequency of the latter is null for unswept wings and becomes unsteady as the sweep angle is increased. The frequencies and wavelength of stall cells obtained with stability analysis are in line with the observation of the URANS simulations. However, discrepancies between the wavelength of buffet cells and the global mode with the largest growth rate are observed. Nevertheless, the frequency of the unstable modes is consistent with that of structures convected at the convection speed observed in the URANS simulations. A mode consistent with a 2-D vortex-shedding in subsonic stall conditions was found, as well as a 2-D buffet mode in transonic buffet conditions. The 2-D vortex shedding is not observed in the URANS simulations because the angle of attack is lower than the one for the onset of this unstable mode. A similar condition where the buffet cell mode is present but not the 2-D buffet mode might allow us to obtain steady buffet cells on an unswept wing.
Nonlinear flow simulations starting from the baseflows effectively shows that the flows diverge following the shapes identified in the stability analyses. In the case of the subsonic stall, the number of cells predicted in the stability analyses stay constant in the nonlinear regime. However, the solution of transonic buffet over swept wings diverges towards buffet cells with a lower wavenumber after the appearance of spanwise flow structures of the length identified with the stability analyses, possibly because of nonlinear effects.
Finally, results of the stability analyses allow us to follow the angle of onset of a 3-D mode from the low speed to the transonic flow regime. This study was done on an NACA0012 aerofoil at a Reynolds number of ![]() $1\times 10^{7}$. Although the wavelength of this mode varies greatly with the Mach number, using the separation height as the reference length allows us to centre the non-dimensional wavenumber around a value
$1\times 10^{7}$. Although the wavelength of this mode varies greatly with the Mach number, using the separation height as the reference length allows us to centre the non-dimensional wavenumber around a value ![]() $\beta h_s \approx 0.25$. This result reinforces the conclusion that the two phenomena are the same and are related to the occurrence of flow separation. Also, the 3-D mode is identified at an angle of attack lower than the 2-D buffet onset angle. This shows that the buffet cells associated with 3-D buffet can be observed without the presence of the 2-D buffet.
$\beta h_s \approx 0.25$. This result reinforces the conclusion that the two phenomena are the same and are related to the occurrence of flow separation. Also, the 3-D mode is identified at an angle of attack lower than the 2-D buffet onset angle. This shows that the buffet cells associated with 3-D buffet can be observed without the presence of the 2-D buffet.
Hence, this paper provides evidence that the buffet cells and the stall cells are in fact the same flow instability. Even though it is convenient to describe the 3-D mode in buffet condition as a 3-D buffet phenomenon in the context of applied aerodynamics, one can show that this mode is oscillatory only when the wings are swept. Moreover, the physical mechanisms involved in the 2-D buffet and the buffet cells are different. As such, one can question the accuracy of naming the so-called buffet cells as 3-D buffet and not just as stall cells.
Acknowledgements
Parts of this paper were presented at the 54th 3AF International Conference AERO2019 (FP63-AERO2019-plante). This work is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). Part of this work made use of the GENCI CINES facilities (Grant DARI no. A0042A10423).
Declaration of interests
The authors report no conflict of interest.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2020.848.
Appendix. OAT15A analysis
As verification for the implementation of the method proposed by Schmid et al. (Reference Schmid, de Pando and Peake2017), we have carried out a global linear stability analysis of transonic buffet of an OAT15A aerofoil in the same regime as in Crouch et al. (Reference Crouch, Garbaruk and Strelets2019). A grid with the same property and the same numerical set-up as the ones used for the OALT25 aerofoil are used. Figure 35 shows the growth rate and the frequency of the 2-D mode with respect to ![]() $\beta$. The results of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) are also presented. One can observe that the frequencies and growth rates are close to the values found by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019). The trend with respect to the wavenumber is also the same. This agreement verifies the method used in this paper.
$\beta$. The results of Crouch et al. (Reference Crouch, Garbaruk and Strelets2019) are also presented. One can observe that the frequencies and growth rates are close to the values found by Crouch et al. (Reference Crouch, Garbaruk and Strelets2019). The trend with respect to the wavenumber is also the same. This agreement verifies the method used in this paper.

Figure 35. Effect of the wavenumber of the 2-D buffet mode (OAT15A, ![]() $Re = 3\times 10^{6}$,
$Re = 3\times 10^{6}$, ![]() $\alpha =3.5^{\circ }$,
$\alpha =3.5^{\circ }$, ![]() $\delta = 0^{\circ }$): (a) growth rate; (b) frequency.
$\delta = 0^{\circ }$): (a) growth rate; (b) frequency.