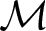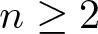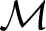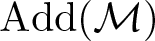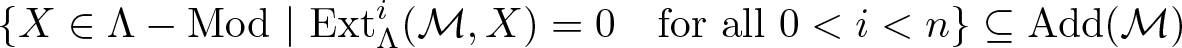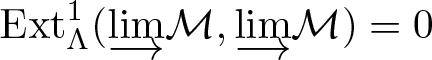1. Introduction
One of the central goals in the representation theory of finite dimensional algebras is to classify finitely generated indecomposable modules up to isomorphism and morphisms between them, but this is considered as ‘impossible’ in general because most algebras have wild representation type. In the modern representation theory of algebras, the main approach to understanding the structure of the module category is to investigate subcategories of the module category having good properties.
In higher-dimensional Auslander–Reiten theory, as introduced by Osamu Iyama in [Reference Iyama27, Reference Iyama28], the module category is replaced by a subcategory with suitable homological properties known as an n-cluster tilting subcategory, where n is a positive integer. Note that Λ-mod itself is the unique 1-cluster tilting subcategory of Λ-mod. If an n-cluster tilting subcategory ![]() $\mathcal{M}$ admits an additive generator, then
$\mathcal{M}$ admits an additive generator, then ![]() $\mathcal{M}$ is called of finite type. The question of finiteness of n-cluster tilting subcategories for
$\mathcal{M}$ is called of finite type. The question of finiteness of n-cluster tilting subcategories for ![]() $n \geq 2$, which is among the first that have been asked by Iyama [Reference Iyama29], is still open. Up to now, all known n-cluster tilting subcategories with
$n \geq 2$, which is among the first that have been asked by Iyama [Reference Iyama29], is still open. Up to now, all known n-cluster tilting subcategories with ![]() $n \geq 2$ are of finite type. Several equivalence conditions for finiteness of n-cluster tilting subcategories are given in [Reference Diyanatnezhad and Nasr-Isfahani14–Reference Ebrahimi and Nasr-Isfahani17, Reference Fazelpour and Nasr-Isfahani21].
$n \geq 2$ are of finite type. Several equivalence conditions for finiteness of n-cluster tilting subcategories are given in [Reference Diyanatnezhad and Nasr-Isfahani14–Reference Ebrahimi and Nasr-Isfahani17, Reference Fazelpour and Nasr-Isfahani21].
Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. It is natural to ask the following question: when does
$n \geq 2$. It is natural to ask the following question: when does ![]() $\mathcal{M}$ induce an n-cluster tilting subcategory in Λ-Mod? Ebrahimi and the second author in [Reference Ebrahimi and Nasr-Isfahani16, Reference Ebrahimi and Nasr-Isfahani17] investigated this question and its relationship to Iyama’s question. They showed that
$\mathcal{M}$ induce an n-cluster tilting subcategory in Λ-Mod? Ebrahimi and the second author in [Reference Ebrahimi and Nasr-Isfahani16, Reference Ebrahimi and Nasr-Isfahani17] investigated this question and its relationship to Iyama’s question. They showed that ![]() ${\rm Add}(\mathcal{M})$ is an n-cluster tilting subcategory of Λ-Mod if and only if
${\rm Add}(\mathcal{M})$ is an n-cluster tilting subcategory of Λ-Mod if and only if ![]() $\mathcal{M}$ is of finite type (see [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12]). For an n-cluster tilting subcategory
$\mathcal{M}$ is of finite type (see [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12]). For an n-cluster tilting subcategory ![]() $\mathcal{M}$ of Λ-mod,
$\mathcal{M}$ of Λ-mod,  ${\underrightarrow{\lim}}\mathcal{M}$, consists of all filtered colimits of objects from
${\underrightarrow{\lim}}\mathcal{M}$, consists of all filtered colimits of objects from ![]() $\mathcal{M}$, is a generating-cogenerating functorially finite subcategory of Λ-Mod. Hence the following question, as has been posed in [Reference Ebrahimi and Nasr-Isfahani17, question 3.5], naturally arises.
$\mathcal{M}$, is a generating-cogenerating functorially finite subcategory of Λ-Mod. Hence the following question, as has been posed in [Reference Ebrahimi and Nasr-Isfahani17, question 3.5], naturally arises.
Question A. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Is
$n \geq 2$. Is  ${\underrightarrow{\lim}}\mathcal{M}$ an n-rigid subcategory of Λ-Mod?
${\underrightarrow{\lim}}\mathcal{M}$ an n-rigid subcategory of Λ-Mod?
They proved  ${\underrightarrow{\lim}}\mathcal{M}$ is the unique n-cluster tilting subcategory of Λ-Mod containing
${\underrightarrow{\lim}}\mathcal{M}$ is the unique n-cluster tilting subcategory of Λ-Mod containing ![]() $\mathcal{M}$ if question A has positive answer (see [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.1]). In the case n = 2, employing cotorsion theory, they showed question A is equivalent to Iyama’s question (see [Reference Ebrahimi and Nasr-Isfahani17, theorem 4.10]).
$\mathcal{M}$ if question A has positive answer (see [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.1]). In the case n = 2, employing cotorsion theory, they showed question A is equivalent to Iyama’s question (see [Reference Ebrahimi and Nasr-Isfahani17, theorem 4.10]).
In this article, we study these questions and their connection to Iyama’s question. We show that question A is equivalent to Iyama’s question when ![]() $n \geq 2$. In fact, we prove the following theorem. Note that the equivalence between (b) and (c) and implication (a) implies (b) is already known by [Reference Ebrahimi and Nasr-Isfahani16, Reference Ebrahimi and Nasr-Isfahani17].
$n \geq 2$. In fact, we prove the following theorem. Note that the equivalence between (b) and (c) and implication (a) implies (b) is already known by [Reference Ebrahimi and Nasr-Isfahani16, Reference Ebrahimi and Nasr-Isfahani17].
Theorem A. (theorem 3.7)
Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then the following statements are equivalent.
$n \geq 2$. Then the following statements are equivalent.
(a)
 $\mathcal{M}$ is of finite type.
$\mathcal{M}$ is of finite type.(b)
 ${\underrightarrow{\lim}}\mathcal{M}$ is an n-cluster tilting subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is an n-cluster tilting subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(c)
 ${\underrightarrow{\lim}}\mathcal{M}$ is an n-rigid subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is an n-rigid subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(d)
 ${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$.
${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$.(e) Every pure submodule N of a module X in
 ${\rm Add}(\mathcal{M})$ is a direct summand of X.
${\rm Add}(\mathcal{M})$ is a direct summand of X.(f)
 ${\underrightarrow{\lim}}\mathcal{M}$ is pure semisimple.
${\underrightarrow{\lim}}\mathcal{M}$ is pure semisimple.
Mittag-Leffler modules occur naturally in algebra, algebraic geometry, and model theory (see [Reference Grothendieck26, Reference Prest33, Reference Raynaud and Gruson35]). Mittag-Leffler modules play a prominent role in Simson’s characterization of perfect functor categories (see [Reference Simson39, theorem 6.3] and see also [Reference Azumaya and Facchini8, theorem 8]). We study the subcategory of all Mittag-Leffler modules in  ${\underrightarrow{\lim}} \mathcal{M}$ when
${\underrightarrow{\lim}} \mathcal{M}$ when ![]() $\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. As a consequence, we show the assumption that every module in
$n \geq 2$. As a consequence, we show the assumption that every module in  ${\underrightarrow{\lim}} \mathcal{M}$ is Mittag-Leffler guarantees that
${\underrightarrow{\lim}} \mathcal{M}$ is Mittag-Leffler guarantees that ![]() $\mathcal{M}$ is of finite type (see corollary 3.10).
$\mathcal{M}$ is of finite type (see corollary 3.10).
1.1. Notation
Throughout this article, all rings are associative with unit unless otherwise stated and n always denotes a fixed positive integer. Also we assume that Λ is an artin algebra. Moreover, we write homomorphisms on the right. Let T be a ring, not necessary with unit. We denote by T-Mod (resp., T-mod) the category of all (finitely generated) left T-modules. We write ![]() $\prod_{i \in I}U_i$ (resp.,
$\prod_{i \in I}U_i$ (resp., ![]() $\bigoplus_{i \in I}U_i$) for the direct product (resp., direct coproduct) of the left T-modules Ui in T-Mod. Moreover, we write
$\bigoplus_{i \in I}U_i$) for the direct product (resp., direct coproduct) of the left T-modules Ui in T-Mod. Moreover, we write ![]() $M^{(K)}$ for the direct coproduct of cardinal K copies of a left T-module M. A left (resp., right) T-module M is called unitary if TM = M (resp., MT = M). We denote by TMod (resp., ModT) the category of all unitary left (resp., right) T-modules. Also, we denote by
$M^{(K)}$ for the direct coproduct of cardinal K copies of a left T-module M. A left (resp., right) T-module M is called unitary if TM = M (resp., MT = M). We denote by TMod (resp., ModT) the category of all unitary left (resp., right) T-modules. Also, we denote by ![]() ${\rm Proj}(T)$ (resp.,
${\rm Proj}(T)$ (resp., ![]() ${\rm proj}(T)$) the full subcategory of TMod consisting of (resp., finitely generated) unitary left T-modules which are projective in TMod. Let
${\rm proj}(T)$) the full subcategory of TMod consisting of (resp., finitely generated) unitary left T-modules which are projective in TMod. Let ![]() $\mathcal{M}$ be an additive full subcategory of Λ-mod. We denote by Mod
$\mathcal{M}$ be an additive full subcategory of Λ-mod. We denote by Mod![]() $(\mathcal{M})$ the category of all contravariant additive functors from
$(\mathcal{M})$ the category of all contravariant additive functors from ![]() $\mathcal{M}$ to the category
$\mathcal{M}$ to the category ![]() $\mathfrak{Ab}$ of all abelian groups. We denote by
$\mathfrak{Ab}$ of all abelian groups. We denote by ![]() ${\rm Add}(\mathcal{M})$ (resp.,
${\rm Add}(\mathcal{M})$ (resp., ![]() ${\rm add}(\mathcal{M})$) the full subcategory of Λ-Mod (resp., Λ-mod) whose objects are direct summands of (resp., finite) direct sums of objects in
${\rm add}(\mathcal{M})$) the full subcategory of Λ-Mod (resp., Λ-mod) whose objects are direct summands of (resp., finite) direct sums of objects in ![]() $\mathcal{M}$. Also, we denote by
$\mathcal{M}$. Also, we denote by  ${\underrightarrow{\lim}} \mathcal{M}$ the full subcategory of Λ-Mod in which each of its objects is a direct limit of objects in
${\underrightarrow{\lim}} \mathcal{M}$ the full subcategory of Λ-Mod in which each of its objects is a direct limit of objects in ![]() $\mathcal{M}$.
$\mathcal{M}$.
2. Preliminaries
Throughout this section, we fix a positive integer n. We first recall from [Reference Jasso30, definition 3.14] the definition of n-cluster tilting subcategories of abelian categories. Then we discuss the (Gabriel) functor rings T associated with n-cluster tilting subcategories ![]() $\mathcal{M}$ of Λ-mod and also the relationship between the functor category
$\mathcal{M}$ of Λ-mod and also the relationship between the functor category ![]() ${\rm Mod}(\mathcal{M})$ and the category TMod. We investigate the weak global dimension of (Gabriel) functor rings associated with n-cluster tilting subcategories of module categories, generalizing results from Fuller [Reference Fuller and Hullinger23, proposition 1.5] and Auslander [Reference Auslander4, proposition 4.2] (see theorem 2.3). By using this outcome, we prove some basic properties of the subcategory of filtered colimit
${\rm Mod}(\mathcal{M})$ and the category TMod. We investigate the weak global dimension of (Gabriel) functor rings associated with n-cluster tilting subcategories of module categories, generalizing results from Fuller [Reference Fuller and Hullinger23, proposition 1.5] and Auslander [Reference Auslander4, proposition 4.2] (see theorem 2.3). By using this outcome, we prove some basic properties of the subcategory of filtered colimit  ${\underrightarrow{\lim}}\mathcal{M}$ of n-cluster tilting subcategory
${\underrightarrow{\lim}}\mathcal{M}$ of n-cluster tilting subcategory ![]() $\mathcal{M}$ of Λ-mod.
$\mathcal{M}$ of Λ-mod.
Osamu Iyama introduced n-cluster tilting modules and higher Auslander algebras, known as n-Auslander algebras, in [Reference Iyama27, Reference Iyama28] to construct a higher Auslander correspondence (see [Reference Iyama27, theorem 0.2]), generalizing the classical correspondence between algebras of finite representation type and Auslander algebras as developed by Auslander in [Reference Auslander4, corollary 4.7].
Let ![]() $\mathcal{M}$ be a full subcategory of an abelian category
$\mathcal{M}$ be a full subcategory of an abelian category ![]() $\mathcal{A}$. Given an object
$\mathcal{A}$. Given an object ![]() $A \in \mathcal{A}$, a morphism
$A \in \mathcal{A}$, a morphism ![]() $\theta: M \rightarrow A$ with
$\theta: M \rightarrow A$ with ![]() $M \in \mathcal{M}$ is called a right
$M \in \mathcal{M}$ is called a right ![]() $\mathcal{M}$-approximation of A if any morphism from an object in
$\mathcal{M}$-approximation of A if any morphism from an object in ![]() $\mathcal{M}$ to A factors through θ. The subcategory
$\mathcal{M}$ to A factors through θ. The subcategory ![]() $\mathcal{M}$ is called contravariantly finite if every object in
$\mathcal{M}$ is called contravariantly finite if every object in ![]() $\mathcal{A}$ admits a right
$\mathcal{A}$ admits a right ![]() $\mathcal{M}$-approximation. Left
$\mathcal{M}$-approximation. Left ![]() $\mathcal{M}$-approximations and covariantly finite subcategories are defined dually. Also
$\mathcal{M}$-approximations and covariantly finite subcategories are defined dually. Also ![]() $\mathcal{M}$ is called functorially finite if it is both contravariantly and covariantly finite. We refer the reader to [Reference Auslander and Reiten5, Reference Auslander and Smalø6] for more details on functorially finite subcategories.
$\mathcal{M}$ is called functorially finite if it is both contravariantly and covariantly finite. We refer the reader to [Reference Auslander and Reiten5, Reference Auslander and Smalø6] for more details on functorially finite subcategories.
For a positive integer n, an abelian category ![]() $\mathcal{A}$ is called an n-Auslander category if
$\mathcal{A}$ is called an n-Auslander category if ![]() $\mathcal{A}$ has enough projectives and satisfies
$\mathcal{A}$ has enough projectives and satisfies ![]() ${\rm gl.dim}\mathcal{A} \leq n + 1 \leq {\rm dom.dim}\mathcal{A}$. Beligiannis in [Reference Beligiannis11] proved a categorified version of higher Auslander’s correspondence for arbitrary abelian categories. He proved that there is a bijection between equivalence classes of contravariantly finite subcategories
${\rm gl.dim}\mathcal{A} \leq n + 1 \leq {\rm dom.dim}\mathcal{A}$. Beligiannis in [Reference Beligiannis11] proved a categorified version of higher Auslander’s correspondence for arbitrary abelian categories. He proved that there is a bijection between equivalence classes of contravariantly finite subcategories ![]() $\mathcal{M}$ in abelian categories
$\mathcal{M}$ in abelian categories ![]() $\mathcal{A}$ with enough injectives that satisfy the following conditions:
$\mathcal{A}$ with enough injectives that satisfy the following conditions:
(i) Any right
 $\mathcal{M}$-approximation is an epimorphism,
$\mathcal{M}$-approximation is an epimorphism,(ii)
 $\mathcal{M} = \mathcal{M}^{\bot_n}=\lbrace Y\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(\mathcal{M},Y)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace$.
$\mathcal{M} = \mathcal{M}^{\bot_n}=\lbrace Y\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(\mathcal{M},Y)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace$.
and equivalence classes of n-Auslander categories (see [Reference Beligiannis11, theorem 8.23]). It is given by ![]() $\mathcal{M} \mapsto {\rm mod}(\mathcal{M})$, where
$\mathcal{M} \mapsto {\rm mod}(\mathcal{M})$, where ![]() ${\rm mod}(\mathcal{M})$ denotes the category of contravariant coherent functors from
${\rm mod}(\mathcal{M})$ denotes the category of contravariant coherent functors from ![]() $\mathcal{M}$ to the category
$\mathcal{M}$ to the category ![]() $\mathfrak{Ab}$ of all abelian groups. An additive functor
$\mathfrak{Ab}$ of all abelian groups. An additive functor ![]() $F: \mathcal{M} \rightarrow \mathfrak{Ab}$ is called coherent if there exists an exact sequence
$F: \mathcal{M} \rightarrow \mathfrak{Ab}$ is called coherent if there exists an exact sequence ![]() $\mathcal{M}(-, M_1) \rightarrow \mathcal{M}(-, M_0) \rightarrow F \rightarrow 0$, where
$\mathcal{M}(-, M_1) \rightarrow \mathcal{M}(-, M_0) \rightarrow F \rightarrow 0$, where ![]() $M_0, M_1 \in \mathcal{M}$ (see [Reference Auslander3]).
$M_0, M_1 \in \mathcal{M}$ (see [Reference Auslander3]).
Before presenting the definition of the n-cluster tilting subcategories of arbitrary abelian categories, let us recall some notions.
Let ![]() $\mathcal{M}$ be a full subcategory of an abelian category
$\mathcal{M}$ be a full subcategory of an abelian category ![]() $\mathcal{A}$. We recall that
$\mathcal{A}$. We recall that ![]() $\mathcal{M}$ is generating if any object in
$\mathcal{M}$ is generating if any object in ![]() $\mathcal{A}$ is a quotient of an object in
$\mathcal{A}$ is a quotient of an object in ![]() $\mathcal{M}$; that is, for every object
$\mathcal{M}$; that is, for every object ![]() $A \in \mathcal{A}$, there exists an exact sequence
$A \in \mathcal{A}$, there exists an exact sequence ![]() $M \rightarrow A \rightarrow 0$ with
$M \rightarrow A \rightarrow 0$ with ![]() $M \in \mathcal{M}$. Cogenerating subcategories are defined dually.
$M \in \mathcal{M}$. Cogenerating subcategories are defined dually. ![]() $\mathcal{M}$ is called a generating-cogenerating subcategory of
$\mathcal{M}$ is called a generating-cogenerating subcategory of ![]() $\mathcal{A}$ if it is both generating and cogenerating.
$\mathcal{A}$ if it is both generating and cogenerating.
Definition 2.1. (See [Reference Jasso30] definition 3.14)
Let ![]() $\mathcal{A}$ be an abelian category and
$\mathcal{A}$ be an abelian category and ![]() $\mathcal{M}$ be a generating-cogenerating full subcategory of
$\mathcal{M}$ be a generating-cogenerating full subcategory of ![]() $\mathcal{A}$. The subcategory
$\mathcal{A}$. The subcategory ![]() $\mathcal{M}$ of
$\mathcal{M}$ of ![]() $\mathcal{A}$ is called n-cluster tilting if it is functorially finite in
$\mathcal{A}$ is called n-cluster tilting if it is functorially finite in ![]() $\mathcal{A}$ and
$\mathcal{A}$ and ![]() $\mathcal{M}^{\bot_n}=\mathcal{M}={^{\bot_n}\mathcal{M}}$, where
$\mathcal{M}^{\bot_n}=\mathcal{M}={^{\bot_n}\mathcal{M}}$, where
 \begin{align*}
{^{\bot_n}\mathcal{M}}&=\lbrace X\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(X,\mathcal{M})=0 ~~~ {\rm for ~all }~ 0 \lt i \lt n \rbrace\\
\mathcal{M}^{\bot_n}&=\lbrace Y\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(\mathcal{M},Y)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace.
\end{align*}
\begin{align*}
{^{\bot_n}\mathcal{M}}&=\lbrace X\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(X,\mathcal{M})=0 ~~~ {\rm for ~all }~ 0 \lt i \lt n \rbrace\\
\mathcal{M}^{\bot_n}&=\lbrace Y\in \mathcal{A}~|~ {\rm Ext}^i_{\mathcal{A}}(\mathcal{M},Y)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace.
\end{align*} Note that ![]() $\mathcal{A}$ itself is the unique 1-cluster tilting subcategory of
$\mathcal{A}$ itself is the unique 1-cluster tilting subcategory of ![]() $\mathcal{A}$.
$\mathcal{A}$.
Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod. Assume that
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod. Assume that ![]() $\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ is a complete set of non-isomorphic indecomposable modules in
$\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ is a complete set of non-isomorphic indecomposable modules in ![]() $\mathcal{M}$. Set
$\mathcal{M}$. Set ![]() $U=\bigoplus_{\alpha \in J} U_{\alpha}$ and for each
$U=\bigoplus_{\alpha \in J} U_{\alpha}$ and for each ![]() $\alpha \in J$ let
$\alpha \in J$ let ![]() $e_{\alpha}=\pi_{\alpha} \varepsilon_{\alpha}$, where
$e_{\alpha}=\pi_{\alpha} \varepsilon_{\alpha}$, where ![]() $\pi_{\alpha}:U \rightarrow U_{\alpha}$ is the canonical projection and
$\pi_{\alpha}:U \rightarrow U_{\alpha}$ is the canonical projection and ![]() $\varepsilon_{\alpha}:U_{\alpha} \rightarrow U$ is the canonical injection. For each object X of Λ-Mod, we define as in [Reference Menini32, p. 242],
$\varepsilon_{\alpha}:U_{\alpha} \rightarrow U$ is the canonical injection. For each object X of Λ-Mod, we define as in [Reference Menini32, p. 242],
 \begin{equation*}
\widehat{\mathrm{Hom}}_{\Lambda}(U,X)=\lbrace f \in {\rm Hom}_{\Lambda}(U,X)~|~ e_{\alpha}f =0~ {\rm for ~almost~ all}~ \alpha \in J \rbrace.
\end{equation*}
\begin{equation*}
\widehat{\mathrm{Hom}}_{\Lambda}(U,X)=\lbrace f \in {\rm Hom}_{\Lambda}(U,X)~|~ e_{\alpha}f =0~ {\rm for ~almost~ all}~ \alpha \in J \rbrace.
\end{equation*} For X = U, we write  $T:= \widehat{{\rm Hom}}_{\Lambda}(U, U)=\widehat{{\rm End}}_{\Lambda}(U)$. Following [Reference Fuller22, p. 40] (see also [Reference Yamagata43, p. 370]),
$T:= \widehat{{\rm Hom}}_{\Lambda}(U, U)=\widehat{{\rm End}}_{\Lambda}(U)$. Following [Reference Fuller22, p. 40] (see also [Reference Yamagata43, p. 370]),  $T=\widehat{{\rm End}}_{\Lambda}(U)$ is called functor ring (or Gabriel ring) of
$T=\widehat{{\rm End}}_{\Lambda}(U)$ is called functor ring (or Gabriel ring) of ![]() $\mathcal{M}$.
$\mathcal{M}$.
A ring S (not necessary with unit) has enough idempotents if there exists a family ![]() $\lbrace q_{\alpha}~|~\alpha \in I \rbrace$ of pairwise orthogonal idempotents of S such that
$\lbrace q_{\alpha}~|~\alpha \in I \rbrace$ of pairwise orthogonal idempotents of S such that ![]() $S=\bigoplus_{\alpha \in I}Sq_{\alpha}=\bigoplus_{\alpha \in I}q_{\alpha}S$ (see [Reference Fuller22, p. 39]). From [Reference Menini32, proposition 2.2(6)], we can see that
$S=\bigoplus_{\alpha \in I}Sq_{\alpha}=\bigoplus_{\alpha \in I}q_{\alpha}S$ (see [Reference Fuller22, p. 39]). From [Reference Menini32, proposition 2.2(6)], we can see that ![]() $T=\bigoplus_{\alpha \in J}Te_{\alpha}=\bigoplus_{\alpha \in J}e_{\alpha}T$ is a ring with enough idempotents. Moreover, the assignment
$T=\bigoplus_{\alpha \in J}Te_{\alpha}=\bigoplus_{\alpha \in J}e_{\alpha}T$ is a ring with enough idempotents. Moreover, the assignment  $X \mapsto \widehat{\mathrm{Hom}}_{\Lambda}(U,X)$ defines a covariant left exact functor
$X \mapsto \widehat{\mathrm{Hom}}_{\Lambda}(U,X)$ defines a covariant left exact functor  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod![]() $ \rightarrow T$Mod (see [Reference Menini32, proposition 2.2(5)]). The functor
$ \rightarrow T$Mod (see [Reference Menini32, proposition 2.2(5)]). The functor  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod ![]() $\rightarrow T$Mod preserves coproducts and induces an additive equivalence between the full subcategory
$\rightarrow T$Mod preserves coproducts and induces an additive equivalence between the full subcategory ![]() ${\rm Add}(\mathcal{M})$ of Λ-Mod and the full subcategory
${\rm Add}(\mathcal{M})$ of Λ-Mod and the full subcategory ![]() ${\rm Proj}(T)$ of TMod with the inverse equivalence
${\rm Proj}(T)$ of TMod with the inverse equivalence ![]() $U \otimes_T -$ (see also [Reference Fuller22, pp. 40–41]). Hence, we can see that
$U \otimes_T -$ (see also [Reference Fuller22, pp. 40–41]). Hence, we can see that  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \mathcal{M} \rightarrow {\rm proj}(T)$ is an additive equivalence with the inverse equivalence
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \mathcal{M} \rightarrow {\rm proj}(T)$ is an additive equivalence with the inverse equivalence ![]() $U \otimes_{T}-$. By [Reference Fazelpour and Nasr-Isfahani20, theorem 3.6], the functor ring of
$U \otimes_{T}-$. By [Reference Fazelpour and Nasr-Isfahani20, theorem 3.6], the functor ring of ![]() $\mathcal{M}$ uniquely determines up to Morita equivalence (see also the proof of [Reference Garcia and Simson25, theorem 3.3]).
$\mathcal{M}$ uniquely determines up to Morita equivalence (see also the proof of [Reference Garcia and Simson25, theorem 3.3]).
It is shown in [Reference Gabriel24, proposition 2, p. 347] (see also [Reference Yamagata43, p. 370]) that there exists an additive equivalence ![]() ${\rm Mod}(\mathcal{M}) \rightarrow T{\rm Mod}$ which preserves and reflects finitely generated projective objects and exact sequences. Hence proposition 2.2 is an immediate consequence of [Reference Beligiannis11, theorem 8.23]. However, we provide an alternative proof for proposition 2.2 using the functor ring technique.
${\rm Mod}(\mathcal{M}) \rightarrow T{\rm Mod}$ which preserves and reflects finitely generated projective objects and exact sequences. Hence proposition 2.2 is an immediate consequence of [Reference Beligiannis11, theorem 8.23]. However, we provide an alternative proof for proposition 2.2 using the functor ring technique.
Proposition 2.2. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod and T be the functor ring of
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod and T be the functor ring of ![]() $\mathcal{M}$. Then the projective dimension of the kernel of any morphism in
$\mathcal{M}$. Then the projective dimension of the kernel of any morphism in ![]() ${\rm proj}(T)$ is less than or equal to n − 1.
${\rm proj}(T)$ is less than or equal to n − 1.
Proof. Let ![]() $\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of non-isomorphic indecomposable modules in
$\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of non-isomorphic indecomposable modules in ![]() $\mathcal{M}$ and
$\mathcal{M}$ and  $T=\widehat{{\rm End}}_{\Lambda}(U)$, where
$T=\widehat{{\rm End}}_{\Lambda}(U)$, where ![]() $U=\bigoplus_{\alpha \in J} U_{\alpha}$. Let
$U=\bigoplus_{\alpha \in J} U_{\alpha}$. Let ![]() $h: Q' \rightarrow Q$ be a morphism in
$h: Q' \rightarrow Q$ be a morphism in ![]() ${\rm proj}(T)$. We show that
${\rm proj}(T)$. We show that ![]() ${\rm pd}({\rm Ker}(h)) \leq n-1$. Since the functor
${\rm pd}({\rm Ker}(h)) \leq n-1$. Since the functor  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod![]() $ \rightarrow T$Mod is left exact and induces an additive equivalence between the full subcategory
$ \rightarrow T$Mod is left exact and induces an additive equivalence between the full subcategory ![]() $\mathcal{M}$ of Λ-Mod and the full subcategory
$\mathcal{M}$ of Λ-Mod and the full subcategory ![]() ${\rm proj}(T)$ of TMod, we have the following commutative diagram
${\rm proj}(T)$ of TMod, we have the following commutative diagram

where ![]() $f: M' \rightarrow M$ is a morphism in
$f: M' \rightarrow M$ is a morphism in ![]() $\mathcal{M}$ and
$\mathcal{M}$ and  $\overline{f}=\widehat{\mathrm{Hom}}_{\Lambda}(U, f)$. Hence
$\overline{f}=\widehat{\mathrm{Hom}}_{\Lambda}(U, f)$. Hence  ${\rm Ker}(h) \cong \widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f))$ as T-modules. Therefore, it is enough to show that
${\rm Ker}(h) \cong \widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f))$ as T-modules. Therefore, it is enough to show that  ${\rm pd}(\widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f))) \leq n-1$. If n = 1, then
${\rm pd}(\widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f))) \leq n-1$. If n = 1, then ![]() $\mathcal{M}=\Lambda$-mod. Since
$\mathcal{M}=\Lambda$-mod. Since ![]() ${\rm Ker}(f)$ is a finitely generated left Λ-module,
${\rm Ker}(f)$ is a finitely generated left Λ-module,  $\widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f)) \in {\rm proj}(T)$ and so the result follows. Now let
$\widehat{\mathrm{Hom}}_{\Lambda}(U, {\rm Ker}(f)) \in {\rm proj}(T)$ and so the result follows. Now let ![]() $n \geq 2$. Since
$n \geq 2$. Since ![]() ${\rm Ker}(f)$ is finitely generated, by [Reference Iyama29, proposition 2.3], we have an exact sequence
${\rm Ker}(f)$ is finitely generated, by [Reference Iyama29, proposition 2.3], we have an exact sequence
 \begin{equation*}0 \rightarrow M_{n-1} \overset{\beta_{n-1}}{\rightarrow} \cdots \rightarrow M_0 \overset{\beta_{0}}{\rightarrow} {\rm Ker}(f) \rightarrow 0\end{equation*}
\begin{equation*}0 \rightarrow M_{n-1} \overset{\beta_{n-1}}{\rightarrow} \cdots \rightarrow M_0 \overset{\beta_{0}}{\rightarrow} {\rm Ker}(f) \rightarrow 0\end{equation*} with terms in ![]() $\mathcal{M}$ such that the sequence
$\mathcal{M}$ such that the sequence
 \begin{equation*}
0 \!\rightarrow {\rm Hom}_{\mathcal{M}}(-,M_{n-1})\! \overset{(-,\beta_{n-1})}{\rightarrow}\! \cdots \rightarrow\! {\rm Hom}_{\mathcal{M}}(-,M_0)\! \overset{(-,\beta_{0})}{\rightarrow}\! {\rm Hom}_{\mathcal{M}}(-,{\rm Ker}(f))\! \rightarrow\! 0 (\star)
\end{equation*}
\begin{equation*}
0 \!\rightarrow {\rm Hom}_{\mathcal{M}}(-,M_{n-1})\! \overset{(-,\beta_{n-1})}{\rightarrow}\! \cdots \rightarrow\! {\rm Hom}_{\mathcal{M}}(-,M_0)\! \overset{(-,\beta_{0})}{\rightarrow}\! {\rm Hom}_{\mathcal{M}}(-,{\rm Ker}(f))\! \rightarrow\! 0 (\star)
\end{equation*}is exact. Now we show that the following sequence is exact
 \begin{equation*}0 \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-1}) \overset{\overline{\beta_{n-1}}}{\rightarrow} \cdots \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,M_0) \overset{\overline{\beta_{0}}}{\rightarrow} \widehat{\mathrm{Hom}}_{\Lambda}(U,{\rm Ker}(f)) \rightarrow 0, (\star \star)\end{equation*}
\begin{equation*}0 \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-1}) \overset{\overline{\beta_{n-1}}}{\rightarrow} \cdots \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,M_0) \overset{\overline{\beta_{0}}}{\rightarrow} \widehat{\mathrm{Hom}}_{\Lambda}(U,{\rm Ker}(f)) \rightarrow 0, (\star \star)\end{equation*} where  $\overline{\beta_{i}}=\widehat{\mathrm{Hom}}_{\Lambda}(U,\beta_{i})$ for each
$\overline{\beta_{i}}=\widehat{\mathrm{Hom}}_{\Lambda}(U,\beta_{i})$ for each ![]() $i \in \lbrace 0, \ldots, n-1 \rbrace$. Since the functor
$i \in \lbrace 0, \ldots, n-1 \rbrace$. Since the functor  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-): \Lambda$-Mod![]() $ \rightarrow T$Mod is left exact, the sequence
$ \rightarrow T$Mod is left exact, the sequence ![]() $(\star \star)$ is exact at
$(\star \star)$ is exact at  $\widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-1})$ and
$\widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-1})$ and  $\widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-2})$. Let
$\widehat{\mathrm{Hom}}_{\Lambda}(U,M_{n-2})$. Let ![]() $l \in \lbrace -1, 0, \ldots, n-3\rbrace$. Set
$l \in \lbrace -1, 0, \ldots, n-3\rbrace$. Set ![]() $M_{-1}= {\rm Ker}(f)$ and
$M_{-1}= {\rm Ker}(f)$ and ![]() $\beta_{-1}=0$. It is sufficient to show that it is exact at
$\beta_{-1}=0$. It is sufficient to show that it is exact at  $\widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$. Let
$\widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$. Let  $g \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$ such that
$g \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$ such that ![]() $g \beta_{l} = 0$. For each
$g \beta_{l} = 0$. For each ![]() $\alpha \in J$ let
$\alpha \in J$ let ![]() $e_{\alpha}=\pi_{\alpha} \varepsilon_{\alpha}$, where
$e_{\alpha}=\pi_{\alpha} \varepsilon_{\alpha}$, where ![]() $\pi_{\alpha}:U \rightarrow U_{\alpha}$ is the canonical projection and
$\pi_{\alpha}:U \rightarrow U_{\alpha}$ is the canonical projection and ![]() $\varepsilon_{\alpha}:U_{\alpha} \rightarrow U$ is the canonical injection. Since
$\varepsilon_{\alpha}:U_{\alpha} \rightarrow U$ is the canonical injection. Since  $g \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$, there exists a finite subset A of J such that
$g \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_l)$, there exists a finite subset A of J such that ![]() $e_{\alpha}g = 0$ for all
$e_{\alpha}g = 0$ for all ![]() $\alpha \in J \setminus A$. Consider the following diagram
$\alpha \in J \setminus A$. Consider the following diagram

where ![]() $M_{-2}=0$ and
$M_{-2}=0$ and ![]() $\varepsilon: \bigoplus_{\alpha \in A}U_{\alpha} \rightarrow U$ and
$\varepsilon: \bigoplus_{\alpha \in A}U_{\alpha} \rightarrow U$ and ![]() $\pi: U \rightarrow \bigoplus_{\alpha \in A}U_{\alpha}$ are the canonical injection and projection, respectively. Since
$\pi: U \rightarrow \bigoplus_{\alpha \in A}U_{\alpha}$ are the canonical injection and projection, respectively. Since ![]() $\bigoplus_{\alpha \in A}U_{\alpha} \in \mathcal{M}$,
$\bigoplus_{\alpha \in A}U_{\alpha} \in \mathcal{M}$, ![]() $\varepsilon g \beta_{l} = 0$, and the sequence
$\varepsilon g \beta_{l} = 0$, and the sequence ![]() $(\star)$ is exact, there exists a morphism
$(\star)$ is exact, there exists a morphism ![]() $\gamma: \bigoplus_{\alpha \in A}U_{\alpha} \rightarrow M_{l+1}$ such that
$\gamma: \bigoplus_{\alpha \in A}U_{\alpha} \rightarrow M_{l+1}$ such that ![]() $\gamma \beta_{l+1} = \varepsilon g$ and so
$\gamma \beta_{l+1} = \varepsilon g$ and so ![]() $\pi \gamma \beta_{l+1} = \pi \varepsilon g$. It is not difficult to see that
$\pi \gamma \beta_{l+1} = \pi \varepsilon g$. It is not difficult to see that ![]() $\pi \varepsilon g =g$ and
$\pi \varepsilon g =g$ and  $\pi \gamma \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_{l+1})$. This implies that the sequence
$\pi \gamma \in \widehat{\mathrm{Hom}}_{\Lambda}(U,M_{l+1})$. This implies that the sequence ![]() $(\star \star)$ is exact and so the result follows.
$(\star \star)$ is exact and so the result follows.
Let R be a ring with enough idempotents. A unitary left R-module N is called flat if the functor ![]() $- \otimes_{R}N: {\rm Mod}R \rightarrow \mathfrak{Ab}$ is an exact functor, where
$- \otimes_{R}N: {\rm Mod}R \rightarrow \mathfrak{Ab}$ is an exact functor, where ![]() $\mathfrak{Ab}$ is the category of abelian groups (see [Reference Garcia and Simson25, p. 115]). Note that a unitary left R-module N is flat if and only if N is a direct limit of finitely generated projective unitary left R-modules (see [Reference Wisbauer42, proposition 49.5]). Moreover, we denote by
$\mathfrak{Ab}$ is the category of abelian groups (see [Reference Garcia and Simson25, p. 115]). Note that a unitary left R-module N is flat if and only if N is a direct limit of finitely generated projective unitary left R-modules (see [Reference Wisbauer42, proposition 49.5]). Moreover, we denote by ![]() ${\rm Flat}(T)$ the full subcategory of
${\rm Flat}(T)$ the full subcategory of ![]() $T{\rm Mod}$ consisting of flat unitary left T-modules.
$T{\rm Mod}$ consisting of flat unitary left T-modules.
Given a unitary left R-module M, the flat dimension of M which is denoted by ![]() ${\rm fd}(M)$ is less than or equal to m if there exists a finite flat resolution
${\rm fd}(M)$ is less than or equal to m if there exists a finite flat resolution
If no such finite resolution exists, then ![]() ${\rm fd}(M)=\infty$. The weak global dimension of R which is denoted by
${\rm fd}(M)=\infty$. The weak global dimension of R which is denoted by ![]() ${\rm w. gl. dim}(R)$ is defined as a supremum of the flat dimension of all unitary left R-modules (see [Reference Del Rio13, p. 210]).
${\rm w. gl. dim}(R)$ is defined as a supremum of the flat dimension of all unitary left R-modules (see [Reference Del Rio13, p. 210]).
Let ![]() $\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod. Beligiannis in [Reference Beligiannis11, theorem 8.23] proved that the projective dimension of any object in
$\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod. Beligiannis in [Reference Beligiannis11, theorem 8.23] proved that the projective dimension of any object in ![]() ${\rm mod}(\mathcal{M})$ is less or equal to n + 1. Using the functor ring technique, in theorem 2.3, we show that flat dimension of any object in
${\rm mod}(\mathcal{M})$ is less or equal to n + 1. Using the functor ring technique, in theorem 2.3, we show that flat dimension of any object in ![]() ${\rm Mod}(\mathcal{M})$ is less or equal to n + 1.
${\rm Mod}(\mathcal{M})$ is less or equal to n + 1.
Theorem 2.3. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod and T be the functor ring of
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod and T be the functor ring of ![]() $\mathcal{M}$. Then
$\mathcal{M}$. Then ![]() ${\rm w.gl.dim}(T) \leq n+1$.
${\rm w.gl.dim}(T) \leq n+1$.
Proof. For any ![]() $N \in T$Mod, we take an exact sequence
$N \in T$Mod, we take an exact sequence
in TMod, where each Qi is projective in TMod. By applying the technique used in the proof of [Reference Fazelpour and Nasr-Isfahani21, theorem 3.1(1)], we can see that  ${\rm Ker}(g)\cong {\underrightarrow{\lim}} {\rm Ker}(g_i)$ as T-modules, where each gi is a morphism in
${\rm Ker}(g)\cong {\underrightarrow{\lim}} {\rm Ker}(g_i)$ as T-modules, where each gi is a morphism in ![]() ${\rm proj}(T)$. By proposition 2.2,
${\rm proj}(T)$. By proposition 2.2, ![]() ${\rm pd}({\rm Ker}(g_i)) \leq n-1$. Let X be a unitary right T-module. Then
${\rm pd}({\rm Ker}(g_i)) \leq n-1$. Let X be a unitary right T-module. Then ![]() ${\rm Tor}_n^{T}(X, {\rm Ker}(g_i))=0$. Since
${\rm Tor}_n^{T}(X, {\rm Ker}(g_i))=0$. Since  ${\rm Tor}_n^{T}(X, {\rm Ker}(g)) \cong {\underrightarrow{\lim}} {\rm Tor}_n^{T}(X, {\rm Ker}(g_i))$, we have
${\rm Tor}_n^{T}(X, {\rm Ker}(g)) \cong {\underrightarrow{\lim}} {\rm Tor}_n^{T}(X, {\rm Ker}(g_i))$, we have ![]() ${\rm Tor}_n^{T}(X, {\rm Ker}(g)) = 0$. This yields K is a flat unitary left T-module. Therefore,
${\rm Tor}_n^{T}(X, {\rm Ker}(g)) = 0$. This yields K is a flat unitary left T-module. Therefore, ![]() ${\rm fd}(N) \leq n+1$ and so
${\rm fd}(N) \leq n+1$ and so ![]() ${\rm w.gl.dim}(T) \leq n+1$.
${\rm w.gl.dim}(T) \leq n+1$.
As a consequence, we have the following results.
Corollary 2.4. ([Reference Fuller and Hullinger23] proposition 1.5)
Let T be the functor ring of Λ-mod. Then ![]() ${{\rm w.gl.dim}(T) \leq 2}$.
${{\rm w.gl.dim}(T) \leq 2}$.
Λ is called of finite type if Λ-mod has an additive generator.
Corollary 2.5. ([Reference Auslander4] proposition 4.2)
Let Λ be of finite type. Then ![]() ${\rm gl.dim}({\rm End}_{\Lambda}(M)) \leq 2$, where M is an additive generator of Λ-mod.
${\rm gl.dim}({\rm End}_{\Lambda}(M)) \leq 2$, where M is an additive generator of Λ-mod.
3. Main results
In this section, we prove the main results of the article. A full subcategory ![]() $\mathcal{M}$ of an abelian category
$\mathcal{M}$ of an abelian category ![]() $\mathcal{A}$ is called n-rigid, if
$\mathcal{A}$ is called n-rigid, if  ${\rm Ext}_{\mathcal{A}}^{k}(\mathcal{M}, \mathcal{M})=0$ for every
${\rm Ext}_{\mathcal{A}}^{k}(\mathcal{M}, \mathcal{M})=0$ for every ![]() $k \in \lbrace 1, \ldots, n-1\rbrace$ (see [Reference Beligiannis11, p. 443]). Clearly, any n-cluster tilting subcategory
$k \in \lbrace 1, \ldots, n-1\rbrace$ (see [Reference Beligiannis11, p. 443]). Clearly, any n-cluster tilting subcategory ![]() $\mathcal{M}$ of
$\mathcal{M}$ of ![]() $\mathcal{A}$ is n-rigid.
$\mathcal{A}$ is n-rigid.
In the following proposition, we list some basic properties of the subcategory  ${\underrightarrow{\lim}}\mathcal{M}$ of Λ-Mod when
${\underrightarrow{\lim}}\mathcal{M}$ of Λ-Mod when ![]() $\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod. Note that proposition 3.1(a) and (b) are consequences of [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.4(i)].
$\mathcal{M}$ is an n-cluster tilting subcategory of Λ-mod. Note that proposition 3.1(a) and (b) are consequences of [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.4(i)].
Proposition 3.1. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then
$n \geq 2$. Then
(a)
 ${\underrightarrow{\lim}}\mathcal{M}$ is a generating-cogenerating subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is a generating-cogenerating subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(b)
 ${\underrightarrow{\lim}}\mathcal{M}$ is a functorially finite subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is a functorially finite subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(c)
 ${\rm Ext}_{\Lambda}^{k}({\rm Add}(\mathcal{M}), {\underrightarrow{\lim}}\mathcal{M})=0$ for every
${\rm Ext}_{\Lambda}^{k}({\rm Add}(\mathcal{M}), {\underrightarrow{\lim}}\mathcal{M})=0$ for every  $k \in \lbrace 1,\ldots,n-1 \rbrace$.
$k \in \lbrace 1,\ldots,n-1 \rbrace$.(d)
 $\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace \subseteq {\underrightarrow{\lim}}\mathcal{M}$.
$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace \subseteq {\underrightarrow{\lim}}\mathcal{M}$.
Proof. (a) We already know that every module is a factor module of a free module and every module is an essential submodule of an injective module. From ![]() $\Lambda , D(\Lambda) \in \mathcal{M}$ and the fact that injective modules are precisely direct summands of direct sums of copies of the
$\Lambda , D(\Lambda) \in \mathcal{M}$ and the fact that injective modules are precisely direct summands of direct sums of copies of the ![]() $D(\Lambda)$, for each left Λ-module M, we obtain homomorphisms
$D(\Lambda)$, for each left Λ-module M, we obtain homomorphisms ![]() $P \rightarrow M$ and
$P \rightarrow M$ and ![]() $M \rightarrow E$ which are epimorphism and monomorphism, respectively, where
$M \rightarrow E$ which are epimorphism and monomorphism, respectively, where ![]() $P, E \in {\rm Add}(\mathcal{M})$. Hence
$P, E \in {\rm Add}(\mathcal{M})$. Hence  ${\underrightarrow{\lim}}\mathcal{M}$ is a generating-cogenerating subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is a generating-cogenerating subcategory of Λ-![]() ${\rm Mod}$.
${\rm Mod}$.
(b) Since ![]() $\mathcal{M}$ is a covariantly finite subcategory of Λ-mod, by [Reference Krause31, proposition 3.11],
$\mathcal{M}$ is a covariantly finite subcategory of Λ-mod, by [Reference Krause31, proposition 3.11],  ${\underrightarrow{\lim}}\mathcal{M}$ is a covariantly finite subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is a covariantly finite subcategory of Λ-![]() ${\rm Mod}$. Also by [Reference El Bashir18, theorem 3.2],
${\rm Mod}$. Also by [Reference El Bashir18, theorem 3.2],  ${\underrightarrow{\lim}}\mathcal{M}$ is a contravariantly finite subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is a contravariantly finite subcategory of Λ-![]() ${\rm Mod}$ (see also [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.4(i)]).
${\rm Mod}$ (see also [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.4(i)]).
(c) By using [Reference Rotman37, proposition 7.21] and [Reference Enochs and Jenda19, proposition 3.1.16], for any ![]() $N \in {\rm Add}(\mathcal{M})$ and
$N \in {\rm Add}(\mathcal{M})$ and  $M \in {\underrightarrow{\lim}}\mathcal{M}$, we have
$M \in {\underrightarrow{\lim}}\mathcal{M}$, we have  ${\rm Ext}_{\Lambda}^k(N,M) \cong \prod_{i \in A}{\underrightarrow{\lim}}_{j \in J} {\rm Ext}_{\Lambda}^k(N_i,M_j)$, where each
${\rm Ext}_{\Lambda}^k(N,M) \cong \prod_{i \in A}{\underrightarrow{\lim}}_{j \in J} {\rm Ext}_{\Lambda}^k(N_i,M_j)$, where each ![]() $N_i, M_j \in \mathcal{M}$. Since
$N_i, M_j \in \mathcal{M}$. Since ![]() $\mathcal{M}$ is n-rigid,
$\mathcal{M}$ is n-rigid, ![]() ${\rm Ext}_{\Lambda}^{k}(N, M)=0$ for every
${\rm Ext}_{\Lambda}^{k}(N, M)=0$ for every ![]() $k \in \lbrace 1,\ldots,n-1 \rbrace$ and the result follows.
$k \in \lbrace 1,\ldots,n-1 \rbrace$ and the result follows.
(d) Let ![]() $\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of representative of the isomorphic classes of indecomposable modules in
$\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of representative of the isomorphic classes of indecomposable modules in ![]() $\mathcal{M}$ and
$\mathcal{M}$ and  $T=\widehat{{\rm End}}_{\Lambda}(U)$, where
$T=\widehat{{\rm End}}_{\Lambda}(U)$, where ![]() $U=\bigoplus _{\alpha \in J} U_{\alpha}$. Assume that X is a left Λ-module such that
$U=\bigoplus _{\alpha \in J} U_{\alpha}$. Assume that X is a left Λ-module such that ![]() ${\rm Ext}_{\Lambda}^{k}(\mathcal{M}, X)=0$ for all
${\rm Ext}_{\Lambda}^{k}(\mathcal{M}, X)=0$ for all ![]() $k \in \lbrace 1, \ldots,n-1 \rbrace$. We show that
$k \in \lbrace 1, \ldots,n-1 \rbrace$. We show that  $X \in {\underrightarrow{\lim}}\mathcal{M}$. Consider the minimal injective resolution of X, namely
$X \in {\underrightarrow{\lim}}\mathcal{M}$. Consider the minimal injective resolution of X, namely
Applying the functor  $\widehat{\mathrm{Hom}}_{\Lambda}(U,-)$ and using the fact that
$\widehat{\mathrm{Hom}}_{\Lambda}(U,-)$ and using the fact that ![]() ${\rm Ext}_{\Lambda}^{k}(\mathcal{M}, X)=0$ for all
${\rm Ext}_{\Lambda}^{k}(\mathcal{M}, X)=0$ for all ![]() ${k \in \lbrace 1, \ldots, n-1 \rbrace}$, we obtain an exact sequence
${k \in \lbrace 1, \ldots, n-1 \rbrace}$, we obtain an exact sequence
 \begin{equation*}
0 \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_0) \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_1) \rightarrow \cdots \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_n).
\end{equation*}
\begin{equation*}
0 \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_0) \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_1) \rightarrow \cdots \rightarrow \widehat{\mathrm{Hom}}_{\Lambda}(U,E_n).
\end{equation*} Since each ![]() $E_l \in {\rm Add}(\mathcal{M})$, each
$E_l \in {\rm Add}(\mathcal{M})$, each  $\widehat{\mathrm{Hom}}_{\Lambda}(U,E_l) \in {\rm Proj}(T)$ and so by theorem 2.3, we can see that
$\widehat{\mathrm{Hom}}_{\Lambda}(U,E_l) \in {\rm Proj}(T)$ and so by theorem 2.3, we can see that  $\widehat{\mathrm{Hom}}_{\Lambda}(U,X) \in {\rm Flat}(T)$. Hence
$\widehat{\mathrm{Hom}}_{\Lambda}(U,X) \in {\rm Flat}(T)$. Hence  $U \otimes_T \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \in {\underrightarrow{\lim}}\mathcal{M}$. On the other hand, by using the fact that
$U \otimes_T \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \in {\underrightarrow{\lim}}\mathcal{M}$. On the other hand, by using the fact that ![]() $\Lambda \in \mathcal{M}$, it is not difficult to see that
$\Lambda \in \mathcal{M}$, it is not difficult to see that  $U \otimes_T \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \cong X$. Therefore,
$U \otimes_T \widehat{\mathrm{Hom}}_{\Lambda}(U,X) \cong X$. Therefore,  $X \in {\underrightarrow{\lim}}\mathcal{M}$ and the result follows.
$X \in {\underrightarrow{\lim}}\mathcal{M}$ and the result follows.
As a consequence, we have the following result.
Corollary 3.2. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then
$n \geq 2$. Then  $\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace = {\underrightarrow{\lim}}\mathcal{M}$.
$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace = {\underrightarrow{\lim}}\mathcal{M}$.
Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then by the proof of proposition 3.1(a),
$n \geq 2$. Then by the proof of proposition 3.1(a), ![]() ${\rm Add}(\mathcal{M})$ is a generating-cogenerating subcategory of Λ-Mod. By [Reference Angeleri-Hugel1, p. 651],
${\rm Add}(\mathcal{M})$ is a generating-cogenerating subcategory of Λ-Mod. By [Reference Angeleri-Hugel1, p. 651], ![]() ${\rm Add}(\mathcal{M})$ is a contravariantly finite subcategory of Λ-Mod. Also, by proposition 3.1(c),
${\rm Add}(\mathcal{M})$ is a contravariantly finite subcategory of Λ-Mod. Also, by proposition 3.1(c), ![]() ${\rm Add}(\mathcal{M})$ is an n-rigid subcategory of Λ-Mod. Therefore, it is natural to ask when
${\rm Add}(\mathcal{M})$ is an n-rigid subcategory of Λ-Mod. Therefore, it is natural to ask when ![]() ${\rm Add}(\mathcal{M})$ is a maximal n-rigid subcategory of Λ-Mod. We present the following proposition based on [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12] and [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4].
${\rm Add}(\mathcal{M})$ is a maximal n-rigid subcategory of Λ-Mod. We present the following proposition based on [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12] and [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4].
Proposition 3.3. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then the following statements are equivalent.
$n \geq 2$. Then the following statements are equivalent.
(a)
 $\mathcal{M}$ is of finite type.
$\mathcal{M}$ is of finite type.(b)
 $\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace = {\rm Add}(\mathcal{M})$.
$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace = {\rm Add}(\mathcal{M})$.(c)
 $\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace \subseteq {\rm Add}(\mathcal{M})$.
$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace \subseteq {\rm Add}(\mathcal{M})$.(d)
 ${\rm Add}(\mathcal{M})$ is an n-cluster tilting subcategory of Λ-
${\rm Add}(\mathcal{M})$ is an n-cluster tilting subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.
Proof. ![]() $(d) \Leftrightarrow (a)$ follows from [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12].
$(d) \Leftrightarrow (a)$ follows from [Reference Ebrahimi and Nasr-Isfahani16, theorem 4.12].
![]() $(d) \Rightarrow (b) \Rightarrow(c)$ is clear.
$(d) \Rightarrow (b) \Rightarrow(c)$ is clear.
![]() $(c) \Rightarrow (a)$ follows from the fact that
$(c) \Rightarrow (a)$ follows from the fact that ![]() $\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace$ is closed under filtered colimits and therefore contain
$\lbrace X\in \Lambda-{\rm Mod}~|~ {\rm Ext}^i_{\Lambda}(\mathcal{M},X)=0 ~~~ {\rm for ~all}~ 0 \lt i \lt n \rbrace$ is closed under filtered colimits and therefore contain  ${\underrightarrow{\lim}}\mathcal{M}$. Therefore,
${\underrightarrow{\lim}}\mathcal{M}$. Therefore,  ${\rm Add}(\mathcal{M})={\underrightarrow{\lim}}\mathcal{M}$ and by [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4],
${\rm Add}(\mathcal{M})={\underrightarrow{\lim}}\mathcal{M}$ and by [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4], ![]() $\mathcal{M}$ is of finite type.
$\mathcal{M}$ is of finite type.
Remark 3.4. In [Reference Iyama29], Iyama has been posed the following question that remains unanswered:
• Let Λ be a finite dimension K-algebra. Does any n-cluster tilting subcategory of Λ-mod with
 $n \geq 2$ have an additive generator?
$n \geq 2$ have an additive generator?
Ebrahimi and the second author in [Reference Ebrahimi and Nasr-Isfahani16, remark 4.13] posed the following question, which is equivalent to Iyama’s question.
• Let
 $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with  $n \geq 2$. Is
$n \geq 2$. Is  ${\rm Add}(\mathcal{M})$ an n-cluster tilting subcategory of Λ-Mod?
${\rm Add}(\mathcal{M})$ an n-cluster tilting subcategory of Λ-Mod?
By proposition 3.3, this question can be restated as:
• Let
 $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with  $n \geq 2$. Does every left Λ-module X with
$n \geq 2$. Does every left Λ-module X with  ${\rm Ext}^{1,\ldots,n-1}_{\Lambda}(\mathcal{M},X)=0$ belong to
${\rm Ext}^{1,\ldots,n-1}_{\Lambda}(\mathcal{M},X)=0$ belong to  ${\rm Add}(\mathcal{M})$?
${\rm Add}(\mathcal{M})$?
Let ![]() $\mathcal{M}$ be an additive full subcategory of Λ-mod which is closed under direct summands. A sequence
$\mathcal{M}$ be an additive full subcategory of Λ-mod which is closed under direct summands. A sequence ![]() $0 \rightarrow A \overset{f}{\rightarrow} B \overset{g}{\rightarrow} C \rightarrow 0$ in
$0 \rightarrow A \overset{f}{\rightarrow} B \overset{g}{\rightarrow} C \rightarrow 0$ in  ${\underrightarrow{\lim}}\mathcal{M}$ (i.e., a pair of maps f and g with fg = 0) is said to be pure-exact if the sequence
${\underrightarrow{\lim}}\mathcal{M}$ (i.e., a pair of maps f and g with fg = 0) is said to be pure-exact if the sequence
 \begin{equation*}0 \rightarrow {\rm Hom}_{\Lambda}(M, A) \overset{{\rm Hom}_{\Lambda}(M, f)}{\rightarrow} {\rm Hom}_{\Lambda}(M, B) \overset{{\rm Hom}_{\Lambda}(M, g)}{\rightarrow} {\rm Hom}_{\Lambda}(M, C) \rightarrow 0\end{equation*}
\begin{equation*}0 \rightarrow {\rm Hom}_{\Lambda}(M, A) \overset{{\rm Hom}_{\Lambda}(M, f)}{\rightarrow} {\rm Hom}_{\Lambda}(M, B) \overset{{\rm Hom}_{\Lambda}(M, g)}{\rightarrow} {\rm Hom}_{\Lambda}(M, C) \rightarrow 0\end{equation*} is exact for each ![]() $M \in \mathcal{M}$ (see [Reference Crawley-Boevey12, p. 1653]).
$M \in \mathcal{M}$ (see [Reference Crawley-Boevey12, p. 1653]).
A homomorphism ![]() $g: M \rightarrow X$ is called right minimal if any endomorphism
$g: M \rightarrow X$ is called right minimal if any endomorphism ![]() $h: M \rightarrow M$ such that hg = g is an isomorphism. Let
$h: M \rightarrow M$ such that hg = g is an isomorphism. Let ![]() $\mathcal{X}$ be a full subcategory of Λ-Mod. A left Λ-module N has an
$\mathcal{X}$ be a full subcategory of Λ-Mod. A left Λ-module N has an ![]() $\mathcal{X}$-cover if there is a right minimal right
$\mathcal{X}$-cover if there is a right minimal right ![]() $\mathcal{X}$-approximation
$\mathcal{X}$-approximation ![]() $X \rightarrow N$ (see [Reference Bazzoni and Positselski9, Section 4]).
$X \rightarrow N$ (see [Reference Bazzoni and Positselski9, Section 4]).
Remark 3.5. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Motivated by proposition 3.3 (see also [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4]), it is natural to ask whether
$n \geq 2$. Motivated by proposition 3.3 (see also [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4]), it is natural to ask whether ![]() ${\rm Add}(\mathcal{M})$ is closed under direct limits. This question is equivalent to Iyama’s question. Let
${\rm Add}(\mathcal{M})$ is closed under direct limits. This question is equivalent to Iyama’s question. Let ![]() $\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of non-isomorphic indecomposable modules in
$\lbrace U_{\alpha}~|~ \alpha \in J \rbrace$ be a complete set of non-isomorphic indecomposable modules in ![]() $\mathcal{M}$ and set
$\mathcal{M}$ and set ![]() $U=\bigoplus_{\alpha \in J} U_{\alpha}$. Let
$U=\bigoplus_{\alpha \in J} U_{\alpha}$. Let ![]() $0 \rightarrow N' \rightarrow N \rightarrow N'' \rightarrow 0$ be a pure exact sequence, where
$0 \rightarrow N' \rightarrow N \rightarrow N'' \rightarrow 0$ be a pure exact sequence, where ![]() $N \in {\rm Add}(U)$. By [Reference Krause31, lemma 3.10],
$N \in {\rm Add}(U)$. By [Reference Krause31, lemma 3.10],  $N' \in {\underrightarrow{\lim}}\mathcal{M}$. Hence by proposition 3.1,
$N' \in {\underrightarrow{\lim}}\mathcal{M}$. Hence by proposition 3.1, ![]() ${\rm Ext}_{\Lambda}^{1}(U, N')=0$. This implies that the sequence of abelian groups
${\rm Ext}_{\Lambda}^{1}(U, N')=0$. This implies that the sequence of abelian groups
is exact. Therefore by using [Reference Bazzoni and Positselski9, corollary 9.6], Iyama’s question is equivalent to the following question.
• Let
 $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with  $n \geq 2$. Does any object of
$n \geq 2$. Does any object of  ${\underrightarrow{\lim}}\mathcal{M}$ have an
${\underrightarrow{\lim}}\mathcal{M}$ have an  ${\rm Add}(\mathcal{M})$-cover?
${\rm Add}(\mathcal{M})$-cover?
Let ![]() $\mathcal{M}$ be an additive full subcategory of Λ-mod which is closed under direct summands. Following [Reference Simson40, Reference Simson41], the category
$\mathcal{M}$ be an additive full subcategory of Λ-mod which is closed under direct summands. Following [Reference Simson40, Reference Simson41], the category  ${\underrightarrow{\lim}}\mathcal{M}$ is defined to be pure semisimple if any pure-exact sequence in
${\underrightarrow{\lim}}\mathcal{M}$ is defined to be pure semisimple if any pure-exact sequence in  ${\underrightarrow{\lim}}\mathcal{M}$ splits (see also [Reference Crawley-Boevey12, Section 3]).
${\underrightarrow{\lim}}\mathcal{M}$ splits (see also [Reference Crawley-Boevey12, Section 3]).
Remark 3.6. Let Δ be a left artinian ring and ![]() $\mathcal{M}$ be a covariantly finite additive full subcategory of Δ-mod which is closed under direct summands. Then by [Reference Crawley-Boevey12, theorem 4.2],
$\mathcal{M}$ be a covariantly finite additive full subcategory of Δ-mod which is closed under direct summands. Then by [Reference Crawley-Boevey12, theorem 4.2],  $\mathcal{A}={\underrightarrow{\lim}}\mathcal{M}$ is a locally finitely presented category with products. By using [Reference Krause31, proposition 3.11 and corollary 2.7] and [Reference Crawley-Boevey12, lemma 4.3], we can see that
$\mathcal{A}={\underrightarrow{\lim}}\mathcal{M}$ is a locally finitely presented category with products. By using [Reference Krause31, proposition 3.11 and corollary 2.7] and [Reference Crawley-Boevey12, lemma 4.3], we can see that ![]() $\mathcal{A}$ is a pure semisimple category if and only if every module in
$\mathcal{A}$ is a pure semisimple category if and only if every module in ![]() $\mathcal{A}$ is a direct sum of indecomposable modules. Equivalently, every module in
$\mathcal{A}$ is a direct sum of indecomposable modules. Equivalently, every module in ![]() $\mathcal{A}$ is a direct sum of finitely generated modules (see [Reference Beligiannis10, Subsection 2.1.1]).
$\mathcal{A}$ is a direct sum of finitely generated modules (see [Reference Beligiannis10, Subsection 2.1.1]).
In the following theorem, we give equivalence conditions for n-rigidity of filtered colimits of n-cluster tilting subcategories of module categories. Note that the equivalence between (b) and (c) and implication (a) implies (b) is already known by [Reference Ebrahimi and Nasr-Isfahani16, Reference Ebrahimi and Nasr-Isfahani17].
Theorem 3.7. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Then the following statements are equivalent.
$n \geq 2$. Then the following statements are equivalent.
(a)
 $\mathcal{M}$ is of finite type.
$\mathcal{M}$ is of finite type.(b)
 ${\underrightarrow{\lim}}\mathcal{M}$ is an n-cluster tilting subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is an n-cluster tilting subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(c)
 ${\underrightarrow{\lim}}\mathcal{M}$ is an n-rigid subcategory of Λ-
${\underrightarrow{\lim}}\mathcal{M}$ is an n-rigid subcategory of Λ- ${\rm Mod}$.
${\rm Mod}$.(d)
 ${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$.
${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$.(e) Every pure submodule N of a module X in
 ${\rm Add}(\mathcal{M})$ is a direct summand of X.
${\rm Add}(\mathcal{M})$ is a direct summand of X.(f)
 ${\underrightarrow{\lim}}\mathcal{M}$ is pure semisimple.
${\underrightarrow{\lim}}\mathcal{M}$ is pure semisimple.
Proof. ![]() $(a) \Rightarrow (b)$ follows from proposition 3.3 and [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4].
$(a) \Rightarrow (b)$ follows from proposition 3.3 and [Reference Ebrahimi and Nasr-Isfahani17, proposition 4.4].
![]() $(b) \Leftrightarrow (c)$ follows from [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.6].
$(b) \Leftrightarrow (c)$ follows from [Reference Ebrahimi and Nasr-Isfahani17, theorem 3.6].
![]() $(c) \Rightarrow (d)$ is clear.
$(c) \Rightarrow (d)$ is clear.
![]() $(d) \Rightarrow (e)$. Let X be a module in
$(d) \Rightarrow (e)$. Let X be a module in ![]() ${\rm Add}(\mathcal{M})$ and N be a pure submodule of X. We show that N is a direct summand of X. Consider the pure exact sequence
${\rm Add}(\mathcal{M})$ and N be a pure submodule of X. We show that N is a direct summand of X. Consider the pure exact sequence
 $X \in {\underrightarrow{\lim}}\mathcal{M}$ and by [Reference Krause31, lemmas 3.9 and 3.10], N and
$X \in {\underrightarrow{\lim}}\mathcal{M}$ and by [Reference Krause31, lemmas 3.9 and 3.10], N and ![]() $X/N$ are modules in
$X/N$ are modules in  ${\underrightarrow{\lim}}\mathcal{M}$. Since
${\underrightarrow{\lim}}\mathcal{M}$. Since  ${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$, the exact sequence
${\rm Ext}_{\Lambda}^1({\underrightarrow{\lim}}\mathcal{M}, {\underrightarrow{\lim}}\mathcal{M})=0$, the exact sequence ![]() $0 \rightarrow N \rightarrow X \rightarrow X/N \rightarrow 0$ is split and so the result follows.
$0 \rightarrow N \rightarrow X \rightarrow X/N \rightarrow 0$ is split and so the result follows.
![]() $(e) \Rightarrow (f)$. By remark 3.6, it is enough to show that every module in
$(e) \Rightarrow (f)$. By remark 3.6, it is enough to show that every module in  ${\underrightarrow{\lim}}\mathcal{M}$ is a direct sum of finitely generated modules. Let X be a module in
${\underrightarrow{\lim}}\mathcal{M}$ is a direct sum of finitely generated modules. Let X be a module in  ${\underrightarrow{\lim}}\mathcal{M}$. Then by [Reference Crawley-Boevey12, lemma 4.1], there exists a pure epimorphism
${\underrightarrow{\lim}}\mathcal{M}$. Then by [Reference Crawley-Boevey12, lemma 4.1], there exists a pure epimorphism ![]() $\varphi: \bigoplus_{\alpha \in A}M_{\alpha} {\rightarrow} X$ with each
$\varphi: \bigoplus_{\alpha \in A}M_{\alpha} {\rightarrow} X$ with each ![]() $M_{\alpha} \in \mathcal{M}$. This implies that
$M_{\alpha} \in \mathcal{M}$. This implies that ![]() ${\rm Ker}(\varphi)$ is a pure submodule of
${\rm Ker}(\varphi)$ is a pure submodule of ![]() $\bigoplus_{\alpha \in A}M_{\alpha}$. Hence by assumption, X is a direct sum of finitely generated modules and so the result follows.
$\bigoplus_{\alpha \in A}M_{\alpha}$. Hence by assumption, X is a direct sum of finitely generated modules and so the result follows.
![]() $(f) \Rightarrow (a)$ follows from [Reference Fazelpour and Nasr-Isfahani21, corollary 4.6].
$(f) \Rightarrow (a)$ follows from [Reference Fazelpour and Nasr-Isfahani21, corollary 4.6].
Remark 3.8. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$. Suppose that
$n \geq 2$. Suppose that ![]() ${(M_i, \varphi_{ij})_{i,j \in I}}$ is a direct system in
${(M_i, \varphi_{ij})_{i,j \in I}}$ is a direct system in ![]() $\mathcal{M}$. Consider the following property
$\mathcal{M}$. Consider the following property
(*) For each family
 $\lbrace \psi_{ij}: M_i \rightarrow N~|~i \lt j \rbrace$ of morphisms with
$\lbrace \psi_{ij}: M_i \rightarrow N~|~i \lt j \rbrace$ of morphisms with  $N \in {\underrightarrow{\lim}}\mathcal{M}$ such that
$N \in {\underrightarrow{\lim}}\mathcal{M}$ such that
 \begin{equation*}
\psi_{ik} = \psi_{ij} + \varphi_{ij}\psi_{jk} \text{for each}\ i, j, k \in I\ \mathrm{with}\ i \lt j \lt k,
\end{equation*}
\begin{equation*}
\psi_{ik} = \psi_{ij} + \varphi_{ij}\psi_{jk} \text{for each}\ i, j, k \in I\ \mathrm{with}\ i \lt j \lt k,
\end{equation*}there exists a family
 $\lbrace \psi_i: M_i \rightarrow N~|~i \in I \rbrace$ of morphisms such that
$\lbrace \psi_i: M_i \rightarrow N~|~i \in I \rbrace$ of morphisms such that
 \begin{equation*}
\psi_i=\psi_{ij} + \varphi_{ij}\psi_j \ \text{for each}\ i, j \in I\ \text{with}\ i \lt j.
\end{equation*}
\begin{equation*}
\psi_i=\psi_{ij} + \varphi_{ij}\psi_j \ \text{for each}\ i, j \in I\ \text{with}\ i \lt j.
\end{equation*}
By theorem 3.7 and [Reference Saroch and Stovicek38, lemma 2.3], Iyama’s question equivalent to the following question:
• Let
 $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with  $n \geq 2$. Does any direct system
$n \geq 2$. Does any direct system  ${(M_i, \varphi_{ij})_{i,j \in I}}$ in
${(M_i, \varphi_{ij})_{i,j \in I}}$ in  $\mathcal{M}$ have the property
$\mathcal{M}$ have the property  $(\ast)$?
$(\ast)$?
A left Λ-module M is called Mittag-Leffler if the canonical map
 \begin{equation*} (\prod_{i \in I} Q_i) \otimes_{\Lambda} M \rightarrow \prod_{i \in I} (Q_i \otimes_{\Lambda}M)\end{equation*}
\begin{equation*} (\prod_{i \in I} Q_i) \otimes_{\Lambda} M \rightarrow \prod_{i \in I} (Q_i \otimes_{\Lambda}M)\end{equation*} is injective, where ![]() $\lbrace Q_i~ |~ i \in I\rbrace$ are arbitrary right Λ-modules (see [Reference Azumaya7, p. 19]). A direct system
$\lbrace Q_i~ |~ i \in I\rbrace$ are arbitrary right Λ-modules (see [Reference Azumaya7, p. 19]). A direct system ![]() $(M_i, \varphi_{ij})_{i, j \in I}$ of left Λ-module is called factorizable if for every
$(M_i, \varphi_{ij})_{i, j \in I}$ of left Λ-module is called factorizable if for every ![]() $i \in I$ there exists
$i \in I$ there exists ![]() $j \geq i$ such that φij factors through each φik with
$j \geq i$ such that φij factors through each φik with ![]() $k \geq i$. Let
$k \geq i$. Let ![]() $(M_i, \varphi_{ij})_{i, j \in I}$ be a direct system of finitely generated left Λ-modules and
$(M_i, \varphi_{ij})_{i, j \in I}$ be a direct system of finitely generated left Λ-modules and  $M={\underrightarrow{\lim}} M_i$. Then by [Reference Raynaud and Gruson35, pp. 69–70, lemma 2.1.2 and propositions 2.1.4 and 2.1.5], M is Mittag-Leffler if and only if
$M={\underrightarrow{\lim}} M_i$. Then by [Reference Raynaud and Gruson35, pp. 69–70, lemma 2.1.2 and propositions 2.1.4 and 2.1.5], M is Mittag-Leffler if and only if ![]() $(M_i, \varphi_{ij})_{i, j \in I}$ is factorizable. For artin algebras, it is known that Mittag-Leffler modules coincide with locally pure projective modules (see [Reference Angeleri-Hugel, Herbera and Trlifaj2, lemma 20]). Recall that a left Λ-module N is called locally pure projective if any pure epimorphism
$(M_i, \varphi_{ij})_{i, j \in I}$ is factorizable. For artin algebras, it is known that Mittag-Leffler modules coincide with locally pure projective modules (see [Reference Angeleri-Hugel, Herbera and Trlifaj2, lemma 20]). Recall that a left Λ-module N is called locally pure projective if any pure epimorphism ![]() $g: Y \rightarrow N$ is locally split, that is, for each
$g: Y \rightarrow N$ is locally split, that is, for each ![]() $x \in N$ there is a map
$x \in N$ there is a map ![]() $\varphi=\varphi_{x}: N \rightarrow Y$ such that
$\varphi=\varphi_{x}: N \rightarrow Y$ such that ![]() $x = (x)\varphi g$.
$x = (x)\varphi g$.
Let ![]() $\mathcal{M}$ be a skeletally small additive full subcategory of Λ-mod which is closed under direct summands. Let
$\mathcal{M}$ be a skeletally small additive full subcategory of Λ-mod which is closed under direct summands. Let ![]() $\lbrace M_i~|~i \in I\rbrace$ be a complete set of isomorphism classes of objects in
$\lbrace M_i~|~i \in I\rbrace$ be a complete set of isomorphism classes of objects in ![]() $\mathcal{M}$ and put
$\mathcal{M}$ and put ![]() $M= \bigoplus_{i \in I}M_i$. We denote by
$M= \bigoplus_{i \in I}M_i$. We denote by ![]() $\mathscr{G}(M)$ the category of all left Λ-modules N which admit a locally split epimorphism
$\mathscr{G}(M)$ the category of all left Λ-modules N which admit a locally split epimorphism ![]() $g: M^{(K)} \rightarrow N$ for some set K. It is clear by definition that
$g: M^{(K)} \rightarrow N$ for some set K. It is clear by definition that ![]() ${\rm Add}(\mathcal{M}) \subseteq \mathscr{G}(M)$. Moreover,
${\rm Add}(\mathcal{M}) \subseteq \mathscr{G}(M)$. Moreover, ![]() $\mathscr{G}(M)$ consists of all modules in
$\mathscr{G}(M)$ consists of all modules in  ${\underrightarrow{\lim}}\mathcal{M}$ which are locally pure projective (see [Reference Angeleri-Hugel1, proposition 2.3]).
${\underrightarrow{\lim}}\mathcal{M}$ which are locally pure projective (see [Reference Angeleri-Hugel1, proposition 2.3]).
Remark 3.9. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $\lbrace U_{\alpha}~|~\alpha \in J\rbrace$ be a complete set of isomorphism classes of modules in
$\lbrace U_{\alpha}~|~\alpha \in J\rbrace$ be a complete set of isomorphism classes of modules in ![]() $\mathcal{M}$. Then
$\mathcal{M}$. Then  ${\rm Add}(\mathcal{M}) \subseteq \mathscr{G}(U) \subseteq {\underrightarrow{\lim}}\mathcal{M}$, where
${\rm Add}(\mathcal{M}) \subseteq \mathscr{G}(U) \subseteq {\underrightarrow{\lim}}\mathcal{M}$, where ![]() $U= \bigoplus_{\alpha \in J}U_{\alpha}$. The locally finitely presented category
$U= \bigoplus_{\alpha \in J}U_{\alpha}$. The locally finitely presented category  ${\underrightarrow{\lim}}\mathcal{M}$ is a covariantly finite subcategory of Λ-Mod and also it is closed under direct product (see [Reference Krause31, proposition 3.11]). By [Reference Rada and Saorin34, corollary 3.5],
${\underrightarrow{\lim}}\mathcal{M}$ is a covariantly finite subcategory of Λ-Mod and also it is closed under direct product (see [Reference Krause31, proposition 3.11]). By [Reference Rada and Saorin34, corollary 3.5], ![]() ${\rm Add}(\mathcal{M})$ is a covariantly finite subcategory of Λ-Mod if and only if
${\rm Add}(\mathcal{M})$ is a covariantly finite subcategory of Λ-Mod if and only if ![]() ${\rm Add}(\mathcal{M})$ is closed under direct products. Note that Rothmaler in [Reference Rothmaler36] studied direct products of Mittag-Leffler modules by using tools in model theory. He showed that all reduced products of Mittag-Leffler left Λ-modules are Mittag-Leffler if and only if all left Λ-modules are Mittag-Leffler if and only if Λ is left pure-semisimple (see [Reference Rothmaler36, corollary 3.2]). Hence one may ask when
${\rm Add}(\mathcal{M})$ is closed under direct products. Note that Rothmaler in [Reference Rothmaler36] studied direct products of Mittag-Leffler modules by using tools in model theory. He showed that all reduced products of Mittag-Leffler left Λ-modules are Mittag-Leffler if and only if all left Λ-modules are Mittag-Leffler if and only if Λ is left pure-semisimple (see [Reference Rothmaler36, corollary 3.2]). Hence one may ask when ![]() $\mathscr{G}(U)$ is a covariantly finite subcategory of Λ-Mod. Also, it is natural to ask whether
$\mathscr{G}(U)$ is a covariantly finite subcategory of Λ-Mod. Also, it is natural to ask whether ![]() $\mathscr{G}(U)$ is closed under direct products. In particular, it is natural and interesting to ask the following question:
$\mathscr{G}(U)$ is closed under direct products. In particular, it is natural and interesting to ask the following question:
• Let
 $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with  $n \geq 2$. Is any direct system in
$n \geq 2$. Is any direct system in  $\mathcal{M}$ factorizable?
$\mathcal{M}$ factorizable?
As a consequence of theorem 3.7 and [Reference Angeleri-Hugel1, theorems 3.4, 4.4, 5.1, and 5.2], we have the following result that shows the questions in remark 3.9 are equivalent to Iyama’s question.
Corollary 3.10. Let ![]() $\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with
$\mathcal{M}$ be an n-cluster tilting subcategory of Λ-mod with ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $\lbrace U_{\alpha}~|~\alpha \in J\rbrace$ be a complete set of isomorphism classes of objects of
$\lbrace U_{\alpha}~|~\alpha \in J\rbrace$ be a complete set of isomorphism classes of objects of ![]() $\mathcal{M}$. Put
$\mathcal{M}$. Put ![]() $U= \bigoplus_{\alpha \in J}U_{\alpha}$. Then the following statements are equivalent.
$U= \bigoplus_{\alpha \in J}U_{\alpha}$. Then the following statements are equivalent.
(a)
 $\mathcal{M}$ is of finite type.
$\mathcal{M}$ is of finite type.(b) All modules in
 ${\underrightarrow{\lim}}\mathcal{M}$ are Mittag-Leffler modules.
${\underrightarrow{\lim}}\mathcal{M}$ are Mittag-Leffler modules.(c)
 $\mathscr{G}(U)$ is closed under direct products.
$\mathscr{G}(U)$ is closed under direct products.(d)
 $\mathscr{G}(U)$ is closed under direct limits.
$\mathscr{G}(U)$ is closed under direct limits.(e)
 $\mathscr{G}(U)$ is a covariantly finite subcategory of Λ-Mod.
$\mathscr{G}(U)$ is a covariantly finite subcategory of Λ-Mod.(f) Every pure submodule N of a module
 $X \in {\rm Add}(\mathcal{M})$ is a direct summand of X.
$X \in {\rm Add}(\mathcal{M})$ is a direct summand of X.
Acknowledgements
The authors would like to thank the referee for a careful reading of this article and making helpful suggestions and comments that improved the article. The work of the first author is based upon research funded by Iran National Science Foundation (INSF) under project No. 4001480. The research of the first author was in part carried out in IPM-Isfahan Branch. The work of the second author is based upon research funded by Iran National Science Foundation (INSF) under project No. 4032107. Also, the research of the second author was in part supported by a grant from IPM (No. 1403160416).