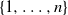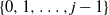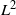1. Introduction
Given a finite group and a generating k-tuple, consider the simple random walk on G associated with this k-tuple. At each integer time, this random walk moves from the current position
$X_n$
to
$X_ng$
, where g is picked uniformly at random among the k generators, independently of all previous steps. To define the hit-and-run walk based on the same generating k-tuple, for any group element g, call
$m_g$
the order (i.e. exponent) of g. At each step, pick one of the k generators uniformly at random, call it g, pick
$\ell$
uniformly in
$\{0,\ldots, m_g-1\}$
, and move to
$X_ng^\ell$
.
This defines a natural variation on simple random walks which allows for long jumps when the orders of some of the generators are relatively large. As often in the study of random walks on finite groups, it is easier to think about the problem for a family of random walks on a sequence of finite groups whose sizes increase to infinity.
Two of the most basic questions one can ask concerning a family of ergodic random walks on some finite groups whose sizes increase to infinity are: How long does the walk take to be approximately uniformly distributed? Does the cut-off phenomenon occur? That is, is there a rapid transition from being far from equilibrium to reaching approximate equilibrium? See [Reference Aldous1], [Reference Diaconis5], and [Reference Diaconis6] for introductions to these problems. In the context of hit-and-run random walks, the following additional question emerges: Does the hit-and-run version converge faster than the simple random walk version? That is, does the extra randomization help, and if so, how much?
We study these problems in the case of the hit-and-run walk associated with one of the classic random walks on the symmetric group, top-to-random. See Example 1.2 below. We show that if convergence is measured in
$L^2$
, the hit-and-run walk and the original top-to-random walk both take order
$n\log n$
to converge. What exactly happens to the hit-and-run walk in total variation is left as an open question, but it seems plausible that, again, it takes order
$n\log n$
to converge, as top-to-random does [Reference Aldous1, Reference Diaconis5]. We give an analysis of the Markov chain consisting in following a fixed single card. While studying this example and based on some numerical evidence, the first and last authors conjectured that the hit-and-run top-to-random walk had only non-negative eigenvalues. The second author provided a proof of this fact, and more, based on earlier works on hit-and-run algorithms [Reference Rudolf and Ullrich11]: for any generating tuple on any finite group, the associated hit-and-run walk has non-negative spectrum. See Theorem 1.1 and Section 4.
1.1. Random walks based on generating k-tuples
Let G be a finite group with identity element e. For any generating k-tuple
$S=(g_1,\ldots, g_k)$
, let
$\mu_S$
be the probability measure
\begin{equation*}\mu_S=\dfrac{1}{k}\sum_{i=1}^k\delta_{g_i},\quad\delta_{g}(h)=\begin{cases} 1 & \text{if $ h=g$,}\\ 0 & \text{otherwise.}\end{cases}\end{equation*}
The random walk on the group G driven by the measure
$\mu_S$
above or any probability measure
$\mu$
, for that matter, is the Markov chain with state space G and Markov kernel
\begin{equation*}M(x,y)=\mu(x^{-1}y).\end{equation*}
The uniform measure
$u=u_G$
on G is always invariant for such a Markov chain and it is useful to consider the (convolution) operator
\begin{equation*}f\mapsto Mf(x)=\sum_yM(x,y)f(y)\end{equation*}
acting on
$L^2=L^2(G,u)$
. At any (discrete) time t, the iterated kernel
$M^t(x,y)$
is given by the t-fold convolution
$\mu^{(t)}$
of
$\mu$
by itself in the form
$M^t(x,y)=\mu^{(t)}(x^{-1}y)$
. The adjoint
$M^*$
of M satisfies
$M=M^*$
if and only if
$\mu$
is symmetric in the sense that
$\check{\mu}(x)=\mu(x^{-1} )=\mu(x)$
.
Example 1.1. The following examples on the symmetric group
$\mathbf S_n$
will be of particular interest to us. See [Reference Aldous1], [Reference Bernstein and Nestoridi2], [Reference Brown and Diaconis3], [Reference Diaconis5], [Reference Diaconis and Saloff-Coste7], [Reference Diaconis and Shahshahani8], [Reference Diaconis, Fill and Pitman9], and [Reference Saloff-Coste13].
-
(Top-to-random.)
$S=(\sigma_i)_1^n$
, where
$\sigma_i$
takes the top card of the deck and places it in position i. In cycle notation,
$\sigma_i=(i,i-1,\ldots, 2,1)$
. The probability measure
$\mu_S$
in this example is not symmetric. -
(Random-to-random or random insertions.)
$S= (\sigma_{ij})_{1\le i, j\le n}$
(ordered lexicographically), where
$\sigma_{ij}$
is ‘take the card in position i and insert it in position j’. In cycle notation, when
$i<j$
,
$\sigma_{ij}=(\,j,j-1,\ldots,i)$
. Note also that
$\sigma_{ij}=\sigma_{ji}^{-1}$
and
$\sigma_{ii}=e$
. The corresponding measure
$\mu_S$
gives probability
$1/n$
to the identity element e and probability
$1/n^2$
to each
$\sigma_{ij}$
,
$i\neq j$
with the caveat that when
$|j-i|=1$
,
$\sigma_{ij}=\sigma_{ji}$
, so that the corresponding transposition
$\tau=\sigma_{ij}=\sigma_{ji}$
actually has probability
$2/n^2$
. -
(Random transposition.) Take
$S=(\tau_{ij})_{1\le i \le j\le n}$
, where
$\tau_{ij}$
transposes the cards in positions i and j (i.e.
$\tau_{ij}=(i,j)$
). This tuple S contains each true transposition (i, j),
$1\le i<j\le n$
, twice, and also includes n copies of the identity (i, i),
$1\le i\le n$
. Equivalently, we can think of (i, j) being picked uniformly independently at random from
$\{1,\ldots,n\}$
so that the probability measure
$\mu_S$
gives probability
$1/n$
to the identity and probability
$2/n^2 $
to any transposition.
All these examples are ergodic in the sense that the distribution at time t of the associated Markov chain converges to the uniform distribution u on
$\mathbf S_n$
.
1.2. Hit-and-run walks based on generating tuples
We now consider the following modification of the measure
$\mu_S$
associated with a fixed generating tuple
$S=(s_1,\ldots,s_k)$
, which we call
$q_S$
. For each
$s_i\in S$
, let
$m_i$
be its order in G (the smallest m such that
$s_i^m=e$
). Define
\begin{equation} q_S=\dfrac{1}{k}\sum_{i=1}^k \dfrac{1}{m_i}\sum_{j=0}^{m_i-1}\delta_{s_i^j}.\end{equation}
To describe
$q_S$
in words,
$q_S$
is the distribution of a random element in G chosen as follows: pick i uniformly in
$\{1,\ldots,k\}$
, pick m uniformly in
$\{0,\ldots,m_i-1\}$
, output
$s_i^m\in G$
. This is reminiscent of the so-called hit-and-run algorithms, hence the name.
The question we want to address is whether or not the random walk driven by
$q_S$
mixes faster than the random walk driven by
$\mu_S$
. Does taking a uniform step in the direction of the generator
$s_i$
, i.e. along the one parameter subgroup
$\{s_i^m\,:\, 0\le m\le m_i-1\}$
instead of just a single
$s_i$
-step, speed up convergence or not?
Example 1.2. (Our main example: hit-and-run for top-to-random.) Top-to-random on
$\mathbf S_n$
is obtained by considering the generating n-tuple
\begin{equation*}S= \{ (k,k-1,\ldots, 2,1)\,:\, k=1,\ldots,n\}=\{\sigma_k\,:\, k=1,\ldots,n\}\end{equation*}
where
$\sigma_k\,:\!=\, (k, k - 1,\ldots,2, 1)$
. The associated simple random walk measure is (as mentioned earlier, it is not symmetric)
\begin{equation*}\mu_S(\sigma) =\begin{cases} \dfrac{1}{n} & \text{if $ \sigma\in S$,} \\[7pt] 0 & \text{otherwise.} \end{cases} \end{equation*}
The associated hit-and-run measure is given by
\begin{equation}q(\sigma)=q_S(\sigma)=\dfrac{1}{n}\sum_{i=1}^n \dfrac{1}{i}\sum_{j=0}^{i-1}\delta_{\sigma_i^j}(\sigma).\end{equation}
This probability measure is symmetric and gives positive probability to order
$n^2$
distinct permutations.
Let us now describe our findings (informally), and related open questions regarding the hit-and-run for top-to-random shuffle.
-
(Facts.) In
$L^2$
, the mixing time for hit-and-run for top-to-random with n cards is of order
$n\log n$
, the same order as the top-to-random shuffle. See Section 3. There is a cut-off in
$L^2$
but the cut-off time is not known. See Theorem 1.2 below. In
$L^1$
(i.e. total variation), the mixing time is at least of order n and no more than order
$n\log n$
. -
(Open questions.) What is the cut-off time in
$L^2$
for the hit-and-run version of top to random? How does it compare precisely with
$n\log n$
, the cut-off time for the top-to-random shuffle? -
(Open questions.) Is there a cut-off in
$L^1$
(i.e. total variation)? What is the order of magnitude of the
$L^1$
-mixing time? Describe a simple statistic that provides a good lower bound for the mixing time in
$L^1$
. -
(Conjecture.) There is a cut-off in
$L^1$
and the rough order of the
$L^1$
cut-off time is
$n\log n$
.
Regarding general hit-and-run walks, we prove the following result.
Theorem 1.1. Let G be a finite group and let
$S=(s_1,\ldots,s_k)$
be a generating tuple. The eigenvalues
$-1\le \beta_{|G|-1}\le \dots\le \beta_1\le \beta_0=1$
of the hit-and-run walk on G based on S driven by the symmetric measure
$q_{S}$
at (1.1) are all non-negative, i.e.
$0\le \beta_{|G|-1}\le \dots\le \beta_1\le \beta_0=1$
.
The proof of this theorem is in Section 4. Section 2 provides exact computations concerning the Markov chains obtained by following a single card. We explore the time to equilibrium for this Markov chain as a function of the starting position of the card that is followed, both in total variation and in
$L^2$
. Section 3 studies the convergence of the hit-and-run top-to-random walk on the symmetric group
$\mathbf S_n$
in the
$L^2$
-norm
$\Vert \cdot \Vert_2$
, that is, we estimate
\begin{equation*}d_2\bigl(q^{(t)},\bigr) = \Vert\bigl( q^{(t)}/u\bigr)-1 \Vert_2.\end{equation*}
We prove the following result, which shows that the
$L^2$
-mixing time is of order
$n\log n$
.
Theorem 1.2. For any n, t, we have
\begin{equation*}d_2\bigl(q^{(t)},u\bigr) \ge \sqrt{n-1} \,\biggl(1-\dfrac{1}{n}\biggr)^{t}.\end{equation*}
The second largest eigenvalue
$\beta_1$
of q satisfies
$\beta_1\in [1-1/n, 1-1/(8n)]$
and, for any n large enough and
$t(n,c) \ge 9 n\log n \, + 12 n c$
,
$c>0$
,
\begin{equation*}d_2\bigl(q^{(t(n,c))},u\bigr)\le (2+{\textrm{o}}(1))\,{\textrm{e}}^{-c}\le \sqrt{5}\,{\textrm{e}}^{-c}.\end{equation*}
The convergence of
$q^{(t)}$
to u in the
$L^2$
sense occurs with a cut-off.
Remark 1.1. The well-known definition of cut-off can be found in the next section. The existence of this
$L^2$
-cut-off follows from the other assertions in the theorem and [Reference Chen and Saloff-Coste4, Theorem 3.3]. Indeed, we know that the spectral gap
$\lambda=1-\beta_1$
for q is at least
$1/(8n)$
and the time to stationarity in
$L^2$
, T, is at least
$\frac{1}{2} n\log n$
so that the product
$\lambda T$
tends to infinity with n. Referring to the vocabulary and definitions from [Reference Chen and Saloff-Coste4], the
$L^2$
-cut-off stated in the theorem occurs at about
$n\log n$
and has a window of order n. We do not know the more precise behavior of the cut-off time. The upper bound on
$d_2(q^{(t)},u)$
is stated ‘for n large enough’. This comes from the proof of Theorem 1 in [Reference Bernstein and Nestoridi2] and whatever ‘large enough’ means in the proof of [Reference Bernstein and Nestoridi2, Theorem 1] works here as well. It seems that
$n\ge 6$
is enough. We do not expect the constants in the definition of t(n, c) to be sharp.
1.3. Notions of convergence
We will discuss convergence to the uniform distribution using two different distances between probability measures (or between their densities with respect to the uniform measure u). Let
$\nu$
be a probability measure on a finite group G and let u be the uniform distribution on G.
Total variation (or
$\frac{1}{2}\hbox{-}L^1(G,u)$
-norm) is defined by
\begin{align*} \|\nu-u\|_{\textrm{TV}}&=\max_{A\subseteq G}\{\nu(A)-u(A)\}\\ &=\max_{A\subseteq G}\{|\nu(A)-u(A)|\}\\ &= \dfrac{1}{2} \|(\nu/u)-1\|_1\\ &= \dfrac{1}{2}\sum_{g\in G}|\nu(g)-u(g)|.\end{align*}
We also set
$d_1(\nu,u)= \|(\nu/u)-1\|_1 =2\|\nu-u\|_{\textrm{TV}}.$
Convergence in
$L^2(G,u)$
is measured using the distance
\begin{align*} d_2(\nu,u)^2&= \|(\nu/u)-1\|^2_2 \\ &= \sum_{g\in G} |(\nu(g)/u(g))-1|^2 u(g)\\ &= |G|\sum_{g\in G}|\nu(g)-u(g)|^2.\end{align*}
Let
$(G_n)_1^\infty$
be a sequence of finite groups such that
$|G_n|$
tends to infinity with n. Let
$u_n$
be the uniform probability on
$G_n$
. We say that a sequence of probability measures
$\mu_n$
on
$G_n$
,
$n=1,2,\ldots,$
has a cut-off at time
$t_n$
in
$L^p$
,
$p=1,2$
, if
$t_n\rightarrow \infty$
and, for any
$\epsilon>0$
,
\begin{equation*}\lim_{n\rightarrow \infty}d_p\bigl(\mu_n^{((1+\epsilon) t_n)},u_n\bigr)=0 \quad\text{and}\quad d_p\bigl(\mu_n^{((1-\epsilon)t_n)},u_n\bigr) =l_\infty(p),\end{equation*}
where
$l_\infty(1)=1$
and
$l_\infty(2)=+\infty$
.
Whenever the probability measure
$\mu$
is symmetric, i.e.
$\check{\mu}=\mu$
, the associated convolution operator
$f\mapsto Mf$
is diagonalizable with real eigenvalues
$-1\le \beta_{|G|-1}\le \dots \le \beta_1 \le\beta_0=1$
and
\begin{equation*}d_2\bigl(\mu^{(t)},u\bigr)^2= \sum_1^{|G|-1} \beta_i^{2t},\quad t=1,2,\ldots.\end{equation*}
This follows from the usual spectral decomposition. See e.g. [Reference Saloff-Coste13, Theorem 5.2]. Moreover,
\begin{equation*}d_\infty\bigl(\mu^{(2t)},u\bigr)=\max_G\biggl\{\biggl|\dfrac{\mu}{\nu}-1\biggr|\biggr\}=|G|\mu^{(2t)}(e)-1 =d_2\bigl(\mu^{(t)},u\bigr)^2.\end{equation*}
The second equality (no absolute value) uses
\begin{equation*}\mu^{(2t)}(e)=\sum_y\mu^{(t)}(y)\mu^{(t)}(y^{-1})=\sum_y|\mu^{(t)}(y)|^2.\end{equation*}
The Cauchy–Schwarz inequality easily gives
$d_\infty\bigl(\mu^{(2t)},u\bigr)\le d_2\bigl(\mu^{(t)},u\bigr)^2$
and it follows that this inequality must be an equality. Let us illustrate these definitions using the classical examples described above.
-
(Top-to-random.) Convergence in total variation occurs at time
$n\log n$
in the sense that if we set
$t(n,c)=n\log n+ cn$
, See [Reference Diaconis5] and [Reference Diaconis, Fill and Pitman9]. With a little work, the results in [Reference Diaconis, Fill and Pitman9] easily imply
\begin{equation*}\lim_{n\rightarrow \infty}\bigl\|\mu^{(t(n,c))}-u\bigr\|_{\textrm{TV}} =\begin{cases} 1 &\text{if $ c<0$,}\\ 0 &\text{if $ c>0$.}\end{cases}\end{equation*}
\begin{equation*}\lim_{n\rightarrow \infty}d_2\bigl(\mu^{(t(n,c))},u\bigr) =\begin{cases} \infty &\text{if $ c<0$,}\\ 0 &\text{if $ c>0$.}\end{cases} \end{equation*}
-
(Random-to-random.) Convergence in total variation (and in
$L^2$
) occurs with a cut-off at time
$(3n/4)\log n$
. See [Reference Bernstein and Nestoridi2]. -
(Random transposition.) Convergence in total variation (and in
$L^2$
) occurs with a cut-off at time
$(n/2)\log n$
. See [Reference Diaconis5], [Reference Diaconis and Shahshahani8], and [Reference Saloff-Coste and Zúñiga14].
2. Single-card Markov chain
To investigate the complex behavior of the hit-and-run top-to-random chain, it behooves us to explore the dynamics of just a single card. We do so by defining a Markov chain
$(X_t)^\infty_{t = 0}$
with state space
$\{1, 2,\ldots, n \}$
that represents the position of an arbitrarily chosen card after t shuffle iterations. This is a classical example of a function of a Markov chain that produces a Markov chain.
2.1. Abstract projection
Before proceeding with the example, we review some general aspects of this situation. Abstractly, we start with a Markov kernel Q on a state space X (in our case
$Q(x,y)= q_S(x^{-1}y)$
on
$\mathbf S_n$
) and a lumping (or projection) map
$p\,:\, X\rightarrow \underline X$
which is surjective and has the property that
\begin{equation*}\sum_{y\in X\,:\, p(y)=\underline{y}}Q(x,y) = \underline{Q}(\underline{x},\underline{y})\end{equation*}
depends only on
$p(x)=\underline{x}$
. This defines a Markov kernel on
$\underline{X}$
. If Q has stationary measure
$\pi$
then its push-forward
$\underline{\pi}(\underline{x})=\pi (p^{-1}(\underline{x}))$
is stationary for
$\underline{Q}$
. Moreover,
\begin{equation*}\|Q^t(x,\cdot)-\pi\|_{\textrm{TV}} \ge \|\underline{Q}^t(\underline{x},\cdot)-\underline{\pi}\|_{\textrm{TV}}.\end{equation*}
This simple comparison does not work well for the
$L^2$
and
$L^\infty$
convergence measured using
$d_2$
and
$d_\infty$
because normalization becomes an issue.
Let
$\beta$
and
$\underline{\phi}$
be an eigenvalue and associated eigenfunction for the chain
$\underline{Q}$
. Then it is plain that the function
$\phi(x)= \underline{\phi}\circ p(x)$
is an eigenfunction for Q with eigenvalue
$\beta$
. Also, two orthogonal eigenfunctions
$\underline{\phi}_1,\underline{\phi}_2$
for
$\underline{Q}$
on
$L^2(\underline{\pi})$
give orthogonal
$\phi_1,\phi_2$
in
$L^2(\pi)$
(we will not use this second fact).
2.2. Single-card chain in L 2
Let q be the measure for the hit-and-run version of top-to-random defined in (1.2). We consider the projection of
$Q(x,y)=q(x^{-1}y)$
on
$\{1,\ldots,n\}$
corresponding to following the position of a single card. To simplify notation, we set
$\underline{Q}=K$
and notice that the stationary (and reversible) measure for K is the uniform measure on
$\{1,\ldots, n\}$
. The transition probabilities K(i, j),
$i,j\in \{1,\ldots, n\}$
are given by
\begin{equation*}K(i,j) = \begin{cases}\displaystyle\dfrac{1}{n}\sum_{k \geq j}^n\dfrac{1}{k} + \dfrac{i - 1}{n} &\text{if $ i = j$,} \\[15pt]\displaystyle\dfrac{1}{n}\sum_{k \geq i}^n\dfrac{1}{k} &\text{if $ j< i$,} \\[15pt]\displaystyle\dfrac{1}{n}\sum_{k \geq j}^n\dfrac{1}{k} &\text{if $ j > i$.}\end{cases}\end{equation*}
The following lemma gives the eigenvalues and eigenvectors of K. The form of the eigenvectors was guessed by extrapolation from the cases
$n \leq 4$
.
Lemma 2.1. The eigenvalues and associated eigenvectors of the stochastic matrix
$(K(i,j))_{1\le i,j\le n}$
are
$\beta_0=1$
,
$\boldsymbol{\Psi}_0=(1,\ldots,1)$
and
\begin{equation*}\beta_i= 1-\dfrac{i}{n},\quad \boldsymbol{\Psi}_i= \biggl(\dfrac{-1}{n - i},\ldots,\dfrac{-1}{n - i}, 1, 0, \ldots, 0\biggr),\quad i=1,\ldots,n-1,\end{equation*}
where, in
$\boldsymbol{\Psi}_i$
, the value
$-1/(n-i)$
is repeated
$n-i$
times.
Proof. It suffices to verify the guessed formula. For
$\beta_{n-j}$
and
$\boldsymbol{\Psi}_{n-j}$
,
$j \in \{1,\ldots,n-1\}$
, and
$k < j + 1$
, we have
\begin{align*}&(K\boldsymbol{\Psi}_{n-j})_k\\[5pt]&\quad =\dfrac{1}{n}\biggl[\dfrac{1}{k} + \dfrac{1}{k+1} + \cdots + \dfrac{1}{n}\biggr][k-1]\dfrac{({-}1)}{j} \notag \\[5pt]&\quad\quad + \biggl[\dfrac{1}{n}\biggl[\dfrac{1}{k} + \dfrac{1}{k+1} + \cdots + \dfrac{1}{n}\biggr] + \dfrac{k-1}{n}\biggr]\dfrac{({-}1)}{j}\notag \\[5pt]&\quad\quad + \dfrac{1}{n}\biggl[\dfrac{1}{k+1} + \dfrac{1}{k+2} + \cdots + \dfrac{1}{n}\biggr]\dfrac{({-}1)}{j} + \cdots + \dfrac{1}{n}\biggl[\dfrac{1}{j} + \dfrac{1}{j+1} + \cdots + \dfrac{1}{n}\biggr] \dfrac{({-}1)}{j}\notag \\[5pt]&\quad\quad + \dfrac{1}{n}\biggl[\dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr]\cdot1 + 0 + \cdots + 0\notag \\[5pt]&\quad = \dfrac{1}{n} \biggl[\dfrac{({-}1)}{j}\biggl(\dfrac{j}{n} + \dfrac{j}{n-1} + \cdots + \dfrac{j}{j+1}\biggr) + \dfrac{({-}1)}{j}[j-k]\cdot1 + \dfrac{({-}1)}{j} k + \dfrac{1}{j} - \dfrac{1}{j}\notag \\[5pt]&\quad\quad + \dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr]\notag \\[5pt]&\quad = -\dfrac{1}{n}.\end{align*}
For
$k = j + 1$
, we obtain
\begin{align*}(K\boldsymbol{\Psi}_{n-j})_k&= \dfrac{1}{n}\biggl(\dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr)j \dfrac{({-}1)}{j}\notag \\[3pt]&\quad + \dfrac{1}{n}\biggl(\dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr) + \dfrac{j}{n} = \dfrac{j}{n}.\end{align*}
Likewise, for
$k > j + 1$
, we find
\begin{align*}(K\boldsymbol{\Psi}_{n-j})_k&=\dfrac{1}{n}\biggl(\dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr)j\dfrac{({-}1)}{j}\notag \\[3pt] &\quad + \dfrac{1}{n}\biggl(\dfrac{1}{j+1} + \dfrac{1}{j+2} + \cdots + \dfrac{1}{n}\biggr) = 0.\end{align*}
These eigenvectors are not normalized and
\begin{equation}\|\boldsymbol{\Psi}_i\|_2^2= \dfrac{1}{n(n-i)} +\dfrac{1}{n}= \dfrac{n-i+1}{n(n-i)}, \quad i=1,\ldots, n-1.\end{equation}
In the next lemma we use this knowledge (including (2.1)) to compute
\begin{align*}d_2(K^t(i,\cdot),u)^2&= n\sum_{j=1}^n \biggl|K^t(i,j)-\dfrac{1}{n}\biggr|^2 = \sum_{k=1}^{n-1} \beta_k^{2t} \dfrac{\boldsymbol{\Psi}_k(i)^2}{\|\boldsymbol{\Psi}_k\|_2^2}. \end{align*}
For the last equality, see e.g. [Reference Saloff-Coste13, equation (5.2)] or [Reference Saloff-Coste12, Lemma 1.3.3].
Lemma 2.2. The quantity
$d_2(K^t(i,\cdot),u)^2$
equals
\begin{equation*}\begin{cases}\displaystyle\sum_{k= 1}^{n - 2} \biggl(1 - \dfrac{k}{n}\biggr)^{2t}\dfrac{n}{(n - k)(n - k + 1)} + \biggl(\dfrac{1}{n}\biggr)^{2t}\dfrac{n}{2} & {if\ i = 1,} \\[15pt]\displaystyle\sum_{k= 1}^{n - i} \biggl(1 - \dfrac{k}{n}\biggr)^{2t}\dfrac{n}{(n - k)(n - k + 1)} + \biggl( \dfrac{i-1}{n}\biggr)^{2t}\dfrac{n(i-1)}{i} & {if\ 1< i < n,} \\[15pt]\biggl(1 - \dfrac{1}{n}\biggr)^{2t}(n-1) & {if\ i= n.}\end{cases}\end{equation*}
We need to understand what these formulas mean. The term
\begin{equation*}\sum_{k= 1}^{n - i} \biggl(1 - \dfrac{k}{n}\biggr)^{2t}\dfrac{n}{(n - k)(n - k + 1)}\end{equation*}
can be bounded above by
\begin{equation*}\dfrac{1}{n}\sum_{k= 1}^{n - i} \biggl(1 - \dfrac{k}{n}\biggr)^{2t-2}\end{equation*}
and bounded below by one-half of this quantity. Set
\begin{equation*}B(n,t,i) \biggl(1-\dfrac{1}{n}\biggr)^{2t-1}=\dfrac{1}{n}\sum_{k= 1}^{n - i} \biggl(1 - \dfrac{k}{n}\biggr)^{2t-2}.\end{equation*}
Lemma 2.3. For
$n\ge 4$
,
$t\ge 1$
, the quantity B(n, t) is bounded as follows.
-
If
$2\le i\le an$
,
$a \le1/2$
,
\begin{equation*}\biggl(\dfrac{1}{n-1}+\dfrac{1}{4(2t-1)}\biggr)\le B(n,t,i)\le \biggl(\dfrac{1}{n-1}+\dfrac{1}{2t-1}\biggr).\end{equation*}
-
If
$i\le an$
,
$ a <1$
, and
$n\ge 2/(1-a)$
, then there exists
$c_a>0$
such that
\begin{equation*}\biggl(\dfrac{1}{n-1}+\dfrac{c_a}{2t-1}\biggr)\le B(n,t,i)\le \biggl(\dfrac{1}{n-1}+\dfrac{1}{2t-1}\biggr).\end{equation*}
-
If
$n-i_0\le i\le n-2$
,
\begin{equation*}\dfrac{1}{n-1} \le B(n,t,i)\le \dfrac{i_0}{n-1}.\end{equation*}
Proof. Observe that
\begin{align*}B(n,t,i)&=\dfrac{1}{n}\biggl(1-\dfrac{1}{n}\biggr)^{\!-1} \sum_{k= 1}^{n - i} \biggl(\dfrac{1 - {k}/{n}}{1-{1}/{n}}\biggr)^{\!2t-2} = \dfrac{1}{n-1} +\dfrac{1}{n-1}\sum_{k=2}^{n-i}\biggl(1-\dfrac{k-1}{n-1}\biggr)^{\!2t-2}. \end{align*}
The stated results easily follow, for example, by comparing Riemann sums with integrals in the first and second cases.
Proposition 2.1.
-
(a) For each fixed
$i=1,2,\ldots, $
set
$t_i(n,c)=({2n}/{i})({\log}\ n \,+c)$
. Then That is, the position of the card starting in position
\begin{equation*}\lim_{n\rightarrow \infty} d_2\bigl(K^{t_i(n,c)}(n-i,\cdot),u\bigr) = \begin{cases} +\infty & if\ c<0,\\ 0 & if\ c>0. \end{cases} \end{equation*}
$n-i$
becomes random in the
$L^2$
sense with a cut-off at time
$({2n}/{i})\log n$
.
-
(b) For each fixed
$i=1,2,\ldots$
and any
$t_n$
tending to infinity, Moreover, there exists a constant
\begin{equation*}\lim_{n\rightarrow \infty} d_2(K^{t_n}(i,\cdot),u) = 0.\end{equation*}
$c_i>0$
such that, for any
$\epsilon \in (2/n,1)$
,
\begin{equation*}d_2(K^{t}(i,\cdot),u)=\epsilon \Rightarrow t(n) \in (c_i/\epsilon^2, 10/\epsilon^2).\end{equation*}
-
(c) For each fixed
$a\in (0,1)$
, set Then
\begin{equation*} t_a(n,c)= \dfrac{1}{2\log\! (1/a)} ({\log}\ n +c). \end{equation*}
That is, the position of the card starting in position [an] becomes random in the
\begin{equation*}\lim_{n\rightarrow \infty} d_2\bigl(K^{t_a(n,c)}([an],\cdot),u\bigr) = \begin{cases} +\infty & {if\ c<0,}\\ 0 &{if\ c>0.}\end{cases} \end{equation*}
$L^2$
sense with a cut-off at time
${\log n}/{(2\log\! (1/a))}$
.
Remark 2.1. The first and second statements are for fixed i, that is, they cannot be applied with i depending on n. Because of this, statement (a) is about starting somewhere near the bottom and statement (b) about starting somewhere near the top. Similarly, in (c), the real
$a\in (0,1)$
is fixed, which means this statement is about starting from somewhere in the middle. In statements (a) and (c), where exactly one starts is important as it appears in the definition of the cut-off time.
Proof. Avoiding the two special cases of the first and last starting positions (which are easily treated), for a starting position
$j\in \{2,\ldots,n-1\}$
, we have
\begin{align*} & \dfrac{1}{2}\biggl(1-\dfrac{1}{n}\biggr)^{2t-1}B(n,j,t)+ \biggl( \dfrac{j-1}{n}\biggr)^{2t}\dfrac{n(\,j-1)}{i} \\ & \quad \le d_2(K^t(\,j,\cdot),u)^2\\ & \quad \le \biggl(1-\dfrac{1}{n}\biggr)^{2t-1}B(n,j,t)+ \biggl( \dfrac{j-1}{n}\biggr)^{2t}\dfrac{n(\,j-1)}{j} .\end{align*}
The stated results follow from Lemma 2.3 and careful inspection.
We end this section with two eigenvalue data plots, shown in Figure 1, which concern different projections, namely, those corresponding to following a given pair or a triplet of cards instead of just one. These chains become more complex and we have not computed all their eigenvalues and eigenfunctions. Instead, these plots are based on computer-assisted computations of the eigenvalues of these chains. The first plot is for the two-card chain on 21 cards and the second is for the three-card chains on 21 cards.
Figure 1. 21 cards. (a) The eigenvalue distribution for the two-card chains. (b) The eigenvalue distribution for the three-card chains. Note that all eigenvalues are positive.
2.3. Single-card chain in L 1
The relatively simple form of the eigenvalues and eigenvectors of the single-card chain K also allows us to determine the
$L^1$
-distance of
$K^{t}(i,\cdot)$
from its stationary measure u. Namely, the diagonalization of K shows that the ith row of
$K^t$
,
$K^t(i,\cdot)$
,
$1\le i\le n-1$
, consists of the repeated entry
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{-(i-1)^t}{i} + \dfrac{i^{t-1}}{i+1} + \dots + \dfrac{(n-1)^{t-1}}{n}\biggr) + \dfrac{1}{n}\end{equation*}
in columns
$j=1$
through
$i-1$
,
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{(i-1)^{t+1}}{i} + \dfrac{i^{t-1}}{i+1} + \dots + \dfrac{(n-1)^{t-1}}{n}\biggr) + \dfrac{1}{n}\end{equation*}
in column i,
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{-(i+k-1)^t}{i+k} + \dfrac{(i+k)^{t-1}}{i+k+1} + \dots + \dfrac{(n-1)^{t-1}}{n}\biggr) + \dfrac{1}{n}\end{equation*}
in column
$j=i+k$
,
$i+1\le i+k<n$
, and
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{-(n-1)^t}{n}\biggr) + \dfrac{1}{n}\end{equation*}
in column n. The last row,
$i=n$
, consists of the entries
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{-(n-1)^t}{n}\biggr)+\dfrac{1}{n} \end{equation*}
in columns 1 through
$n-1$
and
\begin{equation*}\dfrac{1}{n^t}\biggl(\dfrac{(n-1)^{t+1}}{n} \biggr)+ \dfrac{1}{n} \end{equation*}
in column n.
In the case
$i=n$
(single card starting at the bottom of the deck), we find that
\begin{equation*}\|K^t(n,\cdot)-u\|_{\textrm{TV}}= \biggl(1-\dfrac{1}{n}\biggr)^{t+1}\end{equation*}
(indeed, by definition of our shuffling, this card position becomes uniform as soon as it is touched). For
$1\le i\le n-1$
,
\begin{align} 2\|K^t(i,\cdot)-u\|_{\textrm{TV}}&= \dfrac{1}{n^t}\biggl|-\dfrac{(n-1)^{t}}{n}\biggr|+\dfrac{i-1}{n^t}\Biggl|\dfrac{-(i-1)^t}{i} + \sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}\Biggr| \notag \\ & \quad+\dfrac{1}{n^t}\Biggl( \dfrac{(i-1)^{t+1}}{i}+\sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}\Biggr) \notag \\&\quad + \dfrac{1}{n^t} \sum_{k=1}^{n-i-1} \Biggl|\dfrac{-(i+k-1)^t}{i+k} + \sum_{\ell=1}^{n-(i+k)}\dfrac{(i+k+\ell-1)^{t-1}}{i+k+\ell} \Biggr|\notag \\ &=J_1+J_2+J_3+J_4. \end{align}
Looking at
$J_2$
and
$J_4$
for large t, i.e.
$t\ge (n-1)\log n +{(n-1)}/{(n-2)}$
, we have
\begin{equation*}\dfrac{-(i-1)^t}{i} + \sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}\ge 0\end{equation*}
and
\begin{equation*}\dfrac{-(i+k-1)^t}{i+k} + \sum_{\ell=1}^{n-(i+k)}\dfrac{(i+k+\ell-1)^{t-1}}{i+k+\ell}\ge 0 \quad \text{for $ k\in\{ 1,\ldots, n-i-1\}$.}\end{equation*}
Because the sum of all the same terms in
$J_1+J_2+J_3+J_4$
but without any absolute value is
\begin{equation*}\sum_{\ell=1}^n (K^t(i,\ell)-u(\ell))=0,\end{equation*}
it follows that for
$t\ge (n-1)\log n +{(n-1)}/{(n-2)}$
, we have
$2\|K^t(i,\cdot)-u\|_{\textrm{TV}}=2|J_1|$
, that is,
\begin{equation*}\|K^t(i,\cdot)-u\|_{\textrm{TV}}=\dfrac{1}{n}\biggl(1-\dfrac{1}{n}\biggr)^{t},\quad i\in \{1,\ldots, n-1\}.\end{equation*}
This, of course, occurs only after much approximate convergence has taken place. It only describes the long-term asymptotic behavior of
$\|K^t(i,\cdot)-u\|_{\textrm{TV}}$
,
$i<n$
. To describe the shorter-term behavior, we consider three cases: bottom starting positions of the type
$n-i$
for fixed
$i=1,2,\ldots,$
top starting positions of the type
$i=1,2, \ldots,$
and middle of the pack starting positions of the type [an],
$a\in (0,1)$
(see Remark 2.1 above). The key difficulty in these estimates is to identify which of the terms
$J_1,J_2, J_3, J_4$
plays the key role. In what follows, we omit the details regarding upper bounds. The details given for the lower bounds indicate, in each case, which term is dominant and hence what the target should be for upper bounds. Verifying that all terms are upper-bounded appropriately follows from simple careful arguments including basic Riemann sum estimates.
For starting position
$n-i$
, i fixed, we get a reasonable lower bound by focusing on the first and third terms in (2.2). Write
\begin{align*}2 \|K^t(n-i,\cdot)-u\|_{\textrm{TV}}&\ge \dfrac{1}{n}\biggl(1-\dfrac{1}{n}\biggr)^t\\ &\quad +\dfrac{1}{n^t}\Biggl( \dfrac{(n-i-1)^{t+1}}{n-i}+\sum_{\ell=n-i+1}^{n}\dfrac{(\ell-1)^{t-1}}{\ell}\Biggr)\\ &\ge \dfrac{1}{n}\biggl(1-\dfrac{1}{n}\biggr)^t+ \biggl(1-\dfrac{i+1}{n}\biggr)^{t+1}.\end{align*}
An upper bound of the type
\begin{equation*} \|K^t(n-i,\cdot)-u\|_{\textrm{TV}}\le C_i\biggl(\dfrac{1}{n}\biggl(1-\dfrac{1}{n}\biggr)^t+ \biggl(1-\dfrac{i+1}{n}\biggr)^{t}\biggr)\end{equation*}
holds as well. This proves convergence in time of order
$n/(i+1)$
with no cut-off for the bottom cards.
For starting position i, i fixed (starting position towards the top), we have
\begin{equation*}2 \|K^t(i,\cdot)-u\|_{\textrm{TV}}\ge \biggl(\dfrac{1}{n} +\dfrac{c_i}{t}\biggr)\biggl(1-\dfrac{1}{n}\biggr)^t .\end{equation*}
The term
$({c_i}/{t})(1-1/n)^t$
is contributed by the last summand,
$J_4$
, in (2.2). In this last summand, namely
\begin{equation*} \dfrac{1}{n^t} \sum_{k=1}^{n-i-1} \Biggl|\dfrac{-(i+k-1)^t}{i+k} + \sum_{\ell=1}^{n-(i+k)}\dfrac{(i+k+\ell-1)^{t-1}}{i+k+\ell} \Biggr| ,\end{equation*}
restrict the first summation to those k less than, say,
$n/4$
. In this range of k values, the positive term in the absolute value dominates the negative term and we obtain a lower bound of the type (we assume
$t\ge 4$
)
\begin{align*} \dfrac{c_i}{n^t} \sum_{k=1}^{n/4} \sum_{ \ell=n/2}^{n-1}\ell ^{t-2} &\ge c^{\prime}_i \biggl(1-\dfrac{1}{n}\biggr)^{t-1}\Biggl(\dfrac{1}{n-1}\sum_{n/2}^{n-1} \biggl(\dfrac{\ell}{n-1}\biggr)^{t-2}\Biggr)\\ &\ge \dfrac{c^{\prime\prime}_i }{t} \biggl(1-\dfrac{1}{n}\biggr)^t, \end{align*}
where we used an integral to lower-bound the Riemann sum in parentheses. A matching upper bound
\begin{equation*} \|K^t(i,\cdot)-u\|_{\textrm{TV}}\le C_i \biggl(\dfrac{1}{n} +\dfrac{1}{t}\biggr)\biggl(1-\dfrac{1}{n}\biggr)^t \end{equation*}
is easily obtained for all four terms in (2.2). The key rate of convergence is thus in
$1/t$
for the top starting positions.
For a starting position in the middle of the pack,
$i=[an]$
,
$a\in (0,1) $
fixed, a similar analysis shows that
$\|K^t([an],\cdot)-u\|_{\textrm{TV}}$
is also of order
\begin{equation*}\biggl(\dfrac{1}{n}+ \dfrac{1}{t} \biggr)\biggl(1-\dfrac{1}{n}\biggr)^t .\end{equation*}
This time, for the lower bound, we use the second term
\begin{equation*} \dfrac{i-1}{n^t}\Biggl|\dfrac{-(i-1)^t}{i} + \sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}\Biggr| .\end{equation*}
It provides a lower bound of the type
$c_a(1-1/n)^t/t$
. Indeed, for
$i=[an]$
and n large enough,
\begin{align*} \sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}&\ge \dfrac{(n-1)^{t-1}}{2} \sum_{\ell=[an]}^{n-1} \biggl(\dfrac{\ell}{n-1} \biggr)^{t-2}\dfrac{1}{n-1} \\ & \ge \dfrac{(n-1)^{t-1}}{2} \int _{(a+1)/2}^1 x^{t-2}\,{\textrm{d}} x\\ &\ge c_a \dfrac{(n-1)^{t-1}}{t-1}.\end{align*}
For
$t\ge t_a$
, this is larger than twice
$(i-1)^{t-1}$
,
$i=[an]$
. It follows that
\begin{align*} \dfrac{i-1}{n^t}\Biggl|\dfrac{-(i-1)^t}{i} + \sum_{\ell=i}^{n-1}\dfrac{\ell^{t-1}}{\ell+1}\Biggr| &\ge \dfrac{c_a}{2} \dfrac{an}{n^{t} }\dfrac{(n-1)^{t-1}}{t-1} \ge \dfrac{c^{\prime}_a}{t} \biggl(1-\dfrac{1}{n}\biggr)^t .\end{align*}
Again, using similar techniques, all terms in (2.2) can be seen to be bounded above appropriately.
3. Hit-and-run for top-to-random in L 2
In this section we prove Theorem 1.2, which concerns the convergence to stationarity measured in the
$L^2$
sense, that is, using
$d_2(q^{(t)},u)$
for the hit-and-run version of top-to-random driven by the measure q in (1.2).
Proof of the lower bound in Theorem 1.2.In the section concerning following a single card, we learned that
$(1-1/n)$
is an eigenvalue of that chain and consequently also an eigenvalue of convolution by q on
$\mathbf S_n$
. Now, on
$\mathbf S_n$
, each eigenvalue has multiplicity at least equal to the dimension of any irreducible representation at which it occurs. The group
$\mathbf S_n$
has two representations of dimension 1: the trivial representation and the sign representation. All other irreducible representations have dimension at least
$n-1$
. So it suffices to verify that
$(1-1/n)$
does not occur only at the sign representation. This can be seen from the form of the associated eigenvector we have constructed. Alternatively, one easily computes the eigenvalue for the sign representation to be
$1/2$
if n is even and
$(n+1)/2n$
if n is odd (
$(n+1)/2$
is the number of odd integers in
$\{1,\ldots,n\}$
). In any case, this gives the lower bound
$d_2(q^{(t)},u)\ge \sqrt{n-1}(1-1/n)^t$
as stated.
To prove the stated upper bound for
$d_2(q^{(t)},u)$
, we use the comparison technique from [Reference Diaconis and Saloff-Coste7]. Anticipating the next section, we use the fact that hit-and-run walks have non-negative spectrum. It turns out that the most efficient comparison is with the random-to-random walk of Example 1.1 driven by the measure
\begin{equation*}\mu(\sigma)=\begin{cases} 1/n & \text{if $ \sigma=\textrm{id}$,}\\2/n^2 &\text{if $ \sigma=\sigma_{i(i+1)}=\sigma_{(i+1)i}$,}\\1/n^2 &\text{if $ \sigma=\sigma_{ij}$, $ 1\le i\neq j\le n$, $|j-i|>1$,}\end{cases}\end{equation*}
where
$\sigma_{ij}=(\,j,j-1,\ldots,i)$
,
$\sigma_{ji}=\sigma^{-1}_{ij}$
,
$1\le i<j \le n$
. Recall that the Dirichlet form associated with a symmetric probability measure
$\nu$
on a finite group G is
\begin{equation*}\mathcal E_\nu(v,w)= \dfrac{1}{2|G|}\sum_{x,y\in G}(v(xy)-v(x))(w(xy)-w(x))\nu(y),\quad v,w\in L^2(G).\end{equation*}
Lemma 3.1. The Dirichlet form
$\mathcal E_\mu$
associated with the random-to-random measure
$\mu$
and the Dirichlet form
$\mathcal E_q$
associated with hit-and-run version of top-to-random satisfy
\begin{equation*}\mathcal E_\mu (v,v)\le 8 \mathcal E_q(v,v) \quad {{for\ all\ v\in L^2(G).}}\end{equation*}
Proof. Recall that
$\sigma_k=\sigma_{1k}=(k,k-1,\ldots,1)$
. For each
$\sigma_{ij}, 1\le i\neq j\le n$
, we find a product of
$\sigma_k^\ell$
,
$1\le \ell < k\le n$
, which equals
$\sigma_{ij}$
. There are many ways to do this, but the following is efficient. Observe that for
$i < j$
,
$\sigma_{ij} = \sigma_j^i\sigma_{j-1}^{j-i}$
. That is, to move the card in position i down to position j, insert the first i cards at position j, then insert the first
$j - i$
cards now on top at position
$j - 1$
. After the first move, the card originally in position j is at position
$j - i$
, so the second move places it in position
$j - 1$
. The other
$i - 1$
cards moved down to position
$j - 1$
are returned to their original spot in the second move (barring the card originally in position i) by sliding past them all the cards they originally slid past, which were on the top after the first move. For
$i > j$
,
\begin{equation*} \sigma_{ij} = \sigma_{ji}^{-1} = \sigma_{i-1}^{-(i-j)}\sigma_i^{-j} = \sigma_{i-1}^{j-1}\sigma_i^{i-j}. \end{equation*}
Now we use [Reference Diaconis and Saloff-Coste7, Theorem 1] with
$\widetilde{\mathcal E}=\mathcal E_\mu$
,
$\mathcal E=\mathcal E_q$
, which gives
\begin{equation*}\mathcal E_\mu\le A\mathcal E_q,\quad A=\max_{\sigma\,:\, q(\sigma)>0}\Biggl\{\dfrac{1}{q(\sigma)} \sum_{1\le i\neq j\le n} |\sigma_{ij}|N(\sigma,\sigma_{ij})\mu(\sigma_{ij})\Biggr\}.\end{equation*}
In the formula giving A,
$|\sigma_{ij}|$
is the length of the product expressing
$\sigma_{ij}$
, which, in our case, is always equal to 2;
$N(\sigma,\sigma_{ij})$
is the number of times
$\sigma$
appears in the product for
$\sigma_{ij}$
. So, if
$\sigma=\sigma_k^{\ell}$
for some
$2\le k\le n$
and
$1\le \ell\le k-1$
,
$1\le i<j\le n$
,
\begin{equation*}N(\sigma,\sigma_{ij})=\begin{cases} 0 & \text{if $ (k,\ell)\not\in\{(\,j,i),(\,j-1,j-i)\}$,} \\[3pt] 1 &\text{if $ (k,\ell)\in\{(\,j,i),(\,j-1,j-i)\}$.} \end{cases}\end{equation*}
When
$1\le j<i\le n$
, we similarly have
\begin{equation*}N(\sigma,\sigma_{ij})=\begin{cases} 0 & \text{if $ (k,\ell)\not\in\{(i-1,j-1),(i,i-j)\}$,} \\[3pt] 1 &\text{if $ (k,\ell)\in\{(i-1,j-1),(i,i-j)\}$.} \end{cases}\end{equation*}
For
$1\le \ell<k<n$
, this gives
\begin{equation*} \Biggl\{\dfrac{1}{q(\sigma_k^\ell)} \sum_{1\le i\neq j\le n} |\sigma_{ij}|N(\sigma,\sigma_{ij})\mu(\sigma_{ij})\Biggr\}= 8k/n , \end{equation*}
whereas for
$(k,\ell)=(n,\ell)$
the result is 4. See Figure 2 for a comparison of the spectral distributions.
Figure 2. Comparison of the spectrum of random-to-random (a) and hit-and-run for top-to-random (b). The key difference is the higher multiplicity of very small eigenvalues in the random-to-random shuffle (most of those are actually equal to 0). Note the different scales on the y-axes of the two graphics. This is for a deck of seven cards so there are
$7!$
eigenvalues.
Proof of the upper bound in Theorem 1.2.Given the comparison inequality
$\mathcal E_\mu\le 8 \mathcal E_q$
between quadratic forms, Lemma 6 of [Reference Diaconis and Saloff-Coste7] (see also [Reference Saloff-Coste13, Theorem 10.2]) provides a comparison inequality. Here we used the same idea in a slightly tighter way. Let
$0\le \alpha_{|G|-1}\le \dots\le \alpha_1<\alpha_0=1$
be the eigenvalues for random-to-random. By [Reference Diaconis and Saloff-Coste7, Lemma 4], the inequality
$\mathcal E_\mu\le 8 \mathcal E_q$
gives
\begin{equation*}1-\beta_i\ge \dfrac{1}{8} (1-\alpha_i).\end{equation*}
This is enough because there are no negative eigenvalues (to see what happens when there are negative eigenvalues, see [Reference Diaconis and Saloff-Coste7]; the absence of negative eigenvalues is only a small simplification). Split the sum (the inequality here uses the fact that the
$\beta_i$
are all non-negative)
\begin{equation*} d_2\bigl(q^{(t)},u\bigr)^2 =\sum_{i=1}^{|G|-1} \beta_i^{2t} \le \sum_{i=1}^{|G|-1}\,{\textrm{e}}^{-2t(1-\beta_i)}\end{equation*}
into two sums: the sum over those indices i such that
$\alpha_i\le 1/2$
and the sum over the indices for which
$\alpha_i>1/2$
. For the first sum, write
\begin{equation*}\sum_{i\,:\, \alpha_i\le 1/2}\,{\textrm{e}}^{-2t(1-\beta_i)}\le (n!) \,{\textrm{e}}^{- t/8}.\end{equation*}
For the second sum, note that
${\textrm{e}}^{-3(1-x)/2}\le x$
when
$x\in[.5,1]$
, and write
\begin{align*}\sum_{i\,:\, \alpha_i> 1/2} \,{\textrm{e}}^{-2t(1-\beta_i)}&\le \sum_{i\,:\, \alpha_i> 1/2} \,{\textrm{e}}^{-t(1-\alpha_i)/4} \le \sum_{i\,:\, \alpha_i> 1/2} \alpha_i ^{ t/6} \le d_2\bigl(\mu^{([t/12])},u\bigr)^2 .\end{align*}
This gives
\begin{equation} d_2\bigl(q^{(t)},u\bigr)^2\le (n!)\,{\textrm{e}}^{-t/8} +d_2\bigl(\mu^{([t/12])},u\bigr)^2.\end{equation}
In [Reference Bernstein and Nestoridi2, equation (25)], it is proved that the spectral gap for
$\mu$
is asymptotically equal to
$1/n$
(see the beginning of Section 3 in [Reference Bernstein and Nestoridi2]; the exact value is
$(n+2/n^2$
and it occurs with multiplicity at least
$(n-1)$
) and that
\begin{equation*}d_2\bigl(\mu^{(s)},u\bigr)^2\le 4 \,{\textrm{e}}^{-2c}\quad \text{for any $ s\ge \dfrac{3}{4} n \log n +cn$, $c>0$,}\end{equation*}
as long as n is sufficiently large (let us note that this is a rather difficult result). Using this in (3.1) yields the upper bound stated in Theorem 1.2.
4. Positivity of the spectrum
In this final section we prove Theorem 1.1. Given a general hit-and-run random walk driven by the measure
$q_S$
at (1.1) on a finite group G, we set
\begin{equation*}Q(x,y)= q_S(x^{-1}y)=\dfrac{1}{k} \sum_{i=1}^k \dfrac{1}{m_i} \sum_{j=0}^{m_i-1} \delta_{s_i^j}(x^{-1} y), \quad x,y \in G.\end{equation*}
This defines a self-adjoint operator
$f\mapsto Qf=\sum _yQ(\cdot,y)f(y)$
acting on the space
$H=L^2(G,u)$
equipped with the inner product
\begin{equation*}\langle f_1,f_2 \rangle = \dfrac{1}{\vert G \vert} \sum_{x\in G} f_1(x) f_2(x).\end{equation*}
Let
\begin{equation*}\beta_{|G|-1}\le\dots \le \beta_1\le \beta_0=1\end{equation*}
be the
$|G|$
eigenvalues of this operator. Because Q is Markov, these eigenvalues are contained in the interval
$[{-}1,1]$
. The theorem we want to prove, Theorem 1.1, asserts that they are in fact in the interval [0, 1], that is, Q is non-negative in the sense that
$\langle Qf,f\rangle \ge 0$
. The proof follows the main idea of [Reference Rudolf and Ullrich11], which consists in writing Q in the product form
\begin{equation*}Q= P^*RP\end{equation*}
using auxiliary operators
$P,R,P^*$
, where
$R=R^2$
is self-adjoint acting on the extended Hilbert space
$H_{\textrm{aux}}$
, the space of functions on
$G\times \{1,\ldots,k\}$
equipped with its natural inner product
$\langle \cdot,\cdot\rangle _{\textrm{aux}}$
. Because
$R=R^2$
,
$R^*=R$
, and
$P^*$
is the formal adjoint of P, such a decomposition establishes that
\begin{equation*}\langle Qf,f\rangle=\langle P^*RP f,f\rangle =\langle RPf,RPf\rangle_{\textrm{aux}}\ge 0.\end{equation*}
To use such a decomposition is a key insight from [Reference Rudolf and Ullrich11], but it also appears in [Reference Ullrich15, Remark 4.4] and [Reference Dyer, Greenhill and Ullrich10, Lemma 3.1].
Define the auxiliary Hilbert space
$H_{\textrm{aux}} = \mathbb{R}^{G\times \{1,\ldots, k\}}$
equipped with inner product
\begin{equation*}\langle g_1,g_2\rangle_{\textrm{aux}}\,:\!=\, \dfrac{1}{k \vert G \vert} \sum_{x\in G} \sum_{i=1}^k g_1(x,i) g_2(x,i),\end{equation*}
where
$g_1,g_2 \in H_{\textrm{aux}}$
. Let
$P\,:\, H \to H_{\textrm{aux}}$
denote the bounded linear operator given by
\begin{equation*}P f(x,i) = f(x), \quad (x,i) \in G\times\{1,\ldots,k\}.\end{equation*}
Note that the adjoint operator,
$P^*\,:\, H_{\textrm{aux}} \to H$
of P is given by
\begin{equation*}P^* g(x) = \dfrac{1}{k}\sum_{i=1}^k g(x,i).\end{equation*}
That
$P^*$
is the adjoint of P means here that
$\langle P^*g,f \rangle = \langle g,Pf \rangle_{\textrm{aux}}$
for any
$f\in H$
and
$g\in H_{\textrm{aux}}$
, which can be verified by a simple calculation. The matrices (or kernels) of these operators are
\begin{align*}P((x,i),y) & = \delta_x(y),\\ P^*(x,(y,i)) & = \dfrac{\delta_{x}(y)}{k},\end{align*}
for any
$x,y \in G$
and
$i\in \{1,\ldots,k\}$
. For any pair
$(x,i)\in G\times\{1,\ldots,k\}$
, call
\begin{equation*}\mathcal{Z}(x,i) \,:\!=\, \bigl\{ x_0,\ldots,x_{m_i-1} \mid x_i \,:\!=\, x s_i^j, j=0,\ldots, m_i-1 \bigr\}\end{equation*}
the orbit of x in G under the cyclic subgroup
$\langle s_i\rangle=\bigl\{ s_i^j\,:\, j=0,\ldots, m_i-1\bigr\}$
generated by
$s_i$
in G. Define a Markov transition kernel
\begin{equation*}R(\cdot,\cdot) \ \text{on}\ (G\times \{1,\ldots,k\})^2\end{equation*}
by setting
\begin{equation*}R ((x,i_1), (y,i_2)) \,:\!=\, \delta_{i_1}(i_2) \dfrac{\delta_{\mathcal{Z}(x,i_1)}(y)}{m_{i_1}}.\end{equation*}
It induces a Markov operator,
$R \,:\, H_{\textrm{aux}} \to H_{\textrm{aux}}$
, given by
\begin{equation*}Rg (x,i) = \dfrac{1}{m_i} \sum_{z\in \mathcal{Z}(x,i)} g(z,i), \quad g\in H_{\textrm{aux}}.\end{equation*}
Because
\begin{equation*}x\in \mathcal{Z}(y,i) \quad\text{if and only if}\quad y\in \mathcal{Z}(x,i)\end{equation*}
the operator R is symmetric, that is,
\begin{align*}R((x,i_1),(y,i_2))&= \delta_{i_1}(i_2) \dfrac{\delta_{\mathcal{Z}(x,i_1)}(y)}{m_{i_1}}= \delta_{i_2}(i_1) \dfrac{\delta_{\mathcal{Z}(y,i_2)}(x)}{m_{i_2}}= R((y,i_2),(x,i_1)).\end{align*}
Thus the corresponding operator
$R \,:\, H_{\textrm{aux}} \to H_{\textrm{aux}}$
is self-adjoint.
Lemma 4.1. The operator R satisfies
$R^2=R$
and
$Q=P^* RP$
.
Proof of
$R^2=R$
. For arbitrary
$g\in H_{\textrm{aux}}$
, we have
\begin{align*}R^2 g(x,i)& = \dfrac{1}{m_i} \sum_{y\in \mathcal{Z}(x,i)} Rg(y,i) = \dfrac{1}{m_i} \sum_{y\in \mathcal{Z}(x,i)} \sum_{z\in \mathcal{Z}(y,i)} \dfrac{g(z,i)}{m_i} = Rg(x,i).\end{align*}
Here we used the facts that for
$y\in \mathcal{Z}(x,i)$
we have
$ \mathcal{Z}(x,i) = \mathcal{Z}(y,i)$
and
$\vert \mathcal{Z}(x,i)\vert = m_i$
.
Proof of
$Q=P^*RP$
. For any
$x,y \in G$
we have
\begin{align*}P^* R P (x,y)& = \dfrac{1}{k} \sum_{i=1}^k R P ((x,i),y) \\ & = \dfrac{1}{k} \sum_{i=1}^k \sum_{z\in \mathcal{Z}(x,i)} \dfrac{P((z,i),y)}{m_{i}} \\& = \dfrac{1}{k} \sum_{i=1}^k\dfrac{1}{m_i}\sum_{z\in \mathcal{Z}(x,i)} \delta_{y}(z)\\& = \dfrac{1}{k} \sum_{i=1}^k \dfrac{1}{m_i} \sum_{j=0}^{m_i-1} \delta_{y}\bigl(xs_i^j\bigr)\\ & = Q(x,y).\end{align*}
Here we used the definition of
$\mathcal{Z}(x,i)$
and, in the last equality, that
$y=xs_i^j $
if and only if
$s_i^j = x^{-1} y.$
5. Final remarks
Example 5.1. (Example where hit-and-run is faster.) Assume that
$G=(\mathbb Z/n\mathbb Z)^d$
and
$S=(0,e_1,-e_1,\ldots,e_d,-e_d)$
, where
$e_j=(0,\ldots, 0,1,0, \ldots,0)$
with the 1 in position j,
$1\le j\le d$
. In
$L^2$
and
$L^1$
, the walk driven by
$\mu_S$
mixes in time
\begin{equation*} \dfrac{d\log d}{2(1-\cos 2\pi/n)} \end{equation*}
(as d (and possibly) n tends to infinity). The measure
$q_S$
is given by
\begin{equation*}q_S(0)= \dfrac{n+2d}{n(1+2d)}\sim \dfrac{1}{2d}+ \dfrac{1}{n}\end{equation*}
and, for
$m\in \{1,\ldots, n-1\}$
and
$j\in \{1,\ldots,d\}$
,
\begin{equation*}q_S( me_j)=\dfrac{2}{(1+2d)n}\sim \dfrac{1}{dn}.\end{equation*}
This is very close to the walk that simply takes a random step in a random coordinate and thus behaves similarly. The mixing times for
$q_S$
are different in
$L^1$
and in
$L^2$
. In
$L^1$
(or total variation), the mixing time is
$d\log d$
(based on the coupon collector problem). In
$L^2$
, the mixing time is
$d\log\! (dn)$
. In both cases there is a gain over
$\mu_S$
of order
$n^2$
. See [Reference Saloff-Coste13, page 323] and [Reference Diaconis and Saloff-Coste7, page 2154].
Example 5.2. (Example when hit-and-run is a little slower.) Let us consider briefly the example of random-transposition on
$\mathbf S_n$
. Because all generators have order 2, the measure
$q_S$
gives probability
\begin{equation*}\dfrac{1}{n}+ \dfrac{n-1}{2n}=\dfrac{1}{2}\biggl(1+\dfrac{1}{n}\biggr)\end{equation*}
to the identity and probability
${1}/{n^2}$
to any transposition. It follows that the hit-and-run random walk based on random transposition has a cut-off in total variation and
$L^2$
at time
$n\log n$
, a slow-down by a factor of
$1/2$
compared to its simple random walk counterpart.
Remarks regarding hit-and-run for top-to-random. Because the hit-and-run shuffle based on top-to-random is the focus of this paper, it is worth pointing out that it can be described naturally without reference to the general hit-and-run construction. Namely, the measure q at (1.2) can be alternatively obtained as follows. Pick a position i uniformly at random in
$\{1,\ldots, n\}$
and then pick a packet size j uniformly at random in
$\{1,\ldots,i\}$
. Pick up the packet of the top j cards and place it below the card originally at position i. This is clearly different from the top-m-to-random shuffles studied in [Reference Diaconis, Fill and Pitman9]. There are two shuffle mechanisms described in [Reference Diaconis and Saloff-Coste7] which bear some close similarities to the hit-and-run top-to-random shuffle described above. They are as follows.
-
The crude overhand shuffle [Reference Diaconis and Saloff-Coste7, page 2148]. The top, middle, and bottom packets are identified using two random positions
$1\le a\le b\le n$
, and the order of the packets is changed as follows: top goes to the bottom, middle remains in the middle, bottom goes to the top. The pair of positions
$a\le b$
is chosen by picking a uniformly in
$\{1,\ldots, n\}$
and b uniformly in
$\{a,\ldots, n\}$
. Note that this gives weight
$1/n$
to the identity which is obtained for
$a=b=n$
. An
$L^2$
mixing time upper bound of order
$n\log n$
is proved in [Reference Diaconis and Saloff-Coste7] and an
$L^1$
mixing time lower bound based on a coupon collector argument is also stated in [Reference Diaconis and Saloff-Coste7]. However, although the coupon collector argument described in [Reference Diaconis and Saloff-Coste7] makes heuristic sense, it seems that its detailed implementation is unclear because the probability that a pair of adjacent cards is broken up depends on the position of the cards. This is worth mentioning here because the exact same difficulty appears for the hit-and-run version of top-to-random, which is the focus of the present article. -
The Borel shuffle [Reference Diaconis and Saloff-Coste7, page 2150] (which is taken from a book on the game of Bridge by Borel and Chéron from 1940). In this shuffle, a middle packet is removed from the deck and placed on top. If (a, b),
$1\le a\le b\le n$
, describes the position of the top and bottom card of the packet removed, (a, b) is picked with probability
$1/\binom{{n+1}}{2}$
, and this gives probability
$2/(n+1)$
to the identity which is obtained for any of the choices (1, b),
$1\le b\le n$
. An
$L^2$
mixing time upper bound of order
$n\log n$
is proved in [Reference Diaconis and Saloff-Coste7] as well as an
$L^1$
mixing time lower bound based on a coupon collector argument (for this shuffle the coupon collector argument works fine).
Acknowledgements
We wish to thank the anonymous reviewers whose comments helped us improve the readability of the paper.
Funding information
The research of Samuel Boardman was partially supported by the NSF RTG-grant DMS-1645643. The research of Daniel Rudolf was partially supported by DFG project 389483880. The research of Laurent Saloff-Coste was partially supported by NSF grants DMS-1707589 and DMS-2054593.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
