Hostname: page-component-686fd747b7-4b24c Total loading time: 0 Render date: 2025-02-13T12:36:56.282Z Has data issue: false hasContentIssue false
  • English
  • Français

The hit-and-run version of top-to-random

Part of: Stochastic processes Probability theory on algebraic and topological structures Markov processes

Published online by Cambridge University Press:  12 July 2022

Samuel Boardman ,
Daniel Rudolf  and
Laurent Saloff-Coste
Samuel Boardman*
Affiliation:
Cornell University
Daniel Rudolf*
Affiliation:
University of Passau
Laurent Saloff-Coste*
Affiliation:
Cornell University
*
*Postal address: 530 Church St, 2074 East Hall, Ann Arbor, MI 48109, USA. Email address: stb89@cornell.edu
**Postal address: Fakultät für Informatik und Mathematik, Innstraße 33, 94032 Passau, Germany. Email address: daniel.rudolf@uni-passau.de
***Postal address: 567 Malott Hall, Department of Mathematics, Ithaca, NY 14853, USA. Email address: lps2@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study an example of a hit-and-run random walk on the symmetric group $\mathbf S_n$ . Our starting point is the well-understood top-to-random shuffle. In the hit-and-run version, at each single step, after picking the point of insertion j uniformly at random in 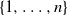$\{1,\ldots,n\}$ , the top card is inserted in the jth position k times in a row, where k is uniform in 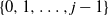$\{0,1,\ldots,j-1\}$ . The question is, does this accelerate mixing significantly or not? We show that, in 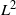$L^2$ and sup-norm, this accelerates mixing at most by a constant factor (independent of n). Analyzing this problem in total variation is an interesting open question. We show that, in general, hit-and-run random walks on finite groups have non-negative spectrum.

Keywords

Markov chaincard shufflingcut-off phenomenon

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 60B10: Convergence of probability measures
Secondary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization 60G51: Processes with independent increments; L'evy processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 860 - 879
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, A. (1983). Random walks on finite groups and rapidly mixing Markov chains. In Seminar on Probability XVII (Lecture Notes Math. 986), pp. 243–297. Springer, Berlin.10.1007/BFb0068322CrossRefGoogle Scholar
Bernstein, M. and Nestoridi, E. (2019). Cutoff for random to random card shuffle. Ann. Prob. 47, 3303–3320.10.1214/19-AOP1340CrossRefGoogle Scholar
Brown, K. S. and Diaconis, P. (1998). Random walks and hyperplane arrangements. Ann. Prob. 26, 1813–1854.10.1214/aop/1022855884CrossRefGoogle Scholar
Chen, G.-Y. and Saloff-Coste, L. (2008). The cutoff phenomenon for ergodic Markov processes. Electron. J. Prob. 13, 26–78.10.1214/EJP.v13-474CrossRefGoogle Scholar
Diaconis, P. (1988). Group Representations in Probability and Statistics (Institute of Mathematical Statistics Lecture Notes: Monograph Series 11). Institute of Mathematical Statistics, Hayward, CA.Google Scholar
Diaconis, P. (1996). The cutoff phenomenon in finite Markov chains. Proc. Nat. Acad. Sci. USA 93, 1659–1664.10.1073/pnas.93.4.1659CrossRefGoogle Scholar
Diaconis, P. and Saloff-Coste, L. (1993). Comparison techniques for random walk on finite groups. Ann. Prob. 21, 2131–2156.10.1214/aop/1176989013CrossRefGoogle Scholar
Diaconis, P. and Shahshahani, M. (1981). Generating a random permutation with random transpositions. Z. Wahrscheinlichkeitsth. 57, 159–179.10.1007/BF00535487CrossRefGoogle Scholar
Diaconis, P., Fill, J. A. and Pitman, J. (1992). Analysis of top to random shuffles. Combinatorics Prob. Comput. 1, 135–155.10.1017/S0963548300000158CrossRefGoogle Scholar
Dyer, M., Greenhill, C. and Ullrich, M. (2014). Structure and eigenvalues of heat-bath Markov chains. Linear Algebra Appl. 454, 57–71.10.1016/j.laa.2014.04.018CrossRefGoogle Scholar
Rudolf, D. and Ullrich, M. (2013). Positivity of hit-and-run and related algorithms. Electron. Commun. Prob. 18, 8.10.1214/ECP.v18-2507CrossRefGoogle Scholar
Saloff-Coste, L. (1997). Lectures on finite Markov chains. In Lectures on Probability Theory and Statistics (Lecture Notes Math. 1665), ed. P. Bernard, pp. 301–413. Springer, Berlin.10.1007/BFb0092621CrossRefGoogle Scholar
Saloff-Coste, L. (2004). Random walks on finite groups. In Probability on Discrete Structures (Encyclopaedia Math. Sci. 110), pp. 263–346. Springer, Berlin.10.1007/978-3-662-09444-0_5CrossRefGoogle Scholar
Saloff-Coste, L. and Zúñiga, J. (2008). Refined estimates for some basic random walks on the symmetric and alternating groups. ALEA Lat. Am. J. Prob. Math. Statist. 4, 359–392.Google Scholar
Ullrich, M. (2014). Rapid mixing of Swendsen–Wang dynamics in two dimensions. Dissertationes Math. 502, 1–64.10.4064/dm502-0-1CrossRefGoogle Scholar