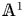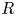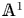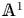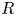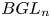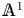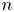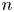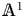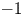1. Introduction
In this paper we build some foundations for localization with respect to a set of primes in the Morel–Voevodsky unstable ![]() ${\mathbb {A}}^1$-homotopy theory [Reference Morel and VoevodskyMV99] and study some applications. Our approach proceeds largely by analogy with the classical topological story [Reference QuillenQui69, Reference Bousfield and KanBK72, Reference SullivanSul05].
${\mathbb {A}}^1$-homotopy theory [Reference Morel and VoevodskyMV99] and study some applications. Our approach proceeds largely by analogy with the classical topological story [Reference QuillenQui69, Reference Bousfield and KanBK72, Reference SullivanSul05].
The Morel–Voevodsky approach to the construction of the ![]() ${\mathbb {A}}^1$-homotopy category is a two-stage localization. One begins with a category of spaces: we choose the model of simplicial presheaves on the category of smooth schemes. At the first stage, one formally inverts ‘Nisnevich local’ weak equivalences to obtain a ‘local homotopy category’. At the second stage, one formally inverts projection maps with one factor the affine line to obtain the unstable
${\mathbb {A}}^1$-homotopy category is a two-stage localization. One begins with a category of spaces: we choose the model of simplicial presheaves on the category of smooth schemes. At the first stage, one formally inverts ‘Nisnevich local’ weak equivalences to obtain a ‘local homotopy category’. At the second stage, one formally inverts projection maps with one factor the affine line to obtain the unstable ![]() ${\mathbb {A}}^1$-homotopy category.
${\mathbb {A}}^1$-homotopy category.
If ![]() $R$ is a subring of the rational numbers, then our goal will be to further localize the
$R$ is a subring of the rational numbers, then our goal will be to further localize the ![]() ${\mathbb {A}}^1$-homotopy category to obtain an
${\mathbb {A}}^1$-homotopy category to obtain an ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-homotopy category. While such localizations formally exist, as in the classical story, we want to isolate a class of spaces for which
${\mathbb {A}}^1$-homotopy category. While such localizations formally exist, as in the classical story, we want to isolate a class of spaces for which ![]() $R$-localization is ‘well behaved’. In the classical situation, for sufficiently nice spaces (e.g. nilpotent spaces), ‘well behaved’ means that localization preserves fiber sequences, and has the effect of simply tensoring homotopy groups with
$R$-localization is ‘well behaved’. In the classical situation, for sufficiently nice spaces (e.g. nilpotent spaces), ‘well behaved’ means that localization preserves fiber sequences, and has the effect of simply tensoring homotopy groups with ![]() $R$.
$R$.
Following the two-stage construction of the ![]() ${\mathbb {A}}^1$-homotopy category above, we begin in § 2 by analyzing nilpotence in the more general context of the local homotopy theory of simplicial presheaves on a site (with enough points in the topos-theoretic sense). In this context, there is a ‘strong’ notion of nilpotence, which is analogous to the classical notion in the sense that Postnikov towers for spaces can be refined to a tower of principal fibrations. However, we also introduce a broader ‘local’ notion of nilpotence, where local nilpotence means ‘stalkwise’ nilpotence, which is natural from the standpoint of local homotopy theory. Section 2 closes with a quick discussion of
${\mathbb {A}}^1$-homotopy category above, we begin in § 2 by analyzing nilpotence in the more general context of the local homotopy theory of simplicial presheaves on a site (with enough points in the topos-theoretic sense). In this context, there is a ‘strong’ notion of nilpotence, which is analogous to the classical notion in the sense that Postnikov towers for spaces can be refined to a tower of principal fibrations. However, we also introduce a broader ‘local’ notion of nilpotence, where local nilpotence means ‘stalkwise’ nilpotence, which is natural from the standpoint of local homotopy theory. Section 2 closes with a quick discussion of ![]() $R$-localization in the local homotopy theory of simplicial presheaves.
$R$-localization in the local homotopy theory of simplicial presheaves.
In § 3 we begin our analysis of nilpotence in ![]() ${\mathbb {A}}^1$-homotopy theory. After reviewing foundational structural facts about
${\mathbb {A}}^1$-homotopy theory. After reviewing foundational structural facts about ![]() ${\mathbb {A}}^1$-homotopy sheaves, the bulk of §§ 3.1 and 3.2 is devoted to an analysis of the relevant ‘group theory’ in the context of
${\mathbb {A}}^1$-homotopy sheaves, the bulk of §§ 3.1 and 3.2 is devoted to an analysis of the relevant ‘group theory’ in the context of ![]() ${\mathbb {A}}^1$-homotopy theory. Then we analyze variants of the above notions of nilpotence in
${\mathbb {A}}^1$-homotopy theory. Then we analyze variants of the above notions of nilpotence in ![]() ${\mathbb {A}}^1$-homotopy theory (see Definition 3.3.1).
${\mathbb {A}}^1$-homotopy theory (see Definition 3.3.1).
A basic motivation for our analysis is that the analogs of spaces that are simple or even simply-connected in classical algebraic topology can fail to be so in ![]() ${\mathbb {A}}^1$-algebraic topology. For example, the projective line or, more generally, the variety parameterizing complete flags in a vector space is
${\mathbb {A}}^1$-algebraic topology. For example, the projective line or, more generally, the variety parameterizing complete flags in a vector space is ![]() ${\mathbb {A}}^1$-nilpotent (see Theorem 3.4.8). However, these examples typically fail to be
${\mathbb {A}}^1$-nilpotent (see Theorem 3.4.8). However, these examples typically fail to be ![]() ${\mathbb {A}}^1$-simple because their
${\mathbb {A}}^1$-simple because their ![]() ${\mathbb {A}}^1$-fundamental sheaves of groups may fail to be abelian (see Remark 3.4.9 for further discussion).
${\mathbb {A}}^1$-fundamental sheaves of groups may fail to be abelian (see Remark 3.4.9 for further discussion).
In § 4 we then proceed to analyze ![]() $R$-localization in
$R$-localization in ![]() ${\mathbb {A}}^1$-homotopy theory, keeping our motivating examples in mind. Classically,
${\mathbb {A}}^1$-homotopy theory, keeping our motivating examples in mind. Classically, ![]() $R$-local equivalences can be characterized as maps that induce isomorphisms on
$R$-local equivalences can be characterized as maps that induce isomorphisms on ![]() $R$-local homology. The natural analog of ‘homology’ in the context of
$R$-local homology. The natural analog of ‘homology’ in the context of ![]() ${\mathbb {A}}^1$-homotopy theory is the
${\mathbb {A}}^1$-homotopy theory is the ![]() ${\mathbb {A}}^1$-homology theory studied by F. Morel in [Reference MorelMor12, § 6.2]. Thus, we analyze morphisms of spaces that induce isomorphisms on
${\mathbb {A}}^1$-homology theory studied by F. Morel in [Reference MorelMor12, § 6.2]. Thus, we analyze morphisms of spaces that induce isomorphisms on ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-homology.
${\mathbb {A}}^1$-homology.
Remark 1 For spaces that are (![]() ${\mathbb {A}}^1$-)simply connected, there is a tight connection between
${\mathbb {A}}^1$-)simply connected, there is a tight connection between ![]() ${\mathbb {A}}^1$-homotopy and
${\mathbb {A}}^1$-homotopy and ![]() ${\mathbb {A}}^1$-homology. In such situations, our approach agrees with previous approaches to localization (e.g. [Reference Wickelgren and WilliamsWW19, § 3]), which use equivalent alternative approaches circumventing discussion of
${\mathbb {A}}^1$-homology. In such situations, our approach agrees with previous approaches to localization (e.g. [Reference Wickelgren and WilliamsWW19, § 3]), which use equivalent alternative approaches circumventing discussion of ![]() ${\mathbb {A}}^1$-homology. On the other hand, more recently, G. Guzman [Reference GuzmanGuz19] has studied localization of the unstable motivic homotopy category with respect to
${\mathbb {A}}^1$-homology. On the other hand, more recently, G. Guzman [Reference GuzmanGuz19] has studied localization of the unstable motivic homotopy category with respect to ![]() ${\mathbb {A}}^1$-homology. Her focus is rather different from ours, as her goal is to obtain a ‘coalgebraic’ description of the associated local homotopy category along the lines of [Reference QuillenQui69] or [Reference GoerssGoe95].
${\mathbb {A}}^1$-homology. Her focus is rather different from ours, as her goal is to obtain a ‘coalgebraic’ description of the associated local homotopy category along the lines of [Reference QuillenQui69] or [Reference GoerssGoe95].
A significant portion of § 4 is devoted to analyzing the relationship between nilpotence and ![]() ${\mathbb {A}}^1$-homology. This section closes with a construction of a model for
${\mathbb {A}}^1$-homology. This section closes with a construction of a model for ![]() $R$-localization that behaves ‘reasonably’ for suitable nilpotent spaces (see Theorems 4.3.9 and 4.3.11): for example, the effect on higher
$R$-localization that behaves ‘reasonably’ for suitable nilpotent spaces (see Theorems 4.3.9 and 4.3.11): for example, the effect on higher ![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $R$-localization amounts to tensoring with
$R$-localization amounts to tensoring with ![]() $R$).
$R$).
Remark 2 Morel's ![]() ${\mathbb {A}}^1$-homology theory does not coincide with motivic homology defined via Voevodsky's triangulated category of motives [Reference Mazza, Voevodsky and WeibelMVW06]. For example, if we consider the motivic Hopf map
${\mathbb {A}}^1$-homology theory does not coincide with motivic homology defined via Voevodsky's triangulated category of motives [Reference Mazza, Voevodsky and WeibelMVW06]. For example, if we consider the motivic Hopf map ![]() $\eta : {\mathbb {A}}^2 \,{\setminus}\, 0 \to {\mathbb {P}}^1$, then the map
$\eta : {\mathbb {A}}^2 \,{\setminus}\, 0 \to {\mathbb {P}}^1$, then the map ![]() $\eta _*$ in motivic homology is the zero map but, as Morel observed, non-zero in
$\eta _*$ in motivic homology is the zero map but, as Morel observed, non-zero in ![]() ${\mathbb {A}}^1$-homology [Reference MorelMor06a, Remark 3.12]. Moreover, this theory is not
${\mathbb {A}}^1$-homology [Reference MorelMor06a, Remark 3.12]. Moreover, this theory is not ![]() ${\mathbb {P}}^1$-stable, that is, representable in the stable
${\mathbb {P}}^1$-stable, that is, representable in the stable ![]() ${\mathbb {A}}^1$-homotopy category of
${\mathbb {A}}^1$-homotopy category of ![]() ${\mathbb {P}}^1$-spectra (if it was, then the
${\mathbb {P}}^1$-spectra (if it was, then the ![]() ${\mathbb {A}}^1$-homology sheaves of a space in the sense of Morel could be equipped with transfers of a suitable form, but they cannot always be equipped with this structure; see [Reference LevineLev10, § 2] for an example).
${\mathbb {A}}^1$-homology sheaves of a space in the sense of Morel could be equipped with transfers of a suitable form, but they cannot always be equipped with this structure; see [Reference LevineLev10, § 2] for an example).
Section 5 focuses on the main applications of our constructions: we establish analogs of some classical results of J.-P. Serre. First, Serre showed that after inverting sufficiently many primes, compact Lie groups split as products of odd-dimensional spheres [Reference SerreSer53]. Serre obtained this decomposition by analyzing explicitly the computation of the cohomology of compact Lie groups. An algebro-geometric analog of a compact Lie group is a split reductive group; once-punctured affine spaces are algebro-geometric analogs of odd-dimensional spheres. With these analogies in mind, we establish the following result.
Theorem 3 Suppose ![]() $k$ is a field that is not formally real and
$k$ is a field that is not formally real and ![]() $n \geq 2$ is an integer. After inverting
$n \geq 2$ is an integer. After inverting ![]() $(n-1)!$, there is an
$(n-1)!$, there is an ![]() ${\mathbb {A}}^1$-weak equivalence of the form
${\mathbb {A}}^1$-weak equivalence of the form
Remark 4 Our proof of this fact is rather different from the classical proof as we make no direct cohomology computations. While the rational Voevodsky motive (or motivic cohomology) of split reductive groups is understood [Reference GrossGro97, Reference BiglariBig12], the ![]() ${\mathbb {A}}^1$-homology has only been analyzed in low degrees [Reference MorelMor11, Appendix A]. We are forced to construct the summands by means of explicit maps and we do this by studying ‘Suslin matrices’ (introduced in [Reference SuslinSus77]). Appealing to (complex) realization, our proof thus yields a new proof of Serre's classical splitting in this case.
${\mathbb {A}}^1$-homology has only been analyzed in low degrees [Reference MorelMor11, Appendix A]. We are forced to construct the summands by means of explicit maps and we do this by studying ‘Suslin matrices’ (introduced in [Reference SuslinSus77]). Appealing to (complex) realization, our proof thus yields a new proof of Serre's classical splitting in this case.
Serre also showed that the homotopy groups of ![]() $S^{2n-1}$ are finite except in degree equal
$S^{2n-1}$ are finite except in degree equal ![]() $2n-1$. Likewise, the homotopy groups of
$2n-1$. Likewise, the homotopy groups of ![]() $S^{2n}$ are finite except in degrees
$S^{2n}$ are finite except in degrees ![]() $2n$ and
$2n$ and ![]() $4n-1$. The first result is a juxtaposition of two results: one shows that odd-dimensional spheres are rationally equivalent to Eilenberg–Mac Lane spaces by analysis of the homotopy fiber of the map
$4n-1$. The first result is a juxtaposition of two results: one shows that odd-dimensional spheres are rationally equivalent to Eilenberg–Mac Lane spaces by analysis of the homotopy fiber of the map ![]() $S^{2n-1} \to K({\mathbb {Z}},2n-1)$ induced by the fundamental class (equivalently, the first non-trivial stage of the Postnikov tower), and one establishes that Eilenberg–Mac Lane spaces have finitely generated cohomology by use of Serre's class theory. The second result follows from the first by construction of a fiber sequence of the form
$S^{2n-1} \to K({\mathbb {Z}},2n-1)$ induced by the fundamental class (equivalently, the first non-trivial stage of the Postnikov tower), and one establishes that Eilenberg–Mac Lane spaces have finitely generated cohomology by use of Serre's class theory. The second result follows from the first by construction of a fiber sequence of the form
We establish some motivic analogs of these results. To phrase the results in a uniform geometric fashion, we use the split affine quadric ![]() $Q_{2n-1}$ (defined by setting the even-dimensional hyperbolic form equal to
$Q_{2n-1}$ (defined by setting the even-dimensional hyperbolic form equal to ![]() $1$) and its corresponding even-dimensional analog
$1$) and its corresponding even-dimensional analog ![]() $Q_{2n}$ (this is not quite obtained by setting the odd-dimensional standard split hyperbolic form equal to
$Q_{2n}$ (this is not quite obtained by setting the odd-dimensional standard split hyperbolic form equal to ![]() $1$, but it is isomorphic to this if
$1$, but it is isomorphic to this if ![]() $k$ has characteristic not equal to
$k$ has characteristic not equal to ![]() $2$; see the beginning of § 5.1 for more details).
$2$; see the beginning of § 5.1 for more details).
Theorem 5 (see Theorems 5.3.3 and 5.3.11)
Assume ![]() $k$ is a field that is not formally real.
$k$ is a field that is not formally real.
1. The map
induced by the fundamental class in motivic cohomology is an \[ Q_{2n-1} \longrightarrow K({\mathbb{Z}}(n),2n-1) \]
\[ Q_{2n-1} \longrightarrow K({\mathbb{Z}}(n),2n-1) \] ${\mathbb {A}}^1$-equivalence for
${\mathbb {A}}^1$-equivalence for  $n = 1$, and a rational
$n = 1$, and a rational  ${\mathbb {A}}^1$-weak equivalence if
${\mathbb {A}}^1$-weak equivalence if  $n \geq 2$.
$n \geq 2$.2. There is a rational
 ${\mathbb {A}}^1$-fiber sequence of the form
where the first map is the fundamental class in motivic cohomology, and second map is the squaring map.
${\mathbb {A}}^1$-fiber sequence of the form
where the first map is the fundamental class in motivic cohomology, and second map is the squaring map. \[ Q_{2n} \longrightarrow K({\mathbb{Z}}(n),2n) \longrightarrow K({\mathbb{Z}}(2n),4n), \]
\[ Q_{2n} \longrightarrow K({\mathbb{Z}}(n),2n) \longrightarrow K({\mathbb{Z}}(2n),4n), \]
Remark 6 The classical proof of the first result uses the Serre spectral sequence to understand the cohomology of the ![]() $(2n-1)$-fold connective cover of
$(2n-1)$-fold connective cover of ![]() $S^{2n-1}$. In the motivic context, we do not have a Serre spectral sequence of the necessary form. Our proof is by necessity quite different from the classical proof and proceeds by appeal to Theorem 3 and rational degeneration of the motivic spectral sequence linking algebraic K-theory and motivic cohomology. Moreover, our result is an unstable analog of Morel's equivalence between the rationalized stable
$S^{2n-1}$. In the motivic context, we do not have a Serre spectral sequence of the necessary form. Our proof is by necessity quite different from the classical proof and proceeds by appeal to Theorem 3 and rational degeneration of the motivic spectral sequence linking algebraic K-theory and motivic cohomology. Moreover, our result is an unstable analog of Morel's equivalence between the rationalized stable ![]() ${\mathbb {A}}^1$-homotopy category and Voevodsky's category of motives (assuming
${\mathbb {A}}^1$-homotopy category and Voevodsky's category of motives (assuming ![]() $-1$ is a sum of squares in
$-1$ is a sum of squares in ![]() $k$). Similar comments apply to the even-dimensional case.
$k$). Similar comments apply to the even-dimensional case.
After Theorem 5, the motivic analog of the finite-generation of the cohomology of classical Eilenberg–Mac Lane spaces is closely related to the Beilinson–Soulé vanishing conjecture and the unstable ![]() ${\mathbb {A}}^1$-homotopy theory of Voevodsky's motivic Eilenberg–Mac Lane spaces. We refer the reader to Corollary 5.3.7 and the surrounding material for further discussion of this relationship.
${\mathbb {A}}^1$-homotopy theory of Voevodsky's motivic Eilenberg–Mac Lane spaces. We refer the reader to Corollary 5.3.7 and the surrounding material for further discussion of this relationship.
With the exception of the case ![]() $n = 1$ of Theorem 5(2), all of the results stated above could be established with a more restrictive version of
$n = 1$ of Theorem 5(2), all of the results stated above could be established with a more restrictive version of ![]() $R$-localization (i.e. for ‘simple’ spaces). Nevertheless, allowing nilpotent spaces yields considerable additional flexibility, for example, good control of fiber sequences under
$R$-localization (i.e. for ‘simple’ spaces). Nevertheless, allowing nilpotent spaces yields considerable additional flexibility, for example, good control of fiber sequences under ![]() $R$-localization (see Remark 4.3.12 for further explanations). As a consequence, the bulk of this paper is devoted to developing localization in generality suitable for future geometric applications. For us, key among these observations is the fact that
$R$-localization (see Remark 4.3.12 for further explanations). As a consequence, the bulk of this paper is devoted to developing localization in generality suitable for future geometric applications. For us, key among these observations is the fact that ![]() $BGL_n$ has a ‘well-behaved’ rationalization, either if
$BGL_n$ has a ‘well-behaved’ rationalization, either if ![]() $n$ is odd or if
$n$ is odd or if ![]() $n$ is even and
$n$ is even and ![]() $-1$ is a sum of squares in the base field (combine Theorems 3.4.6, 3.4.12 and 4.3.9); these results use the full strength of the techniques developed here. A different set of applications is presented in [Reference Asok, Fasel and HopkinsAFH20], where we construct low-rank vector bundles on smooth affine varieties that are
$-1$ is a sum of squares in the base field (combine Theorems 3.4.6, 3.4.12 and 4.3.9); these results use the full strength of the techniques developed here. A different set of applications is presented in [Reference Asok, Fasel and HopkinsAFH20], where we construct low-rank vector bundles on smooth affine varieties that are ![]() ${\mathbb {A}}^1$-weakly equivalent to projective spaces. We refer the reader to the introduction to each section for a more detailed description of its contents.
${\mathbb {A}}^1$-weakly equivalent to projective spaces. We refer the reader to the introduction to each section for a more detailed description of its contents.
Preliminaries and notation. Throughout this paper ![]() $k$ will denote a fixed base field and
$k$ will denote a fixed base field and ![]() $R$ will be a commutative unital ring (typically a subring of the field of rational numbers
$R$ will be a commutative unital ring (typically a subring of the field of rational numbers ![]() ${\mathbb {Q}}$). We remind the reader that a field
${\mathbb {Q}}$). We remind the reader that a field ![]() $k$ is called formally real if
$k$ is called formally real if ![]() $-1$ is not a sum of squares in
$-1$ is not a sum of squares in ![]() $k$ and not formally real otherwise; these notions will reappear later in the paper and we refer the reader to [Reference Elman, Karpenko and MerkurjevEKM08, § 95] for a discussion of some properties of formally real fields.
$k$ and not formally real otherwise; these notions will reappear later in the paper and we refer the reader to [Reference Elman, Karpenko and MerkurjevEKM08, § 95] for a discussion of some properties of formally real fields.
If ![]() $\mathbf {C}$ is a small category, then we use the following notation:
$\mathbf {C}$ is a small category, then we use the following notation:
•
 $\mathrm {Ab}(\mathbf {C})$, the category of presheaves of abelian groups on
$\mathrm {Ab}(\mathbf {C})$, the category of presheaves of abelian groups on  $\mathbf {C}$;
$\mathbf {C}$;•
 $\mathrm {Mod}_R(\mathbf {C})$, the category of presheaves of
$\mathrm {Mod}_R(\mathbf {C})$, the category of presheaves of  $R$-modules on
$R$-modules on  $\mathbf {C}$;
$\mathbf {C}$;•
 $\mathrm {Grp}(\mathbf {C})$, the category of presheaves of groups on
$\mathrm {Grp}(\mathbf {C})$, the category of presheaves of groups on  $\mathbf {C}$;
$\mathbf {C}$;•
 $\mathrm {sPre}(\mathbf {C})$ for the category of simplicial presheaves on
$\mathrm {sPre}(\mathbf {C})$ for the category of simplicial presheaves on  $\mathbf {C}$.
$\mathbf {C}$.
If ![]() $\mathbf {C}$ is equipped with a Grothendieck topology
$\mathbf {C}$ is equipped with a Grothendieck topology ![]() $\tau$, then we use the following notation:
$\tau$, then we use the following notation:
•
 $\mathrm {Ab}_{\tau }(\mathbf {C})$, the full subcategory of
$\mathrm {Ab}_{\tau }(\mathbf {C})$, the full subcategory of  $\mathrm {Ab}(\mathbf {C})$ consisting of
$\mathrm {Ab}(\mathbf {C})$ consisting of  $\tau$-sheaves of abelian groups;
$\tau$-sheaves of abelian groups;•
 $\mathrm {Mod}_{R,\tau }(\mathbf {C})$, the full subcategory of
$\mathrm {Mod}_{R,\tau }(\mathbf {C})$, the full subcategory of  $\mathrm {Mod}_R(\mathbf {C})$ consisting of
$\mathrm {Mod}_R(\mathbf {C})$ consisting of  $\tau$-sheaves of
$\tau$-sheaves of  $R$-modules.
$R$-modules.•
 $\mathrm {Grp}_{\tau }(\mathbf {C})$, the full subcategory of
$\mathrm {Grp}_{\tau }(\mathbf {C})$, the full subcategory of  $\mathrm {Grp}(\mathbf {C})$ consisting of
$\mathrm {Grp}(\mathbf {C})$ consisting of  $\tau$-sheaves of groups.
$\tau$-sheaves of groups.
We will typically use script letters ![]() $\mathscr {X},\mathscr {Y}$ for objects in
$\mathscr {X},\mathscr {Y}$ for objects in ![]() $\mathrm {sPre}(\mathbf {C})$. If
$\mathrm {sPre}(\mathbf {C})$. If ![]() $\mathbf {C}$ is a pointed category with terminal object
$\mathbf {C}$ is a pointed category with terminal object ![]() $\ast$ (i.e.
$\ast$ (i.e. ![]() $\mathbf {C}$ has an initial object and the canonical map from the initial to the terminal object is an isomorphism), then we write
$\mathbf {C}$ has an initial object and the canonical map from the initial to the terminal object is an isomorphism), then we write
•
 $\mathrm {sPre}(\mathbf {C})_{\ast }$ for the category of pointed objects in
$\mathrm {sPre}(\mathbf {C})_{\ast }$ for the category of pointed objects in  $\mathrm {sPre}(\mathbf {C})$,
$\mathrm {sPre}(\mathbf {C})$,
that is, pairs ![]() $(\mathscr {X},x)$ where
$(\mathscr {X},x)$ where ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $x: \ast \to \mathscr {X}$ is a morphism.
$x: \ast \to \mathscr {X}$ is a morphism.
If ![]() $(\mathbf {C},\tau )$ is a site,
$(\mathbf {C},\tau )$ is a site, ![]() $\mathrm {sPre}(\mathbf {C})$ can be equipped with a
$\mathrm {sPre}(\mathbf {C})$ can be equipped with a ![]() $\tau$-local model structure (see § 2.2 for more details); we write
$\tau$-local model structure (see § 2.2 for more details); we write ![]() $\mathrm {Ho}_{\tau }(\mathbf {C})$ for the associated homotopy category and
$\mathrm {Ho}_{\tau }(\mathbf {C})$ for the associated homotopy category and ![]() $\mathrm {Ho}_{\tau,\ast }(\mathbf {C})$ for the pointed homotopy category. We write
$\mathrm {Ho}_{\tau,\ast }(\mathbf {C})$ for the pointed homotopy category. We write ![]() $\mathrm {R}_{\tau }$ for a fixed functorial fibrant replacement functor for the
$\mathrm {R}_{\tau }$ for a fixed functorial fibrant replacement functor for the ![]() $\tau$-local model structure and, given
$\tau$-local model structure and, given ![]() $\mathscr {X},\mathscr {Y} \in \mathrm {sPre}(\mathbf {C})$, we write
$\mathscr {X},\mathscr {Y} \in \mathrm {sPre}(\mathbf {C})$, we write ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y})$ for the associated derived mapping space.
$\operatorname {Map}(\mathscr {X},\mathscr {Y})$ for the associated derived mapping space.
If ![]() $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$, we write
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$, we write ![]() $B\mathbf {G} \in \mathrm {sPre}(\mathbf {C})$ for the associated classifying space; in brief,
$B\mathbf {G} \in \mathrm {sPre}(\mathbf {C})$ for the associated classifying space; in brief, ![]() $\mathbf {G}$-torsors on spaces may be described in terms of maps in
$\mathbf {G}$-torsors on spaces may be described in terms of maps in ![]() $\mathrm {Ho}_{\tau }(\mathbf {C})$; we refer the reader to [Reference JardineJar15, Theorem 9.8] in particular, and [Reference JardineJar15, Chapter 9] more generally, for further discussion of this point. We also write
$\mathrm {Ho}_{\tau }(\mathbf {C})$; we refer the reader to [Reference JardineJar15, Theorem 9.8] in particular, and [Reference JardineJar15, Chapter 9] more generally, for further discussion of this point. We also write ![]() $B_{\tau }\mathbf {G}$ for a
$B_{\tau }\mathbf {G}$ for a ![]() $\tau$-local fibrant replacement for
$\tau$-local fibrant replacement for ![]() $B\mathbf {G}$; we refer the reader to [Reference Asok, Hoyois and WendtAHW18, § 2.3] for more discussion of this notation.
$B\mathbf {G}$; we refer the reader to [Reference Asok, Hoyois and WendtAHW18, § 2.3] for more discussion of this notation.
Similarly, if ![]() $\mathbf {A} \in \mathrm {Ab}_{\tau }(\mathbf {C})$, and
$\mathbf {A} \in \mathrm {Ab}_{\tau }(\mathbf {C})$, and ![]() $n \geq 0$ is an integer, we write
$n \geq 0$ is an integer, we write ![]() $K(\mathbf {A},n) \in \mathrm {sPre}(\mathbf {C})$ for the associated Eilenberg–Mac Lane space [Reference JardineJar15, p. 212]; such objects represent sheaf cohomology with coefficients in
$K(\mathbf {A},n) \in \mathrm {sPre}(\mathbf {C})$ for the associated Eilenberg–Mac Lane space [Reference JardineJar15, p. 212]; such objects represent sheaf cohomology with coefficients in ![]() $\mathbf {A}$ in
$\mathbf {A}$ in ![]() $\mathrm {Ho}_{\tau }(\mathbf {C})$ [Reference JardineJar15, Theorem 8.26]. We will also use the notation
$\mathrm {Ho}_{\tau }(\mathbf {C})$ [Reference JardineJar15, Theorem 8.26]. We will also use the notation ![]() $K(\mathbf {A},n)$ when
$K(\mathbf {A},n)$ when ![]() $\mathbf {A}$ is a chain complex of
$\mathbf {A}$ is a chain complex of ![]() $\tau$-sheaves of abelian groups situated in positive (homological) degrees. In this case,
$\tau$-sheaves of abelian groups situated in positive (homological) degrees. In this case, ![]() $K(\mathbf {A},n)$ represents hypercohomology with coefficients in
$K(\mathbf {A},n)$ represents hypercohomology with coefficients in ![]() $\mathbf {A}$; see [Reference JardineJar15, Chapter 8] for more details.
$\mathbf {A}$; see [Reference JardineJar15, Chapter 8] for more details.
We write ![]() $\mathrm {Sm}_k$ for the category of schemes that are separated, smooth and have finite type over
$\mathrm {Sm}_k$ for the category of schemes that are separated, smooth and have finite type over ![]() $\operatorname {Spec} k$. When
$\operatorname {Spec} k$. When ![]() $\mathbf {C} = \mathrm {Sm}_k$, we set
$\mathbf {C} = \mathrm {Sm}_k$, we set ![]() $\mathrm {Spc}_k := \mathrm {sPre}(\mathrm {Sm}_k)$. Typically, we will take
$\mathrm {Spc}_k := \mathrm {sPre}(\mathrm {Sm}_k)$. Typically, we will take ![]() $\mathbf {C} = \mathrm {Sm}_k$ equipped with the Nisnevich topology, and if no topology is mentioned, the word ‘sheaf’ should be taken to mean Nisnevich sheaf. We set
$\mathbf {C} = \mathrm {Sm}_k$ equipped with the Nisnevich topology, and if no topology is mentioned, the word ‘sheaf’ should be taken to mean Nisnevich sheaf. We set ![]() $\mathrm {Ab}_k := \mathrm {Ab}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ and
$\mathrm {Ab}_k := \mathrm {Ab}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ and ![]() $\mathrm {Grp}_k := \mathrm {Grp}_{\operatorname {Nis}}(\mathrm {Sm}_k)$. When
$\mathrm {Grp}_k := \mathrm {Grp}_{\operatorname {Nis}}(\mathrm {Sm}_k)$. When ![]() $(\mathbf {C},\tau ) = (\mathrm {Sm}_k,\operatorname {Nis})$, the category
$(\mathbf {C},\tau ) = (\mathrm {Sm}_k,\operatorname {Nis})$, the category ![]() $\mathrm {Ho}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ (
$\mathrm {Ho}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ (![]() $\mathrm {Ho}_{\operatorname {Nis},\ast }(\mathrm {Sm}_k)$) will be called the (pointed) simplicial homotopy category.
$\mathrm {Ho}_{\operatorname {Nis},\ast }(\mathrm {Sm}_k)$) will be called the (pointed) simplicial homotopy category.
The Morel–Voeovodsky ![]() ${\mathbb {A}}^1$-homotopy category
${\mathbb {A}}^1$-homotopy category ![]() $\mathrm {Ho}_{k}$ is obtained from
$\mathrm {Ho}_{k}$ is obtained from ![]() $\mathrm {Ho}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ by a further Bousfield localization (see § 3.1 for more details); the pointed
$\mathrm {Ho}_{\operatorname {Nis}}(\mathrm {Sm}_k)$ by a further Bousfield localization (see § 3.1 for more details); the pointed ![]() ${\mathbb {A}}^1$-homotopy category is obtained similarly, beginning with the pointed simplicial homotopy category
${\mathbb {A}}^1$-homotopy category is obtained similarly, beginning with the pointed simplicial homotopy category ![]() $\mathrm {Ho}_{\operatorname {Nis},\ast }(\mathrm {Sm}_k)$ instead. If
$\mathrm {Ho}_{\operatorname {Nis},\ast }(\mathrm {Sm}_k)$ instead. If ![]() $\mathscr {X},\mathscr {Y} \in \mathrm {Spc}_k$, we set
$\mathscr {X},\mathscr {Y} \in \mathrm {Spc}_k$, we set
and similar notation will be used for pointed ![]() ${\mathbb {A}}^1$-homotopy classes of maps.
${\mathbb {A}}^1$-homotopy classes of maps.
2. Nilpotence and  $R$-localization in local homotopy theory
$R$-localization in local homotopy theory
Suppose ![]() $R \subset {\mathbb {Q}}$ is a subring. The main goal of this section is to study a notion of
$R \subset {\mathbb {Q}}$ is a subring. The main goal of this section is to study a notion of ![]() $R$-localization of simplicial presheaves, paying close attention to the behavior of localization for ‘nilpotent spaces’ in a sense we introduce here.
$R$-localization of simplicial presheaves, paying close attention to the behavior of localization for ‘nilpotent spaces’ in a sense we introduce here.
In § 2.1 we begin by formulating sheaf-theoretic notions of nilpotent and ![]() $R$-local sheaves of groups. In § 2.2 we review basic constructions related to the local homotopy theory of simplicial presheaves on a small Grothendieck site [Reference JardineJar15]. In the case where the site has ‘enough points’, we introduce various notions of nilpotent spaces (or maps) in this context. In § 2.3 we analyze functorial
$R$-local sheaves of groups. In § 2.2 we review basic constructions related to the local homotopy theory of simplicial presheaves on a small Grothendieck site [Reference JardineJar15]. In the case where the site has ‘enough points’, we introduce various notions of nilpotent spaces (or maps) in this context. In § 2.3 we analyze functorial ![]() $R$-localizations for nilpotent spaces in the situation under consideration.
$R$-localizations for nilpotent spaces in the situation under consideration.
Presumably, much of what we discuss in this section could be formulated in an arbitrary ![]() $\infty$-topos [Reference LurieLur09], but we restrict our attention to simplicial presheaves on a small Grothendieck site both to simplify the discussion and because that is all we will use in our applications to
$\infty$-topos [Reference LurieLur09], but we restrict our attention to simplicial presheaves on a small Grothendieck site both to simplify the discussion and because that is all we will use in our applications to ![]() ${\mathbb {A}}^1$-homotopy theory.
${\mathbb {A}}^1$-homotopy theory.
Versions of some facts here about ![]() $R$-localization were worked out in [Reference Wickelgren and WilliamsWW19, § 3], though they mainly analyze localization functors for the analogs of simply connected or, more generally, simple spaces. Moreover, it was observed there that various inequivalent versions of the theory exist, just as in the classical situation. Indeed, for non-nilpotent spaces, there are a number of inequivalent
$R$-localization were worked out in [Reference Wickelgren and WilliamsWW19, § 3], though they mainly analyze localization functors for the analogs of simply connected or, more generally, simple spaces. Moreover, it was observed there that various inequivalent versions of the theory exist, just as in the classical situation. Indeed, for non-nilpotent spaces, there are a number of inequivalent ![]() $R$-localization functors (see Remark 2.3.5 for further discussion and references).
$R$-localization functors (see Remark 2.3.5 for further discussion and references).
In any case, upon choosing a model of functorial ![]() $R$-localization for simplicial sets, one may then define
$R$-localization for simplicial sets, one may then define ![]() $R$-localization for pointed simplicial presheaves sectionwise. Then we check that
$R$-localization for pointed simplicial presheaves sectionwise. Then we check that ![]() $R$-localization behaves well with respect to local weak equivalences. Nothing in this section should be surprising to experts; we collected the relevant facts here for lack of a better reference.
$R$-localization behaves well with respect to local weak equivalences. Nothing in this section should be surprising to experts; we collected the relevant facts here for lack of a better reference.
2.1 Nilpotent (pre)sheaves of groups
Suppose throughout this section that ![]() $\mathbf {C}$ is a small category. If
$\mathbf {C}$ is a small category. If ![]() $\mathbf {C}$ is equipped with a Grothendieck topology, then we formulate notions of nilpotence for sheaves of groups and actions of sheaves of groups (see Definitions 2.1.1 and 2.1.3) and study the basic properties of such sheaves of groups. We then study
$\mathbf {C}$ is equipped with a Grothendieck topology, then we formulate notions of nilpotence for sheaves of groups and actions of sheaves of groups (see Definitions 2.1.1 and 2.1.3) and study the basic properties of such sheaves of groups. We then study ![]() $R$-local sheaves of groups when
$R$-local sheaves of groups when ![]() $R \subset {\mathbb {Q}}$ is a subring and discuss the interplay of nilpotence and the property of being
$R \subset {\mathbb {Q}}$ is a subring and discuss the interplay of nilpotence and the property of being ![]() $R$-local; we close with a definition of
$R$-local; we close with a definition of ![]() $R$-nilpotent sheaf of groups (see Definition 2.3.4).
$R$-nilpotent sheaf of groups (see Definition 2.3.4).
Nilpotent sheaves of groups and actions
If ![]() $\mathbf {H},\mathbf {G} \in \mathrm {Grp}(\mathbf {C})$, then an action of
$\mathbf {H},\mathbf {G} \in \mathrm {Grp}(\mathbf {C})$, then an action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\mathbf {H}$ is a homomorphism of presheaves of groups
$\mathbf {H}$ is a homomorphism of presheaves of groups ![]() $\mathbf {G} \to {\mathbf {Aut}}(\mathbf {H})$. If
$\mathbf {G} \to {\mathbf {Aut}}(\mathbf {H})$. If ![]() $(\mathbf {C},\tau )$ is a site (i.e.
$(\mathbf {C},\tau )$ is a site (i.e. ![]() $\tau$ is a Grothendieck topology on
$\tau$ is a Grothendieck topology on ![]() $\mathbf {C}$), then given a sheaf of groups
$\mathbf {C}$), then given a sheaf of groups ![]() $\mathbf {H}$,
$\mathbf {H}$, ![]() ${\mathbf {Aut}}(\mathbf {H})$ is automatically a sheaf of groups. Therefore, an action of a sheaf of groups
${\mathbf {Aut}}(\mathbf {H})$ is automatically a sheaf of groups. Therefore, an action of a sheaf of groups ![]() $\mathbf {G}$ on a sheaf of groups
$\mathbf {G}$ on a sheaf of groups ![]() $\mathbf {H}$ is just an action of the underlying presheaves. We now define a notion of nilpotence for actions.
$\mathbf {H}$ is just an action of the underlying presheaves. We now define a notion of nilpotence for actions.
Definition 2.1.1 Assume ![]() $(\mathbf {C},\tau )$ is a site. Suppose
$(\mathbf {C},\tau )$ is a site. Suppose ![]() $\mathbf {G},\mathbf {H} \in \mathrm {Grp}(\mathbf {C})$.
$\mathbf {G},\mathbf {H} \in \mathrm {Grp}(\mathbf {C})$.
1. Given an action of
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$, a
$\mathbf {H}$, a  $\mathbf {G}$-central series for the given action on
$\mathbf {G}$-central series for the given action on  $\mathbf {H}$ is a finite decreasing filtration
of
$\mathbf {H}$ is a finite decreasing filtration
of \[ \mathbf{H} = \mathbf{H}_0 \supset \cdots \supset \mathbf{H}_n = 1 \]
\[ \mathbf{H} = \mathbf{H}_0 \supset \cdots \supset \mathbf{H}_n = 1 \] $\mathbf {H}$ by
$\mathbf {H}$ by  $\mathbf {G}$-stable normal subgroup presheaves such that:
$\mathbf {G}$-stable normal subgroup presheaves such that:
(a) the successive subquotients
 $\mathbf {H}_i/\mathbf {H}_{i+1}$ are presheaves of abelian groups; and
$\mathbf {H}_i/\mathbf {H}_{i+1}$ are presheaves of abelian groups; and(b) the induced action of
 $\mathbf {G}$ on each subquotient is trivial.
$\mathbf {G}$ on each subquotient is trivial.
2. An action of
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$ is called nilpotent if there exists a
$\mathbf {H}$ is called nilpotent if there exists a  $\mathbf {G}$-central series for the action.
$\mathbf {G}$-central series for the action.3. If
 $\mathbf {G},\mathbf {H} \in \mathrm {Grp}_{\tau }(\mathbf {C})$, then an action of
$\mathbf {G},\mathbf {H} \in \mathrm {Grp}_{\tau }(\mathbf {C})$, then an action of  $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$ is called nilpotent if the underlying action as presheaves is nilpotent.
$\mathbf {H}$ is called nilpotent if the underlying action as presheaves is nilpotent.4. A presheaf of groups
 $\mathbf {G}$ will be called nilpotent if the conjugation action of
$\mathbf {G}$ will be called nilpotent if the conjugation action of  $\mathbf {G}$ on itself is a nilpotent action.
$\mathbf {G}$ on itself is a nilpotent action.5. If
 $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ then
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ then  $\mathbf {G}$ will be called nilpotent if it is nilpotent as a presheaf.
$\mathbf {G}$ will be called nilpotent if it is nilpotent as a presheaf.6. Given a nilpotent action of
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$ and a
$\mathbf {H}$ and a  $\mathbf {G}$-central series for the action, the length of the series is the smallest integer
$\mathbf {G}$-central series for the action, the length of the series is the smallest integer  $c$ such that
$c$ such that  $\mathbf {H}_{c'} = 1$ for all
$\mathbf {H}_{c'} = 1$ for all  $c' \geq c$.
$c' \geq c$.7. The nilpotence class of a nilpotent action is the minimum length of a
 $\mathbf {G}$-central series for the action.
$\mathbf {G}$-central series for the action.
Remark 2.1.2 Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. If a sheaf of groups
$(\mathbf {C},\tau )$ is a site with enough points. If a sheaf of groups ![]() $\mathbf {G}$ acts on a sheaf of groups
$\mathbf {G}$ acts on a sheaf of groups ![]() $\mathbf {H}$, then the action is trivial if and only if the action is stalkwise trivial since one may check that
$\mathbf {H}$, then the action is trivial if and only if the action is stalkwise trivial since one may check that ![]() $\mathbf {G} \to \mathbf {Aut}(\mathbf {H})$ is the trivial homomorphism stalkwise. It follows that one can check whether a given filtration of
$\mathbf {G} \to \mathbf {Aut}(\mathbf {H})$ is the trivial homomorphism stalkwise. It follows that one can check whether a given filtration of ![]() $\mathbf {H}$ by
$\mathbf {H}$ by ![]() $\mathbf {G}$-stable subsheaves is a
$\mathbf {G}$-stable subsheaves is a ![]() $\mathbf {G}$-central series stalkwise.
$\mathbf {G}$-central series stalkwise.
In the sheaf-theoretic context, we also make the following definition.
Definition 2.1.3 Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. An action of a sheaf of groups
$(\mathbf {C},\tau )$ is a site with enough points. An action of a sheaf of groups ![]() $\mathbf {G}$ on a sheaf of groups
$\mathbf {G}$ on a sheaf of groups ![]() $\mathbf {H}$ is locally nilpotent if there exists a decreasing filtration
$\mathbf {H}$ is locally nilpotent if there exists a decreasing filtration
by ![]() $\mathbf {G}$-stable normal subgroup sheaves such that for every point
$\mathbf {G}$-stable normal subgroup sheaves such that for every point ![]() $s$ of
$s$ of ![]() $(\mathbf {C},\tau )$ the induced action of the group
$(\mathbf {C},\tau )$ the induced action of the group ![]() $s^*\mathbf {G}$ on the group
$s^*\mathbf {G}$ on the group ![]() $s^*\mathbf {H}$ is nilpotent (in particular, the induced filtration on each stalk is finite). A filtration as above will be called a locally finite
$s^*\mathbf {H}$ is nilpotent (in particular, the induced filtration on each stalk is finite). A filtration as above will be called a locally finite ![]() $\mathbf {G}$-central series for the action of
$\mathbf {G}$-central series for the action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\mathbf {H}$.
$\mathbf {H}$.
One interesting difference between the classical story for nilpotent actions and the sheaf-theoretic situation we consider is that local nilpotence need not imply nilpotence in general, essentially because the nilpotence class of the action can vary with the stalks.
Example 2.1.4 Consider the unramified Grothendieck–Witt sheaf ![]() $\mathbf {GW}$; this is a Zariski sheaf of rings on
$\mathbf {GW}$; this is a Zariski sheaf of rings on ![]() $\mathrm {Sm}_k$ (in fact it is already a Nisnevich sheaf). This sheaf has a natural action by the sheaf
$\mathrm {Sm}_k$ (in fact it is already a Nisnevich sheaf). This sheaf has a natural action by the sheaf ![]() ${{\mathbf {G}}_{m}^{}}$ of units. Since we will only be interested in phenomena at the level of stalks, we mention that separable, finitely generated extensions of the base field
${{\mathbf {G}}_{m}^{}}$ of units. Since we will only be interested in phenomena at the level of stalks, we mention that separable, finitely generated extensions of the base field ![]() $k$ are examples of stalks in the Nisnevich topology on
$k$ are examples of stalks in the Nisnevich topology on ![]() $\mathrm {Sm}_k$.
$\mathrm {Sm}_k$.
Fix a separable, finitely generated extension ![]() $L/k$. We now describe the action of
$L/k$. We now describe the action of ![]() ${{\mathbf {G}}_{m}^{}}$ on
${{\mathbf {G}}_{m}^{}}$ on ![]() $\mathbf {GW}$ at the level of
$\mathbf {GW}$ at the level of ![]() $L$-points. The abelian group of sections
$L$-points. The abelian group of sections ![]() $\mathbf {GW}(L)$ coincides with
$\mathbf {GW}(L)$ coincides with ![]() $GW(L)$, the usual Grothendieck–Witt group of (stable) isomorphism classes of symmetric bilinear forms over
$GW(L)$, the usual Grothendieck–Witt group of (stable) isomorphism classes of symmetric bilinear forms over ![]() $L$. There is an evident morphism
$L$. There is an evident morphism ![]() ${{\mathbf {G}}_{m}^{}}(L) \to \mathbf {GW}(L)$ that sends a unit
${{\mathbf {G}}_{m}^{}}(L) \to \mathbf {GW}(L)$ that sends a unit ![]() $u$ to the (invertible) one-dimensional form
$u$ to the (invertible) one-dimensional form ![]() $\langle u \rangle$. The action of
$\langle u \rangle$. The action of ![]() ${{\mathbf {G}}_{m}^{}}$ is given by tensoring a given form with the one-dimensional form
${{\mathbf {G}}_{m}^{}}$ is given by tensoring a given form with the one-dimensional form ![]() $\langle u \rangle$.
$\langle u \rangle$.
Consider the filtration of ![]() $GW(L)$ by powers of the fundamental ideal
$GW(L)$ by powers of the fundamental ideal ![]() $I^n(L)$. Note that
$I^n(L)$. Note that ![]() $I(L)$ is additively generated by
$I(L)$ is additively generated by ![]() $1$-fold Pfister forms,
$1$-fold Pfister forms,
by appeal to [Reference Elman, Karpenko and MerkurjevEKM08, Corollary 4.9]. Since ![]() $I(L)$ is generated by
$I(L)$ is generated by ![]() $1$-fold Pfister forms, it follows that
$1$-fold Pfister forms, it follows that ![]() $I^n(L)$ is additively generated by (
$I^n(L)$ is additively generated by (![]() $n$-fold) Pfister forms. A straightforward calculation shows that multiplication by
$n$-fold) Pfister forms. A straightforward calculation shows that multiplication by ![]() $\langle u \rangle$ is trivial on the successive subquotients
$\langle u \rangle$ is trivial on the successive subquotients ![]() $I^n(L)/I^{n+1}(L)$ [Reference FaselFas08, Lemma E.1.3]. It follows from these facts that the filtration
$I^n(L)/I^{n+1}(L)$ [Reference FaselFas08, Lemma E.1.3]. It follows from these facts that the filtration ![]() $I^n(L)$ is the
$I^n(L)$ is the ![]() ${{\mathbf {G}}_{m}^{}}(L)$-lower central series for this action (see, for example, [Reference Hilton, Mislin and RoitbergHMR75, § I.4] for the definition of the latter notion).
${{\mathbf {G}}_{m}^{}}(L)$-lower central series for this action (see, for example, [Reference Hilton, Mislin and RoitbergHMR75, § I.4] for the definition of the latter notion).
Assume furthermore that ![]() $k$ is not formally real and that
$k$ is not formally real and that ![]() $k$ has finite étale
$k$ has finite étale ![]() $2$-cohomological dimension. The Arason–Pfister Hauptsatz shows that
$2$-cohomological dimension. The Arason–Pfister Hauptsatz shows that ![]() $I^n(L)$ is then trivial for
$I^n(L)$ is then trivial for ![]() $n$ large enough (depending on the étale
$n$ large enough (depending on the étale ![]() $2$-cohomological dimension of
$2$-cohomological dimension of ![]() $L$; see [Reference Elman, Karpenko and MerkurjevEKM08, Theorem 6.18] and [Reference Asok and FaselAF14b, Proposition 5.1] for details). Thus, as
$L$; see [Reference Elman, Karpenko and MerkurjevEKM08, Theorem 6.18] and [Reference Asok and FaselAF14b, Proposition 5.1] for details). Thus, as ![]() $L$ varies through the generic points of smooth
$L$ varies through the generic points of smooth ![]() $k$-schemes, we see that the length of the
$k$-schemes, we see that the length of the ![]() ${{\mathbf {G}}_{m}^{}}(L)$-lower central series varies. Later, we will see that variants of this example arise naturally in geometry (see Example 3.2.5, Proposition 3.4.10 and Theorem 3.4.12 for further discussion).
${{\mathbf {G}}_{m}^{}}(L)$-lower central series varies. Later, we will see that variants of this example arise naturally in geometry (see Example 3.2.5, Proposition 3.4.10 and Theorem 3.4.12 for further discussion).
Permanence properties for (locally) nilpotent actions
Suppose ![]() $(\mathbf {C},\tau )$ is a site. If
$(\mathbf {C},\tau )$ is a site. If ![]() $\varphi : \mathbf {G}' \to \mathbf {G}$ is a homomorphism of
$\varphi : \mathbf {G}' \to \mathbf {G}$ is a homomorphism of ![]() $\tau$-sheaves of groups, and
$\tau$-sheaves of groups, and ![]() $\mathbf {H}$ is a sheaf of groups with a
$\mathbf {H}$ is a sheaf of groups with a ![]() $\mathbf {G}$-action, then
$\mathbf {G}$-action, then ![]() $\mathbf {H}$ inherits a
$\mathbf {H}$ inherits a ![]() $\mathbf {G}'$-action via precomposition with
$\mathbf {G}'$-action via precomposition with ![]() $\varphi$.
$\varphi$.
Lemma 2.1.5 If ![]() $\varphi : \mathbf {G}' \to \mathbf {G}$ is a homomorphism of sheaves of groups, and if
$\varphi : \mathbf {G}' \to \mathbf {G}$ is a homomorphism of sheaves of groups, and if ![]() $\mathbf {H}$ carries a (locally) nilpotent
$\mathbf {H}$ carries a (locally) nilpotent ![]() $\mathbf {G}$-action, then the
$\mathbf {G}$-action, then the ![]() $\mathbf {G}'$-action induced by
$\mathbf {G}'$-action induced by ![]() $\varphi$ is (locally) nilpotent as well.
$\varphi$ is (locally) nilpotent as well.
Proof. A (finite) ![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$ gives a (finite)
$\mathbf {H}$ gives a (finite) ![]() $\mathbf {G}'$-central series as well by restriction.
$\mathbf {G}'$-central series as well by restriction.
The next result is a sheaf-theoretic analog of [Reference Bousfield and KanBK72, II.4.2].
Lemma 2.1.6 Suppose ![]() $\mathbf {G}$ is a sheaf of groups,
$\mathbf {G}$ is a sheaf of groups, ![]() $\mathbf {H},\mathbf {H}'$ and
$\mathbf {H},\mathbf {H}'$ and ![]() $\mathbf {H}''$ are sheaves of groups equipped with an action of
$\mathbf {H}''$ are sheaves of groups equipped with an action of ![]() $\mathbf {G}$ and we are given a short exact sequence of the form
$\mathbf {G}$ and we are given a short exact sequence of the form
where the homomorphisms in the exact sequence are ![]() $\mathbf {G}$-equivariant. The action of
$\mathbf {G}$-equivariant. The action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\mathbf {H}$ is (locally) nilpotent if and only if the actions of
$\mathbf {H}$ is (locally) nilpotent if and only if the actions of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\mathbf {H}'$ and
$\mathbf {H}'$ and ![]() $\mathbf {H}''$ are so.
$\mathbf {H}''$ are so.
Proof. Choose a (locally finite) ![]() $\mathbf {G}$-central series
$\mathbf {G}$-central series ![]() $\{\mathbf {H}_i\}$ for
$\{\mathbf {H}_i\}$ for ![]() $\mathbf {H}$. The restriction
$\mathbf {H}$. The restriction ![]() $\mathbf {H}_i \cap \mathbf {H}'$ yields a (locally finite)
$\mathbf {H}_i \cap \mathbf {H}'$ yields a (locally finite) ![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}'$. Likewise, the quotient sheaves
$\mathbf {H}'$. Likewise, the quotient sheaves ![]() $\mathbf {H}_i/(\mathbf {H}' \cap \mathbf {H}_i)$ yield a (locally finite)
$\mathbf {H}_i/(\mathbf {H}' \cap \mathbf {H}_i)$ yield a (locally finite) ![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}''$.
$\mathbf {H}''$.
Conversely, take a (locally finite) ![]() $\mathbf {G}$-central series
$\mathbf {G}$-central series ![]() $\{\mathbf {H}''_i\}$ for
$\{\mathbf {H}''_i\}$ for ![]() $\mathbf {H}''$. The fiber product sheaves
$\mathbf {H}''$. The fiber product sheaves ![]() $\mathbf {H}_i := \mathbf {H} \times _{\mathbf {H}''} \mathbf {H}''_i$ exist for all i and are automatically
$\mathbf {H}_i := \mathbf {H} \times _{\mathbf {H}''} \mathbf {H}''_i$ exist for all i and are automatically ![]() $\mathbf {G}$-stable as all the morphisms defining the fiber product are
$\mathbf {G}$-stable as all the morphisms defining the fiber product are ![]() $\mathbf {G}$-equivariant. Moreover, all of these sheaves contain
$\mathbf {G}$-equivariant. Moreover, all of these sheaves contain ![]() $\mathbf {H}'$ by construction. If we take a (locally finite)
$\mathbf {H}'$ by construction. If we take a (locally finite) ![]() $\mathbf {G}$-central series of
$\mathbf {G}$-central series of ![]() $\mathbf {H}'$, say
$\mathbf {H}'$, say ![]() $\{\mathbf {H}'_j\}$, then we may build a (locally finite)
$\{\mathbf {H}'_j\}$, then we may build a (locally finite) ![]() $\mathbf {G}$-central series of
$\mathbf {G}$-central series of ![]() $\mathbf {H}$ by reindexing.
$\mathbf {H}$ by reindexing.
2.2 Nilpotence in local homotopy theory
The main goal of this section is to study nilpotent spaces in the local homotopy theory of simplicial presheaves. We begin by reviewing some terminology from local homotopy theory following [Reference JardineJar15]. We then define a notion of nilpotent morphism of simplicial presheaves using the definitions of § 2.1. We then deduce analogs of a number of ‘permanence’ properties for nilpotent morphisms of spaces that will be useful later.
Review of local homotopy theory
Suppose ![]() $\mathbf {C}$ is a small category and write
$\mathbf {C}$ is a small category and write ![]() $\mathrm {sPre}(\mathbf {C})$ for the category of simplicial presheaves on
$\mathrm {sPre}(\mathbf {C})$ for the category of simplicial presheaves on ![]() $\mathbf {C}$. We view
$\mathbf {C}$. We view ![]() $\mathrm {sPre}({\mathbf {C}})$ as a model category with the injective model structure: the weak equivalences are objectwise weak equivalences, the cofibrations are the monomorphisms, and the fibrations are determined by the right lifting property. We write
$\mathrm {sPre}({\mathbf {C}})$ as a model category with the injective model structure: the weak equivalences are objectwise weak equivalences, the cofibrations are the monomorphisms, and the fibrations are determined by the right lifting property. We write ![]() $\operatorname {Map}(\mathscr {F},\mathscr {G})$ for the derived mapping space between two objects of
$\operatorname {Map}(\mathscr {F},\mathscr {G})$ for the derived mapping space between two objects of ![]() $\mathrm {sPre}(\mathbf {C})$.
$\mathrm {sPre}(\mathbf {C})$.
The model category ![]() $\mathrm {sPre}(\mathbf {C})$ is known to be simplicial, proper and combinatorial [Reference LurieLur09, Proposition A.2.8.2], and we may appeal to the machinery of Bousfield localization (see [Reference HirschhornHir03] for a detailed treatment of localization). Recall that if
$\mathrm {sPre}(\mathbf {C})$ is known to be simplicial, proper and combinatorial [Reference LurieLur09, Proposition A.2.8.2], and we may appeal to the machinery of Bousfield localization (see [Reference HirschhornHir03] for a detailed treatment of localization). Recall that if ![]() $S$ is a set of morphisms in
$S$ is a set of morphisms in ![]() $\mathrm {sPre}(\mathbf {C})$, then a simplicial presheaf
$\mathrm {sPre}(\mathbf {C})$, then a simplicial presheaf ![]() $\mathscr {F}$ is
$\mathscr {F}$ is ![]() $S$-local if, for every
$S$-local if, for every ![]() $f: \mathscr {G} \to \mathscr {H}$ in
$f: \mathscr {G} \to \mathscr {H}$ in ![]() $S$, the induced map
$S$, the induced map ![]() $f^*: \operatorname {Map}(\mathscr {H},\mathscr {F}) \to \operatorname {Map}(\mathscr {G},\mathscr {F})$ is a weak equivalence. A morphism
$f^*: \operatorname {Map}(\mathscr {H},\mathscr {F}) \to \operatorname {Map}(\mathscr {G},\mathscr {F})$ is a weak equivalence. A morphism ![]() $f: \mathscr {G} \to \mathscr {H}$ is an
$f: \mathscr {G} \to \mathscr {H}$ is an ![]() $S$-local equivalence if, for every
$S$-local equivalence if, for every ![]() $S$-local
$S$-local ![]() $\mathscr {F}$, the map
$\mathscr {F}$, the map ![]() $f^*$ is a weak equivalence.
$f^*$ is a weak equivalence.
The ![]() $S$-local equivalences are the weak equivalences for a new model structure
$S$-local equivalences are the weak equivalences for a new model structure ![]() $\mathrm {sPre}(\mathbf {C})[S^{-1}]$ called the
$\mathrm {sPre}(\mathbf {C})[S^{-1}]$ called the ![]() $S$-local model structure: the cofibrations in
$S$-local model structure: the cofibrations in ![]() $\mathrm {sPre}(\mathbf {C})[S^{-1}]$ are still monomorphisms, and the fibrant objects are the fibrant objects in
$\mathrm {sPre}(\mathbf {C})[S^{-1}]$ are still monomorphisms, and the fibrant objects are the fibrant objects in ![]() $\mathrm {sPre}(\mathbf {C})$ that are
$\mathrm {sPre}(\mathbf {C})$ that are ![]() $S$-local. This new model structure is again left proper, simplicial and combinatorial [Reference LurieLur09, Proposition A.3.7.3]. The identity functors form a Quillen adjunction
$S$-local. This new model structure is again left proper, simplicial and combinatorial [Reference LurieLur09, Proposition A.3.7.3]. The identity functors form a Quillen adjunction
and the associated Quillen derived functor ![]() $\mathrm {Ho}(\mathrm {sPre}(\mathbf {C})[S^{-1}]) \to \mathrm {Ho}(\mathrm {sPre}(\mathbf {C}))$ is fully faithful with essential image the subcategory of
$\mathrm {Ho}(\mathrm {sPre}(\mathbf {C})[S^{-1}]) \to \mathrm {Ho}(\mathrm {sPre}(\mathbf {C}))$ is fully faithful with essential image the subcategory of ![]() $S$-local objects.
$S$-local objects.
If ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site, then one introduces the notion of
$(\mathbf {C},\tau )$ is a small Grothendieck site, then one introduces the notion of ![]() $\tau$-local weak equivalence [Reference JardineJar15, p. 64]. The Bousfield localization of
$\tau$-local weak equivalence [Reference JardineJar15, p. 64]. The Bousfield localization of ![]() $\mathrm {sPre}(\mathbf {C})$ with respect to the class of
$\mathrm {sPre}(\mathbf {C})$ with respect to the class of ![]() $\tau$-local weak equivalences yields the (injective)
$\tau$-local weak equivalences yields the (injective) ![]() $\tau$-local model structure on
$\tau$-local model structure on ![]() $\mathrm {sPre}(\mathbf {C})$, which is again a combinatorial, proper, simplicial model category. We will write
$\mathrm {sPre}(\mathbf {C})$, which is again a combinatorial, proper, simplicial model category. We will write ![]() $\mathrm {R}_{\tau }$ for a fibrant replacement functor in this category. If
$\mathrm {R}_{\tau }$ for a fibrant replacement functor in this category. If ![]() $(\mathbf {C},\tau )$ has enough points, then the functor
$(\mathbf {C},\tau )$ has enough points, then the functor ![]() $\mathrm {R}_{\tau }$ may be assumed to commute with formation of finite products. Indeed, this follows from [Reference Morel and VoevodskyMV99, § 2 Theorem 1.66], which shows that one may use a ‘Godement resolution’ functor for
$\mathrm {R}_{\tau }$ may be assumed to commute with formation of finite products. Indeed, this follows from [Reference Morel and VoevodskyMV99, § 2 Theorem 1.66], which shows that one may use a ‘Godement resolution’ functor for ![]() $R_{\tau }$. Note that Morel and Voevodsky state this assertion under an auxiliary ‘finite type’ hypothesis [Reference Morel and VoevodskyMV99, § 2 Definition 1.31], which ensures that Postnikov towers converge. However, in modern terminology this hypothesis is equivalent to a hypercompleteness hypothesis on the
$R_{\tau }$. Note that Morel and Voevodsky state this assertion under an auxiliary ‘finite type’ hypothesis [Reference Morel and VoevodskyMV99, § 2 Definition 1.31], which ensures that Postnikov towers converge. However, in modern terminology this hypothesis is equivalent to a hypercompleteness hypothesis on the ![]() $\infty$-category attached to the injective model structure on
$\infty$-category attached to the injective model structure on ![]() $\mathrm {sPre}(\mathbf {C})$ [Reference LurieLur09, pp. 666–669]. With that in mind, the hypothesis that
$\mathrm {sPre}(\mathbf {C})$ [Reference LurieLur09, pp. 666–669]. With that in mind, the hypothesis that ![]() $(\mathbf {C},\tau )$ has enough points is sufficient to guarantee hypercompleteness [Reference LurieLur09, Remark 6.5.4.7]. In any case, we write
$(\mathbf {C},\tau )$ has enough points is sufficient to guarantee hypercompleteness [Reference LurieLur09, Remark 6.5.4.7]. In any case, we write ![]() $\operatorname {Ho}_{\tau }(\mathbf {C})$ for the associated homotopy category.
$\operatorname {Ho}_{\tau }(\mathbf {C})$ for the associated homotopy category.
If ![]() $\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$ is a simplicial presheaf, then a base point for
$\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$ is a simplicial presheaf, then a base point for ![]() $\mathscr {X}$ is a morphism
$\mathscr {X}$ is a morphism ![]() $x$ from the final object
$x$ from the final object ![]() $\ast$ to
$\ast$ to ![]() $\mathscr {X}$. The category of pointed simplicial presheaves
$\mathscr {X}$. The category of pointed simplicial presheaves ![]() $\mathrm {sPre}(\mathbf {C})_{\ast }$ can be equipped with a
$\mathrm {sPre}(\mathbf {C})_{\ast }$ can be equipped with a ![]() $\tau$-local model structure as well: a map of pointed simplicial presheaves is a cofibration, weak equivalence or fibration in the
$\tau$-local model structure as well: a map of pointed simplicial presheaves is a cofibration, weak equivalence or fibration in the ![]() $\tau$-local model structure if it is so after forgetting the base point. We use the same notation as above for the fibrant replacement functor in this context. We write
$\tau$-local model structure if it is so after forgetting the base point. We use the same notation as above for the fibrant replacement functor in this context. We write ![]() $\operatorname {Ho}_{\tau,\ast }(\mathbf {C})$ for the associated homotopy category.
$\operatorname {Ho}_{\tau,\ast }(\mathbf {C})$ for the associated homotopy category.
Nilpotent simplicial presheaves
Suppose ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site (which we will assume has enough points when we speak of ‘local’ notions below). Given an object
$(\mathbf {C},\tau )$ is a small Grothendieck site (which we will assume has enough points when we speak of ‘local’ notions below). Given an object ![]() $\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$, we write
$\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$, we write ![]() $\boldsymbol {\pi }_0(\mathscr {X})$ for the
$\boldsymbol {\pi }_0(\mathscr {X})$ for the ![]() $\tau$-sheaf associated with the presheaf
$\tau$-sheaf associated with the presheaf ![]() $U \mapsto \pi _0(\mathscr {X}(U))$. We will say that
$U \mapsto \pi _0(\mathscr {X}(U))$. We will say that ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() $\tau$-connected (or just simplicially connected if
$\tau$-connected (or just simplicially connected if ![]() $\tau$ is clear from context) if the structure map
$\tau$ is clear from context) if the structure map ![]() $\mathscr {X} \to \ast$ induces an isomorphism on
$\mathscr {X} \to \ast$ induces an isomorphism on ![]() $\boldsymbol {\pi }_0$.
$\boldsymbol {\pi }_0$.
If ![]() $(\mathscr {X},x)$ is a pointed simplicial presheaf, we define
$(\mathscr {X},x)$ is a pointed simplicial presheaf, we define ![]() $\tau$-homotopy sheaves
$\tau$-homotopy sheaves ![]() $\boldsymbol {\pi }_i(\mathscr {X},x)$ as the
$\boldsymbol {\pi }_i(\mathscr {X},x)$ as the ![]() $\tau$-sheaves associated with the presheaves
$\tau$-sheaves associated with the presheaves
As usual, these are sheaves of groups for ![]() $i = 1$ and sheaves of abelian groups for
$i = 1$ and sheaves of abelian groups for ![]() $i \geq 2$. For any integer
$i \geq 2$. For any integer ![]() $n > 0$, say that a pointed space
$n > 0$, say that a pointed space ![]() $(\mathscr {X},x)$ is simplicially
$(\mathscr {X},x)$ is simplicially ![]() $n$-connected if
$n$-connected if ![]() $\mathscr {X}$ is simplicially connected, and
$\mathscr {X}$ is simplicially connected, and ![]() $\boldsymbol {\pi }_i(\mathscr {X},x) = 0$ for
$\boldsymbol {\pi }_i(\mathscr {X},x) = 0$ for ![]() $1 \leq i \leq n$.
$1 \leq i \leq n$.
The standard action of the group ![]() $\pi _1(\mathscr {X}(U),x)$ on
$\pi _1(\mathscr {X}(U),x)$ on ![]() $\pi _i(\mathscr {X}(U),x)$ is functorial in
$\pi _i(\mathscr {X}(U),x)$ is functorial in ![]() $U$ and sheafification yields an action of the sheaf
$U$ and sheafification yields an action of the sheaf ![]() $\boldsymbol {\pi }_1(\mathscr {X},x)$ on
$\boldsymbol {\pi }_1(\mathscr {X},x)$ on ![]() $\boldsymbol {\pi }_i(\mathscr {X},x)$. (Frequently, to unburden the notation, we will suppress base points in homotopy sheaves of pointed spaces.)
$\boldsymbol {\pi }_i(\mathscr {X},x)$. (Frequently, to unburden the notation, we will suppress base points in homotopy sheaves of pointed spaces.)
If ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a fiber sequence of pointed simplicial presheaves (henceforth we will refer to such sequences as simplicial fiber sequences), then, for any object
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a fiber sequence of pointed simplicial presheaves (henceforth we will refer to such sequences as simplicial fiber sequences), then, for any object ![]() $U \in \mathrm {sPre}(\mathbf {C})_{\ast }$, applying
$U \in \mathrm {sPre}(\mathbf {C})_{\ast }$, applying ![]() $\operatorname {Hom}_{\operatorname {Ho}_{\tau,\ast }(\mathbf {C})}(U,-)$ to the above fiber sequence yields a long exact sequence [Reference HoveyHov99, Proposition 6.5.3]. Sheafifying this exact sequence then gives a long exact sequence in homotopy sheaves associated with any simplicial fiber sequence.
$\operatorname {Hom}_{\operatorname {Ho}_{\tau,\ast }(\mathbf {C})}(U,-)$ to the above fiber sequence yields a long exact sequence [Reference HoveyHov99, Proposition 6.5.3]. Sheafifying this exact sequence then gives a long exact sequence in homotopy sheaves associated with any simplicial fiber sequence.
If ![]() $f: \mathscr {E} \to \mathscr {B}$ is any morphism of pointed connected spaces, then we may build the simplicial homotopy fiber of
$f: \mathscr {E} \to \mathscr {B}$ is any morphism of pointed connected spaces, then we may build the simplicial homotopy fiber of ![]() $f$ exactly as one does classically. In more detail, consider the map
$f$ exactly as one does classically. In more detail, consider the map ![]() $\mathscr {B} \to \mathrm {R}_{\tau }\mathscr {B}$ and functorially factor the composite
$\mathscr {B} \to \mathrm {R}_{\tau }\mathscr {B}$ and functorially factor the composite ![]() $\mathscr {E} \to \mathrm {R}_{\tau }\mathscr {B}$ as an acyclic cofibration
$\mathscr {E} \to \mathrm {R}_{\tau }\mathscr {B}$ as an acyclic cofibration ![]() $\mathscr {E} \to \mathscr {E}'$ followed by a fibration
$\mathscr {E} \to \mathscr {E}'$ followed by a fibration ![]() $\mathscr {E}' \to \mathrm {R}_{\tau }\mathscr {B}$. If
$\mathscr {E}' \to \mathrm {R}_{\tau }\mathscr {B}$. If ![]() $\mathscr {\ast }$ is the base point of
$\mathscr {\ast }$ is the base point of ![]() $\mathrm {R}_{\tau }\mathscr {B}$, then we define
$\mathrm {R}_{\tau }\mathscr {B}$, then we define ![]() $\operatorname {hofib}(f)$ to be the ordinary fiber of
$\operatorname {hofib}(f)$ to be the ordinary fiber of ![]() $\mathscr {E}' \to \mathrm {R}_{\tau }\mathscr {B}$ over
$\mathscr {E}' \to \mathrm {R}_{\tau }\mathscr {B}$ over ![]() $\ast$. There is a simplicial fiber sequence of the form
$\ast$. There is a simplicial fiber sequence of the form
by construction. If ![]() $U \in \mathbf {C}$, then sheafifying the objectwise action of
$U \in \mathbf {C}$, then sheafifying the objectwise action of ![]() $\pi _1(\mathscr {E}(U))$ on
$\pi _1(\mathscr {E}(U))$ on ![]() $\pi _1(\operatorname {hofib}(f)(U))$ induces an action of the sheaf of groups
$\pi _1(\operatorname {hofib}(f)(U))$ induces an action of the sheaf of groups ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ on the sheaf
$\boldsymbol {\pi }_1(\mathscr {E})$ on the sheaf ![]() $\boldsymbol {\pi }_i(\operatorname {hofib}(f))$. Granted these facts, one makes the following definition.
$\boldsymbol {\pi }_i(\operatorname {hofib}(f))$. Granted these facts, one makes the following definition.
Definition 2.2.1 Suppose ![]() $f: \mathscr {E} \to \mathscr {B}$ is a morphism in
$f: \mathscr {E} \to \mathscr {B}$ is a morphism in ![]() $\mathrm {sPre}(\mathbf {C})_{\ast }$, and write
$\mathrm {sPre}(\mathbf {C})_{\ast }$, and write ![]() $\mathscr {F}$ for the homotopy fiber of
$\mathscr {F}$ for the homotopy fiber of ![]() $f$.
$f$.
1. The morphism
 $f$ is (locally) nilpotent if
$f$ is (locally) nilpotent if  $\mathscr {F}$ is simplicially connected and the action of
$\mathscr {F}$ is simplicially connected and the action of  $\boldsymbol {\pi }_1(\mathscr {E})$ on
$\boldsymbol {\pi }_1(\mathscr {E})$ on  $\boldsymbol {\pi }_i(\mathscr {F})$ is (locally) nilpotent for every
$\boldsymbol {\pi }_i(\mathscr {F})$ is (locally) nilpotent for every  $i \geq 0$ (in the sense of Definition 2.1.1 or Definition 2.1.3).
$i \geq 0$ (in the sense of Definition 2.1.1 or Definition 2.1.3).2. A pointed space
 $(\mathscr {X},x)$ is (locally) nilpotent if the structure morphism is (locally) nilpotent.
$(\mathscr {X},x)$ is (locally) nilpotent if the structure morphism is (locally) nilpotent.
Permanence properties of nilpotence
Proposition 2.2.2 Suppose
is a composable pair of morphisms in ![]() $\mathrm {sPre}(\mathbf {C})_{\ast }$. Assume that the simplicial homotopy fibers of
$\mathrm {sPre}(\mathbf {C})_{\ast }$. Assume that the simplicial homotopy fibers of ![]() $p$,
$p$, ![]() $q$ and
$q$ and ![]() $pq$ are all simplicially connected. If any two elements of
$pq$ are all simplicially connected. If any two elements of ![]() $\{p,q,pq\}$ are nilpotent morphisms, then so is the third.
$\{p,q,pq\}$ are nilpotent morphisms, then so is the third.
Proof. Write ![]() $\mathscr {F}_p$ for the simplicial homotopy fiber of
$\mathscr {F}_p$ for the simplicial homotopy fiber of ![]() $p$,
$p$, ![]() $\mathscr {F}_q$ for the simplicial homotopy fiber of
$\mathscr {F}_q$ for the simplicial homotopy fiber of ![]() $q$ and
$q$ and ![]() $\mathscr {F}_{pq}$ for the simplicial homotopy fiber of the composite. In that case, by the ‘octahedral axiom’ in the pointed homotopy category (e.g. [Reference HoveyHov99, Proposition 6.3.6]) there is an associated simplicial fiber sequence of the form
$\mathscr {F}_{pq}$ for the simplicial homotopy fiber of the composite. In that case, by the ‘octahedral axiom’ in the pointed homotopy category (e.g. [Reference HoveyHov99, Proposition 6.3.6]) there is an associated simplicial fiber sequence of the form
and we may consider the associated long exact sequence of homotopy sheaves, which takes the form
By assumption, ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2)$ acts on the homotopy sheaves of
$\boldsymbol {\pi }_1(\mathscr {E}_2)$ acts on the homotopy sheaves of ![]() $\mathscr {F}_q$ and
$\mathscr {F}_q$ and ![]() $\mathscr {F}_{pq}$ while
$\mathscr {F}_{pq}$ while ![]() $\boldsymbol {\pi }_1(\mathscr {E}_1)$ acts on the homotopy sheaves of
$\boldsymbol {\pi }_1(\mathscr {E}_1)$ acts on the homotopy sheaves of ![]() $\mathscr {F}_p$. Composing with the homomorphism
$\mathscr {F}_p$. Composing with the homomorphism ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2) \to \boldsymbol {\pi }_1(\mathscr {E}_1)$ defines an action of
$\boldsymbol {\pi }_1(\mathscr {E}_2) \to \boldsymbol {\pi }_1(\mathscr {E}_1)$ defines an action of ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2)$ on the higher homotopy sheaves of
$\boldsymbol {\pi }_1(\mathscr {E}_2)$ on the higher homotopy sheaves of ![]() $\mathscr {F}_p$ as well. The long exact sequence of homotopy sheaves is then
$\mathscr {F}_p$ as well. The long exact sequence of homotopy sheaves is then ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariant with respect to these actions.
$\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariant with respect to these actions.
We may break the long exact sequence in homotopy sheaves above ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariantly into short exact sequences. The result then follows from repeated application of Lemma 2.1.6.
$\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariantly into short exact sequences. The result then follows from repeated application of Lemma 2.1.6.
Next, we observe that, under suitable hypotheses, (locally) nilpotent morphisms are stable under homotopy base change.
Proposition 2.2.3 Consider a homotopy Cartesian diagram

in ![]() $\mathrm {sPre}(\mathbf {C})_{\ast }$. If all spaces in the diagram are simplicially connected, and
$\mathrm {sPre}(\mathbf {C})_{\ast }$. If all spaces in the diagram are simplicially connected, and ![]() $f$ is (locally) nilpotent, then so is
$f$ is (locally) nilpotent, then so is ![]() $f'$.
$f'$.
Proof. This follows immediately from Lemma 2.1.5: the action of ![]() $\boldsymbol {\pi }_1(\mathscr {E}')$ on the homotopy fiber of
$\boldsymbol {\pi }_1(\mathscr {E}')$ on the homotopy fiber of ![]() $f'$, which coincides with the homotopy fiber of
$f'$, which coincides with the homotopy fiber of ![]() $f$ by assumption, is induced by the homomorphism
$f$ by assumption, is induced by the homomorphism ![]() $\boldsymbol {\pi }_1(\mathscr {E}') \to \boldsymbol {\pi }_1(\mathscr {E})$.
$\boldsymbol {\pi }_1(\mathscr {E}') \to \boldsymbol {\pi }_1(\mathscr {E})$.
Proposition 2.2.4 Suppose ![]() $g: \mathscr {E} \to \mathscr {B}$ is a morphism in
$g: \mathscr {E} \to \mathscr {B}$ is a morphism in ![]() $\mathrm {sPre}(\mathbf {C})_{\ast }$ with homotopy fiber
$\mathrm {sPre}(\mathbf {C})_{\ast }$ with homotopy fiber ![]() $\mathscr {F}$, and assume
$\mathscr {F}$, and assume ![]() $\mathscr {F},\mathscr {E}$ and
$\mathscr {F},\mathscr {E}$ and ![]() $\mathscr {B}$ are all simplicially connected. If
$\mathscr {B}$ are all simplicially connected. If ![]() $\mathscr {E}$ is (locally) nilpotent, then
$\mathscr {E}$ is (locally) nilpotent, then ![]() $\mathscr {F}$ is (locally) nilpotent.
$\mathscr {F}$ is (locally) nilpotent.
Proof. Consider the following homotopy commutative diagram.

By appeal to Proposition 2.2.3 to check ![]() $\mathscr {F} \to \ast$ is nilpotent, it suffices to show that
$\mathscr {F} \to \ast$ is nilpotent, it suffices to show that ![]() $g$ is (locally) nilpotent, that is, that the
$g$ is (locally) nilpotent, that is, that the ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-action on
$\boldsymbol {\pi }_1(\mathscr {E})$-action on ![]() $\boldsymbol {\pi }_i(\mathscr {F})$ is (locally) nilpotent.
$\boldsymbol {\pi }_i(\mathscr {F})$ is (locally) nilpotent.
To this end, observe that there is a ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-equivariant long exact sequence of the form
$\boldsymbol {\pi }_1(\mathscr {E})$-equivariant long exact sequence of the form
While we do not know that the action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ on
$\boldsymbol {\pi }_1(\mathscr {E})$ on ![]() $\boldsymbol {\pi }_{i+1}(\mathscr {B})$ is (locally) nilpotent, we do know that
$\boldsymbol {\pi }_{i+1}(\mathscr {B})$ is (locally) nilpotent, we do know that ![]() $\operatorname {im} \pi _{i+1}(\mathscr {B})$ in
$\operatorname {im} \pi _{i+1}(\mathscr {B})$ in ![]() $\boldsymbol {\pi }_i(\mathscr {F})$ is central for
$\boldsymbol {\pi }_i(\mathscr {F})$ is central for ![]() $i \geq 1$ and carries a trivial action of
$i \geq 1$ and carries a trivial action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$. In other words, there are
$\boldsymbol {\pi }_1(\mathscr {E})$. In other words, there are ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-equivariant short exact sequences of the form
$\boldsymbol {\pi }_1(\mathscr {E})$-equivariant short exact sequences of the form
where ![]() $\mathbf {M}_{i+1}$ is the image of
$\mathbf {M}_{i+1}$ is the image of ![]() $\boldsymbol {\pi }_{i+1}(\mathscr {B})$ in
$\boldsymbol {\pi }_{i+1}(\mathscr {B})$ in ![]() $\boldsymbol {\pi }_i(\mathscr {F})$. In fact, the action of
$\boldsymbol {\pi }_i(\mathscr {F})$. In fact, the action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ on
$\boldsymbol {\pi }_1(\mathscr {E})$ on ![]() $\mathbf {M}_{i+1}$ is trivial (the classical proof of this result, for example, [Reference Hilton, Mislin and RoitbergHMR75, Proof of Theorem 2.2], discusses this further). As a
$\mathbf {M}_{i+1}$ is trivial (the classical proof of this result, for example, [Reference Hilton, Mislin and RoitbergHMR75, Proof of Theorem 2.2], discusses this further). As a ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-stable subsheaf of
$\boldsymbol {\pi }_1(\mathscr {E})$-stable subsheaf of ![]() $\boldsymbol {\pi }_i(\mathscr {E})$, the kernel in the above statement carries a (locally) nilpotent
$\boldsymbol {\pi }_i(\mathscr {E})$, the kernel in the above statement carries a (locally) nilpotent ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-action. The nilpotence of the
$\boldsymbol {\pi }_1(\mathscr {E})$-action. The nilpotence of the ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-action on
$\boldsymbol {\pi }_1(\mathscr {E})$-action on ![]() $\boldsymbol {\pi }_i(\mathscr {F})$ then follows by appeal to Lemma 2.1.6.
$\boldsymbol {\pi }_i(\mathscr {F})$ then follows by appeal to Lemma 2.1.6.
2.3  $R$-localization of simplicial presheaves
$R$-localization of simplicial presheaves
We now discuss ![]() $R$-localization of simplicial presheaves. Suppose
$R$-localization of simplicial presheaves. Suppose ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site and consider
$(\mathbf {C},\tau )$ is a small Grothendieck site and consider ![]() $\mathrm {sPre}(\mathbf {C})$ with the
$\mathrm {sPre}(\mathbf {C})$ with the ![]() $\tau$-local model structure described above. We use the following notation.
$\tau$-local model structure described above. We use the following notation.
Notation 2.3.1 Suppose ![]() $R$ is a subring of
$R$ is a subring of ![]() ${\mathbb {Q}}$. The elements of
${\mathbb {Q}}$. The elements of ![]() $R$ are fractions with denominator divisible by elements of some (possibly empty) set
$R$ are fractions with denominator divisible by elements of some (possibly empty) set ![]() $P$ of prime numbers:
$P$ of prime numbers: ![]() $R = {\mathbb {Z}}[P^{-1}]$. Henceforth, given
$R = {\mathbb {Z}}[P^{-1}]$. Henceforth, given ![]() $R \subset {\mathbb {Q}}$, we will always write
$R \subset {\mathbb {Q}}$, we will always write ![]() $P$ for this associated set of primes.
$P$ for this associated set of primes.
After reviewing some aspects of ![]() $R$-locality for sheaves of groups, we then introduce a notion of
$R$-locality for sheaves of groups, we then introduce a notion of ![]() $R$-local weak equivalence. We choose definitions that are well adapted to stalkwise analysis, following [Reference Wickelgren and WilliamsWW19]. We then analyze the interaction between nilpotence properties and
$R$-local weak equivalence. We choose definitions that are well adapted to stalkwise analysis, following [Reference Wickelgren and WilliamsWW19]. We then analyze the interaction between nilpotence properties and ![]() $R$-localization for simplicial presheaves
$R$-localization for simplicial presheaves
 $R$-localization for sheaves of groups
$R$-localization for sheaves of groups
If ![]() $\mathbf {G}$ is any presheaf of groups on
$\mathbf {G}$ is any presheaf of groups on ![]() $\mathbf {C}$, and
$\mathbf {C}$, and ![]() $n$ is an integer, then we define the
$n$ is an integer, then we define the ![]() $n$th power map
$n$th power map ![]() $\mathbf {G} \to \mathbf {G}$ to be the sectionwise
$\mathbf {G} \to \mathbf {G}$ to be the sectionwise ![]() $n$th power map of groups. Of course, if
$n$th power map of groups. Of course, if ![]() $\mathbf {G}$ is not a presheaf of abelian groups, this need not be a group homomorphism.
$\mathbf {G}$ is not a presheaf of abelian groups, this need not be a group homomorphism.
Assume ![]() $R \subset {\mathbb {Q}}$ is a subring, and recall Notation 2.3.1. If
$R \subset {\mathbb {Q}}$ is a subring, and recall Notation 2.3.1. If ![]() $\mathbf {G} \in \mathrm {Grp}(\mathbf {C})$, we will say that
$\mathbf {G} \in \mathrm {Grp}(\mathbf {C})$, we will say that ![]() $\mathbf {G}$ is
$\mathbf {G}$ is ![]() $R$-local (or
$R$-local (or ![]() $P$-local) if the
$P$-local) if the ![]() $p$th power map is an isomorphism of presheaves for every
$p$th power map is an isomorphism of presheaves for every ![]() $p \in P$. Similarly, we will say that a sheaf of groups
$p \in P$. Similarly, we will say that a sheaf of groups ![]() $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ is
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ is ![]() $R$-local if the
$R$-local if the ![]() $p$th power map is an isomorphism of sheaves for every
$p$th power map is an isomorphism of sheaves for every ![]() $p \in P$. The following result is immediate from the definitions.
$p \in P$. The following result is immediate from the definitions.
Lemma 2.3.2 Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. A sheaf of groups
$(\mathbf {C},\tau )$ is a site with enough points. A sheaf of groups ![]() $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ is
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ is ![]() $R$-local if and only if, for every point
$R$-local if and only if, for every point ![]() $s$ of
$s$ of ![]() $(\mathbf {C},\tau )$, the group
$(\mathbf {C},\tau )$, the group ![]() $s^*\mathbf {G}$ is
$s^*\mathbf {G}$ is ![]() $R$-local.
$R$-local.
One knows that an abelian group is ![]() $R$-local if and only if it is an
$R$-local if and only if it is an ![]() $R$-module. It follows immediately from the definitions that a (pre)sheaf of abelian groups is
$R$-module. It follows immediately from the definitions that a (pre)sheaf of abelian groups is ![]() $R$-local if and only if it is a (pre)sheaf of
$R$-local if and only if it is a (pre)sheaf of ![]() $R$-modules. More generally, a nilpotent group is
$R$-modules. More generally, a nilpotent group is ![]() $R$-local if and only if it has a finite central series
$R$-local if and only if it has a finite central series ![]() $G = G_0 \supset \cdots \supset G_n = e$ such that each subquotient
$G = G_0 \supset \cdots \supset G_n = e$ such that each subquotient ![]() $G_j/G_{j+1}$ admits a (necessarily unique)
$G_j/G_{j+1}$ admits a (necessarily unique) ![]() $R$-module structure [Reference Bousfield and KanBK72, V.2.7]. The next result follows from this fact by passing to stalks.
$R$-module structure [Reference Bousfield and KanBK72, V.2.7]. The next result follows from this fact by passing to stalks.
Lemma 2.3.3 Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. The following conditions on a (locally) nilpotent sheaf of groups
$(\mathbf {C},\tau )$ is a site with enough points. The following conditions on a (locally) nilpotent sheaf of groups ![]() $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ are equivalent.
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ are equivalent.
1. The sheaf
 $\mathbf {G}$ is
$\mathbf {G}$ is  $R$-local.
$R$-local.2. The sheaf
 $\mathbf {G}$ has a (locally) finite central series with successive subquotients that are sheaves of
$\mathbf {G}$ has a (locally) finite central series with successive subquotients that are sheaves of  $R$-modules.
$R$-modules.
Definition 2.3.4 Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. A sheaf of groups
$(\mathbf {C},\tau )$ is a site with enough points. A sheaf of groups ![]() $\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ will be called (locally)
$\mathbf {G} \in \mathrm {Grp}_{\tau }(\mathbf {C})$ will be called (locally) ![]() $R$-nilpotent if it satisfies either of the equivalent conditions of Lemma 2.3.3.
$R$-nilpotent if it satisfies either of the equivalent conditions of Lemma 2.3.3.
 $R$-local weak equivalences
$R$-local weak equivalences
We continue to follow Notation 2.3.1. Set ![]() $S^1_{\rm rig} := B{\mathbb {Z}}$; this is a Kan complex (in fact a simplicial abelian group) weakly equivalent to
$S^1_{\rm rig} := B{\mathbb {Z}}$; this is a Kan complex (in fact a simplicial abelian group) weakly equivalent to ![]() $\Delta ^1/\partial \Delta ^1$. The multiplication by
$\Delta ^1/\partial \Delta ^1$. The multiplication by ![]() $n$ map induces a self-map
$n$ map induces a self-map ![]() $B{\mathbb {Z}} \to B{\mathbb {Z}}$ that we will call
$B{\mathbb {Z}} \to B{\mathbb {Z}}$ that we will call ![]() $\rho ^1_n$. For
$\rho ^1_n$. For ![]() $r\geq 2$, let
$r\geq 2$, let ![]() $S^{r}_{\rm rig} = S^1_{\rm rig} {\scriptstyle {\wedge }} (\Delta ^{r-1}/\partial \Delta ^{r})_+$. Define
$S^{r}_{\rm rig} = S^1_{\rm rig} {\scriptstyle {\wedge }} (\Delta ^{r-1}/\partial \Delta ^{r})_+$. Define ![]() $\rho ^r_n: S^r_{\rm rig} \to S^r_{\rm rig}$ for
$\rho ^r_n: S^r_{\rm rig} \to S^r_{\rm rig}$ for ![]() $r \geq 2$ by the formula
$r \geq 2$ by the formula ![]() $\rho ^r_n = \rho ^1_n {\scriptstyle {\wedge }} {\rm id}$.
$\rho ^r_n = \rho ^1_n {\scriptstyle {\wedge }} {\rm id}$.
For ![]() $(\mathbf {C},\tau )$ any small Grothendieck site, we set
$(\mathbf {C},\tau )$ any small Grothendieck site, we set
where ![]() $\rho ^n_r$ is now viewed as a morphism of constant simplicial presheaves. The left Bousfield localization of the injective
$\rho ^n_r$ is now viewed as a morphism of constant simplicial presheaves. The left Bousfield localization of the injective ![]() $\tau$-local model structure on
$\tau$-local model structure on ![]() $\mathrm {sPre}(\mathbf {C})$ with respect to the set of morphisms
$\mathrm {sPre}(\mathbf {C})$ with respect to the set of morphisms ![]() $T_R$ will be called the
$T_R$ will be called the ![]() $R$-local model structure on
$R$-local model structure on ![]() $\mathrm {sPre}(\mathbf {C})$; since the site
$\mathrm {sPre}(\mathbf {C})$; since the site ![]() $(\mathbf {C},\tau )$ will be fixed, we hope that suppressing
$(\mathbf {C},\tau )$ will be fixed, we hope that suppressing ![]() $\tau$ from the notation causes no confusion. We write
$\tau$ from the notation causes no confusion. We write ![]() $\operatorname {L}_R$ for the fibrant replacement functor on
$\operatorname {L}_R$ for the fibrant replacement functor on ![]() $\mathrm {sPre}(\mathbf {C})$ for the
$\mathrm {sPre}(\mathbf {C})$ for the ![]() $R$-local model structure so
$R$-local model structure so ![]() $\operatorname {L}_R \mathscr {X}$ is both
$\operatorname {L}_R \mathscr {X}$ is both ![]() $R$-local and
$R$-local and ![]() $\tau$-fibrant.
$\tau$-fibrant.
Remark 2.3.5 In the situation where ![]() $\mathbf {C}$ is the
$\mathbf {C}$ is the ![]() $1$-point site, this definition yields the form of
$1$-point site, this definition yields the form of ![]() $R$-localization on the model category of simplicial sets studied in [Reference Casacuberta and PeschkeCP93]. The a priori strange-looking form of
$R$-localization on the model category of simplicial sets studied in [Reference Casacuberta and PeschkeCP93]. The a priori strange-looking form of ![]() $T_R$ is necessary to ensure that localization is compatible with the action of the fundamental group on higher homotopy groups, already in this classical situation. Various different notions of
$T_R$ is necessary to ensure that localization is compatible with the action of the fundamental group on higher homotopy groups, already in this classical situation. Various different notions of ![]() $R$-localization are compared in [Reference Casacuberta and PeschkeCP93, § 8]: these notions may disagree on non-nilpotent spaces. More generally, suppose
$R$-localization are compared in [Reference Casacuberta and PeschkeCP93, § 8]: these notions may disagree on non-nilpotent spaces. More generally, suppose ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site and
$(\mathbf {C},\tau )$ is a small Grothendieck site and ![]() $s$ is a point of this site. In Proposition 2.3.6(1) below, we investigate the commutation of
$s$ is a point of this site. In Proposition 2.3.6(1) below, we investigate the commutation of ![]() $\operatorname {L}_R$ with
$\operatorname {L}_R$ with ![]() $s^*$; here, we abuse notation and implicitly write
$s^*$; here, we abuse notation and implicitly write ![]() $\operatorname {L}_R$ for localization of both simplicial presheaves and simplicial sets.
$\operatorname {L}_R$ for localization of both simplicial presheaves and simplicial sets.
The next result collects formal properties of ![]() $\operatorname {L}_R$, which will be essential in the sequel; this result restates [Reference Wickelgren and WilliamsWW19, Lemma 3.3 and Propositions 3.4,3.8], but our proof slightly corrects that of [Reference Wickelgren and WilliamsWW19, Lemma 3.3].
$\operatorname {L}_R$, which will be essential in the sequel; this result restates [Reference Wickelgren and WilliamsWW19, Lemma 3.3 and Propositions 3.4,3.8], but our proof slightly corrects that of [Reference Wickelgren and WilliamsWW19, Lemma 3.3].
Proposition 2.3.6 Suppose ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site with enough points, and
$(\mathbf {C},\tau )$ is a small Grothendieck site with enough points, and ![]() $\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$.
$\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$.
1. The
 $R$-localization functor
$R$-localization functor  $\operatorname {L}_R$ commutes with taking stalks, that is, if
$\operatorname {L}_R$ commutes with taking stalks, that is, if  $s$ is a point of
$s$ is a point of  $(\mathbf {C},\tau )$, then
$(\mathbf {C},\tau )$, then  $s^* \operatorname {L}_R \mathscr {X} \cong \operatorname {L}_R s^* \mathscr {X}$.
$s^* \operatorname {L}_R \mathscr {X} \cong \operatorname {L}_R s^* \mathscr {X}$.2. If
 $\mathscr {X}$ is fibrant, then
$\mathscr {X}$ is fibrant, then  $\mathscr {X}$ is
$\mathscr {X}$ is  $R$-local if and only if its stalks are all
$R$-local if and only if its stalks are all  $R$-local for
$R$-local for  $s$ ranging through a conservative family of points for
$s$ ranging through a conservative family of points for  $(\mathbf {C},\tau )$.
$(\mathbf {C},\tau )$.3. The
 $R$-localization functor commutes with formation of finite products.
$R$-localization functor commutes with formation of finite products.
Proof. For (1), we first show that ![]() $s^* \operatorname {L}_R \mathscr {X}$ is
$s^* \operatorname {L}_R \mathscr {X}$ is ![]() $R$-local. Since
$R$-local. Since ![]() $\operatorname {L}_R \mathscr {X}$ is fibrant, so is
$\operatorname {L}_R \mathscr {X}$ is fibrant, so is ![]() $s^* \operatorname {L}_R \mathscr {X}$. Therefore, it suffices to show that if
$s^* \operatorname {L}_R \mathscr {X}$. Therefore, it suffices to show that if ![]() $\rho ^k_n$ is an element of
$\rho ^k_n$ is an element of ![]() $T_R$, then the induced map
$T_R$, then the induced map
is a weak equivalence of simplicial sets. By definition, any point of the site ![]() $(\mathbf {C},\tau )$ may be realized as a filtered colimit over neighborhoods. Explicitly, there is an isomorphism of simplicial sets of the form
$(\mathbf {C},\tau )$ may be realized as a filtered colimit over neighborhoods. Explicitly, there is an isomorphism of simplicial sets of the form
The simplicial set ![]() $S^k_{\tau }$ is not a compact simplicial set (since
$S^k_{\tau }$ is not a compact simplicial set (since ![]() $B{\mathbb {Z}}$ is not finite) so we cannot simply commute the colimit past the mapping space. Instead,
$B{\mathbb {Z}}$ is not finite) so we cannot simply commute the colimit past the mapping space. Instead, ![]() $S^k_{\tau }$ is ‘homotopically small’ in the sense that it is weakly equivalent to a compact object (this notion is related to, but different from, that of [Reference Dwyer and KanDK80, § 2.2]), which allows us to proceed as follows.
$S^k_{\tau }$ is ‘homotopically small’ in the sense that it is weakly equivalent to a compact object (this notion is related to, but different from, that of [Reference Dwyer and KanDK80, § 2.2]), which allows us to proceed as follows.
Set ![]() $S^1 := \Delta ^1/\partial \Delta ^1$ and consider the map
$S^1 := \Delta ^1/\partial \Delta ^1$ and consider the map ![]() $S^1 \to S^1_{\rm rig}$; this map is an acyclic cofibration. There is an induced cofibration
$S^1 \to S^1_{\rm rig}$; this map is an acyclic cofibration. There is an induced cofibration ![]() $S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+) \to S^{k+1}_{\rm rig}$. By the universal property of colimits, this map induces a commutative square of the form
$S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+) \to S^{k+1}_{\rm rig}$. By the universal property of colimits, this map induces a commutative square of the form

Since ![]() $s^*\operatorname {L}_R \mathscr {X}$ and
$s^*\operatorname {L}_R \mathscr {X}$ and ![]() $\operatorname {L}_R \mathscr {X}(U)$ are fibrant simplicial sets, it follows that the maps
$\operatorname {L}_R \mathscr {X}(U)$ are fibrant simplicial sets, it follows that the maps ![]() $\operatorname {Map}(S^k_{\tau },s^*\operatorname {L}_R \mathscr {X}) \to \operatorname {Map}(S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+),s^*\operatorname {L}_R \mathscr {X})$ and
$\operatorname {Map}(S^k_{\tau },s^*\operatorname {L}_R \mathscr {X}) \to \operatorname {Map}(S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+),s^*\operatorname {L}_R \mathscr {X})$ and
are acyclic fibrations. In particular, the bottom horizontal map in the square is a weak equivalence. Since filtered colimits of weak equivalences are again weak equivalences, it follows that the top horizontal map is a weak equivalence as well. Since ![]() $S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+)$ is compact, the right-hand vertical map is an isomorphism of simplicial sets. Altogether, we conclude that the left-hand vertical map is a weak equivalence of simplicial sets.
$S^1 {\scriptstyle {\wedge }} (\Delta ^k/\partial \Delta ^k_+)$ is compact, the right-hand vertical map is an isomorphism of simplicial sets. Altogether, we conclude that the left-hand vertical map is a weak equivalence of simplicial sets.
There is an isomorphism of simplicial sets of the form
As ![]() $\operatorname {L}_R \mathscr {X}$ is
$\operatorname {L}_R \mathscr {X}$ is ![]() $R$-local by assumption,
$R$-local by assumption, ![]() $\rho ^k_n$ induces a weak equivalence on
$\rho ^k_n$ induces a weak equivalence on ![]() $\operatorname {Map}(S^k_{\rm rig} \times U,\operatorname {L}_R \mathscr {X})$.
$\operatorname {Map}(S^k_{\rm rig} \times U,\operatorname {L}_R \mathscr {X})$.
The functor ![]() $s^*$ preserves acyclic cofibrations and therefore the map
$s^*$ preserves acyclic cofibrations and therefore the map ![]() $s^* \mathscr {X} \to s^* \operatorname {L}_R \mathscr {X}$ is an acyclic cofibration with target an object that is fibrant in the
$s^* \mathscr {X} \to s^* \operatorname {L}_R \mathscr {X}$ is an acyclic cofibration with target an object that is fibrant in the ![]() $R$-local model structure on simplicial sets. It follows that
$R$-local model structure on simplicial sets. It follows that ![]() $s^* \operatorname {L}_R \mathscr {X}$ is equivalent in the
$s^* \operatorname {L}_R \mathscr {X}$ is equivalent in the ![]() $R$-local model structure to any other
$R$-local model structure to any other ![]() $R$-local fibrant replacement of
$R$-local fibrant replacement of ![]() $s^* \mathscr {X}$, for example,
$s^* \mathscr {X}$, for example, ![]() $\operatorname {L}_R s^* \mathscr {X}$.
$\operatorname {L}_R s^* \mathscr {X}$.
For (2), observe that the proof of (1) implies that if ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() $R$-local, then so is
$R$-local, then so is ![]() $s^*\mathscr {X}$. Conversely,
$s^*\mathscr {X}$. Conversely, ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() $R$-local if and only if
$R$-local if and only if ![]() $\mathscr {X}$ is fibrant and the map
$\mathscr {X}$ is fibrant and the map ![]() $\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is a simplicial weak equivalence. However, the map
$\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is a simplicial weak equivalence. However, the map ![]() $\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is a simplicial weak equivalence if and only if it is after taking stalks. By the proof of (1), this is the case if and only if
$\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is a simplicial weak equivalence if and only if it is after taking stalks. By the proof of (1), this is the case if and only if ![]() $s^*\mathscr {X} \to \operatorname {L}_R s^* \mathscr {X}$ is a weak equivalence for every point
$s^*\mathscr {X} \to \operatorname {L}_R s^* \mathscr {X}$ is a weak equivalence for every point ![]() $s$. Since
$s$. Since ![]() $s^*\mathscr {X}$ is fibrant, this amounts to the assertion that
$s^*\mathscr {X}$ is fibrant, this amounts to the assertion that ![]() $s^*\mathscr {X}$ is an
$s^*\mathscr {X}$ is an ![]() $R$-local simplicial set.
$R$-local simplicial set.
For (3), it suffices to observe that if ![]() $\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$, then
$\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$, then ![]() $\mathscr {X} \times (-)$ preserves weak equivalences. Indeed, this latter fact follows from Ken Brown's lemma [Reference HoveyHov99, Lemma 1.1.12] because all objects of
$\mathscr {X} \times (-)$ preserves weak equivalences. Indeed, this latter fact follows from Ken Brown's lemma [Reference HoveyHov99, Lemma 1.1.12] because all objects of ![]() $\mathrm {sPre}(\mathbf {C})$ are cofibrant and
$\mathrm {sPre}(\mathbf {C})$ are cofibrant and ![]() $\mathscr {X} \times (-)$ preserves acyclic cofibrations. To conclude, one observes that
$\mathscr {X} \times (-)$ preserves acyclic cofibrations. To conclude, one observes that ![]() $\operatorname {L}_R \mathscr {X} \times \operatorname {L}_R \mathscr {Y}$ is
$\operatorname {L}_R \mathscr {X} \times \operatorname {L}_R \mathscr {Y}$ is ![]() $R$-local and
$R$-local and ![]() $\tau$-fibrant and
$\tau$-fibrant and ![]() $R$-locally weakly equivalent to
$R$-locally weakly equivalent to ![]() $\mathscr {X} \times \mathscr {Y}$ and therefore also to
$\mathscr {X} \times \mathscr {Y}$ and therefore also to ![]() $\operatorname {L}_R (\mathscr {X} \times \mathscr {Y})$.
$\operatorname {L}_R (\mathscr {X} \times \mathscr {Y})$.
Lemma 2.3.7 Suppose ![]() $(\mathbf {C},\tau )$ is a small Grothendieck site with enough points, and
$(\mathbf {C},\tau )$ is a small Grothendieck site with enough points, and ![]() $(\mathscr {X},x) \in \mathrm {sPre}(\mathbf {C})_*$ is a pointed
$(\mathscr {X},x) \in \mathrm {sPre}(\mathbf {C})_*$ is a pointed ![]() $R$-local space. For any integer
$R$-local space. For any integer ![]() $i \geq 0$, the homotopy sheaves
$i \geq 0$, the homotopy sheaves ![]() $\boldsymbol {\pi }_i(\mathscr {X},x)$ are
$\boldsymbol {\pi }_i(\mathscr {X},x)$ are ![]() $R$-local sheaves of groups.
$R$-local sheaves of groups.
Proof. We show that the homotopy presheaves are ![]() $R$-local, and the statement about homotopy sheaves follows by sheafifying. Let
$R$-local, and the statement about homotopy sheaves follows by sheafifying. Let ![]() $U$ be an object of
$U$ be an object of ![]() $\mathbf {C}$. Write
$\mathbf {C}$. Write ![]() $R = {\mathbb {Z}}[P^{-1}]$ for some set of primes
$R = {\mathbb {Z}}[P^{-1}]$ for some set of primes ![]() $P$. We will show that the
$P$. We will show that the ![]() $p$th power map on
$p$th power map on ![]() $\pi _i(\operatorname {L}_R\mathscr {X}(U))$ is a bijection for any
$\pi _i(\operatorname {L}_R\mathscr {X}(U))$ is a bijection for any ![]() $p \in P$. To this end, observe that the
$p \in P$. To this end, observe that the ![]() $p$th power map is the map induced by
$p$th power map is the map induced by ![]() $\rho _p^i \times {\rm id}_{U}$ on
$\rho _p^i \times {\rm id}_{U}$ on ![]() $\pi _0(\operatorname {Map}_{*}(S^i_{\rm rig} \times U,\operatorname {L}_R \mathscr {X}))$. Since
$\pi _0(\operatorname {Map}_{*}(S^i_{\rm rig} \times U,\operatorname {L}_R \mathscr {X}))$. Since ![]() $\operatorname {L}_R\mathscr {X}$ is
$\operatorname {L}_R\mathscr {X}$ is ![]() $R$-local and
$R$-local and ![]() $\rho ^i_p \times {\rm id}_{U}$ lies in
$\rho ^i_p \times {\rm id}_{U}$ lies in ![]() $T_R$, this map is a bijection.
$T_R$, this map is a bijection.
Remark 2.3.8 Lemma 2.3.7 admits a converse in the following sense. If ![]() $(\mathscr {X},x) \in \mathrm {sPre}(\mathbf {C})_*$ is fibrant in the
$(\mathscr {X},x) \in \mathrm {sPre}(\mathbf {C})_*$ is fibrant in the ![]() $\tau$-local model structure and its homotopy sheaves are
$\tau$-local model structure and its homotopy sheaves are ![]() $R$-local, then
$R$-local, then ![]() $(\mathscr {X},x)$ is
$(\mathscr {X},x)$ is ![]() $R$-local as well.
$R$-local as well.
Lemma 2.3.9 Assume ![]() $(\mathbf {C},\tau )$ is a site. If
$(\mathbf {C},\tau )$ is a site. If ![]() $f: \mathscr {X} \to \mathscr {Y}$ is a morphism in
$f: \mathscr {X} \to \mathscr {Y}$ is a morphism in ![]() $\mathrm {sPre}(\mathbf {C})$, then the following conditions are equivalent.
$\mathrm {sPre}(\mathbf {C})$, then the following conditions are equivalent.
1. The morphism
 $f$ is an
$f$ is an  $R$-local weak equivalence.
$R$-local weak equivalence.2. For every
 $R$-local space
$R$-local space  $\mathscr {W}$, the map
is a bijection.
$\mathscr {W}$, the map
is a bijection. \[ f^*: \operatorname{Hom}_{\operatorname{Ho}_{\tau}(\mathbf{C})}(\mathscr{Y},\mathscr{W}) \longrightarrow \operatorname{Hom}_{\operatorname{Ho}_{\tau}(\mathbf{C})}(\mathscr{X},\mathscr{W}) \]
\[ f^*: \operatorname{Hom}_{\operatorname{Ho}_{\tau}(\mathbf{C})}(\mathscr{Y},\mathscr{W}) \longrightarrow \operatorname{Hom}_{\operatorname{Ho}_{\tau}(\mathbf{C})}(\mathscr{X},\mathscr{W}) \]
Proof. The first statement implies the second by taking ![]() $\pi _0$ of the simplicial mapping space. The second statement implies the first by observing that if
$\pi _0$ of the simplicial mapping space. The second statement implies the first by observing that if ![]() $\mathscr {W}$ is
$\mathscr {W}$ is ![]() $R$-local, then so is
$R$-local, then so is ![]() $\Omega ^i \mathscr {W}$ for every
$\Omega ^i \mathscr {W}$ for every ![]() $i \geq 0$.
$i \geq 0$.
Lemma 2.3.10 Suppose ![]() $p: \mathscr {E} \to \mathscr {B}$ is a (locally) nilpotent morphism of pointed simplicially connected spaces. The morphism
$p: \mathscr {E} \to \mathscr {B}$ is a (locally) nilpotent morphism of pointed simplicially connected spaces. The morphism
is also a (locally) nilpotent morphism, and the canonical map ![]() $\operatorname {L}_R(\operatorname {hofib}(p)) \to \operatorname {hofib}(\operatorname {L}_R p)$ is a
$\operatorname {L}_R(\operatorname {hofib}(p)) \to \operatorname {hofib}(\operatorname {L}_R p)$ is a ![]() $\tau$-local weak equivalence.
$\tau$-local weak equivalence.
Proof. Consider the morphism ![]() $\mathscr {B} \to \mathrm {R}_{\tau }\mathscr {B}$ and factor the composite
$\mathscr {B} \to \mathrm {R}_{\tau }\mathscr {B}$ and factor the composite ![]() $\mathscr {E} \to \mathrm {R}_\tau {\mathscr {B}}$ as an acyclic cofibration
$\mathscr {E} \to \mathrm {R}_\tau {\mathscr {B}}$ as an acyclic cofibration ![]() $\mathscr {E} \to \mathscr {E}'$ followed by a
$\mathscr {E} \to \mathscr {E}'$ followed by a ![]() $\tau$-fibration
$\tau$-fibration ![]() $\mathscr {E}' \to \mathrm {R}_{\mathscr {B}}$ so that the homotopy fiber of
$\mathscr {E}' \to \mathrm {R}_{\mathscr {B}}$ so that the homotopy fiber of ![]() $p$ is the actual fiber of
$p$ is the actual fiber of ![]() $p': \mathscr {E}' \to \mathrm {R}_\tau {\mathscr {B}}$. Both conditions in the statement may be checked stalkwise, and stalkwise the hypotheses imply that
$p': \mathscr {E}' \to \mathrm {R}_\tau {\mathscr {B}}$. Both conditions in the statement may be checked stalkwise, and stalkwise the hypotheses imply that ![]() $p'$ is a nilpotent fibration.
$p'$ is a nilpotent fibration.
Next, recall that Bousfield and Kan construct the functor ![]() $R_{\infty }$ [Reference Bousfield and KanBK72, I.4.2] and show that
$R_{\infty }$ [Reference Bousfield and KanBK72, I.4.2] and show that ![]() $R_{\infty }$ models
$R_{\infty }$ models ![]() $R$-localization [Reference Bousfield and KanBK72, V.4.3]. By [Reference Casacuberta and PeschkeCP93, Proposition 8.1] on the category of simplicial sets,
$R$-localization [Reference Bousfield and KanBK72, V.4.3]. By [Reference Casacuberta and PeschkeCP93, Proposition 8.1] on the category of simplicial sets, ![]() $\operatorname {L}_R$ models localization à la Bousfield and Kan. Therefore, the results about preservation of nilpotent fibrations by
$\operatorname {L}_R$ models localization à la Bousfield and Kan. Therefore, the results about preservation of nilpotent fibrations by ![]() $R_{\infty }$ also hold for
$R_{\infty }$ also hold for ![]() $\operatorname {L}_R$. Granted these observations, the result follows directly from [Reference Bousfield and KanBK72, II.4.8].
$\operatorname {L}_R$. Granted these observations, the result follows directly from [Reference Bousfield and KanBK72, II.4.8].
Functorial  $R$-localization for nilpotent sheaves of groups and spaces
$R$-localization for nilpotent sheaves of groups and spaces
We now define a functorial ![]() $R$-localization for sheaves of groups; our goal is to show that this functor is well behaved on the category of (locally) nilpotent sheaves of groups.
$R$-localization for sheaves of groups; our goal is to show that this functor is well behaved on the category of (locally) nilpotent sheaves of groups.
Definition 2.3.11 If ![]() $\mathbf {G}$ is a sheaf of groups, then we define
$\mathbf {G}$ is a sheaf of groups, then we define
the sheaf of groups ![]() $\mathbf {G}_R$ will be called the
$\mathbf {G}_R$ will be called the ![]() $R$-localization of
$R$-localization of ![]() $\mathbf {G}$.
$\mathbf {G}$.
By definition, the assignment ![]() $\mathbf {G} \mapsto \mathbf {G}_R$ is functorial. The properties of this functor upon restriction to the category of (locally) nilpotent sheaves of groups are recorded in the following result.
$\mathbf {G} \mapsto \mathbf {G}_R$ is functorial. The properties of this functor upon restriction to the category of (locally) nilpotent sheaves of groups are recorded in the following result.
Proposition 2.3.12 Suppose ![]() $R \subset {\mathbb {Q}}$ is a ring. The assignment
$R \subset {\mathbb {Q}}$ is a ring. The assignment ![]() $\mathbf {G} \mapsto \mathbf {G}_R$ enjoys the following properties.
$\mathbf {G} \mapsto \mathbf {G}_R$ enjoys the following properties.
1. The functor
 $(-)_R$ is left adjoint to the forgetful functor from the category of (locally)
$(-)_R$ is left adjoint to the forgetful functor from the category of (locally)  $R$-local nilpotent sheaves of groups to the category of (locally) nilpotent sheaves of groups.
$R$-local nilpotent sheaves of groups to the category of (locally) nilpotent sheaves of groups.2. The functor
 $(-)_R$ preserves exact sequences of (locally) nilpotent sheaves of groups.
$(-)_R$ preserves exact sequences of (locally) nilpotent sheaves of groups.3. If
 $R' \subset {\mathbb {Q}}$ is another ring, then the natural transformation
$R' \subset {\mathbb {Q}}$ is another ring, then the natural transformation  $(-)_{R \otimes _{{\mathbb {Z}}} R'} \to ((-)_R)_{R'}$ is an isomorphism of functors from the category of (locally) nilpotent sheaves of groups to the category of
$(-)_{R \otimes _{{\mathbb {Z}}} R'} \to ((-)_R)_{R'}$ is an isomorphism of functors from the category of (locally) nilpotent sheaves of groups to the category of  $R \otimes _{{\mathbb {Z}}} R'$-local (locally) nilpotent sheaves of groups.
$R \otimes _{{\mathbb {Z}}} R'$-local (locally) nilpotent sheaves of groups.
Proof. For the first point, ![]() $(-)_R$ is functorial by construction and it follows from Lemma 2.3.7 that
$(-)_R$ is functorial by construction and it follows from Lemma 2.3.7 that ![]() $\mathbf {G}_R$ is an
$\mathbf {G}_R$ is an ![]() $R$-local sheaf of groups. If
$R$-local sheaf of groups. If ![]() $\mathbf {G}$ is (locally) nilpotent, then we claim
$\mathbf {G}$ is (locally) nilpotent, then we claim ![]() $\mathbf {G}_R$ is (locally) nilpotent and
$\mathbf {G}_R$ is (locally) nilpotent and ![]() $R$-local. Since
$R$-local. Since ![]() $\operatorname {L}_R$ commutes with taking stalks, we may check this stalkwise, in which case it follows immediately from [Reference Bousfield and KanBK72, V.2.2].
$\operatorname {L}_R$ commutes with taking stalks, we may check this stalkwise, in which case it follows immediately from [Reference Bousfield and KanBK72, V.2.2].
To complete the proof of (1), it suffices to prove that ![]() $\mathbf {G} \to \mathbf {G}_R$ is initial among maps from
$\mathbf {G} \to \mathbf {G}_R$ is initial among maps from ![]() $\mathbf {G}$ to (locally) nilpotent
$\mathbf {G}$ to (locally) nilpotent ![]() $R$-local sheaves of groups. If
$R$-local sheaves of groups. If ![]() $\mathbf {H}$ is a (locally) nilpotent
$\mathbf {H}$ is a (locally) nilpotent ![]() $R$-local sheaf of groups equipped with a homomorphism
$R$-local sheaf of groups equipped with a homomorphism ![]() $\mathbf {G} \to \mathbf {H}$, then there is an evident map
$\mathbf {G} \to \mathbf {H}$, then there is an evident map ![]() $\mathrm {R}_{\tau }B\mathbf {G} \to \mathrm {R}_{\tau }B\mathbf {H}$. The space
$\mathrm {R}_{\tau }B\mathbf {G} \to \mathrm {R}_{\tau }B\mathbf {H}$. The space ![]() $\mathrm {R}_{\tau }B\mathbf {H}$ is
$\mathrm {R}_{\tau }B\mathbf {H}$ is ![]() $R$-local by Remark 2.3.8, and therefore, it follows that
$R$-local by Remark 2.3.8, and therefore, it follows that ![]() $\mathrm {R}_{\tau }B\mathbf {G} \to \mathrm {R}_{\tau }B\mathbf {H}$ factors through
$\mathrm {R}_{\tau }B\mathbf {G} \to \mathrm {R}_{\tau }B\mathbf {H}$ factors through ![]() $\operatorname {L}_R B\mathbf {G}$. Applying
$\operatorname {L}_R B\mathbf {G}$. Applying ![]() $\boldsymbol {\pi }_1$ establishes (1).
$\boldsymbol {\pi }_1$ establishes (1).
For (2), suppose
is a short exact sequence of (locally) nilpotent sheaves of groups. In that case, we get a simplicial fiber sequence of the form
Applying ![]() $\operatorname {L}_R$ to this fiber sequence yields a simplicial fiber sequence by appeal to Lemma 2.3.10. Exactness then follows by appeal to [Reference Bousfield and KanBK72, V.2.4], since exactness may be checked stalkwise.
$\operatorname {L}_R$ to this fiber sequence yields a simplicial fiber sequence by appeal to Lemma 2.3.10. Exactness then follows by appeal to [Reference Bousfield and KanBK72, V.2.4], since exactness may be checked stalkwise.
If ![]() $\mathbf {A}$ is an abelian sheaf of groups, then there is an evident isomorphism of functors
$\mathbf {A}$ is an abelian sheaf of groups, then there is an evident isomorphism of functors ![]() $(R \otimes _{{\mathbb {Z}}} R') \otimes \mathbf {A} {\stackrel {\sim }{\;\longrightarrow \;}} R \otimes (R' \otimes \mathbf {A})$. Following [Reference Bousfield and KanBK72, V.2.9], (3) is immediate from (2) and a straightforward induction argument.
$(R \otimes _{{\mathbb {Z}}} R') \otimes \mathbf {A} {\stackrel {\sim }{\;\longrightarrow \;}} R \otimes (R' \otimes \mathbf {A})$. Following [Reference Bousfield and KanBK72, V.2.9], (3) is immediate from (2) and a straightforward induction argument.
Corollary 2.3.13 Suppose ![]() $(\mathscr {X},x)$ is a pointed locally nilpotent space.
$(\mathscr {X},x)$ is a pointed locally nilpotent space.
1. The space
 $\operatorname {L}_R\mathscr {X}$ is an
$\operatorname {L}_R\mathscr {X}$ is an  $R$-local locally nilpotent space.
$R$-local locally nilpotent space.2. For every integer
 $i \geq 1$, the canonical map
$i \geq 1$, the canonical map  $\boldsymbol {\pi }_i(\mathscr {X})_R \to \boldsymbol {\pi }_i(\operatorname {L}_R\mathscr {X})$ is an isomorphism.
$\boldsymbol {\pi }_i(\mathscr {X})_R \to \boldsymbol {\pi }_i(\operatorname {L}_R\mathscr {X})$ is an isomorphism.
Proof. The first point is a special case of Lemma 2.3.10. The second point follows immediately from [Reference Bousfield and KanBK72, V.3.1] because the relevant isomorphism may be checked stalkwise.
3. Nilpotence in  ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
In this section we formulate and study a notion of nilpotence in ![]() ${\mathbb {A}}^1$-homotopy theory. Section 3.1 recalls various results from Morel's foundational work [Reference MorelMor12], in particular the notions of strongly and strictly
${\mathbb {A}}^1$-homotopy theory. Section 3.1 recalls various results from Morel's foundational work [Reference MorelMor12], in particular the notions of strongly and strictly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups (see Definition 3.1.5). We then develop the basic properties of
${\mathbb {A}}^1$-invariant sheaves of groups (see Definition 3.1.5). We then develop the basic properties of ![]() ${\mathbb {A}}^1$-local group theory necessary to formulate suitable notions of nilpotence. The main technical complication that arises is due to failure of existence of cokernels (see Remark 3.1.15 for a precise statement). Section 3.2 then studies nilpotence in the context of
${\mathbb {A}}^1$-local group theory necessary to formulate suitable notions of nilpotence. The main technical complication that arises is due to failure of existence of cokernels (see Remark 3.1.15 for a precise statement). Section 3.2 then studies nilpotence in the context of ![]() ${\mathbb {A}}^1$-local group theory.
${\mathbb {A}}^1$-local group theory.
Section 3.3 introduces various flavors of nilpotence for spaces and morphisms in ![]() ${\mathbb {A}}^1$-homotopy theory (see Definition 3.3.1); we encourage the reader to pay attention to the notion of weakly
${\mathbb {A}}^1$-homotopy theory (see Definition 3.3.1); we encourage the reader to pay attention to the notion of weakly ![]() ${\mathbb {A}}^1$-nilpotent spaces which will play a prominent role later. Moreover, we establish a collection of basic properties for such spaces (e.g. a characterization in terms of existence of Moore–Postnikov factorizations, that is, Theorem 3.3.13). Finally, § 3.4 constructs a host of spaces of geometric interest that exemplify the variant definitions we make.
${\mathbb {A}}^1$-nilpotent spaces which will play a prominent role later. Moreover, we establish a collection of basic properties for such spaces (e.g. a characterization in terms of existence of Moore–Postnikov factorizations, that is, Theorem 3.3.13). Finally, § 3.4 constructs a host of spaces of geometric interest that exemplify the variant definitions we make.
3.1  ${\mathbb {A}}^1$-local group theory
${\mathbb {A}}^1$-local group theory
Morel showed that the ![]() ${\mathbb {A}}^1$-homotopy sheaves of a pointed space in degrees greater than
${\mathbb {A}}^1$-homotopy sheaves of a pointed space in degrees greater than ![]() $1$ have the fundamental property that their cohomology presheaves are themselves
$1$ have the fundamental property that their cohomology presheaves are themselves ![]() ${\mathbb {A}}^1$-invariant. After reviewing the basic definitions in
${\mathbb {A}}^1$-invariant. After reviewing the basic definitions in ![]() ${\mathbb {A}}^1$-homotopy theory, we study what one might call
${\mathbb {A}}^1$-homotopy theory, we study what one might call ![]() ${\mathbb {A}}^1$-local group theory, building on the foundational results of Morel [Reference MorelMor12]. In particular, we analyze functorial
${\mathbb {A}}^1$-local group theory, building on the foundational results of Morel [Reference MorelMor12]. In particular, we analyze functorial ![]() ${\mathbb {A}}^1$-localization of groups and various categorical properties of the resulting category.
${\mathbb {A}}^1$-localization of groups and various categorical properties of the resulting category.
Preliminaries on  ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
Fix a base field ![]() $k$, and write
$k$, and write ![]() $\mathrm {Sm}_k$ for the category of schemes that are separated, smooth and have finite type over
$\mathrm {Sm}_k$ for the category of schemes that are separated, smooth and have finite type over ![]() $\operatorname {Spec} k$. We view
$\operatorname {Spec} k$. We view ![]() $\mathrm {Sm}_k$ as a site by equipping it with the Nisnevich topology. We set
$\mathrm {Sm}_k$ as a site by equipping it with the Nisnevich topology. We set ![]() $\mathrm {Spc}_k := \mathrm {sPre}(\mathrm {Sm}_k)$ and view this as a site equipped with the injective Nisnevich local model structure. Similarly, we write
$\mathrm {Spc}_k := \mathrm {sPre}(\mathrm {Sm}_k)$ and view this as a site equipped with the injective Nisnevich local model structure. Similarly, we write ![]() $\mathrm {Spc}_{k,*}$ for the category of pointed simplicial presheaves on
$\mathrm {Spc}_{k,*}$ for the category of pointed simplicial presheaves on ![]() $\mathrm {Sm}_k$.
$\mathrm {Sm}_k$.
The (pointed) ![]() ${\mathbb {A}}^1$-homotopy category
${\mathbb {A}}^1$-homotopy category ![]() $\mathrm {Ho}_{k}$ can be obtained as a left Bousfield localization of the injective Nisnevich local model structure on
$\mathrm {Ho}_{k}$ can be obtained as a left Bousfield localization of the injective Nisnevich local model structure on ![]() $\mathrm {Spc}_k$ (respectively,
$\mathrm {Spc}_k$ (respectively, ![]() $\mathrm {Spc}_{k,*}$) with respect to the morphisms
$\mathrm {Spc}_{k,*}$) with respect to the morphisms ![]() $\mathscr {X} \times {\mathbb {A}}^1 \to \mathscr {X}$,
$\mathscr {X} \times {\mathbb {A}}^1 \to \mathscr {X}$, ![]() $\mathscr {X} \in \mathrm {Spc}_k$.
$\mathscr {X} \in \mathrm {Spc}_k$.
We write ![]() $\operatorname {L}_{{\mathbb {A}}^1}: \mathrm {Spc}_k \to \mathrm {Spc}_k$ for the
$\operatorname {L}_{{\mathbb {A}}^1}: \mathrm {Spc}_k \to \mathrm {Spc}_k$ for the ![]() ${\mathbb {A}}^1$-localization functor. This functor comes equipped with a natural transformation
${\mathbb {A}}^1$-localization functor. This functor comes equipped with a natural transformation ![]() $\theta : {\rm id} \to \operatorname {L}_{{\mathbb {A}}^1}$ such that for any space
$\theta : {\rm id} \to \operatorname {L}_{{\mathbb {A}}^1}$ such that for any space ![]() $\mathscr {X}$ the following properties hold.
$\mathscr {X}$ the following properties hold.
1. The space
 $\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is fibrant in the injective Nisnevich local model structure, and the map
$\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is fibrant in the injective Nisnevich local model structure, and the map  $\mathscr {X} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is an
$\mathscr {X} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is an  ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.2. If
 $\mathscr {Y}$ is any simplicially fibrant and
$\mathscr {Y}$ is any simplicially fibrant and  ${\mathbb {A}}^1$-local space, and
${\mathbb {A}}^1$-local space, and  $f: \mathscr {X} \to \mathscr {Y}$, then
$f: \mathscr {X} \to \mathscr {Y}$, then  $f$ factors as
$f$ factors as  $\mathscr {X} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {X} \to \mathscr {Y}$.
$\mathscr {X} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {X} \to \mathscr {Y}$.3. The functor
 $\operatorname {L}_{{\mathbb {A}}^1}$ preserves finite limits.
$\operatorname {L}_{{\mathbb {A}}^1}$ preserves finite limits.
Remark 3.1.1 The properties of the ![]() ${\mathbb {A}}^1$-localization construction described here are all explicitly contained in [Reference Morel and VoevodskyMV99], except the last one. That the
${\mathbb {A}}^1$-localization construction described here are all explicitly contained in [Reference Morel and VoevodskyMV99], except the last one. That the ![]() ${\mathbb {A}}^1$-localization functor can be assumed to preserve finite limits follows from a slight modification of the construction described before [Reference Morel and VoevodskyMV99, § 2 Lemma 3.20]. There, the
${\mathbb {A}}^1$-localization functor can be assumed to preserve finite limits follows from a slight modification of the construction described before [Reference Morel and VoevodskyMV99, § 2 Lemma 3.20]. There, the ![]() ${\mathbb {A}}^1$-localization functor is constructed by iterated application of a fibrant resolution functor for the injective Nisnevich local model structure and the singular construction. The singular construction preserves limits [Reference Morel and VoevodskyMV99, § 2 p. 87]. Taking the Godement resolution [Reference Morel and VoevodskyMV99, p. 66–70] as fibrant replacement functor for the injective Nisnevich local model structure, it follows by appeal to [Reference Morel and VoevodskyMV99, § 2 Theorem 1.66] that the fibrant resolution functor can be assumed to preserve finite limits as well.
${\mathbb {A}}^1$-localization functor is constructed by iterated application of a fibrant resolution functor for the injective Nisnevich local model structure and the singular construction. The singular construction preserves limits [Reference Morel and VoevodskyMV99, § 2 p. 87]. Taking the Godement resolution [Reference Morel and VoevodskyMV99, p. 66–70] as fibrant replacement functor for the injective Nisnevich local model structure, it follows by appeal to [Reference Morel and VoevodskyMV99, § 2 Theorem 1.66] that the fibrant resolution functor can be assumed to preserve finite limits as well.
Remark 3.1.2 In [Reference Morel and VoevodskyMV99] the motivic homotopy category ![]() $\mathrm {Ho}_{k}$ is obtained by Bousfield localizing simplicial Nisnevich sheaves on
$\mathrm {Ho}_{k}$ is obtained by Bousfield localizing simplicial Nisnevich sheaves on ![]() $\mathrm {Sm}_k$. By contrast, the model we use builds
$\mathrm {Sm}_k$. By contrast, the model we use builds ![]() $\mathrm {Ho}_{k}$ as a localization of simplicial presheaves on
$\mathrm {Ho}_{k}$ as a localization of simplicial presheaves on ![]() $\mathrm {Sm}_k$. The two constructions yield Quillen equivalent models of
$\mathrm {Sm}_k$. The two constructions yield Quillen equivalent models of ![]() $\mathrm {Ho}_{k}$ by [Reference JardineJar00, Theorems B.4 and B.6].
$\mathrm {Ho}_{k}$ by [Reference JardineJar00, Theorems B.4 and B.6].
It will be important to remember that the category of ![]() ${\mathbb {A}}^1$-local objects is closed under formation of homotopy limits and filtered homotopy colimits. We now recall some results about how
${\mathbb {A}}^1$-local objects is closed under formation of homotopy limits and filtered homotopy colimits. We now recall some results about how ![]() ${\mathbb {A}}^1$-local objects behave in fiber sequences.
${\mathbb {A}}^1$-local objects behave in fiber sequences.
Lemma 3.1.3 If ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence where
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence where ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}$ are
$\mathscr {B}$ are ![]() ${\mathbb {A}}^1$-local spaces, then
${\mathbb {A}}^1$-local spaces, then ![]() $\mathscr {F}$ is
$\mathscr {F}$ is ![]() ${\mathbb {A}}^1$-local as well.
${\mathbb {A}}^1$-local as well.
Lemma 3.1.4 [Reference Asok, Wickelgren and WilliamsAWW17, Lemma 2.2.10]
Suppose ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence of pointed spaces. If
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence of pointed spaces. If ![]() $\mathscr {B}$ and
$\mathscr {B}$ and ![]() $\mathscr {F}$ are both
$\mathscr {F}$ are both ![]() ${\mathbb {A}}^1$-local, and
${\mathbb {A}}^1$-local, and ![]() $\mathscr {B}$ is simplicially connected, then
$\mathscr {B}$ is simplicially connected, then ![]() $\mathscr {E}$ is
$\mathscr {E}$ is ![]() ${\mathbb {A}}^1$-local as well.
${\mathbb {A}}^1$-local as well.
Consequences of Morel's unstable connectivity theorem
If ![]() $\mathscr {X} \in \mathrm {Spc}_k$, then we set
$\mathscr {X} \in \mathrm {Spc}_k$, then we set ![]() $\boldsymbol {\pi }_0^{{\mathbb {A}}^1}(\mathscr {X}) := \boldsymbol {\pi }_0(\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X})$. Similarly, if
$\boldsymbol {\pi }_0^{{\mathbb {A}}^1}(\mathscr {X}) := \boldsymbol {\pi }_0(\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X})$. Similarly, if ![]() $(\mathscr {X},x) \in \mathrm {Spc}_{k,*}$, then we write
$(\mathscr {X},x) \in \mathrm {Spc}_{k,*}$, then we write ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x) := \boldsymbol {\pi }_i(\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X},x)$; these sheaves are called the
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x) := \boldsymbol {\pi }_i(\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X},x)$; these sheaves are called the ![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $\mathscr {X}$. Morel established a number of key structural results for
$\mathscr {X}$. Morel established a number of key structural results for ![]() ${\mathbb {A}}^1$-homotopy sheaves. To state these results, we first recall the following definition.
${\mathbb {A}}^1$-homotopy sheaves. To state these results, we first recall the following definition.
Definition 3.1.5 Assume ![]() $k$ is a base field.
$k$ is a base field.
1. A Nisnevich sheaf of groups
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathrm {Sm}_k$ is called strongly
$\mathrm {Sm}_k$ is called strongly  ${\mathbb {A}}^1$-invariant if
${\mathbb {A}}^1$-invariant if  $B\mathbf {G}$ is
$B\mathbf {G}$ is  ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.2. A Nisnevich sheaf of abelian groups
 $\mathbf {A}$ on
$\mathbf {A}$ on  $\mathrm {Sm}_k$ is called strictly
$\mathrm {Sm}_k$ is called strictly  ${\mathbb {A}}^1$-invariant if
${\mathbb {A}}^1$-invariant if  $K(\mathbf {A},n)$ is
$K(\mathbf {A},n)$ is  ${\mathbb {A}}^1$-local for every
${\mathbb {A}}^1$-local for every  $n \geq 0$.
$n \geq 0$.
Notation 3.1.6 We write ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ for the full subcategory of Nisnevich sheaves of groups consisting of strongly
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ for the full subcategory of Nisnevich sheaves of groups consisting of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups. We write
${\mathbb {A}}^1$-invariant sheaves of groups. We write ![]() $\mathrm {Ab}^{{\mathbb {A}}^1}_k$ for the full subcategory of Nisnevich sheaves of abelian groups consisting of strictly
$\mathrm {Ab}^{{\mathbb {A}}^1}_k$ for the full subcategory of Nisnevich sheaves of abelian groups consisting of strictly ![]() ${\mathbb {A}}^1$-invariant sheaves.
${\mathbb {A}}^1$-invariant sheaves.
Example 3.1.7 If ![]() $G$ is a finite étale group scheme, then the simplicial classifying space
$G$ is a finite étale group scheme, then the simplicial classifying space ![]() $BG$ is
$BG$ is ![]() ${\mathbb {A}}^1$-local by [Reference Morel and VoevodskyMV99, § 4 Proposition 3.5], that is,
${\mathbb {A}}^1$-local by [Reference Morel and VoevodskyMV99, § 4 Proposition 3.5], that is, ![]() $G$ is strongly
$G$ is strongly ![]() ${\mathbb {A}}^1$-invariant. In particular, if
${\mathbb {A}}^1$-invariant. In particular, if ![]() $G$ is a finite group, the associated constant group scheme is strongly
$G$ is a finite group, the associated constant group scheme is strongly ![]() ${\mathbb {A}}^1$-invariant. Thus, sending a finite group to its associated constant group scheme defines a functor from the category of finite groups to the category of strongly
${\mathbb {A}}^1$-invariant. Thus, sending a finite group to its associated constant group scheme defines a functor from the category of finite groups to the category of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups.
${\mathbb {A}}^1$-invariant sheaves of groups.
We recall some key results of Morel on the structure of the categories of strongly and strictly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups.
${\mathbb {A}}^1$-invariant sheaves of groups.
Theorem 3.1.8 (Morel)
Assume ![]() $(\mathscr {X},x) \in \mathrm {Spc}_{k,*}$.
$(\mathscr {X},x) \in \mathrm {Spc}_{k,*}$.
1. The sheaf
 $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ is a strongly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ is a strongly  ${\mathbb {A}}^1$-invariant sheaf of groups.
${\mathbb {A}}^1$-invariant sheaf of groups.2. Any strongly
 ${\mathbb {A}}^1$-invariant sheaf of abelian groups that is pulled back from a perfect subfield is strictly
${\mathbb {A}}^1$-invariant sheaf of abelian groups that is pulled back from a perfect subfield is strictly  ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
Comments on the proof
The first statement in Theorem 3.1.8 is [Reference MorelMor12, Theorem 6.1]. For the second statement, we proceed as follows. Morel proves in [Reference MorelMor12, Theorem 5.46] that if ![]() $k$ is a perfect field, then strongly
$k$ is a perfect field, then strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of abelian groups are strictly
${\mathbb {A}}^1$-invariant sheaves of abelian groups are strictly ![]() ${\mathbb {A}}^1$-invariant. Our claim follows from the Morel's assertion by standard base-change results (see, for example, [Reference HoyoisHoy15, Lemmas A.2 and A.4]). A common application of the above result is that if
${\mathbb {A}}^1$-invariant. Our claim follows from the Morel's assertion by standard base-change results (see, for example, [Reference HoyoisHoy15, Lemmas A.2 and A.4]). A common application of the above result is that if ![]() $(\mathscr {X},x)$ is a space over a field
$(\mathscr {X},x)$ is a space over a field ![]() $k$ that is pulled back from the prime field, then, for any integer
$k$ that is pulled back from the prime field, then, for any integer ![]() $i \geq 2$, the sheaf
$i \geq 2$, the sheaf ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x)$ is strictly
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x)$ is strictly ![]() ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
Remark 3.1.9 The condition that a sheaf of groups be strongly or strictly ![]() ${\mathbb {A}}^1$-invariant implies many useful properties that will be used in the sequel. For example, if
${\mathbb {A}}^1$-invariant implies many useful properties that will be used in the sequel. For example, if ![]() $\mathbf {G}$ is a strongly
$\mathbf {G}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf, then
${\mathbb {A}}^1$-invariant sheaf, then ![]() $\mathbf {G}$ is unramified in the sense of [Reference MorelMor12, Definition 2.1]; this follows from [Reference MorelMor12, Corollary 6.9(2)]. In particular, this means that if
$\mathbf {G}$ is unramified in the sense of [Reference MorelMor12, Definition 2.1]; this follows from [Reference MorelMor12, Corollary 6.9(2)]. In particular, this means that if ![]() $X$ is any irreducible smooth
$X$ is any irreducible smooth ![]() $k$-scheme with function field
$k$-scheme with function field ![]() $k(X)$, then the restriction map
$k(X)$, then the restriction map
is injective. In particular, Theorem 3.1.8 implies that all the higher homotopy sheaves of a pointed space ![]() $(\mathscr {X},x) \in \mathrm {Spc}_k$ that are pulled back from a perfect subfield are unramified.
$(\mathscr {X},x) \in \mathrm {Spc}_k$ that are pulled back from a perfect subfield are unramified.
Theorem 3.1.8 allows one to construct a left adjoint to the inclusion ![]() $\mathrm {Grp}_k^{{\mathbb {A}}^1} \hookrightarrow \mathrm {Grp}_k$.
$\mathrm {Grp}_k^{{\mathbb {A}}^1} \hookrightarrow \mathrm {Grp}_k$.
Definition 3.1.10 If ![]() $\mathbf {G}$ is a Nisnevich sheaf of groups on
$\mathbf {G}$ is a Nisnevich sheaf of groups on ![]() $\mathrm {Sm}_k$, then its
$\mathrm {Sm}_k$, then its ![]() ${\mathbb {A}}^1$-localization is defined by
${\mathbb {A}}^1$-localization is defined by
Example 3.1.11 The evident homomorphism ![]() $\mathbf {G} \to \mathbf {G}_{{\mathbb {A}}^1}$ need not be injective. Take
$\mathbf {G} \to \mathbf {G}_{{\mathbb {A}}^1}$ need not be injective. Take ![]() $\mathbf {G} = SL_n$ (or any
$\mathbf {G} = SL_n$ (or any ![]() ${\mathbb {A}}^1$-connected sheaf of groups); in that case one can show that
${\mathbb {A}}^1$-connected sheaf of groups); in that case one can show that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BSL_n) = 1$.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BSL_n) = 1$.
The next result is a consequence of [Reference MorelMor05, Theorem 6.1.8 and Lemma 6.2.13].
Theorem 3.1.12 (Morel)
The category ![]() $\mathrm {Ab}^{{\mathbb {A}}^1}_k$ is abelian, and the forgetful functor
$\mathrm {Ab}^{{\mathbb {A}}^1}_k$ is abelian, and the forgetful functor ![]() $\mathrm {Ab}^{{\mathbb {A}}^1}_k \to \mathrm {Ab}_k$ is an exact full embedding.
$\mathrm {Ab}^{{\mathbb {A}}^1}_k \to \mathrm {Ab}_k$ is an exact full embedding.
Remark 3.1.13 As observed in [Reference MorelMor05, Remark 6.2.14], the above result means, in particular, that any kernel or cokernel of a morphism of strictly ![]() ${\mathbb {A}}^1$-invariant sheaves is again strictly
${\mathbb {A}}^1$-invariant sheaves is again strictly ![]() ${\mathbb {A}}^1$-invariant. In fact, this consequence will be used repeatedly in the sequel. In what follows, we will study corresponding questions for strongly
${\mathbb {A}}^1$-invariant. In fact, this consequence will be used repeatedly in the sequel. In what follows, we will study corresponding questions for strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups where the situation is more complicated; see, for example, Remark 3.1.15 for further discussion of this point.
${\mathbb {A}}^1$-invariant sheaves of groups where the situation is more complicated; see, for example, Remark 3.1.15 for further discussion of this point.
Strongly  ${\mathbb {A}}^1$-invariant sheaves of groups
${\mathbb {A}}^1$-invariant sheaves of groups
We first examine how various group-theoretic constructions interact with the property of being ![]() ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.
Lemma 3.1.14 Assume ![]() $k$ is a field.
$k$ is a field.
1. The kernel of a morphism in
 $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ is again a strongly
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ is again a strongly  ${\mathbb {A}}^1$-invariant sheaf of groups.
${\mathbb {A}}^1$-invariant sheaf of groups.2. Any extension of strongly
 ${\mathbb {A}}^1$-invariant sheaves of groups is again strongly
${\mathbb {A}}^1$-invariant sheaves of groups is again strongly  ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.3. If
 $\varphi : \mathbf {A} \to \mathbf {G}$ is any injective morphism of strongly
$\varphi : \mathbf {A} \to \mathbf {G}$ is any injective morphism of strongly  ${\mathbb {A}}^1$-invariant sheaves of groups, and
${\mathbb {A}}^1$-invariant sheaves of groups, and  $\mathbf {A}$ is (i) pulled back from a perfect subfield of
$\mathbf {A}$ is (i) pulled back from a perfect subfield of  $k$ and (ii) contained in the center of
$k$ and (ii) contained in the center of  $\mathbf {G}$, then
$\mathbf {G}$, then  $\mathbf {G}/\mathbf {A}$ is strongly
$\mathbf {G}/\mathbf {A}$ is strongly  ${\mathbb {A}}^1$-invariant as well.
${\mathbb {A}}^1$-invariant as well.
Proof. Suppose ![]() $\varphi : \mathbf {H} \to \mathbf {G}$ is a morphism of strongly
$\varphi : \mathbf {H} \to \mathbf {G}$ is a morphism of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups. There is an induced morphism
${\mathbb {A}}^1$-invariant sheaves of groups. There is an induced morphism ![]() $B\mathbf {H} \to B\mathbf {G}$. By assumption, both
$B\mathbf {H} \to B\mathbf {G}$. By assumption, both ![]() $B\mathbf {H}$ and
$B\mathbf {H}$ and ![]() $B\mathbf {G}$ are
$B\mathbf {G}$ are ![]() ${\mathbb {A}}^1$-local. Write
${\mathbb {A}}^1$-local. Write ![]() $\mathscr {F}$ for the simplicial homotopy fiber of
$\mathscr {F}$ for the simplicial homotopy fiber of ![]() $\varphi$. Since
$\varphi$. Since ![]() $\boldsymbol {\pi }_2(B\mathbf {G})$ vanishes by assumption, the associated long exact sequence in homotopy sheaves takes the form
$\boldsymbol {\pi }_2(B\mathbf {G})$ vanishes by assumption, the associated long exact sequence in homotopy sheaves takes the form
Appealing to Lemma 3.1.3 allows us to conclude that ![]() $\mathscr {F}$ is already
$\mathscr {F}$ is already ![]() ${\mathbb {A}}^1$-local, which means that
${\mathbb {A}}^1$-local, which means that ![]() $\boldsymbol {\pi }_1(\mathscr {F}) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is strongly
$\boldsymbol {\pi }_1(\mathscr {F}) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is strongly ![]() ${\mathbb {A}}^1$-invariant by Theorem 3.1.8.
${\mathbb {A}}^1$-invariant by Theorem 3.1.8.
For the second point, suppose ![]() $1 \to \mathbf {G}_1 \to \mathbf {G}_2 \to \mathbf {G}_3 \to 1$ is an exact sequence of Nisnevich sheaves of groups and
$1 \to \mathbf {G}_1 \to \mathbf {G}_2 \to \mathbf {G}_3 \to 1$ is an exact sequence of Nisnevich sheaves of groups and ![]() $\mathbf {G}_3$ is strongly
$\mathbf {G}_3$ is strongly ![]() ${\mathbb {A}}^1$-invariant. In that case, there is a simplicial fiber sequence
${\mathbb {A}}^1$-invariant. In that case, there is a simplicial fiber sequence
Note that ![]() $B\mathbf {G}_3$ is simplicially connected by construction. If
$B\mathbf {G}_3$ is simplicially connected by construction. If ![]() $\mathbf {G}_1$ and
$\mathbf {G}_1$ and ![]() $\mathbf {G}_3$ are strongly
$\mathbf {G}_3$ are strongly ![]() ${\mathbb {A}}^1$-invariant, then
${\mathbb {A}}^1$-invariant, then ![]() $B\mathbf {G}_1$ and
$B\mathbf {G}_1$ and ![]() $B\mathbf {G}_3$ are
$B\mathbf {G}_3$ are ![]() ${\mathbb {A}}^1$-local by assumption. In that case, it follows from Lemma 3.1.4 that
${\mathbb {A}}^1$-local by assumption. In that case, it follows from Lemma 3.1.4 that ![]() $B\mathbf {G}_2$ must be
$B\mathbf {G}_2$ must be ![]() ${\mathbb {A}}^1$-local as well, that is,
${\mathbb {A}}^1$-local as well, that is, ![]() $\mathbf {G}_2$ is strongly
$\mathbf {G}_2$ is strongly ![]() ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
For the third point, by assumption there is a central extension of the form
This central extension is classified by a simplicial fiber sequence of the form
Since ![]() $\mathbf {G}$ is strongly
$\mathbf {G}$ is strongly ![]() ${\mathbb {A}}^1$-invariant,
${\mathbb {A}}^1$-invariant, ![]() $B\mathbf {G}$ is
$B\mathbf {G}$ is ![]() ${\mathbb {A}}^1$-local. Likewise, since
${\mathbb {A}}^1$-local. Likewise, since ![]() $\mathbf {A}$ is strongly
$\mathbf {A}$ is strongly ![]() ${\mathbb {A}}^1$-invariant, abelian and pulled back from a perfect subfield of
${\mathbb {A}}^1$-invariant, abelian and pulled back from a perfect subfield of ![]() $k$ it is strictly
$k$ it is strictly ![]() ${\mathbb {A}}^1$-invariant by appeal to Theorem 3.1.8. Therefore,
${\mathbb {A}}^1$-invariant by appeal to Theorem 3.1.8. Therefore, ![]() $K(\mathbf {A},2)$ is
$K(\mathbf {A},2)$ is ![]() ${\mathbb {A}}^1$-local. Since
${\mathbb {A}}^1$-local. Since ![]() $K(\mathbf {A},2)$ is simplicially connected by construction, we conclude that
$K(\mathbf {A},2)$ is simplicially connected by construction, we conclude that ![]() $B\mathbf {G}$ is
$B\mathbf {G}$ is ![]() ${\mathbb {A}}^1$-local by appeal to Lemma 3.1.4.
${\mathbb {A}}^1$-local by appeal to Lemma 3.1.4.
Remark 3.1.15 In recent work, Choudhury and Hogadi have established that the kernel and image of a morphism of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves are again strongly
${\mathbb {A}}^1$-invariant sheaves are again strongly ![]() ${\mathbb {A}}^1$-invariant [Reference Choudhury and HogadiCH21, Theorem 1.5].
${\mathbb {A}}^1$-invariant [Reference Choudhury and HogadiCH21, Theorem 1.5].
We now analyze the existence of various limits in the category ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$.
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$.
Lemma 3.1.16 The category ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ has all finite limits, and the forgetful functor
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ has all finite limits, and the forgetful functor ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k \to \mathrm {Grp}_k$ creates limits. More precisely,
$\mathrm {Grp}^{{\mathbb {A}}^1}_k \to \mathrm {Grp}_k$ creates limits. More precisely,
1. the trivial group is strongly
 ${\mathbb {A}}^1$-invariant and is a terminal object; and
${\mathbb {A}}^1$-invariant and is a terminal object; and2. the pullback of a diagram of strongly
 ${\mathbb {A}}^1$-invariant sheaves is again strongly
${\mathbb {A}}^1$-invariant sheaves is again strongly  ${\mathbb {A}}^1$-invariant (in particular, the intersection of strongly
${\mathbb {A}}^1$-invariant (in particular, the intersection of strongly  ${\mathbb {A}}^1$-invariant sheaves of groups is again strongly
${\mathbb {A}}^1$-invariant sheaves of groups is again strongly  ${\mathbb {A}}^1$-invariant).
${\mathbb {A}}^1$-invariant).
Proof. For the first point, observe that the trivial group ![]() $1$ is evidently strongly
$1$ is evidently strongly ![]() ${\mathbb {A}}^1$-invariant; that it is a terminal object in
${\mathbb {A}}^1$-invariant; that it is a terminal object in ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ follows from the fact that it is a terminal object in
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ follows from the fact that it is a terminal object in ![]() $\mathrm {Grp}_k$.
$\mathrm {Grp}_k$.
For the second point, suppose ![]() $\mathbf {G}$,
$\mathbf {G}$, ![]() $\mathbf {H}_1$ and
$\mathbf {H}_1$ and ![]() $\mathbf {H}_2$ are sheaves of groups, and assume we are given morphisms
$\mathbf {H}_2$ are sheaves of groups, and assume we are given morphisms ![]() $\varphi _1: \mathbf {H}_1 \to \mathbf {G}$ and
$\varphi _1: \mathbf {H}_1 \to \mathbf {G}$ and ![]() $\varphi _2: \mathbf {H}_2 \to \mathbf {G}$. In that case, the simplicial homotopy fiber product
$\varphi _2: \mathbf {H}_2 \to \mathbf {G}$. In that case, the simplicial homotopy fiber product ![]() $B\mathbf {H}_1 \times ^{h}_{B{\mathbf {G}}} B\mathbf {H}_2$ fits into a fiber sequence of the form
$B\mathbf {H}_1 \times ^{h}_{B{\mathbf {G}}} B\mathbf {H}_2$ fits into a fiber sequence of the form
By [Reference May and PontoMP12, Corollary 2.2.3], for example, this description implies that ![]() $\boldsymbol {\pi }_1^s(B\mathbf {H}_1 \times ^{h}_{B{\mathbf {G}}} B\mathbf {H}_2)$ coincides with the pullback of the diagram
$\boldsymbol {\pi }_1^s(B\mathbf {H}_1 \times ^{h}_{B{\mathbf {G}}} B\mathbf {H}_2)$ coincides with the pullback of the diagram ![]() $\mathbf {H}_1 \to \mathbf {G} \leftarrow \mathbf {H}_2$ (because
$\mathbf {H}_1 \to \mathbf {G} \leftarrow \mathbf {H}_2$ (because ![]() $B \mathbf {H}_1 \times B\mathbf {H}_2$ is
$B \mathbf {H}_1 \times B\mathbf {H}_2$ is ![]() $1$-truncated).
$1$-truncated).
If ![]() $\mathbf {G}$,
$\mathbf {G}$, ![]() $\mathbf {H}_1$ and
$\mathbf {H}_1$ and ![]() $\mathbf {H}_2$ are all strongly
$\mathbf {H}_2$ are all strongly ![]() ${\mathbb {A}}^1$-invariant, then the simplicial homotopy fiber product is
${\mathbb {A}}^1$-invariant, then the simplicial homotopy fiber product is ![]() ${\mathbb {A}}^1$-local, again by Lemma 3.1.4 applied to the simplicial fiber sequence of the previous paragraph (
${\mathbb {A}}^1$-local, again by Lemma 3.1.4 applied to the simplicial fiber sequence of the previous paragraph (![]() $B \mathbf {H}_1 \times B\mathbf {H}_2$ is simplicially connected as before). Thus,
$B \mathbf {H}_1 \times B\mathbf {H}_2$ is simplicially connected as before). Thus,
which is precisely what we wanted to show.
Any category that has pullbacks and a terminal object necessarily possesses all finite limits [Reference Mac LaneMac98, Corollary V.2.1]. Finally, the results above establish that the inclusion functor preserves the terminal object and pullbacks and therefore, creates finite limits as well.
Contractions
Definition 3.1.17 If ![]() $\mathbf {G}$ is a strongly
$\mathbf {G}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups, the contraction of
${\mathbb {A}}^1$-invariant sheaf of groups, the contraction of ![]() $\mathbf {G}$, denoted
$\mathbf {G}$, denoted ![]() $\mathbf {G}_{-1}$, is defined by
$\mathbf {G}_{-1}$, is defined by
The next result summarizes the important formal properties of contraction.
Proposition 3.1.18 (Morel)
Assume ![]() $k$ is a field.
$k$ is a field.
1. The functor
 $\mathbf {G} \mapsto (\mathbf {G})_{-1}$ defines an endofunctor of
$\mathbf {G} \mapsto (\mathbf {G})_{-1}$ defines an endofunctor of  $\mathrm {Grp}_k^{{\mathbb {A}}^1}$.
$\mathrm {Grp}_k^{{\mathbb {A}}^1}$.2. If
 $k$ is perfect, then contraction restricts to an endofunctor of
$k$ is perfect, then contraction restricts to an endofunctor of  $\mathrm {Ab}^{{\mathbb {A}}^1}_k$ to
$\mathrm {Ab}^{{\mathbb {A}}^1}_k$ to  $\mathrm {Ab}^{{\mathbb {A}}^1}_k$.
$\mathrm {Ab}^{{\mathbb {A}}^1}_k$.3. The contraction functor preserves short exact sequences.
Proof. The assignment ![]() $\mathbf {G} \mapsto \mathbf {G}_{-1}$ is evidently functorial. That
$\mathbf {G} \mapsto \mathbf {G}_{-1}$ is evidently functorial. That ![]() $\mathbf {G}_{-1}$ is again strongly
$\mathbf {G}_{-1}$ is again strongly ![]() ${\mathbb {A}}^1$-invariant is [Reference MorelMor12, Lemma 2.32]. The second statement follows from the first and Theorem 3.1.8. The third statement is [Reference MorelMor12, Lemma 7.33].
${\mathbb {A}}^1$-invariant is [Reference MorelMor12, Lemma 2.32]. The second statement follows from the first and Theorem 3.1.8. The third statement is [Reference MorelMor12, Lemma 7.33].
The next result explains the geometric importance of the contraction construction.
Theorem 3.1.19 [Reference MorelMor12, Theorem 6.13]
Suppose ![]() $(\mathscr {X},x)$ is a pointed
$(\mathscr {X},x)$ is a pointed ![]() ${\mathbb {A}}^1$-connected space. The following statements hold.
${\mathbb {A}}^1$-connected space. The following statements hold.
1. The space
 $\Omega _{{{\mathbf {G}}_{m}^{}}}\mathscr {X}$ is again pointed and
$\Omega _{{{\mathbf {G}}_{m}^{}}}\mathscr {X}$ is again pointed and  ${\mathbb {A}}^1$-connected.
${\mathbb {A}}^1$-connected.2.
 $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\Omega _{{{\mathbf {G}}_{m}^{}}}\mathscr {X}) = \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_{-1}$.
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\Omega _{{{\mathbf {G}}_{m}^{}}}\mathscr {X}) = \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_{-1}$.
Strong  ${\mathbb {A}}^1$-invariance of group-theoretic constructions
${\mathbb {A}}^1$-invariance of group-theoretic constructions
If ![]() $\mathbf {G}$ is a sheaf of groups, then we write
$\mathbf {G}$ is a sheaf of groups, then we write ![]() $Z(\mathbf {G})$ for the kernel of the morphism
$Z(\mathbf {G})$ for the kernel of the morphism ![]() $\mathbf {G} \to \mathbf {Aut}(\mathbf {G})$ (sectionwise, sending an element to its corresponding inner automorphism). There is a natural homomorphism
$\mathbf {G} \to \mathbf {Aut}(\mathbf {G})$ (sectionwise, sending an element to its corresponding inner automorphism). There is a natural homomorphism
given by the product.
More generally, suppose we are given a homomorphism of sheaves of groups ![]() $\varphi : \mathbf {H} \to \mathbf {G}$. Consider the sheaf of pointed sets
$\varphi : \mathbf {H} \to \mathbf {G}$. Consider the sheaf of pointed sets ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$. This sheaf of pointed sets comes equipped with an action of the sheaf
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$. This sheaf of pointed sets comes equipped with an action of the sheaf ![]() $\mathbf {G}$ by conjugation on the target. Viewing
$\mathbf {G}$ by conjugation on the target. Viewing ![]() $\varphi$ as a global section of
$\varphi$ as a global section of ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$, we define
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$, we define ![]() $C_{\mathbf {G}}(\varphi )$ to be the sheaf-theoretic stabilizer of the section
$C_{\mathbf {G}}(\varphi )$ to be the sheaf-theoretic stabilizer of the section ![]() $\varphi \in \operatorname {Hom}(\mathbf {H},\mathbf {G})$ under the conjugation action of
$\varphi \in \operatorname {Hom}(\mathbf {H},\mathbf {G})$ under the conjugation action of ![]() $\mathbf {G}$.
$\mathbf {G}$.
The homomorphism ![]() $\varphi$ induces an evaluation homomorphism
$\varphi$ induces an evaluation homomorphism
when ![]() $\varphi$ is the identity homomorphism on
$\varphi$ is the identity homomorphism on ![]() $\mathbf {G}$, this homomorphism coincides with the one defined in the preceding paragraph.
$\mathbf {G}$, this homomorphism coincides with the one defined in the preceding paragraph.
With ![]() $\varphi : \mathbf {H} \to \mathbf {G}$ as above, write
$\varphi : \mathbf {H} \to \mathbf {G}$ as above, write ![]() $\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ for the component of the internal mapping space containing
$\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ for the component of the internal mapping space containing ![]() $B\varphi$. The homomorphism of the preceding paragraph induces a morphism
$B\varphi$. The homomorphism of the preceding paragraph induces a morphism
and applying ![]() $\boldsymbol {\pi }_1$ defines a homomorphism
$\boldsymbol {\pi }_1$ defines a homomorphism
Again, in the special case where ![]() $\varphi$ is the identity map on
$\varphi$ is the identity map on ![]() $\mathbf {G}$, this reduces to a homomorphism
$\mathbf {G}$, this reduces to a homomorphism ![]() $Z(\mathbf {G}) \to \boldsymbol {\pi }_1(\operatorname {Map}(B\mathbf {G},B\mathbf {G})_1)$.
$Z(\mathbf {G}) \to \boldsymbol {\pi }_1(\operatorname {Map}(B\mathbf {G},B\mathbf {G})_1)$.
Proposition 3.1.20 Assume ![]() $k$ is a field, and
$k$ is a field, and ![]() $\varphi : \mathbf {H} \to \mathbf {G}$ is a morphism in
$\varphi : \mathbf {H} \to \mathbf {G}$ is a morphism in ![]() $\mathrm {Grp}_k$.
$\mathrm {Grp}_k$.
1. The morphism
is an isomorphism of sheaves of groups. \[ C_{{\mathbf{G}}}(\varphi) \longrightarrow \boldsymbol{\pi}_1(\operatorname{Map}(B\mathbf{H},B\mathbf{G})_{\varphi}) \]
\[ C_{{\mathbf{G}}}(\varphi) \longrightarrow \boldsymbol{\pi}_1(\operatorname{Map}(B\mathbf{H},B\mathbf{G})_{\varphi}) \]2. If
 $\mathbf {G}$ is strongly
$\mathbf {G}$ is strongly  ${\mathbb {A}}^1$-invariant, then so is
${\mathbb {A}}^1$-invariant, then so is  $C_{{\mathbf {G}}}(\varphi )$.
$C_{{\mathbf {G}}}(\varphi )$.3. If
 $k$ is a perfect field, then
$k$ is a perfect field, then  $Z({\mathbf {G}})$ is strictly
$Z({\mathbf {G}})$ is strictly  ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
Proof. The first statement is a sheaf-theoretic variant of a classical statement about discrete groups, which is essentially an exercise in covering space theory. Indeed, we claim that there is an evaluation morphism ![]() $\operatorname {Map}(B\mathbf {H},B\mathbf {G})_{\varphi } \to B\mathbf {G}$ that fits into a simplicial fiber sequence of the form
$\operatorname {Map}(B\mathbf {H},B\mathbf {G})_{\varphi } \to B\mathbf {G}$ that fits into a simplicial fiber sequence of the form
where ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$ is viewed as a simplicially constant presheaf, that is, all face and degeneracy maps are reduced to the identity. Granting this, taking homotopy sheaves of this fiber sequence with base point
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$ is viewed as a simplicially constant presheaf, that is, all face and degeneracy maps are reduced to the identity. Granting this, taking homotopy sheaves of this fiber sequence with base point ![]() $\varphi$ yields a long exact sequence in homotopy sheaves of the form
$\varphi$ yields a long exact sequence in homotopy sheaves of the form
and the first statement follows immediately from the fact that the action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$ is induced by conjugation on the target, in conjunction with the definition of
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$ is induced by conjugation on the target, in conjunction with the definition of ![]() $C_{{\mathbf {G}}}(\varphi )$.
$C_{{\mathbf {G}}}(\varphi )$.
To produce this fiber sequence, recall that if ![]() $H$ and
$H$ and ![]() $G$ are (discrete) groups, we may form the internal hom-groupoid
$G$ are (discrete) groups, we may form the internal hom-groupoid ![]() $\operatorname {Hom}(BH,BG)$: objects are group homomorphisms
$\operatorname {Hom}(BH,BG)$: objects are group homomorphisms ![]() $H \to G$, and, given two objects
$H \to G$, and, given two objects ![]() $f: H \to G$ and
$f: H \to G$ and ![]() $f': H \to G$, a morphism from
$f': H \to G$, a morphism from ![]() $f$ to
$f$ to ![]() $f'$ is an element
$f'$ is an element ![]() $g \in G$ conjugating
$g \in G$ conjugating ![]() $f$ to
$f$ to ![]() $f'$. Equivalently,
$f'$. Equivalently, ![]() $\operatorname {Hom}(BH,BG)$ is the ‘action groupoid’ attached to the set
$\operatorname {Hom}(BH,BG)$ is the ‘action groupoid’ attached to the set ![]() $\operatorname {Hom}(H,G)$ viewed as a
$\operatorname {Hom}(H,G)$ viewed as a ![]() $G$-set with
$G$-set with ![]() $G$ acting by conjugation on the target. There is an associated morphism of groupoids
$G$ acting by conjugation on the target. There is an associated morphism of groupoids ![]() $\operatorname {Hom}(BH,BG) \to BG$: send an object
$\operatorname {Hom}(BH,BG) \to BG$: send an object ![]() $f: H \to G$ to the unique object of
$f: H \to G$ to the unique object of ![]() $BG$ and an element
$BG$ and an element ![]() $g \in G$ conjugating
$g \in G$ conjugating ![]() $f$ to
$f$ to ![]() $f'$ to the element
$f'$ to the element ![]() $g$. In terms of action groupoids, this is the functor corresponding to the morphism of
$g$. In terms of action groupoids, this is the functor corresponding to the morphism of ![]() $G$-sets
$G$-sets ![]() $\operatorname {Hom}(H,G) \to \ast$. Covering space theory implies that the nerve of the groupoid
$\operatorname {Hom}(H,G) \to \ast$. Covering space theory implies that the nerve of the groupoid ![]() $\operatorname {Hom}(BH,BG)$ coincides with the mapping space
$\operatorname {Hom}(BH,BG)$ coincides with the mapping space ![]() $\operatorname {Map}(BH,BG)$, at which point one immediately deduces the existence of a fiber sequence as above in the category of simplicial sets.
$\operatorname {Map}(BH,BG)$, at which point one immediately deduces the existence of a fiber sequence as above in the category of simplicial sets.
The general case reduces to the case just mentioned using the homotopy-theoretic interpretation of stacks in terms of ![]() $1$-truncated simplicial presheaves (i.e. having no homotopy in degrees
$1$-truncated simplicial presheaves (i.e. having no homotopy in degrees ![]() $\geq 1$; see [Reference HollanderHol08, Reference JardineJar01]). Indeed, consider the action of
$\geq 1$; see [Reference HollanderHol08, Reference JardineJar01]). Indeed, consider the action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$ by conjugation; the homotopy quotient of this action fits into a simplicial fiber sequence of the form
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$ by conjugation; the homotopy quotient of this action fits into a simplicial fiber sequence of the form
where ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})_{h\mathbf {G}}$ is modeled by the usual simplicial Borel construction.
$\operatorname {Hom}(\mathbf {H},\mathbf {G})_{h\mathbf {G}}$ is modeled by the usual simplicial Borel construction.
To establish the original claim, it suffices to show that the middle term is Nisnevich locally weakly equivalent to ![]() $\operatorname {Map}(B\mathbf {H},B\mathbf {G})$, in which case the original statement follows from the discussion above by taking the fiber over the base point corresponding to
$\operatorname {Map}(B\mathbf {H},B\mathbf {G})$, in which case the original statement follows from the discussion above by taking the fiber over the base point corresponding to ![]() $\varphi$. To see this, we use the following model for the mapping space. The space
$\varphi$. To see this, we use the following model for the mapping space. The space ![]() $B\mathbf {G}$ is canonically simplicially weakly equivalent to the simplicial presheaf
$B\mathbf {G}$ is canonically simplicially weakly equivalent to the simplicial presheaf ![]() $B\mathrm {Tors}(\mathbf {G})$ that assigns to
$B\mathrm {Tors}(\mathbf {G})$ that assigns to ![]() $U \in \mathrm {Sm}_k$ the nerve of the groupoid
$U \in \mathrm {Sm}_k$ the nerve of the groupoid ![]() $B\mathrm {Tors}(\mathbf {G})(U)$ of
$B\mathrm {Tors}(\mathbf {G})(U)$ of ![]() $\mathbf {G}$-torsors on
$\mathbf {G}$-torsors on ![]() $U$ by [Reference Asok, Hoyois and WendtAHW18, Lemma 2.3.2(1)].
$U$ by [Reference Asok, Hoyois and WendtAHW18, Lemma 2.3.2(1)].
There is a map ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})_{h\mathbf {G}} \to \operatorname {Map}(B\mathbf {H},B\mathrm {Tors}(\mathbf {G}))$ induced by the classifying space functor: at the level of
$\operatorname {Hom}(\mathbf {H},\mathbf {G})_{h\mathbf {G}} \to \operatorname {Map}(B\mathbf {H},B\mathrm {Tors}(\mathbf {G}))$ induced by the classifying space functor: at the level of ![]() $0$-simplices, a homomorphism
$0$-simplices, a homomorphism ![]() $\mathbf {H} \to \mathbf {G}$ defines a morphism
$\mathbf {H} \to \mathbf {G}$ defines a morphism ![]() $B\mathbf {H} \to B\mathbf {G}$ and conjugate homomorphisms induce the same map. That this map is a Nisnevich local weak equivalence can be checked sectionwise; we treat the case of
$B\mathbf {H} \to B\mathbf {G}$ and conjugate homomorphisms induce the same map. That this map is a Nisnevich local weak equivalence can be checked sectionwise; we treat the case of ![]() $0$-simplices as the general case is similar. A section of
$0$-simplices as the general case is similar. A section of ![]() $\operatorname {Map}(B\mathbf {H},B\mathrm {Tors}(\mathbf {G}))(U)$ is a
$\operatorname {Map}(B\mathbf {H},B\mathrm {Tors}(\mathbf {G}))(U)$ is a ![]() $\mathbf {G}$-torsor over
$\mathbf {G}$-torsor over ![]() $B\mathbf {H} \times U$. By picking a refinement
$B\mathbf {H} \times U$. By picking a refinement ![]() $U' \to U$, the composite map
$U' \to U$, the composite map ![]() $E\mathbf {H} \times U' \to B\mathbf {G}$ admits a trivialization. In that case, a choice of such a trivialization then corresponds to a section of
$E\mathbf {H} \times U' \to B\mathbf {G}$ admits a trivialization. In that case, a choice of such a trivialization then corresponds to a section of ![]() $\operatorname {Hom}(\mathbf {H},\mathbf {G})$ over
$\operatorname {Hom}(\mathbf {H},\mathbf {G})$ over ![]() $U'$. Unwinding the definitions, two local sections determine isomorphic torsors if they differ by conjugation. This construction is evidently inverse to the one given by the ‘classifying space’ map above, which is thus a Nisnevich local weak equivalence.
$U'$. Unwinding the definitions, two local sections determine isomorphic torsors if they differ by conjugation. This construction is evidently inverse to the one given by the ‘classifying space’ map above, which is thus a Nisnevich local weak equivalence.
For the second statement, it suffices to observe that ![]() $\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ is
$\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ is ![]() ${\mathbb {A}}^1$-local. To see this, observe that since
${\mathbb {A}}^1$-local. To see this, observe that since ![]() $B\mathbf {G}$ is
$B\mathbf {G}$ is ![]() ${\mathbb {A}}^1$-local,
${\mathbb {A}}^1$-local, ![]() $\operatorname {Map}(\mathscr {Y},B\mathbf {G})$ is
$\operatorname {Map}(\mathscr {Y},B\mathbf {G})$ is ![]() ${\mathbb {A}}^1$-local for any
${\mathbb {A}}^1$-local for any ![]() $\mathscr {Y}$. Likewise, any component of an
$\mathscr {Y}$. Likewise, any component of an ![]() ${\mathbb {A}}^1$-local space is
${\mathbb {A}}^1$-local space is ![]() ${\mathbb {A}}^1$-local, so it follows that
${\mathbb {A}}^1$-local, so it follows that ![]() $\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ is
$\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi$ is ![]() ${\mathbb {A}}^1$-local is well. In that case,
${\mathbb {A}}^1$-local is well. In that case, ![]() $\boldsymbol {\pi }_1(\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi )$ is strongly
$\boldsymbol {\pi }_1(\operatorname {Map}(B\mathbf {H},B\mathbf {G})_\varphi )$ is strongly ![]() ${\mathbb {A}}^1$-invariant, and the strong
${\mathbb {A}}^1$-invariant, and the strong ![]() ${\mathbb {A}}^1$-invariance of
${\mathbb {A}}^1$-invariance of ![]() $C_{{\mathbf {G}}}(\varphi )$ then follows immediately from the statement (1).
$C_{{\mathbf {G}}}(\varphi )$ then follows immediately from the statement (1).
The third statement follows from the second by taking ![]() $\varphi$ to be the identity map on
$\varphi$ to be the identity map on ![]() $\mathbf {G}$ and using the fact that
$\mathbf {G}$ and using the fact that ![]() $Z({\mathbf {G}})$ is a sheaf of abelian groups.
$Z({\mathbf {G}})$ is a sheaf of abelian groups.
Remark 3.1.21 The assertion that the center of a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf is again strongly
${\mathbb {A}}^1$-invariant sheaf is again strongly ![]() ${\mathbb {A}}^1$-invariant has been recently established by different means by Choudhury and Hogadi [Reference Choudhury and HogadiCH21, Theorem 3.1].
${\mathbb {A}}^1$-invariant has been recently established by different means by Choudhury and Hogadi [Reference Choudhury and HogadiCH21, Theorem 3.1].
If ![]() $\mathbf {G}$ is a sheaf of groups, define a sequence of quotients of
$\mathbf {G}$ is a sheaf of groups, define a sequence of quotients of ![]() $\mathbf {G}$ inductively as follows. Set
$\mathbf {G}$ inductively as follows. Set ![]() $\mathbf {G}_0 = \mathbf {G}$ and define
$\mathbf {G}_0 = \mathbf {G}$ and define ![]() $\mathbf {G}_i$,
$\mathbf {G}_i$, ![]() $i \geq 1$, inductively by setting
$i \geq 1$, inductively by setting ![]() $\mathbf {G}_i = \mathbf {G}_{i-1}/Z(\mathbf {G}_{i-1})$. In that case, we define the
$\mathbf {G}_i = \mathbf {G}_{i-1}/Z(\mathbf {G}_{i-1})$. In that case, we define the ![]() $i$th higher center
$i$th higher center ![]() $Z_i(\mathbf {G})$ as the kernel of the map
$Z_i(\mathbf {G})$ as the kernel of the map ![]() $\mathbf {G} \to \mathbf {G}_i$.
$\mathbf {G} \to \mathbf {G}_i$.
Proposition 3.1.22 Suppose ![]() $\mathbf {G}$ is a strongly
$\mathbf {G}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups. The following statements hold.
${\mathbb {A}}^1$-invariant sheaf of groups. The following statements hold.
1. The higher centers
 $Z_i(\mathbf {G})$ of
$Z_i(\mathbf {G})$ of  $\mathbf {G}$ are all strongly
$\mathbf {G}$ are all strongly  ${\mathbb {A}}^1$-invariant normal subsheaves of groups of
${\mathbb {A}}^1$-invariant normal subsheaves of groups of  $\mathbf {G}$.
$\mathbf {G}$.2. Each of these sheaves is characteristic, that is, it is stable under the natural action of
 $\mathbf {Aut}(\mathbf {G})$.
$\mathbf {Aut}(\mathbf {G})$.3. The quotients
 $\mathbf {G}/Z_i(\mathbf {G})$ are strongly
$\mathbf {G}/Z_i(\mathbf {G})$ are strongly  ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
Proof. The sheaf ![]() $\mathbf {G}_0 := \mathbf {G}$ is strongly
$\mathbf {G}_0 := \mathbf {G}$ is strongly ![]() ${\mathbb {A}}^1$-invariant by assumption. Since
${\mathbb {A}}^1$-invariant by assumption. Since ![]() $\mathbf {G}_i = \mathbf {G}_{i-1}/Z(\mathbf {G}_{i-1})$, it follows inductively by combining Proposition 3.1.20(3) and Lemma 3.1.14(3) that
$\mathbf {G}_i = \mathbf {G}_{i-1}/Z(\mathbf {G}_{i-1})$, it follows inductively by combining Proposition 3.1.20(3) and Lemma 3.1.14(3) that ![]() $\mathbf {G}_i$ is strongly
$\mathbf {G}_i$ is strongly ![]() ${\mathbb {A}}^1$-invariant. The fact that
${\mathbb {A}}^1$-invariant. The fact that ![]() $Z_i(\mathbf {G})$ is strongly
$Z_i(\mathbf {G})$ is strongly ![]() ${\mathbb {A}}^1$-invariant follows from Lemma 3.1.14(1) since it is the kernel of a map of strongly
${\mathbb {A}}^1$-invariant follows from Lemma 3.1.14(1) since it is the kernel of a map of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves. The final statement is immediate since
${\mathbb {A}}^1$-invariant sheaves. The final statement is immediate since ![]() $\mathbf {G}/Z_i(\mathbf {G}) = \mathbf {G}_i$ by definition. The statement about being characteristic subgroup sheaves may be checked stalkwise, in which case it reduces to the corresponding fact in group theory.
$\mathbf {G}/Z_i(\mathbf {G}) = \mathbf {G}_i$ by definition. The statement about being characteristic subgroup sheaves may be checked stalkwise, in which case it reduces to the corresponding fact in group theory.
We also make one further remark, unrelated to the above discussion, for future use.
Remark 3.1.23 If ![]() $\mathscr {S}$ is a pointed sheaf of sets, then the free strongly
$\mathscr {S}$ is a pointed sheaf of sets, then the free strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups on
${\mathbb {A}}^1$-invariant sheaf of groups on ![]() $\mathscr {S}$ is defined to be
$\mathscr {S}$ is defined to be ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\Sigma \mathscr {S})$. One may check that this construction defines a functor from the category of sheaves of sets to the category of strongly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\Sigma \mathscr {S})$. One may check that this construction defines a functor from the category of sheaves of sets to the category of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups that is left adjoint to the evident forgetful functor [Reference MorelMor12, Lemma 7.23]. Morel writes
${\mathbb {A}}^1$-invariant sheaves of groups that is left adjoint to the evident forgetful functor [Reference MorelMor12, Lemma 7.23]. Morel writes ![]() $F_{{\mathbb {A}}^1}(\mathscr {S})$ for this construction in [Reference MorelMor12, p. 189]. For our purposes, it will be important to remember that
$F_{{\mathbb {A}}^1}(\mathscr {S})$ for this construction in [Reference MorelMor12, p. 189]. For our purposes, it will be important to remember that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1) = F_{{\mathbb {A}}^1}({{\mathbf {G}}_{m}^{}})$; we will come back to this observation in Example 3.2.11.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1) = F_{{\mathbb {A}}^1}({{\mathbf {G}}_{m}^{}})$; we will come back to this observation in Example 3.2.11.
3.2  ${\mathbb {A}}^1$-nilpotent groups
${\mathbb {A}}^1$-nilpotent groups
We now define ![]() ${\mathbb {A}}^1$-nilpotent actions and
${\mathbb {A}}^1$-nilpotent actions and ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups in parallel with the classical story: the latter are defined as iterated central extensions of strictly
${\mathbb {A}}^1$-nilpotent sheaves of groups in parallel with the classical story: the latter are defined as iterated central extensions of strictly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups.
${\mathbb {A}}^1$-invariant sheaves of groups.
Definition 3.2.1 Suppose ![]() $\mathbf {G}$ and
$\mathbf {G}$ and ![]() $\mathbf {H}$ are strongly
$\mathbf {H}$ are strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups.
${\mathbb {A}}^1$-invariant sheaves of groups.
1. An action
 $\varphi$ of
$\varphi$ of  $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$ is said to be
$\mathbf {H}$ is said to be  ${\mathbb {A}}^1$-nilpotent (respectively, locally
${\mathbb {A}}^1$-nilpotent (respectively, locally  ${\mathbb {A}}^1$-nilpotent) if
${\mathbb {A}}^1$-nilpotent) if  $\mathbf {H}$ has a finite (respectively, locally finite)
$\mathbf {H}$ has a finite (respectively, locally finite)  $\mathbf {G}$-central series (see Definitions 2.1.1 and 2.1.3)
such that the successive subquotients
$\mathbf {G}$-central series (see Definitions 2.1.1 and 2.1.3)
such that the successive subquotients \[ \mathbf{H} = \mathbf{H}_0 \supset \mathbf{H}_1 \cdots \]
\[ \mathbf{H} = \mathbf{H}_0 \supset \mathbf{H}_1 \cdots \] $\mathbf {H}_i/\mathbf {H}_{i+1}$ are strongly
$\mathbf {H}_i/\mathbf {H}_{i+1}$ are strongly  ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.2. A
 $\mathbf {G}$-central series for
$\mathbf {G}$-central series for  $\mathbf {H}$ as in the preceding point will be called an
$\mathbf {H}$ as in the preceding point will be called an  ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-  $\mathbf {G}$-central series; the smallest integer
$\mathbf {G}$-central series; the smallest integer  $i$ such that
$i$ such that  $\mathbf {H}_j = 1$ for all
$\mathbf {H}_j = 1$ for all  $j \geq i$ will be called the length of the series.
$j \geq i$ will be called the length of the series.3. We will say that
 $\mathbf {G}$ is (locally)
$\mathbf {G}$ is (locally)  ${\mathbb {A}}^1$-nilpotent if the conjugation action of
${\mathbb {A}}^1$-nilpotent if the conjugation action of  $\mathbf {G}$ on itself is (locally)
$\mathbf {G}$ on itself is (locally)  ${\mathbb {A}}^1$-nilpotent, that is,
${\mathbb {A}}^1$-nilpotent, that is,  $\mathbf {G}$ admits a decreasing filtration by normal subgroup sheaves with abelian strongly
$\mathbf {G}$ admits a decreasing filtration by normal subgroup sheaves with abelian strongly  ${\mathbb {A}}^1$-invariant subquotients and such that the induced action of
${\mathbb {A}}^1$-invariant subquotients and such that the induced action of  $\mathbf {G}$ on successive subquotients is trivial; in this case the filtration will be called an
$\mathbf {G}$ on successive subquotients is trivial; in this case the filtration will be called an  ${\mathbb {A}}^1$-central series for
${\mathbb {A}}^1$-central series for  $\mathbf {G}$.
$\mathbf {G}$.
Remark 3.2.2 Given the above definition, a number of remarks are in order.
1. Lemma 3.1.14 states that kernels of morphisms of strongly
 ${\mathbb {A}}^1$-invariant sheaves of groups are again strongly
${\mathbb {A}}^1$-invariant sheaves of groups are again strongly  ${\mathbb {A}}^1$-invariant. Since
${\mathbb {A}}^1$-invariant. Since  $\mathbf {H}_{i+1}$ is the kernel of the morphism
$\mathbf {H}_{i+1}$ is the kernel of the morphism  $\mathbf {H}_i \to \mathbf {H}_i/\mathbf {H}_{i+1}$, and the latter is strongly
$\mathbf {H}_i \to \mathbf {H}_i/\mathbf {H}_{i+1}$, and the latter is strongly  ${\mathbb {A}}^1$-invariant by assumption, we conclude inductively that each
${\mathbb {A}}^1$-invariant by assumption, we conclude inductively that each  $\mathbf {H}_i$ is a strongly
$\mathbf {H}_i$ is a strongly  ${\mathbb {A}}^1$-invariant subsheaf of
${\mathbb {A}}^1$-invariant subsheaf of  $\mathbf {H}$.
$\mathbf {H}$.2. By Theorem 3.1.8, assuming
 $k$ is perfect, the condition
$k$ is perfect, the condition  $\mathbf {H}_i/\mathbf {H}_{i+1}$ is strongly
$\mathbf {H}_i/\mathbf {H}_{i+1}$ is strongly  ${\mathbb {A}}^1$-invariant implies
${\mathbb {A}}^1$-invariant implies  $\mathbf {H}_i/\mathbf {H}_{i+1}$ is strictly
$\mathbf {H}_i/\mathbf {H}_{i+1}$ is strictly  ${\mathbb {A}}^1$-invariant. Indeed,
${\mathbb {A}}^1$-invariant. Indeed,  $\mathbf {H}_i/\mathbf {H}_{i+1}$ is abelian since it arises as a subquotient in a
$\mathbf {H}_i/\mathbf {H}_{i+1}$ is abelian since it arises as a subquotient in a  $\mathbf {G}$-central series.
$\mathbf {G}$-central series.3. If
 $\mathbf {G}$ is an
$\mathbf {G}$ is an  ${\mathbb {A}}^1$-nilpotent sheaf of groups, then the condition that
${\mathbb {A}}^1$-nilpotent sheaf of groups, then the condition that  $\mathbf {G}_i/\mathbf {G}_{i+1}$ is abelian is implied by the assumption that the conjugation action of
$\mathbf {G}_i/\mathbf {G}_{i+1}$ is abelian is implied by the assumption that the conjugation action of  $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {G}_i/\mathbf {G}_{i+1}$ is trivial. As usual, if
$\mathbf {G}_i/\mathbf {G}_{i+1}$ is trivial. As usual, if  $\mathbf {G}$ is
$\mathbf {G}$ is  ${\mathbb {A}}^1$-nilpotent, the extensions
are all central extensions of strongly
${\mathbb {A}}^1$-nilpotent, the extensions
are all central extensions of strongly \[ 1 \longrightarrow \mathbf{G}_i/\mathbf{G}_{i+1} \longrightarrow \mathbf{G}/\mathbf{G}_{i+1} \longrightarrow \mathbf{G}/\mathbf{G}_i \longrightarrow 1 \]
\[ 1 \longrightarrow \mathbf{G}_i/\mathbf{G}_{i+1} \longrightarrow \mathbf{G}/\mathbf{G}_{i+1} \longrightarrow \mathbf{G}/\mathbf{G}_i \longrightarrow 1 \] ${\mathbb {A}}^1$-invariant sheaves.
${\mathbb {A}}^1$-invariant sheaves.
Proposition 3.2.3 Assume ![]() $k$ is a perfect field, and
$k$ is a perfect field, and ![]() $\mathbf {G}$ is a sheaf of groups.
$\mathbf {G}$ is a sheaf of groups.
1. The sheaf
 $\mathbf {G}$ is
$\mathbf {G}$ is  ${\mathbb {A}}^1$-nilpotent if and only if it is strongly
${\mathbb {A}}^1$-nilpotent if and only if it is strongly  ${\mathbb {A}}^1$-invariant and the upper central series terminates in finitely many steps.
${\mathbb {A}}^1$-invariant and the upper central series terminates in finitely many steps.2. In particular, a sheaf of groups
 $\mathbf {G}$ is
$\mathbf {G}$ is  ${\mathbb {A}}^1$-nilpotent if and only if
${\mathbb {A}}^1$-nilpotent if and only if  $\mathbf {G}$ is strongly
$\mathbf {G}$ is strongly  ${\mathbb {A}}^1$-invariant and nilpotent as a sheaf of groups.
${\mathbb {A}}^1$-invariant and nilpotent as a sheaf of groups.
Proof. The standard proof from group theory that a group is nilpotent if and only if its upper central series terminates in finitely many steps works for sheaves of groups. Next, observe that Proposition 3.1.22 guarantees that if ![]() $\mathbf {G}$ is strongly
$\mathbf {G}$ is strongly ![]() ${\mathbb {A}}^1$-invariant then the upper central series has terms that are strongly
${\mathbb {A}}^1$-invariant then the upper central series has terms that are strongly ![]() ${\mathbb {A}}^1$-invariant with strictly
${\mathbb {A}}^1$-invariant with strictly ![]() ${\mathbb {A}}^1$-invariant subquotients. Therefore, if
${\mathbb {A}}^1$-invariant subquotients. Therefore, if ![]() $\mathbf {G}$ has a finite upper central series, it has a finite
$\mathbf {G}$ has a finite upper central series, it has a finite ![]() ${\mathbb {A}}^1$-central series. Conversely, if
${\mathbb {A}}^1$-central series. Conversely, if ![]() $\mathbf {G}$ has a finite
$\mathbf {G}$ has a finite ![]() ${\mathbb {A}}^1$-central series, then the upper central series must terminate in finitely many steps as well. The second statement follows immediately from the first.
${\mathbb {A}}^1$-central series, then the upper central series must terminate in finitely many steps as well. The second statement follows immediately from the first.
Remark 3.2.4 If ![]() $\mathbf {G}$ is a strongly
$\mathbf {G}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups, then one may define its ‘
${\mathbb {A}}^1$-invariant sheaf of groups, then one may define its ‘![]() ${\mathbb {A}}^1$-abelianization’
${\mathbb {A}}^1$-abelianization’ ![]() $\mathbf {G}^{\rm ab} := \mathbf {H}_1^{{\mathbb {A}}^1}(B\mathbf {G})$ (see § 4.1); this sheaf is the initial strictly
$\mathbf {G}^{\rm ab} := \mathbf {H}_1^{{\mathbb {A}}^1}(B\mathbf {G})$ (see § 4.1); this sheaf is the initial strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of abelian groups admitting a morphism from
${\mathbb {A}}^1$-invariant sheaf of abelian groups admitting a morphism from ![]() $\mathbf {G}$. Choudhury and Hogadi prove that the map
$\mathbf {G}$. Choudhury and Hogadi prove that the map ![]() $\mathbf {G} \to \mathbf {G}^{\rm ab}$ is an epimorphism [Reference Choudhury and HogadiCH21, Theorem 1.1]. One may then inductively construct a lower
$\mathbf {G} \to \mathbf {G}^{\rm ab}$ is an epimorphism [Reference Choudhury and HogadiCH21, Theorem 1.1]. One may then inductively construct a lower ![]() ${\mathbb {A}}^1$-central series for
${\mathbb {A}}^1$-central series for ![]() $\mathbf {G}$.
$\mathbf {G}$.
Example 3.2.5 The key example of a locally ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups arises from the scaling action of
${\mathbb {A}}^1$-nilpotent sheaf of groups arises from the scaling action of ![]() ${{\mathbf {G}}_{m}^{}}$ on the first non-vanishing
${{\mathbf {G}}_{m}^{}}$ on the first non-vanishing ![]() ${\mathbb {A}}^1$-homotopy sheaf of
${\mathbb {A}}^1$-homotopy sheaf of ![]() ${\mathbb {A}}^{n} \,{\setminus}\, 0$,
${\mathbb {A}}^{n} \,{\setminus}\, 0$, ![]() $n \geq 2$, at least if we work over a base field that is not formally real. (Note that the action of
$n \geq 2$, at least if we work over a base field that is not formally real. (Note that the action of ![]() ${{\mathbf {G}}_{m}^{}}$ on
${{\mathbf {G}}_{m}^{}}$ on ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ does not preserve base points, but this is irrelevant for the action on the first
${\mathbb {A}}^n \,{\setminus}\, 0$ does not preserve base points, but this is irrelevant for the action on the first ![]() ${\mathbb {A}}^1$-homotopy sheaf because it can be interpreted in terms of
${\mathbb {A}}^1$-homotopy sheaf because it can be interpreted in terms of ![]() ${\mathbb {A}}^1$-homology via the Hurewicz theorem (Theorem 4.2.1).) In this case
${\mathbb {A}}^1$-homology via the Hurewicz theorem (Theorem 4.2.1).) In this case ![]() $\boldsymbol {\pi }_{n-1}^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0) = {{\mathbf {K}}}^{\rm MW}_n$, which has a filtration by the subsheaves
$\boldsymbol {\pi }_{n-1}^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0) = {{\mathbf {K}}}^{\rm MW}_n$, which has a filtration by the subsheaves ![]() $\mathbf {I}^{j}$ for
$\mathbf {I}^{j}$ for ![]() $j \geq n+1$, all of which are stable under multiplication by units. The successive subquotients are isomorphic to either
$j \geq n+1$, all of which are stable under multiplication by units. The successive subquotients are isomorphic to either ![]() ${{\mathbf {K}}}^{\rm M}_n$ or
${{\mathbf {K}}}^{\rm M}_n$ or ![]() ${{\mathbf {K}}}^{\rm M}_{j}/2$,
${{\mathbf {K}}}^{\rm M}_{j}/2$, ![]() $j \geq n+1$, with a trivial action of
$j \geq n+1$, with a trivial action of ![]() ${{\mathbf {G}}_{m}^{}}$ in either. As in Example 2.1.4, the induced filtration on sections over any extension of the base field will be finite.
${{\mathbf {G}}_{m}^{}}$ in either. As in Example 2.1.4, the induced filtration on sections over any extension of the base field will be finite.
Lemma 3.2.6 Suppose ![]() $\varphi : \mathbf {G}' \to \mathbf {G}$ is a morphism of strongly
$\varphi : \mathbf {G}' \to \mathbf {G}$ is a morphism of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups. If
${\mathbb {A}}^1$-invariant sheaves of groups. If ![]() $\mathbf {H}$ is a strongly
$\mathbf {H}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups carrying a (locally)
${\mathbb {A}}^1$-invariant sheaf of groups carrying a (locally) ![]() ${\mathbb {A}}^1$-nilpotent action of
${\mathbb {A}}^1$-nilpotent action of ![]() $\mathbf {G}$, then the action of
$\mathbf {G}$, then the action of ![]() $\mathbf {G}'$ on
$\mathbf {G}'$ on ![]() $\mathbf {H}$ induced by precomposition with
$\mathbf {H}$ induced by precomposition with ![]() $\varphi$ is also (locally)
$\varphi$ is also (locally) ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. Any (locally finite) ![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$ defines, by precomposition with
$\mathbf {H}$ defines, by precomposition with ![]() $\varphi$, a (locally finite)
$\varphi$, a (locally finite) ![]() $\mathbf {G}'$-central series for
$\mathbf {G}'$-central series for ![]() $\mathbf {H}$, that is, this is a special case of Lemma 2.1.5.
$\mathbf {H}$, that is, this is a special case of Lemma 2.1.5.
Lemma 3.2.7 Suppose ![]() $\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$.
$\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$.
1. If
 $\mathbf {G}$ is a (locally)
$\mathbf {G}$ is a (locally)  ${\mathbb {A}}^1$-nilpotent group, then any strongly
${\mathbb {A}}^1$-nilpotent group, then any strongly  ${\mathbb {A}}^1$-invariant subsheaf of groups of
${\mathbb {A}}^1$-invariant subsheaf of groups of  $\mathbf {G}$ is again (locally)
$\mathbf {G}$ is again (locally)  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.2. If
 $k$ is a perfect field, then any strongly
$k$ is a perfect field, then any strongly  ${\mathbb {A}}^1$-invariant quotient of
${\mathbb {A}}^1$-invariant quotient of  $\mathbf {G}$ is again
$\mathbf {G}$ is again  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.3. If
 $\mathbf {A}$ is a strongly
$\mathbf {A}$ is a strongly  ${\mathbb {A}}^1$-invariant sheaf of abelian groups, and
${\mathbb {A}}^1$-invariant sheaf of abelian groups, and  $\mathbf {G}$ is
$\mathbf {G}$ is  ${\mathbb {A}}^1$-nilpotent, then a central extension of
${\mathbb {A}}^1$-nilpotent, then a central extension of  $\mathbf {G}$ by
$\mathbf {G}$ by  $\mathbf {A}$ is again
$\mathbf {A}$ is again  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.4. If
 $\mathbf {H}$ and
$\mathbf {H}$ and  $\mathbf {H}'$ are
$\mathbf {H}'$ are  ${\mathbb {A}}^1$-nilpotent sheaves of groups, and we are given morphisms
${\mathbb {A}}^1$-nilpotent sheaves of groups, and we are given morphisms  $\mathbf {H} \to \mathbf {G}$ and
$\mathbf {H} \to \mathbf {G}$ and  $\mathbf {H}' \to \mathbf {G}$, then
$\mathbf {H}' \to \mathbf {G}$, then  $\mathbf {H} \times _{\mathbf {G}} \mathbf {H}'$ is again
$\mathbf {H} \times _{\mathbf {G}} \mathbf {H}'$ is again  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
In particular, the category of ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups is a subcategory of
${\mathbb {A}}^1$-nilpotent sheaves of groups is a subcategory of ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ that is stable under formation of finite limits.
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ that is stable under formation of finite limits.
Proof. Assume ![]() $\mathbf {G}$ is an
$\mathbf {G}$ is an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups. For the first statement, suppose
${\mathbb {A}}^1$-nilpotent sheaf of groups. For the first statement, suppose ![]() $\mathbf {H}$ is a strongly
$\mathbf {H}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant subsheaf of groups of
${\mathbb {A}}^1$-invariant subsheaf of groups of ![]() $\mathbf {G}$. In that case, Lemma 3.1.16 guarantees that the intersection of the sheaves in an
$\mathbf {G}$. In that case, Lemma 3.1.16 guarantees that the intersection of the sheaves in an ![]() ${\mathbb {A}}^1$-central series for
${\mathbb {A}}^1$-central series for ![]() $\mathbf {G}$ with
$\mathbf {G}$ with ![]() $\mathbf {H}$ provides an
$\mathbf {H}$ provides an ![]() ${\mathbb {A}}^1$-central series for
${\mathbb {A}}^1$-central series for ![]() $\mathbf {H}$. One argues in an identical way to establish local
$\mathbf {H}$. One argues in an identical way to establish local ![]() ${\mathbb {A}}^1$-nilpotence of
${\mathbb {A}}^1$-nilpotence of ![]() $\mathbf {H}$ given the corresponding statement for
$\mathbf {H}$ given the corresponding statement for ![]() $\mathbf {G}$.
$\mathbf {G}$.
For the second statement, observe that any quotient of a nilpotent sheaf of groups is a nilpotent sheaf of groups. Since the quotient is assumed strongly ![]() ${\mathbb {A}}^1$-invariant, the result follows from Proposition 3.2.3.
${\mathbb {A}}^1$-invariant, the result follows from Proposition 3.2.3.
For the third statement, suppose we have a central extension ![]() $\mathbf {G}'$ of
$\mathbf {G}'$ of ![]() $\mathbf {G}$ by
$\mathbf {G}$ by ![]() $\mathbf {A}$. If
$\mathbf {A}$. If ![]() $\mathbf {G}_i$ is a filtration of
$\mathbf {G}_i$ is a filtration of ![]() $\mathbf {G}$ witnessing
$\mathbf {G}$ witnessing ![]() ${\mathbb {A}}^1$-nilpotence with
${\mathbb {A}}^1$-nilpotence with ![]() $\mathbf {G}_n = 1$, then Lemma 3.1.16 implies that
$\mathbf {G}_n = 1$, then Lemma 3.1.16 implies that ![]() $\mathbf {G}'_i := \mathbf {G}_i \times _{\mathbf {G}} \mathbf {G}'$ yields a sequence of strongly
$\mathbf {G}'_i := \mathbf {G}_i \times _{\mathbf {G}} \mathbf {G}'$ yields a sequence of strongly ![]() ${\mathbb {A}}^1$-invariant normal subsheaves containing
${\mathbb {A}}^1$-invariant normal subsheaves containing ![]() $\mathbf {A}$. Setting
$\mathbf {A}$. Setting ![]() $\mathbf {G}'_{n+1} = 1$, one checks that
$\mathbf {G}'_{n+1} = 1$, one checks that ![]() $\mathbf {G}'_i$ provides an
$\mathbf {G}'_i$ provides an ![]() ${\mathbb {A}}^1$-central series for
${\mathbb {A}}^1$-central series for ![]() $\mathbf {G}'$ as in the corresponding statement in classical group theory.
$\mathbf {G}'$ as in the corresponding statement in classical group theory.
For the final assertion, observe that if ![]() $\mathbf {H}$ and
$\mathbf {H}$ and ![]() $\mathbf {H}'$ are
$\mathbf {H}'$ are ![]() ${\mathbb {A}}^1$-nilpotent, then
${\mathbb {A}}^1$-nilpotent, then ![]() $\mathbf {H} \times \mathbf {H}'$ is also
$\mathbf {H} \times \mathbf {H}'$ is also ![]() ${\mathbb {A}}^1$-nilpotent: if
${\mathbb {A}}^1$-nilpotent: if ![]() $\mathbf {H}_i$ and
$\mathbf {H}_i$ and ![]() $\mathbf {H}_i'$ are
$\mathbf {H}_i'$ are ![]() ${\mathbb {A}}^1$-central series (of possibly different lengths) for each group, then
${\mathbb {A}}^1$-central series (of possibly different lengths) for each group, then ![]() $\mathbf {H}_i \times \mathbf {H}_i'$ is an
$\mathbf {H}_i \times \mathbf {H}_i'$ is an ![]() ${\mathbb {A}}^1$-central series for the product. As the fiber product is strongly
${\mathbb {A}}^1$-central series for the product. As the fiber product is strongly ![]() ${\mathbb {A}}^1$-invariant by Lemma 3.1.16, the fact that
${\mathbb {A}}^1$-invariant by Lemma 3.1.16, the fact that ![]() $\mathbf {H} \times _{\mathbf {G}} \mathbf {H}'$ is
$\mathbf {H} \times _{\mathbf {G}} \mathbf {H}'$ is ![]() ${\mathbb {A}}^1$-nilpotent follows from statement (1).
${\mathbb {A}}^1$-nilpotent follows from statement (1).
That the category of ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups is stable under formation of finite limits now follows from the fact that the terminal object in the category of groups (i.e. the trivial sheaf of groups) is
${\mathbb {A}}^1$-nilpotent sheaves of groups is stable under formation of finite limits now follows from the fact that the terminal object in the category of groups (i.e. the trivial sheaf of groups) is ![]() ${\mathbb {A}}^1$-nilpotent, and the fact that this category is closed under pullbacks.
${\mathbb {A}}^1$-nilpotent, and the fact that this category is closed under pullbacks.
Remark 3.2.8 After Lemma 3.2.7, the class of ![]() ${\mathbb {A}}^1$-nilpotent groups can be described as the smallest subcategory of
${\mathbb {A}}^1$-nilpotent groups can be described as the smallest subcategory of ![]() $\mathrm {Grp}^{{\mathbb {A}}^1}_k$ containing all strongly
$\mathrm {Grp}^{{\mathbb {A}}^1}_k$ containing all strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of abelian groups and closed under central extensions. Arbitrary extensions of
${\mathbb {A}}^1$-invariant sheaves of abelian groups and closed under central extensions. Arbitrary extensions of ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups need not be
${\mathbb {A}}^1$-nilpotent sheaves of groups need not be ![]() ${\mathbb {A}}^1$-nilpotent; this follows from Example 3.1.7 since constant group schemes attached to finite groups are strongly
${\mathbb {A}}^1$-nilpotent; this follows from Example 3.1.7 since constant group schemes attached to finite groups are strongly ![]() ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
Definition 3.2.9 If ![]() $\mathbf {G}$ is
$\mathbf {G}$ is ![]() ${\mathbb {A}}^1$-nilpotent, we will say that
${\mathbb {A}}^1$-nilpotent, we will say that ![]() $\mathbf {G}$ has
$\mathbf {G}$ has ![]() ${\mathbb {A}}^1$-nilpotence class
${\mathbb {A}}^1$-nilpotence class ![]() $c$ if the minimum length of an
$c$ if the minimum length of an ![]() ${\mathbb {A}}^1$-central series is
${\mathbb {A}}^1$-central series is ![]() $c$. Similarly, if
$c$. Similarly, if ![]() $\mathbf {H}$ is a strongly
$\mathbf {H}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant group that has an
${\mathbb {A}}^1$-invariant group that has an ![]() ${\mathbb {A}}^1$-nilpotent action of a strongly
${\mathbb {A}}^1$-nilpotent action of a strongly ![]() ${\mathbb {A}}^1$-invariant group
${\mathbb {A}}^1$-invariant group ![]() $\mathbf {G}$, the
$\mathbf {G}$, the ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$- ![]() $\mathbf {G}$-nilpotence class of
$\mathbf {G}$-nilpotence class of ![]() $\mathbf {H}$ is the minimum length of an
$\mathbf {H}$ is the minimum length of an ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$.
$\mathbf {H}$.
Lemma 3.2.10 If ![]() $k$ is a perfect field, and
$k$ is a perfect field, and ![]() $\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$ is an
$\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$ is an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups, then the
${\mathbb {A}}^1$-nilpotent sheaf of groups, then the ![]() ${\mathbb {A}}^1$-nilpotence class of
${\mathbb {A}}^1$-nilpotence class of ![]() $\mathbf {G}$ is the length of the upper central series for
$\mathbf {G}$ is the length of the upper central series for ![]() $\mathbf {G}$.
$\mathbf {G}$.
Proof. This fact follows immediately from the characterization of ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups given in Proposition 3.2.3, and the proof of the corresponding fact in group theory.
${\mathbb {A}}^1$-nilpotent sheaves of groups given in Proposition 3.2.3, and the proof of the corresponding fact in group theory.
Example 3.2.11 The most basic example of an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups is
${\mathbb {A}}^1$-nilpotent sheaf of groups is ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$; this is a non-abelian group which Morel shows is a central extension of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$; this is a non-abelian group which Morel shows is a central extension of ![]() ${{\mathbf {G}}_{m}^{}}$ by
${{\mathbf {G}}_{m}^{}}$ by ![]() ${{\mathbf {K}}}^{\mathrm {MW}}_2$ [Reference MorelMor12, Theorem 7.29 and Remark 7.31]. This example presents the interesting situation that the free strongly
${{\mathbf {K}}}^{\mathrm {MW}}_2$ [Reference MorelMor12, Theorem 7.29 and Remark 7.31]. This example presents the interesting situation that the free strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups on a (non-trivial) sheaf of sets
${\mathbb {A}}^1$-invariant sheaf of groups on a (non-trivial) sheaf of sets ![]() $\mathscr {S}$ may be
$\mathscr {S}$ may be ![]() ${\mathbb {A}}^1$-nilpotent (see Remark 3.1.23 for discussion of the free strongly
${\mathbb {A}}^1$-nilpotent (see Remark 3.1.23 for discussion of the free strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups on a sheaf of sets; in this case
${\mathbb {A}}^1$-invariant sheaf of groups on a sheaf of sets; in this case ![]() $\mathscr {S} = {{\mathbf {G}}_{m}^{}}$). This example will be discussed in greater detail in Remark 3.4.9.
$\mathscr {S} = {{\mathbf {G}}_{m}^{}}$). This example will be discussed in greater detail in Remark 3.4.9.
More on  ${\mathbb {A}}^1$-nilpotent actions
${\mathbb {A}}^1$-nilpotent actions
Momentarily, we will define ![]() ${\mathbb {A}}^1$-nilpotent spaces. We consider in more detail
${\mathbb {A}}^1$-nilpotent spaces. We consider in more detail ![]() ${\mathbb {A}}^1$-nilpotent actions of a strongly
${\mathbb {A}}^1$-nilpotent actions of a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups. The following result will be a key technical tool; it is the analog for
${\mathbb {A}}^1$-invariant sheaf of groups. The following result will be a key technical tool; it is the analog for ![]() ${\mathbb {A}}^1$-nilpotent groups of Lemma 2.1.6, though we note that the statement differs slightly from that one because of the behavior of limits and colimits in the category of strongly
${\mathbb {A}}^1$-nilpotent groups of Lemma 2.1.6, though we note that the statement differs slightly from that one because of the behavior of limits and colimits in the category of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves.
${\mathbb {A}}^1$-invariant sheaves.
Proposition 3.2.12 Assume ![]() $k$ is a perfect field,
$k$ is a perfect field, ![]() $\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$,
$\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$, ![]() $\mathbf {H},\mathbf {H}'$ and
$\mathbf {H},\mathbf {H}'$ and ![]() $\mathbf {H}''$ are strongly
$\mathbf {H}''$ are strongly ![]() ${\mathbb {A}}^1$-invariant sheaves with an action of
${\mathbb {A}}^1$-invariant sheaves with an action of ![]() $\mathbf {G}$, and
$\mathbf {G}$, and
is a ![]() $\mathbf {G}$-equivariant short exact sequence of strongly
$\mathbf {G}$-equivariant short exact sequence of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves.
${\mathbb {A}}^1$-invariant sheaves.
1. If the actions of
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}'$ and
$\mathbf {H}'$ and  $\mathbf {H}''$ are (locally)
$\mathbf {H}''$ are (locally)  ${\mathbb {A}}^1$-nilpotent, then the action on
${\mathbb {A}}^1$-nilpotent, then the action on  $\mathbf {H}$ is (locally)
$\mathbf {H}$ is (locally)  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.2. If the action of
 $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}$ is (locally)
$\mathbf {H}$ is (locally)  ${\mathbb {A}}^1$-nilpotent, then the action of
${\mathbb {A}}^1$-nilpotent, then the action of  $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}'$ is (locally)
$\mathbf {H}'$ is (locally)  ${\mathbb {A}}^1$-nilpotent, and, if the sequence is a central extension, then the action of
${\mathbb {A}}^1$-nilpotent, and, if the sequence is a central extension, then the action of  $\mathbf {G}$ on
$\mathbf {G}$ on  $\mathbf {H}''$ is also (locally)
$\mathbf {H}''$ is also (locally)  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. For the first statement, it suffices to observe that Lemma 3.1.14(2) implies that strongly ![]() ${\mathbb {A}}^1$-invariant sheaves of groups are stable by extensions; the result then follows from the corresponding sheaf-theoretic statement, Lemma 2.1.6.
${\mathbb {A}}^1$-invariant sheaves of groups are stable by extensions; the result then follows from the corresponding sheaf-theoretic statement, Lemma 2.1.6.
For the second statement, we proceed as follows. We prove the statement for locally ![]() ${\mathbb {A}}^1$-nilpotent actions; the proof in the
${\mathbb {A}}^1$-nilpotent actions; the proof in the ![]() ${\mathbb {A}}^1$-nilpotent case follows by simply dropping the word ‘locally;. Suppose we have a locally finite
${\mathbb {A}}^1$-nilpotent case follows by simply dropping the word ‘locally;. Suppose we have a locally finite ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$. Lemma 3.1.16 guarantees that the restriction of the corresponding filtration to
$\mathbf {H}$. Lemma 3.1.16 guarantees that the restriction of the corresponding filtration to ![]() $\mathbf {H}'$ provides a locally finite
$\mathbf {H}'$ provides a locally finite ![]() $\mathbf {G}$-central series of
$\mathbf {G}$-central series of ![]() $\mathbf {H}'$.
$\mathbf {H}'$.
We claim that, if the exact sequence is a central extension, then the image of the locally finite ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$ in
$\mathbf {H}$ in ![]() $\mathbf {H}''$ is also a locally finite
$\mathbf {H}''$ is also a locally finite ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series for the target. To see this, it suffices to show that the image of each term in
$\mathbf {G}$-central series for the target. To see this, it suffices to show that the image of each term in ![]() $\mathbf {H}''$ is again strongly
$\mathbf {H}''$ is again strongly ![]() ${\mathbb {A}}^1$-invariant.
${\mathbb {A}}^1$-invariant.
To this end, let ![]() $\mathbf {H}_i$ be an arbitrary term in the locally finite
$\mathbf {H}_i$ be an arbitrary term in the locally finite ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series for
$\mathbf {G}$-central series for ![]() $\mathbf {H}$. We already know that
$\mathbf {H}$. We already know that ![]() $\mathbf {H}_i \cap \mathbf {H}' =: \mathbf {H}'_i$ is strongly
$\mathbf {H}_i \cap \mathbf {H}' =: \mathbf {H}'_i$ is strongly ![]() ${\mathbb {A}}^1$-invariant. However, since the exact sequence in the statement is a central extension, we conclude that
${\mathbb {A}}^1$-invariant. However, since the exact sequence in the statement is a central extension, we conclude that ![]() $\mathbf {H}'_i$ is contained in the center of
$\mathbf {H}'_i$ is contained in the center of ![]() $\mathbf {H}_i$, in which case the quotient is strongly
$\mathbf {H}_i$, in which case the quotient is strongly ![]() ${\mathbb {A}}^1$-invariant subsheaf
${\mathbb {A}}^1$-invariant subsheaf ![]() $\mathbf {H}''_i \subset \mathbf {H}''$ by appeal to Lemma 3.1.14(3).
$\mathbf {H}''_i \subset \mathbf {H}''$ by appeal to Lemma 3.1.14(3).
Corollary 3.2.13 Suppose ![]() $\mathbf {G}$ is a strongly
$\mathbf {G}$ is a strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups acting on strongly
${\mathbb {A}}^1$-invariant sheaf of groups acting on strongly ![]() ${\mathbb {A}}^1$-invariant groups
${\mathbb {A}}^1$-invariant groups ![]() $\mathbf {H}$,
$\mathbf {H}$, ![]() $\mathbf {H}'$ and
$\mathbf {H}'$ and ![]() $\mathbf {H}''$ and suppose we are given
$\mathbf {H}''$ and suppose we are given ![]() $\mathbf {G}$-equivariant morphisms
$\mathbf {G}$-equivariant morphisms ![]() $\mathbf {H}' \to \mathbf {H}$ and
$\mathbf {H}' \to \mathbf {H}$ and ![]() $\mathbf {H}'' \to \mathbf {H}$. If the
$\mathbf {H}'' \to \mathbf {H}$. If the ![]() $\mathbf {G}$-actions on
$\mathbf {G}$-actions on ![]() $\mathbf {H}'$ and
$\mathbf {H}'$ and ![]() $\mathbf {H}''$ are (locally)
$\mathbf {H}''$ are (locally) ![]() ${\mathbb {A}}^1$-nilpotent, then the induced
${\mathbb {A}}^1$-nilpotent, then the induced ![]() $\mathbf {G}$-action on
$\mathbf {G}$-action on ![]() $\mathbf {H}' \times _{\mathbf {H}} \mathbf {H}''$ is also (locally)
$\mathbf {H}' \times _{\mathbf {H}} \mathbf {H}''$ is also (locally) ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. As before, the fiber product is strongly ![]() ${\mathbb {A}}^1$-invariant by Lemma 3.1.16. Moreover, the fiber product is equipped with a
${\mathbb {A}}^1$-invariant by Lemma 3.1.16. Moreover, the fiber product is equipped with a ![]() $\mathbf {G}$-action: it is a
$\mathbf {G}$-action: it is a ![]() $\mathbf {G}$-stable subsheaf of the product
$\mathbf {G}$-stable subsheaf of the product ![]() $\mathbf {H} \times \mathbf {H}'$ equipped with the diagonal
$\mathbf {H} \times \mathbf {H}'$ equipped with the diagonal ![]() $\mathbf {G}$-action. If
$\mathbf {G}$-action. If ![]() $\mathbf {H}'_i$ and
$\mathbf {H}'_i$ and ![]() $\mathbf {H}''_i$ are (locally finite)
$\mathbf {H}''_i$ are (locally finite) ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\mathbf {G}$-central series, then
$\mathbf {G}$-central series, then ![]() $\mathbf {H}'_i \times _{\mathbf {H}} \mathbf {H}''_i$ yields a
$\mathbf {H}'_i \times _{\mathbf {H}} \mathbf {H}''_i$ yields a ![]() $\mathbf {G}$-central series for the fiber product by appeal to Proposition 3.2.12(1).
$\mathbf {G}$-central series for the fiber product by appeal to Proposition 3.2.12(1).
3.3  ${\mathbb {A}}^1$-nilpotent spaces and
${\mathbb {A}}^1$-nilpotent spaces and  ${\mathbb {A}}^1$-fiber sequences
${\mathbb {A}}^1$-fiber sequences
We now define various notions of ![]() ${\mathbb {A}}^1$-nilpotence for morphisms of spaces by analogy with the situation in classical topology; we defer the explicit construction of examples to § 3.4. Here, we discuss some of the basic formal properties of such morphisms and give some useful criteria for checking nilpotence. We also analyze the interaction between nilpotence and
${\mathbb {A}}^1$-nilpotence for morphisms of spaces by analogy with the situation in classical topology; we defer the explicit construction of examples to § 3.4. Here, we discuss some of the basic formal properties of such morphisms and give some useful criteria for checking nilpotence. We also analyze the interaction between nilpotence and ![]() ${\mathbb {A}}^1$-fiber sequences.
${\mathbb {A}}^1$-fiber sequences.
Definition 3.3.1 Suppose ![]() $f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of spaces with
$f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of spaces with ![]() ${\mathbb {A}}^1$-homotopy fiber
${\mathbb {A}}^1$-homotopy fiber ![]() $\mathscr {F}$.
$\mathscr {F}$.
1. The morphism
 $f$ will be called a (locally)
$f$ will be called a (locally)  ${\mathbb {A}}^1$-nilpotent morphism if
${\mathbb {A}}^1$-nilpotent morphism if  $\mathscr {F}$ is
$\mathscr {F}$ is  ${\mathbb {A}}^1$-connected, and for any choice of base point
${\mathbb {A}}^1$-connected, and for any choice of base point  $\ast$ in
$\ast$ in  $\mathscr {F}$ the action of
$\mathscr {F}$ the action of  $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E},e)$ on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E},e)$ on  $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F},\ast )$ is (locally)
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F},\ast )$ is (locally)  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.2. A pointed space
 $(\mathscr {X},x)$ will be called (locally)
$(\mathscr {X},x)$ will be called (locally)  ${\mathbb {A}}^1$-nilpotent if the structure morphism
${\mathbb {A}}^1$-nilpotent if the structure morphism  $\mathscr {X} \to \ast$ is (locally)
$\mathscr {X} \to \ast$ is (locally)  ${\mathbb {A}}^1$-nilpotent;
${\mathbb {A}}^1$-nilpotent;3. weakly
 ${\mathbb {A}}^1$-nilpotent if
${\mathbb {A}}^1$-nilpotent if  $\mathscr {X}$ is locally
$\mathscr {X}$ is locally  ${\mathbb {A}}^1$-nilpotent and
${\mathbb {A}}^1$-nilpotent and  $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$ is
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$ is  ${\mathbb {A}}^1$-nilpotent; and
${\mathbb {A}}^1$-nilpotent; and4.
 ${\mathbb {A}}^1$-simple if
${\mathbb {A}}^1$-simple if  $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ is abelian and acts trivially on the higher
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ is abelian and acts trivially on the higher  ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of  $\mathscr {X}$.
$\mathscr {X}$.
Proposition 3.3.2 Assume ![]() $k$ is a perfect field, and suppose
$k$ is a perfect field, and suppose ![]() $q: \mathscr {E}_2 \to \mathscr {E}_1$ and
$q: \mathscr {E}_2 \to \mathscr {E}_1$ and ![]() $p: \mathscr {E}_1 \to \mathscr {E}_0$ are pointed morphisms in
$p: \mathscr {E}_1 \to \mathscr {E}_0$ are pointed morphisms in ![]() $\mathrm {Spc}_k$ such that the
$\mathrm {Spc}_k$ such that the ![]() ${\mathbb {A}}^1$-homotopy fibers of
${\mathbb {A}}^1$-homotopy fibers of ![]() $p$,
$p$, ![]() $q$ and
$q$ and ![]() $pq$ are all connected.
$pq$ are all connected.
1. If
 $p$ and
$p$ and  $q$ are (locally)
$q$ are (locally)  ${\mathbb {A}}^1$-nilpotent, then so is
${\mathbb {A}}^1$-nilpotent, then so is  $pq$; if
$pq$; if  $pq$ and
$pq$ and  $p$ are (locally)
$p$ are (locally)  ${\mathbb {A}}^1$-nilpotent, so is
${\mathbb {A}}^1$-nilpotent, so is  $q$.
$q$.2. If
 $pq$ and
$pq$ and  $q$ are (locally)
$q$ are (locally)  ${\mathbb {A}}^1$-nilpotent, and
${\mathbb {A}}^1$-nilpotent, and  $p$ is
$p$ is  $1$-connected, then
$1$-connected, then  $p$ is (locally)
$p$ is (locally)  ${\mathbb {A}}^1$-nilpotent as well.
${\mathbb {A}}^1$-nilpotent as well.
Proof. The proof parallels that of Proposition 2.2.2. In particular, by the ‘octahedral axiom’ in the ![]() ${\mathbb {A}}^1$-homotopy category, there is an
${\mathbb {A}}^1$-homotopy category, there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
where each term is the ![]() ${\mathbb {A}}^1$-homotopy fiber of the map in the subscript. All the spaces in this
${\mathbb {A}}^1$-homotopy fiber of the map in the subscript. All the spaces in this ![]() ${\mathbb {A}}^1$-fiber sequence are
${\mathbb {A}}^1$-fiber sequence are ![]() ${\mathbb {A}}^1$-connected by assumption. There is an induced action of
${\mathbb {A}}^1$-connected by assumption. There is an induced action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on all of the homotopy sheaves of each of these spaces, and a
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on all of the homotopy sheaves of each of these spaces, and a ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant long exact sequence of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant long exact sequence of ![]() ${\mathbb {A}}^1$-homotopy sheaves which ends as follows:
${\mathbb {A}}^1$-homotopy sheaves which ends as follows:
The kernel ![]() $\mathbf {K}$ of
$\mathbf {K}$ of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq})$, which coincides with the image of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq})$, which coincides with the image of ![]() $\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(\mathscr {F}_p)$ in
$\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(\mathscr {F}_p)$ in ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q)$ by exactness, is strongly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q)$ by exactness, is strongly ![]() ${\mathbb {A}}^1$-invariant by Lemma 3.1.14 and
${\mathbb {A}}^1$-invariant by Lemma 3.1.14 and ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-stable by construction. Moreover,
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-stable by construction. Moreover, ![]() $\mathbf {K}$ is contained in the center of
$\mathbf {K}$ is contained in the center of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q)$.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_q)$.
We may then break the above long exact sequence of sheaves ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant short exact sequences of strongly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant short exact sequences of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves. In particular, we obtain the two
${\mathbb {A}}^1$-invariant sheaves. In particular, we obtain the two ![]() $\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariant exact sequences:
$\boldsymbol {\pi }_1(\mathscr {E}_2)$-equivariant exact sequences:
 \begin{align*} 1 \longrightarrow \mathbf{K} \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_q) \longrightarrow &\ker(\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p)) \longrightarrow 1, \\ 1 \longrightarrow \ker(\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p)) \longrightarrow &\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p) \longrightarrow 1, \end{align*}
\begin{align*} 1 \longrightarrow \mathbf{K} \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_q) \longrightarrow &\ker(\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p)) \longrightarrow 1, \\ 1 \longrightarrow \ker(\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p)) \longrightarrow &\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_{pq}) \longrightarrow \boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{F}_p) \longrightarrow 1, \end{align*}which we now analyze.
If ![]() $pq$ and
$pq$ and ![]() $p$ are (locally)
$p$ are (locally) ![]() ${\mathbb {A}}^1$-nilpotent, then we conclude by appeal to Proposition 3.2.12 that the action of
${\mathbb {A}}^1$-nilpotent, then we conclude by appeal to Proposition 3.2.12 that the action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on ![]() $\boldsymbol {\pi }_1(\mathscr {F}_q)$ is (locally)
$\boldsymbol {\pi }_1(\mathscr {F}_q)$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent. If
${\mathbb {A}}^1$-nilpotent. If ![]() $p$ and
$p$ and ![]() $q$ are (locally)
$q$ are (locally) ![]() ${\mathbb {A}}^1$-nilpotent, then observe that since the first exact sequence above is a
${\mathbb {A}}^1$-nilpotent, then observe that since the first exact sequence above is a ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant central extension we may conclude that the action of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-equivariant central extension we may conclude that the action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$ on ![]() $\ker (\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_p))$ is (locally)
$\ker (\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_p))$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, again by appeal to Proposition 3.2.12. Another appeal to this result then implies that the
${\mathbb {A}}^1$-nilpotent, again by appeal to Proposition 3.2.12. Another appeal to this result then implies that the ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-action on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}_2)$-action on ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq})$ is
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}_{pq})$ is ![]() ${\mathbb {A}}^1$-nilpotent. The statements about higher homotopy sheaves are established similarly, by repeated appeal to Proposition 3.2.12 (since all sheaves are strictly
${\mathbb {A}}^1$-nilpotent. The statements about higher homotopy sheaves are established similarly, by repeated appeal to Proposition 3.2.12 (since all sheaves are strictly ![]() ${\mathbb {A}}^1$-invariant; this also treats the case where
${\mathbb {A}}^1$-invariant; this also treats the case where ![]() $pq$ and
$pq$ and ![]() $q$ are (locally)
$q$ are (locally) ![]() ${\mathbb {A}}^1$-nilpotent and
${\mathbb {A}}^1$-nilpotent and ![]() $p$ is
$p$ is ![]() $1$-connected.
$1$-connected.
If ![]() $\mathscr {X}$ is any pointed
$\mathscr {X}$ is any pointed ![]() ${\mathbb {A}}^1$-connected space, then we write
${\mathbb {A}}^1$-connected space, then we write ![]() $\widetilde {\mathscr {X}}$ for the
$\widetilde {\mathscr {X}}$ for the ![]() ${\mathbb {A}}^1$-universal cover of
${\mathbb {A}}^1$-universal cover of ![]() $\mathscr {X}$ in the sense of [Reference MorelMor12, § 7.1]. If
$\mathscr {X}$ in the sense of [Reference MorelMor12, § 7.1]. If ![]() $\boldsymbol {\pi } := \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$, then there is an
$\boldsymbol {\pi } := \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$, then there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
and ![]() $\widetilde {\mathscr {X}}$ is
$\widetilde {\mathscr {X}}$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected. The action of
$1$-connected. The action of ![]() $\boldsymbol {\pi }$ on
$\boldsymbol {\pi }$ on ![]() $\widetilde {\mathscr {X}}$ is by ‘deck transformations’, which do not preserve base points. Nevertheless, analysis of this action in conjunction with Proposition 3.3.2 can be used to produce a computationally useful characterization of
$\widetilde {\mathscr {X}}$ is by ‘deck transformations’, which do not preserve base points. Nevertheless, analysis of this action in conjunction with Proposition 3.3.2 can be used to produce a computationally useful characterization of ![]() ${\mathbb {A}}^1$-nilpotence.
${\mathbb {A}}^1$-nilpotence.
Corollary 3.3.3 Assume ![]() $(\mathscr {X},x)$ is a pointed
$(\mathscr {X},x)$ is a pointed ![]() ${\mathbb {A}}^1$-connected space with
${\mathbb {A}}^1$-connected space with ![]() $\boldsymbol {\pi } := \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ an
$\boldsymbol {\pi } := \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},x)$ an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups. The following conditions are equivalent.
${\mathbb {A}}^1$-nilpotent sheaf of groups. The following conditions are equivalent.
1. The space
 $\mathscr {X}$ is (locally)
$\mathscr {X}$ is (locally)  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.2. The action of
 $\boldsymbol {\pi }$ on
$\boldsymbol {\pi }$ on  $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\widetilde {\mathscr {X}})$ is (locally)
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\widetilde {\mathscr {X}})$ is (locally)  ${\mathbb {A}}^1$-nilpotent for every
${\mathbb {A}}^1$-nilpotent for every  $i > 1$.
$i > 1$.
Proof. Since ![]() $B\boldsymbol {\pi }$ is
$B\boldsymbol {\pi }$ is ![]() ${\mathbb {A}}^1$-nilpotent by assumption, and
${\mathbb {A}}^1$-nilpotent by assumption, and ![]() $\widetilde {\mathscr {X}}$ is
$\widetilde {\mathscr {X}}$ is ![]() ${\mathbb {A}}^1$-simply connected, the statements involving the
${\mathbb {A}}^1$-simply connected, the statements involving the ![]() ${\mathbb {A}}^1$-nilpotence hypothesis follow immediately by applying Proposition 3.3.2 to the composite morphism
${\mathbb {A}}^1$-nilpotence hypothesis follow immediately by applying Proposition 3.3.2 to the composite morphism ![]() $\mathscr {X} \to B\boldsymbol {\pi } \to \ast$. In fact, essentially the same proof works assuming the hypothesis of local
$\mathscr {X} \to B\boldsymbol {\pi } \to \ast$. In fact, essentially the same proof works assuming the hypothesis of local ![]() ${\mathbb {A}}^1$-nilpotence because
${\mathbb {A}}^1$-nilpotence because ![]() $B\boldsymbol {\pi }$ is
$B\boldsymbol {\pi }$ is ![]() $1$-truncated. Indeed, both the forward and reverse implications follow from this observation because the
$1$-truncated. Indeed, both the forward and reverse implications follow from this observation because the ![]() $\boldsymbol {\pi }$-action on the higher homotopy sheaves of
$\boldsymbol {\pi }$-action on the higher homotopy sheaves of ![]() $\widetilde {\mathscr {X}}$ coincides with the
$\widetilde {\mathscr {X}}$ coincides with the ![]() $\boldsymbol {\pi }$-action on the higher homotopy sheaves of
$\boldsymbol {\pi }$-action on the higher homotopy sheaves of ![]() $\mathscr {X}$.
$\mathscr {X}$.
Remark 3.3.4 Just as in classical topology, if the action of ![]() $\boldsymbol {\pi }$ on
$\boldsymbol {\pi }$ on ![]() $\widetilde {\mathscr {X}}$ is null-
$\widetilde {\mathscr {X}}$ is null-![]() ${\mathbb {A}}^1$-homotopic, then the induced action on higher
${\mathbb {A}}^1$-homotopic, then the induced action on higher ![]() ${\mathbb {A}}^1$-homotopy sheaves will be trivial. Because the homotopy sheaves
${\mathbb {A}}^1$-homotopy sheaves will be trivial. Because the homotopy sheaves ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ are all strictly
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ are all strictly ![]() ${\mathbb {A}}^1$-invariant, they are unramified (see Remark 3.1.9), and thus triviality of the necessary actions may be checked on sections over finitely generated extensions of the base field.
${\mathbb {A}}^1$-invariant, they are unramified (see Remark 3.1.9), and thus triviality of the necessary actions may be checked on sections over finitely generated extensions of the base field.
Proposition 3.3.5 Assume we are given a homotopy Cartesian diagram of pointed ![]() ${\mathbb {A}}^1$-connected spaces of the following form.
${\mathbb {A}}^1$-connected spaces of the following form.

If ![]() $f$ is (locally)
$f$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, then so is
${\mathbb {A}}^1$-nilpotent, then so is ![]() $f'$.
$f'$.
Proof. Up to ![]() ${\mathbb {A}}^1$-weak equivalence, we may replace the diagram in question by
${\mathbb {A}}^1$-weak equivalence, we may replace the diagram in question by ![]() $\operatorname {L}_{{\mathbb {A}}^1} f$ and
$\operatorname {L}_{{\mathbb {A}}^1} f$ and ![]() $\operatorname {L}_{{\mathbb {A}}^1} g$. In that case,
$\operatorname {L}_{{\mathbb {A}}^1} g$. In that case, ![]() $\operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times ^h_{\operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}} \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is
$\operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times ^h_{\operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}} \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is ![]() ${\mathbb {A}}^1$-local since there is a simplicial homotopy fiber sequence of the form
${\mathbb {A}}^1$-local since there is a simplicial homotopy fiber sequence of the form
Since ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}'$ are
$\mathscr {B}'$ are ![]() ${\mathbb {A}}^1$-connected by assumption,
${\mathbb {A}}^1$-connected by assumption, ![]() $\operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is simplicially connected as well, so appeal to Lemma 3.1.4 allows us to conclude the middle term is
$\operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is simplicially connected as well, so appeal to Lemma 3.1.4 allows us to conclude the middle term is ![]() ${\mathbb {A}}^1$-local. It also follows that the induced map
${\mathbb {A}}^1$-local. It also follows that the induced map ![]() $\mathscr {E}' \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times ^h_{\operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}} \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is an
$\mathscr {E}' \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {E} \times ^h_{\operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}} \operatorname {L}_{{\mathbb {A}}^1} \mathscr {B}'$ is an ![]() ${\mathbb {A}}^1$-weak equivalence since all spaces are connected. In that case, the result follows from the corresponding result for simplicial presheaves, that is, by appeal to Proposition 2.2.3 (replacing appeal to Lemma 2.1.5 by appeal to Lemma 3.2.6).
${\mathbb {A}}^1$-weak equivalence since all spaces are connected. In that case, the result follows from the corresponding result for simplicial presheaves, that is, by appeal to Proposition 2.2.3 (replacing appeal to Lemma 2.1.5 by appeal to Lemma 3.2.6).
Theorem 3.3.6 Assume ![]() $k$ is a perfect field. Suppose
$k$ is a perfect field. Suppose ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an ![]() ${\mathbb {A}}^1$-fiber sequence of pointed
${\mathbb {A}}^1$-fiber sequence of pointed ![]() ${\mathbb {A}}^1$-connected spaces. If
${\mathbb {A}}^1$-connected spaces. If ![]() $\mathscr {E}$ is (locally)
$\mathscr {E}$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, then
${\mathbb {A}}^1$-nilpotent, then ![]() $\mathscr {F}$ is (locally)
$\mathscr {F}$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. The proof is essentially identical to that of Proposition 2.2.4. By assumption, there is an ![]() ${\mathbb {A}}^1$-homotopy Cartesian square of the following form.
${\mathbb {A}}^1$-homotopy Cartesian square of the following form.

By Proposition 3.3.5, to check that ![]() $\mathscr {F} \to \ast$ is (locally)
$\mathscr {F} \to \ast$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, it suffices to show that
${\mathbb {A}}^1$-nilpotent, it suffices to show that ![]() $f$ is (locally)
$f$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, that is, the action of
${\mathbb {A}}^1$-nilpotent, that is, the action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on ![]() $\boldsymbol {\pi }_i(\mathscr {F})$ is (locally)
$\boldsymbol {\pi }_i(\mathscr {F})$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
There is a ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariant long exact sequence in
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariant long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves associated with the above fibration, which may be
${\mathbb {A}}^1$-homotopy sheaves associated with the above fibration, which may be ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariantly broken into short exact sequences of the form
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariantly broken into short exact sequences of the form
In this case, by exactness of the sequence, both ![]() $\mathbf {K}_{i+1}$ and
$\mathbf {K}_{i+1}$ and ![]() $\ker (\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {E}) \longrightarrow \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {B}))$ are strongly
$\ker (\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {E}) \longrightarrow \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {B}))$ are strongly ![]() ${\mathbb {A}}^1$-invariant by appeal to Lemma 3.1.14. Moreover, as a homotopy exact sequence, the above short exact sequence is actually a central extension of strongly
${\mathbb {A}}^1$-invariant by appeal to Lemma 3.1.14. Moreover, as a homotopy exact sequence, the above short exact sequence is actually a central extension of strongly ![]() ${\mathbb {A}}^1$-invariant sheaves. Now, by assumption,
${\mathbb {A}}^1$-invariant sheaves. Now, by assumption, ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts in a (locally)
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts in a (locally) ![]() ${\mathbb {A}}^1$-nilpotent fashion on
${\mathbb {A}}^1$-nilpotent fashion on ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {E})$ and therefore in a (locally)
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {E})$ and therefore in a (locally) ![]() ${\mathbb {A}}^1$-nilpotent fashion on the kernel in the above short exact sequence by appeal to Lemma 3.2.7. Likewise, the
${\mathbb {A}}^1$-nilpotent fashion on the kernel in the above short exact sequence by appeal to Lemma 3.2.7. Likewise, the ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-action on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-action on ![]() $\mathbf {K}_{i+1}$ is trivial and it follows again by appeal to Lemma 3.2.7 that the extension is (locally)
$\mathbf {K}_{i+1}$ is trivial and it follows again by appeal to Lemma 3.2.7 that the extension is (locally) ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-nilpotent.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-nilpotent.
We record the following special case of the above for later use.
Corollary 3.3.7 If ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an ![]() ${\mathbb {A}}^1$-fiber sequence of connected spaces, and
${\mathbb {A}}^1$-fiber sequence of connected spaces, and ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}$ are weakly
$\mathscr {B}$ are weakly ![]() ${\mathbb {A}}^1$-nilpotent, then
${\mathbb {A}}^1$-nilpotent, then ![]() $\mathscr {F}$ is weakly
$\mathscr {F}$ is weakly ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proposition 3.3.8 Assume ![]() $k$ is a perfect field. Suppose
$k$ is a perfect field. Suppose ![]() $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is an ![]() ${\mathbb {A}}^1$-fiber sequence of pointed
${\mathbb {A}}^1$-fiber sequence of pointed ![]() ${\mathbb {A}}^1$-connected spaces. If
${\mathbb {A}}^1$-connected spaces. If ![]() $\mathscr {B}$ is
$\mathscr {B}$ is ![]() ${\mathbb {A}}^1$-simply connected, and
${\mathbb {A}}^1$-simply connected, and ![]() $\mathscr {F}$ is (locally)
$\mathscr {F}$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent (respectively,
${\mathbb {A}}^1$-nilpotent (respectively, ![]() ${\mathbb {A}}^1$-simple), then
${\mathbb {A}}^1$-simple), then ![]() $\mathscr {E}$ is (locally)
$\mathscr {E}$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent (respectively,
${\mathbb {A}}^1$-nilpotent (respectively, ![]() ${\mathbb {A}}^1$-simple) as well.
${\mathbb {A}}^1$-simple) as well.
Proof. Under the hypotheses, ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is a quotient of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is a quotient of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$, and since all spaces have a
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$, and since all spaces have a ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-action, they inherit an action of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-action, they inherit an action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ by restriction. Now, the image of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ by restriction. Now, the image of ![]() $\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(\mathscr {B})$ in
$\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(\mathscr {B})$ in ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is a central subsheaf. Moreover, by exactness of the long exact sequence, the image of this subsheaf is again strongly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is a central subsheaf. Moreover, by exactness of the long exact sequence, the image of this subsheaf is again strongly ![]() ${\mathbb {A}}^1$-invariant as it is identified with the kernel of the map
${\mathbb {A}}^1$-invariant as it is identified with the kernel of the map ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}) \to \mathscr {E}$. Then, since
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F}) \to \mathscr {E}$. Then, since ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is (locally)
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is (locally) ![]() ${\mathbb {A}}^1$-nilpotent, it follows that (locally)
${\mathbb {A}}^1$-nilpotent, it follows that (locally) ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is also
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is also ![]() ${\mathbb {A}}^1$-nilpotent by appeal to Lemma 3.2.7(2).
${\mathbb {A}}^1$-nilpotent by appeal to Lemma 3.2.7(2).
Next, consider the portion of the long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves:
${\mathbb {A}}^1$-homotopy sheaves:
Since ![]() $k$ is perfect and
$k$ is perfect and ![]() $n \geq 2$, the homotopy sheaves in question are strictly
$n \geq 2$, the homotopy sheaves in question are strictly ![]() ${\mathbb {A}}^1$-invariant (so all images and cokernels are strictly
${\mathbb {A}}^1$-invariant (so all images and cokernels are strictly ![]() ${\mathbb {A}}^1$-invariant as well by appeal to Theorem 3.1.12). Moreover, by assumption
${\mathbb {A}}^1$-invariant as well by appeal to Theorem 3.1.12). Moreover, by assumption ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {B})$ carries a trivial action of
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {B})$ carries a trivial action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$, so the quotient
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$, so the quotient ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {E})/\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a trivial action of
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {E})/\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a trivial action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$, which is, in particular, (locally)
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$, which is, in particular, (locally) ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Thus, to conclude, it suffices by Proposition 3.2.12 to show that ![]() $\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a (locally)
$\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a (locally) ![]() ${\mathbb {A}}^1$-nilpotent action of
${\mathbb {A}}^1$-nilpotent action of ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {E})$. However,
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {E})$. However, ![]() $\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a (locally)
$\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$ carries a (locally) ![]() ${\mathbb {A}}^1$-nilpotent action of
${\mathbb {A}}^1$-nilpotent action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ by assumption. If we pick a (locally finite)
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ by assumption. If we pick a (locally finite) ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$-central series for
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$-central series for ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})$, it induces a (locally finite)
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})$, it induces a (locally finite) ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$-central series
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$-central series ![]() $\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$; this is also a (locally finite)
$\operatorname {im}(\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}))$; this is also a (locally finite) ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series by restriction, which is what we wanted to show.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series by restriction, which is what we wanted to show.
The statement about ![]() ${\mathbb {A}}^1$-simplicity is established similarly. If
${\mathbb {A}}^1$-simplicity is established similarly. If ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is abelian, then
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is abelian, then ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is necessarily abelian as well. If
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ is necessarily abelian as well. If ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ acts trivially on the higher
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ acts trivially on the higher ![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $\mathscr {F}$, then the argument of the preceding paragraph also shows that
$\mathscr {F}$, then the argument of the preceding paragraph also shows that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially on the higher
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially on the higher ![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $\mathscr {E}$.
$\mathscr {E}$.
 ${\mathbb {A}}^1$-nilpotence and Moore–Postnikov factorizations
${\mathbb {A}}^1$-nilpotence and Moore–Postnikov factorizations
A pointed morphism ![]() $f:(\mathscr {E},e)\to (\mathscr {B},b)$ is an
$f:(\mathscr {E},e)\to (\mathscr {B},b)$ is an ![]() ${\mathbb {A}}^1$-principal fibration if there exist a pointed space
${\mathbb {A}}^1$-principal fibration if there exist a pointed space ![]() $(\mathscr {C},c)$ and a pointed ‘classifying’ map
$(\mathscr {C},c)$ and a pointed ‘classifying’ map ![]() $w: \mathscr {B} \to \mathscr {C}$ such that
$w: \mathscr {B} \to \mathscr {C}$ such that ![]() $\mathscr {E}$ is the homotopy pullback of the path-loop fibration along
$\mathscr {E}$ is the homotopy pullback of the path-loop fibration along ![]() $w$. We may consider factorizations of a pointed morphism as a tower of principal fibrations in a sense we now make precise; we largely follow the discussion of [Reference Hilton, Mislin and RoitbergHMR75, II.2].
$w$. We may consider factorizations of a pointed morphism as a tower of principal fibrations in a sense we now make precise; we largely follow the discussion of [Reference Hilton, Mislin and RoitbergHMR75, II.2].
Definition 3.3.9 Suppose ![]() $f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed
$f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed ![]() ${\mathbb {A}}^1$-connected spaces. A factorization of
${\mathbb {A}}^1$-connected spaces. A factorization of ![]() $f$ as a tower of
$f$ as a tower of ![]() ${\mathbb {A}}^1$-fibrations consists of a sequence of pointed spaces
${\mathbb {A}}^1$-fibrations consists of a sequence of pointed spaces ![]() $\tau _{\leq i}f$,
$\tau _{\leq i}f$, ![]() $i \geq 0$, morphisms
$i \geq 0$, morphisms ![]() $p_i: \tau _{\leq i}f \to \tau _{\leq i-1}f$,
$p_i: \tau _{\leq i}f \to \tau _{\leq i-1}f$, ![]() $\mathscr {E} \to \tau _{\leq i}f$ and
$\mathscr {E} \to \tau _{\leq i}f$ and ![]() $\tau _{\leq i}f \to \mathscr {B}$ fitting into a commutative diagram of the form
$\tau _{\leq i}f \to \mathscr {B}$ fitting into a commutative diagram of the form

having the following properties.
1.
 $\tau _{\leq 0}f = \mathscr {B}$ (thus, the composite morphisms
$\tau _{\leq 0}f = \mathscr {B}$ (thus, the composite morphisms  $\mathscr {E} \to \tau _{\leq i}f \to \mathscr {B}$ coincide with
$\mathscr {E} \to \tau _{\leq i}f \to \mathscr {B}$ coincide with  $f$).
$f$).2. The induced morphism
 ${\mathscr E} \to \operatorname {holim}_i \tau _{\leq i}f$ is an
${\mathscr E} \to \operatorname {holim}_i \tau _{\leq i}f$ is an  ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
If, furthermore,
3. for each integer
 $i \geq 0$, the morphism
$i \geq 0$, the morphism  $p_i$ is an
$p_i$ is an  ${\mathbb {A}}^1$-principal fibration in the sense mentioned above,
${\mathbb {A}}^1$-principal fibration in the sense mentioned above,
then we will say that the given factorization of ![]() $f$ is a factorization of
$f$ is a factorization of ![]() $f$ as a tower of
$f$ as a tower of ![]() ${\mathbb {A}}^1$-principal fibrations.
${\mathbb {A}}^1$-principal fibrations.
Example 3.3.10 Suppose ![]() $f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed
$f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed ![]() ${\mathbb {A}}^1$-connected spaces. If the morphism
${\mathbb {A}}^1$-connected spaces. If the morphism ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$ is surjective, then
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$ is surjective, then ![]() $f$ admits a standard factorization as a tower of
$f$ admits a standard factorization as a tower of ![]() ${\mathbb {A}}^1$-fibrations: the
${\mathbb {A}}^1$-fibrations: the ![]() ${\mathbb {A}}^1$-Moore–Postnikov factorization. Indeed, this is a factorization of
${\mathbb {A}}^1$-Moore–Postnikov factorization. Indeed, this is a factorization of ![]() $f$ as a tower of
$f$ as a tower of ![]() ${\mathbb {A}}^1$-fibrations where, in addition to the statements in Definition 3.3.9, the following statements hold.
${\mathbb {A}}^1$-fibrations where, in addition to the statements in Definition 3.3.9, the following statements hold.
1. The morphisms
 $\mathscr {E} \to \tau _{\leq i}f$ induce epimorphisms on
$\mathscr {E} \to \tau _{\leq i}f$ induce epimorphisms on  ${\mathbb {A}}^1$-homotopy sheaves in degrees
${\mathbb {A}}^1$-homotopy sheaves in degrees  $\leq i+1$ that are furthermore isomorphisms in degrees
$\leq i+1$ that are furthermore isomorphisms in degrees  $\leq i$.
$\leq i$.2. The map on
 ${\mathbb {A}}^1$-homotopy sheaves induced by the morphisms
${\mathbb {A}}^1$-homotopy sheaves induced by the morphisms  $\tau _{\leq i}f \to \mathscr {B}$ are isomorphisms in degrees
$\tau _{\leq i}f \to \mathscr {B}$ are isomorphisms in degrees  $>i+1$, and a monomorphism in degree
$>i+1$, and a monomorphism in degree  $i+1$.
$i+1$.
Definition 3.3.11 Suppose ![]() $f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed
$f: (\mathscr {E},e) \to (\mathscr {B},b)$ is a morphism of pointed ![]() ${\mathbb {A}}^1$-connected spaces equipped with a factorization as a tower of
${\mathbb {A}}^1$-connected spaces equipped with a factorization as a tower of ![]() ${\mathbb {A}}^1$-fibrations as in Definition 3.3.9. We will say that this factorization admits an
${\mathbb {A}}^1$-fibrations as in Definition 3.3.9. We will say that this factorization admits an ![]() ${\mathbb {A}}^1$-principal refinement if, for each
${\mathbb {A}}^1$-principal refinement if, for each ![]() $n \geq 1$, there exists an integer
$n \geq 1$, there exists an integer ![]() $c$ (which will depend on
$c$ (which will depend on ![]() $n$) such that
$n$) such that
1. the morphism
 $p_n: \tau _{\leq n}f \to \tau _{\leq n-1}f$ factors as
and
$p_n: \tau _{\leq n}f \to \tau _{\leq n-1}f$ factors as
and \[ \tau_{\leq n} f = \tau_{\leq n,c} f \stackrel{p_{n,c}}{\longrightarrow} \tau_{\leq n,c-1} f \longrightarrow \cdots \longrightarrow \tau_{\leq n,1} f \stackrel{p_{n,0}}{\longrightarrow} \tau_{\leq n,0}f = \tau_{\leq n-1} f, \]
\[ \tau_{\leq n} f = \tau_{\leq n,c} f \stackrel{p_{n,c}}{\longrightarrow} \tau_{\leq n,c-1} f \longrightarrow \cdots \longrightarrow \tau_{\leq n,1} f \stackrel{p_{n,0}}{\longrightarrow} \tau_{\leq n,0}f = \tau_{\leq n-1} f, \]2. the new tower
 $\tau _{\leq n,j}f$ is a factorization of
$\tau _{\leq n,j}f$ is a factorization of  $f$ by
$f$ by  ${\mathbb {A}}^1$-principal fibrations.
${\mathbb {A}}^1$-principal fibrations.
Remark 3.3.12 The statement that the ![]() ${\mathbb {A}}^1$-Moore–Postnikov factorization (Example 3.3.10) admits an
${\mathbb {A}}^1$-Moore–Postnikov factorization (Example 3.3.10) admits an ![]() ${\mathbb {A}}^1$-principal refinement amounts to asking that, for each
${\mathbb {A}}^1$-principal refinement amounts to asking that, for each ![]() $n,i$ as in Definition 3.3.11, the morphism
$n,i$ as in Definition 3.3.11, the morphism ![]() $p_{n,i}$ is an
$p_{n,i}$ is an ![]() ${\mathbb {A}}^1$-principal fibration in the sense that there exist a strictly
${\mathbb {A}}^1$-principal fibration in the sense that there exist a strictly ![]() ${\mathbb {A}}^1$-invariant sheaf
${\mathbb {A}}^1$-invariant sheaf ![]() $\mathbf {G}_{n,i}$ and an
$\mathbf {G}_{n,i}$ and an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
The following result is the ![]() ${\mathbb {A}}^1$-homotopic analog of one of the classical characterizations of nilpotent spaces.
${\mathbb {A}}^1$-homotopic analog of one of the classical characterizations of nilpotent spaces.
Theorem 3.3.13 Suppose ![]() $f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed
$f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed ![]() ${\mathbb {A}}^1$-connected spaces such that the induced morphism
${\mathbb {A}}^1$-connected spaces such that the induced morphism ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$ is an epimorphism. The morphism
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E}) \to \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {B})$ is an epimorphism. The morphism ![]() $f$ is
$f$ is ![]() ${\mathbb {A}}^1$-nilpotent if and only if the
${\mathbb {A}}^1$-nilpotent if and only if the ![]() ${\mathbb {A}}^1$-Moore–Postnikov tower of
${\mathbb {A}}^1$-Moore–Postnikov tower of ![]() $f$ admits an
$f$ admits an ![]() ${\mathbb {A}}^1$-principal refinement.
${\mathbb {A}}^1$-principal refinement.
We give the proof of the forward implication below. We will defer the proof of the reverse implication to Corollary 4.2.4. Note that Theorem 3.3.17 below depends on this characterization of ![]() ${\mathbb {A}}^1$-nilpotence, but is placed in this section (as opposed to after Corollary 4.2.4) for stylistic reasons.
${\mathbb {A}}^1$-nilpotence, but is placed in this section (as opposed to after Corollary 4.2.4) for stylistic reasons.
Proof. See [Reference Hilton, Mislin and RoitbergHMR75, Theorem II.2.14] for the corresponding statement in classical topology, which we essentially follow. Observe that the hypotheses on ![]() $f$ imply that the
$f$ imply that the ![]() ${\mathbb {A}}^1$-homotopy fiber
${\mathbb {A}}^1$-homotopy fiber ![]() $\mathscr {F}$ of
$\mathscr {F}$ of ![]() $f$ is
$f$ is ![]() ${\mathbb {A}}^1$-connected. We show that if the
${\mathbb {A}}^1$-connected. We show that if the ![]() ${\mathbb {A}}^1$-Moore–Postnikov filtration admits an
${\mathbb {A}}^1$-Moore–Postnikov filtration admits an ![]() ${\mathbb {A}}^1$-principal refinement, then
${\mathbb {A}}^1$-principal refinement, then ![]() $f$ is
$f$ is ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
We want to show that the action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on all the higher homotopy sheaves of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on all the higher homotopy sheaves of ![]() $\mathscr {F}$ is
$\mathscr {F}$ is ![]() ${\mathbb {A}}^1$-nilpotent. Assuming
${\mathbb {A}}^1$-nilpotent. Assuming ![]() $p_n$ admits a factorization as in the statement, there is an induced action of
$p_n$ admits a factorization as in the statement, there is an induced action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ on ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\tau _{\leq n}f)$ for every
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\tau _{\leq n}f)$ for every ![]() $n$ and therefore an induced action on
$n$ and therefore an induced action on ![]() $\tau _{\leq n,i}f$ for every
$\tau _{\leq n,i}f$ for every ![]() $i$, making
$i$, making
into a fiber sequence where all the morphisms are ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariant. Repeated application of Proposition 3.2.12 then yields the result.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-equivariant. Repeated application of Proposition 3.2.12 then yields the result.
 ${\mathbb {A}}^1$-nilpotence and mapping spaces
${\mathbb {A}}^1$-nilpotence and mapping spaces
Definition 3.3.14 Assume ![]() $k$ is a field. We will say that
$k$ is a field. We will say that ![]() $\mathscr {X} \in \mathrm {Spc}_k$ has
$\mathscr {X} \in \mathrm {Spc}_k$ has ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $\leq d$ if, for every strictly
$\leq d$ if, for every strictly ![]() ${\mathbb {A}}^1$-invariant sheaf
${\mathbb {A}}^1$-invariant sheaf ![]() $\mathbf {A}$ and every integer
$\mathbf {A}$ and every integer ![]() $i > d$, the group
$i > d$, the group ![]() $H^i_{\operatorname {Nis}}(\mathscr {X},\mathbf {A}) = 0$, and
$H^i_{\operatorname {Nis}}(\mathscr {X},\mathbf {A}) = 0$, and ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $d$ if
$d$ if ![]() $\mathscr {X}$ has
$\mathscr {X}$ has ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $\leq d$ but not
$\leq d$ but not ![]() $\leq d-1$. We will say that
$\leq d-1$. We will say that ![]() $\mathscr {X}$ has finite
$\mathscr {X}$ has finite ![]() ${\mathbb {A}}^1$-cohomological dimension, if it has
${\mathbb {A}}^1$-cohomological dimension, if it has ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $\leq d$ for some integer
$\leq d$ for some integer ![]() $d$, and strongly finite
$d$, and strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension if, for every extension
${\mathbb {A}}^1$-cohomological dimension if, for every extension ![]() $L/k$, the base change
$L/k$, the base change ![]() $\mathscr {X}_L \in \mathrm {Spc}_L$ has
$\mathscr {X}_L \in \mathrm {Spc}_L$ has ![]() ${\mathbb {A}}^1$-cohomological dimension no higher than
${\mathbb {A}}^1$-cohomological dimension no higher than ![]() $d$ for some integer
$d$ for some integer ![]() $d$, independent of
$d$, independent of ![]() $L$.
$L$.
Example 3.3.15 If ![]() $X$ is a smooth
$X$ is a smooth ![]() $k$-scheme of dimension
$k$-scheme of dimension ![]() $d$, then
$d$, then ![]() $X$ has strongly finite
$X$ has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $\leq d$. From this and the suspension isomorphism in Nisnevich cohomology, one deduces that
$\leq d$. From this and the suspension isomorphism in Nisnevich cohomology, one deduces that ![]() $\Sigma ^j X_+$ also has strongly finite
$\Sigma ^j X_+$ also has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension. More generally, if
${\mathbb {A}}^1$-cohomological dimension. More generally, if ![]() $\mathscr {X}$ is any pointed space for which there exist integers
$\mathscr {X}$ is any pointed space for which there exist integers ![]() $i,j$ such that
$i,j$ such that ![]() $\Sigma ^i \mathscr {X}$ has the
$\Sigma ^i \mathscr {X}$ has the ![]() ${\mathbb {A}}^1$-homotopy type of
${\mathbb {A}}^1$-homotopy type of ![]() $\Sigma ^j X_+$ for some smooth scheme
$\Sigma ^j X_+$ for some smooth scheme ![]() $X_+$, then
$X_+$, then ![]() $\mathscr {X}$ has strongly finite
$\mathscr {X}$ has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension. In particular, this last statement holds for any motivic sphere
${\mathbb {A}}^1$-cohomological dimension. In particular, this last statement holds for any motivic sphere ![]() $S^i {\scriptstyle {\wedge }} {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} j}}$ since it holds for
$S^i {\scriptstyle {\wedge }} {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} j}}$ since it holds for ![]() ${{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} j}}$ (use
${{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} j}}$ (use ![]() ${\mathbb {A}}^j \,{\setminus}\, 0$).
${\mathbb {A}}^j \,{\setminus}\, 0$).
Theorem 3.3.16 Assume ![]() $k$ is a perfect field. If
$k$ is a perfect field. If ![]() $\mathscr {X}$ is any pointed
$\mathscr {X}$ is any pointed ![]() ${\mathbb {A}}^1$-nilpotent space, and
${\mathbb {A}}^1$-nilpotent space, and ![]() $\mathscr {Y}$ is a pointed space having strongly finite
$\mathscr {Y}$ is a pointed space having strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension, then for any fixed pointed map
${\mathbb {A}}^1$-cohomological dimension, then for any fixed pointed map ![]() $f: \mathscr {Y} \to \mathscr {X}$, the
$f: \mathscr {Y} \to \mathscr {X}$, the ![]() ${\mathbb {A}}^1$-connected component of the mapping space
${\mathbb {A}}^1$-connected component of the mapping space ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ containing
$\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ containing ![]() $f$ is again
$f$ is again ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. First, suppose ![]() $\mathscr {X} = K(\mathbf {A},n)$ for some integer
$\mathscr {X} = K(\mathbf {A},n)$ for some integer ![]() $n \geq 1$ and a strictly
$n \geq 1$ and a strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups
${\mathbb {A}}^1$-invariant sheaf of groups ![]() $\mathbf {A}$. In that case, consider the space
$\mathbf {A}$. In that case, consider the space
for some map ![]() $f \in H^n(\mathscr {Y},\mathbf {A})$. Observe that
$f \in H^n(\mathscr {Y},\mathbf {A})$. Observe that ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))$ is itself a (possibly
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))$ is itself a (possibly ![]() ${\mathbb {A}}^1$-disconnected)
${\mathbb {A}}^1$-disconnected) ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-space. Indeed, the space
$h$-space. Indeed, the space ![]() $K(\mathbf {A},n)$ is
$K(\mathbf {A},n)$ is ![]() ${\mathbb {A}}^1$-local by assumption, so the mapping space
${\mathbb {A}}^1$-local by assumption, so the mapping space ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))$ is
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))$ is ![]() ${\mathbb {A}}^1$-local as well. Now, any
${\mathbb {A}}^1$-local as well. Now, any ![]() ${\mathbb {A}}^1$-connected component of an
${\mathbb {A}}^1$-connected component of an ![]() ${\mathbb {A}}^1$-local space is again
${\mathbb {A}}^1$-local space is again ![]() ${\mathbb {A}}^1$-local, so
${\mathbb {A}}^1$-local, so ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$ is
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$ is ![]() ${\mathbb {A}}^1$-local also. The identity component
${\mathbb {A}}^1$-local also. The identity component ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_0$ is itself an
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_0$ is itself an ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-space and therefore
$h$-space and therefore ![]() ${\mathbb {A}}^1$-simple. On the other hand, multiplication by
${\mathbb {A}}^1$-simple. On the other hand, multiplication by ![]() $f$ induces an
$f$ induces an ![]() ${\mathbb {A}}^1$-weak equivalence between
${\mathbb {A}}^1$-weak equivalence between ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_0$ and
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_0$ and ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$, so we conclude the latter is
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$, so we conclude the latter is ![]() ${\mathbb {A}}^1$-simple as well. Explicitly,
${\mathbb {A}}^1$-simple as well. Explicitly, ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f)$ coincides with
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f)$ coincides with ![]() $\boldsymbol {\pi }_i((\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f))$; for any
$\boldsymbol {\pi }_i((\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f))$; for any ![]() $i > 0$, this latter sheaf, which is necessarily strictly
$i > 0$, this latter sheaf, which is necessarily strictly ![]() ${\mathbb {A}}^1$-invariant, has sections
${\mathbb {A}}^1$-invariant, has sections ![]() $\tilde {H}^{n-i}_{\operatorname {Nis}}(\mathscr {Y}_L,\mathbf {A}_L)$ over a finitely generated extension
$\tilde {H}^{n-i}_{\operatorname {Nis}}(\mathscr {Y}_L,\mathbf {A}_L)$ over a finitely generated extension ![]() $L/k$.
$L/k$.
Next, assume that the ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $n$-truncated and
$n$-truncated and ![]() ${\mathbb {A}}^1$-nilpotent for some integer
${\mathbb {A}}^1$-nilpotent for some integer ![]() $n$, that is, there exists an integer
$n$, that is, there exists an integer ![]() $n$ such that
$n$ such that ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x)$ vanishes for
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X},x)$ vanishes for ![]() $i > n$. In that case, by appeal to Theorem 3.3.13 we know that the
$i > n$. In that case, by appeal to Theorem 3.3.13 we know that the ![]() ${\mathbb {A}}^1$–Postnikov factorization of the structure morphism admits an
${\mathbb {A}}^1$–Postnikov factorization of the structure morphism admits an ![]() ${\mathbb {A}}^1$-principal refinement, and furthermore that the resulting factorization is a finite tower; in this case, we will say that
${\mathbb {A}}^1$-principal refinement, and furthermore that the resulting factorization is a finite tower; in this case, we will say that ![]() $\mathscr {X}$ has a finite
$\mathscr {X}$ has a finite ![]() ${\mathbb {A}}^1$-principal series. We then proceed by induction. Since applying mapping spaces preserves
${\mathbb {A}}^1$-principal series. We then proceed by induction. Since applying mapping spaces preserves ![]() ${\mathbb {A}}^1$-fiber sequences, we reduce inductively to the following situation: there are
${\mathbb {A}}^1$-fiber sequences, we reduce inductively to the following situation: there are ![]() ${\mathbb {A}}^1$-fiber sequences of the form
${\mathbb {A}}^1$-fiber sequences of the form
where ![]() $\mathscr {X}$ admits a finite
$\mathscr {X}$ admits a finite ![]() ${\mathbb {A}}^1$-principal series and
${\mathbb {A}}^1$-principal series and ![]() $\mathscr {X}'$ admits a finite
$\mathscr {X}'$ admits a finite ![]() ${\mathbb {A}}^1$-principal series of shorter length. By the discussion of the preceding paragraph
${\mathbb {A}}^1$-principal series of shorter length. By the discussion of the preceding paragraph ![]() $\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$ is
$\operatorname {Map}(\mathscr {Y},K(\mathbf {A},n))_f$ is ![]() ${\mathbb {A}}^1$-simple, and one assumes that
${\mathbb {A}}^1$-simple, and one assumes that ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {X}')_f$ is
$\operatorname {Map}(\mathscr {Y},\mathscr {X}')_f$ is ![]() ${\mathbb {A}}^1$-nilpotent by induction. In that case,
${\mathbb {A}}^1$-nilpotent by induction. In that case, ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is necessarily also
$\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is necessarily also ![]() ${\mathbb {A}}^1$-nilpotent by appeal to Corollary 3.3.7. The discussion of the preceding paragraph also implies, by appeal to the long exact sequence in
${\mathbb {A}}^1$-nilpotent by appeal to Corollary 3.3.7. The discussion of the preceding paragraph also implies, by appeal to the long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves of a fibration, that
${\mathbb {A}}^1$-homotopy sheaves of a fibration, that ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ only depends on
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ only depends on ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ for
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ for ![]() $n \leq d+i+1$, if
$n \leq d+i+1$, if ![]() $\mathscr {Y}$ has strongly finite
$\mathscr {Y}$ has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension
${\mathbb {A}}^1$-cohomological dimension ![]() $\leq d$.
$\leq d$.
Now assume that ![]() $\mathscr {X}$ is a general
$\mathscr {X}$ is a general ![]() ${\mathbb {A}}^1$-nilpotent space. To check that
${\mathbb {A}}^1$-nilpotent space. To check that ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is
$\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is ![]() ${\mathbb {A}}^1$-nilpotent, we need to know that
${\mathbb {A}}^1$-nilpotent, we need to know that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ is
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ is ![]() ${\mathbb {A}}^1$-nilpotent and that this sheaf of groups acts
${\mathbb {A}}^1$-nilpotent and that this sheaf of groups acts ![]() ${\mathbb {A}}^1$-nilpotently on
${\mathbb {A}}^1$-nilpotently on ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ for all
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {Map}(\mathscr {Y},\mathscr {X})_f)$ for all ![]() $i > 0$. Thus,
$i > 0$. Thus, ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is
$\operatorname {Map}(\mathscr {Y},\mathscr {X})_f$ is ![]() ${\mathbb {A}}^1$-nilpotent if and only if all its finite Postnikov sections are
${\mathbb {A}}^1$-nilpotent if and only if all its finite Postnikov sections are ![]() ${\mathbb {A}}^1$-nilpotent. We know that
${\mathbb {A}}^1$-nilpotent. We know that ![]() $\mathscr {X}$ is the homotopy limit of its finite
$\mathscr {X}$ is the homotopy limit of its finite ![]() ${\mathbb {A}}^1$-Postnikov sections. The map
${\mathbb {A}}^1$-Postnikov sections. The map ![]() $\mathscr {X} \to \tau _{\leq n} \mathscr {X}$ induces a map
$\mathscr {X} \to \tau _{\leq n} \mathscr {X}$ induces a map
Because ![]() $\mathscr {Y}$ has strongly finite
$\mathscr {Y}$ has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension, it follows that for any
${\mathbb {A}}^1$-cohomological dimension, it follows that for any ![]() $m$, the map of the preceding display induces an
$m$, the map of the preceding display induces an ![]() ${\mathbb {A}}^1$-weak equivalence as
${\mathbb {A}}^1$-weak equivalence as ![]() $n \to \infty$ by the final comment of the preceding paragraph. Indeed, the map on homotopy sheaves is an isomorphism for
$n \to \infty$ by the final comment of the preceding paragraph. Indeed, the map on homotopy sheaves is an isomorphism for ![]() $n$ sufficiently large depending on
$n$ sufficiently large depending on ![]() $m$ and
$m$ and ![]() $d$.
$d$.
The above results have consequences for the contraction construction from Definition 3.1.17. For example, we may analyze ![]() ${\mathbb {A}}^1$-nilpotence of iterated
${\mathbb {A}}^1$-nilpotence of iterated ![]() ${{\mathbf {G}}_{m}^{}}$-loop spaces of
${{\mathbf {G}}_{m}^{}}$-loop spaces of ![]() ${\mathbb {A}}^1$-nilpotent spaces. As a corollary of Theorem 3.3.16, we deduce the following result, which shows that
${\mathbb {A}}^1$-nilpotent spaces. As a corollary of Theorem 3.3.16, we deduce the following result, which shows that ![]() ${{\mathbf {G}}_{m}^{}}$-loop spaces of
${{\mathbf {G}}_{m}^{}}$-loop spaces of ![]() ${\mathbb {A}}^1$-nilpotent spaces are
${\mathbb {A}}^1$-nilpotent spaces are ![]() ${\mathbb {A}}^1$-nilpotent. Unlike the situation in classical homotopy theory,
${\mathbb {A}}^1$-nilpotent. Unlike the situation in classical homotopy theory, ![]() ${{\mathbf {G}}_{m}^{}}$-loop spaces need not automatically have an
${{\mathbf {G}}_{m}^{}}$-loop spaces need not automatically have an ![]() $h$-space structure since
$h$-space structure since ![]() ${{\mathbf {G}}_{m}^{}}$ has no cogroup structure in
${{\mathbf {G}}_{m}^{}}$ has no cogroup structure in ![]() $\mathrm {Ho}_{k}$.
$\mathrm {Ho}_{k}$.
Theorem 3.3.17 Assume ![]() $(\mathscr {X},x)$ is a pointed
$(\mathscr {X},x)$ is a pointed ![]() ${\mathbb {A}}^1$-nilpotent space, then
${\mathbb {A}}^1$-nilpotent space, then ![]() $\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}\mathscr {X}$ is
$\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}\mathscr {X}$ is ![]() ${\mathbb {A}}^1$-nilpotent for every
${\mathbb {A}}^1$-nilpotent for every ![]() $n \geq 0$. In particular, if
$n \geq 0$. In particular, if ![]() $\mathbf {G}$ is an
$\mathbf {G}$ is an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups, then
${\mathbb {A}}^1$-nilpotent sheaf of groups, then ![]() $\mathbf {G}_{-n}$ is again an
$\mathbf {G}_{-n}$ is again an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups for every
${\mathbb {A}}^1$-nilpotent sheaf of groups for every ![]() $n \geq 0$.
$n \geq 0$.
Proof. By appealing to Theorem 3.1.19(1) we conclude that ![]() $\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}} \mathscr {X}$ is always
$\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}} \mathscr {X}$ is always ![]() ${\mathbb {A}}^1$-connected. Furthermore, in Example 3.3.15 we observed that
${\mathbb {A}}^1$-connected. Furthermore, in Example 3.3.15 we observed that ![]() ${{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$ has strongly finite
${{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$ has strongly finite ![]() ${\mathbb {A}}^1$-cohomological dimension. Granted those two facts, the first statement is a consequence of Theorem 3.3.16: take
${\mathbb {A}}^1$-cohomological dimension. Granted those two facts, the first statement is a consequence of Theorem 3.3.16: take ![]() $\mathscr {Y} = {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. The second statement follows from the first by repeated application of Theorem 3.1.19:
$\mathscr {Y} = {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. The second statement follows from the first by repeated application of Theorem 3.1.19: ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}B\mathbf {G}) = \mathbf {G}_{-n}$.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}B\mathbf {G}) = \mathbf {G}_{-n}$.
3.4 Explicit examples
In this subsection we collect a number of examples of spaces as in Definition 3.3.1. After reviewing some basic examples (see Example 3.4.1), we show that ![]() ${\mathbb {P}}^{2n+1}_k$ and
${\mathbb {P}}^{2n+1}_k$ and ![]() $BGL_{2n+1}$ are
$BGL_{2n+1}$ are ![]() ${\mathbb {A}}^1$-simple (see Proposition 3.4.4, and Theorem 3.4.6). Then we show that generalized flag varieties are typically
${\mathbb {A}}^1$-simple (see Proposition 3.4.4, and Theorem 3.4.6). Then we show that generalized flag varieties are typically ![]() ${\mathbb {A}}^1$-nilpotent but not
${\mathbb {A}}^1$-nilpotent but not ![]() ${\mathbb {A}}^1$-simple (see Theorem 3.4.8 and Remark 3.4.9). Finally, we observe that
${\mathbb {A}}^1$-simple (see Theorem 3.4.8 and Remark 3.4.9). Finally, we observe that ![]() ${\mathbb {P}}^{2n}_k$ and
${\mathbb {P}}^{2n}_k$ and ![]() $BGL_{2n}$ are not locally
$BGL_{2n}$ are not locally ![]() ${\mathbb {A}}^1$-nilpotent over general fields
${\mathbb {A}}^1$-nilpotent over general fields ![]() $k$, but are weakly
$k$, but are weakly ![]() ${\mathbb {A}}^1$-nilpotent if
${\mathbb {A}}^1$-nilpotent if ![]() $k$ is a field that is not formally real (see Proposition 3.4.10, Theorem 3.4.12 and the discussion of Remarks 3.4.11 and 3.4.13).
$k$ is a field that is not formally real (see Proposition 3.4.10, Theorem 3.4.12 and the discussion of Remarks 3.4.11 and 3.4.13).
 ${\mathbb {A}}^1$-simple spaces
${\mathbb {A}}^1$-simple spaces
If ![]() $(\mathscr {X},e)$ is an
$(\mathscr {X},e)$ is an ![]() $h$-space in
$h$-space in ![]() $\mathrm {sPre}(\mathrm {Sm}_k)$, then
$\mathrm {sPre}(\mathrm {Sm}_k)$, then ![]() $\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is also an
$\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ is also an ![]() $h$-space since
$h$-space since ![]() $\operatorname {L}_{{\mathbb {A}}^1}$ preserves finite products. If
$\operatorname {L}_{{\mathbb {A}}^1}$ preserves finite products. If ![]() $(\mathscr {X},e)$ is an
$(\mathscr {X},e)$ is an ![]() ${\mathbb {A}}^1$-connected
${\mathbb {A}}^1$-connected ![]() $h$-space, then it follows from the usual Eckmann–Hilton argument that
$h$-space, then it follows from the usual Eckmann–Hilton argument that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},e)$ is abelian and that this sheaf of groups acts trivially on the higher
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X},e)$ is abelian and that this sheaf of groups acts trivially on the higher ![]() ${\mathbb {A}}^1$-homotopy sheaves since this is true stalkwise. Thus, if
${\mathbb {A}}^1$-homotopy sheaves since this is true stalkwise. Thus, if ![]() $\mathscr {X}$ is an
$\mathscr {X}$ is an ![]() ${\mathbb {A}}^1$-connected
${\mathbb {A}}^1$-connected ![]() $h$-space, it follows that
$h$-space, it follows that ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() ${\mathbb {A}}^1$-simple.
${\mathbb {A}}^1$-simple.
Example 3.4.1 The following are well-known examples of ![]() ${\mathbb {A}}^1$-simple spaces (see Definition 3.3.1):
${\mathbb {A}}^1$-simple spaces (see Definition 3.3.1):
1. split, simply connected, semi-simple algebraic groups (the hypotheses guarantee that the resulting space is
 ${\mathbb {A}}^1$-connected and the result is evident for any
${\mathbb {A}}^1$-connected and the result is evident for any  ${\mathbb {A}}^1$-connected sheaf of groups);
${\mathbb {A}}^1$-connected sheaf of groups);2. the space
 $B_{\operatorname {Nis}}A$ for any abelian sheaf of groups
$B_{\operatorname {Nis}}A$ for any abelian sheaf of groups  $A$;
$A$;3. the stable group
 $BGL$ (this is an
$BGL$ (this is an  ${\mathbb {A}}^1$-connected
${\mathbb {A}}^1$-connected  $h$-space);
$h$-space);4. the motivic Eilenberg–Mac Lane space
 $K({\mathbb {Z}}(n),2n)$ or
$K({\mathbb {Z}}(n),2n)$ or  $K({\mathbb {Z}}/m(n),2n)$ for any integers
$K({\mathbb {Z}}/m(n),2n)$ for any integers  $m, n > 0$ (the hypotheses guarantee that the resulting space is
$m, n > 0$ (the hypotheses guarantee that the resulting space is  ${\mathbb {A}}^1$-connected; see § 5.3 for further discussion of this example).
${\mathbb {A}}^1$-connected; see § 5.3 for further discussion of this example).
Remark 3.4.2 In classical algebraic topology, the odd-dimensional real projective spaces ![]() $\mathbb {RP}^{2n+1}$ are all simple spaces (i.e. have abelian fundamental group and the action on higher homotopy groups is trivial), not just nilpotent. In contrast,
$\mathbb {RP}^{2n+1}$ are all simple spaces (i.e. have abelian fundamental group and the action on higher homotopy groups is trivial), not just nilpotent. In contrast, ![]() $\mathbb {P}^1_k$ is not
$\mathbb {P}^1_k$ is not ![]() ${\mathbb {A}}^1$-simple because
${\mathbb {A}}^1$-simple because ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1_k)$ is not even a sheaf of abelian groups. Nevertheless, the
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1_k)$ is not even a sheaf of abelian groups. Nevertheless, the ![]() ${\mathbb {A}}^1$-fundamental sheaves of groups of
${\mathbb {A}}^1$-fundamental sheaves of groups of ![]() ${\mathbb {P}}^n_k$ for
${\mathbb {P}}^n_k$ for ![]() $n \geq 2$ are isomorphic to
$n \geq 2$ are isomorphic to ![]() ${{\mathbf {G}}_{m}^{}}$, which is abelian.
${{\mathbf {G}}_{m}^{}}$, which is abelian.
The ![]() ${\mathbb {A}}^1$-fiber sequences produced by the following result will be essential in our construction of (locally)
${\mathbb {A}}^1$-fiber sequences produced by the following result will be essential in our construction of (locally) ![]() ${\mathbb {A}}^1$-nilpotent spaces to follow.
${\mathbb {A}}^1$-nilpotent spaces to follow.
Theorem 3.4.3 Assume ![]() $k$ is a field and
$k$ is a field and ![]() $G$ is a split, simply connected, semi-simple
$G$ is a split, simply connected, semi-simple ![]() $k$-group scheme. If
$k$-group scheme. If ![]() $H \subset G$ is a closed subgroup scheme, such that the
$H \subset G$ is a closed subgroup scheme, such that the ![]() $H$-torsor
$H$-torsor ![]() $G \to G/H$ is Nisnevich locally trivial, then there is an
$G \to G/H$ is Nisnevich locally trivial, then there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
Proof. Under these hypotheses, there is a simplicial fiber sequence of the form
by [Reference Asok, Hoyois and WendtAHW18, Lemma 2.4.1]. The space ![]() $B_{\operatorname {Nis}}G$ is Nisnevich local by definition and it satisfies Nisnevich excision by [Reference Asok, Hoyois and WendtAHW17, Theorem 3.2.5]. Furthermore,
$B_{\operatorname {Nis}}G$ is Nisnevich local by definition and it satisfies Nisnevich excision by [Reference Asok, Hoyois and WendtAHW17, Theorem 3.2.5]. Furthermore, ![]() $\pi _0(B_{\operatorname {Nis}}G)$ is
$\pi _0(B_{\operatorname {Nis}}G)$ is ![]() ${\mathbb {A}}^1$-invariant on affines by [Reference Asok, Hoyois and WendtAHW20, Theorem 2.4]. Therefore, by appeal to [Reference Asok, Hoyois and WendtAHW18, Theorem 2.2.5], we conclude that the above simplicial fiber sequence is an
${\mathbb {A}}^1$-invariant on affines by [Reference Asok, Hoyois and WendtAHW20, Theorem 2.4]. Therefore, by appeal to [Reference Asok, Hoyois and WendtAHW18, Theorem 2.2.5], we conclude that the above simplicial fiber sequence is an ![]() ${\mathbb {A}}^1$-fiber sequence.
${\mathbb {A}}^1$-fiber sequence.
Proposition 3.4.4 If ![]() $k$ is a field, then for every integer
$k$ is a field, then for every integer ![]() $n > 0$, the space
$n > 0$, the space ![]() ${\mathbb {P}}^{2n+1}_k$ is
${\mathbb {P}}^{2n+1}_k$ is ![]() ${\mathbb {A}}^1$-simple.
${\mathbb {A}}^1$-simple.
Proof. We suppress ![]() $k$ from the notation. We proceed by analogy with the argument establishing nilpotence of odd-dimensional real projective spaces in classical topology. In other words, we will establish the equivalent conditions of Corollary 3.3.3. To this end, let us recall that there is an
$k$ from the notation. We proceed by analogy with the argument establishing nilpotence of odd-dimensional real projective spaces in classical topology. In other words, we will establish the equivalent conditions of Corollary 3.3.3. To this end, let us recall that there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
classifying the tautological ![]() ${{\mathbf {G}}_{m}^{}}$-torsor over
${{\mathbf {G}}_{m}^{}}$-torsor over ![]() ${\mathbb {P}}^{2n+1}$ [Reference MorelMor12, Lemma 7.5]. In particular, the first map is the quotient of the standard scaling action of
${\mathbb {P}}^{2n+1}$ [Reference MorelMor12, Lemma 7.5]. In particular, the first map is the quotient of the standard scaling action of ![]() ${{\mathbf {G}}_{m}^{}}$ on
${{\mathbf {G}}_{m}^{}}$ on ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$.
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$.
For any ![]() $n > 0$,
$n > 0$, ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected, and thus is a model for the
$1$-connected, and thus is a model for the ![]() ${\mathbb {A}}^1$-universal covering space of
${\mathbb {A}}^1$-universal covering space of ![]() ${\mathbb {P}}^{2n+1}$ [Reference MorelMor12, Theorem 7.8]. Thus, it suffices to show that the action of
${\mathbb {P}}^{2n+1}$ [Reference MorelMor12, Theorem 7.8]. Thus, it suffices to show that the action of ![]() ${{\mathbf {G}}_{m}^{}}$ on the higher
${{\mathbf {G}}_{m}^{}}$ on the higher ![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Following the observation of Remark 3.3.4, we will show that the scaling ![]() ${{\mathbf {G}}_{m}^{}}$-action on
${{\mathbf {G}}_{m}^{}}$-action on ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is null
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ is null ![]() ${\mathbb {A}}^1$-homotopic; we prove this in a fashion analogous to [Reference Asok and FaselAF14b, Lemma 4.8]. Since the homotopy sheaves of
${\mathbb {A}}^1$-homotopic; we prove this in a fashion analogous to [Reference Asok and FaselAF14b, Lemma 4.8]. Since the homotopy sheaves of ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ are unramified, to show that the action of
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ are unramified, to show that the action of ![]() ${{\mathbf {G}}_{m}^{}}$ is trivial, it suffices to show that, for every finitely generated separable extension
${{\mathbf {G}}_{m}^{}}$ is trivial, it suffices to show that, for every finitely generated separable extension ![]() $L$ of the base field
$L$ of the base field ![]() $k$ the action of
$k$ the action of ![]() ${{\mathbf {G}}_{m}^{}}(L)$ is null
${{\mathbf {G}}_{m}^{}}(L)$ is null ![]() ${\mathbb {A}}^1$-homotopic.
${\mathbb {A}}^1$-homotopic.
Thus, it suffices to show that for every unit ![]() $u \in L^{\times }$, the endomorphism of
$u \in L^{\times }$, the endomorphism of ![]() ${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ induced by scaling via
${\mathbb {A}}^{2n+2} \,{\setminus}\, 0$ induced by scaling via ![]() $u$ has trivial motivic Brouwer degree. Indeed, the motivic Brouwer degree of the map
$u$ has trivial motivic Brouwer degree. Indeed, the motivic Brouwer degree of the map ![]() $(x_1,\ldots,x_{2n+2}) \to (ux_1,ux_2,\ldots,ux_{2n+2})$ can be computed via the procedure described in [Reference FaselFas12, Remark 2.6]. Following this procedure, one sees that the Brouwer degree of the above map is
$(x_1,\ldots,x_{2n+2}) \to (ux_1,ux_2,\ldots,ux_{2n+2})$ can be computed via the procedure described in [Reference FaselFas12, Remark 2.6]. Following this procedure, one sees that the Brouwer degree of the above map is ![]() $\langle u \rangle ^{2n+2}$, which, as a square class, is trivial in
$\langle u \rangle ^{2n+2}$, which, as a square class, is trivial in ![]() $GW(L)$.
$GW(L)$.
Remark 3.4.5 One can also establish the preceding result as follows. One shows that there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
where ![]() $\mathrm {HP}^n$ is the Panin–Walter model for quaternionic projective space [Reference Panin and WalterPW10, § 3]. By construction,
$\mathrm {HP}^n$ is the Panin–Walter model for quaternionic projective space [Reference Panin and WalterPW10, § 3]. By construction, ![]() $\mathrm {HP}^n = Sp_{2n+2}/(Sp_{2n} \times Sp_2)$, and the map
$\mathrm {HP}^n = Sp_{2n+2}/(Sp_{2n} \times Sp_2)$, and the map ![]() ${\mathbb {P}}^{2n+1} \to \mathrm {HP}^n$ is the map
${\mathbb {P}}^{2n+1} \to \mathrm {HP}^n$ is the map ![]() $Sp_{2n+2}/(Sp_{2n} \times {{\mathbf {G}}_{m}^{}}) \to Sp_{2n+2}/(Sp_{2n} \times Sp_2)$ induced by the inclusion of
$Sp_{2n+2}/(Sp_{2n} \times {{\mathbf {G}}_{m}^{}}) \to Sp_{2n+2}/(Sp_{2n} \times Sp_2)$ induced by the inclusion of ![]() ${{\mathbf {G}}_{m}^{}} \hookrightarrow Sp_2$ as a maximal torus. Here
${{\mathbf {G}}_{m}^{}} \hookrightarrow Sp_2$ as a maximal torus. Here ![]() $Sp_{2n+2}/(Sp_{2n} \times {{\mathbf {G}}_{m}^{}})$ is a model for the standard Jouanolou device over
$Sp_{2n+2}/(Sp_{2n} \times {{\mathbf {G}}_{m}^{}})$ is a model for the standard Jouanolou device over ![]() ${\mathbb {P}}^{2n+1}$ for every
${\mathbb {P}}^{2n+1}$ for every ![]() $n \geq 0$. One may show that
$n \geq 0$. One may show that ![]() $\mathrm {HP}^n$ is
$\mathrm {HP}^n$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected. Then, since
$1$-connected. Then, since ![]() ${\mathbb {P}}^1$ is
${\mathbb {P}}^1$ is ![]() ${\mathbb {A}}^1$-nilpotent by Theorem 3.4.8 below, one may conclude by appealing to Proposition 3.3.8.
${\mathbb {A}}^1$-nilpotent by Theorem 3.4.8 below, one may conclude by appealing to Proposition 3.3.8.
The next result is an analog in ![]() ${\mathbb {A}}^1$-algebraic topology of the classical fact that
${\mathbb {A}}^1$-algebraic topology of the classical fact that ![]() $BO(2n+1)$ is a simple space.
$BO(2n+1)$ is a simple space.
Theorem 3.4.6 If ![]() $k$ is a field, then, for every integer
$k$ is a field, then, for every integer ![]() $n \geq 0$, the
$n \geq 0$, the ![]() $k$-space
$k$-space ![]() $BGL_{2n+1}$ is
$BGL_{2n+1}$ is ![]() ${\mathbb {A}}^1$-simple.
${\mathbb {A}}^1$-simple.
Proof. Again, we suppress ![]() $k$ from the notation. For
$k$ from the notation. For ![]() $n = 0$, the assertion is that
$n = 0$, the assertion is that ![]() $B{{\mathbf {G}}_{m}^{}}$ is
$B{{\mathbf {G}}_{m}^{}}$ is ![]() ${\mathbb {A}}^1$-simple, which follows from the fact that
${\mathbb {A}}^1$-simple, which follows from the fact that ![]() $B{{\mathbf {G}}_{m}^{}}$ admits an
$B{{\mathbf {G}}_{m}^{}}$ admits an ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-space structure. Therefore, we assume
$h$-space structure. Therefore, we assume ![]() $n > 0$.
$n > 0$.
We begin by considering the homomorphism ![]() $GL_m \to SL_{m+1}$ defined at the level of points by sending an invertible
$GL_m \to SL_{m+1}$ defined at the level of points by sending an invertible ![]() $m \times m$ matrix
$m \times m$ matrix ![]() $X$ to the block matrix
$X$ to the block matrix ![]() $(X,\det X^{-1})$. This homomorphism identifies
$(X,\det X^{-1})$. This homomorphism identifies ![]() $GL_m$ as the Levi factor of a parabolic subgroup in
$GL_m$ as the Levi factor of a parabolic subgroup in ![]() $SL_{m+1}$. The quotient morphism
$SL_{m+1}$. The quotient morphism ![]() $SL_{m+1} \to SL_{m+1}/GL_{m}$ is Zariski and hence Nisnevich locally trivial, so Theorem 3.4.3 yields an
$SL_{m+1} \to SL_{m+1}/GL_{m}$ is Zariski and hence Nisnevich locally trivial, so Theorem 3.4.3 yields an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
The fiber here is identified as the standard Jouanolou device over ![]() ${\mathbb {P}}^{m}$ (i.e. the complement of the incidence divisor in the product of
${\mathbb {P}}^{m}$ (i.e. the complement of the incidence divisor in the product of ![]() ${\mathbb {P}}^m \times {\mathbb {P}}^m$, where the second copy of projective space is viewed as the dual of the first).
${\mathbb {P}}^m \times {\mathbb {P}}^m$, where the second copy of projective space is viewed as the dual of the first).
If ![]() $m = 2n+1$ is odd, then it follows from Proposition 3.4.4 and the identifications described in the preceding paragraph that
$m = 2n+1$ is odd, then it follows from Proposition 3.4.4 and the identifications described in the preceding paragraph that ![]() $SL_{2n+2}/GL_{2n+1}$ is
$SL_{2n+2}/GL_{2n+1}$ is ![]() ${\mathbb {A}}^1$-simple. Since
${\mathbb {A}}^1$-simple. Since ![]() $BSL_{m+1}$ is always
$BSL_{m+1}$ is always ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected, the result follows from Proposition 3.3.8.
$1$-connected, the result follows from Proposition 3.3.8.
Examples of  ${\mathbb {A}}^1$-nilpotent spaces
${\mathbb {A}}^1$-nilpotent spaces
Examples of ![]() ${\mathbb {A}}^1$-nilpotent spaces may be built from those in Example 3.4.1 by taking homotopy fibers of maps.
${\mathbb {A}}^1$-nilpotent spaces may be built from those in Example 3.4.1 by taking homotopy fibers of maps.
Example 3.4.7 Any finite product of (![]() ${\mathbb {A}}^1$-connected) spaces of the form
${\mathbb {A}}^1$-connected) spaces of the form ![]() $K(\mathbf {A},i)$ is also an
$K(\mathbf {A},i)$ is also an ![]() ${\mathbb {A}}^1$-simple space and thus
${\mathbb {A}}^1$-simple space and thus ![]() ${\mathbb {A}}^1$-nilpotent. By an
${\mathbb {A}}^1$-nilpotent. By an ![]() ${\mathbb {A}}^1$-polyGEM, we will mean a space contained in the smallest class of spaces that (i) contains finite products of Eilenberg–Mac Lane spaces, and (ii) is closed under the operation of taking homotopy fibers of morphisms of
${\mathbb {A}}^1$-polyGEM, we will mean a space contained in the smallest class of spaces that (i) contains finite products of Eilenberg–Mac Lane spaces, and (ii) is closed under the operation of taking homotopy fibers of morphisms of ![]() ${\mathbb {A}}^1$-polyGEMs. A straightforward induction argument appealing to Corollary 3.3.7 guarantees that such spaces are automatically
${\mathbb {A}}^1$-polyGEMs. A straightforward induction argument appealing to Corollary 3.3.7 guarantees that such spaces are automatically ![]() ${\mathbb {A}}^1$-nilpotent. For example, any finite Postnikov truncation of an
${\mathbb {A}}^1$-nilpotent. For example, any finite Postnikov truncation of an ![]() ${\mathbb {A}}^1$-nilpotent space is an
${\mathbb {A}}^1$-nilpotent space is an ![]() ${\mathbb {A}}^1$-polyGEM.
${\mathbb {A}}^1$-polyGEM.
More interesting examples of ![]() ${\mathbb {A}}^1$-nilpotent spaces are constructed in the following result.
${\mathbb {A}}^1$-nilpotent spaces are constructed in the following result.
Theorem 3.4.8 Suppose ![]() $k$ is a perfect field, assume
$k$ is a perfect field, assume ![]() $G$ is a split, semi-simple, simply connected
$G$ is a split, semi-simple, simply connected ![]() $k$-group scheme, and let
$k$-group scheme, and let ![]() $B$ be a split Borel subgroup. For every integer
$B$ be a split Borel subgroup. For every integer ![]() $n \geq 0$, the space
$n \geq 0$, the space ![]() $\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}G/B$ is
$\Omega _{{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}}G/B$ is ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. We first treat the case ![]() $n = 0$. Fix a split maximal torus
$n = 0$. Fix a split maximal torus ![]() $T \subset G$ and observe that there are induced maps
$T \subset G$ and observe that there are induced maps
The above morphism is Zariski locally trivial with affine space fibers and thus an ![]() ${\mathbb {A}}^1$-weak equivalence. Moreover, the
${\mathbb {A}}^1$-weak equivalence. Moreover, the ![]() $T$-torsor
$T$-torsor ![]() $G \to G/T$ is Zariski and hence Nisnevich locally trivial (and thus Nisnevich locally split). Since the map
$G \to G/T$ is Zariski and hence Nisnevich locally trivial (and thus Nisnevich locally split). Since the map ![]() $G/T \to G/B$ is an
$G/T \to G/B$ is an ![]() ${\mathbb {A}}^1$-weak equivalence, Theorem 3.4.3 allows us to conclude that there is an
${\mathbb {A}}^1$-weak equivalence, Theorem 3.4.3 allows us to conclude that there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
Since ![]() $BT$ is
$BT$ is ![]() ${\mathbb {A}}^1$-nilpotent (
${\mathbb {A}}^1$-nilpotent (![]() ${\mathbb {A}}^1$-simple in fact) and all spaces are
${\mathbb {A}}^1$-simple in fact) and all spaces are ![]() ${\mathbb {A}}^1$-connected, the result follows from Theorem 3.3.6. For
${\mathbb {A}}^1$-connected, the result follows from Theorem 3.3.6. For ![]() $n \geq 0$, we conclude by appeal to Theorem 3.3.17.
$n \geq 0$, we conclude by appeal to Theorem 3.3.17.
Remark 3.4.9 In the simplest case ![]() $G = SL_2$ the above result shows that
$G = SL_2$ the above result shows that ![]() ${\mathbb {P}}^1$ is
${\mathbb {P}}^1$ is ![]() ${\mathbb {A}}^1$-nilpotent. Indeed, in that case
${\mathbb {A}}^1$-nilpotent. Indeed, in that case ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$ is non-abelian by Example 3.2.11. More generally, the fiber sequence in the statement, together with the facts that
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$ is non-abelian by Example 3.2.11. More generally, the fiber sequence in the statement, together with the facts that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BT) = T$ and
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BT) = T$ and ![]() $BT$ is
$BT$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-truncated, yields a central extension of the form
$1$-truncated, yields a central extension of the form
For simplicity, assume ![]() $G$ is a split, simple, simply connected
$G$ is a split, simple, simply connected ![]() $k$-group scheme. In that case, the description of
$k$-group scheme. In that case, the description of ![]() $\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ depends on the Dynkin classification of
$\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ depends on the Dynkin classification of ![]() $G$. For example, if
$G$. For example, if ![]() $G$ is not of type
$G$ is not of type ![]() $C_n$, then
$C_n$, then ![]() $\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ is
$\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ is ![]() ${{\mathbf {K}}}^{\rm M}_2$, while if
${{\mathbf {K}}}^{\rm M}_2$, while if ![]() $G$ is of type
$G$ is of type ![]() $C_n$, then
$C_n$, then ![]() $\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ is
$\boldsymbol {\pi }_2^{{\mathbb {A}}^1}(BG)$ is ![]() ${{\mathbf {K}}}^{\rm MW}_2$. For
${{\mathbf {K}}}^{\rm MW}_2$. For ![]() $G = SL_n$, this result appears in [Reference MorelMor12, Theorem 7.20]. For
$G = SL_n$, this result appears in [Reference MorelMor12, Theorem 7.20]. For ![]() $k$ infinite and general
$k$ infinite and general ![]() $G$, this appears in [Reference Voelkel and WendtVW16]. A uniform proof, without assumption on cardinality of
$G$, this appears in [Reference Voelkel and WendtVW16]. A uniform proof, without assumption on cardinality of ![]() $k$, appears in [Reference Morel and SawantMS20, Theorem 1]. Moreover, it is known that the resulting extension is non-trivial in general and
$k$, appears in [Reference Morel and SawantMS20, Theorem 1]. Moreover, it is known that the resulting extension is non-trivial in general and ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(G/B)$ is a non-abelian sheaf of groups.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(G/B)$ is a non-abelian sheaf of groups.
Examples of locally  ${\mathbb {A}}^1$-nilpotent spaces
${\mathbb {A}}^1$-nilpotent spaces
In contrast to the situation for ![]() $BGL_{2n+1}$ discussed in Theorem 3.4.6, one knows that
$BGL_{2n+1}$ discussed in Theorem 3.4.6, one knows that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BGL_{2n}) = {{\mathbf {G}}_{m}^{}}$ can act non-trivially on
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(BGL_{2n}) = {{\mathbf {G}}_{m}^{}}$ can act non-trivially on ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(BGL_{2n})$ (e.g. for
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(BGL_{2n})$ (e.g. for ![]() $n = 1$, see [Reference Asok and FaselAF14b, Corollary 4.9]). Thus,
$n = 1$, see [Reference Asok and FaselAF14b, Corollary 4.9]). Thus, ![]() $BGL_{2n}$ is not
$BGL_{2n}$ is not ![]() ${\mathbb {A}}^1$-simple. Nevertheless, we will see that under appropriate assumptions on the base field,
${\mathbb {A}}^1$-simple. Nevertheless, we will see that under appropriate assumptions on the base field, ![]() $BGL_{2n}$ is locally
$BGL_{2n}$ is locally ![]() ${\mathbb {A}}^1$-nilpotent. To show this, we first establish a local
${\mathbb {A}}^1$-nilpotent. To show this, we first establish a local ![]() ${\mathbb {A}}^1$-nilpotence result for even-dimensional projective spaces. As discussed in Remark 3.4.11,
${\mathbb {A}}^1$-nilpotence result for even-dimensional projective spaces. As discussed in Remark 3.4.11, ![]() ${\mathbb {P}}^{2n}_k$ is not
${\mathbb {P}}^{2n}_k$ is not ![]() ${\mathbb {A}}^1$-nilpotent for general fields
${\mathbb {A}}^1$-nilpotent for general fields ![]() $k$. Furthermore, we will see that
$k$. Furthermore, we will see that ![]() $BGL_{2n}$ is also not
$BGL_{2n}$ is also not ![]() ${\mathbb {A}}^1$-nilpotent for general fields
${\mathbb {A}}^1$-nilpotent for general fields ![]() $k$.
$k$.
Proposition 3.4.10 Suppose ![]() $n \geq 1$ is an integer. If
$n \geq 1$ is an integer. If ![]() $k$ is not formally real, then
$k$ is not formally real, then ![]() ${\mathbb {P}}^{2n}_k$ is weakly
${\mathbb {P}}^{2n}_k$ is weakly ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. The ![]() ${\mathbb {A}}^1$-fiber sequence
${\mathbb {A}}^1$-fiber sequence
shows that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}) = {{\mathbf {G}}_{m}^{}}$, which is, in particular,
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}) = {{\mathbf {G}}_{m}^{}}$, which is, in particular, ![]() ${\mathbb {A}}^1$-nilpotent. To establish local
${\mathbb {A}}^1$-nilpotent. To establish local ![]() ${\mathbb {A}}^1$-nilpotence, we again appeal to Corollary 3.3.3. As in the proof of Proposition 3.4.4, we reduce to showing that the action of
${\mathbb {A}}^1$-nilpotence, we again appeal to Corollary 3.3.3. As in the proof of Proposition 3.4.4, we reduce to showing that the action of ![]() ${{\mathbf {G}}_{m}^{}}$ on
${{\mathbf {G}}_{m}^{}}$ on ![]() ${\mathbb {A}}^{2n+1} \,{\setminus}\, 0$ is homotopically nilpotent. If
${\mathbb {A}}^{2n+1} \,{\setminus}\, 0$ is homotopically nilpotent. If ![]() $L/k$ is an extension field, and
$L/k$ is an extension field, and ![]() $u \in L^{\times }$ is a unit, then the scaling action by
$u \in L^{\times }$ is a unit, then the scaling action by ![]() $u$ has motivic degree
$u$ has motivic degree ![]() $\langle u^{2n+1} \rangle = \langle u \rangle$. On the other hand,
$\langle u^{2n+1} \rangle = \langle u \rangle$. On the other hand, ![]() $1 - \langle u \rangle$ lies in
$1 - \langle u \rangle$ lies in ![]() $I(L)$. Since
$I(L)$. Since ![]() $k$ is not formally real, so is
$k$ is not formally real, so is ![]() $L$ and a well-known result of Pfister [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 31.4] asserts that
$L$ and a well-known result of Pfister [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 31.4] asserts that ![]() $I(L)$ is the nilradical of
$I(L)$ is the nilradical of ![]() $GW(L)$. Therefore, some power of
$GW(L)$. Therefore, some power of ![]() $1 - \langle u \rangle$ is zero and we conclude.
$1 - \langle u \rangle$ is zero and we conclude.
Remark 3.4.11 If ![]() $k$ is
$k$ is ![]() ${\mathbb {R}}$ or, more generally, any formally real field, then
${\mathbb {R}}$ or, more generally, any formally real field, then ![]() ${\mathbb {P}}^{2n}_k$ is not locally nilpotent. Indeed, under this hypothesis, the filtration discussed in Proposition 3.4.10 remains infinite stalkwise. In fact, the lower central series for the
${\mathbb {P}}^{2n}_k$ is not locally nilpotent. Indeed, under this hypothesis, the filtration discussed in Proposition 3.4.10 remains infinite stalkwise. In fact, the lower central series for the ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}_k)$-action on the homotopy sheaf
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}_k)$-action on the homotopy sheaf ![]() $\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}) = {{\mathbf {K}}}^{\rm MW}_{2n+1}$ is not stalkwise finite. One may write down the
$\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}({\mathbb {P}}^{2n}) = {{\mathbf {K}}}^{\rm MW}_{2n+1}$ is not stalkwise finite. One may write down the ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() ${{\mathbf {G}}_{m}^{}}$-lower central series for this sheaf as follows. The kernel of the canonical epimorphism
${{\mathbf {G}}_{m}^{}}$-lower central series for this sheaf as follows. The kernel of the canonical epimorphism ![]() ${{\mathbf {K}}}^{\rm MW}_{2n+1} \to {{\mathbf {K}}}^{\rm M}_{2n+1}$ is
${{\mathbf {K}}}^{\rm MW}_{2n+1} \to {{\mathbf {K}}}^{\rm M}_{2n+1}$ is ![]() $\mathbf {I}^{2n+2}$; the induced
$\mathbf {I}^{2n+2}$; the induced ![]() ${{\mathbf {G}}_{m}^{}}$-action on
${{\mathbf {G}}_{m}^{}}$-action on ![]() ${{\mathbf {K}}}^{\rm M}_{2n+1}$ is trivial. The induced action of
${{\mathbf {K}}}^{\rm M}_{2n+1}$ is trivial. The induced action of ![]() ${{\mathbf {G}}_{m}^{}}$ on
${{\mathbf {G}}_{m}^{}}$ on ![]() $\mathbf {I}^{2n+2}$ is, upon taking sections over fields, the action by multiplication by units. As a consequence, the powers of
$\mathbf {I}^{2n+2}$ is, upon taking sections over fields, the action by multiplication by units. As a consequence, the powers of ![]() $\mathbf {I}^j \subset \mathbf {I}^{2n+2}$,
$\mathbf {I}^j \subset \mathbf {I}^{2n+2}$, ![]() $j \geq 2n+2$ then yield a filtration for which
$j \geq 2n+2$ then yield a filtration for which ![]() ${{\mathbf {G}}_{m}^{}}$-acts trivially on the successive subquotients.
${{\mathbf {G}}_{m}^{}}$-acts trivially on the successive subquotients.
Theorem 3.4.12 If ![]() $k$ is not formally real, then the
$k$ is not formally real, then the ![]() $k$-space
$k$-space ![]() $BGL_{2n}$ is weakly
$BGL_{2n}$ is weakly ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
Proof. As in the proof of Theorem 3.4.6, there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
where the base is ![]() ${\mathbb {A}}^1$-simply connected. Since the fiber is locally
${\mathbb {A}}^1$-simply connected. Since the fiber is locally ![]() ${\mathbb {A}}^1$-nilpotent by appeal to Proposition 3.4.10, the result then follows by appeal to Proposition 3.3.8.
${\mathbb {A}}^1$-nilpotent by appeal to Proposition 3.4.10, the result then follows by appeal to Proposition 3.3.8.
Remark 3.4.13 Again, if ![]() $k = {\mathbb {R}}$ (or, more generally, any formally real field), then the space
$k = {\mathbb {R}}$ (or, more generally, any formally real field), then the space ![]() $BGL_{2n}$ fails to be locally
$BGL_{2n}$ fails to be locally ![]() ${\mathbb {A}}^1$-nilpotent. Indeed, along the lines of Remark 3.4.11 one can explicitly show that
${\mathbb {A}}^1$-nilpotent. Indeed, along the lines of Remark 3.4.11 one can explicitly show that ![]() $\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_{2n})$ does not have a stalkwise finite
$\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_{2n})$ does not have a stalkwise finite ![]() ${{\mathbf {G}}_{m}^{}}$-central series. To see this, begin by observing that
${{\mathbf {G}}_{m}^{}}$-central series. To see this, begin by observing that ![]() $\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_{2n})$ is described in [Reference Asok and FaselAF14a, Theorem 1.1]: it is an extension of
$\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_{2n})$ is described in [Reference Asok and FaselAF14a, Theorem 1.1]: it is an extension of ![]() ${{\mathbf {K}}}^Q_{2n}$ by a sheaf
${{\mathbf {K}}}^Q_{2n}$ by a sheaf ![]() $\mathbf {T}_{2n+1}$ that is the cokernel of a certain morphism
$\mathbf {T}_{2n+1}$ that is the cokernel of a certain morphism ![]() ${{\mathbf {K}}}^{Q}_{2n+1} \to {{\mathbf {K}}}^{\rm MW}_{2n+1}$. The composite morphism
${{\mathbf {K}}}^{Q}_{2n+1} \to {{\mathbf {K}}}^{\rm MW}_{2n+1}$. The composite morphism ![]() ${{\mathbf {K}}}^Q_{2n+1} \to \mathbf {I}^{2n+1}$ is trivial by [Reference Asok and FaselAF14a, Lemma 3.13], and
${{\mathbf {K}}}^Q_{2n+1} \to \mathbf {I}^{2n+1}$ is trivial by [Reference Asok and FaselAF14a, Lemma 3.13], and ![]() $\mathbf {T}_{2n+1}$ is a fiber product of
$\mathbf {T}_{2n+1}$ is a fiber product of ![]() $\mathbf {I}^{2n+1}$ and another sheaf
$\mathbf {I}^{2n+1}$ and another sheaf ![]() $\mathbf {S}_{2n+1}$ whose precise description is unimportant. Appealing to the long exact sequence in
$\mathbf {S}_{2n+1}$ whose precise description is unimportant. Appealing to the long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves attached to the
${\mathbb {A}}^1$-homotopy sheaves attached to the ![]() ${\mathbb {A}}^1$-fiber sequence appearing in the proof of Theorem 3.4.12, one sees that
${\mathbb {A}}^1$-fiber sequence appearing in the proof of Theorem 3.4.12, one sees that ![]() $\mathbf {T}_{2n+1}$ is precisely the image of
$\mathbf {T}_{2n+1}$ is precisely the image of ![]() $\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}({\mathbb {P}}^{2n})$ in
$\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}({\mathbb {P}}^{2n})$ in ![]() $\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_n)$. The
$\boldsymbol {\pi }_{2n}^{{\mathbb {A}}^1}(BGL_n)$. The ![]() ${{\mathbf {G}}_{m}^{}}$-action on the copy of
${{\mathbf {G}}_{m}^{}}$-action on the copy of ![]() $\mathbf {I}^{2n+1}$ in
$\mathbf {I}^{2n+1}$ in ![]() $\mathbf {T}^{2n+1}$ thus does not have a stalkwise finite
$\mathbf {T}^{2n+1}$ thus does not have a stalkwise finite ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() ${{\mathbf {G}}_{m}^{}}$-central series by the conclusion of Remark 3.4.11.
${{\mathbf {G}}_{m}^{}}$-central series by the conclusion of Remark 3.4.11.
4. Nilpotence,  $R$-localization and
$R$-localization and  ${\mathbb {A}}^1$-homology
${\mathbb {A}}^1$-homology
In this section we study ![]() $R$-localization in
$R$-localization in ![]() ${\mathbb {A}}^1$-homotopy theory. We introduce a notion of
${\mathbb {A}}^1$-homotopy theory. We introduce a notion of ![]() $R$-homology equivalence in
$R$-homology equivalence in ![]() ${\mathbb {A}}^1$-homotopy theory, and show that
${\mathbb {A}}^1$-homotopy theory, and show that ![]() $R$-localization is well behaved on locally
$R$-localization is well behaved on locally ![]() ${\mathbb {A}}^1$-nilpotent spaces. Section 4.1 introduces
${\mathbb {A}}^1$-nilpotent spaces. Section 4.1 introduces ![]() ${\mathbb {A}}^1$-homology (following Morel) and studies its various properties. Section 4.2 considers various refinements of Hurewicz theorems in
${\mathbb {A}}^1$-homology (following Morel) and studies its various properties. Section 4.2 considers various refinements of Hurewicz theorems in ![]() ${\mathbb {A}}^1$-homotopy theory; in particular, we finish the proof that
${\mathbb {A}}^1$-homotopy theory; in particular, we finish the proof that ![]() ${\mathbb {A}}^1$-nilpotent spaces have
${\mathbb {A}}^1$-nilpotent spaces have ![]() ${\mathbb {A}}^1$-Postnikov towers that admit principal refinements (see Theorem 3.3.13). Finally, § 4.3 studies
${\mathbb {A}}^1$-Postnikov towers that admit principal refinements (see Theorem 3.3.13). Finally, § 4.3 studies ![]() $R$-localization for
$R$-localization for ![]() ${\mathbb {A}}^1$-nilpotent spaces; Theorems 4.3.9 and 4.3.11 show that
${\mathbb {A}}^1$-nilpotent spaces; Theorems 4.3.9 and 4.3.11 show that ![]() $R$-localization has good properties for (locally)
$R$-localization has good properties for (locally) ![]() ${\mathbb {A}}^1$-nilpotent spaces.
${\mathbb {A}}^1$-nilpotent spaces.
4.1 Sheaf cohomology and  ${\mathbb {A}}^1$-homology
${\mathbb {A}}^1$-homology
In this section we study ![]() ${\mathbb {A}}^1$-homology theory and establish analogs of classical results about the
${\mathbb {A}}^1$-homology theory and establish analogs of classical results about the ![]() ${\mathbb {A}}^1$-homology of nilpotent spaces. We establish generalizations of the known relative Hurewicz theorems in
${\mathbb {A}}^1$-homology of nilpotent spaces. We establish generalizations of the known relative Hurewicz theorems in ![]() ${\mathbb {A}}^1$-homotopy theory (keeping track of actions of the
${\mathbb {A}}^1$-homotopy theory (keeping track of actions of the ![]() ${\mathbb {A}}^1$-fundamental group).
${\mathbb {A}}^1$-fundamental group).
Sheaf cohomology
We briefly recall some notation related to sheaf cohomology in the context of local homotopy theory; we refer the reader to [Reference JardineJar15, Chapter 8] for a detailed treatment of this circle of ideas, which goes back to the foundational work of Brown and Gersten. Suppose ![]() $(\mathbf {C},\tau )$ is a site with enough points. We write
$(\mathbf {C},\tau )$ is a site with enough points. We write ![]() $\mathrm {Ch}_{\mathbf {C}}$ for the abelian category of chain complexes (i.e. differential of degree
$\mathrm {Ch}_{\mathbf {C}}$ for the abelian category of chain complexes (i.e. differential of degree ![]() $-1$) of presheaves of abelian groups on
$-1$) of presheaves of abelian groups on ![]() $\mathbf {C}$ situated in degrees
$\mathbf {C}$ situated in degrees ![]() $\geq 0$. The category
$\geq 0$. The category ![]() $\mathrm {Ch}_{\mathbf {C}}$ can be equipped with an injective local model structure: cofibrations are monomorphisms, weak equivalences are Nisnevich local quasi-isomorphisms (i.e. morphisms that induce isomorphisms on homology sheaves), and fibrations are defined by the lifting property. We write
$\mathrm {Ch}_{\mathbf {C}}$ can be equipped with an injective local model structure: cofibrations are monomorphisms, weak equivalences are Nisnevich local quasi-isomorphisms (i.e. morphisms that induce isomorphisms on homology sheaves), and fibrations are defined by the lifting property. We write ![]() ${\mathrm D}(\mathrm {Ab}(\mathbf {C}))$ for the homotopy category of
${\mathrm D}(\mathrm {Ab}(\mathbf {C}))$ for the homotopy category of ![]() $\mathrm {Ch}_{\mathbf {C}}$, that is, the derived category of (bounded-below complexes of) presheaves of abelian groups on
$\mathrm {Ch}_{\mathbf {C}}$, that is, the derived category of (bounded-below complexes of) presheaves of abelian groups on ![]() ${\mathbf {C}}$.
${\mathbf {C}}$.
If ![]() $\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$ is a space, the presheaf
$\mathscr {X} \in \mathrm {sPre}(\mathbf {C})$ is a space, the presheaf ![]() ${\mathbb {Z}}[\mathscr {X}]$ is a simplicial abelian group. We abuse terminology and write
${\mathbb {Z}}[\mathscr {X}]$ is a simplicial abelian group. We abuse terminology and write ![]() ${\mathbb {Z}}[\mathscr {X}]$ for the associated normalized chain complex which is an object of
${\mathbb {Z}}[\mathscr {X}]$ for the associated normalized chain complex which is an object of ![]() $\mathrm {Ch}_{\mathbf {C}}$ (the Dold–Kan correspondence). Likewise, if
$\mathrm {Ch}_{\mathbf {C}}$ (the Dold–Kan correspondence). Likewise, if ![]() $A$ is a chain complex in non-negative degree, then we write
$A$ is a chain complex in non-negative degree, then we write ![]() $K(A) \in \mathrm {sPre}(\mathbf {C})$ for the associated Eilenberg–Mac Lane space [Reference JardineJar15, p. 212].
$K(A) \in \mathrm {sPre}(\mathbf {C})$ for the associated Eilenberg–Mac Lane space [Reference JardineJar15, p. 212].
We write ![]() ${{\mathbf {H}}}_i(\mathscr {X})$ for the associated homology sheaves of
${{\mathbf {H}}}_i(\mathscr {X})$ for the associated homology sheaves of ![]() ${\mathbb {Z}}[\mathscr {X}]$, and we write
${\mathbb {Z}}[\mathscr {X}]$, and we write ![]() $\tilde {{{\mathbf {H}}}}_i(\mathscr {X})$ for the associated reduced homology sheaves of
$\tilde {{{\mathbf {H}}}}_i(\mathscr {X})$ for the associated reduced homology sheaves of ![]() $\mathscr {X}$ (i.e. the homology sheaves of the kernel
$\mathscr {X}$ (i.e. the homology sheaves of the kernel ![]() $\tilde {{\mathbb {Z}}}[\mathscr {X}]$ of
$\tilde {{\mathbb {Z}}}[\mathscr {X}]$ of ![]() ${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\ast ]$). Note that taking (reduced) homology sheaves commutes with taking stalks, that is, if
${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\ast ]$). Note that taking (reduced) homology sheaves commutes with taking stalks, that is, if ![]() $s$ is a point of
$s$ is a point of ![]() $(\mathbf {C},\tau )$, then
$(\mathbf {C},\tau )$, then ![]() $s^*{{\mathbf {H}}}_i(\mathscr {X}) = H_i(s^*\mathscr {X})$ (the latter being homology with integral coefficients of a simplicial set); we use this fact freely in the sequel.
$s^*{{\mathbf {H}}}_i(\mathscr {X}) = H_i(s^*\mathscr {X})$ (the latter being homology with integral coefficients of a simplicial set); we use this fact freely in the sequel.
 ${\mathbb {A}}^1$-homology
${\mathbb {A}}^1$-homology
We now recall ![]() ${\mathbb {A}}^1$-homology and Morel's (effective)
${\mathbb {A}}^1$-homology and Morel's (effective) ![]() ${\mathbb {A}}^1$-derived category. The
${\mathbb {A}}^1$-derived category. The ![]() ${\mathbb {A}}^1$-derived category
${\mathbb {A}}^1$-derived category ![]() ${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$ is obtained by Nisnevich and
${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$ is obtained by Nisnevich and ![]() ${\mathbb {A}}^1$-localizing the derived category of presheaves of abelian groups on
${\mathbb {A}}^1$-localizing the derived category of presheaves of abelian groups on ![]() $\mathrm {Sm}_k$ (this is the construction described in [Reference MorelMor12, § 6.2], but our notation for the category contains the superscript
$\mathrm {Sm}_k$ (this is the construction described in [Reference MorelMor12, § 6.2], but our notation for the category contains the superscript ![]() $\operatorname {eff}$ to distinguish from a corresponding ‘
$\operatorname {eff}$ to distinguish from a corresponding ‘![]() ${{\mathbf {G}}_{m}^{}}$-stabilized’ version). We write
${{\mathbf {G}}_{m}^{}}$-stabilized’ version). We write ![]() $\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$ for the endofunctor that effects this localization; this is an exact endofunctor on the category of chain complexes of presheaves of abelian groups on
$\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$ for the endofunctor that effects this localization; this is an exact endofunctor on the category of chain complexes of presheaves of abelian groups on ![]() $\mathrm {Sm}_k$.
$\mathrm {Sm}_k$.
If ![]() $f: \mathscr {X} \to \mathscr {Y}$ is an
$f: \mathscr {X} \to \mathscr {Y}$ is an ![]() ${\mathbb {A}}^1$-weak equivalence in
${\mathbb {A}}^1$-weak equivalence in ![]() $\mathrm {Spc}_k$, then one knows the induced map
$\mathrm {Spc}_k$, then one knows the induced map ![]() ${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\mathscr {Y}]$ is an isomorphism in
${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\mathscr {Y}]$ is an isomorphism in ![]() ${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. Thus, the assignment
${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. Thus, the assignment ![]() $\mathscr {X} \to {\mathbb {Z}}[\mathscr {X}]$ passes to a functor
$\mathscr {X} \to {\mathbb {Z}}[\mathscr {X}]$ passes to a functor ![]() $\mathrm {Ho}_{k} \to {\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. We set
$\mathrm {Ho}_{k} \to {\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. We set
and define ![]() ${\mathbb {A}}^1$-homology sheaves by the formula
${\mathbb {A}}^1$-homology sheaves by the formula
As usual, one may also define analogs of reduced homology, and, following the standard notation, we write ![]() $\tilde {H}_i^{{\mathbb {A}}^1}(\mathscr {X})$ for the reduced
$\tilde {H}_i^{{\mathbb {A}}^1}(\mathscr {X})$ for the reduced ![]() ${\mathbb {A}}^1$-homology sheaves of
${\mathbb {A}}^1$-homology sheaves of ![]() $\mathscr {X}$.
$\mathscr {X}$.
Morel's stable ![]() ${\mathbb {A}}^1$-connectivity theorem [Reference MorelMor05, Theorem 3] implies that if
${\mathbb {A}}^1$-connectivity theorem [Reference MorelMor05, Theorem 3] implies that if ![]() $\mathscr {X}$ is a space, then
$\mathscr {X}$ is a space, then ![]() ${\mathbb {Z}}_{{\mathbb {A}}^1}[\mathscr {X}]$ is a
${\mathbb {Z}}_{{\mathbb {A}}^1}[\mathscr {X}]$ is a ![]() $(-1)$-connected object of the derived category of Nisnevich sheaves of abelian groups. In particular,
$(-1)$-connected object of the derived category of Nisnevich sheaves of abelian groups. In particular, ![]() ${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X}) = 0$ for
${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X}) = 0$ for ![]() $i < 0$.
$i < 0$.
If ![]() $(\mathscr {X},x)$ is a pointed space, then the Hurewicz homomorphism is induced by a morphism
$(\mathscr {X},x)$ is a pointed space, then the Hurewicz homomorphism is induced by a morphism
It follows that there are induced actions of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$ on all the
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X})$ on all the ![]() ${\mathbb {A}}^1$-homology sheaves.
${\mathbb {A}}^1$-homology sheaves.
Remark 4.1.1 Voevodsky's derived category of motives is constructed by starting with the ‘presheaves with transfers’ and then Nisnevich and ![]() ${\mathbb {A}}^1$-localizing. Write
${\mathbb {A}}^1$-localizing. Write ![]() $\mathrm {Sm}\mathrm {Cor}_k$ for the category whose objects are smooth schemes and where morphisms are finite correspondences. One writes
$\mathrm {Sm}\mathrm {Cor}_k$ for the category whose objects are smooth schemes and where morphisms are finite correspondences. One writes ![]() $\mathrm {PST}_k$ for the category of contravariant additive functors on
$\mathrm {PST}_k$ for the category of contravariant additive functors on ![]() $\mathrm {Sm}\mathrm {Cor}_k$; this is called the category of presheaves with transfers. There is a functor
$\mathrm {Sm}\mathrm {Cor}_k$; this is called the category of presheaves with transfers. There is a functor ![]() $\mathrm {Sm}_k \to \mathrm {Sm}\mathrm {Cor}_k$ that induces a restriction functor from presheaves with transfers to presheaves of abelian groups. Voevodsky's derived category of motives
$\mathrm {Sm}_k \to \mathrm {Sm}\mathrm {Cor}_k$ that induces a restriction functor from presheaves with transfers to presheaves of abelian groups. Voevodsky's derived category of motives ![]() ${\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$ is constructed by localizing the derived category of chain complexes of presheaves with transfers with respect to Nisnevich and
${\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$ is constructed by localizing the derived category of chain complexes of presheaves with transfers with respect to Nisnevich and ![]() ${\mathbb {A}}^1$-local weak equivalences. Write
${\mathbb {A}}^1$-local weak equivalences. Write ![]() ${\mathbb {Z}}_{\rm tr}[X]$ for the representable functor on
${\mathbb {Z}}_{\rm tr}[X]$ for the representable functor on ![]() $\mathrm {Sm}\mathrm {Cor}_k$ determined by a smooth scheme.
$\mathrm {Sm}\mathrm {Cor}_k$ determined by a smooth scheme.
The left Kan extension of the assignment ![]() ${\mathbb {Z}}[X] \to {\mathbb {Z}}_{\rm tr}[X]$ yields a functor
${\mathbb {Z}}[X] \to {\mathbb {Z}}_{\rm tr}[X]$ yields a functor ![]() ${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k) \to {\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$ (usually called the functor of ‘adding transfers’). It follows that any morphism of spaces
${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k) \to {\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$ (usually called the functor of ‘adding transfers’). It follows that any morphism of spaces ![]() $f: \mathscr {X} \to \mathscr {Y}$ that induces an isomorphism in the
$f: \mathscr {X} \to \mathscr {Y}$ that induces an isomorphism in the ![]() ${\mathbb {A}}^1$-derived category also induces an isomorphism in
${\mathbb {A}}^1$-derived category also induces an isomorphism in ![]() ${\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$. Nevertheless, the two categories are typically quite far from each other.
${\mathrm {DM}}^{\operatorname {eff}}_{k,{\mathbb {Z}}}$. Nevertheless, the two categories are typically quite far from each other.
 ${\mathbb {A}}^1$-homology equivalences and cohomology equivalences
${\mathbb {A}}^1$-homology equivalences and cohomology equivalences
Suppose ![]() $R \subset {\mathbb {Q}}$ is a subring. We write
$R \subset {\mathbb {Q}}$ is a subring. We write ![]() $R_{{\mathbb {A}}^1}[\mathscr {X}]$ for
$R_{{\mathbb {A}}^1}[\mathscr {X}]$ for ![]() $R \otimes \operatorname {L}_{{\mathbb {A}}^1}^{\rm ab} {\mathbb {Z}}[\mathscr {X}]$. Since tensoring with
$R \otimes \operatorname {L}_{{\mathbb {A}}^1}^{\rm ab} {\mathbb {Z}}[\mathscr {X}]$. Since tensoring with ![]() $R$ is exact and
$R$ is exact and ![]() $\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$ is exact, the order in which we localize and tensor is irrelevant. We set
$\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$ is exact, the order in which we localize and tensor is irrelevant. We set ![]() ${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X},R) := {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(R_{{\mathbb {A}}^1}[\mathscr {X}])$. We now give a number of equivalent characterizations of morphisms inducing an isomorphism on
${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X},R) := {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(R_{{\mathbb {A}}^1}[\mathscr {X}])$. We now give a number of equivalent characterizations of morphisms inducing an isomorphism on ![]() ${\mathbb {A}}^1$-homology.
${\mathbb {A}}^1$-homology.
Proposition 4.1.2 The following conditions on a morphism ![]() $f: \mathscr {X} \to \mathscr {Y}$ of spaces are equivalent.
$f: \mathscr {X} \to \mathscr {Y}$ of spaces are equivalent.
1. The morphism
 $R_{{\mathbb {A}}^1}[f]: R_{{\mathbb {A}}^1}[\mathscr {X}] \to R_{{\mathbb {A}}^1}[\mathscr {Y}]$ is a quasi-isomorphism.
$R_{{\mathbb {A}}^1}[f]: R_{{\mathbb {A}}^1}[\mathscr {X}] \to R_{{\mathbb {A}}^1}[\mathscr {Y}]$ is a quasi-isomorphism.2. For every integer
 $i \geq 0$, the morphism
$i \geq 0$, the morphism  $f_*: {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X},R) \to {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {Y},R)$ is an isomorphism.
$f_*: {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {X},R) \to {{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {Y},R)$ is an isomorphism.3. For any strictly
 ${\mathbb {A}}^1$-invariant sheaf
${\mathbb {A}}^1$-invariant sheaf  $\mathbf {M}$ of
$\mathbf {M}$ of  $R$-modules and any integer
$R$-modules and any integer  $i \geq 0$, the map
$i \geq 0$, the map  $f^*: H^i(\mathscr {Y},\mathbf {M}) \to H^i(\mathscr {X},\mathbf {M})$ is an isomorphism.
$f^*: H^i(\mathscr {Y},\mathbf {M}) \to H^i(\mathscr {X},\mathbf {M})$ is an isomorphism.
Proof. That (1) ![]() $\Leftrightarrow$ (2) is immediate. That (2)
$\Leftrightarrow$ (2) is immediate. That (2) ![]() $\Rightarrow$ (3) follows from the universal coefficient spectral sequence. Indeed, there is a functorial, strongly convergent spectral sequence of the form
$\Rightarrow$ (3) follows from the universal coefficient spectral sequence. Indeed, there is a functorial, strongly convergent spectral sequence of the form
(see [Reference JardineJar15, Lemma 8.30] for the spectral sequence); the strong convergence follows from the fact that the homology sheaves of ![]() $R_{{\mathbb {A}}^1}[\mathscr {X}]$ vanish in degrees
$R_{{\mathbb {A}}^1}[\mathscr {X}]$ vanish in degrees ![]() $< 0$, which is the stable
$< 0$, which is the stable ![]() ${\mathbb {A}}^1$-connectivity theorem.
${\mathbb {A}}^1$-connectivity theorem.
For the implication (3) ![]() $\Rightarrow$ (2), we proceed as follows. If
$\Rightarrow$ (2), we proceed as follows. If ![]() $\mathbf {C}$ is an
$\mathbf {C}$ is an ![]() $(i-1)$-connected and
$(i-1)$-connected and ![]() ${\mathbb {A}}^1$-local chain complex of
${\mathbb {A}}^1$-local chain complex of ![]() $R$-modules, then for any strictly
$R$-modules, then for any strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of
${\mathbb {A}}^1$-invariant sheaf of ![]() $R$-modules
$R$-modules ![]() $\mathbf {M}$, there is a canonical isomorphism of the form
$\mathbf {M}$, there is a canonical isomorphism of the form
In particular, we conclude that if ![]() $\mathrm {RHom}(\mathbf {C},\mathbf {M}[i])$ vanishes for all
$\mathrm {RHom}(\mathbf {C},\mathbf {M}[i])$ vanishes for all ![]() $\mathbf {M}$, then
$\mathbf {M}$, then ![]() $H_i^{{\mathbb {A}}^1}(\mathbf {C})$ vanishes by the Yoneda lemma. Applying this observation inductively to the cone of the map
$H_i^{{\mathbb {A}}^1}(\mathbf {C})$ vanishes by the Yoneda lemma. Applying this observation inductively to the cone of the map ![]() $f$, the hypothesis in (3) implies inductively that the cone of
$f$, the hypothesis in (3) implies inductively that the cone of ![]() $f$ has vanishing
$f$ has vanishing ![]() ${\mathbb {A}}^1$-homology sheaves in all degrees, and the result follows.
${\mathbb {A}}^1$-homology sheaves in all degrees, and the result follows.
Remark 4.1.3 Extending Remark 4.1.1, if ![]() $f$ is a morphism of spaces such that
$f$ is a morphism of spaces such that ![]() $R_{{\mathbb {A}}^1}[f]$ is a quasi-isomorphism, then the induced map of motives with
$R_{{\mathbb {A}}^1}[f]$ is a quasi-isomorphism, then the induced map of motives with ![]() $R$-coefficients is an isomorphism as well.
$R$-coefficients is an isomorphism as well.
A homological connectivity lemma
The next result analyzes how homological connectivity behaves under ![]() ${\mathbb {A}}^1$-localization.
${\mathbb {A}}^1$-localization.
Lemma 4.1.4 Assume ![]() $\mathscr {X}$ is a simplicially connected space and
$\mathscr {X}$ is a simplicially connected space and ![]() $n \geq 1$ is an integer. If
$n \geq 1$ is an integer. If ![]() $\mathscr {X}$ is homologically
$\mathscr {X}$ is homologically ![]() $(n-1)$-connected, that is,
$(n-1)$-connected, that is, ![]() $\tilde {{{\mathbf {H}}}}_i(\mathscr {X})$ vanishes for
$\tilde {{{\mathbf {H}}}}_i(\mathscr {X})$ vanishes for ![]() $i < n$, then the following statements hold.
$i < n$, then the following statements hold.
1. The sheaves
 $\tilde {{{\mathbf {H}}}}_i^{{\mathbb {A}}^1}(\mathscr {X})$ vanish for
$\tilde {{{\mathbf {H}}}}_i^{{\mathbb {A}}^1}(\mathscr {X})$ vanish for  $i < n$.
$i < n$.2. The morphism
 $\tilde {{{\mathbf {H}}}}_n(\mathscr {X}) \to \tilde {{{\mathbf {H}}}}_n^{{\mathbb {A}}^1}(\mathscr {X})$ is the initial morphism from
$\tilde {{{\mathbf {H}}}}_n(\mathscr {X}) \to \tilde {{{\mathbf {H}}}}_n^{{\mathbb {A}}^1}(\mathscr {X})$ is the initial morphism from  $\tilde {{{\mathbf {H}}}}_n(\mathscr {X})$ to a strictly
$\tilde {{{\mathbf {H}}}}_n(\mathscr {X})$ to a strictly  ${\mathbb {A}}^1$-invariant sheaf.
${\mathbb {A}}^1$-invariant sheaf.
Proof. While the first statement is an immediate consequence of the stable ![]() ${\mathbb {A}}^1$-connectivity theorem, we give a different proof that will be useful in setting up the notation to establish the second statement as well. By assumption
${\mathbb {A}}^1$-connectivity theorem, we give a different proof that will be useful in setting up the notation to establish the second statement as well. By assumption ![]() $\mathscr {X}$ is simplicially connected. Therefore, the reduced singular chain complex
$\mathscr {X}$ is simplicially connected. Therefore, the reduced singular chain complex ![]() $\tilde {{\mathbb {Z}}}[\mathscr {X}]$ is a chain complex that has vanishing homology sheaves in negative degrees and is thus a
$\tilde {{\mathbb {Z}}}[\mathscr {X}]$ is a chain complex that has vanishing homology sheaves in negative degrees and is thus a ![]() $0$-connected chain complex. By Morel's stable
$0$-connected chain complex. By Morel's stable ![]() ${\mathbb {A}}^1$-connectivity theorem, the complex
${\mathbb {A}}^1$-connectivity theorem, the complex ![]() $\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}] := \operatorname {L}_{{\mathbb {A}}^1}^{\rm ab} \tilde {{\mathbb {Z}}}[\mathscr {X}]$ is thus also
$\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}] := \operatorname {L}_{{\mathbb {A}}^1}^{\rm ab} \tilde {{\mathbb {Z}}}[\mathscr {X}]$ is thus also ![]() $0$-connected.
$0$-connected.
Since ![]() $\tilde {{\mathbb {Z}}}[\mathscr {X}]$ is
$\tilde {{\mathbb {Z}}}[\mathscr {X}]$ is ![]() $0$-connected, by [Reference MorelMor12, Proposition 6.25], the space
$0$-connected, by [Reference MorelMor12, Proposition 6.25], the space ![]() $K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ is
$K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ is ![]() ${\mathbb {A}}^1$-local. As a consequence, the map
${\mathbb {A}}^1$-local. As a consequence, the map ![]() $K(\tilde {{\mathbb {Z}}}[\mathscr {X}]) \to K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ arising by functoriality factors through a morphism
$K(\tilde {{\mathbb {Z}}}[\mathscr {X}]) \to K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ arising by functoriality factors through a morphism
By [Reference MorelMor12, Corollary 6.27] this morphism is a simplicial weak equivalence.
By construction, the homotopy sheaves of ![]() $K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ are the (reduced) homology sheaves of
$K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ are the (reduced) homology sheaves of ![]() $\mathscr {X}$. Our assumption on the homological connectivity of
$\mathscr {X}$. Our assumption on the homological connectivity of ![]() $\mathscr {X}$ thus implies that the space
$\mathscr {X}$ thus implies that the space ![]() $K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ is simplicially
$K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ is simplicially ![]() $(n-1)$-connected. Therefore, Morel's unstable connectivity theorem guarantees that
$(n-1)$-connected. Therefore, Morel's unstable connectivity theorem guarantees that ![]() $\operatorname {L}_{{\mathbb {A}}^1} K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ is again simplicially
$\operatorname {L}_{{\mathbb {A}}^1} K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ is again simplicially ![]() $(n-1)$-connected. The simplicial weak equivalence of the previous paragraph thus implies
$(n-1)$-connected. The simplicial weak equivalence of the previous paragraph thus implies ![]() $K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ is also simplicially
$K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ is also simplicially ![]() $(n-1)$-connected. However, the homotopy sheaves of
$(n-1)$-connected. However, the homotopy sheaves of ![]() $K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ are precisely the reduced
$K(\tilde {{\mathbb {Z}}}_{{\mathbb {A}}^1}[\mathscr {X}])$ are precisely the reduced ![]() ${\mathbb {A}}^1$-homology sheaves of
${\mathbb {A}}^1$-homology sheaves of ![]() $\mathscr {X}$ and thus vanish in degrees
$\mathscr {X}$ and thus vanish in degrees ![]() $< n$ as well.
$< n$ as well.
For the final statement, observe that [Reference MorelMor12, Corollary 6.60] applied to the simplicially ![]() $(n-1)$-connected space
$(n-1)$-connected space ![]() $K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ shows that the morphism
$K(\tilde {{\mathbb {Z}}}[\mathscr {X}])$ shows that the morphism
has the desired universal property.
4.2 Relative Hurewicz theorems revisited
In this section we refine the Hurewicz theorems in ![]() ${\mathbb {A}}^1$-homotopy theory by keeping track of the action of the
${\mathbb {A}}^1$-homotopy theory by keeping track of the action of the ![]() ${\mathbb {A}}^1$-fundamental sheaf of groups. In particular, we refine the strong form of the relative Hurewicz theorem, which follows from the Blakers–Massey theorem established in [Reference Asok and FaselAF16, Theorem 4.1] (and independently in [Reference StrunkStr12, Theorem 2.3.8]).
${\mathbb {A}}^1$-fundamental sheaf of groups. In particular, we refine the strong form of the relative Hurewicz theorem, which follows from the Blakers–Massey theorem established in [Reference Asok and FaselAF16, Theorem 4.1] (and independently in [Reference StrunkStr12, Theorem 2.3.8]).
The relative Hurewicz theorem and coinvariants
Suppose ![]() $f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed, connected simplicial presheaves with homotopy fiber
$f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed, connected simplicial presheaves with homotopy fiber ![]() $\mathscr {F}$ and homotopy cofiber
$\mathscr {F}$ and homotopy cofiber ![]() $\mathscr {C}$. In that case, there is a morphism of simplicial fiber sequences as follows.
$\mathscr {C}$. In that case, there is a morphism of simplicial fiber sequences as follows.

The sheaf ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ acts on the higher homotopy sheaves
$\boldsymbol {\pi }_1(\mathscr {E})$ acts on the higher homotopy sheaves ![]() $\boldsymbol {\pi }_i(\mathscr {F})$. By functoriality there is also an action of
$\boldsymbol {\pi }_i(\mathscr {F})$. By functoriality there is also an action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ on the higher homotopy of sheaves in the bottom row, though this action is necessarily trivial since
$\boldsymbol {\pi }_1(\mathscr {E})$ on the higher homotopy of sheaves in the bottom row, though this action is necessarily trivial since ![]() $\ast$ is certainly simplicially
$\ast$ is certainly simplicially ![]() $1$-connected.
$1$-connected.
The relative Hurewicz theorem analyzes the connectivity of the morphism ![]() $\mathscr {F} \to \Omega \mathscr {C}$ under suitable hypotheses on the connectivity of
$\mathscr {F} \to \Omega \mathscr {C}$ under suitable hypotheses on the connectivity of ![]() $f$. More precisely, there is an evident morphism
$f$. More precisely, there is an evident morphism ![]() $\boldsymbol {\pi }_i(\mathscr {F}) \to \boldsymbol {\pi }_i(\Omega \mathscr {C})$. The counit of the loop suspension adjunction yields a morphism
$\boldsymbol {\pi }_i(\mathscr {F}) \to \boldsymbol {\pi }_i(\Omega \mathscr {C})$. The counit of the loop suspension adjunction yields a morphism ![]() $\Sigma \Omega \mathscr {C} \to \mathscr {C}$. This morphism in turn yields the composite
$\Sigma \Omega \mathscr {C} \to \mathscr {C}$. This morphism in turn yields the composite
where the isomorphism is the suspension isomorphism. Thus, we obtain a morphism
that we will call the relative Hurewicz homomorphism.
Note that, even if ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}$ are
$\mathscr {B}$ are ![]() ${\mathbb {A}}^1$-local,
${\mathbb {A}}^1$-local, ![]() $\mathscr {C}$ need not be. Nevertheless, the morphism
$\mathscr {C}$ need not be. Nevertheless, the morphism ![]() $\mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$ is an isomorphism on
$\mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$ is an isomorphism on ![]() ${\mathbb {A}}^1$-homology sheaves, and models the
${\mathbb {A}}^1$-homology sheaves, and models the ![]() ${\mathbb {A}}^1$-homotopy cofiber of
${\mathbb {A}}^1$-homotopy cofiber of ![]() $\mathscr {E} \to \mathscr {B}$. The canonical map
$\mathscr {E} \to \mathscr {B}$. The canonical map ![]() $\mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$ yields a map
$\mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$ yields a map ![]() $\Omega \mathscr {C} \to \Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$, and the latter is already
$\Omega \mathscr {C} \to \Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$, and the latter is already ![]() ${\mathbb {A}}^1$-local. Composing with the map
${\mathbb {A}}^1$-local. Composing with the map ![]() $\mathscr {F} \to \Omega \mathscr {C}$ described above, we obtain a map
$\mathscr {F} \to \Omega \mathscr {C}$ described above, we obtain a map
The counit of the loop-suspension adjunction yields a morphism ![]() $\Sigma \Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$. Since the target of this morphism is
$\Sigma \Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C} \to \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}$. Since the target of this morphism is ![]() ${\mathbb {A}}^1$-local (even though the source need not be), there is a factorization
${\mathbb {A}}^1$-local (even though the source need not be), there is a factorization
In a fashion analogous to that described above, we obtain morphisms ![]() $\boldsymbol {\pi }_i(\Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}) \to {{\mathbf {H}}}_{i+1}^{{\mathbb {A}}^1}(\mathscr {C})$ and thus a relative Hurewicz homomorphism
$\boldsymbol {\pi }_i(\Omega \operatorname {L}_{{\mathbb {A}}^1} \mathscr {C}) \to {{\mathbf {H}}}_{i+1}^{{\mathbb {A}}^1}(\mathscr {C})$ and thus a relative Hurewicz homomorphism
that we now analyze.
Theorem 4.2.1 Suppose ![]() $f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed,
$f: \mathscr {E} \to \mathscr {B}$ is a morphism of pointed, ![]() ${\mathbb {A}}^1$-local and simplicially connected spaces. Write
${\mathbb {A}}^1$-local and simplicially connected spaces. Write ![]() $\mathscr {F}$ for the simplicial homotopy fiber of
$\mathscr {F}$ for the simplicial homotopy fiber of ![]() $f$ and
$f$ and ![]() $\mathscr {C}$ for the simplicial homotopy cofiber of
$\mathscr {C}$ for the simplicial homotopy cofiber of ![]() $f$. If
$f$. If ![]() $\mathscr {F}$ is
$\mathscr {F}$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $(n-1)$-connected for some integer
$(n-1)$-connected for some integer ![]() $n \geq 1$, then the following statements hold.
$n \geq 1$, then the following statements hold.
1. The sheaves
 ${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {C})$ vanish for
${{\mathbf {H}}}_i^{{\mathbb {A}}^1}(\mathscr {C})$ vanish for  $i \leq n$.
$i \leq n$.2. The relative Hurewicz homomorphism
is the initial morphism from \[ \boldsymbol{\pi}_n^{{\mathbb{A}}^1}(\mathscr{F}) \longrightarrow {{\mathbf{H}}}_{n+1}^{{\mathbb{A}}^1}(\mathscr{C}) \]
\[ \boldsymbol{\pi}_n^{{\mathbb{A}}^1}(\mathscr{F}) \longrightarrow {{\mathbf{H}}}_{n+1}^{{\mathbb{A}}^1}(\mathscr{C}) \] $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})$ to a strictly
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})$ to a strictly  ${\mathbb {A}}^1$-invariant sheaf on which
${\mathbb {A}}^1$-invariant sheaf on which  $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially.3. If
 $n = 1$ and
$n = 1$ and  $\boldsymbol {\pi }_1(\mathscr {F})$ is strictly
$\boldsymbol {\pi }_1(\mathscr {F})$ is strictly  ${\mathbb {A}}^1$-invariant, or if
${\mathbb {A}}^1$-invariant, or if  $n \geq 2$, then the morphism of the previous statement induces an isomorphism
where the source is the sheaf of coinvariants.
$n \geq 2$, then the morphism of the previous statement induces an isomorphism
where the source is the sheaf of coinvariants. \[ \boldsymbol{\pi}_n^{{\mathbb{A}}^1}(\mathscr{F})_{\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{E})} {\stackrel{\sim}{\;\longrightarrow\;}} {{\mathbf{H}}}_{n+1}^{{\mathbb{A}}^1}(\mathscr{C}), \]
\[ \boldsymbol{\pi}_n^{{\mathbb{A}}^1}(\mathscr{F})_{\boldsymbol{\pi}_1^{{\mathbb{A}}^1}(\mathscr{E})} {\stackrel{\sim}{\;\longrightarrow\;}} {{\mathbf{H}}}_{n+1}^{{\mathbb{A}}^1}(\mathscr{C}), \]
Proof. Since ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}$ are simplicially connected and
$\mathscr {B}$ are simplicially connected and ![]() ${\mathbb {A}}^1$-local by assumption, the simplicial homotopy fiber
${\mathbb {A}}^1$-local by assumption, the simplicial homotopy fiber ![]() $\mathscr {F}$ is
$\mathscr {F}$ is ![]() ${\mathbb {A}}^1$-local by Lemma 3.1.3 and thus
${\mathbb {A}}^1$-local by Lemma 3.1.3 and thus ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F}) = \boldsymbol {\pi }_i(\mathscr {F})$ so
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F}) = \boldsymbol {\pi }_i(\mathscr {F})$ so ![]() $\mathscr {F}$ is simplicially
$\mathscr {F}$ is simplicially ![]() $(n-1)$-connected.
$(n-1)$-connected.
The simplicial homotopy cofiber ![]() $\operatorname {hocofib} f$ need not be
$\operatorname {hocofib} f$ need not be ![]() ${\mathbb {A}}^1$-local, so we consider
${\mathbb {A}}^1$-local, so we consider ![]() $\operatorname {L}_{{\mathbb {A}}^1} \operatorname {hocofib} f$ and we have a commutative diagram of simplicial fiber sequences
$\operatorname {L}_{{\mathbb {A}}^1} \operatorname {hocofib} f$ and we have a commutative diagram of simplicial fiber sequences

where ![]() $\Omega \operatorname {L}_{{\mathbb {A}}^1} \operatorname {hocofib} f$ is already
$\Omega \operatorname {L}_{{\mathbb {A}}^1} \operatorname {hocofib} f$ is already ![]() ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.
Consider the action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ on all of the spaces in the diagram. Since we saw above that
$\boldsymbol {\pi }_1(\mathscr {E})$ on all of the spaces in the diagram. Since we saw above that ![]() $\mathscr {F}$ is simplicially
$\mathscr {F}$ is simplicially ![]() $(n-1)$-connected, the classical relative Hurewicz theorem [Reference WhiteheadWhi78, Theorem IV.7.2] applied stalkwise implies that the map
$(n-1)$-connected, the classical relative Hurewicz theorem [Reference WhiteheadWhi78, Theorem IV.7.2] applied stalkwise implies that the map ![]() $\boldsymbol {\pi }_i(\mathscr {F}) \to {{\mathbf {H}}}_{i+1}(\operatorname {hocofib} f)$ is the map ‘factoring out the action of
$\boldsymbol {\pi }_i(\mathscr {F}) \to {{\mathbf {H}}}_{i+1}(\operatorname {hocofib} f)$ is the map ‘factoring out the action of ![]() $\boldsymbol {\pi }_1(\mathscr {E})$’. More precisely, we conclude that
$\boldsymbol {\pi }_1(\mathscr {E})$’. More precisely, we conclude that ![]() ${{\mathbf {H}}}_{i+1}(\operatorname {hocofib} f)$ vanishes in degrees
${{\mathbf {H}}}_{i+1}(\operatorname {hocofib} f)$ vanishes in degrees ![]() $\leq n$ and that
$\leq n$ and that ![]() ${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$ is the
${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$ is the ![]() $\boldsymbol {\pi }_1(\mathscr {E})$ coinvariants of
$\boldsymbol {\pi }_1(\mathscr {E})$ coinvariants of ![]() $\boldsymbol {\pi }_n(\mathscr {F})$. Since
$\boldsymbol {\pi }_n(\mathscr {F})$. Since ![]() $\operatorname {hocofib} f$ is homologically
$\operatorname {hocofib} f$ is homologically ![]() $n$-connected, it follows by appeal to Lemma 4.1.4(1) that
$n$-connected, it follows by appeal to Lemma 4.1.4(1) that ![]() $\tilde {{{\mathbf {H}}}}_{i+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ also vanishes for
$\tilde {{{\mathbf {H}}}}_{i+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ also vanishes for ![]() $i \leq n$, which establishes the first point of the theorem.
$i \leq n$, which establishes the first point of the theorem.
To establish the second point of the theorem, observe that Lemma 4.1.4(2) implies that ![]() ${{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ is the initial strictly
${{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ is the initial strictly ![]() ${\mathbb {A}}^1$-invariant sheaf admitting a morphism from
${\mathbb {A}}^1$-invariant sheaf admitting a morphism from ![]() ${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$. We observed in the preceding paragraph that the
${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$. We observed in the preceding paragraph that the ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-action on the latter sheaf is already trivial, so the induced action on
$\boldsymbol {\pi }_1(\mathscr {E})$-action on the latter sheaf is already trivial, so the induced action on ![]() ${{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ is also trivial.
${{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$ is also trivial.
To see that the morphism in question is an isomorphism if either ![]() $n = 1$ and
$n = 1$ and ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is strictly ![]() ${\mathbb {A}}^1$-invariant or for
${\mathbb {A}}^1$-invariant or for ![]() $n \geq 2$, we proceed as follows. Let
$n \geq 2$, we proceed as follows. Let ![]() $\mathbf {K}$ be the kernel of the morphism
$\mathbf {K}$ be the kernel of the morphism ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}) \to {{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$. Then
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F}) \to {{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$. Then ![]() $\mathbf {K}$ and the quotient
$\mathbf {K}$ and the quotient ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ are strictly
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ are strictly ![]() ${\mathbb {A}}^1$-invariant by appeal to Theorem 3.1.12. By universality, it follows that the identity map on
${\mathbb {A}}^1$-invariant by appeal to Theorem 3.1.12. By universality, it follows that the identity map on ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ factors through an epimorphism
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ factors through an epimorphism ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K} \to {{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$. Then, as observed above, the ordinary Hurewicz theorem identifies
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K} \to {{\mathbf {H}}}_{n+1}^{{\mathbb {A}}^1}(\operatorname {hocofib} f)$. Then, as observed above, the ordinary Hurewicz theorem identifies ![]() $\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ with
$\boldsymbol {\pi }_n^{{\mathbb {A}}^1}(\mathscr {F})/\mathbf {K}$ with ![]() ${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$ and the latter is precisely the
${{\mathbf {H}}}_{n+1}(\operatorname {hocofib} f)$ and the latter is precisely the ![]() $\boldsymbol {\pi }_1(\mathscr {E})$-coinvariants of
$\boldsymbol {\pi }_1(\mathscr {E})$-coinvariants of ![]() $\boldsymbol {\pi }_n(\mathscr {F})$.
$\boldsymbol {\pi }_n(\mathscr {F})$.
The  ${\mathbb {A}}^1$-Whitehead theorem for
${\mathbb {A}}^1$-Whitehead theorem for  ${\mathbb {A}}^1$-simple spaces
${\mathbb {A}}^1$-simple spaces
The relative Hurewicz theorem above has a number of consequences, including the following result that generalizes other ‘homological’ forms of the ![]() ${\mathbb {A}}^1$-Whitehead theorem in the literature (e.g. [Reference Wickelgren and WilliamsWW19, Corollary 2.22]).
${\mathbb {A}}^1$-Whitehead theorem in the literature (e.g. [Reference Wickelgren and WilliamsWW19, Corollary 2.22]).
Theorem 4.2.2 If ![]() $f: \mathscr {X} \to \mathscr {Y}$ is a morphism of
$f: \mathscr {X} \to \mathscr {Y}$ is a morphism of ![]() ${\mathbb {A}}^1$-simple spaces (see Definition 3.3.1) and
${\mathbb {A}}^1$-simple spaces (see Definition 3.3.1) and ![]() $f_*$ is an isomorphism
$f_*$ is an isomorphism ![]() ${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\mathscr {Y}]$ in
${\mathbb {Z}}[\mathscr {X}] \to {\mathbb {Z}}[\mathscr {Y}]$ in ![]() ${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$, then
${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$, then ![]() $f$ is an
$f$ is an ![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Proof. Since ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ are
$\mathscr {Y}$ are ![]() ${\mathbb {A}}^1$-simple, we know their
${\mathbb {A}}^1$-simple, we know their ![]() ${\mathbb {A}}^1$-fundamental sheaves of groups are strictly
${\mathbb {A}}^1$-fundamental sheaves of groups are strictly ![]() ${\mathbb {A}}^1$-invariant. For any
${\mathbb {A}}^1$-invariant. For any ![]() ${\mathbb {A}}^1$-simple space, the canonical map
${\mathbb {A}}^1$-simple space, the canonical map ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X}) \longrightarrow {{\mathbf {H}}}_1^{{\mathbb {A}}^1}(\mathscr {X})$ is an isomorphism. Indeed, the latter is the initial strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {X}) \longrightarrow {{\mathbf {H}}}_1^{{\mathbb {A}}^1}(\mathscr {X})$ is an isomorphism. Indeed, the latter is the initial strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of (abelian) groups admitting a map from
${\mathbb {A}}^1$-invariant sheaf of (abelian) groups admitting a map from ![]() $\boldsymbol {\pi }_1(\mathscr {X})$, but since the former is strictly
$\boldsymbol {\pi }_1(\mathscr {X})$, but since the former is strictly ![]() ${\mathbb {A}}^1$-invariant already, this map must be an isomorphism. Let
${\mathbb {A}}^1$-invariant already, this map must be an isomorphism. Let ![]() $\mathscr {F}$ be the
$\mathscr {F}$ be the ![]() ${\mathbb {A}}^1$-homotopy fiber of
${\mathbb {A}}^1$-homotopy fiber of ![]() $f$ and consider the associated long exact sequence of homotopy sheaves,
$f$ and consider the associated long exact sequence of homotopy sheaves,
here the map ![]() $f_*$ coincides with the map on
$f_*$ coincides with the map on ![]() ${\mathbb {A}}^1$-homology sheaves induced by
${\mathbb {A}}^1$-homology sheaves induced by ![]() $f$ by the discussion above. Therefore, our assumption on
$f$ by the discussion above. Therefore, our assumption on ![]() $f$ guarantees that the map
$f$ guarantees that the map ![]() $f_*$ is an isomorphism. Thus, we conclude that
$f_*$ is an isomorphism. Thus, we conclude that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is a cokernel of a morphism of strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ is a cokernel of a morphism of strictly ![]() ${\mathbb {A}}^1$-invariant sheaves and thus itself strictly
${\mathbb {A}}^1$-invariant sheaves and thus itself strictly ![]() ${\mathbb {A}}^1$-invariant. Granted that observation, the result follows from Theorem 4.2.1(3) and a straightforward induction.
${\mathbb {A}}^1$-invariant. Granted that observation, the result follows from Theorem 4.2.1(3) and a straightforward induction.
Remark 4.2.3 Theorem 4.2.2 applies to show that a map of pointed, ![]() ${\mathbb {A}}^1$-connected,
${\mathbb {A}}^1$-connected, ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-spaces is an
$h$-spaces is an ![]() ${\mathbb {A}}^1$-weak equivalence if and only if the map is an
${\mathbb {A}}^1$-weak equivalence if and only if the map is an ![]() ${\mathbb {A}}^1$-homology equivalence.
${\mathbb {A}}^1$-homology equivalence.
Nilpotence and Moore–Postnikov factorizations
With the relative Hurewicz theorem in hand, we may establish the reverse implication in Theorem 3.3.13.
Corollary 4.2.4 Assume ![]() $k$ is a perfect field. If
$k$ is a perfect field. If ![]() $f: \mathscr {E} \to \mathscr {B}$ an
$f: \mathscr {E} \to \mathscr {B}$ an ![]() ${\mathbb {A}}^1$-nilpotent morphism of pointed
${\mathbb {A}}^1$-nilpotent morphism of pointed ![]() ${\mathbb {A}}^1$-connected spaces, then the
${\mathbb {A}}^1$-connected spaces, then the ![]() ${\mathbb {A}}^1$-Moore–Postnikov tower admits a principal refinement (see Definition 3.3.11).
${\mathbb {A}}^1$-Moore–Postnikov tower admits a principal refinement (see Definition 3.3.11).
Proof. Consider the morphism ![]() $\tau _{\leq i}f \to \tau _{\leq i-1}f$. We treat two cases:
$\tau _{\leq i}f \to \tau _{\leq i-1}f$. We treat two cases: ![]() $i = 1$ and
$i = 1$ and ![]() $i \geq 2$. For
$i \geq 2$. For ![]() $i = 1$, we want to show that
$i = 1$, we want to show that ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ admits a
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ admits a ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq 1}f) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-invariant central series. Since
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq 1}f) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-invariant central series. Since ![]() $k$ is perfect, by Proposition 3.2.3 we know the
$k$ is perfect, by Proposition 3.2.3 we know the ![]() ${\mathbb {A}}^1$-upper central series witnesses the
${\mathbb {A}}^1$-upper central series witnesses the ![]() ${\mathbb {A}}^1$-nilpotence of
${\mathbb {A}}^1$-nilpotence of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$; furthermore, it is
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$; furthermore, it is ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-invariant by definition of the action and the fact that the terms of the upper central series are characteristic subgroup sheaves (i.e. stable by automorphisms of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-invariant by definition of the action and the fact that the terms of the upper central series are characteristic subgroup sheaves (i.e. stable by automorphisms of ![]() $\mathbf {G}$). By induction, one sees that the subquotients of the
$\mathbf {G}$). By induction, one sees that the subquotients of the ![]() ${\mathbb {A}}^1$-upper central series provide the necessary factorization.
${\mathbb {A}}^1$-upper central series provide the necessary factorization.
For ![]() $i \geq 2$, the result follows directly from the relative
$i \geq 2$, the result follows directly from the relative ![]() ${\mathbb {A}}^1$-Hurewicz theorem as in the classical argument [Reference Hilton, Mislin and RoitbergHMR75, Theorems II.2.9 and II.2.14]. Arguing inductively, the
${\mathbb {A}}^1$-Hurewicz theorem as in the classical argument [Reference Hilton, Mislin and RoitbergHMR75, Theorems II.2.9 and II.2.14]. Arguing inductively, the ![]() ${\mathbb {A}}^1$-relative Hurewicz theorem above yields a canonical strictly
${\mathbb {A}}^1$-relative Hurewicz theorem above yields a canonical strictly ![]() ${\mathbb {A}}^1$-invariant quotient of the
${\mathbb {A}}^1$-invariant quotient of the ![]() $i$th homotopy sheaf of the
$i$th homotopy sheaf of the ![]() ${\mathbb {A}}^1$-homotopy fiber equipped with a trivial action of
${\mathbb {A}}^1$-homotopy fiber equipped with a trivial action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq i}f) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$; in fact, as the sheaf of coinvariants this quotient is the maximal strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq i}f) = \boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$; in fact, as the sheaf of coinvariants this quotient is the maximal strictly ![]() ${\mathbb {A}}^1$-invariant quotient with trivial action of
${\mathbb {A}}^1$-invariant quotient with trivial action of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$. We define the first stage of the refinement to be the pullback of
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$. We define the first stage of the refinement to be the pullback of ![]() $\tau _{\leq i-1}f \to K({{\mathbf {H}}}_i^{{\mathbb {A}}^1}(f), i+1)$ and iterate this procedure. By assumption
$\tau _{\leq i-1}f \to K({{\mathbf {H}}}_i^{{\mathbb {A}}^1}(f), i+1)$ and iterate this procedure. By assumption ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq i}f)$ is an
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\tau _{\leq i}f)$ is an ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-nilpotent sheaf, so has a finite
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-nilpotent sheaf, so has a finite ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series. The
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series. The ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series obtained by iteratively taking coinvariants is thus finite and the iterative procedure just sketched necessarily terminates.
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$-central series obtained by iteratively taking coinvariants is thus finite and the iterative procedure just sketched necessarily terminates.
Remark 4.2.5 In contrast to the standard proof of this result, for ![]() $n = 1$, the
$n = 1$, the ![]() ${\mathbb {A}}^1$-principal refinement constructed above need not be ‘maximal’ because of the form of the relative
${\mathbb {A}}^1$-principal refinement constructed above need not be ‘maximal’ because of the form of the relative ![]() ${\mathbb {A}}^1$-Hurewicz theorem (Theorem 4.2.1). Indeed, the first quotient of
${\mathbb {A}}^1$-Hurewicz theorem (Theorem 4.2.1). Indeed, the first quotient of ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ described above is just some strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {F})$ described above is just some strictly ![]() ${\mathbb {A}}^1$-invariant sheaf on which
${\mathbb {A}}^1$-invariant sheaf on which ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially: a priori there is no reason this quotient has to coincide with the coinvariant subsheaf in general since we do not know that the latter sheaf is actually strictly
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\mathscr {E})$ acts trivially: a priori there is no reason this quotient has to coincide with the coinvariant subsheaf in general since we do not know that the latter sheaf is actually strictly ![]() ${\mathbb {A}}^1$-invariant. Moreover, because we use the
${\mathbb {A}}^1$-invariant. Moreover, because we use the ![]() ${\mathbb {A}}^1$-upper central series, the above principal refinement fails to be a functorial principal refinement.
${\mathbb {A}}^1$-upper central series, the above principal refinement fails to be a functorial principal refinement.
4.3  $R$-localization for
$R$-localization for  ${\mathbb {A}}^1$-nilpotent spaces
${\mathbb {A}}^1$-nilpotent spaces
Finally, in this section, we discuss ![]() $R$-localization of motivic spaces. We show that locally
$R$-localization of motivic spaces. We show that locally ![]() ${\mathbb {A}}^1$-nilpotent spaces have well-behaved localizations and that localization preserves various fiber sequences.
${\mathbb {A}}^1$-nilpotent spaces have well-behaved localizations and that localization preserves various fiber sequences.
The basic definitions
Definition 4.3.1 Suppose ![]() $f: \mathscr {X} \to \mathscr {Y}$ is a morphism in
$f: \mathscr {X} \to \mathscr {Y}$ is a morphism in ![]() $\mathrm {Spc}_k$. If
$\mathrm {Spc}_k$. If ![]() $R \subset {\mathbb {Q}}$ is a subring, then we will say that
$R \subset {\mathbb {Q}}$ is a subring, then we will say that ![]() $f$ is an
$f$ is an ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-weak equivalence or
${\mathbb {A}}^1$-weak equivalence or ![]() $R$-
$R$- ![]() ${\mathbb {A}}^1$-weak equivalence if the induced morphism
${\mathbb {A}}^1$-weak equivalence if the induced morphism ![]() $R_{{\mathbb {A}}^1}[\mathscr {X}] \to R_{{\mathbb {A}}^1}[\mathscr {Y}]$ is an isomorphism in
$R_{{\mathbb {A}}^1}[\mathscr {X}] \to R_{{\mathbb {A}}^1}[\mathscr {Y}]$ is an isomorphism in ![]() ${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. When
${\mathrm D}_{{\mathbb {A}}^1}^{\operatorname {eff}}(k)$. When ![]() $R = {\mathbb {Z}}_{(P)}$ for a set of primes
$R = {\mathbb {Z}}_{(P)}$ for a set of primes ![]() $P$, we will call
$P$, we will call ![]() $f$ a
$f$ a ![]() $P$-local
$P$-local ![]() ${\mathbb {A}}^1$-weak equivalence and a rational
${\mathbb {A}}^1$-weak equivalence and a rational ![]() ${\mathbb {A}}^1$-weak equivalence if
${\mathbb {A}}^1$-weak equivalence if ![]() $P$ is empty; when
$P$ is empty; when ![]() $R = {\mathbb {Z}}[ {1}/{n}]$, we will say that
$R = {\mathbb {Z}}[ {1}/{n}]$, we will say that ![]() $f$ is an
$f$ is an ![]() ${\mathbb {A}}^1$-weak equivalence after inverting
${\mathbb {A}}^1$-weak equivalence after inverting ![]() $n$.
$n$.
Remark 4.3.2 We have defined the notion of ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-weak equivalence above using homology in contrast to our earlier definition of
${\mathbb {A}}^1$-weak equivalence above using homology in contrast to our earlier definition of ![]() $R$-local equivalence using self-maps of the circle (§ 2.3). One reason for this disjunction is simply convenience of referencing. In Theorem 4.3.9 we will see that, for weakly
$R$-local equivalence using self-maps of the circle (§ 2.3). One reason for this disjunction is simply convenience of referencing. In Theorem 4.3.9 we will see that, for weakly ![]() ${\mathbb {A}}^1$-nilpotent spaces, in essence,
${\mathbb {A}}^1$-nilpotent spaces, in essence, ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization can be modeled by first
${\mathbb {A}}^1$-localization can be modeled by first ![]() ${\mathbb {A}}^1$-localizing and then applying the
${\mathbb {A}}^1$-localizing and then applying the ![]() $R$-localization functor studied previously.
$R$-localization functor studied previously.
Granted this definition, we may construct the ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local homotopy category by techniques of Bousfield localization.
${\mathbb {A}}^1$-local homotopy category by techniques of Bousfield localization.
Definition 4.3.3 We write ![]() ${\mathrm {Ho}_{k}}_{R}$ for the
${\mathrm {Ho}_{k}}_{R}$ for the ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local homotopy category, that is, the category obtained by left Bousfield localizing
${\mathbb {A}}^1$-local homotopy category, that is, the category obtained by left Bousfield localizing ![]() $\mathrm {Spc}_k$ at the set of
$\mathrm {Spc}_k$ at the set of ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalences. Likewise, if
${\mathbb {A}}^1$-weak equivalences. Likewise, if ![]() $n \neq 0$, we write
$n \neq 0$, we write ![]() $\mathrm {Ho}_{k}[{1}/{n}]$ for the category
$\mathrm {Ho}_{k}[{1}/{n}]$ for the category ![]() ${\mathrm {Ho}_{k}}_{{\mathbb {Z}}[{1}/{n}]}$.
${\mathrm {Ho}_{k}}_{{\mathbb {Z}}[{1}/{n}]}$.
Definition 4.3.4 A space ![]() $\mathscr {Z}$ is
$\mathscr {Z}$ is ![]() $R$-
$R$- ![]() ${\mathbb {A}}^1$-local if, for every
${\mathbb {A}}^1$-local if, for every ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalence
${\mathbb {A}}^1$-weak equivalence ![]() $f: \mathscr {X} \to \mathscr {Y}$, the map
$f: \mathscr {X} \to \mathscr {Y}$, the map ![]() $\operatorname {Map}(\mathscr {Y},\mathscr {Z}) \to \operatorname {Map}(\mathscr {X},\mathscr {Z})$ of derived mapping spaces is a weak equivalence.
$\operatorname {Map}(\mathscr {Y},\mathscr {Z}) \to \operatorname {Map}(\mathscr {X},\mathscr {Z})$ of derived mapping spaces is a weak equivalence.
The next lemma summarizes some basic facts about ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local spaces.
${\mathbb {A}}^1$-local spaces.
Lemma 4.3.5 The following statements hold.
1. If
 $\mathbf {A}$ is an
$\mathbf {A}$ is an  $R$-local strictly
$R$-local strictly  ${\mathbb {A}}^1$-invariant sheaf of abelian groups, then, for any integer
${\mathbb {A}}^1$-invariant sheaf of abelian groups, then, for any integer  $n \geq 0$,
$n \geq 0$,  $K(\mathbf {A},n)$ is
$K(\mathbf {A},n)$ is  $R$-
$R$- ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.2. If
 $\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence of pointed,
$\mathscr {F} \to \mathscr {E} \to \mathscr {B}$ is a simplicial fiber sequence of pointed,  ${\mathbb {A}}^1$-connected spaces and both
${\mathbb {A}}^1$-connected spaces and both  $\mathscr {E}$ and
$\mathscr {E}$ and  $\mathscr {B}$ are
$\mathscr {B}$ are  $R$-
$R$- ${\mathbb {A}}^1$-local, then
${\mathbb {A}}^1$-local, then  $\mathscr {F}$ is
$\mathscr {F}$ is  $R$-
$R$- ${\mathbb {A}}^1$-local as well; the
${\mathbb {A}}^1$-local as well; the  $R$-
$R$- ${\mathbb {A}}^1$-model structure is right proper.
${\mathbb {A}}^1$-model structure is right proper.3. If
 $\mathbf {G}$ is an
$\mathbf {G}$ is an  $R$-local
$R$-local  ${\mathbb {A}}^1$-nilpotent sheaf of groups, then
${\mathbb {A}}^1$-nilpotent sheaf of groups, then  $B\mathbf {G}$ is
$B\mathbf {G}$ is  $R$-
$R$- ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.4. If
 $\mathscr {X} \in \mathrm {Spc}_k$ is a connected
$\mathscr {X} \in \mathrm {Spc}_k$ is a connected  ${\mathbb {A}}^1$-nilpotent space such that
${\mathbb {A}}^1$-nilpotent space such that  $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ is
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})$ is  $R$-local for every
$R$-local for every  $i > 0$, then
$i > 0$, then  $\mathscr {X}$ is
$\mathscr {X}$ is  $R$-
$R$- ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.
Proof. Since ![]() $K(\mathbf {A},n)$ is
$K(\mathbf {A},n)$ is ![]() ${\mathbb {A}}^1$-local, for any space
${\mathbb {A}}^1$-local, for any space ![]() $\mathscr {X}$ there are identifications of the form
$\mathscr {X}$ there are identifications of the form
Granted these identifications, the fact that ![]() $K(\mathbf {A},n)$ is
$K(\mathbf {A},n)$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local is an immediate consequence of the equivalent conditions listed in Proposition 4.1.2.
${\mathbb {A}}^1$-local is an immediate consequence of the equivalent conditions listed in Proposition 4.1.2.
For the second statement, observe that applying ![]() $\mathrm {Map}(\mathscr {X},-)$ preserves fiber sequences. If
$\mathrm {Map}(\mathscr {X},-)$ preserves fiber sequences. If ![]() $\mathscr {Y} \to \mathscr {X}$ is an
$\mathscr {Y} \to \mathscr {X}$ is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-equivalence, then there is a morphism of simplicial fiber sequences as follows.
${\mathbb {A}}^1$-equivalence, then there is a morphism of simplicial fiber sequences as follows.

By considering the associated long exact sequence in homotopy, for example, one checks that the map ![]() $\mathrm {Map}(\mathscr {X},\mathscr {F}) \to \mathrm {Map}(\mathscr {Y},\mathscr {F})$ in the above diagram is again a weak equivalence. The right properness of the
$\mathrm {Map}(\mathscr {X},\mathscr {F}) \to \mathrm {Map}(\mathscr {Y},\mathscr {F})$ in the above diagram is again a weak equivalence. The right properness of the ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local model structure is now immediate from this observation.
${\mathbb {A}}^1$-local model structure is now immediate from this observation.
For the third statement, consider ![]() $B\mathbf {G}$ where
$B\mathbf {G}$ where ![]() $\mathbf {G}$ is
$\mathbf {G}$ is ![]() $R$-local and
$R$-local and ![]() ${\mathbb {A}}^1$-nilpotent. In that case,
${\mathbb {A}}^1$-nilpotent. In that case, ![]() $\mathbf {G}$ may be written as an iterated central extension by strictly
$\mathbf {G}$ may be written as an iterated central extension by strictly ![]() ${\mathbb {A}}^1$-invariant sheaves of
${\mathbb {A}}^1$-invariant sheaves of ![]() $R$-modules. Given such a central extension, there is an associated
$R$-modules. Given such a central extension, there is an associated ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
The first statement guarantees that ![]() $K(\mathbf {A},2)$ is
$K(\mathbf {A},2)$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local, and we may inductively assume that
${\mathbb {A}}^1$-local, and we may inductively assume that ![]() $B\mathbf {G}'$ is
$B\mathbf {G}'$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local, so we conclude that
${\mathbb {A}}^1$-local, so we conclude that ![]() $B\mathbf {G}$ is
$B\mathbf {G}$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local as well.
${\mathbb {A}}^1$-local as well.
The final statement is immediate from Theorem 3.3.13 and the preceding points.
 $R$-
$R$- ${\mathbb {A}}^1$-localization of
${\mathbb {A}}^1$-localization of  ${\mathbb {A}}^1$-nilpotent groups
${\mathbb {A}}^1$-nilpotent groups
Lemma 4.3.6 If ![]() $\mathbf {A}$ is a strictly
$\mathbf {A}$ is a strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups, then, for every integer
${\mathbb {A}}^1$-invariant sheaf of groups, then, for every integer ![]() $n > 0$,
$n > 0$,
is a functorial ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization of
${\mathbb {A}}^1$-localization of ![]() $K(\mathbf {A},n)$.
$K(\mathbf {A},n)$.
Proof. The space ![]() $K(R \otimes \mathbf {A},n)$ is
$K(R \otimes \mathbf {A},n)$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local by Lemma 4.3.5(1). The canonical morphism
${\mathbb {A}}^1$-local by Lemma 4.3.5(1). The canonical morphism ![]() $\mathbf {A} \to R \otimes \mathbf {A}$ yields a morphism
$\mathbf {A} \to R \otimes \mathbf {A}$ yields a morphism ![]() $K(\mathbf {A},n) \to K(R \otimes \mathbf {A},n)$. We want to show that this morphism is an
$K(\mathbf {A},n) \to K(R \otimes \mathbf {A},n)$. We want to show that this morphism is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalence. In fact, the morphism
${\mathbb {A}}^1$-weak equivalence. In fact, the morphism ![]() $\mathrm {R}_{\operatorname {Nis}} K(\mathbf {A},n) \to \mathrm {R}_{\operatorname {Nis}} K(R \otimes \mathbf {A},n)$ is an
$\mathrm {R}_{\operatorname {Nis}} K(\mathbf {A},n) \to \mathrm {R}_{\operatorname {Nis}} K(R \otimes \mathbf {A},n)$ is an ![]() $R$-local simplicial weak equivalence. Indeed, this can be checked stalkwise, in which case it follows from [Reference Bousfield and KanBK72, Chapter V.3.2].
$R$-local simplicial weak equivalence. Indeed, this can be checked stalkwise, in which case it follows from [Reference Bousfield and KanBK72, Chapter V.3.2].
We may now define a functorial ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization for
${\mathbb {A}}^1$-localization for ![]() ${\mathbb {A}}^1$-nilpotent sheaves of groups.
${\mathbb {A}}^1$-nilpotent sheaves of groups.
Theorem 4.3.7 Assume ![]() $k$ is a perfect field, and suppose
$k$ is a perfect field, and suppose ![]() $\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$ is an
$\mathbf {G} \in \mathrm {Grp}^{{\mathbb {A}}^1}_k$ is an ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups.
${\mathbb {A}}^1$-nilpotent sheaf of groups.
1. The space
 $\operatorname {L}_R B\mathbf {G}$ is
$\operatorname {L}_R B\mathbf {G}$ is  $R$-
$R$- ${\mathbb {A}}^1$-local.
${\mathbb {A}}^1$-local.2. The functor
 $\mathrm {Ab}^{{\mathbb {A}}^1}_k \to \mathrm {Mod}^{{\mathbb {A}}^1}_R$ sending a strictly
$\mathrm {Ab}^{{\mathbb {A}}^1}_k \to \mathrm {Mod}^{{\mathbb {A}}^1}_R$ sending a strictly  ${\mathbb {A}}^1$-invariant sheaf
${\mathbb {A}}^1$-invariant sheaf  $\mathbf {A}$ to
$\mathbf {A}$ to  $R \otimes \mathbf {A}$ extends to a functor
from the category of
$R \otimes \mathbf {A}$ extends to a functor
from the category of \[ \mathbf{G} \to \boldsymbol{\pi}_1(\operatorname{L}_R B_{\operatorname{Nis}}\mathbf{G}) =: \mathbf{G}_R \]
\[ \mathbf{G} \to \boldsymbol{\pi}_1(\operatorname{L}_R B_{\operatorname{Nis}}\mathbf{G}) =: \mathbf{G}_R \] ${\mathbb {A}}^1$-nilpotent sheaves of groups to the category of
${\mathbb {A}}^1$-nilpotent sheaves of groups to the category of  $R$-local
$R$-local  ${\mathbb {A}}^1$-nilpotent sheaves of groups.
${\mathbb {A}}^1$-nilpotent sheaves of groups.3. The functor of (2) preserves short exact sequences of
 ${\mathbb {A}}^1$-nilpotent sheaves of groups.
${\mathbb {A}}^1$-nilpotent sheaves of groups.4. For any
 ${\mathbb {A}}^1$-nilpotent sheaf of groups
${\mathbb {A}}^1$-nilpotent sheaf of groups  $\mathbf {G}$, there is a canonical isomorphism
$\mathbf {G}$, there is a canonical isomorphism  $(\mathbf {G}_{-1})_{R} \cong (\mathbf {G}_R)_{-1}$ (see Definition 3.1.17).
$(\mathbf {G}_{-1})_{R} \cong (\mathbf {G}_R)_{-1}$ (see Definition 3.1.17).
Proof. If ![]() $\mathbf {A}$ is strictly
$\mathbf {A}$ is strictly ![]() ${\mathbb {A}}^1$-invariant, then we know that
${\mathbb {A}}^1$-invariant, then we know that ![]() $\operatorname {L}_R B\mathbf {A}$ is
$\operatorname {L}_R B\mathbf {A}$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local by appeal to Lemma 4.3.6 and
${\mathbb {A}}^1$-local by appeal to Lemma 4.3.6 and ![]() $\boldsymbol {\pi }_1(\operatorname {L}_R B\mathbf {A}) \cong \mathbf {A} \otimes R =: \mathbf {A}_R$.
$\boldsymbol {\pi }_1(\operatorname {L}_R B\mathbf {A}) \cong \mathbf {A} \otimes R =: \mathbf {A}_R$.
To treat the general case, suppose we have a central extension of the form
where ![]() $\mathbf {A}$ is strictly
$\mathbf {A}$ is strictly ![]() ${\mathbb {A}}^1$-invariant and
${\mathbb {A}}^1$-invariant and ![]() $\mathbf {G}$ and
$\mathbf {G}$ and ![]() $\mathbf {G}'$ are
$\mathbf {G}'$ are ![]() ${\mathbb {A}}^1$-nilpotent. In that case, there is a fiber sequence of the form
${\mathbb {A}}^1$-nilpotent. In that case, there is a fiber sequence of the form
in which each term is ![]() ${\mathbb {A}}^1$-local (i.e. this is an
${\mathbb {A}}^1$-local (i.e. this is an ![]() ${\mathbb {A}}^1$-fiber sequence). We claim that the sequence
${\mathbb {A}}^1$-fiber sequence). We claim that the sequence
is a simplicial fiber sequence of ![]() ${\mathbb {A}}^1$-local spaces. To this end, observe that
${\mathbb {A}}^1$-local spaces. To this end, observe that ![]() $\operatorname {L}_R K(\mathbf {A},2)$ is simplicially
$\operatorname {L}_R K(\mathbf {A},2)$ is simplicially ![]() $1$-connected and
$1$-connected and ![]() ${\mathbb {A}}^1$-local by appeal to Lemma 4.3.6. Next, observe that
${\mathbb {A}}^1$-local by appeal to Lemma 4.3.6. Next, observe that ![]() $B\mathbf {G}'$ and
$B\mathbf {G}'$ and ![]() $B\mathbf {G}$ are
$B\mathbf {G}$ are ![]() ${\mathbb {A}}^1$-nilpotent and therefore nilpotent in the classical sense. It follows from Lemma 2.3.10 that the canonical map from the
${\mathbb {A}}^1$-nilpotent and therefore nilpotent in the classical sense. It follows from Lemma 2.3.10 that the canonical map from the ![]() $R$-localization of
$R$-localization of ![]() $B\mathbf {G}$ to the homotopy fiber of
$B\mathbf {G}$ to the homotopy fiber of ![]() $\operatorname {L}_R B\mathbf {G}' \to \operatorname {L}_R K(\mathbf {A},2)$ is a simplicial weak equivalence.
$\operatorname {L}_R B\mathbf {G}' \to \operatorname {L}_R K(\mathbf {A},2)$ is a simplicial weak equivalence.
We claim that by induction ![]() $\operatorname {L}_R B\mathbf {G}$ is
$\operatorname {L}_R B\mathbf {G}$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local. The base case is Lemma 4.3.6: in particular, we may assume inductively that
${\mathbb {A}}^1$-local. The base case is Lemma 4.3.6: in particular, we may assume inductively that ![]() $\operatorname {L}_R B\mathbf {G}'$ is simplicially connected,
$\operatorname {L}_R B\mathbf {G}'$ is simplicially connected, ![]() ${\mathbb {A}}^1$-local, has an
${\mathbb {A}}^1$-local, has an ![]() $R$-local strongly
$R$-local strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups
${\mathbb {A}}^1$-invariant sheaf of groups ![]() $\boldsymbol {\pi }_1(\operatorname {L}_R B\mathbf {G}')$ and is
$\boldsymbol {\pi }_1(\operatorname {L}_R B\mathbf {G}')$ and is ![]() $1$-truncated, that is, all higher homotopy sheaves vanish. In that case, Lemma 4.3.5 guarantees that
$1$-truncated, that is, all higher homotopy sheaves vanish. In that case, Lemma 4.3.5 guarantees that ![]() $\operatorname {L}_R B\mathbf {G}'$ is
$\operatorname {L}_R B\mathbf {G}'$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local. Then combining Lemmas 4.3.6 and 4.3.5 with the fiber sequence of (4.1) implies that
${\mathbb {A}}^1$-local. Then combining Lemmas 4.3.6 and 4.3.5 with the fiber sequence of (4.1) implies that ![]() $\operatorname {L}_R B\mathbf {G}$ is
$\operatorname {L}_R B\mathbf {G}$ is ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local as well.
${\mathbb {A}}^1$-local as well.
Statement (2) is immediate from (1). Statement (3) follows immediately from Lemma 2.3.12. For (4), consider the map ![]() $\mathbf {G} \to \mathbf {G}_R$. Taking contractions yields a morphism
$\mathbf {G} \to \mathbf {G}_R$. Taking contractions yields a morphism ![]() $\mathbf {G}_{-1} \to (\mathbf {G}_R)_{-1}$. The construction of
$\mathbf {G}_{-1} \to (\mathbf {G}_R)_{-1}$. The construction of ![]() $R$-localization, together with the fact that
$R$-localization, together with the fact that ![]() $(-)_{-1}$ preserves exact sequences, implies that
$(-)_{-1}$ preserves exact sequences, implies that ![]() $(\mathbf {G}_R)_{-1}$ is an
$(\mathbf {G}_R)_{-1}$ is an ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups, and therefore there is an induced morphism
${\mathbb {A}}^1$-nilpotent sheaf of groups, and therefore there is an induced morphism ![]() $(\mathbf {G}_{-1})_R \to (\mathbf {G}_R)_{-1}$. By definition of contraction, this map is an isomorphism if
$(\mathbf {G}_{-1})_R \to (\mathbf {G}_R)_{-1}$. By definition of contraction, this map is an isomorphism if ![]() $\mathbf {G}$ is abelian, and one deduces it is an isomorphism in general by induction on the
$\mathbf {G}$ is abelian, and one deduces it is an isomorphism in general by induction on the ![]() ${\mathbb {A}}^1$-nilpotence class of
${\mathbb {A}}^1$-nilpotence class of ![]() $\mathbf {G}$.
$\mathbf {G}$.
A technical result
Before moving on to analyze ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization of
${\mathbb {A}}^1$-localization of ![]() ${\mathbb {A}}^1$-nilpotent spaces, we establish a useful technical result here about the interaction between
${\mathbb {A}}^1$-nilpotent spaces, we establish a useful technical result here about the interaction between ![]() ${\mathbb {A}}^1$-localization and
${\mathbb {A}}^1$-localization and ![]() $R$-localization in the sense of § 2.3.
$R$-localization in the sense of § 2.3.
Proposition 4.3.8 Suppose ![]() $(\mathscr {X},x)$ is a pointed, connected space. If
$(\mathscr {X},x)$ is a pointed, connected space. If ![]() $\mathscr {X}$ is a weakly
$\mathscr {X}$ is a weakly ![]() ${\mathbb {A}}^1$-nilpotent and
${\mathbb {A}}^1$-nilpotent and ![]() ${\mathbb {A}}^1$-local space (see Definition 3.3.1 for the former notion), then
${\mathbb {A}}^1$-local space (see Definition 3.3.1 for the former notion), then ![]() $\operatorname {L}_R \mathscr {X}$ is again
$\operatorname {L}_R \mathscr {X}$ is again ![]() ${\mathbb {A}}^1$-local. Moreover, for each integer
${\mathbb {A}}^1$-local. Moreover, for each integer ![]() $i \geq 1$, there are identifications of the form
$i \geq 1$, there are identifications of the form
and ![]() $\operatorname {L}_R \mathscr {X}$ is again a weakly
$\operatorname {L}_R \mathscr {X}$ is again a weakly ![]() ${\mathbb {A}}^1$-nilpotent space.
${\mathbb {A}}^1$-nilpotent space.
Proof. By [Reference Asok, Wickelgren and WilliamsAWW17, Lemma 2.2.11(2)], to check a connected space ![]() $\mathscr {Y}$ is
$\mathscr {Y}$ is ![]() ${\mathbb {A}}^1$-local, it suffices to show that
${\mathbb {A}}^1$-local, it suffices to show that ![]() $\boldsymbol {\pi }_1(\mathscr {Y})$ is strongly
$\boldsymbol {\pi }_1(\mathscr {Y})$ is strongly ![]() ${\mathbb {A}}^1$-invariant and
${\mathbb {A}}^1$-invariant and ![]() $\boldsymbol {\pi }_i(\mathscr {Y})$ is strictly
$\boldsymbol {\pi }_i(\mathscr {Y})$ is strictly ![]() ${\mathbb {A}}^1$-invariant for
${\mathbb {A}}^1$-invariant for ![]() $i \geq 2$.
$i \geq 2$.
Replacing ![]() $\mathscr {X}$ by
$\mathscr {X}$ by ![]() $\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ if necessary, we may assume that
$\operatorname {L}_{{\mathbb {A}}^1} \mathscr {X}$ if necessary, we may assume that ![]() $\mathscr {X}$ is simplicially fibrant and
$\mathscr {X}$ is simplicially fibrant and ![]() ${\mathbb {A}}^1$-local. Set
${\mathbb {A}}^1$-local. Set ![]() $\boldsymbol {\pi } := \boldsymbol {\pi }_1(\mathscr {X},x)$ and consider the first stage of the
$\boldsymbol {\pi } := \boldsymbol {\pi }_1(\mathscr {X},x)$ and consider the first stage of the ![]() ${\mathbb {A}}^1$-Postnikov tower for
${\mathbb {A}}^1$-Postnikov tower for ![]() $\mathscr {X}$, that is, the morphism
$\mathscr {X}$, that is, the morphism ![]() $\mathscr {X} \to B\boldsymbol {\pi }$. Write
$\mathscr {X} \to B\boldsymbol {\pi }$. Write ![]() $\widetilde {\mathscr {X}}$ for the simplicial homotopy fiber of
$\widetilde {\mathscr {X}}$ for the simplicial homotopy fiber of ![]() $\mathscr {X} \to B\boldsymbol {\pi }$. Since
$\mathscr {X} \to B\boldsymbol {\pi }$. Since ![]() $\boldsymbol {\pi }$ is strongly
$\boldsymbol {\pi }$ is strongly ![]() ${\mathbb {A}}^1$-invariant,
${\mathbb {A}}^1$-invariant, ![]() $B\boldsymbol {\pi }$ is
$B\boldsymbol {\pi }$ is ![]() ${\mathbb {A}}^1$-local as well, so
${\mathbb {A}}^1$-local as well, so ![]() $\widetilde {\mathscr {X}}$ is
$\widetilde {\mathscr {X}}$ is ![]() ${\mathbb {A}}^1$-local by appeal to Lemma 3.1.3. Furthermore,
${\mathbb {A}}^1$-local by appeal to Lemma 3.1.3. Furthermore, ![]() $\widetilde {\mathscr {X}}$ is simplicially
$\widetilde {\mathscr {X}}$ is simplicially ![]() $1$-connected by assumption. Of course,
$1$-connected by assumption. Of course, ![]() $\boldsymbol {\pi }_i(\widetilde {\mathscr {X}}) \cong \boldsymbol {\pi }_i(\mathscr {X})$ for
$\boldsymbol {\pi }_i(\widetilde {\mathscr {X}}) \cong \boldsymbol {\pi }_i(\mathscr {X})$ for ![]() $i \geq 2$ as well.
$i \geq 2$ as well.
The morphism ![]() $\mathscr {X} \to B\boldsymbol {\pi }$ is a locally
$\mathscr {X} \to B\boldsymbol {\pi }$ is a locally ![]() ${\mathbb {A}}^1$-nilpotent morphism of simplicially connected spaces by the identifications of the preceding paragraph. If we apply
${\mathbb {A}}^1$-nilpotent morphism of simplicially connected spaces by the identifications of the preceding paragraph. If we apply ![]() $\operatorname {L}_R$ to this simplicial fiber sequence, then Lemma 2.3.10 guarantees that there is again a simplicial fiber sequence of the form
$\operatorname {L}_R$ to this simplicial fiber sequence, then Lemma 2.3.10 guarantees that there is again a simplicial fiber sequence of the form
Since the simplicial connectivity of ![]() $\operatorname {L}_R \widetilde {\mathscr {X}}$ may be checked stalkwise, and
$\operatorname {L}_R \widetilde {\mathscr {X}}$ may be checked stalkwise, and ![]() $\operatorname {L}_R$ commutes with formation of stalks, since stalkwise
$\operatorname {L}_R$ commutes with formation of stalks, since stalkwise ![]() $R$-localization preserves connectivity, we conclude that
$R$-localization preserves connectivity, we conclude that ![]() $\operatorname {L}_R \widetilde {\mathscr {X}}$ is again simplicially
$\operatorname {L}_R \widetilde {\mathscr {X}}$ is again simplicially ![]() $1$-connected.
$1$-connected.
Corollary 2.3.13 allows us to conclude that ![]() $\boldsymbol {\pi }_i(\operatorname {L}_R \widetilde {\mathscr {X}}) \cong \boldsymbol {\pi }_i(\mathscr {X})_R$. Since
$\boldsymbol {\pi }_i(\operatorname {L}_R \widetilde {\mathscr {X}}) \cong \boldsymbol {\pi }_i(\mathscr {X})_R$. Since ![]() $\boldsymbol {\pi }_i(\mathscr {X})$ is strictly
$\boldsymbol {\pi }_i(\mathscr {X})$ is strictly ![]() ${\mathbb {A}}^1$-invariant as
${\mathbb {A}}^1$-invariant as ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() ${\mathbb {A}}^1$-local, and we know that tensoring with
${\mathbb {A}}^1$-local, and we know that tensoring with ![]() $R$ preserves strict
$R$ preserves strict ![]() ${\mathbb {A}}^1$-invariance, we conclude that
${\mathbb {A}}^1$-invariance, we conclude that ![]() $\boldsymbol {\pi }_i(\operatorname {L}_R \mathscr {X}) \cong \boldsymbol {\pi }_i(\operatorname {L}_R \widetilde {\mathscr {X}})$ is strictly
$\boldsymbol {\pi }_i(\operatorname {L}_R \mathscr {X}) \cong \boldsymbol {\pi }_i(\operatorname {L}_R \widetilde {\mathscr {X}})$ is strictly ![]() ${\mathbb {A}}^1$-invariant for all
${\mathbb {A}}^1$-invariant for all ![]() $i \geq 2$. Likewise, from Theorem 4.3.7, we conclude that
$i \geq 2$. Likewise, from Theorem 4.3.7, we conclude that ![]() $\boldsymbol {\pi }_1(\operatorname {L}_R \mathscr {X}) \cong \boldsymbol {\pi }_1(\operatorname {L}_R B\boldsymbol {\pi })$ is an
$\boldsymbol {\pi }_1(\operatorname {L}_R \mathscr {X}) \cong \boldsymbol {\pi }_1(\operatorname {L}_R B\boldsymbol {\pi })$ is an ![]() $R$-local strongly
$R$-local strongly ![]() ${\mathbb {A}}^1$-invariant sheaf of groups.
${\mathbb {A}}^1$-invariant sheaf of groups.
We already know that ![]() $\boldsymbol {\pi }_1(\mathscr {X})_R$ is an
$\boldsymbol {\pi }_1(\mathscr {X})_R$ is an ![]() $R$-local
$R$-local ![]() ${\mathbb {A}}^1$-nilpotent sheaf of groups. To establish the local
${\mathbb {A}}^1$-nilpotent sheaf of groups. To establish the local ![]() ${\mathbb {A}}^1$-nilpotence of the higher homotopy sheaves, simply observe that because
${\mathbb {A}}^1$-nilpotence of the higher homotopy sheaves, simply observe that because ![]() $R$-localization is given by tensoring with
$R$-localization is given by tensoring with ![]() $R$ and
$R$ and ![]() $R$ is flat as a
$R$ is flat as a ![]() ${\mathbb {Z}}$-module, if we take any locally finite
${\mathbb {Z}}$-module, if we take any locally finite ![]() $\boldsymbol {\pi }$-central series for
$\boldsymbol {\pi }$-central series for ![]() $\boldsymbol {\pi }_i(\mathscr {X})$, then tensoring that series with
$\boldsymbol {\pi }_i(\mathscr {X})$, then tensoring that series with ![]() $R$ provides a locally finite
$R$ provides a locally finite ![]() $\boldsymbol {\pi }_R$-central series for
$\boldsymbol {\pi }_R$-central series for ![]() $\boldsymbol {\pi }_i(\mathscr {X})_R$.
$\boldsymbol {\pi }_i(\mathscr {X})_R$.
 $R$-
$R$- ${\mathbb {A}}^1$-localizations of
${\mathbb {A}}^1$-localizations of  ${\mathbb {A}}^1$-nilpotent spaces
${\mathbb {A}}^1$-nilpotent spaces
We may now construct a convenient functorial model for the ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization of a weakly
${\mathbb {A}}^1$-localization of a weakly ![]() ${\mathbb {A}}^1$-nilpotent spaces.
${\mathbb {A}}^1$-nilpotent spaces.
Theorem 4.3.9 Suppose ![]() $k$ is a perfect field and
$k$ is a perfect field and ![]() $\mathscr {X} \in \mathrm {Spc}_k$ is a pointed, connected,
$\mathscr {X} \in \mathrm {Spc}_k$ is a pointed, connected, ![]() ${\mathbb {A}}^1$-local space. If
${\mathbb {A}}^1$-local space. If ![]() $\mathscr {X}$ is weakly
$\mathscr {X}$ is weakly ![]() ${\mathbb {A}}^1$-nilpotent (see Definition 3.3.1), then the following statements hold.
${\mathbb {A}}^1$-nilpotent (see Definition 3.3.1), then the following statements hold.
1. The canonical map
 $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_R \to \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {L}_R \mathscr {X})$ is an isomorphism for every
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_R \to \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\operatorname {L}_R \mathscr {X})$ is an isomorphism for every  $i \geq 1$. Moreover,
$i \geq 1$. Moreover,  $\operatorname {L}_R \mathscr {X}$ is connected,
$\operatorname {L}_R \mathscr {X}$ is connected,  $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\operatorname {L}_R \mathscr {X})$ is an
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}(\operatorname {L}_R \mathscr {X})$ is an  $R$-local
$R$-local  ${\mathbb {A}}^1$-nilpotent sheaf of groups, and
${\mathbb {A}}^1$-nilpotent sheaf of groups, and  $\operatorname {L}_R \mathscr {X}$ is again locally
$\operatorname {L}_R \mathscr {X}$ is again locally  ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.2. The canonical map
 $\mathscr {X} \to \operatorname {L}_R \mathscr {X}$ is an
$\mathscr {X} \to \operatorname {L}_R \mathscr {X}$ is an  $R$-
$R$- ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.3. The
 $R$-
$R$- ${\mathbb {A}}^1$-localization functor commutes with formation of finite products for weakly
${\mathbb {A}}^1$-localization functor commutes with formation of finite products for weakly  ${\mathbb {A}}^1$-nilpotent spaces.
${\mathbb {A}}^1$-nilpotent spaces.
Proof. The first point is precisely Proposition 4.3.8. To check that ![]() $\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is an
$\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalence, we proceed as follows. Observe that
${\mathbb {A}}^1$-weak equivalence, we proceed as follows. Observe that ![]() $\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is an
$\mathscr {X} \to \operatorname {L}_R\mathscr {X}$ is an ![]() $R$-local simplicial weak equivalence since it is so stalkwise. Therefore, appeal to [Reference Bousfield and KanBK72, Proposition V.3.2] implies that the map
$R$-local simplicial weak equivalence since it is so stalkwise. Therefore, appeal to [Reference Bousfield and KanBK72, Proposition V.3.2] implies that the map ![]() $R[\mathscr {X}] \to R[\operatorname {L}_R \mathscr {X}]$ is stalkwise a weak equivalence, which means it is an isomorphism in the derived category of Nisnevich sheaves of
$R[\mathscr {X}] \to R[\operatorname {L}_R \mathscr {X}]$ is stalkwise a weak equivalence, which means it is an isomorphism in the derived category of Nisnevich sheaves of ![]() $R$-modules. It follows that the map remains an isomorphism after applying
$R$-modules. It follows that the map remains an isomorphism after applying ![]() $\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$, so the map
$\operatorname {L}_{{\mathbb {A}}^1}^{\rm ab}$, so the map ![]() $\mathscr {X} \to \operatorname {L}_R \mathscr {X}$ is an
$\mathscr {X} \to \operatorname {L}_R \mathscr {X}$ is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-equivalence as well.
${\mathbb {A}}^1$-equivalence as well.
For the final point, note that both ![]() $\operatorname {L}_R$ and
$\operatorname {L}_R$ and ![]() $\operatorname {L}_{{\mathbb {A}}^1}$ commute with formation of finite products by construction (see Proposition 2.3.6 for the former). Since products of weakly
$\operatorname {L}_{{\mathbb {A}}^1}$ commute with formation of finite products by construction (see Proposition 2.3.6 for the former). Since products of weakly ![]() ${\mathbb {A}}^1$-nilpotent spaces are weakly
${\mathbb {A}}^1$-nilpotent spaces are weakly ![]() ${\mathbb {A}}^1$-nilpotent, the conclusion of third point follows from the first two.
${\mathbb {A}}^1$-nilpotent, the conclusion of third point follows from the first two.
The above theorem has the following very useful consequence.
Corollary 4.3.10 Suppose ![]() $k$ is a perfect field. A morphism
$k$ is a perfect field. A morphism ![]() $f: \mathscr {X} \to \mathscr {Y}$ of pointed, weakly
$f: \mathscr {X} \to \mathscr {Y}$ of pointed, weakly ![]() ${\mathbb {A}}^1$-nilpotent spaces is an
${\mathbb {A}}^1$-nilpotent spaces is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalence if and only if the induced maps
${\mathbb {A}}^1$-weak equivalence if and only if the induced maps ![]() $f_*: \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_R \to \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {Y})_R$ are isomorphisms for every
$f_*: \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {X})_R \to \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {Y})_R$ are isomorphisms for every ![]() $i \geq 1$.
$i \geq 1$.
We conclude this section by observing that our model for ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization behaves well in fiber sequences.
${\mathbb {A}}^1$-localization behaves well in fiber sequences.
Theorem 4.3.11 Suppose
is an ![]() ${\mathbb {A}}^1$-fiber sequence of pointed
${\mathbb {A}}^1$-fiber sequence of pointed ![]() ${\mathbb {A}}^1$-connected spaces. If
${\mathbb {A}}^1$-connected spaces. If ![]() $\mathscr {E}$ and
$\mathscr {E}$ and ![]() $\mathscr {B}$ are weakly
$\mathscr {B}$ are weakly ![]() ${\mathbb {A}}^1$-nilpotent, then
${\mathbb {A}}^1$-nilpotent, then
is again an ![]() ${\mathbb {A}}^1$-fiber sequence.
${\mathbb {A}}^1$-fiber sequence.
Proof. By applying ![]() $\operatorname {L}_{{\mathbb {A}}^1}$ to the fiber sequence, we may assume that the sequence in question is a simplicial fiber sequence of pointed simplicially connected and
$\operatorname {L}_{{\mathbb {A}}^1}$ to the fiber sequence, we may assume that the sequence in question is a simplicial fiber sequence of pointed simplicially connected and ![]() ${\mathbb {A}}^1$-local spaces. Moreover, Corollary 3.3.7 implies that
${\mathbb {A}}^1$-local spaces. Moreover, Corollary 3.3.7 implies that ![]() $\mathscr {F}$ is weakly
$\mathscr {F}$ is weakly ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
The canonical map ![]() $\operatorname {L}_R \mathscr {F} \to \operatorname {hofib}(\operatorname {L}_R \mathscr {E} \to \operatorname {L}_R \mathscr {B})$ is a simplicial weak equivalence by appeal to Lemma 2.3.10. On the other hand, Theorem 4.3.9 guarantees that the canonical maps
$\operatorname {L}_R \mathscr {F} \to \operatorname {hofib}(\operatorname {L}_R \mathscr {E} \to \operatorname {L}_R \mathscr {B})$ is a simplicial weak equivalence by appeal to Lemma 2.3.10. On the other hand, Theorem 4.3.9 guarantees that the canonical maps ![]() $\mathscr {F} \to \operatorname {L}_R \mathscr {F}$,
$\mathscr {F} \to \operatorname {L}_R \mathscr {F}$, ![]() $\mathscr {E} \to \operatorname {L}_R \mathscr {E}$ and
$\mathscr {E} \to \operatorname {L}_R \mathscr {E}$ and ![]() $\mathscr {B} \to \operatorname {L}_R \mathscr {B}$ are
$\mathscr {B} \to \operatorname {L}_R \mathscr {B}$ are ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalences. In total, we conclude that the map
${\mathbb {A}}^1$-weak equivalences. In total, we conclude that the map
is an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Remark 4.3.12 As in the classical situation, even if ![]() $f: \mathscr {E} \to \mathscr {B}$ is a morphism of
$f: \mathscr {E} \to \mathscr {B}$ is a morphism of ![]() ${\mathbb {A}}^1$-simple spaces, the homotopy fiber of
${\mathbb {A}}^1$-simple spaces, the homotopy fiber of ![]() $f$ may be
$f$ may be ![]() ${\mathbb {A}}^1$-nilpotent. Here is a rather geometric example: over any field
${\mathbb {A}}^1$-nilpotent. Here is a rather geometric example: over any field ![]() $k$, the proof of Theorem 3.4.6 in the case where
$k$, the proof of Theorem 3.4.6 in the case where ![]() $n = 0$ yields an
$n = 0$ yields an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
where we have identified ![]() ${\mathbb {P}}^1$ with
${\mathbb {P}}^1$ with ![]() $SL_2/{{\mathbf {G}}_{m}^{}}$. The middle term is
$SL_2/{{\mathbf {G}}_{m}^{}}$. The middle term is ![]() ${\mathbb {A}}^1$-simple and
${\mathbb {A}}^1$-simple and ![]() $BSL_2$ is even
$BSL_2$ is even ![]() ${\mathbb {A}}^1$-simply connected. As mentioned in Remark 3.4.9,
${\mathbb {A}}^1$-simply connected. As mentioned in Remark 3.4.9, ![]() $\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$ is non-abelian and
$\boldsymbol {\pi }_1^{{\mathbb {A}}^1}({\mathbb {P}}^1)$ is non-abelian and ![]() ${\mathbb {A}}^1$-nilpotent.
${\mathbb {A}}^1$-nilpotent.
5. Applications
H. Hopf observed that compact Lie groups have the same real cohomology as products of spheres [Reference HopfHop45] and J.-P. Serre [Reference SerreSer53, V.4] established the same results after inverting smaller sets of primes. More precisely, suppose one is given a compact Lie group ![]() $G$. Serre called a prime
$G$. Serre called a prime ![]() $p$ regular for
$p$ regular for ![]() $G$ if there exist a product of spheres
$G$ if there exist a product of spheres ![]() $X = \prod _{i = 1}^{\ell } S^{n_i}$ and a map
$X = \prod _{i = 1}^{\ell } S^{n_i}$ and a map ![]() $f: X \to G$ such that
$f: X \to G$ such that ![]() $f_*: H_*(X,{\mathbb {Z}}/p) \to H_*(G,{\mathbb {Z}}/p)$ is an isomorphism. If
$f_*: H_*(X,{\mathbb {Z}}/p) \to H_*(G,{\mathbb {Z}}/p)$ is an isomorphism. If ![]() $p$ is regular for
$p$ is regular for ![]() $G$, then
$G$, then ![]() $G$ is
$G$ is ![]() $p$-locally a product of spheres. Later, B. Harris [Reference HarrisHar61] observed that similar
$p$-locally a product of spheres. Later, B. Harris [Reference HarrisHar61] observed that similar ![]() $p$-local decompositions exist for various homogeneous spaces of compact Lie groups. In this section we study motivic analogs of these and related
$p$-local decompositions exist for various homogeneous spaces of compact Lie groups. In this section we study motivic analogs of these and related ![]() $p$-local decompositions.
$p$-local decompositions.
5.1 Self-equivalences of motivic spheres
We study self-maps of motivic spheres that are weak equivalences after suitable localization. To construct such maps, we review some constructions of Suslin and then analyze computations of motivic Brouwer degree for the relevant self-maps. We begin by recalling some facts about Grothendieck–Witt rings and motivic Brouwer degrees.
Fix an arbitrary field ![]() $k$. We use the notation
$k$. We use the notation ![]() $Q_{2n-1}$ for the odd-dimensional smooth affine quadric defined by the equation
$Q_{2n-1}$ for the odd-dimensional smooth affine quadric defined by the equation ![]() $\sum _{i=1}^n x_iy_i = 1$ in
$\sum _{i=1}^n x_iy_i = 1$ in ![]() ${\mathbb {A}}^{2n}$ with coordinates
${\mathbb {A}}^{2n}$ with coordinates ![]() $x_1,\ldots,x_n,y_1,\ldots,y_n$. Projection onto the
$x_1,\ldots,x_n,y_1,\ldots,y_n$. Projection onto the ![]() $x$-variables determines a morphism
$x$-variables determines a morphism ![]() $Q_{2n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$ that is a torsor under a vector bundle, in particular an
$Q_{2n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$ that is a torsor under a vector bundle, in particular an ![]() ${\mathbb {A}}^1$-weak equivalence; we also refer to this morphism as the ‘universal unimodular row’. For any integer
${\mathbb {A}}^1$-weak equivalence; we also refer to this morphism as the ‘universal unimodular row’. For any integer ![]() $n \geq 1$, the quadric
$n \geq 1$, the quadric ![]() $Q_{2n-1}$ is
$Q_{2n-1}$ is ![]() ${\mathbb {A}}^1$-weakly equivalent to
${\mathbb {A}}^1$-weakly equivalent to ![]() $\Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. We also use the notation
$\Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. We also use the notation ![]() $Q_{2n}$ for the smooth affine quadric defined by the equation
$Q_{2n}$ for the smooth affine quadric defined by the equation ![]() $\sum _{i=1}^n x_iy_i = z(1-z)$ in
$\sum _{i=1}^n x_iy_i = z(1-z)$ in ![]() ${\mathbb {A}}^{2n+1}$ with the evident coordinates. By [Reference Asok, Doran and FaselADF17, Theorem 2], this quadric is
${\mathbb {A}}^{2n+1}$ with the evident coordinates. By [Reference Asok, Doran and FaselADF17, Theorem 2], this quadric is ![]() ${\mathbb {A}}^1$-weakly equivalent to
${\mathbb {A}}^1$-weakly equivalent to ![]() ${{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ (in fact, all of these assertions hold over
${{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ (in fact, all of these assertions hold over ![]() $\operatorname {Spec} {\mathbb {Z}}$).
$\operatorname {Spec} {\mathbb {Z}}$).
Grothendieck–Witt groups and motivic Brouwer degree
Morel described the ring of homotopy endomorphisms of motivic spheres by establishing the following result.
Theorem 5.1.1 (Morel)
Suppose ![]() $k$ is a field. For any integer
$k$ is a field. For any integer ![]() $n \geq 2$, there is an isomorphism of rings:
$n \geq 2$, there is an isomorphism of rings:
Proof. For a casual exposition see [Reference MorelMor06a, § 1], and for a very explicit ‘classical’ description of the above degree map see [Reference CazanaveCaz12]. The result as stated follows by combining a number of statements from [Reference MorelMor12]. We observed above that for any integer ![]() $n \geq 1$,
$n \geq 1$, ![]() $Q_{2n-1}$ is
$Q_{2n-1}$ is ![]() ${\mathbb {A}}^1$-weakly equivalent to
${\mathbb {A}}^1$-weakly equivalent to ![]() $\Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. Appealing to [Reference MorelMor12, Corollary 6.43], one knows that there are isomorphisms of abelian groups of the form
$\Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$. Appealing to [Reference MorelMor12, Corollary 6.43], one knows that there are isomorphisms of abelian groups of the form ![]() $\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(Q_{2n-1}) \cong {{\mathbf {K}}}^{\rm MW}_0(k)$ for
$\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(Q_{2n-1}) \cong {{\mathbf {K}}}^{\rm MW}_0(k)$ for ![]() $n \geq 3$; the corresponding isomorphism for
$n \geq 3$; the corresponding isomorphism for ![]() $n = 2$ follows from [Reference MorelMor12, Theorem 7.20]. By [Reference MorelMor12, Lemma 3.10], one knows that
$n = 2$ follows from [Reference MorelMor12, Theorem 7.20]. By [Reference MorelMor12, Lemma 3.10], one knows that ![]() ${{\mathbf {K}}}^{\rm MW}_0(k) \cong GW(k)$ as abelian groups. The fact that the ring structure on homotopy endomorphism induced by composition corresponds to the ring structure in the Grothendieck–Witt group follows from [Reference MorelMor12, Theorem 7.35].
${{\mathbf {K}}}^{\rm MW}_0(k) \cong GW(k)$ as abelian groups. The fact that the ring structure on homotopy endomorphism induced by composition corresponds to the ring structure in the Grothendieck–Witt group follows from [Reference MorelMor12, Theorem 7.35].
We will refer to the isomorphism ![]() $\operatorname {deg}$ as the motivic Brouwer degree. In order to apply our localization techniques, we will need to observe that
$\operatorname {deg}$ as the motivic Brouwer degree. In order to apply our localization techniques, we will need to observe that ![]() $GW(k)$ simplifies after inverting primes, at least under suitable assumptions on the base field.
$GW(k)$ simplifies after inverting primes, at least under suitable assumptions on the base field.
Lemma 5.1.2 Suppose ![]() $A$ is a ring which is
$A$ is a ring which is ![]() $2$-divisible and
$2$-divisible and ![]() $k$ is a field that is not formally real. The rank map
$k$ is a field that is not formally real. The rank map ![]() $GW(k) \to {\mathbb {Z}}$ induces an isomorphism
$GW(k) \to {\mathbb {Z}}$ induces an isomorphism ![]() $GW(k) \otimes A {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} A$.
$GW(k) \otimes A {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} A$.
Proof. There is an isomorphism of rings ![]() $GW(k) \cong {\mathbb {Z}} \times _{{\mathbb {Z}}/2} W(k)$. If
$GW(k) \cong {\mathbb {Z}} \times _{{\mathbb {Z}}/2} W(k)$. If ![]() $k$ is a field that is not formally real, then
$k$ is a field that is not formally real, then ![]() $W(k)$ is a
$W(k)$ is a ![]() $2$-primary torsion group [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 31.4(6)]. It follows that
$2$-primary torsion group [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 31.4(6)]. It follows that ![]() $GW(k) \otimes A \cong A$ as
$GW(k) \otimes A \cong A$ as ![]() $A$ is
$A$ is ![]() $2$-divisible.
$2$-divisible.
Remark 5.1.3 If ![]() $k$ is formally real the situation is rather different. For example, when
$k$ is formally real the situation is rather different. For example, when ![]() $k = {\mathbb {R}}$, then
$k = {\mathbb {R}}$, then ![]() $GW(k) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}$.
$GW(k) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}$.
Suslin matrices and motivic degree
Recall that there is a quotient morphism
where the latter is isomorphic to ![]() $Q_{2n-1}$ by the map sending a matrix to the first row times the first column of its inverse. This morphism factors the ‘first row’ morphism
$Q_{2n-1}$ by the map sending a matrix to the first row times the first column of its inverse. This morphism factors the ‘first row’ morphism ![]() $SL_n \to {\mathbb {A}}^n \,{\setminus}\, 0$, where the induced map
$SL_n \to {\mathbb {A}}^n \,{\setminus}\, 0$, where the induced map ![]() $SL_n/SL_{n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$ is Zariski locally trivial with affine space fibers and thus an
$SL_n/SL_{n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$ is Zariski locally trivial with affine space fibers and thus an ![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Let ![]() $R$ be any commutative ring, and let
$R$ be any commutative ring, and let ![]() $a = (a_1,\ldots,a_n)$ be a unimodular row in
$a = (a_1,\ldots,a_n)$ be a unimodular row in ![]() $R$. Such a row corresponds to a morphism of schemes
$R$. Such a row corresponds to a morphism of schemes ![]() $\operatorname {Spec} R \to {\mathbb {A}}^n \,{\setminus}\, 0$. In this case, we can always find
$\operatorname {Spec} R \to {\mathbb {A}}^n \,{\setminus}\, 0$. In this case, we can always find ![]() $b = (b_1,\ldots,b_n)$ such that
$b = (b_1,\ldots,b_n)$ such that ![]() $a b^t = 1$. Suslin showed [Reference SuslinSus77, Theorem 2] (see also [Reference SuslinSus77, p. 489, point (b)]), that there exists
$a b^t = 1$. Suslin showed [Reference SuslinSus77, Theorem 2] (see also [Reference SuslinSus77, p. 489, point (b)]), that there exists ![]() $S_n(a,b) \in SL_n(R)$ whose first row is equal to
$S_n(a,b) \in SL_n(R)$ whose first row is equal to ![]() $(a_1,a_2,a_3^2,\ldots,a_n^{n-1})$. The ‘universal’
$(a_1,a_2,a_3^2,\ldots,a_n^{n-1})$. The ‘universal’ ![]() $S_n$ corresponds to a morphism
$S_n$ corresponds to a morphism
we refer to such morphisms as Suslin matrices. The composite map
has a motivic Brouwer degree, which we now compute.
Lemma 5.1.4 Suppose ![]() $k$ is a field. For any integer
$k$ is a field. For any integer ![]() $n \geq 2$, the following formula holds in
$n \geq 2$, the following formula holds in ![]() $GW(k)$:
$GW(k)$:
 \[ \operatorname{deg}(\phi_n) = \begin{cases} \langle 1 \rangle & \text{ if } n = 2, \\ \dfrac{(n-1)!}{2}h & \text{ if } n > 2; \end{cases} \]
\[ \operatorname{deg}(\phi_n) = \begin{cases} \langle 1 \rangle & \text{ if } n = 2, \\ \dfrac{(n-1)!}{2}h & \text{ if } n > 2; \end{cases} \]
here ![]() $h$ is the class of the hyperbolic form.
$h$ is the class of the hyperbolic form.
Proof. The degree of the element in question coincides with the degree of the map ![]() ${\mathbb {A}}^n \,{\setminus}\, 0 \to {\mathbb {A}}^n \,{\setminus}\, 0$ given in coordinates by
${\mathbb {A}}^n \,{\setminus}\, 0 \to {\mathbb {A}}^n \,{\setminus}\, 0$ given in coordinates by ![]() $(a_1,\ldots,a_n) \to (a_1,a_2,a_3^2\ldots,a_n^{n-1})$. As explained in the proof of [Reference Asok and FaselAF14a, Theorem 4.10], the degree of this map can be computed as follows. By elementary manipulations, we can view the element
$(a_1,\ldots,a_n) \to (a_1,a_2,a_3^2\ldots,a_n^{n-1})$. As explained in the proof of [Reference Asok and FaselAF14a, Theorem 4.10], the degree of this map can be computed as follows. By elementary manipulations, we can view the element ![]() $[a_1,a_2,a_3^2\ldots,a_n^{n-1}]$ as a symbol in
$[a_1,a_2,a_3^2\ldots,a_n^{n-1}]$ as a symbol in ![]() ${{\mathbf {K}}}^{\rm MW}_n(k)$. If
${{\mathbf {K}}}^{\rm MW}_n(k)$. If ![]() $n = 2$, the map in question is the identity map.
$n = 2$, the map in question is the identity map.
If ![]() $n > 2$, then we proceed as follows. Following [Reference MorelMor12, p. 51], write
$n > 2$, then we proceed as follows. Following [Reference MorelMor12, p. 51], write ![]() $\epsilon = - \langle -1 \rangle$, then
$\epsilon = - \langle -1 \rangle$, then ![]() $h = 1 - \epsilon$. If
$h = 1 - \epsilon$. If ![]() $r$ is any positive integer, set
$r$ is any positive integer, set ![]() $r_{\epsilon } = \sum _{i=1}^r \langle (-1)^{i-1} \rangle$. A straightforward computation shows that
$r_{\epsilon } = \sum _{i=1}^r \langle (-1)^{i-1} \rangle$. A straightforward computation shows that ![]() $r_{\epsilon }s_{\epsilon } = (rs)_{\epsilon }$. Appealing to [Reference MorelMor12, Lemma 3.14], one knows that
$r_{\epsilon }s_{\epsilon } = (rs)_{\epsilon }$. Appealing to [Reference MorelMor12, Lemma 3.14], one knows that ![]() $[a^m]=m_\epsilon [a]$. Therefore, for any integer
$[a^m]=m_\epsilon [a]$. Therefore, for any integer ![]() $n \geq 3$.
$n \geq 3$.
Since ![]() $n \geq 3$,
$n \geq 3$, ![]() $(n-1)!$ is even, and we conclude that
$(n-1)!$ is even, and we conclude that ![]() $((n-1)!)_{\epsilon } = ({(n-1)!}/{2})h$ as asserted.
$((n-1)!)_{\epsilon } = ({(n-1)!}/{2})h$ as asserted.
Self equivalences of motivic spheres
Proposition 5.1.5 If ![]() $k$ is a field that is not formally real, then the map
$k$ is a field that is not formally real, then the map ![]() $\phi _n$ is an
$\phi _n$ is an ![]() ${\mathbb {A}}^1$-weak equivalence after inverting
${\mathbb {A}}^1$-weak equivalence after inverting ![]() $(n-1)!$.
$(n-1)!$.
Proof. The maps ![]() $\phi _n$ are all defined over
$\phi _n$ are all defined over ![]() $\operatorname {Spec} {\mathbb {Z}}$. By standard base-change results, it suffices to prove that
$\operatorname {Spec} {\mathbb {Z}}$. By standard base-change results, it suffices to prove that ![]() $\phi _n$ is an
$\phi _n$ is an ![]() ${\mathbb {A}}^1$-weak equivalence over a non-formally real perfect subfield (e.g. the prime field if
${\mathbb {A}}^1$-weak equivalence over a non-formally real perfect subfield (e.g. the prime field if ![]() $k$ has positive characteristic or
$k$ has positive characteristic or ![]() ${\mathbb {Q}}[i]$ if
${\mathbb {Q}}[i]$ if ![]() $k$ has characteristic
$k$ has characteristic ![]() $0$).
$0$).
Set ![]() $R = {\mathbb {Z}}[{1}/{(n-1)!}]$. By the equivalent characterizations of what it means for a map to be an
$R = {\mathbb {Z}}[{1}/{(n-1)!}]$. By the equivalent characterizations of what it means for a map to be an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-equivalence (see Definition 4.3.4 and apply the variant of Lemma 2.3.9 in that context), it suffices to show that if
${\mathbb {A}}^1$-equivalence (see Definition 4.3.4 and apply the variant of Lemma 2.3.9 in that context), it suffices to show that if ![]() $\mathscr {W}$ is an arbitrary
$\mathscr {W}$ is an arbitrary ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-local space, then the map induced by
${\mathbb {A}}^1$-local space, then the map induced by ![]() $\phi _n$
$\phi _n$
is a bijection. Because ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ is
${\mathbb {A}}^n \,{\setminus}\, 0$ is ![]() ${\mathbb {A}}^1$-connected, we can assume without loss of generality that
${\mathbb {A}}^1$-connected, we can assume without loss of generality that ![]() $\mathscr {W}$ is pointed and connected. In that case, the canonical map from pointed to free homotopy classes of maps is a surjection. Thus, it suffices to prove that the map of pointed sets is a bijection.
$\mathscr {W}$ is pointed and connected. In that case, the canonical map from pointed to free homotopy classes of maps is a surjection. Thus, it suffices to prove that the map of pointed sets is a bijection.
However, the sets in question are, by definition, ![]() $\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$. For any integer
$\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$. For any integer ![]() $n \geq 2$, the group
$n \geq 2$, the group ![]() $\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$ is a
$\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$ is a ![]() $GW(k)$-module with module structure induced by precomposition. However, we know that
$GW(k)$-module with module structure induced by precomposition. However, we know that ![]() $\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$ is an
$\boldsymbol {\pi }_{n-1,n}^{{\mathbb {A}}^1}(\mathscr {W})(k)$ is an ![]() $R$-module, which means that the
$R$-module, which means that the ![]() $GW(k)$-module structure factors through an action of
$GW(k)$-module structure factors through an action of ![]() $GW(k) \otimes R$. Using Lemma 5.1.2, we conclude that
$GW(k) \otimes R$. Using Lemma 5.1.2, we conclude that ![]() $GW(k) \otimes R \cong R$.
$GW(k) \otimes R \cong R$.
By appeal to Lemma 5.1.4 the self-map ![]() $\phi _n$ has motivic degree
$\phi _n$ has motivic degree ![]() $(n-1)!$ in
$(n-1)!$ in ![]() $GW(k) \otimes R \cong R$. Since
$GW(k) \otimes R \cong R$. Since ![]() $(n-1)!$ is invertible in
$(n-1)!$ is invertible in ![]() $R$ by assumption, the result follows.
$R$ by assumption, the result follows.
5.2 Unstable splittings of special groups and associated homogeneous spaces
We now analyze splittings of classical split reductive groups using the results of the preceding subsection. In particular, we construct unstable splittings of ![]() $SL_n$ and
$SL_n$ and ![]() $Sp_n$ (Theorem 5.2.1 and Corollary 5.2.4) as well as splittings of associated symmetric spaces (see Corollary 5.2.5). We then use these results to deduce splittings for all the stable classical groups (see Proposition 5.2.8 and Corollary 5.2.14).
$Sp_n$ (Theorem 5.2.1 and Corollary 5.2.4) as well as splittings of associated symmetric spaces (see Corollary 5.2.5). We then use these results to deduce splittings for all the stable classical groups (see Proposition 5.2.8 and Corollary 5.2.14).
Splittings for the special linear group
If ![]() $m < n$, then we may consider the composite morphism
$m < n$, then we may consider the composite morphism
where the second morphism is given as the inclusion ![]() $X \mapsto {\rm diag}(X,Id_{n-m})$. Then we obtain a morphism
$X \mapsto {\rm diag}(X,Id_{n-m})$. Then we obtain a morphism
by taking the composite of ![]() $\prod _{m \leq n} \Phi _m$ and the product map
$\prod _{m \leq n} \Phi _m$ and the product map ![]() $SL_n^{\times n-1} \longrightarrow SL_n$. The following result about the morphism
$SL_n^{\times n-1} \longrightarrow SL_n$. The following result about the morphism ![]() $\Phi$ corresponds to Theorem 3 in the introduction.
$\Phi$ corresponds to Theorem 3 in the introduction.
Theorem 5.2.1 Assume ![]() $k$ is a field that is not formally real. The morphism
$k$ is a field that is not formally real. The morphism
becomes an ![]() ${\mathbb {A}}^1$-weak equivalence after inverting
${\mathbb {A}}^1$-weak equivalence after inverting ![]() $(n-1)!$.
$(n-1)!$.
Proof. The map sending ![]() $X \in SL_n$ to its first row and the first column of its inverse defines a morphism
$X \in SL_n$ to its first row and the first column of its inverse defines a morphism ![]() $SL_n \to Q_{2n-1}$. The quotient
$SL_n \to Q_{2n-1}$. The quotient ![]() $SL_n/SL_{n-1}$ exists as a smooth scheme, and the morphism just described defines an isomorphism
$SL_n/SL_{n-1}$ exists as a smooth scheme, and the morphism just described defines an isomorphism ![]() $SL_n/SL_{n-1} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} Q_{2n-1}$. By Theorem 3.4.3, there is an
$SL_n/SL_{n-1} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} Q_{2n-1}$. By Theorem 3.4.3, there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form ![]() $Q_{2n-1} \to BSL_{n-1} \to BSL_{n-1}$, which yields an
$Q_{2n-1} \to BSL_{n-1} \to BSL_{n-1}$, which yields an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
by simplicially looping. By appeal to Theorem 4.3.11, this fiber sequence remains a fiber sequence after ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization for any
${\mathbb {A}}^1$-localization for any ![]() $R \subset {\mathbb {Q}}$.
$R \subset {\mathbb {Q}}$.
Under the hypothesis on ![]() $k$, the composite map
$k$, the composite map ![]() $S_n: Q_{2n-1} \to SL_n \to Q_{2n-1}$ becomes an
$S_n: Q_{2n-1} \to SL_n \to Q_{2n-1}$ becomes an ![]() ${\mathbb {A}}^1$-weak equivalence after inverting
${\mathbb {A}}^1$-weak equivalence after inverting ![]() $(n-1)!$ by appeal to Proposition 5.1.5. Therefore, taking
$(n-1)!$ by appeal to Proposition 5.1.5. Therefore, taking ![]() $R = {\mathbb {Z}}[{1}/{(n-1)!}]$, the fiber sequence is split after
$R = {\mathbb {Z}}[{1}/{(n-1)!}]$, the fiber sequence is split after ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-localization, and the product map
${\mathbb {A}}^1$-localization, and the product map ![]() $Q_{2n-1} \times SL_{n-1} \to SL_n$ is an
$Q_{2n-1} \times SL_{n-1} \to SL_n$ is an ![]() ${\mathbb {A}}^1$-weak equivalence after inverting
${\mathbb {A}}^1$-weak equivalence after inverting ![]() $(n-1)!$. The result then follows by a straightforward induction.
$(n-1)!$. The result then follows by a straightforward induction.
Remark 5.2.2 Since ![]() $R$-localization commutes with the formation of finite products, and since
$R$-localization commutes with the formation of finite products, and since ![]() $Q_{2n-1}$ is a retract of
$Q_{2n-1}$ is a retract of ![]() $SL_n$ after inverting
$SL_n$ after inverting ![]() $(n-1)!$, we conclude that
$(n-1)!$, we conclude that ![]() $Q_{2n-1}$ is an
$Q_{2n-1}$ is an ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-space after inverting
$h$-space after inverting ![]() $(n-1)!$.
$(n-1)!$.
Splittings for the symplectic group
In [Reference Asok and FaselAF17, Proposition 3.3.3], we observed that a slight modification of the Suslin matrix can be viewed as a morphism ![]() $P_n: Q_{4n-1} \to Sp_{2^{n-1}}$.
$P_n: Q_{4n-1} \to Sp_{2^{n-1}}$.
Lemma 5.2.3 The morphism ![]() $P_n: Q_{4n-1} \to Sp_{2^{n-1}}$ lifts uniquely up to
$P_n: Q_{4n-1} \to Sp_{2^{n-1}}$ lifts uniquely up to ![]() ${\mathbb {A}}^1$-homotopy to a morphism
${\mathbb {A}}^1$-homotopy to a morphism ![]() $Q_{4n-1} \to Sp_{2n}$ in such a way that the composite map
$Q_{4n-1} \to Sp_{2n}$ in such a way that the composite map ![]() $Q_{4n-1} \to Sp_{2n} \hookrightarrow SL_{2n}$ is
$Q_{4n-1} \to Sp_{2n} \hookrightarrow SL_{2n}$ is ![]() ${\mathbb {A}}^1$-homotopic to the morphism
${\mathbb {A}}^1$-homotopic to the morphism ![]() $S_{2n}$ considered above.
$S_{2n}$ considered above.
Proof. The modified Suslin matrices are obtained from usual Suslin matrices by left and right multiplying by matrices that are elementary and thus naively ![]() ${\mathbb {A}}^1$-homotopic to the identity. It follows from this observation that the morphism
${\mathbb {A}}^1$-homotopic to the identity. It follows from this observation that the morphism ![]() $P_n$ is
$P_n$ is ![]() ${\mathbb {A}}^1$-homotopic to a morphism
${\mathbb {A}}^1$-homotopic to a morphism ![]() $Q_{4n-1} \to SL_{2^{n-1}}$ defined by the appropriate Suslin matrix. Therefore, if we can lift
$Q_{4n-1} \to SL_{2^{n-1}}$ defined by the appropriate Suslin matrix. Therefore, if we can lift ![]() $P_n$ through
$P_n$ through ![]() $Sp_{2n}$, it follows immediately that the composite with the inclusion
$Sp_{2n}$, it follows immediately that the composite with the inclusion ![]() $Sp_{2n} \to SL_{2n}$ is
$Sp_{2n} \to SL_{2n}$ is ![]() ${\mathbb {A}}^1$-homotopic to
${\mathbb {A}}^1$-homotopic to ![]() $S_{2n}$.
$S_{2n}$.
To that end, recall that there is a Cartesian square of closed-immersion group homomorphisms of the following form.

Here the vertical maps are the usual stabilization maps for symplectic and special linear groups, respectively. This Cartesian square defines an isomorphism of quotients ![]() $Sp_{2n}/Sp_{2n-2} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} SL_{2n}/SL_{2n-1}$ and thus an isomorphism
$Sp_{2n}/Sp_{2n-2} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} SL_{2n}/SL_{2n-1}$ and thus an isomorphism ![]() $Sp_{2n}/Sp_{2n-2} \cong Q_{4n-1}$.
$Sp_{2n}/Sp_{2n-2} \cong Q_{4n-1}$.
Now, there is an ![]() ${\mathbb {A}}^1$-weak equivalence
${\mathbb {A}}^1$-weak equivalence ![]() $Q_{4n-1} \to {\mathbb {A}}^{2n} \,{\setminus}\, 0$, and we know that
$Q_{4n-1} \to {\mathbb {A}}^{2n} \,{\setminus}\, 0$, and we know that ![]() ${\mathbb {A}}^{2n} \,{\setminus}\, 0$ is at least
${\mathbb {A}}^{2n} \,{\setminus}\, 0$ is at least ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $(2n-2)$-connected. Appealing to Theorem 3.4.3 and looping, we deduce that there is an
$(2n-2)$-connected. Appealing to Theorem 3.4.3 and looping, we deduce that there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
that is, the ![]() ${\mathbb {A}}^1$-homotopy fiber of
${\mathbb {A}}^1$-homotopy fiber of ![]() $Sp_{2n-2} \to Sp_{2n}$ is
$Sp_{2n-2} \to Sp_{2n}$ is ![]() $\Omega Q_{4n-1}$, which is at least
$\Omega Q_{4n-1}$, which is at least ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $(2n-3)$-connected.
$(2n-3)$-connected.
We now proceed by induction. Given a morphism ![]() $Q_{4n-1} \to Sp_{2N}$, we can analyze inductively the obstructions to lifting along the inclusion
$Q_{4n-1} \to Sp_{2N}$, we can analyze inductively the obstructions to lifting along the inclusion ![]() $Sp_{2N-2}$. These obstructions live in
$Sp_{2N-2}$. These obstructions live in ![]() $H^i(Q_{4n-1},\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$. The group
$H^i(Q_{4n-1},\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$. The group ![]() $H^i(Q_{4n-1},\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$ vanishes unless
$H^i(Q_{4n-1},\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$ vanishes unless ![]() $i = 0$ or
$i = 0$ or ![]() $2n-1$ [Reference Asok and FaselAF14a, Lemma 4.5], and the sheaf
$2n-1$ [Reference Asok and FaselAF14a, Lemma 4.5], and the sheaf ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$ is trivial if
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^{2N} \,{\setminus}\, 0))$ is trivial if ![]() $i \leq 2N-2$ by the connectivity observation of the previous paragraph. If all of these obstructions vanish, then a lift necessarily exists. The result then follows by a straightforward induction.
$i \leq 2N-2$ by the connectivity observation of the previous paragraph. If all of these obstructions vanish, then a lift necessarily exists. The result then follows by a straightforward induction.
As was the case with the special linear group, these modified Suslin matrices yield a morphism
We then obtain a splitting analogous to that of Theorem 5.2.1.
Corollary 5.2.4 Assume ![]() $k$ is a field that is not formally real. The morphism
$k$ is a field that is not formally real. The morphism
becomes an isomorphism in ![]() $\mathrm {Ho}_{k}$ after inverting
$\mathrm {Ho}_{k}$ after inverting ![]() $(2n-1)!$.
$(2n-1)!$.
Proof. We repeat the proof of Theorem 5.2.1 appealing to the ![]() ${\mathbb {A}}^1$-fiber sequence
${\mathbb {A}}^1$-fiber sequence
Then we simply observe that the morphism ![]() $Q_{4n-1} \to Sp_{2n}$ uniquely lifting
$Q_{4n-1} \to Sp_{2n}$ uniquely lifting ![]() $P_n$ when composed with the map
$P_n$ when composed with the map ![]() $Sp_{2n} \to Q_{4n-1}$ gives an
$Sp_{2n} \to Q_{4n-1}$ gives an ![]() ${\mathbb {A}}^1$-homotopy endomorphism of
${\mathbb {A}}^1$-homotopy endomorphism of ![]() ${\mathbb {A}}^{2n} \,{\setminus}\, 0$ with degree
${\mathbb {A}}^{2n} \,{\setminus}\, 0$ with degree ![]() $(n-1)!$ after Lemma 5.2.3.
$(n-1)!$ after Lemma 5.2.3.
Splittings for some homogeneous spaces
Harris generalized some of Serre's splittings for compact Lie groups to some classes of homogeneous spaces [Reference HarrisHar61]. We now establish some analogs of the splitting results he established. Let ![]() $X_n = SL_{2n}/Sp_{2n}$. Using the isomorphism
$X_n = SL_{2n}/Sp_{2n}$. Using the isomorphism ![]() $X_{n+1} \cong SL_{2n+1}/Sp_{2n}$ obtained from diagram (5.1), one sees that there is an
$X_{n+1} \cong SL_{2n+1}/Sp_{2n}$ obtained from diagram (5.1), one sees that there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
The Suslin morphism ![]() $S_{2n+1}: Q_{4n+1} \to SL_{2n+1}$ thus yields a morphism
$S_{2n+1}: Q_{4n+1} \to SL_{2n+1}$ thus yields a morphism ![]() $Q_{2n+1} \to X_{n+1}$.
$Q_{2n+1} \to X_{n+1}$.
Corollary 5.2.5 Assume ![]() $k$ is a field that is not formally real. There is an
$k$ is a field that is not formally real. There is an ![]() ${\mathbb {A}}^1$-weak equivalence
${\mathbb {A}}^1$-weak equivalence
after inverting ![]() $(2n-1)!$.
$(2n-1)!$.
Proof. There is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
Appealing to the proofs of Theorem 5.2.1 and Corollary 5.2.4 and recalling Lemma 5.2.3, we conclude that after inverting ![]() $(2n-1)!$ the left-hand morphism is split and corresponds to the inclusion
$(2n-1)!$ the left-hand morphism is split and corresponds to the inclusion ![]() $Q_3 \times Q_7 \times \cdots \times Q_{4n-1} \to \prod _{2 \leq m \leq n} Q_{2m-1}$.
$Q_3 \times Q_7 \times \cdots \times Q_{4n-1} \to \prod _{2 \leq m \leq n} Q_{2m-1}$.
Infinite products
We need to make some comments about infinite products of spaces.
Lemma 5.2.6 Suppose ![]() $\mathscr {X}_n \in \mathrm {Spc}_k$,
$\mathscr {X}_n \in \mathrm {Spc}_k$, ![]() $n \in {\mathbb {N}}$, is a sequence of pointed fibrant, simplicially connected and
$n \in {\mathbb {N}}$, is a sequence of pointed fibrant, simplicially connected and ![]() ${\mathbb {A}}^1$-local spaces. Suppose for each positive integer
${\mathbb {A}}^1$-local spaces. Suppose for each positive integer ![]() $m$ there exists an integer
$m$ there exists an integer ![]() $c(m)$ such that
$c(m)$ such that ![]() $\mathscr {X}_N$ is at least
$\mathscr {X}_N$ is at least ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $m$-connected for every
$m$-connected for every ![]() $N > c(m)$. If we consider the system of finite products
$N > c(m)$. If we consider the system of finite products ![]() $\prod _{i=0}^n \mathscr {X}_n$ as a directed system with respect to the evident inclusion maps arising from the base point, then the induced map
$\prod _{i=0}^n \mathscr {X}_n$ as a directed system with respect to the evident inclusion maps arising from the base point, then the induced map
 \[ \operatorname{colim}_n \prod_{i=0}^n \mathscr{X}_i \longrightarrow \prod_{i \in {\mathbb{N}}} \mathscr{X}_i \]
\[ \operatorname{colim}_n \prod_{i=0}^n \mathscr{X}_i \longrightarrow \prod_{i \in {\mathbb{N}}} \mathscr{X}_i \]
is an isomorphism on ![]() ${\mathbb {A}}^1$-homotopy sheaves and thus is an
${\mathbb {A}}^1$-homotopy sheaves and thus is an ![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Proof. Under the stated connectivity hypotheses, for any given integer ![]() $j$, the
$j$, the ![]() $j$th
$j$th ![]() ${\mathbb {A}}^1$-homotopy sheaf of the left-hand side stabilizes at a finite stage; more precisely, the map
${\mathbb {A}}^1$-homotopy sheaf of the left-hand side stabilizes at a finite stage; more precisely, the map ![]() $\boldsymbol {\pi }_j\bigl (\prod _{i=1}^N \mathscr {X_i}\bigr ) \to \boldsymbol {\pi }_j\bigl (\prod _{i=1}^{c(j)} \mathscr {X}_i\bigr )$ induced by the projection is an isomorphism for all
$\boldsymbol {\pi }_j\bigl (\prod _{i=1}^N \mathscr {X_i}\bigr ) \to \boldsymbol {\pi }_j\bigl (\prod _{i=1}^{c(j)} \mathscr {X}_i\bigr )$ induced by the projection is an isomorphism for all ![]() $N > c(j)$. It follows from [Reference Bousfield and KanBK72, Theorem IX.3.1] that the map in the statement induces an isomorphism on homotopy sheaves and is thus an
$N > c(j)$. It follows from [Reference Bousfield and KanBK72, Theorem IX.3.1] that the map in the statement induces an isomorphism on homotopy sheaves and is thus an ![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Example 5.2.7 If ![]() $i < n$, then the spaces
$i < n$, then the spaces ![]() $K({\mathbb {Z}}(n),2n-i)$ are at least
$K({\mathbb {Z}}(n),2n-i)$ are at least ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $(n-i)$-connected. Likewise, the spaces
$(n-i)$-connected. Likewise, the spaces ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ are at least
${\mathbb {A}}^n \,{\setminus}\, 0$ are at least ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $(n-2)$-connected. In the sequel, we will use Lemma 5.2.6 with these sequences of spaces.
$(n-2)$-connected. In the sequel, we will use Lemma 5.2.6 with these sequences of spaces.
Rational splittings of the stable linear and symplectic groups
Using the facts about infinite products discussed above, we now establish splitting results for stable linear and symplectic groups. Before Theorem 5.2.1, we constructed morphisms
 \[ \prod_{i=2}^n Q_{2i-1} \longrightarrow SL_n \]
\[ \prod_{i=2}^n Q_{2i-1} \longrightarrow SL_n \]
for each integer ![]() $n$. If we take the colimit of the maps on the left-hand side with respect to inclusions of base points, and the maps on the right-hand side with respect to the inclusions
$n$. If we take the colimit of the maps on the left-hand side with respect to inclusions of base points, and the maps on the right-hand side with respect to the inclusions ![]() $SL_n \hookrightarrow SL_{n+1}$ described before Theorem 5.2.1, we obtain a morphism
$SL_n \hookrightarrow SL_{n+1}$ described before Theorem 5.2.1, we obtain a morphism
 \[ \operatorname{colim}_n \prod_{i=2}^n Q_{2i-1} \longrightarrow SL. \]
\[ \operatorname{colim}_n \prod_{i=2}^n Q_{2i-1} \longrightarrow SL. \]The same construction can be performed for the symplectic groups (see the discussion preceding Corollary 5.2.4) to obtain a morphism
 \[ \operatorname{colim}_n \prod_{i=2}^n Q_{4i-1} \longrightarrow Sp. \]
\[ \operatorname{colim}_n \prod_{i=2}^n Q_{4i-1} \longrightarrow Sp. \]We use these morphisms in the next statement.
Proposition 5.2.8 There are diagrams of the form
 \begin{align*} \prod_{i\geq 2} Q_{2i-1} \longleftarrow &\operatorname{colim}_n \prod_{2 \leq i \leq n} Q_{2i-1} \longrightarrow SL, \\ \prod_{i\geq 2} Q_{4i-1} \longleftarrow &\operatorname{colim}_n \prod_{2 \leq i \leq n} Q_{4i-1} \longrightarrow Sp, \end{align*}
\begin{align*} \prod_{i\geq 2} Q_{2i-1} \longleftarrow &\operatorname{colim}_n \prod_{2 \leq i \leq n} Q_{2i-1} \longrightarrow SL, \\ \prod_{i\geq 2} Q_{4i-1} \longleftarrow &\operatorname{colim}_n \prod_{2 \leq i \leq n} Q_{4i-1} \longrightarrow Sp, \end{align*}
where all morphisms are ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalences.
${\mathbb {A}}^1$-weak equivalences.
Proof. Theorem 5.2.1 implies that the maps ![]() $\prod _{2 \leq i \leq n} Q_{2i-1} \longrightarrow SL_n$ become
$\prod _{2 \leq i \leq n} Q_{2i-1} \longrightarrow SL_n$ become ![]() ${\mathbb {A}}^1$-weak equivalences after inverting
${\mathbb {A}}^1$-weak equivalences after inverting ![]() $(n-1)!$ and thus are all
$(n-1)!$ and thus are all ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalences. By definition,
${\mathbb {A}}^1$-weak equivalences. By definition, ![]() $SL = \operatorname {colim}_n SL_n$ where the colimit is taken with respect to the standard inclusions as block diagonal matrices. Since filtered colimits of
$SL = \operatorname {colim}_n SL_n$ where the colimit is taken with respect to the standard inclusions as block diagonal matrices. Since filtered colimits of ![]() ${\mathbb {A}}^1$-weak equivalences are
${\mathbb {A}}^1$-weak equivalences are ![]() ${\mathbb {A}}^1$-weak equivalences [Reference Morel and VoevodskyMV99, §Lemma 2.2.12], it follows that the induced morphism
${\mathbb {A}}^1$-weak equivalences [Reference Morel and VoevodskyMV99, §Lemma 2.2.12], it follows that the induced morphism
is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence as well. That the map
${\mathbb {A}}^1$-weak equivalence as well. That the map
is an ![]() ${\mathbb {A}}^1$-weak equivalence is an immediate consequence of Lemma 5.2.6. The argument for
${\mathbb {A}}^1$-weak equivalence is an immediate consequence of Lemma 5.2.6. The argument for ![]() $Sp$ is formally identical to that for
$Sp$ is formally identical to that for ![]() $SL$: one makes appeal to Corollary 5.2.4 instead of Theorem 5.2.1.
$SL$: one makes appeal to Corollary 5.2.4 instead of Theorem 5.2.1.
Rational splittings of the stable orthogonal group
Assume through the remainder of this subsection that one works over a base field ![]() $k$ having characteristic not equal to
$k$ having characteristic not equal to ![]() $2$ (this assumption will be made explicit in theorem statements below, and it simplifies the discussion). We may use the above results to give a corresponding decomposition for the stable orthogonal group as well. Let
$2$ (this assumption will be made explicit in theorem statements below, and it simplifies the discussion). We may use the above results to give a corresponding decomposition for the stable orthogonal group as well. Let ![]() $O_n$ (respectively,
$O_n$ (respectively, ![]() $SO_n$) be the usual split (special) orthogonal group, that is, the (special) orthogonal group of the split quadratic form in
$SO_n$) be the usual split (special) orthogonal group, that is, the (special) orthogonal group of the split quadratic form in ![]() $n$ variables.
$n$ variables.
There are closed immersion group homomorphisms ![]() $O_n \to GL_n$ and
$O_n \to GL_n$ and ![]() $H_n': GL_n \to O_{2n}$ (mapping a matrix
$H_n': GL_n \to O_{2n}$ (mapping a matrix ![]() $M$ to the block-diagonal matrix
$M$ to the block-diagonal matrix ![]() $\mathrm {diag}(M,(M^{-1})^t)$); we will also use the hyperbolic morphism
$\mathrm {diag}(M,(M^{-1})^t)$); we will also use the hyperbolic morphism ![]() $H_n: GL_n \to Sp_{2n}$ defined in an analogous way. Explicitly, if
$H_n: GL_n \to Sp_{2n}$ defined in an analogous way. Explicitly, if ![]() $X$ is a smooth affine scheme, then the composite
$X$ is a smooth affine scheme, then the composite ![]() $X \to BGL_n \to B_{et}O_{2n}$ sends a vector bundle
$X \to BGL_n \to B_{et}O_{2n}$ sends a vector bundle ![]() $\mathscr {V}$ on
$\mathscr {V}$ on ![]() $X$ to the bundle
$X$ to the bundle ![]() $\mathscr {V} \oplus \mathscr {V}^{\vee }$ equipped with its canonical symmetry automorphism: if
$\mathscr {V} \oplus \mathscr {V}^{\vee }$ equipped with its canonical symmetry automorphism: if ![]() $c: \mathscr {V} \to \mathscr {V}^{\vee \vee }$ is the canonical isomorphism, then the symmetric space structure is given by the matrix
$c: \mathscr {V} \to \mathscr {V}^{\vee \vee }$ is the canonical isomorphism, then the symmetric space structure is given by the matrix ![]() $\big (\begin {smallmatrix} 0 & 1 \\ c & 0 \end {smallmatrix}\big )$. Likewise, the composite
$\big (\begin {smallmatrix} 0 & 1 \\ c & 0 \end {smallmatrix}\big )$. Likewise, the composite ![]() $X \to BGL_n \to BSp_{2n}$ sends a vector bundle
$X \to BGL_n \to BSp_{2n}$ sends a vector bundle ![]() $\mathscr {V}$ on
$\mathscr {V}$ on ![]() $X$ to
$X$ to ![]() $\mathscr {V} \oplus \mathscr {V}^{\vee }$ equipped with its canonical antisymmetry automorphism.
$\mathscr {V} \oplus \mathscr {V}^{\vee }$ equipped with its canonical antisymmetry automorphism.
There are stabilization homomorphisms ![]() $O_n \to O_{n+1}$ for every integer
$O_n \to O_{n+1}$ for every integer ![]() $n \geq 2$. The composite homomorphisms
$n \geq 2$. The composite homomorphisms
are compatible with the aforementioned stabilization maps in the sense that the diagrams

are ![]() ${\mathbb {A}}^1$-homotopy commutative. One therefore obtains stable homomorphisms
${\mathbb {A}}^1$-homotopy commutative. One therefore obtains stable homomorphisms
that are well defined in the ![]() ${\mathbb {A}}^1$-homotopy category. We would like to show that these homomorphisms are
${\mathbb {A}}^1$-homotopy category. We would like to show that these homomorphisms are ![]() ${\mathbb {A}}^1$-weak equivalences after inverting suitable primes, but our statements are slightly complicated because of connectivity issues: the stable symplectic group
${\mathbb {A}}^1$-weak equivalences after inverting suitable primes, but our statements are slightly complicated because of connectivity issues: the stable symplectic group ![]() $Sp$ is
$Sp$ is ![]() ${\mathbb {A}}^1$-connected, but as the next remark explains, the stable orthogonal group is not.
${\mathbb {A}}^1$-connected, but as the next remark explains, the stable orthogonal group is not.
Remark 5.2.9 Since ![]() $2$ is invertible in the base field, the stable orthogonal group
$2$ is invertible in the base field, the stable orthogonal group ![]() $O$ has two connected components corresponding to elements of determinant
$O$ has two connected components corresponding to elements of determinant ![]() $\pm 1$. As a consequence we do not know that
$\pm 1$. As a consequence we do not know that ![]() $O$ has a ‘well-behaved’
$O$ has a ‘well-behaved’ ![]() ${\mathbb {A}}^1$-localization because Theorem 4.3.9 does not necessarily apply. In the analogous situation in topology, this problem can be rectified by passing to the special orthogonal group, which is connected as a topological space. However, in the algebro-geometric setting, while the special orthogonal group
${\mathbb {A}}^1$-localization because Theorem 4.3.9 does not necessarily apply. In the analogous situation in topology, this problem can be rectified by passing to the special orthogonal group, which is connected as a topological space. However, in the algebro-geometric setting, while the special orthogonal group ![]() $SO$ is the component of
$SO$ is the component of ![]() $O$ corresponding to elements of determinant
$O$ corresponding to elements of determinant ![]() $1$, it is not
$1$, it is not ![]() ${\mathbb {A}}^1$-connected. Indeed, there is an
${\mathbb {A}}^1$-connected. Indeed, there is an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
classifying the spin double cover. As a consequence of Lemma 5.2.10, it follows that there is an injective morphism ![]() $\boldsymbol {\pi }_0^{{\mathbb {A}}^1}(SO) \to \boldsymbol {\pi }_0^{{\mathbb {A}}^1}(B_{\unicode{x00E9}{\text {t}}}\mu _2)$. The composite morphism
$\boldsymbol {\pi }_0^{{\mathbb {A}}^1}(SO) \to \boldsymbol {\pi }_0^{{\mathbb {A}}^1}(B_{\unicode{x00E9}{\text {t}}}\mu _2)$. The composite morphism ![]() $SO \to \boldsymbol {\pi }_0^{{\mathbb {A}}^1}(B_{\unicode{x00E9}{\text {t}}}\mu _2)$ is a sheafification of the spinor norm homomorphism (see, for example, [Reference BassBas74]; it coincides with this homomorphism on sections over essentially smooth local rings), which is non-trivial in general.
$SO \to \boldsymbol {\pi }_0^{{\mathbb {A}}^1}(B_{\unicode{x00E9}{\text {t}}}\mu _2)$ is a sheafification of the spinor norm homomorphism (see, for example, [Reference BassBas74]; it coincides with this homomorphism on sections over essentially smooth local rings), which is non-trivial in general.
Lemma 5.2.10 Assume ![]() $k$ is a field. The stable group
$k$ is a field. The stable group ![]() $Spin$ is
$Spin$ is ![]() ${\mathbb {A}}^1$-connected and
${\mathbb {A}}^1$-connected and ![]() ${\mathbb {A}}^1$-simple. Moreover, the map
${\mathbb {A}}^1$-simple. Moreover, the map ![]() $Spin \to SO \to O$ induces an isomorphism on
$Spin \to SO \to O$ induces an isomorphism on ![]() ${\mathbb {A}}^1$-homotopy sheaves in degrees
${\mathbb {A}}^1$-homotopy sheaves in degrees ![]() $\geq 1$ (pointed by the identity element).
$\geq 1$ (pointed by the identity element).
Proof. Granted ![]() ${\mathbb {A}}^1$-connectedness,
${\mathbb {A}}^1$-connectedness, ![]() ${\mathbb {A}}^1$-simplicity is immediate since all spaces in question are
${\mathbb {A}}^1$-simplicity is immediate since all spaces in question are ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-groups. To see that
$h$-groups. To see that ![]() $Spin$ is
$Spin$ is ![]() ${\mathbb {A}}^1$-connected, we proceed as follows. To check that a space
${\mathbb {A}}^1$-connected, we proceed as follows. To check that a space ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() ${\mathbb {A}}^1$-connected, it suffices by [Reference MorelMor05, Lemma 6.1.3] to check that
${\mathbb {A}}^1$-connected, it suffices by [Reference MorelMor05, Lemma 6.1.3] to check that ![]() $\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! \mathscr {X}(L))$ consists of a single element for every finitely generated separable extension field
$\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! \mathscr {X}(L))$ consists of a single element for every finitely generated separable extension field ![]() $L/k$. Since
$L/k$. Since ![]() $Spin$ is, by construction, a filtered colimit, every element of
$Spin$ is, by construction, a filtered colimit, every element of ![]() $\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin(L)$ lies in
$\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin(L)$ lies in ![]() $\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n(L)$ for some integer
$\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n(L)$ for some integer ![]() $n$. Thus, it suffices to show that
$n$. Thus, it suffices to show that ![]() $\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n (L))$ is trivial for
$\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n (L))$ is trivial for ![]() $n$ sufficiently large. To to check the latter statement, it suffices to know that every element of
$n$ sufficiently large. To to check the latter statement, it suffices to know that every element of ![]() $Spin_n(L)$ is
$Spin_n(L)$ is ![]() ${\mathbb {A}}^1$-homotopic to the base point. Recall from that if
${\mathbb {A}}^1$-homotopic to the base point. Recall from that if ![]() $G$ is a split, reductive
$G$ is a split, reductive ![]() $k$-group scheme, and
$k$-group scheme, and ![]() $R$ is a
$R$ is a ![]() $k$-algebra, then the elementary subgroup
$k$-algebra, then the elementary subgroup ![]() $E(R)$ is the subgroup of
$E(R)$ is the subgroup of ![]() $G(R)$ generated by root subgroups (see [Reference AbeAbe69, Definition 1.5] for a more precise definition). Any element of the elementary subgroup is
$G(R)$ generated by root subgroups (see [Reference AbeAbe69, Definition 1.5] for a more precise definition). Any element of the elementary subgroup is ![]() ${\mathbb {A}}^1$-homotopic to the identity. It follows from [Reference MatsumotoMat66, Corollary 2], that
${\mathbb {A}}^1$-homotopic to the identity. It follows from [Reference MatsumotoMat66, Corollary 2], that ![]() $Spin_n(L)$ coincides with its elementary subgroup if
$Spin_n(L)$ coincides with its elementary subgroup if ![]() $n \geq 5$ (which guarantees it has rank
$n \geq 5$ (which guarantees it has rank ![]() $\geq 2$) and we conclude that
$\geq 2$) and we conclude that ![]() $\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n(L)) = \ast$ in that range as well.
$\pi _0(\operatorname {Sing}^{{\mathbb {A}}^1}\!\! Spin_n(L)) = \ast$ in that range as well.
Remark 5.2.11 While the blanket assumption that ![]() $k$ has characteristic not equal to
$k$ has characteristic not equal to ![]() $2$ is in place in the preceding statement, the assertion that
$2$ is in place in the preceding statement, the assertion that ![]() $Spin_n$ is
$Spin_n$ is ![]() ${\mathbb {A}}^1$-connected for any
${\mathbb {A}}^1$-connected for any ![]() $n \geq 5$ holds even without that assumption. Thus, the assertion that the stable group
$n \geq 5$ holds even without that assumption. Thus, the assertion that the stable group ![]() $Spin$ is
$Spin$ is ![]() ${\mathbb {A}}^1$-connected also holds without that assumption; for this reason, we have not included any hypothesis on the field explicitly in the statement.
${\mathbb {A}}^1$-connected also holds without that assumption; for this reason, we have not included any hypothesis on the field explicitly in the statement.
We consider the composite map ![]() $Spin \to SO \to Sp$. The homomorphism
$Spin \to SO \to Sp$. The homomorphism ![]() $Sp_{2n} \to O_{4n}$ discussed above lifts uniquely through a morphism
$Sp_{2n} \to O_{4n}$ discussed above lifts uniquely through a morphism ![]() $Sp_{2n} \to Spin_{4n}$ (use [Reference ConradCon14, Exercise 6.5.2(iii)]) and these lifts are compatible with stabilization maps. Therefore, we obtain a morphism
$Sp_{2n} \to Spin_{4n}$ (use [Reference ConradCon14, Exercise 6.5.2(iii)]) and these lifts are compatible with stabilization maps. Therefore, we obtain a morphism ![]() $Sp \to Spin$ factoring the map
$Sp \to Spin$ factoring the map ![]() $Sp \to O$ described above.
$Sp \to O$ described above.
Theorem 5.2.12 Suppose ![]() $k$ is a field that is not formally real and has characteristic not equal to
$k$ is a field that is not formally real and has characteristic not equal to ![]() $2$, and
$2$, and ![]() $R \subset {\mathbb {Q}}$ is a subring in which
$R \subset {\mathbb {Q}}$ is a subring in which ![]() $2$ is invertible. The morphisms
$2$ is invertible. The morphisms ![]() $Spin \to Sp$ and
$Spin \to Sp$ and ![]() $Sp \to Spin$ just defined are mutually inverse
$Sp \to Spin$ just defined are mutually inverse ![]() ${\mathbb {A}}^1$-weak equivalences after inverting
${\mathbb {A}}^1$-weak equivalences after inverting ![]() $2$.
$2$.
Proof. The composite ![]() $O_n \to O_{4n}$ induces a morphism
$O_n \to O_{4n}$ induces a morphism ![]() $B_{\unicode{x00E9}{\text {t}}}O_n \to B_{et}O_{4n}$ that stabilizes to a morphism
$B_{\unicode{x00E9}{\text {t}}}O_n \to B_{et}O_{4n}$ that stabilizes to a morphism ![]() $\psi : B_{\unicode{x00E9}{\text {t}}}O \to B_{\unicode{x00E9}{\text {t}}}O$. For any smooth affine
$\psi : B_{\unicode{x00E9}{\text {t}}}O \to B_{\unicode{x00E9}{\text {t}}}O$. For any smooth affine ![]() $k$-scheme
$k$-scheme ![]() $X$, if
$X$, if ![]() $(\mathscr {V},\varphi )$ is a symmetric bilinear space, then the formulas for the hyperbolic morphisms described above show that the composite
$(\mathscr {V},\varphi )$ is a symmetric bilinear space, then the formulas for the hyperbolic morphisms described above show that the composite ![]() $X \to B_{\unicode{x00E9}{\text {t}}}O \to B_{\unicode{x00E9}{\text {t}}}O$ of the classifying map of
$X \to B_{\unicode{x00E9}{\text {t}}}O \to B_{\unicode{x00E9}{\text {t}}}O$ of the classifying map of ![]() $(\mathscr {V},\varphi )$ with
$(\mathscr {V},\varphi )$ with ![]() $\psi$ sends
$\psi$ sends ![]() $[(\mathscr {V},\varphi )] \mapsto \langle 1, 1, -1,-1 \rangle [(\mathscr {V},\varphi )]$ and therefore induces multiplication by this class at the level of
$[(\mathscr {V},\varphi )] \mapsto \langle 1, 1, -1,-1 \rangle [(\mathscr {V},\varphi )]$ and therefore induces multiplication by this class at the level of ![]() ${\mathbb {A}}^1$-homotopy sheaves. Likewise, one shows that the other composite
${\mathbb {A}}^1$-homotopy sheaves. Likewise, one shows that the other composite ![]() $BSp \to BSp$ induced by
$BSp \to BSp$ induced by ![]() $Sp_{2n} \to Sp_{8n}$ also coincides with multiplication by
$Sp_{2n} \to Sp_{8n}$ also coincides with multiplication by ![]() $\langle 1,1,-1,-1\rangle$ and thus induces multiplication by this class in homotopy sheaves as well.
$\langle 1,1,-1,-1\rangle$ and thus induces multiplication by this class in homotopy sheaves as well.
We now use the observation above to deduce corresponding statements about the induced self-maps of the stable group ![]() $Spin$ by passing to suitable connected covers. The proof of [Reference Schlichting and TripathiST15, Theorem 5] shows that
$Spin$ by passing to suitable connected covers. The proof of [Reference Schlichting and TripathiST15, Theorem 5] shows that ![]() $B_{\operatorname {Nis}}O$ is the
$B_{\operatorname {Nis}}O$ is the ![]() ${\mathbb {A}}^1$-connected component of the trivial torsor in
${\mathbb {A}}^1$-connected component of the trivial torsor in ![]() $B_{\unicode{x00E9}{\text {t}}}O$. Likewise,
$B_{\unicode{x00E9}{\text {t}}}O$. Likewise, ![]() $B_{\operatorname {Nis}}Spin$ is
$B_{\operatorname {Nis}}Spin$ is ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected by appeal to Lemma 5.2.10. The map
$1$-connected by appeal to Lemma 5.2.10. The map ![]() $Spin \to O$ induces a morphism
$Spin \to O$ induces a morphism ![]() $B_{\operatorname {Nis}}Spin \to B_{\operatorname {Nis}}O \to B_{\unicode{x00E9}{\text {t}}}O$ which makes
$B_{\operatorname {Nis}}Spin \to B_{\operatorname {Nis}}O \to B_{\unicode{x00E9}{\text {t}}}O$ which makes ![]() $B_{\operatorname {Nis}}Spin$ into the
$B_{\operatorname {Nis}}Spin$ into the ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $1$-connected cover of
$1$-connected cover of ![]() $B_{\unicode{x00E9}{\text {t}}}O$. Therefore, the composite of
$B_{\unicode{x00E9}{\text {t}}}O$. Therefore, the composite of ![]() $B_{\operatorname {Nis}}Spin \to B_{\unicode{x00E9}{\text {t}}}O$ and the map
$B_{\operatorname {Nis}}Spin \to B_{\unicode{x00E9}{\text {t}}}O$ and the map ![]() $B_{et}O \to B_{\unicode{x00E9}{\text {t}}}O$ described in the previous paragraph lifts uniquely up to
$B_{et}O \to B_{\unicode{x00E9}{\text {t}}}O$ described in the previous paragraph lifts uniquely up to ![]() ${\mathbb {A}}^1$-homotopy through a morphism
${\mathbb {A}}^1$-homotopy through a morphism ![]() $B_{\operatorname {Nis}}Spin \to B_{\operatorname {Nis}}Spin$. By the uniqueness of this lift, this map coincides up to
$B_{\operatorname {Nis}}Spin \to B_{\operatorname {Nis}}Spin$. By the uniqueness of this lift, this map coincides up to ![]() ${\mathbb {A}}^1$-homotopy with the self-map
${\mathbb {A}}^1$-homotopy with the self-map ![]() $Spin \to Spin$ defined as the composite
$Spin \to Spin$ defined as the composite ![]() $Spin \to Sp \to Spin$ after taking loop spaces.
$Spin \to Sp \to Spin$ after taking loop spaces.
It follows from the discussion above that the composite map ![]() $Spin \to Spin$ induces multiplication by the class of
$Spin \to Spin$ induces multiplication by the class of ![]() $\langle 1,1,-1,-1\rangle$ in
$\langle 1,1,-1,-1\rangle$ in ![]() $GW(k)$ after passing to
$GW(k)$ after passing to ![]() ${\mathbb {A}}^1$-homotopy sheaves. If
${\mathbb {A}}^1$-homotopy sheaves. If ![]() $k$ is not formally real, then Lemma 5.1.2 shows that
$k$ is not formally real, then Lemma 5.1.2 shows that ![]() $GW(k) \otimes R \cong R$ via the rank map. Since
$GW(k) \otimes R \cong R$ via the rank map. Since ![]() $\langle 1,1,-1,-1\rangle$ has rank
$\langle 1,1,-1,-1\rangle$ has rank ![]() $4$ we conclude that the induced map on homotopy sheaves is an isomorphism after inverting
$4$ we conclude that the induced map on homotopy sheaves is an isomorphism after inverting ![]() $2$. Likewise, the map
$2$. Likewise, the map ![]() $Sp \to Sp$ is an isomorphism on
$Sp \to Sp$ is an isomorphism on ![]() ${\mathbb {A}}^1$-homotopy sheaves after inverting
${\mathbb {A}}^1$-homotopy sheaves after inverting ![]() $2$.
$2$.
Remark 5.2.13 The assumption that ![]() $k$ has characteristic not equal to
$k$ has characteristic not equal to ![]() $2$ in Theorem 5.2.12 arises implicitly in our appeal to [Reference Schlichting and TripathiST15] where this assumption is used to analyze the higher Grothendieck–Witt space.
$2$ in Theorem 5.2.12 arises implicitly in our appeal to [Reference Schlichting and TripathiST15] where this assumption is used to analyze the higher Grothendieck–Witt space.
The next result, which follows by combining Theorem 5.2.12 and Proposition 5.2.8, is an unstable variant of a result originally announced by Morel [Reference MorelMor06b]; it completes the description of rational ![]() ${\mathbb {A}}^1$-homotopy groups of stable classical groups (away from fields of characteristic
${\mathbb {A}}^1$-homotopy groups of stable classical groups (away from fields of characteristic ![]() $2$).
$2$).
Corollary 5.2.14 If ![]() $k$ is a field that is not formally real and has characteristic not equal to
$k$ is a field that is not formally real and has characteristic not equal to ![]() $2$, then the composite morphism
$2$, then the composite morphism
where the first morphism is that from Proposition 5.2.8 and the second is the morphism constructed just prior to Theorem 5.2.12, is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
5.3 On rational homotopy sheaves of motivic spheres
In this section we combine the results of the previous section with some results about rationalized K-theory to deduce information about the structure of unstable ![]() ${\mathbb {A}}^1$-homotopy sheaves of spheres. We will freely use facts about Voevodsky's motivic Eilenberg–Mac Lane spaces; we refer the reader to [Reference VoevodskyVoe10, § 3] and the references therein for more discussion about these objects. For any integer
${\mathbb {A}}^1$-homotopy sheaves of spheres. We will freely use facts about Voevodsky's motivic Eilenberg–Mac Lane spaces; we refer the reader to [Reference VoevodskyVoe10, § 3] and the references therein for more discussion about these objects. For any integer ![]() $n \geq 0$, we write
$n \geq 0$, we write ![]() ${\mathbb {Z}}(n)$ for a model of Voevodsky motivic complex (see, for example, [Reference Mazza, Voevodsky and WeibelMVW06, Definition 3.1]). Viewing
${\mathbb {Z}}(n)$ for a model of Voevodsky motivic complex (see, for example, [Reference Mazza, Voevodsky and WeibelMVW06, Definition 3.1]). Viewing ![]() ${\mathbb {Z}}(n)$ as a chain complex of Nisnevich sheaves of abelian groups, its homology sheaves are concentrated in degrees
${\mathbb {Z}}(n)$ as a chain complex of Nisnevich sheaves of abelian groups, its homology sheaves are concentrated in degrees ![]() $\geq -n$. If
$\geq -n$. If ![]() $m \geq n$, we use the notation
$m \geq n$, we use the notation
to denote the Eilenberg–Mac Lane space attached to the complex ![]() ${\mathbb {Z}}(n)[m]$; this space represents motivic cohomology in
${\mathbb {Z}}(n)[m]$; this space represents motivic cohomology in ![]() $\mathrm {Ho}_{k}$ (see [Reference VoevodskyVoe03, § 2] for a summary and [Reference DeligneDel09] for details).
$\mathrm {Ho}_{k}$ (see [Reference VoevodskyVoe03, § 2] for a summary and [Reference DeligneDel09] for details).
Rationalized  $K$-theory
$K$-theory
The motivic cohomology of ![]() $BGL_n$ is generated as a module over motivic cohomology of a point by Chern classes
$BGL_n$ is generated as a module over motivic cohomology of a point by Chern classes ![]() $c_1,\ldots,c_n$ in bi-degrees
$c_1,\ldots,c_n$ in bi-degrees ![]() $(2i,i)$ [Reference PushinPus04]. As a consequence, for every integer
$(2i,i)$ [Reference PushinPus04]. As a consequence, for every integer ![]() $n$, and every integer
$n$, and every integer ![]() $i < n$, the
$i < n$, the ![]() $i$th Chern class corresponds to an
$i$th Chern class corresponds to an ![]() ${\mathbb {A}}^1$-homotopy class of maps
${\mathbb {A}}^1$-homotopy class of maps
Since ![]() $BGL_1$ is already
$BGL_1$ is already ![]() ${\mathbb {A}}^1$-local [Reference Morel and VoevodskyMV99, § 4 Proposition 3.8], and
${\mathbb {A}}^1$-local [Reference Morel and VoevodskyMV99, § 4 Proposition 3.8], and ![]() ${\mathbb {Z}}(1) = {{\mathbf {G}}_{m}^{}}[-1]$, the map
${\mathbb {Z}}(1) = {{\mathbf {G}}_{m}^{}}[-1]$, the map ![]() $c_1: BGL_1 \to K({\mathbb {Z}}(1),2)$ is an
$c_1: BGL_1 \to K({\mathbb {Z}}(1),2)$ is an ![]() ${\mathbb {A}}^1$-weak equivalence essentially by definition.
${\mathbb {A}}^1$-weak equivalence essentially by definition.
Taking products of Chern classes, there are induced morphisms ![]() $BGL_n \to \prod _{i=1}^n K({\mathbb {Z}}(i),2i)$ and a morphism
$BGL_n \to \prod _{i=1}^n K({\mathbb {Z}}(i),2i)$ and a morphism
Likewise, Chern classes induce maps ![]() $BSL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i)$ and a morphism
$BSL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i)$ and a morphism
The direct sum of vector bundles equips the classifying spaces ![]() $BGL$ and
$BGL$ and ![]() $BSL$ of the stable general and special linear groups with the structure of
$BSL$ of the stable general and special linear groups with the structure of ![]() ${\mathbb {A}}^1$-
${\mathbb {A}}^1$-![]() $h$-spaces; these spaces are thus
$h$-spaces; these spaces are thus ![]() ${\mathbb {A}}^1$-simple. We know that
${\mathbb {A}}^1$-simple. We know that ![]() $SL_n$ and
$SL_n$ and ![]() $SL$ are all
$SL$ are all ![]() ${\mathbb {A}}^1$-connected spaces. Taking simplicial loops, one obtains a morphism
${\mathbb {A}}^1$-connected spaces. Taking simplicial loops, one obtains a morphism
The next result analyzes these morphisms.
Proposition 5.3.1 The following maps are ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalences:
${\mathbb {A}}^1$-weak equivalences:
1. the map
 $c: BGL \to \prod _{n \geq 1} K({\mathbb {Z}}(n),2n)$;
$c: BGL \to \prod _{n \geq 1} K({\mathbb {Z}}(n),2n)$;2. the map
 $c': BSL \to \prod _{n \geq 2} K({\mathbb {Z}}(n),2n)$;
$c': BSL \to \prod _{n \geq 2} K({\mathbb {Z}}(n),2n)$;3. the map
 $\Omega c': SL \to \prod _{n \geq 2} K({\mathbb {Z}}(n),2n-1)$.
$\Omega c': SL \to \prod _{n \geq 2} K({\mathbb {Z}}(n),2n-1)$.
Proof. For the first statement, it suffices to show that the induced map on homotopy sheaves after rationalization is an isomorphism. The map of the statement induces a morphism of presheaves on ![]() $\mathrm {Sm}_k$ of the form
$\mathrm {Sm}_k$ of the form
 \[ [\Sigma^i U_+,BGL]_{{\mathbb{A}}^1} \longrightarrow \bigg[\Sigma^i U_+, \prod_{n \geq 1} K({\mathbb{Z}}(n),2n)\bigg]_{{\mathbb{A}}^1} \]
\[ [\Sigma^i U_+,BGL]_{{\mathbb{A}}^1} \longrightarrow \bigg[\Sigma^i U_+, \prod_{n \geq 1} K({\mathbb{Z}}(n),2n)\bigg]_{{\mathbb{A}}^1} \]
The left-hand side is precisely ![]() $K_i(U)$ by appeal to [Reference Morel and VoevodskyMV99, § 4 Theorem 3.13] (see [Reference Schlichting and TripathiST15, § 8 Remark 2 p. 1162] for some corrections). Since
$K_i(U)$ by appeal to [Reference Morel and VoevodskyMV99, § 4 Theorem 3.13] (see [Reference Schlichting and TripathiST15, § 8 Remark 2 p. 1162] for some corrections). Since ![]() $[\Sigma ^i U_+, K({\mathbb {Z}}(n),2n)]_{{\mathbb {A}}^1} = H^{2n-i,n}(U)$ the universal property of a product allows us to identify the right-hand side with
$[\Sigma ^i U_+, K({\mathbb {Z}}(n),2n)]_{{\mathbb {A}}^1} = H^{2n-i,n}(U)$ the universal property of a product allows us to identify the right-hand side with ![]() $\prod _{n \geq 1} [\Sigma ^i U_+, K({\mathbb {Z}}(n),2n)]_{{\mathbb {A}}^1}$ and thus
$\prod _{n \geq 1} [\Sigma ^i U_+, K({\mathbb {Z}}(n),2n)]_{{\mathbb {A}}^1}$ and thus ![]() $\prod _{n \geq 1} H^{2n-i,n}(U)$. Now, one knows that, after tensoring the groups on the both sides with
$\prod _{n \geq 1} H^{2n-i,n}(U)$. Now, one knows that, after tensoring the groups on the both sides with ![]() ${\mathbb {Q}}$, this map is an isomorphism; this is the degeneration of the motivic spectral sequence, which identifies the graded pieces for the
${\mathbb {Q}}$, this map is an isomorphism; this is the degeneration of the motivic spectral sequence, which identifies the graded pieces for the ![]() $\gamma$-filtration in K-theory with Bloch's higher Chow groups (this is originally due to Bloch [Reference BlochBlo86], but see [Reference LevineLev94] for a corrected version). In the context of motivic homotopy theory, see [Reference RiouRio10, Theorem 5.3.10] and [Reference RiouRio10, Remark 6.2.3.10].
$\gamma$-filtration in K-theory with Bloch's higher Chow groups (this is originally due to Bloch [Reference BlochBlo86], but see [Reference LevineLev94] for a corrected version). In the context of motivic homotopy theory, see [Reference RiouRio10, Theorem 5.3.10] and [Reference RiouRio10, Remark 6.2.3.10].
For the second statement, observe that there is a commutative diagram

where the left-hand vertical map is induced by the determinant and the right-hand vertical map is projection onto the first factor. As remarked above, the bottom morphism here is an ![]() ${\mathbb {A}}^1$-weak equivalence. The left-hand vertical map fits into an
${\mathbb {A}}^1$-weak equivalence. The left-hand vertical map fits into an ![]() ${\mathbb {A}}^1$-fiber sequence where the
${\mathbb {A}}^1$-fiber sequence where the ![]() ${\mathbb {A}}^1$-homotopy fiber is
${\mathbb {A}}^1$-homotopy fiber is ![]() $BSL$. The
$BSL$. The ![]() ${\mathbb {A}}^1$-homotopy fiber of the right-hand vertical map is
${\mathbb {A}}^1$-homotopy fiber of the right-hand vertical map is ![]() $\prod _{i \geq 2} K({\mathbb {Z}}(i),2i)$. The induced map on homotopy fibers is the morphism
$\prod _{i \geq 2} K({\mathbb {Z}}(i),2i)$. The induced map on homotopy fibers is the morphism ![]() $c'$ by construction. Since the morphisms
$c'$ by construction. Since the morphisms ![]() $c$ and
$c$ and ![]() $c_1$ are
$c_1$ are ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalences, the latter assertion having been discussed before the statement of the proposition, one concludes that
${\mathbb {A}}^1$-weak equivalences, the latter assertion having been discussed before the statement of the proposition, one concludes that ![]() $c'$ is a
$c'$ is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence as well. The final statement follows by looping the previous one.
${\mathbb {A}}^1$-weak equivalence as well. The final statement follows by looping the previous one.
Remark 5.3.2 Looping the map ![]() $BSL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i)$, one obtains a morphism
$BSL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i)$, one obtains a morphism ![]() $SL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i-1)$. Taking colimits on both sides, one obtains a morphism
$SL_n \to \prod _{i=2}^n K({\mathbb {Z}}(i),2i-1)$. Taking colimits on both sides, one obtains a morphism
 \[ \operatorname{colim}_n SL_n \longrightarrow \operatorname{colim}_n \prod_{i=2}^n K({\mathbb{Z}}(i),2i-1). \]
\[ \operatorname{colim}_n SL_n \longrightarrow \operatorname{colim}_n \prod_{i=2}^n K({\mathbb{Z}}(i),2i-1). \]
The colimit on the left-hand side is ![]() $SL$, and there is thus a morphism
$SL$, and there is thus a morphism
By appeal to Lemma 5.2.6 the right-hand map is an ![]() ${\mathbb {A}}^1$-weak equivalence. Since
${\mathbb {A}}^1$-weak equivalence. Since ![]() $S^1$ is a compact object, taking simplicial loops commutes with formation of filtered (homotopy) colimits. It follows that the morphism described in the previous display coincides with
$S^1$ is a compact object, taking simplicial loops commutes with formation of filtered (homotopy) colimits. It follows that the morphism described in the previous display coincides with ![]() $\Omega c'$.
$\Omega c'$.
Rational homotopy of motivic spheres: odd-dimensional quadrics
Another classical result of Serre is that the morphism ![]() $S^{2n-1} \to K({\mathbb {Z}},2n-1)$ corresponding to the fundamental class (alternatively, the first non-trivial stage of the Postnikov tower) is a rational weak equivalence. Because of the weak equivalence
$S^{2n-1} \to K({\mathbb {Z}},2n-1)$ corresponding to the fundamental class (alternatively, the first non-trivial stage of the Postnikov tower) is a rational weak equivalence. Because of the weak equivalence ![]() ${\mathbb {A}}^n \,{\setminus}\, 0 \cong \Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$, we conclude that there is an isomorphism
${\mathbb {A}}^n \,{\setminus}\, 0 \cong \Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$, we conclude that there is an isomorphism ![]() $\mathbf {M}({\mathbb {A}}^n \,{\setminus}\, 0) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n-1]$ in the Voevodsky triangulated category of motives [Reference Mazza, Voevodsky and WeibelMVW06, Corollary 15.3]. Thus, for any integer
$\mathbf {M}({\mathbb {A}}^n \,{\setminus}\, 0) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n-1]$ in the Voevodsky triangulated category of motives [Reference Mazza, Voevodsky and WeibelMVW06, Corollary 15.3]. Thus, for any integer ![]() $n \geq 2$,
$n \geq 2$, ![]() $H^{2n-1,n}({\mathbb {A}}^n \,{\setminus}\, 0,{\mathbb {Z}}) \cong {\mathbb {Z}}$. A choice
$H^{2n-1,n}({\mathbb {A}}^n \,{\setminus}\, 0,{\mathbb {Z}}) \cong {\mathbb {Z}}$. A choice ![]() $\xi$ of generator can thus be realized by an
$\xi$ of generator can thus be realized by an ![]() ${\mathbb {A}}^1$-homotopy class of maps
${\mathbb {A}}^1$-homotopy class of maps ![]() ${\mathbb {A}}^n \,{\setminus}\, 0 \to K({\mathbb {Z}}(n),2n-1)$. Above, we described an
${\mathbb {A}}^n \,{\setminus}\, 0 \to K({\mathbb {Z}}(n),2n-1)$. Above, we described an ![]() ${\mathbb {A}}^1$-weak equivalence
${\mathbb {A}}^1$-weak equivalence ![]() $Q_{2n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$. So the preceding map also defines a morphism
$Q_{2n-1} \to {\mathbb {A}}^n \,{\setminus}\, 0$. So the preceding map also defines a morphism
We now establish an analog of this result in ![]() ${\mathbb {A}}^1$-homotopy theory, which corresponds to the first part of Theorem 5.
${\mathbb {A}}^1$-homotopy theory, which corresponds to the first part of Theorem 5.
Theorem 5.3.3 If ![]() $k$ is a field that is not formally real, then for every integer
$k$ is a field that is not formally real, then for every integer ![]() $n > 1$, the map
$n > 1$, the map
of (5.2) is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence.
${\mathbb {A}}^1$-weak equivalence.
Proof. After Proposition 5.2.8 there is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence of the form
${\mathbb {A}}^1$-weak equivalence of the form ![]() $\prod _{n \geq 2} Q_{2n-1} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} SL$. Composing this
$\prod _{n \geq 2} Q_{2n-1} {\stackrel {{\scriptscriptstyle {\sim }}}{\;\rightarrow \;}} SL$. Composing this ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak with
${\mathbb {A}}^1$-weak with ![]() $\Omega c'$, we conclude that there is an induced
$\Omega c'$, we conclude that there is an induced ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence of the form
${\mathbb {A}}^1$-weak equivalence of the form
and we now give an alternative identification of the component maps.
The map ![]() $Q_{2n-1} \to SL_n$ is given by a Suslin morphism, while the map
$Q_{2n-1} \to SL_n$ is given by a Suslin morphism, while the map ![]() ${SL_n \to K({\mathbb {Z}}(n),2n-1)}$ is given by the loops on the
${SL_n \to K({\mathbb {Z}}(n),2n-1)}$ is given by the loops on the ![]() $n$th Chern class. Since
$n$th Chern class. Since ![]() $Q_{2n-1} \cong \Sigma ^{n-1} {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$, it follows from [Reference Morel and VoevodskyMV99, § 4 Theorem 3.13] that
$Q_{2n-1} \cong \Sigma ^{n-1} {{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$, it follows from [Reference Morel and VoevodskyMV99, § 4 Theorem 3.13] that ![]() $SK_1(Q_{2n-1}) \cong K_0(k) \cong {\mathbb {Z}}$. Suslin showed that the class of the composite map
$SK_1(Q_{2n-1}) \cong K_0(k) \cong {\mathbb {Z}}$. Suslin showed that the class of the composite map ![]() $Q_{2n-1} \to SL_n \to SL$ in
$Q_{2n-1} \to SL_n \to SL$ in ![]() $SK_1(Q_{2n-1})$ is a generator [Reference SuslinSus82, Theorem 2.3 and Corollary 2.7].
$SK_1(Q_{2n-1})$ is a generator [Reference SuslinSus82, Theorem 2.3 and Corollary 2.7].
Since rationally the motivic cohomology of ![]() $Q_{2n-1}$ coincides with the rationalized K-theory, we conclude that the Suslin matrix is a rational multiple of the class
$Q_{2n-1}$ coincides with the rationalized K-theory, we conclude that the Suslin matrix is a rational multiple of the class ![]() $\xi$. In fact, we can be slightly more precise. The motivic cohomology of
$\xi$. In fact, we can be slightly more precise. The motivic cohomology of ![]() $SL_n$ is computed in [Reference WilliamsWil12]. In particular, one knows
$SL_n$ is computed in [Reference WilliamsWil12]. In particular, one knows ![]() $H^{2n-1,n}(SL_n,{\mathbb {Z}}) \cong {\mathbb {Z}}$ and the relevant generator is the image via pullback along the map
$H^{2n-1,n}(SL_n,{\mathbb {Z}}) \cong {\mathbb {Z}}$ and the relevant generator is the image via pullback along the map ![]() $SL_n \to {\mathbb {A}}^n \,{\setminus}\, 0$ of the corresponding generator of
$SL_n \to {\mathbb {A}}^n \,{\setminus}\, 0$ of the corresponding generator of ![]() $H^{2n-1,n}({\mathbb {A}}^n \,{\setminus}\, 0)$. In particular, the composite with the Suslin morphism corresponds to
$H^{2n-1,n}({\mathbb {A}}^n \,{\setminus}\, 0)$. In particular, the composite with the Suslin morphism corresponds to ![]() $(n-1)!$ times the generator. Thus, after inverting
$(n-1)!$ times the generator. Thus, after inverting ![]() $(n-1)!$ this morphism coincides with the map
$(n-1)!$ this morphism coincides with the map ![]() $Q_{2n-1} \to K({\mathbb {Z}}(n),2n-1)$ from (5.2). Therefore, we conclude that the map
$Q_{2n-1} \to K({\mathbb {Z}}(n),2n-1)$ from (5.2). Therefore, we conclude that the map
defined by taking colimits of the finite products of the morphisms in (5.2) is also a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence (see Remark 5.3.2 for related discussion).
${\mathbb {A}}^1$-weak equivalence (see Remark 5.3.2 for related discussion).
Finally, for every integer ![]() $n \geq 2$, the map of (5.2) is, by construction, a retract of the map displayed in the previous paragraph. Therefore, we conclude that (5.2) is a
$n \geq 2$, the map of (5.2) is, by construction, a retract of the map displayed in the previous paragraph. Therefore, we conclude that (5.2) is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence as well, which is what we wanted to show.
${\mathbb {A}}^1$-weak equivalence as well, which is what we wanted to show.
Remark 5.3.4 If ![]() $k$ is a subfield of
$k$ is a subfield of ![]() ${\mathbb {C}}$, then the conclusion of Theorem 5.3.3 is compatible with complex realization. Indeed, the complex realization of
${\mathbb {C}}$, then the conclusion of Theorem 5.3.3 is compatible with complex realization. Indeed, the complex realization of ![]() $K({\mathbb {Z}}(n),2n-1)$ is homotopy equivalent to
$K({\mathbb {Z}}(n),2n-1)$ is homotopy equivalent to ![]() $K({\mathbb {Z}},2n-1)$ [Reference VoevodskyVoe10, Corollary 3.48], while the complex realization of
$K({\mathbb {Z}},2n-1)$ [Reference VoevodskyVoe10, Corollary 3.48], while the complex realization of ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ or
${\mathbb {A}}^n \,{\setminus}\, 0$ or ![]() $Q_{2n-1}$ is homotopy equivalent to
$Q_{2n-1}$ is homotopy equivalent to ![]() $S^{2n-1}$. The induced map on realizations yields the map
$S^{2n-1}$. The induced map on realizations yields the map ![]() $S^{2n-1} \to K({\mathbb {Z}},2n-1)$.
$S^{2n-1} \to K({\mathbb {Z}},2n-1)$.
Remark 5.3.5 Theorem 5.3.3 is an unstable variant of a result due originally to Morel in the stable case ([Reference MorelMor04, Theorem 5.2.2] or [Reference MorelMor06b]): if ![]() $-1$ is a sum of squares in
$-1$ is a sum of squares in ![]() $k$, then the rationalized motivic sphere spectrum is simply the rational motivic Eilenberg–Mac Lane spectrum (see [Reference Cisinski and DégliseCD19, Theorem 16.2.13] for a proof).
$k$, then the rationalized motivic sphere spectrum is simply the rational motivic Eilenberg–Mac Lane spectrum (see [Reference Cisinski and DégliseCD19, Theorem 16.2.13] for a proof).
Theorem 5.3.3 may be used to reformulate the Beilinson–Soulé vanishing conjecture (see, for example, [Reference KahnKah05, II.4.3.4] for a statement of the conjecture). Before stating the reformulation, we include the following result explained to us by F. Déglise.
Lemma 5.3.6 If ![]() $E/k$ is an arbitrary field extension, then the map
$E/k$ is an arbitrary field extension, then the map
is injective. In particular, if the Beilinson–Soulé vanishing conjecture holds for ![]() $E$, then it holds for
$E$, then it holds for ![]() $k$ as well.
$k$ as well.
Proof. One may reduce to the case where ![]() $E/k$ is a finitely generated extension by a continuity argument; this follows from, for example, [Reference DégliseDég07, Proposition 1.24]. To treat the case of finitely generated extensions, it suffices to treat two special cases:
$E/k$ is a finitely generated extension by a continuity argument; this follows from, for example, [Reference DégliseDég07, Proposition 1.24]. To treat the case of finitely generated extensions, it suffices to treat two special cases: ![]() $E/k$ is finite and
$E/k$ is finite and ![]() $E = k(t)$.
$E = k(t)$.
If ![]() $E/k$ is finite, the result follows by existence of transfers in motivic cohomology; indeed, there is a pushforward map
$E/k$ is finite, the result follows by existence of transfers in motivic cohomology; indeed, there is a pushforward map ![]() $H^{p,q}(E,{\mathbb {Q}}) \to H^{p,q}(k,{\mathbb {Q}})$ such that the composite of pushforward and pullback is multiplication by the degree of the extension; injectivity follows immediately. Finally, we treat the case where
$H^{p,q}(E,{\mathbb {Q}}) \to H^{p,q}(k,{\mathbb {Q}})$ such that the composite of pushforward and pullback is multiplication by the degree of the extension; injectivity follows immediately. Finally, we treat the case where ![]() $E = k(t)$. In that case, by [Reference DégliseDég08, Proposition 6.1.1 and Corollaire 6.1.3] we know that
$E = k(t)$. In that case, by [Reference DégliseDég08, Proposition 6.1.1 and Corollaire 6.1.3] we know that
the sum is taken over the codimension-![]() $1$ points of
$1$ points of ![]() ${\mathbb {A}}^1_k$, and the pullback map corresponding to the inclusion
${\mathbb {A}}^1_k$, and the pullback map corresponding to the inclusion ![]() $k \hookrightarrow k(t)$ is the inclusion of the first summand on the right.
$k \hookrightarrow k(t)$ is the inclusion of the first summand on the right.
The injectivity assertion in the case ![]() $E = k(t)$ is actually ‘softer’ than the more precise assertions above, as observed by the referees. Indeed, if
$E = k(t)$ is actually ‘softer’ than the more precise assertions above, as observed by the referees. Indeed, if ![]() $k$ is infinite, which we may assume without loss of generality, injectivity can be deduced as follows. The group
$k$ is infinite, which we may assume without loss of generality, injectivity can be deduced as follows. The group ![]() $H^{p,q}(k(t),{\mathbb {Q}})$ is a colimit of
$H^{p,q}(k(t),{\mathbb {Q}})$ is a colimit of ![]() $H^{p,q}(U,{\mathbb {Q}})$ where
$H^{p,q}(U,{\mathbb {Q}})$ where ![]() $U$ ranges over the non-empty open subschemes of the affine line. Since non-empty open subschemes over an infinite field have a rational point, the pullback along the inclusion of that rational point provides the splitting of the statement.
$U$ ranges over the non-empty open subschemes of the affine line. Since non-empty open subschemes over an infinite field have a rational point, the pullback along the inclusion of that rational point provides the splitting of the statement.
As a consequence, we obtain the following reformulation of the Beilinson–Soulé vanishing conjecture.
Corollary 5.3.7 Suppose ![]() $k$ is a field that is not formally real, and assume
$k$ is a field that is not formally real, and assume ![]() $n > 1$ is an integer. If
$n > 1$ is an integer. If ![]() $L/k$ is an extension, then the following statements are equivalent.
$L/k$ is an extension, then the following statements are equivalent.
1. The Beilinson–Soulé vanishing conjecture holds for every subfield of
 $L$ in weight
$L$ in weight  $n$.
$n$.2. The group
 $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0)_{{\mathbb {Q}}}(L) = 0$ for
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0)_{{\mathbb {Q}}}(L) = 0$ for  $i \geq 2n-1$.
$i \geq 2n-1$.3. The group
 ${{\mathbf {H}}}_i^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0,{\mathbb {Q}})(L) = 0$ for
${{\mathbf {H}}}_i^{{\mathbb {A}}^1}({\mathbb {A}}^n \,{\setminus}\, 0,{\mathbb {Q}})(L) = 0$ for  $i \geq 2n-1$.
$i \geq 2n-1$.
Proof. Note that
The Beilinson–Soulé vanishing conjecture for fields in weight ![]() $n$ is equivalent to
$n$ is equivalent to
The equivalence of the first two statements is then immediate from Theorem 5.3.3 and Lemma 5.3.6.
The equivalence of the second and third statements is an immediate consequence of the Whitehead theorem. Indeed, consider the map ![]() ${\mathbb {A}}^n \,{\setminus}\, 0 \longrightarrow \tau _{\leq 2n-2}{\mathbb {A}}^n \,{\setminus}\, 0$ from punctured affine
${\mathbb {A}}^n \,{\setminus}\, 0 \longrightarrow \tau _{\leq 2n-2}{\mathbb {A}}^n \,{\setminus}\, 0$ from punctured affine ![]() $n$-space to its
$n$-space to its ![]() $(2n-2)$th
$(2n-2)$th ![]() ${\mathbb {A}}^1$–Postnikov truncation. The vanishing of rational homotopy in (2) is equivalent to this map being a
${\mathbb {A}}^1$–Postnikov truncation. The vanishing of rational homotopy in (2) is equivalent to this map being a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-equivalence. Since both spaces in question are simple, this map is a
${\mathbb {A}}^1$-equivalence. Since both spaces in question are simple, this map is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-equivalence if and only if it is a
${\mathbb {A}}^1$-equivalence if and only if it is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-homology equivalence by the Whitehead theorem (see Theorem 4.2.2).
${\mathbb {A}}^1$-homology equivalence by the Whitehead theorem (see Theorem 4.2.2).
Remark 5.3.8 Since the Beilinson–Soulé vanishing conjecture is known to hold for finite fields, totally imaginary number fields or function fields of curves over finite fields, Corollary 5.3.7 can also be viewed as a rational computation of the sections of motivic homotopy sheaves of ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ over such fields.
${\mathbb {A}}^n \,{\setminus}\, 0$ over such fields.
On the other hand, the vanishing of the integral ![]() ${\mathbb {A}}^1$-homology of
${\mathbb {A}}^1$-homology of ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ in degrees
${\mathbb {A}}^n \,{\setminus}\, 0$ in degrees ![]() $> 2n-1$ is a special case of a conjecture of Morel [Reference MorelMor12, Conjecture 6.34]. At least with rational coefficients, and over fields in which
$> 2n-1$ is a special case of a conjecture of Morel [Reference MorelMor12, Conjecture 6.34]. At least with rational coefficients, and over fields in which ![]() $-1$ is a sum of squares, Morel's vanishing conjecture in the case of
$-1$ is a sum of squares, Morel's vanishing conjecture in the case of ![]() ${\mathbb {A}}^n \,{\setminus}\, 0$ is thus equivalent to the Beilinson–Soulé vanishing conjecture over all finitely generated separable extensions of the base field.
${\mathbb {A}}^n \,{\setminus}\, 0$ is thus equivalent to the Beilinson–Soulé vanishing conjecture over all finitely generated separable extensions of the base field.
Corollary 5.3.9 Assume ![]() $k$ is a field that is not formally real. If
$k$ is a field that is not formally real. If ![]() $\mathbf {M}$ is any strictly
$\mathbf {M}$ is any strictly ![]() ${\mathbb {A}}^1$-invariant sheaf of
${\mathbb {A}}^1$-invariant sheaf of ![]() ${\mathbb {Q}}$-vector spaces, then, for any integer
${\mathbb {Q}}$-vector spaces, then, for any integer ![]() $n \geq 2$, the following statement holds:
$n \geq 2$, the following statement holds:
 \[ H^i(K({\mathbb{Z}}(n),2n-1),\mathbf{M}) = \begin{cases} \mathbf{M}(k) & \text{ if } i = 0, \\ 0 & \text{ if } 1 \leq i \leq n-2, \\ \mathbf{M}_{-n}(k) & \text{ if } i = n-1, \text{ and } \\ 0 & \text{ if } i > n-1. \end{cases} \]
\[ H^i(K({\mathbb{Z}}(n),2n-1),\mathbf{M}) = \begin{cases} \mathbf{M}(k) & \text{ if } i = 0, \\ 0 & \text{ if } 1 \leq i \leq n-2, \\ \mathbf{M}_{-n}(k) & \text{ if } i = n-1, \text{ and } \\ 0 & \text{ if } i > n-1. \end{cases} \]Proof. This follows by combining [Reference Asok and FaselAF14a, Lemma 4.5] and Proposition 4.1.2.
Rational homotopy of motivic spheres: even-dimensional quadrics
The motivic analog of even-dimensional spheres are the quadrics ![]() $Q_{2n}$, which are
$Q_{2n}$, which are ![]() ${\mathbb {A}}^1$-homotopy equivalent to
${\mathbb {A}}^1$-homotopy equivalent to ![]() ${{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ (see the beginning of § 5.1). Indeed, the complex realization of such spheres is homotopy equivalent to
${{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ (see the beginning of § 5.1). Indeed, the complex realization of such spheres is homotopy equivalent to ![]() $S^{2n}$. We also obtain the following motivic analog of a result of a classical result of Serre [Reference SerreSer53, IV.4 Corollaire 2]. In order to formulate the statement, we use the
$S^{2n}$. We also obtain the following motivic analog of a result of a classical result of Serre [Reference SerreSer53, IV.4 Corollaire 2]. In order to formulate the statement, we use the ![]() ${\mathbb {A}}^1$-EHP sequence of [Reference Wickelgren and WilliamsWW19].
${\mathbb {A}}^1$-EHP sequence of [Reference Wickelgren and WilliamsWW19].
Proposition 5.3.10 Suppose ![]() $k$ is a field that is not formally real and
$k$ is a field that is not formally real and ![]() $R$ is a subring of
$R$ is a subring of ![]() ${\mathbb {Q}}$ in which
${\mathbb {Q}}$ in which ![]() $2$ is invertible.
$2$ is invertible.
1. There is an
 ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
 \[ Q_{2n-1} \longrightarrow \Omega Q_{2n} \longrightarrow \Omega Q_{4n-1}. \]
\[ Q_{2n-1} \longrightarrow \Omega Q_{2n} \longrightarrow \Omega Q_{4n-1}. \]2. The sequence from (1) splits to yield an
 $R$-
$R$- ${\mathbb {A}}^1$-equivalence of the form
${\mathbb {A}}^1$-equivalence of the form
 \[ \Omega Q_{2n} {\stackrel{\sim}{\;\longrightarrow\;}} Q_{2n-1} \times \Omega Q_{4n-1}. \]
\[ \Omega Q_{2n} {\stackrel{\sim}{\;\longrightarrow\;}} Q_{2n-1} \times \Omega Q_{4n-1}. \]
Proof. The first statement is a special case of [Reference Wickelgren and WilliamsWW19, Theorem 8.3] applied to ![]() $\mathscr {X} = Q_{2n-1} \cong \Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$ (see [Reference Wickelgren and WilliamsWW19, Corollary 1.4]: by hypothesis,
$\mathscr {X} = Q_{2n-1} \cong \Sigma ^{n-1}{{\mathbf {G}}_{m}^{{\scriptstyle {\wedge }} n}}$ (see [Reference Wickelgren and WilliamsWW19, Corollary 1.4]: by hypothesis, ![]() $k$ is not formally real, and the parity condition from their statement is satisfied by construction). Thus, we obtain an
$k$ is not formally real, and the parity condition from their statement is satisfied by construction). Thus, we obtain an ![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
For the second point, the ![]() ${\mathbb {A}}^1$-fiber sequence in question remains an
${\mathbb {A}}^1$-fiber sequence in question remains an ![]() $R$-
$R$-![]() ${\mathbb {A}}^1$-fiber sequence, for example, by appeal to Theorem 4.3.11. The long exact sequence in
${\mathbb {A}}^1$-fiber sequence, for example, by appeal to Theorem 4.3.11. The long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves of the resulting fiber sequence takes the form
${\mathbb {A}}^1$-homotopy sheaves of the resulting fiber sequence takes the form
Since ![]() $k$ is not formally real,
$k$ is not formally real, ![]() $GW(k) \otimes R \cong R$ by Lemma 5.1.2. Consider the Whitehead square
$GW(k) \otimes R \cong R$ by Lemma 5.1.2. Consider the Whitehead square ![]() $[\iota,\iota ]$ of the identity map
$[\iota,\iota ]$ of the identity map ![]() $\iota$ on
$\iota$ on ![]() $Q_{2n}$; this corresponds to an
$Q_{2n}$; this corresponds to an ![]() ${\mathbb {A}}^1$-homotopy class of maps
${\mathbb {A}}^1$-homotopy class of maps ![]() $Q_{4n-1} \to Q_{2n}$ (see [Reference Asok, Wickelgren and WilliamsAWW17, § 4.1] for further discussion of Whitehead products in this motivic setting). The computation of
$Q_{4n-1} \to Q_{2n}$ (see [Reference Asok, Wickelgren and WilliamsAWW17, § 4.1] for further discussion of Whitehead products in this motivic setting). The computation of ![]() $\mathrm {H}$ on the Whitehead square of the identity is contained in [Reference Asok, Wickelgren and WilliamsAWW17, Theorem 4.4.1]; in this case, the relevant class lies in
$\mathrm {H}$ on the Whitehead square of the identity is contained in [Reference Asok, Wickelgren and WilliamsAWW17, Theorem 4.4.1]; in this case, the relevant class lies in ![]() $GW(k) \otimes R$. Indeed, it follows that this class is a unit
$GW(k) \otimes R$. Indeed, it follows that this class is a unit ![]() $GW(k) \otimes R$ under the hypotheses on
$GW(k) \otimes R$ under the hypotheses on ![]() $k$ and
$k$ and ![]() $R$. In other words, the simplicial loops of the Whitehead square of the identity yield a splitting of the
$R$. In other words, the simplicial loops of the Whitehead square of the identity yield a splitting of the ![]() ${\mathbb {A}}^1$-EHP sequence and thus a decomposition of the form
${\mathbb {A}}^1$-EHP sequence and thus a decomposition of the form
In essence, the argument we have given is a straightforward translation of Serre's proof to motivic homotopy theory; the results of [Reference Asok, Wickelgren and WilliamsAWW17, Reference Wickelgren and WilliamsWW19] guarantee that the necessary technology to make this translation sensible is in place.
In classical topology there is a ![]() ${\mathbb {Q}}$-fiber sequence
${\mathbb {Q}}$-fiber sequence ![]() $S^{2n} \to K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$, where the first map is given by the fundamental class and the second map is given by the squaring map. In motivic homotopy theory, the
$S^{2n} \to K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$, where the first map is given by the fundamental class and the second map is given by the squaring map. In motivic homotopy theory, the ![]() ${\mathbb {A}}^1$-weak equivalence
${\mathbb {A}}^1$-weak equivalence ![]() $Q_{2n} \cong {{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ shows that
$Q_{2n} \cong {{\mathbb {P}}^1}^{{\scriptstyle {\wedge }} n}$ shows that ![]() $\mathbf {M}(Q_{2n}) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n]$ in Voevodsky's derived category of motives. As a consequence
$\mathbf {M}(Q_{2n}) \cong {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n]$ in Voevodsky's derived category of motives. As a consequence ![]() $H^{2n,n}(Q_{2n},Z) = {\mathbb {Z}}$, and a choice of generator corresponds to an
$H^{2n,n}(Q_{2n},Z) = {\mathbb {Z}}$, and a choice of generator corresponds to an ![]() ${\mathbb {A}}^1$-homotopy class of maps
${\mathbb {A}}^1$-homotopy class of maps ![]() $Q_{2n} \to K({\mathbb {Z}}(n),2n)$. The following result, which refines and extends Proposition 5.3.10 is the second statement of Theorem 5 from the introduction.
$Q_{2n} \to K({\mathbb {Z}}(n),2n)$. The following result, which refines and extends Proposition 5.3.10 is the second statement of Theorem 5 from the introduction.
Theorem 5.3.11 If ![]() $k$ is a field that is not formally real, then, for any integer
$k$ is a field that is not formally real, then, for any integer ![]() $n \geq 1$, there is a
$n \geq 1$, there is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-fiber sequence of the form
${\mathbb {A}}^1$-fiber sequence of the form
where the first morphism is the fundamental class in motivic cohomology, and the second morphism is the squaring map.
Remark 5.3.12 The standard proof of the corresponding statement in classical topology goes as follows. One considers the squaring map ![]() $K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$, and then computes the rational cohomology of the homotopy fiber by a Serre spectral sequence argument. The map from
$K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$, and then computes the rational cohomology of the homotopy fiber by a Serre spectral sequence argument. The map from ![]() $S^{2n}$ to the homotopy fiber is easily seen to be a rational cohomology isomorphism and the result follows. Just as with Theorem 5.3.3, our proof of the corresponding motivic result is not a direct translation of this standard proof from topology. In addition to our lack of a usable Serre spectral sequence, there are ‘weight’ issues that would arise. In conjunction with Corollary 5.3.7, Theorem 5.3.11 gives another geometric interpretation of the Beilinson–Soulé vanishing conjecture; the resulting statement is our candidate for the natural motivic analog of the vanishing statement for rational homotopy groups of even-dimensional spheres.
$S^{2n}$ to the homotopy fiber is easily seen to be a rational cohomology isomorphism and the result follows. Just as with Theorem 5.3.3, our proof of the corresponding motivic result is not a direct translation of this standard proof from topology. In addition to our lack of a usable Serre spectral sequence, there are ‘weight’ issues that would arise. In conjunction with Corollary 5.3.7, Theorem 5.3.11 gives another geometric interpretation of the Beilinson–Soulé vanishing conjecture; the resulting statement is our candidate for the natural motivic analog of the vanishing statement for rational homotopy groups of even-dimensional spheres.
Proof. The cup square map corresponds to a morphism
As discussed before the statement, we may choose a map ![]() $Q_{2n} \to K({\mathbb {Z}}(n),2n)$ corresponding to a generator of
$Q_{2n} \to K({\mathbb {Z}}(n),2n)$ corresponding to a generator of ![]() $H^{2n,n}(Q_{2n},{\mathbb {Z}})$. Since
$H^{2n,n}(Q_{2n},{\mathbb {Z}})$. Since ![]() $\mathbf {M}(Q_{2n}) = {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n]$, the group
$\mathbf {M}(Q_{2n}) = {\mathbb {Z}} \oplus {\mathbb {Z}}(n)[2n]$, the group ![]() $H^{4n,2n}(Q_{2n},{\mathbb {Z}})$ vanishes and thus the composite map
$H^{4n,2n}(Q_{2n},{\mathbb {Z}})$ vanishes and thus the composite map ![]() $Q_{2n} \to K({\mathbb {Z}}(n),2n) \to K({\mathbb {Z}}(2n),4n)$ is null
$Q_{2n} \to K({\mathbb {Z}}(n),2n) \to K({\mathbb {Z}}(2n),4n)$ is null ![]() ${\mathbb {A}}^1$-homotopic. A choice of a null
${\mathbb {A}}^1$-homotopic. A choice of a null ![]() ${\mathbb {A}}^1$-homotopy yields a morphism fitting into the following diagram:
${\mathbb {A}}^1$-homotopy yields a morphism fitting into the following diagram:

Fix such a choice once and for all for the rest of this proof.
Since the spaces ![]() $K({\mathbb {Z}}(n),2n)$ and
$K({\mathbb {Z}}(n),2n)$ and ![]() $K({\mathbb {Z}}(2n),4n)$ are
$K({\mathbb {Z}}(2n),4n)$ are ![]() ${\mathbb {A}}^1$-simple, it follows from Theorem 3.3.7 that the
${\mathbb {A}}^1$-simple, it follows from Theorem 3.3.7 that the ![]() ${\mathbb {A}}^1$-homotopy fiber is
${\mathbb {A}}^1$-homotopy fiber is ![]() ${\mathbb {A}}^1$-nilpotent. In that case, Theorem 4.3.11 implies that the
${\mathbb {A}}^1$-nilpotent. In that case, Theorem 4.3.11 implies that the ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-localization of the induced fiber sequence
${\mathbb {A}}^1$-localization of the induced fiber sequence
is again an ![]() ${\mathbb {A}}^1$-fiber sequence. We want to show that the map
${\mathbb {A}}^1$-fiber sequence. We want to show that the map ![]() $Q_{2n} \to \mathscr {F}$ corresponding to our choice of null homotopy of the composite is a
$Q_{2n} \to \mathscr {F}$ corresponding to our choice of null homotopy of the composite is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence. Corollary 4.3.10 states that to check this morphism is a
${\mathbb {A}}^1$-weak equivalence. Corollary 4.3.10 states that to check this morphism is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence, it suffices to show that the induced map on
${\mathbb {A}}^1$-weak equivalence, it suffices to show that the induced map on ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-homotopy sheaves is an isomorphism.
${\mathbb {A}}^1$-homotopy sheaves is an isomorphism.
We first compute the ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $\mathscr {F}$. By appeal to Theorem 4.3.9,
$\mathscr {F}$. By appeal to Theorem 4.3.9, ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathrm {L}_{\mathbb {Q}} \mathscr {F}) = \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$. The
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathrm {L}_{\mathbb {Q}} \mathscr {F}) = \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$. The ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $K({\mathbb {Z}}(n),2n)$ and
$K({\mathbb {Z}}(n),2n)$ and ![]() $K({\mathbb {Z}}(2n),4n)$ may be computed by using the path-loop fibration
$K({\mathbb {Z}}(2n),4n)$ may be computed by using the path-loop fibration
and Theorem 5.3.3. In particular, we conclude that
Likewise, we conclude that
Putting these facts together, rationalizing the long exact sequence in ![]() ${\mathbb {A}}^1$-homotopy sheaves yields an exact sequence of the form
${\mathbb {A}}^1$-homotopy sheaves yields an exact sequence of the form
 \begin{align*} \cdots &\longrightarrow \boldsymbol{\pi}_{i}^{{\mathbb{A}}^1}(Q_{2n-1})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_{i}^{{\mathbb{A}}^1}(Q_{4n-1})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_i^{{\mathbb{A}}^1}(\mathscr{F})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_{i-1}^{{\mathbb{A}}^1}(Q_{2n-1})_{{\mathbb{Q}}}\\ &\longrightarrow \boldsymbol{\pi}_{i-1}^{{\mathbb{A}}^1}(Q_{4n-1})_{{\mathbb{Q}}} \longrightarrow \cdots. \end{align*}
\begin{align*} \cdots &\longrightarrow \boldsymbol{\pi}_{i}^{{\mathbb{A}}^1}(Q_{2n-1})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_{i}^{{\mathbb{A}}^1}(Q_{4n-1})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_i^{{\mathbb{A}}^1}(\mathscr{F})_{{\mathbb{Q}}} \longrightarrow \boldsymbol{\pi}_{i-1}^{{\mathbb{A}}^1}(Q_{2n-1})_{{\mathbb{Q}}}\\ &\longrightarrow \boldsymbol{\pi}_{i-1}^{{\mathbb{A}}^1}(Q_{4n-1})_{{\mathbb{Q}}} \longrightarrow \cdots. \end{align*}We claim that this sequence is canonically split.
Consider the cup-squaring map ![]() $K({\mathbb {Z}}(n),2n) \to K({\mathbb {Z}}(2n),4n)$. We claim that this map is null-
$K({\mathbb {Z}}(n),2n) \to K({\mathbb {Z}}(2n),4n)$. We claim that this map is null-![]() ${\mathbb {A}}^1$-homotopic after taking simplicial loops. Indeed, the map obtained by simplicial looping is adjoint to a map
${\mathbb {A}}^1$-homotopic after taking simplicial loops. Indeed, the map obtained by simplicial looping is adjoint to a map
Since cup-products are null-homotopic in a suspension, it follows that the above map is null-![]() ${\mathbb {A}}^1$-homotopic; this observation yields the claimed splitting.
${\mathbb {A}}^1$-homotopic; this observation yields the claimed splitting.
We use this observation now to show that the map ![]() $Q_{2n} \to \mathscr {F}$ described before the statement induces an isomorphism on homotopy sheaves, and is therefore a
$Q_{2n} \to \mathscr {F}$ described before the statement induces an isomorphism on homotopy sheaves, and is therefore a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence. We may directly compute the
${\mathbb {A}}^1$-weak equivalence. We may directly compute the ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-homotopy sheaves of
${\mathbb {A}}^1$-homotopy sheaves of ![]() $Q_{2n}$ by appeal to Proposition 5.3.10. Indeed, we observe that
$Q_{2n}$ by appeal to Proposition 5.3.10. Indeed, we observe that ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})_{{\mathbb {Q}}} \cong \boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}} \oplus \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$. To prove that the induced maps are isomorphisms, we just have to show that the induced maps on each summand are isomorphisms; this involves unwinding the definitions of the various maps.
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})_{{\mathbb {Q}}} \cong \boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}} \oplus \boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$. To prove that the induced maps are isomorphisms, we just have to show that the induced maps on each summand are isomorphisms; this involves unwinding the definitions of the various maps.
To see that the map ![]() $Q_{2n} \to \mathscr {F}$ induces an isomorphism on the summand
$Q_{2n} \to \mathscr {F}$ induces an isomorphism on the summand ![]() $\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ we proceed as follows. The summand of
$\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ we proceed as follows. The summand of ![]() $\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ in the
$\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ in the ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})_{{\mathbb {Q}}}$ arises via the map
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})_{{\mathbb {Q}}}$ arises via the map ![]() $Q_{2n-1} \to \Omega \Sigma Q_{2n-1} \cong \Omega Q_{2n}$ in the
$Q_{2n-1} \to \Omega \Sigma Q_{2n-1} \cong \Omega Q_{2n}$ in the ![]() ${\mathbb {A}}^1$-EHP sequence. Likewise, the summand of
${\mathbb {A}}^1$-EHP sequence. Likewise, the summand of ![]() $\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ in
$\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ in ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$ arises from the map
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$ arises from the map ![]() $\mathscr {F} \to K({\mathbb {Z}}(n),2n)$. We therefore have a diagram of the form
$\mathscr {F} \to K({\mathbb {Z}}(n),2n)$. We therefore have a diagram of the form

where the top left horizontal morphism arises from the EHP sequence, the leftmost vertical morphism is the fundamental class, the middle vertical morphism is obtained by applying ![]() $\Omega \Sigma$ to the leftmost vertical morphism, and the right vertical map is the simplicial loops of the map
$\Omega \Sigma$ to the leftmost vertical morphism, and the right vertical map is the simplicial loops of the map ![]() $\mathscr {F} \to K({\mathbb {Z}}(n),2n)$. By construction the composite of the top right horizontal morphism and the rightmost vertical morphism is the loops on the fundamental class
$\mathscr {F} \to K({\mathbb {Z}}(n),2n)$. By construction the composite of the top right horizontal morphism and the rightmost vertical morphism is the loops on the fundamental class ![]() $Q_{2n} \to K({\mathbb {Z}}(n),2n)$. The bottom right horizontal morphism exists by appeal to the suspension isomorphism in motivic cohomology: there is an isomorphism in motivic cohomology
$Q_{2n} \to K({\mathbb {Z}}(n),2n)$. The bottom right horizontal morphism exists by appeal to the suspension isomorphism in motivic cohomology: there is an isomorphism in motivic cohomology ![]() $H^{2n-1,n}(Q_{2n-1},{\mathbb {Z}}) \cong H^{2n,n}(Q_{2n},{\mathbb {Z}})$, and the resulting square commutes. The claim about the summand
$H^{2n-1,n}(Q_{2n-1},{\mathbb {Z}}) \cong H^{2n,n}(Q_{2n},{\mathbb {Z}})$, and the resulting square commutes. The claim about the summand ![]() $\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ then follows.
$\boldsymbol {\pi }_{i-1}^{{\mathbb {A}}^1}(Q_{2n-1})_{{\mathbb {Q}}}$ then follows.
The statement about the summand ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$ is obtained similarly. Indeed, as in the proof of Proposition 5.3.10, the summand in question in
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$ is obtained similarly. Indeed, as in the proof of Proposition 5.3.10, the summand in question in ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})$ arises from the choice of map
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{2n})$ arises from the choice of map ![]() $Q_{4n-1} \to Q_{2n}$; for concreteness we fix the one given by the
$Q_{4n-1} \to Q_{2n}$; for concreteness we fix the one given by the ![]() ${\mathbb {A}}^1$-homotopy class of the Whitehead square
${\mathbb {A}}^1$-homotopy class of the Whitehead square ![]() $[\iota,\iota ]$. This morphism fits into a square of the form
$[\iota,\iota ]$. This morphism fits into a square of the form

where the left vertical map is the fundamental class, and the bottom horizontal map is the map ![]() $\Omega K({\mathbb {Z}}(2n),4n) \to \mathscr {F}$ from the fiber sequence structure. Under the assumptions on
$\Omega K({\mathbb {Z}}(2n),4n) \to \mathscr {F}$ from the fiber sequence structure. Under the assumptions on ![]() $k$, the left vertical map is a
$k$, the left vertical map is a ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-weak equivalence, and the bottom horizontal map induces the summand of
${\mathbb {A}}^1$-weak equivalence, and the bottom horizontal map induces the summand of ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$ in
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(Q_{4n-1})_{{\mathbb {Q}}}$ in ![]() $\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$. This square commutes after rationalization. Indeed, the composite map
$\boldsymbol {\pi }_i^{{\mathbb {A}}^1}(\mathscr {F})_{{\mathbb {Q}}}$. This square commutes after rationalization. Indeed, the composite map ![]() $Q_{4n-1} \to Q_{2n} \to K({\mathbb {Z}}(n),2n)$ is null, and therefore lifts (rationally) to a map
$Q_{4n-1} \to Q_{2n} \to K({\mathbb {Z}}(n),2n)$ is null, and therefore lifts (rationally) to a map ![]() $Q_{4n-1} \to K({\mathbb {Z}}(2n),4n-1)$. The group of such homomorphisms is isomorphic to
$Q_{4n-1} \to K({\mathbb {Z}}(2n),4n-1)$. The group of such homomorphisms is isomorphic to ![]() ${\mathbb {Q}}$, so it suffices to observe that the lifted map is non-zero, in which case it is a multiple of the fundamental class. Since
${\mathbb {Q}}$, so it suffices to observe that the lifted map is non-zero, in which case it is a multiple of the fundamental class. Since ![]() $[\iota,\iota ]$ splits the
$[\iota,\iota ]$ splits the ![]() ${\mathbb {A}}^1$-EHP sequence, it induces the identity
${\mathbb {A}}^1$-EHP sequence, it induces the identity ![]() $\Omega Q_{4n-1} \to \Omega Q_{4n-1}$ and thus is not null-
$\Omega Q_{4n-1} \to \Omega Q_{4n-1}$ and thus is not null-![]() ${\mathbb {A}}^1$-homotopic.
${\mathbb {A}}^1$-homotopic.
Remark 5.3.13 If ![]() $k$ is a subfield of
$k$ is a subfield of ![]() ${\mathbb {C}}$, then the complex realization of the
${\mathbb {C}}$, then the complex realization of the ![]() ${\mathbb {Q}}$-
${\mathbb {Q}}$-![]() ${\mathbb {A}}^1$-fiber sequence of Theorem 5.3.11 is the
${\mathbb {A}}^1$-fiber sequence of Theorem 5.3.11 is the ![]() ${\mathbb {Q}}$-fiber sequence
${\mathbb {Q}}$-fiber sequence ![]() $S^{2n} \to K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$. This fact follows immediately from the fact that the complex realization of
$S^{2n} \to K({\mathbb {Z}},2n) \to K({\mathbb {Z}},4n)$. This fact follows immediately from the fact that the complex realization of ![]() $Q_{2n}$ is
$Q_{2n}$ is ![]() $S^{2n}$ and that the complex realizations of motivic Eilenberg–Mac Lane spaces of this form are corresponding ordinary Eilenberg–Mac Lane spaces [Reference VoevodskyVoe10, Corollary 3.48]. Indeed, the induced map
$S^{2n}$ and that the complex realizations of motivic Eilenberg–Mac Lane spaces of this form are corresponding ordinary Eilenberg–Mac Lane spaces [Reference VoevodskyVoe10, Corollary 3.48]. Indeed, the induced map ![]() $H^{2n,n}(Q_{2n},{\mathbb {Z}}) \to H^{2n}(S^{2n},{\mathbb {Z}})$ is precisely the cycle class map, which sends the fundamental class to the fundamental class, and a similar statement holds for the squaring map.
$H^{2n,n}(Q_{2n},{\mathbb {Z}}) \to H^{2n}(S^{2n},{\mathbb {Z}})$ is precisely the cycle class map, which sends the fundamental class to the fundamental class, and a similar statement holds for the squaring map.
Acknowledgements
The authors would like to thank Marc Hoyois for various discussions around the notion of nilpotence in ![]() ${\mathbb {A}}^1$-homotopy theory and Frédéric Déglise for discussions around the Beilinson–Soulé vanishing conjecture (in particular, for providing us with Lemma 5.3.6). The authors owe an intellectual debt to Peter Hilton, Guido Mislin and Joseph Roitberg: while there is very little explicit reference to the book [Reference Hilton, Mislin and RoitbergHMR75] elsewhere in this work, our presentation of nilpotence is inspired by theirs. Finally, the authors would like to thank the referees for numerous corrections, questions and helpful comments that clarified the exposition.
${\mathbb {A}}^1$-homotopy theory and Frédéric Déglise for discussions around the Beilinson–Soulé vanishing conjecture (in particular, for providing us with Lemma 5.3.6). The authors owe an intellectual debt to Peter Hilton, Guido Mislin and Joseph Roitberg: while there is very little explicit reference to the book [Reference Hilton, Mislin and RoitbergHMR75] elsewhere in this work, our presentation of nilpotence is inspired by theirs. Finally, the authors would like to thank the referees for numerous corrections, questions and helpful comments that clarified the exposition.