1. Introduction
Internal hydraulic jumps in stably stratified environments are observed in oceans, inland waters and the atmosphere. They occur in areas close to vertical and horizontal constrictions (Baines Reference Baines1984, Reference Baines1998). Internal hydraulic jumps in stably stratified environments can be traced back to studies by Long (Reference Long1953, Reference Long1954), Benton (Reference Benton1954) and Yih and Guha (Reference Yih and Guha1955). Also, Armi (Reference Armi1986) and Lawrence (Reference Lawrence1993) conducted investigations on the hydraulics of two-layer flows and reviewed previous work in this field. Most internal jump investigations have assumed the pressure to remain hydrostatic and, generally, have ignored mixing across the interface.
Entrainment and mixing across density interfaces are relevant in geophysical and environmental applications. Among many natural and industrial thermohaline applications, the brilliant idea of Stommel and Farmer (Reference Stommel and Farmer1953) of controlling mixing in stratified fjords and channels has motivated this ongoing research. Furthermore, this work is related to internal hydraulic jumps observed in the ocean. An example is the well-documented internal hydraulic jump of the Strait of Gibraltar (Armi and Farmer Reference Armi and Farmer1988; Thorpe et al. Reference Thorpe, Malarkey, Voet, Alford, Girton and Carter2018 and others). This narrow passage connects salty warm water from the Mediterranean Sea to less salty and cooler water from the Atlantic Ocean. In this ocean water exchange, the buoyancy arising from temperature and that from salinity are in opposite directions. And, as will be shown in this paper, such a condition can produce significant nonlinear buoyancy effects.
Wilkinson and Wood (Reference Wilkinson and Wood1971) investigated the miscible behaviour of an internal jump. They carried out a stationary miscible jump analysis by applying a one-dimensional momentum equation. They introduced the concept of a density jump by considering entrainment of ambient fluid. Research on miscible internal jumps in two-layer systems has also been carried out by many researchers including Chu and Baddour (Reference Chu and Baddour1977), Baddour and Abbink (Reference Baddour and Abbink1983), Wood and Simpson (Reference Wood and Simpson1984), Baddour (Reference Baddour1987), Holland et al. (Reference Holland, Rosales, Stefanica and Tabak2002), Hassid, Regev & Poreh (Reference Hassid, Regev and Poreh2007), Thorpe and Li (Reference Thorpe and Li2014), Ogden and Helfrich (Reference Ogden and Helfrich2016), Baines (Reference Baines2016) and others.
Baddour (Reference Baddour1991) defined the thermal hydraulic jump as a jump where the density field is only a function of temperature. This function of temperature in water applications is nonlinear. However, a saline hydraulic jump is a jump where the density field is only a function of salinity, and therefore, the temperature is constant. The saline jump is equivalent to the density jump introduced by Wilkinson and Wood (Reference Wilkinson and Wood1971) because the density is practically a linear function of salinity. For the more general case of a thermohaline jump considered here, the temperature and salinity can vary, and both contribute to the buoyancy field.
In water applications of internal hydraulic jumps, the density field has commonly been determined using a simplified linear water equation of state. The accuracy of this assumption was examined by Baddour (Reference Baddour1991), where, under winter conditions, the nonlinearity of the equation of state had profound effects on the flow. In fact, the flow development in the jump region was significantly altered when the temperature of ambient water was between 0 and 15 °C.
This study considers miscible entraining thermohaline jumps. As mentioned above, temperature and salt are both possible contributors to the buoyancy. As clearly demonstrated by Dadonau, Partridge & Linden (Reference Dadonau, Partridge and Linden2020), double diffusive effects in thermohaline jets are diminished, close to the source, as the Reynolds number is increased. It is assumed in this study that the Reynolds number is sufficiently large and double diffusion is not altering the flow dynamics in the jump region.
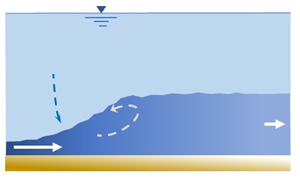
The flows under consideration are illustrated in figure 1, where internal jumps are created by highly turbulent (Reynolds number ![]() $R{e_0} \gg 1$) and supercritical (Froude number
$R{e_0} \gg 1$) and supercritical (Froude number ![]() $F{r_0} > 1$) discharge
$F{r_0} > 1$) discharge ![]() ${Q_0}$, of width
${Q_0}$, of width ![]() ${b_0}$, depth
${b_0}$, depth ![]() ${h_0}$, temperature
${h_0}$, temperature ![]() ${T_0}$ and salinity
${T_0}$ and salinity ![]() ${S_0}$. The flow occurs either at the free surface (see overflow in figure 1a) or along the bottom (see underflow in figure 1b). The deep receiving ambient water has a temperature
${S_0}$. The flow occurs either at the free surface (see overflow in figure 1a) or along the bottom (see underflow in figure 1b). The deep receiving ambient water has a temperature ![]() ${T_a}$, salinity
${T_a}$, salinity ![]() ${S_a}$ and a width
${S_a}$ and a width ![]() ${b_1} \ge \,\,{b_0}$. The temperature and salinity are such that the flow is stably stratified throughout the region of interest. Note, because of nonlinear thermohaline buoyancy, a turbulent flow, which is initially stably stratified, is not necessarily stably stratified after mixing (Turner Reference Turner1966). Thermohaline jumps exhibiting reversible buoyancy arising from entrainment are not considered in this paper.
${b_1} \ge \,\,{b_0}$. The temperature and salinity are such that the flow is stably stratified throughout the region of interest. Note, because of nonlinear thermohaline buoyancy, a turbulent flow, which is initially stably stratified, is not necessarily stably stratified after mixing (Turner Reference Turner1966). Thermohaline jumps exhibiting reversible buoyancy arising from entrainment are not considered in this paper.

Figure 1. Definition sketches of stationary entraining thermohaline jumps upstream of vertical and horizontal constrictions, showing (a) side-view of overflow, (b) side-view of underflow and (c) top-view of overflow and underflow.
The entraining thermohaline jump is a rapidly varying phenomenon associated with changes in velocity, temperature, salinity and depth. Similar to a single-layer open channel flow, the internal jump is a transition from a supercritical flow ![]() $(F{r_0} > 1)$ to a subcritical flow
$(F{r_0} > 1)$ to a subcritical flow ![]() $(F{r_1} < 1)$ (Henderson Reference Henderson1966). Owing to the entrainment of ambient fluid, the discharge (or flow rate) increases in the jump region from
$(F{r_1} < 1)$ (Henderson Reference Henderson1966). Owing to the entrainment of ambient fluid, the discharge (or flow rate) increases in the jump region from ![]() ${Q_0}$ to
${Q_0}$ to ![]() ${Q_1}$, the temperature changes from
${Q_1}$, the temperature changes from ![]() ${T_0}$ to
${T_0}$ to ![]() ${T_1}$ and salinity from
${T_1}$ and salinity from ![]() ${S_0}$ to
${S_0}$ to ![]() ${S_1}$. The depth of the mixed layer downstream of the jump is h 1 and its width is b 1. Two horizontal eddies are observed when the jump is three-dimensional (b 1 > b 0). The temperature and salinity in these horizontal eddies, which are attached to the upstream wall, are Te and Se. The laboratory experiment by Guo (Reference Guo1992) indicated that Te ≈ T 1 and Se ≈ S 1. Further downstream of the jump, vertical and/or horizontal constrictions of height Zc and width bc provide hydraulic controls, through which the flow is critical
${S_1}$. The depth of the mixed layer downstream of the jump is h 1 and its width is b 1. Two horizontal eddies are observed when the jump is three-dimensional (b 1 > b 0). The temperature and salinity in these horizontal eddies, which are attached to the upstream wall, are Te and Se. The laboratory experiment by Guo (Reference Guo1992) indicated that Te ≈ T 1 and Se ≈ S 1. Further downstream of the jump, vertical and/or horizontal constrictions of height Zc and width bc provide hydraulic controls, through which the flow is critical ![]() $(F{r_c} = 1)$.
$(F{r_c} = 1)$.
Thermohaline buoyancy will first be derived in § 2, based on a seawater equation of state, which is nonlinear in temperature and linear in salinity. The thermohaline buoyancy will then be applied in § 3 to the conservation equations of temperature, salt and momentum. These simple basic equations reveal the nonlinear mixing behaviour of thermohaline jumps. Although, the miscible jump solutions obtained are not unique, they are clearly defining maximum entraining conditions, which are of practical interest. A matching technique will be used in § 4 to examine how downstream boundary conditions by vertical and/or horizontal constrictions determine unique jump solutions. Finally, in § 5, the internal jump theory will be compared with the two-dimensional (2-D) and three-dimensional (3-D) experiments by Guo (Reference Guo1992).
2. Thermohaline buoyancy
The international equation of state for seawater (Millero and Poisson Reference Millero and Poisson1981), which has a temperature T (°C) and salinity S (ppt or g kg−1) is shown in figure 2. This equation is nonlinear throughout the range of temperature and salinity of interest (T = 0–40 °C and S = 0–40 ppt), and for all practical purposes can be expressed as
where ρ is the density of water in kg m−3, and f 1 and f 2 are nonlinear functions of temperature. The function f 1 represents the density of pure fresh water, as determined by Bigg (Reference Bigg1967). The function f 2 was determined in this study by fitting the salinity term of (2.1) to the salinity terms of the international equation of state for seawater by Millero and Poisson (Reference Millero and Poisson1981). With f 1 and f 2 expressed as polynomials, the equation of state for seawater becomes
 \begin{equation}\rho (T,S) = \mathop \sum \limits_{i = 0}^n {a_i}{T^i} + S\mathop \sum \limits_{i = 0}^m {b_i}{T^i}.\end{equation}
\begin{equation}\rho (T,S) = \mathop \sum \limits_{i = 0}^n {a_i}{T^i} + S\mathop \sum \limits_{i = 0}^m {b_i}{T^i}.\end{equation}A linearized equation of state, which has been widely adopted for ocean and inland water modelling is (Whitehead Reference Whitehead1995)
where ![]() ${\rho _0}$ is a reference density,
${\rho _0}$ is a reference density, ![]() $\alpha $ a negative thermal expansion coefficient and
$\alpha $ a negative thermal expansion coefficient and ![]() $\beta $ a positive saline contraction coefficient. It will be shown that such linear simplification is not always adequate. Brydon, Sun & Bleck (Reference Brydon, Sun and Bleck1999) and Nycander, Hieronymus & Roquet (Reference Nycander, Hieronymus and Roquet2015) and others have also emphasized the need to apply a nonlinear equation of state for ocean modelling.
$\beta $ a positive saline contraction coefficient. It will be shown that such linear simplification is not always adequate. Brydon, Sun & Bleck (Reference Brydon, Sun and Bleck1999) and Nycander, Hieronymus & Roquet (Reference Nycander, Hieronymus and Roquet2015) and others have also emphasized the need to apply a nonlinear equation of state for ocean modelling.

Figure 2. Contour lines of seawater density ![]() $\rho $ (kg m−3) as a function of temperature T (°C) and salinity S (ppt) in the range of temperature (0–40 °C) and salinity (0–40 ppt).
$\rho $ (kg m−3) as a function of temperature T (°C) and salinity S (ppt) in the range of temperature (0–40 °C) and salinity (0–40 ppt).
The degrees of the polynomials in (2.2) required to obtain accurate densities throughout the range of temperature and salinity of interest are n = 5 and m = 2. The constants of these two polynomials are (Baddour Reference Baddour1994) a 0 = 999.842594, a 1 = 6.793952 × 10−2, a 2 = −9.095290 × 10−3, a 3 = 1.001685 × 10−4, a 4 = −1.120083 × 10−6, a 5 = 6.536332 × 10−9, b 0 = 0.806924, b 1 = −3.042878 × 10−3 and b 2 = 3.280458 × 10−5. Densities calculated with (2.2) and the international equation of state at standard atmospheric pressure by Millero and Poisson (Reference Millero and Poisson1981) are practically identical, with differences not exceeding 0.08 % throughout the range of temperature and salinity of interest. Millero (Reference Millero2010) provided an interesting historical account of the international seawater equation of state.
Density anomalies, and related buoyancy, were obtained in this study by transforming the coordinate system of (2.2) from ![]() $(T,\,S,\,\rho )$ to
$(T,\,S,\,\rho )$ to ![]() $(\Delta T,\,\Delta S,\,\Delta \rho )$, where Δ represents an excess quantity relative to the ambient state (i.e.
$(\Delta T,\,\Delta S,\,\Delta \rho )$, where Δ represents an excess quantity relative to the ambient state (i.e. ![]() $\Delta T = T - {T_a}$,
$\Delta T = T - {T_a}$, ![]() $\Delta S = S - {S_a}$ and
$\Delta S = S - {S_a}$ and ![]() $\Delta \rho = \rho - {\rho _a}$) and suffix a refers to the state of ambient water. This transformation was achieved, as illustrated in figure 3, by moving the origin of the frame of reference from (0,0,0) to
$\Delta \rho = \rho - {\rho _a}$) and suffix a refers to the state of ambient water. This transformation was achieved, as illustrated in figure 3, by moving the origin of the frame of reference from (0,0,0) to ![]() $({T_a},\,{S_a},\,{\rho _a})$. Note the new origin at
$({T_a},\,{S_a},\,{\rho _a})$. Note the new origin at ![]() $({T_a},\,{S_a},\,{\rho _a})$ lies on the equation of state surface (see figure 3).
$({T_a},\,{S_a},\,{\rho _a})$ lies on the equation of state surface (see figure 3).

Figure 3. Transformation of the equation of state obtained by moving the origin of the frame reference from (0,0,0) to ![]() $({T_a},\,{S_a},\,{\rho _a})$.
$({T_a},\,{S_a},\,{\rho _a})$.
The polynomial transformation, defined above, gives the following expression for the density anomaly:
 \begin{equation}\Delta \rho = \sum\limits_{i = 1}^n {{a_i}\Delta {T^i}} + {S_a}\left( {\sum\limits_{i = 1}^m {{\beta_i}\Delta {T^i}} } \right)\,+\, \Delta S\, \left( {{\beta_0} + \sum\limits_{i = 1}^m {{\beta_i}\Delta {T^i}}} \right),\end{equation}
\begin{equation}\Delta \rho = \sum\limits_{i = 1}^n {{a_i}\Delta {T^i}} + {S_a}\left( {\sum\limits_{i = 1}^m {{\beta_i}\Delta {T^i}} } \right)\,+\, \Delta S\, \left( {{\beta_0} + \sum\limits_{i = 1}^m {{\beta_i}\Delta {T^i}}} \right),\end{equation}where
 \begin{gather}{\alpha _i} = \mathop \sum \limits_{j = i}^n \left( {\begin{array}{*{20}{c}} j\\ i \end{array}} \right){a_j}T_a^{j - i};\quad i = 1,n,\end{gather}
\begin{gather}{\alpha _i} = \mathop \sum \limits_{j = i}^n \left( {\begin{array}{*{20}{c}} j\\ i \end{array}} \right){a_j}T_a^{j - i};\quad i = 1,n,\end{gather} \begin{gather}{\beta _0} = \mathop \sum \limits_{j = 0}^m {b_j}T_a^j,\end{gather}
\begin{gather}{\beta _0} = \mathop \sum \limits_{j = 0}^m {b_j}T_a^j,\end{gather} \begin{gather}{\beta _i} = \mathop \sum \limits_{j = i}^m \left( {\begin{array}{*{20}{c}} j\\ i \end{array}} \right){b_j}T_a^{j - i}; \quad i = 1,m.\end{gather}
\begin{gather}{\beta _i} = \mathop \sum \limits_{j = i}^m \left( {\begin{array}{*{20}{c}} j\\ i \end{array}} \right){b_j}T_a^{j - i}; \quad i = 1,m.\end{gather}
For n = 5, the coefficients ![]() ${\alpha _i}$ are
${\alpha _i}$ are
 \begin{equation}\left. {\begin{array}{*{20}{@{}c}} {{\alpha_1} = {a_1} + 2{a_2}{T_a} + 3{a_3}T_a^2 + 4{a_4}T_a^3 + 5{a_5}T_a^4}\\ {{\alpha_2} = {a_2} + 3{a_3}{T_a} + 6{a_4}T_a^2 + 10{a_5}T_a^3}\\ {{\alpha_3} = {a_3} + 4{a_4}{T_a} + 10{a_5}T_a^2}\\ {{\alpha_4} = {a_4} + 5{a_5}{T_a}}\\ {{\alpha_5} = {a_5}} \end{array}} \right\},\end{equation}
\begin{equation}\left. {\begin{array}{*{20}{@{}c}} {{\alpha_1} = {a_1} + 2{a_2}{T_a} + 3{a_3}T_a^2 + 4{a_4}T_a^3 + 5{a_5}T_a^4}\\ {{\alpha_2} = {a_2} + 3{a_3}{T_a} + 6{a_4}T_a^2 + 10{a_5}T_a^3}\\ {{\alpha_3} = {a_3} + 4{a_4}{T_a} + 10{a_5}T_a^2}\\ {{\alpha_4} = {a_4} + 5{a_5}{T_a}}\\ {{\alpha_5} = {a_5}} \end{array}} \right\},\end{equation}
and for m = 2, the coefficients ![]() ${\beta _i}$ are
${\beta _i}$ are
 \begin{equation}\left. {\begin{array}{*{20}{@{}c}} {{\beta_0} = {b_0} + {b_1}{T_a} + {b_2}T_a^2}\\ {{\beta_1} = {b_1} + 2{b_2}{T_a}}\\ {{\beta_2} = {b_2}} \end{array}} \right\}.\end{equation}
\begin{equation}\left. {\begin{array}{*{20}{@{}c}} {{\beta_0} = {b_0} + {b_1}{T_a} + {b_2}T_a^2}\\ {{\beta_1} = {b_1} + 2{b_2}{T_a}}\\ {{\beta_2} = {b_2}} \end{array}} \right\}.\end{equation}
A positive value of Δρ indicates an excess density compared to the ambient state (downward buoyancy), and a negative Δρ is a density deficit (i.e. upward buoyancy). Equation (2.4) is shown in figure 4 for a state of ambient water given by Ta = 20 °C and Sa = 30 ppt. This transformation is defining the positive and negative buoyancy regimes for any combinations of temperature difference ![]() $\Delta T = T - {T_a}$ and salinity difference
$\Delta T = T - {T_a}$ and salinity difference ![]() $\Delta S = S - {S_a}$. Equation (2.4), which is plotted in figure 4, will be applied in the following section to determine the buoyancy associated with temperature and salinity differences in thermohaline jumps.
$\Delta S = S - {S_a}$. Equation (2.4), which is plotted in figure 4, will be applied in the following section to determine the buoyancy associated with temperature and salinity differences in thermohaline jumps.

Figure 4. Density anomaly ![]() $\mathrm{\Delta }\rho = \rho - {\rho _a}$ (kg m−3) calculated with (2.4) as a function of temperature difference
$\mathrm{\Delta }\rho = \rho - {\rho _a}$ (kg m−3) calculated with (2.4) as a function of temperature difference ![]() $\mathrm{\Delta }T = T - {T_a}$ (°C) and salinity difference
$\mathrm{\Delta }T = T - {T_a}$ (°C) and salinity difference ![]() $\mathrm{\Delta }S = S - {S_a}$ (ppt) for ambient water conditions Ta = 20 °C and Sa = 30 ppt.
$\mathrm{\Delta }S = S - {S_a}$ (ppt) for ambient water conditions Ta = 20 °C and Sa = 30 ppt.
3. Thermohaline internal hydraulic jumps
3.1. Governing equations
The basic assumptions in the following analysis are: (i) discharge and ambient water conditions are steady; (ii) velocity, temperature and salinity profiles are uniform at the exit and downstream of the jump; (iii) density difference is everywhere relatively small ![]() $(\Delta \rho /{\rho _a} \ll 1)$, which allows for the Boussinesq's approximation to be applied; (iv) discharge Reynolds number is high, which produces strong mixing with minimal manifestation of double diffusion; (v) the water in the horizontal eddies attached to the vertical upstream wall of three-dimensional jumps has temperature and salinity similar to the mixed water downstream of the jump, and (vi) heat and salt are conserved.
$(\Delta \rho /{\rho _a} \ll 1)$, which allows for the Boussinesq's approximation to be applied; (iv) discharge Reynolds number is high, which produces strong mixing with minimal manifestation of double diffusion; (v) the water in the horizontal eddies attached to the vertical upstream wall of three-dimensional jumps has temperature and salinity similar to the mixed water downstream of the jump, and (vi) heat and salt are conserved.
Based on these assumptions, the governing equations for the temperature, salt and momentum of a stationary internal jump are
In all the equations, subscript 0 refers to the supercritical flow upstream of the jump and subscript 1 to the subcritical flow downstream of the jump. The magnitude of the initial buoyancy (or effective gravity) upstream is ![]() ${g^{\prime}_0} = g|\Delta {\rho _0}|/{\rho _a}$ and downstream is
${g^{\prime}_0} = g|\Delta {\rho _0}|/{\rho _a}$ and downstream is ![]() ${g^{\prime}_1} = g|\Delta {\rho _1}|/{\rho _a}$, and g is the constant gravity.
${g^{\prime}_1} = g|\Delta {\rho _1}|/{\rho _a}$, and g is the constant gravity.
The left-hand side of (3.3) represents the net flux of momentum in the jump region and the right-hand side of (3.3) represents the net hydrostatic force, which includes a component exerted by the upstream wall of width (b 1 – b 0).
In addition to the above governing equations, it is important to recognize that the jump solutions cannot physically be associated with a gain of energy. This condition requires the total energy head of the flow downstream of the jump to be less than upstream of the jump. When the velocity profiles are uniform upstream and downstream of the jump, the total energy head is given by (Henderson Reference Henderson1966)
and ![]() $U = Q/(bh)$ is a cross-sectional average velocity.
$U = Q/(bh)$ is a cross-sectional average velocity.
Hence, the energy constraint on the jump solution is
3.2. Nonlinear thermohaline mixing
Dilution resulting from ambient water entrainment into the jump is directly related to the ratio of discharge downstream and upstream of the jump. Hence, from (3.1) and (3.2), we can define the dilution in the jump as
The effect of dilution (or mixing) on thermohaline buoyancy was first examined using (2.4) and (3.6). For a given dilution ![]() $\mu$ and initial values
$\mu$ and initial values ![]() $\mathrm{\Delta }{T_0}$ and
$\mathrm{\Delta }{T_0}$ and ![]() $\mathrm{\Delta }{S_0}$, (3.6) gives the excess temperature
$\mathrm{\Delta }{S_0}$, (3.6) gives the excess temperature ![]() $\mathrm{\Delta }{T_1}$ and excess salinity
$\mathrm{\Delta }{T_1}$ and excess salinity ![]() $\mathrm{\Delta }{S_1}$ of the mixed fluid downstream of the jump. These properties of the mixed fluid are then translated into excess density
$\mathrm{\Delta }{S_1}$ of the mixed fluid downstream of the jump. These properties of the mixed fluid are then translated into excess density ![]() $\Delta {\rho _1}$ using (2.4). Results obtained in this manner are plotted in figure 5 and compared with the mixing behaviour based on the linearized equation of state (2.3).
$\Delta {\rho _1}$ using (2.4). Results obtained in this manner are plotted in figure 5 and compared with the mixing behaviour based on the linearized equation of state (2.3).

Figure 5. Comparison of linear and nonlinear mixing behaviour for thermohaline underflow and overflow jumps.
The density anomaly ratio ![]() $\Delta {\rho _0}/\Delta {\rho _1}$ for a linear equation of state, is simply
$\Delta {\rho _0}/\Delta {\rho _1}$ for a linear equation of state, is simply
 \begin{equation}\frac{{\mathrm{\Delta }{\rho _0}}}{{\mathrm{\Delta }{\rho _1}}} = \frac{{\alpha \mathrm{\Delta }{T_0} + \beta \mathrm{\Delta }{S_0}}}{{\alpha \mathrm{\Delta }{T_1} + \beta \mathrm{\Delta }{S_1}}} = \frac{{\alpha \mathrm{\Delta }{T_0} + \beta \mathrm{\Delta }{S_0}}}{{\alpha \frac{{\mathrm{\Delta }{T_0}}}{\mu } + \beta \frac{{\mathrm{\Delta }{S_0}}}{\mu }}} = \mu .\end{equation}
\begin{equation}\frac{{\mathrm{\Delta }{\rho _0}}}{{\mathrm{\Delta }{\rho _1}}} = \frac{{\alpha \mathrm{\Delta }{T_0} + \beta \mathrm{\Delta }{S_0}}}{{\alpha \mathrm{\Delta }{T_1} + \beta \mathrm{\Delta }{S_1}}} = \frac{{\alpha \mathrm{\Delta }{T_0} + \beta \mathrm{\Delta }{S_0}}}{{\alpha \frac{{\mathrm{\Delta }{T_0}}}{\mu } + \beta \frac{{\mathrm{\Delta }{S_0}}}{\mu }}} = \mu .\end{equation}This linear mixing behaviour is represented in figure 5 by the 1:1 slope line.
As illustrated in figure 6, the nonlinearity and concave downward curvature of the equation of state are responsible for producing density ratios ![]() ${{\Delta {\rho _o}} / {\Delta {\rho _1}}}\,\gt\,\mu$ for overflows and
${{\Delta {\rho _o}} / {\Delta {\rho _1}}}\,\gt\,\mu$ for overflows and ![]() ${{\Delta {\rho _o}} / {\Delta {\rho _1}}}\,\lt\,\mu$ for underflows.
${{\Delta {\rho _o}} / {\Delta {\rho _1}}}\,\lt\,\mu$ for underflows.

Figure 6. Schematic illustration of linear and nonlinear (concave downward) mixing behaviour for underflows and overflows.
3.3. Non-dimensional governing equations
To generalize the results, the momentum equation (3.3) and the energy equation (3.5) are first expressed in non-dimensional forms as
Momentum Equation:
Energy Equation:
Here, the discharge Froude number ![]() $F{r_0} = {Q_0}/\sqrt {({{g^{\prime}}_0}b_0^2h_0^3)} $, the depth ratio across the jump r = h 1/h 0 and the jump enlargement ratio β = b 1/b 0. Note, because of nonlinear mixing, the buoyancy flux across the jump is not conserved. In other words,
$F{r_0} = {Q_0}/\sqrt {({{g^{\prime}}_0}b_0^2h_0^3)} $, the depth ratio across the jump r = h 1/h 0 and the jump enlargement ratio β = b 1/b 0. Note, because of nonlinear mixing, the buoyancy flux across the jump is not conserved. In other words, ![]() ${g^{\prime}_0}{Q_0} \ne {g^{\prime}_1}{Q_1}$ and therefore the dilution
${g^{\prime}_0}{Q_0} \ne {g^{\prime}_1}{Q_1}$ and therefore the dilution ![]() $\mu = {Q_1}/{Q_0} \ne {g^{\prime}_0}/{g^{\prime}_1}$ . The buoyancy flux for linear mixing is, of course, conserved because
$\mu = {Q_1}/{Q_0} \ne {g^{\prime}_0}/{g^{\prime}_1}$ . The buoyancy flux for linear mixing is, of course, conserved because ![]() $\mu = \mathrm{\Delta }{\rho _0}/\mathrm{\Delta }{\rho _1} = {g^{\prime}_0}/{g^{\prime}_1}$, and (3.8) reduces to
$\mu = \mathrm{\Delta }{\rho _0}/\mathrm{\Delta }{\rho _1} = {g^{\prime}_0}/{g^{\prime}_1}$, and (3.8) reduces to
For a 2-D flow ![]() ${b_1} = {b_0}$, hence
${b_1} = {b_0}$, hence ![]() $\beta = 1$ and
$\beta = 1$ and
from which the classical hydraulic jump equation is correctly recovered by setting the dilution ![]() $\mu$ = 1 (Rouse Reference Rouse1946):
$\mu$ = 1 (Rouse Reference Rouse1946):
And the only positive subcritical solution, shown in figure 7, of this quadratic equation is the well-known hydraulics formula:
The dilution properties of internal hydraulic jumps were next examined by plotting the general (3.8) as ![]() $r = f(\mu )$, by setting both the discharge Froude number Fr 0 and channel enlargement ration
$r = f(\mu )$, by setting both the discharge Froude number Fr 0 and channel enlargement ration ![]() $\beta $ to be constants. These plots were obtained with an exact algorithm for determining all the real and imaginary roots of a cubic equation. The jump immiscible (
$\beta $ to be constants. These plots were obtained with an exact algorithm for determining all the real and imaginary roots of a cubic equation. The jump immiscible (![]() $\mu$ = 1) and miscible (
$\mu$ = 1) and miscible (![]() $\mu$ >1) solutions are illustrated in figure 7. For the quiescent and deep ambient water condition, the miscible jump solutions always form closed loops in the
$\mu$ >1) solutions are illustrated in figure 7. For the quiescent and deep ambient water condition, the miscible jump solutions always form closed loops in the ![]() $\mu$–r plane. The loops are connected to the origin (r = 0,
$\mu$–r plane. The loops are connected to the origin (r = 0, ![]() $\mu$ = 0) and the size of the loop increases vertically with Fr 0 and horizontally with β. The upper branch (solid line in figure 7) of a loop is subcritical
$\mu$ = 0) and the size of the loop increases vertically with Fr 0 and horizontally with β. The upper branch (solid line in figure 7) of a loop is subcritical ![]() $(F{r_1} = {Q_1}/\sqrt {({{g^{\prime}}_1}b_1^2h_1^3)} < 1)$ and the lower branch is supercritical (Fr 1 > 1). The subcritical and supercritical branches meet at the origin (0,0) as well as at a point where the flow is critical (Frc = 1) and where the dilution is reaching a maximum value
$(F{r_1} = {Q_1}/\sqrt {({{g^{\prime}}_1}b_1^2h_1^3)} < 1)$ and the lower branch is supercritical (Fr 1 > 1). The subcritical and supercritical branches meet at the origin (0,0) as well as at a point where the flow is critical (Frc = 1) and where the dilution is reaching a maximum value ![]() $\mu$c.
$\mu$c.

Figure 7. Dilution diagram of internal hydraulic jumps in deep and quiescent ambient water according to the momentum equation (3.8) and for Fr 0 = const. and β = const.
The maximum possible dilution occurring in a channel is of practical interest. Differentiating (3.10) and setting ![]() $\textrm{d}\mu /\textrm{d}r = 0$, the maximum dilution for linear mixing is
$\textrm{d}\mu /\textrm{d}r = 0$, the maximum dilution for linear mixing is
and the critical depth is
Similar results for nonlinear mixing are obtained numerically using (3.8). Figure 8 shows results from (3.8) in the physical domain ![]() $(r \ge 0,\,\mu \ge 1)$ for thermohaline jumps under linear and nonlinear mixing conditions. Effects of nonlinear mixing on maximum dilution
$(r \ge 0,\,\mu \ge 1)$ for thermohaline jumps under linear and nonlinear mixing conditions. Effects of nonlinear mixing on maximum dilution ![]() $\mu$c are also presented in figure 9. It is evident from both figures 8 and 9 that nonlinear mixing increases the dilution and depth of thermohaline overflow jumps and decreases the dilution and depth of thermohaline underflow jumps. The results also indicate that nonlinear mixing effects are more significant when buoyancy arising from temperature and that from salinity are acting in opposite directions.
$\mu$c are also presented in figure 9. It is evident from both figures 8 and 9 that nonlinear mixing increases the dilution and depth of thermohaline overflow jumps and decreases the dilution and depth of thermohaline underflow jumps. The results also indicate that nonlinear mixing effects are more significant when buoyancy arising from temperature and that from salinity are acting in opposite directions.

Figure 8. Dilution properties of stationary entraining thermohaline jumps obtained with (3.8), Fr 0 = 10, Ta = 20 °C and Sa = 30 ppt: (a) overflow, ΔS 0 = −5 ppt; and (b) underflow, ΔS 0 = +5 ppt.

Figure 9. Maximum dilution of stationary entraining thermohaline jumps obtained with (3.8), Ta = 20 °C, Sa = 30 ppt: (a) overflow, ΔS 0 = −5 ppt; and (b) underflow, ΔS 0 = +5 ppt.
3.4. Energy considerations
Energy constraints on miscible jumps given by (3.9) are examined in figure 10. Total energy heads for overflow jumps are plotted in figure 10(a) for linear and nonlinear mixing conditions. Similar results for underflow jumps are presented in figure 10(b). Figure 10(a) shows that nonlinear mixing systematically increases the total head of the supercritical and subcritical branches of the overflow jump. The opposite effect can be seen in figure 10(b), where nonlinear mixing decreases the total head of the underflow jump. Consistent with the results obtained from the momentum equation, the nonlinearity effects on the total energy head were more pronounced when the buoyancy arising from temperature and that from salinity were acting in opposite directions. Furthermore, the total head H/h 0 of the supercritical branches were always smaller than the initial total head H 0/h 0, but always higher than the total head of the subcritical branches. This observation indicates, on energetic grounds, that the miscible entraining thermohaline jump is a physically possible transition from supercritical to subcritical flow, and not vice versa.
4. Downstream hydraulic control
Effects of downstream boundary conditions on the miscible jump solutions obtained in § 3 are analysed here. The assumptions of this analysis are: (i) there is no entrainment of ambient water in the subcritical region downstream of the jump; (ii) there is no loss of energy in the short distance separating the jump from the channel end; (iii) a hydraulic control is established at the section of maximum vertical and/or horizontal contraction, where flow reaches a critical state in a manner similar to single-layer open channel hydraulics (Henderson Reference Henderson1966).
For a maximum height of sill Zc, which coincides with a minimum channel width bc, the critical flow condition is ![]() $Fr_c^2 = Q_1^2/{g^{\prime}_1}b_c^2h_c^3 = 1$ and the critical depth
$Fr_c^2 = Q_1^2/{g^{\prime}_1}b_c^2h_c^3 = 1$ and the critical depth ![]() ${h_c} = {(Q_1^2/{g^{\prime}_1}b_c^2)^{1/3}}$ (Henderson Reference Henderson1966).
${h_c} = {(Q_1^2/{g^{\prime}_1}b_c^2)^{1/3}}$ (Henderson Reference Henderson1966).
Because there is no entrainment downstream of the jump, the discharge remains constant and ![]() ${Q_c} = {Q_1}$. Similarly, the density does not change downstream of the jump and
${Q_c} = {Q_1}$. Similarly, the density does not change downstream of the jump and ![]() ${g^{\prime}_c} = {g^{\prime}_1}$.
${g^{\prime}_c} = {g^{\prime}_1}$.
Furthermore, conserving energy of the subcritical flow through the sill and/or contraction requires the total head ![]() ${H_1} = {Z_c} + {H_c}$. Additionally, from basic hydraulics of rectangular channels, the critical head
${H_1} = {Z_c} + {H_c}$. Additionally, from basic hydraulics of rectangular channels, the critical head ![]() ${H_c} = {\textstyle{3 \over 2}}{h_c}$ (Henderson Reference Henderson1966). Hence, the downstream boundary condition applied to the jump can finally be written as
${H_c} = {\textstyle{3 \over 2}}{h_c}$ (Henderson Reference Henderson1966). Hence, the downstream boundary condition applied to the jump can finally be written as
 \begin{equation}{h_1} + \frac{{Q_1^2}}{{2{{g^{\prime}}_1}b_1^2h_1^2}} = {Z_c} + \frac{3}{2}{\left( {\frac{{Q_1^2}}{{b_c^2{{g^{\prime}}_1}}}} \right)^{1/3}},\end{equation}
\begin{equation}{h_1} + \frac{{Q_1^2}}{{2{{g^{\prime}}_1}b_1^2h_1^2}} = {Z_c} + \frac{3}{2}{\left( {\frac{{Q_1^2}}{{b_c^2{{g^{\prime}}_1}}}} \right)^{1/3}},\end{equation}and in non-dimensional form, the downstream boundary condition is
 \begin{equation}r + \frac{1}{2}{\left( {\frac{{F{r_0}}}{\beta }} \right)^2}{\left( {\frac{\mu }{r}} \right)^2}\left( {\frac{{{{g^{\prime}}_0}}}{{{{g^{\prime}}_1}}}} \right) = {\lambda _c} + \frac{3}{2}{\left( {\frac{{F{r_0}}}{{{\beta_c}}}} \right)^{2/3}}{\mu ^{2/3}}{\left( {\frac{{{{g^{\prime}}_0}}}{{{{g^{\prime}}_1}}}} \right)^{1/3}},\end{equation}
\begin{equation}r + \frac{1}{2}{\left( {\frac{{F{r_0}}}{\beta }} \right)^2}{\left( {\frac{\mu }{r}} \right)^2}\left( {\frac{{{{g^{\prime}}_0}}}{{{{g^{\prime}}_1}}}} \right) = {\lambda _c} + \frac{3}{2}{\left( {\frac{{F{r_0}}}{{{\beta_c}}}} \right)^{2/3}}{\mu ^{2/3}}{\left( {\frac{{{{g^{\prime}}_0}}}{{{{g^{\prime}}_1}}}} \right)^{1/3}},\end{equation}
where ![]() ${\beta _c} = {b_c}/{b_0}$ and
${\beta _c} = {b_c}/{b_0}$ and ![]() ${\lambda _c} = {Z_c}/{h_0}$.
${\lambda _c} = {Z_c}/{h_0}$.
Note, the linear mixing approximation of (4.2) (case of ![]() ${g^{\prime}_0}/{g^{\prime}_1} = \mu$) is
${g^{\prime}_0}/{g^{\prime}_1} = \mu$) is
 \begin{equation}1 + \frac{1}{2}{\left( {\frac{{F{r_0}}}{\beta }} \right)^2}{\left( {\frac{\mu }{r}} \right)^3} = \frac{{{\lambda _c}}}{r} + \frac{3}{2}{\left( {\frac{{F{r_0}}}{{{\beta_c}}}} \right)^{2/3}}\left( {\frac{\mu }{r}} \right).\end{equation}
\begin{equation}1 + \frac{1}{2}{\left( {\frac{{F{r_0}}}{\beta }} \right)^2}{\left( {\frac{\mu }{r}} \right)^3} = \frac{{{\lambda _c}}}{r} + \frac{3}{2}{\left( {\frac{{F{r_0}}}{{{\beta_c}}}} \right)^{2/3}}\left( {\frac{\mu }{r}} \right).\end{equation}
Subcritical branches of the general (4.2), plotted as ![]() $\mu = f(r)$, are superimposed in figure 11 on the momentum equation (3.8), which was formulated in § 3.
$\mu = f(r)$, are superimposed in figure 11 on the momentum equation (3.8), which was formulated in § 3.

Figure 11. Matching solutions for overflow jumps obtained by superimposing (4.2) [downstream control] and (3.8) [momentum equation]; Fr 0 = 10, β = 5, Ta = 20 °C, Sa = 30 ppt, ΔT 0 = +10 °C and ΔS 0 = +5 ppt: (a) vertical sill heights λc ranging from 0 to 5; and (b) horizontal contractions βc ranging from 1 to 5.
The jump solutions are required to satisfy simultaneously the momentum equation (3.8) and the hydraulic control (4.2). The solutions in the ![]() $\mu - r$ plane are, therefore, the points of intersection of (3.8) and (4.2). This matching technique is applied in figure 11 to determine the solutions associated with specified discharge and downstream conditions.
$\mu - r$ plane are, therefore, the points of intersection of (3.8) and (4.2). This matching technique is applied in figure 11 to determine the solutions associated with specified discharge and downstream conditions.
Figure 11(a) demonstrates the effect of a vertical sill on an overflow jump. When the relative height of the sill λc is increased from 0 to 4, the dilution in the jump region decreases from the maximum dilution ![]() $\mu$ =
$\mu$ = ![]() $\mu$c for λc = 0 to the minimum dilution
$\mu$c for λc = 0 to the minimum dilution ![]() $\mu$ = 1 for λc = 4. In figure 11(a), when λc > 4, (4.2) does not intersect (3.8). Such condition (e.g. λc = 5 in figure 11a) indicates that there is no free entraining jump solution. In this case, (4.2) at
$\mu$ = 1 for λc = 4. In figure 11(a), when λc > 4, (4.2) does not intersect (3.8). Such condition (e.g. λc = 5 in figure 11a) indicates that there is no free entraining jump solution. In this case, (4.2) at ![]() $\mu$ = 1 gives r > r*. In other words, the flow cannot simultaneously satisfy both the discharge and the hydraulic control conditions. As previously documented by Baddour and Abbink (Reference Baddour and Abbink1983), this condition produces the so-called drowned jump. The roller of a drowned jump was observed to move all the way upstream and submerge the exit. Entrainment in drowned jumps is suppressed and dilution μ ~ 1 (Baddour Reference Baddour1987).
$\mu$ = 1 gives r > r*. In other words, the flow cannot simultaneously satisfy both the discharge and the hydraulic control conditions. As previously documented by Baddour and Abbink (Reference Baddour and Abbink1983), this condition produces the so-called drowned jump. The roller of a drowned jump was observed to move all the way upstream and submerge the exit. Entrainment in drowned jumps is suppressed and dilution μ ~ 1 (Baddour Reference Baddour1987).
A similar behaviour is observed in figure 11(b), which shows the effect of a downstream horizontal contraction on the jump solutions. As expected, in the absence of a channel contraction (βc = β = 5), the dilution in the jump region is maximized and ![]() $\mu$ =
$\mu$ = ![]() $\mu$c. And, as the downstream control width decreases (βc < 5), the dilution is gradually reduced. Eventually, at some contraction (βc ~ 1 in figure 11b), entrainment is suppressed and the jump becomes drowned.
$\mu$c. And, as the downstream control width decreases (βc < 5), the dilution is gradually reduced. Eventually, at some contraction (βc ~ 1 in figure 11b), entrainment is suppressed and the jump becomes drowned.
Controlling dilution in stratified mixing channels is of practical interest. This work demonstrates how to control dilution in a channel by balancing the effects of upstream and downstream conditions.
5. Comparison with experiment
Guo (Reference Guo1992) carried out a series of 54 overflow internal jump tests in the laboratory using two channels, namely channel A and channel B. Channel A, which was reported in an earlier study by Baddour (Reference Baddour1991), was 0.15 m wide, 2.5 m long and 0.35 m deep. In channel A, the dilution in the jump region could be controlled and measured directly with a flowmeter and indirectly obtained from temperature measurements. Both methods provided consistent results. Channel B was assembled inside a 1 m wide flume to simulate conditions in a stratified mixing channel connected to a larger body of water. Channel B had two setups, 0.2 m or 0.4 m wide, and 3 m long and 0.23 m deep. The dilution in the jump region in channel B was obtained from detailed temperature profiles. In channel A and channel B, temperature data were gathered with vertical and horizontal banks of 0.12 mm diameter type T thermocouples connected to a PC data acquisition system. The response time of the thermocouples was 0.01 s. The data acquisition system was programmed to simultaneously scan, at a frequency of 10 Hz, the output of up to 15 probes for a period of 100 s. The conditions of the tests by Guo (Reference Guo1992) are summarized in table 1.
Table 1. Testing conditions of 2-D and 3-D experiments by Guo (Reference Guo1992).

For channel enlargement ratios β between 1 and 10, the horizontal temperature profiles downstream of the jump were practically uniform across the width of the channel. For higher values of β, the horizontal profiles were expected to gradually become non-uniform and eventually Gaussian in shape when β was very large. For such wide channel enlargement ratios, appropriate profile shape parameters would have to be incorporated in the formulation of (3.8) and (4.2).
The experimental data of Guo (Reference Guo1992) are compared in Figures 12 and 13 with the theory developed in this paper. There was generally good agreement between theory and experiment in the entire range of testing conditions. In particular, figure 12(b) confirms the predicted effects of nonlinear mixing. The experiments by Guo (Reference Guo1992) did not include salinity variations. To the author's best knowledge, detailed experimental data on stationary entraining jumps with buoyancy produced by differences in temperature and salinity, have not yet been published.

Figure 12. Comparison of theory with the experiment by Guo (Reference Guo1992): (a) Fr 0 = 5, Ta = 20 °C, ΔT 0 = 15 °C; (b) Fr 0 = 7.5, β = 10, ΔT 0 = 15 °C.

Figure 13. Comparison of theory with all 2-D and 3-D experiments by Guo (Reference Guo1992).
6. Concluding remarks
The nonlinear buoyancy of stationary thermohaline jumps was investigated in this study with a function derived from a nonlinear seawater equation of state. The proposed buoyancy function was obtained with a polynomial transformation and was accurate throughout the range of temperature and salinity of interest (T = 0–40 °C and S = 0–40 ppt) and can be applied in modelling flows in the ocean and inland waters.
Nonlinear buoyancy effects were found to be significant when buoyancy arising from temperature and that from salt were acting in opposite directions. Thermohaline overflow jumps achieved greater depths and were capable of entraining more ambient fluid than linear saline jumps. However, thermohaline underflow jumps were shallower and less diluted than linear saline jumps. A matching technique was applied to determine the effect of a downstream control on the miscible jump solution.
Two-dimensional and three-dimensional overflow jump experiments by Guo (Reference Guo1992) are in good agreement with the nonlinear jump theory presented in this paper. Nevertheless, further nonlinear mixing experiments designed specifically to examine the combined buoyancy effects of temperature and salinity on the development of stationary overflow and underflow jumps have not yet been published and are highly recommended.
Finally, it is also recommended to incorporate nonlinear buoyancy equations in the models of oceanic internal hydraulic jumps.
Acknowledgements
The author would like to thank the reviewers for their constructive comments and suggestions, which have strengthened and improved the paper. Lu-Li Guo conducted 2-D and 3-D thermal jump experiments in the hydraulics laboratory at the University of Western Ontario. Grants to the author, in support of research on stratified flows, were received from the Natural Sciences and Engineering Research Council of Canada (NSERC).
Declaration of interest
The author reports no conflict of interest.