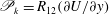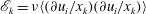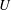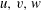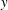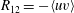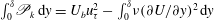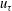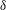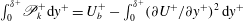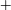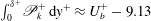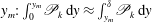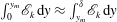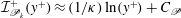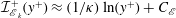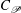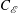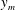1 Introduction
Beginning with Prandtl in 1904, turbulent wall-bounded flows have been intensively investigated by numerous researchers. Reviews of the topic can be found in Cantwell (Reference Cantwell1981), Robinson (Reference Robinson1991), Gad-el Hak & Bandyopadhyay (Reference Gad-el Hak and Bandyopadhyay1994), Fernholz & Finley (Reference Fernholz and Finley1996), Klewicki (Reference Klewicki2010), Marusic et al. (Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b ), Smits, McKeon & Marusic (Reference Smits, McKeon and Marusic2011), Jiménez (Reference Jiménez2013), Smits & Marusic (Reference Smits and Marusic2013), and Marusic, Baars & Hutchins (Reference Marusic, Baars and Hutchins2017). The present work focuses on turbulent-kinetic-energy (TKE) production and dissipation, and specifically on the integral properties of TKE production and dissipation.
Better knowledge of TKE production
![]() $\mathscr{P}_{k}=R_{12}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)$
and TKE dissipation
$\mathscr{P}_{k}=R_{12}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)$
and TKE dissipation
![]() $\mathscr{E}_{k}=\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}u_{i}/x_{k})(\unicode[STIX]{x2202}u_{i}/x_{k})\rangle$
can shed light on how turbulence is (re)generated and sustained. In this work,
$\mathscr{E}_{k}=\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}u_{i}/x_{k})(\unicode[STIX]{x2202}u_{i}/x_{k})\rangle$
can shed light on how turbulence is (re)generated and sustained. In this work,
![]() $U$
represents the mean velocity in the streamwise direction
$U$
represents the mean velocity in the streamwise direction
![]() $x$
, and
$x$
, and
![]() $u,v$
represent the fluctuating velocity component in the streamwise direction
$u,v$
represent the fluctuating velocity component in the streamwise direction
![]() $x$
and the wall-normal direction
$x$
and the wall-normal direction
![]() $y$
, and
$y$
, and
![]() $R_{12}=-\langle uv\rangle$
is the kinematic Reynolds shear stress. Angle brackets denote averaging. While the balance of the TKE budget equation is commonly presented in numerical simulation of turbulent wall-bounded flows, as by Eggels et al. (Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994), Abe, Kawamura & Matsuo (Reference Abe, Kawamura and Matsuo2001), Hoyas & Jiménez (Reference Hoyas and Jiménez2008), Wu & Moin (Reference Wu and Moin2009), Jiménez et al. (Reference Jiménez, Hoyas, Simens and Mizuno2010), the integral of TKE production and dissipation has received less attention.
$R_{12}=-\langle uv\rangle$
is the kinematic Reynolds shear stress. Angle brackets denote averaging. While the balance of the TKE budget equation is commonly presented in numerical simulation of turbulent wall-bounded flows, as by Eggels et al. (Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994), Abe, Kawamura & Matsuo (Reference Abe, Kawamura and Matsuo2001), Hoyas & Jiménez (Reference Hoyas and Jiménez2008), Wu & Moin (Reference Wu and Moin2009), Jiménez et al. (Reference Jiménez, Hoyas, Simens and Mizuno2010), the integral of TKE production and dissipation has received less attention.
Panton (Reference Panton2001) pointed out the important role of TKE production in the generation of Reynolds stress and self-sustaining turbulence in the near-wall region. It is well known that the peak TKE production occurs within the viscous buffer layer at
![]() $y^{+}\approx 12$
(Fernholz & Finley Reference Fernholz and Finley1996). In the present work, superscript
$y^{+}\approx 12$
(Fernholz & Finley Reference Fernholz and Finley1996). In the present work, superscript
![]() $^{+}$
denotes inner scaling. The inner-scaled distance,
$^{+}$
denotes inner scaling. The inner-scaled distance,
![]() $y^{+}$
, from the wall, is
$y^{+}$
, from the wall, is
![]() $y^{+}=y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
where
$y^{+}=y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
where
![]() $u_{\unicode[STIX]{x1D70F}}$
is the friction velocity. Plotting the pre-multiplied TKE production on semilogarithmic axes, Marusic, Mathis & Hutchins (Reference Marusic, Mathis and Hutchins2010a
) have shown that the main contribution to the bulk TKE production comes from the near-wall region at low Reynolds number. At sufficiently high Reynolds number the logarithmic region dominates TKE production, as shown in Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
), Bernardini, Pirozzoli & Orlandi (Reference Bernardini, Pirozzoli and Orlandi2014), Pirozzoli, Bernardini & Orlandi (Reference Pirozzoli, Bernardini and Orlandi2016) and Renard & Deck (Reference Renard and Deck2016).
$u_{\unicode[STIX]{x1D70F}}$
is the friction velocity. Plotting the pre-multiplied TKE production on semilogarithmic axes, Marusic, Mathis & Hutchins (Reference Marusic, Mathis and Hutchins2010a
) have shown that the main contribution to the bulk TKE production comes from the near-wall region at low Reynolds number. At sufficiently high Reynolds number the logarithmic region dominates TKE production, as shown in Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
), Bernardini, Pirozzoli & Orlandi (Reference Bernardini, Pirozzoli and Orlandi2014), Pirozzoli, Bernardini & Orlandi (Reference Pirozzoli, Bernardini and Orlandi2016) and Renard & Deck (Reference Renard and Deck2016).
Orlandi (Reference Orlandi1997) derived a decomposition of the TKE production into two parts, one containing the streamwise component of the fluctuating Lamb vector and the other in a divergence form. Using direct numerical simulation (DNS) data, Bernardini et al. (Reference Bernardini, Pirozzoli and Orlandi2014) examined Orlandi’s decomposition of TKE production. They proposed a scaling for the TKE production and offered an explanation for the mixed scaling
![]() $\sqrt{u_{\unicode[STIX]{x1D70F}}U_{\infty }}$
for the streamwise velocity variance
$\sqrt{u_{\unicode[STIX]{x1D70F}}U_{\infty }}$
for the streamwise velocity variance
![]() $\langle uu\rangle$
, where
$\langle uu\rangle$
, where
![]() $U_{\infty }$
is the free streamwise velocity of zero-pressure-gradient turbulent boundary layer flows (ZPG TBLs).
$U_{\infty }$
is the free streamwise velocity of zero-pressure-gradient turbulent boundary layer flows (ZPG TBLs).
Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016) have investigated the global TKE production for the mean streamwise velocity and scalar. They found that the near-wall region is characterized by nearly equal values of velocity and scalar production, and the global velocity dissipation is found to exceed the global dissipation of the scalar. The difference was attributed to the pressure term in the velocity equation, consistent with the analogy proposed by Abe & Antonia (Reference Abe and Antonia2009).
Laadhari (Reference Laadhari2007) examined the Reynolds number dependence of the dissipation of the mean kinetic energy and TKE in wall-bounded flow. He found that the mean part reaches a constant value at sufficiently high Reynolds number, while the turbulent part follows a logarithmic law. Laadhari (Reference Laadhari2007) pointed out that the logarithmic law of friction can be obtained without any assumption on the mean velocity distribution.
Recently, Abe & Antonia (Reference Abe and Antonia2016) examined the integrals of the mean and TKE dissipation rates using DNS data from turbulent channel flow. They established a logarithmic dependence of the integrated turbulent energy dissipation rate for
![]() $300<\unicode[STIX]{x1D6FF}^{+}<10^{4}$
, and found that the dependence is intimately linked to the logarithmic skin friction law. The scaling of the turbulent energy dissipation rate in the inner region, outer region and overlap region were examined. Abe & Antonia (Reference Abe and Antonia2017) have extended the studies on the integration of the transport equations for the mean and turbulent parts of the scalar dissipation rate, and have obtained a simple relation for the bulk mean scalar and the wall transfer coefficient.
$300<\unicode[STIX]{x1D6FF}^{+}<10^{4}$
, and found that the dependence is intimately linked to the logarithmic skin friction law. The scaling of the turbulent energy dissipation rate in the inner region, outer region and overlap region were examined. Abe & Antonia (Reference Abe and Antonia2017) have extended the studies on the integration of the transport equations for the mean and turbulent parts of the scalar dissipation rate, and have obtained a simple relation for the bulk mean scalar and the wall transfer coefficient.
Renard & Deck (Reference Renard and Deck2016) derived an identity that decomposes the mean skin friction coefficient into a laminar part and a turbulent part. One motive for Renard and Deck’s work was to improve the FIK identity, a decomposition of the mean skin friction coefficient derived by Fukagata, Iwamoto & Kasagi (Reference Fukagata, Iwamoto and Kasagi2002). The Renard and Deck (RD) identity was also independently derived by Abe & Antonia (Reference Abe and Antonia2016). While the FIK identity and the RD identity focus on the decomposition of the mean skin friction coefficient, here we show that the RD identity in fact reveals a very important property of the TKE production, that is, the global integral of the TKE production.
The rest of the paper is organized as follows. In § 2, we present the RD identity in the form of the global integral of TKE production for turbulent channel flows, turbulent pipe flows and ZPG TBL. In § 3.1 we briefly present the distribution of
![]() $\mathscr{P}_{k}$
and
$\mathscr{P}_{k}$
and
![]() $\mathscr{E}_{k}$
. In § 3.2 the RD identity equations are verified using DNS and experimental data from turbulent channel flows, turbulent pipe flows and ZPG TBL. In § 3.3 we briefly review the scaling for the peak Reynolds shear stress location and meso-length scale. In § 3.4 we present the pre-multiplied TKE production and dissipation. In § 3.5 we show the partition of the integral of the TKE production and dissipation around the peak Reynolds shear stress location
$\mathscr{E}_{k}$
. In § 3.2 the RD identity equations are verified using DNS and experimental data from turbulent channel flows, turbulent pipe flows and ZPG TBL. In § 3.3 we briefly review the scaling for the peak Reynolds shear stress location and meso-length scale. In § 3.4 we present the pre-multiplied TKE production and dissipation. In § 3.5 we show the partition of the integral of the TKE production and dissipation around the peak Reynolds shear stress location
![]() $y_{m}$
. In § 3.6 we present the integral profiles of the TKE production and dissipation.
$y_{m}$
. In § 3.6 we present the integral profiles of the TKE production and dissipation.
2 The RD identity and the global integral of the TKE production
Using the mean streamwise kinetic-energy budget equation in an absolute reference frame, Renard & Deck (Reference Renard and Deck2016) derived a decomposition of the mean skin friction coefficient
![]() $C_{f}$
in turbulent wall-bounded flows. For channel flows, the RD identity can be written as
$C_{f}$
in turbulent wall-bounded flows. For channel flows, the RD identity can be written as
where
![]() $\unicode[STIX]{x1D6FF}$
is the channel half-height, the mean skin friction coefficient is defined as
$\unicode[STIX]{x1D6FF}$
is the channel half-height, the mean skin friction coefficient is defined as
![]() $C_{f}=\unicode[STIX]{x1D70F}_{w}/(0.5\unicode[STIX]{x1D70C}U_{b}^{2})=2u_{\unicode[STIX]{x1D70F}}^{2}/U_{b}^{2}$
and
$C_{f}=\unicode[STIX]{x1D70F}_{w}/(0.5\unicode[STIX]{x1D70C}U_{b}^{2})=2u_{\unicode[STIX]{x1D70F}}^{2}/U_{b}^{2}$
and
![]() $U_{b}=(\int _{0}^{\unicode[STIX]{x1D6FF}}U\,\text{d}y)/\unicode[STIX]{x1D6FF}$
is the bulk mean velocity. Renard & Deck (Reference Renard and Deck2016) have thoroughly examined the contribution of turbulence to the mean skin friction. While they focused on the mean skin friction, here we examine the RD identity from the perspective of the global integral of the TKE production. For completeness, we will briefly derive the RD identity using a simplified approach.
$U_{b}=(\int _{0}^{\unicode[STIX]{x1D6FF}}U\,\text{d}y)/\unicode[STIX]{x1D6FF}$
is the bulk mean velocity. Renard & Deck (Reference Renard and Deck2016) have thoroughly examined the contribution of turbulence to the mean skin friction. While they focused on the mean skin friction, here we examine the RD identity from the perspective of the global integral of the TKE production. For completeness, we will briefly derive the RD identity using a simplified approach.
The simplified derivation starts from the mean momentum balance (MMB) equation for fully developed turbulent channel flow:
where
![]() $u_{\unicode[STIX]{x1D70F}}^{2}/\unicode[STIX]{x1D6FF}$
comes from the mean pressure force
$u_{\unicode[STIX]{x1D70F}}^{2}/\unicode[STIX]{x1D6FF}$
comes from the mean pressure force
![]() $-(1/\unicode[STIX]{x1D70C})(\text{d}P/\text{d}x)$
(see Pope Reference Pope2001). The corresponding boundary conditions are
$-(1/\unicode[STIX]{x1D70C})(\text{d}P/\text{d}x)$
(see Pope Reference Pope2001). The corresponding boundary conditions are
Integrating the MMB equation (2.2) in the wall-normal direction and applying boundary conditions yields a relation for the total shear stress, viscous shear stress plus Reynolds shear stress, as
The integral of TKE production can be obtained in two steps. Step one is to multiply the MMB equation (2.2) by a weight function
![]() $U$
$U$
In step two, the weighted MMB equation (2.6) is integrated in the wall-normal direction
![]() $y$
to produce
$y$
to produce
Note that integration by parts was applied to the second and third terms in (2.6), and no-slip boundary conditions were applied for
![]() $U$
and
$U$
and
![]() $R_{12}$
at the channel wall.
$R_{12}$
at the channel wall.
Substituting the relation for
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)+R_{12}$
in (2.5), the integrated equation (2.7) can be rearranged as
$\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)+R_{12}$
in (2.5), the integrated equation (2.7) can be rearranged as
 $$\begin{eqnarray}\int _{0}^{y}\mathscr{P}_{k}\,\text{d}y=\left\{u_{\unicode[STIX]{x1D70F}}^{2}U-u_{\unicode[STIX]{x1D70F}}^{2}\frac{\displaystyle \left(yU-\int _{0}^{y}U\,\text{d}y\right)}{\unicode[STIX]{x1D6FF}}\right\}-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{y}\mathscr{P}_{k}\,\text{d}y=\left\{u_{\unicode[STIX]{x1D70F}}^{2}U-u_{\unicode[STIX]{x1D70F}}^{2}\frac{\displaystyle \left(yU-\int _{0}^{y}U\,\text{d}y\right)}{\unicode[STIX]{x1D6FF}}\right\}-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y.\end{eqnarray}$$
For brevity, we denote the TKE production term as
![]() $\mathscr{P}_{k}=R_{12}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)$
. The global integral identity for TKE production is obtained by setting
$\mathscr{P}_{k}=R_{12}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)$
. The global integral identity for TKE production is obtained by setting
![]() $y=\unicode[STIX]{x1D6FF}$
in the integral equation (2.8)
$y=\unicode[STIX]{x1D6FF}$
in the integral equation (2.8)
It can be easily shown that the identity equation (2.9) is the RD identity equation (2.1).
In the study of turbulent wall-bounded flows,
![]() $u_{\unicode[STIX]{x1D70F}}$
and
$u_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D708}$
are often used to scale the mean velocity, Reynolds shear stress and wall-normal distance as
$\unicode[STIX]{x1D708}$
are often used to scale the mean velocity, Reynolds shear stress and wall-normal distance as
![]() $U^{+}=U/u_{\unicode[STIX]{x1D70F}}$
,
$U^{+}=U/u_{\unicode[STIX]{x1D70F}}$
,
![]() $R_{12}^{+}=R_{12}/u_{\unicode[STIX]{x1D70F}}^{2}$
and
$R_{12}^{+}=R_{12}/u_{\unicode[STIX]{x1D70F}}^{2}$
and
![]() $y^{+}=yu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
. This procedure is commonly referred to as ‘inner scaling’. The inner-scaled integral equation (2.8) can be expressed as
$y^{+}=yu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$
. This procedure is commonly referred to as ‘inner scaling’. The inner-scaled integral equation (2.8) can be expressed as
 $$\begin{eqnarray}\int _{0}^{y^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\left\{U^{+}-\frac{\displaystyle y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+}}{\unicode[STIX]{x1D6FF}^{+}}\right\}-\int _{0}^{y^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\,\text{d}y^{+},\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{y^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\left\{U^{+}-\frac{\displaystyle y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+}}{\unicode[STIX]{x1D6FF}^{+}}\right\}-\int _{0}^{y^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\,\text{d}y^{+},\end{eqnarray}$$
and the global integral identity equation (2.9) in inner scaling can be expressed as
where the inner-scaled TKE production is
![]() $\mathscr{P}_{k}^{+}=R_{12}^{+}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})$
. In other words, the RD identity states that the sum of the global integrals of
$\mathscr{P}_{k}^{+}=R_{12}^{+}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})$
. In other words, the RD identity states that the sum of the global integrals of
![]() $(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}$
and the TKE production
$(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}$
and the TKE production
![]() $\mathscr{P}_{k}^{+}$
always equals
$\mathscr{P}_{k}^{+}$
always equals
![]() $U_{b}^{+}$
in a channel flow, regardless of the Reynolds number. The identity equation (2.9) for the global integral of TKE production was first presented by Laadhari (Reference Laadhari2007). Although Laadhari started with the dissipation equation for the kinetic energy, equating the TKE production to dissipation in turbulent channel flow, he essentially used the mean momentum balance equation to obtain the identity equation. Here the identity equation is derived in a more straightforward fashion.
$U_{b}^{+}$
in a channel flow, regardless of the Reynolds number. The identity equation (2.9) for the global integral of TKE production was first presented by Laadhari (Reference Laadhari2007). Although Laadhari started with the dissipation equation for the kinetic energy, equating the TKE production to dissipation in turbulent channel flow, he essentially used the mean momentum balance equation to obtain the identity equation. Here the identity equation is derived in a more straightforward fashion.
Due to the geometric shape, the global integral identity for the TKE production in turbulent pipe flows is (see appendix B for more details)
where
![]() $\mathscr{P}_{k}^{+}=R_{12}^{+}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})$
for turbulent pipe flow.
$\mathscr{P}_{k}^{+}=R_{12}^{+}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})$
for turbulent pipe flow.
The global integral identity for the TKE production in ZPG TBL is (see appendix A for more details)
 $$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U_{\infty }^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\,\text{d}y^{+}+\left\{\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,U_{\infty }^{+}\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U_{\infty }^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\,\text{d}y^{+}+\left\{\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,U_{\infty }^{+}\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}.\end{eqnarray}$$
The identity equations for the global TKE production in turbulent channel flow, turbulent pipe flow and ZPG TBL have similar form, but there are subtle differences. For example, it is known that the profiles of the mean velocity and Reynolds shear stress of channel and pipe flows are similar, but there are subtle differences, especially in the wake region (see Jiménez et al. Reference Jiménez, Hoyas, Simens and Mizuno2009; Mathis et al. Reference Mathis, Monty, Hutchins and Marusic2009b ; Monty et al. Reference Monty, Hutchins, Ng, Marusic and Chong2009, and Ng et al. Reference Ng, Monty, Hutchins, Chong and Marusic2011). Given the difference in geometry and the ensuing difference in the integration, the global identities for channel flow and pipe flow will not be the same, as we will show in the following.
3 Experimental and numerical data
The calculation of the TKE production
![]() $\mathscr{P}_{k}$
requires data on the mean streamwise velocity gradient
$\mathscr{P}_{k}$
requires data on the mean streamwise velocity gradient
![]() $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
and the kinematic Reynolds shear stress
$\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
and the kinematic Reynolds shear stress
![]() $R_{12}$
. In physical experiments, the spatial resolution is limited, especially in the near-wall region, where the gradient
$R_{12}$
. In physical experiments, the spatial resolution is limited, especially in the near-wall region, where the gradient
![]() $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
varies rapidly. Moreover, in high Reynolds number physical experiments, the first data point of
$\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
varies rapidly. Moreover, in high Reynolds number physical experiments, the first data point of
![]() $R_{12}$
is often beyond the peak Reynolds shear stress location. Thus, it is challenging to obtain TKE production
$R_{12}$
is often beyond the peak Reynolds shear stress location. Thus, it is challenging to obtain TKE production
![]() $\mathscr{P}_{k}$
data in physical experiments, especially in the near-wall region of high Reynolds number flows. The measurement of the TKE dissipation
$\mathscr{P}_{k}$
data in physical experiments, especially in the near-wall region of high Reynolds number flows. The measurement of the TKE dissipation
![]() $\mathscr{E}_{k}$
in physical experiments is even more difficult. The scarcity of the TKE production and dissipation data from physical experiments is one of the reasons why their integrals have not been widely studied in the past.
$\mathscr{E}_{k}$
in physical experiments is even more difficult. The scarcity of the TKE production and dissipation data from physical experiments is one of the reasons why their integrals have not been widely studied in the past.
During the past three decades, however, numerical simulations, especially direct numerical simulation, have provided high quality data for
![]() $\mathscr{P}_{k}$
and
$\mathscr{P}_{k}$
and
![]() $\mathscr{E}_{k}$
. At the same time, higher resolution probes have been developed to obtain data in the near-wall region of high Reynolds number flows (see, for example, Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015). The present work would not have been possible without the aid of the high quality DNS data and experimental data generously shared by the researchers. Here, we use DNS and high resolution experimental data to investigate the integral properties of TKE production and dissipation, including the global integral, partition of the integrals, and shapes of the integral profiles.
$\mathscr{E}_{k}$
. At the same time, higher resolution probes have been developed to obtain data in the near-wall region of high Reynolds number flows (see, for example, Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015). The present work would not have been possible without the aid of the high quality DNS data and experimental data generously shared by the researchers. Here, we use DNS and high resolution experimental data to investigate the integral properties of TKE production and dissipation, including the global integral, partition of the integrals, and shapes of the integral profiles.
3.1 TKE production and dissipation distribution
TKE production
![]() $\mathscr{P}_{k}$
and dissipation
$\mathscr{P}_{k}$
and dissipation
![]() $\mathscr{E}_{k}$
profiles have been commonly presented in DNS studies of turbulent wall-bounded flows (see, for example, Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994; Abe et al.
Reference Abe, Kawamura and Matsuo2001; Hoyas & Jiménez Reference Hoyas and Jiménez2008; Wu & Moin Reference Wu and Moin2009; Jiménez et al.
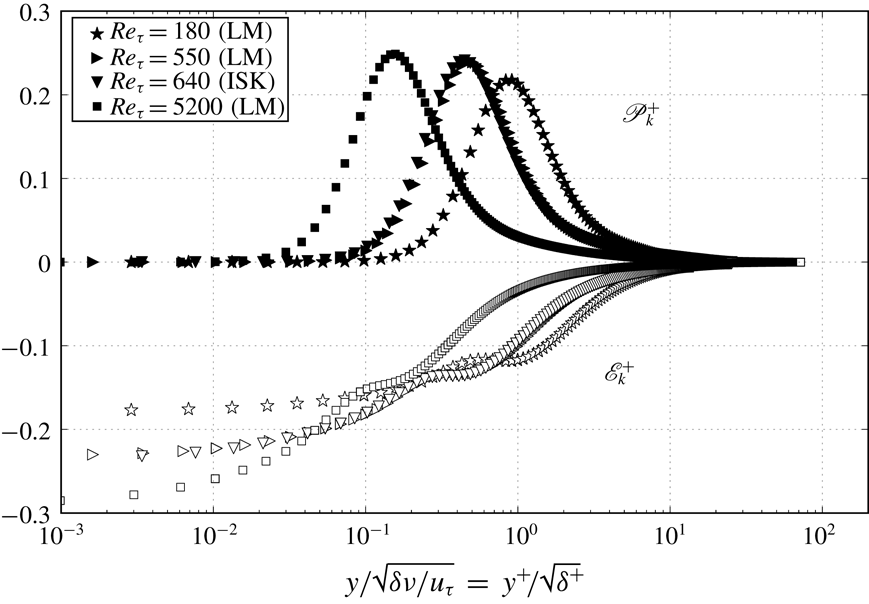
Reference Jiménez, Hoyas, Simens and Mizuno2010). For the convenience of readers, figure 1 presents
$\mathscr{E}_{k}$
profiles have been commonly presented in DNS studies of turbulent wall-bounded flows (see, for example, Eggels et al.
Reference Eggels, Unger, Weiss, Westerweel, Adrian, Friedrich and Nieuwstadt1994; Abe et al.
Reference Abe, Kawamura and Matsuo2001; Hoyas & Jiménez Reference Hoyas and Jiménez2008; Wu & Moin Reference Wu and Moin2009; Jiménez et al.
Reference Jiménez, Hoyas, Simens and Mizuno2010). For the convenience of readers, figure 1 presents
![]() $\mathscr{P}_{k}$
and
$\mathscr{P}_{k}$
and
![]() $\mathscr{E}_{k}$
versus wall-normal distance from two independent DNS studies of turbulent channel flows by Iwamoto, Suzuki & Kasagi (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015). The agreement between the DNS of Lee & Moser (Reference Lee and Moser2015) at
$\mathscr{E}_{k}$
versus wall-normal distance from two independent DNS studies of turbulent channel flows by Iwamoto, Suzuki & Kasagi (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015). The agreement between the DNS of Lee & Moser (Reference Lee and Moser2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=550$
and the DNS of Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) at
$Re_{\unicode[STIX]{x1D70F}}=550$
and the DNS of Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) at
![]() $Re_{\unicode[STIX]{x1D70F}}=640$
indicates the high quality of the simulations.
$Re_{\unicode[STIX]{x1D70F}}=640$
indicates the high quality of the simulations.

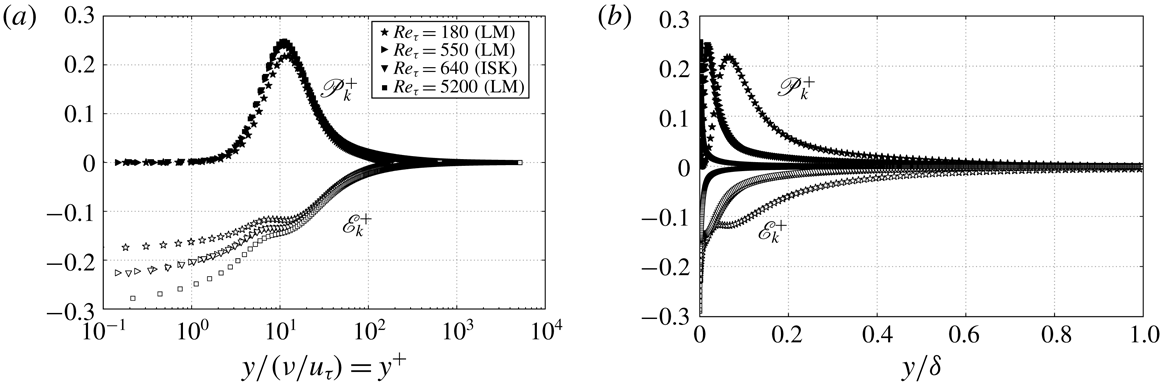
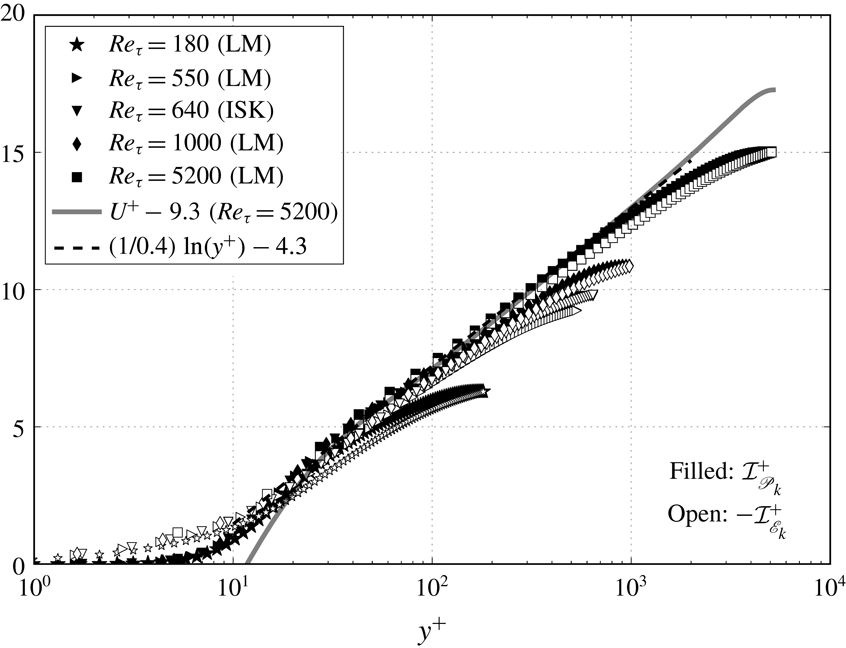
Figure 1. TKE production and dissipation versus wall-normal distance. (a) Inner-scaled wall-normal distance
![]() $y^{+}$
. (b) Outer-scaled wall-normal distance
$y^{+}$
. (b) Outer-scaled wall-normal distance
![]() $y/\unicode[STIX]{x1D6FF}$
. Data are from independent DNS studies by Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
$y/\unicode[STIX]{x1D6FF}$
. Data are from independent DNS studies by Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
In figure 1(a) the wall-normal distance is inner scaled as
![]() $y^{+}=y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
. To better show the near-wall region, the data are plotted on semilogarithmic axes. To show the trend in the outer region, figure 1(b) presents TKE production and dissipation versus the outer-scaled location
$y^{+}=y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
. To better show the near-wall region, the data are plotted on semilogarithmic axes. To show the trend in the outer region, figure 1(b) presents TKE production and dissipation versus the outer-scaled location
![]() $y/\unicode[STIX]{x1D6FF}$
.
$y/\unicode[STIX]{x1D6FF}$
.

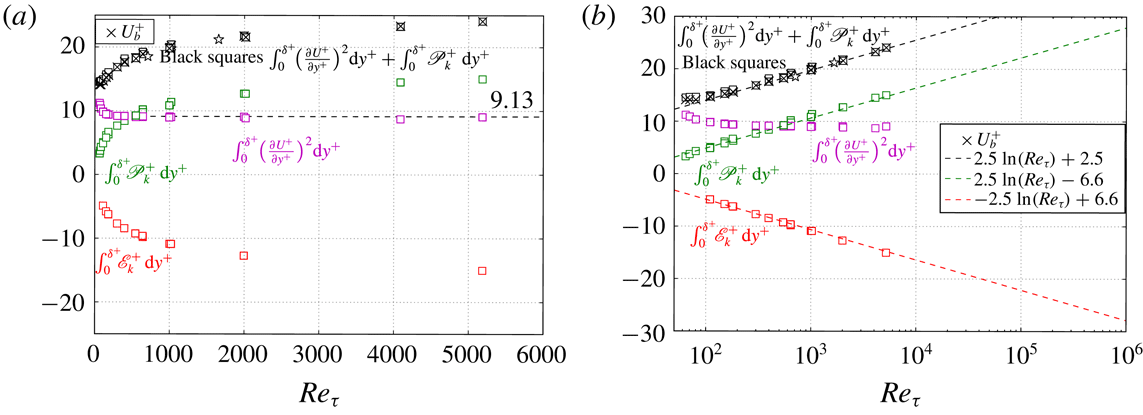
Figure 2. Reynolds number dependence of the global integral of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
(magenta squares),
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
(magenta squares),
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(green squares) and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(green squares) and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
(red squares) in turbulent channel flows. Also shown are the sum of
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
(red squares) in turbulent channel flows. Also shown are the sum of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black squares), the
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black squares), the
![]() $U_{b}^{+}$
from DNS (black
$U_{b}^{+}$
from DNS (black
![]() $\times$
) and
$\times$
) and
![]() $U_{b}^{+}$
from experimental measurement (black star) by Wei & Willmarth (Reference Wei and Willmarth1989). (a) On linear–linear axes. (b) On semilogarithmic axes. DNS data are from four independent studies: Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015), Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016).
$U_{b}^{+}$
from experimental measurement (black star) by Wei & Willmarth (Reference Wei and Willmarth1989). (a) On linear–linear axes. (b) On semilogarithmic axes. DNS data are from four independent studies: Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015), Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016).
Three notable features of figure 1(a) are as follows. (i) The inner-scaled TKE production
![]() $\mathscr{P}_{k}^{+}$
peaks at
$\mathscr{P}_{k}^{+}$
peaks at
![]() $y^{+}\approx 12$
with a maximum value of about
$y^{+}\approx 12$
with a maximum value of about
![]() $\mathscr{P}_{k,max}^{+}\approx 0.25$
, with no apparent Reynolds number dependence (the
$\mathscr{P}_{k,max}^{+}\approx 0.25$
, with no apparent Reynolds number dependence (the
![]() $Re_{\unicode[STIX]{x1D70F}}=180$
case clearly has a low Reynolds number effect). (ii) The inner-scaled TKE dissipation at the wall
$Re_{\unicode[STIX]{x1D70F}}=180$
case clearly has a low Reynolds number effect). (ii) The inner-scaled TKE dissipation at the wall
![]() $\mathscr{E}_{k}^{+}(y=0)$
clearly increases with Reynolds number. (iii) The TKE production
$\mathscr{E}_{k}^{+}(y=0)$
clearly increases with Reynolds number. (iii) The TKE production
![]() $\mathscr{P}_{k}^{+}$
and dissipation
$\mathscr{P}_{k}^{+}$
and dissipation
![]() $\mathscr{E}_{k}^{+}$
are not always in equilibrium. For example, the balance of the TKE budget equation in the viscous sublayer is between the dissipation
$\mathscr{E}_{k}^{+}$
are not always in equilibrium. For example, the balance of the TKE budget equation in the viscous sublayer is between the dissipation
![]() $\mathscr{E}_{k}^{+}$
and the viscous diffusion term. However, the viscous diffusion, turbulent transport and pressure velocity correlation terms in the TKE budget equation only redistribute TKE among different layers, and the global integral of these transport terms can be shown to be zero in turbulent channel flow and turbulent pipe flows. Therefore, the global integral of TKE production and dissipation must have the same magnitude, but with opposite signs. The global identity for the TKE production should also apply to the global integral of the TKE dissipation.
$\mathscr{E}_{k}^{+}$
and the viscous diffusion term. However, the viscous diffusion, turbulent transport and pressure velocity correlation terms in the TKE budget equation only redistribute TKE among different layers, and the global integral of these transport terms can be shown to be zero in turbulent channel flow and turbulent pipe flows. Therefore, the global integral of TKE production and dissipation must have the same magnitude, but with opposite signs. The global identity for the TKE production should also apply to the global integral of the TKE dissipation.
The balance of the TKE budget equation among different terms is commonly presented in DNS studies of turbulent wall-bounded flows, as in Bernardini et al. (Reference Bernardini, Pirozzoli and Orlandi2014) and Lee & Moser (Reference Lee and Moser2015), and is not discussed here. The focus of this work is on the integral properties of the TKE production and dissipation, that is, the area under the
![]() $\mathscr{P}_{k}^{+}$
curve and
$\mathscr{P}_{k}^{+}$
curve and
![]() $\mathscr{E}_{k}^{+}$
curve in figure 1(b).
$\mathscr{E}_{k}^{+}$
curve in figure 1(b).
3.2 Global integral of TKE production and dissipation
Using
![]() $R_{12}$
and
$R_{12}$
and
![]() $U$
data from four independent DNS studies of turbulent channel flows by Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015) and Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016), the global integrals
$U$
data from four independent DNS studies of turbulent channel flows by Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015) and Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016), the global integrals
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
are calculated and presented in figure 2 as a function of Reynolds number. Also shown in the figures is the global integral
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
are calculated and presented in figure 2 as a function of Reynolds number. Also shown in the figures is the global integral
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
calculated from the DNS data of TKE dissipation term. To illustrate the global integral identity equation (2.11) for channel flows, the bulk mean velocity
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
calculated from the DNS data of TKE dissipation term. To illustrate the global integral identity equation (2.11) for channel flows, the bulk mean velocity
![]() $U_{b}^{+}$
from DNS is also plotted in figure 2. As a test of accuracy, the experimental measurement of
$U_{b}^{+}$
from DNS is also plotted in figure 2. As a test of accuracy, the experimental measurement of
![]() $U_{b}^{+}$
by Wei & Willmarth (Reference Wei and Willmarth1989) is plotted in the figure, and can be seen to agree well with the DNS data.
$U_{b}^{+}$
by Wei & Willmarth (Reference Wei and Willmarth1989) is plotted in the figure, and can be seen to agree well with the DNS data.
Figure 2 shows that the sum of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black open squares in the plot) agrees very well with
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black open squares in the plot) agrees very well with
![]() $U_{b}^{+}$
(black
$U_{b}^{+}$
(black
![]() $\times$
or star in the plot), and this supports the validity of the global integral identity equation (2.11).
$\times$
or star in the plot), and this supports the validity of the global integral identity equation (2.11).
Figure 2 shows that in low Reynolds number turbulent channel flow,
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\text{d}y^{+}>\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(in a laminar channel flow,
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\text{d}y^{+}>\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(in a laminar channel flow,
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}=U_{b}^{+}$
). However, as Reynolds number increases,
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}=U_{b}^{+}$
). However, as Reynolds number increases,
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
decreases to a constant value of approximately
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
decreases to a constant value of approximately
![]() $9.13$
for
$9.13$
for
![]() $Re_{\unicode[STIX]{x1D70F}}>300$
. This constant value is consistent with the results of Laadhari (Reference Laadhari2007) and Abe & Antonia (Reference Abe and Antonia2016). Thus, at sufficiently high Reynolds number, the global integral of the TKE production and dissipation in turbulent channel flows can be approximated as
$Re_{\unicode[STIX]{x1D70F}}>300$
. This constant value is consistent with the results of Laadhari (Reference Laadhari2007) and Abe & Antonia (Reference Abe and Antonia2016). Thus, at sufficiently high Reynolds number, the global integral of the TKE production and dissipation in turbulent channel flows can be approximated as
To date, the highest
![]() $U_{b}^{+}$
obtained in superpipe experiments by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) is around
$U_{b}^{+}$
obtained in superpipe experiments by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) is around
![]() $U_{b}^{+}\sim 35$
, so the contribution of
$U_{b}^{+}\sim 35$
, so the contribution of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}\approx 9.13$
is not negligible in the identity equation (3.1). However, at infinite Reynolds number,
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}\approx 9.13$
is not negligible in the identity equation (3.1). However, at infinite Reynolds number,
![]() $U_{b}^{+}\gg 9.13$
and
$U_{b}^{+}\gg 9.13$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}$
.
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}$
.
To better show the Reynolds number dependence, figure 2(b) presents the data on semilogarithmic axes. In figure 2(b) a logarithmic function is used to approximate the Reynolds number dependence of the inner-scaled bulk mean velocity as
![]() $U_{b}^{+}\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})+2.5$
. From (3.1), the approximate function for the global integral of the TKE production and dissipation becomes
$U_{b}^{+}\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})+2.5$
. From (3.1), the approximate function for the global integral of the TKE production and dissipation becomes
Given the complicated nature of turbulent wall-bounded flows, it is unlikely that the exact Reynolds number dependence of
![]() $U_{b}^{+}$
is a simple logarithmic function, but it is not the purpose of this work to determine the best fitting function or parameters for the Reynolds number dependence. Figure 2(b) shows that the increase of
$U_{b}^{+}$
is a simple logarithmic function, but it is not the purpose of this work to determine the best fitting function or parameters for the Reynolds number dependence. Figure 2(b) shows that the increase of
![]() $U_{b}^{+}$
,
$U_{b}^{+}$
,
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
with Reynolds number is in fact nearly logarithmic. Similar logarithmic functions have been used by Laadhari (Reference Laadhari2007), Zanoun, Nagib & Durst (Reference Zanoun, Nagib and Durst2009) and Abe & Antonia (Reference Abe and Antonia2016) to approximate the bulk mean velocity in high Reynolds number turbulent channel flow.
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
with Reynolds number is in fact nearly logarithmic. Similar logarithmic functions have been used by Laadhari (Reference Laadhari2007), Zanoun, Nagib & Durst (Reference Zanoun, Nagib and Durst2009) and Abe & Antonia (Reference Abe and Antonia2016) to approximate the bulk mean velocity in high Reynolds number turbulent channel flow.
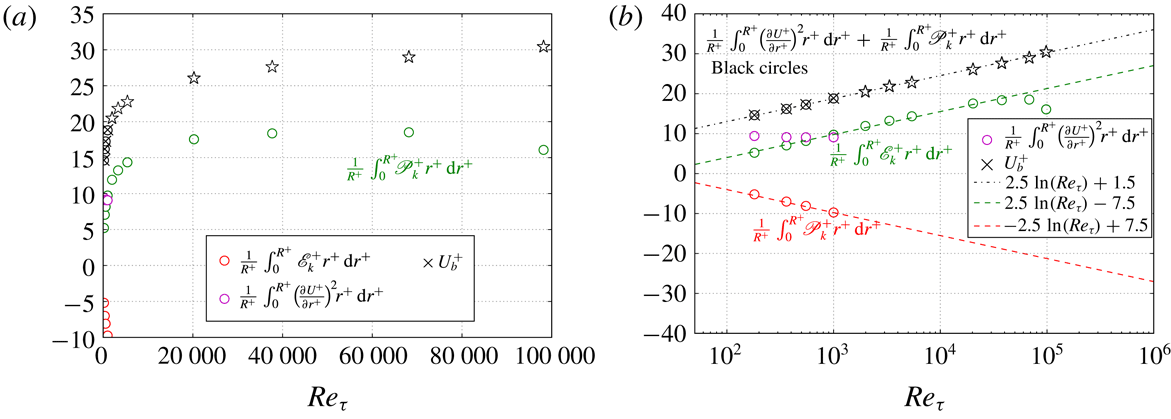
Figure 3 presents the Reynolds number dependence of the global integral results in turbulent pipe flows. As shown in the figures, the sum of
![]() $(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
and
$(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
and
![]() $(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
agrees excellently with the
$(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
agrees excellently with the
![]() $U_{b}^{+}$
data, and this strongly supports the global integral identity equation (2.12). The deviation of the superpipe data from the trend is caused by the spatial resolution in the near-wall region. At such a high Reynolds number, the first data point is close to or beyond the peak Reynolds shear stress location. In the superpipe experiments by Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2015), the Reynolds shear stress
$U_{b}^{+}$
data, and this strongly supports the global integral identity equation (2.12). The deviation of the superpipe data from the trend is caused by the spatial resolution in the near-wall region. At such a high Reynolds number, the first data point is close to or beyond the peak Reynolds shear stress location. In the superpipe experiments by Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2015), the Reynolds shear stress
![]() $R_{12}$
is not measured. For the calculation of
$R_{12}$
is not measured. For the calculation of
![]() $\mathscr{P}_{k}$
,
$\mathscr{P}_{k}$
,
![]() $R_{12}$
is calculated indirectly using
$R_{12}$
is calculated indirectly using
![]() $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
and the once-integrated mean momentum balance equation (see appendix B).
$\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$
and the once-integrated mean momentum balance equation (see appendix B).

Figure 3. Reynolds number dependence of the global integral of
![]() $(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
(magenta circles),
$(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
(magenta circles),
![]() $(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
(green circles) and
$(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
(green circles) and
![]() $(1/R^{+})\int _{0}^{R^{+}}\mathscr{E}_{k}^{+}r^{+}\,\text{d}r^{+}$
(red circles) in turbulent pipe flows. Also shown are the sum of
$(1/R^{+})\int _{0}^{R^{+}}\mathscr{E}_{k}^{+}r^{+}\,\text{d}r^{+}$
(red circles) in turbulent pipe flows. Also shown are the sum of
![]() $(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
and
$(1/R^{+})\int _{0}^{R^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}r^{+})^{2}r^{+}\,\text{d}r^{+}$
and
![]() $(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
(black circles),
$(1/R^{+})\int _{0}^{R^{+}}\mathscr{P}_{k}^{+}r^{+}\,\text{d}r^{+}$
(black circles),
![]() $U_{b}^{+}$
from DNS (black
$U_{b}^{+}$
from DNS (black
![]() $\times$
) by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and
$\times$
) by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and
![]() $U_{b}^{+}$
from superpipe (black star) by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013). (a) On linear–linear axes. (b) On semilogarithmic axes.
$U_{b}^{+}$
from superpipe (black star) by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013). (a) On linear–linear axes. (b) On semilogarithmic axes.
Figure 4 shows the global integral results for ZPG TBL. Due to the advection term (the last two integrals) in (2.13), the sum of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
will be smaller than
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
will be smaller than
![]() $U_{\infty }^{+}$
, as shown in the figure, but figure 4 shows that the difference is small, indicating that the mean advection has a minor role in the global balance of the TKE budget. The deviation of the experimental data at
$U_{\infty }^{+}$
, as shown in the figure, but figure 4 shows that the difference is small, indicating that the mean advection has a minor role in the global balance of the TKE budget. The deviation of the experimental data at
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 10\,000$
is caused by the spatial resolution of data points in the experiments of De Graaff & Eaton (Reference De Graaff and Eaton2000).
$Re_{\unicode[STIX]{x1D70F}}\approx 10\,000$
is caused by the spatial resolution of data points in the experiments of De Graaff & Eaton (Reference De Graaff and Eaton2000).

Figure 4. Reynolds number dependence of the global integral of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
(magenta triangles),
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
(magenta triangles),
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(green triangles) and
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(green triangles) and
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
(red triangles) in ZPG TBL. Also shown are the sum of
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}$
(red triangles) in ZPG TBL. Also shown are the sum of
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}+\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black triangles),
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}+\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
(black triangles),
![]() $U_{\infty }^{+}$
from DNS (black
$U_{\infty }^{+}$
from DNS (black
![]() $\times$
) and
$\times$
) and
![]() $U_{\infty }^{+}$
from experimental measurement (black asterisk) by De Graaff & Eaton (Reference De Graaff and Eaton2000), Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2015). (a) On linear–linear axes. (b) On semilogarithmic axes. DNS data are from two independent studies by Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009) and Schlatter & Örlü (Reference Schlatter and Örlü2010).
$U_{\infty }^{+}$
from experimental measurement (black asterisk) by De Graaff & Eaton (Reference De Graaff and Eaton2000), Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2015). (a) On linear–linear axes. (b) On semilogarithmic axes. DNS data are from two independent studies by Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009) and Schlatter & Örlü (Reference Schlatter and Örlü2010).
To sum up, the global integral identity of the TKE production (2.11)–(2.13) has been verified with high resolution experimental and DNS data from turbulent channel flows, pipe flows and ZPG TBL. Next, we will present the partition of the integral of the TKE production and dissipation in turbulent wall-bounded flows. We find that at sufficiently high Reynolds number, the integrals of the TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location
![]() $y_{m}$
. Given the importance of
$y_{m}$
. Given the importance of
![]() $y_{m}$
and meso-scaling in the partition of the integral of TKE production and dissipation, we will briefly review the meso-layer and meso-scaling before presenting the partition of the integrals.
$y_{m}$
and meso-scaling in the partition of the integral of TKE production and dissipation, we will briefly review the meso-layer and meso-scaling before presenting the partition of the integrals.
3.3 Meso-layer, meso-length scale and peak location of Reynolds shear stress
The concept of a meso-layer has been proposed in a number of studies, including Long & Chen (Reference Long and Chen1981), Afzal (Reference Afzal1982, Reference Afzal1984), Sreenivasan & Sahay (Reference Sreenivasan, Sahay and Panton1997), Wosnik, Castillo & George (Reference Wosnik, Castillo and George2000) and Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005). For example, in Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) a four-layer structure is proposed for turbulent wall-bounded flows, based on the force balance of the mean momentum balance equation. Their Layer III (the meso-layer) centres around the peak Reynolds shear stress location
![]() $y_{m}$
.
$y_{m}$
.
A meso-length scale for turbulent channel/pipe and ZPG TBL flows has been proposed as the geometric mean of the inner length scale
![]() $l_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
and the outer length scale
$l_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
and the outer length scale
![]() $l_{o}=\unicode[STIX]{x1D6FF}$
, as
$l_{o}=\unicode[STIX]{x1D6FF}$
, as
![]() $l_{m}=\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}$
(Fife et al.
Reference Fife, Klewicki, McMurtry and Wei2005a
,Reference Fife, Wei, Klewicki and McMurtry
b
; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). Meso-length scale
$l_{m}=\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}$
(Fife et al.
Reference Fife, Klewicki, McMurtry and Wei2005a
,Reference Fife, Wei, Klewicki and McMurtry
b
; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). Meso-length scale
![]() $l_{m}$
has been advocated as a fundamental length scale in turbulent channel/pipe flow and ZPG TBL, like the
$l_{m}$
has been advocated as a fundamental length scale in turbulent channel/pipe flow and ZPG TBL, like the
![]() $l_{\unicode[STIX]{x1D708}}$
and
$l_{\unicode[STIX]{x1D708}}$
and
![]() $l_{o}$
(Fife et al.
Reference Fife, Klewicki, McMurtry and Wei2005a
,Reference Fife, Wei, Klewicki and McMurtry
b
; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). It has long been known that the peak Reynolds shear stress location
$l_{o}$
(Fife et al.
Reference Fife, Klewicki, McMurtry and Wei2005a
,Reference Fife, Wei, Klewicki and McMurtry
b
; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). It has long been known that the peak Reynolds shear stress location
![]() $y_{m}$
scales as
$y_{m}$
scales as
![]() $y_{m}=O(\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}})$
(see, for example, Long & Chen Reference Long and Chen1981; Sreenivasan Reference Sreenivasan1989; Sreenivasan & Sahay Reference Sreenivasan, Sahay and Panton1997; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). Thus, the peak Reynolds shear stress location
$y_{m}=O(\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}})$
(see, for example, Long & Chen Reference Long and Chen1981; Sreenivasan Reference Sreenivasan1989; Sreenivasan & Sahay Reference Sreenivasan, Sahay and Panton1997; Wei et al.
Reference Wei, Fife, Klewicki and McMurtry2005). Thus, the peak Reynolds shear stress location
![]() $y_{m}$
scales as the meso-length scale.
$y_{m}$
scales as the meso-length scale.

Figure 5. Dependence of Reynolds shear stress peak location
![]() $y_{m}$
on Reynolds numbers. Squares are channel flow data from DNS of Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015), circles are pipe flow data from DNS of El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and superpipe by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) and triangles are ZPG-TBL data from DNS by Schlatter & Örlü (Reference Schlatter and Örlü2010) (filled triangles) and Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009) (open triangles). Note Reynolds shear stress
$y_{m}$
on Reynolds numbers. Squares are channel flow data from DNS of Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015), circles are pipe flow data from DNS of El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013) and superpipe by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) and triangles are ZPG-TBL data from DNS by Schlatter & Örlü (Reference Schlatter and Örlü2010) (filled triangles) and Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009) (open triangles). Note Reynolds shear stress
![]() $R_{12}$
is not directly measured in the superpipe, but calculated indirectly as
$R_{12}$
is not directly measured in the superpipe, but calculated indirectly as
![]() $R_{12}^{+}=1-y^{+}/R^{+}-\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+}$
(see appendix B for more details).
$R_{12}^{+}=1-y^{+}/R^{+}-\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+}$
(see appendix B for more details).
The meso-length scaling is defined as
Given the spatial resolution limitation inherent in physical experiments, it has been challenging to determine
![]() $y_{m}$
precisely. However, during the past thirty years, more DNS data at higher Reynolds numbers, and higher resolution experimental data, have made it possible to determine more precisely the Reynolds number dependence of
$y_{m}$
precisely. However, during the past thirty years, more DNS data at higher Reynolds numbers, and higher resolution experimental data, have made it possible to determine more precisely the Reynolds number dependence of
![]() $y_{m}$
. Figure 5 shows the Reynolds number dependence of the meso-scaled peak location
$y_{m}$
. Figure 5 shows the Reynolds number dependence of the meso-scaled peak location
![]() $y_{m}/l_{m}$
. The experimental and numerical data in figure 5 offer strong evidence that at sufficiently high Reynolds number the peak Reynolds shear stress location
$y_{m}/l_{m}$
. The experimental and numerical data in figure 5 offer strong evidence that at sufficiently high Reynolds number the peak Reynolds shear stress location
![]() $y_{m}$
scales as the meso-length scale:
$y_{m}$
scales as the meso-length scale:
![]() $y_{m}=O(l_{m})$
.
$y_{m}=O(l_{m})$
.
Figure 5 shows that the peak Reynolds shear stress location
![]() $y_{m}$
in turbulent channel flows is approximately
$y_{m}$
in turbulent channel flows is approximately
![]() $y_{m}\approx 1.5l_{m}$
or
$y_{m}\approx 1.5l_{m}$
or
![]() $y_{m}^{+}\approx 1.5\sqrt{\unicode[STIX]{x1D6FF}^{+}}$
for
$y_{m}^{+}\approx 1.5\sqrt{\unicode[STIX]{x1D6FF}^{+}}$
for
![]() $Re_{\unicode[STIX]{x1D70F}}>2000$
. The peak Reynolds shear stress location in ZPG TBL is slightly larger, at
$Re_{\unicode[STIX]{x1D70F}}>2000$
. The peak Reynolds shear stress location in ZPG TBL is slightly larger, at
![]() $y_{m}\approx 2.4l_{m}$
or
$y_{m}\approx 2.4l_{m}$
or
![]() $y_{m}^{+}\approx 2.4\sqrt{\unicode[STIX]{x1D6FF}^{+}}$
. In the 1980s, Long & Chen (Reference Long and Chen1981) proposed a similar scaling but with a numerical factor of 1.87, and Sreenivasan (Reference Sreenivasan1989) suggested a numerical factor of 2.0. Given the spatial resolution of the instrumentation available then, and the Reynolds number range of the data, these predictions are remarkably close to the recent DNS and high resolution experimental data shown in figure 5.
$y_{m}^{+}\approx 2.4\sqrt{\unicode[STIX]{x1D6FF}^{+}}$
. In the 1980s, Long & Chen (Reference Long and Chen1981) proposed a similar scaling but with a numerical factor of 1.87, and Sreenivasan (Reference Sreenivasan1989) suggested a numerical factor of 2.0. Given the spatial resolution of the instrumentation available then, and the Reynolds number range of the data, these predictions are remarkably close to the recent DNS and high resolution experimental data shown in figure 5.
One motivation for the present work is to assess the role of the meso-layer and meso-length scale in the partition of the integrals of TKE production and dissipation. In figure 6 we present the distribution of the TKE production and dissipation versus the meso-scaled distance from the wall, to complement the inner-scaled distance and the outer-scaled distance presented in figure 1. The peak location of TKE production in meso-scaling becomes smaller with increasing Reynolds number. This is not surprising, as the peak location of the TKE production scales with inner scaling.

Figure 6. TKE production and dissipation versus meso-scaled distance from the wall
![]() $y/l_{m}$
. Data from DNS of channel flow Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
$y/l_{m}$
. Data from DNS of channel flow Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
3.4 Pre-multiplied TKE production and dissipation
To better show the near-wall region, it is common to plot the wall-normal distance on a logarithmic scale. For the convenience of depicting the area under the curve (its integral) on semilogarithmic axes, the TKE production and dissipation have been pre-multiplied by the wall-normal distance, because the derivative of a logarithmic function has the following property:
Thus the area under the pre-multiplied TKE production and dissipation curves on semilogarithmic axes equals the integrals of TKE production and dissipation. For the inner-scaled
![]() $y^{+}$
and meso-scaled
$y^{+}$
and meso-scaled
![]() $y/l_{m}$
, the integrals of TKE production (or dissipation) can be written, respectively, as
$y/l_{m}$
, the integrals of TKE production (or dissipation) can be written, respectively, as
where
![]() $y_{1}$
is the location of the first data point above the surface. As
$y_{1}$
is the location of the first data point above the surface. As
![]() $\log (0)$
is undefined, the first data point
$\log (0)$
is undefined, the first data point
![]() $y_{1}$
should not be at the wall. In practice, the first data point is at a small distance from the wall.
$y_{1}$
should not be at the wall. In practice, the first data point is at a small distance from the wall.
In figure 7(a) the pre-multiplied TKE production and dissipation are plotted versus the inner-scaled distance from the wall
![]() $y^{+}$
on semilogarithmic axes. For convenience, the xticks on the bottom show values of
$y^{+}$
on semilogarithmic axes. For convenience, the xticks on the bottom show values of
![]() $y^{+}$
and the xticks on the top show values of
$y^{+}$
and the xticks on the top show values of
![]() $\log _{10}y^{+}$
. As in figure 1(a), the pre-multiplied TKE production also peaks within the viscous buffer layer at
$\log _{10}y^{+}$
. As in figure 1(a), the pre-multiplied TKE production also peaks within the viscous buffer layer at
![]() $y^{+}\approx 12$
.
$y^{+}\approx 12$
.

Figure 7. Pre-multiplied TKE production and dissipation versus distance from the wall on semilogarithmic axes. (a) Distance from the wall is inner scaled
![]() $y^{+}$
. (b) Distance from the wall is meso-scaled
$y^{+}$
. (b) Distance from the wall is meso-scaled
![]() $y/l_{m}$
. The xticks on bottom denote values of
$y/l_{m}$
. The xticks on bottom denote values of
![]() $y^{+}$
or
$y^{+}$
or
![]() $y/l_{m}$
and xticks on top denote values of
$y/l_{m}$
and xticks on top denote values of
![]() $\log _{10}(y^{+})$
or
$\log _{10}(y^{+})$
or
![]() $\log _{10}(y/l_{m})$
.
$\log _{10}(y/l_{m})$
.
Figure 7 shows that as Reynolds number increases the pre-multiplied TKE production and dissipation approach a plateau away from the wall, before dropping sharply towards the channel centre. It has been observed that at sufficiently high Reynolds number, say
![]() $Re_{\unicode[STIX]{x1D70F}}>20\,000$
, a second bump appears away from the wall in the pre-multiplied TKE production profile. For example, using a composite mean velocity profile and the corresponding Reynolds shear stress profile proposed by Perry, Marusic & Jones (Reference Perry, Marusic and Jones2002), Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
) sketched the pre-multiplied TKE production profiles
$Re_{\unicode[STIX]{x1D70F}}>20\,000$
, a second bump appears away from the wall in the pre-multiplied TKE production profile. For example, using a composite mean velocity profile and the corresponding Reynolds shear stress profile proposed by Perry, Marusic & Jones (Reference Perry, Marusic and Jones2002), Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
) sketched the pre-multiplied TKE production profiles
![]() $y^{+}\mathscr{P}_{k}^{+}$
for different Reynolds numbers. The value of the plateau is approximately
$y^{+}\mathscr{P}_{k}^{+}$
for different Reynolds numbers. The value of the plateau is approximately
![]() $y^{+}\mathscr{P}_{k}^{+}\approx 2.5$
. Their sketch for
$y^{+}\mathscr{P}_{k}^{+}\approx 2.5$
. Their sketch for
![]() $Re_{\unicode[STIX]{x1D70F}}=10^{6}$
shows a smaller second bump away from the wall (Marusic et al.
Reference Marusic, Mathis and Hutchins2010a
). The second bump is also observed in the plot by Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016).
$Re_{\unicode[STIX]{x1D70F}}=10^{6}$
shows a smaller second bump away from the wall (Marusic et al.
Reference Marusic, Mathis and Hutchins2010a
). The second bump is also observed in the plot by Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016).
In figure 7(b), the pre-multiplied TKE production and dissipation are plotted versus the meso-scaled distance from the wall
![]() $y/l_{m}$
on semilogarithmic axes. The advantage of the meso-scaled length scale is shown in figure 8, in which the area under the curves of the pre-multiplied TKE production and dissipation is approximated by a rectangle.
$y/l_{m}$
on semilogarithmic axes. The advantage of the meso-scaled length scale is shown in figure 8, in which the area under the curves of the pre-multiplied TKE production and dissipation is approximated by a rectangle.

Figure 8. Sketch approximating the integral of TKE production and dissipation at high Reynolds number. Dashed curves approximate the area under the pre-multiplied TKE production and dissipation curves of DNS data at
![]() $Re_{\unicode[STIX]{x1D70F}}=5300$
by Lee & Moser (Reference Lee and Moser2015). The dot-dashed curves are approximations for a higher Reynolds number at
$Re_{\unicode[STIX]{x1D70F}}=5300$
by Lee & Moser (Reference Lee and Moser2015). The dot-dashed curves are approximations for a higher Reynolds number at
![]() $Re_{\unicode[STIX]{x1D70F}}=10^{6}$
. The trend will be similar as Reynolds number increases further. The vertical dashed black line denotes the peak Reynolds shear stress location
$Re_{\unicode[STIX]{x1D70F}}=10^{6}$
. The trend will be similar as Reynolds number increases further. The vertical dashed black line denotes the peak Reynolds shear stress location
![]() $y_{m}/l_{m}\approx 1.5$
, as shown in figure 5.
$y_{m}/l_{m}\approx 1.5$
, as shown in figure 5.
In figure 8 the dashed rectangle approximates the integral of the TKE production and dissipation at
![]() $Re_{\unicode[STIX]{x1D70F}}=5300$
of Lee & Moser (Reference Lee and Moser2015), and the dot-dashed rectangle is an extrapolation for a higher Reynolds number at
$Re_{\unicode[STIX]{x1D70F}}=5300$
of Lee & Moser (Reference Lee and Moser2015), and the dot-dashed rectangle is an extrapolation for a higher Reynolds number at
![]() $Re_{\unicode[STIX]{x1D70F}}=10^{6}$
. The height of the rectangle is approximately
$Re_{\unicode[STIX]{x1D70F}}=10^{6}$
. The height of the rectangle is approximately
![]() $\ln (10)y^{+}\mathscr{P}_{k}^{+}\approx 5.7$
, which is consistent with the value used in the sketch of Marusic et al. (Reference Marusic, Baars and Hutchins2017), differing by a factor of
$\ln (10)y^{+}\mathscr{P}_{k}^{+}\approx 5.7$
, which is consistent with the value used in the sketch of Marusic et al. (Reference Marusic, Baars and Hutchins2017), differing by a factor of
![]() $\ln (10)$
.
$\ln (10)$
.
The width of the rectangle in figure 8 can be approximated as
![]() $\log _{10}(\unicode[STIX]{x1D6FF}^{+})$
(see the xticks on the top of figure 8). Thus the area under the curves of the pre-multiplied TKE production and dissipation can be approximated as
$\log _{10}(\unicode[STIX]{x1D6FF}^{+})$
(see the xticks on the top of figure 8). Thus the area under the curves of the pre-multiplied TKE production and dissipation can be approximated as
![]() $5.7\log _{10}(\unicode[STIX]{x1D6FF}^{+})\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})$
. This approximation is consistent with the Reynolds number dependence in the global integral identity equation
$5.7\log _{10}(\unicode[STIX]{x1D6FF}^{+})\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})$
. This approximation is consistent with the Reynolds number dependence in the global integral identity equation
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}-9.13$
and the data for
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}-9.13$
and the data for
![]() $U_{b}^{+}\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})+2.5$
, as shown in figure 2(b).
$U_{b}^{+}\approx 2.5\ln (Re_{\unicode[STIX]{x1D70F}})+2.5$
, as shown in figure 2(b).
The vertical dashed line at
![]() $y/l_{m}=1.5$
in figure 8 indicates the peak Reynolds shear stress location, as shown in figure 5. Figure 8 shows that the width of the rectangle on both sides of
$y/l_{m}=1.5$
in figure 8 indicates the peak Reynolds shear stress location, as shown in figure 5. Figure 8 shows that the width of the rectangle on both sides of
![]() $y_{m}$
is of the order of
$y_{m}$
is of the order of
![]() $0.5\log _{10}(\unicode[STIX]{x1D6FF}^{+})$
(see the xticks on the top).
$0.5\log _{10}(\unicode[STIX]{x1D6FF}^{+})$
(see the xticks on the top).
The equal partition of the integral of the TKE production and dissipation around
![]() $y_{m}$
can also be explained using table 1. The ranges of boundary layer around
$y_{m}$
can also be explained using table 1. The ranges of boundary layer around
![]() $y_{m}$
, in meso-scaling, are
$y_{m}$
, in meso-scaling, are
![]() $O((\log _{10}(\unicode[STIX]{x1D6FF}^{+}))/2)$
on both sides. Assuming
$O((\log _{10}(\unicode[STIX]{x1D6FF}^{+}))/2)$
on both sides. Assuming
![]() $A_{k}$
for the height of the rectangle that approximates the pre-multiplied TKE production or dissipation, the area or the integral of TKE production and dissipation between the first data point
$A_{k}$
for the height of the rectangle that approximates the pre-multiplied TKE production or dissipation, the area or the integral of TKE production and dissipation between the first data point
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{m}$
is
$y_{m}$
is
![]() $O((\log _{10}(\unicode[STIX]{x1D6FF}^{+})A_{k})/2)$
, and the area between
$O((\log _{10}(\unicode[STIX]{x1D6FF}^{+})A_{k})/2)$
, and the area between
![]() $y_{m}$
and
$y_{m}$
and
![]() $\unicode[STIX]{x1D6FF}$
is also
$\unicode[STIX]{x1D6FF}$
is also
![]() $O((\log _{10}(\unicode[STIX]{x1D6FF}^{+})A_{k})/2)$
.
$O((\log _{10}(\unicode[STIX]{x1D6FF}^{+})A_{k})/2)$
.
Table 1. Partition of boundary layer around the meso-layer. For convenience, the first data point is taken as
![]() $y_{1}^{+}=1$
. (One can choose other values for
$y_{1}^{+}=1$
. (One can choose other values for
![]() $y_{1}$
. For example, if
$y_{1}$
. For example, if
![]() $y_{1}^{+}=0.1$
, then
$y_{1}^{+}=0.1$
, then
![]() $\log _{10}(0.1)=-1$
, and
$\log _{10}(0.1)=-1$
, and
![]() $\log _{10}(0.1/\sqrt{\unicode[STIX]{x1D6FF}^{+}})\approx -0.5\log _{10}(\unicode[STIX]{x1D6FF}^{+})-1$
. As
$\log _{10}(0.1/\sqrt{\unicode[STIX]{x1D6FF}^{+}})\approx -0.5\log _{10}(\unicode[STIX]{x1D6FF}^{+})-1$
. As
![]() $\unicode[STIX]{x1D6FF}^{+}\rightarrow \infty$
, the constant
$\unicode[STIX]{x1D6FF}^{+}\rightarrow \infty$
, the constant
![]() $-1$
becomes negligible. Furthermore, as
$-1$
becomes negligible. Furthermore, as
![]() $y_{1}$
becomes smaller than 0.1, the pre-multiplied TKE production and dissipation quickly approach 0.)
$y_{1}$
becomes smaller than 0.1, the pre-multiplied TKE production and dissipation quickly approach 0.)

Figure 8 and table 1 indicate that the integrals of the TKE production and dissipation are equally partitioned around
![]() $y_{m}$
with a value of
$y_{m}$
with a value of
![]() $1.25\ln (\unicode[STIX]{x1D6FF}^{+})$
. The advantage and importance of meso-scaled length can be summarized simply: at sufficiently high Reynolds number, the integrals of TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location
$1.25\ln (\unicode[STIX]{x1D6FF}^{+})$
. The advantage and importance of meso-scaled length can be summarized simply: at sufficiently high Reynolds number, the integrals of TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location
![]() $y_{m}$
.
$y_{m}$
.
The approximation of pre-multiplied TKE production or dissipation as a rectangle is crude, but it is interesting that meso-scaled distance from the wall reveals that the TKE production and dissipation seem to centre the integrals evenly across the meso-layer. Next we will use DNS data to assess quantitatively the partition of the integral of the TKE production and TKE dissipation around the peak Reynolds shear stress location
![]() $y_{m}$
.
$y_{m}$
.
3.5 Partition of the TKE production and dissipation around
 $y_{m}$
$y_{m}$
Using the TKE budget data from DNS by Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015) and Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016), the integrals of TKE production from
![]() $0$
to
$0$
to
![]() $y_{m}$
and from
$y_{m}$
and from
![]() $y_{m}$
to
$y_{m}$
to
![]() $\unicode[STIX]{x1D6FF}$
are calculated and presented in figure 9(a). Also plotted is the
$\unicode[STIX]{x1D6FF}$
are calculated and presented in figure 9(a). Also plotted is the
![]() $(U_{b}^{+}-9.13)/2$
from (3.1). To better show the partition, the integrals are divided by
$(U_{b}^{+}-9.13)/2$
from (3.1). To better show the partition, the integrals are divided by
![]() $(U_{b}^{+}-9.13)$
in figure 9(b), which clearly shows that at low Reynolds number, the integral from
$(U_{b}^{+}-9.13)$
in figure 9(b), which clearly shows that at low Reynolds number, the integral from
![]() $0$
to
$0$
to
![]() $y_{m}$
is larger than that from
$y_{m}$
is larger than that from
![]() $y_{m}$
to
$y_{m}$
to
![]() $\unicode[STIX]{x1D6FF}$
. For example, at
$\unicode[STIX]{x1D6FF}$
. For example, at
![]() $Re_{\unicode[STIX]{x1D70F}}=100$
, the value from
$Re_{\unicode[STIX]{x1D70F}}=100$
, the value from
![]() $0$
to
$0$
to
![]() $y_{m}$
(solid green square) is approximately
$y_{m}$
(solid green square) is approximately
![]() $0.6$
, and the value from
$0.6$
, and the value from
![]() $y_{m}$
to
$y_{m}$
to
![]() $\unicode[STIX]{x1D6FF}$
(open green square) is approximately
$\unicode[STIX]{x1D6FF}$
(open green square) is approximately
![]() $0.25$
. Note that they do not add up to 1 because
$0.25$
. Note that they do not add up to 1 because
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
is larger than
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
is larger than
![]() $9.13$
at this low Reynolds number. The dominance of the near-wall region at low Reynolds number is consistent with the observation of Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
).
$9.13$
at this low Reynolds number. The dominance of the near-wall region at low Reynolds number is consistent with the observation of Marusic et al. (Reference Marusic, Mathis and Hutchins2010a
).
At sufficiently high Reynolds number, figure 9(b) shows that the integral of TKE production indeed approaches an equal partition around
![]() $y_{m}$
, with
$y_{m}$
, with
![]() $\int _{0}^{y_{m}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx \int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx 0.5(U_{b}^{+}-9.13)$
.
$\int _{0}^{y_{m}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx \int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx 0.5(U_{b}^{+}-9.13)$
.

Figure 9. Partition of the integral of the TKE production about the peak Reynolds shear stress location
![]() $y_{m}$
. (a) Integral of the TKE production from
$y_{m}$
. (a) Integral of the TKE production from
![]() $0$
to
$0$
to
![]() $y_{m}$
and from
$y_{m}$
and from
![]() $y_{m}$
to
$y_{m}$
to
![]() $\unicode[STIX]{x1D6FF}$
versus Reynolds number. (b) Integrals divided by
$\unicode[STIX]{x1D6FF}$
versus Reynolds number. (b) Integrals divided by
![]() $(U_{b}^{+}-9.13)$
versus Reynolds number. The filled squares represent
$(U_{b}^{+}-9.13)$
versus Reynolds number. The filled squares represent
![]() $\int _{0}^{y_{m}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
calculated from DNS of turbulent channel flow by Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015). The open squares represent
$\int _{0}^{y_{m}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
calculated from DNS of turbulent channel flow by Abe et al. (Reference Abe, Kawamura and Matsuo2001), Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002), Lee & Moser (Reference Lee and Moser2015). The open squares represent
![]() $\int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
. Circles represent turbulent pipe flow data from El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013).
$\int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}$
. Circles represent turbulent pipe flow data from El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013).

Figure 10. Partition of TKE production and dissipation around the peak Reynolds shear stress location
![]() $y_{m}$
. Turbulent channel flows (squares), turbulent pipe flows (circles), ZPG TBL (triangles). A value of
$y_{m}$
. Turbulent channel flows (squares), turbulent pipe flows (circles), ZPG TBL (triangles). A value of
![]() $a=9.13$
is used for turbulent channel and pipe flows and
$a=9.13$
is used for turbulent channel and pipe flows and
![]() $a=12$
is used for ZPG TBL.
$a=12$
is used for ZPG TBL.
Partition of the integral of TKE dissipation is calculated from DNS data and presented in figure 10. It can only be proven that the global integral of the TKE production must equal the global integral of the TKE dissipation in turbulent channel flows and turbulent pipe flows. Given the complicated roles of the transport terms in the different layers, it is not known a priori that the partition of the integral of the TKE dissipation will be the same as that of the TKE production. However, the DNS data shown in figure 10 strongly suggest that the integral of the TKE dissipation data is also equally partitioned around the peak Reynolds shear stress location
![]() $y_{m}$
at sufficiently high Reynolds number,
$y_{m}$
at sufficiently high Reynolds number,
![]() $\int _{0}^{y_{m}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx \int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx 0.5(U_{b}^{+}-9.13)$
.
$\int _{0}^{y_{m}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx \int _{y_{m}^{+}}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx 0.5(U_{b}^{+}-9.13)$
.
3.6 ‘Log layer’ in the integral profiles of TKE production and dissipation
Finally, we investigate the integral profiles of the TKE production and dissipation. Denote the integral of TKE production and dissipation as
Using inner-scaled variables, the inner-scaled integral functions can be written as
 $$\begin{eqnarray}{\mathcal{I}}_{\mathscr{P}_{k}}^{+}(y)=\frac{\displaystyle \int _{0}^{y}\mathscr{P}_{k}\,\text{d}y}{u_{\unicode[STIX]{x1D70F}}^{3}};\quad {\mathcal{I}}_{\mathscr{E}_{k}}^{+}(y)=\frac{\displaystyle \int _{0}^{y}\mathscr{E}_{k}\,\text{d}y}{u_{\unicode[STIX]{x1D70F}}^{3}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{\mathscr{P}_{k}}^{+}(y)=\frac{\displaystyle \int _{0}^{y}\mathscr{P}_{k}\,\text{d}y}{u_{\unicode[STIX]{x1D70F}}^{3}};\quad {\mathcal{I}}_{\mathscr{E}_{k}}^{+}(y)=\frac{\displaystyle \int _{0}^{y}\mathscr{E}_{k}\,\text{d}y}{u_{\unicode[STIX]{x1D70F}}^{3}}.\end{eqnarray}$$
The integral profiles of TKE production and dissipation are calculated from the DNS data of turbulent channel flow by Abe et al. (Reference Abe, Kawamura and Matsuo2001) and Lee & Moser (Reference Lee and Moser2015) and presented in figure 11. Also plotted in the figure is the inner normalized mean streamwise velocity
![]() $U^{+}$
at
$U^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=5200$
shifted downwards by 9.3 and the log-law equation for
$Re_{\unicode[STIX]{x1D70F}}=5200$
shifted downwards by 9.3 and the log-law equation for
![]() $U^{+}$
, but with an additive constant of
$U^{+}$
, but with an additive constant of
![]() $-4.3$
.
$-4.3$
.
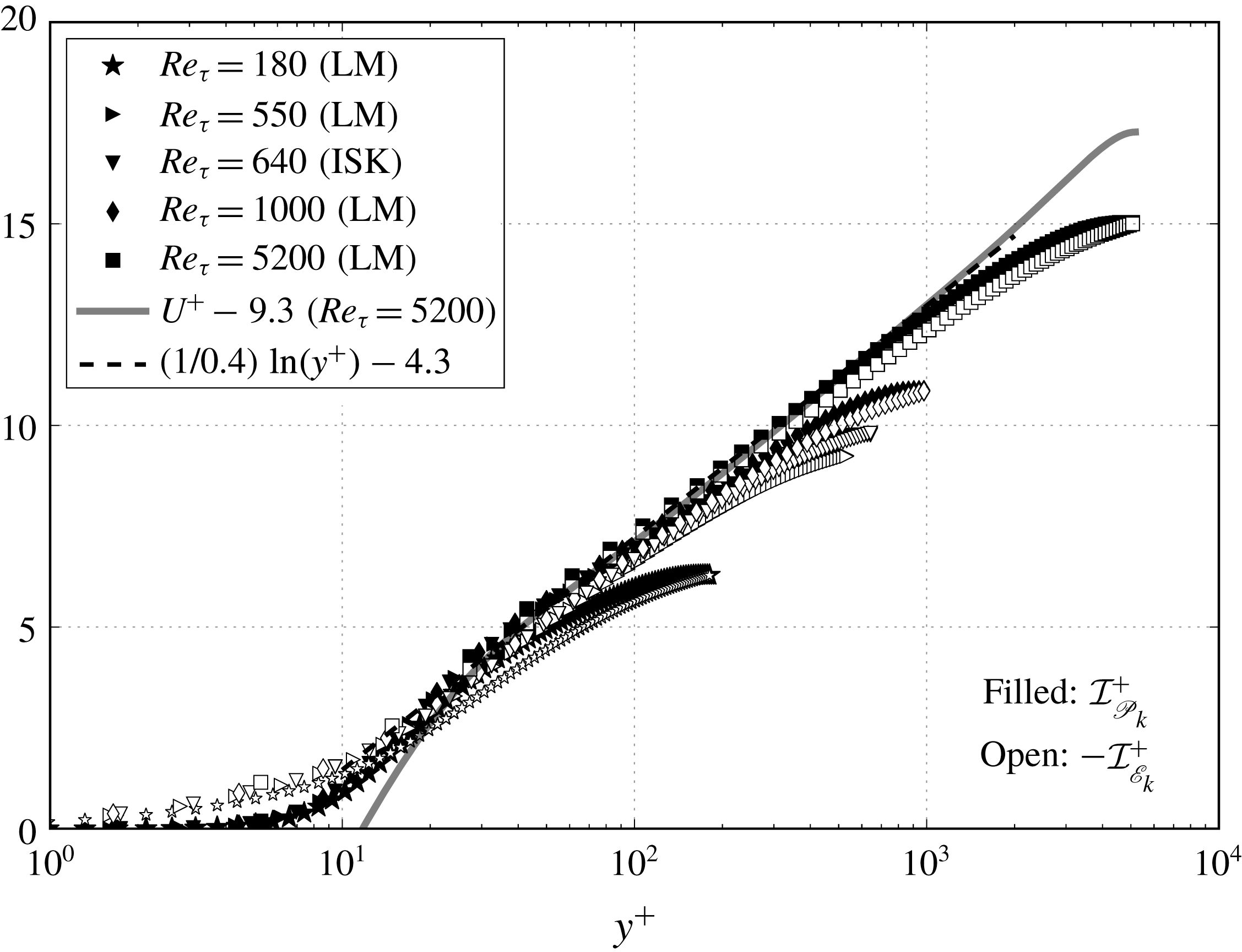
Figure 11. Integral profiles of the TKE production and dissipation versus
![]() $y^{+}$
. Data are from DNS of turbulent channel flows by Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
$y^{+}$
. Data are from DNS of turbulent channel flows by Iwamoto et al. (Reference Iwamoto, Suzuki and Kasagi2002) and Lee & Moser (Reference Lee and Moser2015).
In the viscous sublayer and buffer layer, the integral of the TKE dissipation is larger than the integral of the TKE production. For example, the integral of the TKE production at
![]() $y^{+}\approx 5$
(the end of the viscous sublayer) is
$y^{+}\approx 5$
(the end of the viscous sublayer) is
![]() $\int _{0}^{5}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx 0.06$
. The integral of the TKE dissipation at the end of viscous sublayer is
$\int _{0}^{5}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx 0.06$
. The integral of the TKE dissipation at the end of viscous sublayer is
![]() $\int _{0}^{5}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx 0.8$
. As shown in figure 1(a), in the viscous sublayer the TKE production term is small, and the TKE dissipation is balanced by the viscous diffusion term.
$\int _{0}^{5}\mathscr{E}_{k}^{+}\,\text{d}y^{+}\approx 0.8$
. As shown in figure 1(a), in the viscous sublayer the TKE production term is small, and the TKE dissipation is balanced by the viscous diffusion term.
Figure 12(a) shows the integral profiles of TKE production and dissipation for turbulent pipe flows, and figure 12(b) shows the same profiles for ZPG TBL. To facilitate comparison, the same logarithmic equation
![]() $(1/0.4)\ln (y^{+})-4.3$
is plotted in all three figures. Notable features in figures 11 and 12 are as follows. (i) At the channel or pipe centreline, the magnitude of the global integral of the TKE production is the same as that of the dissipation. However, outside the boundary layer of ZPG TBL, the magnitude of the global integral of TKE production is larger than that of the dissipation, as shown in figure 12(b). (ii) Although all three types of turbulent wall-bounded flows exhibit a logarithmic-like layer at sufficiently high Reynolds number, noticeable differences exist among the three flows, especially in the wake region.
$(1/0.4)\ln (y^{+})-4.3$
is plotted in all three figures. Notable features in figures 11 and 12 are as follows. (i) At the channel or pipe centreline, the magnitude of the global integral of the TKE production is the same as that of the dissipation. However, outside the boundary layer of ZPG TBL, the magnitude of the global integral of TKE production is larger than that of the dissipation, as shown in figure 12(b). (ii) Although all three types of turbulent wall-bounded flows exhibit a logarithmic-like layer at sufficiently high Reynolds number, noticeable differences exist among the three flows, especially in the wake region.

Figure 12. Integral profiles of the TKE production and dissipation versus
![]() $y^{+}$
. (a) Turbulent pipe flows at
$y^{+}$
. (a) Turbulent pipe flows at
![]() $Re_{\unicode[STIX]{x1D70F}}=181,\,550,\,1000$
by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013). (b) ZPG TBL at
$Re_{\unicode[STIX]{x1D70F}}=181,\,550,\,1000$
by El Khoury et al. (Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013). (b) ZPG TBL at
![]() $Re_{\unicode[STIX]{x1D703}}=670,\,2000,\,3270$
(
$Re_{\unicode[STIX]{x1D703}}=670,\,2000,\,3270$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=252,\,671,\,1043$
) by Schlatter & Örlü (Reference Schlatter and Örlü2010).
$Re_{\unicode[STIX]{x1D70F}}=252,\,671,\,1043$
) by Schlatter & Örlü (Reference Schlatter and Örlü2010).
The logarithmic-like layer shown in figures 11 and 12 can be represented as
The von Kármán ‘constant’ in the log law is approximately the same as the one in the
![]() $U^{+}$
profile. Discussions on the existence of the log layer and the ‘universality’ of the von Kármán constant can be found in the work of Nagib & Chauhan (Reference Nagib and Chauhan2008). The downward shift in the integral profiles of TKE production and dissipation is directly related to the constant
$U^{+}$
profile. Discussions on the existence of the log layer and the ‘universality’ of the von Kármán constant can be found in the work of Nagib & Chauhan (Reference Nagib and Chauhan2008). The downward shift in the integral profiles of TKE production and dissipation is directly related to the constant
![]() $-9.13$
in the global integral identity equation (3.1).
$-9.13$
in the global integral identity equation (3.1).
The logarithmic-like behaviour of the TKE production integral in turbulent channel flow can be explained by (2.10):
Thus the integral of TKE production can be approximated by
![]() $U^{+}$
with a downward shift. It has been shown above that, at sufficiently high Reynolds number,
$U^{+}$
with a downward shift. It has been shown above that, at sufficiently high Reynolds number,
![]() $\int _{0}^{y^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}\lesssim 9.13$
. Moreover, outside the viscous sublayer and buffer layer, it can be shown that
$\int _{0}^{y^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}\lesssim 9.13$
. Moreover, outside the viscous sublayer and buffer layer, it can be shown that
![]() $(y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+})/\unicode[STIX]{x1D6FF}^{+}$
is small. In other words, the logarithmic-like behaviour of the TKE production is directly related to the logarithmic-like behaviour of the mean velocity
$(y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+})/\unicode[STIX]{x1D6FF}^{+}$
is small. In other words, the logarithmic-like behaviour of the TKE production is directly related to the logarithmic-like behaviour of the mean velocity
![]() $U^{+}$
.
$U^{+}$
.
The logarithmic-like scaling for the global integrals of the TKE production and dissipation, equation (3.1), is also directly related to the logarithmic-like behaviour of the integral profiles of TKE production and dissipation, equations (3.9) and (3.10). At sufficiently high Reynolds number, equations (3.9) and (3.10) indicate that
It is known that, at sufficiently high Reynolds number,
![]() $y_{m}=O(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
or
$y_{m}=O(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$
or
![]() $y_{m}^{+}=O(\sqrt{\unicode[STIX]{x1D6FF}^{+}})$
. From (3.9) and (3.10), the scaling for the integral of TKE production and dissipation from wall to
$y_{m}^{+}=O(\sqrt{\unicode[STIX]{x1D6FF}^{+}})$
. From (3.9) and (3.10), the scaling for the integral of TKE production and dissipation from wall to
![]() $y_{m}$
can be estimated as
$y_{m}$
can be estimated as
Hence, the equal partition of TKE production around
![]() $y_{m}$
is also directly related to the logarithmic-like behaviour of the integral profiles of TKE production and dissipation, equation (3.9).
$y_{m}$
is also directly related to the logarithmic-like behaviour of the integral profiles of TKE production and dissipation, equation (3.9).
The noticeable difference among the integrals of the TKE production and dissipation in channel flows, pipe flows and ZPG TBL is similar to the differences observed in the low-order statistics on different types of turbulent wall-bounded flows, in particular within the wake region, as discussed by Jiménez et al. (Reference Jiménez, Hoyas, Simens and Mizuno2009), Mathis et al. (Reference Mathis, Monty, Hutchins and Marusic2009b ), Monty et al. (Reference Monty, Hutchins, Ng, Marusic and Chong2009) and Ng et al. (Reference Ng, Monty, Hutchins, Chong and Marusic2011). The differences between the internal flow (channel or pipe flows) and ZPG TBL are traced by Jiménez et al. (Reference Jiménez, Hoyas, Simens and Mizuno2009) to an excess of production of the streamwise turbulent energy in the outer part of the boundary layer.
4 Discussion
The integral properties of the TKE production and dissipation revealed in the present work may provide quantitative measures of the inner and outer interactions and the emergence of the second peak in the streamwise variance. For example, it has been reported by Marusic et al. (Reference Marusic, Baars and Hutchins2017) that a second peak in the streamwise variance appears when
![]() $Re_{\unicode[STIX]{x1D70F}}\gtrapprox 15\,000{-}20\,000$
, which roughly corresponds to two decades of scale separation on both sides of
$Re_{\unicode[STIX]{x1D70F}}\gtrapprox 15\,000{-}20\,000$
, which roughly corresponds to two decades of scale separation on both sides of
![]() $y_{m}$
in figure 8,
$y_{m}$
in figure 8,
![]() $l_{m}/l_{\unicode[STIX]{x1D708}}\sim 100$
and
$l_{m}/l_{\unicode[STIX]{x1D708}}\sim 100$
and
![]() $\unicode[STIX]{x1D6FF}/l_{m}\sim 100$
. Furthermore, the reported location of the second
$\unicode[STIX]{x1D6FF}/l_{m}\sim 100$
. Furthermore, the reported location of the second
![]() $\langle uu\rangle$
peak scales as the meso-length scale
$\langle uu\rangle$
peak scales as the meso-length scale
![]() $O(l_{m})$
as shown in Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009a
), Ng et al. (Reference Ng, Monty, Hutchins, Chong and Marusic2011), and Vincenti et al. (Reference Vincenti, Klewicki, Morrill-Winter, White and Wosnik2013), not as the outer scale
$O(l_{m})$
as shown in Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009a
), Ng et al. (Reference Ng, Monty, Hutchins, Chong and Marusic2011), and Vincenti et al. (Reference Vincenti, Klewicki, Morrill-Winter, White and Wosnik2013), not as the outer scale
![]() $\unicode[STIX]{x1D6FF}$
.
$\unicode[STIX]{x1D6FF}$
.
Interestingly, Tsuji (Reference Tsuji1999) has found that the peak position of the dissipation spectrum in turbulent boundary layers scales the same as the peak Reynolds shear stress location. In other words, both peak locations scale not with inner length scale
![]() $l_{\unicode[STIX]{x1D708}}$
, nor with outer length scale
$l_{\unicode[STIX]{x1D708}}$
, nor with outer length scale
![]() $l_{o}$
, but with the meso-length scale
$l_{o}$
, but with the meso-length scale
![]() $l_{m}$
.
$l_{m}$
.
The integrals of TKE production and dissipation exhibit a logarithmic-like layer in turbulent wall-bounded flows, similar to that for the mean streamwise velocity
![]() $U^{+}$
. In the viscous sublayer, the mean streamwise velocity grows almost linearly,
$U^{+}$
. In the viscous sublayer, the mean streamwise velocity grows almost linearly,
![]() $U^{+}\approx y^{+}$
. In contrast, the integrals of TKE production and dissipation grow much more slowly in the viscous sublayer and buffer layer. As a result, the integral of TKE production and dissipation approaches an equal partition at relatively moderate Reynolds numbers of
$U^{+}\approx y^{+}$
. In contrast, the integrals of TKE production and dissipation grow much more slowly in the viscous sublayer and buffer layer. As a result, the integral of TKE production and dissipation approaches an equal partition at relatively moderate Reynolds numbers of
![]() $Re_{\unicode[STIX]{x1D70F}}\approx 1000{-}2000$
(see figure 9). Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) have shown that the velocity increment
$Re_{\unicode[STIX]{x1D70F}}\approx 1000{-}2000$
(see figure 9). Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) have shown that the velocity increment
![]() $\unicode[STIX]{x0394}U$
would establish an equal partition around the peak Reynolds shear stress location at much higher Reynolds number. This is because
$\unicode[STIX]{x0394}U$
would establish an equal partition around the peak Reynolds shear stress location at much higher Reynolds number. This is because
![]() $U_{c}^{+}$
or
$U_{c}^{+}$
or
![]() $U_{\infty }^{+}$
grows nearly logarithmically with Reynolds number, so the velocity increment within the viscous sublayer and buffer layer of
$U_{\infty }^{+}$
grows nearly logarithmically with Reynolds number, so the velocity increment within the viscous sublayer and buffer layer of
![]() $\unicode[STIX]{x0394}U^{+}\approx 12$
becomes negligible only at very high Reynolds number. The partition of velocity increment reflects the distribution of mean vorticity within the boundary layer, which is important in understanding the structure and underlying physics in turbulent wall-bounded flows.
$\unicode[STIX]{x0394}U^{+}\approx 12$
becomes negligible only at very high Reynolds number. The partition of velocity increment reflects the distribution of mean vorticity within the boundary layer, which is important in understanding the structure and underlying physics in turbulent wall-bounded flows.
5 Conclusions
Direct numerical simulation and high resolution experimental data of turbulent wall-bounded flows (channel, pipe, ZPG TBL) have been used to investigate the integral properties of the turbulent-kinetic-energy production and dissipation. We first verified the RD identity for the global integral of the TKE production for turbulent channel flows, turbulent pipe flows and ZPG TBL. For channel flows, the global integral identity for the TKE production is
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=U_{b}^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
. At low Reynolds number, the global integral
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}=U_{b}^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
. At low Reynolds number, the global integral
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
is larger than the global integral of the TKE production. As Reynolds number increases,
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
is larger than the global integral of the TKE production. As Reynolds number increases,
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
decreases to a constant value of
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$
decreases to a constant value of
![]() $9.13$
for turbulent channel flows, and the global integral of the TKE production can be approximated as
$9.13$
for turbulent channel flows, and the global integral of the TKE production can be approximated as
![]() $\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}-9.13$
for turbulent channel flows. It is observed that at sufficiently high Reynolds number, both
$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}-9.13$
for turbulent channel flows. It is observed that at sufficiently high Reynolds number, both
![]() $U_{b}^{+}$
and the global integral of TKE production and dissipation can be well approximated by a logarithmic function.
$U_{b}^{+}$
and the global integral of TKE production and dissipation can be well approximated by a logarithmic function.
The partition of the TKE production and dissipation can be better shown if the pre-multiplied TKE production and dissipation are plotted versus meso-scaled distance from the wall
![]() $y/l_{m}$
on semilogarithmic axes. At sufficiently high Reynolds number, it is found that the integrals of TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location
$y/l_{m}$
on semilogarithmic axes. At sufficiently high Reynolds number, it is found that the integrals of TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location
![]() $y_{m}$
. This equal partition underlines the important role of the meso-length scale
$y_{m}$
. This equal partition underlines the important role of the meso-length scale
![]() $l_{m}$
in the dynamics of turbulent wall-bounded flows.
$l_{m}$
in the dynamics of turbulent wall-bounded flows.
At sufficiently high Reynolds number, the integral profiles of the TKE production and dissipation are found to exhibit a logarithmic-like layer similar to that of the mean streamwise velocity
![]() $U^{+}$
. The logarithmic-like behaviour of the integral profiles of TKE production and dissipation, the equal partition of the integrals around
$U^{+}$
. The logarithmic-like behaviour of the integral profiles of TKE production and dissipation, the equal partition of the integrals around
![]() $y_{m}$
, and the logarithmic-like scaling for the global integrals of the TKE production and dissipation are intimately related.
$y_{m}$
, and the logarithmic-like scaling for the global integrals of the TKE production and dissipation are intimately related.
Acknowledgements
The author is very grateful to Dr Abe, Dr Bernardini, Dr De Graaff, Dr Eaton, Dr Iwamoto, Dr Jimenez, Dr El Khoury, Dr Hoyas, Dr Hultmark, Dr Kasagi, Dr Kawamura, Dr Lee, Dr Moser, Dr Orlu, Dr Pirozzoli, Dr Schlatter, Dr Simens, Dr Smits and Dr Vallikivi for generously sharing their data.
Appendix A. Derivation of the global identity for TBL
The mean momentum balance (MMB) equation for two-dimensional incompressible turbulent boundary layer flow reads
Note that the mean continuity equation is used to replace
![]() $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}x$
by
$\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}x$
by
![]() $-\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}y$
, so all the derivatives are local. The corresponding boundary conditions are
$-\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}y$
, so all the derivatives are local. The corresponding boundary conditions are
Integrating the MMB equation (A 1) in the wall-normal direction and applying boundary conditions produces a relation for the total shear stress as
Step one in obtaining integral of TKE production is to multiply the MMB equation (A 1) by a weight function
![]() $U$
:
$U$
:
then integration of the weighted equation (A 5) in the wall-normal direction yields
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{0}^{y}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]U\,\text{d}y+\left\{\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}U-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{R_{12}U-\int _{0}^{y}R_{12}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\,\text{d}y\right\}-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\int _{0}^{y}U\,\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{0}^{y}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]U\,\text{d}y+\left\{\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}U-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{R_{12}U-\int _{0}^{y}R_{12}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\,\text{d}y\right\}-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\int _{0}^{y}U\,\text{d}y.\end{eqnarray}$$
Note that integration by parts is applied to the second and third terms in (A 5). Substituting the relation for the total shear stress in (A 4), the integral of TKE production can be expressed as
 $$\begin{eqnarray}\displaystyle \int _{0}^{y}\mathscr{P}_{k}\,\text{d}y & = & \displaystyle u_{\unicode[STIX]{x1D70F}}^{2}U\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\int _{0}^{y}U\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y-U\int _{0}^{y}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\left\{yU-\int _{0}^{y}U\,\text{d}y\right\}-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{y}\mathscr{P}_{k}\,\text{d}y & = & \displaystyle u_{\unicode[STIX]{x1D70F}}^{2}U\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\int _{0}^{y}U\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y-U\int _{0}^{y}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\left\{yU-\int _{0}^{y}U\,\text{d}y\right\}-\unicode[STIX]{x1D708}\int _{0}^{y}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\,\text{d}y,\end{eqnarray}$$
and the global integral identity for TKE production can be expressed as
 $$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}}\mathscr{P}_{k}\,\text{d}y & = & \displaystyle u_{\unicode[STIX]{x1D70F}}^{2}U_{e}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\int _{0}^{\unicode[STIX]{x1D6FF}}U\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y-U_{e}\int _{0}^{\unicode[STIX]{x1D6FF}}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\left\{\unicode[STIX]{x1D6FF}U_{e}-\int _{0}^{\unicode[STIX]{x1D6FF}}U\,\text{d}y\right\}-\unicode[STIX]{x1D708}\int _{0}^{\unicode[STIX]{x1D6FF}}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}}\mathscr{P}_{k}\,\text{d}y & = & \displaystyle u_{\unicode[STIX]{x1D70F}}^{2}U_{e}\nonumber\\ \displaystyle & & \displaystyle +\,\left\{\int _{0}^{\unicode[STIX]{x1D6FF}}U\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y-U_{e}\int _{0}^{\unicode[STIX]{x1D6FF}}\left[U\frac{\unicode[STIX]{x2202}V}{\text{d}y}-V\frac{\unicode[STIX]{x2202}U}{\text{d}y}\right]\text{d}y\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\left\{\unicode[STIX]{x1D6FF}U_{e}-\int _{0}^{\unicode[STIX]{x1D6FF}}U\,\text{d}y\right\}-\unicode[STIX]{x1D708}\int _{0}^{\unicode[STIX]{x1D6FF}}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}y}\right)^{2}\text{d}y.\end{eqnarray}$$
The integral of TKE production in inner scaling becomes
 $$\begin{eqnarray}\displaystyle \int _{0}^{y^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U^{+}+\left\{\int _{0}^{y^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.U^{+}\int _{0}^{y^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}\nonumber\\ \displaystyle & & \displaystyle +\left[\frac{\unicode[STIX]{x1D708}}{u_{\unicode[STIX]{x1D70F}}^{3}}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\right]\left\{y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+}\right\}-\int _{0}^{y^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\text{d}y^{+},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{y^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U^{+}+\left\{\int _{0}^{y^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.U^{+}\int _{0}^{y^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}\nonumber\\ \displaystyle & & \displaystyle +\left[\frac{\unicode[STIX]{x1D708}}{u_{\unicode[STIX]{x1D70F}}^{3}}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\right]\left\{y^{+}U^{+}-\int _{0}^{y^{+}}U^{+}\,\text{d}y^{+}\right\}-\int _{0}^{y^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\text{d}y^{+},\qquad\end{eqnarray}$$
and the global integral of TKE production in inner scaling becomes
 $$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U_{e}^{+}+\left\{\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.U_{e}^{+}\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}\nonumber\\ \displaystyle & & \displaystyle +\left[\frac{\unicode[STIX]{x1D708}}{u_{\unicode[STIX]{x1D70F}}^{3}}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\right]\left\{\unicode[STIX]{x1D6FF}^{+}U_{e}^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\,\text{d}y^{+}\right\}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\text{d}y^{+}.\quad \qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+} & = & \displaystyle U_{e}^{+}+\left\{\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.U_{e}^{+}\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left[U^{+}\frac{\unicode[STIX]{x2202}V^{+}}{\text{d}y^{+}}-V^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\text{d}y^{+}}\right]\text{d}y^{+}\right\}\nonumber\\ \displaystyle & & \displaystyle +\left[\frac{\unicode[STIX]{x1D708}}{u_{\unicode[STIX]{x1D70F}}^{3}}\frac{1}{\unicode[STIX]{x1D70C}}\frac{\text{d}P}{\text{d}x}\right]\left\{\unicode[STIX]{x1D6FF}^{+}U_{e}^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}U^{+}\,\text{d}y^{+}\right\}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}\text{d}y^{+}.\quad \qquad\end{eqnarray}$$
In ZPG TBL, the mean pressure gradient is zero, so the terms involved
![]() $\text{d}P/\text{d}x$
will be zero in (A 9) and (A 10).
$\text{d}P/\text{d}x$
will be zero in (A 9) and (A 10).
Appendix B. Derivation of the global identity for turbulent pipe flows
The mean momentum balance equation for fully developed turbulent pipe flows reads
Note that
![]() $(2u_{\unicode[STIX]{x1D70F}}^{2}/R)$
comes from the mean pressure gradient
$(2u_{\unicode[STIX]{x1D70F}}^{2}/R)$
comes from the mean pressure gradient
![]() $-(1/\unicode[STIX]{x1D70C})(\text{d}P/\text{d}x)$
(see Pope Reference Pope2001). The corresponding boundary conditions are
$-(1/\unicode[STIX]{x1D70C})(\text{d}P/\text{d}x)$
(see Pope Reference Pope2001). The corresponding boundary conditions are
Integration of the MMB equation (B 1) along the
![]() $r$
direction,
$r$
direction,
![]() $\int _{0}^{r}(\text{MMB})2\unicode[STIX]{x03C0}r\,\text{d}r$
, yields a relation for the total shear stress as
$\int _{0}^{r}(\text{MMB})2\unicode[STIX]{x03C0}r\,\text{d}r$
, yields a relation for the total shear stress as
Note that in the cylindrical coordinate system
![]() $r$
starts from the centreline. As a result, both the viscous shear stress
$r$
starts from the centreline. As a result, both the viscous shear stress
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}r$
and the Reynolds shear stress
$\unicode[STIX]{x1D708}\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}r$
and the Reynolds shear stress
![]() $R_{12}$
are negative. This equation is used to calculate
$R_{12}$
are negative. This equation is used to calculate
![]() $R_{12}$
in the superpipe using the measured
$R_{12}$
in the superpipe using the measured
![]() $U$
data.
$U$
data.
Step one in obtaining the integral of TKE production is to multiply the MMB equation (B 1) by a weight function
![]() $U$
$U$
In step two, integration of the weighted equation (B 5),
![]() $\int _{0}^{r}(\text{MMB})U2\unicode[STIX]{x03C0}r\,\text{d}r$
, along the
$\int _{0}^{r}(\text{MMB})U2\unicode[STIX]{x03C0}r\,\text{d}r$
, along the
![]() $r$
direction yields
$r$
direction yields
Substituting the relation for the total shear stress in (B 4), the integral of TKE production can be rearranged as
Setting
![]() $r=R$
in (B 7) yields the global integral identity of TKE production for pipe flows
$r=R$
in (B 7) yields the global integral identity of TKE production for pipe flows
The integral equation (B 7) in inner scaling can be expressed as
 $$\begin{eqnarray}\int _{0}^{r^{+}}r^{+}R_{12}^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}r^{+}}\,\text{d}r^{+}=\frac{\displaystyle \left(2\int _{0}^{r^{+}}r^{+}U^{+}\,\text{d}r^{+}-r^{+2}U^{+}\right)}{R^{+}}-\int _{0}^{r^{+}}r^{+}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}r^{+}}\right)^{2}\text{d}r^{+},\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{r^{+}}r^{+}R_{12}^{+}\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}r^{+}}\,\text{d}r^{+}=\frac{\displaystyle \left(2\int _{0}^{r^{+}}r^{+}U^{+}\,\text{d}r^{+}-r^{+2}U^{+}\right)}{R^{+}}-\int _{0}^{r^{+}}r^{+}\left(\frac{\unicode[STIX]{x2202}U^{+}}{\unicode[STIX]{x2202}r^{+}}\right)^{2}\text{d}r^{+},\end{eqnarray}$$
and the inner-scaled global integral identity for TKE production in pipe flow can be expressed as
For the convenience of comparison with channel flow and TBL flow, pipe flow data are often presented versus distance from the pipe surface
![]() $y=R-r$
. Hence,
$y=R-r$
. Hence,
![]() $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y=-\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}r$
. From (B 4), it can be easily shown that the Reynolds shear stress in turbulent pipe flows can be expressed as
$\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y=-\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}r$
. From (B 4), it can be easily shown that the Reynolds shear stress in turbulent pipe flows can be expressed as
For turbulent channel flow, the Reynolds shear stress can be obtained from (2.5) as
Thus the Reynolds shear stress in turbulent pipe flow and turbulent channel flow have the same function form, but opposite sign, due to the designation of the positive wall-normal direction.