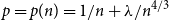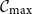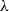1. Introduction
The Erdős–Rényi random graph, denoted by G(n, p), is obtained from the complete graph with vertex set [n] by independently retaining each edge with probability
![]() $p\in [0,1]$
and deleting it with probability
$p\in [0,1]$
and deleting it with probability
![]() $1-p$
. We are interested in the size of the largest connected component
$1-p$
. We are interested in the size of the largest connected component
![]() $\mathcal C_{\max}$
, or a typical connected component
$\mathcal C_{\max}$
, or a typical connected component
![]() $\mathcal{C}(v)$
for
$\mathcal{C}(v)$
for
![]() $v\in[n]$
. It is well known (see e.g [Reference Bollobás7, Reference van der Hofstad32] or [Reference Janson, Luczak and Rucinski15] for more details) that, if
$v\in[n]$
. It is well known (see e.g [Reference Bollobás7, Reference van der Hofstad32] or [Reference Janson, Luczak and Rucinski15] for more details) that, if
![]() $p=p(n)=\gamma/n$
for constant
$p=p(n)=\gamma/n$
for constant
![]() $\gamma$
, then G(n, p) undergoes a phase transition as
$\gamma$
, then G(n, p) undergoes a phase transition as
![]() $\gamma$
passes 1:
$\gamma$
passes 1:
-
i. if
 $\gamma < 1$
(the subcritical case), then
$\gamma < 1$
(the subcritical case), then
 $|\mathcal C_{\max}|$
is of order
$|\mathcal C_{\max}|$
is of order
 $\log n$
;
$\log n$
; -
ii. if
 $\gamma=1$
(the critical case), then
$\gamma=1$
(the critical case), then
 $|\mathcal C_{\max}|$
is of order
$|\mathcal C_{\max}|$
is of order
 $n^{2/3}$
;
$n^{2/3}$
; -
iii. if
 $\gamma > 1$
(the supercritical case), then
$\gamma > 1$
(the supercritical case), then
 $|\mathcal C_{\max}|$
is of order n.
$|\mathcal C_{\max}|$
is of order n.
Motivated by the lack of a simple proof of (ii), Nachmias and Peres [Reference Nachmias and Peres24] used a martingale argument to prove that for any
![]() $n>1000$
and
$n>1000$
and
![]() $A>8$
,
$A>8$
,
and
They also gave bounds when
![]() $p = \frac{1+\lambda n^{-1/3}}{n}$
for fixed
$p = \frac{1+\lambda n^{-1/3}}{n}$
for fixed
![]() $\lambda\in\mathbb{R}$
. The best known bound on the latter quantity is due originally to Pittel [Reference Pittel26] who showed that for p of this form,
$\lambda\in\mathbb{R}$
. The best known bound on the latter quantity is due originally to Pittel [Reference Pittel26] who showed that for p of this form,
converges as
![]() $A\to\infty$
to a specific constant, which is stated to be
$A\to\infty$
to a specific constant, which is stated to be
![]() $(2\pi)^{-1/2}$
but should be
$(2\pi)^{-1/2}$
but should be
![]() $(8/9\pi)^{1/2}$
due to a small oversight in the proof. More details, and a stronger result that allows A and
$(8/9\pi)^{1/2}$
due to a small oversight in the proof. More details, and a stronger result that allows A and
![]() $\lambda$
to depend on n, are available in [Reference Roberts28]. Both [Reference Pittel26] and [Reference Roberts28] rely on a combinatorial formula for the expected number of components with exactly k vertices and
$\lambda$
to depend on n, are available in [Reference Roberts28]. Both [Reference Pittel26] and [Reference Roberts28] rely on a combinatorial formula for the expected number of components with exactly k vertices and
![]() $k+\ell$
edges, which is specific to Erdős–Rényi graphs and appears difficult to adapt to other models, together with analytic approximations.
$k+\ell$
edges, which is specific to Erdős–Rényi graphs and appears difficult to adapt to other models, together with analytic approximations.
We provide a new proof of asymptotics for
![]() $\mathbb{P}(|\mathcal{C}(v)|>An^{2/3})$
and
$\mathbb{P}(|\mathcal{C}(v)|>An^{2/3})$
and
![]() $\mathbb{P}(|\mathcal{C}_{\max}|>An^{2/3})$
that combines the strengths of the results mentioned above:
$\mathbb{P}(|\mathcal{C}_{\max}|>An^{2/3})$
that combines the strengths of the results mentioned above:
-
it gives accurate bounds for large A as
 $n\to\infty$
;
$n\to\infty$
; -
it allows A and
 $\lambda$
to depend on n;
$\lambda$
to depend on n; -
it uses only robust probabilistic tools and therefore has the potential to be adapted to other models of random graphs.
This is the purpose of our main theorem, which we now state.
Theorem 1.1 There exists
![]() $A_0>0$
such that if
$A_0>0$
such that if
![]() $A=A(n)$
satisfies
$A=A(n)$
satisfies
![]() $A_0\le A = o(n^{1/30})$
and
$A_0\le A = o(n^{1/30})$
and
![]() $p=p(n)=1/n+\lambda/n^{4/3}$
with
$p=p(n)=1/n+\lambda/n^{4/3}$
with
![]() $\lambda = \lambda(n)$
such that
$\lambda = \lambda(n)$
such that
![]() $|\lambda|\leq A/3$
, then for sufficiently large n and any vertex
$|\lambda|\leq A/3$
, then for sufficiently large n and any vertex
![]() $v\in[n]$
, we have
$v\in[n]$
, we have
and
for some constants
![]() $0<c_1\le c_2<\infty$
.
$0<c_1\le c_2<\infty$
.
Although our methods are not accurate enough to give the correct constant factor in the asymptotic, identified in [Reference Roberts28], we believe that the substantially more robust approach is worth the small sacrifice in precision. Indeed, the probabilistic arguments in [Reference Nachmias and Peres24] have been adapted to critical random d-regular graphs by Nachmias and Peres [Reference Nachmias and Peres23], the configuration model with bounded degrees by Riordan [Reference Riordan27], and more recently a particular model of inhomogeneous random graphs by the first author and Pachon [Reference De Ambroggio and Pachon11].
At the end of Sections 3 and 4 (see Remarks 3.7 and 4.15) we will comment further on the problem of finding the right constant in the asymptotic using methods similar to the ones in this paper. We believe that it may be possible but would require significantly more technical work. We also remark that Nachmias and Peres [Reference Nachmias and Peres24] gave specific values of n and A for which their bounds hold, namely
![]() $n>1000$
and
$n>1000$
and
![]() $A>8$
. We could do the same, but it would again require significantly more technical details given the more precise nature of our bounds.
$A>8$
. We could do the same, but it would again require significantly more technical details given the more precise nature of our bounds.
We remark that our proofs of the upper bounds in Theorem 1.1 are particularly straightforward, perhaps even more so than those in [Reference Nachmias and Peres24], despite giving a much more accurate bound. A key part of the argument will be the following simple ballot-type result, which may be of independent interest.
Lemma 1.2 Fix
![]() $n\in\mathbb{N}$
. Let
$n\in\mathbb{N}$
. Let
![]() $X_1,\dots,X_n$
be
$X_1,\dots,X_n$
be
![]() $\mathbb{Z}-$
valued random variables and suppose that the law of
$\mathbb{Z}-$
valued random variables and suppose that the law of
![]() $(X_1,\dots,X_n)$
is invariant under rotations (it may depend on n). Define
$(X_1,\dots,X_n)$
is invariant under rotations (it may depend on n). Define
![]() $S_0 = 0$
and
$S_0 = 0$
and
![]() $S_t = \sum_{i=1}^{t}X_i$
, for
$S_t = \sum_{i=1}^{t}X_i$
, for
![]() $t\in [n]$
. Then for any
$t\in [n]$
. Then for any
![]() $j\in\mathbb{N}$
,
$j\in\mathbb{N}$
,
Our proofs of the lower bounds in Theorem 1.1 will be more complicated than those for the upper bounds, although they still use only robust probabilistic techniques such as a generalised ballot theorem, Poisson approximations for the binomial distribution and Brownian approximations to random walks. In future work we intend to demonstrate the adaptability of our new approach by applying our methods to other random graph models. As the first step in this direction, for applications of Lemma 1.2 to a random intersection graph, an inhomogeneous random graph and percolation on a d-regular graph, see [Reference De Ambroggio10].
Structure of the paper. We start by introducing ballot-type results in Section 2, where we prove Lemma 1.2 and a corollary which will be the main tool to obtain the upper bounds in Theorem 1.1. We also state a generalised ballot theorem due to Addario-Berry and Reed [Reference Addario-Berry and Reed2] that will be used for our lower bounds. Subsequently, in Section 3 we prove the upper bounds in (a) and (b) of Theorem 1.1, whereas the corresponding lower bounds will be proved in Section 4.
Notation. We write
![]() $\mathbb{N}_0 = \mathbb{N}\cup\{0\}$
,
$\mathbb{N}_0 = \mathbb{N}\cup\{0\}$
,
![]() $[n]=\{1,2,\ldots,n\}$
, and
$[n]=\{1,2,\ldots,n\}$
, and
![]() $[\![a,b]\!] = [a,b]\cap{\mathbb{Z}}$
. The abbreviation i.i.d. means ‘independent and identically distributed’. The empty sum is defined to be 0, and the empty product is defined to be 1. In particular we use the convention that
$[\![a,b]\!] = [a,b]\cap{\mathbb{Z}}$
. The abbreviation i.i.d. means ‘independent and identically distributed’. The empty sum is defined to be 0, and the empty product is defined to be 1. In particular we use the convention that
![]() $\sum_{i=n+1}^n a_i$
is zero, for any n and any sequence
$\sum_{i=n+1}^n a_i$
is zero, for any n and any sequence
![]() $(a_i)$
. For brevity we simply write A rather than A(n),
$(a_i)$
. For brevity we simply write A rather than A(n),
![]() $\lambda$
instead of
$\lambda$
instead of
![]() $\lambda(n)$
, and p in place of
$\lambda(n)$
, and p in place of
![]() $p(n)=1/n + \lambda n^{-4/3}$
. We will often write c to mean a constant in
$p(n)=1/n + \lambda n^{-4/3}$
. We will often write c to mean a constant in
![]() $(0,\infty)$
and use c many times in a single proof even though the constant may change from line to line.
$(0,\infty)$
and use c many times in a single proof even though the constant may change from line to line.
1.1. Related work
Besides his Proposition 2, which gives asymptotics for
![]() $\mathbb{P}(|\mathcal C_{\max}|>An^{2/3})$
in the case of constant (large) A and
$\mathbb{P}(|\mathcal C_{\max}|>An^{2/3})$
in the case of constant (large) A and
![]() $\lambda$
, Pittel [Reference Pittel26] includes several other results which we make no attempt to rework. These include asymptotics for
$\lambda$
, Pittel [Reference Pittel26] includes several other results which we make no attempt to rework. These include asymptotics for
![]() $\mathbb{P}(|\mathcal C_{\max}|< an^{2/3})$
when a is small. Nachmias and Peres [Reference Nachmias and Peres24] also gave a simple but inaccurate upper bound on this quantity, and it would be interesting to give an intuitive probabilistic proof of more accurate asymptotics. Pittel’s paper is partially based on an earlier article by Luczak, Pittel and Wierman [Reference Łuczak, Pittel and Wierman20].
$\mathbb{P}(|\mathcal C_{\max}|< an^{2/3})$
when a is small. Nachmias and Peres [Reference Nachmias and Peres24] also gave a simple but inaccurate upper bound on this quantity, and it would be interesting to give an intuitive probabilistic proof of more accurate asymptotics. Pittel’s paper is partially based on an earlier article by Luczak, Pittel and Wierman [Reference Łuczak, Pittel and Wierman20].
For G(n, p) outside the critical scaling window, i.e. when
![]() $\lambda$
is not bounded in n,
$\lambda$
is not bounded in n,
![]() $n^{2/3}$
is not the most likely size for the largest component of the graph, and therefore our results—while still true, at least provided
$n^{2/3}$
is not the most likely size for the largest component of the graph, and therefore our results—while still true, at least provided
![]() $|\lambda| \le A/3 = o(n^{1/30})$
—appear less natural than those by Nachmias and Peres [Reference Nachmias and Peres22], Bollobás and Riordan [Reference Bollobás and Riordan8] or Riordan [Reference Riordan27].
$|\lambda| \le A/3 = o(n^{1/30})$
—appear less natural than those by Nachmias and Peres [Reference Nachmias and Peres22], Bollobás and Riordan [Reference Bollobás and Riordan8] or Riordan [Reference Riordan27].
A local limit theorem for the size of the k largest components (for arbitrary k) was given by Van der Hofstad et al. [Reference van der Hofstad, Kager and Müller34]. See also Van der Hofstad et al. [Reference van der Hofstad, Kliem and van Leeuwaarden36], where similar results to those established by Pittel [Reference Pittel26] are proved in the context of inhomogeneous random graphs.
Aldous [Reference Aldous3] used a breadth-first search algorithm to explore G(n, p) for p within the critical window and showed that the sizes of the largest components, if rescaled by
![]() $n^{2/3}$
, converge (in an appropriate sense) to some limit, which he described in detail. The same type of argument has been used by Van der Hofstad [Reference van der Hofstad, Janssen and van Leeuwaarden33] to investigate critical SIR epidemics. The work of Aldous was then developed by Addario-Berry, Broutin and Goldschmidt [Reference Addario-Berry, Broutin and Goldschmidt1] who showed that the rescaled components themselves converge to metric spaces characterised by excursions of Brownian motion with parabolic drift, decorated by a Poisson point process.
$n^{2/3}$
, converge (in an appropriate sense) to some limit, which he described in detail. The same type of argument has been used by Van der Hofstad [Reference van der Hofstad, Janssen and van Leeuwaarden33] to investigate critical SIR epidemics. The work of Aldous was then developed by Addario-Berry, Broutin and Goldschmidt [Reference Addario-Berry, Broutin and Goldschmidt1] who showed that the rescaled components themselves converge to metric spaces characterised by excursions of Brownian motion with parabolic drift, decorated by a Poisson point process.
There are several other models that share similar properties with the near-critical Erdős–Rényi graph. For instance, there are many critical models whose component sizes, when suitably rescaled, converge to the lengths of excursions of Brownian motion with parabolic drift just as for the Erdős–Rényi graph. Some examples include inhomogeneous random graphs (see e.g. [Reference Bhamidi, van der Hofstad and van Leeuwaarden5] and [Reference Bhamidi, van der Hofstad and van Leeuwaarden6]), the configuration model (see [Reference Dhara, van der Hofstad, van Leeuwaarden and Sen13], [Reference Joseph16] and [Reference Riordan27]), and quantum random graphs (see [Reference Dembo, Levit and Vadlamani12]).
In another direction we mention [Reference O’Connell25],where a large deviations rate function is provided for the size of the maximal component divided by n, valid for the
![]() $G(n,\gamma/n)$
model with
$G(n,\gamma/n)$
model with
![]() $\gamma>0$
. For a very recent work in this direction, see [Reference Andreis, König and Patterson4].
$\gamma>0$
. For a very recent work in this direction, see [Reference Andreis, König and Patterson4].
Finally, the results of [Reference Roberts28] were used to show the existence of times when a dynamical version of the Erdős–Rényi graph has an unusually large connected component. Related results about the structure of dynamical Erdős–Rényi graphs were given by Rossignol [Reference Rossignol29].
2. Ballot-style results
Let
![]() $X_1,\dots,X_n \in \{-1,1\}$
be i.i.d. random variables taking values in
$X_1,\dots,X_n \in \{-1,1\}$
be i.i.d. random variables taking values in
![]() $\{-1,1\}$
, with
$\{-1,1\}$
, with
![]() $\mathbb{P}(X_i=1)=\mathbb{P}(X_i=-1)=1/2$
, and let
$\mathbb{P}(X_i=1)=\mathbb{P}(X_i=-1)=1/2$
, and let
![]() $S_t = \sum_{i=1}^{t}X_i$
. In its simplest form the ballot theorem concerns the probability that
$S_t = \sum_{i=1}^{t}X_i$
. In its simplest form the ballot theorem concerns the probability that
![]() $S_t$
stays positive for all times
$S_t$
stays positive for all times
![]() $t\in [n]$
, given that
$t\in [n]$
, given that
![]() $S_n=k \in \mathbb{N}$
, and says that the answer is
$S_n=k \in \mathbb{N}$
, and says that the answer is
![]() $k/n$
; see e.g. [Reference Addario-Berry and Reed2, Reference Kager17, Reference Konstantopoulos19, Reference van der Hofstad and Keane35] and references therein. However, we will be interested in evaluating probabilities of the following type:
$k/n$
; see e.g. [Reference Addario-Berry and Reed2, Reference Kager17, Reference Konstantopoulos19, Reference van der Hofstad and Keane35] and references therein. However, we will be interested in evaluating probabilities of the following type:
where
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $X_1,\dots,X_n$
are i.i.d. random variables taking values in
$X_1,\dots,X_n$
are i.i.d. random variables taking values in
![]() $\{-1,0,1,2,\dots\}$
. A possible solution might be to apply the following generalised ballot theorem.
$\{-1,0,1,2,\dots\}$
. A possible solution might be to apply the following generalised ballot theorem.
Theorem 2.1 (Addario-Berry and Reed [Reference Addario-Berry and Reed2])Suppose X is a random variable satisfying
![]() $\mathbb{E}[X]=0$
,
$\mathbb{E}[X]=0$
,
![]() $\text{Var}(X)>0$
,
$\text{Var}(X)>0$
,
![]() $\mathbb{E}[X^{2+\alpha}]<\infty$
for some
$\mathbb{E}[X^{2+\alpha}]<\infty$
for some
![]() $\alpha >0$
, and X is a lattice random variable with period d (meaning that dX is an integer random variable and d is the smallest positive real number for which this holds). Then given independent random variables
$\alpha >0$
, and X is a lattice random variable with period d (meaning that dX is an integer random variable and d is the smallest positive real number for which this holds). Then given independent random variables
![]() $X_1,X_2,\dots$
distributed as X with associated partial sums
$X_1,X_2,\dots$
distributed as X with associated partial sums
![]() $S_t = \sum_{i=1}^{t}X_i$
, for all j such that
$S_t = \sum_{i=1}^{t}X_i$
, for all j such that
![]() $0\leq j =O\left(\sqrt{n}\right)$
and such that j is a multiple of
$0\leq j =O\left(\sqrt{n}\right)$
and such that j is a multiple of
![]() $1/d$
we have
$1/d$
we have
This result will indeed be useful in the proof of the lower bounds in our Theorem 1.1. However, for the upper bound we will need a result that holds when j is much larger than
![]() $\sqrt{n}$
. Our Lemma 1.2 shows that the upper bound remains true more generally. We now aim to prove that result.
$\sqrt{n}$
. Our Lemma 1.2 shows that the upper bound remains true more generally. We now aim to prove that result.
Fix
![]() $n\in \mathbb{N}$
. Let
$n\in \mathbb{N}$
. Let
![]() $X = (X_1,\dots,X_n)$
be random variables taking values in
$X = (X_1,\dots,X_n)$
be random variables taking values in
![]() $\mathbb{Z}$
. Define
$\mathbb{Z}$
. Define
![]() $S_0 = 0$
and
$S_0 = 0$
and
![]() $S_t = \sum_{i=1}^{t}X_i$
for all
$S_t = \sum_{i=1}^{t}X_i$
for all
![]() $t\in [n]$
. Given
$t\in [n]$
. Given
![]() $r\in [n]$
, define the rotation of
$r\in [n]$
, define the rotation of
![]() $S=(S_0,S_1,\dots,S_n)$
by r as the walk
$S=(S_0,S_1,\dots,S_n)$
by r as the walk
![]() $S^{r}=(S_0^{r},S_1^{r},\dots,S_n^{r})$
corresponding to the rotated sequence
$S^{r}=(S_0^{r},S_1^{r},\dots,S_n^{r})$
corresponding to the rotated sequence
![]() $X^{r} = (X_{r+1},\dots,X_n,X_1,\dots,X_r)$
. That is,
$X^{r} = (X_{r+1},\dots,X_n,X_1,\dots,X_r)$
. That is,
-
if
 $0\leq t\leq n-r$
, then
$0\leq t\leq n-r$
, then
 $S_t^{r} = S_{t+r}-S_r = \sum_{i=r+1}^{t+r}X_i$
;
$S_t^{r} = S_{t+r}-S_r = \sum_{i=r+1}^{t+r}X_i$
; -
if
 $n-r<t\leq n$
, then
$n-r<t\leq n$
, then
 $S_t^{r} = S_n+S_{t+r-n}-S_r = \sum_{i=r+1}^{n}X_i+\sum_{i=1}^{t+r-n}X_i$
.
$S_t^{r} = S_n+S_{t+r-n}-S_r = \sum_{i=r+1}^{n}X_i+\sum_{i=1}^{t+r-n}X_i$
.
In particular,
![]() $S_n^{r}=\sum_{i=r+1}^{n}X_i+\sum_{i=1}^{r}X_i=S_n$
(for every
$S_n^{r}=\sum_{i=r+1}^{n}X_i+\sum_{i=1}^{r}X_i=S_n$
(for every
![]() $r\in [n]$
) and
$r\in [n]$
) and
![]() $S^n=S$
.
$S^n=S$
.
Definition 2.2 We say that
![]() $r\in [n]$
is favourable if
$r\in [n]$
is favourable if
![]() $S_t^{r}>0 $
for every
$S_t^{r}>0 $
for every
![]() $t\in [n]$
.
$t\in [n]$
.
The following lemma contains the key observation needed to prove Lemma 1.2.
Lemma 2.3 Fix
![]() $j\in \mathbb{N}$
. If
$j\in \mathbb{N}$
. If
![]() $S_n=j$
, then
$S_n=j$
, then
Proof. The idea is simply that between each two favourable vertices, the partial sum must increase by at least one. To see this, let
![]() $1\leq I_1<\dots <I_L\leq n$
denote the indices (if any) such that
$1\leq I_1<\dots <I_L\leq n$
denote the indices (if any) such that
![]() $I_k$
is favourable for
$I_k$
is favourable for
![]() $1\leq k\leq L$
. We need to show that
$1\leq k\leq L$
. We need to show that
![]() $L\leq j$
. Observe that for each
$L\leq j$
. Observe that for each
![]() $1\leq k\leq L-1$
, since
$1\leq k\leq L-1$
, since
![]() $I_k$
is favourable and
$I_k$
is favourable and
![]() $X_1,\ldots,X_n$
are integer-valued, we have
$X_1,\ldots,X_n$
are integer-valued, we have
![]() $S^{I_k}_t\ge 1$
for all
$S^{I_k}_t\ge 1$
for all
![]() $t\in[n]$
; in particular
$t\in[n]$
; in particular
![]() $S_{I_{k+1}-I_k}^{I_k}\geq 1$
. For the same reason,
$S_{I_{k+1}-I_k}^{I_k}\geq 1$
. For the same reason,
![]() $S_{(I_1+n)-I_L}^{I_L}\geq 1$
. Consequently
$S_{(I_1+n)-I_L}^{I_L}\geq 1$
. Consequently
 \begin{equation*}S_n= \sum_{k=1}^{L-1}S_{I_{k+1}-I_k}^{I_k}+S_{(I_1+n)-I_L}^{I_L} \ge \sum_{k=1}^{L-1} 1 + 1 = L.\end{equation*}
\begin{equation*}S_n= \sum_{k=1}^{L-1}S_{I_{k+1}-I_k}^{I_k}+S_{(I_1+n)-I_L}^{I_L} \ge \sum_{k=1}^{L-1} 1 + 1 = L.\end{equation*}
But our assumption is that
![]() $S_n=j$
, so we must have
$S_n=j$
, so we must have
![]() $L\le j$
as required.
$L\le j$
as required.
Proof of Lemma 1.2. For any
![]() $r\in[n]$
, since
$r\in[n]$
, since
![]() $(X_1,X_2,\ldots,X_n)$
is invariant under rotations,
$(X_1,X_2,\ldots,X_n)$
is invariant under rotations,
and since
![]() $S_n^r=S_n$
, we obtain that
$S_n^r=S_n$
, we obtain that
Summing over
![]() $r\in[n]$
and applying Lemma 2.3 we have
$r\in[n]$
and applying Lemma 2.3 we have
 \begin{align*}n\mathbb{P}(S_t>0\ \forall t\in [n],\,S_n=j) & = \sum_{r=1}^{n}\mathbb{E}[\unicode{x1D7D9}_{\{r \text{ is favourable}\}}\unicode{x1D7D9}_{\{S_n=j\}}] \\
& = \mathbb{E}\bigg[\unicode{x1D7D9}_{\{S_n=j\}}\sum_{r=1}^{n}\unicode{x1D7D9}_{\{r \text{ is favourable}\}}\bigg]\\
&\leq \mathbb{E}\left[\unicode{x1D7D9}_{\{S_n=j\}}j\right]= j\mathbb{P}(S_n=j)\end{align*}
\begin{align*}n\mathbb{P}(S_t>0\ \forall t\in [n],\,S_n=j) & = \sum_{r=1}^{n}\mathbb{E}[\unicode{x1D7D9}_{\{r \text{ is favourable}\}}\unicode{x1D7D9}_{\{S_n=j\}}] \\
& = \mathbb{E}\bigg[\unicode{x1D7D9}_{\{S_n=j\}}\sum_{r=1}^{n}\unicode{x1D7D9}_{\{r \text{ is favourable}\}}\bigg]\\
&\leq \mathbb{E}\left[\unicode{x1D7D9}_{\{S_n=j\}}j\right]= j\mathbb{P}(S_n=j)\end{align*}
which completes the proof.
The following corollary will be used to prove the upper bounds of Theorem 1.1.
Corollary 2.4 Fix
![]() $n\in\mathbb{N}$
and let
$n\in\mathbb{N}$
and let
![]() $(X_i)_{i\ge 1}$
be i.i.d. random variables taking values in
$(X_i)_{i\ge 1}$
be i.i.d. random variables taking values in
![]() $\mathbb{Z}$
, whose distribution may depend on n. Let
$\mathbb{Z}$
, whose distribution may depend on n. Let
![]() $h\in \mathbb{N}$
, and suppose that
$h\in \mathbb{N}$
, and suppose that
![]() $\mathbb{P}(X_1=h)>0$
. Define
$\mathbb{P}(X_1=h)>0$
. Define
![]() $S_t = \sum_{i=1}^{t}X_i$
for
$S_t = \sum_{i=1}^{t}X_i$
for
![]() $t\in\mathbb{N}_0$
. Then for any
$t\in\mathbb{N}_0$
. Then for any
![]() $j\geq 1$
we have
$j\geq 1$
we have
Proof. Let
![]() $X_0$
be an independent copy of
$X_0$
be an independent copy of
![]() $X_1$
. Define
$X_1$
. Define
![]() $S_t^*=X_0+S_t$
for
$S_t^*=X_0+S_t$
for
![]() $0\leq t\leq n$
. Then
$0\leq t\leq n$
. Then
 \begin{align}&\mathbb{P}(h+S_t>0\ \forall t\in [n],\, h+S_{n}=j)\nonumber\\[2pt]
&=\mathbb{P}(X_0=h)^{-1}\mathbb{P}(h+S_t>0\ \forall t\in [n],\,h+S_{n}=j,\,X_0=h)\nonumber\\[2pt]
&=\mathbb{P}(X_1=h)^{-1}\mathbb{P}(S_t^*>0\ \forall t\in [n],\,S_{n}^*=j,\,S_0^*=h)\nonumber\\[2pt]
&\leq \mathbb{P}(X_1=h)^{-1}\mathbb{P}(S_t^*>0\ \forall t\in \{0\}\cup [n],\,S_{n}^*=j).\end{align}
\begin{align}&\mathbb{P}(h+S_t>0\ \forall t\in [n],\, h+S_{n}=j)\nonumber\\[2pt]
&=\mathbb{P}(X_0=h)^{-1}\mathbb{P}(h+S_t>0\ \forall t\in [n],\,h+S_{n}=j,\,X_0=h)\nonumber\\[2pt]
&=\mathbb{P}(X_1=h)^{-1}\mathbb{P}(S_t^*>0\ \forall t\in [n],\,S_{n}^*=j,\,S_0^*=h)\nonumber\\[2pt]
&\leq \mathbb{P}(X_1=h)^{-1}\mathbb{P}(S_t^*>0\ \forall t\in \{0\}\cup [n],\,S_{n}^*=j).\end{align}
Now since
![]() $(S_0^*,S_1^*,\dots,S_n^*)\overset{d}{=}(S_1,S_2,\dots,S_{n+1})$
, applying Lemma 1.2 we obtain that
$(S_0^*,S_1^*,\dots,S_n^*)\overset{d}{=}(S_1,S_2,\dots,S_{n+1})$
, applying Lemma 1.2 we obtain that
 \begin{align*}\mathbb{P}(S_t^*>0\ \forall t\in \{0\}\cup [n],\,S_{n}^*=j)&=\mathbb{P}(S_t>0\ \forall t\in [n+1]\,,S_{n+1}=j)\\[2pt]
&\leq \frac{j}{n+1}\mathbb{P}(S_{n+1}=j),\end{align*}
\begin{align*}\mathbb{P}(S_t^*>0\ \forall t\in \{0\}\cup [n],\,S_{n}^*=j)&=\mathbb{P}(S_t>0\ \forall t\in [n+1]\,,S_{n+1}=j)\\[2pt]
&\leq \frac{j}{n+1}\mathbb{P}(S_{n+1}=j),\end{align*}
and substituting this into (1) gives the result.
3. Proof of the upper bounds in Theorem 1.1
A main ingredient in our analysis is an exploration process, which is a procedure to sequentially discover the component containing a given vertex, and which reduces the study of component sizes to the analysis of the trajectory of a stochastic process. Such exploration processes are well known, dating back at least to [Reference Martin-Löf21], and several variants exist. Our description closely follows the one appearing in [Reference Roberts28]; see also [Reference Nachmias and Peres24].
Let G be any (undirected) graph with vertex set [n], and let
![]() $v\in [n]$
be any given vertex. Fix an ordering of the n vertices with v first. At each time
$v\in [n]$
be any given vertex. Fix an ordering of the n vertices with v first. At each time
![]() $t\in \{0\}\cup [n]$
of the exploration, each vertex will be active, explored or unseen; the number of explored vertices will be t whereas the (possibly random) number of active vertices will be denoted by
$t\in \{0\}\cup [n]$
of the exploration, each vertex will be active, explored or unseen; the number of explored vertices will be t whereas the (possibly random) number of active vertices will be denoted by
![]() $Y_t$
. At time
$Y_t$
. At time
![]() $t=0$
, vertex v is declared to be active whereas all other vertices are declared unseen, so that
$t=0$
, vertex v is declared to be active whereas all other vertices are declared unseen, so that
![]() $Y_0=1$
. At each step
$Y_0=1$
. At each step
![]() $t\in [n]$
of the procedure, if
$t\in [n]$
of the procedure, if
![]() $Y_{t-1}>0$
then we let
$Y_{t-1}>0$
then we let
![]() $u_t$
be the first active vertex; if
$u_t$
be the first active vertex; if
![]() $Y_{t-1}=0$
, we let
$Y_{t-1}=0$
, we let
![]() $u_t$
be the first unseen vertex (here the term first refers to the ordering that we fixed at the beginning of the procedure). Note that at time
$u_t$
be the first unseen vertex (here the term first refers to the ordering that we fixed at the beginning of the procedure). Note that at time
![]() $t=1$
we have
$t=1$
we have
![]() $u_1=v$
. Denote by
$u_1=v$
. Denote by
![]() $\eta_t$
the number of unseen neighbours of
$\eta_t$
the number of unseen neighbours of
![]() $u_t$
in G and change the status of these vertices to active. Then, set
$u_t$
in G and change the status of these vertices to active. Then, set
![]() $u_t$
itself explored. From this description we see that:
$u_t$
itself explored. From this description we see that:
-
 $Y_t=Y_{t-1}+\eta_t-1$
, if
$Y_t=Y_{t-1}+\eta_t-1$
, if
 $Y_{t-1}>0$
;
$Y_{t-1}>0$
; -
 $Y_t=\eta_t$
, if
$Y_t=\eta_t$
, if
 $Y_{t-1}=0$
.
$Y_{t-1}=0$
.
We now specialise to the Erdős–Rényi random graph, i.e. we now take
![]() $G=G(n,p)$
. Let us denote by
$G=G(n,p)$
. Let us denote by
![]() $U_t=n-Y_t-t$
the number of unseen vertices in G(n, p) at time t, and define
$U_t=n-Y_t-t$
the number of unseen vertices in G(n, p) at time t, and define
![]() $\mathcal{F}_0 = \{\Omega,\emptyset\}$
and
$\mathcal{F}_0 = \{\Omega,\emptyset\}$
and
![]() $\mathcal{F}_t = \sigma(\{\eta_j\,{:}\,1\leq j\leq t\})$
for
$\mathcal{F}_t = \sigma(\{\eta_j\,{:}\,1\leq j\leq t\})$
for
![]() $t\in [n]$
. Then for
$t\in [n]$
. Then for
![]() $t\in [n]$
, given
$t\in [n]$
, given
![]() $\mathcal{F}_{t-1}$
, we see that
$\mathcal{F}_{t-1}$
, we see that
![]() $\eta_t\sim \textrm{Bin}(U_{t-1},p)$
. Since
$\eta_t\sim \textrm{Bin}(U_{t-1},p)$
. Since
![]() $U_t\leq n-t$
, we can couple the process
$U_t\leq n-t$
, we can couple the process
![]() $(\eta_i)_{i \in [n]}$
with a sequence
$(\eta_i)_{i \in [n]}$
with a sequence
![]() $(\tau_i)_{i \in [n]}$
of independent
$(\tau_i)_{i \in [n]}$
of independent
![]() $\textrm{Bin}(n-i,p)$
random variables such that
$\textrm{Bin}(n-i,p)$
random variables such that
![]() $\tau_i\geq \eta_i$
for all i. It follows that, for any
$\tau_i\geq \eta_i$
for all i. It follows that, for any
![]() $k\in[n]$
,
$k\in[n]$
,
 \begin{align}\mathbb{P}(|\mathcal{C}(v)|> k) &= \mathbb{P}(Y_t>0\ \forall t\in [k])\nonumber\\&=\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\eta_i-1)>0\ \forall t\in [k]\bigg)\nonumber\\\
&\leq \mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \bigg).\end{align}
\begin{align}\mathbb{P}(|\mathcal{C}(v)|> k) &= \mathbb{P}(Y_t>0\ \forall t\in [k])\nonumber\\&=\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\eta_i-1)>0\ \forall t\in [k]\bigg)\nonumber\\\
&\leq \mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \bigg).\end{align}
We would like to apply Corollary 2.4 to the sequence
![]() $(1+\sum_{i=1}^{t}(\tau_i-1))_{t\in [k]}$
, and to this end we need to turn the latter process into a random walk with identically distributed increments. This is achieved in Lemma 3.1 below.
$(1+\sum_{i=1}^{t}(\tau_i-1))_{t\in [k]}$
, and to this end we need to turn the latter process into a random walk with identically distributed increments. This is achieved in Lemma 3.1 below.
Lemma 3.1 There exists a finite constant c such that for any
![]() $k\in[n]$
,
$k\in[n]$
,
 \begin{equation*}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \bigg) \leq c\mathbb{P}\left(1+R_t>0\ \forall t\in [k],\, 1+R_{k}\ge \frac{k^2p}{2} - \frac{k}{n^{1/2}}\right),\end{equation*}
\begin{equation*}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \bigg) \leq c\mathbb{P}\left(1+R_t>0\ \forall t\in [k],\, 1+R_{k}\ge \frac{k^2p}{2} - \frac{k}{n^{1/2}}\right),\end{equation*}
where
![]() $(R_t)_{t\geq 0}$
is a random walk with
$(R_t)_{t\geq 0}$
is a random walk with
![]() $R_0=0$
and i.i.d. steps each having distribution
$R_0=0$
and i.i.d. steps each having distribution
![]() $\textrm{Bin}(n,p)-1$
.
$\textrm{Bin}(n,p)-1$
.
The idea behind this lemma is that by adding an independent Bin(i, p) random variable to
![]() $\tau_i$
, we transform it into a Bin(n, p) random variable which forms one of the steps of the random walk
$\tau_i$
, we transform it into a Bin(n, p) random variable which forms one of the steps of the random walk
![]() $R_t$
appearing on the right-hand side. If the sum of the
$R_t$
appearing on the right-hand side. If the sum of the
![]() $\tau_i$
up to t remains positive then
$\tau_i$
up to t remains positive then
![]() $R_t$
, which is larger, must certainly also remain positive; but also the final value
$R_t$
, which is larger, must certainly also remain positive; but also the final value
![]() $R_k$
must be larger than the sum of the additional contributions from the Bin(i, p) random variables. A standard bound shows that these additional contributions are concentrated about their mean, which is approximately
$R_k$
must be larger than the sum of the additional contributions from the Bin(i, p) random variables. A standard bound shows that these additional contributions are concentrated about their mean, which is approximately
![]() $k^2p/2$
.
$k^2p/2$
.
We postpone the details until Section 3.1 and continue with the proof of the upper bounds in Theorem 1.1. By summing over the possible values of
![]() $R_k$
, we can apply Corollary 2.4 with
$R_k$
, we can apply Corollary 2.4 with
![]() $h=1$
to the quantity on the right-hand side of Lemma 3.1: it is at most
$h=1$
to the quantity on the right-hand side of Lemma 3.1: it is at most
 \begin{equation}\frac{c}{k+1}\sum_{j=h(k,n)}^{(k+1)(n-1)} j \mathbb{P}\left( R_{k+1}=j\right),\end{equation}
\begin{equation}\frac{c}{k+1}\sum_{j=h(k,n)}^{(k+1)(n-1)} j \mathbb{P}\left( R_{k+1}=j\right),\end{equation}
where
![]() $h(k,n)=\lceil \frac{k^2}{2}p - \frac{k}{n^{1/2}} \rceil$
, and the upper limit on the sum is due to the fact that
$h(k,n)=\lceil \frac{k^2}{2}p - \frac{k}{n^{1/2}} \rceil$
, and the upper limit on the sum is due to the fact that
![]() $R_{k+1}\leq$
$R_{k+1}\leq$
![]() $(k+1)(n-1)$
(because each step of
$(k+1)(n-1)$
(because each step of
![]() $R_t$
is at most
$R_t$
is at most
![]() $n-1$
, and in
$n-1$
, and in
![]() $R_{k+1}$
we are summing
$R_{k+1}$
we are summing
![]() $k+1$
of them).
$k+1$
of them).
We now rewrite the above sum in a way that is easier to analyse, using the following elementary observation. If X is a random variable taking values in
![]() $\mathbb{Z}\cap(-\infty,N]$
for some
$\mathbb{Z}\cap(-\infty,N]$
for some
![]() $N\in \mathbb{N}$
, then for any
$N\in \mathbb{N}$
, then for any
![]() $h\ge1$
, we have
$h\ge1$
, we have
 \begin{align*}\mathbb{E}[X\unicode{x1D7D9}_{\{X\ge h\}}] = \mathbb{E}\Big[\sum_{i=1}^N \unicode{x1D7D9}_{\{i\le X\}}\unicode{x1D7D9}_{\{X\ge h\}}\Big]&= \mathbb{E}\Big[\sum_{i=1}^h \unicode{x1D7D9}_{\{X\ge h\}}\Big] + \mathbb{E}\Big[\sum_{i=h+1}^N \unicode{x1D7D9}_{\{X\ge i\}}\Big]\\
&= h\mathbb{P}(X\ge h) + \sum_{i=h+1}^N \mathbb{P}(X\ge i).\end{align*}
\begin{align*}\mathbb{E}[X\unicode{x1D7D9}_{\{X\ge h\}}] = \mathbb{E}\Big[\sum_{i=1}^N \unicode{x1D7D9}_{\{i\le X\}}\unicode{x1D7D9}_{\{X\ge h\}}\Big]&= \mathbb{E}\Big[\sum_{i=1}^h \unicode{x1D7D9}_{\{X\ge h\}}\Big] + \mathbb{E}\Big[\sum_{i=h+1}^N \unicode{x1D7D9}_{\{X\ge i\}}\Big]\\
&= h\mathbb{P}(X\ge h) + \sum_{i=h+1}^N \mathbb{P}(X\ge i).\end{align*}
Applying this to
![]() $R_{k+1}$
, and using that
$R_{k+1}$
, and using that
![]() $h(k,n)/(k+1) \le k/n$
when n is large, we have
$h(k,n)/(k+1) \le k/n$
when n is large, we have
 \begin{equation*}\frac{1}{k+1}\sum_{j=h(k,n)}^{(k+1)(n-1)} j \mathbb{P}\left( R_{k+1}=j\right) \le \frac{k}{n} \mathbb{P}(R_{k+1}\ge h(k,n)) + \frac{1}{k+1} \sum_{j=h(k,n)+1}^{(k+1)(n-1)} \mathbb{P}(R_{k+1}\ge j),\end{equation*}
\begin{equation*}\frac{1}{k+1}\sum_{j=h(k,n)}^{(k+1)(n-1)} j \mathbb{P}\left( R_{k+1}=j\right) \le \frac{k}{n} \mathbb{P}(R_{k+1}\ge h(k,n)) + \frac{1}{k+1} \sum_{j=h(k,n)+1}^{(k+1)(n-1)} \mathbb{P}(R_{k+1}\ge j),\end{equation*}
and putting this together with (2), Lemma 3.1 and (3), we have shown that
 \begin{equation*}\mathbb{P}\left(|\mathcal{C}(v)|>k \right)\leq \frac{ck}{n} \mathbb{P}(R_{k+1}\ge h(k,n)) + \frac{c}{k+1} \sum_{j=h(k,n)+1}^{(k+1)(n-1)} \mathbb{P}(R_{k+1}\ge j).\end{equation*}
\begin{equation*}\mathbb{P}\left(|\mathcal{C}(v)|>k \right)\leq \frac{ck}{n} \mathbb{P}(R_{k+1}\ge h(k,n)) + \frac{c}{k+1} \sum_{j=h(k,n)+1}^{(k+1)(n-1)} \mathbb{P}(R_{k+1}\ge j).\end{equation*}
The next two lemmas conclude the proof of the upper bound in part (a) of Theorem 1.1 by showing that, when we take
![]() $k=\lceil An^{2/3}\rceil$
with
$k=\lceil An^{2/3}\rceil$
with
![]() $A\ge1$
, the right-hand side above is bounded by
$A\ge1$
, the right-hand side above is bounded by
![]() $cA^{-1/2}n^{-1/3}\exp\{-A^3/8+\lambda A^2/2-\lambda^2A/2\}$
. Let
$cA^{-1/2}n^{-1/3}\exp\{-A^3/8+\lambda A^2/2-\lambda^2A/2\}$
. Let
Lemma 3.2 Suppose that
![]() $1\le A=o\left(n^{1/12}\right)$
,
$1\le A=o\left(n^{1/12}\right)$
,
![]() $\lambda = o(n^{1/12})$
and
$\lambda = o(n^{1/12})$
and
![]() $\lambda\le A/3$
. There exists a finite constant c such that
$\lambda\le A/3$
. There exists a finite constant c such that
Lemma 3.3 Suppose that
![]() $1\le A=o\left(n^{1/12}\right)$
,
$1\le A=o\left(n^{1/12}\right)$
,
![]() $\lambda = o(n^{1/12})$
and
$\lambda = o(n^{1/12})$
and
![]() $\lambda\le A/3$
. There exists a finite constant c such that
$\lambda\le A/3$
. There exists a finite constant c such that
 \begin{equation*}\frac{1}{\lceil An^{2/3}\rceil+1} \sum_{j=H(A,n)+1}^{(\lceil An^{2/3}\rceil+1)(n-1)} \mathbb{P}(R_{\lceil An^{2/3}\rceil+1}\ge j) \leq \frac{c}{A^2 n^{1/3}}e^{-A^3/8+\lambda A^2/2 - \lambda^2 A/2}.\end{equation*}
\begin{equation*}\frac{1}{\lceil An^{2/3}\rceil+1} \sum_{j=H(A,n)+1}^{(\lceil An^{2/3}\rceil+1)(n-1)} \mathbb{P}(R_{\lceil An^{2/3}\rceil+1}\ge j) \leq \frac{c}{A^2 n^{1/3}}e^{-A^3/8+\lambda A^2/2 - \lambda^2 A/2}.\end{equation*}
Since
![]() $R_{\lceil An^{2/3}\rceil+1}$
is simply a binomial random variable, the proofs of Lemmas 3.2 and 3.3 are exercises in applying standard estimates to binomial random variables. We carry out the details in Section 3.1. Subject to these and the proof of Lemma 3.1, the proof of the upper bound in part (a) of Theorem 1.1 is complete.
$R_{\lceil An^{2/3}\rceil+1}$
is simply a binomial random variable, the proofs of Lemmas 3.2 and 3.3 are exercises in applying standard estimates to binomial random variables. We carry out the details in Section 3.1. Subject to these and the proof of Lemma 3.1, the proof of the upper bound in part (a) of Theorem 1.1 is complete.
The upper bound of part (b) in Theorem 1.1 is deduced from the upper bound in part (a) using the following standard procedure, used for example in [Reference Nachmias and Peres24]. For any
![]() $k\in[n]$
, denote by
$k\in[n]$
, denote by
the number of vertices that are contained in components of size larger than k. If u is any fixed vertex in G(n, p), we have
and then taking
![]() $k=\lceil An^{2/3}\rceil$
and applying part (a), this is at most
$k=\lceil An^{2/3}\rceil$
and applying part (a), this is at most
as required. This concludes the proof for the upper bounds (a) and (b) in Theorem 1.1, subject to proving Lemmas 3.1, 3.2 and 3.3.
3.1. Proofs of Lemmas 3.1, 3.2 and 3.3
To prove Lemmas 3.1, 3.2 and 3.3 we will make use of the following two preliminary results on the concentration of Binomial random variables about their mean. The first of these results is Theorem 1.3 in [Reference Bollobás7], while the second is Theorem 2.1 in [Reference Janson, Luczak and Rucinski15].
Lemma 3.4 Let
![]() $S\sim \textrm{Bin}(n,p)$
, and suppose that
$S\sim \textrm{Bin}(n,p)$
, and suppose that
![]() $np\geq 1$
and
$np\geq 1$
and
![]() $1\leq h\leq (1-p)n/3$
. Then
$1\leq h\leq (1-p)n/3$
. Then
Lemma 3.5 Let
![]() $S\sim \textrm{Bin}(n,p)$
and define
$S\sim \textrm{Bin}(n,p)$
and define
![]() $\phi(x) = (1+x)\log(1+x)-x$
for
$\phi(x) = (1+x)\log(1+x)-x$
for
![]() $x\geq -1$
. Then for every
$x\geq -1$
. Then for every
![]() $t\geq 0$
we have that
$t\geq 0$
we have that
-
a.
 $\mathbb{P}(S\geq \mathbb{E}[S]+t)\leq \exp\{-\mathbb{E}[S]\phi(t/\mathbb{E}[S])\}\leq \exp\left\{-t^2/2(\mathbb{E}[S]+t/3)\right\}$
;
$\mathbb{P}(S\geq \mathbb{E}[S]+t)\leq \exp\{-\mathbb{E}[S]\phi(t/\mathbb{E}[S])\}\leq \exp\left\{-t^2/2(\mathbb{E}[S]+t/3)\right\}$
; -
b.
 $\mathbb{P}(S\leq \mathbb{E}[S]-t)\leq \exp\{-t^2/2\mathbb{E}[S]\}$
.
$\mathbb{P}(S\leq \mathbb{E}[S]-t)\leq \exp\{-t^2/2\mathbb{E}[S]\}$
.
We are now ready to start with the proofs of the lemmas stated in the previous section.
Proof of Lemma 3.1. We want to bound
 \begin{equation*}\mathbb{P}\Big(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \Big)\end{equation*}
\begin{equation*}\mathbb{P}\Big(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t\in [k] \Big)\end{equation*}
from above, where
![]() $\tau_i\sim \textrm{Bin}(n-i,p)$
are independent. We do this by adding extra terms to the sum
$\tau_i\sim \textrm{Bin}(n-i,p)$
are independent. We do this by adding extra terms to the sum
![]() $\sum_{i=1}^{t}(\tau_i-1)$
to create a random walk with identically distributed steps. To this end, let
$\sum_{i=1}^{t}(\tau_i-1)$
to create a random walk with identically distributed steps. To this end, let
![]() $(B_i)_{i\in [n]}$
be a sequence of independent random variables, also independent from
$(B_i)_{i\in [n]}$
be a sequence of independent random variables, also independent from
![]() $(\tau_i)_{i \in [n]}$
, and such that
$(\tau_i)_{i \in [n]}$
, and such that
![]() $B_i\sim \textrm{Bin}(i,p)$
for every
$B_i\sim \textrm{Bin}(i,p)$
for every
![]() $i \in [n]$
. Moreover, define
$i \in [n]$
. Moreover, define
![]() $S_t = \sum_{i=1}^{t}B_i$
for
$S_t = \sum_{i=1}^{t}B_i$
for
![]() $t\in [n]$
. Let
$t\in [n]$
. Let
Since
![]() $S_{k} \sim \textrm{Bin}\left(k(k+1)/2,p\right)$
, an application of Lemma 3.5(b) with
$S_{k} \sim \textrm{Bin}\left(k(k+1)/2,p\right)$
, an application of Lemma 3.5(b) with
![]() $t=kn^{-1/2} + kp/2$
yields that
$t=kn^{-1/2} + kp/2$
yields that
![]() $P\geq c$
for some
$P\geq c$
for some
![]() $c>0$
. Now using the independence of
$c>0$
. Now using the independence of
![]() $(\tau_i)_{i\in [n]}$
and
$(\tau_i)_{i\in [n]}$
and
![]() $(B_i)_{i \in [n]}$
we obtain that
$(B_i)_{i \in [n]}$
we obtain that
 \begin{equation*}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t \in [k] \bigg) =P^{-1}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t \in [k],\, S_{k}\ge\frac{k^2}{2}p-\frac{k}{n^{1/2}}\bigg).\end{equation*}
\begin{equation*}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t \in [k] \bigg) =P^{-1}\mathbb{P}\bigg(1+\sum_{i=1}^{t}(\tau_i-1)>0\ \forall t \in [k],\, S_{k}\ge\frac{k^2}{2}p-\frac{k}{n^{1/2}}\bigg).\end{equation*}
Setting
![]() $R_t = \sum_{i=1}^{t}(\tau_i + B_i-1)$
, we see that the last quantity is bounded from above by
$R_t = \sum_{i=1}^{t}(\tau_i + B_i-1)$
, we see that the last quantity is bounded from above by
so noting that
![]() $\tau_i+B_i \overset{iid}{\sim}\textrm{Bin}(n,p)$
for every
$\tau_i+B_i \overset{iid}{\sim}\textrm{Bin}(n,p)$
for every
![]() $i\in [n]$
completes the proof.
$i\in [n]$
completes the proof.
Proof of Lemma 3.2. Write
and recall that
We want to use Lemma 3.4 to bound from above the quantity
where we recall that
![]() $(R_t)_{t\ge 0}$
is a random walk with
$(R_t)_{t\ge 0}$
is a random walk with
![]() $R_0=0$
and i.i.d. steps each having distribution
$R_0=0$
and i.i.d. steps each having distribution
![]() $\textrm{Bin}(n,p)-1$
. Letting
$\textrm{Bin}(n,p)-1$
. Letting
![]() $B_{j,p}$
be a binomial random variable with parameters j and p, setting
$B_{j,p}$
be a binomial random variable with parameters j and p, setting
![]() $h\,{:}\,{\raise-1.5pt{=}}\, H-K\lambda/n^{1/3}$
(which is of order
$h\,{:}\,{\raise-1.5pt{=}}\, H-K\lambda/n^{1/3}$
(which is of order
![]() $A^2n^{1/3}$
since
$A^2n^{1/3}$
since
![]() $\lambda<A/3$
) and observing that
$\lambda<A/3$
) and observing that
applying Lemma 3.4 we obtain
 \begin{align}\mathbb{P}(R_{K}\ge H) &= \mathbb{P}( B_{nK,p} \geq K+H)\nonumber\\[2pt]
&=\mathbb{P}( B_{nK,p} \geq nKp+H-K\lambda/n^{1/3})\nonumber\\[2pt]
&\leq \frac{(p(1-p)nK)^{1/2}}{h\sqrt{2\pi}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}+\frac{h}{p(1-p)nK}+\frac{h^3}{2(1-p)^3(nK)^3}\right\}\nonumber\\[2pt]
&\leq c \frac{K^{1/2}}{A^2n^{1/3}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}\right\}\nonumber\\[2pt]
&\leq \frac{c}{A^{3/2}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}\right\}.\end{align}
\begin{align}\mathbb{P}(R_{K}\ge H) &= \mathbb{P}( B_{nK,p} \geq K+H)\nonumber\\[2pt]
&=\mathbb{P}( B_{nK,p} \geq nKp+H-K\lambda/n^{1/3})\nonumber\\[2pt]
&\leq \frac{(p(1-p)nK)^{1/2}}{h\sqrt{2\pi}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}+\frac{h}{p(1-p)nK}+\frac{h^3}{2(1-p)^3(nK)^3}\right\}\nonumber\\[2pt]
&\leq c \frac{K^{1/2}}{A^2n^{1/3}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}\right\}\nonumber\\[2pt]
&\leq \frac{c}{A^{3/2}}\exp\left\{-\frac{1}{2}\frac{h^2}{p(1-p)nK}\right\}.\end{align}
Define
Elementary estimates using the fact that
![]() $A=o(n^{1/12})$
and
$A=o(n^{1/12})$
and
![]() $\lambda=o(n^{1/12})$
show that
$\lambda=o(n^{1/12})$
show that
From (4) we therefore have, for large n,
 \begin{align*}\frac{K-1}{n} \mathbb{P}(R_{K}\ge H) &\le c\frac{A}{n^{1/3}} \frac{1}{A^{3/2}}e^{-x(A,n,\lambda)^2/2}\\
&\le \frac{c}{\sqrt{A}n^{1/3}}\exp\left(-\frac{A^3}{8}+\frac{\lambda A^2}{2} - \frac{\lambda^2 A}{2} \right),\end{align*}
\begin{align*}\frac{K-1}{n} \mathbb{P}(R_{K}\ge H) &\le c\frac{A}{n^{1/3}} \frac{1}{A^{3/2}}e^{-x(A,n,\lambda)^2/2}\\
&\le \frac{c}{\sqrt{A}n^{1/3}}\exp\left(-\frac{A^3}{8}+\frac{\lambda A^2}{2} - \frac{\lambda^2 A}{2} \right),\end{align*}
which completes the proof of Lemma 3.2.
Before we prove Lemma 3.3, we will need the following bound, which is an easy application of Lemma 3.5.
Lemma 3.6 Suppose that
![]() $B_{N,p}$
is a binomial random variable with parameters
$B_{N,p}$
is a binomial random variable with parameters
![]() $N\ge 1$
and
$N\ge 1$
and
![]() $p\in[0,1]$
. Let
$p\in[0,1]$
. Let
![]() $C\in(0,\infty)$
be constant. Then for all
$C\in(0,\infty)$
be constant. Then for all
![]() $x\in(0, C(Np)^{2/3}]$
we have that
$x\in(0, C(Np)^{2/3}]$
we have that
where c is another finite constant.
Proof. Applying Lemma 3.5, we have
and since
![]() $\log(1+t)>t-t^2/2$
for every
$\log(1+t)>t-t^2/2$
for every
![]() $t>0$
,
$t>0$
,
 \begin{align*}\mathbb{P}\left(B_{N,p}\ge Np + x\right) &\le \exp\Big(-Np\Big[\Big(1+\frac{x}{Np}\Big)\Big(\frac{x}{Np}-\frac{x^2}{2(Np)^2}\Big)-\frac{x}{Np}\Big]\Big)\\
&= \exp\Big(-Np\Big[\frac{x^2}{2(Np)^2} - \frac{x^3}{2(Np)^3}\Big]\Big)\\
&= \exp\Big(-\frac{x^2}{2Np}+\frac{x^3}{2(Np)^2}\Big),\end{align*}
\begin{align*}\mathbb{P}\left(B_{N,p}\ge Np + x\right) &\le \exp\Big(-Np\Big[\Big(1+\frac{x}{Np}\Big)\Big(\frac{x}{Np}-\frac{x^2}{2(Np)^2}\Big)-\frac{x}{Np}\Big]\Big)\\
&= \exp\Big(-Np\Big[\frac{x^2}{2(Np)^2} - \frac{x^3}{2(Np)^3}\Big]\Big)\\
&= \exp\Big(-\frac{x^2}{2Np}+\frac{x^3}{2(Np)^2}\Big),\end{align*}
which establishes the result with
![]() $c=\exp(C^3/2)$
.
$c=\exp(C^3/2)$
.
Proof of Lemma 3.3. Writing
we aim to bound
 \begin{equation*}\frac{1}{K}\sum_{j=H+1}^{K(n-1)}\mathbb{P}(R_{K} \ge j)\end{equation*}
\begin{equation*}\frac{1}{K}\sum_{j=H+1}^{K(n-1)}\mathbb{P}(R_{K} \ge j)\end{equation*}
from above. We first note that
 \begin{equation}\frac{1}{K}\sum_{j=H+1}^{K(n-1)}\mathbb{P}(R_{K} \ge j) \le \frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(R_K\ge j) + n\mathbb{P}(R_K \ge K^{2/3}).\end{equation}
\begin{equation}\frac{1}{K}\sum_{j=H+1}^{K(n-1)}\mathbb{P}(R_{K} \ge j) \le \frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(R_K\ge j) + n\mathbb{P}(R_K \ge K^{2/3}).\end{equation}
To bound the second term on the right-hand side of (5) observe that, since
![]() $A=o(n^{1/12})$
and
$A=o(n^{1/12})$
and
![]() $\lambda = o(n^{1/12})$
, we have
$\lambda = o(n^{1/12})$
, we have
![]() $K\ge nKp - K^{2/3}/2$
when n is large. Thus, when n is large,
$K\ge nKp - K^{2/3}/2$
when n is large. Thus, when n is large,
 \begin{align}n\mathbb{P}(R_K \ge K^{2/3}) &= n\mathbb{P}(B_{nK,p}\ge K + K^{2/3})\nonumber\\[3pt]
&\leq n\mathbb{P}(B_{nK,p}\ge nKp+K^{2/3}/2).\end{align}
\begin{align}n\mathbb{P}(R_K \ge K^{2/3}) &= n\mathbb{P}(B_{nK,p}\ge K + K^{2/3})\nonumber\\[3pt]
&\leq n\mathbb{P}(B_{nK,p}\ge nKp+K^{2/3}/2).\end{align}
Using the second inequality in part (a) of Lemma 3.5 we obtain
 \begin{align}(6)&\le n \exp\left\{-\frac{K^{4/3}}{8(nKp+\frac{1}{6}K^{2/3})}\right\} \leq n\exp\left\{-cA^{1/3}n^{2/9}\right\}\end{align}
\begin{align}(6)&\le n \exp\left\{-\frac{K^{4/3}}{8(nKp+\frac{1}{6}K^{2/3})}\right\} \leq n\exp\left\{-cA^{1/3}n^{2/9}\right\}\end{align}
and for sufficiently large n we have that
Next, for the first term on the right-hand side of (5), note that
 \begin{align}\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(R_K\ge j)&=\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(B_{nK,p}\ge K+j)\nonumber\\[3pt]
&=\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(B_{nK,p}\ge nKp+j-K\lambda n^{-1/3}).\end{align}
\begin{align}\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(R_K\ge j)&=\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(B_{nK,p}\ge K+j)\nonumber\\[3pt]
&=\frac{1}{K}\sum_{j=H+1}^{\lfloor K^{2/3}\rfloor} \mathbb{P}(B_{nK,p}\ge nKp+j-K\lambda n^{-1/3}).\end{align}
Since
![]() $A=o(n^{1/12})$
and
$A=o(n^{1/12})$
and
![]() $\lambda=o(n^{1/12})$
, we have
$\lambda=o(n^{1/12})$
, we have
![]() $K\lambda n^{-1/3}=o(K^{2/3})$
, and therefore we may apply Lemma 3.6 to obtain
$K\lambda n^{-1/3}=o(K^{2/3})$
, and therefore we may apply Lemma 3.6 to obtain
 \begin{align*}(8)\le \frac{c}{K}\sum_{j=H+1}^{\lfloor K^{2/3} \rfloor}\exp\left\{-\frac{(j-K\lambda n^{-1/3})^2}{2nKp}\right\}\leq \frac{c}{\sqrt{K}}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right),\end{align*}
\begin{align*}(8)\le \frac{c}{K}\sum_{j=H+1}^{\lfloor K^{2/3} \rfloor}\exp\left\{-\frac{(j-K\lambda n^{-1/3})^2}{2nKp}\right\}\leq \frac{c}{\sqrt{K}}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right),\end{align*}
where G denotes a Gaussian random variable with mean zero and unit variance. Recalling the standard bound
![]() $\mathbb{P}(G\geq t)\leq (t\sqrt{2\pi})^{-1}e^{-t^2/2}$
, which is valid for every
$\mathbb{P}(G\geq t)\leq (t\sqrt{2\pi})^{-1}e^{-t^2/2}$
, which is valid for every
![]() $t>0$
, we obtain
$t>0$
, we obtain
 \begin{equation*}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right) \leq \frac{1}{\sqrt{2\pi}}\frac{\sqrt{nKp}}{H+1-K\lambda/n^{1/3}}\exp\Big(-\frac{(H+1-K\lambda/n^{1/3})^2}{2nKp}\Big).\end{equation*}
\begin{equation*}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right) \leq \frac{1}{\sqrt{2\pi}}\frac{\sqrt{nKp}}{H+1-K\lambda/n^{1/3}}\exp\Big(-\frac{(H+1-K\lambda/n^{1/3})^2}{2nKp}\Big).\end{equation*}
An easy computation reveals that
and consequently we obtain
 \begin{align*}\frac{c}{\sqrt{K}}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right) \le \frac{c}{A^2n^{1/3}}\exp\left\{-\frac{A^3}{8}+\lambda\frac{A^2}{2}-\lambda^2\frac{A}{2}\right\},\end{align*}
\begin{align*}\frac{c}{\sqrt{K}}\mathbb{P}\left(G\ge \frac{H+1-K\lambda/n^{1/3}}{\sqrt{nKp}}\right) \le \frac{c}{A^2n^{1/3}}\exp\left\{-\frac{A^3}{8}+\lambda\frac{A^2}{2}-\lambda^2\frac{A}{2}\right\},\end{align*}
as required.
Remark 3.7 Here we comment on the possibility of obtaining the correct constant factor in the upper bound of the asymptotic for
![]() $\mathbb{P}(|\mathcal{C}_{\text{max}}|>An^{2/3})$
using the above methodology. We will give a corresponding comment for the lower bound in Remark 4.15.
$\mathbb{P}(|\mathcal{C}_{\text{max}}|>An^{2/3})$
using the above methodology. We will give a corresponding comment for the lower bound in Remark 4.15.
There are three places in our proof of the upper bounds stated in Theorem 1.1 where unspecified constants appear. One of these is from Lemma 3.1. The constant appearing within this result could be eliminated by amending the argument to use
![]() $k/n^\gamma$
rather than
$k/n^\gamma$
rather than
![]() $k/n^{1/2}$
, for e.g.
$k/n^{1/2}$
, for e.g.
![]() $\gamma=5/12$
, and strengthening our assumption on A appropriately to ensure that the error coming from Lemma 3.5 is smaller than our desired bound.
$\gamma=5/12$
, and strengthening our assumption on A appropriately to ensure that the error coming from Lemma 3.5 is smaller than our desired bound.
Another step requiring a more detailed analysis comes from the application of Lemma 3.4 in the proof of Lemma 3.2. Similarly to the first case above, this should be possible but would require stronger conditions on the relationship between A and
![]() $\lambda$
, or error bounds that depend on
$\lambda$
, or error bounds that depend on
![]() $A/\lambda$
.
$A/\lambda$
.
Finally, a further constant appears when we apply Corollary 2.4 in (3). Finding the correct constant here would require a different approach; either an improvement to Corollary 2.4, or an attempt to apply other results about random walks to
![]() $(R_t)_{t\ge0}$
. The latter option would be complicated by the fact that the step distribution of
$(R_t)_{t\ge0}$
. The latter option would be complicated by the fact that the step distribution of
![]() $R_t$
depends on n.
$R_t$
depends on n.
4. Proof of the lower bounds in Theorem 1.1
Let
![]() $v\in [n]$
be any vertex in G(n, p) from which we start running the exploration process described at the beginning of Section 3. We write
$v\in [n]$
be any vertex in G(n, p) from which we start running the exploration process described at the beginning of Section 3. We write
![]() $T_2 = \lceil An^{2/3}\rceil$
; we will in due course also have a time
$T_2 = \lceil An^{2/3}\rceil$
; we will in due course also have a time
![]() $T_1$
which is smaller than
$T_1$
which is smaller than
![]() $T_2$
.
$T_2$
.
Recall from Section 3 that
![]() $\eta_{i}$
denotes the number of unseen vertices which become active during the ith step of the exploration process, and
$\eta_{i}$
denotes the number of unseen vertices which become active during the ith step of the exploration process, and
![]() $Y_t=1+\sum_{i=1}^{t}(\eta_i-1)$
is the number of active vertices at step t of the procedure. Moreover, recall that
$Y_t=1+\sum_{i=1}^{t}(\eta_i-1)$
is the number of active vertices at step t of the procedure. Moreover, recall that
where
![]() $\mathcal{F}_i = \sigma(\{\eta_{1},\dots,\eta_i\})$
and
$\mathcal{F}_i = \sigma(\{\eta_{1},\dots,\eta_i\})$
and
![]() $p=p(n)=1/n+\lambda n^{-4/3}$
. We will start by proving the lower bound in part (a) of Theorem 1.1; that is, by bounding from below the probability
$p=p(n)=1/n+\lambda n^{-4/3}$
. We will start by proving the lower bound in part (a) of Theorem 1.1; that is, by bounding from below the probability
 \begin{equation*}\mathbb{P}\left(|\mathcal{C}(v)|>T_2\right)=\mathbb{P}\left(1+\sum_{i=1}^{t}(\eta_i-1)>0\ \forall t \in [T_2]\right).\end{equation*}
\begin{equation*}\mathbb{P}\left(|\mathcal{C}(v)|>T_2\right)=\mathbb{P}\left(1+\sum_{i=1}^{t}(\eta_i-1)>0\ \forall t \in [T_2]\right).\end{equation*}
We note that the random variables
![]() $\eta_i$
are not independent, which makes our analysis more difficult. The first part of our argument, therefore, consists of replacing the
$\eta_i$
are not independent, which makes our analysis more difficult. The first part of our argument, therefore, consists of replacing the
![]() $\eta_{i}$
with a sequence of independent binomial random variables which are easier to analyse. The idea is that
$\eta_{i}$
with a sequence of independent binomial random variables which are easier to analyse. The idea is that
![]() $\eta_i$
, which is the number of neighbours of our ith vertex that are unseen, is roughly
$\eta_i$
, which is the number of neighbours of our ith vertex that are unseen, is roughly
![]() $\textrm{Bin}(n-i,p)$
, but the first parameter is slightly smaller due to the (random) number of active vertices that are present at the beginning of the ith step of the exploration process. If we can bound the number of active vertices above by some deterministic value K with high probability, then we can remove this source of randomness and obtain a sequence of independent increments in place of the
$\textrm{Bin}(n-i,p)$
, but the first parameter is slightly smaller due to the (random) number of active vertices that are present at the beginning of the ith step of the exploration process. If we can bound the number of active vertices above by some deterministic value K with high probability, then we can remove this source of randomness and obtain a sequence of independent increments in place of the
![]() $\eta_i$
. To this end, fix
$\eta_i$
. To this end, fix
![]() $K\in\mathbb{N}$
and suppose that
$K\in\mathbb{N}$
and suppose that
![]() $(\delta_i)_{i\in [T_2]}$
is a sequence of independent random variables with
$(\delta_i)_{i\in [T_2]}$
is a sequence of independent random variables with
![]() $\delta_i\sim \textrm{Bin}(n-K-i,p)$
and set
$\delta_i\sim \textrm{Bin}(n-K-i,p)$
and set
![]() $R_t = 1+\sum_{i=1}^{t}(\delta_i-1)$
. We note that the definitions of
$R_t = 1+\sum_{i=1}^{t}(\delta_i-1)$
. We note that the definitions of
![]() $\delta_i$
and
$\delta_i$
and
![]() $R_t$
depend implicitly on K; sometimes for clarity we will write
$R_t$
depend implicitly on K; sometimes for clarity we will write
![]() $\delta_i^{(K)}$
and
$\delta_i^{(K)}$
and
![]() $R_t^{(K)}$
. We will soon fix
$R_t^{(K)}$
. We will soon fix
![]() $K=\lfloor n^{2/5}\rfloor$
, but the following lemma works for any
$K=\lfloor n^{2/5}\rfloor$
, but the following lemma works for any
![]() $K<n-T_2$
. We postpone the proof, which constructs a coupling between
$K<n-T_2$
. We postpone the proof, which constructs a coupling between
![]() $\eta_i$
and
$\eta_i$
and
![]() $\delta_i$
, until Section 4.3.
$\delta_i$
, until Section 4.3.
Lemma 4.1 Suppose that
![]() $K+T_2<n$
. Define
$K+T_2<n$
. Define
![]() $\tau_0\,{:}\,{\raise-1.5pt{=}}\, \min\{t\geq 1:Y_t=0\}$
, the first time at which the set of active vertices becomes empty. Then
$\tau_0\,{:}\,{\raise-1.5pt{=}}\, \min\{t\geq 1:Y_t=0\}$
, the first time at which the set of active vertices becomes empty. Then
Our next result shows that if we choose
![]() $K=\lfloor n^{2/5}\rfloor$
, then we do not have to worry about the last probability on the right-hand side of (10).
$K=\lfloor n^{2/5}\rfloor$
, then we do not have to worry about the last probability on the right-hand side of (10).
Lemma 4.2 Let
![]() $\tau_0$
be as in the previous lemma. As
$\tau_0$
be as in the previous lemma. As
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
The proof of Lemma 4.2, which easily follows from Lemma 3.5, is again postponed toSection 4.3.
Given (11), we can now fix
![]() $K=\lfloor n^{2/5}\rfloor$
and focus on providing a lower bound for
$K=\lfloor n^{2/5}\rfloor$
and focus on providing a lower bound for
Observe that, although we now have a process with independent increments, obtaining a lower bound for (12) remains a non-trivial task, because the
![]() $\delta_i$
that are used to define
$\delta_i$
that are used to define
![]() $R_t$
are not identically distributed. We consider two options to produce a random walk with i.i.d. increments from
$R_t$
are not identically distributed. We consider two options to produce a random walk with i.i.d. increments from
![]() $(R_t)_{t\in [T_2]}$
. The first is to view
$(R_t)_{t\in [T_2]}$
. The first is to view
![]() $\delta_i$
as a sum of i.i.d. Bernoulli random variables, with
$\delta_i$
as a sum of i.i.d. Bernoulli random variables, with
![]() $\delta_1$
summing more Bernoullis than
$\delta_1$
summing more Bernoullis than
![]() $\delta_2$
and so on; and then to rearrange the same Bernoullis amongst sums
$\delta_2$
and so on; and then to rearrange the same Bernoullis amongst sums
![]() $\delta_i^{\prime}$
that all have equal length. The second is simply to add an independent
$\delta_i^{\prime}$
that all have equal length. The second is simply to add an independent
![]() $\textrm{Bin}(K+i,p)$
random variable to
$\textrm{Bin}(K+i,p)$
random variable to
![]() $\delta_i$
for each i.
$\delta_i$
for each i.
It turns out that neither of these two options works on its own. The first has problems if we try to cover too many values of i, since the more Bernoullis that we have to rearrange, the less accurate our estimates become. The second has problems when i is small, as the variance of the added
![]() $\textrm{Bin}(K+i,p)$
random variables is too large when our random walk is near the origin.
$\textrm{Bin}(K+i,p)$
random variables is too large when our random walk is near the origin.
We therefore combine the two techniques. We take
![]() $T_1\in[T_2]$
and carry out the first strategy for times
$T_1\in[T_2]$
and carry out the first strategy for times
![]() $t\in [T_1]$
, and the second strategy for
$t\in [T_1]$
, and the second strategy for
![]() $t\in [\![ T_1, T_2]\!]$
.
$t\in [\![ T_1, T_2]\!]$
.
We note first that for any deterministic
![]() $H\in\mathbb{N}$
and
$H\in\mathbb{N}$
and
![]() $T_1\in[T_2]$
,
$T_1\in[T_2]$
,
 \begin{align}&\mathbb{P}\big(R_t>0\ \forall t \in [T_2]\big)\nonumber\\[3pt] &\quad \geq \mathbb{P}\big(R_t>0\ \forall t\in [T_1],\,\, R_{T_1}\in [H,2H],\,\, R_t>0\ \forall t\in [\![ T_1, T_2]\!]\big)\nonumber\\[3pt]&\quad \ge \mathbb{P}\big(R_t>0\ \forall t\in [T_1],\,\, R_{T_1}\in [H,2H]\big)\mathbb{P}( R_t > 0\ \forall t\in [\![ T_1, T_2]\!] \,\big|\, R_{T_1}=H\big).\end{align}
\begin{align}&\mathbb{P}\big(R_t>0\ \forall t \in [T_2]\big)\nonumber\\[3pt] &\quad \geq \mathbb{P}\big(R_t>0\ \forall t\in [T_1],\,\, R_{T_1}\in [H,2H],\,\, R_t>0\ \forall t\in [\![ T_1, T_2]\!]\big)\nonumber\\[3pt]&\quad \ge \mathbb{P}\big(R_t>0\ \forall t\in [T_1],\,\, R_{T_1}\in [H,2H]\big)\mathbb{P}( R_t > 0\ \forall t\in [\![ T_1, T_2]\!] \,\big|\, R_{T_1}=H\big).\end{align}
We now fix
![]() $T_1 = 2\lfloor n^{2/3}/A^2\rfloor-1$
and
$T_1 = 2\lfloor n^{2/3}/A^2\rfloor-1$
and
![]() $H = \lceil n^{1/3}/A\rceil$
.
$H = \lceil n^{1/3}/A\rceil$
.
Proposition 4.3 There exists
![]() $c>0$
such that for sufficiently large n and A,
$c>0$
such that for sufficiently large n and A,
Proposition 4.4 There exists
![]() $c>0$
such that for sufficiently large n and A,
$c>0$
such that for sufficiently large n and A,
We will prove Proposition 4.3 in Section 4.1 and Proposition 4.4 in Section 4.2. For now we show how these results can be used to complete the proof of the lower bounds in Theorem 1.1.
Proof of lower bounds in Theorem 1.1. By Lemmas 4.1 and 4.2,
In light of (13), it then follows from Propositions 4.3 and 4.4 that
This concludes the proof of the lower bound in part (a) of Theorem 1.1. In order to prove the lower bound in part (b), we will need to use the fact that for any
![]() $\mathbb{N}_0$
-valued random variable X,
$\mathbb{N}_0$
-valued random variable X,
This can be proved by applying the Cauchy–Schwarz inequality to
![]() $X\unicode{x1D7D9}_{\{X\ge 1\}}$
.
$X\unicode{x1D7D9}_{\{X\ge 1\}}$
.
To proceed with the proof of the lower bound in part (b), let us denote by
![]() $X = \sum_{i=1}^{n}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2]\}}$
the number of components of size between
$X = \sum_{i=1}^{n}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2]\}}$
the number of components of size between
![]() $T_2$
and
$T_2$
and
![]() $2T_2$
. Observe that
$2T_2$
. Observe that
![]() $X\geq 1 $
implies
$X\geq 1 $
implies
![]() $|\mathcal{C}_{\max}|\geq T_2$
. Therefore using (15) we obtain
$|\mathcal{C}_{\max}|\geq T_2$
. Therefore using (15) we obtain
For the numerator, we have
Next we bound the denominator from above. Given vertices
![]() $i,j\in [n]$
, write
$i,j\in [n]$
, write
![]() $i\leftrightarrow j$
if there exists a path of opens edges between i and j. Then we can write
$i\leftrightarrow j$
if there exists a path of opens edges between i and j. Then we can write
where
 \begin{equation*}S_1 = \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{j\neq i}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{|\mathcal{C}(j)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{i \nleftrightarrow j \}}\bigg]\end{equation*}
\begin{equation*}S_1 = \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{j\neq i}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{|\mathcal{C}(j)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{i \nleftrightarrow j \}}\bigg]\end{equation*}
and
 \begin{equation*}S_2 = \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{j\neq i}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{|\mathcal{C}(j)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{i \leftrightarrow j \}}\bigg].\end{equation*}
\begin{equation*}S_2 = \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{j\neq i}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{|\mathcal{C}(j)|\in [T_2,2T_2] \}}\unicode{x1D7D9}_{\{i \leftrightarrow j \}}\bigg].\end{equation*}
For
![]() $S_1$
we have
$S_1$
we have
 \begin{align*}S_1&\leq n^2\sum_{k=T_2}^{2T_2}\mathbb{P}\Big(|\mathcal{C}(1)|=k, 1\nleftrightarrow 2\Big)\mathbb{P}\Big(|C(2)|\in [T_2,2T_2] \,\Big|\, |\mathcal{C}(1)|=k, 1\nleftrightarrow 2\Big)\\[3pt] &\leq n^2 \mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2] \right) \mathbb{P}\left(|\mathcal{C}(2)|\ge T_2\right).\end{align*}
\begin{align*}S_1&\leq n^2\sum_{k=T_2}^{2T_2}\mathbb{P}\Big(|\mathcal{C}(1)|=k, 1\nleftrightarrow 2\Big)\mathbb{P}\Big(|C(2)|\in [T_2,2T_2] \,\Big|\, |\mathcal{C}(1)|=k, 1\nleftrightarrow 2\Big)\\[3pt] &\leq n^2 \mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2] \right) \mathbb{P}\left(|\mathcal{C}(2)|\ge T_2\right).\end{align*}
For
![]() $S_2$
we have
$S_2$
we have
 \begin{equation*}\begin{split}S_2=\mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{k=T_2}^{2T_2}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|=k\}}\sum_{j\neq i}\unicode{x1D7D9}_{\{j\in \mathcal{C}(i)\}}\bigg]&\leq \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{k=T_2}^{2T_2}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|=k\}}k\bigg]\\[3pt] &\leq 2T_2 n\mathbb{P}\left(|C(1)|\in [T_2,2T_2]\right).\end{split}\end{equation*}
\begin{equation*}\begin{split}S_2=\mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{k=T_2}^{2T_2}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|=k\}}\sum_{j\neq i}\unicode{x1D7D9}_{\{j\in \mathcal{C}(i)\}}\bigg]&\leq \mathbb{E}\bigg[\sum_{i=1}^{n}\sum_{k=T_2}^{2T_2}\unicode{x1D7D9}_{\{|\mathcal{C}(i)|=k\}}k\bigg]\\[3pt] &\leq 2T_2 n\mathbb{P}\left(|C(1)|\in [T_2,2T_2]\right).\end{split}\end{equation*}
Returning to (18) and recalling that
![]() $T_2 = \lceil An^{2/3}\rceil$
, we obtain
$T_2 = \lceil An^{2/3}\rceil$
, we obtain
 \begin{multline*}\mathbb{E}[X^2]\leq n\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right) + n^2 \mathbb{P}\left(|C(1)|\in [T_2,2T_2] \right)\mathbb{P}\left(|\mathcal{C}(2)|\ge T_2\right)\\[3pt]+ 3An^{5/3}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right).\end{multline*}
\begin{multline*}\mathbb{E}[X^2]\leq n\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right) + n^2 \mathbb{P}\left(|C(1)|\in [T_2,2T_2] \right)\mathbb{P}\left(|\mathcal{C}(2)|\ge T_2\right)\\[3pt]+ 3An^{5/3}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right).\end{multline*}
By the upper bound in part (a) of Theorem 1.1,
and therefore
Substituting this and (17) into (16) and then applying (14), we obtain
 \begin{align}\nonumber\mathbb{P}\left(|\mathcal{C}_{\max}|\geq \lceil An^{2/3} \rceil\right)&\geq\frac{n^{2}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right)^2}{cAn^{5/3}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right)}\\[3pt]&=c\frac{n^{1/3}}{A}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right).\end{align}
\begin{align}\nonumber\mathbb{P}\left(|\mathcal{C}_{\max}|\geq \lceil An^{2/3} \rceil\right)&\geq\frac{n^{2}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right)^2}{cAn^{5/3}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right)}\\[3pt]&=c\frac{n^{1/3}}{A}\mathbb{P}\left(|\mathcal{C}(1)|\in [T_2,2T_2]\right).\end{align}
Observe that
and by applying the upper bound in Theorem 1.1(a) with 2A in place of A, together with (14), for A sufficiently large we may ensure that
![]() $\mathbb{P}(|\mathcal{C}(1)|> 2T_2)\le \mathbb{P}(|\mathcal{C}(1)|\geq T_2)/2$
. Therefore (19) is at least
$\mathbb{P}(|\mathcal{C}(1)|> 2T_2)\le \mathbb{P}(|\mathcal{C}(1)|\geq T_2)/2$
. Therefore (19) is at least
as required. This completes the proof of Theorem 1.2, subject to the proofs of Lemmas 4.1 and 4.2 and Propositions 4.3 and 4.4.
4.1. Rearranging Bernoullis and applying the ballot theorem: proof of Proposition 4.3
We first introduce a technical result which will be used to transform
![]() $(R_t)_{t\in [T_1]}$
into a process with i.i.d. increments.
$(R_t)_{t\in [T_1]}$
into a process with i.i.d. increments.
Lemma 4.5 Suppose that
![]() $N\in\mathbb{N}$
, and that
$N\in\mathbb{N}$
, and that
![]() $L\in[N]$
is odd. Let
$L\in[N]$
is odd. Let
![]() $(I_j^{i})_{i,j\ge 1}$
be i.i.d. non-negative random variables and set
$(I_j^{i})_{i,j\ge 1}$
be i.i.d. non-negative random variables and set
![]() $X_i=\sum_{j=1}^{N-i}I_j^{i}$
for
$X_i=\sum_{j=1}^{N-i}I_j^{i}$
for
![]() $i=1,\ldots,L$
. Then there exist i.i.d. random variables
$i=1,\ldots,L$
. Then there exist i.i.d. random variables
![]() $(\tilde I_j^i)_{i,j\ge1}$
with the same distribution as
$(\tilde I_j^i)_{i,j\ge1}$
with the same distribution as
![]() $I^i_j$
such that if we set
$I^i_j$
such that if we set
![]() $\tilde X_i=\sum_{j=1}^{N-(L+1)/2}\tilde I_j^{i}$
then
$\tilde X_i=\sum_{j=1}^{N-(L+1)/2}\tilde I_j^{i}$
then
-
 $\sum_{i=1}^{t} \tilde X_i\leq \sum_{i=1}^{t}X_i$
for all
$\sum_{i=1}^{t} \tilde X_i\leq \sum_{i=1}^{t}X_i$
for all
 $1\leq t\leq L$
;
$1\leq t\leq L$
; -
 $\sum_{i=1}^{L} \tilde X_i=\sum_{i=1}^{L}X_i$
.
$\sum_{i=1}^{L} \tilde X_i=\sum_{i=1}^{L}X_i$
.
The reader can think of the
![]() $I_j^i$
as Bernoulli(p)-distributed, so that
$I_j^i$
as Bernoulli(p)-distributed, so that
![]() $X_i\sim \textrm{Bin}(N-i,p)$
and
$X_i\sim \textrm{Bin}(N-i,p)$
and
![]() $\tilde X_i\sim \textrm{Bin}(N-(L+1)/2,p)$
. The idea behind the proof is that
$\tilde X_i\sim \textrm{Bin}(N-(L+1)/2,p)$
. The idea behind the proof is that
![]() $X_1$
has more summands than
$X_1$
has more summands than
![]() $X_L$
, so if we transfer some of the summands from
$X_L$
, so if we transfer some of the summands from
![]() $X_1$
to
$X_1$
to
![]() $X_L$
, we do not change the value of
$X_L$
, we do not change the value of
![]() $\sum_{i=1}^L X_i$
but we decrease
$\sum_{i=1}^L X_i$
but we decrease
![]() $X_1$
. Then we move on to
$X_1$
. Then we move on to
![]() $X_2$
and transfer some of its summands to
$X_2$
and transfer some of its summands to
![]() $X_{L-1}$
, which decreases
$X_{L-1}$
, which decreases
![]() $\sum_{i=1}^2 X_i$
without changing
$\sum_{i=1}^2 X_i$
without changing
![]() $\sum_{i=1}^L X_i$
; and so on. We postpone the details until Section 4.3.
$\sum_{i=1}^L X_i$
; and so on. We postpone the details until Section 4.3.
Before we can proceed with the proof of Proposition 4.3, we need one more tool. We can use Lemma 4.5 to transform
![]() $(R_t)_{t\in [T_1]}$
into a process with i.i.d. increments, but in order to apply the generalised ballot theorem, Theorem 2.1, we need our increments also to have mean zero and for their distribution not to depend on n. The following lemma is slightly more general than we will need.
$(R_t)_{t\in [T_1]}$
into a process with i.i.d. increments, but in order to apply the generalised ballot theorem, Theorem 2.1, we need our increments also to have mean zero and for their distribution not to depend on n. The following lemma is slightly more general than we will need.
Lemma 4.6 Take
![]() $n\in\mathbb{N}$
,
$n\in\mathbb{N}$
,
![]() $h_n\ge 0$
,
$h_n\ge 0$
,
![]() $a_n\in(-1,\infty)$
satisfying
$a_n\in(-1,\infty)$
satisfying
![]() $na_n\in\mathbb{Z}$
,
$na_n\in\mathbb{Z}$
,
![]() $b_n\in(-1,n-1)$
and
$b_n\in(-1,n-1)$
and
![]() $t_n\in\mathbb{N}$
. Suppose that
$t_n\in\mathbb{N}$
. Suppose that
![]() $M_t = 1 + \sum_{i=1}^t (W_i-1)$
where the
$M_t = 1 + \sum_{i=1}^t (W_i-1)$
where the
![]() $W_i$
are independent
$W_i$
are independent
![]() $\textrm{Bin}(n(1+a_n),(1+b_n)/n)$
random variables. Let
$\textrm{Bin}(n(1+a_n),(1+b_n)/n)$
random variables. Let
![]() $\mu_n = (1+a_n)(1+b_n)$
. Then
$\mu_n = (1+a_n)(1+b_n)$
. Then
 \begin{multline*}\mathbb{P}\big(M_t>0\,\,\,\,\forall t\in [t_n], \, M_{t_n}\in[h_n,2h_n]\big)\\
\ge (\mu_n\wedge 1)^{2h_n} \mu_n^{t_n-1} e^{(1-\mu_n)t_n}\mathbb{P}\big(\hat M_t > 0 \,\,\,\,\forall t\in[t_n],\, \hat M_{t_n}\in[h_n,2h_n]\big) - \frac{t_n}{n}(1+a_n)(1+b_n)^2\end{multline*}
\begin{multline*}\mathbb{P}\big(M_t>0\,\,\,\,\forall t\in [t_n], \, M_{t_n}\in[h_n,2h_n]\big)\\
\ge (\mu_n\wedge 1)^{2h_n} \mu_n^{t_n-1} e^{(1-\mu_n)t_n}\mathbb{P}\big(\hat M_t > 0 \,\,\,\,\forall t\in[t_n],\, \hat M_{t_n}\in[h_n,2h_n]\big) - \frac{t_n}{n}(1+a_n)(1+b_n)^2\end{multline*}
where
![]() $\hat M_t= 1+\sum_{i=1}^{t}(\hat W_i-1)$
, and
$\hat M_t= 1+\sum_{i=1}^{t}(\hat W_i-1)$
, and
![]() $(\hat W_i)_{i=1}^{t_n}$
is a sequence of independent Poisson random variables with mean one.
$(\hat W_i)_{i=1}^{t_n}$
is a sequence of independent Poisson random variables with mean one.
We delay the proof, which uses a fairly standard Poisson approximation for the binomial distribution and then a simple change of measure to remove the drift, until Section 4.4 and proceed with the proof of Proposition 4.3.
Proof of Proposition 4.3. As previously mentioned, we want to bound
by means of the generalised ballot theorem, Theorem 2.1. To this end, we first need to turn the process
![]() $(R_t)_{t\in [T_1]}$
into a random walk with i.i.d. steps having mean zero. In order to obtain identically distributed steps we will make use of Lemma 4.5.
$(R_t)_{t\in [T_1]}$
into a random walk with i.i.d. steps having mean zero. In order to obtain identically distributed steps we will make use of Lemma 4.5.
Recall that
![]() $H=\lceil n^{1/3}/A\rceil$
and
$H=\lceil n^{1/3}/A\rceil$
and
![]() $R_t=1+\sum_{i=1}^{t}(\delta_i-1)$
, where each
$R_t=1+\sum_{i=1}^{t}(\delta_i-1)$
, where each
![]() $\delta_i$
is the sum of
$\delta_i$
is the sum of
![]() $n-\lfloor n^{2/5} \rfloor -i$
i.i.d. Ber(p) random variables. It follows from Lemma 4.5, with
$n-\lfloor n^{2/5} \rfloor -i$
i.i.d. Ber(p) random variables. It follows from Lemma 4.5, with
![]() $N=n-\lfloor n^{2/5}\rfloor$
and
$N=n-\lfloor n^{2/5}\rfloor$
and
![]() $L=T_1$
, that there exists a sequence
$L=T_1$
, that there exists a sequence
![]() $(\tilde \delta_i)_{i\in [T_1]}$
of i.i.d random variables with
$(\tilde \delta_i)_{i\in [T_1]}$
of i.i.d random variables with
![]() $\tilde \delta_i\sim \textrm{Bin}(n-\lfloor n^{2/5}\rfloor - (T_1+1)/2,p)$
for which, setting
$\tilde \delta_i\sim \textrm{Bin}(n-\lfloor n^{2/5}\rfloor - (T_1+1)/2,p)$
for which, setting
![]() $\tilde R_t = 1+\sum_{i=1}^{t}(\tilde \delta_i-1)$
, we obtain
$\tilde R_t = 1+\sum_{i=1}^{t}(\tilde \delta_i-1)$
, we obtain
In order to evaluate the probabilities appearing in the above sum by means of the generalised ballot theorem, we still have to turn
![]() $(\tilde R_t)_{t\in [T_1]}$
into a process whose increments have mean zero. We do this by applying Lemma 4.6 with
$(\tilde R_t)_{t\in [T_1]}$
into a process whose increments have mean zero. We do this by applying Lemma 4.6 with
![]() $h_n=H$
,
$h_n=H$
,
![]() $t_n=T_1=2\lfloor n^{2/3}/A^2\rfloor-1$
,
$t_n=T_1=2\lfloor n^{2/3}/A^2\rfloor-1$
,
![]() $a_n = -\lfloor n^{2/5}\rfloor/n - (T_1+1)/(2n)$
and
$a_n = -\lfloor n^{2/5}\rfloor/n - (T_1+1)/(2n)$
and
![]() $b_n = \lambda/n^{1/3}$
. Since
$b_n = \lambda/n^{1/3}$
. Since
![]() $|\lambda|\le A/3$
, it is easy to see that there exists a constant
$|\lambda|\le A/3$
, it is easy to see that there exists a constant
![]() $c>0$
(not depending on n) such that
$c>0$
(not depending on n) such that
Also, using the inequality
![]() $1+x\ge e^{x-x^2}$
valid for
$1+x\ge e^{x-x^2}$
valid for
![]() $x\ge -1/2$
, for sufficiently large n we have
$x\ge -1/2$
, for sufficiently large n we have
for some constant
![]() $c>0$
. Finally, since
$c>0$
. Finally, since
from Lemma 4.6 we obtain that
 \begin{align}&\mathbb{P}\left(\tilde R_t>0\ \forall t\in [T_1],\, \tilde R_{T_1}\in [H,2H]\right)\nonumber\\
&\quad \ge c\mathbb{P}\left(\hat R_t>0\ \forall t\in [T_1],\, \hat R_{T_1}\in [H,2H]\right) - \frac{C}{A^2 n^{1/3}} \end{align}
\begin{align}&\mathbb{P}\left(\tilde R_t>0\ \forall t\in [T_1],\, \tilde R_{T_1}\in [H,2H]\right)\nonumber\\
&\quad \ge c\mathbb{P}\left(\hat R_t>0\ \forall t\in [T_1],\, \hat R_{T_1}\in [H,2H]\right) - \frac{C}{A^2 n^{1/3}} \end{align}
for some constants
![]() $c>0$
and
$c>0$
and
![]() $C<\infty$
, where
$C<\infty$
, where
![]() $\hat R_t = 1+\sum_{i=1}^t (\hat \delta_i-1)$
and
$\hat R_t = 1+\sum_{i=1}^t (\hat \delta_i-1)$
and
![]() $(\hat\delta_i)_{i=1}^{T_1}$
is a sequence of independent Poisson random variables with parameter 1.
$(\hat\delta_i)_{i=1}^{T_1}$
is a sequence of independent Poisson random variables with parameter 1.
We are now in a position to apply Theorem 2.1. Recalling that
![]() $H = \lceil n^{1/3}/A\rceil$
and
$H = \lceil n^{1/3}/A\rceil$
and
![]() $T_1 = 2\lfloor n^{2/3}/A^2\rfloor-1$
, for all
$T_1 = 2\lfloor n^{2/3}/A^2\rfloor-1$
, for all
![]() $k\in[H-1,2H-1]$
we have
$k\in[H-1,2H-1]$
we have
![]() $k\leq 2H=O(\sqrt{T_1})$
. We can therefore conclude from Theorem 2.1 that
$k\leq 2H=O(\sqrt{T_1})$
. We can therefore conclude from Theorem 2.1 that
 \begin{align*}&\mathbb{P}\left(\hat R_t>0\ \forall t\in [T_1],\, \hat R_{T_1}\in [H,2H]\right) \\
&\quad \ge \mathbb{P}\left(\hat R_t-1>0\ \forall t\in [T_1],\, \hat R_{T_1}-1\in [H-1,2H-1]\right) \\
&\quad \ge c\sum_{k=H-1}^{2H-1} \frac{k+1}{T_1^{3/2}},\end{align*}
\begin{align*}&\mathbb{P}\left(\hat R_t>0\ \forall t\in [T_1],\, \hat R_{T_1}\in [H,2H]\right) \\
&\quad \ge \mathbb{P}\left(\hat R_t-1>0\ \forall t\in [T_1],\, \hat R_{T_1}-1\in [H-1,2H-1]\right) \\
&\quad \ge c\sum_{k=H-1}^{2H-1} \frac{k+1}{T_1^{3/2}},\end{align*}
which is of order
![]() $An^{-1/3}$
. Substituting this bound into (21) gives
$An^{-1/3}$
. Substituting this bound into (21) gives
Taking A sufficiently large that the first term dominates, and then recalling (20), gives theresult.
4.2. Adding independent binomials and approximating with Brownian motion: Proof of Proposition 4.4
Recall that
![]() $R_t = 1+\sum_{i=1}^t (\delta_i-1)$
where
$R_t = 1+\sum_{i=1}^t (\delta_i-1)$
where
![]() $(\delta_i)_{i=1}^{T_2}$
is a sequence of independent
$(\delta_i)_{i=1}^{T_2}$
is a sequence of independent
![]() $\textrm{Bin}(n-K-i,p)$
random variables. Recall also that
$\textrm{Bin}(n-K-i,p)$
random variables. Recall also that
![]() $H=\lceil n^{1/3}/A\rceil$
,
$H=\lceil n^{1/3}/A\rceil$
,
![]() $K=\lfloor n^{2/5}\rfloor$
,
$K=\lfloor n^{2/5}\rfloor$
,
![]() $T_1 = 2\lfloor n^{2/3}/A^2\rfloor -1$
and
$T_1 = 2\lfloor n^{2/3}/A^2\rfloor -1$
and
![]() $T_2 = \lceil An^{2/3}\rceil$
. Throughout this section we write
$T_2 = \lceil An^{2/3}\rceil$
. Throughout this section we write
![]() $T = T_2-T_1$
.
$T = T_2-T_1$
.
Our first task in this section is to replace
![]() $R_t$
with a sum of i.i.d. random variables. We do this by adding an independent
$R_t$
with a sum of i.i.d. random variables. We do this by adding an independent
![]() $\textrm{Bin}(K+i,p)$
random variable to
$\textrm{Bin}(K+i,p)$
random variable to
![]() $\delta_i$
for each i, and checking that the sum of these additional random variables cannot be too large using Lemma 3.5.
$\delta_i$
for each i, and checking that the sum of these additional random variables cannot be too large using Lemma 3.5.
Lemma 4.7 For
![]() $t\in[0,\infty)$
, define
$t\in[0,\infty)$
, define
Then there exists
![]() $c>0$
such that for all large n,
$c>0$
such that for all large n,
where
![]() $S_t = \sum_{i=1}^t (\Delta_i-1)$
, and
$S_t = \sum_{i=1}^t (\Delta_i-1)$
, and
![]() $(\Delta_i)_{i=1}^{T}$
is a sequence of independent Bin(n,p) random variables.
$(\Delta_i)_{i=1}^{T}$
is a sequence of independent Bin(n,p) random variables.
The proof of Lemma 4.7 is in Section 4.3. Next, in order to apply a Brownian approximation to our random walk, we would like the step distribution not to depend on n.
Lemma 4.8 For
![]() $t\in[0,\infty)$
, define
$t\in[0,\infty)$
, define
Let g and
![]() $(S_t)_{t=0}^T$
be as in Lemma 4.7. Then there exist constants
$(S_t)_{t=0}^T$
be as in Lemma 4.7. Then there exist constants
![]() $c,C\in(0,\infty)$
such that
$c,C\in(0,\infty)$
such that
 \begin{align*}&\mathbb{P}\big(S_t > g(t)\;\; \forall t\in[\![ 1,T]\!]\big)\\
&\ge c e^{\lambda A^2/2 - \lambda^2 A/2}\mathbb{P}\big(\hat S_t > \gamma(t)\;\;\forall t\in[\![ 1,T]\!],\, \hat S_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A}\big) - C\exp\Big(- \frac{n^{1/3}}{4A}\Big),\end{align*}
\begin{align*}&\mathbb{P}\big(S_t > g(t)\;\; \forall t\in[\![ 1,T]\!]\big)\\
&\ge c e^{\lambda A^2/2 - \lambda^2 A/2}\mathbb{P}\big(\hat S_t > \gamma(t)\;\;\forall t\in[\![ 1,T]\!],\, \hat S_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A}\big) - C\exp\Big(- \frac{n^{1/3}}{4A}\Big),\end{align*}
where
![]() $\hat S_t = \sum_{i=1}^t( \hat\Delta_i-1)$
and
$\hat S_t = \sum_{i=1}^t( \hat\Delta_i-1)$
and
![]() $(\hat\Delta_i)_{i=1}^{T}$
is a sequence of independent Poisson random variables of parameter 1.
$(\hat\Delta_i)_{i=1}^{T}$
is a sequence of independent Poisson random variables of parameter 1.
Again we delay the proof, which is similar to the proof of Lemma 4.6, until Section 4.4 and proceed with the proof of Proposition 4.4. As mentioned above, our strategy is to approximate the random walk
![]() $(\hat S_t)_{t=0}^{T}$
appearing in Lemma 4.8 with Brownian motion. We will use an accurate bound of Komlós, Major and Tusnády due to its ease of application, although we will not really need the additional precision gained over the earlier result of Strassen [Reference Strassen31, Theorem 1.5]. The following rephrasing of the original theorem is from [Reference Chatterjee9].
$(\hat S_t)_{t=0}^{T}$
appearing in Lemma 4.8 with Brownian motion. We will use an accurate bound of Komlós, Major and Tusnády due to its ease of application, although we will not really need the additional precision gained over the earlier result of Strassen [Reference Strassen31, Theorem 1.5]. The following rephrasing of the original theorem is from [Reference Chatterjee9].
Theorem 4.9 (Komlós et al. [Reference Komlós, Major and Tusnády18]).Let
![]() $(\xi_i)_{i\geq 1}$
be a sequence of i.i.d. random variables with
$(\xi_i)_{i\geq 1}$
be a sequence of i.i.d. random variables with
![]() $\mathbb{E}[\xi_1]=0$
and
$\mathbb{E}[\xi_1]=0$
and
![]() $\mathbb{E}[\xi_1^{2}]=1$
. Suppose that there exists
$\mathbb{E}[\xi_1^{2}]=1$
. Suppose that there exists
![]() $\theta>0$
such that
$\theta>0$
such that
![]() $\mathbb{E}\left[e^{\theta |\xi_1|}\right]<\infty$
. For each
$\mathbb{E}\left[e^{\theta |\xi_1|}\right]<\infty$
. For each
![]() $k\in\{0\}\cup\mathbb{N}$
, let
$k\in\{0\}\cup\mathbb{N}$
, let
![]() $U_k = \sum_{i=1}^k \xi_i$
. Then for every
$U_k = \sum_{i=1}^k \xi_i$
. Then for every
![]() $N\in \mathbb{N}$
it is possible to construct a version of
$N\in \mathbb{N}$
it is possible to construct a version of
![]() $(U_k)_{k=0}^N$
and a standard Brownian Motion
$(U_k)_{k=0}^N$
and a standard Brownian Motion
![]() $(B_s)_{s\in[0,N]}$
on the same probability space such that, for every
$(B_s)_{s\in[0,N]}$
on the same probability space such that, for every
![]() $x\geq 0$
,
$x\geq 0$
,
where M, C and
![]() $c>0$
do not depend on N.
$c>0$
do not depend on N.
Applying this with
![]() $N=T$
and
$N=T$
and
![]() $U_k = \hat S_k$
, we immediately obtain the following corollary.
$U_k = \hat S_k$
, we immediately obtain the following corollary.
Corollary 4.10 Suppose that
![]() $\hat S_t = \sum_{i=1}^t \hat{\Delta}_i$
, where
$\hat S_t = \sum_{i=1}^t \hat{\Delta}_i$
, where
![]() $(\hat \Delta_i)_{i=1}^{T}$
is a sequence of independent Poisson random variables of parameter 1, and that
$(\hat \Delta_i)_{i=1}^{T}$
is a sequence of independent Poisson random variables of parameter 1, and that
![]() $(B_s)_{s\ge 0}$
is a standard Brownian motion. There exist constants
$(B_s)_{s\ge 0}$
is a standard Brownian motion. There exist constants
![]() $c,C\in(0,\infty)$
such that for any
$c,C\in(0,\infty)$
such that for any
![]() $x_n\ge 0$
and any function
$x_n\ge 0$
and any function
![]() $\gamma:[0,\infty)\to\mathbb{R}$
,
$\gamma:[0,\infty)\to\mathbb{R}$
,
 \begin{align*}\mathbb{P}\big(\hat S_t &> \gamma(t)\;\;\forall t\in[\![ 1,T]\!],\, \hat S_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A}\big)\\
&\ge \mathbb{P}\big(B_s > \gamma(s) + M\log T + x_n\;\;\forall s\in[0,T],\, B_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A} - M\log T - x_n\big) - C e^{-c x_n}.\end{align*}
\begin{align*}\mathbb{P}\big(\hat S_t &> \gamma(t)\;\;\forall t\in[\![ 1,T]\!],\, \hat S_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A}\big)\\
&\ge \mathbb{P}\big(B_s > \gamma(s) + M\log T + x_n\;\;\forall s\in[0,T],\, B_{T}\le\gamma(T)+\tfrac{3n^{1/3}}{8A} - M\log T - x_n\big) - C e^{-c x_n}.\end{align*}
We have now reduced our task to bounding the probability that a Brownian motion remains above a curve up to time T and is not too far above the curve at time T.
Proposition 4.11 There exists a constant
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $x_n$
satisfying
$x_n$
satisfying
![]() $A^3\ll x_n \ll n^{1/3}/A$
, any constant M (not depending on n) and
$A^3\ll x_n \ll n^{1/3}/A$
, any constant M (not depending on n) and
![]() $\gamma$
as in Lemma 4.8, for large n,
$\gamma$
as in Lemma 4.8, for large n,
The proof of Proposition 4.11 involves considering two time intervals,
![]() $[0,T/2]$
and
$[0,T/2]$
and
![]() $[T/2,T]$
, and approximating
$[T/2,T]$
, and approximating
![]() $\gamma(T)$
by a straight line on each of these intervals. We carry out the details in Section 4.5.
$\gamma(T)$
by a straight line on each of these intervals. We carry out the details in Section 4.5.
We now have all the ingredients to prove Proposition 4.4 and therefore Theorem 1.1.
Proof of Proposition 4.4. We simply combine Lemmas 4.7 and 4.8, Corollary 4.10 and Proposition 4.11.
4.3. Proofs of Lemmas 4.1, 4.2, 4.5 and 4.7: creating i.i.d. sequences
We first prove Lemma 4.1, which replaces
![]() $\eta_i$
, the number of unseen vertices that become active at the ith step of the exploration process, with an independent Binomial random variable that does not depend on the history of the exploration process.
$\eta_i$
, the number of unseen vertices that become active at the ith step of the exploration process, with an independent Binomial random variable that does not depend on the history of the exploration process.
Proof of Lemma 4.1. From the description of the exploration process provided at the beginning of Section 3, recall that
![]() $u_t$
is the vertex that is explored at step t. Let us denote by
$u_t$
is the vertex that is explored at step t. Let us denote by
![]() $\mathcal{A}^*_t$
the set of unseen vertices that become active at step
$\mathcal{A}^*_t$
the set of unseen vertices that become active at step
![]() $t-1$
of the process (with
$t-1$
of the process (with
![]() $\mathcal A^*_1 = \{u_1\}$
), and let
$\mathcal A^*_1 = \{u_1\}$
), and let
![]() $\mathcal A_t = \bigcup_{i=0}^t \mathcal A^*_i$
, the set of all active or explored vertices after step
$\mathcal A_t = \bigcup_{i=0}^t \mathcal A^*_i$
, the set of all active or explored vertices after step
![]() $t-1$
. Also, write
$t-1$
. Also, write
![]() $X^t_v$
for the indicator that
$X^t_v$
for the indicator that
![]() $u_t$
is a neighbour of vertex v.
$u_t$
is a neighbour of vertex v.
For each
![]() $t=1,2,\ldots,n-K$
, if
$t=1,2,\ldots,n-K$
, if
![]() $|\mathcal A_t| < K+t$
then let
$|\mathcal A_t| < K+t$
then let
![]() $\mathcal B^*_t$
be any subset of the vertices [n] such that
$\mathcal B^*_t$
be any subset of the vertices [n] such that
-
 $\mathcal A^*_t \subset \mathcal B^*_t$
;
$\mathcal A^*_t \subset \mathcal B^*_t$
; -
 $\mathcal B^*_t \cap \mathcal A_{t-1} = \emptyset$
;
$\mathcal B^*_t \cap \mathcal A_{t-1} = \emptyset$
; -
 $\big|\mathcal B^*_t \cup \mathcal A_{t-1}\big| = K+t$
.
$\big|\mathcal B^*_t \cup \mathcal A_{t-1}\big| = K+t$
.
If
![]() $|\mathcal A_t| \ge K+t$
then let
$|\mathcal A_t| \ge K+t$
then let
![]() $\mathcal B^*_t = \mathcal A^*_t$
. Then let
$\mathcal B^*_t = \mathcal A^*_t$
. Then let
Take a sequence
![]() $\hat X_1^t, \hat X_2^t,\ldots$
of independent Bernoulli random variables of parameter p, also independent of everything else.
$\hat X_1^t, \hat X_2^t,\ldots$
of independent Bernoulli random variables of parameter p, also independent of everything else.
Note that
and define
 \begin{equation*}\delta_t = \sum_{v\not\in\mathcal B^*_t\cup\mathcal A_{t-1}} X^t_v + \sum_{i=1}^{r_t} \hat X^t_j.\end{equation*}
\begin{equation*}\delta_t = \sum_{v\not\in\mathcal B^*_t\cup\mathcal A_{t-1}} X^t_v + \sum_{i=1}^{r_t} \hat X^t_j.\end{equation*}
Then, since
and the random variables
![]() $\{X^i_v \,{:}\, v\in \mathcal A_{i-1}^c\}$
are independent and independent of
$\{X^i_v \,{:}\, v\in \mathcal A_{i-1}^c\}$
are independent and independent of
![]() $\{X^j_v \,{:}\, v\in \mathcal A_{j-1}^c\}$
for any
$\{X^j_v \,{:}\, v\in \mathcal A_{j-1}^c\}$
for any
![]() $j\neq i$
, we see that
$j\neq i$
, we see that
![]() $(\delta_t)_{t=1}^{n-K}$
is a sequence of independent random variables such that
$(\delta_t)_{t=1}^{n-K}$
is a sequence of independent random variables such that
![]() $\delta_t \sim \textrm{Bin}(n-K-t,p)$
.
$\delta_t \sim \textrm{Bin}(n-K-t,p)$
.
We also observe that if
![]() $|\mathcal A_t| < K+t$
, then
$|\mathcal A_t| < K+t$
, then
![]() $|\mathcal B^*_t \cup \mathcal A_{t-1}| = K+t$
and so
$|\mathcal B^*_t \cup \mathcal A_{t-1}| = K+t$
and so
![]() $r_t=0$
. Since we also have
$r_t=0$
. Since we also have
![]() $\mathcal A^*_t \subset \mathcal B^*_t$
, we see that if
$\mathcal A^*_t \subset \mathcal B^*_t$
, we see that if
![]() $|\mathcal A_t| < K+t$
then
$|\mathcal A_t| < K+t$
then
![]() $\eta_t \ge \delta_t$
. Thus, recalling that
$\eta_t \ge \delta_t$
. Thus, recalling that
![]() $\tau_0$
denotes the first time at which the set of active vertices is empty and since
$\tau_0$
denotes the first time at which the set of active vertices is empty and since
![]() $\{\tau_0>T_2\}=\{1+\sum_{i=1}^{t}(\eta_{i}-1)>0\ \forall t\in [T_2]\}$
we obtain
$\{\tau_0>T_2\}=\{1+\sum_{i=1}^{t}(\eta_{i}-1)>0\ \forall t\in [T_2]\}$
we obtain
 \begin{align*}\mathbb{P}\left(|\mathcal{C}(v)|>T_2\right) &= \mathbb{P}\Big(1+\sum_{i=1}^{t}(\eta_i - 1)>0 \forall t\in [T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\eta_i - 1)>0 \forall t\in [T_2]\text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2] \text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big),\end{align*}
\begin{align*}\mathbb{P}\left(|\mathcal{C}(v)|>T_2\right) &= \mathbb{P}\Big(1+\sum_{i=1}^{t}(\eta_i - 1)>0 \forall t\in [T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\eta_i - 1)>0 \forall t\in [T_2]\text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2] \text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big),\end{align*}
where the last inequality follows from the fact that on the event
![]() $\{|\mathcal{A}_t|<K+t\forall t\in [T_2]\}$
we have
$\{|\mathcal{A}_t|<K+t\forall t\in [T_2]\}$
we have
![]() $\eta_{t}\geq \delta_t$
for
$\eta_{t}\geq \delta_t$
for
![]() $t\in [T_2]$
(and
$t\in [T_2]$
(and
![]() $\tau_0\wedge T_2=T_2$
on
$\tau_0\wedge T_2=T_2$
on
![]() $\{1+\sum_{i=1}^{t}(\eta_{i}-1)>0\ \forall t\in [T_2]\}$
). Now
$\{1+\sum_{i=1}^{t}(\eta_{i}-1)>0\ \forall t\in [T_2]\}$
). Now
 \begin{align*}&\mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2] \text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2]\Big) - \mathbb{P}\Big(\exists t\in [\tau_0\wedge T_2] : |\mathcal A_t| \ge K+t\Big).\end{align*}
\begin{align*}&\mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2] \text{ and } |\mathcal A_t|
< K+t \forall t\in [\tau_0 \wedge T_2]\Big)\\
&\ge \mathbb{P}\Big(1+\sum_{i=1}^{t}(\delta_i - 1)>0 \forall t\in [T_2]\Big) - \mathbb{P}\Big(\exists t\in [\tau_0\wedge T_2] : |\mathcal A_t| \ge K+t\Big).\end{align*}
Since
![]() $|\mathcal A_t| = Y_t + t$
, the result follows.
$|\mathcal A_t| = Y_t + t$
, the result follows.
Next we prove Lemma 4.2, which ensures that the probability that the number of active vertices becomes too large is small.
Proof of Lemma 4.2. Let
![]() $\zeta_i\overset{i.i.d.}{\sim}\textrm{Bin}(n,p)$
. A union bound gives
$\zeta_i\overset{i.i.d.}{\sim}\textrm{Bin}(n,p)$
. A union bound gives
 \begin{align}\nonumber\mathbb{P}\left(\exists i\leq \tau_0\wedge T_2\,{:}\,Y_i\geq \lfloor n^{2/5}\rfloor \right) &\leq \sum_{i=1}^{T_2}\mathbb{P}\left(Y_i\geq \lfloor n^{2/5}\rfloor,i\leq \tau_0\right)\\
&\leq\sum_{i=1}^{T_2}\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor,i\leq \tau_0\bigg)\end{align}
\begin{align}\nonumber\mathbb{P}\left(\exists i\leq \tau_0\wedge T_2\,{:}\,Y_i\geq \lfloor n^{2/5}\rfloor \right) &\leq \sum_{i=1}^{T_2}\mathbb{P}\left(Y_i\geq \lfloor n^{2/5}\rfloor,i\leq \tau_0\right)\\
&\leq\sum_{i=1}^{T_2}\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor,i\leq \tau_0\bigg)\end{align}
 \begin{align}&\leq \sum_{i=1}^{T_2}\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor\bigg).\end{align}
\begin{align}&\leq \sum_{i=1}^{T_2}\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor\bigg).\end{align}
Denoting by
![]() $B_{N,q}$
a binomial random variable with parameters N and q, by Lemma 3.5 we see that for
$B_{N,q}$
a binomial random variable with parameters N and q, by Lemma 3.5 we see that for
![]() $i\in [T_2]$
,
$i\in [T_2]$
,
 \begin{align}\nonumber\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor\bigg)&=\mathbb{P}\left(B_{in,p}\geq inp-i\lambda n^{-1/3}+\lfloor n^{2/5}\rfloor-1\right)\\
&\leq \mathbb{P}\left(B_{in,p}\geq inp+ n^{2/5}\left(1-c\frac{A|\lambda|}{n^{1/15}}\right)\right).\end{align}
\begin{align}\nonumber\mathbb{P}\bigg(1+\sum_{j=1}^{i}(\zeta_j-1)\geq \lfloor n^{2/5}\rfloor\bigg)&=\mathbb{P}\left(B_{in,p}\geq inp-i\lambda n^{-1/3}+\lfloor n^{2/5}\rfloor-1\right)\\
&\leq \mathbb{P}\left(B_{in,p}\geq inp+ n^{2/5}\left(1-c\frac{A|\lambda|}{n^{1/15}}\right)\right).\end{align}
Now,
![]() $A=o(n^{1/30})$
and
$A=o(n^{1/30})$
and
![]() $|\lambda|\leq A/3$
, so
$|\lambda|\leq A/3$
, so
![]() $A|\lambda|=o\left(n^{1/15}\right)$
and hence for large enough n we obtain
$A|\lambda|=o\left(n^{1/15}\right)$
and hence for large enough n we obtain
 \begin{align}(24)\leq \mathbb{P}\left(B_{in,p}\geq inp+ n^{2/5}/2 \right)\leq \exp\left\{-\frac{n^{4/5}/4}{2inp+\frac{1}{3}n^{2/5}}\right\}.\end{align}
\begin{align}(24)\leq \mathbb{P}\left(B_{in,p}\geq inp+ n^{2/5}/2 \right)\leq \exp\left\{-\frac{n^{4/5}/4}{2inp+\frac{1}{3}n^{2/5}}\right\}.\end{align}
Since
![]() $i\leq T_2$
we see that (25)
$i\leq T_2$
we see that (25)
![]() $\leq e^{-cn^{2/15}/A}$
for some positive constant
$\leq e^{-cn^{2/15}/A}$
for some positive constant
![]() $c>0$
. Finally, since
$c>0$
. Finally, since
![]() $A,\lambda=o(n^{1/30})$
as
$A,\lambda=o(n^{1/30})$
as
![]() $n\rightarrow \infty$
we conclude that
$n\rightarrow \infty$
we conclude that
Lemma 4.5 involves rearranging Bernoulli random variables to produce an i.i.d. sequence.
Proof of Lemma 4.5. Recall the convention that the empty sum is zero. By hypothesis,
 \begin{equation}X_i=\sum_{j=1}^{N-i}I_j^{i},\end{equation}
\begin{equation}X_i=\sum_{j=1}^{N-i}I_j^{i},\end{equation}
where
![]() $(I_j^{i})_{i,j\geq 1}$
are i.i.d. non-negative random variables. Let
$(I_j^{i})_{i,j\geq 1}$
are i.i.d. non-negative random variables. Let
![]() $\ell = (L+1)/2$
; recall that L is odd, so
$\ell = (L+1)/2$
; recall that L is odd, so
![]() $\ell\in \mathbb{N}$
. Define
$\ell\in \mathbb{N}$
. Define
 \begin{equation*}\tilde{X}_i = \left\{ \begin{aligned}& \sum_{j=1}^{N-\ell}I_j^{i}, && 1\leq i\leq \ell\\
& \sum_{j=1}^{N-i}I_j^{i} + \sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i}, && \ell<i\leq L.\\\end{aligned}\right.\end{equation*}
\begin{equation*}\tilde{X}_i = \left\{ \begin{aligned}& \sum_{j=1}^{N-\ell}I_j^{i}, && 1\leq i\leq \ell\\
& \sum_{j=1}^{N-i}I_j^{i} + \sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i}, && \ell<i\leq L.\\\end{aligned}\right.\end{equation*}
Observe that
![]() $(\tilde{X}_i)_{i=1}^{L}$
is a sequence of i.i.d. random variables and
$(\tilde{X}_i)_{i=1}^{L}$
is a sequence of i.i.d. random variables and
![]() $\tilde{X}_i\overset{d}{=}\sum_{j=1}^{N-\ell}I_j^{1}$
,
$\tilde{X}_i\overset{d}{=}\sum_{j=1}^{N-\ell}I_j^{1}$
,
![]() $1\leq i\leq L$
. Next we claim that
$1\leq i\leq L$
. Next we claim that
 \begin{equation}\sum_{i=1}^{t}\tilde{X}_i\leq \sum_{i=1}^{t}X_i\end{equation}
\begin{equation}\sum_{i=1}^{t}\tilde{X}_i\leq \sum_{i=1}^{t}X_i\end{equation}
for all
![]() $1\leq t\leq L$
. To see this, observe first that when
$1\leq t\leq L$
. To see this, observe first that when
![]() $1\leq t\leq \ell$
we have that
$1\leq t\leq \ell$
we have that
 \begin{align*}\sum_{i=1}^{t}\tilde{X}_i=\sum_{i=1}^{t}\sum_{j=1}^{N-\ell}I_j^{i}\leq \sum_{i=1}^{t}\sum_{j=1}^{N-i}I_j^{i}= \sum_{i=1}^{t}X_i.\end{align*}
\begin{align*}\sum_{i=1}^{t}\tilde{X}_i=\sum_{i=1}^{t}\sum_{j=1}^{N-\ell}I_j^{i}\leq \sum_{i=1}^{t}\sum_{j=1}^{N-i}I_j^{i}= \sum_{i=1}^{t}X_i.\end{align*}
Next, for
![]() $\ell<t\leq L$
we have that
$\ell<t\leq L$
we have that
 \begin{equation*}\sum_{i=1}^{t}\tilde{X}_i = \sum_{i=1}^{\ell}\tilde{X}_i +\sum_{i=\ell+1}^{t}\tilde{X}_i =\sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i}.\end{equation*}
\begin{equation*}\sum_{i=1}^{t}\tilde{X}_i = \sum_{i=1}^{\ell}\tilde{X}_i +\sum_{i=\ell+1}^{t}\tilde{X}_i =\sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i}.\end{equation*}
Making the change of variable
![]() $k=L+1-i$
, we see that
$k=L+1-i$
, we see that
 \begin{equation*}\sum_{i=\ell+1}^{t}\sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i} = \sum_{k=L+1-t}^{\ell-1}\sum_{j=N-\ell+1}^{N-k}I_j^{k} = \sum_{k=L+1-t}^{\ell}\sum_{j=N-\ell+1}^{N-k}I_j^{k},\end{equation*}
\begin{equation*}\sum_{i=\ell+1}^{t}\sum_{j=N-\ell+1}^{N-(L+1-i)}I_j^{L+1-i} = \sum_{k=L+1-t}^{\ell-1}\sum_{j=N-\ell+1}^{N-k}I_j^{k} = \sum_{k=L+1-t}^{\ell}\sum_{j=N-\ell+1}^{N-k}I_j^{k},\end{equation*}
where the last equality follows from the fact that the term corresponding to
![]() $k=\ell$
is zero.
$k=\ell$
is zero.
Therefore
 \begin{align}\sum_{i=1}^{t}\tilde{X}_i &= \sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=L+1-t}^{\ell}\sum_{j=N-\ell+1}^{N-i}I_j^{i}\end{align}
\begin{align}\sum_{i=1}^{t}\tilde{X}_i &= \sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=L+1-t}^{\ell}\sum_{j=N-\ell+1}^{N-i}I_j^{i}\end{align}
 \begin{align}&\le\sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=1}^{\ell}\sum_{j=N-\ell+1}^{N-i}I_j^{i}\nonumber\\ &= \sum_{i=1}^t X_i\nonumber\end{align}
\begin{align}&\le\sum_{i=1}^{\ell}\sum_{j=1}^{N-\ell}I_j^{i}+\sum_{i=\ell+1}^{t}\sum_{j=1}^{N-i}I_j^{i}+\sum_{i=1}^{\ell}\sum_{j=N-\ell+1}^{N-i}I_j^{i}\nonumber\\ &= \sum_{i=1}^t X_i\nonumber\end{align}
as claimed. The second statement of the lemma simply follows by taking
![]() $t=L$
in (28), in which case the subsequent inequality is an equality.
$t=L$
in (28), in which case the subsequent inequality is an equality.
Lemma 4.7 provides an alternative way of producing i.i.d. sequences of Binomial random variables, by adding independent binomials to the original sequence.
Proof of Lemma 4.7. Recall that
![]() $R_t=1+\sum_{i=1}^{t}(\delta_i-1)$
. As we did in Section 4.2, write
$R_t=1+\sum_{i=1}^{t}(\delta_i-1)$
. As we did in Section 4.2, write
![]() $T=T_2-T_1$
. Let
$T=T_2-T_1$
. Let
![]() $(L_i)_{i\in [T_2]}$
be a sequence of independent random variables, also independent of
$(L_i)_{i\in [T_2]}$
be a sequence of independent random variables, also independent of
![]() $(\delta_i)_{i\in [T_2]}$
and such that
$(\delta_i)_{i\in [T_2]}$
and such that
![]() $L_i\sim \textrm{Bin}(K+i,p)$
. Then, setting
$L_i\sim \textrm{Bin}(K+i,p)$
. Then, setting
 \begin{equation}S_t = \sum_{i=T_1+1}^{T_1+t}(\delta_i+L_i-1),\end{equation}
\begin{equation}S_t = \sum_{i=T_1+1}^{T_1+t}(\delta_i+L_i-1),\end{equation}
we see that
![]() $\delta_i+L_i \overset{i.i.d.}{\sim}\textrm{Bin}(n,p)$
. Let
$\delta_i+L_i \overset{i.i.d.}{\sim}\textrm{Bin}(n,p)$
. Let
![]() $\mathcal L_t = \sum_{i=T_1+1}^{T_1+t}L_i$
. Then for any
$\mathcal L_t = \sum_{i=T_1+1}^{T_1+t}L_i$
. Then for any
![]() $f\,{:}\,\mathbb{N}\to\mathbb{R}$
,
$f\,{:}\,\mathbb{N}\to\mathbb{R}$
,
 \begin{align}\mathbb{P}(R_t>0 \;\;\forall t\in [\![ T_1, T_2]\!] \,|\, R_{T_1}=H)&= \mathbb{P}\big(R_{T_1+t}-R_{T_1} > -H \;\;\forall t\in[T] \big)\nonumber\\[3pt] &= \mathbb{P}\big(S_t - \mathcal L_t > -H \;\; \forall t\in[T] \big)\nonumber\\[3pt] &\ge \mathbb{P}\big(S_t > \mathcal L_t - H \;\; \forall t\in[T],\, \mathcal L_t \le f(t)+H\;\;\forall t\in[T] \big)\nonumber\\[3pt] &\ge \mathbb{P}\big(S_t > f(t)\;\;\forall t\in[T]\big) - \mathbb{P}\big(\exists t\in[T] : \mathcal L_t > f(t)+H\big).\end{align}
\begin{align}\mathbb{P}(R_t>0 \;\;\forall t\in [\![ T_1, T_2]\!] \,|\, R_{T_1}=H)&= \mathbb{P}\big(R_{T_1+t}-R_{T_1} > -H \;\;\forall t\in[T] \big)\nonumber\\[3pt] &= \mathbb{P}\big(S_t - \mathcal L_t > -H \;\; \forall t\in[T] \big)\nonumber\\[3pt] &\ge \mathbb{P}\big(S_t > \mathcal L_t - H \;\; \forall t\in[T],\, \mathcal L_t \le f(t)+H\;\;\forall t\in[T] \big)\nonumber\\[3pt] &\ge \mathbb{P}\big(S_t > f(t)\;\;\forall t\in[T]\big) - \mathbb{P}\big(\exists t\in[T] : \mathcal L_t > f(t)+H\big).\end{align}
We now let
![]() $f(t) = \mathbb{E}[\mathcal L_t] + \frac{A^{1/2}}{n^{5/12}}(T_1+t) - H$
and aim to show that
$f(t) = \mathbb{E}[\mathcal L_t] + \frac{A^{1/2}}{n^{5/12}}(T_1+t) - H$
and aim to show that
Indeed, a union bound gives
 \begin{equation*}\mathbb{P}\big(\exists t\in[T] \,{:}\, \mathcal L_t > f(t)+H\big) \le \sum_{t=1}^{T} \mathbb{P}\Big( \mathcal L_t \ge \mathbb{E}[\mathcal L_t] + \frac{A^{1/2}}{n^{5/12}}(T_1+t) \Big),\end{equation*}
\begin{equation*}\mathbb{P}\big(\exists t\in[T] \,{:}\, \mathcal L_t > f(t)+H\big) \le \sum_{t=1}^{T} \mathbb{P}\Big( \mathcal L_t \ge \mathbb{E}[\mathcal L_t] + \frac{A^{1/2}}{n^{5/12}}(T_1+t) \Big),\end{equation*}
and then applying Lemma 3.5 yields
 \begin{equation}\mathbb{P}\big(\exists t\in[T] \,{:}\, \mathcal L_t > f(t)+H\big) \le \sum_{t=1}^{T} \exp\bigg(-\frac{A(T_1+t)^2 n^{-5/6}}{2(K+T_1+1/2)tp+t^2p+\frac{2A^{1/2}(T_1+t)}{3n^{5/12}}}\bigg).\end{equation}
\begin{equation}\mathbb{P}\big(\exists t\in[T] \,{:}\, \mathcal L_t > f(t)+H\big) \le \sum_{t=1}^{T} \exp\bigg(-\frac{A(T_1+t)^2 n^{-5/6}}{2(K+T_1+1/2)tp+t^2p+\frac{2A^{1/2}(T_1+t)}{3n^{5/12}}}\bigg).\end{equation}
One may easily check that for some finite constant C, we have
and
Thus, for some
![]() $c>0$
,
$c>0$
,
 \begin{equation*}\exp\bigg(-\frac{A(T_1+t)^2 n^{-5/6}}{2(K+T_1+1/2)tp+t^2p+\frac{2A^{1/2}(T_1+t)}{3n^{5/12}}}\bigg) \le \exp(-cAn^{1/6})\end{equation*}
\begin{equation*}\exp\bigg(-\frac{A(T_1+t)^2 n^{-5/6}}{2(K+T_1+1/2)tp+t^2p+\frac{2A^{1/2}(T_1+t)}{3n^{5/12}}}\bigg) \le \exp(-cAn^{1/6})\end{equation*}
which combines with (32) to give (31).
Substituting (31) into (30) proves the Lemma with f in place of g. It therefore suffices to check that
![]() $f(t)\le g(t)$
for all t when n is large. This holds since
$f(t)\le g(t)$
for all t when n is large. This holds since
 \begin{equation*}\mathcal L_t\sim \textrm{Bin}\bigg(\sum_{i=T_1+1}^{T_1+t}(K+i),p\bigg) = \textrm{Bin}\big((K+T_1)t + t(t+1)/2,p\big),\end{equation*}
\begin{equation*}\mathcal L_t\sim \textrm{Bin}\bigg(\sum_{i=T_1+1}^{T_1+t}(K+i),p\bigg) = \textrm{Bin}\big((K+T_1)t + t(t+1)/2,p\big),\end{equation*}
and we have
These estimates show that
![]() $f(t)\le g(t)$
and complete the proof.
$f(t)\le g(t)$
and complete the proof.
4.4. Proofs of Lemmas 4.6 and 4.8: Poisson approximation and a change of measure
The proof of Lemma 4.6 uses two standard ingredients: a coupling between Binomial and Poisson random variables, and a change of measure to remove the drift from a random walk.
Proof of Lemma 4.6. Note that
![]() $\mathbb{E}[W_i] = (1+a_n)(1+b_n) = \mu_n$
for each i. By [Reference van der Hofstad32, Theorem 2.10] we can construct a coupling between
$\mathbb{E}[W_i] = (1+a_n)(1+b_n) = \mu_n$
for each i. By [Reference van der Hofstad32, Theorem 2.10] we can construct a coupling between
![]() $(W_i)_{i\in\mathbb{N}}$
and a sequence
$(W_i)_{i\in\mathbb{N}}$
and a sequence
![]() $W_i^{\prime}$
of i.i.d. Poisson random variables with parameter
$W_i^{\prime}$
of i.i.d. Poisson random variables with parameter
![]() $\mu_n$
, such that
$\mu_n$
, such that
 \begin{equation*}\mathbb{P}(W_i\neq W_i^{\prime}) \le \sum_{i=1}^{n(1+a_n)} \Big(\frac{1+b_n}{n}\Big)^2 = \frac{(1+a_n)(1+b_n)^2}{n}.\end{equation*}
\begin{equation*}\mathbb{P}(W_i\neq W_i^{\prime}) \le \sum_{i=1}^{n(1+a_n)} \Big(\frac{1+b_n}{n}\Big)^2 = \frac{(1+a_n)(1+b_n)^2}{n}.\end{equation*}
Let
![]() $M_t^{\prime} = 1 + \sum_{i=1}^t (W_i^{\prime}-1)$
. Then
$M_t^{\prime} = 1 + \sum_{i=1}^t (W_i^{\prime}-1)$
. Then
 \begin{align*}\mathbb{P}\big(M_t>0\,\,\,\,\forall t\in[t_n], \, M_{t_n}&\in[h_n,2h_n]\big)\\
&\ge \mathbb{P}\big(M_t^{\prime}>0\,\,\,\,\forall t\in[t_n], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big) - \mathbb{P}\big(\exists i\in[t_n] : W_i\neq W_i^{\prime}\big),\end{align*}
\begin{align*}\mathbb{P}\big(M_t>0\,\,\,\,\forall t\in[t_n], \, M_{t_n}&\in[h_n,2h_n]\big)\\
&\ge \mathbb{P}\big(M_t^{\prime}>0\,\,\,\,\forall t\in[t_n], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big) - \mathbb{P}\big(\exists i\in[t_n] : W_i\neq W_i^{\prime}\big),\end{align*}
and a union bound gives that
We now seek to remove the drift from the sequence
![]() $M^{\prime}_t$
by using a change of measure. Define a new probability measure
$M^{\prime}_t$
by using a change of measure. Define a new probability measure
![]() $\mathbb{Q}$
by setting, for
$\mathbb{Q}$
by setting, for
![]() $B\in\sigma(W_1^{\prime},\ldots,W_{t_n}^{\prime})$
,
$B\in\sigma(W_1^{\prime},\ldots,W_{t_n}^{\prime})$
,
 \begin{equation*}\mathbb{Q}(B) = \mathbb{E}\bigg[\unicode{x1D7D9}_B \prod_{i=1}^{t_n} \mu_n ^{-W_i^{\prime}}\bigg] \mathbb{E}\Big[\mu_n^{- W_1^{\prime}}\Big]^{-t_n} = \mathbb{E}\left[\unicode{x1D7D9}_B\mu_n^{-\sum_{i=1}^{t_n}W^{\prime}_i}\right]\mathbb{E}\Big[\mu_n^{- W_1^{\prime}}\Big]^{-t_n}.\end{equation*}
\begin{equation*}\mathbb{Q}(B) = \mathbb{E}\bigg[\unicode{x1D7D9}_B \prod_{i=1}^{t_n} \mu_n ^{-W_i^{\prime}}\bigg] \mathbb{E}\Big[\mu_n^{- W_1^{\prime}}\Big]^{-t_n} = \mathbb{E}\left[\unicode{x1D7D9}_B\mu_n^{-\sum_{i=1}^{t_n}W^{\prime}_i}\right]\mathbb{E}\Big[\mu_n^{- W_1^{\prime}}\Big]^{-t_n}.\end{equation*}
Note that
![]() $\sum_{i=1}^{t_n} W^{\prime}_i = M_{t_n}^{\prime}+t_n-1$
and, since
$\sum_{i=1}^{t_n} W^{\prime}_i = M_{t_n}^{\prime}+t_n-1$
and, since
![]() $W_1^{\prime}$
is Poisson with parameter
$W_1^{\prime}$
is Poisson with parameter
![]() $\mu_n$
,
$\mu_n$
,
![]() $\mathbb{E}\big[\mu_n^{- W_1^{\prime}}\big]= e^{\mu_n(1/\mu_n-1)} = e^{1-\mu_n}$
. Thus
$\mathbb{E}\big[\mu_n^{- W_1^{\prime}}\big]= e^{\mu_n(1/\mu_n-1)} = e^{1-\mu_n}$
. Thus
We write
![]() $\mathbb{E}_\mathbb{Q}$
for expectation with respect to the probability measure
$\mathbb{E}_\mathbb{Q}$
for expectation with respect to the probability measure
![]() $\mathbb{Q}$
. It is straightforward to check that, under
$\mathbb{Q}$
. It is straightforward to check that, under
![]() $\mathbb{Q}$
, the
$\mathbb{Q}$
, the
![]() $W_i^{\prime}$
are independent Poisson random variables of parameter 1.
$W_i^{\prime}$
are independent Poisson random variables of parameter 1.
By the definition of
![]() $\mathbb{Q}$
, we have
$\mathbb{Q}$
, we have
 \begin{align*}&\mathbb{P}\big(M_t^{\prime}>0\,\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big)\\[3pt]
&= \mathbb{E}_\mathbb{Q}\Big[\mu_n^{M^{\prime}_{t_n}+t_n-1} \unicode{x1D7D9}_{\{M_t^{\prime}>0\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\}}\Big]e^{(1-\mu_n)t_n}\\[3pt]
&\ge (\mu_n\wedge 1)^{2h_n} \mu_n^{t_n-1}\mathbb{Q}\big(M_t^{\prime}>0\,\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big)e^{(1-\mu_n)t_n}.\end{align*}
\begin{align*}&\mathbb{P}\big(M_t^{\prime}>0\,\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big)\\[3pt]
&= \mathbb{E}_\mathbb{Q}\Big[\mu_n^{M^{\prime}_{t_n}+t_n-1} \unicode{x1D7D9}_{\{M_t^{\prime}>0\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\}}\Big]e^{(1-\mu_n)t_n}\\[3pt]
&\ge (\mu_n\wedge 1)^{2h_n} \mu_n^{t_n-1}\mathbb{Q}\big(M_t^{\prime}>0\,\,\forall t\in[\![ 0,t_n]\!], \, M_{t_n}^{\prime}\in[h_n,2h_n]\big)e^{(1-\mu_n)t_n}.\end{align*}
Since
![]() $(W_i^{\prime})_{i=1}^{t_n}$
is a sequence of independent Poisson random variables of parameter 1 under
$(W_i^{\prime})_{i=1}^{t_n}$
is a sequence of independent Poisson random variables of parameter 1 under
![]() $\mathbb{Q}$
, substituting this and (34) into (33) gives the result.
$\mathbb{Q}$
, substituting this and (34) into (33) gives the result.
The proof of Lemma 4.8 is similar to that of Lemma 4.6, but we will need to delve deeper into the details of the coupling between the Binomial and Poisson random variables.
Proof of Lemma 4.8. We follow almost the same proof as Lemma 4.6, noting that
![]() $\mathbb{E}[\Delta_i] = np$
for each i. By [32, Theorem 2.10] we can couple
$\mathbb{E}[\Delta_i] = np$
for each i. By [32, Theorem 2.10] we can couple
![]() $(\Delta_i)_{i=1}^T$
with a sequence
$(\Delta_i)_{i=1}^T$
with a sequence
![]() $(\Delta_i^{\prime})_{i=1}^T$
of i.i.d. Poisson random variables with parameter np. Write
$(\Delta_i^{\prime})_{i=1}^T$
of i.i.d. Poisson random variables with parameter np. Write
![]() $S_t^{\prime} = \sum_{i=1}^t (\Delta_i^{\prime}-1)$
. Then we obtain
$S_t^{\prime} = \sum_{i=1}^t (\Delta_i^{\prime}-1)$
. Then we obtain
 \begin{align}\nonumber&\mathbb{P}\big(S_t>g(t)\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\[3pt] \nonumber&\geq \mathbb{P}\big(S_t>g(t)\,\,\forall t\in[\![ 0,T]\!],\, S^{\prime}_t>g(t)+\tfrac{n^{1/3}}{4A}\,\,\forall t\in[\![ 0,T]\!]\big) \\[3pt] \nonumber&=\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\[3pt] \nonumber&\quad -\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!],\, \exists t \in [\![ 0,T]\!] \,{:}\, S_t\leq g(t)\big)\\[3pt]&\ge \mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big) - \mathbb{P}\Big(\max_{t\le T}|S_t-S_t^{\prime}|> \tfrac{n^{1/3}}{4A}\Big),\end{align}
\begin{align}\nonumber&\mathbb{P}\big(S_t>g(t)\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\[3pt] \nonumber&\geq \mathbb{P}\big(S_t>g(t)\,\,\forall t\in[\![ 0,T]\!],\, S^{\prime}_t>g(t)+\tfrac{n^{1/3}}{4A}\,\,\forall t\in[\![ 0,T]\!]\big) \\[3pt] \nonumber&=\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\[3pt] \nonumber&\quad -\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!],\, \exists t \in [\![ 0,T]\!] \,{:}\, S_t\leq g(t)\big)\\[3pt]&\ge \mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big) - \mathbb{P}\Big(\max_{t\le T}|S_t-S_t^{\prime}|> \tfrac{n^{1/3}}{4A}\Big),\end{align}
where the last inequality follows from the fact that
 \begin{align*}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!],\,\exists t \in [\![ 0,T]\!] \,{:}\, S_t\leq g(t)\big)\\[3pt] &\quad \leq \mathbb{P}(\exists t \in [\![ 0,T]\!] \,{:}\, |S^{\prime}_t-S_t|>\tfrac{n^{1/3}}{4A})=\mathbb{P}\big(\max_{t\le T}|S_t-S_t^{\prime}|> \tfrac{n^{1/3}}{4A}\big).\end{align*}
\begin{align*}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!],\,\exists t \in [\![ 0,T]\!] \,{:}\, S_t\leq g(t)\big)\\[3pt] &\quad \leq \mathbb{P}(\exists t \in [\![ 0,T]\!] \,{:}\, |S^{\prime}_t-S_t|>\tfrac{n^{1/3}}{4A})=\mathbb{P}\big(\max_{t\le T}|S_t-S_t^{\prime}|> \tfrac{n^{1/3}}{4A}\big).\end{align*}
To estimate the last probability, we see that
 \begin{equation}\mathbb{P}\Big(\max_{t\le T} |S_t - S_t^{\prime}| > \frac{n^{1/3}}{4A}\Big) \le \mathbb{P}\bigg(\sum_{i=1}^T |\Delta_i-\Delta^{\prime}_i| > \frac{n^{1/3}}{4A}\bigg) \le \mathbb{E}[e^{|\Delta_1 - \Delta_1^{\prime}|}]^T e^{-n^{1/3}/(4A)},\end{equation}
\begin{equation}\mathbb{P}\Big(\max_{t\le T} |S_t - S_t^{\prime}| > \frac{n^{1/3}}{4A}\Big) \le \mathbb{P}\bigg(\sum_{i=1}^T |\Delta_i-\Delta^{\prime}_i| > \frac{n^{1/3}}{4A}\bigg) \le \mathbb{E}[e^{|\Delta_1 - \Delta_1^{\prime}|}]^T e^{-n^{1/3}/(4A)},\end{equation}
where for the last inequality we used the i.i.d. property of the increments
![]() $\Delta_i-\Delta_i^{\prime}$
. To continue our bounds we need some more detail about the coupling of
$\Delta_i-\Delta_i^{\prime}$
. To continue our bounds we need some more detail about the coupling of
![]() $\Delta_1$
and
$\Delta_1$
and
![]() $\Delta^{\prime}_1$
from the proof of [Reference van der Hofstad32, Theorem 2.10]. We break
$\Delta^{\prime}_1$
from the proof of [Reference van der Hofstad32, Theorem 2.10]. We break
![]() $\Delta_1$
up into a sum of n i.i.d. Bernoulli random variables of parameter p, which we call
$\Delta_1$
up into a sum of n i.i.d. Bernoulli random variables of parameter p, which we call
![]() $(\beta_j)_{j=1}^n$
, and couple these with n Poisson random variables
$(\beta_j)_{j=1}^n$
, and couple these with n Poisson random variables
![]() $(\beta^{\prime}_j)_{j=1}^n$
of parameter p, so that
$(\beta^{\prime}_j)_{j=1}^n$
of parameter p, so that
 \begin{equation*}\Delta_1 = \sum_{j=1}^n \beta_{j} \text{ and } \Delta^{\prime}_1 = \sum_{j=1}^n \beta^{\prime}_{j}.\end{equation*}
\begin{equation*}\Delta_1 = \sum_{j=1}^n \beta_{j} \text{ and } \Delta^{\prime}_1 = \sum_{j=1}^n \beta^{\prime}_{j}.\end{equation*}
The coupling is arranged so that for each i and j,
-
 $\mathbb{P}(\beta_{j} = \beta^{\prime}_{j} = 0) = 1-p$
,
$\mathbb{P}(\beta_{j} = \beta^{\prime}_{j} = 0) = 1-p$
, -
 $\mathbb{P}(\beta_{j} = \beta^{\prime}_{j} = 1) = pe^{-p}$
,
$\mathbb{P}(\beta_{j} = \beta^{\prime}_{j} = 1) = pe^{-p}$
, -
 $\mathbb{P}(\beta_{j} = 1,\,\beta^{\prime}_{j}=0) = e^{-p}-(1-p)$
and
$\mathbb{P}(\beta_{j} = 1,\,\beta^{\prime}_{j}=0) = e^{-p}-(1-p)$
and -
 $\mathbb{P}(\beta_{j} = 1,\,\beta^{\prime}_{j}=k) = \mathbb{P}(\beta^{\prime}_{j}=k) = \frac{e^{-p}p^k}{k!}$
for
$\mathbb{P}(\beta_{j} = 1,\,\beta^{\prime}_{j}=k) = \mathbb{P}(\beta^{\prime}_{j}=k) = \frac{e^{-p}p^k}{k!}$
for
 $k\ge 2$
.
$k\ge 2$
.
We deduce (using the inequality
![]() $e^{-x}\le 1-x+x^2/2$
, valid for all
$e^{-x}\le 1-x+x^2/2$
, valid for all
![]() $x\ge 0$
) that
$x\ge 0$
) that
 \begin{align*}\mathbb{E}[e^{|\beta_{j}-\beta^{\prime}_{j}|}] &= 1-p+pe^{-p} + e(e^{-p}-(1-p)) + \sum_{k=2}^\infty e^{k-1}\frac{e^{-p}p^k}{k!}\\
&\le 1 + e\frac{p^2}{2} + p^2 e e^{-p} \sum_{k=0}^\infty \frac{(ep)^k}{(k+2)!} \le 1 + cp^2\end{align*}
\begin{align*}\mathbb{E}[e^{|\beta_{j}-\beta^{\prime}_{j}|}] &= 1-p+pe^{-p} + e(e^{-p}-(1-p)) + \sum_{k=2}^\infty e^{k-1}\frac{e^{-p}p^k}{k!}\\
&\le 1 + e\frac{p^2}{2} + p^2 e e^{-p} \sum_{k=0}^\infty \frac{(ep)^k}{(k+2)!} \le 1 + cp^2\end{align*}
for some finite constant c. Thus
and substituting this into (37) gives
for some finite constant C.
We now consider the first quantity on the right-hand side of (36) and use the same change of measure as in (35) with
![]() $\mu_n = pn$
to remove the drift from
$\mu_n = pn$
to remove the drift from
![]() $S_t^{\prime}$
. Noting that
$S_t^{\prime}$
. Noting that
![]() $g(t) + \frac{n^{1/3}}{4A} = \gamma(t)$
, by the definition of
$g(t) + \frac{n^{1/3}}{4A} = \gamma(t)$
, by the definition of
![]() $\mathbb{Q}$
, for any
$\mathbb{Q}$
, for any
![]() $\ell\ge0$
,
$\ell\ge0$
,
 \begin{align}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\nonumber\\[3pt]
&\ge\mathbb{P}\big(S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\big)\nonumber\\[3pt]
&=\mathbb{E}_\mathbb{Q}\Big[(pn)^{S^{\prime}_T + T}\unicode{x1D7D9}_{\{S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\}}\Big]e^{(1-pn)T}\nonumber\\[3pt]
&\ge (pn\wedge 1)^{\ell}(pn)^{\gamma(T)+T} e^{(1-pn)T} \mathbb{Q}\big(S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\big).\end{align}
\begin{align}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\nonumber\\[3pt]
&\ge\mathbb{P}\big(S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\big)\nonumber\\[3pt]
&=\mathbb{E}_\mathbb{Q}\Big[(pn)^{S^{\prime}_T + T}\unicode{x1D7D9}_{\{S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\}}\Big]e^{(1-pn)T}\nonumber\\[3pt]
&\ge (pn\wedge 1)^{\ell}(pn)^{\gamma(T)+T} e^{(1-pn)T} \mathbb{Q}\big(S_t^{\prime}>\gamma(t)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(t)+\ell\big).\end{align}
Taking
![]() $\ell = \frac{3n^{1/3}}{8A}$
and recalling that
$\ell = \frac{3n^{1/3}}{8A}$
and recalling that
![]() $pn = 1+\lambda n^{-1/3}$
and
$pn = 1+\lambda n^{-1/3}$
and
and using that
![]() $|\lambda|\le A/3$
,
$|\lambda|\le A/3$
,
![]() $|A|=o(n^{1/30})$
and
$|A|=o(n^{1/30})$
and
![]() $1+x\geq e^{x-x^2}$
for all
$1+x\geq e^{x-x^2}$
for all
![]() $x>-1/2$
we have
$x>-1/2$
we have
and
and using the more precise inequality
![]() $1+x\ge e^{x-x^2/2-|x|^3}$
for all
$1+x\ge e^{x-x^2/2-|x|^3}$
for all
![]() $x>-1/2$
,
$x>-1/2$
,
Substituting these estimates into (39), we obtain
 \begin{align*}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\ &\quad \ge c e^{\lambda A^2/2 - \lambda^2 A/2}\mathbb{Q}\big(S_t^{\prime}>\gamma(T)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(T)+\tfrac{3n^{1/3}}{8A}\big).\end{align*}
\begin{align*}&\mathbb{P}\big(S_t^{\prime}>g(t) + \tfrac{n^{1/3}}{4A}\,\,\,\,\forall t\in[\![ 0,T]\!]\big)\\ &\quad \ge c e^{\lambda A^2/2 - \lambda^2 A/2}\mathbb{Q}\big(S_t^{\prime}>\gamma(T)\,\,\,\,\forall t\in[\![ 0,T]\!],\, S_T^{\prime} \le \gamma(T)+\tfrac{3n^{1/3}}{8A}\big).\end{align*}
Since
![]() $(S_t^{\prime})_{t=1}^{T}$
is a sum of independent Poisson random variables of parameter 1 under
$(S_t^{\prime})_{t=1}^{T}$
is a sum of independent Poisson random variables of parameter 1 under
![]() $\mathbb{Q}$
, substituting this and (38) into (36) gives the result.
$\mathbb{Q}$
, substituting this and (38) into (36) gives the result.
4.5. The probability a Brownian motion stays above a curve: proof of Proposition 4.11
Recall that
and write
our aim in this section is to bound
![]() $P_n(T)$
from below.
$P_n(T)$
from below.
Define
and
Note that since
![]() $x_n\ll n^{1/3}/A$
, for large n we have
$x_n\ll n^{1/3}/A$
, for large n we have
![]() $M\log T + x_n\le n^{1/3}/(8A)$
, so
$M\log T + x_n\le n^{1/3}/(8A)$
, so
We approximate the curve
![]() $\phi(s)$
given above with two straight lines defined, for
$\phi(s)$
given above with two straight lines defined, for
![]() $s\in [0,T/2]$
, by
$s\in [0,T/2]$
, by
and
Also define
 \begin{align*}I &= \Big[\psi_T/2 - A^{1/2}n^{1/3},\, \psi_T/2\Big]\\
&= \Big[\frac{9T}{2A^2n^{1/3}} + \frac{pT^2}{4} - A^{1/2}n^{1/3},\, \frac{9T}{2A^2n^{1/3}} + \frac{pT^2}{4}\Big].\end{align*}
\begin{align*}I &= \Big[\psi_T/2 - A^{1/2}n^{1/3},\, \psi_T/2\Big]\\
&= \Big[\frac{9T}{2A^2n^{1/3}} + \frac{pT^2}{4} - A^{1/2}n^{1/3},\, \frac{9T}{2A^2n^{1/3}} + \frac{pT^2}{4}\Big].\end{align*}
See Figure 1 for reference. Note that
![]() $\psi_T/2 - A^{1/2}n^{1/3} > \phi(T/2)$
when n is large, so the interval I falls entirely above the curve
$\psi_T/2 - A^{1/2}n^{1/3} > \phi(T/2)$
when n is large, so the interval I falls entirely above the curve
![]() $\phi$
.
$\phi$
.

Figure 1. We want our Brownian motion to stay above the blue curve, and the two green lines
![]() $\ell_1$
and
$\ell_1$
and
![]() $\ell_2$
show linear approximations to this curve on the two half-intervals. The dashed red line shows roughly where we expect our Brownian motion to be, given that it stays above the curve. This is a caricature of the true picture, and not to scale.
$\ell_2$
show linear approximations to this curve on the two half-intervals. The dashed red line shows roughly where we expect our Brownian motion to be, given that it stays above the curve. This is a caricature of the true picture, and not to scale.
Since
![]() $\phi$
is convex, the linear interpolations
$\phi$
is convex, the linear interpolations
![]() $\ell_1$
and
$\ell_1$
and
![]() $\ell_2$
fall above the curve and therefore (40) is at least
$\ell_2$
fall above the curve and therefore (40) is at least
For a lower bound, we may also insist that at time
![]() $T/2$
our Brownian motion falls within the interval I. Moreover, it will be convenient for us to know that at time T, our Brownian motion is some distance above the curve. To this end define
$T/2$
our Brownian motion falls within the interval I. Moreover, it will be convenient for us to know that at time T, our Brownian motion is some distance above the curve. To this end define
Putting all this together we obtain
 \begin{align}&P_n(T) \ge \int_I \mathbb{P}\big(B_s > \ell_1(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in \,\textrm{d} w\big) \nonumber \\[3pt] &\quad \cdot \mathbb{P}_w\big(B_s > \ell_2(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in I'\big).\end{align}
\begin{align}&P_n(T) \ge \int_I \mathbb{P}\big(B_s > \ell_1(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in \,\textrm{d} w\big) \nonumber \\[3pt] &\quad \cdot \mathbb{P}_w\big(B_s > \ell_2(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in I'\big).\end{align}
Here
![]() $\mathbb{P}_w$
denotes a probability measure under which our Brownian motion starts from w rather than 0.
$\mathbb{P}_w$
denotes a probability measure under which our Brownian motion starts from w rather than 0.
Lemma 4.12 For any
![]() $\mu,y\in\mathbb{R}$
,
$\mu,y\in\mathbb{R}$
,
![]() $t>0$
,
$t>0$
,
![]() $x>y$
and
$x>y$
and
![]() $z>y+\mu t$
,
$z>y+\mu t$
,
 \begin{align*}&\mathbb{P}_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z) \\
&\quad = \frac{1}{\sqrt{2\pi t}} \exp\Big(-\frac{(z-x)^2}{2t}\Big)\Big(1-\exp\Big(\frac{2(x-y)(\mu t+y-z)}{t}\Big)\Big)\,\textrm{d} z.\end{align*}
\begin{align*}&\mathbb{P}_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z) \\
&\quad = \frac{1}{\sqrt{2\pi t}} \exp\Big(-\frac{(z-x)^2}{2t}\Big)\Big(1-\exp\Big(\frac{2(x-y)(\mu t+y-z)}{t}\Big)\Big)\,\textrm{d} z.\end{align*}
Proof. We begin with an exponential change of measure to balance the drift
![]() $\mu$
. Letting
$\mu$
. Letting
![]() $(\mathcal{F}_s)_{s\ge 0}$
be the natural filtration of our Brownian motion, define
$(\mathcal{F}_s)_{s\ge 0}$
be the natural filtration of our Brownian motion, define
![]() $\mathcal P_x$
, with expectation operator
$\mathcal P_x$
, with expectation operator
![]() $\mathcal E_x$
, by setting
$\mathcal E_x$
, by setting
Then under
![]() $\mathcal P_x$
,
$\mathcal P_x$
,
![]() $(B_s)_{s\ge 0}$
is a Brownian motion with drift
$(B_s)_{s\ge 0}$
is a Brownian motion with drift
![]() $\mu$
started from x, and therefore
$\mu$
started from x, and therefore
 \begin{align*}\mathbb{P}_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z) &= \mathcal E_x\big[ e^{-\mu B_t + \mu^2 t/2 + \mu x}\unicode{x1D7D9}_{\{B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z\}}\big]\\[3pt]
&= e^{-\mu z + \mu^2 t/2 + \mu x}\mathcal P_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z)\\[3pt]
&= e^{-\mu z + \mu^2 t/2 + \mu x}\mathbb{P}_x(B_s > y \;\;\forall s\le t,\, B_t + \mu t \in \,\textrm{d} z).\end{align*}
\begin{align*}\mathbb{P}_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z) &= \mathcal E_x\big[ e^{-\mu B_t + \mu^2 t/2 + \mu x}\unicode{x1D7D9}_{\{B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z\}}\big]\\[3pt]
&= e^{-\mu z + \mu^2 t/2 + \mu x}\mathcal P_x(B_s > y + \mu s \;\;\forall s\le t,\, B_t \in \,\textrm{d} z)\\[3pt]
&= e^{-\mu z + \mu^2 t/2 + \mu x}\mathbb{P}_x(B_s > y \;\;\forall s\le t,\, B_t + \mu t \in \,\textrm{d} z).\end{align*}
We now recall that, as a consequence of the reflection principle for Brownian motion, for
![]() $x>y$
and
$x>y$
and
![]() $w>y$
,
$w>y$
,
Since the ratio within the second exponential expands as
grouping by
![]() $-(w-x)^2/2t$
we obtain
$-(w-x)^2/2t$
we obtain
 \begin{align*}&\mathbb{P}_x(B_s > y \;\;\forall s\le t,\, B_t \in dw)\\[3pt]
&\quad = \frac{1}{\sqrt{2\pi t}}\exp\Big(-\frac{(w-x)^2}{2t}\Big)\left(1-\exp\Big(\frac{2(yx-wx+yw-y^2)}{t}\Big)\right).\end{align*}
\begin{align*}&\mathbb{P}_x(B_s > y \;\;\forall s\le t,\, B_t \in dw)\\[3pt]
&\quad = \frac{1}{\sqrt{2\pi t}}\exp\Big(-\frac{(w-x)^2}{2t}\Big)\left(1-\exp\Big(\frac{2(yx-wx+yw-y^2)}{t}\Big)\right).\end{align*}
Taking
![]() $w=z-\mu t$
and substituting into the expression above, and then simplifying, gives the result.
$w=z-\mu t$
and substituting into the expression above, and then simplifying, gives the result.
We now use Lemma 4.12 to obtain a lower bound for the probability that
![]() $B_t$
stays above the line
$B_t$
stays above the line
![]() $l_1(s)$
and finishes near
$l_1(s)$
and finishes near
![]() $w\in I$
at time
$w\in I$
at time
![]() $T/2$
.
$T/2$
.
Corollary 4.13 For
![]() $w\in I$
,
$w\in I$
,
Proof. We apply Lemma 4.12 with
![]() $x=0$
,
$x=0$
,
![]() $z=w$
,
$z=w$
,
![]() $y=-n^{1/3}/(8A)$
,
$y=-n^{1/3}/(8A)$
,
![]() $\mu = \frac{9}{A^2 n^{1/3}} + \frac{pT}{4}$
and
$\mu = \frac{9}{A^2 n^{1/3}} + \frac{pT}{4}$
and
![]() $t=T/2$
. With these parameters,
$t=T/2$
. With these parameters,
![]() $w>y+\mu t$
and hence Lemma 4.12 tells us that
$w>y+\mu t$
and hence Lemma 4.12 tells us that
 \begin{align*}\mathbb{P}\big(B_s > \ell_1(s)\;\; \forall s&\in[0,T/2],\, B_{T/2} \in \,\textrm{d} w\big)\\
&= \frac{1}{\sqrt{\pi T}} e^{-w^2/T} \Big(1-\exp\Big(-2\Big(w+\frac{n^{1/3}}{8A} - \frac{9T}{2A^2 n^{1/3}} - \frac{pT^2}{8}\Big)\frac{n^{1/3}}{4AT}\Big)\Big)\,\textrm{d} w.\end{align*}
\begin{align*}\mathbb{P}\big(B_s > \ell_1(s)\;\; \forall s&\in[0,T/2],\, B_{T/2} \in \,\textrm{d} w\big)\\
&= \frac{1}{\sqrt{\pi T}} e^{-w^2/T} \Big(1-\exp\Big(-2\Big(w+\frac{n^{1/3}}{8A} - \frac{9T}{2A^2 n^{1/3}} - \frac{pT^2}{8}\Big)\frac{n^{1/3}}{4AT}\Big)\Big)\,\textrm{d} w.\end{align*}
Since
![]() $w\in I$
, we have
$w\in I$
, we have
![]() $w\ge \frac{9T}{2A^2 n^{1/3}} + \frac{pT^2}{4} - A^{1/2}n^{1/3}$
and therefore
$w\ge \frac{9T}{2A^2 n^{1/3}} + \frac{pT^2}{4} - A^{1/2}n^{1/3}$
and therefore
for some
![]() $c>0$
, and the result follows.
$c>0$
, and the result follows.
Next we bound from below the second probability that appears in the integral (41), again by means of Lemma 4.12.
Corollary 4.14 For
![]() $w\in I$
and A sufficiently large,
$w\in I$
and A sufficiently large,
Proof. We now apply Lemma 4.12 with
![]() $x=w$
,
$x=w$
,
![]() $y=-\frac{n^{1/3}}{8A} + \frac{9T}{2A^2 n^{1/3}} + \frac{pT^2}{8}$
,
$y=-\frac{n^{1/3}}{8A} + \frac{9T}{2A^2 n^{1/3}} + \frac{pT^2}{8}$
,
![]() $\mu = \frac{9}{A^2 n^{1/3}} + \frac{3pT}{4}$
and
$\mu = \frac{9}{A^2 n^{1/3}} + \frac{3pT}{4}$
and
![]() $t=T/2$
. This tells us that
$t=T/2$
. This tells us that
 \begin{align}&\mathbb{P}_w\big(B_s > \ell_2(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in I' \big)\nonumber\\[3pt] &\quad = \frac{1}{\sqrt{\pi T}} \int_{I'}^{} e^{-(z-w)^2/T} \Big(1-\exp\Big(\frac{2(w-y)(\mu t +y - z)}{t}\Big)\Big)\,\textrm{d} z,\end{align}
\begin{align}&\mathbb{P}_w\big(B_s > \ell_2(s)\;\; \forall s\in[0,T/2],\, B_{T/2} \in I' \big)\nonumber\\[3pt] &\quad = \frac{1}{\sqrt{\pi T}} \int_{I'}^{} e^{-(z-w)^2/T} \Big(1-\exp\Big(\frac{2(w-y)(\mu t +y - z)}{t}\Big)\Big)\,\textrm{d} z,\end{align}
we want an upper bound for the exponential term
To this end observe that, since
![]() $z\geq \phi(T)+n^{1/3}/16A$
and
$z\geq \phi(T)+n^{1/3}/16A$
and
then
Also, since
![]() $w\in I$
we obtain
$w\in I$
we obtain
 \begin{align*}(w-y)(\mu t +y -z)\leq -\frac{n^{1/3}}{16A}(w-y)&\leq -\frac{n^{1/3}}{16A}\left(\frac{pT^2}{8}+\frac{n^{1/3}}{8A}-A^{1/2}n^{1/3}\right)\\&=-\frac{n^{1/3}}{16A}\frac{pT^2}{8}(1-o(1)),\end{align*}
\begin{align*}(w-y)(\mu t +y -z)\leq -\frac{n^{1/3}}{16A}(w-y)&\leq -\frac{n^{1/3}}{16A}\left(\frac{pT^2}{8}+\frac{n^{1/3}}{8A}-A^{1/2}n^{1/3}\right)\\&=-\frac{n^{1/3}}{16A}\frac{pT^2}{8}(1-o(1)),\end{align*}
whence
Plugging this estimate into (42) we obtain the desired result.
Proof of Proposition 4.11. Substituting Corollaries 4.13 and 4.14 into (41), and recalling the definition of I
![]() $^{\prime}$
we obtain
$^{\prime}$
we obtain
Using the substitutions
![]() $u = w - \psi_T/2$
and
$u = w - \psi_T/2$
and
![]() $v = z - \psi_T$
, the term on the right-hand side of the inequality in (43) equals
$v = z - \psi_T$
, the term on the right-hand side of the inequality in (43) equals
which, after multiplying out the quadratic terms in the exponent, becomes
Since
![]() $u,v\le 0$
, we have
$u,v\le 0$
, we have
![]() $2uv/T\ge 0$
and therefore the integral over u is at least
$2uv/T\ge 0$
and therefore the integral over u is at least
We deduce that
Now
so the exponent on the right-hand side of (44) is
![]() $e^{-\psi_T^2/2T - O(1)}$
; thus (44) becomes
$e^{-\psi_T^2/2T - O(1)}$
; thus (44) becomes
It then remains only to note that
and the proof is complete.
Remark 4.15 Here we continue the discussion started with Remark 3.7, where we highlighted at which steps within the proof of the upper bounds stated in Theorem 1.1 we saw the appearance of constant factors in front of the probability
![]() $\mathbb{P}(|\mathcal{C}_{\text{max}}|>An^{2/3})$
. For the lower bound, the problem of finding the right constant is similarly involved. For instance, with Proposition 4.3 we see the appearance of a constant which comes not only from some involved computations, which similarly to Remark 3.7 could possibly be tightened subject to further conditions on A and
$\mathbb{P}(|\mathcal{C}_{\text{max}}|>An^{2/3})$
. For the lower bound, the problem of finding the right constant is similarly involved. For instance, with Proposition 4.3 we see the appearance of a constant which comes not only from some involved computations, which similarly to Remark 3.7 could possibly be tightened subject to further conditions on A and
![]() $\lambda$
, but also from an application of Theorem 2.1 (the generalised ballot theorem). Therefore, in order to properly identify this constant, one would need to either go through the proof of the generalised ballot theorem in our setting and check whether it would be possible to keep track of all the constants appearing there; or to apply other results on random walks, for example the probability for a random walk to stay positive [Reference Spitzer30] together with a convergence in law of random walks conditioned to stay positive, e.g. from [Reference Durrett14].
$\lambda$
, but also from an application of Theorem 2.1 (the generalised ballot theorem). Therefore, in order to properly identify this constant, one would need to either go through the proof of the generalised ballot theorem in our setting and check whether it would be possible to keep track of all the constants appearing there; or to apply other results on random walks, for example the probability for a random walk to stay positive [Reference Spitzer30] together with a convergence in law of random walks conditioned to stay positive, e.g. from [Reference Durrett14].
Acknowledgements
Both authors would like to thank Nathanaël Berestycki for some very helpful discussions. We also thank the Royal Society for their generous funding, of a PhD scholarship for UDA and a University Research Fellowship for MR. Finally, we thank two anonymous referees for their thoughtful comments and suggestions, which helped us to improve the paper.