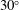1 Introduction
Transonic buffet refers to an unsteady-flow condition involving shock oscillations that can produce large variations in sectional wing lift. These oscillations can be large enough to drive airplane-level normal accelerations well in excess of
![]() $0.1g$
, where
$0.1g$
, where
![]() $g$
is the gravitational acceleration. Predicting the onset of these forced airplane oscillations is an important part of airplane design, since these oscillations can limit the operating envelope of an aircraft.
$g$
is the gravitational acceleration. Predicting the onset of these forced airplane oscillations is an important part of airplane design, since these oscillations can limit the operating envelope of an aircraft.
Early experiments aimed at understanding buffet onset were focused on two-dimensional (2-D) airfoils, e.g. McDevitt & Okuno (Reference McDevitt and Okuno1985), Benoit & Legrain (Reference Benoit and Legrain1987), Bartels & Edwards (Reference Bartels and Edwards1997), Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009). For a given Mach number, as the angle of attack is increased the shock intensifies and moves aft over the airfoil. At large angles of attack, the boundary layer begins to separate at the foot of the shock. The region of separated flow increases with further increase in the angle of attack until it extends from the foot of the shock to the trailing edge. At some stage in this process, the flow begins to show global unsteadiness characterized by an oscillation of the shock synchronized with an oscillation of the separated shear layer. This nominally 2-D oscillation is typically dominated by a single frequency, or a narrow band of frequencies with harmonics. In some cases, the flow downstream of the shock can also exhibit three-dimensional (3-D) structures.
Airfoil buffet onset has been linked to a global flow instability associated with the 2-D base state (Crouch, Garbaruk & Magidov Reference Crouch, Garbaruk and Magidov2007; Crouch et al. Reference Crouch, Garbaruk, Magidov and Travin2009a ,Reference Crouch, Garbaruk, Magidov and Jacquin b ; Iorio, Gonzalez & Ferrer Reference Iorio, Gonzalaz and Ferrer2014; Sartor, Mettot & Sipp Reference Sartor, Mettot and Sipp2015). The onset of unsteadiness is characterized by a Hopf bifurcation leading to the development of shock oscillations. The predicted frequency and unsteady-flow structure appear to be in good agreement with experiments. As the shock moves fore and aft, the post-shock shear layer moves away from and toward the surface in a synchronized fashion. Simulations using unsteady Reynolds averaged Navier–Stokes (URANS) equations (Thiery & Coustols Reference Thiery and Coustols2006; Crouch et al. Reference Crouch, Garbaruk, Magidov and Travin2009a ; Iovnovich & Raveh Reference Iovnovich and Raveh2014; Plante et al. Reference Plante, Laurendeau, Dandois and Sartor2017) or detached eddy simulations (DES) (Deck Reference Deck2005) show general agreement with the experimental observations. Some 3-D simulations of nominally 2-D (‘extruded’) airfoils also show spanwise-varying spatial structures (or local cells) (Iovnovich & Raveh Reference Iovnovich and Raveh2014; Plante et al. Reference Plante, Laurendeau, Dandois and Sartor2017; Plante, Dandois & Laurendeau Reference Plante, Dandois and Laurendeau2019). These structures are more pronounced when the shock is near its upstream limit, but their overall impact on the buffet onset is less clear.
Studies of swept-wing buffet show some distinctly different characteristics when compared with unswept wings (Benoit & Legrain Reference Benoit and Legrain1987; Molton et al. Reference Molton, Dandois, Lepage, Brunet and Bur2013; Iovnovich & Raveh Reference Iovnovich and Raveh2014; Dandois Reference Dandois2016; Ohmichi, Ishida & Hashimoto Reference Ohmichi, Ishida and Hashimoto2017; Sartor & Timme Reference Sartor and Timme2017; Sugioka et al. Reference Sugioka, Koike, Nakakita, Numata, Nonomura and Asai2018). The frequency content is more broad-banded, and the characteristic frequency can be 4–7 times larger than observed on an unswept wing. The shock oscillations also appear to propagate spanwise, which indicates that it is dominated by a 3-D structure. For a finite-span swept wing, the spanwise variations in the flow field result in a more localized region of unsteady onset as compared with the nominally 2-D, or infinite swept, wing. The finite-span swept wing has recently been analysed using global stability analysis with a fully 3-D eigenmode (Timme Reference Timme2018, Reference Timme2019). These results show an unstable mode of limited spanwise extent, which propagates outboard similar to experimental observations, but at a single frequency analogous to the airfoil global instability. Some of the characteristics distinguishing buffet of the unswept and swept wing, of infinite or finite span, are further discussed in the review of Giannelis, Vio & Levinski (Reference Giannelis, Vio and Levinski2017).

Figure 1. Schematic of a section of the infinite swept wing.
In this paper, we investigate the buffet onset for swept wings using a global instability analysis, with specific attention to the potential role of spanwise-varying flow structures. The underlying flow is uniform in the spanwise direction (i.e. infinite swept wing), roughly analogous to a streamwise cut through a finite-span wing. The results are primarily focused on the extruded ONERA OAT15A airfoil section with blunt trailing edge. This supercritical profile has been used in several previous studies, including: airfoil experiments (Jacquin et al. Reference Jacquin, Molton, Deck, Maury and Soulevant2009), swept-wing experiments (Molton et al. Reference Molton, Dandois, Lepage, Brunet and Bur2013; Dandois Reference Dandois2016), numerical simulations (Deck Reference Deck2005; Thiery & Coustols Reference Thiery and Coustols2006; Plante et al. Reference Plante, Laurendeau, Dandois and Sartor2017) and stability analyses (Crouch et al. Reference Crouch, Garbaruk, Magidov and Jacquin2009b ; Sartor et al. Reference Sartor, Mettot and Sipp2015). Some limited results will be discussed for the RA16SC1 airfoil section in order to highlight instability characteristics that are more airfoil dependent. Results from numerical simulations, based on the URANS equations, are also provided to assess and support the findings from the stability analysis.
2 Formulation and analysis
The analysis considers compressible unsteady flow at relatively high Reynolds numbers where the boundary layer is turbulent. However, the time scales associated with buffet are typically much larger than the characteristic eddy time scales of the boundary layer. This permits the application of the URANS equations to govern the flow. A detailed discussion about the suitability of the URANS equations for this flow is given in Crouch et al. (Reference Crouch, Garbaruk, Magidov and Travin2009a ). Closure for the Reynolds stresses is provided using the Spalart–Allmaras turbulence model (Spalart & Allmaras Reference Spalart and Allmaras1994) with compressibility corrections (Spalart Reference Spalart2000). This leads to a set of six equations: continuity, streamwise, spanwise and transverse momentum, energy and eddy viscosity. These equations can be written in terms of the primitive variables in the following homogeneous vector form,
with
![]() $q=\{\unicode[STIX]{x1D70C},u,v,w,T,\tilde{\unicode[STIX]{x1D708}}\}$
, where
$q=\{\unicode[STIX]{x1D70C},u,v,w,T,\tilde{\unicode[STIX]{x1D708}}\}$
, where
![]() $M$
and
$M$
and
![]() $Q$
are linear operators, and
$Q$
are linear operators, and
![]() $N$
contains all nonlinear terms,
$N$
contains all nonlinear terms,
![]() $\unicode[STIX]{x1D70C}$
is the density,
$\unicode[STIX]{x1D70C}$
is the density,
![]() $T$
is the temperature,
$T$
is the temperature,
![]() $u$
,
$u$
,
![]() $v$
,
$v$
,
![]() $w$
are velocities in the
$w$
are velocities in the
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
directions, respectively, and
$z$
directions, respectively, and
![]() $\tilde{\unicode[STIX]{x1D708}}$
is the modified eddy viscosity. The coordinate system is aligned to the wing leading edge, with
$\tilde{\unicode[STIX]{x1D708}}$
is the modified eddy viscosity. The coordinate system is aligned to the wing leading edge, with
![]() $z$
pointing outboard, as shown in figure 1. The boundary conditions on the wing surface are given by
$z$
pointing outboard, as shown in figure 1. The boundary conditions on the wing surface are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u=v=w=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}n}=\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}n}=0,\\ \displaystyle \tilde{\unicode[STIX]{x1D708}}=0,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u=v=w=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}n}=\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}n}=0,\\ \displaystyle \tilde{\unicode[STIX]{x1D708}}=0,\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}n$
is a derivative normal to the surface.
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}n$
is a derivative normal to the surface.
The far-field conditions involve the primitive variables and the Riemann invariants, and are given by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle I_{1}=V_{n}+\frac{2a}{(\unicode[STIX]{x1D6FE}-1)}=k_{x}u+k_{y}v+\frac{2}{(\unicode[STIX]{x1D6FE}-1)}\sqrt{\unicode[STIX]{x1D6FE}RT},\\ \displaystyle I_{2}=V_{n}-\frac{2a}{(\unicode[STIX]{x1D6FE}-1)}=k_{x}u+k_{y}v-\frac{2}{(\unicode[STIX]{x1D6FE}-1)}\sqrt{\unicode[STIX]{x1D6FE}RT},\\ \displaystyle I_{3}=V_{\unicode[STIX]{x1D70F}}=k_{y}u-k_{x}v,\quad I_{4}=w,\quad I_{5}=\frac{RT}{\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FE}-1}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle I_{1}=V_{n}+\frac{2a}{(\unicode[STIX]{x1D6FE}-1)}=k_{x}u+k_{y}v+\frac{2}{(\unicode[STIX]{x1D6FE}-1)}\sqrt{\unicode[STIX]{x1D6FE}RT},\\ \displaystyle I_{2}=V_{n}-\frac{2a}{(\unicode[STIX]{x1D6FE}-1)}=k_{x}u+k_{y}v-\frac{2}{(\unicode[STIX]{x1D6FE}-1)}\sqrt{\unicode[STIX]{x1D6FE}RT},\\ \displaystyle I_{3}=V_{\unicode[STIX]{x1D70F}}=k_{y}u-k_{x}v,\quad I_{4}=w,\quad I_{5}=\frac{RT}{\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6FE}-1}},\end{array}\right\}\end{eqnarray}$$
where
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
are the local directional cosines in the boundary normal. These conditions are imposed on the subsonic boundaries. On the inlet boundary, the invariants
$k_{y}$
are the local directional cosines in the boundary normal. These conditions are imposed on the subsonic boundaries. On the inlet boundary, the invariants
![]() $I_{1}$
,
$I_{1}$
,
![]() $I_{3}$
,
$I_{3}$
,
![]() $I_{4}$
and
$I_{4}$
and
![]() $I_{5}$
are given and
$I_{5}$
are given and
![]() $I_{2}$
is extrapolated from the interior of the computational domain, whereas on the outlet boundary,
$I_{2}$
is extrapolated from the interior of the computational domain, whereas on the outlet boundary,
![]() $I_{1}$
,
$I_{1}$
,
![]() $I_{3}$
,
$I_{3}$
,
![]() $I_{4}$
and
$I_{4}$
and
![]() $I_{5}$
are extrapolated and
$I_{5}$
are extrapolated and
![]() $I_{2}$
is given.
$I_{2}$
is given.
The state vector describing the total flow field is decomposed into a steady base flow and a perturbation vector,
![]() $q=\bar{q}+q^{\prime }$
. The vector
$q=\bar{q}+q^{\prime }$
. The vector
![]() $\bar{q}$
is a solution of the steady form of (2.1) – that is, with
$\bar{q}$
is a solution of the steady form of (2.1) – that is, with
![]() $\unicode[STIX]{x2202}\bar{q}/\unicode[STIX]{x2202}t\equiv 0$
. For conditions close to the steady base flow state, the perturbation component
$\unicode[STIX]{x2202}\bar{q}/\unicode[STIX]{x2202}t\equiv 0$
. For conditions close to the steady base flow state, the perturbation component
![]() $q^{\prime }$
can be considered as small relative to the vector
$q^{\prime }$
can be considered as small relative to the vector
![]() $\bar{q}$
. Substituting
$\bar{q}$
. Substituting
![]() $q=\bar{q}+q^{\prime }$
into (2.1), cancelling the terms governing
$q=\bar{q}+q^{\prime }$
into (2.1), cancelling the terms governing
![]() $\bar{q}$
and linearizing the equations in terms of
$\bar{q}$
and linearizing the equations in terms of
![]() $q^{\prime }$
yields,
$q^{\prime }$
yields,
The linear operator
![]() $M$
contains the terms associated with the time derivatives from the original equation (2.1). The linear operator
$M$
contains the terms associated with the time derivatives from the original equation (2.1). The linear operator
![]() $N_{\bar{q}}$
consists of linear terms from the original equations, and the terms generated by nonlinear interactions between
$N_{\bar{q}}$
consists of linear terms from the original equations, and the terms generated by nonlinear interactions between
![]() $\bar{q}$
and
$\bar{q}$
and
![]() $q^{\prime }$
.
$q^{\prime }$
.
For the infinite swept wing the base flow is quasi-3-D, i.e.
![]() $\bar{w}\neq 0$
, but
$\bar{w}\neq 0$
, but
![]() $\unicode[STIX]{x2202}\bar{q}/\unicode[STIX]{x2202}z\equiv 0$
, and a general perturbation to the steady-state flow
$\unicode[STIX]{x2202}\bar{q}/\unicode[STIX]{x2202}z\equiv 0$
, and a general perturbation to the steady-state flow
![]() $\bar{q}(x,y)$
can be represented by spanwise and temporally harmonic normal modes of the form
$\bar{q}(x,y)$
can be represented by spanwise and temporally harmonic normal modes of the form
The function
![]() $\hat{q}$
describes the mode shape, and
$\hat{q}$
describes the mode shape, and
![]() $\unicode[STIX]{x1D714}$
is the frequency associated with a prescribed spanwise wavenumber
$\unicode[STIX]{x1D714}$
is the frequency associated with a prescribed spanwise wavenumber
![]() $\unicode[STIX]{x1D6FD}$
. In general, both
$\unicode[STIX]{x1D6FD}$
. In general, both
![]() $\hat{q}$
and
$\hat{q}$
and
![]() $\unicode[STIX]{x1D714}$
can be complex, so the physical solution is taken as the real part of (2.5).
$\unicode[STIX]{x1D714}$
can be complex, so the physical solution is taken as the real part of (2.5).
Substituting (2.5) into (2.4) and rescaling the terms yields a system of equations governing the modal perturbations
with
![]() $L$
being a second-order linear differential operator. The quasi-3-D problem formulation and the resulting equation (2.6) have forms similar to the 2-D problem, which is described in detail in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The inclusion of the spanwise velocity component
$L$
being a second-order linear differential operator. The quasi-3-D problem formulation and the resulting equation (2.6) have forms similar to the 2-D problem, which is described in detail in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The inclusion of the spanwise velocity component
![]() $w$
introduces an additional momentum equation, and some additional terms in (2.4). The
$w$
introduces an additional momentum equation, and some additional terms in (2.4). The
![]() $z$
dependence of
$z$
dependence of
![]() $q^{\prime }$
also results in additional terms compared with the 2-D formulation. These
$q^{\prime }$
also results in additional terms compared with the 2-D formulation. These
![]() $z$
-dependent terms appear in the linear operator
$z$
-dependent terms appear in the linear operator
![]() $L$
with
$L$
with
![]() $\unicode[STIX]{x1D6FD}$
multipliers.
$\unicode[STIX]{x1D6FD}$
multipliers.
Equation (2.6) with linearized boundary conditions (2.2), (2.3) describes an eigenvalue problem, which is solved numerically. The results are scaled using the free-stream velocity
![]() $U_{\infty }$
and the wing chord
$U_{\infty }$
and the wing chord
![]() $c$
measured normal to the leading edge. This leads to a Reynolds number of
$c$
measured normal to the leading edge. This leads to a Reynolds number of
![]() $Re=U_{\infty }c/\unicode[STIX]{x1D708}$
, where
$Re=U_{\infty }c/\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. The angular frequency
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. The angular frequency
![]() $\unicode[STIX]{x1D714}_{r}$
can be expressed in terms of the Strouhal number as
$\unicode[STIX]{x1D714}_{r}$
can be expressed in terms of the Strouhal number as
![]() $St=\tilde{f}c/U_{\infty }=\unicode[STIX]{x1D714}_{r}/2\unicode[STIX]{x03C0}$
. The dimensional frequency and spanwise wavelength are denoted by
$St=\tilde{f}c/U_{\infty }=\unicode[STIX]{x1D714}_{r}/2\unicode[STIX]{x03C0}$
. The dimensional frequency and spanwise wavelength are denoted by
![]() $\tilde{f}$
and
$\tilde{f}$
and
![]() $\tilde{\unicode[STIX]{x1D706}}$
, respectively.
$\tilde{\unicode[STIX]{x1D706}}$
, respectively.
The steady RANS equations are solved using the NTS code (Shur, Strelets & Travin Reference Shur, Strelets and Travin2004), which is based on an implicit finite-volume formulation on a structured multi-block overlapping grid. The third-order upwind-biased Roe scheme (Roe Reference Roe1981) is used for approximation of inviscid fluxes, while the viscous momentum and heat fluxes are approximated with the second-order central difference scheme. The convective terms in the eddy-viscosity transport equation of the Spalart–Allmaras model are approximated with the first-order upwind scheme. To calculate the steady base flow, the NTS code uses local time stepping, and is capable of returning a steady solution for nominally unsteady-flow regimes that are close to the unsteady-onset conditions. In this case, the local time stepping does not approximate the unsteady equations, but rather provides an iterative procedure for obtaining a steady solution if it exists. The equations are integrated using a large time step (large Courant–Friedrichs–Lewy (CFL) number) to damp unsteadiness, which is enabled by the use of an implicit scheme. Thus, no artificial dissipation is introduced into the steady base flow solutions.
The stability equations are derived and discretized independently from the steady-flow equations. This enables an assessment of the instability that is not overly sensitive to the level of steady-flow convergence. Thus, in principle, the stability analysis can be done for extreme flow conditions where the steady-flow convergence is more challenging. However, in the current study all steady-flow solutions used in the stability analysis are deeply converged: the maximum residual is less than
![]() $10^{-8}$
. The only modification of the scheme used for the solution of the stability equation (2.6) is that, unlike the original Roe scheme, the upwind finite-difference approximations are linearized and are based on the sign of the cell-face normal component of the steady velocity. In order to reduce the numerical dissipation of the upwind differencing, we use a ‘hybrid’ scheme which is weighted between upwind and central differencing,
$10^{-8}$
. The only modification of the scheme used for the solution of the stability equation (2.6) is that, unlike the original Roe scheme, the upwind finite-difference approximations are linearized and are based on the sign of the cell-face normal component of the steady velocity. In order to reduce the numerical dissipation of the upwind differencing, we use a ‘hybrid’ scheme which is weighted between upwind and central differencing,
The finite difference operators
![]() $\unicode[STIX]{x1D6E5}_{3u}$
and
$\unicode[STIX]{x1D6E5}_{3u}$
and
![]() $\unicode[STIX]{x1D6E5}_{4c}$
correspond to the third-order upwind and fourth-order centred schemes, respectively, and
$\unicode[STIX]{x1D6E5}_{4c}$
correspond to the third-order upwind and fourth-order centred schemes, respectively, and
![]() $\unicode[STIX]{x1D6FC}_{H}$
is the weighting constant. The influence of this parameter on the calculated results is discussed in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The current results are all based on a value
$\unicode[STIX]{x1D6FC}_{H}$
is the weighting constant. The influence of this parameter on the calculated results is discussed in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The current results are all based on a value
![]() $\unicode[STIX]{x1D6FC}_{H}=0.2$
.
$\unicode[STIX]{x1D6FC}_{H}=0.2$
.

Figure 2. Multi-block grid showing local refinement in the neighbourhood of the shock (OAT15A).
All computations (steady flow, unsteady flow, instability) make use of the same
![]() $x$
–
$x$
–
![]() $y$
grid, as shown in figure 2. This is a 2-block C-type grid with approximately 85 000 cells. The grid is refined in the vicinity of the shock with a chordwise grid spacing of
$y$
grid, as shown in figure 2. This is a 2-block C-type grid with approximately 85 000 cells. The grid is refined in the vicinity of the shock with a chordwise grid spacing of
![]() $0.002c$
. The wall normal grid spacing ensures that the first grid point is less than one wall unit from the surface. The grid extends to approximately 30 chord lengths from the airfoil.
$0.002c$
. The wall normal grid spacing ensures that the first grid point is less than one wall unit from the surface. The grid extends to approximately 30 chord lengths from the airfoil.
The eigenvalue problem of (2.6) is solved numerically using the implicitly restarted Arnoldi method (Hernandez et al.
Reference Hernandez, Roman, Tomas and Vidal2007), which is a member of the Krylov subspace projection methods. This yields a large number of eigenvalues, but only a small number of these are physically meaningful. We focus on the least-stable eigenmodes as indicators for the onset of instability and unsteadiness. A small number of modes are calculated in the neighbourhood of a prescribed frequency
![]() $\unicode[STIX]{x1D714}^{\ast }$
, where
$\unicode[STIX]{x1D714}^{\ast }$
, where
![]() $\text{Im}(\unicode[STIX]{x1D714}^{\ast })>0$
. This is done using the shift-invert spectral transformation, as implemented in the library Petsc/Slepc (Hernandez et al.
Reference Hernandez, Roman, Tomas and Vidal2007), with lower–upper factorization. The number of Arnoldi vectors is set to 128, and the solution is considered to be converged when the error estimate is below
$\text{Im}(\unicode[STIX]{x1D714}^{\ast })>0$
. This is done using the shift-invert spectral transformation, as implemented in the library Petsc/Slepc (Hernandez et al.
Reference Hernandez, Roman, Tomas and Vidal2007), with lower–upper factorization. The number of Arnoldi vectors is set to 128, and the solution is considered to be converged when the error estimate is below
![]() $10^{-8}$
. For the grid used in this study, this requires about 50–100 GB memory and approximately 10 min of compute time on 2 nodes of a cluster (
$10^{-8}$
. For the grid used in this study, this requires about 50–100 GB memory and approximately 10 min of compute time on 2 nodes of a cluster (
![]() $2\times$
Intel Xeon CPU E5-2697v3, 28 cores, 2.60 GHz, 64 GB memory). When necessary, physical modes can be distinguished from spurious modes by calculating the average eigenfunction amplitude at the far-field boundary (neglecting the wake region). The physical modes have negligibly small amplitudes in the far field compared with the peak modal amplitude.
$2\times$
Intel Xeon CPU E5-2697v3, 28 cores, 2.60 GHz, 64 GB memory). When necessary, physical modes can be distinguished from spurious modes by calculating the average eigenfunction amplitude at the far-field boundary (neglecting the wake region). The physical modes have negligibly small amplitudes in the far field compared with the peak modal amplitude.
The global instability formulation follows the analysis of Jackson (Reference Jackson1987) and Zebib (Reference Zebib1987) with an extension to compressible high-Reynolds-number flows (Crouch et al. Reference Crouch, Garbaruk and Magidov2007). A more general overview of global stability analysis is provided in the review of Theofilis (Reference Theofilis2011).
3 Stability results for the unswept wing
Earlier studies show that transonic airfoils become unstable to an oscillatory mode through a Hopf bifurcation as the angle of attack is increased at fixed Mach number. The instability is characterized by a shock oscillation synchronized to a downstream oscillation of the post-shock shear-layer thickness. The predicted onset of buffeting is in good agreement with experiments based on small-aspect-ratio wings, say
![]() $b/c\approx 3$
, where
$b/c\approx 3$
, where
![]() $c$
is the chord length and
$c$
is the chord length and
![]() $b$
is the span (Crouch et al.
Reference Crouch, Garbaruk and Magidov2007, Reference Crouch, Garbaruk, Magidov and Travin2009a
,Reference Crouch, Garbaruk, Magidov and Jacquin
b
; Iorio et al.
Reference Iorio, Gonzalaz and Ferrer2014; Sartor et al.
Reference Sartor, Mettot and Sipp2015). The predicted unsteady-flow structure is also in good agreement with experiments, including: the spatial distribution, the phasing, and the frequency of the unsteady fluctuations (Crouch et al.
Reference Crouch, Garbaruk, Magidov and Jacquin2009b
). Recent modal analysis of buffeting flows also shows a flow structure consistent with the instability predictions (Poplingher & Raveh Reference Poplingher and Raveh2018).
$b$
is the span (Crouch et al.
Reference Crouch, Garbaruk and Magidov2007, Reference Crouch, Garbaruk, Magidov and Travin2009a
,Reference Crouch, Garbaruk, Magidov and Jacquin
b
; Iorio et al.
Reference Iorio, Gonzalaz and Ferrer2014; Sartor et al.
Reference Sartor, Mettot and Sipp2015). The predicted unsteady-flow structure is also in good agreement with experiments, including: the spatial distribution, the phasing, and the frequency of the unsteady fluctuations (Crouch et al.
Reference Crouch, Garbaruk, Magidov and Jacquin2009b
). Recent modal analysis of buffeting flows also shows a flow structure consistent with the instability predictions (Poplingher & Raveh Reference Poplingher and Raveh2018).
A general 3-D analysis of an infinite-span wing performed in the present study shows two types of instability: an unsteady oscillatory mode with
![]() $\unicode[STIX]{x1D6FD}\approx 0$
,
$\unicode[STIX]{x1D6FD}\approx 0$
,
![]() $\unicode[STIX]{x1D714}_{r}\neq 0$
and a stationary mode with
$\unicode[STIX]{x1D714}_{r}\neq 0$
and a stationary mode with
![]() $\unicode[STIX]{x1D6FD}>0$
,
$\unicode[STIX]{x1D6FD}>0$
,
![]() $\unicode[STIX]{x1D714}_{r}=0$
. The growth rates
$\unicode[STIX]{x1D714}_{r}=0$
. The growth rates
![]() $\unicode[STIX]{x1D714}_{i}$
for these modes are shown as a function of
$\unicode[STIX]{x1D714}_{i}$
for these modes are shown as a function of
![]() $\unicode[STIX]{x1D6FD}$
in figure 3 for different values of the angle of attack
$\unicode[STIX]{x1D6FD}$
in figure 3 for different values of the angle of attack
![]() $\unicode[STIX]{x1D6FC}$
. These unstable modes are easily discernible from the cloud of non-descript stable modes, similar to airfoil results in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The oscillatory mode is unstable for small values of
$\unicode[STIX]{x1D6FC}$
. These unstable modes are easily discernible from the cloud of non-descript stable modes, similar to airfoil results in Crouch et al. (Reference Crouch, Garbaruk and Magidov2007). The oscillatory mode is unstable for small values of
![]() $\unicode[STIX]{x1D6FD}$
, corresponding to a long spanwise wavelength (
$\unicode[STIX]{x1D6FD}$
, corresponding to a long spanwise wavelength (
![]() $\tilde{\unicode[STIX]{x1D706}}=2\unicode[STIX]{x03C0}c/\unicode[STIX]{x1D6FD}$
) greater than
$\tilde{\unicode[STIX]{x1D706}}=2\unicode[STIX]{x03C0}c/\unicode[STIX]{x1D6FD}$
) greater than
![]() $10c$
. The growth rate is nearly constant for
$10c$
. The growth rate is nearly constant for
![]() $0\leqslant \unicode[STIX]{x1D6FD}<0.45$
, and then drops to zero around
$0\leqslant \unicode[STIX]{x1D6FD}<0.45$
, and then drops to zero around
![]() $\unicode[STIX]{x1D6FD}\approx 0.5$
. The critical wavenumber (at the angle of attack for instability onset) is near
$\unicode[STIX]{x1D6FD}\approx 0.5$
. The critical wavenumber (at the angle of attack for instability onset) is near
![]() $\unicode[STIX]{x1D6FD}\approx 0.48$
. As the angle of attack increases, the 2-D mode with
$\unicode[STIX]{x1D6FD}\approx 0.48$
. As the angle of attack increases, the 2-D mode with
![]() $\unicode[STIX]{x1D6FD}=0$
is dominant. The oscillatory-mode frequency at
$\unicode[STIX]{x1D6FD}=0$
is dominant. The oscillatory-mode frequency at
![]() $\unicode[STIX]{x1D6FD}=0$
is
$\unicode[STIX]{x1D6FD}=0$
is
![]() $\unicode[STIX]{x1D714}_{r}\approx 0.42$
(
$\unicode[STIX]{x1D714}_{r}\approx 0.42$
(
![]() $St\approx 0.07$
), slightly increasing to
$St\approx 0.07$
), slightly increasing to
![]() $\unicode[STIX]{x1D714}_{r}\approx 0.46$
at
$\unicode[STIX]{x1D714}_{r}\approx 0.46$
at
![]() $\unicode[STIX]{x1D6FD}=0.5$
. The stationary mode occurs at larger values of
$\unicode[STIX]{x1D6FD}=0.5$
. The stationary mode occurs at larger values of
![]() $\unicode[STIX]{x1D6FD}$
and is characterized by spanwise wavelengths ranging from approximately
$\unicode[STIX]{x1D6FD}$
and is characterized by spanwise wavelengths ranging from approximately
![]() $0.05c{-}1.5c$
. This mode is unstable over a wide range of
$0.05c{-}1.5c$
. This mode is unstable over a wide range of
![]() $\unicode[STIX]{x1D6FD}$
, and displays two maximums in the growth rate – one with intermediate wavelengths around
$\unicode[STIX]{x1D6FD}$
, and displays two maximums in the growth rate – one with intermediate wavelengths around
![]() $\unicode[STIX]{x1D6FD}=6$
and another with short wavelengths around
$\unicode[STIX]{x1D6FD}=6$
and another with short wavelengths around
![]() $\unicode[STIX]{x1D6FD}=45$
. These modes have significantly higher growth rates and become critical at conditions close to the oscillatory-mode critical conditions.
$\unicode[STIX]{x1D6FD}=45$
. These modes have significantly higher growth rates and become critical at conditions close to the oscillatory-mode critical conditions.

Figure 3. Instability growth rates at
![]() $M=0.73$
,
$M=0.73$
,
![]() $Re=3\times 10^{6}$
as a function of
$Re=3\times 10^{6}$
as a function of
![]() $\unicode[STIX]{x1D6FD}$
for (a) oscillatory modes and (b) stationary modes (OAT15A).
$\unicode[STIX]{x1D6FD}$
for (a) oscillatory modes and (b) stationary modes (OAT15A).
The observation of this spanwise-periodic stationary mode is similar to earlier findings for separated low-Reynolds-number airfoils (Rodriguez & Theofilis Reference Rodriguez and Theofilis2011). In that case, the stationary modes were viewed as a possible mechanism for the origin of stall cells. The role of these modes was later questioned in the work of Gioria et al. (Reference Gioria, He, Perez and Theofilis2016), which showed them to be stable and showed an unsteady mode to be less stable (i.e. more dominant). The stall cells were then linked to a secondary instability associated with the unsteady flow.
In the current analysis, the short-wavelength stationary mode has a wavelength comparable with the shear-layer thickness. This raises questions regarding a potentially non-physical origin for this mode. There is uncertainty about the ability to represent this mode within the RANS framework, since the instability wavelength is comparable with length scales which are modelled within the RANS approach. However, the intermediate-wavelength stationary mode concentrated around
![]() $\unicode[STIX]{x1D6FD}=6$
has a predicted wavelength that is substantially larger than the modelled eddies, and is not suspect as a potential artefact of the RANS modelling.
$\unicode[STIX]{x1D6FD}=6$
has a predicted wavelength that is substantially larger than the modelled eddies, and is not suspect as a potential artefact of the RANS modelling.

Figure 4. Magnitude of
![]() $u$
component of instability for
$u$
component of instability for
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
$\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
![]() $Re=3\times 10^{6}$
with different values of
$Re=3\times 10^{6}$
with different values of
![]() $\unicode[STIX]{x1D6FD}$
: (a)
$\unicode[STIX]{x1D6FD}$
: (a)
![]() $\unicode[STIX]{x1D6FD}=0$
oscillatory, (b)
$\unicode[STIX]{x1D6FD}=0$
oscillatory, (b)
![]() $\unicode[STIX]{x1D6FD}=6$
stationary, (c)
$\unicode[STIX]{x1D6FD}=6$
stationary, (c)
![]() $\unicode[STIX]{x1D6FD}=12$
stationary, (d)
$\unicode[STIX]{x1D6FD}=12$
stationary, (d)
![]() $\unicode[STIX]{x1D6FD}=45$
stationary (OAT15A).
$\unicode[STIX]{x1D6FD}=45$
stationary (OAT15A).
The mode shape for the
![]() $u$
component of the disturbance is shown in figure 4 for different values of
$u$
component of the disturbance is shown in figure 4 for different values of
![]() $\unicode[STIX]{x1D6FD}$
. For
$\unicode[STIX]{x1D6FD}$
. For
![]() $\unicode[STIX]{x1D6FD}=0$
, the oscillatory mode is concentrated around a maximum in the region of the shock with a second concentration in the downstream shear layer that is approximately 20 times weaker than at the shock. The intermediate-wavelength stationary mode (
$\unicode[STIX]{x1D6FD}=0$
, the oscillatory mode is concentrated around a maximum in the region of the shock with a second concentration in the downstream shear layer that is approximately 20 times weaker than at the shock. The intermediate-wavelength stationary mode (
![]() $\unicode[STIX]{x1D6FD}=6$
) has a similar shape, but the magnitude in the shear layer is closer to half the magnitude at the shock. At a value of
$\unicode[STIX]{x1D6FD}=6$
) has a similar shape, but the magnitude in the shear layer is closer to half the magnitude at the shock. At a value of
![]() $\unicode[STIX]{x1D6FD}=12$
, the disturbance magnitude in the shear layer is about the same as in the shock region. Finally, for larger values of
$\unicode[STIX]{x1D6FD}=12$
, the disturbance magnitude in the shear layer is about the same as in the shock region. Finally, for larger values of
![]() $\unicode[STIX]{x1D6FD}$
, the disturbance is concentrated in the shear layer, with minimal impact on the shock. This short-wavelength disturbance corresponds to a spanwise-periodic thickening and thinning of the shear layer downstream of the shock. This can be seen in figure 5, which shows the
$\unicode[STIX]{x1D6FD}$
, the disturbance is concentrated in the shear layer, with minimal impact on the shock. This short-wavelength disturbance corresponds to a spanwise-periodic thickening and thinning of the shear layer downstream of the shock. This can be seen in figure 5, which shows the
![]() $u$
component of the total velocity, constructed by superposing the base flow with a linear finite-amplitude
$u$
component of the total velocity, constructed by superposing the base flow with a linear finite-amplitude
![]() $\unicode[STIX]{x1D6FD}=45$
disturbance (i.e. neglecting any nonlinear mean-flow modification). The disturbance amplitude (the maximum
$\unicode[STIX]{x1D6FD}=45$
disturbance (i.e. neglecting any nonlinear mean-flow modification). The disturbance amplitude (the maximum
![]() $u^{\prime }$
value over
$u^{\prime }$
value over
![]() $U_{\infty }$
) is set to an extremely high value of 30 % to make the spanwise changes to the flow more discernible. The two images correspond to the extremes in the base flow modification and are spaced a half-wavelength apart. Even with this large amplitude, the differences in the total flow field are fairly modest. Table 1 summarizes the key attributes of the different modes of instability.
$U_{\infty }$
) is set to an extremely high value of 30 % to make the spanwise changes to the flow more discernible. The two images correspond to the extremes in the base flow modification and are spaced a half-wavelength apart. Even with this large amplitude, the differences in the total flow field are fairly modest. Table 1 summarizes the key attributes of the different modes of instability.

Figure 5. Total
![]() $u$
-component of velocity
$u$
-component of velocity
![]() $(\bar{u}+u^{\prime })$
for the
$(\bar{u}+u^{\prime })$
for the
![]() $\unicode[STIX]{x1D6FD}=45$
mode at
$\unicode[STIX]{x1D6FD}=45$
mode at
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
$\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
![]() $Re=3\times 10^{6}$
. Cuts at spanwise locations of the (a) minimum shear-layer thickness and (b) maximum shear-layer thickness (OAT15A).
$Re=3\times 10^{6}$
. Cuts at spanwise locations of the (a) minimum shear-layer thickness and (b) maximum shear-layer thickness (OAT15A).

Figure 6. Stability boundaries for different
![]() $\unicode[STIX]{x1D6FD}$
values corresponding to local maxima of the growth rate at
$\unicode[STIX]{x1D6FD}$
values corresponding to local maxima of the growth rate at
![]() $Re=3\times 10^{6}$
(OAT15A).
$Re=3\times 10^{6}$
(OAT15A).
Table 1. Summary of instability-mode attributes for the unswept OAT15A wing.

The angle of attack corresponding to the onset of the instability for the various modes as a function of Mach number is given by the stability boundary of figure 6. This shows that the oscillatory and stationary modes go unstable at roughly the same conditions. At the lower Mach number, the short-wavelength stationary mode (
![]() $\unicode[STIX]{x1D6FD}\approx 45$
) has a critical angle of attack slightly lower than the oscillatory mode. At higher Mach numbers, the oscillatory mode is the first to go unstable with increasing angle of attack. The
$\unicode[STIX]{x1D6FD}\approx 45$
) has a critical angle of attack slightly lower than the oscillatory mode. At higher Mach numbers, the oscillatory mode is the first to go unstable with increasing angle of attack. The
![]() $\unicode[STIX]{x1D6FD}\approx 6$
stationary instability occurs at an angle of attack that is super-critical to the
$\unicode[STIX]{x1D6FD}\approx 6$
stationary instability occurs at an angle of attack that is super-critical to the
![]() $\unicode[STIX]{x1D6FD}\approx 45$
mode at lower Mach number, but sub-critical at higher Mach number. Absent the short-wavelength stationary mode, the oscillatory mode has the lowest critical angle of attack across the assessed range of Mach numbers. The experimental values in figure 6 are from the experiment of Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009).
$\unicode[STIX]{x1D6FD}\approx 45$
mode at lower Mach number, but sub-critical at higher Mach number. Absent the short-wavelength stationary mode, the oscillatory mode has the lowest critical angle of attack across the assessed range of Mach numbers. The experimental values in figure 6 are from the experiment of Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009).
The existence of the stationary modes could impact the onset of buffet at some conditions by altering the unsteady growth characteristics or by superposition of a 3-D flow structure. To fully assess the post-critical effects of the stationary modes, the oscillatory mode would need to be analysed in conjunction with the stationary mode using weakly nonlinear analysis (Herbert Reference Herbert1983) (or Floquet theory if one of the modes has a chance to become dominant). For an ad hoc assessment of the potential impact of this stationary mode, we consider a sectional analysis that includes a finite-amplitude disturbance superposed on the base flow. This composite base flow is taken from a streamwise cut through the total flow field at a
![]() $z$
position corresponding to a minimum or maximum of the stationary disturbance (as given in figure 5). This stationary-mode alteration to the base flow (neglecting any nonlinear mean-flow modification) shows a minimal impact on the oscillatory-mode growth rate. This suggests that for the OAT15A airfoil the likely effect of these stationary modes is to provide a 3-D structure to the nominally 2-D unsteady flow. This is consistent with observations in the experiments of Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009) for the OAT15A airfoil, but may not generalize to other airfoil sections.
$z$
position corresponding to a minimum or maximum of the stationary disturbance (as given in figure 5). This stationary-mode alteration to the base flow (neglecting any nonlinear mean-flow modification) shows a minimal impact on the oscillatory-mode growth rate. This suggests that for the OAT15A airfoil the likely effect of these stationary modes is to provide a 3-D structure to the nominally 2-D unsteady flow. This is consistent with observations in the experiments of Jacquin et al. (Reference Jacquin, Molton, Deck, Maury and Soulevant2009) for the OAT15A airfoil, but may not generalize to other airfoil sections.

Figure 7. Variation with angle of attack for (a) growth rates of the stationary and oscillatory modes, and (b) oscillatory-mode frequencies for the dominant range of
![]() $\unicode[STIX]{x1D6FD}$
. Results at
$\unicode[STIX]{x1D6FD}$
. Results at
![]() $M=0.73$
and
$M=0.73$
and
![]() $Re=3\times 10^{6}$
(RA16SC1).
$Re=3\times 10^{6}$
(RA16SC1).

Figure 8. Contour plot of pressure-coefficient perturbation for (a)
![]() $t\cdot U_{\infty }/c=44.5$
, and a half-period later (b)
$t\cdot U_{\infty }/c=44.5$
, and a half-period later (b)
![]() $t\cdot U_{\infty }/c=51.5$
. Results at
$t\cdot U_{\infty }/c=51.5$
. Results at
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
$\unicode[STIX]{x1D6FC}=3.2^{\circ }$
and
![]() $Re=3\times 10^{6}$
(OAT15A).
$Re=3\times 10^{6}$
(OAT15A).

Figure 9. Contour plot of pressure-coefficient perturbation for (a)
![]() $t\cdot U_{\infty }/c=85$
, (b)
$t\cdot U_{\infty }/c=85$
, (b)
![]() $t\cdot U_{\infty }/c=125$
and (c)
$t\cdot U_{\infty }/c=125$
and (c)
![]() $t\cdot U_{\infty }/c=165$
. Results at
$t\cdot U_{\infty }/c=165$
. Results at
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.3^{\circ }$
and
$\unicode[STIX]{x1D6FC}=3.3^{\circ }$
and
![]() $Re=3\times 10^{6}$
(OAT15A).
$Re=3\times 10^{6}$
(OAT15A).
Results for the RA16SC1 airfoil section also show the short-wavelength mode, but not the intermediate-wavelength mode, for the unswept wing. Figure 7(a) shows the growth rate for the stationary and oscillatory modes for this airfoil as a function of angle of attack for
![]() $M=0.73$
,
$M=0.73$
,
![]() $Re=4\times 10^{6}$
. The shaded zone in this figure corresponds to the observed buffet onset from the experiments of Benoit & Legrain (Reference Benoit and Legrain1987): the flow was steady at
$Re=4\times 10^{6}$
. The shaded zone in this figure corresponds to the observed buffet onset from the experiments of Benoit & Legrain (Reference Benoit and Legrain1987): the flow was steady at
![]() $2.5^{\circ }$
and unsteady at
$2.5^{\circ }$
and unsteady at
![]() $3.0^{\circ }$
. The buffet-onset condition is well predicted by the onset of instability for the oscillatory mode. The oscillatory-mode frequency is shown in figure 7(b) for
$3.0^{\circ }$
. The buffet-onset condition is well predicted by the onset of instability for the oscillatory mode. The oscillatory-mode frequency is shown in figure 7(b) for
![]() $\unicode[STIX]{x1D6FD}=0$
and
$\unicode[STIX]{x1D6FD}=0$
and
![]() $\unicode[STIX]{x1D6FD}=0.5$
. The range between the two curves captures the expected frequency resulting from instability growth. The symbols show the measured frequencies
$\unicode[STIX]{x1D6FD}=0.5$
. The range between the two curves captures the expected frequency resulting from instability growth. The symbols show the measured frequencies
![]() $\tilde{f}$
(with the conversion from Hz
$\tilde{f}$
(with the conversion from Hz
![]() $\unicode[STIX]{x1D714}_{r}/\tilde{f}=2\unicode[STIX]{x03C0}c/U_{\infty }=0.0045s$
), which are in good agreement with the stability analysis. This agreement between the predicted and measured onset conditions further suggests that the short-wavelength mode may be non-physical, or not physically significant for buffet.
$\unicode[STIX]{x1D714}_{r}/\tilde{f}=2\unicode[STIX]{x03C0}c/U_{\infty }=0.0045s$
), which are in good agreement with the stability analysis. This agreement between the predicted and measured onset conditions further suggests that the short-wavelength mode may be non-physical, or not physically significant for buffet.
4 URANS simulations for the unswept wing
To further evaluate the interplay of the different instability modes, URANS simulations are conducted at near-onset conditions. The same code that is used for calculating the steady base flows (Shur et al. Reference Shur, Strelets and Travin2004) is run in a time-accurate mode (i.e. with spatially constant time step ensuring a CFL number less than 1.0) starting with a steady solution. Time derivatives are approximated with second-order backward differences (three-layer scheme) with sub-iterations. Earlier studies have shown the unsteady code to provide accurate and reliable solutions for URANS simulations, large-eddy simulations (LES), and direct numerical simulations (DNS) (Shur et al. Reference Shur, Spalart, Squires, Strelets and Travin2000; Spalart, Strelets & Travin Reference Spalart, Strelets and Travin2006; Spalart et al. Reference Spalart, Belyaev, Garbaruk, Shur, Strelets and Travin2017).
The computational grid uses the identical (
![]() $x,y$
) grid used in the stability analysis, distributed spanwise over the domain
$x,y$
) grid used in the stability analysis, distributed spanwise over the domain
![]() $L_{z}$
with uniform spacing. Two spanwise grids are employed in the simulations:
$L_{z}$
with uniform spacing. Two spanwise grids are employed in the simulations:
![]() $L_{z}=2c$
with
$L_{z}=2c$
with
![]() $\unicode[STIX]{x0394}z=0.005c$
, and
$\unicode[STIX]{x0394}z=0.005c$
, and
![]() $L_{z}=4c$
with
$L_{z}=4c$
with
![]() $\unicode[STIX]{x0394}z=0.01c$
. Periodic boundary conditions are applied at the spanwise ends of the domain. The initial steady-flow field is generated by replicating the deeply converged 2-D RANS solutions (as used for the base flow in the stability analysis) over the spanwise domain with zero spanwise velocity. To investigate conditions very close to the instability onset, the initial steady field is perturbed with an instability mode with a wavelength observed in neighbouring URANS simulations and an amplitude of
$\unicode[STIX]{x0394}z=0.01c$
. Periodic boundary conditions are applied at the spanwise ends of the domain. The initial steady-flow field is generated by replicating the deeply converged 2-D RANS solutions (as used for the base flow in the stability analysis) over the spanwise domain with zero spanwise velocity. To investigate conditions very close to the instability onset, the initial steady field is perturbed with an instability mode with a wavelength observed in neighbouring URANS simulations and an amplitude of
![]() $10^{-5}$
. This is done to decrease the time needed to observe the onset of unsteadiness, which otherwise can be extremely long, thus demanding very large time samples.
$10^{-5}$
. This is done to decrease the time needed to observe the onset of unsteadiness, which otherwise can be extremely long, thus demanding very large time samples.
Simulations are conducted at several angles of attack for
![]() $M=0.72$
, 0.73, 0.74. At
$M=0.72$
, 0.73, 0.74. At
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.2^{\circ }$
the flow goes unsteady with an oscillation frequency of
$\unicode[STIX]{x1D6FC}=3.2^{\circ }$
the flow goes unsteady with an oscillation frequency of
![]() $\unicode[STIX]{x1D714}_{r}=0.46$
and is uniform in the spanwise direction. Figure 8 shows the coefficient of pressure on the wing upper surface for the unsteady perturbation. The two snapshots correspond to extrema in the unsteady oscillation, separated by one half of the oscillation period. At this low amplitude, the shock movement is very small, so the primary difference observed is in the sign of the perturbation.
$\unicode[STIX]{x1D714}_{r}=0.46$
and is uniform in the spanwise direction. Figure 8 shows the coefficient of pressure on the wing upper surface for the unsteady perturbation. The two snapshots correspond to extrema in the unsteady oscillation, separated by one half of the oscillation period. At this low amplitude, the shock movement is very small, so the primary difference observed is in the sign of the perturbation.
A sequence of surface-perturbation snapshots for
![]() $M=0.73$
,
$M=0.73$
,
![]() $\unicode[STIX]{x1D6FC}=3.3^{\circ }$
is shown in figure 9. The flow initially (not shown) goes unsteady with a spanwise-uniform perturbation at
$\unicode[STIX]{x1D6FC}=3.3^{\circ }$
is shown in figure 9. The flow initially (not shown) goes unsteady with a spanwise-uniform perturbation at
![]() $\unicode[STIX]{x1D714}_{r}=0.41$
, similar to figure 8. As the unsteadiness increases, a spanwise-varying disturbance begins to grow as shown in figure 9(a). This perturbation amplifies a few orders of magnitude, resulting in a disturbance field corresponding to the stationary mode at the intermediate wavelength
$\unicode[STIX]{x1D714}_{r}=0.41$
, similar to figure 8. As the unsteadiness increases, a spanwise-varying disturbance begins to grow as shown in figure 9(a). This perturbation amplifies a few orders of magnitude, resulting in a disturbance field corresponding to the stationary mode at the intermediate wavelength
![]() $\tilde{\unicode[STIX]{x1D706}}=c$
. At larger times, the flow becomes essentially unsteady – ultimately resulting in a large-amplitude spanwise-uniform perturbation with a frequency matching the initial oscillatory mode. Simulations with a larger spanwise domain (
$\tilde{\unicode[STIX]{x1D706}}=c$
. At larger times, the flow becomes essentially unsteady – ultimately resulting in a large-amplitude spanwise-uniform perturbation with a frequency matching the initial oscillatory mode. Simulations with a larger spanwise domain (
![]() $L_{z}=4c$
) show essentially the same spanwise wavelength.
$L_{z}=4c$
) show essentially the same spanwise wavelength.
Simulations conducted at
![]() $M=0.72$
result in steady spanwise-uniform flow for
$M=0.72$
result in steady spanwise-uniform flow for
![]() $\unicode[STIX]{x1D6FC}<3.5^{\circ }$
. At
$\unicode[STIX]{x1D6FC}<3.5^{\circ }$
. At
![]() $\unicode[STIX]{x1D6FC}=3.6^{\circ }$
the simulations show the development of an oscillatory mode of instability with a frequency of
$\unicode[STIX]{x1D6FC}=3.6^{\circ }$
the simulations show the development of an oscillatory mode of instability with a frequency of
![]() $\unicode[STIX]{x1D714}_{r}=0.43$
. This mode is uniform in the spanwise direction. At
$\unicode[STIX]{x1D714}_{r}=0.43$
. This mode is uniform in the spanwise direction. At
![]() $\unicode[STIX]{x1D6FC}=3.7^{\circ }$
the flow shows an initial onset of unsteadiness with a frequency of
$\unicode[STIX]{x1D6FC}=3.7^{\circ }$
the flow shows an initial onset of unsteadiness with a frequency of
![]() $\unicode[STIX]{x1D714}_{r}=0.44$
and no significant spanwise variation. At
$\unicode[STIX]{x1D714}_{r}=0.44$
and no significant spanwise variation. At
![]() $\unicode[STIX]{x1D6FC}=3.8^{\circ }$
, the flow initially displays a spanwise-uniform oscillatory mode with a frequency of
$\unicode[STIX]{x1D6FC}=3.8^{\circ }$
, the flow initially displays a spanwise-uniform oscillatory mode with a frequency of
![]() $\unicode[STIX]{x1D714}_{r}=0.41$
. However, after only a few cycles of oscillation a spanwise-varying stationary disturbance rapidly grows: thus suppressing the oscillatory mode. The stationary disturbance grows three orders of magnitude, resulting in a spanwise-periodic flow structure downstream of the shock, with
$\unicode[STIX]{x1D714}_{r}=0.41$
. However, after only a few cycles of oscillation a spanwise-varying stationary disturbance rapidly grows: thus suppressing the oscillatory mode. The stationary disturbance grows three orders of magnitude, resulting in a spanwise-periodic flow structure downstream of the shock, with
![]() $\unicode[STIX]{x1D6FD}=28$
. This is followed by a nonlinear stage, where the flow becomes unsteady.
$\unicode[STIX]{x1D6FD}=28$
. This is followed by a nonlinear stage, where the flow becomes unsteady.

Figure 10. Neutral stability curves for (a) oscillatory modes, and (b) stationary modes, with S and U showing stable and unstable regions, respectively. Solid symbols are results from URANS, and open symbols are extrapolated URANS results at instability onset. Results at
![]() $M=0.72$
, 0.73, 0.74 and
$M=0.72$
, 0.73, 0.74 and
![]() $Re=3\times 10^{6}$
(OAT15A).
$Re=3\times 10^{6}$
(OAT15A).
Figure 10 shows the different URANS simulation results overlayed on neutral stability curves, for oscillatory (
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D714}_{r}$
) and stationary results (
$\unicode[STIX]{x1D714}_{r}$
) and stationary results (
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}$
) from the linear stability analysis. Each solid symbol corresponds to a URANS simulation. The open symbols are derived from extrapolating simulation growth rates to zero to infer the
$\unicode[STIX]{x1D6FD}$
) from the linear stability analysis. Each solid symbol corresponds to a URANS simulation. The open symbols are derived from extrapolating simulation growth rates to zero to infer the
![]() $\unicode[STIX]{x1D6FC}$
for instability onset; corresponding frequency and wavenumber are taken from the nearest observed simulation value. The results show the simulation-based instability onset is shifted approximately 0.1 higher in
$\unicode[STIX]{x1D6FC}$
for instability onset; corresponding frequency and wavenumber are taken from the nearest observed simulation value. The results show the simulation-based instability onset is shifted approximately 0.1 higher in
![]() $\unicode[STIX]{x1D6FC}$
compared with stability theory. This is similar to the 2-D airfoil results presented in (Crouch et al.
Reference Crouch, Garbaruk, Magidov and Travin2009a
), where the delayed onset was attributed to numerical dissipation, needed for accommodating shocks, in the URANS solutions.
$\unicode[STIX]{x1D6FC}$
compared with stability theory. This is similar to the 2-D airfoil results presented in (Crouch et al.
Reference Crouch, Garbaruk, Magidov and Travin2009a
), where the delayed onset was attributed to numerical dissipation, needed for accommodating shocks, in the URANS solutions.
As shown in figure 10(a), the simulation oscillation frequencies are in good agreement with the stability analysis. The lower branch of the neutral stability curve (i.e. smaller
![]() $\unicode[STIX]{x1D714}_{r}$
) corresponds to
$\unicode[STIX]{x1D714}_{r}$
) corresponds to
![]() $\unicode[STIX]{x1D6FD}=0$
, and the upper branch corresponds to
$\unicode[STIX]{x1D6FD}=0$
, and the upper branch corresponds to
![]() $\unicode[STIX]{x1D6FD}\approx 0.5$
. Due to the limited spanwise extent of the URANS-simulation domain, the oscillatory results are essentially uniform in the spanwise direction: corresponding to the lower branch. Figure 10(b) shows that the observed spanwise wavenumber for stationary disturbances is also in general agreement with the stability analysis. For
$\unicode[STIX]{x1D6FD}\approx 0.5$
. Due to the limited spanwise extent of the URANS-simulation domain, the oscillatory results are essentially uniform in the spanwise direction: corresponding to the lower branch. Figure 10(b) shows that the observed spanwise wavenumber for stationary disturbances is also in general agreement with the stability analysis. For
![]() $M=0.73$
and 0.74, the intermediate wavelength is observed in the simulations, with characteristics in good agreement with the stability results. For
$M=0.73$
and 0.74, the intermediate wavelength is observed in the simulations, with characteristics in good agreement with the stability results. For
![]() $M=0.72$
, the short-wavelength mode is observed. The onset of the short wavelength is shifted by approximately 0.3 in
$M=0.72$
, the short-wavelength mode is observed. The onset of the short wavelength is shifted by approximately 0.3 in
![]() $\unicode[STIX]{x1D6FC}$
relative to the stability theory; a larger offset than observed for the other modes. A comparison of growth rates at
$\unicode[STIX]{x1D6FC}$
relative to the stability theory; a larger offset than observed for the other modes. A comparison of growth rates at
![]() $\unicode[STIX]{x1D6FC}=3.3^{\circ }$
for
$\unicode[STIX]{x1D6FC}=3.3^{\circ }$
for
![]() $M=0.73$
shows
$M=0.73$
shows
![]() $\unicode[STIX]{x1D714}_{i}=0.064$
from stability analysis and
$\unicode[STIX]{x1D714}_{i}=0.064$
from stability analysis and
![]() $\unicode[STIX]{x1D714}_{i}=0.051$
from URANS for the oscillatory mode. For the same conditions, the intermediate-wavelength (
$\unicode[STIX]{x1D714}_{i}=0.051$
from URANS for the oscillatory mode. For the same conditions, the intermediate-wavelength (
![]() $\unicode[STIX]{x1D6FD}\approx 6$
) stationary-mode growth rates are
$\unicode[STIX]{x1D6FD}\approx 6$
) stationary-mode growth rates are
![]() $\unicode[STIX]{x1D714}_{i}=0.28$
and
$\unicode[STIX]{x1D714}_{i}=0.28$
and
![]() $\unicode[STIX]{x1D714}_{i}=0.16$
for the stability analysis and the URANS simulations, respectively.
$\unicode[STIX]{x1D714}_{i}=0.16$
for the stability analysis and the URANS simulations, respectively.
The overall agreement between the simulations and the global stability results is very good for the long-wavelength oscillatory mode and for the intermediate-wavelength stationary mode. The simulations show the short-wavelength mode to be less prominent than would be expected from the stability theory. The simulation onset for this mode occurs at higher
![]() $\unicode[STIX]{x1D6FC}$
, and the growth rates are significantly smaller, than predicted by the stability theory.
$\unicode[STIX]{x1D6FC}$
, and the growth rates are significantly smaller, than predicted by the stability theory.
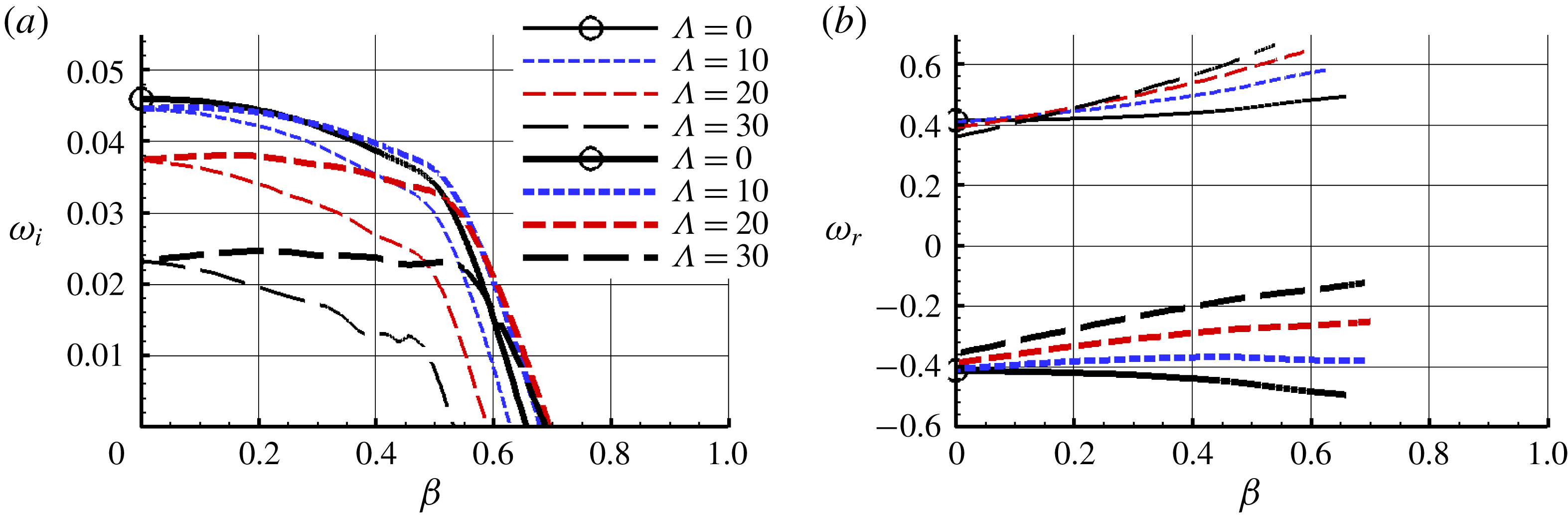
Figure 11. Oscillatory-mode (a) growth rates and (b) frequencies for different sweep angles
![]() $\unicode[STIX]{x1D6EC}=0^{\circ }$
,
$\unicode[STIX]{x1D6EC}=0^{\circ }$
,
![]() $10^{\circ }$
,
$10^{\circ }$
,
![]() $20^{\circ }$
,
$20^{\circ }$
,
![]() $30^{\circ }$
at
$30^{\circ }$
at
![]() $M_{n}=0.73$
,
$M_{n}=0.73$
,
![]() $\unicode[STIX]{x1D6FC}_{n}=3.2^{\circ }$
and
$\unicode[STIX]{x1D6FC}_{n}=3.2^{\circ }$
and
![]() $Re_{n}=3\times 10^{6}$
(OAT15A).
$Re_{n}=3\times 10^{6}$
(OAT15A).
5 Stability results for the swept wing
The infinite-span swept-wing flow is characterized by a quasi-3-D steady state, with the spanwise velocity component
![]() $U_{\infty }\sin \unicode[STIX]{x1D6EC}$
and a normal to the leading edge velocity and Mach number given by
$U_{\infty }\sin \unicode[STIX]{x1D6EC}$
and a normal to the leading edge velocity and Mach number given by
![]() $U_{n}=U_{\infty }\cos \unicode[STIX]{x1D6EC}$
and
$U_{n}=U_{\infty }\cos \unicode[STIX]{x1D6EC}$
and
![]() $M_{n}=M\cos \unicode[STIX]{x1D6EC}$
, respectively, where
$M_{n}=M\cos \unicode[STIX]{x1D6EC}$
, respectively, where
![]() $\unicode[STIX]{x1D6EC}$
is the sweep angle. This leads to a normal to the leading edge Reynolds number of
$\unicode[STIX]{x1D6EC}$
is the sweep angle. This leads to a normal to the leading edge Reynolds number of
![]() $Re_{n}=U_{n}c/\unicode[STIX]{x1D708}$
. To allow direct comparisons between different sweep conditions, we introduce an angle of attack normal to the leading edge defined by
$Re_{n}=U_{n}c/\unicode[STIX]{x1D708}$
. To allow direct comparisons between different sweep conditions, we introduce an angle of attack normal to the leading edge defined by
![]() $\unicode[STIX]{x1D6FC}_{n}=\tan ^{-1}(\tan \unicode[STIX]{x1D6FC}/\cos \unicode[STIX]{x1D6EC})$
; for zero sweep
$\unicode[STIX]{x1D6FC}_{n}=\tan ^{-1}(\tan \unicode[STIX]{x1D6FC}/\cos \unicode[STIX]{x1D6EC})$
; for zero sweep
![]() $\unicode[STIX]{x1D6FC}_{n}\equiv \unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}_{n}\equiv \unicode[STIX]{x1D6FC}$
.
The effect of sweep on the oscillatory-mode growth rate and frequency is shown in figure 11 for fixed values of
![]() $Re_{n}$
,
$Re_{n}$
,
![]() $M_{n}$
and
$M_{n}$
and
![]() $\unicode[STIX]{x1D6FC}_{n}$
. For zero sweep, the growth rate is positive for
$\unicode[STIX]{x1D6FC}_{n}$
. For zero sweep, the growth rate is positive for
![]() $\unicode[STIX]{x1D6FD}$
less than approximately 0.6 with a maximum at
$\unicode[STIX]{x1D6FD}$
less than approximately 0.6 with a maximum at
![]() $\unicode[STIX]{x1D6FD}=0$
. The variation of the frequency is symmetric about the
$\unicode[STIX]{x1D6FD}=0$
. The variation of the frequency is symmetric about the
![]() $\unicode[STIX]{x1D6FD}$
axis, so the spanwise-varying modes show no preferred propagation direction. With the addition of sweep, the symmetry is broken resulting in two distinct branches – one with higher growth rates, and one with lower growth rates for
$\unicode[STIX]{x1D6FD}$
axis, so the spanwise-varying modes show no preferred propagation direction. With the addition of sweep, the symmetry is broken resulting in two distinct branches – one with higher growth rates, and one with lower growth rates for
![]() $\unicode[STIX]{x1D6FD}>0$
. The higher growth-rate branch corresponds to negative frequencies, which suggests a bias toward inboard-propagating waves on a swept wing. As the sweep is increased, the magnitude of the frequency for the inboard-propagating modes becomes lower than for the nominal unswept
$\unicode[STIX]{x1D6FD}>0$
. The higher growth-rate branch corresponds to negative frequencies, which suggests a bias toward inboard-propagating waves on a swept wing. As the sweep is increased, the magnitude of the frequency for the inboard-propagating modes becomes lower than for the nominal unswept
![]() $\unicode[STIX]{x1D6FD}=0$
value.
$\unicode[STIX]{x1D6FD}=0$
value.

Figure 12. Travelling-mode growth rate and frequency as a function of
![]() $\unicode[STIX]{x1D6FD}$
for infinite swept wing with: (a,b)
$\unicode[STIX]{x1D6FD}$
for infinite swept wing with: (a,b)
![]() $\unicode[STIX]{x1D6EC}=10^{\circ }$
, (c,d)
$\unicode[STIX]{x1D6EC}=10^{\circ }$
, (c,d)
![]() $\unicode[STIX]{x1D6EC}=20^{\circ }$
, (e,f)
$\unicode[STIX]{x1D6EC}=20^{\circ }$
, (e,f)
![]() $\unicode[STIX]{x1D6EC}=30^{\circ }$
, at
$\unicode[STIX]{x1D6EC}=30^{\circ }$
, at
![]() $M_{n}=0.73$
and
$M_{n}=0.73$
and
![]() $Re_{n}=3\times 10^{6}$
(OAT15A).
$Re_{n}=3\times 10^{6}$
(OAT15A).
The effect of sweep on the stationary modes is shown in figure 12. For the swept wing, these modes become travelling modes with a positive characteristic frequency that increases with
![]() $\unicode[STIX]{x1D6FD}$
. These modes propagate spanwise in the outboard direction, consistent with observations of buffeting flow in swept-wing experiments. The frequency plots show two characteristic phase speeds
$\unicode[STIX]{x1D6FD}$
. These modes propagate spanwise in the outboard direction, consistent with observations of buffeting flow in swept-wing experiments. The frequency plots show two characteristic phase speeds
![]() $U_{c}=\unicode[STIX]{x1D714}_{r}/\unicode[STIX]{x1D6FD}$
, one for
$U_{c}=\unicode[STIX]{x1D714}_{r}/\unicode[STIX]{x1D6FD}$
, one for
![]() $\unicode[STIX]{x1D6FD}<10$
and another for
$\unicode[STIX]{x1D6FD}<10$
and another for
![]() $\unicode[STIX]{x1D6FD}>10$
. The frequency associated with the short-wavelength mode is roughly an order of magnitude larger than for the intermediate-wavelength mode. As the sweep angle is increased, the intermediate-wavelength mode (
$\unicode[STIX]{x1D6FD}>10$
. The frequency associated with the short-wavelength mode is roughly an order of magnitude larger than for the intermediate-wavelength mode. As the sweep angle is increased, the intermediate-wavelength mode (
![]() $\unicode[STIX]{x1D6FD}\approx 6$
) becomes more dominant at near-critical conditions. For a sweep angle of
$\unicode[STIX]{x1D6FD}\approx 6$
) becomes more dominant at near-critical conditions. For a sweep angle of
![]() $30^{\circ }$
, the wavelengths around
$30^{\circ }$
, the wavelengths around
![]() $\unicode[STIX]{x1D6FD}=6$
(
$\unicode[STIX]{x1D6FD}=6$
(
![]() $\tilde{\unicode[STIX]{x1D706}}\approx c$
) are the first to become unstable with increasing angle of attack. These modes link continuously to the short-wavelength travelling modes with increasing angle of attack. This is seen more clearly in figure 13, which provides a zoomed-in view of the growth rate and frequency at smaller values of
$\tilde{\unicode[STIX]{x1D706}}\approx c$
) are the first to become unstable with increasing angle of attack. These modes link continuously to the short-wavelength travelling modes with increasing angle of attack. This is seen more clearly in figure 13, which provides a zoomed-in view of the growth rate and frequency at smaller values of
![]() $\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6FD}$
for
![]() $\unicode[STIX]{x1D6EC}=30^{\circ }$
.
$\unicode[STIX]{x1D6EC}=30^{\circ }$
.
The critical angles of attack
![]() $\unicode[STIX]{x1D6FC}_{n}$
and
$\unicode[STIX]{x1D6FC}_{n}$
and
![]() $\unicode[STIX]{x1D6FC}$
for the onset of instability for the various modes as functions of the sweep angle
$\unicode[STIX]{x1D6FC}$
for the onset of instability for the various modes as functions of the sweep angle
![]() $\unicode[STIX]{x1D6EC}$
are shown by the stability boundaries of figure 14. The critical
$\unicode[STIX]{x1D6EC}$
are shown by the stability boundaries of figure 14. The critical
![]() $\unicode[STIX]{x1D6FC}_{n}$
for onset of instability is nearly constant with sweep angle, while the critical
$\unicode[STIX]{x1D6FC}_{n}$
for onset of instability is nearly constant with sweep angle, while the critical
![]() $\unicode[STIX]{x1D6FC}$
shows a slight reduction with increasing sweep. The relative ordering of the modes does not change significantly with sweep, except that the
$\unicode[STIX]{x1D6FC}$
shows a slight reduction with increasing sweep. The relative ordering of the modes does not change significantly with sweep, except that the
![]() $\unicode[STIX]{x1D6FD}\approx 6$
modes become subcritical to the short-wavelength travelling modes for
$\unicode[STIX]{x1D6FD}\approx 6$
modes become subcritical to the short-wavelength travelling modes for
![]() $\unicode[STIX]{x1D6EC}>25^{\circ }$
. Similar to the unswept wing, both the oscillatory and the travelling modes can be expected to play some role in the buffet onset. However, in this case both modes are propagating modes with non-zero frequency.
$\unicode[STIX]{x1D6EC}>25^{\circ }$
. Similar to the unswept wing, both the oscillatory and the travelling modes can be expected to play some role in the buffet onset. However, in this case both modes are propagating modes with non-zero frequency.

Figure 13. Travelling-mode (a) growth rate and (b) frequency as a function of
![]() $\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6FD}$
for
![]() $\unicode[STIX]{x1D6EC}=30^{\circ }$
. Results for different values of
$\unicode[STIX]{x1D6EC}=30^{\circ }$
. Results for different values of
![]() $\unicode[STIX]{x1D6FC}_{n}$
with
$\unicode[STIX]{x1D6FC}_{n}$
with
![]() $M_{n}=0.73$
,
$M_{n}=0.73$
,
![]() $Re_{n}=3\times 10^{6}$
(OAT15A).
$Re_{n}=3\times 10^{6}$
(OAT15A).

Figure 14. Stability boundaries as a function of sweep for different
![]() $\unicode[STIX]{x1D6FD}$
values corresponding to local maxima of the growth rate. Results in terms of (a)
$\unicode[STIX]{x1D6FD}$
values corresponding to local maxima of the growth rate. Results in terms of (a)
![]() $\unicode[STIX]{x1D6FC}_{n}$
and (b)
$\unicode[STIX]{x1D6FC}_{n}$
and (b)
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $M_{n}=0.73$
and
$M_{n}=0.73$
and
![]() $Re_{n}=3\times 10^{6}$
(OAT15A).
$Re_{n}=3\times 10^{6}$
(OAT15A).
Focusing on the
![]() $30^{\circ }$
-sweep condition, there are two groups of modes that are expected to contribute to the unsteady-flow structure. First, the generalization of the airfoil oscillatory mode exists within a frequency range of
$30^{\circ }$
-sweep condition, there are two groups of modes that are expected to contribute to the unsteady-flow structure. First, the generalization of the airfoil oscillatory mode exists within a frequency range of
![]() $0.15<\unicode[STIX]{x1D714}_{r}<0.35$
(
$0.15<\unicode[STIX]{x1D714}_{r}<0.35$
(
![]() $0.024<St<0.056$
), which propagates inboard with a phase speed
$0.024<St<0.056$
), which propagates inboard with a phase speed
![]() $U_{c}<-0.2$
. This mode also exists within a frequency range of
$U_{c}<-0.2$
. This mode also exists within a frequency range of
![]() $0.35<\unicode[STIX]{x1D714}_{r}<0.6$
(
$0.35<\unicode[STIX]{x1D714}_{r}<0.6$
(
![]() $0.056<St<0.095$
), which propagates outboard with a phase speed
$0.056<St<0.095$
), which propagates outboard with a phase speed
![]() $U_{c}>1.2$
. These oscillatory modes have spanwise wavelengths of
$U_{c}>1.2$
. These oscillatory modes have spanwise wavelengths of
![]() $\tilde{\unicode[STIX]{x1D706}}>10c$
. Based on the growth rates, the inboard-propagating mode is expected to be more dominant. Second, the intermediate-wavelength mode exists in a frequency band centred around
$\tilde{\unicode[STIX]{x1D706}}>10c$
. Based on the growth rates, the inboard-propagating mode is expected to be more dominant. Second, the intermediate-wavelength mode exists in a frequency band centred around
![]() $\unicode[STIX]{x1D714}_{r}\approx 2.4$
(
$\unicode[STIX]{x1D714}_{r}\approx 2.4$
(
![]() $St\approx 0.38$
). This mode has spanwise wavelengths around
$St\approx 0.38$
). This mode has spanwise wavelengths around
![]() $\tilde{\unicode[STIX]{x1D706}}\approx c$
and an outboard-propagating phase speed of
$\tilde{\unicode[STIX]{x1D706}}\approx c$
and an outboard-propagating phase speed of
![]() $U_{c}\approx 0.4$
.
$U_{c}\approx 0.4$
.
The experiments of Dandois (Reference Dandois2016) on the
![]() $30^{\circ }$
finite-span swept OAT15A also showed two distinct oscillation frequencies. In the mid span, an inboard-propagating disturbance was observed, with a frequency around
$30^{\circ }$
finite-span swept OAT15A also showed two distinct oscillation frequencies. In the mid span, an inboard-propagating disturbance was observed, with a frequency around
![]() $St=0.04$
and a wavelength longer than the model span (
$St=0.04$
and a wavelength longer than the model span (
![]() $\tilde{\unicode[STIX]{x1D706}}>5c$
,
$\tilde{\unicode[STIX]{x1D706}}>5c$
,
![]() $b=3.4c$
). The phase speed for this disturbance was
$b=3.4c$
). The phase speed for this disturbance was
![]() $U_{c}=-0.21$
. The other oscillation frequency was more dominant farther outboard, and was banded around
$U_{c}=-0.21$
. The other oscillation frequency was more dominant farther outboard, and was banded around
![]() $St=0.26$
. These were outboard propagating disturbances with wavelengths around
$St=0.26$
. These were outboard propagating disturbances with wavelengths around
![]() $\tilde{\unicode[STIX]{x1D706}}=c$
and a phase speed of
$\tilde{\unicode[STIX]{x1D706}}=c$
and a phase speed of
![]() $U_{c}\approx 0.4$
. The characteristics of these experimentally observed disturbances are in very good agreement with the dominant modes predicted by the global instability analysis. In particular, the travelling modes on a swept wing (that can co-exist with the low-frequency oscillatory mode) result in a more broad-banded frequency response with a characteristic frequency that is roughly 10 times greater than the swept long-wavelength oscillatory mode, or about 6 times greater than the unswept oscillatory mode for the same airfoil section.
$U_{c}\approx 0.4$
. The characteristics of these experimentally observed disturbances are in very good agreement with the dominant modes predicted by the global instability analysis. In particular, the travelling modes on a swept wing (that can co-exist with the low-frequency oscillatory mode) result in a more broad-banded frequency response with a characteristic frequency that is roughly 10 times greater than the swept long-wavelength oscillatory mode, or about 6 times greater than the unswept oscillatory mode for the same airfoil section.
Table 2. Summary of instability-mode attributes for the swept OAT15A wing, with
![]() $\unicode[STIX]{x1D6EC}=30^{\circ }$
.
$\unicode[STIX]{x1D6EC}=30^{\circ }$
.

The mode shapes associated with the different values of
![]() $\unicode[STIX]{x1D6FD}$
(as shown in figure 4) remain essentially the same with increasing sweep. Thus, the unsteady modes at
$\unicode[STIX]{x1D6FD}$
(as shown in figure 4) remain essentially the same with increasing sweep. Thus, the unsteady modes at
![]() $\unicode[STIX]{x1D6FD}\approx 0$
and
$\unicode[STIX]{x1D6FD}\approx 0$
and
![]() $\unicode[STIX]{x1D6FD}=6$
have similar spatial distributions: concentrated at the shock and the shear layer, consistent with buffeting flow. The
$\unicode[STIX]{x1D6FD}=6$
have similar spatial distributions: concentrated at the shock and the shear layer, consistent with buffeting flow. The
![]() $\unicode[STIX]{x1D6FD}=45$
mode is concentrated in the shear layer and corresponds to a band of higher-frequency undulations of the shear-layer thickness, with
$\unicode[STIX]{x1D6FD}=45$
mode is concentrated in the shear layer and corresponds to a band of higher-frequency undulations of the shear-layer thickness, with
![]() $\unicode[STIX]{x1D714}\approx 12$
(
$\unicode[STIX]{x1D714}\approx 12$
(
![]() $St\approx 2$
). The experiments of Dandois (Reference Dandois2016) also showed shear-layer fluctuations around this frequency, but in the experiments they were linked to the Kelvin–Helmholtz instability. Thus, the experiments do not provide any clear evidence for the predicted short-wavelength modes.
$St\approx 2$
). The experiments of Dandois (Reference Dandois2016) also showed shear-layer fluctuations around this frequency, but in the experiments they were linked to the Kelvin–Helmholtz instability. Thus, the experiments do not provide any clear evidence for the predicted short-wavelength modes.
Table 2 summarizes the key attributes of the different modes of instability for the infinite swept wing. These are all unsteady modes, but the intermediate- and long-wavelength modes are most clearly linked to swept-wing buffet. The short-wavelength modes do not produce a buffet-type flow oscillation. The long-wavelength modes have lower growth rates compared with the intermediate-wavelength modes, but for a given amplitude they would result in a larger wing-lift fluctuation. For the more general finite swept wing, the taper and twist would result in a spanwise localization of the instability. In this case, the instabilities are expected to originate in a spanwise region that carries the highest sectional lift. This is analogous to vortex shedding originating at the location of maximum diameter for a wavy cylinder (Garbaruk & Crouch Reference Garbaruk and Crouch2011). The finite wing 3-D eigenmodes calculated by Timme (Reference Timme2019), while based on a different wing geometry, all display the expected spanwise localization of the instability.
Note finally that the introduction of sweep for the RA16SC1 airfoil section has a minimal effect on the long-wavelength oscillatory-mode characteristics, but a more significant impact on the intermediate- and short-wavelength travelling modes. For sweep angles up to
![]() $20^{\circ }$
, this airfoil shows only one local maximum in the travelling-mode growth rate corresponding to the short-wavelength mode around
$20^{\circ }$
, this airfoil shows only one local maximum in the travelling-mode growth rate corresponding to the short-wavelength mode around
![]() $\unicode[STIX]{x1D6FD}\approx 50$
. At a sweep angle of
$\unicode[STIX]{x1D6FD}\approx 50$
. At a sweep angle of
![]() $30^{\circ }$
, there are two local maximums corresponding to the short-wavelength mode and the intermediate-wavelength mode around
$30^{\circ }$
, there are two local maximums corresponding to the short-wavelength mode and the intermediate-wavelength mode around
![]() $\unicode[STIX]{x1D6FD}\approx 5$
.
$\unicode[STIX]{x1D6FD}\approx 5$
.
6 Summary and conclusions
Earlier studies on airfoils linked the transonic buffet onset to a nominally 2-D global flow instability. Stability analysis predicts the buffet boundary, the buffet frequencies and the post-buffet unsteady-flow characteristics for airfoils. Observations of swept-wing buffet showed distinct characteristics that suggested the global instability approach may not be appropriate for this more complex flow. Experiments at ONERA (Benoit & Legrain Reference Benoit and Legrain1987; Molton et al. Reference Molton, Dandois, Lepage, Brunet and Bur2013; Dandois Reference Dandois2016) show a broad-band of frequencies associated with swept-wing buffet, in contrast to a single dominant frequency for an unswept airfoil. The swept-wing frequencies are also 4–7 times higher than for the unswept airfoil. The experiments, and numerical simulations of Iovnovich & Raveh (Reference Iovnovich and Raveh2014) and Ohmichi et al. (Reference Ohmichi, Ishida and Hashimoto2017), also show the swept-wing buffet has a spanwise dependence that is consistent with a spanwise-propagating disturbance.
This paper extends the global instability analysis to more broadly consider spanwise variations of the buffeting flow and effects of sweep.
For the unswept wing, the analysis reveals stationary modes in addition to the oscillatory mode observed on 2-D airfoils. The stationary modes include a band of short-wavelength modes around
![]() $\tilde{\unicode[STIX]{x1D706}}\approx 0.1c$
and a band of intermediate-wavelength modes around
$\tilde{\unicode[STIX]{x1D706}}\approx 0.1c$
and a band of intermediate-wavelength modes around
![]() $\tilde{\unicode[STIX]{x1D706}}\approx c$
. The short-wavelength modes are concentrated in the shear layer downstream of the shock with wavelengths comparable with the shear-layer thickness. The intermediate-wavelength modes have wavelengths much greater than the shear-layer thickness, and are concentrated both in the shock and the shear layer – similar to the long-wavelength oscillatory mode linked to buffet. These findings from the stability analysis are supported by results from numerical simulations based on the URANS equations.
$\tilde{\unicode[STIX]{x1D706}}\approx c$
. The short-wavelength modes are concentrated in the shear layer downstream of the shock with wavelengths comparable with the shear-layer thickness. The intermediate-wavelength modes have wavelengths much greater than the shear-layer thickness, and are concentrated both in the shock and the shear layer – similar to the long-wavelength oscillatory mode linked to buffet. These findings from the stability analysis are supported by results from numerical simulations based on the URANS equations.
With the introduction of sweep, the stationary modes become traveling modes and propagate outboard along the wing. The continuous band of wavelengths results in a broad-banded frequency content. For a wing sweep of
![]() $30^{\circ }$
, the intermediate-wavelength modes are centred on a frequency that is roughly 6 times greater than the nominal oscillatory-mode frequency predicted for the 2-D airfoil. The overall characteristics (frequency, phase speed and flow structure) of the intermediate-wavelength travelling modes are in good agreement with experimental observations on swept wings. The validity and physical significance of the short-wavelength shear-layer modes is unclear since their wavelengths overlap the scales normally averaged as part of the URANS turbulence modelling, and the experimental evidence for these short-wavelength modes is less definitive. Predicted changes to the long-wavelength oscillatory mode as a result of sweep are also in general agreement with experiments. While these long-wavelength modes have smaller growth rates compared with the intermediate-wavelength modes, their spanwise structure is more conducive to driving significant wing-lift fluctuations.
$30^{\circ }$
, the intermediate-wavelength modes are centred on a frequency that is roughly 6 times greater than the nominal oscillatory-mode frequency predicted for the 2-D airfoil. The overall characteristics (frequency, phase speed and flow structure) of the intermediate-wavelength travelling modes are in good agreement with experimental observations on swept wings. The validity and physical significance of the short-wavelength shear-layer modes is unclear since their wavelengths overlap the scales normally averaged as part of the URANS turbulence modelling, and the experimental evidence for these short-wavelength modes is less definitive. Predicted changes to the long-wavelength oscillatory mode as a result of sweep are also in general agreement with experiments. While these long-wavelength modes have smaller growth rates compared with the intermediate-wavelength modes, their spanwise structure is more conducive to driving significant wing-lift fluctuations.
The overall findings of the analysis suggest that the buffet onset on swept wings also stems from a global flow instability, although with a primary instability mode that differs from the mode responsible for unswept airfoil buffet.
Acknowledgements
A version of this paper was presented as AIAA Paper 2018-3229. All computations performed in Saint Petersburg used resources of the Supercomputer Centre ‘Polytechnichesky’ of the Saint-Petersburg Polytechnic University.