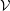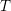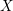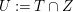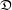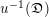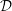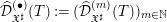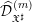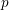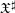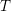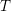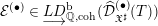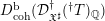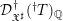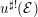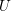Introduction
Soit ![]() ${\mathcal{V}}$ un anneau de valuation discrète complet d’inégales caractéristiques
${\mathcal{V}}$ un anneau de valuation discrète complet d’inégales caractéristiques ![]() $(0,p)$, de corps résiduel parfait et de corps des fractions
$(0,p)$, de corps résiduel parfait et de corps des fractions ![]() $K$. Soit
$K$. Soit ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de ![]() ${\mathcal{V}}$-schémas formels séparés, quasi compacts et lisses,
${\mathcal{V}}$-schémas formels séparés, quasi compacts et lisses, ![]() $T$ un diviseur de
$T$ un diviseur de ![]() $X$ tel que
$X$ tel que ![]() $U:=T\cap Z$ soit un diviseur de
$U:=T\cap Z$ soit un diviseur de ![]() $Z$. Soit
$Z$. Soit ![]() $\mathfrak{D}$ un diviseur à croisements normaux strict de
$\mathfrak{D}$ un diviseur à croisements normaux strict de ![]() $\mathfrak{X}$ tel que
$\mathfrak{X}$ tel que ![]() $u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de
$u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de ![]() ${\mathcal{Z}}$. On pose
${\mathcal{Z}}$. On pose ![]() $\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$,
$\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$, ![]() ${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et
${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et ![]() $u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur
$u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur ![]() ${\mathcal{V}}$. Pour simplifier la présentation de cette introduction, supposons que
${\mathcal{V}}$. Pour simplifier la présentation de cette introduction, supposons que ![]() $u$ soit de codimension pure égale à
$u$ soit de codimension pure égale à ![]() $1$. Pour tout entier
$1$. Pour tout entier ![]() $m\in \mathbb{N}$, on note
$m\in \mathbb{N}$, on note ![]() $\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$, où
$\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$, où ![]() $\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)$ désigne les faisceaux d’anneaux construits par Berthelot dans [Reference BerthelotBer96, 4.2.3] et
$\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)$ désigne les faisceaux d’anneaux construits par Berthelot dans [Reference BerthelotBer96, 4.2.3] et ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{(m)}$ est le faisceau des opérateurs différentiels de niveau
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{(m)}$ est le faisceau des opérateurs différentiels de niveau ![]() $m$ sur
$m$ sur ![]() $\mathfrak{X}$ (voir [Reference BerthelotBer96, 2.2], puis sa version logarithmique dans [Reference MontagnonMon02]), le chapeau signifiant la complétion
$\mathfrak{X}$ (voir [Reference BerthelotBer96, 2.2], puis sa version logarithmique dans [Reference MontagnonMon02]), le chapeau signifiant la complétion ![]() $p$-adique. On dispose de plus des morphismes canoniques de changement de niveaux
$p$-adique. On dispose de plus des morphismes canoniques de changement de niveaux ![]() $\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\rightarrow \widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m+1)}(T)$ (voir [Reference MontagnonMon02] ou, pour sa version non logarithmique, [Reference BerthelotBer96]), ce qui donne le système inductif d’anneaux
$\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\rightarrow \widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m+1)}(T)$ (voir [Reference MontagnonMon02] ou, pour sa version non logarithmique, [Reference BerthelotBer96]), ce qui donne le système inductif d’anneaux ![]() $\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T):=(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T))_{m\in \mathbb{N}}$. Berthelot construit le faisceau des opérateurs différentiels de niveau fini en posant
$\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T):=(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T))_{m\in \mathbb{N}}$. Berthelot construit le faisceau des opérateurs différentiels de niveau fini en posant ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}:=\underset{\underset{m}{\longrightarrow }}{\lim }\,\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\otimes _{\mathbb{Z}}\mathbb{Q}$. Par tensorisation par
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}:=\underset{\underset{m}{\longrightarrow }}{\lim }\,\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\otimes _{\mathbb{Z}}\mathbb{Q}$. Par tensorisation par ![]() $\mathbb{Q}$ et passage à la limite sur le niveau, on obtient le foncteur noté
$\mathbb{Q}$ et passage à la limite sur le niveau, on obtient le foncteur noté ![]() $\varinjlim :D^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$. Afin d’obtenir un foncteur pleinement fidèle qui factorise ce foncteur
$\varinjlim :D^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$. Afin d’obtenir un foncteur pleinement fidèle qui factorise ce foncteur ![]() $\varinjlim$, Berthelot a introduit la catégorie
$\varinjlim$, Berthelot a introduit la catégorie ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ qui est une localisation de
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ qui est une localisation de ![]() $D^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. Il a défini la sous-catégorie pleine des complexes cohérents de
$D^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. Il a défini la sous-catégorie pleine des complexes cohérents de ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ qu’il note
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ qu’il note ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. Il a établi alors que le foncteur
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. Il a établi alors que le foncteur ![]() $\varinjlim$ induit l’équivalence de catégories
$\varinjlim$ induit l’équivalence de catégories
Soit ![]() ${\mathcal{E}}^{(\bullet )}$ un objet de
${\mathcal{E}}^{(\bullet )}$ un objet de ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ et
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ et ![]() ${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ l’objet de
${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ l’objet de ![]() $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ correspondant. On dispose de
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ correspondant. On dispose de ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$ l’image inverse extraordinaire de
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$ l’image inverse extraordinaire de ![]() ${\mathcal{E}}^{(\bullet )}$ par
${\mathcal{E}}^{(\bullet )}$ par ![]() $u$ et de
$u$ et de ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ le foncteur cohomologique local à support strict dans
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ le foncteur cohomologique local à support strict dans ![]() $Z$ de
$Z$ de ![]() ${\mathcal{E}}^{(\bullet )}$. Ces foncteurs s’étendent naturellement à
${\mathcal{E}}^{(\bullet )}$. Ces foncteurs s’étendent naturellement à ![]() $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ et sont compatibles à l’équivalence de catégories (*) ci-dessus, i.e. on bénéficie des isomorphismes canoniques fonctoriels en
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ et sont compatibles à l’équivalence de catégories (*) ci-dessus, i.e. on bénéficie des isomorphismes canoniques fonctoriels en ![]() ${\mathcal{E}}^{(\bullet )}$ de la forme :
${\mathcal{E}}^{(\bullet )}$ de la forme : ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\varinjlim ~\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ et
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\varinjlim ~\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ et ![]() $u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\varinjlim ~\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$. Comme conséquence immédiate de [Reference CaroCar16], on vérifie que les trois propriétés
$u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\varinjlim ~\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$. Comme conséquence immédiate de [Reference CaroCar16], on vérifie que les trois propriétés ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$,
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$, ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ et
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ et ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(T)_{\mathbb{Q}})$ sont équivalentes (voir la preuve de 3.4.8). De plus, si
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(T)_{\mathbb{Q}})$ sont équivalentes (voir la preuve de 3.4.8). De plus, si ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$ alors
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$ alors ![]() $u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$. La réciproque est loin d’être claire. La raison est que pour tout objet
$u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$. La réciproque est loin d’être claire. La raison est que pour tout objet ![]() ${\mathcal{F}}^{(\bullet )}$ de
${\mathcal{F}}^{(\bullet )}$ de ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$, la propriété selon laquelle
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$, la propriété selon laquelle ![]() $\varinjlim ~({\mathcal{F}}^{(\bullet )})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$ n’implique pas en général que
$\varinjlim ~({\mathcal{F}}^{(\bullet )})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$ n’implique pas en général que ![]() ${\mathcal{F}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. Lorsque
${\mathcal{F}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. Lorsque ![]() ${\mathcal{E}}$ est un
${\mathcal{E}}$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent, nous nous intéressons dans ce papier à cette réciproque. Nous prouvons en particulier que si les espaces de cohomologies de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent, nous nous intéressons dans ce papier à cette réciproque. Nous prouvons en particulier que si les espaces de cohomologies de ![]() $u^{\sharp !}({\mathcal{E}})$ sont des isocristaux sur
$u^{\sharp !}({\mathcal{E}})$ sont des isocristaux sur ![]() ${\mathcal{Z}}$ surconvergeant le long d’un diviseur de
${\mathcal{Z}}$ surconvergeant le long d’un diviseur de ![]() $U$, alors
$U$, alors ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$.
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$.
Précisons à présent le contenu de ce papier. Dans le premier chapitre, nous donnons quelques préliminaires topologiques concernant les ![]() $K$-espaces topologiques localement convexes. Nous rappelons notamment la définition des espaces de type LB et nous reprenons quelques points sur les produits tensoriels complétés de modules localement convexes dans le contexte qui nous sera utile dans la suite de ce travail. Dans le deuxième chapitre, nous munissons naturellement les isocristaux surconvergents et le faisceau des opérateurs différentiels de niveau fini à singularités surconvergentes d’une structure canonique d’espace de type LB. Après quelques propriétés topologiques sur les foncteurs images directes et images inverses extraordinaires par une immersion fermée, nous établissons dans le dernier chapitre le résultat principal décrit en début d’introduction de ce papier. Nous finissons par des applications du théorème principal aux log-isocristaux surconvergents satisfaisant certaines propriétés de type non Liouville. Les résultats que l’on déduit généralisent les propositions [Reference Caro and TsuzukiCT12, 1.3.13, 2.2.9, 2.3.4] et nous obtenons en réalité des preuves plus simples (on utilise néanmoins [Reference Caro and TsuzukiCT12, 1.3.13] et l’on démontre le reste). L’une de ces généralisations est, grâce à une remarque apparue dans un travail en commun avec Tomoyuki Abe (plus précisément, voir la remarque 3.5.4), de ne pas supposer que l’on dispose d’une rétraction lisse
$K$-espaces topologiques localement convexes. Nous rappelons notamment la définition des espaces de type LB et nous reprenons quelques points sur les produits tensoriels complétés de modules localement convexes dans le contexte qui nous sera utile dans la suite de ce travail. Dans le deuxième chapitre, nous munissons naturellement les isocristaux surconvergents et le faisceau des opérateurs différentiels de niveau fini à singularités surconvergentes d’une structure canonique d’espace de type LB. Après quelques propriétés topologiques sur les foncteurs images directes et images inverses extraordinaires par une immersion fermée, nous établissons dans le dernier chapitre le résultat principal décrit en début d’introduction de ce papier. Nous finissons par des applications du théorème principal aux log-isocristaux surconvergents satisfaisant certaines propriétés de type non Liouville. Les résultats que l’on déduit généralisent les propositions [Reference Caro and TsuzukiCT12, 1.3.13, 2.2.9, 2.3.4] et nous obtenons en réalité des preuves plus simples (on utilise néanmoins [Reference Caro and TsuzukiCT12, 1.3.13] et l’on démontre le reste). L’une de ces généralisations est, grâce à une remarque apparue dans un travail en commun avec Tomoyuki Abe (plus précisément, voir la remarque 3.5.4), de ne pas supposer que l’on dispose d’une rétraction lisse ![]() $\mathfrak{X}\rightarrow {\mathcal{Z}}$ de
$\mathfrak{X}\rightarrow {\mathcal{Z}}$ de ![]() $u$ (hypothèse qui apparaît par exemple dans le théorème [Reference Caro and TsuzukiCT12, 1.3.13]).
$u$ (hypothèse qui apparaît par exemple dans le théorème [Reference Caro and TsuzukiCT12, 1.3.13]).
Notations
Dans ce papier, on désigne par ![]() ${\mathcal{V}}$ un anneau de valuation discrète complet d’inégales caractéristiques
${\mathcal{V}}$ un anneau de valuation discrète complet d’inégales caractéristiques ![]() $(0,p)$,
$(0,p)$, ![]() $k$ son corps résiduel supposé parfait,
$k$ son corps résiduel supposé parfait, ![]() $K$ son corps des fractions et
$K$ son corps des fractions et ![]() $\unicode[STIX]{x1D70B}$ une uniformisante. Les faisceaux seront notés par des lettres calligraphiques, leurs sections globales par la lettre droite associée. Les modules sont par défaut à gauche. On notera avec des chapeaux les complétions
$\unicode[STIX]{x1D70B}$ une uniformisante. Les faisceaux seront notés par des lettres calligraphiques, leurs sections globales par la lettre droite associée. Les modules sont par défaut à gauche. On notera avec des chapeaux les complétions ![]() $p$-adiques et si
$p$-adiques et si ![]() ${\mathcal{E}}$ est un faisceau en groupes abéliens, alors on posera
${\mathcal{E}}$ est un faisceau en groupes abéliens, alors on posera ![]() ${\mathcal{E}}_{\mathbb{Q}}:={\mathcal{E}}\otimes _{\mathbb{Z}}\mathbb{Q}$. Soit
${\mathcal{E}}_{\mathbb{Q}}:={\mathcal{E}}\otimes _{\mathbb{Z}}\mathbb{Q}$. Soit ![]() ${\mathcal{A}}$ un faisceau d’anneaux sur un espace topologique
${\mathcal{A}}$ un faisceau d’anneaux sur un espace topologique ![]() $X$. Si
$X$. Si ![]() $\ast$ est l’un des symboles
$\ast$ est l’un des symboles ![]() $+$,
$+$, ![]() $-$ ou
$-$ ou ![]() $\text{b}$,
$\text{b}$, ![]() $D^{\ast }({\mathcal{A}})$ désigne la catégorie dérivée des complexes de
$D^{\ast }({\mathcal{A}})$ désigne la catégorie dérivée des complexes de ![]() ${\mathcal{A}}$-modules (à gauche) vérifiant les conditions correspondantes d’annulation des faisceaux de cohomologie. Lorsque l’on souhaite préciser entre droite et gauche, on précise alors comme suit
${\mathcal{A}}$-modules (à gauche) vérifiant les conditions correspondantes d’annulation des faisceaux de cohomologie. Lorsque l’on souhaite préciser entre droite et gauche, on précise alors comme suit ![]() $D^{\ast }(\,^{\text{g}}{\mathcal{A}})$ ou
$D^{\ast }(\,^{\text{g}}{\mathcal{A}})$ ou ![]() $D^{\ast }({\mathcal{A}}^{\text{d}})$. On note
$D^{\ast }({\mathcal{A}}^{\text{d}})$. On note ![]() $D_{\text{coh}}^{\text{b}}({\mathcal{A}})$ la sous-catégorie pleine de
$D_{\text{coh}}^{\text{b}}({\mathcal{A}})$ la sous-catégorie pleine de ![]() $D({\mathcal{A}})$ des complexes à cohomologie cohérente et bornée. On suppose (sans nuire à la généralité) que tous les
$D({\mathcal{A}})$ des complexes à cohomologie cohérente et bornée. On suppose (sans nuire à la généralité) que tous les ![]() $k$-schémas sont réduits et on pourra confondre les diviseurs avec leur support. Les
$k$-schémas sont réduits et on pourra confondre les diviseurs avec leur support. Les ![]() ${\mathcal{V}}$-schémas formels seront indiqués par des lettres calligraphiques ou gothiques et leur fibre spéciale par la lettre droite correspondante.
${\mathcal{V}}$-schémas formels seront indiqués par des lettres calligraphiques ou gothiques et leur fibre spéciale par la lettre droite correspondante.
1 Préliminaires topologiques
Notons ![]() $\mathfrak{C}$ la catégorie des
$\mathfrak{C}$ la catégorie des ![]() $K$-espaces vectoriels topologiques localement convexes. Notons
$K$-espaces vectoriels topologiques localement convexes. Notons ![]() $\mathfrak{D}$ la sous-catégorie pleine de
$\mathfrak{D}$ la sous-catégorie pleine de ![]() $\mathfrak{C}$ des
$\mathfrak{C}$ des ![]() $K$-espaces séparés et complets. On remarque qu’un morphisme surjectif
$K$-espaces séparés et complets. On remarque qu’un morphisme surjectif ![]() $V\rightarrow V\text{sp}\prime \prime$ de
$V\rightarrow V\text{sp}\prime \prime$ de ![]() $\mathfrak{C}$ est le conoyau de son noyau dans
$\mathfrak{C}$ est le conoyau de son noyau dans ![]() $\mathfrak{C}$ si et seulement si
$\mathfrak{C}$ si et seulement si ![]() $V\text{sp}\prime \prime$ est muni de la topologie quotient.
$V\text{sp}\prime \prime$ est muni de la topologie quotient.
1.1 Espaces de type  $LB$
$LB$
Nous agglomérons ce dont nous aurons besoin sur les ![]() $K$-espaces de type
$K$-espaces de type ![]() $LB$, surtout du lemme 1.1.7 mais aussi de sa preuve (voir l’étape
$LB$, surtout du lemme 1.1.7 mais aussi de sa preuve (voir l’étape ![]() $2$ de la preuve de 3.4.6).
$2$ de la preuve de 3.4.6).
1.1.1. Soit ![]() $(V_{i})_{i\in I}$ un système inductif filtrant de
$(V_{i})_{i\in I}$ un système inductif filtrant de ![]() $\mathfrak{C}$. Posons
$\mathfrak{C}$. Posons ![]() $V:=\mathop{\varinjlim }\nolimits_{i}\,V_{i}$ la limite inductive calculée dans
$V:=\mathop{\varinjlim }\nolimits_{i}\,V_{i}$ la limite inductive calculée dans ![]() $\mathfrak{C}$. En tant que
$\mathfrak{C}$. En tant que ![]() $K$-espace vectoriel,
$K$-espace vectoriel, ![]() $V$ est la limite inductive de
$V$ est la limite inductive de ![]() $(V_{i})_{i\in I}$ calculée dans la catégorie des
$(V_{i})_{i\in I}$ calculée dans la catégorie des ![]() $K$-espaces vectoriels. La topologie localement convexe sur
$K$-espaces vectoriels. La topologie localement convexe sur ![]() $V$ est la plus fine rendant continu tous les morphismes canoniques
$V$ est la plus fine rendant continu tous les morphismes canoniques ![]() $V_{i}\rightarrow V$.
$V_{i}\rightarrow V$.
Remarque 1.1.2. Soit ![]() $(V_{i})_{i\in I}$ et
$(V_{i})_{i\in I}$ et ![]() $(W_{i})_{i\in I}$ deux systèmes inductifs filtrants de
$(W_{i})_{i\in I}$ deux systèmes inductifs filtrants de ![]() $\mathfrak{C}$,
$\mathfrak{C}$, ![]() $f_{i}:V_{i}\rightarrow W_{i}$ une famille compatible de morphismes de
$f_{i}:V_{i}\rightarrow W_{i}$ une famille compatible de morphismes de ![]() $\mathfrak{C}$ et
$\mathfrak{C}$ et ![]() $f:\mathop{\varinjlim }\nolimits_{i}\,V_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ le morphisme de
$f:\mathop{\varinjlim }\nolimits_{i}\,V_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ le morphisme de ![]() $\mathfrak{C}$ induit par passage à la limite inductive. Si pour tout
$\mathfrak{C}$ induit par passage à la limite inductive. Si pour tout ![]() $i$ l’image de
$i$ l’image de ![]() $f_{i}$ est dense dans
$f_{i}$ est dense dans ![]() $W_{i}$, alors l’image de
$W_{i}$, alors l’image de ![]() $f$ est dense.
$f$ est dense.
En effet, si ![]() $F$ est un fermé de
$F$ est un fermé de ![]() $\mathop{\varinjlim }\nolimits_{i}\,W_{i}$ contenant l’image de
$\mathop{\varinjlim }\nolimits_{i}\,W_{i}$ contenant l’image de ![]() $f$, alors l’image inverse de
$f$, alors l’image inverse de ![]() $F$ sur
$F$ sur ![]() $W_{i}$ est un fermé contenant l’image de
$W_{i}$ est un fermé contenant l’image de ![]() $f_{i}$ qui est dense dans
$f_{i}$ qui est dense dans ![]() $W_{i}$. La flèche canonique
$W_{i}$. La flèche canonique ![]() $W_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ se factorise donc toujours via
$W_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ se factorise donc toujours via ![]() $W_{i}\rightarrow F$. D’où
$W_{i}\rightarrow F$. D’où ![]() $F=\mathop{\varinjlim }\nolimits_{i}\,W_{i}$.
$F=\mathop{\varinjlim }\nolimits_{i}\,W_{i}$.
Lemme 1.1.3. Soit ![]() $(V_{i})_{i\in I}$ et
$(V_{i})_{i\in I}$ et ![]() $(W_{i})_{i\in I}$ deux systèmes inductifs filtrants de
$(W_{i})_{i\in I}$ deux systèmes inductifs filtrants de ![]() $\mathfrak{C}$,
$\mathfrak{C}$, ![]() $f_{i}:V_{i}\rightarrow W_{i}$ une famille compatible de morphismes surjectifs, stricts de
$f_{i}:V_{i}\rightarrow W_{i}$ une famille compatible de morphismes surjectifs, stricts de ![]() $\mathfrak{C}$ et
$\mathfrak{C}$ et ![]() $f:\mathop{\varinjlim }\nolimits_{i}\,V_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ le morphisme de
$f:\mathop{\varinjlim }\nolimits_{i}\,V_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}\,W_{i}$ le morphisme de ![]() $\mathfrak{C}$ induit par passage à la limite inductive. Alors
$\mathfrak{C}$ induit par passage à la limite inductive. Alors ![]() $f$ est un morphisme surjectif strict.
$f$ est un morphisme surjectif strict.
Démonstration.
La surjectivité de ![]() $f$ est déjà connue. Posons
$f$ est déjà connue. Posons ![]() $W:=\mathop{\varinjlim }\nolimits_{i}\,W_{i}$. Comme le morphisme
$W:=\mathop{\varinjlim }\nolimits_{i}\,W_{i}$. Comme le morphisme ![]() $f$ est continu et surjectif, la propriété énonant que
$f$ est continu et surjectif, la propriété énonant que ![]() $f$ est strict est alors équivalente à la propriété suivante : tout morphisme
$f$ est strict est alors équivalente à la propriété suivante : tout morphisme ![]() $g:W\rightarrow W\text{sp}\prime$ tel que
$g:W\rightarrow W\text{sp}\prime$ tel que ![]() $g\circ f$ soit continu est lui-même continu. Soit
$g\circ f$ soit continu est lui-même continu. Soit ![]() $g:W\rightarrow W\text{sp}\prime$ tel que
$g:W\rightarrow W\text{sp}\prime$ tel que ![]() $g\circ f$ soit continu. Notons
$g\circ f$ soit continu. Notons ![]() $g_{i}:W_{i}\rightarrow W\text{sp}\prime$ le composé du morphisme canonique
$g_{i}:W_{i}\rightarrow W\text{sp}\prime$ le composé du morphisme canonique ![]() $W_{i}\rightarrow W$ avec
$W_{i}\rightarrow W$ avec ![]() $g$. Comme
$g$. Comme ![]() $f_{i}$ est surjectif et strict, et comme
$f_{i}$ est surjectif et strict, et comme ![]() $g_{i}\circ f_{i}:V_{i}\rightarrow W\text{sp}\prime$ est continu (car composé de
$g_{i}\circ f_{i}:V_{i}\rightarrow W\text{sp}\prime$ est continu (car composé de ![]() $V_{i}\rightarrow V$ avec
$V_{i}\rightarrow V$ avec ![]() $g\circ f$), les morphismes
$g\circ f$), les morphismes ![]() $g_{i}$ sont alors continus. D’après la propriété universelle de la limite inductive,
$g_{i}$ sont alors continus. D’après la propriété universelle de la limite inductive, ![]() $g$ est donc aussi continu.
$g$ est donc aussi continu.
Lemme 1.1.4. Soit ![]() $(V_{i})_{i\in I}$ un système inductif filtrant de
$(V_{i})_{i\in I}$ un système inductif filtrant de ![]() $\mathfrak{C}$ et
$\mathfrak{C}$ et ![]() $J$ une partie cofinale de
$J$ une partie cofinale de ![]() $I$. On dispose de l’homéomorphisme canonique
$I$. On dispose de l’homéomorphisme canonique ![]() $\mathop{\varinjlim }\nolimits_{j\in J}V_{j}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{i\in I}V_{i}$ dont la bijection sous-jacente est la bijection canonique.
$\mathop{\varinjlim }\nolimits_{j\in J}V_{j}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{i\in I}V_{i}$ dont la bijection sous-jacente est la bijection canonique.
Démonstration.
Standard.
Définition 1.1.5. Un ![]() $K$-espace de type
$K$-espace de type ![]() $LB$ est un
$LB$ est un ![]() $K$-espace localement convexe séparé
$K$-espace localement convexe séparé ![]() $V$ tel qu’il existe, pour tout entier
$V$ tel qu’il existe, pour tout entier ![]() $m\in \mathbb{N}$, des morphismes continus de
$m\in \mathbb{N}$, des morphismes continus de ![]() $K$-espaces de Banach
$K$-espaces de Banach ![]() $V_{m}\rightarrow V_{m+1}$ et un homéomorphisme de la forme
$V_{m}\rightarrow V_{m+1}$ et un homéomorphisme de la forme ![]() $\mathop{\varinjlim }\nolimits_{m}\,V_{m}\overset{{\sim}}{\longrightarrow }\,V$.
$\mathop{\varinjlim }\nolimits_{m}\,V_{m}\overset{{\sim}}{\longrightarrow }\,V$.
Remarque 1.1.6. Dans la définition de ![]() $K$-espace de type
$K$-espace de type ![]() $LB$ de 1.1.5 et avec ses notations, il n’est pas restrictif de supposer que les morphismes
$LB$ de 1.1.5 et avec ses notations, il n’est pas restrictif de supposer que les morphismes ![]() $V_{m}\rightarrow V_{m+1}$ soient injectifs. En effet, si l’on note
$V_{m}\rightarrow V_{m+1}$ soient injectifs. En effet, si l’on note ![]() $j_{m}:V_{m}\rightarrow V$,
$j_{m}:V_{m}\rightarrow V$, ![]() $W_{m}:=V_{m}/\ker j_{m}$ muni de la topologie quotient, topologie qui en fait un
$W_{m}:=V_{m}/\ker j_{m}$ muni de la topologie quotient, topologie qui en fait un ![]() $K$-espace de Banach (car
$K$-espace de Banach (car ![]() $V$ est séparé donc
$V$ est séparé donc ![]() $W_{m}$ est un quotient séparé d’un
$W_{m}$ est un quotient séparé d’un ![]() $K$-espace de Banach), on vérifie par propriété universelle que les morphismes
$K$-espace de Banach), on vérifie par propriété universelle que les morphismes ![]() $K$-linéaires canoniques réciproques
$K$-linéaires canoniques réciproques ![]() $\mathop{\varinjlim }\nolimits_{m}V_{m}\rightarrow \mathop{\varinjlim }\nolimits_{m}W_{m}$ et
$\mathop{\varinjlim }\nolimits_{m}V_{m}\rightarrow \mathop{\varinjlim }\nolimits_{m}W_{m}$ et ![]() $\mathop{\varinjlim }\nolimits_{m}W_{m}\rightarrow \mathop{\varinjlim }\nolimits_{m}V_{m}$ sont continus.
$\mathop{\varinjlim }\nolimits_{m}W_{m}\rightarrow \mathop{\varinjlim }\nolimits_{m}V_{m}$ sont continus.
Lemme 1.1.7. Un quotient séparé d’un espace de type ![]() $LB$ est un espace de type
$LB$ est un espace de type ![]() $LB$.
$LB$.
Démonstration.
Pour tout entier ![]() $m\in \mathbb{N}$, donnons-nous des monomorphismes continus de
$m\in \mathbb{N}$, donnons-nous des monomorphismes continus de ![]() $K$-espaces de Banach
$K$-espaces de Banach ![]() $V_{m}\rightarrow V_{m+1}$. On note
$V_{m}\rightarrow V_{m+1}$. On note ![]() $V:=\mathop{\varinjlim }\nolimits_{m}\,V_{m}$ et
$V:=\mathop{\varinjlim }\nolimits_{m}\,V_{m}$ et ![]() $i_{m}:V_{m}{\hookrightarrow}V$ les monomorphismes continus canoniques. Soit
$i_{m}:V_{m}{\hookrightarrow}V$ les monomorphismes continus canoniques. Soit ![]() $G:=V/W$ un quotient de
$G:=V/W$ un quotient de ![]() $V$ qui est séparé. Notons
$V$ qui est séparé. Notons ![]() $G^{(m)}:=V_{m}/i_{m}^{-1}(W)$ muni de la topologie quotient, i.e. telle que la surjection canonique
$G^{(m)}:=V_{m}/i_{m}^{-1}(W)$ muni de la topologie quotient, i.e. telle que la surjection canonique ![]() $\unicode[STIX]{x1D70B}_{m}:V_{m}{\twoheadrightarrow}G^{(m)}$ soit stricte. Notons
$\unicode[STIX]{x1D70B}_{m}:V_{m}{\twoheadrightarrow}G^{(m)}$ soit stricte. Notons ![]() $j_{m}:G^{(m)}\rightarrow G$ l’injection canonique. Comme
$j_{m}:G^{(m)}\rightarrow G$ l’injection canonique. Comme ![]() $j_{m}\circ \unicode[STIX]{x1D70B}_{m}$ est continu et comme
$j_{m}\circ \unicode[STIX]{x1D70B}_{m}$ est continu et comme ![]() $\unicode[STIX]{x1D70B}_{m}$ est strict,
$\unicode[STIX]{x1D70B}_{m}$ est strict, ![]() $j_{m}$ est donc continu. Comme
$j_{m}$ est donc continu. Comme ![]() $G$ est séparé, il en est alors de même de
$G$ est séparé, il en est alors de même de ![]() $G^{(m)}$. Ainsi
$G^{(m)}$. Ainsi ![]() $G^{(m)}$ est un
$G^{(m)}$ est un ![]() $K$-espace de Banach. Il découle de 1.1.3 que le morphisme de gauche du diagramme canonique
$K$-espace de Banach. Il découle de 1.1.3 que le morphisme de gauche du diagramme canonique

est un épimorphisme strict. Comme il en est de même du morphisme de droite et comme l’isomorphisme du bas est un homéomorphisme, il en est donc de même de l’isomorphisme du haut.
1.2 Topologie projective d’un produit tensoriel sur une  $K$-algèbre
$K$-algèbre
Soit ![]() $D$ une
$D$ une ![]() $K$-algèbre (sans topologie et non nécessairement commutative) telle que
$K$-algèbre (sans topologie et non nécessairement commutative) telle que ![]() $K$ soit dans le centre de
$K$ soit dans le centre de ![]() $D$. Notons
$D$. Notons ![]() $\mathfrak{C}_{D,g}$ (resp.
$\mathfrak{C}_{D,g}$ (resp. ![]() $\mathfrak{C}_{D,d}$) la sous-catégorie pleine de
$\mathfrak{C}_{D,d}$) la sous-catégorie pleine de ![]() $\mathfrak{C}$ des objets de
$\mathfrak{C}$ des objets de ![]() $\mathfrak{C}$ tels que la structure de
$\mathfrak{C}$ tels que la structure de ![]() $K$-espace vectoriel se prolonge en une structure de
$K$-espace vectoriel se prolonge en une structure de ![]() $D$-module à gauche (resp. à droite).
$D$-module à gauche (resp. à droite).
1.2.1. (Application ![]() $D$-balancée continue et complétion.) Soit
$D$-balancée continue et complétion.) Soit ![]() $V$ un objet de
$V$ un objet de ![]() $\mathfrak{C}_{D,d}$,
$\mathfrak{C}_{D,d}$, ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$ et
$\mathfrak{C}_{D,g}$ et ![]() $U$ un objet de
$U$ un objet de ![]() $\mathfrak{C}$. On munit
$\mathfrak{C}$. On munit ![]() $V\times W$ de la topologie produit, i.e.
$V\times W$ de la topologie produit, i.e. ![]() $V\times W$ est le produit calculé dans
$V\times W$ est le produit calculé dans ![]() $\mathfrak{C}$. Soit
$\mathfrak{C}$. Soit ![]() $\unicode[STIX]{x1D6FD}:V\times W\rightarrow U$ une application
$\unicode[STIX]{x1D6FD}:V\times W\rightarrow U$ une application ![]() $D$-balancée, i.e. une application
$D$-balancée, i.e. une application ![]() $K$-bilinéaire telle que pour tout
$K$-bilinéaire telle que pour tout ![]() $v\in V$, tout
$v\in V$, tout ![]() $w\in W$ et tout
$w\in W$ et tout ![]() $d\in D$, on ait
$d\in D$, on ait ![]() $\unicode[STIX]{x1D6FD}(vd,w)=\unicode[STIX]{x1D6FD}(v,dw)$. Par
$\unicode[STIX]{x1D6FD}(vd,w)=\unicode[STIX]{x1D6FD}(v,dw)$. Par ![]() $K$-bilinéarité de
$K$-bilinéarité de ![]() $\unicode[STIX]{x1D6FD}$, si
$\unicode[STIX]{x1D6FD}$, si ![]() $L$ est un sous-
$L$ est un sous-![]() ${\mathcal{V}}$-module (resp. un réseau de
${\mathcal{V}}$-module (resp. un réseau de ![]() $U$ au sens de [Reference SchneiderSch02, 2.1]) de
$U$ au sens de [Reference SchneiderSch02, 2.1]) de ![]() $U$, alors
$U$, alors ![]() $\unicode[STIX]{x1D6FD}^{-1}(L)$ est un sous-
$\unicode[STIX]{x1D6FD}^{-1}(L)$ est un sous-![]() ${\mathcal{V}}$-module (resp. un réseau) de
${\mathcal{V}}$-module (resp. un réseau) de ![]() $V\times W$. De plus, d’après [Reference SchneiderSch02, 17.1], comme
$V\times W$. De plus, d’après [Reference SchneiderSch02, 17.1], comme ![]() $\unicode[STIX]{x1D6FD}$ est
$\unicode[STIX]{x1D6FD}$ est ![]() $K$-bilinéaire, l’application
$K$-bilinéaire, l’application ![]() $\unicode[STIX]{x1D6FD}$ est continue si et seulement si elle l’est en zéro, i.e. pour tout sous-
$\unicode[STIX]{x1D6FD}$ est continue si et seulement si elle l’est en zéro, i.e. pour tout sous-![]() ${\mathcal{V}}$-module ouvert de
${\mathcal{V}}$-module ouvert de ![]() $L$ de
$L$ de ![]() $U$, il existe des sous-
$U$, il existe des sous-![]() ${\mathcal{V}}$-modules ouverts respectivement
${\mathcal{V}}$-modules ouverts respectivement ![]() $M$ de
$M$ de ![]() $V$ et
$V$ et ![]() $N$ de
$N$ de ![]() $W$ tels que
$W$ tels que ![]() $\unicode[STIX]{x1D6FD}(M\times N)\subset L$.
$\unicode[STIX]{x1D6FD}(M\times N)\subset L$.
Supposons ![]() $\unicode[STIX]{x1D6FD}$ continue. On dispose alors du morphisme
$\unicode[STIX]{x1D6FD}$ continue. On dispose alors du morphisme ![]() $K$-bilinéaire
$K$-bilinéaire ![]() $\underset{M,N}{\varprojlim }\,V\times W/M\times N\rightarrow \underset{L}{\varprojlim }\,V/L$, où
$\underset{M,N}{\varprojlim }\,V\times W/M\times N\rightarrow \underset{L}{\varprojlim }\,V/L$, où ![]() $L$ (resp.
$L$ (resp. ![]() $M$, resp.
$M$, resp. ![]() $N$) parcourt les réseaux ouverts de
$N$) parcourt les réseaux ouverts de ![]() $U$ (resp.
$U$ (resp. ![]() $V$, resp.
$V$, resp. ![]() $W$). On note
$W$). On note ![]() $\widehat{\unicode[STIX]{x1D6FD}}:\widehat{V}\times \widehat{W}\rightarrow \widehat{U}$ cette application. Comme les réseaux ouverts de
$\widehat{\unicode[STIX]{x1D6FD}}:\widehat{V}\times \widehat{W}\rightarrow \widehat{U}$ cette application. Comme les réseaux ouverts de ![]() $\widehat{U}$ sont de la forme
$\widehat{U}$ sont de la forme ![]() $\underset{L}{\varprojlim }\,L_{0}/L$ où
$\underset{L}{\varprojlim }\,L_{0}/L$ où ![]() $L_{0}$ est un réseau ouvert de
$L_{0}$ est un réseau ouvert de ![]() $U$ et
$U$ et ![]() $L$ parcourt les réseaux ouverts de
$L$ parcourt les réseaux ouverts de ![]() $U$ inclus dans
$U$ inclus dans ![]() $L_{0}$ (et de même pour
$L_{0}$ (et de même pour ![]() $\widehat{V}\times \widehat{W}$), on vérifie alors que
$\widehat{V}\times \widehat{W}$), on vérifie alors que ![]() $\widehat{\unicode[STIX]{x1D6FD}}$ est continue. Comme l’image de
$\widehat{\unicode[STIX]{x1D6FD}}$ est continue. Comme l’image de ![]() $V\times W$ dans
$V\times W$ dans ![]() $\widehat{V}\times \widehat{W}$ est dense, on vérifie que
$\widehat{V}\times \widehat{W}$ est dense, on vérifie que ![]() $\widehat{\unicode[STIX]{x1D6FD}}$ est l’unique application
$\widehat{\unicode[STIX]{x1D6FD}}$ est l’unique application ![]() $K$-bilinéaire continue induisant le carré commutatif :
$K$-bilinéaire continue induisant le carré commutatif :

En revanche, pour que ![]() $\widehat{\unicode[STIX]{x1D6FD}}$ soit
$\widehat{\unicode[STIX]{x1D6FD}}$ soit ![]() $D$-balancée, il faut des hypothèses topologiques sur
$D$-balancée, il faut des hypothèses topologiques sur ![]() $D$ (voir 1.3.4).
$D$ (voir 1.3.4).
1.2.2. Soit ![]() $V$ un objet de
$V$ un objet de ![]() $\mathfrak{C}_{D,d}$ et
$\mathfrak{C}_{D,d}$ et ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$. En munissant
$\mathfrak{C}_{D,g}$. En munissant ![]() $V\times W$ de la topologie produit, la topologie projective sur le produit tensoriel
$V\times W$ de la topologie produit, la topologie projective sur le produit tensoriel ![]() $V\otimes _{D}W$ est la topologie
$V\otimes _{D}W$ est la topologie ![]() $K$-localement convexe la plus fine telle que le morphisme
$K$-localement convexe la plus fine telle que le morphisme ![]() $K$-bilinéaire canonique
$K$-bilinéaire canonique ![]() $\unicode[STIX]{x1D70C}_{V,W}:V\times W\rightarrow V\otimes _{D}W$ soit continu. Ainsi, un réseau
$\unicode[STIX]{x1D70C}_{V,W}:V\times W\rightarrow V\otimes _{D}W$ soit continu. Ainsi, un réseau ![]() $L\subset V\otimes _{D}W$ est ouvert si et seulement si
$L\subset V\otimes _{D}W$ est ouvert si et seulement si ![]() $\unicode[STIX]{x1D70C}_{V,W}^{-1}(L)$ est ouvert. Comme nous ne considérerons que des topologies de type projectif sur les produits tensoriels, nous pourrons omettre d’indiquer le qualificatif « projectif ».
$\unicode[STIX]{x1D70C}_{V,W}^{-1}(L)$ est ouvert. Comme nous ne considérerons que des topologies de type projectif sur les produits tensoriels, nous pourrons omettre d’indiquer le qualificatif « projectif ».
L’objet ![]() $V\otimes _{D}W$ vérifie la propriété universelle : pour toute application
$V\otimes _{D}W$ vérifie la propriété universelle : pour toute application ![]() $D$-balancée et continue de la forme
$D$-balancée et continue de la forme ![]() $\unicode[STIX]{x1D719}:V\times W\rightarrow U$, il existe un unique morphisme dans
$\unicode[STIX]{x1D719}:V\times W\rightarrow U$, il existe un unique morphisme dans ![]() $\mathfrak{C}$ de la forme
$\mathfrak{C}$ de la forme ![]() $\unicode[STIX]{x1D703}:V\otimes _{D}W\rightarrow U$ tel que
$\unicode[STIX]{x1D703}:V\otimes _{D}W\rightarrow U$ tel que ![]() $\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D70C}_{V,W}=\unicode[STIX]{x1D719}$.
$\unicode[STIX]{x1D703}\circ \unicode[STIX]{x1D70C}_{V,W}=\unicode[STIX]{x1D719}$.
On en déduit que l’on obtient en réalité le bifoncteur canonique
Lemme 1.2.3. Soit ![]() $V$ un objet de
$V$ un objet de ![]() $\mathfrak{C}_{D,d}$ et
$\mathfrak{C}_{D,d}$ et ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$. On suppose qu’il existe un sous-
$\mathfrak{C}_{D,g}$. On suppose qu’il existe un sous-![]() ${\mathcal{V}}$-module
${\mathcal{V}}$-module ![]() $V_{0}$ de
$V_{0}$ de ![]() $V$ (resp.
$V$ (resp. ![]() $W_{0}$ de
$W_{0}$ de ![]() $W$) tel qu’une base de voisinages de zéro de
$W$) tel qu’une base de voisinages de zéro de ![]() $V$ (resp.
$V$ (resp. ![]() $W$) soit donnée par la famille
$W$) soit donnée par la famille ![]() $(p^{n}V_{0})_{n\in \mathbb{N}}$ (resp.
$(p^{n}V_{0})_{n\in \mathbb{N}}$ (resp. ![]() $(p^{n}W_{0})_{n\in \mathbb{N}}$). Notons
$(p^{n}W_{0})_{n\in \mathbb{N}}$). Notons ![]() $U_{0}:=<\unicode[STIX]{x1D70C}_{V,W}(V_{0}\times W_{0})>$, où
$U_{0}:=<\unicode[STIX]{x1D70C}_{V,W}(V_{0}\times W_{0})>$, où ![]() ${<}?>$ désigne le « sous-
${<}?>$ désigne le « sous-![]() ${\mathcal{V}}$-module de
${\mathcal{V}}$-module de ![]() $V\otimes _{D}W$ engendré par
$V\otimes _{D}W$ engendré par ![]() $?$ ». Alors une base de voisinages sur
$?$ ». Alors une base de voisinages sur ![]() $V\otimes _{D}W$ muni de sa topologie canonique (voir 1.2.2) est donnée par
$V\otimes _{D}W$ muni de sa topologie canonique (voir 1.2.2) est donnée par ![]() $(p^{n}U_{0})_{n\in \mathbb{N}}$.
$(p^{n}U_{0})_{n\in \mathbb{N}}$.
Démonstration.
Comme ![]() $V_{0}$ et
$V_{0}$ et ![]() $W_{0}$ sont des réseaux respectifs de
$W_{0}$ sont des réseaux respectifs de ![]() $V$ et
$V$ et ![]() $W$,
$W$, ![]() $U_{0}$ est un réseau de
$U_{0}$ est un réseau de ![]() $U$. Pour tout entier
$U$. Pour tout entier ![]() $n\in \mathbb{N}$, comme
$n\in \mathbb{N}$, comme ![]() $\unicode[STIX]{x1D70C}_{V,W}^{-1}(p^{n}U_{0})\supset p^{n}(V_{0}\times W_{0})$, les
$\unicode[STIX]{x1D70C}_{V,W}^{-1}(p^{n}U_{0})\supset p^{n}(V_{0}\times W_{0})$, les ![]() $p^{n}U_{0}$ sont donc des ouverts de
$p^{n}U_{0}$ sont donc des ouverts de ![]() $V\otimes _{D}W$. Réciproquement, soit
$V\otimes _{D}W$. Réciproquement, soit ![]() $L$ un sous-
$L$ un sous-![]() ${\mathcal{V}}$-module ouvert de
${\mathcal{V}}$-module ouvert de ![]() $V\otimes _{D}W$. Il existe alors un entier
$V\otimes _{D}W$. Il existe alors un entier ![]() $n$ assez grand tel que
$n$ assez grand tel que ![]() $\unicode[STIX]{x1D70C}_{V,W}^{-1}(L)\supset p^{n}(V_{0}\times W_{0})$. Comme
$\unicode[STIX]{x1D70C}_{V,W}^{-1}(L)\supset p^{n}(V_{0}\times W_{0})$. Comme ![]() $L$ est un
$L$ est un ![]() ${\mathcal{V}}$-module, on a alors
${\mathcal{V}}$-module, on a alors ![]() $L\supset <\unicode[STIX]{x1D70C}_{V,W}(p^{n}(V_{0}\times W_{0}))>=p^{2n}<\unicode[STIX]{x1D70C}_{V,W}(V_{0}\times W_{0})>=p^{2n}U_{0}$.
$L\supset <\unicode[STIX]{x1D70C}_{V,W}(p^{n}(V_{0}\times W_{0}))>=p^{2n}<\unicode[STIX]{x1D70C}_{V,W}(V_{0}\times W_{0})>=p^{2n}U_{0}$.
1.2.4. Soit ![]() $D\text{sp}\prime \rightarrow D$ un homomorphisme de
$D\text{sp}\prime \rightarrow D$ un homomorphisme de ![]() $K$-algèbres tel que
$K$-algèbres tel que ![]() $K$ soit aussi dans le centre de
$K$ soit aussi dans le centre de ![]() $D\text{sp}\prime$. Soit
$D\text{sp}\prime$. Soit ![]() $V$ un objet de
$V$ un objet de ![]() $\mathfrak{C}_{D,d}$ et
$\mathfrak{C}_{D,d}$ et ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$. Comme le composé
$\mathfrak{C}_{D,g}$. Comme le composé ![]() $V\times W\rightarrow V\otimes _{D\text{sp}\prime }W\rightarrow V\otimes _{D}W$ est le morphisme canonique, par définition des topologies définies sur
$V\times W\rightarrow V\otimes _{D\text{sp}\prime }W\rightarrow V\otimes _{D}W$ est le morphisme canonique, par définition des topologies définies sur ![]() $V\otimes _{D\text{sp}\prime }W$ et
$V\otimes _{D\text{sp}\prime }W$ et ![]() $V\otimes _{D}W$, l’épimorphisme
$V\otimes _{D}W$, l’épimorphisme ![]() $V\otimes _{D\text{sp}\prime }W\rightarrow V\otimes _{D}W$ est donc strict.
$V\otimes _{D\text{sp}\prime }W\rightarrow V\otimes _{D}W$ est donc strict.
Lemme 1.2.5. Soit ![]() $V\rightarrow V\text{sp}\prime \prime$ (resp.
$V\rightarrow V\text{sp}\prime \prime$ (resp. ![]() $W\rightarrow W\text{sp}\prime \prime$) un épimorphisme strict de
$W\rightarrow W\text{sp}\prime \prime$) un épimorphisme strict de ![]() $\mathfrak{C}_{D,d}$ (resp.
$\mathfrak{C}_{D,d}$ (resp. ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$). Les épimorphismes
$\mathfrak{C}_{D,g}$). Les épimorphismes ![]() $V\otimes _{D}W\rightarrow V\otimes _{D}W\text{sp}\prime \prime$ et
$V\otimes _{D}W\rightarrow V\otimes _{D}W\text{sp}\prime \prime$ et ![]() $V\otimes _{D}W\rightarrow V\text{sp}\prime \prime \otimes _{D}W$ sont alors stricts.
$V\otimes _{D}W\rightarrow V\text{sp}\prime \prime \otimes _{D}W$ sont alors stricts.
Démonstration.
Par symétrie, vérifions-le seulement pour le premier. Soit ![]() $L$ un réseau de
$L$ un réseau de ![]() $V\otimes _{D}W\text{sp}\prime \prime$. Comme
$V\otimes _{D}W\text{sp}\prime \prime$. Comme ![]() $V\times W\rightarrow V\times W\text{sp}\prime \prime$ est strict, par définition de la topologie sur
$V\times W\rightarrow V\times W\text{sp}\prime \prime$ est strict, par définition de la topologie sur ![]() $V\otimes _{D}W\text{sp}\prime \prime$,
$V\otimes _{D}W\text{sp}\prime \prime$, ![]() $L$ est ouvert si est seulement si son image inverse sur
$L$ est ouvert si est seulement si son image inverse sur ![]() $V\times W$ est un ouvert. Par définition de la topologie sur
$V\times W$ est un ouvert. Par définition de la topologie sur ![]() $V\otimes _{D}W$, cela équivaut au fait que son image inverse sur
$V\otimes _{D}W$, cela équivaut au fait que son image inverse sur ![]() $V\otimes _{D}W$ soit un ouvert. D’où le résultat.
$V\otimes _{D}W$ soit un ouvert. D’où le résultat.
Nous ne devrions pas avoir besoin des deux lemmes qui suivent, mais cela vaut sans doute la peine de les écrire.
Lemme 1.2.6. Soit ![]() $(V_{i})_{i\in I}$ un système inductif filtrant de
$(V_{i})_{i\in I}$ un système inductif filtrant de ![]() $\mathfrak{C}_{D,d}$,
$\mathfrak{C}_{D,d}$, ![]() $(W_{i})_{i\in I}$ un système inductif filtrant de
$(W_{i})_{i\in I}$ un système inductif filtrant de ![]() $\mathfrak{C}_{D,g}$,
$\mathfrak{C}_{D,g}$, ![]() $U$ un objet de
$U$ un objet de ![]() $\mathfrak{C}$,
$\mathfrak{C}$, ![]() $\unicode[STIX]{x1D6FD}_{i}:V_{i}\times W_{i}\rightarrow U$ une famille compatible d’applications
$\unicode[STIX]{x1D6FD}_{i}:V_{i}\times W_{i}\rightarrow U$ une famille compatible d’applications ![]() $D$-balancées continues. Alors l’application
$D$-balancées continues. Alors l’application ![]() $D$-balancée
$D$-balancée ![]() $\unicode[STIX]{x1D6FD}:=\mathop{\varinjlim }\nolimits_{i}V_{i}\times W_{i}\rightarrow U$ est continue.
$\unicode[STIX]{x1D6FD}:=\mathop{\varinjlim }\nolimits_{i}V_{i}\times W_{i}\rightarrow U$ est continue.
Démonstration.
Notons ![]() $g_{i}:V_{i}\times W_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}V_{i}\times W_{i}$ les applications
$g_{i}:V_{i}\times W_{i}\rightarrow \mathop{\varinjlim }\nolimits_{i}V_{i}\times W_{i}$ les applications ![]() $D$-balancées continues canoniques. Soit
$D$-balancées continues canoniques. Soit ![]() $L$ un réseau ouvert de
$L$ un réseau ouvert de ![]() $U$. Le lemme découle alors de l’égalité
$U$. Le lemme découle alors de l’égalité ![]() $\unicode[STIX]{x1D6FD}^{-1}(L)=\sum _{i\in I}g_{i}(\unicode[STIX]{x1D6FD}_{i}^{-1}(L)).$
$\unicode[STIX]{x1D6FD}^{-1}(L)=\sum _{i\in I}g_{i}(\unicode[STIX]{x1D6FD}_{i}^{-1}(L)).$
Lemme 1.2.7. Soit ![]() $(V_{i})_{i\in I}$ un système inductif filtrant de
$(V_{i})_{i\in I}$ un système inductif filtrant de ![]() $\mathfrak{C}_{D,d}$ et
$\mathfrak{C}_{D,d}$ et ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$.
$\mathfrak{C}_{D,g}$.
(1) Le morphisme canonique
 $\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow (\mathop{\varinjlim }\nolimits_{i}\,V_{i})\times W$ est un homéomorphisme.
$\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow (\mathop{\varinjlim }\nolimits_{i}\,V_{i})\times W$ est un homéomorphisme.(2) On dispose alors de l’isomorphisme canonique dans
 $\mathfrak{C}$ de la forme
$\mathfrak{C}$ de la forme  $$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\otimes _{D}W)\overset{{\sim}}{\longrightarrow }\,(\mathop{\varinjlim }\nolimits_{i}\,V_{i})\otimes _{D}W.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\otimes _{D}W)\overset{{\sim}}{\longrightarrow }\,(\mathop{\varinjlim }\nolimits_{i}\,V_{i})\otimes _{D}W.\end{eqnarray}$$
Démonstration.
Notons ![]() $V:=\mathop{\varinjlim }\nolimits_{i}\,V_{i}$ et
$V:=\mathop{\varinjlim }\nolimits_{i}\,V_{i}$ et ![]() $f_{i}:V_{i}\rightarrow V$ les morphismes canoniques. Traitons d’abord la première assertion. Par définition de la topologie sur la limite inductive, la bijection canonique
$f_{i}:V_{i}\rightarrow V$ les morphismes canoniques. Traitons d’abord la première assertion. Par définition de la topologie sur la limite inductive, la bijection canonique ![]() $\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow V\times W$ est continue. Soit
$\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow V\times W$ est continue. Soit ![]() $(L_{i})_{i\in I}$ une famille de réseaux ouverts de
$(L_{i})_{i\in I}$ une famille de réseaux ouverts de ![]() $(V_{i})_{i\in I}$ et
$(V_{i})_{i\in I}$ et ![]() $(M_{i})_{i\in I}$ une famille de réseaux ouverts de
$(M_{i})_{i\in I}$ une famille de réseaux ouverts de ![]() $W$. Il s’agit de vérifier que
$W$. Il s’agit de vérifier que ![]() $\sum _{i\in I}f_{i}(L_{i})\times M_{i}$ est un ouvert de
$\sum _{i\in I}f_{i}(L_{i})\times M_{i}$ est un ouvert de ![]() $V\times W$. Cela résulte immédiatement de l’inclusion
$V\times W$. Cela résulte immédiatement de l’inclusion ![]() $\sum _{i\in I}f_{i}(L_{i})\times M_{i}\supset (\sum _{i\in I}f_{i}(L_{i}))\times M_{i_{0}}$ valable quel que que soit
$\sum _{i\in I}f_{i}(L_{i})\times M_{i}\supset (\sum _{i\in I}f_{i}(L_{i}))\times M_{i_{0}}$ valable quel que que soit ![]() $i_{0}\in I$ (en effet, on utilise la relation
$i_{0}\in I$ (en effet, on utilise la relation ![]() $(x,y)=(x,0)+(0,y)$ pour
$(x,y)=(x,0)+(0,y)$ pour ![]() $x\in \sum _{i\in I}f_{i}(L_{i})$ et
$x\in \sum _{i\in I}f_{i}(L_{i})$ et ![]() $y\in M_{i_{0}}$).
$y\in M_{i_{0}}$).
Vérifions à présent la seconde assertion, i.e. le ![]() $K$-espace localement convexe
$K$-espace localement convexe ![]() $V\otimes _{D}W$ vérifie la propriété universelle de la limite inductive dans
$V\otimes _{D}W$ vérifie la propriété universelle de la limite inductive dans ![]() $\mathfrak{C}$ du système
$\mathfrak{C}$ du système ![]() $(V_{i}\otimes _{D}W)_{i\in I}$ : si l’on se donne une famille compatible de morphismes de
$(V_{i}\otimes _{D}W)_{i\in I}$ : si l’on se donne une famille compatible de morphismes de ![]() $\mathfrak{C}$ de la forme
$\mathfrak{C}$ de la forme ![]() $V_{i}\otimes _{D}W\rightarrow U$, alors ils se factorisent de manière unique en un morphisme
$V_{i}\otimes _{D}W\rightarrow U$, alors ils se factorisent de manière unique en un morphisme ![]() $K$-linéaire de la forme
$K$-linéaire de la forme ![]() $V\otimes _{D}W\rightarrow U$. Pour vérifier que celui-là est continu, il faut et il suffit que le composé
$V\otimes _{D}W\rightarrow U$. Pour vérifier que celui-là est continu, il faut et il suffit que le composé ![]() $V\times W\rightarrow V\otimes _{D}W\rightarrow U$ le soit. Or, comme toutes les applications
$V\times W\rightarrow V\otimes _{D}W\rightarrow U$ le soit. Or, comme toutes les applications ![]() $D$-balancées
$D$-balancées ![]() $V_{i}\times W\rightarrow U$ sont continues, d’après 1.2.6, il en est de même de l’application
$V_{i}\times W\rightarrow U$ sont continues, d’après 1.2.6, il en est de même de l’application ![]() $D$-balancée
$D$-balancée ![]() $\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow U$. On déduit alors de la première assertion du lemme que le morphisme canonique
$\mathop{\varinjlim }\nolimits_{i}\,(V_{i}\times W)\rightarrow U$. On déduit alors de la première assertion du lemme que le morphisme canonique ![]() $V\times W\rightarrow U$ est continu. D’où le résultat.
$V\times W\rightarrow U$ est continu. D’où le résultat.
1.3 Complétions de produit tensoriel de modules localement convexes
1.3.1. Avec les notations de 1.2, soit ![]() $V$ un objet de
$V$ un objet de ![]() $\mathfrak{C}_{D,d}$ et
$\mathfrak{C}_{D,d}$ et ![]() $W$ un objet de
$W$ un objet de ![]() $\mathfrak{C}_{D,g}$. On note
$\mathfrak{C}_{D,g}$. On note ![]() $V\widehat{\otimes }_{D}W$ le séparé complété de
$V\widehat{\otimes }_{D}W$ le séparé complété de ![]() $V\otimes _{D}W$ et
$V\otimes _{D}W$ et ![]() $i_{V,W}:V\otimes _{D}W\rightarrow V\widehat{\otimes }_{D}W$ le morphisme canonique. Il résulte de la propriété universelle du produit tensoriel et de celle du séparé complété la propriété universelle suivante : pour toute application
$i_{V,W}:V\otimes _{D}W\rightarrow V\widehat{\otimes }_{D}W$ le morphisme canonique. Il résulte de la propriété universelle du produit tensoriel et de celle du séparé complété la propriété universelle suivante : pour toute application ![]() $D$-balancée et continue de la forme
$D$-balancée et continue de la forme ![]() $\unicode[STIX]{x1D719}:V\times W\rightarrow U$ avec
$\unicode[STIX]{x1D719}:V\times W\rightarrow U$ avec ![]() $U\in \mathfrak{D}$, il existe alors un unique morphisme dans
$U\in \mathfrak{D}$, il existe alors un unique morphisme dans ![]() $\mathfrak{D}$ de la forme
$\mathfrak{D}$ de la forme ![]() $\unicode[STIX]{x1D703}:V\widehat{\otimes }_{D}W\rightarrow U$ tel que
$\unicode[STIX]{x1D703}:V\widehat{\otimes }_{D}W\rightarrow U$ tel que ![]() $\unicode[STIX]{x1D703}\circ i_{V,W}\circ \unicode[STIX]{x1D70C}_{V,W}=\unicode[STIX]{x1D719}$.
$\unicode[STIX]{x1D703}\circ i_{V,W}\circ \unicode[STIX]{x1D70C}_{V,W}=\unicode[STIX]{x1D719}$.
On obtient ainsi le bifoncteur canonique
Définition 1.3.2. Soit ![]() $D$ une
$D$ une ![]() $K$-algèbre telle que
$K$-algèbre telle que ![]() $K$ soit dans le centre de
$K$ soit dans le centre de ![]() $D$.
$D$.
(1) On dit que
 $D$ est une
$D$ est une  $K$-algèbre localement convexe si
$K$-algèbre localement convexe si  $D$ est munie d’une topologie
$D$ est munie d’une topologie  $K$-localement convexe, telle que la multiplication soit une application
$K$-localement convexe, telle que la multiplication soit une application  $K$-bilinéaire continue. Un morphisme de
$K$-bilinéaire continue. Un morphisme de  $K$-algèbres localement convexes est un morphisme de
$K$-algèbres localement convexes est un morphisme de  $K$-algèbres qui est continu pour les topologies respectives. On dit que
$K$-algèbres qui est continu pour les topologies respectives. On dit que  $D$ est une
$D$ est une  $K$-algèbre de Banach si
$K$-algèbre de Banach si  $D$ est une
$D$ est une  $K$-algèbre localement convexe dont la topologie sous-jacente en fait un
$K$-algèbre localement convexe dont la topologie sous-jacente en fait un  $K$-espace de Banach.
$K$-espace de Banach.(2) Soit
 $D$ une
$D$ une  $K$-algèbre localement convexe. Un
$K$-algèbre localement convexe. Un  $D$-module à gauche localement convexe est un
$D$-module à gauche localement convexe est un  $D$-module à gauche
$D$-module à gauche  $M$ muni d’une topologie
$M$ muni d’une topologie  $K$-localement convexe telle que la loi externe structurale
$K$-localement convexe telle que la loi externe structurale  $D\times M\rightarrow M$ soit une application
$D\times M\rightarrow M$ soit une application  $K$-bilinéaire continue. Un
$K$-bilinéaire continue. Un  $D$-module à gauche de Banach est un
$D$-module à gauche de Banach est un  $D$-module à gauche localement convexe dont la topologie sous-jacente en fait un
$D$-module à gauche localement convexe dont la topologie sous-jacente en fait un  $K$-espace de Banach. Un morphisme de
$K$-espace de Banach. Un morphisme de  $D$-modules à gauche localement convexes (resp. de Banach) est un morphisme de
$D$-modules à gauche localement convexes (resp. de Banach) est un morphisme de  $D$-modules à gauche qui est aussi un morphisme de
$D$-modules à gauche qui est aussi un morphisme de  $K$-espaces localement convexes (resp. de Banach).
$K$-espaces localement convexes (resp. de Banach).De même en remplac˛ant à gauche par à droite.
Lemme 1.3.3. Soit ![]() $D$ une
$D$ une ![]() $K$-algèbre localement convexe et
$K$-algèbre localement convexe et ![]() $\unicode[STIX]{x1D719}:M\rightarrow N$ un morphisme de
$\unicode[STIX]{x1D719}:M\rightarrow N$ un morphisme de ![]() $D$-modules à gauche (resp. à droite) localement convexes.
$D$-modules à gauche (resp. à droite) localement convexes.
(1) La structure de
 $K$-espace localement convexe séparé complet sur
$K$-espace localement convexe séparé complet sur  $\widehat{D}$ se prolonge en une structure canonique de
$\widehat{D}$ se prolonge en une structure canonique de  $K$-algèbre localement convexe. De plus, le morphisme canonique
$K$-algèbre localement convexe. De plus, le morphisme canonique  $D\rightarrow \widehat{D}$ est un morphisme de
$D\rightarrow \widehat{D}$ est un morphisme de  $K$-algèbres localement convexes.
$K$-algèbres localement convexes.(2) Le morphisme induit par séparée complétion
 $\widehat{\unicode[STIX]{x1D719}}:\widehat{M}\rightarrow \widehat{N}$ est un morphisme de
$\widehat{\unicode[STIX]{x1D719}}:\widehat{M}\rightarrow \widehat{N}$ est un morphisme de  $\widehat{D}$-modules localement convexes. De plus, le morphisme canonique
$\widehat{D}$-modules localement convexes. De plus, le morphisme canonique  $M\rightarrow \widehat{M}$ est un morphisme de
$M\rightarrow \widehat{M}$ est un morphisme de  $D$-modules localement convexes.
$D$-modules localement convexes.
Démonstration.
Contentons-nous de prouver le cas non respectif. D’après 2, l’application ![]() $K$-bilinéaire continue structurale canonique
$K$-bilinéaire continue structurale canonique ![]() $\unicode[STIX]{x1D707}_{D}:D\times D\rightarrow D$ induit l’application
$\unicode[STIX]{x1D707}_{D}:D\times D\rightarrow D$ induit l’application ![]() $K$-bilinéaire continue
$K$-bilinéaire continue ![]() $\unicode[STIX]{x1D707}_{\widehat{D}}:=\widehat{\unicode[STIX]{x1D707}_{D}}:\widehat{D}\times \widehat{D}\rightarrow \widehat{D}$ s’inscrivant (de manière unique) dans le diagramme commutatif :
$\unicode[STIX]{x1D707}_{\widehat{D}}:=\widehat{\unicode[STIX]{x1D707}_{D}}:\widehat{D}\times \widehat{D}\rightarrow \widehat{D}$ s’inscrivant (de manière unique) dans le diagramme commutatif :

Comme les deux applications ![]() $\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\unicode[STIX]{x1D707}_{\widehat{D}}\times \text{id}),\,\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\text{id}\times \unicode[STIX]{x1D707}_{\widehat{D}}):\widehat{D}\times \widehat{D}\times \widehat{D}\rightarrow \widehat{D}$ coïncident après composition par le morphisme canonique
$\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\unicode[STIX]{x1D707}_{\widehat{D}}\times \text{id}),\,\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\text{id}\times \unicode[STIX]{x1D707}_{\widehat{D}}):\widehat{D}\times \widehat{D}\times \widehat{D}\rightarrow \widehat{D}$ coïncident après composition par le morphisme canonique ![]() $D\times D\times D\rightarrow \widehat{D}\times \widehat{D}\times \widehat{D}$ dont l’image est dense, on obtient
$D\times D\times D\rightarrow \widehat{D}\times \widehat{D}\times \widehat{D}$ dont l’image est dense, on obtient ![]() $\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\unicode[STIX]{x1D707}_{\widehat{D}}\times \text{id})=\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\text{id}\times \unicode[STIX]{x1D707}_{\widehat{D}})$, i.e. la multiplication est associative. On vérifie de même les autres propriétés qui font de
$\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\unicode[STIX]{x1D707}_{\widehat{D}}\times \text{id})=\unicode[STIX]{x1D707}_{\widehat{D}}\circ (\text{id}\times \unicode[STIX]{x1D707}_{\widehat{D}})$, i.e. la multiplication est associative. On vérifie de même les autres propriétés qui font de ![]() $\widehat{D}$ une
$\widehat{D}$ une ![]() $K$-algèbre localement convexe. Il est clair que le morphisme continu canonique
$K$-algèbre localement convexe. Il est clair que le morphisme continu canonique ![]() $D\rightarrow \widehat{D}$ est alors un morphisme de
$D\rightarrow \widehat{D}$ est alors un morphisme de ![]() $K$-algèbres localement convexes.
$K$-algèbres localement convexes.
D’après 1.2.1, les applications ![]() $K$-bilinéaires continues structurales canoniques
$K$-bilinéaires continues structurales canoniques ![]() $\unicode[STIX]{x1D707}_{M}:D\times M\rightarrow M$ et
$\unicode[STIX]{x1D707}_{M}:D\times M\rightarrow M$ et ![]() $\unicode[STIX]{x1D707}_{N}:D\times N\rightarrow N$ induisent les applications
$\unicode[STIX]{x1D707}_{N}:D\times N\rightarrow N$ induisent les applications ![]() $K$-bilinéaires continues
$K$-bilinéaires continues ![]() $\unicode[STIX]{x1D707}_{\widehat{M}}:=\widehat{\unicode[STIX]{x1D707}_{M}}:\widehat{D}\times \widehat{M}\rightarrow \widehat{M}$ et
$\unicode[STIX]{x1D707}_{\widehat{M}}:=\widehat{\unicode[STIX]{x1D707}_{M}}:\widehat{D}\times \widehat{M}\rightarrow \widehat{M}$ et ![]() $\unicode[STIX]{x1D707}_{\widehat{N}}:=\widehat{\unicode[STIX]{x1D707}_{N}}:\widehat{D}\times \widehat{N}\rightarrow \widehat{N}$. De même, on vérifie que
$\unicode[STIX]{x1D707}_{\widehat{N}}:=\widehat{\unicode[STIX]{x1D707}_{N}}:\widehat{D}\times \widehat{N}\rightarrow \widehat{N}$. De même, on vérifie que ![]() $\unicode[STIX]{x1D707}_{\widehat{M}}$ et
$\unicode[STIX]{x1D707}_{\widehat{M}}$ et ![]() $\unicode[STIX]{x1D707}_{\widehat{N}}$ induisent respectivement une structure canonique de
$\unicode[STIX]{x1D707}_{\widehat{N}}$ induisent respectivement une structure canonique de ![]() $\widehat{D}$-modules localement convexes sur
$\widehat{D}$-modules localement convexes sur ![]() $\widehat{M}$ et
$\widehat{M}$ et ![]() $\widehat{N}$. Comme le diagramme
$\widehat{N}$. Comme le diagramme

est commutatif après composition par ![]() $D\times M\rightarrow \widehat{D}\times \widehat{M}$ dont l’image est dense, celui-là est commutatif. D’où le résultat.
$D\times M\rightarrow \widehat{D}\times \widehat{M}$ dont l’image est dense, celui-là est commutatif. D’où le résultat.
Lemme 1.3.4. Soit ![]() $D$ une
$D$ une ![]() $K$-algèbre localement convexe,
$K$-algèbre localement convexe, ![]() $M$ un
$M$ un ![]() $D$-module à droite localement convexe,
$D$-module à droite localement convexe, ![]() $N$ un
$N$ un ![]() $D$-module à gauche localement convexe et
$D$-module à gauche localement convexe et ![]() $U$ un
$U$ un ![]() $K$-espace localement convexe. Soit
$K$-espace localement convexe. Soit ![]() $\unicode[STIX]{x1D6FD}:M\times N\rightarrow U$ une application
$\unicode[STIX]{x1D6FD}:M\times N\rightarrow U$ une application ![]() $D$-balancée et continue. L’application
$D$-balancée et continue. L’application ![]() $\widehat{\unicode[STIX]{x1D6FD}}:\widehat{M}\times \widehat{N}\rightarrow \widehat{U}$ (voir 1.2.1) est alors une application
$\widehat{\unicode[STIX]{x1D6FD}}:\widehat{M}\times \widehat{N}\rightarrow \widehat{U}$ (voir 1.2.1) est alors une application ![]() $\widehat{D}$-balancée et continue.
$\widehat{D}$-balancée et continue.
Démonstration.
On sait déjà que l’application ![]() $\widehat{\unicode[STIX]{x1D6FD}}$ est continue. Considérons le carré :
$\widehat{\unicode[STIX]{x1D6FD}}$ est continue. Considérons le carré :

où ![]() $\unicode[STIX]{x1D707}_{\widehat{M}}:\widehat{M}\times \widehat{D}\rightarrow \widehat{M}$ et
$\unicode[STIX]{x1D707}_{\widehat{M}}:\widehat{M}\times \widehat{D}\rightarrow \widehat{M}$ et ![]() $\unicode[STIX]{x1D707}_{\widehat{N}}:\widehat{D}\times \widehat{N}\rightarrow \widehat{N}$ sont les applications
$\unicode[STIX]{x1D707}_{\widehat{N}}:\widehat{D}\times \widehat{N}\rightarrow \widehat{N}$ sont les applications ![]() $K$-bilinéaires continues structurales canoniques. Comme l’image de
$K$-bilinéaires continues structurales canoniques. Comme l’image de ![]() $M\times D\times N$ dans
$M\times D\times N$ dans ![]() $\widehat{M}\times \widehat{D}\times \widehat{N}$ est dense, le carré
$\widehat{M}\times \widehat{D}\times \widehat{N}$ est dense, le carré
est donc commutatif car il l’est sans les chapeaux.
Proposition 1.3.5. Soit ![]() $D$ une
$D$ une ![]() $K$-algèbre localement convexe,
$K$-algèbre localement convexe, ![]() $M$ un
$M$ un ![]() $D$-module à droite localement convexe et
$D$-module à droite localement convexe et ![]() $N$ un
$N$ un ![]() $D$-module à gauche localement convexe. On dispose alors de l’isomorphisme canonique dans
$D$-module à gauche localement convexe. On dispose alors de l’isomorphisme canonique dans ![]() $\mathfrak{D}$ de la forme :
$\mathfrak{D}$ de la forme :
Démonstration.
Par fonctorialité du foncteur séparée complétion, on dispose du morphisme dans ![]() $\mathfrak{D}$ de la forme :
$\mathfrak{D}$ de la forme : ![]() $M\widehat{\otimes }_{D}N\rightarrow \widehat{M}\widehat{\otimes }_{\widehat{D}}\widehat{N}.$ Pour construire le morphisme quasi inverse, par propriété universelle du produit tensoriel, il s’agit de définir canoniquement une application continue de la forme
$M\widehat{\otimes }_{D}N\rightarrow \widehat{M}\widehat{\otimes }_{\widehat{D}}\widehat{N}.$ Pour construire le morphisme quasi inverse, par propriété universelle du produit tensoriel, il s’agit de définir canoniquement une application continue de la forme ![]() $\widehat{M}\times \widehat{N}\rightarrow M\widehat{\otimes }_{D}N$ qui soit
$\widehat{M}\times \widehat{N}\rightarrow M\widehat{\otimes }_{D}N$ qui soit ![]() $\widehat{D}$-balancée, ce qui résulte aussitôt du lemme 1.3.4 appliqué à
$\widehat{D}$-balancée, ce qui résulte aussitôt du lemme 1.3.4 appliqué à ![]() $\unicode[STIX]{x1D6FD}$ égale à l’application canonique
$\unicode[STIX]{x1D6FD}$ égale à l’application canonique ![]() $M\times N\rightarrow M\otimes _{D}N$.
$M\times N\rightarrow M\otimes _{D}N$.
2 Espaces de type  $LB$ en théorie des
$LB$ en théorie des  $D$-modules arithmétiques
$D$-modules arithmétiques
Sauf mention explicite du contraire, nous utiliserons les notations et hypothèses suivantes : soit ![]() $\mathfrak{X}$ un
$\mathfrak{X}$ un ![]() ${\mathcal{V}}$-schéma formel affine, lisse, muni de coordonnées locales
${\mathcal{V}}$-schéma formel affine, lisse, muni de coordonnées locales ![]() $t_{1},\ldots ,t_{d}$ et soit
$t_{1},\ldots ,t_{d}$ et soit ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{d}$ les dérivations correspondantes. On note
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{d}$ les dérivations correspondantes. On note ![]() ${\mathcal{Z}}:=\bigcap _{i=1}^{e}V(t_{i})$ et
${\mathcal{Z}}:=\bigcap _{i=1}^{e}V(t_{i})$ et ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ l’immersion fermée induite. Soit
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ l’immersion fermée induite. Soit ![]() $\mathfrak{D}=V(t_{e+1}\cdots t_{f})$ un diviseur à croisements normaux strict de
$\mathfrak{D}=V(t_{e+1}\cdots t_{f})$ un diviseur à croisements normaux strict de ![]() $\mathfrak{X}$ tel que
$\mathfrak{X}$ tel que ![]() $u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de
$u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de ![]() ${\mathcal{Z}}$. On pose
${\mathcal{Z}}$. On pose ![]() $\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$,
$\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$, ![]() ${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et
${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et ![]() $u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur
$u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur ![]() ${\mathcal{V}}$. Soit
${\mathcal{V}}$. Soit ![]() $f\in O_{\mathfrak{X}}$ et
$f\in O_{\mathfrak{X}}$ et ![]() $f_{0}\in O_{X}$ sa réduction modulo
$f_{0}\in O_{X}$ sa réduction modulo ![]() $\unicode[STIX]{x1D70B}$ telle que
$\unicode[STIX]{x1D70B}$ telle que ![]() $T:=V(f_{0})$ soit un diviseur de
$T:=V(f_{0})$ soit un diviseur de ![]() $X$ tel que
$X$ tel que ![]() $U:=T\cap Z$ soit un diviseur de
$U:=T\cap Z$ soit un diviseur de ![]() $Z$. Soit
$Z$. Soit ![]() $\unicode[STIX]{x1D706}_{0}:\mathbb{N}\rightarrow \mathbb{N}$ une application croissante telle que
$\unicode[STIX]{x1D706}_{0}:\mathbb{N}\rightarrow \mathbb{N}$ une application croissante telle que ![]() $\unicode[STIX]{x1D706}_{0}(m)\geqslant m$, pour tout
$\unicode[STIX]{x1D706}_{0}(m)\geqslant m$, pour tout ![]() $m\in \mathbb{N}$. Pour alléger les notations, on pose alors
$m\in \mathbb{N}$. Pour alléger les notations, on pose alors ![]() $\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(\unicode[STIX]{x1D706}_{0}(m))}(T)$,
$\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(\unicode[STIX]{x1D706}_{0}(m))}(T)$, ![]() $\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U):=\widehat{{\mathcal{B}}}_{{\mathcal{Z}}}^{(\unicode[STIX]{x1D706}_{0}(m))}(U)$,
$\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U):=\widehat{{\mathcal{B}}}_{{\mathcal{Z}}}^{(\unicode[STIX]{x1D706}_{0}(m))}(U)$, ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ et
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ et ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}$. De même, on pose alors
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}$. De même, on pose alors ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}:=\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)$,
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}:=\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)$, ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$,
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et enfin
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et enfin ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$.
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$.
2.1 Topologies canoniques
2.1.1. (Topologie de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe canonique (resp. de
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe canonique (resp. de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée) sur
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée) sur ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$.) On définit les topologies suivantes.
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$.) On définit les topologies suivantes.
∙ Pour tout entier
 $m$, la topologie canonique de
$m$, la topologie canonique de  $O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe sur
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe sur  $\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$ est celle dont une base de voisinages de zéro est
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$ est celle dont une base de voisinages de zéro est  $(p^{n}\widetilde{B}_{\mathfrak{X}}^{(m)}(T))_{n\in \mathbb{N}}$.
$(p^{n}\widetilde{B}_{\mathfrak{X}}^{(m)}(T))_{n\in \mathbb{N}}$.∙ On munit
 $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ d’une topologie canonique de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ d’une topologie canonique de  $O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe telle que l’isomorphisme canonique
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe telle que l’isomorphisme canonique  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{m}\,\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$ soit un homéomorphisme (on remarque que d’après 1.1.4, cela ne dépend pas de l’application
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{m}\,\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$ soit un homéomorphisme (on remarque que d’après 1.1.4, cela ne dépend pas de l’application  $\unicode[STIX]{x1D706}_{0}$).
$\unicode[STIX]{x1D706}_{0}$).∙ Comme
 $\bigcap _{n\in \mathbb{N}}p^{n}{O_{\mathfrak{X}}[\frac{1}{f}]}^{\dagger }=\{0\}$ et comme on dispose de l’isomorphisme canonique
$\bigcap _{n\in \mathbb{N}}p^{n}{O_{\mathfrak{X}}[\frac{1}{f}]}^{\dagger }=\{0\}$ et comme on dispose de l’isomorphisme canonique  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$ (voir la preuve de [Reference BerthelotBer96, 4.3.2]), on munit alors
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$ (voir la preuve de [Reference BerthelotBer96, 4.3.2]), on munit alors  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ d’une structure de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ d’une structure de  $O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée (à ne pas confondre avec la topologie canonique induite par la limite inductive) dont une base de voisinages de zéro est donnée par
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée (à ne pas confondre avec la topologie canonique induite par la limite inductive) dont une base de voisinages de zéro est donnée par  $(p^{n}O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })_{n\in \mathbb{N}}$. Muni de cette topologie,
$(p^{n}O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })_{n\in \mathbb{N}}$. Muni de cette topologie,  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est normée mais pas de Banach : son séparé complété est
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est normée mais pas de Banach : son séparé complété est  $O_{\mathfrak{X}}\{\frac{1}{f}\}_{K}$. Rappelons enfin que comme
$O_{\mathfrak{X}}\{\frac{1}{f}\}_{K}$. Rappelons enfin que comme  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$, alors
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$, alors  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est noethérien (voir [Reference FultonFul69]).
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est noethérien (voir [Reference FultonFul69]).∙ Comme nous préférons travailler avec des
 $K$-espaces de type
$K$-espaces de type  $LB$ (voir le lemme 2.2.5), nous prenons par défaut la topologie canonique de
$LB$ (voir le lemme 2.2.5), nous prenons par défaut la topologie canonique de  $O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe sur
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe sur  $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ (définie dans le deuxième point).
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ (définie dans le deuxième point).
2.1.2. (Faisceaux des opérateurs différentiels.)
∙ Pour tout entier
 $m\geqslant 0$, on munit canoniquement
$m\geqslant 0$, on munit canoniquement  $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ d’une topologie de
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ d’une topologie de  $\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$-module de Banach, i.e. les
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$-module de Banach, i.e. les  $p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$ avec
$p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$ avec  $n\in \mathbb{N}$ forment une base de voisinages de zéro. On dispose de même d’une structure canonique de
$n\in \mathbb{N}$ forment une base de voisinages de zéro. On dispose de même d’une structure canonique de  $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach sur respectivement
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach sur respectivement  $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$,
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$,  $\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et  $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$via la base de voisinages de zéro d’ouverts donnée par respectivement
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$via la base de voisinages de zéro d’ouverts donnée par respectivement  $(p^{n}\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$,
$(p^{n}\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$,  $(p^{n}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$ et
$(p^{n}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$ et  $(p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$.
$(p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)})_{n\in \mathbb{N}}$.∙ La topologie canonique sur la
 $O_{\mathfrak{X},\mathbb{Q}}$-algèbre
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre  $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ est la topologie limite inductive dans
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ est la topologie limite inductive dans  $\mathfrak{C}$via
$\mathfrak{C}$via  $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$, où les
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$, où les  $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ sont munis de la topologie définie ci-dessus. Une base de voisinages de zéro de
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ sont munis de la topologie définie ci-dessus. Une base de voisinages de zéro de  $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ est donc donnée par la famille
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ est donc donnée par la famille  $\sum _{m=0}^{\infty }p^{n_{m}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$, où
$\sum _{m=0}^{\infty }p^{n_{m}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$, où  $(n_{m})_{m\in \mathbb{N}}$ parcourt les suites d’entiers positifs et où l’on a noté
$(n_{m})_{m\in \mathbb{N}}$ parcourt les suites d’entiers positifs et où l’on a noté  $\sum _{m=0}^{\infty }p^{n_{m}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}:=\underset{n\in \mathbb{N}}{\varinjlim }\sum _{m=0}^{n}p^{n_{m}}\widetilde{D}_{\mathfrak{ X}^{\sharp }}^{(m)}$.
$\sum _{m=0}^{\infty }p^{n_{m}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}:=\underset{n\in \mathbb{N}}{\varinjlim }\sum _{m=0}^{n}p^{n_{m}}\widetilde{D}_{\mathfrak{ X}^{\sharp }}^{(m)}$.∙ De même, on définit respectivement sur
 $D_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$,
$D_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$,  $\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et  $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ une topologie canonique de
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ une topologie canonique de  $O_{{\mathcal{Z}},\mathbb{Q}}$-module localement convexe. On remarque que d’après le lemme 1.1.4, on peut remplacer l’indice
$O_{{\mathcal{Z}},\mathbb{Q}}$-module localement convexe. On remarque que d’après le lemme 1.1.4, on peut remplacer l’indice  $\mathbb{N}$ par un sous-ensemble cofinal sans changer la topologie.
$\mathbb{N}$ par un sous-ensemble cofinal sans changer la topologie.
2.1.3. (Topologie canonique d’un ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent.) Soit
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent.) Soit ![]() $E$ un
$E$ un ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. On le munit d’une topologie canonique de
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. On le munit d’une topologie canonique de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-module localement convexe de la manière suivante. D’après [Reference BerthelotBer96, 3.6], il existe pour
$O_{\mathfrak{X},\mathbb{Q}}$-module localement convexe de la manière suivante. D’après [Reference BerthelotBer96, 3.6], il existe pour ![]() $m_{0}$ assez grand un
$m_{0}$ assez grand un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini ![]() $E^{(m_{0})}$ et un isomorphisme
$E^{(m_{0})}$ et un isomorphisme ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme ![]() $\unicode[STIX]{x1D716}:D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour tout entier
$\unicode[STIX]{x1D716}:D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour tout entier ![]() $m\geqslant m_{0}$, posons
$m\geqslant m_{0}$, posons ![]() $E^{(m)}:=\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}$. On munit
$E^{(m)}:=\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}$. On munit ![]() $E^{(m)}$ de la topologie canonique qui en fait un
$E^{(m)}$ de la topologie canonique qui en fait un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module de type fini de Banach (égale à la topologie quotient via un épimorphisme de la forme
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module de type fini de Banach (égale à la topologie quotient via un épimorphisme de la forme ![]() $(\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow E^{(m)}$). Comme pour tout
$(\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow E^{(m)}$). Comme pour tout ![]() $m$ les morphismes canoniques de la forme
$m$ les morphismes canoniques de la forme ![]() $(\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m+1)})^{r}$ sont continus, on en déduit que le morphisme canonique
$(\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m+1)})^{r}$ sont continus, on en déduit que le morphisme canonique ![]() $E^{(m)}\rightarrow E^{(m+1)}$ est continu. On munit
$E^{(m)}\rightarrow E^{(m+1)}$ est continu. On munit ![]() $E$ d’une topologie de
$E$ d’une topologie de ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent localement convexe qui fait de
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent localement convexe qui fait de ![]() $\unicode[STIX]{x1D716}:\mathop{\varinjlim }\nolimits_{m}E^{(m)}\overset{{\sim}}{\longrightarrow }\,E$ un homéomorphisme. Cela ne dépend pas du choix de
$\unicode[STIX]{x1D716}:\mathop{\varinjlim }\nolimits_{m}E^{(m)}\overset{{\sim}}{\longrightarrow }\,E$ un homéomorphisme. Cela ne dépend pas du choix de ![]() $(m_{0},E^{(m_{0})},\unicode[STIX]{x1D716})$. En effet, soit pour
$(m_{0},E^{(m_{0})},\unicode[STIX]{x1D716})$. En effet, soit pour ![]() $m\text{sp}\prime _{0}$ assez grand un
$m\text{sp}\prime _{0}$ assez grand un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime _{0})}$-module de type fini
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime _{0})}$-module de type fini ![]() $E^{\prime (m\text{sp}\prime _{0})}$ et un isomorphisme
$E^{\prime (m\text{sp}\prime _{0})}$ et un isomorphisme ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme ![]() $\unicode[STIX]{x1D716}\text{sp}\prime :D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{\prime (m\text{sp}\prime _{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour
$\unicode[STIX]{x1D716}\text{sp}\prime :D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{\prime (m\text{sp}\prime _{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour ![]() $m\geqslant m\text{sp}\prime _{0}$, posons
$m\geqslant m\text{sp}\prime _{0}$, posons ![]() $E^{\prime (m)}:=\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime _{0})}}E^{\prime (m\text{sp}\prime _{0})}$. D’après [Reference BerthelotBer96, 3.6.2], pour
$E^{\prime (m)}:=\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime _{0})}}E^{\prime (m\text{sp}\prime _{0})}$. D’après [Reference BerthelotBer96, 3.6.2], pour ![]() $m\text{sp}\prime \prime _{0}$ assez grand, il existe pour tout
$m\text{sp}\prime \prime _{0}$ assez grand, il existe pour tout ![]() $m\geqslant m\text{sp}\prime \prime _{0}$ des isomorphismes
$m\geqslant m\text{sp}\prime \prime _{0}$ des isomorphismes ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaires
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaires ![]() $\unicode[STIX]{x1D716}_{m}:E^{\prime (m)}\overset{{\sim}}{\longrightarrow }\,E^{(m)}$ tels que
$\unicode[STIX]{x1D716}_{m}:E^{\prime (m)}\overset{{\sim}}{\longrightarrow }\,E^{(m)}$ tels que ![]() $\unicode[STIX]{x1D716}\circ \unicode[STIX]{x1D716}^{\dagger }=\unicode[STIX]{x1D716}\text{sp}\prime$, avec
$\unicode[STIX]{x1D716}\circ \unicode[STIX]{x1D716}^{\dagger }=\unicode[STIX]{x1D716}\text{sp}\prime$, avec ![]() $\unicode[STIX]{x1D716}^{\dagger }:=\mathop{\varinjlim }\nolimits_{m}\,\unicode[STIX]{x1D716}_{m}$. Or, d’après [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3] (en effet, on remarque que la commutativité des anneaux est superflue), les
$\unicode[STIX]{x1D716}^{\dagger }:=\mathop{\varinjlim }\nolimits_{m}\,\unicode[STIX]{x1D716}_{m}$. Or, d’après [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3] (en effet, on remarque que la commutativité des anneaux est superflue), les ![]() $\unicode[STIX]{x1D716}_{m}$ sont des homéomorphismes. Par passage à la limite, on en déduit que
$\unicode[STIX]{x1D716}_{m}$ sont des homéomorphismes. Par passage à la limite, on en déduit que ![]() $\unicode[STIX]{x1D716}^{\dagger }$ est un homéomorphisme. D’où la canonicité de la topologie (on utilise aussi 1.1.4).
$\unicode[STIX]{x1D716}^{\dagger }$ est un homéomorphisme. D’où la canonicité de la topologie (on utilise aussi 1.1.4).
2.1.4. (Topologie canonique d’un ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini.) Soit
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini.) Soit ![]() $E$ un
$E$ un ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini. D’après [Reference BerthelotBer96, 3.6.2], il existe, pour
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini. D’après [Reference BerthelotBer96, 3.6.2], il existe, pour ![]() $m_{0}$ assez grand, un
$m_{0}$ assez grand, un ![]() $\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini
$\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini ![]() $E^{(m_{0})}$ et un isomorphisme
$E^{(m_{0})}$ et un isomorphisme ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire de la forme ![]() $\unicode[STIX]{x1D716}:O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}}E^{(m_{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour tout entier
$\unicode[STIX]{x1D716}:O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}}E^{(m_{0})}\overset{{\sim}}{\longrightarrow }\,E$. Pour tout entier ![]() $m\geqslant m_{0}$, posons
$m\geqslant m_{0}$, posons ![]() $E^{(m)}:=\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}\otimes _{\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}}E^{(m_{0})}$. On munit
$E^{(m)}:=\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}\otimes _{\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}}E^{(m_{0})}$. On munit ![]() $E^{(m)}$ de la topologie canonique qui en fait un
$E^{(m)}$ de la topologie canonique qui en fait un ![]() $\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$-module de type fini de Banach (égale à la topologie quotient via un épimorphisme de la forme
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}$-module de type fini de Banach (égale à la topologie quotient via un épimorphisme de la forme ![]() $(\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}})^{r}\rightarrow E^{(m)}$). Comme, pour tout
$(\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}})^{r}\rightarrow E^{(m)}$). Comme, pour tout ![]() $m$, les morphismes canoniques de la forme
$m$, les morphismes canoniques de la forme ![]() $(\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}})^{r}\rightarrow (\widetilde{B}_{\mathfrak{X}}^{(m+1)}(T)_{\mathbb{Q}})^{r}$ sont continus, on en déduit que le morphisme canonique
$(\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}})^{r}\rightarrow (\widetilde{B}_{\mathfrak{X}}^{(m+1)}(T)_{\mathbb{Q}})^{r}$ sont continus, on en déduit que le morphisme canonique ![]() $E^{(m)}\rightarrow E^{(m+1)}$ est continu. On munit
$E^{(m)}\rightarrow E^{(m+1)}$ est continu. On munit ![]() $E$ d’une topologie de
$E$ d’une topologie de ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini localement convexe qui fait de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini localement convexe qui fait de ![]() $\unicode[STIX]{x1D716}:\mathop{\varinjlim }\nolimits_{m}E^{(m)}\overset{{\sim}}{\longrightarrow }\,E$ un homéomorphisme. De manière analogue à 2.1.3, on vérifie que cela ne dépend pas du choix de
$\unicode[STIX]{x1D716}:\mathop{\varinjlim }\nolimits_{m}E^{(m)}\overset{{\sim}}{\longrightarrow }\,E$ un homéomorphisme. De manière analogue à 2.1.3, on vérifie que cela ne dépend pas du choix de ![]() $(m_{0},E^{(m_{0})},\unicode[STIX]{x1D716})$.
$(m_{0},E^{(m_{0})},\unicode[STIX]{x1D716})$.
2.2 Cas des isocristaux surconvergents
Rappelons les conventions suivantes.
Définition 2.2.1. Un isocristal sur ![]() $\mathfrak{X}^{\sharp }$ surconvergeant le long de
$\mathfrak{X}^{\sharp }$ surconvergeant le long de ![]() $T$ est un
$T$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent qui est aussi un
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent qui est aussi un ![]() ${\mathcal{O}}_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module localement projectif de type fini.
${\mathcal{O}}_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module localement projectif de type fini.
Lemme 2.2.2. (Topologie canonique d’un log-isocristal surconvergent)
Soit ![]() $E$ un
$E$ un ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent qui soit aussi un
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent qui soit aussi un ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module projectif de type fini pour la structure induite. La topologie sur
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module projectif de type fini pour la structure induite. La topologie sur ![]() $E$ en tant que
$E$ en tant que ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent est la même que celle en tant que
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent est la même que celle en tant que ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini. On l’appellera donc topologie canonique sur l’isocristal surconvergent
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini. On l’appellera donc topologie canonique sur l’isocristal surconvergent ![]() $E$.
$E$.
Démonstration.
De manière analogue à [Reference BerthelotBer96, 4.4.5] (voir aussi [Reference BerthelotBer96, 4.4.7]), quitte à augmenter ![]() $\unicode[STIX]{x1D706}_{0}$, il existe pour
$\unicode[STIX]{x1D706}_{0}$, il existe pour ![]() $m_{0}$ assez grand un
$m_{0}$ assez grand un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini topologiquement nilpotent
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini topologiquement nilpotent ![]() $E^{(m_{0})}$ qui est pour la structure induite un
$E^{(m_{0})}$ qui est pour la structure induite un ![]() $\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini et tel que
$\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini et tel que ![]() $E\overset{{\sim}}{\longrightarrow }\,D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}$. Or, d’après [Reference BerthelotBer96, 4.1.2], la topologie canonique de
$E\overset{{\sim}}{\longrightarrow }\,D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}E^{(m_{0})}$. Or, d’après [Reference BerthelotBer96, 4.1.2], la topologie canonique de ![]() $E^{(m_{0})}$ en tant que
$E^{(m_{0})}$ en tant que ![]() $\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini est la même que celle en tant que
$\widetilde{B}_{\mathfrak{X}}^{(m_{0})}(T)_{\mathbb{Q}}$-module de type fini est la même que celle en tant que ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini. De manière analogue à [Reference BerthelotBer96, 4.4.11], on vérifie que le morphisme canonique
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini. De manière analogue à [Reference BerthelotBer96, 4.4.11], on vérifie que le morphisme canonique
est un isomorphisme. D’où le résultat.
Lemme 2.2.3. Soit ![]() $\unicode[STIX]{x1D719}:E\rightarrow E\text{sp}\prime$ un morphisme de
$\unicode[STIX]{x1D719}:E\rightarrow E\text{sp}\prime$ un morphisme de ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. de
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. de ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini). Avec
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini). Avec ![]() $E$ et
$E$ et ![]() $E\text{sp}\prime$ munis des topologies canoniques (voir respectivement 2.1.3 et 2.1.4), le morphisme
$E\text{sp}\prime$ munis des topologies canoniques (voir respectivement 2.1.3 et 2.1.4), le morphisme ![]() $\unicode[STIX]{x1D719}$ est continu.
$\unicode[STIX]{x1D719}$ est continu.
Démonstration.
D’après [Reference BerthelotBer96, 3.6], il existe pour un entier positif ![]() $m_{0}$ assez grand un morphisme de
$m_{0}$ assez grand un morphisme de ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-modules de type fini
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-modules de type fini ![]() $\unicode[STIX]{x1D719}^{(m_{0})}:E^{(m_{0})}\rightarrow E^{\prime (m_{0})}$ tel que
$\unicode[STIX]{x1D719}^{(m_{0})}:E^{(m_{0})}\rightarrow E^{\prime (m_{0})}$ tel que ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$ soit isomorphe à
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$ soit isomorphe à ![]() $\unicode[STIX]{x1D719}$. Comme
$\unicode[STIX]{x1D719}$. Comme ![]() $\unicode[STIX]{x1D719}^{(m_{0})}$ est continu pour les topologies canoniques (voir [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3]), il en résulte que
$\unicode[STIX]{x1D719}^{(m_{0})}$ est continu pour les topologies canoniques (voir [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3]), il en résulte que ![]() $\unicode[STIX]{x1D719}$ est continu. Le cas respectif se traite de la même manière.
$\unicode[STIX]{x1D719}$ est continu. Le cas respectif se traite de la même manière.
Lemme 2.2.4. Soit ![]() $\unicode[STIX]{x1D719}:E{\twoheadrightarrow}E\text{sp}\prime$ un épimorphisme de
$\unicode[STIX]{x1D719}:E{\twoheadrightarrow}E\text{sp}\prime$ un épimorphisme de ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. de
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. de ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini). Alors
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini). Alors ![]() $\unicode[STIX]{x1D719}$ est un morphisme strict.
$\unicode[STIX]{x1D719}$ est un morphisme strict.
Démonstration.
D’après [Reference BerthelotBer96, 3.6], il existe pour un entier positif ![]() $m_{0}$ assez grand un morphisme de
$m_{0}$ assez grand un morphisme de ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-modules de type fini
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-modules de type fini ![]() $\unicode[STIX]{x1D719}^{(m_{0})}:E^{(m_{0})}\rightarrow E^{\prime (m_{0})}$ tel que
$\unicode[STIX]{x1D719}^{(m_{0})}:E^{(m_{0})}\rightarrow E^{\prime (m_{0})}$ tel que ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$ soit isomorphe à
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$ soit isomorphe à ![]() $\unicode[STIX]{x1D719}$. Comme on a
$\unicode[STIX]{x1D719}$. Comme on a ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\text{coker}(\unicode[STIX]{x1D719}^{(m_{0})})=\{0\}$, quitte à augmenter
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\text{coker}(\unicode[STIX]{x1D719}^{(m_{0})})=\{0\}$, quitte à augmenter ![]() $m_{0}$, on peut supposer que
$m_{0}$, on peut supposer que ![]() $\unicode[STIX]{x1D719}^{(m_{0})}$ est surjectif. Il en est alors de même de
$\unicode[STIX]{x1D719}^{(m_{0})}$ est surjectif. Il en est alors de même de ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$, pour tout entier
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}}\unicode[STIX]{x1D719}^{(m_{0})}$, pour tout entier ![]() $m\geqslant m_{0}$, ces derniers étant d’ailleurs continus et stricts pour les topologies de Banach respectives (voir [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3, corollary 5]). Par passage à la limite, il en résulte que
$m\geqslant m_{0}$, ces derniers étant d’ailleurs continus et stricts pour les topologies de Banach respectives (voir [Reference Bosch, Güntzer and RemmertBGR84, 3.7.3, corollary 5]). Par passage à la limite, il en résulte que ![]() $\unicode[STIX]{x1D719}$ est strict (voir 1.1.3). Le cas respectif se traite de la même manière.
$\unicode[STIX]{x1D719}$ est strict (voir 1.1.3). Le cas respectif se traite de la même manière.
Lemme 2.2.5. La topologie de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe canonique sur
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre localement convexe canonique sur ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est plus riche que celle induite par sa structure de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est plus riche que celle induite par sa structure de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée. Pour la topologie canonique, on en déduit que
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée. Pour la topologie canonique, on en déduit que ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est une
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est une ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre de type LB.
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre de type LB.
Démonstration.
On dispose des isomorphismes canoniques ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$ et
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}[\frac{1}{f}]_{K}^{\dagger }$ et ![]() $\widetilde{B}_{\mathfrak{X}}^{(m)}(T)\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}\{\frac{p}{f^{p^{m+1}}}\}$ (voir la preuve de [Reference BerthelotBer96, 4.3.2]). Il en résulte le morphisme de
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T)\overset{{\sim}}{\longrightarrow }\,O_{\mathfrak{X}}\{\frac{p}{f^{p^{m+1}}}\}$ (voir la preuve de [Reference BerthelotBer96, 4.3.2]). Il en résulte le morphisme de ![]() ${\mathcal{V}}$-algèbres
${\mathcal{V}}$-algèbres ![]() $\widetilde{B}_{\mathfrak{X}}^{(m)}(T){\hookrightarrow}O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ (pour l’injectivité, voir [Reference BerthelotBer96, 4.3.3.(ii)]). Le morphisme canonique de
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T){\hookrightarrow}O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ (pour l’injectivité, voir [Reference BerthelotBer96, 4.3.3.(ii)]). Le morphisme canonique de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbres
$O_{\mathfrak{X},\mathbb{Q}}$-algèbres ![]() $\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}{\hookrightarrow}O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est donc continu, avec
$\widetilde{B}_{\mathfrak{X}}^{(m)}(T)_{\mathbb{Q}}{\hookrightarrow}O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ est donc continu, avec ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ muni de sa topologie de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$ muni de sa topologie de ![]() $O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée. En passant à la limite, on en déduit le résultat.
$O_{\mathfrak{X},\mathbb{Q}}$-algèbre normée. En passant à la limite, on en déduit le résultat.
Lemme 2.2.6. Soit ![]() $I\subset (O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un monomorphisme de
$I\subset (O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un monomorphisme de ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules. Alors
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules. Alors ![]() $I$ est fermé dans
$I$ est fermé dans ![]() $(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ pour la topologie induite par la topologie canonique de
$(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ pour la topologie induite par la topologie canonique de ![]() $(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$.
$(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$.
Démonstration.
Notons ![]() $M:=(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}/I$ et
$M:=(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}/I$ et ![]() $M_{0}$ l’image du morphisme composé
$M_{0}$ l’image du morphisme composé ![]() $(O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })^{r}\subset (O_{\mathfrak{ X}}(\text{}^{\dagger }T)_{\mathbb{ Q}})^{r}{\twoheadrightarrow}M$. Munissons
$(O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })^{r}\subset (O_{\mathfrak{ X}}(\text{}^{\dagger }T)_{\mathbb{ Q}})^{r}{\twoheadrightarrow}M$. Munissons ![]() $M$ de la topologie quotient (pour la topologie canonique de
$M$ de la topologie quotient (pour la topologie canonique de ![]() $(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$). Il s’agit ainsi de vérifier que
$(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$). Il s’agit ainsi de vérifier que ![]() $M$ est séparé pour cette topologie. Or, comme pour tout entier
$M$ est séparé pour cette topologie. Or, comme pour tout entier ![]() $n$ le
$n$ le ![]() ${\mathcal{V}}$-module
${\mathcal{V}}$-module ![]() $p^{n}(O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })^{r}$ est un ouvert de
$p^{n}(O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger })^{r}$ est un ouvert de ![]() $(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ (voir 2.2.5), le
$(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ (voir 2.2.5), le ![]() ${\mathcal{V}}$-module
${\mathcal{V}}$-module ![]() $p^{n}M_{0}$ est alors un ouvert de
$p^{n}M_{0}$ est alors un ouvert de ![]() $M$. En outre, comme
$M$. En outre, comme ![]() $O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ est noethérien et comme
$O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ est noethérien et comme ![]() $O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }\rightarrow O_{\mathfrak{ X}}\{\frac{1}{f}\}$ est fidèlement plat, comme
$O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }\rightarrow O_{\mathfrak{ X}}\{\frac{1}{f}\}$ est fidèlement plat, comme ![]() $M_{0}$ est un
$M_{0}$ est un ![]() $O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$-module de type fini, alors
$O_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$-module de type fini, alors ![]() $M_{0}$ est séparé pour la topologie
$M_{0}$ est séparé pour la topologie ![]() $p$-adique (voir [Reference MatsumuraMat89, Théorèmes 8.10 et 8.12]), i.e.
$p$-adique (voir [Reference MatsumuraMat89, Théorèmes 8.10 et 8.12]), i.e. ![]() $\bigcap _{n\in \mathbb{N}}p^{n}M_{0}=\{0\}$. Il en résulte que
$\bigcap _{n\in \mathbb{N}}p^{n}M_{0}=\{0\}$. Il en résulte que ![]() $M$ est séparé.
$M$ est séparé.
Proposition 2.2.7. Les ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini sont des
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de type fini sont des ![]() $O_{\mathfrak{X},\mathbb{Q}}$-modules de type LB pour la topologie canonique. De plus, les sous-
$O_{\mathfrak{X},\mathbb{Q}}$-modules de type LB pour la topologie canonique. De plus, les sous-![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules d’un
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules d’un ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini ![]() $M$ sont fermés dans
$M$ sont fermés dans ![]() $M$ pour la topologie canonique de
$M$ pour la topologie canonique de ![]() $M$.
$M$.
Démonstration.
Soit ![]() $M$ un
$M$ un ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini muni de sa topologie canonique. Il existe un épimorphisme de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de type fini muni de sa topologie canonique. Il existe un épimorphisme de ![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de la forme
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules de la forme ![]() $(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}{\twoheadrightarrow}M$. D’après 2.2.4, ce morphisme est strict pour les topologies canoniques respectives. Il résulte alors de 2.2.6 que
$(O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}{\twoheadrightarrow}M$. D’après 2.2.4, ce morphisme est strict pour les topologies canoniques respectives. Il résulte alors de 2.2.6 que ![]() $M$ est séparé et donc
$M$ est séparé et donc ![]() $M$ est un
$M$ est un ![]() $O_{\mathfrak{X},\mathbb{Q}}$-module de type LB. Si
$O_{\mathfrak{X},\mathbb{Q}}$-module de type LB. Si ![]() $M\text{sp}\prime$ est un sous-
$M\text{sp}\prime$ est un sous-![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module de ![]() $M$, alors, grâce à 2.2.4, le module
$M$, alors, grâce à 2.2.4, le module ![]() $M/M\text{sp}\prime$ est séparé pour la topologie quotient induite par
$M/M\text{sp}\prime$ est séparé pour la topologie quotient induite par ![]() $M$. D’où le résultat.
$M$. D’où le résultat.
Remarque 2.2.8. Soit ![]() $I\subset (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un sous-
$I\subset (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un sous-![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Soit
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Soit ![]() $J\subset (O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un sous-
$J\subset (O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$ un sous-![]() $O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module. Il n’est pas clair que ces inclusions soient strictes pour les topologies canoniques respectives ni que
$O_{\mathfrak{X}}(\text{}^{\dagger }T)_{\mathbb{Q}}$-module. Il n’est pas clair que ces inclusions soient strictes pour les topologies canoniques respectives ni que ![]() $I$ soit fermé dans
$I$ soit fermé dans ![]() $(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$. Cependant, d’après une communication de Tomoyuki Abe, les
$(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}$. Cependant, d’après une communication de Tomoyuki Abe, les ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents sont aussi des espaces de type LB.
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents sont aussi des espaces de type LB.
2.3 Cas du faisceau des opérateurs différentiels de niveau fini à singularités surconvergentes
Proposition 2.3.1. Soit ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de ![]() ${\mathcal{V}}$-schémas formels affines et lisses,
${\mathcal{V}}$-schémas formels affines et lisses, ![]() $\mathfrak{D}$ un diviseur à croisements normaux strict de
$\mathfrak{D}$ un diviseur à croisements normaux strict de ![]() $\mathfrak{X}$ tel que
$\mathfrak{X}$ tel que ![]() $u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de
$u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de ![]() ${\mathcal{Z}}$. On pose
${\mathcal{Z}}$. On pose ![]() $\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$,
$\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$, ![]() ${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et
${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et ![]() $u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur
$u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur ![]() ${\mathcal{V}}$. Soit
${\mathcal{V}}$. Soit ![]() $\unicode[STIX]{x1D719}$ un morphisme
$\unicode[STIX]{x1D719}$ un morphisme ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire à gauche de la forme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire à gauche de la forme ![]() $\unicode[STIX]{x1D719}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Soit
$\unicode[STIX]{x1D719}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Soit ![]() $\unicode[STIX]{x1D713}$ un morphisme
$\unicode[STIX]{x1D713}$ un morphisme ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire à droite de la forme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-linéaire à droite de la forme ![]() $\unicode[STIX]{x1D713}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Notons
$\unicode[STIX]{x1D713}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Notons ![]() $u_{g}^{\ast }(\unicode[STIX]{x1D719}):(D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{r}\rightarrow (D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{s}$ et
$u_{g}^{\ast }(\unicode[STIX]{x1D719}):(D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{r}\rightarrow (D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{s}$ et ![]() $u_{d}^{\ast }(\unicode[STIX]{x1D713}):(D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger })^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger })^{s}$ les morphismes
$u_{d}^{\ast }(\unicode[STIX]{x1D713}):(D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger })^{r}\rightarrow (D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger })^{s}$ les morphismes ![]() $D_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaires induits par fonctorialité. Les morphismes
$D_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaires induits par fonctorialité. Les morphismes ![]() $\unicode[STIX]{x1D719}$,
$\unicode[STIX]{x1D719}$, ![]() $u_{g}^{\ast }(\unicode[STIX]{x1D719})$,
$u_{g}^{\ast }(\unicode[STIX]{x1D719})$, ![]() $u_{d}^{\ast }(\unicode[STIX]{x1D713})$ sont continus pour les topologies canoniques respectives (voir les définitions de 2.1.2).
$u_{d}^{\ast }(\unicode[STIX]{x1D713})$ sont continus pour les topologies canoniques respectives (voir les définitions de 2.1.2).
Démonstration.
(1) La continuité de ![]() $\unicode[STIX]{x1D719}$ résulte du lemme 2.2.3.
$\unicode[STIX]{x1D719}$ résulte du lemme 2.2.3.
(2) Vérifions à présent que ![]() $u_{g}^{\ast }(\unicode[STIX]{x1D719})$ est continu. Notons
$u_{g}^{\ast }(\unicode[STIX]{x1D719})$ est continu. Notons ![]() $\unicode[STIX]{x1D70B}$ les morphismes
$\unicode[STIX]{x1D70B}$ les morphismes ![]() $O_{\mathfrak{X},\mathbb{Q}}$-linéaires surjectifs de la forme
$O_{\mathfrak{X},\mathbb{Q}}$-linéaires surjectifs de la forme ![]() $\unicode[STIX]{x1D70B}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{n}{\twoheadrightarrow}(D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{n}$, pour un certain entier positif
$\unicode[STIX]{x1D70B}:(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{n}{\twoheadrightarrow}(D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })^{n}$, pour un certain entier positif ![]() $n$. Comme
$n$. Comme ![]() $u_{g}^{\ast }(\unicode[STIX]{x1D719})\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D719}$, il suffit d’établir que
$u_{g}^{\ast }(\unicode[STIX]{x1D719})\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D719}$, il suffit d’établir que ![]() $\unicode[STIX]{x1D70B}$ est un morphisme continu et strict. Comme la surjection canonique
$\unicode[STIX]{x1D70B}$ est un morphisme continu et strict. Comme la surjection canonique ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ envoie
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ envoie ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$ sur
$\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$ sur ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, celle-là est donc continue. D’après le théorème de l’application ouverte de Banach, ce morphisme surjectif et continu de
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, celle-là est donc continue. D’après le théorème de l’application ouverte de Banach, ce morphisme surjectif et continu de ![]() $K$-espaces de Banach est donc strict. Il découle alors du lemme 1.1.3 qu’il en est de même par passage à la limite sur le niveau de
$K$-espaces de Banach est donc strict. Il découle alors du lemme 1.1.3 qu’il en est de même par passage à la limite sur le niveau de ![]() $\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70B}$.
(3) On procède de même que pour l’étape (2) pour valider la continuité de ![]() $u_{d}^{\ast }(\unicode[STIX]{x1D713})$.
$u_{d}^{\ast }(\unicode[STIX]{x1D713})$.
Proposition 2.3.2. Soit ![]() $(N_{m})_{m\in \mathbb{N}}$ une suite strictement croissante d’entiers positifs. Le
$(N_{m})_{m\in \mathbb{N}}$ une suite strictement croissante d’entiers positifs. Le ![]() $K$-espace localement convexe
$K$-espace localement convexe ![]() $\underset{m}{\varinjlim }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(N_{m})}$ (muni de la topologie limite inductive dans la catégorie des
$\underset{m}{\varinjlim }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(N_{m})}$ (muni de la topologie limite inductive dans la catégorie des ![]() $K$-espaces localement convexes) est un espace de type
$K$-espaces localement convexes) est un espace de type ![]() $LB$.
$LB$.
Démonstration.
D’après 1.1.4, il suffit de traiter le cas où ![]() $N_{m}=m$. Comme les
$N_{m}=m$. Comme les ![]() $K$-espaces
$K$-espaces ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ sont de Banach, il s’agit de vérifier la séparation de
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ sont de Banach, il s’agit de vérifier la séparation de ![]() $\underset{m}{\varinjlim }~\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$. Notons
$\underset{m}{\varinjlim }~\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$. Notons ![]() $L$ le sous-
$L$ le sous-![]() ${\mathcal{V}}$-module de
${\mathcal{V}}$-module de ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ des éléments qui s’écrivent sous la forme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ des éléments qui s’écrivent sous la forme ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{d}}a_{\text{}\underline{k}}\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{[\text{}\underline{k}]}$ avec
$\sum _{\text{}\underline{k}\in \mathbb{N}^{d}}a_{\text{}\underline{k}}\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{[\text{}\underline{k}]}$ avec ![]() $a_{\text{}\underline{k}}\in {\mathcal{O}}_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ (on demande bien sûr que la série converge dans
$a_{\text{}\underline{k}}\in {\mathcal{O}}_{\mathfrak{X}}[\frac{1}{f}]^{\dagger }$ (on demande bien sûr que la série converge dans ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$). Or, comme
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$). Or, comme ![]() $p^{n}L\supset p^{n}D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)=\sum _{m=0}^{\infty }p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$, alors
$p^{n}L\supset p^{n}D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)=\sum _{m=0}^{\infty }p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}$, alors ![]() $p^{n}L$ est un ouvert de
$p^{n}L$ est un ouvert de ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ pour tout entier
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$ pour tout entier ![]() $n$. Par unicité de l’écriture sous la forme
$n$. Par unicité de l’écriture sous la forme ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{d}}a_{\text{}\underline{k}}\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{[\text{}\underline{k}]}$ des éléments de
$\sum _{\text{}\underline{k}\in \mathbb{N}^{d}}a_{\text{}\underline{k}}\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{[\text{}\underline{k}]}$ des éléments de ![]() $L$, on vérifie que
$L$, on vérifie que ![]() $\bigcap _{n\in \mathbb{N}}p^{n}L=\{0\}$. On obtient donc la séparation voulue.
$\bigcap _{n\in \mathbb{N}}p^{n}L=\{0\}$. On obtient donc la séparation voulue.
Proposition 2.3.3. Les topologies canoniques sont celles définies en 2.1.2.
(1) Pour tout entier
 $m\in \mathbb{N}$, soit
$m\in \mathbb{N}$, soit  $V^{(m)}$ un
$V^{(m)}$ un  $D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$-module à gauche localement convexe et
$D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$-module à gauche localement convexe et  $V^{(m)}\rightarrow V^{(m+1)}$ un morphisme continu. Soit
$V^{(m)}\rightarrow V^{(m+1)}$ un morphisme continu. Soit  $(N_{m})_{m\in \mathbb{N}}$ et
$(N_{m})_{m\in \mathbb{N}}$ et  $(N\text{sp}\prime _{m})_{m\in \mathbb{N}}$ deux suites strictement croissantes d’entiers positifs. Avec les notations de 1.3.1, l’isomorphisme canonique (5)est alors un homéomorphisme.
$(N\text{sp}\prime _{m})_{m\in \mathbb{N}}$ deux suites strictement croissantes d’entiers positifs. Avec les notations de 1.3.1, l’isomorphisme canonique (5)est alors un homéomorphisme. $$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(N\text{sp}\prime _{m})}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}V^{(N_{m})}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}V^{(m)}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(N\text{sp}\prime _{m})}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}V^{(N_{m})}\overset{{\sim}}{\longrightarrow }\,\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}V^{(m)}\end{eqnarray}$$(2) Les
 $K$-espaces localement convexes sont des
$K$-espaces localement convexes sont des $$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{m}\,\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(N_{m})}\text{ et }\mathop{\varinjlim }\nolimits_{m}\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varinjlim }\nolimits_{m}\,\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(N_{m})}\text{ et }\mathop{\varinjlim }\nolimits_{m}\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\end{eqnarray}$$ $K$-espaces de type LB.
$K$-espaces de type LB.
3 Préservation de la cohérence par foncteur cohomologique local
Soit ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ une immersion fermée de ![]() ${\mathcal{V}}$-schémas formels séparés, quasi compacts et lisses, et
${\mathcal{V}}$-schémas formels séparés, quasi compacts et lisses, et ![]() $T$ un diviseur de
$T$ un diviseur de ![]() $X$ tel que
$X$ tel que ![]() $U:=T\cap Z$ soit un diviseur de
$U:=T\cap Z$ soit un diviseur de ![]() $Z$. Soit
$Z$. Soit ![]() $\mathfrak{D}$ un diviseur à croisements normaux strict de
$\mathfrak{D}$ un diviseur à croisements normaux strict de ![]() $\mathfrak{X}$ tel que
$\mathfrak{X}$ tel que ![]() $u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de
$u^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de ![]() ${\mathcal{Z}}$. On pose
${\mathcal{Z}}$. On pose ![]() $\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$,
$\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$, ![]() ${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et
${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ et ![]() $u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur
$u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte de schémas formels logarithmiques lisses sur ![]() ${\mathcal{V}}$. Soit
${\mathcal{V}}$. Soit ![]() $\unicode[STIX]{x1D706}_{0}:\mathbb{N}\rightarrow \mathbb{N}$ une application croissante telle que
$\unicode[STIX]{x1D706}_{0}:\mathbb{N}\rightarrow \mathbb{N}$ une application croissante telle que ![]() $\unicode[STIX]{x1D706}_{0}(m)\geqslant m$, pour tout
$\unicode[STIX]{x1D706}_{0}(m)\geqslant m$, pour tout ![]() $m\in \mathbb{N}$. Pour alléger les notations, on pose alors
$m\in \mathbb{N}$. Pour alléger les notations, on pose alors ![]() $\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(\unicode[STIX]{x1D706}_{0}(m))}(T)$,
$\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T):=\widehat{{\mathcal{B}}}_{\mathfrak{X}}^{(\unicode[STIX]{x1D706}_{0}(m))}(T)$, ![]() $\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U):=\widehat{{\mathcal{B}}}_{{\mathcal{Z}}}^{(\unicode[STIX]{x1D706}_{0}(m))}(U)$,
$\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U):=\widehat{{\mathcal{B}}}_{{\mathcal{Z}}}^{(\unicode[STIX]{x1D706}_{0}(m))}(U)$, ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ et
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{\mathfrak{X}}^{(m)}(T)\widehat{\otimes }_{{\mathcal{O}}_{\mathfrak{X}}}\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ et ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}$. De même,
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}$. De même, ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}:=\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)$,
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}:=\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)$, ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$,
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)\widehat{\otimes }_{{\mathcal{O}}_{{\mathcal{Z}}}}\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$.
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$.
3.1 Images inverses par une immersion fermée de  ${\mathcal{V}}$-schémas formels affines et lisses
${\mathcal{V}}$-schémas formels affines et lisses
On suppose dans cette section que ![]() $\mathfrak{X}$ est affine.
$\mathfrak{X}$ est affine.
Lemme 3.1.1. (Théorèmes de type A et B)
Les morphismes canoniques ![]() $O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$,
$O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, ![]() $O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et
$O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ et ![]() $O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\rightarrow D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }$ sont des isomorphismes.
$O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\rightarrow D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }$ sont des isomorphismes.
De plus, pour tout entier ![]() $q\geqslant 1$,
$q\geqslant 1$, ![]() $H^{q}({\mathcal{Z}},\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})=0$,
$H^{q}({\mathcal{Z}},\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})=0$, ![]() $H^{q}({\mathcal{Z}},\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})=0$ et
$H^{q}({\mathcal{Z}},\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})=0$ et ![]() $H^{q}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })=0$.
$H^{q}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger })=0$.
Démonstration.
Comme le foncteur ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ commute aux limites projectives, on vérifie que le morphisme canonique
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ commute aux limites projectives, on vérifie que le morphisme canonique ![]() $O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est un isomorphisme. Comme le foncteur
$O_{{\mathcal{Z}}}\otimes _{O_{\mathfrak{X}}}\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est un isomorphisme. Comme le foncteur ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ et le produit tensoriel commutent à la tensorisation par
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ et le produit tensoriel commutent à la tensorisation par ![]() $\mathbb{Q}$ (car
$\mathbb{Q}$ (car ![]() ${\mathcal{Z}}$ est noethérien) et aux limites inductives filtrantes de faisceaux sur
${\mathcal{Z}}$ est noethérien) et aux limites inductives filtrantes de faisceaux sur ![]() ${\mathcal{Z}}$, on en déduit les deux autres isomorphismes.
${\mathcal{Z}}$, on en déduit les deux autres isomorphismes.
On procède de même pour les annulations, les propriétés satisfaites par le foncteur ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ que l’on a utilisées étant toujours valables pour les foncteurs dérivés
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ que l’on a utilisées étant toujours valables pour les foncteurs dérivés ![]() $H^{q}({\mathcal{Z}},-)$ (voir [Reference BerthelotBer96, 3.3.2, 3.4.0.1 et 3.6.5]).
$H^{q}({\mathcal{Z}},-)$ (voir [Reference BerthelotBer96, 3.3.2, 3.4.0.1 et 3.6.5]).
Notations 3.1.2. (Images inverses dérivées gauches.) Soit ![]() $E^{(m)}$ un
$E^{(m)}$ un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module cohérent à gauche. On pose
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module cohérent à gauche. On pose ![]() ${\mathcal{E}}^{(m)}:=\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$,
${\mathcal{E}}^{(m)}:=\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$, ![]() $E:=D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$ et
$E:=D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$ et ![]() ${\mathcal{E}}:={\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$. On définit les foncteurs images inverses dérivées gauches en posant
${\mathcal{E}}:={\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}E^{(m)}$. On définit les foncteurs images inverses dérivées gauches en posant ![]() $\mathbb{L}u^{\ast }(E^{(m)}):=\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}E^{(m)}$,
$\mathbb{L}u^{\ast }(E^{(m)}):=\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}E^{(m)}$, ![]() $\mathbb{L}u^{\ast }({\mathcal{E}}^{(m)}):=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}{\mathcal{E}}^{(m)}$. De la même manière,
$\mathbb{L}u^{\ast }({\mathcal{E}}^{(m)}):=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}{\mathcal{E}}^{(m)}$. De la même manière, ![]() $\mathbb{L}u^{\ast }(E):=D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}E$ et
$\mathbb{L}u^{\ast }(E):=D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}E$ et ![]() $\mathbb{L}u^{\ast }({\mathcal{E}}):={\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{{\mathcal{D}}_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}{\mathcal{E}}$. On remarque que les notations sont justifiées par le lemme 3.1.1 et correspondent aux foncteurs
$\mathbb{L}u^{\ast }({\mathcal{E}}):={\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{{\mathcal{D}}_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}{\mathcal{E}}$. On remarque que les notations sont justifiées par le lemme 3.1.1 et correspondent aux foncteurs ![]() $\mathbb{L}u^{\ast }$ calculés dans la catégorie des
$\mathbb{L}u^{\ast }$ calculés dans la catégorie des ![]() $O_{\mathfrak{X},\mathbb{Q}}$-modules ou
$O_{\mathfrak{X},\mathbb{Q}}$-modules ou ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules. Enfin, d’après les théorèmes de type
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules. Enfin, d’après les théorèmes de type ![]() $A$, tous les
$A$, tous les ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-modules cohérents et les
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-modules cohérents et les ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents sont de cette forme (voir respectivement [Reference BerthelotBer96, 3.4 et 3.6.5]).
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents sont de cette forme (voir respectivement [Reference BerthelotBer96, 3.4 et 3.6.5]).
De même, en remplac˛ant ![]() $?_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}$ par
$?_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}$ par ![]() $?_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}$, on définit le foncteur
$?_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}$, on définit le foncteur ![]() $\mathbb{L}u^{\ast }$ pour les modules à droite. Par exemple, si
$\mathbb{L}u^{\ast }$ pour les modules à droite. Par exemple, si ![]() $E^{(m)}$ est un
$E^{(m)}$ est un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module cohérent à droite, on pose
$\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-module cohérent à droite, on pose ![]() $\mathbb{L}u^{\ast }(E^{(m)}):=E\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$. Enfin, si l’on veut préciser que l’on a affaire à des modules à gauche (resp. à droite), on pourra noter
$\mathbb{L}u^{\ast }(E^{(m)}):=E\otimes _{\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)}}^{\mathbb{L}}\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$. Enfin, si l’on veut préciser que l’on a affaire à des modules à gauche (resp. à droite), on pourra noter ![]() $\mathbb{L}u_{g}^{\ast }$ (resp.
$\mathbb{L}u_{g}^{\ast }$ (resp. ![]() $\mathbb{L}u_{d}^{\ast }$) à la place de
$\mathbb{L}u_{d}^{\ast }$) à la place de ![]() $\mathbb{L}u^{\ast }$.
$\mathbb{L}u^{\ast }$.
Lemme 3.1.3. Avec les notations et hypothèses de 3.1.2, on dispose alors des isomorphismes canoniques
Démonstration.
Le premier se traitant de manière analogue, contentons-nous de vérifier le dernier isomorphisme. Soit ![]() $P^{\bullet }$ une résolution gauche de
$P^{\bullet }$ une résolution gauche de ![]() $E$ par des
$E$ par des ![]() $D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules libres de type fini. Le complexe
$D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules libres de type fini. Le complexe ![]() ${\mathcal{P}}^{\bullet }:={\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet }$ est alors une résolution gauche de
${\mathcal{P}}^{\bullet }:={\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet }$ est alors une résolution gauche de ![]() ${\mathcal{E}}$ par des
${\mathcal{E}}$ par des ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules libres de type fini. On dispose alors des isomorphismes canoniques :
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules libres de type fini. On dispose alors des isomorphismes canoniques :
 $$\begin{eqnarray}\displaystyle \hspace{-4.0pt} & \displaystyle D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}E\overset{{\sim}}{\longleftarrow }\,D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet } & \displaystyle \nonumber\\ \displaystyle \hspace{-4.0pt} & \displaystyle \overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet })\overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)}u^{-1}{\mathcal{P}}^{\bullet })\overset{{\sim}}{\longrightarrow }\, & \displaystyle \nonumber\\ \displaystyle \hspace{-4.0pt} & \displaystyle \mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}u^{-1}{\mathcal{P}}^{\bullet })\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}u^{-1}{\mathcal{E}}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{-4.0pt} & \displaystyle D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}E\overset{{\sim}}{\longleftarrow }\,D_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet } & \displaystyle \nonumber\\ \displaystyle \hspace{-4.0pt} & \displaystyle \overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}P^{\bullet })\overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)}u^{-1}{\mathcal{P}}^{\bullet })\overset{{\sim}}{\longrightarrow }\, & \displaystyle \nonumber\\ \displaystyle \hspace{-4.0pt} & \displaystyle \mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}u^{-1}{\mathcal{P}}^{\bullet })\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }\otimes _{u^{-1}{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}^{\mathbb{L}}u^{-1}{\mathcal{E}}), & \displaystyle \nonumber\end{eqnarray}$$ l’avant-dernier isomorphisme résultant du fait que les ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }$-modules libres sont
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{\dagger }$-modules libres sont ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$-acycliques (voir le lemme 3.1.1).
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$-acycliques (voir le lemme 3.1.1).
Remarque 3.1.4. Comme les ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. les
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents (resp. les ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-modules cohérents) vérifient le théorème de type
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-modules cohérents) vérifient le théorème de type ![]() $B$ (voir [Reference BerthelotBer96, 3.6.4]), on aurait pu utiliser les résolutions de Koszul pour valider le lemme 3.1.3 ci-dessus.
$B$ (voir [Reference BerthelotBer96, 3.6.4]), on aurait pu utiliser les résolutions de Koszul pour valider le lemme 3.1.3 ci-dessus.
3.2 Image directe de niveau  $m$ : exactitude
$m$ : exactitude
Pour faire des calculs en coordonnées locales, nous utiliserons les notations et hypothèses suivantes : on suppose que ![]() $\mathfrak{X}$ est affine, muni de coordonnées locales
$\mathfrak{X}$ est affine, muni de coordonnées locales ![]() $t_{1},\ldots ,t_{d}$ telles que
$t_{1},\ldots ,t_{d}$ telles que ![]() ${\mathcal{Z}}:=\bigcap _{i=1}^{e}V(t_{i})$,
${\mathcal{Z}}:=\bigcap _{i=1}^{e}V(t_{i})$, ![]() $\mathfrak{D}=V(t_{e+1}\cdots t_{f})$ et que
$\mathfrak{D}=V(t_{e+1}\cdots t_{f})$ et que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ soit l’immersion fermée induite.
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ soit l’immersion fermée induite.
Notations 3.2.1. Pour tout entier ![]() $m\geqslant 0$, on pose
$m\geqslant 0$, on pose ![]() $D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U):=\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)\otimes _{{\mathcal{O}}_{{\mathcal{Z}}}}D_{{\mathcal{Z}}^{\sharp }}^{(m)}$ et
$D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U):=\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)\otimes _{{\mathcal{O}}_{{\mathcal{Z}}}}D_{{\mathcal{Z}}^{\sharp }}^{(m)}$ et ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U):=D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$. On munit
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U):=D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{{\mathcal{O}}_{{\mathcal{Z}}}}\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$. On munit ![]() $D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$ (resp.
$D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$ (resp. ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$) d’une structure de
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$) d’une structure de ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-algèbre normée dont une base de voisinages de zéro est donnée par la famille
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-algèbre normée dont une base de voisinages de zéro est donnée par la famille ![]() $(p^{n}D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U))_{n\in \mathbb{N}}$ (resp.
$(p^{n}D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U))_{n\in \mathbb{N}}$ (resp. ![]() $(p^{n}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U))_{n\in \mathbb{N}}$). En d’autres termes, ce sont les topologies provenant des normes induites via les inclusions
$(p^{n}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U))_{n\in \mathbb{N}}$). En d’autres termes, ce sont les topologies provenant des normes induites via les inclusions ![]() $D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\hookrightarrow}\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ et
$D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\hookrightarrow}\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ et ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\hookrightarrow}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$. De plus, on remarque que le séparé complété de
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\hookrightarrow}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$. De plus, on remarque que le séparé complété de ![]() $D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$ (resp.
$D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$ (resp. ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$) est
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$) est ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ (resp.
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ (resp. ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$).
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$).
Lemme 3.2.2. Soit ![]() $V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime$ une suite exacte de
$V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime$ une suite exacte de ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-modules de Banach (voir la définition 1.3.2 et la topologie canonique de 2.1.2). On suppose de plus que
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-modules de Banach (voir la définition 1.3.2 et la topologie canonique de 2.1.2). On suppose de plus que ![]() $\unicode[STIX]{x1D719}$ et
$\unicode[STIX]{x1D719}$ et ![]() $\unicode[STIX]{x1D713}$ sont des morphismes stricts. Les suites
$\unicode[STIX]{x1D713}$ sont des morphismes stricts. Les suites
sont alors exactes et leurs morphismes sont stricts.
Démonstration.
(1) Supposons d’abord que l’on dispose en réalité de la suite exacte ![]() $0\rightarrow V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime \rightarrow 0$. Pour tout
$0\rightarrow V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime \rightarrow 0$. Pour tout ![]() $\text{}\underline{k}\in \mathbb{N}^{e}$, en identifiant
$\text{}\underline{k}\in \mathbb{N}^{e}$, en identifiant ![]() $\mathbb{N}^{e}$ à un sous-ensemble de
$\mathbb{N}^{e}$ à un sous-ensemble de ![]() $\mathbb{N}^{d}$via l’inclusion
$\mathbb{N}^{d}$via l’inclusion ![]() $\text{}\underline{k}=(k_{1},\ldots ,k_{e})\mapsto (k_{1},\ldots ,k_{e},0,\ldots ,0)$, notons
$\text{}\underline{k}=(k_{1},\ldots ,k_{e})\mapsto (k_{1},\ldots ,k_{e},0,\ldots ,0)$, notons ![]() $\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}$ l’image de
$\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}$ l’image de ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m)}}$ (comme
$\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m)}}$ (comme ![]() $\text{}\underline{k}\in \mathbb{N}^{e}$, on remarque que
$\text{}\underline{k}\in \mathbb{N}^{e}$, on remarque que ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m)}}=\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{{<}\text{}\underline{k}{>}_{(m)}}$) via la surjection canonique
$\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m)}}=\text{}\underline{\unicode[STIX]{x2202}}_{\sharp }^{{<}\text{}\underline{k}{>}_{(m)}}$) via la surjection canonique ![]() $D_{\mathfrak{X}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\twoheadrightarrow}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$. Les éléments du
$D_{\mathfrak{X}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}{\twoheadrightarrow}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}$. Les éléments du ![]() $K$-espace vectoriel
$K$-espace vectoriel ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ s’écrivent de manière unique sous la forme
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ s’écrivent de manière unique sous la forme ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}$, la somme étant finie et
$\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}$, la somme étant finie et ![]() $x_{\text{}\underline{k}}\in V$. D’après 1.2.3, si l’on note
$x_{\text{}\underline{k}}\in V$. D’après 1.2.3, si l’on note ![]() $V_{0}$ le sous-
$V_{0}$ le sous-![]() ${\mathcal{V}}$-module de
${\mathcal{V}}$-module de ![]() $V$ des éléments de norme inférieure ou égale à
$V$ des éléments de norme inférieure ou égale à ![]() $1$ et
$1$ et ![]() $U_{0}$ le sous-
$U_{0}$ le sous-![]() ${\mathcal{V}}$-module de
${\mathcal{V}}$-module de ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ engendré par l’image canonique de la flèche
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ engendré par l’image canonique de la flèche ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)\times V_{0}\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$, alors une base de voisinage de
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)\times V_{0}\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$, alors une base de voisinage de ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ est donnée par la famille
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ est donnée par la famille ![]() $(p^{n}U_{0})_{n\in \mathbb{N}}$. On en déduit que la topologie canonique sur
$(p^{n}U_{0})_{n\in \mathbb{N}}$. On en déduit que la topologie canonique sur ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ est induite par la norme
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V$ est induite par la norme ![]() $\Vert \!\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}\!\Vert =\max _{\text{}\underline{k}}\Vert \!x_{\text{}\underline{k}}\!\Vert$. On a la même description pour
$\Vert \!\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}\!\Vert =\max _{\text{}\underline{k}}\Vert \!x_{\text{}\underline{k}}\!\Vert$. On a la même description pour ![]() $V\text{sp}\prime$ ou
$V\text{sp}\prime$ ou ![]() $V\text{sp}\prime \prime$ à la place de
$V\text{sp}\prime \prime$ à la place de ![]() $V$. On obtient alors la suite exacte courte de
$V$. On obtient alors la suite exacte courte de ![]() $K$-espaces normés
$K$-espaces normés
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V\text{sp}\prime \rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{ Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}\nonumber\\ \displaystyle & & \displaystyle \qquad V\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V\text{sp}\prime \prime \rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V\text{sp}\prime \rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{ Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}\nonumber\\ \displaystyle & & \displaystyle \qquad V\rightarrow D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\otimes _{D_{{\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}}V\text{sp}\prime \prime \rightarrow 0,\end{eqnarray}$$ dont tous les morphismes sont stricts (pour celle de l’injection, c’est évident d’après la description de leur norme ; pour celle de la surjection, on peut par exemple invoquer 1.2.5 ou bien faire le calcul). Or, d’après la proposition 1.3.5, comme ![]() $V$ est un
$V$ est un ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach, le morphisme canonique
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach, le morphisme canonique ![]() $D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp }}^{(m)}}(U)_{\mathbb{Q}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V$ est un isomorphisme. Comme le foncteur de séparée complétion transforme les suites exactes courtes dont les applications sont des morphismes stricts de
$D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\widehat{\otimes }_{D_{{\mathcal{Z}}^{\sharp }}^{(m)}}(U)_{\mathbb{Q}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V$ est un isomorphisme. Comme le foncteur de séparée complétion transforme les suites exactes courtes dont les applications sont des morphismes stricts de ![]() $K$-espaces normés en des suites exactes courtes dont les applications sont des morphismes stricts, on obtient la suite exacte
$K$-espaces normés en des suites exactes courtes dont les applications sont des morphismes stricts, on obtient la suite exacte
dont les morphismes sont stricts. Comme ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ est plat à gauche sur
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$ est plat à gauche sur ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$, on dispose de la même suite exacte que 10 où l’on remplace
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$, on dispose de la même suite exacte que 10 où l’on remplace ![]() $\widehat{\otimes }$ par
$\widehat{\otimes }$ par ![]() $\otimes$. Le morphisme surjectif de cette dernière suite exacte est strict grâce à 1.2.5. Enfin, le caractère strict du morphisme injectif résulte quant à lui du fait qu’en le composant avec le monomorphisme strict
$\otimes$. Le morphisme surjectif de cette dernière suite exacte est strict grâce à 1.2.5. Enfin, le caractère strict du morphisme injectif résulte quant à lui du fait qu’en le composant avec le monomorphisme strict ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V$, on obtienne encore un monomorphisme strict.
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V$, on obtienne encore un monomorphisme strict.
(2) En décomposant les suites exactes en suites exactes courtes, on obtient le résultat.
Lemme 3.2.3. Soit ![]() $m\text{sp}\prime \geqslant m$ deux entiers,
$m\text{sp}\prime \geqslant m$ deux entiers, ![]() $V$ un
$V$ un ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach et
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach et ![]() $V\text{sp}\prime$ un
$V\text{sp}\prime$ un ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}$-module de Banach (voir la définition 1.3.2). Soit
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}$-module de Banach (voir la définition 1.3.2). Soit ![]() $\unicode[STIX]{x1D719}:V{\hookrightarrow}V\text{sp}\prime$ un monomorphisme de
$\unicode[STIX]{x1D719}:V{\hookrightarrow}V\text{sp}\prime$ un monomorphisme de ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire. Le morphisme continu
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire. Le morphisme continu ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ canoniquement induit par
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ canoniquement induit par ![]() $\unicode[STIX]{x1D719}$ est alors injectif.
$\unicode[STIX]{x1D719}$ est alors injectif.
Démonstration.
Notons ![]() $\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}$ l’image de
$\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}$ l’image de ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m\text{sp}\prime )}}$via la surjection canonique
$\text{}\underline{\unicode[STIX]{x2202}}^{{<}\text{}\underline{k}{>}_{(m\text{sp}\prime )}}$via la surjection canonique ![]() $D_{\mathfrak{X}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{Q}}{\twoheadrightarrow}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{Q}}$. D’après la preuve de 3.2.2, le
$D_{\mathfrak{X}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{Q}}{\twoheadrightarrow}D_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{Q}}$. D’après la preuve de 3.2.2, le ![]() $K$-espace de Banach
$K$-espace de Banach ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ est le
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ est le ![]() $K$-espace des éléments s’écrivant de manière unique sous la forme
$K$-espace des éléments s’écrivant de manière unique sous la forme ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}\otimes x_{\text{}\underline{k}}$, la somme étant infinie mais la suite des éléments
$\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}\otimes x_{\text{}\underline{k}}$, la somme étant infinie mais la suite des éléments ![]() $x\text{sp}\prime _{\text{}\underline{k}}\in V\text{sp}\prime$ tendant vers zéro lorsque
$x\text{sp}\prime _{\text{}\underline{k}}\in V\text{sp}\prime$ tendant vers zéro lorsque ![]() $|\text{}\underline{k}|$ tend vers l’infini. Comme
$|\text{}\underline{k}|$ tend vers l’infini. Comme ![]() $\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}=\unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}$, pour un certain
$\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}=\unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}$, pour un certain ![]() $\unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\in {\mathcal{V}}\setminus \{0\}$, on vérifie alors que le morphisme canonique
$\unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\in {\mathcal{V}}\setminus \{0\}$, on vérifie alors que le morphisme canonique ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{ Q}}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ envoie la somme
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}(U)_{\mathbb{Q}}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}V\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m\text{sp}\prime )}(U)_{\mathbb{ Q}}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m\text{sp}\prime )}}V\text{sp}\prime$ envoie la somme ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}$ sur
$\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m)}\otimes x_{\text{}\underline{k}}$ sur ![]() $\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}\otimes \unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\unicode[STIX]{x1D719}(x_{\text{}\underline{k}})$. D’où le résultat.
$\sum _{\text{}\underline{k}\in \mathbb{N}^{e}}\unicode[STIX]{x1D709}_{\text{}\underline{k},(m\text{sp}\prime )}\otimes \unicode[STIX]{x1D706}_{\text{}\underline{k},(m,m\text{sp}\prime )}\unicode[STIX]{x1D719}(x_{\text{}\underline{k}})$. D’où le résultat.
Nous n’aurons pas besoin de la proposition 3.2.4, mais elle résulte immédiatement des lemmes 3.2.2 et 3.2.3 que nous utiliserons.
Proposition 3.2.4. Soit ![]() $0\rightarrow V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime$ une suite exacte de
$0\rightarrow V\text{sp}\prime \underset{\unicode[STIX]{x1D719}}{\longrightarrow }V\underset{\unicode[STIX]{x1D713}}{\longrightarrow }V\text{sp}\prime \prime$ une suite exacte de ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-modules de Banach (voir la définition 1.3.2). On suppose de plus que
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-modules de Banach (voir la définition 1.3.2). On suppose de plus que ![]() $\unicode[STIX]{x1D719}$ est un morphisme strict. La suite
$\unicode[STIX]{x1D719}$ est un morphisme strict. La suite
est alors exacte et ![]() $\text{id}\widehat{\otimes }\unicode[STIX]{x1D719}$ est strict.
$\text{id}\widehat{\otimes }\unicode[STIX]{x1D719}$ est strict.
Démonstration.
En munissant ![]() $W:=V/V\text{sp}\prime$ de la topologie quotient, on obtient le morphisme
$W:=V/V\text{sp}\prime$ de la topologie quotient, on obtient le morphisme ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire, injectif et continu
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire, injectif et continu ![]() $W{\hookrightarrow}V\text{sp}\prime \prime$. On en déduit que
$W{\hookrightarrow}V\text{sp}\prime \prime$. On en déduit que ![]() $W$ est un
$W$ est un ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach, car il est un quotient séparé de
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-module de Banach, car il est un quotient séparé de ![]() $V$. On applique alors respectivement les lemmes 3.2.2 et 3.2.3 à la suite exacte
$V$. On applique alors respectivement les lemmes 3.2.2 et 3.2.3 à la suite exacte ![]() $0\rightarrow V\text{sp}\prime \rightarrow V\rightarrow W\rightarrow 0$ et au monomorphisme
$0\rightarrow V\text{sp}\prime \rightarrow V\rightarrow W\rightarrow 0$ et au monomorphisme ![]() $W\rightarrow V\text{sp}\prime \prime$.
$W\rightarrow V\text{sp}\prime \prime$.
3.2.5. Le module ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est séparé pour la topologie
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est séparé pour la topologie ![]() $p$-adique. En effet, si
$p$-adique. En effet, si ![]() $E$ est un sous-
$E$ est un sous-![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}$-module à gauche de type fini de
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}$-module à gauche de type fini de ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, comme
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$, comme ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}$ est le séparé complété
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}$ est le séparé complété ![]() $p$-adique d’un
$p$-adique d’un ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}$-module à droite libre, alors
$\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}$-module à droite libre, alors ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}E$ est séparé et complet pour la topologie
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}E$ est séparé et complet pour la topologie ![]() $p$-adique (voir [Reference BerthelotBer96, 3.2.4]). On en déduit aussi que le morphisme canonique de la forme
$p$-adique (voir [Reference BerthelotBer96, 3.2.4]). On en déduit aussi que le morphisme canonique de la forme ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}E\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est un monomorphisme. En passant à la limite inductive sur
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}E\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est un monomorphisme. En passant à la limite inductive sur ![]() $E$, on en déduit que le morphisme canonique
$E$, on en déduit que le morphisme canonique ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est injectif.
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}\rightarrow \widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ est injectif.
On munit ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ de la topologie produit tensoriel définie dans 1.2.2, i.e. d’après le lemme 1.2.3, c’est la topologie dont une base de voisinages de zéro est donnée par la famille
$\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ de la topologie produit tensoriel définie dans 1.2.2, i.e. d’après le lemme 1.2.3, c’est la topologie dont une base de voisinages de zéro est donnée par la famille ![]() $p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ avec
$p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ avec ![]() $n$ parcourant
$n$ parcourant ![]() $\mathbb{N}$. On munit naturellement
$\mathbb{N}$. On munit naturellement ![]() $(\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{\mathbb{ Q}}$ de la topologie dont une base de voisinages de zéro est donnée par la famille
$(\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{\mathbb{ Q}}$ de la topologie dont une base de voisinages de zéro est donnée par la famille ![]() $p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ avec
$p^{n}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)}$ avec ![]() $n$ parcourant
$n$ parcourant ![]() $\mathbb{N}$, ce qui en fait un
$\mathbb{N}$, ce qui en fait un ![]() $K$-espace de Banach. On obtient alors le monomorphisme strict de
$K$-espace de Banach. On obtient alors le monomorphisme strict de ![]() $K$-espaces normés
$K$-espaces normés
Par construction des séparées complétions de ![]() $K$-espaces localement connexes (par exemple voir la preuve de [Reference SchneiderSch02, 7.5]), on vérifie que le morphisme 12 se factorise en l’isomorphisme canonique (indépendant des coordonnées locales) de
$K$-espaces localement connexes (par exemple voir la preuve de [Reference SchneiderSch02, 7.5]), on vérifie que le morphisme 12 se factorise en l’isomorphisme canonique (indépendant des coordonnées locales) de ![]() $K$-espaces de Banach :
$K$-espaces de Banach :
3.3 Stabilité de la cohérence par foncteur cohomologique local en degré zéro
3.3.1. (Rappels.) On rappelle que d’après [Reference CaroCar16, 5.3.8], les foncteurs ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ et
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ et ![]() $u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ sont isomorphes. On dispose aussi du foncteur
$u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ sont isomorphes. On dispose aussi du foncteur ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ défini de telle sorte que l’on ait l’isomorphisme de foncteurs
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ défini de telle sorte que l’on ait l’isomorphisme de foncteurs ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }\circ \varinjlim \overset{{\sim}}{\longrightarrow }\,\varinjlim \circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$, où
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }\circ \varinjlim \overset{{\sim}}{\longrightarrow }\,\varinjlim \circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$, où ![]() $\varinjlim$ désigne le foncteur canonique
$\varinjlim$ désigne le foncteur canonique ![]() $\varinjlim :\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ qui induit l’équivalence de catégories
$\varinjlim :\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow D^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ qui induit l’équivalence de catégories
(voir [Reference CaroCar16, 2] ou [Reference BerthelotBer02, 4.2.4] énoncé sans structure logarithmique). Si le besoin de distinguer les deux foncteurs ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ se fait sentir, on notera alors dans ce cas
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ se fait sentir, on notera alors dans ce cas ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{(\bullet )}:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$. Enfin, pour tout
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{(\bullet )}:\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})\rightarrow \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$. Enfin, pour tout ![]() $n\in \mathbb{N}$, on note
$n\in \mathbb{N}$, on note ![]() ${\mathcal{H}}_{Z}^{\dagger n}:={\mathcal{H}}^{n}\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})\rightarrow M({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$, où
${\mathcal{H}}_{Z}^{\dagger n}:={\mathcal{H}}^{n}\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }:D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})\rightarrow M({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$, où ![]() $M({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ désigne la catégorie des
$M({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ désigne la catégorie des ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche.
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche.
Pour établir la proposition qui suit, nous aurons besoin des deux lemmes suivants.
Lemme 3.3.2. (Berthelot-Kashiwara)
Soit ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent à support dans
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent à support dans ![]() ${\mathcal{Z}}$.
${\mathcal{Z}}$.
(1) Le complexe
 $u^{\sharp !}({\mathcal{E}})$ est isomorphe à
$u^{\sharp !}({\mathcal{E}})$ est isomorphe à  ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$, ce dernier étant un
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$, ce dernier étant un  ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. De plus, le morphisme canonique
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. De plus, le morphisme canonique  $u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})\rightarrow {\mathcal{E}}$ est un isomorphisme.
$u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})\rightarrow {\mathcal{E}}$ est un isomorphisme.(2) Le morphisme canonique
 $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\rightarrow {\mathcal{E}}$ est un isomorphisme.
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\rightarrow {\mathcal{E}}$ est un isomorphisme.
Démonstration.
Modulo l’isomorphisme ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{(\bullet )}\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}$, c’est une reformulation des versions arithmétiques de Berthelot du théorème de Kashiwara de [Reference CaroCar16, 5.3.7] et [Reference CaroCar16, A.8].
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{(\bullet )}\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}$, c’est une reformulation des versions arithmétiques de Berthelot du théorème de Kashiwara de [Reference CaroCar16, 5.3.7] et [Reference CaroCar16, A.8].
Lemme 3.3.3. Soit ![]() $Y$ un sous-schéma fermé de
$Y$ un sous-schéma fermé de ![]() $X$ et
$X$ et ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Le morphisme canonique
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Le morphisme canonique ![]() ${\mathcal{H}}_{Y}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{E}}$ est injectif.
${\mathcal{H}}_{Y}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{E}}$ est injectif.
Démonstration.
Via le triangle de localisation de ![]() ${\mathcal{E}}$ par rapport à
${\mathcal{E}}$ par rapport à ![]() $Y$, il s’agit d’établir
$Y$, il s’agit d’établir ![]() ${\mathcal{H}}^{-1}({\mathcal{E}}(\text{}^{\dagger }Y))=0$. Lorsque
${\mathcal{H}}^{-1}({\mathcal{E}}(\text{}^{\dagger }Y))=0$. Lorsque ![]() $Y$ est un diviseur, cela résulte de l’exactitude du foncteur
$Y$ est un diviseur, cela résulte de l’exactitude du foncteur ![]() $(\text{}^{\dagger }Y)$ sur la catégorie des
$(\text{}^{\dagger }Y)$ sur la catégorie des ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents. On en déduit le cas général via les triangles distingués de Mayer-Vietoris (voir [Reference CaroCar16, 4.4.5]) en procédant par récurrence sur le nombre minimal de diviseurs dont l’intersection donne
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents. On en déduit le cas général via les triangles distingués de Mayer-Vietoris (voir [Reference CaroCar16, 4.4.5]) en procédant par récurrence sur le nombre minimal de diviseurs dont l’intersection donne ![]() $Y$.
$Y$.
Proposition 3.3.4. Soit ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Alors,
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent. Alors, ![]() ${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ est un
${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent si et seulement si
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent si et seulement si ![]() ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. Si l’une de ces deux conditions est satisfaite, on a alors l’isomorphisme
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. Si l’une de ces deux conditions est satisfaite, on a alors l’isomorphisme ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$.
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$.
Démonstration.
(1) Supposons que ![]() ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. On dispose alors du morphisme canonique de
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent. On dispose alors du morphisme canonique de ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents de la forme
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents de la forme ![]() $\unicode[STIX]{x1D719}:u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\rightarrow {\mathcal{E}}$. Comme le noyau de
$\unicode[STIX]{x1D719}:u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\rightarrow {\mathcal{E}}$. Comme le noyau de ![]() $\unicode[STIX]{x1D719}$ est un
$\unicode[STIX]{x1D719}$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent à support dans
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent à support dans ![]() $Z$, comme
$Z$, comme ![]() ${\mathcal{H}}^{0}u^{\sharp !}$ est exact à gauche (sur la catégorie des
${\mathcal{H}}^{0}u^{\sharp !}$ est exact à gauche (sur la catégorie des ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents) et comme le noyau de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents) et comme le noyau de ![]() ${\mathcal{H}}^{0}u^{\sharp !}(\unicode[STIX]{x1D719})$ est nul, on déduit alors du théorème de Berthelot-Kashiwara (voir la première partie de 3.3.2) que
${\mathcal{H}}^{0}u^{\sharp !}(\unicode[STIX]{x1D719})$ est nul, on déduit alors du théorème de Berthelot-Kashiwara (voir la première partie de 3.3.2) que ![]() $\unicode[STIX]{x1D719}$ est injectif.
$\unicode[STIX]{x1D719}$ est injectif.
Comme le morphisme canonique ![]() ${\mathcal{H}}_{Z}^{\dagger 0}(u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}))\rightarrow u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un isomorphisme (voir la seconde partie de 3.3.2), on en déduit que l’injection canonique
${\mathcal{H}}_{Z}^{\dagger 0}(u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}))\rightarrow u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un isomorphisme (voir la seconde partie de 3.3.2), on en déduit que l’injection canonique ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{E}}$ se factorise par les inclusions
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{E}}$ se factorise par les inclusions ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}}){\hookrightarrow}{\mathcal{E}}$ (la seconde flèche est bien injective grâce à 3.3.3). Par l’absurde, l’inclusion
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}}){\hookrightarrow}{\mathcal{E}}$ (la seconde flèche est bien injective grâce à 3.3.3). Par l’absurde, l’inclusion ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ n’est pas un isomorphisme. Dans ce cas, il existe un ouvert affine
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}}){\hookrightarrow}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ n’est pas un isomorphisme. Dans ce cas, il existe un ouvert affine ![]() $\mathfrak{U}$ de
$\mathfrak{U}$ de ![]() $\mathfrak{X}$, une section
$\mathfrak{X}$, une section ![]() $s$ sur
$s$ sur ![]() $\mathfrak{U}$ de
$\mathfrak{U}$ de ![]() ${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ qui n’est pas une section sur
${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ qui n’est pas une section sur ![]() $\mathfrak{U}$ de
$\mathfrak{U}$ de ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$. Soit
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$. Soit ![]() ${\mathcal{G}}$ le sous-
${\mathcal{G}}$ le sous-![]() ${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module de
${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module de ![]() ${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})|\mathfrak{U}$ engendré par
${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})|\mathfrak{U}$ engendré par ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$ et par la section
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$ et par la section ![]() $s$. Comme le faisceau associé à un sous-préfaisceau d’un faisceau contient le sous-préfaisceau,
$s$. Comme le faisceau associé à un sous-préfaisceau d’un faisceau contient le sous-préfaisceau, ![]() ${\mathcal{G}}$ contient strictement
${\mathcal{G}}$ contient strictement ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$. De plus,
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$. De plus, ![]() ${\mathcal{G}}$ est à support dans
${\mathcal{G}}$ est à support dans ![]() $\mathfrak{U}\cap Z$ car
$\mathfrak{U}\cap Z$ car ![]() ${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})|\mathfrak{U}$ l’est. Comme
${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})|\mathfrak{U}$ l’est. Comme ![]() ${\mathcal{G}}$ est un sous-
${\mathcal{G}}$ est un sous-![]() ${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module de type fini du
${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module de type fini du ![]() ${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module cohérent
${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module cohérent ![]() ${\mathcal{E}}|\mathfrak{U}$,
${\mathcal{E}}|\mathfrak{U}$, ![]() ${\mathcal{G}}$ est alors un sous-
${\mathcal{G}}$ est alors un sous-![]() ${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module cohérent. Or, en appliquant le foncteur exact à gauche
${\mathcal{D}}_{\mathfrak{U}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\cap U)_{\mathbb{Q}}$-module cohérent. Or, en appliquant le foncteur exact à gauche ![]() ${\mathcal{H}}^{0}u^{\sharp !}$ aux inclusions
${\mathcal{H}}^{0}u^{\sharp !}$ aux inclusions ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}{\hookrightarrow}{\mathcal{G}}{\hookrightarrow}{\mathcal{E}}|\mathfrak{U}$, on obtient les isomorphismes
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}{\hookrightarrow}{\mathcal{G}}{\hookrightarrow}{\mathcal{E}}|\mathfrak{U}$, on obtient les isomorphismes ![]() ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{G}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$. Via le théorème de Berthelot-Kashiwara, le premier de ces deux isomorphismes entraîne alors que
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{G}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}$. Via le théorème de Berthelot-Kashiwara, le premier de ces deux isomorphismes entraîne alors que ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{G}}$, ce qui est une contradiction.
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})|\mathfrak{U}\overset{{\sim}}{\longrightarrow }\,{\mathcal{G}}$, ce qui est une contradiction.
(2) Supposons que ![]() ${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ soit
${\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$ soit ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérent. Si
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérent. Si ![]() ${\mathcal{G}}$ est un
${\mathcal{G}}$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent, on obtient les isomorphismes
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent, on obtient les isomorphismes ![]() $u^{\sharp !}({\mathcal{G}})\overset{{\sim}}{\longrightarrow }\,\mathbb{L}u^{\ast }({\mathcal{G}})[d_{Z/X}]\overset{{\sim}}{\longrightarrow }\,\mathbb{R}{\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{G}})$. Si
$u^{\sharp !}({\mathcal{G}})\overset{{\sim}}{\longrightarrow }\,\mathbb{L}u^{\ast }({\mathcal{G}})[d_{Z/X}]\overset{{\sim}}{\longrightarrow }\,\mathbb{R}{\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{G}})$. Si ![]() $Z_{1}$ est un diviseur de
$Z_{1}$ est un diviseur de ![]() $X$ contenant
$X$ contenant ![]() $Z$, on calcule que
$Z$, on calcule que ![]() ${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{E}}(\text{}^{\dagger }Z_{1}))=0$. Via des suites spectrales de Mayer-Vietoris, on en déduit, par récurrence sur le nombre de diviseurs dont l’intersection est égale à
${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{E}}(\text{}^{\dagger }Z_{1}))=0$. Via des suites spectrales de Mayer-Vietoris, on en déduit, par récurrence sur le nombre de diviseurs dont l’intersection est égale à ![]() $Z$, l’annulation
$Z$, l’annulation ![]() ${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{H}}^{0}({\mathcal{E}}(\text{}^{\dagger }Z)))={\mathcal{H}}^{0}\left(\mathbb{R}{\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{E}}(\text{}^{\dagger }Z))\right)=0.$ En appliquant à la suite exacte
${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{H}}^{0}({\mathcal{E}}(\text{}^{\dagger }Z)))={\mathcal{H}}^{0}\left(\mathbb{R}{\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}{\mathcal{E}}(\text{}^{\dagger }Z))\right)=0.$ En appliquant à la suite exacte ![]() $0\rightarrow {\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{E}}\rightarrow {\mathcal{H}}^{0}({\mathcal{E}}(\text{}^{\dagger }Z))$ le foncteur
$0\rightarrow {\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{E}}\rightarrow {\mathcal{H}}^{0}({\mathcal{E}}(\text{}^{\dagger }Z))$ le foncteur ![]() ${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}-)$, on en déduit que le morphisme canonique
${\mathcal{H}}om_{{\mathcal{O}}_{\mathfrak{X}}}({\mathcal{O}}_{{\mathcal{Z}}},\unicode[STIX]{x1D714}_{{\mathcal{Z}}/\mathfrak{X}}\otimes _{{\mathcal{O}}_{\mathfrak{X}}}-)$, on en déduit que le morphisme canonique ![]() ${\mathcal{H}}^{0}u^{\sharp !}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un isomorphisme. Via la première partie de 3.3.2, on en déduit l’isomorphisme
${\mathcal{H}}^{0}u^{\sharp !}{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})\rightarrow {\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ est un isomorphisme. Via la première partie de 3.3.2, on en déduit l’isomorphisme ![]() $u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$.
$u_{+}^{\sharp }{\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}_{Z}^{\dagger 0}({\mathcal{E}})$.
3.4 Stabilité de la cohérence par foncteur cohomologique local en degré maximal
Notations 3.4.1. Soit ![]() $\mathfrak{B}$ la base de voisinages de
$\mathfrak{B}$ la base de voisinages de ![]() $\mathfrak{X}$ des ouverts affines et munis de coordonnées locales. Pour tout
$\mathfrak{X}$ des ouverts affines et munis de coordonnées locales. Pour tout ![]() $\mathfrak{U}\in \mathfrak{B}$, on note
$\mathfrak{U}\in \mathfrak{B}$, on note ![]() $\mathfrak{U}^{\sharp }:=(\mathfrak{U},\mathfrak{U}\cap \mathfrak{D})$.
$\mathfrak{U}^{\sharp }:=(\mathfrak{U},\mathfrak{U}\cap \mathfrak{D})$.
∙ On note
 $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ le faisceau (d’ensemble) sur
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ le faisceau (d’ensemble) sur  $\mathfrak{X}$ associé au préfaisceau sur
$\mathfrak{X}$ associé au préfaisceau sur  $\mathfrak{B}$ définie de la manière suivante
$\mathfrak{B}$ définie de la manière suivante  $\mathfrak{U}\in \mathfrak{B}\mapsto \widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}$, les morphismes de restriction étant les morphismes canoniques (la séparée complétion est un foncteur).
$\mathfrak{U}\in \mathfrak{B}\mapsto \widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}$, les morphismes de restriction étant les morphismes canoniques (la séparée complétion est un foncteur).∙ Comme les morphismes canoniques
sont fonctoriels en $$\begin{eqnarray}\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{D}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\end{eqnarray}$$ $\mathfrak{U}$, on obtient donc le morphisme canonique de faisceaux : (14)
$\mathfrak{U}$, on obtient donc le morphisme canonique de faisceaux : (14) $$\begin{eqnarray}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow \widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}.\end{eqnarray}$$∙ Soit
 $\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ un morphisme
$\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ un morphisme  $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire à gauche. En utilisant la fonctorialité en
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire à gauche. En utilisant la fonctorialité en  $\mathfrak{U}$ des morphismes
$\mathfrak{U}$ des morphismes  $\text{id}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)})):\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow \widetilde{D}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ , on obtient le morphisme de faisceaux : (15)
$\text{id}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)})):\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow \widetilde{D}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ , on obtient le morphisme de faisceaux : (15) $$\begin{eqnarray}\displaystyle & & \displaystyle \text{id}\widehat{\otimes }u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)}):\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{id}\widehat{\otimes }u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)}):\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}.\end{eqnarray}$$
(1) Avec les notations de 3.4.1, on dispose du diagramme canonique commutatif de faisceaux :
(16)dont la flèche du haut est un isomorphisme.
(2) Soit
 $\unicode[STIX]{x1D716}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$ un morphisme
$\unicode[STIX]{x1D716}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$ un morphisme  $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$-linéaire à gauche et
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$-linéaire à gauche et  $\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme induit par tensorisation par
$\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme induit par tensorisation par  $\mathbb{Q}$. On dispose alors du carré commutatif (17)dont les isomorphismes verticaux sont induites par la factorisation de (16).
$\mathbb{Q}$. On dispose alors du carré commutatif (17)dont les isomorphismes verticaux sont induites par la factorisation de (16).
Démonstration.
Soit ![]() $\mathfrak{U}\in \mathfrak{B}$. Pour tout entier positif
$\mathfrak{U}\in \mathfrak{B}$. Pour tout entier positif ![]() $i$, on note
$i$, on note ![]() $X_{i}$,
$X_{i}$, ![]() $X_{i}^{\sharp }$,
$X_{i}^{\sharp }$, ![]() $Z_{i}$,
$Z_{i}$, ![]() $Z_{i}^{\sharp }$,
$Z_{i}^{\sharp }$, ![]() $U_{i}$ et
$U_{i}$ et ![]() $U_{i}^{\sharp }$ les réductions modulo
$U_{i}^{\sharp }$ les réductions modulo ![]() $\unicode[STIX]{x1D70B}^{i+1}$ de
$\unicode[STIX]{x1D70B}^{i+1}$ de ![]() $\mathfrak{X}$,
$\mathfrak{X}$, ![]() $\mathfrak{X}^{\sharp }$,
$\mathfrak{X}^{\sharp }$, ![]() ${\mathcal{Z}}$,
${\mathcal{Z}}$, ![]() ${\mathcal{Z}}^{\sharp }$,
${\mathcal{Z}}^{\sharp }$, ![]() $\mathfrak{U}$ et
$\mathfrak{U}$ et ![]() $\mathfrak{U}^{\sharp }$ respectivement. On dispose des
$\mathfrak{U}^{\sharp }$ respectivement. On dispose des ![]() ${\mathcal{B}}_{Z_{i}\cap U_{i}}^{(m)}(T\cap Z_{i}\cap U_{i})$-modules quasi cohérents
${\mathcal{B}}_{Z_{i}\cap U_{i}}^{(m)}(T\cap Z_{i}\cap U_{i})$-modules quasi cohérents ![]() $\widetilde{{\mathcal{D}}}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$,
$\widetilde{{\mathcal{D}}}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$, ![]() $\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$ et enfin
$\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$ et enfin ![]() $\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$. Comme le foncteur sections globales commute aux limites projectives et par quasi-cohérence de nos faisceaux sur
$\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)}\otimes _{{\mathcal{V}}}{\mathcal{V}}/\unicode[STIX]{x1D70B}^{i+1}$. Comme le foncteur sections globales commute aux limites projectives et par quasi-cohérence de nos faisceaux sur ![]() $X_{i}$, on obtient les isomorphismes canoniques
$X_{i}$, on obtient les isomorphismes canoniques
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widetilde{{\mathcal{D}}}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)})\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\mathop{\varprojlim }\nolimits_{i}\unicode[STIX]{x1D6E4}(U_{i},\widetilde{{\mathcal{D}}}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)})\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\mathop{\varprojlim }\nolimits_{i}\widetilde{D}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}}\widetilde{D}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widetilde{{\mathcal{D}}}_{\mathfrak{ U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)})\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\mathop{\varprojlim }\nolimits_{i}\unicode[STIX]{x1D6E4}(U_{i},\widetilde{{\mathcal{D}}}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)})\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\mathop{\varprojlim }\nolimits_{i}\widetilde{D}_{U_{i}^{\sharp }\leftarrow Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}\otimes _{\widetilde{D}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }}^{(m)}}\widetilde{D}_{Z_{i}^{\sharp }\cap U_{i}^{\sharp }\rightarrow U_{i}^{\sharp }}^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{{\sim}}{\longrightarrow }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)}.\end{eqnarray}$$ Or, pour tout ![]() $\mathfrak{U}\in \mathfrak{B}$, le foncteur
$\mathfrak{U}\in \mathfrak{B}$, le foncteur ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},-)$ commute au produit tensoriel par
$\unicode[STIX]{x1D6E4}(\mathfrak{U},-)$ commute au produit tensoriel par ![]() $\mathbb{Q}$. On en déduit alors que le faisceau
$\mathbb{Q}$. On en déduit alors que le faisceau ![]() $(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{\mathbb{ Q}}$ sur
$(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})_{\mathbb{ Q}}$ sur ![]() $\mathfrak{X}$ est associé au faisceau sur
$\mathfrak{X}$ est associé au faisceau sur ![]() $\mathfrak{B}$ défini par
$\mathfrak{B}$ défini par ![]() $\mathfrak{U}\in \mathfrak{B}\mapsto (\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)})_{\mathbb{ Q}}$. Les isomorphismes canoniques (13) nous permettent de conclure le premier point. La seconde assertion se vérifie de même facilement.
$\mathfrak{U}\in \mathfrak{B}\mapsto (\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }}^{(m)}}\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }\rightarrow \mathfrak{U}^{\sharp }}^{(m)})_{\mathbb{ Q}}$. Les isomorphismes canoniques (13) nous permettent de conclure le premier point. La seconde assertion se vérifie de même facilement.
Remarque 3.4.3. Avec les notations de 3.4.1, le faisceau sur ![]() $\mathfrak{B}$ en
$\mathfrak{B}$ en ![]() $K$-espaces vectoriels
$K$-espaces vectoriels ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ est aussi un faisceau sur
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$ est aussi un faisceau sur ![]() $\mathfrak{B}$ à valeur dans la catégorie des
$\mathfrak{B}$ à valeur dans la catégorie des ![]() $K$-espaces topologiques (on vérifie que les morphismes de restriction sont injectifs et stricts).
$K$-espaces topologiques (on vérifie que les morphismes de restriction sont injectifs et stricts).
Lemme 3.4.4. On suppose que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure ![]() $e$. Soit
$e$. Soit ![]() $\unicode[STIX]{x1D6FC}$ un morphisme de
$\unicode[STIX]{x1D6FC}$ un morphisme de ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche qui soit de la forme
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche qui soit de la forme ![]() $\unicode[STIX]{x1D6FC}:({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow ({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Soit
$\unicode[STIX]{x1D6FC}:({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\rightarrow ({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Soit ![]() $m_{0}$ assez grand tel qu’il existe un morphisme
$m_{0}$ assez grand tel qu’il existe un morphisme ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-linéaire à gauche de la forme
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}$-linéaire à gauche de la forme ![]() $\unicode[STIX]{x1D6FC}^{(m_{0})}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m_{0})})^{s}$ induisant
$\unicode[STIX]{x1D6FC}^{(m_{0})}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m_{0})})^{s}$ induisant ![]() $\unicode[STIX]{x1D6FC}$ par extension via
$\unicode[STIX]{x1D6FC}$ par extension via ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}\rightarrow {\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{ Q}}$. Pour
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m_{0})}\rightarrow {\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{ Q}}$. Pour ![]() $m\geqslant m_{0}$, on note
$m\geqslant m_{0}$, on note ![]() $\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme induit par extension de
$\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme induit par extension de ![]() $\unicode[STIX]{x1D6FC}^{(m_{0})}$.
$\unicode[STIX]{x1D6FC}^{(m_{0})}$.
On dispose alors du diagramme commutatif

dont les flèches verticales sont des isomorphismes.
Démonstration.
Quitte à multiplier ![]() $\unicode[STIX]{x1D6FC}^{(m_{0})}$ par une puissance de
$\unicode[STIX]{x1D6FC}^{(m_{0})}$ par une puissance de ![]() $p$ assez grande, on peut supposer que
$p$ assez grande, on peut supposer que ![]() $\unicode[STIX]{x1D6FC}^{(m_{0})}$ provient par extension d’un morphisme
$\unicode[STIX]{x1D6FC}^{(m_{0})}$ provient par extension d’un morphisme ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-linéaire à gauche de la forme
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-linéaire à gauche de la forme ![]() $\unicode[STIX]{x1D716}^{(m_{0})}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m_{0})})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp }}^{(m_{0})})^{s}$. Notons
$\unicode[STIX]{x1D716}^{(m_{0})}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m_{0})})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp }}^{(m_{0})})^{s}$. Notons ![]() $\unicode[STIX]{x1D716}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$ les morphismes induits par extension. On obtient ainsi le foncteur dans
$\unicode[STIX]{x1D716}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$ les morphismes induits par extension. On obtient ainsi le foncteur dans ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ de la forme
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ de la forme
Or,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\ast }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})}):\mathop{\varinjlim }\nolimits_{m}\,\left(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})^{r}\right)_{\mathbb{Q}}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \mathop{\varinjlim }\nolimits_{m}\,\left(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})^{s}\right)_{\mathbb{Q}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\ast }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})}):\mathop{\varinjlim }\nolimits_{m}\,\left(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})^{r}\right)_{\mathbb{Q}}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \mathop{\varinjlim }\nolimits_{m}\,\left(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(m)}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }\rightarrow \mathfrak{X}^{\sharp }}^{(m)})^{s}\right)_{\mathbb{Q}}.\nonumber\end{eqnarray}$$ De plus, comme par définition ![]() $\varinjlim =\mathop{\varinjlim }\nolimits_{m}\circ (\mathbb{Q}\otimes _{\mathbb{Z}}-)$, en appliquant le foncteur
$\varinjlim =\mathop{\varinjlim }\nolimits_{m}\circ (\mathbb{Q}\otimes _{\mathbb{Z}}-)$, en appliquant le foncteur ![]() $\mathop{\varinjlim }\nolimits_{m}$ au carré commutatif (17), on obtient que
$\mathop{\varinjlim }\nolimits_{m}$ au carré commutatif (17), on obtient que ![]() $\varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\ast }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})})$ et
$\varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\ast }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})})$ et ![]() $\mathop{\varinjlim }\nolimits_{m}(\text{id}\widehat{\otimes }u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$ sont canoniquement isomorphes. Comme par définition
$\mathop{\varinjlim }\nolimits_{m}(\text{id}\widehat{\otimes }u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$ sont canoniquement isomorphes. Comme par définition ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }(\unicode[STIX]{x1D6FC})=\varinjlim \circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})})$, comme les deux foncteurs
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }(\unicode[STIX]{x1D6FC})=\varinjlim \circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }(\unicode[STIX]{x1D716}^{(\bullet +m_{0})})$, comme les deux foncteurs ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ et
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }$ et ![]() $u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}$ sont isomorphes et comme
$u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}$ sont isomorphes et comme ![]() $u^{\ast }=u^{\sharp (\bullet )!}[e]$, on en déduit alors le résultat.
$u^{\ast }=u^{\sharp (\bullet )!}[e]$, on en déduit alors le résultat.
Remarque 3.4.5. Avec les notations de 3.4.4, supposons ![]() $\mathfrak{X}$ affine. Soit
$\mathfrak{X}$ affine. Soit ![]() $E^{(m_{0})}$ un
$E^{(m_{0})}$ un ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-module cohérent sans
$\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-module cohérent sans ![]() $p$-torsion,
$p$-torsion, ![]() ${\mathcal{E}}^{(\bullet )}:=\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}}E^{(m_{0})}$ le
${\mathcal{E}}^{(\bullet )}:=\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}}E^{(m_{0})}$ le ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}$-module localement de présentation finie associé et
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}$-module localement de présentation finie associé et ![]() ${\mathcal{E}}:=\varinjlim ({\mathcal{E}}^{\bullet })$ le
${\mathcal{E}}:=\varinjlim ({\mathcal{E}}^{\bullet })$ le ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent associé. En prenant une résolution de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent associé. En prenant une résolution de ![]() $E^{(m_{0})}$ par des
$E^{(m_{0})}$ par des ![]() $\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-modules libres de type fini qui induit, après application du foncteur
$\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}$-modules libres de type fini qui induit, après application du foncteur ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}}-$, une résolution de
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}\otimes _{\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m_{0})}}-$, une résolution de ![]() ${\mathcal{E}}^{(\bullet )}$ par des
${\mathcal{E}}^{(\bullet )}$ par des ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}$-modules libres de type fini, on vérifie que le complexe
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet +m_{0})}$-modules libres de type fini, on vérifie que le complexe ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ est isomorphe à un complexe dont les termes sont de la forme
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ est isomorphe à un complexe dont les termes sont de la forme ![]() ${\mathcal{H}}_{Z}^{\dagger e}(({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{N})$ pour certains entiers
${\mathcal{H}}_{Z}^{\dagger e}(({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{N})$ pour certains entiers ![]() $N$.
$N$.
Théorème 3.4.6. On suppose que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure ![]() $e$. Soit
$e$. Soit ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent vérifiant les deux propriétés suivantes :
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent vérifiant les deux propriétés suivantes :
(1) pour
 $i=0,\ldots ,e-1$, localement en
$i=0,\ldots ,e-1$, localement en  ${\mathcal{Z}}$, les
${\mathcal{Z}}$, les  ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-modules
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-modules  ${\mathcal{H}}^{i}u^{\sharp !}({\mathcal{E}})$ sont
${\mathcal{H}}^{i}u^{\sharp !}({\mathcal{E}})$ sont  $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$-acycliques ;
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$-acycliques ;(2) le module
 $u^{\ast }({\mathcal{E}})$ est un
$u^{\ast }({\mathcal{E}})$ est un  ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui est aussi
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui est aussi  ${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-localement projectif de type fini pour la structure induite.
${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-localement projectif de type fini pour la structure induite.
Le ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module ![]() ${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$ est alors cohérent.
${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$ est alors cohérent.
Démonstration.
(0) Hypothèses 1 : passage aux sections globales, quelques notations.
Comme la ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérence de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérence de ![]() ${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$ est locale, on peut reprendre les notations et hypothèses du chapitre 2. Dans ce cas, posons
${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$ est locale, on peut reprendre les notations et hypothèses du chapitre 2. Dans ce cas, posons ![]() $E:=\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{E}})$. Avec les notations de 3.1.2, les hypothèses d’acyclicité sur
$E:=\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{E}})$. Avec les notations de 3.1.2, les hypothèses d’acyclicité sur ![]() ${\mathcal{E}}$ impliquent l’isomorphisme
${\mathcal{E}}$ impliquent l’isomorphisme ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}(\mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},\mathbb{L}u^{\ast }{\mathcal{E}}))$ (on utilise la suite spectrale d’hypercohomologie du foncteur dérivé de
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}(\mathbb{R}\unicode[STIX]{x1D6E4}({\mathcal{Z}},\mathbb{L}u^{\ast }{\mathcal{E}}))$ (on utilise la suite spectrale d’hypercohomologie du foncteur dérivé de ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$). On déduit alors du lemme 3.1.3 l’isomorphisme
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$). On déduit alors du lemme 3.1.3 l’isomorphisme ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}(\mathbb{L}u^{\ast }(E))=u^{\ast }(E)$.
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,{\mathcal{H}}^{0}(\mathbb{L}u^{\ast }(E))=u^{\ast }(E)$.
Choisissons une présentation finie ![]() $(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{a}{\longrightarrow }(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{b}{\longrightarrow }E\rightarrow 0$ de
$(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{a}{\longrightarrow }(D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{b}{\longrightarrow }E\rightarrow 0$ de ![]() $E$ (voir le théorème de type
$E$ (voir le théorème de type ![]() $A$ de Berthelot de [Reference BerthelotBer96, 3.6.5] qui est valable pour les
$A$ de Berthelot de [Reference BerthelotBer96, 3.6.5] qui est valable pour les ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents). En appliquant à cette présentation finie le foncteur
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents). En appliquant à cette présentation finie le foncteur ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}-$, on en déduit la suite exacte de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}\otimes _{D_{\mathfrak{ X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}}-$, on en déduit la suite exacte de ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules à gauche ![]() $({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{\unicode[STIX]{x1D6FC}}{\longrightarrow }({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{\unicode[STIX]{x1D6FD}}{\longrightarrow }{\mathcal{E}}\rightarrow 0$. Par exactitude à droite des deux foncteurs de la forme
$({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{\unicode[STIX]{x1D6FC}}{\longrightarrow }({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{\unicode[STIX]{x1D6FD}}{\longrightarrow }{\mathcal{E}}\rightarrow 0$. Par exactitude à droite des deux foncteurs de la forme ![]() $u^{\ast }$ (voir les définitions de 3.1.2), on obtient les suites exactes
$u^{\ast }$ (voir les définitions de 3.1.2), on obtient les suites exactes ![]() $(u^{\ast }{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{u^{\ast }(\unicode[STIX]{x1D6FC})}{\longrightarrow }(u^{\ast }{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{u^{\ast }(\unicode[STIX]{x1D6FD})}{\longrightarrow }u^{\ast }({\mathcal{E}})\rightarrow 0$ et
$(u^{\ast }{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{u^{\ast }(\unicode[STIX]{x1D6FC})}{\longrightarrow }(u^{\ast }{\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{u^{\ast }(\unicode[STIX]{x1D6FD})}{\longrightarrow }u^{\ast }({\mathcal{E}})\rightarrow 0$ et ![]() $(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{u^{\ast }(a)}{\longrightarrow }(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{u^{\ast }(b)}{\longrightarrow }u^{\ast }(E)\rightarrow 0$. Comme
$(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{u^{\ast }(a)}{\longrightarrow }(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{u^{\ast }(b)}{\longrightarrow }u^{\ast }(E)\rightarrow 0$. Comme ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}))=u^{\ast }(a)$ et comme le morphisme canonique
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}))=u^{\ast }(a)$ et comme le morphisme canonique ![]() $u^{\ast }(E)\rightarrow \unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})$ est un isomorphisme, en appliquant le foncteur
$u^{\ast }(E)\rightarrow \unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }{\mathcal{E}})$ est un isomorphisme, en appliquant le foncteur ![]() $\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ à l’avant-dernière suite exacte, on obtient encore une suite exacte (canoniquement isomorphe à la dernière). En posant
$\unicode[STIX]{x1D6E4}({\mathcal{Z}},-)$ à l’avant-dernière suite exacte, on obtient encore une suite exacte (canoniquement isomorphe à la dernière). En posant ![]() ${\mathcal{M}}:=u^{\ast }({\mathcal{E}})$,
${\mathcal{M}}:=u^{\ast }({\mathcal{E}})$, ![]() $M:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{M}})$,
$M:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{M}})$, ![]() $\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}))$ et
$\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}))$ et ![]() $\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FD}))$, on obtient donc la suite exacte suivante
$\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FD}))$, on obtient donc la suite exacte suivante ![]() $(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{\unicode[STIX]{x1D719}}{\longrightarrow }(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{\unicode[STIX]{x1D713}}{\longrightarrow }M\rightarrow 0$.
$(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}\underset{\unicode[STIX]{x1D719}}{\longrightarrow }(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}\underset{\unicode[STIX]{x1D713}}{\longrightarrow }M\rightarrow 0$.
(0 bis) Hypothèses 2 : niveaux ![]() $m\geqslant m_{0}$, quelques notations.
$m\geqslant m_{0}$, quelques notations.
Soit ![]() $m_{0}\geqslant 0$ assez grand tel que, pour tout
$m_{0}\geqslant 0$ assez grand tel que, pour tout ![]() $m\geqslant m_{0}$, il existe un morphisme
$m\geqslant m_{0}$, il existe un morphisme ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire à gauche de la forme
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire à gauche de la forme ![]() $\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ et induisant
$\unicode[STIX]{x1D6FC}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ et induisant ![]() $\unicode[STIX]{x1D6FC}$ par extension via
$\unicode[STIX]{x1D6FC}$ par extension via ![]() $\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow {\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$. D’après la seconde partie de nos hypothèses,
$\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)}\rightarrow {\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$. D’après la seconde partie de nos hypothèses, ![]() ${\mathcal{M}}$ est associé à un isocristal sur
${\mathcal{M}}$ est associé à un isocristal sur ![]() $Z^{\sharp }\setminus U$ surconvergeant le long de
$Z^{\sharp }\setminus U$ surconvergeant le long de ![]() $U$ (voir [Reference Caro and TsuzukiCT12]). Donc, comme
$U$ (voir [Reference Caro and TsuzukiCT12]). Donc, comme ![]() $M=\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{M}})$ et comme
$M=\unicode[STIX]{x1D6E4}({\mathcal{Z}},{\mathcal{M}})$ et comme ![]() ${\mathcal{Z}}$ est affine et lisse, le
${\mathcal{Z}}$ est affine et lisse, le ![]() $O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module
$O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module ![]() $M$ est alors projectif et de type fini. De plus, de manière analogue à [Reference BerthelotBer96, 4.4.5] (et aussi [Reference BerthelotBer96, 4.4.7]), quitte à augmenter
$M$ est alors projectif et de type fini. De plus, de manière analogue à [Reference BerthelotBer96, 4.4.5] (et aussi [Reference BerthelotBer96, 4.4.7]), quitte à augmenter ![]() $\unicode[STIX]{x1D706}_{0}$ et
$\unicode[STIX]{x1D706}_{0}$ et ![]() $m_{0}$, il existe un
$m_{0}$, il existe un ![]() $\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini et topologiquement nilpotent
$\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}$-module de type fini et topologiquement nilpotent ![]() ${\mathcal{M}}^{(m_{0})}$ qui est, pour la structure induite de
${\mathcal{M}}^{(m_{0})}$ qui est, pour la structure induite de ![]() $\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module, un
$\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module, un ![]() $\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module (localement projectif) de type fini et un isomorphisme
$\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module (localement projectif) de type fini et un isomorphisme ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaire de la forme
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaire de la forme ![]() ${\mathcal{M}}\overset{{\sim}}{\longrightarrow }\,{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}}{\mathcal{M}}^{(m_{0})}$. Pour tout
${\mathcal{M}}\overset{{\sim}}{\longrightarrow }\,{\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}}{\mathcal{M}}^{(m_{0})}$. Pour tout ![]() $m\geqslant m_{0}$, on pose alors
$m\geqslant m_{0}$, on pose alors ![]() ${\mathcal{M}}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}}{\mathcal{M}}^{(m_{0})}$.
${\mathcal{M}}^{(m)}:=\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\otimes _{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m_{0})}}{\mathcal{M}}^{(m_{0})}$.
Notons ![]() $\unicode[STIX]{x1D6FD}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow {\mathcal{E}}$ le composé du morphisme
$\unicode[STIX]{x1D6FD}^{(m)}:(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow {\mathcal{E}}$ le composé du morphisme ![]() $\unicode[STIX]{x1D6FD}$ avec l’inclusion canonique
$\unicode[STIX]{x1D6FD}$ avec l’inclusion canonique ![]() $(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\hookrightarrow}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Posons enfin
$(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\hookrightarrow}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Posons enfin ![]() $\unicode[STIX]{x1D719}^{(m)}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)}))$ et
$\unicode[STIX]{x1D719}^{(m)}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FC}^{(m)}))$ et ![]() $\unicode[STIX]{x1D713}^{(m)}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FD}^{(m)}))$. Avec les définitions et notations de 3.1.2, on obtient ainsi la suite
$\unicode[STIX]{x1D713}^{(m)}:=\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }(\unicode[STIX]{x1D6FD}^{(m)}))$. Avec les définitions et notations de 3.1.2, on obtient ainsi la suite ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D719}^{(m)}}{\longrightarrow }(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D713}^{(m)}}{\longrightarrow }M\rightarrow 0$. On remarque que cette suite devient exacte seulement après passage à la limite sur le niveau.
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D719}^{(m)}}{\longrightarrow }(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D713}^{(m)}}{\longrightarrow }M\rightarrow 0$. On remarque que cette suite devient exacte seulement après passage à la limite sur le niveau.
(1) Hypothèses 2 : topologie de type LB sur M, niveaux ![]() $m\geqslant m_{1}$, sections continues
$m\geqslant m_{1}$, sections continues ![]() $\unicode[STIX]{x1D703}$,
$\unicode[STIX]{x1D703}$, ![]() $\unicode[STIX]{x1D703}^{(m)}$.
$\unicode[STIX]{x1D703}^{(m)}$.
On munit ![]() $M$ de la topologie canonique de
$M$ de la topologie canonique de ![]() $O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module de type fini qui en fait un
$O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module de type fini qui en fait un ![]() $O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module de type LB (voir 2.2.2 et 2.2.7). Comme
$O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module de type LB (voir 2.2.2 et 2.2.7). Comme ![]() $M$ est un
$M$ est un ![]() $O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module projectif, il existe alors un morphisme
$O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module projectif, il existe alors un morphisme ![]() $O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaire
$O_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-linéaire ![]() $\unicode[STIX]{x1D703}:M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ tel que
$\unicode[STIX]{x1D703}:M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ tel que ![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D703}=id$. Comme
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D703}=id$. Comme ![]() $M^{(m_{0})}$ est un
$M^{(m_{0})}$ est un ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module de type fini, il existe
$\widetilde{B}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-module de type fini, il existe ![]() $m_{1}\geqslant m_{0}$ tel que, pour tout
$m_{1}\geqslant m_{0}$ tel que, pour tout ![]() $m\geqslant m_{1}$, on ait
$m\geqslant m_{1}$, on ait ![]() $\unicode[STIX]{x1D703}(M^{(m_{0})})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$. Ainsi, cette section
$\unicode[STIX]{x1D703}(M^{(m_{0})})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$. Ainsi, cette section ![]() $\unicode[STIX]{x1D703}$ se factorise (de manière unique) en un morphisme
$\unicode[STIX]{x1D703}$ se factorise (de manière unique) en un morphisme ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-linéaire de la forme
$\widetilde{B}_{{\mathcal{Z}}}^{(m_{0})}(U)_{\mathbb{Q}}$-linéaire de la forme ![]() $M^{(m_{0})}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$. D’où la factorisation
$M^{(m_{0})}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$. D’où la factorisation ![]() $\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire unique
$\widetilde{{\mathcal{B}}}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire unique ![]() $\unicode[STIX]{x1D703}^{(m)}:M^{(m)}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ pour tout
$\unicode[STIX]{x1D703}^{(m)}:M^{(m)}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ pour tout ![]() $m\geqslant m_{1}$. Soit
$m\geqslant m_{1}$. Soit ![]() $\overset{\circ }{M}^{(m)}$ un
$\overset{\circ }{M}^{(m)}$ un ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$-module de type fini induisant l’isomorphisme
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$-module de type fini induisant l’isomorphisme ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire. Or, une base de voisinages de zéro sur
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire. Or, une base de voisinages de zéro sur ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ (resp.
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ (resp. ![]() $M^{(m)}$) est donnée par la famille de
$M^{(m)}$) est donnée par la famille de ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$-modules
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)$-modules ![]() $(p^{n}(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)})^{s})_{n\in \mathbb{N}}$ (resp.
$(p^{n}(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)})^{s})_{n\in \mathbb{N}}$ (resp. ![]() $(p^{n}(\overset{\circ }{M}^{(m)})_{n\in \mathbb{N}})$). Pour
$(p^{n}(\overset{\circ }{M}^{(m)})_{n\in \mathbb{N}})$). Pour ![]() $n$ assez grand, on a l’inclusion
$n$ assez grand, on a l’inclusion ![]() $\unicode[STIX]{x1D703}^{(m)}(p^{n}\overset{\circ }{M}^{(m)})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$. On en déduit que le morphisme
$\unicode[STIX]{x1D703}^{(m)}(p^{n}\overset{\circ }{M}^{(m)})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp }}^{(m)})^{s}$. On en déduit que le morphisme ![]() $\unicode[STIX]{x1D703}^{(m)}$ de
$\unicode[STIX]{x1D703}^{(m)}$ de ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-modules de Banach est continu. Par composition de morphismes continus, il en est donc de même de
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-modules de Banach est continu. Par composition de morphismes continus, il en est donc de même de ![]() $M^{(m)}\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Par passage à la limite sur le niveau
$M^{(m)}\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$. Par passage à la limite sur le niveau ![]() $m\geqslant m_{1}$, la section
$m\geqslant m_{1}$, la section ![]() $\unicode[STIX]{x1D703}:M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ est alors continue.
$\unicode[STIX]{x1D703}:M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ est alors continue.
(2) Le ![]() $K$-espace
$K$-espace ![]() $G$de type
$G$de type ![]() $LB$, les
$LB$, les ![]() $K$-espaces de Banach
$K$-espaces de Banach ![]() $G^{(m)}$. Avec les topologies canoniques respectives (voir les définitions de 2.1.2), d’après la proposition 2.3.1, l’application
$G^{(m)}$. Avec les topologies canoniques respectives (voir les définitions de 2.1.2), d’après la proposition 2.3.1, l’application ![]() $\unicode[STIX]{x1D719}$ est un morphisme continu de
$\unicode[STIX]{x1D719}$ est un morphisme continu de ![]() $K$-espaces de type
$K$-espaces de type ![]() $LB$ (voir 2.3.3). Notons
$LB$ (voir 2.3.3). Notons ![]() $G:=(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}/\ker (\unicode[STIX]{x1D719})$ le
$G:=(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}/\ker (\unicode[STIX]{x1D719})$ le ![]() $K$-espace localement convexe dont la topologie est celle qui fait de la projection canonique
$K$-espace localement convexe dont la topologie est celle qui fait de la projection canonique ![]() $\unicode[STIX]{x1D70B}:(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}{\twoheadrightarrow}G$ un morphisme strict. Notons
$\unicode[STIX]{x1D70B}:(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{r}{\twoheadrightarrow}G$ un morphisme strict. Notons ![]() $\unicode[STIX]{x1D704}:G{\hookrightarrow}(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ le monomorphisme tel que
$\unicode[STIX]{x1D704}:G{\hookrightarrow}(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ le monomorphisme tel que ![]() $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D719}$. Comme
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D70B}=\unicode[STIX]{x1D719}$. Comme ![]() $\unicode[STIX]{x1D719}$ est continue, alors
$\unicode[STIX]{x1D719}$ est continue, alors ![]() $\unicode[STIX]{x1D704}$ est continu. Comme
$\unicode[STIX]{x1D704}$ est continu. Comme ![]() $(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ est séparé (voir 2.3.3), il en est alors de même de
$(u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ est séparé (voir 2.3.3), il en est alors de même de ![]() $G$. Ainsi
$G$. Ainsi ![]() $G$ est un quotient séparé d’un espace de type
$G$ est un quotient séparé d’un espace de type ![]() $LB$. D’après 1.1.7, cela entraîne que
$LB$. D’après 1.1.7, cela entraîne que ![]() $G$ est aussi un espace de type
$G$ est aussi un espace de type ![]() $LB$. Plus précisément, d’après sa preuve, en notant
$LB$. Plus précisément, d’après sa preuve, en notant ![]() $G^{(m)}:=(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}/(\ker (\unicode[STIX]{x1D719})\cap (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r})$ muni de la topologie quotient,
$G^{(m)}:=(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}/(\ker (\unicode[STIX]{x1D719})\cap (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r})$ muni de la topologie quotient, ![]() $G^{(m)}$ est un
$G^{(m)}$ est un ![]() $K$-espace de Banach et l’isomorphisme canonique
$K$-espace de Banach et l’isomorphisme canonique ![]() $\mathop{\varinjlim }\nolimits_{m}G^{(m)}\overset{{\sim}}{\longrightarrow }\,G$ est aussi un homéomorphisme. Comme par définition le morphisme
$\mathop{\varinjlim }\nolimits_{m}G^{(m)}\overset{{\sim}}{\longrightarrow }\,G$ est aussi un homéomorphisme. Comme par définition le morphisme ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow G^{(m)}$ est strict, il découle de 3.2.2 que l’on dispose de l’épimorphisme strict
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow G^{(m)}$ est strict, il découle de 3.2.2 que l’on dispose de l’épimorphisme strict
Il résulte alors de 1.1.3 que l’on dispose de l’épimorphisme strict :
(3) Les applications ![]() $\unicode[STIX]{x1D719}$,
$\unicode[STIX]{x1D719}$, ![]() $\unicode[STIX]{x1D704}$et
$\unicode[STIX]{x1D704}$et ![]() $\unicode[STIX]{x1D713}$sont des morphismes stricts.
$\unicode[STIX]{x1D713}$sont des morphismes stricts.
D’après ce qui précède, on dispose du morphisme ![]() $O_{{\mathcal{Z}},\mathbb{Q}}$-linéaire
$O_{{\mathcal{Z}},\mathbb{Q}}$-linéaire ![]() $(\unicode[STIX]{x1D704},\unicode[STIX]{x1D703}):G\oplus M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ qui est aussi une application continue et bijective entre deux
$(\unicode[STIX]{x1D704},\unicode[STIX]{x1D703}):G\oplus M\rightarrow (u^{\ast }D_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})^{s}$ qui est aussi une application continue et bijective entre deux ![]() $K$-espaces de type
$K$-espaces de type ![]() $LB$. D’après le théorème de l’application ouverte de Banach (voir [Reference SchneiderSch02, 8.8]), le morphisme
$LB$. D’après le théorème de l’application ouverte de Banach (voir [Reference SchneiderSch02, 8.8]), le morphisme ![]() $(\unicode[STIX]{x1D704},\unicode[STIX]{x1D703})$ est donc un homéomorphisme. Comme
$(\unicode[STIX]{x1D704},\unicode[STIX]{x1D703})$ est donc un homéomorphisme. Comme ![]() $\unicode[STIX]{x1D719}$ est le morphisme composé
$\unicode[STIX]{x1D719}$ est le morphisme composé
le morphisme ![]() $\unicode[STIX]{x1D719}$ est alors strict (ce qui est équivalent d’ailleurs à la propriété selon laquelle le morphisme
$\unicode[STIX]{x1D719}$ est alors strict (ce qui est équivalent d’ailleurs à la propriété selon laquelle le morphisme ![]() $\unicode[STIX]{x1D704}$ est strict). On remarque que, comme
$\unicode[STIX]{x1D704}$ est strict). On remarque que, comme ![]() $M$ est un
$M$ est un ![]() $K$-espace séparé, alors
$K$-espace séparé, alors ![]() $G$ est un fermé de
$G$ est un fermé de ![]() $G\oplus M$ (car homéomorphe au fermé
$G\oplus M$ (car homéomorphe au fermé ![]() $G\oplus \{0\}$). Enfin, comme
$G\oplus \{0\}$). Enfin, comme ![]() $\unicode[STIX]{x1D704}(G)=\text{Im}(\unicode[STIX]{x1D719})=\ker (\unicode[STIX]{x1D713})$, on obtient le carré commutatif canonique
$\unicode[STIX]{x1D704}(G)=\text{Im}(\unicode[STIX]{x1D719})=\ker (\unicode[STIX]{x1D713})$, on obtient le carré commutatif canonique

dont on sait déjà que toutes les flèches autres que ![]() $\unicode[STIX]{x1D713}$ sont continues et dont la flèche du haut est un homéomorphisme. On en déduit la continuité de
$\unicode[STIX]{x1D713}$ sont continues et dont la flèche du haut est un homéomorphisme. On en déduit la continuité de ![]() $\unicode[STIX]{x1D713}$. Comme
$\unicode[STIX]{x1D713}$. Comme ![]() $\unicode[STIX]{x1D713}$ est un morphisme continu et surjectif entre deux espaces de type
$\unicode[STIX]{x1D713}$ est un morphisme continu et surjectif entre deux espaces de type ![]() $LB$, on en déduit que
$LB$, on en déduit que ![]() $\unicode[STIX]{x1D713}$ est un morphisme strict.
$\unicode[STIX]{x1D713}$ est un morphisme strict.
(4) Constructions et propriétés de ![]() $H^{(m)}$et
$H^{(m)}$et ![]() $N^{(m)}$.
$N^{(m)}$.
Dans toute la suite de la preuve, ![]() $m$ sera toujours par défaut un entier plus grand que
$m$ sera toujours par défaut un entier plus grand que ![]() $m_{1}\geqslant m_{0}$. Notons
$m_{1}\geqslant m_{0}$. Notons ![]() $H^{(m)}:=\unicode[STIX]{x1D704}^{-1}((u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s})$ et
$H^{(m)}:=\unicode[STIX]{x1D704}^{-1}((u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s})$ et ![]() $\unicode[STIX]{x1D704}^{(m)}:H^{(m)}{\hookrightarrow}(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme
$\unicode[STIX]{x1D704}^{(m)}:H^{(m)}{\hookrightarrow}(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ le morphisme ![]() $\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire induit par
$\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}$-linéaire induit par ![]() $\unicode[STIX]{x1D704}$. On munit
$\unicode[STIX]{x1D704}$. On munit ![]() $H^{(m)}$ de l’unique topologie telle que
$H^{(m)}$ de l’unique topologie telle que ![]() $\unicode[STIX]{x1D704}^{(m)}$ soit un morphisme strict (avec
$\unicode[STIX]{x1D704}^{(m)}$ soit un morphisme strict (avec ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ muni de sa topologie canonique de
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ muni de sa topologie canonique de ![]() $K$-espace de Banach). On a vu au cours de l’étape
$K$-espace de Banach). On a vu au cours de l’étape ![]() $3$ que
$3$ que ![]() $\unicode[STIX]{x1D704}(G)$ est fermé. Il en résulte que
$\unicode[STIX]{x1D704}(G)$ est fermé. Il en résulte que ![]() $\unicode[STIX]{x1D704}^{(m)}(H^{(m)})$ est un fermé de
$\unicode[STIX]{x1D704}^{(m)}(H^{(m)})$ est un fermé de ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ qui est un
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ qui est un ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach. Ainsi,
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach. Ainsi, ![]() $H^{(m)}$ est aussi un
$H^{(m)}$ est aussi un ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach. Notons alors
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach. Notons alors ![]() $N^{(m)}:=\text{Im}(\unicode[STIX]{x1D713}^{(m)})$ et
$N^{(m)}:=\text{Im}(\unicode[STIX]{x1D713}^{(m)})$ et ![]() $\unicode[STIX]{x1D713}^{\prime (m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\twoheadrightarrow}N^{(m)}$ l’épimorphisme canonique factorisant
$\unicode[STIX]{x1D713}^{\prime (m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\twoheadrightarrow}N^{(m)}$ l’épimorphisme canonique factorisant ![]() $\unicode[STIX]{x1D713}^{(m)}$. On obtient alors sur
$\unicode[STIX]{x1D713}^{(m)}$. On obtient alors sur ![]() $N^{(m)}$ une structure de
$N^{(m)}$ une structure de ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach qui fait de l’épimorphisme
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-module de Banach qui fait de l’épimorphisme ![]() $\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire
$\widetilde{B}_{{\mathcal{Z}}}^{(m)}(U)_{\mathbb{Q}}$-linéaire ![]() $\unicode[STIX]{x1D713}^{\prime (m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\twoheadrightarrow}N^{(m)}$ une application stricte. On dispose ainsi du diagramme commutatif
$\unicode[STIX]{x1D713}^{\prime (m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}{\twoheadrightarrow}N^{(m)}$ une application stricte. On dispose ainsi du diagramme commutatif

dont les morphismes horizontaux sont stricts et forment deux suites exactes courtes (la première est d’ailleurs scindée via ![]() $\unicode[STIX]{x1D703}$). Comme le composé de
$\unicode[STIX]{x1D703}$). Comme le composé de ![]() $H^{(m)}\subset G$ avec
$H^{(m)}\subset G$ avec ![]() $\unicode[STIX]{x1D704}$ est continu et comme
$\unicode[STIX]{x1D704}$ est continu et comme ![]() $\unicode[STIX]{x1D704}$ est un monomorphisme strict, on remarque que l’inclusion
$\unicode[STIX]{x1D704}$ est un monomorphisme strict, on remarque que l’inclusion ![]() $H^{(m)}\subset G$ est alors continue. Enfin, comme
$H^{(m)}\subset G$ est alors continue. Enfin, comme ![]() $\unicode[STIX]{x1D713}^{(m)}$ est continu, l’inclusion
$\unicode[STIX]{x1D713}^{(m)}$ est continu, l’inclusion ![]() $N^{(m)}\subset M$ l’est aussi.
$N^{(m)}\subset M$ l’est aussi.
Grâce à 3.2.2, la suite exacte courte du bas de (24) induit la suite exacte avec morphismes stricts :
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D704}^{(m)}}{\rightarrow }\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{\rightarrow }\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D704}^{(m)}}{\rightarrow }\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{\rightarrow }\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\rightarrow 0.\end{eqnarray}$$En passant à la limite sur le niveau, il en résulte la suite exacte avec morphismes continus :
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\rightarrow 0.\end{eqnarray}$$ (5) Passage à la limite sur le niveau pour ![]() $G^{(m)}$et
$G^{(m)}$et ![]() $H^{(m)}$ : comparaison.
$H^{(m)}$ : comparaison.
Notons ![]() $j_{m}:G^{(m)}\rightarrow G$ le monomorphisme canonique continu. Pour tout
$j_{m}:G^{(m)}\rightarrow G$ le monomorphisme canonique continu. Pour tout ![]() $m\geqslant m_{1}$, comme le morphisme
$m\geqslant m_{1}$, comme le morphisme ![]() $\unicode[STIX]{x1D719}$ se factorise par le morphisme continu
$\unicode[STIX]{x1D719}$ se factorise par le morphisme continu ![]() $\unicode[STIX]{x1D719}^{(m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$, on obtient alors l’inclusion
$\unicode[STIX]{x1D719}^{(m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\rightarrow (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$, on obtient alors l’inclusion ![]() $\unicode[STIX]{x1D704}\circ j_{m}(G^{(m)})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ et donc
$\unicode[STIX]{x1D704}\circ j_{m}(G^{(m)})\subset (u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}$ et donc ![]() $j_{m}(G^{(m)})\subset H^{(m)}$. Le monomorphisme continu
$j_{m}(G^{(m)})\subset H^{(m)}$. Le monomorphisme continu ![]() $j_{m}$ se factorise donc (de manière unique) par un monomorphisme continu de la forme
$j_{m}$ se factorise donc (de manière unique) par un monomorphisme continu de la forme ![]() $G^{(m)}\rightarrow H^{(m)}$.
$G^{(m)}\rightarrow H^{(m)}$.
Réciproquement, comme ![]() $H^{(m)}$ est un
$H^{(m)}$ est un ![]() $K$-espace de Banach et comme on a l’égalité
$K$-espace de Banach et comme on a l’égalité ![]() $G=\bigcup _{m\in \mathbb{N}}j_{m}(G^{(m)})$, d’après [Reference SchneiderSch02, 8.9], il existe alors
$G=\bigcup _{m\in \mathbb{N}}j_{m}(G^{(m)})$, d’après [Reference SchneiderSch02, 8.9], il existe alors ![]() $N_{m}\geqslant m$ assez grand tel que
$N_{m}\geqslant m$ assez grand tel que ![]() $H^{(m)}\subset G$ est le composé d’un morphisme (unique) continu de la forme
$H^{(m)}\subset G$ est le composé d’un morphisme (unique) continu de la forme ![]() $H^{(m)}\rightarrow G^{(N_{m})}$ suivi de
$H^{(m)}\rightarrow G^{(N_{m})}$ suivi de ![]() $j_{N_{m}}$. Il ne coûte rien de supposer que la suite
$j_{N_{m}}$. Il ne coûte rien de supposer que la suite ![]() $(N_{m})_{m\geqslant m_{1}}$ est strictement croissante.
$(N_{m})_{m\geqslant m_{1}}$ est strictement croissante.
D’après 3.2.3, on dispose alors des monomorphismes continus :
 $$\begin{eqnarray}\displaystyle \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)} & {\hookrightarrow} & \displaystyle \widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}G^{(N_{m})}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(N_{m})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)} & {\hookrightarrow} & \displaystyle \widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}G^{(N_{m})}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(N_{m})}.\end{eqnarray}$$En passant la suite (27) à la limite inductive sur le niveau, grâce à( 5), son composé est un homéomorphisme. Comme le foncteur de passage à la limite inductive sur le niveau préserve la continuité et l’injectivité, on en déduit que le morphisme canonique horizontal du haut du carré

est un homéomorphisme. Comme les morphismes verticaux sont des homéomorphismes (voir (5)), il en est de même de la flèche du bas.
(6) Passage à la limite sur le niveau pour ![]() $M^{(m)}$et
$M^{(m)}$et ![]() $N^{(m)}$: comparaison.
$N^{(m)}$: comparaison.
Comme ![]() $\unicode[STIX]{x1D713}^{(m)}$ est continu, pour tout
$\unicode[STIX]{x1D713}^{(m)}$ est continu, pour tout ![]() $m\geqslant m_{1}$, d’après [Reference SchneiderSch02, 8.9], il existe
$m\geqslant m_{1}$, d’après [Reference SchneiderSch02, 8.9], il existe ![]() $N_{m}\geqslant m$ assez grand tel que
$N_{m}\geqslant m$ assez grand tel que ![]() $\unicode[STIX]{x1D713}^{(m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M$ soit la composition d’un morphisme continu (forcément unique) de la forme
$\unicode[STIX]{x1D713}^{(m)}:(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M$ soit la composition d’un morphisme continu (forcément unique) de la forme ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M^{(N_{m})}$ suivi du monomorphisme
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M^{(N_{m})}$ suivi du monomorphisme ![]() $M^{(N_{m})}{\hookrightarrow}M$. Comme
$M^{(N_{m})}{\hookrightarrow}M$. Comme ![]() $N^{(m)}=\text{Im}(\unicode[STIX]{x1D713}^{(m)})=\text{Im}(\unicode[STIX]{x1D713}^{\prime (m)})$, ce morphisme
$N^{(m)}=\text{Im}(\unicode[STIX]{x1D713}^{(m)})=\text{Im}(\unicode[STIX]{x1D713}^{\prime (m)})$, ce morphisme ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M^{(N_{m})}$ se décompose de manière unique en
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow M^{(N_{m})}$ se décompose de manière unique en ![]() $(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}N^{(m)}{\hookrightarrow}M^{(N_{m})}$. Le morphisme
$(u^{\ast }\widetilde{D}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}N^{(m)}{\hookrightarrow}M^{(N_{m})}$. Le morphisme ![]() $\unicode[STIX]{x1D713}^{(m)}$ induit donc le morphisme composé ci-dessous noté abusivement
$\unicode[STIX]{x1D713}^{(m)}$ induit donc le morphisme composé ci-dessous noté abusivement
 $$\begin{eqnarray}\displaystyle & & \displaystyle u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)}):\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)}):\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}.\nonumber\end{eqnarray}$$ La notation ![]() $u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)})$ est justifiée par le fait que ce morphisme composé ne dépend pas du choix de
$u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)})$ est justifiée par le fait que ce morphisme composé ne dépend pas du choix de ![]() $N_{m}$, mais seulement du niveau
$N_{m}$, mais seulement du niveau ![]() $m$ fixé, de
$m$ fixé, de ![]() $\unicode[STIX]{x1D713}^{(m)}$ et de l’immersion fermée
$\unicode[STIX]{x1D713}^{(m)}$ et de l’immersion fermée ![]() $u$. En passant à la limite sur le niveau, on obtient les morphismes continus :
$u$. En passant à la limite sur le niveau, on obtient les morphismes continus :
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\text{id}\widehat{\otimes }\unicode[STIX]{x1D713}^{\prime (m)}}{{\twoheadrightarrow}}\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}N^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}\end{eqnarray}$$ dont le composé est ![]() $\underset{m}{\varinjlim }\,u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)})$. Comme, pour tout
$\underset{m}{\varinjlim }\,u_{+}^{\sharp (m)}(\unicode[STIX]{x1D713}^{(m)})$. Comme, pour tout ![]() $m\geqslant m_{1}$, le morphisme
$m\geqslant m_{1}$, le morphisme ![]() $\unicode[STIX]{x1D713}^{(m)}\circ \unicode[STIX]{x1D703}^{(m)}$ est l’inclusion canonique
$\unicode[STIX]{x1D713}^{(m)}\circ \unicode[STIX]{x1D703}^{(m)}$ est l’inclusion canonique ![]() $M^{(m)}{\hookrightarrow}M$, ce dernier se factorise alors canoniquement en
$M^{(m)}{\hookrightarrow}M$, ce dernier se factorise alors canoniquement en ![]() $M^{(m)}{\hookrightarrow}N^{(m)}\subset M$. On en déduit comme pour l’étape
$M^{(m)}{\hookrightarrow}N^{(m)}\subset M$. On en déduit comme pour l’étape ![]() $(5)$ que la flèche de droite de (29) est un homéomorphisme.
$(5)$ que la flèche de droite de (29) est un homéomorphisme.
(7) Première conclusion.
En composant (21) avec l’isomorphisme du bas de (28), on obtient l’épimorphisme strict de la suite :
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}{\twoheadrightarrow}\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad {\hookrightarrow}\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}{\twoheadrightarrow}\mathop{\varinjlim }\nolimits_{m}\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}H^{(m)}\nonumber\\ \displaystyle & & \displaystyle \qquad {\hookrightarrow}\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s},\end{eqnarray}$$la seconde flèche étant le monomorphisme de (26). On déduit alors de la suite exacte (26) et du fait que la flèche de droite de (29) est un homéomorphisme, la suite exacte :
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D6FC}_{Z}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FD}_{Z}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D6FC}_{Z}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{ X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{D}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FD}_{Z}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}M^{(m)}\rightarrow 0,\end{eqnarray}$$ où ![]() $\unicode[STIX]{x1D6FC}_{Z}^{\dagger }:=\text{id}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$, qui est égale au composé des morphismes de (30), et, avec les notations de l’étape (
$\unicode[STIX]{x1D6FC}_{Z}^{\dagger }:=\text{id}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$, qui est égale au composé des morphismes de (30), et, avec les notations de l’étape (![]() $6$),
$6$), ![]() $\unicode[STIX]{x1D6FD}_{Z}^{\dagger }:=\underset{m}{\varinjlim }\,u_{+}^{\sharp (m)}(\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FD}^{(m)}))$.
$\unicode[STIX]{x1D6FD}_{Z}^{\dagger }:=\underset{m}{\varinjlim }\,u_{+}^{\sharp (m)}(\unicode[STIX]{x1D6E4}({\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FD}^{(m)}))$.
(8) Faisceautisation.
(i) Soit ![]() $\mathfrak{B}$ la base de voisinages de
$\mathfrak{B}$ la base de voisinages de ![]() $\mathfrak{X}$ définie par ses ouverts affines. Le préfaisceau sur
$\mathfrak{X}$ définie par ses ouverts affines. Le préfaisceau sur ![]() $\mathfrak{B}$ défini par
$\mathfrak{B}$ défini par ![]() $\mathfrak{U}\in \mathfrak{B}\mapsto \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},{\mathcal{M}}^{(m)})$ est, par définition de
$\mathfrak{U}\in \mathfrak{B}\mapsto \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},{\mathcal{M}}^{(m)})$ est, par définition de ![]() ${\mathcal{M}}^{(m)}$, en réalité un faisceau dont le faisceau sur
${\mathcal{M}}^{(m)}$, en réalité un faisceau dont le faisceau sur ![]() $\mathfrak{X}$ est
$\mathfrak{X}$ est ![]() $u_{+}^{\sharp }({\mathcal{M}})$.
$u_{+}^{\sharp }({\mathcal{M}})$.
(ii) Avec les notations de 3.4.1, comme le foncteur faisceau associé à un préfaisceau (d’ensemble) commute aux limites inductives filtrantes, alors le faisceau associé au préfaisceau ![]() $\mathfrak{U}\in \mathfrak{B}\mapsto \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}))$ est
$\mathfrak{U}\in \mathfrak{B}\mapsto \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}))$ est ![]() $\underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}$, de même pour un autre entier que
$\underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}$, de même pour un autre entier que ![]() $r$.
$r$.
(iii) Pour tout ![]() $\mathfrak{U}\in \mathfrak{B}$, notons
$\mathfrak{U}\in \mathfrak{B}$, notons ![]() $u^{\sharp }|\mathfrak{U}:{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }{\hookrightarrow}\mathfrak{U}^{\sharp }$ l’immersion fermée exacte induite par
$u^{\sharp }|\mathfrak{U}:{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp }{\hookrightarrow}\mathfrak{U}^{\sharp }$ l’immersion fermée exacte induite par ![]() $u^{\sharp }$. Pour tout
$u^{\sharp }$. Pour tout ![]() $m\geqslant m_{1}$, on dispose de la suite (pas forcément exacte) :
$m\geqslant m_{1}$, on dispose de la suite (pas forcément exacte) : ![]() $(\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D6FC}^{(m)}|\mathfrak{U}}{\longrightarrow }(\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D6FD}^{(m)}|\mathfrak{U}}{\longrightarrow }{\mathcal{E}}|\mathfrak{U}\rightarrow 0$. Comme pour (31) (il suffit de remplacer
$(\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{r}\underset{\unicode[STIX]{x1D6FC}^{(m)}|\mathfrak{U}}{\longrightarrow }(\widetilde{{\mathcal{D}}}_{\mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)})^{s}\underset{\unicode[STIX]{x1D6FD}^{(m)}|\mathfrak{U}}{\longrightarrow }{\mathcal{E}}|\mathfrak{U}\rightarrow 0$. Comme pour (31) (il suffit de remplacer ![]() $u^{\sharp }$ par
$u^{\sharp }$ par ![]() $u^{\sharp }|\mathfrak{U}$), on obtient alors la suite exacte
$u^{\sharp }|\mathfrak{U}$), on obtient alors la suite exacte
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}))\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FC}_{\mathfrak{U}}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}))\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FD}_{\mathfrak{U}}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }({\mathcal{M}}^{(m)}))\rightarrow 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{r}))\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FC}_{\mathfrak{U}}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }((\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp },\mathbb{Q}}^{(m)})^{s}))\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\unicode[STIX]{x1D6FD}_{\mathfrak{U}}^{\dagger }}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{D}_{\mathfrak{U}\leftarrow {\mathcal{Z}}\cap \mathfrak{U},\mathbb{Q}}^{(m)}\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }({\mathcal{M}}^{(m)}))\rightarrow 0,\nonumber\end{eqnarray}$$ où ![]() $\widehat{\otimes }:=\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}$,
$\widehat{\otimes }:=\widehat{\otimes }_{\widetilde{D}_{{\mathcal{Z}}^{\sharp }\cap \mathfrak{U}^{\sharp },\mathbb{Q}}^{(m)}}$, ![]() $\unicode[STIX]{x1D6FC}_{\mathfrak{U}}^{\dagger }:=id\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$ et
$\unicode[STIX]{x1D6FC}_{\mathfrak{U}}^{\dagger }:=id\widehat{\otimes }\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FC}^{(m)})$ et ![]() $\unicode[STIX]{x1D6FD}_{\mathfrak{U}}^{\dagger }:=\underset{m}{\varinjlim }\,(u^{\sharp }|\mathfrak{U})_{+}^{(m)}(\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FD}^{(m)}))$. Comme ces suites exactes sont fonctorielles en
$\unicode[STIX]{x1D6FD}_{\mathfrak{U}}^{\dagger }:=\underset{m}{\varinjlim }\,(u^{\sharp }|\mathfrak{U})_{+}^{(m)}(\unicode[STIX]{x1D6E4}(\mathfrak{U}\cap {\mathcal{Z}},u^{\ast }\unicode[STIX]{x1D6FD}^{(m)}))$. Comme ces suites exactes sont fonctorielles en ![]() $\mathfrak{U}$ et comme le foncteur faisceau associé à un préfaisceau est exact, on obtient alors la suite exacte:
$\mathfrak{U}$ et comme le foncteur faisceau associé à un préfaisceau est exact, on obtient alors la suite exacte:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\underset{m}{\varinjlim }\,\text{id}\widehat{\otimes }u^{\ast }\unicode[STIX]{x1D6FC}^{(m)}}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow u_{+}^{\sharp }({\mathcal{M}})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{r}\nonumber\\ \displaystyle & & \displaystyle \qquad \underset{\underset{m}{\varinjlim }\,\text{id}\widehat{\otimes }u^{\ast }\unicode[STIX]{x1D6FC}^{(m)}}{\longrightarrow }\underset{m}{\varinjlim }\,\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }\leftarrow {\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}\widehat{\otimes }_{\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp },\mathbb{Q}}^{(m)}}(u^{\ast }\widetilde{{\mathcal{D}}}_{\mathfrak{ X}^{\sharp },\mathbb{Q}}^{(m)})^{s}\rightarrow u_{+}^{\sharp }({\mathcal{M}})\rightarrow 0.\end{eqnarray}$$ (9) Fin de la preuve. Comme le foncteur ![]() ${\mathcal{H}}_{Z}^{\dagger e}$ est exact à droite (dans la catégorie des
${\mathcal{H}}_{Z}^{\dagger e}$ est exact à droite (dans la catégorie des ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents), alors le conoyau de
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-modules cohérents), alors le conoyau de ![]() ${\mathcal{H}}_{Z}^{\dagger e}(\unicode[STIX]{x1D719})$ est isomorphe à
${\mathcal{H}}_{Z}^{\dagger e}(\unicode[STIX]{x1D719})$ est isomorphe à ![]() ${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$. Or, il découle du lemme 3.4.4 et de la suite exacte (32) que le conoyau de
${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})$. Or, il découle du lemme 3.4.4 et de la suite exacte (32) que le conoyau de ![]() ${\mathcal{H}}_{Z}^{\dagger e}(\unicode[STIX]{x1D719})$ est isomorphe à
${\mathcal{H}}_{Z}^{\dagger e}(\unicode[STIX]{x1D719})$ est isomorphe à ![]() $u_{+}^{\sharp }{\mathcal{M}}$. Comme
$u_{+}^{\sharp }{\mathcal{M}}$. Comme ![]() $u^{\ast }({\mathcal{E}})={\mathcal{M}}$, on a démontré ainsi que
$u^{\ast }({\mathcal{E}})={\mathcal{M}}$, on a démontré ainsi que ![]() ${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp }u^{\ast }({\mathcal{E}})$. Enfin, comme
${\mathcal{H}}_{Z}^{\dagger e}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp }u^{\ast }({\mathcal{E}})$. Enfin, comme ![]() $u$ est propre et
$u$ est propre et ![]() $u^{\ast }({\mathcal{E}})$ est un
$u^{\ast }({\mathcal{E}})$ est un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent, alors
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent, alors ![]() $u_{+}^{\sharp }u^{\ast }({\mathcal{E}})$ est un
$u_{+}^{\sharp }u^{\ast }({\mathcal{E}})$ est un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent.
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent.
Corollaire 3.4.7. On suppose que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure ![]() $1$. Soit
$1$. Soit ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent tel que
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent tel que ![]() ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent et que
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent et que ![]() ${\mathcal{H}}^{1}u^{\sharp !}({\mathcal{E}})$ soit un
${\mathcal{H}}^{1}u^{\sharp !}({\mathcal{E}})$ soit un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui soit aussi un
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui soit aussi un ![]() ${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module localement projectif de type fini pour la structure induite. Le complexe
${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module localement projectif de type fini pour la structure induite. Le complexe ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ est alors
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ est alors ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérent.
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérent.
Démonstration.
Via le triangle distingué ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\rightarrow {\mathcal{E}}\rightarrow (\text{}^{\dagger }Z)({\mathcal{E}})\rightarrow +1$, comme
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\rightarrow {\mathcal{E}}\rightarrow (\text{}^{\dagger }Z)({\mathcal{E}})\rightarrow +1$, comme ![]() $(\text{}^{\dagger }Z)({\mathcal{E}})$ est un module, on en déduit que
$(\text{}^{\dagger }Z)({\mathcal{E}})$ est un module, on en déduit que ![]() ${\mathcal{H}}_{Z}^{\dagger i}({\mathcal{E}})$ pour tout
${\mathcal{H}}_{Z}^{\dagger i}({\mathcal{E}})$ pour tout ![]() $i\not \in \{0,1\}$. La
$i\not \in \{0,1\}$. La ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérence du complexe
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-cohérence du complexe ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ résulte alors de 3.3.4 et de 3.4.6.
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ résulte alors de 3.3.4 et de 3.4.6.
Le théorème qui suit est juste une reformulation et un corollaire de [Reference CaroCar16, 3.5.2].
Théorème 3.4.8. [Reference CaroCar16, 3.5.2]
On suppose que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure ![]() $1$. Soit
$1$. Soit ![]() ${\mathcal{E}}^{(\bullet )}$ un objet de
${\mathcal{E}}^{(\bullet )}$ un objet de ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ et
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ et ![]() ${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ l’objet de
${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ l’objet de ![]() $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ correspondant. Les assertions suivantes sont équivalentes :
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ correspondant. Les assertions suivantes sont équivalentes :
(1)
 $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$,
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$,(2)
 $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$,
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$,(3)
 $(\text{}^{\dagger }Z)({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$,
$(\text{}^{\dagger }Z)({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$,(4)
 $(\text{}^{\dagger }Z)({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$,
$(\text{}^{\dagger }Z)({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$,(5)
 $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$.
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$.
Démonstration.
Les équivalences ![]() $(2)\Leftrightarrow (3)$ et
$(2)\Leftrightarrow (3)$ et ![]() $(4)\Leftrightarrow (5)$ résultent du triangle distingué de localisation
$(4)\Leftrightarrow (5)$ résultent du triangle distingué de localisation ![]() $\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\rightarrow {\mathcal{E}}^{(\bullet )}\rightarrow (\text{}^{\dagger }Z)({\mathcal{E}}^{(\bullet )})\rightarrow +1$. L’équivalence
$\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\rightarrow {\mathcal{E}}^{(\bullet )}\rightarrow (\text{}^{\dagger }Z)({\mathcal{E}}^{(\bullet )})\rightarrow +1$. L’équivalence ![]() $(3)\Leftrightarrow (4)$ est exactement le corollaire [Reference CaroCar16, 3.5.2]. L’équivalence
$(3)\Leftrightarrow (4)$ est exactement le corollaire [Reference CaroCar16, 3.5.2]. L’équivalence ![]() $(1)\Leftrightarrow (2)$ découle de l’isomorphisme canonique
$(1)\Leftrightarrow (2)$ découle de l’isomorphisme canonique ![]() $u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ (voir [Reference CaroCar16, 5.3.8.1]), de l’isomorphisme canonique
$u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})$ (voir [Reference CaroCar16, 5.3.8.1]), de l’isomorphisme canonique ![]() $u^{\sharp (\bullet )!}\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\overset{{\sim}}{\longrightarrow }\,u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$, ainsi que du théorème de Berthelot-Kashiwara toujours valable dans le contexte des catégories de la forme
$u^{\sharp (\bullet )!}\circ \mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}}^{(\bullet )})\overset{{\sim}}{\longrightarrow }\,u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})$, ainsi que du théorème de Berthelot-Kashiwara toujours valable dans le contexte des catégories de la forme ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ (voir [Reference CaroCar16, 5.3.7]).
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ (voir [Reference CaroCar16, 5.3.7]).
Corollaire 3.4.9. On suppose que ![]() $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ est de codimension pure ![]() $1$. Soit
$1$. Soit ![]() ${\mathcal{E}}$ un
${\mathcal{E}}$ un ![]() ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent tel que
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module cohérent tel que ![]() ${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un
${\mathcal{H}}^{0}u^{\sharp !}({\mathcal{E}})$ soit un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent et que
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent et que ![]() ${\mathcal{H}}^{1}u^{\sharp !}({\mathcal{E}})$ soit un
${\mathcal{H}}^{1}u^{\sharp !}({\mathcal{E}})$ soit un ![]() ${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui soit aussi un
${\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}}$-module cohérent qui soit aussi un ![]() ${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module localement projectif de type fini pour la structure induite. Soit
${\mathcal{O}}_{{\mathcal{Z}}}(\text{}^{\dagger }U)_{\mathbb{Q}}$-module localement projectif de type fini pour la structure induite. Soit ![]() ${\mathcal{E}}^{(\bullet )}$ un objet de
${\mathcal{E}}^{(\bullet )}$ un objet de ![]() $\underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ tel que
$\underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}(\widetilde{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )})$ tel que ![]() ${\mathcal{E}}\overset{{\sim}}{\longrightarrow }\,\varinjlim ~({\mathcal{E}}^{(\bullet )})$. Alors
${\mathcal{E}}\overset{{\sim}}{\longrightarrow }\,\varinjlim ~({\mathcal{E}}^{(\bullet )})$. Alors ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$.
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$.
Remarque 3.4.10. On garde les notations et hypothèses du théorème 3.4.8.
![]() $\bullet$ Si l’une des conditions équivalentes du théorème 3.4.8 est satisfaite, alors on dispose de l’isomorphisme
$\bullet$ Si l’une des conditions équivalentes du théorème 3.4.8 est satisfaite, alors on dispose de l’isomorphisme ![]() $u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ (dans le terme de gauche, les foncteurs
$u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$ (dans le terme de gauche, les foncteurs ![]() $u_{+}^{\sharp }$ et
$u_{+}^{\sharp }$ et ![]() $u^{\sharp !}$ sont calculés sur les catégories respectives de
$u^{\sharp !}$ sont calculés sur les catégories respectives de ![]() ${\mathcal{D}}^{\dagger }$-modules cohérents).
${\mathcal{D}}^{\dagger }$-modules cohérents).
![]() $\bullet$ En revanche, si l’on suppose seulement que
$\bullet$ En revanche, si l’on suppose seulement que ![]() $u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$, alors il n’est pas clair que
$u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$, alors il n’est pas clair que ![]() $u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})$ (les foncteurs
$u_{+}^{\sharp }\circ u^{\sharp !}({\mathcal{E}})$ (les foncteurs ![]() $u_{+}^{\sharp }$ et
$u_{+}^{\sharp }$ et ![]() $u^{\sharp !}$ sont calculés sur les catégories respectives de
$u^{\sharp !}$ sont calculés sur les catégories respectives de ![]() ${\mathcal{D}}^{\dagger }$-modules cohérents) soit isomorphe à
${\mathcal{D}}^{\dagger }$-modules cohérents) soit isomorphe à ![]() $\varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})=\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$. En effet, il n’est alors pas évident que la cohérence de
$\varinjlim \circ u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})=\mathbb{R}\text{}\underline{\unicode[STIX]{x1D6E4}}_{Z}^{\dagger }({\mathcal{E}})$. En effet, il n’est alors pas évident que la cohérence de ![]() $u^{\sharp !}({\mathcal{E}})$ implique
$u^{\sharp !}({\mathcal{E}})$ implique ![]() $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$. A priori, pour garantir une telle implication, on a besoin de conditions supplémentaires (par exemple 3.4.9).
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widetilde{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )})$. A priori, pour garantir une telle implication, on a besoin de conditions supplémentaires (par exemple 3.4.9).
3.5 Applications aux log-isocristaux surconvergents
Rappelons les conditions de non-liouvillité apparaissant dans [Reference Caro and TsuzukiCT12, 1.1.1].
Définition 3.5.1. Soit ![]() ${\mathcal{E}}$ un isocristal sur
${\mathcal{E}}$ un isocristal sur ![]() $\mathfrak{X}^{\sharp }$ surconvergeant le long de
$\mathfrak{X}^{\sharp }$ surconvergeant le long de ![]() $T$. On dit que
$T$. On dit que ![]() ${\mathcal{E}}$ satisfait respectivement les conditions (a), (b) et (p) si le long de chacune des composantes irréductibles de
${\mathcal{E}}$ satisfait respectivement les conditions (a), (b) et (p) si le long de chacune des composantes irréductibles de ![]() $D$ non incluse dans
$D$ non incluse dans ![]() $T$ on a :
$T$ on a :
(a) aucune différence des exposants de
 ${\mathcal{E}}$ n’est un nombre
${\mathcal{E}}$ n’est un nombre  $p$-adic de Liouville ;
$p$-adic de Liouville ;(b) aucun des exposants de
 ${\mathcal{E}}$ n’est un nombre
${\mathcal{E}}$ n’est un nombre  $p$-adic de Liouville ;
$p$-adic de Liouville ;
(p) aucun des exposants de
 ${\mathcal{E}}$ n’est un entier strictement positif.
${\mathcal{E}}$ n’est un entier strictement positif.
Nous aurons besoin de la définition suivante.
Définition 3.5.2. Soit ![]() ${\mathcal{E}}\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$.
${\mathcal{E}}\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$.
∙ On dit que
 ${\mathcal{E}}$ est strictement
${\mathcal{E}}$ est strictement  $0$-dévissable en log-isocristaux surconvergeant sur
$0$-dévissable en log-isocristaux surconvergeant sur  $\mathfrak{X}^{\sharp }$ s’il existe un diviseur
$\mathfrak{X}^{\sharp }$ s’il existe un diviseur  $T\text{sp}\prime$ contenant
$T\text{sp}\prime$ contenant  $T$, une immersion fermée de
$T$, une immersion fermée de  ${\mathcal{V}}$-schémas formels lisses
${\mathcal{V}}$-schémas formels lisses  $i:{\mathcal{Z}}\text{sp}\prime {\hookrightarrow}\mathfrak{X}$ tels que
$i:{\mathcal{Z}}\text{sp}\prime {\hookrightarrow}\mathfrak{X}$ tels que  $i^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de
$i^{-1}(\mathfrak{D})$ soit un diviseur à croisements normaux strict de  ${\mathcal{Z}}\text{sp}\prime$,
${\mathcal{Z}}\text{sp}\prime$,  $T\text{sp}\prime \cap Z\text{sp}\prime$ soit un diviseur de
$T\text{sp}\prime \cap Z\text{sp}\prime$ soit un diviseur de  $Z\text{sp}\prime$,
$Z\text{sp}\prime$,  ${\mathcal{E}}\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\text{sp}\prime )_{\mathbb{Q}})$,
${\mathcal{E}}\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T\text{sp}\prime )_{\mathbb{Q}})$,  ${\mathcal{E}}$ soit à support dans
${\mathcal{E}}$ soit à support dans  ${\mathcal{Z}}\text{sp}\prime$ et, si l’on note
${\mathcal{Z}}\text{sp}\prime$ et, si l’on note  ${\mathcal{Z}}^{\prime \sharp }:=({\mathcal{Z}}\text{sp}\prime ,i^{-1}({\mathcal{D}}))$ et
${\mathcal{Z}}^{\prime \sharp }:=({\mathcal{Z}}\text{sp}\prime ,i^{-1}({\mathcal{D}}))$ et  $i^{\sharp }:{\mathcal{Z}}^{\prime \sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte induite, alors les espaces de cohomologie de
$i^{\sharp }:{\mathcal{Z}}^{\prime \sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ l’immersion fermée exacte induite, alors les espaces de cohomologie de  $i^{\sharp !}({\mathcal{E}})$ sont des isocristaux sur
$i^{\sharp !}({\mathcal{E}})$ sont des isocristaux sur  ${\mathcal{Z}}^{\prime \sharp }$ surconvergeant le long de
${\mathcal{Z}}^{\prime \sharp }$ surconvergeant le long de  $T\text{sp}\prime \cap Z\text{sp}\prime$.
$T\text{sp}\prime \cap Z\text{sp}\prime$.∙ Par récurrence sur
 $n\in \mathbb{N}$, on dit que
$n\in \mathbb{N}$, on dit que  ${\mathcal{E}}$ est strictement
${\mathcal{E}}$ est strictement  $n+1$-dévissable en log-isocristaux surconvergeant sur
$n+1$-dévissable en log-isocristaux surconvergeant sur  $\mathfrak{X}^{\sharp }$, s’il existe un triangle distingué dans
$\mathfrak{X}^{\sharp }$, s’il existe un triangle distingué dans  $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ de la forme où
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$ de la forme où $$\begin{eqnarray}{\mathcal{E}}\text{sp}\prime \rightarrow {\mathcal{E}}\rightarrow {\mathcal{E}}\text{sp}\prime \prime \rightarrow {\mathcal{E}}\text{sp}\prime [1],\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}\text{sp}\prime \rightarrow {\mathcal{E}}\rightarrow {\mathcal{E}}\text{sp}\prime \prime \rightarrow {\mathcal{E}}\text{sp}\prime [1],\end{eqnarray}$$ ${\mathcal{E}}\text{sp}\prime ,{\mathcal{E}}\text{sp}\prime \prime$ sont strictement
${\mathcal{E}}\text{sp}\prime ,{\mathcal{E}}\text{sp}\prime \prime$ sont strictement  $n$-dévissables en log-isocristaux surconvergeant sur
$n$-dévissables en log-isocristaux surconvergeant sur  $\mathfrak{X}^{\sharp }$.
$\mathfrak{X}^{\sharp }$.
Notations 3.5.3. On suppose que ![]() ${\mathcal{Z}}\cup \mathfrak{D}$ est un diviseur à croisements normaux strict de
${\mathcal{Z}}\cup \mathfrak{D}$ est un diviseur à croisements normaux strict de ![]() $\mathfrak{X}$. On note
$\mathfrak{X}$. On note ![]() $\mathfrak{X}^{\flat }:=(\mathfrak{X},{\mathcal{Z}}\cup \mathfrak{D})$ le log-schéma formel logarithmique lisse, et
$\mathfrak{X}^{\flat }:=(\mathfrak{X},{\mathcal{Z}}\cup \mathfrak{D})$ le log-schéma formel logarithmique lisse, et ![]() $\unicode[STIX]{x1D6FC}:\mathfrak{X}^{\flat }\rightarrow \mathfrak{X}^{\sharp }$ et
$\unicode[STIX]{x1D6FC}:\mathfrak{X}^{\flat }\rightarrow \mathfrak{X}^{\sharp }$ et ![]() $\unicode[STIX]{x1D6FD}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}$ les morphismes canoniques.
$\unicode[STIX]{x1D6FD}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}$ les morphismes canoniques.
Remarque 3.5.4. On garde les notations et hypothèses de 3.5.3. D’après une remarque apparue dans un travail en commun avec Tomoyuki Abe (voir [Reference Abe and CaroAC18, 4]), il existe un diagramme de la forme du carré de gauche :

où ![]() $f$ est un morphisme étale,
$f$ est un morphisme étale, ![]() $g\text{sp}\prime$ est un morphisme lisse qui est une rétraction de
$g\text{sp}\prime$ est un morphisme lisse qui est une rétraction de ![]() $u\text{sp}\prime$ et tel que, en posant
$u\text{sp}\prime$ et tel que, en posant ![]() $\mathfrak{D}\text{sp}\prime :=f^{-1}\mathfrak{D}$, on ait
$\mathfrak{D}\text{sp}\prime :=f^{-1}\mathfrak{D}$, on ait ![]() $\mathfrak{D}\text{sp}\prime =g^{\prime -1}\circ u^{\prime -1}(\mathfrak{D}\text{sp}\prime )$, où les trois autres carrés sont cartésiens par définition (on remarque alors que tous les morphismes sont exacts).
$\mathfrak{D}\text{sp}\prime =g^{\prime -1}\circ u^{\prime -1}(\mathfrak{D}\text{sp}\prime )$, où les trois autres carrés sont cartésiens par définition (on remarque alors que tous les morphismes sont exacts).
Le corollaire qui suit étend le théorème [Reference Caro and TsuzukiCT12, 1.3.13].
Corollaire 3.5.5. On garde les notations et hypothèses de 3.5.3. Soit ![]() ${\mathcal{E}}$ un isocristal sur
${\mathcal{E}}$ un isocristal sur ![]() $\mathfrak{X}^{\flat }$ surconvergeant le long de
$\mathfrak{X}^{\flat }$ surconvergeant le long de ![]() $T$ et satisfaisant les conditions (a) et (b) de 3.5.1. Les propriétés suivantes sont alors satisfaites.
$T$ et satisfaisant les conditions (a) et (b) de 3.5.1. Les propriétés suivantes sont alors satisfaites.
(1) Le complexe
 $u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est un complexe d’isocristaux sur
$u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est un complexe d’isocristaux sur  ${\mathcal{Z}}^{\sharp }$ surconvergeant le long de
${\mathcal{Z}}^{\sharp }$ surconvergeant le long de  $U$ et satisfaisant les conditions (a) et (b) de 3.5.1.
$U$ et satisfaisant les conditions (a) et (b) de 3.5.1.(2) On dispose du triangle distingué dans
 $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(T)_{\mathbb{Q}})$ de la forme : En particulier,
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(T)_{\mathbb{Q}})$ de la forme : En particulier, $$\begin{eqnarray}u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }Z)\rightarrow u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})[1].\end{eqnarray}$$
$$\begin{eqnarray}u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }Z)\rightarrow u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})[1].\end{eqnarray}$$ $\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est strictement
$\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est strictement  $1$-dévissable en log-isocristaux surconvergeant sur
$1$-dévissable en log-isocristaux surconvergeant sur  $\mathfrak{X}^{\sharp }$.
$\mathfrak{X}^{\sharp }$.(3) Si
 ${\mathcal{E}}$ vérifie en outre la condition (p) de 3.5.1, alors le morphisme canonique
${\mathcal{E}}$ vérifie en outre la condition (p) de 3.5.1, alors le morphisme canonique  $\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }Z)$ est un isomorphisme.
$\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }Z)$ est un isomorphisme.
Démonstration.
Grâce à la remarque 3.5.4 et grâce à l’isomorphisme de changement de base par un morphisme lisse (voir [Reference CaroCar16, 5.4.6]) qui donne l’isomorphisme ![]() $f^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}\circ f^{\flat !}({\mathcal{E}})$, on se ramène au cas où il existe un morphisme lisse
$f^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\overset{{\sim}}{\longrightarrow }\,\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}\circ f^{\flat !}({\mathcal{E}})$, on se ramène au cas où il existe un morphisme lisse ![]() $g:\mathfrak{X}\rightarrow {\mathcal{Z}}$ tel que
$g:\mathfrak{X}\rightarrow {\mathcal{Z}}$ tel que ![]() $g\circ u=id$ et
$g\circ u=id$ et ![]() $\mathfrak{D}=g^{-1}\circ u^{-1}(\mathfrak{D})$. On note alors
$\mathfrak{D}=g^{-1}\circ u^{-1}(\mathfrak{D})$. On note alors ![]() $g^{\sharp }:\mathfrak{X}^{\sharp }\rightarrow {\mathcal{Z}}^{\sharp }$ le morphisme induit par
$g^{\sharp }:\mathfrak{X}^{\sharp }\rightarrow {\mathcal{Z}}^{\sharp }$ le morphisme induit par ![]() $g$ et
$g$ et ![]() $g^{\flat }:=g^{\sharp }\circ u$. Soit
$g^{\flat }:=g^{\sharp }\circ u$. Soit ![]() ${\mathcal{E}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\flat }}^{(\bullet )}(T))$ un objet tel que
${\mathcal{E}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\flat }}^{(\bullet )}(T))$ un objet tel que ![]() $\varinjlim ~{\mathcal{E}}^{(\bullet )}\overset{{\sim}}{\longrightarrow }\,{\mathcal{E}}$. Comme
$\varinjlim ~{\mathcal{E}}^{(\bullet )}\overset{{\sim}}{\longrightarrow }\,{\mathcal{E}}$. Comme ![]() $(\text{}^{\dagger }Z)\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})={\mathcal{E}}^{(\bullet )}(\text{}^{\dagger }Z)$, on dispose alors du triangle distingué dans
$(\text{}^{\dagger }Z)\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})={\mathcal{E}}^{(\bullet )}(\text{}^{\dagger }Z)$, on dispose alors du triangle distingué dans ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$:
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$:
 $$\begin{eqnarray}\displaystyle & & \displaystyle u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\rightarrow \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\rightarrow {\mathcal{E}}^{(\bullet )}(\text{}^{\dagger }Z)\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})[1].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\rightarrow \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\rightarrow {\mathcal{E}}^{(\bullet )}(\text{}^{\dagger }Z)\nonumber\\ \displaystyle & & \displaystyle \qquad \rightarrow u_{+}^{\sharp (\bullet )}\circ u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})[1].\end{eqnarray}$$ En appliquant le foncteur ![]() $g_{+}^{\sharp (\bullet )}$ au triangle (34), comme
$g_{+}^{\sharp (\bullet )}$ au triangle (34), comme ![]() $g_{+}^{\sharp (\bullet )}\circ u_{+}^{\sharp (\bullet )}=id$ et comme
$g_{+}^{\sharp (\bullet )}\circ u_{+}^{\sharp (\bullet )}=id$ et comme ![]() $g_{+}^{\sharp (\bullet )}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}=g_{+}^{\flat (\bullet )}$, on obtient alors le triangle distingué dans
$g_{+}^{\sharp (\bullet )}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}=g_{+}^{\flat (\bullet )}$, on obtient alors le triangle distingué dans ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$ :
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{qc}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$ :
En appliquant le foncteur ![]() $\varinjlim$ à (35), comme
$\varinjlim$ à (35), comme ![]() $\unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$, avec [Reference CaroCar16, 5.1.7], on obtient :
$\unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LM}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$, avec [Reference CaroCar16, 5.1.7], on obtient :
Grâce au théorème [Reference Caro and TsuzukiCT12, 1.3.13], on déduit de 36 que ![]() $u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est un complexe d’isocristaux sur
$u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est un complexe d’isocristaux sur ![]() ${\mathcal{Z}}^{\sharp }$ surconvergeant le long de
${\mathcal{Z}}^{\sharp }$ surconvergeant le long de ![]() $U$ et satisfaisant les conditions (a) et (b) de 3.5.1. Il résulte alors de 3.4.7 et 3.4.8 que
$U$ et satisfaisant les conditions (a) et (b) de 3.5.1. Il résulte alors de 3.4.7 et 3.4.8 que ![]() $u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. Le triangle (34) est donc un triangle distingué de
$u^{\sharp (\bullet )!}\circ \unicode[STIX]{x1D6FC}_{+}^{(\bullet )}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. Le triangle (34) est donc un triangle distingué de ![]() $\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. On en déduit la partie (2) du corollaire. Lorsque
$\underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$. On en déduit la partie (2) du corollaire. Lorsque ![]() ${\mathcal{E}}$ satisfait les conditions (a), (b) et (p) de 3.5.1, il découle de [Reference Caro and TsuzukiCT12, 1.1.22.1] que
${\mathcal{E}}$ satisfait les conditions (a), (b) et (p) de 3.5.1, il découle de [Reference Caro and TsuzukiCT12, 1.1.22.1] que ![]() $g_{+}^{\flat }({\mathcal{E}})\rightarrow g_{+}^{\flat }({\mathcal{E}}(\text{}^{\dagger }Z))$ est un isomorphisme (cela se vérifie comme [Reference Caro and TsuzukiCT12, 1.3.13] découle de [Reference Caro and TsuzukiCT12, 1.1.22.1]). Via (36), cela entraîne que
$g_{+}^{\flat }({\mathcal{E}})\rightarrow g_{+}^{\flat }({\mathcal{E}}(\text{}^{\dagger }Z))$ est un isomorphisme (cela se vérifie comme [Reference Caro and TsuzukiCT12, 1.3.13] découle de [Reference Caro and TsuzukiCT12, 1.1.22.1]). Via (36), cela entraîne que ![]() $u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})=0$ et donc
$u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})=0$ et donc ![]() $u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})=0$. On a validé ainsi la partie (3) du corollaire.
$u_{+}^{\sharp }\circ u^{\sharp !}\circ \unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})=0$. On a validé ainsi la partie (3) du corollaire.
Le corollaire qui suit étend [Reference Caro and TsuzukiCT12, 2.2.9] et [Reference Caro and TsuzukiCT12, 2.3.4].
Corollaire 3.5.6. Supposons pour simplifier les énoncés que ![]() $\mathfrak{X}$ soit intègre. Soit
$\mathfrak{X}$ soit intègre. Soit ![]() $\mathfrak{D}_{1},\ldots ,\mathfrak{D}_{s}$ les composantes irréductibles de
$\mathfrak{D}_{1},\ldots ,\mathfrak{D}_{s}$ les composantes irréductibles de ![]() $\mathfrak{D}$. Soit
$\mathfrak{D}$. Soit ![]() $1\leqslant r\leqslant s$,
$1\leqslant r\leqslant s$, ![]() $\mathfrak{D}\text{sp}\prime \prime :=\bigcup _{1\leqslant i\leqslant r}~\mathfrak{D}_{i}$,
$\mathfrak{D}\text{sp}\prime \prime :=\bigcup _{1\leqslant i\leqslant r}~\mathfrak{D}_{i}$, ![]() $\mathfrak{D}\text{sp}\prime :=\bigcup _{r+1\leqslant i\leqslant s}~\mathfrak{D}_{i}$,
$\mathfrak{D}\text{sp}\prime :=\bigcup _{r+1\leqslant i\leqslant s}~\mathfrak{D}_{i}$, ![]() $\mathfrak{X}^{\flat }:=(\mathfrak{X},\mathfrak{D}\text{sp}\prime )$ et
$\mathfrak{X}^{\flat }:=(\mathfrak{X},\mathfrak{D}\text{sp}\prime )$ et ![]() $\unicode[STIX]{x1D6FC}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}^{\flat }$ le morphisme canonique. Soit
$\unicode[STIX]{x1D6FC}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}^{\flat }$ le morphisme canonique. Soit ![]() ${\mathcal{E}}$ un isocristal sur
${\mathcal{E}}$ un isocristal sur ![]() $\mathfrak{X}^{\sharp }$ surconvergeant le long de
$\mathfrak{X}^{\sharp }$ surconvergeant le long de ![]() $T$.
$T$.
(1) Si
 ${\mathcal{E}}$ vérifie les conditions (a) et (b) de 3.5.1, alors
${\mathcal{E}}$ vérifie les conditions (a) et (b) de 3.5.1, alors  $\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est strictement
$\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})$ est strictement  $r$-dévissable en log-isocristaux surconvergeant sur
$r$-dévissable en log-isocristaux surconvergeant sur  $\mathfrak{X}^{\flat }$ satisfaisant les conditions (a) et (b) de 3.5.1.
$\mathfrak{X}^{\flat }$ satisfaisant les conditions (a) et (b) de 3.5.1.(2) Si
 ${\mathcal{E}}$ vérifie les conditions (a), (b) et (p) de 3.5.1, le morphisme canonique
${\mathcal{E}}$ vérifie les conditions (a), (b) et (p) de 3.5.1, le morphisme canonique  $\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }D\text{sp}\prime \prime )$ est un isomorphisme.
$\unicode[STIX]{x1D6FC}_{+}({\mathcal{E}})\rightarrow {\mathcal{E}}(\text{}^{\dagger }D\text{sp}\prime \prime )$ est un isomorphisme.
Démonstration.
Vérifions d’abord (1). On procède par récurrence sur ![]() $r$. Le cas où
$r$. Le cas où ![]() $r=1$ est le corollaire 3.5.5. Supposons donc
$r=1$ est le corollaire 3.5.5. Supposons donc ![]() $r\geqslant 2$. Posons
$r\geqslant 2$. Posons ![]() ${\mathcal{Z}}:=\mathfrak{D}_{1}$,
${\mathcal{Z}}:=\mathfrak{D}_{1}$, ![]() $\mathfrak{D}_{{\geqslant}2}:=\bigcup _{2\leqslant i\leqslant s}~\mathfrak{D}_{i}$,
$\mathfrak{D}_{{\geqslant}2}:=\bigcup _{2\leqslant i\leqslant s}~\mathfrak{D}_{i}$, ![]() $\mathfrak{X}^{\sharp \flat }:=(\mathfrak{X},\mathfrak{D}_{{\geqslant}2})$,
$\mathfrak{X}^{\sharp \flat }:=(\mathfrak{X},\mathfrak{D}_{{\geqslant}2})$, ![]() ${\mathcal{Z}}^{\sharp \flat }:=({\mathcal{Z}},{\mathcal{Z}}\cap \mathfrak{D}_{{\geqslant}2})$ et
${\mathcal{Z}}^{\sharp \flat }:=({\mathcal{Z}},{\mathcal{Z}}\cap \mathfrak{D}_{{\geqslant}2})$ et ![]() ${\mathcal{Z}}^{\flat }:=({\mathcal{Z}},{\mathcal{Z}}\cap \mathfrak{D}\text{sp}\prime )$. On note
${\mathcal{Z}}^{\flat }:=({\mathcal{Z}},{\mathcal{Z}}\cap \mathfrak{D}\text{sp}\prime )$. On note ![]() $\unicode[STIX]{x1D6FC}_{1}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}^{\sharp \flat }$,
$\unicode[STIX]{x1D6FC}_{1}:\mathfrak{X}^{\sharp }\rightarrow \mathfrak{X}^{\sharp \flat }$, ![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime :\mathfrak{X}^{\sharp \flat }\rightarrow \mathfrak{X}^{\flat }$,
$\unicode[STIX]{x1D6FC}\text{sp}\prime :\mathfrak{X}^{\sharp \flat }\rightarrow \mathfrak{X}^{\flat }$, ![]() $\unicode[STIX]{x1D6FD}\text{sp}\prime :{\mathcal{Z}}^{\sharp \flat }\rightarrow {\mathcal{Z}}^{\sharp }$,
$\unicode[STIX]{x1D6FD}\text{sp}\prime :{\mathcal{Z}}^{\sharp \flat }\rightarrow {\mathcal{Z}}^{\sharp }$, ![]() $u^{\sharp \flat }:{\mathcal{Z}}^{\sharp \flat }\rightarrow \mathfrak{X}^{\sharp \flat }$ et
$u^{\sharp \flat }:{\mathcal{Z}}^{\sharp \flat }\rightarrow \mathfrak{X}^{\sharp \flat }$ et ![]() $u^{\flat }:{\mathcal{Z}}^{\flat }\rightarrow \mathfrak{X}^{\flat }$ les morphismes canoniques. Lorsque
$u^{\flat }:{\mathcal{Z}}^{\flat }\rightarrow \mathfrak{X}^{\flat }$ les morphismes canoniques. Lorsque ![]() $T\supset Z$, on calcule facilement (voir par exemple [Reference Caro and TsuzukiCT12, 2.2.1]) que
$T\supset Z$, on calcule facilement (voir par exemple [Reference Caro and TsuzukiCT12, 2.2.1]) que ![]() $\unicode[STIX]{x1D6FC}_{1+}({\mathcal{E}})={\mathcal{E}}$. Supposons alors que
$\unicode[STIX]{x1D6FC}_{1+}({\mathcal{E}})={\mathcal{E}}$. Supposons alors que ![]() $T\cap Z$ soit un diviseur de
$T\cap Z$ soit un diviseur de ![]() $Z$. D’après 3.5.5, on dispose alors du triangle distingué de localisation dans
$Z$. D’après 3.5.5, on dispose alors du triangle distingué de localisation dans ![]() $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp \flat }}^{\dagger }(T)_{\mathbb{Q}})$
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp \flat }}^{\dagger }(T)_{\mathbb{Q}})$
tel que ![]() ${\mathcal{F}}:=u^{\sharp \flat !}\circ \unicode[STIX]{x1D6FC}_{1+}({\mathcal{E}})$ soit un complexe d’isocristaux sur
${\mathcal{F}}:=u^{\sharp \flat !}\circ \unicode[STIX]{x1D6FC}_{1+}({\mathcal{E}})$ soit un complexe d’isocristaux sur ![]() ${\mathcal{Z}}^{\sharp \flat }$ surconvergeant le long de
${\mathcal{Z}}^{\sharp \flat }$ surconvergeant le long de ![]() $T\cap Z$ satisfaisant les conditions (a) et (b) de 3.5.1. Or, par hypothèse de récurrence (et aussi parce que le foncteur
$T\cap Z$ satisfaisant les conditions (a) et (b) de 3.5.1. Or, par hypothèse de récurrence (et aussi parce que le foncteur ![]() $\unicode[STIX]{x1D6FD}\text{sp}\prime _{+}$ est exact sur la catégorie des isocristaux sur
$\unicode[STIX]{x1D6FD}\text{sp}\prime _{+}$ est exact sur la catégorie des isocristaux sur ![]() ${\mathcal{Z}}^{\sharp \flat }$ surconvergeant le long de
${\mathcal{Z}}^{\sharp \flat }$ surconvergeant le long de ![]() $T\cap Z$),
$T\cap Z$), ![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}({\mathcal{E}}(\text{}^{\dagger }Z_{1}))$ (resp.
$\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}({\mathcal{E}}(\text{}^{\dagger }Z_{1}))$ (resp. ![]() $\unicode[STIX]{x1D6FD}\text{sp}\prime _{+}({\mathcal{F}})$) est strictement
$\unicode[STIX]{x1D6FD}\text{sp}\prime _{+}({\mathcal{F}})$) est strictement ![]() $r-1$-dévissable en log-isocristaux surconvergeant sur
$r-1$-dévissable en log-isocristaux surconvergeant sur ![]() $\mathfrak{X}^{\flat }$ (resp.
$\mathfrak{X}^{\flat }$ (resp. ![]() ${\mathcal{Z}}^{\flat }$). L’isomorphisme canonique
${\mathcal{Z}}^{\flat }$). L’isomorphisme canonique ![]() $\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}\circ u_{+}^{\sharp \flat }({\mathcal{F}})\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp \flat }\circ \unicode[STIX]{x1D6FD}\text{sp}\prime _{+}({\mathcal{F}})$ nous permet de conclure (1). On établit (2) de manière identique.
$\unicode[STIX]{x1D6FC}\text{sp}\prime _{+}\circ u_{+}^{\sharp \flat }({\mathcal{F}})\overset{{\sim}}{\longrightarrow }\,u_{+}^{\sharp \flat }\circ \unicode[STIX]{x1D6FD}\text{sp}\prime _{+}({\mathcal{F}})$ nous permet de conclure (1). On établit (2) de manière identique.
Remerciements
Je remercie Tomoyuki Abe pour ses commentaires concernant le fait que les ![]() ${\mathcal{D}}$-modules arithmétiques cohérents sont de type LB et notre travail en commun qui a conduit à la remarque 3.5.4.
${\mathcal{D}}$-modules arithmétiques cohérents sont de type LB et notre travail en commun qui a conduit à la remarque 3.5.4.