2.1 Laminar base flow

Equations (2.1)–(2.3) with boundary conditions (2.4)–(2.5) admit a laminar solution that only depends on the wall-normal coordinate $z$ and is spatially uniform in $x$ and $y$

(2.6)$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{U}_{0}(z)={\displaystyle \frac{\sin (\unicode[STIX]{x1D6FE})}{6\tilde{\unicode[STIX]{x1D708}}}}\left(z^{3}-{\displaystyle \frac{1}{4}}z\right)\boldsymbol{e}_{x}, & \displaystyle\end{eqnarray}$$

(2.7)$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{T}}_{0}(z)=-z, & \displaystyle\end{eqnarray}$$

(2.8)$$\begin{eqnarray}\displaystyle & \displaystyle p_{0}(z)=\unicode[STIX]{x1D6F1}-\cos (\unicode[STIX]{x1D6FE})z^{2}/2, & \displaystyle\end{eqnarray}$$

with arbitrary pressure constant $\unicode[STIX]{x1D6F1}$. The linear temperature profile and the cubic velocity profile of this laminar base flow are sketched in figure 1 (grey lines). Within the laminar solution, buoyancy forces caused by the linear temperature profile as well as shear forces due to the velocity gradients in the buoyancy driven cubic velocity profile are present. The former is destabilizing for $-90^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$ while shear can lead to instabilities at all non-zero inclination angles. At sufficiently strong driving, instabilities create overturning convective motion so that the laminar solution is no longer observed and the symmetries of ILC are broken.

2.2 Symmetries

Inclined layer convection at zero inclination ($\unicode[STIX]{x1D6FE}=0^{\circ }$) corresponds to Rayleigh–Bénard convection with isotropy and homogeneity in the $x$–$y$ plane. At all inclinations $0^{\circ }\neq \unicode[STIX]{x1D6FE}\neq 180^{\circ }$, the isotropy of the horizontal layer is broken by the wall-parallel component of gravity, driving the laminar flow along the $x$ dimension. The laminar flow in ILC is still homogeneous and thereby invariant under continuous translations

(2.9)$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{\prime }(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y)[U,V,W,{\mathcal{T}}](x,y,z)\equiv [U,V,W,{\mathcal{T}}](x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y,z).\end{eqnarray}$$

Moreover, ILC is invariant under discrete reflections

(2.10)$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x03C0}_{y}[U,V,W,{\mathcal{T}}](x,y,z)\equiv [U,-V,W,{\mathcal{T}}](x,-y,z), & \displaystyle\end{eqnarray}$$

(2.11)$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x03C0}_{xz}[U,V,W,{\mathcal{T}}](x,y,z)\equiv [-U,V,-W,-{\mathcal{T}}](-x,y,-z). & \displaystyle\end{eqnarray}$$

The symmetry group of ILC consists of all products of the generators $\{\unicode[STIX]{x03C0}_{y},\unicode[STIX]{x03C0}_{xz},\unicode[STIX]{x1D70F}^{\prime }(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y)\}$. We indicate this group by $S_{ILC}=\langle \unicode[STIX]{x03C0}_{y},\unicode[STIX]{x03C0}_{xz},\unicode[STIX]{x1D70F}^{\prime }(\unicode[STIX]{x0394}x,\unicode[STIX]{x0394}y)\rangle$, where angle brackets $\langle \rangle$ imply all products of elements given in the brackets. Inclined layer convection has the same symmetries as plane Couette flow where analogous notation is commonly used (e.g Gibson & Brand Reference Gibson and Brand2014).

Instead of considering an infinite fluid layer, we consider a finite periodic fluid layer by imposing periodic boundary conditions in $x$ and in $y$, $[U,V,W,{\mathcal{T}}](x,y,z)=[U,V,W,{\mathcal{T}}](x+L_{x},y,z)$ and $[U,V,W,{\mathcal{T}}](x,y,z)=[U,V,W,{\mathcal{T}}](x,y+L_{y},z)$, respectively. Due to the periodic boundary conditions, we express continuous translations as

(2.12)$$\begin{eqnarray}\unicode[STIX]{x1D70F}(a_{x},a_{y})[U,V,W,{\mathcal{T}}](x,y,z)\equiv [U,V,W,{\mathcal{T}}](x+a_{x}L_{x},y+a_{y}L_{y},z),\end{eqnarray}$$

with shift factors $a_{x},a_{y}\in [0,1)$ scaling the spatial periods $L_{x}$ and $L_{y}$ of the periodic domain. Continuous translations in periodic domains are cyclic and shifts by $L_{x}$ or $L_{y}$ correspond to the identity operator $\unicode[STIX]{x1D70F}(0,0)$. Since the streamwise direction $x$ and the spanwise direction $y$ of ILC can be rotated and reflected, the symmetry group of ILC in $x$–$y$-periodic domains is isomorphic to the direct product of two copies of the orthogonal group in two dimensions, $O(2)$, that is $O(2)\times O(2)$. In the product, one term refers to the $x$ dimension, the other to the $y$ dimension.

The relevance of the system’s symmetries for the dynamics is that once a state is invariant under a symmetry transformation of the equivariance group $S_{ILC}$, $[\boldsymbol{U},{\mathcal{T}}]=\unicode[STIX]{x1D70E}[\boldsymbol{U},{\mathcal{T}}]$ with $\unicode[STIX]{x1D70E}\in S_{ILC}$, the evolution under the full nonlinear governing equations (2.1)–(2.3) will preserve the symmetry and the evolving trajectory will remain in the symmetry subspace of all possible states invariant under $\unicode[STIX]{x1D70E}$ (e.g. Cvitanović et al. Reference Cvitanović, Artuso, Mainieri, Tanner and Vattay2017). Consequently, trajectories and invariant states of the infinitely extended system without any symmetry constraints can be computed in symmetry subspaces, including those defined by the discrete translation symmetries imposed by periodic boundary conditions. To compute states in symmetry subspaces defined by a discrete symmetry $\unicode[STIX]{x1D70E}\in S_{ILC}$ satisfying $\unicode[STIX]{x1D70E}^{2}=1$, we impose $\unicode[STIX]{x1D70E}$ using a projection $([\boldsymbol{U},{\mathcal{T}}]+\unicode[STIX]{x1D70E}[\boldsymbol{U},{\mathcal{T}}])/2$ during simulations. Any exact solution in a symmetry subspace remains a valid solution of the full unconstrained infinite system. Imposing symmetries does not affect the state but may disallow instabilities breaking the imposed symmetries and thereby simplifies numerical access to invariant states with symmetries.

All invariant states discussed in the present article are invariant under transformations of subgroups of $S_{ILC}=\langle \unicode[STIX]{x03C0}_{y},\unicode[STIX]{x03C0}_{xz},\unicode[STIX]{x1D70F}(a_{x},a_{y})\rangle$. We will specify the generators of the symmetry group $S$ of invariant states in terms of the combinations of $\unicode[STIX]{x03C0}_{y}$, $\unicode[STIX]{x03C0}_{xz}$ and $\unicode[STIX]{x1D70F}(a_{x},a_{y})$. The choice of generators is not unique because translations $\unicode[STIX]{x1D70F}(a_{x},a_{y})$ define conjugacy classes of group elements, corresponding to the free choice of the spatial phase of invariant states in $x$ and $y$. We choose the spatial phase such that three-dimensional inversion $\unicode[STIX]{x03C0}_{xyz}=\unicode[STIX]{x03C0}_{y}\unicode[STIX]{x03C0}_{xz}$, where applicable to invariant states, applies with respect to the domain origin at $(x,y,z)=(0,0,0)$.

2.3 Energy transfer

Inclined layer convection is a thermally driven dissipative system. The externally imposed temperature difference results in the thermal energy flux that is required to sustain temperature gradients. These gradients, together with gravity, generate buoyancy forces that drive the fluid flow. Thereby thermal energy is converted to kinetic energy that is eventually dissipated by conversion into heat through internal viscous friction. The kinetic energy balance is obtained by multiplying (2.1) with $\boldsymbol{U}$ and space averaging equation (2.1) over the entire domain volume $\unicode[STIX]{x1D6FA}$, denoted by $\langle \rangle _{\unicode[STIX]{x1D6FA}}$,

(2.13)$$\begin{eqnarray}\displaystyle \frac{1}{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle U^{2}\rangle _{\unicode[STIX]{x1D6FA}}=\langle \hat{\boldsymbol{g}}\boldsymbol{U}{\mathcal{T}}\rangle _{\unicode[STIX]{x1D6FA}}-\tilde{\unicode[STIX]{x1D708}}\langle (\unicode[STIX]{x1D735}\times \boldsymbol{U})^{2}\rangle _{\unicode[STIX]{x1D6FA}}=I-D. & & \displaystyle\end{eqnarray}$$

The rate of change of kinetic energy in $\unicode[STIX]{x1D6FA}$ is given by the difference between energy input $I$, the work due to buoyancy forces and viscous dissipation $D$ (Malkus Reference Malkus1964). These rates may be normalized by the laminar transfer rate

(2.14)$$\begin{eqnarray}\displaystyle I_{0}=D_{0}=\sin ^{2}(\unicode[STIX]{x1D6FE})/(720\,\tilde{\unicode[STIX]{x1D708}}) & & \displaystyle\end{eqnarray}$$

for non-zero inclination, $\unicode[STIX]{x1D6FE}\neq 0^{\circ }$.

Since the kinetic energy of all equilibrium states remains constant, energy transfer rates need to be balanced, implying $I=D$. A periodic orbit will be characterized by instantaneously unbalanced rates but the net energy transfer integrated over one period $T$ of the orbit vanishes, $\int _{0}^{T}(I-D)\,\text{d}t=0$. For equilibria with relative dissipation $D/I=1$, equation (2.13) allows to distinguish two destabilising mechanisms. When buoyancy forces drive an instability of an equilibrium state, $I$ increases over $D$ implying $D/I<1$ for the initial dynamics triggered by the instability. A shear driven instability of an equilibrium leads initially to $D/I>1$ because rising shear increases $D$ over $I$. Local oscillatory instabilities of equilibrium states discussed in the present paper cause oscillation amplitudes to grow symmetrically around $D/I=1$ with an exponential growth rate. The symmetry around $D/I=1$ suggests that buoyancy and shear forces contribute equally to the destabilising mechanism underlying an oscillatory instability. We will characterize all invariant states and their instabilities in terms of energy transfer.

On average, the thermal heat flux through any plane parallel to the walls is independent of the height $z$. At the walls, the transport is purely diffusive but in the centre of the domain convective heat transport can be significant. To quantify the instantaneous, time-dependent, heat transport due to convective effects, we formulate the energy balance equation for heat not averaged over the full but over the lower half of the domain. This generates boundary flux terms at the midplane between the walls, where convective transport is expected to be largest. The volume average of (2.2) over the lower half of the domain volume $\unicode[STIX]{x1D6FA}/2$, yields

(2.15)$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle {\mathcal{T}}\rangle _{\unicode[STIX]{x1D6FA}/2}=\left\langle -\tilde{\unicode[STIX]{x1D705}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}{\mathcal{T}}\right\rangle _{A(-0.5)}-\left\langle W{\mathcal{T}}-\tilde{\unicode[STIX]{x1D705}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}{\mathcal{T}}\right\rangle _{A(0)}=J-\mathit{Nu}. & & \displaystyle\end{eqnarray}$$

Here $\langle \rangle _{A(z)}$ denote averages over planes at height $z$ parallel to the walls. The rate of change of thermal energy averaged over the lower half of the domain $\unicode[STIX]{x1D6FA}/2$ is given by the diffusive boundary heat flux $J$ at the lower wall and the instantaneous Nusselt number $\mathit{Nu}$ at the midplane. The laminar diffusive heat flux is

(2.16)$$\begin{eqnarray}\displaystyle J_{0}=\mathit{Nu}_{0}=\tilde{\unicode[STIX]{x1D705}}. & & \displaystyle\end{eqnarray}$$

As for the kinetic energy balance, equilibrium states imply $J=\mathit{Nu}$. Periodic orbits will have unbalanced instantaneous fluxes that average to vanishing net thermal energy change over one period.

3.1 Direct numerical simulations

The Oberbeck–Boussinesq equations for inclined layers (2.1)–(2.3) in a $x$–$y$-periodic domain are solved in direct numerical simulations (DNS) using a pseudo-spectral method (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang2006, p. 133ff). After substituting the base-fluctuation decomposition $[\boldsymbol{U},{\mathcal{T}}]=[\boldsymbol{U}_{0},{\mathcal{T}}_{0}]+[\boldsymbol{u},\unicode[STIX]{x1D703}]$ into (2.1)–(2.3), the continuous field variables of the fluctuations $[\boldsymbol{u},\unicode[STIX]{x1D703}](x,y,z,t)$ are numerically approximated by Fourier and Chebyshev expansions of the form

(3.1)$$\begin{eqnarray}\displaystyle [\boldsymbol{u},\unicode[STIX]{x1D703}](\boldsymbol{x},t)=\mathop{\sum }_{k_{x}=-K_{x}}^{K_{x}}\mathop{\sum }_{k_{y}=-K_{y}}^{K_{y}}\mathop{\sum }_{j=0}^{N_{z}-1}[\tilde{\boldsymbol{u}},\tilde{\unicode[STIX]{x1D703}}]_{k_{x},k_{y},j}(t){\mathcal{C}}_{j}(z)\text{e}^{2\unicode[STIX]{x03C0}\text{i}(k_{x}x/L_{x}+k_{y}y/L_{y})}, & & \displaystyle\end{eqnarray}$$

where ${\mathcal{C}}_{j}(z)$ is the $j$th Chebyshev polynomial of the first kind, linearly rescaled to the interval $z\in [-0.5,0.5]$. Velocity and temperature are fixed at the walls of the domain at $\boldsymbol{u}(z=\pm 0.5)=0$ and $\unicode[STIX]{x1D703}(z=\pm 0.5)=0$, as the inhomogeneous boundary conditions are absorbed in ${\mathcal{T}}_{0}(z)$. Owing to incompressibility, the pressure $p$ is a dependent variable and fully determined by $\boldsymbol{u}$. The pressure is obtained by solving a Tau problem with the influence matrix method (Kleiser & Schumann Reference Kleiser, Schumann and Hirschel1980; Canuto & Landriani Reference Canuto and Landriani1986). To completely specify the problem with periodic boundary conditions, an integral constraint on either pressure gradient or mean flux is required. We keep the mean-pressure gradient along the $x$ and the $y$ direction constant, specifically $\int _{0}^{L_{y}}\int _{0}^{L_{x}}\unicode[STIX]{x1D735}p\,\text{d}x\,\text{d}y=0$. Technically, we modify pressure as $p=p^{\prime }+\boldsymbol{U}^{2}/2$ which allows expressing the nonlinear term in (2.1) in rotational form $\boldsymbol{U}\times (\unicode[STIX]{x1D735}\times \boldsymbol{U})=(\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{U}-\boldsymbol{U}^{2}/2$. After evaluation of the nonlinear terms in (2.1) and (2.2) in physical space, the products are transformed to a spectral representation using the ‘fastest Fourier transform in the West’ (known as FFTW) library (Frigo & Johnson Reference Frigo and Johnson2005) and dealiased using the $2/3$ rule (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang2006, p. 133f). Due to dealiasing, a grid of size $N_{x}\times N_{y}\times N_{z}$ in physical space implies spectral summation bounds of $K_{x}=N_{x}/3-1$ and $K_{y}=N_{y}/3-1$ in (3.1). We use e.g. $[N_{x},N_{y},N_{z}]=[32,32,25]$ to resolve a single pair of convection rolls in a domain of extent $[L_{x},L_{y}]=[2.2211,2.0162]$. This choice is discussed in § 3.3. For time-marching, an implicit–explicit multistep algorithm of third-order is implemented solving the diffusion terms and the pressure term fully implicitly, and the nonlinear terms and the buoyancy term explicitly. See appendix A for the details of the time-stepping algorithm. The code is written in C + + as an extension module to the MPI-parallel software Channelflow 2.0 (Gibson et al. Reference Gibson, Reetz, Azimi, Ferraro, Kreilos, Schrobsdorff, Farano, Yesil, Schütz and Culpo2019).

The numerical implementation of the extension module Channelflow-ILC (publically available at channelflow.ch) has been validated by reproducing three key results with different levels of importance of nonlinear effects. First, a highly resolved critical threshold for the linear onset of convection in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) is accurately reproduced (see § 3.3). Second, numerical continuations in $\unicode[STIX]{x1D6FE}$ and $\mathit{Ra}$ of invariant states underlying longitudinal convection rolls reproduce an analytic scaling invariance of the nonlinear Oberbeck–Boussinesq equations (2.1)–(2.3), as discussed in § 3 of the accompanying article (Reetz, Subramanian & Schneider Reference Reetz, Subramanian and Schneider2020). Third, the statistics of fully turbulent Rayleigh–Bénard convection match previous results on the scaling of $\mathit{Nu}\sim \mathit{Ra}$ (appendix B).

3.2 Computation of invariant states

We not only simulate the time evolution of ILC but also compute invariant states. Any state of ILC can be expressed as a state vector $\boldsymbol{x}(t)=[\boldsymbol{u},\unicode[STIX]{x1D703}](x,y,z,t)$ in a state space of ILC for given boundary conditions. The unique time evolution of state vectors $\boldsymbol{x}(t)$ is computed using DNS. Invariant states are defined as particular state vectors $\boldsymbol{x}^{\ast }$ such that

(3.2)$$\begin{eqnarray}{\mathcal{G}}(\boldsymbol{x}^{\ast })=\unicode[STIX]{x1D70E}{\mathcal{F}}^{\text{T}}(\boldsymbol{x}^{\ast })-\boldsymbol{x}^{\ast }=0,\end{eqnarray}$$

where ${\mathcal{F}}^{\text{T}}$ is the evolution operator for (2.1)–(2.3) over a finite time period $T$ defining a dynamical system for ILC. Operator $\unicode[STIX]{x1D70E}$ is an element of the symmetry group $S_{\mathit{ILC}}$ and applies a discrete coordinate transformation in terms of (2.10)–(2.12). Since (2.1)–(2.3) are partial differential equations, the state space of this dynamical system is of infinite dimension. The numerical representation of ILC discussed in § 3.1 renders the state space dimension finite. The spatially discretized partial differential equations correspond to a set of coupled ordinary differential equations, one for each of the four fields $[u,v,w,\unicode[STIX]{x1D703}]$ at each spatial collocation point. Thus, the dynamical system has a state space with $N=4\times N_{x}\times N_{y}\times N_{z}\times 4/9$ dimensions. The factor $4/9$ accounts for the cutoff wavenumbers due to dealiasing. To solve (3.2) efficiently in an $N$-dimensional state space, Channelflow-ILC employs a matrix-free Newton–Raphson iteration, based on the generalized minimal residual method (known as GMRES) to construct a Krylov subspace, together with a hookstep trust region optimization (Viswanath Reference Viswanath2007). The trust region optimization increases the radius of convergence. To be within a radius of convergence of the Newton–Raphson method, the initial state of the iteration must be close to an invariant state. Full convergence within double-precision arithmetic requires the residual of (3.2) to be $\Vert {\mathcal{G}}(\boldsymbol{x})\Vert _{2}=\mathit{O}(10^{-16})$. Here, we define the normalized $L_{2}$ norm of state vectors as

(3.3)$$\begin{eqnarray}\Vert \boldsymbol{x}\Vert _{2}=\left(\frac{1}{L_{x}L_{y}}\int _{0}^{L_{x}}\int _{0}^{L_{y}}\int _{-0.5}^{0.5}u^{2}+v^{2}+w^{2}+\unicode[STIX]{x1D703}^{2}\,\text{d}x\,\text{d}y\,\text{d}z\right)^{1/2}.\end{eqnarray}$$

Once invariant states have converged in a Newton iteration, their spectrum of eigenvalues can be computed using Arnoldi iteration (Viswanath Reference Viswanath2007) and bifurcation branches can be computed using continuation methods (see Dijkstra et al. (Reference Dijkstra, Wubs, Cliffe, Doedel, Hazel, Lucarini, Salinger, Phipps, Sanchez-Umbria and Schuttelaars2014) for a review).

We distinguish two types of invariant states, namely equilibrium states (EQs) and periodic orbits (POs). If the period $T$ in (3.2) can be arbitrarily chosen a priori, then invariant states are steady states or EQs. We use $T=20$ to compute an EQ. If invariant states require $T$ to match a specific time period, the state is unsteady but exactly recurrent over $T$ and the invariant state is a PO. The period $T$ of a PO is determined in the Newton iteration. There are additional classifications of EQs and POs. If $\unicode[STIX]{x1D70E}\in S_{ILC}$ in (3.2) with $\unicode[STIX]{x1D70E}\neq 1$, the invariant state is a relative invariant state. Relative EQs are travelling wave states (known as TWs) that are steady states in a co-moving frame of reference. Travelling wave states satisfy (3.2) with $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(a_{x},a_{y})$, where shift factors $a_{x}$ and $a_{y}$ must be determined in the Newton iteration. A relative PO might also travel over its period $T$ requiring a specific $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(a_{x},a_{y})$. Some periodic orbits that have $\unicode[STIX]{x1D70E}=1$ after a full period $T$ still may exploit a discrete symmetry operation $\unicode[STIX]{x1D70E}\neq 1$ after a relative period $T^{\prime }=T/n$ with $n\in \mathbb{N}$. This type of relative PO is a ‘pre-periodic orbit’ (see e.g. Budanur & Cvitanović Reference Budanur and Cvitanović2017).

Where possible, we name invariant states according to the existing names of observed convection patterns and instabilities in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). We will show that specific nonlinear invariant states underlie specific convection patterns and that the specific states can be linked, in most cases, to bifurcation points corresponding to specific instabilities. To reflect the link between observed patterns, invariant states and instabilities but also to clearly distinguish between the three distinct objects, we use different symbols/fonts to indicate: an observed ‘pattern X’ as ${\mathcal{P}}{\mathcal{X}}$, instabilities linked to this pattern as $PX_{i}$, and exact invariant states underlying the pattern as $PX$.

3.3 Straight convection rolls as equilibrium states

Figure 2. (a) Critical thresholds $\mathit{Ra}_{c}(\unicode[STIX]{x1D6FE})$ for the instabilities to longitudinal rolls ($LR_{i}$) and transverse rolls ($TR_{i}$) from linear stability analysis of $B$ at $\mathit{Pr}=1.07$ (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). (b) Bifurcation branches of invariant states $LR$ and $TR$ at $\unicode[STIX]{x1D6FE}_{c2}$ bifurcate together from $B$ at $\mathit{Ra}_{c2}=8053.1$. When computing $LR$ and $TR$ in a minimal domain of size $[L_{x},L_{y}]=[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$, $LR$ is stable (solid line) and $TR$ is unstable (dotted line).

The simplest invariant state in ILC is the laminar base flow (2.6)–(2.8), denoted as $B$ and representing a zero-state for the fluctuations $[\boldsymbol{u},\unicode[STIX]{x1D703}]=0$. When $B$ becomes dynamically unstable, straight convection rolls may form. In ILC at $\unicode[STIX]{x1D6FE}=0^{\circ }$, the case corresponding to Rayleigh–Bénard convection, the critical threshold for the onset of convection is $\mathit{Ra}_{c}(\unicode[STIX]{x1D6FE}=0^{\circ })=1707.76$ (Busse Reference Busse1978). In ILC at $\unicode[STIX]{x1D6FE}\neq 0^{\circ }$, two types of straight roll patterns can emerge from a primary instability, either longitudinal rolls (${\mathcal{L}}{\mathcal{R}}$), with orientation along $x$, or transverse rolls (${\mathcal{T}}{\mathcal{R}}$), with orientation along $y$. The type of rolls to which $B$ becomes first unstable when $\mathit{Pr}$ is fixed and $\mathit{Ra}$ is increased depends on $\unicode[STIX]{x1D6FE}$ (Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969; Hart Reference Hart1971a). Figure 2(a) shows the curves for critical thresholds $\mathit{Ra}_{c}(\unicode[STIX]{x1D6FE})$ at $\mathit{Pr}=1.07$. The point in the $\unicode[STIX]{x1D6FE}$–$\mathit{Ra}$ plane where $LR_{i}$ and $TR_{i}$ have the same critical threshold is a codimension-2 point. We reproduce this point at $\unicode[STIX]{x1D6FE}=77.7567^{\circ }\equiv \unicode[STIX]{x1D6FE}_{c2}$ and $\mathit{Ra}_{c}(\unicode[STIX]{x1D6FE}_{c2})=8053.1\equiv \mathit{Ra}_{c2}$ via numerical continuation of equilibrium states $LR$ and $TR$ down in $\mathit{Ra}$ to their exact bifurcation point from $B$ (figure 2b). Here, $LR$ is invariant under the symmetry group $S_{\mathit{LR}}=\langle \unicode[STIX]{x03C0}_{xz}\unicode[STIX]{x1D70F}(0,0.5),\unicode[STIX]{x03C0}_{y}\unicode[STIX]{x1D70F}(0,0.5),\unicode[STIX]{x1D70F}(a_{x},0)\rangle$ and $TR$ is invariant under $S_{\mathit{TR}}=\langle \unicode[STIX]{x03C0}_{xz},\unicode[STIX]{x03C0}_{y},\unicode[STIX]{x1D70F}(0,a_{y})\rangle$. Both equilibrium states, $LR$ and $TR$, are numerically fully converged to satisfy (3.2). Useful initial states for the Newton iteration are obtained from a ‘phase portrait’ analysis as explained in the following section.

Linear stability analysis suggests streamwise and spanwise wavelengths for the primary instability to longitudinal and transverse rolls at the codimension-2 point (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). Accordingly we choose the periodic domain to match wavelengths $\unicode[STIX]{x1D706}_{x}=2.2211$ and $\unicode[STIX]{x1D706}_{y}=2.0162$ of instabilities $TR_{i}$ and $LR_{i}$, respectively. For the domain size $[L_{x},L_{y}]=[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$, we have reproduced the codimension-2 point at $[\unicode[STIX]{x1D6FE}_{c2},\mathit{Ra}_{c2}]=[77.7567^{\circ },8053.1]$. We confirmed that all given digits are significant. The step size of the continuation was chosen sufficiently small to indicate the bifurcation point at this accuracy. Moreover, increasing the grid resolution beyond $[n_{x},n_{y},n_{z}]=[32,32,25]$ does not change the result. We fix $\unicode[STIX]{x1D706}_{x}=2.2211$ and $\unicode[STIX]{x1D706}_{y}=2.0162$ as constants in this paper, and choose all periodic domains to be periodic over $[L_{x},L_{y}]=[l\,\unicode[STIX]{x1D706}_{x},m\,\unicode[STIX]{x1D706}_{y}]$ and to be discretized with $[N_{x},N_{y},N_{z}]=[l\,n_{x},m\,n_{y},n_{z}]$ with $l,m\in \mathbb{N}$. Thus, the invariant states discussed here have prescribed pattern wavelengths, unlike pattern forming instabilities calculated using a Floquet analysis (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016).

3.4 Phase portrait analysis

Temporal transitions from laminar flow to longitudinal or transverse rolls are studied by initialising a simulation with small perturbations around the dynamically unstable base state $B$ and visualizing the time evolution in a state space projection representing a ‘phase portrait’. Two state vector trajectories $\boldsymbol{x}(t)$ are simulated just above the codimension-2 point, at $\unicode[STIX]{x1D6FE}_{c2}$ and $\mathit{Ra}=8500>\mathit{Ra}_{c2}$. Each trajectory starts from $B$ perturbed by small amplitude noise of $\mathit{O}(10^{-5})$. The evolution of $\boldsymbol{x}(t)$ is simulated in the symmetry subspace of $[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$-periodicity, corresponding to the domain size, and either $S_{\mathit{LR}}$ or $S_{\mathit{TR}}$. Imposing either $S_{\mathit{LR}}$ or $S_{\mathit{TR}}$ causes $\boldsymbol{x}(t)$ to remain in the symmetry subspace since (2.1)–(2.3) are equivariant under $S_{\mathit{LR}}$ and $S_{\mathit{TR}}$. Each symmetry subspace contains only one type of straight convection rolls. Thus, the choice of either $S_{\mathit{LR}}$ or $S_{\mathit{TR}}$ selects whether longitudinal or transverse rolls emerge.

The longitudinal and the transverse state trajectories are analysed in a ‘phase plane’ spanned by kinetic energy input $I$ and relative viscous dissipation $D/I$ defined in (2.13). The $D/I$-axis allows to distinguish two types of instabilities of equilibrium states in ILC satisfying $D=I$. The transition towards $LR$ is triggered by a buoyancy driven instability of $B$ that initially increases $I$ over $D$. The transition towards $TR$ is triggered by a shear driven instability of $B$ that initially increases $D$ over $I$. The phase portrait illustrates that the state $LR$ is reached via a temporal transition from a buoyancy driven instability of $B$, and $TR$ is reached via a temporal transition from a shear driven instability of $B$ (figure 3a).

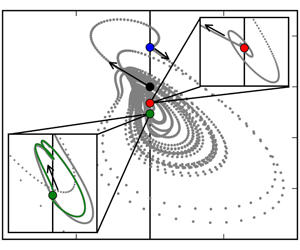
Figure 3. (a) Simulated state trajectories (grey dots) evolving from noise around the unstable laminar base flow $B$ at $\unicode[STIX]{x1D6FE}_{c2}$ and $\mathit{Ra}=8500$ over time $t$ (left), and plotted as phase portraits in a plane of normalized kinetic energy input $I/I_{0}$ and relative dissipation $D/I$ (right). The DNS is confined to either $S_{\mathit{LR}}$ and $S_{\mathit{TR}}$, allowing either a buoyancy driven instability to initiate a temporal transition to $LR$ or a shear driven instability to initiate a temporal transition to $TR$. Arrows indicate the direction of the evolution. Exact equilibrium states $LR$ and $TR$ are visualized by three-dimensional contours at $1/3[\min (\unicode[STIX]{x1D703}),\max (\unicode[STIX]{x1D703})]$ and the in-plane components of $\boldsymbol{u}$ at the domain sides. (b) Without imposing discrete symmetries, $TR$ is dynamically unstable. Perturbing $TR$ initiates a dynamical connection to $LR$ with fast dynamics near the unstable manifold of $TR$ and slow dynamics near the stable manifold of $LR$.

The phase portrait analysis not only characterizes the forces driving an instability but also helps to identify good initial guesses for Newton iterations that may converge to invariant states. After a stage of exponential growth in the transition from $B$, the two state trajectories saturate and the dynamics slows down exponentially (figure 3a). Exponential slowdown near $D/I=1$ suggests the presence of an equilibrium state, and indeed, the two final state vectors $\boldsymbol{x}(t=1000)$ are close to invariant states and good initial guesses for a Newton iteration. They converge to $LR$ and $TR$, respectively, and provide the starting point for the numerical continuation shown in figure 2(b). Consequently, the phase portrait analysis is useful for finding invariant states during temporal transitions. Moreover, the phase portrait clearly illustrates how the dynamics follow dynamical connections between invariant states, in this case $B\rightarrow LR$ and $B\rightarrow TR$. We use the term ‘dynamical connection’ for state trajectories connecting the state space neighbourhood of two invariant states in a finite time. Dynamical connections indicate the existence of a nearby heteroclinic connection requiring infinite time to be traversed (e.g. Farano et al. Reference Farano, Cherubini, Robinet, De Palma and Schneider2019).

The dynamical stability of $LR$ and $TR$ at $\unicode[STIX]{x1D6FE}_{c2}$ and $\mathit{Ra}=8500$ is characterized using Arnoldi iteration in the symmetry subspace of the $[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$-periodic domain. Here, $LR$ is stable and $TR$ is weakly unstable with respect to two shift-symmetry related three-dimensional, longitudinally oriented, eigenmodes with linear growth rate of $\unicode[STIX]{x1D714}_{r}=0.044$. These unstable eigenmodes of $TR$ do not exist in the symmetry subspace defined by $S_{\mathit{TR}}$ where the temporal transition to stable $TR$ was simulated. However, the simulated dynamical connection $B\rightarrow TR$ also exists in the larger subspace where $S_{\mathit{TR}}$ is not imposed and $B\rightarrow TR$ connects two unstable invariant states. When perturbing unstable $TR$, a buoyancy driven instability triggers a dynamical connection $TR\rightarrow LR$. Along this connection the dynamics undergo a rapid slowdown suggesting a transition from the fast unstable manifold of $TR$ to the slow stable manifold of $LR$ whose leading eigenvalue is $\unicode[STIX]{x1D714}_{r}=-0.016$ (figure 3b).

In summary, the phase portrait analysis serves three purposes. First, high-dimensional state space trajectories can be visualized in a two-dimensional projection. Second, close approaches to invariant states and a slowdown of the dynamics provide useful initial guesses for Newton iterations to converge. Thus, the phase portrait analysis gives access to invariant states. Third, the type of instability triggering a transition from an equilibrium state can be characterized as either buoyancy driven or shear driven via the departure from the $D/I=1$ line in the phase portrait.

4.1 Transitions with equilibrium state attractor

4.1.1 Wavy rolls

The convection pattern of wavy rolls (${\mathcal{W}}{\mathcal{R}}$) has been observed in early experiments (Hart Reference Hart1971a) and associated with the wavy instability $WR_{i}$ of $LR$ (Clever & Busse Reference Clever and Busse1977), also found for longitudinal rolls in Bénard–Couette flow (Clever, Busse & Kelly Reference Clever, Busse and Kelly1977). Hart (Reference Hart1971b) already hypothesized a relation between ${\mathcal{W}}{\mathcal{R}}$ and wavy vortex flow in Taylor–Couette experiments (Coles Reference Coles1965). Such a relation was later found to exist, and exploited in the first constructions of invariant states underlying wavy velocity streaks in subcritical shear flows (Nagata Reference Nagata1990; Clever & Busse Reference Clever and Busse1992). The convection pattern of wavy rolls is observed in ILC at control parameter values $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[40^{\circ },0.07,1.07]$ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000). We simulate a temporal transition starting from small-amplitude noise around the unstable base flow at these values of the control parameters. The size of the periodic domain is $[L_{x},L_{y}]=[2\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$ and no additional discrete symmetries are imposed.

Figure 4. (a) State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=40^{\circ }$ and $\mathit{Ra}=2385$ ($\unicode[STIX]{x1D716}=0.07$). After a transient in the vicinity of $LR$, the shear driven instability $WR_{i}$ of $LR$ makes the trajectory follow a stable spiral towards equilibrium state $WR$. (b) Flow structure of $WR$ in a periodic domain of size $[L_{x},L_{y}]=[2\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$.

The phase portrait reveals a two-stage transition from the base flow $B$ to wavy rolls. First, a buoyancy driven instability of $B$ leads to a slow transient over $700<t<1400$ in the vicinity of $LR$. Second, a shear driven instability of $LR$ leads to a spiralling trajectory on which the dynamics approach the equilibrium state $WR$ (figure 4a). The spectrum of eigenvalues of $WR$ has the complex pair $(\unicode[STIX]{x1D714}_{r},\pm \unicode[STIX]{x1D714}_{i})=(-0.007,\pm 0.039)$ closest to the imaginary axis. The imaginary part suggests an oscillation period on the spiralling trajectory of $T=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{i}=161$. The decaying oscillations of the trajectory for $t>1500$ match this period. The flow structure of equilibrium state $WR$ shows the characteristic wavy modulations observed in experiments and simulations (figure 4b). The invariant state $WR$ is invariant under shift-reflect and shift-rotate symmetries $S_{\mathit{WR}}=\langle \unicode[STIX]{x03C0}_{y}\unicode[STIX]{x1D70F}(0.5,0.5),\unicode[STIX]{x03C0}_{xz}\unicode[STIX]{x1D70F}(0.5,0.5)\rangle$. These symmetries are analogous to the symmetries of wavy velocity streaks in plane Couette flow (e.g. Gibson et al. Reference Gibson, Halcrow and Cvitanović2008).

Figure 5. (a) Spectrum of leading eigenvalues of $LR$ explains exponential approach and escape rates relative to $LR$. (b) $L_{2}$-distance between $LR$ and the state trajectory shown in figure 4(a) illustrates exponential approach and escape dynamics in the state space neighbourhood of $LR$. The dotted line marks the exponential rates given by the leading stable and unstable eigenvalues of $LR$.

The state trajectory follows a sequence of dynamical connections $B\rightarrow LR\rightarrow WR$. The transient close to $LR$, a saddle point with stable and unstable eigendirections, follows exponential dynamics. The leading eigenvalues of $LR$ are real, $[\unicode[STIX]{x1D714}_{1,2},\unicode[STIX]{x1D714}_{3},\unicode[STIX]{x1D714}_{4}]=[0.038,10^{-9},-0.039]$, and define the exponential rate of approach, ${\sim}\text{e}^{\unicode[STIX]{x1D714}_{4}t}$, and escape, ${\sim}\text{e}^{\unicode[STIX]{x1D714}_{1,2}t}$ (figure 5). The double multiplicity of the positive eigenvalue is a result of the continuous translation symmetry $\unicode[STIX]{x1D70F}(a_{x},0)$ of $LR$ allowing two orthonormal eigenmodes of arbitrary $x$ phase. Continuous translations $\unicode[STIX]{x1D70F}(0,a_{y})$ are not an invariance of $LR$ but change the $y$ phase of $LR$ and generate a continuum of equivalent states. The Goldstone mode corresponding to the translation invariance of $LR$ is the marginally stable eigenmode with eigenvalue $\unicode[STIX]{x1D714}_{3}$. Therefore, the pitchfork bifurcation creating $LR$ is a circle pitchfork bifurcation (Crawford & Knobloch Reference Crawford and Knobloch1991). The non-zero finite value of $\unicode[STIX]{x1D714}_{3}$ is a measure for the accuracy of the Arnoldi iteration. The minimal distance of the state trajectory to $LR$ is $\Vert \boldsymbol{x}(t=1050)-LR\Vert _{2}/\Vert LR\Vert _{2}\approx 10^{-8}$. Consequently, the transition dynamics from $B$ generate a trajectory transiently visiting the state space neighbourhood of the unstable equilibrium state $LR$, as already suggested by the phase portrait.

When increasing thermal driving, the ${\mathcal{W}}{\mathcal{R}}$ pattern is succeeded by weakly turbulent wavy rolls, also called ‘crawling rolls’ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000). A DNS at $\unicode[STIX]{x1D716}=0.5$ leads to a much more complicated phase portrait than at $\unicode[STIX]{x1D716}=0.07$. At these control parameter values, the state trajectory initially still undergoes the transition sequence $B\rightarrow LR\rightarrow WR$. However, $WR$ is now unstable. After a transient visit close to $WR$ at $t=500$, a buoyancy driven instability of $WR$ leads to a sequence of large-amplitude, fast oscillations before the state trajectory is attracted to a small-amplitude, slow bursting cycle (figure 6). The fast transient oscillations have clockwise revolving trajectories in the $D/I$–$I$ plane and dominate the phase portrait. We suspect the existence of an unstable periodic orbit with similar shaped phase portrait underlying the transient oscillations. Finding and analysing this periodic orbit is beyond the scope of this work but will be discussed elsewhere (authors’ unpublished observations). Here, we discuss the slow dynamical attractor at these values of the control parameters.

Figure 6. State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=40^{\circ }$ and $\mathit{Ra}=3344$ ($\unicode[STIX]{x1D716}=0.5$). The trajectory visits unstable $LR$, followed by a transient visit of $WR$ (inset c). Subsequently, the trajectory undergoes a sequence of rapid oscillations and is finally attracted to a heteroclinic cycle between equilibrium state $OWR$ and a symmetry related equilibrium. The time series for $2000<t<10\,000$ in inset (a) indicates the increasing time spent near the equilibrium states. The phase portrait of the heteroclinic cycle is magnified in inset (b). Since the energy transfer rates do not differ for symmetry related states, the heteroclinic cycle appears as a homoclinic cycle. See figure 7(a) for a projection that distinguishes the two equilibrium states.

Figure 7. Robust heteroclinic cycle between two symmetry related equilibrium states at $\unicode[STIX]{x1D6FE}=40^{\circ }$ and $\mathit{Ra}=3344$ ($\unicode[STIX]{x1D716}=0.5$). (a) $L_{2}$-distance relative to the two symmetry related equilibrium states, $OWR$ and $\unicode[STIX]{x1D70F}_{xy}OWR$, visualizes how the simulated state trajectory (grey dots) approaches the heteroclinic cycle (black line). The direction of the dynamics is indicated by black arrows. (b) Flow structure of $OWR$ in a periodic domain of size $[2\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$. (c) Temperature contours at midplane illustrate the spatial phase of $OWR$, $\unicode[STIX]{x1D70F}_{xy}OWR$, and their unstable eigenmodes $\boldsymbol{e}^{u}$ and $\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}$, respectively, along the diagonal of the domain (dotted line). The pattern wavenumbers of equilibria and unstable eigenmodes along the domain diagonals suggest a nearby 1 : 2 resonance.

The temporal dynamics of ILC at $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[40^{\circ },0.5,1.07]$ in a periodic domain of size $[2\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$ is attracted to a heteroclinic cycle. The cycle dynamically connects an equilibrium state, which we name oblique wavy rolls ($OWR$), with a symmetry related equilibrium state $\unicode[STIX]{x1D70F}_{xy}OWR$ (figure 7). Here, $\unicode[STIX]{x1D70F}_{xy}=\unicode[STIX]{x1D70F}(0.25,0.25)$ is a shift operator translating the wavy flow structure by half a pattern wavelength in the direction of the domain diagonal along which the wavy convection rolls of $OWR$ are aligned. The invariant states $OWR$ and $\unicode[STIX]{x1D70F}_{xy}OWR$ show two spatial periods of the wavy pattern along the domain diagonal and both are invariant under transformations of $S_{\mathit{OWR}}=\langle \unicode[STIX]{x03C0}_{xyz},\unicode[STIX]{x1D70F}(0.5,0.5)\rangle$. Without imposing the symmetries in $S_{\mathit{OWR}}$, $OWR$ and $\unicode[STIX]{x1D70F}_{xy}OWR$ have each a single purely real unstable eigenmode, denoted as state vector $\boldsymbol{e}^{u}$ and $\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}$, respectively, that breaks the $\unicode[STIX]{x1D70F}(0.5,0.5)$-symmetry by having only one spatial period along the domain diagonal (figure 7c). Perturbing $OWR$ with $\boldsymbol{e}^{u}$ initiates the temporal transition $OWR\rightarrow \unicode[STIX]{x1D70F}_{xy}OWR$. Perturbing $\unicode[STIX]{x1D70F}_{xy}OWR$ with $\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}$ initiates the temporal transition $\unicode[STIX]{x1D70F}_{xy}OWR\rightarrow OWR$. Together, the two dynamical connections form a heteroclinic cycle. The two involved unstable eigenmodes $\boldsymbol{e}^{u}$ and $\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}$ preserve the symmetries $\unicode[STIX]{x03C0}_{xyz}$ and $\unicode[STIX]{x03C0}_{xyz}\unicode[STIX]{x1D70F}(0.5,0.5)$, respectively. Thus, they are analogous to sine- and cosine-eigenmodes in that they, first, are orthogonal such that the $L_{2}$ inner product is $\langle \boldsymbol{e}^{u},\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}\rangle =0$, and, second, have a reflection symmetry with respect to different reflection points, namely $\unicode[STIX]{x03C0}_{xyz}$ and $\unicode[STIX]{x03C0}_{xyz}\unicode[STIX]{x1D70F}(0.5,0.5)$ (figure 7c). When imposing $\unicode[STIX]{x03C0}_{xyz}$-symmetry, the unstable eigenmode $\unicode[STIX]{x1D70F}_{xy}\boldsymbol{e}^{u}$ is disallowed, $\unicode[STIX]{x1D70F}_{xy}OWR$ becomes dynamically stable, and the associated symmetry subspace $\unicode[STIX]{x1D6F4}_{1}$ contains only the dynamical connection $OWR\rightarrow \unicode[STIX]{x1D70F}_{xy}OWR$. When imposing $\unicode[STIX]{x03C0}_{xyz}\unicode[STIX]{x1D70F}(0.5,0.5)$-symmetry, the unstable eigenmode $\boldsymbol{e}^{u}$ is disallowed, $OWR$ becomes dynamically stable, and the associated symmetry subspace $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D70F}}$ contains only the dynamical connection $\unicode[STIX]{x1D70F}_{xy}OWR\rightarrow OWR$. Hence, the heteroclinic cycle satisfies all three conditions for the existence of a robust heteroclinic cycle between two symmetry related equilibrium states (Krupa Reference Krupa1997):

1. (i) $OWR$ is a saddle and $\unicode[STIX]{x1D70F}_{xy}OWR$ is an attractor (or sink) in a symmetry subspace $\unicode[STIX]{x1D6F4}_{1}$ of the entire state space of the $[2\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$-periodic domain.

2. (ii) There is a saddle-attractor connection $OWR\rightarrow \unicode[STIX]{x1D70F}_{xy}OWR$ in $\unicode[STIX]{x1D6F4}_{1}$.

3. (iii) There is a symmetry relation between the two equilibrium states, mediated by $\unicode[STIX]{x1D70F}_{xy}\in S_{\mathit{ILC}}$.

Robust heteroclinic cycles of this type have been previously described in systems with $O(2)$-symmetry that are near a codimension-2 point where bifurcating eigenmodes show a spatial 1 : 2 resonance (Armbruster, Guckenheimer & Holmes Reference Armbruster, Guckenheimer and Holmes1988; Proctor & Jones Reference Proctor and Jones1988; Mercader, Prat & Knobloch Reference Mercader, Prat and Knobloch2002; Nore et al. Reference Nore, Tuckerman, Daube and Xin2003). In the present case, the existence of $OWR$ with wavenumber $m=2$ along the domain diagonal and with an instability of wavenumber $m=1$ suggests a nearby codimension-2 point where oblique straight rolls become simultaneously unstable to $m=1$ and $m=2$ wavy modulations. Oblique straight rolls are not discussed here but are a known instability of laminar ILC (Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969). Reetz et al. (Reference Reetz, Subramanian and Schneider2020) demonstrate that $OWR$ of both wavenumbers, $m=1$ and $m=2$, indeed bifurcate off oblique straight rolls in two pitchfork bifurcations at only slightly different values of the control parameters, suggesting a 1 : 2 resonance.

The robust heteroclinic cycle is numerically identified as an attractor of the dynamics suggesting its dynamical stability. The stability of robust heteroclinic cycles depends on the leading eigenvalues of the involved equilibrium states (Krupa & Melbourne Reference Krupa and Melbourne1995). The leading eigenvalues of $OWR$ without imposing additional discrete symmetries are $[\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3,4}]=[0.016,-0.023,-0.037\pm 0.050]$. When imposing $\unicode[STIX]{x03C0}_{xyz}$, the contracting eigenvalue $\unicode[STIX]{x1D714}_{2}$ vanishes. When imposing $\unicode[STIX]{x03C0}_{xyz}\unicode[STIX]{x1D70F}(0.5,0.5)$, the expanding eigenvalue $\unicode[STIX]{x1D714}_{1}$ vanishes. Thus, the leading expanding and contracting eigenvalues belong to two different symmetry subspaces. The complex eigenvalue $\unicode[STIX]{x1D714}_{3,4}$ is radial as it belongs to both subspaces and does not influence the stability of the cycle. Since $|\unicode[STIX]{x1D714}_{1}|/|\unicode[STIX]{x1D714}_{2}|<1$, the heteroclinic cycle is dynamically stable (Krupa & Melbourne Reference Krupa and Melbourne1995).

Figure 8. (a) State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=80^{\circ }$ and $\unicode[STIX]{x1D716}=0.05$ ($\mathit{Ra}=8525$). After a transient in the vicinity of $TR$, the buoyancy driven instability $KN_{i}$ causes the trajectory to follow a stable spiral towards equilibrium state $KN$. (b) Flow structure of $KN$ in a periodic domain of size $[L_{x},L_{y}]=[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$.

We do not expect this heteroclinic cycle to be stable in larger domains. However, oblique wavy rolls are observed to evolve slowly in experiments and simulations at lower thermal driving (Daniels et al. Reference Daniels, Brausch, Pesch and Bodenschatz2008). At the control parameter values selected here, observations in larger domains indicate chaotic dynamics on a faster time scale than the time scale of the approach to the heteroclinic cycle (authors’ unpublished observations). The time period $\unicode[STIX]{x0394}t$ over which the state trajectory remains close to an equilibrium increases with time (figure 6a). It should eventually diverge but here saturates at $\unicode[STIX]{x0394}t\approx \mathit{O}(10^{3})$. This saturation effect is due to the numerical double-precision of the DNS. The unstable eigenvalue $\unicode[STIX]{x1D714}_{1}=0.016$ of $OWR$ amplifies the numerical noise on a time scale of $\log (10^{16})/\unicode[STIX]{x1D714}_{1}=\mathit{O}(10^{3})$.

4.1.2 Knots

The convection pattern of knots (${\mathcal{K}}{\mathcal{N}}$) is experimentally observed as ‘knotted’ superposition of ${\mathcal{T}}{\mathcal{R}}$ and ${\mathcal{L}}{\mathcal{R}}$ just above inclination $\unicode[STIX]{x1D6FE}_{c2}$ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000). Stability analysis confirms the existence of a $KN_{i}$ instability of $TR$ (Fujimura & Kelly Reference Fujimura and Kelly1993). We refer to experimental and numerical observations of ${\mathcal{K}}{\mathcal{N}}$ at $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[80^{\circ },0.05,1.07]$ (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). At these control parameter values, a temporal transition from the noise-perturbed unstable base flow is simulated in a periodic domain of size $[L_{x},L_{y}]=[\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{y}]$. No additional discrete symmetries are imposed.

After the initial shear driven transition $B\rightarrow TR$, the buoyancy driven instability $KN_{i}$ of $TR$ leads to a stable spiral approaching $KN$, an equilibrium state underlying the observed ${\mathcal{K}}{\mathcal{N}}$ pattern (figure 8). The spectrum of eigenvalues of stable $KN$ has a complex pair $(\unicode[STIX]{x1D714}_{r},\unicode[STIX]{x1D714}_{i})=(-0.0085,\pm 0.0304)$ closest to the imaginary axis. The linear period of $T=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{i}=207$ matches the simulated oscillations on the stable spiral trajectory. The flow structure of $KN$ shows the characteristic bimodal mix of longitudinal and transverse modes, here, with a stronger transverse contribution (figure 8b). Here, $KN$ is invariant under symmetries $S_{\mathit{KN}}=\langle \unicode[STIX]{x03C0}_{y}\unicode[STIX]{x1D70F}(0,0.5),\unicode[STIX]{x03C0}_{xyz}\rangle$.

Close to the values of the control parameters where stationary ${\mathcal{K}}{\mathcal{N}}$ are observed, Daniels et al. (Reference Daniels, Plapp and Bodenschatz2000) report on bursting dynamics. When simulating a transition at increased $\unicode[STIX]{x1D716}=0.15$ ($\mathit{Ra}=9338$), the state trajectory, after transiently visiting $TR$, does not approach $KN$ that has become unstable. Instead, the trajectory visits again the laminar base flow ($TR\rightarrow B$) from where it approaches a stable periodic orbit with period $T=251$ and $S_{\mathit{KN}}$ symmetries. We call this orbit bursting knots ($BKN$). The $BKN$ orbit describes a bursting cycle with slow dynamics near $B$ and fast dynamics along a clockwise revolving trajectory in the $D/I$ plane (figure 9). The fast stage shows growth of a transient ${\mathcal{K}}{\mathcal{N}}$ pattern that ultimately forms decaying longitudinal plumes (figure 9b). Longitudinal modes decay because $LR_{i}$ exists only at higher $\unicode[STIX]{x1D716}$ at $\unicode[STIX]{x1D6FE}=80^{\circ }$. During the slow stage, the phase portrait of the orbit shows sharp turns near $B$ suggesting an influence of the stable and unstable manifold of $B$ on the orbit (inset in figure 9). The bursting dynamics of this specific periodic orbit appears similar to a nonlinear limit cycle found in natural doubly diffusive convection (Bergeon & Knobloch Reference Bergeon and Knobloch2002) but does not match the travelling dynamics of the longitudinal bursts observed in ILC at these control parameter values Daniels et al. (Reference Daniels, Plapp and Bodenschatz2000). The next section discusses two periodic orbits clearly underlying experimental observations.

Figure 9. (a) State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=80^{\circ }$, as in figure 8, but at increased $\unicode[STIX]{x1D716}=0.15$ ($\mathit{Ra}=9338$). Instead of terminating in a stable spiral, the trajectory returns to laminar flow from where it approaches the stable periodic orbit $BKN$ along which knots emerge as bursts. The inset magnifies the phase portrait close to the laminar base state $B$. (b) Flow structure of an instance along the periodic orbit $BKN$ illustrates decaying longitudinal plumes that bring the state trajectory close to laminar flow.

4.2 Transitions with periodic attractors

4.2.1 Subharmonic oscillations

An oscillatory instability of $LR$ at small inclinations gives rise to a convection pattern of spatially subharmonic oscillations observed in experiments at $\mathit{Pr}=1.07$ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000) and studied using Floquet analysis at $\mathit{Pr}=0.71$ (Busse & Clever Reference Busse and Clever2000). Here, we depart from our convention to follow the naming of Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) and name this pattern subharmonic standing wave (${\mathcal{S}}{\mathcal{S}}{\mathcal{W}}$) instead of longitudinal subharmonic oscillations to stress the standing wave nature of the pattern. We refer to observations of ${\mathcal{S}}{\mathcal{S}}{\mathcal{W}}$ at $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[17^{\circ },1.5,1.07]$ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000; Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). A temporal transition is simulated in a periodic domain of size $[L_{x},L_{y}]=[2\unicode[STIX]{x1D706}_{x},2\unicode[STIX]{x1D706}_{y}]$, closely matching the results of the Floquet analysis in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). Unexpectedly, the dynamics transiently exhibits spatially subharmonic oscillations but does not saturate at a stable oscillatory pattern at these values of the control parameters. Therefore, we reduce the angle of inclinations to $\unicode[STIX]{x1D6FE}=15^{\circ }$. No additional discrete symmetries are imposed.

Figure 10. State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=15^{\circ }$ and $\unicode[STIX]{x1D716}=1.5$ ($\mathit{Ra}=4420$). The phase portrait illustrates how the instability $SSW_{i}$ leads to an oscillatory transition $LR\rightarrow SSW$ along a symmetric unstable spiral approaching periodic orbit $SSW$ (red solid line). The inset magnifies the phase portrait of the transition $LR\rightarrow SSW$.

After a rapid transient visit near $LR$, the dynamics along a drifting spiral trajectory is attracted to a stable limit cycle, a periodic orbit named $SSW$ (figure 10). The initial part of the transition $LR\rightarrow SSW$ is symmetric around $D/I=1$ indicating that buoyancy and shear forces equally drive this instability. The periodic orbit $SSW$ revolves clockwise in the $D/I$ plane. $SSW$ is also a pre-periodic orbit satisfying condition (3.2) with $\unicode[STIX]{x1D70E}_{\mathit{SSW}}=\unicode[STIX]{x03C0}_{y}\unicode[STIX]{x1D70F}(0.25,0.25)$ and a pre-period of $T_{\mathit{SSW}}^{\prime }=12.03$. The local oscillatory instability of $LR$ suggests $T=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{i}=45.11$, close to the observed full orbit period of $T_{\mathit{SSW}}=4T_{\mathit{SSW}}^{\prime }=48.12$. After $2T_{\mathit{SSW}}^{\prime }$, condition (3.2) requires $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(0.5,0)$. The orbit is invariant under inversion and half-box shifts $S_{\mathit{SSW}}=\langle \unicode[STIX]{x03C0}_{xyz},\unicode[STIX]{x1D70F}(0.5,0.5)\rangle$.

Figure 11. Transfer rates of kinetic energy (solid) and thermal energy (dashed) over one pre-period $T_{\mathit{SSW}}^{\prime }=12.03$ of the $SSW$ orbit at $\unicode[STIX]{x1D6FE}=15^{\circ }$ and $\unicode[STIX]{x1D716}=1.5$ ($\mathit{Ra}=4420$). Temperature contours at midplane show instances of kinetic energy balance $I-D=0$ (b,d) or thermal energy balance $J-\mathit{Nu}=0$ (a,c,a’) along the orbit. States $a$ and $a^{\prime }$ are related by symmetry transformation $\unicode[STIX]{x1D70E}=\unicode[STIX]{x03C0}_{y}\unicode[STIX]{x1D70F}(0.25,0.25)$.

Periodic orbits in ILC must exactly balance net transfer of kinetic energy and heat over one period $\int _{0}^{T_{\mathit{SSW}}^{\prime }}(I-D)\,\text{d}t=0$. The terms in the energy equations (2.13)–(2.15) oscillate approximately harmonically with one relative period of $SSW$. Instances of $I-D=0$ or $J-\mathit{Nu}=0$ correspond to local extrema of $\langle U^{2}/2\rangle _{\unicode[STIX]{x1D6FA}}$ and $\langle T\rangle _{\unicode[STIX]{x1D6FA}/2}$, respectively. The phase lag between kinetic energy and heat phase is $0.37T_{\mathit{SSW}}^{\prime }$ (figure 11). The Nusselt number varies between $1.88\leqslant \mathit{Nu}\leqslant 1.90$, close but below the convective heat transfer of $LR$ with $\mathit{Nu}=1.98$. The pattern of $SSW$ over one period can be described as standing wave modulation (panels in figure 11), a consequence of counter-propagating travelling waves along the hot and cold plumes of $LR$ (Busse & Clever Reference Busse and Clever2000).

4.2.2 Transverse oscillations

Transverse oscillations (${\mathcal{T}}{\mathcal{O}}$) are observed experimentally as chaotic bending modulations of ${\mathcal{T}}{\mathcal{R}}$, a pattern also named ‘switching diamond panes’ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000). An oscillatory $TO_{i}$ instability is found as a secondary instability of $TR$ in the interval $83.2^{\circ }<\unicode[STIX]{x1D6FE}\leqslant 120^{\circ }$ for $\mathit{Pr}=1.07$ (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). We refer to observations of ${\mathcal{T}}{\mathcal{O}}$ at $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[100^{\circ },0.1,1.07]$ (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000; Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016), and simulate a temporal transition at these control parameter values in a periodic domain of size $[L_{x},L_{y}]=[12\unicode[STIX]{x1D706}_{x},6\unicode[STIX]{x1D706}_{y}]$, close to the pattern wavelengths used to simulate $TO$ in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). Without imposing additional discrete symmetries, no stable periodic orbit is found. Therefore, a transition is simulated in a symmetry subspace defined by $S_{\mathit{TO}}=\langle \unicode[STIX]{x03C0}_{y},\unicode[STIX]{x03C0}_{xz},\unicode[STIX]{x1D70F}(0.5,0.5)\rangle$.

Figure 12. State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=100^{\circ }$ and $\unicode[STIX]{x1D716}=0.1$ ($\mathit{Ra}=10050$). The phase portrait illustrates how the TO instability leads to an oscillatory transition $LR\rightarrow TO$ along an unstable spiral approaching periodic orbit $TO$ (red solid line). Initial oscillations triggered by $TO_{i}$ are symmetric with respect to $D/I=1$. The inset magnifies the initial symmetric trajectory from $TR$.

The transition $B\rightarrow TR$ gives rise to 12 pairs of straight transverse rolls before slow and weak bending modulations set in. Like $SSW_{i}$, the instability $TO_{i}$ of $TR$ generates a state trajectory that is initially symmetric around $D/I=1$ suggesting that buoyancy and shear forces drive this instability equally. The state trajectory from $TR$ approaches the stable periodic orbit $TO$ within a few oscillation periods (figure 12). Here, $TO$ is a pre-periodic orbit solving condition (3.2) with $\unicode[STIX]{x1D70E}_{\mathit{TO}}=\unicode[STIX]{x1D70F}(0.5,0)$ and a pre-period of $T_{\mathit{TO}}^{\prime }=122.1$, i.e. half of the full period. As observed experimentally (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000), the oscillation period is on the order of one diffusion time scale $\mathit{O}(T_{d})=\mathit{O}(\sqrt{\mathit{Ra }\mathit{ Pr}}T_{f})$. Without the imposed discrete symmetries $S_{\mathit{TO}}$, $TO$ has six eigenvalues with positive real part at the given parameters. The associated eigenmodes break all symmetries in $S_{\mathit{TO}}$.

Heat and kinetic energy oscillate non-harmonically and almost in phase over a relative period of $TO$ at these control parameter values. The pattern of $TO$ resembles $TR$ at the kinetic energy minimum. Near the energy maximum, the transverse rolls are maximally bent (figure 13). The weak subharmonic varicose oscillations have a much larger pattern wavelength than all other invariant states discussed in the present work. In very large domains, observations show spatial-temporal chaos at these control parameter values (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000; Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016), suggesting that the periodic orbit $TO$ in larger domains is embedded in a chaotic attractor.

Figure 13. Transfer rates of kinetic (solid) and thermal energy (dashed) over one pre-period $T_{\mathit{TO}}^{\prime }=122.1$ of the $TO$ orbit at $\unicode[STIX]{x1D6FE}=100^{\circ }$ and $\unicode[STIX]{x1D716}=0.1$ ($\mathit{Ra}=10050$). Temperature contours at midplane show instances of thermal energy balance $J-\mathit{Nu}=0$. States $a$ and $a^{\prime }$ are related by symmetry transformation $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(0.5,0)$.

4.3 Transient skewed varicose pattern in Rayleigh–Bénard convection

Various secondary instabilities are known in Rayleigh–Bénard convection, namely Eckhaus, zigzag, knot, skewed varicose, cross-rolls and oscillatory instability (Busse Reference Busse1978). At $\mathit{Pr}=1.07$, the skewed varicose instability $SV_{i}$ is the first to destabilize convection rolls as demonstrated by experiments (Bodenschatz, Pesch & Ahlers Reference Bodenschatz, Pesch and Ahlers2000) and stability analysis (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). We refer to observations of the skewed varicose pattern (${\mathcal{S}}{\mathcal{V}}$) at $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[0^{\circ },2.26,1.07]$ (Bodenschatz et al. Reference Bodenschatz, Pesch and Ahlers2000, figure 7). A normalized Rayleigh number of $\unicode[STIX]{x1D716}=2.26$ is far above the critical threshold for $SV_{i}$. Here, we simulate a temporal transition at $\unicode[STIX]{x1D716}=1.05$, much closer to threshold. The periodic domain is of size $[L_{x},L_{y}]=[4\unicode[STIX]{x1D706}_{x},4\unicode[STIX]{x1D706}_{y}]$, and no additional discrete symmetries are imposed.

The conducting state of the Rayleigh–Bénard system before convection onset is isotropic in the $x$–$y$ plane and rolls have no preferred orientation in the infinite system. Therefore, we denote straight convection rolls in the isotropic system as $R_{\unicode[STIX]{x1D706}}$ with a subscript indicating the approximate pattern wavelength $\unicode[STIX]{x1D706}$ if $\unicode[STIX]{x1D6FE}=0^{\circ }$. The attributes ‘longitudinal’ and ‘transverse’ relate to the direction of rolls relative to the base flow and are only used in the inclined case. At control parameters $[\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D716},\mathit{Pr}]=[0^{\circ },1.05,1.07]$, rolls of various wavelengths are unstable. To promote the growth of rolls at $\unicode[STIX]{x1D706}_{y}$, we perturb the base state with small-amplitude rolls at $\unicode[STIX]{x1D706}_{y}$ and aligned with the $x$ dimension. In addition, we add small-amplitude noise to break the translational symmetries. This perturbation of $B$ triggers the growth of four pairs of convection rolls $R_{\unicode[STIX]{x1D706}2}$, comparable to the pattern of $LR$ at $\unicode[STIX]{x1D6FE}\neq 0^{\circ }$ in the present study. After a rapid transition $B\rightarrow R_{\unicode[STIX]{x1D706}2}$ over $\unicode[STIX]{x0394}t=40$, the shear driven instability $SV_{i}$ generates a slow departure from $R_{\unicode[STIX]{x1D706}2}$ over $\unicode[STIX]{x0394}t=20\,000$. The shear forces that drive $SV_{i}$ are generated solely by the convective motion of the secondary state, $R_{\unicode[STIX]{x1D706}2}$, as the primary base state, $B$, does not generate shear at $\unicode[STIX]{x1D6FE}=0^{\circ }$. The exponential escape rate from $R_{\unicode[STIX]{x1D706}2}$ is given by the only positive real eigenvalue of $R_{\unicode[STIX]{x1D706}2}$, $\unicode[STIX]{x1D714}_{r}=3.8\times 10^{-4}$, with quadruple multiplicity. The associated eigenmodes show the characteristic three-dimensional oblique pattern of the skewed varicose instability (Busse & Clever Reference Busse and Clever1979). While escaping from $R_{\unicode[STIX]{x1D706}2}$, the convection rolls $R_{\unicode[STIX]{x1D706}2}$ start tilting and form a thin skewed region along the domain diagonal where rolls become strongly sheared ($t_{1}=20\,680$), pinch off ($t_{2}=20\,782$), reconnect and form rolls $R_{\unicode[STIX]{x1D706}3}$ at increased wavelength $\unicode[STIX]{x1D706}=2.5731$ and rotated by $16.8^{\circ }$ against the $x$ direction (figure 14). $R_{\unicode[STIX]{x1D706}3}$ are linearly stable at these control parameter values.

Figure 14. State trajectory evolution from the unstable base state $B$ at $\unicode[STIX]{x1D6FE}=0^{\circ }$ and $\unicode[STIX]{x1D716}=1.05$ ($\mathit{Ra}=3500$). Initially for $0<t<40$, a fast transition along $B\rightarrow R_{\unicode[STIX]{x1D706}2}$ gives rise to straight convection rolls at wavelength $\unicode[STIX]{x1D706}_{y}$ (not shown). After a very long transient close to $R_{\unicode[STIX]{x1D706}2}$, the shear driven instability $SV_{i}$ of straight convection rolls $R_{\unicode[STIX]{x1D706}2}$ leads to rolls $R_{\unicode[STIX]{x1D706}3}$ at increased wavelength. The inset magnifies the phase portrait of the transition $R_{\unicode[STIX]{x1D706}2}\rightarrow R_{\unicode[STIX]{x1D706}3}$. During the transition $R_{\unicode[STIX]{x1D706}2}\rightarrow R_{\unicode[STIX]{x1D706}3}$ around $t_{1}=20\,680$, a skewed varicose pattern emerges transiently. The midplane temperature contours (b) illustrate different instances along the state trajectory (cross markers). Unlike in previous figures, the kinetic energy input $I$ is not normalized by the laminar input $I_{0}$ since $I_{0}=0$ at $\unicode[STIX]{x1D6FE}=0^{\circ }$ (see (2.14)).

The simulated sequence of dynamical connections $B\rightarrow R_{\unicode[STIX]{x1D706}2}\rightarrow R_{\unicode[STIX]{x1D706}3}$ is invariant under $S_{\mathit{SV}}=\langle \unicode[STIX]{x03C0}_{xyz},\unicode[STIX]{x1D70F}(0.25,0.25)\rangle$ and at $t_{2}$, resembles the experimentally observed ${\mathcal{S}}{\mathcal{V}}$ pattern (figure 7 in Bodenschatz et al. (Reference Bodenschatz, Pesch and Ahlers2000)). However, the phase portrait does not indicate a transiently visited invariant state. The state trajectory crosses $D/I=1$ without slowdown (figure 14). Simulating the instability $SV_{i}$ at other values of the control parameters does not change this observation. Thus, the transient dynamics of the ${\mathcal{S}}{\mathcal{V}}$ pattern seems to occur in the absence of an underlying invariant state.