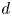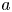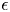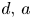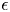1. Introduction
The development of projective birational geometry has been deeply connected with the understanding of singularities [Reference Xu38]. In particular, global theories shed light on the singularities of the minimal model program [Reference Kollár22]. However, singularities of dimension greater than three seem too complicated to have an explicit characterization [Reference Kollár23]. Therefore, a more qualitative and intrinsic description of these singularities is desirable.
A common technique to study singularities using birational geometry is to apply certain monoidal transformation to the singularity to extract an exceptional projective divisor over it and then try to deduce some local information of the singularity from the global information of the exceptional divisor. This approach has been successful in many cases: the study of dual complexes of singularities [Reference de Fernex, Kollár and Xu10, Reference Kollár and Xu26], the finiteness of the algebraic fundamental group of a klt singularity [Reference Xu37], the ascending chain condition for log canonical thresholds [Reference de Fernex, Ein and Mustaţă9, Reference Hacon, McKernan and Xu16], the study of the normalized volume function on klt singularities [Reference Li27–Reference Li and Xu29], and the theory of log canonical complements [Reference Birkar7, Reference Prokhorov and Shokurov31, Reference Prokhorov and Shokurov32], among others.
In this article, we use this approach to study the minimal log discrepancies of klt singularities [Reference Ambro3, Reference Shokurov36]. We aim to explain how a bound on the singularities of a plt blow-up implies finiteness of the possible minimal log discrepancies. More precisely, we say that a plt blow-up $\pi \colon Y\rightarrow X$![]() at a point $x$
at a point $x$![]() of a klt pair $(X,\,\Delta )$
of a klt pair $(X,\,\Delta )$![]() is $\epsilon$
is $\epsilon$![]() -plt if the log discrepancies of the corresponding plt pair $(Y,\,\Delta _Y+E)$
-plt if the log discrepancies of the corresponding plt pair $(Y,\,\Delta _Y+E)$![]() are either zero or greater than $\epsilon$
are either zero or greater than $\epsilon$![]() (see Definition 2.5). Here, $E$
(see Definition 2.5). Here, $E$![]() is the exceptional divisor and $\Delta _Y$
is the exceptional divisor and $\Delta _Y$![]() the strict transform of $\Delta$
the strict transform of $\Delta$![]() on $Y$
on $Y$![]() . We say that the point $x$
. We say that the point $x$![]() of the klt pair $(X,\,\Delta )$
of the klt pair $(X,\,\Delta )$![]() admits an $\epsilon$
admits an $\epsilon$![]() -plt blow-up if there exists $\pi$
-plt blow-up if there exists $\pi$![]() as above. For $\epsilon$
as above. For $\epsilon$![]() a positive real number, adjunction [Reference Hacon13, Theorem 0.1] and the boundedness of Fano varieties [Reference Birkar6, Theorem 1.1], allows us to conclude that the normal projective varieties $E$
a positive real number, adjunction [Reference Hacon13, Theorem 0.1] and the boundedness of Fano varieties [Reference Birkar6, Theorem 1.1], allows us to conclude that the normal projective varieties $E$![]() belong to a bounded family. By [Reference Xu37, Lemma 1], we know that every klt singularity admits a plt blow-up and a simple argument using the resolution of singularities proves that every klt singularity admits an $\epsilon$
belong to a bounded family. By [Reference Xu37, Lemma 1], we know that every klt singularity admits a plt blow-up and a simple argument using the resolution of singularities proves that every klt singularity admits an $\epsilon$![]() -plt blow-up for some positive real number $\epsilon$
-plt blow-up for some positive real number $\epsilon$![]() (see Proposition 2.7).
(see Proposition 2.7).
Using the above notation, we can introduce the set of minimal log discrepancies of $a$![]() -log canonical pairs admitting an $\epsilon$
-log canonical pairs admitting an $\epsilon$![]() -plt blow-up:
-plt blow-up:
We recall the conjecture known as the ascending chain condition for minimal log discrepancies:
Conjecture 1 (cf. [Reference Shokurov36, ACC])
Let $d$![]() be a positive integer and $\mathcal {R}$
be a positive integer and $\mathcal {R}$![]() be a set of real numbers satisfying the descending chain condition. Then the set $\mathcal {M}(d,\,\mathcal {R})_{0,0}$
be a set of real numbers satisfying the descending chain condition. Then the set $\mathcal {M}(d,\,\mathcal {R})_{0,0}$![]() satisfies the ascending chain condition.
satisfies the ascending chain condition.
The above conjecture is equivalent to Shokurov's ACC for mld's conjecture by means of Proposition 2.7. The importance of the ACC conjecture is that, together with the semicontinuity conjecture for minimal log discrepancies [Reference Shokurov36, LSC], they imply the termination of flips. This last problem is one of the main obstacles to complete the Minimal Model Program.
The ascending chain condition for minimal log discrepancies is known for surface singularities [Reference Alexeev1], for certain terminal threefold singularities [Reference Shokurov34, Lemma 4.4.1], and for toric singularities [Reference Ambro4, Reference Borisov8]. However, in higher dimensions, there is not much that we can say about the possible mld's in a fixed dimension. In this paper, we give a first step towards the understanding of higher dimensional minimal log discrepancies. The following theorem can be understood as a natural geometric stratification of the possible mld's of a fixed dimension by finite sets:
Theorem 1 Let $d$![]() be a positive integer and let $a$
be a positive integer and let $a$![]() and $\epsilon$
and $\epsilon$![]() be positive real numbers, and $\mathcal {S}$
be positive real numbers, and $\mathcal {S}$![]() the set of standard rational numbers, i.e., $\mathcal {S}:=\{ 1-\frac {1}{n} \mid n\in \mathbb {Z}_{>0}\}$
the set of standard rational numbers, i.e., $\mathcal {S}:=\{ 1-\frac {1}{n} \mid n\in \mathbb {Z}_{>0}\}$![]() . Then the set $\mathcal {M}(d,\,\mathcal {S})_{a,\epsilon }$
. Then the set $\mathcal {M}(d,\,\mathcal {S})_{a,\epsilon }$![]() is finite.
is finite.
The theorem implies the following corollary towards the ascending chain condition.
Corollary 1 Let $d$![]() be a positive integer, $\epsilon$
be a positive integer, $\epsilon$![]() a positive real number, and $\mathcal {S}$
a positive real number, and $\mathcal {S}$![]() the set of standard rational numbers. The set $\mathcal {M}(d,\,\mathcal {S})_{0,\epsilon }$
the set of standard rational numbers. The set $\mathcal {M}(d,\,\mathcal {S})_{0,\epsilon }$![]() satisfies the ascending chain condition.
satisfies the ascending chain condition.
In the above setting, $0$![]() -log canonical means just log canonical. In § 2.5, we give two examples that show that the theorem does not hold if $a$
-log canonical means just log canonical. In § 2.5, we give two examples that show that the theorem does not hold if $a$![]() and $\epsilon$
and $\epsilon$![]() are not positive. We also prove that $a$
are not positive. We also prove that $a$![]() -log canonical singularities which admit an $\epsilon$
-log canonical singularities which admit an $\epsilon$![]() -plt blow-up have bounded Cartier index.
-plt blow-up have bounded Cartier index.
Theorem 2 Let $d$![]() be a positive integer, and let $a$
be a positive integer, and let $a$![]() and $\epsilon$
and $\epsilon$![]() be positive real numbers. There exists $p$
be positive real numbers. There exists $p$![]() only depending on $d,\,a$
only depending on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() satisfying the following. Let $(X,\,\Delta )$
satisfying the following. Let $(X,\,\Delta )$![]() be a $d$
be a $d$![]() -dimensional $a$
-dimensional $a$![]() -log canonical pair with standard coefficients which admits an $\epsilon$
-log canonical pair with standard coefficients which admits an $\epsilon$![]() -plt blow-up at $x\in X$
-plt blow-up at $x\in X$![]() . Then $p(K_X+\Delta )$
. Then $p(K_X+\Delta )$![]() is a Cartier divisor on a neighbourhood of $x\in X$
is a Cartier divisor on a neighbourhood of $x\in X$![]() .
.
Exceptional singularities are those klt singularities for which any log canonical threshold is computed at a unique divisorial valuation [Reference Shokurov35, Definition 1.5]. The exceptional Du Val surface singularities are the $E_6,\,E_7$![]() and $E_8$
and $E_8$![]() singularities. Hypersurfaces exceptional singularities were studied by Ishii and Prokhorov [Reference Ishii and Prokhorov19]. In dimension $3$
singularities. Hypersurfaces exceptional singularities were studied by Ishii and Prokhorov [Reference Ishii and Prokhorov19]. In dimension $3$![]() , Prokhorov and Markusevich proved that there are only finitely many $\epsilon$
, Prokhorov and Markusevich proved that there are only finitely many $\epsilon$![]() -log canonical exceptional quotient singularities [Reference Markushevich and Prokhorov30]. However, a classification of exceptional singularities in higher dimensions seems unfeasable. In this direction, we prove the following application of our main theorem:
-log canonical exceptional quotient singularities [Reference Markushevich and Prokhorov30]. However, a classification of exceptional singularities in higher dimensions seems unfeasable. In this direction, we prove the following application of our main theorem:
Corollary 2 The ascending chain condition for minimal log discrepancies of exceptional singularities with standard coefficients holds.
It is worth mentioning that Corollary 2 follows almost directly from the proof of [Reference Prokhorov and Shokurov31, Theorem 4.4] and [Reference Birkar6, Theorem 1.1]. These two results together with [Reference Ishii18] and [Reference Fujino12] are the main motivation of Theorem 1. The proof of [Reference Prokhorov and Shokurov31, Theorem 4.4] already contains some of the ideas used in this article.
After completing this project, the author was informed that J. Han, J. Liu and V. Shokurov have obtained the results of this paper with more general coefficients [Reference Han, Liu and Shokurov17]. The proof of this manuscript goes along that of [Reference Shokurov35] in dimension $3$![]() . In the following remark, we give a detailed account of this generalization.
. In the following remark, we give a detailed account of this generalization.
Remark 1.1 Corollary 1 (respectively Corollary 2) is generalized by [Reference Han, Liu and Shokurov17, Theorem 1.3] (respectively [Reference Han, Liu and Shokurov17, Theorem 1.2]), where the authors prove the statement with general coefficients. Theorem 1 and Theorem 2 are implied by Theorem [Reference Han, Liu and Shokurov17, Theorem 1.6], where the authors prove a uniform bound for the regional fundamental group.
2. Preliminaries
All varieties in this paper are quasi-projective over a fixed algebraically closed field of characteristic zero unless stated otherwise. In this section, we collect some definitions and preliminary results which will be used in the proof of the main theorem.
2.1. Singularities
In this subsection, we recall the singularities of the minimal model program, the set of standard coefficients and exceptional singularities. We also prove some basic properties about singularities.
Definition 2.1 In this paper, a sub-pair $(X,\,\Delta )$![]() consists of a normal quasi-projective variety $X$
consists of a normal quasi-projective variety $X$![]() and a $\mathbb {Q}$
and a $\mathbb {Q}$![]() -divisor $\Delta$
-divisor $\Delta$![]() so that $K_X+\Delta$
so that $K_X+\Delta$![]() is a $\mathbb {Q}$
is a $\mathbb {Q}$![]() -Cartier $\mathbb {Q}$
-Cartier $\mathbb {Q}$![]() -divisor. If the coefficients of $\Delta$
-divisor. If the coefficients of $\Delta$![]() are non-negative then we say that $(X,\,\Delta )$
are non-negative then we say that $(X,\,\Delta )$![]() is a log pair, or simply a pair.
is a log pair, or simply a pair.
Let $\pi \colon W \rightarrow X$![]() be a log resolution of the pair $(X,\,\Delta )$
be a log resolution of the pair $(X,\,\Delta )$![]() and denote by $K_W+\Delta _W+F_W$
and denote by $K_W+\Delta _W+F_W$![]() the log pull-back of $K_X+\Delta$
the log pull-back of $K_X+\Delta$![]() , where $\Delta _W$
, where $\Delta _W$![]() is the strict transform of $\Delta$
is the strict transform of $\Delta$![]() on $W$
on $W$![]() and $F_W$
and $F_W$![]() is an exceptional divisor. The discrepancy of a prime divisor $E$
is an exceptional divisor. The discrepancy of a prime divisor $E$![]() on $W$
on $W$![]() with respect to the pair $(X,\,\Delta )$
with respect to the pair $(X,\,\Delta )$![]() is
is
The log discrepancy of a prime divisor $E$![]() on $W$
on $W$![]() with respect to the pair $(X,\,\Delta )$
with respect to the pair $(X,\,\Delta )$![]() is the value
is the value
The center of $E$![]() on $X$
on $X$![]() is its image on $X$
is its image on $X$![]() via the morphism $\pi$
via the morphism $\pi$![]() . We denote by $c_X(E)$
. We denote by $c_X(E)$![]() the centre of the prime divisor $E$
the centre of the prime divisor $E$![]() on the variety $X$
on the variety $X$![]() . A prime divisor over $X$
. A prime divisor over $X$![]() is a prime effective divisor $E$
is a prime effective divisor $E$![]() on a normal quasi-projective variety $W$
on a normal quasi-projective variety $W$![]() which admits a projective birational morphism $W\rightarrow X$
which admits a projective birational morphism $W\rightarrow X$![]() .
.
We say that the sub-pair $(X,\,\Delta )$![]() is sub- $\epsilon$
is sub- $\epsilon$![]() -log canonical if
-log canonical if
for every prime divisor $E$![]() on $W$
on $W$![]() . If $(X,\,\Delta )$
. If $(X,\,\Delta )$![]() is a pair then we say that is $\epsilon$
is a pair then we say that is $\epsilon$![]() -log canonical in the above situation. If $\epsilon >0$
-log canonical in the above situation. If $\epsilon >0$![]() is arbitrary, we may also say that $(X,\,\Delta )$
is arbitrary, we may also say that $(X,\,\Delta )$![]() is Kawamata log terminal (or klt) and if $\epsilon =0$
is Kawamata log terminal (or klt) and if $\epsilon =0$![]() we just say that the pair is log canonical, equivalently, the centre of a log canonical place. The total discrepancy $a(X,\,\Delta )$
we just say that the pair is log canonical, equivalently, the centre of a log canonical place. The total discrepancy $a(X,\,\Delta )$![]() of the pair $(X,\,\Delta )$
of the pair $(X,\,\Delta )$![]() is the infimum among all discrepancies $a_E(X,\,\Delta )$
is the infimum among all discrepancies $a_E(X,\,\Delta )$![]() with $E$
with $E$![]() a prime divisor over $X$
a prime divisor over $X$![]() . Thus, $(X,\,\Delta )$
. Thus, $(X,\,\Delta )$![]() is $a$
is $a$![]() -log canonical if and only if $a(X,\,\Delta )+1\geq a$
-log canonical if and only if $a(X,\,\Delta )+1\geq a$![]() .
.
Let $(X,\,\Delta )$![]() be a log canonical pair. A log canonical place of $(X,\,\Delta )$
be a log canonical pair. A log canonical place of $(X,\,\Delta )$![]() is a prime divisor $E$
is a prime divisor $E$![]() on a birational model of $X$
on a birational model of $X$![]() so that $a_E(X,\,\Delta )=-1$
so that $a_E(X,\,\Delta )=-1$![]() . A log canonical center of $(X,\,\Delta )$
. A log canonical center of $(X,\,\Delta )$![]() is the image on $X$
is the image on $X$![]() of a log canonical place.
of a log canonical place.
Definition 2.2 Let $(X,\,\Delta )$![]() be a log pair and $x\in X$
be a log pair and $x\in X$![]() . The minimal log discrepancy of $(X,\,\Delta )$
. The minimal log discrepancy of $(X,\,\Delta )$![]() at $x$
at $x$![]() is
is
If $(X,\,\Delta )$![]() is a log canonical pair, taking a log resolution and using [Reference Kollár and Mori25, Lemma 2.29], we can see that the above infimum is indeed a minimum. Observe that $\textrm {mld}_x(X,\,\Delta )\geq 0$
is a log canonical pair, taking a log resolution and using [Reference Kollár and Mori25, Lemma 2.29], we can see that the above infimum is indeed a minimum. Observe that $\textrm {mld}_x(X,\,\Delta )\geq 0$![]() if and only if the pair $(X,\,\Delta )$
if and only if the pair $(X,\,\Delta )$![]() is log canonical at $x\in X$
is log canonical at $x\in X$![]() . Moreover, $\textrm {mld}_x(X,\,\Delta )>0$
. Moreover, $\textrm {mld}_x(X,\,\Delta )>0$![]() if and only if the pair $(X,\,\Delta )$
if and only if the pair $(X,\,\Delta )$![]() is klt at $x\in X$
is klt at $x\in X$![]() . On the other hand, if $(X,\,\Delta )$
. On the other hand, if $(X,\,\Delta )$![]() is not log canonical at $x\in X$
is not log canonical at $x\in X$![]() , then $\textrm {mld}_x(X,\,\Delta )=-\infty$
, then $\textrm {mld}_x(X,\,\Delta )=-\infty$![]() (see, e.g. [Reference Kollár and Mori25, Corollary 2.32]).
(see, e.g. [Reference Kollár and Mori25, Corollary 2.32]).
Definition 2.3 We say that the pair $(X,\,\Delta )$![]() is divisorial log terminal (or dlt) if the following conditions hold:
is divisorial log terminal (or dlt) if the following conditions hold:
(1) there exists a closed subset $Z\subset X$
 so that $X\setminus Z$
so that $X\setminus Z$ is smooth,
is smooth,(2) $\Delta |_{X\setminus Z}$
 has simple normal crossing support, and
has simple normal crossing support, and(3) every divisor $E$
 over $X$
over $X$ with centre in $Z$
with centre in $Z$ has positive log discrepancy with respect to $(X,\,\Delta )$
has positive log discrepancy with respect to $(X,\,\Delta )$ .
.
A pair $(X,\,\Delta )$![]() is called purely log terminal (or plt) if the log discrepancy of every exceptional prime divisor over $X$
is called purely log terminal (or plt) if the log discrepancy of every exceptional prime divisor over $X$![]() is strictly positive. In this case, $\lfloor \Delta \rfloor$
is strictly positive. In this case, $\lfloor \Delta \rfloor$![]() is a disjoint union of normal prime divisors.
is a disjoint union of normal prime divisors.
Definition 2.4 Given a finite set $\mathcal {R}$![]() of rational numbers, we denote by
of rational numbers, we denote by
and call $\mathcal {H}(\mathcal {R})$![]() the set of hyperstandard coefficients associated with $\mathcal {R}$
the set of hyperstandard coefficients associated with $\mathcal {R}$![]() . We denote $\mathcal {S}:=\mathcal {H}(\{1\})$
. We denote $\mathcal {S}:=\mathcal {H}(\{1\})$![]() and call this the set of standard coefficients.
and call this the set of standard coefficients.
Definition 2.5 A plt blow-up of a log pair $(X,\,\Delta )$![]() at a point $x\in X$
at a point $x\in X$![]() is a projective birational morphism $\pi \colon Y \rightarrow X$
is a projective birational morphism $\pi \colon Y \rightarrow X$![]() with the following properties:
with the following properties:
(1) $Y$
 is a quasi-projective normal variety,
is a quasi-projective normal variety,(2) the exceptional locus of $\pi$
 is an irreducible divisor $E$
is an irreducible divisor $E$ whose image on $X$
whose image on $X$ is $x$
is $x$ ,
,(3) the pair $(Y,\,\Delta _Y+E)$
 is purely log terminal, where $\Delta _Y$
is purely log terminal, where $\Delta _Y$ is the strict transform of $\Delta$
is the strict transform of $\Delta$ on $Y$
on $Y$ , and
, and(4) $-E$
 is ample over $X$
is ample over $X$ .
.
We say that the pair $(X,\,\Delta )$![]() admits a plt blow-up at $x\in X$
admits a plt blow-up at $x\in X$![]() if there exists $\pi$
if there exists $\pi$![]() with the above conditions. Moreover, we say that the plt blow-up is an $\epsilon$
with the above conditions. Moreover, we say that the plt blow-up is an $\epsilon$![]() -plt blow-up if any log discrepancy of $(Y,\,\Delta _Y+E)$
-plt blow-up if any log discrepancy of $(Y,\,\Delta _Y+E)$![]() is either zero or greater than $\epsilon$
is either zero or greater than $\epsilon$![]() . Analogously, we say that the pair $(X,\,\Delta )$
. Analogously, we say that the pair $(X,\,\Delta )$![]() admits an $\epsilon$
admits an $\epsilon$![]() -plt blow-up at $x\in X$
-plt blow-up at $x\in X$![]() if there exists $\pi$
if there exists $\pi$![]() with the above conditions.
with the above conditions.
Definition 2.6 The exceptional divisor of a plt blow-up is often called a Kollár component of the singularity [Reference Li and Xu28, Definition 1.1]. We may use both acceptions on this paper. We may also call the log Fano pair $(E,\,\Delta _E)$![]() , where
, where
is obtained by adjunction to $E$![]() , a Kollár component over the klt pair $(X,\,\Delta )$
, a Kollár component over the klt pair $(X,\,\Delta )$![]() . Observe that $-(K_E+\Delta _E)$
. Observe that $-(K_E+\Delta _E)$![]() is ample and $(E,\,\Delta _E)$
is ample and $(E,\,\Delta _E)$![]() is klt. Hence, $(E,\,\Delta _E)$
is klt. Hence, $(E,\,\Delta _E)$![]() is a log Fano pair [Reference Birkar7, 2.10].
is a log Fano pair [Reference Birkar7, 2.10].
Proposition 2.7 Let $(X,\,\Delta )$![]() be a klt pair and $x\in X$
be a klt pair and $x\in X$![]() . There exists an $\epsilon$
. There exists an $\epsilon$![]() -plt blow-up of $(X,\,\Delta )$
-plt blow-up of $(X,\,\Delta )$![]() at $x$
at $x$![]() for some positive $\epsilon$
for some positive $\epsilon$![]() .
.
Proof. By [Reference Xu37, Lemma 1], we can construct a plt blow-up $\pi \colon Y \rightarrow X$![]() of $(X,\,\Delta )$
of $(X,\,\Delta )$![]() over $x$
over $x$![]() . Let $\pi _Y \colon W\rightarrow Y$
. Let $\pi _Y \colon W\rightarrow Y$![]() be a log resolution of $(Y,\,\Delta _Y+E)$
be a log resolution of $(Y,\,\Delta _Y+E)$![]() , so we can write
, so we can write
where $\Delta _W$![]() is the strict transform of $\Delta _Y$
is the strict transform of $\Delta _Y$![]() on $W$
on $W$![]() , and $F_W$
, and $F_W$![]() is an exceptional divisor. We can take $\epsilon$
is an exceptional divisor. We can take $\epsilon$![]() small enough so that
small enough so that
for all exceptional prime divisors $D$![]() , where $E_W$
, where $E_W$![]() is the strict transform of $E$
is the strict transform of $E$![]() on $W$
on $W$![]() . By [Reference Kollár and Mori25, Lemma 2.29], we conclude that every exceptional divisor over $W$
. By [Reference Kollár and Mori25, Lemma 2.29], we conclude that every exceptional divisor over $W$![]() has log discrepancy either zero or greater than $\epsilon$
has log discrepancy either zero or greater than $\epsilon$![]() with respect to the purely log terminal pair $(Y,\,\Delta _Y+E)$
with respect to the purely log terminal pair $(Y,\,\Delta _Y+E)$![]() .
.
Theorem 1 motivates the following natural invariant of klt singularities.
Definition 2.8 Let $(X,\,\Delta )$![]() be a klt pair and $x\in X$
be a klt pair and $x\in X$![]() . We define the mildest component, or $\mathcal {M}\mathcal {C}$
. We define the mildest component, or $\mathcal {M}\mathcal {C}$![]() for simplicity, of $(X,\,\Delta )$
for simplicity, of $(X,\,\Delta )$![]() at the point $x\in X$
at the point $x\in X$![]() to be:
to be:
In Proposition 2.25, we will prove that the $\mathcal {M}\mathcal {C}$![]() is indeed attained by some Kollár component over $x\in X$
is indeed attained by some Kollár component over $x\in X$![]() . In this setting, the conditions of Theorem 1 and Theorem 2 can be abbreviated as $(X,\,\Delta )$
. In this setting, the conditions of Theorem 1 and Theorem 2 can be abbreviated as $(X,\,\Delta )$![]() is a $d$
is a $d$![]() -dimensional pair which is $a$
-dimensional pair which is $a$![]() -log canonical at $x\in X$
-log canonical at $x\in X$![]() and $\mathcal{M}\mathcal{C}_x(X,\,\Delta )\geq \epsilon$
and $\mathcal{M}\mathcal{C}_x(X,\,\Delta )\geq \epsilon$![]() .
.
Remark 2.9 In general, one could define the mildest component of $(X,\,\Delta )$![]() at $x\in X$
at $x\in X$![]() for every Grothendieck point of the variety $X$
for every Grothendieck point of the variety $X$![]() . However, by cutting down with general hyperplanes, the study of minimal log discrepancies on a variety $X$
. However, by cutting down with general hyperplanes, the study of minimal log discrepancies on a variety $X$![]() of dimension $d$
of dimension $d$![]() at a point $x\in X$
at a point $x\in X$![]() of codimension $k$
of codimension $k$![]() is equivalent to the study of minimal log discrepancies on a variety $X$
is equivalent to the study of minimal log discrepancies on a variety $X$![]() of dimension $d-k$
of dimension $d-k$![]() at a closed point.
at a closed point.
Definition 2.10 A dlt modification of a log canonical pair $(X,\,\Delta )$![]() is a projective birational morphism $\pi \colon Y\rightarrow X$
is a projective birational morphism $\pi \colon Y\rightarrow X$![]() so that $\pi ^{*}(K_X+\Delta )=K_Y+\Delta _Y+E_Y$
so that $\pi ^{*}(K_X+\Delta )=K_Y+\Delta _Y+E_Y$![]() , where $\Delta _Y$
, where $\Delta _Y$![]() is the strict transform of $\Delta$
is the strict transform of $\Delta$![]() on $X$
on $X$![]() and $E_Y$
and $E_Y$![]() is an exceptional divisor over $X$
is an exceptional divisor over $X$![]() so that the sub-pair $(Y,\,\Delta _Y+E_Y)$
so that the sub-pair $(Y,\,\Delta _Y+E_Y)$![]() is a dlt pair. It is known that every log canonical pair admits a dlt modification [Reference Kollár and Kovács24, Theorem 3.1].
is a dlt pair. It is known that every log canonical pair admits a dlt modification [Reference Kollár and Kovács24, Theorem 3.1].
Definition 2.11 We say that a klt pair $(X,\,\Delta )$![]() is exceptional at $x\in X$
is exceptional at $x\in X$![]() if for every boundary $\Gamma \geq 0$
if for every boundary $\Gamma \geq 0$![]() on $X$
on $X$![]() so that $(X,\,\Delta +\Gamma )$
so that $(X,\,\Delta +\Gamma )$![]() is a log canonical pair, any dlt modification of $(X,\,\Delta +\Gamma )$
is a log canonical pair, any dlt modification of $(X,\,\Delta +\Gamma )$![]() is indeed plt.
is indeed plt.
Remark 2.12 It is known that if $(X,\,\Delta )$![]() is exceptional at $x$
is exceptional at $x$![]() and $X$
and $X$![]() is $\mathbb {Q}$
is $\mathbb {Q}$![]() -factorial, then there exists a unique prime divisor over $X$
-factorial, then there exists a unique prime divisor over $X$![]() which determines all log canonical thresholds over $x\in X$
which determines all log canonical thresholds over $x\in X$![]() [Reference Markushevich and Prokhorov30, Proposition 2.7].
[Reference Markushevich and Prokhorov30, Proposition 2.7].
Definition 2.13 Let $(X,\,\Delta )$![]() be a log canonical pair and $X\rightarrow Z$
be a log canonical pair and $X\rightarrow Z$![]() be a contraction of normal quasi-projective varieties. We say that $\Gamma \geq 0$
be a contraction of normal quasi-projective varieties. We say that $\Gamma \geq 0$![]() is a strong $(\delta,\,n)$
is a strong $(\delta,\,n)$![]() -complement over $z\in Z$
-complement over $z\in Z$![]() of $(X,\,\Delta )$
of $(X,\,\Delta )$![]() if the following conditions hold:
if the following conditions hold:
• $(X,\,\Delta +\Gamma )$
 is an $\delta$
is an $\delta$ -log canonical pair, and
-log canonical pair, and• $n(K_X+\Delta +\Gamma )\sim 0$
 over a neighbourhood of $z$
over a neighbourhood of $z$ .
.
In the case that $X\rightarrow Z$![]() is the identity, then we say that $\Gamma$
is the identity, then we say that $\Gamma$![]() is a local strong $(\delta,\,n)$
is a local strong $(\delta,\,n)$![]() -complement around $x\in X$
-complement around $x\in X$![]() for $(X,\,\Delta )$
for $(X,\,\Delta )$![]() . On the other hand, if $Z=\textrm {Spec}(k)$
. On the other hand, if $Z=\textrm {Spec}(k)$![]() for some field $k$
for some field $k$![]() , then we say that $\Gamma$
, then we say that $\Gamma$![]() is a global strong $(\delta,\,n)$
is a global strong $(\delta,\,n)$![]() -complement for the pair $(X,\,\Delta )$
-complement for the pair $(X,\,\Delta )$![]() . A strong $n$
. A strong $n$![]() -complement is a strong $(0,\,n)$
-complement is a strong $(0,\,n)$![]() -complement.
-complement.
Lemma 2.14 Let $(X,\,\Delta )$![]() be a klt pair which is exceptional at $x\in X$
be a klt pair which is exceptional at $x\in X$![]() . Assume that the coefficients of $\Delta$
. Assume that the coefficients of $\Delta$![]() are standard. There exists an $\epsilon _d$
are standard. There exists an $\epsilon _d$![]() -blow-up of $(X,\,\Delta )$
-blow-up of $(X,\,\Delta )$![]() at $x,$
at $x,$![]() for some positive real number $\epsilon _d$
for some positive real number $\epsilon _d$![]() which only depends on the dimension $d$
which only depends on the dimension $d$![]() of $X$
of $X$![]() .
.
Proof. By Lemma 2.7, we can extract an $\epsilon$![]() -plt blow-up over $x\in X$
-plt blow-up over $x\in X$![]() for some real number $\epsilon$
for some real number $\epsilon$![]() . By [Reference Birkar7, Theorem 1.8] there exists a strong $n$
. By [Reference Birkar7, Theorem 1.8] there exists a strong $n$![]() -complement $K_Y+\Delta _Y+\Gamma _Y+E$
-complement $K_Y+\Delta _Y+\Gamma _Y+E$![]() for $K_Y+\Delta _Y+E$
for $K_Y+\Delta _Y+E$![]() over $x$
over $x$![]() , for $n$
, for $n$![]() only depending on $d$
only depending on $d$![]() and $\mathcal {S}$
and $\mathcal {S}$![]() . Since $\mathcal {S}$
. Since $\mathcal {S}$![]() is a fixed set then $n$
is a fixed set then $n$![]() only depends on $d$
only depends on $d$![]() . Since $K_Y+\Delta _Y+\Gamma _Y+E$
. Since $K_Y+\Delta _Y+\Gamma _Y+E$![]() is $\mathbb {Q}$
is $\mathbb {Q}$![]() -linearly trivial over $x\in X$
-linearly trivial over $x\in X$![]() then we can write
then we can write
for some boundary $\Gamma$![]() on $X$
on $X$![]() so that $(X,\,\Delta +\Gamma )$
so that $(X,\,\Delta +\Gamma )$![]() is a log canonical pair. By the exceptionality of $(X,\,\Delta )$
is a log canonical pair. By the exceptionality of $(X,\,\Delta )$![]() at $x$
at $x$![]() we deduce that $(X,\,\Delta +\Gamma )$
we deduce that $(X,\,\Delta +\Gamma )$![]() has a unique log canonical place and hence $(Y,\,\Delta _Y+\Gamma _Y+E)$
has a unique log canonical place and hence $(Y,\,\Delta _Y+\Gamma _Y+E)$![]() has a unique log canonical place $E$
has a unique log canonical place $E$![]() . Moreover, since $n(K_Y+\Delta _Y+\Gamma _Y+E)$
. Moreover, since $n(K_Y+\Delta _Y+\Gamma _Y+E)$![]() is Cartier over $x$
is Cartier over $x$![]() , we conclude that
, we conclude that
for every divisor $F$![]() over $Y$
over $Y$![]() which is not equal to $E$
which is not equal to $E$![]() . Thus, it suffices to take $\epsilon _d=\frac {1}{n}$
. Thus, it suffices to take $\epsilon _d=\frac {1}{n}$![]() .
.
2.2. Bounded families
In this subsection, we recall the definition of a log bounded family and prove some properties of such families.
Definition 2.15 We say that a set of pairs $\mathcal {P}$![]() is log bounded if there exists a projective morphism $\mathcal {X} \rightarrow T$
is log bounded if there exists a projective morphism $\mathcal {X} \rightarrow T$![]() of possibly reducible varieties and a divisor $\mathcal {B}$
of possibly reducible varieties and a divisor $\mathcal {B}$![]() on $\mathcal {X}$
on $\mathcal {X}$![]() so that for every pair $(X,\,\Delta )\in \mathcal {P}$
so that for every pair $(X,\,\Delta )\in \mathcal {P}$![]() there exists a closed point $t\in T$
there exists a closed point $t\in T$![]() and an isomorphism $\phi \colon \mathcal {X}_t \rightarrow X$
and an isomorphism $\phi \colon \mathcal {X}_t \rightarrow X$![]() so that $(\mathcal {X}_t,\,\mathcal {B}_t)$
so that $(\mathcal {X}_t,\,\mathcal {B}_t)$![]() is a pair and $\phi _*^{-1}\Delta \leq \mathcal {B}_t$
is a pair and $\phi _*^{-1}\Delta \leq \mathcal {B}_t$![]() . If, moreover, $\phi$
. If, moreover, $\phi$![]() induces an isomorphism of pairs between $(X,\,\Delta )$
induces an isomorphism of pairs between $(X,\,\Delta )$![]() and $(\mathcal {X}_t,\, \mathcal {B}_t)$
and $(\mathcal {X}_t,\, \mathcal {B}_t)$![]() , meaning that for any prime divisor $D$
, meaning that for any prime divisor $D$![]() on $X$
on $X$![]() , we have that
, we have that
we will say that the set of pairs $\mathcal {P}$![]() is strictly log bounded. We say that $\mathcal {X}\rightarrow T$
is strictly log bounded. We say that $\mathcal {X}\rightarrow T$![]() is a bounding family for the varieties $X$
is a bounding family for the varieties $X$![]() and that $\mathcal {B}$
and that $\mathcal {B}$![]() is a bounding divisor for the set of divisors $\{ \Delta \mid (X,\,\Delta )\in \mathcal {P}\}$
is a bounding divisor for the set of divisors $\{ \Delta \mid (X,\,\Delta )\in \mathcal {P}\}$![]() .
.
The following lemma follows from the definition of strictly log bounded family.
Lemma 2.16 Let $\mathcal {P}$![]() be a log bounded family of pairs so that the set $\{ \textrm {coeff}(\Delta ) \mid (X,\,\Delta ) \in \mathcal {P}\}$
be a log bounded family of pairs so that the set $\{ \textrm {coeff}(\Delta ) \mid (X,\,\Delta ) \in \mathcal {P}\}$![]() is finite. Then the family $\mathcal {P}$
is finite. Then the family $\mathcal {P}$![]() is strictly log bounded.
is strictly log bounded.
Lemma 2.17 Let $\mathcal {P}$![]() be a bounded family of $d$
be a bounded family of $d$![]() -dimensional projective varieties so that $-K_X$
-dimensional projective varieties so that $-K_X$![]() is pseudo-effective for every $X\in \mathcal {P}$
is pseudo-effective for every $X\in \mathcal {P}$![]() . Then, there exists a positive constant $C,$
. Then, there exists a positive constant $C,$![]() only depending on $\mathcal {P},$
only depending on $\mathcal {P},$![]() satisfying the following: for every $X\in \mathcal {P},$
satisfying the following: for every $X\in \mathcal {P},$![]() we can find a very ample Cartier divisor $A$
we can find a very ample Cartier divisor $A$![]() with $A^{d}\leq C$
with $A^{d}\leq C$![]() and $A^{d-1}(-K_X)\leq C$
and $A^{d-1}(-K_X)\leq C$![]() .
.
Proof. Let $\mathcal {X}\rightarrow T$![]() be the bounding family. By Notherian induction, we can stratify the base $T$
be the bounding family. By Notherian induction, we can stratify the base $T$![]() into finitely many locally closed subvarieties $T_i\subset T$
into finitely many locally closed subvarieties $T_i\subset T$![]() , satisfying the following: For each fibre over $t\in T_i$
, satisfying the following: For each fibre over $t\in T_i$![]() of $\mathcal {X}_i\rightarrow T_i$
of $\mathcal {X}_i\rightarrow T_i$![]() we have that $K_{\mathcal {X}_i}|_{\mathcal {X}_t}=K_{\mathcal {X}_t}$
we have that $K_{\mathcal {X}_i}|_{\mathcal {X}_t}=K_{\mathcal {X}_t}$![]() . We may assume that the $T_i$
. We may assume that the $T_i$![]() 's are disjoint by successively replacing $T_i,\,T_j$
's are disjoint by successively replacing $T_i,\,T_j$![]() with $T_i\setminus \operatorname {supp}(T_i\cap T_j),\, T_j\setminus \operatorname {supp}(T_i\cap T_j)$
with $T_i\setminus \operatorname {supp}(T_i\cap T_j),\, T_j\setminus \operatorname {supp}(T_i\cap T_j)$![]() and $T_i\cap T_j$
and $T_i\cap T_j$![]() . For each $i$
. For each $i$![]() , we can consider a very ample effective Cartier divisor $\mathcal {A}_i$
, we can consider a very ample effective Cartier divisor $\mathcal {A}_i$![]() on $\mathcal {X}_i$
on $\mathcal {X}_i$![]() . For each fibre, we define $\mathcal {A}_{\mathcal {X}_t}:=\mathcal {A}_i|_{\mathcal {X}_t}$
. For each fibre, we define $\mathcal {A}_{\mathcal {X}_t}:=\mathcal {A}_i|_{\mathcal {X}_t}$![]() . Then, we have that $\mathcal {A}_{\mathcal {X}_t}^{d}(-K_{\mathcal {X}_t}) = \mathcal {A}^{d-1}(-K_{\mathcal {X}})|_{\mathcal {X}_t}$
. Then, we have that $\mathcal {A}_{\mathcal {X}_t}^{d}(-K_{\mathcal {X}_t}) = \mathcal {A}^{d-1}(-K_{\mathcal {X}})|_{\mathcal {X}_t}$![]() for each $t\in T_i$
for each $t\in T_i$![]() . Thus, the intersection $\mathcal {A}_{\mathcal {X}_t}^{d}(-K_{\mathcal {X}_t})$
. Thus, the intersection $\mathcal {A}_{\mathcal {X}_t}^{d}(-K_{\mathcal {X}_t})$![]() only takes finitely many values over $T_i$
only takes finitely many values over $T_i$![]() . Analogously, $\mathcal {A}_{\mathcal {X}_t}^{d}$
. Analogously, $\mathcal {A}_{\mathcal {X}_t}^{d}$![]() only takes finitely many values over $T_i$
only takes finitely many values over $T_i$![]() . We define $C$
. We define $C$![]() to be the maximum of all these intersection numbers among all the $T_i$
to be the maximum of all these intersection numbers among all the $T_i$![]() 's. Then, for each $X\in \mathcal {P}$
's. Then, for each $X\in \mathcal {P}$![]() it suffices to consider $A$
it suffices to consider $A$![]() to be the pull-back of $\mathcal {A}_{\mathcal {X}_t}$
to be the pull-back of $\mathcal {A}_{\mathcal {X}_t}$![]() to $X$
to $X$![]() via the isomorphism $X\rightarrow \mathcal {X}_t$
via the isomorphism $X\rightarrow \mathcal {X}_t$![]() .
.
Lemma 2.18 Let $\mathcal {P}$![]() be a bounded family of $d$
be a bounded family of $d$![]() -dimensional projective varieties and $\mathcal {Q}$
-dimensional projective varieties and $\mathcal {Q}$![]() a set of pairs $\{ (X,\,\Delta ) \mid X \in \mathcal {P}\},$
a set of pairs $\{ (X,\,\Delta ) \mid X \in \mathcal {P}\},$![]() so that $\textrm {coeff}(\Delta )$
so that $\textrm {coeff}(\Delta )$![]() satisfies the descending chain condition and for every $(X,\,\Delta )\in \mathcal {Q}$
satisfies the descending chain condition and for every $(X,\,\Delta )\in \mathcal {Q}$![]() we have that $-(K_X+\Delta )$
we have that $-(K_X+\Delta )$![]() is pseudo-effective. Then $\mathcal {Q}$
is pseudo-effective. Then $\mathcal {Q}$![]() is a log bounded set of pairs.
is a log bounded set of pairs.
Proof. By Lemma 2.17, we can find a positive constant $C$![]() so that for each $X\in \mathcal {P}$
so that for each $X\in \mathcal {P}$![]() there is a very ample Cartier divisor $A$
there is a very ample Cartier divisor $A$![]() with $A^{d}\leq C$
with $A^{d}\leq C$![]() and $A^{d-1}(-K_X) \leq C$
and $A^{d-1}(-K_X) \leq C$![]() . The set $\textrm {coeff}(\Delta )$
. The set $\textrm {coeff}(\Delta )$![]() satisfies the descending chain condition, so there exists $\delta >0$
satisfies the descending chain condition, so there exists $\delta >0$![]() small enough so that $\delta < \textrm {coeff}(\Delta )$
small enough so that $\delta < \textrm {coeff}(\Delta )$![]() for every boundary $\Delta$
for every boundary $\Delta$![]() of a pair $(X,\,\Delta )$
of a pair $(X,\,\Delta )$![]() on $\mathcal {Q}$
on $\mathcal {Q}$![]() . Since $-(K_X+\Delta )$
. Since $-(K_X+\Delta )$![]() is pseudo-effective we have that $A^{d-1}\cdot (-K_X-\Delta ) \geq 0$
is pseudo-effective we have that $A^{d-1}\cdot (-K_X-\Delta ) \geq 0$![]() , hence we conclude that
, hence we conclude that
where $\Delta _\textrm {red}$![]() is $\Delta$
is $\Delta$![]() with the reduced structure. Thus, we get that $A^{d-1}\cdot \Delta _\textrm {red}\leq \delta ^{-1} C$
with the reduced structure. Thus, we get that $A^{d-1}\cdot \Delta _\textrm {red}\leq \delta ^{-1} C$![]() , so by [Reference Alexeev2, Lemma 3.7.(2)], we conclude that the set of pairs $\mathcal {Q}$
, so by [Reference Alexeev2, Lemma 3.7.(2)], we conclude that the set of pairs $\mathcal {Q}$![]() is log bounded.
is log bounded.
Lemma 2.19 Let $\mathcal {P}$![]() be a strictly log bounded family of log Fano pairs. Then, there exists $m$
be a strictly log bounded family of log Fano pairs. Then, there exists $m$![]() only depending on $\mathcal {P},$
only depending on $\mathcal {P},$![]() so that $|-m(K_X+\Delta )|$
so that $|-m(K_X+\Delta )|$![]() is base point free for $(X,\,\Delta )\in \mathcal {P}$
is base point free for $(X,\,\Delta )\in \mathcal {P}$![]() .
.
Proof. Note that the dimension of the varieties of $\mathcal {P}$![]() is bounded. Let $(\mathcal {X},\,\mathcal {B})\rightarrow T$
is bounded. Let $(\mathcal {X},\,\mathcal {B})\rightarrow T$![]() be a log bounding family for $\mathcal {P}$
be a log bounding family for $\mathcal {P}$![]() . We can stratify the base $T$
. We can stratify the base $T$![]() into finitely many locally closed subvarieties $T_i\subset T$
into finitely many locally closed subvarieties $T_i\subset T$![]() , satisfying the following: For each fibre over $t\in T_i$
, satisfying the following: For each fibre over $t\in T_i$![]() of $\mathcal {X}_i\rightarrow T_i$
of $\mathcal {X}_i\rightarrow T_i$![]() , we have that $(K_{\mathcal {X}_i}+\mathcal {B}_i)|_{\mathcal {X}_t}=K_{\mathcal {X}_t}+\mathcal {B}_t$
, we have that $(K_{\mathcal {X}_i}+\mathcal {B}_i)|_{\mathcal {X}_t}=K_{\mathcal {X}_t}+\mathcal {B}_t$![]() . In particular, we conclude that there exists a constant $c$
. In particular, we conclude that there exists a constant $c$![]() , only depending on $\mathcal {P}$
, only depending on $\mathcal {P}$![]() , so that $c(K_X+\Delta )$
, so that $c(K_X+\Delta )$![]() is Cartier for every $(X,\,\Delta )\in \mathcal {P}$
is Cartier for every $(X,\,\Delta )\in \mathcal {P}$![]() . Then, applying Kollár's effective base point freeness [Reference Kollár21, Theorem 1.1] with $a=1$
. Then, applying Kollár's effective base point freeness [Reference Kollár21, Theorem 1.1] with $a=1$![]() and $L=-c(K_X+\Delta )$
and $L=-c(K_X+\Delta )$![]() , we conclude that there exists a constant $m$
, we conclude that there exists a constant $m$![]() , only depending on $\mathcal {P}$
, only depending on $\mathcal {P}$![]() , so that $|-m(K_X+\Delta )|$
, so that $|-m(K_X+\Delta )|$![]() is base point free.
is base point free.
Definition 2.20 Let $X$![]() be an irreducible projective variety of dimension $d$
be an irreducible projective variety of dimension $d$![]() and let $D$
and let $D$![]() be a $\mathbb {Q}$
be a $\mathbb {Q}$![]() -Cartier divisor on $X$
-Cartier divisor on $X$![]() . The volume of $D$
. The volume of $D$![]() is
is
In particular, a big divisor has positive volume.
Lemma 2.21 Let $\mathcal {P}$![]() be a strictly log bounded family of $d$
be a strictly log bounded family of $d$![]() -dimensional klt pairs. Then there exist positive real numbers $v_1$
-dimensional klt pairs. Then there exist positive real numbers $v_1$![]() and $v_2,$
and $v_2,$![]() only depending on $\mathcal {P}$
only depending on $\mathcal {P}$![]() , so that for every $(X,\,\Delta ) \in \mathcal {P}$
, so that for every $(X,\,\Delta ) \in \mathcal {P}$![]() with $-(K_X+\Delta )$
with $-(K_X+\Delta )$![]() ample we have that
ample we have that
Proof. Since ampleness is open in families, we may restrict to an open set $U\subset T$![]() so that $-(K_{\mathcal {X}_t} +\mathcal {B}_t)$
so that $-(K_{\mathcal {X}_t} +\mathcal {B}_t)$![]() is ample for every $t\in U$
is ample for every $t\in U$![]() . Furthermore, by Noetherian induction, we may assume that the induced morphism $\mathcal {X}_U \rightarrow U$
. Furthermore, by Noetherian induction, we may assume that the induced morphism $\mathcal {X}_U \rightarrow U$![]() is a projective smooth morphism of relative dimension $d$
is a projective smooth morphism of relative dimension $d$![]() with normal fibres. In this case, we have that
with normal fibres. In this case, we have that
is an upper-semicontinuous function on $t\in U$![]() . Hence, it takes finitely many values on $U$
. Hence, it takes finitely many values on $U$![]() .
.
Lemma 2.22 Let $\mathcal {P}$![]() be a strictly log bounded family of log Fano pairs. We can find a positive real number $M,$
be a strictly log bounded family of log Fano pairs. We can find a positive real number $M,$![]() only depending on $\mathcal {P},$
only depending on $\mathcal {P},$![]() so that for every $(X,\,\Delta )\in \mathcal {P}$
so that for every $(X,\,\Delta )\in \mathcal {P}$![]() there exists an ample curve $C$
there exists an ample curve $C$![]() on $X$
on $X$![]() so that
so that
Proof. By Lemma 2.19, we can find a positive natural number $m$![]() , only depending on $\mathcal {P}$
, only depending on $\mathcal {P}$![]() , so that $|-m(K_X+\Delta )|$
, so that $|-m(K_X+\Delta )|$![]() is a base point free linear system for any $(X,\,\Delta ) \in \mathcal {P}$
is a base point free linear system for any $(X,\,\Delta ) \in \mathcal {P}$![]() . Hence, a general curve $C$
. Hence, a general curve $C$![]() on the rational equivalence class of $(-m(K_X+\Delta ))^{d-1}$
on the rational equivalence class of $(-m(K_X+\Delta ))^{d-1}$![]() will be an ample curve. Moreover, by Lemma 2.21, we have that
will be an ample curve. Moreover, by Lemma 2.21, we have that
Thus, it suffices to take $M=m^{d-1}v_2$![]() .
.
Lemma 2.23 Let $d$![]() be a positive integer and $\epsilon$
be a positive integer and $\epsilon$![]() a positive real number. There exists a constant $l$
a positive real number. There exists a constant $l$![]() only depending on $d$
only depending on $d$![]() and $\epsilon$
and $\epsilon$![]() satisfying the following. Let $X$
satisfying the following. Let $X$![]() be a $d$
be a $d$![]() -dimensional klt variety so that $K_X$
-dimensional klt variety so that $K_X$![]() is Cartier at $x\in X$
is Cartier at $x\in X$![]() . Assume that $X$
. Assume that $X$![]() admits an $\epsilon$
admits an $\epsilon$![]() -plt blow-up at $x\in X$
-plt blow-up at $x\in X$![]() extracting a divisor $E$
extracting a divisor $E$![]() . Then we have that
. Then we have that
In particular, there are finitely many possible values for $a_E(X,\,0)$![]() .
.
Proof. Let $\pi \colon Y \rightarrow X$![]() be the $\epsilon$
be the $\epsilon$![]() -plt blow-up at $x\in X$
-plt blow-up at $x\in X$![]() and write
and write
By assumption of $X$![]() being klt and $K_X$
being klt and $K_X$![]() being Cartier at $x$
being Cartier at $x$![]() we know that $a_E(X,\,0)$
we know that $a_E(X,\,0)$![]() is a non-negative integer. We write
is a non-negative integer. We write
Thus, the pair $(E,\,\Delta _E)$![]() is $\epsilon$
is $\epsilon$![]() -lc and $-(K_E+\Delta _E)$
-lc and $-(K_E+\Delta _E)$![]() is ample. By boundedness of Fano varieties [Reference Birkar6, Theorem 1.1], we conclude that the projective varieties $E$
is ample. By boundedness of Fano varieties [Reference Birkar6, Theorem 1.1], we conclude that the projective varieties $E$![]() belong to a bounded family. By [Reference Hacon and Kovács15, Theorem 3.34], we know that the coefficients of $\Delta _E$
belong to a bounded family. By [Reference Hacon and Kovács15, Theorem 3.34], we know that the coefficients of $\Delta _E$![]() are standard, therefore the pairs $(E,\,\Delta _E)$
are standard, therefore the pairs $(E,\,\Delta _E)$![]() are log bounded by Lemma 2.18. Moreover, since $(E,\,\Delta _E)$
are log bounded by Lemma 2.18. Moreover, since $(E,\,\Delta _E)$![]() is $\epsilon$
is $\epsilon$![]() -log canonical then the coefficients of $\Delta _E$
-log canonical then the coefficients of $\Delta _E$![]() are at most $1-\epsilon$
are at most $1-\epsilon$![]() , hence belong to a finite set of rational numbers. By Lemma 2.16, conclude that the pairs $(E,\,\Delta _E)$
, hence belong to a finite set of rational numbers. By Lemma 2.16, conclude that the pairs $(E,\,\Delta _E)$![]() belong to a strictly log bounded family $\mathcal {P}$
belong to a strictly log bounded family $\mathcal {P}$![]() , which only depends on the dimension $d$
, which only depends on the dimension $d$![]() and the positive real number $\epsilon$
and the positive real number $\epsilon$![]() .
.
By [Reference Shokurov33, Proposition 3.9], we know that at codimension $2$![]() points of $Y$
points of $Y$![]() , every Weil divisor has Cartier index bounded by $p$
, every Weil divisor has Cartier index bounded by $p$![]() , for some constant $p$
, for some constant $p$![]() which only depends on $\epsilon$
which only depends on $\epsilon$![]() . Hence, there exists a closed subset $Z$
. Hence, there exists a closed subset $Z$![]() on $Y$
on $Y$![]() of codimension at least $3$
of codimension at least $3$![]() , so that the Cartier index of $E$
, so that the Cartier index of $E$![]() is a divisor of $p$
is a divisor of $p$![]() outside $Z$
outside $Z$![]() . By Lemma 2.22, we may find an ample curve $C$
. By Lemma 2.22, we may find an ample curve $C$![]() so that
so that
for some constant $M$![]() which only depends on $\mathcal {P}$
which only depends on $\mathcal {P}$![]() . Thus, up to replacing $C$
. Thus, up to replacing $C$![]() with a rationally equivalent curve, we may assume that $C$
with a rationally equivalent curve, we may assume that $C$![]() does not intersect $Z$
does not intersect $Z$![]() , so we have $p E \cdot C$
, so we have $p E \cdot C$![]() is a negative integer, or equivalently,
is a negative integer, or equivalently,
Moreover, since $(E,\,\Delta _E)$![]() belongs to a strictly log bounded family, we conclude that the Cartier index of $-(K_E+\Delta _E)$
belongs to a strictly log bounded family, we conclude that the Cartier index of $-(K_E+\Delta _E)$![]() is bounded by a constant which only depends on $\mathcal {P}$
is bounded by a constant which only depends on $\mathcal {P}$![]() [Reference Birkar7, Lemma 2.25]. In particular,
[Reference Birkar7, Lemma 2.25]. In particular,
belongs to a finite set $\mathcal {F}$![]() of positive rational numbers, which only depends on $\mathcal {P}$
of positive rational numbers, which only depends on $\mathcal {P}$![]() . Finally, observe that from the relation
. Finally, observe that from the relation
we conclude that
so
where the right-hand side only depends on $\epsilon$![]() and $\mathcal {F}$
and $\mathcal {F}$![]() . Since $\mathcal {F}$
. Since $\mathcal {F}$![]() only depends on $\mathcal {P}$
only depends on $\mathcal {P}$![]() , and $\mathcal {P}$
, and $\mathcal {P}$![]() only depends on $d$
only depends on $d$![]() and $\epsilon$
and $\epsilon$![]() , we deduce that $l=p \max \{ \mathcal {F}\}-1$
, we deduce that $l=p \max \{ \mathcal {F}\}-1$![]() only depends on $d$
only depends on $d$![]() and $\epsilon$
and $\epsilon$![]() . This proves the first statement. Since $a_E(X,\,0)$
. This proves the first statement. Since $a_E(X,\,0)$![]() is a non-negative integer, we conclude that there are finitely many possible values for it, proving the second statement.
is a non-negative integer, we conclude that there are finitely many possible values for it, proving the second statement.
Lemma 2.24 Let $\mathcal {P}$![]() be a strictly log bounded family of log Fano pairs. Then, the total discrepancies of pairs $(X,\,\Delta )\in \mathcal {P}$
be a strictly log bounded family of log Fano pairs. Then, the total discrepancies of pairs $(X,\,\Delta )\in \mathcal {P}$![]() take only finitely many values.
take only finitely many values.
Proof. Let $\mathcal {X}\rightarrow T$![]() be a bounding family. Let $\mathcal {B}\subset \mathcal {X}$
be a bounding family. Let $\mathcal {B}\subset \mathcal {X}$![]() be an effective divisor so that $(\mathcal {X},\,\mathcal {B})$
be an effective divisor so that $(\mathcal {X},\,\mathcal {B})$![]() strictly log bound the family $\mathcal {P}$
strictly log bound the family $\mathcal {P}$![]() . By Noetherian induction, we can stratify the base $T$
. By Noetherian induction, we can stratify the base $T$![]() into finitely many locally closed subvarieties $T_i\subset T$
into finitely many locally closed subvarieties $T_i\subset T$![]() , satisfying the following: For each induced family $\mathcal {X}_i\rightarrow T_i$
, satisfying the following: For each induced family $\mathcal {X}_i\rightarrow T_i$![]() , we can find a log resolution of $(\mathcal {X}_i,\,\mathcal {B}_i)$
, we can find a log resolution of $(\mathcal {X}_i,\,\mathcal {B}_i)$![]() so that admits a log resolution over $T_i$
so that admits a log resolution over $T_i$![]() and each blow-up is horizontal over $T_i$
and each blow-up is horizontal over $T_i$![]() . By [Reference Kollár and Mori25, Corollary 2.32.(2)], we conclude that the total discrepancy of each fibre of $(\mathcal {X}_i,\,\mathcal {B}_i)\rightarrow T_i$
. By [Reference Kollár and Mori25, Corollary 2.32.(2)], we conclude that the total discrepancy of each fibre of $(\mathcal {X}_i,\,\mathcal {B}_i)\rightarrow T_i$![]() belongs to a finite set. Hence, the total discrepancy of each fibre of $(\mathcal {X},\,\mathcal {B})\rightarrow T$
belongs to a finite set. Hence, the total discrepancy of each fibre of $(\mathcal {X},\,\mathcal {B})\rightarrow T$![]() belongs to a finite set. Then, the same holds for pairs $(X,\,\Delta )\in \mathcal {P}$
belongs to a finite set. Then, the same holds for pairs $(X,\,\Delta )\in \mathcal {P}$![]() .
.
To conclude this subsection, we will prove that the mildest component of a klt singularity is indeed attained by a Kollár component, or equivalently, the infimum in Definition 2.8 is a minimum.
Proposition 2.25 Let $(X,\,\Delta )$![]() be a pair which is klt at $x$
be a pair which is klt at $x$![]() . Assume that the coefficients of $\Delta$
. Assume that the coefficients of $\Delta$![]() are rational numbers. There exists a Kollár component $\pi \colon Y \rightarrow X$
are rational numbers. There exists a Kollár component $\pi \colon Y \rightarrow X$![]() extracting a divisor $E\subset Y$
extracting a divisor $E\subset Y$![]() so that
so that
Proof. We proceed by contradiction. Recall that
We want to prove that the supremum on the right is actually a maximum. Assume it is not. Then, we can find a sequence of Kollár components $\pi _i \colon Y_i \rightarrow X$![]() over $x\in X$
over $x\in X$![]() for the pair $(X,\,\Delta )$
for the pair $(X,\,\Delta )$![]() so that the total discrepancies of the pairs $(E_i,\, \Delta _{E_i})$
so that the total discrepancies of the pairs $(E_i,\, \Delta _{E_i})$![]() are in an infinite increasing sequence. Since each $(E_i,\,\Delta _{E_i})$
are in an infinite increasing sequence. Since each $(E_i,\,\Delta _{E_i})$![]() is klt, its total log discrepancy is positive. We are assuming that the total discrepancy of the sequence $(E_i,\,\Delta _{E_i})$
is klt, its total log discrepancy is positive. We are assuming that the total discrepancy of the sequence $(E_i,\,\Delta _{E_i})$![]() is infinite and strictly increasing. Hence, there exists $\epsilon >0$
is infinite and strictly increasing. Hence, there exists $\epsilon >0$![]() so that each $(E_i,\,\Delta _{E_i})$
so that each $(E_i,\,\Delta _{E_i})$![]() is $\epsilon$
is $\epsilon$![]() -log canonical. Thus, by [Reference Birkar7, Theorem 1.1], we conclude that the varieties $E_i$
-log canonical. Thus, by [Reference Birkar7, Theorem 1.1], we conclude that the varieties $E_i$![]() belong to a bounded family.
belong to a bounded family.
Since the coefficients of $\Delta _{Y_i}$![]() are fixed by $\textrm {coeff}(\Delta )$
are fixed by $\textrm {coeff}(\Delta )$![]() , we conclude that the coefficients of $\Delta _{E_i}$
, we conclude that the coefficients of $\Delta _{E_i}$![]() belong to a finite set of rational numbers which only depend on $\textrm {coeff}(\Delta )$
belong to a finite set of rational numbers which only depend on $\textrm {coeff}(\Delta )$![]() [Reference Filipazzi and Moraga11, Lemma 5.3]. By Lemma 2.18, we conclude that the pairs $(E_i,\,\Delta _{E_i})$
[Reference Filipazzi and Moraga11, Lemma 5.3]. By Lemma 2.18, we conclude that the pairs $(E_i,\,\Delta _{E_i})$![]() are log bounded. By Lemma 2.16, we conclude that the pairs $(E_i,\,\Delta _{E_i})$
are log bounded. By Lemma 2.16, we conclude that the pairs $(E_i,\,\Delta _{E_i})$![]() are strictly log bounded. Since the pairs $(E_i,\,\Delta _{E_i})$
are strictly log bounded. Since the pairs $(E_i,\,\Delta _{E_i})$![]() belong to a strictly log bounded family, then their total discrepancies can take only finitely many values (see Lemma 2.24). This leads to a contradiction. We conclude that there is no such infinite sequence, hence the supremum is a maximum.
belong to a strictly log bounded family, then their total discrepancies can take only finitely many values (see Lemma 2.24). This leads to a contradiction. We conclude that there is no such infinite sequence, hence the supremum is a maximum.
2.3. Finite morphisms
In this subsection, we recall the index one cover of a log canonical singularity and the behaviour of log discrepancies under finite dominant morphisms.
Definition 2.26 Let $(X,\,\Delta )$![]() be a pair and write $\Delta =\sum \nolimits _i d_i \Delta _i$
be a pair and write $\Delta =\sum \nolimits _i d_i \Delta _i$![]() where the $\Delta _i$
where the $\Delta _i$![]() 's are pairwise different prime divisors on $X$
's are pairwise different prime divisors on $X$![]() . Given a quasi-finite morphism $\phi \colon X'\rightarrow X$
. Given a quasi-finite morphism $\phi \colon X'\rightarrow X$![]() between normal varieties, we can write
between normal varieties, we can write
where
and $r_j$![]() is the ramification index at the generic point of $E_j$
is the ramification index at the generic point of $E_j$![]() [Reference Shokurov33, 2.1]. The above formula is called the pull-back formula for quasi-finite morphisms.
[Reference Shokurov33, 2.1]. The above formula is called the pull-back formula for quasi-finite morphisms.
The following lemma follows from the pull-back formula for quasi-finite morphisms.
Lemma 2.27 Let $(X,\,\Delta )$![]() be a pair with standard coefficients and $\phi \colon X'\rightarrow X$
be a pair with standard coefficients and $\phi \colon X'\rightarrow X$![]() be a finite morphism of normal varieties. Assume that for every prime divisor $E$
be a finite morphism of normal varieties. Assume that for every prime divisor $E$![]() on $X'$
on $X'$![]() , we have that $r_E+1$
, we have that $r_E+1$![]() divides $(1-d_i)^{-1},$
divides $(1-d_i)^{-1},$![]() where $r_E$
where $r_E$![]() is the ramification index of $\phi$
is the ramification index of $\phi$![]() at $E$
at $E$![]() and $d_i$
and $d_i$![]() is the coefficient of $\phi (E)$
is the coefficient of $\phi (E)$![]() at $\Delta$
at $\Delta$![]() . Then $\Delta '$
. Then $\Delta '$![]() is an effective divisor whose coefficients are standard.
is an effective divisor whose coefficients are standard.
The following is a theorem of Zariski that is often used instead of resolution of singularities [Reference Zariski39].
Theorem 2.28 Let $Y'$![]() and $X$
and $X$![]() be two integral schemes of finite type over a field over $\mathbb {Z},$
be two integral schemes of finite type over a field over $\mathbb {Z},$![]() and $f \colon Y'\rightarrow X$
and $f \colon Y'\rightarrow X$![]() a dominant morphism. Let $D\subset Y'$
a dominant morphism. Let $D\subset Y'$![]() be a prime divisor and $\eta \in D$
be a prime divisor and $\eta \in D$![]() the generic point. Assume that $Y'$
the generic point. Assume that $Y'$![]() is normal at $\eta$
is normal at $\eta$![]() . We can define a sequence of schemes and rational maps as follows:
. We can define a sequence of schemes and rational maps as follows:
(1) $X_0=X$
 and $f_0=f,$
and $f_0=f,$
(2) If $f_i \colon Y' \dashrightarrow X_i$
 is defined, then let $Z_i\subset X_i$
is defined, then let $Z_i\subset X_i$ the closure of $f_i(\eta )$
the closure of $f_i(\eta )$ . We define $X_{i+1}$
. We define $X_{i+1}$ to be the blow-up of $X_i$
to be the blow-up of $X_i$ at $Z_i$
at $Z_i$ and $f_{i+1}\colon Y' \dashrightarrow X_{i+1}$
and $f_{i+1}\colon Y' \dashrightarrow X_{i+1}$ the induced rational map.
the induced rational map.
For $j$![]() large enough $\dim (Z_j)\geq \dim (X)-1$
large enough $\dim (Z_j)\geq \dim (X)-1$![]() and $X_j$
and $X_j$![]() is regular at the generic point of $Z_j$
is regular at the generic point of $Z_j$![]() .
.
Lemma 2.29 With the assumptions of Lemma 2.27, the following conditions hold:
(1) For $\epsilon$
 a non-negative real number, the pair $(X',\,\Delta ')$
a non-negative real number, the pair $(X',\,\Delta ')$ is $\epsilon$
is $\epsilon$ -log canonical if and only if $(X,\,\Delta )$
-log canonical if and only if $(X,\,\Delta )$ is $\epsilon$
is $\epsilon$ -log canonical, and
-log canonical, and(2) if $(X,\,\Delta )$
 is a log canonical pair with a unique log canonical centre $x\in X,$
is a log canonical pair with a unique log canonical centre $x\in X,$ $(X,\,\Delta )$
$(X,\,\Delta )$ has a unique log canonical place, and $x'=\phi ^{-1}(x)$
has a unique log canonical place, and $x'=\phi ^{-1}(x)$ is a point, then $(X',\,\Delta ')$
is a point, then $(X',\,\Delta ')$ has a unique log canonical place.
has a unique log canonical place.
Proof. Let $\pi \colon Y \rightarrow X$![]() be a projective birational morphism and $Y'\rightarrow Y\times _{X} X'$
be a projective birational morphism and $Y'\rightarrow Y\times _{X} X'$![]() the normalization of the main component of the fibre product, then we have a commutative diagram
the normalization of the main component of the fibre product, then we have a commutative diagram

and we can write
Here $\Delta '_{Y'}$![]() is the strict transform of $\Delta '$
is the strict transform of $\Delta '$![]() on $Y'$
on $Y'$![]() . By Lemma 2.27, we know that $(X',\,\Delta ')$
. By Lemma 2.27, we know that $(X',\,\Delta ')$![]() is a log pair. Thus, we have the relation
is a log pair. Thus, we have the relation
Therefore, by the pull-back formula for quasi-finite morphisms we have that
where $r_E$![]() is the ramification index of $\phi _Y$
is the ramification index of $\phi _Y$![]() at the generic point of $E$
at the generic point of $E$![]() . By Theorem 2.28, we know that for every divisorial valuation on $X'$
. By Theorem 2.28, we know that for every divisorial valuation on $X'$![]() we can find $\pi \colon Y \rightarrow X$
we can find $\pi \colon Y \rightarrow X$![]() so that the centre of this valuation on $Y'$
so that the centre of this valuation on $Y'$![]() is a divisor, where $Y'$
is a divisor, where $Y'$![]() is as in the commutative diagram (
is as in the commutative diagram (
). This proves the first statement.
Now we turn to prove the second statement by contradiction. By the proof of the first statement, we know that the log canonical pair $(X',\,\Delta ')$![]() has at least one log canonical place, and all its log canonical places map onto $x'\in X'$
has at least one log canonical place, and all its log canonical places map onto $x'\in X'$![]() . Assume that $(X',\,\Delta ')$
. Assume that $(X',\,\Delta ')$![]() has more than one log canonical place. Let $\pi \colon Y'\rightarrow X'$
has more than one log canonical place. Let $\pi \colon Y'\rightarrow X'$![]() be a dlt modification of $(X',\,\Delta ')$
be a dlt modification of $(X',\,\Delta ')$![]() and write
and write
Applying [Reference Kollár and Mori25, Theorem 5.48] to a log resolution of $(Y',\,\Delta '_Y)$![]() , we deduce that $\lfloor \Delta '_{Y'} \rfloor$
, we deduce that $\lfloor \Delta '_{Y'} \rfloor$![]() is connected. Moreover, since $(X',\,\Delta ')$
is connected. Moreover, since $(X',\,\Delta ')$![]() has more than one log canonical place, the divisor $\lfloor \Delta '_{Y'}\rfloor$
has more than one log canonical place, the divisor $\lfloor \Delta '_{Y'}\rfloor$![]() is connected and has at least two irreducible components. Since the intersection of two log canonical centres is a union of log canonical centres [Reference Ambro5, Theorem 1.1], we deduce that $(Y',\,\Delta '_{Y'})$
is connected and has at least two irreducible components. Since the intersection of two log canonical centres is a union of log canonical centres [Reference Ambro5, Theorem 1.1], we deduce that $(Y',\,\Delta '_{Y'})$![]() has infinitely many log canonical places. Thus, $(X',\,\Delta ')$
has infinitely many log canonical places. Thus, $(X',\,\Delta ')$![]() has infinitely many log canonical places. By Theorem 2.28, we conclude that each of those log canonical places appears in a commutative diagram as in (2.1). Moreover, at least one log canonical place of $(X',\,\Delta ')$
has infinitely many log canonical places. By Theorem 2.28, we conclude that each of those log canonical places appears in a commutative diagram as in (2.1). Moreover, at least one log canonical place of $(X',\,\Delta ')$![]() is exceptional over the dlt model $(Y,\,\Delta _Y)$
is exceptional over the dlt model $(Y,\,\Delta _Y)$![]() of $(X,\,\Delta )$
of $(X,\,\Delta )$![]() . Therefore, $(X,\,\Delta )$
. Therefore, $(X,\,\Delta )$![]() has at least two log canonical places. This provides the needed contradiction and the claim follows.
has at least two log canonical places. This provides the needed contradiction and the claim follows.
Definition 2.30 Let $(X,\,\Delta )$![]() be a klt pair with standard coefficients and $x\in X$
be a klt pair with standard coefficients and $x\in X$![]() a point. Consider $a$
a point. Consider $a$![]() the smallest positive integer so that $a(K_X+\Delta )\sim 0$
the smallest positive integer so that $a(K_X+\Delta )\sim 0$![]() on a neighborhood of $x\in X$
on a neighborhood of $x\in X$![]() , or equivalently, $a$
, or equivalently, $a$![]() is the Cartier index of $K_X+\Delta$
is the Cartier index of $K_X+\Delta$![]() at $x\in X$
at $x\in X$![]() . Therefore, we have an isomorphism $\mathcal {O}_X(a(K_X+\Delta ))\simeq \mathcal {O}_X$
. Therefore, we have an isomorphism $\mathcal {O}_X(a(K_X+\Delta ))\simeq \mathcal {O}_X$![]() , we can choose a nowhere zero section
, we can choose a nowhere zero section
and consider $\phi \colon X'\rightarrow X$![]() the corresponding cyclic cover. The ramification index of $\phi$
the corresponding cyclic cover. The ramification index of $\phi$![]() at a prime divisor $E$
at a prime divisor $E$![]() which maps onto $\Delta _i$
which maps onto $\Delta _i$![]() is exactly $d_i-1$
is exactly $d_i-1$![]() , where $d_i=\textrm {coeff}_{\Delta _i}(\Delta )$
, where $d_i=\textrm {coeff}_{\Delta _i}(\Delta )$![]() . Moreover, $\phi$
. Moreover, $\phi$![]() is ramified only at the support of $\Delta$
is ramified only at the support of $\Delta$![]() . Therefore, from the pull-back formula for quasi-finite morphisms, we know that
. Therefore, from the pull-back formula for quasi-finite morphisms, we know that
We call $\phi$![]() the index one cover of the klt pair $(X,\,\Delta )$
the index one cover of the klt pair $(X,\,\Delta )$![]() locally at $x\in X$
locally at $x\in X$![]() [Reference Fujino12, Notation 4.1].
[Reference Fujino12, Notation 4.1].
2.4. Complements
In this subsection, we prove that klt singularities with plt blow-ups admit local complements with a unique log canonical place.
Remark 2.31 In this notation, a pair $(X,\,\Delta )$![]() is exceptional at $x\in X$
is exceptional at $x\in X$![]() if and only if every local complement at $x\in X$
if and only if every local complement at $x\in X$![]() has a unique log canonical place.
has a unique log canonical place.
Lemma 2.32 Let $(X,\,\Delta )$![]() be a $d$
be a $d$![]() -dimensional klt pair with standard coefficients. Assume that $(X,\,\Delta )$
-dimensional klt pair with standard coefficients. Assume that $(X,\,\Delta )$![]() admits an $\epsilon$
admits an $\epsilon$![]() -plt blow-up at $x\in X$
-plt blow-up at $x\in X$![]() extracting the exceptional divisor $E$
extracting the exceptional divisor $E$![]() . There exists a natural number $n,$
. There exists a natural number $n,$![]() only depending on $d$
only depending on $d$![]() and $\epsilon,$
and $\epsilon,$![]() and a boundary $\Gamma$
and a boundary $\Gamma$![]() on $X$
on $X$![]() so that the following conditions hold:
so that the following conditions hold:
• $n(K_X+\Delta +\Gamma ) \sim 0$
 on a neighbourhood of $x\in X,$
on a neighbourhood of $x\in X,$ and
and• $K_Y+\Delta _Y+\Gamma _Y +E =\pi ^{*}(K_X+\Delta +\Gamma )$
 is an $\epsilon$
is an $\epsilon$ -plt pair on a neighbourhood of $x\in X$
-plt pair on a neighbourhood of $x\in X$ .
.
Moreover, we may assume that the boundary divisors $\Gamma$![]() and $\Delta$
and $\Delta$![]() do not share prime components.
do not share prime components.
Proof. We will construct a strong $(0,\,n)$![]() -complement for the divisor $-(K_Y+\Delta _Y+E)$
-complement for the divisor $-(K_Y+\Delta _Y+E)$![]() with respect to the morphism $\pi \colon Y \rightarrow X$
with respect to the morphism $\pi \colon Y \rightarrow X$![]() around $x\in X$
around $x\in X$![]() . This complement will push-forward to a $(0,\,n)$
. This complement will push-forward to a $(0,\,n)$![]() -complement for $(X,\,\Delta )$
-complement for $(X,\,\Delta )$![]() locally around $x\in X$
locally around $x\in X$![]() . In order to do so, we will do adjunction to $E$
. In order to do so, we will do adjunction to $E$![]() , produce a global complement on $E$
, produce a global complement on $E$![]() and then pull-back to a neighbourhood of $E$
and then pull-back to a neighbourhood of $E$![]() .
.
By adjunction, we can write
where $(E,\,\Delta _E)$![]() is an $\epsilon$
is an $\epsilon$![]() -log canonical pair and the coefficients of $\Delta _E$
-log canonical pair and the coefficients of $\Delta _E$![]() belong to a set of rational numbers satisfying the descending chain condition with rational accumulation points (see, e.g. [Reference Filipazzi and Moraga11, Lemma 5.3]). Hence, by [Reference Filipazzi and Moraga11, Theorem 1.3.2], we can find $n$
belong to a set of rational numbers satisfying the descending chain condition with rational accumulation points (see, e.g. [Reference Filipazzi and Moraga11, Lemma 5.3]). Hence, by [Reference Filipazzi and Moraga11, Theorem 1.3.2], we can find $n$![]() only depending on $d$
only depending on $d$![]() and $\epsilon$
and $\epsilon$![]() , and a global strong $(\epsilon,\,n)$
, and a global strong $(\epsilon,\,n)$![]() -complement $\Gamma _E$
-complement $\Gamma _E$![]() for the pair $(E,\,\Delta _E)$
for the pair $(E,\,\Delta _E)$![]() . From the proof of [Reference Filipazzi and Moraga11, Theorem 1.3], we may assume that $\Gamma _E$
. From the proof of [Reference Filipazzi and Moraga11, Theorem 1.3], we may assume that $\Gamma _E$![]() does not share prime components with $\Delta _E$
does not share prime components with $\Delta _E$![]() . Without loss of generality, we may assume that $n\Delta _Y$
. Without loss of generality, we may assume that $n\Delta _Y$![]() is a Weil divisor. Indeed, since $(Y,\,\Delta _Y+E)$
is a Weil divisor. Indeed, since $(Y,\,\Delta _Y+E)$![]() is $\epsilon$
is $\epsilon$![]() -plt and the coefficients of $\Delta _Y$
-plt and the coefficients of $\Delta _Y$![]() are standard, then they belong to a finite set.
are standard, then they belong to a finite set.
Let $\pi _Y \colon W \rightarrow Y$![]() be a log resolution of $(Y,\,\Delta _Y+E)$
be a log resolution of $(Y,\,\Delta _Y+E)$![]() , and write
, and write
where $E_W$![]() is the strict transform of $E$
is the strict transform of $E$![]() on $W$
on $W$![]() . We define
. We define
Let $P_W$![]() be the unique integral effective divisor on $W$
be the unique integral effective divisor on $W$![]() so that
so that
is a boundary on $W$![]() so that $(W,\,\Lambda _W)$
so that $(W,\,\Lambda _W)$![]() is plt and $\lfloor \Lambda _W \rfloor =E_W$
is plt and $\lfloor \Lambda _W \rfloor =E_W$![]() . We claim that $P_W$
. We claim that $P_W$![]() is an exceptional divisor over $Y$
is an exceptional divisor over $Y$![]() . Assume it is not. Indeed, if $D$
. Assume it is not. Indeed, if $D$![]() is a prime divisor on $W$
is a prime divisor on $W$![]() which is not contracted on $Y$
which is not contracted on $Y$![]() then, we have that
then, we have that
because $n\Delta _Y$![]() is integral. Therefore
is integral. Therefore
Hence, if $\textrm {coeff}_D(P_W)>0$![]() , then $\textrm {coeff}_P(P_W)\geq 1$
, then $\textrm {coeff}_P(P_W)\geq 1$![]() , so $\textrm {coeff}_P(\Lambda _W)>1$
, so $\textrm {coeff}_P(\Lambda _W)>1$![]() . In particular, $(W,\,\Lambda _W)$
. In particular, $(W,\,\Lambda _W)$![]() is not plt. This leads to a contradiction. We conclude that $P_W$
is not plt. This leads to a contradiction. We conclude that $P_W$![]() is exceptional over $Y$
is exceptional over $Y$![]() .
.
By definition, we have that
is the sum of the klt pair $(W,\,\Lambda _W-E_W)$![]() and the nef and big divisor $(n+1)N_W$
and the nef and big divisor $(n+1)N_W$![]() over a neighbourhood of $x\in X$
over a neighbourhood of $x\in X$![]() . Note that $(W,\,\Lambda _W-E_W)$
. Note that $(W,\,\Lambda _W-E_W)$![]() is klt given that $(W,\,\Lambda _W)$
is klt given that $(W,\,\Lambda _W)$![]() is plt with $\lfloor \Lambda _W\rfloor =E_W$
is plt with $\lfloor \Lambda _W\rfloor =E_W$![]() . Shrinking around $x\in X$
. Shrinking around $x\in X$![]() we may assume that $X$
we may assume that $X$![]() is affine, then $(n+1)N_W$
is affine, then $(n+1)N_W$![]() is nef and big over $X$
is nef and big over $X$![]() . By the relative version of Kawamata–Viehweg theorem [Reference Kawamata, Matsuda and Matsuki20, Theorem 1-2-5], we have a surjection
. By the relative version of Kawamata–Viehweg theorem [Reference Kawamata, Matsuda and Matsuki20, Theorem 1-2-5], we have a surjection
We denote by $\Gamma _{E_W}$![]() the pull-back of $\Gamma _E$
the pull-back of $\Gamma _E$![]() to $E_W$
to $E_W$![]() . Observe that we have
. Observe that we have
where $P_{E_W}:=P_W|_{E_W}$![]() and $\Delta _{E_W}:=\Delta _W|_{E_W}$
and $\Delta _{E_W}:=\Delta _W|_{E_W}$![]() . The divisor $G_{E_W}$
. The divisor $G_{E_W}$![]() is integral and its coefficients are strictly greater than $-1$
is integral and its coefficients are strictly greater than $-1$![]() , therefore it is indeed effective. By the surjectivity of (2.2), there exists $0\leq G_W \sim L_W+P_W$
, therefore it is indeed effective. By the surjectivity of (2.2), there exists $0\leq G_W \sim L_W+P_W$![]() which restricts to $G_{E_W}$
which restricts to $G_{E_W}$![]() . We denote by $G_Y$
. We denote by $G_Y$![]() the push-forward of $G_W$
the push-forward of $G_W$![]() to $Y$
to $Y$![]() . By pushing-forward the linear equivalence $L_W+P_W\sim G_W$
. By pushing-forward the linear equivalence $L_W+P_W\sim G_W$![]() to $Y$
to $Y$![]() , and using the fact that $P_W$
, and using the fact that $P_W$![]() is $Y$
is $Y$![]() -exceptional, we get that
-exceptional, we get that
We define $\Gamma _Y := \frac {G_Y}{n}$![]() . Observe that by construction, we have
. Observe that by construction, we have
on a neighbourhood of $x\in X$![]() . We claim that $\Gamma _Y|_{E}= \Gamma _E$
. We claim that $\Gamma _Y|_{E}= \Gamma _E$![]() . Indeed, observe that we can define
. Indeed, observe that we can define
and $n\Gamma _W$![]() pushes-forward to $G_Y$
pushes-forward to $G_Y$![]() on $Y$
on $Y$![]() , hence $\Gamma _W = \pi _Y^{*}(\Gamma _Y)$
, hence $\Gamma _W = \pi _Y^{*}(\Gamma _Y)$![]() . On the other hand, we have $n\Gamma _{E_W}= n \Gamma _W|_{E_W}$
. On the other hand, we have $n\Gamma _{E_W}= n \Gamma _W|_{E_W}$![]() , which means that $\Gamma _{E_W}=\Gamma _W|_{E_W}$
, which means that $\Gamma _{E_W}=\Gamma _W|_{E_W}$![]() . Thus, we have $\Gamma _Y|_E=\Gamma _E$
. Thus, we have $\Gamma _Y|_E=\Gamma _E$![]() as claimed.
as claimed.
Finally, observe that
so by inversion of adjunction, we conclude that $(Y,\,\Delta _Y+\Gamma _Y+E)$![]() is $\epsilon$
is $\epsilon$![]() -plt. Moreover, since $\Gamma _E$
-plt. Moreover, since $\Gamma _E$![]() and $\Delta _E$
and $\Delta _E$![]() prime components, then $\Delta _Y$
prime components, then $\Delta _Y$![]() and $\Gamma _Y$
and $\Gamma _Y$![]() do not share prime components as well. Define $\Gamma =\pi _*(\Gamma _Y)$
do not share prime components as well. Define $\Gamma =\pi _*(\Gamma _Y)$![]() , and observe that
, and observe that
Thus, $(X,\,\Delta +\Gamma )$![]() is a log canonical pair with a unique log canonical place so that $n(K_X+\Delta +\Gamma ) \sim 0$
is a log canonical pair with a unique log canonical place so that $n(K_X+\Delta +\Gamma ) \sim 0$![]() on a neighbourhood of $x\in X$
on a neighbourhood of $x\in X$![]() . Moreover, $\Delta$
. Moreover, $\Delta$![]() and $\Gamma$
and $\Gamma$![]() do not share prime components.
do not share prime components.
2.5. Examples
In this subsection, we give two examples to show that the $a$![]() -log canonical and $\epsilon$
-log canonical and $\epsilon$![]() -plt blow-up conditions of Theorem 1 and Theorem 2 are indeed necessary.
-plt blow-up conditions of Theorem 1 and Theorem 2 are indeed necessary.
Example 2.33 Let $X_n$![]() be the cone over a rational curve of degree $n$
be the cone over a rational curve of degree $n$![]() . Blowing-up the vertex $\pi _n \colon Y_n \rightarrow X_n$
. Blowing-up the vertex $\pi _n \colon Y_n \rightarrow X_n$![]() gives a log resolution so that the pair $(Y_n,\,E_n)$
gives a log resolution so that the pair $(Y_n,\,E_n)$![]() is log smooth. Hence, $\pi _n$
is log smooth. Hence, $\pi _n$![]() is a $1$
is a $1$![]() -plt blow-up. However, $a_{E_n}(X_n,\,0)= -1+\frac {2}{n}$
-plt blow-up. However, $a_{E_n}(X_n,\,0)= -1+\frac {2}{n}$![]() , and the Cartier index of $X_n$
, and the Cartier index of $X_n$![]() at the vertex depends on $n$
at the vertex depends on $n$![]() . In this case, the condition of Theorem 1 that is violated, is the fact that the minimal log discrepancy is bounded away from zero. Indeed, the discrepancies $a_{E_n}(X_n,\,0)$
. In this case, the condition of Theorem 1 that is violated, is the fact that the minimal log discrepancy is bounded away from zero. Indeed, the discrepancies $a_{E_n}(X_n,\,0)$![]() are converging to $-1$
are converging to $-1$![]() .
.
Example 2.34 By [Reference Hayakawa14, Proposition 5.1], we can construct terminal threefold singularities $X_m$![]() of index $m$
of index $m$![]() and extract two different divisors with discrepancies $1/m$
and extract two different divisors with discrepancies $1/m$![]() and $2/m$
and $2/m$![]() , respectively. Hence, if there is any plt blow-up of $X_m$
, respectively. Hence, if there is any plt blow-up of $X_m$![]() it is an $\epsilon$
it is an $\epsilon$![]() -plt blow-up for some $\epsilon \leq 2/m$
-plt blow-up for some $\epsilon \leq 2/m$![]() . In this case, the condition of Theorem 1 that is violated, is the existence of a plt blow-up with total discrepancy bounded away from zero.
. In this case, the condition of Theorem 1 that is violated, is the existence of a plt blow-up with total discrepancy bounded away from zero.
3. Proof of the main Theorem
Proof of Theorem 1. Let $(X,\,\Delta )$![]() be a log pair which admits an $\epsilon$
be a log pair which admits an $\epsilon$![]() -plt blow-up $\pi \colon Y \rightarrow X$
-plt blow-up $\pi \colon Y \rightarrow X$![]() at $x\in X$
at $x\in X$![]() . By assumption $(X,\,\Delta )$
. By assumption $(X,\,\Delta )$![]() is $a$
is $a$![]() -lc at $x\in X$
-lc at $x\in X$![]() . In particular, the minimal log discrepancy $\textrm {mld}_x(X,\,\Delta )$
. In particular, the minimal log discrepancy $\textrm {mld}_x(X,\,\Delta )$![]() is strictly positive.
is strictly positive.
Let $\phi \colon X'\rightarrow X$![]() be the index one cover of the klt pair $(X,\,\Delta )$
be the index one cover of the klt pair $(X,\,\Delta )$![]() locally at $x$
locally at $x$![]() so that $\phi ^{*}(K_X+\Delta )=K_{X'}$
so that $\phi ^{*}(K_X+\Delta )=K_{X'}$![]() (see [Reference Fujino12, Notation 4.1] or Definition 2.30). We denote by $Y'$
(see [Reference Fujino12, Notation 4.1] or Definition 2.30). We denote by $Y'$![]() the normalization of the main component of $X'\times _X Y$
the normalization of the main component of $X'\times _X Y$![]() . Hence, we have a commutative diagram
. Hence, we have a commutative diagram

where $\pi '$![]() is birational and $\phi _Y$
is birational and $\phi _Y$![]() is finite with the same degree as $\phi$
is finite with the same degree as $\phi$![]() . We can write
. We can write
where $E'$![]() is the reduced exceptional divisor contracted by $\pi '$
is the reduced exceptional divisor contracted by $\pi '$![]() . We claim that the pair $(Y',\, E')$
. We claim that the pair $(Y',\, E')$![]() is $\epsilon$
is $\epsilon$![]() -plt. Indeed, by Lemma 2.32, we may find an effective divisor $\Gamma$
-plt. Indeed, by Lemma 2.32, we may find an effective divisor $\Gamma$![]() on $X$
on $X$![]() so that
so that
is an $\epsilon$![]() -plt pair, where $\Gamma _Y$
-plt pair, where $\Gamma _Y$![]() is the strict transform of $\Gamma$
is the strict transform of $\Gamma$![]() on $Y$
on $Y$![]() . By the equality (3.1), we know that log canonical places of $(X,\,\Delta +\Gamma )$
. By the equality (3.1), we know that log canonical places of $(X,\,\Delta +\Gamma )$![]() are the same as log canonical places of $(Y,\,\Delta _Y+\Gamma _Y+E)$
are the same as log canonical places of $(Y,\,\Delta _Y+\Gamma _Y+E)$![]() , i.e., the morphism is crepant for these pairs. The pair $(Y,\,\Delta _Y+\Gamma _Y+E)$
, i.e., the morphism is crepant for these pairs. The pair $(Y,\,\Delta _Y+\Gamma _Y+E)$![]() has a unique log canonical place which corresponds to $E$
has a unique log canonical place which corresponds to $E$![]() . Hence, $(X,\,\Delta +\Gamma )$
. Hence, $(X,\,\Delta +\Gamma )$![]() has a unique log canonical place which corresponds to $E$
has a unique log canonical place which corresponds to $E$![]() . By construction, the divisors $\Delta$
. By construction, the divisors $\Delta$![]() and $\Gamma$
and $\Gamma$![]() do not share prime components. Therefore, by Lemma 2.27 and Lemma 2.29, we conclude that
do not share prime components. Therefore, by Lemma 2.27 and Lemma 2.29, we conclude that
is indeed a pair which has a unique log canonical place and its log discrepancies are either zero or greater than $\epsilon$![]() . By the commutativy of the diagram, we have that
. By the commutativy of the diagram, we have that
is an $\epsilon$![]() -plt pair. Hence $(Y',\,E')$
-plt pair. Hence $(Y',\,E')$![]() is $\epsilon$
is $\epsilon$![]() -plt as well. In particular, $\pi ' \colon Y'\rightarrow X'$
-plt as well. In particular, $\pi ' \colon Y'\rightarrow X'$![]() is an $\epsilon$
is an $\epsilon$![]() -plt blow-up at $x'\in X'$
-plt blow-up at $x'\in X'$![]() .
.
Observe that by construction the $\mathbb {Q}$![]() -divisors $K_Y+\Delta _Y+E$
-divisors $K_Y+\Delta _Y+E$![]() and $K_{Y'}+E'$
and $K_{Y'}+E'$![]() are both $\epsilon$
are both $\epsilon$![]() -plt and anti-ample over $X$
-plt and anti-ample over $X$![]() and $X'$
and $X'$![]() , respectively. We define the following pairs by adjunction:
, respectively. We define the following pairs by adjunction:
By the above considerations, we know that both pairs $(E',\,\Delta _{E'})$![]() and $(E,\,\Delta _E)$
and $(E,\,\Delta _E)$![]() are log Fano and $\epsilon$
are log Fano and $\epsilon$![]() -lc. By [Reference Birkar6, Theorem 1.1], we know that the algebraic varieties $E$
-lc. By [Reference Birkar6, Theorem 1.1], we know that the algebraic varieties $E$![]() and $E'$
and $E'$![]() belong to a bounded family which only depends on $d-1$
belong to a bounded family which only depends on $d-1$![]() and $\epsilon$
and $\epsilon$![]() . Moreover, the boundary divisors $\Delta _{E}$
. Moreover, the boundary divisors $\Delta _{E}$![]() and $\Delta _{E'}$
and $\Delta _{E'}$![]() have coefficients that belong to a set with the descending chain condition. By Lemma 2.18, we conclude that the log pairs $(E,\,\Delta _{E})$
have coefficients that belong to a set with the descending chain condition. By Lemma 2.18, we conclude that the log pairs $(E,\,\Delta _{E})$![]() and $(E',\,\Delta _{E'})$
and $(E',\,\Delta _{E'})$![]() belong to a log bounded family which only depends on $d-1$
belong to a log bounded family which only depends on $d-1$![]() , $\epsilon$
, $\epsilon$![]() , and the derived set of standard coefficients. Furthermore, by [Reference Birkar7, Lemma 3.3], we know that the coefficients of $\Delta _{E}$
, and the derived set of standard coefficients. Furthermore, by [Reference Birkar7, Lemma 3.3], we know that the coefficients of $\Delta _{E}$![]() and $\Delta _{E'}$
and $\Delta _{E'}$![]() belong to a set of hyperstandard coefficients $\mathcal {H}(\mathcal {R})$
belong to a set of hyperstandard coefficients $\mathcal {H}(\mathcal {R})$![]() corresponding to a finite set of rational numbers $\mathcal {R}$
corresponding to a finite set of rational numbers $\mathcal {R}$![]() , which only depends on $\mathcal {S}$
, which only depends on $\mathcal {S}$![]() . By the $\epsilon$
. By the $\epsilon$![]() -log canonical condition of the pairs $(E,\,\Delta _E)$
-log canonical condition of the pairs $(E,\,\Delta _E)$![]() and $(E',\,\Delta _{E'})$
and $(E',\,\Delta _{E'})$![]() and the fact that the only accumulation point of $\mathcal {H}(\mathcal {R})$
and the fact that the only accumulation point of $\mathcal {H}(\mathcal {R})$![]() is $1$
is $1$![]() , we conclude that $\Delta _{E}$
, we conclude that $\Delta _{E}$![]() and $\Delta _{E'}$
and $\Delta _{E'}$![]() have coefficients in the finite set $\mathcal {H}(\mathcal {R})\cap [0,\,1-\epsilon )$
have coefficients in the finite set $\mathcal {H}(\mathcal {R})\cap [0,\,1-\epsilon )$![]() which only depends on $\epsilon$
which only depends on $\epsilon$![]() . By Lemma 2.16, we deduce that the pairs $(E,\,\Delta _E)$
. By Lemma 2.16, we deduce that the pairs $(E,\,\Delta _E)$![]() and $(E',\,\Delta _{E'})$
and $(E',\,\Delta _{E'})$![]() belong to a strictly log bounded family. Denote by $\phi _E$
belong to a strictly log bounded family. Denote by $\phi _E$![]() the restriction of $\phi _Y$
the restriction of $\phi _Y$![]() to $E'$
to $E'$![]() and observe that
and observe that
where $r_E$![]() denotes the ramification index of $\phi _Y$
denotes the ramification index of $\phi _Y$![]() at the generic point of $E'$
at the generic point of $E'$![]() .
.
Now we turn to prove that $\deg (\phi )$![]() has an upper bound which only depends on $d,\,a$
has an upper bound which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() . In order to do so, we just need to provide that there is an upper bound for $\phi _E$
. In order to do so, we just need to provide that there is an upper bound for $\phi _E$![]() and $r_E$
and $r_E$![]() . Observe that we have
. Observe that we have
Therefore, by Lemma 2.21, there is an upper bound $C(d,\,\epsilon )$![]() for $\deg (\phi _E)$
for $\deg (\phi _E)$![]() , which only depends on $d-1$
, which only depends on $d-1$![]() and $\epsilon$
and $\epsilon$![]() . On the other hand, we have the relation
. On the other hand, we have the relation
By Lemma 2.23, we know that $a_{E'}(X',\,0)+1$![]() has an upper bound $C'(d,\,\epsilon )$
has an upper bound $C'(d,\,\epsilon )$![]() which only depends on $d$
which only depends on $d$![]() and $\epsilon$
and $\epsilon$![]() . We conclude that $deg(\phi )$
. We conclude that $deg(\phi )$![]() has an upper bound which only depends on $d,\,a$
has an upper bound which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() . Indeed, we have that
. Indeed, we have that
This proves the claim that $\deg (\phi )$![]() is bounded above by a constant which only depends on $d,\,a$
is bounded above by a constant which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() . Hence, the index of $K_X+\Delta$
. Hence, the index of $K_X+\Delta$![]() around $x$
around $x$![]() is bounded by a constant which only depends on $d,\,a$
is bounded by a constant which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() (see, e.g. [Reference Kollár22, 2.49]).
(see, e.g. [Reference Kollár22, 2.49]).
Thus, $\textrm {mld}_x(X,\,\Delta )$![]() belongs to a discrete set which only depends on $d,\,a$
belongs to a discrete set which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() . Finally, by Lemma 2.29, we have that
. Finally, by Lemma 2.29, we have that
therefore $\textrm {mld}_x(X,\,\Delta )$![]() belongs to a finite set which only depends on $d,\,a$
belongs to a finite set which only depends on $d,\,a$![]() and $\epsilon$
and $\epsilon$![]() .
.
Proof of Theorem 2. It follows from the bound on $\deg (\phi )$![]() given in the proof of Theorem 1. See equation (3.2).
given in the proof of Theorem 1. See equation (3.2).
Proof of Corollary 1. If there exists a sequence in $\mathcal {M}(d,\,\mathcal {S})_{0,\epsilon }$![]() which contradicts the ascending chain condition, passing to a subsequence we may assume the sequence is strictly increasing. Therefore, such infinite sequence belongs to $\mathcal {M}(d,\,\mathcal {S})_{a,\epsilon }$
which contradicts the ascending chain condition, passing to a subsequence we may assume the sequence is strictly increasing. Therefore, such infinite sequence belongs to $\mathcal {M}(d,\,\mathcal {S})_{a,\epsilon }$![]() for some positive real number $a$
for some positive real number $a$![]() . This contradicts Theorem 1.
. This contradicts Theorem 1.
Acknowledgements
The author would like to thank Caucher Birkar, Christopher Hacon, Harold Blum, Stefano Filipazzi, and Yuri Prokhorov for many useful comments. The author was partially supported by NSF research grants no: DMS-1300750, DMS-1265285 and by a grant from the Simons Foundation; Award Number: 256202. After completing this project, the author was informed