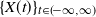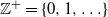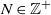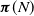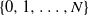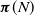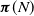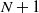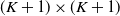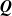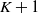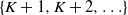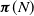1. Introduction
We consider a time-homogeneous, continuous-time Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
on a countably infinite state space
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
on a countably infinite state space
![]() $\mathbb{Z}^+ = \{0,1,\dots\}$
. Let
$\mathbb{Z}^+ = \{0,1,\dots\}$
. Let
![]() $q_{i,j}$
(
$q_{i,j}$
(
![]() $i,j \in \mathbb{Z}^+, i \neq j$
) denote the transition rate from state i to state j. The infinitesimal generator
$i,j \in \mathbb{Z}^+, i \neq j$
) denote the transition rate from state i to state j. The infinitesimal generator
![]() $\textbf{\textit{Q}}$
of the Markov chain
$\textbf{\textit{Q}}$
of the Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
is then given by
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
is then given by
 \begin{equation*}\textbf{\textit{Q}}=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}-q_0 & q_{0,1} & q_{0,2} & q_{0,3} & \dots\\ \\[-5pt] q_{1, 0} & -q_1 & q_{1,2} & q_{1,3} & \dots\\ \\[-5pt] q_{2, 0} & q_{2,1} & -q_2 & q_{2,3} & \dots\\ \\[-5pt] q_{3, 0} & q_{3,1} & q_{3,2} & -q_3 & \dots\\ \\[-5pt] \vdots &\vdots &\vdots & \vdots & \ddots\end{array}\right),\end{equation*}
\begin{equation*}\textbf{\textit{Q}}=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}-q_0 & q_{0,1} & q_{0,2} & q_{0,3} & \dots\\ \\[-5pt] q_{1, 0} & -q_1 & q_{1,2} & q_{1,3} & \dots\\ \\[-5pt] q_{2, 0} & q_{2,1} & -q_2 & q_{2,3} & \dots\\ \\[-5pt] q_{3, 0} & q_{3,1} & q_{3,2} & -q_3 & \dots\\ \\[-5pt] \vdots &\vdots &\vdots & \vdots & \ddots\end{array}\right),\end{equation*}
where
 \begin{equation*}q_i = \sum_{\substack{j \in \mathbb{Z}^+\\ j \neq i}} q_{i,j},\quad i \in \mathbb{Z}^+.\end{equation*}
\begin{equation*}q_i = \sum_{\substack{j \in \mathbb{Z}^+\\ j \neq i}} q_{i,j},\quad i \in \mathbb{Z}^+.\end{equation*}
We assume that
![]() $q_i < \infty$
(
$q_i < \infty$
(
![]() $i \in \mathbb{Z}^+$
) and
$i \in \mathbb{Z}^+$
) and
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
is stationary and ergodic. We then define
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
is stationary and ergodic. We then define
![]() $\boldsymbol{\pi}$
as the stationary distribution of
$\boldsymbol{\pi}$
as the stationary distribution of
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
:
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
:
where
![]() $\pi_i = \mathbb{P}(X(0)=i)$
(
$\pi_i = \mathbb{P}(X(0)=i)$
(
![]() $i \in \mathbb{Z}^+$
). Note that
$i \in \mathbb{Z}^+$
). Note that
![]() $\boldsymbol{\pi}$
is determined uniquely by
$\boldsymbol{\pi}$
is determined uniquely by
where
![]() $\textbf{\textit{e}}$
denotes a column vector of the appropriate dimension whose elements are all equal to one.
$\textbf{\textit{e}}$
denotes a column vector of the appropriate dimension whose elements are all equal to one.
In general, it is hard to obtain the stationary distribution of the Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty, \infty)}$
because there are infinitely many unknowns
$\{X(t)\}_{t \in (\!-\infty, \infty)}$
because there are infinitely many unknowns
![]() $\pi_i$
(
$\pi_i$
(
![]() $i \in \mathbb{Z}^+$
) in (1.1). In the past, this problem has been tackled mainly by two approaches: the augmented truncation approximation [Reference Hart and Tweedie4, Reference Liu, Li and Masuyama7, Reference Seneta12, Reference Zhao and Liu16] and the matrix-analytic method [Reference Latouche and Ramaswami6, Reference Neuts10, Reference Neuts11]. In the augmented truncation approximation, we choose a sufficiently large
$i \in \mathbb{Z}^+$
) in (1.1). In the past, this problem has been tackled mainly by two approaches: the augmented truncation approximation [Reference Hart and Tweedie4, Reference Liu, Li and Masuyama7, Reference Seneta12, Reference Zhao and Liu16] and the matrix-analytic method [Reference Latouche and Ramaswami6, Reference Neuts10, Reference Neuts11]. In the augmented truncation approximation, we choose a sufficiently large
![]() $N \in \mathbb{Z}^+$
and partition
$N \in \mathbb{Z}^+$
and partition
![]() $\mathbb{Z}^+$
into a finite subset
$\mathbb{Z}^+$
into a finite subset
![]() $\mathbb{Z}_0^N$
and its complement
$\mathbb{Z}_0^N$
and its complement
![]() $\mathbb{Z}_{N+1}^{\infty}$
, where
$\mathbb{Z}_{N+1}^{\infty}$
, where
![]() $\mathbb{Z}_m^{\ell}$
(
$\mathbb{Z}_m^{\ell}$
(
![]() $m,\ell \in\mathbb{Z}^+$
) and
$m,\ell \in\mathbb{Z}^+$
) and
![]() $\mathbb{Z}_m^{\infty}$
(
$\mathbb{Z}_m^{\infty}$
(
![]() $m \in \mathbb{Z}^+$
) are defined as
$m \in \mathbb{Z}^+$
) are defined as
 \begin{equation*}\mathbb{Z}_m^{\ell}=\begin{cases}\{m, m+1, \dots, \ell\}, & m \leq \ell,\\[4pt] \emptyset, &m > \ell,\end{cases}\qquad\mathbb{Z}_m^{\infty}=\{m, m+1,\dots\},\quad m \in \mathbb{Z}^+.\end{equation*}
\begin{equation*}\mathbb{Z}_m^{\ell}=\begin{cases}\{m, m+1, \dots, \ell\}, & m \leq \ell,\\[4pt] \emptyset, &m > \ell,\end{cases}\qquad\mathbb{Z}_m^{\infty}=\{m, m+1,\dots\},\quad m \in \mathbb{Z}^+.\end{equation*}
We also partition the stationary distribution
![]() $\boldsymbol{\pi}$
in conformance with the partition of the state space:
$\boldsymbol{\pi}$
in conformance with the partition of the state space:
We then construct a finite-state Markov chain on
![]() $\mathbb{Z}_0^N$
, using the
$\mathbb{Z}_0^N$
, using the
![]() $(N+1) \times (N+1)$
northwest corner block
$(N+1) \times (N+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator
$\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator
![]() $\textbf{\textit{Q}}$
. This finite-state Markov chain on
$\textbf{\textit{Q}}$
. This finite-state Markov chain on
![]() $\mathbb{Z}_0^N$
can be regarded as an approximation to the original Markov chain on
$\mathbb{Z}_0^N$
can be regarded as an approximation to the original Markov chain on
![]() $\mathbb{Z}^+$
. Specifically, we construct an infinitesimal generator
$\mathbb{Z}^+$
. Specifically, we construct an infinitesimal generator
![]() $\textbf{\textit{Q}}^{(1,1)}(N) +\textbf{\textit{Q}}_{\textrm{A}}(N)$
of a Markov chain on
$\textbf{\textit{Q}}^{(1,1)}(N) +\textbf{\textit{Q}}_{\textrm{A}}(N)$
of a Markov chain on
![]() $\mathbb{Z}_0^N$
, where
$\mathbb{Z}_0^N$
, where
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
is an augmentation matrix such that
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
is an augmentation matrix such that
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)\geq \textbf{\textit{O}}$
and
$\textbf{\textit{Q}}_{\textrm{A}}(N)\geq \textbf{\textit{O}}$
and
![]() $\big[\textbf{\textit{Q}}^{(1,1)}(N) + \textbf{\textit{Q}}_{\textrm{A}}(N)\big] \textbf{\textit{e}}= \textbf{0}$
. Usually,
$\big[\textbf{\textit{Q}}^{(1,1)}(N) + \textbf{\textit{Q}}_{\textrm{A}}(N)\big] \textbf{\textit{e}}= \textbf{0}$
. Usually,
![]() $[\textbf{\textit{Q}}^{(1,1)}(N)+\textbf{\textit{Q}}_{\textrm{A}}(N)]$
is assumed to be irreducible. Let
$[\textbf{\textit{Q}}^{(1,1)}(N)+\textbf{\textit{Q}}_{\textrm{A}}(N)]$
is assumed to be irreducible. Let
![]() $\boldsymbol{\pi}(N)$
(
$\boldsymbol{\pi}(N)$
(
![]() $N \in \mathbb{Z}^+$
) denote the conditional stationary distribution given
$N \in \mathbb{Z}^+$
) denote the conditional stationary distribution given
![]() $X(0) \in \mathbb{Z}_0^N$
:
$X(0) \in \mathbb{Z}_0^N$
:
where
![]() $\pi_i(N)=\mathbb{P}(X(0)=i \mid X(0) \in \mathbb{Z}_0^N)$
(
$\pi_i(N)=\mathbb{P}(X(0)=i \mid X(0) \in \mathbb{Z}_0^N)$
(
![]() $i \in \mathbb{Z}_0^N$
). By definition, we have
$i \in \mathbb{Z}_0^N$
). By definition, we have
where
![]() $\boldsymbol{\pi}^{(1)}(N)$
is given in (1.2). In the augmented truncation approximation, an approximation
$\boldsymbol{\pi}^{(1)}(N)$
is given in (1.2). In the augmented truncation approximation, an approximation
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N)$
to
$\boldsymbol{\pi}^{\textrm{trunc}}(N)$
to
![]() $\boldsymbol{\pi}(N)$
is determined by
$\boldsymbol{\pi}(N)$
is determined by
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N) [\textbf{\textit{Q}}^{(1,1)}(N) + \textbf{\textit{Q}}_{\textrm{A}}(N)] = \textbf{0}$
and
$\boldsymbol{\pi}^{\textrm{trunc}}(N) [\textbf{\textit{Q}}^{(1,1)}(N) + \textbf{\textit{Q}}_{\textrm{A}}(N)] = \textbf{0}$
and
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N) \textbf{\textit{e}} = 1$
. We then adopt
$\boldsymbol{\pi}^{\textrm{trunc}}(N) \textbf{\textit{e}} = 1$
. We then adopt
![]() $\boldsymbol{\pi}^{\textrm{approx},N} = (\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
as an approximation to the stationary distribution
$\boldsymbol{\pi}^{\textrm{approx},N} = (\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
as an approximation to the stationary distribution
![]() $\boldsymbol{\pi}$
of the original Markov chain. Under some technical conditions,
$\boldsymbol{\pi}$
of the original Markov chain. Under some technical conditions,
![]() $\boldsymbol{\pi}^{\textrm{approx},N}$
is known to converge to
$\boldsymbol{\pi}^{\textrm{approx},N}$
is known to converge to
![]() $\boldsymbol{\pi}$
as N goes to infinity [Reference Hart and Tweedie4, Reference Seneta12]. Therefore,
$\boldsymbol{\pi}$
as N goes to infinity [Reference Hart and Tweedie4, Reference Seneta12]. Therefore,
![]() $\boldsymbol{\pi}^{\textrm{approx},N}$
will be a good approximation if N is sufficiently large.
$\boldsymbol{\pi}^{\textrm{approx},N}$
will be a good approximation if N is sufficiently large.
On the other hand, the matrix-analytic method utilizes structures of Markov chains which appear often in applications. Specifically, the standard matrix-analytic method is applicable to block-structured Markov chains with the following features: the state space
![]() $\mathbb{Z}^+$
can be partitioned into finite and disjoint subsets
$\mathbb{Z}^+$
can be partitioned into finite and disjoint subsets
![]() $\mathcal{L}_m$
(
$\mathcal{L}_m$
(
![]() $m \in \mathbb{Z}^+$
), called levels, in such a way that direct transitions between levels are skip-free in one direction (or both). In particular, Markov chains are called M/G/1-type if transitions between levels are skip-free to the left [Reference Neuts11], and they are called G/M/1-type if transitions between levels are skip-free to the right [Reference Neuts10]. If transitions between levels are skip-free in both directions, they are called quasi-birth-and-death processes [Reference Bright and Taylor1, Reference Neuts10]. In the matrix-analytic method, the exact computation of the stationary distribution is targeted.
$m \in \mathbb{Z}^+$
), called levels, in such a way that direct transitions between levels are skip-free in one direction (or both). In particular, Markov chains are called M/G/1-type if transitions between levels are skip-free to the left [Reference Neuts11], and they are called G/M/1-type if transitions between levels are skip-free to the right [Reference Neuts10]. If transitions between levels are skip-free in both directions, they are called quasi-birth-and-death processes [Reference Bright and Taylor1, Reference Neuts10]. In the matrix-analytic method, the exact computation of the stationary distribution is targeted.
In both of the above-mentioned approaches, the (conditional) stationary distribution is characterized by systems of linear equations. By contrast, this paper studies the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
(
$\boldsymbol{\pi}(N)$
(
![]() $N \in \mathbb{Z}^+$
) via systems of linear inequalities. It is known that the boundary vector in block-structured Markov chains of level-dependent M/G/1 type can be obtained by the solution of an infinite number of inequalities; based on this, computational algorithms for the conditional stationary distribution
$N \in \mathbb{Z}^+$
) via systems of linear inequalities. It is known that the boundary vector in block-structured Markov chains of level-dependent M/G/1 type can be obtained by the solution of an infinite number of inequalities; based on this, computational algorithms for the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
have been developed in [Reference Kimura and Takine5, Reference Takine15].
$\boldsymbol{\pi}(N)$
have been developed in [Reference Kimura and Takine5, Reference Takine15].
The purpose of this paper is to characterize the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
via systems of linear inequalities, without assuming any regular structures. In other words, we will attempt to find minimum regions on the first orthant
$\boldsymbol{\pi}(N)$
via systems of linear inequalities, without assuming any regular structures. In other words, we will attempt to find minimum regions on the first orthant
![]() $\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \geq \textbf{0}\}$
of
$\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \geq \textbf{0}\}$
of
![]() $\mathbb{R}^{N+1}$
which contain
$\mathbb{R}^{N+1}$
which contain
![]() $\boldsymbol{\pi}(N)$
. Specifically, we first consider
$\boldsymbol{\pi}(N)$
. Specifically, we first consider
![]() $\boldsymbol{\pi}(N)$
based only on the
$\boldsymbol{\pi}(N)$
based only on the
![]() $(N+1) \times (N+1)$
northwest corner block
$(N+1) \times (N+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator
$\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator
![]() $\textbf{\textit{Q}}$
, and we obtain a system of
$\textbf{\textit{Q}}$
, and we obtain a system of
![]() $N+1$
linear inequalities that
$N+1$
linear inequalities that
![]() $\boldsymbol{\pi}(N)$
satisfies. It immediately follows that
$\boldsymbol{\pi}(N)$
satisfies. It immediately follows that
![]() $\boldsymbol{\pi}(N)$
lies in an N-simplex
$\boldsymbol{\pi}(N)$
lies in an N-simplex
![]() $\mathcal{P}(N)$
on the first orthant of
$\mathcal{P}(N)$
on the first orthant of
![]() $\mathbb{R}^{N+1}$
, where vertices of
$\mathbb{R}^{N+1}$
, where vertices of
![]() $\mathcal{P}(N)$
are determined only by
$\mathcal{P}(N)$
are determined only by
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
. As we will see, the derivation of these results is absurdly simple. Nonetheless, the
$\textbf{\textit{Q}}^{(1,1)}(N)$
. As we will see, the derivation of these results is absurdly simple. Nonetheless, the
![]() $N+1$
vertices of the N-simplex
$N+1$
vertices of the N-simplex
![]() $\mathcal{P}(N)$
(i.e.,
$\mathcal{P}(N)$
(i.e.,
![]() $N+1$
linearly independent probability vectors that span
$N+1$
linearly independent probability vectors that span
![]() $\mathcal{P}(N)$
) are essential for
$\mathcal{P}(N)$
) are essential for
![]() $\boldsymbol{\pi}(N)$
; in any ergodic, continuous-time Markov chain with
$\boldsymbol{\pi}(N)$
; in any ergodic, continuous-time Markov chain with
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
,
$\textbf{\textit{Q}}^{(1,1)}(N)$
,
![]() $\boldsymbol{\pi}(N)$
can be expressed as a convex combination of those vertices. We also provide a probabilistic interpretation of this result.
$\boldsymbol{\pi}(N)$
can be expressed as a convex combination of those vertices. We also provide a probabilistic interpretation of this result.
Next we consider the case that a subset
of
![]() $\mathbb{Z}_0^N$
is available, as well as
$\mathbb{Z}_0^N$
is available, as well as
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
. Note that
$\textbf{\textit{Q}}^{(1,1)}(N)$
. Note that
![]() $\mathcal{J}(N)$
can be regarded as a kind of structural information, because it is the subset of states in
$\mathcal{J}(N)$
can be regarded as a kind of structural information, because it is the subset of states in
![]() $\mathbb{Z}_0^N$
which are directly reachable from at least one state in
$\mathbb{Z}_0^N$
which are directly reachable from at least one state in
![]() $\mathbb{Z}_{N+1}^{\infty}$
. We show that the role of
$\mathbb{Z}_{N+1}^{\infty}$
. We show that the role of
![]() $\mathcal{J}(N)$
is to eliminate redundant vertices of
$\mathcal{J}(N)$
is to eliminate redundant vertices of
![]() $\mathcal{P}(N)$
, and we obtain a
$\mathcal{P}(N)$
, and we obtain a
![]() $(|\mathcal{J}(N)|-1)$
-simplex
$(|\mathcal{J}(N)|-1)$
-simplex
![]() $\mathcal{P}^+(N)$
whose relative interior contains
$\mathcal{P}^+(N)$
whose relative interior contains
![]() $\boldsymbol{\pi}(N)$
, where for any set
$\boldsymbol{\pi}(N)$
, where for any set
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
![]() $|\mathcal{X}|$
stands for the cardinality of
$|\mathcal{X}|$
stands for the cardinality of
![]() $\mathcal{X}$
. In other words, when
$\mathcal{X}$
. In other words, when
![]() $\mathcal{J}(N)$
is available,
$\mathcal{J}(N)$
is available,
![]() $\boldsymbol{\pi}(N)$
is given by a convex combination of
$\boldsymbol{\pi}(N)$
is given by a convex combination of
![]() $|\mathcal{J}(N)|$
vertices of
$|\mathcal{J}(N)|$
vertices of
![]() $\mathcal{P}^+(N)$
with positive weights. These results are closely related to the augmented truncation approximation (ATA), and we provide some practical implications for it. In particular, the linear ATA has the same degree of freedom as the general ATA does, and
$\mathcal{P}^+(N)$
with positive weights. These results are closely related to the augmented truncation approximation (ATA), and we provide some practical implications for it. In particular, the linear ATA has the same degree of freedom as the general ATA does, and
![]() $\mathcal{J}(N)$
is useful in choosing an augmentation matrix in the linear ATA.
$\mathcal{J}(N)$
is useful in choosing an augmentation matrix in the linear ATA.
Next we consider an extension of the above results, using state transitions in peripheral states of
![]() $\mathbb{Z}_0^N$
. Specifically, for a fixed K (
$\mathbb{Z}_0^N$
. Specifically, for a fixed K (
![]() $K > N$
), we obtain an N-simplex
$K > N$
), we obtain an N-simplex
![]() $\widetilde{\mathcal{P}}(K,N)$
(
$\widetilde{\mathcal{P}}(K,N)$
(
![]() $\subseteq \mathcal{P}(N)$
) that contains
$\subseteq \mathcal{P}(N)$
) that contains
![]() $\boldsymbol{\pi}(N)$
, which is determined only by the
$\boldsymbol{\pi}(N)$
, which is determined only by the
![]() $(K+1) \times (K+1)$
northwest corner block
$(K+1) \times (K+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
of
$\textbf{\textit{Q}}^{(1,1)}(K)$
of
![]() $\textbf{\textit{Q}}$
. Furthermore, when both
$\textbf{\textit{Q}}$
. Furthermore, when both
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
are available, we show that redundant vertices of
$\mathcal{J}(K)$
are available, we show that redundant vertices of
![]() $\widetilde{\mathcal{P}}(K,N)$
can be eliminated.
$\widetilde{\mathcal{P}}(K,N)$
can be eliminated.
The common feature of all of the above results is that we characterize
![]() $\boldsymbol{\pi}(N)$
by specifying simplices on the first orthant of
$\boldsymbol{\pi}(N)$
by specifying simplices on the first orthant of
![]() $\mathbb{R}^{N+1}$
which contain
$\mathbb{R}^{N+1}$
which contain
![]() $\boldsymbol{\pi}(N)$
. In order to refine these results further, we consider general convex polytopes, using
$\boldsymbol{\pi}(N)$
. In order to refine these results further, we consider general convex polytopes, using
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
. For this purpose, we introduce a new structure called (K, N)-skip-free sets, and using them, we obtain the minimum convex polytope that contains
$\mathcal{J}(K)$
. For this purpose, we introduce a new structure called (K, N)-skip-free sets, and using them, we obtain the minimum convex polytope that contains
![]() $\boldsymbol{\pi}(N)$
, under the condition that only
$\boldsymbol{\pi}(N)$
, under the condition that only
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
are available.
$\mathcal{J}(K)$
are available.
The rest of this paper is organized as follows. In Section 2, we obtain simplices that contain
![]() $\boldsymbol{\pi}(N)$
, based on
$\boldsymbol{\pi}(N)$
, based on
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
(and
$\textbf{\textit{Q}}^{(1,1)}(N)$
(and
![]() $\mathcal{J}(N)$
). We also provide some practical implications for the augmented truncation approximation. In Section 3, we extend the result in the preceding section, using state transitions in peripheral states. In Section 4, we introduce skip-free sets and obtain the minimum convex polytope that contains
$\mathcal{J}(N)$
). We also provide some practical implications for the augmented truncation approximation. In Section 3, we extend the result in the preceding section, using state transitions in peripheral states. In Section 4, we introduce skip-free sets and obtain the minimum convex polytope that contains
![]() $\boldsymbol{\pi}(N)$
. Finally, some concluding remarks are provided in Section 5.
$\boldsymbol{\pi}(N)$
. Finally, some concluding remarks are provided in Section 5.
2. The characterization of
 $\boldsymbol{\pi}(N)$
by linear inequalities: fundamental results
$\boldsymbol{\pi}(N)$
by linear inequalities: fundamental results
In this section, we characterize the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
via systems of linear inequalities, based on the
$\boldsymbol{\pi}(N)$
via systems of linear inequalities, based on the
![]() $(N+1) \times (N+1)$
northwest corner block of the infinitesimal generator
$(N+1) \times (N+1)$
northwest corner block of the infinitesimal generator
![]() $\textbf{\textit{Q}}$
.
$\textbf{\textit{Q}}$
.
2.1. Preliminaries
We will construct a convex polytope
![]() $\mathcal{P}$
, by considering the intersection of a polyhedral convex cone
$\mathcal{P}$
, by considering the intersection of a polyhedral convex cone
![]() $\mathcal{C}$
on the first orthant
$\mathcal{C}$
on the first orthant
![]() $\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \geq \textbf{0}\}$
of
$\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \geq \textbf{0}\}$
of
![]() $\mathbb{R}^{N+1}$
and a hyperplane containing all probability vectors in
$\mathbb{R}^{N+1}$
and a hyperplane containing all probability vectors in
![]() $\mathbb{R}^{N+1}$
. As we will see,
$\mathbb{R}^{N+1}$
. As we will see,
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{P}$
take the following forms:
$\mathcal{P}$
take the following forms:
 \begin{align}\mathcal{C}&=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{A}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0}\},\nonumber\\[3pt] \mathcal{P}&=\mathcal{C} \cap \{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{e}} =1 \}=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{A}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\},\end{align}
\begin{align}\mathcal{C}&=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{A}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0}\},\nonumber\\[3pt] \mathcal{P}&=\mathcal{C} \cap \{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{e}} =1 \}=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}\textbf{\textit{A}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\},\end{align}
where
![]() $\textbf{\textit{A}}$
and
$\textbf{\textit{A}}$
and
![]() $\textbf{\textit{B}}$
denote appropriate matrices with
$\textbf{\textit{B}}$
denote appropriate matrices with
![]() $N+1$
rows. Note that we allow
$N+1$
rows. Note that we allow
![]() $\textbf{\textit{B}} = \textbf{\textit{O}}$
, and in that case, we can ignore the constraint
$\textbf{\textit{B}} = \textbf{\textit{O}}$
, and in that case, we can ignore the constraint
![]() $\textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0}$
in (2.1). In general, a convex polytope
$\textbf{\textit{x}}\textbf{\textit{B}} = \textbf{0}$
in (2.1). In general, a convex polytope
![]() $\mathcal{P}$
can also be represented by a set of convex combinations of vertices of
$\mathcal{P}$
can also be represented by a set of convex combinations of vertices of
![]() $\mathcal{P}$
. Specifically, by using an appropriate nonnegative matrix
$\mathcal{P}$
. Specifically, by using an appropriate nonnegative matrix
![]() $\overline{\textbf{\textit{C}}}$
with
$\overline{\textbf{\textit{C}}}$
with
![]() $N+1$
columns such that
$N+1$
columns such that
![]() $\overline{\textbf{\textit{C}}}\textbf{\textit{e}}=\textbf{\textit{e}}$
,
$\overline{\textbf{\textit{C}}}\textbf{\textit{e}}=\textbf{\textit{e}}$
,
![]() $\mathcal{P}$
in (2.1) can also be represented as
$\mathcal{P}$
in (2.1) can also be represented as
Note that
![]() $\overline{\textbf{\textit{C}}}$
is composed of
$\overline{\textbf{\textit{C}}}$
is composed of
![]() $1 \times (N+1)$
probability vectors
$1 \times (N+1)$
probability vectors
![]() $\overline{\textbf{\textit{c}}}_i$
(
$\overline{\textbf{\textit{c}}}_i$
(
![]() $i=0,1,\ldots,M$
) that span
$i=0,1,\ldots,M$
) that span
![]() $\mathcal{P}$
. If the M vectors
$\mathcal{P}$
. If the M vectors
![]() $\overline{\textbf{\textit{c}}}_1 - \overline{\textbf{\textit{c}}}_0$
,
$\overline{\textbf{\textit{c}}}_1 - \overline{\textbf{\textit{c}}}_0$
,
![]() $\overline{\textbf{\textit{c}}}_2-\overline{\textbf{\textit{c}}}_0$
,
$\overline{\textbf{\textit{c}}}_2-\overline{\textbf{\textit{c}}}_0$
,
![]() $\ldots$
,
$\ldots$
,
![]() $\overline{\textbf{\textit{c}}}_M-\overline{\textbf{\textit{c}}}_0$
are linearly independent,
$\overline{\textbf{\textit{c}}}_M-\overline{\textbf{\textit{c}}}_0$
are linearly independent,
![]() $\mathcal{P}$
is called an M-simplex. Let
$\mathcal{P}$
is called an M-simplex. Let
![]() $\textrm{ri}\, \mathcal{P}$
denote the relative interior of the convex polytope
$\textrm{ri}\, \mathcal{P}$
denote the relative interior of the convex polytope
![]() $\mathcal{P}$
:
$\mathcal{P}$
:
 \begin{align}\textrm{ri}\, \mathcal{P}&=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \textbf{\textit{A}} > \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}}=\textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}}=1\}\\[3pt] &= \{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \boldsymbol{\alpha}\overline{\textbf{\textit{C}}},\boldsymbol{\alpha} > \textbf{0},\ \boldsymbol{\alpha}\textbf{\textit{e}}=1\}.\nonumber\end{align}
\begin{align}\textrm{ri}\, \mathcal{P}&=\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} \textbf{\textit{A}} > \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{B}}=\textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}}=1\}\\[3pt] &= \{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \boldsymbol{\alpha}\overline{\textbf{\textit{C}}},\boldsymbol{\alpha} > \textbf{0},\ \boldsymbol{\alpha}\textbf{\textit{e}}=1\}.\nonumber\end{align}
2.2. Characterization of
 $\boldsymbol{\pi}(N)$
in terms of
$\boldsymbol{\pi}(N)$
in terms of
 $\textbf{\textit{Q}}^{(1,1)}(N)$
$\textbf{\textit{Q}}^{(1,1)}(N)$
In this subsection, we assume that for an arbitrarily fixed
![]() $N \in\mathbb{Z}^+$
, the stationary distribution
$N \in\mathbb{Z}^+$
, the stationary distribution
![]() $\boldsymbol{\pi}$
of an ergodic, continuous-time Markov chain
$\boldsymbol{\pi}$
of an ergodic, continuous-time Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
is partitioned as in (1.2) and the infinitesimal generator
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
is partitioned as in (1.2) and the infinitesimal generator
![]() $\textbf{\textit{Q}}$
is partitioned as follows:
$\textbf{\textit{Q}}$
is partitioned as follows:
 \begin{equation}\textbf{\textit{Q}} = \kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{\infty}\\ \\[-5pt] \mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N) \\ \\[-5pt] \mathbb{Z}_{N+1}^{\infty} & \textbf{\textit{Q}}^{(2,1)}(N) &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation}
\begin{equation}\textbf{\textit{Q}} = \kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{\infty}\\ \\[-5pt] \mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N) \\ \\[-5pt] \mathbb{Z}_{N+1}^{\infty} & \textbf{\textit{Q}}^{(2,1)}(N) &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation}
We define
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
as the collection of ergodic, continuous-time Markov chains on
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
as the collection of ergodic, continuous-time Markov chains on
![]() $\mathbb{Z}^+$
whose infinitesimal generators have the specific
$\mathbb{Z}^+$
whose infinitesimal generators have the specific
![]() $(N+1) \times (N+1)$
northwest corner block
$(N+1) \times (N+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
.
$\textbf{\textit{Q}}^{(1,1)}(N)$
.
We first characterize the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
of Markov chains in
$\boldsymbol{\pi}(N)$
of Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
. Owing to the ergodicity,
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
. Owing to the ergodicity,
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular whether it is irreducible or not. We then define
$\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular whether it is irreducible or not. We then define
![]() $\textbf{\textit{H}}(N)$
as
$\textbf{\textit{H}}(N)$
as
By definition,
![]() $\textbf{\textit{H}}(N) \geq \textbf{\textit{O}}$
and
$\textbf{\textit{H}}(N) \geq \textbf{\textit{O}}$
and
![]() $\textbf{\textit{H}}(N) \textbf{\textit{e}} >\textbf{0}$
. Let
$\textbf{\textit{H}}(N) \textbf{\textit{e}} >\textbf{0}$
. Let
![]() $\overline{\textbf{\textit{H}}}(N)$
denote an
$\overline{\textbf{\textit{H}}}(N)$
denote an
![]() $(N+1) \times (N+1)$
matrix obtained by normalizing each row of
$(N+1) \times (N+1)$
matrix obtained by normalizing each row of
![]() $\textbf{\textit{H}}(N)$
in such a way that
$\textbf{\textit{H}}(N)$
in such a way that
![]() $\overline{\textbf{\textit{H}}}(N) \textbf{\textit{e}} = \textbf{\textit{e}}$
:
$\overline{\textbf{\textit{H}}}(N) \textbf{\textit{e}} = \textbf{\textit{e}}$
:
where for any
![]() $(n+1)$
-dimensional vector
$(n+1)$
-dimensional vector
![]() $\textbf{\textit{x}}$
,
$\textbf{\textit{x}}$
,
![]() $\textrm{diag}(\textbf{\textit{x}})$
denotes an
$\textrm{diag}(\textbf{\textit{x}})$
denotes an
![]() $(n+1)$
-dimensional diagonal matrix whose ith diagonal element is given by the ith element
$(n+1)$
-dimensional diagonal matrix whose ith diagonal element is given by the ith element
![]() $[\textbf{\textit{x}}]_i$
of
$[\textbf{\textit{x}}]_i$
of
![]() $\textbf{\textit{x}}$
. We also define
$\textbf{\textit{x}}$
. We also define
![]() $\Gamma(n)$
(
$\Gamma(n)$
(
![]() $n \in \mathbb{Z}^+$
) as the set of all
$n \in \mathbb{Z}^+$
) as the set of all
![]() $(n+1)$
-dimensional probability vectors:
$(n+1)$
-dimensional probability vectors:
Theorem 2.1. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, we have
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, we have
where
![]() $\mathcal{P}(N)$
$\mathcal{P}(N)$
![]() $(N \in \mathbb{Z}^+)$
denotes an N-simplex on the first orthant of
$(N \in \mathbb{Z}^+)$
denotes an N-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
which is given by
$\mathbb{R}^{N+1}$
which is given by
Proof. The starting point of the proof is the global balance equations (1.1) for
![]() $\boldsymbol{\pi}^{(1)}(N)$
:
$\boldsymbol{\pi}^{(1)}(N)$
:
It then follows from (1.3) and (2.9) that
Because
![]() $\boldsymbol{\pi}^{(2)}(N)/\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}}>\textbf{0}$
and
$\boldsymbol{\pi}^{(2)}(N)/\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}}>\textbf{0}$
and
![]() $\textbf{\textit{Q}}^{(2,1)}(N) \geq \textbf{\textit{O}}$
,
$\textbf{\textit{Q}}^{(2,1)}(N) \geq \textbf{\textit{O}}$
,
![]() $\boldsymbol{\pi}(N)$
satisfies
$\boldsymbol{\pi}(N)$
satisfies
from which (2.6) with (2.7) follows.
Next, we show the equivalence between (2.7) and (2.8). We rewrite (2.7) as
 \begin{align*}&\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{\textit{y}},\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \textbf{\textit{y}} \textbf{\textit{H}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N) \textbf{\textit{e}}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}.\end{align*}
\begin{align*}&\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{\textit{y}},\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \textbf{\textit{y}} \textbf{\textit{H}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}\\&\quad =\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N) \textbf{\textit{e}}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\}.\end{align*}
Let
![]() $\boldsymbol{\alpha} = \textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
. Since
$\boldsymbol{\alpha} = \textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
. Since
![]() $\textbf{\textit{x}} =\boldsymbol{\alpha} \overline{\textbf{\textit{H}}}(N)$
, we have
$\textbf{\textit{x}} =\boldsymbol{\alpha} \overline{\textbf{\textit{H}}}(N)$
, we have
![]() $\textbf{\textit{x}}\textbf{\textit{e}} = \boldsymbol{\alpha}\textbf{\textit{e}}$
. Furthermore, if
$\textbf{\textit{x}}\textbf{\textit{e}} = \boldsymbol{\alpha}\textbf{\textit{e}}$
. Furthermore, if
![]() $\textbf{\textit{y}} \geq \textbf{0}$
, we have
$\textbf{\textit{y}} \geq \textbf{0}$
, we have
![]() $\boldsymbol{\alpha} =\textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N) \textbf{\textit{e}}) \geq \textbf{0}$
and vice versa, since
$\boldsymbol{\alpha} =\textbf{\textit{y}} \textrm{diag}(\textbf{\textit{H}}(N) \textbf{\textit{e}}) \geq \textbf{0}$
and vice versa, since
![]() $\textbf{\textit{H}}(N)\textbf{\textit{e}} > \textbf{0}$
. We thus have
$\textbf{\textit{H}}(N)\textbf{\textit{e}} > \textbf{0}$
. We thus have
Because
![]() $\overline{\textbf{\textit{H}}}(N)$
is composed of
$\overline{\textbf{\textit{H}}}(N)$
is composed of
![]() $N+1$
linearly independent probability vectors,
$N+1$
linearly independent probability vectors,
![]() $\mathcal{P}(N)$
is an N-simplex on the first orthant of
$\mathcal{P}(N)$
is an N-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
. □
$\mathbb{R}^{N+1}$
. □
Theorem 2.1 implies that the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
of any Markov chain in
$\boldsymbol{\pi}(N)$
of any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
is given by a convex combination of row vectors of
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
is given by a convex combination of row vectors of
![]() $\overline{\textbf{\textit{H}}}(N)$
; i.e., there exists
$\overline{\textbf{\textit{H}}}(N)$
; i.e., there exists
![]() $\boldsymbol{\alpha}^*(N)$
such that
$\boldsymbol{\alpha}^*(N)$
such that
Remark 2.1. Since
![]() $\overline{\textbf{\textit{H}}}(N)$
is nonsingular, there is a one-to-one correspondence between
$\overline{\textbf{\textit{H}}}(N)$
is nonsingular, there is a one-to-one correspondence between
![]() $\boldsymbol{\pi}(N)$
and
$\boldsymbol{\pi}(N)$
and
![]() $\boldsymbol{\alpha}^*(N)$
, i.e.,
$\boldsymbol{\alpha}^*(N)$
, i.e.,
![]() $\boldsymbol{\alpha}^*(N) = \boldsymbol{\pi}(N) (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textrm{diag}(\overline{\textbf{\textit{H}}}(N)\textbf{\textit{e}})$
. Consequently, obtaining the conditional stationary distribution
$\boldsymbol{\alpha}^*(N) = \boldsymbol{\pi}(N) (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textrm{diag}(\overline{\textbf{\textit{H}}}(N)\textbf{\textit{e}})$
. Consequently, obtaining the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
in an ergodic, continuous-time Markov chain is equivalent to obtaining the nonnegative weight vector
$\boldsymbol{\pi}(N)$
in an ergodic, continuous-time Markov chain is equivalent to obtaining the nonnegative weight vector
![]() $\boldsymbol{\alpha}^*(N)$
.
$\boldsymbol{\alpha}^*(N)$
.
The following corollary can be used to evaluate the accuracy of an approximation to
![]() $\boldsymbol{\pi}(N)$
.
$\boldsymbol{\pi}(N)$
.
Corollary 2.1. For an arbitrary probability vector
![]() $\textbf{\textit{x}} \in \Gamma(N)$
, we have
$\textbf{\textit{x}} \in \Gamma(N)$
, we have
where
![]() $\| \cdot \|_1$
stands for the
$\| \cdot \|_1$
stands for the
![]() $\ell_1$
norm and
$\ell_1$
norm and
![]() $\overline{\textbf{\textit{h}}}_i(N)$
(
$\overline{\textbf{\textit{h}}}_i(N)$
(
![]() $i \in \mathbb{Z}_0^N$
) denotes the ith row vector of
$i \in \mathbb{Z}_0^N$
) denotes the ith row vector of
![]() $\overline{\textbf{\textit{H}}}(N)$
. Furthermore, if
$\overline{\textbf{\textit{H}}}(N)$
. Furthermore, if
![]() $\textbf{\textit{x}} \in \mathcal{P}(N)$
, we have
$\textbf{\textit{x}} \in \mathcal{P}(N)$
, we have
Proof. (2.13) immediately follows from Theorem 2.1 and the convexity of
![]() $\mathcal{P}(N)$
. Furthermore, if
$\mathcal{P}(N)$
. Furthermore, if
![]() $\textbf{\textit{x}} \in \mathcal{P}(N)$
, there exists a probability vector
$\textbf{\textit{x}} \in \mathcal{P}(N)$
, there exists a probability vector
![]() $\boldsymbol{\beta}=(\beta_0\ \beta_1\ \cdots\ \beta_N) \in \Gamma(N)$
such that
$\boldsymbol{\beta}=(\beta_0\ \beta_1\ \cdots\ \beta_N) \in \Gamma(N)$
such that
from which (2.14) follows. □
We now provide a probabilistic interpretation of (2.12). We partition the state space
![]() $\mathbb{Z}^+$
into
$\mathbb{Z}^+$
into
![]() $\mathbb{Z}_0^N$
and
$\mathbb{Z}_0^N$
and
![]() $\mathbb{Z}_{N+1}^{\infty}$
and regard
$\mathbb{Z}_{N+1}^{\infty}$
and regard
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
as an alternating Markov renewal process. For an integer n, let
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
as an alternating Markov renewal process. For an integer n, let
![]() $T_n^{(1)}$
(resp.
$T_n^{(1)}$
(resp.
![]() $T_n^{(2)}$
) denote the nth time instant at which
$T_n^{(2)}$
) denote the nth time instant at which
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
enters into
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
enters into
![]() $\mathbb{Z}_0^N$
from
$\mathbb{Z}_0^N$
from
![]() $\mathbb{Z}_{N+1}^{\infty}$
(resp. into
$\mathbb{Z}_{N+1}^{\infty}$
(resp. into
![]() $\mathbb{Z}_{N+1}^{\infty}$
from
$\mathbb{Z}_{N+1}^{\infty}$
from
![]() $\mathbb{Z}_0^N$
), where we assume
$\mathbb{Z}_0^N$
), where we assume
![]() $T_n^{(1)} < T_n^{(2)} < T_{n+1}^{(1)}$
without loss of generality. We define I(t) (
$T_n^{(1)} < T_n^{(2)} < T_{n+1}^{(1)}$
without loss of generality. We define I(t) (
![]() $t \in (\!-\infty, \infty)$
) as the state at the last renewal epoch before time t, i.e.,
$t \in (\!-\infty, \infty)$
) as the state at the last renewal epoch before time t, i.e.,
 \begin{equation*}I(t)=\begin{cases}X(T_n^{(1)}),&T_n^{(1)} \leq t < T_n^{(2)},\\ X(T_n^{(2)}),&T_n^{(2)} \leq t
< T_{n+1}^{(1)}.\end{cases}\end{equation*}
\begin{equation*}I(t)=\begin{cases}X(T_n^{(1)}),&T_n^{(1)} \leq t < T_n^{(2)},\\ X(T_n^{(2)}),&T_n^{(2)} \leq t
< T_{n+1}^{(1)}.\end{cases}\end{equation*}
We then consider the joint process
![]() $\{(X(t),I(t))\}_{t \in (\!-\infty,\infty)}$
, which is assumed to be stationary.
$\{(X(t),I(t))\}_{t \in (\!-\infty,\infty)}$
, which is assumed to be stationary.
Corollary 2.2. For any Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
in
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, the (i,j)th
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, the (i,j)th
![]() $(i,j \in \mathbb{Z}_0^N)$
element of
$(i,j \in \mathbb{Z}_0^N)$
element of
![]() $\overline{\textbf{\textit{H}}}(N)$
is given by
$\overline{\textbf{\textit{H}}}(N)$
is given by
and the ith
![]() $(i \in \mathbb{Z}_0^N)$
element of
$(i \in \mathbb{Z}_0^N)$
element of
![]() $\boldsymbol{\alpha}^*(N)$
is given by
$\boldsymbol{\alpha}^*(N)$
is given by
We thus interpret (2.12) as
The proof of Corollary 2.2 is given in Appendix A. Note that for a given
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
,
$\textbf{\textit{Q}}^{(1,1)}(N)$
,
![]() $\mathcal{P}(N)$
in Theorem 2.1 may not be tight in
$\mathcal{P}(N)$
in Theorem 2.1 may not be tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
. For example,
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
. For example,
![]() $\mathcal{P}(N)$
may include
$\mathcal{P}(N)$
may include
![]() $\textbf{\textit{x}} \in\mathbb{R}^{N+1}$
such that
$\textbf{\textit{x}} \in\mathbb{R}^{N+1}$
such that
![]() $[\textbf{\textit{x}}]_i = 0$
for some
$[\textbf{\textit{x}}]_i = 0$
for some
![]() $i \in \mathbb{Z}_0^N$
, whereas
$i \in \mathbb{Z}_0^N$
, whereas
![]() $\boldsymbol{\pi}(N) > \textbf{0}$
since Markov chains in
$\boldsymbol{\pi}(N) > \textbf{0}$
since Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
are ergodic. In the next subsection, we eliminate redundancy in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
are ergodic. In the next subsection, we eliminate redundancy in
![]() $\mathcal{P}(N)$
using the structural information
$\mathcal{P}(N)$
using the structural information
![]() $\mathcal{J}(N)$
in (1.4).
$\mathcal{J}(N)$
in (1.4).
2.3. Characterization of
 $\boldsymbol{\pi}(\textbf{\textit{N}})$
in terms of
$\boldsymbol{\pi}(\textbf{\textit{N}})$
in terms of
 $\textbf{\textit{Q}}^{(1,1)}(\textbf{\textit{N}})$
and
$\textbf{\textit{Q}}^{(1,1)}(\textbf{\textit{N}})$
and
 $\mathcal{J}(\textbf{\textit{N}})$
$\mathcal{J}(\textbf{\textit{N}})$
For specific
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
and
$\textbf{\textit{Q}}^{(1,1)}(N)$
and
![]() $\mathcal{J}(N)$
, we define
$\mathcal{J}(N)$
, we define
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
as the collection of ergodic, continuous-time Markov chains on
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
as the collection of ergodic, continuous-time Markov chains on
![]() $\mathbb{Z}^+$
whose infinitesimal generators have
$\mathbb{Z}^+$
whose infinitesimal generators have
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
and
$\textbf{\textit{Q}}^{(1,1)}(N)$
and
![]() $\mathcal{J}(N)$
. By definition,
$\mathcal{J}(N)$
. By definition,
Note here that
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
may be empty for some pairs of
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
may be empty for some pairs of
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
and
$\textbf{\textit{Q}}^{(1,1)}(N)$
and
![]() $\mathcal{J}(N)$
. For example, if
$\mathcal{J}(N)$
. For example, if
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
is a diagonal matrix,
$\textbf{\textit{Q}}^{(1,1)}(N)$
is a diagonal matrix,
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N)) = \emptyset$
unless
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N)) = \emptyset$
unless
![]() $\mathcal{J}(N) = \mathbb{Z}_0^N$
, owing to ergodicity. In the rest of this subsection, we assume that if
$\mathcal{J}(N) = \mathbb{Z}_0^N$
, owing to ergodicity. In the rest of this subsection, we assume that if
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N)) \neq \emptyset$
, then
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N)) \neq \emptyset$
, then
![]() $\mathcal{J}(N)=\{0,1,\dots,|\mathcal{J}(N)|-1\}$
without loss of generality.
$\mathcal{J}(N)=\{0,1,\dots,|\mathcal{J}(N)|-1\}$
without loss of generality.
If
![]() $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
, we partition
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
, we partition
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
and
$\textbf{\textit{Q}}^{(1,1)}(N)$
and
![]() $\textbf{\textit{Q}}^{(2,1)}(N)$
in (2.3) into two matrices:
$\textbf{\textit{Q}}^{(2,1)}(N)$
in (2.3) into two matrices:
 \begin{align}\begin{pmatrix}\textbf{\textit{Q}}^{(1,1)}(N)\\ \\[-5pt] \textbf{\textit{Q}}^{(2,1)}(N)\end{pmatrix}=\kbordermatrix{& \mathcal{J}(N) & \mathbb{Z}_0^N \setminus \mathcal{J}(N)\\ \\[-5pt] \mathbb{Z}_0^N & \textbf{\textit{Q}}_+^{(1,1)}(N) &\quad \textbf{\textit{Q}}_0^{(1,1)}(N)\\ \\[-5pt] \mathbb{Z}_{N+1}^{\infty} & \textbf{\textit{Q}}_+^{(2,1)}(N) &\quad \textbf{\textit{O}}}.\end{align}
\begin{align}\begin{pmatrix}\textbf{\textit{Q}}^{(1,1)}(N)\\ \\[-5pt] \textbf{\textit{Q}}^{(2,1)}(N)\end{pmatrix}=\kbordermatrix{& \mathcal{J}(N) & \mathbb{Z}_0^N \setminus \mathcal{J}(N)\\ \\[-5pt] \mathbb{Z}_0^N & \textbf{\textit{Q}}_+^{(1,1)}(N) &\quad \textbf{\textit{Q}}_0^{(1,1)}(N)\\ \\[-5pt] \mathbb{Z}_{N+1}^{\infty} & \textbf{\textit{Q}}_+^{(2,1)}(N) &\quad \textbf{\textit{O}}}.\end{align}
(2.10) is then rewritten as
 \begin{align}\boldsymbol{\pi}(N)\cdot\kbordermatrix{& \mathcal{J}(N) &\quad \mathbb{Z}_0^N \setminus \mathcal{J}(N)\\ \\[-5pt]& -\textbf{\textit{Q}}_+^{(1,1)}(N)&\quad -\textbf{\textit{Q}}_0^{(1,1)}(N)}=\kbordermatrix{& \mathcal{J}(N)&\quad \hbox to 7mm{\hss$\scriptstyle \mathbb{Z}_0^N \setminus \mathcal{J}(N)$\hss}\\ \\[-5pt]&\displaystyle\frac{\boldsymbol{\pi}^{(2)}(N)}{\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}}} \cdot \textbf{\textit{Q}}_+^{(2,1)}(N)&\quad \textbf{0}}.\end{align}
\begin{align}\boldsymbol{\pi}(N)\cdot\kbordermatrix{& \mathcal{J}(N) &\quad \mathbb{Z}_0^N \setminus \mathcal{J}(N)\\ \\[-5pt]& -\textbf{\textit{Q}}_+^{(1,1)}(N)&\quad -\textbf{\textit{Q}}_0^{(1,1)}(N)}=\kbordermatrix{& \mathcal{J}(N)&\quad \hbox to 7mm{\hss$\scriptstyle \mathbb{Z}_0^N \setminus \mathcal{J}(N)$\hss}\\ \\[-5pt]&\displaystyle\frac{\boldsymbol{\pi}^{(2)}(N)}{\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}}} \cdot \textbf{\textit{Q}}_+^{(2,1)}(N)&\quad \textbf{0}}.\end{align}
We define
![]() $\Gamma^+(N)$
as
$\Gamma^+(N)$
as
Theorem 2.2. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, we have
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, we have
where
![]() $\mathcal{P}^+(N)$
$\mathcal{P}^+(N)$
![]() $(N \in \mathbb{Z}^+)$
denotes a
$(N \in \mathbb{Z}^+)$
denotes a
![]() $(|\mathcal{J}(N)|-1)$
-simplex on the first orthant of
$(|\mathcal{J}(N)|-1)$
-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
which is given by
$\mathbb{R}^{N+1}$
which is given by
![]() $\mathcal{P}^+(N) = \mathcal{P}(N)$
if
$\mathcal{P}^+(N) = \mathcal{P}(N)$
if
![]() $\mathcal{J}(N) = \mathbb{Z}_0^N$
, and by
$\mathcal{J}(N) = \mathbb{Z}_0^N$
, and by
otherwise.
Proof. If
![]() $\mathcal{J}(N)=\mathbb{Z}_0^N$
, we have
$\mathcal{J}(N)=\mathbb{Z}_0^N$
, we have
![]() $\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}^{(2,1)}(N) >\textbf{0}$
since
$\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}^{(2,1)}(N) >\textbf{0}$
since
![]() $\boldsymbol{\pi}^{(2)}(N) > \textbf{0}$
. Theorem 2.2 for
$\boldsymbol{\pi}^{(2)}(N) > \textbf{0}$
. Theorem 2.2 for
![]() $\mathcal{J}(N)=\mathbb{Z}_0^N$
then follows from (2.2), (2.10), and Theorem 2.1. On the other hand, if
$\mathcal{J}(N)=\mathbb{Z}_0^N$
then follows from (2.2), (2.10), and Theorem 2.1. On the other hand, if
![]() $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
, then
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
, then
![]() $\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}_+^{(2,1)}(N) > \textbf{0}$
. In this case, (2.21) with (2.22) follows from (2.2) and (2.19). The equivalence between (2.22) and (2.23) for
$\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}_+^{(2,1)}(N) > \textbf{0}$
. In this case, (2.21) with (2.22) follows from (2.2) and (2.19). The equivalence between (2.22) and (2.23) for
![]() $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
can be shown in a way similar to the proof of Theorem 2.1, as shown in Appendix B. Since
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
can be shown in a way similar to the proof of Theorem 2.1, as shown in Appendix B. Since
![]() $\overline{\textbf{\textit{H}}}(N)$
is nonnegative and nonsingular,
$\overline{\textbf{\textit{H}}}(N)$
is nonnegative and nonsingular,
![]() $\mathcal{P}^+(N)$
is a
$\mathcal{P}^+(N)$
is a
![]() $(|\mathcal{J}(N)|-1)$
-simplex on the first orthant of
$(|\mathcal{J}(N)|-1)$
-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
. □
$\mathbb{R}^{N+1}$
. □
By definition, we have
![]() $\Gamma^+(N)\subseteq \Gamma(N)$
, and therefore
$\Gamma^+(N)\subseteq \Gamma(N)$
, and therefore
where
![]() $\mathcal{P}^+(N) = \mathcal{P}(N)$
iff
$\mathcal{P}^+(N) = \mathcal{P}(N)$
iff
![]() $\mathcal{J}(N) = \mathbb{Z}_0^N$
. Theorem 2.2 indicates the importance of the structural information
$\mathcal{J}(N) = \mathbb{Z}_0^N$
. Theorem 2.2 indicates the importance of the structural information
![]() $\mathcal{J}(N)$
about direct transitions from
$\mathcal{J}(N)$
about direct transitions from
![]() $\mathbb{Z}_{N+1}^{\infty}$
to
$\mathbb{Z}_{N+1}^{\infty}$
to
![]() $\mathbb{Z}_0^N$
. For example, if
$\mathbb{Z}_0^N$
. For example, if
![]() $\mathcal{J}(N)$
is a singleton for a certain N, say,
$\mathcal{J}(N)$
is a singleton for a certain N, say,
![]() $\mathcal{J}(N)=\{i\}$
(
$\mathcal{J}(N)=\{i\}$
(
![]() $i \in \mathbb{Z}_0^N$
),
$i \in \mathbb{Z}_0^N$
),
![]() $\boldsymbol{\pi}(N)$
is given by the ith row vector of
$\boldsymbol{\pi}(N)$
is given by the ith row vector of
![]() $\overline{\textbf{\textit{H}}}(N)$
, as pointed out in [16, Corollary 3]. Numerical algorithms for block-structured Markov chains of level-dependent M/G/1-type in [Reference Kimura and Takine5, Reference Takine15] also utilize (2.21) with (2.22) implicitly.
$\overline{\textbf{\textit{H}}}(N)$
, as pointed out in [16, Corollary 3]. Numerical algorithms for block-structured Markov chains of level-dependent M/G/1-type in [Reference Kimura and Takine5, Reference Takine15] also utilize (2.21) with (2.22) implicitly.
The corollary below follows from Theorem 2.2; its proof is omitted because it is almost the same as that of Corollary 2.1.
Corollary 2.3. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For an arbitrary probability vector
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For an arbitrary probability vector
![]() $\textbf{\textit{x}} \in \Gamma(N)$
, we have
$\textbf{\textit{x}} \in \Gamma(N)$
, we have
Furthermore, if
![]() $\textbf{\textit{x}} \in \mathcal{P}^+(N)$
, we have
$\textbf{\textit{x}} \in \mathcal{P}^+(N)$
, we have
Example 2.1. Consider an ergodic, level-dependent M
![]() ${}^{\text{X}}\!$
/M/1 queue with disasters, whose infinitesimal generator
${}^{\text{X}}\!$
/M/1 queue with disasters, whose infinitesimal generator
![]() $\textbf{\textit{Q}}$
takes the following form:
$\textbf{\textit{Q}}$
takes the following form:
 \begin{equation}\textbf{\textit{Q}}=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}-q_0 & q_{0,1} & q_{0,2} & q_{0,3} & q_{0,4} & q_{0,5} & \dots\\ \\[-7pt] q_{1,0} & -q_1 & q_{1,2} & q_{1,3} & q_{1,4} & q_{1,5} & \dots\\ \\[-7pt] q_{2,0} & q_{2,1} & -q_2 & q_{2,3} & q_{2,4} & q_{2,5} & \dots\\ \\[-7pt] q_{3,0} & 0 & q_{3,2} & -q_3 & q_{3,4} & q_{3,5} & \dots\\ \\[-7pt] q_{4,0} & 0 & 0 & q_{4,3} & -q_4 & q_{4,5} & \dots\\ \\[-7pt] q_{5,0} & 0 & 0 & 0 & q_{5,4} & -q_5 & \dots\\ \\[-7pt] \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\end{array}\right),\notag\end{equation}
\begin{equation}\textbf{\textit{Q}}=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}-q_0 & q_{0,1} & q_{0,2} & q_{0,3} & q_{0,4} & q_{0,5} & \dots\\ \\[-7pt] q_{1,0} & -q_1 & q_{1,2} & q_{1,3} & q_{1,4} & q_{1,5} & \dots\\ \\[-7pt] q_{2,0} & q_{2,1} & -q_2 & q_{2,3} & q_{2,4} & q_{2,5} & \dots\\ \\[-7pt] q_{3,0} & 0 & q_{3,2} & -q_3 & q_{3,4} & q_{3,5} & \dots\\ \\[-7pt] q_{4,0} & 0 & 0 & q_{4,3} & -q_4 & q_{4,5} & \dots\\ \\[-7pt] q_{5,0} & 0 & 0 & 0 & q_{5,4} & -q_5 & \dots\\ \\[-7pt] \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\end{array}\right),\notag\end{equation}
where
![]() $q_{i,0} > 0$
and
$q_{i,0} > 0$
and
![]() $q_{i,i-1} > 0$
(
$q_{i,i-1} > 0$
(
![]() $i \in \mathbb{Z}^+ \setminus\{0\}$
). We then have
$i \in \mathbb{Z}^+ \setminus\{0\}$
). We then have
because the state immediately after a downward transition from state i (
![]() $i \geq N+1$
) is either state 0 or state
$i \geq N+1$
) is either state 0 or state
![]() $i-1$
. It then follows that
$i-1$
. It then follows that
and
Note here that
![]() $\overline{\textbf{\textit{h}}}_i(N)$
(
$\overline{\textbf{\textit{h}}}_i(N)$
(
![]() $i \in \mathbb{Z}_0^N$
) can be obtained by (i) solving
$i \in \mathbb{Z}_0^N$
) can be obtained by (i) solving
![]() $\textbf{\textit{x}}_i (\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{\textit{e}}_i(N)$
for
$\textbf{\textit{x}}_i (\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{\textit{e}}_i(N)$
for
![]() $\textbf{\textit{x}}_i \in \mathbb{R}^{N+1}$
and (ii) letting
$\textbf{\textit{x}}_i \in \mathbb{R}^{N+1}$
and (ii) letting
![]() $\overline{\textbf{\textit{h}}}_i(N)=\textbf{\textit{x}}_i/\textbf{\textit{x}}_i\textbf{\textit{e}}$
, where
$\overline{\textbf{\textit{h}}}_i(N)=\textbf{\textit{x}}_i/\textbf{\textit{x}}_i\textbf{\textit{e}}$
, where
![]() $\textbf{\textit{e}}_i(N) \in \mathbb{R}^{N+1}$
denotes a
$\textbf{\textit{e}}_i(N) \in \mathbb{R}^{N+1}$
denotes a
![]() $1 \times (N+1)$
unit vector whose ith element is equal to one. The simplest way to obtain an approximation
$1 \times (N+1)$
unit vector whose ith element is equal to one. The simplest way to obtain an approximation
![]() $\boldsymbol{\pi}^{\textrm{approx}}(N) \in\textrm{ri}\, \mathcal{P}^+(N)$
to
$\boldsymbol{\pi}^{\textrm{approx}}(N) \in\textrm{ri}\, \mathcal{P}^+(N)$
to
![]() $\boldsymbol{\pi}(N)$
might be to solve
$\boldsymbol{\pi}(N)$
might be to solve
![]() $\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}) = \beta_0 \textbf{\textit{e}}_0(N)+ (1-\beta_0) \textbf{\textit{e}}_N(N)$
for an arbitrary
$\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}) = \beta_0 \textbf{\textit{e}}_0(N)+ (1-\beta_0) \textbf{\textit{e}}_N(N)$
for an arbitrary
![]() $\beta_0 \in (0,1)$
and let
$\beta_0 \in (0,1)$
and let
![]() $\boldsymbol{\pi}^{\textrm{approx}}(N) = \textbf{\textit{x}}/\textbf{\textit{x}}\textbf{\textit{e}}$
.
$\boldsymbol{\pi}^{\textrm{approx}}(N) = \textbf{\textit{x}}/\textbf{\textit{x}}\textbf{\textit{e}}$
.
We now show that
![]() $\mathcal{P}^+(N)$
is tight in
$\mathcal{P}^+(N)$
is tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
.
Lemma 2.1. If
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
and
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
and
![]() $\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(N)$
, we have
$\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(N)$
, we have
![]() $\textbf{\textit{x}} > \textbf{0}$
.
$\textbf{\textit{x}} > \textbf{0}$
.
Proof. We assume
![]() $[\textbf{\textit{x}}]_{j^*} = 0$
for some
$[\textbf{\textit{x}}]_{j^*} = 0$
for some
![]() $j^* \in \mathbb{Z}_0^N$
and derive a contradiction. Since
$j^* \in \mathbb{Z}_0^N$
and derive a contradiction. Since
![]() $\textbf{\textit{x}} = \boldsymbol{\alpha}(\textbf{\textit{x}})\overline{\textbf{\textit{H}}}(N)$
for some
$\textbf{\textit{x}} = \boldsymbol{\alpha}(\textbf{\textit{x}})\overline{\textbf{\textit{H}}}(N)$
for some
![]() $\boldsymbol{\alpha}(\textbf{\textit{x}}) \in\textrm{ri}\, \Gamma^+(N)$
,
$\boldsymbol{\alpha}(\textbf{\textit{x}}) \in\textrm{ri}\, \Gamma^+(N)$
,
![]() $[\textbf{\textit{x}}]_{j^*} = 0$
is equivalent to
$[\textbf{\textit{x}}]_{j^*} = 0$
is equivalent to
![]() $[\boldsymbol{\alpha}(\textbf{\textit{x}}) \overline{\textbf{\textit{H}}}(N)]_{j^*} = 0$
for some
$[\boldsymbol{\alpha}(\textbf{\textit{x}}) \overline{\textbf{\textit{H}}}(N)]_{j^*} = 0$
for some
![]() $\boldsymbol{\alpha}(\textbf{\textit{x}}) \in \textrm{ri}\, \Gamma^+(N)$
. This implies that
$\boldsymbol{\alpha}(\textbf{\textit{x}}) \in \textrm{ri}\, \Gamma^+(N)$
. This implies that
![]() $[\overline{\textbf{\textit{H}}}(N)]_{i,j^*} = 0$
for all
$[\overline{\textbf{\textit{H}}}(N)]_{i,j^*} = 0$
for all
![]() $i \in \mathcal{J}(N)$
since
$i \in \mathcal{J}(N)$
since
![]() $[\boldsymbol{\alpha}(\textbf{\textit{x}})]_i > 0$
for all
$[\boldsymbol{\alpha}(\textbf{\textit{x}})]_i > 0$
for all
![]() $i \in \mathcal{J}(N)$
and
$i \in \mathcal{J}(N)$
and
![]() $\overline{\textbf{\textit{H}}}(N) \geq \textbf{\textit{O}}$
. It then follows from (2.15) that
$\overline{\textbf{\textit{H}}}(N) \geq \textbf{\textit{O}}$
. It then follows from (2.15) that
![]() $\mathbb{P}(X(0) = j^* \mid I(0) \in \mathcal{J}(N)) = 0$
for any Markov chain in
$\mathbb{P}(X(0) = j^* \mid I(0) \in \mathcal{J}(N)) = 0$
for any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
. Furthermore,
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
. Furthermore,
![]() $\mathbb{P}(I(0) \in \mathbb{Z}_0^N \setminus \mathcal{J}(N)) = 0$
and
$\mathbb{P}(I(0) \in \mathbb{Z}_0^N \setminus \mathcal{J}(N)) = 0$
and
![]() $\mathbb{P}(X(0) = j^* \mid I(0) \in \mathbb{Z}_{N+1}^{\infty}) = 0$
by definition. We thus have
$\mathbb{P}(X(0) = j^* \mid I(0) \in \mathbb{Z}_{N+1}^{\infty}) = 0$
by definition. We thus have
 \begin{align*}\mathbb{P}(X(0)=j^*)&=\mathbb{P}(I(0) \in \mathcal{J}(N)) \mathbb{P}(X(0)=j^* \mid I(0) \in \mathcal{J}(N))\\[3pt] & \qquad\qquad {}+\mathbb{P}(I(0) \in \mathbb{Z}_{N+1}^{\infty})\mathbb{P}(X(0) = j^* \mid I(0) \in \mathbb{Z}_{N+1}^{\infty})\\[3pt] &= 0,\end{align*}
\begin{align*}\mathbb{P}(X(0)=j^*)&=\mathbb{P}(I(0) \in \mathcal{J}(N)) \mathbb{P}(X(0)=j^* \mid I(0) \in \mathcal{J}(N))\\[3pt] & \qquad\qquad {}+\mathbb{P}(I(0) \in \mathbb{Z}_{N+1}^{\infty})\mathbb{P}(X(0) = j^* \mid I(0) \in \mathbb{Z}_{N+1}^{\infty})\\[3pt] &= 0,\end{align*}
for any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, which contradicts the ergodicity. □
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, which contradicts the ergodicity. □
Theorem 2.3. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
, there exists a Markov chain in
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
, there exists a Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
whose
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
whose
![]() $\boldsymbol{\pi}(N)$
is given by
$\boldsymbol{\pi}(N)$
is given by
![]() $\textbf{\textit{x}}$
.
$\textbf{\textit{x}}$
.
Proof. It follows from (2.24) that if
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
, we have
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
, we have
![]() $\textbf{\textit{x}} \in \mathcal{P}(N)$
, i.e.,
$\textbf{\textit{x}} \in \mathcal{P}(N)$
, i.e.,
![]() $\textbf{\textit{x}} (\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq\textbf{0}$
and
$\textbf{\textit{x}} (\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq\textbf{0}$
and
![]() $\textbf{\textit{x}}\textbf{\textit{e}}=1$
. Note also that
$\textbf{\textit{x}}\textbf{\textit{e}}=1$
. Note also that
![]() $\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \neq \textbf{0}$
, because if
$\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \neq \textbf{0}$
, because if
![]() $\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{0}$
held, we would have
$\textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) = \textbf{0}$
held, we would have
![]() $\textbf{\textit{x}}= \textbf{0}\cdot (\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1} = \textbf{0}$
, which contradicts
$\textbf{\textit{x}}= \textbf{0}\cdot (\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1} = \textbf{0}$
, which contradicts
![]() $\textbf{\textit{x}}\textbf{\textit{e}}=1$
. We then define
$\textbf{\textit{x}}\textbf{\textit{e}}=1$
. We then define
![]() $\boldsymbol{\zeta}(\textbf{\textit{x}})$
as
$\boldsymbol{\zeta}(\textbf{\textit{x}})$
as
It is easy to see that
![]() $\boldsymbol{\zeta}(\textbf{\textit{x}}) \in \textrm{ri}\, \Gamma^+(N)$
for
$\boldsymbol{\zeta}(\textbf{\textit{x}}) \in \textrm{ri}\, \Gamma^+(N)$
for
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
. For an arbitrarily chosen
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(N)$
. For an arbitrarily chosen
![]() $\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(N)$
, we consider a Markov chain whose infinitesimal generator
$\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(N)$
, we consider a Markov chain whose infinitesimal generator
![]() $\textbf{\textit{Q}}$
is given by
$\textbf{\textit{Q}}$
is given by
 \begin{equation}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^N & \mathbb{Z}_{N+1}^{\infty}\\ \\[-7pt]\mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N)\\ \\[-7pt] \mathbb{Z}_{N+1}^{\infty}& (\!-\textbf{\textit{Q}}^{(2,2)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}}) &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation}
\begin{equation}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^N & \mathbb{Z}_{N+1}^{\infty}\\ \\[-7pt]\mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N)\\ \\[-7pt] \mathbb{Z}_{N+1}^{\infty}& (\!-\textbf{\textit{Q}}^{(2,2)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}}) &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation}
The global balance equations are then given by
From (2.25) and (2.27), we observe that the special form of
![]() $\textbf{\textit{Q}}^{(2,1)}(N) =(\!-\textbf{\textit{Q}}^{(2,2)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}})$
ensures
$\textbf{\textit{Q}}^{(2,1)}(N) =(\!-\textbf{\textit{Q}}^{(2,2)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}})$
ensures
![]() $\boldsymbol{\pi}^{(1)}(N) = c_1 \textbf{\textit{x}}$
for some positive constant
$\boldsymbol{\pi}^{(1)}(N) = c_1 \textbf{\textit{x}}$
for some positive constant
![]() $c_1$
. We now set
$c_1$
. We now set
where
![]() $\textbf{\textit{z}}$
denotes a
$\textbf{\textit{z}}$
denotes a
![]() $1 \times \infty$
positive probability vector. Equation (2.28) is then reduced to
$1 \times \infty$
positive probability vector. Equation (2.28) is then reduced to
which indicates that (2.29) ensures
![]() $\boldsymbol{\pi}^{(2)}(N) = c_2 \textbf{\textit{z}} > \textbf{0}$
for some positive constant
$\boldsymbol{\pi}^{(2)}(N) = c_2 \textbf{\textit{z}} > \textbf{0}$
for some positive constant
![]() $c_2$
. In fact, solving (2.27) and (2.30) with
$c_2$
. In fact, solving (2.27) and (2.30) with
![]() $\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}} +\boldsymbol{\pi}^{(2)}(N)\textbf{\textit{e}} = 1$
, we obtain
$\boldsymbol{\pi}^{(1)}(N)\textbf{\textit{e}} +\boldsymbol{\pi}^{(2)}(N)\textbf{\textit{e}} = 1$
, we obtain
We thus conclude that the Markov chain with the infinitesimal generator
![]() $\textbf{\textit{Q}}$
defined by (2.26) and (2.29) is a member of
$\textbf{\textit{Q}}$
defined by (2.26) and (2.29) is a member of
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
and it has
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N),\mathcal{J}(N))$
and it has
![]() $\boldsymbol{\pi}(N) = \textbf{\textit{x}}$
. □
$\boldsymbol{\pi}(N) = \textbf{\textit{x}}$
. □
Example 2.2. (Example 2.1 continued.) Consider
![]() $\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Theorem 2.2 implies that there exists
$\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Theorem 2.2 implies that there exists
![]() $\alpha_0 = \alpha_0^* \in (0,1)$
such that
$\alpha_0 = \alpha_0^* \in (0,1)$
such that
![]() $\boldsymbol{\pi}(N) = \alpha_0^* \overline{\textbf{\textit{h}}}_0(N) + (1-\alpha_0^*)\overline{\textbf{\textit{h}}}_N(N)$
. As stated in Theorem 2.3, however,
$\boldsymbol{\pi}(N) = \alpha_0^* \overline{\textbf{\textit{h}}}_0(N) + (1-\alpha_0^*)\overline{\textbf{\textit{h}}}_N(N)$
. As stated in Theorem 2.3, however,
![]() $\textrm{ri}\, \mathcal{P}^+(N)$
is tight in
$\textrm{ri}\, \mathcal{P}^+(N)$
is tight in
![]() $\mathcal{M}( \textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
. Therefore, we cannot identify the exact
$\mathcal{M}( \textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
. Therefore, we cannot identify the exact
![]() $\alpha_0^* \in (0, 1)$
if only
$\alpha_0^* \in (0, 1)$
if only
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
and
$\textbf{\textit{Q}}^{(1,1)}(N)$
and
![]() $\mathcal{J}(N)=\{0,N\}$
are available.
$\mathcal{J}(N)=\{0,N\}$
are available.
2.4. Implications for the augmented truncation approximation
We provide some practical implications of the results in Sections 2.2 and 2.3 for the augmented truncation approximation (ATA). As mentioned in Section 1, an ATA solution
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N)$
to
$\boldsymbol{\pi}^{\textrm{trunc}}(N)$
to
![]() $\boldsymbol{\pi}(N)$
is obtained by
$\boldsymbol{\pi}(N)$
is obtained by
where
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
denotes an augmentation matrix, i.e., an
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
denotes an augmentation matrix, i.e., an
![]() $(N+1) \times (N+1)$
nonnegative matrix satisfying
$(N+1) \times (N+1)$
nonnegative matrix satisfying
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)\textbf{\textit{e}} = (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}}$
. The central topic in the literature on the ATA is the convergence of
$\textbf{\textit{Q}}_{\textrm{A}}(N)\textbf{\textit{e}} = (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}}$
. The central topic in the literature on the ATA is the convergence of
![]() $\boldsymbol{\pi}^{\textrm{approx},N}=(\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
to the stationary distribution
$\boldsymbol{\pi}^{\textrm{approx},N}=(\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
to the stationary distribution
![]() $\boldsymbol{\pi}$
as N goes to infinity. Note that our interest is different from this; that is to say, we are interested in what kind of
$\boldsymbol{\pi}$
as N goes to infinity. Note that our interest is different from this; that is to say, we are interested in what kind of
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
is reasonable for a given N.
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
is reasonable for a given N.
Although
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
is usually chosen in such a way that
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
is usually chosen in such a way that
![]() $[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)]$
is irreducible, we allow reducible
$[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)]$
is irreducible, we allow reducible
![]() $[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)]$
as well. Note that the error bound for the approximation
$[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)]$
as well. Note that the error bound for the approximation
![]() $\boldsymbol{\pi}^{\textrm{approx},N} =(\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
to the stationary distribution
$\boldsymbol{\pi}^{\textrm{approx},N} =(\boldsymbol{\pi}^{\textrm{trunc}}(N)\ \ \textbf{0})$
to the stationary distribution
![]() $\boldsymbol{\pi}$
is given by
$\boldsymbol{\pi}$
is given by
(see [Reference Kimura and Takine5]), where
![]() $\epsilon^{\textrm{trunc}}(N)$
denotes an upper bound of
$\epsilon^{\textrm{trunc}}(N)$
denotes an upper bound of
![]() $\| \boldsymbol{\pi}^{\textrm{trunc}}(N) - \boldsymbol{\pi}(N)\|_1$
:
$\| \boldsymbol{\pi}^{\textrm{trunc}}(N) - \boldsymbol{\pi}(N)\|_1$
:
It is clear that
![]() $\mathbb{P}(X(0) > N)$
is a decreasing function of N and that for a given N,
$\mathbb{P}(X(0) > N)$
is a decreasing function of N and that for a given N,
![]() $\boldsymbol{\pi}^{\textrm{approx},N}$
will be the best approximation to
$\boldsymbol{\pi}^{\textrm{approx},N}$
will be the best approximation to
![]() $\boldsymbol{\pi}$
when
$\boldsymbol{\pi}$
when
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N) = \boldsymbol{\pi}(N)$
(i.e.,
$\boldsymbol{\pi}^{\textrm{trunc}}(N) = \boldsymbol{\pi}(N)$
(i.e.,
![]() $\epsilon^{\textrm{trunc}}(N) = 0$
) [Reference Zhao and Liu16]. In what follows, we first consider Markov chains in
$\epsilon^{\textrm{trunc}}(N) = 0$
) [Reference Zhao and Liu16]. In what follows, we first consider Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
and discuss some implications of our results in Section 2.2 for the ATA.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
and discuss some implications of our results in Section 2.2 for the ATA.
We define
![]() $\mathcal{T}(N)$
as the set of all possible ATA solutions satisfying (2.31):
$\mathcal{T}(N)$
as the set of all possible ATA solutions satisfying (2.31):
where
![]() $\mathcal{A}(N)$
denotes the set of all possible augmentation matrices,
$\mathcal{A}(N)$
denotes the set of all possible augmentation matrices,
In the literature, the ATA is called linear if the rank of
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
is equal to one [Reference Gibson and Seneta2]. We then define
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
is equal to one [Reference Gibson and Seneta2]. We then define
![]() $\mathcal{T}_{\textrm{L}}(N)$
as the set of all possible approximations obtained by the linear ATA:
$\mathcal{T}_{\textrm{L}}(N)$
as the set of all possible approximations obtained by the linear ATA:
where
![]() $\mathcal{A}_{\textrm{L}}(N)$
denotes the set of all possible linear augmentation matrices,
$\mathcal{A}_{\textrm{L}}(N)$
denotes the set of all possible linear augmentation matrices,
Recall that
![]() $\Gamma(N)$
is the set of all
$\Gamma(N)$
is the set of all
![]() $1 \times (N+1)$
probability vectors, which is defined in (2.5).
$1 \times (N+1)$
probability vectors, which is defined in (2.5).
Lemma 2.2. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, we have
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N))$
, we have
where
![]() $\mathcal{P}(N)$
is given by (2.8).
$\mathcal{P}(N)$
is given by (2.8).
The proof of Lemma 2.2 is given in Appendix C. Lemma 2.2 implies the following.
Implication 2.1. In view of Remark 2.1, we can consider that the ATA attempts to find an approximation to the weight vector
![]() $\boldsymbol{\alpha}^*(N)$
for
$\boldsymbol{\alpha}^*(N)$
for
![]() $\overline{\textbf{\textit{H}}}(N)$
in (2.12) by setting the augmentation matrix
$\overline{\textbf{\textit{H}}}(N)$
in (2.12) by setting the augmentation matrix
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)$
appropriately. In this sense, the linear ATA has the same degree of freedom as the general ATA does.
$\textbf{\textit{Q}}_{\textrm{A}}(N)$
appropriately. In this sense, the linear ATA has the same degree of freedom as the general ATA does.
We thus restrict our attention to the linear ATA with
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N)= (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}$
, where
$\textbf{\textit{Q}}_{\textrm{A}}(N)= (\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}$
, where
![]() $\boldsymbol{\zeta} \in\Gamma(N)$
. In this case, (2.31) is reduced to
$\boldsymbol{\zeta} \in\Gamma(N)$
. In this case, (2.31) is reduced to
Note here that
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
in (2.32) is closely related to
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
in (2.32) is closely related to
![]() $\boldsymbol{\pi}(N)$
in a Markov chain with the infinitesimal generator
$\boldsymbol{\pi}(N)$
in a Markov chain with the infinitesimal generator
![]() $\textbf{\textit{Q}}$
in (2.26). Specifically, using the cut-flow balance equation
$\textbf{\textit{Q}}$
in (2.26). Specifically, using the cut-flow balance equation
we can rewrite (2.27) to be
We thus have
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) = \boldsymbol{\pi}(N) =\textbf{\textit{x}}\in \mathcal{P}(N)$
if we set
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) = \boldsymbol{\pi}(N) =\textbf{\textit{x}}\in \mathcal{P}(N)$
if we set
![]() $\boldsymbol{\zeta} = \boldsymbol{\zeta}(\textbf{\textit{x}})$
in (2.32).
$\boldsymbol{\zeta} = \boldsymbol{\zeta}(\textbf{\textit{x}})$
in (2.32).
Implication 2.2. The linear ATA solution
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
for a specific
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
for a specific
![]() $\boldsymbol{\zeta}$
is identical to
$\boldsymbol{\zeta}$
is identical to
![]() $\boldsymbol{\pi}(N)$
in an ergodic Markov chain whose infinitesimal generator takes the following form:
$\boldsymbol{\pi}(N)$
in an ergodic Markov chain whose infinitesimal generator takes the following form:
 \begin{equation*}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^N & \mathbb{Z}_{N+1}^{\infty}\\ \\[-7pt]\mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N) \\ \\[-7pt] \mathbb{Z}_{N+1}^{\infty}& (\!-\textbf{\textit{Q}}^{(2,2)}(N)\textbf{\textit{e}}) \boldsymbol{\zeta} &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation*}
\begin{equation*}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^N & \mathbb{Z}_{N+1}^{\infty}\\ \\[-7pt]\mathbb{Z}_0^N & \textbf{\textit{Q}}^{(1,1)}(N) &\quad \textbf{\textit{Q}}^{(1,2)}(N) \\ \\[-7pt] \mathbb{Z}_{N+1}^{\infty}& (\!-\textbf{\textit{Q}}^{(2,2)}(N)\textbf{\textit{e}}) \boldsymbol{\zeta} &\quad \textbf{\textit{Q}}^{(2,2)}(N)}.\end{equation*}
Since
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \in \mathcal{T}_{\textrm{L}}(N) = \mathcal{P}(N)$
, it follows from Theorem 2.1 that
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \in \mathcal{T}_{\textrm{L}}(N) = \mathcal{P}(N)$
, it follows from Theorem 2.1 that
for some
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \in \Gamma(N)$
. Recall that there is a one-to-one correspondence between
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \in \Gamma(N)$
. Recall that there is a one-to-one correspondence between
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta})$
and
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta})$
and
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
, as stated in Remark 2.1. Note also that there are one-to-one correspondences between
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
, as stated in Remark 2.1. Note also that there are one-to-one correspondences between
![]() $\boldsymbol{\zeta}$
and
$\boldsymbol{\zeta}$
and
![]() $\boldsymbol{\alpha}(N;\,\boldsymbol{\zeta})$
,
$\boldsymbol{\alpha}(N;\,\boldsymbol{\zeta})$
,
and between
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
and
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
and
![]() $\boldsymbol{\zeta}$
,
$\boldsymbol{\zeta}$
,
From (2.33), we also observe that
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta})$
is given by a convex combination of the row vectors
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta})$
is given by a convex combination of the row vectors
![]() $\overline{\textbf{\textit{h}}}_i(N)$
(
$\overline{\textbf{\textit{h}}}_i(N)$
(
![]() $i \in \mathbb{Z}_0^N$
) of
$i \in \mathbb{Z}_0^N$
) of
![]() $\overline{\textbf{\textit{H}}}(N)$
with the nonnegative weight vector
$\overline{\textbf{\textit{H}}}(N)$
with the nonnegative weight vector
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
. It then follows from (2.13) that
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
. It then follows from (2.13) that
This error bound tempts us to set
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
in such a way that
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
in such a way that
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is located at the center of the
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is located at the center of the
![]() $\mathcal{P}(N)$
spanned by the
$\mathcal{P}(N)$
spanned by the
![]() $\overline{\textbf{\textit{h}}}_i(N)$
(
$\overline{\textbf{\textit{h}}}_i(N)$
(
![]() $i\in \mathbb{Z}_0^N$
). For example, if we set
$i\in \mathbb{Z}_0^N$
). For example, if we set
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) =\textbf{\textit{e}}^T/(N+1)$
, where T stands for the transpose operator, then
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) =\textbf{\textit{e}}^T/(N+1)$
, where T stands for the transpose operator, then
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is given by the center of gravity of
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is given by the center of gravity of
![]() $\mathcal{P}(N)$
. Note here that (2.33) is equivalent to
$\mathcal{P}(N)$
. Note here that (2.33) is equivalent to
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) (\!-\textbf{\textit{Q}}^{(1,1)}(N)) =\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \textrm{diag}^{-1}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
.
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) (\!-\textbf{\textit{Q}}^{(1,1)}(N)) =\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \textrm{diag}^{-1}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
.
Implication 2.3 If we have a desirable
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
rather than
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
rather than
![]() $\boldsymbol{\zeta}$
itself,
$\boldsymbol{\zeta}$
itself,
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
for such an
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
for such an
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
can be computed as follows:
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
can be computed as follows:
-
(i) We first obtain
 $\boldsymbol{\eta}(N)\coloneqq \textbf{\textit{H}}(N)\textbf{\textit{e}}$
by solving
$\boldsymbol{\eta}(N)\coloneqq \textbf{\textit{H}}(N)\textbf{\textit{e}}$
by solving
 $(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \boldsymbol{\eta}(N) = \textbf{\textit{e}}$
.
$(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \boldsymbol{\eta}(N) = \textbf{\textit{e}}$
. -
(ii) We then obtain
 $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
by solving
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
by solving
 \begin{equation*}\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) (\!-\textbf{\textit{Q}}^{(1,1)}(N)) =\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \textrm{diag}^{-1}(\boldsymbol{\eta}(N)).\end{equation*}
\begin{equation*}\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) (\!-\textbf{\textit{Q}}^{(1,1)}(N)) =\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) \textrm{diag}^{-1}(\boldsymbol{\eta}(N)).\end{equation*}
In the above procedure, we have to solve two systems of linear equations with
![]() $-\textbf{\textit{Q}}^{(1,1)}(N)$
. Therefore, relative to the procedure for solving (2.32) directly for a specific
$-\textbf{\textit{Q}}^{(1,1)}(N)$
. Therefore, relative to the procedure for solving (2.32) directly for a specific
![]() $\boldsymbol{\zeta}$
, the computational cost increases by
$\boldsymbol{\zeta}$
, the computational cost increases by
![]() $(N+1)^2$
in terms of the number of multiplications/divisions, if we utilize the LU decomposition. This increase can be regarded as the cost of specifying the weight vector
$(N+1)^2$
in terms of the number of multiplications/divisions, if we utilize the LU decomposition. This increase can be regarded as the cost of specifying the weight vector
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
directly, instead of specifying
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta})$
directly, instead of specifying
![]() $\boldsymbol{\zeta}$
.
$\boldsymbol{\zeta}$
.
Next we consider Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, where the structural information
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, where the structural information
![]() $\mathcal{J}(N)$
is assumed to be available. It follows from (2.34) that for all
$\mathcal{J}(N)$
is assumed to be available. It follows from (2.34) that for all
![]() $i \in \mathbb{Z}_0^N$
,
$i \in \mathbb{Z}_0^N$
,
We then define
![]() $\mathcal{T}_{\textrm{L}}^+(N)$
as the set of all possible approximations obtained by the linear ATA when
$\mathcal{T}_{\textrm{L}}^+(N)$
as the set of all possible approximations obtained by the linear ATA when
![]() $\mathcal{J}(N)$
is available:
$\mathcal{J}(N)$
is available:
where
![]() $\Gamma^+(N)$
is given by (2.20). By definition, we have
$\Gamma^+(N)$
is given by (2.20). By definition, we have
![]() $\mathcal{T}_{\textrm{L}}^+(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
.
$\mathcal{T}_{\textrm{L}}^+(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
.
Lemma 2.3. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, we have
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N), \mathcal{J}(N))$
, we have
where
![]() $\mathcal{P}^+(N)$
is given by (2.23).
$\mathcal{P}^+(N)$
is given by (2.23).
The proof of Lemma 2.3 is given in Appendix D. We thus have
![]() $\boldsymbol{\pi}(N) \in \textrm{ri}\, \mathcal{T}_{\textrm{L}}^+(N)$
from Theorem 2.2. It also follows from (2.36) that if
$\boldsymbol{\pi}(N) \in \textrm{ri}\, \mathcal{T}_{\textrm{L}}^+(N)$
from Theorem 2.2. It also follows from (2.36) that if
![]() $[\boldsymbol{\zeta}]_i > 0$
for some
$[\boldsymbol{\zeta}]_i > 0$
for some
![]() $i \in \mathbb{Z}_0^N \setminus \mathcal{J}(N)$
, we have
$i \in \mathbb{Z}_0^N \setminus \mathcal{J}(N)$
, we have
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta}) \notin \mathcal{P}^+(N)$
, because the
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\,\boldsymbol{\zeta}) \notin \mathcal{P}^+(N)$
, because the
![]() $\overline{\textbf{\textit{h}}}_j(N)$
(
$\overline{\textbf{\textit{h}}}_j(N)$
(
![]() $j\in \mathbb{Z}_0^N$
) are linearly independent. Moreover, it follows from Corollary 2.3 that
$j\in \mathbb{Z}_0^N$
) are linearly independent. Moreover, it follows from Corollary 2.3 that
which is tighter than (2.35). In summary, we have the following.
Implication 2.4. If the structural information
![]() $\mathcal{J}(N)$
is available, it is natural that we should choose
$\mathcal{J}(N)$
is available, it is natural that we should choose
![]() $\boldsymbol{\zeta}$
from
$\boldsymbol{\zeta}$
from
![]() $\textrm{ri}\, \Gamma^+(N)$
in obtaining a linear ATA solution, where
$\textrm{ri}\, \Gamma^+(N)$
in obtaining a linear ATA solution, where
![]() $\Gamma^+(N)$
is given by (2.20). For example, we may choose
$\Gamma^+(N)$
is given by (2.20). For example, we may choose
![]() $\boldsymbol{\zeta}$
whose ith (
$\boldsymbol{\zeta}$
whose ith (
![]() $i \in \mathbb{Z}_0^N$
) element is given by
$i \in \mathbb{Z}_0^N$
) element is given by
![]() $1/|\mathcal{J}(N)|$
if
$1/|\mathcal{J}(N)|$
if
![]() $i\in \mathcal{J}(N)$
and by 0 otherwise.
$i\in \mathcal{J}(N)$
and by 0 otherwise.
Implication 2.4 indicates that the last-column augmentation
![]() $\boldsymbol{\zeta} =(0\ 0\ \cdots\ 0\ 1)$
, which is one of the common augmentation strategies in the literature, may not be effective unless
$\boldsymbol{\zeta} =(0\ 0\ \cdots\ 0\ 1)$
, which is one of the common augmentation strategies in the literature, may not be effective unless
![]() $\mathcal{J}(N) =\{N\}$
, because if
$\mathcal{J}(N) =\{N\}$
, because if
![]() $\mathcal{J}(N) \neq \{N\}$
, we have
$\mathcal{J}(N) \neq \{N\}$
, we have
![]() $\boldsymbol{\zeta} = (0\ 0\ \cdots\ 0\ 1) \not\in \textrm{ri}\, \Gamma^+(N)$
and therefore
$\boldsymbol{\zeta} = (0\ 0\ \cdots\ 0\ 1) \not\in \textrm{ri}\, \Gamma^+(N)$
and therefore
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \not\in \textrm{ri}\, \mathcal{P}^+(N)$
, while
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \not\in \textrm{ri}\, \mathcal{P}^+(N)$
, while
![]() $\boldsymbol{\pi}(N) \in \textrm{ri}\, \mathcal{P}^+(N)$
.
$\boldsymbol{\pi}(N) \in \textrm{ri}\, \mathcal{P}^+(N)$
.
Example 2.3. (Example 2.1 continued.) Consider
![]() $\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Since
$\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Since
![]() $\mathcal{J}(N) = \{0,N\}$
, we may set
$\mathcal{J}(N) = \{0,N\}$
, we may set
![]() $\boldsymbol{\zeta} = (\zeta_0\ \ 0\ \ 0\ \ \cdots\ \ 0\ \ 1-\zeta_0) \in\textrm{ri}\, \Gamma^+(N)$
for an arbitrary
$\boldsymbol{\zeta} = (\zeta_0\ \ 0\ \ 0\ \ \cdots\ \ 0\ \ 1-\zeta_0) \in\textrm{ri}\, \Gamma^+(N)$
for an arbitrary
![]() $\zeta_0 \in (0,1)$
. The ATA solution
$\zeta_0 \in (0,1)$
. The ATA solution
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is then obtained by solving
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta})$
is then obtained by solving
with
![]() $\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \textbf{\textit{e}} = 1$
. If we are concerned with the error bound in (2.37), we first compute
$\boldsymbol{\pi}^{\textrm{trunc}}(N;\, \boldsymbol{\zeta}) \textbf{\textit{e}} = 1$
. If we are concerned with the error bound in (2.37), we first compute
![]() $\overline{\textbf{\textit{h}}}_i$
(
$\overline{\textbf{\textit{h}}}_i$
(
![]() $i=0,N$
) by the procedure described in Example 2.1 and then adopt
$i=0,N$
) by the procedure described in Example 2.1 and then adopt
![]() $(\overline{\textbf{\textit{h}}}_0+\overline{\textbf{\textit{h}}}_N)/2$
as the ATA solution (or alternatively, we perform the procedure in Implication 2.3 with
$(\overline{\textbf{\textit{h}}}_0+\overline{\textbf{\textit{h}}}_N)/2$
as the ATA solution (or alternatively, we perform the procedure in Implication 2.3 with
![]() $\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) =(1/2\ 0\ 0\ \cdots\ 0\ 1/2)$
). Note that this choice yields the minimum error bound of (2.37) in this specific example, which is half the error bound of the last-column augmentation.
$\boldsymbol{\alpha}(N;\, \boldsymbol{\zeta}) =(1/2\ 0\ 0\ \cdots\ 0\ 1/2)$
). Note that this choice yields the minimum error bound of (2.37) in this specific example, which is half the error bound of the last-column augmentation.
Remark 2.2. As shown in (A.1), we have
which satisfies
![]() $\boldsymbol{\pi}(N)[\textbf{\textit{Q}}^{(1,1)}(N)+(\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}^*] = \textbf{0}$
. Therefore, in order to obtain a good one-point approximation to the conditional stationary distribution
$\boldsymbol{\pi}(N)[\textbf{\textit{Q}}^{(1,1)}(N)+(\!-\textbf{\textit{Q}}^{(1,1)}(N))\textbf{\textit{e}} \boldsymbol{\zeta}^*] = \textbf{0}$
. Therefore, in order to obtain a good one-point approximation to the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
, we need some information about
$\boldsymbol{\pi}(N)$
, we need some information about
![]() $\boldsymbol{\pi}^{(2)}(N)$
, as in the Iterative Aggregation/Disaggregation methods for finite-state Markov chains [Reference Stewart13, Reference Takahashi14].
$\boldsymbol{\pi}^{(2)}(N)$
, as in the Iterative Aggregation/Disaggregation methods for finite-state Markov chains [Reference Stewart13, Reference Takahashi14].
3. Extensions using state transitions in peripheral states
In this section, we consider extensions of the results in Sections 2.2 and 2.3 by using the
![]() $(K+1) \times (K+1)$
northwest corner block of the infinitesimal generator
$(K+1) \times (K+1)$
northwest corner block of the infinitesimal generator
![]() $\textbf{\textit{Q}}$
, where
$\textbf{\textit{Q}}$
, where
![]() $K > N$
. For this purpose, we partition
$K > N$
. For this purpose, we partition
![]() $\boldsymbol{\pi}$
and
$\boldsymbol{\pi}$
and
![]() $\textbf{\textit{Q}}$
as follows:
$\textbf{\textit{Q}}$
as follows:
 \begin{align}\includegraphics{inline1.eps}\end{align}
\begin{align}\includegraphics{inline1.eps}\end{align}
Note here that from (1.2) and (2.3),
In order to utilize the results in the preceding section, we consider the censored Markov chain
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
obtained by observing the Markov chain
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
obtained by observing the Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
only when
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
only when
![]() $X(t) \in\mathbb{Z}_0^N\cup\mathbb{Z}_{K+1}^{\infty}$
. The infinitesimal generator of
$X(t) \in\mathbb{Z}_0^N\cup\mathbb{Z}_{K+1}^{\infty}$
. The infinitesimal generator of
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
is then given by
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
is then given by
 \begin{equation}\widetilde{\textbf{\textit{Q}}}(K,N)=\kbordermatrix{& \mathbb{Z}_0^N &\quad \mathbb{Z}_{K+1}^{\infty} \\ \\[-7pt] \mathbb{Z}_0^N & \widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)&\quad \widetilde{\textbf{\textit{Q}}}^{(1,3)}(K,N)\\ \\[-7pt] \mathbb{Z}_{K+1}^{\infty} & \widetilde{\textbf{\textit{Q}}}^{(3,1)}(K,N)&\quad \widetilde{\textbf{\textit{Q}}}^{(3,3)}(K,N)},\end{equation}
\begin{equation}\widetilde{\textbf{\textit{Q}}}(K,N)=\kbordermatrix{& \mathbb{Z}_0^N &\quad \mathbb{Z}_{K+1}^{\infty} \\ \\[-7pt] \mathbb{Z}_0^N & \widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)&\quad \widetilde{\textbf{\textit{Q}}}^{(1,3)}(K,N)\\ \\[-7pt] \mathbb{Z}_{K+1}^{\infty} & \widetilde{\textbf{\textit{Q}}}^{(3,1)}(K,N)&\quad \widetilde{\textbf{\textit{Q}}}^{(3,3)}(K,N)},\end{equation}
where for
![]() $i,j=1,3$
,
$i,j=1,3$
,
In particular, we have
where
Note that
![]() $(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))$
in (3.4) is nonsingular because
$(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))$
in (3.4) is nonsingular because
![]() $\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)$
and
$\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)$
and
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
are nonsingular.
$\textbf{\textit{Q}}^{(1,1)}(N)$
are nonsingular.
Clearly, Theorem 2.1 is applicable to the censored Markov chain
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
on
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
on
![]() $\mathbb{Z}_0^N \cup \mathbb{Z}_{K+1}^{\infty}$
. Note also that the conditional stationary distribution of
$\mathbb{Z}_0^N \cup \mathbb{Z}_{K+1}^{\infty}$
. Note also that the conditional stationary distribution of
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
given
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
given
![]() $\widetilde{X}(0) \in \mathbb{Z}_0^N$
is identical to
$\widetilde{X}(0) \in \mathbb{Z}_0^N$
is identical to
![]() $\boldsymbol{\pi}(N)$
. We define
$\boldsymbol{\pi}(N)$
. We define
![]() $\widetilde{\Gamma}(K,N)$
(
$\widetilde{\Gamma}(K,N)$
(
![]() $K > N$
) as
$K > N$
) as
 \begin{align}\widetilde{\Gamma}(K,N)&=\bigl\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\ \nonumber\\[3pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\boldsymbol{\beta} \in \Gamma(N)\bigr\},\end{align}
\begin{align}\widetilde{\Gamma}(K,N)&=\bigl\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\ \nonumber\\[3pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\boldsymbol{\beta} \in \Gamma(N)\bigr\},\end{align}
where
Remark 3.1. It can be verified that
![]() $\widetilde{\textbf{\textit{H}}}(K,N)$
is identical to the
$\widetilde{\textbf{\textit{H}}}(K,N)$
is identical to the
![]() $(N+1) \times (N+1)$
northwest corner block of the
$(N+1) \times (N+1)$
northwest corner block of the
![]() $(K+1) \times(K+1)$
matrix
$(K+1) \times(K+1)$
matrix
![]() $\textbf{\textit{H}}(K) = (\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
.
$\textbf{\textit{H}}(K) = (\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
.
For a specific
![]() $(K+1) \times (K+1)$
northwest corner block
$(K+1) \times (K+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
, we define
$\textbf{\textit{Q}}^{(1,1)}(K)$
, we define
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K))$
as the collection of ergodic, continuous-time Markov chains on
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K))$
as the collection of ergodic, continuous-time Markov chains on
![]() $\mathbb{Z}^+$
whose infinitesimal generators have
$\mathbb{Z}^+$
whose infinitesimal generators have
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
.
$\textbf{\textit{Q}}^{(1,1)}(K)$
.
Theorem 3.1. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K))$
, we have
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K))$
, we have
where
![]() $\widetilde{\mathcal{P}}(K,N)$
denotes an N-simplex on the first orthant of
$\widetilde{\mathcal{P}}(K,N)$
denotes an N-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
which is given by
$\mathbb{R}^{N+1}$
which is given by
with
![]() $\textbf{\textit{R}}(K,N)$
as in (3.5).
$\textbf{\textit{R}}(K,N)$
as in (3.5).
Proof. Associated with
![]() $\widetilde{\textbf{\textit{H}}}(K,N)$
in (3.7), we define
$\widetilde{\textbf{\textit{H}}}(K,N)$
in (3.7), we define
![]() $\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
as
$\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
as
Applying Theorem 2.1 to (3.2), we obtain
![]() $\boldsymbol{\pi}(N) \in \widehat{\mathcal{P}}(K,N)$
, where
$\boldsymbol{\pi}(N) \in \widehat{\mathcal{P}}(K,N)$
, where
![]() $\widehat{\mathcal{P}}(K,N)$
has two equivalent expressions:
$\widehat{\mathcal{P}}(K,N)$
has two equivalent expressions:
 \begin{align}\widehat{\mathcal{P}}(K,N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)) \geq \textbf{0},\textbf{\textit{x}}\textbf{\textit{e}}=1\big\}\nonumber\\[3pt] &=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N),\boldsymbol{\beta} \in \Gamma(N)\big\}.\end{align}
\begin{align}\widehat{\mathcal{P}}(K,N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)) \geq \textbf{0},\textbf{\textit{x}}\textbf{\textit{e}}=1\big\}\nonumber\\[3pt] &=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N),\boldsymbol{\beta} \in \Gamma(N)\big\}.\end{align}
Because of (3.4),
![]() $\widetilde{\mathcal{P}}(K,N)$
in (3.8) is identical to
$\widetilde{\mathcal{P}}(K,N)$
in (3.8) is identical to
![]() $\widehat{\mathcal{P}}(K,N)$
.
$\widehat{\mathcal{P}}(K,N)$
.
Next, we show the equivalence between (3.9) and (3.11). It follows from (3.4) and (3.7) that
 \begin{align}\widetilde{\textbf{\textit{H}}}(K,N)=(\!-\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N))^{-1}&=(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} (\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1}\nonumber\\[3pt] &=(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N).\end{align}
\begin{align}\widetilde{\textbf{\textit{H}}}(K,N)=(\!-\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N))^{-1}&=(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} (\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1}\nonumber\\[3pt] &=(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N).\end{align}
Therefore, for an arbitrary
![]() $\boldsymbol{\beta} \in \Gamma(N)$
, we have from (3.10) and (3.12) that
$\boldsymbol{\beta} \in \Gamma(N)$
, we have from (3.10) and (3.12) that
 \begin{align}\boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N)&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N)\nonumber\\[3pt] &= \boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})\overline{\textbf{\textit{H}}}(N)\nonumber\\[3pt] &=\boldsymbol{\alpha} \overline{\textbf{\textit{H}}}(N),\end{align}
\begin{align}\boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N)&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N)\nonumber\\[3pt] &= \boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})\overline{\textbf{\textit{H}}}(N)\nonumber\\[3pt] &=\boldsymbol{\alpha} \overline{\textbf{\textit{H}}}(N),\end{align}
where
which shows the equivalence between (3.9) and (3.11). We thus conclude that
![]() $\widetilde{\mathcal{P}}(K,N)$
is an N-simplex on the first orthant of
$\widetilde{\mathcal{P}}(K,N)$
is an N-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
because of the nonsingularity of
$\mathbb{R}^{N+1}$
because of the nonsingularity of
![]() $\overline{\widetilde{\textbf{\textit{H}}}}(K,N) \geq \textbf{\textit{O}}$
, (3.11), and (3.15). □
$\overline{\widetilde{\textbf{\textit{H}}}}(K,N) \geq \textbf{\textit{O}}$
, (3.11), and (3.15). □
Corollary 3.1.
![]() $\widetilde{\Gamma}(K,N)$
in (3.6) is a subset of
$\widetilde{\Gamma}(K,N)$
in (3.6) is a subset of
![]() $\Gamma(N)$
:
$\Gamma(N)$
:
Furthermore,
and therefore
where
![]() $\mathcal{P}(N)$
is as given in Theorem 2.1.
$\mathcal{P}(N)$
is as given in Theorem 2.1.
The proof of Corollary 3.1 is given in Appendix E.
Next, we consider an extension of the results in Section 2.3. For specific
![]() $(K+1) \times (K\,{+}\,1)$
northwest corner block
$(K+1) \times (K\,{+}\,1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and the structural information
$\textbf{\textit{Q}}^{(1,1)}(K)$
and the structural information
![]() $\mathcal{J}(K)$
(
$\mathcal{J}(K)$
(
![]() $K > N$
), we define
$K > N$
), we define
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
as the collection of ergodic, continuous-time Markov chains on
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
as the collection of ergodic, continuous-time Markov chains on
![]() $\mathbb{Z}^+$
whose infinitesimal generators have
$\mathbb{Z}^+$
whose infinitesimal generators have
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
. For Markov chains in
$\mathcal{J}(K)$
. For Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
, we define
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
, we define
![]() $\widetilde{\mathcal{J}}(K,N)$
(
$\widetilde{\mathcal{J}}(K,N)$
(
![]() $K > N$
) as the set of states in
$K > N$
) as the set of states in
![]() $\mathbb{Z}_0^N$
which are reachable from some states in
$\mathbb{Z}_0^N$
which are reachable from some states in
![]() $\mathbb{Z}_{K+1}^{\infty}$
either directly or only via some states in
$\mathbb{Z}_{K+1}^{\infty}$
either directly or only via some states in
![]() $\mathbb{Z}_{N+1}^K$
:
$\mathbb{Z}_{N+1}^K$
:
Note here that
![]() $\widetilde{\mathcal{J}}(K,N) \neq \emptyset$
because of the ergodicity. Note also that
$\widetilde{\mathcal{J}}(K,N) \neq \emptyset$
because of the ergodicity. Note also that
![]() $\widetilde{\mathcal{J}}(K,N)$
is determined completely by
$\widetilde{\mathcal{J}}(K,N)$
is determined completely by
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
, because from (1.4), (3.1), and (3.3),
$\mathcal{J}(K)$
, because from (1.4), (3.1), and (3.3),
 \begin{gather*}\mathcal{J}(K)=\{j \in \mathbb{Z}_0^N;\ \bigl[\textbf{\textit{e}}^T \textbf{\textit{Q}}^{(3,1)}(K,N) \bigr]_j > 0\}\cup\{j \in \mathbb{Z}_{N+1}^K;\ \bigl[ \textbf{\textit{e}}^T \textbf{\textit{Q}}^{(3,2)}(K,N) \bigr]_j > 0\},\\[3pt] \widetilde{\textbf{\textit{Q}}}^{(3,1)}(K,N)=\textbf{\textit{Q}}^{(3,1)}(K,N)+\textbf{\textit{Q}}^{(3,2)}(K,N)\cdot(\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N).\end{gather*}
\begin{gather*}\mathcal{J}(K)=\{j \in \mathbb{Z}_0^N;\ \bigl[\textbf{\textit{e}}^T \textbf{\textit{Q}}^{(3,1)}(K,N) \bigr]_j > 0\}\cup\{j \in \mathbb{Z}_{N+1}^K;\ \bigl[ \textbf{\textit{e}}^T \textbf{\textit{Q}}^{(3,2)}(K,N) \bigr]_j > 0\},\\[3pt] \widetilde{\textbf{\textit{Q}}}^{(3,1)}(K,N)=\textbf{\textit{Q}}^{(3,1)}(K,N)+\textbf{\textit{Q}}^{(3,2)}(K,N)\cdot(\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N).\end{gather*}
Furthermore, by definition,
and states in
![]() $\mathcal{J}(N) \setminus \widetilde{\mathcal{J}}(K,N)$
, if any, can be reached from
$\mathcal{J}(N) \setminus \widetilde{\mathcal{J}}(K,N)$
, if any, can be reached from
![]() $\mathbb{Z}_{K+1}^{\infty}$
only after visiting some states in
$\mathbb{Z}_{K+1}^{\infty}$
only after visiting some states in
![]() $\widetilde{\mathcal{J}}(K,N)$
.
$\widetilde{\mathcal{J}}(K,N)$
.
Example 3.1. (Example 2.1 continued.) Consider
![]() $\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. By definition,
$\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. By definition,
![]() $\mathcal{J}(K)=\{0,K\}$
and
$\mathcal{J}(K)=\{0,K\}$
and
![]() $\widetilde{\mathcal{J}}(K,N) = \{0,N\} = \mathcal{J}(N)$
.
$\widetilde{\mathcal{J}}(K,N) = \{0,N\} = \mathcal{J}(N)$
.
Without loss of generality, we assume
![]() $\widetilde{\mathcal{J}}(K,N) =\{0,1,\dots,|\widetilde{\mathcal{J}}(K,N)|-1\}$
. We then partition
$\widetilde{\mathcal{J}}(K,N) =\{0,1,\dots,|\widetilde{\mathcal{J}}(K,N)|-1\}$
. We then partition
![]() $\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)$
in (3.2) into two matrices,
$\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)$
in (3.2) into two matrices,
 \begin{align}\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)&=\kbordermatrix{&\widetilde{\mathcal{J}}(K,N) &\quad \mathbb{Z}_0^N\setminus\widetilde{\mathcal{J}}(K,N)\\ \\[-9pt] &\widetilde{\textbf{\textit{Q}}}^{(1,1)}_+(K,N)&\quad \widetilde{\textbf{\textit{Q}}}_0^{(1,1)}(K,N)\\},\end{align}
\begin{align}\widetilde{\textbf{\textit{Q}}}^{(1,1)}(K,N)&=\kbordermatrix{&\widetilde{\mathcal{J}}(K,N) &\quad \mathbb{Z}_0^N\setminus\widetilde{\mathcal{J}}(K,N)\\ \\[-9pt] &\widetilde{\textbf{\textit{Q}}}^{(1,1)}_+(K,N)&\quad \widetilde{\textbf{\textit{Q}}}_0^{(1,1)}(K,N)\\},\end{align}
and define
![]() $\widetilde{\Gamma}^+(K,N)$
as
$\widetilde{\Gamma}^+(K,N)$
as
 \begin{align}\widetilde{\Gamma}^+(K,N)&=\bigl\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\ \nonumber\\&{\boldsymbol{\beta}} \in \Gamma(N),\ [\boldsymbol{\beta}]_i=0\ (i \in \mathbb{Z}_0^N\setminus\widetilde{\mathcal{J}}(K,N))\bigr\}.\end{align}
\begin{align}\widetilde{\Gamma}^+(K,N)&=\bigl\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\ \nonumber\\&{\boldsymbol{\beta}} \in \Gamma(N),\ [\boldsymbol{\beta}]_i=0\ (i \in \mathbb{Z}_0^N\setminus\widetilde{\mathcal{J}}(K,N))\bigr\}.\end{align}
Theorem 3.2. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
(
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
(
![]() $K > N$
), we have
$K > N$
), we have
where
![]() $\widetilde{\mathcal{P}}^+(K,N)$
denotes a
$\widetilde{\mathcal{P}}^+(K,N)$
denotes a
![]() $(|\widetilde{\mathcal{J}}(K,N)|-1)$
-simplex on the first orthant of
$(|\widetilde{\mathcal{J}}(K,N)|-1)$
-simplex on the first orthant of
![]() $\ \mathbb{R}^{N+1}$
which is given by
$\ \mathbb{R}^{N+1}$
which is given by
![]() $\widetilde{\mathcal{P}}(K,N)$
if
$\widetilde{\mathcal{P}}(K,N)$
if
![]() $\widetilde{\mathcal{J}}(K,N) = \mathbb{Z}_0^N$
, and by
$\widetilde{\mathcal{J}}(K,N) = \mathbb{Z}_0^N$
, and by
 \begin{align}\widetilde{\mathcal{P}}^+(K,N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\widetilde{\textbf{\textit{Q}}}_+^{(1,1)}(K,N)) \geq \textbf{0},\nonumber\\& \quad \textbf{\textit{x}}(\!-\widetilde{\textbf{\textit{Q}}}_0^{(1,1)}(K,N)) = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\big\} \end{align}
\begin{align}\widetilde{\mathcal{P}}^+(K,N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\widetilde{\textbf{\textit{Q}}}_+^{(1,1)}(K,N)) \geq \textbf{0},\nonumber\\& \quad \textbf{\textit{x}}(\!-\widetilde{\textbf{\textit{Q}}}_0^{(1,1)}(K,N)) = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\big\} \end{align}
otherwise.
Proof. If
![]() $\widetilde{\mathcal{J}}(K,N) = \mathbb{Z}_0^N$
, Theorem 3.2 can be shown in the same way as Theorem 2.2 for
$\widetilde{\mathcal{J}}(K,N) = \mathbb{Z}_0^N$
, Theorem 3.2 can be shown in the same way as Theorem 2.2 for
![]() $\mathcal{J}(N)=\mathbb{Z}_0^N$
. We thus assume that
$\mathcal{J}(N)=\mathbb{Z}_0^N$
. We thus assume that
![]() $\widetilde{\mathcal{J}}(K,N) \neq \mathbb{Z}_0^N$
. Applying Theorem 2.2 to the censored Markov chain with infinitesimal generator
$\widetilde{\mathcal{J}}(K,N) \neq \mathbb{Z}_0^N$
. Applying Theorem 2.2 to the censored Markov chain with infinitesimal generator
![]() $\widetilde{\textbf{\textit{Q}}}(K,N)$
in (3.2) with partition (3.21), we obtain (3.23) with (3.24), where (3.24) can also be expressed as follows:
$\widetilde{\textbf{\textit{Q}}}(K,N)$
in (3.2) with partition (3.21), we obtain (3.23) with (3.24), where (3.24) can also be expressed as follows:
 \begin{align}\widetilde{\mathcal{P}}^+(K,N) = & \bigl\{ \textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N),\nonumber\\[3pt]
&\boldsymbol{\beta} \in \Gamma(N),\ [\boldsymbol{\beta}]_i=0\ (i \in \mathbb{Z}_0^N \setminus \widetilde{\mathcal{J}}(K,N))\bigr\},\end{align}
\begin{align}\widetilde{\mathcal{P}}^+(K,N) = & \bigl\{ \textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} = \boldsymbol{\beta} \overline{\widetilde{\textbf{\textit{H}}}}(K,N),\nonumber\\[3pt]
&\boldsymbol{\beta} \in \Gamma(N),\ [\boldsymbol{\beta}]_i=0\ (i \in \mathbb{Z}_0^N \setminus \widetilde{\mathcal{J}}(K,N))\bigr\},\end{align}
where
![]() $\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
is given by (3.10). Equation (3.25) now follows from (3.13) and (3.26). Since
$\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
is given by (3.10). Equation (3.25) now follows from (3.13) and (3.26). Since
![]() $\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
is nonnegative and nonsingular, (3.26) implies that
$\overline{\widetilde{\textbf{\textit{H}}}}(K,N)$
is nonnegative and nonsingular, (3.26) implies that
![]() $\widetilde{\mathcal{P}}^+(K,N)$
is a
$\widetilde{\mathcal{P}}^+(K,N)$
is a
![]() $(|\widetilde{\mathcal{J}}(K,N)|-1)$
-simplex on the first orthant of
$(|\widetilde{\mathcal{J}}(K,N)|-1)$
-simplex on the first orthant of
![]() $\mathbb{R}^{N+1}$
. □
$\mathbb{R}^{N+1}$
. □
By definition,
where
![]() $\widetilde{\Gamma}(K,N)$
is given by (3.6). We thus have
$\widetilde{\Gamma}(K,N)$
is given by (3.6). We thus have
where
![]() $\widetilde{\mathcal{P}}(K,N)$
is given in Theorem 3.1.
$\widetilde{\mathcal{P}}(K,N)$
is given in Theorem 3.1.
Corollary 3.2.
![]() $\widetilde{\Gamma}^+(K,N)$
in (3.22) is a subset of
$\widetilde{\Gamma}^+(K,N)$
in (3.22) is a subset of
![]() $\Gamma^+(N)$
in (2.20):
$\Gamma^+(N)$
in (2.20):
Furthermore,
and therefore
The proof of Corollary 3.2 is given in Appendix F. Since
![]() $\widetilde{\mathcal{P}}(K,N)$
in Theorem 3.1 and
$\widetilde{\mathcal{P}}(K,N)$
in Theorem 3.1 and
![]() $\widetilde{\mathcal{P}}^+(K, N)$
in Theorem 3.2 are compact, Corollaries 3.1 and 3.2 suggest that those simplices converge to certain sets as K goes to infinity. In fact, we have the following proposition.
$\widetilde{\mathcal{P}}^+(K, N)$
in Theorem 3.2 are compact, Corollaries 3.1 and 3.2 suggest that those simplices converge to certain sets as K goes to infinity. In fact, we have the following proposition.
Proposition 3.1. ([8, Theorem 2.3]) In any ergodic, continuous-time Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
on
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
on
![]() $\mathbb{Z}^+$
,
$\mathbb{Z}^+$
,
The corollary below follows immediately from (3.11), (3.15), (3.18), (3.26), (3.28), (3.31), and Proposition 3.1.
Corollary 3.3. In any ergodic, continuous-time Markov chain
![]() $\{X(t);\ t \geq0\}$
on
$\{X(t);\ t \geq0\}$
on
![]() $\mathbb{Z}^+$
,
$\mathbb{Z}^+$
,
and
Since
![]() $\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N) \subseteq\widetilde{\mathcal{P}}^+(K,N)$
,
$\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N) \subseteq\widetilde{\mathcal{P}}^+(K,N)$
,
![]() $\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N)$
also converges to
$\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N)$
also converges to
![]() $\{\boldsymbol{\pi}(N)\}$
as K goes to infinity. Note here that
$\{\boldsymbol{\pi}(N)\}$
as K goes to infinity. Note here that
![]() $\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N)$
may not be tight in
$\textrm{ri}\, \widetilde{\mathcal{P}}^+(K,N)$
may not be tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
for a finite K. For example, we consider
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
for a finite K. For example, we consider
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N+1), \mathcal{J}(N+1))$
, where
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N+1), \mathcal{J}(N+1))$
, where
![]() $K=N+1$
,
$K=N+1$
,
![]() $\mathcal{J}(N+1) = \{N+1\}$
, and
$\mathcal{J}(N+1) = \{N+1\}$
, and
![]() $q_{N+1,j} > 0$
for all
$q_{N+1,j} > 0$
for all
![]() $j \in \mathbb{Z}_0^N$
. We then have
$j \in \mathbb{Z}_0^N$
. We then have
![]() $\widetilde{\mathcal{J}}(N+1,N) = \mathbb{Z}_0^N$
, and therefore
$\widetilde{\mathcal{J}}(N+1,N) = \mathbb{Z}_0^N$
, and therefore
![]() $\widetilde{\mathcal{P}}^+(N+1,N)$
is an N-simplex spanned by
$\widetilde{\mathcal{P}}^+(N+1,N)$
is an N-simplex spanned by
![]() $(N+1)$
row vectors of
$(N+1)$
row vectors of
![]() $\overline{\widetilde{\textbf{\textit{H}}}}(N+1,N)$
, as shown in the proof of Theorem 3.2. On the other hand, it follows from Theorem 2.2 that
$\overline{\widetilde{\textbf{\textit{H}}}}(N+1,N)$
, as shown in the proof of Theorem 3.2. On the other hand, it follows from Theorem 2.2 that
![]() $\mathcal{P}^+(N+1)$
is given by a singleton with the
$\mathcal{P}^+(N+1)$
is given by a singleton with the
![]() $(N+1)$
th row vector
$(N+1)$
th row vector
![]() $\overline{\textbf{\textit{h}}}_{N+1}(N+1)$
of
$\overline{\textbf{\textit{h}}}_{N+1}(N+1)$
of
![]() $\overline{\textbf{\textit{H}}}(N+1)$
. In other words, all Markov chains in
$\overline{\textbf{\textit{H}}}(N+1)$
. In other words, all Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N+1), \{N+1\})$
have the same
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(N+1), \{N+1\})$
have the same
![]() $\boldsymbol{\pi}(N)$
(i.e. the normalized vector of the first
$\boldsymbol{\pi}(N)$
(i.e. the normalized vector of the first
![]() $N+1$
elements of
$N+1$
elements of
![]() $\overline{\textbf{\textit{h}}}_{N+1}(N+1)$
), so that
$\overline{\textbf{\textit{h}}}_{N+1}(N+1)$
), so that
![]() $\textrm{ri}\, \widetilde{\mathcal{P}}^+(N+1,N)$
is not tight. In the next section, we find the minimum convex polytope that contains
$\textrm{ri}\, \widetilde{\mathcal{P}}^+(N+1,N)$
is not tight. In the next section, we find the minimum convex polytope that contains
![]() $\boldsymbol{\pi}(N)$
, in the sense that it is tight in
$\boldsymbol{\pi}(N)$
, in the sense that it is tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
4. Minimum convex polytopes for
 $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
In this section, we consider minimum convex polytopes that contain
![]() $\boldsymbol{\pi}(N)$
for Markov chains in
$\boldsymbol{\pi}(N)$
for Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
. The outline of our approach can be summarized as follows. For convenience, we partition
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
. The outline of our approach can be summarized as follows. For convenience, we partition
![]() $\textbf{\textit{H}}(K)=(\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
and
$\textbf{\textit{H}}(K)=(\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
and
![]() $\boldsymbol{\pi}(K)$
as follows:
$\boldsymbol{\pi}(K)$
as follows:
Since
![]() $\boldsymbol{\pi}(K) \in \textrm{ri}\, \mathcal{P}^+(K)$
by Theorem 2.2,
$\boldsymbol{\pi}(K) \in \textrm{ri}\, \mathcal{P}^+(K)$
by Theorem 2.2,
![]() $\boldsymbol{\pi}(N)=\boldsymbol{\pi}^{(1)}(K;\,N)/\boldsymbol{\pi}^{(1)}(K;\, N)\textbf{\textit{e}}$
is given by a convex combination of normalized row vectors of
$\boldsymbol{\pi}(N)=\boldsymbol{\pi}^{(1)}(K;\,N)/\boldsymbol{\pi}^{(1)}(K;\, N)\textbf{\textit{e}}$
is given by a convex combination of normalized row vectors of
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
corresponding to
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
corresponding to
![]() $\mathcal{J}(K)$
.
$\mathcal{J}(K)$
.
Note here that in all sample paths of the first passage from
![]() $\mathbb{Z}_{K+1}^{\infty}$
to
$\mathbb{Z}_{K+1}^{\infty}$
to
![]() $\mathbb{Z}_0^N$
,
$\mathbb{Z}_0^N$
,
![]() $\{X(t)\}_{t \in (-\infty, \infty)}$
must visit at least one state in
$\{X(t)\}_{t \in (-\infty, \infty)}$
must visit at least one state in
![]() $\mathcal{J}(K)$
. In view of this fact, we first introduce (K,N)-skip-free sets. Roughly speaking, a (K, N)-skip-free set
$\mathcal{J}(K)$
. In view of this fact, we first introduce (K,N)-skip-free sets. Roughly speaking, a (K, N)-skip-free set
![]() $\mathcal{X}$
is a proper subset of
$\mathcal{X}$
is a proper subset of
![]() $\mathbb{Z}_0^K$
such that in all sample paths of the first passage from
$\mathbb{Z}_0^K$
such that in all sample paths of the first passage from
![]() $\mathbb{Z}_{K+1}^{\infty}$
to
$\mathbb{Z}_{K+1}^{\infty}$
to
![]() $\mathbb{Z}_{0}^{K}$
,
$\mathbb{Z}_{0}^{K}$
,
![]() $\{X(t)\}_{t \in (-\infty, \infty)}$
must visit at least one state in
$\{X(t)\}_{t \in (-\infty, \infty)}$
must visit at least one state in
![]() $\mathcal{X}$
. We then show in Theorem 4.1 that
$\mathcal{X}$
. We then show in Theorem 4.1 that
![]() $\boldsymbol{\pi}(N)=\boldsymbol{\pi}^{(1)}(K;\,N)/\boldsymbol{\pi}^{(1)}(K;\, N)\textbf{\textit{e}}$
is given by a convex combination of normalized row vectors of
$\boldsymbol{\pi}(N)=\boldsymbol{\pi}^{(1)}(K;\,N)/\boldsymbol{\pi}^{(1)}(K;\, N)\textbf{\textit{e}}$
is given by a convex combination of normalized row vectors of
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
corresponding to members of
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
corresponding to members of
![]() $\mathcal{X}$
.
$\mathcal{X}$
.
To find the minimum convex polytopes that contain
![]() $\boldsymbol{\pi}(N)$
, we introduce a partial order among (K, N)-skip-free sets, considering the first passage time from
$\boldsymbol{\pi}(N)$
, we introduce a partial order among (K, N)-skip-free sets, considering the first passage time from
![]() $\mathbb{Z}_{K+1}^{\infty}$
to them. We then show the inclusion relation among convex polytopes associated with (K, N)-skip-free sets in Lemma 4.1. Finally, in Theorem 4.2, we find the smallest (K, N)-skip-free set and the corresponding minimum convex polytope, which is shown to be tight in
$\mathbb{Z}_{K+1}^{\infty}$
to them. We then show the inclusion relation among convex polytopes associated with (K, N)-skip-free sets in Lemma 4.1. Finally, in Theorem 4.2, we find the smallest (K, N)-skip-free set and the corresponding minimum convex polytope, which is shown to be tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
4.1. (K, N)-skip-free sets
For an arbitrary non-empty subset
![]() $\mathcal{B}$
of
$\mathcal{B}$
of
![]() $\mathbb{Z}^+$
, we define
$\mathbb{Z}^+$
, we define
![]() $F(\mathcal{B})$
as the first passage time to
$F(\mathcal{B})$
as the first passage time to
![]() $\mathcal{B}$
:
$\mathcal{B}$
:
Definition 4.1. ((K, N)-skip-free set.) For arbitrarily fixed
![]() $K, N \in \mathbb{Z}^+$
(
$K, N \in \mathbb{Z}^+$
(
![]() $K > N$
), consider a Markov chain
$K > N$
), consider a Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
in
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
. We refer to a subset
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
. We refer to a subset
![]() $\mathcal{X}$
of
$\mathcal{X}$
of
![]() $\mathbb{Z}_0^K$
as a (K, N)-skip-free set if
$\mathbb{Z}_0^K$
as a (K, N)-skip-free set if
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
starting from any state in
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
starting from any state in
![]() $\mathbb{Z}_{K+1}^{\infty}$
must visit
$\mathbb{Z}_{K+1}^{\infty}$
must visit
![]() $\mathcal{X}$
by the first passage time to
$\mathcal{X}$
by the first passage time to
![]() $\mathbb{Z}_0^N$
, i.e.,
$\mathbb{Z}_0^N$
, i.e.,
In particular, a (K, N)-skip-free set
![]() $\mathcal{X}$
is called proper if for any proper subset
$\mathcal{X}$
is called proper if for any proper subset
![]() $\mathcal{Y}$
of
$\mathcal{Y}$
of
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
Let
![]() $\mathcal{S}(K,N)$
denote the family of all (K, N)-skip-free sets and
$\mathcal{S}(K,N)$
denote the family of all (K, N)-skip-free sets and
![]() $\mathcal{S}^*(K,N)$
the family of all proper (K, N)-skip-free sets.
$\mathcal{S}^*(K,N)$
the family of all proper (K, N)-skip-free sets.
Remark 4.1. By definition,
-
(i) (K, N)-skip-free sets are determined only by
 $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
 $\mathcal{J}(K)$
,
$\mathcal{J}(K)$
, -
(ii)
 $\mathcal{S}^*(K,N)\subseteq\mathcal{S}(K,N)$
,
$\mathcal{S}^*(K,N)\subseteq\mathcal{S}(K,N)$
, -
(iii)
 $\mathcal{J}(K) \in \mathcal{S}(K,N)$
and
$\mathcal{J}(K) \in \mathcal{S}(K,N)$
and
 $\widetilde{\mathcal{J}}(K,N) \in \mathcal{S}^*(K,N)$
, where
$\widetilde{\mathcal{J}}(K,N) \in \mathcal{S}^*(K,N)$
, where
 $\widetilde{\mathcal{J}}(K,N)$
is given by (3.19), and
$\widetilde{\mathcal{J}}(K,N)$
is given by (3.19), and -
(iv)
 $\mathcal{J}(K) \cap \mathbb{Z}_0^N \subseteq \mathcal{X}\ \mbox{for all}\ \mathcal{X} \in\mathcal{S}(K,N)$
.
$\mathcal{J}(K) \cap \mathbb{Z}_0^N \subseteq \mathcal{X}\ \mbox{for all}\ \mathcal{X} \in\mathcal{S}(K,N)$
.
We can provide an equivalent definition of (K, N)-skip-free sets by considering a directed graph associated with
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
. Specifically, for arbitrarily fixed
$\mathcal{J}(K)$
. Specifically, for arbitrarily fixed
![]() $K, N \in \mathbb{Z}^+$
(
$K, N \in \mathbb{Z}^+$
(
![]() $K > N$
), we define the directed graph
$K > N$
), we define the directed graph
where V(K, N) and E(K, N) denote sets of nodes and arcs defined as
 \begin{align*}V(K,N) &= \{s,t\} \cup \mathbb{Z}_0^K,\\[3pt] E(K,N) &=\{(s,j);\ j \in \mathcal{J}(K)\} \cup \{(i,t);\ i \in \mathbb{Z}_0^N\}\\[3pt]&\quad {}\cup\{(i,j);\ i \in \mathbb{Z}_{N+1}^K,\ j \in \mathbb{Z}_0^K, q_{i,j}>0\}.\end{align*}
\begin{align*}V(K,N) &= \{s,t\} \cup \mathbb{Z}_0^K,\\[3pt] E(K,N) &=\{(s,j);\ j \in \mathcal{J}(K)\} \cup \{(i,t);\ i \in \mathbb{Z}_0^N\}\\[3pt]&\quad {}\cup\{(i,j);\ i \in \mathbb{Z}_{N+1}^K,\ j \in \mathbb{Z}_0^K, q_{i,j}>0\}.\end{align*}
Node s represents the set of states in
![]() $\mathbb{Z}_{K+1}^{\infty}$
, and node t is a virtual terminal node for the first passage to
$\mathbb{Z}_{K+1}^{\infty}$
, and node t is a virtual terminal node for the first passage to
![]() $\mathbb{Z}_0^N$
. It is readily seen from Definition 4.1 that a subset
$\mathbb{Z}_0^N$
. It is readily seen from Definition 4.1 that a subset
![]() $\mathcal{X}$
of
$\mathcal{X}$
of
![]() $\mathbb{Z}_0^K$
is a (K, N)-skip-free set iff
$\mathbb{Z}_0^K$
is a (K, N)-skip-free set iff
![]() $\mathcal{X}$
is an (s,t)-node cut in G(K, N), and that
$\mathcal{X}$
is an (s,t)-node cut in G(K, N), and that
![]() $\mathcal{X}$
is proper iff it is a minimal (s, t)-node cut.
$\mathcal{X}$
is proper iff it is a minimal (s, t)-node cut.
For a given G(K, N), nodes in
![]() $\mathbb{Z}_0^K$
can be classified into two classes, depending on whether they appear on the way of at least one path from node s to node t. That is,
$\mathbb{Z}_0^K$
can be classified into two classes, depending on whether they appear on the way of at least one path from node s to node t. That is,
where nodes in
![]() $\mathcal{N}_+(K,N)$
are reachable from node s and each of them has at least one path to node t. Note here that
$\mathcal{N}_+(K,N)$
are reachable from node s and each of them has at least one path to node t. Note here that
![]() $\mathcal{N}_0(K,N)= \mathbb{Z}_0^K \setminus \mathcal{N}_+(K,N)$
is given by
$\mathcal{N}_0(K,N)= \mathbb{Z}_0^K \setminus \mathcal{N}_+(K,N)$
is given by
where
![]() $\mathcal{N}_0^{(\ell)}(K,N)$
(
$\mathcal{N}_0^{(\ell)}(K,N)$
(
![]() $\ell=1,2,3$
) are defined as follows:
$\ell=1,2,3$
) are defined as follows:
 \begin{align*}\mathcal{N}_0^{(1)}(K,N)&=\mathbb{Z}_0^N \setminus \widetilde{\mathcal{J}}(K,N)=\{i \in \mathbb{Z}_0^N;\ \mathbb{P}(X(F(\mathbb{Z}_0^N)) = i \mid X(0) \in \mathbb{Z}_{K+1}^{\infty}) = 0\},\\[3pt] \mathcal{N}_0^{(2)}(K,N)&=\{i \in \mathbb{Z}_{N+1}^K;\ \\[3pt] &\qquad\qquad\mathbb{P}(X(t) \in \mathbb{Z}_{N+1}^{\infty} \mbox{ for all } t \in (0,F(\{i\})]\mid X(0) \in \mathbb{Z}_{K+1}^{\infty}) = 0\},\\[3pt] \mathcal{N}_0^{(3)}(K,N)&=\{i \in \mathbb{Z}_{N+1}^K;\ \mathbb{P}(X(t) \in \mathbb{Z}_{N+1}^K \mbox{ for all } t \in (0,F(\mathbb{Z}_0^N)]\mid X(0) = i) = 0\}.\end{align*}
\begin{align*}\mathcal{N}_0^{(1)}(K,N)&=\mathbb{Z}_0^N \setminus \widetilde{\mathcal{J}}(K,N)=\{i \in \mathbb{Z}_0^N;\ \mathbb{P}(X(F(\mathbb{Z}_0^N)) = i \mid X(0) \in \mathbb{Z}_{K+1}^{\infty}) = 0\},\\[3pt] \mathcal{N}_0^{(2)}(K,N)&=\{i \in \mathbb{Z}_{N+1}^K;\ \\[3pt] &\qquad\qquad\mathbb{P}(X(t) \in \mathbb{Z}_{N+1}^{\infty} \mbox{ for all } t \in (0,F(\{i\})]\mid X(0) \in \mathbb{Z}_{K+1}^{\infty}) = 0\},\\[3pt] \mathcal{N}_0^{(3)}(K,N)&=\{i \in \mathbb{Z}_{N+1}^K;\ \mathbb{P}(X(t) \in \mathbb{Z}_{N+1}^K \mbox{ for all } t \in (0,F(\mathbb{Z}_0^N)]\mid X(0) = i) = 0\}.\end{align*}
Roughly speaking, states in
![]() $\mathcal{N}_0^{(1)}(K,N) \subseteq \mathbb{Z}_0^N$
and states in
$\mathcal{N}_0^{(1)}(K,N) \subseteq \mathbb{Z}_0^N$
and states in
![]() $\mathcal{N}_0^{(2)}(K,N) \subseteq \mathbb{Z}_{N+1}^K$
can be reached from any states in
$\mathcal{N}_0^{(2)}(K,N) \subseteq \mathbb{Z}_{N+1}^K$
can be reached from any states in
![]() $\mathbb{Z}_{K+1}^{\infty}$
only after visiting
$\mathbb{Z}_{K+1}^{\infty}$
only after visiting
![]() $\widetilde{\mathcal{J}}(K,N) \subseteq \mathbb{Z}_0^N$
. On the other hand, states in
$\widetilde{\mathcal{J}}(K,N) \subseteq \mathbb{Z}_0^N$
. On the other hand, states in
![]() $\mathcal{N}_0^{(3)}(K,N) \in \mathbb{Z}_{N+1}^K$
have no paths to
$\mathcal{N}_0^{(3)}(K,N) \in \mathbb{Z}_{N+1}^K$
have no paths to
![]() $\widetilde{\mathcal{J}}(K,N)$
without visiting
$\widetilde{\mathcal{J}}(K,N)$
without visiting
![]() $\mathbb{Z}_{K+1}^{\infty}$
.
$\mathbb{Z}_{K+1}^{\infty}$
.
By definition,
![]() $\mathcal{X} \cap \mathcal{N}_0(K,N) = \emptyset$
if
$\mathcal{X} \cap \mathcal{N}_0(K,N) = \emptyset$
if
![]() $\mathcal{X} \in\mathcal{S}^*(K,N)$
, whereas there may exist
$\mathcal{X} \in\mathcal{S}^*(K,N)$
, whereas there may exist
![]() $\mathcal{X} \in \mathcal{S}(K,N)$
such that
$\mathcal{X} \in \mathcal{S}(K,N)$
such that
![]() $\mathcal{X}\cap \mathcal{N}_0(K,N) \neq \emptyset$
. As we will see, all states in
$\mathcal{X}\cap \mathcal{N}_0(K,N) \neq \emptyset$
. As we will see, all states in
![]() $\mathcal{N}_0(K,N)$
can be excluded from consideration when we study
$\mathcal{N}_0(K,N)$
can be excluded from consideration when we study
![]() $\boldsymbol{\pi}(N)$
for Markov chains in
$\boldsymbol{\pi}(N)$
for Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
.
Before considering minimum convex polytopes for Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
, we provide a remark on (K, N)-skip-free sets. Note that (K, N)-skip-free sets can be regarded as a natural extension of levels with the skip-free-to-the-left property in Markov chains of M/G/1-type. Suppose a Markov chain
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
, we provide a remark on (K, N)-skip-free sets. Note that (K, N)-skip-free sets can be regarded as a natural extension of levels with the skip-free-to-the-left property in Markov chains of M/G/1-type. Suppose a Markov chain
![]() $\{X(t)\}_{t\in(\!-\infty, \infty)}$
is of M/G/1-type; i.e., its state space
$\{X(t)\}_{t\in(\!-\infty, \infty)}$
is of M/G/1-type; i.e., its state space
![]() $\mathbb{Z}^+$
is partitioned into disjoint levels
$\mathbb{Z}^+$
is partitioned into disjoint levels
![]() $\{\mathcal{L}_m;\ m\in \mathbb{Z}^+\}$
, and transitions between two levels are skip-free to the left. We now consider the first passage time from
$\{\mathcal{L}_m;\ m\in \mathbb{Z}^+\}$
, and transitions between two levels are skip-free to the left. We now consider the first passage time from
![]() $\mathcal{L}_{K+1}$
to
$\mathcal{L}_{K+1}$
to
![]() $\mathcal{L}_N$
(
$\mathcal{L}_N$
(
![]() $K > N$
). It then follows that each level
$K > N$
). It then follows that each level
![]() $\mathcal{L}_m$
(
$\mathcal{L}_m$
(
![]() $m=N,N+1,\ldots,K$
) can be regarded as a
$m=N,N+1,\ldots,K$
) can be regarded as a
![]() $(\hat{K},\hat{N})$
-skip-free set, where
$(\hat{K},\hat{N})$
-skip-free set, where
![]() $\hat{K}$
and
$\hat{K}$
and
![]() $\hat{N}$
denote the total number of states in
$\hat{N}$
denote the total number of states in
![]() $\bigcup_{m=0}^K \mathcal{L}_m$
and
$\bigcup_{m=0}^K \mathcal{L}_m$
and
![]() $\bigcup_{m=0}^N \mathcal{L}_m$
. One of the most notable differences between (K, N)-skip-free sets and levels with the skip-free-to-the-left property is that (K, N)-skip-free sets are not disjoint, while levels are disjoint.
$\bigcup_{m=0}^N \mathcal{L}_m$
. One of the most notable differences between (K, N)-skip-free sets and levels with the skip-free-to-the-left property is that (K, N)-skip-free sets are not disjoint, while levels are disjoint.
4.2. Minimum convex polytopes
We consider convex polytopes associated with (K, N)-skip-free sets. We partition
![]() $\textbf{\textit{H}}(K)=(\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
into two matrices as in (4.1). Note here that
$\textbf{\textit{H}}(K)=(\!-\textbf{\textit{Q}}^{(1,1)}(K))^{-1}$
into two matrices as in (4.1). Note here that
and
![]() $[\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}}]_{i} > 0$
for all
$[\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}}]_{i} > 0$
for all
![]() $i \in \mathbb{Z}_0^K\setminus \mathcal{N}_0^{(3)}(K,N)$
. For any
$i \in \mathbb{Z}_0^K\setminus \mathcal{N}_0^{(3)}(K,N)$
. For any
![]() $(K+1)$
-dimensional vector
$(K+1)$
-dimensional vector
![]() $\textbf{\textit{x}}$
, we define
$\textbf{\textit{x}}$
, we define
![]() $\textrm{diag}^*(\textbf{\textit{x}})$
as a
$\textrm{diag}^*(\textbf{\textit{x}})$
as a
![]() $(K+1)$
-dimensional diagonal matrix whose ith (
$(K+1)$
-dimensional diagonal matrix whose ith (
![]() $i \in \mathbb{Z}_0^K$
) diagonal element is given by
$i \in \mathbb{Z}_0^K$
) diagonal element is given by
 \begin{equation*}[\textrm{diag}^*(\textbf{\textit{x}})]_{i,i}=\begin{cases}\displaystyle\frac{1}{[\textbf{\textit{x}}]_i}, & [\textbf{\textit{x}}]_i \neq 0,\\[3pt] 0, & \textrm{otherwise}.\end{cases}\end{equation*}
\begin{equation*}[\textrm{diag}^*(\textbf{\textit{x}})]_{i,i}=\begin{cases}\displaystyle\frac{1}{[\textbf{\textit{x}}]_i}, & [\textbf{\textit{x}}]_i \neq 0,\\[3pt] 0, & \textrm{otherwise}.\end{cases}\end{equation*}
We then define
![]() $\Gamma(K,N;\,\mathcal{B})$
(
$\Gamma(K,N;\,\mathcal{B})$
(
![]() $K,N \in \mathbb{Z}^+$
,
$K,N \in \mathbb{Z}^+$
,
![]() $K > N$
,
$K > N$
,
![]() $\mathcal{B} \subseteq\mathbb{Z}_0^K$
) as
$\mathcal{B} \subseteq\mathbb{Z}_0^K$
) as
 \begin{align*}\Gamma(K,N;\,\mathcal{B})&=\big\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta}\textbf{\textit{U}}(K,N),\boldsymbol{\beta} \in \Gamma(K),\\[3pt]& {}[\boldsymbol{\beta}]_i \geq 0\ (i \in \mathcal{B}),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K\setminus\mathcal{B})\},\end{align*}
\begin{align*}\Gamma(K,N;\,\mathcal{B})&=\big\{\boldsymbol{\alpha} \in \mathbb{R}^{N+1};\ \boldsymbol{\alpha}=\boldsymbol{\beta}\textbf{\textit{U}}(K,N),\boldsymbol{\beta} \in \Gamma(K),\\[3pt]& {}[\boldsymbol{\beta}]_i \geq 0\ (i \in \mathcal{B}),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K\setminus\mathcal{B})\},\end{align*}
where
![]() $\Gamma(n)$
(
$\Gamma(n)$
(
![]() $n \in \mathbb{Z}^+$
) is defined in (2.5) and
$n \in \mathbb{Z}^+$
) is defined in (2.5) and
![]() $\textbf{\textit{U}}(K,N)$
is given by
$\textbf{\textit{U}}(K,N)$
is given by
 \begin{align*}\textbf{\textit{U}}(K,N)&=\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\begin{pmatrix}\textbf{\textit{I}}\\ (\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N)\end{pmatrix}\\&\cdot(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}).\end{align*}
\begin{align*}\textbf{\textit{U}}(K,N)&=\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\begin{pmatrix}\textbf{\textit{I}}\\ (\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N)\end{pmatrix}\\&\cdot(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}).\end{align*}
Moreover, for
![]() $\mathcal{X} \in \mathcal{S}(K,N)$
, we define
$\mathcal{X} \in \mathcal{S}(K,N)$
, we define
![]() $\mathcal{X}^*$
as
$\mathcal{X}^*$
as
Note that
We then have the following theorem, whose proof is given in Appendix G.
Theorem 4.1. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\break \mathcal{J}(K))$
, we have for
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\break \mathcal{J}(K))$
, we have for
![]() $\mathcal{X} \in\mathcal{S}(K,N)$
(
$\mathcal{X} \in\mathcal{S}(K,N)$
(
![]() $K>N$
) that
$K>N$
) that
where
![]() $\mathcal{P}^+(K,N;\, \mathcal{X}^*)$
denotes a convex polytope on the first orthant of
$\mathcal{P}^+(K,N;\, \mathcal{X}^*)$
denotes a convex polytope on the first orthant of
![]() $\mathbb{R}^{N+1}$
which is given by
$\mathbb{R}^{N+1}$
which is given by
 \begin{align}\mathcal{P}^+(K,N;\, \mathcal{X}^{*})&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \big[(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))]_i \geq 0\ (i \in \mathcal{X}^*),\nonumber\\[3pt] &\quad\,\big[(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^{*}),\nonumber\\[3pt] &\quad \textbf{\textit{x}}\textbf{\textit{e}}=1,\ \textbf{\textit{y}}\geq\textbf{0}\big\}\end{align}
\begin{align}\mathcal{P}^+(K,N;\, \mathcal{X}^{*})&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \big[(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))]_i \geq 0\ (i \in \mathcal{X}^*),\nonumber\\[3pt] &\quad\,\big[(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^{*}),\nonumber\\[3pt] &\quad \textbf{\textit{x}}\textbf{\textit{e}}=1,\ \textbf{\textit{y}}\geq\textbf{0}\big\}\end{align}
In particular,
Remark 4.2. Consider two (K, N)-skip-free sets
![]() $\mathcal{X}_A, \mathcal{X}_B \in \mathcal{S}(K,N)$
. If
$\mathcal{X}_A, \mathcal{X}_B \in \mathcal{S}(K,N)$
. If
![]() $\mathcal{X}_A \subseteq \mathcal{X}_B$
, we have
$\mathcal{X}_A \subseteq \mathcal{X}_B$
, we have
![]() $\mathcal{X}_A^* \subseteq \mathcal{X}_B^*$
by definition. Therefore, it follows from (4.5) that
$\mathcal{X}_A^* \subseteq \mathcal{X}_B^*$
by definition. Therefore, it follows from (4.5) that
![]() $\mathcal{P}^+(K,N;\, \mathcal{X}_A^*) \subseteq \mathcal{P}^+(K,N;\, \mathcal{X}_B^*)$
if
$\mathcal{P}^+(K,N;\, \mathcal{X}_A^*) \subseteq \mathcal{P}^+(K,N;\, \mathcal{X}_B^*)$
if
![]() $\mathcal{X}_A\subseteq \mathcal{X}_B$
.
$\mathcal{X}_A\subseteq \mathcal{X}_B$
.
Lemma 4.1. For Markov chains in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
with
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
with
![]() $\mathcal{X}_A,\mathcal{X}_B \in \mathcal{S}(K,N)$
, we consider the first passage times
$\mathcal{X}_A,\mathcal{X}_B \in \mathcal{S}(K,N)$
, we consider the first passage times
![]() $F(\mathcal{X}_A^*)$
,
$F(\mathcal{X}_A^*)$
,
![]() $F(\mathcal{X}_B^*)$
, and
$F(\mathcal{X}_B^*)$
, and
![]() $F(\mathbb{Z}_0^N)$
. If the statements
$F(\mathbb{Z}_0^N)$
. If the statements
and
hold sample-path-wise, we have
The proof of Lemma 4.1 is given in Appendix H. By definition,
![]() $\widetilde{\mathcal{J}}(K,N) \in \mathcal{S}^*(K,N)$
, and
$\widetilde{\mathcal{J}}(K,N) \in \mathcal{S}^*(K,N)$
, and
![]() $\mathcal{P}^+(K,N;\,\widetilde{\mathcal{J}}(K,N))$
is identical to
$\mathcal{P}^+(K,N;\,\widetilde{\mathcal{J}}(K,N))$
is identical to
![]() $\widetilde{\mathcal{P}}^+(K,N)$
in (3.24). Recall that
$\widetilde{\mathcal{P}}^+(K,N)$
in (3.24). Recall that
![]() $\widetilde{\mathcal{J}}(K,N) \subseteq \mathbb{Z}_0^N$
. Therefore, for any
$\widetilde{\mathcal{J}}(K,N) \subseteq \mathbb{Z}_0^N$
. Therefore, for any
![]() $\mathcal{X}\in \mathcal{S}(K,N)$
,
$\mathcal{X}\in \mathcal{S}(K,N)$
,
![]() $F(\mathcal{X}) \leq F(\widetilde{\mathcal{J}}(K,N))$
holds sample-path-wise, given
$F(\mathcal{X}) \leq F(\widetilde{\mathcal{J}}(K,N))$
holds sample-path-wise, given
![]() $X(0) \in \mathbb{Z}_{K+1}^{\infty}$
. On the other hand,
$X(0) \in \mathbb{Z}_{K+1}^{\infty}$
. On the other hand,
![]() $\mathcal{J}(K) \in\mathcal{S}(K,N)$
, and each state in
$\mathcal{J}(K) \in\mathcal{S}(K,N)$
, and each state in
![]() $\mathcal{J}(K)$
is reachable from some states in
$\mathcal{J}(K)$
is reachable from some states in
![]() $\mathbb{Z}_{K+1}^{\infty}$
by direct transitions. Note here that
$\mathbb{Z}_{K+1}^{\infty}$
by direct transitions. Note here that
We thus have
![]() $F(\mathcal{J}^*(K)) \leq F(\mathcal{X}^*)$
sample-path-wise, given
$F(\mathcal{J}^*(K)) \leq F(\mathcal{X}^*)$
sample-path-wise, given
![]() $X(0) \in \mathbb{Z}_{K+1}^{\infty}$
. The corollary below follows from Theorem 4.1 and the above observations.
$X(0) \in \mathbb{Z}_{K+1}^{\infty}$
. The corollary below follows from Theorem 4.1 and the above observations.
Corollary 4.1. Among (K, N)-skip-free sets,
![]() $\widetilde{\mathcal{J}}(K,N)$
in (3.19) gives a maximum convex polytope, i.e.,
$\widetilde{\mathcal{J}}(K,N)$
in (3.19) gives a maximum convex polytope, i.e.,
On the other hand, among (K, N)-skip-free sets,
![]() $\mathcal{J}^*(K)$
gives a minimum convex polytope, i.e.,
$\mathcal{J}^*(K)$
gives a minimum convex polytope, i.e.,
Note here that
![]() $\mathcal{J}^*(K)$
is not proper in general. We thus consider a proper (K, N)-skip-free set that gives the minimum convex polytope
$\mathcal{J}^*(K)$
is not proper in general. We thus consider a proper (K, N)-skip-free set that gives the minimum convex polytope
![]() $\mathcal{P}^+(K,N;\,\mathcal{J}^*(K))$
. Specifically, we introduce a subset
$\mathcal{P}^+(K,N;\,\mathcal{J}^*(K))$
. Specifically, we introduce a subset
![]() $\mathcal{D}(K,N)$
of
$\mathcal{D}(K,N)$
of
![]() $\mathcal{J}(K)$
, which is generated by the following procedure.
$\mathcal{J}(K)$
, which is generated by the following procedure.
Procedure 4.1. ([Reference Nagamochi9].)
-
(i) We obtain a directed graph
 $G^*(K,N)$
from G(K, N) in (4.2) by removing all incoming edges to nodes in
$G^*(K,N)$
from G(K, N) in (4.2) by removing all incoming edges to nodes in
 $\mathcal{J}(K)$
.
$\mathcal{J}(K)$
. -
(ii) We then find the subset
 $\mathcal{D}(K,N)$
of nodes in
$\mathcal{D}(K,N)$
of nodes in
 $\mathcal{J}(K)$
from which node t is reachable in
$\mathcal{J}(K)$
from which node t is reachable in
 $G^*(K,N)$
.
$G^*(K,N)$
.
Note that Step (ii) can be performed with O(K) operations, by considering reverse paths from node t to node s in the graph
![]() $G^*(K,N)$
.
$G^*(K,N)$
.
Lemma 4.2. ([Reference Nagamochi9].) Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
(
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\mathcal{J}(K))$
(
![]() $K>N$
), we have
$K>N$
), we have
![]() $\mathcal{D}(K,N) \in \mathcal{S}^*(K,N)$
. Furthermore,
$\mathcal{D}(K,N) \in \mathcal{S}^*(K,N)$
. Furthermore,
![]() $\mathcal{D}(K,N) \subseteq \mathcal{X}$
for all
$\mathcal{D}(K,N) \subseteq \mathcal{X}$
for all
![]() $\mathcal{X} \subseteq \mathcal{J}(K)$
such that
$\mathcal{X} \subseteq \mathcal{J}(K)$
such that
![]() $\mathcal{X} \in \mathcal{S}(K,N)$
.
$\mathcal{X} \in \mathcal{S}(K,N)$
.
The proof of Lemma 4.2 is given in Appendix I.
Lemma 4.3. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\break \mathcal{J}(K))$
(
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K),\break \mathcal{J}(K))$
(
![]() $K>N$
), we have
$K>N$
), we have
where
![]() $\mathcal{J}^*(K)$
is given by (4.8).
$\mathcal{J}^*(K)$
is given by (4.8).
Proof. Since
![]() $\mathcal{D}(K,N) \in \mathcal{S}^*(K,N)$
, we have
$\mathcal{D}(K,N) \in \mathcal{S}^*(K,N)$
, we have
![]() $\mathcal{D}^*(K,N) = \mathcal{D}(K,N)$
from (4.4). It then follows from Remark 4.2 and
$\mathcal{D}^*(K,N) = \mathcal{D}(K,N)$
from (4.4). It then follows from Remark 4.2 and
![]() $\mathcal{D}(K,N) \subseteq \mathcal{J}(K)$
that
$\mathcal{D}(K,N) \subseteq \mathcal{J}(K)$
that
On the other hand, it follows from Lemma 4.2 that
![]() $F(\mathcal{J}^*(K)) \leq F(\mathcal{D}(K,N))$
if
$F(\mathcal{J}^*(K)) \leq F(\mathcal{D}(K,N))$
if
![]() $X(0) \in\mathbb{Z}_{K+1}^{\infty}$
and
$X(0) \in\mathbb{Z}_{K+1}^{\infty}$
and
![]() $F(\mathcal{D}(K,N)) \leq F(\mathbb{Z}_0^N)$
if
$F(\mathcal{D}(K,N)) \leq F(\mathbb{Z}_0^N)$
if
![]() $X(0) \in\mathcal{J}^*(K)$
. We thus have
$X(0) \in\mathcal{J}^*(K)$
. We thus have
![]() $\mathcal{P}^+(K,N;\, \mathcal{J}^*(K)) \subseteq \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
from Lemma 4.1, which completes the proof. □
$\mathcal{P}^+(K,N;\, \mathcal{J}^*(K)) \subseteq \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
from Lemma 4.1, which completes the proof. □
The following theorem shows that the minimum convex polytope
![]() $\mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
is tight in
$\mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
is tight in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
.
Theorem 4.2. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For any
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
, there exists a Markov chain in
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
, there exists a Markov chain in
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
whose
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
whose
![]() $\boldsymbol{\pi}(N)$
is given by
$\boldsymbol{\pi}(N)$
is given by
![]() $\textbf{\textit{x}}$
.
$\textbf{\textit{x}}$
.
The proof of Theorem 4.2 is given in Appendix J. As shown in the proof, if
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
and
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
and
![]() $\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
, we have
$\textbf{\textit{x}} \in\textrm{ri}\, \mathcal{P}^+(K,N;\,\mathcal{D}(K,N))$
, we have
![]() $\textbf{\textit{x}} > \textbf{0}$
. The following corollary comes from the fact that
$\textbf{\textit{x}} > \textbf{0}$
. The following corollary comes from the fact that
![]() $\mathcal{P}^+(K,N;\ \mathcal{D}(K,N))$
is a convex polytope spanned by
$\mathcal{P}^+(K,N;\ \mathcal{D}(K,N))$
is a convex polytope spanned by
![]() $\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
for
$\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
for
![]() $i \in\mathcal{D}(K,N)$
(cf. (H.1)), where
$i \in\mathcal{D}(K,N)$
(cf. (H.1)), where
![]() $\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
(
$\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
(
![]() $i \in \mathbb{Z}_0^K$
) denotes the ith normalized row vector of
$i \in \mathbb{Z}_0^K$
) denotes the ith normalized row vector of
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
in (4.1).
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
in (4.1).
Corollary 4.2. Suppose
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For an arbitrary probability vector
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K)) \neq \emptyset$
. For an arbitrary probability vector
![]() $\textbf{\textit{x}} \in \Gamma(N)$
, we have
$\textbf{\textit{x}} \in \Gamma(N)$
, we have
Furthermore, if
![]() $\textbf{\textit{x}} \in \mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
, we have
$\textbf{\textit{x}} \in \mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
, we have
 \begin{align*}\max_{i \in \mathcal{D}(K,N)}\| \textbf{\textit{x}} - \overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N) \|_1&\leq\max_{i,j \in \mathcal{D}(K,N)}\| \overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\, N)-\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N) \|_1,\\& \qquad\qquad\qquad\qquad\qquad\qquad\textbf{\textit{x}} \in \mathcal{P}^+(K,N;\, \mathcal{D}(K,N)).\end{align*}
\begin{align*}\max_{i \in \mathcal{D}(K,N)}\| \textbf{\textit{x}} - \overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N) \|_1&\leq\max_{i,j \in \mathcal{D}(K,N)}\| \overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\, N)-\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N) \|_1,\\& \qquad\qquad\qquad\qquad\qquad\qquad\textbf{\textit{x}} \in \mathcal{P}^+(K,N;\, \mathcal{D}(K,N)).\end{align*}
Example 4.2.
(Example 2.1 continued.) Consider
![]() $\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Note that
$\textbf{\textit{Q}}$
in Example 2.1 of Section 2.3. Note that
![]() $\mathcal{J}(N)=\{0,N\}$
and
$\mathcal{J}(N)=\{0,N\}$
and
![]() $\mathcal{J}(K)= \mathcal{J}^*(K) = \mathcal{D}(K,N) = \{0,K\}$
. We set
$\mathcal{J}(K)= \mathcal{J}^*(K) = \mathcal{D}(K,N) = \{0,K\}$
. We set
![]() $q_{i,j} = \lambda_i b_{j-i}$
(
$q_{i,j} = \lambda_i b_{j-i}$
(
![]() $i \in \mathbb{Z}^+, j > i$
),
$i \in \mathbb{Z}^+, j > i$
),
![]() $q_{i,i-1} = \mu_i$
(
$q_{i,i-1} = \mu_i$
(
![]() $i \in \mathbb{Z}^+ \setminus\{0\}$
), and
$i \in \mathbb{Z}^+ \setminus\{0\}$
), and
![]() $q_{i,0} = \gamma_i$
(
$q_{i,0} = \gamma_i$
(
![]() $i \in \mathbb{Z}^+ \setminus \{0,1\}$
), where
$i \in \mathbb{Z}^+ \setminus \{0,1\}$
), where
 \begin{gather*}\lambda_i = 2 - \frac{1}{i+1}\quad (i \in \mathbb{Z}^+),\qquad \hspace*{-12pt}b_i = \frac{1}{2^i}\quad (i \in \mathbb{Z}^+ \setminus \{0\}),\\ \mu_i = \frac{i}{10}\quad (i \in \mathbb{Z}^+ \setminus \{0\}),\qquad\gamma_i = \frac{\lambda_i}{i}\quad (i \in \mathbb{Z}^+ \setminus \{0,1\}).\end{gather*}
\begin{gather*}\lambda_i = 2 - \frac{1}{i+1}\quad (i \in \mathbb{Z}^+),\qquad \hspace*{-12pt}b_i = \frac{1}{2^i}\quad (i \in \mathbb{Z}^+ \setminus \{0\}),\\ \mu_i = \frac{i}{10}\quad (i \in \mathbb{Z}^+ \setminus \{0\}),\qquad\gamma_i = \frac{\lambda_i}{i}\quad (i \in \mathbb{Z}^+ \setminus \{0,1\}).\end{gather*}
Table 1 shows the worst-case error bound
of Corollary 4.2, where
![]() $N=50$
, and the result for
$N=50$
, and the result for
![]() $K=N$
indicates the worst-case error bound
$K=N$
indicates the worst-case error bound
of Corollary 2.3. We observe that the worst-case error bound steadily decreases as K increases and that if
![]() $K=150$
, any probability vector
$K=150$
, any probability vector
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
is a good approximation to
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\, \mathcal{D}(K,N))$
is a good approximation to
![]() $\boldsymbol{\pi}(N)$
in this specific case.
$\boldsymbol{\pi}(N)$
in this specific case.
Table 1. The worst-case error bounds in Example 4.2 (
![]() $N=50$
).
$N=50$
).

5. Concluding remarks
This paper studied the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
in ergodic, continuous-time Markov chains on
$\boldsymbol{\pi}(N)$
in ergodic, continuous-time Markov chains on
![]() $\mathbb{Z}^+$
via systems of linear inequalities. Specifically, we first obtained an N-simplex
$\mathbb{Z}^+$
via systems of linear inequalities. Specifically, we first obtained an N-simplex
![]() $\mathcal{P}(N)$
containing
$\mathcal{P}(N)$
containing
![]() $\boldsymbol{\pi}(N)$
, assuming only the knowledge of the
$\boldsymbol{\pi}(N)$
, assuming only the knowledge of the
![]() $(N+1) \times (N+1)$
northwest corner block
$(N+1) \times (N+1)$
northwest corner block
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator. We then refined this result and eliminated unnecessary vertices from
$\textbf{\textit{Q}}^{(1,1)}(N)$
of the infinitesimal generator. We then refined this result and eliminated unnecessary vertices from
![]() $\mathcal{P}(N)$
, using the structural information
$\mathcal{P}(N)$
, using the structural information
![]() $\mathcal{J}(N)$
. These results are closely related to the augmented truncation approximation (ATA), and we provided some practical implications for it. In particular, we observed that the linear ATA is sufficient for computing an ATA solution, and the structural information
$\mathcal{J}(N)$
. These results are closely related to the augmented truncation approximation (ATA), and we provided some practical implications for it. In particular, we observed that the linear ATA is sufficient for computing an ATA solution, and the structural information
![]() $\mathcal{J}(N)$
, if available, is useful for obtaining a reasonable ATA solution.
$\mathcal{J}(N)$
, if available, is useful for obtaining a reasonable ATA solution.
Next, we extended our results to the cases where the
![]() $(K+1) \times (K+1)$
(
$(K+1) \times (K+1)$
(
![]() $K > N$
) northwest corner block (and
$K > N$
) northwest corner block (and
![]() $\mathcal{J}(K)$
) are available. Furthermore, we introduced new state transition structures called (K, N)-skip-free sets, and we obtained a tight convex polytope that contains
$\mathcal{J}(K)$
) are available. Furthermore, we introduced new state transition structures called (K, N)-skip-free sets, and we obtained a tight convex polytope that contains
![]() $\boldsymbol{\pi}(N)$
, under the condition that only
$\boldsymbol{\pi}(N)$
, under the condition that only
![]() $\textbf{\textit{Q}}^{(1,1)}(K)$
and
$\textbf{\textit{Q}}^{(1,1)}(K)$
and
![]() $\mathcal{J}(K)$
are available.
$\mathcal{J}(K)$
are available.
Note that the results in this paper are also applicable to a time-homogeneous, discrete-time Markov chain on
![]() $\mathbb{Z}^+$
. Specifically, in a discrete-time Markov chain with a state transition probability matrix
$\mathbb{Z}^+$
. Specifically, in a discrete-time Markov chain with a state transition probability matrix
![]() $\textbf{\textit{P}}_D$
, the stationary distribution
$\textbf{\textit{P}}_D$
, the stationary distribution
![]() $\boldsymbol{\pi}_D$
, if it exists, satisfies
$\boldsymbol{\pi}_D$
, if it exists, satisfies
![]() $\boldsymbol{\pi}_D = \boldsymbol{\pi}_D \textbf{\textit{P}}_D$
and
$\boldsymbol{\pi}_D = \boldsymbol{\pi}_D \textbf{\textit{P}}_D$
and
![]() $\boldsymbol{\pi}_D \textbf{\textit{e}}=1$
. Therefore, we can study
$\boldsymbol{\pi}_D \textbf{\textit{e}}=1$
. Therefore, we can study
![]() $\boldsymbol{\pi}_D$
by considering the corresponding continuous-time Markov chain with the infinitesimal generator
$\boldsymbol{\pi}_D$
by considering the corresponding continuous-time Markov chain with the infinitesimal generator
![]() $\textbf{\textit{Q}}=\textbf{\textit{P}}_D-\textbf{\textit{I}}$
.
$\textbf{\textit{Q}}=\textbf{\textit{P}}_D-\textbf{\textit{I}}$
.
In this paper, the state space of a Markov chain
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
was assumed to be countably infinite. Except for Corollary 3.3, however, all the results in this paper also hold for Markov chains with finite state space
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
was assumed to be countably infinite. Except for Corollary 3.3, however, all the results in this paper also hold for Markov chains with finite state space
![]() $\mathbb{Z}_0^{K^*}$
for some
$\mathbb{Z}_0^{K^*}$
for some
![]() $K^* \in \mathbb{Z}^+$
such that
$K^* \in \mathbb{Z}^+$
such that
![]() $N < K < K^*$
, if we replace
$N < K < K^*$
, if we replace
![]() $\mathbb{Z}_N^{\infty}$
and
$\mathbb{Z}_N^{\infty}$
and
![]() $\mathbb{Z}_K^{\infty}$
by
$\mathbb{Z}_K^{\infty}$
by
![]() $\mathbb{Z}_N^{K^*}$
and
$\mathbb{Z}_N^{K^*}$
and
![]() $\mathbb{Z}_K^{K^*}$
.
$\mathbb{Z}_K^{K^*}$
.
We scarcely ever discussed one-point approximations to the conditional stationary distribution
![]() $\boldsymbol{\pi}(N)$
, except in Section 2.4. In view of the error bounds in Corollaries 2.3 and 4.2, it seems to be reasonable to choose the center of a convex polytope that contains
$\boldsymbol{\pi}(N)$
, except in Section 2.4. In view of the error bounds in Corollaries 2.3 and 4.2, it seems to be reasonable to choose the center of a convex polytope that contains
![]() $\boldsymbol{\pi}(N)$
as a one-point approximation to
$\boldsymbol{\pi}(N)$
as a one-point approximation to
![]() $\boldsymbol{\pi}(N)$
. Note, however, that we cannot identify the exact location of
$\boldsymbol{\pi}(N)$
. Note, however, that we cannot identify the exact location of
![]() $\boldsymbol{\pi}(N)$
within the convex polytopes unless further information is available. Therefore, for a specific problem, the choice of the center may or may not work well. The development of new approximation algorithms for the (un)conditional stationary distributions of Markov chains remains as future work.
$\boldsymbol{\pi}(N)$
within the convex polytopes unless further information is available. Therefore, for a specific problem, the choice of the center may or may not work well. The development of new approximation algorithms for the (un)conditional stationary distributions of Markov chains remains as future work.
Appendix A. Proof of Corollary 2.2
Substituting (2.15) and (2.16) into (2.12) yields (2.17). We thus consider (2.15) and (2.16) below. Because
we have
and therefore
 \begin{equation*}[\overline{\textbf{\textit{H}}}(N)]_{i,j}=\displaystyle\frac{1}{\mathbb{E}\bigl[ T_n^{(2)} - T_n^{(1)} \mid X(T_n^{(1)}) = i \bigr]}\mathbb{E}\Bigl[ \int_{T_n^{(1)}}^{T_n^{(2)}} \mathbb{I}(X(t)=j) \textrm{d} t\mid X(T_n^{(1)}) = i \Bigr],\end{equation*}
\begin{equation*}[\overline{\textbf{\textit{H}}}(N)]_{i,j}=\displaystyle\frac{1}{\mathbb{E}\bigl[ T_n^{(2)} - T_n^{(1)} \mid X(T_n^{(1)}) = i \bigr]}\mathbb{E}\Bigl[ \int_{T_n^{(1)}}^{T_n^{(2)}} \mathbb{I}(X(t)=j) \textrm{d} t\mid X(T_n^{(1)}) = i \Bigr],\end{equation*}
from which (2.15) follows.
We also have
![]() $\boldsymbol{\pi}^{(1)}(N)=\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}^{(2,1)}(N)\textbf{\textit{H}}(N)$
from (2.4) and (2.9), so that
$\boldsymbol{\pi}^{(1)}(N)=\boldsymbol{\pi}^{(2)}(N) \textbf{\textit{Q}}^{(2,1)}(N)\textbf{\textit{H}}(N)$
from (2.4) and (2.9), so that
It then follows from (2.10) and (2.12) that
where
It is readily seen that
We thus have
 \begin{equation*}[\boldsymbol{\alpha}^*(N)]_i=\displaystyle\frac{1}{\mathbb{E}\bigl[ T_n^{(2)} - T_n^{(1)} \bigr]}\mathbb{E}\Bigl[ \displaystyle\int_{T_n^{(1)}}^{T_n^{(2)}} \mathbb{I}( I(t) = i) \textrm{d} t \Bigr],\quad i \in \mathbb{Z}_0^N,\end{equation*}
\begin{equation*}[\boldsymbol{\alpha}^*(N)]_i=\displaystyle\frac{1}{\mathbb{E}\bigl[ T_n^{(2)} - T_n^{(1)} \bigr]}\mathbb{E}\Bigl[ \displaystyle\int_{T_n^{(1)}}^{T_n^{(2)}} \mathbb{I}( I(t) = i) \textrm{d} t \Bigr],\quad i \in \mathbb{Z}_0^N,\end{equation*}
from which (2.16) follows.
Appendix B. Equivalence between (2.22) and (2.23) for
 $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
Suppose
![]() $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
. We partition
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
. We partition
![]() $\overline{\textbf{\textit{H}}}(N)$
into two matrices:
$\overline{\textbf{\textit{H}}}(N)$
into two matrices:
 \begin{equation*}\overline{\textbf{\textit{H}}}(N)=\kbordermatrix{ & \mathbb{Z}_0^N\\ \mathcal{J}(N) & \overline{\textbf{\textit{H}}}_+(N)\\ \mathbb{Z}_0^N \setminus \mathcal{J}(N)\quad & \overline{\textbf{\textit{H}}}_0(N)}.\end{equation*}
\begin{equation*}\overline{\textbf{\textit{H}}}(N)=\kbordermatrix{ & \mathbb{Z}_0^N\\ \mathcal{J}(N) & \overline{\textbf{\textit{H}}}_+(N)\\ \mathbb{Z}_0^N \setminus \mathcal{J}(N)\quad & \overline{\textbf{\textit{H}}}_0(N)}.\end{equation*}
Note that (2.23) for
![]() $\mathcal{J}(N) \neq \mathbb{Z}_0^N$
is equivalent to
$\mathcal{J}(N) \neq \mathbb{Z}_0^N$
is equivalent to
We now rewrite (2.22) as
 \begin{align*}\mathcal{P}^+(N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) \geq \textbf{0},\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\big\}\\[2pt]&=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) = \textbf{\textit{y}},\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0},\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!- \textbf{\textit{Q}}_+^{(1,1)}(N)\ \ -\textbf{\textit{Q}}_0^{(1,1)}(N)) = (\textbf{\textit{y}}\ \ \textbf{0}),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}^{(1,1)}(N)) = (\textbf{\textit{y}}\ \ \textbf{0}),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\ \ \textbf{0}) \textbf{\textit{H}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\ \ \textbf{0}) \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\textrm{diag}(\textbf{\textit{H}}_+(N)\textbf{\textit{e}})\ \ \textbf{0}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= \textbf{\textit{y}}\textrm{diag}(\textbf{\textit{H}}_+(N)\textbf{\textit{e}}) \overline{\textbf{\textit{H}}}_+(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] & =\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= \boldsymbol{\alpha} \overline{\textbf{\textit{H}}}_+(N),\boldsymbol{\alpha} \geq \textbf{0},\ \boldsymbol{\alpha}\textbf{\textit{e}} =1\bigr\},\end{align*}
\begin{align*}\mathcal{P}^+(N)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) \geq \textbf{0},\ \textbf{\textit{x}}(\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} = 1\big\}\\[2pt]&=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) = \textbf{\textit{y}},\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0},\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!- \textbf{\textit{Q}}_+^{(1,1)}(N)\ \ -\textbf{\textit{Q}}_0^{(1,1)}(N)) = (\textbf{\textit{y}}\ \ \textbf{0}),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}} (\!-\textbf{\textit{Q}}^{(1,1)}(N)) = (\textbf{\textit{y}}\ \ \textbf{0}),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\ \ \textbf{0}) \textbf{\textit{H}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\ \ \textbf{0}) \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= (\textbf{\textit{y}}\textrm{diag}(\textbf{\textit{H}}_+(N)\textbf{\textit{e}})\ \ \textbf{0}) \overline{\textbf{\textit{H}}}(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] &=\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= \textbf{\textit{y}}\textrm{diag}(\textbf{\textit{H}}_+(N)\textbf{\textit{e}}) \overline{\textbf{\textit{H}}}_+(N),\ \textbf{\textit{y}} \geq \textbf{0},\ \textbf{\textit{x}}\textbf{\textit{e}} =1\bigr\}\\[2pt] & =\bigl\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}= \boldsymbol{\alpha} \overline{\textbf{\textit{H}}}_+(N),\boldsymbol{\alpha} \geq \textbf{0},\ \boldsymbol{\alpha}\textbf{\textit{e}} =1\bigr\},\end{align*}
where the last equality follows from the same reasoning as in (2.11).
Appendix C. Proof of Lemma 2.2
Since
![]() $\mathcal{A}_{\textrm{L}}(N)\subseteq\mathcal{A}(N)$
, we have
$\mathcal{A}_{\textrm{L}}(N)\subseteq\mathcal{A}(N)$
, we have
![]() $\mathcal{T}_{\textrm{L}}(N) \subseteq\mathcal{T}(N)$
. We thus show
$\mathcal{T}_{\textrm{L}}(N) \subseteq\mathcal{T}(N)$
. We thus show
![]() $\mathcal{T}(N) \subseteq \mathcal{P}(N)$
and
$\mathcal{T}(N) \subseteq \mathcal{P}(N)$
and
![]() $\mathcal{P}(N) \subseteq\mathcal{T}_{\textrm{L}}(N)$
, from which the lemma follows.
$\mathcal{P}(N) \subseteq\mathcal{T}_{\textrm{L}}(N)$
, from which the lemma follows.
We first prove
![]() $\mathcal{T}(N) \subseteq \mathcal{P}(N)$
. Suppose
$\mathcal{T}(N) \subseteq \mathcal{P}(N)$
. Suppose
![]() $\textbf{\textit{x}}\in\mathcal{T}(N)$
; i.e.,
$\textbf{\textit{x}}\in\mathcal{T}(N)$
; i.e.,
![]() $\textbf{\textit{x}}[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)] =\textbf{0}$
for some
$\textbf{\textit{x}}[\textbf{\textit{Q}}^{(1,1)}(N)+ \textbf{\textit{Q}}_{\textrm{A}}(N)] =\textbf{0}$
for some
![]() $\textbf{\textit{Q}}_{\textrm{A}}(N) \in \mathcal{A}(N)$
. Post-multiplying both sides of this equation by
$\textbf{\textit{Q}}_{\textrm{A}}(N) \in \mathcal{A}(N)$
. Post-multiplying both sides of this equation by
![]() $\textbf{\textit{H}}(N)=(\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1}$
and rearranging terms, we obtain
$\textbf{\textit{H}}(N)=(\!-\textbf{\textit{Q}}^{(1,1)}(N))^{-1}$
and rearranging terms, we obtain
where
![]() $\boldsymbol{\alpha} = \textbf{\textit{x}} \textbf{\textit{Q}}_{\textrm{A}}(N) \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
. Note here that
$\boldsymbol{\alpha} = \textbf{\textit{x}} \textbf{\textit{Q}}_{\textrm{A}}(N) \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})$
. Note here that
![]() $\boldsymbol{\alpha} \in \Gamma(N)$
because
$\boldsymbol{\alpha} \in \Gamma(N)$
because
![]() $\boldsymbol{\alpha} \geq\textbf{0}$
,
$\boldsymbol{\alpha} \geq\textbf{0}$
,
![]() $\textbf{\textit{x}} \textbf{\textit{e}} = 1$
, and
$\textbf{\textit{x}} \textbf{\textit{e}} = 1$
, and
![]() $\textbf{\textit{x}} \textbf{\textit{e}} = \boldsymbol{\alpha}\overline{\textbf{\textit{H}}}(N) \textbf{\textit{e}} = \boldsymbol{\alpha} \textbf{\textit{e}}$
. We thus obtain
$\textbf{\textit{x}} \textbf{\textit{e}} = \boldsymbol{\alpha}\overline{\textbf{\textit{H}}}(N) \textbf{\textit{e}} = \boldsymbol{\alpha} \textbf{\textit{e}}$
. We thus obtain
![]() $\textbf{\textit{x}} \in \mathcal{P}(N)$
from (2.8), so that
$\textbf{\textit{x}} \in \mathcal{P}(N)$
from (2.8), so that
![]() $\mathcal{T}(N)\subseteq \mathcal{P}(N)$
.
$\mathcal{T}(N)\subseteq \mathcal{P}(N)$
.
Next, we prove
![]() $\mathcal{P}(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
. For an arbitrarily fixed
$\mathcal{P}(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
. For an arbitrarily fixed
![]() $\textbf{\textit{x}} \in \mathcal{P}(N)$
, let
$\textbf{\textit{x}} \in \mathcal{P}(N)$
, let
![]() $\textbf{\textit{y}} = \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq \textbf{0}$
(cf. (2.7)). Since
$\textbf{\textit{y}} = \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N)) \geq \textbf{0}$
(cf. (2.7)). Since
![]() $\textbf{\textit{x}}\textbf{\textit{e}} = 1$
and
$\textbf{\textit{x}}\textbf{\textit{e}} = 1$
and
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular, we have
$\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular, we have
![]() $\textbf{\textit{y}} \neq \textbf{0}$
. We then consider a linear augmentation matrix
$\textbf{\textit{y}} \neq \textbf{0}$
. We then consider a linear augmentation matrix
![]() $\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N)$
given by
$\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N)$
given by
It is clear that
![]() $\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N) \in \mathcal{A}_{\textrm{L}}(N)$
and
$\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N) \in \mathcal{A}_{\textrm{L}}(N)$
and
which implies
![]() $\textbf{\textit{x}} \in \mathcal{T}_{\textrm{L}}(N)$
, so that
$\textbf{\textit{x}} \in \mathcal{T}_{\textrm{L}}(N)$
, so that
![]() $\mathcal{P}(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
.
$\mathcal{P}(N) \subseteq \mathcal{T}_{\textrm{L}}(N)$
.
Appendix D. Proof of Lemma 2.3
If
![]() $\mathcal{J}(N) = \mathbb{Z}_0^N$
, Lemma 2.3 immediately follows from Lemma 2.2. We thus assume
$\mathcal{J}(N) = \mathbb{Z}_0^N$
, Lemma 2.3 immediately follows from Lemma 2.2. We thus assume
![]() $\mathcal{J}(N)\neq \mathbb{Z}_0^N$
. Implication 2.2 with
$\mathcal{J}(N)\neq \mathbb{Z}_0^N$
. Implication 2.2 with
![]() $\boldsymbol{\zeta} \in \Gamma^+(N)$
implies
$\boldsymbol{\zeta} \in \Gamma^+(N)$
implies
![]() $\mathcal{T}_{\textrm{L}}^+(N) \subseteq\mathcal{P}^+(N)$
. We thus show
$\mathcal{T}_{\textrm{L}}^+(N) \subseteq\mathcal{P}^+(N)$
. We thus show
![]() $\mathcal{P}^+(N) \subseteq \mathcal{T}_{\textrm{L}}^+(N)$
below. For an arbitrarily fixed
$\mathcal{P}^+(N) \subseteq \mathcal{T}_{\textrm{L}}^+(N)$
below. For an arbitrarily fixed
![]() $\textbf{\textit{x}} \in \mathcal{P}^+(N)$
, let
$\textbf{\textit{x}} \in \mathcal{P}^+(N)$
, let
![]() $\textbf{\textit{y}} = \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N))$
. Since
$\textbf{\textit{y}} = \textbf{\textit{x}}(\!-\textbf{\textit{Q}}^{(1,1)}(N))$
. Since
![]() $\textbf{\textit{x}}\textbf{\textit{e}}=1$
and
$\textbf{\textit{x}}\textbf{\textit{e}}=1$
and
![]() $\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular,
$\textbf{\textit{Q}}^{(1,1)}(N)$
is nonsingular,
![]() $\textbf{\textit{y}} \neq \textbf{0}$
. Furthermore, by definition,
$\textbf{\textit{y}} \neq \textbf{0}$
. Furthermore, by definition,
![]() $\textbf{\textit{x}}(\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) \geq \textbf{0}$
and
$\textbf{\textit{x}}(\!-\textbf{\textit{Q}}_+^{(1,1)}(N)) \geq \textbf{0}$
and
![]() $\textbf{\textit{x}}(\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0}$
, where
$\textbf{\textit{x}}(\!-\textbf{\textit{Q}}_0^{(1,1)}(N)) = \textbf{0}$
, where
![]() $\textbf{\textit{Q}}_+^{(1,1)}(N)$
and
$\textbf{\textit{Q}}_+^{(1,1)}(N)$
and
![]() $\textbf{\textit{Q}}_0^{(1,1)}(N)$
are given in (2.18). We then partition
$\textbf{\textit{Q}}_0^{(1,1)}(N)$
are given in (2.18). We then partition
![]() $\textbf{\textit{y}}$
into two parts:
$\textbf{\textit{y}}$
into two parts:
where
![]() $\textbf{\textit{y}}+ \geq \textbf{0}$
and
$\textbf{\textit{y}}+ \geq \textbf{0}$
and
![]() $\textbf{\textit{y}}_+ \textbf{\textit{e}} > 0$
. We now consider a linear augmentation matrix
$\textbf{\textit{y}}_+ \textbf{\textit{e}} > 0$
. We now consider a linear augmentation matrix
![]() $\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N)$
given by
$\textbf{\textit{Q}}_{\textrm{A}}^{\dag}(N)$
given by
It is clear that
and
which implies
![]() $\textbf{\textit{x}} \in \mathcal{T}_{\textrm{L}}^+(N)$
, so that
$\textbf{\textit{x}} \in \mathcal{T}_{\textrm{L}}^+(N)$
, so that
![]() $\mathcal{P}^+(N) \subseteq \mathcal{T}_{\textrm{L}}^+(N)$
.
$\mathcal{P}^+(N) \subseteq \mathcal{T}_{\textrm{L}}^+(N)$
.
Appendix E. Proof of Corollary 3.1
We first prove (3.16) by showing that
![]() $\boldsymbol{\beta} \in \Gamma(N) \Rightarrow \boldsymbol{\alpha}\in \Gamma(N)$
in (3.14), i.e., that
$\boldsymbol{\beta} \in \Gamma(N) \Rightarrow \boldsymbol{\alpha}\in \Gamma(N)$
in (3.14), i.e., that
For this purpose, we consider (3.5). By definition, we have for
![]() $i,j \in \mathbb{Z}_0^N$
,
$i,j \in \mathbb{Z}_0^N$
,
and therefore
![]() $\textbf{\textit{R}}(K,N)$
is substochastic; i.e.,
$\textbf{\textit{R}}(K,N)$
is substochastic; i.e.,
It follows that
Recall that
![]() $\textbf{\textit{H}}(N) \geq \textbf{\textit{O}}$
and
$\textbf{\textit{H}}(N) \geq \textbf{\textit{O}}$
and
![]() $\widetilde{\textbf{\textit{H}}}(K,N) \geq\textbf{\textit{O}}$
. We thus conclude
$\widetilde{\textbf{\textit{H}}}(K,N) \geq\textbf{\textit{O}}$
. We thus conclude
![]() $\boldsymbol{\beta} \geq\textbf{0}\ \Rightarrow\ \boldsymbol{\alpha} \geq \textbf{0}$
from (3.14). Furthermore, we have
$\boldsymbol{\beta} \geq\textbf{0}\ \Rightarrow\ \boldsymbol{\alpha} \geq \textbf{0}$
from (3.14). Furthermore, we have
 \begin{align*}\boldsymbol{\alpha}\textbf{\textit{e}}&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N)\textbf{\textit{e}}\\&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\widetilde{\textbf{\textit{H}}}(K,N) \textbf{\textit{e}}\\&=\boldsymbol{\beta}\textbf{\textit{e}}.\end{align*}
\begin{align*}\boldsymbol{\alpha}\textbf{\textit{e}}&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textbf{\textit{H}}(N)\textbf{\textit{e}}\\&=\boldsymbol{\beta} \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\widetilde{\textbf{\textit{H}}}(K,N) \textbf{\textit{e}}\\&=\boldsymbol{\beta}\textbf{\textit{e}}.\end{align*}
Next we show (3.17). For this purpose, we consider the censored process on
![]() $\mathbb{Z}_0^N \cup \mathbb{Z}_{K_1+1}^{\infty}$
whose generator is given by
$\mathbb{Z}_0^N \cup \mathbb{Z}_{K_1+1}^{\infty}$
whose generator is given by
![]() $\widetilde{\textbf{\textit{Q}}}(K_1,N)$
. We then apply Theorem 2.1 with
$\widetilde{\textbf{\textit{Q}}}(K_1,N)$
. We then apply Theorem 2.1 with
![]() $N = K = K_1$
and obtain
$N = K = K_1$
and obtain
![]() $\widetilde{\Gamma}(K_1,N)$
. Moreover, we apply Theorem 3.1 to the above censored process on
$\widetilde{\Gamma}(K_1,N)$
. Moreover, we apply Theorem 3.1 to the above censored process on
![]() $\mathbb{Z}_0^N \cup\mathbb{Z}_{K_1+1}^{\infty}$
with
$\mathbb{Z}_0^N \cup\mathbb{Z}_{K_1+1}^{\infty}$
with
![]() $K=K_2$
and obtain
$K=K_2$
and obtain
![]() $\widetilde{\Gamma}(K_2,N)$
. Now (3.17) follows from (3.16), with
$\widetilde{\Gamma}(K_2,N)$
. Now (3.17) follows from (3.16), with
![]() $\widetilde{\Gamma}(K_1,N)$
and
$\widetilde{\Gamma}(K_1,N)$
and
![]() $\widetilde{\Gamma}(K_2,N)$
corresponding to
$\widetilde{\Gamma}(K_2,N)$
corresponding to
![]() $\Gamma(N)$
and
$\Gamma(N)$
and
![]() $\widetilde{\Gamma}(K,N)$
in (3.16).
$\widetilde{\Gamma}(K,N)$
in (3.16).
Appendix F. Proof of Corollary 3.2
We first consider (3.29). If
![]() $\mathcal{J}(N) = \mathbb{Z}_0^N$
, (3.29) is immediate because
$\mathcal{J}(N) = \mathbb{Z}_0^N$
, (3.29) is immediate because
We thus assume
![]() $\mathcal{J}(N)\neq\mathbb{Z}_0^N$
. Noting (3.20), we partition
$\mathcal{J}(N)\neq\mathbb{Z}_0^N$
. Noting (3.20), we partition
![]() $\mathbb{Z}_0^N$
into the three subsets
$\mathbb{Z}_0^N$
into the three subsets
![]() $\widetilde{\mathcal{J}}(K,N)$
,
$\widetilde{\mathcal{J}}(K,N)$
,
![]() $\mathcal{J}(N)\setminus\widetilde{\mathcal{J}}(K,N)$
, and
$\mathcal{J}(N)\setminus\widetilde{\mathcal{J}}(K,N)$
, and
![]() $\mathbb{Z}_0^N\setminus\mathcal{J}(N)$
:
$\mathbb{Z}_0^N\setminus\mathcal{J}(N)$
:
Note here that
![]() $\mathcal{J}(N)\setminus\widetilde{\mathcal{J}}(K,N)$
may be empty; if this is the case, we simply ignore the corresponding terms. It follows from (3.5) that
$\mathcal{J}(N)\setminus\widetilde{\mathcal{J}}(K,N)$
may be empty; if this is the case, we simply ignore the corresponding terms. It follows from (3.5) that
where
Suppose
![]() $\boldsymbol{\alpha} \in \widetilde{\Gamma}^+(K,N)$
, i.e., there exists a nonnegative vector
$\boldsymbol{\alpha} \in \widetilde{\Gamma}^+(K,N)$
, i.e., there exists a nonnegative vector
![]() $\boldsymbol{\beta}$
such that
$\boldsymbol{\beta}$
such that
and
 \begin{align*}\boldsymbol{\alpha}&= \kbordermatrix{& \widetilde{\mathcal{J}}(K,N)&\quad \mathcal{J}(N) \setminus \widetilde{\mathcal{J}}(K,N)&\quad \mathbb{Z}_0^N\setminus\mathcal{J}(N)\\[3pt] & \boldsymbol{\alpha}_1 &\quad \boldsymbol{\alpha}_2 &\quad \boldsymbol{\alpha}_3}\\[3pt] &= (\boldsymbol{\beta}_1\ \ \textbf{0}\ \ \textbf{0})\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}).\end{align*}
\begin{align*}\boldsymbol{\alpha}&= \kbordermatrix{& \widetilde{\mathcal{J}}(K,N)&\quad \mathcal{J}(N) \setminus \widetilde{\mathcal{J}}(K,N)&\quad \mathbb{Z}_0^N\setminus\mathcal{J}(N)\\[3pt] & \boldsymbol{\alpha}_1 &\quad \boldsymbol{\alpha}_2 &\quad \boldsymbol{\alpha}_3}\\[3pt] &= (\boldsymbol{\beta}_1\ \ \textbf{0}\ \ \textbf{0})\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})(\textbf{\textit{I}} - \textbf{\textit{R}}(K,N))^{-1} \textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}).\end{align*}
It follows from (3.16) and (3.27) that
![]() $\widetilde{\Gamma}^+(K,N) \subseteq \Gamma(N)$
, so that
$\widetilde{\Gamma}^+(K,N) \subseteq \Gamma(N)$
, so that
![]() $\boldsymbol{\alpha}\textbf{\textit{e}}=1$
and
$\boldsymbol{\alpha}\textbf{\textit{e}}=1$
and
![]() $\boldsymbol{\alpha} \geq \textbf{0}$
. Moreover, using (F.1) and (F.2), we can rewrite
$\boldsymbol{\alpha} \geq \textbf{0}$
. Moreover, using (F.1) and (F.2), we can rewrite
![]() $\boldsymbol{\alpha}$
as
$\boldsymbol{\alpha}$
as
 \begin{align*}\boldsymbol{\alpha}&= (\boldsymbol{\beta}_1\ \ \textbf{0}\ \ \textbf{0})\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})\\[3pt] & +\boldsymbol{\beta}\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\textbf{\textit{B}}\bigl(\textbf{\textit{Q}}_+^{(2,1)}(K,N)\ \ \textbf{\textit{Q}}_{++}^{(2,1)}(K,N)\ \ \textbf{\textit{O}}\bigr)\textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\end{align*}
\begin{align*}\boldsymbol{\alpha}&= (\boldsymbol{\beta}_1\ \ \textbf{0}\ \ \textbf{0})\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}})\\[3pt] & +\boldsymbol{\beta}\textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,N)\textbf{\textit{e}})\textbf{\textit{B}}\bigl(\textbf{\textit{Q}}_+^{(2,1)}(K,N)\ \ \textbf{\textit{Q}}_{++}^{(2,1)}(K,N)\ \ \textbf{\textit{O}}\bigr)\textrm{diag}(\textbf{\textit{H}}(N)\textbf{\textit{e}}),\end{align*}
and therefore
![]() $\boldsymbol{\alpha}_3=\textbf{0}$
, which completes the proof of (3.29).
$\boldsymbol{\alpha}_3=\textbf{0}$
, which completes the proof of (3.29).
We omit the proof of (3.30) because it is almost the same as the proof of (3.17) in Corollary 3.1, except that the former uses Theorem 2.2, Theorem 3.2, and (3.29) where the latter uses Theorem 2.1, Theorem 3.1, and (3.16), respectively.
Appendix G. Proof of Theorem 4.1
Without loss of generality, we assume
![]() $\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
, where
$\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
, where
![]() $M = |\mathbb{Z}_0^N \cup \mathcal{X}^*|-1$
. It then follows from Theorem 3.1 with
$M = |\mathbb{Z}_0^N \cup \mathcal{X}^*|-1$
. It then follows from Theorem 3.1 with
![]() $N\coloneqq M$
that
$N\coloneqq M$
that
Note here that if
![]() $X(0) \in \mathbb{Z}_{K+1}^{\infty}$
, the first passage time to
$X(0) \in \mathbb{Z}_{K+1}^{\infty}$
, the first passage time to
![]() $\mathbb{Z}_0^M$
ends on
$\mathbb{Z}_0^M$
ends on
![]() $\mathcal{X}^*$
. Therefore, following a discussion similar to the proof of Theorem 3.2, we obtain
$\mathcal{X}^*$
. Therefore, following a discussion similar to the proof of Theorem 3.2, we obtain
where
 \begin{align}\widehat{\mathcal{P}}^+(K,M;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{M+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}_M \overline{\widetilde{\textbf{\textit{H}}}}(K,M),\ \nonumber\\& \boldsymbol{\beta}_M \in \Gamma(M),[\boldsymbol{\beta}_M]_i = 0\ (i \in \mathbb{Z}_0^M \setminus \mathcal{X}^*)\big\}.\end{align}
\begin{align}\widehat{\mathcal{P}}^+(K,M;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{M+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}_M \overline{\widetilde{\textbf{\textit{H}}}}(K,M),\ \nonumber\\& \boldsymbol{\beta}_M \in \Gamma(M),[\boldsymbol{\beta}_M]_i = 0\ (i \in \mathbb{Z}_0^M \setminus \mathcal{X}^*)\big\}.\end{align}
For a proper
![]() $\mathcal{X}^*$
, we have
$\mathcal{X}^*$
, we have
![]() $\mathcal{X}^* \cap \mathcal{N}_0(K,N) = \emptyset$
; i.e., the probability that the first passage time from
$\mathcal{X}^* \cap \mathcal{N}_0(K,N) = \emptyset$
; i.e., the probability that the first passage time from
![]() $\mathbb{Z}_{K+1}^{\infty}$
to
$\mathbb{Z}_{K+1}^{\infty}$
to
![]() $\mathbb{Z}_0^M$
ends on state i is strictly positive for all
$\mathbb{Z}_0^M$
ends on state i is strictly positive for all
![]() $i \in \mathcal{X}^*$
. We thus have
$i \in \mathcal{X}^*$
. We thus have
![]() $\mathcal{X}^* = \widetilde{\mathcal{J}}(K,M)$
for
$\mathcal{X}^* = \widetilde{\mathcal{J}}(K,M)$
for
![]() $\mathcal{X}^* \in \mathcal{S}^*(K,N)$
, and therefore from Theorem 3.2,
$\mathcal{X}^* \in \mathcal{S}^*(K,N)$
, and therefore from Theorem 3.2,
Since
![]() $\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
,
$\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
,
![]() $\boldsymbol{\pi}(N)$
can be expressed in terms of
$\boldsymbol{\pi}(N)$
can be expressed in terms of
![]() $\boldsymbol{\pi}(M)$
. Specifically, we first partition
$\boldsymbol{\pi}(M)$
. Specifically, we first partition
![]() $\boldsymbol{\pi}(M)$
and
$\boldsymbol{\pi}(M)$
and
![]() $\widetilde{\textbf{\textit{H}}}(K,M)$
as follows:
$\widetilde{\textbf{\textit{H}}}(K,M)$
as follows:
 \begin{align*}\boldsymbol{\pi}(M)&=\kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{M}\\& \boldsymbol{\pi}^{(1)}(M;\, N) &\quad \boldsymbol{\pi}^{(2)}(M;\, N)},\\ \widetilde{\textbf{\textit{H}}}(K,M)&=\kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{M}\\& \widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N)&\quad \widetilde{\textbf{\textit{H}}}^{(*,2)}(K,M;\, N)}.\end{align*}
\begin{align*}\boldsymbol{\pi}(M)&=\kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{M}\\& \boldsymbol{\pi}^{(1)}(M;\, N) &\quad \boldsymbol{\pi}^{(2)}(M;\, N)},\\ \widetilde{\textbf{\textit{H}}}(K,M)&=\kbordermatrix{&\mathbb{Z}_0^N &\quad \mathbb{Z}_{N+1}^{M}\\& \widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N)&\quad \widetilde{\textbf{\textit{H}}}^{(*,2)}(K,M;\, N)}.\end{align*}
It then follows from (G.1) and (G.2) that
![]() $\boldsymbol{\pi}^{(1)}(M;\, N) \in\widehat{\mathcal{P}}_M^{+(1)}(K,M;\, \mathcal{X}^*)$
, where
$\boldsymbol{\pi}^{(1)}(M;\, N) \in\widehat{\mathcal{P}}_M^{+(1)}(K,M;\, \mathcal{X}^*)$
, where
 \begin{align}\widehat{\mathcal{P}}_M^{+(1)}(K,M;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}_M \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,M)\textbf{\textit{e}})\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N),\ \nonumber\\&\quad \boldsymbol{\beta}_M \in \Gamma(M),\ [\boldsymbol{\beta}_M]_i = 0\ (i \in \mathbb{Z}_0^M \setminus \mathcal{X}^*)\big\}.\end{align}
\begin{align}\widehat{\mathcal{P}}_M^{+(1)}(K,M;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}_M \textrm{diag}^{-1}(\widetilde{\textbf{\textit{H}}}(K,M)\textbf{\textit{e}})\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N),\ \nonumber\\&\quad \boldsymbol{\beta}_M \in \Gamma(M),\ [\boldsymbol{\beta}_M]_i = 0\ (i \in \mathbb{Z}_0^M \setminus \mathcal{X}^*)\big\}.\end{align}
By definition,
![]() $\boldsymbol{\pi}(N) = \boldsymbol{\pi}^{(1)}(M;\, N) /\boldsymbol{\pi}^{(1)}(M;\, N) \textbf{\textit{e}}$
. It follows from (G.3) that
$\boldsymbol{\pi}(N) = \boldsymbol{\pi}^{(1)}(M;\, N) /\boldsymbol{\pi}^{(1)}(M;\, N) \textbf{\textit{e}}$
. It follows from (G.3) that
![]() $\boldsymbol{\pi}^{(1)}(M;\, N)$
is given by a weighted sum of row vectors of
$\boldsymbol{\pi}^{(1)}(M;\, N)$
is given by a weighted sum of row vectors of
![]() $\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\,N)$
. On the other hand, it follows from Remark 3.1 that if
$\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\,N)$
. On the other hand, it follows from Remark 3.1 that if
![]() $\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
, then
$\mathbb{Z}_0^N \cup \mathcal{X}^* = \mathbb{Z}_0^M$
, then
![]() $\widetilde{\textbf{\textit{H}}}(K,M)$
is identical to the
$\widetilde{\textbf{\textit{H}}}(K,M)$
is identical to the
![]() $(M+1) \times(M+1)$
northwest corner block of
$(M+1) \times(M+1)$
northwest corner block of
![]() $\textbf{\textit{H}}(K)$
. Therefore, the row vectors corresponding to state
$\textbf{\textit{H}}(K)$
. Therefore, the row vectors corresponding to state
![]() $i \in \mathcal{X}^*$
in
$i \in \mathcal{X}^*$
in
![]() $\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N)$
and in
$\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\, N)$
and in
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
are identical. Therefore, replacing
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
are identical. Therefore, replacing
![]() $\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\,N)$
by
$\widetilde{\textbf{\textit{H}}}^{(*,1)}(K,M;\,N)$
by
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
and normalizing
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
and normalizing
![]() $\boldsymbol{\pi}^{(1)}(M;\,N)$
, we obtain
$\boldsymbol{\pi}^{(1)}(M;\,N)$
, we obtain
where
 \begin{align}\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\textbf{\textit{H}}^{(*,1)}(K;\, N),\nonumber\\& \quad\boldsymbol{\beta}\in\Gamma(K),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^*)\big\}.\end{align}
\begin{align}\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\textbf{\textit{H}}^{(*,1)}(K;\, N),\nonumber\\& \quad\boldsymbol{\beta}\in\Gamma(K),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^*)\big\}.\end{align}
In particular, for a proper
![]() $\mathcal{X}^*$
, we have
$\mathcal{X}^*$
, we have
Note that
![]() $\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)$
in (G.4) is a convex polytope on the first orthant of
$\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)$
in (G.4) is a convex polytope on the first orthant of
![]() $\mathbb{R}^{N+1}$
.
$\mathbb{R}^{N+1}$
.
The proof of (4.5) will be complete if we can show that
this will be done below. Note that
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
is given in terms of
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
is given in terms of
![]() $\widetilde{\textbf{\textit{H}}}(K,N)$
in (3.7):
$\widetilde{\textbf{\textit{H}}}(K,N)$
in (3.7):
It then follows from (3.12) and (G.6) that
 \begin{align*}&\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\textbf{\textit{H}}^{(*,1)}(K;\, N)\quad \\&=\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\begin{pmatrix}\textbf{\textit{I}}\nonumber\\ (\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N)\end{pmatrix}\widetilde{\textbf{\textit{H}}}(K,N)\\&=\boldsymbol{\beta}\textbf{\textit{U}}(K,N)\overline{\textbf{\textit{H}}}(N),\end{align*}
\begin{align*}&\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\textbf{\textit{H}}^{(*,1)}(K;\, N)\quad \\&=\boldsymbol{\beta}\textrm{diag}^*(\textbf{\textit{H}}^{(*,1)}(K;\, N)\textbf{\textit{e}})\begin{pmatrix}\textbf{\textit{I}}\nonumber\\ (\!-\textbf{\textit{Q}}^{(2,2)}(K,N))^{-1}\textbf{\textit{Q}}^{(2,1)}(K,N)\end{pmatrix}\widetilde{\textbf{\textit{H}}}(K,N)\\&=\boldsymbol{\beta}\textbf{\textit{U}}(K,N)\overline{\textbf{\textit{H}}}(N),\end{align*}
so that
![]() $\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)$
is identical to
$\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)$
is identical to
![]() $\mathcal{P}^+(K,N;\,\mathcal{X}^*)$
in (4.6). The equivalence between (4.5) and (4.6) can be shown in the same way as in the proof of Theorem 2.2, so that we omit it.
$\mathcal{P}^+(K,N;\,\mathcal{X}^*)$
in (4.6). The equivalence between (4.5) and (4.6) can be shown in the same way as in the proof of Theorem 2.2, so that we omit it.
Appendix H. Proof of Lemma 4.1
If
![]() $\mathcal{X}_A^* = \mathcal{X}_B^*$
, Lemma 4.1 holds. We thus assume
$\mathcal{X}_A^* = \mathcal{X}_B^*$
, Lemma 4.1 holds. We thus assume
![]() $\mathcal{X}_A^* \neq \mathcal{X}_B^*$
. Note that for
$\mathcal{X}_A^* \neq \mathcal{X}_B^*$
. Note that for
![]() $\mathcal{X} \in S(K,N)$
,
$\mathcal{X} \in S(K,N)$
,
![]() $\mathcal{P}^+(K,N;\, \mathcal{X}^*)$
is equivalent to
$\mathcal{P}^+(K,N;\, \mathcal{X}^*)$
is equivalent to
![]() $\widehat{\mathcal{P}}^+(K,N;\,\mathcal{X}^*)$
in (G.4); i.e.,
$\widehat{\mathcal{P}}^+(K,N;\,\mathcal{X}^*)$
in (G.4); i.e.,
 \begin{align}\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta} \overline{\textbf{\textit{H}}}^{(*,1)}(K;\, N),\nonumber\\&\quad \boldsymbol{\beta}\in\Gamma(K),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^*)\big\},\end{align}
\begin{align}\widehat{\mathcal{P}}^+(K,N;\, \mathcal{X}^*)&=\big\{\textbf{\textit{x}} \in \mathbb{R}^{N+1};\ \textbf{\textit{x}}=\boldsymbol{\beta} \overline{\textbf{\textit{H}}}^{(*,1)}(K;\, N),\nonumber\\&\quad \boldsymbol{\beta}\in\Gamma(K),\ [\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus \mathcal{X}^*)\big\},\end{align}
where
Let
![]() $\textbf{\textit{h}}_j^{(*,1)}(K;\, N)$
and
$\textbf{\textit{h}}_j^{(*,1)}(K;\, N)$
and
![]() $\overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\,N)$
(
$\overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\,N)$
(
![]() $j \in \mathbb{Z}_0^K$
) denote the jth row vectors of
$j \in \mathbb{Z}_0^K$
) denote the jth row vectors of
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
and
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
and
![]() $\overline{\textbf{\textit{H}}}^{(*,1)}(K;\, N)$
. Note that the lemma is proven if
$\overline{\textbf{\textit{H}}}^{(*,1)}(K;\, N)$
. Note that the lemma is proven if
It is clear that (H.2) holds for
![]() $i \in \mathcal{X}_A^* \cap\mathcal{X}_B^*$
. We thus show (H.2) for
$i \in \mathcal{X}_A^* \cap\mathcal{X}_B^*$
. We thus show (H.2) for
![]() $i \in \mathcal{X}_A^*\setminus \mathcal{X}_B^*$
below.
$i \in \mathcal{X}_A^*\setminus \mathcal{X}_B^*$
below.
For a fixed
![]() $i \in \mathcal{X}_A^* \setminus \mathcal{X}_B^*$
, we consider a censored Markov chain
$i \in \mathcal{X}_A^* \setminus \mathcal{X}_B^*$
, we consider a censored Markov chain
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
by observing
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
by observing
![]() $\{X(t)\}_{t \in (\!-\infty,\infty)}$
only when
$\{X(t)\}_{t \in (\!-\infty,\infty)}$
only when
![]() $X(t) \in\mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\} \cup \mathbb{Z}_{K+1}^{\infty}$
. The infinitesimal generator
$X(t) \in\mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\} \cup \mathbb{Z}_{K+1}^{\infty}$
. The infinitesimal generator
![]() $\widetilde{\textbf{\textit{Q}}}\coloneqq \widetilde{\textbf{\textit{Q}}}(K,N,\mathcal{X}_B^*,i)$
of the censored Markov chain
$\widetilde{\textbf{\textit{Q}}}\coloneqq \widetilde{\textbf{\textit{Q}}}(K,N,\mathcal{X}_B^*,i)$
of the censored Markov chain
![]() $\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
takes the following form:
$\{\widetilde{X}(t)\}_{t \in (\!-\infty,\infty)}$
takes the following form:
 \begin{equation*}\widetilde{\textbf{\textit{Q}}}=\kbordermatrix{&\mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\} &\quad \mathbb{Z}_{K+1}^{\infty}\\ \\[-9pt] \mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\}\quad &\widetilde{\textbf{\textit{Q}}}^{(1,1)} &\quad \widetilde{\textbf{\textit{Q}}}^{(1,2)} \\ \\[-9pt] \mathbb{Z}_{K+1}^{\infty} & \widetilde{\textbf{\textit{Q}}}^{(2,1)} &\quad \widetilde{\textbf{\textit{Q}}}^{(2,2)}},\end{equation*}
\begin{equation*}\widetilde{\textbf{\textit{Q}}}=\kbordermatrix{&\mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\} &\quad \mathbb{Z}_{K+1}^{\infty}\\ \\[-9pt] \mathbb{Z}_0^N \cup \mathcal{X}_B^* \cup \{i\}\quad &\widetilde{\textbf{\textit{Q}}}^{(1,1)} &\quad \widetilde{\textbf{\textit{Q}}}^{(1,2)} \\ \\[-9pt] \mathbb{Z}_{K+1}^{\infty} & \widetilde{\textbf{\textit{Q}}}^{(2,1)} &\quad \widetilde{\textbf{\textit{Q}}}^{(2,2)}},\end{equation*}
where, with
![]() $\mathbb{Z}_B=\mathbb{Z}_0^N \cup \mathcal{X}_B^*$
,
$\mathbb{Z}_B=\mathbb{Z}_0^N \cup \mathcal{X}_B^*$
,
 \begin{equation*}\widetilde{\textbf{\textit{Q}}}^{(1,1)}=\kbordermatrix{& \mathbb{Z}_B \quad& \{i\}\quad \\ \mathbb{Z}_B &\widetilde{\textbf{\textit{Q}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} &\quad \widetilde{\textbf{\textit{q}}}_{\mathbb{Z}_B,i}^{(1,1)}\\ \\[-9pt] \{i\} &\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} &\quad -\widetilde{q}_{i,i}^{(1,1)}}.\end{equation*}
\begin{equation*}\widetilde{\textbf{\textit{Q}}}^{(1,1)}=\kbordermatrix{& \mathbb{Z}_B \quad& \{i\}\quad \\ \mathbb{Z}_B &\widetilde{\textbf{\textit{Q}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} &\quad \widetilde{\textbf{\textit{q}}}_{\mathbb{Z}_B,i}^{(1,1)}\\ \\[-9pt] \{i\} &\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} &\quad -\widetilde{q}_{i,i}^{(1,1)}}.\end{equation*}
Note here that
since
![]() $i \in \mathcal{X}_A^* \setminus \mathcal{X}_B^*$
and (4.7) holds sample-path-wise. We define
$i \in \mathcal{X}_A^* \setminus \mathcal{X}_B^*$
and (4.7) holds sample-path-wise. We define
![]() $\widetilde{\textbf{\textit{H}}}\coloneqq \widetilde{\textbf{\textit{H}}}(K,N,\mathcal{X}_B^*,i)$
as
$\widetilde{\textbf{\textit{H}}}\coloneqq \widetilde{\textbf{\textit{H}}}(K,N,\mathcal{X}_B^*,i)$
as
 \begin{align*}\widetilde{\textbf{\textit{H}}}=\big(\!- \widetilde{\textbf{\textit{Q}}}^{(1,1)} \big)^{-1}&=\kbordermatrix{& \mathbb{Z}_B & \{i\}\\ \mathbb{Z}_B &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B} &\quad \widetilde{\textbf{\textit{h}}}_{\mathbb{Z}_B,i}\\ \\[-9pt]\{i\} & \widetilde{\textbf{\textit{h}}}_{i,\mathbb{Z}_B} &\quad \widetilde{h}_{i,i}}\\ \\[-9pt] &=\kbordermatrix{& \mathbb{Z}_B & \{i\}\\ \\[-9pt] \mathbb{Z}_B & \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B} & \widetilde{\textbf{\textit{h}}}_{\mathbb{Z}_B,i}\\ \\[-9pt] \{i\} & (\widetilde{q}_{i,i}^{(1,1)})^{-1}\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}&\quad \widetilde{h}_{i,i}}.\end{align*}
\begin{align*}\widetilde{\textbf{\textit{H}}}=\big(\!- \widetilde{\textbf{\textit{Q}}}^{(1,1)} \big)^{-1}&=\kbordermatrix{& \mathbb{Z}_B & \{i\}\\ \mathbb{Z}_B &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B} &\quad \widetilde{\textbf{\textit{h}}}_{\mathbb{Z}_B,i}\\ \\[-9pt]\{i\} & \widetilde{\textbf{\textit{h}}}_{i,\mathbb{Z}_B} &\quad \widetilde{h}_{i,i}}\\ \\[-9pt] &=\kbordermatrix{& \mathbb{Z}_B & \{i\}\\ \\[-9pt] \mathbb{Z}_B & \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B} & \widetilde{\textbf{\textit{h}}}_{\mathbb{Z}_B,i}\\ \\[-9pt] \{i\} & (\widetilde{q}_{i,i}^{(1,1)})^{-1}\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}&\quad \widetilde{h}_{i,i}}.\end{align*}
Note here that if we partition
![]() $\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}$
as
$\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}$
as
 \begin{equation*}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}=\kbordermatrix{& \mathbb{Z}_0^N &\quad \mathbb{Z}_B \setminus \mathbb{Z}_0^N\\ \\[-9pt] \mathbb{Z}_0^N \setminus \mathcal{X}_B^* &\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,2)}\\ \\[-7pt] \mathcal{X}_B^* &\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)} &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}},\end{equation*}
\begin{equation*}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}=\kbordermatrix{& \mathbb{Z}_0^N &\quad \mathbb{Z}_B \setminus \mathbb{Z}_0^N\\ \\[-9pt] \mathbb{Z}_0^N \setminus \mathcal{X}_B^* &\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,2)}\\ \\[-7pt] \mathcal{X}_B^* &\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)} &\quad \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}},\end{equation*}
the row vector of
![]() $\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}$
corresponding to
$\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}$
corresponding to
![]() $j \in \mathcal{X}_B^*$
is identical to
$j \in \mathcal{X}_B^*$
is identical to
![]() $\textbf{\textit{h}}_j^{(*,1)}(K;\, N)$
. Furthermore, noting (H.3), we have
$\textbf{\textit{h}}_j^{(*,1)}(K;\, N)$
. Furthermore, noting (H.3), we have
 \begin{align*}\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}&=\left(\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \begin{pmatrix}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} \\ \\[-9pt] \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}\end{pmatrix} \widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)}\begin{pmatrix}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,2)} \\ \\[-9pt] \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}\end{pmatrix}\right)\\ \\[-8pt] &=\big(\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B,+}^{(1,1)}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}\quad \widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B,+}^{(1,1)}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}\big),\end{align*}
\begin{align*}\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}&=\left(\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)} \begin{pmatrix}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,1)} \\ \\[-9pt] \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}\end{pmatrix} \widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B}^{(1,1)}\begin{pmatrix}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(1,2)} \\ \\[-9pt] \widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}\end{pmatrix}\right)\\ \\[-8pt] &=\big(\widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B,+}^{(1,1)}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,1)}\quad \widetilde{\textbf{\textit{q}}}_{i,\mathbb{Z}_B,+}^{(1,1)}\widetilde{\textbf{\textit{H}}}_{\mathbb{Z}_B,\mathbb{Z}_B}^{(2,2)}\big),\end{align*}
and
Therefore,
![]() $\textbf{\textit{h}}_i^{(*,1)}(K;\, N)$
(
$\textbf{\textit{h}}_i^{(*,1)}(K;\, N)$
(
![]() $i \in \mathcal{X}_A^* \setminus\mathcal{X}_B^*$
) is given by a linear combination of the
$i \in \mathcal{X}_A^* \setminus\mathcal{X}_B^*$
) is given by a linear combination of the
![]() $\textbf{\textit{h}}_j^{(*,1)}(K;\,N)$
(
$\textbf{\textit{h}}_j^{(*,1)}(K;\,N)$
(
![]() $j \in \mathcal{X}_B^*$
) with nonnegative weights
$j \in \mathcal{X}_B^*$
) with nonnegative weights
![]() $\alpha_{i,j}$
:
$\alpha_{i,j}$
:
We thus conclude that
![]() $\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
(
$\overline{\textbf{\textit{h}}}_i^{(*,1)}(K;\, N)$
(
![]() $i \in\mathcal{X}_A^* \setminus \mathcal{X}_B^*$
) is given by a convex combination of
$i \in\mathcal{X}_A^* \setminus \mathcal{X}_B^*$
) is given by a convex combination of
![]() $\overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\, N)$
(
$\overline{\textbf{\textit{h}}}_j^{(*,1)}(K;\, N)$
(
![]() $j \in \mathcal{X}_B^*$
); i.e.,
$j \in \mathcal{X}_B^*$
); i.e.,
where
 \begin{equation*}\beta_{i,j}=\frac{\alpha_{i,j} \textbf{\textit{h}}_j^{(*,1)}(K;\, N) \textbf{\textit{e}}}{\textbf{\textit{h}}_i^{(*,1)}(K;\, N) \textbf{\textit{e}}},\quad j \in \mathcal{X}_B^*.\end{equation*}
\begin{equation*}\beta_{i,j}=\frac{\alpha_{i,j} \textbf{\textit{h}}_j^{(*,1)}(K;\, N) \textbf{\textit{e}}}{\textbf{\textit{h}}_i^{(*,1)}(K;\, N) \textbf{\textit{e}}},\quad j \in \mathcal{X}_B^*.\end{equation*}
Note that
![]() $\beta_{i,j} \geq 0$
and
$\beta_{i,j} \geq 0$
and
![]() $\sum_{j \in \mathcal{X}_B^*} \beta_{i,j} =1$
, which completes the proof.
$\sum_{j \in \mathcal{X}_B^*} \beta_{i,j} =1$
, which completes the proof.
Appendix I. Proof of Lemma 4.2
We first prove that
![]() $\mathcal{D}(K,N)$
is an (s, t)-node cut in G(K, N), and then we show its minimality. To prove the former, we show that the graph
$\mathcal{D}(K,N)$
is an (s, t)-node cut in G(K, N), and then we show its minimality. To prove the former, we show that the graph
![]() $G(K,N;\, -\mathcal{D}(K,N))$
, which is obtained from G(K, N) by removing all nodes in
$G(K,N;\, -\mathcal{D}(K,N))$
, which is obtained from G(K, N) by removing all nodes in
![]() $\mathcal{D}(K,N)$
, has no directed paths from s to t. To prove this, we assume that
$\mathcal{D}(K,N)$
, has no directed paths from s to t. To prove this, we assume that
![]() $G(K,N;\, -\mathcal{D}(K,N))$
has a directed path P from s to t and derive a contradiction. Since
$G(K,N;\, -\mathcal{D}(K,N))$
has a directed path P from s to t and derive a contradiction. Since
![]() $\mathcal{J}(K)$
is the set of all neighboring nodes of s, P must contain a node
$\mathcal{J}(K)$
is the set of all neighboring nodes of s, P must contain a node
![]() $v \in\mathcal{J}(K) \setminus \mathcal{D}(K,N)$
, where we assume that if P contains more than one node in
$v \in\mathcal{J}(K) \setminus \mathcal{D}(K,N)$
, where we assume that if P contains more than one node in
![]() $\mathcal{J}(K) \setminus\mathcal{D}(K,N)$
, then v is the node closest to t. Because the directed path from v to t has no edges incoming to any nodes in
$\mathcal{J}(K) \setminus\mathcal{D}(K,N)$
, then v is the node closest to t. Because the directed path from v to t has no edges incoming to any nodes in
![]() $\mathcal{J}(K)$
,
$\mathcal{J}(K)$
,
![]() $G^*(K,N)$
should contain the subpath
$G^*(K,N)$
should contain the subpath
![]() $P_{v,t}$
of P from v to t. This, however, contradicts the fact that
$P_{v,t}$
of P from v to t. This, however, contradicts the fact that
![]() $\mathcal{D}(K,N)$
contains all nodes in
$\mathcal{D}(K,N)$
contains all nodes in
![]() $\mathcal{J}(K)$
from which t is reachable in
$\mathcal{J}(K)$
from which t is reachable in
![]() $G^*(K,N)$
.
$G^*(K,N)$
.
Next we show the minimality of
![]() $\mathcal{D}(K,N)$
. For each node
$\mathcal{D}(K,N)$
. For each node
![]() $v \in\mathcal{D}(K,N)$
,
$v \in\mathcal{D}(K,N)$
,
![]() $G^*(K,N)$
contains a directed path
$G^*(K,N)$
contains a directed path
![]() $P_{v,t}$
from v that visits t without passing through any other nodes in
$P_{v,t}$
from v that visits t without passing through any other nodes in
![]() $\mathcal{J}(K)$
. As a result, the edge
$\mathcal{J}(K)$
. As a result, the edge
![]() $(s,v) \in E(K,N)$
and
$(s,v) \in E(K,N)$
and
![]() $P_{v,t}$
form a directed path from s to t in G(K, N), and therefore
$P_{v,t}$
form a directed path from s to t in G(K, N), and therefore
![]() $v \in \mathcal{D}(K,N)$
must be included in any (s,t)-node cut
$v \in \mathcal{D}(K,N)$
must be included in any (s,t)-node cut
![]() $\mathcal{X} \subseteq \mathcal{J}(K)$
in G(K, N). We thus conclude that
$\mathcal{X} \subseteq \mathcal{J}(K)$
in G(K, N). We thus conclude that
![]() $\mathcal{D}(K,N) \subseteq \mathcal{X}$
for any
$\mathcal{D}(K,N) \subseteq \mathcal{X}$
for any
![]() $\mathcal{X}$
such that
$\mathcal{X}$
such that
![]() $\mathcal{X} \subseteq \mathcal{J}(K)$
and
$\mathcal{X} \subseteq \mathcal{J}(K)$
and
![]() $\mathcal{X} \in S(K,N)$
, which completes the proof.
$\mathcal{X} \in S(K,N)$
, which completes the proof.
Appendix J. Proof of Theorem 4.2
Note that
![]() $\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\, \mathcal{J}^*(K))$
from Lemma 4.3 and
$\textbf{\textit{x}} \in \textrm{ri}\, \mathcal{P}^+(K,N;\, \mathcal{J}^*(K))$
from Lemma 4.3 and
![]() $\mathcal{P}^+(K,N;\,\mathcal{J}^*(K))=\widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
from (G.5), where
$\mathcal{P}^+(K,N;\,\mathcal{J}^*(K))=\widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
from (G.5), where
![]() $\widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
is given in (G.5). We thus have
$\widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
is given in (G.5). We thus have
![]() $\textbf{\textit{x}} \in\textrm{ri}\, \widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
; therefore there exists
$\textbf{\textit{x}} \in\textrm{ri}\, \widehat{\mathcal{P}}^+(K,N;\, \mathcal{J}^*(K))$
; therefore there exists
![]() $\boldsymbol{\beta} \in \Gamma(K)$
such that
$\boldsymbol{\beta} \in \Gamma(K)$
such that
![]() $[\boldsymbol{\beta}]_i > 0\ (i\in \mathcal{J}^*(K))$
,
$[\boldsymbol{\beta}]_i > 0\ (i\in \mathcal{J}^*(K))$
,
![]() $[\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus\mathcal{J}^*(K))$
, and
$[\boldsymbol{\beta}]_i = 0\ (i \in \mathbb{Z}_0^K \setminus\mathcal{J}^*(K))$
, and
On the other hand, it follows from (4.8) that
![]() $\mathcal{J}(K) \setminus \mathcal{J}^*(K) = \mathcal{J}(K) \cap \mathcal{N}_0^{(3)}(K,N)$
. Therefore, we have from (4.3) that
$\mathcal{J}(K) \setminus \mathcal{J}^*(K) = \mathcal{J}(K) \cap \mathcal{N}_0^{(3)}(K,N)$
. Therefore, we have from (4.3) that
where
![]() $\textbf{\textit{h}}_i^{(*,1)}(K;\, N)$
(
$\textbf{\textit{h}}_i^{(*,1)}(K;\, N)$
(
![]() $i \in \mathbb{Z}_0^K$
) denotes the ith row vector of
$i \in \mathbb{Z}_0^K$
) denotes the ith row vector of
![]() $\textbf{\textit{H}}^{(*,1)}(K;\, N)$
. Let
$\textbf{\textit{H}}^{(*,1)}(K;\, N)$
. Let
![]() $\boldsymbol{\gamma} \in\mathbb{R}^{K+1}$
be defined by
$\boldsymbol{\gamma} \in\mathbb{R}^{K+1}$
be defined by
where
![]() $\textbf{\textit{e}}_i \in \Gamma(K)$
(
$\textbf{\textit{e}}_i \in \Gamma(K)$
(
![]() $i \in \mathbb{Z}_0^K$
) denotes the unit vector whose ith element is equal to one. Note here that
$i \in \mathbb{Z}_0^K$
) denotes the unit vector whose ith element is equal to one. Note here that
We thus have
Let
![]() $\textbf{\textit{y}}=\boldsymbol{\gamma}\textbf{\textit{H}}^{(*,2)}(K;\, N)$
. We then have
$\textbf{\textit{y}}=\boldsymbol{\gamma}\textbf{\textit{H}}^{(*,2)}(K;\, N)$
. We then have
It follows from (J.1) and (J.2) that
Furthermore,
![]() $(\textbf{\textit{x}}\ \textbf{\textit{y}}) \textbf{\textit{e}} = \boldsymbol{\gamma} \textbf{\textit{H}}(K)\textbf{\textit{e}} >\textbf{0}$
since
$(\textbf{\textit{x}}\ \textbf{\textit{y}}) \textbf{\textit{e}} = \boldsymbol{\gamma} \textbf{\textit{H}}(K)\textbf{\textit{e}} >\textbf{0}$
since
![]() $\textbf{\textit{H}}(K)\textbf{\textit{e}} > \textbf{0}$
. We thus have
$\textbf{\textit{H}}(K)\textbf{\textit{e}} > \textbf{0}$
. We thus have
![]() $(\textbf{\textit{x}}\ \textbf{\textit{y}})/((\textbf{\textit{x}}\ \textbf{\textit{y}})\textbf{\textit{e}}) \in \textrm{ri}\, \mathcal{P}^+(K)$
, and therefore
$(\textbf{\textit{x}}\ \textbf{\textit{y}})/((\textbf{\textit{x}}\ \textbf{\textit{y}})\textbf{\textit{e}}) \in \textrm{ri}\, \mathcal{P}^+(K)$
, and therefore
from Lemma 2.1. We then define
![]() $\boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}})$
as
$\boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}})$
as
Note that
![]() $\boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}}) \in \textrm{ri}\, \Gamma^+(K)$
, where
$\boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}}) \in \textrm{ri}\, \Gamma^+(K)$
, where
We now consider a Markov chain whose infinitesimal generator
![]() $\textbf{\textit{Q}}$
is given by
$\textbf{\textit{Q}}$
is given by
 \begin{equation}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^K & \mathbb{Z}_{K+1}^{\infty}\\ \\[-9pt] \mathbb{Z}_0^K & \textbf{\textit{Q}}^{(1,1)}(K) &\quad (\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}}\textbf{\textit{z}}\\ \\[-9pt] \mathbb{Z}_{K+1}^{\infty}& \textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}}) &\quad -\textbf{\textit{I}},},\end{equation}
\begin{equation}\textbf{\textit{Q}}= \kbordermatrix{&\mathbb{Z}_0^K & \mathbb{Z}_{K+1}^{\infty}\\ \\[-9pt] \mathbb{Z}_0^K & \textbf{\textit{Q}}^{(1,1)}(K) &\quad (\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}}\textbf{\textit{z}}\\ \\[-9pt] \mathbb{Z}_{K+1}^{\infty}& \textbf{\textit{e}} \boldsymbol{\zeta}(\textbf{\textit{x}},\textbf{\textit{y}}) &\quad -\textbf{\textit{I}},},\end{equation}
where
![]() $\textbf{\textit{z}}$
denotes a
$\textbf{\textit{z}}$
denotes a
![]() $1 \times \infty$
positive probability vector. Note here that the Markov chain with
$1 \times \infty$
positive probability vector. Note here that the Markov chain with
![]() $\textbf{\textit{Q}}$
given by (J.3) is a member of
$\textbf{\textit{Q}}$
given by (J.3) is a member of
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
if it is ergodic, i.e., if the global balance equation
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
if it is ergodic, i.e., if the global balance equation
![]() $\boldsymbol{\pi}\textbf{\textit{Q}}=\textbf{0}$
has a unique positive solution
$\boldsymbol{\pi}\textbf{\textit{Q}}=\textbf{0}$
has a unique positive solution
![]() $\boldsymbol{\pi}$
satisfying
$\boldsymbol{\pi}$
satisfying
![]() $\boldsymbol{\pi}\textbf{\textit{e}} = 1$
, where
$\boldsymbol{\pi}\textbf{\textit{e}} = 1$
, where
![]() $\boldsymbol{\pi}\textbf{\textit{Q}}=\textbf{0}$
is written as
$\boldsymbol{\pi}\textbf{\textit{Q}}=\textbf{0}$
is written as
Solving the above with
![]() $\boldsymbol{\pi}^{(1)}(K)\textbf{\textit{e}} +\boldsymbol{\pi}^{(2)}(K)\textbf{\textit{e}} = 1$
, we obtain
$\boldsymbol{\pi}^{(1)}(K)\textbf{\textit{e}} +\boldsymbol{\pi}^{(2)}(K)\textbf{\textit{e}} = 1$
, we obtain
 \begin{align*}\boldsymbol{\pi}&=\begin{pmatrix}\boldsymbol{\pi}^{(1)}(K) & \boldsymbol{\pi}^{(2)}(K)\end{pmatrix}\\&=\frac{1}{(\textbf{\textit{x}}\ \textbf{\textit{y}})\textbf{\textit{e}} +(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}}}\begin{pmatrix}(\textbf{\textit{x}}\ \textbf{\textit{y}}) &\quad (\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}} \cdot \textbf{\textit{z}}\end{pmatrix}\\&=\frac{1}{1 + \textbf{\textit{y}}\textbf{\textit{e}} + \boldsymbol{\gamma}\textbf{\textit{e}}}\begin{pmatrix}(\textbf{\textit{x}}\ \textbf{\textit{y}}) &\quad \boldsymbol{\gamma}\textbf{\textit{e}} \cdot \textbf{\textit{z}}\end{pmatrix}> \textbf{0};\end{align*}
\begin{align*}\boldsymbol{\pi}&=\begin{pmatrix}\boldsymbol{\pi}^{(1)}(K) & \boldsymbol{\pi}^{(2)}(K)\end{pmatrix}\\&=\frac{1}{(\textbf{\textit{x}}\ \textbf{\textit{y}})\textbf{\textit{e}} +(\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}}}\begin{pmatrix}(\textbf{\textit{x}}\ \textbf{\textit{y}}) &\quad (\textbf{\textit{x}}\ \textbf{\textit{y}})(\!-\textbf{\textit{Q}}^{(1,1)}(K))\textbf{\textit{e}} \cdot \textbf{\textit{z}}\end{pmatrix}\\&=\frac{1}{1 + \textbf{\textit{y}}\textbf{\textit{e}} + \boldsymbol{\gamma}\textbf{\textit{e}}}\begin{pmatrix}(\textbf{\textit{x}}\ \textbf{\textit{y}}) &\quad \boldsymbol{\gamma}\textbf{\textit{e}} \cdot \textbf{\textit{z}}\end{pmatrix}> \textbf{0};\end{align*}
in particular,
We thus conclude that the Markov chain with
![]() $\textbf{\textit{Q}}$
in (J.3) is a member of
$\textbf{\textit{Q}}$
in (J.3) is a member of
![]() $\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
, and it has
$\mathcal{M}(\textbf{\textit{Q}}^{(1,1)}(K), \mathcal{J}(K))$
, and it has
![]() $\boldsymbol{\pi}(N) = \textbf{\textit{x}}$
.
$\boldsymbol{\pi}(N) = \textbf{\textit{x}}$
.
Acknowledgements
The authors would like to thank Dr. Hiroshi Nagamochi for his instructive comments on the minimal node cuts of directed graphs. The research of the second author was supported in part by JSPS KAKENHI Grant No. 19K11841.