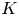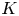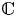1. Introduction
1.1 Search for motivic complexes
For an arbitrary field ![]() $F$ and integers
$F$ and integers ![]() $n$ and
$n$ and ![]() $m$, Beilinson [Reference BeilinsonBei87] suggested a definition of motivic cohomology groups
$m$, Beilinson [Reference BeilinsonBei87] suggested a definition of motivic cohomology groups ![]() $H^n(F,\mathbb {Q}(m))$ as appropriate pieces of higher algebraic
$H^n(F,\mathbb {Q}(m))$ as appropriate pieces of higher algebraic ![]() $K$-theory groups, defined earlier by Quillen. In several cases (
$K$-theory groups, defined earlier by Quillen. In several cases (![]() $n=m$ and
$n=m$ and ![]() $n=1, m=2$) Suslin [Reference SuslinSus85, Reference SuslinSus91] proved that these groups could be identified with the cohomology groups of very explicit complexes. For the case
$n=1, m=2$) Suslin [Reference SuslinSus85, Reference SuslinSus91] proved that these groups could be identified with the cohomology groups of very explicit complexes. For the case ![]() $n=m$ this implies an isomorphism between motivic cohomology and Milnor
$n=m$ this implies an isomorphism between motivic cohomology and Milnor ![]() $K$-theory.
$K$-theory.
One may hope that this construction can be generalized to arbitrary integers ![]() $n$ and
$n$ and ![]() $m$. This leads to a definition of very explicit complexes (polylogarithmic motivic complexes), whose cohomology groups conjecturally coincide with rational motivic cohomology groups; see [Reference GoncharovGon95b]. The beauty and elegance of this construction come with a price: proving functoriality in
$m$. This leads to a definition of very explicit complexes (polylogarithmic motivic complexes), whose cohomology groups conjecturally coincide with rational motivic cohomology groups; see [Reference GoncharovGon95b]. The beauty and elegance of this construction come with a price: proving functoriality in ![]() $F$ is very hard. Difficulties already exist in the case of Milnor
$F$ is very hard. Difficulties already exist in the case of Milnor ![]() $K$-theory, which we will discuss in detail below.
$K$-theory, which we will discuss in detail below.
The main goal of this paper is to establish existence of norm maps for the cohomology groups of polylogarithmic motivic complexes for the case ![]() $n=m-1$, namely the degree ‘next to Milnor
$n=m-1$, namely the degree ‘next to Milnor ![]() $K$-theory’. This implies some corollaries, including the strong Suslin reciprocity law conjectured by Goncharov [Reference GoncharovGon05, p. 53 and Conjecture 6.2]. We will also formulate an application to hyperbolic scissors congruence theory, which was the author's original motivation behind this project.
$K$-theory’. This implies some corollaries, including the strong Suslin reciprocity law conjectured by Goncharov [Reference GoncharovGon05, p. 53 and Conjecture 6.2]. We will also formulate an application to hyperbolic scissors congruence theory, which was the author's original motivation behind this project.
1.2 Main definitions and results
Let ![]() $A$ be an abelian group. Denote by
$A$ be an abelian group. Denote by ![]() $A_\mathbb {Q}=A\otimes _{\mathbb {Z}} \mathbb {Q}$ its rationalization.
$A_\mathbb {Q}=A\otimes _{\mathbb {Z}} \mathbb {Q}$ its rationalization.
Let ![]() $F$ be an arbitrary field. We will associate several
$F$ be an arbitrary field. We will associate several ![]() $\mathbb {Q}$-vector spaces with
$\mathbb {Q}$-vector spaces with ![]() $F$. We start with
$F$. We start with ![]() $F^{\times }_{\mathbb {Q}}:=F^{\times }\otimes _{\mathbb {Z}} \mathbb {Q}$: the multiplicative group of a field, made rational. We have an exact sequence
$F^{\times }_{\mathbb {Q}}:=F^{\times }\otimes _{\mathbb {Z}} \mathbb {Q}$: the multiplicative group of a field, made rational. We have an exact sequence
where ![]() $\mathbb {Q}[F]_1$ is a
$\mathbb {Q}[F]_1$ is a ![]() $\mathbb {Q}$-vector space freely generated by vectors
$\mathbb {Q}$-vector space freely generated by vectors ![]() $[p]_1$ for
$[p]_1$ for ![]() $p\in {\mathbb {P}}^1_F= F\cup \{\infty \}$ subject to the relations
$p\in {\mathbb {P}}^1_F= F\cup \{\infty \}$ subject to the relations ![]() $[0]_1=[1]_1=[\infty ]_1=0$. The subscript
$[0]_1=[1]_1=[\infty ]_1=0$. The subscript ![]() $1$ in the symbol
$1$ in the symbol ![]() $\mathbb {Q}[F]_1$ is only for bookkeeping and refers to the motivic weight. The subspace
$\mathbb {Q}[F]_1$ is only for bookkeeping and refers to the motivic weight. The subspace ![]() $R_1(F)$ is generated by elements
$R_1(F)$ is generated by elements ![]() $[x_1,x_2]_1=[x_1]_1+[x_2]_1-[x_1x_2]_1$. These symbols satisfy the following cocycle relation:
$[x_1,x_2]_1=[x_1]_1+[x_2]_1-[x_1x_2]_1$. These symbols satisfy the following cocycle relation:
Next, we define the second Bloch group Footnote 1 ![]() $B_2(F)_{\mathbb {Q}}$ as the cokernel of a map
$B_2(F)_{\mathbb {Q}}$ as the cokernel of a map
Here the vector space ![]() $\mathbb {Q}[F]_2$ is defined just as
$\mathbb {Q}[F]_2$ is defined just as ![]() $\mathbb {Q}[F]_1$ is defined and the space
$\mathbb {Q}[F]_1$ is defined and the space ![]() $R_2(F)$ is freely generated by the symbols
$R_2(F)$ is freely generated by the symbols ![]() $[x_1,x_2]_2$, whose image in
$[x_1,x_2]_2$, whose image in ![]() $\mathbb {Q}[F]_2$ equals the sum
$\mathbb {Q}[F]_2$ equals the sum
where the terms ![]() $x_i$ satisfy the following
$x_i$ satisfy the following ![]() $5$-periodic recurrence:
$5$-periodic recurrence:
Explicitly,
For some values of ![]() $x_1$ and
$x_1$ and ![]() $x_2$ in the formulas above an indeterminate term of the form
$x_2$ in the formulas above an indeterminate term of the form ![]() $0/0$ or
$0/0$ or ![]() $\infty / \infty$ may appear. In this case we omit such terms in the formula for the map
$\infty / \infty$ may appear. In this case we omit such terms in the formula for the map ![]() $R_2(F)\longrightarrow \mathbb {Q}[F]_2$. We will denote the image of
$R_2(F)\longrightarrow \mathbb {Q}[F]_2$. We will denote the image of ![]() $[x]_2\in \mathbb {Q}[F]_2$ in
$[x]_2\in \mathbb {Q}[F]_2$ in ![]() $B_2(F)_{\mathbb {Q}}$ by
$B_2(F)_{\mathbb {Q}}$ by ![]() $\{x\}_2$. It is easy to see that the following relations hold in
$\{x\}_2$. It is easy to see that the following relations hold in ![]() $B_2(F)_{\mathbb {Q}}$:
$B_2(F)_{\mathbb {Q}}$:
 \begin{equation} \begin{aligned} & \{a\}_2+\{1-a\}_2=0,\\ & \{a\}_2+\bigg\{ \frac{1}{a} \bigg\}_2=0, \\ & \{a\}_2- \{b\}_2+\bigg\{ \frac{b}{a} \bigg\}_2-\bigg\{ \frac{1-a^{{-}1}}{1-b^{{-}1}}\bigg\}_2+\bigg\{ \frac{1-a}{1-b} \bigg\}_2=0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \{a\}_2+\{1-a\}_2=0,\\ & \{a\}_2+\bigg\{ \frac{1}{a} \bigg\}_2=0, \\ & \{a\}_2- \{b\}_2+\bigg\{ \frac{b}{a} \bigg\}_2-\bigg\{ \frac{1-a^{{-}1}}{1-b^{{-}1}}\bigg\}_2+\bigg\{ \frac{1-a}{1-b} \bigg\}_2=0. \end{aligned} \end{equation}
The third relation is called the five-term relation and is often used in defining ![]() $B_2(F)$.
$B_2(F)$.
Remark The definition above is motivated by the fact that for ![]() $F=\mathbb {C}$ the map
$F=\mathbb {C}$ the map
sending ![]() $[x]_2$ to the Bloch–Wigner dilogarithm
$[x]_2$ to the Bloch–Wigner dilogarithm ![]() $\mathcal {L}_2(x)$ is well-defined, thanks to Abel's equation for the dilogarithm; see [Reference GoncharovGon95a]. We omit the rationalization sign, because
$\mathcal {L}_2(x)$ is well-defined, thanks to Abel's equation for the dilogarithm; see [Reference GoncharovGon95a]. We omit the rationalization sign, because ![]() $B_2(\mathbb {C})$ is uniquely divisible; see [Reference SuslinSus91, Remark 5.1].
$B_2(\mathbb {C})$ is uniquely divisible; see [Reference SuslinSus91, Remark 5.1].
The following complex ![]() ${\mathcal {B}}(F,2)$ is called the weight-two polylogarithmic complex:
${\mathcal {B}}(F,2)$ is called the weight-two polylogarithmic complex:
where ![]() $\delta \{x\}_2=(1-x)\wedge x$. The fact that
$\delta \{x\}_2=(1-x)\wedge x$. The fact that ![]() $\delta$ annihilates the five-term relation can be checked by a direct computation:
$\delta$ annihilates the five-term relation can be checked by a direct computation:
 \[ \delta\bigg(\sum_{i=1}^5 \{x_i\}_2\bigg)=\sum_{i=1}^5 (1-x_i) \wedge x_i=\sum_{i=1}^5 (x_{i-1}x_{i+1})\wedge x_i=\sum_{i=1}^5 x_{i-1}\wedge x_i - \sum_{i=1}^5 x_{i}\wedge x_{i+1}=0. \]
\[ \delta\bigg(\sum_{i=1}^5 \{x_i\}_2\bigg)=\sum_{i=1}^5 (1-x_i) \wedge x_i=\sum_{i=1}^5 (x_{i-1}x_{i+1})\wedge x_i=\sum_{i=1}^5 x_{i-1}\wedge x_i - \sum_{i=1}^5 x_{i}\wedge x_{i+1}=0. \] Conjectures of Goncharov [Reference GoncharovGon95b, p. 5 and Conjecture B] imply that the vector spaces ![]() $F^{\times }_{\mathbb {Q}}$ and
$F^{\times }_{\mathbb {Q}}$ and ![]() $B_2(F)_{\mathbb {Q}}$ are the first two graded components of a conjectural graded Lie coalgebra
$B_2(F)_{\mathbb {Q}}$ are the first two graded components of a conjectural graded Lie coalgebra ![]() $\mathcal {L}_{F}$, the Lie coalgebra of mixed Tate motives over
$\mathcal {L}_{F}$, the Lie coalgebra of mixed Tate motives over ![]() $F$. The category of finite-dimensional graded corepresentations of
$F$. The category of finite-dimensional graded corepresentations of ![]() $\mathcal {L}_{F}$ should be equivalent to a conjectural abelian category of mixed Tate motives over
$\mathcal {L}_{F}$ should be equivalent to a conjectural abelian category of mixed Tate motives over ![]() $F$. The cohomology of the Chevalley–Eilenberg complex of
$F$. The cohomology of the Chevalley–Eilenberg complex of ![]() $\mathcal {L}_{F}$ in each graded component should coincide with rational motivic cohomology groups of the field
$\mathcal {L}_{F}$ in each graded component should coincide with rational motivic cohomology groups of the field ![]() $F$:
$F$:
This suggests the existence of a very explicit presentation for motivic cohomology groups. The above is known for ![]() $i=j=n>0$: the corresponding cohomology of
$i=j=n>0$: the corresponding cohomology of ![]() $\mathcal {L}_{F}$ is equal to the cokernel of the map
$\mathcal {L}_{F}$ is equal to the cokernel of the map
which coincides with the rationalized Milnor ![]() $K$-theory of
$K$-theory of ![]() $F$. It follows from the results of Suslin [Reference SuslinSus85] that
$F$. It follows from the results of Suslin [Reference SuslinSus85] that
Results of Goncharov [Reference GoncharovGon94] suggest that the third graded component of ![]() $\mathcal {L}_{F}$ should be generated by elements
$\mathcal {L}_{F}$ should be generated by elements ![]() $[x]_3 \in \mathbb {Q}[F]_3$ for
$[x]_3 \in \mathbb {Q}[F]_3$ for ![]() $x \in \mathbb {P}^1_F$ subject to the relations representing functional equations for the single-valued version of the classical trilogarithm function
$x \in \mathbb {P}^1_F$ subject to the relations representing functional equations for the single-valued version of the classical trilogarithm function ![]() $\mathcal {L}_3$, defined in [Reference GoncharovGon95b]. This motivates the introduction of truncated polylogarithmic complexes
$\mathcal {L}_3$, defined in [Reference GoncharovGon95b]. This motivates the introduction of truncated polylogarithmic complexes ![]() ${\mathcal {B}}_2(F,n)$:
${\mathcal {B}}_2(F,n)$:
where the first term is defined as the cokernel of the map
sending ![]() $[x]_3\otimes y_3 \wedge \cdots \wedge y_n$ to
$[x]_3\otimes y_3 \wedge \cdots \wedge y_n$ to ![]() $\{x\}_2\otimes x \wedge y_3 \wedge \cdots \wedge y_n$.
$\{x\}_2\otimes x \wedge y_3 \wedge \cdots \wedge y_n$.
Conjecture 1.1 (Goncharov) For an arbitrary field ![]() $F$ and
$F$ and ![]() $n\geq 2$, the kernel of the map
$n\geq 2$, the kernel of the map
is isomorphic to the motivic cohomology group ![]() $H^{n-1}_{\mathcal {M}}(F, \mathbb {Q}(n))$.
$H^{n-1}_{\mathcal {M}}(F, \mathbb {Q}(n))$.
This is known for ![]() $n=2$ thanks to the work of Suslin [Reference SuslinSus91]. We will denote this kernel by
$n=2$ thanks to the work of Suslin [Reference SuslinSus91]. We will denote this kernel by ![]() $H^{n-1}_{{\rm G}}(F, \mathbb {Q}(n))$. Our main result is the following theorem.
$H^{n-1}_{{\rm G}}(F, \mathbb {Q}(n))$. Our main result is the following theorem.
Theorem 1.2 Let ![]() $k$ be an arbitrary field and
$k$ be an arbitrary field and ![]() $n\geq 3$. Then the following sequence is exact:
$n\geq 3$. Then the following sequence is exact:
Here ![]() $k_P$ is the residue field at the point
$k_P$ is the residue field at the point ![]() $P \in \mathbb {A}^1_k$. The residue maps
$P \in \mathbb {A}^1_k$. The residue maps ![]() $\partial _P$ will be defined below. We will formulate and prove a similar statement for Milnor
$\partial _P$ will be defined below. We will formulate and prove a similar statement for Milnor ![]() $K$-theory, which was used by Bass and Tate [Reference Bass and TateBT73] and by Suslin [Reference SuslinSus79] to construct norm maps in Milnor
$K$-theory, which was used by Bass and Tate [Reference Bass and TateBT73] and by Suslin [Reference SuslinSus79] to construct norm maps in Milnor ![]() $K$-theory. Their construction works in our case as well.
$K$-theory. Their construction works in our case as well.
Corollary 1.3 Let ![]() $F$ be a perfect field. For every finite field extension
$F$ be a perfect field. For every finite field extension ![]() $L/F$ there is a norm homomorphism
$L/F$ there is a norm homomorphism
that makes the functor ![]() $H^{n-1}_{{\rm G}}(-, \mathbb {Q}(n))$ into a Rost cycle module as defined in [Reference RostRos96].
$H^{n-1}_{{\rm G}}(-, \mathbb {Q}(n))$ into a Rost cycle module as defined in [Reference RostRos96].
This implies the following conjecture of Goncharov [Reference GoncharovGon05, p. 53 and Conjecture 6.2]:
Corollary 1.4 (Strong reciprocity law) Let ![]() $X$ be a compact smooth algebraic curve over
$X$ be a compact smooth algebraic curve over ![]() $\mathbb {C}$. For every
$\mathbb {C}$. For every ![]() $n\geq 3$ the map
$n\geq 3$ the map
is null-homotopic. Here the total residue map ![]() $Res$ is a sum over all points
$Res$ is a sum over all points ![]() $P\in X$ of local residue maps
$P\in X$ of local residue maps ![]() $\partial _P$.
$\partial _P$.
Remark For curves of genus ![]() $g\leq 1$, Goncharov found a formula for a contracting homotopy [Reference GoncharovGon05, Theorems 6.5 and 6.14]. For curves of higher genus explicit construction of
$g\leq 1$, Goncharov found a formula for a contracting homotopy [Reference GoncharovGon05, Theorems 6.5 and 6.14]. For curves of higher genus explicit construction of ![]() $h$ remains unknown.
$h$ remains unknown.
To formulate the next corollary, we recall some notions from the theory of scissors congruences. Let ![]() $\mathcal {P}(\mathbb {H}^3)$ be a
$\mathcal {P}(\mathbb {H}^3)$ be a ![]() $\mathbb {Q}$-vector space generated by classes of hyperbolic polytopes modulo the scissors congruence equivalence relation. The so-called Dehn invariant
$\mathbb {Q}$-vector space generated by classes of hyperbolic polytopes modulo the scissors congruence equivalence relation. The so-called Dehn invariant
associates to a polytope the sum ![]() $\sum _{e\in E} l_e \otimes \alpha _e$, where
$\sum _{e\in E} l_e \otimes \alpha _e$, where ![]() $E$ is the set of edges of a polytope,
$E$ is the set of edges of a polytope, ![]() $l_e$ is the length of the corresponding edge and
$l_e$ is the length of the corresponding edge and ![]() $\alpha _e$ is the corresponding dihedral angle. There is a chain map
$\alpha _e$ is the corresponding dihedral angle. There is a chain map ![]() $S[i]$,
$S[i]$,

where map ![]() $S[1]\colon B_2(\mathbb {C}) \longrightarrow \mathcal {P}(\mathbb {H}^3)$ sends an element
$S[1]\colon B_2(\mathbb {C}) \longrightarrow \mathcal {P}(\mathbb {H}^3)$ sends an element ![]() $\{z\}_2$ to the scissors congruence class of the ideal tetrahedron with vertices
$\{z\}_2$ to the scissors congruence class of the ideal tetrahedron with vertices ![]() $\infty ,0,1, z$ and
$\infty ,0,1, z$ and
 \begin{align} S[2]\bigl((1-z) \wedge z\bigr)&={-}(1-z) \wedge z+(1-\bar{z}) \wedge \bar{z}\nonumber\\ & = 2\big(|z|\otimes \arg(1-z)-|1-z|\otimes \arg(z) \big)\in \mathbb{R} \otimes \mathbb{R}/ 2 \pi \mathbb{Z}. \end{align}
\begin{align} S[2]\bigl((1-z) \wedge z\bigr)&={-}(1-z) \wedge z+(1-\bar{z}) \wedge \bar{z}\nonumber\\ & = 2\big(|z|\otimes \arg(1-z)-|1-z|\otimes \arg(z) \big)\in \mathbb{R} \otimes \mathbb{R}/ 2 \pi \mathbb{Z}. \end{align}Corollary 1.5 Let ![]() $X$ be a smooth projective curve over
$X$ be a smooth projective curve over ![]() $\mathbb {C}$. Then there is a map
$\mathbb {C}$. Then there is a map
such that for any three meromorphic functions ![]() $f_1, f_2, f_3$ the Dehn invariant of a polytope
$f_1, f_2, f_3$ the Dehn invariant of a polytope ![]() $h(f_1 \wedge f_2 \wedge f_3)$ is equal to
$h(f_1 \wedge f_2 \wedge f_3)$ is equal to ![]() $(S[2] \circ Res)(f_1 \wedge f_2 \wedge f_3)$ and the hyperbolic volume of the polytope
$(S[2] \circ Res)(f_1 \wedge f_2 \wedge f_3)$ and the hyperbolic volume of the polytope ![]() $h(f_1 \wedge f_2 \wedge f_3)$ is given by the convergent integral
$h(f_1 \wedge f_2 \wedge f_3)$ is given by the convergent integral
where the form ![]() $r_2(f_1,f_2,f_3)$ is equal to
$r_2(f_1,f_2,f_3)$ is equal to
Remark The statement of the Corollary 1.5 was the original motivation behind this project. It was prompted by scissors congruence properties of Schläfli orthoschemes, discovered by J.-P. Sydler [Reference SydlerSyd65]. Hyperbolic orthoschemes appear in the image of the map ![]() $h$ from Corollary 1.5 for
$h$ from Corollary 1.5 for ![]() $X=\mathbb {P}^1$.
$X=\mathbb {P}^1$.
1.3 The structure of this paper
Towards proving Theorem 1.2, we start by discussing the classical proof of an exact sequence for Milnor ![]() $K$-theory: Theorem 2.1. There is nothing original in our exposition, but the proof of Theorem 1.2 is based on it. This proof is based on the properties of a certain filtration, which we will use extensively in the proof of Theorem 1.2. We do not write in detail proofs of Corollaries 1.3 and 1.4 because they are not different from the Milnor
$K$-theory: Theorem 2.1. There is nothing original in our exposition, but the proof of Theorem 1.2 is based on it. This proof is based on the properties of a certain filtration, which we will use extensively in the proof of Theorem 1.2. We do not write in detail proofs of Corollaries 1.3 and 1.4 because they are not different from the Milnor ![]() $K$-theory case, which is explained in [Reference SuslinSus79]. Corollary 1.5 follows from results of [Reference GoncharovGon05] and [Reference DupontDup01].
$K$-theory case, which is explained in [Reference SuslinSus79]. Corollary 1.5 follows from results of [Reference GoncharovGon05] and [Reference DupontDup01].
Our proof of the main result occupies §§ 3–7. In § 3 one can find the proof modulo two key statements: Lemmas 3.3 and 3.4. Proofs of Lemma 3.3 and 3.4 are based on the study of the coresidue map, which are defined in the derived category only. The most non-trivial step in the proof of Theorem 1.2 is to show that these maps are well-defined, which is done in §§ 5.4 and 5.5.
1.4 Notation and conventions
All our results are valid only modulo torsion, so we work everywhere with ![]() $\mathbb {Q}$-vector spaces. Thus it is convenient to omit the rationalization sign from the notation, which we do everywhere, starting with § 2, except in § 4.2. In particular, we will use
$\mathbb {Q}$-vector spaces. Thus it is convenient to omit the rationalization sign from the notation, which we do everywhere, starting with § 2, except in § 4.2. In particular, we will use ![]() $F^{\times }$ instead of
$F^{\times }$ instead of ![]() $F^{\times }_{\mathbb {Q}}$,
$F^{\times }_{\mathbb {Q}}$, ![]() $K_n^M(F)$ instead of
$K_n^M(F)$ instead of ![]() $K_n^M(F)_{\mathbb {Q}}$,
$K_n^M(F)_{\mathbb {Q}}$, ![]() $B_2(F)$ instead of
$B_2(F)$ instead of ![]() $B_2(F)_{\mathbb {Q}}$, and so on.
$B_2(F)_{\mathbb {Q}}$, and so on.
We use notation ![]() $\mathbb {S}^k V$ and
$\mathbb {S}^k V$ and ![]() $\Lambda ^k V$ for symmetric and wedge powers of a vector space. The tensor product
$\Lambda ^k V$ for symmetric and wedge powers of a vector space. The tensor product ![]() $V\otimes W$ is understood as the tensor product over
$V\otimes W$ is understood as the tensor product over ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
Next, for ![]() $n\geq 3$ we denote the cokernel of the map
$n\geq 3$ we denote the cokernel of the map
by the symbol ![]() $[B_2(F)\otimes \Lambda ^{n-2} F^{\times }]_t$. For every subfactor space
$[B_2(F)\otimes \Lambda ^{n-2} F^{\times }]_t$. For every subfactor space ![]() $X$ of the space
$X$ of the space ![]() $B_2(F)\otimes \Lambda ^{n-2} F^{\times }$ we will denote by the symbol
$B_2(F)\otimes \Lambda ^{n-2} F^{\times }$ we will denote by the symbol ![]() $[X]_t$ its projection to
$[X]_t$ its projection to ![]() $[B_2(F)\otimes \Lambda ^{n-2} F^{\times }]_t$.
$[B_2(F)\otimes \Lambda ^{n-2} F^{\times }]_t$.
A few remarks about filtered vector spaces are in order. By a filtered vector space ![]() $(V,\mathcal {F})$ we mean a vector space
$(V,\mathcal {F})$ we mean a vector space ![]() $V$ equipped with an increasing filtration
$V$ equipped with an increasing filtration
We will denote by ![]() $gr_k^{\mathcal {F}}V$ the associated graded space
$gr_k^{\mathcal {F}}V$ the associated graded space ![]() $\mathcal {F}_k V / \mathcal {F}_{k-1} V$. A morphism
$\mathcal {F}_k V / \mathcal {F}_{k-1} V$. A morphism
of filtered vector spaces is called strictly compatible with filtration if
Every subspace or factor space of a filtered vector space inherits the filtration. Similarly, there exists a natural filtration on the tensor product of a finite number of filtered vector spaces. A detailed exposition of these notions can be found in [Reference DeligneDel71].
2. Results of Bass, Tate and Milnor
2.1 Milnor  $K$-theory
$K$-theory
We start by discussing a well-known analogue of Theorem 1.2 for Milnor ![]() $K$-theory. It was proved by Bass and Tate [Reference Bass and TateBT73] for
$K$-theory. It was proved by Bass and Tate [Reference Bass and TateBT73] for ![]() $n=2$ and by Milnor [Reference MilnorMil70] in general.
$n=2$ and by Milnor [Reference MilnorMil70] in general.
Let ![]() $F$ be an arbitrary field. For every integer
$F$ be an arbitrary field. For every integer ![]() $n$ we define
$n$ we define ![]() $K_n^M(F)$, the Milnor
$K_n^M(F)$, the Milnor ![]() $K$-group of
$K$-group of ![]() $F$, to be the quotient of the abelian group
$F$, to be the quotient of the abelian group ![]() $\Lambda ^n F^{\times }$ by the subgroup generated by tensors
$\Lambda ^n F^{\times }$ by the subgroup generated by tensors ![]() $(1-x)\wedge x \wedge y_3 \wedge \cdots \wedge y_n$. The image of an element
$(1-x)\wedge x \wedge y_3 \wedge \cdots \wedge y_n$. The image of an element ![]() $y_1 \wedge y_2 \wedge \cdots \wedge y_n$ in
$y_1 \wedge y_2 \wedge \cdots \wedge y_n$ in ![]() $K_n^M(F)$ is denoted by
$K_n^M(F)$ is denoted by ![]() $\{y_1, y_2,\ldots ,y_n\}$. Our definition agrees with the classical one modulo
$\{y_1, y_2,\ldots ,y_n\}$. Our definition agrees with the classical one modulo ![]() $2$-torsion. In accordance with the convention from § 1.4, we denote by
$2$-torsion. In accordance with the convention from § 1.4, we denote by ![]() $K_n^M(F)$ the
$K_n^M(F)$ the ![]() $\mathbb {Q}$-vector space
$\mathbb {Q}$-vector space ![]() $K_n^M(F)_{\mathbb {Q}}$.
$K_n^M(F)_{\mathbb {Q}}$.
Our next goal is to define residue maps. Suppose that ![]() $\nu$ is a discrete valuation of
$\nu$ is a discrete valuation of ![]() $F$ with residue field
$F$ with residue field ![]() $F_{\nu }$ and uniformizer
$F_{\nu }$ and uniformizer ![]() $f_\nu$. We define a map
$f_\nu$. We define a map
For any elements ![]() $u_1, \ldots , u_n \in F^\times$ with vanishing discrete valuation we let
$u_1, \ldots , u_n \in F^\times$ with vanishing discrete valuation we let
and
Here ![]() $\bar {u}$ is the residue of
$\bar {u}$ is the residue of ![]() $u$ in
$u$ in ![]() $F_\nu ^{\times }$. This map can be uniquely extended by linearity to
$F_\nu ^{\times }$. This map can be uniquely extended by linearity to ![]() $\Lambda ^n F^{\times }$. It is easy to see that it induces a well-defined map from
$\Lambda ^n F^{\times }$. It is easy to see that it induces a well-defined map from ![]() $K_n^M(F)$ to
$K_n^M(F)$ to ![]() $K_{n-1}^M (F_{\nu })$.
$K_{n-1}^M (F_{\nu })$.
We will be especially interested in the case when ![]() $F=k(t)$ and the valuation
$F=k(t)$ and the valuation ![]() $\nu _P$ corresponds to a point
$\nu _P$ corresponds to a point ![]() $P\in \mathbb {A}^1_k$. We will denote the residue field by
$P\in \mathbb {A}^1_k$. We will denote the residue field by ![]() $k_P$, and a uniformizer by
$k_P$, and a uniformizer by ![]() $f_P$.The uniformizer will always be chosen to be a monic polynomial.
$f_P$.The uniformizer will always be chosen to be a monic polynomial.
Theorem 2.1 (Milnor, Tate) The following sequence is exact for ![]() $n\geq 2$:
$n\geq 2$:
Here the map ![]() $K_n^M(k) \stackrel {j}{\longrightarrow } K_n^M(k(t))$ is induced by an inclusion of
$K_n^M(k) \stackrel {j}{\longrightarrow } K_n^M(k(t))$ is induced by an inclusion of ![]() $k$ in
$k$ in ![]() $k(t)$.
$k(t)$.
2.2 Some corollaries of Theorem 2.1
Assume that ![]() $F$ is perfect. Theorem 2.1 can be used to construct a norm map
$F$ is perfect. Theorem 2.1 can be used to construct a norm map
for any finite field extension ![]() $L/F$. For this consider any point
$L/F$. For this consider any point ![]() $P\in \mathbb {A}^1_F$ with residue field
$P\in \mathbb {A}^1_F$ with residue field ![]() $L$ (such a point exists by the primitive element theorem). Thanks to Theorem 2.1, for any element
$L$ (such a point exists by the primitive element theorem). Thanks to Theorem 2.1, for any element ![]() $w\in K_n^M(L)$ there exists an element
$w\in K_n^M(L)$ there exists an element ![]() $W \in K_{n+1}^M(F(t))$ with residue (at the point
$W \in K_{n+1}^M(F(t))$ with residue (at the point ![]() $P$) equal to
$P$) equal to ![]() $w$ and with vanishing residues at all other points. Then one can define
$w$ and with vanishing residues at all other points. Then one can define ![]() $Nm_{L/F}(w)$ to be the residue of
$Nm_{L/F}(w)$ to be the residue of ![]() $W$ at
$W$ at ![]() $\infty \in \mathbb {P}^1$.
$\infty \in \mathbb {P}^1$.
One can show that this construction does not depend on the choice of ![]() $P$. The proof is straightforward for the case when one works modulo torsion, as we do. Using the norm map, one can establish all usual properties of norms. In particular, we obtain the following non-trivial result.
$P$. The proof is straightforward for the case when one works modulo torsion, as we do. Using the norm map, one can establish all usual properties of norms. In particular, we obtain the following non-trivial result.
Corollary 2.2 (Suslin reciprocity law) Let ![]() $X$ be a compact smooth algebraic curve over
$X$ be a compact smooth algebraic curve over ![]() $\mathbb {C}$. Then for
$\mathbb {C}$. Then for ![]() $n\geq 1$ the map
$n\geq 1$ the map
is equal to zero. Here the total residue map ![]() $Res$ is a sum over all points
$Res$ is a sum over all points ![]() $P\in X$ of local residue maps
$P\in X$ of local residue maps ![]() $\partial _P$.
$\partial _P$.
All the details of these constructions can be found in [Reference SuslinSus79].
2.3 Proof of Theorem 2.1
Proof. Denote the ![]() $\mathbb {Q}$-vector space
$\mathbb {Q}$-vector space ![]() $k(t)^{\times }$ by
$k(t)^{\times }$ by ![]() $D$. It is naturally graded by the degree
$D$. It is naturally graded by the degree ![]() $d$:
$d$: ![]() $D_0=k^{\times }$ and for
$D_0=k^{\times }$ and for ![]() $d$ greater than zero
$d$ greater than zero ![]() $D_d$ is freely generated by monic irreducible polynomials of degree
$D_d$ is freely generated by monic irreducible polynomials of degree ![]() $d$. We will use interchangeably the notation
$d$. We will use interchangeably the notation ![]() $D_{\leq d}$ and
$D_{\leq d}$ and ![]() $\mathcal {F}_d D$ for
$\mathcal {F}_d D$ for ![]() ${\bigoplus}_{i \leq d} D_i$. The filtration
${\bigoplus}_{i \leq d} D_i$. The filtration ![]() $\mathcal {F}_\bullet$ can be extended to all wedge powers of
$\mathcal {F}_\bullet$ can be extended to all wedge powers of ![]() $k(t)^{\times }$ and thus defines a filtration on
$k(t)^{\times }$ and thus defines a filtration on ![]() $K_n^M(k(t))$. Explicitly,
$K_n^M(k(t))$. Explicitly, ![]() $\mathcal {F}_d K_n^M(k(t))$ is generated by symbols
$\mathcal {F}_d K_n^M(k(t))$ is generated by symbols ![]() $\{f_1,\ldots , f_n\}$, where
$\{f_1,\ldots , f_n\}$, where ![]() $f_i$ are irreducible polynomials of degree
$f_i$ are irreducible polynomials of degree ![]() $\leq d$.
$\leq d$.
Let ![]() $P \in \mathbb {A}^1_k$ be a point of degree
$P \in \mathbb {A}^1_k$ be a point of degree ![]() $d$. Then the map
$d$. Then the map ![]() $\partial _P$ vanishes on all symbols
$\partial _P$ vanishes on all symbols ![]() $\{g_1,\ldots , g_n\}$, where
$\{g_1,\ldots , g_n\}$, where ![]() $g_i$ are irreducible polynomials of degree less than
$g_i$ are irreducible polynomials of degree less than ![]() $d$. We deduce that the following map is well-defined:
$d$. We deduce that the following map is well-defined:
We claim that this map is an isomorphism. To see that this map ![]() $\oplus \partial _P$ is surjective, consider any element
$\oplus \partial _P$ is surjective, consider any element ![]() $\{r_1, r_2, \ldots , r_{n-1}\} \in K_{n-1}^M (k_P)$. For each
$\{r_1, r_2, \ldots , r_{n-1}\} \in K_{n-1}^M (k_P)$. For each ![]() $i$ let
$i$ let ![]() $\widetilde {r_i}$ be a polynomial of minimal degree with residue
$\widetilde {r_i}$ be a polynomial of minimal degree with residue ![]() $r_i$. Then
$r_i$. Then
If ![]() $Q$ is any other point of degree
$Q$ is any other point of degree ![]() $d$,
$d$,
This implies that the map ![]() $\oplus \partial _P$ is surjective.
$\oplus \partial _P$ is surjective.
To see that ![]() $\oplus \partial _P$ is injective, for every point
$\oplus \partial _P$ is injective, for every point ![]() $P$ we construct coresidue maps
$P$ we construct coresidue maps
The definition is straightforward: for every element ![]() $\{r_1, r_2, \ldots , r_{n-1}\} \in K_{n-1}^M (k_P)$ we put
$\{r_1, r_2, \ldots , r_{n-1}\} \in K_{n-1}^M (k_P)$ we put
Lemma 2.3 The coresidue map
is well-defined.
Proof To begin, we show that the map ![]() $c_P$ is linear in each variable. Consider a pair of elements in
$c_P$ is linear in each variable. Consider a pair of elements in ![]() $K_{n-1}^M (k_P)$:
$K_{n-1}^M (k_P)$:
Then
It is easy to see that
 \begin{equation} \begin{aligned} c_P(S_1) & =\{f_P, \widetilde{s_1}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \\ c_P(S_2) & =\{f_P, \widetilde{s_2}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \\ c_P(S_1+S_2) & =\{f_P, \widetilde{s_1s_2}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} c_P(S_1) & =\{f_P, \widetilde{s_1}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \\ c_P(S_2) & =\{f_P, \widetilde{s_2}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \\ c_P(S_1+S_2) & =\{f_P, \widetilde{s_1s_2}, \widetilde{r_2}, \ldots, \tilde{r}_{n-1}\}, \end{aligned} \end{equation}so
Note that from the division algorithm it follows that there exists a polynomial ![]() $q(t)$ such that
$q(t)$ such that
so that
This implies
 \begin{align} c_P(S_1)+c_P(S_2)-c_P(S_1+S_2)&= \bigg\{ f_P, \dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}\nonumber\\ & = \bigg\{ f_P, 1-\frac{-q f_P}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}\nonumber\\ &=\bigg\{ \frac{-q f_P}{\widetilde{s_1s_2}}, 1-\frac{-q f_P}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\} \!-\!\bigg\{ \frac{-q}{\widetilde{s_1s_2}},\dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}} ,\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\} \nonumber\\ & = -\bigg\{ \frac{-q}{\widetilde{s_1s_2}},\dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}} ,\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}. \end{align}
\begin{align} c_P(S_1)+c_P(S_2)-c_P(S_1+S_2)&= \bigg\{ f_P, \dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}\nonumber\\ & = \bigg\{ f_P, 1-\frac{-q f_P}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}\nonumber\\ &=\bigg\{ \frac{-q f_P}{\widetilde{s_1s_2}}, 1-\frac{-q f_P}{\widetilde{s_1s_2}},\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\} \!-\!\bigg\{ \frac{-q}{\widetilde{s_1s_2}},\dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}} ,\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\} \nonumber\\ & = -\bigg\{ \frac{-q}{\widetilde{s_1s_2}},\dfrac{\widetilde{s_1} \widetilde{s_2}}{\widetilde{s_1s_2}} ,\widetilde{r_2}, \ldots, \tilde{r}_{n-1} \bigg\}. \end{align}Since
the expression
lies in ![]() $\mathcal {F}_{d-1} K_n^M(k(t))$, so it vanishes in
$\mathcal {F}_{d-1} K_n^M(k(t))$, so it vanishes in ![]() $gr_d^{\mathcal {F}} K_n^M(k(t))$. Thus
$gr_d^{\mathcal {F}} K_n^M(k(t))$. Thus ![]() $c_P(S_1)+c_P(S_2)=c_P(S_1+S_2)$.
$c_P(S_1)+c_P(S_2)=c_P(S_1+S_2)$.
It is easy to see that ![]() $c_P$ is antisymmetric and vanishes on elements
$c_P$ is antisymmetric and vanishes on elements ![]() $\{r_1, 1-r_1, r_3,\ldots , r_{n-1}\}$, so this map is well-defined.
$\{r_1, 1-r_1, r_3,\ldots , r_{n-1}\}$, so this map is well-defined.
We claim that the map ![]() $\sum c_P$ is the inverse of
$\sum c_P$ is the inverse of ![]() $\oplus \partial _P$. Obviously
$\oplus \partial _P$. Obviously ![]() $\partial _P \circ c_P=id$ and
$\partial _P \circ c_P=id$ and ![]() $\partial _P \circ c_Q=0$ if points
$\partial _P \circ c_Q=0$ if points ![]() $P$ and
$P$ and ![]() $Q$ are distinct. It remains to show that
$Q$ are distinct. It remains to show that
Notice that this equality holds for elements in ![]() $gr_d^{\mathcal {F}}K_n^M \big (k(t)\big )$ of the form
$gr_d^{\mathcal {F}}K_n^M \big (k(t)\big )$ of the form ![]() $\{f_P,\widetilde {r_1}, \widetilde {r_2}, \ldots , \widetilde {r_{n-1}}\}$ where
$\{f_P,\widetilde {r_1}, \widetilde {r_2}, \ldots , \widetilde {r_{n-1}}\}$ where ![]() $\widetilde {r_i}$ are elements of degree less than
$\widetilde {r_i}$ are elements of degree less than ![]() $d$.
$d$.
Lemma 2.4 The vector space ![]() $gr_d^{\mathcal {F}} K_n^M (k(t))$ is generated by elements
$gr_d^{\mathcal {F}} K_n^M (k(t))$ is generated by elements
for polynomials ![]() $f$ and
$f$ and ![]() $g_i$ such that
$g_i$ such that ![]() $\deg (f)=d$ and
$\deg (f)=d$ and ![]() $\deg (g_i) < d$.
$\deg (g_i) < d$.
Proof. Denote by ![]() $\mathcal {G}_s gr_d^{\mathcal {F}} K_n^M (k(t))$ a subspace of
$\mathcal {G}_s gr_d^{\mathcal {F}} K_n^M (k(t))$ a subspace of ![]() $gr_d^{\mathcal {F}} K_n^M (k(t))$ generated by elements
$gr_d^{\mathcal {F}} K_n^M (k(t))$ generated by elements
where ![]() $k\leq s$, the polynomials
$k\leq s$, the polynomials ![]() $f_i$ are monic irreducible of degree
$f_i$ are monic irreducible of degree ![]() $d$ and the degree of the polynomials
$d$ and the degree of the polynomials ![]() $g_i$ is less than
$g_i$ is less than ![]() $d$. Clearly,
$d$. Clearly,
To prove the lemma it is sufficient to show that
for ![]() $2\leq s \leq n$.
$2\leq s \leq n$.
We present a proof for ![]() $n=2$, the general case being similar. Consider two distinct monic polynomials
$n=2$, the general case being similar. Consider two distinct monic polynomials ![]() $f_1, f_2$ of degree
$f_1, f_2$ of degree ![]() $d$. Then
$d$. Then
Note that since ![]() $f_2$ and
$f_2$ and ![]() $f_1$ are monic,
$f_1$ are monic, ![]() $\deg (f_2-f_1) < d$, so
$\deg (f_2-f_1) < d$, so
From this the statement follows.
We conclude that the map
is an isomorphism, from which Theorem 2.1 easily follows.
3. The plan of the proof of Theorem 1.2
To give a precise statement of Theorem 1.2, we need to extend the definition of the residue map ![]() $\partial _P$ to truncated polylogarithmic complexes.
$\partial _P$ to truncated polylogarithmic complexes.
3.1 Residue map
Let ![]() $F$ be a field with discrete valuation
$F$ be a field with discrete valuation ![]() $\nu$ and residue field
$\nu$ and residue field ![]() $F_{\nu }$. Denote by
$F_{\nu }$. Denote by ![]() $f_\nu$ a uniformizer. Our goal is to define a chain map
$f_\nu$ a uniformizer. Our goal is to define a chain map ![]() $\partial _{\nu }$,
$\partial _{\nu }$,

for ![]() $n\geq 3$. We have already defined this map on
$n\geq 3$. We have already defined this map on ![]() $\Lambda ^{n}F^{\times }$ in the previous section. On
$\Lambda ^{n}F^{\times }$ in the previous section. On
we define it by the formula
It is easy to see that ![]() $\partial _{\nu }$ is a chain map of complexes
$\partial _{\nu }$ is a chain map of complexes
Theorem 1.2 is equivalent to the statement that the complex of chain maps
is exact on cohomology.
3.2 Filtration by degree
The main tool in the proof of Theorem 2.1 was an auxiliary filtration ![]() $\mathcal {F}_{\bullet }$ on
$\mathcal {F}_{\bullet }$ on ![]() $K_n^M(k(t))$ induced by the degree filtration on
$K_n^M(k(t))$ induced by the degree filtration on ![]() $k(t)^{\times }$. This filtration can be extended to the complex
$k(t)^{\times }$. This filtration can be extended to the complex ![]() ${\mathcal {B}}_2(k(t),n)$. For this we first define a filtration
${\mathcal {B}}_2(k(t),n)$. For this we first define a filtration ![]() $\mathcal {F}_{\bullet }$ on the Bloch group
$\mathcal {F}_{\bullet }$ on the Bloch group ![]() $B_2(k(t))$ as a pre-image of the filtration
$B_2(k(t))$ as a pre-image of the filtration ![]() $\mathcal {F}_{\bullet }$ on
$\mathcal {F}_{\bullet }$ on ![]() $\Lambda ^2 k(t)^{\times }$ under
$\Lambda ^2 k(t)^{\times }$ under ![]() $\delta$. In the next section we will use results of Suslin to describe this filtration more explicitly. This defines a filtration on
$\delta$. In the next section we will use results of Suslin to describe this filtration more explicitly. This defines a filtration on ![]() $B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times }$, which descends to
$B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times }$, which descends to ![]() $[ B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times }]_t$.
$[ B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times }]_t$.
Recall that a map
of filtered spaces is called strictly compatible with the filtration if
Lemma 3.1 The map
is strictly compatible with the filtration ![]() $\mathcal {F}$.
$\mathcal {F}$.
Proof. The statement follows from the proof of Theorem 2.1.
Lemma 3.2 To prove Theorem 1.2 it is sufficient to show that for every positive degree ![]() $d$ the map
$d$ the map
is a quasi-isomorphism.
Proof. Assume that (11) is a quasi-isomorphism. We will use the fact that ![]() $\mathcal {F}_0B_2(k(t))=B_2(k)$, which will be proved in the next section. Our goal is to show that the complex
$\mathcal {F}_0B_2(k(t))=B_2(k)$, which will be proved in the next section. Our goal is to show that the complex
is exact for ![]() $n\geq 3$, where
$n\geq 3$, where ![]() $H^{n-1}_{{\rm G}}(F, \mathbb {Q}(n))$ is the kernel of the map
$H^{n-1}_{{\rm G}}(F, \mathbb {Q}(n))$ is the kernel of the map
Consider an element ![]() $x \in H^{n-1}_{{\rm G}}(k(t), \mathbb {Q}(n))$ in the kernel of
$x \in H^{n-1}_{{\rm G}}(k(t), \mathbb {Q}(n))$ in the kernel of ![]() $\oplus \partial _P$. Then
$\oplus \partial _P$. Then
by (11). But
so ![]() $x \in H^{n-1}_{{\rm G}}(k, \mathbb {Q}(n))$. So the complex (12) is exact in the middle term. To show that
$x \in H^{n-1}_{{\rm G}}(k, \mathbb {Q}(n))$. So the complex (12) is exact in the middle term. To show that ![]() $\oplus \partial _P$ is surjective, notice that
$\oplus \partial _P$ is surjective, notice that ![]() $\delta$ is strictly compatible with
$\delta$ is strictly compatible with ![]() $\mathcal {F}$, so
$\mathcal {F}$, so ![]() $gr_d^{\mathcal {F}} H^{n-1}_{{\rm G}}(k(t), \mathbb {Q}(n))$ is the kernel of the map
$gr_d^{\mathcal {F}} H^{n-1}_{{\rm G}}(k(t), \mathbb {Q}(n))$ is the kernel of the map
It follows from the quasi-isomorphism (11) that this kernel is isomorphic to
From this the lemma follows.
3.3 Filtration by support
It remains to prove that the map
is a quasi-isomorphism. For this we introduce another filtration on ![]() $gr^{\mathcal {F}}_d{\mathcal {B}}_2(k(t),n)$: filtration by support. This is an increasing filtration
$gr^{\mathcal {F}}_d{\mathcal {B}}_2(k(t),n)$: filtration by support. This is an increasing filtration ![]() $\mathcal {G}_1\subset \mathcal {G}_2\subset \cdots \subset \mathcal {G}_n$. On
$\mathcal {G}_1\subset \mathcal {G}_2\subset \cdots \subset \mathcal {G}_n$. On ![]() $gr_d^{\mathcal {F}} \big (\Lambda ^n k(t)^{\times }\big )$ we define the filtration by placing tensors
$gr_d^{\mathcal {F}} \big (\Lambda ^n k(t)^{\times }\big )$ we define the filtration by placing tensors
with polynomials ![]() $f_i, g_i$ such that
$f_i, g_i$ such that ![]() $\deg (f_i)=d,$ and
$\deg (f_i)=d,$ and ![]() $\deg (g_i) < d$ in
$\deg (g_i) < d$ in ![]() $\mathcal {G}_s$. It is easy to see that
$\mathcal {G}_s$. It is easy to see that
On ![]() $gr^{\mathcal {F}}_d(B_2(k(x)))$ we define the filtration as the pre-image of the filtration
$gr^{\mathcal {F}}_d(B_2(k(x)))$ we define the filtration as the pre-image of the filtration ![]() $\mathcal {G}$ on
$\mathcal {G}$ on ![]() $gr_d^{\mathcal {F}} \big (\Lambda ^2 k(t)^{\times }\big )$ under
$gr_d^{\mathcal {F}} \big (\Lambda ^2 k(t)^{\times }\big )$ under ![]() $\delta$. It will be computed explicitly in the next section. Finally, on
$\delta$. It will be computed explicitly in the next section. Finally, on ![]() $gr^{\mathcal {F}}_d [B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times } ]_t$ the filtration is obtained by projecting the tensor product of the corresponding filtrations on the components.
$gr^{\mathcal {F}}_d [B_2(k(t)) \otimes \Lambda ^{n-2}k(t)^{\times } ]_t$ the filtration is obtained by projecting the tensor product of the corresponding filtrations on the components.
3.4 What remains to be proved
Theorem 1.2 follows from Lemmas 3.3 and 3.4.
Lemma 3.3 The complex
is quasi-isomorphic to
Lemma 3.3 will be proved in § 6 using a construction of coresidue maps ![]() $c_P$. The difficulty is that the coresidue maps can be defined in the derived category only.
$c_P$. The difficulty is that the coresidue maps can be defined in the derived category only.
Lemma 3.4 For ![]() $s>1$, the complex
$s>1$, the complex
is acyclic.
Lemma 3.4 is not very hard and will be proved in § 7. To see that Lemmas 3.3 and 3.4 imply Theorem 1.2 we also need to show that the map
is strictly compatible with filtration ![]() $\mathcal {G}$; compatibility will follow from the proof of Lemma 3.4.
$\mathcal {G}$; compatibility will follow from the proof of Lemma 3.4.
4. Anatomy of the group  $B_2(k(t))$
$B_2(k(t))$
4.1 Introduction
The goal of this section is to describe a set of generators for the group ![]() $B_2(k(t))$. The results of this section can be formulated very explicitly (see Corollary 4.4) but the proofs use the connection with higher algebraic
$B_2(k(t))$. The results of this section can be formulated very explicitly (see Corollary 4.4) but the proofs use the connection with higher algebraic ![]() $K$-theory, established by Suslin.
$K$-theory, established by Suslin.
Recall from § 2.3 that for ![]() $d\geq 1$ the vector space
$d\geq 1$ the vector space ![]() $D_d\subset k(t)^{\times }$ is freely generated by monic irreducible polynomials of degree
$D_d\subset k(t)^{\times }$ is freely generated by monic irreducible polynomials of degree ![]() $d$. Also,
$d$. Also, ![]() $D_0=k^{\times }$.
$D_0=k^{\times }$.
Definition 4.1 For a point ![]() $P\in \mathbb {A}^1_k$ of degree
$P\in \mathbb {A}^1_k$ of degree ![]() $d$ consider a linear map
$d$ consider a linear map
which sends a polynomial ![]() $f\in k(t)^{\times }$ of degree less than
$f\in k(t)^{\times }$ of degree less than ![]() $\deg (P)$ to its residue
$\deg (P)$ to its residue ![]() $\bar {f}$. We denote the kernel of the map
$\bar {f}$. We denote the kernel of the map ![]() $\rho _P$ by
$\rho _P$ by ![]() $B_P$.
$B_P$.
The map ![]() $\rho _P$ is surjective: any residue class
$\rho _P$ is surjective: any residue class ![]() $r \in k_{P}^{\times }$ is the image of a unique polynomial of degree less than
$r \in k_{P}^{\times }$ is the image of a unique polynomial of degree less than ![]() $\deg (P)$, which we denote by
$\deg (P)$, which we denote by ![]() $\tilde {r}$.
$\tilde {r}$.
Consider a map
defined on generators ![]() $[r_1,r_2]_1$ by the formula
$[r_1,r_2]_1$ by the formula
and extended to ![]() $R_1(k_{P})$ by linearity. Clearly, this map is well-defined and surjective.
$R_1(k_{P})$ by linearity. Clearly, this map is well-defined and surjective.
Remark We will later use the fact that ![]() $D_d$ is rather close to the rational group ring of
$D_d$ is rather close to the rational group ring of ![]() $k_P^{\times }$ and
$k_P^{\times }$ and ![]() $B_P$ is related to the square of the augmentation ideal of the group ring. More precisely, there exists a surjective map
$B_P$ is related to the square of the augmentation ideal of the group ring. More precisely, there exists a surjective map
sending ![]() $r$ to
$r$ to ![]() $\tilde {r}$. The kernel is generated by elements
$\tilde {r}$. The kernel is generated by elements ![]() $[r_1]+[r_2]-[r_1r_2]$, where
$[r_1]+[r_2]-[r_1r_2]$, where ![]() $\deg (\widetilde {r_1})+ \deg (\widetilde {r_2}) < d$.
$\deg (\widetilde {r_1})+ \deg (\widetilde {r_2}) < d$.
4.2 A result of Suslin
The second cohomology group of the weight-two polylogarithmic complex ![]() ${\mathcal {B}}^\bullet (F,2)$ is naturally identified with a rationalized Milnor
${\mathcal {B}}^\bullet (F,2)$ is naturally identified with a rationalized Milnor ![]() $K$-group. Suslin provedFootnote 2 in [Reference SuslinSus91] that its first cohomology group is naturally identified with the indecomposable part of
$K$-group. Suslin provedFootnote 2 in [Reference SuslinSus91] that its first cohomology group is naturally identified with the indecomposable part of ![]() $K_3(F)_{\mathbb {Q}}$. Hence, the following sequence is exact:
$K_3(F)_{\mathbb {Q}}$. Hence, the following sequence is exact:
We will use two other results from ![]() $K$-theory coming from the relation between the
$K$-theory coming from the relation between the ![]() $K$-theory of
$K$-theory of ![]() $k$ and
$k$ and ![]() $k(t)$. First, the following exact sequence is a special case of Theorem 2.1:
$k(t)$. First, the following exact sequence is a special case of Theorem 2.1:
Second, from the localization sequence and ![]() $\mathbb {A}^1$-homotopy invariance for algebraic
$\mathbb {A}^1$-homotopy invariance for algebraic ![]() $K$-theory it follows that the embedding
$K$-theory it follows that the embedding
is an isomorphism. Combining these two results with Suslin's theorem, we get the following statement.
Corollary 4.2 The following sequence is exact:
 \[ 0 \longrightarrow B_2(k)_{\mathbb{Q}}\longrightarrow B_2(k(t))_{\mathbb{Q}} \longrightarrow \dfrac{\Lambda^2 k(t)^\times_{\mathbb{Q}}}{\Lambda^2 k^\times_{\mathbb{Q}}} \longrightarrow \mathop{\bigoplus} \limits_{P\in \mathbb{A}^1_k} \big( k_P^{{\times}} \big)_{\mathbb{Q}} \longrightarrow 0. \]
\[ 0 \longrightarrow B_2(k)_{\mathbb{Q}}\longrightarrow B_2(k(t))_{\mathbb{Q}} \longrightarrow \dfrac{\Lambda^2 k(t)^\times_{\mathbb{Q}}}{\Lambda^2 k^\times_{\mathbb{Q}}} \longrightarrow \mathop{\bigoplus} \limits_{P\in \mathbb{A}^1_k} \big( k_P^{{\times}} \big)_{\mathbb{Q}} \longrightarrow 0. \]4.3 A degree filtration on the truncated weight-two polylogarithmic complex
The associated graded factor ![]() $gr_d^\mathcal {F}(\Lambda ^2 k(t)^\times )$ can be described explicitly:
$gr_d^\mathcal {F}(\Lambda ^2 k(t)^\times )$ can be described explicitly:
The vector space ![]() $B_2(k(t))$ carries a filtration induced from the filtration on
$B_2(k(t))$ carries a filtration induced from the filtration on ![]() $\Lambda ^2 k(t)^\times$, which we will also denote by
$\Lambda ^2 k(t)^\times$, which we will also denote by ![]() $\mathcal {F}$. It follows from Corollary 4.2 that
$\mathcal {F}$. It follows from Corollary 4.2 that ![]() $\mathcal {F}_0 B_2(k(t))=B_2(k)$ and that the following sequence is exact for
$\mathcal {F}_0 B_2(k(t))=B_2(k)$ and that the following sequence is exact for ![]() $d>0$:
$d>0$:
Lemma 4.3 The following sequence is exact:
Proof. The projection ![]() $gr_d^{\mathcal {F}}[ B_2(k(t))] \longrightarrow \Lambda ^2 D_d$ is surjective. Indeed, given two irreducible monic polynomials
$gr_d^{\mathcal {F}}[ B_2(k(t))] \longrightarrow \Lambda ^2 D_d$ is surjective. Indeed, given two irreducible monic polynomials ![]() $f$ and
$f$ and ![]() $g$ of degree
$g$ of degree ![]() $d$, consider the symbol
$d$, consider the symbol ![]() $\{ {f}/{g}\}_2 \in B_2(k(t))$. Since
$\{ {f}/{g}\}_2 \in B_2(k(t))$. Since
and ![]() $g-f$ has degree less than
$g-f$ has degree less than ![]() $d$, it follows that
$d$, it follows that ![]() $\{ {f}/{g}\}_2$ projects to
$\{ {f}/{g}\}_2$ projects to ![]() $f \wedge g$ in
$f \wedge g$ in ![]() $\Lambda ^2 D_d$. Consider the following commutative diagram with exact rows and surjective columns:
$\Lambda ^2 D_d$. Consider the following commutative diagram with exact rows and surjective columns:

Applying the snake lemma, we get an exact sequence
On the other hand, ![]() $B_P$ was defined as the kernel of the map
$B_P$ was defined as the kernel of the map ![]() $D_{ < d} \stackrel {\rho _P}{\longrightarrow } k_P^{\times }$, so
$D_{ < d} \stackrel {\rho _P}{\longrightarrow } k_P^{\times }$, so
is isomorphic to ![]() ${\bigoplus}_{\deg (P)=d} B_P$.
${\bigoplus}_{\deg (P)=d} B_P$.
Let ![]() $P\in \mathbb {A}^1_k$ be a point of degree
$P\in \mathbb {A}^1_k$ be a point of degree ![]() $d$. A composition of the map
$d$. A composition of the map
and an embedding
is a map
More explicitly, ![]() $\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}}\}_2$.
$\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}}\}_2$.
Remark The map ![]() $\beta _P$ is well-defined by construction. This is equivalent to the following relation in
$\beta _P$ is well-defined by construction. This is equivalent to the following relation in ![]() $gr_d^\mathcal {F}[B_2(k(t))]$:
$gr_d^\mathcal {F}[B_2(k(t))]$:
This relation could also be derived independently by applying the ![]() $5$-term relation several times.
$5$-term relation several times.
Corollary 4.4 The vector space ![]() $B_2(k(t))$ is generated over its subspace
$B_2(k(t))$ is generated over its subspace ![]() $B_2(k)$ by the following two types of elements:
$B_2(k)$ by the following two types of elements:
(1) symbols
 $\{{f(t)}/{g(t)}\}_2$, where
$\{{f(t)}/{g(t)}\}_2$, where  $f$ and
$f$ and  $g$ are irreducible monic polynomials of the same degree;
$g$ are irreducible monic polynomials of the same degree;(2) symbols
 $\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}} \}_2,$ where
$\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}} \}_2,$ where  $r_1$ and
$r_1$ and  $r_2$ are two elements in
$r_2$ are two elements in  $k_P^{\times }$ for some point
$k_P^{\times }$ for some point  $P$.
$P$.
Remark Though this corollary is formulated in a completely elementary way, the author was not able to derive it from the five-term relation without using algebraic ![]() $K$-theory. If
$K$-theory. If ![]() $k$ is algebraically closed this is known as the Rogers dilogarithm identity; see [Reference DupontDup01, Theorem 8.14].
$k$ is algebraically closed this is known as the Rogers dilogarithm identity; see [Reference DupontDup01, Theorem 8.14].
5. Coresidue map in the derived category
Our goal is to prove Lemma 3.3, claiming that the complex
is quasi-isomorphic to
For this we will construct a coresidue chain map from a complex, which is quasi-isomorphic to ![]() ${\mathcal {B}}_2(k_P,n-1)$, to
${\mathcal {B}}_2(k_P,n-1)$, to ![]() $gr_d^{\mathcal {F}}{\mathcal {B}}_2(k(t),n)$ with image in
$gr_d^{\mathcal {F}}{\mathcal {B}}_2(k(t),n)$ with image in ![]() $\mathcal {G}_1$. The main difficulty will be to prove the fact that this map is well-defined.
$\mathcal {G}_1$. The main difficulty will be to prove the fact that this map is well-defined.
5.1 Free resolution of the truncated polylogarithmic complex
To construct a free resolution of the polylogarithmic complex
recall the presentation of ![]() $B_2$,
$B_2$, ![]() $F^{\times }$ and
$F^{\times }$ and ![]() $B_2 \otimes _a F^{\times }$ by generators and relations:
$B_2 \otimes _a F^{\times }$ by generators and relations:
 \begin{equation} \begin{aligned} & 0 \longrightarrow R_1(F) \longrightarrow \mathbb{Q}[F]_1 \longrightarrow F^\times \longrightarrow 0,\\ & R_2(F) \longrightarrow \mathbb{Q}[F]_2 \longrightarrow B_2(F) \longrightarrow 0,\\ & \mathbb{Q}[F]_3 \otimes \Lambda^{n-3}F^\times \longrightarrow B_2(F)\otimes \Lambda^{n-2} F^\times \longrightarrow [B_2(F)\otimes \Lambda^{n-2} F^\times]_t \longrightarrow 0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & 0 \longrightarrow R_1(F) \longrightarrow \mathbb{Q}[F]_1 \longrightarrow F^\times \longrightarrow 0,\\ & R_2(F) \longrightarrow \mathbb{Q}[F]_2 \longrightarrow B_2(F) \longrightarrow 0,\\ & \mathbb{Q}[F]_3 \otimes \Lambda^{n-3}F^\times \longrightarrow B_2(F)\otimes \Lambda^{n-2} F^\times \longrightarrow [B_2(F)\otimes \Lambda^{n-2} F^\times]_t \longrightarrow 0. \end{aligned} \end{equation}
Using standard properties of wedge powers, one obtains the following resolution of ![]() $\Lambda ^n F^{\times }$:
$\Lambda ^n F^{\times }$:
One also obtains the following resolution of ![]() $[B_2(F)\otimes \Lambda ^{n-2} F^\times ]_t$:
$[B_2(F)\otimes \Lambda ^{n-2} F^\times ]_t$:
 \begin{equation} \begin{aligned} & \mathbb{Q}[F]_3 \otimes \Lambda^{n-3}\mathbb{Q}[F]_1\\ & \qquad\qquad \oplus \\ & \mathbb{Q}[F]_2 \otimes R_1(F) \otimes \Lambda^{n-3} \mathbb{Q}[F]_1\longrightarrow \mathbb{Q}[F]_2 \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \longrightarrow [B_2(F)\otimes \Lambda^{n-2} F^\times ]_t \longrightarrow 0\\ & \qquad\qquad \oplus\\ & R_2(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1.\end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \mathbb{Q}[F]_3 \otimes \Lambda^{n-3}\mathbb{Q}[F]_1\\ & \qquad\qquad \oplus \\ & \mathbb{Q}[F]_2 \otimes R_1(F) \otimes \Lambda^{n-3} \mathbb{Q}[F]_1\longrightarrow \mathbb{Q}[F]_2 \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \longrightarrow [B_2(F)\otimes \Lambda^{n-2} F^\times ]_t \longrightarrow 0\\ & \qquad\qquad \oplus\\ & R_2(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1.\end{aligned} \end{equation}
The map ![]() $\delta =\delta [0]\colon [B_2(F)\otimes \Lambda ^{n-2} F^\times ]_t\longrightarrow \Lambda ^{n} F^\times$ can be lifted to a map
$\delta =\delta [0]\colon [B_2(F)\otimes \Lambda ^{n-2} F^\times ]_t\longrightarrow \Lambda ^{n} F^\times$ can be lifted to a map ![]() $\delta [i]$ between the resolutions above. Clearly, we have to define
$\delta [i]$ between the resolutions above. Clearly, we have to define
by the formula
The map ![]() $\delta [2]$ can be defined in many different ways. We put
$\delta [2]$ can be defined in many different ways. We put ![]() $\delta [2]$ equal to zero on
$\delta [2]$ equal to zero on ![]() $\mathbb {Q}[F]_3 \otimes \Lambda ^{n-3}\mathbb {Q}[F]_1$. Next, define
$\mathbb {Q}[F]_3 \otimes \Lambda ^{n-3}\mathbb {Q}[F]_1$. Next, define ![]() $\delta [2]$ on
$\delta [2]$ on ![]() $\mathbb {Q}[F]_2 \otimes R_1(F) \otimes \Lambda ^{n-3} \mathbb {Q}[F]_1$ by the formula
$\mathbb {Q}[F]_2 \otimes R_1(F) \otimes \Lambda ^{n-3} \mathbb {Q}[F]_1$ by the formula
Finally, we need to define ![]() $\delta [2]$ on
$\delta [2]$ on ![]() $R_2(F) \otimes \Lambda ^{n-2} \mathbb {Q}[F]_1$. It is sufficient to define
$R_2(F) \otimes \Lambda ^{n-2} \mathbb {Q}[F]_1$. It is sufficient to define ![]() $\delta [2]$ on
$\delta [2]$ on ![]() $R_2(F)$.
$R_2(F)$.
For that recall the simplest proof of the five-term relation. The element ![]() $[x_1,x_2]_2\in R_2(F)$ is mapped to the element
$[x_1,x_2]_2\in R_2(F)$ is mapped to the element ![]() $\sum _{i=1}^5 [x_i]_2\in \mathbb {Q}[F]_2$, where the
$\sum _{i=1}^5 [x_i]_2\in \mathbb {Q}[F]_2$, where the ![]() $x_i\in F$ satisfy the following
$x_i\in F$ satisfy the following ![]() $5$-periodic recurrence:
$5$-periodic recurrence:
Then
 \[ \delta \bigg(\sum_{i=1}^5[x_{i}]_2\bigg)=\sum_{i=1}^5(1-x_{i})\wedge x_{i} \in \Lambda^2 F^{{\times}} . \]
\[ \delta \bigg(\sum_{i=1}^5[x_{i}]_2\bigg)=\sum_{i=1}^5(1-x_{i})\wedge x_{i} \in \Lambda^2 F^{{\times}} . \]
Since ![]() $(1-x_{i})\wedge x_{i}=x_{i-1}\wedge x_{i}-x_{i}\wedge x_{i+1}$, the sum vanishes telescopically. This suggests the following definition of the map
$(1-x_{i})\wedge x_{i}=x_{i-1}\wedge x_{i}-x_{i}\wedge x_{i+1}$, the sum vanishes telescopically. This suggests the following definition of the map ![]() $R_2(F) \stackrel {\delta [2]}{\longrightarrow } R_1(F)\otimes \mathbb {Q}[F]_1$:
$R_2(F) \stackrel {\delta [2]}{\longrightarrow } R_1(F)\otimes \mathbb {Q}[F]_1$:
 \[ \delta[2][x_1,x_2]_2={-}\sum_{i=1}^5 [x_{i-1},x_{i+1}]_1 \otimes [x_i]_1. \]
\[ \delta[2][x_1,x_2]_2={-}\sum_{i=1}^5 [x_{i-1},x_{i+1}]_1 \otimes [x_i]_1. \] Finally, denote by ![]() $\tilde {\mathcal {B}}_2(F,n)$ the cone of the map
$\tilde {\mathcal {B}}_2(F,n)$ the cone of the map ![]() $\delta [\bullet ]$. For the convenience of the reader, we list here the terms of the complex
$\delta [\bullet ]$. For the convenience of the reader, we list here the terms of the complex ![]() $\tilde {\mathcal {B}}_2(F,n)$ in each degree:
$\tilde {\mathcal {B}}_2(F,n)$ in each degree:
 \begin{equation} \begin{aligned} & { \rm Degree\ 1:}\quad \Lambda^n \mathbb{Q}[F]_1, \\ & { \rm Degree\ 2:}\quad \bigl ( R_1(F)\otimes \Lambda^{n-1} \mathbb{Q}[F]_1 \bigr)\oplus\bigl ( \mathbb{Q}[F]_2 \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr),\\ & { \rm Degree\ 3:}\quad \bigl ( \mathbb{S}^2 R_1(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr) \oplus \bigl (\mathbb{Q}[F]_3 \otimes \Lambda^{n-3}\mathbb{Q}[F]_1 \bigr )\\ & \hspace{4.8pc} \oplus \bigl ( \mathbb{Q}[F]_2 \otimes R_1(F) \otimes \Lambda^{n-3} \mathbb{Q}[F]_1 \bigr) \oplus \bigl(R_2(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr ). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & { \rm Degree\ 1:}\quad \Lambda^n \mathbb{Q}[F]_1, \\ & { \rm Degree\ 2:}\quad \bigl ( R_1(F)\otimes \Lambda^{n-1} \mathbb{Q}[F]_1 \bigr)\oplus\bigl ( \mathbb{Q}[F]_2 \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr),\\ & { \rm Degree\ 3:}\quad \bigl ( \mathbb{S}^2 R_1(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr) \oplus \bigl (\mathbb{Q}[F]_3 \otimes \Lambda^{n-3}\mathbb{Q}[F]_1 \bigr )\\ & \hspace{4.8pc} \oplus \bigl ( \mathbb{Q}[F]_2 \otimes R_1(F) \otimes \Lambda^{n-3} \mathbb{Q}[F]_1 \bigr) \oplus \bigl(R_2(F) \otimes \Lambda^{n-2} \mathbb{Q}[F]_1 \bigr ). \end{aligned} \end{equation}Denote by
the cone chain morphism. We have proven the following statement.
Lemma 5.1 The map ![]() $\pi$ induces an isomorphism on the cohomology groups in degrees 1 and 2.
$\pi$ induces an isomorphism on the cohomology groups in degrees 1 and 2.
5.2 Coresidue map
Let ![]() $P$ be a point of the degree
$P$ be a point of the degree ![]() $d$ in
$d$ in ![]() $\mathbb {A}^1_k$. Our goal is to define a coresidue map
$\mathbb {A}^1_k$. Our goal is to define a coresidue map ![]() $c_P$ in the derived category,
$c_P$ in the derived category,
with the property that the composition ![]() $\partial _P \circ c_P$ is a quasi-isomorphism. Because of Lemma 5.1, it is sufficient to construct a map from
$\partial _P \circ c_P$ is a quasi-isomorphism. Because of Lemma 5.1, it is sufficient to construct a map from ![]() $\tilde {\mathcal {B}}_2(k_P,n)$ to
$\tilde {\mathcal {B}}_2(k_P,n)$ to ![]() $gr_d^{\mathcal {F}}{\mathcal {B}}_2(k(t),n+1)$, which we will also denote by
$gr_d^{\mathcal {F}}{\mathcal {B}}_2(k(t),n+1)$, which we will also denote by ![]() $c_P$.
$c_P$.
The definition of ![]() $c_P$ is completely straightforward, but checking that it is a chain morphism is non-trivial. First, define
$c_P$ is completely straightforward, but checking that it is a chain morphism is non-trivial. First, define
by the formula
Next, define
by the formula
Here ![]() $\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1} \widetilde {r_2}}/{\widetilde {r_1 r_2}} \}_2 \in B_P \subset gr_d^{\mathcal {F}} B_2(k(t))$. Finally, define
$\beta _P([r_1,r_2]_1)=\{ {\widetilde {r_1} \widetilde {r_2}}/{\widetilde {r_1 r_2}} \}_2 \in B_P \subset gr_d^{\mathcal {F}} B_2(k(t))$. Finally, define
by the formula
To check that ![]() $c_P$ is a chain map it is enough to show that the composition
$c_P$ is a chain map it is enough to show that the composition ![]() $c_P[2]\circ \delta$ vanishes. Its domain
$c_P[2]\circ \delta$ vanishes. Its domain ![]() $\widetilde {{\mathcal {B}}}_2(k_P,n)[3]$ has four direct summands. On
$\widetilde {{\mathcal {B}}}_2(k_P,n)[3]$ has four direct summands. On ![]() $\mathbb {Q}[k_P]_3 \otimes \Lambda ^{n-3}\mathbb {Q}[k_P]_1$ the map vanishes by definition of
$\mathbb {Q}[k_P]_3 \otimes \Lambda ^{n-3}\mathbb {Q}[k_P]_1$ the map vanishes by definition of ![]() $\delta [2]$. We continue in the next sections.
$\delta [2]$. We continue in the next sections.
5.3 Vanishing of  $c_P[2]\circ \delta$ on
$c_P[2]\circ \delta$ on  $\mathbb {Q}[k_P]_2 \otimes R_1(k_P) \otimes \Lambda ^{n-3} \mathbb {Q}[k_P]_1$
$\mathbb {Q}[k_P]_2 \otimes R_1(k_P) \otimes \Lambda ^{n-3} \mathbb {Q}[k_P]_1$
Obviously, it is sufficient to consider the case ![]() $n=3$.
$n=3$.
Lemma 5.2 The following identity holds in ![]() $[B_2(F)\otimes \Lambda ^2 F^{\times }]_t$:
$[B_2(F)\otimes \Lambda ^2 F^{\times }]_t$:
Proof. Consider the five-term relation
and multiply it by ![]() $(a/b) \wedge (({1-a})/({1-b}))$. We get the expression above modulo terms
$(a/b) \wedge (({1-a})/({1-b}))$. We get the expression above modulo terms ![]() $\{x\}_2\otimes x \wedge y=\delta (\{x\}_3\otimes y)$.
$\{x\}_2\otimes x \wedge y=\delta (\{x\}_3\otimes y)$.
For ![]() $a=\widetilde {r_1}$ and
$a=\widetilde {r_1}$ and ![]() $b={\widetilde {r_2}\widetilde {r_3}}/{\widetilde {r_2r_3}}$ we use Lemma 5.2 and get that, in
$b={\widetilde {r_2}\widetilde {r_3}}/{\widetilde {r_2r_3}}$ we use Lemma 5.2 and get that, in ![]() $B_2(k(t))\otimes \Lambda ^2 k(t)^{\times }$,
$B_2(k(t))\otimes \Lambda ^2 k(t)^{\times }$,
Moreover, using arguments as in the proof of Lemma 2.3, the following equality holds in ![]() $gr_d^{\mathcal {F}} \big ( B_2(k(t))\otimes \Lambda ^2 k(t)^{\times } \big )$:
$gr_d^{\mathcal {F}} \big ( B_2(k(t))\otimes \Lambda ^2 k(t)^{\times } \big )$:
so
Equivalently,
5.4 Vanishing of  $c_P[2]\circ \delta$ on
$c_P[2]\circ \delta$ on  $\mathbb {S}^2 R_1(k_P) \otimes \Lambda ^{n-2} \mathbb {Q}[k_P]_1$
$\mathbb {S}^2 R_1(k_P) \otimes \Lambda ^{n-2} \mathbb {Q}[k_P]_1$
It is enough to check the vanishing of ![]() $c_P[2]\circ \delta$ on
$c_P[2]\circ \delta$ on ![]() $\mathbb {S}^2 R_1(k_P) \otimes \Lambda ^{n-2} \mathbb {Q}[k_P]_1$ for
$\mathbb {S}^2 R_1(k_P) \otimes \Lambda ^{n-2} \mathbb {Q}[k_P]_1$ for ![]() $n=2$. For this we use Lemma 5.3.
$n=2$. For this we use Lemma 5.3.
Lemma 5.3 Let ![]() $r_1, r_2, r_3 , r_4$ be some elements in
$r_1, r_2, r_3 , r_4$ be some elements in ![]() $k_P$. Then
$k_P$. Then
in ![]() $gr^{\mathcal {F}}_d [B_2(k(t))\otimes k(t)^{\times }]_t$.
$gr^{\mathcal {F}}_d [B_2(k(t))\otimes k(t)^{\times }]_t$.
This is probably the strangest part of the proof. We will prove Lemma 5.3 after Lemma 5.4.
Lemma 5.4 Let ![]() $A$ be an abelian group, and
$A$ be an abelian group, and ![]() $I<\mathbb {Q}[A]$ be the augmentation ideal. Then the elements of the form
$I<\mathbb {Q}[A]$ be the augmentation ideal. Then the elements of the form ![]() $([a_1]+[a_2]-[a_3]-[a_4])^2$ with
$([a_1]+[a_2]-[a_3]-[a_4])^2$ with ![]() $a_1 a_2=a_3 a_4 \in A$ generate
$a_1 a_2=a_3 a_4 \in A$ generate ![]() $\mathbb {S}^2 I^2$.
$\mathbb {S}^2 I^2$.
Proof. Obviously, elements of the form
generate ![]() $\mathbb {S}^2 I^2$. The statement of the lemma follows from the following identity, which can be checked by direct computation:
$\mathbb {S}^2 I^2$. The statement of the lemma follows from the following identity, which can be checked by direct computation:
 \begin{align} &-4([a]+[b]-[ab]-[1])\cdot([c]+[d]-[cd]-[1])\nonumber\\ &\quad+([ab]+[cd]-[bd]-[ac])^2+([ab]+[cd]-[ad]-[bc])^2-([bd]+[ac]-[ad]-[bc])^2\nonumber\\ &\quad-([a]+[bd]-[d]-[ab])^2-([ad]+[b]-[ab]-[d])^2+ ([a]+[bd]-[ad]-[b])^2\nonumber\\ &\quad-([a]+[bc]-[c]-[ab])^2 - ([ac]+[b]-[ab]-[c])^2 + ([a]+[bc]-[ac]-[b])^2\nonumber\\ &\quad-([c]+[ad]-[a]-[cd])^2-([ac]+[d]-[cd]-[a])^2+([c]+[ad]-[ac]-[d]) ^2\nonumber\\ &\quad-([c]+[bd]-[b]-[cd])^2- ([bc]+[d]-[cd]-[b])^2+ ([c]+[bd]-[bc]-[d])^2\nonumber\\ &\quad+ 2([a]+[b]-[ab]-[1])^2 + 2 ([c]+[d] -[cd]-[1])^2=0. \end{align}
\begin{align} &-4([a]+[b]-[ab]-[1])\cdot([c]+[d]-[cd]-[1])\nonumber\\ &\quad+([ab]+[cd]-[bd]-[ac])^2+([ab]+[cd]-[ad]-[bc])^2-([bd]+[ac]-[ad]-[bc])^2\nonumber\\ &\quad-([a]+[bd]-[d]-[ab])^2-([ad]+[b]-[ab]-[d])^2+ ([a]+[bd]-[ad]-[b])^2\nonumber\\ &\quad-([a]+[bc]-[c]-[ab])^2 - ([ac]+[b]-[ab]-[c])^2 + ([a]+[bc]-[ac]-[b])^2\nonumber\\ &\quad-([c]+[ad]-[a]-[cd])^2-([ac]+[d]-[cd]-[a])^2+([c]+[ad]-[ac]-[d]) ^2\nonumber\\ &\quad-([c]+[bd]-[b]-[cd])^2- ([bc]+[d]-[cd]-[b])^2+ ([c]+[bd]-[bc]-[d])^2\nonumber\\ &\quad+ 2([a]+[b]-[ab]-[1])^2 + 2 ([c]+[d] -[cd]-[1])^2=0. \end{align}Proof of Lemma 5.3 We will apply Lemma 5.4 to the group ![]() $A=k_P^{\times }$. There is a map
$A=k_P^{\times }$. There is a map ![]() $\varphi _1$ from the group ring
$\varphi _1$ from the group ring ![]() $\mathbb {Q}[k_P^{\times }]$ to
$\mathbb {Q}[k_P^{\times }]$ to ![]() $D_{ < d}$, sending
$D_{ < d}$, sending ![]() $[r]$ to
$[r]$ to ![]() $\tilde {r}$. The image of
$\tilde {r}$. The image of ![]() $I^2$ under this map is contained in
$I^2$ under this map is contained in ![]() $B_P$, because the sequence
$B_P$, because the sequence
is exact. Furthermore,
Denote the composition of the map ![]() $\varphi _1\colon I^2 \longrightarrow B_P$ with the embedding
$\varphi _1\colon I^2 \longrightarrow B_P$ with the embedding ![]() $B_P \hookrightarrow gr_d^{\mathcal {F}} B_2(t)$ by
$B_P \hookrightarrow gr_d^{\mathcal {F}} B_2(t)$ by ![]() $\varphi _2$:
$\varphi _2$:
This map can be used to construct a map
sending ![]() $\lambda _1\cdot \lambda _2 \in \mathbb {S}^2I^2$ to
$\lambda _1\cdot \lambda _2 \in \mathbb {S}^2I^2$ to ![]() $\varphi _2(\lambda _1) \otimes \varphi _1(\lambda _2)+ \varphi _2(\lambda _2) \otimes \varphi _1(\lambda _1)$.
$\varphi _2(\lambda _1) \otimes \varphi _1(\lambda _2)+ \varphi _2(\lambda _2) \otimes \varphi _1(\lambda _1)$.
To conclude the proof of Lemma 5.3, we need to show that the map ![]() $(\varphi _1\cdot \varphi _2)$ vanishes on
$(\varphi _1\cdot \varphi _2)$ vanishes on ![]() $\mathbb {S}^2I^2$, because the expression
$\mathbb {S}^2I^2$, because the expression
is equal to ![]() $(\varphi _1\cdot \varphi _2)(([r_1]-[1])([r_2]-[1]) \cdot ([r_3]-[1])([r_4]-[1]) )$.
$(\varphi _1\cdot \varphi _2)(([r_1]-[1])([r_2]-[1]) \cdot ([r_3]-[1])([r_4]-[1]) )$.
It follows from Lemma 5.4 that it is sufficient to check the vanishing of the map ![]() $(\varphi _1\cdot \varphi _2)$ on elements
$(\varphi _1\cdot \varphi _2)$ on elements
where ![]() $r_1r_2=r_3r_4$ in
$r_1r_2=r_3r_4$ in ![]() $k_P^{\times }$. Notice that in this case
$k_P^{\times }$. Notice that in this case
 \begin{equation} \begin{aligned} & \varphi_1([r_1]+[r_2]-[r_3]-[r_4])=\frac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_3}\widetilde{r_4}},\\ & \varphi_2([r_1]+[r_2]-[r_3]-[r_4])=\bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1r_2}}\bigg\}_2-\bigg\{ \dfrac{\widetilde{r_3}\widetilde{r_4}}{\widetilde{r_3r_4 }} \bigg\}_2. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \varphi_1([r_1]+[r_2]-[r_3]-[r_4])=\frac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_3}\widetilde{r_4}},\\ & \varphi_2([r_1]+[r_2]-[r_3]-[r_4])=\bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1r_2}}\bigg\}_2-\bigg\{ \dfrac{\widetilde{r_3}\widetilde{r_4}}{\widetilde{r_3r_4 }} \bigg\}_2. \end{aligned} \end{equation}
The last expression is equal to ![]() $\{{\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_3} \widetilde {r_4}}\}_2$. To see that, it is enough to check that the coproduct
$\{{\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_3} \widetilde {r_4}}\}_2$. To see that, it is enough to check that the coproduct
vanishes in ![]() $gr_d^{\mathcal {F}}[\Lambda ^2 k(t)^{\times }]$, which is obvious.
$gr_d^{\mathcal {F}}[\Lambda ^2 k(t)^{\times }]$, which is obvious.
From this we get that
which finishes the proof of Lemma 5.3.
5.5 Vanishing of  $c_P[2]\circ \delta$ on
$c_P[2]\circ \delta$ on  $R_2(F) \otimes \Lambda ^{n-2} \mathbb {Q}[F]_1$
$R_2(F) \otimes \Lambda ^{n-2} \mathbb {Q}[F]_1$
Clearly, it is enough to consider the case ![]() $n=2$. Our goal is to show the following lemma.
$n=2$. Our goal is to show the following lemma.
Lemma 5.5 For any ![]() $r_1, r_2 \in k_P^{\times }$ define
$r_1, r_2 \in k_P^{\times }$ define ![]() $r_{i+1}=({1-r_i})/{r_{i-1}}$,
$r_{i+1}=({1-r_i})/{r_{i-1}}$, ![]() $i=3,4,5$. Then the expression
$i=3,4,5$. Then the expression
 \begin{align} &(\{\widetilde{r_1}\}_2+\{\widetilde{r_2}\}_2+\{\widetilde{r_3}\}_2+\{\widetilde{r_4}\}_2+\{\widetilde{r_5}\}_2)\otimes f_P+\bigg\{ \frac{\widetilde{r_1} \widetilde{r_3}}{1-\widetilde{r_2}} \bigg\}_2\otimes \widetilde{r_2}+\bigg\{ \frac{\widetilde{r_2} \widetilde{r_4}}{1-\widetilde{r_3}} \bigg\}_2\nonumber\\ &\quad \otimes \widetilde{r_3}+\bigg\{ \frac{\widetilde{r_3} \widetilde{r_5}}{1-\widetilde{r_4}} \bigg\}_2\otimes \widetilde{r_4}+\bigg\{ \frac{\widetilde{r_4} \widetilde{r_1}}{1-\widetilde{r_5}} \bigg\}_2\otimes \widetilde{r_5}+\bigg\{ \frac{\widetilde{r_5} \widetilde{r_2}}{1-\widetilde{r_1}} \bigg\}_2\otimes \widetilde{r_1} \end{align}
\begin{align} &(\{\widetilde{r_1}\}_2+\{\widetilde{r_2}\}_2+\{\widetilde{r_3}\}_2+\{\widetilde{r_4}\}_2+\{\widetilde{r_5}\}_2)\otimes f_P+\bigg\{ \frac{\widetilde{r_1} \widetilde{r_3}}{1-\widetilde{r_2}} \bigg\}_2\otimes \widetilde{r_2}+\bigg\{ \frac{\widetilde{r_2} \widetilde{r_4}}{1-\widetilde{r_3}} \bigg\}_2\nonumber\\ &\quad \otimes \widetilde{r_3}+\bigg\{ \frac{\widetilde{r_3} \widetilde{r_5}}{1-\widetilde{r_4}} \bigg\}_2\otimes \widetilde{r_4}+\bigg\{ \frac{\widetilde{r_4} \widetilde{r_1}}{1-\widetilde{r_5}} \bigg\}_2\otimes \widetilde{r_5}+\bigg\{ \frac{\widetilde{r_5} \widetilde{r_2}}{1-\widetilde{r_1}} \bigg\}_2\otimes \widetilde{r_1} \end{align}
vanishes in ![]() $gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$.
$gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$.
This will finish showing how ![]() $c_P[2]\circ \delta$ vanishes, because
$c_P[2]\circ \delta$ vanishes, because
We start with a lemma whose proof is inspired by the Gauss lemma, used in the classical proof of quadratic reciprocity.
Lemma 5.6 For ![]() $1\leq i\leq 5$ there exist polynomials
$1\leq i\leq 5$ there exist polynomials ![]() $g_i(t), h_i(t)$ of degrees less than
$g_i(t), h_i(t)$ of degrees less than ![]() $d$, such that
$d$, such that ![]() $r_i={\overline {h_i}}/{\overline {g_i}}$ in
$r_i={\overline {h_i}}/{\overline {g_i}}$ in ![]() $k_P^{\times }$ and the sequence
$k_P^{\times }$ and the sequence ![]() $\lambda _i={g_i}/{h_i}$ satisfies the recurrence
$\lambda _i={g_i}/{h_i}$ satisfies the recurrence
Proof. We will suppose that ![]() $d$ is odd: the even case is similar. For the residue
$d$ is odd: the even case is similar. For the residue ![]() $r_1\in k_P$ there exist polynomials
$r_1\in k_P$ there exist polynomials ![]() $g_1(t), h_1(t)\in k(t)$ of degrees less or equal to
$g_1(t), h_1(t)\in k(t)$ of degrees less or equal to ![]() $\lfloor {d}/{2}\rfloor$, such that the residue of
$\lfloor {d}/{2}\rfloor$, such that the residue of ![]() ${g_1}/{h_1}$ is equal to
${g_1}/{h_1}$ is equal to ![]() $r_1$. Indeed, consider
$r_1$. Indeed, consider ![]() $k_P$ as a vector space over
$k_P$ as a vector space over ![]() $k$ with basis
$k$ with basis ![]() $1, \bar {t}, \ldots , \overline {t^{d-1}}$ and denote by
$1, \bar {t}, \ldots , \overline {t^{d-1}}$ and denote by ![]() $V$ its subspace, spanned by
$V$ its subspace, spanned by ![]() $1, \bar {t}, \ldots , \overline {t^{\lfloor d/2 \rfloor }}$. Multiplication by
$1, \bar {t}, \ldots , \overline {t^{\lfloor d/2 \rfloor }}$. Multiplication by ![]() $r_1$ is a linear automorphism of
$r_1$ is a linear automorphism of ![]() $k_P$ and
$k_P$ and ![]() $\dim (V)>{\dim (k_P)}/{2}$, so there exists a vector
$\dim (V)>{\dim (k_P)}/{2}$, so there exists a vector ![]() $g_1 \in V$ such that
$g_1 \in V$ such that ![]() $r_1 g_1=f_1 \in V$.
$r_1 g_1=f_1 \in V$.
Similarly, we can find ![]() $g_2(t), h_2(t)\in k(t)$ of degrees less or equal to
$g_2(t), h_2(t)\in k(t)$ of degrees less or equal to ![]() $\lfloor {d}/{2} \rfloor$, such that the residue of
$\lfloor {d}/{2} \rfloor$, such that the residue of ![]() ${g_2}/{h_2}$ is equal to
${g_2}/{h_2}$ is equal to ![]() $r_2$. There exists a unique sequence
$r_2$. There exists a unique sequence ![]() $\lambda _i$, such that
$\lambda _i$, such that ![]() $\lambda _1={g_1}/{h_1}$ and
$\lambda _1={g_1}/{h_1}$ and ![]() $\lambda _2={g_2}/{h_2}$, which satisfies the required recurrence. Then
$\lambda _2={g_2}/{h_2}$, which satisfies the required recurrence. Then
and we define ![]() $g_3=(h_2-g_2)h_1$ and
$g_3=(h_2-g_2)h_1$ and ![]() $h_3=h_2g_1$. Similarly,
$h_3=h_2g_1$. Similarly,
and
Obviously, ![]() $\deg (g_i), \deg (h_i)$ are less than
$\deg (g_i), \deg (h_i)$ are less than ![]() $d$ for
$d$ for ![]() $1\leq i\leq 5$ as required.
$1\leq i\leq 5$ as required.
To simplify the notation a little bit we will omit the ![]() $\tilde {\ }$ and
$\tilde {\ }$ and ![]() $\bar {\ }$ symbols till the end of § 5.5. First we want to rewrite
$\bar {\ }$ symbols till the end of § 5.5. First we want to rewrite ![]() $\bigl (\sum _{i=1}^{5}\{r_i\}_2\bigr )\otimes f_P$ as an element of
$\bigl (\sum _{i=1}^{5}\{r_i\}_2\bigr )\otimes f_P$ as an element of ![]() $[B_P \otimes D_{ < d}]_t$.
$[B_P \otimes D_{ < d}]_t$.
Lemma 5.7 Consider ![]() $r_i\in k_P^{\times }$,
$r_i\in k_P^{\times }$, ![]() $1\leq i\leq 5$, as in Lemma 5.5 and
$1\leq i\leq 5$, as in Lemma 5.5 and ![]() $\lambda _i\in k(t)$,
$\lambda _i\in k(t)$, ![]() $1\leq i\leq 5$, as in Lemma 5.6. The following equality holds in
$1\leq i\leq 5$, as in Lemma 5.6. The following equality holds in ![]() $gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$:
$gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$:
Proof. Thanks to the five-term relation, for every ![]() $1\leq i \leq 5$,
$1\leq i \leq 5$,
We will simplify each of the three terms on the right-hand side of (21) in ![]() $gr_d^{\mathcal {F}}[ B_2(k(t)) \otimes k(t)^{\times }]_t$. Suppose that
$gr_d^{\mathcal {F}}[ B_2(k(t)) \otimes k(t)^{\times }]_t$. Suppose that
Since the degrees of ![]() $g_i$ and
$g_i$ and ![]() $h_i$ are less than
$h_i$ are less than ![]() $d$, the degree of
$d$, the degree of ![]() $q_i$ is also less than
$q_i$ is also less than ![]() $d$. Then
$d$. Then
 \begin{align} -\bigg\{\frac{\lambda_i}{r_i} \bigg\}_2 \otimes f_P&={-}\bigg\{\frac{g_i}{h_ir_i} \bigg\}_2 \otimes f_P=\bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes f_P\nonumber\\ & = \bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes \bigg(\frac{h_ir_i}{g_i}-1 \bigg)-\bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes \frac{q_i}{g_i}={-}\bigg\{\frac{r_i}{\lambda_i} \bigg\}_2 \otimes \frac{q_i}{g_i}. \end{align}
\begin{align} -\bigg\{\frac{\lambda_i}{r_i} \bigg\}_2 \otimes f_P&={-}\bigg\{\frac{g_i}{h_ir_i} \bigg\}_2 \otimes f_P=\bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes f_P\nonumber\\ & = \bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes \bigg(\frac{h_ir_i}{g_i}-1 \bigg)-\bigg\{\frac{h_ir_i}{g_i} \bigg\}_2 \otimes \frac{q_i}{g_i}={-}\bigg\{\frac{r_i}{\lambda_i} \bigg\}_2 \otimes \frac{q_i}{g_i}. \end{align}
We used here the following equalities in ![]() $[B_2(F)\otimes F^{\times }]_t$:
$[B_2(F)\otimes F^{\times }]_t$:
Similarly,
and
So, we get the following:
From the five-term relation, we see that
 \begin{align} &-\bigg\{\frac{\lambda_i}{r_i} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}-\bigg\{\frac{1-\lambda_i^{{-}1}}{1-r_i^{{-}1}} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}-\bigg\{\frac{1-r_i}{1-\lambda_i} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}\nonumber\\ &\quad =(\{r_i\} -\{\lambda_i\})\otimes \frac{q_i}{(r_i-1)g_i}=0. \end{align}
\begin{align} &-\bigg\{\frac{\lambda_i}{r_i} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}-\bigg\{\frac{1-\lambda_i^{{-}1}}{1-r_i^{{-}1}} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}-\bigg\{\frac{1-r_i}{1-\lambda_i} \bigg\}_2 \otimes \frac{q_i}{(r_i-1)g_i}\nonumber\\ &\quad =(\{r_i\} -\{\lambda_i\})\otimes \frac{q_i}{(r_i-1)g_i}=0. \end{align}After adding it to the previous equality, we get that
which finishes the proof of the statement of Lemma 5.7.
Proof (End of Lemma 5.5) Observe that the following relation holds in ![]() $B_P\subset gr_d^{\mathcal {F}} B_2(k(t))$:
$B_P\subset gr_d^{\mathcal {F}} B_2(k(t))$:
Indeed, the map ![]() $\delta$ applied to this expression lands in
$\delta$ applied to this expression lands in ![]() $\mathcal {F}_{d}\Lambda ^2 k(t)^{\times }$ and vanishes there modulo terms of lower degree.
$\mathcal {F}_{d}\Lambda ^2 k(t)^{\times }$ and vanishes there modulo terms of lower degree.
Our goal is to prove that
 \[ \sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P +\bigg\{\frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggr) \]
\[ \sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P +\bigg\{\frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggr) \]
vanishes in ![]() $gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$. Using the five-term relation for
$gr_d^{\mathcal {F}} [B_2(k(t))\otimes k(t)^{\times }]_t$. Using the five-term relation for ![]() $\lambda _i$ and the lemma above, we get that
$\lambda _i$ and the lemma above, we get that
 \begin{align} &\sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggl)\nonumber\\ &\quad = \sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P -\{\lambda_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggr)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(-\bigg\{\frac{r_i}{\lambda_i} \bigg\}_2 \otimes (r_i-1)+\bigg\{\frac{r_i-1}{\lambda_i-1} \bigg\}_2 \otimes \lambda_i +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \nonumber\\ &\qquad \otimes \frac{r_i}{\lambda_i} +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes \lambda_i \bigg). \end{align}
\begin{align} &\sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggl)\nonumber\\ &\quad = \sum_{i=1}^5 \biggl(\{r_i\}_2\otimes f_P -\{\lambda_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \biggr)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(-\bigg\{\frac{r_i}{\lambda_i} \bigg\}_2 \otimes (r_i-1)+\bigg\{\frac{r_i-1}{\lambda_i-1} \bigg\}_2 \otimes \lambda_i +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \nonumber\\ &\qquad \otimes \frac{r_i}{\lambda_i} +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes \lambda_i \bigg). \end{align}By Lemma 5.3,
We obtain
 \begin{align} &\sum_{i=1}^5 \bigg(\{r_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \bigg)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(\bigg\{\frac{r_i-1}{\lambda_i-1} \bigg\}_2 \otimes \lambda_i -\bigg\{ \frac{r_i}{\lambda_i}\bigg\}_2 \otimes (r_{i-1}r_{i+1})+\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes \lambda_i \bigg)\nonumber\\ &\quad= \sum_{i=1}^5 \bigg(\bigg\{\frac{r_{i-1}}{\lambda_{i-1}} \bigg\}_2 \otimes \lambda_i+\bigg\{\frac{r_{i+1}}{\lambda_{i+1}} \bigg\}_2 \otimes \lambda_i-\bigg\{ \frac{r_i}{\lambda_i}\bigg\}_2 \otimes (r_{i-1}r_{i+1}) \bigg)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(\bigg\{\frac{r_{i-1}}{\lambda_{i-1}} \bigg\}_2 \otimes \frac{\lambda_i}{r_i} \bigg) + \sum_{i=1}^5 \biggl(\bigg\{\frac{r_{i+1}}{\lambda_{i+1}} \bigg\}_2 \otimes \frac{\lambda_i}{r_i} \biggr). \end{align}
\begin{align} &\sum_{i=1}^5 \bigg(\{r_i\}_2\otimes f_P +\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes r_i \bigg)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(\bigg\{\frac{r_i-1}{\lambda_i-1} \bigg\}_2 \otimes \lambda_i -\bigg\{ \frac{r_i}{\lambda_i}\bigg\}_2 \otimes (r_{i-1}r_{i+1})+\bigg\{ \frac{r_{i-1}r_{i+1}}{1-r_i}\bigg\}_2 \otimes \lambda_i \bigg)\nonumber\\ &\quad= \sum_{i=1}^5 \bigg(\bigg\{\frac{r_{i-1}}{\lambda_{i-1}} \bigg\}_2 \otimes \lambda_i+\bigg\{\frac{r_{i+1}}{\lambda_{i+1}} \bigg\}_2 \otimes \lambda_i-\bigg\{ \frac{r_i}{\lambda_i}\bigg\}_2 \otimes (r_{i-1}r_{i+1}) \bigg)\nonumber\\ &\quad = \sum_{i=1}^5 \bigg(\bigg\{\frac{r_{i-1}}{\lambda_{i-1}} \bigg\}_2 \otimes \frac{\lambda_i}{r_i} \bigg) + \sum_{i=1}^5 \biggl(\bigg\{\frac{r_{i+1}}{\lambda_{i+1}} \bigg\}_2 \otimes \frac{\lambda_i}{r_i} \biggr). \end{align}The last expression vanishes, because by Lemma 5.3,
6. Proof of Lemma 3.3
For this we need to show that the chain map

is a quasi-isomorphism. That the chain map is a quasi-isomorphism when restricted to the second cohomology group follows from Theorem 2.1. Denote by ![]() $K$ the kernel of the map
$K$ the kernel of the map
We must show that the induced map on the first cohomology group which is induced by the chain map ![]() $\oplus \partial _P$ is an isomorphism:
$\oplus \partial _P$ is an isomorphism:
Recall that we defined the coresidue map ![]() $\sum c_P$ going in the opposite direction from the chain map
$\sum c_P$ going in the opposite direction from the chain map ![]() $\oplus \partial _P$. Since
$\oplus \partial _P$. Since ![]() $\partial _P \circ c_P$ is the identity for
$\partial _P \circ c_P$ is the identity for ![]() $P=Q$ and vanishes otherwise,
$P=Q$ and vanishes otherwise, ![]() $\oplus \partial _P$ induces a surjective map on cohomology. Let us prove that it is also injective.
$\oplus \partial _P$ induces a surjective map on cohomology. Let us prove that it is also injective.
Lemma 6.1 Vector space ![]() $gr_1^{\mathcal {G}} gr_d^{\mathcal {F}}[ B_2(k(t)) \otimes \Lambda ^{n-2} k(t)^{\times }]_t$ is generated by elements
$gr_1^{\mathcal {G}} gr_d^{\mathcal {F}}[ B_2(k(t)) \otimes \Lambda ^{n-2} k(t)^{\times }]_t$ is generated by elements
 \begin{equation} \begin{aligned} & (1)\quad \beta_{P}([r_1,r_2]_1)\otimes g_{3} \wedge \cdots \wedge g_n,\\ & (2)\quad \big\{ \tilde{r} \big\}_2\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & (1)\quad \beta_{P}([r_1,r_2]_1)\otimes g_{3} \wedge \cdots \wedge g_n,\\ & (2)\quad \big\{ \tilde{r} \big\}_2\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
where ![]() $r, r_1, r_2 \in k_P$ and
$r, r_1, r_2 \in k_P$ and ![]() $\deg (g_i) < d$.
$\deg (g_i) < d$.
Proof. From Corollary 4.4 it follows that the space
is generated by elements of the following three types:
 \begin{equation} \begin{aligned} & (a)\quad \beta_{P}([r_1,r_2]_1)\otimes g_{3} \wedge \cdots \wedge g_n,\\ & (b)\quad \bigg\{ \frac{g_1}{g_2} \bigg\}_2\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \\ & (c)\quad \beta_{g_1}([r_1,r_2]_1)\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & (a)\quad \beta_{P}([r_1,r_2]_1)\otimes g_{3} \wedge \cdots \wedge g_n,\\ & (b)\quad \bigg\{ \frac{g_1}{g_2} \bigg\}_2\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \\ & (c)\quad \beta_{g_1}([r_1,r_2]_1)\otimes f_P \wedge g_{4} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
where ![]() $g_1$ and
$g_1$ and ![]() $g_2$ are both irreducible polynomials of the same degree less than
$g_2$ are both irreducible polynomials of the same degree less than ![]() $d$. It is sufficient to consider the case
$d$. It is sufficient to consider the case ![]() $n=3$. Our goal is to express elements of type
$n=3$. Our goal is to express elements of type ![]() $(b)$ and
$(b)$ and ![]() $(c)$ via elements of type
$(c)$ via elements of type ![]() $(1)$ and
$(1)$ and ![]() $(2)$. We will show that this is true for elements of type
$(2)$. We will show that this is true for elements of type ![]() $(b)$; type
$(b)$; type ![]() $(c)$ is similar. Let
$(c)$ is similar. Let ![]() $r$ be the residue of
$r$ be the residue of ![]() ${g_1}/{g_2}$ modulo
${g_1}/{g_2}$ modulo ![]() $f_P$. By the five-term relation
$f_P$. By the five-term relation
the expression
lies in ![]() $B_P$, because
$B_P$, because ![]() $\delta$ sends it to
$\delta$ sends it to ![]() $D_{ < d}\otimes f_P$.
$D_{ < d}\otimes f_P$.
Finally, notice that for every ![]() $r_1, r_2 \in k_P$, such that
$r_1, r_2 \in k_P$, such that ![]() $r_1 r_2=q f_P+\overline {r_1r_2}$,
$r_1 r_2=q f_P+\overline {r_1r_2}$,
because ![]() $\{ {r_1 r_2}/{\overline {r_1r_2}} \}_2\otimes ( 1- {r_1 r_2}/{\overline {r_1r_2}} )=0$. So,
$\{ {r_1 r_2}/{\overline {r_1r_2}} \}_2\otimes ( 1- {r_1 r_2}/{\overline {r_1r_2}} )=0$. So,
is a linear combination of elements of type ![]() $(1)$.
$(1)$.
End of the proof of Lemma 3.3 Let ![]() $x \in gr_1^\mathcal {G}gr_d^{\mathcal {F}} [ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }]_t$ be an element in the kernel of
$x \in gr_1^\mathcal {G}gr_d^{\mathcal {F}} [ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }]_t$ be an element in the kernel of ![]() $\delta$ with vanishing residues
$\delta$ with vanishing residues ![]() $\partial _P$ at all points of degree
$\partial _P$ at all points of degree ![]() $d$. Then
$d$. Then ![]() $x$ is lying in the subspace generated by elements of type
$x$ is lying in the subspace generated by elements of type ![]() $(1)$ in the notation of Lemma 6.1. Indeed, the map
$(1)$ in the notation of Lemma 6.1. Indeed, the map ![]() $id-\sum c_P \partial _P$ is well-defined and vanishes on elements of type (2). On the other hand,
$id-\sum c_P \partial _P$ is well-defined and vanishes on elements of type (2). On the other hand, ![]() $(id-\sum c_P \partial _P)x=x$. It remains to notice that map
$(id-\sum c_P \partial _P)x=x$. It remains to notice that map ![]() $\delta$ is injective on the space of elements of type
$\delta$ is injective on the space of elements of type ![]() $(1)$, which follows from the exact sequence
$(1)$, which follows from the exact sequence
 \begin{align*} \mathop{\bigoplus} \limits_{\deg(P)=d} \mathbb{S}^2 B_P \otimes \Lambda^{d-3} D_{{<}d} &\longrightarrow \mathop{\bigoplus} \limits_{\deg(P)=d} B_P \otimes \Lambda^{d-2} D_{{<}d} \\ &\longrightarrow \mathop{\bigoplus} \limits_{\deg(P)=d} f_P \otimes \Lambda^{d-1} D_{{<}d} \longrightarrow \Lambda^{d-1} F_P^{{\times}}\longrightarrow 0 \end{align*}
\begin{align*} \mathop{\bigoplus} \limits_{\deg(P)=d} \mathbb{S}^2 B_P \otimes \Lambda^{d-3} D_{{<}d} &\longrightarrow \mathop{\bigoplus} \limits_{\deg(P)=d} B_P \otimes \Lambda^{d-2} D_{{<}d} \\ &\longrightarrow \mathop{\bigoplus} \limits_{\deg(P)=d} f_P \otimes \Lambda^{d-1} D_{{<}d} \longrightarrow \Lambda^{d-1} F_P^{{\times}}\longrightarrow 0 \end{align*}and Lemma 5.3.
7. Proof of Lemma 3.4
Here we prove Lemma 3.4, claiming that for ![]() $s>1$ the complex
$s>1$ the complex
is exact. Recall that the space ![]() $gr_s^\mathcal {G}gr_d^{\mathcal {F}} \Lambda ^n k(t)^{\times }$ coincides with
$gr_s^\mathcal {G}gr_d^{\mathcal {F}} \Lambda ^n k(t)^{\times }$ coincides with ![]() $\Lambda ^s D_d \otimes \Lambda ^{n-s} D_{ < d}$. Let
$\Lambda ^s D_d \otimes \Lambda ^{n-s} D_{ < d}$. Let ![]() $h$ be a map in the opposite direction
$h$ be a map in the opposite direction
sending
to
Here we suppose that the ![]() $f_i$ are monic, irreducible, distinct polynomials of degree
$f_i$ are monic, irreducible, distinct polynomials of degree ![]() $d$ and the degrees of
$d$ and the degrees of ![]() $g_i$ are less than
$g_i$ are less than ![]() $d$.
$d$.
Lemma 7.1 Map ![]() $h$ is well-defined.
$h$ is well-defined.
Proof. It is sufficient to check that
vanishes in ![]() $gr_3^\mathcal {G}gr_d^{\mathcal {F}}\big ( B_2(k(t))\otimes _a k(t)^{\times }\big )$. From the five-term relation it follows that
$gr_3^\mathcal {G}gr_d^{\mathcal {F}}\big ( B_2(k(t))\otimes _a k(t)^{\times }\big )$. From the five-term relation it follows that
After multiplication by
we get the following equality in ![]() $B_2(k(t))\otimes _a k(t)^{\times }$:
$B_2(k(t))\otimes _a k(t)^{\times }$:
 \begin{align} & \bigg\{\frac{f_1}{f_2} \bigg\}_2\otimes f_3 +\bigg\{\frac{f_3}{f_2} \bigg\}_2\otimes f_1\nonumber\\ &\quad ={-}\bigg\{\frac{f_1}{f_2} \bigg\}_2\otimes \frac{f_1-f_2}{(f_3-f_2)f_1} + \bigg\{\frac{f_3}{f_2} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{f_3-f_2}\nonumber\\ &\qquad -\bigg\{\frac{f_3}{f_1} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{(f_3-f_2)f_1}- \bigg\{\frac{1-f_1/f_2}{1-f_3/f_2} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{(f_3-f_2)f_1}. \end{align}
\begin{align} & \bigg\{\frac{f_1}{f_2} \bigg\}_2\otimes f_3 +\bigg\{\frac{f_3}{f_2} \bigg\}_2\otimes f_1\nonumber\\ &\quad ={-}\bigg\{\frac{f_1}{f_2} \bigg\}_2\otimes \frac{f_1-f_2}{(f_3-f_2)f_1} + \bigg\{\frac{f_3}{f_2} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{f_3-f_2}\nonumber\\ &\qquad -\bigg\{\frac{f_3}{f_1} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{(f_3-f_2)f_1}- \bigg\{\frac{1-f_1/f_2}{1-f_3/f_2} \bigg\}_2\otimes \frac{(f_1-f_2)f_3}{(f_3-f_2)f_1}. \end{align}
All four expressions on the right-hand side of this equality lie in ![]() $\mathcal {G}_{2}gr_d^{\mathcal {F}}\big [ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }\big ]_t$.
$\mathcal {G}_{2}gr_d^{\mathcal {F}}\big [ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }\big ]_t$.
Obviously, ![]() $\delta \circ h=id$, so to finish Lemma 3.4 it is sufficient to show that
$\delta \circ h=id$, so to finish Lemma 3.4 it is sufficient to show that ![]() $h$ is surjective. From Corollary 4.4 it follows that the space
$h$ is surjective. From Corollary 4.4 it follows that the space
is generated by elements of the following three types:
 \begin{equation} \begin{aligned} & (1)\quad \beta_{f_1}([r_1,r_2]_1)\otimes f_2 \wedge\cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n,\\ & (2)\quad \bigg\{ \frac{f_1}{f_2} \bigg\}_2\otimes f_3 \wedge\cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n, \\ & (3)\quad B \otimes f_1 \wedge f_2 \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & (1)\quad \beta_{f_1}([r_1,r_2]_1)\otimes f_2 \wedge\cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n,\\ & (2)\quad \bigg\{ \frac{f_1}{f_2} \bigg\}_2\otimes f_3 \wedge\cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n, \\ & (3)\quad B \otimes f_1 \wedge f_2 \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n, \end{aligned} \end{equation}
where ![]() $f_1, \ldots , f_s$ are monic, distinct, irreducible polynomials of degree
$f_1, \ldots , f_s$ are monic, distinct, irreducible polynomials of degree ![]() $d$,
$d$, ![]() $g_{s+1}, \ldots , g_n$ are polynomials of degrees less than
$g_{s+1}, \ldots , g_n$ are polynomials of degrees less than ![]() $d$ and
$d$ and ![]() $B$ lies in
$B$ lies in ![]() $\mathcal {F}_{ < d}B_2(k(t))$.
$\mathcal {F}_{ < d}B_2(k(t))$.
Lemma 7.2 Elements of type (1)–(3) lie in the image of ![]() $h$.
$h$.
Proof. For elements of type (2) there is nothing to prove.
Let us prove the lemma for elements of type (1). From Lemma 5.2 it follows that for any elements ![]() $X,Y \in B_2(F)$ we have that
$X,Y \in B_2(F)$ we have that
vanishes in ![]() $[B_2(F) \otimes \Lambda ^2 F^{\times }]_t$. This can be applied to
$[B_2(F) \otimes \Lambda ^2 F^{\times }]_t$. This can be applied to ![]() $X=B \in \mathcal {F}_{ < d}B_2(k(x))$ and
$X=B \in \mathcal {F}_{ < d}B_2(k(x))$ and ![]() $Y=\{ {f_1}/{f_2}\}_2$. We get that
$Y=\{ {f_1}/{f_2}\}_2$. We get that
Since in ![]() $gr_s^\mathcal {G}gr_d^{\mathcal {F}}[ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }]_t$ the element
$gr_s^\mathcal {G}gr_d^{\mathcal {F}}[ B_2(k(t))\otimes \Lambda ^{n-2} k(t)^{\times }]_t$ the element ![]() $B \otimes f_1 \wedge f_2 \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n$ is equal to
$B \otimes f_1 \wedge f_2 \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n$ is equal to ![]() $B \otimes (1-{f_1}/{f_2}) \wedge {f_1}/{f_2} \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n$, elements of type (1) lie in the image of
$B \otimes (1-{f_1}/{f_2}) \wedge {f_1}/{f_2} \wedge \cdots \wedge f_s \wedge g_{s+1} \wedge \cdots \wedge g_n$, elements of type (1) lie in the image of ![]() $h$.
$h$.
It remains to deal with elements of type (3). It is enough to consider the case ![]() $s=2$. Let
$s=2$. Let ![]() $r$ be the residue of
$r$ be the residue of ![]() ${\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}}$ modulo
${\widetilde {r_1}\widetilde {r_2}}/{\widetilde {r_1r_2}}$ modulo ![]() $f_2$. From the five-term relation we see that
$f_2$. From the five-term relation we see that
 \begin{align} \bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1r_2}} \bigg\}_2\otimes f_2&= \{r \}_2\otimes f_2-\bigg\{ \dfrac{\widetilde{r_1r_2} r}{\widetilde{r_1}\widetilde{r_2}} \bigg\}_2\otimes f_2\nonumber\\ &\quad + \bigg\{ \dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2- \bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}}{\widetilde{r_1r_2}(r-1)} \bigg\}_2\otimes f_2. \end{align}
\begin{align} \bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1r_2}} \bigg\}_2\otimes f_2&= \{r \}_2\otimes f_2-\bigg\{ \dfrac{\widetilde{r_1r_2} r}{\widetilde{r_1}\widetilde{r_2}} \bigg\}_2\otimes f_2\nonumber\\ &\quad + \bigg\{ \dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2- \bigg\{ \dfrac{\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}}{\widetilde{r_1r_2}(r-1)} \bigg\}_2\otimes f_2. \end{align}
All terms on the right-hand side of the equality lie in the image of ![]() $h$. We will show this for the second term; for the other three the proof is similar. Since
$h$. We will show this for the second term; for the other three the proof is similar. Since ![]() $\deg (r) < d$, there exists a polynomial
$\deg (r) < d$, there exists a polynomial ![]() $q$ of degree less than
$q$ of degree less than ![]() $d$, such that
$d$, such that
So in ![]() $B_2(k(t))\otimes _a k(t)^{\times }$ we have
$B_2(k(t))\otimes _a k(t)^{\times }$ we have
 \begin{align} \bigg\{ \dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2&={-}\bigg\{ 1-\dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2,\nonumber\\ -\bigg\{ \dfrac{\widetilde{r_1r_2} r-\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2&={-}\bigg\{ \dfrac{-qf_2}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2=\bigg\{ \dfrac{-qf_2}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes \dfrac{-q}{\widetilde{r_1}\widetilde{r_2}(r-1)}. \end{align}
\begin{align} \bigg\{ \dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2&={-}\bigg\{ 1-\dfrac{(\widetilde{r_1}\widetilde{r_2}-\widetilde{r_1r_2}) r}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2,\nonumber\\ -\bigg\{ \dfrac{\widetilde{r_1r_2} r-\widetilde{r_1}\widetilde{r_2}}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2&={-}\bigg\{ \dfrac{-qf_2}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes f_2=\bigg\{ \dfrac{-qf_2}{\widetilde{r_1}\widetilde{r_2}(r-1)} \bigg\}_2\otimes \dfrac{-q}{\widetilde{r_1}\widetilde{r_2}(r-1)}. \end{align}Clearly
so by Corollary 4.4,
lies in ![]() $\mathcal {G}_1 gr_d^\mathcal {F}B_2(k(t))$. So
$\mathcal {G}_1 gr_d^\mathcal {F}B_2(k(t))$. So
vanishes in ![]() $gr_2^\mathcal {G}gr_d^\mathcal {F} [B_2(k(t))\otimes k(t)^{\times } ]_t$.
$gr_2^\mathcal {G}gr_d^\mathcal {F} [B_2(k(t))\otimes k(t)^{\times } ]_t$.
Acknowledgements
I would like to thank S. Gorchinskiy, A. Levin, O. Martin and A. Goncharov for their invaluable help with preparing this paper. Also I thank Gerhard Paseman for his help on a draft of the paper.