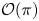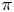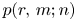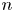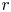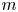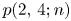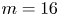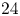1. Introduction
Let $\pi$![]() be an integer partition and $\pi '$
be an integer partition and $\pi '$![]() its conjugate. Stanley [Reference Stanley9, Reference Stanley10] introduced a new integral partition statistic
its conjugate. Stanley [Reference Stanley9, Reference Stanley10] introduced a new integral partition statistic
where $\mathcal {O}(\pi )$![]() denotes the number of odd parts in the partition $\pi$
denotes the number of odd parts in the partition $\pi$![]() . This statistic is called the Stanley rank.
. This statistic is called the Stanley rank.
Let $n\geq 1$![]() and $m\geq 2$
and $m\geq 2$![]() be integers. For any integer $r$
be integers. For any integer $r$![]() with $0\leq r\leq m-1$
with $0\leq r\leq m-1$![]() , define
, define
From the fact that
it is easy to see that for $n\geq 1$![]() ,
,
where $p(n)$![]() is the number of partitions of $n$
is the number of partitions of $n$![]() . Moreover, if $m$
. Moreover, if $m$![]() is even and $r$
is even and $r$![]() is odd, then
is odd, then
Stanley [Reference Stanley9, Reference Stanley10] also established the following generating function for $p(0,\,4;n)- p(2,\,4;n)$![]() :
:
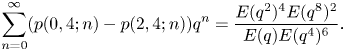
Here and throughout this paper,

Following the work of Stanley, Andrews [Reference Andrews2] then obtained the generating function for $p(0,\,4;n)$![]() :
:

Furthermore, he proved that for $n\geq 0$![]() ,
,
which is a refinement of the following famous congruence due to Ramanujan:
At the end of his paper [Reference Andrews2], Andrews asked for a partition statistic that would give a combinatorial interpretation of (1.2) since his proof of (1.2) is analytic. Berkovich and Garvan [Reference Berkovich and Garvan4] later provided three such statistics and answered Andrews’ inquiry.
In 2010, Swisher [Reference Swisher13] proved that (1.2) is just one of infinitely many similar congruences satisfied by $p(0,\,4;n)$![]() . In her Ph.D. thesis [Reference Swisher12], Swisher also established the following elegant results:
. In her Ph.D. thesis [Reference Swisher12], Swisher also established the following elegant results:
and for sufficiently large $n$![]() ,
,
Berkovich and Garvan [Reference Berkovich and Garvan3] also gave elementary proofs of (1.3)–(1.7) with the restriction of “$n$![]() sufficiently large” removed. Further, Berkovich and Garvan presented a handful of new results, including
sufficiently large” removed. Further, Berkovich and Garvan presented a handful of new results, including
and for $n\ge 1$![]() ,
,
In this paper, we establish the generating functions for $p(r,\, m;n)$![]() with $m=16$
with $m=16$![]() and $24$
and $24$![]() . It should be pointed out that if we define
. It should be pointed out that if we define
then in view of (1.1) and (1.9),
It follows from [Reference Berkovich and Garvan4, (2.8) and (2.9)] that
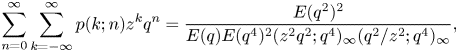
where the $q$![]() -Pochhammer symbol is defined as usual by
-Pochhammer symbol is defined as usual by

From (1.11), we observe that
and then from (1.10),
Therefore, we merely list the generating functions for $p(r,\,m;n)$![]() with $m\in \{16,\,24\}$
with $m\in \{16,\,24\}$![]() and $0\leq r\leq \frac {m}{2}$
and $0\leq r\leq \frac {m}{2}$![]() .
.
Theorem 1.1 We have

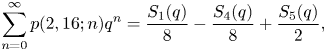



where

Theorem 1.2 We have







where

Remark Noticing that
one may therefore obtain the generating functions for $p(r,\,m;n)$![]() with $m\in \{6,\,8,\,12\}$
with $m\in \{6,\,8,\,12\}$![]() with the assistance of Theorems 1.1 and 1.2.
with the assistance of Theorems 1.1 and 1.2.
In light of Theorems 1.1 and 1.2, we prove the following results which are refinements of (1.3)–(1.7).
Theorem 1.3 Let $m\in \{4,\,6\}$![]() and $i$
and $i$![]() be an integer with $0\leq i \le m-1$
be an integer with $0\leq i \le m-1$![]() . Then
. Then
and
Also, for sufficiently large $n,$![]()
2. Proof of Theorem 1.1
In this section, we always set $\zeta =e^{\pi \mathrm {i}/8}$![]() . In order to prove Theorem 1.1, we first establish a lemma.
. In order to prove Theorem 1.1, we first establish a lemma.
Lemma 2.1 We have

and

Proof. Noticing that $\zeta ^{2}=\frac {\sqrt {2}}{2}(1+\mathrm {i})$![]() , we have
, we have
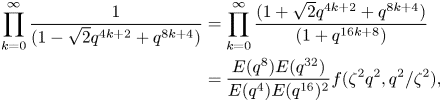
where Ramanujan's general theta function is given by
It follows from Entry 30 (ii) and (iii) on page 46 of Berndt's book [Reference Berndt5] that
Taking $a=\zeta ^{2}q^{2}$![]() and $b=q^{2}/\zeta ^{2}$
and $b=q^{2}/\zeta ^{2}$![]() in (2.4) yields
in (2.4) yields
By the fact that $\zeta ^{4}=\mathrm {i}$![]() , we have
, we have
and
Making use of (2.5)–(2.7) and the fact that $\zeta ^{2}=\frac {\sqrt {2}}{2}(1+\mathrm {i})$![]() , we arrive at
, we arrive at
Now, (2.1) follows from (2.3) and (2.8). Also, replacing $q$![]() by $\mathrm {i}\,q$
by $\mathrm {i}\,q$![]() in (2.1) leads to (2.2).
in (2.1) leads to (2.2).
Now, we are ready to prove Theorem 1.1.
Proof Proof of Theorem 1.1
Employing (1.10), (1.11) and the fact that

we have, for $0\le a\le 15$![]() ,
,
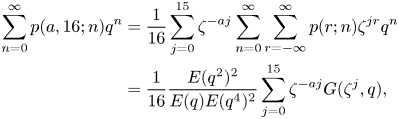
where
It is easy to check that for $k,\, j\geq 0$![]() ,
,
In light of (2.11) and (2.12),

Using (2.1), (2.2), (2.10) and (2.13), we find that

Theorem 1.1 follows from (2.14) and the fact that $\zeta =\frac {\sqrt {2+\sqrt {2}}}{2}+ \frac {\sqrt {2-\sqrt {2}}}{2} \,\mathrm {i}$![]() .
.
3. Proof of Theorem 1.2
In this section, we prove Theorem 1.2. Throughout our proof, we always write $\omega =e^{\pi \mathrm {i} /12}$![]() . We first prove the following lemma.
. We first prove the following lemma.
Lemma 3.1 We have
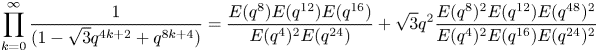
and

Proof. Notice that $\omega ^{2}=\frac {\sqrt {3}}{2}+\frac {1}{2}\,\mathrm {i}$![]() . Therefore,
. Therefore,

where $f(a,\,b)$![]() is as defined in (2.4). It follows from the quintuple product identity [Reference Berndt5, (38.2), p. 80] that
is as defined in (2.4). It follows from the quintuple product identity [Reference Berndt5, (38.2), p. 80] that
Setting $B=-\omega ^{2}$![]() in (3.4), we deduce that
in (3.4), we deduce that
By the fact that $\omega ^{4}=\frac {1}{2}+\frac {\sqrt {3}}{2}\,\mathrm {i}$![]() ,
,

Therefore,
Taking $a=-\mathrm {i}\,q^{2}$![]() and $b=-q^{10}/\mathrm {i}$
and $b=-q^{10}/\mathrm {i}$![]() in (2.4) yields
in (2.4) yields

On the other hand, if we put $a=- q^{2}/\mathrm {i}$![]() and $b=-\mathrm {i}\,q^{10}$
and $b=-\mathrm {i}\,q^{10}$![]() in (2.4), then
in (2.4), then

Finally, (3.1) follows from (3.3) and (3.5)–(3.8). Also, replacing $q$![]() by $\mathrm {i}\,q$
by $\mathrm {i}\,q$![]() in (3.1) yields (3.2).
in (3.1) yields (3.2).
Now, we prove Theorem 1.2.
Proof of Theorem 1.2 Utilizing (1.10), (1.11) and the fact that

we arrive at

where $G(z,\,q)$![]() is as defined in (2.11). In light of (2.11) and (2.12),
is as defined in (2.11). In light of (2.11) and (2.12),
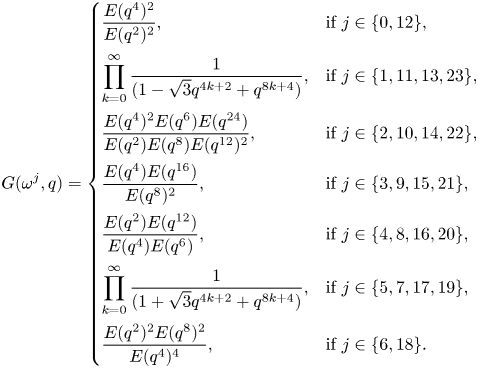
By (3.1), (3.2), (3.9) and (3.10),

Theorem 1.2 follows from (3.11) and the fact that $\omega = \frac {\sqrt {6}+\sqrt {2}}{4}+\frac {\sqrt {6} -\sqrt {2}}{4}\,\mathrm {i}$![]() .
.
4. Proof of Theorem 1.3
In this section, we prove Theorem 1.3 using Theorems 1.1 and 1.2 along with a result due to Sussman [Reference Sussman11].
In [Reference Sussman11], applying the standard circle method due to Rademacher [Reference Rademacher8], Sussman obtained an exact formula for $g(n)$![]() , the coefficients in
, the coefficients in

where $\mathbf {m}=(m_1,\,\ldots,\,m_J)$![]() is a sequence of distinct positive integers and $\mathbf {d}=(\delta _1,\,\ldots,\,\delta _J)$
is a sequence of distinct positive integers and $\mathbf {d}=(\delta _1,\,\ldots,\,\delta _J)$![]() is a sequence of non-zero integers such that $\sum \nolimits _{j=1}^{J} \delta _{j}<0$
is a sequence of non-zero integers such that $\sum \nolimits _{j=1}^{J} \delta _{j}<0$![]() .
.
To state Sussman's result, we first fix some notation. Let $k$![]() be a positive integer. We define
be a positive integer. We define

Further, for any integer $h$![]() such that $\gcd (h,\,k)=1$
such that $\gcd (h,\,k)=1$![]() , we define
, we define

where $s(d,\,c)$![]() is the Dedekind sum defined by
is the Dedekind sum defined by

with

Let $L=\operatorname {lcm}(m_1,\,\ldots,\,m_J)$![]() . We divide the set $\{1,\,2,\,\ldots,\,L\}$
. We divide the set $\{1,\,2,\,\ldots,\,L\}$![]() into two disjoint subsets:
into two disjoint subsets:
Theorem 4.1 Sussman
If $\Sigma > 0$![]() and the inequality
and the inequality
holds for all $1\le \ell \le L,$![]() then for positive integers $n>-\Omega /24,$
then for positive integers $n>-\Omega /24,$![]()

where $I_s(x)$![]() is the modified Bessel function of the first kind.
is the modified Bessel function of the first kind.
Remark We also frequently make use of the asymptotic expansion of $I_s(x)$![]() (see [Reference Abramowitz and Stegun1, p. 377, (9.7.1)]): for fixed $s$
(see [Reference Abramowitz and Stegun1, p. 377, (9.7.1)]): for fixed $s$![]() , when $|\arg x|<\frac {\pi }{2}$
, when $|\arg x|<\frac {\pi }{2}$![]() ,
,
Remark In [Reference Chern6], Chern considered the case where $\Sigma \le 0$![]() in (4.1) and obtained a similar asymptotic formula for $g(n)$
in (4.1) and obtained a similar asymptotic formula for $g(n)$![]() .
.
Let us define, for $i=1,\,\ldots,\,5$![]() ,
,

where $S_i(q)$![]() 's are as defined in Theorem 1.1. First, we know from a famous result due to Hardy and Ramanujan [Reference Hardy and Ramanujan7] that, as $n\to \infty$
's are as defined in Theorem 1.1. First, we know from a famous result due to Hardy and Ramanujan [Reference Hardy and Ramanujan7] that, as $n\to \infty$![]() ,
,
Next, we show that, as $n\to \infty$![]() ,
,

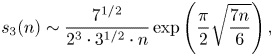


We only prove (4.6) and (4.8) as instances. The rest can be shown analogously by Sussman's result (4.3).
First, we show (4.6). In (4.1), let us put
Thus, we have $\Sigma =\frac {1}{2}$![]() and $\Omega =-1$
and $\Omega =-1$![]() . Also, $L=64$
. Also, $L=64$![]() . We compute that
. We compute that

Next, we verify that assumption (4.2) is satisfied. Then, it can be computed that when $k=1$![]() , the $I$
, the $I$![]() -Bessel term has the largest order, which is
-Bessel term has the largest order, which is

Further, when $k=1$![]() , we have
, we have

It follows from (4.3), with (4.4) utilized, that

For (4.8), we put
in (4.1). Thus, $\Sigma =\frac {1}{2}$![]() and $\Omega =-1$
and $\Omega =-1$![]() . Further, $L=8$
. Further, $L=8$![]() . We compute that
. We compute that
Next, we verify that assumption (4.2) is satisfied. Then, it can be computed that when $k=4$![]() , the $I$
, the $I$![]() -Bessel term has the largest order, which is
-Bessel term has the largest order, which is

Further, when $k=4$![]() , we have
, we have

It follows from (4.3), with (4.4) utilized, that

Notice that, for the exponential terms in (4.5)–(4.9), we have, numerically,
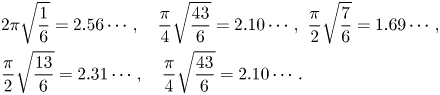
Recall that, for any integer $i$![]() with $1\le i\le 4$
with $1\le i\le 4$![]() , we have $p(2i,\,16,\,n)=p(16-2i,\,16,\,n)$
, we have $p(2i,\,16,\,n)=p(16-2i,\,16,\,n)$![]() . We conclude from the numerical calculations in (4.10) that
. We conclude from the numerical calculations in (4.10) that
as $n\to \infty$![]() for any integer $i$
for any integer $i$![]() with $0\le i\le 7$
with $0\le i\le 7$![]() , and therefore (1.24) follows when $m=4$
, and therefore (1.24) follows when $m=4$![]() .
.
We also deduce from the numerical calculations in (4.10) that, for $0\le i<4$![]() ,
,
as $n\to \infty$![]() . We know from (4.8) that
. We know from (4.8) that

Hence, (1.26) and (1.27) hold when $m=4$![]() . Finally, since
. Finally, since
we see that (1.25) is true when $m=4$![]() .
.
Next, we prove Theorem 1.3 when $m=6$![]() . Let us define, for $i=1,\,\ldots,\,7$
. Let us define, for $i=1,\,\ldots,\,7$![]() ,
,

where $F_i(q)$![]() 's are as defined in Theorem 1.2. Applying Sussman's result (4.3), we have, as $n\to \infty$
's are as defined in Theorem 1.2. Applying Sussman's result (4.3), we have, as $n\to \infty$![]() ,
,





Moreover, we notice that, for the exponential terms in (4.11)–(4.17), we have, numerically,

Recall that, for any integer $i$![]() with $1\le i\le 6$
with $1\le i\le 6$![]() , we have $p(2i,\,24;n) =p(24-2i,\,24;n)$
, we have $p(2i,\,24;n) =p(24-2i,\,24;n)$![]() . We conclude from the numerical calculations in (4.18) that
. We conclude from the numerical calculations in (4.18) that
as $n\to \infty$![]() for any integer $i$
for any integer $i$![]() with $0\le i\le 11$
with $0\le i\le 11$![]() , and therefore (1.24) follows when $m=6$
, and therefore (1.24) follows when $m=6$![]() . We also have, for $0\le i<6$
. We also have, for $0\le i<6$![]() ,
,
as $n\to \infty$![]() . Hence, in (1.25)–(1.27), the case of $m=6$
. Hence, in (1.25)–(1.27), the case of $m=6$![]() follows by arguments akin to those for the case of $m=4$
follows by arguments akin to those for the case of $m=4$![]() . Therefore, the proof of Theorem 1.3 is completed.
. Therefore, the proof of Theorem 1.3 is completed.
5. Conclusion and conjectures
In this paper, we first established the generating functions of $p(r,\,m;n)$![]() with $m=16$
with $m=16$![]() and $24$
and $24$![]() by making use of theta function identities and then proved some inequalities for $p(r,\,m;n)$
by making use of theta function identities and then proved some inequalities for $p(r,\,m;n)$![]() based on their generating functions and Sussman's asymptotic formulas for quotients of Dedekind eta functions. According to the work of Berkovich and Garvan [Reference Berkovich and Garvan3], it would be appealing to find elementary proofs of Theorem 1.3 with the restriction of “$n$
based on their generating functions and Sussman's asymptotic formulas for quotients of Dedekind eta functions. According to the work of Berkovich and Garvan [Reference Berkovich and Garvan3], it would be appealing to find elementary proofs of Theorem 1.3 with the restriction of “$n$![]() sufficiently large” removed.
sufficiently large” removed.
Moreover, based on our numerical calculations, we present the following two conjectures.
Conjecture 5.1 For any integer $0\leq i < m$![]() with $m$
with $m$![]() an arbitrary positive integer, there always exists a positive integer $N(m,\,i)$
an arbitrary positive integer, there always exists a positive integer $N(m,\,i)$![]() such that for all $n\geq N(m,\,i)$
such that for all $n\geq N(m,\,i)$![]() ,
,
Conjecture 5.2 For any integer $0\leq k \leq m$![]() with $m$
with $m$![]() an arbitrary positive integer,
an arbitrary positive integer,
and
Acknowledgements
The authors cordially thank the anonymous referee for his/her helpful comments. The first, third and fourth authors were supported by the National Science Foundation of China (no. 11971203) and the Natural Science Foundation of Jiangsu Province of China (no. BK20180044). The second author was supported by a Killam Postdoctoral Fellowship from the Killam Trusts.