1. Introduction
The study of minimal submanifolds and its characteristics are considered classical in Riemannian geometry. In particular, problems about the Morse index. Roughly speaking, if $\Sigma ^{n}$![]() is a closed minimal submanifold in a Riemannian manifold $M$
is a closed minimal submanifold in a Riemannian manifold $M$![]() , its Morse index, $\hbox{Index}(\Sigma)$
, its Morse index, $\hbox{Index}(\Sigma)$![]() , measures how far $\Sigma$
, measures how far $\Sigma$![]() is from being a local minimum of the area functional. There are many papers highlighting the relation between the index and geometric and topological aspects of minimal submanifolds. In his celebrated work[Reference Simons19], Simons proved that all closed minimal submanifolds $\Sigma ^{n}$
is from being a local minimum of the area functional. There are many papers highlighting the relation between the index and geometric and topological aspects of minimal submanifolds. In his celebrated work[Reference Simons19], Simons proved that all closed minimal submanifolds $\Sigma ^{n}$![]() of the unit sphere $\mathbb {S}^{n+p+1}$
of the unit sphere $\mathbb {S}^{n+p+1}$![]() have ${{\rm {Index}}(\Sigma )} \geq p+1$
have ${{\rm {Index}}(\Sigma )} \geq p+1$![]() , with equality only when $\Sigma$
, with equality only when $\Sigma$![]() is totally geodesic. After this, others papers were made describing families of minimal submanifolds with same index and providing estimates of the Morse index in other special ambient manifolds, see for instance [Reference do Carmo, Ritoré and Ros7, Reference Lawson and Simons13, Reference Ohnita15, Reference Perdomo16, Reference Torralbo and Urbano20]. We point out some results in these works. Lawson and Simons in [Reference Lawson and Simons13] characterized the complex submanifolds as the only stable minimal submanifolds in the complex projective space $\mathbb {CP}^{m}$
is totally geodesic. After this, others papers were made describing families of minimal submanifolds with same index and providing estimates of the Morse index in other special ambient manifolds, see for instance [Reference do Carmo, Ritoré and Ros7, Reference Lawson and Simons13, Reference Ohnita15, Reference Perdomo16, Reference Torralbo and Urbano20]. We point out some results in these works. Lawson and Simons in [Reference Lawson and Simons13] characterized the complex submanifolds as the only stable minimal submanifolds in the complex projective space $\mathbb {CP}^{m}$![]() . Ohnita in [Reference Ohnita15] completed the classification of stable minimal submanifolds in compact rank-one symmetric spaces. Futhermore, do Carmo, Ritoré and Ros obtained in [Reference do Carmo, Ritoré and Ros7] a classification for two-sided closed minimal hypersurfaces $\Sigma ^{n}$
. Ohnita in [Reference Ohnita15] completed the classification of stable minimal submanifolds in compact rank-one symmetric spaces. Futhermore, do Carmo, Ritoré and Ros obtained in [Reference do Carmo, Ritoré and Ros7] a classification for two-sided closed minimal hypersurfaces $\Sigma ^{n}$![]() with index one in the real projective spaces $\mathbb {R}\mathbb {P}^{n+1}$
with index one in the real projective spaces $\mathbb {R}\mathbb {P}^{n+1}$![]() . Recently, Torralbo and Urbano in [Reference Torralbo and Urbano20] classified minimal submanifolds into a product of a sphere by an arbitrary Riemannian manifold, and Perdomo in [Reference Perdomo16] characterized the Clifford tori as the only closed orientable minimal hypersurfaces with antipodal symmetry and index $n + 3$
. Recently, Torralbo and Urbano in [Reference Torralbo and Urbano20] classified minimal submanifolds into a product of a sphere by an arbitrary Riemannian manifold, and Perdomo in [Reference Perdomo16] characterized the Clifford tori as the only closed orientable minimal hypersurfaces with antipodal symmetry and index $n + 3$![]() into the unit Euclidean sphere. We must also mention the work done by Ros in [Reference Ros17], where the author used harmonic forms in a clever way to obtain lower bounds of the Morse index as a function of the genus of minimal surfaces immersed in a flat $3$
into the unit Euclidean sphere. We must also mention the work done by Ros in [Reference Ros17], where the author used harmonic forms in a clever way to obtain lower bounds of the Morse index as a function of the genus of minimal surfaces immersed in a flat $3$![]() -torus $T^{3}$
-torus $T^{3}$![]() and in $\mathbb {R}^{3}$
and in $\mathbb {R}^{3}$![]() . Finally, we highlight that Savo in [Reference Savo18] performed an ingenious trick to obtain a comparison theorem between the spectrums of the stability operator acting on functions and the Hodge–Laplacian acting on $1$
. Finally, we highlight that Savo in [Reference Savo18] performed an ingenious trick to obtain a comparison theorem between the spectrums of the stability operator acting on functions and the Hodge–Laplacian acting on $1$![]() -form of closed orientable minimal hypersurfaces of $\mathbb {S}^{n+p+1}$
-form of closed orientable minimal hypersurfaces of $\mathbb {S}^{n+p+1}$![]() , and such comparison implies a lower estimate of the Morse index by a linear function of its first Betti's number. This technique was refined in many directions, see for instances the breakthrough done in [Reference Ambrozio, Carlotto and Sharp2, Reference Gorodski, Mendes and Radeschi11]. Also, due to the fruitfulness of this technique, very recently such method was successfully adapted for the constant mean curvature and weighted minimal hypersurfaces settings, see for instance [Reference Aiex and Hong1, Reference Cavalcante and de Oliveira3, Reference Cavalcante and Oliveira4, Reference Impera and Rimoldi9, Reference Impera, Rimoldi and Savo10].
, and such comparison implies a lower estimate of the Morse index by a linear function of its first Betti's number. This technique was refined in many directions, see for instances the breakthrough done in [Reference Ambrozio, Carlotto and Sharp2, Reference Gorodski, Mendes and Radeschi11]. Also, due to the fruitfulness of this technique, very recently such method was successfully adapted for the constant mean curvature and weighted minimal hypersurfaces settings, see for instance [Reference Aiex and Hong1, Reference Cavalcante and de Oliveira3, Reference Cavalcante and Oliveira4, Reference Impera and Rimoldi9, Reference Impera, Rimoldi and Savo10].
Focusing on the higher codimensional case, we apply the Savo's approach to a new family of normal sections inspired by the works of Simons [Reference Simons19] and Savo [Reference Savo18] and we thus obtain a comparison result between the spectrums of the stability operator acting on sections of the normal bundle and the Hodge–Laplacian acting on $1$![]() -forms of a closed minimal submanifold $\Sigma ^{n}$
-forms of a closed minimal submanifold $\Sigma ^{n}$![]() into $\mathbb {S}^{n+p+1}$
into $\mathbb {S}^{n+p+1}$![]() and thus we generalize, in some sense, the Savo's results to closed minimal submanifolds. We point out that whether the codimension is at least $2$
and thus we generalize, in some sense, the Savo's results to closed minimal submanifolds. We point out that whether the codimension is at least $2$![]() , our comparison theorem uses topological and geometrical features of the submanifold, but in codimension one we get the same estimates of Savo, which only requires topological features. As a consequence we obtain a theorem that shows that the Morse index is bounded from below by a linear function of the first Betti's number $b_1(\Sigma )$
, our comparison theorem uses topological and geometrical features of the submanifold, but in codimension one we get the same estimates of Savo, which only requires topological features. As a consequence we obtain a theorem that shows that the Morse index is bounded from below by a linear function of the first Betti's number $b_1(\Sigma )$![]() .
.
The main result of the paper compares the spectrums of the stability operator acting on sections of the normal bundle and the Hodge–Laplacian acting on $1$![]() -forms.
-forms.
The result reads as follows:
Let $\Sigma ^{n}$![]() be a closed minimal submanifold of $\mathbb {S}^{n+p+1}$
be a closed minimal submanifold of $\mathbb {S}^{n+p+1}$![]() , $p\geq 0$
, $p\geq 0$![]() , and let $L$
, and let $L$![]() be the stability operator acting on the space of normal sections. Then,
be the stability operator acting on the space of normal sections. Then,
where $m(\alpha )= {{n+p+2}\choose {2}}(\alpha - 1)+1$![]() and $C$
and $C$![]() is a lower bound for the Ricci curvature of $\Sigma$
is a lower bound for the Ricci curvature of $\Sigma$![]()
As a by product of the technique we obtain the following result:
Let $\Sigma ^{n}$![]() be a closed minimal submanifold of $\mathbb {S}^{n+p+1}$
be a closed minimal submanifold of $\mathbb {S}^{n+p+1}$![]() , $p\geq 0$
, $p\geq 0$![]() , and let $L$
, and let $L$![]() be the stability operator acting on the space of normal sections. If
be the stability operator acting on the space of normal sections. If
then
We observe that our curvature hypothesis is less restrictive than the hypotheses in [Reference Chern, do Carmo and Kobayashi5, Reference Leung14], and since the spaces of closed minimal surfaces in $\mathbb {S}^{3}$![]() and in $\mathbb {S}^{5}$
and in $\mathbb {S}^{5}$![]() are abundant, see for instance [Reference Lawson12], we believe that our curvature hypothesis is not so restrictive, see remark 4.5.
are abundant, see for instance [Reference Lawson12], we believe that our curvature hypothesis is not so restrictive, see remark 4.5.
Finally, we point out that the last result provides evidence for a positive answer to a well-known conjecture proposed by Schoen and Marques–Neves in the setting of higher codimension.
The paper is organized in the following way: In the second section we give a brief summary about the minimal submanifolds theory and about $p$![]() -forms. In the third section we establish conventions that will be used later in the paper and also some technical results that will be necessary in the proof of the main results. In the last section, we provide the proof of the main results.
-forms. In the third section we establish conventions that will be used later in the paper and also some technical results that will be necessary in the proof of the main results. In the last section, we provide the proof of the main results.
2. Background material
In this section we present some concepts and notations that will be useful throughout this manuscript.
2.1 Rough Laplacian
Let $E^{N}$![]() be a Riemannian bundle over a closed Riemannian manifold $\Sigma ^{n}$
be a Riemannian bundle over a closed Riemannian manifold $\Sigma ^{n}$![]() and denote by ${\rm Hom}(T\Sigma, E)$
and denote by ${\rm Hom}(T\Sigma, E)$![]() the homomorphism bundle endowed with a metric $\langle \cdot, \cdot \rangle$
the homomorphism bundle endowed with a metric $\langle \cdot, \cdot \rangle$![]() and a linear connection $\nabla$
and a linear connection $\nabla$![]() given by
given by
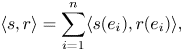
where $\{e_1,\dots, e_n\}$![]() is an orthonormal frame on $\Sigma$
is an orthonormal frame on $\Sigma$![]() , and
, and
for all sections $s$![]() and $r$
and $r$![]() in ${\rm Hom}(T\Sigma, E)$
in ${\rm Hom}(T\Sigma, E)$![]() and tangent vectors $X$
and tangent vectors $X$![]() and $Y$
and $Y$![]() on $\Sigma$
on $\Sigma$![]() . It is easy to show that $\langle \cdot, \cdot \rangle$
. It is easy to show that $\langle \cdot, \cdot \rangle$![]() is well defined and ${\rm Hom}(T\Sigma, E)$
is well defined and ${\rm Hom}(T\Sigma, E)$![]() endowed with $\nabla$
endowed with $\nabla$![]() and $\langle \cdot, \cdot \rangle$
and $\langle \cdot, \cdot \rangle$![]() is a Riemannian bundle over $\Sigma$
is a Riemannian bundle over $\Sigma$![]() . For all section $s$
. For all section $s$![]() in $E$
in $E$![]() , we note that $\nabla s$
, we note that $\nabla s$![]() is a section in ${\rm Hom}(T\Sigma, E)$
is a section in ${\rm Hom}(T\Sigma, E)$![]() , which is given by
, which is given by
for any vector field $X$![]() on $\Sigma$
on $\Sigma$![]() . Using the connection on ${\rm Hom}(T\Sigma, E)$
. Using the connection on ${\rm Hom}(T\Sigma, E)$![]() , consider $\nabla _{X,Y}s$
, consider $\nabla _{X,Y}s$![]() given by
given by
for any $X,Y \in \Gamma (T\Sigma )$![]() .
.
Definition 2.1 Given $s \in \Gamma (E)$![]() , the rough Laplacian $\nabla ^{2}\,s$
, the rough Laplacian $\nabla ^{2}\,s$![]() of $s$
of $s$![]() is the trace of the bilinear form $(X,Y) \to \nabla _{X,Y}s$
is the trace of the bilinear form $(X,Y) \to \nabla _{X,Y}s$![]() .
.
Proposition 2.2 Given an arbitrary geodesic frame $\{e_1,\ldots,e_n\}$![]() on $\Sigma$
on $\Sigma$![]() at $p,$
at $p,$![]() for any section $s$
for any section $s$![]() in $E,$
in $E,$![]() we have
we have

Proof. See [Reference Simons19, proposition 1.2.1].
2.2 Minimal immersions and stability operator
A closed submanifold $\Sigma$![]() of a Riemannian manifold $M$
of a Riemannian manifold $M$![]() is called minimal if it is a critical point of the area functional associated to admissible variations. That is, for all smooth maps $\phi :(-\varepsilon,\varepsilon )\times \Sigma \to M$
is called minimal if it is a critical point of the area functional associated to admissible variations. That is, for all smooth maps $\phi :(-\varepsilon,\varepsilon )\times \Sigma \to M$![]() , such that at each $t \in (-\varepsilon,\varepsilon )$
, such that at each $t \in (-\varepsilon,\varepsilon )$![]() , $\phi _t := \phi |_{\{t\}\times \Sigma }$
, $\phi _t := \phi |_{\{t\}\times \Sigma }$![]() is an immersion of $\Sigma$
is an immersion of $\Sigma$![]() and $\phi _0$
and $\phi _0$![]() is the inclusion map, we have that
is the inclusion map, we have that
where $\Sigma _t:=\phi _t(\Sigma )$![]() and $|\Omega |$
and $|\Omega |$![]() means the area of $\Omega$
means the area of $\Omega$![]() . A straightforward computation gives us
. A straightforward computation gives us
where $X = \frac {\partial \phi }{\partial t}(0,\cdot )$![]() and $H$
and $H$![]() is the trace of the second fundamental form of $\Sigma$
is the trace of the second fundamental form of $\Sigma$![]() in $M$
in $M$![]() . From this previous formula, we have that $\Sigma$
. From this previous formula, we have that $\Sigma$![]() is a minimal submanifold if and only if $H$
is a minimal submanifold if and only if $H$![]() vanishes.
vanishes.
Furthermore, if $\Sigma$![]() is minimal, for any $Z \in \Gamma (T\Sigma ^{\perp })$
is minimal, for any $Z \in \Gamma (T\Sigma ^{\perp })$![]() and $\phi (t,x) = \exp _x(tZ(x))$
and $\phi (t,x) = \exp _x(tZ(x))$![]() for $t\in (-\epsilon, \epsilon )$
for $t\in (-\epsilon, \epsilon )$![]() , where ${\rm {exp}}$
, where ${\rm {exp}}$![]() is the exponential map of $M$
is the exponential map of $M$![]() , we have
, we have
with $\tilde {R}(Z) = \sum _i\bar {R}(Z,e_i)e_i$![]() and $\tilde {B}(Z) = \sum _{i,j}\langle Z, B(e_i,e_j) \rangle B(e_i,e_j)$
and $\tilde {B}(Z) = \sum _{i,j}\langle Z, B(e_i,e_j) \rangle B(e_i,e_j)$![]() for an orthonormal frame $\{e_1,...,e_n\}$
for an orthonormal frame $\{e_1,...,e_n\}$![]() on $\Sigma$
on $\Sigma$![]() , where $\bar {R}$
, where $\bar {R}$![]() is the curvature tensor of $M$
is the curvature tensor of $M$![]() and $B$
and $B$![]() is the second fundamental form of $\Sigma$
is the second fundamental form of $\Sigma$![]() . The right-hand side of the above equation defines a quadratic form on $\Gamma (T\Sigma ^{\perp })$
. The right-hand side of the above equation defines a quadratic form on $\Gamma (T\Sigma ^{\perp })$![]() given by
given by
and it is known in the literature as Index form. The linear operator associated to the quadratic form is
and it is called the stability operator. Simons proved in [Reference Simons19] that $L$![]() is a strongly elliptic operator on a compact manifold, its spectrum is discrete and consists of an increasing sequence of eigenvalues converging to infinity:
is a strongly elliptic operator on a compact manifold, its spectrum is discrete and consists of an increasing sequence of eigenvalues converging to infinity:
which is counted with multiplicity. Notice that we can estimate the eigenvalues of $L$![]() using the min-max quotient associated to the quadratic form induced by the operator $L$
using the min-max quotient associated to the quadratic form induced by the operator $L$![]() as follows:
as follows:
for any $Z$![]() orthogonal to $\mathcal {L}_{k-1}$
orthogonal to $\mathcal {L}_{k-1}$![]() which is the direct sum of the first $k-1$
which is the direct sum of the first $k-1$![]() eigenspaces of $L$
eigenspaces of $L$![]() , see [Reference Davies6, chapter 4].
, see [Reference Davies6, chapter 4].
Finally, we recall that the ${{\rm {Index}}(\Sigma )}$![]() of a minimal submanifold $\Sigma$
of a minimal submanifold $\Sigma$![]() is the number of negative eigenvalues of $L$
is the number of negative eigenvalues of $L$![]() . Furthermore, $\Sigma$
. Furthermore, $\Sigma$![]() is called stable if ${{\rm {Index}}(\Sigma )} = 0$
is called stable if ${{\rm {Index}}(\Sigma )} = 0$![]() and unstable otherwise. The ${{\rm {Index}}(\Sigma )}$
and unstable otherwise. The ${{\rm {Index}}(\Sigma )}$![]() measures how far $\Sigma$
measures how far $\Sigma$![]() is from being a local minimum of the area functional.
is from being a local minimum of the area functional.
2.3 The Hodge–Laplacian and harmonic forms
In a closed Riemaniann manifold $\Sigma$![]() , the Hodge–Laplacian on the space of $p$
, the Hodge–Laplacian on the space of $p$![]() -forms $\Omega ^{p}(\Sigma )$
-forms $\Omega ^{p}(\Sigma )$![]() is the second order differential operator $\Delta _p$
is the second order differential operator $\Delta _p$![]() given by
given by
where $d$![]() is the exterior differential and $d^{*}$
is the exterior differential and $d^{*}$![]() is its formal adjoint with respect to the $L^{2}$
is its formal adjoint with respect to the $L^{2}$![]() -inner product. The eigenvalues of $\Delta _p$
-inner product. The eigenvalues of $\Delta _p$![]() , counted with multiplicity, are
, counted with multiplicity, are
A $p$![]() -form $\omega \in \Omega ^{p}(\Sigma )$
-form $\omega \in \Omega ^{p}(\Sigma )$![]() is called harmonic if $\Delta _p\omega = 0$
is called harmonic if $\Delta _p\omega = 0$![]() . The Hodge's Theorem asserts that in a closed Riemannian manifold $\Sigma$
. The Hodge's Theorem asserts that in a closed Riemannian manifold $\Sigma$![]() , the space of harmonics $p$
, the space of harmonics $p$![]() -forms is isomorphic to the $p$
-forms is isomorphic to the $p$![]() -th de Rham cohomology space of $\Sigma$
-th de Rham cohomology space of $\Sigma$![]() . Hence, the space of $p$
. Hence, the space of $p$![]() -harmonics forms has dimension equal to the $p$
-harmonics forms has dimension equal to the $p$![]() -th Betti's number $b_p(\Sigma )$
-th Betti's number $b_p(\Sigma )$![]() of $\Sigma$
of $\Sigma$![]() . In particular, $\lambda _i(\Delta _p) =0$
. In particular, $\lambda _i(\Delta _p) =0$![]() for all $i=1,\dots,b_p(\Sigma )$
for all $i=1,\dots,b_p(\Sigma )$![]() .
.
The Bochner–Weitzenböck formula relates the Hodge–Laplacian and the rough Laplacian. More precisely, on $\Omega ^{1}(\Sigma )$![]() the Bochner–Weitzenböck formula reads as follows:
the Bochner–Weitzenböck formula reads as follows:
for any $1$![]() -form $\omega$
-form $\omega$![]() , where $\nabla^{2}$
, where $\nabla^{2}$![]() is the rough Laplacian on $1$
is the rough Laplacian on $1$![]() -forms and ${{\rm {Ric}}}$
-forms and ${{\rm {Ric}}}$![]() is the Ricci tensor of $\Sigma$
is the Ricci tensor of $\Sigma$![]() .
.
3. Preliminary results
In this section, we will present some results and computations that will simplify the arguments and notation in the proof of the main results.
Let $\eta (x)=-x$![]() be a unit normal vector field on $\mathbb {S}^{n+p+1}$
be a unit normal vector field on $\mathbb {S}^{n+p+1}$![]() and so the second fundamental form of the standard embedding of $\mathbb {S}^{n+p+1}$
and so the second fundamental form of the standard embedding of $\mathbb {S}^{n+p+1}$![]() in $\mathbb {R}^{n+p+2}$
in $\mathbb {R}^{n+p+2}$![]() is $\tilde AX=-D_X\eta = X$
is $\tilde AX=-D_X\eta = X$![]() for all $X \in \Gamma (T\mathbb {S}^{n+p+1})$
for all $X \in \Gamma (T\mathbb {S}^{n+p+1})$![]() , where $D$
, where $D$![]() is the standard derivative of maps on $\mathbb {R}^{n+p+2}$
is the standard derivative of maps on $\mathbb {R}^{n+p+2}$![]() . Let $\Sigma$
. Let $\Sigma$![]() be an oriented closed minimal submanifold of $\mathbb {S}^{n+p+1}$
be an oriented closed minimal submanifold of $\mathbb {S}^{n+p+1}$![]() , whose second fundamental form will be indicated by $B$
, whose second fundamental form will be indicated by $B$![]() and its associated shape operator in direction of $Z \in \Gamma (T\Sigma ^{\perp })$
and its associated shape operator in direction of $Z \in \Gamma (T\Sigma ^{\perp })$![]() is denoted by $A_Z$
is denoted by $A_Z$![]() . Precisely, $B(X, Y) = (\bar \nabla _XY)^{\perp }$
. Precisely, $B(X, Y) = (\bar \nabla _XY)^{\perp }$![]() and $\langle A_ZX,Y\rangle = \langle B(X,Y), Z\rangle$
and $\langle A_ZX,Y\rangle = \langle B(X,Y), Z\rangle$![]() , for $X$
, for $X$![]() and $Y$
and $Y$![]() tangent vectors on $\Sigma$
tangent vectors on $\Sigma$![]() , where $\bar \nabla$
, where $\bar \nabla$![]() is the Levi–Civita connection on the sphere.
is the Levi–Civita connection on the sphere.
The next result summarizes some simple computations.
Lemma 3.1 Let $V$![]() be a parallel vector field of $\mathbb {R}^{n+p+2}$
be a parallel vector field of $\mathbb {R}^{n+p+2}$![]() . If $V^{\perp }$
. If $V^{\perp }$![]() and $V^{\top }$
and $V^{\top }$![]() are the normal and tangential components of $V$
are the normal and tangential components of $V$![]() along $\Sigma$
along $\Sigma$![]() in the sphere $\mathbb {S}^{n+p+1},$
in the sphere $\mathbb {S}^{n+p+1},$![]() then:
then:
(a) For all $X\in \Gamma (T\Sigma )$
 one has $\nabla^{\perp }_X V^{\perp } = -B(X,V^{\top });$
one has $\nabla^{\perp }_X V^{\perp } = -B(X,V^{\top });$
(b) For all $X\in \Gamma (T\Sigma )$
 one has $\nabla_X V^{\top } = \langle V,\eta \rangle X + A_{V^{\bot }}X;$
one has $\nabla_X V^{\top } = \langle V,\eta \rangle X + A_{V^{\bot }}X;$
(c) $\nabla\langle V,\eta \rangle = -V^{\top };$

(d) $\Delta \langle V,\eta \rangle = -n\langle V,\eta \rangle ;$

(e) $\nabla^{2}V^{\perp } = -\tilde {B}(V^{\perp }),$

where $\nabla$![]() and $\nabla ^{\perp }$
and $\nabla ^{\perp }$![]() are the connections induced by the Levi–Civita connection of the sphere on the tangent and normal bundle of $\Sigma$
are the connections induced by the Levi–Civita connection of the sphere on the tangent and normal bundle of $\Sigma$![]() in $\mathbb {S}^{n+p+1}$
in $\mathbb {S}^{n+p+1}$![]() .
.
Proof. Noticing that $V = \langle V, \eta \rangle \eta + V^{\perp } + V^{\top }$![]() and differentiating this identity we obtain
and differentiating this identity we obtain

Taking the normal and tangential component along $\Sigma$![]() in $\mathbb {S}^{n+p+1}$
in $\mathbb {S}^{n+p+1}$![]() of the formula above we get items (a) and (b). Next, note that
of the formula above we get items (a) and (b). Next, note that
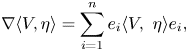
for $\{e_1\cdots, e_n\}$![]() a geodesic frame on $\Sigma$
a geodesic frame on $\Sigma$![]() at $p$
at $p$![]() . Therefore,
. Therefore,

and thus

and so we get item (c).
Using the definition of Laplacian of functions and items (b) and (c) we have:

where we used the minimality of $\Sigma$![]() here.
here.
Let $\{e_1,...,e_n\}$![]() be an orthonormal geodesic frame on $\Sigma$
be an orthonormal geodesic frame on $\Sigma$![]() at $p$
at $p$![]() . Using the proposition 2.2 and item (a) we have
. Using the proposition 2.2 and item (a) we have
and therefore, using item (b) and Codazzi equation and omitting the summation sign, we get

Since $\Sigma$![]() is minimal and $\{e_1,..,e_n\}$
is minimal and $\{e_1,..,e_n\}$![]() is an orthonormal geodesic frame, the second and last terms in equation above are equal to zero. Using minimality again and the commutativity of tracing and derivative we get
is an orthonormal geodesic frame, the second and last terms in equation above are equal to zero. Using minimality again and the commutativity of tracing and derivative we get
and thus we conclude the desired results.
We now recall the definition of the Laplacian of a vector field on $\Sigma$![]() . First of all, given a vector field $X$
. First of all, given a vector field $X$![]() on $\Sigma$
on $\Sigma$![]() , we can produce an $1$
, we can produce an $1$![]() -form by the formula
-form by the formula
for any $Y$![]() tangent vector to $\Sigma$
tangent vector to $\Sigma$![]() . Moreover, given an $1$
. Moreover, given an $1$![]() -form $\omega$
-form $\omega$![]() , the Riesz representation on a Hilbert space gives us a vector field $\omega ^{\sharp }$
, the Riesz representation on a Hilbert space gives us a vector field $\omega ^{\sharp }$![]() defined by
defined by
for any $Y$![]() tangent vector to $\Sigma$
tangent vector to $\Sigma$![]() . Such operations $^{\sharp }$
. Such operations $^{\sharp }$![]() and $^{\flat }$
and $^{\flat }$![]() are known as musical isomorphisms.
are known as musical isomorphisms.
Using the Hodge–Laplacian on $1$![]() -forms and the musical isomorphisms above, we introduce the following concept.
-forms and the musical isomorphisms above, we introduce the following concept.
Definition 3.2 For a vector field $X \in \Gamma (T\Sigma )$![]() , the Laplacian of $X$
, the Laplacian of $X$![]() is defined by
is defined by
The next result provides a relation between the rough Laplacian and the Laplacian introduced above.
Lemma 3.3 For any vector field $X\in \Gamma (T\Sigma )$![]() we have
we have
where $\{e_1,...,e_n\}$![]() is a local orthonormal frame on $\Sigma$
is a local orthonormal frame on $\Sigma$![]() . Moreover,
. Moreover,
In particular,
Proof. Using the Bochner–Weitzenböck formula 2.1 we have
for all $Y \in \Gamma (T\Sigma )$![]() . On the other hand, the Gauss equation and minimality of $\Sigma$
. On the other hand, the Gauss equation and minimality of $\Sigma$![]() yields us
yields us
Replacing this equality in the previous equation we deduce the first formula asserted.
Since the Hodge–Laplacian $\Delta _1$![]() and exterior differential $d$
and exterior differential $d$![]() commutes, we have from items (c) and (d) of lemma 3.1 that
commutes, we have from items (c) and (d) of lemma 3.1 that
and so we conclude the proof.
Lemma 3.4 For any vector $V$![]() of $\mathbb {R}^{n+p+2}$
of $\mathbb {R}^{n+p+2}$![]() and any vector field $X \in \Gamma (T\Sigma )$
and any vector field $X \in \Gamma (T\Sigma )$![]() we have:
we have:
(a) $\nabla\langle V,X\rangle = \langle V,\eta \rangle X + A_{V^{\perp }} X +\sum _i \langle V,\nabla_{e_i}X\rangle e_i;$

(b) $\Delta \langle V,X\rangle = (n-2)\langle V,X\rangle -\langle V,\Delta X\rangle + 2\mathrm {div}(X)\langle V,\eta \rangle - 2\sum _i\langle B(e_i,V^{\top }),$
 $B(e_i,X)\rangle + 2\sum _i\langle A_{V^{\perp }}e_i , \nabla_{e_i}X\rangle,$
$B(e_i,X)\rangle + 2\sum _i\langle A_{V^{\perp }}e_i , \nabla_{e_i}X\rangle,$
where $\{e_1,...,e_n\}$![]() is a local orthonormal frame on $\Sigma$
is a local orthonormal frame on $\Sigma$![]() at $q$
at $q$![]() .
.
Proof. Let $\{e_1,\cdots, e_n\}$![]() be an orthonormal geodesic frame on $\Sigma$
be an orthonormal geodesic frame on $\Sigma$![]() at $q$
at $q$![]() . Using the definition of Laplacian and rough Laplacian we obtain
. Using the definition of Laplacian and rough Laplacian we obtain
and
Using the equalities above, lemma 3.3 and lemma 3.1 we get the desired formulas.
Next we have a simple and useful formula that will be used many times in our computations. Its expression is the following:
Lemma 3.5 For all pair of vector $X,Y$![]() of $\mathbb {R}^{n+p+2},$
of $\mathbb {R}^{n+p+2},$![]() we have
we have
where $C(n,p)= \frac {\omega _{n+p+1}}{n+p+2}$![]() and $\omega _k$
and $\omega _k$![]() is the area of the $k$
is the area of the $k$![]() -dimensional unit sphere.
-dimensional unit sphere.
Proof. Using the Divergence Theorem for the vector field $V(q) = \langle q ,Y\rangle X$![]() on the unit ball $\mathbb {B}^{n+p+2}$
on the unit ball $\mathbb {B}^{n+p+2}$![]() and noticing that $\mathbb {S}^{n+p+1}$
and noticing that $\mathbb {S}^{n+p+1}$![]() is its boundary, we deduce the equality directly.
is its boundary, we deduce the equality directly.
Now we introduce a new family of normal vector fields on $\Sigma$![]() which depends on a given $X \in \Gamma (T\mathbb {R}^{n+p+2})$
which depends on a given $X \in \Gamma (T\mathbb {R}^{n+p+2})$![]() and given vectors $V,W$
and given vectors $V,W$![]() of $\mathbb {R}^{n+p+2}$
of $\mathbb {R}^{n+p+2}$![]() . Such family of vector fields $Z_X \in \Gamma (T\mathbb {S}^{n+p+1})$
. Such family of vector fields $Z_X \in \Gamma (T\mathbb {S}^{n+p+1})$![]() are given by:
are given by:
We point out that such vector field $Z$![]() can be seen as tri-linear function from the space $\Gamma (T\mathbb {S}^{n+p+1})\times \Gamma (\mathbb {R}^{n+p+2})\times \Gamma (\mathbb {R}^{n+p+2})$
can be seen as tri-linear function from the space $\Gamma (T\mathbb {S}^{n+p+1})\times \Gamma (\mathbb {R}^{n+p+2})\times \Gamma (\mathbb {R}^{n+p+2})$![]() to $\Gamma (T\Sigma ^{\perp } )$
to $\Gamma (T\Sigma ^{\perp } )$![]() and it is skew-symmetric in the variables $V$
and it is skew-symmetric in the variables $V$![]() and $W$
and $W$![]() , and this fact will be very useful in this manuscript.
, and this fact will be very useful in this manuscript.
Using the notation established above we are able to prove the following result:
Proposition 3.6 For any $X \in \Gamma (T\Sigma )$![]() and $L$
and $L$![]() the stability operator, we have
the stability operator, we have
and here
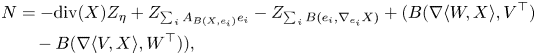
and $V$![]() and $W$
and $W$![]() are vectors of $\mathbb {R}^{n+p+2}$
are vectors of $\mathbb {R}^{n+p+2}$![]() and $\{e_1,...,e_n\}$
and $\{e_1,...,e_n\}$![]() is a local orthonormal frame on $\Sigma$
is a local orthonormal frame on $\Sigma$![]() .
.
Proof. By definition of $Z_X$![]() it is enough to compute $\nabla ^{2}(\langle W, X \rangle V^{\perp })$
it is enough to compute $\nabla ^{2}(\langle W, X \rangle V^{\perp })$![]() . Notice that
. Notice that
Using lemma 3.4, lemma 3.1 items (a) and (e) and $\tilde R(V^{\perp }) = nV^{\perp }$![]() , we get
, we get
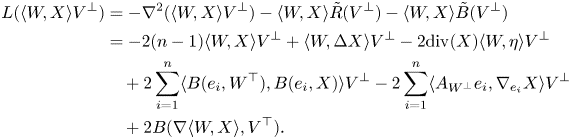
In a similar fashion we obtain

Thus, summing these two formulas and using the notation introduced before we conclude the desired formula.
The last result in this section provide us a useful and direct formula for the $L^{2}$![]() -inner product of elements of the form $Z_{(\cdot )}$
-inner product of elements of the form $Z_{(\cdot )}$![]() . In this result we denote by $\mu$
. In this result we denote by $\mu$![]() the measure $C(n,p)^{-1}\mathcal {H}^{n+p+1}$
the measure $C(n,p)^{-1}\mathcal {H}^{n+p+1}$![]() .
.
The computations are:
Lemma 3.7 For any $X$![]() and $Y$
and $Y$![]() in $\Gamma (T\mathbb {R}^{n+p+2})$
in $\Gamma (T\mathbb {R}^{n+p+2})$![]() the following formulas hold:
the following formulas hold:
(a) $\displaystyle \int _{U}|V^{\perp }|^{2}\, {\rm d}\mu (V) = p+1;$

(b) $\displaystyle \int _{U\times U} \langle Z_X, Z_Y\rangle \, {\rm d}\mu (V) {\rm d}\mu (W) = 2p\langle X, Y\rangle + 2\langle X^{\top }, Y^{\top }\rangle +2\langle X,\eta \rangle \langle Y,\eta \rangle,$

and here $U=\mathbb {S}^{n+p+1}$![]() and $(\cdot )^{\top }$
and $(\cdot )^{\top }$![]() is the projection on $T\Sigma$
is the projection on $T\Sigma$![]() .
.
Proof. The first item follows directly from lemma 3.5, because $|V^{\perp }|^{2} = \sum _i\langle V, \eta _i\rangle ^{2}$![]() , where $\{\eta _1,\cdots, \eta _{p+1}\}$
, where $\{\eta _1,\cdots, \eta _{p+1}\}$![]() is an orthonormal frame of $T\Sigma ^{\perp }$
is an orthonormal frame of $T\Sigma ^{\perp }$![]() .
.
For the last item, note that

and so, using lemma 3.5 and item (1) in this lemma, we obtain:

and in the last equality we used that $T\mathbb {R}^{n+p+2} = T\Sigma \oplus T\Sigma ^{\perp } \oplus \langle \eta \rangle$![]() .
.
4. Statements and proof of the main results
We restate our main results, and provide a proof for each one of them. The first result reads as follows:
Theorem 4.1 Let $\Sigma ^{n}$![]() be a closed minimal submanifold of $\mathbb {S}^{n+p+1},$
be a closed minimal submanifold of $\mathbb {S}^{n+p+1},$![]() $p\geq 0,$
$p\geq 0,$![]() and let $L$
and let $L$![]() be the stability operator acting on the space of normal sections. Then,
be the stability operator acting on the space of normal sections. Then,
where $m(\alpha )= {{n+p+2}\choose {2}}(\alpha - 1)+1$![]() and $C$
and $C$![]() is a lower bound for the Ricci curvature of $\Sigma$
is a lower bound for the Ricci curvature of $\Sigma$![]() .
.
Proof. Let $\{N_1,N_2,\dots, N_k, \dots \}$![]() be an orthonormal basis of the space of normal sections $\Gamma (T\Sigma ^{\perp })$
be an orthonormal basis of the space of normal sections $\Gamma (T\Sigma ^{\perp })$![]() formed by eigensections of $L$
formed by eigensections of $L$![]() , where $N_i$
, where $N_i$![]() is an eigensection associated to $\lambda _i(L)$
is an eigensection associated to $\lambda _i(L)$![]() . Given a positive integer $\alpha$
. Given a positive integer $\alpha$![]() , if $\mathcal {L}_{m}$
, if $\mathcal {L}_{m}$![]() denotes the direct sum of the $m$
denotes the direct sum of the $m$![]() first eigenspaces of $\Delta$
first eigenspaces of $\Delta$![]() , we want to find a non-zero $X \in \Gamma (T\Sigma )$
, we want to find a non-zero $X \in \Gamma (T\Sigma )$![]() such that
such that
for all pairs of parallel vector fields $V$![]() and $W$
and $W$![]() . As $Z$
. As $Z$![]() is a skew symmetric bilinear form on the variables $V$
is a skew symmetric bilinear form on the variables $V$![]() and $W$
and $W$![]() and the space of parallel vector fields of $\mathbb {R}^{n+p+2}$
and the space of parallel vector fields of $\mathbb {R}^{n+p+2}$![]() has dimension equal to $n+p+2$
has dimension equal to $n+p+2$![]() , the problem of finding X is equivalent to the problem of finding a non-zero solution to a homogeneous system with ${{n+p+2}\choose {2}}(\alpha - 1)$
, the problem of finding X is equivalent to the problem of finding a non-zero solution to a homogeneous system with ${{n+p+2}\choose {2}}(\alpha - 1)$![]() equations and $m$
equations and $m$![]() unknown variables. So, $X$
unknown variables. So, $X$![]() satisfying 4.1 exists if
satisfying 4.1 exists if
Thus, under the previous condition, the min-max principle for quadratic forms gives us
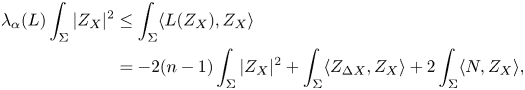
and here and from now on we omit the Riemannian volume element ${\rm d}v_g$![]() on $\Sigma$
on $\Sigma$![]() .
.
Using lemma 3.7 item (b) we get, for $U=\mathbb {S}^{n+p+1}$![]() :
:

where $\{e_1,\cdots, e_n\}$![]() is an orthonormal frame on $\Sigma$
is an orthonormal frame on $\Sigma$![]() . For the last term, we consider $\{\eta _1,\cdots, \eta _{p+1}\}$
. For the last term, we consider $\{\eta _1,\cdots, \eta _{p+1}\}$![]() a local orthonormal frame for $T\Sigma ^{\perp }$
a local orthonormal frame for $T\Sigma ^{\perp }$![]() . Denoting
. Denoting
by $\Omega$![]() , and after a direct computation we have:
, and after a direct computation we have:

and so

On the other hand, we have
and by the Gauss equation and minimality of $\Sigma$![]() we deduce
we deduce
Integrating inequality (4.2) with respect to $(V,W) \in U\times U$![]() and using Fubini theorem we deduce, from the previous equalities, that
and using Fubini theorem we deduce, from the previous equalities, that
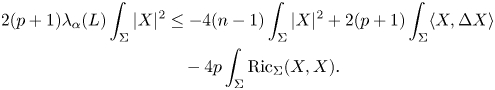
Since $X$![]() is a non-zero vector field in $\mathcal {L}_{m(\alpha )}$
is a non-zero vector field in $\mathcal {L}_{m(\alpha )}$![]() , it verifies the inequality
, it verifies the inequality
and hence we get
Remark 4.2 As we pointed out before, in codimension one case $(p=0)$![]() we do not have geometric constraints on the submanifold, i.e., the lower bound on the Ricci curvature of the submanifold is not necessary.
we do not have geometric constraints on the submanifold, i.e., the lower bound on the Ricci curvature of the submanifold is not necessary.
Following the same arguments used by Savo in [Reference Savo18] and under a suitable hypothesis we are able to prove the following lower bound to the Morse index:
Theorem 4.3 Let $\Sigma ^{n}$![]() be a closed minimal submanifold of $\mathbb {S}^{n+p+1},$
be a closed minimal submanifold of $\mathbb {S}^{n+p+1},$![]() $p\geq 0$
$p\geq 0$![]() , and let $L$
, and let $L$![]() be the stability operator acting on the space of normal sections. If $p\cdot {{\rm {Ric}}}^{}_\Sigma > -(n-1),$
be the stability operator acting on the space of normal sections. If $p\cdot {{\rm {Ric}}}^{}_\Sigma > -(n-1),$![]() then
then
Proof. Taking

where $\lfloor x \rfloor$![]() is the denoting the largest integer which is $\leq$
is the denoting the largest integer which is $\leq$![]() $x$
$x$![]() . By definition, we have $m(\alpha ) \leq b_1(\Sigma )$
. By definition, we have $m(\alpha ) \leq b_1(\Sigma )$![]() and thus, using theorem 4.1, we obtain
and thus, using theorem 4.1, we obtain

and by our hypothesis on the Ricci curvature of $\Sigma$![]() , we get
, we get
Since $\alpha \geq \frac {b_1(\Sigma ) }{{{n+p+2}\choose {2}}}$![]() , follows from the inequality above that
, follows from the inequality above that
So, a direct consequence is the following:
Corollary 4.4 Let $\Sigma ^{n}$![]() be a closed minimal submanifold of $\mathbb {S}^{n+2},$
be a closed minimal submanifold of $\mathbb {S}^{n+2},$![]() and let $L$
and let $L$![]() be the stability operator acting on the space of normal sections. If ${{\rm {Ric}}}^{}_\Sigma > -(n-1),$
be the stability operator acting on the space of normal sections. If ${{\rm {Ric}}}^{}_\Sigma > -(n-1),$![]() then
then
Remark 4.5 It would be interesting to know whether there is a sequence of $n$![]() -dimensional closed minimal submanifolds in the unit sphere with codimension $p$
-dimensional closed minimal submanifolds in the unit sphere with codimension $p$![]() , and $p\cdot {{\rm {Ric}}}_\Sigma >-(n-1)$
, and $p\cdot {{\rm {Ric}}}_\Sigma >-(n-1)$![]() and also unbounded first Betti number. What we already know is that the first Betti's number, under the lower bound of the Ricci curvature, has an upper bound depending on the codimension and the diameter, see [Reference Gromov8, theorem 5.21], which can be large for big values of the diameter.
and also unbounded first Betti number. What we already know is that the first Betti's number, under the lower bound of the Ricci curvature, has an upper bound depending on the codimension and the diameter, see [Reference Gromov8, theorem 5.21], which can be large for big values of the diameter.
Acknowledgments
The authors would like to express their gratitude to Alessandro Savo and Lucas Ambrozio for carefully reading this manuscript and also for their valuable and encouraging comments and suggestions. The authors would also like to thank the referee for providing careful and thoughtful feedback which helped improve this work.
Funding
This work was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brazil [CNPq: grants 303613/2018-1 to M.B.] and [CAPES: Finance code - 001 to both authors].