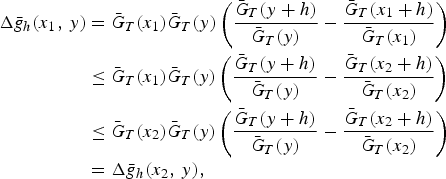1. INTRODUCTION
Aging concepts constitute by far one of the most challenging issues in reliability theory. Thus, the consequences derived from an increasing failure rate (IFR) in maintenance problems have caused many researchers to address their efforts to study this condition. The books of Barlow and Proschan [Reference Barlow and Proschan1,Reference Barlow and Proschan2] are pioneers in this field and have become classical references. In a recent work, Ross, Shanthikumar, and Zhu [Reference Ross, Shanthikumar and Zhu12] also focus on this issue, providing conditions for different types of random variable to be IFR.
Stochastic orders play an essential role in reliability problems to assess how a system deteriorates or not with age. Thus, they can be used to describe notions of aging. Nevertheless, stochastic orders turn out to be a valuable tool in applied probability, with important applications in engineering, economics, and others. Müller and Stoyan [Reference Müller and Stoyan10] as well as Shaked and Shanthikumar [Reference Shaked and Shanthikumar14] provide a comprehensive treatment of stochastic orders. The work of Lai and Xie [Reference Lai and Xie9] is devoted to both stochastic aging and dependence concepts and constitutes a useful reference in reliability engineering.
Lately, researchers are concerned with the reversed hazard rate function in assessing system reliability. This function represents the probability that the maintenance of a system is fulfilled by a given period, providing a measure of its reparability [Reference Sunoj and Maya16]. The works of Block, Savits, and Singh [Reference Block, Savits and Singh4], Finkelstein [Reference Finkelstein8], Chandra and Roy [Reference Chandra and Roy5], among others, deal with this function.
In this work we deal with renewal processes and the number of events occurring before a certain random time, T, independent of the process. We focus on the reliability properties of T which are preserved under the renewal process.
As far as we know, one of the first works dealing with such preservation properties is by Esary, Marshall, and Proschan [Reference Esary, Marshall and Proschan7]. This work is mainly concerned with the preservation of reliability classes under shock models, although Sections 4 and 5 consider preservation properties of the so-called cumulative damage models along with the obvious application to the underlying renewal processes. Moreover, a counterexample proves that T being IFR, does not necessarily imply that N(T) is also IFR. In a recent work, Ross et al. [12 Thm. 3.1.] showed that for a general renewal process under certain stochastic order conditions, if T is IFR so is N(T). This property constitutes the starting point to prove the IFR property for random variables arising under different stochastic models. The particular case of mixed Poisson models, which has attracted much of researchers' attention, should also be mentioned (Grandell [Reference Grandell6, Chap. 7], and the references therein). Thus, it is known that these models preserve the classical reliability classes of T (Vinogradov [Reference Vinogradov17] and Block and Savits [Reference Block and Savits3]).
This work aims at analyzing the preservation of reliability classes under mixtures of renewal processes. Previous works focus on the failure rate and positive aging (Esary et al. [Reference Esary, Marshall and Proschan7]); however, negative aging and the reversed hazard rate are now subject to more attention. Ross et al. [Reference Ross, Shanthikumar and Zhu12] provided some results related to the reversed hazard ratio ordering in renewal processes and Markov chains. Following Ross et al. [Reference Ross, Shanthikumar and Zhu12] and the stochastic orders theory, we obtain reliability classes that are preserved when the renewal times verify appropriate ordering conditions.
The article is organized as follows. Section 2 contains definitions and results on aging classes to be used throughout the article; new results are stated in Sections 3 and 4. Thus, in Section 3 is shown that both properties—the logconvexity and the decreasing failure rate (DFR)—are, in general, preserved. Section 4 deals with the preservation of reliability classes when certain order conditions for the renewal periods are imposed. In particular, if such periods are ordered in the likelihood ratio order, both properties—the increasing and decreasing failure rate average (IFRA and DFRA, respectively)—are preserved. We also give some insight into the preservation of the IFR property when the renewal periods are ordered in the reversed hazard rate order (Ross et al. [Reference Ross, Shanthikumar and Zhu12]), providing a different proof for the particular case of a renewal process. Then, we carry out a similar study on the preservation of the decreasing reversed hazard rate (DRHR), provided that the renewal times are ordered in the hazard rate order.
2. PRELIMINARIES
This section contains a list of definitions (Barlow and Proschan [Reference Barlow and Proschan2]) used in the article to simplify its reading. The terms “increasing” and “decreasing” mean, as usual, “nondecreasing” and “nonincreasing,” respectively.
Definition 2.1
Let X be a nonnegative random variable with G and G¯ the corresponding distribution and reliability functions, respectively. G is said to be
(i) logconcave if G has a density g such that log g is concave, that is,
(ii) increasing failure rate if
(iii) increasing failure rate average if [G¯(t)]1/tis decreasing in t > 0.
(iv) New better than used (NBU) if
The following implications hold among the foregoing classes:
Further classes can be defined by reversing the direction of monotonicity and the appropriate change in the signs of inequalities. These properties are (i)′ logconvex, (ii)′ decreasing failure rate, (iii)′ decreasing failure rate average, and (iv)′ new worse than used (NWU).
Remark 2.2
IFR distributions can show a jump only at the right-hand end of its interval, whereas DFR distributions show a jump only at the origin [1, p. 26]. We will assume that a constant nonnegative random variable belongs to the IFR class to be coherent with Definition 2.1 and Theorem 4.7(i).
There exist different ways of defining the corresponding counterparts of the preceding classes for discrete random variables (cf. Lai and Xie [Reference Lai and Xie9]). We will follow the definitions usually considered in renewal processes (Esary et al. [Reference Esary, Marshall and Proschan7] or Grandell [Reference Grandell6, Chap. 7]).
Definition 2.3
Let X be a nonnegative integer-valued random variable and p nits corresponding probability mass function
The distribution function is said to be
(i) discrete logconcave if the probability mass function satisfies
(ii) Discrete increasing failure rate (d-IFR) if P(X = n)/P(X ≥ n) is increasing in n or, equivalently, if
(iii) Discrete increasing failure rate average (d-IFRA) if [P(X ≥n)1/nis decreasing in n = 1, 2, … .
(iv) Discrete new better than used (d-NBU) if
As in the previous case, no other implications apart from the following ones hold: 
.
As earlier, the corresponding discrete classes reversing the direction of monotonicity and the signs of the inequalities are also defined.
Additional classes concerning the reversed hazard rate are presented next. This function exhibits a more recent use in reliability analysis and turns out to be more natural when the timescale is reversed (Shaked and Shanthikumar [Reference Shaked and Shanthikumar14], Block et al. [Reference Block, Savits and Singh4], Sengupta and Nanda [Reference Sengupta and Nanda13], and Nanda and Sengupta [Reference Nanda and Sengupta11]).
Definition 2.4
A distribution function G is said to be decreasing reversed hazard rate if log G is concave, namely if G(z + t)/G(t) is decreasing in t for all z > 0.
Remark 2.5
Note that in the case that G has no density, Definition 2.4 is still valid although the reversed hazard rate cannot be defined (Sengupta and Nanda [Reference Sengupta and Nanda13]). In addition, a DRHR random variable is absolutely continuous except, at most, at the left end point of its interval of support [13, p. 427]. As in the IFR case, we assume that a nonnegative constant random variable is DRHR, which turns out to be coherent with the proof of Theorem 4.7(ii). Observe that there is no nonnegative random variable having an IRHR distribution. If a reversed hazard rate is increasing, its interval of support must have a finite upper point.
Next, the concept of discrete reversed hazard rate is presented (Nanda and Sengupta [Reference Nanda and Sengupta11]).
Definition 2.6
Let X be a nonnegative integer-valued random variable with distribution function G. X is said to have discrete decreasing reversed hazard rate if
This is equivalent to the following two statements: G(n)/G(n + 1) is increasing in n, or
The next section is devoted to reliability classes preserved under renewal processes when general conditions are assumed.
3. PRESERVATION OF RELIABILITY PROPERTIES UNDER RENEWAL PROCESSES
Consider now a renewal process {N(t) : t ≥ 0}, with (S n)n=1, 2, … being the time of the nth event; that is,
(X n)n=1,2,… constitute a set of independent and identically distributed nonnegative random variables with common distribution function F. In what follows, we assume that the interarrival times cannot be concentrated at zero. Thus, P(X n = 0) < 1, n = 1, 2, ….
N(t) represents the number of events by time t; therefore,
In addition, let T be a nonnegative random variable, independent of (X n)n=1,2,…, with G T and G¯T being the corresponding distribution and reliability functions, respectively. For technical purposes we assume that G T has no common discontinuity points with the distribution functions corresponding to (S n)n=1,2,…. Hence, it can be proved that (see Esary et al. [7, p. 642])
and, therefore,
Esary et al. [Reference Esary, Marshall and Proschan7] analyzed the preservation of reliability classes for a system subject to shocks with immediate applications to renewal processes. In particular, these authors show that N(t) is IFRA for all t > 0 [7, Lemma 4.1]. Moreover, it is also proved, by means of a counterexample, that is not possible for N(t) to be IFR without strengthening the hypotheses [7, Example 4.6].
In the case of T being IFR or logconcave, N(T) does not necessarily preserve such properties [7, p. 645]. However, the following results show that when the direction of the monotonicity is reversed, N(T) inherits some aging properties of T in particular, the logconvexity and the DFR condition.
Theorem 3.1
Consider T a random variable with density g Tindependent of (S n)n=1, 2,…. If T is logconvex, then N(T) is discrete logconvex.
Proof
Recall first that (0, ∞) is the interval of support for logconvex distributions [2, p. 79, Exercise 11]. Let X 1, X 2, … , X n, 
, 
, … 
, U, V, X, and Y be independent, identically distributed random variables with common distribution F. Let S n be as in (2) and define 
:= ∑i=1n
. From (5), it follows that for all n = 0, 1, … ,
![P\lpar N\lpar T\rpar =n\rpar = E \lsqb G_T \lpar S_n +X\rpar - G_T \lpar S_n \rpar \rsqb = E \left[\vint_0^X g_T \lpar x+S_n\rpar \; dx \right]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn6.gif?pub-status=live){kind=small}
as well as
![\eqalign{P\lpar N\lpar T\rpar =n+1\rpar ^2=E \Bigg[\vint_0^X \vint_0^Y g_{T} \lpar x+S_n +U\rpar \, g_T \lpar\, y+ S_n^{\ast} + V \rpar \; dx\; dy\Bigg].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn7.gif?pub-status=live)
Note that
In the above expressions, consider that U/(U + V) := V/(U + V) := 1/2 if U = V = 0.
Applying the logconvexity of g T first and then the inequality z αw 1−α ≤ αz + (1 − α)w, z, w ≥ 0 and 0 ≤ α ≤ 1, we have that for all x ≥ 0 and y ≥ 0,
Next, calculations aim at obtaining a bound for the expression in (7). By first taking the conditional expectation with respect to S n, 
, X, Y, and U + V and using the foregoing inequality, we get
![\eqalign{E & \left[\vint_0^X \vint_0^Y g_T \lpar x+S_n +U\rpar g_T \lpar y+ S_n^{\,\ast} + V \rpar \ dx\; dy\, \vert\, S_n\comma\; S_n^{\,\ast}\comma\; X\comma\; Y\comma\; U+V \right]\cr & \quad \le E \left[{V \over U+V} \vert U+V \right]\vint_0^X \vint_0^Y g_T\, \lpar x+S_n\rpar g_T\, \lpar \,y+S_n^{\,\ast} + U + V \rpar \; dx\; dy\cr & \quad +E \left[{U \over U+V} \vert U+V \right]\vint_0^X \vint_0^Y g_T \,\lpar y+S_n^{\,\ast} \rpar g_T\, \lpar x+ S_n + U + V \rpar \; dx\; dy\cr & = {1 \over 2} \vint_0^X \vint_0^Y g_T\, \lpar x+S_n\rpar g_T\, \lpar \,y+ S_n^{\,\ast} + U + V \rpar \; dx\; dy \cr & +{1 \over 2} \vint_0^X \vint_0^Y g_T\, \lpar\, y+S_n^{\ast} \rpar g_T \,\lpar x+ S_n + U + V \rpar \; dx\; dy. }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU12.gif?pub-status=live)
Next, note that both summands in the last expression are identically distributed, so taking expectations in the previous inequality leads to
![\eqalign {E & \left[\vint_0^X \vint_0^Y g_T \lpar x+S_n +U\rpar g_T \lpar \, y+ S_n^{\ast} + V \rpar \; dx\; dy \right]\cr & \le E\left[\vint_0^X g_T \lpar x+S_n\rpar\ dx\right]E\left[\vint_0^Y g_T \lpar \,y+ S_n^{\ast} + U + V \rpar \; dy\right]. }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU13.gif?pub-status=live)
Expressions in (6) and (7) yield
and the result in Theorem 3.1 holds.■
The following result is concerned with the DFR property.
Theorem 3.2
Let N(t) be a renewal process, as defined in ( 3), and T a random variable independent from (Sn)n=1,2,…given in ( 2). Consider that the distribution function of T has no common discontinuity points with the distribution functions corresponding to (Sn)n=1,2,…. If T is DFR, then N(T) is d-DFR.
Proof
The assertion follows by induction on n. From (4), it follows that N(T) is d-DFR if and only if for all n = 0, 1, … , the following inequality is satisfied:
For n = 0, the above inequality follows immediately from the fact that T being DFR implies that T is also NWU and, therefore,
Taking expectations, both the independence and the identical distribution assumptions yield (8).
Hence, assume that (8) holds for n. Take b := sup{x ≥ 0 : G¯T(x) > 0}. Then
Note that G¯T(· + x)/G¯T(x) is a DFR distribution for all 0 ≤ x < b. Using first the induction hypothesis and then the Cauchy-Schwartz inequality, it follows that
Therefore, the result in (8) also holds for n + 1 and the proof of Theorem 3.2 is complete.■
4. PRESERVATION OF RELIABILITY CLASSES UNDER SOME ORDER CONDITIONS OF THE RENEWAL PERIODS
Regarding the IFRA property, Esary et al. [7, p. 643] showed that T being IFR implies that N(T) is IFRA. As far as we know, the question of whether N(T) is IFRA provided that T is also IFRA remains open. It is shown in Theorem 4.3 that this property holds if (S n)n=1,2,… are ordered in the likelihood ratio order.
Next, we recall the following definition of the likelihood ratio order (Müller and Stoyan [10, p. 12]) or Shaked and Shanthikumar [14, p. 27]), so that our results hold either in continuous, discrete, or more general conditions of the arrival times.
Definition 4.1
Let X and Y be two absolutely continuous random variables with respect to some dominating measure μ, with f Xand f Yits respective density functions. X is said to be smaller than Y in the likelihood ratio order (denoted X ≤lrY) if
(a/0 is assumed to be ∞ if a > 0). A sequence of random variables (S n)n=1,2,…is said to be increasing in the likelihood ratio order if S n ≤lrS n+1for all n = 1, 2, … .
Note that in the foregoing definition, the absolutely continuous case is obtained provided that μ is the Lebesgue measure, whereas the discrete case turns out by taking μ as the counting measure on the nonnegative integers.
Remark 4.2
From the previous definition it follows that if X ≤lrY, then for any t 0 that is not in the support of X and that is less than the supremum of the support of X, it follows that t 0 is not in the support of Y. This fact will be used in proof of the following theorem.
Theorem 4.3
Let N(t) be a renewal process as in (3) and (S n)n=1,2,…an increasing sequence in the likelihood ratio order. Consider T a random variable, independent of (S n)n=1,2,…and assume that the distribution function of T has no common discontinuity points with the distribution functions corresponding to (S n)n=1,2,…. If T is IFRA (DFRA), then N(T) is d-IFRA (d-DFRA).
Proof
Let us consider the IFRA case. According to the definition, we will prove that
From now on, we will assume that 0 < P(N(T) ≥ n) < 1 because condition (9) is trivially verified otherwise. Let 0 < λn < ∞ be such that
implying that
![E \left[{\it \bar {G}}_T\lpar S_n\rpar \right]=P\lpar N\lpar T\rpar \ge n \rpar =E\lpar e^{-\lambda_{n}S_{n}}\rpar](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn11.gif?pub-status=live){kind=small}
and, therefore,
![E \left[{\it \bar{G}}_T\lpar S_n\rpar -e^{-\lambda_{n}S_{n}}\right]=0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn12.gif?pub-status=live){kind=small}
Next, it is shown that
![E \left[{\it \bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\right]\le 0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn13.gif?pub-status=live){kind=small}
Recall that T being IFRA implies that −log G¯T is star-shaped. G¯T and e −λx change sign at most once on (0, ∞) and from + to − if this happens [2, p. 89]. Therefore, there exist some t 0 ≥ 0 such that
Note that t 0 = 0 (resp. t 0 = ∞) means that G¯T (x) ≤ e −λnx, x > 0 (resp. G¯T (x) > e −λnx, x > 0). Observe first that (12) implies that S n cannot be concentrated at [0, t 0). The preliminary hypotheses showed that the interarrival times cannot be concentrated at zero, so P(S n = 0) < 1. Assume that P(0 < S n < t 0) = 1 − P(S n = 0) and denote by f *n the density function of S n. Thus,
![E\left[{\bar {G}}_T\lpar S_n\rpar -e^{-\lambda_{n}S_{n}}\right]=\vint_{\lpar 0\comma t_{0}\rpar }\lpar {\bar {G}}_T\lpar x\rpar -e^{-\lambda_{n}x}\rpar f^{\ast n}\lpar x\rpar \; d\!\mu\lpar x\rpar \gt 0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU20.gif?pub-status=live){kind=small}
The last integral concerns a strictly positive function over a set of strictly positive probability; hence, the last inequality holds, contradicting (12). Therefore, P(S n ≥ t 0) > 0. Now define
Denote by 1A(·) the indicator function of the set A and by A c its complementary. Since s n ≥ t 0, then G¯T (x) − e −λnx ≤ 0, x ≥ s n, and, therefore,
![E \left[\lpar {\bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\rpar 1_{\lsqb s_{n}\comma \infty\rpar {\bigcap} A_{n}^{c} }\lpar S_{n+1}\rpar \right]\le 0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn14.gif?pub-status=live){kind=small}
On the other hand, taking into account Remark 4.2, we also have
![E \left[\lpar {\bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\rpar 1_{\lsqb 0\comma s_{n}\rpar {\bigcap} A_{n}^{c} }\lpar S_{n+1}\rpar \right]=0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn15.gif?pub-status=live){kind=small}
From (14) and (15) we deduce that
![\eqalignno{E & \left [{\bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\right] \cr & \quad\le E \left[\lpar {\bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\rpar 1_{ A_{n}}\lpar S_{n+1}\rpar \right] \cr & \quad =\vint_{A_{n}}\lpar {\bar {G}}_T\lpar x\rpar -e^{-\lambda_{n}x}\rpar {f^{{\ast}\lpar n+1\rpar }\lpar x\rpar \over f^{{\ast} n}\lpar x\rpar }f^{{\ast} n}\lpar x\rpar \; d\mu\lpar x\rpar \cr & \quad=E \left[\lpar {\bar {G}}_T\lpar S_{n}\rpar -e^{-\lambda_{n}S_{n}}\rpar {f^{{\ast}\lpar n+1\rpar }\lpar S_n\rpar \over f^{{\ast} n}\lpar S_n\rpar }\right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn16.gif?pub-status=live)
Since (S n)n=1,2,… are ordered in the likelihood ratio order, then 
is an increasing function on A n. Set t 0′ := inf{x ≥ t 0 : f *n(x) > 0}. If t′0 ∉ A n, then define
From (12) and (16) along with the fact that 
is an increasing function, we get
![\eqalign{E & \left [{\bar {G}}_T\lpar S_{n+1}\rpar -e^{-\lambda_{n}S_{n+1}}\right]\cr & \qquad \le E \left[\lpar {\bar {G}}_T\lpar S_{n}\rpar -e^{-\lambda_{n}S_{n}}\rpar {f^{\ast\lpar {n}+1\rpar }\lpar S_n\rpar \over f^{\ast {n}}\lpar S_n\rpar }\right]\cr & \qquad =E \left[\lpar {\bar {G}}_T\lpar S_{n}\rpar -e^{-\lambda_{n}S_{n}}\rpar \left({f^{\ast\lpar {n}+1\rpar }\lpar S_n\rpar \over f^{\ast {n}}\lpar S_n\rpar }-{f^{\ast\lpar {n}+1\rpar }\lpar t_{0}^\prime\rpar \over f^{\ast {n}}\lpar t_{0}^\prime\rpar }\right)\right]\le 0.}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU23.gif?pub-status=live)
The two factors inside the expectation always have opposite signs; hence, the last inequality holds and, thus, the proof of (13) is completed. Finally, (10) and (13) lead to
![P\lpar N\lpar T\rpar \ge n+1 \rpar =E \left[{\bar {G}}_T\lpar S_{n+1}\rpar \right]\le E\left(e^{-\lambda_{n}S_{n+1}}\right)=P\lpar N\lpar T\rpar \ge n \rpar ^{(n+1)/n}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU24.gif?pub-status=live){kind=small}
and the d-IFRA property is shown. An analogous proof can be carried out for the d-DFRA case by reversing the signs of inequalities.■
Remark 4.4
Theorem 4.3 includes the mixed Poisson model as a particular case. Since in this case the interarrival times (X n)n=1,2,… are exponential random variables that have logconcave density functions, Theorem 1.C.5 in Shaked and Shanthikumar [14, p. 30] yields
This section is also concerned with the preservation of the IFR property. Being more precise, we prove that if (S n)n=1,2,… are ordered in the reversed hazard rate order, then T being IFR implies that N(T) is also IFR. It should be pointed out that this result follows from Theorem 3.1. in Ross et al. [Reference Ross, Shanthikumar and Zhu12], who showed this property for a more general definition of renewal process than that considered in (3). Dealing with this particular case, we make use of the general definition for T being IFR (see Remark 2.2), as well as the general definitions for both the hazard rate and reversed hazard rate order (see Definition 4.5). A similar approach lead us to prove that if (S n)n=1,2,… are ordered in the hazard rate order and T is DRHR, then N(T) is also DRHR.
First, we recall the definitions of both the hazard rate order and the reversed hazard rate order.
Definition 4.5
Let X and Y be two random variables with distribution functions F X and F Yand survival functions F¯Xand F¯Y, respectively.
(i) X is said to be smaller than Y with respect to the hazard rate order (X ≤hrY) if
for t in the union of the intervals of support of X and Y.(ii) X is said to be smaller than Y with respect to the reversed hazard rate order (X ≤rhY) if
for t in the union of the intervals of support of X and Y.
A sequence of random variables (S n)n=1,2,…is said to be increasing with respect to the hazard rate order (resp. the reversed hazard rate order) if S n ≤hrS n+1(resp. S n≤rhS n+1) for all n = 1, 2, … .
Regarding the previous orders, we will make use of the characterization below [Reference Müller and Stoyan10]. Part (i) is due to Shanthikumar and Yao [Reference Shanthikumar and Yao15].
Theorem 1.9.3 (Müller and Stoyen [10, p. 53])
(i) X ≤hrY if and only if
for all g:ℝ2 → ℝ such that Δg(x, y) := g(x, y) − g(y, x) is increasing in x for all x ≥ y with X *and Y *being independent with X * =st X and Y * =stY (=stdenotes identical distribution).(ii) X ≤rhY if and only if
for g:ℝ2 → ℝ such that Δg(x, y) := g(x, y) − g(y, x) is increasing in x for all x ≤ y with X *and Y *being independent with X * =stX and Y * =stY.
The following lemma aims at providing technical aid to prove the preservation of both IFR and DRHR properties.
Lemma 4.6
Let T be a nonnegative random variable with survival function G¯Tand h ≥ 0.
(i) Define the function
(18)and assume that T is IFR; thenis increasing in x for x ≤ y.(ii) Define the function
(19)and assume that T is DRHR; thenis increasing in x for x ≥ y.
Proof
(i) Set h ≥ 0 and y ∈ ℝ. It has to be shown that
(20)If G¯T (y) = 0, then (20) holds since G¯T(y + h) ≤ G¯T (y) = 0 and, hence, Δg¯h (x 1, y) = 0 = Δg¯h (x 2, y). Assume that G¯T (y) > 0; then G¯T (x 1) ≥ G¯T (x 2) ≥ G¯T (y) > 0. Since T is IFR from part (ii) in Definition 2.1, it follows thatThen, by taking into account the above inequalities, it can be stated thatthus showing (20).
A similar approach leads to the proof of part (ii), replacing the survival function by the distribution function and using Definition (2.4).■
The next assertions refer to the preservation of the IFR and DRHR properties.
Theorem 4.7
Let N(t) be a renewal process as in (3) and T a random variable, independent of (S n)n=1,2,…. Consider that the distribution function of T and the corresponding (S n)n=1,2,…have no common discontinuity points. The following statements hold:
(i) T being IFR implies that N(T) is also IFR, provided that (S n)n=1,2,…are increasing in the reversed hazard rate order.
(ii) T being DRHR implies that N(T) is also DRHR, provided that (S n)n=1,2,…are increasing in the hazard rate order.
Proof
(i) Let h ≥ 0 and y ∈ ℝ. Consider g¯h(x, y) as in (18). Since T is IFR, part (i) in Lemma 4.6 yields
Consider S n+1* a random variable identically distributed to S n+1 and independent of the initial interarrival times. Since S n ≤rhS n+1, from part (ii) in Theorem 1.9.3, it follows thatfurther implyingBy using the foregoing expression with h := X n+1 and taking expectations with respect to h, it can also be written that(21)As the interarrival times are identically distributed, then S n+2* =stS n+1* + X n+1. Then(22)From (4), (21), and (22) we deduce thatthus concluding that N(T) is IFR.(ii) A similar proof yields the result in this part. Let h ≥ 0 and y ∈ ℝ. Consider g h(x, y) as in (19). Since T is DRHR, from part (ii) in Lemma 4.6, it follows that
Consider S n+1* a random variable identically distributed to S n+1 and independent of the initial interarrival times. Since S n ≤hrS n+1, from part (i) in Theorem 1.9.3,is derived and, as in the proof of part (i), we obtain(23)As S n+2* =stS n+1* + X n+1, we also have(24)Then, (5), (23), and (24) lead tothus implying that N(T) is the discrete decreasing reversed hazard rate [following the formula in (1)].■
![E\left[{\it \bar{g}}_h\lpar S_{n}\comma\, S_{n+1}^{\,\ast}\rpar \right]\le E\left[{\it \bar{g}}_h\lpar S_{n+1}^{\,\ast}\comma\; S_{n}\rpar \right]\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU34.gif?pub-status=live){kind=small}
![E\left[{\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+1}^{\ast}+h\rpar \right] \le E [{\it \bar{G}}_T\lpar S_{n+1}^{\ast} \rpar {\it \bar{G}}_T\lpar S_{n} + h\rpar ]\comma \qquad h\ge 0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU35.gif?pub-status=live){kind=small}
![E\left[{\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+1}^{\ast}+X_{n+1}\rpar \right]\le E\left[{\it \bar{G}}_T\lpar S_{n+1}^{\ast}\rpar {\it \bar{G}}_T\lpar S_{n}+X_{n+1}\rpar \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn21.gif?pub-status=live){kind=small}
![E\lsqb {\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+2}^{\ast}\rpar \rsqb =E\left[{\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+1}^{\ast}+X_{n+1}\rpar \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqn22.gif?pub-status=live){kind=small}
Remark 4.8
The proof of Theorem 4.7 can be easily extended to the case of renewal processes with interarrival times X n independent but not necessarily identically distributed. However, for the IFR property, we need the additional assumption that
whereas for the DRHR property, we need that
As both proofs follow a parallel treatment, we focus our attention on the IFR property. The proof of part (i) would be the same up to (21). We need condition (25), as it ensures us that S *n+1 + X n+1 ≤stS *n+2 and then we can replace (22) by
![E\lsqb {\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+2}^{\ast}\rpar \rsqb \le E\left[{\it \bar{G}}_T\lpar S_{n}\rpar {\it \bar{G}}_T\lpar S_{n+1}^{\ast}+X_{n+1}\rpar \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022131819267-0421:S0269964808000016_eqnU41.gif?pub-status=live){kind=small}
Afterward, the proof remains the same. Note that (25) is equivalent to condition (c) in Theorem 3.1 in Ross et al. [Reference Ross, Shanthikumar and Zhu12] for the case of independent interarrival times.
In fact, if (25) is not verified, the preservation of the IFR property is not guaranteed. Take, for instance, T a uniform random variable on (0, 1) (which, according to Definition 2.1(i) is an IFR random variable) and take constant interarrival times X 1 = 1/4 and X 2 = 1/8. Clearly, 1/4 = S 1 ≤hrS 2 = 3/8. Moreover, we deduce from (4) that
In this case,
and, therefore, N(T) is not an IFR random variable, as Definition 2.3(ii) is not satisfied for n = 0.
Remark 4.9
Recall that the hazard rate and the reversed hazard rate orders are weaker conditions than the likelihood ratio order. Therefore, taking into account (17), it follows that the renewal periods of a Poisson process, (S n)n=1,2,…, are increasing in both the hazard rate order and the reversed hazard rate order. Thus, the preservation of the IFR property (Vinogradov [Reference Vinogradov17]) and the DRHR property for a mixed Poisson model can be respectively deduced as a consequence of parts (i) and (ii) in Theorem 4.7.
The next corollary is immediately derived from Theorem 4.7.
Corollary 4.10
Let {N(t) : t ≥ 0} be a renewal process as in (3).
(i) If (S n)n=1,2,…are increasing in the reversed hazard rate order, then, for each t > 0, N(t) is IFR.
(ii) If (S n)n=1,2,…, are increasing in the hazard rate order, then, for each t > 0, N (t) is DRHR.
Proof
(i) For every t > 0, the constant random variable t is IFR (see Remark 2.2). As a consequence of part (i) in Theorem 4.7, if (S n)n=1,2,… is increasing in the reversed hazard rate order, then N(t) is IFR, provided that t does not belong to the set of discontinuity points of (S n)n=1,2,…, thus showing (i) in this case. Nevertheless, observe that the discontinuity points of (S n)n=1,2,… constitute a numerable set. Then if t is a discontinuity point of (S n)n=1,2,…, we can take a decreasing sequence of nonnegative numbers (t k)k=1,2,… such that t k ↓ t, with t k not belonging to the set of discontinuity points of (S n)n=1,2,…. Since for each k = 1, 2, … , N(t k) satisfy the IFR property, it can be written that
that isThus, by taking limits in the expression above the discrete IFR property for N(t) is deduced and, hence, part (i) is completed.(ii) The proof is shown by similar means.■
Corollary 4.10 provides an extension for some well-known results concerning the duality in the relationship of N(t) and the distribution function of interarrival times. This is pointed out in the next remark.
Remark 4.11
Sengupta and Nanda [13, Thm. 6] showed that if (X n)n=1,2,… are IFR (resp. DRHR), then N(t) is DRHR (resp. IFR) for each t > 0. Note that this is a particular case of Corollary 4.10 since if (X n)n=1,2,… are IFR (resp. DRHR), from Theorem 1.C.8 in Shaked in Shanthikumar [Reference Shaked and Shanthikumar14], it can be deduced that
Acknowledgments
We want to express our gratitude to Lola Berrade for valuable discussion and inestimable help in writing this manuscript and also to an anonymous referee for helpful comments. This research has been supported by grant 2006-CIE-03 of the University of Zaragoza. The authors acknowledge support of DGA S11 (FGB) and E64 (CS), respectively.
