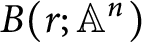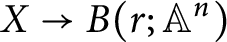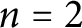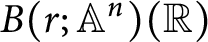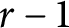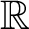1 Introduction
Given a topological group G, one may form the classifying space, well-defined up to homotopy equivalence, as the base space of any numerable principal G-bundle
![]() $EG \to BG$
where the total space is contractible, [Reference Dold3, Theorem 7.5]. The space
$EG \to BG$
where the total space is contractible, [Reference Dold3, Theorem 7.5]. The space
![]() $BG$
is a universal space for G-bundles, in that the set of homotopy classes of maps
$BG$
is a universal space for G-bundles, in that the set of homotopy classes of maps
![]() $[X, BG]$
is in natural bijection with the set of numerable principal G-bundles on X.
$[X, BG]$
is in natural bijection with the set of numerable principal G-bundles on X.
If G is a finite nontrivial group, then
![]() $BG$
is necessarily infinite dimensional, [Reference Swan20], and so there is no hope of producing
$BG$
is necessarily infinite dimensional, [Reference Swan20], and so there is no hope of producing
![]() $BG$
as a variety even over
$BG$
as a variety even over
![]() ${\mathbb {C}}$
. Nonetheless, as in [Reference Totaro22], one can approximate
${\mathbb {C}}$
. Nonetheless, as in [Reference Totaro22], one can approximate
![]() $BG$
by taking a large representation V of G on which G acts freely outside of a high-codimension closed set Z, and such that
$BG$
by taking a large representation V of G on which G acts freely outside of a high-codimension closed set Z, and such that
![]() $(V-Z)/G$
is defined as a quasiprojective scheme. The higher the codimension of Z in V, the better an approximation
$(V-Z)/G$
is defined as a quasiprojective scheme. The higher the codimension of Z in V, the better an approximation
![]() $(V-Z)/G$
is to the notional
$(V-Z)/G$
is to the notional
![]() $BG$
.
$BG$
.
In this paper, we consider the case of
![]() $G=S_n$
, the symmetric group on n letters. The representations we consider as our Vs are the most obvious ones, r copies of the permutation representation of
$G=S_n$
, the symmetric group on n letters. The representations we consider as our Vs are the most obvious ones, r copies of the permutation representation of
![]() $S_n$
on
$S_n$
on
![]() ${\mathbb {A}}^n$
. The closed loci we consider are minimal: the loci where the action is not free. We use the language of étale algebras to give an interpretation of the resulting spaces. Our main result, Theorem 3.13, says that the scheme
${\mathbb {A}}^n$
. The closed loci we consider are minimal: the loci where the action is not free. We use the language of étale algebras to give an interpretation of the resulting spaces. Our main result, Theorem 3.13, says that the scheme
![]() $B(r; {\mathbb {A}}^n):=(V-Z)/S_n$
produced by this machine represents “étale algebras equipped with r generating global sections” up to isomorphism of these data. The schemes
$B(r; {\mathbb {A}}^n):=(V-Z)/S_n$
produced by this machine represents “étale algebras equipped with r generating global sections” up to isomorphism of these data. The schemes
![]() $B(r; {\mathbb {A}}^n)$
are therefore in the same relation to the group
$B(r; {\mathbb {A}}^n)$
are therefore in the same relation to the group
![]() $S_n$
as the projective spaces
$S_n$
as the projective spaces
![]() ${\mathbb {P}}^r$
are to the group scheme
${\mathbb {P}}^r$
are to the group scheme
![]() ${\mathbb {G}_{m}}$
.
${\mathbb {G}_{m}}$
.
Section 2 is concerned with preliminary results on generation of étale algebras. The main construction of the paper, that of
![]() $B(r; {\mathbb {A}}^n)$
, is made in Section 3, and the functor it represents is described. Since we are working with schemes, and not in a homotopy category, the space
$B(r; {\mathbb {A}}^n)$
, is made in Section 3, and the functor it represents is described. Since we are working with schemes, and not in a homotopy category, the space
![]() $B(r; {\mathbb {A}}^n)$
does not classify bundles; rather it represents a functor of “bundles along with chosen generators”, which we now explain.
$B(r; {\mathbb {A}}^n)$
does not classify bundles; rather it represents a functor of “bundles along with chosen generators”, which we now explain.
A choice of r global sections generating an étale algebra
![]() ${\mathcal {A}}$
of degree n on a scheme X corresponds to a map
${\mathcal {A}}$
of degree n on a scheme X corresponds to a map
![]() $\phi : X \to B(r; {\mathbb {A}}^n)$
. While the map
$\phi : X \to B(r; {\mathbb {A}}^n)$
. While the map
![]() $\phi $
is dependent on the chosen generating sections, we show in Section 4 that if one is prepared to pass to a limit, in a sense made precise there, the
$\phi $
is dependent on the chosen generating sections, we show in Section 4 that if one is prepared to pass to a limit, in a sense made precise there, the
![]() ${\mathbb {A}^{1}}$
-homotopy class of a composite
${\mathbb {A}^{1}}$
-homotopy class of a composite
![]() $\tilde \phi : X \to B(r; {\mathbb {A}}^n) \to B(\infty ; {\mathbb {A}}^n)$
depends only on the isomorphism class of
$\tilde \phi : X \to B(r; {\mathbb {A}}^n) \to B(\infty ; {\mathbb {A}}^n)$
depends only on the isomorphism class of
![]() ${\mathcal {A}}$
and not the generators. As a practical matter, this means that for a wide range of cohomology theories,
${\mathcal {A}}$
and not the generators. As a practical matter, this means that for a wide range of cohomology theories,
![]() $E^*$
, the map
$E^*$
, the map
![]() $E^*(\tilde \phi )$
depends only on
$E^*(\tilde \phi )$
depends only on
![]() ${\mathcal {A}}$
and not on the generators used to define it.
${\mathcal {A}}$
and not on the generators used to define it.
In Section 5, working over a field, we observe that the motivic cohomology, and therefore the Chow groups, of the varieties
![]() $B(r; {\mathbb {A}}^2)$
has already been calculated in [Reference Dugger and Isaksen4].
$B(r; {\mathbb {A}}^2)$
has already been calculated in [Reference Dugger and Isaksen4].
A degree-2 or quadratic étale algebra
![]() ${\mathcal {A}}$
over a ring R carries an involution
${\mathcal {A}}$
over a ring R carries an involution
![]() $\sigma $
and a trace map
$\sigma $
and a trace map
![]() ${Tr}: {\mathcal {A}} \to R$
. There is a close connection between
${Tr}: {\mathcal {A}} \to R$
. There is a close connection between
![]() ${\mathcal {A}}$
and the rank-
${\mathcal {A}}$
and the rank-
![]() $1$
projective module
$1$
projective module
![]() ${\mathcal {L}} = \ker ({Tr})$
. In Section 6, we show that the algebra
${\mathcal {L}} = \ker ({Tr})$
. In Section 6, we show that the algebra
![]() ${\mathcal {A}}$
can be generated by r elements if and only if the projective module
${\mathcal {A}}$
can be generated by r elements if and only if the projective module
![]() ${\mathcal {L}}$
can be generated by r elements.
${\mathcal {L}}$
can be generated by r elements.
A famous counterexample of S. Chase, appearing in [Reference Swan21], shows that there is a smooth affine
![]() $r-1$
-dimensional
$r-1$
-dimensional
![]() ${\mathbb {R}}$
-variety
${\mathbb {R}}$
-variety
![]() $\operatorname {\mathrm {Spec}} R$
and a line bundle
$\operatorname {\mathrm {Spec}} R$
and a line bundle
![]() ${\mathcal {L}}$
on
${\mathcal {L}}$
on
![]() $\operatorname {\mathrm {Spec}} R$
requiring r global sections to generate. This shows a that a bound of O. Forster [Reference Forster8] on the minimal number of sections required to generate a line bundle on
$\operatorname {\mathrm {Spec}} R$
requiring r global sections to generate. This shows a that a bound of O. Forster [Reference Forster8] on the minimal number of sections required to generate a line bundle on
![]() $\operatorname {\mathrm {Spec}} R$
, namely
$\operatorname {\mathrm {Spec}} R$
, namely
![]() $\dim\; R +1$
, is sharp. In light of Section 6, the same smooth affine
$\dim\; R +1$
, is sharp. In light of Section 6, the same smooth affine
![]() ${\mathbb {R}}$
-variety of dimension
${\mathbb {R}}$
-variety of dimension
![]() $r-1$
can be used to produce étale algebras
$r-1$
can be used to produce étale algebras
![]() ${\mathcal {A}}$
, of arbitrary degree n, requiring r global sections to generate. This fact was observed independently by M. Ojanguren. It shows that a bound established by U. First and Z. Reichstein in [Reference First and Reichstein6] is sharp in the case of étale algebras: they can always be generated by
${\mathcal {A}}$
, of arbitrary degree n, requiring r global sections to generate. This fact was observed independently by M. Ojanguren. It shows that a bound established by U. First and Z. Reichstein in [Reference First and Reichstein6] is sharp in the case of étale algebras: they can always be generated by
![]() $\dim\; R + 1$
global sections and this cannot be improved in general. The details are worked out in Section 7, and we incidentally show that the example of S. Chase follows easily from our construction of
$\dim\; R + 1$
global sections and this cannot be improved in general. The details are worked out in Section 7, and we incidentally show that the example of S. Chase follows easily from our construction of
![]() $B(r; {\mathbb {A}}^2)$
and some elementary calculations in the singular cohomology of
$B(r; {\mathbb {A}}^2)$
and some elementary calculations in the singular cohomology of
![]() $B(r; {\mathbb {A}}^2)({\mathbb {R}})$
.
$B(r; {\mathbb {A}}^2)({\mathbb {R}})$
.
Finally, we offer some thoughts about determining whether the bound of First and Reichstein is sharp if one restricts to varieties over algebraically closed fields.
1.1 Notation and other preliminaries
-
• All rings in this paper are assumed to be unital, associative, and commutative.
-
• k denotes a base ring.
-
• A variety X is a geometrically reduced, separated scheme of finite type over a field. We do not require the base field to be algebraically closed, nor do we require varieties to be irreducible.
-
•
 $C_2$
denotes the cyclic group of order
$C_2$
denotes the cyclic group of order
 $2$
.
$2$
.
We use the functor-of-points formalism ([Reference Eisenbud and Harris5, Part IV]) heavily throughout, which is to say we view a scheme X as the sheaf of sets it represents on the big Zariski site of all schemes
2 Étale algebras
Let R be a ring and S an R-algebra. Then there is a morphism of rings
![]() $\mu :S\otimes _R S^{\text {op}}\to S$
sending
$\mu :S\otimes _R S^{\text {op}}\to S$
sending
![]() $a\otimes b$
to
$a\otimes b$
to
![]() $ab$
. We obtain an exact sequence
$ab$
. We obtain an exact sequence
 $$ \begin{align*} 0\to \ker(\mu) \to S\otimes_R S^{\text{op}} \xrightarrow{\mu} S\to 0 \end{align*} $$
$$ \begin{align*} 0\to \ker(\mu) \to S\otimes_R S^{\text{op}} \xrightarrow{\mu} S\to 0 \end{align*} $$
We recall ([Reference Ford7, Chapter 4]) that an R-algebra S is called separable if S is a projective
![]() $S\otimes _R S^{\text {op}}$
-module.
$S\otimes _R S^{\text {op}}$
-module.
Definition 2.1 Let R be a ring. A commutative R-algebra S is called étale if S is a flat, separable, finitely presented R-algebra.
Proposition 2.2 Let R be a commutative ring, and S a commutative R-algebra. Then the following are equivalent:
-
1. S is an étale R-algebra.
-
2. S is a finitely presented R-algebra and
 $\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$
is formally étale in the sense of [Reference Grothendieck9, Section 17.1].
$\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$
is formally étale in the sense of [Reference Grothendieck9, Section 17.1].
Proof By [Reference Ford7, Corollary 4.7.3], we see that 1 implies 2. Conversely, a finitely generated and formally étale map is flat and unramified [Reference Grothendieck9, Corollaire 17.6.2], and a finitely generated commutative unramified R-algebra S is separable [Reference Ford7, Theorem 8.3.6]. ▪
Definition 2.3 An R-algebra S is called finite étale if S is an étale R-algebra and a finitely generated R-module.
Remark 2.4 If S is a finitely presented R-algebra that is finitely generated as an R-module then it is also finitely presented as an R-module ([Reference Grothendieck11, 1.4.7]). Moreover, finitely presented and flat modules are projective ([Reference de Jong2, tag 058Q]), so a finite étale algebra S over R is, in particular, a projective R-module of finite rank.
Definition 2.5 We say that an étale algebra is of degree n if the rank of S as a projective R-module is n. A degree-n étale algebra is necessarily finite étale.
Over a ring R, and for any integer
![]() $n>0$
, there exists the trivial rank n étale algebra
$n>0$
, there exists the trivial rank n étale algebra
![]() $R^n$
with componentwise addition and multiplication. The next lemma states that all étale algebras are étale-locally isomorphic to the trivial one.
$R^n$
with componentwise addition and multiplication. The next lemma states that all étale algebras are étale-locally isomorphic to the trivial one.
Lemma 2.6 Let R be a ring and S an R-algebra. The following statements are equivalent:
-
• S is an étale algebra of degree n.
-
• There is a finite étale R-algebra T such that
 $S\otimes _R T\cong T^n$
as T-algebras.
$S\otimes _R T\cong T^n$
as T-algebras.
A proof may be found in [Reference Ford7, Corollary 1.1.16, Corollary 4.4.6, Proposition 4.6.11].
We may extend this definition to schemes. Fix a ground ring k throughout.
Definition 2.7 Let X be a k-scheme. Let
![]() $\mathcal {A}$
be a locally free sheaf of
$\mathcal {A}$
be a locally free sheaf of
![]() $\mathcal {O}_X$
-algebras of constant rank n. We say that
$\mathcal {O}_X$
-algebras of constant rank n. We say that
![]() $\mathcal {A}$
is an étale X-algebra or étale algebra over X if for every open affine subset
$\mathcal {A}$
is an étale X-algebra or étale algebra over X if for every open affine subset
![]() $U\subset X$
the
$U\subset X$
the
![]() ${\mathcal {O}}_X(U)$
-algebra
${\mathcal {O}}_X(U)$
-algebra
![]() $\mathcal {A}(U)$
is an étale algebra. If the algebras
$\mathcal {A}(U)$
is an étale algebra. If the algebras
![]() ${\mathcal {A}}(U)$
are étale of rank n, we say
${\mathcal {A}}(U)$
are étale of rank n, we say
![]() ${\mathcal {A}}$
is a degree-n étale algebra.
${\mathcal {A}}$
is a degree-n étale algebra.
By Remark 2.4 it is clear that a sheaf of degree-n étale algebras
![]() $\mathcal {A}$
over X is a quasi-coherent sheaf of
$\mathcal {A}$
over X is a quasi-coherent sheaf of
![]() $\mathcal {O}_X$
-modules.
$\mathcal {O}_X$
-modules.
If X is a k-scheme and n a positive integer, then there exists a trivial rank-n étale algebra
![]() $\mathcal {O}^n_X$
with componentwise addition and multiplication.
$\mathcal {O}^n_X$
with componentwise addition and multiplication.
Lemma 2.8 Let X be a k-scheme and
![]() $\mathcal {A}$
be a finitely presented, quasi-coherent sheaf of
$\mathcal {A}$
be a finitely presented, quasi-coherent sheaf of
![]() $\mathcal {O}_X$
-algebras. Then the following are equivalent:
$\mathcal {O}_X$
-algebras. Then the following are equivalent:
-
•
 $\mathcal {A}$
is an étale X-algebra of degree n.
$\mathcal {A}$
is an étale X-algebra of degree n. -
• There is an affine étale cover
 $\{ U_i\xrightarrow {f_i} X\}$
such that
$\{ U_i\xrightarrow {f_i} X\}$
such that
 $f_i^*\mathcal {A}\cong \mathcal {O}_{U_i}^n$
as
$f_i^*\mathcal {A}\cong \mathcal {O}_{U_i}^n$
as
 $\mathcal {O}_{U_i}$
-algebras.
$\mathcal {O}_{U_i}$
-algebras.
Proof This is immediate from Lemma 2.6. ▪
Definition 2.9 If A is an algebra over a ring R, then a subset
![]() $\Lambda \subset A$
is said to generate A over R if no strict R-subalgebra of A contains
$\Lambda \subset A$
is said to generate A over R if no strict R-subalgebra of A contains
![]() $\Lambda $
.
$\Lambda $
.
If
![]() $\Lambda = \{ a_1, \dots , a_r\} \subset A$
is a finite subset, then the smallest subalgebra of A containing
$\Lambda = \{ a_1, \dots , a_r\} \subset A$
is a finite subset, then the smallest subalgebra of A containing
![]() $\Lambda $
agrees with the image of the evaluation map
$\Lambda $
agrees with the image of the evaluation map
 $k[x_1, \dots , x_r] \overset {(a_1,\dots , a_r)}{\to } A$
. Therefore, saying that
$k[x_1, \dots , x_r] \overset {(a_1,\dots , a_r)}{\to } A$
. Therefore, saying that
![]() $\Lambda $
generates A is equivalent to saying this map is surjective.
$\Lambda $
generates A is equivalent to saying this map is surjective.
Proposition 2.10 Let
![]() $\Lambda = \{a_1, \dots , a_r\}$
be a finite set of elements of A, an algebra over a ring R. The following are equivalent:
$\Lambda = \{a_1, \dots , a_r\}$
be a finite set of elements of A, an algebra over a ring R. The following are equivalent:
-
1.
 $\Lambda $
generates A as an R-algebra.
$\Lambda $
generates A as an R-algebra. -
2. There exists a set of elements
 $\{\;f_1, \dots , f_n\} \subset R$
that generate the unit ideal and such that, for each
$\{\;f_1, \dots , f_n\} \subset R$
that generate the unit ideal and such that, for each
 $i \in \{1, \dots , n\}$
, the image of
$i \in \{1, \dots , n\}$
, the image of
 $\Lambda $
in
$\Lambda $
in
 $A_{f_i}$
generates
$A_{f_i}$
generates
 $A_{f_i}$
as an
$A_{f_i}$
as an
 $R_{f_i}$
-algebra.
$R_{f_i}$
-algebra. -
3. For each
 $\mathfrak m \in \operatorname {\mathrm {MaxSpec}} R$
, the image of
$\mathfrak m \in \operatorname {\mathrm {MaxSpec}} R$
, the image of
 $\Lambda $
in
$\Lambda $
in
 $A_{\mathfrak m}$
generates
$A_{\mathfrak m}$
generates
 $A_{\mathfrak m}$
as an
$A_{\mathfrak m}$
as an
 $R_{\mathfrak m}$
-algebra.
$R_{\mathfrak m}$
-algebra. -
4. Let
 $k(\mathfrak m)$
denote the residue field of the local ring
$k(\mathfrak m)$
denote the residue field of the local ring
 $R_{\mathfrak m}$
. For each
$R_{\mathfrak m}$
. For each
 $\mathfrak m\in \operatorname {\mathrm {MaxSpec}} R$
, the image of
$\mathfrak m\in \operatorname {\mathrm {MaxSpec}} R$
, the image of
 $\Lambda $
in
$\Lambda $
in
 $A\otimes _R k(\mathfrak m)$
generates
$A\otimes _R k(\mathfrak m)$
generates
 $A\otimes _R k(\mathfrak m)$
as a
$A\otimes _R k(\mathfrak m)$
as a
 $k({\mathfrak m})$
-algebra.
$k({\mathfrak m})$
-algebra.
Proof In the case of a finite subset,
![]() $\Lambda = \{ a_1, \dots , a_r\}$
, the condition that
$\Lambda = \{ a_1, \dots , a_r\}$
, the condition that
![]() $\Lambda $
generates A is equivalent to the surjectivity of the evaluation map
$\Lambda $
generates A is equivalent to the surjectivity of the evaluation map
![]() $R[x_1, \dots , x_r] \to A$
.
$R[x_1, \dots , x_r] \to A$
.
The question of generation is therefore a question of whether a certain map is an epimorphism in the category of R-modules, and conditions (2)–(4) are well-known equivalent conditions saying that this map is an epimorphism. ▪
Using Proposition 2.10, we extend the definition of “generation of an algebra” from the case where the base is affine to the case of a general scheme.
Definition 2.11 Let
![]() $\mathcal {A}$
be an algebra over a scheme X. For
$\mathcal {A}$
be an algebra over a scheme X. For
![]() $ \Lambda \subset \Gamma (X,\mathcal {A})$
we say that
$ \Lambda \subset \Gamma (X,\mathcal {A})$
we say that
![]() $\Lambda\; $
generates
$\Lambda\; $
generates
![]() $\mathcal {A}$
if, for each open affine
$\mathcal {A}$
if, for each open affine
![]() $U\subset X$
the
$U\subset X$
the
![]() $\mathcal {O}_X(U)$
-algebra
$\mathcal {O}_X(U)$
-algebra
![]() $\mathcal {A}(U)$
is generated by restriction of sections in
$\mathcal {A}(U)$
is generated by restriction of sections in
![]() $\Lambda $
to U.
$\Lambda $
to U.
2.1 Generation of trivial algebras
Let
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $r \ge 1$
. Consider the trivial étale algebra
$r \ge 1$
. Consider the trivial étale algebra
![]() ${\mathcal {O}}_X^n$
over a scheme X. A global section of this algebra is equivalent to a morphism
${\mathcal {O}}_X^n$
over a scheme X. A global section of this algebra is equivalent to a morphism
![]() $X \to {\mathbb {A}}^n$
, and an r-tuple
$X \to {\mathbb {A}}^n$
, and an r-tuple
![]() $\Lambda $
of sections is a morphism
$\Lambda $
of sections is a morphism
![]() $X \to \left ({\mathbb {A}}^n\right )^r$
. One might hope that the subfunctor
$X \to \left ({\mathbb {A}}^n\right )^r$
. One might hope that the subfunctor
![]() ${\mathcal {F}} \subseteq \left ({\mathbb {A}}^n\right )^r$
of r-tuples of sections generating
${\mathcal {F}} \subseteq \left ({\mathbb {A}}^n\right )^r$
of r-tuples of sections generating
![]() ${\mathcal {O}}_X^n$
as an étale algebra is representable, and this turns out to be the case.
${\mathcal {O}}_X^n$
as an étale algebra is representable, and this turns out to be the case.
In order to define subschemes of
![]() $\left ({\mathbb {A}}^n\right )^r$
, it will be necessary to name coordinates:
$\left ({\mathbb {A}}^n\right )^r$
, it will be necessary to name coordinates:
It will also be useful to retain the grouping into n-tuples, so we define
![]() $\vec x_l = (x_{l1}, x_{l2}, \dots , x_{ln})$
.
$\vec x_l = (x_{l1}, x_{l2}, \dots , x_{ln})$
.
Notation 2.12 Fix n and r as above. For
![]() $(i,j) \in \{1, \dots , n\}^2$
with
$(i,j) \in \{1, \dots , n\}^2$
with
![]() $i<j$
, let
$i<j$
, let
 $Z_{ij} \subset \left ({\mathbb {A}}^n\right )^r$
denote the closed subscheme given by the sum of the ideals
$Z_{ij} \subset \left ({\mathbb {A}}^n\right )^r$
denote the closed subscheme given by the sum of the ideals
![]() $(x_{ki} - x_{kj})$
where k varies from
$(x_{ki} - x_{kj})$
where k varies from
![]() $\;1$
to n.
$\;1$
to n.
Write
![]() $U(r; {\mathbb {A}}^n)$
, or
$U(r; {\mathbb {A}}^n)$
, or
![]() $\;U(r)$
when n is clear from the context, for the open subscheme of
$\;U(r)$
when n is clear from the context, for the open subscheme of
![]() $\left ( {\mathbb {A}}^n \right )^r$
given by
$\left ( {\mathbb {A}}^n \right )^r$
given by
 $$\begin{align*}U(r; {\mathbb{A}}^n) = \left( {\mathbb{A}}^n\right)^r - \bigcup_{i < j} Z_{ij} \end{align*}$$
$$\begin{align*}U(r; {\mathbb{A}}^n) = \left( {\mathbb{A}}^n\right)^r - \bigcup_{i < j} Z_{ij} \end{align*}$$
Proposition 2.13 Let
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $r \ge 1$
. The open subscheme
$r \ge 1$
. The open subscheme
![]() $U(r; {\mathbb {A}}^n ) \subset \left ({\mathbb {A}}^n\right )^r$
represents the functor sending a scheme X to r-tuples
$U(r; {\mathbb {A}}^n ) \subset \left ({\mathbb {A}}^n\right )^r$
represents the functor sending a scheme X to r-tuples
![]() $(a_1, \dots , a_r)$
of global sections of
$(a_1, \dots , a_r)$
of global sections of
![]() ${\mathcal {O}}_X^n$
that generate it as an
${\mathcal {O}}_X^n$
that generate it as an
![]() ${\mathcal {O}}_X$
-algebra.
${\mathcal {O}}_X$
-algebra.
Proof Temporarily, let
![]() ${\mathcal {F}}$
denote the subfunctor of
${\mathcal {F}}$
denote the subfunctor of
![]() $\left ({\mathbb {A}}^n\right )^r$
defined by
$\left ({\mathbb {A}}^n\right )^r$
defined by
It follows from Proposition 2.10 and Definition 2.11 that
![]() ${\mathcal {F}}$
is actually a sheaf on the big Zariski site.
${\mathcal {F}}$
is actually a sheaf on the big Zariski site.
Both
![]() $U(r; {\mathbb {A}}^n)$
and
$U(r; {\mathbb {A}}^n)$
and
![]() ${\mathcal {F}}$
are subsheaves of the sheaf represented by
${\mathcal {F}}$
are subsheaves of the sheaf represented by
![]() $({\mathbb {A}}^n)^r$
, and therefore in order to show they agree, it suffices to show
$({\mathbb {A}}^n)^r$
, and therefore in order to show they agree, it suffices to show
![]() $U(r; {\mathbb {A}}^n)(R) = {\mathcal {F}}(R)$
when R is a local ring.
$U(r; {\mathbb {A}}^n)(R) = {\mathcal {F}}(R)$
when R is a local ring.
Let R be a local ring. The set
![]() $U(r; {\mathbb {A}}^n)(R)$
consists of certain r-tuples
$U(r; {\mathbb {A}}^n)(R)$
consists of certain r-tuples
![]() $(\vec a_1, \dots , \vec a_r )$
of elements of
$(\vec a_1, \dots , \vec a_r )$
of elements of
![]() $R^n$
. Letting
$R^n$
. Letting
![]() $a_{ki}$
denote the ith element of
$a_{ki}$
denote the ith element of
![]() $\vec a_k$
, then the r-tuples are those with the property that for each
$\vec a_k$
, then the r-tuples are those with the property that for each
![]() $i \neq j$
, there exists some k such that
$i \neq j$
, there exists some k such that
![]() $a_{ki} - a_{kj} \in R^\times $
. The proposition now follows from Lemma 2.14 below. ▪
$a_{ki} - a_{kj} \in R^\times $
. The proposition now follows from Lemma 2.14 below. ▪
Lemma 2.14 Let R be a local ring, with maximal ideal
![]() $\mathfrak m$
. Let
$\mathfrak m$
. Let
![]() $(\vec a_1, \dots , \vec a_r)$
denote an r-tuple of elements in
$(\vec a_1, \dots , \vec a_r)$
denote an r-tuple of elements in
![]() $R^n$
, and let
$R^n$
, and let
![]() $a_{ki}$
denote the ith element of
$a_{ki}$
denote the ith element of
![]() $\vec a_k$
. The following are equivalent:
$\vec a_k$
. The following are equivalent:
-
• The set
 $\{\vec a_1, \dots , \vec a_r \}$
generates the (trivial) étale R-algebra
$\{\vec a_1, \dots , \vec a_r \}$
generates the (trivial) étale R-algebra
 $R^n$
.
$R^n$
. -
• For each pair
 $(i,j)$
satisfying
$(i,j)$
satisfying
 $1 \le i < j \le n$
, there is some
$1 \le i < j \le n$
, there is some
 $k \in \{1 ,\dots , r\}$
such that the element
$k \in \{1 ,\dots , r\}$
such that the element
 $a_{ki} - a_{kj}$
is a unit in
$a_{ki} - a_{kj}$
is a unit in
 $R^\times $
.
$R^\times $
.
Proof Each condition is equivalent to the same condition over
![]() $R/\mathfrak m$
: the first by virtue of 2.10, and the second by elementary algebra. Therefore, it suffices to prove this when R is a field.
$R/\mathfrak m$
: the first by virtue of 2.10, and the second by elementary algebra. Therefore, it suffices to prove this when R is a field.
Suppose
![]() $\{\vec a_1, \dots , \vec a_r \}$
generates
$\{\vec a_1, \dots , \vec a_r \}$
generates
![]() $R^n$
as an algebra. Then, for any pair of indices
$R^n$
as an algebra. Then, for any pair of indices
![]() $(i,j)$
with
$(i,j)$
with
![]() $1 \le i < j \le n$
, it is possible to find a polynomial
$1 \le i < j \le n$
, it is possible to find a polynomial
![]() $p \in R[X_1, \dots , X_r]$
such that
$p \in R[X_1, \dots , X_r]$
such that
![]() $p(a_{1i}, a_{2i}, \dots , a_{ri}) = 1$
and
$p(a_{1i}, a_{2i}, \dots , a_{ri}) = 1$
and
![]() $p(a_{1j}, a_{2j}, \dots , a_{rj}) = 0$
. In particular, there exists some l such that
$p(a_{1j}, a_{2j}, \dots , a_{rj}) = 0$
. In particular, there exists some l such that
![]() $a_{li} \neq a_{lj}$
.
$a_{li} \neq a_{lj}$
.
Conversely, suppose that for each pair
![]() $i<j$
, we can find some l such that
$i<j$
, we can find some l such that
![]() $a_{li} \neq a_{lj}$
. For each pair
$a_{li} \neq a_{lj}$
. For each pair
![]() $i \neq j$
, we can find a polynomial
$i \neq j$
, we can find a polynomial
![]() $p_{i,j} \in R[x_1, \dots , x_r]$
with the property that
$p_{i,j} \in R[x_1, \dots , x_r]$
with the property that
![]() $p_{i,j}(a_{1i} , \dots , a_{ri}) = 1$
and
$p_{i,j}(a_{1i} , \dots , a_{ri}) = 1$
and
![]() $p_{i,j}(a_{1j}, \dots , a_{rj}) = 0$
by taking
$p_{i,j}(a_{1j}, \dots , a_{rj}) = 0$
by taking
 $$\begin{align*}p_{i,j}= (a_{ki}- a_{kj})^{-1}(x_k - a_{kj}) \end{align*}$$
$$\begin{align*}p_{i,j}= (a_{ki}- a_{kj})^{-1}(x_k - a_{kj}) \end{align*}$$
for instance. Consequently, we may produce a polynomial
![]() $p_i \in R[x_1, \dots , x_r]$
with the property that
$p_i \in R[x_1, \dots , x_r]$
with the property that
![]() $p_i(a_{1j} , \dots , a_{rj}) = \delta _{i,j}$
(Kronecker delta). It follows that
$p_i(a_{1j} , \dots , a_{rj}) = \delta _{i,j}$
(Kronecker delta). It follows that
![]() $\{\vec a_1, \dots , \vec a_r \}$
generates the trivial algebra. ▪
$\{\vec a_1, \dots , \vec a_r \}$
generates the trivial algebra. ▪
3 Classifying spaces
Fix
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $r \ge 1$
.
$r \ge 1$
.
Notation 3.1 For a given k-scheme X, a degree-n étale algebra
![]() $\;{\mathcal {A}}\;$
with r generating sections denotes the data of a degree-n étale algebra
$\;{\mathcal {A}}\;$
with r generating sections denotes the data of a degree-n étale algebra
![]() ${\mathcal {A}}\;$
over X, and an r-tuple of sections
${\mathcal {A}}\;$
over X, and an r-tuple of sections
![]() $(a_1, \dots , a_r) \in \Gamma ( X, {\mathcal {A}})$
that generate
$(a_1, \dots , a_r) \in \Gamma ( X, {\mathcal {A}})$
that generate
![]() ${\mathcal {A}}$
. These data will be briefly denoted
${\mathcal {A}}$
. These data will be briefly denoted
![]() $({\mathcal {A}} , a_1, \dots , a_r)$
. A morphism
$({\mathcal {A}} , a_1, \dots , a_r)$
. A morphism
![]() $\psi : ({\mathcal {A}}, a_1, \dots , a_r) \to ({\mathcal {A}}', a_1' ,\dots , a_r')$
of such data consists of a map
$\psi : ({\mathcal {A}}, a_1, \dots , a_r) \to ({\mathcal {A}}', a_1' ,\dots , a_r')$
of such data consists of a map
![]() $\psi : {\mathcal {A}} \to {\mathcal {A}}'$
of étale algebras over X such that
$\psi : {\mathcal {A}} \to {\mathcal {A}}'$
of étale algebras over X such that
![]() $\psi (a_i) =a_i'$
for all
$\psi (a_i) =a_i'$
for all
![]() $i \in \{1, \dots , r\}$
. It is immediate that all morphisms are isomorphisms, and between any two objects, there is at most one isomorphism. The isomorphism class of
$i \in \{1, \dots , r\}$
. It is immediate that all morphisms are isomorphisms, and between any two objects, there is at most one isomorphism. The isomorphism class of
![]() $({\mathcal {A}}, a_1, \dots , a_r)$
will be denoted
$({\mathcal {A}}, a_1, \dots , a_r)$
will be denoted
![]() $[{\mathcal {A}}, a_1, \dots , a_r]$
.
$[{\mathcal {A}}, a_1, \dots , a_r]$
.
Definition 3.2 For a given X, there is a set, rather than a proper class, of isomorphism classes of degree-n étale algebras over X, and so there is a set of isomorphism classes of degree-n étale algebras with r generating sections. Since generation is a local condition by Proposition 2.10, it follows that there is a functor
 $$ \begin{align*} {\mathcal{F}}(r;{\mathbb{A}}^n) & : k{\text{-}}{\mathbf{Sch}} \to {\mathbf{Set}}, \\ {\mathcal{F}}(r;{\mathbb{A}}^n)(X) & = \{ [{\mathcal{A}}, a_1, \dots , a_r] \mid ({\mathcal{A}}, a_1, \dots, a_r) \text{ is a degree-}n \\ & \text{ 'etale algebra over } X \text{ and } r \text{ generating sections} \} \end{align*} $$
$$ \begin{align*} {\mathcal{F}}(r;{\mathbb{A}}^n) & : k{\text{-}}{\mathbf{Sch}} \to {\mathbf{Set}}, \\ {\mathcal{F}}(r;{\mathbb{A}}^n)(X) & = \{ [{\mathcal{A}}, a_1, \dots , a_r] \mid ({\mathcal{A}}, a_1, \dots, a_r) \text{ is a degree-}n \\ & \text{ 'etale algebra over } X \text{ and } r \text{ generating sections} \} \end{align*} $$
The purpose of this section is to produce a variety
![]() $B(r;{\mathbb {A}}^n)$
representing the functor
$B(r;{\mathbb {A}}^n)$
representing the functor
![]() ${\mathcal {F}}(r;{\mathbb {A}}^n)$
on the category of k-schemes.
${\mathcal {F}}(r;{\mathbb {A}}^n)$
on the category of k-schemes.
3.1 Descent for
 ${\mathcal {F}}(r, {\mathbb {A}}^n)$
${\mathcal {F}}(r, {\mathbb {A}}^n)$
Proposition 3.3 The functor
![]() ${\mathcal {F}}(r; {\mathbb {A}}^n)$
is a sheaf on the big étale site of
${\mathcal {F}}(r; {\mathbb {A}}^n)$
is a sheaf on the big étale site of
![]() $\operatorname {\mathrm {Spec}} k$
.
$\operatorname {\mathrm {Spec}} k$
.
In fact, it is a sheaf on the big fpqc site, but we will require only the étale descent condition.
Proof Suppose X is a k-scheme and
![]() $\{\; f_i : Y_i \to X \}_{i \in I}$
is an étale covering. We must identify
$\{\; f_i : Y_i \to X \}_{i \in I}$
is an étale covering. We must identify
![]() ${\mathcal {F}}(r ; {\mathbb {A}}^n)(X)$
with the equalizer in
${\mathcal {F}}(r ; {\mathbb {A}}^n)(X)$
with the equalizer in
 $$\begin{align*}E \to \prod_{i \in I} {\mathcal{F}}(r, {\mathbb{A}}^n)(Y_i) \rightrightarrows \prod_{i,j \in I^2} {\mathcal{F}}(r; {\mathbb{A}}^n)(Y_i \times_X Y_j). \end{align*}$$
$$\begin{align*}E \to \prod_{i \in I} {\mathcal{F}}(r, {\mathbb{A}}^n)(Y_i) \rightrightarrows \prod_{i,j \in I^2} {\mathcal{F}}(r; {\mathbb{A}}^n)(Y_i \times_X Y_j). \end{align*}$$
There is clearly a map
![]() ${\mathcal {F}}(r; {\mathbb {A}}^n)(X) \to E$
.
${\mathcal {F}}(r; {\mathbb {A}}^n)(X) \to E$
.
Suppose we have an i-tuple of elements
![]() $([{\mathcal {A}}_i, \vec a(i) ])_{i \in I}$
in this equalizer. Choosing representatives in each case, we have degree-n étale algebras
$([{\mathcal {A}}_i, \vec a(i) ])_{i \in I}$
in this equalizer. Choosing representatives in each case, we have degree-n étale algebras
![]() ${\mathcal {A}}_i$
on each
${\mathcal {A}}_i$
on each
![]() $Y_i$
, along with chosen generating global sections. The equalizer condition is that there is an isomorphism over
$Y_i$
, along with chosen generating global sections. The equalizer condition is that there is an isomorphism over
![]() $Y_i \times _X Y_j$
of the form
$Y_i \times _X Y_j$
of the form
 $\phi _{ij}: {\operatorname {pr}}_1^*({\mathcal {A}}_i, \vec a(i)) {\overset {\cong }{\longrightarrow }} {\operatorname {pr}}_2^*({\mathcal {A}}_j, \vec {a}(\;j))$
. The fact that there is at most one isomorphism between étale algebras with r generating sections implies that we have a descent datum
$\phi _{ij}: {\operatorname {pr}}_1^*({\mathcal {A}}_i, \vec a(i)) {\overset {\cong }{\longrightarrow }} {\operatorname {pr}}_2^*({\mathcal {A}}_j, \vec {a}(\;j))$
. The fact that there is at most one isomorphism between étale algebras with r generating sections implies that we have a descent datum
![]() $( {\mathcal {A}}_i, \phi _{ij})$
, and it is well known, [Reference de Jong2, Tag 023S], that quasi-coherent sheaves satisfy étale descent. We therefore obtain a quasi-coherent sheaf of algebras
$( {\mathcal {A}}_i, \phi _{ij})$
, and it is well known, [Reference de Jong2, Tag 023S], that quasi-coherent sheaves satisfy étale descent. We therefore obtain a quasi-coherent sheaf of algebras
![]() ${\mathcal {A}}$
on X, and since
${\mathcal {A}}$
on X, and since
![]() ${\mathcal {A}}$
is an étale sheaf, the generating sections of each
${\mathcal {A}}$
is an étale sheaf, the generating sections of each
![]() ${\mathcal {A}}_i$
glue to give generating sections of
${\mathcal {A}}_i$
glue to give generating sections of
![]() ${\mathcal {A}}$
. This implies that
${\mathcal {A}}$
. This implies that
![]() ${\mathcal {F}}(r; {\mathbb {A}}^n)(X) \to E$
is surjective.
${\mathcal {F}}(r; {\mathbb {A}}^n)(X) \to E$
is surjective.
To see it is injective, suppose
![]() $({\mathcal {A}}, \vec {a})$
and
$({\mathcal {A}}, \vec {a})$
and
![]() $({\mathcal {A}}', \vec {a}')$
become isomorphic when restricted to each
$({\mathcal {A}}', \vec {a}')$
become isomorphic when restricted to each
![]() $Y_i$
. Then, since there can be at most a unique isomorphism between two étale algebras with generating sections, the local isomorphisms between
$Y_i$
. Then, since there can be at most a unique isomorphism between two étale algebras with generating sections, the local isomorphisms between
![]() $({\mathcal {A}}, \vec {a})$
and
$({\mathcal {A}}, \vec {a})$
and
![]() $({\mathcal {A}}', \vec {a}')$
assemble to give an isomorphism of descent data. Since there is an equivalence of categories between descent data and quasi-coherent sheaves, [Reference de Jong2, Tag 023S], it follows that there is an isomorphism
$({\mathcal {A}}', \vec {a}')$
assemble to give an isomorphism of descent data. Since there is an equivalence of categories between descent data and quasi-coherent sheaves, [Reference de Jong2, Tag 023S], it follows that there is an isomorphism
![]() $\phi : {\mathcal {A}} \overset {\sim }{\to } {\mathcal {A}}'$
. This isomorphism takes
$\phi : {\mathcal {A}} \overset {\sim }{\to } {\mathcal {A}}'$
. This isomorphism takes
![]() $\vec {a}$
to
$\vec {a}$
to
![]() $\vec {a}'$
, as required. ▪
$\vec {a}'$
, as required. ▪
3.2 Construction of
 $B(r; {\mathbb {A}}^n)$
$B(r; {\mathbb {A}}^n)$
Proposition 3.4 Let R be a nonzero connected ring. Then the automorphism group of the trivial étale R-algebra
![]() $R^n$
is the symmetric group
$R^n$
is the symmetric group
![]() $S_n$
, acting on the terms.
$S_n$
, acting on the terms.
Proof Since the equation
![]() $x^2-x=0$
has only the two solutions
$x^2-x=0$
has only the two solutions
![]() $1, 0$
in R, the condition
$1, 0$
in R, the condition
![]() $a^2=a$
for
$a^2=a$
for
![]() $a \in R^n$
implies that each component of a is either
$a \in R^n$
implies that each component of a is either
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Consider the elements
The set of these elements is determined by the conditions:
![]() $e_i^2 = e_i$
,
$e_i^2 = e_i$
,
![]() $e_i \neq 0$
,
$e_i \neq 0$
,
![]() $e_i e_j = 0$
for
$e_i e_j = 0$
for
![]() $i \neq j$
and
$i \neq j$
and
![]() $\sum _{i=1}^n e_i = 1 \in R^n$
.
$\sum _{i=1}^n e_i = 1 \in R^n$
.
Therefore any automorphism of
![]() $R^n$
as an R-algebra permutes the
$R^n$
as an R-algebra permutes the
![]() $e_i$
and is determined by this permutation. ▪
$e_i$
and is determined by this permutation. ▪
There is an action of the symmetric group
![]() $S_n$
on
$S_n$
on
![]() ${\mathbb {A}}^n$
, given by permuting the coordinates, and from there, there is a diagonal action of
${\mathbb {A}}^n$
, given by permuting the coordinates, and from there, there is a diagonal action of
![]() $S_n$
on
$S_n$
on
![]() $\left ( {\mathbb {A}}^n \right )^r$
, and the action restricts to the open subscheme
$\left ( {\mathbb {A}}^n \right )^r$
, and the action restricts to the open subscheme
![]() $U(r; {\mathbb {A}}^n)$
.
$U(r; {\mathbb {A}}^n)$
.
Proposition 3.5 The action of
![]() $S_n$
on
$S_n$
on
![]() $U(r; {\mathbb {A}}^n)$
is scheme-theoretically free.
$U(r; {\mathbb {A}}^n)$
is scheme-theoretically free.
Proof It suffices to verify that the action is free on the sets
![]() $U(r;{\mathbb {A}}^n)(K)$
where K is a separably closed field over k. Here one is considering the diagonal
$U(r;{\mathbb {A}}^n)(K)$
where K is a separably closed field over k. Here one is considering the diagonal
![]() $S_n$
action on r-tuples
$S_n$
action on r-tuples
![]() $(\vec a_1, \dots , \vec a_r)$
where each
$(\vec a_1, \dots , \vec a_r)$
where each
![]() $\vec a_l \in K^n$
is a vector and such that for all indices
$\vec a_l \in K^n$
is a vector and such that for all indices
![]() $i \neq j$
, there exists some
$i \neq j$
, there exists some
![]() $\vec a_l$
such that the ith and jth entries of
$\vec a_l$
such that the ith and jth entries of
![]() $\vec a_l$
are different. The result follows. ▪
$\vec a_l$
are different. The result follows. ▪
Construction 3.6 There is a free diagonal action of
![]() $S_n$
on
$S_n$
on
![]() $U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n$
, such that the projection
$U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n$
, such that the projection
![]() $p: U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n \to U(r;{\mathbb {A}}^n)$
is equivariant. The quotient schemes for these actions exist by reference to [Reference Grothendieck10, Exposé V, Proposition 1.8] and [Reference Liu and Erne15, Proposition 3.3.36]. Write
$p: U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n \to U(r;{\mathbb {A}}^n)$
is equivariant. The quotient schemes for these actions exist by reference to [Reference Grothendieck10, Exposé V, Proposition 1.8] and [Reference Liu and Erne15, Proposition 3.3.36]. Write
![]() $q: E(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
for the induced map of quotient schemes. There is a commutative square
$q: E(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
for the induced map of quotient schemes. There is a commutative square

Proposition 3.7 In the notation above, the maps
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are finite.
$\pi '$
are finite.
Proof We concentrate on the case of
![]() $\pi $
; that of
$\pi $
; that of
![]() $\pi '$
is similar. The map
$\pi '$
is similar. The map
![]() $\pi $
is formed as follows (see [Reference Grothendieck10, Exposé V, §1]): it is possible to cover
$\pi $
is formed as follows (see [Reference Grothendieck10, Exposé V, §1]): it is possible to cover
![]() $U(r; {\mathbb {A}}^n)$
by
$U(r; {\mathbb {A}}^n)$
by
![]() $S_n$
-invariant open affine subschemes
$S_n$
-invariant open affine subschemes
![]() $\operatorname {\mathrm {Spec}} R \subseteq {\mathbb {A}}^{nr}$
. Then
$\operatorname {\mathrm {Spec}} R \subseteq {\mathbb {A}}^{nr}$
. Then
![]() $\pi |_{\operatorname {\mathrm {Spec}} R} : \operatorname {\mathrm {Spec}} R \to \operatorname {\mathrm {Spec}} R^{S_n}$
, induced by the inclusion of
$\pi |_{\operatorname {\mathrm {Spec}} R} : \operatorname {\mathrm {Spec}} R \to \operatorname {\mathrm {Spec}} R^{S_n}$
, induced by the inclusion of
![]() $R^{S_n}$
in R. The map
$R^{S_n}$
in R. The map
![]() $R^{S_n} \to R$
is of finite type, since R is of finite type over k. By [Reference Atiyah and Macdonald1, Exercise 5.12, p68], the extension
$R^{S_n} \to R$
is of finite type, since R is of finite type over k. By [Reference Atiyah and Macdonald1, Exercise 5.12, p68], the extension
![]() $R^{S_n} \to R$
is integral, and being of finite type, it is finite. ▪
$R^{S_n} \to R$
is integral, and being of finite type, it is finite. ▪
Corollary 3.8 The maps
![]() $\pi : U(r; {\mathbb {A}}^n) \to B(r; {\mathbb {A}}^n)$
and
$\pi : U(r; {\mathbb {A}}^n) \to B(r; {\mathbb {A}}^n)$
and
![]() $\pi ': U(r; {\mathbb {A}}^n) \times {\mathbb {A}}^n \to E(r; {\mathbb {A}}^n)$
are
$\pi ': U(r; {\mathbb {A}}^n) \times {\mathbb {A}}^n \to E(r; {\mathbb {A}}^n)$
are
![]() $S_n$
-torsors.
$S_n$
-torsors.
That is, each satisfies the conditions of [Reference Grothendieck10, Exposé V, Proposition 2.6].
Remark 3.9 The sheaf of sections of the map
![]() $p: U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n \to U(r;{\mathbb {A}}^n)$
is the trivial degree-n étale algebra
$p: U(r;{\mathbb {A}}^n) \times {\mathbb {A}}^n \to U(r;{\mathbb {A}}^n)$
is the trivial degree-n étale algebra
 ${\mathcal {O}}_{U(r;{\mathbb {A}}^n)}^n$
on
${\mathcal {O}}_{U(r;{\mathbb {A}}^n)}^n$
on
![]() $U(r;{\mathbb {A}}^n)$
. The action of
$U(r;{\mathbb {A}}^n)$
. The action of
![]() $S_n$
on these sections is by algebra automorphisms, and so the sheaf of sections of the quotient map
$S_n$
on these sections is by algebra automorphisms, and so the sheaf of sections of the quotient map
![]() $q: E(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
is endowed with the structure of a degree-n étale algebra
$q: E(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
is endowed with the structure of a degree-n étale algebra
![]() ${\mathcal {E}}(r;{\mathbb {A}}^n)$
on
${\mathcal {E}}(r;{\mathbb {A}}^n)$
on
![]() $B(r;{\mathbb {A}}^n)$
. We will often confuse the scheme
$B(r;{\mathbb {A}}^n)$
. We will often confuse the scheme
![]() $E(r;{\mathbb {A}}^n)$
over
$E(r;{\mathbb {A}}^n)$
over
![]() $B(r;{\mathbb {A}}^n)$
with the étale algebra of sections
$B(r;{\mathbb {A}}^n)$
with the étale algebra of sections
![]() ${\mathcal {E}}(r;{\mathbb {A}}^n)$
.
${\mathcal {E}}(r;{\mathbb {A}}^n)$
.
The map p has r canonical sections
 $\{s_j \}_{j=1}^r$
given as follows:
$\{s_j \}_{j=1}^r$
given as follows:
These sections are
![]() $S_n$
-equivariant, and so induce sections
$S_n$
-equivariant, and so induce sections
![]() $\{t_i: B(r;{\mathbb {A}}^n) \to E(r;{\mathbb {A}}^n)\}_{i=1}^r$
of the map q.
$\{t_i: B(r;{\mathbb {A}}^n) \to E(r;{\mathbb {A}}^n)\}_{i=1}^r$
of the map q.
Remark 3.10 By reference to [Reference de Jong2, Lemma 05B5], the quotient k-scheme
![]() $B(r;{\mathbb {A}}^n)$
is smooth over k since
$B(r;{\mathbb {A}}^n)$
is smooth over k since
![]() $U(r;{\mathbb {A}}^n)$
is and
$U(r;{\mathbb {A}}^n)$
is and
![]() $\pi $
is faithfully flat ([Reference Grothendieck10, Exposé V, Proposition 2.6]) and locally finitely presented. Since
$\pi $
is faithfully flat ([Reference Grothendieck10, Exposé V, Proposition 2.6]) and locally finitely presented. Since
![]() $\pi $
is finite it is a proper map. When the base k is a field, the variety
$\pi $
is finite it is a proper map. When the base k is a field, the variety
![]() $B(r;{\mathbb {A}}^n)$
is a quasiprojective variety but not projective. Indeed, if
$B(r;{\mathbb {A}}^n)$
is a quasiprojective variety but not projective. Indeed, if
![]() $B(r;{\mathbb {A}}^n)\to \operatorname {\mathrm {Spec}}(k)$
were proper then
$B(r;{\mathbb {A}}^n)\to \operatorname {\mathrm {Spec}}(k)$
were proper then
![]() $U(r;{\mathbb {A}}^n)\to \operatorname {\mathrm {Spec}}(k)$
would be proper too, but
$U(r;{\mathbb {A}}^n)\to \operatorname {\mathrm {Spec}}(k)$
would be proper too, but
![]() $U(r;{\mathbb {A}}^n)$
is a nonempty open subvariety of affine space.
$U(r;{\mathbb {A}}^n)$
is a nonempty open subvariety of affine space.
3.3 The functor represented by
 $B(r,{\mathbb {A}}^n)$
$B(r,{\mathbb {A}}^n)$
We now establish the identity of functors
![]() $B(r,{\mathbb {A}}^n)(X) = {\mathcal {F}}(r;{\mathbb {A}}^n)(X)$
.
$B(r,{\mathbb {A}}^n)(X) = {\mathcal {F}}(r;{\mathbb {A}}^n)(X)$
.
Construction 3.11 There is a canonical element
![]() $[\mathcal {E}(r;{\mathbb {A}}^n),t_1,\ldots ,t_r]$
in
$[\mathcal {E}(r;{\mathbb {A}}^n),t_1,\ldots ,t_r]$
in
![]() ${\mathcal {F}}(r;{\mathbb {A}}^n)(B(r;{\mathbb {A}}^n))$
, see 3.9. Therefore, there exists a natural transformation of presheaves of k-schemes
${\mathcal {F}}(r;{\mathbb {A}}^n)(B(r;{\mathbb {A}}^n))$
, see 3.9. Therefore, there exists a natural transformation of presheaves of k-schemes
![]() $B(r, {\mathbb {A}}^n)(\cdot ) \to {\mathcal {F}}(r; {\mathbb {A}}^n)(\cdot )$
given by sending a map
$B(r, {\mathbb {A}}^n)(\cdot ) \to {\mathcal {F}}(r; {\mathbb {A}}^n)(\cdot )$
given by sending a map
![]() $\phi : X \to B(r; {\mathbb {A}}^n)$
to the pull-back of the canonical element.
$\phi : X \to B(r; {\mathbb {A}}^n)$
to the pull-back of the canonical element.
Lemma 3.12 If
![]() $[A,s_1,\ldots ,s_r]\in {\mathcal {F}}(r;{\mathbb {A}}^n)(R)$
where R is a strictly henselian local ring, then there exists a unique morphism of schemes
$[A,s_1,\ldots ,s_r]\in {\mathcal {F}}(r;{\mathbb {A}}^n)(R)$
where R is a strictly henselian local ring, then there exists a unique morphism of schemes
![]() $\phi :\operatorname {\mathrm {Spec}}(R)\to B(r;{\mathbb {A}}^n)$
such that
$\phi :\operatorname {\mathrm {Spec}}(R)\to B(r;{\mathbb {A}}^n)$
such that
Proof Since R is a strictly henselian local ring, there exists an R-isomorphism
![]() $A\xrightarrow {\psi } R^n$
of algebras, by virtue of [Reference Milne17, Proposition 1.4.4]. Let
$A\xrightarrow {\psi } R^n$
of algebras, by virtue of [Reference Milne17, Proposition 1.4.4]. Let
![]() $\{\psi (s_i) \} \subset R^n$
denote the corresponding sections of
$\{\psi (s_i) \} \subset R^n$
denote the corresponding sections of
![]() $R^n$
.
$R^n$
.
We thus obtain a map
![]() $\tilde {\phi }:\operatorname {\mathrm {Spec}}(R)\to U(r;{\mathbb {A}}^n)$
defined by giving the R-point
$\tilde {\phi }:\operatorname {\mathrm {Spec}}(R)\to U(r;{\mathbb {A}}^n)$
defined by giving the R-point
![]() $(\psi (s_1),\ldots ,\psi (s_r))$
. Post-composing this map with the projection
$(\psi (s_1),\ldots ,\psi (s_r))$
. Post-composing this map with the projection
![]() $U(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
, we obtain a morphism
$U(r;{\mathbb {A}}^n) \to B(r;{\mathbb {A}}^n)$
, we obtain a morphism
![]() $\phi : \operatorname {\mathrm {Spec}}(R)\to B(r;{\mathbb {A}}^n)$
. It is a tautology that
$\phi : \operatorname {\mathrm {Spec}}(R)\to B(r;{\mathbb {A}}^n)$
. It is a tautology that
![]() $\phi ^*(\mathcal {E}(r;{\mathbb {A}}^n))=A$
and
$\phi ^*(\mathcal {E}(r;{\mathbb {A}}^n))=A$
and
![]() $\phi ^*(t_i)=s_i$
.
$\phi ^*(t_i)=s_i$
.
It now behooves us to show that
![]() $\phi $
does not depend on the choices made in the construction.
$\phi $
does not depend on the choices made in the construction.
Suppose
![]() $\phi ': \operatorname {\mathrm {Spec}} R \to B(r;{\mathbb {A}}^n)$
is another morphism satisfying the conditions of the lemma. We may lift this R-point of
$\phi ': \operatorname {\mathrm {Spec}} R \to B(r;{\mathbb {A}}^n)$
is another morphism satisfying the conditions of the lemma. We may lift this R-point of
![]() $B(r;{\mathbb {A}}^n)$
to an R-point
$B(r;{\mathbb {A}}^n)$
to an R-point
![]() $\tilde \phi ' : \operatorname {\mathrm {Spec}} R \to U(r;{\mathbb {A}}^n)$
, since
$\tilde \phi ' : \operatorname {\mathrm {Spec}} R \to U(r;{\mathbb {A}}^n)$
, since
![]() $\pi $
is an étale covering, and therefore represents an epimorphism of étale sheaves [Reference de Jong2, Lemma 00WT]. By hypothesis we have
$\pi $
is an étale covering, and therefore represents an epimorphism of étale sheaves [Reference de Jong2, Lemma 00WT]. By hypothesis we have
Thus
![]() $\tilde \phi $
and
$\tilde \phi $
and
![]() $\tilde \phi '$
differ by an automorphism of
$\tilde \phi '$
differ by an automorphism of
![]() $R^n$
, i.e., by an element of
$R^n$
, i.e., by an element of
![]() $S_n$
since local rings are connected so 3.4 applies. Therefore
$S_n$
since local rings are connected so 3.4 applies. Therefore
![]() $\phi =\phi '$
as required. ▪
$\phi =\phi '$
as required. ▪
Theorem 3.13 If X is a k-scheme, then the map
is a bijection.
Proof We note that
![]() $B(r, {\mathbb {A}}^n)$
represents a sheaf on the big étale site of
$B(r, {\mathbb {A}}^n)$
represents a sheaf on the big étale site of
![]() $\operatorname {\mathrm {Spec}} k$
, since it is a k-scheme. The presheaf
$\operatorname {\mathrm {Spec}} k$
, since it is a k-scheme. The presheaf
![]() ${\mathcal {F}}(r; {\mathbb {A}}^n)$
is also an étale sheaf, by virtue of Proposition 3.3. It therefore suffices to prove that
${\mathcal {F}}(r; {\mathbb {A}}^n)$
is also an étale sheaf, by virtue of Proposition 3.3. It therefore suffices to prove that
![]() $B(r, {\mathbb {A}}^n)(\operatorname {\mathrm {Spec}} R) \to {\mathcal {F}}(r; {\mathbb {A}}^n)(\operatorname {\mathrm {Spec}} R)$
when R is a strictly henselian local ring, but this is Lemma 3.12. ▪
$B(r, {\mathbb {A}}^n)(\operatorname {\mathrm {Spec}} R) \to {\mathcal {F}}(r; {\mathbb {A}}^n)(\operatorname {\mathrm {Spec}} R)$
when R is a strictly henselian local ring, but this is Lemma 3.12. ▪
Example 3.14 Let us consider the toy example where k is a field and
![]() $X = \operatorname {\mathrm {Spec}} K$
for some field extension
$X = \operatorname {\mathrm {Spec}} K$
for some field extension
![]() $K/k$
, where
$K/k$
, where
![]() $n \ge 2$
, and where
$n \ge 2$
, and where
![]() $r=1$
. That is, we are considering étale algebras
$r=1$
. That is, we are considering étale algebras
![]() $A/K$
along with a chosen generating element
$A/K$
along with a chosen generating element
![]() $a \in A$
. After base change to the separable closure,
$a \in A$
. After base change to the separable closure,
![]() $K^s$
, we obtain an
$K^s$
, we obtain an
![]() $S_n$
-equivariant isomorphism of
$S_n$
-equivariant isomorphism of
![]() $K^s$
-algebras:
$K^s$
-algebras:
 $$\begin{align*}\psi : A_{K^s} {\overset{\cong}{\longrightarrow}} (K^s)^{\times n}.\end{align*}$$
$$\begin{align*}\psi : A_{K^s} {\overset{\cong}{\longrightarrow}} (K^s)^{\times n}.\end{align*}$$
For the sake of the exposition, use
![]() $\psi $
to identify source and target. The element
$\psi $
to identify source and target. The element
![]() $a \in A$
yields a chosen generating element
$a \in A$
yields a chosen generating element
![]() $\tilde a \in (K^s)^n$
. The element
$\tilde a \in (K^s)^n$
. The element
![]() $\tilde a$
is a vector of n pairwise distinct elements of
$\tilde a$
is a vector of n pairwise distinct elements of
![]() $K^s$
. The element
$K^s$
. The element
![]() $\tilde a$
is a
$\tilde a$
is a
![]() $K^s$
-point of
$K^s$
-point of
![]() $U(1; {\mathbb {A}}^n)$
. In general, this point is not defined over K, but its image in
$U(1; {\mathbb {A}}^n)$
. In general, this point is not defined over K, but its image in
![]() $B(1;{\mathbb {A}}^n)$
is.
$B(1;{\mathbb {A}}^n)$
is.
Since
![]() $U(1;{\mathbb {A}}^n) \subseteq {\mathbb {A}}^n$
, and
$U(1;{\mathbb {A}}^n) \subseteq {\mathbb {A}}^n$
, and
![]() $B(1;{\mathbb {A}}^n)=U(1;{\mathbb {A}}^n)/\Sigma _n$
, the image of
$B(1;{\mathbb {A}}^n)=U(1;{\mathbb {A}}^n)/\Sigma _n$
, the image of
![]() $\tilde a$
in
$\tilde a$
in
![]() $B(1;{\mathbb {A}}^n)(K^s)$
may be presented as the elementary symmetric polynomials in the
$B(1;{\mathbb {A}}^n)(K^s)$
may be presented as the elementary symmetric polynomials in the
![]() $a_i$
. To say that the image of
$a_i$
. To say that the image of
![]() $\tilde a = (a_1, \dots , a_n)$
in
$\tilde a = (a_1, \dots , a_n)$
in
![]() $B(1;{\mathbb {A}}^n)$
is defined over K is to say that the coefficients of the polynomial
$B(1;{\mathbb {A}}^n)$
is defined over K is to say that the coefficients of the polynomial
![]() $\prod _{i=1}^n (x-a_i)$
are defined in K.
$\prod _{i=1}^n (x-a_i)$
are defined in K.
The variety
![]() $B(1;{\mathbb {A}}^n)$
is the k-variety parametrizing degree-n polynomials with distinct roots, i.e., with invertible discriminant.
$B(1;{\mathbb {A}}^n)$
is the k-variety parametrizing degree-n polynomials with distinct roots, i.e., with invertible discriminant.
Example 3.15 To reduce the toy example even further, let us consider the case of
![]() $k=K$
a field of characteristic different from
$k=K$
a field of characteristic different from
![]() $2$
, and
$2$
, and
![]() $n=2$
.
$n=2$
.
The variety
![]() $B(1;{\mathbb {A}}^2)$
may be presented as spectrum of the
$B(1;{\mathbb {A}}^2)$
may be presented as spectrum of the
![]() $C_2$
-fixed subring of
$C_2$
-fixed subring of
![]() $k[x,y, (x-y)^{-1}]$
under the action interchanging x and y. This is
$k[x,y, (x-y)^{-1}]$
under the action interchanging x and y. This is
![]() $k[(x+y), (x-y)^2, (x-y)^{-2}]$
, although it is more elegant to present it after the change of coordinates
$k[(x+y), (x-y)^2, (x-y)^{-2}]$
, although it is more elegant to present it after the change of coordinates
![]() $c_1= x+ y$
and
$c_1= x+ y$
and
![]() $c_0=xy$
:
$c_0=xy$
:
A quadratic étale k-algebra equipped with the generating element a corresponds to the point
![]() $(c_1, c_0) \in B(1;{\mathbb {A}}^2)(k)$
where a satisfies the minimal polynomial
$(c_1, c_0) \in B(1;{\mathbb {A}}^2)(k)$
where a satisfies the minimal polynomial
![]() $a^2 - c_1 a + c_0 = 0$
.
$a^2 - c_1 a + c_0 = 0$
.
For instance if
![]() $k={\mathbb {R}}$
, the quadratic étale algebra of complex numbers
$k={\mathbb {R}}$
, the quadratic étale algebra of complex numbers
![]() ${\mathbb {C}}$
with generator
${\mathbb {C}}$
with generator
![]() $s+ti$
over
$s+ti$
over
![]() ${\mathbb {R}}$
(here
${\mathbb {R}}$
(here
![]() $t \neq 0$
), corresponds to the point
$t \neq 0$
), corresponds to the point
![]() $(2s, s^2+t^2) \in B(1;{\mathbb {A}}^2)({\mathbb {R}})$
, whereas
$(2s, s^2+t^2) \in B(1;{\mathbb {A}}^2)({\mathbb {R}})$
, whereas
![]() ${\mathbb {R}} \times {\mathbb {R}}$
, generated by
${\mathbb {R}} \times {\mathbb {R}}$
, generated by
![]() $(s+t,s-t)$
over
$(s+t,s-t)$
over
![]() ${\mathbb {R}}$
(again
${\mathbb {R}}$
(again
![]() $t\neq 0$
), corresponds to the point
$t\neq 0$
), corresponds to the point
![]() $(2s,s^2-t^2)$
.
$(2s,s^2-t^2)$
.
4 Stabilization in cohomology
We might wish to use the schemes
![]() $B(r;{\mathbb {A}}^n)$
to define cohomological invariants of étale algebras. The idea is the following: suppose given such an algebra
$B(r;{\mathbb {A}}^n)$
to define cohomological invariants of étale algebras. The idea is the following: suppose given such an algebra
![]() ${\mathcal {A}}$
on a k-scheme X, and suppose one can find generators
${\mathcal {A}}$
on a k-scheme X, and suppose one can find generators
![]() $(a_1, \dots a_r)$
for
$(a_1, \dots a_r)$
for
![]() ${\mathcal {A}}$
. Then one has a classifying map
${\mathcal {A}}$
. Then one has a classifying map
![]() $\phi : X \to B(r;{\mathbb {A}}^n)$
, and one may apply a cohomology functor
$\phi : X \to B(r;{\mathbb {A}}^n)$
, and one may apply a cohomology functor
![]() $E^*$
, such as Chow groups or algebraic K-theory, to obtain “characteristic classes” for
$E^*$
, such as Chow groups or algebraic K-theory, to obtain “characteristic classes” for
![]() ${\mathcal {A}}$
-along-with-
${\mathcal {A}}$
-along-with-
![]() $\!\!(a_1, \dots , a_r)$
, in the form of
$\!\!(a_1, \dots , a_r)$
, in the form of
![]() $\phi ^* : E^*(B(r;{\mathbb {A}}^n)) \to E^*(X)$
. The dependence on the specific generators chosen is a nuisance, and we see in this section that this dependence goes away provided we are prepared to pass to a limit “
$\phi ^* : E^*(B(r;{\mathbb {A}}^n)) \to E^*(X)$
. The dependence on the specific generators chosen is a nuisance, and we see in this section that this dependence goes away provided we are prepared to pass to a limit “
![]() $\!\!B(\infty )$
” and assume that the theory
$\!\!B(\infty )$
” and assume that the theory
![]() $E^*$
is
$E^*$
is
![]() ${\mathbb {A}^{1}}$
-invariant, in that
${\mathbb {A}^{1}}$
-invariant, in that
![]() $E^*(X) \to E^*(X \times {\mathbb {A}^{1}})$
is an isomorphism.
$E^*(X) \to E^*(X \times {\mathbb {A}^{1}})$
is an isomorphism.
Definition 4.1 There are stabilization maps
![]() $U(r;{\mathbb {A}}^n)\to U(r+1;{\mathbb {A}}^n)$
obtained by augmenting an r-tuple of n-tuples by the n-tuple
$U(r;{\mathbb {A}}^n)\to U(r+1;{\mathbb {A}}^n)$
obtained by augmenting an r-tuple of n-tuples by the n-tuple
![]() $(0,0,\dots ,0)$
. These stabilization maps are
$(0,0,\dots ,0)$
. These stabilization maps are
![]() $S_n$
-equivariant and therefore descend to maps
$S_n$
-equivariant and therefore descend to maps
![]() $B(r;{\mathbb {A}}^n) \to B(r+1;{\mathbb {A}}^n)$
.
$B(r;{\mathbb {A}}^n) \to B(r+1;{\mathbb {A}}^n)$
.
The stabilization maps defined above may be composed with one another, to yield maps
![]() $B(r;{\mathbb {A}}^n) \to B(r';{\mathbb {A}}^n)$
for all
$B(r;{\mathbb {A}}^n) \to B(r';{\mathbb {A}}^n)$
for all
![]() $r < r'$
. These maps will also be called stabilization maps.
$r < r'$
. These maps will also be called stabilization maps.
Proposition 4.2 Let X be a k-scheme. Suppose
have the property that
![]() ${\mathcal {A}}\; {\cong }\; {\mathcal {A}}'$
as étale algebras. Let
${\mathcal {A}}\; {\cong }\; {\mathcal {A}}'$
as étale algebras. Let
![]() $\phi : X\to B(r;{\mathbb {A}}^n)$
and
$\phi : X\to B(r;{\mathbb {A}}^n)$
and
![]() $\phi ':X\to B(r';{\mathbb {A}}^n)$
be the corresponding classifying morphism. For
$\phi ':X\to B(r';{\mathbb {A}}^n)$
be the corresponding classifying morphism. For
![]() $R= r + r'$
, the composite maps
$R= r + r'$
, the composite maps
![]() $\tilde \phi : X \to B(r;{\mathbb {A}}^n) \to B(R;{\mathbb {A}}^n)$
and
$\tilde \phi : X \to B(r;{\mathbb {A}}^n) \to B(R;{\mathbb {A}}^n)$
and
![]() $\tilde \phi ': X \to B(r';{\mathbb {A}}^n) \to B(R;{\mathbb {A}}^n)$
given by stabilization are naively
$\tilde \phi ': X \to B(r';{\mathbb {A}}^n) \to B(R;{\mathbb {A}}^n)$
given by stabilization are naively
![]() ${\mathbb {A}^{1}}$
-homotopic.
${\mathbb {A}^{1}}$
-homotopic.
An “elementary
![]() ${\mathbb {A}^{1}}$
-homotopy” between maps
${\mathbb {A}^{1}}$
-homotopy” between maps
![]() $\phi , \phi ': X \to B$
is a map
$\phi , \phi ': X \to B$
is a map
![]() $\Phi : X \times {\mathbb {A}^{1}} \to B$
specializing to
$\Phi : X \times {\mathbb {A}^{1}} \to B$
specializing to
![]() $\phi $
at
$\phi $
at
![]() $0$
and
$0$
and
![]() $\phi '$
at
$\phi '$
at
![]() $1$
. Two maps
$1$
. Two maps
![]() $\phi , \phi ': X \to B$
are “naively
$\phi , \phi ': X \to B$
are “naively
![]() ${\mathbb {A}^{1}}$
-homotopic” if they may be joined by a finite sequence of elementary homotopies. Two naively homotopic maps between smooth finite-type k-schemes are identified in the
${\mathbb {A}^{1}}$
-homotopic” if they may be joined by a finite sequence of elementary homotopies. Two naively homotopic maps between smooth finite-type k-schemes are identified in the
![]() ${\mathbb{A}^{1}}$
-homotopy theory of schemes of [Reference Morel and Voevodsky18], but they do not account for all identifications in that theory.
${\mathbb{A}^{1}}$
-homotopy theory of schemes of [Reference Morel and Voevodsky18], but they do not account for all identifications in that theory.
Proof We may assume that
![]() ${\mathbb {A}} = {\mathcal {A}}'$
. We may also assume that
${\mathbb {A}} = {\mathcal {A}}'$
. We may also assume that
![]() $r=r'$
—if
$r=r'$
—if
![]() $r < r'$
, then pad the vector
$r < r'$
, then pad the vector
![]() $(a_1, \dots , a_r)$
with
$(a_1, \dots , a_r)$
with
![]() $0$
s to produce a vector
$0$
s to produce a vector
![]() $(a_1, \dots , a_r, 0, \dots , 0)$
of length
$(a_1, \dots , a_r, 0, \dots , 0)$
of length
![]() $r'$
, and similarly in the other case.
$r'$
, and similarly in the other case.
Write t for the parameter of
![]() ${\mathbb {A}^{1}}$
. Let
${\mathbb {A}^{1}}$
. Let
![]() ${\mathcal {A}}[t]$
denote the pull-back of
${\mathcal {A}}[t]$
denote the pull-back of
![]() ${\mathcal {A}}$
along the projection
${\mathcal {A}}$
along the projection
![]() $X \times {\mathbb {A}^{1}} \to X$
.
$X \times {\mathbb {A}^{1}} \to X$
.
Consider the sections
![]() $((1-t)a_1, \dots , (1-t)a_r, ta^{\prime }_1, \dots , ta^{\prime }_r)$
of
$((1-t)a_1, \dots , (1-t)a_r, ta^{\prime }_1, \dots , ta^{\prime }_r)$
of
![]() ${\mathcal {A}}[t]$
. Since either t or
${\mathcal {A}}[t]$
. Since either t or
![]() $(1-t)$
is a unit at all local rings of points
$(1-t)$
is a unit at all local rings of points
![]() ${\mathbb {A}}^1$
, by appeal to Proposition 2.10 and consideration of the restrictions to
${\mathbb {A}}^1$
, by appeal to Proposition 2.10 and consideration of the restrictions to
![]() $X \times ({\mathbb {A}^{1}} -\{0\})$
and
$X \times ({\mathbb {A}^{1}} -\{0\})$
and
![]() $X \times ({\mathbb {A}^{1}} - \{1\})$
, we see that
$X \times ({\mathbb {A}^{1}} - \{1\})$
, we see that
![]() $((1-t)a_1, \dots , (1-t)a_r, ta^{\prime }_1, \dots , ta^{\prime }_r)$
furnish a set of generators for
$((1-t)a_1, \dots , (1-t)a_r, ta^{\prime }_1, \dots , ta^{\prime }_r)$
furnish a set of generators for
![]() ${\mathcal {A}}[t]$
. At
${\mathcal {A}}[t]$
. At
![]() $t=0$
, they specialize to
$t=0$
, they specialize to
![]() $(a_1, \dots , a_r, 0, \dots , 0)$
, viz., the generators specified by the stabilized map
$(a_1, \dots , a_r, 0, \dots , 0)$
, viz., the generators specified by the stabilized map
![]() $\phi : X \to B(r;{\mathbb {A}}^n) \to B(2r;{\mathbb {A}}^n)$
. At
$\phi : X \to B(r;{\mathbb {A}}^n) \to B(2r;{\mathbb {A}}^n)$
. At
![]() $t=1$
, they specialize to
$t=1$
, they specialize to
![]() $(0, \dots , 0, a^{\prime }_1, \dots , a^{\prime }_r)$
, which is not precisely the list of generators specified by
$(0, \dots , 0, a^{\prime }_1, \dots , a^{\prime }_r)$
, which is not precisely the list of generators specified by
![]() $\phi ': X \to B(r;{\mathbb {A}}^n) \to B(2r;{\mathbb {A}}^n)$
, but may be brought to this form by another elementary
$\phi ': X \to B(r;{\mathbb {A}}^n) \to B(2r;{\mathbb {A}}^n)$
, but may be brought to this form by another elementary
![]() ${\mathbb {A}^{1}}$
-homotopy. ▪
${\mathbb {A}^{1}}$
-homotopy. ▪
Corollary 4.3 Let
![]() $\phi $
and
$\phi $
and
![]() $\phi '$
be as in the previous proposition. If
$\phi '$
be as in the previous proposition. If
![]() $E^*$
denotes any
$E^*$
denotes any
![]() ${\mathbb {A}^{1}}$
-invariant cohomology theory, then
${\mathbb {A}^{1}}$
-invariant cohomology theory, then
![]() $E^*(\tilde \phi )=E^*(\tilde \phi ')$
.
$E^*(\tilde \phi )=E^*(\tilde \phi ')$
.
5 The motivic cohomology of the spaces
 $B(r; {\mathbb {A}}^2)$
$B(r; {\mathbb {A}}^2)$
For this section, let k denote a fixed field of characteristic different from
![]() $2$
. The motivic cohomology of the spaces
$2$
. The motivic cohomology of the spaces
![]() $B(r; {\mathbb {A}}^2)$
has already been calculated in [Reference Dugger and Isaksen4].
$B(r; {\mathbb {A}}^2)$
has already been calculated in [Reference Dugger and Isaksen4].
5.1 Change of coordinates
Lemma 5.1 There is an equivariant isomorphism
![]() $ U(r;{\mathbb {A}}^2) \cong \mathbb {A}^r\setminus \{0\} \times \mathbb {A}^r$
, where
$ U(r;{\mathbb {A}}^2) \cong \mathbb {A}^r\setminus \{0\} \times \mathbb {A}^r$
, where
![]() $C_2$
acts as multiplication by
$C_2$
acts as multiplication by
![]() $-1$
on the first factor
$-1$
on the first factor
![]() $\mathbb {A}^r\setminus \{0\}$
and trivially on the second factor
$\mathbb {A}^r\setminus \{0\}$
and trivially on the second factor
![]() $\mathbb {A}^r$
. Taking quotient by
$\mathbb {A}^r$
. Taking quotient by
![]() $C_2$
-action yields
$C_2$
-action yields
![]() $B(r;{\mathbb {A}}^2) \cong (\mathbb {A}^r\setminus \{0\})/C_2\times \mathbb {A}^r.$
$B(r;{\mathbb {A}}^2) \cong (\mathbb {A}^r\setminus \{0\})/C_2\times \mathbb {A}^r.$
Proof By means of the change of coordinates
we see that
![]() $U(r; {\mathbb {A}}^2) {\cong } ({\mathbb {A}}^r {\setminus } \{0\}) \times {\mathbb {A}}^r$
. Moreover, the action of
$U(r; {\mathbb {A}}^2) {\cong } ({\mathbb {A}}^r {\setminus } \{0\}) \times {\mathbb {A}}^r$
. Moreover, the action of
![]() $C_2$
on
$C_2$
on
![]() $U(r;{\mathbb {A}}^2)$
is given by
$U(r;{\mathbb {A}}^2)$
is given by
![]() $z_i \mapsto -z_i$
and
$z_i \mapsto -z_i$
and
![]() $w_i \mapsto w_i$
. We therefore obtain an isomorphism
$w_i \mapsto w_i$
. We therefore obtain an isomorphism
![]() $B(r; {\mathbb {A}}^2)= U(r;{\mathbb {A}}^2)/ C_2 {\cong } ({\mathbb {A}}^r {\setminus } \{0\}) / C_2 \times {\mathbb {A}}^r$
. Write
$B(r; {\mathbb {A}}^2)= U(r;{\mathbb {A}}^2)/ C_2 {\cong } ({\mathbb {A}}^r {\setminus } \{0\}) / C_2 \times {\mathbb {A}}^r$
. Write
![]() $V(r;{\mathbb {A}}^2)$
for
$V(r;{\mathbb {A}}^2)$
for
![]() ${\mathbb {A}}^r {\setminus } \{0\}/C_2$
. It is immediate that
${\mathbb {A}}^r {\setminus } \{0\}/C_2$
. It is immediate that
![]() $B(r;{\mathbb {A}}^2) {\cong } V(r;{\mathbb {A}}^2) \times {\mathbb {A}}^r$
, and so there is a split inclusion
$B(r;{\mathbb {A}}^2) {\cong } V(r;{\mathbb {A}}^2) \times {\mathbb {A}}^r$
, and so there is a split inclusion
![]() $V(r;{\mathbb {A}}^2) \to B(r;{\mathbb {A}}^2)$
which is moreover an
$V(r;{\mathbb {A}}^2) \to B(r;{\mathbb {A}}^2)$
which is moreover an
![]() ${\mathbb {A}^{1}}$
-equivalence.▪
${\mathbb {A}^{1}}$
-equivalence.▪
5.2 The deleted quadric presentation
Definition 5.2 Endow
![]() ${\mathbb {P}}^{2r-1}$
with the projective coordinates
${\mathbb {P}}^{2r-1}$
with the projective coordinates
![]() $a_1, \dots , a_r$
,
$a_1, \dots , a_r$
,
![]() $b_1 , \dots , b_r$
. Let
$b_1 , \dots , b_r$
. Let
![]() $Q_{2r-2}$
denote the closed subvariety given by the vanishing of
$Q_{2r-2}$
denote the closed subvariety given by the vanishing of
![]() $\sum _{i=1}^r a_i b_i$
, and let
$\sum _{i=1}^r a_i b_i$
, and let
![]() $DQ_{2r-1}$
denote the open complement
$DQ_{2r-1}$
denote the open complement
![]() ${\mathbb {P}}^{2r-1} \setminus Q_{2r-2}$
.
${\mathbb {P}}^{2r-1} \setminus Q_{2r-2}$
.
The main computation of [Reference Dugger and Isaksen4] is a calculation of the modulo-
![]() $2$
motivic cohomology of
$2$
motivic cohomology of
![]() $DQ_{2r-1}$
, and of a family of related spaces
$DQ_{2r-1}$
, and of a family of related spaces
![]() $DQ_{2r}$
. Our reference for the motivic cohomology of k-varieties is [Reference Mazza, Voevodsky and Weibel16]. For a given abelian group A, either
$DQ_{2r}$
. Our reference for the motivic cohomology of k-varieties is [Reference Mazza, Voevodsky and Weibel16]. For a given abelian group A, either
![]() ${\mathbb {Z}}$
or
${\mathbb {Z}}$
or
![]() ${\mathbb {F}}_2$
in this paper, and a given variety X, the motivic cohomology
${\mathbb {F}}_2$
in this paper, and a given variety X, the motivic cohomology
![]() ${\mathrm {H}}^{*,*}(X; A)$
is a bigraded algebra over the cohomology of the ground field,
${\mathrm {H}}^{*,*}(X; A)$
is a bigraded algebra over the cohomology of the ground field,
![]() $\operatorname {\mathrm {Spec}} k$
.
$\operatorname {\mathrm {Spec}} k$
.
Denote the modulo-
![]() $2$
motivic cohomology of
$2$
motivic cohomology of
![]() $\operatorname {\mathrm {Spec}} k$
by
$\operatorname {\mathrm {Spec}} k$
by
![]() ${\mathbb {M}}_2$
. This is a bigraded ring,
${\mathbb {M}}_2$
. This is a bigraded ring,
 $$\begin{align*}{\mathbb{M}}_2 = \bigoplus_{i,n} {\mathbb{M}}_2^{n,i},\end{align*}$$
$$\begin{align*}{\mathbb{M}}_2 = \bigoplus_{i,n} {\mathbb{M}}_2^{n,i},\end{align*}$$
nonzero only in degrees
![]() $0 \le n \le i$
. There are two notable classes,
$0 \le n \le i$
. There are two notable classes,
![]() $\rho \in {\mathbb {M}}^{1,1}_2$
, the reduction modulo
$\rho \in {\mathbb {M}}^{1,1}_2$
, the reduction modulo
![]() $2$
of
$2$
of
![]() $\{-1\} \in K^M_1(k) = {\mathrm {H}}^{1,1}(\operatorname {\mathrm {Spec}} k, {\mathbb {Z}})$
, and
$\{-1\} \in K^M_1(k) = {\mathrm {H}}^{1,1}(\operatorname {\mathrm {Spec}} k, {\mathbb {Z}})$
, and
![]() $\tau \in {\mathbb {M}}^{0,1}_2$
, corresponding to the identity
$\tau \in {\mathbb {M}}^{0,1}_2$
, corresponding to the identity
![]() $(-1)^2 = 1$
. If
$(-1)^2 = 1$
. If
![]() $-1$
is a square in k, then
$-1$
is a square in k, then
![]() $\rho = 0$
, but
$\rho = 0$
, but
![]() $\tau $
is always a nonzero class.
$\tau $
is always a nonzero class.
Proposition 5.3. (Dugger–Isaksen, [4] Theorem 4.9)
There is an isomorphism of graded rings
 $$\begin{align*}{\mathrm{H}}^{\ast, \ast} (DQ_{2r-1}; {\mathbb{F}}_2) {\cong} \frac{{\mathbb{M}}_2 [a, b]}{ (a^2 - \rho a - \tau b, b^{r})} \end{align*}$$
$$\begin{align*}{\mathrm{H}}^{\ast, \ast} (DQ_{2r-1}; {\mathbb{F}}_2) {\cong} \frac{{\mathbb{M}}_2 [a, b]}{ (a^2 - \rho a - \tau b, b^{r})} \end{align*}$$
where
![]() $|a| = (1,1)$
and
$|a| = (1,1)$
and
![]() $|b| = (2,1)$
.
$|b| = (2,1)$
.
Moreover, the inclusion
![]() $DQ_{2r-1} \to DQ_{2r+1}$
given by
$DQ_{2r-1} \to DQ_{2r+1}$
given by
![]() $a_{r+1} = b_{r+1} = 0$
induces the map
$a_{r+1} = b_{r+1} = 0$
induces the map
![]() ${\mathrm {H}}^{\ast , \ast } (DQ_{2r+1}; {\mathbb {F}}_2) \to {\mathrm {H}}^{\ast , \ast } (DQ_{2r-1}; {\mathbb {F}}_2)$
sending a to a and b to b.
${\mathrm {H}}^{\ast , \ast } (DQ_{2r+1}; {\mathbb {F}}_2) \to {\mathrm {H}}^{\ast , \ast } (DQ_{2r-1}; {\mathbb {F}}_2)$
sending a to a and b to b.
This proposition subsumes two other notable calculations of invariants. In the first place, owing to the Beilinson–Lichtenbaum conjecture [Reference Voevodsky23], it subsumes the calculation of
![]() ${\mathrm {H}}^\ast _{{\text {'et}}} (DQ_{2r-1};{\mathbb {F}}_2)$
. For instance, if k is algebraically closed, then
${\mathrm {H}}^\ast _{{\text {'et}}} (DQ_{2r-1};{\mathbb {F}}_2)$
. For instance, if k is algebraically closed, then
![]() ${\mathbb {M}}_2 = {\mathbb {F}}[\tau ]$
, and one deduces that
${\mathbb {M}}_2 = {\mathbb {F}}[\tau ]$
, and one deduces that
![]() ${\mathrm {H}}^\ast _{{\text {'et}}}( DQ_{2r-1}; {\mathbb {F}}_2) {\cong } {\mathbb {F}}_2[a, b] /( a^2 -b , b^{r}) = {\mathbb {F}}_2[a]/(a^{2r})$
.
${\mathrm {H}}^\ast _{{\text {'et}}}( DQ_{2r-1}; {\mathbb {F}}_2) {\cong } {\mathbb {F}}_2[a, b] /( a^2 -b , b^{r}) = {\mathbb {F}}_2[a]/(a^{2r})$
.
In the second, since
![]() ${\mathrm {H}}^{2n,n}(\cdot ; {\mathbb {F}}_2)$
is identified with
${\mathrm {H}}^{2n,n}(\cdot ; {\mathbb {F}}_2)$
is identified with
![]() ${\mathrm {CH}}^n(\cdot ) {\otimes }_{\mathbb {Z}} {\mathbb {F}}_2$
, the calculation of the proposition subsumes that of the Chow groups modulo
${\mathrm {CH}}^n(\cdot ) {\otimes }_{\mathbb {Z}} {\mathbb {F}}_2$
, the calculation of the proposition subsumes that of the Chow groups modulo
![]() $2$
. In fact, the extension problems that prevented Dugger and Isaksen from calculating
$2$
. In fact, the extension problems that prevented Dugger and Isaksen from calculating
![]() ${\mathrm {H}}^{\ast , \ast }(DQ_{2r-1} ; {\mathbb {Z}})$
do not arise in this range, and by reference to the appendix of [Reference Dugger and Isaksen4], which in turn refers to [Reference Karpenko and Merkurjev13], one can calculate the integral Chow rings. This is done in the first two paragraphs of the proof of [Reference Dugger and Isaksen4, Theorem 4.9].
${\mathrm {H}}^{\ast , \ast }(DQ_{2r-1} ; {\mathbb {Z}})$
do not arise in this range, and by reference to the appendix of [Reference Dugger and Isaksen4], which in turn refers to [Reference Karpenko and Merkurjev13], one can calculate the integral Chow rings. This is done in the first two paragraphs of the proof of [Reference Dugger and Isaksen4, Theorem 4.9].
Proposition 5.4 One may present
 $$\begin{align*}{\mathrm{CH}}^\ast(DQ_{2r-1}) = \frac{{\mathbb{Z}}[\tilde b]}{(2\tilde b, \tilde b^{r})}, \quad |b| = 1.\end{align*}$$
$$\begin{align*}{\mathrm{CH}}^\ast(DQ_{2r-1}) = \frac{{\mathbb{Z}}[\tilde b]}{(2\tilde b, \tilde b^{r})}, \quad |b| = 1.\end{align*}$$
As before, the map
![]() $DQ_{2r-1} \to DQ_{2r+1}$
given by adding
$DQ_{2r-1} \to DQ_{2r+1}$
given by adding
![]() $0$
s induces the map
$0$
s induces the map
![]() $b \mapsto b$
on Chow rings. Moreover
$b \mapsto b$
on Chow rings. Moreover
![]() ${\mathrm {CH}}^\ast (DQ_{2r-1}) {\otimes }_{\mathbb {Z}} {\mathbb {F}}_2$
can be identified with the subring of
${\mathrm {CH}}^\ast (DQ_{2r-1}) {\otimes }_{\mathbb {Z}} {\mathbb {F}}_2$
can be identified with the subring of
![]() $ {\mathrm {H}}^{\ast , \ast } (DQ_{2r-1}; {\mathbb {F}}_2)$
generated by b.
$ {\mathrm {H}}^{\ast , \ast } (DQ_{2r-1}; {\mathbb {F}}_2)$
generated by b.
The reason we have explained all this is that there is a composite of maps
both of which are
![]() ${\mathbb {A}^{1}}$
-equivalences, and so Propositions 5.3 and 5.4 amount to a calculation of the motivic and étale cohomologies and Chow rings of
${\mathbb {A}^{1}}$
-equivalences, and so Propositions 5.3 and 5.4 amount to a calculation of the motivic and étale cohomologies and Chow rings of
![]() $B(r; {\mathbb {A}}^2)$
. Both maps in diagram (5.2) are compatible in the evident way with an increase in r, so that we may use the material of this section to compute the stable invariants of
$B(r; {\mathbb {A}}^2)$
. Both maps in diagram (5.2) are compatible in the evident way with an increase in r, so that we may use the material of this section to compute the stable invariants of
![]() $B(r; {\mathbb {A}}^2)$
in the sense of Section 4.
$B(r; {\mathbb {A}}^2)$
in the sense of Section 4.
The
![]() ${\mathbb {A}^{1}}$
-equivalence
${\mathbb {A}^{1}}$
-equivalence
![]() $B(r; {\mathbb {A}}^2) \to ({\mathbb {A}}^{r} {\setminus } \{0\})/ C_2$
was constructed above in Lemma 5.1, so it remains to prove the following.
$B(r; {\mathbb {A}}^2) \to ({\mathbb {A}}^{r} {\setminus } \{0\})/ C_2$
was constructed above in Lemma 5.1, so it remains to prove the following.
Lemma 5.5 Let
![]() $r \ge 1$
. The variety
$r \ge 1$
. The variety
![]() $DQ_{2r-1}$
is affine and has coordinate ring
$DQ_{2r-1}$
is affine and has coordinate ring
 $$\begin{align*}R = \left[\frac{k[x_1,\dots, x_r, y_1, \dots, y_r]}{\big(1-\sum_{i=1}^r x_iy_i \big)}\right]^{C_2} \end{align*}$$
$$\begin{align*}R = \left[\frac{k[x_1,\dots, x_r, y_1, \dots, y_r]}{\big(1-\sum_{i=1}^r x_iy_i \big)}\right]^{C_2} \end{align*}$$
where the
![]() $C_2$
action on
$C_2$
action on
![]() $x_i$
and
$x_i$
and
![]() $y_i$
is by
$y_i$
is by
![]() $x_i \mapsto -x_i$
and
$x_i \mapsto -x_i$
and
![]() $y_i \mapsto -y_i$
.
$y_i \mapsto -y_i$
.
Proof The variety
![]() $DQ_{2r-1}$
is a complement of a hypersurface in
$DQ_{2r-1}$
is a complement of a hypersurface in
![]() ${\mathbb {P}}^{2r-1}$
, and is therefore affine.
${\mathbb {P}}^{2r-1}$
, and is therefore affine.
Let Q denote
![]() $a_1 b_1 + \dots + a_r b_r$
. The coordinate ring of
$a_1 b_1 + \dots + a_r b_r$
. The coordinate ring of
![]() $DQ_{2r-1}$
is the ring of degree-
$DQ_{2r-1}$
is the ring of degree-
![]() $0$
terms in the graded ring
$0$
terms in the graded ring
![]() $S=k[a_1, \dots , a_r, b_1, \dots , b_r, Q^{-1}]$
, where
$S=k[a_1, \dots , a_r, b_1, \dots , b_r, Q^{-1}]$
, where
![]() $|a_i| = |b_i| = 1$
and
$|a_i| = |b_i| = 1$
and
![]() $|Q^{-1}| = -2$
. This ring is the subring of S generated by the terms
$|Q^{-1}| = -2$
. This ring is the subring of S generated by the terms
![]() $a_ia_j Q^{-1}$
,
$a_ia_j Q^{-1}$
,
![]() $a_i b_j Q^{-1}$
and
$a_i b_j Q^{-1}$
and
![]() $b_i b_j Q^{-1}$
.
$b_i b_j Q^{-1}$
.
Consider the ring
 $$\begin{align*}T = \frac{k[ x_1, \dots, x_r, y_1 , \dots , y_r]}{( 1- \sum_{i=1}^r x_i y_i )}. \end{align*}$$
$$\begin{align*}T = \frac{k[ x_1, \dots, x_r, y_1 , \dots , y_r]}{( 1- \sum_{i=1}^r x_i y_i )}. \end{align*}$$
One may define a map of rings
![]() $\phi : S \to T$
by sending
$\phi : S \to T$
by sending
![]() $a_i \mapsto x_i$
and
$a_i \mapsto x_i$
and
![]() $b_i \mapsto y_i$
, since
$b_i \mapsto y_i$
, since
![]() $Q \mapsto 1$
under this assignment. Restricting to
$Q \mapsto 1$
under this assignment. Restricting to
![]() $\Gamma (DQ_{2r-1}, {\mathcal {O}}_{DQ_{2r-1}}) \subset S$
, one obtains a map
$\Gamma (DQ_{2r-1}, {\mathcal {O}}_{DQ_{2r-1}}) \subset S$
, one obtains a map
![]() $\Gamma (DQ_{2r-1}, {\mathcal {O}}_{DQ_{2r-1}}) \to T$
for which the image is precisely the subring generated by terms
$\Gamma (DQ_{2r-1}, {\mathcal {O}}_{DQ_{2r-1}}) \to T$
for which the image is precisely the subring generated by terms
![]() $x_ix_j$
,
$x_ix_j$
,
![]() $x_i y_j$
and
$x_i y_j$
and
![]() $y_i y_j$
, i.e., the fixed subring under the
$y_i y_j$
, i.e., the fixed subring under the
![]() $C_2$
action given by
$C_2$
action given by
![]() $x_i \mapsto -x_i$
and
$x_i \mapsto -x_i$
and
![]() $y_i \mapsto -y_i$
.
$y_i \mapsto -y_i$
.
It remains to establish this map is injective. We show that the kernel of the map
![]() $\phi : S \to T$
contains only one homogeneous element,
$\phi : S \to T$
contains only one homogeneous element,
![]() $0$
, so that the restriction of this map to the subring of degree-
$0$
, so that the restriction of this map to the subring of degree-
![]() $\!\!0$
terms in S is injective. The kernel of
$\!\!0$
terms in S is injective. The kernel of
![]() $\phi $
is the ideal
$\phi $
is the ideal
![]() $(Q-1)$
. Since S is an integral domain, degree considerations imply that no nonzero multiple of
$(Q-1)$
. Since S is an integral domain, degree considerations imply that no nonzero multiple of
![]() $(Q-1)$
is homogeneous. ▪
$(Q-1)$
is homogeneous. ▪
Proposition 5.6 For all r, there is an
![]() ${\mathbb {A}^{1}}$
-equivalence
${\mathbb {A}^{1}}$
-equivalence
Proof Let T be as in the proof of Lemma 5.5. It is well known that
![]() $\operatorname {\mathrm {Spec}} T$
is an affine vector bundle torsor over
$\operatorname {\mathrm {Spec}} T$
is an affine vector bundle torsor over
![]() ${\mathbb {A}}^r \setminus \{0\}$
. In fact, for each
${\mathbb {A}}^r \setminus \{0\}$
. In fact, for each
![]() $j \in \{1, \dots , r\}$
, if we define
$j \in \{1, \dots , r\}$
, if we define
![]() $U_j {\cong } {\mathbb {A}}^1{\setminus }\{0\} \times {\mathbb {A}}^{r-1}$
to be the open subscheme of
$U_j {\cong } {\mathbb {A}}^1{\setminus }\{0\} \times {\mathbb {A}}^{r-1}$
to be the open subscheme of
![]() ${\mathbb {A}}^r {\setminus } \{0\}$
where the jth coordinate is invertible, then we arrive at a pull-back diagram
${\mathbb {A}}^r {\setminus } \{0\}$
where the jth coordinate is invertible, then we arrive at a pull-back diagram

Since
![]() $U_j$
inherits a free
$U_j$
inherits a free
![]() $C_2$
-action, it follows that in the quotient we obtain a vector bundle
$C_2$
-action, it follows that in the quotient we obtain a vector bundle
![]() $({\mathbb {A}}^{r-1} \times U_j)/C_2 \to U_j/C_2$
, and so the map
$({\mathbb {A}}^{r-1} \times U_j)/C_2 \to U_j/C_2$
, and so the map
![]() $(\operatorname {\mathrm {Spec}} T) / C_2 \to ({\mathbb {A}}^r {\setminus } \{0\})/ C_2$
is an
$(\operatorname {\mathrm {Spec}} T) / C_2 \to ({\mathbb {A}}^r {\setminus } \{0\})/ C_2$
is an
![]() ${\mathbb {A}}^1$
-equivalence, as claimed. ▪
${\mathbb {A}}^1$
-equivalence, as claimed. ▪
As a consequence of Proposition 5.6 we observe that the affine variety
![]() $DQ_{2r-1}$
is an affine approximation of
$DQ_{2r-1}$
is an affine approximation of
![]() $B(r;{\mathbb {A}}^2)$
.
$B(r;{\mathbb {A}}^2)$
.
6 Relation to line bundles in the quadratic case
We continue to work over a field k, and to require that the characteristic of k be different from
![]() $2$
.
$2$
.
In the case where
![]() $n=2$
, the structure group of the degree-n étale algebra is
$n=2$
, the structure group of the degree-n étale algebra is
![]() $C_2$
, the cyclic group of order
$C_2$
, the cyclic group of order
![]() $2$
, which happens to be a subgroup of
$2$
, which happens to be a subgroup of
![]() ${\mathbb {G}_{m}}$
. More explicitly,
${\mathbb {G}_{m}}$
. More explicitly,
![]() ${\mathrm {H}}^1_{{\text {'et}}}(\operatorname {\mathrm {Spec}} R ; C_2)$
is an abelian group which is isomorphic to the isomorphism classes of quadratic étale algebras on
${\mathrm {H}}^1_{{\text {'et}}}(\operatorname {\mathrm {Spec}} R ; C_2)$
is an abelian group which is isomorphic to the isomorphism classes of quadratic étale algebras on
![]() $\operatorname {\mathrm {Spec}} R$
. On the other hand due to the Kummer sequence and
$\operatorname {\mathrm {Spec}} R$
. On the other hand due to the Kummer sequence and
![]() $C_2\subset {\mathbb {G}_{m}}$
we have
$C_2\subset {\mathbb {G}_{m}}$
we have
which means that
![]() ${\mathrm {H}}^1_{{\text {'et}}}(\operatorname {\mathrm {Spec}} R ; C_2)$
is identified with the set of isomorphism classes of
${\mathrm {H}}^1_{{\text {'et}}}(\operatorname {\mathrm {Spec}} R ; C_2)$
is identified with the set of isomorphism classes of
![]() $2$
-torsion line bundles
$2$
-torsion line bundles
![]() ${\mathcal {L}}$
with a choice of trivialization
${\mathcal {L}}$
with a choice of trivialization
 $\phi :{\mathcal {L}} \otimes {\mathcal {L}} {\overset {\cong }{\longrightarrow }} {\mathcal {O}}_R$
.
$\phi :{\mathcal {L}} \otimes {\mathcal {L}} {\overset {\cong }{\longrightarrow }} {\mathcal {O}}_R$
.
This is the basis of the following construction.
Construction 6.1 Let X be a scheme such that
![]() $2$
is invertible in all residue fields, and let
$2$
is invertible in all residue fields, and let
![]() ${\mathcal {A}}$
be a quadratic étale algebra on X. There is a trace map [Reference Knus14, Section I.1]:
${\mathcal {A}}$
be a quadratic étale algebra on X. There is a trace map [Reference Knus14, Section I.1]:
and an involution
![]() $\sigma : {\mathcal {A}} \to {\mathcal {A}}$
given by
$\sigma : {\mathcal {A}} \to {\mathcal {A}}$
given by
![]() $\sigma = {Tr} - \operatorname {\mathrm {id}}$
. Define
$\sigma = {Tr} - \operatorname {\mathrm {id}}$
. Define
![]() ${\mathcal {L}}$
to be the kernel of
${\mathcal {L}}$
to be the kernel of
![]() ${Tr}: {\mathcal {A}} \to {\mathcal {O}}$
. The sequence of sheaves on X
${Tr}: {\mathcal {A}} \to {\mathcal {O}}$
. The sequence of sheaves on X
is split short exact, where the splitting
![]() ${\mathcal {O}} \to {\mathcal {A}}$
is given on sections by
${\mathcal {O}} \to {\mathcal {A}}$
is given on sections by
 $x \mapsto \frac {1}{2} x$
.
$x \mapsto \frac {1}{2} x$
.
The construction of
![]() ${\mathcal {L}}$
from
${\mathcal {L}}$
from
![]() ${\mathcal {A}}$
gives an explicit instantiation of the map
${\mathcal {A}}$
gives an explicit instantiation of the map
![]() ${\mathrm {H}}^1_{{\text {'et}}}(X , C_2) \to {\mathrm {H}}^1_{{\text {'et}}} (X, {\mathbb {G}_{m}})$
on isomorphism classes. We note that
${\mathrm {H}}^1_{{\text {'et}}}(X , C_2) \to {\mathrm {H}}^1_{{\text {'et}}} (X, {\mathbb {G}_{m}})$
on isomorphism classes. We note that
![]() ${\mathcal {L}}$
must necessarily be a
${\mathcal {L}}$
must necessarily be a
![]() $2$
-torsion line bundles, in that
$2$
-torsion line bundles, in that
![]() ${\mathcal {L}} {\otimes } {\mathcal {L}} $
is trivial.
${\mathcal {L}} {\otimes } {\mathcal {L}} $
is trivial.
It is partly possible to reverse the construction of
![]() ${\mathcal {L}}$
from
${\mathcal {L}}$
from
![]() ${\mathcal {A}}$
.
${\mathcal {A}}$
.
Construction 6.2 Let X be as above, and let
![]() ${\mathcal {L}}$
be a line-bundle on X such that there is an isomorphism
${\mathcal {L}}$
be a line-bundle on X such that there is an isomorphism
![]() ${\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
. Let
${\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
. Let
![]() $\phi : {\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
be a specific choice of isomorphism. From the data
$\phi : {\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
be a specific choice of isomorphism. From the data
![]() $({\mathcal {L}}, \phi )$
, we may produce an étale algebra
$({\mathcal {L}}, \phi )$
, we may produce an étale algebra
![]() ${\mathcal {A}} = {\mathcal {O}} \oplus {\mathcal {L}}$
on which the multiplication is given, on sections, by
${\mathcal {A}} = {\mathcal {O}} \oplus {\mathcal {L}}$
on which the multiplication is given, on sections, by
![]() $(r, x) \cdot (r', x') = (rr' + \phi (x {\otimes } x'), rx' + r' x)$
.
$(r, x) \cdot (r', x') = (rr' + \phi (x {\otimes } x'), rx' + r' x)$
.
Proposition 6.3 Let X be a scheme such that
![]() $2$
is invertible in all residue fields of points of X. Let
$2$
is invertible in all residue fields of points of X. Let
![]() ${\mathcal {A}}$
a quadratic étale algebra on X. Let
${\mathcal {A}}$
a quadratic étale algebra on X. Let
![]() ${\mathcal {L}}$
be the associated line bundle to
${\mathcal {L}}$
be the associated line bundle to
![]() ${\mathcal {A}}$
, as in Construction 6.1. Suppose
${\mathcal {A}}$
, as in Construction 6.1. Suppose
![]() $a_1, \dots , a_r$
are global sections of
$a_1, \dots , a_r$
are global sections of
![]() ${\mathcal {A}}$
. Then
${\mathcal {A}}$
. Then
![]() $a_1, \dots , a_r$
generate
$a_1, \dots , a_r$
generate
![]() ${\mathcal {A}}$
as an algebra if and only if
${\mathcal {A}}$
as an algebra if and only if
 $a_1 - \frac {1}{2} {Tr}(a_1), \dots , a_r - \frac {1}{2} {Tr}(a_r)$
generate
$a_1 - \frac {1}{2} {Tr}(a_1), \dots , a_r - \frac {1}{2} {Tr}(a_r)$
generate
![]() ${\mathcal {L}}$
as a line bundle.
${\mathcal {L}}$
as a line bundle.
Proof Write q for the map
 $a \mapsto a - \frac {1}{2} {Tr}(a)$
. The questions of generation of
$a \mapsto a - \frac {1}{2} {Tr}(a)$
. The questions of generation of
![]() ${\mathcal {A}}$
and of
${\mathcal {A}}$
and of
![]() ${\mathcal {L}}$
may be reduced to residue fields at points of X, by Proposition 2.10 for the algebra and Nakayama’s lemma for the line bundle.
${\mathcal {L}}$
may be reduced to residue fields at points of X, by Proposition 2.10 for the algebra and Nakayama’s lemma for the line bundle.
We may therefore suppose F is a field of characteristic different from
![]() $2$
, and that
$2$
, and that
![]() $A/ F$
is a quadratic étale algebra. Since
$A/ F$
is a quadratic étale algebra. Since
![]() $2$
is invertible, we may write
$2$
is invertible, we may write
![]() $A = F[z]/(z^2 - c)$
for some element
$A = F[z]/(z^2 - c)$
for some element
![]() $c \in F^\times $
. In this presentation,
$c \in F^\times $
. In this presentation,
![]() $\sigma (z) = -z$
and
$\sigma (z) = -z$
and
![]() ${Tr}(az + b) = 2b$
. The kernel of the trace map, i.e.
${Tr}(az + b) = 2b$
. The kernel of the trace map, i.e.
![]() $\;{\mathcal {L}}$
, is therefore
$\;{\mathcal {L}}$
, is therefore
![]() $Fz$
. The map
$Fz$
. The map
![]() $q: A \to Fz$
is given by
$q: A \to Fz$
is given by
![]() $q(a z + b) = az$
.
$q(a z + b) = az$
.
An r-tuple
![]() $\vec a = (a_1 z + b_1, \dots , a_r z + b_r)$
of elements of A generate it as an F-algebra if and only if
$\vec a = (a_1 z + b_1, \dots , a_r z + b_r)$
of elements of A generate it as an F-algebra if and only if
![]() $q(\vec a) = (a_1z , \dots a_rz)$
do. This tuple generates A as an algebra if and only if at least one of the
$q(\vec a) = (a_1z , \dots a_rz)$
do. This tuple generates A as an algebra if and only if at least one of the
![]() $a_i$
is nonzero, which is exactly the condition for it to generate
$a_i$
is nonzero, which is exactly the condition for it to generate
![]() $Fz$
as an F-vector space.▪
$Fz$
as an F-vector space.▪
Remark 6.4 Let k be a field of characteristic different from
![]() $2$
. Let X be a k-variety. An étale algebra of degree
$2$
. Let X be a k-variety. An étale algebra of degree
![]() $2$
generated by r global sections corresponds to a map
$2$
generated by r global sections corresponds to a map
![]() $X \to B(r; {\mathbb {A}}^2)$
. A line bundle generated by r global sections corresponds to a map
$X \to B(r; {\mathbb {A}}^2)$
. A line bundle generated by r global sections corresponds to a map
![]() $X\to {\mathbb {P}}^{r-1}$
. In light of Proposition 6.3, there must be a map of varieties
$X\to {\mathbb {P}}^{r-1}$
. In light of Proposition 6.3, there must be a map of varieties
![]() $B(r; {\mathbb {A}}^2) \to {\mathbb {P}}^{r-1}$
. This map is given by
$B(r; {\mathbb {A}}^2) \to {\mathbb {P}}^{r-1}$
. This map is given by
 $$\begin{align*}B(r; {\mathbb{A}}^2) \overset{{\cong}}{\to } ({\mathbb{A}}^r{\setminus}\{0\})/C_2 \times {\mathbb{A}}^r \overset{p_1}{\to} ({\mathbb{A}}^r {\setminus} \{0\}) / C_2\to ({\mathbb{A}}^r {\setminus} \{0\} )/ {\mathbb{G}_{m}} {\overset{\cong}{\longrightarrow}} {\mathbb{P}}^{r-1} \end{align*}$$
$$\begin{align*}B(r; {\mathbb{A}}^2) \overset{{\cong}}{\to } ({\mathbb{A}}^r{\setminus}\{0\})/C_2 \times {\mathbb{A}}^r \overset{p_1}{\to} ({\mathbb{A}}^r {\setminus} \{0\}) / C_2\to ({\mathbb{A}}^r {\setminus} \{0\} )/ {\mathbb{G}_{m}} {\overset{\cong}{\longrightarrow}} {\mathbb{P}}^{r-1} \end{align*}$$
where the morphisms are, left to right, the isomorphism of Lemma 5.1, projection onto the second factor, and the map induced by the inclusion
![]() $C_2 \subset {\mathbb {G}_{m}}$
.
$C_2 \subset {\mathbb {G}_{m}}$
.
7 The example of Chase
The following will be referred to as “the example of Chase”.
Construction 7.1 Let
 $S = {\mathbb {R}}[ z_1, \dots , z_r ]/\Big ( \sum _{i=1}^r z_i^2 - 1 \Big )$
and equip this with the
$S = {\mathbb {R}}[ z_1, \dots , z_r ]/\Big ( \sum _{i=1}^r z_i^2 - 1 \Big )$
and equip this with the
![]() $C_2$
-action given by
$C_2$
-action given by
![]() $z_i \mapsto -z_i$
. Let
$z_i \mapsto -z_i$
. Let
![]() $R = S^{C_2}$
. The dimension of both R and S is
$R = S^{C_2}$
. The dimension of both R and S is
![]() $r-1$
.
$r-1$
.
The ring R carries a projective module of rank
![]() $1$
, i.e., a line bundle, that requires r global sections in order to generate it. This example is given in [Reference Swan21, Theorem 4].
$1$
, i.e., a line bundle, that requires r global sections in order to generate it. This example is given in [Reference Swan21, Theorem 4].
Remark 7.2 In fact, the line bundle in question is of order
![]() $2$
in the Picard group, so Proposition 6.3 applies and there is an associated quadratic étale algebra on
$2$
in the Picard group, so Proposition 6.3 applies and there is an associated quadratic étale algebra on
![]() $\operatorname {\mathrm {Spec}} R = Y(r)$
requiring r generators. The algebra is, of course, dependent on a choice of trivialization of the square of the line bundle, but one may choose the trivialization so the étale algebra in question is S itself as an R-algebra.
$\operatorname {\mathrm {Spec}} R = Y(r)$
requiring r generators. The algebra is, of course, dependent on a choice of trivialization of the square of the line bundle, but one may choose the trivialization so the étale algebra in question is S itself as an R-algebra.
Remark 7.3 This construction shows that the bound of First and Reichstein, [Reference First and Reichstein6], on the number of generators required by an étale algebra of degree
![]() $2$
is tight. This was first observed, to the best of our knowledge, by M. Ojanguren in private communication.
$2$
is tight. This was first observed, to the best of our knowledge, by M. Ojanguren in private communication.
Even better, replacing S by
![]() $S \times R^{n-2}$
over R, one produces a degree-n étale algebra over R requiring r elements to generate, so the bound is tight in the case of étale algebras of arbitrary degrees. We owe this observation to Zinovy Reichstein.
$S \times R^{n-2}$
over R, one produces a degree-n étale algebra over R requiring r elements to generate, so the bound is tight in the case of étale algebras of arbitrary degrees. We owe this observation to Zinovy Reichstein.
The original method of proof that the line bundle in the example of Chase cannot be generated by fewer than r global sections uses the Borsuk–Ulam theorem. Here we show that a variation on that proof follows naturally from our general theory of classifying objects. The Borsuk–Ulam theorem is a theorem about the topology of
![]() ${\mathbb {R}}P^r$
, so it can be no surprise that it is replaced here by facts about the singular cohomology of
${\mathbb {R}}P^r$
, so it can be no surprise that it is replaced here by facts about the singular cohomology of
![]() ${\mathbb {R}}P^r$
.
${\mathbb {R}}P^r$
.
7.1 The homotopy type of the real points of
 $B(r;{\mathbb {A}}^2)$
$B(r;{\mathbb {A}}^2)$
In addition to the general results about the motivic cohomology of
![]() $B(r; {\mathbb {A}}^2)$
, we can give a complete description of the homotopy type of the real points
$B(r; {\mathbb {A}}^2)$
, we can give a complete description of the homotopy type of the real points
![]() $B(r; {\mathbb {A}}^2)({\mathbb {R}})$
.
$B(r; {\mathbb {A}}^2)({\mathbb {R}})$
.
If X is a nonsingular
![]() ${\mathbb {R}}$
-variety, then it is possible to produce a complex manifold from X by first extending scalars to
${\mathbb {R}}$
-variety, then it is possible to produce a complex manifold from X by first extending scalars to
![]() ${\mathbb {C}}$
and then employing the usual Betti realization functor to produce a manifold
${\mathbb {C}}$
and then employing the usual Betti realization functor to produce a manifold
![]() $X({\mathbb {C}})$
. Since X is defined over
$X({\mathbb {C}})$
. Since X is defined over
![]() ${\mathbb {R}}$
, however, the resulting manifold is equipped with an action of the Galois group
${\mathbb {R}}$
, however, the resulting manifold is equipped with an action of the Galois group
![]() $\operatorname {Gal}({\mathbb {C}}/{\mathbb {R}}) {\cong } C_2$
. We write
$\operatorname {Gal}({\mathbb {C}}/{\mathbb {R}}) {\cong } C_2$
. We write
![]() $X({\mathbb {R}})$
for the Galois-fixed points of
$X({\mathbb {R}})$
for the Galois-fixed points of
![]() $X({\mathbb {C}})$
.
$X({\mathbb {C}})$
.
Remark 7.4 The real realization functor
![]() $X \leadsto X({\mathbb {R}})$
preserves finite products, so that if
$X \leadsto X({\mathbb {R}})$
preserves finite products, so that if
![]() $f,g: X\to Y$
are two maps of varieties and
$f,g: X\to Y$
are two maps of varieties and
![]() $H: X \times {\mathbb {A}^{1}} \to X'$
is an
$H: X \times {\mathbb {A}^{1}} \to X'$
is an
![]() ${\mathbb {A}^{1}}$
-homotopy between them, then
${\mathbb {A}^{1}}$
-homotopy between them, then
![]() $f({\mathbb {R}}), g({\mathbb {R}})$
are homotopic maps of varieties, via the homotopy obtained by restricting
$f({\mathbb {R}}), g({\mathbb {R}})$
are homotopic maps of varieties, via the homotopy obtained by restricting
![]() $H({\mathbb {R}}): X({\mathbb {R}}) \times {\mathbb {A}^{1}}({\mathbb {R}}) = X({\mathbb {R}}) \times {\mathbb {R}} \to X'({\mathbb {R}})$
to the subspace
$H({\mathbb {R}}): X({\mathbb {R}}) \times {\mathbb {A}^{1}}({\mathbb {R}}) = X({\mathbb {R}}) \times {\mathbb {R}} \to X'({\mathbb {R}})$
to the subspace
![]() $X({\mathbb {R}}) \times [0,1]$
.
$X({\mathbb {R}}) \times [0,1]$
.
Using Lemma 5.1, present
![]() $U(r; {\mathbb {A}}^2)$
as the variety of
$U(r; {\mathbb {A}}^2)$
as the variety of
![]() $2r$
-tuples
$2r$
-tuples
This variety carries an action by
![]() $C_2$
sending
$C_2$
sending
![]() $z_i \mapsto -z_i$
and fixing the
$z_i \mapsto -z_i$
and fixing the
![]() $w_i$
. We know
$w_i$
. We know
![]() $U(r;{\mathbb {A}}^2)$
and
$U(r;{\mathbb {A}}^2)$
and
![]() $B(r;{\mathbb {A}}^2)$
are naively homotopy equivalent to
$B(r;{\mathbb {A}}^2)$
are naively homotopy equivalent to
![]() $\mathbb {A}^r\setminus \{0\}$
and
$\mathbb {A}^r\setminus \{0\}$
and
![]() $\mathbb {A}^r\setminus \{0\}/C_2$
respectively.
$\mathbb {A}^r\setminus \{0\}/C_2$
respectively.
Construction 7.5 We now consider an inclusion that is not, in general, an equivalence. Let
![]() $P(r) = \operatorname {\mathrm {Spec}} S$
denote the subvariety of
$P(r) = \operatorname {\mathrm {Spec}} S$
denote the subvariety of
![]() ${\mathbb {A}}^r{\setminus } \{0\}$
consisting of r-tuples
${\mathbb {A}}^r{\setminus } \{0\}$
consisting of r-tuples
![]() $(z_1, \dots , z_r)$
such that
$(z_1, \dots , z_r)$
such that
![]() $\sum _{i=1}^r z_i^2 = 1$
. This is an
$\sum _{i=1}^r z_i^2 = 1$
. This is an
![]() $(r-1)$
-dimensional closed affine subscheme of
$(r-1)$
-dimensional closed affine subscheme of
![]() ${\mathbb {A}}^r {\setminus } \{0\}$
, invariant under the
${\mathbb {A}}^r {\setminus } \{0\}$
, invariant under the
![]() $C_2$
action on
$C_2$
action on
![]() ${\mathbb {A}}^r {\setminus } \{0\}$
. The quotient of
${\mathbb {A}}^r {\setminus } \{0\}$
. The quotient of
![]() $P(r)$
by
$P(r)$
by
![]() $C_2$
is
$C_2$
is
![]() $Y(r) = \operatorname {\mathrm {Spec}} R$
, and is equipped with an evident map
$Y(r) = \operatorname {\mathrm {Spec}} R$
, and is equipped with an evident map
![]() $Y(r) \to ({\mathbb {A}}^r {\setminus } \{0\}) /C_2 \to B(r; {\mathbb {A}}^2)$
. Here S and R take on the same meanings as in Construction 7.1.
$Y(r) \to ({\mathbb {A}}^r {\setminus } \{0\}) /C_2 \to B(r; {\mathbb {A}}^2)$
. Here S and R take on the same meanings as in Construction 7.1.
Proposition 7.6 Let notation be as in Construction 7.5. The real manifold
![]() $B(r;{\mathbb {A}}^2)({\mathbb {R}})$
has the homotopy type of
$B(r;{\mathbb {A}}^2)({\mathbb {R}})$
has the homotopy type of
The closed inclusion
![]() $Y(r) \to B(r;{\mathbb {A}}^2)$
includes
$Y(r) \to B(r;{\mathbb {A}}^2)$
includes
![]() $Y(r)({\mathbb {R}}) \to B(r;{\mathbb {A}}^2)({\mathbb {R}})$
as a deformation retract of one of the connected components.
$Y(r)({\mathbb {R}}) \to B(r;{\mathbb {A}}^2)({\mathbb {R}})$
as a deformation retract of one of the connected components.
Proof By Lemma 5.1 and Remark 7.4, the manifold
![]() $B(r,{\mathbb {A}}^2)({\mathbb {R}})$
is homotopy equivalent to
$B(r,{\mathbb {A}}^2)({\mathbb {R}})$
is homotopy equivalent to
![]() $({\mathbb {A}}^r{\setminus } \{0\}/C_2)({\mathbb {R}})$
. The manifold
$({\mathbb {A}}^r{\setminus } \{0\}/C_2)({\mathbb {R}})$
. The manifold
![]() $({\mathbb {A}}^r{\setminus } \{0\}/C_2)({\mathbb {C}})$
consists of equivalence classes of r-tuples of complex numbers
$({\mathbb {A}}^r{\setminus } \{0\}/C_2)({\mathbb {C}})$
consists of equivalence classes of r-tuples of complex numbers
![]() $(z_1,...,z_r)$
, where the
$(z_1,...,z_r)$
, where the
![]() $z_i$
are not all
$z_i$
are not all
![]() $0$
, under the relation
$0$
, under the relation
The real points of
![]() $({\mathbb {A}}^r{\setminus } \{0\})/C_2$
consist of Galois-invariant equivalence classes. There are two components of this manifold: either the terms in
$({\mathbb {A}}^r{\setminus } \{0\})/C_2$
consist of Galois-invariant equivalence classes. There are two components of this manifold: either the terms in
![]() $(z_1, \dots ,z_r)$
are all real or they are all imaginary. In either case, the connected component is homeomorphic to the manifold
$(z_1, \dots ,z_r)$
are all real or they are all imaginary. In either case, the connected component is homeomorphic to the manifold
![]() ${\mathbb {R}} P^{r-1}$
.
${\mathbb {R}} P^{r-1}$
.
We now consider the manifold
![]() $Y(r)({\mathbb {R}})$
. This arises as the Galois-fixed points of
$Y(r)({\mathbb {R}})$
. This arises as the Galois-fixed points of
![]() $Y(r)({\mathbb {C}})$
, which in turn is the quotient of
$Y(r)({\mathbb {C}})$
, which in turn is the quotient of
![]() $P(r)({\mathbb {C}})$
by a sign action. That is,
$P(r)({\mathbb {C}})$
by a sign action. That is,
![]() $P(r)({\mathbb {C}})$
is the complex manifold of r-tuples
$P(r)({\mathbb {C}})$
is the complex manifold of r-tuples
![]() $(z_1, \dots , z_r)$
satisfying
$(z_1, \dots , z_r)$
satisfying
![]() $\sum _{i=1}^r z_i^2 = 1$
. Again, in the
$\sum _{i=1}^r z_i^2 = 1$
. Again, in the
![]() ${\mathbb {R}}$
-points, the
${\mathbb {R}}$
-points, the
![]() $z_i$
are either all real or all purely imaginary. The condition
$z_i$
are either all real or all purely imaginary. The condition
![]() $\sum _{i=1}^r z_i^2 = 1$
is incompatible with purely imaginary
$\sum _{i=1}^r z_i^2 = 1$
is incompatible with purely imaginary
![]() $z_i$
, so
$z_i$
, so
![]() $Y(r)({\mathbb {R}})$
is the manifold of r-tuples of real numbers
$Y(r)({\mathbb {R}})$
is the manifold of r-tuples of real numbers
![]() $(z_1, \dots , z_r)$
satisfying
$(z_1, \dots , z_r)$
satisfying
![]() $\sum _{i=1}^r z_i^2 =1$
, taken up to sign. In short,
$\sum _{i=1}^r z_i^2 =1$
, taken up to sign. In short,
![]() $Y^r({\mathbb {R}}) = {\mathbb {R}}P^{r-1}$
.
$Y^r({\mathbb {R}}) = {\mathbb {R}}P^{r-1}$
.
As for the inclusion
![]() $Y(r)({\mathbb {R}}) \to B(r;{\mathbb {A}}^2)({\mathbb {R}})$
, it admits the following description, as can be seen by tracing through all the morphisms defined so far. Suppose given an equivalence class of real numbers
$Y(r)({\mathbb {R}}) \to B(r;{\mathbb {A}}^2)({\mathbb {R}})$
, it admits the following description, as can be seen by tracing through all the morphisms defined so far. Suppose given an equivalence class of real numbers
![]() $(z_1, \dots , z_r)$
, satisfying
$(z_1, \dots , z_r)$
, satisfying
![]() $\sum _{i=1}^r z_i^2 = 1$
, taken up to sign. Then embed
$\sum _{i=1}^r z_i^2 = 1$
, taken up to sign. Then embed
![]() $(z_1, \dots , z_r)$
as the point of
$(z_1, \dots , z_r)$
as the point of
![]() $B(r;{\mathbb {A}}^2)({\mathbb {R}})$
given by the class of
$B(r;{\mathbb {A}}^2)({\mathbb {R}})$
given by the class of
![]() $(z_1, z_2, \dots , z_r, 0, \dots , 0)$
. That is, embed
$(z_1, z_2, \dots , z_r, 0, \dots , 0)$
. That is, embed
![]() ${\mathbb {R}}P^{r-1}$
in
${\mathbb {R}}P^{r-1}$
in
 ${\mathbb {R}}^r \times \left ({\mathbb {R}}^{r-1} {\setminus } \{0\} \right ) /C_2$
by embedding
${\mathbb {R}}^r \times \left ({\mathbb {R}}^{r-1} {\setminus } \{0\} \right ) /C_2$
by embedding
![]() ${\mathbb {R}}P^{r-1} \subset ({\mathbb {R}}^r {\setminus } \{0\})/ C_2$
as a deformation retract, and then embedding the latter space as the zero section of the trivial bundle. It is elementary that this composite is also a deformation retract. ▪
${\mathbb {R}}P^{r-1} \subset ({\mathbb {R}}^r {\setminus } \{0\})/ C_2$
as a deformation retract, and then embedding the latter space as the zero section of the trivial bundle. It is elementary that this composite is also a deformation retract. ▪
Remark 7.7 We remark that the functor
![]() $X \leadsto X({\mathbb {R}})$
does not commute with colimits. For instance
$X \leadsto X({\mathbb {R}})$
does not commute with colimits. For instance
![]() $U(r;{\mathbb {A}}^2)({\mathbb {R}}) / C_2$
, which is connected, is not the same as
$U(r;{\mathbb {A}}^2)({\mathbb {R}}) / C_2$
, which is connected, is not the same as
![]() $B(r;{\mathbb {A}}^2)({\mathbb {R}})$
.
$B(r;{\mathbb {A}}^2)({\mathbb {R}})$
.
In fact, the two components of
![]() $B(r;{\mathbb {A}}^2)({\mathbb {R}})$
as calculated above correspond to two isomorphism classes of quadratic étale
$B(r;{\mathbb {A}}^2)({\mathbb {R}})$
as calculated above correspond to two isomorphism classes of quadratic étale
![]() ${\mathbb {R}}$
-algebras: one component corresponds to the split algebra
${\mathbb {R}}$
-algebras: one component corresponds to the split algebra
![]() ${\mathbb {R}} \times {\mathbb {R}}$
, and the other to the nonsplit
${\mathbb {R}} \times {\mathbb {R}}$
, and the other to the nonsplit
![]() ${\mathbb {C}}$
.
${\mathbb {C}}$
.
We will need two properties of
![]() ${\mathrm {H}}^*({\mathbb {R}}P^r; {\mathbb {F}}_2)$
here. Both are standard and may be found in [Reference Hatcher12].
${\mathrm {H}}^*({\mathbb {R}}P^r; {\mathbb {F}}_2)$
here. Both are standard and may be found in [Reference Hatcher12].
-
•
 ${\mathrm {H}}^*({\mathbb {R}}P^r ;{\mathbb {F}}_2) {\cong } {\mathbb {F}}_2[\theta ]/(\theta ^{r+1})$
where
${\mathrm {H}}^*({\mathbb {R}}P^r ;{\mathbb {F}}_2) {\cong } {\mathbb {F}}_2[\theta ]/(\theta ^{r+1})$
where
 $|\theta | = 1$
.
$|\theta | = 1$
. -
• The standard inclusion of
 ${\mathbb {R}}P^r \hookrightarrow {\mathbb {R}}P^{r+1}$
given by augmenting by
${\mathbb {R}}P^r \hookrightarrow {\mathbb {R}}P^{r+1}$
given by augmenting by
 $0$
induces the evident reduction map
$0$
induces the evident reduction map
 $\theta \mapsto \theta $
on cohomology.
$\theta \mapsto \theta $
on cohomology.
Proposition 7.8 We continue to work over
![]() $k = {\mathbb {R}}$
. Let
$k = {\mathbb {R}}$
. Let
![]() $s_r:B(r;{\mathbb {A}}^2)\to B(r+1;{\mathbb {A}}^2)$
be the stabilization map of Definition 4.1. The induced map on cohomology groups
$s_r:B(r;{\mathbb {A}}^2)\to B(r+1;{\mathbb {A}}^2)$
be the stabilization map of Definition 4.1. The induced map on cohomology groups
is an isomorphism when
![]() $j \le r$
and is
$j \le r$
and is
![]() $0$
otherwise.
$0$
otherwise.
Proof The map
![]() $s_r^*$
is arrived at by considering the inclusion
$s_r^*$
is arrived at by considering the inclusion
![]() $U(r;{\mathbb {A}}^2) \to U(r+1;{\mathbb {A}}^2)$
, which is given by augmenting an r-tuple of pairs
$U(r;{\mathbb {A}}^2) \to U(r+1;{\mathbb {A}}^2)$
, which is given by augmenting an r-tuple of pairs
![]() $(a_1, b_1, \dots , a_r, b_r)$
by
$(a_1, b_1, \dots , a_r, b_r)$
by
![]() $(0,0)$
, and then taking the quotient by
$(0,0)$
, and then taking the quotient by
![]() $C_2$
. After
$C_2$
. After
![]() ${\mathbb {R}}$
-realization, one is left with a map
${\mathbb {R}}$
-realization, one is left with a map
![]() $B(r;{\mathbb {A}}^2)({\mathbb {R}}) \to B(r+1;{\mathbb {A}}^2)({\mathbb {R}})$
which on each connected component is homotopy equivalent to the standard inclusion
$B(r;{\mathbb {A}}^2)({\mathbb {R}}) \to B(r+1;{\mathbb {A}}^2)({\mathbb {R}})$
which on each connected component is homotopy equivalent to the standard inclusion
![]() ${\mathbb {R}}P^r \to {\mathbb {R}}P^{r+1}$
. The result follows.▪
${\mathbb {R}}P^r \to {\mathbb {R}}P^{r+1}$
. The result follows.▪
Proposition 7.9 (Ojanguren)
Let S and R be as in Construction 7.1. The quadratic étale algebra
![]() $S/R$
cannot be generated by fewer than r elements.
$S/R$
cannot be generated by fewer than r elements.
Sketch of proofWrite
![]() $Y(r) = \operatorname {\mathrm {Spec}} R$
as in Construction 7.5. The morphism
$Y(r) = \operatorname {\mathrm {Spec}} R$
as in Construction 7.5. The morphism
![]() $Y(r) \to B(r ; {\mathbb {A}}^2)$
of Construction 7.5 classifies a quadratic étale algebra over
$Y(r) \to B(r ; {\mathbb {A}}^2)$
of Construction 7.5 classifies a quadratic étale algebra over
![]() $Y(r)$
, and we can identify this algebra as S.
$Y(r)$
, and we can identify this algebra as S.
The map
![]() $\phi : Y(r) \to B(r; {\mathbb {A}}^2)$
induces stable maps
$\phi : Y(r) \to B(r; {\mathbb {A}}^2)$
induces stable maps
![]() $\tilde \phi : Y(r) \to B(R; {\mathbb {A}}^2)$
. Any such stable map induces a surjective map
$\tilde \phi : Y(r) \to B(R; {\mathbb {A}}^2)$
. Any such stable map induces a surjective map
by Proposition 7.6 and 7.8. In particular, it is a surjection when
![]() $\ast = r-1$
.
$\ast = r-1$
.
Suppose S can be generated by
![]() $r-1$
elements, then there is a classifying map
$r-1$
elements, then there is a classifying map
![]() $\phi ' : Y(r) \to B(r-1; {\mathbb {A}}^2)$
, from which one can produce a stable map
$\phi ' : Y(r) \to B(r-1; {\mathbb {A}}^2)$
, from which one can produce a stable map
By reference to Corollary 4.3, for sufficiently large values of R, the maps
![]() $\tilde \phi ^*$
and
$\tilde \phi ^*$
and
![]() $(\tilde \phi ')^*$
agree. But
$(\tilde \phi ')^*$
agree. But
![]() $(\tilde \phi ')^*$
induces the
$(\tilde \phi ')^*$
induces the
![]() $0$
-map when
$0$
-map when
![]() $\ast = r-1$
, since
$\ast = r-1$
, since
![]() ${\mathrm {H}}^*(B(r-1; {\mathbb {A}}^2)({\mathbb {R}}); {\mathbb {F}}_2)$
is a direct sum of two copies of
${\mathrm {H}}^*(B(r-1; {\mathbb {A}}^2)({\mathbb {R}}); {\mathbb {F}}_2)$
is a direct sum of two copies of
![]() ${\mathbb {F}}_2[\theta ]/(\theta ^{r-1})$
. This contradicts the surjectivity of
${\mathbb {F}}_2[\theta ]/(\theta ^{r-1})$
. This contradicts the surjectivity of
![]() $\tilde \phi ^*$
in this degree.
$\tilde \phi ^*$
in this degree.
7.2 Algebras over fields containing a square root of
 $-1$
$-1$
Remark 7.10 When the field k contains a square root i of
![]() $-1$
, the analogous construction to that of Chase exhibits markedly different behaviour. For simplicity, suppose r is an even integer. Consider the ring
$-1$
, the analogous construction to that of Chase exhibits markedly different behaviour. For simplicity, suppose r is an even integer. Consider the ring
 $$\begin{align*}S'=\dfrac{k[z_1, \dots , z_r]}{\big(\sum_{i=1}^r z_i^2-1\big)} \end{align*}$$
$$\begin{align*}S'=\dfrac{k[z_1, \dots , z_r]}{\big(\sum_{i=1}^r z_i^2-1\big)} \end{align*}$$
with the action of
![]() $C_2$
given by
$C_2$
given by
![]() $z_i \mapsto -z_i$
. Let
$z_i \mapsto -z_i$
. Let
![]() $R' = (S')^{C_2}$
. After making the change of variables
$R' = (S')^{C_2}$
. After making the change of variables
![]() $x_{j} =z_{2j-1}+iz_{2j}$
and
$x_{j} =z_{2j-1}+iz_{2j}$
and
![]() $y_j=z_{2j-1} - iz_{2j}$
, we see that
$y_j=z_{2j-1} - iz_{2j}$
, we see that
![]() $S'$
is isomorphic to
$S'$
is isomorphic to
 $$\begin{align*}\frac{k[x_1, \dots, x_{r/2}, y_1, \dots, y_{r/2}]}{\Big( \sum_{j=1}^{r/2} x_jy_j -1 \Big)}\end{align*}$$
$$\begin{align*}\frac{k[x_1, \dots, x_{r/2}, y_1, \dots, y_{r/2}]}{\Big( \sum_{j=1}^{r/2} x_jy_j -1 \Big)}\end{align*}$$
and
![]() $R'$
is isomorphic to the subring consisting of terms of even degree. The smallest
$R'$
is isomorphic to the subring consisting of terms of even degree. The smallest
![]() $R'$
-subalgebra of
$R'$
-subalgebra of
![]() $S'$
containing the
$S'$
containing the
![]() $r/2$
-terms
$r/2$
-terms
![]() $x_1, \dots , x_{r/2}$
contains each of the
$x_1, \dots , x_{r/2}$
contains each of the
![]() $y_j$
because of the relation
$y_j$
because of the relation
 $$\begin{align*}y_j = \sum_{l=1}^{r/2} x_l (y_l y_j) \end{align*}$$
$$\begin{align*}y_j = \sum_{l=1}^{r/2} x_l (y_l y_j) \end{align*}$$
so
![]() $S'$
may be generated over
$S'$
may be generated over
![]() $R'$
by
$R'$
by
![]() $r/2$
elements. In fact,
$r/2$
elements. In fact,
![]() $R'$
is the coordinate ring of
$R'$
is the coordinate ring of
![]() $DQ_{r-1}$
, by Lemma 5.5. In Proposition 7.13 below, we show that
$DQ_{r-1}$
, by Lemma 5.5. In Proposition 7.13 below, we show that
![]() $S'$
cannot be generated by fewer than
$S'$
cannot be generated by fewer than
![]() $r/2$
elements over
$r/2$
elements over
![]() $R'$
.
$R'$
.
One may reasonably ask, therefore, over a field k containing a square root of
![]() $-1$
:
$-1$
:
Question 7.11 For a given dimension d, is there a smooth d-dimensional affine variety
![]() $\operatorname {\mathrm {Spec}} R$
and a finite étale algebra
$\operatorname {\mathrm {Spec}} R$
and a finite étale algebra
![]() ${\mathcal {A}}$
over
${\mathcal {A}}$
over
![]() $\operatorname {\mathrm {Spec}} R$
such that
$\operatorname {\mathrm {Spec}} R$
such that
![]() ${\mathcal {A}}$
cannot be generated by fewer than
${\mathcal {A}}$
cannot be generated by fewer than
![]() $d +1$
elements?
$d +1$
elements?
The result of [Reference First and Reichstein6] implies that if
![]() $d+1$
is increased, then the answer is negative.
$d+1$
is increased, then the answer is negative.
Remark 7.12 If
![]() $d=1$
, the answer to the question is positive. An example can be produced using any smooth affine curve Y for which
$d=1$
, the answer to the question is positive. An example can be produced using any smooth affine curve Y for which
![]() ${}_2 \text{Pic}(Y) \neq 0$
. Specifically, one may take a smooth elliptic curve and discard a point to produce such a Y. A nontrivial
${}_2 \text{Pic}(Y) \neq 0$
. Specifically, one may take a smooth elliptic curve and discard a point to produce such a Y. A nontrivial
![]() $2$
-torsion line bundle
$2$
-torsion line bundle
![]() ${\mathcal {L}}$
on Y cannot be generated by
${\mathcal {L}}$
on Y cannot be generated by
![]() $1$
section, since it is not trivial. One may choose a trivialization
$1$
section, since it is not trivial. One may choose a trivialization
![]() $\phi : {\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
, and therefore endow
$\phi : {\mathcal {L}} {\otimes } {\mathcal {L}} \to {\mathcal {O}}$
, and therefore endow
![]() ${\mathcal {L}} \oplus {\mathcal {O}}$
with the structure of a quadratic étale algebra, as in Construction 6.2, and this algebra also cannot be generated by
${\mathcal {L}} \oplus {\mathcal {O}}$
with the structure of a quadratic étale algebra, as in Construction 6.2, and this algebra also cannot be generated by
![]() $1$
element.
$1$
element.
Proposition 7.13 Let k be a field containing a square root i of
![]() $-1$
. Let T denote the ring
$-1$
. Let T denote the ring
 $$\begin{align*}T = \frac{ k [x_1 ,\dots, x_r, y_1, \dots, y_r] }{ ( \sum_{i=1}^r x_i y_i - 1 ) } \end{align*}$$
$$\begin{align*}T = \frac{ k [x_1 ,\dots, x_r, y_1, \dots, y_r] }{ ( \sum_{i=1}^r x_i y_i - 1 ) } \end{align*}$$
endowed with the
![]() $C_2$
action given by
$C_2$
action given by
![]() $x_i \mapsto -x_i$
and
$x_i \mapsto -x_i$
and
![]() $y_i \mapsto -y_i$
. Let
$y_i \mapsto -y_i$
. Let
![]() $R =T^{C_2}$
. Then the quadratic étale algebra T over R can be generated by the r elements
$R =T^{C_2}$
. Then the quadratic étale algebra T over R can be generated by the r elements
![]() $x_1, \dots , x_r$
, but cannot be generated by fewer than r elements.
$x_1, \dots , x_r$
, but cannot be generated by fewer than r elements.
Proof The ring R is the coordinate ring of the variety
![]() $DQ_{2r-1}$
in Lemma 5.5. In particular, there is an
$DQ_{2r-1}$
in Lemma 5.5. In particular, there is an
![]() ${\mathbb {A}^{1}}$
-equivalence
${\mathbb {A}^{1}}$
-equivalence
![]() $\phi : DQ_{2r-1} \to B(r; {\mathbb {A}}^2)$
, as in equation (5.2). Tracing through this composite, one sees it classifies the quadratic étale algebra generated by
$\phi : DQ_{2r-1} \to B(r; {\mathbb {A}}^2)$
, as in equation (5.2). Tracing through this composite, one sees it classifies the quadratic étale algebra generated by
![]() $x_1, \dots , x_r$
, i.e., T itself—the argument being as given for
$x_1, \dots , x_r$
, i.e., T itself—the argument being as given for
![]() $DQ_{r-1}$
in Remark 7.10.
$DQ_{r-1}$
in Remark 7.10.
Suppose for the sake of contradiction that T can be generated by
![]() $r-1$
elements over R. Let
$r-1$
elements over R. Let
![]() $\phi ' : DQ_{2r-1} \to B(r-1; {\mathbb {A}}^2)$
be a classifying map for some such
$\phi ' : DQ_{2r-1} \to B(r-1; {\mathbb {A}}^2)$
be a classifying map for some such
![]() $r-1$
-tuple of generators. Let
$r-1$
-tuple of generators. Let
![]() $\tilde \phi $
and
$\tilde \phi $
and
![]() $\tilde \phi '$
denote the composite maps
$\tilde \phi '$
denote the composite maps
![]() $DQ_{2r-1} \to B(2r-1; {\mathbb {A}}^2)$
. By Corollary 4.3, these maps induce the same map on Chow groups. But in degree
$DQ_{2r-1} \to B(2r-1; {\mathbb {A}}^2)$
. By Corollary 4.3, these maps induce the same map on Chow groups. But in degree
![]() $r-1$
, the map
$r-1$
, the map
![]() $\tilde \phi ^* : {\mathrm {CH}}^{r-1} ( B(2r-1; {\mathbb {A}}^2)) \to {\mathrm {CH}}^{r-1}( B(r; {\mathbb {A}}^2) ) \to {\mathrm {CH}}^{r-1}(DQ_{2r-1})$
is an isomorphism of cyclic groups of order
$\tilde \phi ^* : {\mathrm {CH}}^{r-1} ( B(2r-1; {\mathbb {A}}^2)) \to {\mathrm {CH}}^{r-1}( B(r; {\mathbb {A}}^2) ) \to {\mathrm {CH}}^{r-1}(DQ_{2r-1})$
is an isomorphism of cyclic groups of order
![]() $2$
, by reference to Proposition 5.4, while by the same proposition,
$2$
, by reference to Proposition 5.4, while by the same proposition,
![]() $(\tilde \phi ')^* : {\mathrm {CH}}^{r-1} ( B(2r-1; {\mathbb {A}}^2)) \to {\mathrm {CH}}^{r-1}( B(r-1; {\mathbb {A}}^2) ) \to {\mathrm {CH}}^{r-1}(DQ_{2r-1})$
is
$(\tilde \phi ')^* : {\mathrm {CH}}^{r-1} ( B(2r-1; {\mathbb {A}}^2)) \to {\mathrm {CH}}^{r-1}( B(r-1; {\mathbb {A}}^2) ) \to {\mathrm {CH}}^{r-1}(DQ_{2r-1})$
is
![]() $0$
. ▪
$0$
. ▪
The following shows that the bound of [Reference First and Reichstein6] is not quite sharp when applied to quadratic étale algebras over smooth
![]() $\bar k$
-algebras where
$\bar k$
-algebras where
![]() $\bar k$
is an algebraically closed field.
$\bar k$
is an algebraically closed field.
Proposition 7.14 Let
![]() $\bar k$
be an algebraically closed field. Let
$\bar k$
be an algebraically closed field. Let
![]() $n\geq 2$
, and
$n\geq 2$
, and
![]() $\operatorname {\mathrm {Spec}} R$
an n-dimensional smooth affine
$\operatorname {\mathrm {Spec}} R$
an n-dimensional smooth affine
![]() $\bar k$
-variety. If
$\bar k$
-variety. If
![]() ${\mathcal {A}}$
is a quadratic étale algebra on
${\mathcal {A}}$
is a quadratic étale algebra on
![]() $\operatorname {\mathrm {Spec}} R$
, then
$\operatorname {\mathrm {Spec}} R$
, then
![]() ${\mathcal {A}}$
may be generated by n global sections.
${\mathcal {A}}$
may be generated by n global sections.
Proof Let
![]() ${\mathcal {L}}$
be a torsion line bundle on
${\mathcal {L}}$
be a torsion line bundle on
![]() $\operatorname {\mathrm {Spec}} R$
, or, equivalently, a rank-
$\operatorname {\mathrm {Spec}} R$
, or, equivalently, a rank-
![]() $1$
projective module on R. A result of Murthy’s, [Reference Pavaman Murthy19, Corollary 3.16], implies that
$1$
projective module on R. A result of Murthy’s, [Reference Pavaman Murthy19, Corollary 3.16], implies that
![]() ${\mathcal {L}}$
may be generated by n elements if and only if
${\mathcal {L}}$
may be generated by n elements if and only if
![]() $c_1({\mathcal {L}})^n = 0$
. By another result of Murthy’s, [Reference Pavaman Murthy19, Theorem 2.14], the group
$c_1({\mathcal {L}})^n = 0$
. By another result of Murthy’s, [Reference Pavaman Murthy19, Theorem 2.14], the group
![]() ${\mathrm {CH}}^n(R)$
is torsion free, so it follows that if
${\mathrm {CH}}^n(R)$
is torsion free, so it follows that if
![]() ${\mathcal {L}}$
is a
${\mathcal {L}}$
is a
![]() $2$
-torsion line bundle, then
$2$
-torsion line bundle, then
![]() ${\mathcal {L}}$
can be generated by n elements. The proposition follows by Proposition 6.3. ▪
${\mathcal {L}}$
can be generated by n elements. The proposition follows by Proposition 6.3. ▪
Acknowledgment
This paper owes several great debts to Zinovy Reichstein, who introduced each author, separately, to the question at hand and who also supplied the argument in the introduction reducing the question of étale algebras of degree n to that of degree
![]() $2$
. We would also like to thank Uriya First, who very graciously read an earlier draft. We would like to thank Manuel Ojanguren who read an early draft of this paper, explained the construction of the example he had given to Uriya First, and encouraged the authors.
$2$
. We would also like to thank Uriya First, who very graciously read an earlier draft. We would like to thank Manuel Ojanguren who read an early draft of this paper, explained the construction of the example he had given to Uriya First, and encouraged the authors.