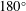2.1 Trisonic wind tunnel (TWT)

Experiments were conducted in the blowdown-to-atmosphere TWT. Trisonic refers to the fact that the TWT can operate at subsonic, transonic and supersonic Mach numbers. The facility uses air as the test gas and has a test section enclosed in a pressurized plenum. Data were obtained at a free-stream Mach number $M_{\infty }$ of 0.94 ( $U_{\infty }=311~\text{m}~\text{s}^{-1}$ ), which was determined using a free-stream velocity measurement at the cavity entrance location and the assumption of isentropic expansion. Forty-nine wind tunnel runs were made at this condition. Typical flow conditions for the experiments conducted in the $305~\text{mm}^{2}\times 305~\text{mm}^{2}$ test section are given in table 1. The tunnel wall boundary layers developed naturally and were fully turbulent upon arrival at the test section. Previous PIV measurements have indicated that the 99 % wall boundary layer thickness at the cavity entrance is approximately 13 mm or approximately half the cavity depth. The boundary layer displacement and momentum thicknesses were approximately 1.7 mm and 1.4 mm, respectively.

Figure 1. Cavity photos: (a) cavity in the lower wall of the test section and the PIV laser sheet and (b) cavity installed in the upper test section wall for PSP experiments.

Table 1. Typical TWT experimental conditions. $T_{0}$ , stagnation temperature; $R_{e}$ , Reynolds number.

In subsonic cavity flows it is necessary to mitigate the undesirable acoustical interference associated with solid wind tunnel walls by placing an acoustic absorber in the wall opposite to the cavity (Song Reference Song2008; Murray, Sallstrom & Ukeiley Reference Murray, Sallstrom and Ukeiley2009; Wagner et al. Reference Wagner, Casper, Beresh, Henfling, Spillers and Pruett2015a ). The spanwise walls of subsonic test sections can also lead to acoustical contamination if untreated (Wagner et al. Reference Wagner, Casper, Beresh, Henfling, Spillers and Pruett2015a ). To reduce these effects, the wall opposite the cavity and one spanwise wall were replaced with acoustic dampeners, which consisted of a porous wall, used typically for transonic testing, backed by acoustical absorption foam. The opposite spanwise wall was solid with a window providing a view for the PIV cameras. This acoustic dampener configuration was found to significantly reduce acoustical contamination in comparison to those using either a solid opposite or solid spanwise wall.

2.2 Cavity hardware

The cavity had a length $L$ of 127 mm, width $W$ of 127 mm and depth $D$ of 25.4 mm and was installed in the lower wall of the test section in experiments using PIV (figure 1 a). In separate experiments using TR-PSP, the cavity was instead installed in the ceiling of the wind tunnel and the cavity floor was viewed through windows in the lower walls of the test section and plenum (figure 1 b). In both cases the leading edge of the cavity was 410 mm downstream of the test section entrance and the turbulent boundary layer had similar properties. With an $L/D$ of 5, the cavity flow category is ‘open’ and expected to resonate (Tracy & Plentovich Reference Tracy and Plentovich1997). The streamwise ( $x$ ), wall-normal ( $y$ ), spanwise ( $z$ ) coordinate system originates at the spanwise centre of the cavity leading edge (figure 1 a). The wind tunnel floor is defined to be at $y=0$ , with positive $y$ pointing away from cavity.

2.3 Unsteady pressures

Two dynamic pressure sensors (Kulite XCQ-062-30A) having a range of approximately 207 kPa and a flat frequency response up until approximately 50 kHz were placed in the spanwise centre of the cavity fore and the aft wall. The fore wall sensor was located at $y=-0.5D$ and the aft wall probe was at a position of $-0.63D$ . The sampling frequency $f_{s}$ was 200 kHz and the data were lowpass filtered at 50 kHz. One million samples were obtained at each location. Previous experiments have confirmed the experiments to be repeatable having a precision uncertainty on the mean of approximately 0.5 % (Wagner et al. Reference Wagner, Casper, Beresh, Hunter, Henfling, Spillers and Pruett2015b ).

High-frequency PSP from Innovative Scientific Solutions, Inc. (ISSI) was sprayed onto the entire floor of the cavity (figure 1 b). The paint used a platinum-tetra-fluoro-phenyl-porphyrin (PtTFPP) luminophore added on top of a porous ceramic binder. The porosity of the base layer added surface area to allow fast response of the paint. Specifically, a frequency response of approximately 10 kHz (Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017) was possible making it essentially time resolved for the resonance dynamics characterized herein. Moreover, the paint measurements have been shown to be in good agreement with pressure sensors (Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017).

Three ISSI LM2XX-DM-400 water-cooled light arrays excited the PSP over a range of approximately $400~\text{nm}\pm 30~\text{nm}$ . The lights were placed in the plenum surrounding the tunnel to locate them as close as possible to the cavity. The majority of emission from the paint was centred at a wavelength near 650 nm. A high-speed camera (Photron SA-Z) fitted with a 50 mm lens was used to acquire full-view images of the cavity at framing rates of 20 kHz. At 20 kHz, the camera had a resolution of $1024~\text{pixel}\times 1024~\text{pixel}$ with a quantum efficiency of 49 % at 630 nm. A 590 nm longpass filter removed the 400 nm excitation light and 20 000 images were acquired and used for spectral analysis.

Raw images were post-processed using an adaptive Wiener filter in the Mathworks software package Matlab. This acted as a lowpass filter to reduce additive noise in the images. Static calibrations were used to convert the intensity ratios to pressure ratios, yielding the unsteady pressure fluctuations within the cavity. Additional details on the calibration and TR-PSP set-up can be found in Casper et al. (Reference Casper, Wagner, Beresh, Spillers and Henfling2017).

2.4 Time-resolved particle image velocimetry

Seeding was provided by a smoke generator that delivered a large quantity of mineral oil particles to the tunnel stagnation chamber. Measurement of the particle response across a shock wave has shown the particle size to be approximately $0.8~\unicode[STIX]{x03BC}\text{m}$ , which returns Stokes numbers of approximately 0.04 based on a posteriori measurements of typical cavity shear layer eddies. The particles, therefore, rapidly attain the local velocity even in the presence of velocity gradients in the shear layer (Samimy & Lele Reference Samimy and Lele1991). Visual inspection of the PIV images showed adequate seeding in all portions of the cavity, including the recirculation region.

A quasi-continuous burst-mode laser (QuasiModo-1000, Spectral Energies, LLC) with both diode and flashlamp Nd:YAG amplifiers was used to produce a high energy pulse train at a wavelength of 532 nm. The laser design is based on a master oscillator power amplifier architecture and is similar to previously reported pulse-burst lasers (Slipchenko et al. Reference Slipchenko, Miller, Roy, Gord, Danczyk and Meyer2012, Reference Slipchenko, Miller, Roy, Gord and Meyer2014). As detailed in Beresh et al. (Reference Beresh, Kearney, Wagner, Guildenbecher, Henfling, Spillers, Pruett, Jiang, Slipchenko and Mance2015a ), the laser is capable of producing doublets with the variable inter-pulse spacing time and at varying pulse frequencies (repetition rates). Here, the laser was operated at 37.5 kHz with doublets separated in time by $3~\unicode[STIX]{x03BC}\text{s}$ . A 10.2 ms burst was generated every 8 s and the energy per pulse was approximately 27 mJ. Five bursts per wind tunnel run brought the total number of independent bursts (independent time series) to 245 and the total number of image pairs to approximately 94 000. The beam was shaped into a laser sheet covering the streamwise length of the cavity having a spanwise thickness of 1.5 mm and was located at the spanwise centre of the cavity.

Images were acquired using two high-speed cameras (Photron SA-Zs). Each camera was operated at 75 kHz at a resolution of $640~\text{pixel}\times 360~\text{pixel}$ . The two pulses in a doublet were frame straddled around the inter-frame transfer time of the cameras to produce separate images for cross-correlation analysis. As a result, the PIV repetition rate was half that of the framing rate, or 37.5 kHz. In a manner similar to Beresh et al. (Reference Beresh, Kearney, Wagner, Guildenbecher, Henfling, Spillers, Pruett, Jiang, Slipchenko and Mance2015a ), the two cameras were angled downward at $12^{\circ }$ to peer into the cavity and placed side by side to extend the field of view in the streamwise direction. The views were joined using a linear interpolation method to give the vectors equidistant spacing across the entire field. The combined field of view was approximately $120\times 30~\text{mm}$ . The cameras imaged approximately 50 % of the cavity depth in contrast to the 100 % depth covered in previous 10 Hz stereoscopic PIV experiments, which utilized a mirror in the test section plenum to increase optical access (Beresh et al. Reference Beresh, Wagner, Pruett, Henfling and Spillers2015c ). Resonance dynamics as determined from the TR-PIV is compared to that given using this 10 Hz dataset.

The image pairs were processed using the LaVision PIV software package DaVis v8.2 to a final interrogation window size of $24~\text{pixel}\times 24~\text{pixel}$ in the same fashion as described in Beresh et al. (Reference Beresh, Kearney, Wagner, Guildenbecher, Henfling, Spillers, Pruett, Jiang, Slipchenko and Mance2015a ).

3.1 Power spectral densities

Power spectral densities of the pressure and velocity data were computed in Matlab using the Welch windowing algorithm (pwelch function). A window overlap of 50 % was used. PSDs based on the pressure sensor data utilized a window length $\unicode[STIX]{x0394}f$ of 10 Hz, whereas the window lengths in the TR-PSP and TR-PIV PSDs were 50  Hz and 100 Hz, respectively.

For the velocity data, the square root of the PSD is reported, which is normalized by the free-stream velocity $U_{\infty }$ to yield units of $\text{Hz}^{-0.5}$ . In the case of the pressure data, frequency spectra are reported in decibels as sound pressure level (SPL):

(3.1) $$\begin{eqnarray}\text{SPL}(f)=10\log _{10}\left[\frac{\text{PSD}_{p}(f)\unicode[STIX]{x0394}f_{ref}}{p_{ref}^{2}}\right],\end{eqnarray}$$

where $\text{PSD}_{p}$ represents the power spectral density of pressure, $p_{ref}$ is a reference pressure set to the standard $20~\unicode[STIX]{x03BC}\text{Pa}$ and $\unicode[STIX]{x0394}f_{ref}$ is a reference frequency set here to 1 Hz. Spatial distributions of the PSD amplitude at frequencies corresponding to cavity tones are shown herein to highlight the spatial variation associated with resonance in both the pressure (TR-PSP) and velocity (TR-PIV) fields.

3.2 Bandpass filtering of TR-PIV

The time-resolved velocity fields were bandpass filtered in the time domain about each of the first three cavity tone frequencies using a Butterworth filter based on the algorithm in Russell (Reference Russell2006). This algorithm uses a cascade of first-order filters and hence is precise for narrow-band applications. The filter results in very little signal attenuation at the desired frequency band and is designed to produce zero phase shift. A bandwidth of 100 Hz was chosen to narrowly focus on the resonance frequencies.

3.3 Conditioning of the TR-PIV data (active mode definition)

The bandpass-filtered velocities ( $v_{fm}$ , where $m$ is integer mode number) are used to condition the TR-PIV data as follows. The standard deviation of the wall-normal filtered velocity was calculated for each of the 245 TR-PIV series at a location observed to contain prominent resonance peaks in the TR-PIV PSDs. As described in the results, in the case of modes two and three, a location of $x=3.6D$ and $y=0.1D$ was chosen to satisfy this criterion. In contrast, turbulent fluctuations in the vicinity of mode one overwhelmed any resonance peak at this location. Thus, for mode one a point above the cavity and more upstream ( $x=2D$ and $y=0.6D$ ) was chosen where mode one did exhibit a prominent PSD peak. An ‘active’ mode is defined to occur when at the conditioning location, the standard deviation of $v_{fm}$ is in the top forty per cent in comparison to all 245 time sequences. This leaves about 100 cases of active modes for subsequent spectral and cross-correlation analysis. Unless otherwise specified only active cases were used in the analysis.

3.4 Continuous wavelet transform

Joint-time frequency analysis (JTFA) on the pressure sensor and time-resolved velocity data was conducted using a continuous wavelet transform (CWT). This technique shows the frequency content of the disturbances as a function of time. The transform provides good time resolution for identifying intermittent mode switching within the cavity. As in Kegerise et al. (Reference Kegerise, Spina and Cattefesta2004), the transform utilized a Morlet mother wavelet. The mathematical formulation to provide the CWT coefficients is described in detail in Torrence & Compo (Reference Torrence and Compo1998). Moreover, the CWT coefficients were computed using a Matlab script that utilized an algorithm based on the discrete Fourier transform. The script was also provided by Torrence & Compo (Reference Torrence and Compo1998). Finally, results are presented as an intermittency function:

(3.2) $$\begin{eqnarray}I_{n}(s)=\frac{|W_{n}(s)|^{2}}{\langle |W_{n}(s)|^{2}\rangle _{s}},\end{eqnarray}$$

where $W_{n}(s)$ is the CWT coefficient. This serves to normalize the transform with respect to the average spectrum over the wavelet scale (frequency range) of interest.

The wavelet transform was applied to both the pressure sensor data and the TR-PIV data with two primary purposes: (i) to investigate whether the mode switching observed in the pressure signals is also evident in simultaneous PIV fields and (ii) to conditionally average the previous 10 Hz dataset of Beresh et al. (Reference Beresh, Wagner, Pruett, Henfling and Spillers2015c ).

3.5 Determination of coherent flow structure using 10 Hz PIV

Coherent flow structures during resonance, based on the previous 10 Hz PIV data (Beresh et al. Reference Beresh, Wagner, Pruett, Henfling and Spillers2015b ), were found by conditionally averaging the velocity fields. The fore wall pressure sensor was used in this process since turbulent fluctuations are lower in the upstream portion of the cavity. The wavelet transform was applied to the pressure sensor time traces. The traces were then effectively bandpass filtered by setting wavelet transform coefficients other than those at the cavity tone frequencies to zero and then computing an inverse wavelet transform. Importantly, this served to filter the pressure data without a time delay to maintain synchronization with the 10 Hz PIV data. An example of bandpass-filtered pressures using this methodology is shown in figure 2(a), where each trace is offset in pressure for clarity. The filtering is clearly able to reveal modulation of modal amplitude.

Figure 2. Bandpass filtering of pressure sensor data: (a) unfiltered and bandpass-filtered traces of the fore wall pressure sensor in the vicinity of PIV acquisition time and (b) illustration of the binning regions used to produce phase-averaged vector fields.

The bandpass-filtered pressures were used to conditionally average the simultaneously acquired 10 Hz PIV data as follows. For a given mode, the amplitude of the filtered trace at the PIV acquisition time was first determined. The local maximum amplitude in the 25 ms surrounding the PIV time was also found. If the amplitude at the PIV time was at least 50 % of the local maximum then the mode was considered active and the PIV vector field was used for conditional averaging. As illustrated in figure 2(b), the waveforms were binned into six phases. In the current paper, only conditionally averaged fields in the vicinity of the peak (region 2 at $90^{\circ }$ ) and the trough (region 5 at $270^{\circ }$ ) are shown for brevity.

Approximately 10 % (300) of the 10 Hz vector fields were used for each phase-averaged result. Finally, the mean wall-normal velocity field ( $V$ ) was subtracted from the phase-averaged field ( $V_{\unicode[STIX]{x1D703}m}$ ) to reveal the coherent flow structure (Hussain Reference Hussain1986) associated with resonance tones.

3.6 Convective and phase velocities based on cross-correlations

Cross-correlation coefficients between time sequences of wall-normal velocity $v$ at points separated by fixed streamwise distance $\unicode[STIX]{x0394}x$ and variable time delay $\unicode[STIX]{x0394}t$ were calculated.

The time delay at which the correlation was at a maximum and the known streamwise separation were used to compute the streamwise convection velocity $U_{c}$ between the points. The analysis was performed in a row-by-row fashion, at every point within the row, thereby revealing spatial distributions of streamwise convective velocity. This methodology captures $U_{c}$ over the entire measurement domain, although the data are essentially smoothed by a moving-average, lowpass filter.

The cross-correlation analysis was also performed on the bandpass-filtered data corresponding to cavity modes one–three ( $v_{f1}{-}v_{f3}$ ). In this case, the velocity returned is by definition the phase velocity $U_{pm}$ , where $U_{p}$ is phase velocity and $m$ is integer mode number.

The streamwise separation $\unicode[STIX]{x0394}x$ between measurements locations was varied between ten and twenty vector spacings ( $0.45D{-}0.90D$ ). A spacing less than approximately ten vectors was generally too low for the temporal resolution of the measurements, whereas a spacing greater than approximately twenty vectors overly smoothed the convective velocity fields. Comparisons between calculations using separations within this range typically fell within the precision uncertainty of the measurements quantified in the results. Hence, the smaller spacing of $0.45D$ was utilized to maximize spatial resolution with one exception being the unfiltered case where a larger spacing of $0.68D$ was used to reduce a non-physical jump in $U_{c}$ observed at the interface between the two side-by-side measurements.

4.1 Basic cavity flow properties

Some basic cavity characteristics and definitions are first given here prior to discussing resonance dynamics. The mean flow field over nearly the entire height and length of the cavity, obtained from 10 Hz, stereoscopic PIV measurements (Beresh et al. Reference Beresh, Wagner, Pruett, Henfling and Spillers2015c ), is shown in figure 3(a).

The flow in figure 3(a) demonstrates the expected behaviour of a mixing layer that grows with streamwise distance (Murray et al. Reference Murray, Sallstrom and Ukeiley2009). A single recirculation region centred at approximately $x=3.4D$ is also evident. Below the cavity lip line ( $y=0$ ), the flow is turned downward in the mixing layer. Eventually the mixing layer impinges on the aft wall to produce the acoustical disturbances responsible for the resonance feedback loop.

Figure 3. Basic cavity flow properties: (a) mean streamwise velocity $U$ contours with superposed streamlines (Beresh et al. Reference Beresh, Wagner, Pruett, Henfling and Spillers2015c ) and (b) SPL at the fore wall and aft wall of the cavity. Dashed lines represent frequencies predicted by the modified Rossiter relation of Heller & Bliss (Reference Heller and Bliss1975).

Sound pressure level SPL spectra obtained at the fore wall and aft wall of the cavity are shown in figure 3(b). The spectra were calculated using the pressure transducers. At Mach 0.94, the first three Rossiter modes have similar amplitude. A fourth cavity tone is also observed, but discussion of this mode is omitted from the paper as its behaviour is consistent with modes two and three. The expected frequencies of the cavity tones can be given with the Rossiter (Reference Rossiter1964) relation modified by Heller & Bliss (Reference Heller and Bliss1975):

(4.1) $$\begin{eqnarray}St_{m}=\frac{f_{m}L}{U_{\infty }}=\frac{m-\unicode[STIX]{x1D6FC}}{\left[M_{\infty }\left(1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}-1}{2}}M_{\infty }\right)^{-1/2}+{\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}\right]},\end{eqnarray}$$

where $f$ is frequency, $U_{\infty }$ is free-stream velocity and $\unicode[STIX]{x1D6FE}$ is the ratio of specific heats. This semi-empirical equation is based on the assumption that vortical disturbances associated with resonance propagate downstream at a constant convection velocity of $\unicode[STIX]{x1D705}\times U_{\infty }$ . When a disturbance reaches the aft wall, there is a phase lag $\unicode[STIX]{x1D6FC}$ (in fractions of a wavelength), which occurs before an upstream-propagating disturbance is formed. According to this view, the upstream-propagating disturbance then moves at the speed of sound based on the stagnation temperature $a_{0}$ . Throughout the literature, commonly used constants for phase lag and convective velocity are 0.25 and 0.57, respectively (Tracy & Plentovich Reference Tracy and Plentovich1997; Murray et al. Reference Murray, Sallstrom and Ukeiley2009). Although the semi-empirical relation is a simplification of the cavity resonance physics (e.g. it is known that disturbances in the shear layer do not move at constant velocity (Larchevêque et al. Reference Larchevêque, Sagaut, Le and Compte2004; Hassan et al. Reference Hassan, Labraga and Keirsbulck2007)), it often provides good predictions of cavity tone frequencies. The current work is no exception. For instance, as shown in figure 3(b), using the common values for $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D705}$ gives agreement between the measured and predicted frequencies to within 2 %.

Finally, for linear stability considerations presented later, it is also useful to normalize the modal frequencies as circular shear layer forcing frequency:

(4.2) $$\begin{eqnarray}\unicode[STIX]{x1D714}_{m}=\frac{2\unicode[STIX]{x03C0}f_{m}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FA},0}}{U_{\infty }},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FA},0}$ is the initial vorticity thickness at the cavity entrance, which was measured to be 4.8 mm (Beresh et al. Reference Beresh, Wagner and Casper2016). The cavity frequencies $f_{m}$ along with their non-dimensional counterparts $St_{m}$ and $\unicode[STIX]{x1D714}_{m}$ are summarized in table 2.

Table 2. Cavity tone frequencies.

4.2 Modulations of cavity pressure and velocity

The dynamic events during cavity flows do not occur uniformly with time. Rather, modal amplitudes are known to vary temporally through mode switching. Examples of this tonal modulation are shown in figure 4, which gives the time-varying frequency content of pressure measured at the fore wall during two separate wind tunnel experiments. Contour levels are CWT coefficients normalized according to (3.2). The average used for normalization in each case is that over the time and frequency range corresponding to each panel. Dashed lines appear in the figures to mark the first three cavity mode frequencies ( $f_{1}$ , $f_{2}$ , and $f_{3}$ ). Modes two and three exhibit substantial differences between the two cases. For example, mode two is more active in figure 4(a). Specifically, on average, the CWT amplitude at mode two is 1.9 times greater than that in figure 4(b). On the other hand, mode three is more active in figure 4(b) and has a CWT amplitude 1.8 times greater than that in figure 4(a).

Figure 4. Time–frequency content of fore wall pressure from two separate Mach 0.94 time sequences.

Figure 5. Time–frequency content of wall-normal velocity at $x=3.6D$ and $y=0.1D$ : (a) same time sequence as figure 4(a) and (b) same time sequence as figure 4(b).

The corresponding variation of frequency content in the time-resolved velocity data is shown in figure 5. The JTFA was performed on the wall-normal velocity component $v$ at a location of $x=3.6D$ and $y=0.1D$ where modes two and three exhibited prominent peaks at in the TR-PIV PSDs (subsequently shown in § 4.7). Note that as discussed in § 3.3, this is the same location used to condition the TR-PIV data to define active modes. The left panel corresponds to the same time sequence of figure 4(a) and the right panel corresponds to that in figure 4(b). Similar to the pressure frequency content, the third cavity tone is observed to be much more active in the right panel than in the left (the amplitude at mode three is two times greater than that in figure 5 a). Also, like the pressure data, mode two contains greater fluctuations in the left panel (the amplitude at mode two is 1.8 times greater than that in figure 5 b). In both figures 4(a) and in 5(a), mode two exhibits a peak around a time of 0.003 s (labels A and A $^{\prime }$ ). Though less pronounced, some correlation between figures 4(b) and 5(b) can also be seen for the third cavity mode (B–B $^{\prime }$ and C–C $^{\prime }$ ).

On the other hand, the correlation between the pressure and velocity figures at $f_{1}$ is more limited. At mode one, turbulent fluctuations overwhelm resonance at this particular velocity location as is detailed subsequently in § 4.7. A clearer correlation between the pressure and velocity fields can be observed if instead the location of $x=2.0D$ and $y=0.6D$ is chosen. At this location, mode one exhibits a prominent peak in the TR-PIV PSDs (shown later in § 4.7), which is the reason this location was also used to condition the TR-PIV data. Normalized CWT coefficients at $x=2.0D$ and $y=0.6D$ are shown in figure 6, where a stronger similarity to the mode one pressure fluctuations in figure 4 can be observed. For instance, the peak in mode one velocity fluctuations (label E in figure 6 a) is also present in the pressure fluctuations (label E $^{\prime }$ in figure 4 a). Similarly, the mode one peaks in figure 6(b) (labels F and G) occur at similar times to those in figure 4(b) (F $^{\prime }$ and G $^{\prime }$ ).

Figure 6. Time–frequency content of wall-normal velocity at $x=2.0D$ and $y=0.6D$ : (a) same time sequence as figure 4(a) and (b) same time sequence as figure 4(b).

4.3 Coherent structures based on 10 Hz PIV

Coherent flow structures during resonance, based on the previous 10 Hz PIV data of Beresh et al. (Reference Beresh, Wagner, Pruett, Henfling and Spillers2015c ), are first briefly presented. The primary purpose of this is to ensure that coherent structures returned using a more conventional process (Hussain Reference Hussain1986) are similar to those given using the bandpass-filtered TR-PIV.

Coherent wall-normal velocity fields ( $V_{\unicode[STIX]{x1D703}}-V$ ) corresponding to resonance modes two and three are shown in figure 7. As expected, moving from the case when the modal pressure is at a peak ( $\unicode[STIX]{x1D703}=90^{\circ }$ ) to when it is at a trough ( $\unicode[STIX]{x1D703}=270^{\circ }$ ) results in a velocity sign inversion. The coherent velocities show a spatial modulation in structure size with streamwise distance. For instance, the mode two fields show a significant growth in coherent structures to occur in the vicinity of $x=3D$ , while a decrease in structure size occurs in the aft end of the cavity for $x>4D$ . Modulation is also seen for mode three, particularly at $\unicode[STIX]{x1D703}_{3}=270^{\circ }$ , where structure size increases in the region $1D<x<2D$ and in the region $3D<x<4D$ . These observations are explained subsequently using the TR-PIV and TR-PSP data.

Figure 7. Coherent flow structures ( $V_{\unicode[STIX]{x1D703}}-V$ ) obtained with phase averaging of 10 Hz PIV data: mode two (a,c) and mode three (b,d). Solid and dashed lines correspond to $0.017U_{\infty }$ and $-0.017U_{\infty }$ , respectively.

4.4 Resonant flow structure using TR-PIV

4.4.1 Bandpass-filtered sequences

To characterize resonance dynamics, the TR-PIV data were bandpass filtered about the modal frequencies. This allows for the contributions of each cavity mode to be separated and analysed. As discussed subsequently, modes two and three show behaviour more consistent with the classical view (Rossiter Reference Rossiter1964) that resonance occurs in part through the downstream propagation of vortical disturbances. Thus, these modes are described prior to mode one.

An example of flow structure during resonance is shown in figure 8, which gives the bandpass-filtered, wall-normal velocity $v_{f2}$ (a,c,e,g,i,k) and streamwise velocity $u_{f2}$ (b,d,f,h,j,l) fields corresponding to a cycle of mode two ( $St=0.68$ ) lasting for a period $T_{2}$ . The figure was generated from a single experiment, namely the same as in figures 4(a) and 5(a) when mode two was active and is representative of other mode two cycles. The wall-normal velocities associated with mode two reveal a clear convection of organized structure as time increases. At $t=0$ , a region of organized positive vertical velocity appears near $x/D=1$ (label A). With continuing time, this structure convects downstream reaching a position near $x/D=3.4$ at $t=0.87T_{2}$ . Upon completion of a full cycle at $T_{2}$ (not shown) it is apparent that the upstream region of positive vertical velocity (A) moves downstream to become the larger region of positive vertical velocity (A $^{\prime }$ ). Similar observations are seen in the regions of negative vertical velocities (B and B $^{\prime }$ ).

Figure 8. Mode two ( $St=0.68$ ) bandpass-filtered velocities: wall normal (a,c,e,g,i,k) and streamwise (b,d,f,h,j,l). Solid and dashed lines correspond to $0.017U_{\infty }$ and $-0.017U_{\infty }$ , respectively.

The streamwise modal velocities exhibit a more complex flow structure than the wall normal. A region of negative velocity tends to reside below a region of higher velocity and vice versa, an observation consistent with propagating vortical structures. Regardless, similar to the wall-normal component, an overall downstream convection of negative (C and C $^{\prime }$ ) and positive velocities (D and D $^{\prime }$ ) is also observed in the streamwise velocities.

Figure 9. Mode three ( $St=1.04$ ) bandpass-filtered velocities: wall normal (a,c,e,g,i,k) and streamwise (b,d,f,h,j,l). Solid and dashed lines correspond to $0.017U_{\infty }$ and $-0.017U_{\infty }$ , respectively.

Bandpass-filtered velocities corresponding to a mode three cycle ( $St=1.04$ ) of resonance having period $T_{3}$ are displayed in figure 9. The figure was generated from the same time sequence as in figures 4(b) and 5(b) when mode three was active and is representative of other mode three cycles. Like mode two, an obvious convection of wall-normal flow structures is seen with increasing time, though as expected, the structures are smaller and more closely spaced, consistent with a lower wavelength. Once again, in the streamwise case, regions of opposite signed velocity appear under the structures propagating in the shear layer. Again this observation is related to the fact that resonance occurs through the propagation of vortices as is emphasized with the annotations in the $t=0.21T_{3}$ panels.

As the structures propagate downstream they reside at higher wall-normal locations within the cavity. A similar upward trajectory of resonant flow structures has been observed in several incompressible (Lee, Seena & Sung Reference Lee, Seena and Sung2010; Seena & Sung Reference Seena and Sung2013) and compressible (Li, Nonomura & Fujii Reference Li, Nonomura and Fujii2013) numerical studies. A possible explanation for this observation may be related to the fact that the thickness of turbulent mixing layer grows with downstream distance. If turbulent fluctuations serve to disrupt the coherent vortices associated with resonance, then the height at which vortices are less susceptible to disruption would continually increase with downstream distance as the turbulent mixing layer grows. Thus, a structure at a greater $y/D$ may be statistically more likely to remain intact with downstream propagation.

Inspection of the mode two and mode three bandpass-filtered sequences reveals a modulation of structure size with streamwise distance. This is summarized subsequently with a more rigorous approach that calculates structure size as a function of streamwise distance based on phase-averaged fields of the TR-PIV data.

Bandpass-filtered velocity fields corresponding to cavity mode one ( $St=0.28$ ) are displayed in figure 10. The time sequence was obtained during the same experiment as in figure 4(b), when mode one was active. Like modes two and three, a convection of wall-normal flow structure is evident. As time progresses through the full cycle period $T_{1}$ , the regions of positive (A) and negative (B) wall-normal velocity move downstream. A major difference with respect to the two higher-frequency modes, however, is that this convection takes place at a lower wall-normal location. In fact, comparison to the mean flow field in figure 3 suggests that wall-normal flow structures are moving through a region in the shear layer more influenced by recirculation.

Figure 10. Mode one bandpass-filtered velocities: wall normal (a,c,e,g,i,k) and streamwise (b,d,f,h,j,l). Solid and dashed lines correspond to $0.017U_{\infty }$ and $-0.017U_{\infty }$ in the wall-normal panels and $0.034U_{\infty }$ and $-0.034U_{\infty }$ in the streamwise panels.

A convection of resonant flow structure is also seen in the streamwise filtered velocity $u_{f1}$ . As time progresses, regions of negative (C) and positive (D) streamwise velocity propagate downstream once again lower in the cavity. In comparison to the wall-normal modal velocities, however, the streamwise velocities exhibit larger variations above $y=0$ . For instance, at $t=0.20T_{1}$ , a large region of positive velocity extends across the cavity length. A similar instance of a large negative velocity region can also be seen at $t=0.60T_{1}$ . These regions were observed to occur with downstream propagation beginning at the upstream limit of the measurement domain. The velocity fluctuations are perhaps related to a large-scale flapping of the shear layer that has been observed in several incompressible (Rockwell & Knisely Reference Rockwell and Knisely1978; Knisely & Rockwell Reference Knisely and Rockwell1982; Najm & Ghoneim Reference Najm and Ghoneim1991; Lin & Rockwell Reference Lin and Rockwell2001; Liu & Katz Reference Liu and Katz2013) and compressible (Murray et al. Reference Murray, Sallstrom and Ukeiley2009) cavity flows. This flapping has been suggested to be associated with low-frequency dynamics in the recirculation region.

An additional look at mode one flow structure is given figure 11 where coherent streamwise velocity fields ( $U_{\unicode[STIX]{x1D703}1}-U$ ) are shown. The fields shown are $180^{\circ }$ out of phase corresponding to instances where mode one is a peak with respect to the upstream pressure sensor ( $90^{\circ }$ ) and when it is a trough ( $270^{\circ }$ ). Similar to the bandpass-filtered sequence in figure 10, mode one is seen to occur with coherent motion over a significant streamwise extent of the cavity length as well as in the recirculation region.

Figure 11. Mode one coherent flow structures ( $U_{\unicode[STIX]{x1D703}1}-U$ ) obtained with phase averaging of 10 Hz PIV data. Solid and dashed lines correspond to $0.017U_{\infty }$ and $-0.017U_{\infty }$ , respectively.

4.4.2 Phase-averaged bandpass-filtered TR-PIV fields

The bandpass-filtered TR-PIV data at modes two and three were phase averaged to resolve the resonant flow structure in a more statistical fashion. In this case, the averaging was achieved using the TR-PIV data alone without comparison to the pressure sensor data. The signal location for the phase averaging was the same as that used for conditioning, namely $x=3.6D$ , $y=0.1D$ . Phase-averaged, bandpass-filtered velocity fields corresponding to modes two and three are shown in figure 12. A single phase (or time) is shown for each mode. The phase was chosen for each mode such that the fields qualitatively matched those based on the 10 Hz PIV data shown in figure 7.

Figure 12. Phase-averaged fields based on the bandpass-filtered TR-PIV data: (a) mode two streamwise velocity, (b) mode three streamwise velocity, (c) mode two wall-normal velocity, (d) mode three wall-normal velocity, (e) mode two spanwise vorticity and (f) mode three spanwise vorticity. Streamlines are overlaid on each figure.

The fields yield similar results to the previous sequences displayed in figures 8 and 9 that were based on single experiments. In the streamwise velocities (figure 12 a,b), regions of oppositely signed velocity tend to reside under those higher in the shear layer, an observation which is clearer in the case of mode three (figure 12 b). In the wall-normal velocity fields (figure 12 c,d), large structures with alternating sign are prevalent throughout the shear layer. The streamlines overlaid on each panel show the expected result that resonance occurs with the propagation of vortical disturbances. Plots of phase-averaged spanwise vorticity (figure 12 e,f), based on bandpass-filtered vorticity fields, further confirm this to be the case.

4.5 Comparison of flow structure using 10 Hz PIV and TR-PIV

The TR-PIV bandpass-filtered and the 10 Hz PIV phase-averaged fields look qualitatively similar. To facilitate quantitative comparisons, the wall-normal velocity fields in figure 12 (TR-PIV) and in figure 7 (10 Hz PIV) were averaged over the wall-normal coordinate as is shown in figure 13. In the case of both mode two (figure 13 a) and mode three (figure 13 b) the independent methods produce excellent agreement in terms of phase and wavelength indicating that either technique is well suited to produce coherent structures associated with resonance. The differences in amplitude likely stem from the different methodologies used to produce the 10 Hz PIV and TR-PIV phase averages.

Figure 13. Modal wall-normal velocities, normalized by $U_{\infty }$ , obtained from phase averaging the bandpass-filtered TR-PIV data and those found by phase averaging previous 10 Hz PIV data: (a) mode two and (b) mode three.

An obvious advantage that the TR-PIV gives in comparison to the 10 Hz PIV is substantially improved temporal resolution. This allows for allows for PSDs to be calculated at each available vector location as well as calculations of convective velocity fields. Such insight would be impossible with the 10 Hz data. The TR-PIV is also able to provide much more detailed information on coherent structure modulation as opposed to the 10 Hz data since many more phases can be obtained.

4.6 Modulation of coherent structure size with streamwise distance

An in-depth look at coherent structure modulation provided by the TR-PIV data is shown in figures 14 and 15. In each case, the coherent structures over an entire resonance cycle are superposed. This effectively captures the envelope of resonant flow structure size. The figures were generated using the phase-averaged, bandpass-filtered velocities described in § 4.4.2. The contours are lines of constant velocity with the thresholds chosen to most effectively maximize dynamic range in the figure (i.e. show the smallest and largest structures simultaneously).

Figure 14. Modulation of resonant flow structure based on bandpass-filtered, phase-averaged, wall-normal velocity fields: (a) mode two and (b) mode three. The contours in each figure are lines of constant $0.017U_{\infty }$ showing superposed structures for an entire resonance cycle.

Figure 15. Modulation of resonant flow structure based on bandpass-filtered, phase-averaged, streamwise velocity fields: (a) mode two and (b) mode three. The contours in each figure are lines of constant $0.015U_{\infty }$ showing superposed structures for an entire resonance cycle.

Coherent structures based on the wall-normal component of velocity are displayed in figure 14. During mode two (figure 14 a), the coherent structure size increases to a maximum near $x=3D$ before reaching a local minimum near $x=4D$ . Mode three (figure 14 b) also shows variation in structure size with streamwise distance, albeit over an apparently shorter wavelength. For both modes, this modulation occurs primarily in the shear layer.

Coherent structures returned using the streamwise velocity component are given in figure 15. Like the sequences of bandpass-filtered velocity, the distribution of streamwise coherent flow structure is more complex than the wall normal. Both mode two (figure 15 a) and mode three (figure 15 b) demonstrate significant variation in structure size within the mixing layer. Additionally, however, the structure size also varies in the region under the mixing layer. This is because the streamwise distributions are influenced by vortical structures where positive regions lie under negative regions and vice versa.

Structure size is quantified further in figure 16 where the height of the wall-normal velocity structures as a function of axial position is given. The size here is defined using the envelope in figure 14. The profiles returned using the streamwise velocity structures of figure 15 are very similar and are omitted here for brevity. Note that the modulation of structure size seen in figure 16 in the context of resonance dynamics is discussed subsequently along with the PSD profiles in the figure.

Figure 16. Resonant flow structure size using the wall-normal velocity fields (left ordinate) compared to the modal PSD amplitude averaged across the height of the measurement domain (right ordinate): (a) mode two and (b) mode three.

4.7 Spatial distributions of velocity PSD modal amplitude

Many of the preceding observations related to the bandpass-filtered velocity fields can be summarized concisely with spatial distributions of PSD amplitude at the given cavity mode frequencies. Along these lines, PSD amplitude distributions of wall-normal and streamwise velocity at frequencies corresponding to cavity modes one through three (i.e. $\text{PSD}_{v}(f_{m})$ and $\text{PSD}_{u}(f_{m})$ ) are shown in figure 17. The contours display the square root of PSD amplitude as to maintain units of normalized velocity.

Figure 17. Spatial distributions showing the square root of velocity PSD amplitudes at the cavity tone frequencies normalized by $U_{\infty }$ : (a) mode one, wall normal, (b) mode one, streamwise, (c) mode two, wall normal, (d) mode two, streamwise, (e) mode three, wall normal and (f) mode three, streamwise.

In the case of mode one (figure 17 a,b), the PSD peaks lie near the recirculation region (figure 3 a). As the cavity mode number increases to two and three, the extent of resonance activity grows to reach higher portions within the cavity mixing layer. Such an observation is consistent with the bandpass-filtered results, which in general showed that resonant flow structures propagated at higher wall-normal locations as the mode number was increased.

As the mode number increases, the extent of modal activity not only moves upward within the cavity, but also upstream. This is especially evident in the wall-normal distributions. This observation can be explained using linear stability analysis. The overall gain describing the amplitude of an instability wave in an acoustically forced free shear layer is the product of a receptivity factor, describing the creation of the instability wave, and an exponential growth rate factor, describing subsequent growth of the instability wave. Both of these factors are frequency dependent; however, for subsonic and transonic Mach numbers, the optimal frequency is very close to the most unstable instability mode frequency (Barone Reference Barone2003). For the present Mach number, the optimal non-dimensional circular forcing frequency $\unicode[STIX]{x1D714}$ (4.2) is approximately 0.4 (Barone Reference Barone2003). Therefore, as displayed in table 2, when the mode frequency increases, $\unicode[STIX]{x1D714}_{m}$ approaches the optimal value. Recall that $\unicode[STIX]{x1D714}_{m}$ is based on the initial vorticity thickness within the cavity. This means that the shear layer is initially more receptive to higher-frequency instabilities, which explains why the modal activity moves upstream with mode number.

A spatial periodicity, more obviously present in the wall-normal PSD distributions, is evident. As the mode number increases, the spatial wavelength decreases accordingly. Kegerise (Reference Kegerise1999) also noted a spatial periodicity above the cavity using hot wire and optical deflectometry measurements. Moreover, Garg & Cattafesta (Reference Garg and Cattafesta2001) observed coherent structures in the density field above a resonating cavity flow. The current work seeks to further build on these observations by explaining the mechanism for the periodicity with the TR-PIV measurements.

The streamwise PSD distributions exhibit periodicity, although in comparison to the wall-normal distributions, a much greater dependence on $y$ is observed. In the case of both mode two (figure 17 d) and mode three (figure 17 f), a distinct waveform is observed near $y=0$ , while another is present within the cavity. Dashed lines appear in each panel to clarify the locations of the upper and lower waveforms. The mode two and mode three streamwise contour plots each indicate there to be a phase shift between the upper and lower waveforms. This is quantified further in figure 18, which shows line plots of streamwise PSD amplitude along the two different dashed lines annotated in figure 17(d). Near the aft end of the cavity there is a phase shift approximately 0.3 times the mode two wavelength. As annotated in figure, this phase shift is apparent when the peak-to-peak distance or the peak-to-trough distance is used. An intuitive, though qualitative, explanation for this observation lies in the phase delay built into the Rossiter model (4.1). The Rossiter model prescribes a phase delay between the time when a vortical structure impinges on the aft wall and when an acoustical disturbance propagates upstream, typically near a value corresponding to a phase lag of $0.25\unicode[STIX]{x1D706}$ . The fact that a similar phase delay is observed here between the upper shear layer wave and that lower within the cavity indicates that the streamwise PSD amplitude plots may simply be providing visualization of the phase lag.

Figure 18. Mode two profiles of streamwise velocity PSD amplitude at two different $y$ locations corresponding to the dashed lines in figure 17(d). As illustrated above, the mode two wavelength $\unicode[STIX]{x1D706}_{2}$ is estimated using the shear layer waveform along $y/D=0.06$ .

The mode two and mode three PSD amplitude contours are visually similar to figures 14 and 15, which plot variation of coherent structure size. This suggests that the PSD amplitude distributions are influenced primarily by velocity fluctuations associated with the modulation of coherent flow structure. To estimate the integrated behaviour across cavity height, the wall-normal velocity PSD amplitude distributions of figure 17 were averaged across the entire wall-normal extent of the measurement region. In figure 16, line plots of the resulting averaged PSD amplitude are compared to the coherent structure size returned using the bandpass-filtered, phase-averaged TR-PIV fields. As is shown in this figure, the cavity modal PSD distributions closely follow the coherent structure size indicating they are dominated by resonant fluctuations. It should be noted, however, that turbulent contributions can play a role in the spatial distributions for weaker resonant tones (Beresh et al. Reference Beresh, Wagner, Casper, DeMauro, Henfling and Spillers2017). Moreover, mode one PSD amplitude distributions are more influenced by broadband fluctuations.

To further investigate mode one acoustics, PSDs of wall-normal velocity at five points within the cavity are shown in figure 19. At locations of $y=0$ or lower, peaks corresponding to mode one tend to have little prominence. In fact, in the recirculation region ( $x=4D$ and $y=-0.3D$ ), broadband fluctuations have completely overwhelmed any evidence of a peak at $f_{1}$ . On the other hand, the points above $y=0$ do show evidence of mode one in the spectra. The relevance of this point will become apparent when comparing to the mode one pressure fluctuations given by the TR-PSP.

Figure 19. Mode one PSD spectra at five points within the cavity using all 245 time sequences.

4.8 Relationship between the modal pressure and velocity fields

Distributions of surface pressure fluctuations along the cavity floor given from the TR-PSP are presented in figure 20(a–c). The spatial distributions show the SPL value at each of the three modal frequencies (i.e. $\text{SPL}(f_{m})$ ). Note that the lines at $z/D=-1.8$ and the semicircles near $z/D=-2.5$ are measurement artefacts where shading by the wind tunnel and cavity geometry prevented adequate lighting of the cavity floor. Overall, the pressure distributions are fairly one-dimensional and show little variation in pressure fluctuations across the spanwise dimension of the cavity. Like the velocity PSD amplitude distributions, the spatial wavelengths of the SPL fields decrease with mode number. For instance, the mode one distribution exhibits a single minimum near $x=2D$ , whereas modes two and three have two and three local minima, respectively.

Figure 20. Spatial distributions of cavity floor SPL amplitudes corresponding to modes (a) one, (b) two and (c) three. Streamwise profiles of centreline SPL amplitude compared to streamwise and wall-normal velocity PSD amplitudes for modes the for modes (d) one, (e) two and (f) three.

The primary purpose of the TR-PSP here is to use its excellent spatial and temporal resolution to map pressure variations as a function of streamwise distance. This allows for detailed comparisons to the TR-PIV to better understand resonance dynamics. Towards this end, the streamwise variation of PSD amplitude at the spanwise centre of the cavity is plotted for modes one (figure 20 d), two (figure 20 e) and three (figure 20 f). Several previous cavity studies (Tracy & Plentovich Reference Tracy and Plentovich1997; Lee Reference Lee2010; Flaherty et al. Reference Flaherty, Reedy, Elliot, Austin, Schmit and Crafton2013; Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017) have observed similar spatial distributions, which look similar to patterns produced by standing waves.

Casper et al. (Reference Casper, Wagner, Beresh, Spillers and Henfling2017) recently showed that these spatial amplitude variations can be better explained using Rossiter’s model of cavity resonance which consists of downstream-propagating shear layer disturbances and weaker upstream-propagating acoustic waves. Because the waves moving upstream and downstream have different speeds, the phase velocity is not zero and a true standing wave is not generated. However, an interference pattern is developed by the wave superposition. Importantly, since the interfering waves have the same frequency, the group velocity of the wave summation is zero. In other words, the minima and maxima do not move with time (Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017).

Of prime importance is how the velocity field is coupled to the pressure field. (Even though the velocity and pressure data were obtained on opposite walls of the wind tunnel, the incipient boundary layers and cavity acoustics are essentially identical at the two locations making for effective comparisons.) The streamwise velocity PSD amplitudes of figure 17, averaged across the wall-normal direction of the measurement, are also shown in figure 20. For modes two and three, the averaging was performed over the entire wall-normal extent of the measurement, whereas for mode one, the region above $y=0$ was used to avoid the influence of turbulent fluctuations (figure 19).

In the case of modes two (figure 20 e) and three (figure 20 f), the locations of local minima in the pressure PSDs correspond to local maxima in the streamwise velocity PSDs. Similarly, local maxima in the pressure PSDs correspond to local minima in the streamwise modal velocities. Because the streamwise modal pressure distributions have fixed local minima and maxima (Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017), these observations can be explained with analogy to a standing wave, where nodes in modal pressure correspond to antinodes in streamwise modal velocity and vice versa. In other words, the very same constructive and destructive interference responsible for the periodic pressure distributions is apparent in the velocity fields due to cavity acoustics.

Wall-normal modal velocity PSD amplitudes, averaged across the measurement height, are also plotted in figure 20. At modes two and three, the wall-normal distributions take on a wave-like form similar to the streamwise distributions. Since cavity resonance occurs with the propagation of vortical structures, a coupling between the streamwise and wall-normal velocity fluctuations through rotation is to be expected. Though in close proximity, local wall-normal velocity maxima no longer occur at the location of pressure minima. Rather, the wall-normal waveforms precede the streamwise waveforms in $x$ . This is consistent with regions of upwash preceding streamwise velocity variations (figure 12).

Similar behaviour is observed at mode one where a local maximum is observed in the streamwise and wall-normal velocity amplitude profiles near the SPL minimum. The increasing velocity fluctuations at $x>3D$ are likely explained by increasing turbulence as the aft wall is approached (e.g. Zhuang et al. Reference Zhuang, Alvi, Alkislar and Shih2006). Likewise, a diminishing contribution of mode one resonance with increasing $x$ was also observed in figure 19 in the spectra corresponding to $y=0.6D$ .

The preceding experimental observations suggest a 180-degree phase difference to exist between the modal pressure and velocity fluctuations. In conjunction with Rossiter-based models to predict pressure fluctuation distributions (Kegerise Reference Kegerise1999; Casper et al. Reference Casper, Wagner, Beresh, Spillers and Henfling2017), this can be used to predict velocity fluctuation distributions at resonance frequencies in the flow above the cavity.

4.9 Convective and modal propagation velocities

4.9.1 Convective velocities based on unfiltered velocities

The spatial distribution of convective velocity within the cavity using the unfiltered velocity data is displayed in figure 21(a). The convection velocity is based on correlations of wall-normal velocity since $v$ is less influenced by upstream-propagating pressure waves than $u$ and is thereby more likely to give a better measurement of $U_{c}$ (Larchevêque et al. Reference Larchevêque, Sagaut, Le and Compte2004). The non-physical jump seen near the centre of the figure is related to the fact that the two vector fields were combined to produce the single field.

Figure 21. Unfiltered convective velocities based on the wall-normal component of raw velocity: (a) distribution within the cavity and (b) centreline profile compared to the simulations of Larchevêque et al. (Reference Larchevêque, Sagaut, Le and Compte2004). Dashed line corresponds to $U_{c}=0.57U_{\infty }$ .

The unfiltered convective velocity demonstrates some expected trends. At a constant streamwise station, $U_{c}$ increases with $y$ . Moreover, at constant $y$ , the convective velocity tends to increase with increasing streamwise distance. These trends are consistent with the mean flow field (figure 3), which shows the shear layer dives downward into the cavity with increasing streamwise distance to increase the convective velocity at a given $y$ location. The convective velocity profile at $y=0$ is plotted in figure 21(b), where the precision uncertainty based on 95 % confidence intervals is approximately $\pm 0.01U_{\infty }$ . The convective velocity increases as $x$ increases from $1D$ through $4D$ . Over this same region, the slope of the profile decreases until a plateau region is reached between approximately $3D$ and $3.8D$ . The convection velocity then begins to decrease for the rest of the measurement domain. As discussed in Larchevêque et al. (Reference Larchevêque, Sagaut, Le and Compte2004), the relatively constant acceleration observed in the upstream portion of the cavity corresponds to a region where the flow is predominantly two dimensional, whereas the sudden decrease in the downstream portion is associated with the aft wall.

These measurements are in line with previous cavity flow studies. Hassan et al. (Reference Hassan, Labraga and Keirsbulck2007), for example, measured similar convective velocity profiles in incompressible cavity flows, including a region of increasing slope, a plateau region, and a region of decreasing velocity following the plateau. The average convective velocities in Hassan et al. (Reference Hassan, Labraga and Keirsbulck2007) resided between approximately $0.40U_{\infty }$ and $0.50U_{\infty }$ , similar to the values reported in the incompressible studies of Haigermoser et al. (Reference Haigermoser, Vesely, Novara and Onorato2008) and Bian et al. (Reference Bian, Driscoll, Elbing and Ceccio2011). In comparison, in the available measurement region, the average convective velocity here computes to $0.48U_{\infty }$ , below the $0.57U_{\infty }$ used in the Rossiter relation to correctly predict the tone frequencies. It is possible that a new combination of constants using the lower measured $U_{c}$ could instead be used, although such an investigation is beyond the scope of the current work. The simulated convective velocity profile of Larchevêque et al. (Reference Larchevêque, Sagaut, Le and Compte2004), computed at similar flow conditions ( $M_{\infty }=0.85$ , $L/D=5$ ) to those herein, is also shown in figure 21. The current measurements show similar trends, although the simulated profile has an overall higher average convective velocity of  $0.52U_{\infty }$ .

4.9.2 Modal propagation (phase) velocities

Modal propagation (phase) velocities ( $U_{p}$ ), based on the cross-correlation of bandpass-filtered, wall-normal velocity fields are shown in figure 22. The non-physical jump is no longer present, indicating the source of the discontinuity was in the mean flow. The propagation velocity fields present a unique view of resonance dynamics in cavity flows. Unlike the measurements of unfiltered velocity data shown here in figure 21 and in other studies, a periodicity is observed when the bandpass-filtered velocities are used to compute the cross-correlations. There is a wavelength in the propagation velocity, which decreases with increasing mode number in a fashion analogous to the decreasing spatial wavelengths in the modal velocity and surface pressure fluctuations.

Figure 22. Modal phase velocities based on the wall-normal component of filtered velocity: (a) mode 1, (b) mode 2, (c) mode 3 and (d) streamwise profiles at $y=0$ . Error bars represent the precision uncertainty with 95 % confidence intervals.

Propagation velocity profiles obtained at $y=0$ for all three cavity modes are plotted in figure 22(d). On average, the propagation velocity increases with cavity mode number. Specifically, the average $U_{p}$ of modes one, two and three in the figure is $0.11U_{\infty }$ , $0.42U_{\infty }$ and $0.47U_{\infty }$ , respectively. This is likely related to the fact that as the cavity mode number increases, the coherent structures tend to reside at higher locations within the flow field reaching a higher portion of the shear layer where the mean local velocity is higher (figure 3 a).

The propagation velocity distributions in figure 22(d) corresponding to modes two and three show a clear periodicity. Casper et al. (Reference Casper, Wagner, Beresh, Spillers and Henfling2017) also measured a periodic propagation velocity based on correlations of bandpass-filtered surface pressures using TR-PSP. Moreover, their wave interference model, based on Rossiter’s interpretation of upstream-travelling acoustic disturbances superposed with downstream-travelling shear layer disturbances, predicted oscillations in propagation velocity. The modal propagation velocity exhibits periodicity because the superposed waves travel at different velocities. Since the propagation velocity represents motion of a resulting travelling wave at a distinct frequency, it is more appropriate to refer to the distributions in figure 22 as modal phase velocities. Here, the fact the phase velocity in the shear layer ( $y=0$ ) is positive for modes one through three indicates that the downstream-propagating disturbances overwhelm their upstream-propagating counterparts at this location.