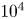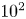2. Basic equations

We study a plasma confined in a magnetic field $\boldsymbol {B}$ and having negligible macroscopic motion, i.e. its fluid velocity $\boldsymbol {v}$ identically vanishes. The plasma is also characterized by a finite electric conductivity $\sigma \simeq \textrm {const.}$ The electric field in the plasma is then provided, via the current density, according to the generalized Ohm's law

(2.1)\begin{equation} \boldsymbol{E} = \frac{1}{\sigma}\boldsymbol{J}.\end{equation}

Expressing the electric field via the scalar and vector potentials ($\varphi$ and $\boldsymbol {A}$, respectively), i.e.

(2.2)\begin{equation} \boldsymbol{E} ={-} \boldsymbol{\nabla} \varphi - \partial _t\boldsymbol{A}/c, \end{equation}

observing that $\boldsymbol {B} = \boldsymbol {\nabla } \wedge \boldsymbol {A}$ and noting that in the Coulomb gauge (i.e. $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {A} = 0$) $\boldsymbol {J} =- (c/4{\rm \pi} ){\rm \Delta} \boldsymbol {A}$ ($c$ is the speed of light), we can finally rewrite (2.1) as follows:

(2.3)\begin{equation} \partial _t\boldsymbol{A} ={-}c\boldsymbol{\nabla} \varphi+ \frac{c^2}{4{\rm \pi} \sigma}{\rm \Delta} \boldsymbol{A}.\end{equation}

We now consider an axial symmetry, associated with a toroidal topology by the choice of cylindrical coordinates $r$, $\phi$ and $z$, having the following ranges of variation: $R_0-a\leqslant r \leqslant R_0+a$, $0\leqslant \phi < 2{\rm \pi}$. Here, $R_0$ denotes the major radius of a standard tokamak configuration, while $a$ is the minor radius (we also have $|z|\lesssim a$). The axial symmetry is implemented by requiring the independence of all the physical quantities from $\phi$.

We write the vector potential as follows:

(2.4)\begin{equation} \boldsymbol{A} = \boldsymbol{A}_p + \frac{\psi}{2{\rm \pi} r} \hat{e}_{\phi} ,\end{equation}

where $\hat {e}_{\phi }$ is the toroidal versor and the poloidal (radial–axial) vector potential $\boldsymbol {A}_p$ is described by the relations

(2.5a,b)\begin{equation} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{A}_p = 0,\quad \boldsymbol{\nabla} \wedge \boldsymbol{A}_p = B_{\phi} \equiv \frac{2}{c}\frac{I}{r}, \end{equation}

The functions $\psi = \psi (t, r, z)$ and $I = I(t, r, z)$ denote the flux function and the axial current function (in the cross-section ${\rm \pi} r^2$), respectively, and they are the considered dynamical degrees of freedom.

Since the scalar electric potential gradient is poloidal in axial symmetry, we easily get the dynamics of $\psi$ from the toroidal component of (2.3), and that of $I$ by taking the curl of the remaining poloidal components (so eliminating the gradient of $\varphi$) and by taking into account (2.4) and (2.5a,b). Thus, we arrive to the following two (identical) dynamical equations:

(2.6)\begin{gather} \partial _t\psi = \frac{c^2}{4{\rm \pi} \sigma}{\rm \Delta}^*\psi , \end{gather}

(2.7)\begin{gather}\partial _tI = \frac{c^2}{4{\rm \pi} \sigma}{\rm \Delta}^{*} I , \end{gather}

where we have defined ${\rm \Delta} ^*(\cdots ) \equiv r\partial _r(1/r\partial _r(\cdots )) + \partial ^2_z(\cdots )$. Now, the toroidal component of the momentum conservation equation ($p$ denoting the plasma pressure), i.e.

(2.8)\begin{equation} \boldsymbol{\nabla} p = (\boldsymbol{\nabla}\wedge\boldsymbol{B})\wedge\boldsymbol{B}/4{\rm \pi} , \end{equation}

reduces to the constraint $\partial _r\psi \partial _zI - \partial _z\psi \partial _rI = 0$, implying the basic restriction $I = I(\psi )$. Once we substitute this expression into (2.7), the compatibility with (2.6) leads to the condition

(2.9)\begin{equation} \frac{\textrm{d}^2 I}{\textrm{d} \psi^2} |\boldsymbol{\nabla} \psi|^2 = 0, \end{equation}

which is either trivially solved by $\psi =\textrm {const.}$, or by letting

(2.10)\begin{equation} \frac{\textrm{d}^2I}{\textrm{d} \psi^2} = 0 \Rightarrow I = A_1\psi + A_0,\end{equation}

where $A_{1,0}$ are two integration constants. Near the magnetic axis, (2.10) would correspond to considering a first-order expansion of $I(\psi )$, in a similar fashion as in Solov'ev (Reference Solov'ev1968), where analytical solutions of the GSE in the same regime are found by expanding the quantities $\textrm {d} p/\textrm {d} \psi$ and $I \,\textrm {d} I/\textrm {d} \psi$. In this context, however, the Solov'ev solution fails to guarantee the compatibility of the resistive system, de facto neglecting (2.7). In § 5, we study this incompatible scenario in detail, providing a comparison with the formally correct solution, which is derived in the following section.

The poloidal components of (2.8) reduce to the usual GSE,

(2.11)\begin{equation} {\rm \Delta}^*\psi ={-} 16{\rm \pi}^3 r^2 \frac{\textrm{d} p}{\textrm{d} \psi} - \frac{16{\rm \pi}^2}{c^2}I\frac{\textrm{d} I}{\textrm{d} \psi},\end{equation}

in which we also implement choice (2.10), i.e.

(2.12)\begin{equation} {\rm \Delta}^*\psi ={-} 16{\rm \pi}^3 r^2 \frac{\textrm{d} p}{\textrm{d} \psi} - \frac{16{\rm \pi}^2}{c^2}(A_1^2\psi+A_1 A_0).\end{equation}

Finally, the mass conservation equation ($\rho$ being the plasma mass density), i.e.

(2.13)\begin{equation} \partial _t\rho + \boldsymbol{\nabla} \boldsymbol{\cdot}(\rho \boldsymbol{v}) = 0,\end{equation}

becomes, in the present scenario, the simple relation $\rho \equiv \rho _0(r,z)$, where $\rho _0$ denotes is the time-independent plasma mass density.

3. Dynamical implications

The discussion above clarified how $\psi (t,r,z)$ is the only dynamical variable of the system, which has to obey (2.6) and (2.12). These two equations can be combined into a new one

(3.1)\begin{equation} \partial_t \psi = \frac{c^2}{4{\rm \pi} \sigma}\left( - 16{\rm \pi}^3 r^2 \frac{\textrm{d} p}{\textrm{d} \psi} - \frac{16{\rm \pi}^2}{c^2}(A_1^2\psi+A_1 A_0) \right),\end{equation}

which remains coupled to (2.12).

In order to look for analytical solutions, having to deal with a $dp/d\psi$ term, we preserve the linearity of the system by assuming the following expression for the pressure:

(3.2)\begin{equation} p(\psi) = C_2 \psi^2 /2 + C_1 \psi + C_0,\end{equation}

where $C_{2,1,0}$ are generic real constants. Taking (3.2) into account, it is easy to check that the general solution of (3.1) takes the form

(3.3)\begin{equation} \psi (t,r,z) = \psi _0(r,z) \,\textrm{e}^{ - \gamma(r) t}+ \delta (r),\end{equation}

where $\psi _0(r,z)$ is a generic function yet to be determined, while the quantities $\gamma (r)$ and $\delta (r)$ are given by

(3.4a,b)\begin{equation} \gamma(r) \equiv \frac{4{\rm \pi} }{\sigma} (A_1^2+{\rm \pi} c^2 C_2 r^2 ) ,\quad \delta (r) \equiv{-}\frac{{\rm \pi} c^2C_1 r^2 + A_1A_0}{{\rm \pi} c^2 C_2 r^2 + A_1^2} .\end{equation}

By substituting (3.3) and (3.4a,b) into (2.12), we obtain an equation for $\psi _0(r,z)$

(3.5)\begin{align} &\textrm{e}^{-\gamma(r)t} \left[ {\rm \Delta}^*\psi_0 +\frac{8{\rm \pi}^2c^2}{\sigma} C_2 r t \left({-}2\partial_r\psi_0 + \frac{8{\rm \pi}^2c^2}{\sigma}C_2 r t \psi_0 \right) \right]+\frac{8{\rm \pi}^2 c^4 A_1 C_2 (A_1C_1 - A_0C_2)}{({\rm \pi} c^2 C_2 r^2+A_1^2)^3} \nonumber\\ &\quad ={-}16{\rm \pi}^3 r^2[ C_2 (\psi_0 \,\textrm{e}^{-\gamma(r)t}+\delta(r))+C_1 ] - \frac{16{\rm \pi}^2}{c^2}[ A_1^2 (\psi_0\, \textrm{e}^{-\gamma(r)t}+\delta(r))+A_1A_0 ] , \end{align}

which involves terms proportional to $1$, $t$ and $t^2$, which of course must be equated separately. In order to solve the time-dependent equations, the constant $C_2$ must be set to 0, which implies that also the pressure must be linear in the flux function, like the axial current function $I$. This kind of choice for the functions $p$ and $I$ has been previously studied in Mc Carthy (Reference Mc Carthy1999), although in our work we show how such an assumption is naturally motivated by dynamical considerations.

After choosing $C_2=0$, (3.3) and (3.4a,b) reduce to

(3.6)\begin{equation} \psi (t,r,z) = \psi _0(r,z)\, \textrm{e}^{ - \gamma t}+ \delta (r),\end{equation}

and

(3.7a,b)\begin{equation} \gamma \equiv \frac{4{\rm \pi} A_1^2}{\sigma},\quad \delta (r) \equiv{-}\frac{{\rm \pi} c^2C_1}{A_1^2}r^2- \frac{A_0}{A_1},\end{equation}

respectively. Finally, the equation for $\psi _0(r,z)$ takes the form

(3.8)\begin{equation} {\rm \Delta}^* \psi _0 ={-}16{\rm \pi} ^2 A_1^2 \psi _0/c^2.\end{equation}

Before studying the morphology of the plasma profile, we observe that the magnetic configuration is always damped in time by a constant rate $\gamma$, which we associate with a resistive diffusion time scale, towards an asymptotic constant field $\boldsymbol {B}_{\infty } = (c^2C_1/A_1^2)\hat {e}_z$.

The present study has the merit of defining quantitatively a lifetime for a given plasma configuration, once resistive diffusion is consistently taken into account. In particular, we showed how the lifetime is very sensitive to $A_1$, i.e. the proportionality constant between $I$ and $\psi$. This approach in not intended as an alternative choice to standard transport studies on assigned equilibria. In fact, we simply clarify the influence of the considered correction to Ohm's law on the evolution of a plasma profile, which could play a significant role in the physics of future steady-state tokamak machines.

4. Magnetic profile

In order to investigate the constant poloidal flux function $\psi _0(r,z)$ predicted by (3.8), we observe that its linearity allows us to consider the following Fourier expansion:

(4.1)\begin{equation} \psi_0(r,z) = \int^{\infty}_{0} \textrm{d} k \chi_k(r)\, \textrm{e}^{\textrm{i}kz}+\textrm{c.c.},\end{equation}

where c.c. indicates the complex conjugate, and $\chi _k(r)$ verifies the eigenvalue problem

(4.2)\begin{equation} \frac{\textrm{d}^2\chi_k}{\textrm{d} r^2} - \frac{1}{r} \frac{\textrm{d} \chi_k}{\textrm{d} r} = E_k \chi_k, \quad E_k \equiv k^2 - \frac{16{\rm \pi}^2A_1^2}{c^2}.\end{equation}

The equation for $\chi _k$ admits an analytical solution in terms of Bessel functions. In particular, defining $x\equiv r |E_k|^{1/2}$ and setting $\chi _k\equiv r\varepsilon (k,x)$, (4.2) can be rewritten as

(4.3)\begin{equation} x^2\frac{\textrm{d}^2\varepsilon}{{\textrm{d} x}^2} + x\frac{\textrm{d}\varepsilon}{\textrm{d} x} - ( 1 \pm x^2)\varepsilon = 0, \end{equation}

where the sign $-$ corresponds to $E_k<0$, i.e. to $k< k^*$, where $k^*=4{\rm \pi} A_1/c$, while the sign $+$ to the case $E_k>0$, i.e. to $k>k^*$.

In correspondence to the sign $\mp$, the solutions of (4.3) are

(4.4)\begin{gather} \varepsilon _-(k,x) = \varepsilon _1(k) J_1(x) + \varepsilon _2(k) Y_1(x) , \end{gather}

(4.5)\begin{gather}\varepsilon _+ (k,x) = \varepsilon _3(k) I_1(x) + \varepsilon _4(k) K_1(x), \end{gather}

where $J_1$, $Y_1$ ($I_1$, $K_1$) denote ordinary (modified) Bessel functions of index 1, while the coefficients $\varepsilon _j(k)$ (with $j=1,2,3,4$) have to be assigned via the initial condition $\psi (0,r,z) = \psi _0(r,z) + \delta (r)$. In this scheme, taking into account that the $r$ variable is bounded and that $I_1(\infty )$ is divergent, the flux function $\psi (t,r,z)$ admits the following representation:

(4.6)\begin{align} \psi(t,r,z)&={-}{A_0}/{A_1}+\varLambda r^{2}\nonumber\\ &\quad +\textrm{e}^{-\gamma t} \int_{k_0}^{k^*} \textrm{d} k[[r\varepsilon_1(k)J_1(r\sqrt{|k^2-k^{*2}|})\nonumber\\ &\quad +r\varepsilon _2(k) Y_1(r\sqrt{|k^2-k^{*2}|})]\, \textrm{e}^{\textrm{i}kz}+ \textrm{c.c.}] \nonumber\\ &\quad +\textrm{e}^{-\gamma t}\int_{k^*}^{\infty}\, \textrm{d} k[r\varepsilon_4(k) K_1(r\sqrt{|k^2-k^{*2}|})\,\textrm{e}^{\textrm{i}kz}+\textrm{c.c.}]. \end{align}

Here, $\varLambda =-{\rm \pi} c^2C_1/A_1^2$ and, to exclude wavelengths greater than the machine diameter, we have introduced a minimum wavenumber $k_0={\rm \pi} /a$, i.e. $k\geqslant k_0$. We also remark that, by suitably choosing the constant $C_0$ in (3.2) for the plasma pressure, the basic requirement $p\geqslant 0$ can be easily implemented in our confined plasma region.

4.1. Specific implementation

In order to investigate the morphology of the plasma configuration, we analyse the level surfaces of $\psi (r,z,t)$ at given times, together with the surface $p=0$ (representing the plasma boundary layer). The general solution for $\psi$ as in (4.6) can be adapted to a given scenario by imposing specific initial conditions. In this respect, for the sake of simplicity, we assign to the functions $\varepsilon _j(k)$ a set of sufficiently narrow Gaussians, centred around arbitrarily given wave vectors $k_{j,i}$ and weighted by amplitudes ${\bar {\varepsilon}}_{j,i}$. Then, a given set of points $(r_l,z_l)$ lying along the boundary curve of the addressed scenario generates an associated set of algebraic equations of the form $\psi (r_l,z_l,0)=\psi _B$, where $\psi _B$ is the value of the magnetic flux at the plasma boundary. Since we require $p=0$ on the same surface, recalling (3.2) and that $C_2=0$, we set $C_0=-C_1\psi _B$. The rest of the constants have to be determined according to the relevant plasma parameters.

As an illustrative example, let us assume the parameters characterizing a tokamak equilibrium specified for the DTT facility, as in Albanese et al. (Reference Albanese, Crisanti, Martin, Martone and Pizzuto2019). In particular, the main machine parameters are major radius $R_0=2.11$ m, minor radius $a=0.64$ m, averaged electron density $n_e=1.8\times 10^{20}$ m$^{-3}$ and electron temperature $T_e=6.1$ keV. The resulting plasma frequency is $\omega _p=7.57\times 10^{11}$ s$^{-1}$ and, considering the Spitzer electric conductivity for a hydrogen plasma (with the Coulomb logarithm of ${O}(10)$), we obtain $\sigma =5.34\times 10^{8}\varOmega ^{-1}$ m$^{-1}$. We implement an initial condition matching the double-null scenario, with main plasma parameters as reported in table 1. In the same table, we also report the fitted values associated with our analytic solution, which is able to correctly reproduce most of the parameters. In this scheme, we obtain a configuration characteristic time of $\gamma ^{-1} = 1.1\times 10^4$ s. As a stability check, the safety factor $q$ meets the Kruskal–Shafranov condition for stability $q>1$ over the whole plasma region, with an average value of $2.6$.

Table 1. Data relative to the double-null DTT scenario, as in Albanese et al. (Reference Albanese, Crisanti, Martin, Martone and Pizzuto2019), and the corresponding fitted values from our solution and the Solov'ev configuration, which is introduced in § 5. The subscript $\text {A}$ refers to quantities along the magnetic axis, $\psi _{B}$ is the magnetic flux at the plasma boundary, $\beta _{p}$ is the ratio of the plasma pressure to the poloidal magnetic pressure, $I_{P}$ is the total plasma current and $l_{i}$ is the internal inductance.

In figure 1, we plot the level surfaces of the flux function $\psi (t,r,z)$ at different times, where the initial condition at $t=0$ is shown in the first panel. At later stages, the allowed domain for the plasma configuration decreases, and the central pressure is correspondingly suppressed (cf. (3.2)). Since the area inside the separatrix is decreasing in time, the axial symmetry implies that the confined plasma volume is also diminishing, but keeping a constant plasma density $\rho \equiv \rho _0$. As a consequence, the plasma evolution has to be associated with a loss of particles through the boundary layer of the toroidal plasma profile. The behaviour of this outgoing flux of matter must be described in a different physical setting, having to deal with the behaviour of non-confined plasma in the scrape-off layer.

Figure 1. Contour plot of the flux function (in the physical plane $(r,z)$) integrated from (4.6) according to the proposed double-null scenario for DTT (Albanese et al. Reference Albanese, Crisanti, Martin, Martone and Pizzuto2019), for different instants as indicated over the panels (colour scheme from beige ($\psi =2.50$ Vs, also red line) to purple ($\psi =8$ Vs)). The separatrix $p=0$ is enlightened in red. The initial condition is imposed through 14 boundary points, plus two conditions on the derivatives of $\psi$ at the x-point. Wavenumbers $k$ run from $0.52$ to $1.72$ in steps of $0.2$.

Concerning the lifetime of the configuration, it is important to stress that we observe the opening of all magnetic lines, determining the loss of confinement, at $t=99$ s. This time scale is two orders of magnitude shorter than $\gamma ^{-1}$, and is comparable to the predicted duration of the discharge of about $\simeq 50$ s. This behaviour can be understood if we consider that the plasma region can also be defined as the points satisfying $\psi \geqslant \psi _{B}$. Indicating the initial peak value of the magnetic flux as $\psi _{A}$, in correspondence to the magnetic axis, it is clear that after an overall decrease in $\psi$ of the order ${\rm \Delta} \psi \equiv |\psi _{A}-\psi _{B}|$ the whole profile will lie below the $\psi _{B}$ threshold, i.e. all magnetic lines will be open. Then, it is natural to define an effective lifetime according to the condition $\bar {\psi }_0 ( 1-\textrm {e}^{-\gamma t^*})={\rm \Delta} \psi$ (where $\bar {\psi }_0$ is the order of magnitude of the function $\psi _0(r,z)$), which provides the expression

(4.7)\begin{equation} t^*={-}\gamma^{{-}1}\ln(1-{\rm \Delta}\psi/\bar{\psi}_0).\end{equation}

In the case under study, ${\rm \Delta} \psi \simeq 5.5$ Vs and $\bar {\psi }_0\simeq 600$ Vs, so that $t^*=99$ s, as shown in the plots.

We also remark that the solution outside the boundary layer takes a different character, being described by a vacuum problem at the initial stage of the evolution. In this outer region the current density must be set to zero, according to the pressure profile. Therefore, outside the separatrix $p=0$, we must require that $A_1=A_0=C_1=C_0\equiv 0$ and also that the toroidal current $J_{\phi }$ vanishes. This last condition leads to the equation

(4.8)\begin{equation} {\rm \Delta}^* \psi(t,r,z)=0,\end{equation}

which is the only surviving equation for the vacuum configuration. Clearly, the time dependence of the magnetic flux function in vacuum is ensured by the matching conditions on the boundary layer.

4.2. Implications of temperature dynamics

As already noted at the end of § 2, the continuity equation (2.13), in the absence of velocity fields, implies a time-independent profile of the mass density $\rho =\rho _0(r,z)$. In the limit of applicability of the perfect gas law to the plasma (coherent with a non-zero resistivity), we thus see that the temperature must decay in time like the pressure does, as implied by (3.2) and (3.6).

From this point of view, the assumption of dealing with a constant conductivity, on which the present analysis is based, is questionable. In fact, it is well known from Spitzer & Härm (Reference Spitzer and Härm1953) that the plasma conductivity increases as $\sigma \sim T^{3/2}$, therefore the validity of the present scheme extends as far as a time-averaged value of this quantity can be considered, namely for a time scale $t \ll \gamma ^{-1}$.

The question could be addressed in a more rigorous way by including the temperature dynamics in the model, via the conservation equation for energy. The simple diffusive equation we could assign for the temperature evolution in cylindrical coordinates is the following:

(4.9)\begin{equation} \partial _tT = \frac{2}{3n_0K_B}\frac{1}{r} \partial_r(r \kappa _T\partial _rT) + \frac{2}{3n_0K_B} \partial_z(\kappa _T \partial _zT),\end{equation}

where $\kappa _T$ denotes the thermal conductivity coefficient, $K_B$ is the Boltzmann constant and $n_0(r,z)$ is the equilibrium plasma particle density, equal to $\rho _0(r,z)/m_i$ in the case of a single atomic species plasma with ion mass $m_i$. However, assuming the validity of the perfect gas law for the plasma, we must also have $T = p(\psi )/n_0$, which clearly opens a problem of compatibility between the equation above and (3.6), describing the flux function evolution.

This compatibility request cannot be easily solved and shows, once again, how the complete self-consistency of a plasma evolution implies serious restrictions on the relations among the involved physical quantities. Our analysis calls attention to how fixing the equilibria and then evolving transport on that configuration, recalculating it in a later step and iterating the procedure, as in typical fusion codes, could cut off all these mathematical questions from the problem. In general, this procedure is reliable and efficient due to the different time scale of the equilibrium variation with respect to the transport phenomena, but it could lead to non-trivial miscalculations when the magnetic flux function and the other physical plasma quantities, for instance the velocity field, evolve together in a coherent and consistent MHD scheme. Our study of resistive diffusion acting on equilibria is just a simple example of a more general problem of consistency which could emerge when equilibrium and transport codes are matched together.

Coming back to the question of the temperature behaviour, we observe that, as discussed in Montani, Rizzo & Carlevaro (Reference Montani, Rizzo and Carlevaro2018), where an astrophysical context has been investigated, the compatibility of the system for $T=T(\psi )$ is still possible for a local model, where all the background quantities are considered constant, and the perturbations have a sufficiently short wavelength. A similar picture, with some minor modifications of the physical framework, could also be applied to a tokamak configuration, if we were interested to study local effects of diffusion near a given regular magnetic surface $\psi (r,z) = \psi _0$. This study could be of interest in determining the stochastization of the magnetic flux dynamics and the onset of an island formation. This process is clearly absent in the present model, in which the magnetic flux surfaces are differentiable topological sets and evolve in time, preserving this main feature and their basic shape. Using a local model near each assigned background surface, considering also a space-dependent resistivity, could allow a study of the instability of this scenario versus a stochastic domain.

Before closing this section, it is worth recalling the hypotheses at the heart of the present analysis and their physical motivation or interpretation. We consider a non-steady (slowly varying) axisymmetric plasma configuration, characterized by zero velocity fields, a space–time-independent temperature and a constant conductivity coefficient.

The assumption to deal with zero advective flows is rather natural in the analysis of equilibria (Biskamp Reference Biskamp1993) and it is justified by the absence of evidence for macroscopic plasma motion during a wide class of discharges in tokamak devices. However, the observation of spontaneous toroidal and poloidal rotation, as well as rotation due to plasma interaction with hot neutral beams and other power sources (Rice Reference Rice2016) suggests that, under specific conditions, the present analysis needs to be extended in this direction. In the present work, the main task is to investigate the role of resistive diffusion by slowly altering an equilibrium configuration over time. Thus, we focus our attention on the resistive time scale as the fundamental one which drives the plasma evolution. In this sense, the introduction of a velocity field is surely of interest, but only after the basic resistive mechanism of diffusion is understood in its intrinsic nature.

The assumption of a uniform plasma temperature is more serious and definitely unrealistic close to the separatrix region of the plasma, but it is also commonly employed in the study of tokamak physics, when the equilibrium configuration is viewed in its most basic features (see, e.g. Tamain et al. Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016). More precisely, the possibility of considering a constant temperature must be implicitly thought of as a restriction on the considered plasma space and time region. In the present case, this restriction must be referred to what we defined as the effective lifetime of the configuration, corresponding to the disappearance of a closed separatrix (see § 4.1). In fact, since this time scale is approximately two orders of magnitude shorter than the resistive diffusion time (derived in § 3), it is safe to consider the plasma as isothermal during the evolution. As far as the plasma is sufficiently hot so that its collisional nature is negligible (e.g. the thermal conductivity discussed above), the isothermal nature of the plasma within the separatrix is a satisfactory approximation, up to the beginning of a disruption, before the thermal quench has occurred (Nedospasov Reference Nedospasov2008).

For what concerns the constant nature of the conductivity coefficient, we can develop similar considerations about its restriction to a limited space and time region of the plasma, as argued for the temperature. However, in view of capturing the basic feature of a slowly varying equilibrium due to resistive diffusion, the uniformity of $\sigma$ seems to be natural. In fact, a non-uniform coefficient $\sigma$ would only affect the diffusion properties in different space regions, without introducing any new conceptual modification of the present picture.

Although some of the above hypotheses could be weakened in a future semi-analytical analysis, we stress once more that the loss of an analytical treatment for a more general configuration outlines possible shortcomings in the complete separation between equilibria and transport, often introduced in plasma transport codes.

5. Comparison to alternative approaches

In order to compare our self-consistent approach to other standard methods, we begin by studying an alternative analytical solution in correspondence to the well-known Solov'ev configuration (Solov'ev Reference Solov'ev1968). In this sense, we go back to the original GSE, (2.11), and assume its right-hand side to be independent of $\psi$

(5.1)\begin{equation} {\rm \Delta}^*\psi={-}16{\rm \pi}^3C_{1s} r^2 -\frac{16{\rm \pi}^2}{c^2}A_{1s} ,\end{equation}

where $C_{1s}$ and $A_{1s}$ are constants (the subscript $s$ indicates quantities relative to the Solov'ev scenario). The corresponding choices for $p(\psi )$ and $I(\psi )$ are the following:

(5.2a,b)\begin{equation} p_s(\psi)=C_{1s}\psi+C_{0s},\quad I_s(\psi)=\sqrt{2A_{1s}\psi+A_{0s}},\end{equation}

so that the pressure is of the same kind as previously considered (remember that $C_2=0$), while the axial current has a different functional form. It is important to remark that substituting the latter expression into (2.9) we get

(5.3)\begin{equation} \frac{\textrm{d}^2I_s}{\textrm{d}\psi^2}|\boldsymbol{\nabla}\psi|^2={-}\frac{A_{1s}^2}{(2 A_{1s} \psi + A_{0s})^{3/2}}|\boldsymbol{\nabla}\psi|^2=0, \end{equation}

which admits only the trivial solutions $A_{1s}=0$ or $\psi =\textrm {const.}$ However, if the equation above is excluded from the model, (2.6) and (5.1) lead to the expression

(5.4)\begin{equation} \psi_s(r,z,t)={-} a(r) t + b(r) + \psi_0(r,z) ,\end{equation}

with

(5.5)\begin{gather} a(r)=\frac{4{\rm \pi}^2 c^2}{\sigma}\left(C_{1s} r^2 +\frac{A_{1s}}{{\rm \pi} c^2}\right), \end{gather}

(5.6)\begin{gather}b(r)=2{\rm \pi}^3 r^2\left[{-}C_{1s} r^2 +\frac{2 A_{1s}}{{\rm \pi} c^2} ( 1-2\log r ) \right]. \end{gather}

Here, $\psi _0(r,z)$ is formally equivalent to the solution already considered in § 4, since it must satisfy (4.1) and (4.2), with the only difference that now $E_k=k^2$. The most striking feature of $\psi _s(r,z,t)$ is the linear time dependence, which differs from the exponential decay of the consistent solution.

To test this discrepancy, we fit the new expression, (5.4), to the same double-null scenario of § 4.1. The agreement is sufficiently good, as can be noted from the fitted values in table 1. Moreover, the time evolutions of the two profiles follow the same dynamics up to the loss of confinement, which, in this case, takes place after $98$ s. This similarity between exponential and linear decays can be explained noting that confinement is lost on a time scale much shorter than $\gamma ^{-1}$, when the exponential in (4.6) is still in its linear phase.

Although this result suggests that (2.9) can be safely disregarded in the DTT plasma scenario, this cannot be considered as a general proof. The Solov'ev case has the good property of preserving the linearity of the system, which instead is usually broken in the context of numerical equilibrium solvers, such as EFIT (Lao et al. Reference Lao, St. John, Stambaugh, Kellman and Pfeiffer1985), where nonlinear forms of $\textrm {d} p/ \textrm {d} \psi$ and $I \, \textrm {d} I/\textrm {d}\psi$ are assumed. In such scenarios, (2.11) cannot be solved through simple analytic means, so an exact comparison lies outside the scope of the present work. We propose an effective estimate of the incompatibility of the nonlinear case, by considering the following generalization of (2.10):

(5.7)\begin{equation} I_n(\psi)=A_{1,n}\psi^n+A_{0,n},\end{equation}

where the coefficients $A_{1,n}$ and $A_{0,n}$ are determined according to the relevant plasma parameters of table 1. Assuming $|\boldsymbol {\nabla }\psi |^2$ to be of the same order of magnitude in all configurations (i.e. $\sim ({\rm \Delta} \psi /a)^2$), the error committed in (2.9) is quantified by the second derivative of $I_n$ with respect to $\psi$

(5.8)\begin{equation} \frac{\textrm{d}^2I_n}{\textrm{d} \psi^2}=n(n-1) A_{1,n} \psi^{n-2}.\end{equation}

The same quantity, calculated for the Solov'ev configuration, is taken as a reference, so we study the function

(5.9)\begin{equation} \epsilon(\psi,n)\equiv\log_{10}\left| \left.\frac{\textrm{d}^2I_n}{\textrm{d}\psi^2} \right/ \frac{\textrm{d}^2I_s}{\textrm{d}\psi^2}\right|= \left|A^2_{1s}\frac{n(n-1) A_{1,n} \psi^{n-2}}{(2 A_{1s}\psi+A_{0s})^{3/2}}\right|, \end{equation}

defined as a logarithm for convenience.

In figure 2, it clearly emerges that the magnitude of $\epsilon$ grows quickly for $n$ different than 0 and 1 (the only two analytically correct values). In particular, the whole region below $n=0$ takes up values larger than 3, i.e. the left-hand side of (2.9) is at least three times larger in these cases than in the Solov'ev case. A fiducial interval can be defined around $n=1$, in which the discrepancy is less than one order of magnitude. According to this estimate, more detailed studies should be performed on the viability of the coupling of evolutive codes with nonlinear GSE configurations.

Figure 2. Variation of $\epsilon (\psi ,n)$ for values of $\psi$ corresponding to the DTT double-null plasma scenario (Albanese et al. Reference Albanese, Crisanti, Martin, Martone and Pizzuto2019), and $n\in (-2,5)$. The colour scheme goes from white ($\epsilon <0$) to red ($\epsilon >5$), while each contour is labelled by the corresponding value, with shorter dashes indicating greater values.

6. Concluding remarks

We analysed a varying tokamak plasma equilibrium, in which the magnetic field profile is damped by resistive effects. In such a dynamical scheme, the GSE is coupled with an evolutionary equation for the magnetic flux function dynamics, i.e. the induction equation.

The main result has been the determination of a lifetime for the plasma confinement, here discussed in the particular case of an initial condition corresponding to the $5$ MA double-null scenario for the DTT tokamak proposal, as in Albanese et al. (Reference Albanese, Crisanti, Martin, Martone and Pizzuto2019). A secondary, effective lifetime also arises from the observation of the loss of magnetic confinement on a time scale much shorter than expected, and comparable to the duration of the discharge.

Clearly, the present analysis cannot be directly applied to the discharge evolution of a tokamak machine. In fact, during a discharge, the current is governed by inductive processes associated with the time dependence of the current running in the magnetic field coils. Furthermore, when a flat-top configuration is reached, it is maintained with a steady profile also via different current drive mechanisms, such as radio frequencies coupled to the plasma.

Our analysis is mainly aimed at providing some physical insight in view of the following delicate matter. The ideal GSE is usually assumed to describe the plasma equilibrium at any given time, while the generalized Ohm's law, on which transport computations are based, takes into account all the non-ideal processes involved in the construction of the steady current profile, including the resistive diffusion. Hence, from a rigorous mathematical point of view, the matching of such different pictures is inconsistent since the evolution of transport quantities would clearly influence the behaviour in time of the magnetic flux function, which instead is taken as fixed between different steps of an iterating procedure. Moreover, even ideal effects like the presence of velocity fields pose similar questions, whenever particle transport is calculated over an underlying equilibrium obtained from a static version of the GSE.

The physical predictivity of this standard strategy in describing tokamak physics relies on the different time scales of the transport processes and of the equilibrium variation, but this approximation clearly fails when the plasma configuration is subject to abrupt modifications, as during the L–H transition (Wagner Reference Wagner2007) or disruptions.

For instance, we show that the compatibility of the dynamics requires the poloidal current function $I$ to have a linear dependence on the magnetic flux function. As discussed in § 5, this constraint could produce significant deviations between the steady and the dynamical versions of the GSE, namely when nonlinear contributions to $I(\psi )$ are considered, as it is often the case in numerical codes (Lao et al. Reference Lao, St. John, Stambaugh, Kellman and Pfeiffer1985).

In other words, the present analysis cannot be directly applied to the operation of a tokamak device, but it suggests a more careful understanding of the underlying physical assumptions with which different codes separately face different pieces of tokamak physics. In large sized machines, having also large discharge durations, the consistency of the dynamics, raised here, could play a significant role.

For what concerns the application of our model to the DTT scenario, it is worth observing that our capability to analytically reproduce the plasma configuration is affected by a certain degree of approximation, since our solution lacks the sufficient number of parameters to constrain all the relevant plasma quantities. In this respect, the number of parameters that can be fixed is naturally related to the linear prescription $I\propto \psi$, which is a remarkable conceptual implication of including resistivity into the magnetic flux function dynamics.

We also studied two cases where this prescription is not respected, de facto disregarding (2.9). In the Solov'ev configuration, which keeps the system linear, no dramatic changes are observed on the profile, while in nonlinear cases we obtain numerical evidence of a larger discrepancy. We conclude that, before saying a definitive word on the relevance of resistive diffusion to the equilibrium properties, a more systematic study on commonly used nonlinear plasma codes could be of interest.