1. INTRODUCTION
In the past years, great efforts have been devoted to modeling and identification of nonlinear systems due to the inherent nonlinearities in real-life industrial plants and processes. For such systems, assumption of linearity fails, and an accurate mathematical model based on the physics of the system is infeasible due to large number of parameters, some of which can be unknown (Ronen et al., Reference Ronen, Shabtai and Guterman2002). Researchers have proposed several nonlinear identification methods (e.g., DeVeaux et al., Reference DeVeaux, Psichogios and Ungar1993; Kashiwagi & Rong, Reference Kashiwagi and Rong2002; Billings, Reference Billings2013; de Costa Martins & de Araujo, Reference da Costa Martins and de Araujo2015; Scarpiniti et al., Reference Scarpiniti, Comminiello, Parisi and Uncini2015; Pan et al., Reference Pan, Yuan, Goncalves and Stan2016), and demonstrated that these methods are capable of identifying nonlinear systems with different degrees of performance. However, they have several drawbacks. An excellent review on these methods can be found in Yassin et al. (Reference Yassin, Taib and Adnan2013).
A multimodel-based alternative approach to modeling and identification of these systems has attracted many researchers recently. In contrast to the conventional modeling technique, a system is represented by a set of models that are combined, with different degree of validity, to form the global model. Each model represents the system in a specific region of operation. Owing to its potential benefits, this effective field of research has received several contributions, and has gained lots of interest in many fields of application such as biochemical (Dunlop et al., Reference Dunlop, Franco and Murray2007), process control (Xue & Li, Reference Xue and Li2005), communication (Abbas & Tufvesson, Reference Abbas and Tufvesson2011), and power systems (Gan & Wang, Reference Gan and Wang2011). Despite its benefits, the approach still faces several challenges.
One main challenge of the multimodel approach is the partitioning of the system's operating space to a number of subspaces. This further raises the question of how many submodels are required to adequately represent the entire operating region of the nonlinear system when combined within the multimodel framework. One solution to this problem is the design of identification experiments for known operating spaces (e.g., Dunlop et al., Reference Dunlop, Franco and Murray2007; Gregorčič & Lightbody, Reference Gregorčič and Lightbody2007; Novak et al., Reference Novak, Chalupa and Bobal2009; Wernholt & Moberg, Reference Wernholt and Moberg2011). Data are collected for each operating space, and a submodel is identified for each a priori known region.
However, the knowledge involved in any industrial systems and processes, especially chemical process, is often incomplete. In addition, they may be subjected to unknown parameter variations and exhibit wide operating ranges. Therefore, in such situations, partitioning of the operating space and identification of the submodels can be very challenging due to lack of prior information on the system's operating conditions.
The problem of identifying the parameters of the submodels is coupled with the data partition problem, whereby each data point needs to be associated with the most suitable submodel. In the partitioning process, optimization of number of submodels and their parameters is very crucial for the correct identification of the system. While too few submodels can deteriorate the systems, increasing the number of submodels does not necessarily improve the performances obtained (Ksouri-Lahmari et al., Reference Ksouri-Lahmari, Borne and Benrejeb2004).
In the literature, many interesting algorithms have been proposed to address this challenge. Ronen et al. (Reference Ronen, Shabtai and Guterman2002) used fuzzy clustering for operating space partition and utilized both cluster and model validities methods to find the optimal number of clusters. The approach repeats the procedure for a number of submodels until a satisfactory number is obtained. Venkat et al. (Reference Venkat, Vijaysai and Gudi2003) proposed a loss function, linear model based reconstruction error, to determine the optimal number of clusters resulting in minimum model error. Samia et al. (Reference Samia, Ben Abdennour, Kamel and Borne2002, Reference Samia, Kamel, Ridha and Mekki2008) utilized a heuristic method based on the number of neurons in the output layer of a Kohonen network. In their approach, the network has to be trained repeatedly until a satisfactory number of clusters is obtained. Moreover, the training of the network is very slow and increases with the number of data samples. Ltaief et al. (Reference Ltaief, Abderrahim and Ben Abdennour2008), Mohamed et al. (Reference Mohamed, Ben Nasr and Sahli2011), and Bedoui et al. (Reference Bedoui, Ltaief and Abderrahim2012) utilized subtractive clustering that automatically determines the number of clusters. The accuracy of their algorithm was known to depend on proper selection of its parameters (Demirli et al., Reference Demirli, Chengs and Muthukumaran2003).
In Gugaliya and Gudi (Reference Gugaliya and Gudi2010) and Novak et al. (Reference Novak, Chalupa and Bobal2011) large number of clusters was initially assumed and later reduced by merging similar clusters. Teslic et al. (Reference Teslic, Hartmann, Nelles and Škrjanc2011) proposed an iterative incremental partitioning algorithm using G-K clustering. Numbers of clusters are iteratively increased by splitting the worst modeled cluster if its standard deviation error is greater than a certain threshold. Elfelly et al. (Reference Elfelly, Dieulot, Benrejeb and Borne2010) proposed the use of a separate clustering algorithm called the rival penalized competitive learning neural network. Adequate numbers of clusters are determined by visual consideration of only clusters' centers that are enclosed by the data distribution when the initial number of clusters is larger than the real number of operating clusters. In general, all the aforementioned methods partitioned the operating space and/or determined the number of adequate submodels based on data distribution only, which may not reflect the complexity of the system's behavior.
In this paper, an efficient three-stage algorithm is proposed to obtain a multimodel representation of nonlinear systems without prior knowledge of the operating conditions. In the first stage, estimation of the initial parameters and the number of submodels are both obtained through a reinforced combinatorial particle swarm optimization (RCPSO). To identify more efficient submodels, hybrid K-means is used to obtain the final submodels in the second stage. Finally, based on a constrained Kalman filter, the identified submodels are interpolated to form the multimodel output that has the capability to approximate the real system. The main advantage of the proposed framework is its automatic optimization of the required number of submodels with respect to submodel complexity. This implies that the operating space of the system can be partitioned into a parsimonious number of submodels, and the structure of the submodels can be assumed without prior knowledge. Thus, the algorithm can automatically converge to a good compromise between the number of submodels and complexity. Another interesting advantage is that the partition and selection of number of submodels is based not only on data distribution but also on the linearity of the operating region and that of the assumed model structure. Benchmark simulation examples, including a continuous stirred tank reactor system, are provided to illustrate the effectiveness of the proposed method.
The rest of this paper is organized as follows: Section 2 describes the multimodel framework and problem formulation. In Section 3, the first stage of the proposed multimodel approach is discussed, followed by the second and third stages in Sections 4 and 5, respectively. Simulation examples are provided in Section 6, to demonstrate the effectiveness of the proposed method. Finally, a brief conclusion is given in Section 7.
2. MULTIMODEL FRAMEWORK AND PROBLEM FORMULATION
Multimodel representation of complex nonlinear system generally involves interpolation of a number of submodels to form the global system (see Fig. 1). Considering a nonlinear system of the form
$$\eqalign{y\lpar k \rpar = \ & F\lpar {\,y\lpar {k - 1} \rpar \comma \ y\lpar {k - 2} \rpar \comma \;\ldots\comma\, y\lpar {k - na} \rpar\comma } \cr & {u\lpar {k - 1} \rpar \comma \ u\lpar {k - 2} \rpar \comma \ldots\comma\, u\lpar {k - nb} \rpar } \rpar\comma } $$
where u(k) and y(k) are the input and output of the system respectively at instant k. The integers nb and na are the time lag of the input and output, respectively. The multimodel representation of the system can be described by
$$y\lpar k \rpar = \mathop \sum \limits_{i = 1}^m \, f_i\lpar {x\lpar k \rpar } \rpar {\rm \phi}_i\lpar k \rpar\comma $$
where m is the number of submodels and f i (·) and φ i (k) are the ith submodel and its validity (weight), respectively. The validity describes the contribution of each submodel to the observed output and allows smooth transition between the local models when the system moves from one operating point to another. For easy interpretation, the validity satisfies the convexity property (Shorten et al., Reference Shorten, Murry-Smith, Bjorgan and Gollee1999; Orjuela et al., Reference Orjuela, Maquin and Ragot2006):
$$\mathop \sum \limits_{i = 1}^m {\rm \varphi}_i\lpar k \rpar = 1\comma \quad \forall k\semicolon $$
$$0 \le {\rm \varphi}_i\lpar k \rpar \le 1\comma \;\quad \forall k\comma \; \forall i \in 1\comma \ldots\comma\, M.\; $$
Given a set of input–output data, the multimodel identification problem is to estimate the number of submodels (m), the parameters of each submodel (f i (·)), and the validity (φ i ) for each submodel.
Fig. 1. Output blended multimodel identification structure.
Note that submodel f i (·) can be linear, nonlinear, or a combination of the two submodels. In this study, linear submodels are considered. Therefore, the function f i (x(k)) can be written as
$$f_i\lpar {x\lpar k \rpar } \rpar = x_i\lpar k \rpar {\rm \theta}_i^T \lpar k \rpar \comma $$
where θ i is the vector of parameters of ith the submodel, which can be estimated from the data pairs:
$$z\left( k \right) = \left\{ {x\left( k \right)\comma \; y\left( k \right):k = 1\comma \ldots\comma\,N} \right\}\comma $$
where
$$\eqalign{x\left( k \right) = \ & \left[ {y\left( {k - 1} \right)\comma\; y\left( {k - 2} \right)\comma \ldots\comma\, y\left( {k - na} \right)\comma} \right. \cr & \left. {u\left( {k - 1} \right)\comma\; u\left( {k - 2} \right)\comma \ldots\comma\, u\left( {k - nb} \right)} \right]} $$
is the regressor vector.
The multimodel identification of complex nonlinear systems from a finite set of input–output data is quite involving as the submodels identification is dependents on the data partition. In order to solve the aforementioned problem, a three-stage algorithm is proposed:
-
1. Obtaining the number of submodels and the initial submodel: This stage involves application of RCPSO to obtain m number of partitions and the representative data sets for each partition. The m number of clusters obtained from RCPSO is then used to estimate the initial submodels and initial cluster centers.
-
2. Obtain the final submodels: In this stage hybrid a K-means criterion is applied to the result of the previous stage to refine the submodels.
-
3. Interpolation of the submodels: Finally, the validity of each submodel is estimated to realize the multimodel output.
The details of these stages are provided in the subsequent sections.
3. STAGE 1: OBTAINING THE NUMBER OF SUBMODELS AND THE INITIAL PARTITION
The aim of this stage is to determine the number of partitions and to evolve a partition representing a possible grouping of the given data set. That is, given a data set Z = [z
1, z
2, … , z
N
] in
${{\rm \cal R}}^d$
, that is, N points each with d dimension (d = na + nb), we need to simultaneously find the number of partition (m) and divide Z into m exhaustive and mutually exclusive clusters C = [c
1, c
2, … , c
m
] with respect to a predefined criteria such that
-
1.
$c_1 \ne \emptyset\comma \ i = 1\comma \ldots\comma\, m\semicolon $
-
2.
$c_i \cap c_l = \emptyset\comma \ i = 1\comma \ldots\comma\, m\comma\ i \ne l\semicolon\; $
-
3.
$\mathop \cup \nolimits_{i = 1}^m \!c_i = Z$
.
To achieve this objective with partitional algorithm, a modification to combinatorial PSO (CPSO; Jarboui et al., Reference Jarboui, Cheikh, Siarry and Rebai2007) is proposed. The modification is necessary because the CPSO algorithm required the number of clusters to be fixed a prior. In what follows, particle swarm optimization, CPSO, and its modification for the determination of the initial submodels are described.
3.1. PSO
PSO (Kennedy & Eberhart, Reference Kennedy and Eberhart1995) is a metaheuristic search algorithm, mimicking the movement of organisms in a bird flock or fish school. Due to its simple concept and fast convergence, PSO has attracted much attention and wide applications in various fields, including systems identification problems (e.g., Modares et al., Reference Modares, Alfi and Fateh2010; Tang et al., Reference Tang, Qiao and Guan2010; Majhi & Panda, Reference Majhi and Panda2011; Cornoiu et al., Reference Cornoiu, Bara and Popescu2013; Hu et al., Reference Hu, Wang, Wang, Wang and Zhang2014; Zeng et al., Reference Zeng, Tan, Dong and Yang2014; Kramar et al., Reference Kramar, Cica, Sredanovic and Kopac2015). PSO combines self and social experience for directing search to an optimal solution. The position of individuals referred to as particles is influenced by its best position ever attained (called Pbest), the position of the best in the swarm (Gbest), and the current velocity V
i
that drives the particles. At each generation t, each particle i adjusts its velocity
$V_{ij}^t \; $
and position
$p_{ij}^t \; $
for each dimension j by referring to its personal best, Pbest, and the global best, Gbest. The following equations are used by the original PSO for velocity and particle updates:
$$V_{ij}^{t + 1} = {\rm \omega} V_{ij}^t + c_1r_1\lpar {{\rm Pbest}_{ij}^t - p_{ij}^t} \rpar + c_2r_2\lpar {{\rm Gbest}^t - p_{ij}^t} \rpar\comma $$
$$ p_{ij}^{t + 1} = xp_{ij}^t + V_{ij}^{t + 1}\comma $$
where
$$V_{ij}^t $
and
$p_{ij}^t $
are the jth element of the ith velocity and particle vector, respectively, at generation t;
$\hbox{Pbest}_{ij}^t $
is the personal best position of the ith particle and
$\hbox{Gbest}_{}^t \; $
is the global best during iterations 1 to t; ω is the inertia weight that controls the impact of the previous velocities on the current velocity; r
1 and r
2 are uniformly distributed random variables in range [0, 1]; and c
1 and c
2 are the acceleration constants.
3.2. CPSO-based partition
CPSO (Jarboui et al., Reference Jarboui, Cheikh, Siarry and Rebai2007) is an extension to the original PSO to be able to cope with the clustering problem. It has a similar procedure as the original PSO except that it differs in two characteristics: particle and velocity representation. In CPSO, particles P i are encoded with label-based representation, where P i = [p i1, p i2, … , p iN ] provides integer numbers representing the cluster's number of data points, such that p ij ∈ {1, 2, … , m}, where m is the number of clusters. The velocity of each particle uses a dummy variable that permits transition from combinatorial to continuous state and vice versa. Thus, the velocity and particle are updated through the following equations:
$$v_{ij}^{t + 1} = wv_{ij}^t + r_1c_1\lpar { - 1 - y_{ij}^t} \rpar + r_2c_2\lpar {1 - y_{ij}^t} \rpar\comma $$
where
$y_{ij}^t $
is a dummy variable defined by
$$y_{ij}^t = \left\{ \matrix{1 \hfill & {\rm if} \ p_{ij}^t = {\rm Gbest}_j^t \hfill \cr - 1 \hfill & {\rm if} \ p_{ij}^t = {\rm Pbest}_j^t \hfill \cr - 1\; {\rm or} \;1 \hfill & \hbox{randomly if} \ p_{ij}^t = {\rm Pbest}_j^t = {\rm Gbest}_j^t \hfill \cr 0 \hfill & {\rm otherwise}\hfill & \hfill \cr} \right. .$$
After velocity update, the position of each particle is updated through the dummy variable according to the following equations:
$$\lambda _{ij}^{t + 1} = y_{ij}^t + v_{ij}^{t + 1}\comma $$
$$y_{ij}^t = \left\{ {\matrix{ 1 \hfill & {\rm if}\; {\rm \lambda}_{ij}^t \; \gt \; {\rm \alpha} \hfill \cr - 1 \hfill & {\rm if}\; {\rm \lambda}_{ij}^t \lt - {\rm \alpha} \hfill \cr 0 \hfill & {\rm otherwise} \hfill \cr}} \right.\comma $$
$$p_{ij}^t = \left\{ {\matrix{ {\rm Gbest}_j^t\hfill &\hfill\!\!\!\!\!\!{\rm if}\; y_{ij}^t = 1 \hfill \cr {\rm Pbest}_{ij}^t\hfill & \hfill{\rm if}\; y_{ij}^t = - 1\comma \cr \hbox{randomly selected} & \!\!\!\!{\rm otherwise} \cr}} \right. $$
where α is a design parameter determined by the user.
3.3. RCPSO-based partition
This section introduces the RCPSO and how it is used to determine the number of partitions and the initial partition. As mentioned earlier, the CPSO algorithm is reinforced as, contrary to our case, the number of partitions in the algorithm is fixed a priori. In addition, the CPSO objective is not adequate for use in submodel identification, which is of paramount important. The following four new features distinguish RCPSO from CPSO:
-
1. Particles encoding: Similar to CPSO, RCPSO uses the label-based integer encoding to represent each particle. However, instead of assigning the same number of clusters to all particles, in RCPSO each particle evolve with its own number of clusters at each iteration. Each particle position P i = [p i1, p i2, … , p iN ], characterized by N elements, where N is the number of data points, provides integer numbers representing the cluster number of each data point, such that p ij ∈ {1, 2, … , m i } represents the cluster number of the jth data point in the ith particle and m i is the number of clusters associated with the ith particle. In addition, m i is assumed to lie in the range [m min, m max], where m min is 2 by default and m max is manually specified. The particle and velocity updates follow that of CPSO [Eqs. (9)–(13)].
-
2. Avoiding empty clusters: In the label-based representation, it is possible to generate a solution with an empty cluster if the number of its clusters is smaller than the largest cluster number associated with the particle solution. To avoid this, new positions of particles are checked. At each generation, particles with an empty cluster are corrected by changing the largest cluster number to the smallest unused cluster number.
-
3. Fitness function: The fitness criterion used in CPSO are the variance ratio criterion (VRC) and sum of square error of the cluster. The sum of square error is not appropriate when the number of clusters is not known in advance. This is because the maximum number of clusters will always be favored because its value will decrease as the number of cluster increases. In contrast, VRC has been used when the number of clusters is not known. However, in RCPSO, the use of a fitness function based on cluster regression error fused in minimum descriptive length reflects the peculiar nature of the problem at hand. Cluster regression error criterion guides toward a linear submodel in each cluster, while the minimum descriptive length discourage large number of clusters. Thus, unlike VRC, the peculiarity of the problem at hand resides in our objective to use a linear model for each cluster while minimizing the number of unknown clusters.
Given the data set Z defined in Eq. (6), the cluster regression error (CRE) is defined by
(14)where
$$\; {\rm CRE} = \mathop \sum \limits_{i - 1}^{m_{{\rm max}}^{\prime}} {\rm SE}\comma $$
(15)In Eqs. (14) and (15), m′max is the maximum number of clusters assigned to a solution, n i is the number of data points in the ith cluster, and θ i is the parameter of the linear model associated with the ith cluster. This can be obtained using the least square technique as follows:
$${\rm SE} = \sqrt {\left( {\displaystyle{1 \over {n_i}}\mathop \sum \nolimits_{\,j = 1}^{n_i} {\left( {y_j - x_j{\rm \theta}_i^T} \right) }^2} \right)}. \; $$
(16)Finally, the fitness function is defined by
$${\rm \theta} _i = \left[ {\; \mathop \sum \limits_{\,j = 1}^{n_i} x_jx_j^T} \right]^{ - 1}\left[ {\; \mathop \sum \limits_{\,j = 1}^{n_i} y_jx_j} \right]. $$
(17)where N is the total number of data points. The smaller the fitness value, the better the clustering solution.
$${\rm fitness} = \displaystyle{{m_{{\rm max}}^{\prime}\! \log \lpar N \rpar + N\log \lpar {{\rm CRE}^2} \rpar } \over 2}\comma $$
-
4. Avoiding small size data: A situation may occur where the number of data points assigned to a cluster is too small. On the one hand, if the number of data points n i is less than the dimension of the data, d = na + nb, then the model obtained from the cluster will be singular. On the other hand, if n i ≥ d but n i < td, where td signifies a reasonable minimum number of data points (i.e., 5% of data points), then the model obtained may not be well defined. In order to avoid these two situations, the SE in Eq. (15) is not calculated from the data when n i < 0.05N; instead, a penalty value is assigned to the SE to discourage having a small number of data points in a cluster. This penalty value can be an arbitrary value higher than the SE value for an acceptable number of data points. As such, a penalty value of 1000 has been chosen in all simulation examples.
After the encoding of the particles as discussed above, the execution of RCPSO to obtain the number of clusters and the initial partition is done according to the following steps:
-
Step 1. Initialize particle position vector X and associated velocity V in the population randomly. For each particle i, the number of clusters m i is randomly generated in the range [m min, m max], then each data point is randomly assigned to one cluster.
-
Step 2. Evaluate the fitness function for each particle using Eq. (17).
-
Step 3. Compare the fitness value of each particle with it previous best solution (Pbset) fitness and update Pbest with the current solution if it is better than the previous value (Pbest).
-
Step 4. Compare the fitness value with the overall previous best (Gbest) fitness. Update Gbest to the current solution if its fitness values is better than Gbest fitness value.
-
Step 5. Update positions and velocities of particles using Eqs. (9) to (13).
-
Step 6. Check for empty clusters in all particle solutions and correct if they exist.
-
Step 7. Repeat Step 2 to Step 6 until the maximum number of iterations is completed.
3.4. Estimation of the initial submodels
Given a set of cluster representatives
$$\tilde z = \left\{ {{\tilde z}_i = \left( {{\tilde x}_i\comma\,{\tilde y}_i} \right)\comma\; \quad i = 1\comma \ldots\comma\, m} \right\}\comma $$
from the RCPSO algorithm, where m is the number of clusters, the next task is to estimate the initial submodels. For this purpose, a least square estimation is applied to the data set in each cluster to find the initial submodel. The coefficients vector θ i for each submodel is computed through the formula
$$\tilde {\rm \theta} _i = (\tilde {\rm \phi} _i^T \!\tilde {\rm \phi} _i^T \} ^{ - 1}\; \tilde {\rm \phi} _i^T \tilde y_i\comma $$
where
$\tilde {\rm \phi} _i = \lsqb {{\tilde x}_i\lpar 1 \rpar\comma \ldots\comma\, {\tilde x}_i\lpar {n_i} \rpar} \rsqb ^T$
and
$\tilde y_i$
are the regression matrix and output vector belonging to the ith cluster, respectively and n
i
is the number data in the ith partition.
In addition, the centers of the data are calculated by finding the mean of the data in each cluster produced by the previous stage. The center of each cluster is given as
$$\tilde c_i = \displaystyle{1 \over {n_i}}\; \mathop \sum \limits_{\,j = 1}^{n_i} {\tilde{x}}_{ij}\quad i = 1\comma\ 2\comma\ldots\comma \; m.\; $$
4. STAGE 2: OBTAIN THE FINAL SUBMODELS
This stage involves a refinement to the submodels produced in the previous stage. In order to achieve this objective, a hybrid K-means criterion (Stanforth et al., Reference Stanforth, Kolossov, Mirkin, Brito, Cucumel, Bertrand and Carvalho2007) is adopted. Given a data set Z = [z
1, z
2, . . . . , z
N
] in
${{\rm \cal R}}^d$
, K-means algorithm group the data Z into k clusters such that an objective function is minimized. The K-means objective function is defined as the sum of the square error between each data point and the corresponding cluster center:
$$J_1\lpar c \rpar = \mathop \sum \limits_{i = 1}^m \mathop \sum \limits_{z_{\,j} \in u_i}^{} \lpar {z_j - c_i} \rpar ^2\comma$$
where z i and c i are the data point and cluster center, respectively. The objective function is minimized using an alternating optimization procedure. It starts with an arbitrary k centers and assigns each data point to the nearest center. The assignment of each data point is defined by a binary membership matrix U, such that
$$u_{ij} = \left\{ {\matrix{ 1 & {\rm if}\; {\lpar {z_j - c_i} \rpar }^2\le {\lpar {z_j - c_k} \rpar }^2\comma\quad i \ne k \hfill \cr 0 & {\rm otherwise} \hfill \cr}} \right. . $$
Each center is updated as the mean of all points assigned to it. These two steps are carried out iteratively until a predefined termination criterion is met, which occurs when with RCPSO there is no change in the objective function.
In the same spirit of K-mean algorithm, the following linear regression loss function can also be formulated:
$$J_2\lpar {\rm\theta} \rpar = \mathop \sum \limits_{i = 1}^m \mathop \sum \limits_{{\tilde x}_{\,j} \in u_i}^{} \lpar {y_j - {\tilde x}_j {\rm \theta}_j^T} \rpar ^2 . $$
Thus, instead of minimizing the cluster error objective function, a linear regression objective function is minimized. Combining the two objectives J 1 and J 2, the hybrid K-means objective can be written as
$$J\lpar {{\rm \theta}\comma\, c} \rpar = {\rm \lambda} \; J_1\lpar c \rpar + J_2\lpar {\rm \theta} \rpar\comma $$
where λ ∈ [0, 1] is a constant term to be defined by the user to specify a relative weight of the objective function. This formulation allows not only partitioning of the data set but also associating a submodel to each partition. In addition, the partitions formed are guided toward linear regions. This fits perfectly into the problem definition, as the aim of partitioning the input space is to form a linear submodel for each partition. Furthermore, the inclusion of J 1 will allow us to assign new data to a partition in a situation where the submodels need to be updated online.
The description of how this stage utilizes the hybrid K-means algorithm is shown in Figure 2. It begins with using the previously estimated cluster centers and associated model parameters as initialization of the algorithm. This eliminates the burden of the determination of the number of clusters, diminishes the effect of initialization, and increases the convergence rate of the K-means algorithm. Line 2 starts a loop that repeats itself for as long as there is a significant change in the objective function. It begins by determining the membership matrix U by Eq. (21), which assign each data point to a cluster. Line 4 estimates the parameter vector θ i and the center c i for each cluster. Next, from Lines 5 to 13, undefined clusters are detected and removed from subsequent updates. An undefined cluster is characterized by singular cluster, which may result when the size of the cluster falls below the number of regressors.
Fig. 2. Stage 2: estimating final submodels.
Lines 8 to 13 remove a cluster from the pool if the number of data points in the cluster is less than the number of regressors. In addition, the number of cluster is reduced by 1. The break statement in Line 12 ensure only one cluster is removed at each iteration when an undefined cluster is detected. This is to allows other undefined clusters, if they exist, to readjust during the next iteration and probably to circumvent undefined status. Line 15 computes the objective function J according to Eq. (23) while Line 16 increments the number of iteration. Next, the loop goes back to Line 3 to repeat the procedure.
Once the algorithm is completed, the final parameters θ of each submodel are obtained along with their associated centroid c i . The submodels are now ready for interpolation in the next stage to obtain the final global model that will represent the system under consideration.
5. STAGE 3: INTERPOLATION OF THE SUBMODELS
This is the final stage where the multimodel output is realized by combining the estimated final submodels obtained in the previous stage (Fig. 2). To achieve this, the validity of each submodel has to be estimated. In the literature, different realizations exist to combine the submodels along with their validity. In this study, a weighted sum of the output of the submodels is used to form the output of the multimodel, where the weight signifies the validity of each submodel.
Among many possible candidates for validity estimation, constrained Kalman filter (CKF) validity estimation is an effective technique introduced in our earlier work (Adeniran & Elferik, Reference Adeniran and Elferik2014). The CKF estimates the validity of each submodel at every time instant while satisfying the convexity property in Eqs. (3) and (4). The final output of the system in computed using Eq. (2). Detail description of the CKF algorithm can be found in Appendix A.
6. SIMULATIONS
The effectiveness of the proposed multimodel approach is demonstrated in this section. Four simulation examples were carried out. To illustrate flexibility of the proposed method on the number of parameters assumed for the submodels, two- and four-parameter submodel structures are examined. The two- and four-parameter submodel structures, subsequently refer to as two-parameter and four-parameter structures, respectively, are described by
$$y_i\lpar k \rpar = a_{i1}y\lpar {k - 1} \rpar + b_{i1} u\lpar {k - 1} \rpar\comma $$
$$\eqalign{y_{i\lpar k \rpar } = & a_{i1}y_i\lpar {k - 1} \rpar + a_{i2}y_i\lpar {k - 2} \rpar \cr & + b_{i1}u\lpar {k - 1} \rpar + b_{i2}u\lpar {k - 2} \rpar\comma }$$
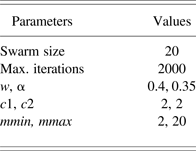
where a i1, a i2, b i1, b i2 are the ith submodel scalar parameters to be identified by Stage 1 and Stage 2. Unless it is stated otherwise, the parameter settings of RCPSO used are given in Table 1. Throughout the simulations, λ = 0.01 is used in Stage 2. In Stage 3, estimation of the validity using the CKF algorithm, setting W = P −1(k) and W = I, are both utilized, with the matrix P initialized as a diagonal matrix 100I. The validity of each submodel, ϕ, is initialized randomly while satisfying the convexity property. The obtained multimodel is evaluated based on the validation data using the mean square error (MSE) and variance accounted for (VAF) performance measures:
$$\hbox{MSE} = \displaystyle{1 \over N}\; \mathop \sum \limits_{i = 1}^N \; \lpar {y\lpar i \rpar - \tilde y\lpar i \rpar } \rpar\comma $$
$${\rm VAF} = \max \left( {100 \times \left( {1 - \displaystyle{{{\rm var}\lpar {y - \tilde y} \rpar } \over {{\rm var}\lpar y \rpar }}} \right)\comma\;0} \right)\comma $$
where y is the real system output and
$\hat y\; $
is the multimodel estimated output. All simulations are performed using MATLAB 2012b on a 2.4-GHz i3 64-bit Windows machine with 4 G of RAM.
Table 1. Reinforced combinatorial particle swarm optimization parameter settings
6.1. Example 1
In the first example, a discrete-time system from Elfelly et al. (Reference Elfelly, Dieulot, Benrejeb and Borne2010) is considered. The system is described by
$$\eqalign{y\left( k \right) & = a_1\left( k \right)y\left( {k - 1} \right) + a_2\left( k \right)y\left( {k - 2} \right) \cr & \quad + b_1\left( k \right)u\left( {k - 1} \right) + b_2u\left( {k - 2} \right).\; } $$
The variation laws of different parameters of the process is given by
$$\eqalign{a_1\lpar k \rpar &= 0.04\; \hbox{sin}\lpar {0.035k} \rpar + 0.8\comma \cr a_2\lpar k \rpar &= 0.005\; \hbox{sin}\lpar {0.03k} \rpar + 0.1\comma \cr b_1\lpar k \rpar &= 0.02\; \hbox{sin}\lpar {0.03k} \rpar + 0.5\comma \cr b_2\left( k \right) &= 0.01\; {\rm sin}\left( {0.035k} \right) + 0.2.}$$
The system was excited with uniform random signal u(k) on the range [−1, 1]. A total of 600 data points were generated for the two submodel structures above. The initial and final submodels obtained in Stage 1 and Stage 2 are shown in Table B.1 and Table B.2 in Appendix B, respectively. It can be observed from the tables that four and two submodels were identified in Stage 1 for two-parameter and four-parameter structures, respectively. The convergence paths of the objective function in the developed RCPSO are shown in Figure 3. Although the figures show faster convergence for four-parameter structures compared to two-parameter structures, this is not always the case. It is possible that the algorithm started with particle positions closer to the final solution in the four-parameter structures than the two-parameter structure because of random initialization of the particle positions. The convergence of the hybrid K-means in Stage 2 is shown in Figure 4. Faster convergence can also be noticed in the four-parameter structures than in the two-parameter structures.
Fig. 3. Reinforced combinatorial particle swarm optimization objective function convergence plot.
Fig. 4. Hybrid K-means objective function convergence plot.
In the validation stage, a different input signal [u(k) = 1 + sin(0.06k)] was injected into the real systems and the identified submodels. The submodels were interpolated with CKF validity estimation as described in Stage 3 to form the multimodel output. The real system's output and the multimodel output for the two submodels' structures are compared using the MSE and VAF. To evaluate the significance of the refinement in Stage 2, the multimodel output is estimated based on the initial and final submodels obtained in Stage 1 and Stage 2, respectively.
The multimodel identification results are shown in Tables 2 and 3 for the combined final submodels and initial submodels, respectively. It can be observed that the performance of the proposed algorithm is better when all the final submodels are combined, and can well approximate the real system either with two-parameter or four-parameter structure using both CKF settings. However, the two-parameter structure shows better performance than the four-parameter structure. In addition, the CKF with settings W = I has slightly better performance values in the two-parameter submodel structure. Furthermore, it can be pointed out that fewer parameters (8) have been achieved in comparison to the multimodel approach adopted in Elfelly et al. (Reference Elfelly, Dieulot, Benrejeb and Borne2010; 12 parameters). Figures 5 and 6 show the comparison between the real system output and the multimodel output for the three-stage algorithm.
Fig. 5. Multimodel identification outputs using validation data.
Fig. 6. Multimodel identification error using validation data.
Table 2. Performance of proposed multimodel based on the initial submodels
Table 3. Performance of proposed multimodel based on final submodels
6.2. Example 2
A nonlinear dynamical system taken from Orjuela et al. (Reference Orjuela, Marx, Ragot and Maquin2013) is considered for multimodel identification:
$$y\lpar {k + 1} \rpar = \lpar {0.6 - 0.1 a\lpar k \rpar } \rpar y\lpar k \rpar + a\lpar k \rpar u\lpar k \rpar\comma $$
$$ a\lpar k \rpar = \displaystyle{{6 - 0.006y\lpar k \rpar } \over {1 + 0.2y\lpar k \rpar }}\comma $$
The identification was carried out using the proposed approach with a data set of 600 samples of uniform random signal within the range of [−0.9,0.9]. Tables B.3 and B.4 in Appendix B show the initial and final submodels parameters with their associated centers.
The proposed multimodel approach identified two submodels for both two-parameter and four-parameter structures. Figures 7 and 8 show the convergence of the objective function in Stages 1 and 2, respective.
Fig. 7. Reinforced combinatorial particle swarm optimization objective function convergence plot.
Fig. 8. Hybrid K-means objective function convergence plot.
To verify the accuracy of the proposed approach, the output of the nonlinear system was compared with the output of the proposed multimodel approach using the validation data under the following input:
$$u\lpar k \rpar = \sin \left( {\displaystyle{{2{\rm \pi}} \over {25}}k} \right).$$
Figures 9 and 10 show the output of the multimodel approach and the error obtained, respectively, when the final submodels are combined during the validation, while Table 4 shows their performance measure. It can be observed that both submodels' structures can approximate the real system. In addition, both CKF settings show the same performance. Table 5 shows the performance of the proposed technique using the initial submodels (without Stage 2). Although the significance of Stage 2 seems not pronounced in this example, its inclusion does provide slightly better performance as seen in Table 4.
Fig. 9. Multimodel identification outputs using validation data.
Fig. 10. Multimodel identification error using validation data.
Table 4. Performance of proposed multimodel based on final submodels
Table 5. Performance of proposed multimodel based on initial submodels
6.3. Example 3
In the third example, the following highly nonlinear dynamical system is considered for identification:
$$\eqalign{y\lpar {k + 1} \rpar =& \displaystyle{{u\lpar k \rpar } \over {1 + y^2\lpar {k - 1} \rpar + y^2\lpar {k - 2} \rpar }} \cr & + \displaystyle{{y\lpar k \rpar y\lpar {k - 1} \rpar y\lpar {k - 2} \rpar u\lpar {k - 1} \rpar \lpar {y\lpar {k - 2} \rpar - 1} \rpar } \over {1 + y^2\lpar {k - 1} \rpar + y^2\lpar {k - 2} \rpar }}.}$$
It is a benchmark system proposed in (Narendra & Parthasarathy, Reference Narendra and Parthasarathy1990) and subsequently has been used in (Chen & Khalil, Reference Chen and Khalil1995; Verdult et al., Reference Verdult, Ljung and Verhaegen2002; Wen et al., Reference Wen, Wang, Jin and Ma2007; Orjuela et al., Reference Orjuela, Marx, Ragot and Maquin2013). The system was excited by uniformly distributed random signal in the interval [−1, 1]. The identification was carried out with a data set of 800 samples.
Using the proposed multimodel approach, four and two submodels were identified for two-parameter and four-parameter structures, respectively. The convergence of the objective functions in Stages 1 and 2 for both structures are shown in Figures 11 and 12, respectively. The initial and final submodel parameters with their associated centers for the two stages are shown in Tables B.5 and B.6 in Appendix B.
Fig. 11. Reinforced combinatorial particle swarm optimization objective function convergence plot.
Fig. 12. Hybrid K-means objective function convergence plot.
Validation of the multimodel identification was done with a second data set of 800 samples generated by an input signal given by
$$u\lpar k \rpar = \left\{ {\matrix{ \sin \left( {\displaystyle{{2{\rm \pi}} \over {250}}k} \right)\hfill &{\rm if}\; k \le 500 \hfill \cr 0.8\; \sin \left( {\displaystyle{{2{\rm \pi}} \over {250}}k} \right) + 0.2\; \sin \left( {\displaystyle{{2{\rm \pi}} \over {25}}k} \right) & {\rm if}\; k \gt 500 \hfill \cr}} \right.\;.$$
Simulation results obtained from Figures 13 and 14 show that the model outputs closely agree with the system output for both submodels' structures when the final submodels were combined. In addition, it can be concluded from Table 6 that the two-parameter structure with CKF setting W = I shows the best performance. Furthermore, a slightly degraded performance can be observed in Table 7 that shows the results obtained when the initial submodels were combined instead of the final submodels.
Fig. 13. Outputs of multimodel identification using validation data.
Fig. 14. Multimodel identification error using validation data.
Table 6. Performance of proposed multimodel based on final submodels
Table 7. Performance of proposed multimodel based on initial submodels
As mentioned earlier, this system has been identified with other multimodel approaches in the literature. Using the same validation data set, Verdult et al. (Reference Verdult, Ljung and Verhaegen2002) achieved MSE of 0.0002 and VAF of 99.9% with four third-order models (24 parameters), Wen et al. (Reference Wen, Wang, Jin and Ma2007) achieved MSE of 0.112 and VAF of 97.9% with 10 BPWA functions (306 parameters), and Orjuela et al. (Reference Orjuela, Marx, Ragot and Maquin2013) achieved MSE of 0.00067 and VAF of 99.7% with 16 parameters. It is quite noteworthy to point out that the proposed multimodel approach does yield close performances to other techniques in the literature but with fewer parameters (8).
6.4. Example 4
In this example, a benchmark continuous stirred tank reactor nonlinear chemical system is considered. The system is described by the following equation in which all variables are dimensionless (Galan et al., Reference Galan, Romagnoli, Palazoǧlu and Arkun2003; Du et al., Reference Du, Song and Li2009):
$$\eqalign{{\dot x}_1 &= - x_1 + D_a \lpar {1 - x_1} \rpar \exp \left( \displaystyle{x_2 \over 1 + \displaystyle{x_2 \over {\rm \gamma}}} \right)\comma \cr {\dot x}_2 &= - x_2 + BD_a \lpar {1 - x_1} \rpar \exp \left( \displaystyle{x_2 \over 1 + \displaystyle{x_2 \over \gamma}} \right) + {\rm \beta} \lpar {u - x_2} \rpar\comma \cr y &= x_2\comma}$$
where x 1 is the reagent conversion, x 2 is the reactor temperature, and u is the coolant temperature. In addition, u and x 2 are the input and output of the system, respectively. The nominal values for the constants are D a = 0.072, γ = 20, B = 8, and β = 0.3.
To test the ability of the proposed multimodel identification method, a random white noise step signal between [−1.51.5] is used as input to the system. The system is simulated with a sampling time of 0.2 min, and 700 pairs of input–output data were collected for the identification process and another 300 pairs for validation.
Based on the proposed method, four and three submodels were identified for the two-parameter and four-parameter structures, respectively. The initial and final submodel parameters with their associated centers are shown in Appendix B (Tables B.7 and B.8). However, the roots of the poles (a parameters) of the identified final submodels show that submodels 3 and 1 are unstable for two-parameter and four-parameter structures, respectively. The convergence of the objective functions in Stages 1 and 2 are shown in Figures 15 and 16, respectively.
Fig. 15. Reinforced combinatorial particle swarm optimization objective function convergence plot.
Fig. 16. Hybrid K-means objective function convergence plot.
The validation results using the second data pairs are shown in Figures 17 and 18 and Table 8 for both structures. It can be observed that the estimated output matched the real output.
Fig. 17. Outputs of multimodel identification using validation data.
Contrary to the notion that all the submodels must be stable for a decoupled multimodel to be stable (Orjuela, Reference Orjuela, Marx, Ragot and Maquin2007), it can be observed from Figure 17 that the multimodel output is stable. This is because the validity estimated by the CKF algorithm is able to filter out the unstable submodel during the blending operation. Figure 19 shows the validity values of the submodels for the four-parameter structure. It can be observed that the validity of submodel 1 is zero at instant 25. It shows that the identified decoupled multimodel acts like a Takagi–Sugeno multiple model where its stability depends not only on the stability of the submodels but also on the validity values. However, further study on this issue would be necessary to the conditions for this behavior. Furthermore, comparison of the results in Tables 8 and 9 indicates that significant improvement was obtained when the final submodels were blended together. This emphasized the significance of including Stage 2 into the methodology to refine the initial submodels for better approximation.
Fig. 18. Multimodel identification error using validation data.
Fig. 19. Validity of four-parameter structure with constrained Kalman filter setting W = P− 1(k).
Table 8. Performance of proposed multimodel based on final submodels
Table 9. Performance of proposed multimodel based on initial submodels
7. CONCLUSION
This paper presents a novel multimodel approach for the identification of nonlinear systems having several possible models depending on the operating region. In the proposed approach, the number of the submodels are not known a priori. The proposed method consists of three stages. In the first stage, a reinforced combinatorial particle swarm optimization was developed to obtain the number of submodels and initial estimate of their parameters. In the second stage, hybrid K-means is used to refine the submodels in the first stage. The submodels are interpolated using a constrained Kalman filter in the third stage. Four simulated nonlinear systems examples that had been studied previously in the literature are presented to illustrate the performance of the method. The examples show that the proposed multimodel approach is effective in the identification of nonlinear systems. Although the proposed algorithm is designed for single-input/single-output systems, an extension to multiple-input/multiple-output systems should be easy by using a multiple-input/single-output formulation. Contrary to the notion that all the submodels must be stable for a decoupled multimodel to be stable, the CKF algorithm for the interpolation is shown to be able to produce a stable system when one of the submodels is unstable. In future research, we would like to further study the conditions necessary for the occurrence of this behavior and develop a control algorithm based on the identified submodels with the CKF algorithm.
ACKNOWLEDGMENTS
The authors acknowledge the support of King Fahd University of Petroleum and Minerals under Project IN141048.
Ahmed A. Adeniran received his BS degree (with honors) in electrical and electronics engineering and his MS degree in computer science from the University of Ibadan. He also received MS and PhD degrees in systems engineering (control option) from King Fahd University of Petroleum and Minerals. Dr. Adeniran's research interests include dynamic system identification and control, fault diagnosis, and artificial intelligence, focusing on the development of data mining and machine learning methods for a variety of tasks and their applications to practical problems in science and engineering.
Sami El Ferik is an Associate Professor in control and instrumentation in the Department of Systems Engineering at King Fahd University of Petroleum and Minerals. He obtained his BS in electrical engineering from Laval University, Quebec, and his MS and PhD both in electrical and computer engineering from Ecole Polytechnique, University of Montreal. Dr. El Ferik's PhD work on flexible manufacturing systems modeling and control was cosupervised with mechanical engineering. After completion of his PhD and postdoctoral positions, he worked with Pratt and Whitney Canada as a Staff Control Analyst at the Research and Development Center of Systems, Controls, and Accessories. His research interests are in sensing, monitoring, and control with strong multidisciplinary research and applications. His research contributions are in control of drug administration, process control and control loop performance monitoring, control of systems with delays, modeling and control of stochastic systems, analysis of network stability, condition monitoring, and conditions.
APPENDIX A The CKF algorithm for validity estimation
The CKF algorithm considered the multimodel representation in Eq. (2) as a parameter estimation problem as follows:
Given the multimodel output in Eq. (2), that is,
$$\; y\lpar k \rpar = \mathop \sum \limits_{i = 1}^M \ f_i \lpar {{\rm \varphi}_i\lpar k \rpar \comma\ {\rm \theta}_i} \rpar {\rm \phi} _i\lpar k \rpar. $$
the vector form, Eq. (2), can be written as
$$\; y\lpar k \rpar = \tilde y\lpar k \rpar {\rm \Phi} \lpar k \rpar\comma$$
where
$\tilde y\lpar k \rpar = \lsqb {y_1\comma\, y_2\comma \ldots\comma\, y_M} \rsqb $
is the known vector of local model outputs and Φ(k) = [ϕ1, ϕ2, . . . , ϕ
M
]
T
is the unknown vector of weights for the local models.
Casting the parameter estimation to a state estimation problem, we have the following state equation:
$$\; \matrix{ {{\rm \Phi} \lpar {k + 1} \rpar = {\rm \Phi} \lpar k \rpar\comma} \hfill \cr\qquad {y\lpar k \rpar = \tilde y\lpar k \rpar {\rm \Phi} \lpar k \rpar + {\rm \upsilon} \lpar k \rpar\comma}}$$
where Φ is the vector of unknown parameter (validity) to be estimated, and v(k) is the measurement noise with covariance
E
[υ(k)v(k)
T
] = R(k). In the case where υ(k) is a white and Gaussian, the Kalman filter theory says that the posterior distribution of ϕ(k), given all the observation up to k − 1, is Gaussian mean value
$\hat {\rm \phi} \lpar k \rpar $
and error covariance matrix P. One should note that an artificial noise w(k) with variance
E
[w(k)w
T
(k)] = Q could be added to Φ(k + 1) in the case of time-varying parameters and also to ensure persistence excitation and avoid ill conditioned numerical computation.
Furthermore, in order for the validity computation (Φ) to satisfy the partition of unity, the equality constraint in Eq. (3) needs to be added. In addition, as at any time instant it is possible for any local model to fully contribute or not to contribute to the system's output, there is a need to impose an inequality constraint [Eq. (4)]. Therefore, these two constraints need to be included in the estimation of (Φ) to give the following full state estimation equation:
$$\; \matrix{ {{\rm \Phi} \lpar {k + 1} \rpar = {\rm \Phi} \lpar k \rpar + {\rm \omega} \lpar k \rpar\comma} \hfill \cr\qquad {y\lpar k \rpar = {\tilde{y}} \lpar k \rpar {\rm \Phi} \lpar k \rpar + {\rm \upsilon} \lpar k \rpar\comma}}$$
such that
$$\; \matrix{ {{\rm \beta \Phi} \lpar k \rpar = 1}\comma \hfill \quad {0\, \le\, {\rm \phi} _i\lpar k \rpar \le 1}\comma}$$
where β is a row vector of [1, 1, … , 1, 1]. The problem is thus formulated as the following: given state Eq. (A.3a), minimize the minimum mean square error estimate of the state Φ(k) [Eq. (A.4)] subject to constraints in Eq. (A.3b).
$$\; \mathop {\min} \limits_{\rm \Phi} {\bi E}\lsqb {{\lpar {{\rm \Phi} \lpar {k} \rpar - \hat{\rm \Phi} \lpar k \rpar } \rpar }^2} \rsqb\comma$$
where
E
[.] is the expectation operation, β is a row vector of [1, 1, … , 1, 1], Φ is the unknown parameter, and
$\hat{\rm \Phi}$
is the estimated one.
The above problems are solved in two steps. In the first step, the equality constraint is solved using the projection techniques (Simon & Chia, Reference Simon and Chia2002; Simon, Reference Simon2006), where the unconstrained estimate
$\hat{\rm \Phi} \lpar k \rpar $
is projected onto the constraint space. The equality constrained optimization problem can be written as
$$\; \mathop {\min} \limits_{\rm \Phi} {\bi E}\lsqb {{\lpar {{\rm \Phi} \lpar {k} \rpar - \hat{\rm \Phi} \lpar {k} \rpar } \rpar }^{T}W\lpar {{\rm \Phi} \lpar {k} \rpar - \hat{\rm \Phi} \lpar k \rpar } \rpar } \rsqb$$
subject to
$$\; {\rm \beta \Phi} \lpar k \rpar = 1\comma$$
where W is a positive define matrix. The solution to this problem is given as
\eqalign{\hat{\rm \Phi}^{\ast}\lpar k \rpar &= \hat{\rm \Phi} \lpar k \rpar + K^{\ast}\lpar k \rpar \; \lsqb 1 - {\rm \beta} \hat{\rm \Phi} \lpar k \rpar \rsqb \comma \cr K^{\ast}\lpar k \rpar &= W^{ - 1}\; {\rm \beta} ^T \lsqb R + {\rm \beta} W^{ - 1}{\rm \beta}^T \rsqb ^{ - 1} \comma \cr P^{\ast}\lpar k \rpar &= \lsqb I - K^{\ast}\lpar k \rpar {\rm \beta} \rsqb W^{ - 1} + Q \comma}$$
where
$\hat{\rm \Phi} $
is the unconstrained estimate,
$\hat{\rm \Phi} ^{\ast} $
is the updated equality constrained estimate that satisfy Eq. (3), and W is a positive definite matrix weight. Setting W = P−
1(k) in Eq. (A.7) results in minimum variance estimate, and setting W = I gives least square estimate of Φ(k) (Simon, Reference Simon2010). Both settings are implemented in this study. This implies that the unconstrained problem is first solved with the standard solution of the Kalman filter after which the obtained unconstrained estimate
$\hat{\rm \Phi} $
is used to update the constrained estimate in Eq. (A.7). Given observations y(k), y(k − 1), … , y(1) and local model outputs
$\tilde y\lpar k \rpar\comma\,\tilde y\lpar {k - 1} \rpar\comma \ldots\comma\, \tilde y\lpar 1 \rpar\comma $
the optimal unconstrained estimate
$\hat{\rm \Phi} $
can be computed using the following Kalman filter equation
$$\eqalign{\hat{\rm \Phi} ^ - \lpar k \rpar &= \hat{\rm \Phi} \lpar {k - 1} \rpar\comma \cr P^{ - \lpar k \rpar } &= P\lpar {k - 1} \rpar + Q \lpar {k - 1} \rpar \cr \hat{\rm \Phi} \lpar k \rpar &= \hat{\rm \Phi} ^ - \lpar k \rpar + K\lpar k \rpar \lsqb {y\lpar k \rpar - \tilde y\lpar k \rpar {\hat{\rm \Phi}}^ - \lpar k \rpar } \rsqb\comma \cr K\lpar k \rpar &= P^ - \lpar k \rpar \tilde y\lpar k \rpar ^T\lsqb {\tilde y\lpar k \rpar P^ - \lpar k \rpar \tilde y{\lpar k \rpar }^T\lpar k \rpar + R\lpar k \rpar } \rsqb ^{ - 1}\comma \cr P\lpar k \rpar &= \lsqb {I - K\lpar k \rpar \tilde y\lpar k \rpar } \rsqb P^ - \lpar k \rpar\comma }$$
where
$P^ - \lpar k \rpar\comma\, \hat{\rm \Phi} ^ - \lpar k \rpar \; $
are the a priori estimate of the error covariance and the validity estimate, respectively;
$P\lpar k \rpar\comma\, \hat{\rm \Phi} \lpar k \rpar \; $
are the a posteriori estimate of the error covariance and the validity estimate respectively; and K(k) is the Kalman gain.
In the second step truncation and normalization (Nihan & Davis, Reference Nihan and Davis1987) are adopted for the inequality constraints. The truncation is used to readjust each element of
$\hat{\rm \Phi} ^{\ast}\lpar k \rpar \; $
in order not to violate the inequality constraint in Eq. (A.4) as follows:
$$\; {\rm \; \hat \Phi} _i^{\ast\ast} \lpar k \rpar = 0\comma \;\; {\rm if}\; \hat{\rm \Phi} ^{\ast}\lpar k \rpar \lt 0.$$
Finally,
$\hat{\rm \Phi} _i^{\ast\ast} \lpar k \rpar \; $
is normalized since the truncation can violate the equality constraint in Eq. (3) and to satisfy the other part of the inequality constraint.
$$\; \hat{\rm \Phi }_i^{\ast\ast\ast} \left( k \right) = \displaystyle{{\hat{\rm \Phi }_i^{\ast\ast} \left( k \right)} \over {\mathop \sum \nolimits_{i = 1}^{} \hat{\rm \Phi }_i^{\ast\ast} \left( k \right)}}\comma$$
where
$ \hat{\rm \Phi} _i^{\ast\ast\ast} \lpar k \rpar = \lsqb {\hat {\rm \phi}_1^{\ast\ast\ast} \lpar k \rpar\comma\, \hat {\rm \phi}_2^{\ast\ast\ast} \lpar k \rpar\comma \ldots\comma\, \hat {\rm \phi}_M^{\ast\ast\ast} \lpar k \rpar } \rsqb ^T$
is the final estimated validity computation at instant k. Note that the
$\hat{\rm \Phi} _i^{\ast\ast\ast} \lpar k \rpar $
and P*(k) are now the new a posteriori estimate of the error covariance and the validity estimate respectively at instant k. The summary of the CKF algorithm is shown in Figure A.1.
Fig. A.1. Stage 3: CFK for validity estimation.
One important feature of the proposed CKF algorithm is the intrinsic ability to handle modeling error and measure noise through the covariance matrices Q and R. In the context of this work, the covariance R represents the measurements noise and the noise resulting from model mismatch (R = σ r + σ b ). The measurement noise σ r can be estimated by taken the variance of the output noise while the model mismatch σ b can be estimated from the error obtained from the submodels.
In contrast, the covariance matrix Q is considered as the parameter that incorporate only the noise resulting from model mismatch Q ≡ σ b . Because the submodels were estimated from the least square criterion, the model mismatch noise σ b can be estimated from data by computing the empirical covariance from the classical result in least square theory (Ljung, Reference Ljung1999) for each submodel:
$${\rm \sigma} _{bi} = \left \Vert {\displaystyle{1 \over {n_i - ({d + 1})}} \mathop \sum \limits_{\,j = 1}^{n_i} \,(y_{ij} - {\hat y}_{ij}) \mathop \sum \limits_{\,j = 1}^{n_i} \,[{\rm \varphi} _{ij}\, {\rm \varphi} _{ij}^T ]^{\wedge} \left\{{- 1} \right\}} \right\Vert\comma$$
where φ
i
are the vectors of the regressors for ith submodel, and n
i
is the number of data points used for estimating the ith submodel. In addition, d is the number of parameters, and y
i
and
$\widehat{{y_i}}\; $
are the actual and predicted output, respectively, for ith submodel. Hence, Q (a diagonal matrix) and R are computed as
$$\; {\bi Q} = {\bi \;} \left[ {\matrix{ {{\bf \sigma}_{{\bi bi}}} & \cdots & 0 \cr \vdots & \ddots & \vdots \cr 0 & \cdots & {{\bf \sigma}_{{\bi bm}}} \cr}} \right]\comma$$
$${\bi R} = {\bi \; }{\bf \sigma }_{\bi r} + \Vert{\bi Q}\Vert.$$
APPENDIX B Submodel coefficients and centers
Table B.1. Initial submodels for Example 1
Table B.2. Final submodels for Example 1
Table B.3. Initial submodels for Example 2
Table B.4. Final submodels for Example 2
Table B.5. Initial submodels for Example 3
Table B.6. Final submodels for Example 3
Table B.7. Initial submodels for Example 4
Table B.8. Final submodels for Example 4
Table B.9. Convergence time
