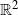1. Introduction
1.1. Model
We use the following framework that is essentially the same as that used in [Reference Biermé, Estrade and Kaj4], [Reference Breton and Dombry5], and [Reference Kaj, Leskelä, Norros and Schmidt18]. Let B(x,u) denote the two-dimensional rectangular box in
![]() $\mathbb{R}^2$
with centre at x and edge lengths
$\mathbb{R}^2$
with centre at x and edge lengths
![]() $u_i$
for
$u_i$
for
![]() $i=1,2$
. We consider a family of rectangles
$i=1,2$
. We consider a family of rectangles
![]() $\smash{(B({X}^{(j)},U^{(j)}))_j}$
in
$\smash{(B({X}^{(j)},U^{(j)}))_j}$
in
![]() $\mathbb{R}^2$
(also referred to as boxes) which are generated by a Poisson point process
$\mathbb{R}^2$
(also referred to as boxes) which are generated by a Poisson point process
![]() $\smash{(X^{(j)},U^{(j)})_j}$
in
$\smash{(X^{(j)},U^{(j)})_j}$
in
![]() $\mathbb{R}^2 \times \mathbb{R}_+^2$
. Let N be a Poisson random measure with intensity measure given by
$\mathbb{R}^2 \times \mathbb{R}_+^2$
. Let N be a Poisson random measure with intensity measure given by
![]() $n(\mathrm{d} x, \mathrm{d}
u) = \lambda \mathrm{d} x F(\mathrm{d} u)$
, where the intensity
$n(\mathrm{d} x, \mathrm{d}
u) = \lambda \mathrm{d} x F(\mathrm{d} u)$
, where the intensity
![]() $\lambda$
is a positive constant. The probability measure F on
$\lambda$
is a positive constant. The probability measure F on
![]() $\mathbb{R}_+^2$
is given by
$\mathbb{R}_+^2$
is given by
where
![]() $c_F>0$
is the normalising constant and
$c_F>0$
is the normalising constant and
![]() $f_i(u_i) \sim
\smash{{1}/{u_i^{\gamma_i+1}}}$
as
$f_i(u_i) \sim
\smash{{1}/{u_i^{\gamma_i+1}}}$
as
![]() $u_i \to \infty$
for
$u_i \to \infty$
for
![]() $i=1,2$
with
$i=1,2$
with
![]() $\gamma_i > 1$
. We assume for the sake of convenience that we have
$\gamma_i > 1$
. We assume for the sake of convenience that we have
![]() $c_F=1$
(because one could simply think that
$c_F=1$
(because one could simply think that
![]() $c_F$
is included in
$c_F$
is included in
![]() $\lambda$
in the case of
$\lambda$
in the case of
![]() $c_F \neq 1$
) and we write
$c_F \neq 1$
) and we write
![]() $f(y) \sim g(y)$
if
$f(y) \sim g(y)$
if
![]() ${f(y)}/{g(y)} \to 1$
. Note that, for
${f(y)}/{g(y)} \to 1$
. Note that, for
![]() $i=1,2$
,
$i=1,2$
,
i.e. the expected length and the expected width (and thus area) of a box are finite.
We discuss random fields defined on certain spaces of signed measures. Let us denote by
![]() $\mathcal{M}_2$
the linear space of signed measures
$\mathcal{M}_2$
the linear space of signed measures
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}^2$
with finite total variation
$\mathbb{R}^2$
with finite total variation
![]() $\Vert \mu \Vert\,:\!=
\vert \mu \vert (\mathbb{R}^2) < \infty$
, where
$\Vert \mu \Vert\,:\!=
\vert \mu \vert (\mathbb{R}^2) < \infty$
, where
![]() $\vert \mu \vert$
is the total variation measure of
$\vert \mu \vert$
is the total variation measure of
![]() $\mu$
(see, e.g. [Reference Rudin26, p. 116]). We are interested in the cumulative volume induced by the boxes and measured by
$\mu$
(see, e.g. [Reference Rudin26, p. 116]). We are interested in the cumulative volume induced by the boxes and measured by
![]() $\mu \in \mathcal{M}_2$
. Therefore, we define the random field
$\mu \in \mathcal{M}_2$
. Therefore, we define the random field
![]() $J\,:\!= (J(\mu))_{\mu}$
on
$J\,:\!= (J(\mu))_{\mu}$
on
![]() $\mathcal{M}_2$
by
$\mathcal{M}_2$
by
Since our purpose is to deal with centred random fields, we introduce the notation for the corresponding centred Poisson random measure
![]() $\smash{\widetilde{N}}\,:\!= N-n$
and centred integral
$\smash{\widetilde{N}}\,:\!= N-n$
and centred integral
![]() $\smash{\skew5\widetilde{J}(\mu)}\,:\!= J(\mu)-\mathbb{E} J(\mu)$
.
$\smash{\skew5\widetilde{J}(\mu)}\,:\!= J(\mu)-\mathbb{E} J(\mu)$
.
The goal of this paper is to obtain scaling limits for the random field
![]() $\,{\skew5\widetilde{J}}$
. By scaling, we mean that the length and the width of the boxes are shrinking to zero, i.e. the scaled edge lengths are
$\,{\skew5\widetilde{J}}$
. By scaling, we mean that the length and the width of the boxes are shrinking to zero, i.e. the scaled edge lengths are
![]() $\rho u_i$
with scaling parameter
$\rho u_i$
with scaling parameter
![]() $\rho \to 0$
, and that the expected number of boxes is increasing, i.e. the intensity
$\rho \to 0$
, and that the expected number of boxes is increasing, i.e. the intensity
![]() $\lambda$
of the Poisson point process is tending to infinity as a function of
$\lambda$
of the Poisson point process is tending to infinity as a function of
![]() $\rho$
. The precise behaviour of
$\rho$
. The precise behaviour of
![]() $\lambda=\lambda(\rho) \to \infty$
is specified in the different scaling regimes below. Following the notational convention from above, we denote by
$\lambda=\lambda(\rho) \to \infty$
is specified in the different scaling regimes below. Following the notational convention from above, we denote by
![]() $\,{\skew5\widetilde{J}}_\rho$
the centred random field corresponding to the Poisson random measure
$\,{\skew5\widetilde{J}}_\rho$
the centred random field corresponding to the Poisson random measure
![]() $N_\rho$
with the modified intensity
$N_\rho$
with the modified intensity
![]() $\lambda_\rho :\!= \lambda(\rho)$
and scaled edge lengths, i.e.
$\lambda_\rho :\!= \lambda(\rho)$
and scaled edge lengths, i.e.
![]() $F_\rho$
is the image measure of F by the change
$F_\rho$
is the image measure of F by the change
![]() $u
\mapsto \rho u$
.
$u
\mapsto \rho u$
.
We mention that random germ–grain models have received significant attention in the literature (cf. [Reference Biermé, Durieu and Wang3]–[Reference Breton, Clarenne and Gobard8], [Reference Gobard14], [Reference Kaj, Leskelä, Norros and Schmidt18], [Reference Lifshits23], and [Reference Pilipauskaitė and Surgailis25]). In a nutshell, our paper extends the work from Biermé et al. [Reference Biermé, Estrade and Kaj4] and Kaj et al. [Reference Kaj, Leskelä, Norros and Schmidt18] to a random boxes model where the size of a grain depends on two differently heavy-tailed-distributed random variables instead of just one random variable for the volume of the grain. To be more precise, the shape of the grains is rectangular with a random length and a random width (mutually independent). Therefore, our model differs from those in that the volume is given by the product of the length and the width, and each box simultaneously gets a random length-to-width ratio. As a consequence, the main novelty of this work is that our random boxes model leads to a greater number of scaling regimes than other random balls models (e.g. [Reference Biermé, Estrade and Kaj4], [Reference Breton and Dombry5], and [Reference Kaj, Leskelä, Norros and Schmidt18]). In particular, the so-called Poisson-lines scaling regime with its distinctive graphical representation has not arisen so far (see Section 2.3.2). The class of limiting random fields contains linear random fields that are Gaussian, compensated Poisson integrals, and integrals with respect to a stable random measure.
Next, we want to say a few words about the applications of random balls models. The motivation comes from telecommunication networks models. A list of some references can be found at the beginning of Chapter 3 of [Reference Lifshits23]. In dimension
![]() $d=1$
, the model applies to the random variation in packet network traffic, where the traffic is generated by independent sources over time. The quantity of interest is the limiting distribution of the aggregated traffic as the time and the number of sources both tend to infinity (possibly with different rates). These different rates can result in different scaling regimes of the superposed network traffic. In some papers, the ‘traffic’ additionally has a weight, which can be interpreted as the amount of required resources, the transmission power, or the file sizes (see, e.g. [Reference Breton and Dombry5], [Reference Fasen12], [Reference Kaj and Taqqu17], and [Reference Lifshits23]). Our model can be interpreted in the same way, when the length of the rectangle is thought to be the transmission time and the width a weight representing, e.g. a transmission rate. Alternatively, our random rectangles model could model a simplified two-dimensional wireless network. Imagine that there are spatially uniformly distributed stations which are equipped with emitters. In our case, the range for transmission (with constant power) of each station is given by a rectangular area and the total power of emission is measured by
$d=1$
, the model applies to the random variation in packet network traffic, where the traffic is generated by independent sources over time. The quantity of interest is the limiting distribution of the aggregated traffic as the time and the number of sources both tend to infinity (possibly with different rates). These different rates can result in different scaling regimes of the superposed network traffic. In some papers, the ‘traffic’ additionally has a weight, which can be interpreted as the amount of required resources, the transmission power, or the file sizes (see, e.g. [Reference Breton and Dombry5], [Reference Fasen12], [Reference Kaj and Taqqu17], and [Reference Lifshits23]). Our model can be interpreted in the same way, when the length of the rectangle is thought to be the transmission time and the width a weight representing, e.g. a transmission rate. Alternatively, our random rectangles model could model a simplified two-dimensional wireless network. Imagine that there are spatially uniformly distributed stations which are equipped with emitters. In our case, the range for transmission (with constant power) of each station is given by a rectangular area and the total power of emission is measured by
![]() $\mu \in
\mathcal{M}_2$
.
$\mu \in
\mathcal{M}_2$
.
1.2 Related work
A basic reference on limit theorems of Poisson integrals is the book by Lifshits [Reference Lifshits23]. The main references for us are [Reference Biermé, Estrade and Kaj4] and [Reference Kaj, Leskelä, Norros and Schmidt18].
Kaj et al. [Reference Kaj, Leskelä, Norros and Schmidt18] studied the limits of a spatial random field generated by independently and uniformly scattered random sets in
![]() $\mathbb{R}^d$
. The sets (also referred to as grains) have a random volume but a predetermined shape. The size of a grain is given by a single heavy-tailed distribution, i.e. scaling means that the intensity
$\mathbb{R}^d$
. The sets (also referred to as grains) have a random volume but a predetermined shape. The size of a grain is given by a single heavy-tailed distribution, i.e. scaling means that the intensity
![]() $\lambda$
grows to infinity while the mean volume
$\lambda$
grows to infinity while the mean volume
![]() $\rho$
of the sets tends to zero. They obtained three different limits depending on the relative speed at which
$\rho$
of the sets tends to zero. They obtained three different limits depending on the relative speed at which
![]() $\lambda$
and
$\lambda$
and
![]() $\rho$
are scaled. Furthermore, they provided statistical properties of the limits.
$\rho$
are scaled. Furthermore, they provided statistical properties of the limits.
Biermé et al. [Reference Biermé, Estrade and Kaj4] considered a random balls model of germ–grain type as well. The predetermined shape of the grains is a ball, whose size depends on the scaling parameter
![]() $\rho$
and the random radius. The radius distribution has a power-law behaviour either in zero or at infinity, i.e. they dealt with zooming in and zooming out. As a main result, they can construct all self-similar, translation, and rotation invariant Gaussian fields through zooming procedures in the random balls model.
$\rho$
and the random radius. The radius distribution has a power-law behaviour either in zero or at infinity, i.e. they dealt with zooming in and zooming out. As a main result, they can construct all self-similar, translation, and rotation invariant Gaussian fields through zooming procedures in the random balls model.
Breton and Dombry [Reference Breton and Dombry5] investigated weighted random balls models, in which the balls additionally have random weights, whose law belongs to the normal domain of attraction of the
![]() $\alpha$
-stable distribution with
$\alpha$
-stable distribution with
![]() $\alpha \in (1,2]$
. They obtained different limiting random fields depending on the regimes and gave statistical properties.
$\alpha \in (1,2]$
. They obtained different limiting random fields depending on the regimes and gave statistical properties.
An anisotropic scaling was examined by Pilipauskait and Surgailis [Reference Pilipauskaitė and Surgailis25]. They studied the scaling limits of the random grain model on the plane with heavy-tailed grain area distribution. The anisotropy was implemented by scaling the x- and y-directions at different rates. Therefore, in the case of the grains being rectangles, the ratio of the edge lengths of all rectangles tends either to zero or to infinity under the scaling. This property distinguishes their model from our random boxes model, where each rectangle has a random length-to-width ratio that does not change under the scaling.
Moreover, limits of random balls models have been well investigated in the literature (e.g. [Reference Biermé, Durieu and Wang3], [Reference Breton and Dombry6], [Reference Breton and Gobard7], [Reference Breton, Clarenne and Gobard8], [Reference Gobard14]) and, in particular, limits of ‘teletraffic’ models (see [Reference Fasen12], [Reference Faÿ, González-Arévalo, Mikosch and Samorodnitsky13], [Reference Kaj and Taqqu17], and a list of further references in [Reference Lifshits23]).
Finally, we would also like to mention the notion of Poisson shot noise, which is related to random balls models and for which many limit theorems are available. The Poisson shot noise process generalises the compound Poisson process, where the summands (‘jump sizes’) can consist of further stochastic processes. Usually, the underlying process is on the real line that can be interpreted as time (see [Reference Çağlar10], [Reference Klüppelberg and Kühn20], [Reference Klüppelberg, Mikosch and Schärf21], and [Reference Lane22] for Poisson processes, and [Reference Iksanov, Marynych and Meiners15] and [Reference Pang and Zhou24] for further processes). Poisson shot noise fields on
![]() $\mathbb{R}^d$
are considered in [Reference Baccelli and Biswas1], [Reference Biermé and Desolneux2], [Reference Bulinskiĭ9], and [Reference Dombry11], where the summands are governed by a response function rather than consisting of stochastic processes.
$\mathbb{R}^d$
are considered in [Reference Baccelli and Biswas1], [Reference Biermé and Desolneux2], [Reference Bulinskiĭ9], and [Reference Dombry11], where the summands are governed by a response function rather than consisting of stochastic processes.
1.3 Overview
Let us outline different scaling regimes which result in different limits. As mentioned above, the scaling regimes are defined by the joint behaviour of the scaling parameter
![]() $\rho$
and the intensity
$\rho$
and the intensity
![]() $\lambda_\rho$
of the Poisson point process as
$\lambda_\rho$
of the Poisson point process as
![]() $\rho \to 0$
. We distinguish the following regimes.
$\rho \to 0$
. We distinguish the following regimes.
High-intensity regime:
 $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to
\infty$
.
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to
\infty$
.Intermediate-intensity regime:
 $ \lambda_\rho \rho^{\gamma_1+\gamma_2}
\to a \in (0,\infty)$
.
$ \lambda_\rho \rho^{\gamma_1+\gamma_2}
\to a \in (0,\infty)$
.Low-intensity regime:
 $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 0$
.
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 0$
.
The low-intensity regime has to be divided once more into three different subregimes. Here, we assume without loss of generality that the tail of the distribution of the length is heavier than that of the width, i.e.
![]() $\gamma_1 < \gamma_2$
. Our naming of these subregimes is based on the limits and on the objects that can be spotted in a graphical representation. We distinguish the following subregimes.
$\gamma_1 < \gamma_2$
. Our naming of these subregimes is based on the limits and on the objects that can be spotted in a graphical representation. We distinguish the following subregimes.
Gaussian-lines scaling regime:
 $\lambda_\rho \rho^{\gamma_1+\eta} \to a
\in (0,\infty)$
for a constant
$\lambda_\rho \rho^{\gamma_1+\eta} \to a
\in (0,\infty)$
for a constant
 $\eta \in (0,\gamma_2)$
and, thus,
$\eta \in (0,\gamma_2)$
and, thus,
 $
\lambda_\rho \rho^{\gamma_1} \to \infty$
. With regard to the scaling limit, it is of no importance to take care of the precise behaviour of
$
\lambda_\rho \rho^{\gamma_1} \to \infty$
. With regard to the scaling limit, it is of no importance to take care of the precise behaviour of
 $\lambda_\rho \rho^{\gamma_2}$
(as long as
$\lambda_\rho \rho^{\gamma_2}$
(as long as
 $\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to 0$
).
$\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to 0$
).Poisson-lines scaling regime:
 $ \lambda_\rho \rho^{\gamma_1} \to a \in
(0,\infty)$
and, thus,
$ \lambda_\rho \rho^{\gamma_1} \to a \in
(0,\infty)$
and, thus,
 $\lambda_\rho \rho^{\gamma_2} \to 0$
.
$\lambda_\rho \rho^{\gamma_2} \to 0$
.Points scaling regime:
 $\lambda_\rho \rho^{\gamma_1} \to 0$
.
$\lambda_\rho \rho^{\gamma_1} \to 0$
.
So far, we have additionally assumed that
![]() $\gamma_1 < 2$
. For
$\gamma_1 < 2$
. For
![]() $2 <
\gamma_1 \leq \gamma_2$
, the length and the width of the boxes have finite variances. In this case, there is only one scaling limit and we just require that
$2 <
\gamma_1 \leq \gamma_2$
, the length and the width of the boxes have finite variances. In this case, there is only one scaling limit and we just require that
![]() $\lambda_\rho \to \infty$
as
$\lambda_\rho \to \infty$
as
![]() $\rho \to 0$
, i.e. there is no further condition on the joint behaviour of
$\rho \to 0$
, i.e. there is no further condition on the joint behaviour of
![]() $\rho$
and
$\rho$
and
![]() $\lambda_\rho$
.
$\lambda_\rho$
.
Let us comment on the parameter a in the intermediate-intensity regime, the Gaussian-lines scaling regime, and the Poisson-lines scaling regime, respectively. For the sake of clarity, the respective results will only be given for the value
![]() $a=1$
. For the general cases where
$a=1$
. For the general cases where
![]() $a \in
(0,\infty)$
not necessarily equals 1, we refer the reader to Remarks 4.1, 4.3, and 4.2 below, respectively.
$a \in
(0,\infty)$
not necessarily equals 1, we refer the reader to Remarks 4.1, 4.3, and 4.2 below, respectively.
The remainder of this paper is structured as follows. Section 2 contains the theorems of convergence to the limiting random fields (subdivided into the different scaling regimes in Sections 2.1, 2.2, and 2.3, respectively) and a comparison to the model where the length and the width of the boxes have finite variances (Section 2.4). A comparison of the different regimes, further facts on statistical properties of the limits, and a modified model with randomly rotated boxes are given in Sections 2.5, 2.6, and 2.7, respectively. We collect some preliminaries in Section 3 in order to prove the main results in Section 4.
2 Main results
The following results are theorems of convergence of the finite-dimensional distributions of the centred and renormalised random field
to a limiting random field, where the corresponding space of signed measures
![]() $\mathcal{M}$
and the function
$\mathcal{M}$
and the function
![]() $n_\rho\,:\!= n(\rho)$
are respectively defined in the theorems below. We denote this convergence by
$n_\rho\,:\!= n(\rho)$
are respectively defined in the theorems below. We denote this convergence by
![]() ${}\smash{{\skew5\widetilde{J}_\rho(\cdot)}/{n_\rho} \xrightarrow{\mathcal{M}}
W(\cdot)}$
, where in each case the limiting random field
${}\smash{{\skew5\widetilde{J}_\rho(\cdot)}/{n_\rho} \xrightarrow{\mathcal{M}}
W(\cdot)}$
, where in each case the limiting random field
![]() $(W(\mu))_\mu$
is specified there.
$(W(\mu))_\mu$
is specified there.
2.1 High-intensity regime
We look at the high-intensity regime where
![]() $\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to \infty$
. First, we define the space of signed measures
$\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to \infty$
. First, we define the space of signed measures
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
where the theorem of convergence holds.
$\mathcal{M}^{\gamma_1,\gamma_2}$
where the theorem of convergence holds.
Definition 2.1. Let
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
be the subset of
$\mathcal{M}^{\gamma_1,\gamma_2}$
be the subset of
![]() $\mathcal{M}_2$
with the following property. For each
$\mathcal{M}_2$
with the following property. For each
![]() $\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, there exist constants
$\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, there exist constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha_i$
with
$\alpha_i$
with
![]() $\gamma_i < \alpha_i \leq 2$
for
$\gamma_i < \alpha_i \leq 2$
for
![]() $i=1,2$
such that, for all
$i=1,2$
such that, for all
![]() $u \in \mathbb{R}_+^2$
,
$u \in \mathbb{R}_+^2$
,
In order to proceed quickly to the results, we postpone a discussion of the space
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
to Section 3.1. Here, we only note that this subspace is closed under translation and dilation; cf. Section 2.6.
$\mathcal{M}^{\gamma_1,\gamma_2}$
to Section 3.1. Here, we only note that this subspace is closed under translation and dilation; cf. Section 2.6.
The limiting random field is given by a centred Gaussian linear random field.
Theorem 2.1. Let
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2, \lambda_\rho \to \infty,$
and
$i=1,2, \lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to \infty$
as
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to \infty$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $(Z(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
$(Z(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
2.2 Intermediate-intensity regime
In the intermediate intensity regime where
![]() $ \lambda_\rho
\rho^{\gamma_1+\gamma_2} \to a \in (0,\infty)$
, the space of signed measures is identical with that in the high-intensity regime. The limiting random field consists of compensated Poisson integrals.
$ \lambda_\rho
\rho^{\gamma_1+\gamma_2} \to a \in (0,\infty)$
, the space of signed measures is identical with that in the high-intensity regime. The limiting random field consists of compensated Poisson integrals.
Theorem 2.2. Let
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2, \lambda_\rho \to \infty,$
and
$i=1,2, \lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
as
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $ (J_I(\mu))_\mu$
is the linear random field of compensated Poisson integrals
$ (J_I(\mu))_\mu$
is the linear random field of compensated Poisson integrals
where the intensity measure is given by
2.3 Low-intensity regime
The low-intensity regime is defined by
![]() $\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to 0$
with
$\lambda_\rho
\rho^{\gamma_1+\gamma_2} \to 0$
with
![]() $\gamma_1 < \gamma_2$
, which is divided once more into three different subregimes. In these subregimes, we additionally have to assume that the density function of the length of a box for small values is bounded, i.e. we assume that there is some
$\gamma_1 < \gamma_2$
, which is divided once more into three different subregimes. In these subregimes, we additionally have to assume that the density function of the length of a box for small values is bounded, i.e. we assume that there is some
![]() $c_{f_1}>0$
such that the inequality
$c_{f_1}>0$
such that the inequality
holds for all
![]() $u_1 \in \mathbb{R}_+$
. This technical assumption ensures the existence of a suitable majorant for
$u_1 \in \mathbb{R}_+$
. This technical assumption ensures the existence of a suitable majorant for
![]() $f_1$
in the proofs below. From now on, we treat the three subregimes separately.
$f_1$
in the proofs below. From now on, we treat the three subregimes separately.
2.3.1 Gaussian-lines scaling regime
We define the space of signed measures
![]() $\mathcal{M}_{L}$
for the Gaussian-lines scaling regime where
$\mathcal{M}_{L}$
for the Gaussian-lines scaling regime where
![]() $\lambda_\rho \rho^{\gamma_1+\eta}
\to a \in (0,\infty)$
for some
$\lambda_\rho \rho^{\gamma_1+\eta}
\to a \in (0,\infty)$
for some
![]() $\eta \in (0,\gamma_2)$
.
$\eta \in (0,\gamma_2)$
.
Definition 2.2. Let
![]() $\mathcal{M}_{L}$
be the subset of
$\mathcal{M}_{L}$
be the subset of
![]() $\mathcal{M}_2$
where
$\mathcal{M}_2$
where
each
 $\mu \in \mathcal{M}_{L}$
has a density function
$\mu \in \mathcal{M}_{L}$
has a density function
 $f_\mu$
, i.e.
$f_\mu$
, i.e.
 $\mu(\mathrm{d} x) = f_\mu(x) {\rm d} x$
;
$\mu(\mathrm{d} x) = f_\mu(x) {\rm d} x$
;for each
 $\mu \in \mathcal{M}_{L},$
the density function
$\mu \in \mathcal{M}_{L},$
the density function
 $f_\mu$
is bounded and decays at least exponentially fast, i.e. there exist constants
$f_\mu$
is bounded and decays at least exponentially fast, i.e. there exist constants
 $C_\mu>0$
and
$C_\mu>0$
and
 $c_\mu>0$
such that, for all
$c_\mu>0$
such that, for all
 $x \in \mathbb{R}^2$
, (2.4)
$x \in \mathbb{R}^2$
, (2.4) $$
\begin{equation}
\vert \kern2ptf_\mu(x) \vert \leq C_\mu {\rm e}^{-c_\mu(\vert x_1 \vert + \vert x_2
\vert)};
\label{eqn5}
\end{equation}
$$
$$
\begin{equation}
\vert \kern2ptf_\mu(x) \vert \leq C_\mu {\rm e}^{-c_\mu(\vert x_1 \vert + \vert x_2
\vert)};
\label{eqn5}
\end{equation}
$$
for each
 $\mu \in \mathcal{M}_{L},$
the pointwise convergence (2.5)as
$\mu \in \mathcal{M}_{L},$
the pointwise convergence (2.5)as $$
\begin{equation}
\frac{1}{{\varepsilon}} \int_{B( x, \binom{u_1}{{\varepsilon}})} f_\mu(y) \mathrm{d} y \to
\int_{[x_1-{u_1}/{2},x_1+{u_1}/{2}]} f_\mu(y_1,x_2) {\rm d} y_1
\label{eqn6}
\end{equation}
$$
$$
\begin{equation}
\frac{1}{{\varepsilon}} \int_{B( x, \binom{u_1}{{\varepsilon}})} f_\mu(y) \mathrm{d} y \to
\int_{[x_1-{u_1}/{2},x_1+{u_1}/{2}]} f_\mu(y_1,x_2) {\rm d} y_1
\label{eqn6}
\end{equation}
$$
 ${\varepsilon} \to 0$
holds for all
${\varepsilon} \to 0$
holds for all
 $(x,u_1) \in \mathbb{R}^2 \times \mathbb{R}_+$
.
$(x,u_1) \in \mathbb{R}^2 \times \mathbb{R}_+$
.
We note that this subspace is closed under translation and dilation; cf. Section 2.6. For a discussion about the properties of this space and the relation to
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
, we refer the reader to Section 3.1.
$\mathcal{M}^{\gamma_1,\gamma_2}$
, we refer the reader to Section 3.1.
In the Gaussian-lines scaling regime, we require a further condition on the ‘lighter’ tail index
![]() $\gamma_2$
, namely
$\gamma_2$
, namely
![]() $\gamma_2>2$
. Consequently, the width of a box has a finite variance. The limiting random field is a centred Gaussian linear random field.
$\gamma_2>2$
. Consequently, the width of a box has a finite variance. The limiting random field is a centred Gaussian linear random field.
Theorem 2.3. Let
![]() $\gamma_1 \in (1,2)$
,
$\gamma_1 \in (1,2)$
,
![]() $\gamma_2>2, \lambda_\rho \to \infty,$
and
$\gamma_2>2, \lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1+\eta} \to 1$
for some
$\lambda_\rho \rho^{\gamma_1+\eta} \to 1$
for some
![]() $\eta \in
(0,\gamma_2)$
as
$\eta \in
(0,\gamma_2)$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $(Y(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
$(Y(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
2.3.2 Poisson-lines scaling regime
In the Poisson-lines scaling regime where
![]() $ \lambda_\rho \rho^{\gamma_1}
\to a \in (0,\infty)$
, we provide the theorem of convergence to a random field consisting of compensated Poisson integrals. The corresponding space of signed measures coincides with that from the Gaussian-lines scaling regime.
$ \lambda_\rho \rho^{\gamma_1}
\to a \in (0,\infty)$
, we provide the theorem of convergence to a random field consisting of compensated Poisson integrals. The corresponding space of signed measures coincides with that from the Gaussian-lines scaling regime.
Theorem 2.4. Let
![]() $\gamma_1 \in (1,2)$
,
$\gamma_1 \in (1,2)$
,
![]() $\gamma_1 < \gamma_2, \lambda_\rho \to \infty,$
and
$\gamma_1 < \gamma_2, \lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1} \to 1$
as
$\lambda_\rho \rho^{\gamma_1} \to 1$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $(J_L(\mu))_\mu$
is the linear random field of compensated Poisson integrals
$(J_L(\mu))_\mu$
is the linear random field of compensated Poisson integrals
where the intensity measure is given by
In the Poisson-lines scaling regime, we have
![]() $ \lambda_\rho
\rho^{\gamma_1} \to a \in (0,\infty)$
and
$ \lambda_\rho
\rho^{\gamma_1} \to a \in (0,\infty)$
and
![]() $ \lambda_\rho \rho^{\gamma_2}
\to 0$
as
$ \lambda_\rho \rho^{\gamma_2}
\to 0$
as
![]() $\rho \to 0$
. This indicates a different behaviour for the length and the width of the boxes. For a graphical representation, we ran simulations of the Poisson point processes for some small
$\rho \to 0$
. This indicates a different behaviour for the length and the width of the boxes. For a graphical representation, we ran simulations of the Poisson point processes for some small
![]() $\rho$
and appropriate
$\rho$
and appropriate
![]() $\lambda_\rho$
. We generated random Poisson points, where we chose Pareto distributions for the length and the width of the boxes. Then, we plotted the boxes that are filled with black colour, i.e. black rectangles. Two samples of the random boxes model in the Poisson-lines scaling regime are given in Figure 1. Besides points, we spot horizontal lines in the sample on the left-hand side. In the sample on the right-hand side, each box is just additionally randomly rotated around the center point of itself (cf. Section 2.7 below for the definition of this modified model).
$\lambda_\rho$
. We generated random Poisson points, where we chose Pareto distributions for the length and the width of the boxes. Then, we plotted the boxes that are filled with black colour, i.e. black rectangles. Two samples of the random boxes model in the Poisson-lines scaling regime are given in Figure 1. Besides points, we spot horizontal lines in the sample on the left-hand side. In the sample on the right-hand side, each box is just additionally randomly rotated around the center point of itself (cf. Section 2.7 below for the definition of this modified model).

Figure 1 Poisson-lines scaling regime.
2.3.3 Points scaling regime
In the points scaling regime where
![]() $\lambda_\rho \rho^{\gamma_1} \to 0$
, we investigate the scaling behaviour of
$\lambda_\rho \rho^{\gamma_1} \to 0$
, we investigate the scaling behaviour of
![]() $\,\skew5\widetilde{J}_\rho$
on the space of signed measures
$\,\skew5\widetilde{J}_\rho$
on the space of signed measures
![]() $\mathcal{M}_{P}$
which is given as follows.
$\mathcal{M}_{P}$
which is given as follows.
Definition 2.3. Let
![]() $\mathcal{M}_{P}$
be the subset of
$\mathcal{M}_{P}$
be the subset of
![]() $\mathcal{M}_2$
where
$\mathcal{M}_2$
where
each signed measure
 $\mu \in \mathcal{M}_{P}$
has a continuous density function
$\mu \in \mathcal{M}_{P}$
has a continuous density function
 $f_\mu$
, i.e.
$f_\mu$
, i.e.
 $\mu(\mathrm{d} x) = f_\mu(x) {\rm d} x$
;
$\mu(\mathrm{d} x) = f_\mu(x) {\rm d} x$
;for each
 $\mu \in \mathcal{M}_{P},$
the density function
$\mu \in \mathcal{M}_{P},$
the density function
 $f_\mu$
is bounded and decays at least exponentially fast, i.e. there exist constants
$f_\mu$
is bounded and decays at least exponentially fast, i.e. there exist constants
 $C_\mu>0$
and
$C_\mu>0$
and
 $c_\mu>0$
such that, for all
$c_\mu>0$
such that, for all
 $x \in \mathbb{R}^2$
,
$x \in \mathbb{R}^2$
,  $$
\begin{equation*}
\vert \kern2ptf_\mu(x) \vert \leq C_\mu {\rm e}^{-c_\mu(\vert x_1 \vert + \vert x_2
\vert)}.
\end{equation*}
$$
$$
\begin{equation*}
\vert \kern2ptf_\mu(x) \vert \leq C_\mu {\rm e}^{-c_\mu(\vert x_1 \vert + \vert x_2
\vert)}.
\end{equation*}
$$
We note that this subspace is closed under translation and dilation; cf. Section 2.6. A further discussion of the space is given in Section 3.1.
The limiting random field consists of integrals with respect to an
![]() $\alpha$
-stable random measure. For
$\alpha$
-stable random measure. For
![]() $\alpha \in (1,2)$
, we denote by
$\alpha \in (1,2)$
, we denote by
![]() $\Lambda_\alpha$
the independently scattered
$\Lambda_\alpha$
the independently scattered
![]() $\alpha$
-stable random measure with unit skewness and Lebesgue control measure (cf., e.g. [Reference Samorodnitsky and Taqqu27]). We define the random linear functional
$\alpha$
-stable random measure with unit skewness and Lebesgue control measure (cf., e.g. [Reference Samorodnitsky and Taqqu27]). We define the random linear functional
by its characteristic function at 1, i.e.
where (excluding the trivial case
![]() $\Vert \kern2ptf_\mu \Vert_{\gamma_1} = 0$
)
$\Vert \kern2ptf_\mu \Vert_{\gamma_1} = 0$
)
and
![]() ${f_\mu}_+\,:\!= \max({\kern2ptf_\mu},0 )$
,
${f_\mu}_+\,:\!= \max({\kern2ptf_\mu},0 )$
,
![]() ${f_\mu}_-\,:\!= - \min({\kern2ptf_\mu},0)$
.
${f_\mu}_-\,:\!= - \min({\kern2ptf_\mu},0)$
.
Theorem 2.5. Let
![]() $\gamma_1 \in (1,2)$
,
$\gamma_1 \in (1,2)$
,
![]() $\gamma_1 < \gamma_2$
,
$\gamma_1 < \gamma_2$
,
![]() $\lambda_\rho \to
\infty,$
and
$\lambda_\rho \to
\infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1} \to 0$
as
$\lambda_\rho \rho^{\gamma_1} \to 0$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where the linear random field of functionals
$\rho \to 0$
, where the linear random field of functionals
![]() $(S_{\gamma_1}(\mu))_\mu$
and the constant
$(S_{\gamma_1}(\mu))_\mu$
and the constant
![]() $c_{\gamma_1,\gamma_2}$
are defined in (2.9) and (4.8) below, respectively.
$c_{\gamma_1,\gamma_2}$
are defined in (2.9) and (4.8) below, respectively.
2.4 The finite-variance case
Finally, we want to investigate the scaling behaviour in the case where the area of a box has a finite variance. We assume that the length and the width of the boxes have finite second moments instead of heavy tails. Similar to above, let F be a probability measure on
![]() $\mathbb{R}_+^2$
given by
$\mathbb{R}_+^2$
given by
Furthermore, we define, for
![]() $i=1,2$
,
$i=1,2$
,
The following result shows that the centred and renormalised random field on the space
![]() $\mathcal{M}_{P}$
converges to a centred Gaussian linear random field. We emphasise that there does not exist a diversity of regimes to distinguish in the finite-variance case, which is also the much simpler case. Nevertheless, the proof of this result can be viewed as a ‘prototype proof’ for all other regimes.
$\mathcal{M}_{P}$
converges to a centred Gaussian linear random field. We emphasise that there does not exist a diversity of regimes to distinguish in the finite-variance case, which is also the much simpler case. Nevertheless, the proof of this result can be viewed as a ‘prototype proof’ for all other regimes.
Moreover, we conjecture that the following theorem holds for a larger space of signed measures than
![]() $\mathcal{M}_{P}$
(but our proof cannot be adapted to this larger space). Actually, the limiting random field is well defined for
$\mathcal{M}_{P}$
(but our proof cannot be adapted to this larger space). Actually, the limiting random field is well defined for
![]() $f_\mu \in L^1(\mathbb{R}^2) \cap L^2(\mathbb{R}^2)$
.
$f_\mu \in L^1(\mathbb{R}^2) \cap L^2(\mathbb{R}^2)$
.
Theorem 2.6. Let
![]() $\lambda_\rho \to \infty$
as
$\lambda_\rho \to \infty$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $v_i$
is defined in (2.11) for
$v_i$
is defined in (2.11) for
![]() $i=1,2$
and where
$i=1,2$
and where
![]() $( X(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
$( X(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
2.5 Comparison of the different regimes
First, we make a remark regarding the comparison of the different regimes among each other. In each low intensity subregime, the different parameters
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
contribute in different ways to the limit. This contrasts the limits in the high- and intermediate-intensity regimes, where both parameters
$\gamma_2$
contribute in different ways to the limit. This contrasts the limits in the high- and intermediate-intensity regimes, where both parameters
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
are present in a homogeneous way in each limit. For example, in the points scaling regime the ‘heavier’ tail index
$\gamma_2$
are present in a homogeneous way in each limit. For example, in the points scaling regime the ‘heavier’ tail index
![]() $\gamma_1$
for the length of a box appears primarily in the limit, i.e. the ‘lighter’ tail index
$\gamma_1$
for the length of a box appears primarily in the limit, i.e. the ‘lighter’ tail index
![]() $\gamma_2$
only enters into a constant (see Theorem 2.5). More precisely, the limit
$\gamma_2$
only enters into a constant (see Theorem 2.5). More precisely, the limit
![]() $S_{\gamma_1}(\mu)$
is a
$S_{\gamma_1}(\mu)$
is a
![]() $\gamma_1$
-stable random variable and the constant
$\gamma_1$
-stable random variable and the constant
![]() $c_{\gamma_1,\gamma_2}$
given in (4.8) below is the only quantity depending on the tail index
$c_{\gamma_1,\gamma_2}$
given in (4.8) below is the only quantity depending on the tail index
![]() $\gamma_2$
.
$\gamma_2$
.
Second, we want to say a few words about the comparison to previous work. Two limiting random fields in this paper have already arisen in identical form. The centred Gaussian linear random field with covariance function given in (2.12) coincides with the corresponding one in the finite-variance case of the random grain model where the size of a grain is given by a single distribution (cf. Theorem 1 of [Reference Kaj, Leskelä, Norros and Schmidt18]). Moreover, the limiting random field consisting of integrals with respect to a stable random measure in the points scaling regime has also appeared there (cf. Equation (13) of [Reference Kaj, Leskelä, Norros and Schmidt18]). The index of stability is given by the index of the regularly varying tail of the volume of a grain there and by the ‘heavier’ tail index
![]() $\gamma_1$
for the length of a box in our random boxes model. All other limiting random fields seem to be new.
$\gamma_1$
for the length of a box in our random boxes model. All other limiting random fields seem to be new.
2.6 Statistical properties
In the following paragraphs, we give some statistical properties of the different scaling limits
![]() $Z, J_I, Y, J_L$
,
$Z, J_I, Y, J_L$
,
![]() $S_{\gamma_1},$
and X on their respective spaces of signed measures. With regard to these properties, we note that these subspaces are closed under translation and dilation. We will omit the proofs of all these facts because they can be verified easily.
$S_{\gamma_1},$
and X on their respective spaces of signed measures. With regard to these properties, we note that these subspaces are closed under translation and dilation. We will omit the proofs of all these facts because they can be verified easily.
Covariance. The covariance functions of the Gaussian random fields Z, Y, and X are given in (2.2), (2.6), and (2.12), respectively. The covariance function of
![]() $J_I$
in the intermediate-intensity regime is exactly the same as in the high-intensity regime (see (2.2)), but the limit
$J_I$
in the intermediate-intensity regime is exactly the same as in the high-intensity regime (see (2.2)), but the limit
![]() $J_I$
is not a Gaussian random field. In the points scaling regime, the scaling limit
$J_I$
is not a Gaussian random field. In the points scaling regime, the scaling limit
![]() $S_{\gamma_1}(\mu)$
is
$S_{\gamma_1}(\mu)$
is
![]() $\gamma_1$
-stable and thus does not have a finite variance. We distinguish two cases in the Poisson-lines scaling regime. If
$\gamma_1$
-stable and thus does not have a finite variance. We distinguish two cases in the Poisson-lines scaling regime. If
![]() $\gamma_2 < 2$
, the compensated Poisson integral
$\gamma_2 < 2$
, the compensated Poisson integral
![]() $J_L(\mu)$
does not have a finite variance. In contrast, if we assume that
$J_L(\mu)$
does not have a finite variance. In contrast, if we assume that
![]() $\gamma_2 > 2$
, i.e. the width of a box has a finite variance, the scaling limit
$\gamma_2 > 2$
, i.e. the width of a box has a finite variance, the scaling limit
![]() $J_L(\mu)$
has a finite variance as well and the covariance function coincides with that in the Gaussian-lines scaling regime (see (2.6)).
$J_L(\mu)$
has a finite variance as well and the covariance function coincides with that in the Gaussian-lines scaling regime (see (2.6)).
Translation invariance. Let
![]() $s \in \mathbb{R}^2$
. We define the translation of a signed measure
$s \in \mathbb{R}^2$
. We define the translation of a signed measure
![]() $\tau_s \mu$
by
$\tau_s \mu$
by
![]() $\tau_s \mu (A)\,:\!=
\mu(A-s)$
for any Borel set A. We call a random field W on
$\tau_s \mu (A)\,:\!=
\mu(A-s)$
for any Borel set A. We call a random field W on
![]() $\mathcal{M}_W$
translation invariant (cf. Definition 3.1 of [Reference Biermé, Estrade and Kaj4]) if we have
$\mathcal{M}_W$
translation invariant (cf. Definition 3.1 of [Reference Biermé, Estrade and Kaj4]) if we have
in finite-dimensional distributions for all
![]() $s \in \mathbb{R}^2$
(
$s \in \mathbb{R}^2$
(
![]() $\mathcal{M}_W$
has to be closed under translations
$\mathcal{M}_W$
has to be closed under translations
![]() $\tau_s$
). All limiting random fields Z,
$\tau_s$
). All limiting random fields Z,
![]() $J_I$
, Y,
$J_I$
, Y,
![]() $J_L$
,
$J_L$
,
![]() $S_{\gamma_1},$
and X are translation invariant on the respective spaces of signed measures.
$S_{\gamma_1},$
and X are translation invariant on the respective spaces of signed measures.
Dilation. For all
![]() $a >0,$
the dilation of a signed measure
$a >0,$
the dilation of a signed measure
![]() $\mu_a$
is given by
$\mu_a$
is given by
![]() $\mu_a (A)\,:\!= \mu(a^{-1}A)$
for any Borel set A. We call a random field W on
$\mu_a (A)\,:\!= \mu(a^{-1}A)$
for any Borel set A. We call a random field W on
![]() $\mathcal{M}_W$
self-similar with index H (cf. Definition 3.3 of [Reference Biermé, Estrade and Kaj4]) if we have
$\mathcal{M}_W$
self-similar with index H (cf. Definition 3.3 of [Reference Biermé, Estrade and Kaj4]) if we have
in finite-dimensional distributions for all
![]() $a >0$
(
$a >0$
(
![]() $\mathcal{M}_W$
has to be closed under dilations
$\mathcal{M}_W$
has to be closed under dilations
![]() $\mu_a$
).
$\mu_a$
).
The limiting (Gaussian) random fields Z, Y, and X are self-similar with indices
![]() $H = (2-\gamma_1 - \gamma_2)/{2}$
,
$H = (2-\gamma_1 - \gamma_2)/{2}$
,
![]() $H=-\gamma_1/{2},$
and
$H=-\gamma_1/{2},$
and
![]() $H=-1$
, respectively. In the points scaling regime, the limit
$H=-1$
, respectively. In the points scaling regime, the limit
![]() $S_{\gamma_1}$
is self-similar with index
$S_{\gamma_1}$
is self-similar with index
![]() $H=2 / \gamma_1 - 2$
. We emphasise that H is negative in these cases. If the reader expects H to be positive, a reason may be found in the way of defining the dilation of a signed measure which, however, is common in the literature. We can also verify that the random field
$H=2 / \gamma_1 - 2$
. We emphasise that H is negative in these cases. If the reader expects H to be positive, a reason may be found in the way of defining the dilation of a signed measure which, however, is common in the literature. We can also verify that the random field
![]() $J_I$
in the intermediate intensity regime is not self-similar (cf. [18, p.537]).
$J_I$
in the intermediate intensity regime is not self-similar (cf. [18, p.537]).
We call a random field W with
![]() $\mathbb{E} W=0$
on
$\mathbb{E} W=0$
on
![]() $\mathcal{M}_W$
(which has to be again closed under dilation) aggregate-similar (cf. Definition 3.5 of [Reference Biermé, Estrade and Kaj4] and [Reference Kaj16]) if there is a positive sequence
$\mathcal{M}_W$
(which has to be again closed under dilation) aggregate-similar (cf. Definition 3.5 of [Reference Biermé, Estrade and Kaj4] and [Reference Kaj16]) if there is a positive sequence
![]() $(a_m)_{m\geq 1}$
such that we have
$(a_m)_{m\geq 1}$
such that we have
in finite-dimensional distributions for all
![]() $m \geq 1$
, where
$m \geq 1$
, where
![]() $(W^k)_{k
\geq 1}$
are independent and identically distributed (i.i.d.) copies of W.
$(W^k)_{k
\geq 1}$
are independent and identically distributed (i.i.d.) copies of W.
We find that the random fields Z, Y, X,
![]() $J_I,$
and
$J_I,$
and
![]() $S_{\gamma_1}$
are aggregate-similar, where we have
$S_{\gamma_1}$
are aggregate-similar, where we have
![]() $a_m=\smash{m^{1/(2-\gamma_1-\gamma_2)}}$
,
$a_m=\smash{m^{1/(2-\gamma_1-\gamma_2)}}$
,
![]() $a_m=\smash{m^{-1/\gamma_1}}$
,
$a_m=\smash{m^{-1/\gamma_1}}$
,
![]() $a_m=m^{-1/2}$
,
$a_m=m^{-1/2}$
,
![]() $a_m=\smash{m^{1/(2-\gamma_1-\gamma_2)}},$
and
$a_m=\smash{m^{1/(2-\gamma_1-\gamma_2)}},$
and
![]() $a_m=\smash{m^{1/(2-2\gamma_1)}}$
, respectively. Regarding the dilation in the Poisson-lines scaling regime, we mention that the scaling limit
$a_m=\smash{m^{1/(2-2\gamma_1)}}$
, respectively. Regarding the dilation in the Poisson-lines scaling regime, we mention that the scaling limit
![]() $J_L$
does not fulfil aggregate-similarity. In fact, it fulfils the following property, which is some kind of aggregate-similarity with dilation:
$J_L$
does not fulfil aggregate-similarity. In fact, it fulfils the following property, which is some kind of aggregate-similarity with dilation:
Here
![]() $a_m=\smash{m^{1/(4-\gamma_1)}}$
and
$a_m=\smash{m^{1/(4-\gamma_1)}}$
and
![]() $\smash{(J_{L,a_m}^k)_{k \geq
1}}$
are i.i.d. copies of
$\smash{(J_{L,a_m}^k)_{k \geq
1}}$
are i.i.d. copies of
![]() $J_{L,a_m}$
. The modification
$J_{L,a_m}$
. The modification
![]() $J_{L,a_m}$
here is also given by (2.7), but
$J_{L,a_m}$
here is also given by (2.7), but
![]() $f_2(\cdot)$
in (2.8) has to be replaced by
$f_2(\cdot)$
in (2.8) has to be replaced by
![]() $\smash{a_m^{-1}f_2(a_m \cdot)}$
, i.e. the measure for the width is dilated simultaneously.
$\smash{a_m^{-1}f_2(a_m \cdot)}$
, i.e. the measure for the width is dilated simultaneously.
2.7 Extension to randomly rotated boxes
A modification of the random boxes model consists in additionally endowing the rectangles with independent and uniformly distributed orientations. A similar model was considered in Section 3.3 of [Reference Kaj, Leskelä, Norros and Schmidt18]. We introduce the Haar measure
![]() $\mathrm{d} \theta$
on the group of rotations
$\mathrm{d} \theta$
on the group of rotations
![]() ${\rm SO}(2)$
in
${\rm SO}(2)$
in
![]() $\mathbb{R}^2$
and consider the Poisson random measure
$\mathbb{R}^2$
and consider the Poisson random measure
![]() $N^\circ_\rho$
on
$N^\circ_\rho$
on
![]() $\mathbb{R}^2 \times \mathbb{R}_+^2 \times {\rm SO}(2)$
with intensity measure given by
$\mathbb{R}^2 \times \mathbb{R}_+^2 \times {\rm SO}(2)$
with intensity measure given by
Then the centred Poisson integral
is the object of interest, where
![]() $B_{\theta}(0,u)\,:\!= \theta B(0,u)$
denotes the rectangle B(0,u) rotated by
$B_{\theta}(0,u)\,:\!= \theta B(0,u)$
denotes the rectangle B(0,u) rotated by
![]() $\theta$
and
$\theta$
and
![]() $B_{\theta}(x,u)$
for
$B_{\theta}(x,u)$
for
![]() $x \neq 0$
is defined by
$x \neq 0$
is defined by
In order to obtain results for this modified random boxes model, we have to adapt the spaces of signed measures slightly. In the following, we treat the high- and intermediate-intensity regimes as an example.
Definition 2.4 Let
![]() $\smash{\mathcal{M}_\circ^{\gamma_1,\gamma_2}}$
be the subset of
$\smash{\mathcal{M}_\circ^{\gamma_1,\gamma_2}}$
be the subset of
![]() $\mathcal{M}_2$
where, for each
$\mathcal{M}_2$
where, for each
![]() $\smash{\mu \in
\mathcal{M}_\circ^{\gamma_1,\gamma_2}}$
, there exist constants
$\smash{\mu \in
\mathcal{M}_\circ^{\gamma_1,\gamma_2}}$
, there exist constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha_i$
with
$\alpha_i$
with
![]() $\gamma_i < \alpha_i \leq 2$
for
$\gamma_i < \alpha_i \leq 2$
for
![]() $i=1,2$
such that, for all
$i=1,2$
such that, for all
![]() $u \in \smash{\mathbb{R}_+^2}$
,
$u \in \smash{\mathbb{R}_+^2}$
,
Using this new subspace of signed measures, we get analogous theorems of convergence. For the high-intensity regime, the limiting random field is again Gaussian.
Theorem 2.7. Let
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2$
,
$i=1,2$
,
![]() $\lambda_\rho \to \infty,$
and
$\lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to \infty$
as
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to \infty$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
 $$
\begin{equation*}
\frac{\skew5\widetilde{J}^\circ_\rho(\cdot)}{\sqrt{ \lambda_\rho
\rho^{\gamma_1+\gamma_2}}\,}
\xrightarrow{\mathcal{M}_\circ^{\gamma_1,\gamma_2}} Z^\circ(\cdot)
\end{equation*}
$$
$$
\begin{equation*}
\frac{\skew5\widetilde{J}^\circ_\rho(\cdot)}{\sqrt{ \lambda_\rho
\rho^{\gamma_1+\gamma_2}}\,}
\xrightarrow{\mathcal{M}_\circ^{\gamma_1,\gamma_2}} Z^\circ(\cdot)
\end{equation*}
$$
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $(Z^\circ(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
$(Z^\circ(\mu))_\mu$
is the centred Gaussian linear random field with covariance function
In the intermediate-intensity regime, the limiting field is again a compensated Poisson random field.
Theorem 2.8. Let
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2$
,
$i=1,2$
,
![]() $\lambda_\rho \to \infty,$
and
$\lambda_\rho \to \infty,$
and
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
as
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
as
![]() $\rho \to 0$
. Then, we have
$\rho \to 0$
. Then, we have
as
![]() $\rho \to 0$
, where
$\rho \to 0$
, where
![]() $\smash{ (J^\circ_I(\mu))_\mu}$
is the linear random field of compensated Poisson integrals
$\smash{ (J^\circ_I(\mu))_\mu}$
is the linear random field of compensated Poisson integrals
where the intensity measure is given by
Since the probability measure
![]() $\mathrm{d} \theta$
on the group
$\mathrm{d} \theta$
on the group
![]() ${\rm SO}(2)$
is not affected by the scaling of the edge lengths as
${\rm SO}(2)$
is not affected by the scaling of the edge lengths as
![]() $\rho \to 0$
, we obtain for each regime the same type of limiting random field as in the model without rotations. Moreover, we can proceed in the proofs as in Theorems 2.1 and 2.2. We just have to use the new subspace of signed measures in order to obtain the analogous limiting random fields for this modified random boxes model. To keep the exposition comprehensible, we will not enter into more details for the proofs in this paper and omit the low-intensity regime, where the modified subspaces are more complicated and technical.
$\rho \to 0$
, we obtain for each regime the same type of limiting random field as in the model without rotations. Moreover, we can proceed in the proofs as in Theorems 2.1 and 2.2. We just have to use the new subspace of signed measures in order to obtain the analogous limiting random fields for this modified random boxes model. To keep the exposition comprehensible, we will not enter into more details for the proofs in this paper and omit the low-intensity regime, where the modified subspaces are more complicated and technical.
In addition, further extensions of our random boxes model are feasible. For example, it is possible to allow nonnegative
![]() $\sigma$
-finite measures F instead of restricting ourselves to probability measures or to consider boxes (hyper-rectangles) in
$\sigma$
-finite measures F instead of restricting ourselves to probability measures or to consider boxes (hyper-rectangles) in
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $d \geq 3$
.
$d \geq 3$
.
3 Preliminaries and technical tools
First, we define the function
![]() $\Psi$
by
$\Psi$
by
which we often require in order to represent characteristic functions. Moreover, note that we use c and C from now on for constants which can differ from line to line as well as within a line.
3.1 Spaces of signed measures
We investigate the spaces of signed measures where the theorems of convergence in the high-, intermediate-, and low-intensity regimes hold, respectively. The following proposition, which we can prove easily, ensures the linearity of these subspaces.
Proposition 3.1. The subsets
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
,
$\mathcal{M}^{\gamma_1,\gamma_2}$
,
![]() $\mathcal{M}_{L},$
and
$\mathcal{M}_{L},$
and
![]() $\mathcal{M}_{P}$
are linear subspaces of
$\mathcal{M}_{P}$
are linear subspaces of
![]() $\mathcal{M}_2$
.
$\mathcal{M}_2$
.
Remark 3.1. The linear space
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
, where the theorems of convergence in the high- and intermediate-intensity regimes hold, is not yet the technically largest possible. We are able to weaken the condition in (2.1) as follows. For each
$\mathcal{M}^{\gamma_1,\gamma_2}$
, where the theorems of convergence in the high- and intermediate-intensity regimes hold, is not yet the technically largest possible. We are able to weaken the condition in (2.1) as follows. For each
![]() $\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, there exist some constants
$\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, there exist some constants
![]() $C>0$
,
$C>0$
,
![]() $\underline{\alpha}_i,$
and
$\underline{\alpha}_i,$
and
![]() $\overline{\alpha}_i$
with
$\overline{\alpha}_i$
with
![]() $0<\underline{\alpha}_i< \gamma_i < \overline{\alpha}_i \leq 2$
for
$0<\underline{\alpha}_i< \gamma_i < \overline{\alpha}_i \leq 2$
for
![]() $i=1,2$
such that the inequality
$i=1,2$
such that the inequality
holds for all
![]() $u \in \smash{\mathbb{R}_+^2}$
.
$u \in \smash{\mathbb{R}_+^2}$
.
Remark 3.2. In Theorems 2.1 and 2.2 in the high- and intermediate-intensity regimes, we additionally assume that
![]() $\gamma_2<2$
instead of just
$\gamma_2<2$
instead of just
![]() $\gamma_2>\gamma_1$
. The reason for that can be motivated in a natural way: On the one hand, we have to require that there exists some
$\gamma_2>\gamma_1$
. The reason for that can be motivated in a natural way: On the one hand, we have to require that there exists some
![]() $\alpha_2 > \gamma_2$
in Definition 2.1 in order to prove the theorems of convergence. On the other hand, we want at least measures whose density functions have compact support to be contained in
$\alpha_2 > \gamma_2$
in Definition 2.1 in order to prove the theorems of convergence. On the other hand, we want at least measures whose density functions have compact support to be contained in
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
. As a consequence,
$\mathcal{M}^{\gamma_1,\gamma_2}$
. As a consequence,
![]() $\alpha_2 \leq 2$
also has to be fulfilled. Therefore, both inequalities can only be satisfied simultaneously for
$\alpha_2 \leq 2$
also has to be fulfilled. Therefore, both inequalities can only be satisfied simultaneously for
![]() $\gamma_2<2$
.
$\gamma_2<2$
.
Remark 3.3. We briefly comment on the characteristics of the spaces of signed measures in the low-intensity subregimes (see Definitions 2.2 and 2.3). The assumption that each signed measure has a density function is obviously necessary since the density function appears explicitly in the limiting random fields. In contrast, we do not conjecture that the technical assumption on the decay of the density function in (2.4) is necessary as well. Nevertheless, the reason for restricting the density functions to functions that decay at least exponentially fast is related to the maximal function of the signed measure given in (3.18) below. We have to ensure that Lemma 3.4(ii) below holds in order to prove the theorems of convergence.
Next, we touch on the comparison of these spaces of signed measures for
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2$
. We observe that the space
$i=1,2$
. We observe that the space
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
contains measures which do not have to have a density. Therefore, there exist some
$\mathcal{M}^{\gamma_1,\gamma_2}$
contains measures which do not have to have a density. Therefore, there exist some
![]() $\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, but
$\mu \in
\mathcal{M}^{\gamma_1,\gamma_2}$
, but
![]() $\mu \notin \mathcal{M}_{k}$
for
$\mu \notin \mathcal{M}_{k}$
for
![]() $k
\in \{L,P\}$
. Conversely, we obtain the following result.
$k
\in \{L,P\}$
. Conversely, we obtain the following result.
Proposition 3.2. Let
![]() $\gamma_i \in (1,2)$
for
$\gamma_i \in (1,2)$
for
![]() $i=1,2$
. We have
$i=1,2$
. We have
![]() $\mathcal{M}_{k} \subseteq
\mathcal{M}^{\gamma_1,\gamma_2}$
for
$\mathcal{M}_{k} \subseteq
\mathcal{M}^{\gamma_1,\gamma_2}$
for
![]() $k \in \{L,P\}$
.
$k \in \{L,P\}$
.
Sketch of the proof. Note that the density function of a signed measure in
![]() $\mathcal{M}_{k}$
for
$\mathcal{M}_{k}$
for
![]() $k \in \{L,P\}$
satisfies
$k \in \{L,P\}$
satisfies
for all
![]() $x \in \mathbb{R}^2$
for some
$x \in \mathbb{R}^2$
for some
![]() $C_\mu>0$
and
$C_\mu>0$
and
![]() $c_\mu>0$
. We can compute that
$c_\mu>0$
. We can compute that
by a case distinction for
![]() $0 \leq u_1 \leq 1$
and
$0 \leq u_1 \leq 1$
and
![]() $u_1 > 1$
. Using the product form, the validity of inequality (2.1) follows.
$u_1 > 1$
. Using the product form, the validity of inequality (2.1) follows.
In order to obtain signed measures which are contained in the spaces
![]() $\mathcal{M}_{k}$
for
$\mathcal{M}_{k}$
for
![]() $k \in \{L,P\}$
, we can stick closely to the definitions of these spaces. For example, we can consider the measure
$k \in \{L,P\}$
, we can stick closely to the definitions of these spaces. For example, we can consider the measure
![]() $\mu$
given by
$\mu$
given by
![]() $\mu(\mathrm{d} x)\,:\!= {\rm e}^{-\vert x_1\vert}{\rm e}^{-\vert
x_2\vert}{\rm d} x$
.
$\mu(\mathrm{d} x)\,:\!= {\rm e}^{-\vert x_1\vert}{\rm e}^{-\vert
x_2\vert}{\rm d} x$
.
3.2 Existence of the random fields
We deal with the existence of the random field
![]() $\,\smash{\skew5\widetilde{J}}$
of interest and all the limiting random fields in the different scaling regimes. Using Lemma 12.13 of [Reference Kallenberg19], we can verify that the random fields J and
$\,\smash{\skew5\widetilde{J}}$
of interest and all the limiting random fields in the different scaling regimes. Using Lemma 12.13 of [Reference Kallenberg19], we can verify that the random fields J and
![]() $\,\smash{\skew5\widetilde{J}}$
exist because we have
$\,\smash{\skew5\widetilde{J}}$
exist because we have
Furthermore, by standard facts on Poisson integrals and Fubini’s theorem, the expected value of
![]() $J(\mu)$
is finite and given by
$J(\mu)$
is finite and given by
Using the function
![]() $\Psi$
defined in (3.1), the characteristic function of
$\Psi$
defined in (3.1), the characteristic function of
![]() $\,\skew5\widetilde{J}(\mu)$
is given by
$\,\skew5\widetilde{J}(\mu)$
is given by
Lemma 3.1 We have, for all
![]() $\mu \in \mathcal{M}^{\gamma_1,\gamma_2}$
,
$\mu \in \mathcal{M}^{\gamma_1,\gamma_2}$
,
Proof. This follows directly from Definition 2.1 of the space
![]() $\mathcal{M}^{\gamma_1,\gamma_2}$
by using the estimate in (0.2) for the function
$\mathcal{M}^{\gamma_1,\gamma_2}$
by using the estimate in (0.2) for the function
![]() $\varphi$
defined by
$\varphi$
defined by
for
![]() $u \in \mathbb{R}_+^2$
.
$u \in \mathbb{R}_+^2$
.
In the following, we briefly note that all the limiting random fields obtained in Theorems 2.1, 2.2, 2.3, 2.4, 2.5, and 2.6 are well defined.
Using Lemma 3.1, we can easily check that the right-hand side of (2.2) is a symmetric, positive-semidefinite function such that there is a centred Gaussian linear random field Z with covariance function given by (2.2).
The existence of
 $J_I$
follows from Lemma 12.13 of [Reference Kallenberg19] and Lemma 3.1.
$J_I$
follows from Lemma 12.13 of [Reference Kallenberg19] and Lemma 3.1.The proof of Theorem 2.3 shows that
 $\sigma^2$
given in (4.17) is finite. Hence, it can serve to construct the covariance function of a centred Gaussian linear random field Y.
$\sigma^2$
given in (4.17) is finite. Hence, it can serve to construct the covariance function of a centred Gaussian linear random field Y.The existence of the compensated Poisson integral
 $J_L(\mu)$
for
$J_L(\mu)$
for
 $\mu \in
\mathcal{M}_{L}$
given in (2.7) can be verified by Lemma 12.13 of [Reference Kallenberg19]. We just have to show that where
$\mu \in
\mathcal{M}_{L}$
given in (2.7) can be verified by Lemma 12.13 of [Reference Kallenberg19]. We just have to show that where $$
\begin{equation*}
\int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \min ( \vert g(x,u) \vert, g(x,u) ^2
)\frac{1}{u_1^{\gamma_1+1}} f_2 ( u_2 ) {\rm d} x {\rm d} u < \infty,
\end{equation*}
$$
$$
\begin{equation*}
\int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \min ( \vert g(x,u) \vert, g(x,u) ^2
)\frac{1}{u_1^{\gamma_1+1}} f_2 ( u_2 ) {\rm d} x {\rm d} u < \infty,
\end{equation*}
$$
 $$
\begin{equation*}
g(x,u)\,:\!= u_2 \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]} f_\mu(y_1,x_2){\rm d}
y_1.
\end{equation*}
$$
$$
\begin{equation*}
g(x,u)\,:\!= u_2 \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]} f_\mu(y_1,x_2){\rm d}
y_1.
\end{equation*}
$$
This can be seen by a case distinction. Let us start with the following general consideration. There is an
![]() ${\varepsilon} >0$
such that
${\varepsilon} >0$
such that
with
![]() $1<\gamma_1 - {\varepsilon} $
and
$1<\gamma_1 - {\varepsilon} $
and
![]() $\gamma_1 + {\varepsilon} < \min ( \gamma_2, 2 )$
. Furthermore, we observe that
$\gamma_1 + {\varepsilon} < \min ( \gamma_2, 2 )$
. Furthermore, we observe that
We use (3.3), (3.4), and assumption (2.4) from Definition 2.2 to obtain
 $$
\begin{align}
&\min ( \vert g(x,u) \vert, g(x,u) ^2 ) \nonumber
\\
&\qquad\leq \min ( (C_\mu g_1(x_1,u_1) {\rm e}^{-c_\mu \vert x_2 \vert}
)^{\gamma_1-{\varepsilon}} , (C_\mu g_1(x_1,u_1) {\rm e}^{-c_\mu \vert x_2
\vert})^{\gamma_1+{\varepsilon}} )\nonumber
\\
&\qquad \times (\vert u_2 \vert^{\gamma_1-{\varepsilon}}+\vert u_2
\vert^{\gamma_1+{\varepsilon}}),
\label{eqn18}\end{align}
$$
$$
\begin{align}
&\min ( \vert g(x,u) \vert, g(x,u) ^2 ) \nonumber
\\
&\qquad\leq \min ( (C_\mu g_1(x_1,u_1) {\rm e}^{-c_\mu \vert x_2 \vert}
)^{\gamma_1-{\varepsilon}} , (C_\mu g_1(x_1,u_1) {\rm e}^{-c_\mu \vert x_2
\vert})^{\gamma_1+{\varepsilon}} )\nonumber
\\
&\qquad \times (\vert u_2 \vert^{\gamma_1-{\varepsilon}}+\vert u_2
\vert^{\gamma_1+{\varepsilon}}),
\label{eqn18}\end{align}
$$
where
Since
due to
![]() $\gamma_1 + {\varepsilon} < \gamma_2$
and the asymptotic behaviour of
$\gamma_1 + {\varepsilon} < \gamma_2$
and the asymptotic behaviour of
![]() $f_2$
, and since
$f_2$
, and since
it remains to show that
is finite. For
![]() $0 \leq u_1 \leq 1$
, we obtain
$0 \leq u_1 \leq 1$
, we obtain
 $$
\begin{align*}
\int_{\mathbb{R} } g_1(x_1,u_1) ^{\gamma_1+{\varepsilon}} {\rm d} x_1 &= \int_{\mathbb{R} } \bigg(
\int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]} {\rm e}^{-c_\mu \vert y_1 \vert } \mathrm{d}
y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&\leq 2 \int_{\mathbb{R}_+ } \bigg( \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]}
{\rm e}^{-c_\mu y_1} \mathrm{d} y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&\leq 2 \int_{\mathbb{R}_+ } \bigg( \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]}
{\rm e}^{-c_\mu ( x_1-{u_1}/{2}) } \mathrm{d} y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&= 2 {\rm e}^{c_\mu {u_1}({\gamma_1+{\varepsilon}})/{2}} u_1^{\gamma_1+{\varepsilon}}\int_{\mathbb{R}_+
} {\rm e}^{-c_\mu ({\gamma_1+{\varepsilon}}) x_1}{\rm d} x_1
\\
&\leq C u_1^{\gamma_1+{\varepsilon}}.
\end{align*}
$$
$$
\begin{align*}
\int_{\mathbb{R} } g_1(x_1,u_1) ^{\gamma_1+{\varepsilon}} {\rm d} x_1 &= \int_{\mathbb{R} } \bigg(
\int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]} {\rm e}^{-c_\mu \vert y_1 \vert } \mathrm{d}
y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&\leq 2 \int_{\mathbb{R}_+ } \bigg( \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]}
{\rm e}^{-c_\mu y_1} \mathrm{d} y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&\leq 2 \int_{\mathbb{R}_+ } \bigg( \int_{[x_1-{u_1}/{2}, x_1+{u_1}/{2}]}
{\rm e}^{-c_\mu ( x_1-{u_1}/{2}) } \mathrm{d} y_1 \bigg)^{\gamma_1+{\varepsilon}} \mathrm{d} x_1
\\
&= 2 {\rm e}^{c_\mu {u_1}({\gamma_1+{\varepsilon}})/{2}} u_1^{\gamma_1+{\varepsilon}}\int_{\mathbb{R}_+
} {\rm e}^{-c_\mu ({\gamma_1+{\varepsilon}}) x_1}{\rm d} x_1
\\
&\leq C u_1^{\gamma_1+{\varepsilon}}.
\end{align*}
$$
In the case of
![]() $u_1 \geq 1$
, we observe that
$u_1 \geq 1$
, we observe that
 $$
\begin{align*}
& \int_{\mathbb{R} } g_1(x_1,u_1) ^{\gamma_1-{\varepsilon}} {\rm d} x_1
\\
&\qquad\leq \int_{[-{u_1}/{2}, {u_1}/{2}]} \bigg( \int_{\mathbb{R}} {\rm e}^{-c_\mu
\vert y_1 \vert} {\rm d} y_1 \bigg)^{\gamma_1-{\varepsilon}} \mathrm{d} x_1 + 2
\int_{({u_1}/{2}, \infty )} g_1(x_1,u_1) ^{\gamma_1-{\varepsilon}} \mathrm{d} x_1
\\
&\qquad = \bigg( \frac{2}{c_\mu} \bigg) ^{\gamma_1-{\varepsilon}} u_1 +
\frac{2}{c_\mu^{\gamma_1-{\varepsilon}}} \int_{({u_1}/{2}, \infty )} ( {\rm e}^{-c_\mu
x_1} ( {\rm e}^{c_\mu {u_1}/{2}} - {\rm e}^{-c_\mu {u_1}/{2}} ) )^{\gamma_1-{\varepsilon}}
\mathrm{d} x_1
\\
&\qquad\leq C \bigg( u_1 + ( {\rm e}^{c_\mu {u_1}/{2}} - {\rm e}^{-c_\mu {u_1}/{2}}
)^{\gamma_1-{\varepsilon}} \frac{1}{c_\mu({\gamma_1-{\varepsilon}})} {\rm e}^{-c_\mu
({\gamma_1-{\varepsilon}}) {u_1}/{2}}\bigg)
\\
&\qquad\leq C ( u_1 + ( {\rm e}^{c_\mu {u_1}/{2}} )^{\gamma_1-{\varepsilon}} {\rm e}^{-c_\mu
({\gamma_1-{\varepsilon}}) {u_1}/{2}})
\\
&\qquad\leq C ( u_1 +1 )
\\
&\qquad\leq C u_1.
\end{align*}
$$
$$
\begin{align*}
& \int_{\mathbb{R} } g_1(x_1,u_1) ^{\gamma_1-{\varepsilon}} {\rm d} x_1
\\
&\qquad\leq \int_{[-{u_1}/{2}, {u_1}/{2}]} \bigg( \int_{\mathbb{R}} {\rm e}^{-c_\mu
\vert y_1 \vert} {\rm d} y_1 \bigg)^{\gamma_1-{\varepsilon}} \mathrm{d} x_1 + 2
\int_{({u_1}/{2}, \infty )} g_1(x_1,u_1) ^{\gamma_1-{\varepsilon}} \mathrm{d} x_1
\\
&\qquad = \bigg( \frac{2}{c_\mu} \bigg) ^{\gamma_1-{\varepsilon}} u_1 +
\frac{2}{c_\mu^{\gamma_1-{\varepsilon}}} \int_{({u_1}/{2}, \infty )} ( {\rm e}^{-c_\mu
x_1} ( {\rm e}^{c_\mu {u_1}/{2}} - {\rm e}^{-c_\mu {u_1}/{2}} ) )^{\gamma_1-{\varepsilon}}
\mathrm{d} x_1
\\
&\qquad\leq C \bigg( u_1 + ( {\rm e}^{c_\mu {u_1}/{2}} - {\rm e}^{-c_\mu {u_1}/{2}}
)^{\gamma_1-{\varepsilon}} \frac{1}{c_\mu({\gamma_1-{\varepsilon}})} {\rm e}^{-c_\mu
({\gamma_1-{\varepsilon}}) {u_1}/{2}}\bigg)
\\
&\qquad\leq C ( u_1 + ( {\rm e}^{c_\mu {u_1}/{2}} )^{\gamma_1-{\varepsilon}} {\rm e}^{-c_\mu
({\gamma_1-{\varepsilon}}) {u_1}/{2}})
\\
&\qquad\leq C ( u_1 +1 )
\\
&\qquad\leq C u_1.
\end{align*}
$$
Finally, we can split the integral in (3.7) into two parts following this case distinction and see that these are bounded by
respectively. Therefore, the existence of the compensated Poisson integral
![]() $J_L(\mu)$
for
$J_L(\mu)$
for
![]() $\mu \in \mathcal{M}_{L}$
is proven since the integral in (3.7) is finite. We note that in inequality (3.5) the particular exponent
$\mu \in \mathcal{M}_{L}$
is proven since the integral in (3.7) is finite. We note that in inequality (3.5) the particular exponent
![]() $\gamma_1-{\varepsilon}$
is not required for this proof and we could also replace
$\gamma_1-{\varepsilon}$
is not required for this proof and we could also replace
![]() $\gamma_1-{\varepsilon}$
by 1. However, we stick to the exponent
$\gamma_1-{\varepsilon}$
by 1. However, we stick to the exponent
![]() $\gamma_1-{\varepsilon}$
because we will need the estimates here for later purposes, for instance, in the proof of Theorem 2.4.
$\gamma_1-{\varepsilon}$
because we will need the estimates here for later purposes, for instance, in the proof of Theorem 2.4.
Since
 $f_\mu \in L^{\gamma_1}(\mathbb{R}^2)$
for
$f_\mu \in L^{\gamma_1}(\mathbb{R}^2)$
for
 $\mu \in \mathcal{M}_{P}$
, the random linear functional
$\mu \in \mathcal{M}_{P}$
, the random linear functional
 $S_{\gamma_1}(\mu)$
given in (2.9) is well defined. We refer the reader to Chapter 3 of [Reference Samorodnitsky and Taqqu27] for an extensive discussion.
$S_{\gamma_1}(\mu)$
given in (2.9) is well defined. We refer the reader to Chapter 3 of [Reference Samorodnitsky and Taqqu27] for an extensive discussion.We can deduce from the proof of Theorem 2.6 that the integral in (2.12) is finite and serves to construct the covariance function of a centred Gaussian linear random field X.
3.3 Further useful lemmas
We continue with some useful lemmas that we use in the proofs of the main results in Section 4. These new lemmas are inspired by Lemma 2.4 of [Reference Biermé, Estrade and Kaj4], and Lemmas 4 and 6 of [Reference Kaj, Leskelä, Norros and Schmidt18].
Lemma 3.2
Let F be a measure on
![]() $\mathbb{R}_+^2$
according to (1.1) and to the asymptotic behaviour specified there. Furthermore, let g be a continuous function on
$\mathbb{R}_+^2$
according to (1.1) and to the asymptotic behaviour specified there. Furthermore, let g be a continuous function on
![]() $\smash{\mathbb{R}_+^2}$
such that there is a constant
$\smash{\mathbb{R}_+^2}$
such that there is a constant
![]() $C>0$
for some
$C>0$
for some
![]() $\alpha_i>\gamma_i$
for
$\alpha_i>\gamma_i$
for
![]() $i=1,2$
such that
$i=1,2$
such that
for all
![]() $u \in \mathbb{R}_+^2$
. Then, we have, as
$u \in \mathbb{R}_+^2$
. Then, we have, as
![]() $\rho \to 0$
,
$\rho \to 0$
,
Proof. The idea of the proof is to split the integral
![]() $\smash{\int_{\mathbb{R}_+^2} g(u)
F_\rho(\mathrm{d} u)}$
into four parts and treat the four integrals separately.
$\smash{\int_{\mathbb{R}_+^2} g(u)
F_\rho(\mathrm{d} u)}$
into four parts and treat the four integrals separately.
Let
![]() ${\varepsilon}>0$
be given and define the constant
${\varepsilon}>0$
be given and define the constant
![]() $c_0$
by
$c_0$
by
where we note that
because of inequality (3.8) and that we have to treat the special case with
slightly differently. Therefore, we can assume that
![]() $c_0>0$
.
$c_0>0$
.
Choose
![]() $N=N({\varepsilon})$
such that, for all
$N=N({\varepsilon})$
such that, for all
![]() $u_i>N$
for
$u_i>N$
for
![]() $i=1,2,$
we have
$i=1,2,$
we have
and
which is feasible due to the power-law assumption on the measure F. We write
![]() $\mathbb{R}_+^2 = \smash{\bigcup_{k=1}^4 \Omega_k}$
with
$\mathbb{R}_+^2 = \smash{\bigcup_{k=1}^4 \Omega_k}$
with
From now on, we discuss the four corresponding integrals separately.
1. Using (3.11), we obtain
(3.13) $$
\begin{align}
& \bigg\vert \int_{\Omega_1} g(u) F_\rho(\mathrm{d} u) -
\rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} g(u) \frac{1}{u_1^{\gamma_1+1}}
\frac{1}{u_2^{\gamma_2+1}} {\rm d} u \bigg\vert \nonumber
\\
&\qquad\leq \int_{\Omega_1} \vert g(u) \vert \bigg\vert \kern2ptf_1\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} - \rho^{\gamma_1+\gamma_2}
\frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} \bigg\vert \mathrm{d} u
\nonumber
\\
&\qquad + \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2 \setminus \Omega_1}
\vert g(u) \vert \frac{ 1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}}
{\rm d} u \nonumber
\\
&\qquad\leq c_0 \frac{{\varepsilon}}{2} \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} \vert
g(u) \vert \frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} {\rm d} u
\nonumber
\\
&\qquad + \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2 \setminus \Omega_1}
\vert g(u) \vert \frac{ 1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}}
{\rm d} u \label{eqn26}\end{align}
$$
for small enough
$$
\begin{align}
& \bigg\vert \int_{\Omega_1} g(u) F_\rho(\mathrm{d} u) -
\rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} g(u) \frac{1}{u_1^{\gamma_1+1}}
\frac{1}{u_2^{\gamma_2+1}} {\rm d} u \bigg\vert \nonumber
\\
&\qquad\leq \int_{\Omega_1} \vert g(u) \vert \bigg\vert \kern2ptf_1\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} - \rho^{\gamma_1+\gamma_2}
\frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} \bigg\vert \mathrm{d} u
\nonumber
\\
&\qquad + \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2 \setminus \Omega_1}
\vert g(u) \vert \frac{ 1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}}
{\rm d} u \nonumber
\\
&\qquad\leq c_0 \frac{{\varepsilon}}{2} \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} \vert
g(u) \vert \frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} {\rm d} u
\nonumber
\\
&\qquad + \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2 \setminus \Omega_1}
\vert g(u) \vert \frac{ 1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}}
{\rm d} u \label{eqn26}\end{align}
$$
for small enough $$
\begin{align}
&\qquad\leq c_0 {\varepsilon} \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} \vert g(u) \vert
\frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} {\rm d} u \nonumber
\end{align}
$$
$$
\begin{align}
&\qquad\leq c_0 {\varepsilon} \rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} \vert g(u) \vert
\frac{1}{u_1^{\gamma_1+1}} \frac{1}{u_2^{\gamma_2+1}} {\rm d} u \nonumber
\end{align}
$$
 $\rho$
, where we also used the fact that the integral in (3.13) converges to zero by the dominated convergence theorem. Hence, we can deduce together with the definition of
$\rho$
, where we also used the fact that the integral in (3.13) converges to zero by the dominated convergence theorem. Hence, we can deduce together with the definition of
 $c_0$
in (3.9) that there exists some
$c_0$
in (3.9) that there exists some
 $\rho_1 > 0$
such that, for all
$\rho_1 > 0$
such that, for all
 $\rho < \rho_1,$
we obtain
$\rho < \rho_1,$
we obtain  $$
\begin{equation*}
\bigg\vert\frac{ \int_{\Omega_1} g(u) F_\rho(\mathrm{d}
u)}{\rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} g(u) (1/u_1^{\gamma_1+1})(1/u_2^{\gamma_2+1}) {\rm d} u} -1\bigg\vert \leq {\varepsilon}.
\end{equation*}
$$
$$
\begin{equation*}
\bigg\vert\frac{ \int_{\Omega_1} g(u) F_\rho(\mathrm{d}
u)}{\rho^{\gamma_1+\gamma_2} \int_{\mathbb{R}_+^2} g(u) (1/u_1^{\gamma_1+1})(1/u_2^{\gamma_2+1}) {\rm d} u} -1\bigg\vert \leq {\varepsilon}.
\end{equation*}
$$
2. We show that
 $\smash{\vert \int_{\Omega_2} g(u) F_\rho(\mathrm{d} u) \vert} =
o(\rho^{\gamma_1+\gamma_2}).$
Indeed, using (3.8), we obtain where we recall that
$\smash{\vert \int_{\Omega_2} g(u) F_\rho(\mathrm{d} u) \vert} =
o(\rho^{\gamma_1+\gamma_2}).$
Indeed, using (3.8), we obtain where we recall that $$
\begin{align*}
\bigg\vert \int_{\Omega_2} g(u) F_\rho(\mathrm{d} u) \bigg\vert & \leq C
\int_0^{\rho N} \int_0^{\rho N} u_1^{\alpha_1} u_2^{\alpha_2}
f_1\bigg(\frac{u_1}{\rho} \bigg)
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho^2} {\rm d} u_1 {\rm d} u_2
\\
&= C \rho^{\alpha_1+\alpha_2} \int_0^N \int_0^N u_1^{\alpha_1}
u_2^{\alpha_2} f_1(u_1)f_2(u_2) {\rm d} u_1 {\rm d} u_2
\\
&\leq C \rho^{\alpha_1+\alpha_2} N^{\alpha_1+\alpha_2},
\end{align*}
$$
$$
\begin{align*}
\bigg\vert \int_{\Omega_2} g(u) F_\rho(\mathrm{d} u) \bigg\vert & \leq C
\int_0^{\rho N} \int_0^{\rho N} u_1^{\alpha_1} u_2^{\alpha_2}
f_1\bigg(\frac{u_1}{\rho} \bigg)
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho^2} {\rm d} u_1 {\rm d} u_2
\\
&= C \rho^{\alpha_1+\alpha_2} \int_0^N \int_0^N u_1^{\alpha_1}
u_2^{\alpha_2} f_1(u_1)f_2(u_2) {\rm d} u_1 {\rm d} u_2
\\
&\leq C \rho^{\alpha_1+\alpha_2} N^{\alpha_1+\alpha_2},
\end{align*}
$$
 $ \smash{\int_0^\infty \int_0^\infty
f_1(u_1)f_2(u_2) {\rm d} u_1 {\rm d} u_2}=1$
according to (1.1) and the assumption that
$ \smash{\int_0^\infty \int_0^\infty
f_1(u_1)f_2(u_2) {\rm d} u_1 {\rm d} u_2}=1$
according to (1.1) and the assumption that
 $c_F=1$
there. Since
$c_F=1$
there. Since
 $\alpha_1+\alpha_2 >
\gamma_1+\gamma_2$
, the assertion of 2 follows upon
$\alpha_1+\alpha_2 >
\gamma_1+\gamma_2$
, the assertion of 2 follows upon
 $\rho \to 0$
.
$\rho \to 0$
.3. We show that
 $\smash{\vert \int_{\Omega_3} g(u) F_\rho(\mathrm{d} u) \vert }=
o(\rho^{\gamma_1+\gamma_2}).$
We obtain, for N satisfying (3.10), for sufficiently small
$\smash{\vert \int_{\Omega_3} g(u) F_\rho(\mathrm{d} u) \vert }=
o(\rho^{\gamma_1+\gamma_2}).$
We obtain, for N satisfying (3.10), for sufficiently small $$
\begin{align*}
\bigg\vert \int_{\Omega_3} g(u) F_\rho(\mathrm{d} u) \bigg\vert & \leq
\int_{\rho N}^\infty \int_0^{\rho N} \vert g(u) \vert \kern2ptf_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_2 f_1
\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho} {\rm d} u_1
\\
&\leq C \int_{\rho N}^\infty \int_0^{\rho N} \min(u_1,u_1^{\alpha_1} )
\min(u_2,u_2^{\alpha_2} ) f_2 \bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho}
{\rm d} u_2 \frac{\rho^{\gamma_1}}{u_1^{\gamma_1+1}} {\rm d} u_1
\\
&\leq C \rho^{\gamma_1} \int_{\rho N}^\infty \min(u_1,u_1^{\alpha_1})
\frac{1}{u_1^{\gamma_1+1}} {\rm d} u_1 \int_0^{\rho N} u_2^{\alpha_2}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_2
\\
& = C \rho^{\gamma_1} \rho^{\alpha_2} \int_0^{N} u_2^{\alpha_2} f_2(u_2)
{\rm d} u_2
\\
&\leq C \rho^{\gamma_1+\alpha_2} N^{\alpha_2}
\\
&\leq {\varepsilon} \rho^{\gamma_1+\gamma_2}
\end{align*}
$$
$$
\begin{align*}
\bigg\vert \int_{\Omega_3} g(u) F_\rho(\mathrm{d} u) \bigg\vert & \leq
\int_{\rho N}^\infty \int_0^{\rho N} \vert g(u) \vert \kern2ptf_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_2 f_1
\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho} {\rm d} u_1
\\
&\leq C \int_{\rho N}^\infty \int_0^{\rho N} \min(u_1,u_1^{\alpha_1} )
\min(u_2,u_2^{\alpha_2} ) f_2 \bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho}
{\rm d} u_2 \frac{\rho^{\gamma_1}}{u_1^{\gamma_1+1}} {\rm d} u_1
\\
&\leq C \rho^{\gamma_1} \int_{\rho N}^\infty \min(u_1,u_1^{\alpha_1})
\frac{1}{u_1^{\gamma_1+1}} {\rm d} u_1 \int_0^{\rho N} u_2^{\alpha_2}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_2
\\
& = C \rho^{\gamma_1} \rho^{\alpha_2} \int_0^{N} u_2^{\alpha_2} f_2(u_2)
{\rm d} u_2
\\
&\leq C \rho^{\gamma_1+\alpha_2} N^{\alpha_2}
\\
&\leq {\varepsilon} \rho^{\gamma_1+\gamma_2}
\end{align*}
$$
 $\rho$
since
$\rho$
since
 $\gamma_1+\alpha_2 >
\gamma_1+\gamma_2$
.
$\gamma_1+\alpha_2 >
\gamma_1+\gamma_2$
.4. Proceeding analogously to 3, we show that
 $\smash{\vert \int_{\Omega_4}
g(u) F_\rho(\mathrm{d} u) \vert} = o(\rho^{\gamma_1+\gamma_2}).$
$\smash{\vert \int_{\Omega_4}
g(u) F_\rho(\mathrm{d} u) \vert} = o(\rho^{\gamma_1+\gamma_2}).$
Finally, we are able to deduce the assertion of the lemma using the results from the four parts above.
The following lemma is also inspired by Lemma 2.4 of [Reference Biermé, Estrade and Kaj4].
Lemma 3.3
Let F be a measure on
![]() $\smash{\mathbb{R}_+^2}$
according to (1.1) and to the asymptotic behaviour specified there. Furthermore, let
$\smash{\mathbb{R}_+^2}$
according to (1.1) and to the asymptotic behaviour specified there. Furthermore, let
![]() $( g_\rho
)$
be a family of continuous functions on
$( g_\rho
)$
be a family of continuous functions on
![]() $\smash{\mathbb{R}_+^2}$
with
$\smash{\mathbb{R}_+^2}$
with
for all
![]() $u \in \mathbb{R}_+^2$
and
$u \in \mathbb{R}_+^2$
and
for some constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha_i>\gamma_i$
for
$\alpha_i>\gamma_i$
for
![]() $i=1,2$
for all
$i=1,2$
for all
![]() $u
\in \smash{\mathbb{R}_+^2}$
. Then, we have
$u
\in \smash{\mathbb{R}_+^2}$
. Then, we have
Proof. The assumptions on
![]() $g_\rho$
ensure that, for all
$g_\rho$
ensure that, for all
![]() $\rho >0$
,
$\rho >0$
,
that there is an integrable majorant, and that we obtain
by the dominated convergence theorem.
Due to the power-law assumption on F, we can choose
![]() $N>0$
such that, for all
$N>0$
such that, for all
![]() $u_i>N$
for
$u_i>N$
for
![]() $i=1,2,$
we have
$i=1,2,$
we have
We use the same definition of the domains
![]() $\Omega_k$
for
$\Omega_k$
for
![]() $k=1,\ldots,4$
as in (3.12) and continue discussing the corresponding four integrals separately. First, using (3.16), we obtain
$k=1,\ldots,4$
as in (3.12) and continue discussing the corresponding four integrals separately. First, using (3.16), we obtain
 $$
\begin{align*}
\bigg\vert \int_{\Omega_1} g_\rho(u) F_\rho(\mathrm{d} u) \bigg\vert &\leq
\int_{\rho N}^\infty \int_{\rho N}^\infty \vert g_\rho(u) \vert \kern2ptf_1
\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_1 {\rm d} u_2
\\
&\leq \int_{0}^\infty \int_{0}^\infty \rho^{\gamma_1+\gamma_2} \vert
g_\rho(u) \vert\frac{2}{u_1^{\gamma_1+1}} \frac{2}{u_2^{\gamma_2+1}} {\rm d}
u_1 {\rm d} u_2.
\end{align*}
$$
$$
\begin{align*}
\bigg\vert \int_{\Omega_1} g_\rho(u) F_\rho(\mathrm{d} u) \bigg\vert &\leq
\int_{\rho N}^\infty \int_{\rho N}^\infty \vert g_\rho(u) \vert \kern2ptf_1
\bigg(\frac{u_1}{\rho}\bigg) \frac{1}{\rho}
f_2\bigg(\frac{u_2}{\rho}\bigg)\frac{1}{\rho} {\rm d} u_1 {\rm d} u_2
\\
&\leq \int_{0}^\infty \int_{0}^\infty \rho^{\gamma_1+\gamma_2} \vert
g_\rho(u) \vert\frac{2}{u_1^{\gamma_1+1}} \frac{2}{u_2^{\gamma_2+1}} {\rm d}
u_1 {\rm d} u_2.
\end{align*}
$$
Therefore, we obtain, together with (3.15),
Using the second assumption on
![]() $g_\rho$
and (3.16), we can check that
$g_\rho$
and (3.16), we can check that
as
![]() $\rho \to 0$
for
$\rho \to 0$
for
![]() $k=2,3,4$
by proceeding analogously to the corresponding parts in the proof of Lemma 3.2. Combining all four partial results, we can deduce (3.14).
$k=2,3,4$
by proceeding analogously to the corresponding parts in the proof of Lemma 3.2. Combining all four partial results, we can deduce (3.14).
We introduce for a signed measure
![]() $\mu \in \mathcal{M}_{k}$
for
$\mu \in \mathcal{M}_{k}$
for
![]() $k \in
\{L,P\}$
the local averages
$k \in
\{L,P\}$
the local averages
![]() $m_\mu(x,u)$
by
$m_\mu(x,u)$
by
and the maximal function
![]() $m_\mu^*$
by
$m_\mu^*$
by
Similar to Lemma 4 of [Reference Kaj, Leskelä, Norros and Schmidt18], we obtain the following facts.
Lemma 3.4
Let
![]() $n_i(\rho) \to 0$
as
$n_i(\rho) \to 0$
as
![]() $\rho \to 0$
for
$\rho \to 0$
for
![]() $i=1,2$
.
$i=1,2$
.
(i) For
 $\mu \in \mathcal{M}_{P}$
, we have
$\mu \in \mathcal{M}_{P}$
, we have  $$
\begin{equation*}
\lim_{\rho \to 0} m_\mu \bigg( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2}
\bigg)= f_\mu(x) \quad \text{for all $(x,u) \in \mathbb{R}^2 \times \mathbb{R}_+^2$.}
\end{equation*}
$$
$$
\begin{equation*}
\lim_{\rho \to 0} m_\mu \bigg( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2}
\bigg)= f_\mu(x) \quad \text{for all $(x,u) \in \mathbb{R}^2 \times \mathbb{R}_+^2$.}
\end{equation*}
$$
(ii) Let
 $\beta>1$
. For
$\beta>1$
. For
 $\mu \in \mathcal{M}_{k}$
for
$\mu \in \mathcal{M}_{k}$
for
 $k \in \{L,P\}$
, there is a function
$k \in \{L,P\}$
, there is a function
 $g \in L^\beta(\mathbb{R}^2)$
such that
$g \in L^\beta(\mathbb{R}^2)$
such that
 $m_\mu^*(x) \leq g(x)$
for all
$m_\mu^*(x) \leq g(x)$
for all
 $x \in \mathbb{R}^2$
.
$x \in \mathbb{R}^2$
.
Proof. (i) The assertion is true because the function
![]() $f_\mu$
is continuous and because there exists, for all
$f_\mu$
is continuous and because there exists, for all
![]() $\delta>0,$
some small enough
$\delta>0,$
some small enough
![]() $\rho_0>0$
such that the set
$\rho_0>0$
such that the set
![]() $\smash{B ( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2} )}$
is contained in the
$\smash{B ( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2} )}$
is contained in the
![]() $\ell^\infty$
-ball with centre x and radius
$\ell^\infty$
-ball with centre x and radius
![]() $\delta$
for all
$\delta$
for all
![]() $\rho<\rho_0$
.
$\rho<\rho_0$
.
(ii) We only require assumption (2.4) on
![]() $\mu \in \mathcal{M}_{k}$
for
$\mu \in \mathcal{M}_{k}$
for
![]() $k \in \{L,P\}$
. We obtain
$k \in \{L,P\}$
. We obtain
 $$
\begin{align}
m_\mu^*(x) &\leq C_\mu \sup_{u \in \mathbb{R}^2_+} \frac{1}{u_1 u_2}
\int_{B(x,u)} {\rm e}^{-c_\mu \vert y_1 \vert} {\rm e}^{-c_\mu \vert y_2 \vert}
{\rm d} y \nonumber
\\
&= C_\mu \prod_{i=1,2} \sup_{u_i \in \mathbb{R}_+} \frac{1}{u_i}
\int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i \vert} {\rm d}
y_i,
\label{eqn32}\end{align}
$$
$$
\begin{align}
m_\mu^*(x) &\leq C_\mu \sup_{u \in \mathbb{R}^2_+} \frac{1}{u_1 u_2}
\int_{B(x,u)} {\rm e}^{-c_\mu \vert y_1 \vert} {\rm e}^{-c_\mu \vert y_2 \vert}
{\rm d} y \nonumber
\\
&= C_\mu \prod_{i=1,2} \sup_{u_i \in \mathbb{R}_+} \frac{1}{u_i}
\int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i \vert} {\rm d}
y_i,
\label{eqn32}\end{align}
$$
and study the supremum in (3.19) by a case distinction. Let
![]() $x_i>0$
. We estimate
$x_i>0$
. We estimate
 $$
\begin{align*}
& \sup_{u_i >0} \frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]}
{\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i
\\
&\qquad\leq \sup_{0< {u_i}/{2} \leq x_i} \frac{1}{u_i} \int_{[x_i-{u_i}/{2},
x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i + \sup_{{u_i}/{2}
\geq x_i} \frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]}
{\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i,
\end{align*}
$$
$$
\begin{align*}
& \sup_{u_i >0} \frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]}
{\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i
\\
&\qquad\leq \sup_{0< {u_i}/{2} \leq x_i} \frac{1}{u_i} \int_{[x_i-{u_i}/{2},
x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i + \sup_{{u_i}/{2}
\geq x_i} \frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]}
{\rm e}^{-c_\mu\vert y_i \vert} {\rm d} y_i,
\end{align*}
$$
and treat the two terms in the last line separately. For
![]() $0<
{u_i}/{2}\leq x_i$
, we obtain
$0<
{u_i}/{2}\leq x_i$
, we obtain
 $$
\begin{align}
\frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i
\vert} \mathrm{d} y_i &= \frac{1}{u_i} \frac{1}{c_\mu} ( {\rm e}^{-c_\mu(x_i -
{u_i}/{2})} - {\rm e}^{-c_\mu (x_i + {u_i}/{2})} ) \nonumber
\\
&= \frac{{\rm e}^{-c_\mu x_i}}{c_\mu} \frac{{\rm e}^{{c_\mu u_i}/{2}} -
{\rm e}^{-{c_\mu u_i}/{2}}}{u_i} \nonumber
\\
&\leq \frac{{\rm e}^{-c_\mu x_i}}{c_\mu} \frac{{\rm e}^{c_\mu x_i} - {\rm e}^{-c_\mu
x_i}}{2x_i} \label{eqn33}\end{align}
$$
$$
\begin{align}
\frac{1}{u_i} \int_{[x_i-{u_i}/{2}, x_i+{u_i}/{2}]} {\rm e}^{-c_\mu\vert y_i
\vert} \mathrm{d} y_i &= \frac{1}{u_i} \frac{1}{c_\mu} ( {\rm e}^{-c_\mu(x_i -
{u_i}/{2})} - {\rm e}^{-c_\mu (x_i + {u_i}/{2})} ) \nonumber
\\
&= \frac{{\rm e}^{-c_\mu x_i}}{c_\mu} \frac{{\rm e}^{{c_\mu u_i}/{2}} -
{\rm e}^{-{c_\mu u_i}/{2}}}{u_i} \nonumber
\\
&\leq \frac{{\rm e}^{-c_\mu x_i}}{c_\mu} \frac{{\rm e}^{c_\mu x_i} - {\rm e}^{-c_\mu
x_i}}{2x_i} \label{eqn33}\end{align}
$$
where we used the fact that the function
is increasing for
![]() $u_i\geq 0$
in (3.20). This can be seen by
$u_i\geq 0$
in (3.20). This can be seen by
because the last term is increasing in
![]() $u_i$
. For
$u_i$
. For
![]() ${u_i}/{2} \geq x_i$
, we observe that
${u_i}/{2} \geq x_i$
, we observe that
Combining the estimates, we obtain
The corresponding estimate with
![]() $\vert x_i \vert$
for
$\vert x_i \vert$
for
![]() $x_i<0$
follows directly because of symmetry. Furthermore, we can bound the supremum in (3.19) by
$x_i<0$
follows directly because of symmetry. Furthermore, we can bound the supremum in (3.19) by
Hence, we are able to conclude that
![]() $m_\mu^*(x) \leq g(x)$
for all
$m_\mu^*(x) \leq g(x)$
for all
![]() $x \in
\mathbb{R}^2$
, where g is defined by
$x \in
\mathbb{R}^2$
, where g is defined by
and we see that
![]() $g^\beta$
is integrable with respect to x for any
$g^\beta$
is integrable with respect to x for any
![]() $\beta>1$
.
$\beta>1$
.
Remark 3.4. We briefly point out why the continuity condition of the density function
![]() $f_\mu$
is essential in the point scaling regime, in particular in Lemma 3.4(i). If the boxes
$f_\mu$
is essential in the point scaling regime, in particular in Lemma 3.4(i). If the boxes
![]() $B( x, \binom{n_1(\rho)
u_1}{n_2(\rho) u_2} )$
had been nicely shrinking sets in the sense of [Reference Rudin26, p. 140], the condition
$B( x, \binom{n_1(\rho)
u_1}{n_2(\rho) u_2} )$
had been nicely shrinking sets in the sense of [Reference Rudin26, p. 140], the condition
![]() $f_\mu \in L^1(\mathbb{R}^2)$
would have been sufficient instead of requiring continuity (see Theorem 7.10 of [Reference Rudin26]). In short, the crucial point for shrinking sets in order to be a sequence of nicely shrinking sets is that each set must occupy at least a certain portion of some spherical neighbourhood. For example, a shrinking grain in the random balls model, where the size of a grain (with predetermined shape) depends only on a single distribution, is nicely shrinking. In contrast, the boxes
$f_\mu \in L^1(\mathbb{R}^2)$
would have been sufficient instead of requiring continuity (see Theorem 7.10 of [Reference Rudin26]). In short, the crucial point for shrinking sets in order to be a sequence of nicely shrinking sets is that each set must occupy at least a certain portion of some spherical neighbourhood. For example, a shrinking grain in the random balls model, where the size of a grain (with predetermined shape) depends only on a single distribution, is nicely shrinking. In contrast, the boxes
![]() $B( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2} )$
in the proof of Theorem 2.5, where we apply Lemma 3.4(i), are not nicely shrinking sets because the length-to-width ratio of the boxes tends to infinity there. Hence, we assume in Definition 2.3 that the density function
$B( x, \binom{n_1(\rho) u_1}{n_2(\rho) u_2} )$
in the proof of Theorem 2.5, where we apply Lemma 3.4(i), are not nicely shrinking sets because the length-to-width ratio of the boxes tends to infinity there. Hence, we assume in Definition 2.3 that the density function
![]() $f_\mu$
is continuous such that Lemma 3.4(i) holds.
$f_\mu$
is continuous such that Lemma 3.4(i) holds.
Lemma 3.5. For each
![]() $\mu \in \mathcal{M}_2$
, the functions
$\mu \in \mathcal{M}_2$
, the functions
are continuous on
![]() $\mathbb{R}_+^2$
.
$\mathbb{R}_+^2$
.
Proof. The idea and the steps of the proof are identical to those in the proof of Lemma 6 of [Reference Kaj, Leskelä, Norros and Schmidt18]. Therefore, we only point out the difference. We start to proceed as there and then obtain
for
![]() $u,v \in \smash{\mathbb{R}_+^2}$
, where
$u,v \in \smash{\mathbb{R}_+^2}$
, where
![]() $B(0,u) \triangle B(0,v)$
denotes the symmetric difference of the sets B(0,u) and B(0,v). Since the sets are just rectangles, we can deduce that
$B(0,u) \triangle B(0,v)$
denotes the symmetric difference of the sets B(0,u) and B(0,v). Since the sets are just rectangles, we can deduce that
![]() $\lim_{u \to v} d(u,v) = 0 $
for all
$\lim_{u \to v} d(u,v) = 0 $
for all
![]() $v \in \smash{\mathbb{R}_+^2}$
and complete the proof together with the other parts.
$v \in \smash{\mathbb{R}_+^2}$
and complete the proof together with the other parts.
4. Proofs of the main results
Due to the linearity of the mapping
![]() $\mu \mapsto
\smash{\skew5\widetilde{J}_\rho(\mu)}$
as well as the linearity of the limiting random fields Z,
$\mu \mapsto
\smash{\skew5\widetilde{J}_\rho(\mu)}$
as well as the linearity of the limiting random fields Z,
![]() $J_I$
, Y,
$J_I$
, Y,
![]() $J_L$
,
$J_L$
,
![]() $S_{\gamma_1},$
and X, the convergence of the finite-dimensional distributions of the centred and renormalised versions of
$S_{\gamma_1},$
and X, the convergence of the finite-dimensional distributions of the centred and renormalised versions of
![]() ${J}_\rho$
is equivalent to the convergence of the one-dimensional distributions. This can be seen using the Cramér–Wold device. Therefore, we have to only deal with the convergence of the characteristic function (without loss of generality at 1)
${J}_\rho$
is equivalent to the convergence of the one-dimensional distributions. This can be seen using the Cramér–Wold device. Therefore, we have to only deal with the convergence of the characteristic function (without loss of generality at 1)
![]() $\mathbb{E} \exp({\rm i}{\,\smash{\skew5\widetilde{J}_\rho(\mu)}}/{n_\rho}).$
The strategy of the following proofs is similar to [Reference Biermé, Estrade and Kaj4] and [Reference Kaj, Leskelä, Norros and Schmidt18]. As mentioned above, we use c and C for constants which can differ from line to line and we often make use of the function
$\mathbb{E} \exp({\rm i}{\,\smash{\skew5\widetilde{J}_\rho(\mu)}}/{n_\rho}).$
The strategy of the following proofs is similar to [Reference Biermé, Estrade and Kaj4] and [Reference Kaj, Leskelä, Norros and Schmidt18]. As mentioned above, we use c and C for constants which can differ from line to line and we often make use of the function
![]() $\Psi$
defined in (3.1).
$\Psi$
defined in (3.1).
4.1 Intermediate-intensity regime
Proof of Theorem 2.2. We recall the characteristic function of
![]() $\smash{\skew5\widetilde{J}_\rho(\mu)}$
:
$\smash{\skew5\widetilde{J}_\rho(\mu)}$
:
The characteristic function of
![]() $J_I(\mu)$
is given by
$J_I(\mu)$
is given by
First, we define the function
![]() $\widetilde{\varphi}$
by
$\widetilde{\varphi}$
by
We note that
![]() $\widetilde{\varphi}$
is continuous due to Lemma 3.5. Using
$\widetilde{\varphi}$
is continuous due to Lemma 3.5. Using
![]() $\vert \Psi(v) \vert \leq {v^2}/{2}$
and (2.1), there are constants
$\vert \Psi(v) \vert \leq {v^2}/{2}$
and (2.1), there are constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha_i$
with
$\alpha_i$
with
![]() $\gamma_i < \alpha_i \leq 2$
for
$\gamma_i < \alpha_i \leq 2$
for
![]() $i=1,2$
such that
$i=1,2$
such that
Now, we apply Lemma 3.2 with
![]() $g\,:\!= \widetilde{\varphi}$
to obtain
$g\,:\!= \widetilde{\varphi}$
to obtain
Using this and the scaling
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
shows the assertion.
$\lambda_\rho \rho^{\gamma_1+\gamma_2} \to 1$
shows the assertion.
Remark 4.1. In the general case, let us say
![]() $\lambda_\rho \rho^{\gamma_1+\gamma_2}
\to a^{2-\gamma_1-\gamma_2} \in (0,\infty)$
with
$\lambda_\rho \rho^{\gamma_1+\gamma_2}
\to a^{2-\gamma_1-\gamma_2} \in (0,\infty)$
with
![]() $a>0$
as
$a>0$
as
![]() $\rho \to 0$
, the limiting compensated Poisson integral equals
$\rho \to 0$
, the limiting compensated Poisson integral equals
![]() $J_I(\mu_a)$
, where
$J_I(\mu_a)$
, where
![]() $\mu_a(\cdot)\,:\!= \mu(a^{-1} \, \cdot)$
. In order to see this, we can apply Theorem 2.2 to
$\mu_a(\cdot)\,:\!= \mu(a^{-1} \, \cdot)$
. In order to see this, we can apply Theorem 2.2 to
![]() $\smash{\skew5\widetilde{J}'_\rho(\cdot)}$
where
$\smash{\skew5\widetilde{J}'_\rho(\cdot)}$
where
![]() $\lambda'_\rho\,:\!= \lambda_\rho / a^{2-\gamma_1-\gamma_2}$
. Then the result follows after an appropriate substitution.
$\lambda'_\rho\,:\!= \lambda_\rho / a^{2-\gamma_1-\gamma_2}$
. Then the result follows after an appropriate substitution.
4.2. High-intensity regime
Proof of Theorem 2.1. For the sake of simplicity, we introduce
with
![]() $n_\rho\,:\!= \smash{\sqrt{\lambda_\rho \rho^{\gamma_1+\gamma_2}}}$
and recall that the characteristic function of
$n_\rho\,:\!= \smash{\sqrt{\lambda_\rho \rho^{\gamma_1+\gamma_2}}}$
and recall that the characteristic function of
![]() ${\skew5\widetilde{J}_\rho(\mu)}
/{n_\rho}$
is given by
${\skew5\widetilde{J}_\rho(\mu)}
/{n_\rho}$
is given by
The goal is to show the convergence of this characteristic function to
which corresponds to a centred Gaussian random variable. The covariance function given in (2.2) can then be obtained by the linearity of Z.
Since, by assumption,
![]() $n_\rho \to \infty$
as
$n_\rho \to \infty$
as
![]() $\rho \to 0$
, we know that
$\rho \to 0$
, we know that
![]() $\Psi({\mu(B(x,u))}/{n_\rho} ) $
can be approximated by
$\Psi({\mu(B(x,u))}/{n_\rho} ) $
can be approximated by
![]() $\smash{-\tfrac{1}{2}} ({\mu(B(x,u))}/{n_\rho} )^2.$
To be more precise, we write
$\smash{-\tfrac{1}{2}} ({\mu(B(x,u))}/{n_\rho} )^2.$
To be more precise, we write
where
![]() $\varphi$
is given in (3.2) and
$\varphi$
is given in (3.2) and
Using Lemma 3.2 together with (2.1), the first integral on the right-hand side of (4.1) converges to
Here, we again refer to Lemma 3.5 for the continuity of
![]() $\varphi$
.
$\varphi$
.
It remains to show that the second integral on the right-hand side of (4.1) converges to zero. For this purpose, we show that
![]() $\Delta_\rho$
satisfies the assumptions on
$\Delta_\rho$
satisfies the assumptions on
![]() $g_\rho$
in Lemma 3.3.
$g_\rho$
in Lemma 3.3.
First, we can show that the estimates
![]() $\vert \Psi(v) + {v^2}/{2}\vert
\leq \vert v \vert ^3$
and
$\vert \Psi(v) + {v^2}/{2}\vert
\leq \vert v \vert ^3$
and
hold. Therefore, we obtain
as
![]() $\rho \to 0$
, which shows that the first assumption of Lemma 3.3 is satisfied. Using
$\rho \to 0$
, which shows that the first assumption of Lemma 3.3 is satisfied. Using
![]() $\vert \Psi(v)\vert \leq
{v^2}/{2}$
and (2.1), the second assumption is also satisfied because we obtain
$\vert \Psi(v)\vert \leq
{v^2}/{2}$
and (2.1), the second assumption is also satisfied because we obtain
 $$
\begin{align*}
\rho^{\gamma_1+\gamma_2}\vert \Delta_\rho(u) \vert &=
\bigg\vert\frac{n_\rho^2}{\lambda_\rho} \Delta_\rho(u) \bigg\vert
\\
&\leq n_\rho^2 \int_{\mathbb{R}^2}\bigg( \bigg\vert
\Psi\bigg(\frac{\mu(B(x,u))}{n_\rho} \bigg) \bigg\vert+ \frac{1}{2}
\bigg( \frac{\mu(B(x,u))}{n_\rho} \bigg)^2 \bigg) {\rm d} x
\\
&\leq n_\rho^2 \int_{\mathbb{R}^2} \bigg( \frac{\mu(B(x,u))}{n_\rho} \bigg)^2 {\rm d}
x
\\
&= \int_{\mathbb{R}^2} \mu(B(x,u))^2 {\rm d} x
\\
& \leq C \min(u_1,u_1^{\alpha_1} ) \min(u_2,u_2^{\alpha_2}
).\tag*{\qedhere}
\end{align*}
$$
$$
\begin{align*}
\rho^{\gamma_1+\gamma_2}\vert \Delta_\rho(u) \vert &=
\bigg\vert\frac{n_\rho^2}{\lambda_\rho} \Delta_\rho(u) \bigg\vert
\\
&\leq n_\rho^2 \int_{\mathbb{R}^2}\bigg( \bigg\vert
\Psi\bigg(\frac{\mu(B(x,u))}{n_\rho} \bigg) \bigg\vert+ \frac{1}{2}
\bigg( \frac{\mu(B(x,u))}{n_\rho} \bigg)^2 \bigg) {\rm d} x
\\
&\leq n_\rho^2 \int_{\mathbb{R}^2} \bigg( \frac{\mu(B(x,u))}{n_\rho} \bigg)^2 {\rm d}
x
\\
&= \int_{\mathbb{R}^2} \mu(B(x,u))^2 {\rm d} x
\\
& \leq C \min(u_1,u_1^{\alpha_1} ) \min(u_2,u_2^{\alpha_2}
).\tag*{\qedhere}
\end{align*}
$$
4.3. Low-intensity regime
4.3.1 Points scaling regime
Proof of Theorem 2.5. In a first step, we prove that
where
![]() $c_2$
is defined in (4.4) below. In a second step, we show that the right-hand side is the characteristic function of an integral with respect to a stable random measure.
$c_2$
is defined in (4.4) below. In a second step, we show that the right-hand side is the characteristic function of an integral with respect to a stable random measure.
Step 1. We recall that the characteristic function of
 $\,{\skew5\widetilde{J}}_\rho(\mu) / (\lambda_\rho^{{1}/{\gamma_1}}\rho^2)$
can be written as (4.2)We use the definition of
$\,{\skew5\widetilde{J}}_\rho(\mu) / (\lambda_\rho^{{1}/{\gamma_1}}\rho^2)$
can be written as (4.2)We use the definition of $$
\begin{equation}
\exp \bigg( \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y) {\rm d}
y\bigg) \lambda_\rho {\rm d} x\ F_\rho(\mathrm{d} u) \bigg).
\label{eqn35}
\end{equation}
$$
$$
\begin{equation}
\exp \bigg( \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y) {\rm d}
y\bigg) \lambda_\rho {\rm d} x\ F_\rho(\mathrm{d} u) \bigg).
\label{eqn35}
\end{equation}
$$
 $m_\mu(x,u)$
in (3.17) and the density of the scaled measure F from (1.1) to obtain (4.3)where we substituted first
$m_\mu(x,u)$
in (3.17) and the density of the scaled measure F from (1.1) to obtain (4.3)where we substituted first $$
\begin{align}
& \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y)
\mathrm{d} y\bigg) \lambda_\rho {\rm d} x\ F_\rho(\mathrm{d} u) \nonumber
\\
&\qquad= \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{u_1
u_2}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} m_\mu(x,u) \bigg) \lambda_\rho
f_1 \bigg( \frac{u_1}{\rho}\bigg) \frac{1}{\rho} f_2 \bigg(
\frac{u_2}{\rho}\bigg) \frac{1}{\rho} {\rm d} x {\rm d} u \nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_1 m_\mu \bigg
(x,\binom{\lambda_\rho^{{1}/{\gamma_1}}\rho {u_1}/ {u_2}}{\rho u_2}
\bigg) \bigg) \frac{ \lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg)\ f_2(u_2) {\rm d} x {\rm d}
u,
\label{eqn36}\end{align}
$$
$$
\begin{align}
& \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y)
\mathrm{d} y\bigg) \lambda_\rho {\rm d} x\ F_\rho(\mathrm{d} u) \nonumber
\\
&\qquad= \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{u_1
u_2}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} m_\mu(x,u) \bigg) \lambda_\rho
f_1 \bigg( \frac{u_1}{\rho}\bigg) \frac{1}{\rho} f_2 \bigg(
\frac{u_2}{\rho}\bigg) \frac{1}{\rho} {\rm d} x {\rm d} u \nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_1 m_\mu \bigg
(x,\binom{\lambda_\rho^{{1}/{\gamma_1}}\rho {u_1}/ {u_2}}{\rho u_2}
\bigg) \bigg) \frac{ \lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg)\ f_2(u_2) {\rm d} x {\rm d}
u,
\label{eqn36}\end{align}
$$
 $u_2 = \rho \widetilde{u}_2$
and then
$u_2 = \rho \widetilde{u}_2$
and then
 $u_1 =
\smash{{\lambda_\rho^{{1}/{\gamma_1}} \rho}
{\widetilde{u}_1}/{\widetilde{u}_2}}$
in the last line. We note that because of Lemma 3.4(i) and that
$u_1 =
\smash{{\lambda_\rho^{{1}/{\gamma_1}} \rho}
{\widetilde{u}_1}/{\widetilde{u}_2}}$
in the last line. We note that because of Lemma 3.4(i) and that $$
\begin{equation*}
\lim_{\rho \to 0} m_\mu \bigg (x,\binom{
\lambda_\rho^{{1}/{\gamma_1}}\rho {u_1}/ {u_2}}{\rho u_2} \bigg) =
f_\mu(x)
\end{equation*}
$$
as
$$
\begin{equation*}
\lim_{\rho \to 0} m_\mu \bigg (x,\binom{
\lambda_\rho^{{1}/{\gamma_1}}\rho {u_1}/ {u_2}}{\rho u_2} \bigg) =
f_\mu(x)
\end{equation*}
$$
as $$
\begin{align*}
\frac{ \lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) &= \frac{
\lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{
u_2}\bigg)^{\gamma_1+1-\gamma_1-1}
\\
&= f_1 \bigg( \lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg)^{\gamma_1+1} \frac{
u_2^{\gamma_1}}{ u_1^{\gamma_1+1}}
\\
&\to \frac{ u_2^{\gamma_1}}{ u_1^{\gamma_1+1}}
\end{align*}
$$
$$
\begin{align*}
\frac{ \lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) &= \frac{
\lambda_\rho^{1+{1}/{\gamma_1}}}{ u_2} f_1 \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{
u_2}\bigg)^{\gamma_1+1-\gamma_1-1}
\\
&= f_1 \bigg( \lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg) \bigg(
\lambda_\rho^{{1}/{\gamma_1}} \frac{u_1}{ u_2}\bigg)^{\gamma_1+1} \frac{
u_2^{\gamma_1}}{ u_1^{\gamma_1+1}}
\\
&\to \frac{ u_2^{\gamma_1}}{ u_1^{\gamma_1+1}}
\end{align*}
$$
 $\rho \to 0$
because of
$\rho \to 0$
because of
 $\smash{\lambda_\rho^{1/{\gamma_1}}} \to
\infty$
and the asymptotic behaviour of
$\smash{\lambda_\rho^{1/{\gamma_1}}} \to
\infty$
and the asymptotic behaviour of
 $f_1$
. Therefore, the integrand in (4.3) converges to If we can also find an integrable majorant of the integrand in (4.3), we obtain
$f_1$
. Therefore, the integrand in (4.3) converges to If we can also find an integrable majorant of the integrand in (4.3), we obtain $$
\begin{equation*}
\Psi ( u_1 f_\mu(x) ) \frac{1}{u_1^{\gamma_1+1}}u_2^{\gamma_1}f_2(u_2).
\end{equation*}
$$
by the dominated convergence theorem, where
$$
\begin{equation*}
\Psi ( u_1 f_\mu(x) ) \frac{1}{u_1^{\gamma_1+1}}u_2^{\gamma_1}f_2(u_2).
\end{equation*}
$$
by the dominated convergence theorem, where $$
\begin{align*}
& \lim_{\rho \to 0} \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y) {\rm d}
y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u)
\\
&\qquad= c_2^{\gamma_1} \int_{\mathbb{R}^2} \int_{\mathbb{R}_+} \Psi(u_1 f_\mu(x))
\frac{1}{u_1^{\gamma_1+1}} {\rm d} u_1 {\rm d} x
\end{align*}
$$
$$
\begin{align*}
& \lim_{\rho \to 0} \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg(
\frac{1}{\lambda_\rho^{{1}/{\gamma_1}} \rho^2} \int_{B(x,u)} f_\mu(y) {\rm d}
y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u)
\\
&\qquad= c_2^{\gamma_1} \int_{\mathbb{R}^2} \int_{\mathbb{R}_+} \Psi(u_1 f_\mu(x))
\frac{1}{u_1^{\gamma_1+1}} {\rm d} u_1 {\rm d} x
\end{align*}
$$
 $c_2$
is defined by (4.4)In order to find such a majorant, we can show that
$c_2$
is defined by (4.4)In order to find such a majorant, we can show that $$
\begin{equation}
c_2\,:\!= \bigg( \int_{\mathbb{R}_+} u_2^{\gamma_1}f_2(u_2) {\rm d} u_2
\bigg)^{{1}/{\gamma_1}}.
\label{eqn37}
\end{equation}
$$
(4.5)and we note that there is an
$$
\begin{equation}
c_2\,:\!= \bigg( \int_{\mathbb{R}_+} u_2^{\gamma_1}f_2(u_2) {\rm d} u_2
\bigg)^{{1}/{\gamma_1}}.
\label{eqn37}
\end{equation}
$$
(4.5)and we note that there is an $$
\begin{equation}
\vert \Psi(v) \vert \leq 2\min ( \vert v \vert , v^2 ),
\label{eqn38}
\end{equation}
$$
$$
\begin{equation}
\vert \Psi(v) \vert \leq 2\min ( \vert v \vert , v^2 ),
\label{eqn38}
\end{equation}
$$
 ${\varepsilon} >0$
with
${\varepsilon} >0$
with
 $1<\gamma_1-{\varepsilon}<\gamma_1+{\varepsilon} <2$
such that (3.3) and (3.4) hold. For all
$1<\gamma_1-{\varepsilon}<\gamma_1+{\varepsilon} <2$
such that (3.3) and (3.4) hold. For all
 $\rho<\rho_0$
with small enough
$\rho<\rho_0$
with small enough
 $\rho_0$
, the integrand (see (4.3)) is therefore dominated by (4.6)where we also used the technical assumption in (2.3). Finally, we can see that (4.6) is integrable because of Lemma 3.4(ii) and
$\rho_0$
, the integrand (see (4.3)) is therefore dominated by (4.6)where we also used the technical assumption in (2.3). Finally, we can see that (4.6) is integrable because of Lemma 3.4(ii) and $$
\begin{equation}
2\min (\vert u_1 \vert^{\gamma_1- {\varepsilon}} , \vert u_1 \vert^{\gamma_1 +
{\varepsilon}} ) ( \vert m_\mu^*(x) \vert^{\gamma_1- {\varepsilon}} + \vert m_\mu^*(x)
\vert^{\gamma_1+ {\varepsilon}}) \frac{c_{f_1}}{u_1^{\gamma_1+1}} u_2^{\gamma_1}
f_2(u_2),
\label{eqn39}
\end{equation}
$$
$$
\begin{equation}
2\min (\vert u_1 \vert^{\gamma_1- {\varepsilon}} , \vert u_1 \vert^{\gamma_1 +
{\varepsilon}} ) ( \vert m_\mu^*(x) \vert^{\gamma_1- {\varepsilon}} + \vert m_\mu^*(x)
\vert^{\gamma_1+ {\varepsilon}}) \frac{c_{f_1}}{u_1^{\gamma_1+1}} u_2^{\gamma_1}
f_2(u_2),
\label{eqn39}
\end{equation}
$$
 $1<\gamma_1 - {\varepsilon}$
.
$1<\gamma_1 - {\varepsilon}$
.Step 2. We deal with the integral
(4.7)We split the integration over $$
\begin{equation}
\int_{\mathbb{R}^2} \int_{\mathbb{R}_+} \Psi(u_1 f_\mu(x)) \frac{1}{u_1^{\gamma_1+1}} {\rm d}
u_1 {\rm d} x.
\label{eqn40}
\end{equation}
$$
$$
\begin{equation}
\int_{\mathbb{R}^2} \int_{\mathbb{R}_+} \Psi(u_1 f_\mu(x)) \frac{1}{u_1^{\gamma_1+1}} {\rm d}
u_1 {\rm d} x.
\label{eqn40}
\end{equation}
$$
 $\mathbb{R}^2$
into
$\mathbb{R}^2$
into
 $\{x \colon f_\mu(x) \geq 0 \}$
and
$\{x \colon f_\mu(x) \geq 0 \}$
and
 $\{x \colon f_\mu(x) < 0 \},$
and note that
$\{x \colon f_\mu(x) < 0 \},$
and note that
 $\Psi(0)=0$
. We recall that
$\Psi(0)=0$
. We recall that
 ${f_\mu}_+\,:\!= \max({\kern2ptf_\mu},0)$
and
${f_\mu}_+\,:\!= \max({\kern2ptf_\mu},0)$
and
 ${f_\mu}_-\,:\!= - \min({\kern2ptf_\mu},0)$
. The substitution
${f_\mu}_-\,:\!= - \min({\kern2ptf_\mu},0)$
. The substitution
 $\widetilde{u}_1=u_1 f_\mu(x)$
shows that (4.7) equals where
$\widetilde{u}_1=u_1 f_\mu(x)$
shows that (4.7) equals where $$
\begin{equation*}
d_{\gamma_1} \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} +
\bar{d}_{\gamma_1}\Vert {f_\mu}_- \Vert_{\gamma_1}^{\gamma_1},
\end{equation*}
$$
$$
\begin{equation*}
d_{\gamma_1} \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} +
\bar{d}_{\gamma_1}\Vert {f_\mu}_- \Vert_{\gamma_1}^{\gamma_1},
\end{equation*}
$$
 $\smash{\bar{d}_{\gamma_1}}$
is the complex conjugate of
$\smash{\bar{d}_{\gamma_1}}$
is the complex conjugate of
 $d_{\gamma_1}\,:\!= \int_{\mathbb{R}_+} ({\Psi(u_1)}/{u_1^{\gamma_1+1}}) {\rm d} u_1 $
. We obtain due to [Reference Samorodnitsky and Taqqu27, p.170]. Therefore, we can finally conclude that
$d_{\gamma_1}\,:\!= \int_{\mathbb{R}_+} ({\Psi(u_1)}/{u_1^{\gamma_1+1}}) {\rm d} u_1 $
. We obtain due to [Reference Samorodnitsky and Taqqu27, p.170]. Therefore, we can finally conclude that $$
\begin{equation*}
d_{\gamma_1}= \frac{\Gamma(2-\gamma_1)}{\gamma_1(\gamma_1-1)} \cos \bigg(
\frac{\pi \gamma_1}{2}\bigg) \bigg(1-{\rm i} \tan \bigg( \frac{\pi
\gamma_1}{2} \bigg) \bigg)
\end{equation*}
$$
where
$$
\begin{equation*}
d_{\gamma_1}= \frac{\Gamma(2-\gamma_1)}{\gamma_1(\gamma_1-1)} \cos \bigg(
\frac{\pi \gamma_1}{2}\bigg) \bigg(1-{\rm i} \tan \bigg( \frac{\pi
\gamma_1}{2} \bigg) \bigg)
\end{equation*}
$$
where $$
\begin{align*}
& \lim_{\rho \to 0} \log \mathbb{E} \exp
\bigg({{\rm i}\frac{\skew5\widetilde{J}_\rho(\mu)}{ c_{\gamma_1,\gamma_2}
\lambda_\rho^{{1}/{\gamma_1}} \rho^2}}\bigg)
\\
&\qquad= c_2^{\gamma_1} \bigg( d_{\gamma_1} \bigg\Vert
\frac{{f_\mu}_+}{c_{\gamma_1} c_2} \bigg\Vert_{\gamma_1}^{\gamma_1} +
\bar{d}_{\gamma_1} \bigg\Vert \frac{{f_\mu}_-}{c_{\gamma_1} c_2}
\bigg\Vert_{\gamma_1}^{\gamma_1} \bigg)
\\
&\qquad = - ( \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} + \Vert {f_\mu}_-
\Vert_{\gamma_1}^{\gamma_1} ) + {\rm i} \tan \bigg( \frac{\pi \gamma_1}{2}
\bigg) ( \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} - \Vert {f_\mu}_-
\Vert_{\gamma_1}^{\gamma_1} )
\\
&\qquad= -\sigma_\mu^{\gamma_1} \bigg(1-{\rm i} \beta_\mu \tan \bigg( \frac{\pi
\gamma_1}{2} \bigg) \bigg),
\end{align*}
$$
(4.8)
$$
\begin{align*}
& \lim_{\rho \to 0} \log \mathbb{E} \exp
\bigg({{\rm i}\frac{\skew5\widetilde{J}_\rho(\mu)}{ c_{\gamma_1,\gamma_2}
\lambda_\rho^{{1}/{\gamma_1}} \rho^2}}\bigg)
\\
&\qquad= c_2^{\gamma_1} \bigg( d_{\gamma_1} \bigg\Vert
\frac{{f_\mu}_+}{c_{\gamma_1} c_2} \bigg\Vert_{\gamma_1}^{\gamma_1} +
\bar{d}_{\gamma_1} \bigg\Vert \frac{{f_\mu}_-}{c_{\gamma_1} c_2}
\bigg\Vert_{\gamma_1}^{\gamma_1} \bigg)
\\
&\qquad = - ( \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} + \Vert {f_\mu}_-
\Vert_{\gamma_1}^{\gamma_1} ) + {\rm i} \tan \bigg( \frac{\pi \gamma_1}{2}
\bigg) ( \Vert {f_\mu}_+ \Vert_{\gamma_1}^{\gamma_1} - \Vert {f_\mu}_-
\Vert_{\gamma_1}^{\gamma_1} )
\\
&\qquad= -\sigma_\mu^{\gamma_1} \bigg(1-{\rm i} \beta_\mu \tan \bigg( \frac{\pi
\gamma_1}{2} \bigg) \bigg),
\end{align*}
$$
(4.8) $$
\begin{equation}
c_{\gamma_1,\gamma_2}\,:\!= c_{\gamma_1} c_2, \qquad c_{\gamma_1}\,:\!= \bigg(
- \frac{\Gamma(2-\gamma_1)}{\gamma_1(\gamma_1-1)} \cos \bigg( \frac{\pi
\gamma_1}{2}\bigg) \bigg)^{{1}/{\gamma_1}},
\label{eqn41}
\end{equation}
$$
$$
\begin{equation}
c_{\gamma_1,\gamma_2}\,:\!= c_{\gamma_1} c_2, \qquad c_{\gamma_1}\,:\!= \bigg(
- \frac{\Gamma(2-\gamma_1)}{\gamma_1(\gamma_1-1)} \cos \bigg( \frac{\pi
\gamma_1}{2}\bigg) \bigg)^{{1}/{\gamma_1}},
\label{eqn41}
\end{equation}
$$
 $c_2$
is given in (4.4), and
$c_2$
is given in (4.4), and
 $\sigma_\mu$
,
$\sigma_\mu$
,
 $
\beta_\mu$
are given in (2.10).
$
\beta_\mu$
are given in (2.10).
4.3.2 Poisson-lines scaling regime
Proof of Theorem 2.4. We recall the characteristic function of
![]() $\,\smash{{\skew5\widetilde{J}_\rho(\mu)}/{\rho}}$
given in (4.2). We proceed as in the proof of Theorem 2.5. Using the definition of
$\,\smash{{\skew5\widetilde{J}_\rho(\mu)}/{\rho}}$
given in (4.2). We proceed as in the proof of Theorem 2.5. Using the definition of
![]() $m_\mu(x,u)$
in (3.17) and the density of the scaled measure F from (1.1), we obtain
$m_\mu(x,u)$
in (3.17) and the density of the scaled measure F from (1.1), we obtain
 $$
\begin{align}
& \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{1}{\rho} \int_{B(x,u)}
f_\mu(y) {\rm d} y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u) \nonumber
\\
&\qquad= \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{u_1 u_2}{\rho}
m_\mu(x,u) \bigg) \lambda_\rho f_1 \bigg( \frac{u_1}{\rho}\bigg)
\frac{1}{\rho} f_2 \bigg( \frac{u_2}{\rho}\bigg) \frac{1}{\rho} {\rm d} x {\rm d}
u \nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_1 u_2 m_\mu
\bigg(x,\binom{u_1}{\rho u_2} \bigg) \bigg) \frac{\lambda_\rho}{\rho} f_1
\bigg( \frac{u_1}{\rho}\bigg) f_2 ( u_2 ) {\rm d} x {\rm d} u,
\label{eqn42}\end{align}
$$
$$
\begin{align}
& \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{1}{\rho} \int_{B(x,u)}
f_\mu(y) {\rm d} y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u) \nonumber
\\
&\qquad= \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{u_1 u_2}{\rho}
m_\mu(x,u) \bigg) \lambda_\rho f_1 \bigg( \frac{u_1}{\rho}\bigg)
\frac{1}{\rho} f_2 \bigg( \frac{u_2}{\rho}\bigg) \frac{1}{\rho} {\rm d} x {\rm d}
u \nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_1 u_2 m_\mu
\bigg(x,\binom{u_1}{\rho u_2} \bigg) \bigg) \frac{\lambda_\rho}{\rho} f_1
\bigg( \frac{u_1}{\rho}\bigg) f_2 ( u_2 ) {\rm d} x {\rm d} u,
\label{eqn42}\end{align}
$$
where we substituted
![]() $u_2 = \rho \widetilde{u}_2$
in the last line. We note that, due to (2.5) in Definition 2.2 of the space
$u_2 = \rho \widetilde{u}_2$
in the last line. We note that, due to (2.5) in Definition 2.2 of the space
![]() $\mathcal{M}_{L}$
,
$\mathcal{M}_{L}$
,
(pointwise for all
![]() $(x,u) \in \mathbb{R}^2 \times \mathbb{R}_+^2$
) and that
$(x,u) \in \mathbb{R}^2 \times \mathbb{R}_+^2$
) and that
 $$
\begin{align*}
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho}\bigg)& =
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho}\bigg) \bigg(
\frac{u_1}{\rho}\bigg) ^{\gamma_1+1} \bigg(
\frac{\rho}{u_1}\bigg)^{\gamma_1+1}
\\
&= f_1 \bigg( \frac{u_1}{\rho}\bigg) \bigg( \frac{u_1}{\rho}\bigg)
^{\gamma_1+1} \lambda_\rho \rho^{\gamma_1} \frac{1}{u_1^{\gamma_1+1}}
\\
& \to \frac{1}{u_1^{\gamma_1+1}}
\end{align*}
$$
$$
\begin{align*}
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho}\bigg)& =
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho}\bigg) \bigg(
\frac{u_1}{\rho}\bigg) ^{\gamma_1+1} \bigg(
\frac{\rho}{u_1}\bigg)^{\gamma_1+1}
\\
&= f_1 \bigg( \frac{u_1}{\rho}\bigg) \bigg( \frac{u_1}{\rho}\bigg)
^{\gamma_1+1} \lambda_\rho \rho^{\gamma_1} \frac{1}{u_1^{\gamma_1+1}}
\\
& \to \frac{1}{u_1^{\gamma_1+1}}
\end{align*}
$$
as
![]() $\rho \to 0$
because of
$\rho \to 0$
because of
![]() $1 / \rho \to \infty$
, the asymptotic behaviour of
$1 / \rho \to \infty$
, the asymptotic behaviour of
![]() $f_1,$
and the fact that
$f_1,$
and the fact that
![]() $\lambda_\rho \rho^{\gamma_1} \to
1$
. Therefore, the integrand in (4.9) converges to
$\lambda_\rho \rho^{\gamma_1} \to
1$
. Therefore, the integrand in (4.9) converges to
If we can also find an integrable majorant of the integrand in (4.9), we obtain
 $$
\begin{align}
& \lim_{\rho \to 0} \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{1}{\rho}
\int_{B(x,u)} f_\mu(y) {\rm d} y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u)
\nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_2
\int_{[x_1-{u_1}/{2},x_1+{u_1}/{2}]} f_\mu(y_1,x_2){\rm d} y_1
\bigg)\frac{1}{u_1^{\gamma_1+1}} f_2 ( u_2 ) {\rm d} x {\rm d} u
\label{eqn43}\end{align}
$$
$$
\begin{align}
& \lim_{\rho \to 0} \int_{\mathbb{R}_+^2}\int_{\mathbb{R}^2} \Psi \bigg( \frac{1}{\rho}
\int_{B(x,u)} f_\mu(y) {\rm d} y\bigg) \lambda_\rho {\rm d} x F_\rho(\mathrm{d} u)
\nonumber
\\
&\qquad= \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi \bigg( u_2
\int_{[x_1-{u_1}/{2},x_1+{u_1}/{2}]} f_\mu(y_1,x_2){\rm d} y_1
\bigg)\frac{1}{u_1^{\gamma_1+1}} f_2 ( u_2 ) {\rm d} x {\rm d} u
\label{eqn43}\end{align}
$$
by the dominated convergence theorem. Using the estimates in (4.5) and (3.3), an extended version of (3.4) and the technical assumption in (2.3), we see that the integrand in (4.9) is dominated by
for all
![]() $\rho<\rho_0$
with small enough
$\rho<\rho_0$
with small enough
![]() $\rho_0$
. Here, we have to choose
$\rho_0$
. Here, we have to choose
![]() ${\varepsilon} >0$
such that
${\varepsilon} >0$
such that
![]() ${1<\gamma_1 - {\varepsilon}}$
,
${1<\gamma_1 - {\varepsilon}}$
,
![]() ${\gamma_1 + {\varepsilon} < 2},$
as well as
${\gamma_1 + {\varepsilon} < 2},$
as well as
![]() $\gamma_1 + {\varepsilon} < \gamma_2$
. These conditions together with Lemma 3.4(ii) ensure that (4.11) is integrable.
$\gamma_1 + {\varepsilon} < \gamma_2$
. These conditions together with Lemma 3.4(ii) ensure that (4.11) is integrable.
Since the characteristic function
![]() $\mathbb{E} ({\rm e}^{{\rm i} J_L(\mu)} )$
of the limit
$\mathbb{E} ({\rm e}^{{\rm i} J_L(\mu)} )$
of the limit
![]() $J_L(\mu)$
is given by the exponential of (4.10), the convergence of the characteristic function is proven.
$J_L(\mu)$
is given by the exponential of (4.10), the convergence of the characteristic function is proven.
Remark 4.2. In the general case, let us say
![]() $\lambda_\rho \rho^{\gamma_1} \to
a^{2-\gamma_1} \in (0,\infty)$
with
$\lambda_\rho \rho^{\gamma_1} \to
a^{2-\gamma_1} \in (0,\infty)$
with
![]() $a>0$
as
$a>0$
as
![]() $\rho \to 0$
, we obtain
$\rho \to 0$
, we obtain
![]() $\,\smash{\skew5\widetilde{J}_\rho(\mu) / (a \rho)} \to J_L(\mu_{a}), $
where we recall that
$\,\smash{\skew5\widetilde{J}_\rho(\mu) / (a \rho)} \to J_L(\mu_{a}), $
where we recall that
![]() $\mu_a(\cdot)\,:\!= \mu(a^{-1} \, \cdot)$
. In order to prove this, we note that we obtain (4.10) with the additional factor
$\mu_a(\cdot)\,:\!= \mu(a^{-1} \, \cdot)$
. In order to prove this, we note that we obtain (4.10) with the additional factor
![]() $a^{2-\gamma_1}$
for the logarithm of the characteristic function of the limit in the general case. Then, we can deduce the result after an appropriate substitution.
$a^{2-\gamma_1}$
for the logarithm of the characteristic function of the limit in the general case. Then, we can deduce the result after an appropriate substitution.
4.3.3 Gaussian-lines scaling regime
Proof of Theorem 2.3. We recall the characteristic function of
![]() $\,\smash{{\skew5\widetilde{J}_\rho(\mu)
}/ {{\rho}^{1-\eta / 2}}}$
, which, after the substitution
$\,\smash{{\skew5\widetilde{J}_\rho(\mu)
}/ {{\rho}^{1-\eta / 2}}}$
, which, after the substitution
![]() $u_2 = \rho
\widetilde{u}_2$
, equals
$u_2 = \rho
\widetilde{u}_2$
, equals
The goal is to show for some
![]() $\sigma^2>0$
the convergence of this characteristic function to
$\sigma^2>0$
the convergence of this characteristic function to
![]() $\exp ( - \sigma^2 /2 )$
, which corresponds to a centred Gaussian random variable.
$\exp ( - \sigma^2 /2 )$
, which corresponds to a centred Gaussian random variable.
To be more precise, we write
 $$
\begin{align}
& \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi\bigg( \frac{ \mu (B (x,\binom{u_1}{\rho
u_2} ))}{{\rho}^{1-\eta / 2}} \bigg) \frac{ \lambda_\rho}{\rho} f_1
\bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) {\rm d} x {\rm d} u \nonumber
\\
&\qquad= - \frac{1}{2} \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} u_2^2 \bigg( \frac{\mu (B
(x,\binom{u_1}{\rho u_2} ))}{\rho u_2} \bigg)^2 \rho^\eta
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) {\rm d}
x {\rm d} u \label{eqn45}\end{align}
$$
$$
\begin{align}
& \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} \Psi\bigg( \frac{ \mu (B (x,\binom{u_1}{\rho
u_2} ))}{{\rho}^{1-\eta / 2}} \bigg) \frac{ \lambda_\rho}{\rho} f_1
\bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) {\rm d} x {\rm d} u \nonumber
\\
&\qquad= - \frac{1}{2} \int_{\mathbb{R}^2 \times \mathbb{R}_+^2} u_2^2 \bigg( \frac{\mu (B
(x,\binom{u_1}{\rho u_2} ))}{\rho u_2} \bigg)^2 \rho^\eta
\frac{\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) {\rm d}
x {\rm d} u \label{eqn45}\end{align}
$$
where
First, we discuss the integral in (4.13) in the case of
![]() $\gamma_2>3$
. Due to
$\gamma_2>3$
. Due to
![]() $\vert \Psi(v) + {v^2}/{2}\vert \leq \vert v \vert
^3$
, we can bound (4.14) and can thus bound the integrand by
$\vert \Psi(v) + {v^2}/{2}\vert \leq \vert v \vert
^3$
, we can bound (4.14) and can thus bound the integrand by
 $$
\begin{align}
& \rho^{3 \eta/2} u_2^3 \bigg( \frac{ \vert \mu (B (x,\binom{u_1}{\rho
u_2} )) \vert}{\rho u_2} \bigg)^3 \frac{ \lambda_\rho}{\rho} f_1 \bigg(
\frac{u_1}{\rho} \bigg) f_2(u_2) \nonumber
\\
&\qquad\leq \rho^{\eta/2} u_2^3 \bigg( \frac{C_\mu}{\rho u_2} \int_{B
(x,\binom{u_1}{\rho u_2})} {\rm e}^{-c_\mu \vert y_1 \vert} {\rm e}^{-c_\mu \vert
y_2 \vert} {\rm d} y \bigg) ^3 \lambda_\rho \rho^{\eta-1} c_{f_1} \bigg(
\frac{\rho}{u_1} \bigg)^{\gamma_1+1} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{\eta/2} u_2^3 g_1(x_1,u_1) ^3 g_2(x_2) ^3
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2)
\label{eqn48}\end{align}
$$
$$
\begin{align}
& \rho^{3 \eta/2} u_2^3 \bigg( \frac{ \vert \mu (B (x,\binom{u_1}{\rho
u_2} )) \vert}{\rho u_2} \bigg)^3 \frac{ \lambda_\rho}{\rho} f_1 \bigg(
\frac{u_1}{\rho} \bigg) f_2(u_2) \nonumber
\\
&\qquad\leq \rho^{\eta/2} u_2^3 \bigg( \frac{C_\mu}{\rho u_2} \int_{B
(x,\binom{u_1}{\rho u_2})} {\rm e}^{-c_\mu \vert y_1 \vert} {\rm e}^{-c_\mu \vert
y_2 \vert} {\rm d} y \bigg) ^3 \lambda_\rho \rho^{\eta-1} c_{f_1} \bigg(
\frac{\rho}{u_1} \bigg)^{\gamma_1+1} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{\eta/2} u_2^3 g_1(x_1,u_1) ^3 g_2(x_2) ^3
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2)
\label{eqn48}\end{align}
$$
for
![]() $\rho<\rho_0$
with small enough
$\rho<\rho_0$
with small enough
![]() $\rho_0$
, where
$\rho_0$
, where
![]() $g_1$
is given in (3.6) and
$g_1$
is given in (3.6) and
Here, we used assumption (2.4) from Definition 2.2, the technical assumption in (2.3), and the fact that
![]() $\lambda_\rho
\rho^{\gamma_1+\eta} \to 1$
. Furthermore, we used
$\lambda_\rho
\rho^{\gamma_1+\eta} \to 1$
. Furthermore, we used
from the proof of Lemma 3.4(ii). By (4.15), we see that the integrand in (4.13) has an integrable majorant since we assumed that
![]() $\gamma_2 > 3,$
and because
$\gamma_2 > 3,$
and because
![]() $g_2^3$
is integrable with respect to
$g_2^3$
is integrable with respect to
![]() $x_2$
and
$x_2$
and
![]() $\smash{g_1(x_1,u_1)^3
/{u_1^{\gamma_1+1}}} $
is also integrable (in order to check this, we just have to follow the lines below (3.7)). Moreover, the majorant converges to zero because of
$\smash{g_1(x_1,u_1)^3
/{u_1^{\gamma_1+1}}} $
is also integrable (in order to check this, we just have to follow the lines below (3.7)). Moreover, the majorant converges to zero because of
![]() $\rho^{\eta/2} \to 0$
.
$\rho^{\eta/2} \to 0$
.
In the case of
![]() $2 < \gamma_2 \leq 3$
, we note that there is an
$2 < \gamma_2 \leq 3$
, we note that there is an
![]() ${\varepsilon}>0$
such that
${\varepsilon}>0$
such that
![]() $2 < \gamma_2 - {\varepsilon} < 3$
as well as
$2 < \gamma_2 - {\varepsilon} < 3$
as well as
![]() $\vert \Psi(v) +
{v^2}/{2}\vert \leq \vert v \vert ^{\gamma_2 - {\varepsilon}}$
. The last-mentioned estimate can be deduced from Lemma 1 of [Reference Kaj, Leskelä, Norros and Schmidt18] by a case distinction (cf. (3.3)). Similar to above, we can bound the integrand in (4.13) by
$\vert \Psi(v) +
{v^2}/{2}\vert \leq \vert v \vert ^{\gamma_2 - {\varepsilon}}$
. The last-mentioned estimate can be deduced from Lemma 1 of [Reference Kaj, Leskelä, Norros and Schmidt18] by a case distinction (cf. (3.3)). Similar to above, we can bound the integrand in (4.13) by
 $$
\begin{align}
& \rho^{{(\gamma_2 - {\varepsilon})} \eta/2} \bigg( \frac{ \vert \mu (B
(x,\binom{u_1}{\rho u_2} )) \vert}{\rho} \bigg)^{\gamma_2 - {\varepsilon}} \frac{
\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) \nonumber
\\
&\qquad\leq \rho^{{(\gamma_2 - {\varepsilon}-2+2)} \eta/2} u_2^{\gamma_2-{\varepsilon}} \bigg(
\frac{\vert \mu (B (x,\binom{u_1}{\rho u_2} )) \vert}{\rho u_2}
\bigg)^{\gamma_2-{\varepsilon}} \frac{ \lambda_\rho}{\rho} c_{f_1} \bigg(
\frac{\rho}{u_1} \bigg)^{\gamma_1+1} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{{(\gamma_2 - {\varepsilon}-2)} \eta/2} u_2^{\gamma_2-{\varepsilon}} (
g_1(x_1,u_1) g_2(x_2) )^{\gamma_2-{\varepsilon}} \lambda_\rho \rho^{\gamma_1+\eta}
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{{(\gamma_2 - {\varepsilon}-2)} \eta/2} u_2^{\gamma_2-{\varepsilon}}
g_1(x_1,u_1) ^{\gamma_2-{\varepsilon}} g_2(x_2)^{\gamma_2-{\varepsilon}}
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2)
\label{eqn49}\end{align}
$$
$$
\begin{align}
& \rho^{{(\gamma_2 - {\varepsilon})} \eta/2} \bigg( \frac{ \vert \mu (B
(x,\binom{u_1}{\rho u_2} )) \vert}{\rho} \bigg)^{\gamma_2 - {\varepsilon}} \frac{
\lambda_\rho}{\rho} f_1 \bigg( \frac{u_1}{\rho} \bigg) f_2(u_2) \nonumber
\\
&\qquad\leq \rho^{{(\gamma_2 - {\varepsilon}-2+2)} \eta/2} u_2^{\gamma_2-{\varepsilon}} \bigg(
\frac{\vert \mu (B (x,\binom{u_1}{\rho u_2} )) \vert}{\rho u_2}
\bigg)^{\gamma_2-{\varepsilon}} \frac{ \lambda_\rho}{\rho} c_{f_1} \bigg(
\frac{\rho}{u_1} \bigg)^{\gamma_1+1} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{{(\gamma_2 - {\varepsilon}-2)} \eta/2} u_2^{\gamma_2-{\varepsilon}} (
g_1(x_1,u_1) g_2(x_2) )^{\gamma_2-{\varepsilon}} \lambda_\rho \rho^{\gamma_1+\eta}
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2) \nonumber
\\
&\qquad\leq C \rho^{{(\gamma_2 - {\varepsilon}-2)} \eta/2} u_2^{\gamma_2-{\varepsilon}}
g_1(x_1,u_1) ^{\gamma_2-{\varepsilon}} g_2(x_2)^{\gamma_2-{\varepsilon}}
\frac{1}{u_1^{\gamma_1+1}} f_2(u_2)
\label{eqn49}\end{align}
$$
for
![]() $\rho<\rho_0$
with small enough
$\rho<\rho_0$
with small enough
![]() $\rho_0$
. Using
$\rho_0$
. Using
![]() $\gamma_1<\gamma_2-{\varepsilon}$
, we can see by (4.16) that the integrand in (4.13) has an integrable majorant because
$\gamma_1<\gamma_2-{\varepsilon}$
, we can see by (4.16) that the integrand in (4.13) has an integrable majorant because
![]() $g_2^{\gamma_2-{\varepsilon}}$
and
$g_2^{\gamma_2-{\varepsilon}}$
and
![]() $\smash{g_1(x_1,u_1)^{\gamma_2-{\varepsilon}}/{u_1^{\gamma_1+1}}}$
are integrable (with the same reasons as above) and that it converges to zero because of
$\smash{g_1(x_1,u_1)^{\gamma_2-{\varepsilon}}/{u_1^{\gamma_1+1}}}$
are integrable (with the same reasons as above) and that it converges to zero because of
![]() ${\gamma_2-{\varepsilon}-2}>0$
. Therefore, we obtain in both cases that the integral in (4.13) converges to zero by the dominated convergence theorem.
${\gamma_2-{\varepsilon}-2}>0$
. Therefore, we obtain in both cases that the integral in (4.13) converges to zero by the dominated convergence theorem.
Next, we deal with the integral in (4.12) and show that it converges to
The convergence of the integrand can be seen similar to above using Definition 2.2 of the space
![]() $\mathcal{M}_{L}$
, the asymptotic behaviour of
$\mathcal{M}_{L}$
, the asymptotic behaviour of
![]() $f_1,$
and the fact that
$f_1,$
and the fact that
![]() $\lambda_\rho
\rho^{\gamma_1+\eta} \to 1$
. A majorant of the integrand is given by
$\lambda_\rho
\rho^{\gamma_1+\eta} \to 1$
. A majorant of the integrand is given by
which is integrable for
![]() $\gamma_2>2$
. Applying the dominated convergence theorem, the convergence of the characteristic function is proven. By linearity, the covariance function given in (2.6) follows from (4.17).
$\gamma_2>2$
. Applying the dominated convergence theorem, the convergence of the characteristic function is proven. By linearity, the covariance function given in (2.6) follows from (4.17).
Remark 4.3. In the general case, let us say
![]() $\lambda_\rho \rho^{\gamma_1+\eta} \to
a^{2} \in (0,\infty)$
with
$\lambda_\rho \rho^{\gamma_1+\eta} \to
a^{2} \in (0,\infty)$
with
![]() $a>0$
as
$a>0$
as
![]() $\rho \to 0$
, the limit is a centred Gaussian linear random field which is given by
$\rho \to 0$
, the limit is a centred Gaussian linear random field which is given by
![]() $( Y(a \mu))_\mu$
, where
$( Y(a \mu))_\mu$
, where
![]() $a \mu$
has the density
$a \mu$
has the density
![]() $a f_\mu$
and the variance of
$a f_\mu$
and the variance of
![]() $ Y(a \mu)$
is just
$ Y(a \mu)$
is just
![]() $ a^2 \sigma^2$
. This can be seen since we obtain the additional factor
$ a^2 \sigma^2$
. This can be seen since we obtain the additional factor
![]() $a^{2}$
in (4.17).
$a^{2}$
in (4.17).
4.4 The finite-variance case
Proof of Theorem 2.6. We use the definition of
![]() $m_\mu(x,u)$
in (3.17) to obtain, for the logarithm of the characteristic function of
$m_\mu(x,u)$
in (3.17) to obtain, for the logarithm of the characteristic function of
![]() $\,\smash{\skew5\widetilde{J}_\rho(\mu) / (\rho^2 \sqrt{\lambda_\rho v_1v_2})}$
,
$\,\smash{\skew5\widetilde{J}_\rho(\mu) / (\rho^2 \sqrt{\lambda_\rho v_1v_2})}$
,
 $$\int_{\mathbb {R}_ + ^2} {\int_{{\mathbb {R}^2}} \Psi } (\frac{1}{{\lambda _\rho ^{1/{\gamma _1}}{\rho ^2}}}\int_{B(x,u)} {{f_\mu }} (y){\text{d}}y){\lambda _\rho }{\text{d}}x\;{F_\rho }({\text{d}}u){\text{ }} = \int_{\mathbb {R}_ + ^2} {\int_{{\mathbb {R}^2}} \Psi } (\frac{{{u_1}{u_2}}}{{\lambda _\rho ^{1/{\gamma _1}}{\rho ^2}}}{m_\mu }(x,u)){\lambda _\rho }{f_1}(\frac{{{u_1}}}{\rho })\frac{1}{\rho }{f_2}(\frac{{{u_2}}}{\rho })\frac{1}{\rho }{\text{d}}x{\text{d}}u{\text{ }} = \int_{{\mathbb {R}^2} \times \mathbb {R}_ + ^2} \Psi ({u_1}{m_\mu }(x,\left( {{\text{ }}\lambda _\rho ^{1/{\gamma _1}}\rho {u_1}/{u_2}{\text{ }}\rho {u_2}{\text{ }}} \right)))\frac{{\lambda _\rho ^{1 + 1/{\gamma _1}}}}{{{u_2}}}{f_1}(\lambda _\rho ^{1/{\gamma _1}}\frac{{{u_1}}}{{{u_2}}})\;{f_2}({u_2}){\text{d}}x{\text{d}}u,$$
$$\int_{\mathbb {R}_ + ^2} {\int_{{\mathbb {R}^2}} \Psi } (\frac{1}{{\lambda _\rho ^{1/{\gamma _1}}{\rho ^2}}}\int_{B(x,u)} {{f_\mu }} (y){\text{d}}y){\lambda _\rho }{\text{d}}x\;{F_\rho }({\text{d}}u){\text{ }} = \int_{\mathbb {R}_ + ^2} {\int_{{\mathbb {R}^2}} \Psi } (\frac{{{u_1}{u_2}}}{{\lambda _\rho ^{1/{\gamma _1}}{\rho ^2}}}{m_\mu }(x,u)){\lambda _\rho }{f_1}(\frac{{{u_1}}}{\rho })\frac{1}{\rho }{f_2}(\frac{{{u_2}}}{\rho })\frac{1}{\rho }{\text{d}}x{\text{d}}u{\text{ }} = \int_{{\mathbb {R}^2} \times \mathbb {R}_ + ^2} \Psi ({u_1}{m_\mu }(x,\left( {{\text{ }}\lambda _\rho ^{1/{\gamma _1}}\rho {u_1}/{u_2}{\text{ }}\rho {u_2}{\text{ }}} \right)))\frac{{\lambda _\rho ^{1 + 1/{\gamma _1}}}}{{{u_2}}}{f_1}(\lambda _\rho ^{1/{\gamma _1}}\frac{{{u_1}}}{{{u_2}}})\;{f_2}({u_2}){\text{d}}x{\text{d}}u,$$
where we substituted
![]() $u_2 = \rho \widetilde{u}_2$
and
$u_2 = \rho \widetilde{u}_2$
and
![]() $u_1 = \rho
\widetilde{u}_1$
in the last line. We note that
$u_1 = \rho
\widetilde{u}_1$
in the last line. We note that
because of Lemma 3.4(i). Due to the estimate
![]() $\vert \Psi(v) +
{v^2}/{2}\vert \leq \vert v \vert ^3$
and
$\vert \Psi(v) +
{v^2}/{2}\vert \leq \vert v \vert ^3$
and
![]() $\lambda_\rho \to \infty$
, we obtain
$\lambda_\rho \to \infty$
, we obtain
Furthermore, we use
![]() $\vert \Psi(v)\vert \leq {v^2}/{2}$
and the definition of
$\vert \Psi(v)\vert \leq {v^2}/{2}$
and the definition of
![]() $m_\mu^*(x)$
in (3.18) to obtain
$m_\mu^*(x)$
in (3.18) to obtain
Since the right-hand side can serve as an integrable majorant, we can apply the dominated convergence theorem and obtain
which is the characteristic function of a Gaussian random variable. Finally, we can conclude that the limiting random field is a centred Gaussian linear random field with covariance function given in (2.12).
Acknowledgements
We would like to thank the anonymous referee for their detailed comments which helped to improve the presentation of the paper.
The work of S. Schwinn is supported by the ‘Excellence Initiative’ of the German Federal and State Governments and the Graduate School of Computational Engineering at Technische Universität Darmstadt.