1 Introduction
As a fundamental topology-transforming process, vortex reconnection has been extensively studied both in classical (Melander & Hussain Reference Melander and Hussain1988; Kida & Takaoka Reference Kida and Takaoka1994) and quantum (Koplik & Levine Reference Koplik and Levine1993; Bewley et al. Reference Bewley, Paoletti, Sreenivasan and Lathrop2008; Zuccher et al. Reference Zuccher, Caliari, Baggaley and Barenghi2012) turbulence. In addition to its physical relevance to turbulence phenomena, such as energy cascade, fine scale mixing and noise generation (Hussain & Duraisamy Reference Hussain and Duraisamy2011), reconnection also represents a stand-alone mathematical problem related to the possible occurrence of a finite-time singularity (FTS), which can be stated as: can any initially smooth velocity field of finite energy in an incompressible fluid become singular at finite time under the evolution of the Navier–Stokes (N–S)/Euler equations? Based on the theorem of Beale, Kato & Majda (Reference Beale, Kato and Majda1984), if a (strictly mathematical) FTS occurs at time 
$t_{c}$, then 
$\int _{0}^{t_{c}}\Vert \unicode[STIX]{x1D74E}(\boldsymbol{x},t)\Vert _{\infty }\,\text{d}t$ must go to infinity, or, in other words, the vorticity 
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$ must become unbounded as 
$t\rightarrow t_{c}$. The FTS question also has important applications concerning the energy dissipation in turbulent flows at high Reynolds numbers (i.e. dissipation anomaly): whether (or how) the rate of dissipation 
$\unicode[STIX]{x1D716}=2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}$ can remain finite in the limit of vanishing kinematic viscosity 
$\unicode[STIX]{x1D708}$ (Sreenivasan Reference Sreenivasan1984; Kerr Reference Kerr2018; Moffatt Reference Moffatt2019)? Here, 
$\unicode[STIX]{x1D6FA}=\langle \unicode[STIX]{x1D74E}^{2}\rangle =\int \unicode[STIX]{x1D74E}^{2}\,\text{d}V$ is the enstrophy, where 
$V$ is the volume.
Originally raised by Leray (Reference Leray1934), the FTS question has since then drawn intense attention (see Doering (Reference Doering2009) and references therein). It is widely believed that the configuration most likely to lead to a singularity consists of two interacting vortex tubes (De Waele & Aarts Reference De Waele and Aarts1994; Constantin, Fefferman & Majda Reference Constantin, Fefferman and Majda1996). Hence, previous searches for a singularity mainly focus on this type of geometry. This search was initiated by Siggia (Reference Siggia1985) using the Biot–Savart (B–S) model, and has been followed by many others, such as Siggia & Pumir (Reference Siggia and Pumir1985), De Waele & Aarts (Reference De Waele and Aarts1994) and Kimura & Moffatt (Reference Kimura and Moffatt2017). They found that ‘pyramid’ or ‘tent-like’ structures tend to emerge during the interaction, and their curvatures at the tipping points increase significantly and the associated core sizes approach zero – suggesting a possible FTS. Note that the B–S model is based on the Euler equations (i.e. vanishing viscosity). Also, to regularize the singular kernel of the B–S integral, a cutoff needs to be employed. With such regularization, the B–S integration always diverges near the singular time of reconnection (Kimura & Moffatt Reference Kimura and Moffatt2017).
Possible formation of a FTS has been extensively studied also with the aid of direct numerical simulation (DNS) (see, for example, Boratav & Pelz (Reference Boratav and Pelz1994), Grauer, Marliani & Germaschewski (Reference Grauer, Marliani and Germaschewski1998), Kerr (Reference Kerr2013)). The existence of a FTS has been reported at times – however, most such singularities turned out to be either numerical artefacts or incorrect predictions. For example, Kerr (Reference Kerr1993) performed an Euler simulation for the anti-parallel vortex tubes and suggested that this initial condition tends to evolve towards a FTS. However, by repeating this computation with higher resolution, Hou & Li (Reference Hou and Li2006) showed that a FTS does not occur. Interestingly, by focusing on solutions with rotational symmetry, Luo & Hou (Reference Luo and Hou2014, Reference Luo and Hou2019) found a class of potentially singular solutions to the three-dimensional axisymmetric Euler equations in a radially bounded, axially periodic cylinder. Note that DNS cannot give conclusive evidence of the existence of a FTS, because the length scale of the phenomenon always decreases to less than the computational resolution (MK1).
Recently, Moffatt & Kimura (Reference Moffatt and Kimura2019a) (hereinafter cited as MK1) have developed a model that governs the evolution of two initially inclined circular vortices. It is based on the argument that the behaviour near the points of closest approach of the vortices (the ‘tipping points’) is determined solely by the curvature, the separation and the core radius. By using the B–S law to obtain analytical expressions for the rate of change of these quantities, they obtain a nonlinear dynamical system of ordinary differential equations (ODEs). The solution for the 
$\unicode[STIX]{x1D708}=0$ case indicates that a FTS can occur for the Euler flow. In a follow-up paper, Moffatt & Kimura (Reference Moffatt and Kimura2019b) (hereinafter cited as MK2) further modified the model to take into account the reconnection process for the viscous flow. They claimed that, although a strictly ‘mathematical singularity’ does not occur, the peak vorticity amplification becomes so large that it can be described as a ‘physical singularity’ for vortex Reynolds number 
$Re(\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708})\gtrsim 4000$. One debatable issue for their model is whether the vortex core remains compact and circular throughout the interaction process. Recent DNS of both the Euler (Brenner, Hormoz & Pumir Reference Brenner, Hormoz and Pumir2016) and N–S equations (Kerr Reference Kerr2018; Yao & Hussain Reference Yao and Hussain2020, hereinafter cited as YH) have demonstrated that there is a strong core flattening during the interaction process. MK1 argued that the core flattening does not occur if the separation of the vortices is small compared with their radius of curvature at the tipping points and if 
$Re$ is large enough. They further claimed that the core flattening should decrease with increasing 
$Re$, as the vortices are spinning so rapidly that they experienced an effectively axisymmetric strain. It is of particular interest to perform DNS for this type of initial configuration to provide insight into this controversy.
2 Initial configuration and numerical set-up
Following MK1 and MK2, we study the interaction of two initially circular vortex rings of radius 
$R=1/\unicode[STIX]{x1D705}$ and circulation 
$\unicode[STIX]{x1D6E4}$ (figure 1). The vortices are symmetrically placed on planes 
$z=\pm x\tan \unicode[STIX]{x1D6FC}$, and are assumed to have a Gaussian cross-section 
$\unicode[STIX]{x1D714}(r)=\unicode[STIX]{x1D6E4}/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}_{0}^{2})\exp [-r^{2}/4\unicode[STIX]{x1D6FF}_{0}^{2}]$ of initial radial scale 
$\unicode[STIX]{x1D6FF}_{0}$. The initial separation distance between the two tipping points 
$T$ is 
$2s_{0}$. Time is non-dimensionalized as 
$\unicode[STIX]{x1D70F}=t/(R^{2}/\unicode[STIX]{x1D6E4})$. In the present paper, we adopt the same initial values as in MK2 – namely,
$$\begin{eqnarray}R=1/\unicode[STIX]{x1D705}_{0}=1,\quad s_{0}=0.1,\quad \unicode[STIX]{x1D6FF}_{0}=0.01\quad \text{and}\quad \unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4.\end{eqnarray}$$ Note that a similar configuration was studied by Kida, Takaoka & Hussain (Reference Kida, Takaoka and Hussain1991) with a much larger core size (i.e. 
$\unicode[STIX]{x1D6FF}_{0}/R\approx 0.2$) to better illustrate the reconnection process.
Figure 1. (a) Schematic of the initial configuration for two circular rings of circulation 
$\unicode[STIX]{x1D6E4}$ and radius 
$R=\unicode[STIX]{x1D705}_{0}^{-1}$ located on inclined planes 
$z=\pm x\tan \unicode[STIX]{x1D6FC}$, with (b) showing the corresponding top view. 
$T$ in (a) represents the tipping point, while 
$S_{s}$ and 
$S_{c}$ in (b) denote the symmetry and collision planes, respectively. The vortices have a Gaussian profile of scale 
$\unicode[STIX]{x1D6FF}_{0}=0.01R$ and the separation between the tipping points 
$T$ is 
$2s_{0}$, with 
$s_{0}=0.1R$.
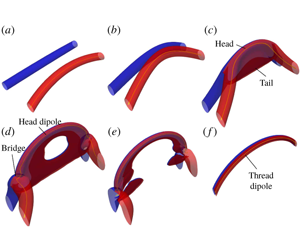
Figure 2. Evolution of the flow structure (represented by vorticity isosurface at 5 % of maximum initial vorticity 
$|\unicode[STIX]{x1D74E}|=0.05\unicode[STIX]{x1D714}_{0}$) near the tipping points for 
$Re=4000$ at: (a) 
$\unicode[STIX]{x1D70F}=0$; (b) 0.25; (c) 0.35; (d) 0.4; (e) 0.43; (f) 0.6. Lines in the structure represent the vortex lines that go through the peak vorticity. See the supplementary movie for the time evolution of different 
$Re$ cases.
MK1 argued that the behaviour near the tipping points 
$T$ is determined solely by the curvature 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70F})$ at those points and by the separation 
$s(\unicode[STIX]{x1D70F})$ and core scale 
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70F})$. On this basis, the dimensionless equations describing their behaviour are (MK1)
$$\begin{eqnarray}\frac{\text{d}s}{\text{d}\unicode[STIX]{x1D70F}}=-\unicode[STIX]{x1D6FE}\frac{\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D6FC}}{4\unicode[STIX]{x03C0}}\left[\log \left(\frac{s}{\unicode[STIX]{x1D6FF}}\right)+\unicode[STIX]{x1D6FD}_{1}\right],\quad \frac{\text{d}\unicode[STIX]{x1D705}}{\text{d}\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FE}\frac{\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}{4\unicode[STIX]{x03C0}s^{2}},\quad \frac{\text{d}\unicode[STIX]{x1D6FF}^{2}}{\text{d}\unicode[STIX]{x1D70F}}=\frac{1}{Re}-\unicode[STIX]{x1D6FE}\frac{\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D6FC}}{4\unicode[STIX]{x03C0}s}\unicode[STIX]{x1D6FF}^{2},\vphantom{\mathop{\sum }_{\sum }}\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6FD}_{1}=0.4417$ and 
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6E4}_{y}/\unicode[STIX]{x1D6E4}$ (with 
$\unicode[STIX]{x1D6E4}_{y}$ the remaining, i.e. unreconnected, circulation in the symmetry plane). 
$\unicode[STIX]{x1D6FE}$ is incorporated to include the reconnection effect when 
$\unicode[STIX]{x1D6FF}/s$ becomes 
$O(1)$ and its governing equation is given as (MK2)
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}\unicode[STIX]{x1D70F}}=-\frac{s\unicode[STIX]{x1D6FE}}{2Re\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6FF}^{3}}\exp [-s^{2}/4\unicode[STIX]{x1D6FF}^{2}].\end{eqnarray}$$Equations (2.2) and (2.3) – a dynamical system of four coupled ODEs (hereinafter referred to as the ‘MK model’) – can be integrated numerically with the initial condition (2.1) to obtain the evolution of vortex interaction and reconnection.
In the present work, DNS of the incompressible N–S equations for this initial configuration is performed using the same pseudospectral algorithm as that in YH. The Reynolds number 
$Re$ (varied by changing the viscosity 
$\unicode[STIX]{x1D708}$) spans from 1000 to 4000, with the domain size 
$2\unicode[STIX]{x03C0}^{3}$ and grid points ranging from 15363 to 40963. To suppress the symmetry-breaking (planar-jet) instability and reduce the computational cost, two-fold symmetry regarding the symmetry 
$S_{s}$ and collision 
$S_{c}$ planes is further employed – hence only a quarter of the domain (
$L_{x}=2L_{y}=2L_{z}=2\unicode[STIX]{x03C0}$) is simulated. The adequacy of the numerical resolution has been confirmed by performing additional simulations at lower resolution, with all quantities checked (energy, enstrophy, peak vorticity, etc.) showing no notable difference (less than 1 %).
3 Results
Figure 2 (and the supplementary movie, available at https://doi.org/10.1017/jfm.2020.58) shows the time progression of the reconnection (based on the vorticity isosurface 
$|\unicode[STIX]{x1D74E}|$) near the tipping points 
$T$ for 
$Re=4000$. (To capture details of the evolution, a relatively low threshold 
$|\unicode[STIX]{x1D74E}|=0.05\unicode[STIX]{x1D714}_{0}$ is chosen here.) The overall dynamics are quite similar to the previous studies on anti-parallel vortex tubes (Melander & Hussain Reference Melander and Hussain1988, YH). Under self-induction, the curved vortex tubes approach each other and collide (figure 2b). Then, the closest vortex lines of opposite directions cut and connect via cross-diffusion to form two sharp cusps, which rapidly recede away from each other through their curvature-driven self-induction. The remnant, unreconnected vortex lines continuously approach each other and form two parallel thin sheet-like structures (called threads). Mutual induction causes the peak vorticity regions of the threads to advect faster than the remainder, forming head–tail structures (figure 2c). Successive reconnected vorticity lines are similarly laid on top of each other so that their accumulations form a transverse vortex (called a bridge, figure 2d). In addition, at this 
$Re$, the head moves so much faster that it separates from the tail to form a dipole at the top of the thread. Recently, YH showed that, for the anti-parallel vortex case, a series of vortex dipoles form at higher 
$Re$, and we expect similar structures for this configuration also. The bridges, then, retract away from the visualized domain and the tails are diffused out (figure 2e). The remaining thread dipoles, as they advect upwards, continuously undergo slow planar reconnection due to cross-diffusion (figure 2e).
Figure 3. Evolution of the vortex core shape (represented by the vorticity iso-contours 
$\unicode[STIX]{x1D714}_{y}=[0.05\,:\,0.1\,:\,2]\unicode[STIX]{x1D714}_{0}$) in the 
$S_{s}$ plane for (a) 
$Re=1000$; (b) 2000; (c) 3000; (d) 4000. The dashed line (- - - -) in each panel denotes the vortex core trajectory and the times are the same in all the panels. The insets in (b–d) are the zoomed-in views of the vortex head dipole at 
$\unicode[STIX]{x1D70F}=0.4$, with the dash-dotted black circle indicating the equivalent core scale 
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70F})$. See the supplementary movie for the full-time evolution of the vortex core.
The spatial and temporal variations of the vortex core (represented by the vorticity iso-contours) in the symmetry 
$S_{s}$ plane are shown in figure 3. As expected, the collision and upward motion of the rings causes the initial circular core to deform into a non-circular shape. As 
$Re$ increases, the vortex cores move closer and upwards faster with smaller sizes. It is clear that the core flattening and stripping, particularly near the tail, increases with 
$Re$ – contradicting the argument by MK1 that the vortex core would be more circular. In addition, at late time, as the dipoles move upwards as a result of mutual induction, they also separate from each other. The reason for this apparently surprising fact is that the inward (towards each other) self-induced velocity of each vortex is smaller (due to increased radius of curvature 
$1/\unicode[STIX]{x1D705}$) than the outward mutual-induced velocity.
Figure 4. Evolution of the bridge vortex core (represented by the vorticity iso-contours 
$\unicode[STIX]{x1D714}_{z}=[0.05\,:\,0.1\,:\,2]\unicode[STIX]{x1D714}_{0}$) on the 
$S_{c}$ plane for 
$Re=4000$. The dashed line (- - - -) denotes the vortex core trajectory; see the supplementary movie for the full-time evolution of the vortex core for different 
$Re$ cases.
To better illustrate the process of bridge formation, figure 4 shows the evolution of the vorticity distribution 
$\unicode[STIX]{x1D714}_{z}$ in the collision plane 
$S_{c}$ for 
$Re=4000$. The initiation of reconnection starts at the contact point (
$y=z=0$) by viscous cross-diffusion. Then the reconnected vortex lines continuously recede away from the contact point due to both self-induction and stretching by the unreconnected vortices. These vortex lines are accumulated to form a thin vortex sheet (i.e. the bridge). Through roll-up at the head of the sheet, the bridge then slowly develops into a circular shape but with non-concentric distributions (i.e. at 
$\unicode[STIX]{x1D70F}=0.5$), similar to the anti-parallel thicker vortex (YH). The vorticity distribution in the bridge core is found to become more concentric at a later time (i.e. 
$\unicode[STIX]{x1D70F}=1$).
Figure 5(a) shows the evolution of the separation 
$s(\unicode[STIX]{x1D70F})$ (half the distance between the two vortex centres in the symmetry plane) for different 
$Re$ values. (Note that, in MK2, there appears to be some error in their calculation when incorporating the remaining circulation 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})$ equation. As reconnection plays a role only when 
$\unicode[STIX]{x1D6FF}/s$ is approximately 
$O(1)$, it should not affect the overall behaviour during early times (i.e. 
$\unicode[STIX]{x1D70F}<0.2$). However, when comparing results without (figure 1 in MK2) and with (figure 5 in MK2) incorporating the 
$\unicode[STIX]{x1D6FE}$ equation for the same 
$Re$ (i.e. 3000), significant differences incorrectly occur; in particular, the reported critical time 
$\unicode[STIX]{x1D70F}_{c}$ is altered from 0.24452 to 1.93916.) As discussed above, the vortex undergoes significant core deformation into non-circular shapes. Following Hussain & Duraisamy (Reference Hussain and Duraisamy2011), we take the vorticity centroid (computed as the centroid of 
$\unicode[STIX]{x1D714}_{y}$ which is above 75 % of its maximum) to be the vortex centre. For a given 
$Re$, 
$s(\unicode[STIX]{x1D70F})$ first decreases rapidly, but then slows down when approaching reconnection. For different 
$Re$ cases, 
$s(\unicode[STIX]{x1D70F})$ almost collapses initially and then gradually departs for low 
$Re$ through strong viscous diffusion. After reconnection, 
$s(\unicode[STIX]{x1D70F})$ increases slowly with the growth rate decreasing slightly as 
$Re$ increases. In addition, the difference of 
$s(\unicode[STIX]{x1D70F})$ between different 
$Re$ cases becomes smaller at higher 
$Re$, suggesting an asymptotic limit for 
$Re\rightarrow \infty$ – akin to the findings by Kimura & Moffatt (Reference Kimura and Moffatt2014) and YH.
Figure 5. Time evolution of (a) 
$s(\unicode[STIX]{x1D70F})$; (b) 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$; (c) 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$ for different 
$Re$ cases; (d) the minimum values for 
$s^{2}(\unicode[STIX]{x1D70F})$, 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ and 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$ as a function of 
$Re$. The dashed line (- - - -) denotes the MK model for 
$Re=4000$.
The inset in figure 5(a) further shows a comparison of the early evolution (
$\unicode[STIX]{x1D70F}<0.3$) of 
$s^{2}(\unicode[STIX]{x1D70F})$ between the DNS result and the MK model for 
$Re=4000$. For this very thin vortex (i.e. 
$\unicode[STIX]{x1D6FF}/R=0.01$), 
$s^{2}(\unicode[STIX]{x1D70F})$ follows a linear scaling 
$s^{2}(\unicode[STIX]{x1D70F})\approx -0.0377(\unicode[STIX]{x1D70F}-0.2626)$ obtained by least-squares fitting between 
$0<\unicode[STIX]{x1D70F}<0.15$. This scaling is the first observed for viscous reconnection using DNS and is consistent with 
$s(\unicode[STIX]{x1D70F})\sim (\unicode[STIX]{x1D6E4}t)^{1/2}$ scaling based on the dimensional analysis, which has been confirmed in prior studies for quantum reconnection (Baggaley et al. Reference Baggaley, Sherwin, Barenghi and Sergeev2012; Villois, Proment & Krstulovic Reference Villois, Proment and Krstulovic2017; Fonda, Sreenivasan & Lathrop Reference Fonda, Sreenivasan and Lathrop2019) and also for classical reconnection using the B–S model (Kimura & Moffatt Reference Kimura and Moffatt2018). It also validates our previous argument (YH) that the failure of satisfying 1/2 scaling observed in Hussain & Duraisamy (Reference Hussain and Duraisamy2011) is due to the core size effect. Note that 
$s^{2}(\unicode[STIX]{x1D70F})$ calculated on the basis of the MK model for 
$Re=4000$ slightly deviates from our DNS result: larger at an early time, but smaller near the start of reconnection. In addition, the critical time (when 
$s\rightarrow 0$) based on the MK model, which is 
$\unicode[STIX]{x1D70F}_{c}=0.2522$, is a little less than 
$\unicode[STIX]{x1D70F}_{c}=0.2632$ based on the linear scaling.
Figure 5(b) shows the time evolution of 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ at the tipping points 
$T$, along with the calculation based on the MK model. (Note that the curvature 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70F})$ is calculated based on the vortex line crossing each tipping point 
$T$, and here 
$T$ is chosen as the position of peak vorticity 
$\unicode[STIX]{x1D714}_{y,p}(=\Vert \unicode[STIX]{x1D714}_{y}\Vert _{\infty })$ in the 
$S_{s}$ plane. Choosing the vorticity centroid as 
$T$ produces no significant difference in 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70F})$, especially for the early evolution (i.e. 
$\unicode[STIX]{x1D70F}<0.4$).) First, a strong decrease of radius of curvature is observed for 
$\unicode[STIX]{x1D70F}<0.3$, which is consistent with the MK model, although at a much slower rate than the model. Note that as reconnection happens, 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ increases – a feature that is missed by the MK model. The increase of 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ (or equivalently the decrease of curvature 
$\unicode[STIX]{x1D705}$) at the tipping points 
$T$ is mainly due to the induced velocity of the bridges – similar to the curvature reversal observed for anti-parallel vortex reconnection cases (Melander & Hussain Reference Melander and Hussain1988). In addition, the head and tail separate at high 
$Re$, causing circulation loss, which results in a slowdown of the mutual upward advection; this also contributes slightly to the increase of 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$. Note that these two effects are also the main reasons for the lower peak vorticity growth observed in our DNS (discussed later). At a later time, as the bridges move far apart, the induced velocity by the bridges becomes weaker at the tipping points, and hence 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ slowly decreases again.
Since the vortex in the 
$S_{s}$ plane experiences strong core deformation, it is non-trivial to determine the scale of the core. Here, an equivalent core scale 
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70F})$ is obtained using the following procedure. (i) We first calculate the area 
$A$ in the vortex core based on the iso-contour of the 
$\unicode[STIX]{x1D706}_{2}$ criterion (Jeong & Hussain Reference Jeong and Hussain1995) (here, 0.1 % of 
$-\unicode[STIX]{x1D706}_{2}$ peak is chosen as the threshold). Note that, when the tail is separated from the head (for example, at 
$\unicode[STIX]{x1D70F}=0.4$ for 
$Re=3000$, figure 3c), only the head is considered. (ii) An equivalent core size is calculated by equating the actual core area to that of a circle of radius 
$\tilde{\unicode[STIX]{x1D6FF}}$ such that 
$\tilde{\unicode[STIX]{x1D6FF}}=\sqrt{A/\unicode[STIX]{x03C0}}$. (iii) Finally, normalization is performed to obtain 
$\unicode[STIX]{x1D6FF}=\tilde{\unicode[STIX]{x1D6FF}}/2.24$, based on the fact that the core size 
$\tilde{\unicode[STIX]{x1D6FF}}_{0}$ for a Gaussian cross-section 
$\unicode[STIX]{x1D714}(r)\sim \exp [-r^{2}/4\unicode[STIX]{x1D6FF}_{0}^{2}]$ calculated using this method is 
$2.24\unicode[STIX]{x1D6FF}_{0}$. 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$ (figure 5c) initially increases almost linearly with 
$\unicode[STIX]{x1D70F}$ due to viscous diffusion. Then it falls rapidly due to the dominant stretching and cross-annihilation. After reconnection, it increases again, but the growth rate now is smaller than the initial rate, due to the combined effect of viscous diffusion and stretching. As 
$Re$ increases, 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$ becomes smaller due to the decreasing viscous effect. 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$ calculated on the basis of the MK model matches well with the DNS result for 
$\unicode[STIX]{x1D70F}<0.1$; however, it drops earlier, which is the consequence of the MK model’s overestimation of the curvature 
$\unicode[STIX]{x1D705}$ and the associated vortex stretching (figure 5b).
Table 1. Reynolds number dependence of minimum/maximum values for 
$s_{min}^{2}$, 
$\unicode[STIX]{x1D6FF}_{min}^{2}$, 
$(\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2})_{min}$ and 
$(\unicode[STIX]{x1D714}_{y,p}/\unicode[STIX]{x1D714}_{0})_{max}$.
The minimum values for 
$s^{2}$, 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}$ and 
$\unicode[STIX]{x1D6FF}^{2}$ for different 
$Re$ are summarized in table 1 and plotted in figure 5(d). All three quantities decrease with increasing 
$Re$. However, the decay rate is much slower than that reported by MK2. For example, while 
$\unicode[STIX]{x1D6FF}_{min}^{2}$ decreases from 
$2.67412\times 10^{-8}$ to 
$2.75\times 10^{-55}$ based on MK2, here 
$\unicode[STIX]{x1D6FF}_{min}^{2}$ only reduces from 
$2.936\times 10^{-5}$ to 
$1.373\times 10^{-5}$ as 
$Re$ increases from 2000 to 4000.
During reconnection, circulation is continuously transferred from the symmetry plane 
$S_{s}$ to the collision plane 
$S_{c}$ – namely, from 
$\unicode[STIX]{x1D6E4}_{y}=\int _{S_{s}}\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{s}\,\text{d}S$ to 
$\unicode[STIX]{x1D6E4}_{z}=\int _{S_{c}}\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{n}_{c}\,\text{d}S$, with 
$\boldsymbol{n}_{s}$ and 
$\boldsymbol{n}_{c}$ denoting the unit vectors normal to 
$S_{s}$ and 
$S_{c}$, respectively. Figure 6(a) shows the variation of 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D6E4}_{y}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D6E4}$ and figure 6(b) shows the corresponding circulation transfer rate 
$-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t$. During the approaching phase, 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})$ is almost unchanged. Then, a sudden drop in 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})$ occurs during the reconnection process. With increasing 
$Re$, reconnection is delayed due to the decreasing viscous effect. However, as bridging commences, the accumulation of successive reconnected vortex lines in the bridge is rapid, and the reconnection process is accelerated as 
$Re$ increases. It can be clearly seen in figure 6(b) that the maximum of 
$-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t$ increases continuously with 
$Re$, and the maximum occurs slightly earlier as 
$Re$ increases. However, the rate of increase for 
$(-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t)_{max}$ (inset of figure 6b) decreases with increasing 
$Re$. At the late stage of reconnection, 
$-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t$ is found to decrease with 
$Re$, again due to the decreasing viscous effect. As a result, the total circulation transfer might decrease at even higher 
$Re$, as already evident from 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})$ between 
$Re=3000$ and 4000 at 
$\unicode[STIX]{x1D70F}\approx 1$ – akin to the finding by YH.
Figure 6. Evolution of (a) 
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F})$ and (b) the circulation transfer rate 
$-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t$, with the inset showing the 
$Re$ dependence of the maximum of the circulation transfer rate 
$(-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t)_{max}$.
Finally, we examine the evolution of the peak vorticity 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ in the symmetry 
$S_{s}$ plane. 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ first decreases due to viscous diffusion, which is consistent with the increase of 
$\unicode[STIX]{x1D6FF}^{2}(\unicode[STIX]{x1D70F})$, and then increases due to the vortex stretching, reaching a maximum almost at the same time as 
$\unicode[STIX]{x1D6FF}_{min}^{2}$. Note that the time for the maximum of 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ occurs later than the peak of 
$-\text{d}\unicode[STIX]{x1D6FE}/\text{d}t$ – similar to the finding of MK2. Figure 7(b) (see also table 1) further shows the maximum of 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ as a function of 
$Re$. As expected, the maximum increases with 
$Re$, but with a decreasing growth rate. Most importantly, the values are much smaller than those reported by MK2! For example, the peak value from our DNS is only 0.842 for 
$Re=2000$, 1.237 for 
$Re=3000$ and 1.589 for 
$Re=4000$. It indicates that even the physical singularity suggested by MK2 for 
$Re\sim 4000$ cannot occur. As discussed, the slower increase of the maximum of 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ for our DNS is because of the braking effect of the core deformation and bridging – two essential processes missed by the MK model.
Figure 7. (a) Time evolution of the peak vorticity amplification 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ and (b) the 
$Re$ dependence of the maximum of the peak vorticity amplification 
$(\unicode[STIX]{x1D714}_{y,p}/\unicode[STIX]{x1D714}_{0})_{max}$.
4 Concluding remarks
We performed DNS of the reconnection of two slender inclined vortex rings for Reynolds number 
$Re$ up to 4000. Compared to those based on the MK model, initially 
$\unicode[STIX]{x1D705}_{0}^{2}/\unicode[STIX]{x1D705}^{2}(\unicode[STIX]{x1D70F})$ decreases much more slowly, but increases during reconnection. More importantly, the growth of the maximum of 
$\unicode[STIX]{x1D714}_{y,p}(\unicode[STIX]{x1D70F})/\unicode[STIX]{x1D714}_{0}$ with 
$Re$ is substantially smaller than the exponential scaling found by MK2. Two physical processes, which suppress the vorticity growth, were overlooked in the MK model: (1) the inevitable core flattening and the subsequent head–tail separation at the tipping points and (2) the braking effect of the bridges. Needless to say, despite large discrepancies with respect to the DNS results, the MK model still has great value, as it does provide a basis for constructing a viable physical model for better understanding vortex interaction and reconnection. An imperative improvement of the MK model is to include the analysis for bridge formation to better capture the reconnection process.
Several additional points deserve to be commented on when comparing vortex reconnection of inclined rings with the standard anti-parallel tubes. First, the core flattening and the formation of thread dipoles are quite generic, regardless of the initial configuration. In addition, the 1/2 scaling of the separation 
$s(\unicode[STIX]{x1D70F})$ for the inclined ring case confirms our previous claim that the core size plays an important role in the evolution of reconnection, and needs to be included for theoretical modelling. Finally, although the peak circulation transfer rate increases with 
$Re$, the total circulation transfer may be decreased at higher 
$Re$. It indicates that the off-centre reconnection and subsequent formation/avalanche of secondary vortices observed by YH for the anti-parallel case may also occur for the ring case.
Acknowledgements
Computational and visualization resources provided by Texas Tech University HPCC, TACC Lonestar and XSEDE are acknowledged.
Declaration of interests
The authors report no conflict of interest.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2020.58.
