1. INTRODUCTION
The nonlinear propagation of an intense electromagnetic beam through a plasma has been an important area of research in the last few decades and gives rise to a variety of nonlinear effects, including self-focusing (Fuchs et al., Reference Fuchs, d'Humires, Sentoku, Antici, Atzeni, Bandulet, Depierreux, Labaune and Schiavi2010; Niknam et al., Reference Niknam, Aliakbari, Majedi, Haji Mirzaei and Hashemzadeh2011; Bokaei et al., Reference Bokaei, Niknam and Milani2013), self-compression (Shorokhov et al., Reference Shorokhov, Pukhov and Kostyukov2003; Couairon et al., Reference Couairon, Biegert, Hauri, Kornelis, Helbing, Keller and Mysyrowicz2006) and parametric instabilities (Saini et al., Reference Saini and Gill2006). These effects have been investigated in the inertial confinement fusion, X-ray generation (Deutsch et al., Reference Deutsch, Furukawa, Mima, Murakami and Nishihara1996), laser-driven acceleration (Tajima et al., Reference Tajima and Dawson1979) and optical harmonic generation (Lin et al., Reference Lin, Chen and Kieffer2002). The propagation of an intense electromagnetic beam through plasma is also subject to many instabilities such as stimulated Brillouin instability (Mauger et al., Reference Mauger, Berge and Skupin2010; Niknam et al., Reference Niknam, Barzegar and Hashemzadeh2013), Raman instability (Pathak et al., Reference Pathak and Tripathi2006) and self-modulational instability (Gill et al., Reference Gill, Kaur and Mahajan2011). Stimulated Brillouin scattering is a three-wave parametric mixing process coupling two radiation fields with an acoustic wave in a medium. In the plasma, this low frequency instability occurs due to ion-acoustic wave excitation. The Raman instability can be most simply characterized as the resonant decay of an incident photon into a scattered photon plus an electron plasma wave (or plasmon).
The modulational instability, that is the subject of this paper, is one of the most important phenomenon in high intensity laser–plasma interaction. In this process, the change in local refraction index gradient due to nonlinear effects such as relativistic and ponderomotive nonlinearities, induces a change of local laser phase velocity, which modulates the local laser frequency. As a consequence, the local group velocity varies according to the modulated frequency and causes the distortion of the pulse envelope. So the wave amplitude becomes spatially modulated and affects the propagation of laser energy in the plasma.
The modulational instability of electromagnetic waves in the relativistic laser–plasma interaction (Sen, Reference Sen1978; Guerin et al., Reference Guerin, Laval, Mora, Adam, Heron and Bendib1995) have been extensively studied. Quesnel et al. (Reference Quesnel, Mora, Adam, Heron and Laval1997) have presented a general two-dimensional (2D) dispersion relation for circularly polarized electromagnetic waves in a cold plasma and studied the electron parametric instabilities such as the relativistic modulational instability. Sprangle et al. (Reference Sprangle, Hafizi and Penano2000) have obtained a 3D wave equation for intense laser beam propagating through a plasma channel and discussed the modulational instability of electromagnetic waves. Their analysis was based on a systematic approach that includes finite-perturbation-length effects, nonlinearities, group velocity dispersion, and transverse effects. In most of the mentioned works, the propagation of laser pulses are considered in un-magnetized plasmas. While the experiments as well as simulations have confirmed that both quasi-static transverse and axial magnetic fields can be generated in the interaction of intense laser fields with plasmas. So the interaction of intense laser pulses with magnetized plasma is an important and relatively new area of study in the laser–plasma interaction field. In this regard, Jha et al. (Reference Jha, Kumar, Raj and Upadhyaya2005) have investigated the modulation instability of a linearly polarized electromagnetic wave in a collisionless magnetized underdense plasma using a 1D model. They have observed that the presence of uniform magnetic field leads to generation of an additional perturbed transverse plasma current density which affects the modulational interaction. Chen et al. (Reference Chen, Liu and Li2010) have used a generalized method to investigate the modulational instability of an intense right-hand elliptically polarized laser beam in magnetized plasmas in the presence of the relativistic and ponderomotive nonlinearities. In these works the effect of collision has been simply ignored. However, in the cases in which the laser pulse length is larger than the collision time scale that is, τ > τcoll, the collision effect can play an important role in determining the propagation properties. Recently, the modulational instability of electromagnetic waves in a collisional quantum magnetoplasma has been studied by Niknam et al. (Reference Niknam, Rastbood, Bafandeh and Khorashadizadeh2014). They have shown that the increment of modulational instability in a quantum plasma depends on the Fermi electron temperature, plasma number density, collision frequency, and the value of modulation wavenumber.
The present paper is devoted to the study of longitudinal modulational instability by considering the effects of relativistic electron mass variation and ponderomotive force nonlinearity. We estimated the importance of considering collision effect between electrons and ions in relativistic, magnetized plasma. Calculation shows that the modulational instability exists for full range of allowable unstable wavelengths in the presence of collisional effects. It is also observed that the growth rate of the modulational instability increases with rising collisional effects. The equations solved using the perturbative expansion technique and in all calculations ω0 ≫ (ωp, ωc) is supposed, where ωp and ωc are the plasma and cyclotron frequency, respectively. This work is organized into four Sections and two Appendices. A wave equation for the laser electric field is derived which includes nonlinear effects and collisions effect in Section 2. In Section 3, the modulational instability is analyzed. Finally, a summary and conclusions are given in Section 4.
2. DERIVATION OF THE REDUCED WAVE EQUATION
We assume an electromagnetic field propagating through magnetized plasma along the z-direction. The electric field along the x-axis is represented by
$${\bf E}({\bf r},t) = {\hat a_x}{E_0}({\bf r},t)\cos ({k_0}z - {{\rm \omega} _0}t),$$
where E 0, ω0, and k 0 are the amplitude of radiation field, wave frequency, and wavenumber, respectively. The plasma is surrounded by a constant magnetic field along y-direction, 
${{\bf B}_{\bf 0}} = {B_0}{\hat a_y}$. The wave equation governing the propagation of laser beam in the presence of current density sources is
$$\left( {{\nabla ^2} - \displaystyle{1 \over {{c^2}}}\displaystyle{{{\partial ^2}} \over {\partial t}}} \right){\bf E} = \displaystyle{{4{\rm \pi}} \over {{c^2}}}\displaystyle{{\partial {\bf J}} \over {\partial t}},$$
where 
${\bf J} = - ne{\bf V}$ is the current density in the plasma and n, −e, and 
${\bf V}$ are the electron density, the electron's charge and its velocity. On the other hand, in the relativistic regime, the momentum transfer equation in the presence of collisions is
$$\displaystyle{d \over {dt}}(m{\rm \gamma} {\bf V}) = - e{\bf E} - \displaystyle{e \over c}{\bf V} \times ({\bf B} + {{\bf B}_0}) - m{\rm \gamma} {\rm \nu} {\bf V},$$
where m is the rest mass of electron, γ is the relativistic factor, ν is the collision frequency and 
${\bf B}$ is the magnetic field of the laser beam. Moreover, the continuity equation is as
$$\displaystyle{{\partial n} \over {\partial t}} + \nabla. (n{\bf V}) = 0.$$It is assumed that the electron's initial velocity in the absence of laser field is zero that is, V 0 = 0. Considering the first three terms of perturbation expansion, electron density, electron velocity, and current density can be expanded in the orders of the radiation field.
Using Eqs (3) and (4) and the perturbation method, the first-order component of the electron velocity is given by
$$\eqalign{{V_{{\rm 1}x}} & = \displaystyle{{ - e{E_0}{\rm \nu}} \over {m({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\cos ({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{e{E_0}{{\rm \omega} _0}} \over {m({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\sin ({k_0}z - {{\rm \omega} _0}t),}$$
$${V_{{\rm 1}z}} = 0$$and the third-order velocity is as follows:
$$\eqalign{{V_{{\rm 3}x}} & = \left[ {\displaystyle{{3{e^3}E_0^3 {\rm \nu}} \over {8{m^3}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}} - \displaystyle{{{e^3}B_0^2 {E_0}{\rm \nu}} \over {{m^3}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}} \right]\cos ({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \left[ {\displaystyle{{3{e^3}E_0^3 {{\rm \omega} _0}(3{{\rm \nu} ^2} - {\rm \omega} _0^2 )} \over {8{m^3}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^3}}} + \displaystyle{{{e^3}B_0^2 {E_0}{{\rm \omega} _0}} \over {{m^3}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}} \right] \cr & \quad \times \sin ({k_0}z - {{\rm \omega} _0}t).} $$In the above equation, all harmonics have been neglected. Eqn. (7) indicates that the third-order velocity is achieved due to the influence of radiation field and external magnetic field on electrons and the collision effect which modifies it. On the other hand, the electron density is perturbed by the high power laser field. One can obtain electron perturbations using the continuity equation Eq. (4)
$$\displaystyle{{\partial {n_1}} \over {\partial t}} + {n_0}(\nabla \cdot {{\bf V}_1}) = 0,$$where n 0 is unperturbed electron density. According to Eq. (8) and transverse coulomb gauge, the first-order electron density perturbation is zero (n 1 = 0) due to v 1z = 0. The second-order continuity equation is
$$\displaystyle{{\partial {n_2}} \over {\partial t}} + \nabla \cdot ({n_0}{V_2} + {n_1}{{\bf V}_1}) = 0.$$Therefore the second-order electron density is obtained as follows (see Appendix A for detailed discussion):
$$\eqalign{{n_2} & = \displaystyle{{ - {e^2}k_0^2 {n_0}E_0^2 (2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {2{m^2}{\rm \omega} _0^2 ({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\cos 2({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{ - 3{e^2}k_0^2 {n_0}E_0^2 {\rm \nu}} \over {2{m^2}{{\rm \omega} _0}({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\sin 2({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{ - {k_0}{e^2}{E_0}{B_0}{n_0}({\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {{m^2}c{{\rm \omega} _0}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\cos ({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{2{k_0}{e^2}{E_0}{B_0}{n_0}{\rm \nu}} \over {{m^2}c{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\sin ({k_0}z - {{\rm \omega} _0}t).} $$The first two terms in Eq. (10) are due to the ponderomotive force excited by the propagating laser pulse in the plasma, the last two terms show the constant magnetic field effect and collision parameter is emerged in all terms.
2.1. Linear source term
The linear part of the plasma current density is given by
$${J_{{\rm 1}x}} = - e{n_0}{V_{x{\rm 1}}}.$$Substituting Eq. (5) into Eq. (11) yields
$$\eqalign{{{\bf J}_1} & = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \pi}}} \left[ {\displaystyle{{\rm \nu} \over {{\rm \omega} _0^2 + {{\rm \nu} ^2}}}{E_0}\cos ({k_0}z - {{\rm \omega} _0}t){{\hat a}_x}} \right. \cr & \quad \left. {- \displaystyle{{{{\rm \omega} _0}} \over {{\rm \omega} _0^2 + {{\rm \nu} ^2}}}{E_0}\sin ({k_0}z - {{\rm \omega} _0}.t){{\hat a}_x}} \right],}$$where ωp = (4πe 2n 0/m)1/2 is the plasma frequency.
To obtain an envelop equation describing the evolution of E(r, t) it is convenient to first neglect the nonlinear contribution from the plasma current density. Taking a Fourier transform of Eq. (2) without the nonlinear source terms gives
$$\left( {{\nabla ^2} + \displaystyle{4 \over {r_0^2}} + \displaystyle{{{\rm \omega} ^2} \over {{c^2}}}{\rm \lambda}_{\rm L}^2 ({\rm \omega} )} \right){\bf E}({\bf r},{\rm \omega} - {{\rm \omega} _0})\;exp(i{k_0}z) = 0,$$where r 0 is the minimum spot size and λL(ω) is the linear refractive index in collisional plasma which is defined as
$${{\rm \lambda} _{\rm L}}({\rm \omega} ) = {\left[ {1 - \displaystyle{{{\rm \omega} _{\rm p}^2 ({{\rm \omega} ^2} + i{\rm \nu} {\rm \omega} )} \over {{{\rm \omega} ^2}({{\rm \omega} ^2} + {{\rm \nu} ^2})}} - \displaystyle{{4{c^2}} \over {{{\rm \omega} ^2}r_0^2}}} \right]^{1/2}}.$$and the mode propagation constant (wavenumber) is β(ω) = ωλ L(ω)/c. Substituting β(ω) in Eq. (13) we get the following equation
$$\left[ {{\nabla ^2} + 2{k_0}\left( {i\displaystyle{\partial \over {\partial z}} + \displaystyle{{{{\rm \beta} ^2}({\rm \omega} ) - k_0^2} \over {2{k_0}}} + \displaystyle{2 \over {{k_0}r_0^2}}} \right)} \right]{\bf E}({\bf r},{\rm \omega} - {{\rm \omega} _0}) = 0,$$
where k 0 is the unperturbed wavenumber. Since 
${\bf E}({\bf r},{\rm \omega} - {{\rm \omega} _0})$ is the Fourier transform of the slowly varying amplitude 
${\bf E}({\bf r},t)$ the propagation wave number β(ω) can be expanded about ω0
$${\rm \beta} ({\rm \omega} ) = {{\rm \beta} _0} + ({\rm \omega} - {{\rm \omega} _0}){{\rm \beta} _1} + \displaystyle{1 \over 2}{({\rm \omega} - {{\rm \omega} _0})^2}{{\rm \beta} _2} +..., $$
where 
${{\rm \beta} _{\rm n}} = [{d^{\rm n}}{\rm \beta} ({\rm \omega} )/d{{\rm \omega} ^{\rm n}}{]_{{\rm \omega} = {{\rm \omega} _0}}}$. In Eq. (16) β0 = k 0 is the wave number in the vacuum, β1 is the first-order dispersion or inverse group velocity and β2 is the second-order dispersion and related to the group velocity dispersion (GVD). Substituting Eq. (16) in Eq. (15) and using the approximation of 
$({{\rm \beta} ^2} - k_0^2 )/2{k_0} \approx {\rm \beta} ({\rm \omega} ) - {k_0}$ and taking the inverse Fourier transform (Sprangle et al., Reference Sprangle, Hafizi and Penano2000) one can obtain
$$\eqalign{&\left[ {{\nabla ^2} + 2{k_0}\left( {i\displaystyle{\partial \over {\partial z}} + {{\rm \beta} _0} - {k_0} + \displaystyle{2 \over {{k_0}r_0^2}} + i{{\rm \beta} _1}\displaystyle{\partial \over {\partial t}} - \displaystyle{{{{\rm \beta} _2}} \over 2}\displaystyle{{{\partial ^2}} \over {\partial {t^2}}}} \right)} \right] \cr & \times {E_0}({\bf r},t) = 0,}$$where the GVD parameter β2 can be defined as follows:
$${{\rm \beta} _2} = - \displaystyle{1 \over {{{\rm \omega} _0}c}}\left[ {\displaystyle{{{\rm \omega} _{\rm p}^2 ({\rm \omega} _0^2 + i{\rm \nu} {{\rm \omega} _0})} \over {{\rm \omega} _0^2 ({\rm \omega} _0^2 + {{\rm \nu} ^2})}} + \displaystyle{{4{c^2}} \over {{\rm \omega} _0^2 r_0^2}}} \right],$$and the higher order terms in β(ω) are neglected. It is also supposed that the nonlinear effects and perturbed current densities of collisional plasma are small.
2.2. Nonlinear source term
The nonlinear contribution to the plasma current density originates from ponderomotive force, relativistic mass, and represents perturbations due to effects of the constant magnetic field and collisions. The nonlinear part of the plasma current density is given by
$${{\bf J}_{\bf 3}} = - e({n_0}{{\bf V}_3} + {n_2}{{\bf V}_1}),$$where V1 is the transverse quiver velocity and V3 is the third-order velocity. Substituting Eqs (5), (7), and (10) into Eq. (19) one obtains
$${{\bf J}_3} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \pi}}} \left[ {\displaystyle{{{d_1}} \over {{{\rm \omega} _0}}}{E_0}\cos ({k_0}z - {{\rm \omega} _0}t){{\hat a}_x} - \displaystyle{{{d_2}} \over {{{\rm \omega} _0}}}{E_0}\sin ({k_0}z - {{\rm \omega} _0}t){{\hat a}_x}} \right],$$in which all harmonics have been neglected. In addition, d 1 and d 2 are given, respectively, as follows:
$$\eqalign{{d_1} & = \displaystyle{{ - {e^2}k_0^2 E_0^2 {\rm \nu} (2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {4{m^2}{{\rm \omega} _0}({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^2}}} + \displaystyle{{3{e^2}k_0^2 E_0^2 {\rm \nu} {{\rm \omega} _0}} \over {4{m^2}({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^2}}} \cr & \quad + \displaystyle{{ - 3{e^2}E_0^2 {\rm \nu} {{\rm \omega} _0}} \over {8{m^2}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}} + \displaystyle{{{\rm \omega} _c^2 {{\rm \omega} _0}{\rm \nu}} \over {{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}},}$$and
$$\eqalign{{d_2} & = \displaystyle{{3{e^2}k_0^2 E_0^2 {{\rm \nu} ^2}} \over {4{m^2}({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^2}}} + \displaystyle{{{e^2}k_0^2 E_0^2 (2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {4{m^2}({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^2}}} \cr & \quad + \displaystyle{{3{e^2}E_0^2 {\rm \omega} _0^2 (3{{\rm \nu} ^2} - {\rm \omega} _0^2 )} \over {8{m^2}{c^2}{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^3}}} + \displaystyle{{{\rm \omega} _c^2 {\rm \omega} _0^2} \over {{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}},}$$where ωc = eB 0/mc. The nonlinear current J3 contains the contributions due to collision effect, magnetic field, and nonlinearities which are generated by radiation pressure.
Replacing the third-order derivative of current density, Eq. (20) in the right hand side of the Eq. (17) gives a good approximation of nonlinear wave equation for the propagation of laser beam in the collisional magnetized plasma as
$$\eqalign{& \left[ {{\nabla ^2} + 2{k_0}\left( {i\displaystyle{\partial \over {\partial z}} + {{\rm \beta} _0} - {k_0} + \displaystyle{2 \over {{k_0}r_0^2}} + i{{\rm \beta} _1}\displaystyle{\partial \over {\partial t}} - \displaystyle{{{{\rm \beta} _2}} \over 2}\displaystyle{{{\partial ^2}} \over {\partial {t^2}}}} \right)} \right]a({\bf r},t) \cr & = - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{c^2}}} \vert a({\bf r},t{) \vert ^2}\left[ {{c_1} + i{c_2}} \right]a({\bf r},t),}$$
where 
$a({\bf r},t) = e{E_0}({\bf r},t)/mc{{\rm \omega} _0}$ is the normalized amplitude of the electric field and ωc = eB/m 0c. In addition, c 1 and c 2 are given, respectively, as follows:
$$\eqalign{{c_1} & = \displaystyle{{ - 3k_0^2 {{\rm \nu} ^2}{c^2}{\rm \omega} _0^2} \over {({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _{\rm o}^2 + {{\rm \nu} ^2}{)^2}}} + \displaystyle{{ - k_0^2 (2{\rm \omega} _0^2 - {{\rm \nu} ^2}){c^2}{\rm \omega} _0^2} \over {({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({\rm \omega} _{\rm o}^2 + {{\rm \nu} ^2}{)^2}}} \cr & \quad + \displaystyle{{ - 3{\rm \omega} _0^4 (3{{\rm \nu} ^2} - {\rm \omega} _0^2 )} \over {2({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^3}}} + \displaystyle{{ - 4{\rm \omega} _{\rm c}^2 {\rm \omega} _0^2} \over {b_{{\rm s0}}^2 {{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}},}$$and
$$\eqalign{{c_2} & = \displaystyle{{k_0^2 {c^2}{\rm \nu} {{\rm \omega} _0}(2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({{\rm \nu} ^2} + {\rm \omega} _0^2 {)^2}}} + \displaystyle{{ - 3k_0^2 {\rm \nu} {\rm \omega} _0^3 {c^2}} \over {({{\rm \nu} ^2} + 4{\rm \omega} _0^2 )({{\rm \nu} ^2} + {\rm \omega} _0^2 {)^2}}} \cr & \quad + \displaystyle{{3{\rm \nu} {\rm \omega} _0^3} \over {2({\rm \omega} _0^2 + {{\rm \nu} ^2}{)^2}}} + \displaystyle{{ - 4{\rm \omega} _{\rm c}^2 {\rm \nu} {\rm \omega} _0^2} \over {b_{{\rm s0}}^2 {{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}.}$$ It is convenient here to change variables from (z, t) to coordinate system in the pulse-stationary frame of reference (z, ξ), where ξ = z − V gt and V g is the group velocity of the laser pulse. So ∂/∂t = −V g∂/∂ξ and 
${\partial ^2}/\partial {t^2} = V_{\rm g}^2 {\partial ^2}/\partial {{\rm \xi} ^2}$ and the Laplacian operator can be written as 
${\nabla ^2} = \nabla _ \bot ^2 + {\partial ^2}/\partial {z^2}$ where its vertical component is 
$\nabla _ \bot ^2 = (1/r)(\partial /\partial r)(r(\partial /\partial r))$, z is the axial propagation direction and r is the radial coordinate. By neglecting 1/k 0 in comparison with 
${{\rm \beta} _2}V_{\rm g}^2 $ (paraxial approximation) and substituting β0 = k 0 and β1 = 1/V g, the Eq. (23) reduces to
$$\eqalign{& \left[ {\nabla _ \bot ^2 + 2{k_0}\left( {i\displaystyle{\partial \over {\partial z}} + \displaystyle{2 \over {{k_0}r_0^2}} - \displaystyle{1 \over 2}{{\rm \beta} _2}V_{\rm g}^2 \displaystyle{{{\partial ^2}} \over {\partial {{\rm \xi} ^2}}}} \right) + 2\displaystyle{{{\partial ^2}} \over {\partial z\partial {\rm \xi}}}} \right]a({\bf r},z,{\rm \xi} ) \cr & = - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{c^2}}} \vert a({\bf r},z,{\rm \xi} {) \vert ^2}\left[ {{c_1} + i{c_2}} \right]a({\bf r},z,{\rm \xi} ).} $$In Eq. (26), the amplitude of radiation field is a slowly varying function of z so ∂2/∂z 2 is negligible in comparison with 2k 0∂/∂z.
3. 1D MODULATIONAL INSTABILITY
In this section, we study the longitudinal modulational instability in the interaction of laser pulse with collisional magnetized plasma. Ignoring the transverse variations of the amplitude of the laser field in the limit of plane wave (r 0 → ∞), the Eq. (26) reduces to
$$\eqalign{&\left[ {2{k_0}\left( {i\displaystyle{\partial \over {\partial z}} - \displaystyle{1 \over 2}{{\rm \beta} _2}V_{\rm g}^2 \displaystyle{{{\partial ^2}} \over {\partial {{\rm \xi} ^2}}}} \right) + 2\displaystyle{{{\partial ^2}} \over {\partial z\partial {\rm \xi}}} + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{c^2}}}\left[ {{c_1} + i{c_2}} \right]{a^2}({\bf r},z,{\rm \xi} )} \right] \cr & \times a({\bf r},z,{\rm \xi} ) = 0.}$$In the long pulse limit, we get
$${a_0}(z) = {a_{{\rm s0}}}\;exp\left( {\displaystyle{{2izP} \over {{Z_{{\rm R0}}}}}} \right),$$
where a s0 is the initial normalized peak amplitude and 
${Z_{{\rm R0}}} =$
${k_0}r_0^2 /2$ is the Rayleigh length. The normalized laser power P is as
$$P = \displaystyle{1 \over 8}\displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{c^2}}}\left[ {{c_1} + i{c_2}} \right]a_{{\rm s0}}^2 r_0^2, $$and r 0 is the minimum spot size. The first-order solution of Eq. (27) depends on ξ variations and this perturbation results in modulational instability, thus the total perturbed amplitude is
$${a_{\rm s}}(z,{\rm \xi} ) = {a_{{\rm s0}}}\;exp\left( {\displaystyle{{2iPz} \over {{Z_{{\rm R0}}}}}} \right) + {a_{{\rm s1}}}\;exp\left( {\displaystyle{{2iPz} \over {{Z_{{\rm R0}}}}}} \right),$$where a s1 is the perturbed amplitude of the beam in collisional plasma and it is complex. Considering condition of |a s1| ≪ |a s0| and substituting Eq. (30) in Eq. (27) we obtain
$$i\displaystyle{{\partial {a_{{\rm s1}}}} \over {\partial z}} - \displaystyle{1 \over 2}{{\rm \beta} _2}V_{\rm g}^2 \displaystyle{{{\partial ^2}{a_{{\rm s1}}}} \over {\partial {{\rm \xi} ^2}}} + \displaystyle{1 \over {{k_0}}}\displaystyle{{{\partial ^2}{a_{{\rm s1}}}} \over {\partial z\partial {\rm \xi}}} + \displaystyle{{2iP} \over {{k_0}{Z_{{\rm R0}}}}}\displaystyle{{\partial {a_{{\rm s1}}}} \over {\partial {\rm \xi}}} + \displaystyle{{4P} \over {{Z_{{\rm R0}}}}}{a_{{\rm s1}}} = 0,$$and a s1 can be considered as follows:
$${a_{{\rm s1}}}(z,{\rm \xi} ) = exp[i(Kz + k{\rm \xi} )] + exp[ - i(Kz + k{\rm \xi} )].$$In the above equation K is the modulation wavenumber and its imaginary part represents the spatial growth and K is the propagation wave number of the perturbed wave amplitude. In the following, we obtain the dispersion relation by substituting Eq. (32) in Eq. (31) as
$$(1 - {\hat k^2}){\hat K^2} + 8(P + {\hat {\rm \beta}_2}{\hat k^2})\hat k\hat K - 16\left( {{{\hat {\rm \beta}} _2}{{\hat k}^2} + P{{\hat {\rm \beta}}_2} - \displaystyle{{{P^2}} \over 4}} \right){\hat k^2} = 0.$$ The quantities of 
$\hat k = k/{k_0}$, 
$\hat K = {Z_{{\rm R0}}}K$ and 
${\hat {\rm \beta} _2} = 1/8(V_{\rm g}^2 k_0^2$
${Z_{{\rm R0}}}{{\rm \beta} _2})$ are dimensionless. Replacing the expansion of β(ω), we get 
${\hat {\rm \beta} _2} \approx - 1/4(1 + {\rm \omega} _{\rm p}^2 ({\rm \omega} _0^2 + i{\rm \nu} {{\rm \omega} _0})r_0^2 /4({\rm \omega} _0^2 + {{\rm \nu} ^2}){c^2})$. Then the roots of dispersion relation, Eq. (33), are obtained as follows:
$$\eqalign{\hat K & = \displaystyle{{ - 4(P + {{\hat {\rm \beta}} _2}{{\hat k}^2})\hat k} \over {1 - {{\hat k}^2}}}\cr & \quad \pm \displaystyle{{4\sqrt {{{\hat k}^2}{{(P + {{\hat {\rm \beta}} _2}{{\hat k}^2})}^2} + (1 - {{\hat k}^2})(\hat {\rm \beta} _2^2 {{\hat k}^2} + P{{\hat {\rm \beta}} _2} - \displaystyle{{{P^2}} \over 4}){{\hat k}^2}}} \over {1 - {{\hat k}^2}}}.}$$ Since calculated quantities 
${\hat {\rm \beta} _2}$, P, and 
$\hat k$ are complex, we can choose 
$\hat {\rm \beta} = {\hat {\rm \beta} _{\rm r}} + i{\hat {\rm \beta} _{\rm i}}$, 
$\hat k = {\hat k_{\rm r}} + i{\hat k_{\rm i}}$, and P = P r + iP i. Substituting these quantities in Eq. (34) we can write 
$\hat K = {\hat K_{\rm r}} + i\Gamma $, which the modulational instability is associated with the imaginary part that is, Γ (see Appendix B for detailed discussion).
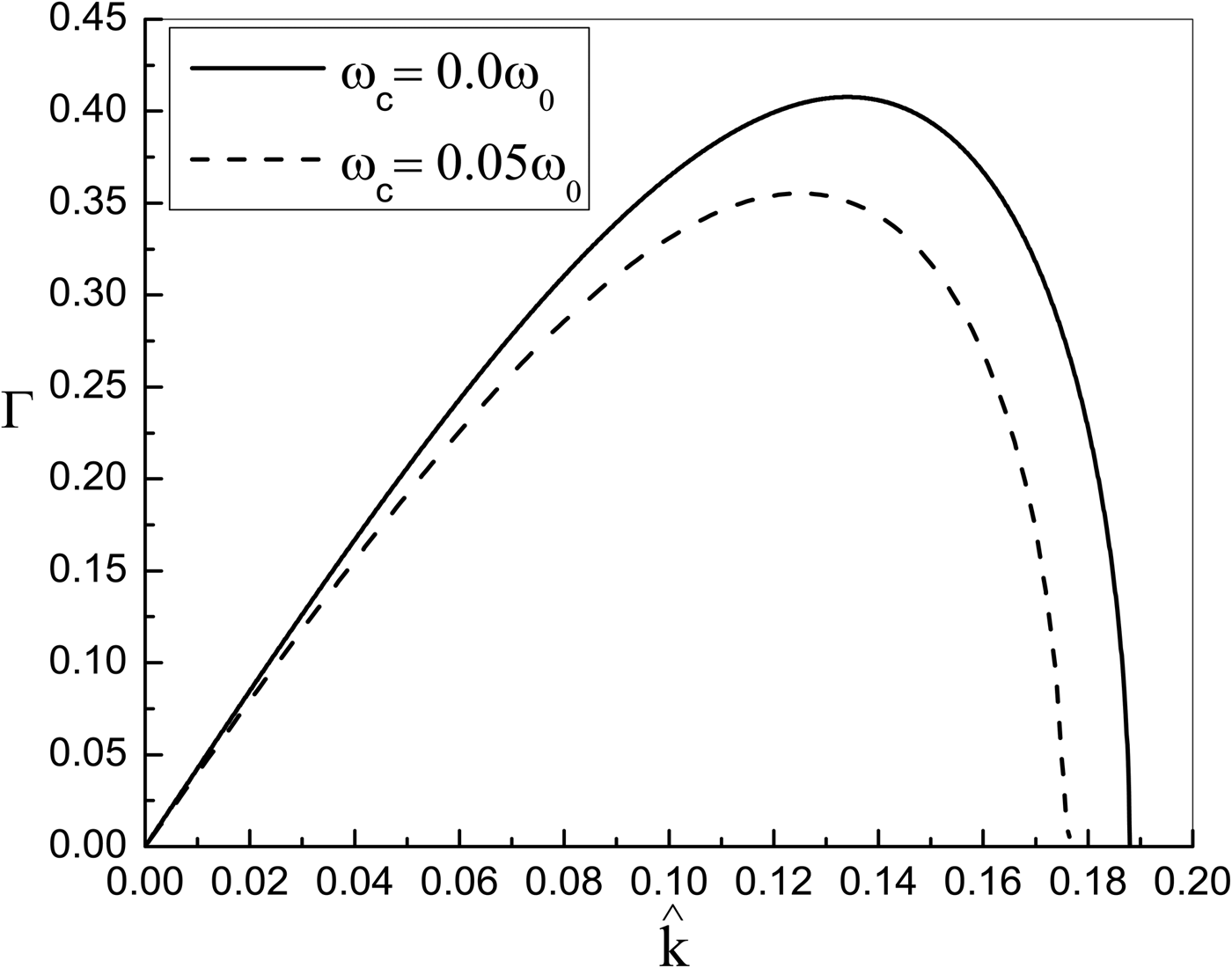
The spatial growth rate of modulational instability in a collisional transversely magnetized plasma is obtained by the imaginary part of the Eq. (34). In Figure 1, the imaginary part of 
$\hat k$ is plotted as a function of normalized wavenumber 
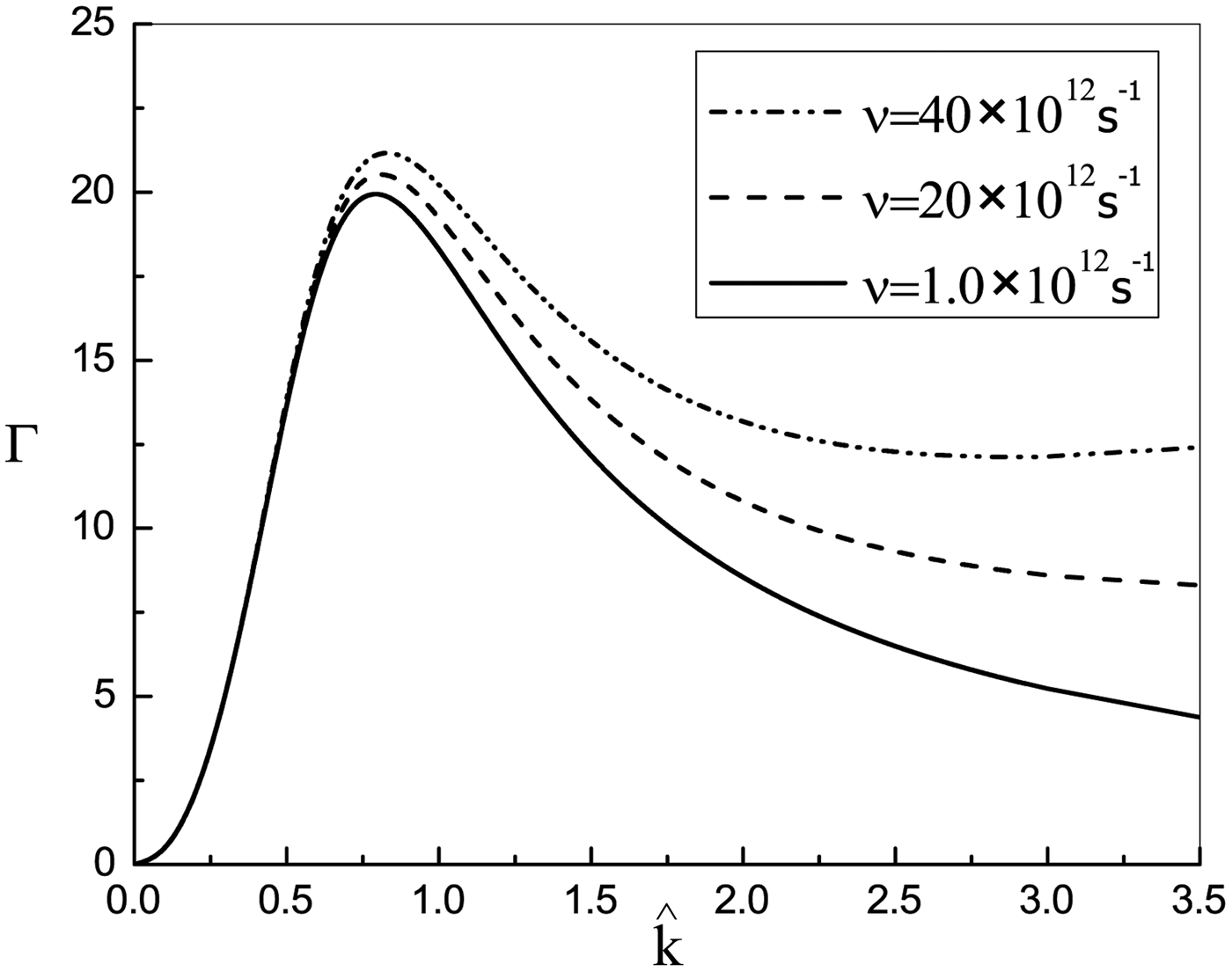
$\hat k$, for two different values of ωc/ω0. It is shown that in the absence of collisional effects the modulational instability is restricted to small wavenumber region and the instability can occur when 
${\hat k^2} \le - P((3P/4) + {\hat {\rm \beta} _2})/((P/2) + {\hat {\rm \beta} _2}^2 )$. Moreover, Figure 1 displays that spatial growth rate of modulational instability in the collisionless plasma decreases by increasing the external magnetic field. Since the perturbed transverse plasma current density due to constant magnetic field results in reducing the combined effects of relativistic and ponderomotive nonlinearities. But in Figure 2, we show that in a collisional magnetized plasma the modulational instability exists for full range of unstable wavenumbers. This figure represents the spatial growth rate of modulational instability in a collisional magnetoactive plasma as a function of normalized wavenumber 
$\hat k$, for three different values of the collision frequency. From this figure, it is observed that in the large wavenumber region, there is a significant increase in instability growth rate due to the collisional effects. These effects tend to change the transverse plasma current density in such a way that the combined effects of relativistic and ponderomotive nonlinearities increase, consequently, the instability growth rate increases. Figure 3 shows the modulational instability growth rate for different values of magnetic field in the presence of collisions. In contrary to the collisionless case, the instability growth rate increases with increase in magnetic field. This happens because the external magnetic field enhances the collisional effects.
Fig. 1. The spatial growth rate of modulational instability as a function of normalized wavenumber in a collisionless plasma for two different values of ωc/ω0. The parameters are ω0 = 1.88 × 1015s −1, a s0 = 0.271, r 0 = 15 μm, and ωp/ω0 = 0.1.
Fig. 2. The spatial growth rate of modulational instability as a function of normalized wavenumber in a collisional, magnetized plasma for three different values of collision frequency, ν. The parameters are ω0 = 1.88 × 1015s −1, a s0 = 0.271, r 0 = 15 μm, ωp/ω0 = 0.1, and ωc/ω0 = 0.1.
Fig. 3. The spatial growth rate of modulational instability as a function of normalized wavenumber for three different values of ωc/ω0 = 0.0, ωc/ω0 = 0.2 and ωc/ω0 = 0.3. The parameters are ωp = 0.1ωp, ν = 20 × 1012s −1.
The effect of plasma frequency on the spatial growth rate of modulational instability in the collisionless and collisional magnetized plasmas are presented in Figures 4a and 4b, respectively. It is observed that increasing plasma frequency has a great effect on the modulational instability. In fact, by increasing the plasma frequency, the effects of relativistic and ponderomotive nonlinearities would be strengthened. Therefore, the modulational instability growth rate is significantly enhanced over the range of unstable wavenumbers.
Fig. 4. The spatial growth rate of modulational instability as a function of normalized wavenumber for two different values of ωp/ω0, (a) ν = 0.0s −1, (b) ν = 1.0 × 1012s −1. The parameters are ω0 = 1.88 × 1015s −1, a s0 = 0.271, r 0 = 15 μm, and ωc/ω0 = 0.1.
4. SUMMARY AND CONCLUSION
In the present paper, we applied the source dependent expansion method to study the modulational instability of a linear polarized laser pulse propagating in a collisional magnetoactive plasma. The longitudinal modulational instability, in which the relativistic and ponderomotive nonlinearities are taken into account, was obtained for the propagating wave in the plasma. The nonlinear dispersion relation in the limit of long pulse was obtained for the perturbed laser beam amplitude. It is observed that in the absence of collisional effects the modulational instability is restricted to the small wavenumber region and the constant magnetic field reduces the growth rate of the instability. In contrast, the spatial growth rate of modulational instability exists for full range of allowable wavelengths of perturbed wave amplitude in the presence of collisional effects. It was illustrated that the spatial growth rate is greatly enhanced in the presence of collisional effects and the applied magnetic field also increases the instability growth rate in the case of collisional plasma. Moreover, the results show that the modulational instability growth rate is significantly enhanced by increasing the plasma frequency due to the nonlinearity reinforcement. Indeed, the modulational interactions in collisional plasma make the important restriction on laser-driven fusion mechanism and play significant role during the laser thermonuclear synthesis.
APPENDIX A
Perturbation approach to obtain Eq. (10)
In this section, application of perturbation method to calculate Eq. (10) has been illustrated in more depth. Using Eqs (3) and (4) the second-order electron velocity will be
$$\eqalign{{V_{{\rm 2}x}} & = \displaystyle{{ - {e^2}{k_0}E_0^2 (2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {2{m^2}{{\rm \omega} _0}(4{\rm \omega} _0^2 + {{\rm \nu} ^2})({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\cos 2({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{3{e^2}{k_0}E_0^2 {\rm \nu}} \over {2{m^2}(4{\rm \omega} _0^2 + {{\rm \nu} ^2})({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\sin 2({k_0}z - {{\rm \omega} _0}t),}$$
$$\eqalign{{V_{{\rm 2}z}} & = \displaystyle{{{e^2}{E_0}{B_0}({\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {{m^2}c{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\cos ({k_0}z - {{\rm \omega} _0}t) \cr & \quad + \displaystyle{{2{e^2}{E_0}{B_0}{\rm \nu} {{\rm \omega} _0}} \over {{m^2}c{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\sin ({k_0}z - {{\rm \omega} _0}t).}$$Substituting second-order velocity into Eq. (9), we get
$$\eqalign{\displaystyle{{\partial {n_2}} \over {\partial t}} & + \displaystyle{\partial \over {\partial z}}\left( {\displaystyle{{ - {n_0}{e^2}{k_0}E_0^2 (2{\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {2{m^2}{{\rm \omega} _0}(4{\rm \omega} _0^2 + {{\rm \nu} ^2})({\rm \omega} _0^2 + {{\rm \nu} ^2})}}} \right.\cos 2({k_0}z - {{\rm \omega} _0}t) \cr & + \displaystyle{{3{n_0}{e^2}{k_0}E_0^2 {\rm \nu}} \over {2{m^2}(4{\rm \omega} _0^2 + {{\rm \nu} ^2})({\rm \omega} _0^2 + {{\rm \nu} ^2})}}\sin 2({k_0}z - {{\rm \omega} _0}t) \cr & + \displaystyle{{{n_0}{e^2}{E_0}{B_0}({\rm \omega} _0^2 - {{\rm \nu} ^2})} \over {{m^2}c{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\cos ({k_0}z - {{\rm \omega} _0}t) \cr & \left. { + \displaystyle{{2{n_0}{e^2}{E_0}{B_0}{\rm \nu} {{\rm \omega} _0}} \over {{m^2}c{{({\rm \omega} _0^2 + {{\rm \nu} ^2})}^2}}}\sin ({k_0}z - {{\rm \omega} _0}t)} \right) = 0.}$$By differentiating and integrating Eq. (A3), one can obtain Eq. (10).
APPENDIX B
Calculation of the instability growth rate
The instability growth rate which is acquired from the imaginary part of Eq. (34), is written as
$$\Gamma = {{\rm \gamma} _1} + 4{{\rm \gamma} _2},$$where γ1 and γ2 are the imaginary parts of first and second terms on the right hand side of Eq. (34), respectively. The parameter γ1 is defined as follows:
$$\eqalign{{\gamma _1} & = - 4\displaystyle{\matrix{{{\hat k}_{\rm r}}\left( {{P_i} + {{\hat \beta} _i}(\hat k_{\rm r}^2 - \hat k_i^2 ) + 2{{\hat k}_i}{{\hat k}_{\rm r}}{{\hat \beta} _{\rm r}}} \right) \hfill \cr \quad + {{\hat k}_i}\left( {{P_{\rm r}} + {{\hat \beta} _{\rm r}}(\hat k_{\rm r}^2 - \hat k_i^2 ) - 2{{\hat \beta} _i}{{\hat k}_i}{{\hat k}_{\rm r}})(1 - \hat k_{\rm r}^2 + \hat k_i^2 )} \right) \hfill} \over {{{(1 - \hat k_{\rm r}^2 + \hat k_i^2 )}^2} + 4\hat k_{\rm r}^2 \hat k_i^2}} \cr & \qquad+ 32\displaystyle{\matrix{{{\hat k}_{\rm r}}\left( {{P_{\rm r}} + {{\hat \beta} _{\rm r}}(\hat k_{\rm r}^2 - \hat k_i^2 ) - 2{{\hat \beta} _i}{{\hat k}_i}{{\hat k}_{\rm r}}} \right) \hfill \cr \quad - {{\hat k}_i}\left( {{P_i} + {{\hat \beta} _i}(\hat k_{\rm r}^2 - \hat k_i^2 + 2{{\hat k}_{\rm r}}{{\hat k}_i}{{\hat \beta} _{\rm r}})} \right) \hfill} \over {{{(1 - \hat k_{\rm r}^2 + \hat k_i^2 )}^2} + 4\hat k_{\rm r}^2 \hat k_i^2}},}$$and the parameter γ2 will be given as
$${{\rm \gamma} _2} = \displaystyle{1 \over {\sqrt 2}} \sqrt { - {G_1} + \sqrt {G_1^2 + G_2^2}},$$where parameters G 1 and G 2 are specified as follows:
$${G_1} = \displaystyle{{{g_1}{g_3} + {g_2}{g_4}} \over {g_3^2 + g_4^2}},$$
$${G_2} = \displaystyle{{{g_2}{g_3} - {g_1}{g_4}} \over {g_3^2 + g_4^2}},$$in which g 1, g 2, g 3, and g 4 are
$$\eqalign{{g_1} & = \displaystyle{3 \over 4}\Big( {(P_{\rm r}^2 - P_i^2 )(\hat k_{\rm r}^2 - \hat k_i^2 ) - 4{P_{\rm r}}{P_i}{{\hat k}_{\rm r}}{{\hat k}_i}} \Big) + ({P_{\rm r}}{{\hat {\rm \beta}} _{\rm r}} - {P_i}{{\hat {\rm \beta}} _i}) \cr & \quad \times \left( {{{(\hat k_{\rm r}^2 - \hat k_i^2 )}^2} - 4\hat k_{\rm r}^2 \hat k_i^2} \right) - 4{{\hat k}_i}{{\hat k}_{\rm r}}(\hat k_{\rm r}^2 - \hat k_i^2 )({P_i}{{\hat {\rm \beta}} _{\rm r}} + {P_{\rm r}}{{\hat {\rm \beta}} _i}) \cr & \quad + (\hat {\rm \beta} _{\rm r}^2 - \hat {\rm \beta} _i^2 ) \left( {{{(\hat k_{\rm r}^2 - \hat k_i^2 )}^2} - 4\hat k_i^2 \hat k_{\rm r}^2} \right) - 8{{\hat {\rm \beta}} _i}{{\hat {\rm \beta}} _{\rm r}}{{\hat k}_i}{{\hat k}_{\rm r}}(\hat k_{\rm r}^2 - \hat k_i^2 ) \cr & \quad + (\hat k_{\rm r}^2 - \hat k_i^2 )({P_{\rm r}}{{\hat {\rm \beta}} _{\rm r}} - {P_i}{{\hat {\rm \beta}} _i}) - 2({P_i}{{\hat {\rm \beta}} _{\rm r}} + {P_{\rm r}}{{\hat {\rm \beta}} _i}){{\hat k}_{\rm r}}{{\hat k}_i} + \displaystyle{1 \over 4}(P_{\rm r}^2 - P_i^2 ) \cr & \quad \times \Big( {(\hat k_{\rm r}^2 - \hat k_i^2 - 4\hat k_{\rm r}^2 \hat k_i^2 ) - 8{P_i}{P_{\rm r}}{{\hat k}_{\rm r}}{{\hat k}_i}(\hat k_{\rm r}^2 - \hat k_i^2 )} \Big),}$$
$$\eqalign{{g_2} & = \displaystyle{3 \over 2}\Big( {{P_{\rm r}}{P_i}(\hat k_{\rm r}^2 - \hat k_i^2 ) + {{\hat k}_{\rm r}}{{\hat k}_i}(P_{\rm r}^2 - P_i^2 )} \Big) + 4\Big(\hat k_{\rm r}^2 - \hat k_i^2 \Big) \cr & \quad \times ({P_{\rm r}}{{\hat {\rm \beta}} _{\rm r}} - {P_i}{{\hat {\rm \beta}} _i}){{\hat k}_{\rm r}}{{\hat k}_i} + ({P_i}{{\hat {\rm \beta}} _{\rm r}} + {P_{\rm r}}{{\hat {\rm \beta}} _i})\left( {{{(\hat k_{\rm r}^2 - \hat k_i^2 )}^2} - 4\hat k_{\rm r}^2 \hat k_i^2} \right) \cr & \quad + 2{{\hat {\rm \beta}} _{\rm r}}{{\hat {\rm \beta}} _i}\left( {{{(\hat k_{\rm r}^2 - \hat k_i^2 )}^2} - 4\hat k_{\rm r}^2 \hat k_i^2} \right) + 4{{\hat k}_{\rm r}}{{\hat k}_i}(\hat k_{\rm r}^2 - \hat k_i^2 )(\hat {\rm \beta} _{\rm r}^2 - \hat {\rm \beta} {i^2}) \cr & \quad + ({P_i}{{\hat {\rm \beta}} _{\rm r}} + {P_{\rm r}}{{\hat {\rm \beta}} _i})(\hat k_{\rm r}^2 - \hat k_i^2 ) + 2{{\hat k}_{\rm r}}{{\hat k}_i}({P_{\rm r}}{{\hat {\rm \beta}} _{\rm r}} - {P_i}{{\hat {\rm \beta}} _i}) \cr & \quad \times \displaystyle{1 \over 2}{P_{\rm r}}{P_i}\left( {{{(\hat k_{\rm r}^2 - \hat k_i^2 )}^2} - 4\hat k_{\rm r}^2 \hat k_i^2} \right) + {{\hat k}_{\rm r}}{{\hat k}_i}(\hat k_{\rm r}^2 - \hat k_i^2 )(P_{\rm r}^2 - P_i^2 ),}$$
$${g_3} = (1 - \hat k_{\rm r}^2 + \hat k_i^2 {)^2} - 4k_{\rm r}^2 k_i^2,$$
$${g_4} = 4(1 - \hat k_{\rm r}^2 + \hat k_i^2 ){\hat k_{\rm r}}{\hat k_i}.$$
