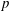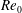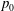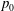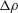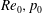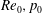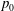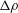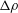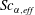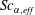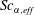1 Introduction
Mixing of several species under high-pressure (high-
![]() $p$
) conditions is encountered in many chemical engineering processes and in virtually all combustion systems used for either transportation or propulsion, e.g. diesel engines, gas turbine engines and rocket engines. In many of these systems the fuel used is a complex mixture of many chemical species (Edwards & Maurice Reference Edwards and Maurice2001; Edwards Reference Edwards2003; Edwards et al.
Reference Edwards, Minus, Harrison and Corporan2004). Chemical reactions in these engineering applications produce additional species compared to the mixture of reactants. Frequently in chemical engineering applications and in all the above-mentioned combustion systems, one encounters high-
$p$
) conditions is encountered in many chemical engineering processes and in virtually all combustion systems used for either transportation or propulsion, e.g. diesel engines, gas turbine engines and rocket engines. In many of these systems the fuel used is a complex mixture of many chemical species (Edwards & Maurice Reference Edwards and Maurice2001; Edwards Reference Edwards2003; Edwards et al.
Reference Edwards, Minus, Harrison and Corporan2004). Chemical reactions in these engineering applications produce additional species compared to the mixture of reactants. Frequently in chemical engineering applications and in all the above-mentioned combustion systems, one encounters high-
![]() $p$
turbulent reactive flows. Understanding these flows is challenging due to the coupling among transport, thermodynamics and dynamics of the flow. Experimental and simulation challenges in discerning the control parameters in these applications are similar. For example, conducting experiments and simulations at high
$p$
turbulent reactive flows. Understanding these flows is challenging due to the coupling among transport, thermodynamics and dynamics of the flow. Experimental and simulation challenges in discerning the control parameters in these applications are similar. For example, conducting experiments and simulations at high
![]() $p$
is demanding and financially expensive. Could perhaps these be conducted at atmospheric
$p$
is demanding and financially expensive. Could perhaps these be conducted at atmospheric
![]() $p$
with no penalty on the resulting outcome in finding the control parameters at high
$p$
with no penalty on the resulting outcome in finding the control parameters at high
![]() $p$
? Both experiments (e.g. Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi, Talley & Coy Reference Chehroudi, Talley and Coy2002) and simulations (e.g. Okong’o & Bellan Reference Okong’o and Bellan2002, Reference Okong’o and Bellan2004) have shown that the high-
$p$
? Both experiments (e.g. Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi, Talley & Coy Reference Chehroudi, Talley and Coy2002) and simulations (e.g. Okong’o & Bellan Reference Okong’o and Bellan2002, Reference Okong’o and Bellan2004) have shown that the high-
![]() $p$
regime displays fundamentally different features from the atmospheric-
$p$
regime displays fundamentally different features from the atmospheric-
![]() $p$
regime, thus indicating the necessity of exploring high-
$p$
regime, thus indicating the necessity of exploring high-
![]() $p$
turbulent reactive flows in their specific
$p$
turbulent reactive flows in their specific
![]() $(p,T)$
realm, where
$(p,T)$
realm, where
![]() $T$
is the temperature.
$T$
is the temperature.
No comparable study exists addressing the complexity of the species mixture, despite the pivotal role it has in tailoring both the fuel composition and combustion processes for increased power and reduced pollutants. Experimental investigations of high-
![]() $p$
turbulent flows have been primarily limited to two species. Such experiments observed a jet injected into a chamber of different composition than the jet. Notable experiments have been conducted for liquid oxygen (LOX) into H2 (Mayer et al.
Reference Mayer, Schik, Schweitzer and Schaeffler1996; Mayer & Tamura Reference Mayer and Tamura1996), LOX into N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into N2 (Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into H2 (Oschwald et al.
Reference Oschwald, Schik, Klar and Mayer1999), He into N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into He (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), a fluoroketone into N2 (Roy, Clement Joly & Corin Segal Reference Roy, Clement Joly and Corin Segal2013), and butanol, n-dodecane or n-hexadecane into N2 (Falgout et al.
Reference Falgout, Rahm, Sedarsky and Linne2016). Few exceptions from the binary-species arrangements exist, but they are not sufficiently quantitatively documented for understanding the influence of particular species, particularly since in some experiments the composition is uncertain. For example, N2 was injected into 10 % CO and 90 % N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002) but only limited jet spreading information is available. On the other hand, Crua, Manin & Pickett (Reference Crua, Manin and Pickett2015b
) injected n-heptane, n-dodecane or n-hexadecane into a mixture of C2H2, H2, N2 and O2 of indefinite composition, while Crua, Heikal & Gold (Reference Crua, Heikal and Gold2015a
) used a rapid compression machine to inject fuels of uncertain chemical composition (e.g. diesel, kerosene) into air.
$p$
turbulent flows have been primarily limited to two species. Such experiments observed a jet injected into a chamber of different composition than the jet. Notable experiments have been conducted for liquid oxygen (LOX) into H2 (Mayer et al.
Reference Mayer, Schik, Schweitzer and Schaeffler1996; Mayer & Tamura Reference Mayer and Tamura1996), LOX into N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into N2 (Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into H2 (Oschwald et al.
Reference Oschwald, Schik, Klar and Mayer1999), He into N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), N2 into He (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002), a fluoroketone into N2 (Roy, Clement Joly & Corin Segal Reference Roy, Clement Joly and Corin Segal2013), and butanol, n-dodecane or n-hexadecane into N2 (Falgout et al.
Reference Falgout, Rahm, Sedarsky and Linne2016). Few exceptions from the binary-species arrangements exist, but they are not sufficiently quantitatively documented for understanding the influence of particular species, particularly since in some experiments the composition is uncertain. For example, N2 was injected into 10 % CO and 90 % N2 (Chehroudi et al.
Reference Chehroudi, Talley and Coy2002) but only limited jet spreading information is available. On the other hand, Crua, Manin & Pickett (Reference Crua, Manin and Pickett2015b
) injected n-heptane, n-dodecane or n-hexadecane into a mixture of C2H2, H2, N2 and O2 of indefinite composition, while Crua, Heikal & Gold (Reference Crua, Heikal and Gold2015a
) used a rapid compression machine to inject fuels of uncertain chemical composition (e.g. diesel, kerosene) into air.
For combustion investigations, the importance of the composition representation of a given fuel according to the identity and number of species in the mixture enters consideration from two important viewpoints. First, in order to tailor the composition of fuels to benefit combustion and reduce emissions, it is generally accepted that, instead of studying the real fuel it is more attractive to construct a surrogate for more tractable and comprehensive investigations. Diesel surrogates have been proposed by Mueller et al. (Reference Mueller, Cannella, Bays, Bruno, DeFabio, Dettman, Gieleciak, Huber, Kweon, McConnell, Pitz and Ratcliff2016) containing four, five and eight species, and kerosene surrogates were proposed by Dagaut & Cathonnet (Reference Dagaut and Cathonnet2006); but although these surrogates may well reproduce physical properties, thermodynamic characteristics and global chemical properties, there is uncertainty that the molecular transport of the species in the surrogate fuel will duplicate that in the real fuel. The importance of molecular transport in high-
![]() $p$
turbulent flows is directly associated with the reduced molecular mass diffusivities, resulting in reduced species-specific effective diffusivities (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013) that measure the combined effect of molecular and turbulent processes. These reduced mass diffusivities are responsible for the formation of high density-gradient magnitude (HDGM) regions seen both in simulations (Okong’o & Bellan Reference Okong’o and Bellan2002; Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013) and in experiments (Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi et al.
Reference Chehroudi, Talley and Coy2002; Falgout et al.
Reference Falgout, Rahm, Sedarsky and Linne2016), including those of the engine combustion network (ECN) Sandia data as detected by Falgout et al. (Reference Falgout, Rahm, Wang and Linne2015). The significance of the HDGM regions is that experimental observations indicate that high density gradients act akin to solid surfaces and influence the vortical distribution in flows, damping turbulence in the perpendicular direction to them and enhancing it in the tangential direction (Hannoun, Fernando & List Reference Hannoun, Fernando and List1988). Additionally, in reactive flows, diffusion is responsible for bringing reactive species into contact and therefore determines whether reactions occur, thus being one of the governing processes.
$p$
turbulent flows is directly associated with the reduced molecular mass diffusivities, resulting in reduced species-specific effective diffusivities (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013) that measure the combined effect of molecular and turbulent processes. These reduced mass diffusivities are responsible for the formation of high density-gradient magnitude (HDGM) regions seen both in simulations (Okong’o & Bellan Reference Okong’o and Bellan2002; Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013) and in experiments (Oschwald & Schik Reference Oschwald and Schick1999; Chehroudi et al.
Reference Chehroudi, Talley and Coy2002; Falgout et al.
Reference Falgout, Rahm, Sedarsky and Linne2016), including those of the engine combustion network (ECN) Sandia data as detected by Falgout et al. (Reference Falgout, Rahm, Wang and Linne2015). The significance of the HDGM regions is that experimental observations indicate that high density gradients act akin to solid surfaces and influence the vortical distribution in flows, damping turbulence in the perpendicular direction to them and enhancing it in the tangential direction (Hannoun, Fernando & List Reference Hannoun, Fernando and List1988). Additionally, in reactive flows, diffusion is responsible for bringing reactive species into contact and therefore determines whether reactions occur, thus being one of the governing processes.
This discussion introduces the second viewpoint highlighting the importance of the particular representation of a complex mixture of species by a selected smaller number of species: since each neat-hydrocarbon combustion is described by a set of tens of thousands of elementary reactions among thousands of species (e.g. Simmie Reference Simmie2003; Silke, Pitz & Westbrook Reference Silke, Pitz and Westbrook2007), such chemical mechanisms are not utilizable in turbulent combustion simulations due to the extreme computational burden needed to solve such a set of equations. To make the simulations tractable, elementary reaction mechanisms are reduced to a much smaller set of species and a representative set of reactions yielding information about the auto-ignition time and the time-wise evolution of species and temperature (Hernández, Ballesteros & Sanz-Argent Reference Hernández, Ballesteros and Sanz-Argent2010; Kourdis & Bellan Reference Kourdis and Bellan2014). These reduced chemical kinetic models are typically included in turbulent reactive codes together with drastic assumptions on transport processes (e.g. the popular assumption that
![]() $Le=1$
, where
$Le=1$
, where
![]() $Le$
is the Lewis number), and results thus obtained are evaluated with experimental data which are reliably available only at atmospheric-
$Le$
is the Lewis number), and results thus obtained are evaluated with experimental data which are reliably available only at atmospheric-
![]() $p$
conditions; many pitfalls are involved in these studies (Bellan Reference Bellan2017b
). Lam (Reference Lam2007), Harstad & Bellan (Reference Harstad and Bellan2013) and Bellan (Reference Bellan2017b
) highlighted the necessity of accounting for the global diffusional influence of the neglected species when using reduced kinetic mechanisms to predict laminar flame propagation. Without focusing specifically on reduced kinetics, the interest is here to assess whether representing a mixture by a reduced number of species would bias the development of a flow resulting from species turbulent mixing, compared to using a larger number of species. Currently, this information is not available.
$p$
conditions; many pitfalls are involved in these studies (Bellan Reference Bellan2017b
). Lam (Reference Lam2007), Harstad & Bellan (Reference Harstad and Bellan2013) and Bellan (Reference Bellan2017b
) highlighted the necessity of accounting for the global diffusional influence of the neglected species when using reduced kinetic mechanisms to predict laminar flame propagation. Without focusing specifically on reduced kinetics, the interest is here to assess whether representing a mixture by a reduced number of species would bias the development of a flow resulting from species turbulent mixing, compared to using a larger number of species. Currently, this information is not available.
This study is devoted to elucidating the effect of the representation of a mixture of species in high-
![]() $p$
turbulent flows by a selected number of its species constituents, including minor species. Effectively, we focus on the number of species and remove the influence of the species identity by considering an increasingly larger number of minor species while the major species have the same identity in all mixtures considered. Essentially, the mixture composition is increasingly refined by the additional number of minor species. Since well-conducted direct numerical simulation (DNS) presents a special opportunity to explore details which are difficult to unravel in other computational methods (e.g. large-eddy simulation or Reynolds-averaged Navier–Stokes) because of embedded approximate submodels, DNS is here selected as the method of choice. This paper is organized as follows. In § 2 we recall the governing equations consisting of the conservation equations and the equation of state, all coupled to the transport properties. The numerical method is briefly addressed in § 3. The configuration, boundary conditions and initial conditions for the 13 conducted DNS realizations are presented in § 4. The results are examined in § 5, encompassing the global characteristics of the layer, instantaneous flow visualizations, the density gradients, effective transport coefficients, the dissipation and the joint probability density function between normalized mass fractions and the normalized
$p$
turbulent flows by a selected number of its species constituents, including minor species. Effectively, we focus on the number of species and remove the influence of the species identity by considering an increasingly larger number of minor species while the major species have the same identity in all mixtures considered. Essentially, the mixture composition is increasingly refined by the additional number of minor species. Since well-conducted direct numerical simulation (DNS) presents a special opportunity to explore details which are difficult to unravel in other computational methods (e.g. large-eddy simulation or Reynolds-averaged Navier–Stokes) because of embedded approximate submodels, DNS is here selected as the method of choice. This paper is organized as follows. In § 2 we recall the governing equations consisting of the conservation equations and the equation of state, all coupled to the transport properties. The numerical method is briefly addressed in § 3. The configuration, boundary conditions and initial conditions for the 13 conducted DNS realizations are presented in § 4. The results are examined in § 5, encompassing the global characteristics of the layer, instantaneous flow visualizations, the density gradients, effective transport coefficients, the dissipation and the joint probability density function between normalized mass fractions and the normalized
![]() $T$
. The findings from this study are summarized in § 6 and conclusions synthesize the aspects impacting future investigations.
$T$
. The findings from this study are summarized in § 6 and conclusions synthesize the aspects impacting future investigations.
2 Governing equations
2.1 Differential conservation equations
The conservation equations are
where
![]() $\unicode[STIX]{x1D6FC}\in [1,N-1]$
,
$\unicode[STIX]{x1D6FC}\in [1,N-1]$
,
![]() $N$
is the number of species,
$N$
is the number of species,
![]() $t$
denotes the time,
$t$
denotes the time,
![]() $x$
is a Cartesian coordinate, subscripts
$x$
is a Cartesian coordinate, subscripts
![]() $i$
and
$i$
and
![]() $j$
refer to the spatial coordinates,
$j$
refer to the spatial coordinates,
![]() $u_{i}$
is the velocity,
$u_{i}$
is the velocity,
![]() $e_{t}=e+u_{i}u_{i}/2$
is the total energy (i.e. internal energy,
$e_{t}=e+u_{i}u_{i}/2$
is the total energy (i.e. internal energy,
![]() $e$
, plus kinetic energy),
$e$
, plus kinetic energy),
![]() $Y_{\unicode[STIX]{x1D6FC}}$
is the mass fraction of species
$Y_{\unicode[STIX]{x1D6FC}}$
is the mass fraction of species
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D61B}_{ij}$
is the Newtonian viscous stress tensor
$\unicode[STIX]{x1D61B}_{ij}$
is the Newtonian viscous stress tensor
where
![]() $\unicode[STIX]{x1D707}$
is the viscosity,
$\unicode[STIX]{x1D707}$
is the viscosity,
![]() $\unicode[STIX]{x1D61A}_{ij}$
is the strain-rate tensor, and
$\unicode[STIX]{x1D61A}_{ij}$
is the strain-rate tensor, and
![]() $J_{\unicode[STIX]{x1D6FC}j}$
and
$J_{\unicode[STIX]{x1D6FC}j}$
and
![]() $q_{j}$
are the
$q_{j}$
are the
![]() $j$
-direction
$j$
-direction
![]() $\unicode[STIX]{x1D6FC}$
-species mass flux and heat flux, respectively.
$\unicode[STIX]{x1D6FC}$
-species mass flux and heat flux, respectively.
Because of the different constitutive relations used for expressing
![]() $\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
and
$\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\boldsymbol{q}$
, equations (2.1)–(2.4) under high-
$\boldsymbol{q}$
, equations (2.1)–(2.4) under high-
![]() $p$
conditions have ultimately a different form from that used under atmospheric-
$p$
conditions have ultimately a different form from that used under atmospheric-
![]() $p$
conditions. The present
$p$
conditions. The present
![]() $\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
and
$\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\boldsymbol{q}$
expressions utilize the full matrices of mass-diffusion coefficients and thermal-diffusion factors derived by Harstad & Bellan (Reference Harstad and Bellan2004a
). In order to enforce global mass conservation, we consider a set of (
$\boldsymbol{q}$
expressions utilize the full matrices of mass-diffusion coefficients and thermal-diffusion factors derived by Harstad & Bellan (Reference Harstad and Bellan2004a
). In order to enforce global mass conservation, we consider a set of (
![]() $N-1$
) species equations rather than the complete set of
$N-1$
) species equations rather than the complete set of
![]() $N$
dependent species; in these (
$N$
dependent species; in these (
![]() $N-1$
) equations, the original molar-fraction fluxes and the heat flux were rewritten to account for only (
$N-1$
) equations, the original molar-fraction fluxes and the heat flux were rewritten to account for only (
![]() $N-1$
) gradients. The final form is
$N-1$
) gradients. The final form is
where
Here,
![]() $X_{\unicode[STIX]{x1D6FC}}=Y_{\unicode[STIX]{x1D6FC}}m/m_{\unicode[STIX]{x1D6FC}}$
represents the species molar fraction;
$X_{\unicode[STIX]{x1D6FC}}=Y_{\unicode[STIX]{x1D6FC}}m/m_{\unicode[STIX]{x1D6FC}}$
represents the species molar fraction;
![]() $m_{\unicode[STIX]{x1D6FC}}$
is the species molar mass;
$m_{\unicode[STIX]{x1D6FC}}$
is the species molar mass;
![]() $m$
is the mixture molar mass,
$m$
is the mixture molar mass,
![]() $m=\sum _{\unicode[STIX]{x1D6FE}=1}^{N}m_{\unicode[STIX]{x1D6FE}}X_{\unicode[STIX]{x1D6FE}}$
;
$m=\sum _{\unicode[STIX]{x1D6FE}=1}^{N}m_{\unicode[STIX]{x1D6FE}}X_{\unicode[STIX]{x1D6FE}}$
;
![]() $v_{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FC}})_{T,p,X_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC})}$
is the partial molar volume, where the molar volume is
$v_{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FC}})_{T,p,X_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC})}$
is the partial molar volume, where the molar volume is
![]() $v=1/n$
and
$v=1/n$
and
![]() $n=\unicode[STIX]{x1D70C}/m$
is the molar density;
$n=\unicode[STIX]{x1D70C}/m$
is the molar density;
![]() $h_{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FC}})_{T,p,X_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC})}$
is the partial molar enthalpy, where the molar enthalpy is
$h_{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FC}})_{T,p,X_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC})}$
is the partial molar enthalpy, where the molar enthalpy is
![]() $h=G-T(\unicode[STIX]{x2202}G/\unicode[STIX]{x2202}T)_{p,X}$
with
$h=G-T(\unicode[STIX]{x2202}G/\unicode[STIX]{x2202}T)_{p,X}$
with
![]() $G$
being the Gibbs energy;
$G$
being the Gibbs energy;
![]() $R_{u}$
is the universal gas constant;
$R_{u}$
is the universal gas constant;
![]() $D_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
are the pairwise mass-diffusion coefficients;
$D_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
are the pairwise mass-diffusion coefficients;
![]() $\unicode[STIX]{x1D6FC}_{T,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
are the binary thermal-diffusion factors; and
$\unicode[STIX]{x1D6FC}_{T,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
are the binary thermal-diffusion factors; and
![]() $\unicode[STIX]{x1D706}$
is the thermal conductivity. The mass-diffusion factors,
$\unicode[STIX]{x1D706}$
is the thermal conductivity. The mass-diffusion factors,
![]() $\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
, are calculated from thermodynamics as
$\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
, are calculated from thermodynamics as
with
![]() $1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
,
$1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
,
![]() $1\leqslant \unicode[STIX]{x1D6FD}\leqslant N-1$
, and
$1\leqslant \unicode[STIX]{x1D6FD}\leqslant N-1$
, and
with
![]() $1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
and
$1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
and
![]() $1\leqslant \unicode[STIX]{x1D6FD}\leqslant N$
. In (2.12) and (2.13),
$1\leqslant \unicode[STIX]{x1D6FD}\leqslant N$
. In (2.12) and (2.13),
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
is the chemical potential of species
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
is the chemical potential of species
![]() $\unicode[STIX]{x1D6FC}$
written in terms of
$\unicode[STIX]{x1D6FC}$
written in terms of
![]() $N-1$
species;
$N-1$
species;
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}\equiv \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{o}$
where
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}\equiv \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{o}$
where
![]() $\unicode[STIX]{x1D711}$
is the fugacity coefficient written in terms of
$\unicode[STIX]{x1D711}$
is the fugacity coefficient written in terms of
![]() $N$
species and the superscript
$N$
species and the superscript
![]() $o$
denotes the pure (
$o$
denotes the pure (
![]() $X_{\unicode[STIX]{x1D6FC}}=1$
) limit. Matrix elements
$X_{\unicode[STIX]{x1D6FC}}=1$
) limit. Matrix elements
![]() $\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
are the solution of the mixing rules equations (Harstad & Bellan Reference Harstad and Bellan2004a
)
$\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
are the solution of the mixing rules equations (Harstad & Bellan Reference Harstad and Bellan2004a
)
where
 $$\begin{eqnarray}\bar{{\mathcal{D}}}_{\unicode[STIX]{x1D6FC}}=1\left/\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}=1 \\ \unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC}}}^{N}\left({\displaystyle \frac{X_{\unicode[STIX]{x1D6FD}}}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}}}\right).\right.\end{eqnarray}$$
$$\begin{eqnarray}\bar{{\mathcal{D}}}_{\unicode[STIX]{x1D6FC}}=1\left/\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}=1 \\ \unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC}}}^{N}\left({\displaystyle \frac{X_{\unicode[STIX]{x1D6FD}}}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}}}\right).\right.\end{eqnarray}$$
Solutions for
![]() $\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
may be obtained by an approximate inversion (Ern & Giovangigli Reference Ern and Giovangigli1998) as follows:
$\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}$
may be obtained by an approximate inversion (Ern & Giovangigli Reference Ern and Giovangigli1998) as follows:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}=\frac{m_{\unicode[STIX]{x1D6FC}}}{m}(1+Y_{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}=1 \\ \unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC}}}^{N}Y_{\unicode[STIX]{x1D6FD}}\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FD}}^{\ast }}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}},\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}=\frac{m_{\unicode[STIX]{x1D6FC}}}{m}(1+Y_{\unicode[STIX]{x1D6FC}})+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}=1 \\ \unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FC}}}^{N}Y_{\unicode[STIX]{x1D6FD}}\frac{{\mathcal{D}}_{\unicode[STIX]{x1D6FD}}^{\ast }}{{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}},\qquad & \displaystyle\end{eqnarray}$$
where
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
is the full approximation binary-diffusion matrix. This method leads to a singularity when the mixture is composed of only one species (as, for instance, in pure fuel zones). In that case (2.15) is no longer used and the diffusion coefficients are evaluated using the binary-diffusion matrix, by setting
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
is the full approximation binary-diffusion matrix. This method leads to a singularity when the mixture is composed of only one species (as, for instance, in pure fuel zones). In that case (2.15) is no longer used and the diffusion coefficients are evaluated using the binary-diffusion matrix, by setting
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}^{\ast }={\mathcal{D}}_{\unicode[STIX]{x1D6FC}N}^{b}$
where
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}^{\ast }={\mathcal{D}}_{\unicode[STIX]{x1D6FC}N}^{b}$
where
![]() $N$
represents the index associated with the solvent. This method was tested against an exact Gauss inversion (not shown) and it gave the same results, with an additional gain in computational time. Defining
$N$
represents the index associated with the solvent. This method was tested against an exact Gauss inversion (not shown) and it gave the same results, with an additional gain in computational time. Defining
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
as the first approximation of the binary diffusion matrix and realizing that the deviation of the ratio
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
as the first approximation of the binary diffusion matrix and realizing that the deviation of the ratio
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}/{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
from unity is comparable to uncertainties in binary diffusion coefficients values (Harstad & Bellan Reference Harstad and Bellan2004a
), we assume
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}/{\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
from unity is comparable to uncertainties in binary diffusion coefficients values (Harstad & Bellan Reference Harstad and Bellan2004a
), we assume
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}={\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
. The computation of
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}={\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
. The computation of
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
and
![]() $\unicode[STIX]{x1D6FC}_{T,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
is described in appendix A along with the other transport properties.
$\unicode[STIX]{x1D6FC}_{T,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{b}$
is described in appendix A along with the other transport properties.
2.2 Equation of state
Equations (2.1)–(2.4) are coupled with the Peng–Robinson (PR) equation of state (EOS)
 $$\begin{eqnarray}p={\displaystyle \frac{R_{u}T\left(\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{\unicode[STIX]{x1D6FC}=N}X_{\unicode[STIX]{x1D6FC}}\right)}{(v_{PR}-b_{mix})}}-{\displaystyle \frac{a_{mix}}{(v_{PR}^{2}+2b_{mix}v_{PR}-b_{mix}^{2})}},\end{eqnarray}$$
$$\begin{eqnarray}p={\displaystyle \frac{R_{u}T\left(\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{\unicode[STIX]{x1D6FC}=N}X_{\unicode[STIX]{x1D6FC}}\right)}{(v_{PR}-b_{mix})}}-{\displaystyle \frac{a_{mix}}{(v_{PR}^{2}+2b_{mix}v_{PR}-b_{mix}^{2})}},\end{eqnarray}$$
from which
![]() $T$
and
$T$
and
![]() $p$
are obtained as an iterative solution which satisfies both values of
$p$
are obtained as an iterative solution which satisfies both values of
![]() $\unicode[STIX]{x1D70C}$
and of
$\unicode[STIX]{x1D70C}$
and of
![]() $e$
, as obtained from the conservation equations (Okong’o, Harstad & Bellan Reference Okong’o, Harstad and Bellan2002). Here
$e$
, as obtained from the conservation equations (Okong’o, Harstad & Bellan Reference Okong’o, Harstad and Bellan2002). Here
![]() $v_{PR}$
is the molar PR volume, and
$v_{PR}$
is the molar PR volume, and
![]() $v=v_{PR}+v_{s}$
, where
$v=v_{PR}+v_{s}$
, where
![]() $v_{s}$
is the volume shift introduced for improving the accuracy of the PR EOS at high
$v_{s}$
is the volume shift introduced for improving the accuracy of the PR EOS at high
![]() $p$
;
$p$
;
![]() $a_{mix}$
and
$a_{mix}$
and
![]() $b_{mix}$
are functions of
$b_{mix}$
are functions of
![]() $T$
and
$T$
and
![]() $X_{i}$
(see appendix B). The
$X_{i}$
(see appendix B). The
![]() $v_{s}$
computation was described in detail elsewhere (Okong’o et al.
Reference Okong’o, Harstad and Bellan2002).
$v_{s}$
computation was described in detail elsewhere (Okong’o et al.
Reference Okong’o, Harstad and Bellan2002).
3 Numerical method
The differential equations combined with the EOS described in § 2 were numerically solved using a fourth-order explicit Runge–Kutta time integration and a sixth-order compact scheme spatial discretization (Lele Reference Lele1992). In order to ensure time stability, the conservative variables were filtered using the eighth-order compact filter described in Gaitonde & Visbal (Reference Gaitonde and Visbal1998). The transfer function of this filter is sharper than that associated with the high-order explicit filters of the Kennedy & Carpenter (Reference Kennedy and Carpenter1994) family used for similar simulations in the past (e.g. Masi et al. Reference Masi, Bellan, Harstad and Okong’o2013; Bellan Reference Bellan2017a ). A parametric study (not shown) using several filter coefficients (0.4, 0.45, 0.475 and 0.49) indicated that the value 0.475 was sufficiently large to ensure that the filter only acts on the shortest wavelengths which can be resolved on the grid and it does not affect the physical content of the data. The code was parallelized using three-dimensional domain decomposition and message passing. The tridiagonal solvers for the compact derivative scheme and the compact filter were efficiently parallelized using the method of Muller & Scheerer (Reference Muller and Scheerer1991).
4 Configuration, boundary conditions and initial conditions
The configuration is that of a temporal mixing layer with periodic boundary conditions in the streamwise (
![]() $x_{1}$
) and spanwise (
$x_{1}$
) and spanwise (
![]() $x_{3}$
) directions and non-reflecting boundary conditions in the cross-stream (
$x_{3}$
) directions and non-reflecting boundary conditions in the cross-stream (
![]() $x_{2}$
) direction. The cross-stream domain size (
$x_{2}$
) direction. The cross-stream domain size (
![]() $L_{2}$
) is sufficiently large so that there is no interference of the mixing region at any time with the domain boundaries. The layer is not symmetric in extent in the
$L_{2}$
) is sufficiently large so that there is no interference of the mixing region at any time with the domain boundaries. The layer is not symmetric in extent in the
![]() $x_{2}$
direction, so as to accommodate the larger layer growth in the stream hosting the lighter mixture; specifically, the upper stream is 1.5 times larger than the lower stream. The domain lengths
$x_{2}$
direction, so as to accommodate the larger layer growth in the stream hosting the lighter mixture; specifically, the upper stream is 1.5 times larger than the lower stream. The domain lengths
![]() $L_{i}$
are the same for all simulations, i.e.
$L_{i}$
are the same for all simulations, i.e.
![]() $L_{1}=0.2$
m,
$L_{1}=0.2$
m,
![]() $L_{2}=0.22$
m and
$L_{2}=0.22$
m and
![]() $L_{3}=0.12$
m. The domain size in the streamwise and spanwise directions is such that it accommodates initially four vortices associated with the wavelengths
$L_{3}=0.12$
m. The domain size in the streamwise and spanwise directions is such that it accommodates initially four vortices associated with the wavelengths
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{3}$
of perturbations:
$\unicode[STIX]{x1D706}_{3}$
of perturbations:
![]() $\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=7.29$
and
$\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=7.29$
and
![]() $\unicode[STIX]{x1D706}_{3}=0.6\unicode[STIX]{x1D706}_{1}$
as in Moser & Rogers (Reference Moser and Rogers1991). The amplitudes of the initial perturbations are
$\unicode[STIX]{x1D706}_{3}=0.6\unicode[STIX]{x1D706}_{1}$
as in Moser & Rogers (Reference Moser and Rogers1991). The amplitudes of the initial perturbations are
![]() $F_{3D}=0.048$
and
$F_{3D}=0.048$
and
![]() $F_{2D}=0.05$
; details about the initial mean flow and the initial analytical perturbation used to hasten the flow transition to turbulence characteristics may be found in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013). The upper-stream and lower-stream temperatures are
$F_{2D}=0.05$
; details about the initial mean flow and the initial analytical perturbation used to hasten the flow transition to turbulence characteristics may be found in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013). The upper-stream and lower-stream temperatures are
![]() $T_{U}=1000$
K and
$T_{U}=1000$
K and
![]() $T_{L}=600$
K, with subscripts
$T_{L}=600$
K, with subscripts
![]() $U$
and
$U$
and
![]() $L$
labelling the upper and lower streams, respectively, for all simulations. The initial Reynolds number is defined as
$L$
labelling the upper and lower streams, respectively, for all simulations. The initial Reynolds number is defined as
 $$\begin{eqnarray}Re_{0}\equiv \frac{0.5(\unicode[STIX]{x1D70C}_{U}+\unicode[STIX]{x1D70C}_{L})\unicode[STIX]{x0394}U_{0}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}}{\unicode[STIX]{x1D707}_{R}}\quad \text{with}~\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=\frac{\unicode[STIX]{x0394}U_{0}}{\left.{\displaystyle \frac{\unicode[STIX]{x2202}u_{0}}{\unicode[STIX]{x2202}x_{2}}}\right|_{max}},\end{eqnarray}$$
$$\begin{eqnarray}Re_{0}\equiv \frac{0.5(\unicode[STIX]{x1D70C}_{U}+\unicode[STIX]{x1D70C}_{L})\unicode[STIX]{x0394}U_{0}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}}{\unicode[STIX]{x1D707}_{R}}\quad \text{with}~\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=\frac{\unicode[STIX]{x0394}U_{0}}{\left.{\displaystyle \frac{\unicode[STIX]{x2202}u_{0}}{\unicode[STIX]{x2202}x_{2}}}\right|_{max}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
is the initial vorticity thickness computed using
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
is the initial vorticity thickness computed using
![]() $u_{0}$
, which is the
$u_{0}$
, which is the
![]() $(x_{1},x_{3})$
planar average of the initial velocity in the streamwise direction;
$(x_{1},x_{3})$
planar average of the initial velocity in the streamwise direction;
![]() $\unicode[STIX]{x1D70C}_{U}$
and
$\unicode[STIX]{x1D70C}_{U}$
and
![]() $\unicode[STIX]{x1D70C}_{L}$
are mixture initial densities,
$\unicode[STIX]{x1D70C}_{L}$
are mixture initial densities,
![]() $\unicode[STIX]{x0394}U_{0}=U_{U}-U_{L}$
is the initial free-stream velocity difference across the layer and
$\unicode[STIX]{x0394}U_{0}=U_{U}-U_{L}$
is the initial free-stream velocity difference across the layer and
![]() $\unicode[STIX]{x1D707}_{R}$
is a reference viscosity. A physical initial mixture viscosity
$\unicode[STIX]{x1D707}_{R}$
is a reference viscosity. A physical initial mixture viscosity
![]() $\unicode[STIX]{x1D707}_{ph,0}$
is computed based on the physical initial species viscosities (see § A.1), then the reference value
$\unicode[STIX]{x1D707}_{ph,0}$
is computed based on the physical initial species viscosities (see § A.1), then the reference value
![]() $\unicode[STIX]{x1D707}_{R}$
is obtained from the chosen value of
$\unicode[STIX]{x1D707}_{R}$
is obtained from the chosen value of
![]() $Re_{0}$
, and finally a factor
$Re_{0}$
, and finally a factor
![]() ${\mathcal{F}}\equiv \unicode[STIX]{x1D707}_{R}/\unicode[STIX]{x1D707}_{ph,0}$
is defined. All transport properties computed during the simulation are then scaled by
${\mathcal{F}}\equiv \unicode[STIX]{x1D707}_{R}/\unicode[STIX]{x1D707}_{ph,0}$
is defined. All transport properties computed during the simulation are then scaled by
![]() ${\mathcal{F}}$
, a procedure which allows the computation of accurate dimensionless numbers, which according to Batchelor (Reference Batchelor1999) define the character of the solution. The value of
${\mathcal{F}}$
, a procedure which allows the computation of accurate dimensionless numbers, which according to Batchelor (Reference Batchelor1999) define the character of the solution. The value of
![]() ${\mathcal{F}}$
was computed at the initial time, for the initial constant
${\mathcal{F}}$
was computed at the initial time, for the initial constant
![]() $p_{0}$
and
$p_{0}$
and
![]() $T_{0}$
, using a mixture composed of two to seven species, each species being averaged over the entire domain. In this manner, a unique
$T_{0}$
, using a mixture composed of two to seven species, each species being averaged over the entire domain. In this manner, a unique
![]() ${\mathcal{F}}$
value is employed in the computational domain. The value of
${\mathcal{F}}$
value is employed in the computational domain. The value of
![]() $\unicode[STIX]{x0394}U_{0}$
is calculated from a specified value of the convective Mach number,
$\unicode[STIX]{x0394}U_{0}$
is calculated from a specified value of the convective Mach number,
![]() $M_{c}$
, through an expression valid for a general fluid
$M_{c}$
, through an expression valid for a general fluid
where
![]() $a$
is the speed of sound, being computed from the EOS. The convective Mach number is set to
$a$
is the speed of sound, being computed from the EOS. The convective Mach number is set to
![]() $M_{c}=0.4$
for all simulations.
$M_{c}=0.4$
for all simulations.
Table 1. Species properties: molecular weight
![]() $m_{\unicode[STIX]{x1D6FC}}$
, critical temperature
$m_{\unicode[STIX]{x1D6FC}}$
, critical temperature
![]() $T_{c}$
, pressure
$T_{c}$
, pressure
![]() $p_{c}$
and volume
$p_{c}$
and volume
![]() $v_{c}$
, acentric factor
$v_{c}$
, acentric factor
![]() $\unicode[STIX]{x1D6FA}$
and dipole moment
$\unicode[STIX]{x1D6FA}$
and dipole moment
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.

The number of species considered in the DNS range from two to seven and their identity is selected for their relevance to combustion. The fuel is represented by n-heptane (C7H16) because it has similar cetane number (CN) value to diesel fuel (CN of
![]() ${\approx}56$
versus
${\approx}56$
versus
![]() ${\approx}50$
); the significance of CN is that it measures the ignition delay time. Air is here represented by its major species, N2 and O2, in suitable proportions. The principal products of complete combustion, CO2 and H2O, are part of the set of species. Finally, the products of incomplete combustion leading to CO2 and H2O (i.e. CO and H2) complete the set of seven species. The properties of these species are listed in table 1. The initial compositions used for the simulations are listed in table 2, where both the mass and molar fractions are listed for each species and each case. The abbreviation of the cases is as follows: the first digit indicates the number of species; R1, R2 and R3 designate the initial Reynolds number (1000, 2000 and 3500, respectively); p60 and p80 stand for the initial pressure (60 and 80 atm, respectively). The last letter represents the methodology used to specify the initial composition: Y indicates that the initial mass fractions
${\approx}50$
); the significance of CN is that it measures the ignition delay time. Air is here represented by its major species, N2 and O2, in suitable proportions. The principal products of complete combustion, CO2 and H2O, are part of the set of species. Finally, the products of incomplete combustion leading to CO2 and H2O (i.e. CO and H2) complete the set of seven species. The properties of these species are listed in table 1. The initial compositions used for the simulations are listed in table 2, where both the mass and molar fractions are listed for each species and each case. The abbreviation of the cases is as follows: the first digit indicates the number of species; R1, R2 and R3 designate the initial Reynolds number (1000, 2000 and 3500, respectively); p60 and p80 stand for the initial pressure (60 and 80 atm, respectively). The last letter represents the methodology used to specify the initial composition: Y indicates that the initial mass fractions
![]() $Y_{\unicode[STIX]{x1D6FC}}$
have been specified; whereas X means that the initial molar fractions
$Y_{\unicode[STIX]{x1D6FC}}$
have been specified; whereas X means that the initial molar fractions
![]() $X_{\unicode[STIX]{x1D6FC}}$
were chosen. The advantage of specifying initial molar fractions rather than mass fractions is that the former can be used to spatially distribute these species stoichiometrically in both streams whereas the latter are not amenable to stipulate stoichiometric spatial distributions. For the two-species configuration, two different initial compositions are considered: s2R2p60Y, in which N2 and C7H16 are initially unmixed; and s2R2p60Ya, in which a small amount of N2 is mixed with C7H16 in the lower stream. The composition in the latter case is chosen such that the initial density ratio,
$X_{\unicode[STIX]{x1D6FC}}$
were chosen. The advantage of specifying initial molar fractions rather than mass fractions is that the former can be used to spatially distribute these species stoichiometrically in both streams whereas the latter are not amenable to stipulate stoichiometric spatial distributions. For the two-species configuration, two different initial compositions are considered: s2R2p60Y, in which N2 and C7H16 are initially unmixed; and s2R2p60Ya, in which a small amount of N2 is mixed with C7H16 in the lower stream. The composition in the latter case is chosen such that the initial density ratio,
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
, matches the s7R2p60X case; comparison of the results from s2R2p60Ya and s7R2p60X permits one to discriminate between the influence of the initial composition, of the number of species, and that of (
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
, matches the s7R2p60X case; comparison of the results from s2R2p60Ya and s7R2p60X permits one to discriminate between the influence of the initial composition, of the number of species, and that of (
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
); it is well known that
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
); it is well known that
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
has a strong effect in turbulence dynamics, even in simpler variable-density shear flows (Almagro, Garcia-Villalba & Flores Reference Almagro, Garcia-Villalba and Flores2017). Regarding the five species initial compositions, s5R2p60Y corresponds to the case studied in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013), in which the mass fractions of the two major products of combustion, CO2 and H2O, were initially distributed uniformly, as minor species, over the entire domain. With the perspective of addressing combustion-relevant situations, we also consider the configuration s5R2p60X, where the composition is fixed as follows: first, the initial molar fraction of one of the products is arbitrarily fixed (e.g.
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
has a strong effect in turbulence dynamics, even in simpler variable-density shear flows (Almagro, Garcia-Villalba & Flores Reference Almagro, Garcia-Villalba and Flores2017). Regarding the five species initial compositions, s5R2p60Y corresponds to the case studied in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013), in which the mass fractions of the two major products of combustion, CO2 and H2O, were initially distributed uniformly, as minor species, over the entire domain. With the perspective of addressing combustion-relevant situations, we also consider the configuration s5R2p60X, where the composition is fixed as follows: first, the initial molar fraction of one of the products is arbitrarily fixed (e.g.
![]() $X_{\text{H}_{2}\text{O}}=0.04$
); then, the molar fractions of the other products are chosen according to stoichiometry; lastly, the sum of the molar fractions of these minor species is subtracted from the sum of
$X_{\text{H}_{2}\text{O}}=0.04$
); then, the molar fractions of the other products are chosen according to stoichiometry; lastly, the sum of the molar fractions of these minor species is subtracted from the sum of
![]() $X_{\unicode[STIX]{x1D6FC}}$
of the major species, that is, air in the upper stream and fuel in the lower stream. The same procedure is used for the seven-species case, in which H2 and CO are also present. All simulations are performed for a free-stream pressure
$X_{\unicode[STIX]{x1D6FC}}$
of the major species, that is, air in the upper stream and fuel in the lower stream. The same procedure is used for the seven-species case, in which H2 and CO are also present. All simulations are performed for a free-stream pressure
![]() $p_{0}=60$
atm, except s7R2p80X for which
$p_{0}=60$
atm, except s7R2p80X for which
![]() $p_{0}=80$
atm.
$p_{0}=80$
atm.
Table 2. Acronyms denoting each case, with a case name being the string of the acronyms under the column ‘Case’ (e.g. s2R1p60Y; see also table 3). All simulations in the same case bin have the same initial condition composition as specified by the initial mass (
![]() $Y_{\unicode[STIX]{x1D6FC}}$
) and molar (
$Y_{\unicode[STIX]{x1D6FC}}$
) and molar (
![]() $X_{\unicode[STIX]{x1D6FC}}$
) fractions (in %) for upper and lower streams; s2, s3, s5 and s7 indicate the number of species considered; R1 denotes
$X_{\unicode[STIX]{x1D6FC}}$
) fractions (in %) for upper and lower streams; s2, s3, s5 and s7 indicate the number of species considered; R1 denotes
![]() $Re_{0}=1000$
, R2 denotes
$Re_{0}=1000$
, R2 denotes
![]() $Re_{0}=2000$
, R3 denotes
$Re_{0}=2000$
, R3 denotes
![]() $Re_{0}=3500$
, as listed in table 3; p60 and p80 denote 60 atm and 80 atm, as also listed in table 3.
$Re_{0}=3500$
, as listed in table 3; p60 and p80 denote 60 atm and 80 atm, as also listed in table 3.

In conducting simulations of temporal configurations the results of which we wish to compare, it is mandatory to ensure that differences in results can be attributed to specific differences in initial conditions. Thus, for all realizations the initial momentum ratio
![]() $|\unicode[STIX]{x1D70C}U|_{L}/|\unicode[STIX]{x1D70C}U|_{U}$
has an approximately similar value, varying in the small range [3.0, 3.6], a fact which is intentional while considering the substantial variation in composition. Had CO2, H2O, CO and H2 been major rather than minor species, it would have been extremely difficult to conduct simulations within such a narrow range of
$|\unicode[STIX]{x1D70C}U|_{L}/|\unicode[STIX]{x1D70C}U|_{U}$
has an approximately similar value, varying in the small range [3.0, 3.6], a fact which is intentional while considering the substantial variation in composition. Had CO2, H2O, CO and H2 been major rather than minor species, it would have been extremely difficult to conduct simulations within such a narrow range of
![]() $|\unicode[STIX]{x1D70C}U|_{L}/|\unicode[STIX]{x1D70C}U|_{U}$
values. Additionally, the five- and seven-species compositions can be thought to mimic mixing under exhaust gas recirculation (EGR) conditions; the three-species composition mimics mixing without EGR; finally, the binary-species compositions relate to most experiments described in § 1. The ECN Spray A Sandia data of C7H16 injection also included EGR and was obtained at an ambient
$|\unicode[STIX]{x1D70C}U|_{L}/|\unicode[STIX]{x1D70C}U|_{U}$
values. Additionally, the five- and seven-species compositions can be thought to mimic mixing under exhaust gas recirculation (EGR) conditions; the three-species composition mimics mixing without EGR; finally, the binary-species compositions relate to most experiments described in § 1. The ECN Spray A Sandia data of C7H16 injection also included EGR and was obtained at an ambient
![]() $p=60$
atm and ambient
$p=60$
atm and ambient
![]() $T=900$
K, similar to some of the upper free-stream conditions of the present study. These latter data are described on the Sandia website as ‘The Spray A condition is a low-temperature combustion condition relevant to engines that use moderate EGR’, which is entirely consistent with the composition listed in table 2.
$T=900$
K, similar to some of the upper free-stream conditions of the present study. These latter data are described on the Sandia website as ‘The Spray A condition is a low-temperature combustion condition relevant to engines that use moderate EGR’, which is entirely consistent with the composition listed in table 2.
The grid spacing,
![]() $\unicode[STIX]{x0394}x_{i}$
, is uniform and is selected to ensure that the smallest scales relevant to dissipation are resolved and that there is no accumulation of energy at those scales (see § 5.1). For fully turbulent flows, the relationship
$\unicode[STIX]{x0394}x_{i}$
, is uniform and is selected to ensure that the smallest scales relevant to dissipation are resolved and that there is no accumulation of energy at those scales (see § 5.1). For fully turbulent flows, the relationship
![]() $l/\unicode[STIX]{x1D702}_{K}\sim Re^{3/4}$
(where
$l/\unicode[STIX]{x1D702}_{K}\sim Re^{3/4}$
(where
![]() $l$
is the integral scale and
$l$
is the integral scale and
![]() $\unicode[STIX]{x1D702}_{K}$
is the Kolmogorov scale) suggests that the grid points should increase as a power law of
$\unicode[STIX]{x1D702}_{K}$
is the Kolmogorov scale) suggests that the grid points should increase as a power law of
![]() $Re$
(Tennekes & Lumley Reference Tennekes and Lumley1989). However, for transitional flows where turbulence is not fully developed and the small structures not yet defined, such scaling is not necessarily expected. Moreover, for flows in which the Prandtl or Schmidt number,
$Re$
(Tennekes & Lumley Reference Tennekes and Lumley1989). However, for transitional flows where turbulence is not fully developed and the small structures not yet defined, such scaling is not necessarily expected. Moreover, for flows in which the Prandtl or Schmidt number,
![]() $Pr$
or
$Pr$
or
![]() $Sc$
, may have values larger than unity, the smallest active scales could be the thermodynamic (rather than dynamic) scales, which thus become the limiting length in resolution. It is difficult to preliminarily rely on one criterion to determine the correct resolution; therefore, a certain amount of experimentation led to the grids listed in table 3. More quantitative resolution assessments are made in § 5.1. The number of grid points used in various realizations ranges from
$Sc$
, may have values larger than unity, the smallest active scales could be the thermodynamic (rather than dynamic) scales, which thus become the limiting length in resolution. It is difficult to preliminarily rely on one criterion to determine the correct resolution; therefore, a certain amount of experimentation led to the grids listed in table 3. More quantitative resolution assessments are made in § 5.1. The number of grid points used in various realizations ranges from
![]() $73\times 10^{6}$
to
$73\times 10^{6}$
to
![]() $1.04\times 10^{9}$
.
$1.04\times 10^{9}$
.
Table 3. List of the DNS realizations and associated resolution. Information regarding the initial upper stream and lower stream compositions is provided in table 2. The subscript
![]() $tr$
denotes the transitional time.
$tr$
denotes the transitional time.

In summary, the database of DNS generated and listed in table 3 allows a thorough study that takes into account the influence of
![]() $Re_{0}$
,
$Re_{0}$
,
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
,
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}\equiv \unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{U}$
, the number of species, the composition and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}\equiv \unicode[STIX]{x1D70C}_{L}-\unicode[STIX]{x1D70C}_{U}$
, the number of species, the composition and
![]() $p_{0}$
.
$p_{0}$
.
5 Results
Considering the present interest in high-
![]() $p$
turbulent flows, each simulation is conducted for time units
$p$
turbulent flows, each simulation is conducted for time units
![]() $t^{\ast }=t\unicode[STIX]{x0394}U_{0}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
until a time denoted
$t^{\ast }=t\unicode[STIX]{x0394}U_{0}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
until a time denoted
![]() $t_{tr}^{\ast }$
at which the one-dimensional fluctuation-based energy spectra become smooth, except for the forcing frequency, indicating that the flow, having started from laminar conditions, has achieved turbulent characteristics;
$t_{tr}^{\ast }$
at which the one-dimensional fluctuation-based energy spectra become smooth, except for the forcing frequency, indicating that the flow, having started from laminar conditions, has achieved turbulent characteristics;
![]() $t_{tr}^{\ast }$
is labelled the transitional time, and most, although not all, of the analysis is conducted at
$t_{tr}^{\ast }$
is labelled the transitional time, and most, although not all, of the analysis is conducted at
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.
To show the quality of the database, we first focus in § 5.1 on numerical resolution aspects by examining the properties of the database at
![]() $t_{tr}^{\ast }$
. Then, in § 5.2 we discuss the evolution of the global quantities up to transition. Flow visualizations are examined in § 5.3 followed by an analysis of the density gradients, their impact on the momentum through the Korteweg tensor and an inquiry into the HDGM composition in § 5.4. We examine both the interaction among species for a specified number of species in a selected realization and the effect of the number of species across the database. The transport properties and non-dimensional numbers related to species and heat transport are addressed in § 5.5. Since dissipation is a gradient-induced process which is due to transport properties, we investigate in § 5.6 the irreversible entropy production. Finally, in § 5.7 we examine whether a reduced, as contrasted to a more detailed, chemical representation of the mixture influences the functional relationship between each species and
$t_{tr}^{\ast }$
. Then, in § 5.2 we discuss the evolution of the global quantities up to transition. Flow visualizations are examined in § 5.3 followed by an analysis of the density gradients, their impact on the momentum through the Korteweg tensor and an inquiry into the HDGM composition in § 5.4. We examine both the interaction among species for a specified number of species in a selected realization and the effect of the number of species across the database. The transport properties and non-dimensional numbers related to species and heat transport are addressed in § 5.5. Since dissipation is a gradient-induced process which is due to transport properties, we investigate in § 5.6 the irreversible entropy production. Finally, in § 5.7 we examine whether a reduced, as contrasted to a more detailed, chemical representation of the mixture influences the functional relationship between each species and
![]() $T$
; maintaining this relationship is one of the important aspects in the modelling of reactive flows using reduced kinetic mechanisms.
$T$
; maintaining this relationship is one of the important aspects in the modelling of reactive flows using reduced kinetic mechanisms.
5.1 Numerical resolution and spectra at transition
A crucial aspect in numerical experiments is to ensure that the computational aspects are conducive to exploring the physics under investigation. To this purpose, we inspect the resolution and the spectra at the transitional time.
Turbulent flows are characterized by the activity of a wide range of scales, the smallest dynamic ones being related to the turbulent kinetic energy dissipation
![]() $\langle \unicode[STIX]{x1D700}\rangle \equiv \langle \unicode[STIX]{x1D61B}_{ij}^{\prime }\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j}\rangle$
, where
$\langle \unicode[STIX]{x1D700}\rangle \equiv \langle \unicode[STIX]{x1D61B}_{ij}^{\prime }\unicode[STIX]{x2202}u_{i}^{\prime }/\unicode[STIX]{x2202}x_{j}\rangle$
, where
![]() $\langle \,\rangle$
symbolizes averages over homogeneous
$\langle \,\rangle$
symbolizes averages over homogeneous
![]() $(x_{1},x_{3})$
planes and
$(x_{1},x_{3})$
planes and
![]() $(\cdot )^{\prime }$
denotes fluctuations from the average. Generally, it is possible to associate a characteristic length scale with the dynamic, the thermal-diffusion and the mass-diffusion phenomena. A measure of the smallest dynamic active scale is provided by the Kolmogorov scale, defined as (e.g. Jagannathan & Donzis Reference Jagannathan and Donzis2016)
$(\cdot )^{\prime }$
denotes fluctuations from the average. Generally, it is possible to associate a characteristic length scale with the dynamic, the thermal-diffusion and the mass-diffusion phenomena. A measure of the smallest dynamic active scale is provided by the Kolmogorov scale, defined as (e.g. Jagannathan & Donzis Reference Jagannathan and Donzis2016)
Thermal processes are related to the Prandtl number
![]() $Pr$
, which measures the importance of momentum transfer with respect to heat transfer. An estimate of the smallest thermal length scale is provided by
$Pr$
, which measures the importance of momentum transfer with respect to heat transfer. An estimate of the smallest thermal length scale is provided by
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D702}_{K}Pr^{-0.5}$
(Goto & Kida Reference Goto and Kida1999), which suggests that, at locations where
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D702}_{K}Pr^{-0.5}$
(Goto & Kida Reference Goto and Kida1999), which suggests that, at locations where
![]() $Pr>1$
, thermal phenomena involve scales smaller than
$Pr>1$
, thermal phenomena involve scales smaller than
![]() $\unicode[STIX]{x1D702}_{K}$
. Similarly, mixing may also occur at scales smaller than
$\unicode[STIX]{x1D702}_{K}$
. Similarly, mixing may also occur at scales smaller than
![]() $\unicode[STIX]{x1D702}_{K}$
; for reactive flows, resolving the mixing scales is of paramount importance since species can react only if they are brought together. The Schmidt number, which measures the importance of momentum transfer with respect to species-mass transfer, can provide an estimate of the mixing scales. For a binary species mixture the mixing scale is the Batchelor scale,
$\unicode[STIX]{x1D702}_{K}$
; for reactive flows, resolving the mixing scales is of paramount importance since species can react only if they are brought together. The Schmidt number, which measures the importance of momentum transfer with respect to species-mass transfer, can provide an estimate of the mixing scales. For a binary species mixture the mixing scale is the Batchelor scale,
![]() $\unicode[STIX]{x1D702}_{B}$
, related to
$\unicode[STIX]{x1D702}_{B}$
, related to
![]() $\unicode[STIX]{x1D702}_{K}$
by
$\unicode[STIX]{x1D702}_{K}$
by
![]() $\unicode[STIX]{x1D702}_{B}=\unicode[STIX]{x1D702}_{K}\,Sc^{-0.5}$
, but it is noted that then
$\unicode[STIX]{x1D702}_{B}=\unicode[STIX]{x1D702}_{K}\,Sc^{-0.5}$
, but it is noted that then
![]() $Sc$
is only defined for a single species mass-diffusion coefficient. Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) circumvented this problem for a mixture of several species modelled utilizing a complete mass-diffusion matrix, by defining an effective species-specific Schmidt number,
$Sc$
is only defined for a single species mass-diffusion coefficient. Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) circumvented this problem for a mixture of several species modelled utilizing a complete mass-diffusion matrix, by defining an effective species-specific Schmidt number,
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, which accounts for all relevant species’ mass-diffusion coefficients, for
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, which accounts for all relevant species’ mass-diffusion coefficients, for
![]() $D_{T,\unicode[STIX]{x1D6FC}}$
and
$D_{T,\unicode[STIX]{x1D6FC}}$
and
![]() $D_{p,\unicode[STIX]{x1D6FC}}$
of (2.6) and for the state of the flow represented by
$D_{p,\unicode[STIX]{x1D6FC}}$
of (2.6) and for the state of the flow represented by
![]() $\unicode[STIX]{x1D735}T$
,
$\unicode[STIX]{x1D735}T$
,
![]() $\unicode[STIX]{x1D735}p$
and
$\unicode[STIX]{x1D735}p$
and
![]() $\unicode[STIX]{x1D735}Y_{\unicode[STIX]{x1D6FC}}$
. The corresponding effective Prandtl number,
$\unicode[STIX]{x1D735}Y_{\unicode[STIX]{x1D6FC}}$
. The corresponding effective Prandtl number,
![]() $Pr_{\mathit{eff}}$
, is defined in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) using the same strategy.
$Pr_{\mathit{eff}}$
, is defined in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) using the same strategy.
Figure 1 shows the cross-stream profile of
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
and
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
and
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
at
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
at
![]() $t_{tr}^{\ast }$
for the
$t_{tr}^{\ast }$
for the
![]() $Re=2000$
cases, and for the two-species
$Re=2000$
cases, and for the two-species
![]() $Re=1000$
and
$Re=1000$
and
![]() $Re=3500$
cases;
$Re=3500$
cases;
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
was computed as
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
was computed as
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D702}_{K}\langle Pr_{\mathit{eff}}\rangle ^{-0.5}$
using the model of Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) to compute
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D702}_{K}\langle Pr_{\mathit{eff}}\rangle ^{-0.5}$
using the model of Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) to compute
![]() $Pr_{\mathit{eff}}$
. The resolution is assessed at
$Pr_{\mathit{eff}}$
. The resolution is assessed at
![]() $t_{tr}^{\ast }$
because the core of the analysis is performed at this time; moreover,
$t_{tr}^{\ast }$
because the core of the analysis is performed at this time; moreover,
![]() $t_{tr}^{\ast }$
is the time of most severe grid requirements since
$t_{tr}^{\ast }$
is the time of most severe grid requirements since
![]() $\unicode[STIX]{x1D702}_{K}$
increases monotonically past this station. The results show that
$\unicode[STIX]{x1D702}_{K}$
increases monotonically past this station. The results show that
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}\lesssim O(1)$
, indicating that all the relevant turbulent scales are well resolved. The maximum values are in the range
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}\lesssim O(1)$
, indicating that all the relevant turbulent scales are well resolved. The maximum values are in the range
![]() $0.9<(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<1.15$
for all p60 simulations; case s7R2p80X displays an even better resolution, with
$0.9<(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<1.15$
for all p60 simulations; case s7R2p80X displays an even better resolution, with
![]() $(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<0.8$
. The resolution is comparable for R1, R2 and R3 cases, highlighting the suitability of the scaling of the computational grids with the
$(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<0.8$
. The resolution is comparable for R1, R2 and R3 cases, highlighting the suitability of the scaling of the computational grids with the
![]() $Re_{0}$
value. The thermal resolution requirements are shown to be here slightly more demanding than the dynamic requirements (
$Re_{0}$
value. The thermal resolution requirements are shown to be here slightly more demanding than the dynamic requirements (
![]() $\langle Pr_{\mathit{eff}}\rangle$
being larger than unity), with
$\langle Pr_{\mathit{eff}}\rangle$
being larger than unity), with
![]() $(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}})_{max}\lesssim 1.3$
. The computational grids are thus slightly finer compared to the atmospheric-
$(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}})_{max}\lesssim 1.3$
. The computational grids are thus slightly finer compared to the atmospheric-
![]() $p$
temporal mixing layer simulations of Almagro et al. (Reference Almagro, Garcia-Villalba and Flores2017) (
$p$
temporal mixing layer simulations of Almagro et al. (Reference Almagro, Garcia-Villalba and Flores2017) (
![]() $(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<1.8$
) and Pantano & Sarkar (Reference Pantano and Sarkar2002) (
$(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}<1.8$
) and Pantano & Sarkar (Reference Pantano and Sarkar2002) (
![]() $(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}\approx 3{-}4$
), so as to satisfy the more stringent thermal- and mass-diffusion requirements.
$(\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K})_{max}\approx 3{-}4$
), so as to satisfy the more stringent thermal- and mass-diffusion requirements.

Figure 1. Averaged resolution in terms of (a) local Kolmogorov length scale
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
and (b) local thermal length scale
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
and (b) local thermal length scale
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
at the transition time
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D703}}$
at the transition time
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.

Figure 2. One-dimensional spectra at
![]() $t_{tr}^{\ast }$
for several simulations: streamwise spectra of (a)
$t_{tr}^{\ast }$
for several simulations: streamwise spectra of (a)
![]() $u_{1}$
, (b)
$u_{1}$
, (b)
![]() $u_{2}$
, (c)
$u_{2}$
, (c)
![]() $u_{3}$
, (g)
$u_{3}$
, (g)
![]() $T$
and (h)
$T$
and (h)
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
; and spanwise spectra of (d)
$Y_{\text{C}_{7}\text{H}_{16}}$
; and spanwise spectra of (d)
![]() $u_{1}$
, (e)
$u_{1}$
, (e)
![]() $u_{2}$
, (f)
$u_{2}$
, (f)
![]() $u_{3}$
, (i)
$u_{3}$
, (i)
![]() $T$
and (j)
$T$
and (j)
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
. Dashed, solid and dashed-dotted lines represent cases R1, R2 and R3, respectively. Same colour legend as in figure 1.
$Y_{\text{C}_{7}\text{H}_{16}}$
. Dashed, solid and dashed-dotted lines represent cases R1, R2 and R3, respectively. Same colour legend as in figure 1.
Further, the excellent resolution of all simulations is highlighted in figure 2 illustrating the spanwise and streamwise spectra,
![]() $E(k)$
, of the three velocity components
$E(k)$
, of the three velocity components
![]() $u_{i}$
, and of the scalars
$u_{i}$
, and of the scalars
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
and
$Y_{\text{C}_{7}\text{H}_{16}}$
and
![]() $T$
at
$T$
at
![]() $t_{tr}^{\ast }$
, as a function of the wavenumber
$t_{tr}^{\ast }$
, as a function of the wavenumber
![]() $k$
. Because, as explained above, the relationship
$k$
. Because, as explained above, the relationship
![]() $\unicode[STIX]{x1D702}_{B}=\unicode[STIX]{x1D702}_{K}\,Sc^{-0.5}$
is only valid for a binary-species mixture, examining the
$\unicode[STIX]{x1D702}_{B}=\unicode[STIX]{x1D702}_{K}\,Sc^{-0.5}$
is only valid for a binary-species mixture, examining the
![]() $Y_{\unicode[STIX]{x1D6FC}}$
-values resolution through the spectra is just as important as assessing the resolution of the dynamic scales; the
$Y_{\unicode[STIX]{x1D6FC}}$
-values resolution through the spectra is just as important as assessing the resolution of the dynamic scales; the
![]() $T$
spectra re-ascertain the resolution of the thermal scales. The results show the spectra smoothness associated with turbulent characteristics (except for the small peak at the perturbation frequency in the spanwise direction), and the appropriate filter behaviour manifested by the lack of energy accumulation at the smallest scales. As expected, the simulations at the larger
$T$
spectra re-ascertain the resolution of the thermal scales. The results show the spectra smoothness associated with turbulent characteristics (except for the small peak at the perturbation frequency in the spanwise direction), and the appropriate filter behaviour manifested by the lack of energy accumulation at the smallest scales. As expected, the simulations at the larger
![]() $Re_{0}$
values have spectra which extend over a wider range of scales and have more energy in the smallest scales than at the smaller
$Re_{0}$
values have spectra which extend over a wider range of scales and have more energy in the smallest scales than at the smaller
![]() $Re_{0}$
values. Increasing
$Re_{0}$
values. Increasing
![]() $p_{0}$
from 60 atm to 80 atm has no visible influence on the spectra, as well as the number of species and the different initial density ratio.
$p_{0}$
from 60 atm to 80 atm has no visible influence on the spectra, as well as the number of species and the different initial density ratio.
As an additional test, the streamwise and spanwise correlation coefficients of the three velocity components and of the temperature were computed at
![]() $t_{tr}^{\ast }$
. The coefficients decrease rapidly to zero in both homogeneous directions (not shown), thereby ensuring that the domain lengths
$t_{tr}^{\ast }$
. The coefficients decrease rapidly to zero in both homogeneous directions (not shown), thereby ensuring that the domain lengths
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{3}$
are sufficiently large to enable the unconstrained evolution of the largest turbulent scales in the computational box.
$L_{3}$
are sufficiently large to enable the unconstrained evolution of the largest turbulent scales in the computational box.
5.2 Evolution of the global quantities
The parameter typically considered to understand and measure the growth of the mixing layer is the momentum thickness, computed as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{m}={\displaystyle \frac{\displaystyle \int _{x_{2},min}^{x_{2},max}[\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},max}-\langle \unicode[STIX]{x1D70C}u_{1}\rangle ][\langle \unicode[STIX]{x1D70C}u_{1}\rangle -\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},min}]\,\text{d}x_{2}}{(\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},max}-\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},min})^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{m}={\displaystyle \frac{\displaystyle \int _{x_{2},min}^{x_{2},max}[\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},max}-\langle \unicode[STIX]{x1D70C}u_{1}\rangle ][\langle \unicode[STIX]{x1D70C}u_{1}\rangle -\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},min}]\,\text{d}x_{2}}{(\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},max}-\langle \unicode[STIX]{x1D70C}u_{1}\rangle _{x_{2},min})^{2}}},\end{eqnarray}$$
where
![]() $x_{2,min}=-0.4L_{2}$
and
$x_{2,min}=-0.4L_{2}$
and
![]() $x_{2,max}=0.6L_{2}$
, the values being consistent with the asymmetric extent of the mixing layer, as stated in § 4. Figure 3 displays
$x_{2,max}=0.6L_{2}$
, the values being consistent with the asymmetric extent of the mixing layer, as stated in § 4. Figure 3 displays
![]() $\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
as a function of
$\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
as a function of
![]() $t^{\ast }$
for the runs listed in table 3. The analytical perturbation ensures a fast transition to a state close to self-similarity, in which the layer grows at a constant rate. The time history of
$t^{\ast }$
for the runs listed in table 3. The analytical perturbation ensures a fast transition to a state close to self-similarity, in which the layer grows at a constant rate. The time history of
![]() $\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
exhibits a similar behaviour in each realization; namely, the initial constant growth rate is slightly reduced after the enstrophy peak (discussed below), but increases monotonically. The change of the slope is more evident for
$\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
exhibits a similar behaviour in each realization; namely, the initial constant growth rate is slightly reduced after the enstrophy peak (discussed below), but increases monotonically. The change of the slope is more evident for
![]() $Re=2000$
cases because of the stronger dampening of vortical structures. Simultaneously with layer growth, the vorticity content of the mixing layer rapidly grows as shown in figure 4, where the domain-averaged positive spanwise vorticity
$Re=2000$
cases because of the stronger dampening of vortical structures. Simultaneously with layer growth, the vorticity content of the mixing layer rapidly grows as shown in figure 4, where the domain-averaged positive spanwise vorticity
![]() $\langle \langle \unicode[STIX]{x1D714}_{3}^{+}\rangle \rangle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0}$
and the domain-averaged enstrophy
$\langle \langle \unicode[STIX]{x1D714}_{3}^{+}\rangle \rangle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0}$
and the domain-averaged enstrophy
![]() $\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
are illustrated (where
$\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
are illustrated (where
![]() $\langle \langle \,\rangle \rangle$
denotes entire domain averaging). The amount of positive spanwise vorticity is representative of the small-scale formation (the initial value being negative), whereas the total enstrophy acts as an indicator of the turbulence activity, i.e. the balance between vorticity production by stretching and tilting mechanisms and its destruction by dissipation effects.
$\langle \langle \,\rangle \rangle$
denotes entire domain averaging). The amount of positive spanwise vorticity is representative of the small-scale formation (the initial value being negative), whereas the total enstrophy acts as an indicator of the turbulence activity, i.e. the balance between vorticity production by stretching and tilting mechanisms and its destruction by dissipation effects.

Figure 3. Time-wise evolution of the normalized momentum thickness
![]() $\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
.
$\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
.

Figure 4. Time-wise evolution of integral quantities: (a) normalized positive spanwise vorticity
![]() $\langle \langle \unicode[STIX]{x1D714}_{3}^{+}\rangle \rangle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0}$
, and (b) normalized enstrophy
$\langle \langle \unicode[STIX]{x1D714}_{3}^{+}\rangle \rangle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0}$
, and (b) normalized enstrophy
![]() $\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
. Legend as in figure 3.
$\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
. Legend as in figure 3.
The spanwise vorticity and enstrophy exhibit similar time-wise evolution for the same Reynolds number, regardless of the number of species. For the
![]() $Re=2000$
cases, a peak is observed at
$Re=2000$
cases, a peak is observed at
![]() $t^{\ast }\approx 45$
, after which viscosity effects tend to emerge. The higher velocity gradients lead to a faster enstrophy decay due to the stronger dissipation with respect to
$t^{\ast }\approx 45$
, after which viscosity effects tend to emerge. The higher velocity gradients lead to a faster enstrophy decay due to the stronger dissipation with respect to
![]() $Re=1000$
cases that show less pronounced and delayed peaks (reflecting also in delayed transition as shown by
$Re=1000$
cases that show less pronounced and delayed peaks (reflecting also in delayed transition as shown by
![]() $t_{tr}^{\ast }$
in table 3). Similarly, case s2R3p60Y exhibits higher vorticity content, peaks around
$t_{tr}^{\ast }$
in table 3). Similarly, case s2R3p60Y exhibits higher vorticity content, peaks around
![]() $t^{\ast }\approx 40$
and experiences faster enstrophy decay with respect to R1 and R2 cases.
$t^{\ast }\approx 40$
and experiences faster enstrophy decay with respect to R1 and R2 cases.
The difference among
![]() $\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
values for realizations with equal
$\langle \langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle \rangle (\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}/\unicode[STIX]{x0394}U_{0})^{2}$
values for realizations with equal
![]() $Re_{0}$
and different number of species is related to
$Re_{0}$
and different number of species is related to
![]() $(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
: a larger
$(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
: a larger
![]() $(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
value reduces the vorticity content, as already shown for both variable-density (Almagro et al.
Reference Almagro, Garcia-Villalba and Flores2017) and compressible flows (Pantano & Sarkar Reference Pantano and Sarkar2002). Moreover, here enstrophy increases with the number of species because, if species other than n-heptane must be accommodated in the lower stream, the
$(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
value reduces the vorticity content, as already shown for both variable-density (Almagro et al.
Reference Almagro, Garcia-Villalba and Flores2017) and compressible flows (Pantano & Sarkar Reference Pantano and Sarkar2002). Moreover, here enstrophy increases with the number of species because, if species other than n-heptane must be accommodated in the lower stream, the
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
value must be reduced; since
$Y_{\text{C}_{7}\text{H}_{16}}$
value must be reduced; since
![]() $m_{\text{C}_{7}\text{H}_{16}}$
has the largest value among all species by a substantial margin, through this
$m_{\text{C}_{7}\text{H}_{16}}$
has the largest value among all species by a substantial margin, through this
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
reduction process
$Y_{\text{C}_{7}\text{H}_{16}}$
reduction process
![]() $(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
decreases. This vortical behaviour is further confirmed by inspection of cases s2R2p60Ya and s7R2p60X, both of which have
$(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
decreases. This vortical behaviour is further confirmed by inspection of cases s2R2p60Ya and s7R2p60X, both of which have
![]() $(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})_{0}\approx 9$
: the time history of the global vortical quantities is essentially the same. Similar considerations hold for the
$(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})_{0}\approx 9$
: the time history of the global vortical quantities is essentially the same. Similar considerations hold for the
![]() $p_{0}$
dependence; the value of
$p_{0}$
dependence; the value of
![]() $(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
has more impact than the number of species as shown by the vortical evolution of case s7R2p80X being closer to s5R2p60Y than to s7R2p60X (
$(\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U})$
has more impact than the number of species as shown by the vortical evolution of case s7R2p80X being closer to s5R2p60Y than to s7R2p60X (
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}=9.492$
, 9.8 and 9.015, respectively).
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}=9.492$
, 9.8 and 9.015, respectively).
As an indication of turbulence level achieved, the value of the momentum-thickness-based Reynolds number,
![]() $Re_{m}\equiv Re_{0}\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
, corresponding to the
$Re_{m}\equiv Re_{0}\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
, corresponding to the
![]() $\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
value at transition, is provided in table 3. Clearly, similar growth rates of different mixing layers translate into approximately equal
$\unicode[STIX]{x1D6FF}_{m}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
value at transition, is provided in table 3. Clearly, similar growth rates of different mixing layers translate into approximately equal
![]() $Re_{m,tr}$
, which in turn explain the similarities in the vortical aspects of the mixing layers: for
$Re_{m,tr}$
, which in turn explain the similarities in the vortical aspects of the mixing layers: for
![]() $Re_{0}=1000$
,
$Re_{0}=1000$
,
![]() $Re_{m,tr}\simeq 1800$
; for
$Re_{m,tr}\simeq 1800$
; for
![]() $Re_{0}=2000$
,
$Re_{0}=2000$
,
![]() $Re_{m,tr}\simeq 3200$
. Table 3 also shows the Reynolds number based on the Taylor microscale, defined as
$Re_{m,tr}\simeq 3200$
. Table 3 also shows the Reynolds number based on the Taylor microscale, defined as
![]() $Re_{\unicode[STIX]{x1D706},tr}=q^{2}\sqrt{5\unicode[STIX]{x1D70C}/(\unicode[STIX]{x1D707}\unicode[STIX]{x1D700})}$
,
$Re_{\unicode[STIX]{x1D706},tr}=q^{2}\sqrt{5\unicode[STIX]{x1D70C}/(\unicode[STIX]{x1D707}\unicode[STIX]{x1D700})}$
,
![]() $q^{2}$
being twice the turbulent kinetic energy. The
$q^{2}$
being twice the turbulent kinetic energy. The
![]() $Re_{\unicode[STIX]{x1D706},tr}$
value displays slight variations for the
$Re_{\unicode[STIX]{x1D706},tr}$
value displays slight variations for the
![]() $Re=2000$
cases and larger variations for the
$Re=2000$
cases and larger variations for the
![]() $Re=1000$
cases; this finding is consistent with the different
$Re=1000$
cases; this finding is consistent with the different
![]() $t_{tr}^{\ast }$
at which transition is achieved for the lower-Reynolds-number simulations. For case s2R3p60Y, values as high as
$t_{tr}^{\ast }$
at which transition is achieved for the lower-Reynolds-number simulations. For case s2R3p60Y, values as high as
![]() $Re_{m,tr}\approx 5000$
and
$Re_{m,tr}\approx 5000$
and
![]() $Re_{\unicode[STIX]{x1D706},tr}\approx 450$
are achieved at transition.
$Re_{\unicode[STIX]{x1D706},tr}\approx 450$
are achieved at transition.
Thus, the analysis of the global quantities indicates that
![]() $Re_{0}$
and
$Re_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
are the main parameters governing the dynamics of the layer evolution.
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
are the main parameters governing the dynamics of the layer evolution.
5.3 Uphill diffusion
Considering the large number of species and the wide range of their initial mass fractions in the free streams, it is useful to introduce a normalized mass fraction variable
where
![]() $Y_{\unicode[STIX]{x1D6FC},ref}^{max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{U},Y_{\unicode[STIX]{x1D6FC}}^{L})$
and
$Y_{\unicode[STIX]{x1D6FC},ref}^{max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{U},Y_{\unicode[STIX]{x1D6FC}}^{L})$
and
![]() $Y_{\unicode[STIX]{x1D6FC},ref}^{min}=\min (Y_{\unicode[STIX]{x1D6FC}}^{U},Y_{\unicode[STIX]{x1D6FC}}^{L})$
. In this manner,
$Y_{\unicode[STIX]{x1D6FC},ref}^{min}=\min (Y_{\unicode[STIX]{x1D6FC}}^{U},Y_{\unicode[STIX]{x1D6FC}}^{L})$
. In this manner,
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}=0$
and
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}=0$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}=1$
represent the initial species’ mass fraction of the upper and lower streams or vice versa, depending on the free-stream location of the species. For example, in the s7R2p60X case, a local value of
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}=1$
represent the initial species’ mass fraction of the upper and lower streams or vice versa, depending on the free-stream location of the species. For example, in the s7R2p60X case, a local value of
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}=0$
means that
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}=0$
means that
![]() $Y_{\text{C}_{7}\text{H}_{16}}=Y_{\text{C}_{7}\text{H}_{16},\mathit{ref}}^{min}=Y_{\text{C}_{7}\text{H}_{16}}^{U}$
; similarly,
$Y_{\text{C}_{7}\text{H}_{16}}=Y_{\text{C}_{7}\text{H}_{16},\mathit{ref}}^{min}=Y_{\text{C}_{7}\text{H}_{16}}^{U}$
; similarly,
![]() $\unicode[STIX]{x1D6EF}_{\text{H}_{2}\text{O}}=1$
implies
$\unicode[STIX]{x1D6EF}_{\text{H}_{2}\text{O}}=1$
implies
![]() $Y_{\text{H}_{2}\text{O}}=Y_{\text{H}_{2}\text{O},\mathit{ref}}^{max}=Y_{\text{H}_{2}\text{O}}^{U}$
. This allows the evaluation of the degree of mixing for species inside the mixing layer compared to the relative reference stream values.
$Y_{\text{H}_{2}\text{O}}=Y_{\text{H}_{2}\text{O},\mathit{ref}}^{max}=Y_{\text{H}_{2}\text{O}}^{U}$
. This allows the evaluation of the degree of mixing for species inside the mixing layer compared to the relative reference stream values.

Figure 5. P.d.f. of
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for all species of case s7R2p60X at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for all species of case s7R2p60X at
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.
Since in the present situation each case of tables 2 and 3 has a different initial composition, the mixing layer region is identified by using a variable threshold. The bounds of the mixing layer are chosen as
where
![]() $k=0.05$
and
$k=0.05$
and
![]() $\unicode[STIX]{x0394}Y_{\text{C}_{7}\text{H}_{16},ref}=Y_{\text{C}_{7}\text{H}_{16}}^{L}-Y_{\text{C}_{7}\text{H}_{16}}^{U}$
. A sensitivity analysis to the value of
$\unicode[STIX]{x0394}Y_{\text{C}_{7}\text{H}_{16},ref}=Y_{\text{C}_{7}\text{H}_{16}}^{L}-Y_{\text{C}_{7}\text{H}_{16}}^{U}$
. A sensitivity analysis to the value of
![]() $k$
is shown in appendix C and the conclusion is that the choice of the bounding value does not affect the physics derived from the analysis.
$k$
is shown in appendix C and the conclusion is that the choice of the bounding value does not affect the physics derived from the analysis.
The advantage of the
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
definition is immediately apparent when examining the probability density functions (p.d.f.s) of
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
definition is immediately apparent when examining the probability density functions (p.d.f.s) of
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
illustrated in figure 5: the probability of the most likely value is the same for all species, although the most likely value is not the same for all species (
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
illustrated in figure 5: the probability of the most likely value is the same for all species, although the most likely value is not the same for all species (
![]() $\simeq 0.65$
for
$\simeq 0.65$
for
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}},\simeq 0.35$
for
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}},\simeq 0.35$
for
![]() $\unicode[STIX]{x1D6EF}_{\text{O}_{2}}$
and
$\unicode[STIX]{x1D6EF}_{\text{O}_{2}}$
and
![]() $\simeq 0.4$
for all minor species
$\simeq 0.4$
for all minor species
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
). However, although for n-heptane and oxygen the p.d.f.s only extend over the
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
). However, although for n-heptane and oxygen the p.d.f.s only extend over the
![]() $[0,1]$
interval, meaning that all the corresponding
$[0,1]$
interval, meaning that all the corresponding
![]() $Y_{\unicode[STIX]{x1D6FC}}$
values are between those specified in the free streams, for all minor species the p.d.f.s extend outside of the
$Y_{\unicode[STIX]{x1D6FC}}$
values are between those specified in the free streams, for all minor species the p.d.f.s extend outside of the
![]() $[0,1]$
interval, hence
$[0,1]$
interval, hence
![]() $Y_{\unicode[STIX]{x1D6FC}}$
values outside the range bounded by the free-stream values occur. This situation for the minor species is the first evidence that uphill diffusion occurs (Taylor & Krishna Reference Taylor and Krishna1993) wherein due to strong coupling among fluxes, species mass diffusion may occur against a species’ gradient. Comparing the p.d.f.s of all minor species, it appears that H2 has the broadest p.d.f. (i.e. it exhibits the largest standard deviation corresponding to heaviest tails of the p.d.f.).
$Y_{\unicode[STIX]{x1D6FC}}$
values outside the range bounded by the free-stream values occur. This situation for the minor species is the first evidence that uphill diffusion occurs (Taylor & Krishna Reference Taylor and Krishna1993) wherein due to strong coupling among fluxes, species mass diffusion may occur against a species’ gradient. Comparing the p.d.f.s of all minor species, it appears that H2 has the broadest p.d.f. (i.e. it exhibits the largest standard deviation corresponding to heaviest tails of the p.d.f.).
To examine the effect of uphill diffusion on the species’ spatial distribution and assess how it relates to
![]() $T$
and the compressibility factor
$T$
and the compressibility factor
![]() $Z=p/(\unicode[STIX]{x1D70C}TR_{u}/m)$
which indicates the deviation from the perfect-gas behaviour, in figure 6 are displayed the spatial distributions of all
$Z=p/(\unicode[STIX]{x1D70C}TR_{u}/m)$
which indicates the deviation from the perfect-gas behaviour, in figure 6 are displayed the spatial distributions of all
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
(except for N2),
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
(except for N2),
![]() $T$
and
$T$
and
![]() $Z$
in the braid plane for case s7R2p60X. Regions having
$Z$
in the braid plane for case s7R2p60X. Regions having
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}<0$
and
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}<0$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
are highlighted in white and black, respectively. The values of
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
are highlighted in white and black, respectively. The values of
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for the first five species display similar values, except for the peripheral regions of the mixing layer: here, the minor species experience uphill diffusion (hydrogen being the most affected species) whereas oxygen is only subjected to regular diffusion, as shown by the p.d.f. As expected,
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for the first five species display similar values, except for the peripheral regions of the mixing layer: here, the minor species experience uphill diffusion (hydrogen being the most affected species) whereas oxygen is only subjected to regular diffusion, as shown by the p.d.f. As expected,
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
shows the opposite distribution, with small fuel-rich pockets (red zones in figure 6
h) penetrating in the upper stream. As apparent in figure 6, uphill diffusion is not dependent on the value of either
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
shows the opposite distribution, with small fuel-rich pockets (red zones in figure 6
h) penetrating in the upper stream. As apparent in figure 6, uphill diffusion is not dependent on the value of either
![]() $T$
or
$T$
or
![]() $Z$
, that is, it occurs over a wide range of
$Z$
, that is, it occurs over a wide range of
![]() $T$
values and, according to the
$T$
values and, according to the
![]() $Z$
values, does not depend on whether the fluid behaves as a perfect gas (
$Z$
values, does not depend on whether the fluid behaves as a perfect gas (
![]() $Z\simeq 1$
) or a real gas (e.g. here it occurs at
$Z\simeq 1$
) or a real gas (e.g. here it occurs at
![]() $Z<0.65$
). The functional relationship between
$Z<0.65$
). The functional relationship between
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
is analysed in § 5.7.
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
is analysed in § 5.7.

Figure 6. Braid plane (
![]() $x_{3}/L_{3}=1/16$
) distribution of different quantities at
$x_{3}/L_{3}=1/16$
) distribution of different quantities at
![]() $t_{tr}^{\ast }$
for s7R2p60X: (a) temperature
$t_{tr}^{\ast }$
for s7R2p60X: (a) temperature
![]() $T$
(K), (b) local compressibility factor
$T$
(K), (b) local compressibility factor
![]() $Z$
, and normalized mass fractions (c)
$Z$
, and normalized mass fractions (c)
![]() $\unicode[STIX]{x1D6EF}_{\text{H}_{2}\text{O}}$
, (d)
$\unicode[STIX]{x1D6EF}_{\text{H}_{2}\text{O}}$
, (d)
![]() $\unicode[STIX]{x1D6EF}_{\text{H}_{2}}$
, (e)
$\unicode[STIX]{x1D6EF}_{\text{H}_{2}}$
, (e)
![]() $\unicode[STIX]{x1D6EF}_{\text{CO}}$
, (f)
$\unicode[STIX]{x1D6EF}_{\text{CO}}$
, (f)
![]() $\unicode[STIX]{x1D6EF}_{\text{CO2}}$
, (g)
$\unicode[STIX]{x1D6EF}_{\text{CO2}}$
, (g)
![]() $\unicode[STIX]{x1D6EF}_{\text{O}_{2}}$
and (h)
$\unicode[STIX]{x1D6EF}_{\text{O}_{2}}$
and (h)
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
. In panels (c–h), white and black denote regions having
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
. In panels (c–h), white and black denote regions having
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}<0$
and
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}<0$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
, respectively.
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
, respectively.
5.4 Density gradients
The Navier–Stokes equations rely on the hypothesis that all dependent variables are infinitely differentiable, and thus no discontinuities can be accommodated. The definition of a discontinuity depends on the scale of interest. For example, whereas material surfaces separating two phases were considered to be discontinuities prior to the studies of van der Waals, he showed that by magnifying the linear extent of the interface it is possible to study the density change from one phase to another as manifested by large density gradients. It has been experimentally shown that, in flows, large density gradients act as material surfaces do, and modify the vortical character of the flow (Hannoun et al.
Reference Hannoun, Fernando and List1988). Korteweg (Reference Korteweg1901) proposed an elegant way to modify the momentum equation should there be large density gradients, and thus to account for the additional vorticity created by these density gradients. Since uphill diffusion results in the formation of density gradients, it is pertinent to examine the
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
field, and correspondingly whether modifications are necessary to (2.2) due to possible significant influence of the Korteweg stresses, before focusing on the other effects of uphill diffusion in § 5.5. Effectively, the magnitude of the Korteweg stresses provides here the criterion enabling one to determine whether the magnitude of the density gradients is sufficiently large to warrant modification of the Navier–Stokes equations.
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
field, and correspondingly whether modifications are necessary to (2.2) due to possible significant influence of the Korteweg stresses, before focusing on the other effects of uphill diffusion in § 5.5. Effectively, the magnitude of the Korteweg stresses provides here the criterion enabling one to determine whether the magnitude of the density gradients is sufficiently large to warrant modification of the Navier–Stokes equations.
Figure 7 shows visualizations of
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
![]() $t_{tr}^{\ast }$
for several realizations;
$t_{tr}^{\ast }$
for several realizations;
![]() $|\cdot |$
denotes here the
$|\cdot |$
denotes here the
![]() ${\mathcal{L}}2$
norm. Clearly, higher turbulence levels (i.e. larger values of
${\mathcal{L}}2$
norm. Clearly, higher turbulence levels (i.e. larger values of
![]() $Re_{0}$
) enhance the complexity of the morphological features of
$Re_{0}$
) enhance the complexity of the morphological features of
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
because of an increase in stirring; this aspect is seen by comparing figure 7(a), 7(b) and 7(c) representing cases s2R1p60Y, s2R2p60Y and s2R3p60Y, respectively. At the same conditions otherwise, an increase in
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
because of an increase in stirring; this aspect is seen by comparing figure 7(a), 7(b) and 7(c) representing cases s2R1p60Y, s2R2p60Y and s2R3p60Y, respectively. At the same conditions otherwise, an increase in
![]() $p_{0}$
does not significantly change the morphological complexity of the HDGM regions, but it clearly results in an increase of
$p_{0}$
does not significantly change the morphological complexity of the HDGM regions, but it clearly results in an increase of
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values. This increase of the
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values. This increase of the
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
value occurs because both the molecular mass diffusion and effective mass diffusion decrease with larger
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
value occurs because both the molecular mass diffusion and effective mass diffusion decrease with larger
![]() $p_{0}$
, these phenomena governing the composition at relatively low and relatively high turbulence levels, respectively. Changing the number of species does not seem to influence the distribution or complexity of the HDGM regions, except for the indirect effect due to change in
$p_{0}$
, these phenomena governing the composition at relatively low and relatively high turbulence levels, respectively. Changing the number of species does not seem to influence the distribution or complexity of the HDGM regions, except for the indirect effect due to change in
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
. Further, the p.d.f.s of
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
. Further, the p.d.f.s of
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for some of the runs listed in table 3 are displayed in figure 8. For clarity, only the R2 category of cases, which contains the largest number of realizations, is completely shown; all R1 cases have p.d.f.s in the vicinity of the illustrated case s2R1p60Y and there is a single run in the R3 category. Inspection of these p.d.f.s in figure 8(a) shows that there is a quantifiable difference among the realizations: the right tails of the p.d.f.s clearly become heavier with increasing
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for some of the runs listed in table 3 are displayed in figure 8. For clarity, only the R2 category of cases, which contains the largest number of realizations, is completely shown; all R1 cases have p.d.f.s in the vicinity of the illustrated case s2R1p60Y and there is a single run in the R3 category. Inspection of these p.d.f.s in figure 8(a) shows that there is a quantifiable difference among the realizations: the right tails of the p.d.f.s clearly become heavier with increasing
![]() $Re_{0}$
and
$Re_{0}$
and
![]() $p_{0}$
(the maximum values being obtained for case s2R3p60Y and, among R2 simulations, for s7R2p80X). The influence of
$p_{0}$
(the maximum values being obtained for case s2R3p60Y and, among R2 simulations, for s7R2p80X). The influence of
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
is highlighted by comparing the R2p60 cases; namely, the heavier tails are obtained for s2R2p60Y and s3R2p60Y (for which
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
is highlighted by comparing the R2p60 cases; namely, the heavier tails are obtained for s2R2p60Y and s3R2p60Y (for which
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
is in the range [12.5–13]), and the lighter tails for s2R2p60Ya and s7R2p60X (having
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
is in the range [12.5–13]), and the lighter tails for s2R2p60Ya and s7R2p60X (having
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}\approx 9$
). Of note, cases s2R2p60Ya and s7R2p60X show that the number of species is unimportant as far as the HDGM regions are concerned, provided that the initial composition does not change
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}\approx 9$
). Of note, cases s2R2p60Ya and s7R2p60X show that the number of species is unimportant as far as the HDGM regions are concerned, provided that the initial composition does not change
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
. Normalization of
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
. Normalization of
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
by
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
(
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
(
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
has similar variation to
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
has similar variation to
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
as a function of the runs listed in table 3) in figure 8(b) shows that indeed
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
as a function of the runs listed in table 3) in figure 8(b) shows that indeed
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
scales with
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
scales with
![]() $\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
to a great extent. Furthermore, it is also clear that the maximum values attained by
$\unicode[STIX]{x1D70C}_{L}/\unicode[STIX]{x1D70C}_{U}$
to a great extent. Furthermore, it is also clear that the maximum values attained by
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
increase with increasing
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
increase with increasing
![]() $Re_{0}$
. The explanation is that turbulence acts only on the continuum scales and thus cannot influence diffusion, which occurs at molecular scales. Since
$Re_{0}$
. The explanation is that turbulence acts only on the continuum scales and thus cannot influence diffusion, which occurs at molecular scales. Since
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
represents the manifestation of diffusion at the continuum scales, the present results confirm the competition at the continuum scales of mass-diffusion manifestation with turbulence in creating the HDGM regions. Essentially, as turbulence is higher, its characteristic time is smaller, a fact which only permits limited diffusion, thus maintaining larger density gradients.
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
represents the manifestation of diffusion at the continuum scales, the present results confirm the competition at the continuum scales of mass-diffusion manifestation with turbulence in creating the HDGM regions. Essentially, as turbulence is higher, its characteristic time is smaller, a fact which only permits limited diffusion, thus maintaining larger density gradients.

Figure 7. Braid plane (
![]() $x_{3}/L_{3}=1/16$
) distribution of the local
$x_{3}/L_{3}=1/16$
) distribution of the local
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
in logarithmic scale
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
in logarithmic scale
![]() $\log _{10}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
$\log _{10}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
![]() $t_{tr}^{\ast }$
for (a) s2R1p60Y, (b) s2R2p60Y, (c) s2R3p60Y, (d) s3R2p60Y, (e) s5R2p60Y, (f) s5R2p60X, (g) s7R2p60X and (h) s7R2p80X. Units are
$t_{tr}^{\ast }$
for (a) s2R1p60Y, (b) s2R2p60Y, (c) s2R3p60Y, (d) s3R2p60Y, (e) s5R2p60Y, (f) s5R2p60X, (g) s7R2p60X and (h) s7R2p80X. Units are
![]() $\text{kg}~\text{m}^{-4}$
.
$\text{kg}~\text{m}^{-4}$
.
The composition of the HDGM regions is examined in figure 9, depicting the conditional averages of
![]() $Y_{\unicode[STIX]{x1D6FC}}$
on
$Y_{\unicode[STIX]{x1D6FC}}$
on
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for case s7R2p60X at
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for case s7R2p60X at
![]() $t_{tr}^{\ast }$
. For low
$t_{tr}^{\ast }$
. For low
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values,
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values,
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
increases rapidly with
$Y_{\text{C}_{7}\text{H}_{16}}$
increases rapidly with
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
, reaching
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
, reaching
![]() $Y_{\text{C}_{7}\text{H}_{16}}\approx 0.8$
already at
$Y_{\text{C}_{7}\text{H}_{16}}\approx 0.8$
already at
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\approx 5\times 10^{4}~\text{kg}~\text{m}^{-4}$
and asymptotically reaching 0.875. Thus, the composition of the regions of largest
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\approx 5\times 10^{4}~\text{kg}~\text{m}^{-4}$
and asymptotically reaching 0.875. Thus, the composition of the regions of largest
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values is dominated by n-heptane. The other species exhibit the opposite behaviour, with a decreased presence in higher-
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values is dominated by n-heptane. The other species exhibit the opposite behaviour, with a decreased presence in higher-
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
regions. This is distinctly shown in figure 9(b) where all
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
regions. This is distinctly shown in figure 9(b) where all
![]() $Y_{\unicode[STIX]{x1D6FC}}$
values are normalized with respect to
$Y_{\unicode[STIX]{x1D6FC}}$
values are normalized with respect to
![]() $Y_{\unicode[STIX]{x1D6FC},max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{L},Y_{\unicode[STIX]{x1D6FC}}^{U})$
. This variation confirms the observation of Bellan (Reference Bellan2017a
) stating that the HDGM regions appear to initiate in regions of relatively small (with respect to the maximum) amount of fuel. Similarly, figure 10 displays the values of
$Y_{\unicode[STIX]{x1D6FC},max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{L},Y_{\unicode[STIX]{x1D6FC}}^{U})$
. This variation confirms the observation of Bellan (Reference Bellan2017a
) stating that the HDGM regions appear to initiate in regions of relatively small (with respect to the maximum) amount of fuel. Similarly, figure 10 displays the values of
![]() $\langle Y_{\text{C}_{7}\text{H}_{16}}\rangle$
and
$\langle Y_{\text{C}_{7}\text{H}_{16}}\rangle$
and
![]() $\langle Y_{\text{C}_{7}\text{H}_{16}}/Y_{\text{C}_{7}\text{H}_{16}}^{max}\rangle$
conditioned on
$\langle Y_{\text{C}_{7}\text{H}_{16}}/Y_{\text{C}_{7}\text{H}_{16}}^{max}\rangle$
conditioned on
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for different realizations. The trend is similar for all simulations, and the normalization with respect to
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
for different realizations. The trend is similar for all simulations, and the normalization with respect to
![]() $Y_{\text{C}_{7}\text{H}_{16}}^{max}$
(different value for each case in order to accommodate the minor species) narrows the range of variation of the R2p60 profiles. For s7R2p80X, the n-heptane contribution to HDGM regions is slightly smaller and is here attributed to the larger difficulty of entraining a denser fluid.
$Y_{\text{C}_{7}\text{H}_{16}}^{max}$
(different value for each case in order to accommodate the minor species) narrows the range of variation of the R2p60 profiles. For s7R2p80X, the n-heptane contribution to HDGM regions is slightly smaller and is here attributed to the larger difficulty of entraining a denser fluid.

Figure 8. P.d.f.s at
![]() $t_{tr}^{\ast }$
of (a)
$t_{tr}^{\ast }$
of (a)
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
(units are
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
(units are
![]() $\text{kg}~\text{m}^{-4}$
), and (b)
$\text{kg}~\text{m}^{-4}$
), and (b)
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
(units are
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
(units are
![]() $\text{m}^{-1}$
). Legend as in figure 3.
$\text{m}^{-1}$
). Legend as in figure 3.

Figure 9. Conditional average of species mass fraction conditioned on local density-gradient magnitude for case s7R2p60X at
![]() $t_{tr}^{\ast }$
: (a)
$t_{tr}^{\ast }$
: (a)
![]() $\langle Y_{\unicode[STIX]{x1D6FC}}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, and (b)
$\langle Y_{\unicode[STIX]{x1D6FC}}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, and (b)
![]() $\langle Y_{\unicode[STIX]{x1D6FC}}/Y_{\unicode[STIX]{x1D6FC}}^{max}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, where
$\langle Y_{\unicode[STIX]{x1D6FC}}/Y_{\unicode[STIX]{x1D6FC}}^{max}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, where
![]() $Y_{\unicode[STIX]{x1D6FC}}^{max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{L},Y_{\unicode[STIX]{x1D6FC}}^{U})$
. Units for
$Y_{\unicode[STIX]{x1D6FC}}^{max}=\max (Y_{\unicode[STIX]{x1D6FC}}^{L},Y_{\unicode[STIX]{x1D6FC}}^{U})$
. Units for
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
are
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
are
![]() $\text{kg}~\text{m}^{-4}$
.
$\text{kg}~\text{m}^{-4}$
.

Figure 10. Average value of the n-heptane mass fraction conditioned on local density-gradient magnitude at
![]() $t_{tr}^{\ast }$
: (a)
$t_{tr}^{\ast }$
: (a)
![]() $\langle Y_{\text{C}_{7}\text{H}_{16}}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, and (b)
$\langle Y_{\text{C}_{7}\text{H}_{16}}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, and (b)
![]() $\langle Y_{\text{C}_{7}\text{H}_{16}}/Y_{\text{C}_{7}\text{H}_{16}}^{max}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, where
$\langle Y_{\text{C}_{7}\text{H}_{16}}/Y_{\text{C}_{7}\text{H}_{16}}^{max}\mid |\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\rangle$
, where
![]() $Y_{\text{C}_{7}\text{H}_{16}}^{max}=\max (Y_{\text{C}_{7}\text{H}_{16}}^{L},Y_{\text{C}_{7}\text{H}_{16}}^{U})$
. Units for
$Y_{\text{C}_{7}\text{H}_{16}}^{max}=\max (Y_{\text{C}_{7}\text{H}_{16}}^{L},Y_{\text{C}_{7}\text{H}_{16}}^{U})$
. Units for
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
are
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
are
![]() $\text{kg}~\text{m}^{-4}$
. Legend as in figure 3.
$\text{kg}~\text{m}^{-4}$
. Legend as in figure 3.
The large
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values encountered in the mixing region motivate an inspection of whether sufficiently large Korteweg stresses are created, thus potentially necessitating a revision of (2.2) to accommodate the effect of interfaces. The second-gradient theory (van der Waals Reference van der Waals1893; Korteweg Reference Korteweg1901) naturally allows one to account for the contribution of large density gradients in the Navier–Stokes equations. This theory represents the theoretical basis for the formulation of the well-known diffuse interface models (Anderson, McFadden & Wheeler Reference Anderson, McFadden and Wheeler1998; Jamet et al.
Reference Jamet, Lebaigue, Coutris and Delhaye2001), widely employed to describe gas–liquid interfaces in multiphase flows. The changes to the momentum, species and energy equations originating from the second-gradient theory are derived in appendix D for a multi-species situation in concert with the mixing rules of Harstad & Bellan (Reference Harstad and Bellan2004a
). To summarize these derivations, including these second-gradient terms in the momentum equation yields (in compact notation)
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
values encountered in the mixing region motivate an inspection of whether sufficiently large Korteweg stresses are created, thus potentially necessitating a revision of (2.2) to accommodate the effect of interfaces. The second-gradient theory (van der Waals Reference van der Waals1893; Korteweg Reference Korteweg1901) naturally allows one to account for the contribution of large density gradients in the Navier–Stokes equations. This theory represents the theoretical basis for the formulation of the well-known diffuse interface models (Anderson, McFadden & Wheeler Reference Anderson, McFadden and Wheeler1998; Jamet et al.
Reference Jamet, Lebaigue, Coutris and Delhaye2001), widely employed to describe gas–liquid interfaces in multiphase flows. The changes to the momentum, species and energy equations originating from the second-gradient theory are derived in appendix D for a multi-species situation in concert with the mixing rules of Harstad & Bellan (Reference Harstad and Bellan2004a
). To summarize these derivations, including these second-gradient terms in the momentum equation yields (in compact notation)
where
are the reversible and irreversible components of the momentum flux, respectively,
![]() $\boldsymbol{u}$
is the velocity vector,
$\boldsymbol{u}$
is the velocity vector,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the species-dependent influence parameter,
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the species-dependent influence parameter,
![]() $\unicode[STIX]{x1D644}$
is the identity matrix, and
$\unicode[STIX]{x1D644}$
is the identity matrix, and
![]() $\hat{\unicode[STIX]{x1D707}}$
and
$\hat{\unicode[STIX]{x1D707}}$
and
![]() $\unicode[STIX]{x1D707}$
are the bulk and shear viscosities. The term multiplying the identity matrix in (5.6) can be interpreted as an equivalent pressure incorporating capillarity effects; whereas the last term is commonly known as the Korteweg tensor. Compared to the typical single-phase flow momentum equation, the additional terms in
$\unicode[STIX]{x1D707}$
are the bulk and shear viscosities. The term multiplying the identity matrix in (5.6) can be interpreted as an equivalent pressure incorporating capillarity effects; whereas the last term is commonly known as the Korteweg tensor. Compared to the typical single-phase flow momentum equation, the additional terms in
![]() $\unicode[STIX]{x1D64B}$
do not produce entropy because they are associated with reversible processes. The irreversible component
$\unicode[STIX]{x1D64B}$
do not produce entropy because they are associated with reversible processes. The irreversible component
![]() $\unicode[STIX]{x1D64F}$
of (5.7) is not modified by the gradient energy, and represents the classical irreversible processes related to viscous dissipation.
$\unicode[STIX]{x1D64F}$
of (5.7) is not modified by the gradient energy, and represents the classical irreversible processes related to viscous dissipation.
By comparing the magnitudes of the gradient of the capillarity terms and the pressure gradient, an order-of-magnitude analysis can be performed in order to estimate the influence of the Korteweg stresses in the momentum equation. Since at
![]() $t_{tr}^{\ast }$
the density-gradient p.d.f. scales with
$t_{tr}^{\ast }$
the density-gradient p.d.f. scales with
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
practically independent of the number of species, and since additionally the highest-
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$
practically independent of the number of species, and since additionally the highest-
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
regions primarily contain n-heptane, a representative magnitude of the Korteweg tensor can be computed for all cases by reducing the complexity of the Korteweg tensor to the situation of a single species: n-heptane. This procedure furthermore avoids confronting the issue of uncertainty in some values of
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
regions primarily contain n-heptane, a representative magnitude of the Korteweg tensor can be computed for all cases by reducing the complexity of the Korteweg tensor to the situation of a single species: n-heptane. This procedure furthermore avoids confronting the issue of uncertainty in some values of
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
. Thus, the influence parameter is chosen to be
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
. Thus, the influence parameter is chosen to be
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}\approx 10^{-5}~\text{cm}^{7}~\text{g}^{-1}~\text{s}^{-2}=10^{-16}~\text{m}^{7}~\text{kg}^{-1}~\text{s}^{-2}$
, a value slightly larger than that reported in the literature (Cornelisse Reference Cornelisse1997) so as to provide an upper bound of the Korteweg effects. Figure 11 displays a comparison between the magnitude of the pressure gradient,
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}\approx 10^{-5}~\text{cm}^{7}~\text{g}^{-1}~\text{s}^{-2}=10^{-16}~\text{m}^{7}~\text{kg}^{-1}~\text{s}^{-2}$
, a value slightly larger than that reported in the literature (Cornelisse Reference Cornelisse1997) so as to provide an upper bound of the Korteweg effects. Figure 11 displays a comparison between the magnitude of the pressure gradient,
![]() $|\unicode[STIX]{x1D735}p|$
, and the term
$|\unicode[STIX]{x1D735}p|$
, and the term
![]() $|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
. The case considered is s2R3p60Y, for which density gradients reach values as high as
$|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
. The case considered is s2R3p60Y, for which density gradients reach values as high as
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\approx 8\times 10^{5}~\text{kg}~\text{m}^{-4}$
and for which there are only two species. The gradient term is shown to be almost nine orders of magnitude smaller than the pressure gradient, yielding thus a negligible contribution to
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|\approx 8\times 10^{5}~\text{kg}~\text{m}^{-4}$
and for which there are only two species. The gradient term is shown to be almost nine orders of magnitude smaller than the pressure gradient, yielding thus a negligible contribution to
![]() $\unicode[STIX]{x1D64B}$
. Even in the regions of the largest
$\unicode[STIX]{x1D64B}$
. Even in the regions of the largest
![]() $|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
values, figure 11 shows that the value of
$|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
values, figure 11 shows that the value of
![]() $|\unicode[STIX]{x1D735}p|$
at those locations is orders of magnitude larger than the values of
$|\unicode[STIX]{x1D735}p|$
at those locations is orders of magnitude larger than the values of
![]() $|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
. A grid convergence analysis, presented in appendix E, shows that the criteria used in § 5.1 for the grid resolution are very stringent because, when the grid is refined by a factor of 50 % in each direction, the quantitative results obtained with the coarser grid are recovered. The conclusion is that the modification to the actual thermodynamic pressure is also negligible, and thus that the present DNS database is appropriate for the purpose of this study, enabling one to pursue the examination of the specific features bringing a deeper understanding of uphill diffusion.
$|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
. A grid convergence analysis, presented in appendix E, shows that the criteria used in § 5.1 for the grid resolution are very stringent because, when the grid is refined by a factor of 50 % in each direction, the quantitative results obtained with the coarser grid are recovered. The conclusion is that the modification to the actual thermodynamic pressure is also negligible, and thus that the present DNS database is appropriate for the purpose of this study, enabling one to pursue the examination of the specific features bringing a deeper understanding of uphill diffusion.
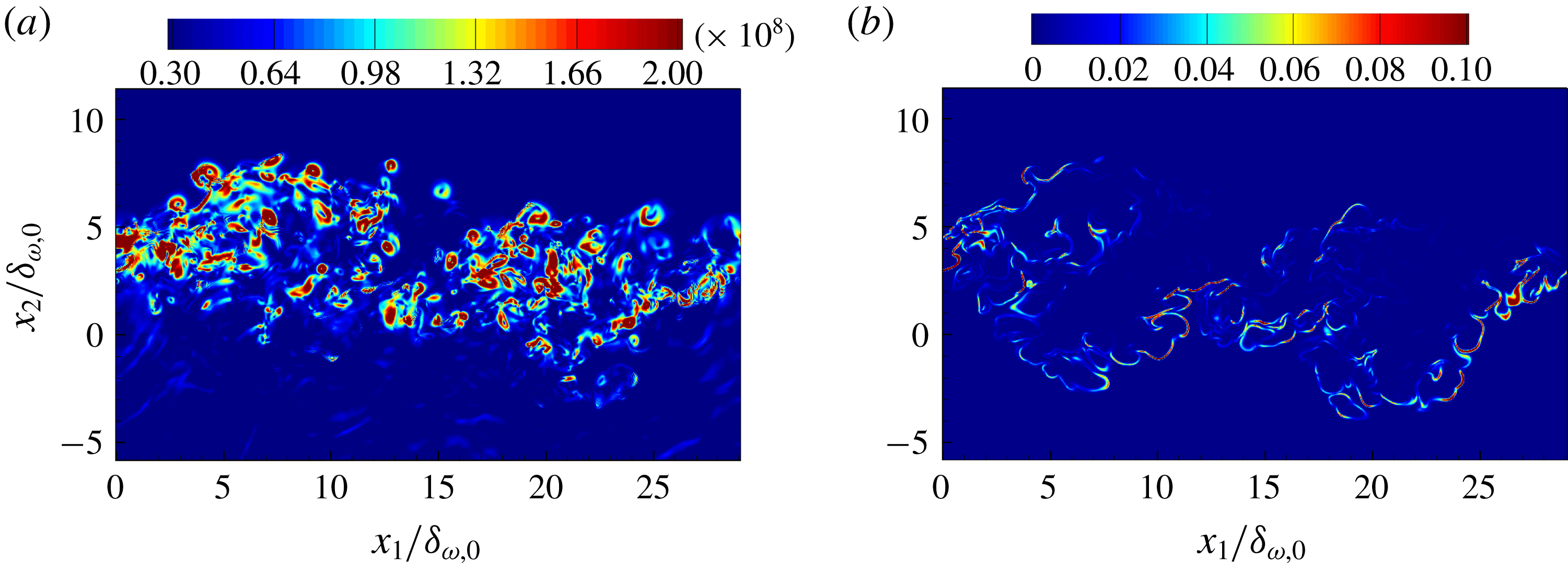
Figure 11. Values of (a)
![]() $|\unicode[STIX]{x1D735}p|$
and (b)
$|\unicode[STIX]{x1D735}p|$
and (b)
![]() $|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
for case s2R3p60Y. Units are
$|\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}[(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C})^{2}]|$
for case s2R3p60Y. Units are
![]() $\text{kg}~\text{m}^{-2}~\text{s}^{-2}$
.
$\text{kg}~\text{m}^{-2}~\text{s}^{-2}$
.
5.5 Effective transport properties
In fluid mechanics, non-dimensional numbers are useful in providing a single length scale, or equivalently a single time scale, associated with a process; comparison of these length (or time) scales related to various phenomena yields crucial information on the physics governing a situation. However, unlike for a binary-species mixture, in a situation involving several species equation (2.6) shows that it is not possible to define a single diffusion length scale. To overcome this difficulty Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013) derived a methodology to express the species diffusive fluxes and heat flux as a function of single effective coefficients. Under the assumption of non-null gradients, valid for mixing layers and in turbulent flows, equation (2.4) can be rewritten as
where
represents a single species diffusion coefficient accounting for the entire flux matrix and
![]() $\unicode[STIX]{x1D6FF}$
signifies functional derivatives. Then
$\unicode[STIX]{x1D6FF}$
signifies functional derivatives. Then
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
can be used to define a species-effective Schmidt number
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
can be used to define a species-effective Schmidt number
Similarly, equation (2.3) can be recast in the form
where
Thus
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
represents an effective thermal conductivity accounting for the entire heat flux pertaining to all species. Therefore, an effective Prandtl number can be defined as
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
represents an effective thermal conductivity accounting for the entire heat flux pertaining to all species. Therefore, an effective Prandtl number can be defined as
along with a species-effective Lewis number,
The functional derivatives
![]() $\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D6FF}T$
,
$\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D6FF}T$
,
![]() $\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D6FF}T/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}Y_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}T$
are modelled as in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013). For example, defining coefficients of type
$\unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}T$
are modelled as in Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013). For example, defining coefficients of type
![]() $C_{pT}\equiv \unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}T$
which exactly satisfy the relation
$C_{pT}\equiv \unicode[STIX]{x1D6FF}p/\unicode[STIX]{x1D6FF}T$
which exactly satisfy the relation
![]() $C_{pT}\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}x_{i}=\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x_{i}$
, the model employing contracted products
$C_{pT}\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}x_{i}=\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x_{i}$
, the model employing contracted products
eliminates directional variations and has a finite value everywhere in the mixing layer. The model accuracy was validated by comparing the modelled fluxes with those computed from the DNS database, showing excellent agreement.

Figure 12. P.d.f.s for case s7R2p60X at
![]() $t_{tr}^{\ast }$
: (a)
$t_{tr}^{\ast }$
: (a)
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
(
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
(
![]() $10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
$10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
![]() ${\mathcal{F}}$
-scaled), (b)
${\mathcal{F}}$
-scaled), (b)
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, and (c)
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, and (c)
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
.
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
.

Figure 13. Braid plane (
![]() $x_{3}/L_{3}=1/16$
) distribution of the local effective Schmidt number
$x_{3}/L_{3}=1/16$
) distribution of the local effective Schmidt number
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for different species at
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for different species at
![]() $t_{tr}^{\ast }$
for s7R2p60X: (a) O2, (b) C7H16 (c) CO, (d) CO2, (e) H2O, and (f) H2.
$t_{tr}^{\ast }$
for s7R2p60X: (a) O2, (b) C7H16 (c) CO, (d) CO2, (e) H2O, and (f) H2.

Figure 14. P.d.f.s computed over the three-dimensional mixing layer at
![]() $t_{tr}^{\ast }$
: (a)
$t_{tr}^{\ast }$
: (a)
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
(
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
(
![]() $10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
$10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
![]() ${\mathcal{F}}$
-scaled), (b)
${\mathcal{F}}$
-scaled), (b)
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
, (c)
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
, (c)
![]() $D_{\text{H}_{2}\text{O},\mathit{eff}}$
(
$D_{\text{H}_{2}\text{O},\mathit{eff}}$
(
![]() $10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
$10^{-7}~\text{m}^{2}~\text{s}^{-1}$
, not
![]() ${\mathcal{F}}$
-scaled), and (d)
${\mathcal{F}}$
-scaled), and (d)
![]() $Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
.
$Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
.
We proceed by first investigating statistical aspects and further scrutinizing details not available through the statistical analysis. Figures 12(a) and 12(b) exhibit the p.d.f.s of the effective diffusion coefficients and of the species-effective Schmidt number. Oxygen and n-heptane have relatively narrow
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
distributions (figure 12
a) with a mean
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
distributions (figure 12
a) with a mean
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx D_{\text{O}_{2},\mathit{eff}}\approx 4.5\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
(a value which is approximately midway between the range of
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx D_{\text{O}_{2},\mathit{eff}}\approx 4.5\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
(a value which is approximately midway between the range of
![]() $O(10^{-5})~\text{m}^{2}~\text{s}^{-1}$
for gases and
$O(10^{-5})~\text{m}^{2}~\text{s}^{-1}$
for gases and
![]() $O(10^{-9})~\text{m}^{2}~\text{s}^{-1}$
for liquids) and the p.d.f.s are located in the
$O(10^{-9})~\text{m}^{2}~\text{s}^{-1}$
for liquids) and the p.d.f.s are located in the
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}>0$
range. Conversely, the
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}>0$
range. Conversely, the
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
of all minor species exhibit much broader symmetric bell-shaped p.d.f.s in a range encompassing both positive and negative
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
of all minor species exhibit much broader symmetric bell-shaped p.d.f.s in a range encompassing both positive and negative
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
with mean values
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
with mean values
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}\approx 3\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
; the
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}\approx 3\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
; the
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
region corresponds to the locations experiencing uphill diffusion. All minor species’ p.d.f.s are similar except for that of H2, which is the widest, and correspondingly has the heaviest tails. We attribute the peculiar H2 behaviour compared to all other minor species to H2 being a much smaller (i.e.
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
region corresponds to the locations experiencing uphill diffusion. All minor species’ p.d.f.s are similar except for that of H2, which is the widest, and correspondingly has the heaviest tails. We attribute the peculiar H2 behaviour compared to all other minor species to H2 being a much smaller (i.e.
![]() $0.74\times 10^{-10}$
m diameter) and lighter (i.e.
$0.74\times 10^{-10}$
m diameter) and lighter (i.e.
![]() $2.016~\text{kg}~\text{kmol}^{-1}$
molar mass) molecule which makes it very mobile, thus enhancing its diffusional interaction with other molecules, compared to species of larger and heavier molecules. This interaction manifests in the H2 flux being more strongly coupled to those of the other species, thereby inducing enhanced uphill diffusion. For all minor species, their Gaussian-like p.d.f. shape is representative of tracer diffusion.
$2.016~\text{kg}~\text{kmol}^{-1}$
molar mass) molecule which makes it very mobile, thus enhancing its diffusional interaction with other molecules, compared to species of larger and heavier molecules. This interaction manifests in the H2 flux being more strongly coupled to those of the other species, thereby inducing enhanced uphill diffusion. For all minor species, their Gaussian-like p.d.f. shape is representative of tracer diffusion.
According to the p.d.f.s of figure 12(b), the most probable value of
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
![]() $Sc_{\text{O}_{2},\mathit{eff}}$
is approximately 1.2. In contrast to n-heptane and oxygen, the minor species exhibit a much broader distribution having symmetric bell-shaped p.d.f.s similar in concept to those of
$Sc_{\text{O}_{2},\mathit{eff}}$
is approximately 1.2. In contrast to n-heptane and oxygen, the minor species exhibit a much broader distribution having symmetric bell-shaped p.d.f.s similar in concept to those of
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
and extending to
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
and extending to
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
values. Correspondingly, the p.d.f.s of
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
values. Correspondingly, the p.d.f.s of
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for the minor species span a much wider range than those of the major species; the most probable values of
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for the minor species span a much wider range than those of the major species; the most probable values of
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
are between 1.5 and 2 for CO, CO2 and H2O, whereas it is approximately 0.7 for H2, for which heavier tails are observed than those of all other minor species. These mean values, more representative for the major species than the minor species, indicate that the constant
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
are between 1.5 and 2 for CO, CO2 and H2O, whereas it is approximately 0.7 for H2, for which heavier tails are observed than those of all other minor species. These mean values, more representative for the major species than the minor species, indicate that the constant
![]() $Sc=0.7$
value, widely employed in modelling species mass transfer, is not appropriate for either the major or the minor species, but it would especially fail in describing the diffusion behaviour of minor species, except for H2 for which however the mean is not very representative considering its wide
$Sc=0.7$
value, widely employed in modelling species mass transfer, is not appropriate for either the major or the minor species, but it would especially fail in describing the diffusion behaviour of minor species, except for H2 for which however the mean is not very representative considering its wide
![]() $Sc_{\text{H}_{2},\mathit{eff}}$
p.d.f.
$Sc_{\text{H}_{2},\mathit{eff}}$
p.d.f.
To assess the commonly used assumption
![]() $Le=1$
, the
$Le=1$
, the
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
p.d.f.s are displayed in figure 12(c) (the corresponding
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
p.d.f.s are displayed in figure 12(c) (the corresponding
![]() $Pr_{\mathit{eff}}$
is discussed in the following). For all species, the most likely values
$Pr_{\mathit{eff}}$
is discussed in the following). For all species, the most likely values
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
are in the range
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
are in the range
![]() $[0,1]$
, but they can locally be as large as 3 or as small as
$[0,1]$
, but they can locally be as large as 3 or as small as
![]() $-1$
, the negative values being due to
$-1$
, the negative values being due to
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
, according to (5.13) and (5.14). The
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
, according to (5.13) and (5.14). The
![]() $Le=1$
assumption appears inaccurate, the most probable
$Le=1$
assumption appears inaccurate, the most probable
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
values being
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
values being
![]() ${\approx}0.45$
for n-C7H16 and O2,
${\approx}0.45$
for n-C7H16 and O2,
![]() ${\approx}0.75$
for CO, CO2 and H2O, and
${\approx}0.75$
for CO, CO2 and H2O, and
![]() ${\approx}0.35$
for H2. The narrower p.d.f.s for the major species indicate that the mean values for these species are more representative than for the minor species.
${\approx}0.35$
for H2. The narrower p.d.f.s for the major species indicate that the mean values for these species are more representative than for the minor species.
The above analysis highlights the range of values of effective non-dimensional numbers but does not provide an indication of their local distribution in the mixing layer. Such local distribution of
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
is illustrated in figure 13 for species involved in case s7R2p60X. The major species, namely O2 and n-C7H16, display small variations of
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
is illustrated in figure 13 for species involved in case s7R2p60X. The major species, namely O2 and n-C7H16, display small variations of
![]() $Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, with the larger values occurring at the upper bound of the mixing layer. This small increase from the lower to the upper mixing layer domain results from the opposite variation of, for example,
$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
, with the larger values occurring at the upper bound of the mixing layer. This small increase from the lower to the upper mixing layer domain results from the opposite variation of, for example,
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
in
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
in
![]() $(x_{1},x_{3})$
planes and the local value of
$(x_{1},x_{3})$
planes and the local value of
![]() $\unicode[STIX]{x1D70C}$
: the former increases as a consequence of the larger
$\unicode[STIX]{x1D70C}$
: the former increases as a consequence of the larger
![]() $T$
, whereas the latter decreases. The minor species CO, CO2 and H2O display a common behaviour; they exhibit higher variations compared to the major species, and negative local values indicate that these species undergo uphill diffusion primarily, but not exclusively, in the lower stream. Lastly, a specific behaviour is observed for H2 for which
$T$
, whereas the latter decreases. The minor species CO, CO2 and H2O display a common behaviour; they exhibit higher variations compared to the major species, and negative local values indicate that these species undergo uphill diffusion primarily, but not exclusively, in the lower stream. Lastly, a specific behaviour is observed for H2 for which
![]() $Sc_{\text{H}_{2},\mathit{eff}}>0$
and
$Sc_{\text{H}_{2},\mathit{eff}}>0$
and
![]() $Sc_{\text{H}_{2},\mathit{eff}}<0$
regions occur over the entire mixing layer. We attribute this H2 prevalence of uphill diffusion over the entire mixing layer to a combination of the aforementioned properties of H2, conferring to it greater mobility, and to the fact that
$Sc_{\text{H}_{2},\mathit{eff}}<0$
regions occur over the entire mixing layer. We attribute this H2 prevalence of uphill diffusion over the entire mixing layer to a combination of the aforementioned properties of H2, conferring to it greater mobility, and to the fact that
![]() $Y_{\text{H}_{2},ref}^{max}<0.01$
in both free streams, making it strongly influenced by turbulent stirring.
$Y_{\text{H}_{2},ref}^{max}<0.01$
in both free streams, making it strongly influenced by turbulent stirring.
Having analysed the different behaviour of the species in a single realization, the focus is now on two species – n-heptane and water – and their behaviour in realizations obtained with different number of species and
![]() $Re_{0}=2000$
is assessed. Case s7R1p60X is also considered in order to address the influence of the
$Re_{0}=2000$
is assessed. Case s7R1p60X is also considered in order to address the influence of the
![]() $Re$
value. Figures 14(a) and 14(b) show the p.d.f.s of
$Re$
value. Figures 14(a) and 14(b) show the p.d.f.s of
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
for different realizations. Compared to the effect of
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
for different realizations. Compared to the effect of
![]() $p_{0}$
, the initial composition only has a relatively small influence on
$p_{0}$
, the initial composition only has a relatively small influence on
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
. Indeed, as the number of species increases, the n-heptane molecules encounter a greater variety of molecules, both size-wise and mass-wise, a fact which increases the irregularity of the possible molecular pathways and slightly widens the p.d.f., resulting in a modest reduction of the mean value of
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
. Indeed, as the number of species increases, the n-heptane molecules encounter a greater variety of molecules, both size-wise and mass-wise, a fact which increases the irregularity of the possible molecular pathways and slightly widens the p.d.f., resulting in a modest reduction of the mean value of
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
. In contrast, pressure plays a greater role since an increase in
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
. In contrast, pressure plays a greater role since an increase in
![]() $p_{0}$
causes a decrease of the molecular diffusivity and of the
$p_{0}$
causes a decrease of the molecular diffusivity and of the
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013). As a consequence, the most likely value of
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013). As a consequence, the most likely value of
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is similar for all the
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is similar for all the
![]() $p_{0}=60$
atm cases (
$p_{0}=60$
atm cases (
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx 1.15$
), whereas it is shifted to
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx 1.15$
), whereas it is shifted to
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx 1.45$
for
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}\approx 1.45$
for
![]() $p_{0}=80$
atm due the smaller
$p_{0}=80$
atm due the smaller
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values. Although
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values. Although
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is smaller for
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is smaller for
![]() $p_{0}=80$
atm, the maximum
$p_{0}=80$
atm, the maximum
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values are
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
values are
![]() ${\approx}1.85$
for all cases, this behaviour being attributed to
${\approx}1.85$
for all cases, this behaviour being attributed to
![]() $\unicode[STIX]{x1D70C}$
increasing with
$\unicode[STIX]{x1D70C}$
increasing with
![]() $p_{0}$
. The R1 case is mostly indistinguishable from the equivalent R2 case except for the most probable value of
$p_{0}$
. The R1 case is mostly indistinguishable from the equivalent R2 case except for the most probable value of
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
which slightly decreases, indicating that the most probable value of
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
which slightly decreases, indicating that the most probable value of
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is susceptible to stirring. Figures 14(c) and 14(d) show the p.d.f.s of
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
is susceptible to stirring. Figures 14(c) and 14(d) show the p.d.f.s of
![]() $D_{\text{H}_{2}\text{O},\mathit{eff}}$
and
$D_{\text{H}_{2}\text{O},\mathit{eff}}$
and
![]() $Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
for realizations in which water is present in the initial composition. Case s5R2p60Y has a uniform initial distribution of H2O, meaning small
$Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
for realizations in which water is present in the initial composition. Case s5R2p60Y has a uniform initial distribution of H2O, meaning small
![]() $Y_{\text{H}_{2}\text{O}}$
gradients, leading to uphill diffusion; on the contrary, s5R2p60X has substantial initial gradients in
$Y_{\text{H}_{2}\text{O}}$
gradients, leading to uphill diffusion; on the contrary, s5R2p60X has substantial initial gradients in
![]() $Y_{\text{H}_{2}\text{O}}$
, explaining why uphill diffusion is small despite this being a minor species. The value of
$Y_{\text{H}_{2}\text{O}}$
, explaining why uphill diffusion is small despite this being a minor species. The value of
![]() $Re$
is seen to make a smaller impact on
$Re$
is seen to make a smaller impact on
![]() $D_{\text{H}_{2}\text{O},\mathit{eff}}$
than on the equivalent for C7H16, this being attributed to the smaller initial gradients than those of
$D_{\text{H}_{2}\text{O},\mathit{eff}}$
than on the equivalent for C7H16, this being attributed to the smaller initial gradients than those of
![]() $Y_{\text{C}_{7}\text{H}_{16}},$
leading to more subdued diffusion. Pressure has a definite effect in that it makes the most probable value more statistically significant, just as for C7H16, but unlike for C7H16, the most probable value only decreases very slightly. The result of this behaviour is seen in the
$Y_{\text{C}_{7}\text{H}_{16}},$
leading to more subdued diffusion. Pressure has a definite effect in that it makes the most probable value more statistically significant, just as for C7H16, but unlike for C7H16, the most probable value only decreases very slightly. The result of this behaviour is seen in the
![]() $Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
: all simulations having the same initial composition exhibit similar p.d.f.s, independent of the number of species, and only slightly dependent on pressure (the most probable value increasing slightly with pressure). However, the initial composition has a major impact, as indeed it should, by substantially increasing the values of
$Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
: all simulations having the same initial composition exhibit similar p.d.f.s, independent of the number of species, and only slightly dependent on pressure (the most probable value increasing slightly with pressure). However, the initial composition has a major impact, as indeed it should, by substantially increasing the values of
![]() $Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
in the negative range.
$Sc_{\text{H}_{2}\text{O},\mathit{eff}}$
in the negative range.

Figure 15. P.d.f.s computed over the three-dimensional mixing layer at
![]() $t_{tr}^{\ast }$
: (a)
$t_{tr}^{\ast }$
: (a)
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
(
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
(
![]() $\text{W}~\text{m}^{-1}~\text{K}^{-1}$
), and (b)
$\text{W}~\text{m}^{-1}~\text{K}^{-1}$
), and (b)
![]() $Pr_{\mathit{eff}}$
. J.p.d.f.s of
$Pr_{\mathit{eff}}$
. J.p.d.f.s of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
(
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
(
![]() $\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
) for cases (c,d) s5R2p60Y and (e,f) s7R2p60X. All the coefficients are not
$\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
) for cases (c,d) s5R2p60Y and (e,f) s7R2p60X. All the coefficients are not
![]() ${\mathcal{F}}$
-scaled.
${\mathcal{F}}$
-scaled.
The p.d.f.s of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
![]() $Pr_{\mathit{eff}}$
are displayed in figures 15(a) and 15(b), respectively. That for
$Pr_{\mathit{eff}}$
are displayed in figures 15(a) and 15(b), respectively. That for
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
exhibits small variations from the most likely value (
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
exhibits small variations from the most likely value (
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}\approx 0.02{-}0.03$
W
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}\approx 0.02{-}0.03$
W
![]() $\text{m}^{-1}~\text{K}^{-1}$
). Although
$\text{m}^{-1}~\text{K}^{-1}$
). Although
![]() $\unicode[STIX]{x1D706}>0$
as molecular transport theory states,
$\unicode[STIX]{x1D706}>0$
as molecular transport theory states,
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
is primarily positive, but negative values also occur in the mixing layer due to transport of enthalpy caused by the species-mass flux, as clearly shown by (5.12). The significance of
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
is primarily positive, but negative values also occur in the mixing layer due to transport of enthalpy caused by the species-mass flux, as clearly shown by (5.12). The significance of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
regions is that heat is transported against
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
regions is that heat is transported against
![]() $\unicode[STIX]{x1D735}T$
. However, negative
$\unicode[STIX]{x1D735}T$
. However, negative
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
values have small probabilities, leading to statistically insignificant
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
values have small probabilities, leading to statistically insignificant
![]() $Pr_{\mathit{eff}}<0$
regions. To verify the fact that uphill conduction is statistically insignificant, p.d.f.s of a normalized
$Pr_{\mathit{eff}}<0$
regions. To verify the fact that uphill conduction is statistically insignificant, p.d.f.s of a normalized
![]() $T$
,
$T$
,
were computed (not shown) for all cases shown in figure 15(a). All p.d.f.s have most probable values in the
![]() $\unicode[STIX]{x1D703}\in [0.1,0.2]$
range, the most probable value becomes less statistically significant with increased number of species, and uphill conduction is confined to regions where
$\unicode[STIX]{x1D703}\in [0.1,0.2]$
range, the most probable value becomes less statistically significant with increased number of species, and uphill conduction is confined to regions where
![]() $\unicode[STIX]{x1D703}<0$
and
$\unicode[STIX]{x1D703}<0$
and
![]() $|\unicode[STIX]{x1D703}|<0.05$
, thus being negligible; also, the region
$|\unicode[STIX]{x1D703}|<0.05$
, thus being negligible; also, the region
![]() $\unicode[STIX]{x1D703}<0$
becomes reduced with increasing number of species. Of note,
$\unicode[STIX]{x1D703}<0$
becomes reduced with increasing number of species. Of note,
![]() $\unicode[STIX]{x1D703}<0$
values are mainly found along the lower limit of the mixing layer region, whereas negative values for the effective thermal diffusivity are registered across the entire mixing layer: this fact highlights that uphill thermal conduction is not limited to the peripheral zones, but its occurrence is widespread across the layer. Independent of the case, the p.d.f. assumes null values past
$\unicode[STIX]{x1D703}<0$
values are mainly found along the lower limit of the mixing layer region, whereas negative values for the effective thermal diffusivity are registered across the entire mixing layer: this fact highlights that uphill thermal conduction is not limited to the peripheral zones, but its occurrence is widespread across the layer. Independent of the case, the p.d.f. assumes null values past
![]() $\unicode[STIX]{x1D703}>0.9$
; this fact is a manifestation of the definition of the mixing layer that is based on the
$\unicode[STIX]{x1D703}>0.9$
; this fact is a manifestation of the definition of the mixing layer that is based on the
![]() $(x_{1},x_{3})$
-averaged mass fraction of heptane (initially present only in the lower colder stream), thus resulting in the temperature of the mixture at the upper limit of the mixing layer being slightly lower than the reference temperature in the upper, unperturbed stream.
$(x_{1},x_{3})$
-averaged mass fraction of heptane (initially present only in the lower colder stream), thus resulting in the temperature of the mixture at the upper limit of the mixing layer being slightly lower than the reference temperature in the upper, unperturbed stream.
Globally, there is no direct clear influence of the initial composition on the
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
values, whereas an increase of
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
values, whereas an increase of
![]() $p_{0}$
seems to slightly shift the distribution towards positive values. As a consequence of both positive and negative values of
$p_{0}$
seems to slightly shift the distribution towards positive values. As a consequence of both positive and negative values of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
, the same variation holds for
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
, the same variation holds for
![]() $Pr_{\mathit{eff}}$
having generally values in the range
$Pr_{\mathit{eff}}$
having generally values in the range
![]() $[0,7]$
, with most probable values as small as
$[0,7]$
, with most probable values as small as
![]() ${\approx}2.5$
and as large as
${\approx}2.5$
and as large as
![]() ${\approx}3$
. These values are representative of dense gases; typically
${\approx}3$
. These values are representative of dense gases; typically
![]() $Pr_{\mathit{eff}}\approx 4$
–5 for liquid refrigerants and
$Pr_{\mathit{eff}}\approx 4$
–5 for liquid refrigerants and
![]() ${\approx}7$
for liquid H2O. As the number of species increases, the most probable value of the p.d.f. shifts towards lower values, being
${\approx}7$
for liquid H2O. As the number of species increases, the most probable value of the p.d.f. shifts towards lower values, being
![]() ${\approx}3$
for case s3R2p60Y to
${\approx}3$
for case s3R2p60Y to
![]() ${\approx}2$
for case s7R2p60X. The p.d.f.s for the seven-species cases exhibit lower dispersion, and higher
${\approx}2$
for case s7R2p60X. The p.d.f.s for the seven-species cases exhibit lower dispersion, and higher
![]() $Pr_{\mathit{eff}}$
values are less probable. An increase of the free-stream pressure
$Pr_{\mathit{eff}}$
values are less probable. An increase of the free-stream pressure
![]() $p_{0}$
results in a slightly lower dispersion, whereas the most likely value remains unchanged. To examine the influence of the
$p_{0}$
results in a slightly lower dispersion, whereas the most likely value remains unchanged. To examine the influence of the
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
values on the corresponding
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}<0$
values on the corresponding
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for C7H16 and H2O, figures 15(c–f) display joint probability density functions (j.p.d.f.s) of
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for C7H16 and H2O, figures 15(c–f) display joint probability density functions (j.p.d.f.s) of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for cases s5R2p60Y and s7R2p60X. According to (5.14),
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
for cases s5R2p60Y and s7R2p60X. According to (5.14),
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
only if
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}<0$
only if
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
![]() $D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
have different signs. The j.p.d.f.s show that
$D_{\unicode[STIX]{x1D6FC},\mathit{eff}}$
have different signs. The j.p.d.f.s show that
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
has much more extensive domain correlation with
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
has much more extensive domain correlation with
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
(which is always positive) than with
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
(which is always positive) than with
![]() $D_{\text{H}_{2}\text{O},\mathit{eff}}$
(which can also become negative). Moreover, that larger correlation is increasingly in the
$D_{\text{H}_{2}\text{O},\mathit{eff}}$
(which can also become negative). Moreover, that larger correlation is increasingly in the
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}>0$
region as the number of species increases. Additionally, figures 15(c) and 15(f) also show the presence (even if statistically small) of
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}>0$
region as the number of species increases. Additionally, figures 15(c) and 15(f) also show the presence (even if statistically small) of
![]() $Le_{\text{H}_{2}\text{O}}>0$
regions given by simultaneous negative values of
$Le_{\text{H}_{2}\text{O}}>0$
regions given by simultaneous negative values of
![]() $\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
$\unicode[STIX]{x1D6EC}_{\mathit{eff}}$
and
![]() $D_{\text{H}_{2}\text{O},\mathit{eff}}$
. Thus, uphill diffusion may occur for species
$D_{\text{H}_{2}\text{O},\mathit{eff}}$
. Thus, uphill diffusion may occur for species
![]() $\unicode[STIX]{x1D6FC}$
, yet
$\unicode[STIX]{x1D6FC}$
, yet
![]() $Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}>0$
.
$Le_{\unicode[STIX]{x1D6FC},\mathit{eff}}>0$
.

Figure 16. Braid plane (
![]() $x_{3}/L_{3}=1/16$
) distribution of the local effective Prandtl number
$x_{3}/L_{3}=1/16$
) distribution of the local effective Prandtl number
![]() $Pr_{\mathit{eff}}$
at
$Pr_{\mathit{eff}}$
at
![]() $t_{tr}^{\ast }$
: (a) 2pR260Y, (b) s3R2p60Y, (c) s5R2p60Y, (d) s5R2p60X, (e) s7R2p60X and (f) s7R2p80X.
$t_{tr}^{\ast }$
: (a) 2pR260Y, (b) s3R2p60Y, (c) s5R2p60Y, (d) s5R2p60X, (e) s7R2p60X and (f) s7R2p80X.
To inquire about the variation of the local distribution of
![]() $Pr_{\mathit{eff}}$
with the number of species, portrayed in figure 16 are visualizations of these fields at
$Pr_{\mathit{eff}}$
with the number of species, portrayed in figure 16 are visualizations of these fields at
![]() $t_{tr}^{\ast }$
for realizations initiated with
$t_{tr}^{\ast }$
for realizations initiated with
![]() $Re_{0}=2000$
. The general observation is that high
$Re_{0}=2000$
. The general observation is that high
![]() $Pr_{\mathit{eff}}$
values are intermingled over the entire mixing layer with low and negative values for all initial compositions. However, with increasing number of species, large values as well as negative values (i.e. uphill heat conduction) occur at a smaller number of locations, rendering the
$Pr_{\mathit{eff}}$
values are intermingled over the entire mixing layer with low and negative values for all initial compositions. However, with increasing number of species, large values as well as negative values (i.e. uphill heat conduction) occur at a smaller number of locations, rendering the
![]() $Pr_{\mathit{eff}}$
field more uniform. That is, the transport of enthalpy by the species has a thermal-transport homogenizing effect on the mixture with increasing mixture complexity, whereas it has the opposite effect for a smaller number of species in the mixture.
$Pr_{\mathit{eff}}$
field more uniform. That is, the transport of enthalpy by the species has a thermal-transport homogenizing effect on the mixture with increasing mixture complexity, whereas it has the opposite effect for a smaller number of species in the mixture.
5.6 Dissipation
The above analysis addressed both the generation of density gradients (and therefore of
![]() $\unicode[STIX]{x1D735}T$
,
$\unicode[STIX]{x1D735}T$
,
![]() $\unicode[STIX]{x1D735}p$
and
$\unicode[STIX]{x1D735}p$
and
![]() $\unicode[STIX]{x1D735}Y_{\unicode[STIX]{x1D6FC}}$
) and the difference in transport properties when the complexity of a mixture was increased by adding species to a baseline mixture. Since the dissipation is the combined result of gradients and molecular transport properties, it is natural to inquire about the effect of species complexity on the dissipation.
$\unicode[STIX]{x1D735}Y_{\unicode[STIX]{x1D6FC}}$
) and the difference in transport properties when the complexity of a mixture was increased by adding species to a baseline mixture. Since the dissipation is the combined result of gradients and molecular transport properties, it is natural to inquire about the effect of species complexity on the dissipation.
Considering the entropy conservation equation (e.g. de Groot & Mazur Reference de Groot and Mazur1984) and using the transport coefficient calculation through the mixing rules (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013), a generalized formulation for the dissipation
![]() $g$
, i.e. the irreversible entropy production, which is the source term in the entropy equation, has been derived (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013). The dissipation is written as the sum of three terms accounting for viscous, thermal and species-mass contributions,
$g$
, i.e. the irreversible entropy production, which is the source term in the entropy equation, has been derived (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013). The dissipation is written as the sum of three terms accounting for viscous, thermal and species-mass contributions,
![]() $g_{visc},g_{temp}$
and
$g_{visc},g_{temp}$
and
![]() $g_{mass}$
,
$g_{mass}$
,
 $$\begin{eqnarray}g=\underbrace{{\displaystyle \frac{\unicode[STIX]{x1D707}}{T}}\left(2\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}-{\textstyle \frac{2}{3}}\unicode[STIX]{x1D61A}_{kk}\unicode[STIX]{x1D61A}_{ll}\right)}_{g_{visc}}+\underbrace{\unicode[STIX]{x1D706}{\displaystyle \frac{1}{T^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}}_{g_{temp}}+\underbrace{{\displaystyle \frac{1}{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FD}=1}^{N}\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{N}{\displaystyle \frac{R_{u}}{(-\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})}}{\displaystyle \frac{\unicode[STIX]{x1D70C}}{m_{\unicode[STIX]{x1D6FC}}Y_{\unicode[STIX]{x1D6FD}}}}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}}_{g_{mass}},\end{eqnarray}$$
$$\begin{eqnarray}g=\underbrace{{\displaystyle \frac{\unicode[STIX]{x1D707}}{T}}\left(2\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}-{\textstyle \frac{2}{3}}\unicode[STIX]{x1D61A}_{kk}\unicode[STIX]{x1D61A}_{ll}\right)}_{g_{visc}}+\underbrace{\unicode[STIX]{x1D706}{\displaystyle \frac{1}{T^{2}}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}}_{g_{temp}}+\underbrace{{\displaystyle \frac{1}{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FD}=1}^{N}\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{N}{\displaystyle \frac{R_{u}}{(-\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}})}}{\displaystyle \frac{\unicode[STIX]{x1D70C}}{m_{\unicode[STIX]{x1D6FC}}Y_{\unicode[STIX]{x1D6FD}}}}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}}_{g_{mass}},\end{eqnarray}$$
where
![]() $(-\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}m)/(Y_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FD}})$
is a symmetric positive semidefinite matrix (Keizer Reference Keizer1987; Giovangigli, Matuszewsky & Dupoirieux Reference Giovangigli, Matuszewsky and Dupoirieux2011) and
$(-\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}m)/(Y_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FD}})$
is a symmetric positive semidefinite matrix (Keizer Reference Keizer1987; Giovangigli, Matuszewsky & Dupoirieux Reference Giovangigli, Matuszewsky and Dupoirieux2011) and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j} & = & \displaystyle -X_{\unicode[STIX]{x1D6FD}}\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\left[\left(\frac{m_{\unicode[STIX]{x1D6FC}}}{m}\bar{\unicode[STIX]{x1D6FC}}_{T,\unicode[STIX]{x1D6FD}}^{b}-{\displaystyle \frac{m_{\unicode[STIX]{x1D6FD}}}{m}}\bar{\unicode[STIX]{x1D6FC}}_{T,\unicode[STIX]{x1D6FC}}^{b}\right){\displaystyle \frac{1}{T}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}+{\displaystyle \frac{m_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FD}}}{mR_{u}T}}\left(\frac{v_{\unicode[STIX]{x1D6FC}}}{m_{\unicode[STIX]{x1D6FC}}}-\frac{v_{\unicode[STIX]{x1D6FD}}}{m_{\unicode[STIX]{x1D6FD}}}\right){\displaystyle \frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{j}}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}=1}^{N-1}\left({\displaystyle \frac{m_{\unicode[STIX]{x1D6FD}}}{m_{\unicode[STIX]{x1D6FE}}}}\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}-{\displaystyle \frac{m_{\unicode[STIX]{x1D6FC}}}{m_{\unicode[STIX]{x1D6FE}}}}\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}\right)\left[{\displaystyle \frac{\unicode[STIX]{x2202}Y_{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x2202}x_{j}}}-Y_{\unicode[STIX]{x1D6FE}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}=1}^{N-1}\left({\displaystyle \frac{m}{m_{\unicode[STIX]{x1D6FF}}}}-{\displaystyle \frac{m}{m_{N}}}\right){\displaystyle \frac{\unicode[STIX]{x2202}Y_{\unicode[STIX]{x1D6FF}}}{\unicode[STIX]{x2202}x_{j}}}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j} & = & \displaystyle -X_{\unicode[STIX]{x1D6FD}}\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\left[\left(\frac{m_{\unicode[STIX]{x1D6FC}}}{m}\bar{\unicode[STIX]{x1D6FC}}_{T,\unicode[STIX]{x1D6FD}}^{b}-{\displaystyle \frac{m_{\unicode[STIX]{x1D6FD}}}{m}}\bar{\unicode[STIX]{x1D6FC}}_{T,\unicode[STIX]{x1D6FC}}^{b}\right){\displaystyle \frac{1}{T}}{\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{j}}}+{\displaystyle \frac{m_{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FD}}}{mR_{u}T}}\left(\frac{v_{\unicode[STIX]{x1D6FC}}}{m_{\unicode[STIX]{x1D6FC}}}-\frac{v_{\unicode[STIX]{x1D6FD}}}{m_{\unicode[STIX]{x1D6FD}}}\right){\displaystyle \frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{j}}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}=1}^{N-1}\left({\displaystyle \frac{m_{\unicode[STIX]{x1D6FD}}}{m_{\unicode[STIX]{x1D6FE}}}}\mathbb{D}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}-{\displaystyle \frac{m_{\unicode[STIX]{x1D6FC}}}{m_{\unicode[STIX]{x1D6FE}}}}\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}_{D\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}\right)\left[{\displaystyle \frac{\unicode[STIX]{x2202}Y_{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x2202}x_{j}}}-Y_{\unicode[STIX]{x1D6FE}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}=1}^{N-1}\left({\displaystyle \frac{m}{m_{\unicode[STIX]{x1D6FF}}}}-{\displaystyle \frac{m}{m_{N}}}\right){\displaystyle \frac{\unicode[STIX]{x2202}Y_{\unicode[STIX]{x1D6FF}}}{\unicode[STIX]{x2202}x_{j}}}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}j}=0$
and
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}j}=0$
and
![]() $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}=-\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}j}$
. The
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}j}=-\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}j}$
. The
![]() $g$
form of (5.19) has been previously used by Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013).
$g$
form of (5.19) has been previously used by Masi et al. (Reference Masi, Bellan, Harstad and Okong’o2013).
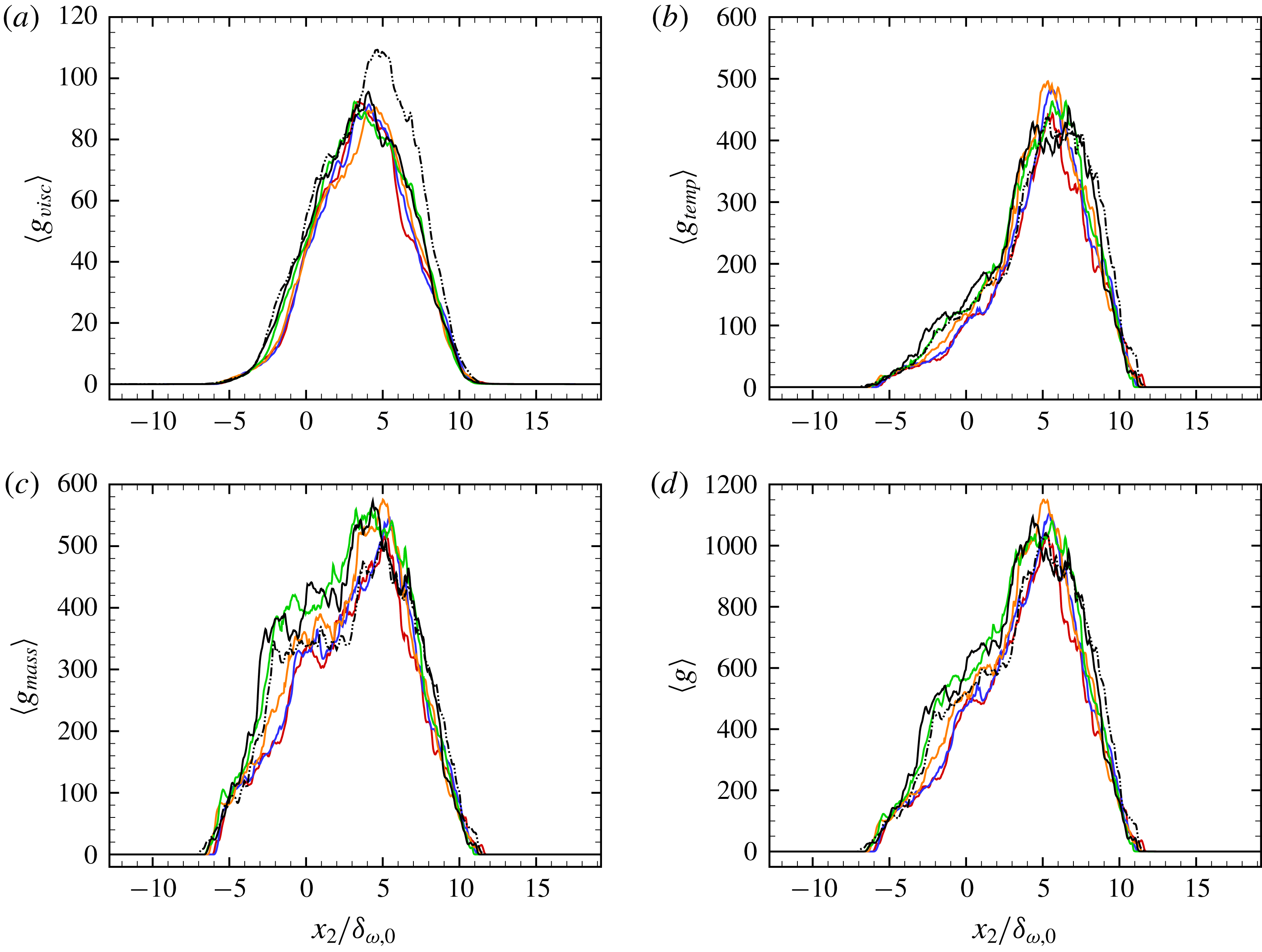
Figure 17. Planar averages in
![]() $(x_{1},x_{3})$
planes of the three modes, (a)
$(x_{1},x_{3})$
planes of the three modes, (a)
![]() $\langle g_{\mathit{visc}}\rangle$
, (b)
$\langle g_{\mathit{visc}}\rangle$
, (b)
![]() $\langle g_{\mathit{temp}}\rangle$
and (c)
$\langle g_{\mathit{temp}}\rangle$
and (c)
![]() $\langle g_{\mathit{mass}}\rangle$
, and of (d)
$\langle g_{\mathit{mass}}\rangle$
, and of (d)
![]() $g$
at the respective
$g$
at the respective
![]() $t_{tr}^{\ast }$
. Units are
$t_{tr}^{\ast }$
. Units are
![]() $\text{W}~\text{m}^{-3}~\text{K}^{-1}$
. Same colour legend as in figure 1.
$\text{W}~\text{m}^{-3}~\text{K}^{-1}$
. Same colour legend as in figure 1.
The
![]() $g_{visc}$
,
$g_{visc}$
,
![]() $g_{temp}$
and
$g_{temp}$
and
![]() $g_{mass}$
(
$g_{mass}$
(
![]() $x_{1},x_{3}$
) planar averages are here computed for the realizations presented in figure 1, and are separately illustrated as a function of
$x_{1},x_{3}$
) planar averages are here computed for the realizations presented in figure 1, and are separately illustrated as a function of
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
in figure 17(a), (b) and (c), respectively. The values of the transport coefficients are not
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}$
in figure 17(a), (b) and (c), respectively. The values of the transport coefficients are not
![]() ${\mathcal{F}}$
-scaled and units are
${\mathcal{F}}$
-scaled and units are
![]() $\text{W}~\text{m}^{-3}~\text{K}^{-1}$
. Comparing the magnitude of these terms,
$\text{W}~\text{m}^{-3}~\text{K}^{-1}$
. Comparing the magnitude of these terms,
![]() $\langle g_{visc}\rangle$
is the smallest by approximately a factor of 5 with respect to
$\langle g_{visc}\rangle$
is the smallest by approximately a factor of 5 with respect to
![]() $\langle g_{temp}\rangle$
and
$\langle g_{temp}\rangle$
and
![]() $\langle g_{mass}\rangle$
; this ordering is attributed to the relatively modest values of
$\langle g_{mass}\rangle$
; this ordering is attributed to the relatively modest values of
![]() $Re_{m,tr}$
compared to fully turbulent flows. The
$Re_{m,tr}$
compared to fully turbulent flows. The
![]() $(x_{1},x_{3})$
planar average
$(x_{1},x_{3})$
planar average
![]() $\langle g_{visc}\rangle$
profiles are not symmetric with respect to
$\langle g_{visc}\rangle$
profiles are not symmetric with respect to
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=0$
but are rather heavily skewed to the upper free-stream side where the fluid is lighter and is thus more amenable to experiencing larger velocities and perhaps larger velocity gradients. While the values of all p60 simulations nearly coincide, a larger
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}=0$
but are rather heavily skewed to the upper free-stream side where the fluid is lighter and is thus more amenable to experiencing larger velocities and perhaps larger velocity gradients. While the values of all p60 simulations nearly coincide, a larger
![]() $p_{0}$
value (case s7R2p80X) induces a slightly larger
$p_{0}$
value (case s7R2p80X) induces a slightly larger
![]() $\langle g_{visc}\rangle$
with respect to p60 cases on the lighter free-stream side, primarily caused by the more elevated values of the dynamic viscosity in the core of the mixing layer (not shown). Even though the single-species viscosity of the minor species can be largely different from that of the major species, the mixture viscosity (computed using the Wilke method, equation (A 1)) is strongly dependent on the molar fractions, explaining the small influence of the minor species for the p60 cases.
$\langle g_{visc}\rangle$
with respect to p60 cases on the lighter free-stream side, primarily caused by the more elevated values of the dynamic viscosity in the core of the mixing layer (not shown). Even though the single-species viscosity of the minor species can be largely different from that of the major species, the mixture viscosity (computed using the Wilke method, equation (A 1)) is strongly dependent on the molar fractions, explaining the small influence of the minor species for the p60 cases.
The cross-stream profiles of
![]() $\langle g_{temp}\rangle$
exhibit similar values for all realizations, a fact which is conjectured to reflect the dominance of
$\langle g_{temp}\rangle$
exhibit similar values for all realizations, a fact which is conjectured to reflect the dominance of
![]() $X_{\unicode[STIX]{x1D6FC}}$
, and thus of the major species’ contribution in the computation of
$X_{\unicode[STIX]{x1D6FC}}$
, and thus of the major species’ contribution in the computation of
![]() $\unicode[STIX]{x1D706}$
(see (A 4)). The
$\unicode[STIX]{x1D706}$
(see (A 4)). The
![]() $\langle g_{temp}\rangle$
profiles are very heavily skewed towards the hotter upper free stream where according to figure 6 is the region of the larger
$\langle g_{temp}\rangle$
profiles are very heavily skewed towards the hotter upper free stream where according to figure 6 is the region of the larger
![]() $\unicode[STIX]{x1D735}T$
, and unlike
$\unicode[STIX]{x1D735}T$
, and unlike
![]() $\langle g_{visc}\rangle$
,
$\langle g_{visc}\rangle$
,
![]() $\langle g_{temp}\rangle$
is unaffected by
$\langle g_{temp}\rangle$
is unaffected by
![]() $p_{0}$
.
$p_{0}$
.
Among all dissipation modes,
![]() $\langle g_{mass}\rangle$
has the largest values; it also exhibits a slight increase with the number of species as a result of the larger interdiffusion in the seven- and five-species cases with respect to the two- and three-species realizations. The
$\langle g_{mass}\rangle$
has the largest values; it also exhibits a slight increase with the number of species as a result of the larger interdiffusion in the seven- and five-species cases with respect to the two- and three-species realizations. The
![]() $\langle g_{mass}\rangle$
profile is less skewed towards the upper stream than those of
$\langle g_{mass}\rangle$
profile is less skewed towards the upper stream than those of
![]() $\langle g_{visc}\rangle$
and
$\langle g_{visc}\rangle$
and
![]() $\langle g_{temp}\rangle$
, and unlike the latter shows a substantial contribution from the lower-stream side. While all
$\langle g_{temp}\rangle$
, and unlike the latter shows a substantial contribution from the lower-stream side. While all
![]() $\langle g_{mass}\rangle$
profiles nearly coincide on the upper-stream side of the
$\langle g_{mass}\rangle$
profiles nearly coincide on the upper-stream side of the
![]() $\langle g_{mass}\rangle$
peak, there is substantial variability among realizations on the lower-stream side that is indicative of the changes in mass-diffusion characteristics as the number of species varies. Compared to s7R2p60X, case s7R2p80X exhibits relatively lower
$\langle g_{mass}\rangle$
peak, there is substantial variability among realizations on the lower-stream side that is indicative of the changes in mass-diffusion characteristics as the number of species varies. Compared to s7R2p60X, case s7R2p80X exhibits relatively lower
![]() $\langle g_{mass}\rangle$
values because of the reduced values of the diffusion coefficients in higher-
$\langle g_{mass}\rangle$
values because of the reduced values of the diffusion coefficients in higher-
![]() $p$
environments.
$p$
environments.
Of note,
![]() $\langle g_{visc}\rangle$
,
$\langle g_{visc}\rangle$
,
![]() $\langle g\rangle$
and
$\langle g\rangle$
and
![]() $\langle g_{mass}\rangle$
all culminate at
$\langle g_{mass}\rangle$
all culminate at
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
, suggesting that most mixing layer activity occurs at this location. As a result,
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
, suggesting that most mixing layer activity occurs at this location. As a result,
![]() $\langle g\rangle$
, portrayed in figure 17(d), also culminates at the
$\langle g\rangle$
, portrayed in figure 17(d), also culminates at the
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
location and, while it retains the near-coincidence of all profiles on the upper-stream side of the layer, it also shows the number-of-species variability effect on the lower-stream side of
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
location and, while it retains the near-coincidence of all profiles on the upper-stream side of the layer, it also shows the number-of-species variability effect on the lower-stream side of
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
. Thus, while the effect of the number of species on
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}\approx 5$
. Thus, while the effect of the number of species on
![]() $g$
is modest, it is not negligible.
$g$
is modest, it is not negligible.
5.7 Relationship between species and temperature
In simulations of reacting flows using reduced kinetic mechanisms, one of the important considerations is maintaining the relationship between
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
(Bellan Reference Bellan2017b
). The DNS database generated here provides a unique opportunity to inquire about the possible deviations in this relationship as the mixture composition is considered in coarser detail. For example, possible causes of deviation would be the observed uphill diffusion of neglected minor species as the composition is simplified. To determine the relationship between
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
(Bellan Reference Bellan2017b
). The DNS database generated here provides a unique opportunity to inquire about the possible deviations in this relationship as the mixture composition is considered in coarser detail. For example, possible causes of deviation would be the observed uphill diffusion of neglected minor species as the composition is simplified. To determine the relationship between
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D703}$
, we compute j.p.d.f.s which, being pointwise functions, provide very detailed information. A less stringent test of this relationship is obtained by computing conditional averages of
$\unicode[STIX]{x1D703}$
, we compute j.p.d.f.s which, being pointwise functions, provide very detailed information. A less stringent test of this relationship is obtained by computing conditional averages of
![]() $\unicode[STIX]{x1D703}$
given
$\unicode[STIX]{x1D703}$
given
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
. These investigations are performed at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
. These investigations are performed at
![]() $t_{tr}^{\ast }$
and they address the relationship for both major and minor species.
$t_{tr}^{\ast }$
and they address the relationship for both major and minor species.

Figure 18. J.p.d.f. of
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for heptane at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for heptane at
![]() $t_{tr}^{\ast }$
, in logarithmic scale: (a) s2R2p60Y, (b) s5R2p60X and (c) s7R2p60X. The p.d.f. is computed inside the mixing layer, defined according to (5.4).
$t_{tr}^{\ast }$
, in logarithmic scale: (a) s2R2p60Y, (b) s5R2p60X and (c) s7R2p60X. The p.d.f. is computed inside the mixing layer, defined according to (5.4).

Figure 19. J.p.d.f. in logarithmic scale of
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for cases s7R2p60X (top line) and s5R2p60X (bottom line): (a,d) O2, (b,e) CO2 and (c,f) H2O. The p.d.f. is computed inside the mixing layer, according to (5.4), at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for cases s7R2p60X (top line) and s5R2p60X (bottom line): (a,d) O2, (b,e) CO2 and (c,f) H2O. The p.d.f. is computed inside the mixing layer, according to (5.4), at
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.
Figure 18 illustrates the j.p.d.f.s for n-heptane in cases s2R2p60Y, s5R2p60X and s7R2p60X; discussing the j.p.d.f. for n-heptane does not imply that n-heptane will preserve its chemical structure at the higher
![]() $T$
values in the domain rather than pyrolysing. Upon careful scrutiny, the j.p.d.f. for s2R2p60Y extends perceptibly to
$T$
values in the domain rather than pyrolysing. Upon careful scrutiny, the j.p.d.f. for s2R2p60Y extends perceptibly to
![]() $\unicode[STIX]{x1D703}<0$
regions; however, these
$\unicode[STIX]{x1D703}<0$
regions; however, these
![]() $\unicode[STIX]{x1D703}<0$
regions are negligible for s5R2p60X and s7R2p60X, consistent with the discussion of § 5.5. Examination of figure 18 shows that, as expected given the initial conditions wherein n-heptane resides in the lower
$\unicode[STIX]{x1D703}<0$
regions are negligible for s5R2p60X and s7R2p60X, consistent with the discussion of § 5.5. Examination of figure 18 shows that, as expected given the initial conditions wherein n-heptane resides in the lower
![]() $T$
stream, the j.p.d.f. exhibits a decreasing relationship between
$T$
stream, the j.p.d.f. exhibits a decreasing relationship between
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
and
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
and
![]() $\unicode[STIX]{x1D703}$
; the width of the j.p.d.f. becomes larger with decreasing
$\unicode[STIX]{x1D703}$
; the width of the j.p.d.f. becomes larger with decreasing
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
and increasing
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
and increasing
![]() $\unicode[STIX]{x1D703}$
, this being a manifestation of the mixing and heat transfer occurring between the two streams. The j.p.d.f. values corresponding to the smallest
$\unicode[STIX]{x1D703}$
, this being a manifestation of the mixing and heat transfer occurring between the two streams. The j.p.d.f. values corresponding to the smallest
![]() $\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
values and largest
$\unicode[STIX]{x1D6EF}_{\text{C}_{7}\text{H}_{16}}$
values and largest
![]() $\unicode[STIX]{x1D703}$
values correspond to the largest values of
$\unicode[STIX]{x1D703}$
values correspond to the largest values of
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}>0$
at which n-heptane is present in the upper stream (see figure 6
a,h). The j.p.d.f.s do not show much visual variation from s2R2p60Y to s5R2p60X, but it is visually apparent that the width of the j.p.d.f. increases from s5R2p60X to s7R2p60X. However, comparison of figures 18(b) and 18(c) indicates that regions with large j.p.d.f. values are less susceptible to change by the addition of species if these species are minor, and the width increase seems to affect only the tails of the j.p.d.f.; that is, the presence of the additional species decreases the preponderance of n-heptane as
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}>0$
at which n-heptane is present in the upper stream (see figure 6
a,h). The j.p.d.f.s do not show much visual variation from s2R2p60Y to s5R2p60X, but it is visually apparent that the width of the j.p.d.f. increases from s5R2p60X to s7R2p60X. However, comparison of figures 18(b) and 18(c) indicates that regions with large j.p.d.f. values are less susceptible to change by the addition of species if these species are minor, and the width increase seems to affect only the tails of the j.p.d.f.; that is, the presence of the additional species decreases the preponderance of n-heptane as
![]() $\unicode[STIX]{x1D703}$
increases, this situation representing regions at larger
$\unicode[STIX]{x1D703}$
increases, this situation representing regions at larger
![]() $x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}>0$
locations within the mixing layer (see figure 6
a,h). To show that the findings for n-heptane are not an isolated conclusion, the j.p.d.f.s for O2, CO2 and H2O are displayed in figure 19. Since their corresponding
$x_{2}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714},0}>0$
locations within the mixing layer (see figure 6
a,h). To show that the findings for n-heptane are not an isolated conclusion, the j.p.d.f.s for O2, CO2 and H2O are displayed in figure 19. Since their corresponding
![]() $Y_{\unicode[STIX]{x1D6FC}}$
is initially larger in the upper stream compared to the lower stream, the j.p.d.f.s exhibit an increasing relationship between
$Y_{\unicode[STIX]{x1D6FC}}$
is initially larger in the upper stream compared to the lower stream, the j.p.d.f.s exhibit an increasing relationship between
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D703}$
. These j.p.d.f.s visually confirm the findings of figure 18: minor species addition widens the tails of the j.p.d.f.s but does not substantially affect the j.p.d.f.s large value region. Finally, figure 20 presents for information the j.p.d.f.s of CO and H2 computed for s7R2p60X, the single simulation in which these species are present. Despite their initial
$\unicode[STIX]{x1D703}$
. These j.p.d.f.s visually confirm the findings of figure 18: minor species addition widens the tails of the j.p.d.f.s but does not substantially affect the j.p.d.f.s large value region. Finally, figure 20 presents for information the j.p.d.f.s of CO and H2 computed for s7R2p60X, the single simulation in which these species are present. Despite their initial
![]() $Y_{\unicode[STIX]{x1D6FC}}$
value being smaller than those of CO2 and H2O, the j.p.d.f.s of CO and H2 are the widest, this being due to uphill diffusion, which for CO and H2 enlarged the range of
$Y_{\unicode[STIX]{x1D6FC}}$
value being smaller than those of CO2 and H2O, the j.p.d.f.s of CO and H2 are the widest, this being due to uphill diffusion, which for CO and H2 enlarged the range of
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
values more than for CO2 and H2O (see figure 5).
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
values more than for CO2 and H2O (see figure 5).

Figure 20. J.p.d.f. in logarithmic scale of
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for case s7R2p60X: (a) CO and (b) H2. The p.d.f. is computed inside the mixing layer, according to (5.4), at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for case s7R2p60X: (a) CO and (b) H2. The p.d.f. is computed inside the mixing layer, according to (5.4), at
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.
To quantify the differences between the j.p.d.f.s obtained as the composition is simplified, relative errors were calculated. The relative deviations of the j.p.d.f.s,
![]() $dev_{\unicode[STIX]{x1D6FC}}$
, for the four common species to s5R2p60X and s7R2p60X, is computed using
$dev_{\unicode[STIX]{x1D6FC}}$
, for the four common species to s5R2p60X and s7R2p60X, is computed using
 $$\begin{eqnarray}\mathit{dev}_{\unicode[STIX]{x1D6FC}}=\frac{\sqrt{\left[(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s7R2p60X}}-(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s5R2p60X}}\right]^{2}}}{(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s7R2p60X}}+\unicode[STIX]{x1D716}},\end{eqnarray}$$
$$\begin{eqnarray}\mathit{dev}_{\unicode[STIX]{x1D6FC}}=\frac{\sqrt{\left[(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s7R2p60X}}-(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s5R2p60X}}\right]^{2}}}{(\text{j.p.d.f.})_{\unicode[STIX]{x1D6FC}}^{\text{s7R2p60X}}+\unicode[STIX]{x1D716}},\end{eqnarray}$$
where the small parameter
![]() $\unicode[STIX]{x1D716}=10^{-16}$
is added to the denominator in order to avoid division by zero. The addition of
$\unicode[STIX]{x1D716}=10^{-16}$
is added to the denominator in order to avoid division by zero. The addition of
![]() $\unicode[STIX]{x1D716}$
does not affect the
$\unicode[STIX]{x1D716}$
does not affect the
![]() $\mathit{dev}_{\unicode[STIX]{x1D6FC}}$
evaluation in regions of large j.p.d.f. values representing the significant combustion localities, but does affect the regions of small j.p.d.f. values in which the relative deviation thus computed may be inaccurate; however, this range of values has negligible contribution to combustion. Figure 21 shows that for all species under consideration – n-heptane, O2, CO2 and H2O –
$\mathit{dev}_{\unicode[STIX]{x1D6FC}}$
evaluation in regions of large j.p.d.f. values representing the significant combustion localities, but does affect the regions of small j.p.d.f. values in which the relative deviation thus computed may be inaccurate; however, this range of values has negligible contribution to combustion. Figure 21 shows that for all species under consideration – n-heptane, O2, CO2 and H2O –
![]() $\mathit{dev}_{\unicode[STIX]{x1D6FC}}$
is very small in the regions of maximum and large j.p.d.f. values and is only large on the periphery of the j.p.d.f.s. These peripheral values occur primarily where the temperature is too low for combustion to occur. The fact that the deviation is small in the region of larger probability is here interpreted as a confirmation that conditional averages may be considered as a sufficient test of the change in j.p.d.f.s as the composition of a mixture of species is refined. The
$\mathit{dev}_{\unicode[STIX]{x1D6FC}}$
is very small in the regions of maximum and large j.p.d.f. values and is only large on the periphery of the j.p.d.f.s. These peripheral values occur primarily where the temperature is too low for combustion to occur. The fact that the deviation is small in the region of larger probability is here interpreted as a confirmation that conditional averages may be considered as a sufficient test of the change in j.p.d.f.s as the composition of a mixture of species is refined. The
![]() $\langle \unicode[STIX]{x1D703}\mid \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}\rangle$
conditional averages are depicted in figure 22 and show that, with the exception of the uphill diffusion regime of CO2 and H2O, where
$\langle \unicode[STIX]{x1D703}\mid \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}\rangle$
conditional averages are depicted in figure 22 and show that, with the exception of the uphill diffusion regime of CO2 and H2O, where
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
, the conditional averages are primarily similar. Thus, we conclude that the simplification of the mixture composition by eliminating minor species does not affect the relationship between the remaining mass fractions and temperature, with the exception of the regions of uphill diffusion of those species that experience it, and in those regions the conditional averages of those species are different.
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}>1$
, the conditional averages are primarily similar. Thus, we conclude that the simplification of the mixture composition by eliminating minor species does not affect the relationship between the remaining mass fractions and temperature, with the exception of the regions of uphill diffusion of those species that experience it, and in those regions the conditional averages of those species are different.

Figure 21. Estimation of the relative deviation (in logarithmic scale) between the j.p.d.f.s of
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for cases s5R2p60X and s7R2p60X (defined by (5.21)), for the same species: (a) O2, (b) C7H16, (c) CO2 and (d) H2O.
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
for cases s5R2p60X and s7R2p60X (defined by (5.21)), for the same species: (a) O2, (b) C7H16, (c) CO2 and (d) H2O.

Figure 22. Conditional average of the normalized temperature
![]() $\unicode[STIX]{x1D703}$
given
$\unicode[STIX]{x1D703}$
given
![]() $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
at
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D6FC}}$
at
![]() $t_{tr}^{\ast }$
for cases (a) s7R2p60X and (b) s5R2p60X.
$t_{tr}^{\ast }$
for cases (a) s7R2p60X and (b) s5R2p60X.
6 Summary and conclusions
This study addressed the potential changes in the characteristics of a turbulent mixture under high-pressure conditions when its composition is simplified by neglecting some chemical species. To perform this investigation, direct numerical simulation (DNS) was used to generate a database representing a three-dimensional temporal mixing layer initially having two streams of different composition that are promoted to mix when the four initial spanwise vortices hosted by the layer experience a double pairing thereby creating an ultimate vortex in which small scales proliferate. Owing to the high-pressure condition, the smallest scale is not necessarily the Kolmogorov scale, but rather the thermodynamic scale. The database was obtained by varying the composition (two, three, five and seven species), by varying the initial Reynolds-number value (1000, 2000 and to 3500) and by varying the pressure (60 atm and 80 atm); a total of 13 realizations were generated. To ensure that the initial momentum ratio has essentially the same value for all layers, only minor composition variations in the mass fraction or mole fractions could be accommodated; as a result, the initial density ratio also varied in a narrow range. The resolution requirements were such that the two largest simulations were performed on
![]() $6.6\times 10^{8}$
and
$6.6\times 10^{8}$
and
![]() $1.037\times 10^{9}$
grid nodes, respectively. All layers were initially perturbed and eventually reached a state which had turbulence characteristics, that is, at that time station the spectra were smooth except for the perturbation frequency. Most, but not all, of the analysis was performed at this state.
$1.037\times 10^{9}$
grid nodes, respectively. All layers were initially perturbed and eventually reached a state which had turbulence characteristics, that is, at that time station the spectra were smooth except for the perturbation frequency. Most, but not all, of the analysis was performed at this state.
General vortical and enstrophy time-wise evolution results indicated that the values of these quantities exhibited substantial differences according to the Reynolds-number value, and increased with the initial Reynolds number. However, within each category defined by the initial Reynolds-number value, there were smaller but definite variations with the number of species, and typically the vortical/enstrophy aspects increased with the density ratio between free streams, indicating the coupling between dynamics and thermodynamics.
To examine the influence of the mixture composition representation, the species were partitioned into major species (n-heptane, oxygen and nitrogen) and minor species (carbon monoxide, carbon dioxide, hydrogen and water). The results first addressed the behaviour of major and minor species within a single realization, and then their variation with composition across realizations. Within each realization, all major species experienced regular mass diffusion, whereas all minor species experienced uphill mass diffusion whereby diffusion occurs in the opposite direction to the mass fraction gradient of the species. Most, but not all, uphill mass diffusion occurred at the periphery of the layer. The species exhibiting most uphill diffusion was hydrogen, and this occurrence was attributed to it having the smallest mass fraction in the composition as well as to its molecular size and mass; all these aspects couple its flux most tightly to those of other species, this being the requirement for obtaining uphill diffusion.
Since the present flows exhibit strong density-gradient regions which were shown in the past to affect the vortical characteristics of the flow (Masi et al.
Reference Masi, Bellan, Harstad and Okong’o2013), an examination was conducted focusing on potential scaling of these aspects, on the composition of these regions and on whether these density gradients affect the flow through the Korteweg tensor. Considerations of the p.d.f. of the density-gradient magnitude scaled by the initial density difference between streams revealed that at the same initial momentum ratio and initial density difference, the realization displaying the largest scaled density-gradient magnitude was that having the largest initial Reynolds-number value. This result was attributed to the fact that turbulence only acts on continuum scales and cannot access the much smaller molecular scales: at the shorter characteristic time of higher turbulence, diffusion is less effective in reducing gradients. For the same initial Reynolds-number value, the scaled
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
was observed to be only slightly dependent on the number of the species in the mixture. Moreover, conditional averages of the mass fractions on the density-gradient magnitude showed that the overwhelming species in these HDGM regions is n-heptane. Employing a comprehensive formulation developed here to account for the Korteweg tensor influence on the conservation equations in the general case of an indefinite number of species, the
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
was observed to be only slightly dependent on the number of the species in the mixture. Moreover, conditional averages of the mass fractions on the density-gradient magnitude showed that the overwhelming species in these HDGM regions is n-heptane. Employing a comprehensive formulation developed here to account for the Korteweg tensor influence on the conservation equations in the general case of an indefinite number of species, the
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
scaling, which is quasi-independent of the number of species, and the fact that n-heptane is the preponderant species in these HDGM regions, permitted the a priori estimation of the influence of the Korteweg stresses in the momentum equation. This computation indicated that, even for the largest density gradients present (
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
scaling, which is quasi-independent of the number of species, and the fact that n-heptane is the preponderant species in these HDGM regions, permitted the a priori estimation of the influence of the Korteweg stresses in the momentum equation. This computation indicated that, even for the largest density gradients present (
![]() $O(10^{6})~\text{kg}~\text{m}^{-4}$
), the Korteweg tensor magnitude is negligible with respect to the pressure gradient magnitude, which is orders of magnitude larger than the Korteweg tensor; this situation prevails even in the regions where the Korteweg tensor has maximum magnitude. Despite the substantial Reynolds-number value achieved at transition for the case initiated with the largest initial Reynolds number, in all realizations, the Reynolds numbers at transition is of the same order of magnitude, with values typically of
$O(10^{6})~\text{kg}~\text{m}^{-4}$
), the Korteweg tensor magnitude is negligible with respect to the pressure gradient magnitude, which is orders of magnitude larger than the Korteweg tensor; this situation prevails even in the regions where the Korteweg tensor has maximum magnitude. Despite the substantial Reynolds-number value achieved at transition for the case initiated with the largest initial Reynolds number, in all realizations, the Reynolds numbers at transition is of the same order of magnitude, with values typically of
![]() $O(10^{3})$
. Since it has been shown that the HDGM regions proliferate increasingly with increasing Reynolds number and the largest density-gradient magnitude rises with the Reynolds number, it is difficult to assert to what extent conclusions on
$O(10^{3})$
. Since it has been shown that the HDGM regions proliferate increasingly with increasing Reynolds number and the largest density-gradient magnitude rises with the Reynolds number, it is difficult to assert to what extent conclusions on
![]() $O(10^{3})$
Reynolds-number flows can be applied to
$O(10^{3})$
Reynolds-number flows can be applied to
![]() $O(10^{4}){-}O(10^{6})$
Reynolds-number flows. Given the necessity to resolve the smallest scales in order to extract the correct density gradients, large-eddy simulations are unable to provide the information for this small-scale analysis. Since DNS is currently unfeasible at the Reynolds-number values of practical interest, whether or not the Korteweg stresses are also negligible in very high-Reynolds-number flows remains an open question that will be addressed in the future.
$O(10^{4}){-}O(10^{6})$
Reynolds-number flows. Given the necessity to resolve the smallest scales in order to extract the correct density gradients, large-eddy simulations are unable to provide the information for this small-scale analysis. Since DNS is currently unfeasible at the Reynolds-number values of practical interest, whether or not the Korteweg stresses are also negligible in very high-Reynolds-number flows remains an open question that will be addressed in the future.
Probability density functions of the effective Schmidt number and effective Lewis number of each of these species revealed that the major species have narrow distributions (and therefore the peak value is statistically significant) whereas the minor species have wide distributions indicating the tight coupling to the local conditions experienced by the species. For the major species, the peak effective Schmidt-number value was a strong function of the pressure, being 1.15 at 60 atm and 1.5 at 80 atm for n-heptane, but showed much more subdued variation according to the number of species in the mixture. The peak effective Lewis number was
![]() ${\sim}0.45$
for n-heptane and varied for the minor species in the range 0.3–0.8. The effective Prandtl-number p.d.f. displayed large values, in the range of refrigerants, and became generally (but not always) narrower for more compositionally complex mixtures, this aspect resulting from the homogenizing effect of the transport of enthalpy by the species. Thus, it is clear that these mixtures show characteristics unlike perfect gases and that the mixture composition has an impact, the extent of which must be determined for each intended application. For example, retaining the relationship between mass fractions and temperature is one of the requirements when proposing reduced chemical kinetic mechanisms. To determine whether this relationship is maintained when simplifying the composition by using reduced chemical kinetic mechanisms, joint p.d.f.s were examined for several species according to the number of the species in the mixture. The present results show that reducing the complexity of the mixture negligibly affects the relationship between mass fractions and temperature in regions where this relationship is strongest and thus likely to sustain combustion; however, reduction in the mixture complexity has a larger influence in regions of uphill diffusion for those remaining species in the mixture that are subject to it, and this influence will be felt through mixing and eventual species availability in combustion regions. Thus, uphill diffusion makes the reduction in the number of species nonlinear and thus invalidates usage of linearity-based methods in the study of species reduction for combustion applications.
${\sim}0.45$
for n-heptane and varied for the minor species in the range 0.3–0.8. The effective Prandtl-number p.d.f. displayed large values, in the range of refrigerants, and became generally (but not always) narrower for more compositionally complex mixtures, this aspect resulting from the homogenizing effect of the transport of enthalpy by the species. Thus, it is clear that these mixtures show characteristics unlike perfect gases and that the mixture composition has an impact, the extent of which must be determined for each intended application. For example, retaining the relationship between mass fractions and temperature is one of the requirements when proposing reduced chemical kinetic mechanisms. To determine whether this relationship is maintained when simplifying the composition by using reduced chemical kinetic mechanisms, joint p.d.f.s were examined for several species according to the number of the species in the mixture. The present results show that reducing the complexity of the mixture negligibly affects the relationship between mass fractions and temperature in regions where this relationship is strongest and thus likely to sustain combustion; however, reduction in the mixture complexity has a larger influence in regions of uphill diffusion for those remaining species in the mixture that are subject to it, and this influence will be felt through mixing and eventual species availability in combustion regions. Thus, uphill diffusion makes the reduction in the number of species nonlinear and thus invalidates usage of linearity-based methods in the study of species reduction for combustion applications.
Acknowledgements
This study was conducted at the California Institute of Technology and sponsored by the Department of Energy, Basic Energy Sciences under the direction of Dr W. Sisk. The computational resources were provided by NASA Advanced Supercomputing at Ames Research Center and by National Energy Research Supercomputing Center of the Department of Energy.
Appendix A. Transport properties
Unlike for atmospheric-
![]() $p$
flows, where three transport properties are generally sufficient (viscosity, diffusivity and thermal conductivity), for high-
$p$
flows, where three transport properties are generally sufficient (viscosity, diffusivity and thermal conductivity), for high-
![]() $p$
conditions there are four relevant transport properties, as follows.
$p$
conditions there are four relevant transport properties, as follows.
A.1 Mixture viscosity
To compute the individual species viscosity,
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
, the Lucas method (Poling, Prausnitz & O’Connell Reference Poling, Prausnitz and O’Connell2001) has been selected due to its high-
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
, the Lucas method (Poling, Prausnitz & O’Connell Reference Poling, Prausnitz and O’Connell2001) has been selected due to its high-
![]() $p$
accuracy capabilities. Moreover, unlike other widespread methods used for similar configurations (such as the one provided by Chung et al. (Reference Chung, Ajlan, Lee and Starling1988)), it contains a correction factor for quantum effects that ensures accurate predictions also for gases having negative acentric factors, such as hydrogen. To compute the mixture physical viscosity,
$p$
accuracy capabilities. Moreover, unlike other widespread methods used for similar configurations (such as the one provided by Chung et al. (Reference Chung, Ajlan, Lee and Starling1988)), it contains a correction factor for quantum effects that ensures accurate predictions also for gases having negative acentric factors, such as hydrogen. To compute the mixture physical viscosity,
![]() $\unicode[STIX]{x1D707}_{ph},$
the Wilke method (Poling et al.
Reference Poling, Prausnitz and O’Connell2001) is utilized providing
$\unicode[STIX]{x1D707}_{ph},$
the Wilke method (Poling et al.
Reference Poling, Prausnitz and O’Connell2001) is utilized providing
where
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{M}$
are weighting factors (Poling et al.
Reference Poling, Prausnitz and O’Connell2001). We distinguish between the physical viscosity
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{M}$
are weighting factors (Poling et al.
Reference Poling, Prausnitz and O’Connell2001). We distinguish between the physical viscosity
![]() $\unicode[STIX]{x1D707}_{ph}$
, the reference viscosity
$\unicode[STIX]{x1D707}_{ph}$
, the reference viscosity
![]() $\unicode[STIX]{x1D707}_{R}$
defined in § 4, and the computational viscosity
$\unicode[STIX]{x1D707}_{R}$
defined in § 4, and the computational viscosity
![]() $\unicode[STIX]{x1D707}$
used to enable resolution to scales of
$\unicode[STIX]{x1D707}$
used to enable resolution to scales of
![]() $O(\unicode[STIX]{x1D702}_{K})$
, as explained in § 4.
$O(\unicode[STIX]{x1D702}_{K})$
, as explained in § 4.
A.2 Mixture thermal conductivity
To compute the physical mixture thermal conductivity,
![]() $\unicode[STIX]{x1D706}_{ph}$
, the species conductivities
$\unicode[STIX]{x1D706}_{ph}$
, the species conductivities
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}$
are first calculated using the Stiel–Thodos method. The ideal specific heat at constant pressure, needed for the computation of the low-pressure thermal conductivity component, is a temperature-dependent third-order polynomial whose coefficients are listed in Poling et al. (Reference Poling, Prausnitz and O’Connell2001) for each of the fluids considered in this study. Then, the Wassiljewa–Mason–Saxena method (Poling et al.
Reference Poling, Prausnitz and O’Connell2001) is utilized to compute
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}$
are first calculated using the Stiel–Thodos method. The ideal specific heat at constant pressure, needed for the computation of the low-pressure thermal conductivity component, is a temperature-dependent third-order polynomial whose coefficients are listed in Poling et al. (Reference Poling, Prausnitz and O’Connell2001) for each of the fluids considered in this study. Then, the Wassiljewa–Mason–Saxena method (Poling et al.
Reference Poling, Prausnitz and O’Connell2001) is utilized to compute
![]() $\unicode[STIX]{x1D706}_{ph}$
from
$\unicode[STIX]{x1D706}_{ph}$
from
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}$
as
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FC}}$
as
where
In § 4 we explain how a scaled thermal conductivity,
![]() $\unicode[STIX]{x1D706}$
, is computed that is used to perform DNS.
$\unicode[STIX]{x1D706}$
, is computed that is used to perform DNS.
A.3 Binary mass diffusivities
Matrix elements
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{b}$
are the building blocks of
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{b}$
are the building blocks of
![]() $\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
and ultimately of
$\mathbb{D}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
and ultimately of
![]() $D_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }$
. To compute
$D_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }$
. To compute
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{b}={\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
, we adopt the method of Harstad & Bellan (Reference Harstad and Bellan2004b
) which gives (in cgs units)
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{b}={\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
, we adopt the method of Harstad & Bellan (Reference Harstad and Bellan2004b
) which gives (in cgs units)
Here
![]() $f_{D,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}(T)$
is generically defined for each matrix element as
$f_{D,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}(T)$
is generically defined for each matrix element as
![]() $f_{D}(T)\equiv (T_{red})^{s}$
, with
$f_{D}(T)\equiv (T_{red})^{s}$
, with
![]() $\ln s=\sum _{\unicode[STIX]{x1D701}=0}^{5}a_{\unicode[STIX]{x1D701}}^{s}(\ln T_{red})^{\unicode[STIX]{x1D701}}$
, where the
$\ln s=\sum _{\unicode[STIX]{x1D701}=0}^{5}a_{\unicode[STIX]{x1D701}}^{s}(\ln T_{red})^{\unicode[STIX]{x1D701}}$
, where the
![]() $a^{s}$
vector has elements
$a^{s}$
vector has elements
![]() $\{-0.84211,-0.32643,-0.10053,0.07747,0.0127,-0.00995\}$
;
$\{-0.84211,-0.32643,-0.10053,0.07747,0.0127,-0.00995\}$
;
![]() $r_{D}$
is a constant
$r_{D}$
is a constant
![]() $O(1)$
which provides an empirical adjustment for the specifics of the collisional interactions of a selected pair of species;
$O(1)$
which provides an empirical adjustment for the specifics of the collisional interactions of a selected pair of species;
![]() $T_{red,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
, with
$T_{red,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
, with
![]() $T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
defined in appendix B; and
$T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
defined in appendix B; and
![]() $v_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
is defined in appendix B as well. Values of
$v_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
is defined in appendix B as well. Values of
![]() $r_{D}$
are listed elsewhere (Harstad & Bellan Reference Harstad and Bellan2004b
) for species pairs relevant to combustion.
$r_{D}$
are listed elsewhere (Harstad & Bellan Reference Harstad and Bellan2004b
) for species pairs relevant to combustion.
A.4 Binary thermal-diffusion factors
According to Harstad & Bellan (Reference Harstad and Bellan2004a ):
where
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{Q}$
is computed from (A 2) and (A 5), and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}^{Q}$
is computed from (A 2) and (A 5), and
![]() $C_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\ast }$
is given by Hirshfelder, Curtis & Bird (Reference Hirshfelder, Curtis and Bird1964) and is function of a normalized temperature including the characteristic molecular interaction potential (Harstad & Bellan Reference Harstad and Bellan2004a
).
$C_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\ast }$
is given by Hirshfelder, Curtis & Bird (Reference Hirshfelder, Curtis and Bird1964) and is function of a normalized temperature including the characteristic molecular interaction potential (Harstad & Bellan Reference Harstad and Bellan2004a
).
Appendix B. Relationships for the equation of state
Miscellaneous relationships relevant to the EOS are
where indices do not follow the Einstein notation, and
where
![]() $T_{red,\unicode[STIX]{x1D6FC}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}}$
,
$T_{red,\unicode[STIX]{x1D6FC}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}}$
,
![]() $T_{c,\unicode[STIX]{x1D6FC}}$
is the critical temperature and
$T_{c,\unicode[STIX]{x1D6FC}}$
is the critical temperature and
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}$
is the acentric factor. Also,
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}$
is the acentric factor. Also,
with
![]() $T_{red,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
,
$T_{red,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}\equiv T/T_{c,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
,
![]() $Z_{c,\unicode[STIX]{x1D6FC}}$
being the critical compression factor with the compression factor defined as
$Z_{c,\unicode[STIX]{x1D6FC}}$
being the critical compression factor with the compression factor defined as
![]() $Z=p/(\unicode[STIX]{x1D70C}TR_{u}/m)$
,
$Z=p/(\unicode[STIX]{x1D70C}TR_{u}/m)$
,
![]() $v_{c,\unicode[STIX]{x1D6FC}}$
being the critical volume,
$v_{c,\unicode[STIX]{x1D6FC}}$
being the critical volume,
![]() $p_{c,\unicode[STIX]{x1D6FC}}$
being the critical pressure, and where
$p_{c,\unicode[STIX]{x1D6FC}}$
being the critical pressure, and where
![]() $k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
is an empirical mixing parameter. The relationship between parameters
$k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
is an empirical mixing parameter. The relationship between parameters
![]() $k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
and
$k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
and
![]() $k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }$
is
$k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }$
is
and for all pairs not in table 4,
![]() $k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }=0$
is used.
$k_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}^{\prime }=0$
is used.
Table 4. Values of
![]() $k^{\prime }$
for species pairs.
$k^{\prime }$
for species pairs.
Appendix C. Mixing layer bounds
The mixing layer is identified using a threshold,
![]() $k$
, for the local
$k$
, for the local
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
value, as shown from (5.4). The value of
$Y_{\text{C}_{7}\text{H}_{16}}$
value, as shown from (5.4). The value of
![]() $k$
is rather arbitrary, and thus it is useful to inquire about the sensitivity of the results to it. Four different thresholds are chosen, varying from 0.01 to 0.1. Figure 23 shows the p.d.f.s of
$k$
is rather arbitrary, and thus it is useful to inquire about the sensitivity of the results to it. Four different thresholds are chosen, varying from 0.01 to 0.1. Figure 23 shows the p.d.f.s of
![]() $Pr_{\mathit{eff}}$
,
$Pr_{\mathit{eff}}$
,
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
,
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
,
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
![]() $Sc_{\text{H}_{2},\mathit{eff}}$
for case s7R2p60X computed with the four different values of
$Sc_{\text{H}_{2},\mathit{eff}}$
for case s7R2p60X computed with the four different values of
![]() $k$
. It is clearly shown that (i) the influence on the species-effective Schmidt numbers is unimportant, (ii) a small bump on the lower bound of the
$k$
. It is clearly shown that (i) the influence on the species-effective Schmidt numbers is unimportant, (ii) a small bump on the lower bound of the
![]() $Pr_{\mathit{eff}}$
p.d.f. appears for smaller thresholds, and (iii) the shape of the
$Pr_{\mathit{eff}}$
p.d.f. appears for smaller thresholds, and (iii) the shape of the
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
p.d.f. is slightly modified, with cases
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
p.d.f. is slightly modified, with cases
![]() $k=0.01$
and
$k=0.01$
and
![]() $k=0.02$
exhibiting a relative maximum near the lower bound. This behaviour, however, does not affect the results significantly, since the most probable value of the p.d.f. is unchanged and the modifications due to the
$k=0.02$
exhibiting a relative maximum near the lower bound. This behaviour, however, does not affect the results significantly, since the most probable value of the p.d.f. is unchanged and the modifications due to the
![]() $k$
value are not physically significant. The value
$k$
value are not physically significant. The value
![]() $k=0.05$
is thus retained for this study.
$k=0.05$
is thus retained for this study.

Figure 23. Influence of the threshold value
![]() $k$
used to identify the mixing layer bounds: (a)
$k$
used to identify the mixing layer bounds: (a)
![]() $Pr_{\mathit{eff}}$
, (b)
$Pr_{\mathit{eff}}$
, (b)
![]() $D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
, (c)
$D_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
, (c)
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and (d)
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and (d)
![]() $Sc_{\text{H}_{2},\mathit{eff}}$
.
$Sc_{\text{H}_{2},\mathit{eff}}$
.
Appendix D. Diffuse interface models for a multi-species mixture
Diffuse interface models (DIMs) employ the second-gradient theory to arrive at formulations used to describe the continuous change of fluid properties across liquid–gas interfaces in subcritical conditions. Pioneering contributions to DIM are due to van der Waals (Reference van der Waals1893), Korteweg (Reference Korteweg1901), Cahn & Hilliard (Reference Cahn and Hilliard1958) and Cahn (Reference Cahn1959). A variety of problems have been successfully described utilizing DIM, e.g. the dynamics of contact lines (Seppecher Reference Seppecher1996), the description of near-critical points (Rowlinson & Widom Reference Rowlinson and Widom2002), and liquid–gas interfaces with topological changes (Jamet et al. Reference Jamet, Lebaigue, Coutris and Delhaye2001). A thorough review of DIM applications is available in Anderson et al. (Reference Anderson, McFadden and Wheeler1998). While the theory is usually initiated by including many chemical species, it invariably becomes focused on a binary-species system. The goal of the derivation below is to provide a general formulation that retains the multi-species aspect up to the end result, and to make this formulation compatible with the mixing rules of Harstad & Bellan (Reference Harstad and Bellan2004a ) used in § 2.1.
According to the gradient theory, the Helmholtz free energy is
where the superscript
![]() $(\cdot )^{0}$
denotes standard bulk properties that do not involve gradients. Assuming symmetric binary capillary coefficients (
$(\cdot )^{0}$
denotes standard bulk properties that do not involve gradients. Assuming symmetric binary capillary coefficients (
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}$
), one can reformulate (D 1) as
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}}$
), one can reformulate (D 1) as
Moreover, assuming constant capillarity coefficients, the following thermodynamic relation is obtained:
where
![]() $S^{0}$
is the bulk entropy per unit volume,
$S^{0}$
is the bulk entropy per unit volume,
![]() $g_{\unicode[STIX]{x1D6FC}}^{0}$
the bulk Gibbs function of species
$g_{\unicode[STIX]{x1D6FC}}^{0}$
the bulk Gibbs function of species
![]() $\unicode[STIX]{x1D6FC}$
per unit mass and
$\unicode[STIX]{x1D6FC}$
per unit mass and
![]() $\text{d}$
represents a differential. Combining (D 3) with standard thermodynamic relations, one finds that
$\text{d}$
represents a differential. Combining (D 3) with standard thermodynamic relations, one finds that
![]() $S=S^{0}$
,
$S=S^{0}$
,
![]() $G=G^{0}$
and
$G=G^{0}$
and
![]() $H=H^{0}$
. On the other hand,
$H=H^{0}$
. On the other hand,
![]() $p=p^{0}-\sum _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}=1}^{N}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FD}}$
and
$p=p^{0}-\sum _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}=1}^{N}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FD}}$
and
![]() $E=E^{0}+\sum _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}=1}^{N}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FD}}$
. In the main sections of this paper, i.e. except for this appendix,
$E=E^{0}+\sum _{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}=1}^{N}\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FD}}$
. In the main sections of this paper, i.e. except for this appendix,
![]() $p\equiv p^{0}$
since the gradient terms are not taken into account in the DNS realizations; thus, in the DNS realizations
$p\equiv p^{0}$
since the gradient terms are not taken into account in the DNS realizations; thus, in the DNS realizations
![]() $p$
only depends on bulk (e.g. local) quantities. The system of conservation equations can be written in the following general formulation
$p$
only depends on bulk (e.g. local) quantities. The system of conservation equations can be written in the following general formulation
where
![]() $\text{D}(\cdot )/\text{D}t$
is the material derivative,
$\text{D}(\cdot )/\text{D}t$
is the material derivative,
![]() $\unicode[STIX]{x1D70C}$
is the density,
$\unicode[STIX]{x1D70C}$
is the density,
![]() $\boldsymbol{u}$
is the velocity,
$\boldsymbol{u}$
is the velocity,
![]() $e_{t}=e+(1/2)\Vert \boldsymbol{u}\Vert ^{2}$
is the total energy,
$e_{t}=e+(1/2)\Vert \boldsymbol{u}\Vert ^{2}$
is the total energy,
![]() $e$
is the internal energy,
$e$
is the internal energy,
![]() $Y_{\unicode[STIX]{x1D6FC}}$
is the mass fraction of the species
$Y_{\unicode[STIX]{x1D6FC}}$
is the mass fraction of the species
![]() $\unicode[STIX]{x1D6FC}$
(with
$\unicode[STIX]{x1D6FC}$
(with
![]() $1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
and
$1\leqslant \unicode[STIX]{x1D6FC}\leqslant N$
and
![]() $\sum _{\unicode[STIX]{x1D6FC}}Y_{\unicode[STIX]{x1D6FC}}=1$
),
$\sum _{\unicode[STIX]{x1D6FC}}Y_{\unicode[STIX]{x1D6FC}}=1$
),
![]() $\unicode[STIX]{x1D64F}$
is the stress tensor,
$\unicode[STIX]{x1D64F}$
is the stress tensor,
![]() $\boldsymbol{J}_{e}=\boldsymbol{q}+\unicode[STIX]{x1D652}\boldsymbol{\cdot }\boldsymbol{u}$
is the energy flux, and
$\boldsymbol{J}_{e}=\boldsymbol{q}+\unicode[STIX]{x1D652}\boldsymbol{\cdot }\boldsymbol{u}$
is the energy flux, and
![]() $\boldsymbol{q}$
and
$\boldsymbol{q}$
and
![]() $\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
are the heat- and mass-diffusion fluxes, respectively. It is possible to decompose the stress tensor into the sum of a reversible part
$\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
are the heat- and mass-diffusion fluxes, respectively. It is possible to decompose the stress tensor into the sum of a reversible part
![]() $\unicode[STIX]{x1D64B}$
and an irreversible one,
$\unicode[STIX]{x1D64B}$
and an irreversible one,
![]() $\unicode[STIX]{x1D64F}$
, i.e.
$\unicode[STIX]{x1D64F}$
, i.e.
![]() $\unicode[STIX]{x1D652}=\unicode[STIX]{x1D64B}+\unicode[STIX]{x1D64F}$
. In order to determine the reversible part of the stress tensor, one may take advantage of the Euler–Lagrange equations and Hamilton’s principle, and solve a constrained minimization problem for the free energy
$\unicode[STIX]{x1D652}=\unicode[STIX]{x1D64B}+\unicode[STIX]{x1D64F}$
. In order to determine the reversible part of the stress tensor, one may take advantage of the Euler–Lagrange equations and Hamilton’s principle, and solve a constrained minimization problem for the free energy
![]() $F$
through the method of Lagrange multipliers (Anderson et al.
Reference Anderson, McFadden and Wheeler1998), obtaining
$F$
through the method of Lagrange multipliers (Anderson et al.
Reference Anderson, McFadden and Wheeler1998), obtaining
where
![]() $p^{0}$
is the thermodynamic pressure and
$p^{0}$
is the thermodynamic pressure and
![]() $\unicode[STIX]{x1D644}$
is the identity matrix.
$\unicode[STIX]{x1D644}$
is the identity matrix.
The term
![]() $\sum _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
is commonly known as the Korteweg tensor. The additional, interface-related terms in
$\sum _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
is commonly known as the Korteweg tensor. The additional, interface-related terms in
![]() $\unicode[STIX]{x1D64B}$
do not produce entropy and are associated with reversible processes. The expressions for the dissipative viscous, heat and mass fluxes can be obtained through application of the thermodynamics of irreversible processes theory (Keizer Reference Keizer1987), which leads to
$\unicode[STIX]{x1D64B}$
do not produce entropy and are associated with reversible processes. The expressions for the dissipative viscous, heat and mass fluxes can be obtained through application of the thermodynamics of irreversible processes theory (Keizer Reference Keizer1987), which leads to
where
![]() $\hat{\unicode[STIX]{x1D707}}$
is the bulk viscosity,
$\hat{\unicode[STIX]{x1D707}}$
is the bulk viscosity,
![]() $\unicode[STIX]{x1D707}$
is the viscosity,
$\unicode[STIX]{x1D707}$
is the viscosity,
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}$
is the chemical potential of the species
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}$
is the chemical potential of the species
![]() $\unicode[STIX]{x1D6FD}$
, and
$\unicode[STIX]{x1D6FD}$
, and
![]() $L_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the Onsager matrix of positive semidefinite phenomenological coefficients (de Groot & Mazur Reference de Groot and Mazur1984). This shows that
$L_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
is the Onsager matrix of positive semidefinite phenomenological coefficients (de Groot & Mazur Reference de Groot and Mazur1984). This shows that
![]() $\unicode[STIX]{x1D64F}$
is unchanged by the second-gradient term contribution; in contrast, both the species and heat fluxes contain an additional term leading to the definition of an equivalent chemical potential,
$\unicode[STIX]{x1D64F}$
is unchanged by the second-gradient term contribution; in contrast, both the species and heat fluxes contain an additional term leading to the definition of an equivalent chemical potential,
![]() $\widetilde{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$
. Moreover, the heat flux contains also a second term which can be written as a function of
$\widetilde{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}}$
. Moreover, the heat flux contains also a second term which can be written as a function of
![]() $\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
. Starting from (D 10) and recalling that the mass-diffusion factors and the partial molar enthalpies are defined as
$\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}$
. Starting from (D 10) and recalling that the mass-diffusion factors and the partial molar enthalpies are defined as
![]() $\unicode[STIX]{x1D6FC}_{D_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}}=(\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FE}})(X_{\unicode[STIX]{x1D6FD}}/T)$
and
$\unicode[STIX]{x1D6FC}_{D_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}}}=(\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x2202}X_{\unicode[STIX]{x1D6FE}})(X_{\unicode[STIX]{x1D6FD}}/T)$
and
![]() $h_{\unicode[STIX]{x1D6FD}}=T(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}/T+s_{\unicode[STIX]{x1D6FD}})$
, respectively, the thermodynamic driving forces can be rewritten as
$h_{\unicode[STIX]{x1D6FD}}=T(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FD}}/T+s_{\unicode[STIX]{x1D6FD}})$
, respectively, the thermodynamic driving forces can be rewritten as
The coefficients of the Onsager matrix, assumed to be independent of the second-gradient defined energy, are calculated as
where subscript
![]() $IK$
labels a quantity associated with the Irwing–Kirkwood (IK) heat-flux formulation (Sarman & Evans Reference Sarman and Evans1992). Since conservation of fluxes and of mass in the system imply that
$IK$
labels a quantity associated with the Irwing–Kirkwood (IK) heat-flux formulation (Sarman & Evans Reference Sarman and Evans1992). Since conservation of fluxes and of mass in the system imply that
![]() $\sum _{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FC}}\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}=0$
and
$\sum _{\unicode[STIX]{x1D6FC}}m_{\unicode[STIX]{x1D6FC}}\boldsymbol{J}_{\unicode[STIX]{x1D6FC}}=0$
and
![]() $\sum _{\unicode[STIX]{x1D6FC}}L_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}m_{\unicode[STIX]{x1D6FC}}=0$
, and since
$\sum _{\unicode[STIX]{x1D6FC}}L_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}m_{\unicode[STIX]{x1D6FC}}=0$
, and since
![]() $Y_{\unicode[STIX]{x1D6FC}}/m_{\unicode[STIX]{x1D6FC}}=X_{\unicode[STIX]{x1D6FC}}/m$
, one obtains
$Y_{\unicode[STIX]{x1D6FC}}/m_{\unicode[STIX]{x1D6FC}}=X_{\unicode[STIX]{x1D6FC}}/m$
, one obtains
Replacing these relations in equation (D 10), one obtains the mass flux as
where
By comparing the formulations with and without the second-gradient term (Harstad & Bellan Reference Harstad and Bellan2000), one finds that
![]() $D_{p,\unicode[STIX]{x1D6FC}}$
and
$D_{p,\unicode[STIX]{x1D6FC}}$
and
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
are unchanged; there is an additional term depending on the Laplacian of the density potential,
${\mathcal{D}}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}}$
are unchanged; there is an additional term depending on the Laplacian of the density potential,
![]() $D_{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}}$
, and the temperature-dependent coefficient
$D_{\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}}$
, and the temperature-dependent coefficient
![]() $\widetilde{D}_{T,\unicode[STIX]{x1D6FC}}$
is slightly modified. It is then possible to define a modified partial enthalpy,
$\widetilde{D}_{T,\unicode[STIX]{x1D6FC}}$
is slightly modified. It is then possible to define a modified partial enthalpy,
![]() $\widetilde{h}_{\unicode[STIX]{x1D6FC}}=h_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}$
, which allows one to recover the classical functional form for
$\widetilde{h}_{\unicode[STIX]{x1D6FC}}=h_{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FC}}$
, which allows one to recover the classical functional form for
![]() $D_{T,\unicode[STIX]{x1D6FC}}$
.
$D_{T,\unicode[STIX]{x1D6FC}}$
.
Similar mathematical developments lead to the general form of the heat flux
![]() $\boldsymbol{q}$
, here derived in the IK form (Sarman & Evans Reference Sarman and Evans1992):
$\boldsymbol{q}$
, here derived in the IK form (Sarman & Evans Reference Sarman and Evans1992):
with
which shows, again, the slight modification in
![]() $\widetilde{\unicode[STIX]{x1D706}}_{IK}^{\prime }$
and the new term
$\widetilde{\unicode[STIX]{x1D706}}_{IK}^{\prime }$
and the new term
![]() $D_{q\unicode[STIX]{x1D719}}$
.
$D_{q\unicode[STIX]{x1D719}}$
.
Appendix E. Grid convergence study
A sensitivity study to the grid resolution has been performed in order to check the numerical quality of the results, particularly those in § 5.4 that could be sensitive to the selected grid. Given the high computational cost of R2 cases, this study has been performed for a R1 case, namely s2R1p60Y. The baseline resolution being approximately the same for all runs (i.e.
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}\approx 1$
in the core of the mixing layer), the significance of the results of this grid convergence study can be extended to all runs. The baseline grid for R1 cases (
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}\approx 1$
in the core of the mixing layer), the significance of the results of this grid convergence study can be extended to all runs. The baseline grid for R1 cases (
![]() $N_{1}\times N_{2}\times N_{3}=480\times 530\times 288$
) has been refined by 50 % for each direction, i.e.
$N_{1}\times N_{2}\times N_{3}=480\times 530\times 288$
) has been refined by 50 % for each direction, i.e.
![]() $N_{1}\times N_{2}\times N_{3}=720\times 795\times 432$
. Consequently, the total number of grid points increases from 73 million to 247 million, approximately.
$N_{1}\times N_{2}\times N_{3}=720\times 795\times 432$
. Consequently, the total number of grid points increases from 73 million to 247 million, approximately.

Figure 24. Grid convergence study for case s2R1p60Y. (a) Time history of normalized enstrophy; (b) averaged resolution in terms of local Kolmogorov length scale
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
at
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}_{K}$
at
![]() $t_{tr}^{\ast }$
; (c) streamwise and (d) spanwise spectra of
$t_{tr}^{\ast }$
; (c) streamwise and (d) spanwise spectra of
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
at
$Y_{\text{C}_{7}\text{H}_{16}}$
at
![]() $t_{tr}^{\ast }$
; and p.d.f.s of (e)
$t_{tr}^{\ast }$
; and p.d.f.s of (e)
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and (f)
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and (f)
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
at
![]() $t_{tr}^{\ast }$
.
$t_{tr}^{\ast }$
.
Figure 24 shows the comparison of several quantities between the results obtained with the two computational grids. The time-wise evolutions of normalized enstrophy are undistinguishable, as well as the streamwise and spanwise spectra of
![]() $Y_{\text{C}_{7}\text{H}_{16}}$
at
$Y_{\text{C}_{7}\text{H}_{16}}$
at
![]() $t_{tr}^{\ast }$
. The spectra for the finer grid span a larger wavenumber range, in concert with the higher resolution, and do not exhibit energy accumulation at the smallest scales. Lastly, the differences between the p.d.f.s of
$t_{tr}^{\ast }$
. The spectra for the finer grid span a larger wavenumber range, in concert with the higher resolution, and do not exhibit energy accumulation at the smallest scales. Lastly, the differences between the p.d.f.s of
![]() $Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
$Sc_{\text{C}_{7}\text{H}_{16},\mathit{eff}}$
and
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
computed with the two grids are very subdued and do not modify either qualitatively or quantitatively the analyses performed in § 5.
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}|$
computed with the two grids are very subdued and do not modify either qualitatively or quantitatively the analyses performed in § 5.