Published online by Cambridge University Press: 09 February 2006
In applied work economists often seek to relate a given response variable y to some causal parameter μ* associated with it. This parameter usually represents a summarization based on some explanatory variables of the distribution of y, such as a regression function, and treating it as a conditional expectation is central to its identification and estimation. However, the interpretation of μ* as a conditional expectation breaks down if some or all of the explanatory variables are endogenous. This is not a problem when μ* is modeled as a parametric function of explanatory variables because it is well known how instrumental variables techniques can be used to identify and estimate μ*. In contrast, handling endogenous regressors in nonparametric models, where μ* is regarded as fully unknown, presents difficult theoretical and practical challenges. In this paper we consider an endogenous nonparametric model based on a conditional moment restriction. We investigate identification-related properties of this model when the unknown function μ* belongs to a linear space. We also investigate underidentification of μ* along with the identification of its linear functionals. Several examples are provided to develop intuition about identification and estimation for endogenous nonparametric regression and related models.We thank Jeff Wooldridge and two anonymous referees for comments that greatly improved this paper.
Models with endogenous regressors arise frequently in microeconometrics. For example, suppose we want to estimate the cost function of a competitive firm; i.e., we want to estimate the model y = μ*(p,q) + ε, where y is the observed cost of production, μ* the firm's cost function, (p,q) the vector of factor prices and output, and ε an unobserved error term. Because the firm is assumed to be a price taker in its input markets, it is reasonable to assume that the factor prices are exogenously set and are uncorrelated with ε. On the other hand, because an inefficient or high-cost firm will, ceteris paribus, tend to produce less output than an efficient firm, q may be correlated with ε. Hence, q is endogenous. Similarly, endogenous regressors may also arise in production function estimation. For instance, suppose we want to estimate the model y = μ*(l,k) + ε, where y is the firm's output, μ* the production function, and (l,k) the vector of labor and capital factor inputs. In some cases it may be reasonable to believe that the firm's usage of certain inputs (say, labor) may depend upon the unobserved quality of management. In that case, such factors will be endogenous. Endogeneity can also be encountered in estimating wage equations of the form y = μ*(s,c) + ε, where y is log of wage rate, s is the years of schooling, and c denotes agent characteristics such as experience and ethnicity. Because years of schooling are correlated with unobservable factors such as ability and family background, s is endogenous. Another classic example of endogeneity is due to simultaneity. For instance, suppose we want to estimate the market demand for a certain good given by y = μ*(p,d) + ε, where y is the quantity demanded in equilibrium, p the equilibrium price, d a vector of demand shifters, and μ* the market demand function. Because prices and quantities are determined simultaneously in equilibrium, p is endogenous. Several additional examples of regression models with endogenous regressors can be found in econometrics texts; see, e.g., Wooldridge (2002).
These models can be written generically as follows. Let y denote a response variable and x a vector of explanatory variables. Suppose that, corresponding to y, there exist an unknown function μ*(x) (we temporarily suppress the dependence of μ* on y for pedagogical convenience) and an unobservable random variable ε such that y = μ*(x) + ε. The parameter of interest in this model is μ*, and its interpretation in terms of the distribution of (y,x) depends upon the assumptions regarding the joint distribution of x and ε; e.g., if

then
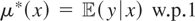
. In this paper we investigate models defined by more general conditions on the distribution of (x,ε). In particular, we allow some or all of the explanatory variables to be endogenous, i.e., correlated with ε, so that the mean independence of ε and x does not hold.
In the parametric case, i.e., when μ* is known up to a finite-dimensional parameter, it is well known how to handle endogeneity. Basically, if we have instrumental variables w that suffice to identify μ*, then we can use two-stage least squares (2SLS), if μ* is linear, or the more efficient generalized method of moments (GMM) to estimate μ*. For instance, in the cost function example described previously, the size of the market served by the firm can serve as an instrument for q; in the production function example we could take the wage paid by the firm as an instrument for l if the former is exogenously set; when estimating the wage equation, mother's education can be used to instrument for years of schooling; and, in the market demand example, variables that shift the market supply function but are uncorrelated with ε, such as weather or other exogenous supply shocks, can serve as instruments for p in the demand equation.
Recently there has been a surge of interest in studying nonparametric (i.e., where the functional form of μ* is completely unknown) models with endogenous regressors; see, e.g., Darolles, Florens, and Renault (2002), Ai and Chen (2003), Blundell and Powell (2003), Newey and Powell (2003), and the references therein. In endogenous nonparametric regression models it is typically assumed that μ* lies in L2(x), the set of functions of x that are square integrable with respect to the distribution of x, and the instruments w satisfy the conditional moment restriction

. However, in this paper we allow the parameter space for μ* to be different from L2(x) (see Section 2 for the motivation). Hence, our results are applicable to any endogenous nonparametric linear model and not just to the regression models described earlier. Apart from this, the main contributions of our paper are as follows. (i) We develop the properties of the function that maps the reduced form into the structural form in a very general setting under minimal assumptions. For instance, we show that it is a closed map (i.e., its graph is closed) although it may not be continuous. Although lack of continuity of this mapping has been noted in earlier papers, the result that it is closed and further characterization of its continuity properties as done in Lemma 2.4 seem to be new to the literature. (ii) Newey and Powell (2003) characterize identification of μ* in terms of the completeness of the conditional distribution of x given w. But, in the absence of any parametric assumptions on the conditional distribution of x given w, it is not clear how completeness can be verified in practice. In fact, as Blundell and Powell (2003) point out, the existing literature in this area basically assumes that μ* is identified and focuses on estimating it. Because failure of identification is not easily detected in nonparametric models (in Section 3 we provide some interesting examples showing that μ* can be unidentified in relatively simple designs), we investigate what happens if the identification condition for μ* fails to hold or cannot be easily checked by showing how to determine the “identifiable part” of μ* by projecting onto an appropriately defined subspace of the parameter space, something that does not seem to have been done earlier in the literature. (iii) In Section 4 we examine the identification of linear functionals of μ* when μ* itself may not be identified. We relate identification of μ* to the identification of its linear functionals by showing that μ* is identified if and only if all bounded linear functionals of μ* are identified. To the best of our knowledge, the results in this section are also new to the literature.
We do not focus on estimation in this paper. In addition to the papers mentioned earlier, readers interested in estimating endogenous nonparametric models should see, e.g., Pinkse (2000), Das (2001), Linton, Mammen, Nielsen, and Tanggaard (2001), Carrasco, Florens, and Renault (2002), Florens (2003), Hall and Horowitz (2003), Newey, Powell, and Vella (2003), and the references therein. Additional works related to this literature include Li (1984) and Roehrig (1988). Note that our identification analysis is global in nature because the nonparametric models we consider are linear in μ*. We hope our results will motivate other researchers to study local properties of nonlinear models of the kind considered by Blundell and Powell (2003) and Newey and Powell (2003).
The introduction was motivated by looking at endogenous nonparametric regression models of the form y = μ*(x) + ε, where
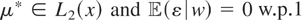
. But in many cases the parameter space for μ* can be a linear function space different than L2(x). For instance, suppose that x = (x1,x2) and μ* is additive in the components
1A good discussion of these models, though without any endogeneity, can be found in Hastie and Tibshirani (1990).
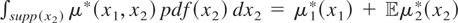
and a similar operation can be carried out to recover μ2*. An alternative model may be based on the assumption that μ*(x) = x1′θ* + μ2*(x2), where θ* is a finite-dimensional parameter and μ2* ∈ L2(x2). This leads to an endogenous version of the partially linear model proposed by Engle, Granger, Rice, and Weiss (1986) and Robinson (1988). Sometimes we may have information regarding the differentiability of μ* that we want to incorporate into the model; in this case, we might assume that μ* is an element of a Sobolev space. We could also allow for μ* to have certain shape restrictions. In particular, because we assume that μ* belongs to a linear space, shape restrictions such as homogeneity and symmetry are permissible for μ*. These variations clearly illustrate the advantage of framing our problem in a general setting. So we now frame our problem in a general Hilbert space setting. The geometric nature of Hilbert spaces allows us to derive a lot of mileage from a few relatively simple concepts.
Let y denote the response variable that is assumed to be an element of
, a separable Hilbert space with inner product 〈·,·〉 and induced norm ∥·∥. Also, let
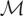
denote a known linear subspace of

(note that
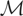
is not assumed to be closed). Assume that, corresponding to y, there exists an element
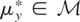
. The vector μy* is a summarization of the distribution of y and may be viewed as the parameter of interest. If y − μy* is orthogonal to

, then μy* is simply the orthogonal projection of y onto
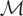
. Here we assume instead that there exists a known linear subspace of

, denoted by

, such that 〈y − μy*,w〉 = 0 for all
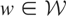
; i.e., y − μy* is orthogonal to

, which we write as
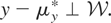
We call

the “model space” and
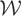
the “instrument space.” The symbol

denotes the set of all

for which the model holds; i.e., for each

there exists a

such that (2.1) holds. Because there is a one-to-one correspondence between random variables and distribution functions,

can also be interpreted as the set of all distributions for which (2.1) holds. Note that because
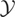
always includes
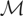
, it is nonempty. Also, continuity of the inner product implies that whenever (2.1) holds, y − μy* is orthogonal to the closure of
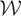
. Therefore,
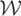
can be assumed to be closed without loss of generality.
Clearly, the endogenous nonparametric regression models described in the introduction are a special case of (2.1) by letting

, and

be the set of random variables of the form y = μy*(x) + ε, where

.
It is easy to see that μy* is identified, i.e., uniquely defined, if and only if the following condition holds.
Condition (I). If

satisfies
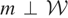
, then m = 0.
Henceforth, we refer to Condition (I) as the “identification condition.” Let

denote orthogonal projection from
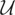
onto
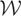
using the inner product 〈·,·〉. Then the identification condition can be alternatively stated as follows: if
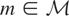
satisfies
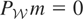
, then m = 0.
Let
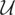
be the familiar Hilbert space of random variables with finite second moments equipped with the usual inner product
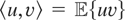
. Also, x (the s × 1 vector of explanatory variables) and w (the d × 1 vector of instrumental variables) are random vectors whose coordinates are elements of
. Moreover,
(resp.
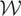
) is the linear space spanned by the coordinates of x (resp. w). Note that in this example
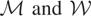
are both finite-dimensional subspaces of
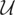
. By (2.1), for a given
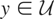
there exists a linear function μy*(x) = x′θy* such that 〈y − x′θy*,w′α〉 = 0 for all

; i.e.,
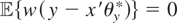
. Condition (I) states that if 〈x′θy*,w′α〉 = 0 for all
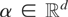
, then θy* = 0. Hence, μy* or, equivalently, θy* are uniquely defined if and only if
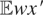
has full column rank. Obviously, the order condition d ≥ s is necessary for

to have full column rank.
Again,

is the Hilbert space of random variables with finite second moments equipped with the usual inner product and (x,w) are random vectors whose components are elements of
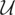
. But, unlike the previous example,

are now infinite-dimensional linear subspaces of
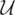
consisting of square integrable functions. By (2.1), for a given y in

there exists a function μy* in L2(x) such that

holds for all g ∈ L2(w). Condition (I) states that if a function f ∈ L2(x) satisfies

for all g ∈ L2(w), then f = 0 w.p.1;
2Because L2(x) and L2(w) are equivalence classes of functions, equality statements in L2(x) and L2(w) hold w.p.1.

for any f in L2(x), then f = 0 w.p.1. But this corresponds to the completeness of pdf (x|w). Therefore, μy* is uniquely defined if and only if the conditional distribution of x|w is complete, a result obtained earlier by Florens, Mouchart, and Rolin (1990, Ch. 5) and Newey and Powell (2003). To get some intuition behind the notion of completeness, observe that if x and w are independent, then completeness fails (of course, if w is independent of the regressors then it is not a good instrument and cannot be expected to help identify μy*). On the other extreme, if x is fully predictable by w then completeness is satisfied trivially, and the endogeneity and identification problems disappear altogether. In fact, we can show the following result.
LEMMA 2.1. The conditional distribution of x|w is complete if and only if for each function f (x) such that

, there exists a function g(w) such that f (x) and g(w) are correlated.
Hence, in the context of nonparametric regression we can think of completeness as a measure of the correlation between the model space L2(x) and the instrument space L2(w).
Let us assume that Condition (I) holds for the remainder of Section 2. Hence, for each
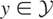
there exists a unique
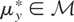
such that
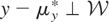
. It follows that

is a linear subspace of

and the map y [map ] μy* is a linear transformation on
. Therefore, from now on we write Vy for μy* so that

denotes a linear map such that μy* = Vy. Employing well-known terminology, V is just the function that maps the reduced form into the structural form. Hence, a clear description of the properties of V is central to understanding the identification and estimation problems in nonparametric linear models with endogenous regressors.
We now study the properties of V. Define
. Because it is straightforward to show that
is the smallest linear subspace of
satisfying Condition (I), we may view

as the “minimal” instrument space. Let
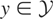
. Because
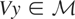
, by definition of

we know that

. But, letting I denote the identity operator, we can write y = Vy + (I − V)y, where

. Hence,

. Furthermore, because
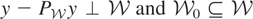
, we have
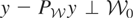
. This shows that when applied to elements of
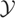
, the projection

has the same properties as orthogonal projection on
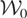
. Next, let
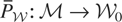
denote the restriction of
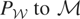
. Then

is a continuous linear mapping from
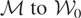
with inverse
3Because
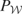
is bounded, its restriction to
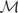
is also bounded and, hence, continuous. Now let m1 and m2 denote elements of

. Suppose w1 = w2. Then
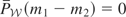
. Hence,
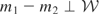
. It follows from Condition (I) that m1 = m2 so that
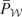
is one-to-one and, by definition, the range of
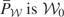
. Therefore, because

is one-to-one and onto, it has an inverse

.

. Clearly,

is also a linear map. Therefore, we can characterize V as

The next example describes how V looks in some familiar settings.
In Example 2.1,
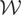
is the linear space spanned by the coordinates of w. Hence,

corresponds to the best linear predictor given w; i.e.,
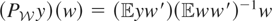
. It is easy to show that
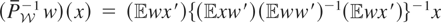
. Therefore, the map
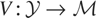
is given by

. But because (Vy)(x) can be written as x′θy*, it follows that θy* here is just the population version of the usual 2SLS estimator. By contrast,
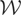
in Example 2.2 is the infinite-dimensional space L2(w). Hence,

is the best prediction operator
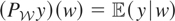
. Therefore, in Example 2.2 we have

.
Before describing additional properties of V, in Lemma 2.2 we propose a series-based approach for determining V. As illustrated by the examples given subsequently, this approach may also be useful as the basis of a practical computational method for estimating V. However, as noted earlier, a full consideration of estimation issues is beyond the scope of the current paper. Instead, the reader is referred to Pinkse (2000), Darolles et al. (2002), Ai and Chen (2003), Hall and Horowitz (2003), and Newey and Powell (2003) for series estimation of endogenous nonparametric models.
LEMMA 2.2. Let m0,m1,m2,… be a basis for

such that

for i ≠ j. Then,

This result is similar in spirit to the eigenvector-based decomposition of Darolles et al. (2002) although we use a different basis in our representation. It demonstrates that if μy* is identified then it can be explicitly characterized in the population by a series representation using a special set of basis vectors (if

so that endogeneity disappears, then Vy is just the projection onto

as expected). The basis functions needed in Lemma 2.2 can be constructed from an arbitrary basis by using the well-known Gram–Schmidt procedure as follows. Let d0,d1,d2,… be a basis for
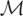
. Define m0 = d0 and let
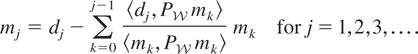
Then m0,m1,m2,… is a basis for
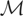
satisfying

for i ≠ j.
The following example illustrates the usefulness of Lemma 2.2.
Let x, w, and ε be real-valued random variables such that x and ε are correlated,
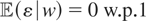
, and (x,w) has a bivariate normal distribution with mean zero and variance
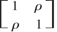
where ρ ∈ (−1,1)[setmn ]{0}. Suppose y = μy*(x) + ε, where μy* is unknown and

. Because
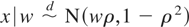
, the conditional distribution of x given w is complete. Hence, μy* is identified. Now let φ be the standard normal probability density function (p.d.f.) and
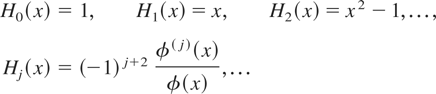
denote Hermite polynomials that are orthogonal with respect to the usual inner product on L2(x). From Granger and Newbold (1976, p. 202) we know that if

, then

. This result ensures that the Hermite basis satisfies the requirement in Lemma 2.2.
4Basis vectors that satisfy Lemma 2.2 for more general bivariate distributions can be constructed by using some of the results discussed in Buja (1990).

, shows that we can write μy* explicitly as
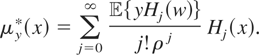
There are some interesting consequences of (2.4). For instance, if
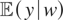
happens to be a polynomial of degree p, then μy* will also be a polynomial of degree p because
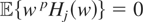
for all j > p. As a particular example, suppose that

. Then it is easily seen that μy*(x) = a − c/ρ2 + bx/ρ + cx2/ρ2. It is also clear from (2.4) that an estimator for μy* can be based on the truncated series for Vy. This is discussed in the next example.
As mentioned earlier, an estimator for μy* can be obtained by truncating the series in (2.4). Suppose we have a random sample (y1,x1,w1),…,(yn,xn,wn) from the distribution of (y,x,w). Let
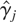
denote the sample analog of
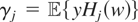
based on these observations; i.e.,

. By (2.4), an estimator of μy* is given by

where kn is a function of the sample size such that kn ↑ ∞ as n ↑ ∞. In this example we show that
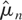
is mean-square consistent and derive its rate of convergence. Suppose for convenience that

are bounded. Then, as shown in the Appendix, for some α > 0 the mean integrated squared error (MISE) of

is given by
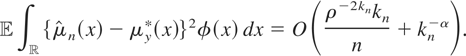
Although (2.5) holds for a stylized setup, it is very informative; e.g., it is clear that the MISE is asymptotically negligible if kn ↑ ∞ sufficiently slowly. Hence,
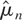
is mean-square consistent for μy*, though its rate of convergence is slow. It converges even more slowly if the instrument is “weak,” i.e., if |ρ| is small. In fact, because the MISE converges to zero if and only if kn log ρ−2 + log kn − log n ↓ −∞, it follows that kn must be O(log n) or smaller. Therefore, even in this simple setting where the joint normality of regressors and instruments is known and imposed in constructing an estimator, the best attainable rate of decrease for the MISE is only O({log n}−α). This suggests that rates of convergence that are powers of 1/log n, rather than 1/n, are relevant for endogenous nonparametric regression models when the distribution of (x,w) is unknown. Rates better than O({log n}−α) can be obtained by imposing additional restrictions on μy*; e.g., Darolles et al. (2002, Thm. 4.2) and Hall and Horowitz (2003, Thm. 4.1) achieve faster rates by making the eigenvalues of certain integral operators decay to zero at a fast enough rate, thereby further restricting μy* implicitly.
Let y = μ1*(x) + μ2*(z) + ε, where μ1* and μ2* are unknown functions such that
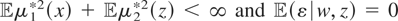
; i.e., x is the only endogenous regressor. In this example, the model space is L2(x) + L2(z), and the instrument space is L2(w,z). Assume that (x,z,w) is trivariate normal with mean zero and positive definite variance-covariance matrix

. Because the conditional distribution of x given (w,z) is normal with mean depending on (w,z) and the family of one-dimensional Gaussian distributions with varying mean is complete, μ1*(x) + μ2*(z) is identified. We now use the approach of Lemma 2.2 to recover μ1* and μ2*. Let μ*(x,z) = μ1*(x) + μ2*(z). Note that
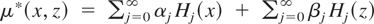
for constants {αj}j=0∞ and {βj}j=0∞. But because
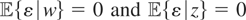
, we have
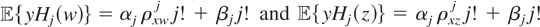
. Solving these simultaneous equations for each j, it follows that

Therefore, using the fact that
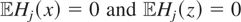
for j ≥ 1,

Hence, μ1* and μ2* are identified.
Next, we consider an iterative scheme for determining V.
5See Petryshyn (1963) for a detailed treatment of recursive methods of this type.
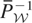
. We only need
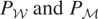
, where the latter denotes orthogonal projection onto the closure of

. In contrast, the series approach of Lemma 2.2 did not require any knowledge of
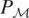
.
LEMMA 2.3. Fix

and consider the equation
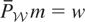
for

. Let m0 denote its solution and define
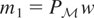
. If there exist a constant a ≠ 0 and an

such that
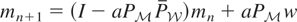
converges to m* as n ↑ ∞, then m* = m0.
This result, which is related to the Landweber–Fridman procedure described in Kress (1999, Ch. 15) and Carrasco et al. (2002), shows that if the sequence mn converges, then it converges to m0. Therefore, given y, we can obtain Vy by applying this procedure to
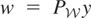
. Because

, convergence in Lemma 2.3 is ensured if there exists a nonzero constant a such that the partial sum

converges pointwise for each

. A well-known sufficient condition for this to happen is that

. Of course, if

so that there is no endogeneity, then

, and there are no further adjustments to m1.
The iterative procedure of Lemma 2.3 also works for Example 2.4. To see this, let a = 1 and note that

, where

. Hence,

, and by (2.4) it follows that

as n ↑ ∞; i.e., mn converges in mean-square to μy*.
Before ending this section, we comment briefly on the pervasiveness of “ill-posed” endogenous nonparametric models. Recall that Condition (I) guarantees that for each

the vector μy* is uniquely defined, i.e., V : y [map ] μy* is a function from

into
. But Condition (I) is not strong enough to ensure that this function is continuous;
6Discontinuity of V means that slight perturbations in the response variable can lead to unbounded changes in μy*, the parameter of interest associated with it. This lack of stability makes precise the sense in which some endogenous nonparametric models can be called “ill-posed.” Note that sometimes a statistical problem is said to be ill-posed because of data issues; e.g., classic nonparametric regression itself can be called ill-posed because we cannot estimate the graph of an unknown function using only a finite amount of data. However, the notion of ill-posedness described here has nothing to do with sample information but is inherent to the model.
such that

as n ↑ ∞ and suppose that

as n ↑ ∞. To show that V is closed, it suffices to show that

. Note that, for each
and, because yn − Vyn → y − m as

. Hence, by definition of

. The next result characterizes the continuity of V.
LEMMA 2.4. The following statements are equivalent: (i) V is continuous on
; (ii)

is closed; (iii) if m1,m2,… is a sequence in

such that

as n ↑ ∞, then mn → 0 as n ↑ ∞; (iv)
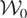
is closed; (v) there exists a closed linear subspace

of

such that

.
The restrictive nature of this lemma reveals that well-posed endogenous nonparametric models are an exception rather than the rule; e.g., even the simple Gaussian setting of Example 2.4 is not sufficient to make the problem there well-posed. To see this, let

denote the normalized nth Hermite polynomial. It is then easy to verify that

converges to zero in mean-square whereas fn does not. Therefore, (iii) does not hold, and, hence, V is not continuous. Of course, if

is finite-dimensional (as in parametric models, or, in nonparametric models where the regressors are discrete random variables with finite support),
7 then (iii) holds and V is continuous. Similarly, if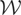
is finite-dimensional then

will be finite-dimensional and, hence, closed, implying that V is continuous. But these are clearly very special cases. A practical consequence of ill-posedness is that some type of “regularization” is needed in estimation procedures to produce estimators with good asymptotic properties. For instance, a truncation-based regularization ensures convergence of the estimator described in Example 2.5. For more about the different regularization schemes used in the literature, see, e.g., Wahba (1990, Ch. 8), Kress (1999, Ch. 15), Carrasco et al. (2002), Loubes and Vanhems (2003), and the references therein.
In this section, we investigate the case where μy* in (2.1) fails to be uniquely defined. As mentioned earlier in Example 2.2, Newey and Powell (2003) and others have characterized identification of the endogenous nonparametric regression model in terms of completeness of the conditional distribution of x given w. They also point out that it is sufficient to restrict pdf (x|w) to the class of full rank exponential densities for it to be complete. However, Examples 3.2 and 3.3 illustrate that this sufficient condition can fail to hold in relatively simple cases. Furthermore, if the distribution of x|w is not assumed to be parametric, completeness can be very hard to verify. Hence, it is important to know what happens when completeness fails or cannot be checked. We now focus on this issue.
Let

be the set of all “identification-destroying” perturbations of μy*. From Condition (I) it follows that μy* is identified if and only if

. Note that

is a closed linear subspace of

. The properties of

play an important role in the identification of μy*.
We maintain the setup of Example 2.1. For linear instrumental variables regression it is easily seen that

. Hence, the identification condition fails to hold, i.e.,
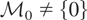
, if

is not of full column rank.
Let y = μy*(x) + ε, where μy* ∈ L2(x) is unknown. The regressor is endogenous, but we have an instrument w satisfying

. Suppose that x = w + v, where

. Hence,

for a.a. w ∈ [−½,½]}. Because
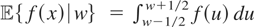
, it is straightforward to show that

holds for a.a. w ∈ [−½,½] if and only if f is periodic in the sense that f (x) = f (1 + x) for a.a.

. Thus,
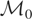
can be explicitly characterized as

for a.a.
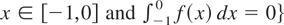
. Because
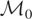
is clearly not equal to {0}, Condition (I) does not hold. Therefore, μy* is not uniquely defined and, hence, cannot be estimated even for the simple design given in this example.
Let y = μ1*(x) + μ2*(z) + ε, where μ1* and μ2* are unknown functions L2(x) and L2(z), respectively, and
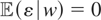
; i.e., both x and z are endogenous, but we only have one instrument w. Obviously, here the model space is L2(x) + L2(z), but the instrument space is L2(w). As in Example 2.6, assume that (x,z,w) are jointly normal with mean zero and variance Ω. Because the conditional distribution of x,z|w is not complete, it follows that μ1*(x) + μ2*(z) is not identified. In fact, it can be shown that
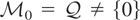
, where

.
8Because
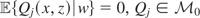
for each j; i.e.,
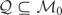
. Next, let

. Then m0(x,z) = f (x) + g(z) for some f ∈ L2(x) and g ∈ L2(z) such that
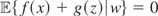
; i.e.,
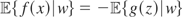
. Hence, writing

, it follows that
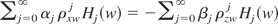
if and only if

. By the completeness of Hermite polynomials in L2(w), this implies that αj ρxwj + βj ρzwj = 0 for each j. Therefore,
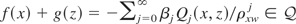
; i.e.,

.
Suppose that a μy* satisfying (2.1) is not uniquely defined. Loosely speaking, this means that the model space is “too large”; i.e., it contains more than one element satisfying (2.1). Hence, to obtain identifiability, we may choose a smaller model space. This approach is analogous to eliminating redundant regressors in an underidentified linear regression model. We now formalize this intuition. For a given

, define

. Identification holds when
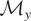
consists of a single element. Otherwise,
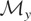
is a collection of elements that cannot be distinguished based on (2.1). A nice property of

is that each of its elements has the same projection onto
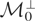
, the orthogonal complement of
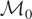
. Hence,
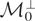
is a natural choice for the reduced model space;
9There is an analogy to
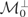
in the specification testing literature. Suppose we want to test the null hypothesis

against the alternative that it is false. Consider the alternative
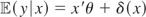
, where δ denotes a deviation from the null. It is obvious that no test will be able to reject the null if δ is a linear function of x. The only detectable perturbations are those that are orthogonal to linear functions, i.e., those satisfying

.
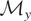
onto
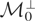
, then μy** can be regarded as the “identifiable part” of μy*. In technical terms, when Condition (I) does not hold, the “true parameter” of the model is, in effect, an equivalence class of elements of

, which we have denoted by the symbol
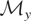
. This class of true parameters may be described in terms of their common features as follows. Because

, each
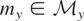
may be decomposed into two components
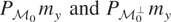
. But because
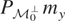
is the same for all
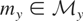
, each equivalence class
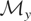
may be described by a single element μy**, which we refer to as the identifiable part of μy*. We may take this canonical element to be

. It is easy to show that μy** is an element of

.
10Let

be arbitrary. Then
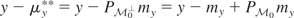
. But

by definition of
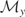
, and
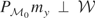
because

. Therefore,

. Because

, it follows that

.
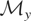
are those

such that
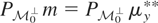
; i.e., all

of the form
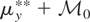
.
Suppose that
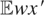
is not of full column rank so the identification condition fails to hold. Here,
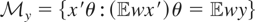
. Because

, where
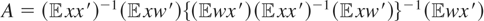
, we have

. Hence, we can only identify linear functions of the form x′Aθ. Of course, if the identification condition holds, i.e.,

is of full column rank, then A reduces to the identity matrix and

with θ* as defined in Example 2.3.
The identifiable part of μy* is given by projecting

onto

, where

for a.a. w ∈ [−½,½]}. Recall that x has the triangular distribution on [−1,1]; i.e., the p.d.f. of x is given by h(x) = 1 + x for −1 ≤ x ≤ 0 and h(x) = 1 − x for 0 ≤ x ≤ 1. It can be shown that

, where
11Showing

is easy. Next, by the projection theorem,

Now let

. Because g is an element of
, its projection onto
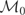
is the zero function. Hence, using the expression for

, it follows that

; i.e.,

. Therefore,

.

Hence, the identifiable part of μy* is a function f satisfying f (x)h(x) = −f (x + 1)h(x + 1) + c for a.a. x ∈ [−1,0] and some constant c.
Now let us determine the identifiable part of the underidentified model in Example 3.3. It can be shown that
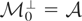
, where

.
12Recall that
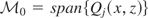
. Now let

. Because
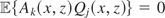
for all

. Therefore,
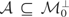
. Next, let
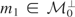
. Then m1(x,z) = f (x) + g(z) for some f ∈ L2(x) and g ∈ L2(z). But because m1 is orthogonal to
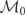
by definition,
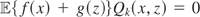
for all k. Hence, writing

, we have

. Thus (ρxzj ρxwj − ρzwj)αj + βj(ρxwj − ρxzj ρzwj) = 0 for j ≥ 1, and

. It follows that

; i.e.,

.
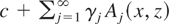
, where c denotes a constant. For example, suppose that ρxw = ρzw; i.e., the instrument has the same correlation with each regressor. Then

consists of functions of the form

; i.e., only elements of L2(x) + L2(z) of the form c + f (x) + f (z) are identified.
As mentioned earlier, underidentification may be viewed as a consequence of the fact that the model space

is too big. Hence, to obtain identifiability, we may choose a smaller model space. A natural choice for this reduced model space is
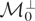
. But to use

in place of

, we must verify that it satisfies two conditions. The first is that for each

there exists a
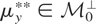
such that

. The second is that
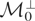
satisfies Condition (I). It is easy to see that both these conditions are satisfied: Fix
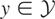
. Then by (2.1), there exists

such that
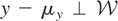
. Let
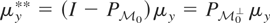
. Then
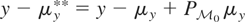
. Because

is an element of

and, hence, orthogonal to
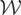
, it follows that

. This shows that

satisfies the first requirement. Next, let m denote an element of
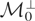
that is orthogonal to
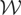
. By definition, there exists

such that
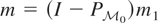
. Because

, for any

we have
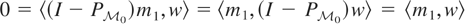
. It follows that

and, hence, that

. Therefore, for

implies that m = 0, proving that

also satisfies the second requirement.
Note that to describe μy**, we can use

in place of
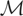
in the theory developed in Section 2. Because Condition (I) is satisfied by

, all of the previous results hold with respect to this choice and μy** = Vy, where V is now based on

.
Economists are often interested in estimating real-valued functions of conditional expectations. For example, letting y denote the market demand for a certain good and x the price, Newey and McFadden (1994) consider estimating

, the approximate change in consumer surplus for a given price change on interval D. In this section we consider an endogenous version of their problem by characterizing the identification of bounded linear functionals of μy* when the latter itself may not be identified (obviously, if μy* is uniquely defined then so is ρ(μy*)). The results of Ai and Chen (2003) can be used to estimate linear functionals of μy* when the latter is identified.
Let
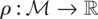
denote a continuous linear functional on
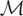
, where a possibly nonunique

satisfies
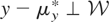
; i.e., we let (2.1) hold though we do not assume that Condition (I) necessarily holds. We now introduce the condition under which ρ(μy*) is uniquely defined.
Condition (I-F). If

satisfies

, then ρ(m) = 0.
As shown subsequently, Condition (I-F) is necessary and sufficient for ρ(μy*) to be identified.
THEOREM 4.1. ρ(μy*) is identified if and only if Condition (I-F) holds.
The next example illustrates the usefulness of this result.
Let y = μy*(x) + ε, where μy* ∈ L2(x) is unknown. The regressors are endogenous, but we have instruments satisfying
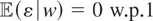
. Assume that the conditional distribution of x given w is not complete. Hence, μy* is not identified. Now consider the expectation functional
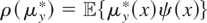
, where ψ is a known weight function satisfying
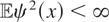
. Theorem 4.1 reveals that
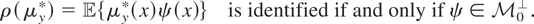
The case ψ(x) = 1 is a special case of (4.1) because

contains all constant functions (in fact, because
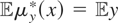
, it is obvious that
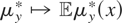
is identified irrespective of whether μy* is identified or not). From (4.1) we can immediately see that in applications where μy* is not identified certain expectation functionals of μy* may still be identified. Of course, if μy* is identified to begin with, then

; hence, ρ(μy*) is identified for all square integrable weight functions. We can also use (4.1) to characterize the identification of bounded linear functionals of the form
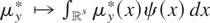
. In particular, it is easily seen that
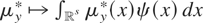
is identified if and only if ψ/h lies in

, where h denotes the unknown Lebesgue density of x. Note that for
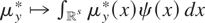
to be a bounded linear functional on L2(x) it is implicitly understood that the random vector x is continuously distributed and

. Of course,
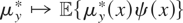
is bounded on L2(x) even when some components of x are discrete.
Finally, we show that Condition (I) holds if and only if Condition (I-F) holds for all bounded linear functionals of μy*. Hence, identification of μy* can also be characterized as follows.
THEOREM 4.2. μy* is identified if and only if all bounded linear functionals of μy* are identified.
For endogenous nonparametric regression, this result provides a direct link between identification of μy* and its expectation functionals by revealing that μy* is identified if and only if all its expectation functionals are identified; i.e., μy* is identified if and only if

is identified for all ψ ∈ L2(x).
We now formulate (2.1) in terms of moment conditions generated by linear operators and also provide an example to illustrate the usefulness of this characterization. Although this formulation may seem different from the manner in which (2.1) is stated, we show that the two representations are in fact logically equivalent. Let y denote an element of
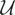
and let

be a known linear subspace of
. Suppose that corresponding to y is an element of

, denoted by μy*, defined as follows: “There exists a linear subspace of
, denoted by
, and a continuous linear operator

such that T(y − μy*) = 0.” Let

denote the set of

for which this model holds; i.e., for each
there exists

such that T(y − μy*) = 0. Note that because

, the domain of T may be taken to be

.
Condition (I-M). If
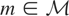
satisfies Tm = 0, then m = 0.
Condition (I-M) is necessary and sufficient for μy* to be uniquely defined (the proof is straightforward and hence is omitted). We say that

is a “moment-condition” model if there is a linear subspace
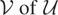
and a continuous linear function

such that for each

there exists
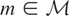
satisfying T(y − m) = 0 and Condition (I-M) holds. We call T the “identification function.” Similarly, we say that
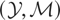
is an “instrumental variables” model if there is a closed linear subspace
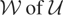
such that for each
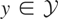
there exists
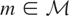
satisfying
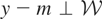
and Condition (I) holds. In fact, it can be easily shown that

is a moment-condition model if and only if it is an instrumental variables model.
The following example illustrates a situation where the nature of the available information makes it easier to write an endogenous nonparametric regression model as a moment-condition model.
Let y = μy*(x) + ε, where

for s > 1 and μy* ∈ L2(x) is unknown. The regressors are correlated with the error term such that the conditional distribution of ε given x satisfies the index restriction
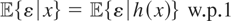
for some known function h with dim h(x) < s. This, e.g., is related to the exclusion restriction assumption maintained in Florens, Heckman, Meghir, and Vytlacil (2002). Let

. Our model has content if the linear moment condition T(y − μy*) = 0 holds for some μy* ∈ L2(x). For μy* to be uniquely defined, by Condition (I-M) we need that
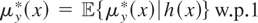
only for μy*(x) = 0 w.p.1. This reveals that μy*'s of the form μy*(x) = f (h(x)) are not identifiable. Therefore, letting
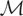
denote the set of all functions in L2(x) that are not functions of h(x), it follows that

is a moment-condition model with identification function T. Next, we show how to write

as an instrumental variables model. Let

be the null space of T; i.e.,

is the set of all random variables ε such that
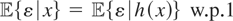
. Because

is a moment-condition model with identification function T, by definition there exists a unique

such that

. It follows that

is also an instrumental variables model with instrument space
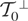
, where

.
13Define
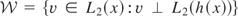
and let v and ε denote arbitrary elements of
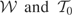
, respectively. Then by the properties of ε and v,

; i.e.,
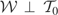
, implying that

. Next, let

. Because the random variable

satisfies
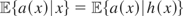
, we obtain that

is an element of

. Hence,

, which implies that

. Therefore, u ⊥ L2(h(x)). Now write u = u1 + u2, where u1 ∈ L2(x) and u2 ∈ L2⊥(x). Because
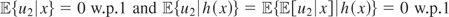
, it follows that

; i.e.,
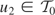
0. But because
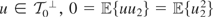
implies that u2 = 0 w.p.1. Hence, u = u1 ∈ L2(x). Thus u ∈ L2(x) and u ⊥ L2(h(x)); i.e.,

. Because u was chosen arbitrarily in

, we conclude that

.
In this paper we investigate some identification issues in nonparametric linear models with endogenous regressors. Our results suggest that identification in such models can fail to hold for even relatively simple designs. Therefore, if researchers are not careful, simply assuming identification and then proceeding to estimation can lead to statistical inference that may be seriously misleading. Because lack of identification here is not easily detected, we show how to determine the identifiable part of the structural function when it is underidentified by orthogonally projecting onto an appropriately defined subspace of the model space. We also examine the connection between identification of the unknown structural function and identification of its linear functionals and show that the two are closely related.
Proof of (2.5). By the orthogonality of Hermite polynomials,
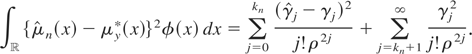
Hence,

But because
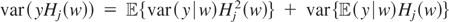
and the maps

are bounded by assumption,
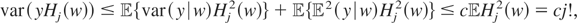
where c is a generic constant. Thus,

. It follows that the MISE is majorized by

. But
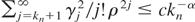
for some α > 0 under some smoothness conditions on μy*; see, e.g., Milne (1929, Cor. I). The desired result follows. █
Proof of Lemma 2.1. Let S denote the statement “For each function f (x) such that

, there exists a function g(w) such that f (x) and g(w) are correlated.” First, suppose that S is not true. Hence, there exists a nonzero function f (x) satisfying
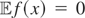
such that

for all g(w). But this implies that
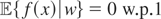
; i.e., pdf (x|w) is not complete. Next, suppose that the conditional distribution of x|w is not complete. Hence, there exists a function f (x) such that

but f (x) ≠ 0; i.e., var f (x) > 0. Clearly, this implies that f (x) is uncorrelated with all functions of w. The desired result follows. █
Proof of Lemma 2.2. We first consider the series expansion for Vy. Let

. Hence, there exists a unique (because Condition (I) is assumed to hold)

such that

. This implies that

. Because
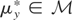
, we can write

for some constants α0,α1,…. Hence,

, and using the fact that
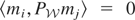
for i ≠ j, it follows that
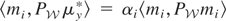
. Hence,
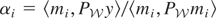
because

. Therefore,

. Next, we consider the series for
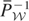
. Let

be any element of

and let
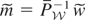
. Note that

by definition of

. Because

is contained in

, by the previous result
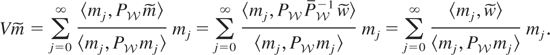
But by (2.2),

. The desired result follows. █
Proof of Lemma 2.3. Note that

. If limn↑∞ mn exists, then mn+1 − mn → 0 as n ↑ ∞ so that

as n ↑ ∞. Because

as n ↑ ∞, it follows that
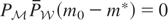
. Let m = m0 − m*; then

. Hence,

so that
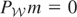
. It follows from Condition (I) that m = 0, i.e., that m* = m0, proving the result. █
Proof of Lemma 2.4. We show that (i) ⇒ (iii) ⇒ (ii) ⇒ (i) and (i) ⇒ (iv) ⇒ (v) ⇒ (i).
First, suppose V is continuous. Let m1,m2,… be a sequence in
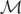
such that

and let

. Note that for each

so that

. Hence, mn = Vyn. Because yn → 0 as n ↑ ∞, it follows that mn → 0. Therefore, (iii) holds.
Next, assume that (iii) holds. Let y1,y2,… denote a sequence in

such that limn↑∞ yn = y for some
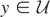
. We need to show that
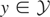
. Observe that because
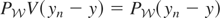
by (2.2) and
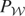
is continuous, it follows that

as n ↑ ∞. But as

is in

, by (iii) we have
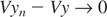
as n ↑ ∞. This shows that yn − Vyn − (y − Vy) → 0 as n ↑ ∞. Because

, we know that

for each n. Thus, by the continuity of the inner product, 〈y − Vy,w〉 = 0 for all

. Hence,

is closed.
Next, suppose that

is closed. Then because V is a closed linear operator with domain

, continuity of V follows by the closed graph theorem; see, e.g., Kreyszig (1978).
Now, let (i) hold. This implies that

is closed. Let w1,w2,… denote a sequence in

with limit

and, for each n = 1,2,…, let
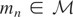
satisfy
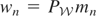
. Because

, it follows that

. Thus

because
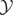
is closed. Next,

by continuity of V. Hence,
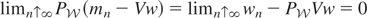
, so that
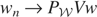
as n ↑ ∞. Because

, we know that

. Hence,
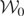
is closed.
Next, assume that

is closed. Because

, the result follows by taking

.
Finally, suppose that (v) holds. Then the restriction of

is closed, and, because

is closed, that restriction is continuous by the closed graph theorem. Let m1,m2,… denote a sequence in
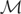
such that

as n ↑ ∞ and let
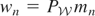
so that w1,w2,… is a sequence in

such that wn → 0 as n ↑ ∞. Note that
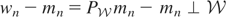
for each n, implying that
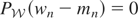
; i.e.,
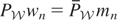
because

is the restriction of

. Hence, mn = Vwn by (2.2). Because V is continuous on
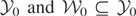
, it follows that limn↑∞ mn = V limn↑∞ wn = 0. Thus (iii) holds. But we have already shown that (iii) implies (i). The desired result follows. █
Proof of Theorem 4.1. ρ(μy*) is identified if and only if all

for which
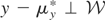
yield the same value of ρ(μy*). Suppose that Condition (I-F) holds and that m1,m2 are elements of
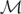
satisfying

for j = 1,2. Then

, so, by Condition (I-F), ρ(m1 − m2) = ρ(m1) − ρ(m2) = 0. Hence, ρ(μy*) is identified. Next, suppose that all m for which

yield the same value of ρ(m). Suppose

satisfies
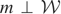
. Then

. Because ρ(μy*) is identified, ρ(m1 + m) = ρ(m1) + ρ(m) = ρ(m1) so that ρ(m) = 0. Hence, Condition (I-F) holds. █
Proof of Theorem 4.2. Suppose Condition (I) holds and

satisfies

. Then, by Condition (I), m = 0 so that ρ(m) = 0 for any linear functional ρ. Next, suppose that Condition (I-F) holds for any continuous linear functional ρ and let

satisfy

. Consider the bounded linear functional ρ(m1) = 〈m,m1〉, where
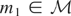
. Because Condition (I-F) holds, it follows that 〈m,m〉 = 0. But this implies that m = 0. Hence, Condition (I) holds. █