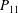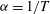1 Introduction
A fascinating dynamic feature of the large-scale circulation in Rayleigh–Bénard convection (RBC) is the cessation and reversal phenomenon, which has been exhibited by many experiments and numerical simulations (see Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Xia Reference Xia2013, and references therein). It is therefore of great importance to explore the mechanism of the flow reversal phenomenon. For instance, it could provide us with insights into the occasional magnetic polarity reversal associated with convection in the Earth’s mantle (Glatzmaier & Roberts Reference Glatzmaier and Roberts1995; Glatzmaier et al. Reference Glatzmaier, Coe, Hongre and Roberts1999).
There are two categories of flow reversal classified by distinct physical mechanisms. One is rotation-led reversal, which occurs only in a cylinder sample caused by incessant azimuthal meandering of the circulating plane (see Brown & Ahlers Reference Brown and Ahlers2006, for example). The other is cessation-led reversal, in which large-scale circulation (LSC) sometimes stops and then randomly restarts in a different direction (see Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010, for example). The cessation-led reversal can occur both in a cylindrical cell and in a box. In order to explain and predict the observed reversal phenomenon, several theoretical models have been prompted including either stochastic differential equations (Sreenivasan, Bershadskii & Niemela Reference Sreenivasan, Bershadskii and Niemela2002; Benzi Reference Benzi2005; Brown & Ahlers Reference Brown and Ahlers2007a
) or deterministic ones (Fontenele Araujo, Grossmann & Lohse Reference Fontenele Araujo, Grossmann and Lohse2005; Resagk et al.
Reference Resagk, du Puits, Thess, Dolzhansky, Grossmann, Araujo and Lohse2006; Gissinger Reference Gissinger2012). The physical model proposed by Sreenivasan et al. (Reference Sreenivasan, Bershadskii and Niemela2002) showed that the imbalance between buoyancy effects and friction might possibly be responsible for the reversals of LSC. Deriving it directly from the equations of motion, Brown & Ahlers (Reference Brown and Ahlers2007a
) proposed a model consisting of two coupled stochastic ordinary differential equations that were able to reproduce some of the important features of the LSC in three-dimensional (3D) RBC, such as cessations and azimuthal meandering. Fontenele Araujo et al. (Reference Fontenele Araujo, Grossmann and Lohse2005) assumed, in their model, that a long-lived plume carried by LSC tends to act against the prevailing flow in the far side. Thus their model is suited to flows with large Prandtl numbers. By incorporating the effects of corner rolls, Ni, Huang & Xia (Reference Ni, Huang and Xia2015) proposed a stochastic model that bridges the discrepancy found in quasi-two-dimensional (2D) and 3D systems. The experimental study in a 3D box by Huang et al. (Reference Huang, Wang, Xi and Xia2015) reported a decoupling of the flow strength and stability of LSC or wind, i.e. reversal behaviour. They claimed that flow reversal is a process of symmetry restoration and found that the more symmetric the system is, the more frequently the flow reversals occur. Later, Huang & Xia (Reference Huang and Xia2016) further showed that the reversal frequency increased dramatically in smaller
![]() ${\it\Gamma}$
cells and confirmed the conclusion proposed by Ni et al. (Reference Ni, Huang and Xia2015).
${\it\Gamma}$
cells and confirmed the conclusion proposed by Ni et al. (Reference Ni, Huang and Xia2015).
Free from complicated and puzzling 3D structures, 2D rectangular samples have been exploited in studying cessation-led reversals (Sugiyama et al. Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2013; Podvin & Sergent Reference Podvin and Sergent2015; Verma, Ambhire & Pandey Reference Verma, Ambhire and Pandey2015). It is concluded by Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010) that two diagonally arranged corner-rolls and moderate Prandtl numbers are necessary in cessation-led reversals. Chandra & Verma (Reference Chandra and Verma2011, Reference Chandra and Verma2013) used the Fourier decomposition method to study the reversals. They proved that flow reversals occur only at a narrow band of Rayleigh numbers with Prandtl numbers equal to 1, where both the Fourier modes (1, 1) and (2, 2) are comparatively strong with nearly equal energy. Podvin & Sergent (Reference Podvin and Sergent2015) applied proper orthogonal decomposition to the velocity and temperature fields of RBC in a 2D square cell. A three-mode model was proposed based on the interaction of the LSC, the quadrupolar flow and horizontal rolls.
Recently, the influence of non-Oberbeck–Boussinesq (NOB) effects on flow dynamics and heat transfer has been studied extensively in turbulent thermal convection (Ahlers et al. Reference Ahlers, Brown, Araujo, Funfschilling, Grossmann and Lohse2006, Reference Ahlers, Araujo, Funfschilling, Grossmann and Lohse2007, Reference Ahlers, Calzavarini, Araujo, Funfschilling, Grossmann, Lohse and Sugiyama2008; Brown & Ahlers Reference Brown and Ahlers2007b ; Sugiyama et al. Reference Sugiyama, Calzavarini, Grossmann and Lohse2007, Reference Sugiyama, Calzavarini, Grossmann and Lohse2009; Sameen, Verzicco & Sreenivasan Reference Sameen, Verzicco and Sreenivasan2008; Horn, Shishkina & Wagner Reference Horn, Shishkina and Wagner2013; Horn & Shishkina Reference Horn and Shishkina2014). To the best of our knowledge, flow reversals in RBC with NOB effects have not been investigated yet. Therefore, the major objective of this study is to show the scenarios of the flow reversals due to NOB effects, which are quite different in large-scale dynamics from those found under the Oberbeck–Boussinesq (OB) approximation. Moreover, in the NOB case, detailed physical mechanisms of flow reversals are studied from the perspective of vortex dynamics. The remainder of the paper is organized as follows. Section 2 introduces the governing equations and numerical methods. In § 3, the main results are presented and discussed. Finally, a short summary is given in § 4.
2 Governing equations and numerical methods
2.1 Governing equations
Consider thermal convection in a square box with height
![]() ${\hat{H}}$
as the reference length (hatted quantities are dimensional). The bottom and upper walls have high and low constant temperatures
${\hat{H}}$
as the reference length (hatted quantities are dimensional). The bottom and upper walls have high and low constant temperatures
![]() $\hat{T}_{h}$
and
$\hat{T}_{h}$
and
![]() $\hat{T}_{c}$
respectively, the average of which serves as the reference temperature
$\hat{T}_{c}$
respectively, the average of which serves as the reference temperature
![]() $\hat{T}_{0}=(\hat{T}_{c}+\hat{T}_{h})/2$
. The side walls are insulated. All four walls are assumed to be no-slip. OB approximation is not applicable for large temperature differences because of the variable physical properties and nonlinear relation between temperature and density in buoyancy force. Thus low-Mach-number equations (Paolucci Reference Paolucci1982) are adopted in this paper. Free-fall velocity
$\hat{T}_{0}=(\hat{T}_{c}+\hat{T}_{h})/2$
. The side walls are insulated. All four walls are assumed to be no-slip. OB approximation is not applicable for large temperature differences because of the variable physical properties and nonlinear relation between temperature and density in buoyancy force. Thus low-Mach-number equations (Paolucci Reference Paolucci1982) are adopted in this paper. Free-fall velocity
![]() $\hat{U} =\displaystyle (2{\it\epsilon}{\hat{g}}{\hat{H}})^{1/2}$
is chosen for the reference velocity with
$\hat{U} =\displaystyle (2{\it\epsilon}{\hat{g}}{\hat{H}})^{1/2}$
is chosen for the reference velocity with
![]() ${\it\epsilon}$
defined later. Other reference quantities include
${\it\epsilon}$
defined later. Other reference quantities include
![]() $\hat{p}_{0}$
,
$\hat{p}_{0}$
,
![]() $\hat{{\it\rho}}_{0}$
,
$\hat{{\it\rho}}_{0}$
,
![]() ${\hat{c}}_{p0}$
,
${\hat{c}}_{p0}$
,
![]() $\hat{{\it\mu}}_{0}$
,
$\hat{{\it\mu}}_{0}$
,
![]() $\hat{k}_{0}$
and
$\hat{k}_{0}$
and
![]() ${\hat{g}}$
. These dimensional quantities are not always independent, e.g.
${\hat{g}}$
. These dimensional quantities are not always independent, e.g.
![]() $\hat{p}_{0}=\hat{{\it\rho}}_{0}\hat{R}\hat{T}_{0}$
with
$\hat{p}_{0}=\hat{{\it\rho}}_{0}\hat{R}\hat{T}_{0}$
with
![]() $\hat{R}$
the gas constant
$\hat{R}$
the gas constant
![]() $8.314~\text{J}~\text{K}^{-1}~\text{mol}^{-1}$
and
$8.314~\text{J}~\text{K}^{-1}~\text{mol}^{-1}$
and
![]() $\hat{{\it\mu}}_{0}$
,
$\hat{{\it\mu}}_{0}$
,
![]() $\hat{k}_{0}$
are functions of
$\hat{k}_{0}$
are functions of
![]() $\hat{T}_{0}$
at reference state with 300 K, unless otherwise stated. Moreover the dynamic pressure is non-dimensionalized by
$\hat{T}_{0}$
at reference state with 300 K, unless otherwise stated. Moreover the dynamic pressure is non-dimensionalized by
![]() $\hat{{\it\rho}}_{0}\hat{U} ^{2}$
. The non-dimensional low-Mach-number Navier–Stokes (NS) equations in which the acoustic wave is filtered are cast in the form of a Cartesian tensor
$\hat{{\it\rho}}_{0}\hat{U} ^{2}$
. The non-dimensional low-Mach-number Navier–Stokes (NS) equations in which the acoustic wave is filtered are cast in the form of a Cartesian tensor
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\mu}=\displaystyle T^{1.5}\frac{1+S_{{\it\mu}}}{T+S_{{\it\mu}}},\\ k=\displaystyle T^{1.5}\frac{1+S_{k}}{T+S_{k}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\it\mu}=\displaystyle T^{1.5}\frac{1+S_{{\it\mu}}}{T+S_{{\it\mu}}},\\ k=\displaystyle T^{1.5}\frac{1+S_{k}}{T+S_{k}},\end{array}\right\}\end{eqnarray}$$
where
![]() $S_{k}=0.648$
and
$S_{k}=0.648$
and
![]() $S_{{\it\mu}}=0.368$
for the reference temperature
$S_{{\it\mu}}=0.368$
for the reference temperature
![]() $T_{0}=300~\text{K}$
. Since
$T_{0}=300~\text{K}$
. Since
![]() $S_{k}\neq S_{{\it\mu}}$
, the Prandtl number is not globally constant. Temperature differential
$S_{k}\neq S_{{\it\mu}}$
, the Prandtl number is not globally constant. Temperature differential
![]() ${\it\epsilon}$
is bound to
${\it\epsilon}$
is bound to
![]() $0.005\leqslant {\it\epsilon}\leqslant 0.6$
. To achieve OB approximation, we set
$0.005\leqslant {\it\epsilon}\leqslant 0.6$
. To achieve OB approximation, we set
![]() ${\it\epsilon}=0.005$
,
${\it\epsilon}=0.005$
,
![]() ${\it\mu}=k=p=1$
,
${\it\mu}=k=p=1$
,
![]() $u_{j,j}=0$
and
$u_{j,j}=0$
and
![]() ${\it\rho}=1$
except in buoyancy term
${\it\rho}=1$
except in buoyancy term
![]() ${\it\rho}=1-{\rm\Delta}T$
.
${\it\rho}=1-{\rm\Delta}T$
.
For a closed system with no-slip and no-penetrative boundary conditions, the time derivative of thermodynamic pressure and divergence of velocity are displayed as follows
which is only a function of temperature. Clearly we see that equations (2.1) to (2.3) coupled with (2.5), (2.6) and (2.7) form an integro-differential system, so the aforementioned model equations are global rather than local.
2.2 Numerical method and validation
The low-Mach-number NS equations (2.1)–(2.3) along with proper boundary conditions are solved by the finite difference method. A non-uniform grid with clustered points near walls is adopted to improve the grid resolution. Scalar and vector variables are staggered in space in order to avoid pressure-velocity decoupling. All spatial derivative terms are approximated by a second-order central difference scheme which intrinsically conserves energy. It has been further illustrated by Moin & Verzicco (Reference Moin and Verzicco2016) that staggered second-order finite difference schemes can produce comparatively accurate simulations at lower computational cost. A fractional-step approach is used to solve momentum equations (2.2). Pressure is also staggered in time with other physical variables to further couple pressure-velocity fields. A multi-grid strategy is exploited to accelerate the iteration process in the Poisson equation.
To validate the code called lMn2d, typical cases in thermal convection are computed and compared with existing results. As illustrated in table 1, under OB approximation, the errors between present results and those of de Vahl Davis & Jones (Reference de Vahl Davis and Jones1983) are less than 0.1 %. In the NOB case with
![]() ${\it\epsilon}=0.6$
, our code also gives a relatively small error which is less than 0.1 % compared with those of Le Quéré et al. (Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005). Note that the reference temperature
${\it\epsilon}=0.6$
, our code also gives a relatively small error which is less than 0.1 % compared with those of Le Quéré et al. (Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005). Note that the reference temperature
![]() $\hat{T}_{0}=600~\text{K}$
is just used here and we set
$\hat{T}_{0}=600~\text{K}$
is just used here and we set
![]() $S_{{\it\mu}}=S_{k}=0.1842$
in the Sutherland law to keep the Prandtl number constant. Another 2D thermal convection is also preformed in a tall side-heated box with an aspect ratio of length to height
$S_{{\it\mu}}=S_{k}=0.1842$
in the Sutherland law to keep the Prandtl number constant. Another 2D thermal convection is also preformed in a tall side-heated box with an aspect ratio of length to height
![]() $L/H=1/8$
. The oscillating frequency is 3.42 which agrees well with the results in Bathe, Brezzi & Pironneau (Reference Bathe, Brezzi and Pironneau2001). For 2D RBC in a square cavity with adiabatic sidewalls, the critical Rayleigh number given by our code is
$L/H=1/8$
. The oscillating frequency is 3.42 which agrees well with the results in Bathe, Brezzi & Pironneau (Reference Bathe, Brezzi and Pironneau2001). For 2D RBC in a square cavity with adiabatic sidewalls, the critical Rayleigh number given by our code is
![]() $Ra_{c}=2584.12$
, which is excellently in agreement with 2585.27 by Sugiyama et al. (Reference Sugiyama, Calzavarini, Grossmann and Lohse2009).
$Ra_{c}=2584.12$
, which is excellently in agreement with 2585.27 by Sugiyama et al. (Reference Sugiyama, Calzavarini, Grossmann and Lohse2009).

Figure 1. (a)
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $k$
as functions of rescaled
$k$
as functions of rescaled
![]() $T$
. (b)
$T$
. (b)
![]() $Pr$
as a function of rescaled
$Pr$
as a function of rescaled
![]() $T$
. Temperature differentials are
$T$
. Temperature differentials are
![]() ${\it\epsilon}=0.2$
, 0.4 and 0.6. Red solid vertical lines show the case under OB approximation for comparison.
${\it\epsilon}=0.2$
, 0.4 and 0.6. Red solid vertical lines show the case under OB approximation for comparison.
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() $k$
and subsequently
$k$
and subsequently
![]() $Pr$
are all subject to Sutherland laws with reference temperature 300 K.
$Pr$
are all subject to Sutherland laws with reference temperature 300 K.
Table 1. Comparison of the averaged Nusselt numbers
![]() $Nu$
of the present computations and those of de Vahl Davis & Jones (Reference de Vahl Davis and Jones1983)
$Nu$
of the present computations and those of de Vahl Davis & Jones (Reference de Vahl Davis and Jones1983)
![]() $^{\ast }$
, Le Quéré et al. (Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005)
$^{\ast }$
, Le Quéré et al. (Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005)
![]() $^{\flat }$
.
$^{\flat }$
.
3 Results and discussion
3.1 Cessation-led reversals by the single corner roll
The Rayleigh number covers a range of
![]() $10^{5}\leqslant Ra\leqslant 5\times 10^{7}$
. Three meshes have been adopted, the grid points of which are between
$10^{5}\leqslant Ra\leqslant 5\times 10^{7}$
. Three meshes have been adopted, the grid points of which are between
![]() $128^{2}$
and
$128^{2}$
and
![]() $384^{2}$
. Since the NOB effects are included, the boundary layer (BL) near the cold wall is much thinner and more grid points should be clustered there. To meet the Courant–Friedrichs–Lewy condition, the time step is of an order of magnitude
$384^{2}$
. Since the NOB effects are included, the boundary layer (BL) near the cold wall is much thinner and more grid points should be clustered there. To meet the Courant–Friedrichs–Lewy condition, the time step is of an order of magnitude
![]() $O({\rm\Delta}x)$
, i.e. approximately
$O({\rm\Delta}x)$
, i.e. approximately
![]() $10^{-3}$
dimensionless time unit. The mesh size
$10^{-3}$
dimensionless time unit. The mesh size
![]() ${\rm\Delta}x$
stringently satisfies the Kolmogorov and Batchelor length scales, both in BLs and bulk regime (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010).
${\rm\Delta}x$
stringently satisfies the Kolmogorov and Batchelor length scales, both in BLs and bulk regime (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010).
3.1.1 Variable physical properties beyond OB approximation
Figure 1 shows that dynamic viscosity
![]() ${\it\mu}$
, conductivity
${\it\mu}$
, conductivity
![]() $k$
and also Prandtl number
$k$
and also Prandtl number
![]() $Pr$
vary with temperature.
$Pr$
vary with temperature.
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $k$
are computed with (2.4). As shown in figure 1(a),
$k$
are computed with (2.4). As shown in figure 1(a),
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $k$
vary greatly with
$k$
vary greatly with
![]() $T$
in the NOB case. For example,
$T$
in the NOB case. For example,
![]() ${\it\mu}$
is reduced by more than 50 % near the cold wall and increased by approximately 40 % near the hot wall when
${\it\mu}$
is reduced by more than 50 % near the cold wall and increased by approximately 40 % near the hot wall when
![]() ${\it\epsilon}=0.6$
. It is also observed that
${\it\epsilon}=0.6$
. It is also observed that
![]() $k$
varies with
$k$
varies with
![]() $T$
a bit faster than
$T$
a bit faster than
![]() ${\it\mu}$
. In figure 1(b),
${\it\mu}$
. In figure 1(b),
![]() $Pr$
also varies with temperature because of the asynchronous changes of
$Pr$
also varies with temperature because of the asynchronous changes of
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $k$
. The red solid vertical line helps to reveal that for the reference state and OB case
$k$
. The red solid vertical line helps to reveal that for the reference state and OB case
![]() $Pr=0.71$
. Compared with the OB approximation, the Prandtl number increases near the cold top wall and decreases near the hot bottom wall. Even with
$Pr=0.71$
. Compared with the OB approximation, the Prandtl number increases near the cold top wall and decreases near the hot bottom wall. Even with
![]() ${\it\epsilon}=0.6$
, the Prandtl number is approximately 0.8 which is still less than unity, and thus the viscous BL is always nested in the thermal one. Since the change of thermal pressure is relatively small (Le Quéré et al.
Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005) and perfect gas is used as the working fluid,
${\it\epsilon}=0.6$
, the Prandtl number is approximately 0.8 which is still less than unity, and thus the viscous BL is always nested in the thermal one. Since the change of thermal pressure is relatively small (Le Quéré et al.
Reference Le Quéré, Weisman, Paillère, Vierendeels, Dick, Becker, Braack and Locke2005) and perfect gas is used as the working fluid,
![]() ${\it\rho}=p/T$
becomes larger near the cold wall and smaller near the hot wall. Thus near the cold wall, kinematic viscosity
${\it\rho}=p/T$
becomes larger near the cold wall and smaller near the hot wall. Thus near the cold wall, kinematic viscosity
![]() ${\it\nu}={\it\mu}/{\it\rho}$
becomes smaller and similarly for the thermal diffusivity
${\it\nu}={\it\mu}/{\it\rho}$
becomes smaller and similarly for the thermal diffusivity
![]() ${\it\kappa}=k/{\it\rho}c_{p}=k/{\it\rho}$
. Near the hot wall,
${\it\kappa}=k/{\it\rho}c_{p}=k/{\it\rho}$
. Near the hot wall,
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
are increased. As regards the thermal isobaric expansion coefficient, clearly
${\it\kappa}$
are increased. As regards the thermal isobaric expansion coefficient, clearly
![]() ${\it\alpha}=1/T$
becomes larger in magnitude near the cold wall.
${\it\alpha}=1/T$
becomes larger in magnitude near the cold wall.

Figure 2. Log–log plots of
![]() $Nu$
as a function of
$Nu$
as a function of
![]() $Ra$
for various temperature differentials. (a) OB approximation, (b)
$Ra$
for various temperature differentials. (a) OB approximation, (b)
![]() ${\it\epsilon}=0.2$
, (c)
${\it\epsilon}=0.2$
, (c)
![]() ${\it\epsilon}=0.4$
, (d)
${\it\epsilon}=0.4$
, (d)
![]() ${\it\epsilon}=0.6$
. Grey square symbols are flow pattern
${\it\epsilon}=0.6$
. Grey square symbols are flow pattern
![]() $P_{11}$
. Grey triangular symbols are flow pattern
$P_{11}$
. Grey triangular symbols are flow pattern
![]() $P_{12}$
. Grey circle symbols are specially mixed patterns with both
$P_{12}$
. Grey circle symbols are specially mixed patterns with both
![]() $P_{11}$
with definite period and
$P_{11}$
with definite period and
![]() $P_{12}$
with random period in the process of flow reversals. Red symbols ‘
$P_{12}$
with random period in the process of flow reversals. Red symbols ‘
![]() $+$
’ represent where there exist flow reversals and the dashed lines denote that the growth of corner rolls is observed only once and
$+$
’ represent where there exist flow reversals and the dashed lines denote that the growth of corner rolls is observed only once and
![]() $P_{12}$
is achieved in the end.
$P_{12}$
is achieved in the end.
3.1.2 New flow reversals
Figure 2 shows plots of
![]() $Nu$
as a function of
$Nu$
as a function of
![]() $Ra$
for various temperature differentials and the phenomenon of the co-existence of multiple solutions is identified. In general, two flow patterns
$Ra$
for various temperature differentials and the phenomenon of the co-existence of multiple solutions is identified. In general, two flow patterns
![]() $P_{11}$
and
$P_{11}$
and
![]() $P_{12}$
are identified where
$P_{12}$
are identified where
![]() $P_{11}$
has one dominant cavity-sizable roll with two diagonally arranged secondary rolls and
$P_{11}$
has one dominant cavity-sizable roll with two diagonally arranged secondary rolls and
![]() $P_{12}$
has two vertically stacked dominant rolls. Under the OB approximation, pattern
$P_{12}$
has two vertically stacked dominant rolls. Under the OB approximation, pattern
![]() $P_{11}$
is unchanged in the full Rayleigh number range. When the temperature differential increases, with
$P_{11}$
is unchanged in the full Rayleigh number range. When the temperature differential increases, with
![]() ${\it\epsilon}\geqslant 0.2$
, we observed the corner roll growth at Rayleigh numbers denoted by dashed lines and symbols ‘
${\it\epsilon}\geqslant 0.2$
, we observed the corner roll growth at Rayleigh numbers denoted by dashed lines and symbols ‘
![]() $+$
’, and the symbols ‘
$+$
’, and the symbols ‘
![]() $+$
’ in particular show cases of flow reversals. Phenomenally, flow reversal is caused by corner roll growth. However, corner roll growth does not always result in flow reversal. Dashed lines mean that the corner roll in pattern
$+$
’ in particular show cases of flow reversals. Phenomenally, flow reversal is caused by corner roll growth. However, corner roll growth does not always result in flow reversal. Dashed lines mean that the corner roll in pattern
![]() $P_{11}$
grows in size but ends up with pattern
$P_{11}$
grows in size but ends up with pattern
![]() $P_{12}$
. It is conjectured that sometimes, in the phase space the trajectory of pairs of
$P_{12}$
. It is conjectured that sometimes, in the phase space the trajectory of pairs of
![]() $P_{11}$
passes by the stable pattern
$P_{11}$
passes by the stable pattern
![]() $P_{12}$
and is attracted by the stationary point or limiting cycle of
$P_{12}$
and is attracted by the stationary point or limiting cycle of
![]() $P_{12}$
. In figure 2(d), it is noteworthy that with strong NOB effects two counter-rotating flow patterns
$P_{12}$
. In figure 2(d), it is noteworthy that with strong NOB effects two counter-rotating flow patterns
![]() $P_{11}$
could switch back and forth with an unstable intermediate pattern
$P_{11}$
could switch back and forth with an unstable intermediate pattern
![]() $P_{12}$
in
$P_{12}$
in
![]() $3\times 10^{6}\leqslant Ra\leqslant 4\times 10^{6}$
. In short, as
$3\times 10^{6}\leqslant Ra\leqslant 4\times 10^{6}$
. In short, as
![]() ${\it\epsilon}\geqslant 0.2$
, we could observe the growth of the cold corner roll at a large range of Rayleigh numbers, for some of which cession-led flow reversals are clearly found. To some extent, the newly found flow reversals may be related to the tendency for symmetry restoration of an asymmetric system.
${\it\epsilon}\geqslant 0.2$
, we could observe the growth of the cold corner roll at a large range of Rayleigh numbers, for some of which cession-led flow reversals are clearly found. To some extent, the newly found flow reversals may be related to the tendency for symmetry restoration of an asymmetric system.
Currently, the vertical velocity component
![]() $w$
at
$w$
at
![]() $y=0.1$
and
$y=0.1$
and
![]() $z=0.5$
is selected as an indicator of flow reversal, since the flow field is well organized by LSC, corner rolls and BLs rather than plumes (Breuer & Hansen Reference Breuer and Hansen2009; Chandra & Verma Reference Chandra and Verma2011). Figure 3(a,b) shows the time evolution of
$z=0.5$
is selected as an indicator of flow reversal, since the flow field is well organized by LSC, corner rolls and BLs rather than plumes (Breuer & Hansen Reference Breuer and Hansen2009; Chandra & Verma Reference Chandra and Verma2011). Figure 3(a,b) shows the time evolution of
![]() $w$
at
$w$
at
![]() $Ra=7\times 10^{5}$
and
$Ra=7\times 10^{5}$
and
![]() $10^{7}$
, in which flow reversals can be clearly found. At
$10^{7}$
, in which flow reversals can be clearly found. At
![]() $Ra=7\times 10^{5}$
, the flow is laminar and the period of reversal is definite. At
$Ra=7\times 10^{5}$
, the flow is laminar and the period of reversal is definite. At
![]() $Ra=10^{7}$
, the flow is chaotic or turbulent with random periods of reversal. As shown by the inset closeups, at
$Ra=10^{7}$
, the flow is chaotic or turbulent with random periods of reversal. As shown by the inset closeups, at
![]() $Ra=7\times 10^{5}$
, the flow reversals only include pattern
$Ra=7\times 10^{5}$
, the flow reversals only include pattern
![]() $P_{11}$
which circulates clockwise, counter-clockwise and back (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2013). At
$P_{11}$
which circulates clockwise, counter-clockwise and back (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2013). At
![]() $Ra=10^{7}$
, flow pattern
$Ra=10^{7}$
, flow pattern
![]() $P_{12}$
sometimes appears, which has been recently reported by Podvin & Sergent (Reference Podvin and Sergent2015). In other words, the process of flow reversals in this case contains two flow patterns
$P_{12}$
sometimes appears, which has been recently reported by Podvin & Sergent (Reference Podvin and Sergent2015). In other words, the process of flow reversals in this case contains two flow patterns
![]() $P_{11}$
and
$P_{11}$
and
![]() $P_{12}$
.
$P_{12}$
.

Figure 3. Time evolution of vertical velocity component at
![]() $(y,z)=(0.1,0.5)$
. (a)
$(y,z)=(0.1,0.5)$
. (a)
![]() $Ra=7\times 10^{5}$
,
$Ra=7\times 10^{5}$
,
![]() ${\it\epsilon}=0.4$
; (b)
${\it\epsilon}=0.4$
; (b)
![]() $Ra=10^{7}$
,
$Ra=10^{7}$
,
![]() ${\it\epsilon}=0.4$
. Green solid diamonds correspond to the closeups near them. In (a), times for the two closeups are 1560 and 3270. In (b), times for the three closeups are 1250, 6250 and 18 750. Corresponding flow animations are shown in supplementary movies 1 and 2, available at http://dx.doi.org/10.1017/jfm.2016.338.
${\it\epsilon}=0.4$
. Green solid diamonds correspond to the closeups near them. In (a), times for the two closeups are 1560 and 3270. In (b), times for the three closeups are 1250, 6250 and 18 750. Corresponding flow animations are shown in supplementary movies 1 and 2, available at http://dx.doi.org/10.1017/jfm.2016.338.

Figure 4. Snapshots of four characteristic temperature fields during a half-period of a flow reversal. Red indicates hot fluid and blue cold fluid. Black arrows represent velocity vectors.
![]() $Ra=10^{7}$
,
$Ra=10^{7}$
,
![]() ${\it\epsilon}=0.4$
and the time is near
${\it\epsilon}=0.4$
and the time is near
![]() $t=17\,000$
in figure 3(b).
$t=17\,000$
in figure 3(b).
3.2 The mechanism of growth of the cold corner roll
3.2.1 Kinematics of reversals
In the work of Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), flow reversals occur due to the growth in size of corner rolls. The flow satisfies top-down symmetry under OB approximation, two diagonally arranged corner rolls grow simultaneously and merge as a new LSC, and finally the preceding LSC is then divided into two new corner rolls (see also Chandra & Verma Reference Chandra and Verma2013). When NOB effects are included, the top-down symmetry breaks, which greatly influences the behaviour of large-scale dynamics and consequently flow reversal. Figure 4 shows a half-period of flow reversal for
![]() $Ra=10^{7}$
and
$Ra=10^{7}$
and
![]() ${\it\epsilon}=0.4$
. It is found that only the top-right corner roll in figure 4(a), which is larger in size and more energetic than the bottom-left one, grows alone and eventually replaces the LSC. The preceding LSC is divided into two parts. One merges with the existing left hot corner roll and both of them die away finally. The other shrinks to a new hot corner roll near the right wall. Compared with the OB case, two major differences in the reversal process have been identified in the NOB case. On the one hand, the hot corner roll with comparatively small size is weak and no visible expansion is observed. This is caused by both buoyancy reduction and larger viscous dissipation near the bottom wall due to the higher temperature. On the other hand, only the single cold corner roll grows and when it reaches the opposite wall, the buildup of a new cold corner roll can be seen in figure 4(b), which is caused by adverse pressure gradient. As seen in figure 4(c), a portion of descending hot plume is observed near the right wall. Huang & Zhou (Reference Huang and Zhou2013) found that there exists strong counter-gradient local heat flux with a magnitude much larger than the global Nusselt number
${\it\epsilon}=0.4$
. It is found that only the top-right corner roll in figure 4(a), which is larger in size and more energetic than the bottom-left one, grows alone and eventually replaces the LSC. The preceding LSC is divided into two parts. One merges with the existing left hot corner roll and both of them die away finally. The other shrinks to a new hot corner roll near the right wall. Compared with the OB case, two major differences in the reversal process have been identified in the NOB case. On the one hand, the hot corner roll with comparatively small size is weak and no visible expansion is observed. This is caused by both buoyancy reduction and larger viscous dissipation near the bottom wall due to the higher temperature. On the other hand, only the single cold corner roll grows and when it reaches the opposite wall, the buildup of a new cold corner roll can be seen in figure 4(b), which is caused by adverse pressure gradient. As seen in figure 4(c), a portion of descending hot plume is observed near the right wall. Huang & Zhou (Reference Huang and Zhou2013) found that there exists strong counter-gradient local heat flux with a magnitude much larger than the global Nusselt number
![]() $Nu$
. Two mechanisms were proposed to be responsible for the local reverse heat flux. One is due to bulk dynamics and the other comes from the competition between LSC and corner rolls. It is the first mechanism that is recognized presently. This descending hot plume forced by the velocity field originated from the newly formed bulk produces counter-gradient local heat flux which results in even negative average
$Nu$
. Two mechanisms were proposed to be responsible for the local reverse heat flux. One is due to bulk dynamics and the other comes from the competition between LSC and corner rolls. It is the first mechanism that is recognized presently. This descending hot plume forced by the velocity field originated from the newly formed bulk produces counter-gradient local heat flux which results in even negative average
![]() $Nu$
(Chandra & Verma Reference Chandra and Verma2013; Yanagisawa, Hamano & Sakuraba Reference Yanagisawa, Hamano and Sakuraba2015; Huang & Xia Reference Huang and Xia2016).
$Nu$
(Chandra & Verma Reference Chandra and Verma2013; Yanagisawa, Hamano & Sakuraba Reference Yanagisawa, Hamano and Sakuraba2015; Huang & Xia Reference Huang and Xia2016).

Figure 5. (a) Distribution of dilation defined by equation (2.6); only the field of the top-left quarter of the box is shown.
![]() $Ra=10^{7}$
,
$Ra=10^{7}$
,
![]() ${\it\epsilon}=0.4$
. (b) Sketch of th control volume related to (a). The time is the same as figure 4(d). Dashed lines are contours of vorticity density of zero value and roughly serve as dividing lines between LSC and corner rolls.
${\it\epsilon}=0.4$
. (b) Sketch of th control volume related to (a). The time is the same as figure 4(d). Dashed lines are contours of vorticity density of zero value and roughly serve as dividing lines between LSC and corner rolls.
3.2.2 Physical mechanism from dynamics of vorticity transport
As aforementioned, the growth of the single cold corner roll induces flow reversals when NOB effects are included, but the physical mechanisms corresponding to the corner roll growth have not yet been analysed. In this subsection, we attempt to understand the detailed mechanisms of growth of the cold corner roll from the perspective of vortex dynamics. First, based on the low-Mach-number momentum equations (2.2) and Reynolds transport theorem, we derive the vorticity transport equation in the NOB case. It is believed that vorticity in corner rolls and LSC is in dynamic balance under OB approximation. And thus possibly the balance is broken by vorticity generation in corner rolls when flow reversals occur with NOB effects. Our aim is to pinpoint which terms in this equation are dominant for the vorticity generation in the corner roll. The vorticity transport equation can be expressed as
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\partial }{\partial t}\int _{V_{0}}\,\text{d}V{\it\Omega}_{i} & = & \displaystyle \underbrace{-\oint _{S_{0}}n_{j}\,\text{d}S{\it\Omega}_{i}u_{j}}_{\text{I}}\underbrace{-\int _{V_{0}}\,\text{d}V{\it\Omega}_{i}\partial _{j}u_{j}}_{\text{II}}\underbrace{-\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}T\partial _{k}{\rm\pi}}_{\text{III}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\underbrace{\left(\frac{Pr}{Ra}\right)^{0.5}\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}(T\partial _{l}{\it\tau}_{lk})}_{\text{IV}}\underbrace{-\frac{1}{2{\it\epsilon}}\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}Tn_{k}}_{\text{V}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\partial }{\partial t}\int _{V_{0}}\,\text{d}V{\it\Omega}_{i} & = & \displaystyle \underbrace{-\oint _{S_{0}}n_{j}\,\text{d}S{\it\Omega}_{i}u_{j}}_{\text{I}}\underbrace{-\int _{V_{0}}\,\text{d}V{\it\Omega}_{i}\partial _{j}u_{j}}_{\text{II}}\underbrace{-\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}T\partial _{k}{\rm\pi}}_{\text{III}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\underbrace{\left(\frac{Pr}{Ra}\right)^{0.5}\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}(T\partial _{l}{\it\tau}_{lk})}_{\text{IV}}\underbrace{-\frac{1}{2{\it\epsilon}}\int _{V_{0}}\,\text{d}V\frac{1}{T}\unicode[STIX]{x1D626}_{ijk}\partial _{j}Tn_{k}}_{\text{V}},\end{eqnarray}$$
where
![]() $S_{0}$
and
$S_{0}$
and
![]() $V_{0}$
are the control surface and volume in figure 5(b). The control volume in (3.1) is roughly surrounded by the zero-value vorticity lines near the top-left corner and two other straight lines
$V_{0}$
are the control surface and volume in figure 5(b). The control volume in (3.1) is roughly surrounded by the zero-value vorticity lines near the top-left corner and two other straight lines
![]() $y\approx 0.35$
and
$y\approx 0.35$
and
![]() $z\approx 0.75$
. Since 2D RBC is considered, the term ‘control volume’ is actually a fixed area and
$z\approx 0.75$
. Since 2D RBC is considered, the term ‘control volume’ is actually a fixed area and
![]() $S_{0}$
the line surrounding it. With no stretching and tilting of the vortex filament,
$S_{0}$
the line surrounding it. With no stretching and tilting of the vortex filament,
![]() ${\it\Omega}_{i}={\it\rho}{\it\omega}_{i}$
is the vorticity density with
${\it\Omega}_{i}={\it\rho}{\it\omega}_{i}$
is the vorticity density with
![]() $i=1$
in 2D simulation.
$i=1$
in 2D simulation.
![]() $\unicode[STIX]{x1D626}_{ijk}$
is the permutation tensor. The left integral term is the time rate of change of total vorticity surrounded by
$\unicode[STIX]{x1D626}_{ijk}$
is the permutation tensor. The left integral term is the time rate of change of total vorticity surrounded by
![]() $S_{0}$
. On the right-hand side of the equality, term I means vorticity transport by convection; term II represents the change of vorticity by dilation or compressibility, vanishing under the OB limit; term III is the interaction of gradient of temperature and hydrodynamic pressure, i.e. baroclinity; term IV is the vorticity diffusion by viscous force; and the last term V indicates the vorticity generation by buoyancy force.
$S_{0}$
. On the right-hand side of the equality, term I means vorticity transport by convection; term II represents the change of vorticity by dilation or compressibility, vanishing under the OB limit; term III is the interaction of gradient of temperature and hydrodynamic pressure, i.e. baroclinity; term IV is the vorticity diffusion by viscous force; and the last term V indicates the vorticity generation by buoyancy force.

Figure 6. Intensities of contributions to the time rate of change of vorticity in the control volume in ten snapshots. The intensities are normalized by the grey area in figure 5(b) for integration.
![]() $Ra=10^{7}$
,
$Ra=10^{7}$
,
![]() ${\it\epsilon}=0.4$
.
${\it\epsilon}=0.4$
.
Figure 5(a) shows distributions of dilation for
![]() $Ra=10^{7}$
with
$Ra=10^{7}$
with
![]() ${\it\epsilon}=0.4$
. LSC and corner rolls could be divided by black-dashed auxiliary vorticity contour lines with zero value. Qualitatively, term I becomes stronger when the Rayleigh number increases and subsequently more plumes detach from the unstable corner roll. For term II, the maximum and minimum regions of dilation in figure 5(a), denoted ‘1’, ‘2’ and ‘3’, are all approximately within the corner roll. The zero contour line of vorticity density goes through ‘1’. The maximum ‘2’ and minimum ‘3’ are near each other, and thus their contributions would approximately offset each other. Since low-Mach-number flow with large temperature difference is barotropic, term III, baroclinity, may possibly change with temperature gradient. The contribution should be specified quantitatively. Term IV, associated with viscosity force, is always negative, corresponding to the vorticity diffusion and dissipation. When the Rayleigh number increases, the viscous effect decreases and concentrates near the wall and the thin region between the corner rolls and LSC. The last term, V, shows the interaction between gravity and temperature gradient. When NOB effects become stronger, it can be affected by
${\it\epsilon}=0.4$
. LSC and corner rolls could be divided by black-dashed auxiliary vorticity contour lines with zero value. Qualitatively, term I becomes stronger when the Rayleigh number increases and subsequently more plumes detach from the unstable corner roll. For term II, the maximum and minimum regions of dilation in figure 5(a), denoted ‘1’, ‘2’ and ‘3’, are all approximately within the corner roll. The zero contour line of vorticity density goes through ‘1’. The maximum ‘2’ and minimum ‘3’ are near each other, and thus their contributions would approximately offset each other. Since low-Mach-number flow with large temperature difference is barotropic, term III, baroclinity, may possibly change with temperature gradient. The contribution should be specified quantitatively. Term IV, associated with viscosity force, is always negative, corresponding to the vorticity diffusion and dissipation. When the Rayleigh number increases, the viscous effect decreases and concentrates near the wall and the thin region between the corner rolls and LSC. The last term, V, shows the interaction between gravity and temperature gradient. When NOB effects become stronger, it can be affected by
![]() $T_{,i}/2{\it\epsilon}$
and the reciprocal of temperature
$T_{,i}/2{\it\epsilon}$
and the reciprocal of temperature
![]() $1/T$
. The coefficient
$1/T$
. The coefficient
![]() $1/T$
of terms III and V introduces some extent of asymmetry between the diagonally arranged top and bottom corner rolls. The asymmetry in term IV is
$1/T$
of terms III and V introduces some extent of asymmetry between the diagonally arranged top and bottom corner rolls. The asymmetry in term IV is
![]() ${\it\mu}$
in
${\it\mu}$
in
![]() ${\it\tau}_{ij}$
rather than
${\it\tau}_{ij}$
rather than
![]() $1/T$
.
$1/T$
.
To quantify the contributions of the five terms in (3.1) to the time rate of change of vorticity, we compute their normalized intensities in ten snapshots at
![]() $Ra=10^{7}$
with
$Ra=10^{7}$
with
![]() ${\it\epsilon}=0.4$
in figure 6. Ten snapshots with an equal time interval are carefully chosen to ensure that they are all at the initial phase of a flow reversal. Compared to the duration of growth of corner rolls, the ten snapshots are taken within a short time. In general, terms IV and V are dominant. From flow fields, term I is found to be related to the oscillations of unstable corner rolls where plume detachment from the corner rolls by convection causes vorticity and energy loss. The plume detachment could also be found in the OB case (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Plume detachment occurs frequently, which could interrupt the growth of corner rolls whether or not NOB effects are included. In NOB cases, term II is small and negligible, which is consistent with the previous qualitative analysis. Term III is of an order of magnitude of 0.01 and thus can be neglected as well. This is because the temperature gradient within the cold corner rolls may still be small and so is the gradient of velocity, although
${\it\epsilon}=0.4$
in figure 6. Ten snapshots with an equal time interval are carefully chosen to ensure that they are all at the initial phase of a flow reversal. Compared to the duration of growth of corner rolls, the ten snapshots are taken within a short time. In general, terms IV and V are dominant. From flow fields, term I is found to be related to the oscillations of unstable corner rolls where plume detachment from the corner rolls by convection causes vorticity and energy loss. The plume detachment could also be found in the OB case (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). Plume detachment occurs frequently, which could interrupt the growth of corner rolls whether or not NOB effects are included. In NOB cases, term II is small and negligible, which is consistent with the previous qualitative analysis. Term III is of an order of magnitude of 0.01 and thus can be neglected as well. This is because the temperature gradient within the cold corner rolls may still be small and so is the gradient of velocity, although
![]() ${\it\epsilon}$
is increased up to 0.4.
${\it\epsilon}$
is increased up to 0.4.

Figure 7. Buoyancy force
![]() $f_{i}=\displaystyle ({\it\rho}-1)n_{i}/2{\it\epsilon}$
varying with height
$f_{i}=\displaystyle ({\it\rho}-1)n_{i}/2{\it\epsilon}$
varying with height
![]() $z$
providing linear distribution of temperature
$z$
providing linear distribution of temperature
![]() $T=1+{\it\epsilon}(1-2z)$
. The black hollow up-triangles represent the distribution of equivalent buoyancy force with respect to the reference state with modelled gravity acceleration. The red solid line is to show the case under OB approximation for comparison.
$T=1+{\it\epsilon}(1-2z)$
. The black hollow up-triangles represent the distribution of equivalent buoyancy force with respect to the reference state with modelled gravity acceleration. The red solid line is to show the case under OB approximation for comparison.
As stated previously, the interesting difference is that only the cold corner roll grows, while the hot corner roll is found to be nearly quiescent. As we can see in figure 6, terms IV and V are two decisive factors. It is obvious that term V is always positive and thus of vital importance in vorticity generation. The asymmetries caused by
![]() $1/T$
(isobaric thermal expansion coefficient
$1/T$
(isobaric thermal expansion coefficient
![]() ${\it\alpha}=1/T$
) in this term other than
${\it\alpha}=1/T$
) in this term other than
![]() $1/T_{0}=1$
under OB approximation may play key roles in the growth of the cold corner roll. Term V originates from the buoyancy force
$1/T_{0}=1$
under OB approximation may play key roles in the growth of the cold corner roll. Term V originates from the buoyancy force
![]() $f_{i}={\it\delta}{\it\rho}n_{i}/2{\it\epsilon}$
in (2.2). Under the OB approximation,
$f_{i}={\it\delta}{\it\rho}n_{i}/2{\it\epsilon}$
in (2.2). Under the OB approximation,
![]() $f_{i}=-{\it\delta}Tn_{i}/2{\it\epsilon}$
is proportional to
$f_{i}=-{\it\delta}Tn_{i}/2{\it\epsilon}$
is proportional to
![]() ${\it\delta}T$
while this relation does not hold in the NOB case
${\it\delta}T$
while this relation does not hold in the NOB case
![]() $f_{i}=(1/T-1)n_{i}/2{\it\epsilon}\approx (-{\it\delta}T+{\it\delta}^{2}T)n_{i}/2{\it\epsilon}$
with
$f_{i}=(1/T-1)n_{i}/2{\it\epsilon}\approx (-{\it\delta}T+{\it\delta}^{2}T)n_{i}/2{\it\epsilon}$
with
![]() ${\it\delta}T=T-1$
. In figure 7, due to NOB-effects-led asymmetry, the buoyancy force has increased by up to 150 % on the cold wall and reduced by approximately 40 % near the hot wall. Equivalently, we modified the gravity acceleration to model a similar buoyancy force based on the OB approximation. In figure 7, the up-triangular symbols display a buoyancy force to model that of
${\it\delta}T=T-1$
. In figure 7, due to NOB-effects-led asymmetry, the buoyancy force has increased by up to 150 % on the cold wall and reduced by approximately 40 % near the hot wall. Equivalently, we modified the gravity acceleration to model a similar buoyancy force based on the OB approximation. In figure 7, the up-triangular symbols display a buoyancy force to model that of
![]() ${\it\epsilon}=0.4$
. The expression of acceleration is
${\it\epsilon}=0.4$
. The expression of acceleration is
![]() $f_{i}=-{\it\delta}T(n_{i}+dg_{i})/2{\it\epsilon}$
with
$f_{i}=-{\it\delta}T(n_{i}+dg_{i})/2{\it\epsilon}$
with
![]() $dg_{i}=-2.0{\it\chi}z+{\it\chi}$
in which
$dg_{i}=-2.0{\it\chi}z+{\it\chi}$
in which
![]() ${\it\chi}={\it\chi}_{1}=0.3$
when
${\it\chi}={\it\chi}_{1}=0.3$
when
![]() $z\leqslant 0.5$
and
$z\leqslant 0.5$
and
![]() ${\it\chi}={\it\chi}_{2}=0.7$
when
${\it\chi}={\it\chi}_{2}=0.7$
when
![]() $z>0.5$
. By adding this equivalent buoyancy force to the OB case, not surprisingly, we reproduced flow reversals (see supplementary movie 3). In this case, the hot corner roll still grows at a smaller rate than its cold counterpart, although the buoyancy force is reduced near the hot wall. The modified buoyancy force by NOB effects increases the probability of the balance breaking (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Liu et al.
Reference Liu, Zhang and others2008) between the corner roll and LSC, and thus leads to flow reversal. In addition, the variation in viscous dissipation in term IV by NOB effects, as seen in figure 1, is also very important for the growth of the cold corner roll. Near the hot wall, viscous dissipation is largely enhanced, which helps to suppress the growth of the hot corner roll. Conversely, the viscous dissipation near the cold wall is considerably attenuated, which promotes the growth of the cold corner roll. Moreover, it is noteworthy that thermal conductivity
$z>0.5$
. By adding this equivalent buoyancy force to the OB case, not surprisingly, we reproduced flow reversals (see supplementary movie 3). In this case, the hot corner roll still grows at a smaller rate than its cold counterpart, although the buoyancy force is reduced near the hot wall. The modified buoyancy force by NOB effects increases the probability of the balance breaking (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Liu et al.
Reference Liu, Zhang and others2008) between the corner roll and LSC, and thus leads to flow reversal. In addition, the variation in viscous dissipation in term IV by NOB effects, as seen in figure 1, is also very important for the growth of the cold corner roll. Near the hot wall, viscous dissipation is largely enhanced, which helps to suppress the growth of the hot corner roll. Conversely, the viscous dissipation near the cold wall is considerably attenuated, which promotes the growth of the cold corner roll. Moreover, it is noteworthy that thermal conductivity
![]() $k$
is also temperature-dependent. Although thermal conductivity
$k$
is also temperature-dependent. Although thermal conductivity
![]() $k$
does not appear explicitly in vorticity transport equation (3.1), as stated by Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), small
$k$
does not appear explicitly in vorticity transport equation (3.1), as stated by Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010), small
![]() $k$
near the cold wall has small thermal dissipation similar to
$k$
near the cold wall has small thermal dissipation similar to
![]() ${\it\mu}$
. In figure 1(b), the Prandtl number does not change much and is always smaller than one. Therefore the effect of change of the Prandtl number could probably be ignored.
${\it\mu}$
. In figure 1(b), the Prandtl number does not change much and is always smaller than one. Therefore the effect of change of the Prandtl number could probably be ignored.
3.2.3 Mass transport and the role of BLs
In the previous section, we conclude that the asymmetry of isobaric thermal expansion coefficient
![]() ${\it\alpha}=1/T$
is the point that results in the growth of the cold corner roll. A very important issue, from the point of view of conservation, is that the process of mass transport between corner rolls and other regimes is still unknown. Figure 8 shows the distribution of density near the top-left corner and the trajectories of two ‘tracer particles’. The trajectories are computed by the predictor–corrector method with accuracy of second order, which is consistent with that of the present code. The corner roll and LSC interact with the top wall and two parts of the BLs form with the joint point marked ‘O’. When the corner roll grows, point ‘O’ moves rightward. Figure 8(a) shows that the density in the cold corner roll changes from
${\it\alpha}=1/T$
is the point that results in the growth of the cold corner roll. A very important issue, from the point of view of conservation, is that the process of mass transport between corner rolls and other regimes is still unknown. Figure 8 shows the distribution of density near the top-left corner and the trajectories of two ‘tracer particles’. The trajectories are computed by the predictor–corrector method with accuracy of second order, which is consistent with that of the present code. The corner roll and LSC interact with the top wall and two parts of the BLs form with the joint point marked ‘O’. When the corner roll grows, point ‘O’ moves rightward. Figure 8(a) shows that the density in the cold corner roll changes from
![]() $1.6$
to approximately
$1.6$
to approximately
![]() $1$
. The initial positions of the tracer particles are located on either side of the joint point ‘O’. In figure 8(b), tracer particle ‘A’ is initially located in the left part of the BL and we find that it always circles in the corner roll and is superimposed by a small velocity pointing to LSC, corresponding to the expansion of the corner roll. The tracer particle ‘B’ is located initially in the right part of the BL related to LSC. It is found that the tracer particle ‘B’ moves rightward initially (black arrow in figure 8(c)) and circles the bulk. After six rounds, when the time is approximately 390 in figure 8(c), tracer particle ‘B’ turns left into the corner roll at the seventh round. At this moment, the flow field shows us that the joint point ‘O’ has a horizontal location
$1$
. The initial positions of the tracer particles are located on either side of the joint point ‘O’. In figure 8(b), tracer particle ‘A’ is initially located in the left part of the BL and we find that it always circles in the corner roll and is superimposed by a small velocity pointing to LSC, corresponding to the expansion of the corner roll. The tracer particle ‘B’ is located initially in the right part of the BL related to LSC. It is found that the tracer particle ‘B’ moves rightward initially (black arrow in figure 8(c)) and circles the bulk. After six rounds, when the time is approximately 390 in figure 8(c), tracer particle ‘B’ turns left into the corner roll at the seventh round. At this moment, the flow field shows us that the joint point ‘O’ has a horizontal location
![]() $y\approx 0.5$
so that particle ‘B’ just after the six rounds has been contained in the left part of the BL. The trajectory of tracer particle ‘B’ clearly shows how the fluid parcel transports from LSC into the cold corner roll. This process could partially explain why the cold corner roll grows from the point of view of mass conservation. Then, it is easy to imagine that when the joint point ‘O’ moves to
$y\approx 0.5$
so that particle ‘B’ just after the six rounds has been contained in the left part of the BL. The trajectory of tracer particle ‘B’ clearly shows how the fluid parcel transports from LSC into the cold corner roll. This process could partially explain why the cold corner roll grows from the point of view of mass conservation. Then, it is easy to imagine that when the joint point ‘O’ moves to
![]() $y=1$
, all the fluid parcels in the BL would transport into the cold corner roll and the preceding bulk could eventually be replaced. Moreover, the asymmetry by NOB effects manifests itself as a thinner BL near the cold upper plate. We could speculate that the relatively small viscosity there helps to transport mass from the BL to the corner roll.
$y=1$
, all the fluid parcels in the BL would transport into the cold corner roll and the preceding bulk could eventually be replaced. Moreover, the asymmetry by NOB effects manifests itself as a thinner BL near the cold upper plate. We could speculate that the relatively small viscosity there helps to transport mass from the BL to the corner roll.

Figure 8. (a) Distribution of density near top-left corner. (b) Trajectory of ‘tracer particle’ A for time duration of 400 dimensionless time units. (c) Trajectory of ‘tracer particle’ B for time duration of 400 dimensionless time units.
![]() $Ra=7\times 10^{5}$
,
$Ra=7\times 10^{5}$
,
![]() ${\it\epsilon}=0.4$
. Initial coordinates of A and B are
${\it\epsilon}=0.4$
. Initial coordinates of A and B are
![]() $y=0.1978$
,
$y=0.1978$
,
![]() $z=0.9862$
and
$z=0.9862$
and
![]() $y=0.3974$
,
$y=0.3974$
,
![]() $z=0.9862$
, respectively shown as black squares. The initial locations are also shown in (b) and (c) and the nearby black arrows reveal the moving directions at the beginning.
$z=0.9862$
, respectively shown as black squares. The initial locations are also shown in (b) and (c) and the nearby black arrows reveal the moving directions at the beginning.
4 Summary and conclusion
In this work, by employing low-Mach-number NS equations, we focus on studying flow reversals in 2D RBC, considering the NOB effects caused by large temperature difference. In OB cases, no flow reversal is found in the present parameter space. Interestingly, once the NOB effects are included, flow reversals are observed for certain ranges of Rayleigh number. Moreover, it is found that the flow reversal occurring at low
![]() $Ra$
usually has a definitive period, while this period tends to be random with increasing
$Ra$
usually has a definitive period, while this period tends to be random with increasing
![]() $Ra$
. In general, as the temperature differential
$Ra$
. In general, as the temperature differential
![]() ${\it\epsilon}$
increases, the parameter range of
${\it\epsilon}$
increases, the parameter range of
![]() $Ra$
in which the corner roll grows and flow reversals occur is widened. This can be viewed as a symmetry restoration process. Phenomenally, in NOB cases, all flow reversals are led by growth of the single cold corner roll, which is quite different from that in OB cases. From the perspective of vortex dynamics, we find that the asymmetries of buoyancy force by variable isobaric thermal coefficient, temperature-dependent viscosity are the major reason why only the cold corner roll grows and eventually replaces the LSC, resulting in flow reversals. In the NOB case, the buoyancy force is increased and viscous dissipation is greatly reduced near the cold wall, both of which are beneficial for the growth of the cold corner roll and thus increase the probability of flow reversals. Lastly, from examining the trajectories of tracer particles, we find that the rightward-moving joint point separating the two sections of BLs near the cold wall plays an important role in mass transport from LSC to corner roll.
$Ra$
in which the corner roll grows and flow reversals occur is widened. This can be viewed as a symmetry restoration process. Phenomenally, in NOB cases, all flow reversals are led by growth of the single cold corner roll, which is quite different from that in OB cases. From the perspective of vortex dynamics, we find that the asymmetries of buoyancy force by variable isobaric thermal coefficient, temperature-dependent viscosity are the major reason why only the cold corner roll grows and eventually replaces the LSC, resulting in flow reversals. In the NOB case, the buoyancy force is increased and viscous dissipation is greatly reduced near the cold wall, both of which are beneficial for the growth of the cold corner roll and thus increase the probability of flow reversals. Lastly, from examining the trajectories of tracer particles, we find that the rightward-moving joint point separating the two sections of BLs near the cold wall plays an important role in mass transport from LSC to corner roll.
Acknowledgements
The authors appreciate the reviewers’ constructive comments and suggestions that helped to improve the manuscript. We thank Dr B. Wang at Durham University for helpful discussions. This work was supported by the National Natural Science Foundation of China under grant nos. 11572314, 11232011 and 11402262, and the Fundamental Research Funds for the Central Universities.
Supplementary movies
Supplementary movies are available at http://dx.doi.org/10.1017/jfm.2016.338.