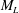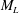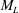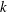1. Introduction
The continued existence of magnetic fields in most astrophysical systems is thought to be due to dynamo action which converts kinetic energy of the plasma into magnetic energy. In particular, fluctuation dynamos are generic, and operate with minimal requirements of the underlying fluid flow. A random flow with modest magnetic Reynolds number
$R_{M}\sim 100$
is sufficient to activate the fluctuation dynamo. Here
$R_{M}=u/(q{\it\eta})$
with
$u$
and
$q$
respectively the characteristic velocity and wavenumber of the flow and
${\it\eta}$
the resistivity. Hence fluctuation dynamos are considered to be ubiquitous in all astrophysical plasmas.
The analytical theory for the fluctuation dynamo was given by Kazantsev (Reference Kazantsev1967). A dynamical equation for the two-point magnetic correlator was derived by using a simple model for the velocity field which is delta-correlated in time. This assumption of delta-correlation allows one to convert the stochastic induction equation for the magnetic field to a partial differential equation in real space for the longitudinal magnetic correlation function
$M_{L}(r,t)$
. Its solution clearly showed for the first time that a random flow with modest
$R_{M}$
can lead to the growth of the field. Kazantsev then also predicted that the magnetic power spectrum for a single scale or a large magnetic Prandtl number,
$P_{M}$
, turbulent flow scales asymptotically as
$M(k)\propto k^{3/2}$
, for
$q\ll k\ll k_{{\it\eta}}$
, with
$k_{{\it\eta}}$
the wavenumber at which resistive dissipation becomes important. This spectrum is known as the Kazantsev spectrum.
Following the seminal work of Kazantsev (Reference Kazantsev1967), there has been considerable interest in fluctuation dynamos, in terms of theoretical developments, in terms of their direct simulation and in terms of various astrophysical applications (Molchanov, Ruzmaĭkin & Sokolov Reference Molchanov, Ruzmaĭkin and Sokolov1985; Zeldovich, Ruzmaikin & Sokoloff Reference Zeldovich, Ruzmaikin and Sokoloff1990; Kulsrud & Anderson Reference Kulsrud and Anderson1992; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin1997; Subramanian Reference Subramanian1997, Reference Subramanian1999; Chertkov et al.
Reference Chertkov, Falkovich, Kolokolov and Vergassola1999; Haugen, Brandenburg & Dobler Reference Haugen, Brandenburg and Dobler2004; Schekochihin et al.
Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004, Reference Schekochihin, Haugen, Brandenburg, Cowley, Maron and McWilliams2005; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Enßlin & Vogt Reference Enßlin and Vogt2006; Subramanian, Shukurov & Haugen Reference Subramanian, Shukurov and Haugen2006; Cho et al.
Reference Cho, Vishniac, Beresnyak, Lazarian and Ryu2009; Malyshkin & Boldyrev Reference Malyshkin and Boldyrev2010; Federrath et al.
Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011; Tobias, Cattaneo & Boldyrev Reference Tobias, Cattaneo and Boldyrev2011; Beresnyak Reference Beresnyak2012; Brandenburg, Sokoloff & Subramanian Reference Brandenburg, Sokoloff and Subramanian2012; Schober et al.
Reference Schober, Schleicher, Bovino and Klessen2012; Sur et al.
Reference Sur, Federrath, Schleicher, Banerjee and Klessen2012; Bhat & Subramanian Reference Bhat and Subramanian2013). These works have clearly demonstrated that random (or turbulent) flows in a conducting plasma, with
$R_{M}>R_{crit}\sim 30{-}500$
, lead to the amplification of magnetic fields on the fast eddy turnover time scale, usually much smaller than the age of the astrophysical system. The value of
$R_{crit}$
depends on
$P_{M}={\it\nu}/{\it\eta}$
, where
${\it\nu}$
is the viscosity, and could even depend on the forcing wavenumber (Subramanian & Brandenburg Reference Subramanian and Brandenburg2014). This rapid growth implies that fluctuation dynamos are crucial for the early generation of magnetic fields in primordial stars, galaxies and galaxy clusters. It is therefore important to obtain a clear understanding of the fluctuation dynamo.
Note that the feature of delta-correlation in time, assumed by Kazantsev (Reference Kazantsev1967), is not realistic in turbulent astrophysical plasmas. There the correlation time,
${\it\tau}$
, is expected to be at least of the order of the smallest eddy turnover time. Thus, its important to understand the effects of finite time correlation on the fluctuation dynamo. This is the main motivation of the present work.
The effect of having a finite-
${\it\tau}$
on the magnetic energy growth has been considered by Chandran (Reference Chandran1997), while Schekochihin & Kulsrud (Reference Schekochihin and Kulsrud2001) examined its consequences for the single-point probability distribution function in the ideal limit. The correction to the evolution of the two-point correlator due to having a finite-
${\it\tau}$
was considered by Kleeorin, Rogachevskii & Sokoloff (Reference Kleeorin, Rogachevskii and Sokoloff2002); they, however, seem to have kept only a subset of the terms we derive here. It was shown by Mason et al. (Reference Mason, Malyshkin, Boldyrev and Cattaneo2011) that the results from simulations involving finite-
${\it\tau}$
velocity flows can be matched to the predictions using the Kazantsev equation provided the diffusivity spectrum is appropriately filtered out at small scales. An analytic understanding of the magnetic spectrum at finite-
${\it\tau}$
is, however, still lacking.
The present work uses random flows with finite time correlation, known as renewing (or renovating) flows, to develop an analytic generalization of the results of Kazantsev (Reference Kazantsev1967) to include the effects of a finite correlation time. Zeldovich et al. (Reference Zeldovich, Molchanov, Ruzmaikin and Sokoloff1988) had used renewing flows for studying the diffusion of scalars and the generation of vectors in random flows. Such flows have also been used to study the effect of finite correlation time on mean field dynamos (Dittrich et al.
Reference Dittrich, Molchanov, Sokolov and Ruzmaikin1984; Gilbert & Bayly Reference Gilbert and Bayly1992; Kolekar, Subramanian & Sridhar Reference Kolekar, Subramanian and Sridhar2012). In an earlier letter (Bhat & Subramanian Reference Bhat and Subramanian2014, hereafter BS14), we gave a brief account of our work on fluctuation dynamos using renewing flows, emphasizing an intriguing result that the Kazantsev spectrum is in fact preserved even for such finite-
${\it\tau}$
. In the present paper, we present our detailed derivations of the generalized Kazantsev equation and the results in BS14, as well as some new WKBJ analysis. In the next section, we formulate the basic problem of fluctuation dynamos in renewing flows. The detailed derivation of the evolution equation for
$M_{L}(r,t)$
which incorporates finite-
${\it\tau}$
effects, to the leading order, is given in § 3. Scaling and WKBJ analysis of this generalized evolution equation are taken up in § 4, and we end with a discussion of our results.
2. Fluctuation dynamos in renewing flows
The evolution of magnetic field, in a conducting fluid with velocity
$\boldsymbol{u}$
, is given by the induction equation,
$$\begin{eqnarray}\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{{\rm\nabla}}\times (\boldsymbol{u}\times \boldsymbol{B}-{\it\eta}\boldsymbol{{\rm\nabla}}\times \boldsymbol{B}).\end{eqnarray}$$
The velocity field here is a random flow which renews itself every time interval
${\it\tau}$
(Dittrich et al.
Reference Dittrich, Molchanov, Sokolov and Ruzmaikin1984; Gilbert & Bayly Reference Gilbert and Bayly1992) and was given by Gilbert & Bayly (Reference Gilbert and Bayly1992) (GB) as
$$\begin{eqnarray}\boldsymbol{u}(\boldsymbol{x})=\boldsymbol{a}\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}+{\it\psi}),\end{eqnarray}$$
with
$\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{q}=0$
for an incompressible flow. In each time interval
$[(n-1){\it\tau},n{\it\tau}]$
:
-
(i)
${\it\psi}$
is chosen uniformly random between 0 and
$2{\rm\pi}$
; -
(ii)
$\boldsymbol{q}$
is uniformly distributed on a sphere of radius
$q=|\boldsymbol{q}|$
; -
(iii) for every fixed
$\hat{\boldsymbol{q}}=\boldsymbol{q}/q$
, the direction of
$\boldsymbol{a}$
is uniformly distributed in the plane perpendicular to
$\boldsymbol{q}$
.
Specifically, for computational ease, we modify the GB ensemble and use
$$\begin{eqnarray}a_{i}=\tilde{P}_{ij}A_{j},\quad \tilde{P}_{ij}(\hat{\boldsymbol{q}})={\it\delta}_{ij}-\hat{q}_{i}\hat{q}_{j},\end{eqnarray}$$
where
$\boldsymbol{A}$
is uniformly distributed on a sphere of radius
$A$
, and
$\tilde{P}_{ij}$
projects
$\boldsymbol{A}$
to the plane perpendicular to
$\boldsymbol{q}$
. Then, on averaging over
$a_{i}$
and using the fact that
$\boldsymbol{A}$
is independent of
$\boldsymbol{q}$
, we have
$\left\langle \boldsymbol{u}\right\rangle =0$
and
$$\begin{eqnarray}\displaystyle \langle a_{i}a_{l}\rangle & = & \displaystyle \langle a^{2}\rangle \frac{{\it\delta}_{il}}{3}=\left\langle A_{j}A_{k}\tilde{P}_{ij}\tilde{P}_{lk}\right\rangle =A^{2}\frac{{\it\delta}_{jk}}{3}\left\langle \tilde{P}_{ij}\tilde{P}_{lk}\right\rangle =\frac{A^{2}}{3}\left\langle \tilde{P}_{il}\right\rangle =\frac{2A^{2}}{3}\frac{{\it\delta}_{il}}{3}\nonumber\\ \displaystyle & \Rightarrow & \displaystyle \langle a^{2}\rangle =(2/3)(A^{2}).\end{eqnarray}$$
This modification in ensemble does not affect any result obtained using the renewing flows. Condition (i) on
${\it\psi}$
ensures statistical homogeneity, while (ii) and (iii) ensure statistical isotropy of the flow.
The magnetic field evolution in any time interval
$[(n-1){\it\tau},n{\it\tau}]$
is
$$\begin{eqnarray}B_{i}(\boldsymbol{x},n{\it\tau})=\int {\mathcal{G}}_{ij}(\boldsymbol{x},\boldsymbol{x}_{0},{\it\tau})B_{j}(\boldsymbol{x}_{0},(n-1){\it\tau})\,\text{d}^{3}\boldsymbol{x}_{0},\end{eqnarray}$$
where
${\mathcal{G}}_{ij}(\boldsymbol{x},\boldsymbol{x}_{0})$
is the Green’s function of (2.1). We define the magnetic two-point spatial correlation function as
$$\begin{eqnarray}\langle B_{j}(\boldsymbol{x},t)B_{l}(\boldsymbol{y},t)\rangle =M_{jl}(r,t),\quad \text{where }r=|\boldsymbol{r}|=|(\boldsymbol{x}-\boldsymbol{y})|,\end{eqnarray}$$
and
$\left\langle \cdot \right\rangle$
denotes an ensemble average. Here we have assumed the statistical homogeneity and isotropy of the magnetic field. Note that if the initial field is statistically homogeneous and isotropic, then this is preserved by the renewing flow as we show explicitly below. Then the evolution of the fluctuating field defined by the two-point correlation is
$$\begin{eqnarray}M_{ih}((\boldsymbol{x}-\boldsymbol{y}),n{\it\tau})=\int \tilde{{\mathcal{G}}}_{ijhl}(\boldsymbol{x},\boldsymbol{x}_{0},\boldsymbol{y},\boldsymbol{y}_{0},{\it\tau})M_{jl}((\boldsymbol{x}_{0}-\boldsymbol{y}_{0}),(n-1){\it\tau})\,\text{d}^{3}\boldsymbol{x}_{0}\,\text{d}^{3}\boldsymbol{y}_{0},\end{eqnarray}$$
where
$\tilde{{\mathcal{G}}}_{ijhl}=\left\langle {\mathcal{G}}_{ij}(\boldsymbol{x},\boldsymbol{x}_{0},{\it\tau}){\mathcal{G}}_{hl}(\boldsymbol{y},\boldsymbol{y}_{0},{\it\tau})\right\rangle$
. Here we could split the averaging on the right-hand side of equation between the Green’s function and the initial magnetic correlator, because the renewing nature of the flow implies that the Green’s function in the current interval is uncorrelated to the magnetic correlator from the previous interval. The renewing nature of the flow also implies that
$\tilde{{\mathcal{G}}}$
depends only on the time difference
${\it\tau}$
and not separately on the initial and final times in the interval
$[(n-1){\it\tau},n{\it\tau}]$
.
To obtain
$\tilde{{\mathcal{G}}}_{ij}(\boldsymbol{x},\boldsymbol{x}_{0},\boldsymbol{y},\boldsymbol{y}_{0},{\it\tau})$
in the renewing flow, we use the method of operator splitting as introduced by GB. The renewal time,
${\it\tau}$
, is split into two equal sub-intervals. In the first sub-interval
${\it\tau}/2$
, resistivity is neglected and the frozen field is advected with twice the original velocity. In the second sub-interval,
$\boldsymbol{u}$
is neglected and the field is diffused with twice the resistivity. This method, plausible in the small-
${\it\tau}$
limit, has been used to recover the standard mean field dynamo equations in renewing flows (Gilbert & Bayly Reference Gilbert and Bayly1992; Kolekar et al.
Reference Kolekar, Subramanian and Sridhar2012). It is further discussed in appendix A.
From the advective part of (2.1), we obtain the standard Cauchy solution, in the first sub-interval
${\it\tau}/2=t_{1}-t_{0}$
,
$$\begin{eqnarray}B_{i}(\boldsymbol{x},t_{1})=\frac{\partial x_{i}}{\partial x_{0j}}B_{j}(\boldsymbol{x}_{0},t_{0})\equiv J_{ij}(\boldsymbol{x}(\boldsymbol{x}_{0}))B_{j}(\boldsymbol{x}_{0},t_{0}).\end{eqnarray}$$
Here
$B_{j}(\boldsymbol{x}_{0},t_{0})$
is the initial field, which propagates from
$\boldsymbol{x}_{0}$
at time
$t_{0}$
, to
$\boldsymbol{x}$
at time
$t_{1}=t_{0}+{\it\tau}/2$
. In (2.2), the phase
${\it\Phi}=\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}+{\it\psi}$
is constant in time as
$\text{d}{\it\Phi}/\text{d}t=\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{u}=0$
, from the condition of incompressibility. Then at time
$t_{1}=t_{0}+{\it\tau}/2$
, we integrate
$\text{d}\boldsymbol{x}/\text{d}t=2\boldsymbol{u}$
to obtain
$$\begin{eqnarray}\boldsymbol{x}=\boldsymbol{x}_{0}+{\it\tau}\boldsymbol{u}=\boldsymbol{x}_{0}+{\it\tau}\boldsymbol{a}\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}_{0}+{\it\psi}).\end{eqnarray}$$
Thus the Jacobian is
$$\begin{eqnarray}J_{ij}(\boldsymbol{x}(\boldsymbol{x}_{0}))={\it\delta}_{ij}+{\it\tau}a_{i}q_{j}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}_{0}+{\it\psi}).\end{eqnarray}$$
It will be more convenient to work with the resulting field in Fourier space,
$$\begin{eqnarray}\hat{B}_{i}(\boldsymbol{k},t_{1})=\int J_{ij}(\boldsymbol{x}(\boldsymbol{x}_{0}))B_{j}(\boldsymbol{x}_{0},t_{0})\text{e}^{-\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}}\,\text{d}^{3}\boldsymbol{x}.\end{eqnarray}$$
Then in the second sub-interval (
$t_{1},t=t_{1}+{\it\tau}/2$
), only diffusion operates with resistivity
$2{\it\eta}$
, to give
$$\begin{eqnarray}\hat{B}_{i}(\boldsymbol{k},t)=G^{{\it\eta}}(\boldsymbol{k},{\it\tau})\hat{B}_{i}(\boldsymbol{k},t_{1})=\text{e}^{-({\it\eta}{\it\tau}\boldsymbol{k}^{2})}\hat{B}_{i}(\boldsymbol{k},t_{1}),\end{eqnarray}$$
where
$G^{{\it\eta}}$
is the resistive Green’s function. We combine (2.11) and (2.12) to derive the evolution equation for the magnetic two-point correlation function,
$$\begin{eqnarray}\langle \hat{B}_{i}(\boldsymbol{k},t)\hat{B}_{h}^{\ast }(\boldsymbol{p},t)\rangle =\text{e}^{-{\it\eta}{\it\tau}(\boldsymbol{k}^{2}+\boldsymbol{p}^{2})}\int \left\langle J_{ij}(\boldsymbol{x}_{0})J_{hl}(\boldsymbol{y}_{0})\text{e}^{-\text{i}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{y})}\right\rangle M_{jl}(\boldsymbol{r}_{0},t_{0})\,\text{d}^{3}\boldsymbol{x}\,\text{d}^{3}\boldsymbol{y}.\end{eqnarray}$$
The statistical homogeneity of the field also implies that the two-point magnetic correlator in Fourier space will be given by
$$\begin{eqnarray}\langle \hat{B}_{i}(\boldsymbol{k},t)\hat{B}_{h}^{\ast }(\boldsymbol{p},t)\rangle =(2{\rm\pi})^{3}{\it\delta}^{3}(\boldsymbol{k}-\boldsymbol{p})\hat{M}_{ih}(\boldsymbol{p},t).\end{eqnarray}$$
Then we use (2.9) to transform from
$(\boldsymbol{x},\boldsymbol{y})$
in (2.13) to
$(\boldsymbol{x}_{0},\boldsymbol{y}_{0})$
. Due to the incompressibility of the flow, the Jacobian of this transformation is unity. We also write
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}_{0}-\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{y}_{0}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}_{0}+\boldsymbol{y}_{0}\boldsymbol{\cdot }(\boldsymbol{k}-\boldsymbol{p})$
in (2.13), transform from
$(\boldsymbol{x}_{0},\boldsymbol{y}_{0})$
to a new set of variables
$(\boldsymbol{r}_{0},{\boldsymbol{y}_{0}}^{\prime }=\boldsymbol{y}_{0})$
, and integrate over
${\boldsymbol{y}_{0}}^{\prime }$
. This leads to a delta function in
$(\boldsymbol{k}-\boldsymbol{p})$
and (2.13) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{M}_{ih}(\boldsymbol{p},t)=\text{e}^{-2{\it\eta}{\it\tau}\boldsymbol{p}^{2}}\int \langle R_{ijhl}\rangle M_{jl}(\boldsymbol{r}_{0},t_{0})\text{e}^{-\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{r}_{0}}\,\text{d}^{3}\boldsymbol{r}_{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \langle R_{ijhl}\rangle =\left\langle J_{ij}(\boldsymbol{x}_{0})J_{hl}(\boldsymbol{y}_{0})\text{e}^{-\text{i}{\it\tau}(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{p})(\sin A-\sin B)}\right\rangle , & \displaystyle\end{eqnarray}$$
$A=(\boldsymbol{x}_{0}\boldsymbol{\cdot }\boldsymbol{q}+{\it\psi})$
and
$B=(\boldsymbol{y}_{0}\boldsymbol{\cdot }\boldsymbol{q}+{\it\psi})$
. Due to the statistical homogeneity of the renewing flow, we expect
$\langle R_{ijhl}\rangle$
to be only a function of
$\boldsymbol{r}_{0}$
, which we will see explicitly later. We now take the inverse Fourier transform of
$\hat{M}_{ih}(\boldsymbol{p},t)$
, 
$$\begin{eqnarray}\displaystyle M_{ih}(\boldsymbol{r},t) & = & \displaystyle \int (1-2{\it\eta}{\it\tau}\boldsymbol{p}^{2})\langle R_{ijhl}\rangle M_{jl}(\boldsymbol{r}_{0},t_{0})\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{0})}\,\text{d}^{3}\boldsymbol{r}_{0}\frac{\text{d}^{3}\boldsymbol{p}}{(2{\rm\pi})^{3}}\nonumber\\ \displaystyle & = & \displaystyle \int \left\langle R_{ijhl}\right\rangle M_{jl}(\boldsymbol{r}_{0},t_{0})\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{0})}\,\text{d}^{3}\boldsymbol{r}_{0}\frac{\text{d}^{3}\boldsymbol{p}}{(2{\rm\pi})^{3}}+2{\it\eta}{\it\tau}{\rm\nabla}^{2}M_{ih}(\boldsymbol{r},t).\end{eqnarray}$$
Here we have also expanded the exponential in the resistive Green’s function and considered only the leading-order term in
${\it\eta}$
, relevant in the independent small-
${\it\eta}$
(or
$R_{M}\gg 1$
) limit. In the resistive term of (2.17), we consider only the
${\it\tau}$
-independent term in
$\left\langle R_{ijhl}\right\rangle$
,
${\it\delta}_{ij}{\it\delta}_{hl}$
, to multiply with
$2{\it\eta}{\it\tau}\boldsymbol{p}^{2}$
since all the other terms will be of the order
${\it\eta}{\it\tau}^{2}$
or higher. (Specifically we neglect terms like
${\it\eta}{\it\tau}^{2}$
compared to
${\it\tau}^{3}$
and
${\it\tau}^{4}$
.) Then we write
$(-\boldsymbol{p}^{2})(\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{r}})$
as
${\rm\nabla}^{2}\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{r}}$
and can take
${\rm\nabla}^{2}$
out of the integral. We have also considered in appendix A the effect of reversing the operator ordering of advection and diffusion and have shown that (2.17) is still obtained. We now turn to the evaluation of
$\langle R_{ijhl}\rangle$
.
3. The generalized Kazantsev equation
Exact evaluation of
$\langle R_{ijhl}\rangle$
is difficult. However, we can motivate a Taylor series expansion of the exponential in
$\langle R_{ijhl}\rangle$
for small Strouhal number
$\mathit{St}=q|\boldsymbol{a}|{\it\tau}=qa{\it\tau}$
, as follows. Firstly, in the argument of the exponential we have
$(\sin A-\sin B)=\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0}/2)\cos ({\it\psi}+\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{R}_{0})$
, where
$\boldsymbol{R}_{0}=(\boldsymbol{x}_{0}+\boldsymbol{y}_{0})/2$
. Also, for the kinematic fluctuation dynamo, the magnetic correlation function peaks around the resistive scale
$r_{0}=|\boldsymbol{r}_{0}|\sim 1/(qR_{M}^{1/2})$
, or the spectrum peaks around
$p\sim (qR_{M}^{1/2})$
(here
$p=|\boldsymbol{p}|$
). Also
$R_{M}\sim a/(q{\it\eta})\gg 1$
. Thus,
$qr_{0}\ll 1$
and
$\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\sim \boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0}$
. Consequently the phase of the exponential in (2.16) is of order
$(pa{\it\tau}qr_{0})\sim qa{\it\tau}=\mathit{St}$
. Thus for
$\mathit{St}\ll 1$
, one can expand the exponential in (2.16) in
${\it\tau}$
. We do this retaining terms up to
${\it\tau}^{4}$
order; on keeping terms up to
${\it\tau}^{2}$
in (2.16), we recover the Kazantsev equation, while the
${\it\tau}^{4}$
terms give finite-
${\it\tau}$
corrections. On expansion we have
$$\begin{eqnarray}\langle R_{ijhl}\rangle =\left\langle H_{ijhl}\left[1-\text{i}{\it\tau}{\it\sigma}-\frac{{\it\tau}^{2}{\it\sigma}^{2}}{2!}+\frac{\text{i}{\it\tau}^{3}{\it\sigma}^{3}}{3!}+\frac{{\it\tau}^{4}{\it\sigma}^{4}}{4!}\right]\right\rangle ,\end{eqnarray}$$
where
${\it\sigma}=(\boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{p})(\sin A-\sin B)$
and
$H_{ijhl}=J_{ij}(\boldsymbol{x}_{0})J_{hl}(\boldsymbol{y}_{0})$
contains terms up to order
${\it\tau}^{2}$
. We note that Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) seem to have kept only terms up to
$p^{2}$
in (3.1). (Each factor of
$p_{i}$
in
${\it\sigma}$
becomes a derivative
$\partial /\partial r_{i}$
, when transiting from Fourier to real space. As Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) have kept terms containing up to the second derivative in
$r_{i}$
(see their (B1)), it would seem that they have kept only up to
$p^{2}$
-type terms in (3.1). However, if one wants the evolution equation to be correct to order
${\it\tau}^{4}$
, as is required to get the finite-
${\it\tau}$
correction to the Kazantsev equation, neglecting terms proportional to
$p^{3}$
and
$p^{4}$
as done by Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) will not give correct results.)
3.1. Kazantsev equation from terms up to order
${\it\tau}^{2}$
We now consider all terms in (3.1) one by one up to the order
${\it\tau}^{2}$
and average over
${\it\psi}$
,
$\hat{\boldsymbol{a}}$
and
$\hat{\boldsymbol{q}}$
. First consider
$\langle H_{ijhl}\rangle$
from (3.1),
$$\begin{eqnarray}\displaystyle \langle H_{ijhl}\rangle & = & \displaystyle \left\langle \vphantom{\frac{1}{2}}{\it\delta}_{ij}{\it\delta}_{hl}+{\it\delta}_{ij}a_{h}q_{l}\cos A+{\it\delta}_{hl}a_{i}q_{j}\cos B\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,a_{i}a_{h}q_{j}q_{l}\frac{{\it\tau}^{2}}{2}(\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})+\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{R}_{0}+2{\it\psi}))\right\rangle .\end{eqnarray}$$
In (3.2), the second, third and last term on the right are proportional to
$\cos (\dots +n{\it\psi})$
and hence go to zero on averaging over
${\it\psi}$
. The survival of such terms, which depend explicitly on
$\boldsymbol{x}_{0}$
,
$\boldsymbol{y}_{0}$
or
$\boldsymbol{R}_{0}$
, would break statistical homogeneity. The resulting expression after averaging over
${\it\psi}$
is
$$\begin{eqnarray}\langle H_{ijhl}\rangle =\left\langle {\it\delta}_{ij}{\it\delta}_{hl}+a_{i}a_{h}q_{j}q_{l}\frac{{\it\tau}^{2}}{2}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\right\rangle ={\it\delta}_{ij}{\it\delta}_{hl}-\frac{{\it\tau}^{2}}{2}\partial _{j}\partial _{l}\left\langle a_{i}a_{h}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\right\rangle ,\end{eqnarray}$$
where we have expressed
$q_{j}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})$
as
$\partial _{j}\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})$
. We find that the expression in (3.3) contains the two-point velocity correlator or the turbulent diffusion tensor, given by
$$\begin{eqnarray}T_{ih}=\frac{{\it\tau}}{2}\langle u_{i}(\boldsymbol{x}_{0})u_{h}(\boldsymbol{y}_{0})\rangle =\frac{{\it\tau}}{2}\langle a_{i}a_{h}\sin A\sin B\rangle =\frac{{\it\tau}}{4}\langle a_{i}a_{h}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\rangle .\end{eqnarray}$$
Then we can express (3.3) as
$$\begin{eqnarray}\langle H_{ijhl}\rangle ={\it\delta}_{ij}{\it\delta}_{hl}-2{\it\tau}\partial _{j}\partial _{l}T_{ih}.\end{eqnarray}$$
Consider now the second term in (3.1),
$\text{i}{\it\tau}\left\langle H_{ijhl}\,{\it\sigma}\right\rangle$
. We average over
${\it\psi}$
and obtain statistically homogeneous terms,
$$\begin{eqnarray}\displaystyle \left\langle \text{i}{\it\tau}H_{ijhl}\,{\it\sigma}\right\rangle & = & \displaystyle \frac{\text{i}{\it\tau}^{2}}{2}\left\langle \boldsymbol{a}\boldsymbol{\cdot }\boldsymbol{p}~[{\it\delta}_{ij}~a_{h}q_{l}~\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})+{\it\delta}_{hl}~a_{i}q_{j}~\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})]\right\rangle \nonumber\\ \displaystyle & = & \displaystyle \frac{-\text{i}{\it\tau}^{2}}{2}~p_{m}[{\it\delta}_{ij}\partial _{l}\left\langle a_{h}a_{m}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\right\rangle +{\it\delta}_{hl}\partial _{j}\left\langle a_{i}a_{m}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\right\rangle ]\nonumber\\ \displaystyle & = & \displaystyle -2\text{i}{\it\tau}p_{m}~[{\it\delta}_{ij}~\partial _{l}T_{hm}+{\it\delta}_{hl}~\partial _{j}T_{im}],\end{eqnarray}$$
where again in the last equation we have identified and expressed in terms of the turbulent diffusion tensor. Similarly, for the third term in (3.1) of order
${\it\tau}^{2}$
, we have
$$\begin{eqnarray}\displaystyle \left\langle H_{ijhl}\frac{{\it\tau}^{2}{\it\sigma}^{2}}{2}\right\rangle & = & \displaystyle \frac{{\it\tau}^{2}}{2}{\it\delta}_{ij}{\it\delta}_{hl}p_{m}p_{n}\left\langle a_{m}a_{n}[1-\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})]\right\rangle \nonumber\\ \displaystyle & = & \displaystyle 2{\it\tau}{\it\delta}_{ij}{\it\delta}_{hl}p_{m}p_{n}[T_{mn}(0)-T_{mn}].\end{eqnarray}$$
Now collecting all the simplified expressions of terms in (3.1) up to the order
${\it\tau}^{2}$
, as given in (3.5)–(3.7), we obtain
$$\begin{eqnarray}\displaystyle \left\langle R_{ijhl}\right\rangle & = & \displaystyle {\it\delta}_{ij}{\it\delta}_{hl}-2{\it\tau}\partial _{j}\partial _{l}T_{ih}-\text{i}2{\it\tau}p_{m}[{\it\delta}_{ij}\partial _{l}T_{hm}+{\it\delta}_{hl}\partial _{j}T_{im}]\nonumber\\ \displaystyle & & \displaystyle +\,2{\it\tau}{\it\delta}_{ij}{\it\delta}_{hl}p_{m}p_{n}[T_{mn}(0)-T_{mn}].\end{eqnarray}$$
We then substitute (3.8) into (2.17). In the case of the first two terms in
$\left\langle R_{ijhl}\right\rangle$
multiplying with unity, the integral in (2.17) is trivial with integration over
$\boldsymbol{p}$
first giving a delta function
${\it\delta}^{3}(\boldsymbol{r}-\boldsymbol{r}_{0})$
which then leads to all functions of
$\boldsymbol{r}_{0}$
simply turning into functions of
$\boldsymbol{r}$
, on integrating over
$\boldsymbol{r}_{0}$
. The other terms containing
$p_{i}$
can be first written as derivatives with respect to
$r_{i}$
. For example, consider the integral in (2.17) containing the fourth term in
$\langle R_{ijhl}\rangle$
from (3.8),
$$\begin{eqnarray}\displaystyle & & \displaystyle \int 2{\it\tau}~{\it\delta}_{ij}{\it\delta}_{hl}~p_{m}p_{n}~[T_{mn}(0)-T_{mn}]M_{jl}(\boldsymbol{r}_{0},t_{0})~\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{0})}\,\text{d}^{3}\boldsymbol{r}_{0}\frac{\text{d}^{3}\boldsymbol{p}}{(2{\rm\pi})^{3}}\nonumber\\ \displaystyle & & \displaystyle \quad =\int 2{\it\tau}\left(\frac{\partial _{m}}{\text{i}}\right)\left(\frac{\partial _{n}}{\text{i}}\right)[T_{mn}(0)-T_{mn}]M_{ih}(\boldsymbol{r}_{0},t_{0})~\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{0})}\,\text{d}^{3}\boldsymbol{r}_{0}\frac{\text{d}^{3}\boldsymbol{p}}{(2{\rm\pi})^{3}}\nonumber\\ \displaystyle & & \displaystyle \quad =-2{\it\tau}~\partial _{m}\partial _{n}[(T_{L}(0)-T_{mn})M_{ih}(\boldsymbol{r}_{0},t_{0})],\end{eqnarray}$$
where we have used the fact that for a statistically homogeneous, isotropic and non-helical velocity field, the correlation function is
$$\begin{eqnarray}T_{ih}=({\it\delta}_{ih}-\hat{r}_{i}\hat{r}_{h})T_{N}(r,t)+\hat{r}_{i}\hat{r}_{h}T_{L}(r,t),\end{eqnarray}$$
where
$\hat{r_{i}}=r_{i}/r$
and hence
$T_{mn}(0)={\it\delta}_{mn}T_{L}(0)$
. Here
$T_{L}(r,t)=\hat{r}_{i}\hat{r}_{h}T_{ih}$
and
$T_{N}(r,t)=(1/2r)[\partial (r^{2}T_{L})/\partial r]$
are, respectively, the longitudinal and transversal correlation functions of the velocity field.
Carrying out all the steps, and noting that
$(M_{ih}(\boldsymbol{r},t)-M_{ih}(\boldsymbol{r},t_{0}))/{\it\tau}=\partial M_{ih}/\partial t$
in the limit
${\it\tau}\rightarrow 0$
, the resulting equation for
$M_{ih}$
is given by
$$\begin{eqnarray}\displaystyle \frac{\partial M_{ih}(\boldsymbol{r},t)}{\partial t} & = & \displaystyle 2(-[T_{ih}M_{jl}]_{,jl}+[T_{mh}M_{il}]_{,ml}+[T_{im}M_{jh}]_{,jm}-[T_{mn}M_{ih}]_{,mn})\nonumber\\ \displaystyle & & \displaystyle +\,(2T_{L}(0)+2{\it\eta})~{\rm\nabla}^{2}M_{ih}.\end{eqnarray}$$
Note that we have a statistically homogeneous, isotropic and non-helical magnetic field, and hence, similar to the velocity correlation function, we have
$M_{ih}=({\it\delta}_{ih}-\hat{r}_{i}\hat{r}_{h})M_{N}(r,t)+\hat{r}_{i}\hat{r}_{h}M_{L}(r,t)$
. Here
$M_{L}(r,t)$
and
$M_{N}(r,t)$
are the longitudinal and transversal correlation functions of the magnetic field. Then on contracting equation (3.11) with
$\hat{r}_{i}\hat{r}_{h}$
we would obtain the dynamical equation for
$M_{L}(r,t)$
, the Kazantsev equation. Note that we have not yet performed averages over
$\boldsymbol{a}$
and
$\boldsymbol{q}$
because we have simply identified the two-point velocity correlator from (3.4) in expressions evaluated after averaging over
${\it\psi}$
(as in (3.5)–(3.7)). We will perform the averages over
$\boldsymbol{a}$
and
$\boldsymbol{q}$
later when we explicitly evaluate velocity correlators.
3.2. Extending the Kazantsev equation to higher order in
${\it\tau}$
Next, we will consider the terms of higher order in
${\it\tau}$
, starting with
${\it\tau}^{3}$
and then
${\it\tau}^{4}$
. Interestingly, it turns out that all the terms of order
${\it\tau}^{3}$
go to 0 on averaging. For example, from the second term in equation (3.1), we obtain
${\it\tau}^{3}\left\langle \text{i}(\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{a})a_{i}a_{h}q_{j}q_{l}\cos A\cos B(\sin A-\sin B)\right\rangle$
. Here, terms in
$\cos A\cos B\sin A=(1/2)\sin (2A)\cos B=(1/4)[\sin (2A+B)-\sin (2A-B)]$
contain
${\it\psi}$
in their argument and hence go to 0 on averaging.
Now we consider the terms of order
${\it\tau}^{4}$
. The first contribution is from the third term in (3.1),
${\it\tau}^{4}\left\langle -[(\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{a})^{2}/2]~a_{i}a_{h}q_{j}q_{l}~\cos A\cos B[\sin A-\sin B]^{2}\right\rangle$
. On averaging over
${\it\psi}$
, we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{{\it\tau}^{4}}{8}\left\langle a_{i}a_{h}~(a_{n}p_{n}a_{m}p_{m})~q_{j}q_{l}[\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})-\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})]\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{{\it\tau}^{4}}{8}\left\langle a_{i}a_{h}~(a_{n}p_{n}a_{m}p_{m})~\partial _{j}\partial _{l}\left[\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})-\frac{\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})}{4}\right]\right\rangle .\end{eqnarray}$$
We identify the terms in (3.12) with two-point fourth-order velocity correlators. Three such velocity correlators can be defined:
$$\begin{eqnarray}\displaystyle T_{mnih}^{x^{2}y^{2}} & = & \displaystyle {\it\tau}^{2}\langle u_{m}(\boldsymbol{x})u_{n}(\boldsymbol{y})u_{i}(\boldsymbol{x})u_{h}(\boldsymbol{y})\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{mnih}^{x^{3}y} & = & \displaystyle {\it\tau}^{2}\langle u_{m}(\boldsymbol{x})u_{n}(\boldsymbol{x})u_{i}(\boldsymbol{x})u_{h}(\boldsymbol{y})\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{mnih}^{x^{4}} & = & \displaystyle {\it\tau}^{2}\langle u_{m}(\boldsymbol{x})u_{n}(\boldsymbol{x})u_{i}(\boldsymbol{x})u_{h}(\boldsymbol{x})\rangle .\end{eqnarray}$$
${\it\tau}^{2}$
, as we envisage that
$T_{ijkl}$
will be finite even in the
${\it\tau}\rightarrow 0$
limit, behaving like products of turbulent diffusion. Note that the renewing flow is not Gaussian random, and hence higher-order correlators of
$\boldsymbol{u}$
are not the product of two-point correlators. We consider the
${\it\psi}$
averaging of the velocity correlators in (3.13), to obtain 
$$\begin{eqnarray}\displaystyle & \displaystyle T_{mnih}^{x^{2}y^{2}}={\it\tau}^{2}\left\langle a_{m}a_{n}a_{i}a_{h}\sin ^{2}A\sin ^{2}B\right\rangle =\frac{{\it\tau}^{2}}{4}\left\langle a_{m}a_{n}a_{i}a_{h}\left(1+\frac{\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})}{2}\right)\right\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{mnih}^{x^{3}y}={\it\tau}^{2}\left\langle a_{m}a_{n}a_{i}a_{h}\sin ^{3}A\sin B\right\rangle =\frac{3{\it\tau}^{2}}{8}\left\langle a_{m}a_{n}a_{i}a_{h}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})\right\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{mnih}^{x^{4}}={\it\tau}^{2}\left\langle a_{m}a_{n}a_{i}a_{h}\sin ^{4}A\right\rangle =\frac{3{\it\tau}^{2}}{8}\left\langle a_{m}a_{n}a_{i}a_{h}\right\rangle . & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}-{\it\tau}^{2}p_{n}p_{m}\partial _{j}\partial _{l}\left[\frac{T_{mnih}^{x^{2}y^{2}}}{4}-\frac{T_{mnih}^{x^{3}y}}{3}\right].\end{eqnarray}$$
Note that the first term in (3.14) does not survive due to the derivatives in (3.17). Similarly, from the fourth term in (3.1), the contribution of order
${\it\tau}^{4}$
is given by
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}{\it\tau}^{4}\frac{(\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{a})^{3}}{6}[{\it\delta}_{ij}a_{h}q_{l}\cos B+{\it\delta}_{hl}a_{i}q_{j}\cos A](\sin A-\sin B)^{3}\nonumber\\ \displaystyle & & \displaystyle \quad =\text{i}\frac{{\it\tau}^{4}}{8}p_{n}p_{m}p_{r}\left(\left\langle {\it\delta}_{ij}a_{k}a_{n}a_{m}a_{r}\partial _{l}\left[2\sin (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})-\frac{\sin (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})}{2}\right]\right\rangle \right)\nonumber\\ \displaystyle & & \displaystyle \quad =-{\it\tau}^{2}2p_{n}p_{m}p_{r}\left({\it\delta}_{ij}\partial _{l}\left[\frac{T_{mnih}^{x^{2}y^{2}}}{4}-\frac{T_{mnih}^{x^{3}y}}{3}\right]\right),\end{eqnarray}$$
where we have again expressed in terms of velocity correlators from (3.14) and (3.15). Lastly, from the fifth term in (3.1), we have
$({\it\tau}^{4}/24){\it\delta}_{ij}{\it\delta}_{hl}\left\langle (\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{a})^{4}(\sin A-\sin B)^{4}\right\rangle$
, which is given by,
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{{\it\tau}^{4}}{16}{\it\delta}_{ij}{\it\delta}_{hl}p_{m}p_{n}p_{r}p_{s}\left\langle a_{m}a_{n}a_{r}a_{s}\left(\frac{3}{2}-2\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})+\frac{\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}_{0})}{2}\right)\right\rangle \nonumber\\ \displaystyle & & \displaystyle \quad ={\it\tau}^{2}{\it\delta}_{ij}{\it\delta}_{hl}p_{m}p_{n}p_{r}p_{s}\left[\frac{T_{mnih}^{x^{2}y^{2}}}{4}-\frac{T_{mnih}^{x^{3}y}}{3}+\frac{T_{mnih}^{x^{4}}}{12}\right].\end{eqnarray}$$
We substitute the above equations (3.17)–(3.19), which form the
${\it\tau}^{2}$
contributions from
$\langle R_{ijhl}\rangle$
, into (2.17). We again find that the integrand determining the magnetic spectral tensor
$\hat{M}_{ih}(\boldsymbol{p},t)$
is of the form
$G(\boldsymbol{p})F_{ih}(\boldsymbol{r}_{0},t_{0})$
, where
$G(\boldsymbol{p})$
is a polynomial up to fourth order in
$p_{i}$
. The inverse Fourier transform of
$\hat{M}_{ih}(\boldsymbol{p},t)$
, as in (2.17), now gives
$$\begin{eqnarray}M_{ih}(\boldsymbol{r},t)=\int G(\boldsymbol{p})F_{ih}(\boldsymbol{r}_{0},t_{0})\text{e}^{\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{0})}\,\text{d}^{3}\boldsymbol{r}_{0}\frac{\text{d}^{3}\boldsymbol{p}}{(2{\rm\pi})^{3}}.\end{eqnarray}$$
The
$p_{i}$
in
$G(\boldsymbol{p})$
above can be written as derivatives with respect to
$r_{i}$
. Then the integral over
$\boldsymbol{p}$
simply gives a delta function
${\it\delta}^{3}(\boldsymbol{r}-\boldsymbol{r}_{0})$
and this makes the integral over
$\boldsymbol{r}_{0}$
trivial. This was explicitly demonstrated earlier in (3.9).
We then divide all the three contributions of order
${\it\tau}^{4}$
in (3.17)–(3.19) by
${\it\tau}$
. From the remaining factor of
${\it\tau}^{3}$
, the
${\it\tau}^{2}$
part is absorbed into
$T_{ijkl}$
, leaving one
${\it\tau}$
which is treated as a small effective finite time parameter. The resulting extended equation for
$M_{ih}$
is given by
$$\begin{eqnarray}\displaystyle \frac{\partial M_{ih}}{\partial t} & = & \displaystyle 2(-[T_{ih}M_{jl}]_{,jl}+[T_{jh}M_{il}]_{,jl}+[T_{il}M_{jh}]_{,jl}-[T_{jl}M_{ih}]_{,jl})+(2T_{L}(0)+2{\it\eta})~{\rm\nabla}^{2}M_{ih}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\tau}\left([\tilde{T}_{mnih}M_{jl}]_{,mnjl}-2[\tilde{T}_{mnrh}M_{il}]_{,mnrl}+\left[\left(\tilde{T}_{mnrs}+\frac{T_{mnrs}^{x^{4}}}{12}\right)M_{ih}\right]_{,mnrs}\right)\!,\qquad\end{eqnarray}$$
where
$\tilde{T}_{mnih}=T_{mnih}^{x^{2}y^{2}}/4-T_{mnih}^{x^{3}y}/3$
. The first two lines in (3.21) contains the terms which give the Kazantsev equation as in (3.11), while the third line contains the finite-
${\it\tau}$
corrections. We write these latter terms as fourth derivatives of the combined velocity and magnetic correlators; however as both the velocity and magnetic fields are divergence free, each spatial derivative only acts on one or the other.
We then contract (3.21) with
$\hat{r}_{i}\hat{r}_{h}$
to obtain the dynamical equation for
$M_{L}(r,t)$
. On such a contraction, the terms in the first two lines lead to the original Kazantsev equation for
$M_{L}$
. In order to perform such a contraction, we need to know the explicit form of the fourth-order velocity correlator,
$\tilde{T}_{mnih}$
. A fourth-order two-point correlator for a homogeneous and isotropic velocity field can be expressed as
$$\begin{eqnarray}T_{mnih}=\hat{r}_{mnih}\overline{T}_{L}+\hat{P}_{(mn}\hat{P}_{ih)}\overline{T}_{N}+\hat{r}_{(mn}\hat{P}_{ih)}\overline{T}_{LN},\end{eqnarray}$$
where
$\hat{r}_{mn}=\hat{r}_{m}\hat{r}_{n}$
and similarly
$\hat{r}_{mnih}=\hat{r}_{m}\hat{r}_{n}\hat{r}_{i}\hat{r}_{h}$
.
$\hat{P}_{mn}={\it\delta}_{mn}-\hat{r}_{mn}$
is the configuration space projection operator. The correlation functions are defined as
$$\begin{eqnarray}\overline{T}_{L}=\hat{r}_{mnih}\tilde{T}_{mnih},\quad \overline{T}_{LN}=\hat{r}_{mn}\hat{P}_{ih}~\tilde{T}_{mnih},\quad \overline{T}_{N}=\hat{P}_{mn}\hat{P}_{ih}~\tilde{T}_{mnih}/16.\end{eqnarray}$$
Lastly, the brackets
$(\,)$
in the subscripts of the two second-rank tensors denote the addition of all terms from different permutations of the four indices considered in pairs. We will henceforth refer to all ten terms in (3.22), namely
$\hat{r}_{mnih},\hat{P}_{mn}\hat{P}_{ih}$
(and two other terms with permutations of the indices),
$\hat{r}_{mn}\hat{P}_{ih}$
(and five other terms with permutations of the indices), as the basis tensors (although not all of them are orthogonal to each other). For a divergence-free (or incompressible) velocity field, the different correlation functions,
$\overline{T}_{L}$
,
$\overline{T}_{N}$
and
$\overline{T}_{LN}$
, are related as
$$\begin{eqnarray}\overline{T}_{LN}=\frac{1}{6r}\frac{\text{d}(r^{2}\overline{T}_{L})}{\text{d}r},\quad \overline{T}_{LN}=\overline{T}_{N}+\frac{r}{4}\frac{\text{d}(\overline{T}_{N})}{\text{d}r}.\end{eqnarray}$$
Consider the contraction of
$\hat{r}_{ih}$
with the first term in the third line in equation (3.21),
$\hat{r}_{ih}[\tilde{T}_{mnih}M_{jl}]_{,mnjl}=\hat{r}_{ih}\tilde{T}_{mnih,jl}M_{jl,mn}$
. Then we have
$$\begin{eqnarray}\displaystyle \hat{r}_{ih}\tilde{T}_{mnih,jl}M_{jl,mn} & = & \displaystyle \frac{1}{r^{2}}([r_{ih}\tilde{T}_{mnih}]_{,jl}-[{\it\delta}_{ij}r_{h}\tilde{T}_{mnih}]_{,j}-[{\it\delta}_{il}r_{h}\tilde{T}_{mnih}]_{,l}\nonumber\\ \displaystyle & & \displaystyle -\,[{\it\delta}_{jh}r_{i}\tilde{T}_{mnih}]_{,j}-[{\it\delta}_{hl}r_{i}\tilde{T}_{mnih}]_{,j}+({\it\delta}_{ij}{\it\delta}_{hl}+{\it\delta}_{il}{\it\delta}_{jh})\tilde{T}_{mnih})M_{jl,mn}.\qquad\end{eqnarray}$$
We obtain a fourth-order tensor from
$\hat{r}_{ih}\tilde{T}_{mnih,jl}$
which multiplies another fourth-order tensor
$M_{jl,mn}$
. To make this computation tractable, we construct a table where we list the coefficients of all the basis tensors. We provide such a table in appendix B, (table 1). Similarly, for the second term in the third line in (3.21),
$$\begin{eqnarray}\displaystyle \hat{r}_{ih}[\tilde{T}_{mnrh}M_{il}]_{,lmnr} & = & \displaystyle (\hat{r}_{h}\tilde{T}_{mnrh,l})(\hat{r}_{i}M_{il,mnr})=\frac{1}{r^{2}}([r_{h}\tilde{T}_{mnrh}]_{,l}-{\it\delta}_{lh}\tilde{T}_{mnrh})\nonumber\\ \displaystyle & & \displaystyle \times \,([r_{i}M_{il}]_{,mnr}-{\it\delta}_{ir}M_{il,mn}-{\it\delta}_{in}M_{il,mr}-{\it\delta}_{im}M_{il,nr}).\end{eqnarray}$$
Again we give the expansion of the fourth-order objects
$(\hat{r}_{h}\tilde{T}_{mnrh,l})$
and
$(\hat{r}_{i}M_{il,mnr})$
(in terms of basis tensors) in table 2 in appendix B. Then lastly we have the third term from the third line in (3.21),
$$\begin{eqnarray}\displaystyle r_{ih}[\tilde{T}_{mnrs}M_{ih}]_{,mnrs} & = & \displaystyle \tilde{T}_{mnrs}([r_{ih}M_{ih}]_{,mnrs}-(r_{ih})_{,m}M_{ih,nrs}-(r_{ih})_{,n}M_{ih,mrs}\nonumber\\ \displaystyle & & \displaystyle -\,(r_{ih})_{,r}M_{ih,nms}-(r_{ih})_{,s}M_{ih,nrm}-(r_{ih})_{,mn}M_{ih,rs}-(r_{ih})_{,mr}M_{ih,ns}\nonumber\\ \displaystyle & & \displaystyle -\,(r_{ih})_{,ms}M_{ih,rn}-(r_{ih})_{,ns}M_{ih,mr}-(r_{ih})_{,rs}M_{ih,mn}-(r_{ih})_{,rn}M_{ih,ms}).\qquad\end{eqnarray}$$
Here the two fourth-order tensor objects multiplying each other are
$\tilde{T}_{mnrs}$
and
$r_{il}M_{jl,mnrs}$
and the expansion of these fourth-order objects in terms of basis tensors can again be found in table 3, in appendix B.
Tables 1–3 in appendix B are useful in making the algebra of all the the fourth-order terms in (3.25)–(3.27) tractable. In each of the tables, we list the expansion of all the individual fourth-order objects in terms of the basis tensors. The basis tensors form the rows, while the expansion coefficients in (3.25)–(3.27) are listed as columns. Note that the first column is the list of the basis tensors. Then the subsequent columns list the expansion coefficients (of the respective basis tensor) for each fourth-order term in (3.25)–(3.27). Then we sum the contributions from each row, separately for the magnetic and velocity parts. The last but one column in table 1 and the last columns in tables 2 and 3 give the resulting sum divided by
$r^{2}$
. We then finally multiply the sum obtained for the magnetic part with the sum from the velocity part.
Here, we note that typically when we multiply one group of the basis tensors with another, all of them go to zero, but yield a constant when multiplied within the same group. For example, the product of
$\hat{r}_{mnih}$
and
$\hat{r}_{mn}\hat{P}_{ih}$
goes to zero, but the product of
$\hat{r}_{mnih}$
with itself naturally produces unity. Then the product of
$\hat{r}_{mn}\hat{P}_{ih}$
with
$\hat{r}_{ih}\hat{P}_{mn}$
(or the other four similar kind of terms) goes to zero, but with itself gives a value of 2. Lastly, the product of
$\hat{P}_{mn}\hat{P}_{ih}$
with
$\hat{P}_{mi}\hat{P}_{nh}$
(or
$\hat{P}_{ni}\hat{P}_{mh}$
) gives a value of 2, but with itself gives a value of 4.
By multiplying the velocity part with the magnetic part in this manner, we finally obtain the additional terms from the contractions, due to finite-
${\it\tau}$
, and extend the Kazantsev equation to the form
$$\begin{eqnarray}\displaystyle \frac{\partial M_{L}(r,t)}{\partial t} & = & \displaystyle \frac{2}{r^{4}}\frac{\partial }{\partial r}\left(r^{4}{\it\eta}_{tot}\frac{\partial M_{L}}{\partial r}\right)+GM_{L}\nonumber\\ \displaystyle & & \displaystyle +\,{\it\tau}M_{L}^{\prime \prime \prime \prime }\left(\overline{T}_{L}+\frac{\overline{T}_{L}(0)}{12}\right)+{\it\tau}M_{L}^{\prime \prime \prime }\left(2\overline{T}_{L}^{\prime }+\frac{8\overline{T}_{L}}{r}+\frac{2\overline{T}_{L}(0)}{3r}\right)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\tau}M_{L}^{\prime \prime }\left(\frac{5\overline{T}_{L}^{\prime \prime }}{3}+\frac{11\overline{T}_{L}^{\prime }}{r}+\frac{8\overline{T}_{L}}{r^{2}}+\frac{2\overline{T}_{L}(0)}{3r^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\tau}M_{L}^{\prime }\left(\frac{2\overline{T}_{L}^{\prime \prime \prime }}{3}+\frac{17\overline{T}_{L}^{\prime \prime }}{3r}+\frac{5\overline{T}_{L}^{\prime }}{r^{2}}-\frac{8\overline{T}_{L}}{r^{3}}-\frac{2\overline{T}_{L}(0)}{3r^{3}}\right).\end{eqnarray}$$
Here,
${\it\eta}_{tot}={\it\eta}+T_{L}(0)-T_{L}(r)$
and
$G=-2(T_{L}^{\prime \prime }+4T_{L}^{\prime }/r)$
. Again the first line gives us the original Kazantsev equation and the rest of the terms form the extended part and have the parameter
${\it\tau}$
multiplying them. We will refer to (3.28) as the generalized Kazantsev equation incorporating finite-
${\it\tau}$
effects. To proceed further, and solve the generalized Kazantsev equation (3.28), we need to first evaluate the second- and fourth-order velocity correlators explicitly for the renewing flow from (3.4) and (3.14), (3.15) and (3.16) respectively.
Consider first the two-point velocity correlator,
$$\begin{eqnarray}T_{ij}=\frac{{\it\tau}}{4}\langle A_{l}A_{m}P_{il}P_{jm}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r})\rangle =\frac{A^{2}{\it\tau}}{12}\langle P_{ij}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r})\rangle =\frac{a^{2}{\it\tau}}{8}\left[{\it\delta}_{ij}+\frac{1}{q^{2}}\frac{\partial ^{2}}{\partial r_{i}r_{j}}\right]j_{0}(qr).\end{eqnarray}$$
Here, we have made use of the results in (2.3) and (2.4), i.e. we have substituted for
$\boldsymbol{a}$
in terms of
$\boldsymbol{A}$
, and first averaged over
$\boldsymbol{A}$
. Similarly, in the expression for
$T_{mnih}^{x^{2}y^{2}}$
in (3.14), we substitute
$a_{m}=A_{s}\tilde{P}_{ms}$
,
$a_{n}=A_{t}\tilde{P}_{nt}$
,
$a_{i}=A_{u}\tilde{P}_{iu}$
and
$a_{h}=A_{v}\tilde{P}_{hv}$
. Then we have
$$\begin{eqnarray}T_{mnih}^{x^{2}y^{2}}=\frac{{\it\tau}^{2}A^{4}}{60}\left\langle \tilde{P}_{(mn}\tilde{P}_{ih)}(1+\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r}))\right\rangle .\end{eqnarray}$$
The first part of (3.30) is evaluated to be
$\langle \tilde{P}_{(mn}\tilde{P}_{ih)}\rangle =8/15({\it\delta}_{(mn}{\it\delta}_{ih)})$
. And the second part of (3.30) is given as
$$\begin{eqnarray}\displaystyle \left\langle \tilde{P}_{(mn}\tilde{P}_{ih)}\cos (2\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r})\right\rangle & = & \displaystyle [({\it\delta}_{mn}+\partial _{m}\partial _{n})({\it\delta}_{ih}+\partial _{i}\partial _{h})+({\it\delta}_{mi}+\partial _{m}\partial _{i})({\it\delta}_{nh}+\partial _{n}\partial _{h})\nonumber\\ \displaystyle & & \displaystyle +\,({\it\delta}_{mh}+\partial _{m}\partial _{h})({\it\delta}_{in}+\partial _{i}\partial _{n})]\,j_{0}(2qr)\nonumber\\ \displaystyle & = & \displaystyle -24\left(\frac{j_{0}(2z)}{(2z)^{2}}+\frac{3\partial _{2z}j_{0}(2z)}{(2z)^{3}}\right)\hat{r}_{mnih}\nonumber\\ \displaystyle & & \displaystyle +\left(j_{0}+\frac{2\partial _{2z}j_{0}(2z)}{2z}-\frac{3\partial _{2z}j_{0}(2z)}{(2z)^{2}}-\frac{9\partial _{2z}j_{0}(2z)}{(2z)^{3}}\right)[\hat{P}_{(mn}\hat{P}_{ih)}]\nonumber\\ \displaystyle & & \displaystyle +\left(\!-\frac{4\partial _{2z}j_{0}(2z)}{z}+\frac{12\partial _{2z}j_{0}(2z)}{(2z)^{2}}+\frac{36\partial _{2z}j_{0}(2z)}{(2z)^{3}}\right)\![\hat{r}_{(mn}\hat{P}_{ih)}],\quad \qquad\end{eqnarray}$$
where
$z=qr$
and
$\partial _{2z}$
is the derivative with respect to
$2z$
. We get a similar expression to (3.31) for
$T_{mnih}^{x^{3}y}=(A^{4}/40)\left\langle \tilde{P}_{(mn}\tilde{P}_{ih)}\cos (\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{r})\right\rangle$
, with all the
$(2z)$
replaced by
$z$
and
$\partial _{2z}$
by
$\partial _{z}$
. Finally, for
$\overline{T}_{L}^{x^{2}y^{2}}$
and
$\overline{T}_{L}^{x^{3}y}$
we get
$$\begin{eqnarray}\displaystyle \overline{T}_{L}^{x^{2}y^{2}}=\frac{-9a^{4}{\it\tau}^{2}}{10}\left(\frac{3\partial _{2z}j_{0}(2z)}{(2z)^{3}}+\frac{j_{0}(2z)}{(2z)^{2}}\right),\quad \overline{T}_{L}^{x^{3}y}=\frac{-27a^{4}{\it\tau}^{2}}{20}\left(\frac{3\partial _{z}j_{0}(z)}{z^{3}}+\frac{j_{0}(z)}{z^{2}}\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
(The above expressions correct the missing
${\sim}a^{4}{\it\tau}^{2}$
factors in (18) of BS14.) These latter equalities give the explicit expressions of these fourth-order correlators for the renewing flow. The generalized Kazantsev equation (3.28) allows eigen-solutions of the form
$M_{L}(z,t)=\tilde{M}_{L}(z)\text{e}^{{\it\gamma}\tilde{t}}$
, where
$\tilde{t}=t{\it\eta}_{t}q^{2}$
, with
${\it\eta}_{t}=T_{L}(0)=a^{2}{\it\tau}/12=A^{2}{\it\tau}/18$
, and
${\it\gamma}$
is the growth rate. Boundary conditions are given as
$M_{L}^{\prime }(0,t)=0$
and
$M_{L}\rightarrow 0$
as
$r\rightarrow \infty$
. Implications of the higher spatial derivative terms are discussed below.
4. Growth rate and magnetic spectrum at finite correlation time
We now discuss the solution of (3.28) to examine the finite correlation time modification to the growth rate and magnetic correlation function or its energy spectrum. For the latter, we focus particularly on the large-
$k$
(or small-
$r$
) behaviour. Recall that in the
${\it\tau}\rightarrow 0$
limit the magnetic spectrum is of the Kazantsev form,
$M(k)\propto k^{3/2}$
for
$q\ll k\ll k_{{\it\eta}}$
. Our aim is to determine how this gets modified in the presence of finite correlation time effects. For this purpose, we employ two different approaches. First, we recall in more detail the scaling solution discussed in BS14. We also then present a WKBJ analysis to derive
$M_{L}(r,t)$
in the small-
$r$
limit, and hence the magnetic spectrum.
In both approaches, to derive the standard Kazantsev spectrum in the large-
$k$
limit, and its finite-
${\it\tau}$
modifications, it suffices to go to the limit of small
$z=qr\ll 1$
. Expanding the Bessel functions in (3.29) and (3.32) in this limit, and substituting
$M_{L}(z,t)=\tilde{M}_{L}(z)\text{e}^{{\it\gamma}\tilde{t}}$
, (3.28) becomes
$$\begin{eqnarray}\displaystyle {\it\gamma}\tilde{M}_{L}(z) & = & \displaystyle \left(\frac{2{\it\eta}}{{\it\eta}_{t}}+\frac{z^{2}}{5}\right)\tilde{M}_{L}^{\prime \prime }+\left(\frac{8{\it\eta}}{{\it\eta}_{t}}+\frac{6z^{2}}{5}\right)\frac{\tilde{M}_{L}^{\prime }}{z}+2\tilde{M}_{L}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{9\bar{{\it\tau}}}{175}\left(\frac{z^{4}}{2}\tilde{M}_{L}^{\prime \prime \prime \prime }+8z^{3}\tilde{M}_{L}^{\prime \prime \prime }+36z^{2}\tilde{M}_{L}^{\prime \prime }+48z\tilde{M}_{L}^{\prime }\right),\end{eqnarray}$$
where
$\bar{{\it\tau}}={\it\tau}{\it\eta}_{t}q^{2}=(\mathit{St})^{2}/12$
and the prime now denotes a
$z$
-derivative.
For the solution near the origin, where
$z\ll \sqrt{{\it\eta}/{\it\eta}_{t}}$
, it suffices to approximate
$\tilde{M}_{L}$
as a parabola and write
$\tilde{M}_{L}(z)=M_{0}(1-z^{2}/z_{{\it\eta}}^{2})$
. From (4.1), we find
$z_{{\it\eta}}=qr_{{\it\eta}}=[240/(2-{\it\gamma})]^{1/2}[R_{M}(\mathit{St})]^{-1/2}$
. The
$\bar{{\it\tau}}$
-dependent terms, which are small because both
$z$
and
$\bar{{\it\tau}}$
are small, do not affect this result. Thus for
$R_{M}\gg 1$
, the resistive scale
$r_{{\it\eta}}\ll 1/q$
(or
$k_{{\it\eta}}=1/r_{{\it\eta}}\gg q$
), although one has to go to sufficiently large
$R_{M}\gg 240/((2-{\it\gamma})\mathit{St})$
for this conclusion to obtain.
In order to determine the magnetic correlation function for spatial scales larger than
$z_{{\it\eta}}$
, and also obtain the growth rate, we have to more fully analyse (4.1). We see that this evolution equation (or (3.28)), also has higher-order (third and fourth) spatial derivatives when going to the finite-
${\it\tau}$
case. This indicates that for finite-
${\it\tau}$
, the
$M_{L}$
evolution is actually non-local, determined by an integral type equation; but whose leading approximation for small
$\bar{{\it\tau}}$
is the local equation (4.1). However, these higher-derivative terms only appear as perturbative terms multiplied by the small parameter
$\bar{{\it\tau}}$
. Then it is possible to use the Landau–Lifshitz type approximation, earlier used in treating the effect of radiation reaction force in electrodynamics (see Landau & Lifshitz Reference Landau and Lifshitz1975, Section 75). In this treatment, one first ignores the perturbative terms proportional to
$\bar{{\it\tau}}$
, which gives basically the Kazantsev equation for
$\tilde{M}_{L}$
, and uses this to express
$\tilde{M}_{L}^{\prime \prime \prime }$
and
$\tilde{M}_{L}^{\prime \prime \prime \prime }$
in terms of the lower-order derivatives
$\tilde{M}_{L}^{\prime \prime }$
and
$\tilde{M}_{L}^{\prime }$
.
We will find that both for the scaling solution and for determining the asymptotic WKBJ solution, these higher-order derivatives are only required in the limit
$z\gg z_{{\it\eta}}$
. In this limit we have from (4.1), at the zeroth order in
$\bar{{\it\tau}}$
,
$$\begin{eqnarray}\frac{z^{2}}{5}\tilde{M}_{L}^{\prime \prime }=-\frac{6z}{5}\tilde{M}_{L}^{\prime }+({\it\gamma}-2)\tilde{M}_{L}.\end{eqnarray}$$
Differentiating this expression first once and then twice gives
$$\begin{eqnarray}z^{3}\tilde{M}_{L}^{\prime \prime \prime }=-8z^{2}\tilde{M}_{L}^{\prime \prime }-z(16-5{\it\gamma}_{0})\tilde{M}_{L}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}z^{4}\tilde{M}_{L}^{\prime \prime \prime \prime }=(56+5{\it\gamma}_{0})z^{2}\tilde{M}_{L}^{\prime \prime }+10(16-5{\it\gamma}_{0})z\tilde{M}_{L}^{\prime }.\end{eqnarray}$$
Here
${\it\gamma}_{0}$
is the growth rate which obtains for the Kazantsev equation in the
${\it\tau}\rightarrow 0$
limit. We now turn to the scaling solution approach.
4.1. Growth rate and magnetic correlations from a scaling solution
Consider the solution for
$z_{{\it\eta}}\ll z\ll 1$
. In this limit, ignoring terms depending on
${\it\eta}/{\it\eta}_{t}$
, (4.1) itself is scale free, as the scaling
$z\rightarrow cz$
leaves it invariant. Thus the resulting equation has power law solutions of the form
$\tilde{M}(z)=\bar{M}_{0}z^{-{\it\lambda}}$
. To find the form of this solution, we first substitute the expressions in (4.3) back into the full equation (4.1). We get, after neglecting the
${\it\eta}/{\it\eta}_{t}$
terms,
$$\begin{eqnarray}\tilde{M}_{L}^{\prime \prime }z^{2}\left(\bar{{\it\tau}}{\it\gamma}_{0}{\textstyle \frac{9}{70}}+{\textstyle \frac{1}{5}}\right)+\tilde{M}_{L}^{\prime }z\left(\bar{{\it\tau}}{\it\gamma}_{0}{\textstyle \frac{27}{35}}+{\textstyle \frac{6}{5}}\right)+(2-{\it\gamma})\tilde{M}_{L}=0.\end{eqnarray}$$
We find the interesting result that the coefficients of the perturbative terms in (4.1) are such that all perturbative terms which do not depend on
${\it\gamma}_{0}$
cancel out in (4.4)!
As already mentioned (4.4) admits power law solutions of the form
$\tilde{M}_{L}(z)=\bar{M}_{0}z^{-{\it\lambda}}$
, with
${\it\lambda}$
determined by
$$\begin{eqnarray}{\it\lambda}^{2}-5{\it\lambda}+\frac{5(2-{\it\gamma})}{\displaystyle 1+{\textstyle \frac{9}{14}}{\it\gamma}_{0}\bar{{\it\tau}}}=0;\quad \text{so }{\it\lambda}=\frac{5}{2}\pm \text{i}{\it\lambda}_{I},~{\it\lambda}_{I}=\frac{1}{2}\left[\frac{20(2-{\it\gamma})}{(1+9{\it\gamma}_{0}\bar{{\it\tau}}/14)}-25\right]^{1/2}\!.\end{eqnarray}$$
More important is the fact that the real part of
${\it\lambda}$
is
${\it\lambda}_{R}=5/2$
, independent of the value of
$\bar{{\it\tau}}$
. We can also get the approximate growth rate assuming
$R_{M}\gg 1$
, following an argument from Gruzinov, Cowley & Sudan (Reference Gruzinov, Cowley and Sudan1996). These authors looked at (4.5) as an equation for
${\it\gamma}({\it\lambda})$
and argued that the growth rate is determined by substituting into (4.5) the value of
${\it\lambda}={\it\lambda}_{m}$
where
$\text{d}{\it\gamma}/\text{d}{\it\lambda}=0$
. This gives
$$\begin{eqnarray}{\it\gamma}_{0}\approx {\textstyle \frac{3}{4}},\quad \text{and}\quad {\it\gamma}\approx \left({\textstyle \frac{3}{4}}\right)\left(1-\left({\textstyle \frac{45}{56}}\right)\bar{{\it\tau}}\right).\end{eqnarray}$$
Note that (4.6) also implies
${\it\lambda}_{I}\approx 0$
. (Including the effects of resistivity gives
${\it\lambda}_{I}$
a small positive non-zero value
$\propto 1/\ln (R_{M})$
as will be shown below.) The
${\it\gamma}_{0}$
we get matches with that of Kulsrud & Anderson (Reference Kulsrud and Anderson1992), obtained from the evolution equation of
$M(k,t)$
. It is also important to note that the growth rate is reduced for a finite-
$\bar{{\it\tau}}$
. This was found in simulations which directly compare with an equivalent Kazantsev model (Mason et al.
Reference Mason, Malyshkin, Boldyrev and Cattaneo2011).
The form of the magnetic correlation
$M_{L}$
for
$z_{{\it\eta}}\ll z\ll 1$
can also be found from (4.5). It is given by
$$\begin{eqnarray}M_{L}(z,t)=\text{e}^{{\it\gamma}\tilde{t}}\tilde{M}_{0}z^{-5/2}\sin ({\it\lambda}_{I}\ln (z)+{\it\phi}),\end{eqnarray}$$
where
$\tilde{M}_{0}$
and
${\it\phi}$
are constants. Thus in this range,
$M_{L}$
varies dominantly as
$z^{-5/2}$
, modulated by the weakly varying sine factor (as
${\it\lambda}_{I}$
is small). We will use this below to determine the asymptotic magnetic spectrum. Before that, we turn to the alternative approach to determining
${\it\gamma}$
and
$M_{L}$
, using the WKBJ approximation, which also allows one to incorporate the effects of the small resistive terms.
4.2. Growth rate and Magnetic correlation function using WKBJ analysis
First it is convenient to define a scaled coordinate
$\bar{z}=(\sqrt{{\it\eta}_{t}/{\it\eta}})~z$
. In terms of this new coordinate the resistive scale will have
$\bar{z}\sim 1$
, whereas the forcing scale,
$z=1$
, corresponds to
$\bar{z}\sim \sqrt{R_{M}}\gg 1$
. Now substituting the expressions in (4.3) back into the full equation (4.1) we get
$$\begin{eqnarray}\frac{\text{d}^{2}\tilde{M}_{L}}{\text{d}\bar{z}^{2}}\left(2+\bar{{\it\tau}}{\it\gamma}_{0}\frac{9\bar{z}^{2}}{70}+\frac{\bar{z}^{2}}{5}\right)+\frac{\text{d}\tilde{M}_{L}}{\text{d}\bar{z}}\left(\frac{8}{\bar{z}}+\bar{{\it\tau}}{\it\gamma}_{0}\frac{27\bar{z}}{35}+\frac{6\bar{z}}{5}\right)+(2-{\it\gamma})\tilde{M}_{L}=0.\end{eqnarray}$$
As remarked earlier, the coefficients of the perturbative terms in (4.1) are such that all perturbative terms which do not depend on
${\it\gamma}_{0}$
cancel out in (4.8).
Further, in order to implement the boundary condition at
$\bar{z}=0$
, under the WKBJ approximation, it is better to transform to a new variable
$x$
, where
$\bar{z}=\text{e}^{x}$
. Also, to eliminate first-derivative terms in the resulting equation we substitute
$\tilde{M}_{L}(x)=g(x)W(x)$
, and choose
$g(x)$
to satisfy the differential equation
$$\begin{eqnarray}\frac{1}{g}\frac{\text{d}g}{\text{d}x}=-\frac{5}{2}\frac{(6+\bar{z}^{2}F)}{(10+\bar{z}^{2}F)},\quad \text{with }F=\left(1+\left(\frac{9}{14}\right)\bar{{\it\tau}}{\it\gamma}_{0}\right).\end{eqnarray}$$
Then
$W$
satisfies
$$\begin{eqnarray}\frac{\text{d}^{2}W}{\text{d}x^{2}}+p(x)W=0,\end{eqnarray}$$
where
$$\begin{eqnarray}p(x)=\frac{A_{0}\bar{z}^{4}-B_{0}\bar{z}^{2}-225}{(10+F\bar{z}^{2})^{2}},\end{eqnarray}$$
$$\begin{eqnarray}A_{0}=5F\left({\textstyle \frac{3}{4}}-{\textstyle \frac{45}{56}}\bar{{\it\tau}}{\it\gamma}_{0}-{\it\gamma}\right),\quad B_{0}=5\left(10{\it\gamma}+{\textstyle \frac{171}{14}}\bar{{\it\tau}}{\it\gamma}_{0}-1\right).\end{eqnarray}$$
The WKBJ solutions to this equation are linear combinations of
$$\begin{eqnarray}W=\frac{1}{p^{1/4}}\exp \left(\pm \text{i}\int ^{x}p^{1/2}\,\text{d}x\right).\end{eqnarray}$$
Note that as
$\bar{z}\rightarrow 0$
,
$x\rightarrow -\infty$
and
$p\rightarrow -9/4$
; so the WKBJ solutions are in the form of growing and decaying exponentials in this limit. And as
$\bar{z}$
increases to a large enough value,
$p(x)$
goes through a zero at say
$\bar{z}=\bar{z}_{0}$
(or
$x=x_{0}$
) and becomes positive for
$\bar{z}>\bar{z}_{0}$
. The solution then becomes oscillatory. Note that when
$\bar{z}\rightarrow +\infty$
, one would again want the solution to decay, and so
$p(x)$
should become negative. This cannot be seen in (4.11), as it is valid only for
$z\ll 1$
(or
$\bar{z}\ll \sqrt{R_{M}}$
), but would require one to consider (3.28) in the opposite limit of
$z\gg 1$
(or
$\bar{z}\gg \sqrt{R_{M}}$
). In such a limit one has
$T_{L}(r)\rightarrow 0$
,
$\overline{T}_{L}(r)\rightarrow 0$
, and again using the Landau–Lifshitz ansatz to eliminate
$\tilde{M}_{L}^{\prime \prime \prime \prime }$
,
$\tilde{M}_{L}(z)$
now satisfies
$$\begin{eqnarray}{\it\gamma}\tilde{M}_{L}(z)=\left(\frac{2{\it\eta}}{{\it\eta}_{t}}+2+\bar{{\it\tau}}{\it\alpha}\right)\tilde{M}_{L}^{\prime \prime }+8\left(\frac{{\it\eta}}{{\it\eta}_{t}}+1\right)\frac{\tilde{M}_{L}^{\prime }}{z},\end{eqnarray}$$
where
${\it\alpha}=(q^{2}\overline{T}_{L}(0){\it\gamma}_{0})/[12({\it\eta}+{\it\eta}_{t})]$
. We can again transform to the
$x$
-coordinate, and write
$\tilde{M}_{L}=gW$
. Then in this limit of
$z\gg 1$
,
$W$
again satisfies (4.10) with now
$$\begin{eqnarray}\frac{1}{g}\frac{\text{d}g}{\text{d}x}=-\text{e}^{x}\frac{(1+{\it\eta}_{t}/{\it\eta})}{2(2+2{\it\eta}_{t}/{\it\eta}+\bar{{\it\tau}}{\it\alpha})},\quad p(x)=-\text{e}^{2x}\frac{(1+{\it\eta}_{t}/{\it\eta})+{\it\gamma}}{(2+2{\it\eta}_{t}/{\it\eta}+\bar{{\it\tau}}{\it\alpha})^{2}}.\end{eqnarray}$$
We see that
$p(x)$
is now negative definite and so again one has exponentially damped solutions for
$W$
. Since
$p(x)>0$
for
$\bar{z}>\bar{z}_{0}$
, and is negative at
$\bar{z}\gg \sqrt{R_{M}}$
, there would again be a point, say
$\bar{z}=\bar{z}_{c}$
(or
$x=x_{c}$
), where it would go to zero. We approximate our WKBJ treatment by assuming that (4.8) is valid for
$z<1$
and (4.14) is valid for
$z>1$
. The outer transition point
$\bar{z}_{c}$
then can be taken to be the boundary between these two regions. We will see that the
$\bar{z}_{c}$
dependence, in the determination of the growth rate and
$\tilde{M}_{L}$
, only comes within a logarithm, and so our results are not very sensitive to its exact value. This feature has been remarked upon earlier by several authors (Kulsrud & Anderson Reference Kulsrud and Anderson1992; Gruzinov et al.
Reference Gruzinov, Cowley and Sudan1996; Schekochihin, Boldyrev & Kulsrud Reference Schekochihin, Boldyrev and Kulsrud2002; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005).
The requirement that the oscillatory solution in the region
$\bar{z}_{0}<\bar{z}<\bar{z}_{c}$
match onto the growing exponential near
$\bar{z}\ll \bar{z}_{0}$
and the decaying exponential when
$\bar{z}\gg \bar{z}_{c}$
, gives the standard condition (Bender & Orszag Reference Bender and Orszag1978; Mestel & Subramanian Reference Mestel and Subramanian1991; Subramanian Reference Subramanian1997) on the eigenvalue
${\it\gamma}$
:
$$\begin{eqnarray}\int _{x_{0}}^{x_{c}}p^{1/2}(x)\,\text{d}x=\frac{(2n+1){\rm\pi}}{2},\quad n=0,1.\end{eqnarray}$$
We will find that
$\bar{z}_{0}$
is large enough that one can neglect the constant terms in (4.11). Then the integral in (4.16) can be done exactly and leads to the condition
$$\begin{eqnarray}A_{0}^{1/2}\left[\ln \left(\frac{\bar{z}_{c}}{\bar{z}_{0}}+\left(\frac{\bar{z}_{c}^{2}}{\bar{z}_{0}^{2}}-1\right)^{1/2}\right)-\left(1-\frac{\bar{z}_{0}^{2}}{\bar{z}_{c}^{2}}\right)^{1/2}\right]=\frac{{\rm\pi}F}{2}.\end{eqnarray}$$
Here we have taken
$n=0$
which corresponds to the fastest growing eigenfunction. We will also find self-consistently that for large
$R_{M}$
,
$\bar{z}_{c}^{2}/\bar{z}_{0}^{2}\gg 1$
. In this case (4.17) gives for the growth rate
$$\begin{eqnarray}{\it\gamma}=\frac{3}{4}-\frac{45}{56}\bar{{\it\tau}}{\it\gamma}_{0}-\frac{{\rm\pi}^{2}}{5}\frac{\displaystyle \left(1+\left({\textstyle \frac{9}{14}}\right)\bar{{\it\tau}}{\it\gamma}_{0}\right)}{(\ln (2\bar{z}_{c}/\bar{z}_{0}))^{2}}\approx \frac{3}{4}\left[1-\frac{45}{56}\bar{{\it\tau}}\right]-\frac{{\rm\pi}^{2}}{5}\frac{\displaystyle \left(1+\left({\textstyle \frac{27}{56}}\right)\bar{{\it\tau}}\right)}{(\ln (R_{M}))^{2}}.\end{eqnarray}$$
In the latter part of (4.18), we have used self-consistent estimates of
${\it\gamma}_{0}\sim 3/4$
,
$\bar{z}_{c}\sim \sqrt{{\it\eta}_{t}/{\it\eta}}z_{c}\sim \sqrt{R_{M}}$
and
$\bar{z}_{0}\sim \sqrt{B_{0}/A_{0}}\sim \ln (R_{M})$
, and so also neglected
$\ln \bar{z}_{0}$
compared to
$\ln \bar{z}_{c}$
. This result for the growth rate exactly matches with that obtained earlier by BS14 in the limit of large
$R_{M}$
using a scaling solution (see (4.6) above). It of course corrects this estimate for finite
$R_{M}$
. We also see from (4.18) that the growth rate is not sensitive (more correctly only logarithmically sensitive) to the exact value of
$\bar{z}_{c}$
, the upper zero of
$p(x)$
.
The WKBJ analysis also gives the form of the eigenfunction between the two zeros:
$$\begin{eqnarray}W(x)\approx \frac{1}{p^{1/4}}\sin \left[\int _{x_{1}}^{x}(p)^{1/2}\,\text{d}x+\frac{{\rm\pi}}{4}\right]\approx \frac{(\ln R_{M})^{1/2}}{{\rm\pi}^{1/2}}\sin \left[\frac{{\rm\pi}}{\ln R_{M}}\ln \left(\frac{\bar{z}}{\bar{z}_{0}}\right)+\frac{{\rm\pi}}{4}\right],\end{eqnarray}$$
where for the latter expression we have taken the large
$\bar{z}>\bar{z}_{0}\gg 1$
limit which is applicable here. Also, for
$\bar{z}\gg 1$
, we can see from (4.9) that
$(1/g)(\text{d}g/\text{d}x)\rightarrow -5/2$
independent of the value of
$\bar{{\it\tau}}$
. Thus in this limit
$g(x)\propto \exp (-5x/2)$
. Since
$M_{L}(z)\propto \text{e}^{{\it\gamma}\tilde{t}}gW$
, the WKBJ solution for the region
$z_{{\it\eta}}\ll z\ll 1$
is then given by
$$\begin{eqnarray}M_{L}(z,t)=\text{e}^{{\it\gamma}\tilde{t}}\tilde{M}_{0}z^{-5/2}\sin \left[\frac{{\rm\pi}}{\ln R_{M}}\ln \left(\frac{z}{z_{0}}\right)+\frac{{\rm\pi}}{4}\right].\end{eqnarray}$$
This again matches with the result obtained from the scaling solution, improving it by fixing the constants there, in particular
${\it\lambda}_{I}$
. We see that the dominant variation of
$M_{L}(z,t)$
in this regime is the power law behaviour
$M_{L}\propto z^{-5/2}$
, modulated by the weakly varying sine factor, as before.
4.3. Magnetic spectrum at finite-
${\it\tau}$
The power law scaling of the magnetic correlation function can be translated to the scaling of the magnetic power spectrum. It is straightforward to show that the magnetic power spectrum is related to the longitudinal correlation function
$M_{L}$
by (cf. Brandenburg & Subramanian Reference Brandenburg and Subramanian2000)
$$\begin{eqnarray}M(k,t)=\int \text{d}r\,(kr)^{3}M_{L}(r,t)j_{1}(kr).\end{eqnarray}$$
The spherical Bessel function
$j_{1}(kr)$
is peaked around
$k\sim 1/r$
, and every value of
$k$
in
$M(k,t)$
gets a dominant contribution in the integral in (4.21) from values of
$r\sim 1/k$
. Therefore a power law behaviour of
$M_{L}\propto z^{-{\it\lambda}_{R}}$
for a range of
$z_{{\it\eta}}\ll z=qr\ll 1$
, translates into a power law for the spectrum
$M(k)\propto k^{{\it\lambda}_{R}-1}$
in the corresponding wavenumber range
$q\ll k\ll q/z_{{\it\eta}}$
. Both the scaling solution in (4.7) and the WKBJ solution given in (4.20), show that in the range
$z_{{\it\eta}}\ll z\ll 1$
,
$M_{L}$
dominantly varies as a power law with
${\it\lambda}_{R}=5/2$
, independent of
${\it\tau}$
. This then leads to the remarkable result emphasized by BS14 that the magnetic spectrum is of the Kazantsev form with
$M(k)\propto k^{3/2}$
in
$k$
-space, independent of
${\it\tau}$
!
5. Discussion and conclusions
Fluctuation dynamos, generic to any turbulent plasma, are likely to be crucial for rapid generation of magnetic fields in astrophysical systems. We have given here an analytical treatment of fluctuation dynamos at finite correlation times, by modelling the velocity as a flow which renews itself after every time step
${\it\tau}$
. In particular we present a detailed derivation of the evolution equation for the two-point magnetic correlation function in such a flow, earlier spelled out briefly in BS14. This generalizes the Kazantsev equation, which was derived under the assumption that the velocity is delta-correlated in time, to the situation where the correlation time is finite. The correlation time will indeed be finite in any turbulent flow. Our generalized evolution equation for
$M_{L}(r,t)$
, (3.28), reduces to the Kazantsev equation when
${\it\tau}\rightarrow 0$
, and extends it to the next order in
${\it\tau}$
.
The evolution equation for such a finite-
${\it\tau}$
involves both higher- (fourth-) order velocity correlators and also higher-order (third and fourth) spatial derivatives of
$M_{L}$
, signalling that non-local effects are important in this case. However, these higher-order derivatives appear only perturbatively, multiplied by the small parameter
$\bar{{\it\tau}}={\it\tau}{\it\eta}_{t}q^{2}$
. This allows us to use the Landau–Lifshitz approach, earlier used to treat the effect of the radiation reaction force in electrodynamics. In this approach, to the zeroth order in
$\bar{{\it\tau}}$
, one retains the standard Kazantsev equation. This is then used to express the third and fourth derivatives of
$M_{L}$
in terms of the lower-order derivatives, to finally get an evolution equation which at most involves second derivatives of
$M_{L}$
.
The resulting evolution equation is analysed both using a scaling solution and the WKBJ approximation. The scaling solution is valid in the range of scales where resistivity can be neglected, while the WKBJ treatment also takes into account the effect of a finite resistivity. From both treatments we see that the effect of a finite-
${\it\tau}$
is to cause a reduction in the dynamo growth rate. This result agrees with the result of simulations which directly compare with an equivalent Kazantsev model (Mason et al.
Reference Mason, Malyshkin, Boldyrev and Cattaneo2011).
The asymptotic form of the correlation function on scales
$z_{{\it\eta}}\ll z\ll 1/q$
is very nearly a power law,
$M_{L}\propto z^{-5/2}$
, independent of
${\it\tau}$
! This leads to the important and intriguing result that the Kazantsev spectrum of
$M(k)\propto k^{3/2}$
is preserved even at finite-
${\it\tau}$
.
Although we have derived the effects of a finite-
${\it\tau}$
using a particular renewing velocity field, the resulting evolution equation for
$M_{ih}$
(3.21) or
$M_{L}$
(3.28) can be cast completely in terms of the general velocity correlators,
$T_{ij}$
and
$T_{ijkl}$
. It also matches exactly with the Kazantsev equation for the
${\it\tau}\rightarrow 0$
case. Moreover, we expect the forms of
$T_{ij}$
and
$T_{ijkl}$
for
$r\ll 1/q$
to be universal due to their symmetries and divergence-free properties. We would therefore conjecture that our results on the magnetic spectrum could have a more general validity than the context (of a renewing velocity) in which they are derived. Future work would involve a numerical study of (3.28) without making the small-
$z$
approximation. The general methodology developed here also holds the promise of being systematically extendable to the non-perturbative regime of
$\mathit{St}\sim 1$
, at least by a series of numerical integrations to implement the averaging. The inclusion of shear and helicity are also the next obvious extensions that need to be studied, issues which we hope to address in the future.
Acknowledgements
We thank D. Sokoloff for very helpful correspondence, A. Brandenburg, N. Singh and S. Sridhar for several useful discussions. P.B. acknowledges support from CSIR. We thank the referees for useful comments which helped in improving our paper.
Appendix A. Operator splitting for the magnetic two-point correlator
In § 2, we obtained the expression for the two-point magnetic correlator,
$M_{ih}(\boldsymbol{r},t)$
, in (2.17), by using the technique of operator splitting as introduced by GB. We give here a brief exposition of the operator splitting technique (Holden et al.
Reference Holden, Karlsen, Li and Risebro2010). Suppose we have a linear equation, given by the addition of two linear operators
$$\begin{eqnarray}\frac{\partial f}{\partial t}=Af+Df\end{eqnarray}$$
whose true solution can be given by
$f(t)=\text{e}^{t(A+D)}f_{0}$
, where
$f_{0}=f(0)$
. On splitting we have
$f_{L}=\text{e}^{hA}\text{e}^{hD}f_{0}$
, also known as Lie splitting. Here
$h$
is a small time step. Then the splitting error after a time step is given by
$$\begin{eqnarray}f_{L}-f(h)=(\text{e}^{hA}\text{e}^{hD}-\text{e}^{t(A+D)})f_{0}=\frac{h^{2}}{2}[A,D]\,f_{0}+O(h^{3})\ast g([A,D]),\end{eqnarray}$$
where all the terms on the right-hand side are essentially functions of the commutator,
$[A,D]$
. Hence if the two operators commute, i.e.
$[A,D]=0$
, then the splitting error goes to 0.
In our case,
$A$
can be the advection operator and then
$D$
is the diffusion operator. In § 2, we first advected the field in (2.8), ignoring the diffusion operator in the first sub-interval, and then subsequently diffused it, ignoring the advection operator. In the following we do the reverse and show that the resulting expression for the magnetic correlator in configuration space,
$M_{ih}(\boldsymbol{r},t)$
, is identical to that obtained in (2.17), in the limit of small
${\it\eta}$
or large
$R_{M}$
. This limit has been assumed to hold even in the earlier case and thus we had considered only the leading-order terms in the expansion of the Green’s function for diffusion,
$\text{e}^{-2{\it\eta}{\it\tau}\boldsymbol{p}^{2}}$
.
Now if we consider only diffusion first, in the first sub-interval,
${\it\tau}/2$
, we have in Fourier space
$$\begin{eqnarray}\hat{B}_{i}(\boldsymbol{m},t_{1})=\text{e}^{-({\it\eta}{\it\tau}\boldsymbol{m}^{2})}\hat{B}_{i}(\boldsymbol{m},t_{0}),\end{eqnarray}$$
where
$\boldsymbol{m}$
is the wavevector. Then, in the next sub-interval, we consider only advection,
$$\begin{eqnarray}B_{i}(\boldsymbol{x},t)=J_{ij}(\boldsymbol{x}(\boldsymbol{x}_{1}))B_{j}(\boldsymbol{x}_{1},t_{1}).\end{eqnarray}$$
We take the Fourier transform of both
$B_{i}(\boldsymbol{x},t)$
and
$B_{j}(\boldsymbol{x}_{1},t_{1})$
, and then substitute (A 3) into the resulting equation,
$$\begin{eqnarray}\hat{B}_{i}(\boldsymbol{k},t)=\int J_{ij}(\boldsymbol{x}(\boldsymbol{x}_{1}))(\text{e}^{-({\it\eta}{\it\tau}\boldsymbol{m}^{2})}\hat{B}_{i}(\boldsymbol{m},t_{0}))\text{e}^{\text{i}(\boldsymbol{m}\boldsymbol{\cdot }\boldsymbol{x}_{1}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})}\,\text{d}^{3}\boldsymbol{x}\frac{\text{d}^{3}\boldsymbol{m}}{(2{\rm\pi})^{3}}.\end{eqnarray}$$
Using (A 5), we can obtain the two-point magnetic correlator,
$$\begin{eqnarray}\displaystyle \langle \hat{B}_{i}(\boldsymbol{k},t)\hat{B}_{h}^{\ast }(\boldsymbol{p},t)\rangle & = & \displaystyle \left\langle \int \text{e}^{-{\it\eta}{\it\tau}(\boldsymbol{m}^{2}+\boldsymbol{n}^{2})}J_{ij}(\boldsymbol{x}_{1})J_{hl}(\boldsymbol{y}_{1})\hat{B}_{j}(\boldsymbol{m})\hat{B}_{l}(\boldsymbol{n})\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \,\text{e}^{\text{i}(\boldsymbol{m}\boldsymbol{\cdot }\boldsymbol{x}_{1}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x})}\text{e}^{\text{i}(-\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{y}_{1}+\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{y})}\,\text{d}^{3}\boldsymbol{x}\,\text{d}^{3}\boldsymbol{y}\frac{(\text{d}^{3}\boldsymbol{m}\,\text{d}^{3}\boldsymbol{n})}{(2{\rm\pi})^{6}}\right\rangle .\end{eqnarray}$$
We follow the same steps as used in § 2 and arrive at the following expression:
$$\begin{eqnarray}\hat{M}_{ih}(\boldsymbol{p},t)=\int \text{e}^{-2{\it\eta}{\it\tau}\boldsymbol{m}^{2}}\left\langle R_{ijhl}\right\rangle \text{e}^{\text{i}\boldsymbol{r}_{1}\boldsymbol{\cdot }(\boldsymbol{m}-\boldsymbol{p})}\hat{M}_{jl}(\boldsymbol{m})\,\text{d}^{3}\boldsymbol{r}_{1}\,\text{d}^{3}\boldsymbol{m}/(2{\rm\pi})^{3},\end{eqnarray}$$
where
$R_{ijhl}$
is as defined in (2.16). The expression in (A 7) differs from the one in (2.16) because the Gaussian,
$\text{e}^{-2{\it\eta}{\it\tau}\boldsymbol{m}^{2}}$
, is now within the integral. In the limit of
${\it\eta}\rightarrow 0$
, we recover the results as in (2.17). To see this, we Fourier transform
$\hat{M}_{ih}(\boldsymbol{p},t)$
back to configuration space,
$$\begin{eqnarray}\displaystyle M_{ih}(\boldsymbol{r}) & = & \displaystyle \int (1-2{\it\eta}{\it\tau}\boldsymbol{m}^{2})\left\langle R_{ijhl}\right\rangle \text{e}^{\text{i}\boldsymbol{r}_{1}\boldsymbol{\cdot }\boldsymbol{m}}\text{e}^{-\text{i}\boldsymbol{p}\boldsymbol{\cdot }(\boldsymbol{r}_{1}-\boldsymbol{r})}\hat{M}_{jl}(\boldsymbol{m})\,\text{d}^{3}\boldsymbol{r}_{1}\,(\text{d}^{3}\boldsymbol{m}\,\text{d}^{3}\boldsymbol{p})/(2{\rm\pi})^{6}\nonumber\\ \displaystyle & = & \displaystyle \int \left\langle R_{ijhl}\right\rangle M_{jl}(\boldsymbol{r}_{1})\text{e}^{\text{i}\boldsymbol{m}\boldsymbol{\cdot }(\boldsymbol{r}-\boldsymbol{r}_{1})}\,\text{d}^{3}\boldsymbol{r}_{1}\frac{\text{d}^{3}\boldsymbol{m}}{(2{\rm\pi})^{3}}+2{\it\eta}{\rm\nabla}^{2}M_{ih}(\boldsymbol{r},t),\end{eqnarray}$$
which now matches with the expression in (2.17). Actually, in the case of the induction equation,
$A$
(advection) and
$D$
(diffusion) do not commute. But here we have shown that these operations do commute, if one looks at the evolution of the magnetic correlation function (which is a statistically averaged quantity), in the limit of small enough
${\it\eta}$
or high
$R_{M}$
. While this is not a proof, it is an encouraging result and suggests the validity of our approach.
We end with a comment on the corresponding evolution equation for
$M_{ij}$
obtained by Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) using the Weiner path integral approach to incorporate microscopic diffusion (Dittrich et al.
Reference Dittrich, Molchanov, Sokolov and Ruzmaikin1984; Zeldovich et al.
Reference Zeldovich, Molchanov, Ruzmaikin and Sokoloff1988, Reference Zeldovich, Ruzmaikin and Sokoloff1990). Their evolution equation for
$M_{ij}$
is given in an integral form by equations (A20) and (A21) of their paper. The corresponding evolution equation that we derive is given by (2.16) in Fourier space and (2.17) in real space. First, for small
${\it\tau}$
, when one keeps terms to the order
${\it\tau}^{2}$
, both approaches agree and the Kazantsev evolution equation is obtained. Also, the only effect of resistivity, to the lowest order in
${\it\tau}$
, even in the path integral approach, as shown by equations (B5) and (B6) of Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002), is to introduce an extra diffusion term of the form
$2{\it\eta}{\rm\nabla}^{2}M_{ij}$
into the evolution equation for
$M_{ij}$
. This is also exactly what happens in our case (see (3.11) or (3.21)), where we have used the operator splitting method. Thus it would seem that our approach of using operator splitting to derive the effect of finite resistivity on
$M_{ij}$
evolution, matches with the more exact path integral methodology of Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) in the limit of small
${\it\tau}$
and small
${\it\eta}$
. Of course, as we pointed out above, Kleeorin et al. (Reference Kleeorin, Rogachevskii and Sokoloff2002) seem to have kept only the terms up to
$p^{2}$
in (3.1). Thus they are missing some of the terms in their evolution equation which correct the Kazantsev equation to leading order in
${\it\tau}$
. Hence, a comparison of the
${\it\eta}$
-independent terms to the generalized Kazantsev equation that we derive here is beyond the scope of the present paper, but would be of interest in the future.
