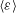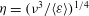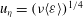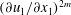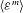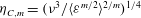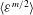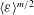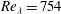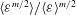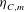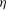1 Introduction
Kolmogorov (Reference Kolmogorov1941b
) introduced the idea of local isotropy, i.e. that turbulence is isotropic at small scales (and possibly universally), provided that the Reynolds number is large enough so that a scale separation occurs, while the large scales are determined by the flow geometry and boundary conditions. Furthermore, Kolmogorov proposed two similarity laws. The first similarity hypothesis states that, for locally homogeneous and isotropic turbulence, the statistics of structure functions, defined as the velocity difference between two points separated by a distance
![]() $r$
, are determined by the viscosity
$r$
, are determined by the viscosity
![]() ${\it\nu}$
and the mean dissipation
${\it\nu}$
and the mean dissipation
![]() $\langle {\it\varepsilon}\rangle$
. For
$\langle {\it\varepsilon}\rangle$
. For
![]() $r$
situated in the inertial range between the very small scales and the large scales, the dependence on the viscosity
$r$
situated in the inertial range between the very small scales and the large scales, the dependence on the viscosity
![]() ${\it\nu}$
should vanish according to the second hypothesis of similarity. From the two quantities
${\it\nu}$
should vanish according to the second hypothesis of similarity. From the two quantities
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $\langle {\it\varepsilon}\rangle$
relevant at the very small scales, he introduced
$\langle {\it\varepsilon}\rangle$
relevant at the very small scales, he introduced
![]() ${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
and
${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
and
![]() $u_{{\it\eta}}=({\it\nu}/\langle {\it\varepsilon}\rangle )^{1/2}$
as characteristic length and velocity scales, which were derived for the second order. The main focus of the present work is to revisit these results and generalise them for higher orders under the same assumptions, i.e. (local) isotropy, (local) homogeneity and incompressibility. We are able to present some new and exact results for longitudinal, even-ordered structure functions.
$u_{{\it\eta}}=({\it\nu}/\langle {\it\varepsilon}\rangle )^{1/2}$
as characteristic length and velocity scales, which were derived for the second order. The main focus of the present work is to revisit these results and generalise them for higher orders under the same assumptions, i.e. (local) isotropy, (local) homogeneity and incompressibility. We are able to present some new and exact results for longitudinal, even-ordered structure functions.
In a second paper, Kolmogorov (Reference Kolmogorov1941a
) proceeded to rewrite the Kármán–Howarth equation (cf. de Karman & Howarth Reference de Karman and Howarth1938) in terms of the second-order longitudinal structure function. This led to analytic solutions for the second-order structure function for
![]() $r\rightarrow 0$
, which agrees with his previously derived result using only isotropy and Taylor series, as given in the first 1941 paper, and the third-order structure function in the inertial range
$r\rightarrow 0$
, which agrees with his previously derived result using only isotropy and Taylor series, as given in the first 1941 paper, and the third-order structure function in the inertial range
![]() ${\it\eta}\ll r\ll L$
under the assumption of very large (infinite) Reynolds number, where
${\it\eta}\ll r\ll L$
under the assumption of very large (infinite) Reynolds number, where
![]() $L$
is the integral length scale.
$L$
is the integral length scale.
The two papers had a huge impact, as they provided specific predictions about the nature of turbulent flows stemming directly from the governing Navier–Stokes equations, one of which is that in the inertial range the structure functions should follow a power law in terms of the separation distance
![]() $r$
. Furthermore, Kolmogorov’s postulate that velocity differences at small scales are isotropic, leading to the idea that some small-scale properties should be flow-independent, is quite appealing (see Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) for an overview). It was found that, although Kolmogorov’s results for the second- and third-order structure functions are in very good agreement with measurements (see e.g. Anselmet, Gagne & Hopfinger Reference Anselmet, Gagne and Hopfinger1984), the generalisation to higher orders is rather poor. For instance, the experimentally observed inertial range power-law exponents
$r$
. Furthermore, Kolmogorov’s postulate that velocity differences at small scales are isotropic, leading to the idea that some small-scale properties should be flow-independent, is quite appealing (see Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) for an overview). It was found that, although Kolmogorov’s results for the second- and third-order structure functions are in very good agreement with measurements (see e.g. Anselmet, Gagne & Hopfinger Reference Anselmet, Gagne and Hopfinger1984), the generalisation to higher orders is rather poor. For instance, the experimentally observed inertial range power-law exponents
![]() ${\it\zeta}_{m}$
at higher orders deviate significantly from the values one would obtain by applying Kolmogorov’s original postulate that only the mean dissipation
${\it\zeta}_{m}$
at higher orders deviate significantly from the values one would obtain by applying Kolmogorov’s original postulate that only the mean dissipation
![]() $\langle {\it\varepsilon}\rangle$
and
$\langle {\it\varepsilon}\rangle$
and
![]() ${\it\nu}$
are relevant. For that matter, Kolmogorov (Reference Kolmogorov1962) modified his theory following Obukhov (Reference Obukhov1962) based on the phenomenological observation that turbulent fluctuations of the dissipation play a crucial role in turbulence. In particular, they substituted a locally averaged dissipation
${\it\nu}$
are relevant. For that matter, Kolmogorov (Reference Kolmogorov1962) modified his theory following Obukhov (Reference Obukhov1962) based on the phenomenological observation that turbulent fluctuations of the dissipation play a crucial role in turbulence. In particular, they substituted a locally averaged dissipation
![]() ${\it\varepsilon}_{r}$
for the overall dissipation
${\it\varepsilon}_{r}$
for the overall dissipation
![]() $\langle {\it\varepsilon}\rangle$
and assumed a log-normal distribution for
$\langle {\it\varepsilon}\rangle$
and assumed a log-normal distribution for
![]() ${\it\varepsilon}_{r}$
. This led the way to (multi-)fractal models providing equations for
${\it\varepsilon}_{r}$
. This led the way to (multi-)fractal models providing equations for
![]() ${\it\zeta}_{m}$
using some additional parameters (see Sreenivasan (Reference Sreenivasan1991) and Frisch (Reference Frisch1995) for overviews). Equations for structure functions of all orders were derived by Hill (Reference Hill2001) and Yakhot (Reference Yakhot2001), using different methods.
${\it\zeta}_{m}$
using some additional parameters (see Sreenivasan (Reference Sreenivasan1991) and Frisch (Reference Frisch1995) for overviews). Equations for structure functions of all orders were derived by Hill (Reference Hill2001) and Yakhot (Reference Yakhot2001), using different methods.
The notion of order-dependent cut-off length scales is also related to the multi-fractal framework – see, for example, Paladin & Vulpiani (Reference Paladin and Vulpiani1987a ,Reference Paladin and Vulpiani b ), who used the multi-fractal model to estimate grid resolution scaling. Frisch & Vergassola (Reference Frisch and Vergassola1991) used the notion of scales smaller than the Kolmogorov scale to modify the second-order structure function as well as the energy spectrum in the so-called intermediate dissipation range (situated in between the Kolmogorov scale and the smallest scale determined by the lowest fractal exponent). They then proposed a renormalisation of the energy spectrum to collapse it to a universal curve.
Meneveau (Reference Meneveau1996) examined the dissipative range by employing an order-dependent interpolation formula accompanied by using a multi-fractal model to examine order- and Reynolds-number-dependent collapse of structure functions in the dissipative range. He showed that order-dependent cut-off length scales as given by a multi-fractal model are consistent with extended self-similarity (ESS; cf. Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) for small Reynolds numbers, but that the collapse of ESS worsens for high Reynolds numbers and order.
Yakhot (Reference Yakhot2003) derived order-dependent cut-off length scales by matching the dissipative range and the inertial range, and related these cut-off scales to the inertial range exponents
![]() ${\it\zeta}_{m}$
. Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005) then used Yakhot’s result and derived additional constraints on the inertial range scaling exponents. Furthermore, they considered the implications regarding the grid resolution of numerical studies in the context of Yakhot’s theory. More recently, Schumacher, Sreenivasan & Yakhot (Reference Schumacher, Sreenivasan and Yakhot2007) examined structure functions using highly resolved direct numerical simulations (DNS) and found that they collapse in the dissipation range when normalised with the cut-off lengths defined by the inertial range exponents given by Yakhot (Reference Yakhot2003).
${\it\zeta}_{m}$
. Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005) then used Yakhot’s result and derived additional constraints on the inertial range scaling exponents. Furthermore, they considered the implications regarding the grid resolution of numerical studies in the context of Yakhot’s theory. More recently, Schumacher, Sreenivasan & Yakhot (Reference Schumacher, Sreenivasan and Yakhot2007) examined structure functions using highly resolved direct numerical simulations (DNS) and found that they collapse in the dissipation range when normalised with the cut-off lengths defined by the inertial range exponents given by Yakhot (Reference Yakhot2003).
The approach presented in this paper differs from those described above inasmuch as we derive cut-off scales by using information gained from the (isotropic) tensorial properties of the velocity gradient tensor, for which we do not need any specific assumptions other than isotropy, homogeneity and incompressibility. This allows us to define the cut-off scales with dissipative quantities only (namely, the moments of the dissipation), and we find exact relations for the longitudinal structure functions of arbitrary even order, using only the same assumptions as in Kolmogorov’s seminal 1941 work (henceforth often abbreviated as K41).
The paper is organised as follows. We use data from DNS, which are described in § 2. In § 3, we look at velocity structure functions in the dissipative range and find analytical relations for even-order longitudinal structure functions. From these follow new
![]() $m$
th-order cut-off length scales
$m$
th-order cut-off length scales
![]() ${\it\eta}_{C,m}$
and velocities
${\it\eta}_{C,m}$
and velocities
![]() $u_{C,m}$
, resulting in Reynolds-number-independent non-dimensional structure functions in the dissipation range, which we discuss and check against our DNS data. We want to emphasise that these results are not connected in any way to the multi-fractal models, in the sense that those models are not needed to derive the results presented here. However, any theory predicting the scaling of the dissipation
$u_{C,m}$
, resulting in Reynolds-number-independent non-dimensional structure functions in the dissipation range, which we discuss and check against our DNS data. We want to emphasise that these results are not connected in any way to the multi-fractal models, in the sense that those models are not needed to derive the results presented here. However, any theory predicting the scaling of the dissipation
![]() ${\it\varepsilon}_{r}$
predicts the scaling of the normalised moments of the dissipation in the dissipative range and therefore also of
${\it\varepsilon}_{r}$
predicts the scaling of the normalised moments of the dissipation in the dissipative range and therefore also of
![]() ${\it\eta}_{C,m}$
. This is examined in detail in § 4, and we compare the results obtained from some well-known models to our DNS. The new scales
${\it\eta}_{C,m}$
. This is examined in detail in § 4, and we compare the results obtained from some well-known models to our DNS. The new scales
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
lead to modifications of grid resolution requirements for DNS and to a modified scaling of the number of grid points as discussed in § 5. Different from previous studies (e.g. Yakhot & Sreenivasan Reference Yakhot and Sreenivasan2005), we use the exact results of § 3 instead of those stemming from multi-fractal models. We then summarise the results in § 6.
$u_{C,m}$
lead to modifications of grid resolution requirements for DNS and to a modified scaling of the number of grid points as discussed in § 5. Different from previous studies (e.g. Yakhot & Sreenivasan Reference Yakhot and Sreenivasan2005), we use the exact results of § 3 instead of those stemming from multi-fractal models. We then summarise the results in § 6.
2 Direct numerical simulations
For the analysis carried out in the present paper, we use data from DNS of forced homogeneous isotropic turbulence with six different sets of Taylor-based Reynolds numbers, ranging from
![]() $Re_{{\it\lambda}}=88$
to
$Re_{{\it\lambda}}=88$
to
![]() $Re_{{\it\lambda}}=754$
, where
$Re_{{\it\lambda}}=754$
, where
![]() $Re_{{\it\lambda}}=u_{rms}{\it\lambda}/{\it\nu}$
,
$Re_{{\it\lambda}}=u_{rms}{\it\lambda}/{\it\nu}$
,
![]() ${\it\lambda}$
denotes the Taylor scale
${\it\lambda}$
denotes the Taylor scale
![]() ${\it\lambda}=\sqrt{10{\it\nu}\langle k\rangle /\langle {\it\varepsilon}\rangle }$
,
${\it\lambda}=\sqrt{10{\it\nu}\langle k\rangle /\langle {\it\varepsilon}\rangle }$
,
![]() $u_{rms}=\langle u_{i}u_{i}/3\rangle$
is the root-mean-square velocity,
$u_{rms}=\langle u_{i}u_{i}/3\rangle$
is the root-mean-square velocity,
![]() $\langle k\rangle =\langle u_{i}u_{i}\rangle /2$
is the mean kinetic energy and
$\langle k\rangle =\langle u_{i}u_{i}\rangle /2$
is the mean kinetic energy and
![]() $\langle {\it\varepsilon}\rangle =2{\it\nu}\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle$
is the mean energy dissipation, with the strain tensor
$\langle {\it\varepsilon}\rangle =2{\it\nu}\langle \unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}\rangle$
is the mean energy dissipation, with the strain tensor
![]() $\unicode[STIX]{x1D61A}_{ij}=(\partial u_{i}/\partial x_{j}+\partial u_{j}/\partial x_{i})/2$
. Angle brackets
$\unicode[STIX]{x1D61A}_{ij}=(\partial u_{i}/\partial x_{j}+\partial u_{j}/\partial x_{i})/2$
. Angle brackets
![]() $\langle \,\cdots \,\rangle$
denote ensemble averages over the full box and several time steps spanning more than an integral turnover time after the simulation has reached its statistically steady state (as given by the ratio
$\langle \,\cdots \,\rangle$
denote ensemble averages over the full box and several time steps spanning more than an integral turnover time after the simulation has reached its statistically steady state (as given by the ratio
![]() $t_{avg}/{\it\tau}$
). We use
$t_{avg}/{\it\tau}$
). We use
![]() $M$
to denote the number of time steps used to compute the averages.
$M$
to denote the number of time steps used to compute the averages.
The six datasets have been computed on the JUQUEEN supercomputer at Forschungszentrum Jülich using a pseudo-spectral code with MPI/OpenMP parallelisation. The three-dimensional Navier–Stokes equations were solved in rotational form, where all terms except the nonlinear term were evaluated in spectral space. For a faster computation, the nonlinear term is evaluated in physical space. The computational domain is a box with periodic boundary conditions and length
![]() $2{\rm\pi}$
. For dealiasing, the scheme of Hou & Li (Reference Hou and Li2007) has been used. For the temporal advancement, a second-order Adams–Bashforth scheme is used in the case of the nonlinear term, while the linear terms are updated using a Crank–Nicolson scheme. To keep the simulation statistically steady, the stochastic forcing scheme of Eswaran & Pope (Reference Eswaran and Pope1988) is applied. The 2DECOMP and FFT library (Li & Laizet Reference Li and Laizet2010) has been used for spatial decomposition and to perform the fast Fourier transforms. The only parameter varied to increase the Reynolds number is the viscosity
$2{\rm\pi}$
. For dealiasing, the scheme of Hou & Li (Reference Hou and Li2007) has been used. For the temporal advancement, a second-order Adams–Bashforth scheme is used in the case of the nonlinear term, while the linear terms are updated using a Crank–Nicolson scheme. To keep the simulation statistically steady, the stochastic forcing scheme of Eswaran & Pope (Reference Eswaran and Pope1988) is applied. The 2DECOMP and FFT library (Li & Laizet Reference Li and Laizet2010) has been used for spatial decomposition and to perform the fast Fourier transforms. The only parameter varied to increase the Reynolds number is the viscosity
![]() ${\it\nu}$
; the forcing parameters have been held constant. The properties of the DNS cases can be found in table 1. The five datasets were computed on a computational mesh with
${\it\nu}$
; the forcing parameters have been held constant. The properties of the DNS cases can be found in table 1. The five datasets were computed on a computational mesh with
![]() $512^{3}$
grid points for case R0 up to
$512^{3}$
grid points for case R0 up to
![]() $4096^{3}$
grid points for case R5. There,
$4096^{3}$
grid points for case R5. There,
![]() ${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
is the Kolmogorov length scale with corresponding time scale
${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
is the Kolmogorov length scale with corresponding time scale
![]() ${\it\tau}_{{\it\eta}}=({\it\nu}/\langle {\it\varepsilon}\rangle )^{1/2}$
,
${\it\tau}_{{\it\eta}}=({\it\nu}/\langle {\it\varepsilon}\rangle )^{1/2}$
,
![]() $L$
is the integral length scale, computed here using the energy spectrum function
$L$
is the integral length scale, computed here using the energy spectrum function
 $$\begin{eqnarray}\displaystyle L=\frac{3{\rm\pi}}{4}\frac{\displaystyle \int {\it\kappa}^{-1}E({\it\kappa})\,\text{d}{\it\kappa}}{\displaystyle \int E({\it\kappa})\,\text{d}{\it\kappa}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L=\frac{3{\rm\pi}}{4}\frac{\displaystyle \int {\it\kappa}^{-1}E({\it\kappa})\,\text{d}{\it\kappa}}{\displaystyle \int E({\it\kappa})\,\text{d}{\it\kappa}}, & & \displaystyle\end{eqnarray}$$
and
![]() ${\it\tau}=\langle k\rangle /\langle {\it\varepsilon}\rangle$
is the integral time scale. The integral length scale
${\it\tau}=\langle k\rangle /\langle {\it\varepsilon}\rangle$
is the integral time scale. The integral length scale
![]() $L$
is small compared to the size of the boxes in order to reduce the influence of the periodic boundary condition. Our data are well resolved with
$L$
is small compared to the size of the boxes in order to reduce the influence of the periodic boundary condition. Our data are well resolved with
![]() ${\it\kappa}_{max}{\it\eta}\geqslant 1.7$
for all five datasets, where
${\it\kappa}_{max}{\it\eta}\geqslant 1.7$
for all five datasets, where
![]() ${\it\kappa}_{max}$
is the largest resolved wavenumber. In turn, this also implies that the Reynolds number is not as high as for other DNS with comparable mesh size reported in the literature. We discuss this in more detail in § 5.
${\it\kappa}_{max}$
is the largest resolved wavenumber. In turn, this also implies that the Reynolds number is not as high as for other DNS with comparable mesh size reported in the literature. We discuss this in more detail in § 5.
Table 1. Characteristics of DNS cases.

3 Dissipative cut-off scales
Kolmogorov’s first similarity hypothesis (cf. Kolmogorov Reference Kolmogorov1941b
) states that ‘for the locally isotropic turbulence the distributions
![]() $F_{n}$
are uniquely determined by the quantities
$F_{n}$
are uniquely determined by the quantities
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $\langle {\it\varepsilon}\rangle$
’, where
$\langle {\it\varepsilon}\rangle$
’, where
![]() $F_{n}$
are the distributions of the velocity increments (note that Frisch (Reference Frisch1995) interprets
$F_{n}$
are the distributions of the velocity increments (note that Frisch (Reference Frisch1995) interprets
![]() $F_{n}$
as ‘small-scale properties’). In other words, all structure functions
$F_{n}$
as ‘small-scale properties’). In other words, all structure functions
![]() $D_{p,q}=\langle [{\rm\Delta}u_{1}]^{p}[{\rm\Delta}u_{2}]^{q}\rangle$
(where
$D_{p,q}=\langle [{\rm\Delta}u_{1}]^{p}[{\rm\Delta}u_{2}]^{q}\rangle$
(where
![]() ${\rm\Delta}u_{j}=u_{j}(\boldsymbol{x}_{i}+\boldsymbol{r}_{i})-u_{j}(\boldsymbol{x}_{i})$
and the separation vector
${\rm\Delta}u_{j}=u_{j}(\boldsymbol{x}_{i}+\boldsymbol{r}_{i})-u_{j}(\boldsymbol{x}_{i})$
and the separation vector
![]() $\boldsymbol{r}_{i}$
with magnitude
$\boldsymbol{r}_{i}$
with magnitude
![]() $r$
is aligned without loss of generality with the
$r$
is aligned without loss of generality with the
![]() $x_{1}$
axis) are supposed to be uniquely determined by the viscosity
$x_{1}$
axis) are supposed to be uniquely determined by the viscosity
![]() ${\it\nu}$
and the mean dissipation
${\it\nu}$
and the mean dissipation
![]() $\langle {\it\varepsilon}\rangle$
for
$\langle {\it\varepsilon}\rangle$
for
![]() $r\rightarrow 0$
. Kolmogorov backed up this claim by determining the solution for the second-order structure functions in the dissipative range,
$r\rightarrow 0$
. Kolmogorov backed up this claim by determining the solution for the second-order structure functions in the dissipative range,
where he obtained the factor
![]() $15$
by relating the mean dissipation
$15$
by relating the mean dissipation
![]() $\langle {\it\varepsilon}\rangle$
to
$\langle {\it\varepsilon}\rangle$
to
![]() $\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
(Kolmogorov Reference Kolmogorov1941b
). Indeed, it is possible to express the full tensor
$\langle (\partial u_{1}/\partial x_{1})^{2}\rangle$
(Kolmogorov Reference Kolmogorov1941b
). Indeed, it is possible to express the full tensor
![]() $\langle (\partial u_{i}/\partial x_{j})(\partial u_{k}/\partial x_{l})\rangle$
by a single scalar (e.g. the mean dissipation) under the assumption of isotropy, homogeneity and incompressibility, which implies that
$\langle (\partial u_{i}/\partial x_{j})(\partial u_{k}/\partial x_{l})\rangle$
by a single scalar (e.g. the mean dissipation) under the assumption of isotropy, homogeneity and incompressibility, which implies that
![]() $D_{2,0}$
and
$D_{2,0}$
and
![]() $D_{0,2}$
are exactly related in the dissipative range. Figure 1 shows the second-order structure function
$D_{0,2}$
are exactly related in the dissipative range. Figure 1 shows the second-order structure function
![]() $D_{2,0}$
normalised in this way for the different Reynolds numbers given in § 2, which we show here to allow a visual comparison with higher-order structure functions normalised with the Kolmogorov scales
$D_{2,0}$
normalised in this way for the different Reynolds numbers given in § 2, which we show here to allow a visual comparison with higher-order structure functions normalised with the Kolmogorov scales
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
as presented below. In that spirit, the ‘goodness of collapse’ of the different curves onto a single curve as seen in figure 1 can be used as reference for the collapse or non-collapse of higher orders. We find that
$u_{{\it\eta}}$
as presented below. In that spirit, the ‘goodness of collapse’ of the different curves onto a single curve as seen in figure 1 can be used as reference for the collapse or non-collapse of higher orders. We find that
![]() $D_{2,0}$
collapses indeed as expected and scales as
$D_{2,0}$
collapses indeed as expected and scales as
![]() $r^{2}$
for
$r^{2}$
for
![]() $r\rightarrow 0$
. The dissipative range extends to
$r\rightarrow 0$
. The dissipative range extends to
![]() $r/{\it\eta}\sim 10$
and is followed by a transitional region. For larger
$r/{\it\eta}\sim 10$
and is followed by a transitional region. For larger
![]() $r/{\it\eta}$
, there is the inertial range which increases with increasing Reynolds number, in agreement with the classical picture of turbulent flows.
$r/{\it\eta}$
, there is the inertial range which increases with increasing Reynolds number, in agreement with the classical picture of turbulent flows.

Figure 1. Longitudinal structure function
![]() $D_{20}$
normalised with
$D_{20}$
normalised with
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
for: *,
$u_{{\it\eta}}$
for: *,
![]() $Re_{{\it\lambda}}=88$
; ♢,
$Re_{{\it\lambda}}=88$
; ♢,
![]() $Re_{{\it\lambda}}=119$
; ▵,
$Re_{{\it\lambda}}=119$
; ▵,
![]() $Re_{{\it\lambda}}=184$
; ▫,
$Re_{{\it\lambda}}=184$
; ▫,
![]() $Re_{{\it\lambda}}=215$
; ▿,
$Re_{{\it\lambda}}=215$
; ▿,
![]() $Re_{{\it\lambda}}=331$
; and ○,
$Re_{{\it\lambda}}=331$
; and ○,
![]() $Re_{{\it\lambda}}=754$
. The dashed line corresponds to (3.16) with
$Re_{{\it\lambda}}=754$
. The dashed line corresponds to (3.16) with
![]() $\widetilde{K}_{2,0}=1/15$
.
$\widetilde{K}_{2,0}=1/15$
.
Generalising Kolmogorov’s first similarity hypothesis implies
where the constant
![]() $K_{m,0}$
should depend on the order
$K_{m,0}$
should depend on the order
![]() $m$
only and is supposed to be independent of the Reynolds number. Non-dimensionalising this relation with the Kolmogorov velocity
$m$
only and is supposed to be independent of the Reynolds number. Non-dimensionalising this relation with the Kolmogorov velocity
![]() $u_{{\it\eta}}=({\it\nu}\langle {\it\varepsilon}\rangle )^{1/4}$
and the Kolmogorov length
$u_{{\it\eta}}=({\it\nu}\langle {\it\varepsilon}\rangle )^{1/4}$
and the Kolmogorov length
![]() ${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
gives
${\it\eta}=({\it\nu}^{3}/\langle {\it\varepsilon}\rangle )^{1/4}$
gives
This implies that the structure functions should collapse for small
![]() $r\rightarrow 0$
according to (3.3) if normalised with
$r\rightarrow 0$
according to (3.3) if normalised with
![]() $u_{{\it\eta}}$
and
$u_{{\it\eta}}$
and
![]() ${\it\eta}$
. Taylor-expanding the structure functions of arbitrary order
${\it\eta}$
. Taylor-expanding the structure functions of arbitrary order
![]() $m=p+q$
, one finds
$m=p+q$
, one finds
In the following, we focus on longitudinal structure functions, for which there are exact results as presented below. We then have for
![]() $r\rightarrow 0$
$r\rightarrow 0$
Similarly to Kolmogorov’s approach for the second order, we then relate the moments of the longitudinal velocity gradient to the moments of the dissipation. One would immediately estimate that
i.e.
in disagreement with Kolmogorov’s first similarity hypothesis and (3.2), as the exponent and the averaging operator do not commute. The question then becomes whether
![]() $C_{m,0}$
is Reynolds-number-independent. For even
$C_{m,0}$
is Reynolds-number-independent. For even
![]() $m$
, it is possible to find the exact values of
$m$
, it is possible to find the exact values of
![]() $C_{m,0}$
following Siggia (Reference Siggia1981), as carried out by Boschung (Reference Boschung2015). From this, we have
$C_{m,0}$
following Siggia (Reference Siggia1981), as carried out by Boschung (Reference Boschung2015). From this, we have
![]() $C_{2}=15/2$
(cf. (3.1)),
$C_{2}=15/2$
(cf. (3.1)),
![]() $C_{4,0}=105/4$
(cf. Siggia Reference Siggia1981),
$C_{4,0}=105/4$
(cf. Siggia Reference Siggia1981),
![]() $C_{6,0}=567/8$
,
$C_{6,0}=567/8$
,
![]() $C_{8,0}=2673/16$
and so on, and in general (for
$C_{8,0}=2673/16$
and so on, and in general (for
![]() $m$
even)
$m$
even)
Consequently, for even
![]() $m$
we have
$m$
we have
with
![]() $\widetilde{K}_{m,0}=(2^{m/2}C_{m,0})^{-1}$
and where the
$\widetilde{K}_{m,0}=(2^{m/2}C_{m,0})^{-1}$
and where the
![]() $C_{m,0}$
are exact, Reynolds-number-independent values as given by (3.8). Therefore, the even longitudinal structure function of order
$C_{m,0}$
are exact, Reynolds-number-independent values as given by (3.8). Therefore, the even longitudinal structure function of order
![]() $m$
is determined by the moment
$m$
is determined by the moment
![]() $\langle {\it\varepsilon}^{m/2}\rangle$
of the dissipation and the viscosity
$\langle {\it\varepsilon}^{m/2}\rangle$
of the dissipation and the viscosity
![]() ${\it\nu}$
for
${\it\nu}$
for
![]() $r\rightarrow 0$
and we also have the exact solutions of some of the structure function equations for
$r\rightarrow 0$
and we also have the exact solutions of some of the structure function equations for
![]() $r\rightarrow 0$
as the prefactor
$r\rightarrow 0$
as the prefactor
![]() $C_{m,0}$
is also known. In other words, we have found the exact solution for arbitrary even-order structure functions in the dissipative range analogously to Kolmogorov’s result at the second order. Note that it is not possible to arrive at these conclusions simply on dimensional grounds, because
$C_{m,0}$
is also known. In other words, we have found the exact solution for arbitrary even-order structure functions in the dissipative range analogously to Kolmogorov’s result at the second order. Note that it is not possible to arrive at these conclusions simply on dimensional grounds, because
![]() $\langle {\it\varepsilon}^{m}\rangle$
and
$\langle {\it\varepsilon}^{m}\rangle$
and
![]() $\langle {\it\varepsilon}\rangle ^{m}$
have the same dimensions.
$\langle {\it\varepsilon}\rangle ^{m}$
have the same dimensions.
What about the mixed and transverse structure functions at even orders? We note that these structure functions are not uniquely determined this way except for the second order
![]() $m=2$
, because the mixed derivatives
$m=2$
, because the mixed derivatives
![]() $\langle (\partial u_{1}/\partial x_{1})^{p}(\partial u_{2}/\partial x_{1})^{q}\rangle$
are not completely determined by
$\langle (\partial u_{1}/\partial x_{1})^{p}(\partial u_{2}/\partial x_{1})^{q}\rangle$
are not completely determined by
![]() $\langle {\it\varepsilon}^{(p+q)/2}\rangle$
. In other words, the higher-order tensors are not determined by only a single scalar function under the constraints of homogeneity and incompressibility. For instance, the general eighth-order velocity gradient tensor is determined by the four invariants
$\langle {\it\varepsilon}^{(p+q)/2}\rangle$
. In other words, the higher-order tensors are not determined by only a single scalar function under the constraints of homogeneity and incompressibility. For instance, the general eighth-order velocity gradient tensor is determined by the four invariants
![]() $I_{1}$
,
$I_{1}$
,
![]() $I_{2}$
,
$I_{2}$
,
![]() $I_{3}$
and
$I_{3}$
and
![]() $I_{4}$
given by Siggia (Reference Siggia1981) (cf. also Hierro & Dopazo Reference Hierro and Dopazo2003). In particular,
$I_{4}$
given by Siggia (Reference Siggia1981) (cf. also Hierro & Dopazo Reference Hierro and Dopazo2003). In particular,

Figure 2. Longitudinal structure functions
![]() $D_{m,0}$
: (a,b)
$D_{m,0}$
: (a,b)
![]() $D_{4,0}$
, (c,d)
$D_{4,0}$
, (c,d)
![]() $D_{6,0}$
, and (e,f)
$D_{6,0}$
, and (e,f)
![]() $D_{8,0}$
. (a,c,e) Kolmogorov scaling with
$D_{8,0}$
. (a,c,e) Kolmogorov scaling with
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
. (b,d,f) Scaling with
$u_{{\it\eta}}$
. (b,d,f) Scaling with
![]() ${\it\eta}_{C}$
(3.14) and
${\it\eta}_{C}$
(3.14) and
![]() $u_{C}$
(3.15). Symbols: *,
$u_{C}$
(3.15). Symbols: *,
![]() $Re_{{\it\lambda}}=88$
; ♢,
$Re_{{\it\lambda}}=88$
; ♢,
![]() $Re_{{\it\lambda}}=119$
; ▵,
$Re_{{\it\lambda}}=119$
; ▵,
![]() $Re_{{\it\lambda}}=184$
; ▫,
$Re_{{\it\lambda}}=184$
; ▫,
![]() $Re_{{\it\lambda}}=215$
; ▿,
$Re_{{\it\lambda}}=215$
; ▿,
![]() $Re_{{\it\lambda}}=331$
; and ○,
$Re_{{\it\lambda}}=331$
; and ○,
![]() $Re_{{\it\lambda}}=754$
. Dashed lines correspond to (3.16) with
$Re_{{\it\lambda}}=754$
. Dashed lines correspond to (3.16) with
![]() $\widetilde{K}_{4,0}=1/105$
(b),
$\widetilde{K}_{4,0}=1/105$
(b),
![]() $\widetilde{K}_{6,0}=1/567$
(d) and
$\widetilde{K}_{6,0}=1/567$
(d) and
![]() $\widetilde{K}_{8,0}=1/2673$
(f).
$\widetilde{K}_{8,0}=1/2673$
(f).
We show higher even orders
![]() $D_{4,0}$
,
$D_{4,0}$
,
![]() $D_{6,0}$
and
$D_{6,0}$
and
![]() $D_{8,0}$
normalised by
$D_{8,0}$
normalised by
![]() $u_{{\it\eta}}$
and
$u_{{\it\eta}}$
and
![]() ${\it\eta}$
in the left column of figure 2 for different Reynolds numbers. Noticeably, these higher orders do not collapse and the disparity increases with Reynolds number and order
${\it\eta}$
in the left column of figure 2 for different Reynolds numbers. Noticeably, these higher orders do not collapse and the disparity increases with Reynolds number and order
![]() $m$
. This was anticipated by Landau & Lifshitz (Reference Landau and Lifshitz1959) (cf. also Frisch Reference Frisch1995), who argued that
$m$
. This was anticipated by Landau & Lifshitz (Reference Landau and Lifshitz1959) (cf. also Frisch Reference Frisch1995), who argued that
![]() $\langle {\it\varepsilon}\rangle$
could not be the relevant quantity for all orders
$\langle {\it\varepsilon}\rangle$
could not be the relevant quantity for all orders
![]() $m$
, i.e. that the proportionality factor
$m$
, i.e. that the proportionality factor
![]() $K_{m,0}$
of (3.3) should be flow-dependent. Normalising (3.9), K41 scaling then implies
$K_{m,0}$
of (3.3) should be flow-dependent. Normalising (3.9), K41 scaling then implies
where the Reynolds-number dependence of
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
increases with increasing order
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
increases with increasing order
![]() $m$
. Consequently, Kolmogorov scaling cannot collapse structure functions different from those at the second order (
$m$
. Consequently, Kolmogorov scaling cannot collapse structure functions different from those at the second order (
![]() $m=2$
) in the dissipative range, as is clearly seen in the left column of figure 2. By introducing a modified order-dependent cut-off length scale,
$m=2$
) in the dissipative range, as is clearly seen in the left column of figure 2. By introducing a modified order-dependent cut-off length scale,
and a cut-off velocity,
we find (3.9) normalised as
in the spirit of Kolmogorov’s 1941 work on the dissipative range for the second order, where the prefactor is constant. This scaling is shown in the right column of figure 2, again for
![]() $D_{4,0}$
,
$D_{4,0}$
,
![]() $D_{6,0}$
and
$D_{6,0}$
and
![]() $D_{8,0}$
for different Reynolds numbers. Thus, (3.16) indeed collapses the structure functions for
$D_{8,0}$
for different Reynolds numbers. Thus, (3.16) indeed collapses the structure functions for
![]() $r\rightarrow 0$
, and
$r\rightarrow 0$
, and
![]() $\widetilde{K}_{m,0}$
is universal in the sense that it does not depend on the Reynolds number but is an order-dependent constant with the exact values
$\widetilde{K}_{m,0}$
is universal in the sense that it does not depend on the Reynolds number but is an order-dependent constant with the exact values
![]() $\widetilde{K}_{2,0}=1/15$
,
$\widetilde{K}_{2,0}=1/15$
,
![]() $\widetilde{K}_{4,0}=1/105$
and so on. This collapse also serves as a numerical confirmation of the relation between the moments of the dissipation and the even moments of the longitudinal velocity gradient as reported by Boschung (Reference Boschung2015). We find (3.16) to hold for
$\widetilde{K}_{4,0}=1/105$
and so on. This collapse also serves as a numerical confirmation of the relation between the moments of the dissipation and the even moments of the longitudinal velocity gradient as reported by Boschung (Reference Boschung2015). We find (3.16) to hold for
![]() $r=0$
to
$r=0$
to
![]() $r/{\it\eta}_{C,m}\approx 10$
independent of the order. That is, the order-dependent dissipation range scales with
$r/{\it\eta}_{C,m}\approx 10$
independent of the order. That is, the order-dependent dissipation range scales with
![]() ${\it\eta}_{C,m}$
as expected. As seen in figure 2, this clearly holds for even orders in general, due to (3.9). We note in passing that
${\it\eta}_{C,m}$
as expected. As seen in figure 2, this clearly holds for even orders in general, due to (3.9). We note in passing that
as we might have expected, i.e. that inertial and viscous forces balance. Consequently,
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
are indeed viscous scales; for order
$u_{C,m}$
are indeed viscous scales; for order
![]() $m=2$
, K41 scaling (i.e. the classical Kolmogorov scaling) is recovered, as
$m=2$
, K41 scaling (i.e. the classical Kolmogorov scaling) is recovered, as
![]() ${\it\eta}_{C,2}={\it\eta}$
and
${\it\eta}_{C,2}={\it\eta}$
and
![]() $u_{C,2}=u_{{\it\eta}}$
.
$u_{C,2}=u_{{\it\eta}}$
.
Let us look at the cut-off length from a slightly different point of view. Considering only the longitudinal even-ordered structure functions, which are determined by the velocity gradients
![]() $\langle (\partial u_{1}/\partial x_{1})^{m}\rangle$
with dimensional units
$\langle (\partial u_{1}/\partial x_{1})^{m}\rangle$
with dimensional units
![]() $[\text{s}^{-m}]$
, one needs a second quantity with dimensions
$[\text{s}^{-m}]$
, one needs a second quantity with dimensions
![]() $[\text{m}^{{\it\alpha}}~\text{s}^{{\it\beta}}]$
(with
$[\text{m}^{{\it\alpha}}~\text{s}^{{\it\beta}}]$
(with
![]() ${\it\alpha}\neq 0$
and
${\it\alpha}\neq 0$
and
![]() ${\it\beta}\neq 0$
) to find a characteristic length scale
${\it\beta}\neq 0$
) to find a characteristic length scale
![]() $l_{m}$
with dimensional units
$l_{m}$
with dimensional units
![]() $[\text{m}]$
. As we are concerned with the dissipative range, the viscosity
$[\text{m}]$
. As we are concerned with the dissipative range, the viscosity
![]() ${\it\nu}$
with dimensions
${\it\nu}$
with dimensions
![]() $[\text{m}^{2}~\text{s}^{-1}]$
is a natural choice. We then have
$[\text{m}^{2}~\text{s}^{-1}]$
is a natural choice. We then have
 $$\begin{eqnarray}\displaystyle l_{m}=\left[\frac{{\it\nu}^{m}}{\langle (\partial u_{1}/\partial x_{1})^{m}\rangle }\right]^{1/(2m)} & = & \displaystyle \left[\frac{{\it\nu}^{(3/2)m}}{{\it\nu}^{m/2}\langle (\partial u_{1}/\partial x_{1})^{m}\rangle }\right]^{1/(2m)}\nonumber\\ \displaystyle & {\sim} & \displaystyle \left[\frac{{\it\nu}^{3}}{\langle {\it\varepsilon}^{m/2}\rangle ^{2/m}}\right]^{1/4}={\it\eta}_{C,m}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle l_{m}=\left[\frac{{\it\nu}^{m}}{\langle (\partial u_{1}/\partial x_{1})^{m}\rangle }\right]^{1/(2m)} & = & \displaystyle \left[\frac{{\it\nu}^{(3/2)m}}{{\it\nu}^{m/2}\langle (\partial u_{1}/\partial x_{1})^{m}\rangle }\right]^{1/(2m)}\nonumber\\ \displaystyle & {\sim} & \displaystyle \left[\frac{{\it\nu}^{3}}{\langle {\it\varepsilon}^{m/2}\rangle ^{2/m}}\right]^{1/4}={\it\eta}_{C,m}\end{eqnarray}$$
and similarly for
![]() $u_{C,m}$
. That is, when choosing the viscosity as the second quantity to build the length scale,
$u_{C,m}$
. That is, when choosing the viscosity as the second quantity to build the length scale,
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
naturally follow. Different scales can only be obtained by choosing a different quantity than
$u_{C,m}$
naturally follow. Different scales can only be obtained by choosing a different quantity than
![]() ${\it\nu}$
.
${\it\nu}$
.
Different from the dissipative range, it is not possible to determine a priori how to normalise
![]() $D_{m,0}=C_{m,0}r^{{\it\zeta}_{m}}$
in the inertial range so that
$D_{m,0}=C_{m,0}r^{{\it\zeta}_{m}}$
in the inertial range so that
![]() $C_{m,0}$
does not depend on the Reynolds number. This is due to the fact that we do not know the exact value of
$C_{m,0}$
does not depend on the Reynolds number. This is due to the fact that we do not know the exact value of
![]() ${\it\zeta}_{m}$
and thus cannot choose suitable velocity and length scales so that
${\it\zeta}_{m}$
and thus cannot choose suitable velocity and length scales so that
![]() $C_{m}$
is non-dimensional; therefore we cannot expect the structure functions to collapse in the inertial range. The only exception is of course the third-order structure function
$C_{m}$
is non-dimensional; therefore we cannot expect the structure functions to collapse in the inertial range. The only exception is of course the third-order structure function
![]() $D_{3,0}=-(4/5)\langle {\it\varepsilon}\rangle r$
, which collapses using the K41 scales
$D_{3,0}=-(4/5)\langle {\it\varepsilon}\rangle r$
, which collapses using the K41 scales
![]() $u_{{\it\eta}}$
and
$u_{{\it\eta}}$
and
![]() ${\it\eta}$
. Deviations from K41 for the second-order structure functions in the inertial range are usually attributed to intermittency effects. For higher orders, it is therefore necessary to consider deviations of the higher-order structure functions normalised in such a way that they collapse for
${\it\eta}$
. Deviations from K41 for the second-order structure functions in the inertial range are usually attributed to intermittency effects. For higher orders, it is therefore necessary to consider deviations of the higher-order structure functions normalised in such a way that they collapse for
![]() $r\rightarrow 0$
(as do the second-order structure functions when normalised with the K41 quantities), i.e. not with
$r\rightarrow 0$
(as do the second-order structure functions when normalised with the K41 quantities), i.e. not with
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
but with
$u_{{\it\eta}}$
but with
![]() ${\it\eta}_{C,m}$
(3.14) and
${\it\eta}_{C,m}$
(3.14) and
![]() $u_{C,m}$
(3.15). If one examines deviations of higher-order structure functions normalised with the second-order quantities
$u_{C,m}$
(3.15). If one examines deviations of higher-order structure functions normalised with the second-order quantities
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
, one includes the well-known increase of higher-order derivative moments scaled by the second moment. These effects are not present when using
$u_{{\it\eta}}$
, one includes the well-known increase of higher-order derivative moments scaled by the second moment. These effects are not present when using
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
, as with these scales the Reynolds-number dependence cancels out.
$u_{C,m}$
, as with these scales the Reynolds-number dependence cancels out.
Next, we also look at the odd orders, which should be determined by
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
(third order),
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
(third order),
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ik}\unicode[STIX]{x1D61A}_{kl}{\it\omega}_{l}\rangle$
(fifth order) and so on. We find that their behaviour resembles that of the even orders, inasmuch as Kolmogorov scaling (3.3) does not collapse the structure functions for
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ik}\unicode[STIX]{x1D61A}_{kl}{\it\omega}_{l}\rangle$
(fifth order) and so on. We find that their behaviour resembles that of the even orders, inasmuch as Kolmogorov scaling (3.3) does not collapse the structure functions for
![]() $r\rightarrow 0$
(cf. the left column of figure 3). Again, we find that deviations increase with increasing order and Reynolds number, as was the case for the even orders. Using
$r\rightarrow 0$
(cf. the left column of figure 3). Again, we find that deviations increase with increasing order and Reynolds number, as was the case for the even orders. Using
![]() ${\it\eta}_{C,m}$
(3.14) and
${\it\eta}_{C,m}$
(3.14) and
![]() $u_{C,m}$
(3.15) collapses the data and again we have an order-dependent dissipation range up to
$u_{C,m}$
(3.15) collapses the data and again we have an order-dependent dissipation range up to
![]() $r/{\it\eta}_{C,m}\sim 10$
. Thus, the general relation (3.16) also holds for odd orders, although we cannot determine the prefactors
$r/{\it\eta}_{C,m}\sim 10$
. Thus, the general relation (3.16) also holds for odd orders, although we cannot determine the prefactors
![]() $\widetilde{K}_{m,0}$
analytically. Furthermore, we would expect the odd moments of the (longitudinal) velocity gradient probability density function (p.d.f.) to scale with
$\widetilde{K}_{m,0}$
analytically. Furthermore, we would expect the odd moments of the (longitudinal) velocity gradient probability density function (p.d.f.) to scale with
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
, if
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
, if
![]() $\langle (\partial u_{1}/\partial x_{1})^{m}\rangle \sim {\it\nu}^{m/2}\langle {\it\varepsilon}^{m/2}\rangle$
for odd orders as well, as our data suggest. Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) find
$\langle (\partial u_{1}/\partial x_{1})^{m}\rangle \sim {\it\nu}^{m/2}\langle {\it\varepsilon}^{m/2}\rangle$
for odd orders as well, as our data suggest. Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) find
![]() $0.11\pm 0.1$
for the Reynolds-number dependence of the skewness of
$0.11\pm 0.1$
for the Reynolds-number dependence of the skewness of
![]() $\partial u_{1}/\partial x_{1}$
, which agrees with the scaling
$\partial u_{1}/\partial x_{1}$
, which agrees with the scaling
![]() $\langle {\it\varepsilon}^{3/2}\rangle /\langle {\it\varepsilon}\rangle ^{3/2}\sim Re_{{\it\lambda}}^{0.12}$
from our DNS. This implies that
$\langle {\it\varepsilon}^{3/2}\rangle /\langle {\it\varepsilon}\rangle ^{3/2}\sim Re_{{\it\lambda}}^{0.12}$
from our DNS. This implies that
![]() $\langle {\it\varepsilon}^{3/2}\rangle \sim {\it\nu}^{3/2}\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
and so on, with constant proportionality factors. However, these factors cannot be determined by the isotropic form of the general velocity gradient tensor, as
$\langle {\it\varepsilon}^{3/2}\rangle \sim {\it\nu}^{3/2}\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
and so on, with constant proportionality factors. However, these factors cannot be determined by the isotropic form of the general velocity gradient tensor, as
![]() $\langle {\it\varepsilon}^{3/2}\rangle$
etc. cannot be expressed in terms of it.
$\langle {\it\varepsilon}^{3/2}\rangle$
etc. cannot be expressed in terms of it.
To summarise,
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
are the right quantities to non-dimensionalise structure functions in the dissipative range, as shown in figures 2 and 3. Using the new scales
$u_{C,m}$
are the right quantities to non-dimensionalise structure functions in the dissipative range, as shown in figures 2 and 3. Using the new scales
![]() ${\it\eta}_{C,m}$
and
${\it\eta}_{C,m}$
and
![]() $u_{C,m}$
collapses the higher orders as well as
$u_{C,m}$
collapses the higher orders as well as
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
in the case of the second order (cf. figure 1).
$u_{{\it\eta}}$
in the case of the second order (cf. figure 1).

Figure 3. Longitudinal structure functions
![]() $D_{m,0}$
: (a,b)
$D_{m,0}$
: (a,b)
![]() $D_{3,0}$
, (c,d)
$D_{3,0}$
, (c,d)
![]() $D_{5,0}$
, and (e,f)
$D_{5,0}$
, and (e,f)
![]() $D_{7,0}$
. (a,c,e) Kolmogorov scaling with
$D_{7,0}$
. (a,c,e) Kolmogorov scaling with
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
. (b,d,f) Scaling with
$u_{{\it\eta}}$
. (b,d,f) Scaling with
![]() ${\it\eta}_{C}$
(3.14) and
${\it\eta}_{C}$
(3.14) and
![]() $u_{C}$
(3.15). Symbols: *,
$u_{C}$
(3.15). Symbols: *,
![]() $Re_{{\it\lambda}}=88$
; ♢,
$Re_{{\it\lambda}}=88$
; ♢,
![]() $Re_{{\it\lambda}}=119$
; ▵,
$Re_{{\it\lambda}}=119$
; ▵,
![]() $Re_{{\it\lambda}}=184$
; ▫,
$Re_{{\it\lambda}}=184$
; ▫,
![]() $Re_{{\it\lambda}}=215$
; ▿,
$Re_{{\it\lambda}}=215$
; ▿,
![]() $Re_{{\it\lambda}}=331$
; and ○,
$Re_{{\it\lambda}}=331$
; and ○,
![]() $Re_{{\it\lambda}}=754$
.
$Re_{{\it\lambda}}=754$
.
Naturally, the question arises how
![]() ${\it\eta}_{C,m}$
scales with
${\it\eta}_{C,m}$
scales with
![]() ${\it\eta}$
. From (3.14) we find
${\it\eta}$
. From (3.14) we find
Figure 4 shows the scaling of
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
as a function of the Reynolds number
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
as a function of the Reynolds number
![]() $Re_{{\it\lambda}}$
as evaluated from our DNS,
$Re_{{\it\lambda}}$
as evaluated from our DNS,
where the dashed lines correspond to a least-squares fit and we use the values of
![]() ${\it\alpha}_{m/2}$
from our DNS in the following. Noticeably, the scaling exponent
${\it\alpha}_{m/2}$
from our DNS in the following. Noticeably, the scaling exponent
![]() ${\it\alpha}_{m/2}$
of (3.20) increases with
${\it\alpha}_{m/2}$
of (3.20) increases with
![]() $m$
, in agreement with the notion of intermittency of
$m$
, in agreement with the notion of intermittency of
![]() ${\it\varepsilon}$
. Donzis, Yeung & Sreenivasan (Reference Donzis, Yeung and Sreenivasan2008) compared
${\it\varepsilon}$
. Donzis, Yeung & Sreenivasan (Reference Donzis, Yeung and Sreenivasan2008) compared
![]() $\langle {\it\varepsilon}^{m/2}\rangle$
and
$\langle {\it\varepsilon}^{m/2}\rangle$
and
![]() $\langle {\it\varepsilon}\rangle ^{m/2}$
as well as the ratio for different orders
$\langle {\it\varepsilon}\rangle ^{m/2}$
as well as the ratio for different orders
![]() $m/2=2,3,4$
as a function of the Reynolds number and grid resolution. They find that a grid resolution
$m/2=2,3,4$
as a function of the Reynolds number and grid resolution. They find that a grid resolution
![]() ${\it\kappa}_{max}{\it\eta}$
somewhere between
${\it\kappa}_{max}{\it\eta}$
somewhere between
![]() ${\it\kappa}_{max}{\it\eta}=1$
and
${\it\kappa}_{max}{\it\eta}=1$
and
![]() ${\it\kappa}_{max}{\it\eta}=3$
is sufficient to resolve the second to fourth moments of
${\it\kappa}_{max}{\it\eta}=3$
is sufficient to resolve the second to fourth moments of
![]() ${\it\varepsilon}$
. Interestingly enough, the sensitivity of the normalised moments with respect to the resolution
${\it\varepsilon}$
. Interestingly enough, the sensitivity of the normalised moments with respect to the resolution
![]() ${\it\kappa}_{max}{\it\eta}$
seems to decrease with increasing Reynolds number, at least for the two cases
${\it\kappa}_{max}{\it\eta}$
seems to decrease with increasing Reynolds number, at least for the two cases
![]() $Re_{{\it\lambda}}=140$
and
$Re_{{\it\lambda}}=140$
and
![]() $Re_{{\it\lambda}}=240$
that they considered (their figure 4 and table 2). For that matter, we feel rather confident that the data shown in our figure 4(a,b) are adequate for the issues addressed in the present study, although we cannot claim that there might be no (small) errors in the values of
$Re_{{\it\lambda}}=240$
that they considered (their figure 4 and table 2). For that matter, we feel rather confident that the data shown in our figure 4(a,b) are adequate for the issues addressed in the present study, although we cannot claim that there might be no (small) errors in the values of
![]() ${\it\alpha}_{m/2}$
used below. In a recent paper, Schumacher et al. (Reference Schumacher, Scheel, Krasnov, Donzis, Yakhot and Sreenivasan2014) compared different flows for
${\it\alpha}_{m/2}$
used below. In a recent paper, Schumacher et al. (Reference Schumacher, Scheel, Krasnov, Donzis, Yakhot and Sreenivasan2014) compared different flows for
![]() $m/2=2,3,4$
and found that the Reynolds-number dependence of
$m/2=2,3,4$
and found that the Reynolds-number dependence of
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
is the same for the different flows they examined (homogeneous isotropic turbulence, a turbulent channel flow and turbulent Rayleigh–Bénard convection). This implies that the moments of the (longitudinal) velocity gradient should also have the same Reynolds-number dependence for the different flow types. This seems to be the case; Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) and Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) compiled data of different flows and found a good collapse of the skewness and flatness of the longitudinal velocity gradient.
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
is the same for the different flows they examined (homogeneous isotropic turbulence, a turbulent channel flow and turbulent Rayleigh–Bénard convection). This implies that the moments of the (longitudinal) velocity gradient should also have the same Reynolds-number dependence for the different flow types. This seems to be the case; Sreenivasan & Antonia (Reference Sreenivasan and Antonia1997) and Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) compiled data of different flows and found a good collapse of the skewness and flatness of the longitudinal velocity gradient.

Figure 4. (a) Scaling of
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
as a function of the Reynolds number. (b) Plot of
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
as a function of the Reynolds number. (b) Plot of
![]() ${\it\alpha}_{m/2}/(2m)$
as a function of
${\it\alpha}_{m/2}/(2m)$
as a function of
![]() $m/2$
. Symbols, DNS data; solid line, K62 theory with
$m/2$
. Symbols, DNS data; solid line, K62 theory with
![]() ${\it\mu}=0.25$
; dashed line, p-model with
${\it\mu}=0.25$
; dashed line, p-model with
![]() $p_{1}=0.7$
; dotted line, She–Leveque model.
$p_{1}=0.7$
; dotted line, She–Leveque model.
Thus, the cut-off length
![]() ${\it\eta}_{C,m}$
decreases with increasing Reynolds number
${\it\eta}_{C,m}$
decreases with increasing Reynolds number
![]() $Re_{{\it\lambda}}$
, while the order dependence needs to be examined more closely. Figure 4(b) shows the ratio
$Re_{{\it\lambda}}$
, while the order dependence needs to be examined more closely. Figure 4(b) shows the ratio
![]() ${\it\alpha}_{m/2}/(2m)$
for
${\it\alpha}_{m/2}/(2m)$
for
![]() $m=1,\ldots ,8$
, where
$m=1,\ldots ,8$
, where
![]() ${\it\alpha}_{m/2}$
has been obtained by fitting the data of figure 4(a). We find that
${\it\alpha}_{m/2}$
has been obtained by fitting the data of figure 4(a). We find that
![]() ${\it\alpha}_{m/2}/(2m)$
plotted over
${\it\alpha}_{m/2}/(2m)$
plotted over
![]() $m/2$
is concave and non-decreasing, at least for the orders observed. This can also be seen in figure 2, where the transitional range is shifted towards smaller scales with increasing order. This immediately raises the question of the asymptotic behaviour of
$m/2$
is concave and non-decreasing, at least for the orders observed. This can also be seen in figure 2, where the transitional range is shifted towards smaller scales with increasing order. This immediately raises the question of the asymptotic behaviour of
![]() ${\it\alpha}_{m/2}$
at high orders, as it would imply that there is a myriad of smaller and smaller scales (
${\it\alpha}_{m/2}$
at high orders, as it would imply that there is a myriad of smaller and smaller scales (
![]() $m/2$
is unbounded in principle). If there is no upper limit of
$m/2$
is unbounded in principle). If there is no upper limit of
![]() ${\it\alpha}$
for
${\it\alpha}$
for
![]() $m\rightarrow \infty$
, then the smallest scale
$m\rightarrow \infty$
, then the smallest scale
![]() ${\it\eta}_{m\rightarrow \infty }\rightarrow 0$
independent of the Reynolds number, as seen from (3.19).
${\it\eta}_{m\rightarrow \infty }\rightarrow 0$
independent of the Reynolds number, as seen from (3.19).
4 Scaling of the normalised dissipation
With the definition of the scales
![]() ${\it\eta}_{C,m}$
, it is natural to write
${\it\eta}_{C,m}$
, it is natural to write
where
![]() ${\it\varepsilon}_{r}$
is the volume-averaged dissipation as proposed by Obukhov (Reference Obukhov1962) and where
${\it\varepsilon}_{r}$
is the volume-averaged dissipation as proposed by Obukhov (Reference Obukhov1962) and where
![]() ${\it\gamma}_{m/2}$
is the scaling exponent of the normalised dissipation,
${\it\gamma}_{m/2}$
is the scaling exponent of the normalised dissipation,
With (3.19) and (3.20), we then find with
![]() ${\it\eta}/L\sim Re_{{\it\lambda}}^{-3/2}$
that
${\it\eta}/L\sim Re_{{\it\lambda}}^{-3/2}$
that
and consequently any model specifying
![]() ${\it\gamma}_{m/2}$
can be used to determine
${\it\gamma}_{m/2}$
can be used to determine
![]() ${\it\alpha}_{m/2}$
. If one assumes together with Kolmogorov (Reference Kolmogorov1962) the ansatz
${\it\alpha}_{m/2}$
. If one assumes together with Kolmogorov (Reference Kolmogorov1962) the ansatz
as is widely accepted, also
![]() ${\it\gamma}_{m/2}={\it\zeta}_{3(m/2)}-m/2$
, and therefore any theory predicting the structure function scaling exponents
${\it\gamma}_{m/2}={\it\zeta}_{3(m/2)}-m/2$
, and therefore any theory predicting the structure function scaling exponents
![]() ${\it\zeta}_{3(m/2)}$
predicts
${\it\zeta}_{3(m/2)}$
predicts
![]() ${\it\alpha}_{m/2}$
. One could also look at
${\it\alpha}_{m/2}$
. One could also look at
![]() ${\it\alpha}$
in a different way: given
${\it\alpha}$
in a different way: given
![]() ${\it\alpha}$
, e.g. by some theory or measurements, one can solve for
${\it\alpha}$
, e.g. by some theory or measurements, one can solve for
![]() ${\it\gamma}$
and then use
${\it\gamma}$
and then use
![]() ${\it\gamma}_{m/2}={\it\zeta}_{3(m/2)}-m/2$
to compute the scaling exponents,
${\it\gamma}_{m/2}={\it\zeta}_{3(m/2)}-m/2$
to compute the scaling exponents,
Then, the larger
![]() ${\it\alpha}_{m/2}$
, the larger are the deviations from K41 scaling
${\it\alpha}_{m/2}$
, the larger are the deviations from K41 scaling
![]() ${\it\zeta}_{3(m/2)}=m/2$
for a given
${\it\zeta}_{3(m/2)}=m/2$
for a given
![]() $m$
. As larger values of
$m$
. As larger values of
![]() ${\it\alpha}_{m/2}$
imply larger higher moments of the dissipation, this is consonant with the notion that anomalous scaling is connected to the intermittency of the dissipation.
${\it\alpha}_{m/2}$
imply larger higher moments of the dissipation, this is consonant with the notion that anomalous scaling is connected to the intermittency of the dissipation.
Since
![]() ${\it\zeta}_{3(m/2)}>0$
for all
${\it\zeta}_{3(m/2)}>0$
for all
![]() $m$
, we find from (4.5) an upper limit for the scaling of the normalised dissipation as well as the ratio of the order-dependent scales,
$m$
, we find from (4.5) an upper limit for the scaling of the normalised dissipation as well as the ratio of the order-dependent scales,
Because
![]() ${\it\alpha}_{m/2}$
increases with increasing
${\it\alpha}_{m/2}$
increases with increasing
![]() $m/2$
and
$m/2$
and
![]() ${\it\alpha}_{1}=0$
, this implies that
${\it\alpha}_{1}=0$
, this implies that
![]() ${\it\alpha}_{m/2}/(2m)$
is concave and that
${\it\alpha}_{m/2}/(2m)$
is concave and that
![]() ${\it\alpha}_{m/2}/(2m)$
increases linearly for large
${\it\alpha}_{m/2}/(2m)$
increases linearly for large
![]() $m$
.
$m$
.
Let us now briefly look at some well-known theories found in the literature and compare their predictions with our DNS. For the rest of this section, we consider even
![]() $m$
, i.e.
$m$
, i.e.
![]() $m/2=1,2,3,\ldots .$
$m/2=1,2,3,\ldots .$
K62 theory (Kolmogorov Reference Kolmogorov1962) assumes a log-normal distribution for the dissipation, which gives
where
![]() ${\it\mu}$
is a coefficient parametrising the intermittency. Sreenivasan & Kailasnath (Reference Sreenivasan and Kailasnath1993) concluded that
${\it\mu}$
is a coefficient parametrising the intermittency. Sreenivasan & Kailasnath (Reference Sreenivasan and Kailasnath1993) concluded that
![]() ${\it\mu}=0.25\pm 0.05$
. From (4.7),
${\it\mu}=0.25\pm 0.05$
. From (4.7),
![]() ${\it\alpha}_{1,K62}=0$
as required. However, K62 gives
${\it\alpha}_{1,K62}=0$
as required. However, K62 gives
![]() ${\it\alpha}_{m/2,K62}\rightarrow \infty$
for
${\it\alpha}_{m/2,K62}\rightarrow \infty$
for
![]() $m/2\rightarrow 8/{\it\mu}+1$
and negative
$m/2\rightarrow 8/{\it\mu}+1$
and negative
![]() ${\it\alpha}_{m/2,K62}$
for
${\it\alpha}_{m/2,K62}$
for
![]() $m/2>8/{\it\mu}+1$
. Similarly, the ratio
$m/2>8/{\it\mu}+1$
. Similarly, the ratio
![]() ${\it\eta}_{C,m}/{\it\eta}\rightarrow 0$
for
${\it\eta}_{C,m}/{\it\eta}\rightarrow 0$
for
![]() $m/2\rightarrow 8/{\it\mu}+1$
, while
$m/2\rightarrow 8/{\it\mu}+1$
, while
![]() ${\it\eta}_{C,m}>{\it\eta}$
for
${\it\eta}_{C,m}>{\it\eta}$
for
![]() $m/2>8/{\it\mu}+1$
. This is at odds with the observation that the normalised moments
$m/2>8/{\it\mu}+1$
. This is at odds with the observation that the normalised moments
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
increase with increasing Reynolds number for
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
increase with increasing Reynolds number for
![]() $m/2>1$
, i.e.
$m/2>1$
, i.e.
![]() ${\it\alpha}_{m/2}>0$
for all
${\it\alpha}_{m/2}>0$
for all
![]() $m/2>1$
. When using K62, at first the moments
$m/2>1$
. When using K62, at first the moments
![]() $\langle {\it\varepsilon}^{m/2}\rangle$
strongly increase with
$\langle {\it\varepsilon}^{m/2}\rangle$
strongly increase with
![]() $Re_{{\it\lambda}}$
and then strongly decrease when
$Re_{{\it\lambda}}$
and then strongly decrease when
![]() $m/2$
is increased further. Similarly, the order-dependent scales
$m/2$
is increased further. Similarly, the order-dependent scales
![]() ${\it\eta}_{C,m}$
become smaller and smaller than the Kolmogorov scale and then jump to
${\it\eta}_{C,m}$
become smaller and smaller than the Kolmogorov scale and then jump to
![]() ${\it\eta}_{C,m}>{\it\eta}$
after a critical threshold. With
${\it\eta}_{C,m}>{\it\eta}$
after a critical threshold. With
![]() ${\it\mu}=0.25$
, we find the singularity for the
${\it\mu}=0.25$
, we find the singularity for the
![]() $33$
rd moment of the normalised dissipation and a reduced intermittency for
$33$
rd moment of the normalised dissipation and a reduced intermittency for
![]() $m/2>33$
.
$m/2>33$
.
Multi-fractality of the dissipation (4.2) has been examined in detail by Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1991). An example for such a multi-fractal model is, for example, the p-model (see Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987), which assumes that an eddy breaks up into two smaller eddies receiving fractions
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}=1-p_{1}$
of the energy. The p-model then yields
$p_{2}=1-p_{1}$
of the energy. The p-model then yields
The p-model then gives
![]() ${\it\alpha}_{1,p}=0$
, while for
${\it\alpha}_{1,p}=0$
, while for
![]() $m/2\rightarrow \infty$
,
$m/2\rightarrow \infty$
,
![]() ${\it\alpha}_{m/2,p}\rightarrow m$
because the parameter
${\it\alpha}_{m/2,p}\rightarrow m$
because the parameter
![]() $p_{1}\leqslant 1$
.
$p_{1}\leqslant 1$
.
Different from the (multi-)fractal framework, She & Leveque (Reference She and Leveque1994) proposed a hierarchy of powers of the dissipation moments
![]() ${\it\epsilon}_{r}^{m/2}=\langle {\it\varepsilon}_{r}^{m/2+1}\rangle /\langle {\it\varepsilon}^{m/2}\rangle$
. They then assumed that
${\it\epsilon}_{r}^{m/2}=\langle {\it\varepsilon}_{r}^{m/2+1}\rangle /\langle {\it\varepsilon}^{m/2}\rangle$
. They then assumed that
![]() ${\it\epsilon}_{r}^{m/2+1}$
is determined by
${\it\epsilon}_{r}^{m/2+1}$
is determined by
![]() ${\it\epsilon}_{r}^{m/2}$
and
${\it\epsilon}_{r}^{m/2}$
and
![]() ${\it\epsilon}_{r}^{\infty }$
for all
${\it\epsilon}_{r}^{\infty }$
for all
![]() $m/2$
. Dubrulle (Reference Dubrulle1994) and She & Waymire (Reference She and Waymire1995) found that the She–Leveque model corresponds to the assumption of a log-Poisson distribution for the dissipation. The She–Leveque model yields
$m/2$
. Dubrulle (Reference Dubrulle1994) and She & Waymire (Reference She and Waymire1995) found that the She–Leveque model corresponds to the assumption of a log-Poisson distribution for the dissipation. The She–Leveque model yields
 $$\begin{eqnarray}\displaystyle {\it\alpha}_{m/2,SL}=6\,\frac{m/2-3\left[1-\displaystyle \left(\frac{2}{3}\right)^{m/2}\right]}{5+\displaystyle \frac{3}{m/2}\left[1-\left(\frac{2}{3}\right)^{m/2}\right]}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\alpha}_{m/2,SL}=6\,\frac{m/2-3\left[1-\displaystyle \left(\frac{2}{3}\right)^{m/2}\right]}{5+\displaystyle \frac{3}{m/2}\left[1-\left(\frac{2}{3}\right)^{m/2}\right]}, & & \displaystyle\end{eqnarray}$$
which contains no parameters, different from the other models examined in this section. The She–Leveque model has been found to be in excellent agreement with structure function exponents obtained by measurements and DNS (see e.g. Anselmet et al.
Reference Anselmet, Gagne and Hopfinger1984; Benzi et al.
Reference Benzi, Ciliberto, Baudet and Chavarria1995; Gotoh, Fukayama & Nakano Reference Gotoh, Fukayama and Nakano2002). Similarly to the other models examined here, the She–Leveque model gives
![]() ${\it\alpha}_{1,SL}=0$
and, for
${\it\alpha}_{1,SL}=0$
and, for
![]() $m/2\rightarrow \infty$
,
$m/2\rightarrow \infty$
,
![]() ${\it\alpha}_{m/2,SL}\rightarrow (6/5)(m/2)$
, i.e. for very large
${\it\alpha}_{m/2,SL}\rightarrow (6/5)(m/2)$
, i.e. for very large
![]() $m$
,
$m$
,
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
scales linearly. Therefore, the order-dependent cut-off scales
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
scales linearly. Therefore, the order-dependent cut-off scales
![]() ${\it\eta}_{C,m}/{\it\eta}$
scale as
${\it\eta}_{C,m}/{\it\eta}$
scale as
![]() ${\it\alpha}_{m/2}/2m\rightarrow 3/10$
for large
${\it\alpha}_{m/2}/2m\rightarrow 3/10$
for large
![]() $m/2$
and the She–Leveque model satisfies (4.6), i.e. the cut-off scales remain bounded at finite Reynolds numbers.
$m/2$
and the She–Leveque model satisfies (4.6), i.e. the cut-off scales remain bounded at finite Reynolds numbers.
The
![]() ${\it\alpha}_{m/2}$
as computed from the three models above are shown in figure 4(b). While K62 overpredicts
${\it\alpha}_{m/2}$
as computed from the three models above are shown in figure 4(b). While K62 overpredicts
![]() ${\it\alpha}_{m/2}$
as expected, both the p-model and the She–Leveque model are in very good agreement with our DNS. Structure function exponents as computed with (4.5) using the
${\it\alpha}_{m/2}$
as expected, both the p-model and the She–Leveque model are in very good agreement with our DNS. Structure function exponents as computed with (4.5) using the
![]() ${\it\alpha}_{m/2}$
from our DNS are shown in table 2, together with the measurements of Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984) and Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002), which we have averaged when more than one value was reported. While we find very good agreement, it should be kept in mind that the higher orders (for both the measurements of Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984) and the DNS of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002) as well as the ones computed from our data) might be subject to significant error bands. It is also worth mentioning that numerical errors in
${\it\alpha}_{m/2}$
from our DNS are shown in table 2, together with the measurements of Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984) and Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002), which we have averaged when more than one value was reported. While we find very good agreement, it should be kept in mind that the higher orders (for both the measurements of Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984) and the DNS of Gotoh et al. (Reference Gotoh, Fukayama and Nakano2002) as well as the ones computed from our data) might be subject to significant error bands. It is also worth mentioning that numerical errors in
![]() ${\it\alpha}_{m/2}$
translate to smaller errors in
${\it\alpha}_{m/2}$
translate to smaller errors in
![]() ${\it\zeta}_{3(m/2)}$
, at least up to
${\it\zeta}_{3(m/2)}$
, at least up to
![]() $m/2=4$
. This error decreases with increasing
$m/2=4$
. This error decreases with increasing
![]() $m/2$
: for instance,
$m/2$
: for instance,
![]() ${\it\alpha}_{2}\pm 10\,\%$
yields
${\it\alpha}_{2}\pm 10\,\%$
yields
![]() ${\it\zeta}_{6}\pm 3.77\,\%$
, while
${\it\zeta}_{6}\pm 3.77\,\%$
, while
![]() ${\it\alpha}_{4}\pm 10\,\%$
yields
${\it\alpha}_{4}\pm 10\,\%$
yields
![]() ${\it\zeta}_{12}\pm 1.16\,\%$
.
${\it\zeta}_{12}\pm 1.16\,\%$
.
Table 2. Comparison of
![]() ${\it\zeta}_{3(m/2)}$
computed with (4.5) using
${\it\zeta}_{3(m/2)}$
computed with (4.5) using
![]() ${\it\alpha}_{m/2}$
from our DNS and literature.
${\it\alpha}_{m/2}$
from our DNS and literature.

5 Resolution requirements
From the existence of scales smaller than the Kolmogorov scale, it follows that this might influence the resolution requirements of DNS, as characterised by the product
![]() ${\it\kappa}_{max}{\it\eta}$
, where
${\it\kappa}_{max}{\it\eta}$
, where
![]() ${\it\kappa}_{max}$
is the maximum wavenumber resolved by the simulation. Different from earlier work, e.g. by Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005), where the multi-fractal model was used to determine the cut-off scales, we use here the exact length scales (3.14). It is therefore worthwhile to examine the required grid resolution in some detail, although it has been studied in the literature by employing different approaches before. Naturally, there is a trade-off for a given number of grid points corresponding to a given
${\it\kappa}_{max}$
is the maximum wavenumber resolved by the simulation. Different from earlier work, e.g. by Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005), where the multi-fractal model was used to determine the cut-off scales, we use here the exact length scales (3.14). It is therefore worthwhile to examine the required grid resolution in some detail, although it has been studied in the literature by employing different approaches before. Naturally, there is a trade-off for a given number of grid points corresponding to a given
![]() ${\it\kappa}_{max}$
between a highly resolved simulation (i.e. a large
${\it\kappa}_{max}$
between a highly resolved simulation (i.e. a large
![]() ${\it\kappa}_{max}{\it\eta}$
) and a high Reynolds number implying a low
${\it\kappa}_{max}{\it\eta}$
) and a high Reynolds number implying a low
![]() ${\it\kappa}_{max}{\it\eta}$
. Common wisdom is to resolve at least
${\it\kappa}_{max}{\it\eta}$
. Common wisdom is to resolve at least
![]() $k_{max}{\it\eta}=1$
and usually
$k_{max}{\it\eta}=1$
and usually
![]() ${\it\kappa}_{max}{\it\eta}=1.3$
is considered high enough. Note that some studies require a higher resolution, especially if the examined quantities depend on high-order derivatives of the velocity field. An example is the study of Jiménez et al. (Reference Jiménez, Wray, Saffman and Rogallo1993), which required
${\it\kappa}_{max}{\it\eta}=1.3$
is considered high enough. Note that some studies require a higher resolution, especially if the examined quantities depend on high-order derivatives of the velocity field. An example is the study of Jiménez et al. (Reference Jiménez, Wray, Saffman and Rogallo1993), which required
![]() ${\it\kappa}_{max}{\it\eta}=2$
.
${\it\kappa}_{max}{\it\eta}=2$
.
It is evident that
![]() ${\it\kappa}_{max}{\it\eta}>1$
is needed to resolve the higher moments of the velocity gradient p.d.f., as these are linked to the higher moments of the dissipation. The higher the order of the moment, the higher the necessary resolution. This can also be seen from the data of Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) as well as Donzis et al. (Reference Donzis, Yeung and Sreenivasan2008), where the velocity gradient p.d.f. did not collapse at similar Reynolds number with
${\it\kappa}_{max}{\it\eta}>1$
is needed to resolve the higher moments of the velocity gradient p.d.f., as these are linked to the higher moments of the dissipation. The higher the order of the moment, the higher the necessary resolution. This can also be seen from the data of Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007) as well as Donzis et al. (Reference Donzis, Yeung and Sreenivasan2008), where the velocity gradient p.d.f. did not collapse at similar Reynolds number with
![]() ${\it\kappa}_{max}{\it\eta}=1$
and
${\it\kappa}_{max}{\it\eta}=1$
and
![]() ${\it\kappa}_{max}{\it\eta}=2$
; the dissimilarity is less in the core of the p.d.f. and stronger in the tails, which are determined by the higher moments.
${\it\kappa}_{max}{\it\eta}=2$
; the dissimilarity is less in the core of the p.d.f. and stronger in the tails, which are determined by the higher moments.
From (3.19), we see that the cut-off lengths
![]() ${\it\eta}_{C,m}$
are less resolved for a given
${\it\eta}_{C,m}$
are less resolved for a given
![]() ${\it\kappa}_{max}{\it\eta}$
with increasing order
${\it\kappa}_{max}{\it\eta}$
with increasing order
![]() $m$
. In order to compare these influences, the normalised resolution
$m$
. In order to compare these influences, the normalised resolution
is provided in table 3, where we have used the values of
![]() $\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
from our data. We also give extrapolated resolutions for
$\langle {\it\varepsilon}^{m/2}\rangle /\langle {\it\varepsilon}\rangle ^{m/2}$
from our data. We also give extrapolated resolutions for
![]() $Re_{{\it\lambda}}=10^{3}$
and
$Re_{{\it\lambda}}=10^{3}$
and
![]() $Re_{{\it\lambda}}=10^{4}$
, which were computed using the fits shown in figure 4(a). These resolutions are not meant to give exactly the required resolution to resolve the eighth order at
$Re_{{\it\lambda}}=10^{4}$
, which were computed using the fits shown in figure 4(a). These resolutions are not meant to give exactly the required resolution to resolve the eighth order at
![]() $Re_{{\it\lambda}}=10^{3}$
, say, but rather to provide an estimate and to show the influence of the Reynolds number and order. For instance,
$Re_{{\it\lambda}}=10^{3}$
, say, but rather to provide an estimate and to show the influence of the Reynolds number and order. For instance,
![]() ${\it\kappa}_{max}{\it\eta}=1.3$
would suggest that the fourth-order structure function (and with it the flatness of the velocity gradient p.d.f.) is completely resolved at
${\it\kappa}_{max}{\it\eta}=1.3$
would suggest that the fourth-order structure function (and with it the flatness of the velocity gradient p.d.f.) is completely resolved at
![]() $Re_{{\it\lambda}}=10^{4}$
, while higher orders are only partially resolved. Equivalently, we would expect
$Re_{{\it\lambda}}=10^{4}$
, while higher orders are only partially resolved. Equivalently, we would expect
![]() ${\it\kappa}_{max}{\it\eta}=1.3$
at
${\it\kappa}_{max}{\it\eta}=1.3$
at
![]() $Re_{{\it\lambda}}=215$
to fully resolve the sixth-order structure function, i.e. this rule of thumb ensures a well enough resolved DNS, if one is interested in lower-order moments at (from the present point of view) low to intermediate Reynolds numbers.
$Re_{{\it\lambda}}=215$
to fully resolve the sixth-order structure function, i.e. this rule of thumb ensures a well enough resolved DNS, if one is interested in lower-order moments at (from the present point of view) low to intermediate Reynolds numbers.
To summarise, if
![]() ${\it\kappa}_{max}{\it\eta}={\it\kappa}_{max}{\it\eta}_{C,2}=1$
completely resolves the second-order structure function, the variance of the velocity gradient p.d.f., the mean dissipation
${\it\kappa}_{max}{\it\eta}={\it\kappa}_{max}{\it\eta}_{C,2}=1$
completely resolves the second-order structure function, the variance of the velocity gradient p.d.f., the mean dissipation
![]() $\langle {\it\varepsilon}\rangle$
and low-order statistics like the mean kinetic energy
$\langle {\it\varepsilon}\rangle$
and low-order statistics like the mean kinetic energy
![]() $\langle k\rangle$
(cf. Yeung & Pope Reference Yeung and Pope1989), then
$\langle k\rangle$
(cf. Yeung & Pope Reference Yeung and Pope1989), then
![]() ${\it\kappa}_{max}{\it\eta}_{C,3}=1$
additionally completely resolves the third-order structure function, the skewness of the velocity gradient p.d.f. and the vortex stretching
${\it\kappa}_{max}{\it\eta}_{C,3}=1$
additionally completely resolves the third-order structure function, the skewness of the velocity gradient p.d.f. and the vortex stretching
![]() $\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
, while
$\langle {\it\omega}_{i}\unicode[STIX]{x1D61A}_{ij}{\it\omega}_{j}\rangle$
, while
![]() ${\it\kappa}_{max}{\it\eta}_{C,4}=1$
also resolves the flatness of the velocity gradient p.d.f., the variance of the p.d.f.
${\it\kappa}_{max}{\it\eta}_{C,4}=1$
also resolves the flatness of the velocity gradient p.d.f., the variance of the p.d.f.
![]() $P({\it\varepsilon})$
and the fourth-order structure function, and so on.
$P({\it\varepsilon})$
and the fourth-order structure function, and so on.
Table 3. Normalised resolution
![]() $[{\it\kappa}_{max}{\it\eta}_{C,m}]^{\ast }={\it\kappa}_{max}{\it\eta}_{C,m}/{\it\kappa}_{max}{\it\eta}$
as a function of Reynolds number
$[{\it\kappa}_{max}{\it\eta}_{C,m}]^{\ast }={\it\kappa}_{max}{\it\eta}_{C,m}/{\it\kappa}_{max}{\it\eta}$
as a function of Reynolds number
![]() $Re_{{\it\lambda}}$
and order
$Re_{{\it\lambda}}$
and order
![]() $m$
.
$m$
.

Thus, we need more grid points to resolve a certain order when increasing the Reynolds number than the classical estimate using K41 would suggest. There are several estimates of the scaling of numbers of grid points with the Reynolds number – see, for instance, Paladin & Vulpiani (Reference Paladin and Vulpiani1987b
), Davidson (Reference Davidson2004) and Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005). In the following, we will use (3.19). If we assume that
![]() ${\it\alpha}_{m/2}/(2m)$
converges to a finite number for
${\it\alpha}_{m/2}/(2m)$
converges to a finite number for
![]() $m\rightarrow \infty$
, we can use (3.19) to estimate the number of grid points to completely resolve all scales, sometimes also called the number of degrees of freedom of the flow. That is, we can estimate the scaling of grid points with the Reynolds number via
$m\rightarrow \infty$
, we can use (3.19) to estimate the number of grid points to completely resolve all scales, sometimes also called the number of degrees of freedom of the flow. That is, we can estimate the scaling of grid points with the Reynolds number via
 $$\begin{eqnarray}\displaystyle N\sim \left(\frac{L_{Box}}{{\rm\Delta}x}\right)^{3} & {\sim} & \displaystyle \left(\frac{L_{Box}}{L}\right)^{3}\left(\frac{L}{{\it\eta}_{C,m\rightarrow \infty }}\right)^{3}\sim \left(\frac{L_{Box}}{L}\right)^{3}\left(\frac{L}{{\it\eta}}\right)^{3}\left(\frac{{\it\eta}}{{\it\eta}_{C,m\rightarrow \infty }}\right)^{3}\nonumber\\ \displaystyle & {\sim} & \displaystyle \left(\frac{L_{Box}}{L}\right)^{3}Re_{L}^{9/4[1+{\it\alpha}_{m/2}/(3m)]},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N\sim \left(\frac{L_{Box}}{{\rm\Delta}x}\right)^{3} & {\sim} & \displaystyle \left(\frac{L_{Box}}{L}\right)^{3}\left(\frac{L}{{\it\eta}_{C,m\rightarrow \infty }}\right)^{3}\sim \left(\frac{L_{Box}}{L}\right)^{3}\left(\frac{L}{{\it\eta}}\right)^{3}\left(\frac{{\it\eta}}{{\it\eta}_{C,m\rightarrow \infty }}\right)^{3}\nonumber\\ \displaystyle & {\sim} & \displaystyle \left(\frac{L_{Box}}{L}\right)^{3}Re_{L}^{9/4[1+{\it\alpha}_{m/2}/(3m)]},\end{eqnarray}$$
where
![]() ${\rm\Delta}x$
is the grid spacing,
${\rm\Delta}x$
is the grid spacing,
![]() $L_{Box}$
the length of the DNS box (cube) and
$L_{Box}$
the length of the DNS box (cube) and
![]() $L$
the integral length. Consequently,
$L$
the integral length. Consequently,
![]() $N$
is larger than the K41 estimate
$N$
is larger than the K41 estimate
![]() $N\sim Re_{L}^{9/4}$
since
$N\sim Re_{L}^{9/4}$
since
![]() ${\it\alpha}_{m/2}\geqslant 0$
and the scaling of
${\it\alpha}_{m/2}\geqslant 0$
and the scaling of
![]() $N$
depends on the asymptotic behaviour of
$N$
depends on the asymptotic behaviour of
![]() ${\it\alpha}_{m/2}/(2m)$
for
${\it\alpha}_{m/2}/(2m)$
for
![]() $m/2\rightarrow \infty$
. From (4.6),
$m/2\rightarrow \infty$
. From (4.6),
![]() ${\it\alpha}_{m/2}/(2m)\leqslant 1/2$
(i.e.
${\it\alpha}_{m/2}/(2m)\leqslant 1/2$
(i.e.
![]() ${\it\alpha}_{m/2}/(3m)\leqslant 1/3$
) and therefore
${\it\alpha}_{m/2}/(3m)\leqslant 1/3$
) and therefore
as upper bound. Paladin & Vulpiani (Reference Paladin and Vulpiani1987b
) used the multi-fractal framework to also obtain
![]() $N\sim Re_{L}^{3}$
as the largest Reynolds-number scaling possible (see also Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005), where also a
$N\sim Re_{L}^{3}$
as the largest Reynolds-number scaling possible (see also Yakhot & Sreenivasan (Reference Yakhot and Sreenivasan2005), where also a
![]() $Re_{L}^{3}$
scaling has been found). For the She–Leveque model,
$Re_{L}^{3}$
scaling has been found). For the She–Leveque model,
![]() ${\it\alpha}_{m/2}/(2m)\rightarrow 3/10$
and one obtains
${\it\alpha}_{m/2}/(2m)\rightarrow 3/10$
and one obtains
![]() $N\sim Re_{L}^{27/10}$
. Paladin & Vulpiani (Reference Paladin and Vulpiani1987b
) reported
$N\sim Re_{L}^{27/10}$
. Paladin & Vulpiani (Reference Paladin and Vulpiani1987b
) reported
![]() $N\sim Re_{L}^{2.3}$
using data from Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984).
$N\sim Re_{L}^{2.3}$
using data from Anselmet et al. (Reference Anselmet, Gagne and Hopfinger1984).
6 Conclusion
Let us briefly summarise the main results. Using relations between the moments of the longitudinal velocity gradient and the moments of the dissipation, we find the exact solution of longitudinal structure functions in the dissipative range without ambiguity or any free parameters for arbitrary even orders as given by (3.9), where the
![]() $C_{m,0}$
are known universal (Reynolds-number-independent) constants. That is, we can precisely and without ambiguity show how the moments of the dissipation enter the structure function solutions in the dissipative range. The only required assumptions are (local) isotropy, (local) homogeneity and incompressibility. From this, we find generalised cut-off scales as given by (3.14) and (3.15). These scales are exact under the above assumptions and can be interpreted as a generalisation of the Kolmogorov scales
$C_{m,0}$
are known universal (Reynolds-number-independent) constants. That is, we can precisely and without ambiguity show how the moments of the dissipation enter the structure function solutions in the dissipative range. The only required assumptions are (local) isotropy, (local) homogeneity and incompressibility. From this, we find generalised cut-off scales as given by (3.14) and (3.15). These scales are exact under the above assumptions and can be interpreted as a generalisation of the Kolmogorov scales
![]() ${\it\eta}$
and
${\it\eta}$
and
![]() $u_{{\it\eta}}$
and are determined by dissipative quantities (the moments of the dissipation and the kinematic viscosity) only. The question then becomes whether the same results hold for mixed and transverse structure functions as well as odd orders. We find empirically from our data that this is indeed the case for the mixed and transverse structure functions, because the ratio of the velocity gradients
$u_{{\it\eta}}$
and are determined by dissipative quantities (the moments of the dissipation and the kinematic viscosity) only. The question then becomes whether the same results hold for mixed and transverse structure functions as well as odd orders. We find empirically from our data that this is indeed the case for the mixed and transverse structure functions, because the ratio of the velocity gradients
![]() $\langle (\partial u_{2}/\partial x_{1})^{p+q}\rangle$
and
$\langle (\partial u_{2}/\partial x_{1})^{p+q}\rangle$
and
![]() $\langle (\partial u_{1}/\partial x_{1})^{p}(\partial u_{2}/\partial x_{1})^{q}\rangle$
to
$\langle (\partial u_{1}/\partial x_{1})^{p}(\partial u_{2}/\partial x_{1})^{q}\rangle$
to
![]() $\langle (\partial u_{1}/\partial x_{1})^{p+q}\rangle$
is constant at sufficiently high Reynolds number, as was previously shown by Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007). However, these constants can only be determined numerically. Also, we find that using moments
$\langle (\partial u_{1}/\partial x_{1})^{p+q}\rangle$
is constant at sufficiently high Reynolds number, as was previously shown by Ishihara et al. (Reference Ishihara, Kaneda, Yokokawa, Itakura and Uno2007). However, these constants can only be determined numerically. Also, we find that using moments
![]() $\langle {\it\varepsilon}^{m/2}\rangle$
with odd
$\langle {\it\varepsilon}^{m/2}\rangle$
with odd
![]() $m$
collapses the odd-order structure functions, although the required connectors again cannot be derived. As the normalised moments of the dissipation increase with increasing Reynolds number and order, the cut-off length scales
$m$
collapses the odd-order structure functions, although the required connectors again cannot be derived. As the normalised moments of the dissipation increase with increasing Reynolds number and order, the cut-off length scales
![]() ${\it\eta}_{C,m}$
decrease. Again, we want to emphasise that we only employ the same assumptions as Kolmogorov in his 1941 papers (Kolmogorov Reference Kolmogorov1941a
,Reference Kolmogorov
b
) and the results of the present paper can be viewed as a generalisation of Kolmogorov’s work for higher orders in the dissipative range. This implies that K41 scaling is only correct for the second order (and for the third order in the inertial range), while for higher orders the new scales should be used, which are defined by (3.14) and (3.15) without any ambiguity or additional assumptions. At scales
${\it\eta}_{C,m}$
decrease. Again, we want to emphasise that we only employ the same assumptions as Kolmogorov in his 1941 papers (Kolmogorov Reference Kolmogorov1941a
,Reference Kolmogorov
b
) and the results of the present paper can be viewed as a generalisation of Kolmogorov’s work for higher orders in the dissipative range. This implies that K41 scaling is only correct for the second order (and for the third order in the inertial range), while for higher orders the new scales should be used, which are defined by (3.14) and (3.15) without any ambiguity or additional assumptions. At scales
![]() $r\sim O({\it\eta}_{C,m})$
, the normalised moments of the dissipation cross over to the volume-averaged dissipation
$r\sim O({\it\eta}_{C,m})$
, the normalised moments of the dissipation cross over to the volume-averaged dissipation
![]() ${\it\varepsilon}_{r}$
. Consequently, any theory predicting the scaling of
${\it\varepsilon}_{r}$
. Consequently, any theory predicting the scaling of
![]() ${\it\varepsilon}_{r}$
or the structure function exponents in the inertial range,
${\it\varepsilon}_{r}$
or the structure function exponents in the inertial range,
![]() ${\it\zeta}$
, can be used to determine the scaling of
${\it\zeta}$
, can be used to determine the scaling of
![]() ${\it\eta}_{C,m}$
. We find that K62 makes unphysical predictions, while both the multi-fractal p-model as well as the She–Leveque model agree very well with our DNS. As there is a myriad of order-dependent (and Reynolds-number-dependent) cut-off length scales, the grid needs to be finer with increasing order and Reynolds number, an effect well known in the literature, which is not captured by K41. We use the exact cut-off lengths of § 5 and our DNS data to estimate the grid resolution at a given order, which gives satisfactory agreement with previous results in the literature. Thus when carrying out DNS studies, one should consider the desired Reynolds number that one is aiming at as well as the order that needs to be fully resolved. Resolving the (K41) Kolmogorov scale
${\it\eta}_{C,m}$
. We find that K62 makes unphysical predictions, while both the multi-fractal p-model as well as the She–Leveque model agree very well with our DNS. As there is a myriad of order-dependent (and Reynolds-number-dependent) cut-off length scales, the grid needs to be finer with increasing order and Reynolds number, an effect well known in the literature, which is not captured by K41. We use the exact cut-off lengths of § 5 and our DNS data to estimate the grid resolution at a given order, which gives satisfactory agreement with previous results in the literature. Thus when carrying out DNS studies, one should consider the desired Reynolds number that one is aiming at as well as the order that needs to be fully resolved. Resolving the (K41) Kolmogorov scale
![]() ${\it\eta}$
is sufficient to resolve the transport of kinetic energy down the cascade and its dissipation. Higher resolution is necessary if one is interested in higher-order statistics, which consequently need higher orders correctly resolved. This is evident inasmuch as the moments of the velocity gradient p.d.f. can be obtained from the limit of
${\it\eta}$
is sufficient to resolve the transport of kinetic energy down the cascade and its dissipation. Higher resolution is necessary if one is interested in higher-order statistics, which consequently need higher orders correctly resolved. This is evident inasmuch as the moments of the velocity gradient p.d.f. can be obtained from the limit of
![]() $D_{p,q}/r^{p+q}$
for
$D_{p,q}/r^{p+q}$
for
![]() $r\rightarrow 0$
.
$r\rightarrow 0$
.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft through the grant Pe 241/44-1 and benefited from many helpful discussions with Dr R. J. Hill. The authors gratefully acknowledge the computing time granted by the JARA-HPC-Vergabegremium provided on the JARA-HPC Partition part of the supercomputer JUQUEEN at the Forschungszentrum Jülich.