Published online by Cambridge University Press: 22 August 2005
This paper develops an asymptotic theory for integrated and near-integrated time series whose range is constrained in some ways. Such a framework arises when integration and cointegration analyses are applied to time series that are bounded either by construction or because they are subject to control. The asymptotic properties of some commonly used integration tests are discussed; the bounded unit root distribution is introduced to describe the limiting distribution of the sample first-order autoregressive coefficient of a random walk under range constraints. The theoretical results show that the presence of such constraints can lead to drastically different asymptotics. Because deviations from the standard unit root theory are measured through two noncentrality parameters that can be consistently estimated, simple measures of the impact of range constraints on the asymptotic distributions are obtained. Generalizations of standard unit root tests that are robust to the presence of range constraints are also provided. Finally, it is shown that the proposed asymptotic framework provides an adequate approximation to the finite-sample properties of the unit root statistics under range constraints.Partial financial support from Italian MIUR grants is gratefully acknowledged. I thank, without implicating, Pentti Saikkonen (the co-editor), an anonymous referee, Attilio Gardini, Martin Jacobsen, Robert de Jong, Paolo Paruolo, Anders Rahbek, and participants at the 58th European Meeting of the Econometric Society, Stockholm, August 21–24, 2003, for helpful comments. I also thank the Bank of International Settlements for providing the European monetary system exchange rate data.
Despite the extensive literature on modeling nonstationary economic time series and on limited-dependent variables, a controversial and rarely discussed topic is how to interpret and analyze time series whose behaviors can be well approximated by means of integrated processes, I(1), but are “limited” in the sense that their range is constrained by fixed bounds. Common cases arise in the context of composition ratios, such as expenditure shares or unemployment rates, or in the presence of nonnegativity restrictions, e.g., for nominal interest rates. Moreover, range constraints represent the standard framework in the context of target zone exchange rates and, more generally, of time series that are subject to control. In the following discussion, time series satisfying (one-sided or two-sided) range restrictions are called “limited” or “bounded.”
Although limited time series cannot be integrated in the usual sense, in many theoretical and econometric studies they are modeled in the I(1) framework. For example, several empirical models of European Monetary System exchange rates have been specified by using (co-)integrated vector autoregressive (VAR) models without taking account of the presence of the target zones (see, among many others, Anthony and MacDonald, 1998; Svensson, 1993; see also Phillips, 2001, and references therein). Similarly, in their influential paper Nelson and Plosser (1982) reject the unit root hypothesis in the U.S. unemployment rate (see the discussions in Caner and Hansen, 2001; Abadir and Taylor, 1999), whereas several authors have looked for possible cointegrating relations linking unemployment rates to other variables. Some theoretical models consistent with a unit root in the unemployment rate have also been proposed (Blanchard and Summers, 1986; Lindbeck and Snower, 1989). In some cases, preliminary data transformations are applied to deal with time series with infinite support. However, such transformations (i) may worsen the overall model fit (Caner and Hansen, 2001, pp. 1581–1582, for the U.S. male unemployment rate) and (ii) cannot be applied when the time series of interest reaches the upper or the lower bound.
A partial attempt to define I(1) processes with range constraints is made by Barr and Cuthbertson (1991, n. 21), regarding investment shares. They observe that
although shares are I(1) in the data there is a theoretical problem in that shares are bounded. Shares cannot be a random walk since such a series is unbounded. However, a random walk is a very special case of an I(1) series, namely linear with an additive Gaussian error. Near the boundary shares must have a non-Gaussian error. Similar considerations apply to variables such as the percentage unemployment and bilateral exchange rates (which are bounded below) which have been examined using cointegration techniques.
A more formal explanation is given by Nicolau (2002), who shows that (quasi-) integrated dynamics can arise when there are nominal bounds also. What is not generally discussed in the literature is (i) why in some cases the constraints can reasonably be neglected and therefore standard I(1) modeling is still appropriate, (ii) to what extent the misspecification depending on the omission of the range constraints affects standard (co-)integration tests, and (iii) how to test for unit roots (or cointegration) in the presence of range constraints.
The existence of range constraints makes the interpretation of the outcome of unit root tests controversial. Suppose, e.g., that the unit root hypothesis is rejected. Should such a rejection be attributed to the absence of a unit root, or does it depend on the presence of range constraints? Standard unit root tests cannot provide an answer to this question.
In this paper all of these issues will be addressed within a unified framework. This aim will be achieved by developing a new asymptotic theory that accounts for both nonstationarity and presence of bounds. This approach allows us to generalize the large-sample theory for integrated and near-integrated processes to the case of range constraints. The unit root distribution can be extended to the case of bounds; the standard theory (see, e.g., Phillips, 1987a, 1987b) is obtained as a special case. The limiting “bounded unit root” distribution depends on two noncentrality parameters that are expressed in terms of the position of the bounds. Such parameters can be estimated and allow a rapid evaluation of the impact of the range constraints on the properties of unit root tests. Moreover, they allow generalization of unit root inference to limited time series.
The paper is organized as follows. The next section defines integrated and near-integrated processes under range constraints, and some basic asymptotic results are obtained. In Section 3 the bounded unit root distribution is derived and analyzed in the context of the unit root statistics. Implications for unit root tests are discussed in Section 4. In Section 5 the problem of testing for unit roots in the presence of bounds is tackled. Two illustrative applications are reported in Section 6. Section 7 concludes with a discussion on some possible extensions of the results obtained.
We start by considering a standard, integrated or near-integrated (NI(1)), real-valued AR(1) process {St}

where ρT is unity or near unity, and a stochastic process {Xt} that is obtained by properly mapping the sample paths of {St} onto an interval [b,b]. This can be done by requiring that {ΔXt} depends on {ΔSt} in such a way that the constraint

holds almost surely for all t (i.e., ΔXt ∈ [b − Xt−1,b − Xt−1] a.s., all t). The simplest process satisfying these requirements is obtained by assuming that, conditionally on Xt−1, ΔXt is determined by truncating ΔSt at b − Xt−1 and b − Xt−1; alternatively, by censoring ΔSt at b − Xt−1 and b − Xt−1. Both (censored and truncated) types of behavior near the bounds can be nested within a more general class of limited processes. The conditions that define such a class are given as follows.1
In the following discussion,

denotes the space of all continuous, real valued functions on [0,1], whereas
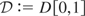
denotes the space of all real valued “cadlag” functions on [0,1], i.e., real valued functions that are right continuous at each point of [0,1) with left limit existing at each point of (0,1]. Finally,

denote weak convergence and convergence in probability, respectively.
DEFINITION 1. A stochastic process {Xt}0T is called “limited near-integrated of order 1,” or “bounded near-integrated of order 1,” briefly BNI(1), if the range constraint
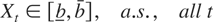
and the following assumptions hold:
(A1) the differenced process ΔXt =: ut can be decomposed as ut = ΔSt + ξt − ξt, where
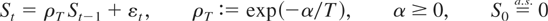
and {ξt},{ξt} are nonnegative processes such that ξt > 0 iff Xt−1 + ΔSt < b and ξt > 0 iff Xt−1 + ΔSt > b; specifically, if Xt−1 + ΔSt < b, then ξt satisfies the constraint
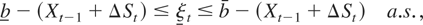
and, similarly, if Xt−1 + ΔSt > b, then ξt satisfies the constraint
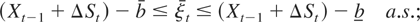
(A2) {εt} (see eqn. (2)), is a zero-mean process satisfying restrictions sufficient to ensure that, for some

, B being a standard Brownian motion;
(A3) {ξt} and {ξt} satisfy restrictions sufficient to ensure that maxt=1,…,T|ξt| and maxt=1,…,T|ξt| are of op(T1/2);
(A4) b = cλT1/2, b = cλT1/2, X0 = c0 λT1/2, c ≤ c0 ≤ c, |c0| < ∞, c ≠ c.
When α = 0, {Xt} is called “limited integrated of order 1” or “bounded integrated of order 1,” briefly BI(1).
Remarks.
2.1. Assumption
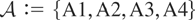
defines the time series behavior of {Xt}. The basic idea is to separate the effect of the bounds from the dynamics that characterize {ΔXt} in the absence of range restrictions. This is achieved through the decomposition of the differenced process {ut} given in Assumption (A1). Specifically, (A1) implies that {Xt} has the component representation ΔXt = ΔSt + ξt − ξt, and hence

. Because in the absence of bounds Xt = X0 + St, the difference Mt = (Xt − X0) − St represents the (cumulated) amount that controls the trajectory of {Xt} to satisfy the range constraint (1). Note that ξt and ξt are different from zero if and only if Xt−1 + ΔSt does not respect the range constraint. When Xt−1 + ΔSt > b (Xt−1 + ΔSt < b), ξt (ξt) is large enough to ensure that Xt satisfies (1). The rationale behind Assumption

is that any truncated/censored/reflected random variable (r.v.) can be written as a random transformation of a r.v. with infinite support.
2Consider for ease of notation the lower bound case only, and suppose that a r.v. u is censored at b and that its cumulative distribution function (c.d.f.) has the form

, where G(·) is an uncensored c.d.f. The same distribution can be obtained by taking u := ε + ξ, where ε is a r.v. with c.d.f. G(·) on all the real set and

. Truncation at b, i.e.,

can be obtained by simply taking ε as a r.v. with c.d.f. G(·) and by taking ξ as a r.v. such that

. Reflection at b, i.e.,

is given by taking ε with c.d.f. G(·) and defining
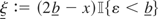
.
2.2. The process {εt} (see (A2)) satisfies an invariance principle and is therefore Rényi-mixing (Phillips and Ouliaris, 1990), or I(0) in a broad sense; see also Davidson (2002). Hence, the local-to-unity asymptotics of Phillips (1987b) imply that
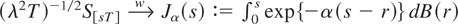
, i.e., an Ornstein–Uhlenbeck process. For α > 0, {St} is therefore near-integrated. In the special case α = 0, ΔSt = εt and {St} is I(1). Note that (A2) also implies that the running maximum of |εt| does not diverge too much, i.e., that maxt=1,…,T|εt| is of op(T1/2).
3A formal proof is provided in the Appendix, Proof of Theorem 1.
2.3. Assumption (A3) is a technical condition that is needed to prevent {Xt} from “jumping” at the bounds. Specifically, (A2) and (A3) together imply that maxt=1,…,T|ΔXt| is of op(T1/2). It is also worth noting that for some bounded processes Assumption (A3) automatically follows from (A1), (A2), and (A4). Consider, e.g., the simple bounded random walk {Xt}, recursively obtained by censoring Xt−1 + εt at b and b (see Cox and Miller, 1965), which is a bounded I(1) process with

. In this case ξt,ξt ≤ |εt| and by Assumption (A2) maxt=1,…,T ξt,maxt=1,…,T ξt ≤ maxt=1,…,T|εt| = op(T1/2) (see Remark 2.2); hence, (A3) holds. In general, however, (A3) does not follow from (A1), (A2), and (A4) as these assumptions do not rule out jumps of magnitude Op(T1/2) when the process breaches the bounds. To see this fact, suppose, e.g., that ξt is defined in a slightly different way:
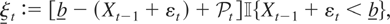
where

. In this case, once the lower bound is breached, the process jumps to the middle of the interval [b,b]. It therefore follows that

with

, so that if Pr{AT = 1} ≠ op(1), Assumptions (A1), (A2), and (A4) do not imply (A3). In this respect, Assumption (A3) allows us to rule out jumps that are not asymptotically negligible (i.e., that are not of op(T1/2)).
2.4. Assumption (A4) may appear unusual. It states a relation between the position of the bounds (b,b) and the sample size T. (A4) is a key condition to assess both empirically and theoretically to what extent the bounds impact on the behavior of the process. As will be stressed later on, c and c in (A4) provide a way to measure the influence of such bounds in finite samples. Moreover, they allow derivation of an asymptotic theory in the presence of range restrictions without modeling the behavior of the process near the bounds in a parametric fashion. Finally, (A4) enables us to obtain a convenient unification of the (near-)unit root asymptotic theory with the limited-dependent variable framework, and also to modify standard unit root inference to take account of the range constraints properly.
2.5. Because the bound parameters b and b (and also the initial value X0) depend on T, a time series generated according to Definition 1 formally constitutes a triangular array of the type {XTt : t = 0,1,…,T; T = 0,1,…} (see, e.g., Phillips, 1987b). This notation is not essential to the discussion that follows; hence, limited (near-)integrated processes will be simply denoted as {Xt}. Note that this richer notation would also allow us to justify Assumption (A4) by referring to the so-called triangular array asymptotics (Andrews and McDermott, 1995), where the sample size is fixed at T0 and the model is imbedded in the triangular array {XTt} (see also Saikkonen and Choi, 2004).
A bounded near-integrated process reverts (i) because of the bounds [b,b] and, if α > 0 in equation (2), (ii) because its driving process {St} has no unit roots. In the special case of bounded integrated dynamics, i.e., α = 0, the process is mean reverting in the close neighborhood of b and b only; hence BI(1) processes have a unit root but differ from standard I(1) processes because of the range constraints. In Section 5 it will be shown how the constraint α = 0 implied by the BI(1) model can be tested against the alternative hypothesis of limited autoregressive dynamics without a unit root.
A basic result of this paper is that BI(1) processes satisfy an invariance principle as in the standard I(1) framework; in this case, however, the limiting process is not a Brownian motion in general but depends on the parameters c0, c, and c of Assumption (A4). To derive this property, we need to introduce the following definition.
DEFINITION 2. Let Z be a stochastic process in
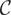
with Z(0) ∈ [a,b], a < b. The bivariate process (L,U) is said to be a “two-sided regulator” of Z, with bounds a,b, if (i) Zab(s) := Z(s) + L(s) − U(s) ∈ [a,b], (ii) L and U are increasing and continuous with L(0) = U(0) = 0 a.s., (iii) L and U increase only when Zab = a and Zab = b, respectively. If Z = B, i.e., a standard Brownian motion, then Zab is called “regulated Brownian motion.”
The two-sided regulator controls the trajectory of a process in

by keeping its sample paths between the given bounds a,b; the regulated process lies in
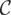
also. Note that for s = 0 the (nondecreasing) regulators L and U equal 0 and hence Zab = Z until the first time at which Z is about to cross one of the two bounds a,b. Then, although Z could escape out of the interval [a,b], the regulated process is forced to lie within the interval because of the two-sided regulator (L,U). The reader can refer to Harrison (1985) and Dixit (1993) for further insights.
Consider the following continuous-time approximant of {Xt}:
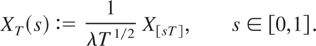
Then, in the unit root case (α = 0) the next theorem follows.
THEOREM 1. Let {Xt} be a BNI(1) process (see Definition 1). Moreover, let XT(·) be defined as in (5). Then, if

, where Bc−c0c−c0 is a regulated Brownian motion with bounds at c − c0, c − c0.
This result differs from standard I(1) asymptotics mainly because the limiting process is not a standard Brownian motion, as, e.g., in Phillips (1987a), but is a regulated Brownian motion. The sample paths of the limiting process are therefore bounded between c − c0 and c − c0. Theorem 1 obviously nests usual asymptotics because, for c0 − c and c − c0 equal to infinity, the standard invariance principle follows. Finally, note also that the weak convergence given in Theorem 1 allows us to consider a BI(1) process as a discrete analog of the regulated Brownian motion.
Remark.
2.7. When b = ∞ and a is finite, the regulator in Definition 2 is said to be a “one-sided regulator” and the regulated process can equivalently be defined as
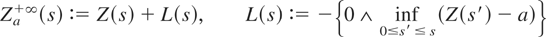
(see Harrison, 1985, Prop. 2.3). Hence, if c = +∞ the (one-sided) regulated Brownian motion in Theorem 1 can be expressed as Bc−c0+∞(s) := B(s) − {0 ∧ inf0≤s′≤s(B(s′) − (c − c0))}. The case of an upper bound follows similarly.
In this section we will show how the presence of range constraints modifies the asymptotic framework of unit root tests. Specifically, by relying on the weak convergence result given in the previous section, the so-called unit root distribution will be generalized to the case of bounds.
Given a sample {Xt}0T drawn from a BI(1) process, with X0 = 0, let
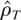
be the sample first-order autoregressive coefficient, which solves
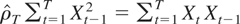
. It is well known that if no range constraints are imposed, namely, if c = −∞ and c = +∞, under well-known conditions
4See, e.g., Assumption (B1) in this section.
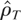
has the following asymptotic distribution (see Phillips, 1987a):
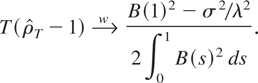
In the special case λ2 = σ2, the asymptotic distribution (7) is known as the unit root (or Dickey–Fuller) distribution,

in the following discussion. By referring to Theorem 1, it is straightforward to extend the asymptotics summarized in (7) to the case of bounds. To this purpose, we strengthen Definition 1 by requiring that the following assumption holds.
Assumption

. (B1) {εt} (see (A2) of Definition 1) is the linear process

, where
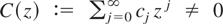
for all

is a martingale difference sequence with respect to some filtration
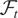
satisfying
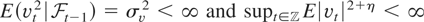
for some η > 0; (B2) for some η,η > 0, {ξt} and {ξt} (see (A3) of Definition 1) satisfy supt=1,…,T E|ξt|2+η < ∞ and supt=1,…,T E|ξt|2+η < ∞.
The unit root distribution in the presence of range constraints is presented in the next theorem.
THEOREM 2. Let {Xt} be a BNI(1) process (see Definition 1); moreover, suppose that Assumption
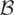
also holds. Then, if α = 0 and X0 = 0, as T ↑ ∞,
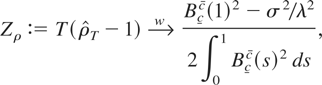
where Bcc is a regulated Brownian motion with bounds at
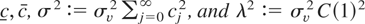
.
For λ2 = σ2 the sample autoregressive coefficient is asymptotically distributed as (2 ∫Bcc(s)2 ds)−1(Bcc(1)2 − 1), which differs from the usual unit root distribution only because it is expressed in terms of functionals of a regulated Brownian motion and not of a standard Brownian motion. This distribution is called a “bounded unit root distribution,” with parameters c and c, and denoted as
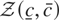
.
Kernel estimates of the probability density function (p.d.f.) associated with the bounded unit root distribution for various values of c = −c =: c > 0, i.e., under symmetric bounds around the origin, are reported in Figure 1. These are based on 50,000 Monte Carlo (MC) replications where the limiting regulated Brownian motion is obtained as Bcc(s) = φcc(B(s)), where φcc(·) is the reflection function (Karatzas and Shreve, 1988, p. 97, for c = 0 and c = a) and the Brownian motion is approximated by its discrete realization from a sample of size N = 20,000; the rationale behind this algorithm is that
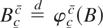
(see Harrison, 1985).
5It is worth noting that, although this algorithm allows exact simulation of the regulated Brownian motion over a discrete grid, simulation of functionals such as
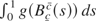
requires the discretized time increment 1/N to be extremely fine to obtain an accurate assessment of the limiting distribution (see Asmussen, Glynn, and Pitman, 1995).

Probability density function of the bounded unit root distribution for c = 0.3, 0.5, 1.1,+∞ (standard unit root distribution). Kernel estimates with Epanechnikov weights.
The 5% quantile of the bounded unit root distribution

is reported in Figure 2 for various values of c.
6Quantiles of the bounded unit root distribution (and also the quantiles of the various statistics discussed in the paper) have been estimated over a grid of values for c = 0.20, 0.21,…, 1.00, 1.02,…, 2.00.

The 5% quantile of the bounded unit root distribution for various values of c: (a) raw data; (b) demeaned data.
Critical values of the Phillips–Perron unit root tests in the two-bound (at −c and at c) case

Several implications can be derived from the preceding results. First, in the presence of range constraints the large-sample distribution of the first-order autoregressive coefficient is nonstandard. With respect to the usual unit root distribution, the limiting “bounded unit root” distribution has two more noncentrality parameters, c and c. Second, the quantiles of the bounded unit root distribution can be extremely different from those of the standard unit root distribution. To which extent the quantiles differ depends (i) on the distance of the bounds from the initial value of the process (through the parameters c,c) and (ii) on the variability of the innovations to {Xt} (through the long-run variance λ2). Third, only for bounds sufficiently far from the starting value of the process the quantiles of the bounded unit root distribution are well approximated by the quantiles of the standard unit root distribution.
Remarks.
3.1 (Initial conditions). The previous derivation of the bounded unit root distribution is based on the condition X0 = 0. However, if the process starts in X0 := c0 λT1/2, where c0 ∈ [c,c], the weak convergence (8) still holds with (c,c) replaced by (c − c0,c − c0), provided that
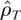
is based on the deviations from the initial value, i.e., on {Xt − X0}. Note that the (5%) quantiles of the bounded unit root distribution are highly sensitive to the presence of asymmetric bounds (i.e., −(c − c0) ≠ c − c0); see Table 1, third column (Zρ).
3.2. (One-sided bounds). One-sided bounds can be treated as a special case by setting c = +∞ (lower bound only) or c = −∞ (upper bound only). By letting X0 = 0 and c = +∞ the 5% quantile of the bounded unit root distribution
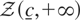
is reported in Figure 3 for various values of c := −c, and a selection of 5% quantiles is reported in Table 2, second column (Zρ). It is interesting to observe that, as c ↑ 0, i.e., the process starts at the lower bound, the quantiles converge to those of the standard unit root distribution. This result—which has already been pointed out in Cavaliere (2003) under more restrictive assumptions—follows from the distribution equality

(see Harrison, 1985, p. xii), which implies that

.

The 5% quantile of the bounded unit root distribution for various values of c: (a) raw data; (b) demeaned data.
Critical values of the Phillips–Perron unit root tests in the one-bound (at −c) case

3.3 (Deterministic term corrections). If the computation of the sample first-order autoregressive coefficient
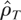
is based on the demeaned series {Xt − X}, the bounded unit root distribution has the form
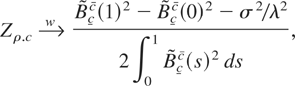
where

is a demeaned regulated Brownian motion. On the other hand, the Zρ statistic calculated after local generalized least squares (GLS) demeaning at ρ := 1 − αT−1 (see Elliott, Rothenberg, and Stock, 1996) has the limiting representation given in (8). In a similar way, if the computation of
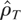
involves fitting a linear time trend by ordinary least squares (OLS) the limiting distribution is given by (9) with
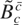
replaced by a demeaned and detrended regulated Brownian motion, namely,

. Finally, Zρ computed on data obtained from local GLS linear detrending at ρ := 1 − αT−1 has the limiting representation given in (8) with Bcc(s) replaced by

, where

.
3.4. It is straightforward to notice that Assumption
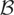
is stronger than (A2) and (A3) of Definition 1. Specifically, under (B1) {εt} satisfies the weak convergence given in (A2) with λ2 as in Theorem 2 (see Phillips and Solo, 1992). Similarly, by standard arguments

hence, (B2) implies (A3). Under Assumption

, the process {εt} is a quite general linear process in terms of a martingale difference. It is worth noting that the conditions given in Assumption (B1), although allowing a neat derivation of the results presented in Theorem 2, are not strictly necessary. For instance, the strong mixing conditions given in Phillips (1987a, Thm. 3.1), could have also been considered. Similarly, (B2) is not strictly necessary for the results given in Theorem 2 and could have been replaced by any set of conditions ensuring that both maxt=1,…,T ξt and maxt=1,…,T ξt are of op(T1/2).
There are important implications of the convergence results outlined previously for unit root testing. Such implications are examined in the next section.
The most common approach to testing for a unit root against stable alternatives is to refer to statistic (8) as a left-sided test, i.e., to reject the null of a unit root for large negative values of
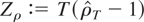
. By using the distribution results of the previous section it can be reasonably argued that in some cases the rejection rate of the test can be substantially affected by the range constraints.
To stress this result, assume that the data generating process (DGP) is BI(1) with uncorrelated homoskedastic innovations (σ2 = λ2). The rejection probabilities of the Zρ test when standard critical values are employed (estimated through MC simulation; see the previous section) are reported in Figure 4; the significance level is set to 5%. As expected, the rejection frequency is strongly related to the position of the bounds. There are at least two important consequences deriving from this result.

Size of the unit root tests in the two-bound case for various values of c = −c =: c and c0 = 0. DF-rho: Zρ unit root test; DF-t: Zt unit root test; VNR: von Neumann ratio test; VR: variance-ratio test, τ = 0.5. (a) Tests based on raw data; (b) tests based on demeaned data.
On the one hand, in the framework of limited time series tests based on conventional critical values could point to the rejection of the unit root hypothesis and the researcher might erroneously conclude that the process has no unit roots, whereas it has a unit root but it is also subject to (one-sided or two-sided) range constraints. When testing for unit roots in the presence of limited time series, an analysis of the “negligibility” of the bounds is therefore a necessary step before interpreting the outcome of standard unit root tests in the usual way. Such a step is usually missing when unit root techniques are applied to the analysis of bounded time series.
On the other hand, Figure 4 also explains why the practitioner might fail to reject the (false) standard I(1) model in the presence of bounds. When the bounds are sufficiently far away, the rejection frequencies of the unit root test when the DGP is I(1) or BI(1) are in fact identical. That is, unit root tests are not always able to detect the presence of the bounds.
A further important implication is that, despite the fact that the bounded unit root distribution (and also the asymptotic distributions of other unit root test statistics; see the discussion that follows) depends on three nuisance parameters, namely, (c − c0,c − c0,σ/λ), the unit root statistic (8) can be rearranged to eliminate σ/λ from its asymptotic distribution; this can be achieved by following the approach of Phillips (1987a). Let
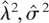
be two consistent estimators for λ2,σ2 in the absence of bounds (i.e., when c = +∞ and c = −∞); for simplicity we assume that
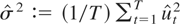
, where

denotes the OLS residuals obtained by regressing Xt on Xt−1 (and, if necessary, on a constant term), and that
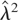
is a conventional sum-of-covariances (SC) estimator of the form
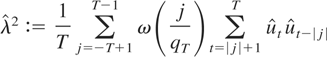
(see, e.g., de Jong and Davidson, 2000, and references therein). We further require the following assumption to hold (see Jansson, 2002).
Assumption
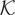
. (K1) For all
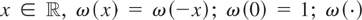
is continuous at zero; ω(0) < ∞, and ∫[0,∞) ω(x) dx < ∞, where ω(x) := supx′≥x|ω(x′)|; (K2) qT ∈ (0,∞) and limT→∞(qT−1 + T−δqT) = 0 for some δ ∈ (0,½].
Assumption

places some restrictions on the kernel function ω(·) and on the bandwidth/lag truncation parameter qT, which needs to grow just more slowly than T1/2; such restrictions, however, are rather general and almost standard in the literature. When Assumption

holds and {εt} satisfies (B1) of Assumption
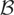
, then the idealized estimator
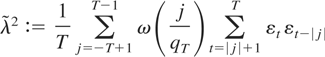
satisfies
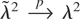
(Jansson, 2002, Thm. 2), and, if there are no bounds (i.e., c = −∞ and c = +∞) and {Xt} has a unit or near unit root, also

is a consistent estimator of λ2.
7Consistency follows, e.g., from Theorem 3 of Hansen (1992).
When there are bounds, consistency can still be preserved given that the bandwidth/lag truncation parameter qT satisfies a regularity condition that is slightly stronger than the one given in (K2) of Assumption

. The following lemma summarizes this result.
LEMMA 3. Under the assumptions of Theorem 2, as T ↑ ∞,

. Moreover, if Assumption

holds with (K2) replaced by the following assumption:
(K2′). qT ∈ (0,∞) and, for some δ ∈ (0,δ*], limT→∞(qT−1 + T−δqT) = 0, where δ* := ½[η*/(2 + η*)], η* := min{η,η,η};
then, as
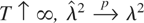
.
Note that (K2′) simply slows down the growth rate of qT by establishing a trade-off between the rate at which qT is allowed to diverge and the moments of εt, ξt, and ξt (recall from Assumption

that η, η, and η control the existing moments of εt, ξt, and ξt, respectively). Now, qT is allowed to grow just more slowly than T1/2 only in the very special case that η* = +∞, i.e., all moments exist. If, e.g., η* = 2 (i.e., fourth-order moments exist) then δ* = ¼, and the well-known o(T1/4) rate suggested in Phillips (1987a) is obtained.
The main consequence of Lemma 3 is that the unit root statistic of Phillips (1987a)

and also the asymptotically equivalent “modified” statistic (Ng and Perron, 2001)

satisfy

, i.e., weak convergence to a bounded unit root distribution with parameters (c,c). Hence, the presence of range constraints does not affect the consistency of the estimators of the nuisance parameters (σ2,λ2), which do not enter the asymptotic distribution of the test statistics. However, c and c are still two noncentrality parameters affecting the asymptotic distributions and, consequently, the outcome of the tests.
Remarks.
4.1. (One-sided bounds). Consider the one-sided bound case (see Remark 3.2). Such a case arises, e.g., in the (co-)integration analysis of nominal interest rates (see, among others, Bec and Rahbek, 2004). For X0 = 0 and c = +∞ the asymptotic rejection frequencies of the
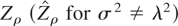
unit root test are reported in Figure 5 for various values of −c := c; the nominal level of the test is 5%. As in the two-bound case, the rejection frequency essentially depends on the distance between the starting value of the process and the position of the bound. However, if such a distance is negligible, i.e., c ≈ 0, the quantiles are identical to those of the standard unit root distribution (see Remark 3.2); this result does not apply when the test involves OLS demeaning (or detrending) of the original time series. In general, in the one-bound case the rejection rate is not as high as in the two-bound case; nevertheless, it can considerably exceed the significance level.

Size of the unit root tests in the one-bound case for various values of −c =: c and c0 = 0. DF-rho: Zρ unit root test; DF-t: Zt unit root test; VNR: von Neumann ratio test; VR: variance-ratio test, τ = 0.5. (a) Tests based on raw data; (b) tests based on demeaned data.
4.2 (Other unit root tests). Comparable evidence affects most of the procedures usually employed to test for unit roots. The t-ratio unit root test (Zt) based on the t-statistic associated to

in the regression equation ΔXt = πXt−1+ error has asymptotic distribution (λ/σ)(4 ∫Bcc(s)2 ds)−1/2(Bcc(1)2 − (σ/λ)2). By Lemma 3, Phillips' t-test

and the corresponding “modified” statistic

converge weakly to

, which differs from the usual asymptotic distribution because Bcc replaces the Brownian motion B. The von Neumann ratio test of Sargan and Bhargava (1983), based on the statistic
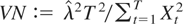
, satisfies the convergence

, which assumes larger values with respect to the standard limiting distribution
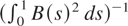
. The variance-ratio test, based on
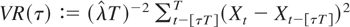
, satisfies

, which is closer to 0 than the standard limiting distribution
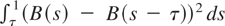
. Asymptotic sizes at the 5% nominal level are plotted in Figures 4 (two-bound case) and 5 (one-bound case). See also Tables 1 and 2 for the 5% quantiles of the

test.
4.3 (Deterministic term corrections). As noticed for the bounded unit root distribution (see Remark 3.1), if the initial condition is X0 = c0 λT1/2, the results do not change provided that the tests are based on {Xt − X0} (or on GLS-demeaned data) and c,c are replaced by c − c0,c − c0. If the tests are based on OLS-demeaned (demeaned and detrended) variables the limiting distributions depend on a demeaned (demeaned and detrended) regulated Brownian motion

as follows:
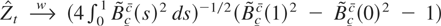
;

;
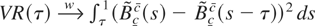
. When the tests are based on GLS linear detrending, the limiting distributions are those given in Remark 4.2 with the regulated Brownian motion replaced by the functional Vc,αc given in Remark 3.3.
4.4 (Empirical assessment of the impact of the bounds). Figures 2 and 4 provide simple tools for understanding to what extent in the basic BI(1) model with symmetric bounds the rejection of the unit root hypothesis could depend on the presence of the bounds. Figures 3 and 5 can be referred to in the case of a lower (upper) bound; similar pictures can be easily obtained by simulation for any value of (c − c0,c − c0). Note, however, that because c − c0 and c − c0 are not generally known, they should at least be consistently estimated. Section 5 tackles this issue.
We end this section by briefly investigating the power function of the Zρ unit root test in the presence of near-integrated dynamics and range constraints. The DGP is therefore BNI(1) with α > 0. Note that the I(1) hypothesis is violated (i) because the DGP has no unit roots and (ii) because of the range constraints. We might therefore expect the rejection frequency to be higher than in the usual near-integrated, NI(1), case.
To explore this issue we need to derive the asymptotic distribution of the unit root test statistics when the DGP is BNI(1) with α > 0. The next result provides the result for the
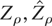
statistics.
THEOREM 4. Under the assumptions of Theorem 2 with α = 0 replaced by α > 0 then, as T ↑ ∞,
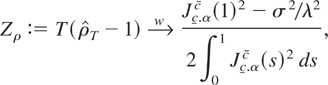
where Jc.αc(s) := Jα(s) + L(s) − U(s), Jα being the diffusion
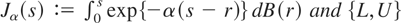
being the two-sided regulator of Jα with bounds at c,c. The heteroskedasticity and autocorrelation robust statistic
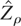
satisfies (12) with σ2/λ2 replaced by unity, provided that Assumption

holds with (K2) replaced by (K2′).
Hence, with respect to the near-integrated framework, the asymptotic distribution of Zρ depends on a regulated Ornstein–Uhlenbeck process. For σ2 = λ2 the distribution (12) can be denoted as “bounded near-unit root distribution,”
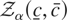
. The theorem can be easily extended to the various unit root tests and to the case of (OLS or GLS) deterministic corrections.
The asymptotic rejection frequency of the

test is plotted for various values of α and c := c = −c under c0 = 0 (symmetric case) in Figure 6. The figures are based on an MC experiment with 50,000 replications where the limiting regulated Ornstein–Uhlenbeck process is obtained by applying the two-sided regulator (see Definition 2) to a discrete realization of the Ornstein–Uhlenbeck process over a grid of 20,000 points. In the left panel of the figure, the test is based on raw data, whereas in the right panel it is based on OLS-demeaned data. For c = +∞ the usual rejection rate of the Zρ test when the DGP is near-integrated is obtained (see, e.g., Elliott et al., 1996, Figs. 1,2). In addition, the figure shows that in the presence of symmetric bounds, the unit root Zρ test tends to reject more often than in the absence of constraints.

Asymptotic power function of the unit root Zρ test against bounded near-integrated alternatives for various values of c = −c =: c, c0 = 0, and α ranging from 0 to 30: (a) tests based on raw data; (b) tests based on demeaned data.
When there are bounds, instead of testing the (trivially false) I(1) hypothesis the researcher should be more interested in testing the “bounded I(1)” hypothesis against a bounded alternative with no unit roots, e.g., the bounded, near-I(1) model. Our framework allows us to tackle this testing problem. Specifically, despite the fact that the bounded unit root distribution (and also the asymptotic distributions of the other unit root test statistics) depends on three nuisance parameters, (c − c0,c − c0,σ/λ), it is possible to define a proper rejection region to test the BI(1) hypothesis at a given significance level, hence avoiding spurious rejections caused by the presence of the bounds.
The main result needed to develop a BI(1) test is given by the following corollary of Lemma 3, which shows that the two unknown parameters (c − c0,c − c0) can be consistently estimated.
COROLLARY 5. Let the assumptions of Theorem 2 hold and suppose that Assumption
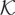
holds with (K2) replaced by (K2′). Then, as

, where

.
Hence, given that the bounds (b,b) are known, from the consistency of
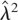
it follows that the two nuisance parameters of the bounded unit root distribution, c − c0 and c − c0, can be consistently estimated by

, respectively.
Therefore, if the DGP is a BI(1) process, the rejection frequency of the

unit root test equalizes the selected significance level in large samples as far as the quantiles of the

distribution are used; such quantiles can easily be computed by MC simulation.
8A selection of 5% quantiles and a GAUSS program for simulating the asymptotic quantiles of unit root tests for any choice of (c,c) are available from the web page http://www2.stat.unibo.it/cavaliere/rconstr/.
It is interesting to compare the asymptotic power function of BI(1) tests against BNI(1) with the asymptotic power function of standard unit root tests in the absence of range constraints. To analyze this issue we do not need any further theoretical result because (i) the distribution of the unit root statistics under BNI(1) dynamics has already been obtained in Section 4, Theorem 4, and (ii) Corollary 5 remains valid.
To assess to what extent the triple {α,c,c} affects the asymptotic power function of the “bounded unit root” tests, in Figure 7 the asymptotic power function of the BI(1) Zρ test
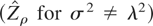
against BNI(1) is plotted for various values of α and c := c = −c under c0 = 0 (symmetric case). In the left panel of the figure the test is applied to raw data, whereas in the right panel the test refers to OLS-demeaned data.

Asymptotic power function of the “bounded unit root” Zρ test against bounded near-integrated alternatives for various values of c = −c =: c, c0 = 0, and α ranging from 0 to 30: (a) tests based on raw data; (b) tests based on demeaned data.
As expected, tests of the BI(1) hypothesis are less powerful than standard I(1) tests; i.e., in the presence of range constraints it is more difficult to assess whether a given series has a unit root than in the usual case of no constraints. Specifically, the smaller c is, the lower the power of the test is. It is also worth noting that, in the case of symmetric bounds, OLS demeaning reduces the power of the test (for α close to zero the test has no power against BNI(1) alternatives). This evidence, however, does not necessarily hold when the bounds are either asymmetric or one-sided; in particular, when the bounds are asymmetric, the tests based on OLS demeaning can outperform the tests based either on the deviations from the initial value or on GLS demeaning. This result suggests that the practitioner should compute both OLS and GLS demeaning-based tests when the null of interest is the BI(1) hypothesis.
In this section we briefly report the outcome of a set of MC simulations on the small-sample size of the bound-corrected unit root tests outlined earlier. Because a key assumption ((A4) of Definition 1) of BI(1) asymptotics is that the position of the bounds depends on T, one could reasonably argue that the small-sample accuracy of the test (at least in terms of size) might be inadequate. In the following discussion it will be shown that this is not the case.9
We do not report the results related to the power properties of the tests in finite samples because the asymptotic local power analysis provides a good description of the finite-sample performance, with all tests approaching the corresponding asymptotic local power function relatively fast as T increases.
Initially, a BI(1) process {Xt} is chosen with {εt} being a Gaussian independent and identically distributed (i.i.d.) process with zero mean and unit variance. The (conditional) distribution of {εt} is reflected at the bounds (see note 2); the results for different truncation mechanisms do not substantially differ. Attention is paid to the case of two symmetric bounds (c = −c =: c > 0 and X0 = 0) and also to the case of a single bound (c = ∞, −c =: c > 0 and X0 = 0). We consider the Zρ and Zt unit root tests, both based on the deviations of the observed series from the initial value and from the sample average; the results for tests based on GLS demeaned variables, and also for the modified MZ tests, do not differ from those discussed here. Because λ2 = σ2, c is estimated by
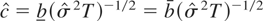
. The critical values of the asymptotic distribution under the null hypothesis are then retrieved through a linear interpolation of the critical values obtained by simulation in Sections 3 and 4. The selected sample sizes are T = 50, 100, 250, 500, and the number of MC replications is 20,000.
The results are summarized in Table 3. The small-sample performance of the tests is excellent. The empirical rejection frequency exceeds the significance level only in the two-bound case, for c = 0.3 and T = 50, when the tests are based on raw data. Nevertheless, when c = 0.3 and T = 100 the rejection rate is already very close to the nominal size for most tests. For the other values of (c,T) the asymptotic approximation of the distribution of the tests considered is extremely well behaving.
Finite-sample null rejection probabilities white noise (WN) model in the one-bound (at −c) and in the two-bound (at −c and c) cases

We now turn to the two-bound case in the presence of autocorrelated errors.
10When the errors are autocorrelated and there is one bound only, the size performance of the tests (not reported) is very close to the size performance in the no-bound case (c = ∞).
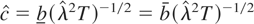
; see Corollary 5) becomes crucial. Hence, together with the Phillips–Perron tests based on the SC estimator of Andrews (1991)
11Specifically, the SC e??stimator is based on the OLS residuals obtained by regressing Xt on Xt−1 (on (Xt−11)′ for the constant-corrected tests) and employs a quadratic spectral kernel with bandwidth parameter chosen according to the Andrews (1991) automatic data-dependent procedure using the plug-in method based on an AR(1) model fit to the data. Note that the quadratic spectral kernel satisfies Assumption (K1); cf. Andrews (1991, p. 837) and Jansson (2002, p. 1450).

, we also report the results obtained by the modified coefficient test (MZρAR) based on an autoregressive estimator of

in the following discussion, with the number of lags chosen according to the modified Akaike information criterion (MAIC) defined in Ng and Perron (2001). Finally, together with the tests based on raw data, tests based on OLS and GLS demeaning (MZρ.cAR and MZρ.cAR, respectively) are included in the tables.
Finite-sample null rejection probabilities AR(1) model; two-bound (at −c and c) case

Finite sample null rejection probabilities MA(1) model; two-bound (at −c and c) case

In the AR(1) case (Table 4) with positively autocorrelated errors, the simulation evidence is comparable to that obtained in the white noise case, although the tests tend to be slightly conservative when the bounds are very close to each other (c = 0.3). The various tests have almost the same size. When the errors are negatively autocorrelated, the tests based on

perform better than the tests based on the SC estimator (as in the standard I(1) framework, c = ∞ in the table). The MA(1) case (Table 5) does not significantly differ from the AR(1) case when the errors are positively correlated, but size distortions are more pronounced when the errors are negatively correlated and the SC estimator of λ2 is employed. On the contrary, the tests based on
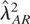
behave very well also in the presence of negatively correlated MA errors. In general, when the errors are autocorrelated, tests employing an autoregressive estimator of the long-run variance deliver the best results in terms of size accuracy.
Overall, the small-sample performance of the asymptotic approximation combined with the use of appropriate empirical estimates of the bound parameters seems to be adequate, and the small-sample size of the BI(1) test appears to be largely satisfactory.
In this section, we briefly discuss two common applications of unit root tests to limited time series, namely, testing for exchange rate mean reversion within a target zone and testing for a unit root in the unemployment rate.
We start by examining an empirical problem that has often been tackled in the literature, i.e., testing for exchange rate mean reversion in the presence of a target zone. The reader can refer to Svensson (1993) and Anthony and MacDonald (1998). Economic theories of target zone exchange rates usually associate the rejection of the unit root hypothesis with the presence of either intramarginal Central Bank interventions or mean reverting fundamentals (Delgado and Dumas, 1992). However, as noticed by Svensson (1993), the presence of the target zone can be the source of mean reversion of the exchange rate. In this framework, we will briefly show how the outcome of unit root tests in the presence of (target zone–) range constraints can lead to wrong economic conclusions and how the researcher can properly modify the conventional test procedures to take the target zone into account.
The exchange rates of four currencies are considered, namely, the Danish krone (DK), the French franc (FF), the Irish pound (IP), and the Dutch guilder (NG), all against the Deutsche mark (DM);12
The data were obtained from Ecu rates extracted from the Bank of International Settlements (BIS) database. All exchange rates are spot Ecu rates recorded at a daily Central Bank telephone conference at 2.30 p.m. Swiss time. The bilateral exchange rates have been calculated from these Ecu rates.

European monetary system exchange rates of the Danish krone (DK), the French franc (FF), the Irish pound (IP), and the Dutch guilder (NG), all against the Deutsche mark, 1987:01–1993:01. Percentage deviations from the central parity.
In Table 6 the (constant-corrected) Phillips–Perron coefficient and t-tests

are reported; the long-run variance λ2 is estimated according to the SC estimator of Andrews (1991) with quadratic spectral kernel and AR(1)-automatic bandwidth selection; see the previous section. Together with the Phillips–Perron tests, we also show the results obtained by using the modified coefficient test, MZρ.cAR, which employs an autoregressive estimator of the long-run variance with the number of lags k chosen by both the MAIC criterion of Ng and Perron (2001) and the Bayesian information criterion (BIC) (MZρ.cAR and MZρ.cbic, respectively) under the constraint k ≤ [12(T/100)1/4].
European monetary system exchange rates: Unit root tests, estimates of the bound parameters, and bound-corrected critical values

Evidence against the I(1) hypothesis is generally found for the French franc, the Irish pound, and the Dutch guilder at the 5% significance level and for the Danish krone at the 10% significance level. Therefore, the researcher might erroneously conclude that the four European monetary system exchange rates considered do not have a unit root and that they are mean reverting within the band.
However, because there are nominal bounds, the relevant question is whether the rejection of the I(1) hypothesis depends on the presence of the target zone (i.e., the DGP is a bounded process with a unit root, BI(1)) or whether it should be interpreted as evidence of mean reversion within the band (i.e., the DGP is a bounded process with no unit roots, BNI(1)). Standard unit root analysis does not provide an answer to this question. However, an answer can be given by employing the BI(1) test introduced in Section 5. In the second half of Table 6 the estimates of the bound parameters (c − c0,c − c0) are reported, in addition to the asymptotic 5% and 10% quantiles associated to the corresponding test statistics under the “bounded unit root” null hypothesis. For the DM/IP and the DM/NG exchange rates, almost all tests reject the null of a unit root even when bound-corrected critical values are employed. Therefore, for these two exchange rates there is evidence of mean reversion that cannot be attributed to the presence of the target zone alone (i.e., the DM/IP and the DM/NG exchange rates are mean reverting within the band).
The results for the DM/DK exchange rate and for the DM/FF exchange rates are opposite. Contrary to the results obtained when standard critical values are employed, the “bounded unit root” tests do not substantially lead to the rejection of the hypothesis of a unit root: the observed mean reversion can be explained by the presence of the target zone alone (i.e., the DM/DK and the DM/FF exchange rates are not mean reverting within the band).
In this section we analyze the monthly U.S. unemployment rate among adult males from January 1948 through August 1999; see Figure 9. These data have recently been analyzed by Caner and Hansen (2001) by means of threshold autoregression methods; the reader can refer to their paper for further details on data definition.

Monthly U.S. percentage unemployment rate among adult males from January 1948 through August 1999.
Our first question is whether the I(1) hypothesis is rejected over the considered sample. By construction, the unemployment rate is bounded, and therefore the I(1) specification should not provide an adequate representation of the data. We explore this issue by referring to the tests previously discussed; we also consider the rescaled range unit root test based on the statistic

, which has been applied to U.S. unemployment by Cavaliere (2001). For the
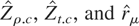
tests, the long-run variance λ2 is estimated through the Andrews (1991) quadratic spectral kernel SC estimator based on first-order autoregression residuals with 12 lags to take account of the peak at the 12-month frequency in the autocorrelation function of the unemployment rate changes. For the modified coefficient test, MZρ.cAR, λ2 is estimated by the autoregressive estimator

with number of lags k equal to 12, which corresponds to the lag length selected by means of the BIC and the MAIC criteria; k = 12 is also the lag length selected by Caner and Hansen (2001). The range statistic based on

, is also reported.
The results are summarized in Table 7, first row. All tests suggest rejecting the I(1) model at the 5% significance level, with the

test rejecting at the 1% level (the standard 1% critical value of the
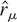
test is 0.833). The researcher should therefore investigate whether such a rejection depends on the existence of an upper and a lower bound or if it can be attributed to the absence of a unit root. In the third, fourth, and fifth rows of Table 7 the estimates of λ2, c − c0, and c − c0 are reported. Because c − c0 is between −0.32 and −0.33 whereas c − c0 is between 9.86 and 10.28, the presence of the upper barrier at b = 100 seems to be negligible. Conversely, according to Figure 5, a lower barrier at −0.32 inflates the asymptotic rejection frequency of the (5% nominal level) OLS-demeaned tests to 18% for
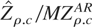
and to 13% for
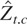
; similarly, the asymptotic rejection frequency of

is found to be about 30%. Therefore, the outcome of unit root tests is likely to be affected by the presence of the lower bound.
U.S. male unemployment rate: Unit root tests, estimates of the bound parameters, and bound-corrected critical values

Bound-corrected critical values can easily be obtained by referring to the criteria outlined in Section 5. The estimates of the 5% and 10% critical values for testing the BI(1) hypothesis are presented in the last two rows of Table 7. Now, two tests reject the BI(1) null hypothesis at the 10% level, with the remaining tests leading to the maintenance of the null hypothesis even at the 10% level. Hence, once one has properly taken account of the bounds, the evidence against the unit root hypothesis in the postwar U.S. male unemployment rate is much weaker than the evidence obtained without accounting for the bounds.
This paper shows how the presence of range constraints affects the asymptotic distribution of unit root tests. Testing for unit roots in bounded time series should always be carried out with caution because, when the unit root hypothesis is rejected, the range constraints can be the leading cause of the rejection. The approach suggested in the paper provides a way to assess the role of range constraints, and it can be implemented easily. It allows a quick evaluation of the relevance of the bounds and also allows the researcher to test statistically whether a given limited time series reverts because of the presence of the bounds alone (the “bounded unit root” hypothesis) or because it does not have a unit root (the “bounded, near-unit root” hypothesis). Moreover, the proposed asymptotic framework provides an adequate approximation of the finite-sample properties of unit root tests under range constraints.
The asymptotics and the finite-sample methods discussed in this paper can be extended to a multivariate framework. Specifically, it can be shown that the stronger the range constraints on the data, the higher the probability that cointegration tests will point toward (spurious) cointegration.
Finally, it is worth noting that the asymptotics obtained also provide a basis for (asymptotic) power comparisons when the researcher wants to test whether a given time series with integrated behavior is bounded by unobservable bounds. For example, in the context of floating nominal exchange rates one might be interested in testing whether a given bilateral exchange rate is regulated within an undeclared target zone (see Nicolau, 2002, and references therein). The asymptotics of Section 4 allow us to understand which tests are preferable in terms of power when the standard I(1) hypothesis is tested against the bounded I(1) alternative.
Proof of Theorem 1. Consider the process

defined recursively as
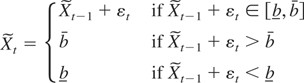
with initial condition

. By setting
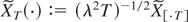
the following theorem holds.
THEOREM 6. Under the conditions of Theorem 1, as
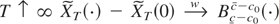
, where Bc−c0c−c0 is a regulated Brownian motion with bounds at c − c0,c − c0.
Proof. The proof consists of two steps. First, we define a continuous approximant of
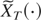
that satisfies Harrison's construction of the regulated Brownian motion, and weak convergence is proved. Then, it is shown that weak convergence holds for

too.
The process

can be recursively defined as
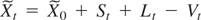
, where
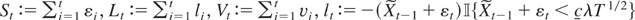
, and
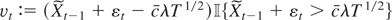
. Obviously,

, all t. To define a continuous approximant of

, say,
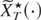
, let us define continuous approximants for all its normalized components, i.e., (λ2T)−1/2St, (λ2T)−1/2Lt, and (λ2T)−1/2Vt. For the partial sum St we can set
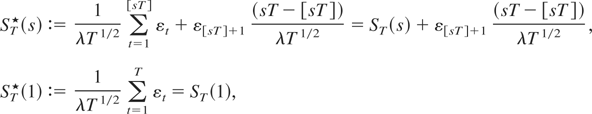
which represents the process obtained by joining the points (t/T,(λ2T)−1/2St) by means of straight lines. For Vt and Lt we define this approximation in a slightly different way:

With respect to linear interpolations like (A.2), this construction still interpolates (λ2T)−1/2Xt but also satisfies the following properties:

From Harrison (1985, Prop. 2.6), the continuous mapping
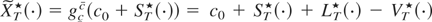
is the unique functional that regulates

to lie within the interval [c,c] and that satisfies properties 1–3. This allows us to obtain the limiting distribution of

by applying the continuous mapping theorem (CMT) (see Billingsley, 1968) to the limit of

. Specifically, if we prove that

under Assumption (A2), then the CMT would imply that

, which is a Brownian motion with initial value c0, regulated at c and at c. To show that
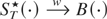
, it suffices to consider the following result:
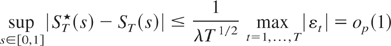
under Assumption (A2), so that from Billingsley (1968, Theorem 4.1),

implies
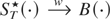
. To see that the last equality in (A.3) holds, note that because weak convergence on a compact space implies stochastic equicontinuity (see, e.g., Pollard, 1990), we have for all ε > 0,

Now, maxt=1,…,T|εt| = λT1/2 maxt=1,…,T|ST(t/T) − ST((t − 1)/T)|, and hence

which converges to 0 as T diverges; see (A.4).
To prove weak convergence of
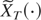
it is sufficient to prove that the process
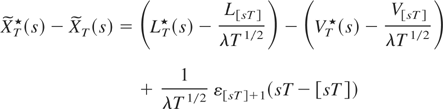
converges to 0 uniformly in probability. Because both
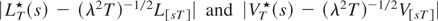
are smaller than (λ2T)−1/2|ε[sT]+1|, and because the set of increasing points of

and the set of increasing points of

are disjoint, it follows that
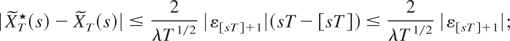
therefore,

, which is of op(1) (see equation (A.3)), and hence the weak convergence of

follows. The proof is completed by noting that because

converges weakly to a Brownian motion starting at c0 and regulated at c,c, the convergence of

to a standard Brownian motion, regulated at c − c0,c − c0, also follows. █
To complete the proof of Theorem 1 it is sufficient to refer to the following lemma.
LEMMA 7.

satisfy the relation
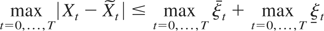
for all T ≥ 0.
Proof. Let

. As

we prove the lemma by showing that the relation
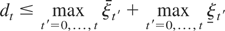
holds for all t = 0,1,…,T. The relation (A.8) is proved by induction. When t = 0,

, and (A.8) holds; therefore it suffices to show that dt+1 ≤ maxt′=0,…,t+1 ξt′ + maxt′=0,…,t+1 ξt′ given that relation (A.8) holds at time t. Suppose that

. If

, also Xt + εt+1 ≥ b, so that ξt+1 = ξt+1 = 0, dt+1 = dt, and relation (A.8) holds because maxt′=0,…,t ξt′ + maxt′=0,…,t ξt′ = maxt′=0,…,t+1 ξt′ + maxt′=0,…,t+1 ξt′. If
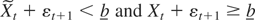
, then ξt+1 = ξt+1 = 0; hence, as

with

, relation (A.8) holds as dt+1 < dt = maxt′=0,…,t ξt′ + maxt′=0,…,t ξt′ = maxt′=0,…,t+1 ξt′ + maxt′=0,…,t+1 ξt′. If both
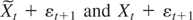
are smaller than b, then
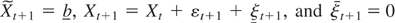
; because

(as Xt + εt+1 < b), we have dt+1 ≤ maxt′=0,…,t+1 ξt′ + maxt′=0,…,t+1 ξt′, so that relation (A.8) holds. By similar arguments, the induction proof also holds when

and, symmetrically, when εt+1 ≥ 0. █
Under (A3), maxt=0,…,T ξt + maxt=0,…,T ξt is of op(T1/2), and hence Lemma 7 implies that

. Consequently, we can apply Billingsley (1968, Theorem 4.1), to conclude that Theorem 6 holds for XT(·) − XT(0) also. █
Proof of Theorem 2. As in Phillips (1987a), we begin by writing the unit root statistics as the ratio between

. Under Assumption

, the weak convergence in (A2) of Definition 1 holds with λ2 := σv2C(1)2 (Phillips and Solo, 1992, Thm. 3.15); consequently, Theorem 1 and the CMT imply the joint weak convergence of

to

with λ2 as previously defined. Finally, the convergence

(see the proof of Lemma 3, which follows), the CMT, and Theorem 4.1 of Billingsley (1968) give the desired result. █
Proof of Lemma 3. For ease of notation and without loss of generality, we prove the lemma for the case of one bound at c < c0. Initially, we consider the estimator of λ2 based on first-differenced data:
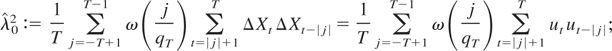
later, we generalize the proof to the residual-based estimator. First, decompose

as

where
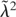
is the idealized estimator given in equation (11). Under Assumptions

and (A2), Theorem 2 in Jansson (2002) shows that
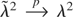
, and hence to complete the proof we only need to prove that the last term on the right-hand side of equation (A.9) goes to 0 in probability. As ξt ≥ 0, all t, we can focus on the following inequalities:

with
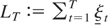
. Recursive substitutions allow us to express XT as
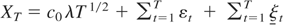
, implying that

converges weakly to the well-defined random variable λ(Bc−c0+∞(1) − B(1)). Moreover, consider the following equality:

By (B1), (B2), and (K2′),

To check this result note that because (K2′) implies that δ*,η* solve (½ − δ*) × (2 + η*) − 1 = 0, it follows that

and, similarly,
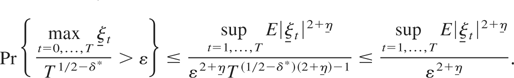
As (A.13) and (A.14) can be made arbitrarily small by choosing ε appropriately, the result (A.12) is proved. Consequently, because (i) qTT−δ* → 0 (see (K2′)); (ii) (K1) implies

(see Jansson, 2002); (iii) T−(1/2−δ*) × (maxt=1,…,T|εt| + maxt=1,…,T|ξt|) = Op(1); (iv) T−1/2LT = Op(1), it holds that (A.10), and hence

, are of op(1).
By setting

and using the weak law of large numbers

(which holds under (B1), see, e.g., Jansson, 2002, p. 1450), it also follows that

; note that this result holds irrespective of Assumption

.
Now, consider the difference

, where

is given in (10). Because

, simple algebra allows us to show that

which is op(1) because (i)
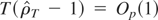
(Theorem 2); (ii) T−δ*qT → 0 and
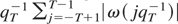
is asymptotically bounded (Assumption
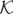
); (iii) maxt=1,…,T T−1/2|Xt| is of op(1) (Theorem 1 and the CMT); and (iv) maxt=1,…,T T−(1/2−δ*)|ut| ≤ maxt=1,…,T T−(1/2−δ*)|ξt| + maxt=1,…,T T−(1/2−δ*)|εt| = Op(1) (see equation (A.12)). Therefore,

also. As before, by setting

it also follows that

, which does not require Assumption

to hold.
Extension to the two-bound case and to the case of demeaned data follows similarly. █
Proof of Theorem 4. We initially prove that when α > 0, Theorem 1 holds with
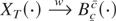
replaced by

. First, under (A2), Lemma 1(a) of Phillips (1987b) holds and implies that

. The same weak convergence holds for the approximant

Second, convergence to the regulated diffusion Jc.αc is obtained by following the proof of Theorem 1, where (A.2) is now replaced by STα(s); see the preceding discussion.
As in the proof of Theorem 2, the weak convergence in (12) holds if
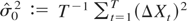
converges to σ2 in probability. But this result follows from the decomposition

because (i)

(see Lemma 3); (ii)

(as ρT − 1 = −α/T + O(T−2)); and (iii)

To prove the second part of the theorem, we only need to show that if the DGP is BNI(1), Lemma 3 continues to hold, and hence

. This can be done by following mechanically the proof of Lemma 3, and it is therefore omitted for brevity. █
Proof of Corollary 5. Because by Assumption (A4),

, consistency follows from

; see Lemma 3. The same proof applies to
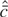
and to

. █

Probability density function of the bounded unit root distribution for c = 0.3, 0.5, 1.1,+∞ (standard unit root distribution). Kernel estimates with Epanechnikov weights.

The 5% quantile of the bounded unit root distribution for various values of c: (a) raw data; (b) demeaned data.

Critical values of the Phillips–Perron unit root tests in the two-bound (at −c and at c) case

The 5% quantile of the bounded unit root distribution for various values of c: (a) raw data; (b) demeaned data.

Critical values of the Phillips–Perron unit root tests in the one-bound (at −c) case

Size of the unit root tests in the two-bound case for various values of c = −c =: c and c0 = 0. DF-rho: Zρ unit root test; DF-t: Zt unit root test; VNR: von Neumann ratio test; VR: variance-ratio test, τ = 0.5. (a) Tests based on raw data; (b) tests based on demeaned data.

Size of the unit root tests in the one-bound case for various values of −c =: c and c0 = 0. DF-rho: Zρ unit root test; DF-t: Zt unit root test; VNR: von Neumann ratio test; VR: variance-ratio test, τ = 0.5. (a) Tests based on raw data; (b) tests based on demeaned data.

Asymptotic power function of the unit root Zρ test against bounded near-integrated alternatives for various values of c = −c =: c, c0 = 0, and α ranging from 0 to 30: (a) tests based on raw data; (b) tests based on demeaned data.

Asymptotic power function of the “bounded unit root” Zρ test against bounded near-integrated alternatives for various values of c = −c =: c, c0 = 0, and α ranging from 0 to 30: (a) tests based on raw data; (b) tests based on demeaned data.

Finite-sample null rejection probabilities white noise (WN) model in the one-bound (at −c) and in the two-bound (at −c and c) cases

Finite-sample null rejection probabilities AR(1) model; two-bound (at −c and c) case

Finite sample null rejection probabilities MA(1) model; two-bound (at −c and c) case

European monetary system exchange rates of the Danish krone (DK), the French franc (FF), the Irish pound (IP), and the Dutch guilder (NG), all against the Deutsche mark, 1987:01–1993:01. Percentage deviations from the central parity.

European monetary system exchange rates: Unit root tests, estimates of the bound parameters, and bound-corrected critical values

Monthly U.S. percentage unemployment rate among adult males from January 1948 through August 1999.

U.S. male unemployment rate: Unit root tests, estimates of the bound parameters, and bound-corrected critical values